内蒙古赤峰市田家炳中学2010-2011学年高二数学4月月考文
内蒙古赤峰市田家炳中学2010-2011学年高一下学期第一次月考语文试卷

赤峰市田家炳中学高一年级2010—2011学年度下学期第一次月考语文试卷本试卷分第I卷(选择题)和第II卷两部分,考试时间150分钟,总分150分。
考试结束后,将第二卷和答题卡一并交回。
第I卷(本卷共15小题,每小题3分,共45分。
)注意事项:1.答题前,考生在答题卡上务必将自己的姓名、考号、班级填写清楚,请认真核准条形码上的考号、姓名和科目。
2.每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案标号,在试题卷上作答无效。
一、基础知识(每小题3分)1.下列各项词语中加点字的注音,完全正确的一项是(3分)( )A.掌舵(tuó)崔嵬(wéi)荻花(dí)环珮(pèi)B.抚膺(yīnɡ) 锦瑟(sè) 恬然(tián) 霓裳(shǎnɡ)C.栈道(zhàn) 嗟叹(jiē) 商贾(ɡǔ) 钿头(diàn)D.溯源(sù) 惘然(mǎnɡ) 悯然(mǐn) 江渚(zhǔ)2、下列各组词语,有错别字的一项是()A. 钩连潦倒地崩山摧群山万壑B. 峥嵘谪居冲波逆折抚赝C. 咨嗟惘然扪参历井海誓山盟D. 崔嵬整顿司马青衫杜鹃啼血3.下列各句中,加点的成语使用正确的一句是()A.作为领导干部,对下岗职工的生活困难决不能掉以轻心....。
B.在这场足球友谊赛中,我校队员前仆后继....,大显身手,终于取得了胜利。
C.这处游览胜地的环境脏乱差到如此地步,简直令人叹为观止....。
D.对于这次活动,同学们有的赞成,有的反对,有的主张改期,议论纷纷,莫衷一是....。
4.下列各句中,没有语病的一句是()A.全球化经营已经成为当今众多大公司的发展战略,而企业兼并则是它们调整经济结构和生产布局的重要手段。
B.99年我省大学招收的本科自费生,是自恢复高考制度以来最多的一年。
C.“海协”和“海基”两会能否继续会谈,汪道涵会长能否访台,关键在于李登辉收回“两国论”,坚持“一个中国”的原则。
内蒙古赤峰市田家炳中学2010-2011学年高二历史4月月考(无答案)人民版

内蒙古赤峰市田家炳中学2010-2011学年高二历史4月月考(无答案)人民版(时间:90分钟分值:100分)一、选择题(本大题共30小题,每小题2分,共计60分。
每小题只有一个选项符合题意。
)1.最早动摇井田制,标志土地国有制开始瓦解的措施是 ( )A.“相地而衰征” B.“废沟洫”C.“尽地力” D.“为田开阡陌封疆”2.北魏孝文帝改革措施中大大加快了各民族人民融合进程的是 ( )A.推行均田制 B.实行三长制 C.整顿吏治 D.实行汉制和移风易俗3.世人对秦国人有着“薄恩礼,好生分”的印象,这与商鞅变法哪一措施有关 ( )A.奖励军功B.奖励耕种 C.焚烧诗书 D.什伍连坐和告奸制度4.下列改革中含有土地所有制变革的是 ( )A.商鞅变法 B.管仲改革 C.王安石变法 D.张居正改革5.我国的古代改革对推动社会进步起了推动作用,但商鞅因变法而车裂,王安石因变法而革职,张居正因变法而死后被抄家。
由此得出的最主要结论是( )A.改革有助于社会进步,但改革者不会有好结果B.改革有风险,改革者应注意保护自己C.改革需要改革者的奉献和牺牲精神D.改革应对反动势力进行彻底镇压6.德国宗教改革的直接原因是 ( )A.天主教会到德国兜售赎罪券B.马丁·路德提出宗教改革的政治主张C.加尔文在瑞士日内瓦进行宗教改革试验D.天主教会对德国的压榨7.以下活动与加尔文有关的是 ( )①主张信仰得救,并把其解释为先定论②主张简化教会组织和宗教仪式,制定严格的道德标准③提出建立民族教会的主张④创立的加尔文宗不符合新兴资产阶级的利益A.①②③ B.②③④ C.①②④ D.①③④8.在俄国历史上,对外战争与国内的改革往往有一定的联系。
下列说法中正确的是 ( ) A.对外战争的失败是俄国在国内实行改革的根本原因B.对外战争失败后,俄国国内改革受到外来势力的干预C.克里木战争的失败促使俄国社会发出要求变革的呼声D.日俄战争的失败再次动摇了沙皇政府的根基,促使沙皇政府实行地方自治改革9.下列说法中不正确的是 ( )A.穆罕默德·阿里改革前,埃及存在着土耳其、英国和马木路克三股外来势力B.日本倒幕派联合外来势力推翻了幕府统治C.戊戌变法是在中华民族面临亡国灭种的形势下展开的D.西方列强集中力量侵略中国,客观上为日本的明治维新提供了一个相对有利的国际环境10.下列关于明治维新时期政府提倡“文明开化”,大力吸收西方的思想文化的说法,不正确的是 ( )A.在政府开放的政策下,进步知识分子掀起传播启蒙思想的热潮B.在这一时期,新闻出版事业获得很大发展C.日本彻底抛弃传统文化,全盘西化D.这一时期日本人的衣食住行各方面发生了深刻变化11.梁启超在《变法通议》中写道:同治初年,德相俾斯麦对人说:“三十年后,日本其兴,中国其弱乎?日人之游欧洲者,讨论学业,讲究官制,归而行之;中人之游一欧洲者,询某厂船炮之利,某厂价值之廉,购而用之。
数学-高二-内蒙古赤峰二中高二(下)4月月考数学试卷(文科)

2015-2016学年内蒙古赤峰二中高二(下)4月月考数学试卷(文科)一、选择题(本大题包括12小题,每小题5分,共60分,每小题给出的四个选项中,只有一项是符合题目要求的,请将正确选项填涂在答题卡上)1.复数的共轭复数的虚部是()A.i B.1 C.﹣i D.﹣12.用反证法证明命题“三角形三个内角至少有一个不大于60°”时,应假设()A.三个内角都不大于60°B.三个内角都大于60°C.三个内角至多有一个大于60°D.三个内角至多有两个大于60°3.如图是根据变量x,y的观测数据(x i,y i)(i=1,2,…10)得到的散点图,由这些散点图可以判断变量x,y具有相关关系的图是()A.①②B.①④C.②③D.③④4.正弦函数是奇函数,f(x)=sin(x2+1)是正弦函数,因此f(x)=sin(x2+1)是奇函数,以上推理()A.小前提不正确 B.大前提不正确 C.结论正确 D.全不正确5.某单位有840名职工,现采用系统抽样方法,抽取42人做问卷调查,将840人按1,2,…,840随机编号,则抽取的42人中,编号落入区间的人数为()A.11 B.12 C.13 D.146.已知x与y之间的一组数据:x 0 1 2 3y m 3 5.5 7已求得关于y与x的线性回归方程为=2.1x+0.85,则m的值为()A.1 B.0.85 C.0.7 D.0.57.从6名男同学和4名女同学中随机选出3名同学参加一项竞技测试,选出的三位同学中至少有一名女同学的概率是()A.B.C.D.8.已知x>0,y>0,x+2y+2xy=8,则x+2y的最小值是()A.3 B.4 C.D.9.用数学归纳法证明不等式“1+++…+<n(n∈N*,n≥2)”时,由n=k(k≥2)不等式成立,推证n=k+1时,左边应增加的项数是()A.2k﹣1B.2k﹣1 C.2k D.2k+110.执行如图所示的程序框图,则输出的结果为()A.4 B.9 C.7 D.511.在区间上随机取一个数x,使得|x+1|﹣|x﹣2|≥1成立的概率是()A.B.C.D.12.设a、b、c是互不相等的正数,现给出下列不等式(1)|a﹣b|≤|a﹣c|+|b﹣c|;(2);(3);(4),则其中正确个数是()A.0 B.1 C.2 D.3二、填空题(每小题5分,共4小题,满分20分.把答案填在答题卡上.)13.已知复数z满足:(1+i)z=i(i为虚数单位),则|z|等于.14.解不等式:x+|2x﹣1|<3.15.若x>0,y>0,且x+2y=1,则+的取值范围是.16.观察下列等式:…照此规律,第n个等式可为.三、解答题(本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤.)17.为了解某班学生喜爱打篮球是否与性别有关,对本班50人进行了问卷调查得到了如下的列联表:喜爱打篮球不喜爱打篮球合计男生 5女生10合计50已知在全部50人中随机抽取1人抽到喜爱打篮球的学生的概率为.(1)请将上面的列联表补充完整;(2)是否有99.5%的把握认为喜爱打篮球与性别有关?说明你的理由;下面的临界值表供参考:p(K2≥k)0.15 0.10 0.05 0.025 0.010 0.005 0.001k 2.072 2.706 3.841 5.024 6.635 7.879 10.828(参考公式:,其中n=a+b+c+d)18.以下茎叶图记录了甲、乙两组各三名同学在期末考试中的数学成绩.乙组记录中有一个数字模糊,无法确认,假设这个数字具有随机性,并在图中以a表示.(Ⅰ)若甲、乙两个小组的数学平均成绩相同,求a的值;(Ⅱ)当a=3时,分别从甲、乙两组同学中各随机选取一名同学,求这两名同学中乙同学的成绩比甲同学的成绩好的概率.(Ⅲ)求乙组平均成绩超过甲组平均成绩的概率.19.(1)已知x∈R,m=x2﹣1,n=2x+2.求证:m,n中至少有一个是非负数.(2)已知a,b,c均为正实数,且a+b+c=1,求证:(﹣1)(﹣1)(﹣1)≥8.20.某种产品的年销售额y与该年广告费用支出x有关,现收集了4组观测数据列于下表:x(万元) 1 4 5 6y(万元)30 40 60 50(1)已知这两个变量满足线性相关关系,求y与x之间的回归方程=x+(2)计划2016年的销售额为100万元,请根据你得到的模型,预测该年广告费用支出应为多少万元?(线性回归方程系数公式==,=﹣,参考数据)21.某校从高一年级学生中随机抽取40名学生作为样本,将他们的期中考试数学成绩(满分100分,成绩均为不低于40分的整数)分成六段:50,60),40,50)与两个分数段内的学生中随机选取2名学生,试用列举法求这两名学生的数学成绩之差的绝对值不大于10的概率.22.已知函数f(x)=|x﹣a|,其中a>1(1)当a=2时,求不等式f(x)≥4﹣|x﹣4|的解集;(2)已知关于x的不等式|f(2x+a)﹣2f(x)|≤2的解集{x|1≤x≤2},求a的值.2015-2016学年内蒙古赤峰二中高二(下)4月月考数学试卷(文科)参考答案与试题解析一、选择题(本大题包括12小题,每小题5分,共60分,每小题给出的四个选项中,只有一项是符合题目要求的,请将正确选项填涂在答题卡上)1.复数的共轭复数的虚部是()A.i B.1 C.﹣i D.﹣1【考点】复数代数形式的乘除运算.【专题】转化思想;数系的扩充和复数.【分析】利用复数的运算法则、共轭复数与虚部的定义即可得出.【解答】解:复数===2+i的共轭复数2﹣i的虚部为﹣1.故选:D.【点评】本题考查了复数的运算法则、共轭复数与虚部的定义,考查了推理能力与计算能力,属于基础题.2.用反证法证明命题“三角形三个内角至少有一个不大于60°”时,应假设()A.三个内角都不大于60°B.三个内角都大于60°C.三个内角至多有一个大于60°D.三个内角至多有两个大于60°【考点】反证法的应用.【专题】证明题;推理和证明.【分析】熟记反证法的步骤,从命题的反面出发假设出结论,直接得出答案即可.【解答】解:∵用反证法证明在一个三角形中,至少有一个内角不大于60°,∴第一步应假设结论不成立,即假设三个内角都大于60°.故选:B.【点评】此题主要考查了反证法的步骤,熟记反证法的步骤:(1)假设结论不成立;(2)从假设出发推出矛盾;(3)假设不成立,则结论成立.3.如图是根据变量x,y的观测数据(x i,y i)(i=1,2,…10)得到的散点图,由这些散点图可以判断变量x,y具有相关关系的图是()A.①②B.①④C.②③D.③④【考点】散点图.【专题】计算题.【分析】通过观察散点图可以知道,y随x的增大而减小,各点整体呈下降趋势,x与y负相关,u随v的增大而增大,各点整体呈上升趋势,u与v正相关.【解答】解:由题图③可知,y随x的增大而减小,各点整体呈下降趋势,x与y负相关,由题图④可知,u随v的增大而增大,各点整体呈上升趋势,u与v正相关.故选D.【点评】本题考查散点图,是通过读图来解决问题,考查读图能力,粗略的反应两个变量之间的关系,是不是线性相关,是正相关还是负相关.4.正弦函数是奇函数,f(x)=sin(x2+1)是正弦函数,因此f(x)=sin(x2+1)是奇函数,以上推理()A.小前提不正确 B.大前提不正确 C.结论正确 D.全不正确【考点】演绎推理的基本方法.【专题】阅读型.【分析】根据三段论的要求:找出大前提,小前提,结论,再判断正误即可.【解答】解:大前提:正弦函数是奇函数,正确;小前提:f(x)=sin(x2+1)是正弦函数,因为该函数为复合函数,故错误;结论:f(x)=sin(x2+1)是奇函数,因为该函数为偶函数,故错误.故选A【点评】本题考查演绎推理的基本方法,属基础题.5.某单位有840名职工,现采用系统抽样方法,抽取42人做问卷调查,将840人按1,2,…,840随机编号,则抽取的42人中,编号落入区间的人数为()A.11 B.12 C.13 D.14【考点】系统抽样方法.【专题】概率与统计.【分析】根据系统抽样方法,从840人中抽取42人,那么从20人抽取1人.从而得出从编号481~720共240人中抽取的人数即可.【解答】解:使用系统抽样方法,从840人中抽取42人,即从20人抽取1人.所以从编号1~480的人中,恰好抽取=24人,接着从编号481~720共240人中抽取=12人.故:B.【点评】本题主要考查系统抽样的定义和方法,属于基础题.6.已知x与y之间的一组数据:x 0 1 2 3y m 3 5.5 7已求得关于y与x的线性回归方程为=2.1x+0.85,则m的值为()A.1 B.0.85 C.0.7 D.0.5【考点】线性回归方程.【专题】计算题;概率与统计.【分析】求出这组数据的横标和纵标的平均数,写出这组数据的样本中心点,把样本中心点代入线性回归方程求出m的值.【解答】解:∵==,=,∴这组数据的样本中心点是(,),∵关于y与x的线性回归方程=2.1x+0.85,∴=2.1×+0.85,解得m=0.5,∴m的值为0.5.故选:D.【点评】本题考查回归分析,考查样本中心点满足回归直线的方程,考查求一组数据的平均数,是一个运算量比较小的题目,并且题目所用的原理不复杂,是一个好题.7.从6名男同学和4名女同学中随机选出3名同学参加一项竞技测试,选出的三位同学中至少有一名女同学的概率是()A.B.C.D.【考点】列举法计算基本事件数及事件发生的概率.【专题】综合题;方程思想;综合法;概率与统计.【分析】选出的3名同学中,至少有一名女同学的对立事件是选出的3名同学都是男同学,由此利用对立事件概率计算公式能求出选出的3名同学中,至少有一名女同学的概率.【解答】解:∵从6名男同学和4名女同学中随机选出3名同学参加一项竞技测试,∴基本事件总数n=,选出的3名同学中,至少有一名女同学的对立事件是选出的3名同学都是男同学,选出的3名同学中,至少有一名女同学的概率:P=1﹣=.故选:A.【点评】本题考查概率的求法,是基础题,解题时要认真审题,注意对立事件概率计算公式的合理运用.8.已知x>0,y>0,x+2y+2xy=8,则x+2y的最小值是()A.3 B.4 C.D.【考点】基本不等式.【专题】计算题.【分析】首先分析题目由已知x>0,y>0,x+2y+2xy=8,求x+2y的最小值,猜想到基本不等式的用法,利用代入已知条件,化简为函数求最值.【解答】解:考察基本不等式,整理得(x+2y)2+4(x+2y)﹣32≥0即(x+2y﹣4)(x+2y+8)≥0,又x+2y>0,所以x+2y≥4故选B.【点评】此题主要考查基本不等式的用法,对于不等式在求最大值最小值的问题中应用非常广泛,需要同学们多加注意.9.用数学归纳法证明不等式“1+++…+<n(n∈N*,n≥2)”时,由n=k(k≥2)不等式成立,推证n=k+1时,左边应增加的项数是()A.2k﹣1B.2k﹣1 C.2k D.2k+1【考点】数学归纳法.【专题】对应思想;综合法;推理和证明.【分析】分别写出n=k和n=k+1时,不等式左边的所有项,根据分母特点计算多出的项数.【解答】解:n=k时,左边=1+++…+,当n=k+1时,左边=1+++…++++…+.∴左边增加的项数为2k+1﹣1﹣(2k﹣1)=2k+1﹣2k=2k.故选:C.【点评】本题考查了数学归纳法的证明步骤,属于基础题.10.执行如图所示的程序框图,则输出的结果为()A.4 B.9 C.7 D.5【考点】程序框图.【专题】算法和程序框图.【分析】由已知中的程序语句可知:该程序的功能是利用循环结构计算并输出变量n的值,模拟程序的运行过程,分析循环中各变量值的变化情况,可得答案.【解答】解:当n=1时,执行循环体后,T=2,S=18,n=3,不满足退出循环的条件,当n=3时,执行循环体后,T=8,S=36,n=5,不满足退出循环的条件,当n=5时,执行循环体后,T=32,S=54,n=7,不满足退出循环的条件,当n=7时,执行循环体后,T=128,S=72,n=9,满足退出循环的条件,故输出的n值为9,故选:B【点评】本题考查了程序框图的应用问题,解题时应模拟程序框图的运行过程,以便得出正确的结论,是基础题.11.在区间上随机取一个数x,使得|x+1|﹣|x﹣2|≥1成立的概率是()A.B.C.D.【考点】几何概型.【专题】计算题;方程思想;综合法;概率与统计.【分析】本题利用几何概型求概率.先解绝对值不等式,再利用解得的区间长度与区间的长度求比值即得.【解答】解:利用几何概型,其测度为线段的长度.由不等式|x+1|﹣|x﹣2|≥1 可得①,或②,③.解①可得x∈∅,解②可得1≤x<2,解③可得x≥2.故原不等式的解集为{x|x≥1},∴在区间上随机取一个数x使得|x+1|﹣|x﹣2|≥1的概率为P==.故选:B.【点评】本题主要考查了几何概型,简单地说,如果每个事件发生的概率只与构成该事件区域的长度(面积或体积)成比例,则称这样的概率模型为几何概率模型,简称为几何概型.12.设a、b、c是互不相等的正数,现给出下列不等式(1)|a﹣b|≤|a﹣c|+|b﹣c|;(2);(3);(4),则其中正确个数是()A.0 B.1 C.2 D.3【考点】不等式比较大小.【专题】计算题.【分析】利用绝对值不等式的性质可判断(1),利用换元法与作差法、配方法可判断(2),利用基本不等式可判断(3),利用分析法可判断(4).【解答】解:(1)∵)|a﹣b|=|(a﹣c)+(c﹣b)|≤|a﹣c|+|b﹣c|,故(1)正确;(2)由于a>0,令t=a+(t≥2),则a2+﹣(a+)=t2﹣t﹣2=t(t﹣1)﹣2≥2×1﹣2=0,即则a2+≥a+,故(2)正确;(3)不妨令a=1,b=2,则|a﹣b|+=1﹣1=0<2,故(3)错误;(4)要证﹣≤﹣,需证+≤+,即证2a+3+2≤2a+3+2,即证a2+3a≤a2+3a+2,即0≤2,显然成立,故原式成立,故(4)正确;综上所述,正确个数是3.故选D.【点评】本题考查不等式比较大小,考查绝对值不等式、基本不等式、配方法与分析法的应用,属于中档题.二、填空题(每小题5分,共4小题,满分20分.把答案填在答题卡上.)13.已知复数z满足:(1+i)z=i(i为虚数单位),则|z|等于.【考点】复数代数形式的乘除运算.【专题】方程思想;转化思想;数系的扩充和复数.【分析】利用复数运算法则、模的计算公式即可得出.【解答】解:∵(1+i)z=i,∴(1﹣i)(1+i)z=i(1﹣i),∴z=,则|z|==.故答案为:.【点评】本题考查了复数运算法则、模的计算公式,考查了推理能力与计算能力,属于基础题.14.解不等式:x+|2x﹣1|<3.【考点】绝对值不等式的解法.【专题】计算题.【分析】通过对2x﹣1的正负讨论将原不等式中的绝对值符号去掉,转化为或,分别解之,再取其并集即可.【解答】解:原不等式可化为或,解得:或,∴原不等式得解集为.【点评】本题考查绝对值不等式的解法,着重考查分类讨论去绝对值符号的方法,属于中档题.15.若x>0,y>0,且x+2y=1,则+的取值范围是3+,+∞)故答案为:90+91+(90+a)40,50),90,100)后得到如图的频率分布直方图.(Ⅰ)求图中实数a的值;(Ⅱ)根据频率分布直方图,试估计该校高一年级学生其中考试数学成绩的平均数;(Ⅲ)若从样本中数学成绩在90,10040,50)内的学生人数为40×0.05=2,这两人分别记为A,B,数学成绩在40,50)或都在40,50)内的学生人数为40×0.05=2,这两人分别记为A,B,数学成绩在40,50)与40,50)或都在hslx3y3h90,100)内,则这两名学生的数学成绩之差的绝对值不大于10,记“这两名学生的数学成绩之差的绝对值不大于10”为事件M,则事件M包含的基本事件有:(A,B),(C,D),(C,E),(C,F),(D,E),(D,F),(E,F),共7个,所以这两名学生的数学成绩之差的绝对值不大于10的概率P=.【点评】本题考查频率和概率的求法,二查平均分的求法,是中档题,解题时要认真审题,注意频率分布直方图和列举法的合理运用.22.已知函数f(x)=|x﹣a|,其中a>1(1)当a=2时,求不等式f(x)≥4﹣|x﹣4|的解集;(2)已知关于x的不等式|f(2x+a)﹣2f(x)|≤2的解集{x|1≤x≤2},求a的值.【考点】带绝对值的函数;绝对值不等式的解法.【专题】压轴题;不等式的解法及应用.【分析】(1)当a=2时,f(x)≥4﹣|x﹣4|可化为|x﹣2|+|x﹣4|≥4,直接求出不等式|x ﹣2|+|x﹣4|≥4的解集即可.(2)设h(x)=f(2x+a)﹣2f(x),则h(x)=.由|h(x)|≤2解得,它与1≤x≤2等价,然后求出a的值.【解答】解:(1)当a=2时,f(x)≥4﹣|x﹣4|可化为|x﹣2|+|x﹣4|≥4,当x≤2时,得﹣2x+6≥4,解得x≤1;当2<x<4时,得2≥4,无解;当x≥4时,得2x﹣6≥4,解得x≥5;故不等式的解集为{x|x≥5或x≤1}.(2)设h(x)=f(2x+a)﹣2f(x),则h(x)=由|h(x)|≤2得,又已知关于x的不等式|f(2x+a)﹣2f(x)|≤2的解集{x|1≤x≤2},所以,故a=3.【点评】本题是中档题,考查绝对值不等式的解法,注意分类讨论思想的应用,考查计算能力,常考题型.2016年10月26日。
内蒙古赤峰市田家炳中学1011学年下学期高一第一次月考数学(附答案)

赤峰市田家炳中学高一年级2010—2011学年度下学期第一次月考数学科试卷 时间:120分钟 满分:150分第I 卷(选择题, 共60分)一 、选择题(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的) 1.下列说法中,正确的是( ) (A )第二象限的角是钝角(B )第三象限的角必大于第二象限的角 (C ) 831-是第二象限角(D )///40264,40984,2095 -是终边相同的角 2.下面各组角中,终边相同的是( ) A. 690,390 B.750,330- C. 420,480- D.840,3000-3.半径为1cm ,中心角为0150的角所对的弧长为( )A.cm 32B.cm 32πC.cm 65D.cm 65π4.若角θ的终边过点P (4,3)(0)a a a -≠,则sin cos θθ+等于( ) A 、15- B 、15C 、15± D 、不能确定,与a 的值有关5.已知θ为第三象限角,则θ2sin 1-化简的结果为 ( )A .θcos B. θcos - C .θcos ± D. 以上都不对6.如果4π<θ<2π,那么下列各式中正确的是( )A . cos θ<sin θ<tan θB .cos θ<tan θ<sin θC .tan θ<sin θ<cos θD .sin θ<cos θ<tan θ7.设A 、B 、C 是三角形的三个内角,下列关系恒成立的是( ) A .cos (A +B )=cos C B .sin (A +B )=sin C C .tan (A +B )=tan CD .sin 2B A +=sin 2C8. 函数x x y sin cos 2-=的值域是( )A . ⎥⎦⎤⎢⎣⎡-45,1 B .⎥⎦⎤⎢⎣⎡45,1 C .[]2,0 D .[]1,1-9.函数y =2tan (3x -4π)的一个对称中心是( )A .(3π,0) B .(6π,0) C .(-4π,0) D .(-2π,0)10.要得到2sin(2)3y x π=-的图像, 需将函数sin 2y x =的图像( ) A .向左平移23π个单位. B .向右平移23π个单位C .向左平移3π个单位D .向右平移3π个单位 11.函数)sin(ϕω+=x y 的部分图象如右图,则ϕ、ω可以取的一组值是( ) A. ,24ππωϕ==B. ,36ππωϕ==C. ,44ππωϕ== D.5,44ππωϕ==12.下列函数中同时满足:①在)2,0(π上是增函数;②奇函数;③以π为最小正周期的函数的是( ) A.x y tan = B.x y cos = C.2tanxy = D.|sin |x y =xO y1 2 3第II 卷(非选择题, 共90分)二、填空题(本大题共4小题,每题5分,共20分,把答案填在题 中横线上)13. 比较大小 (1)0508cos 0144cos ,)413tan(π-)517tan(π- 14.若角α的终边落在直线x y 3-=上,则ααcos sin = 。
内蒙古赤峰市高二下学期数学月考试卷
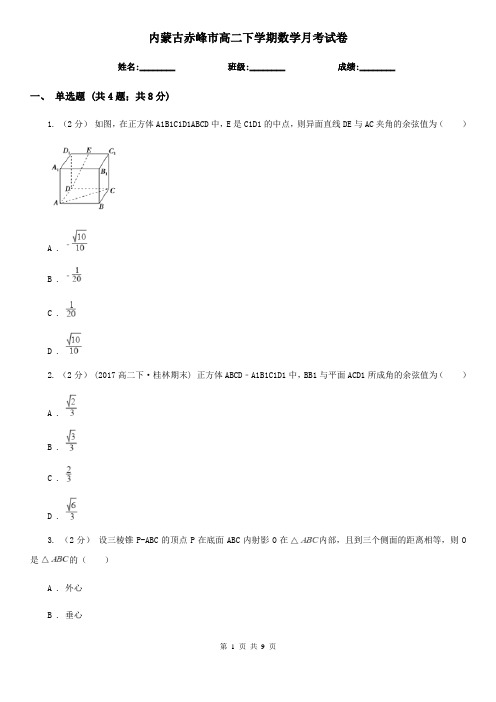
内蒙古赤峰市高二下学期数学月考试卷姓名:________ 班级:________ 成绩:________一、单选题 (共4题;共8分)1. (2分)如图,在正方体A1B1C1D1ABCD中,E是C1D1的中点,则异面直线DE与AC夹角的余弦值为()A .B .C .D .2. (2分) (2017高二下·桂林期末) 正方体ABCD﹣A1B1C1D1中,BB1与平面ACD1所成角的余弦值为()A .B .C .D .3. (2分)设三棱锥P-ABC的顶点P在底面ABC内射影O在内部,且到三个侧面的距离相等,则O 是的()A . 外心B . 垂心C . 内心D . 重心4. (2分) (2017高一下·吉林期末) 已知正方体ABCD-A1B1C1D1棱长为1,点P在线段BD1上,当∠APC 最大时,三棱锥P-ABC的体积为()A .B .C .D .二、填空题 (共10题;共10分)5. (1分)已知,正方形ABCD的边长为1,AP⊥平面ABCD,且AP= ,则PC与平面PAB所成的角是________.6. (1分)如果y=f(x)的定义域为R,对于定义域内的任意x,存在实数a使得f(x+a)=f(﹣x)成立,则称此函数具有“P(a)性质”.给出下列命题:①函数y=sinx具有“P(a)性质”;②若奇函数y=f(x)具有“P(2)性质”,且f(1)=1,则f(2015)=1;③若函数y=f(x)具有“P(4)性质”,图象关于点(1,0)成中心对称,且在(﹣1,0)上单调递减,则y=f(x)在(﹣2,﹣1)上单调递减,在(1,2)上单调递增;④若不恒为零的函数y=f(x)同时具有“P(0)性质”和“P(3)性质”,且函数y=g(x)对,都有|f(x1)﹣f(x2)|≥2成立,则∀x1 , x2∈R,都有|f(x1)﹣f(x2)|≥2成立.其中正确的是________ (写出所有正确命题的编号).7. (1分)如图1,在矩形ABCD中,AB=2BC,E、F分别是AB、CD的中点,现在沿EF把这个矩形折成一个直二面角A﹣EF﹣C(如图2),则在图2中直线AF与平面EBCF所成的角的大小为________.8. (1分) (2017高二下·温州期末) 在正四面体P﹣ABC中,点M是棱PC的中点,点N是线段AB上一动点,且,设异面直线 NM 与 AC 所成角为α,当时,则cosα的取值范围是________.9. (1分) (2019高三上·牡丹江月考) 如图正方体的棱长为,、、,分别为、、的中点.则下列命题:①直线与平面平行;②直线与直线垂直;③平面截正方体所得的截面面积为;④点与点到平面的距离相等;⑤平面截正方体所得两个几何体的体积比为 .其中正确命题的序号为________.10. (1分)(2019高二上·山西月考) 在四面体中,,,,则四面体外接球的表面积是________.11. (1分) (2019高一下·上海月考) 不等式的解为________12. (1分)设直线l与球O有且只有一个公共点P,从直线l出发的两个半平面α,β截球O的两个截面圆的半径分别为1和,二面角α﹣l﹣β的平面角为,则球O的表面积为________ .13. (1分) (2019高一下·上海期末) 函数,的值域是________.14. (1分)某物流公司为了配合“北改”项目顺利进行,决定把三环内的租用仓库搬迁到北三环外重新租地建设.已知仓库每月占用费y1与仓库到车站的距离成反比,而每月车载货物的运费y2与仓库到车站的距离成正比.据测算,如果在距离车站10千米处建仓库,这两项费用y1 , y2分别是2万元和8万元,那么要使这两项费用之和最小,仓库应建在离车站________千米处.三、解答题 (共4题;共50分)15. (10分)正方体ABCD﹣A'B'C'D'的棱长为a,连接A'C',A'D,A'B,BD,BC',C'D,得到一个三棱锥A'﹣BC'D.求:(1)求异面直线A'D与C'D′所成的角;(2)三棱锥A'﹣BC'D的体积.16. (10分)(2017·枣庄模拟) 在四边形ABCD中(如图①),AB∥CD,AB⊥BC,G为AD上一点,且AB=AG=1,GD=CD=2,M为GC的中点,点P为边BC上的点,且满足BP=2PC.现沿GC折叠使平面GCD⊥平面ABCG(如图②).(1)求证:平面BGD⊥平面GCD:(2)求直线PM与平面BGD所成角的正弦值.17. (15分)如下图所示的图形绕虚线旋转一周后形成的几何体是由哪些简单几何体组成的?18. (15分)如图,在四棱柱ABCD﹣A1B1C1D1中,侧棱AA1⊥底面ABCD,AB⊥AC,AB=1,AC=AA1=2,AD=CD=,且点M和N分别为B1C和D1D的中点.(Ⅰ)求证:MN∥平面ABCD(Ⅱ)求二面角D1﹣AC﹣B1的正弦值;(Ⅲ)设E为棱A1B1上的点,若直线NE和平面ABCD所成角的正弦值为,求线段A1E的长.参考答案一、单选题 (共4题;共8分)1-1、2-1、3-1、4-1、二、填空题 (共10题;共10分)5-1、6-1、7-1、8-1、9-1、10-1、11-1、12-1、13-1、14-1、三、解答题 (共4题;共50分)15-1、15-2、16-1、16-2、17-1、18-1、。
2015-2016年内蒙古赤峰二中高二(下)4月月考数学试卷(文科)(解析版)

2015-2016学年内蒙古赤峰二中高二(下)4月月考数学试卷(文科)一、选择题(本大题包括12小题,每小题5分,共60分,每小题给出的四个选项中,只有一项是符合题目要求的,请将正确选项填涂在答题卡上)1.(5分)复数的共轭复数的虚部是()A.i B.1C.﹣i D.﹣12.(5分)用反证法证明命题“三角形的内角至少有一个角不大于60°”时,应假设()A.三角形的三个内角都不大于60°B.三角形的三个内角都大于60°C.三角形的三个内角至多有一个大于60°D.三角形的三个内角至少有两个大于60°3.(5分)如图是根据变量x,y的观测数据(x i,y i)(i=1,2,…10)得到的散点图,由这些散点图可以判断变量x,y具有相关关系的图是()A.①②B.①④C.②③D.③④4.(5分)正弦函数是奇函数,f(x)=sin(x2+1)是正弦函数,因此f(x)=sin(x2+1)是奇函数,以上推理()A.小前提不正确B.大前提不正确C.结论正确D.全不正确5.(5分)某单位有840名职工,现采用系统抽样方法,抽取42人做问卷调查,将840人按1,2,…,840随机编号,则抽取的42人中,编号落入区间[481,720]的人数为()A.11B.12C.13D.146.(5分)已知x与y之间的一组数据:已求得关于y与x的线性回归方程为=2.1x+0.85,则m的值为()A.1B.0.85C.0.7D.0.57.(5分)从6名男同学和4名女同学中随机选出3名同学参加一项竞技测试,选出的三位同学中至少有一名女同学的概率是()A.B.C.D.8.(5分)已知x>0,y>0,x+2y+2xy=8,则x+2y的最小值是()A.3B.4C.D.9.(5分)用数学归纳法证明不等式“1+++…+<n(n∈N*,n≥2)”时,由n=k (k≥2)不等式成立,推证n=k+1时,左边应增加的项数是()A.2k﹣1B.2k﹣1C.2k D.2k+110.(5分)执行如图所示的程序框图,则输出的结果为()A.4B.9C.7D.511.(5分)在区间[﹣3,3]上随机取一个数x,使得|x+1|﹣|x﹣2|≥1成立的概率是()A.B.C.D.12.(5分)设a、b、c是互不相等的正数,现给出下列不等式(1)|a﹣b|≤|a﹣c|+|b﹣c|;(2);(3);(4),则其中正确个数是()A.0B.1C.2D.3二、填空题(每小题5分,共4小题,满分20分.把答案填在答题卡上.)13.(5分)已知复数z满足:(1+i)z=i(i为虚数单位),则|z|等于.14.(5分)解不等式:x+|2x﹣1|<3.15.(5分)若x>0,y>0,且x+2y=1,则+的取值范围是.16.(5分)观察下列等式:…照此规律,第n个等式可为.三、解答题(本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤.)17.(10分)为了解某班学生喜爱打篮球是否与性别有关,对本班50人进行了问卷调查得到了如下的列联表:已知在全部50人中随机抽取1人抽到喜爱打篮球的学生的概率为.(1)请将上面的列联表补充完整;(2)是否有99.5%的把握认为喜爱打篮球与性别有关?说明你的理由;下面的临界值表供参考:(参考公式:,其中n=a+b+c+d)18.(12分)以下茎叶图记录了甲、乙两组各三名同学在期末考试中的数学成绩.乙组记录中有一个数字模糊,无法确认,假设这个数字具有随机性,并在图中以a表示.(Ⅰ)若甲、乙两个小组的数学平均成绩相同,求a的值;(Ⅱ)当a=3时,分别从甲、乙两组同学中各随机选取一名同学,求这两名同学中乙同学的成绩比甲同学的成绩好的概率.(Ⅲ)求乙组平均成绩超过甲组平均成绩的概率.19.(12分)(1)已知x∈R,m=x2﹣1,n=2x+2.求证:m,n中至少有一个是非负数.(2)已知a,b,c均为正实数,且a+b+c=1,求证:(﹣1)(﹣1)(﹣1)≥8.20.(12分)某种产品的年销售额y与该年广告费用支出x有关,现收集了4组观测数据列于下表:(1)已知这两个变量满足线性相关关系,求y与x之间的回归方程=x+(2)计划2016年的销售额为100万元,请根据你得到的模型,预测该年广告费用支出应为多少万元?(线性回归方程系数公式==,=﹣,参考数据)21.(12分)某校从高一年级学生中随机抽取40名学生作为样本,将他们的期中考试数学成绩(满分100分,成绩均为不低于40分的整数)分成六段:[40,50),[50,60),[90,100)后得到如图的频率分布直方图.(Ⅰ)求图中实数a的值;(Ⅱ)根据频率分布直方图,试估计该校高一年级学生其中考试数学成绩的平均数;(Ⅲ)若从样本中数学成绩在[40,50)与[90,100]两个分数段内的学生中随机选取2名学生,试用列举法求这两名学生的数学成绩之差的绝对值不大于10的概率.22.(12分)已知函数f(x)=|x﹣a|,其中a>1(1)当a=2时,求不等式f(x)≥4﹣|x﹣4|的解集;(2)已知关于x的不等式|f(2x+a)﹣2f(x)|≤2的解集{x|1≤x≤2},求a的值.2015-2016学年内蒙古赤峰二中高二(下)4月月考数学试卷(文科)参考答案与试题解析一、选择题(本大题包括12小题,每小题5分,共60分,每小题给出的四个选项中,只有一项是符合题目要求的,请将正确选项填涂在答题卡上)1.(5分)复数的共轭复数的虚部是()A.i B.1C.﹣i D.﹣1【解答】解:复数===2+i的共轭复数2﹣i的虚部为﹣1.故选:D.2.(5分)用反证法证明命题“三角形的内角至少有一个角不大于60°”时,应假设()A.三角形的三个内角都不大于60°B.三角形的三个内角都大于60°C.三角形的三个内角至多有一个大于60°D.三角形的三个内角至少有两个大于60°【解答】解:∵用反证法证明在一个三角形中,至少有一个内角不大于60°,∴第一步应假设结论不成立,即假设三个内角都大于60°.故选:B.3.(5分)如图是根据变量x,y的观测数据(x i,y i)(i=1,2,…10)得到的散点图,由这些散点图可以判断变量x,y具有相关关系的图是()A.①②B.①④C.②③D.③④【解答】解:由题图③可知,y随x的增大而减小,各点整体呈下降趋势,x与y负相关,由题图④可知,u随v的增大而增大,各点整体呈上升趋势,u与v正相关.故选:D.4.(5分)正弦函数是奇函数,f(x)=sin(x2+1)是正弦函数,因此f(x)=sin(x2+1)是奇函数,以上推理()A.小前提不正确B.大前提不正确C.结论正确D.全不正确【解答】解:大前提:正弦函数是奇函数,正确;小前提:f(x)=sin(x2+1)是正弦函数,因为该函数为复合函数,故错误;结论:f(x)=sin(x2+1)是奇函数,因为该函数为偶函数,故错误.故选:A.5.(5分)某单位有840名职工,现采用系统抽样方法,抽取42人做问卷调查,将840人按1,2,…,840随机编号,则抽取的42人中,编号落入区间[481,720]的人数为()A.11B.12C.13D.14【解答】解:使用系统抽样方法,从840人中抽取42人,即从20人抽取1人.所以从481~720共240人中抽取=12人.故选:B.6.(5分)已知x与y之间的一组数据:已求得关于y与x的线性回归方程为=2.1x+0.85,则m的值为()A.1B.0.85C.0.7D.0.5【解答】解:∵==,=,∴这组数据的样本中心点是(,),∵关于y与x的线性回归方程=2.1x+0.85,∴=2.1×+0.85,解得m=0.5,∴m的值为0.5.故选:D.7.(5分)从6名男同学和4名女同学中随机选出3名同学参加一项竞技测试,选出的三位同学中至少有一名女同学的概率是()A.B.C.D.【解答】解:∵从6名男同学和4名女同学中随机选出3名同学参加一项竞技测试,∴基本事件总数n=,选出的3名同学中,至少有一名女同学的对立事件是选出的3名同学都是男同学,选出的3名同学中,至少有一名女同学的概率:P=1﹣=.故选:A.8.(5分)已知x>0,y>0,x+2y+2xy=8,则x+2y的最小值是()A.3B.4C.D.【解答】解:考察基本不等式,整理得(x+2y)2+4(x+2y)﹣32≥0即(x+2y﹣4)(x+2y+8)≥0,又x+2y>0,所以x+2y≥4故选:B.9.(5分)用数学归纳法证明不等式“1+++…+<n(n∈N*,n≥2)”时,由n=k (k≥2)不等式成立,推证n=k+1时,左边应增加的项数是()A.2k﹣1B.2k﹣1C.2k D.2k+1【解答】解:n=k时,左边=1+++…+,当n=k+1时,左边=1+++…++++…+.∴左边增加的项数为2k+1﹣1﹣(2k﹣1)=2k+1﹣2k=2k.故选:C.10.(5分)执行如图所示的程序框图,则输出的结果为()A.4B.9C.7D.5【解答】解:当n=1时,执行循环体后,T=2,S=18,n=3,不满足退出循环的条件,当n=3时,执行循环体后,T=8,S=36,n=5,不满足退出循环的条件,当n=5时,执行循环体后,T=32,S=54,n=7,不满足退出循环的条件,当n=7时,执行循环体后,T=128,S=72,n=9,满足退出循环的条件,故输出的n值为9,故选:B.11.(5分)在区间[﹣3,3]上随机取一个数x,使得|x+1|﹣|x﹣2|≥1成立的概率是()A.B.C.D.【解答】解:利用几何概型,其测度为线段的长度.由不等式|x+1|﹣|x﹣2|≥1 可得①,或②,③.解①可得x∈∅,解②可得1≤x<2,解③可得x≥2.故原不等式的解集为{x|x≥1},∴在区间[﹣3,3]上随机取一个数x使得|x+1|﹣|x﹣2|≥1的概率为P==.故选:B.12.(5分)设a、b、c是互不相等的正数,现给出下列不等式(1)|a﹣b|≤|a﹣c|+|b﹣c|;(2);(3);(4),则其中正确个数是()A.0B.1C.2D.3【解答】解:(1)∵)|a﹣b|=|(a﹣c)+(c﹣b)|≤|a﹣c|+|b﹣c|,故(1)正确;(2)由于a>0,令t=a+(t≥2),则a2+﹣(a+)=t2﹣t﹣2=t(t﹣1)﹣2≥2×1﹣2=0,即则a2+≥a+,故(2)正确;(3)不妨令a=1,b=2,则|a﹣b|+=1﹣1=0<2,故(3)错误;(4)要证﹣≤﹣,需证+≤+,即证2a+3+2≤2a+3+2,即证a2+3a≤a2+3a+2,即0≤2,显然成立,故原式成立,故(4)正确;综上所述,正确个数是3.故选:D.二、填空题(每小题5分,共4小题,满分20分.把答案填在答题卡上.)13.(5分)已知复数z满足:(1+i)z=i(i为虚数单位),则|z|等于.【解答】解:∵(1+i)z=i,∴(1﹣i)(1+i)z=i(1﹣i),∴z=,则|z|==.故答案为:.14.(5分)解不等式:x+|2x﹣1|<3.【解答】解:原不等式可化为或,解得:或,∴原不等式得解集为.15.(5分)若x>0,y>0,且x+2y=1,则+的取值范围是[3+,+∞).【解答】解:∵x>0,y>0,x+2y=1,那么:=()(x+2y)=1+≥3+2=3+.当且仅当x=y,即x=,y=时取等号.所以:的取值范围是[3+,+∞)故答案为:[3+,+∞).16.(5分)观察下列等式:…照此规律,第n个等式可为(n+1)(n+2)…(n+n)=2n×1×3×…×(2n﹣1).【解答】解:观察规律知,左边为n项的积,最小项和最大项依次为(n+1),(n+n),右边为连续奇数之积乘以2n,则第n个等式为:(n+1)(n+2)…(n+n)=2n×1×3×…×(2n ﹣1).故答案为:(n+1)(n+2)…(n+n)=2n×1×3×…×(2n﹣1).三、解答题(本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤.)17.(10分)为了解某班学生喜爱打篮球是否与性别有关,对本班50人进行了问卷调查得到了如下的列联表:已知在全部50人中随机抽取1人抽到喜爱打篮球的学生的概率为.(1)请将上面的列联表补充完整;(2)是否有99.5%的把握认为喜爱打篮球与性别有关?说明你的理由;下面的临界值表供参考:(参考公式:,其中n=a+b+c+d)【解答】解:(1)根据在全部50人中随机抽取1人抽到喜爱打篮球的学生的概率为,可得喜爱打篮球的学生为30人,故可得列联表补充如下:﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(6分)(2)∵﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(12分)∴有99.5%的把握认为喜爱打篮球与性别有关.﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(14分)18.(12分)以下茎叶图记录了甲、乙两组各三名同学在期末考试中的数学成绩.乙组记录中有一个数字模糊,无法确认,假设这个数字具有随机性,并在图中以a表示.(Ⅰ)若甲、乙两个小组的数学平均成绩相同,求a的值;(Ⅱ)当a=3时,分别从甲、乙两组同学中各随机选取一名同学,求这两名同学中乙同学的成绩比甲同学的成绩好的概率.(Ⅲ)求乙组平均成绩超过甲组平均成绩的概率.【解答】解:(Ⅰ)由甲、乙两个小组的数学平均成绩相等,得(88+92+92)=[90+91+(90+a)],解得a=1;(Ⅱ)设“这两名同学中乙同学的成绩比甲同学的成绩好”为事件B,当a=3时,分别从甲、乙两组同学中各随机选取一名同学,所有可能的成绩结果有3×3=9种,它们是:(88,90),(88,91),(88,93),(92,90),(92,91),(92,93),(92,90),(92,91),(92,93).∴事件B的结果有5种,它们是:(88,90),(88,91),(88,93),(92,93),(92,93).∴P(B)=.(Ⅲ)设“乙组平均成绩超过甲组平均成绩”为事件A,a的取值有:0,1,2,…,9共有10种可能.由(Ⅰ)可知,当a=1时甲、乙两个小组的数学平均成绩相同,∴当a=2,…,9时,乙组平均成绩超过甲组平均成绩,共有8种可能.∴乙组平均成绩超过甲组平均成绩的概率P(A)==.19.(12分)(1)已知x∈R,m=x2﹣1,n=2x+2.求证:m,n中至少有一个是非负数.(2)已知a,b,c均为正实数,且a+b+c=1,求证:(﹣1)(﹣1)(﹣1)≥8.【解答】(1)证明:假设m<0且n<0,所以m+n<0.又m+n=x2﹣1+2x+2=x2+2x+1=(x+1)2≥0,这与假设所得结论矛盾,故假设不成立,所以,m,n中至少有一个是非负数;(2)证明:因为a,b,c均为正实数,且a+b+c=1,则:(﹣1)(﹣1)(﹣1)=••=••≥2•2•2=8,当且仅当a=b=c=时取等号.20.(12分)某种产品的年销售额y与该年广告费用支出x有关,现收集了4组观测数据列于下表:(1)已知这两个变量满足线性相关关系,求y与x之间的回归方程=x+(2)计划2016年的销售额为100万元,请根据你得到的模型,预测该年广告费用支出应为多少万元?(线性回归方程系数公式==,=﹣,参考数据)【解答】解:(1)由题意,=4,=45,,=78∴==5,=45﹣5×4=25,∴回归直线方程为=5x+25;(2)由已知y=100时,5x+25=100,可得x=15万元.答:(1)回归直线方程为=5x+25;(2)预测该年广告费用支出应为15万元.21.(12分)某校从高一年级学生中随机抽取40名学生作为样本,将他们的期中考试数学成绩(满分100分,成绩均为不低于40分的整数)分成六段:[40,50),[50,60),[90,100)后得到如图的频率分布直方图.(Ⅰ)求图中实数a的值;(Ⅱ)根据频率分布直方图,试估计该校高一年级学生其中考试数学成绩的平均数;(Ⅲ)若从样本中数学成绩在[40,50)与[90,100]两个分数段内的学生中随机选取2名学生,试用列举法求这两名学生的数学成绩之差的绝对值不大于10的概率.【解答】解:(Ⅰ)由频率分布直方图,得:10×(0.005+0.01+0.025+a+0.01)=1,解得a=0.03.(Ⅱ)由频率分布直方图得到平均分:=0.05×45+0.1×55+0.2×65+0.3×75+0.25×85+0.1×95=74(分).(Ⅲ)由频率分布直方图,得数学成绩在[40,50)内的学生人数为40×0.05=2,这两人分别记为A,B,数学成绩在[90,100)内的学生人数为40×0.1=4,这4人分别记为C,D,E,F,若从数学成绩在[40,50)与[90,100)两个分数段内的学生中随机选取2名学生,则所有的基本事件有:(A,B),(A,C),(A,D),(A,E),(A,F),(B,C),(B,D),(B,E),(B,F),(C,D),(C,E),(C,F),(D,E),(D,F),(E,F),共15个,如果这两名学生的数学成绩都在[40,50)或都在[90,100)内,则这两名学生的数学成绩之差的绝对值不大于10,记“这两名学生的数学成绩之差的绝对值不大于10”为事件M,则事件M包含的基本事件有:(A,B),(C,D),(C,E),(C,F),(D,E),(D,F),(E,F),共7个,所以这两名学生的数学成绩之差的绝对值不大于10的概率P=.22.(12分)已知函数f(x)=|x﹣a|,其中a>1(1)当a=2时,求不等式f(x)≥4﹣|x﹣4|的解集;(2)已知关于x的不等式|f(2x+a)﹣2f(x)|≤2的解集{x|1≤x≤2},求a的值.【解答】解:(1)当a=2时,f(x)≥4﹣|x﹣4|可化为|x﹣2|+|x﹣4|≥4,当x≤2时,得﹣2x+6≥4,解得x≤1;当2<x<4时,得2≥4,无解;当x≥4时,得2x﹣6≥4,解得x≥5;故不等式的解集为{x|x≥5或x≤1}.(2)设h(x)=f(2x+a)﹣2f(x),则h(x)=由|h(x)|≤2得,又已知关于x的不等式|f(2x+a)﹣2f(x)|≤2的解集{x|1≤x≤2},所以,故a=3.。
内蒙古包市高二下学期4月月考数学试题(文科)(解析版)20

高二(下)4月月考数学试卷(文科)一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.(5分)复数(1﹣i)•(1+i)的值是()A.﹣2i B.2i C.2 D.﹣22.(5分)下列命题中是真命题的是()A.如果a>b,那么ac>bc B.如果a>b,那么ac2>bc2C.如果a>b,那么a n>b n(n∈N*) D.如果a>b,c<D那么a﹣c>b﹣d 3.(5分)已知函数f(x)=2cosx﹣3sinx的导数为f'(x),则f'(x)=()A.f'(x)=﹣2sinx﹣3cosx B.f'(x)=﹣2cosx+3sinxC.f'(x)=﹣2sinx+3cosx D.f'(x)=2sinx﹣3cosx4.(5分)下面是关于复数z=的四个命题:其中的真命题为(),p1:|z|=2,p2:z2=2i,p3:z的共轭复数为1+i,p4:z的虚部为﹣1.A.p2,p3B.p1,p2C.p2,p4D.p3,p45.(5分)某样本数据如表:由该样本数据得到的回归方程为=x+.若=7.9,则的值为()A.1.4 B.﹣1.4 C.1.2 D.﹣1.26.(5分)如图,在复平面内,复数z1,z2对应的向量分别是,,则复数对应的点位于()A.第一象限B.第二象限C.第三象限D.第四象限7.(5分)函数y=f(x)的图象过原点且它的导函数y=f′(x)的图象是如图所示的一条直线,y=f(x)的图象的顶点在()A.第Ⅰ象限B.第Ⅱ象限C.第Ⅲ象限D.第Ⅳ象限8.(5分)已知f(x)=x3﹣ax在[1,+∞)上是单调增函数,则a的最大值是()A.0 B.1 C.2 D.39.(5分)等比数列{a n}中,公比q=2,首项a1=2,函数f(x)=x(x﹣a1)(x﹣a2),则f'(0)=()A.8 B.﹣8 C.28D.﹣2810.(5分)已知f(x)=2x3﹣6x2+m(m为常数)在[﹣2,2]上有最大值3,那么此函数在[﹣2,2]上的最小值为()A.﹣5 B.﹣11 C.﹣29 D.﹣3711.(5分)已知二次函数f(x)=ax2+bx+c的导数为f′(x),f′(0)>0,对于任意实数x都有f(x)≥0,则的最小值为()A.3 B.C.2 D.12.(5分)设函数f(x)=x3﹣4x+a(0<a<2)有三个零点x1,x2,x3,且x1<x2<x3,则下列结论正确的是()A.x1>﹣1 B.x2<0 C.x3>2 D.0<x2<1二、填空题:本大题共4小题,每小题5分,共20分.13.(5分)若z l=a+2i,z2=3﹣4i,且为纯虚数,则实数a的值为.14.(5分)若x<0,则函数的最大值为.15.(5分)已知函数f(x)是R上的奇函数,且在(0,+∞)上有f'(x)>0,若f(﹣1)=0,那么关于x的不等式xf(x)<0的解集是.16.(5分)已知点P在曲线上,α为曲线在点P处的切线的倾斜角,则α的取值范围是.三、简答题:本大题共6个小题,第一小题10分,其余每小题各12分. 17.(10分)已知点P在函数f(x)=xe x的图象上.(Ⅰ)求曲线y=f(x)在点P(1,f(1))处的切线方程;(II)求函数y=f(x)的单调区间和极值.18.(12分)已知函数f(x)=|x+1|+2|x﹣a|.(Ⅰ)若a=1,求不等式f(x)>2的解集;(II)若函数y=f(x)的最小值为5,求实数a的值.19.(12分)如图是我国2010年至2016年生活垃圾无害化处理量(单位:亿吨)的折线图.(Ⅰ)由折线图看出,可用线性回归模型拟合y与t的关系,请用相关系数加以说明;(Ⅱ)建立y关于t的回归方程(系数精确到0.01),预测2018年我国生活垃圾无害化处理量.附注:参考数据:=9.32,=40.17,=0.55,≈2.646.参考公式:r=回归方程=+t中斜率和截距的最小二乘估计公式分别为:==,.20.(12分)为了调查某大学学生在周日上网的时间,随机对100名男生和100名女生进行了不记名的问卷调查.得到了如下的统计结果; 表1:男生上网时间与频数分布表表2:女生上网时间与频数分布表(1)若该大学共有女生750人,试估计其中上网时间不少于60分钟的人数; (2)完成下面的2×2列联表,并回答能否有90%的把握认为“大学生周日上网时间与性别有关”? 表3附:K 2=21.(12分)已知函数f(x)=x3+ax2﹣x+c,且a=f′().(1)求a的值;(2)求函数f(x)的单调区间;(3)设函数g(x)=[f(x)﹣x3]•e x,若函数g(x)在x∈[﹣3,2]上单调递增,求实数c的取值范围.22.(12分)已知函数f(x)=xlnx.(I)求函数f(x)的单调递减区间;(II)若f(x)≥﹣x2+ax﹣6在(0,+∞)上恒成立,求实数a的取值范围;(III)过点A(﹣e﹣2,0)作函数y=f(x)图象的切线,求切线方程.高二(下)4月月考数学试卷(文科)参考答案与试题解析一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.(5分)复数(1﹣i)•(1+i)的值是()A.﹣2i B.2i C.2 D.﹣2【分析】直接利用复数代数形式的乘法运算化简得答案.【解答】解:(1﹣i)•(1+i)=12﹣i2=1+1=2.故选:C.【点评】本题考查复数代数形式的乘法运算,是基础的计算题.2.(5分)下列命题中是真命题的是()A.如果a>b,那么ac>bc B.如果a>b,那么ac2>bc2C.如果a>b,那么a n>b n(n∈N*)D.如果a>b,c<D那么a﹣c>b﹣d 【分析】对于A,举反例c≤0时,结论不成立;对于B,举反例c=0时,结论不成立;对于C,讨论0>a>b时,n为奇数或偶数时,结论不一定成立;对于D,应用不等式的性质证明结论成立.【解答】解:对于A,当c≤0时,由a>b,得ac≤bc,∴A是假命题;对于B,当c=0时,由a>b,得ac2=bc2,∴B是假命题;对于C,当0>a>b时,若n为正奇数,由a>b,得a n>b n(n∈N*),若n为正偶数,由a>b,得a n<b n(n∈N*),∴C是假命题;对于D,∵a>b,c<d,∴﹣c>﹣d,∴a﹣c>b﹣d,∴D正确.故选:D.【点评】本题考查了不等式的性质与应用问题,解题时应通过举反例的方法,以及推理证明的方法进行分析与判断,是综合题目.3.(5分)已知函数f(x)=2cosx﹣3sinx的导数为f'(x),则f'(x)=()A.f'(x)=﹣2sinx﹣3cosx B.f'(x)=﹣2cosx+3sinxC.f'(x)=﹣2sinx+3cosx D.f'(x)=2sinx﹣3cosx【分析】根据基本导数公式求导即可【解答】解:f'(x)=﹣2sinx﹣3cosx,故选:A【点评】本题考查导数的运算法则,属于基础题.4.(5分)下面是关于复数z=的四个命题:其中的真命题为(),p1:|z|=2,p2:z2=2i,p3:z的共轭复数为1+i,p4:z的虚部为﹣1.A.p2,p3B.p1,p2C.p2,p4D.p3,p4【分析】由z===﹣1﹣i,知,,p 3:z的共轭复数为﹣1+i,p4:z的虚部为﹣1,由此能求出结果.【解答】解:∵z===﹣1﹣i,∴,,p3:z的共轭复数为﹣1+i,p4:z的虚部为﹣1,故选C.【点评】本题考查复数的基本概念,是基础题.解题时要认真审题,仔细解答.5.(5分)某样本数据如表:由该样本数据得到的回归方程为=x+.若=7.9,则的值为()A.1.4 B.﹣1.4 C.1.2 D.﹣1.2【分析】由该样本数据计算、,根据回归方程过样本中心点,代入求出的值.【解答】解:由该样本数据计算=×(3+4+5+6+7)=5,=×(4.0+2.5﹣0.5+0.5﹣2.0)=0.9,且回归方程=x+中,=7.9,则==﹣1.4.故选:B.【点评】本题考查了线性回归方程过样本中心点的应用问题,是基础题.6.(5分)如图,在复平面内,复数z1,z2对应的向量分别是,,则复数对应的点位于()A.第一象限B.第二象限C.第三象限D.第四象限【分析】通过向量的表示求出向量对应的复数,利用复数的除法运算,求出复数对应的点的象限即可.【解答】解:由题意可知z1=﹣2﹣i,z2=i.∴===﹣1+2i,复数对应的点位于第二象限.故选B.【点评】本题考查复数的基本运算,复数与向量的对应关系,复数的几何意义.7.(5分)函数y=f(x)的图象过原点且它的导函数y=f′(x)的图象是如图所示的一条直线,y=f(x)的图象的顶点在()A.第Ⅰ象限B.第Ⅱ象限C.第Ⅲ象限D.第Ⅳ象限【分析】根据导函数的图象和函数f(x)过原点,设f(x)=ax2+bx并求出f′(x),由图得判断出a、b的符号,再判断出二次函数f(x)的顶点坐标的符号,即可确定顶点所在的象限.【解答】解:由导函数的图象和y=f(x)的图象过原点,设f(x)=ax2+bx,所以f′(x)=2ax+b,由图得a>0,b>0,则<0,=<0则函数f(x)=ax2+bx图象的顶点(,)在第三象限,故选:C.【点评】本题考查利用导数研究函数,以及一次函数和二次函数的图象与性质,考查了数形结合思想,属于基础题.8.(5分)已知f(x)=x3﹣ax在[1,+∞)上是单调增函数,则a的最大值是()A.0 B.1 C.2 D.3【分析】由f(x)=x3﹣ax在[1,+∞)上是单调增函数,得到在[1,+∞)上,f′(x)≥0恒成立,从而解得a≤3,故a的最大值为3.【解答】解:∵f(x)=x3﹣ax在[1,+∞)上是单调增函数∴f′(x)=3x2﹣a≥0在[1,+∞)上恒成立.即a≤3x2∵x∈[1,+∞)时,3x2≥3恒成立∴a≤3∴a的最大值是3故选D【点评】本题主要考查三次函数的单调性的应用、不等式的解法、恒成立问题的解决方法等基础知识,考查了运算求解能力,化归与转化思想.9.(5分)等比数列{a n}中,公比q=2,首项a1=2,函数f(x)=x(x﹣a1)(x﹣a2),则f'(0)=()A.8 B.﹣8 C.28D.﹣28【分析】先根据等比数列的性质求出a2,化简f(x),根据导数的运算法则求导即可.【解答】解:等比数列{a n}中,公比q=2,首项a1=2,∴a2=4,∴f(x)=x(x﹣2)(x﹣4)=x3﹣6x2+8x,∴f′(x)=3x2﹣12x+8,∴f′(0)=8,故选:A【点评】本题考查了等比数列的运算性质以及导数的运算法则,属于基础题.10.(5分)已知f(x)=2x3﹣6x2+m(m为常数)在[﹣2,2]上有最大值3,那么此函数在[﹣2,2]上的最小值为()A.﹣5 B.﹣11 C.﹣29 D.﹣37【分析】求函数的导数,利用导数结合函数的最大值求出m,即可求出函数的最小值.【解答】解:函数的导数为f′(x)=6x2﹣12x=6x(x﹣2),由f′(x)>0得x>2或x<0,此时函数递增,由f′(x)<0得0<x<2,此时函数递减,∵x∈[﹣2,2],∴函数在[﹣2,0]上递增,则[0,2]上递减,则函数的最大值为f(0)=m=3,则f(x)=2x3﹣6x2+3,∵f(2)=2×23﹣6×22+3=﹣5,f(﹣2)=2×(﹣2)3﹣6×(﹣2)2+3=﹣37,∴当x=﹣2时,函数取得最小值为﹣37,故选:D【点评】本题主要考查函数最值的求解,求函数的导数,利用导数研究函数在闭区间上的最值是解决本题的关键.11.(5分)已知二次函数f(x)=ax2+bx+c的导数为f′(x),f′(0)>0,对于任意实数x都有f(x)≥0,则的最小值为()A.3 B.C.2 D.【分析】先求导,由f′(0)>0可得b>0,因为对于任意实数x都有f(x)≥0,所以结合二次函数的图象可得a>0且b2﹣4ac≤0,又因为,利用均值不等式即可求解.【解答】解:∵f'(x)=2ax+b,∴f'(0)=b>0;∵对于任意实数x都有f(x)≥0,∴a>0且b2﹣4ac≤0,∴b2≤4ac,∴c>0;∴,当a=c时取等号.故选C.【点评】本题考查了求导公式,二次函数恒成立问题以及均值不等式,综合性较强.12.(5分)设函数f(x)=x3﹣4x+a(0<a<2)有三个零点x1,x2,x3,且x1<x2<x3,则下列结论正确的是()A.x1>﹣1 B.x2<0 C.x3>2 D.0<x2<1【分析】判断f(x)的单调性,得出三个零点的大致范围,再根据函数零点的存在性定理进行判断.【解答】解:f′(x)=3x2﹣4,令f′(x)=0得x=﹣或x=.∴f(x)在(﹣∞,﹣)上单调递增,在(﹣,)上单调递减,在(,+∞)上单调递增.∴f(x)在(﹣∞,﹣),(﹣,),(,+∞)上各有一个零点.∴x1<﹣<﹣1,故A错误;∵f(﹣)>0,f(0)=a>0,f(1)=﹣3+a<0,f()<0,∴0<x2<1,故B错误;D正确.∵f(2)=a>0,∴x3<2,故C错误.故选D.【点评】本题考查了函数零点的存在性定理,函数单调性的判断,属于中档题.二、填空题:本大题共4小题,每小题5分,共20分.13.(5分)若z l=a+2i,z2=3﹣4i,且为纯虚数,则实数a的值为.【分析】把z l=a+2i,z2=3﹣4i代入,然后化简,复数分子、分母同乘分母的共轭复数,利用实部等于0,虚部不为0,求出a即可.【解答】解:=它是纯虚数,所以3a﹣8=0,且4a+6≠0,解得a=故答案为:【点评】本题考查复数代数形式的乘除运算,复数的基本概念,是基础题.14.(5分)若x<0,则函数的最大值为﹣2.【分析】利用基本不等式得出答案.【解答】解:当x<0时,﹣x>0,∴(﹣x)+≥2=2,∴x+=﹣[(﹣x)+]≤﹣2.故答案为:﹣2.【点评】本题考查了基本不等式与函数最值的计算,属于基础题.15.(5分)已知函数f(x)是R上的奇函数,且在(0,+∞)上有f'(x)>0,若f(﹣1)=0,那么关于x的不等式xf(x)<0的解集是(﹣1,0)∪(0,1).【分析】根据题意,由导数与函数单调性的关系,可得函数f(x)在(0,+∞)为增函数,结合函数的奇偶性可得f(x)在(﹣∞,0)上也为增函数,且f(1)=﹣f(﹣1)=0;由不等式的性质可得xf(x)<0⇒或,解可得x的取值范围,即可得答案.【解答】解:根据题意,函数f(x)在(0,+∞)上有f'(x)>0,则函数在(0,+∞)为增函数,又由函数f(x)是R上的奇函数,则函数f(x)在(﹣∞,0)上也为增函数;且f(1)=﹣f(﹣1)=0当x>0时,xf(x)<0⇒,则有0<x<1,即(0,1),当x<0时,xf(x)<0⇒,则有﹣1<x<0,即(﹣1,0),综合可得:xf(x)<0的解集为:(﹣1,0)∪(0,1);故答案为:(﹣1,0)∪(0,1).【点评】本题考查函数的奇偶性与单调性的综合应用,涉及函数的导数与单调性的关系,关键是利用函数奇偶性的性质进行分类讨论.16.(5分)已知点P在曲线上,α为曲线在点P处的切线的倾斜角,则α的取值范围是(,π).【分析】求出函数的导数,计算切线的斜率,从而求出倾斜角的范围即可.【解答】解:y′=﹣e﹣x,y′|x=0=﹣1,根据倾斜角的范围是(0,π),而函数y=在(0,+∞)递减,故﹣1<tanα<0,故<α<π,故答案为:(,π).【点评】本题考查了切线斜率问题,考查切线的倾斜角,是一道基础题.三、简答题:本大题共6个小题,第一小题10分,其余每小题各12分. 17.(10分)已知点P在函数f(x)=xe x的图象上.(Ⅰ)求曲线y=f(x)在点P(1,f(1))处的切线方程;(II)求函数y=f(x)的单调区间和极值.【分析】(Ⅰ)求得切点坐标和函数的导数,可得切线的斜率,运用点斜式方程可得切线的方程;(II)求导,根据导数与函数单调性及极值的关系,即可求得函数y=f(x)的单调区间和极值.【解答】解:(Ⅰ)由f(x)=xe x,f(1)=e,求导f′(x)=e x+xe x=(1+x)e x,∴f′(1)=2e,∴点P(1,f(1))处的切线方程y﹣f(1)=f′(1)(x﹣1),即y﹣e=2e(x﹣1),整理得:y=2ex﹣e,曲线y=f(x)在点P(1,f(1))处的切线方程y=2ex﹣e;(II)∵函数f(x)=xe x的定义域为R,f'(x)=(xe x)′=x′e x+x(e x)′=e x+xe x,令f'(x)=e x+xe x=e x(1+x)=0,解得:x=﹣1.则x,f′(x),f(x)的变化:∴可知函数f(x)=xe x的单调递减区间为(﹣∞,﹣1),单调递增区间为(﹣1,+∞).当x=﹣1时,函数f(x)=xe x的极小值为f(﹣1)=﹣,无极大值.【点评】本题考查导数的运用:求切线的方程,考查导数的几何意义,利用导数求函数的单调性及极值,考查转化思想,属于中档题.18.(12分)已知函数f(x)=|x+1|+2|x﹣a|.(Ⅰ)若a=1,求不等式f(x)>2的解集;(II)若函数y=f(x)的最小值为5,求实数a的值.【分析】(Ⅰ)通过讨论x的范围,求出各个区间上的不等式的解集,取并集即可;(Ⅱ)通过讨论a的范围,求出各个区间上的函数的最小值,得到关于a的方程,解出即可.【解答】解:(Ⅰ)a=1时,f(x)=|x+1|+2|x﹣1|,x≥1时,f(x)=x+1+2x﹣2=3x﹣1>2,解得:x>1,﹣1<x<1时,f(x)=x+1+2﹣2x=﹣x+3>2,解得:x<1,x≤﹣1时,f(x)=﹣x﹣1+2﹣2x=﹣3x+1>2,解得:x<﹣,综上,不等式的解集是(﹣∞,1)∪(1,+∞);(II)①a>﹣1时,x≥a时,f(x)=x+1+2x﹣2a=3x+1﹣2a,此时,f(x)min=f(a)=a+1,﹣1≤x≤a时,f(x)=x+1+2a﹣2x=﹣x+2a+1,此时,f(x)min=f(a)=a+1;x≤﹣1时,f(x)=﹣x﹣1+2a﹣2x=﹣3x+2a﹣1,此时,f(x)min=f(﹣1)=2a+2,由a>﹣1,得2a+2>a+1,综上,f(x)的最小值是f(a)=a+1=5,解得:a=4;②a<﹣1时,x≥﹣1时,f(x)=x+1+2x﹣2a=3x+1﹣2a,此时,f(x)min=f(﹣1)=﹣2a﹣2,a≤x≤﹣1时,f(x)=﹣x﹣1+2x﹣2a=x﹣1﹣2a,此时,f(x)min=f(a)=﹣a﹣1,x≤a时,f(x)=﹣x﹣1﹣2x+2a=﹣3x+2a﹣1,此时,f(x)min=f(a)=﹣a﹣1,由a<﹣1,则﹣a﹣1<﹣2a﹣2,故f(x)的最小值是f(a)=﹣a﹣1=5,解得:a=﹣6,综合①②a=4或a=﹣6.【点评】本题考查了解绝对值不等式问题,考查分类讨论思想以及函数最值问题,是一道中档题.19.(12分)如图是我国2010年至2016年生活垃圾无害化处理量(单位:亿吨)的折线图.(Ⅰ)由折线图看出,可用线性回归模型拟合y与t的关系,请用相关系数加以说明;(Ⅱ)建立y关于t的回归方程(系数精确到0.01),预测2018年我国生活垃圾无害化处理量.附注:参考数据:=9.32,=40.17,=0.55,≈2.646.参考公式:r=回归方程=+t中斜率和截距的最小二乘估计公式分别为:==,.【分析】(Ⅰ)由折线图中数据和附注中参考数据,计算相关系数,根据相关系数的值得出结论;(Ⅱ)计算回归系数,写出y关于t的回归方程;将2018年对应的t值代入回归方程,计算对应的函数值即可.【解答】解:(Ⅰ)由折线图中数据和附注中参考数据得,,,,所以相关系数为;…(4分)因为y与t的相关系数近似为0.99,说明y与t的线性相关程度相当高,从而可以用线性回归模型拟合y与t的关系;…(6分)(Ⅱ)由及(Ⅰ)得,,;所以,y 关于t的回归方程为:;…(10分)将2018年对应的t=9代入回归方程得:;所以预测2016年我国生活垃圾无害化处理量将约1.82亿吨…(12分) 【点评】本题考查了相关系数与回归直线方程的求法和应用问题,是中档题.20.(12分)为了调查某大学学生在周日上网的时间,随机对100名男生和100名女生进行了不记名的问卷调查.得到了如下的统计结果; 表1:男生上网时间与频数分布表表2:女生上网时间与频数分布表(1)若该大学共有女生750人,试估计其中上网时间不少于60分钟的人数; (2)完成下面的2×2列联表,并回答能否有90%的把握认为“大学生周日上网时间与性别有关”? 表3附:K 2=【分析】(1)女生网时间不少于60分钟的人数的比例为,即可得出结论;(2)根据所给数据完成表3的2×2列联表,利用公式求出k 2,与临界值比较,可得结论.【解答】解:(1)若该大学共有女生750人,估计其中上网时间不少于60分钟的人数750×=225人;(2)因为2.198<2.706,所以不能有90%的把握认为“学生周日上网时间与性别有关”. 【点评】本题考查概率知识的运用,考查独立性检验知识,考查学生的计算能力,属于中档题.21.(12分)已知函数f (x )=x 3+ax 2﹣x +c ,且a=f′(). (1)求a 的值;(2)求函数f (x )的单调区间;(3)设函数g (x )=[f (x )﹣x 3]•e x ,若函数g (x )在x ∈[﹣3,2]上单调递增,求实数c 的取值范围.【分析】(1)先求出函数的导数,得到f′()=3×+2f′()×﹣1,解出即可;(2)先求出函数的导数,解关于导函数的方程,从而得到函数的单调区间;(3)问题等价于h (x )=﹣x 2﹣3x +c ﹣1≥0在x ∈[﹣3,2]上恒成立,只要h (2)≥0,解出即可.【解答】解:(1)f′(x )=3x 2+2ax ﹣1,当x=时,得a=f′()=3×+2f′()×﹣1,解之,得a=﹣1.(2)∵f (x )=x 3﹣x 2﹣x +c ,∴f′(x )=3(x +)(x ﹣1),列表如下: ,所以f (x )的单调递增区间是(﹣∞,﹣)和(1,+∞);f (x )的单调递减区间是(﹣,1).(3)函数g (x )=(﹣x 2﹣x +c )e x ,有g′(x )=(﹣x 2﹣3x +c ﹣1)e x ,因为函数在区间x ∈[﹣3,2]上单调递增,等价于h (x )=﹣x 2﹣3x +c ﹣1≥0在x ∈[﹣3,2]上恒成立,只要h (2)≥0,解得c ≥11,所以c 的取值范围是:c ≥11.【点评】本题考查了函数的单调性问题,考查导数的应用,函数恒成立问题,是一道中档题.22.(12分)已知函数f (x )=xlnx .(I )求函数f (x )的单调递减区间;(II )若f (x )≥﹣x 2+ax ﹣6在(0,+∞)上恒成立,求实数a 的取值范围; (III )过点A (﹣e ﹣2,0)作函数y=f (x )图象的切线,求切线方程.【分析】(Ⅰ)由f′(x )=lnx +1,知f′(x )<0得lnx <﹣1,由此能求出函数f (x )的单调递减区间.(Ⅱ)由f (x )≥﹣x 2+ax ﹣6,得,设,则,由此能求出g (x )最小值g (2)=5+ln2,从而能求出实数a 的取值范围.(Ⅲ)设切点T (x 0,y 0)则k AT =f′(x 0),故,由此能求出切线方程.【解答】解:(Ⅰ)∵f′(x )=lnx +1∴f′(x )<0得lnx <﹣1 (2分) ∴∴函数f (x )的单调递减区间是; (4分)(Ⅱ)∵f (x )≥﹣x 2+ax ﹣6即 设, 则 (7分)当x ∈(0,2)时g′(x )<0,函数g (x )单调递减;当x ∈(2,+∞)时g′(x )>0,函数g (x )单调递增;∴g (x )最小值g (2)=5+ln2,∴实数a 的取值范围是(﹣∞,5+ln2]; (10分)(Ⅲ)设切点T (x 0,y 0)则k AT =f′(x 0), ∴即e 2x 0+lnx 0+1=0设h (x )=e 2x +lnx +1,当x >0时h′(x )>0,∴h (x )是单调递增函数 (13分)∴h (x )=0最多只有一个根, 又,∴由f'(x0)=﹣1得切线方程是.(16分)【点评】本题考查利用导数求闭区间上函数的最值的灵活运用,考查化归与转化、分类与整合的数学思想,培养学生的抽象概括能力、推理论证能力、运算求解能力和创新意识.。
内蒙古赤峰市田家炳中学10-11学年高二4月月考(数学理)

赤峰市田家炳中学高二理科数学月考试卷考试时间150分钟第一卷一、选择题1.下列结论中正确的是( ) (A)导数为零的点一定是极值点(B)如果在0x 附近的左侧0)('>x f ,右侧0)('<x f ,那么)(0x f 是极大值 (C)如果在0x 附近的左侧0)('>x f ,右侧0)('<x f ,那么)(0x f 是极小值 (D)如果在0x 附近的左侧0)('<x f ,右侧0)('>x f ,那么)(0x f 是极大值 2“∵四边形ABCD 是等腰梯形,∴四边形ABCD 的对角线相等.”补充以上推理的大前提( ) A.正方形都是对角线相等的四边形 B. 矩形都是对角线相等的四边形C.等腰梯形都是对角线相等的四边形D.矩形都是对边平行且相等的四边形 3函数()f x 可导,则0(1)(1)2limx f x f x∆→+∆-∆等于( )A '(1)fB '2(1)f C'1(1)2f D '(2)f 34.()34([0,1])1()1()()0()12f x x x x A B C D =-∈-函数的最大值是( )5.已知{}n b 为等比数列,25=b ,则993212=b b b b .若{}n a 为等差数列,25=a ,则{}n a 的类似结论为 ( )A.993212=a a a aB. 91292a a a +++=C. 929321⨯=a a a aD. 12929a a a +++=⨯6. ()f x 与()g x 是R 定义在上的两个可导函数,若()f x 与()g x 满足()()f x g x ''=,则()f x 与()g x 满足:A.()()f x g x = B.()()f x g x - 为常数函数C.()()0f x g x ==D.()()f x g x +为常数函数7. 求曲线2y x =与y x =所围成图形的面积,其中正确的是( ) A .120()S x x dx =-⎰B .120()S x x dx =-⎰C .120()S y y dy =-⎰D .10(S y dy =⎰8.右图是函数b ax x x f ++=2)(的部分图象,则函数()ln ()g x x f x '=+的零点所在的区间是 ( )A 11(,)42B (1,2)C 1(,1)2D (2,3) 9. 函数xx y 142+=单调递增区间是( )A .),0(+∞B .)1,(-∞C .),21(+∞ D .),1(+∞ 10.函数xxy ln =的最大值为( ) A .1-e B .e C .2e D .31011. 设a ∈R ,若函数()3axy e x x R =+∈有大于零的极值点,则( ).3A a >- .3B a <-1.3C a >-1.3D a <-12. 对于R 上可导的任意函数f (x ),且'(1)0f =若满足(x -1)f x '()>0,则必有 ( )A 、f (0)+f (2)<2f (1)B 、f (0)+f (2)≥2f (1)C 、f (0)+f (2)>2f (1)D 、f (0)+f (2)≥2f (1)第二卷各题得分二 填空题13. 函数322(),f x x ax bx a =+++在1=x 时有极值10,那么b a ,的值分别为 。
内蒙古赤峰市田家炳中学2010-2011学年高二下学期第一次月考试题(生物)

内蒙古赤峰市田家炳中学2010-2011学年高二下学期第一次月考试题(生物)1、本试卷分选择题和非选择题两部分,满分为100分。
考试用时90分钟。
2、单选题答案用2B铅笔填涂在答题卡上,非选择题答案用黑色字迹钢笔或签字笔写在试卷上。
第Ⅰ卷(选择题,共60分)一、单选题(每小题只有一个选项最符合题意。
每题1.5分,共60分。
)1.关于人体激素的叙述,错误..的是()A.激素在人体内作为信息物而发挥作用B.激素在人体内含量较低,但有高效的生物催化作用C.人体激素产生后没有专门的导管运输,而是弥散到体液中D.正常人体内,激素的分泌受反馈调节2.有关人体内环境稳态的叙述,错误..的是()A.有3种以上的生理系统参与维持体内环境稳态B.人体内环境稳态的失调与外界环境无关C.人体维持内环境稳态的调节能力有限D.稳态有利于参与其调节的器官保持机能正常3.人体中占体液总量百分比最大的是()A.细胞内液 B.细胞外液C.血液D.淋巴和组织液4.下列各组化合物中,是内环境成分的是()A、纤维蛋白原B、血红蛋白C、受体蛋白D、载体蛋白5.剧烈运动时,血浆中乳酸含量大增而pH基本不变,对此现象的不正确解释是()A.血浆是一种缓冲溶液体系B.乳酸与NaHCO3反应生成弱酸H2CO3和乳酸钠C.产生的H2CO3分解成的CO2可经呼吸排出D.大量乳酸进入血液后马上被稀释或被彻底分解6.下列叙述中,不正确的是()A.血浆成分渗出毛细血管就成为组织液B.组织液渗入毛细血管就成为血浆C.组织液渗入毛细淋巴管就成为淋巴D.淋巴渗出毛细淋巴管壁就成为组织液7.下列关于内环境的叙述中,正确的一组是()①内环境是体内细胞赖以生存的液体环境②内环境是细胞内的环境,即细胞内液③细胞只有通过内环境才能与外界进行物质、能量的交换④内环境主要由血浆、组织液、淋巴构成A、①④B、①③④C、①②③D、③④8.右图是人体内环境示意图。
若某人长期营养不良,血浆蛋白质降低,会引起图中哪一部分的液体增多()A.① B.② C.③ D.④9.反射和反射弧的关系正确的是( )A.反射活动可以不完全通过反射弧实现B.反射活动的完成必须通过反射弧来实现C.只要反射弧完整,必然出现反射活动D.反射和反射弧在性质上是完全相同的10.在反射弧中,能够对刺激起分析和综合作用的是 ( )A.传入神经B.效应器C.感受器 D.神经中枢11.下列有关人体糖代谢及调节的叙述,不正确的是()A.血糖浓度升高能使胰岛A细胞分泌增强B.饥饿时首先被利用的是肝糖元,其后是脂肪C.糖类氧化分解释放的能量的主要贮存形式是ATPD.多食少动,糖类易转变成脂肪而使人肥胖12.胰岛主要有两种分泌细胞,分别是A细胞、B细胞,当血液中葡萄糖量偏高时 ( )A.A细胞、B细胞的分泌功能均增强B.A细胞、B细胞的分泌功能均减弱C.A细胞分泌功能大大增强,B细胞分泌功能大大减弱D.A细胞分泌功能大大减弱,B细胞分泌功能大大增强13.许多淡水鱼在人工饲养的条件下不产卵,如取同种鱼的脑下垂体研碎入鱼体内,可促其产卵,这主要是利用垂体中含有的 ( )A.性激素 B.促甲状腺激素 C.促性腺激素 D.肾上腺素14.人体稳态的调节能力是有一定限度的。
内蒙古赤峰市高二数学下学期第一次月考试题 文

内蒙古赤峰二中2016-2017学年高二下学期第一次月考数学(文)试题试卷类型:A 2017.04.07一.选择题:(本大题共12小题,每小题5分,共60分) 1.复数的11-=i Z 模为( )A .21 B .22 C .2 D .22.角4πα≠是1tan ≠α的( )A.充分不必要条件B.必要不充分条件C.充要条件D.以上都不对3.用反证法证明命题“设a ,b 为实数,则方程x 2+ax +b =0至少有一个实根”时,要做 的假设是( )A .方程x 2+ax +b =0没有实根 B .方程x 2+ax +b =0至多有一个实根 C .方程x 2+ax +b =0至多有两个实根 D .方程x 2+ax +b =0恰好有两个实根 4.函数x x y ln 212-=的单调递减区间为( ) A.(-1,1] B.(0,1] C.[1,+∞) D.(0,+∞)5. 下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量x (吨)与相应的生产耗y (吨标准煤)的几对照数据根据上述数据,得到线性回归方程为35.07.0+=∧x y ,则a =( ) A. 3B. 4C. 5D. 66.为了解高中生作文成绩与课外阅读量之间的关系,某研究机构随机抽取60名高中生做问卷调查,得到以下数据:( ). A .在样本数据中没有发现足够证据支持结论 “作文成绩优秀与课外阅读量大有关”B .在犯错误的概率不超过0.001的前提下认为作文成绩优秀与课外阅读量大有关C .在犯错误的概率不超过0.05的前提下认为作文成绩优秀与课外阅读量大有关D .在犯错误的概率不超过0.005的前提下认为作文成绩优秀与课外阅读量大有关 7.命题“∀x ∈[1,2],x 2-a ≤0”为真命题的一个充分不必要条( ) A .a ≥4 B .a ≤4 C .a ≥5 D .a ≤58.已知函数(a 3)x 5,1(x)2,1x f a x x-+≤⎧⎪=⎨>⎪⎩ 是(-∞,+∞)上的减函数,则a 的取值范围是( )A .(0,3) B.(0,3] C.(0,2) D.(0,2]9.等轴双曲线C 的中心在原点,焦点在x 轴上,C 与抛物线x y 162=的准线交于,A B两点,AB =;则C 的实轴长为( )A. 2B. 22C.4D.810.若函数b bx x x f 33)(3+-=在)(1,0内有极小值,则( )A.10<<bB. 1<bC.0>bD. 21<b 11. 已知点A (2,0),抛物线C :x 2=4y 的焦点为F ,射线FA 与抛物线C 相交于点M ,与其准线相交于点N ,则|FM|:|MN|=( )12如图,P (x 0 , f (x 0))是函数y =f (x )图像上一点,曲线y =f (x)在点P 处的切线交x 轴于点A,PB ⊥x轴,垂足为B. 若ΔPAB 则 0f x '()与0()f x 满足关系式( ) A. 00f x f x ='()() B. 200f x f x ⎡⎤=⎣⎦'()() C. 00f x f x =-'()() D. 200f x f x ⎡⎤=⎣⎦'()()二、填空题:(本大题共4小题,每小题5分,共20分。
内蒙古赤峰二中高二数学4月月考试题文

内蒙古赤峰二中2017-2018 学年高二数学 4 月月考试题文一、选择题 : 本大题共12小题 ,每题 5分 , 共 60 分 , 在每题给出的四个选项中, 只有一项为哪一项切合题目要求的.101.已知复数z=3+i- 2i ( 此中 i 为虚数单位 ) ,则 | z| =A.3 3B. 3 2C.23D.2 22.设会合A= {(x, y)| x2+ y2=1}, B={( x, y)| y=3x},则 A∩ B 的子集的个数是A. 4B.3C.2D.13.为了研究某班学生的脚长 x (单位:厘米)和身高y(单位:厘米)的关系,从该班随机抽取 10名学生,依据丈量数据的散点图能够看出y 与x之间有线性有关关系,设其回归直线方?1010?4 .该班某学生的脚长为程为a?.已知x i 225 ,y i24,据此y? bx1600 ,bi 1i 1预计其身高为A 160B163C166D170[4. 我国古代数学名著《九章算术》有“米谷粒分”题:粮仓开仓收粮,有人送来米1534 石,验得米内夹谷,抽样取米一把,数得254 粒内夹谷28 粒,则这批米内夹谷约为()A.134 石B.169 石C.338 石D. 1365 石5.某校从高一年级学生中随机抽取部分学生,将他们的模块测试成绩分红 6 组:[40,50),[50,60),[60,70),[70,80),[80,90),[90,100]加以统计, 获得如下图的频次散布直方图.已知高一年级共有学生600 名 , 据此预计 , 该模块测试成绩许多于60 分的学生人数为() .A.588B.480 C .450 D .1206.已知 1 是 lga 与 lgb的等比中项,若 a>1, b> 1,则 ab 有()A.最小值 10B.最大值 100C.最大值 10 D.最小值 1007. 设函数 f ( x)=sin (ω x+φ) +cos(ω x+φ)的最小正周期为π,且 f (﹣ x) =f (x),则A . f ( x)在单一递减 B. f(x)在(,)单一递减C. f ( x)在( 0,)单一递加 D .f( x)在(,)单一递加8.如下图的程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术” .执行该程序框图,若输入的a, b 分别为72,27,则输出的aA. 18B.9C. 6D.39. 有5支彩笔(除颜色外无差异),颜色分别为红、黄、蓝、绿、紫. 从这 5 支彩笔中任取 2支不一样颜色的彩笔,则拿出的 2 支彩笔中含有红色彩笔的概率为4321A5B5C5D510 圆柱被一个平面截去一部分后与半球( 半径为r )构成一个几何体,该几何体三视图中的正视图和俯视图如下图. 若该几何体的表面积为16 + 20,则r=()A 1B 8C4D22x t(t 0)相切于 M ( t,6),则线段 AB的长为()A.12B. 18C. 16D. 2412.已知曲线 C1:y=e x上一点 A( x1,y1),曲线 C2:y=1+ln ( x﹣ m)( m>0)上一点 B( x2,y2),当 y1=y2时,对于随意x1, x2,都有 |AB| ≥ e 恒成立,则 m的最小值为()A. 1B. C . e﹣ 1D. e+1二.填空题:本大题共 4 小题,每题 5 分,共 20 分.13.已知实数x,y 知足则z=2x+y的最大值是.14 如图,在边长为 1 的正方形中,随机撒1000 粒豆子,有180 粒落到暗影部分,据此预计阴影部分的面积为___________.设双曲线 x2y2 1 a0,b 0 的左、右极点分别为A ,B,点P在双曲线上且异于A,B15.a2b2两点, O 为坐标原点.若直线PA 与 PB 的斜率之积为7,则双曲线的离心率为 ________.916, 已知函数 f ( x) 是定义在R 上的奇函数,当x0 时, f ( x)xe x,给出以下命题:①当 x0 时, f ( x )xe x;②函数 f ( x) 的单一递减区间是 (, 1),(1,) ;③ 对x1 , x2R ,都有 | f ( x1 ) f ( x2 ) |2.e此中正确的命题是(只填序号)三.解答题:解答应写出文字说明,证明过程或演算步骤.17 (本小题满分12 分)记 S n为等差数列a n的前n项和,已知,a2a1224 . S11121(1) 求a n的通项公式;(2) 令b n1, T n b1 b2 ...... b n,若24T n m 0 对一an 1an 2切n N 成立,务实数m的最大值.18.(本小题满分12 分)如图,四棱锥P- ABCD中,底面ABCD为平行四边形,∠DAB=60°, AB=2AD, M为 AB的中点,△ PAD为等边三角形,且平面 PAD⊥平 ABCD.(1)证明: PM⊥ BC;(2)若 PD=1,求点 D到平面 PAB的距离.19.(本小题满分12 分)跟着资本市场的强势进入,互联网共享单车“忽如一夜春风来”,遍及了一二线城市的大街小巷 . 为认识共享单车在A市的使用状况,某检查机构借助网络进行了问卷检查,并从参加检查的网友中抽取了 200 人进行抽样剖析,获得表格:(单位:人)常常使用有时或不用共计30 岁及以下703010030 岁以上6040100共计13070200( 1)依据以上数据,可否在出错误的概率不超出0.15 的前提下以为A市使用共享单车状况与年纪有关?( 2)现从所抽取的30 岁以上的网友中利用分层抽样的方法再抽取 5 人 .( i )分别求这 5 人中常常使用、有时或不用共享单车的人数;( ii )从这 5人中,再随机选出 2 人赠予一件礼物,求选出的 2 人中起码有 1 人常常使用共享单车的概率 .2参照公式:K2n ad bc,此中 n a b c d .a b c d a c b d参照数据:P K 2k00.150.100.050.0250.010k 02.072 2.7063.841 5.024 6.63520. (本小题满分 12 分)椭 圆 C :x2y 2 1(a b 0) 的 中 心 在 原 点, 焦 点 在 x 轴 上, 焦 距 为 2 , 且与 椭 圆a 2b 2x 2y 2 有同样离心率.12( 1)求椭圆 C 的方程;( 2)若直线 l : ykx m 与椭圆 C 交于不一样的 A, B 两点,且椭圆 C 上存在点 Q ,知足OA OB OQ ,( O 为坐标原点),务实数 取值范围.21 (本小题满分 12 分)已知函数 f ( x ) x 2 ln x ax , g( x)x 2 bx3( 1)若函数 f ( x ) 在 (1, f (1)) 处的切线与直线 2 x y 1 0 垂直,务实数 a 的值;( 2)当 a 0 时,若对于 x 的方程 xg ( x)2 f ( x ) 在区间 ( 1 , 2) 内有两个不相等的实根,2 务实数 b 的取值范围(已知 ln2 0.69 )请考生在第 22、23 两题中任选一题作答.注意:只好做所选定的题目. 假如多做,则按所做的第一个题目计分.22. ( 本小题满分 10 分 ) 选修 4-4 :坐标系与参数方程xOyx = 2+ 2cos α,为参数 ) ,曲线在直角坐标系中,曲线1的参数方程为(α2的Cy = 2sin αCx =2cos β,参数方程为( β 为参数 ) ,以 O 为极点, x 轴的正半轴为极轴成立极坐标系.y =2+ 2sin β(1) 求曲线 C 1 和曲线 C 2 的极坐标方程;ππ π(2) 已知射线 l 1:θ= α(0< α< 2 ) ,将射线 l 1 顺时针旋转 6 获得射线 l2:θ = α- 6 , 且射线 l 1 与曲线 1 交于 , 两点, 射线 l 2 与曲线 2 交于 , 两点,求| |·| | 的最大值.C O P C O Q OP OQ23.(本小题满分10 分)选修4— 5;不等式选讲已知函数 f ( x)2a |. | 2 x(Ⅰ)若 f (0) f (1)3| a |,务实数 a 的取值范围;a(Ⅱ)对随意 | x |≤ 1, f ( x) ≤ 1 恒成立,务实数 a 的值.赤峰二中2016 级高二放学期第一次月考文科数学答案选择题 1---12 BACBB DABCD DC13【答案】 1 0 14【答案】15.16答案. 2,317. (12 分)解:(1) ∵等差数列中,,.∴,解得.⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 2 分,⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 3 分.⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 5 分(2)⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯7 分,⋯⋯⋯ 9 分是增数列,,,∴实数的最大值为. ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯12 分19试题分析:( 1)由列联表可知,.因为,3分所以能在犯错误的概率不超过0.15的前提下认为市使用共享单车状况与年纪有关. 4分( 2 )(i)依题意可知,所抽取的 5 名30 岁以上的网友中,常常使用共享单车的有(人),有时或不用共享单车的有(人).7分(ii)设这5人中,经常使用共享单车的3人分别为,,;有时或不用共享单车的2人分别为,. 则从 5 人中选出 2 人的全部可能结果为,,,,,,,,,共10种. 9分此中没有 1 人常常使用共享单车的可能结果为共1种,故选出的2人中至少有1人经常使用共享单车的概率.12分20.解:(1)由已知可解得.⋯⋯⋯⋯⋯⋯⋯⋯⋯ 3 分所求的方程.⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 4 分( 2)成立方程组消去,整理得..由于直线直线与椭圆交于不同的两点,,有.①⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 6 分, 于是,.⋯⋯⋯⋯⋯⋯⋯⋯⋯8 分当时,易知点对于原点对称,则;当时,易知点不关于原点对称,则.此时,由,得即点在椭圆上,∴.化简得..②由①②两式可得.综上可得实数的取值范围是.⋯⋯⋯⋯⋯⋯⋯⋯⋯12 分21、---------------2分所在点处的切线斜率----------------4分----5分(2)由得因为,整理得:-----------------7分--8分所以当时,单一递减,当时,单一递减,所以在区间内-------------10分,所以所以----------------------------12分注,结果写成也正确221分22. (1) 曲线C的直角坐标方程为 ( x-2) +y= 41因此 C 的极坐标方程为ρ=4cosθ2分1曲线 C2的直角坐标方程为x2+( y-2)2=4,3分因此 C2的极坐标方程为ρ=4sinθ.4分(2) 设点P的极坐标为 ( ρ1,α) ,5分即ρ =4cosα,点Q的极坐标为(ρππ,( α- 6 )) ,即ρ= 4sin(α-6 ),6122分π31则 | OP| ·|OQ|=ρ1ρ2=4cos α·4sin( α- 6 ) = 16cos α·(2sin α-2cos α)= 8sin(2ππα-6 )-4.∵α∈(0,2 ),8分ππ5ππππ∴2α- 6 ∈ ( - 6 , 6 ) .当 2α- 6 = 2 ,即α= 3 时, | OP| ·| OQ|取最大值 4. 10(23)(本小题满分 10 分)选修 4-5 :不等式选讲解析:(Ⅰ)当时,可转化为,该不等式恒成立;当时,可转化为.上可得,数的取范是⋯5 分(Ⅱ)任意恒成立,可得,即,①又,即,②由①②可知.验证时恒成立 .⋯10 分。
内蒙古赤峰市数学高二下学期文数第三次月考试卷

内蒙古赤峰市数学高二下学期文数第三次月考试卷姓名:________ 班级:________ 成绩:________一、单选题 (共12题;共24分)1. (2分)集合,则=()A . (0,2)B . (0,2]C . [0,2]D . [0,2)2. (2分) (2017高二下·中山期末) 若复数z满足z﹣2i=﹣i•z,则z=()A . ﹣1+iB . 1﹣iC . 1+iD . ﹣1﹣i3. (2分) (2019高二下·汕头月考) 有人收集了春节期间平均气温与某取暖商品销售额的有关数据如下表:平均气温(℃)-2-3-5-6销售额(万元)20232730根据以上数据,用线性回归的方法,求得销售额y与平均气温x之间线性回归方程的系数 .则预测平均气温为-8℃时该商品销售额为()A . 34.6万元B . 35.6万元C . 36.6万元D . 37.6万元4. (2分)若从区间(0,e)内随机取两个数,则这两个数之积不小于e的概率为()A . 1-B . 1-C .D .5. (2分)函数的图象与方程的曲线有着密切的联系,如把抛物线的图象绕原点沿逆时针方向旋转90度就得到函数的图象.若把双曲线绕原点按逆时针方向旋转一定角度后,能得到某一个函数的图象,则旋转角可以是()A .B .C .D .6. (2分)执行如右图所示的程序框图.则输出的所有点(x,y)都在函数()的图象上.A . y=x+1B . y=2xC .D .7. (2分)在等差数列中,则的值为()A . 5B . 6C . 8D . 108. (2分) (2016高二上·晋江期中) 若实数x、y满足,则Z= 的取值范围为()A . (﹣∞,﹣4]∪[ ,+∞)B . (﹣∞,﹣2]∪[ ,+∞)C . [﹣2, ]D . [﹣4, ]9. (2分)若f(x)=是R上的增函数,那么a的取值范围是()A . [,3)B . [,1)C . [,3)D . [,1)10. (2分)函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<)的图象如图所示,则f(0)等于()A .B . -C .D . -11. (2分) (2016高三上·沙市模拟) 已知边长为的菱形ABCD中,∠BAD=60°,沿对角线BD折成二面角A﹣BD﹣C为120°的四面体ABCD,则四面体的外接球的表面积为()A . 25πB . 26πC . 27πD . 28π12. (2分) (2019高三上·广东月考) 已知函数(为自然对数的底数)在上有两个零点,则的范围是()A .B .C .D .二、填空题 (共5题;共9分)13. (1分)(2020·杨浦期末) 在直角坐标平面中,,动点在圆上,则的取值范围为________.14. (1分)要得到的图象,只要将的图象________.15. (1分) (2016高二上·福田期中) 已知P(4,﹣1),F为抛物线y2=8x的焦点,M为此抛物线上的点,且使|MP|+|MF|的值最小,则M点的坐标为________.16. (1分)已知数列的各项均为正,为其前项和,满足,数列为等差数列,且,则数列的前项和 ________.17. (5分)现有甲、乙两个靶.某射手向甲靶射击两次,每次命中的概率为,每命中一次得1分,没有命中得0分;向乙靶射击一次,命中的概率为,命中得2分,没有命中得0分.该射手每次射击的结果相互独立.假设该射手完成以上三次射击.(I)求该射手恰好命中两次的概率;(II)求该射手的总得分X的分布列及数学期望EX.三、解答题 (共6题;共55分)18. (10分) (2019高二上·中山月考) 在中,角所对的边分别为,的面积为, .(1)求角的大小;(2)若,,求的值.19. (5分)如图,在底面是直角梯形的四棱锥S﹣ABCD中,∠ABC=90°,SA⊥面ABCD,SA=AB=BC=1,AD=.(Ⅰ)求四棱锥S﹣ABCD的体积;(Ⅱ)求面SCD与面SBA所成的二面角的正切值.20. (10分)在平面直角坐标系xOy中,椭圆C1= 1(a>b>0)上任意一点到点P(﹣1,0)的最小距离为1,且椭圆C的离心率为.(1)求椭圆C的方程;(2)若直线l与椭圆C交于点M、N,且△MON的面积为,问|OM|2+|ON|2是否为定值?若是,求出该定值,并求出sin∠MON的最小值;若不是,说明理由.21. (10分) (2019高三上·西湖期中) 设函数,其图象与轴交于,两点,且 .(1)求的取值范围;(2)证明: .22. (10分)(2018·广东模拟) 选修4-4:坐标系与参数方程在直角坐标系中,直线的参数方程为(为参数),在以原点为极点,轴正半轴为极轴的极坐标系中,圆的方程为.(1)写出直线的普通方程和圆的直角坐标方程;(2)设点,直线与圆相交于两点,求的值.23. (10分)(2012·新课标卷理) 已知函数f(x)=|x+a|+|x﹣2| (1)当a=﹣3时,求不等式f(x)≥3的解集;(2)若f(x)≤|x﹣4|的解集包含[1,2],求a的取值范围.参考答案一、单选题 (共12题;共24分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、11-1、12-1、二、填空题 (共5题;共9分)13-1、14-1、15-1、16-1、17-1、三、解答题 (共6题;共55分)18-1、18-2、19-1、20-1、20-2、21-1、21-2、22-1、22-2、23-1、23-2、。
内蒙古赤峰市田家炳中学10-11学年高二上学期期中考试(语文)

赤峰市田家炳中学2010——2011学年上学期期中考试高二语文试卷(第一卷)第Ⅰ卷(选择题,共30分)一、(每小题3分,共12分)1、下列词语中加点字的读音有错的一组是()A、辖.制(xiá)央浼.(měi)憎.恶(zēng)迤逦..(yǐlǐ)B、讥诮.(qiào)拮.据(jié)欺侮.(wǔ)傩.送(nuó)C、提.防(tí)埋.怨(mán)滑稽.(jī)震颤.(chàn)D、双眸.(móu)翘.首(qiáo)庇.佑(bì)悖.时(bèi)2、下列加点成语使用恰当....的一项是()A、近日,乌鲁木齐市中级法院对7·5事件中3起案件进行一审公开审判,其中6人因罪行极其严重被判处死刑,一人有重大立功表现,罪不容诛....,被依法从轻判处无期徒刑。
B、在共和国成立六十周年之际,各地都举行一系列纪念活动,对这些有意义的活动,人们趋.之若鹜...,热情参与。
C、崔颢的《黄鹤楼》诗的首句是“昔人已乘黄鹤去”不是“昔人已乘白云去”,自唐以来,因版本记录不同,评论家莫衷一是....。
D、古建筑之所以卓尔不群....,不在于它的创新,而在于它代表了某个时代;当代的建筑最不应该照搬古代,需要有时代气息。
3、下列各句中,没有语病的一句是()A、记者又到学校采访到了许多张老师的事迹。
B、通过中国男子足球队的表现,使我们认识到良好的心理素质的重要。
C、我们对于“比较文学”是个比较陌生的概念,读读钱钟书的《谈中国诗》或许能引你走出陌生的境地。
D、“北京人”头盖骨化石,如果不是在“二战”中神秘失踪,他的科研价值一定会在诸多学科中得到充分体现。
4、依次填入下面一段文字横线处的语句,衔接最恰当的一组是()热爱语文吧!因为是语文给了我们聆听美的耳朵,发现美的眼睛,领悟美的头脑。
___________,___________,___________,___________,___________,___________。
内蒙古赤峰市田家炳中学10-11学年高二4月月考(数学理)

赤峰市田家炳中学高二理科数学月考试卷考试时间150分钟第一卷一、选择题1.下列结论中正确的是( ) (A)导数为零的点一定是极值点(B)如果在0x 附近的左侧0)('>x f ,右侧0)('<x f ,那么)(0x f 是极大值 (C)如果在0x 附近的左侧0)('>x f ,右侧0)('<x f ,那么)(0x f 是极小值 (D)如果在0x 附近的左侧0)('<x f ,右侧0)('>x f ,那么)(0x f 是极大值 2“∵四边形ABCD 是等腰梯形,∴四边形ABCD 的对角线相等.”补充以上推理的大前提( ) A.正方形都是对角线相等的四边形 B. 矩形都是对角线相等的四边形C.等腰梯形都是对角线相等的四边形D.矩形都是对边平行且相等的四边形 3函数()f x 可导,则0(1)(1)2limx f x f x∆→+∆-∆等于( )A '(1)fB '2(1)f C'1(1)2f D '(2)f 34.()34([0,1])1()1()()0()12f x x x x A B C D =-∈-函数的最大值是( )5.已知{}n b 为等比数列,25=b ,则993212=b b b b .若{}n a 为等差数列,25=a ,则{}n a 的类似结论为 ( )A.993212=a a a aB. 91292a a a +++=C. 929321⨯=a a a aD. 12929a a a +++=⨯6. ()f x 与()g x 是R 定义在上的两个可导函数,若()f x 与()g x 满足()()f x g x ''=,则()f x 与()g x 满足:A.()()f x g x = B.()()f x g x - 为常数函数C.()()0f x g x ==D.()()f x g x +为常数函数7. 求曲线2y x =与y x =所围成图形的面积,其中正确的是( ) A .120()S x x dx =-⎰B .120()S x x dx =-⎰C .120()S y y dy =-⎰D .10(S y dy =⎰8.右图是函数b ax x x f ++=2)(的部分图象,则函数()ln ()g x x f x '=+的零点所在的区间是 ( )A 11(,)42B (1,2)C 1(,1)2D (2,3) 9. 函数xx y 142+=单调递增区间是( )A .),0(+∞B .)1,(-∞C .),21(+∞ D .),1(+∞ 10.函数xxy ln =的最大值为( ) A .1-e B .e C .2e D .31011. 设a ∈R ,若函数()3axy e x x R =+∈有大于零的极值点,则( ).3A a >- .3B a <-1.3C a >-1.3D a <-12. 对于R 上可导的任意函数f (x ),且'(1)0f =若满足(x -1)f x '()>0,则必有 ( )A 、f (0)+f (2)<2f (1)B 、f (0)+f (2)≥2f (1)C 、f (0)+f (2)>2f (1)D 、f (0)+f (2)≥2f (1)第二卷各题得分二 填空题13. 函数322(),f x x ax bx a =+++在1=x 时有极值10,那么b a ,的值分别为 。
内蒙古赤峰市田家炳中学10-11学年高二上学期期中考试(数学)

赤峰市田家炳中学2010——2011学年上学期期中考试高二数学试卷(第一卷)一:选择题:(在每小题给出的四个选项中,只有一项是符合题目要求的。
每小题5分,共60分)1.ΔABC 中, a =1, b=3, ∠A=30°,则∠B 等于 ( )A .60°B .60°或120°C .30°或150°D .120°2.在△ABC 中,a =10,B=60°,C=45°,则c 等于 ( )A .310+B . 310C .13+D .()1310- 3. 已知集合{}{}0|032|2<-=<-+=a x x B x x x A ,集合若B A ⊆,则a 的取值范围是( ) A.1≤a B. 1≥a C. 1<a D. 1>a4.设{}n a 是等差数列,若273,13a a ==,则数列{}n a 前8项的和为 ( )A.128B.80C.64D.565.设等比数列{}n a 的公比2q =,前n 项和为n S ,则42S a =( ) A .215 B .4 C .2 D .217 6.在下列函数中,最小值是2的是 ( ) A.xx y 22+= B.21222+++=x x y C.x x y sin 1sin += D.55x x y -+= 7.已知,01,0<<-<b a 则 ( )A .2ab ab a >> B.a ab ab >>2C.a ab ab >>2 D .2ab a ab >>8.已知三角形ABC 的顶点坐标A(2,4),B(-1,2),C(1,0),点),(y x P 在三角形内部及边界上运动,则y x z -=的最大值和最小值分别是 ( )A. 3,1 B . -1,-3C. 1,-3 D . 3,-19.已知M={x|x2-2x -3>0}N={x |x2+ax+b ≤0},若M∪N =R ,M∩N=(3,]4,则a+b =( )A.—7 B.-1 C.1 D. 7( )A .(-∞,0)∪(3,+∞)B .(0 ,2)]C .(-1,3)D .(-∞,-1)∪(3,+∞)11.非常数数列}{n a 是等差数列,且}{n a 的第5、10、20项成等比数列,则此等比数列的公比为 ( )A .51B .5C .2D .21 12.函数y =log a (x +3)-1(a >0,a ≠1)的图象恒过定点A ,若点A 在函数1mx y n n =--的图像上,其中mn >0,则n m 21+的最小值为 ( )A .8B .6C .4D .2二:填空题:(每题5分,共20分。
内蒙古赤峰市田家炳中学10-11学年高二4月月考(语文)

锦山中学高二下学期4月份月考试卷语文第Ⅰ卷 阅读题一、现代文阅读(9分,每小题3分。
)阅读下面的文字,完成1—3题。
儒释道互补的和合文化对于和合文化,可以从多角度来解读。
有人从中读出一种文化战略,有人从中读出一种社会理想,都讲出了一番道理。
我别出心裁,想把和合文化解读为一种健全的心态。
在我看来,“和合”一词中的“合”,应该是指人的多种精神诉求的集合。
道理很简单,只有在具备两个以上要素的情况下,才能谈得上“合”;倘若只是单一要素,根本就谈不上“合”了。
多种要素凑在一起,有可能发生冲突,也未必就一定发生冲突。
即便发生冲突,也未尝不可以化解。
成功地化解冲突,便进入了“和”的状态。
/所谓“和”,应该是指多样性的统一,是指冲突的化解。
显而易见,这种意义上的“和”,有别于“同”,故而孔子力主“和而不同”。
要想把人的多方面的精神需求统一起来、协调起来,进入“和”的心态,绝非易事,仅靠一种学说,显然也是不可能做到的,必须综合运用多种学说。
在传统文化资源中,对于和合心态的养成,儒释道三家都是不可或缺的元素。
三教分别满足中国人精神生活中某方面的需要,帮助人们养成和合的心态。
儒家的精神趣旨,可以概括成三个字,那就是“拿得起”;用两个字来概括,那就是“有为”;用一个字来概括,那就是“张”。
儒家主张立德、立功、立言,主张干事,主张积极有为。
儒家好比是粮食店,是精神的加油站。
人没有饭吃,活不成;没有精神食粮,同样也活不成。
/道家的精神趣旨是“想得开”;用两个字来说,叫做“无为”;用一个字来说,叫做“弛”。
道家的趣旨与儒家似乎相反,实际上互为补充。
学会紧张,是一门学问;学会放松,同样也是一门学问。
道家好比是药店,当人遇到了精神困惑的时候,光吃粮食是不行的,还需要吃药,上药店。
/佛教精神趣旨是“放得下”;用一个字来说,那就是“空”。
用佛教的术语说,“放得下”就是看破红尘,去除我执和法执,把精神追求的目标定位在彼岸的极乐世界。
佛教是一个精品店,它要化解人生中的烦恼,达到精神上的解脱,使心灵得以净化。
内蒙古赤峰市田家炳中学10-11学年高二上学期期中考试(物理)

赤峰市田家炳中学2010——2011学年上学期期中考试高二物理试卷(第一卷)第Ⅰ卷(选择题,共48分)一. 选择题:(本题共16小题,每小题3分,共计48分.每小题有一个或多个选项符合题意,全部选对的得3分,选对但不全的得2分,错选或不答的得0分.)1.下列有关电场线的说法中正确的是( )A .电场线越密的地方,同一试探电荷受到的电场力就越大B .电场线就是点电荷在电场中的运动轨迹C .电场线弯曲的地方是非匀强电场, 电场线为直线的地方是匀强电场D .不存在两条平行的电场线 2. 以下说法中正确的是( )A .根据t QI = ,可知电流强度与电量成正比B .根据IUR =,可知导体的电阻与它两端的电压成正比C .1伏/安=1欧D .在I -U 图线上,图线斜率等于导体的电阻3.下面能从本质上解释磁场产生原因的话不正确的是: A .磁极产生磁场 B .电荷产生磁场C .运动电荷产生磁场D .永久磁体产生磁场4.当电子在小磁针正下方由A 不断运动到B 的过程中,如图所示,小磁针如何运动( ) A .不动B .N 极向纸里,S 极向纸外旋转C .向上运动D .N 极向纸外,S 极向纸里旋转5. 如图所示,三根长直导线通电电流大小相同,通电方向为b 导线和d 导线垂直纸面向里,C 导线向纸外,a 点为bd 的中点,ac 垂直bd ,且ab=ad=ac 。
则a 点磁感应强度的方向为( ) A .垂直纸面指向纸外 B .垂直纸面指向纸里 C .沿纸面由d 指向b D .沿纸面由a 指向c6. 对于通电螺线管,下列说法中正确的是( )A .通电螺线管表现出来的磁性相当于条形磁铁,一 端相当于N 极,另一端相当于S 极B .通电螺线管外部的磁感线是从N 极出来,进入S 极的C .通电螺线管内部的磁感线与螺线管轴线平行,由S 极指向N 极D .把小磁针放在通电螺线管内,小磁针静止时,小磁针的N 极指向螺线管的S 极7. 如图所示,一个有质量的金属棒MN ,两端用细软导线连接后悬挂于a 、b 两点。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
内蒙古赤峰市田家炳中学2010-2011学年高二数学4月月考 文
一、选择题:(本大题共12小题,每小题5分,共60分 。
在每小题给出的四个选项中,
只有一项是符合题目要求的)
1.下列函数中,定义域为R 的是 ( ) A. x y =
B. x y 2log =
C. 3x y =
D. x
y 1=
2.复数i z 21+-=,则 z 的虚部为( ) (A)1
(B)-1
(C)2
(D)-2
3.已知0>x ,则函数29
++
=x
x y 有( ) A .最小值8 B .最大值8 C .最小值11
D .最大值11
4.已知ABC △中,a =b =60B =,那么角A 等于( )
A .135
B .90
C .45
D .135或45
5.如果命题“
p q ∧”是假命题,“p ⌝” 是真命题,那么
( )A.命题p 一定是真命题 B.命题q 一定是真命题 C.命题q 可以是真命题也可以是假命题 D.命题q 一定是假命题 6.函数16)(2
3
+-=x x x f 是减函数的区间为( )
A .),4(+∞
B .(0,4)
C .)4,(-∞
D .)0,(-∞ 7.若1
sin cos 2
z i θθ=-
+是纯虚数,则θtan 的值为( )
A
B .
C D .8. 类比平面正三角形的“三边相等,三内角相等”的性质,可知正四面体的下列哪些性质,你认为比较恰当的是( )
① 各棱长相等,同一顶点上的任两条棱的夹角都相等;
② 各个面都是全等的正三角形,相邻两个面所成的二面角都相等; ③ 各个面都是全等的正三角形,同一顶点上的任两条棱的夹角都相等。
A .① B .①② C .①②③ D .③
9.在复平面上的平行四边形ABCD 中,AC =6+8i, BD =-4+6i.则DA 对应的复数是( ) (A )2+14i
(B )1+7i (C )2-14i (D )-1-7i
10. 按流程图的程序计算,若开始输入的值为3x =,则输出的x 的值是 ( )
A .6
B .21
C .156
D .231
11. 投掷两粒骰子,得到其向上的点数分别为n m ,,则复数))((mi n ni m -+为实数的概率为( ) (A )
13
(B )
14 (C )16
(D )
1
12
12.已知lg lg 0a b +=,则函数()x f x a =与函数()log b g x x =-的图象可能是 ( ) A . B . C . D .
二、填空题:( 本大题共4小题,每小题5分,共20分) 13.命题“x ∃∈R ,20x
≤”的否定是 _______________;
14.在等比数列}{n a 中,公比为2,前3项和为21,则=++543a a a ___________
15.在约束条件24120x y x y x +≤⎧⎪
-≤⎨⎪+≥⎩
下,目标函数23+-=y x z 的最大值为____________
16.已知双曲线)0,0(122
22>>=-b a b
y a x 的左、右焦点分别为,,21F F 着在双曲线的右支
上存在一点P ,使得|,|3||21PF PF =则双曲线的离心率e 的取值范围为_____.
三、解答题:(共6题,计70分)
17. (10分)如图,要计算西湖岸边两景点B 与C 的距离,由于地形的限制,需要在岸上
x
选取A 和D 两点,现测得AD CD ⊥,10AD km =,14AB km =,60BDA ︒
∠= ,
135BCD ︒∠=,求两景点B 与C 的距离(精确到0.1km ).参考数据:
1.414, 1.732,
2.236.===
18.(本小题满分12分)
设数列{}n a 的前n 项和为n S ,且满足2n n a S =-()n *∈N . (Ⅰ)求1a ,2a ,3a ,4a 的值并猜想这个数列的通项公式 (Ⅱ)证明数列{}n a 是等比数列.
19、 (本小题满分12分)
已知复数),(R y x yi x z ∈+=满足3)21()21(=⋅++⋅-+⋅z i z i z z .求复数z 在复平面上对应点的轨迹.
已知△ABC 的三边长为a 、b 、c ,且其中任意两边长均不相等.若 111,,a b c
成等差数列.
(1);
(2)求证B 不可能是钝角.
21.(本小题满分12分)
已知直线:2l x =-,l 与x 轴交于点A ,动点(,)M x y 到直线l 的距离比到点(1,0)F 的
距离大1.
(Ⅰ)求点M 的轨迹E 的方程;
(Ⅱ)过点A 作直线交曲线E 于,B C 两点,若2AB BC =,求此直线的方程.
设函数),,,(42)(2
3
R d c b a d cx bx ax x f ∈++-=图象关于原点对称, 且1=x 时,)(x f 取极小值.3
2- (1)求d c b a ,,,的值;
(2)当]1,1[-∈x 时,图象上是否存在两点,使得过此两点处的切线互相垂直?
试证明你的结论;
(3)若]1,1[,21-∈x x 时,求证:3
4|)()(|21≤-x f x f .
高二月考数学试题(文科)答案
一.选择题: CDACC,BDCDD,CB
二.填空题: 13.]2,1(.61 ;715. ;84.14 ;02,>∈∀x
R x 三.解答题:
17.解:在△ABD 中,设BD=x ,
则BDA AD BD AD BD BA ∠⋅⋅-+=cos 2222, 即 60cos 1021014222⋅⋅-+=x x ,
整理得:096102=--x x , 解之:161=x ,62-=x (舍去), 由正弦定理,得:
BCD
BD
CDB BC ∠=
∠sin sin , ∴2830sin 135
sin 16=⋅=
BC ≈11.3 (km)。
19
20.解:(1)
b
c
a b <,证明如下:
21.解:(Ⅰ)解法 1.依题意,动点(,)M x y 到直线1x =-和点(1,0)N 的距离相等,所以
1x =+,即24y x =.……………………………………………………4分
由跟与系数的关系得
2122
44k x x k -+=
124x x ⋅=…………………………………………………………………………………10分
由①、③得,124,33x x =
=,代入②,得212
25
k =
,
所以所求直线方程为2)y x =+…………………………………………………12分 22.(1)0,1,0,3
1
=-===
d c b a ; (2)不存在; (3)证明略.。
