§4 功和能
大学物理第四章--功和能

a
l
xdx
2l
前已得出:
Af
mg(l a)2
2l
mg(l 2 a2 ) mg(l a)2 1 mv2
2l
2l
2
得v
g l
1
(l 2 a 2 ) (l a)2 2
§3 保守力的功与势能 一、 保守力
rB
B
两个质点之间的引力
B
第四章 功和能
§4.1 功 §4.2 动能定理 §4.3 保守力功与势能 §4.4 功能原理机械能守恒定律
§1 功和功率
一、恒力做功 直线运动
A=Fcos S
记作A F S F r
F
F
M
M
S
位移无限小时:
dA
F
dr
dA称为元功
功等于质点受的力和它的位移的点积(标积)
例1一水平放置的弹簧,其一端固定,另一端系一小球,求小
球的位置由A到B的过程中弹力对它所做的功。(在O处弹簧无 形变)
解:根据胡克定律 F F kx
W F dr
xB Fdx
xA
xB xA
kxdx
O
1 2
A
k xB2
B
xA2
1 2
k xA2
作用在质点
上.在该质点从坐标原点运动到(0,2R)位
置过程中,力
F
对它所作的功为多少?
y
b
b
A a F.dr a (Fxdx Fydy)
R
x O
例4 如图,水平桌面上有质点 m ,桌面的摩 擦系数为μ 求:两种情况下摩擦力作的功
专题四功和能

专题四:功和能【知识梳理】一、功 1、功的定义: 一个物体受到力的作用,如果在力的方向上发生一段位移,我们就说这个力对物体做了功。
功是能量改变的量度。
2、公式:αcos FS W =功的正负:功是标量但有正负,当090≤<︒α时,力对物体做正功;90180︒<≤︒α时,力对物体做负功(物体克服某力做功,取正值)。
当︒=90α时,力对物体不功; 3、计算功的常用方法(1)用公式 W =Fs cos α计算功.该方法只能求恒力的功.该公式可写成 W =F ·(s ·cos α)=(F ·cos α)·s ,即功等于力与力方向上位移的乘积或等于位移与位移方向上力的乘积.(2)用公式 W =Pt 来计算.该式一般用于求功率恒定但力变化的情况,例如恒定功率启动的汽车. (3)利用功能原理求功.该方法在考试中最常用,注意功是能量转化的量度,某个力做功对应某一能量转化,例如合外力的功对应物体动能的变化,重力做功对应重力势能的变化,电场力做功对应电势能的变化.(4)等值法求功.当求某个力的功比较困难(一般是变力),且该力做功与某一力做功相同(一般是恒力),可以用等值替代来求.例1、某物体同时受到三个力作用而做匀减速直线运动,其中 F 1 与加速度 a 的方向相同,F 2 与速度 v 的方向相同,F 3 与 速度 v 的方向相反,则A .F 1对物体做正功B .F 2对物体做正功C .F 3对物体做正功D .合外力对物体做负功【解析】因物体做匀减速运动,a 的方向与 v 的方向相反,故F 1对物体做负功,A 错;F 2与速度 v 方向相同,做正功,B 正确;F 3 与 v 方向相反,做负功,C 错误;做匀减速直线运动时,合外力的方向与运动方向相反,做负功,故 D 正确.例2、如图8-3所示,用恒力F 通过光滑的定滑轮,将静止于水平面上的物体从位置A 拉到位置B ,物体可视为质点,定滑轮距水平面高为h ,物体在位置A 、B 时,细绳与水平面的夹角分别为α和β,求绳的拉力F 对物体做的功.【解析】从题设的条件看,作用于物体上的绳的拉力T ,大小与外力F 相等,但物体从A 运动至B 的过程中,拉力T 的方向与水平面的夹角由α变为β,显然拉力T 为变力.此时恒力功定义式W=F ·S·cos α就不适用了.如何化求变力功转而求恒力功就成为解题的关键.由于绳拉物体的变力T 对物体所做的功与恒力F 拉绳做的功相等,根据力对空间积累效应的等效替代便可求出绳的拉力对物体做的功.解:设物体在位置A 时,滑轮左侧绳长为l 1,当物体被绳拉至位置B 时,绳长变为l 2,因此物体由A 到B ,绳长的变化量又因T=F ,则绳的拉力T 对物体做的功例3、质量为m 的物体放在光滑的水平面上,绳经滑轮与水平方向成α角,大小为F 的力作用下,如图所示,求使物体前进位移为S 的过程中对物体做的功。
第四章功和能1

F
b
如果力是位置的函数,设质点在力的作
用元下位沿移一:曲d线r运动,则功的计算如下:
dr
段在位元移位上移的中元将功力为视d为A恒力F,无dr限小 a
在元位移中将力视为恒力,力沿ab的 F
b
功为dA所有F无 d限r小F段c位os移d上r的元F 功cos之d和s 。 dr
A
b
dA
b
F
dr
a
a
分量式: A
A
yb
ya
mgdy
mg
(
yb
ya
)
O
yb
x
可见,重力是保守力。
z
A mg ( yb ya ) -(E pb EPa ) EP
重力的功等于重力势能增量的负值。
重力势能可以某一水平面为零势能点,
EP 为势能增量
EP mgy
•弹力的功和弹性势能
F kx
A
xb xa
Fx
dx
ba
xb xa
这种力称为保守力。
L
2、势能:在具有保守力相互作用的系统内,只 由系统内质点间的相对位置决定的能量称为势 能。
3、几种保守力和相应的势能
•重力的功和重力势能
m在重力作用下由a运动到b,取地面为坐标原点,y
轴d向A上 为m正g,dar、b的Fyy坐d标y 分别m为gyda、yyb。
y b
ma c
mg ya
a
0
例2:有一倔强系数为k的轻弹簧,原长为l0,将 它掉在天花板上,当它下端挂一托盘平衡时,其 长度变为l1,然后托盘中放一重物,弹簧长度变 为l2,则由l1伸长至l2的过程中,弹簧弹性力所做 的功为(以弹簧原长处为坐标原点)
第四章 功和能

第一篇力学第4章功和能第4章功和能Work & Energy第1节功功率第2节动能动能定理第3节保守力势能第4节功能原理机械能守恒定律d rαrr 'ab Fod d A F r =⋅所做的总功d b ab a A F r =⋅⎰d cos b F S α=⎰d cos b aF r α=⎰Work & Power第1节功功率1.功——力的空间积累效应将质点由a 移动到b ,F力相应于元位移d rF , 力对质点所做的功为:——元功tt +d t合力做的功:注意:d b ab aA F r=⋅⎰可见:合力对物体所做的功等于其中各个分力分别对该物体所做功的代数和。
若有多个力同时作用在质点上,则d bab a A F r =⋅⎰ d 12(...)b a F F r=++⋅⎰d d 12...b b a a F r F r =⋅+⋅+⎰⎰...A A ++=21(1)力对质点所做的功, 不仅与始、末位置有关,而且往往与路径有关。
2.功率平均功率:瞬时功率(功率):——做功的快慢功率:力在单位时间内所做的功A P t∆∆=d d 0lim t A A P tt ∆∆∆→==d d A F r=⋅ d d r F F v t =⋅=⋅ P F v∴=⋅单位: 瓦特符号W 1W =1J·s -1当额定功率一定时,负荷力越大,可达到的速率就越小;负荷力越小,可达到的速率就越大。
这就是为什么汽车在上坡时走得慢,下坡时走得例1.如图所示,一匹马以平行于圆弧形路面的拉力拉着质量为m 的车沿半径为R 的圆弧形路面极缓慢地匀速移动,车与路面的滑动摩擦系数为μ,求:车由底端A 被拉上顶端B 时,各力对车所做的功。
解:车受4个力的作用拉力F 、摩擦力f ,沿切向路面支持力N 指向圆心O重力mg 竖直向下在切向与法向有:sin 0F f mg θ--=Nf μ=而()cos sin F mg μθθ∴=+cos 0N mg θ-=拉力的功:d B F A A F S=⎰31[]mgR μ=+d 600(cos sin )mg R μθθθ=+⎰R O R AB θo60重力的功d 600sin g A mg R θθ=-⋅⎰d()600cos mgR θ=⎰/2mgR =-摩擦力的功d 0Sf A f S=-⎰d 600cos mg R μθθ=-⋅⎰μmgR 23-=路面支持力N 的功为零.RORABθo60例2.一人从H =10m 深的水井中提水,开始时,桶中装有M =10kg 的水(忽略桶的质量).由于水桶漏水,每升高1m 要漏出0.2kg 的水,求将水桶匀速地从井中提到井口的过程中,人所做的功。
4 功和能

功能原理
A内非 0
封闭系统:不受外界作用的系统。 封闭系统内有非保守力做功时,机械能不守恒,能 量的形式可能变化,也可能在物体之间转移。
例7:在平面两相同的球做完全弹性碰撞,其中一球开始时 处于静止状态,另一球速度 v。 求证:碰撞后两球速度总互相垂直 解:设碰撞后两球速度 由动量守恒 两边平方
A
Aext Aint EkB EkA
质点组的动能定理: 外力功与内力功的总和,等于 质点系动能的增量。 内力可以改变系统的总动能(电荷的作用、爆炸)
但内力不能改变系统的总动量! (守恒条件)
例4:有一面为1/4凹圆柱面(半径R)的物体(质量M)放置 在光滑水平面,一小球(质量m),从静止开始沿圆面从顶端 无摩擦下落(如图),小球从水平方向飞离大物体时速度 v , 求:1)重力所做的功;2)内力所做的功。 解:重力只对小球做功 m M R A重力 mgs cos mgh A重力 mgR 水平方向无外力,系统水平方向动量守 恒。
A A B dv m dr m vdv A dt A 1 2 1 2 mvB mvA 2 2
B
dv Ft m dt
动能定理: 合外力对质点做的功等于质点动能的增量。
2.质点系的动能定理 B B1 B1 1 1 2 F1 dr1 f1 dr1 m1v 1B m1v 21 A F2 A1 f2 A1 2 2 F1 f1 m2 B2 B2 1 1 2 m1 F2 dr2 f 2 dr2 m2v 2 B m2v 2 2 A A2 A2 2 2
l2
(A) kxdx
l1 l 2 l0
l2
(B )
功和能(4)

了解常见力做功的特点重力做功和路径无关,只与物体始末位置的高度差h有关:W=mg h,当末位置高于初位置时,W>0,即重力做正功;反之则重力做负功。
滑动摩擦力做功与路径有关。
当某物体在一固定平面上运动时,滑动摩擦力做功的绝对值等于摩擦力与路程的乘积。
在弹性范围内,弹簧做功与始末状态弹簧的形变量有关系。
4.理解力和功率的关系。
某力做功的瞬时功率P与该瞬时力的大小F,速度υ及它们的夹角α有关:P=Fυcosα。
应用此式时注意两点:一是明确F指的哪个力;二是明确α是力与速度的夹角。
当我们用P=Fυ分析汽车或汽船(此时cosα=1)的运动时,要注意条件。
如果汽车启动时可以看作匀加速直线运动,阻力可看作大小不变的力,则汽车的牵引力F的大小不变,由P=Fυ可知发动机的功率是逐渐增大的。
但是当功率达到额定功率时不再增大,由P=Fυ可知牵引力F将逐渐减小,即汽车启动时做匀加速运动的时间是有限度的。
在发动机功率不变的条件下,汽车加速运动的加速度将不断减小。
5.掌握动能和动能定理动能E K=mυ2是物体运动的状态量,功是与物理过程有关的过程量。
动能定理是:在某一物理过程中,外力对某物体做功等于该物体末态动能与初态动能之差,即动能增量,用数学表示为åW=-。
动能定理表达了过程量功与状态量动能之间的关系。
在应用动能定理分析一个具体过程时,要做到三个“明确”,即明确研究对象(研究哪个物体的运动情况),明确研究过程(从初状态到末状态)及明确各个力做功的情况。
6.理解势能势能与相互作用的物体之间的相对位置有关,是系统的状态量。
例如重力势能与物体相对地面的高度有关,弹性势能与物体的形变有关。
势能的大小与参考点(此处势能为零)的选取有关,但势能的变化与参考点无关。
重力势能的变化与重力做功的关系是W G=E p1-E p2=mgh1-mgh2;弹性势能的变化与弹簧做功有类似的关系。
要区分重力做功W G=mgh中的“h”和重力势能E p=mgh 中的“h”,前者是始末位置的高度差,后者是物体相对参考面的高度。
大学物理功和能

例4-4、一质量为m的质点,在xoy平面上运动。
其r位置a矢c量os为:ti
b
sin
tj
y
b
B
r
m
t A
x
其中a , b , 为正值常数,a > b 。 o
a
(1)求质点在A (a,0)点和B(0,b)点时的动能。
(2)求质点所受的作用力以及当质点从A运动到B的
解:(过1)程由中分r力
Fx
a
、Fy
cos
rdr
G rb ra 0
Mm r3
rdr
b
Mm
Mm
确定 (两G个0 质r点a ,) 则(MG、0 mrb
1 2
kx22
1 2
kx12
4 8102 (J )
例2:用铁锤把钉子敲入墙面木板。设木板对钉子的阻力
与钉子进入木板的深度成正比。若第一次敲击,能把钉
子钉入木板1cm。第二次敲击时,保持第一次敲击钉子
的速度,那么第二次能把钉子钉入多深?
分析:由于两次锤击的条件相同,锤击后钉子获得的速
度也相同,所具有的初动能也相同;由动能定理
两式相加得:
即: 外力的功之和+内力的功之和 =系统末动能-系统初动能
记作:W外+W内=EKB - EKA
质点系动能定理
所有外力对质点系做的功和内力对质点系做的功 之和等于质点系总动能的增量。
注意:内力能改变系统的总动能, 但不能改变系统的总动量。
说明: 1、动能是状态量,任一运动状态对应一 定的动能。 2、功是过程量,它与能量的改变有联系。 3、动能是质点因运动而具有的做功本领。 4、动能与动量的异同:
F cos
S ab Fdr cos
2023届高考物理一轮复习讲义:专题四 功和能

专题四 功和能重点1. 机械能守恒的条件及其表达方式。
2.以正确的步骤运用机械能守恒定律。
3.动能定理及其导出过程。
4.动能定理的应用。
难点1.如何判断机械能是否守恒,及如何运用机械能守恒定律解决实际问题。
2.建立物理模型、状态分析和寻找物理量之间的关系。
3.多过程和变力做功情况下动能定理的应用。
易错点1. 如何判断机械能是否守恒,及如何运用机械能守恒定律解决实际问题。
2.多过程和变力做功情况下动能定理的应用。
高频考点 1.动能定理的应用。
2. 运用机械能守恒定律解决实际问题。
考情分析:能量问题是历年来高考的重点和热点,考查比较全面而且有较强的综合性。
其中动能定理和功能关系更是重中之重,明确功是能量转化的途径和量度;而机械能守恒定律是另一个重点,要求学生能用守恒观点去解决问题,压轴题也会与此部分知识有关。
本专题内容常与牛顿定律、圆周运动、电磁学知识综合,高考对本部分知识的考查核心会在分析综合能力上。
考点预测:功和功率、动能和动能定理、机械能守恒定律、能量守恒定律是力学的重点,也是高考考查的重点,常以选择题、计算题的形式出现,考题常与生产生活实际联系紧密,题目的综合性较强.预计在高考中,仍将对该部分知识进行考查,复习中要特别注意功和功率的计算,动能定理、机械能守恒定律的应用以及与平抛运动、圆周运动知识的综合应用。
【解读】功和功率是物理学中两个重要的基本概念,是学习动能定理、机械能守恒定律、功能原理的基础,也往往是用能量观点分析问题的切入点。
复习时重点把握好功德概念、正功和负功;变力的功;功率的概念;平均功率和瞬时功率,发动机的额定功率和实际功率问题;与生产生活相关的功率问题。
解决此问题必须准确理解功和功率的意义,建立相关的物理模型,对能力要求较高。
动能定理是一条适用范围很广的物理规律,一般在处理不含时间的动力学问题时应优先考虑动能定理,特别涉及到求变力做功的问题,动能定理几乎是唯一的选择。
大学物理课件4质点动力学-功能

l-a
O
对链条应用动能定理:
1 2 1 A=AG+A f mV mV02 2 2 1 V0 0 AG+A f mV 2 2 mg( l 2 a 2 ) l l mg AG a G dr a xdx l 2l
a
x
前已得出:
2
Af
2
mg ( l a )
3 势能曲线:
E p f 空间位置
故可作出曲线:Ep~h, Ep~x, Ep~r, 统称势能曲线。
重力势能: E p mgh
1 2 弹性势能: E p kx 2 mM 引力势能: E p G r
E p f ( x)
Ep
E p f ( h)
xh r
E p f (r )
2 保守力作功的数学表达式:
L F dr 0
四、势能:
1 概念: 与质点位置有关的能量即为势能Ep。
重力势能: E p mgh
重力功 引力功 弹性力功
mM 引力势能: E p G r 1 2 弹性势能: E p kx 2
A mg( h1 h2 )
1 1 A GmM ( ) rb ra 1 2 2 A k ( x1 x2 ) 2
力 F 在△Si 上的功可写为:
S i a ri r F r ri
·
·
b
Ai F ri cos i
当 n →∞时,则为:
i ( F , r i )
dA F dr cos F dr ——力 F 在位移元 dr 上的元功 则:自a →b的过程,变力 F的功为:
a
rb r F
第4章 功和能ppt课件

4-5 人造地球卫星绕地球做椭圆轨道运动,地球在椭圆的一个焦 点上,则卫星的( C )。 (A)动量不守恒,动能守恒 (B)动量守恒,动能不守恒 (C)对地心的角动量守恒,动能不守恒 (D)对地心的角动量不守恒,动能守恒
解:卫星受地球的力始终指向地球,故卫星运动过程中受到地球的 引力矩始终为零,进而角动量守恒;但地球对卫星的引力的 功不为零,故动能不守恒
yj )
(dxi
d yj )
o
(0,0)
(0,2R)
0
2R
F0 xdx ydy F0( xdx ydy)
(0,0)
0
0
2F0R2
.
4-2 质量为m = 0.5 kg 的质点,在Oxy坐标平面内运动,其运 动方程为x = 5t, y = 0.5t2 (SI),从t = 2 s到t = 4 s这段时间内, 外力对质点做的功为( B )。
解:略
.
4-9 有一人造地球卫星,质量为m,在地球表面上空2倍于地球半 径的高度沿圆轨道运行,用m、R、引力常数G和地球质量M表示 (1)卫星的动能 GMm(6R);(2)卫星的引力势能 GM(m 3R)。
解:略
.
4-10 一质量为 1.0×10-2kg 的子弹,在枪膛中前进时受到的合
力 F1.2 8140 (12x)(N),子弹在枪口的速度为800 m/s.试计算 枪筒的长度.
.
4-6 如图所示,把质量为m,各边长均为2a的均质木箱,由位置1 翻转到位置2,则人力所做的功为 ( 2 1)amg 。
解:略
(a)
(b)
.
4-7一质量为m的质点在指向圆心的平方反比力 Fk 的k作r2用下,
做半径为r的圆周运动,此质点的速率为
4_4 克里希定理
第四章功和能
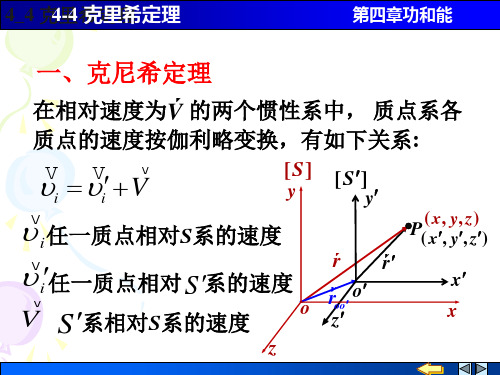
在相对速度为V 的两个惯性系中, 质点系各 质点的速度按伽利略变换,有如下关系:
一、克尼希定理
i 任一质点相对S系的速度 i任一质点相对 S 系的速度
V S 系相对S系的速度
z
i i V
[S]
y
[ S ]
i
1 2 m c (克尼希定理) Ek Ek 2
4-4 克里希定理 4_4 克里希定理
第四章功和能
1 2 克尼希定理写为 Ek m c Ekc 2 1 2 mc 质心的动能 — 整体随质心运动 2
Ekc 质点系相对于质心的动能 Nhomakorabea克尼希定理说明:在实验室参考系中,质点系 的动能等于质点系随质心一起的平动动能加上 质点系相对于质心的动能。 一般不 随便两个参考系之间的动能关系是 为零
m22 0 m11
m1 2 u m1 m2
m2 1 u m1 m2
4-4 克里希定理 4_4 克里希定理
第四章功和能
在质心系中,质点系的动能
1 1 2 2 m11 m22 Ek 2 2 2 2 1 m1m2 m1 m2 2 [ ]u 2 2 2 (m1 m2 ) (m1 m2 ) 1 m1m2 2 u 1 2 2 m1 m2 Ekr u EKC 2 m1m2 令 相对(质心)动能 m1 m2
称为约化质量 (或折合质量)
高能物理实验中称为 资用能
1 2 EK Ek mV ( mii) V 2 i
4-4 克里希定理 4_4 克里希定理
第四章功和能
二、两质点系统
1. 约化质量(或折合质量) 两质点相对速度为:
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
二、 保守力和非保守力: 保守力和非保守力:
1、定义:保守力做功大小与路径无关。 定义:保守力做功大小与路径无关。
a c ha mg b
∆Wi = mg cosθ ∆si = mg ∆hi W = ∑ mg ∆hi = mg ∑ ∆hi = mg ( ha − hb )
∆hi
n n
Σ∆hi
i =1
W外 + W保守内力 + W非保守内力 = Ek − Ek0 W保守内力 = EP 0 − EP 则 W外 + W非保守内力 = Ek + EP) Ek0 + EP 0) ( − (
W + 非保守内 = E − E0 外 W
三、机械能守恒
如果 W外 + W非保守内力 = 0, 则
E = cons.
x2 x2
解:
v v v 2 dr = 5t dti + 2dtj 2w v v d r F = m 2 = ti dt v v 3 dW = F ⋅ dr = 5t dt
2 3 0
W = ∫ 5t dt = 20( J )
二、质点的动能定理: 质点的动能定理:
F 2 2 v − v 0 = 2ax = 2 x m 1 1 2 2 ∴ Fx = mv − mv 0 2 2
合外力所作的功等于 质点动能的增量。 质点动能的增量。
动能定理把过程量功和两个状态的状态量动能联系在一起。
[例题 例题] 一个外力作用在 m=3 kg的物体上,其运动方程为 x=3t的物体上, 的物体上 4t2+t3 (SI)求最初 秒内该力所做的功。 秒内该力所做的功。 )求最初4秒内该力所做的功
1 2 1 2 = kxa − kxb 2 2
1 2 c = − kxa 2
1 2 ∴U ( x ) = kx 2 1 2 1 2 U ( x ) = kx − kxa 2 2
: 竖 悬 的 簧 劲 系 为 端 一 体, 例 一 直 挂 弹 ( 度 数 k)下 挂 物 , 以 体 平 体 若 物的 位 为轴 原 , 作 弹势 和 力 能 零, 证 物 点, 衡 置 Y 的 点 并 为 性能 重 势 的 点试 : 1 y时 其 性 能 重 势 的 和 ky2 体 位 坐 为 的 置 标 , 弹 势 和 力能 总 为 2
x1 y1 z1
x2
y2
z2
v dr
1
2
一维时
v v dW F ⋅ dr v v 3、 率 p = 、 率: 功 : = = F⋅v dt dt
W = ∫ F x dx
x1
x2
[例题 一物体在外力 Fx=3x+2 (SI)作用下,从 x=0 移动到 例题] 移动到x=4m )作用下, 求该力对物体所做的功。 处,求该力对物体所做的功。 解:这是一维变力做功的问题
解法一:在直角坐标系中 GMm ∂U Fx = − =− r2 ∂x ∂U GMm Fy = − =− r2 ∂y
x r y r
v v ∂U v ∂U v v GMm r ∂U F = −( i+ j+ k) = - 2 r r ∂y ∂z ∂x
解法二:在球面坐标系中
GMm z ∂U Fz = − =− 2 r r ∂y
Fx = − ∂E p ∂x , Fy = − ∂E p ∂y , Fz = − ∂E p ∂z
v ∂E p v ∂E p v ∂E p v F = −( i+ j+ k) ∂x ∂y ∂z
例:已知万有引力势能为 已知万有引力势能为
U(r ) = −G
M m r
应用保守力与势能的微分关系, 应用保守力与势能的微分关系,求万有引力
四、能量守恒定律
能量既不能产生,也不能消灭, 能量既不能产生,也不能消灭,它只能从一种形式转换到 另一种形式,但总能量是守恒的。 另一种形式,但总能量是守恒的。
例题:一质量为M的小车与地面光滑接触,初始静止,一质 例题:一质量ቤተ መጻሕፍቲ ባይዱM的小车与地面光滑接触,初始静止, 量为m物体以初速度v 滑到小车上, 量为m物体以初速度v0滑到小车上,物体与小车间摩擦系数 小车长为d 当物体碰到小车前挡板时速度为v 为µ,小车长为d,当物体碰到小车前挡板时速度为v,此时 小车移动了距离为l 试问系统动量守恒吗?机械能守恒吗? 小车移动了距离为l。试问系统动量守恒吗?机械能守恒吗? 解:系统水平方向所 受合外力为零, 受合外力为零, 动 量守恒。 量守恒。 外力作功为零, 外力作功为零, 内力(摩擦力) 内力(摩擦力)作功 不为零, 不为零,故动能不守 恒。
保守力作功等于系统势能的减少。 保守力作功等于系统势能的减少。
1、重力势能 、
W = ∑ mg ∆hi = mg ∑ ∆hi = mg ( ha − hb )
i =1 i =1
n
n
若U(a)=mgha+c, U(b)=mghb +c ,c为任意常数,可 为任意常数, 为任意常数 的值只有c值确定后才能确定 见U(a)的值只有 值确定后才能确定。这就是确定势能 的值只有 值确定后才能确定。 零点。 零点。
=G
r
2
cosα dr
O
M
r rb
b
万有引力的功
r m M dW = G 2 cosα dr r r r r r Q−dr cosα = dr cos(π −α)
a
r r
r F
m
r dr
α
dr
a
= dr
b m M M ∴dW = −G 2 dr r r 1 1 rb m M b M W = ∫ dW = ∫r −G 2 dr= −G m ( − ) ra rb ra a r
dU dU 解:( ) = 0, 2 > 0 1 dx dx 2a ⇒x=6 b
2
dU 12a 6b F =− = 13 − 7 dx x x
§4.4 机械能守恒定律
一、质点系的动能定理
∑W
i外
+ ∑ Wi内 = ∑ E ik − ∑ E ik 0
W外 + W内 = E k − E k 0
二、功能原理
预备知识
矢量的乘法 1. 矢量与标量相乘
v v v v v v v ca = c(a x i + a y j + a z k ) = ca x i + ca y j + ca z k
b φ a
2. 矢量的点乘(标量积)
v v v v c = a ⋅ b = a b cosφ = abcosφ
按照这个定义,
非稳定平衡点x5:
稳定平衡点在势能极小值处。
例:双原子分子中两原 子的相互作用势能函数 可近似写成 a b U ( x ) = 12 − 6 x x 均为正的常量, 为原子间的距离。 式中a , b均为正的常量, x为原子间的距离。求: 为何值时, 为极小? (1)x为何值时, U ( x )为极小? 为多少? (2)两原子间的力 F为多少?
1
r
v v′ F 21
m2
v r1
xO
v r2
r r r r dW = F ⋅ dr1 + F21 ⋅ dr2 12 r r r r v = F ⋅ dr1 + F21 ⋅ d(r1 + r′) 12 r v dW = F21 ⋅ dr′
y
作用力与反作用力的功不一定为0 (1)一对作用力与反作用力的功不一定为0 )一对作用力与反作用力的功不一定为 注意: 注意: (2)一对内力作功之和与相对位移有关。 )一对内力作功之和与相对位移有关。 (3)两质点之间内力作功之和与参照系无关(包括非 )两质点之间内力作功之和与参照系无关( 惯性系),可选相对m 静止的参照系来计算。 ),可选相对 惯性系),可选相对 1静止的参照系来计算。
3 2 W = ∫ Fd x = ∫ ( 3 x + 2)d x = ( x + 2 x ) 4 = 32 J 0 x1 x1 2 v v 5 3v 例:质量为0.1kg的质点,沿曲线r = t i + 2tj ( SI )运动,求在t = 0 3 到t=2 s时间内,作用在该质点的合外力对质点所做的功
M m ra
+c
∴U(ra ) = −G
M m ra
§4.3 保守力和势能函数的微分关系 一、微分关系
v v − dE p = F ⋅ dl = F cos φdl = Fl dl dE p Fl = − dl
在直角坐标系 中,势能为 势能为Ep(x,y,z)
v v − dE p = F • dr = Fx dx + F y dy + Fz dz
i =1
hb
保守力沿闭合路径作功为零。 保守力沿闭合路径作功为零。 v v ∫ F ⋅ ds = 0
三、势能
因为保守力做功与路径无关,只与物体间相互位置有关, 因为保守力做功与路径无关,只与物体间相互位置有关, 叫势能函数。 所以可定义一个位置的函数U(r),叫势能函数。
W =∫ 保
b
a
v v v v F ⋅ dr = −∆U =U(ra ) −U(rb )
O
r rb
由此可见, 由此可见 , 万有引力作功也仅仅与质点的始 末位置有关,与具体路径无关。 末位置有关,与具体路径无关。
引力势能
Mm r v Mm Mm ∫ − G r 2 r ⋅ dr = −G ra − (−G rb ) ra
rb
∴U(ra ) = −G
若选无穷远为势能零点, 若选无穷远为势能零点,则c=0, ,
dx 解: v = = 3 − 8t + 3t 2 dt t = 0 v0 = 3 m ⋅ s -1 t = 4 v4 = 19 m ⋅ s -1 1 1 2 2 W = mv 4 − mv 0 = 528 J 2 2
