0-v-0模型
零维模型

0.8
(Cm是活塞平均速度)
如果活塞和缸壁之间会发生漏气,质量方程写为
dm d mCR d d
mCR表示穿过环缝泄漏的气体质量,可以根据环缝的容积 VCR和压力,并利用状态方程计算
d mCR V CR dp d RT W d
系统做功
dW dV pV h sin cos p sin 2 2 d d 2 1 sin 180
壁面传热量
d QW h C A T T W d
Woschni公式
hC K D
0.2
p T 0.55C 0. d mb 1 C m sin d d 2 b b
对于Wiebe函数
n 1 mb 0 1 exp a m b
(调节参数a,n为常数)
n n 1 d QC d mb Cma(n 1) 0 0 C exp a d d b b b
内能的变化
dE dT mC V d d
b
0 mb 1 1 cos m 2 b
利用上述已知条件,给出燃烧室温度T和曲轴转角 的关 系表达式。
根据热力学第一定律,可得
d Q C dE dW d QW d d d d
控制容积示意图
有关假定如下: ① 压力随曲轴转角 的变化由实测的示功图给出,即 p p( ) 是已知的; ② 混合气的比热是已知的常数,活塞是绝对密封的,不 会发生漏气; ③ 缸壁的传热面积 A A( ) 是已知量,温度TW和传热系 数hC为已知常数; ④ 发动机的角速度ω是已知常数,气缸的体积可以由下 式给出:
6章30内燃机燃烧模型-2010

/ d
dW/d
其中,VCR 为环缝的容积。
dQB dT dV dQW dmCR mCV p (h u0 ) d d d d d
燃烧模型
单韦伯公式(燃烧放热百分率) 1 mb 6 .908Biblioteka y m 0 x 1 e y m z
(2)微分模型
通过求解空间平均湍流参数的简化常微分方程来确定这 些湍流参数。 ① 单方程模型。针对求解湍能 k。 ② 双方程模型。求解湍能 k和耗散率ε。
1)代数湍流模型
由现象分析提出的假设:
①火焰的传播首先是由于流场中大的湍流涡团把新鲜混合气 卷入火焰锋面,卷吸速度正比于湍流强度,然后在Taylor微 尺度量级的小涡团内以层流的方式进行燃烧,在此尺度下扩 散过程是分子过程。 ②质量燃烧率正比于涡团对未燃气体的卷吸率。 ③湍流的强度和特征尺度取决于发动机的转速和结构。即湍 流度与转速成正比,积分尺度与气阀升程或点火时燃烧室的 高度成正比。
0
1)混合气准备模型Whitehouse
B — —准备率(蒸发率), R — —反应率 (B R ) d0为预混合燃烧期,燃烧
0
取决于反应率 R 决于蒸发率 B
(B R ) d 0为扩散燃烧期,燃烧取
0
C1 p o 2 exp( C2 / T ) I dx f (C i , ) Gf N T d C5 C4) C G C 4 G ( C1 p u o2 / G f 3 i I
两类方法
① 从物理概念出发的半经验公式:如单韦伯公式 ② 从现象出发的偏重数学技巧的经验公式:如双韦伯公式
(1)零维模型
1) 混合气准备模型Whitehouse 观点
2020版高考一轮物理复习数字课件第6章专题七 动量观点和能量观点综合应用的“四个模型”

模型一 “子弹打木块”模型
解析:(1)第一颗子弹射入木块的过程,系统动量守恒,即 mv0=(m+M)v1 系统由 O 到 C 的运动过程中机械能守恒,即12(m+M)v21=(m+M)gR m+M 联立以上两式解得 v0= m 2gR=31 m/s。 (2)由动量守恒定律可知,第 2 颗子弹射入木块后,木块的速度为 0 当第 3 颗子弹射入木块时,由动量守恒定律得 mv0=(3m+M)v3 解得 v3=3mm+v0M=2.4 m/s。
设长木板 B 的质量为 M,对长木板 B, 由牛顿第二定律,μmg=Ma2,解得 M
积,即为 ΔE=μmgL=0.1×2×10×1 J =2 J,选项 D 错误。
=2 kg,选项 B 正确;根据 v -t 图线与 答案: AB 横轴所围的面积等于位移可知,木块 A
模型二 滑块——木板模型问题
[多维练透] 2.如图所示,质量为 m=245 g 的物块(可视为质点)放在质量为 M=0.5 kg 的木板左 端,足够长的木板静止在光滑水平面上,物块与木板间的动摩擦因数为 μ=0.4。质 量为 m0=5 g的子弹以速度 v0=300 m/s 沿水平方向射入物块并留在其中(时间极短), g 取 10 m/s2。子弹射入后,求: (1)物块相对木板滑行的时间。 (2)物块相对木板滑行的位移。
模型一 “子弹打木块”模型
(2019·福建龙岩质检)(多选)如图所示,两个质量和速度均相同的子弹分别水平射入 静止在光滑水平地面上质量相同、材料不同的两矩形滑块 A、B 中,射入 A 中的深度是射 入 B 中深度的两倍。上述两种射入过程相比较( ) A.射入滑块 A 的子弹速度变化大 B.整个射入过程中两滑块受到的冲量一样大 C.两个过程中系统产生的热量相同 D.射入滑块 A 中时阻力对子弹做功是射入滑块 B 中时的两倍
VCO
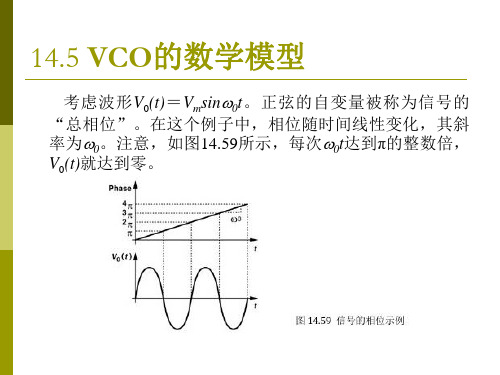
14.5 VCO的数学模型
例14.16 VCO的控制线受一个在V1和V2之间以 周期Tm来回切换的矩形信号激励。画出频率、相 位和输出电压的时间函数波形。 解 w = w0 + KVCOVcont 输出频率在 w1 = w0 + KVCOV1 因为 , out 和w2 w0 KVCOV2 之间来回跳变(图14.62)。相位 是此结果对时间的积分,在输入周期的一半时间 随时间以斜率w1线性增长,在另一半周期以斜率 w2线性增长。VCO的输出波形与图14.61所示的 相似,所以VCO可以被当作频率调制器。
= V0 cos(w 0 t + KVCO
= V0 cosw 0t cos(KVCO -V0 sin w 0t sin(KVCO
wm
wm
Vm
Vm
sin w mt )
sin w mt )
wm
Vm
sin w mt ).
14.5 VCO的数学模型
如果Vm足够小使得KVCOVm/wm<<1 rad,那么
现 在 考 虑 两 个 波 形
14.5 VCO的数学模型
从上述的研究可以看出,波形的相位变化越快, 波形的频率越高,表示频率可以被定义成相位对 时间的微分:
dj w= . dt
14.5 VCO的数学模型
例14.15:图14.61(a)显示的是一个振幅固定的 正弦波形的相位随时间变化的情况。请在时间域 画出此波形。
式(14.73)指出,如果已知波形的频率是时间 的函数,那么相位可以由下式计算
j = ò w dt + j 0 .
wout = w0 + KVCOVcont 特别是,因为对于VCO, 我们有 Vout (t ) = Vm cos( ò wout dt + j 0 )
零模型方法

零模型方法【原创版3篇】篇1 目录1.零模型方法的定义和概述2.零模型方法的数学原理3.零模型方法的应用领域4.零模型方法的优缺点篇1正文零模型方法是一种广泛应用于统计学和机器学习领域的方法。
该方法的基本思想是建立一个概率模型,使得在给定一些已知变量的条件下,另一个变量的概率为零。
这种方法被广泛应用于回归分析、分类和预测等领域。
零模型方法的数学原理主要基于贝叶斯定理和最大似然估计。
贝叶斯定理指出,给定一些已知条件,我们可以计算出一个变量的后验概率。
最大似然估计则是一种求解概率模型参数的方法,它通过最大化模型的似然函数来估计参数。
零模型方法在多个应用领域都取得了良好的效果。
在回归分析中,零模型可以用于识别哪些自变量对因变量的预测有显著影响。
在分类和预测中,零模型可以识别那些对预测结果没有影响的特征,从而提高模型的预测精度。
尽管零模型方法在实际应用中取得了良好的效果,但它也存在一些优缺点。
首先,零模型方法的计算复杂度较高,需要大量的计算资源。
其次,零模型方法的高度依赖于数据质量,如果数据存在噪声或者缺失值,可能会对模型的预测结果产生影响。
然而,零模型方法的优点在于它可以有效地识别出对预测结果有显著影响的变量,从而提高模型的预测精度。
总的来说,零模型方法是一种在统计学和机器学习领域中广泛应用的方法,它具有很多优点,如计算效率高、预测精度高等,但也存在一些缺点,如计算资源需求大、依赖数据质量等。
篇2 目录1.零模型方法的概述2.零模型方法的数学原理3.零模型方法在实际应用中的案例4.零模型方法的优缺点5.零模型方法的发展前景篇2正文【1.零模型方法的概述】零模型方法是一种数学建模方法,主要用于解决实际问题中的优化问题。
零模型方法的基本思想是将问题转化为一个数学模型,通过求解该模型的最优解,从而得到问题的解决方案。
零模型方法广泛应用于多个领域,如经济学、工程学、生物学等。
【2.零模型方法的数学原理】零模型方法的数学原理主要包括两个方面:线性规划和非线性规划。
物理 性必修第一册第1章 动量守恒定律专题课:“子弹打木块”模型和“滑块—木板”模型导学案含答案

2023-2024(上)全品学练考高中物理选择性必修第一册第1章动量守恒定律专题课:“子弹打木块”模型和“滑块—木板”模型学习任务一“子弹打木块”模型[模型建构]模型图示模型特点(1)子弹水平打进木块的过程中,系统的动量守恒.(2)系统的机械能有损失.两种情景(1)子弹嵌入木块中,两者速度相等,机械能损失最多(完全非弹性碰撞)动量守恒:mv0=(m+M)v能量守恒:Q=F f·x=12m v02-12(M+m)v2(2)子弹穿透木块动量守恒:mv0=mv1+Mv2能量守恒:Q=F f·d=12m v02-(12M v22+12m v12)例1一质量为M的木块放在光滑的水平面上,一质量为m的子弹以初速度v0水平打进木块并留在其中.设子弹与木块之间的相互作用力大小为F f.(1)子弹、木块相对静止时的速度为多大?(2)子弹在木块内运动的时间为多长?(3)子弹、木块相互作用过程中,子弹、木块发生的位移以及子弹打进木块的深度分别为多少?(4)系统损失的机械能、系统增加的内能分别为多少?(5)要使子弹不射出木块,木块至少为多长?变式1如图所示,木块静止在光滑水平面上,两颗不同的子弹A、B从木块两侧同时射入木块,最终都停在木块内,这一过程中木块始终保持静止.若子弹A射入的深度大于子弹B射入的深度,则()A .子弹A 的质量一定比子弹B 的质量大B .入射过程中子弹A 受到的阻力比子弹B 受到的阻力大C .子弹A 在木块中运动的时间比子弹B 在木块中运动的时间长D .子弹A 射入木块时的初动能一定比子弹B 射入木块时的初动能大变式2 如图所示,A 、B 两个木块用弹簧连接,它们静止在光滑水平面上,A 和B 的质量分别为99m 和100m.一颗质量为m 的子弹以速度v 0水平射入木块A 内没有穿出,则在之后的运动过程中弹簧的最大弹性势能为多少?学习任务二 “滑块—木板”模型[模型建构]模型 图示模型 特点(1)系统的动量守恒,但机械能不守恒,摩擦力与两者相对位移的乘积等于系统减少的机械能.(2)若滑块未从木板上滑下,当两者速度相同时,木板速度最大,相对位移最大. 求解 方法 (1)求速度:根据动量守恒定律求解,研究对象为一个系统;(2)求时间:根据动量定理求解,研究对象为一个物体;(3)求系统产生的内能或相对位移:根据能量守恒定律Q=F f Δx 或Q=E 初-E 末,研究对象为一个系统.例2 如图所示,质量m=4 kg 的物体,以水平速度v 0=5 m/s 滑上静止在光滑水平面上的平板小车,小车质量M=6 kg,物体与小车车面之间的动摩擦因数μ=0.3,g 取10 m/s 2,设小车足够长,求:(1)小车和物体的共同速度; (2)物体在小车上滑行的时间;(3)在物体相对小车滑动的过程中,系统产生的摩擦热.变式3 如图所示,在光滑水平地面上固定足够高的挡板,距离挡板s=3 m 处静止放置质量M=1 kg 、长L=4 m 的小车,一质量m=2 kg 的滑块(可视为质点)以v 0=6 m/s的初速度滑上小车左端,带动小车向右运动,小车与挡板碰撞时被粘住不动,已知滑块与小车表面间的动摩擦因数μ=0.2,g取10 m/s2.(1)求滑块与小车的共同速度大小;(2)当滑块与小车共速时,小车与挡板的距离和滑块与小车右端的距离分别为多少?(3)若滑块与挡板碰撞时为弹性碰撞,求全过程中滑块克服摩擦力做的功.例3 (多选)[2022·浙江学军中学月考] 如图所示,质量为8m,长度一定的长木板放在光滑的水平面上,质量为m,可视为质点的物块放在长木板的最左端,质量为m的子弹以水平向右的速度v0射入物块且未穿出(该过程的作用时间极短可忽略不计),经时间t0物块以v0的速度离开5长木板的最右端,重力加速度为g,则下列说法正确的是()A.长木板最终的速度大小为v010B.长木板的长度为5v0t016m v02C.子弹射入物块的过程中损失的机械能为920D.物块与长木板间的动摩擦因数为3v010gt01.(子弹打木块模型)(多选)矩形滑块由不同材料的上、下两层粘合在一起组成,将其放在光滑的水平面上,质量为m的子弹以速度v水平射向滑块,若射击下层,子弹刚好不射出.若射击上层,则子弹刚好能射进一半厚度,如图所示,上述两种情况相比较()A.子弹损失的动能一样多B.子弹射击上层时,从射入到共速所经历时间较长C.系统产生的热量一样多D.子弹与上层摩擦力较大2.(滑块—木板模型)(多选)[2022·厦门双十中学月考] 如图甲所示,一长木板静止于光滑水平桌面上,t=0时,小物块以速度v0滑到长木板上,图乙为物块与木板运动的v-t图像,图中t1、v0、v1已知,重力加速度大小为g,由此可求得()A.木板的长度B.物块与木板的质量之比C.物块与木板之间的动摩擦因数D.从t=0开始到t1时刻,木板获得的动能3.(动量综合应用)如图所示,一质量m1=0.45 kg的平顶小车静止在光滑的水平轨道上.质量m2=0.5 kg的小物块(可视为质点)静止在车顶的右端.一质量为m0=0.05 kg的子弹、以水平速度v0=100 m/s射中小车左端并留在车中,最终小物块相对地面以2 m/s的速度滑离小车.已知子弹与车的作用时间极短,物块与车顶面的动摩擦因数μ=0.8,认为最大静摩擦力等于滑动摩擦力.g取10 m/s2,求:(1)子弹相对小车静止时小车速度的大小;(2)小车的长度L.[反思感悟]专题课:“子弹打木块”模型和“滑块—木板”模型例1(1)mM+m v0(2)Mmv0F f(M+m)(3)Mm(M+2m)v022F f(M+m)2Mm2v022F f(M+m)2Mmv022F f(M+m)(4)Mmv022(M+m)Mmv022(M+m)(5)Mmv022F f(M+m)[解析] (1)设子弹、木块相对静止时的速度为v,以子弹初速度的方向为正方向,由动量守恒定律得mv0=(M+m)v解得v=mM+mv0(2)设子弹在木块内运动的时间为t,对木块,由动量定理得F f t=Mv-0解得t=Mmv0F f(M+m)(3)设子弹、木块发生的位移分别为x 1、x 2,如图所示.对子弹,由动能定理得-F f x 1=12mv 2-12m v 02解得x 1=Mm (M+2m )v 022F f (M+m )2对木块,由动能定理得F f x 2=12Mv 2 解得x 2=Mm 2v 022F f (M+m )2子弹打进木块的深度等于相对位移的大小,即x 相=x 1-x 2=Mmv 022F f(M+m ) (4)系统损失的机械能为E损=12m v 02-12(M+m )v 2=Mmv 022(M+m )系统增加的内能为Q=F f ·x 相=Mmv 022(M+m )系统增加的内能等于系统损失的机械能(5)假设子弹恰好不射出木块,有F f L=12m v 02-12(M+m )v 2解得L=Mmv 022F f(M+m )因此木块的长度至少为Mmv 022F f(M+m )变式1 D [解析] 由于木块始终保持静止状态,则两子弹对木块的推力大小相等,即两子弹所受的阻力大小相等,设为F f ,根据动能定理得,对子弹A 有-F f d A =0-E k A ,得E k A =F f d A ,对子弹B 有-F f d B =0-E k B ,得E k B =F f d B ,由于d A >d B ,则有子弹射入时的初动能E k A >E k B ,故B 错误,D 正确.两子弹和木块组成的系统动量守恒,则有√2m A E kA =√2m B E kB ,而E k A >E k B ,则m A <m B ,故A 错误.子弹A 、B 从木块两侧同时射入木块,木块始终保持静止,分析得知,两子弹在木块中运动的时间必定相等,否则木块就会运动,故C 错误. 变式21400m v 02[解析] 子弹射入木块A 的极短时间内,弹簧未发生形变(实际上是形变很小,忽略不计),设子弹和木块A 获得共同速度v ,由动量守恒定律得mv 0=(m+99m )v之后木块A (含子弹)开始压缩弹簧推动B 前进,当A 、B 速度相等时,弹簧的压缩量最大,设此时弹簧的弹性势能为E p ,A 、B 的共同速度为v 1,对A (含子弹)、B 组成的系统,由动量守恒定律得(m+99m )v=(m+99m+100m )v 1由机械能守恒定律得12(m+99m )v 2=12(m+99m+100m )v 12+E p联立解得E p =1400m v 02.例2 (1)2 m/s (2)1 s (3)30 J[解析] (1)小车和物体组成的系统动量守恒,规定向右为正方向,则mv 0=(m+M )v解得v=mv 0m+M =4×54+6 m/s =2 m/s(2)物体在小车上做匀减速直线运动 根据牛顿第二定律可知-μmg=ma 解得a=-μg=-3 m/s 2则物体在小车上滑行的时间为t=v -v 0a=2-5-3s =1 s(3)根据能量守恒定律,系统产生的摩擦热为ΔQ=12m v 02-12(m+M )v 2=12×4×52 J -12×(4+6)×22 J =30 J变式3 (1)4 m/s (2)1 m 1 m (3)36 J[解析] (1)设滑块与小车的共同速度为v 1,二者相对运动过程中根据动量守恒定律,有mv 0=(M+m )v 1 解得v 1=4 m/s(2)设达到共速时小车移动的距离为s 1,对小车,根据动能定理有μmgs 1=12M v 12-0代入数据解得s 1=2 m小车与挡板的距离s 2=s-s 1=1 m设滑块与小车的相对位移为L 1,对系统,根据能量守恒定律,有μmgL 1=12m v 02-12(m+M )v 12代入数据解得L 1=3 m滑块与小车右端的距离L 2=L-L 1=1 m 其位置情况如图乙所示(3)共速后小车未碰撞挡板时小车与滑块间的摩擦力消失而没有做功,如图丙所示.直到小车碰撞挡板被粘住静止,滑块又开始在小车上继续向右做初速度v 1=4 m/s 的匀减速直线运动,由于与挡板发生弹性碰撞,滑块速度大小不变,设返回的路程为L 3,由动能定理,有-μmg (L 2+L 3)=0-12m v 12解得L 3=3 m,说明滑块不会从车左端掉下 全过程中滑块克服摩擦力做的功 W=μmg (L+s 1-L 2)+μmg (L 2+L 3)=36 J .例3 BD [解析] 子弹、物块、木板整个系统,整个过程根据动量守恒定律,有mv 0=2m ·v 05+8m ·v ,求得长木板最终的速度大小为v=340v 0,故A 错误;子弹射入物块的过程中,时间极短.子弹及物块根据动量守恒定律有mv 0=2m ·v',求得v'=v02,该过程系统损失的机械能为ΔE=12m v 02-12·2mv'2,联立两式可求得ΔE=14m v 02,故C 错误;子弹射入物块后到从长木板滑离时,运动的位移大小为x 1=v t 0=v '+25v 02=(v 02+v 05)2t 0=720v 0t 0,长木板滑动位移大小为x 2=v2t 0=340v 02t 0=380v 0t 0,则长木板的长度为L=x 1-x 2=516v 0t 0,故B 正确;对长木板,整个过程根据动量定理有μ·2mgt 0=8mv ,可求得物块与长木板间的动摩擦因数为μ=3v10gt 0,故D 正确.随堂巩固1.ACD [解析] 子弹射入滑块的过程中,将子弹和滑块看成一个整体,合外力为0,动量守恒,所以两种情况下子弹和滑块的最终速度相同,所以末动能相同,故系统损失的动能一样多,产生的热量一样多,A 、C 正确;子弹射击滑块上层能射进一半厚度,射击滑块下层刚好不射出,说明在上层所受的摩擦力比下层大,根据动量定理可知,两种情况下滑块对子弹的冲量相同,子弹射击上层所受摩擦力大,所以从入射到共速经历的时间短,B 错误,D 正确.2.BC [解析] 木板在光滑水平桌面上,物块滑上木板后,系统动量守恒,由图像可知,最终物块与木板以共同速度v 1运动,有mv 0=(M+m )v 1,-μmg Δx=12(M+m )v 12-12m v 02,Δx=(v 0+v 12-v 12)t 1,可求出物块与木板的质量之比及物块与木板之间的动摩擦因数,但求不出木板的长度,A 错误,B 、C 正确;由于木板质量未知,故不能求出木板获得的动能,D 错误. 3.(1)10 m/s (2)2 m[解析] (1)子弹进入小车的过程中,子弹与小车组成的系统动量守恒,由动量守恒定律得 m 0v 0=(m 0+m 1)v 1 解得v 1=10 m/s .(2)三物体组成的系统动量守恒,由动量守恒定律得 (m 0+m 1)v 1=(m 0+m 1)v 2+m 2v 3 解得v 2=8 m/s由能量守恒可得12(m 0+m 1)v 12=μm 2gL+12(m 0+m 1)v 22+12m 2v 32解得L=2 m .专题课:“子弹打木块”模型和“滑块—木板”模型建议用时:40分钟1.(多选)[2022·北京西城区期中] 如图,一表面光滑的平板小车放在光滑水平面上,木块和轻弹簧置于小车表面,轻弹簧一端与固定在小车上的挡板连接,整个装置静止.一颗子弹以一定速度水平射入木块,留在木块中并与木块一起向前滑行,与弹簧接触后压缩弹簧.不计挡板与弹簧质量,弹簧始终在弹性限度内.下列说法正确的是 ( )A .子弹射入木块过程中,子弹与木块组成的系统动量及机械能均守恒B .子弹和木块一起压缩弹簧过程中,子弹、木块、小车组成的系统动量及机械能均守恒C .整个过程,子弹、木块、小车组成的系统所损失的机械能等于子弹与木块摩擦产生的热量及弹簧的弹性势能之和D .其他条件不变时,若增大小车的质量,弹簧的最大压缩量增大2.(多选)如图所示,小车在光滑的水平面上向左运动,木块水平向右在小车的水平车板上运动,且未滑出小车.下列说法中正确的是 ( )A .若小车的初动量大于木块的初动量,则木块先减速运动再加速运动后匀速运动B .若小车的初动量大于木块的初动量,则小车先减速运动再加速运动后匀速运动C .若小车的初动量小于木块的初动量,则木块先减速运动后匀速运动D .若小车的初动量小于木块的初动量,则小车先减速运动后匀速运动 3.(多选)[2022·湖南常德期中] 质量为M 、内壁间距为L 的箱子静止于光滑的水平面上,箱子中间有一质量为m 的小物块,小物块与箱子底板间的动摩擦因数为μ.初始时小物块停在箱子正中间,如图所示.现给小物块一水平向右的初速度v ,小物块与箱壁碰撞N 次后恰又回到箱子正中间,并与箱子保持相对静止.重力加速度为g ,设碰撞都是弹性的,则整个过程中,系统损失的动能为 ( )A .12mv 2B .12·mMm+Mv 2C .12NμmgLD .NμmgL4.如图所示,质量为2 kg 的小车以2.5 m/s 的速度沿光滑的水平面向右运动,现在小车上表面上方1.25 m 高度处将一质量为0.5 kg 的可视为质点的物块由静止释放,经过一段时间物块落在小车上,最终两者一起水平向右匀速运动.重力加速度g 取10 m/s 2,忽略空气阻力,下列说法正确的是 ( )A .物块释放0.3 s 后落到小车上B .若只增大物块的释放高度,则物块与小车的共同速度变小C .物块与小车相互作用的过程中,物块和小车的动量守恒D.物块与小车相互作用的过程中,系统损失的能量为7.5 J5.长木板A放在光滑的水平面上,质量为m=2 kg的另一物体B以水平速度v0=2 m/s滑上原来静止的长木板A的上表面,由于A、B间存在摩擦,之后A、B速度随时间变化情况如图所示,重力加速度g取10 m/s2.则下列说法正确的是()A.木板获得的动能为2 JB.系统损失的机械能为4 JC.木板A的最小长度为2 mD.A、B间的动摩擦因数为0.16.[2022·江苏镇江期中] 质量为m的子弹以某一初速度v0击中静止在水平地面上质量为M的木块,并陷入木块一定深度后与木块相对静止,甲、乙两图表示了这一过程开始和结束时子弹和木块可能的相对位置,设地面粗糙程度均匀,木块对子弹的阻力大小恒定,则下列说法中正确的是()A.无论m、M、v0的大小和地面粗糙程度如何,都只可能是甲图所示的情形B.若M较大,则可能是甲图所示情形;若M较小,则可能是乙图所示情形C.若v0较小,则可能是甲图所示情形;若v0较大,则可能是乙图所示情形D.若地面较粗糙,则可能是甲图所示情形;若地面较光滑,则可能是乙图所示情形7.[2022·石家庄二中月考] 如图所示,一轻质弹簧两端分别连着质量均为m的滑块A和的子弹以水平速度v0射入A中不再穿出B,两滑块都置于光滑的水平面上.今有质量为m4(时间极短),则弹簧在什么状态下滑块B具有最大动能?其值是多少?8.[2022·杭二中月考] 如图所示,质量为m=245 g的物块(可视为质点)放在质量为M=0.5 kg的木板左端,足够长的木板静止在光滑水平面上,物块与木板间的动摩擦因数为μ=0.4.质量为m0=5 g的子弹以速度v0=300 m/s沿水平方向射入物块并留在其中(时间极短),重力加速度g取10 m/s2.子弹射入后,求:(1)子弹和物块一起向右滑行的最大速度v1;(2)木板向右滑行的最大速度v2;(3)物块在木板上滑行的时间t.专题课:“子弹打木块”模型和“滑块—木板”模型建议用时:40分钟1.(多选)[2022·北京西城区期中] 如图,一表面光滑的平板小车放在光滑水平面上,木块和轻弹簧置于小车表面,轻弹簧一端与固定在小车上的挡板连接,整个装置静止.一颗子弹以一定速度水平射入木块,留在木块中并与木块一起向前滑行,与弹簧接触后压缩弹簧.不计挡板与弹簧质量,弹簧始终在弹性限度内.下列说法正确的是()A.子弹射入木块过程中,子弹与木块组成的系统动量及机械能均守恒B.子弹和木块一起压缩弹簧过程中,子弹、木块、小车组成的系统动量及机械能均守恒C.整个过程,子弹、木块、小车组成的系统所损失的机械能等于子弹与木块摩擦产生的热量及弹簧的弹性势能之和D.其他条件不变时,若增大小车的质量,弹簧的最大压缩量增大2.(多选)如图所示,小车在光滑的水平面上向左运动,木块水平向右在小车的水平车板上运动,且未滑出小车.下列说法中正确的是()A.若小车的初动量大于木块的初动量,则木块先减速运动再加速运动后匀速运动B.若小车的初动量大于木块的初动量,则小车先减速运动再加速运动后匀速运动C.若小车的初动量小于木块的初动量,则木块先减速运动后匀速运动D .若小车的初动量小于木块的初动量,则小车先减速运动后匀速运动 3.(多选)[2022·湖南常德期中] 质量为M 、内壁间距为L 的箱子静止于光滑的水平面上,箱子中间有一质量为m 的小物块,小物块与箱子底板间的动摩擦因数为μ.初始时小物块停在箱子正中间,如图所示.现给小物块一水平向右的初速度v ,小物块与箱壁碰撞N 次后恰又回到箱子正中间,并与箱子保持相对静止.重力加速度为g ,设碰撞都是弹性的,则整个过程中,系统损失的动能为 ( )A .12mv 2B .12·mMm+Mv 2C .12NμmgLD .NμmgL4.如图所示,质量为2 kg 的小车以2.5 m/s 的速度沿光滑的水平面向右运动,现在小车上表面上方1.25 m 高度处将一质量为0.5 kg 的可视为质点的物块由静止释放,经过一段时间物块落在小车上,最终两者一起水平向右匀速运动.重力加速度g 取10 m/s 2,忽略空气阻力,下列说法正确的是 ( )A .物块释放0.3 s 后落到小车上B .若只增大物块的释放高度,则物块与小车的共同速度变小C .物块与小车相互作用的过程中,物块和小车的动量守恒D .物块与小车相互作用的过程中,系统损失的能量为7.5 J5.长木板A 放在光滑的水平面上,质量为m=2 kg 的另一物体B 以水平速度v 0=2 m/s 滑上原来静止的长木板A 的上表面,由于A 、B 间存在摩擦,之后A 、B 速度随时间变化情况如图所示,重力加速度g 取10 m/s 2.则下列说法正确的是( )A .木板获得的动能为2 JB .系统损失的机械能为4 JC .木板A 的最小长度为2 mD.A、B间的动摩擦因数为0.16.[2022·江苏镇江期中] 质量为m的子弹以某一初速度v0击中静止在水平地面上质量为M的木块,并陷入木块一定深度后与木块相对静止,甲、乙两图表示了这一过程开始和结束时子弹和木块可能的相对位置,设地面粗糙程度均匀,木块对子弹的阻力大小恒定,则下列说法中正确的是()A.无论m、M、v0的大小和地面粗糙程度如何,都只可能是甲图所示的情形B.若M较大,则可能是甲图所示情形;若M较小,则可能是乙图所示情形C.若v0较小,则可能是甲图所示情形;若v0较大,则可能是乙图所示情形D.若地面较粗糙,则可能是甲图所示情形;若地面较光滑,则可能是乙图所示情形7.[2022·石家庄二中月考] 如图所示,一轻质弹簧两端分别连着质量均为m的滑块A和的子弹以水平速度v0射入A中不再穿出B,两滑块都置于光滑的水平面上.今有质量为m4(时间极短),则弹簧在什么状态下滑块B具有最大动能?其值是多少?8.[2022·杭二中月考] 如图所示,质量为m=245 g的物块(可视为质点)放在质量为M=0.5 kg的木板左端,足够长的木板静止在光滑水平面上,物块与木板间的动摩擦因数为μ=0.4.质量为m0=5 g的子弹以速度v0=300 m/s沿水平方向射入物块并留在其中(时间极短),重力加速度g取10 m/s2.子弹射入后,求:(1)子弹和物块一起向右滑行的最大速度v1;(2)木板向右滑行的最大速度v2;(3)物块在木板上滑行的时间t.专题课:“子弹打木块”模型和“滑块—木板”模型1.CD [解析] 子弹射入木块并留在木块中,子弹与木块组成的系统受合外力等于零,因此动量守恒,因子弹与木块是完全非弹性碰撞,机械能减少最多,即机械能不守恒,A 错误;子弹和木块一起压缩弹簧过程中,子弹、木块、小车组成的系统受合外力等于零,动量守恒,由于压缩弹簧,即对弹簧做功,弹簧的弹性势能增加,子弹、木块、小车组成的系统机械能减少,机械能不守恒,B 错误;由能量守恒定律可知,整个过程,子弹、木块、小车组成的系统所损失的机械能等于子弹与木块摩擦产生的热量及弹簧的弹性势能之和,C 正确;设子弹的质量为m 1,速度为v 0,木块的质量为m ,小车的质量为M ,子弹射入木块后速度为v 1,向右为正方向,由动量守恒定律可得m 1v 0=(m 1+m )v 1,解得v 1=m 1vm 1+m ,此后对子弹、木块、小车组成的系统,规定向右为正方向,由动量守恒定律可得(m 1+m )v 1=(m 1+m+M )v 2,由机械能守恒定律可得12(m 1+m )v 12-12(m 1+m+m )v 22=E pm ,联立解得弹簧的弹性势能为E pm =m 12v 022(m 1+mM+1)(m 1+m ),由此可见其他条件不变时,若增大小车的质量,弹簧的弹性势能增大,弹簧的最大压缩量增大,D 正确.2.AC [解析] 小车和木块组成的系统在水平方向上不受外力,系统在水平方向上动量守恒,若小车的初动量大于木块的初动量,则最后相对静止时整体的动量方向向左,木块先减速运动再反向加速运动后匀速运动,小车先减速运动再匀速运动,故A 正确,B 错误;同理若小车的初动量小于木块的初动量,则最后相对静止时整体的动量方向向右,则木块先减速运动后匀速运动,小车先减速运动再加速运动后匀速运动,C 正确,D 错误.3.BD [解析] 设物块与箱子相对静止时共同速度为v 1,则由动量守恒定律得mv=(M+m )v 1,得v 1=mvM+m ,系统损失的动能为ΔE k 系=12mv 2-12(M+m )v 12=Mmv 22(M+m ),A错误,B 正确.根据能量守恒定律得知,系统产生的内能等于系统损失的动能,根据功能关系得知,系统产生的内能等于系统克服摩擦力做的功,则有Q=ΔE k 系=NμmgL.C 错误,D 正确. 4.D [解析] 物块下落的时间为t=√2ℎg =√2×1.2510s=0.5 s,A 错误;物块与小车相互作用的过程中,物块与小车组成的系统在水平方向的动量守恒,在竖直方向的动量不守恒,由水平方向动量守恒得Mv 0=(M+m )v ,可知,释放高度变大,水平方向的共同速度不变,B 、C 错误;在整个过程中,由能量守恒定律得系统损失的机械能ΔE=mgh+12M v 02-12(M+m )v 2,代入数据可得ΔE=7.5 J,D 正确.5.D [解析] 由题图可知,最终木板获得的速度为v=1 m/s,A 、B 组成的系统动量守恒,以B 的初速度方向为正方向,由动量守恒定律得mv 0=(M+m )v ,解得M=2 kg,则木板获得的动能为E k =12Mv 2=12×2×12 J =1 J,故A 错误;系统损失的机械能ΔE=12m v 02-12(m+M )v 2,代入数据解得ΔE=2 J,故B 错误;v-t 图像中图线与t 轴所围的面积表示位移,由题图得到0~1 s 内B 的位移为x B =12×(2+1)×1 m =1.5 m,A 的位移为x A =12×1×1 m =0.5 m,则木板A 的最小长度为L=x B -x A =1 m,故C 错误;由题图可知,B 的加速度a=Δv Δt=1-21m/s 2=-1 m/s 2,负号表示加速度的方向,由牛顿第二定律得-μmg=ma ,解得μ=0.1,故D 正确.6.A [解析] 在子弹射入木块的瞬间,子弹与木块间的摩擦力远远大于木块与地面间的摩擦力,故地面光滑与粗糙效果相同,子弹和木块构成一系统,在水平方向上合外力为零,在水平方向上动量守恒,规定向右为正方向,设子弹与木块的共同速度为v ,根据动量守恒定律有mv 0=(m+M )v ,木块在水平面上滑行的距离为s ,子弹射入并穿出木块的过程中对木块运用动能定理得F f s=12Mv 2=Mm 2v 022(m+M )2,根据能量守恒定律得Q=F f d=12m v 02-12(m+M )v 2=Mmv 022(M+m ),则d>s ,不论速度、质量大小关系和地面粗糙程度如何,都只可能是甲图所示的情形,故选A . 7.当弹簧第一次恢复原长时281m v 02[解析] 子弹射入A 中时,因时间极短,且A 与B 用弹簧相连,故可认为B 未参与此过程,则子弹与A 组成的系统动量守恒.设子弹与A 的共同速度为v A ,则有m4v 0=(m +m4)v A 解得v A =v05此后,弹簧被压缩,B 加速,当弹簧再次恢复原长时,弹簧的弹性势能为零,B 有最大速度v B m ,即有最大动能E km .此过程相当于以速度v A 运动的滑块A (内含子弹)与静止滑块B 发生弹性碰撞,应用弹性正碰的结论,有v B m =2(m+m4)m+m+m 4·v05=29v 0 E km =12m (29v 0)2=281m v 02.8.(1)6 m/s (2)2 m/s (3)1 s[解析] (1)子弹射入物块后和物块一起向右滑行的初速度即最大速度,由动量守恒定律得m 0v 0=(m 0+m )v 1, 解得v 1=6 m/s .(2)当子弹、物块、木板三者共速时,木板的速度最大,由动量守恒定律得(m 0+m )v 1=(m 0+m+M )v 2, 解得v 2=2 m/s .(3)对物块和子弹组成的系统,由动量定理得-μ(m 0+m )gt=(m 0+m )v 2-(m 0+m )v 1, 解得t=1 s .。
滑块木板模型-2024届新课标高中物理模型与方法(解析版)

2024版新课标高中物理模型与方法--滑块木板模型目录【模型归纳】1模型一光滑面上外力拉板模型二光滑面上外力拉块模型三粗糙面上外力拉板模型四粗糙面上外力拉块模型五粗糙面上刹车减速【常见问题分析】问题1.板块模型中的运动学单过程问题问题2.板块模型中的运动学多过程问题1--至少作用时间问题问题3.板块模型中的运动学多过程问题2--抽桌布问题问题4.板块模型中的运动学粗糙水平面减速问题【模型例析】5【模型演练】13【模型归纳】模型一光滑面上外力拉板加速度分离不分离m1最大加速度a1max=μgm2加速度a2=(F-μm1g) /m2条件:a2>a1max即F>μg(m1+m2)条件:a2≤a1max即F≤μg(m1+m2)整体加速度a=F/(m1+m2)内力f=m1F/(m1+m2)模型二光滑面上外力拉块加速度分离不分离m2最大加速度a2max=μm1g/m2 m1加速度a1=(F-μm1g)/m1条件:a1>a2max即F>μm1g(1+m1/m2)条件:a2≤a1max即F≤μm1g(1+m1/m2)整体加速度a=F/(m1+m2)内力f=m2F/(m1+m2)模型三粗糙面上外力拉板不分离(都静止)不分离(一起加速)分离条件:F≤μ2(m1+m2)g 条件:a2≤a1max即μ2(m1+m2)g<F≤(μ1+μ2)g(m1+m2)整体加速度a=[F-μ2(m1+m2)g)]/(m1条件:a2>a1max=μ1g即F>(μ1+μ2)g(m1+m2)+m2)内力f=m1a外力区间范围模型四粗糙面上外力拉块μ1m1g>μ2(m1+m2)g一起静止一起加速分离条件:F≤μ2(m1+m2)g 条件:μ2(m1+m2)g<F≤(μ1-μ2)m1g(1+m1/m2)整体加速度a=[F-μ2(m1+m2)g)]/(m1+m2)内力f1=μ2(m1+m2)g+m2a条件:a1>a2max=[μ1m1g-μ2(m1+m2)g]/m2即F>(μ1-μ2)m1g(1+m1/m2)外力区间范围模型五粗糙面上刹车减速一起减速减速分离m1最大刹车加速度:a1max=μ1g 整体刹车加速度a=μ2g条件:a≤a1max即μ2≤μ1条件:a>a1max即μ2>μ1m1刹车加速度:a1=μ1gm2刹车加速度:a2=μ2(m1+m2)g-μ1m1g)]/m2加速度关系:a1<a2【常见问题分析】问题1.板块模型中的运动学单过程问题恒力拉板恒力拉块分离,位移关系:x 相对=½a 2t 20-½a 1t 20=L 分离,位移关系:x 相对=½a 1t 20-½a 2t 20=L问题2.板块模型中的运动学多过程问题1--至少作用时间问题问题:板块分离,F 至少作用时间?过程①:板块均加速过程:②板加速、块减速位移关系:x 1相对+x 2相对=L 即Δv ·(t 1+t 2)/2=L ;利用相对运动Δv =(a 2-a 1)t 1、Δv =(a 2+a 1')t 2问题3.板块模型中的运动学多过程问题2--抽桌布问题抽桌布问题简化模型过程①:分离过程:②匀减速分离,位移关系:x2-x1=L10v0多过程问题,位移关系:x1+x1'=L2问题4.板块模型中的运动学粗糙水平面减速问题块带板板带块μ1≥μ2μ1<μ2【模型例析】1一长木板置于粗糙水平地面上,木板左端放置一小物块;在木板右方有一墙壁,木板右端与墙壁的距离为4.5m,如图(a)所示。
专题十一 动量守恒中的四类典型模型-2025届高中物理

第七章动量守恒定律专题十一动量守恒中的四类典型模型核心考点五年考情命题分析预测子弹打木块模型本专题是本章的难点,滑块+弹簧模型和滑块+滑板模型是高考的热点.预计2025年高考会出现考查滑块+滑板模型的选择题或滑块+弹簧模型的计算题.滑块+弹簧模型2023:辽宁T15,浙江6月T18;2022:全国乙T25;2021:天津T10;2019:全国ⅢT25滑块+斜(曲)面模型2023:湖南T15,山东T18滑块+滑板模型2023:辽宁T15;2022:山东T18,河北T13题型1子弹打木块模型1.模型图示2.模型特点(1)子弹水平打进木块的过程中,系统的动量守恒.(2)系统的机械能有损失.3.两种情境(1)子弹嵌入木块中,两者速度相等,机械能损失最多(完全非弹性碰撞)动量守恒:mv 0=(m +M )v .能量守恒:Q =F f s =12m 02-12(M +m )v 2.(2)子弹穿透木块动量守恒:mv 0=mv 1+Mv 2.能量守恒:Q=F f d=12m02-(12M22+12m12).1.[子弹未穿透木块/2024江苏淮安模拟]如图所示,质量为M=0.45kg的木块静止于光滑水平面上,一质量为m=0.05kg的子弹以水平速度v0=100m/s打入木块并停在木块中,下列说法正确的是(A)A.子弹打入木块后子弹和木块的共同速度为v=10m/sB.子弹对木块做的功W=25JC.木块对子弹做正功D.子弹打入木块过程中产生的热量Q=175J解析根据动量守恒定律可得mv0=(M+m)v,解得子弹打入木块后子弹和木块的共同速度为v=B0+=10m/s,故A正确;根据动能定理可知,子弹对木块做的功为W=12Mv2-0=22.5J,故B错误;由于子弹的动能减小,根据动能定理可知,木块对子弹做负功,故C错误;根据能量守恒定律可知,子弹打入木块过程中产生的热量为Q=12m02−12(M+m)v2=225J,故D错误.2.[子弹穿透木块]如图所示,在光滑的水平桌面上静止放置一个质量为980g的匀质木块,现有一颗质量为20g的子弹以大小为300m/s的水平速度沿木块的中心轴线射向木块,最终留在木块中没有射出,和木块一起以共同的速度运动.已知木块沿子弹运动方向的长度为10cm,子弹打进木块的深度为6cm.设木块对子弹的阻力保持不变.(1)求子弹和木块的共同速度以及它们在此过程中所产生的内能.(2)若子弹是以大小为400m/s的水平速度从同一方向水平射向该木块,则在射中木块后能否射穿该木块?答案(1)6m/s882J(2)能解析(1)设子弹射入木块后与木块的共同速度为v,对子弹和木块组成的系统,由动量守恒定律得mv0=(M+m)v解得v=6m/s此过程系统所增加的内能ΔE=12m02-12(M+m)v2=882J.(2)假设子弹以v'0=400m/s的速度入射时没有射穿木块,则对以子弹和木块组成的系统,由动量守恒定律得mv'0=(M+m)v'解得v'=8m/s此过程系统所损耗的机械能为ΔE'=12mv'20-12(M +m )v'2=1568J 由功能关系有ΔE =F 阻x 相=F 阻d ΔE'=F 阻x'相=F 阻d'则ΔΔ'=阻阻'='解得d'=1568147cm因为d'>10cm ,所以假设不成立,能射穿木块.题型2滑块+弹簧模型模型图示水平地面光滑模型特点(1)两个或两个以上的物体与弹簧相互作用的过程中,若系统所受外力的矢量和为零,则系统动量守恒;(2)在能量方面,由于弹簧形变会使弹性势能发生变化,系统的总动能将发生变化;若系统所受的外力和除弹簧弹力以外的内力不做功,系统机械能守恒;(3)弹簧处于最长(最短)状态时两物体速度相等,弹性势能最大,系统动能通常最小(完全非弹性碰撞拓展模型);(4)弹簧恢复原长时,弹性势能为零,系统动能最大(弹性碰撞拓展模型,相当于碰撞结束时)3.[滑块与弹簧连接/多选]如图甲所示,一个轻弹簧的两端与质量分别为m 1和m 2的两物块A 、B 相连接并静止在光滑的水平地面上.现使A 以3m/s 的速度向B 运动压缩弹簧,速度—时间图像如图乙,则有(CD)A.在t 1、t 3时刻两物块达到共同速度1m/s ,且弹簧都处于压缩状态B.从t3到t4时刻弹簧由压缩状态恢复原长C.两物块的质量之比为m1:m2=1:2D.在t2时刻A与B的动能之比E k1:E k2=1:8解析由题图乙可知t1、t3时刻两物块达到共同速度1m/s,且此时系统动能最小,根据系统机械能守恒可知,此时弹性势能最大,t1时刻弹簧处于压缩状态,而t3时刻处于伸长状态,故A错误;结合图像弄清两物块的运动过程,开始时A逐渐减速,B逐渐加速,弹簧被压缩,t1时刻二者速度相同,系统动能最小,势能最大,弹簧被压缩到最短,然后弹簧逐渐恢复原长,B仍然加速,A先减速为零,然后反向加速,t2时刻,弹簧恢复原长状态,由于此时两物块速度相反,因此弹簧的长度将逐渐增大,两物块均减速,在t3时刻,两物块速度相等,系统动能最小,弹簧最长,因此从t3到t4过程中弹簧由伸长状态恢复原长,故B错误;根据动量守恒定律,可知t=0时刻和t=t1时刻系统总动量相等,有m1v1=(m1+m2)v2,其中v1=3m/s,v2=1m/s,解得m1:m2=1:2,故C正确;在t2时刻A的速度为v A=-1m/s,B的速度为v B=2m/s,根据m1:m2=1:2,求出E k1:E k2=1:8,故D正确.命题拓展命题条件不变,一题多设问下列说法不正确的是(C)A.t1~t2时间内B的加速度在减小B.t1和t3时刻弹簧的弹性势能相等C.t2时刻弹簧处于压缩状态D.t3时刻弹簧的弹性势能最大解析由v-t图像可知t1~t2时间内B的加速度在减小,A正确,不符合题意;t1和t3时刻,A和B的速度均相等,则A和B系统的总动能相等,弹簧的弹性势能相等,B正确,不符合题意;t2时刻,A和B的加速度均为零,说明弹簧弹力为零,则弹簧在t2时刻处于原长状态,C错误,符合题意;t3时刻,A和B的速度相等,弹簧的弹性势能最大,D正确,不符合题意.4.[滑块与弹簧不连接]如图所示,一木板放在光滑水平面上,木板的右端与一根沿水平方向放置的轻质弹簧相连,弹簧的自由端在Q点.木板的上表面左端点P与Q点之间是粗糙的,P、Q之间的距离为L,Q点右侧表面是光滑的.一质量为m=0.2kg的滑块(可视为质点)以水平速度v0=3m/s从木板的左端沿板面向右滑行,压缩弹簧后又被弹回.已知木板质量M=0.3kg,滑块与木板表面P、Q之间的动摩擦因数为μ=0.2,g=10m/s2.(1)若L=0.8m,求滑块滑上木板后的运动过程中弹簧的最大弹性势能;(2)要使滑块既能挤压弹簧,最终又没有滑离木板,则木板上P 、Q 之间的距离L 应在什么范围内?答案(1)0.22J(2)0.675m≤L <1.35m解析(1)滑块滑上木板后将弹簧压缩到最短时,弹簧具有最大弹性势能,此时滑块、木板共速,取向右为正方向,由动量守恒定律得mv 0=(m +M )v 共由能量守恒定律得E p =12m 02-12(m +M )共2-μmgL解得E p =0.22J(2)滑块最终没有离开木板,滑块和木板具有共同的末速度,设为u ,滑块与木板组成的系统动量守恒,有mv 0=(m +M )u设共速时滑块恰好滑到Q 点,由能量守恒定律得μmgL 1=12m 02-12(m +M )u2解得L 1=1.35m设共速时滑块恰好回到木板的左端P 点处,由能量守恒定律得2μmgL 2=12m 02-12(m +M )u 2解得L 2=0.675m所以P 、Q 之间的距离L 应满足0.675m≤L <1.35m.题型3滑块+斜(曲)面模型模型图示水平地面光滑、曲面光滑模型特点(1)最高点:m 与M 具有共同水平速度v 共,m 不会从此处或提前偏离轨道,系统水平方向动量守恒,mv 0=(M +m )v 共;系统机械能守恒,12m v 02=12(M +m )v 共2+mgh ,其中h 为滑块上升的最大高度,不一定等于圆弧轨道的高度(完全非弹性碰撞拓展模型);(2)最低点:m 与M 分离点,系统水平方向动量守恒,mv 0=mv 1+Mv 2;系统机械能守恒,12m 02=12m 12+12M 22(弹性碰撞拓展模型)5.[滑块脱离曲面]如图所示,在光滑的水平地面上,静置一质量为m的四分之一光滑圆弧滑块,圆弧半径为R,一质量也为m的小球,以水平速度v0自滑块的左端A处滑上滑块,当二者共速时,小球刚好到达圆弧上端B.若将小球的初速度增大为2v0,不计空气阻力,则小球能达到距B点的最大高度为(C)A.RB.1.5RC.3RD.4R解析若小球以水平速度v0滑上滑块,小球上升到圆弧的上端时,小球与滑块速度相同,设为v1,以小球的初速度v0的方向为正方向,在水平方向上,由动量守恒定律得mv0=2mv1,由机械能守恒定律得12m02=12×2m12+mgR,代入数据解得v0=2g,若小球以水平速度2v0冲上滑块,小球上升到圆弧的上端时,小球与滑块水平方向上速度相同,设为v2,以小球的初速度方向为正方向,在水平方向上,由动量守恒定律得2mv0=2mv2,由能量守恒定律得12m×(2v0)2=12×2m22+mgR+12m2,解得v y=6g,小球离开圆弧后做斜抛运动,竖直方向做匀减速运动,则h=22=3R,故距B点的最大高度为3R,故选C.命题拓展情境不变,一题多设问以水平速度v0自滑块的左端A处滑上滑块,小球与滑块分离时的速度是多少?答案0解析从小球滑上滑块至小球离开滑块的过程中,根据能量守恒定律得12m02=12m球2+12m块2,小球和滑块系统水平方向动量守恒,有mv0=mv球+mv块,解得v球=0.6.[滑块不脱离曲面/2024广东广州部分学校联考]如图所示,质量m0=5g的小球用长l=1m的轻绳悬挂在固定点O,质量m1=10g的物块静止在质量m2=30g的14光滑圆弧轨道的最低点,圆弧轨道静止在光滑水平面上,悬点O在物块m1的正上方,将小球拉至轻绳与竖直方向成37°角后,由静止释放小球,小球下摆至最低点时与物块发生弹性正碰,碰后物块恰能到达圆弧轨道的最上端.若小球、物块可视为质点,不计空气阻力,重力加速度g取10m/s2,sin37°=0.6,cos37°=0.8.求:(1)小球与物块碰撞前瞬间小球的速度v0;(2)小球与物块碰撞后瞬间物块的速度v1;(3)圆弧轨道的半径R.答案(1)v0=2m/s(2)v1=43m/s(3)R=115m解析(1)小球下摆至最低点,满足机械能守恒定律,有m0gl(1-cos37°)=12m002解得v0=2g(1-Hs37°)=2m/s(2)小球与物块碰撞,满足动量守恒定律、机械能守恒定律,有m0v0=m0v01+m1v1 12m002=12m0012+12m112解得v1=43m/s(3)物块滑到圆弧轨道最高点的过程,满足动量守恒定律、机械能守恒定律,则有m1v1=(m1+m2)v212m112=12(m1+m2)22+m1gR解得R=115m.7.[滑块与斜面结合]如图,光滑冰面上静止放置一表面光滑的斜面体,斜面体右侧一蹲在滑板上的小孩和其面前的冰块均静止于冰面上.某时刻小孩将冰块以相对冰面3m/s的速度向斜面体推出,冰块平滑地滑上斜面体,在斜面体上上升的最大高度为h=0.3m(h小于斜面体的高度).已知小孩与滑板的总质量为m1=30kg,冰块的质量为m2=10kg,小孩与滑板始终无相对运动.取重力加速度的大小g=10m/s2.(1)求斜面体的质量;(2)通过计算判断,冰块与斜面体分离后能否追上小孩?答案(1)20kg(2)不能,理由见解析解析(1)规定向左为正方向.冰块在斜面体上上升到最大高度时两者达到共同速度,设此共同速度为v,斜面体的质量为m3.对冰块与斜面体,由水平方向动量守恒和机械能守恒定律得m2v0=(m2+m3)v①12m202=12(m2+m3)v2+m2gh②式中v0=3m/s为冰块推出时的速度,联立①②式并代入题给数据得v=1m/s,m3=20kg ③.(2)设小孩推出冰块后的速度为v1,对小孩与冰块,由动量守恒定律有m1v1+m2v0=0④代入数据得v1=-1m/s⑤设冰块与斜面体分离后的速度分别为v2和v3,对冰块与斜面体,由动量守恒定律和机械能守恒定律有m2v0=m2v2+m3v3⑥12m 202=12m 222+12m 332⑦联立③⑥⑦式并代入数据得v 2=-1m/s⑧由于冰块与斜面体分离后的速度与小孩推出冰块后的速度相同且冰块处在小孩后方,故冰块不能追上小孩.题型4滑块+滑板模型示意图木板初速度为零且足够长木板有初速度且足够长,板块反向地面光滑地面光滑v -t 图像8.[滑块、滑板同向运动]如图所示,质量为M 、长为L 的长木板放在光滑水平面上,一个质量也为M 的物块(可视为质点)以一定的初速度从左端冲上木板,如果长木板是固定的,物块恰好停在木板的右端,如果长木板不固定,则物块冲上木板后在木板上滑行的距离为(C)A.LB.34C.2 D.4解析设物块受到的滑动摩擦力为F f ,物块的初速度为v 0.如果长木板是固定的,物块恰好停在长木板的右端,对物块的滑动过程运用动能定理得-F f L =0-12M 02,如果长木板不固定,物块冲上木板后,物块向右减速的同时,木板要加速,最终两者一起做匀速运动,该过程系统所受外力的合力为零,动量守恒,规定向右为正方向,根据动量守恒定律得Mv 0=(M +M )v 1,对系统运用能量守恒定律有F f L'=12M 02−12(2M )12,联立解得L'=2,C 正确,A 、B 、D 错误.9.[滑块、滑板反向运动]质量为M=1.0kg的长木板A在光滑水平面上以v1=0.5m/s的速度向左运动,某时刻质量为m=0.5kg的小木块B以v2=4m/s的速度从左端向右滑上长木板,经过时间t=0.6s小木块B相对A静止,已知重力加速度g取10m/s2,求:(1)两者相对静止时的运动速度v;(2)从木块滑上木板到相对木板静止的过程中,木板A的动量变化量的大小;(3)小木块与长木板间的动摩擦因数μ.答案(1)1m/s,方向水平向右(2)1.5kg·m/s(3)0.5解析设水平向右为正方向(1)从开始到相对静止,系统在水平方向动量守恒-Mv1+mv2=(M+m)v解得v=1m/s,方向水平向右.(2)长木板的动量变化量大小Δp=Mv-(-Mv1)=1.5kg·m/s.(3)对小木块B,根据动量定理得-μmgt=mv-mv2解得μ=0.5.10.[多个滑块综合考查/2024辽宁沈阳模拟]如图,粗糙水平地面上放着两个相同的木板B和C,可视为质点的物块A以初速度v0冲上木板B.已知A质量为2m,与B、C间动摩擦因数均为μ;B、C质量均为m,与地面间动摩擦因数均为12μ.当A运动至B最右端时,A、B速度相同且B、C恰好相撞(碰撞时间极短),撞后B、C粘在一起.重力加速度为g.求:(1)开始时B、C间的距离;(2)A最终离C右端的距离;(3)从A冲上木板B到最终C静止的整个过程系统因摩擦产生的热量.答案(1)029B(2)230272B(3)3536m02解析(1)A在B上滑动时,对A有2μmg=2ma A故a A=μg对B有2μmg-32μmg=ma B故a B=12μg设经过t1时间A、B速度相同,则有v0-a A t1=a B t1解得t1=203B由于x B=12a B12,解得x B=029B,此即B、C的初始距离(2)木板B的长度等于A、B共速时的相对位移,有L=(v0t1-12a A12)-12a B12解得L=023B由动量守恒定律可得,A滑到B最右端时,A、B共速的速度v1=13v0此时B与C发生完全非弹性碰撞,有mv1=2mv2故碰撞后瞬间B、C的速度为v2=16v0A以13v0的速度滑上C,继续以a A=μg的加速度减速,而此时B、C整体所受合力为零,做匀速直线运动,设经过时间t2后A与B、C共速,则有v1-a A t2=v2解得t2=06B此过程中A相对C的位移大小为x AC=(v1t2-12a A22)-v2t2解得x AC=0272B此后A、C相对静止,故A最终离C右端的距离为L-x AC=230272B(3)B、C碰撞过程损失的机械能为12m12-12×2m22=136m02整个过程系统的总机械能损失为12×2m02-0=m02因此整个过程系统因摩擦产生的热量Q=3536m02.1.[滑块+曲面/2023山东]如图所示,物块A和木板B置于水平地面上,固定光滑弧形轨道末端与B的上表面所在平面相切,竖直挡板P固定在地面上.作用在A上的水平外力,使A 与B以相同速度v0向右做匀速直线运动.当B的左端经过轨道末端时,从弧形轨道某处无初速度下滑的滑块C恰好到达最低点,并以水平速度v滑上B的上表面,同时撤掉外力,此时B右端与P板的距离为s.已知v0=1m/s,v=4m/s,m A=m C=1kg,m B=2kg,A与地面间无摩擦,B与地面间动摩擦因数μ1=0.1,C与B间动摩擦因数μ2=0.5,B足够长,使得C 不会从B上滑下.B与P、A的碰撞均为弹性碰撞,不计碰撞时间,取重力加速度大小g=10m/s2.(1)求C下滑的高度H;(2)与P碰撞前,若B与C能达到共速,且A、B未发生碰撞,求s的范围;(3)若s=0.48m,求B与P碰撞前,摩擦力对C做的功W;(4)若s=0.48m,自C滑上B开始至A、B、C三个物体都达到平衡状态,求这三个物体总动量的变化量Δp的大小.答案(1)0.8m(2)0.625m≤s≤2+2m(3)-6J(4)(6+322)N·s解析(1)C下滑过程,由动能定理有m C gH=12m C v2,解得H=0.8m(2)设C滑上B以后,C的加速度大小为a C,B的加速度大小为a1,B、C共速时间为t1,s的最小值为s1,B、C共同的加速度大小为a2,经过t2时间A追上B,s的最大值为s2,则由牛顿第二定律有μ2m C g=m C a C解得a C=5m/s2μ2m C g-μ1(m B+m C)g=m B a1解得a1=1m/s2又v0+a1t1=v-a C t1解得t1=0.5s由运动学规律有s1=v0t1+12a112联立解得s1=58m=0.625mB、C共速后,由牛顿第二定律得μ1(m B+m C)g=(m B+m C)a2解得a2=1m/s2由运动学公式得s2=s1+(v0+a1t1)t2-12a222s2=v0(t1+t2)联立解得s2=2+2m故s的范围为0.625m≤s≤2+2m(3)由题意知s<s1,所以B与P碰撞时,B与C未共速.设C在B板上滑动的时间为t3,B与P相碰时C的速度大小为v1,则由运动学公式得s=v0t3+12a132解得t3=0.4s(另一解舍去)v1=v-a C t3解得v1=2m/s对物体C从刚滑上B到B与P碰撞前的过程,由动能定理有W=12m C(12-v2)解得W=-6J(4)设B与P碰撞前瞬间的速度大小为v2,B与P碰撞后瞬间的速度为v3,B向左运动的加速度大小为a3,B向左运动时间t4与A相遇.设A、B碰撞前瞬间B的速度大小为v4;A、B碰撞后瞬间,A的速度为v5,B的速度为v6,C的速度大小为v7,则由运动学公式得v2=v0+a1t3解得v2=1.4m/s由于P固定在地面上,B与P的碰撞为弹性碰撞,所以有v3=v2=1.4m/sB与P碰撞后向左运动的过程中,对B由牛顿第二定律得μ2m C g+μ1(m B+m C)g=m B a3解得a3=4m/s2自B、P碰撞后至A、B发生碰撞的过程,由运动学公式得s-v0t3=v0t4+v3t4-12a342解得t4(另一解舍去)v4=v3-a3t4解得v41)m/sv7=v1-a C t4解得v7=(22-1)m/s以向右为正方向,A、B发生弹性碰撞,由动量守恒定律得m A v0-m B v4=m A v5+m B v6由机械能守恒定律得12m A02+12m B42=12m A+12m B62联立解得v5=(1m/s、v6=(1m/s(另一组解舍去)即A、B碰撞后,A以速度v5向左运动,B以初速度v6向右运动经分析可得,B、C最终静止,A最终以速度v5向左运动,故自C滑上B开始至三物体达到平衡状态,这三个物体总动量的变化量为Δp=m A v5-[(m A+m B)v0+m C v]解得Δ=(6N·s2.[滑块+弹簧/2022全国乙]如图(a),一质量为m的物块A与轻质弹簧连接,静止在光滑水平面上;物块B向A运动,t=0时与弹簧接触,到t=2t0时与弹簧分离,第一次碰撞结束,A、B的v-t图像如图(b)所示.已知从t=0到t=t0时间内,物块A运动的距离为0.36v0t0.A、B分离后,A滑上粗糙斜面,然后滑下,与一直在水平面上运动的B再次碰撞,之后A再次滑上斜面,达到的最高点与前一次相同.斜面倾角为θ(sinθ=0.6),与水平面光滑连接.碰撞过程中弹簧始终处于弹性限度内.求(1)第一次碰撞过程中,弹簧弹性势能的最大值;(2)第一次碰撞过程中,弹簧压缩量的最大值;(3)物块A与斜面间的动摩擦因数.图(a)图(b)答案(1)0.6m02(2)0.768v0t0(3)0.45解析(1)水平面光滑,故在水平面上两物块碰撞过程动量守恒,从B与弹簧接触到弹簧第一次压缩到最短过程中有m B v1=(m B+m A)v0其中v1=1.2v0可得m B=5m该过程中机械能守恒,设弹簧最大弹性势能为E p,得E p+12(m A+m B)02=12m B12由上式得E p=0.6m02(2)由图像知0~t0内物块B与物块A的位移差等于弹簧的最大压缩量,也就是题图中该段时间物块A、B图像所夹面积,物块A在0~t0时间内的位移S A=0.36v0t0,即为0~t0内,v-t图像中A线与t轴所夹面积.解法1在压缩弹簧的过程中,物块A、B所受弹簧弹力大小相等,方向相反,则物块A的加速度始终是物块B加速度的5倍,有a A=5a B若两者均做初速度为零的变速运动,则两者的位移满足S A=5S'B在图1中深灰色阴影面积为S A,浅灰色阴影面积为S'B.最大压缩量为X=1.2v0t0-S A-S'B=0.768v0t0图1图2解法20~t0过程,由动量守恒定律有mv A+5mv B=(m+5m)v0结合运动学知识有mS A+5mS B=6mv0t0解得S B=1.128v0t0(B在0~t0内的位移)最大压缩量为X=S B-S A=1.128v0t0-0.36v0t0=0.768v0t0(3)设物块A第一次从斜面滑到平面上时的速度为v x,物块A(含弹簧)回到水平面,第二次与B相互作用过程系统机械能守恒、动量守恒.则有m B v2-m A v x=m B v3+m A·2v012m B22+12m A2=12m B32+12m A(2v0)2其中v2=0.8v0可得v x=v0(另一解舍去)物块A第一次从斜面底端滑到最高点的过程,由动能定理有-mgμs cosθ-mgs sinθ=0-12m(20)2物块A第一次从最高点滑到水平面的过程,由动能定理有-mgμs cosθ+mgs sinθ=12m02-0由上式得μ=0.45.1.[多选]如图所示,在光滑的水平面上放有两个小球A和B,mA>m B,B球上固定一轻质弹簧.A球以速率v去碰撞静止的B球,则(BD)A.A球的最小速率为零B.B球的最大速率为2+vC.当弹簧压缩到最短时,B球的速率最大D.两球的动能最小值为222(+)解析A球与弹簧接触后,弹簧被压缩,弹簧对A球产生向左的弹力,对B球产生向右的弹力,故A球做减速运动,B球做加速运动,当B球的速度等于A球的速度时弹簧的压缩量最大,此后A球继续减速,B球继续加速,弹簧压缩量减小,当弹簧恢复原长时,B球速度最大,A球速度最小,此过程满足动量守恒定律和能量守恒定律,有m A v=m A v1+m B v2,12m A v2=12m A12+12m B22,解得v1=−+v,v2=2+v,因为m A>m B,可知A球的最小速率不为零,B球的最大速率为2+v,故A、C错误,B正确;两球共速时,弹簧压缩到最短,弹性势能最大,此时两球动能最小,根据动量守恒定律有m A v=(m A+m B)v共,E k=12(m A+m B)共2,联立可得E k=222(+),故D正确.2.[2024北京八一中学校考/多选]如图所示,静止在光滑水平桌面上的物块A和B用一轻质弹簧拴接在一起,弹簧处于原长.一颗子弹沿弹簧轴线方向射入物块A并留在其中,射入时间极短.下列说法中正确的是(BD)A.子弹射入物块A的过程中,子弹和物块A的机械能守恒B.子弹射入物块A的过程中,子弹对物块A的冲量大小等于物块A对子弹的冲量大小C.子弹射入物块A后,两物块与子弹的动能之和等于射入物块A前子弹的动能D.两物块运动过程中,弹簧最短时的弹性势能等于弹簧最长时的弹性势能解析子弹射入物块A的过程为完全非弹性碰撞,有动能损失,则子弹和物块A的机械能不守恒,故A错误;子弹射入物块A的过程中,子弹对物块A的作用力与物块A对子弹的作用力是一对相互作用力,等大反向,而且两个力作用时间相等,由I=Ft知,子弹对物块A的冲量大小等于物块A对子弹的冲量大小,故B正确;子弹射入物块A后,两物块与子弹的动能之和小于射入物块A前子弹的动能,因为子弹射入物块A过程中有动能转化为内能,故C错误;两物块运动过程中,弹簧最短时与弹簧最长时都是两物块具有共同速度时,有(m A+m子)v1=(m A+m子+m B)v2,ΔE p=12(m A+m子)12−12(m A+m子+m B)22,则弹簧最短时的弹性势能等于弹簧最长时的弹性势能,故D正确.3.[2024河南三门峡模拟/多选]光滑水平面上停放着质量为m、装有光滑弧形槽的小车,一质量也为m的小球以水平速度v0沿槽口向小车滑去,到达某一高度后,小球又返回右端,图甲小车放置在无阻碍的光滑水平面上,图乙小车靠墙停放,已知重力加速度为g,则(BC)A.图甲中小球返回右端将向右做平抛运动B.图乙中小球返回右端将向右做平抛运动C.图甲中小球在弧形槽内上升的最大高度为024D.图甲中全过程小球对小车压力的冲量为mv0解析题图甲中,小球离开小车时,设小球的速度为v1,小车的速度为v2,整个过程中系统在水平方向上动量守恒,以向左为正方向,由动量守恒定律得mv0=mv1+mv2,对系统由机械能守恒定律得12m02=12m12+12m22,联立解得v1=0,v2=v0,所以题图甲中小球返回右端将做自由落体运动,A错误;题图乙中小车静止不动,因此小球返回右端将向右做平抛运动,B正确;设题图甲中小球在弧形槽内上升的最大高度为h,由系统水平方向动量守恒得mv0=2mv,由能量守恒定律得12m02=12×2mv2+mgh,解得h=024,C正确;由以上分析可知,题图甲中小球返回右端将做自由落体运动,小车将向左做匀速直线运动,速度为v0,对小车水平方向,由动量定理可得I x=Δp=mv0,由于小球对小车一直有竖直向下的压力分量,故全过程小球对小车压力的冲量不等于mv0,D错误.4.[多选]如图所示,光滑水平面上有一质量为2M、半径为R(R足够大)的14光滑圆弧曲面C,质量为M的小球B置于其底端,质量为2的小球A以v0=6m/s的速度向B运动,并与B发生弹性碰撞,两小球均可视为质点,则(AD)A.B的最大速率为4m/sB.B运动到最高点时的速率为34m/sC.B能与A再次发生碰撞D.B不能与A再次发生碰撞解析A与B发生弹性碰撞,取水平向右为正方向,根据动量守恒定律和机械能守恒定律得2v0=2v A+Mv B,12·202=12·22+12M2,解得v A=-2m/s,v B=4m/s,故B的最大速率为4m/s,A正确;B冲上C并运动到最高点时二者共速,设为v,则Mv B=(M+2M)v,得v=43m/s,B错误;B冲上C然后又滑下的过程,设B、C分离时速度分别为v'B、v'C,由水平方向动量守恒有Mv B=Mv'B+2Mv'C,由机械能守恒有12M2=12Mv'2B+12·2Mv'2C,联立解得v'B=-43m/s,由于|v'B|<|v A|,所以二者不会再次发生碰撞,C错误,D正确.5.[设问创新/2024江苏盐城模拟]如图所示,一质量为M=3.0kg的长木板B放在光滑水平地面上,在其右端放一个质量为m=1.0kg的小木块A.同时给A和B大小均为v=5.0m/s、方向相反的初速度,使A开始向左运动,B开始向右运动,A始终没有滑离B.在A做加速运动的时间内,B的速度大小可能是(C)A.1.8m/sB.2.4m/sC.2.8m/sD.3.5m/s解析以A、B组成的系统为研究对象,因为系统不受外力,则系统动量守恒,选择水平向右的方向为正方向,从A、B开始运动到A的速度为零,根据动量守恒定律可得(M-m)v=Mv B1,解得v B1=103m/s,从A、B开始运动到A、B共速,根据动量守恒定律可得(M-m)v=(M+m)v B2,解得v B2=2.5m/s,木块A加速运动的过程为其速度减为零到与B共速的过程,此过程中B始终减速,则在木块A做加速运动的时间内,B的速度范围为2.5m/s≤v B≤103m/s,故C正确,ABD错误.6.[2024湖南长沙南雅中学校考]质量为M,长度为d的木块放在光滑的水平面上,在木块的右边有一个销钉把木块挡住,使木块不能向右滑动,质量为m的子弹以水平速度v0射入静止的木块,刚好能将木块射穿.现拔去销钉,使木块能在水平面上自由滑动,而子弹仍以水平速度v0射入静止的木块,设子弹在木块中受到的阻力大小恒定,则(C)A.拔去销钉,木块和子弹组成的系统动量守恒,机械能也守恒B.子弹在木块中受到的阻力大小为B02C.拔去销钉,子弹在木块中运动的时间为2B(+)0D.拔去销钉,子弹射入木块的深度为B+解析拔去销钉,木块和子弹之间的摩擦力是系统内力,故木块和子弹组成的系统动量守恒;但因摩擦力要做功,故系统机械能不守恒,故A错误.当木块固定时,由动能定理可知-fd=0-12m02,解得f=B022,故B错误.拔去销钉,子弹与木块系统动量守恒,则根据动量守恒定律可得mv0=(m+M)v,解得v=B0+,对木块根据动量定理可得ft=Mv,子弹在木块中运动的时间为2B(+p0,故C正确.拔去销钉,由C选项分析可知最终速度,故整个过程根据动能定理有-fx=12(m+M)v2-12m02,解得x=B+,D错误.7.[2024江西南昌模拟]质量相等的A、B两球之间压缩一根轻质弹簧,静置于光滑水平桌面上,当用挡板挡住A球而只释放B球时,B球被弹出落到距桌边水平距离为x的地面上,如图所示,若再次以相同力压缩该弹簧,取走A左边的挡板,将A、B同时释放,则B球的落地点距桌边水平距离为(D)A.2 B.2x C.x解析当用挡板挡住A球而只释放B球时,B球做平抛运动,设高度为h,则有h=12gt2,x=v0t,所以弹簧的弹性势能为E p=12m02.若再次以相同力压缩该弹簧,取走A左边的挡板,将A、B同时释放,取向右为正方向,由动量守恒定律可得0=mv1-。
SVO原理解析

SVO原理解析最近空闲时间在研究Semi-Direct Monocular Visual Odometry(SVO)[1,2],觉得它值得写⼀写。
另外,SVO的运算量相对较⼩,我想在⼿机上尝试实现它。
关于SVO的介绍,有两篇博客介绍得⾮常好,因此我这⾥只简单提⼀下⼤概的思路,重点讲解了⼀下深度滤波器的原理。
姿态估计估计初始姿态利⽤相邻两帧之间的特征点对,计算相对位姿。
计算第k帧和第k−1帧中的特征点对的patch的灰度差。
特征点对指的是第k−1帧时深度已知的地图点(3D)在两帧中的投影点(2D)。
特征点patch是特征点周围4×4的区域。
利⽤Gauss-Newton迭代法求解ˆTk,k−1。
给k−1帧加⼀个⼩扰动δ,通过灰度差优化δ。
这步叫Inverse compositional formulation。
ˆTk,k−1←ˆTk,k−1⋅T(δ)−1这⼀步忽略patch的变形,不做warping。
因为相邻帧之间的形变很⼩。
Inverse compositional formulation保证Jacobian在迭代中保持不变,因此可以预先计算,降低计算量。
关于⽂章中导数的求解,请参考⾼博的,⾮常详细。
参考⽂献见[3]。
优化匹配关系利⽤初始位姿,寻找更多的地图点(3D)到当前帧投影点(2D)的对应关系。
对每个当前帧能观察到的地图点p(已经收敛的深度估计),找到观察p⾓度最⼩的关键帧r上的对应点u i,优化得到p在当前帧上的投影u′i。
优化的⽬标函数是仿射变换下的灰度差。
u′i=arg minu′i12∥Ik(u′i)−A i I r(u i)∥2∀i这⼀步中的patch采⽤的是8×8邻域,A i表⽰⼀个仿射变换。
这步不考虑极线约束,因为此时的位姿还是不准确的。
第⼆步和第三步需要⼀定量的地图点,不能在⼀开始就使⽤,猜测这是作者强调深度估计收敛快的原因之⼀。
BA优化利⽤第⼆步建⽴起的(p i,u i)的对应关系,优化世界坐标系下的位姿T k,w,标准motion only bundle adjustment。
测试模型的V模型,W模型,X模型,H模型

V模型,W模型,X模型,H模型一、V模型在软件测试方面,V模型是最广为人知的模型,尽管很多富有实际经验的测试人员还是不太熟悉V模型,或者其它的模型。
V模型已存在了很长时间,和瀑布开发模型有着一些共同的特性,由此也和瀑布模型一样地受到了批评和质疑。
V模型中的过程从左到右,描述了基本的开发过程和测试行为。
V模型的价值在于它非常明确地标明了测试过程中存在的不同级别,并且清楚地描述了这些测试阶段和开发过程期间各阶段的对应关系。
局限性:把测试作为编码之后的最后一个活动,需求分析等前期产生的错误直到后期的验收测试才能发现.1.从水平对应关系看左边是设计和分析,是软件设计实现的过程,同时伴随着质量保证活动——审核的过程,也就是静态的测试过程;右边是对左边结果的验证,是动态测试的过程,即对设计和分析的结果进行测试,以确认是否满足用户的需求。
如:需求分析和功能设计对应验收测试,说明在做需求分析、产品功能设计的同时,测试人员就可以阅读、审查需求分析的结果,从而了解产品的设计特性、用户的真正需求,确定测试目标,可以准备用例(Use Case)并策划测试活动。
当系统设计人员在做系统设计时,测试人员可以了解系统是如何实现的,基于什么样的平台,这样可以设计系统的测试方案和测试计划,并事先准备系统的测试环境,包括硬件和第三方软件的采购。
因为这些准备工作,实际上是要花去很多时间。
当设计人员在做在做详细设计时,测试人员可以参与设计,对设计进行评审,找出设计的缺陷,同时设计功能、新特性等各方面的测试用例,完善测试计划,并基于这些测试用例以开发测试脚本。
在编程的同时,进行单元测试,是一种很有效的办法,可以尽快找出程序中的错误,充分的单元测试可以大幅度提高程序质量、减少成本。
从中可以看出,V模型使我们能清楚地看到质量保证活动和项目同时展开, 项目一启动,软件测试的工作也就启动了,避免了瀑布模型所带来的误区——软件测试是在代码完成之后进行。
动量守恒中几种常见的模型

模型四:
带弹簧的木板与滑块模型
如图所示,坡道顶端距水平面高度为h,质量为m1的小物块 A从坡道顶端由静止滑下,进入水平面上的滑道时无机械能 损失,为使A制动,将轻弹簧的一端固定在水平滑道延长线 M处的墙上,另一端与质量为m2的档板B相连,弹簧处于原 长时,B恰位于滑道的末端O点.A与B碰撞时间极短,碰后 结合在一起共同压缩弹簧,已知在OM段A、B与水平面间的 动摩擦因数均为μ,其余各处的摩擦不计,重力加速度为g, 求: (1)物块A在与挡板B碰撞前瞬间速度v的大小; (2)弹簧最大压缩量为d时的弹性势能Ep(设弹簧处于原长 时弹性势能为零).
解:当人从船头走到船尾的过程中,人和船组成的系统都
在水平方向上不受力的作用,故系统水平方向动量守恒。
设某时刻人对地的速度为V2,船对地的速度为V1,则
mV2-MV1=0,即
V1 M V2 m
在人从船头走到船尾的过程中每一时刻系统的动量均守恒, 故mV2t-MV1t=0,即 m所s以2-Ms1 s1m=m0LM,而, ss21+msM2=LML。,
从AB碰撞到弹簧压缩最短过程:
1 2
m1
m2
v'2
Ep
W
代入数据得:Ep m12 gh μm1 m2gd
m1 m2
思考:如果题目让你求解整个系统所产生的热量和压缩 弹簧过程产生的热量,又该怎么求?
规律总结:带弹簧的木板与滑块的模型,可以分为三 个过程:A物体下滑过程,遵循的是机械能守恒定律或 动能定理; A物体碰撞B物体过程,由于内力远大于外力,遵循动 量守恒定律; A、B压缩弹簧的过程,又遵循能量守恒定律(摩擦力 做功,机械能不守恒),分清物理过程,应用物理规 律建立方程,是解决这类问题的关键。
模型7子弹打木块模型(解析版)-动量守恒的十种模型解读和针对性训练

动量守恒的十种模型解读和针对性训练模型7 子弹打木块模型模型解读子弹打木块模型,,一般要用到动量守恒,动量定理,动能定理及动力学等规律,综合性强,能力要求高,是高中物理中常见的题型之一,也是高考中经常出现的题型,。
两种情景情景1 子弹嵌入木块中,两者速度相等,类似于完全非弹性碰撞,机械能损失最多。
情景2 子弹穿透木块,从木块中飞出,类似于非完全弹性碰撞,机械能有损失,损失的机械能等于子弹与木块之间作用力乘以L。
【典例精析】【典例】. (2024山西运城3月质检)如图所示,AOB是光滑水平轨道,BC是半径为R的光滑的14固定圆弧轨道,两轨道恰好相切。
质量为M的小木块静止在O点,一个质量为m的子弹以某一初速度水平向右射入长为L木块内,恰好没穿出木块,然后与木块一起继续运动,且恰能到达圆弧轨道的最高点C(木块和子弹均可以看成质点)。
求:(1)子弹射入木块前的速度;(2)子弹打入木块过程中产生的热量Q;(3)若每当小木块返回到O点或停止在O点时,立即有相同的子弹射入小木块,并留在其中,则当第9颗子弹射入小木块后,小木块沿圆弧轨道能上升的最大高度为多少?【参考答案】(1;(2)()M M m gR Q m+=(3)92R m M M m +æöç÷+èø【名师解析】(1)第一颗子弹射入木块的过程,系统动量守恒,以子弹的初速度方向为正方向,由动量守恒定律得()01mv m M v =+系统由O 到C 的运动过程中机械能守恒,由机械能守恒定律得()()2112m M v m M gR +=+由以上两式解得0v =(2)由()22011122Q mv M m v =-+得()M M m gRQ m+=(3)由动量守恒定律可知,第2,4,6…颗子弹射入木块后,木块的速度为0,第1,3,5…颗子弹射入后,木块运动。
当第9颗子弹射入木块时,以子弹初速度方向为正方向,由动量守恒定律得()099mv m M v =+设此后木块沿圆弧上升的最大高度为H ,由机械能守恒得()()291992m M v m M gH +=+由以上各式可得29m M H R M m +æö=ç÷+èø【针对性训练】1. (2024江苏镇江质检)一木块静止在光滑水平面上,现有一个水平飞来的子弹射入此木块并深入2cm 后相对于木块静止,同一时间内木块被带动前移了1cm ,则子弹损失的动能、木块获得动能之比为( )A. 3:2B. 3:1C. 2:1D. 2:3【参考答案】B【名师解析】在运动的过程中,子弹相对运动的位移12cmx =木块向前运动位移为21cmx =子弹的位移为123cmx x x =+=根据动能定理得,对子弹有k1fx E -=D 子弹损失的动能大小为k1E fxD =对于木块,有2k2fx E =D 木块获得动能k22E fx =则子弹损失的动能、木块获得动能之比为k1k 2:3:1E E D =故选B 。
RT系统中的0维燃烧模型

Zero-Dimensional Combustion Simulation in Real TimeThe development and validation of engine control device functions relies more and more on modern simulation and modelling techniques. The en-Dyna Themos models not only provide a realistic description of the physical behaviour of the entire internal combustion engine, they also satisfy the need for high computational efficiency mandated by the real-time application in Software-in-the Loop and Hardware-in-the-Loop environments.The latest engine technology has a strong impact onthe model-based development and validation of con-trol device functions. Whereas well-known mass-flow based models were sufficiently accurate in the past, more detailed model approaches are required nowa-days to consider the signals measured by new sensors or regard the influence of new actuators. A typical example is the introduction of cylinder pressure sen-sors on diesel engines. The sensor signals have to be physically consistent to pass the plausibility checks of diagnosis functions, for example those demanded by OBD II (Onboard-Diagnostic System) legislation.The model presented here maps all of the main components of modern internal combustion engines, including the compressor, turbine, EGR valve, particu-late filter and oxidizing catalytic converter, to form Simulink blocks. In this paper, we focus on the simu-lation of the combustion process within the cylinder of a diesel engine, which is akin to the model of a spark-ignition engine not presented here. The chosen approach is a zero-dimensional description of the combustion, which takes into account the inert gas portion from the recycled exhaust gas as well as mul-tiple injections in the cylinder pressure calculation. It provides the required degree of physical detail and enables simulation step sizes commonly used in HiL applications, such as 1 ms and above, whereasother model approaches either require smaller step sizes in order to ensure accurate simulation or the computational cost depends strongly on, for exam-ple, the engine speed.Accuracy and computational performance are enhanced by an innovative step size control system that maintains upper limits for the computing time and a maximum angle increment essential for the accuracy of the simulation independent of the step size of the overall simulation.Engine Modelling FrameworkThe modelling framework depicted in Figure 1 com-prises two main parts:• Simulink block libraries representing all promi-nent parts of the engine and the vehicle, such as the cylinder, throttle, manifold, injector and transmission. This modular structure of fully ge-neric model blocks enables almost all engine model configurations to be implemented quickly.• A data preparation tool — so-called Preprocessing — to derive the model parameters in a fast and reproducible process from measurements and data sheet information. For each model block, Preproc-essing provides appropriate methods to calculate the required parameters.Components of combustion engine modelsby Oliver Philipp, Robert Hoepler, Cornelius Chucholowski, Tesis DynawareThermodyna-mical engine dynamics simulation paves the way to faster ECU function deve-lopment.C -T e c h n o l o g i e sFigure 2 shows a typical engine model with its major components. The intake part is composed of individual model blocks for the com-pressor, intercooler and throttle as well as containers between the inter-cooler and throttle and between the throttle and the engine. The ex-haust part consists of models for a turbine, an oxidising catalytic converter, a number of lambda sensors and a container model located between the engine and the turbine. The compressor and turbine are rigidly linked by a shaft. The intake and exhaust manifolds are con-nected by an EGR valve and an EGR cooler. Each cylinder is modelled by an individual instance of a generic library block.The model is adapted to specific requirements by either changing the number of blocks, for example the cylinder blocks, or rearranging existing model blocks. For instance, two-stage charging can be realised by the arrangement of two compressor and turbine blocks connected by a container block. The operating point-dependent bypass of a compres-sor or a turbine can be modelled by throttle blocks connected to adja-cent containers. In order to exploit the full capability and accuracy of the model library, it is necessary to have correct model parameters, as the overall quality of the simulation results is determined by the modelFigure 1: Process for setting up anHiL/SiL applica-tion.Figure 2: Schematic view of a typical model.C -T e c h n o l o g i e sequations and algorithms as well as the parameteri-sation. Preparing the parameters for a new modelcan be a tedious and error-prone task. To alleviate this work, the model library is accompanied by a data preparation system called Preprocessing. It cal-culates the model parameters from standard meas-urements and data sheet information usually avail-able during engine development [4].One important step of this process calculates the characteristic map of the Arrhenius coefficient K arrh , shown in Figure 3, which is required by the combus-tion model. An optimisation algorithm adapts the coefficient for each operating point in such a way that the sum of the mean combustion torques of the cylinders in the simulation matches the combustion torque calculated from the measurement data.In the same way, heat transfer coefficients and parameters describing turbine and compressor blocks, for example, are calculated by Preprocessing. Many of these calculations are also based on results of the engine characteristic map measurement.Gas Dynamics and CombustionAppropriate simulation of the processes inside the cylinder in engine control device test applications requires (i) treatment of the gas dynamics describing the inflowing and outflowing gas, (ii) calculation of the heat release and pressure during combustion, and (iii) determination of the gas composition.The gas state in the manifolds, for example the intake and exhaust manifolds, is simulated by con-tainer models. These calculate the pressure, tempera-ture and gas composition, presuming the gas to be ideal.A realistic temperature calculation considers the heat loss to the surroundings of each container. The following approach is used in the model to calculate the temperature of the exhaust gas from the weight-ed mean temperature of the inflowing mass flows T in ,where kA is the heat transfer coefficient between the container and its surroundings. This leads to the or-dinary differential equation (ODE):m Container c v T˙Container = kA · (T Container – T Ambient ) + ∑m ˙in c p T in – m ˙out c p T Containerp ˙container = m ˙ · p _____ m + T ˙ · p ____ TThis ODE is solved in the presented approach with a fully implicit integration method in order to guarantee a stable calculation of the container pres-sure even in the case of simulation step sizes >1 ms and small container volumes. If this problem is treat-ed by explicit or partially implicit integration meth-ods, the solution of the ODE may become unstable [3].The gas under consideration is composed of O 2, N 2, CO 2, C x H y , CO, NO x and particles. The composition of the exhaust mass flow is calculated as a weighted average of the composition of the inflowing mass flows.The simulation of the combustion is based on the laws of thermodynamics: the gas state in the cylin-der is determined by the balance of mass and energy. It is assumed that the gas state is homogenous in the entire cylinder, also known as a zero-dimensional model approach. The calculation of the heat release and heat losses forms the basis for simulating the pressure inside the cylinder synchronously to the crank angle and the resulting cylinder torque. Syn-chronous in this context denotes that the crank an-gle is provided by an external source, for example HiL hardware or a separate model block, to ensure that the current model calculation uses the present crank angle.Using equilibrium thermodynamics, the gas temper-ature is determined byT ˙= Q ˙wall +Q ˙combustion –p·V ˙+c p ·m ˙in ·T in +c p ·m ˙out ·T out –m ˙·c v ·T__________________________________ m·c v. (1)The time-dependent cylinder volume is deter-mined from the current crank angle and the kine-matics of the crank drive [1]. The wall heat transfercoefficient a used in Q˙wall = a wall (T – T wall ) is calcu-lated using various simplifying assumptions in ac-cordance with the approach by Woschni [2].The reaction kinetics of the combustion of fuel is ap-proximated by the following chemical reactionC x H y + (x + y _4O 2)→ xCO 2 + y _2H 2O.Hence, the heat release dQ combustion /dt during com-bustion can be represented by the concentration ofCO 2dQ combustion _ dt = 1 _x · d(c(CO 2)) _ dt· m Cylinder · H Fuel In the approach presented here, the change in theconcentration of CO 2 is determined by an Arrhenius equation, where K Arrh is the operating point-depend-ent Arrhenius parameter [2]:Figure 3: Characteristic map of the Arrhenius coefficient K arrh resulting from Pre-processing.The simulation ofthe combustion isbased on the laws of thermo-dynamicsC -T e c h n o l o g i e sd(c(CO2)) _dt = KArrh· exp (– 4650K_T)· c(O2) · c(C x H y)The concentrations of O2, H2O, CO2and C x H y inthe exhaust gas are calculated from the reaction ki-netics, while the concentrations of CO, NO x and par-ticles are determined by characteristic maps.The ignition delay time of the injected fuel has a considerable influence on the heat release with re-spect to time. The delay time between injection and ignition is considered by [2]:t delay = 4.4 · 10– 4 · p–1.2 · exp (4650K_T)The influence of multiple injections on the heat release rate during combustion, as depicted in Fig-ure4 for the case of a double injection, is taken into account by an abrupt change in the concentration of C x H y in accordance with the quantity of fuel injected. This assumption is justified by the fact that, during the simulation, injection signals are evaluated dis-cretely at each time step.Solving the differential equation (1) requires a method of high order and low computational effort to calculate the crank angle-resolved values of tem-perature, pressure and torque with adequate pre- cision. The approach presented here is based on DOPRI5, which permits a maximum angle increment of Da = 2° at a simulation step size of 1 ms and a maximum engine speed of 6000 rpm to achieve an accuracy comparable with the explicit Runge-Kutta method (RK 4) with an increment of Da=1°.An innovative step size control system (SCS) was designed to enable real-time operation of the model mandatory for HiL operation. During the combustion phase, the SCS subdivides one step into several mi-cro-steps [3]. A time-based solution ensures that the CPU load is almost independent of the engine speed and leads to sufficient precision of the combustion process even for step sizes >1 ms. Values such as the crank shaft-synchronous combustion torque are mapped to mean values at each simulation step.An important aspect to be considered is the con-tinuous consideration of the injection signals in HiL operation. When the measurement technology used in this scenario is able to continuously pass injection signals to the model, alterations in the injection sig-nal directly effect the simulation without delay. Application ScenariosThe presented model facilitates the development process of an engine control unit (ECU) at various stages. In controller design, a graphical specification of the controller function may be interfaced to the engine model to validate the conceptual design. Pa-rameter studies up to pre-calibration of the controller before it is run with the real engine can reveal sensi-tivity to controller parameters. Tests of the ECU on an HiL test rig take place later in the development, either for the ECU alone or as a part of a network of con-trollers for integration tests. In a recent application, a car manufacturer developed controller functions with cylinder pressure feedback. At first, it was planned to test these functions on the real engine.However, since an HiL test rig with the presented model wasavailable, the controller design was tested on theHiL. The simulation results obtained allowed for anearly optimisation of the controller design and its parameters. Thus, development results were availablemuch earlier than expected.ConclusionReal-time engine simulation including gas dynamicsand combustion is a key enabler for testing leading-edge engine control device functions and can be ap-plied to design control algorithms at an early stageof the development process, with the model simulat-ing the engine as a controlled system. The high-fi-delity approach presented here includes a zero-di-mensional model for the simulation of combustionthat guarantees a realistic calculation of the crank-shaft-related combustion torque and the pressure inthe cylinder.The problem of very small time scales introducedby treating the combustion process in detail on theone hand and expensive computations on the otheris solved by an innovative step size control to main-tain real-time capability. Hence, the same model isapplicable in SiL and HiL applications for designingand testing control device functions.[1] Pischinger, Rudolf; Kell, Manfred; Sams, Theodor: Thermo-dynamik der Verbrennungskraftmaschine; Springer Verlag,Berlin, 2002.[2] Urlaub, Alfred: Verbrennungsmotoren; Springer Verlag,Berlin,1995.[3] Philipp, Oliver, Thalhauser, Josef: A Diesel Engine Modelwith Turbocharging, EGR and Cylinder-pressure Calcula-tion for HiL and SiL, 5th IAV Symposium, 2005.[4] Philipp, Oliver; Röhlich, Stefan: The enDYNA Preprocess-ing tool for model parameterisation, Simulation und Test inder Funktions- und Softwareentwicklung für die Automo-bilindustrie, 2005.Early optimisa-tion of the con-troller design andits parameters Figure 4: Heat release in the case of double injection.C-T e c h n o l o g i e s。
三大力场中的碰撞模型(解析版)--2024年物理二轮常见模型

三大力场中的碰撞模型特训目标特训内容目标1动碰静完全弹性碰撞模型(1T -5T )目标2动碰动完全弹性碰撞模型(6T -10T )目标3完全非弹性碰撞模型(11T -15T )【特训典例】一、动碰静完全弹性碰撞模型1碰碰车深受青少年的喜爱,因此大多数游乐场都设置了碰碰车,如图所示为两游客分别驾驶碰碰车进行游戏。
在某次碰撞时,红车静止在水平面上,黄车以恒定的速度与红车发生正撞;已知黄车和红车连同游客的质量分别为m 1、m 2,碰后两车的速度大小分别为v 1、v 2,假设碰撞的过程没有机械能损失。
则下列说法正确的是()A.若碰后两车的运动方向相同,则一定有m 1>m 2B.若碰后黄车反向运动,则碰撞前后黄车的速度大小之比可能为5∶6C.若碰后黄车反向运动且速度大于红车,则一定有m 2>3m 1D.碰后红车的速度与碰前黄车的速度大小之比可能为3∶1【答案】AC【详解】A .根据动量守恒与机械能守恒m 1v =m 1v 1+m 2v 2;12m 1v 2=12m 1v 21+12m 2v 22得v 1=m 1-m 2m 1+m 2v ,v 2=2m 1m 1+m 2v 可知,当m 1>m 2时,两车速度方向相同,A 正确;B .若碰后黄车反向运动,则m 1<m 2则碰撞后黄车速度小于碰撞前的速度,碰撞前后黄车的速度大小之比不可能为5∶6,B 错误;C .若碰后黄车反向运动且速度大于红车,即m 2-m 1m 1+m 2v >2m 1m 1+m 2v 得m 2>3m 1,C 正确;D .设碰后红车的速度与碰前黄车的速度大小之为3∶1,即v 2:v =3:1得m 1+3m 2=0不符合实际情况,D 错误。
故选AC 。
2一质量为m 的小球A 以初速度v 0与正前方另一小球B 发生碰撞,碰撞过程A 、B 两球的v -t 图像如图所示。
已知地面光滑,则下列说法正确的是()A.图线P 反映的是碰撞过程中A 球的v -t 图像B.B 球的质量可表示为v 0-ccmC.一定存在b -a =v 0D.碰撞过程中A 、B 两球的最大弹性势能为mv 0v 0-c2【答案】ABD【详解】A .A 与B 碰撞过程,对A 、B 进行受力分析可知,A 球受力方向和速度方向相反,A 的速度应减小,则P 反映的是A 球的情况,A 正确;B .由动量守恒定律有mv 0=mv 1+m B v 2=m +m B c 得m B =v 0-ccm ,B 正确;C .由弹性碰撞有12mv 20=12mv 21+12m B v 22得v 2=2mv 0m B +m ,v 1=m -m B v 0m B +m 知v 2-v 1=v 0则发生弹性碰撞才有b -a =v 0,C 错误;D .AB 碰撞过程中速度相等时两球有最大弹性势能,则有mv 0=m +m B c ;12mv 20=12m +m B c 2+E pm 解得E pm =mv 0v 0-c2,D 正确。
系统工程双V模型(Ⅰ)

系统工程双V模型(Ⅰ)经典系统工程过程的可视化表达有多种模型,1978年Kevin Forsberg & Harold Mooz提出V模型,V模型非常准确地表示了从系统分解到集成活动的系统演进过程,使系统工程过程变得可视化、且易于管理。
受到业界广泛的关注与应用。
V模型提出后,不断地在工程实践中应用、演化与改进,在1991年,Kevin Forsberg and Harold Mooz在NCOSE第一届年会上又提出系统工程双V模型,双V模型以一种立体的视角来审视系统开发过程,从而使得系统工程过程的可视化表达更加完善。
下面,我们先从不同模型来了解系统工程过程可视化表达的发展情况。
1、系统工程椭圆模型1974年正式发布的美军标MIL-STD-499A和之后直到90年代初在不断更新的MIL-STD-499B(但从未正式发布)为经典系统工程做了相对完整的总结。
如下图所示,我们称之为椭圆模型。
椭圆模型包括需求分析、功能分析和分配、综合这三步构成的串行技术过程,以及系统分析与控制构成的技术管理过程,用来支持技术过程。
基于技术过程的需求回路、设计回路和验证回路,以及技术过程与技术管理过程的接口,形成自上而下、全面综合、反复迭代、循环递进的问题求解过程,来保证全部系统需求被完整定义、追踪和验证由需求分析、功能分析和分配、综合、系统分析和控制四部分构成的经典系统工程过程被迭代应用于系统生命期各阶段。
国内有学者将经典的系统工程理解为3 个过程,4个回路(验证),生成3个文档。
3个过程的第一步需求分析负责把用户的需求及外部环境的约束变换成系统要求;第二步功能分析与分配负责把系统要求变换成系统的功能, 并把功能分解为系统的一个一个的小动作, 形成的文档是功能架构;第三步设计综合, 则根据现有的产品及技术条件, 把功能架构/映射到物理架构上, 完成设计过程。
4个回路则负责把3个步骤各自的产出和输入进行对比, 看是否匹配, 这个过程叫作验证。
四类经典的直线运动模型(解析版)

四类经典的直线运动模型目录【模型一】“0-v -0”运动模型【模型二】“等位移折返”模型【模型三】三倍加速度运动模型----等时间折返模型【模型四】两类常见非匀变速直线运动模型类型一:力随时间均匀变化类型二:力随位移均匀变化【模型一】“0-v -0”运动模型1.特点:初速度为零,末速度为v ,两段初末速度相同,平均速度相同。
三个比例式:①速度公式v 0=a 1t 1v 0=a 2t 2推导可得:a1a 2=t 2t 1②速度位移公式v 20=2a 1x 1v 20=2a 2x 2推导可得:a1a 2=x 2x 1③平均速度位移公式x 1=v 0t 12x 2=v 0t 22推导可得:x 1x 2=t1t 22.位移三个公式:x =v 02(t 1+t 2);x =v 202a 1+v 202a 2;x =12a 1t 21+12a 2t 223.平均速度:v 1=v 2=v=v 021【多选】(2021·全国·高考真题)水平桌面上,一质量为m 的物体在水平恒力F 拉动下从静止开始运动,物体通过的路程等于s 0时,速度的大小为v 0,此时撤去F ,物体继续滑行2s 0的路程后停止运动,重力加速度大小为g ,则()A.在此过程中F 所做的功为12mv 20 B.在此过中F 的冲量大小等于32mv 0C.物体与桌面间的动摩擦因数等于v 24s 0g D.F 的大小等于物体所受滑动摩擦力大小的2倍【答案】BC【详解】CD .外力撤去前,由牛顿第二定律可知F -μmg =ma 1 ①由速度位移公式有v 20=2a 1s 0②外力撤去后,由牛顿第二定律可知-μmg =ma 2 ③由速度位移公式有-v20=2a2(2s0) ④由①②③④可得,水平恒力F=3mv20 4s0动摩擦因数μ=v20 4gs0滑动摩擦力F f=μmg=mv20 4s0可知F的大小等于物体所受滑动摩擦力大小的3倍,故C正确,D错误;A.在此过程中,外力F做功为W=Fs0=34mv20故A错误;B.由平均速度公式可知,外力F作用时间t1=s00+v02=2s0v0在此过程中,F的冲量大小是I=Ft1=32mv0故B正确。
零维模型

零维模型
-热力学平衡假定 -应用范围: (1)根据示功图计算放热率曲线 (2)用经验的放热规律预测示功图 -柴油机放热率公式: Whitehouse、Weibe、林慰梓等
对于火花点火汽油机的燃烧过程,用零维系统描述的燃 烧室控制容积如图所示,其中,p,T,m,V分别是燃烧 室的压力,温度,混合气质量和体积,QW是缸壁散热引 起的热量损失。
1 2 1 V Vh 1 cos 1 1 2sin 2 2 1
其中气缸工作容积 V ,压缩比 及 都是已知的常数; ⑤ 燃料的燃烧热C是已知常数,混合气的质量燃烧率mb 可用余弦函数计算
h
其中燃烧开始的曲轴转角 ,燃烧持续角 都是已 0 知常数。
(调节参数a,n为常数)
n n 1 d QC d mb Cma(n 1) 0 0 C exp a d d b b b
内能的变化
dE dT mC V d d
b
0 mb 1 1 cos m 2 b
利用上述已知条件,给出燃烧室温度T和曲轴转角 的关 系表达式。
根据热力学第一定律,可得
d Q C dE dW d QW d d d d
0.8
(Cm是活塞平均速度)
如果活塞和缸壁之间会发生漏气,质量方程写为
dm d mCR d d
mCR表示穿过环缝泄漏的气体质量,可以根据环缝的容积 VCR和压力,并利用状态方程计算
d mCR V CR dp d RT W d
化学反应放热
0 d QC d mb 1 C m sin d d 2 b b
