直线与圆的位置关系第一课时课件
合集下载
2.5.1 直线与圆位置关系 课件(共23张PPT)

2
(
3
)
4 1 2= 1 > 0
因为
所以,直线 l 与圆相交,有两个公共点.
由 2 − 3 + 2 = 0 ,解得1 = 2, 2 = 1.
把 1 = 2代入方程①,得 1 = 0 ;
把 2 = 1代入方程① ,得 2 = 3.
所以,直线 l 与圆的两个交点是:
(2,0),(1,3)
【分析】如图,点(2,1)位于圆: 2 + 2 = 1外,经过圆外一点有两条直线与这个圆相切.我们设切线方
程为 − 1 = ( − 2), k为斜率.由直线与圆相切可求出k的值.
y
解法1:设切线的斜率为,则切线的方程为 − 1= − 2 ,
P.
即kx-y+1-2k=0
由圆心(0,0)到切线l的距离等于圆的半径1,得
【分析】思路一 判断直线l与圆的位置关系,就是看由它们的方程组成的方程组有无实数解;
思路二 可以依据圆心到直线的距离与半径长的关系,判断直线与圆的位置关系.
解法一:由直线 l 与圆的方程,得:
3x y 6 0,
2
2
x
y
2 y 4 0.
消去y,得 x 2 3x 2 0
①当切线l的斜率存在时, 即 − + 2 − = 0,
由圆心(0,0)到切线l的距离等于圆的半径1,得
|2 − |
2
+1
= 1, 解得
3
=4 ,
y
.
P
此时,切线l的方程为3 − 4 + 5 = 0.
②当切线l的斜率不存在时,此时直线x=1也符合题意.
(
3
)
4 1 2= 1 > 0
因为
所以,直线 l 与圆相交,有两个公共点.
由 2 − 3 + 2 = 0 ,解得1 = 2, 2 = 1.
把 1 = 2代入方程①,得 1 = 0 ;
把 2 = 1代入方程① ,得 2 = 3.
所以,直线 l 与圆的两个交点是:
(2,0),(1,3)
【分析】如图,点(2,1)位于圆: 2 + 2 = 1外,经过圆外一点有两条直线与这个圆相切.我们设切线方
程为 − 1 = ( − 2), k为斜率.由直线与圆相切可求出k的值.
y
解法1:设切线的斜率为,则切线的方程为 − 1= − 2 ,
P.
即kx-y+1-2k=0
由圆心(0,0)到切线l的距离等于圆的半径1,得
【分析】思路一 判断直线l与圆的位置关系,就是看由它们的方程组成的方程组有无实数解;
思路二 可以依据圆心到直线的距离与半径长的关系,判断直线与圆的位置关系.
解法一:由直线 l 与圆的方程,得:
3x y 6 0,
2
2
x
y
2 y 4 0.
消去y,得 x 2 3x 2 0
①当切线l的斜率存在时, 即 − + 2 − = 0,
由圆心(0,0)到切线l的距离等于圆的半径1,得
|2 − |
2
+1
= 1, 解得
3
=4 ,
y
.
P
此时,切线l的方程为3 − 4 + 5 = 0.
②当切线l的斜率不存在时,此时直线x=1也符合题意.
3《直线与圆的位置关系》课件1.ppt

思考:
(1)当d>r时,能否得出直线和圆的位置关系为相离. (2)当d=r时,能否得出直线和圆的位置关系为相切. (3)当d<r时,能否得出直线和圆的位置关系为相交.
(d为圆心O到直线L的距离,r为圆O的半径)
பைடு நூலகம்
直线和圆的位置关系:
• 直线L和⊙O相交 • 直线L和⊙o相切 • 直线L和⊙o相离 d<r d=r d>r
注明:符号” “读作”等价于”.它表示从左端可以 推出右端,并且从右端也可以推出左端.
由方程组的解确定直线与圆的位置关系
设直线l和圆C的方程分别为: Ax+By+C=0, X2+y2+Dx+Ey+F=0
如果直线l与圆C有公共点,由于公共点同时在l和C上, 所以公共点的坐标一定是这两个 方程的公共解;反之,如果这两个方程有公共解, 那么以公共解为坐标的点必是l与C的公共点. 由直线l和圆C的方程联立方程组 Ax+By+C=0 X2+y2+Dx+Ey+F=0 有如下结论:
L
圆心O到直线L的距离d
.
o
半径r
d>r (1)直线L和⊙O的相离,此时d与r大小关系为_________
圆心O到直线L的距离d
.
o
L
L
半径r
d=r (2)直线L和⊙O相切,此时d与r大小关系为_________
L
圆心O到直线L的距离d
.
o
L
半径r
d<r (3)直线L和⊙O相交,此时d与r大小关系为_________
AB AC
2
C (图1) B D C (图2) B D C A
直线与圆的位置关系ppt课件

新知讲解
想一想:自一点引圆的切线的条数 (1)若点在圆外,则过此点可以作几条切线? 若点在圆外,则过此点可以作圆的两条切线. (2)若点在圆上,则过此点只能作几条切线? 若点在圆上,则过此点只能作圆的一条切线,且此点是切点. (3)若点在圆内,则过此点能作几条切线? 若点在圆内,则过此点不能作圆的切线,即可以作0条. 问题:如何刻画直线与圆相切? 公共点的个数只有1个; 圆心到直线的距离等于半径.
2
因此所求切线l的方程为y=-2x或y= 1 x.
2
新知讲解
例2:已知直线l经过点 O (0,0),且与圆C:(x-1)2 + (y-3)2 =5相切,求直线l的方程.
解法2:当直线l的斜率不存在时,直线l的方程为x=0,圆
心C(1,3)到直线l的距离为1≠ 5 ,不合题意.
当直线l的斜率存在时,设直线l的方程为y=kx,即kx-y=0,
新知讲解
例2:已知直线l经过点 O (0,0),且与圆C:(x-1)2 + (y-3)2 =5相切,求直线l的方程.
思路1 直线与圆相切
直线的方程,
圆的方程
0
直线方程
思路2
d r
新知讲解
例2:已知直线l经过点 O (0,0),且与圆C:(x-1)2 + (y-3)2 =5相切,求直线l的方程.
当堂检测
1.(1)直线x+y-2=0与圆x2+y2=2的位置关系为__相__切____ (2)直线x-y-2=0与圆(x-1)2+(y-1)2=1的位置关系为___相__离___ (3)直线x+2y-1=0和圆x2-2x+y2-y+1=0的位置关系为__相__交____
直线和圆的位置关系 -PPT课件

A
Bl
特点:直线和圆有_____的公共点, 叫做直线和圆_____
这时的直线叫_____,
唯一的公共点叫_____。 特点:直线和圆_____公共点,
叫做直线和圆_____。
.O
.
l
切点 A
.O l
用圆心o到直线l的距离d与圆的半径r的关系来区分
2.直线和圆的位置关系
O
dr
—— 数量特征
l 直线 l 和⊙O相交
24.2.2.直线与圆的位置关系(1)
复习提问:
1、在白板上拖动点A说明点和圆的位置关系有 几种?在用数量关系判别一下点和圆的位置关 系?
.A
微课展示: 一、直线与圆的位置关系
(用公共点的个数来区分)
特点:直线和圆有_____公共点,
叫直线和圆_____, 这时的直线叫做圆的_____。
.O
..
B
4
C3
A
练习二
2.在Rt△ABC中,∠C=90°,AC=3cm,BC=4cm, 以C为圆心,r为半径作圆。
(1)当 r 满足______时,⊙C与直线AB相离。
(2)当 r 满足_____ 时,⊙C与直线AB相切。 B
(3)当r 满足_____ _时,⊙C与直线AB相交。 (4)当r满足____时,⊙C与线段AB只有 一个公共 点.
x2 9x 20 0 的两个根,则直线m与⊙O的位置
关系是
。
若d,r是方程 x2 4x a 0 的两个根,且直线m
与⊙O的位置关系是相切,则a的值是 。
再见
B
A
O
小结:本节课里,你学到了哪 些知识,它们是如何应用的?
说说收获
直线与圆的 位置关系
2.5.1直线与圆的位置关系 课件【可编辑图片版】【共40张PPT】

题型三 有关圆的弦长问题 例 2 求直线 l:3x+y-6=0 被圆 C:x2+y2-2y-4=0 截得 的弦长.
分析:弦心距、半弦长与半径构成的直角三角形求解.
解析:法一:圆C:x2+y2-2y-4=0 可化为x2+(y-1)2=5, 其圆心坐标为(0,1),半径r= 5. 点(0,1)到直线l的距离为d=|3×03+2+11-2 6|= 210, l=2 r2-d2= 10,所以截得的弦长为 10. 法二:设直线l与圆C交于A、B两点.
所成的切点处时,DE为最短距离.此时DE的最小值为
|0+0-8| 2
-
1=(4 2-1) km.
即DE的最短距离为(4 2-1) km.
[方法技巧] 求解直线与圆的方程的实际应用问题的四个步骤
1.认真审题,明确题意. 2.建立平面直角坐标系,用方程表示直线和圆,从而在实际 问题中建立直线与圆的方程. 3.利用直线与圆的方程的有关知识求解问题. 4.把代数结果还原为实际问题的解释.
将A′(x0,-3)代入圆的方程,得x0= 51, ∴当水面下降1 m后,水面宽为2x0=2 51(m).
答案:(1)B (2)2 51
易错辨析 忽略了圆的一个隐含条件 例 4 已知圆的方程为 x2+y2+ax+2y+a2=0,一定点 A(1,2), 要使过定点 A(1,2)作圆的切线有两条,则 a 的取值范围为________.
5,则弦长=2
r2-d2=4
5.
答案:4 5
题型一 直线与圆位置关系的判断
1.直线 y=x+1 与圆 x2+y2=1 的位置关系为( )
A.相切
B.相交但直线不过圆心
C.直线过圆心 D.相离
解析:圆心(0,0)到直线y=x+1的距离d=
直线与圆的位置关系(说课课件)

选择具有代表性的案例,如几何问题、 实际问题等。
分析过程
引导学生分析案例,运用直线与圆的 位置关系的知识点,解决问题。同时, 让学生了解数学知识的实际应用价值, 提高其解决问题的能力。
05
课堂练习与作业
练习题布置
基础练习题
针对直线与圆的基本概念和性质, 设计一些简单的判断题和选择题,
帮助学生理解基本概念。
04
课堂互动与讨论
提问与回答
提问
教师向学生提出问题,引导学生思考直线与圆的位置关系。
回答
学生回答问题,阐述自己的理解和观点,教师给予反馈和指导。
分组讨论
分组
学生分成小组,每组进行讨论。
讨论内容
小组内成员交流自己的想法和观点,共同探讨直线与圆的位置关系,以及在实际 问题中的应用。
案例分析
案例选择
提出问题
提出“直线与圆有哪些位置关系 ?”的问题,引发学生思考和讨 论。
回顾相关知识
回顾直线与圆的基本概念
回顾直线的方程、圆的标准方程等基础知识,为后续学习奠 定基础。
知识关联
强调直线与圆的位置关系与初中数学中点与圆的位置关系之 间的联系,引导学生进行知识迁移。
02
直线与圆的位置关系概述
定义与分类
直线与圆的位置关系说课课件
$number {01}
目 录
• 课程导入 • 直线与圆的位置关系概述 • 直线与圆的位置关系的应用 • 课堂互动与讨论 • 课堂练习与作业 • 课程总结与展望
01 课程导入
引入话题
话题引入
通过展示生活中的直线与圆实例 (如自行车轮、汽车轮胎等), 引导学生思考直线与圆的关系, 激发学习兴趣。
求解角度
通过直线与圆的交点,可以求出直线之间的夹角,或者直线与坐标轴之间的夹角。
分析过程
引导学生分析案例,运用直线与圆的 位置关系的知识点,解决问题。同时, 让学生了解数学知识的实际应用价值, 提高其解决问题的能力。
05
课堂练习与作业
练习题布置
基础练习题
针对直线与圆的基本概念和性质, 设计一些简单的判断题和选择题,
帮助学生理解基本概念。
04
课堂互动与讨论
提问与回答
提问
教师向学生提出问题,引导学生思考直线与圆的位置关系。
回答
学生回答问题,阐述自己的理解和观点,教师给予反馈和指导。
分组讨论
分组
学生分成小组,每组进行讨论。
讨论内容
小组内成员交流自己的想法和观点,共同探讨直线与圆的位置关系,以及在实际 问题中的应用。
案例分析
案例选择
提出问题
提出“直线与圆有哪些位置关系 ?”的问题,引发学生思考和讨 论。
回顾相关知识
回顾直线与圆的基本概念
回顾直线的方程、圆的标准方程等基础知识,为后续学习奠 定基础。
知识关联
强调直线与圆的位置关系与初中数学中点与圆的位置关系之 间的联系,引导学生进行知识迁移。
02
直线与圆的位置关系概述
定义与分类
直线与圆的位置关系说课课件
$number {01}
目 录
• 课程导入 • 直线与圆的位置关系概述 • 直线与圆的位置关系的应用 • 课堂互动与讨论 • 课堂练习与作业 • 课程总结与展望
01 课程导入
引入话题
话题引入
通过展示生活中的直线与圆实例 (如自行车轮、汽车轮胎等), 引导学生思考直线与圆的关系, 激发学习兴趣。
求解角度
通过直线与圆的交点,可以求出直线之间的夹角,或者直线与坐标轴之间的夹角。
直线与圆的位置关系ppt课件

x 2 y 2 Dx Ey F 0
( D 2 +E 2 4 F 0)
代数方法
几何
图形性质究过程,如何通过代数方法,
研究直线与圆的位置关系?
联立两直线方程
两直线的位置关系
方程组解的情况
直线与圆的位置关系
联立直线与圆方程
方程组解的情况
求直线被圆截得的弦长.
(法1) 圆心为C (1, 2), 半径为r 2,
圆心C到直线l的距离d
| 2 2+2 |
2 5 2 8 5
2 2 5
2
弦长为2 (2) (
)
.
=
2
5
5
5
5
22 12
x2 y 2 2x 4 y 1 0
(法2)解 : 联立
2.5.1直线与圆的位置关系
春
来
江
水
绿
如
蓝
日
出
江
花
红
胜
火
问题1:把太阳看作一个圆,海天交线看作一条直线,那么在日出的过程中,
体现了直线和圆的哪些位置关系?
相交
相切
相离
探究交流
问题2:如何判断直线与圆的位置关系?
d
d
d
r
r
r
地平线
直线与圆相切
直线与圆相交
1.通过直线与圆的公共点个数判断
直线与圆有两个公共点
2.弦心距:圆心到弦所在直线的距离;
弦心距
A
O
l
C
O
3.垂径定理:垂直于弦的直径平分这条弦,且平分弦所对的两条弧。
4.求弦长:
①两点距离:联立直线与圆的方程求两交点A,B的坐标
高中数学选择性必修一《2.5.1 第一课时 直线与圆的位置关系》课件

答案:4 5
题型一 直线与圆位置关系的判断 [学透用活]
[典例 1] 求实数 m 的取值范围,使直线 x-my+3=0 与圆 x2+y2-6x+5=0 分别满足:
(1)相交;(2)相切;(3)相离.
[解] 圆的方程化为标准形式为(x-3)2+y2=4,
故圆心(3,0)到直线 x-my+3=0 的距离为 d= m62+1,圆
)
A.0 或 2
B.2
C. 2
D.无解
解析:由圆心(0,0)到直线
x+y+m=0
的距离为半径得|m|= 2
m,解得 m=2.
答案:B
4.直线 y=2x+3 被圆 x2+y2-6x-8y=0 所截得方 程 可 化 为 (x - 3)2 + (y - 4)2 = 25. 故 圆 心 为 (3,4),半径 r=5.又直线方程为 2x-y+3=0,所以圆心到 直线的距离为 d=|2×34-+41+3|= 5,所以弦长为 2 r2-d2 =2× 25-5=4 5.
2.[变条件]若将本例中条件“与直线 y=x+2 平行”换为“过 点 P(5,1)”其他条件不变,结论又如何呢?
解:设所求切线方程为 y-1=k(x-5), 即 kx-y-5k+1=0. 由|2k-3k-2+5k1+1|=2 2.得 k=-6±2 10. 故所求切线方程为(-6+2 10)x-y+31-10 10=0 或(-6 -2 10)x-y+31+10 10=0.
[课堂思维激活] 一、综合性——强调融会贯通 1.已知圆 C:(x-3)2+(y-4)2=4 和直线 l:kx-y-4k+3=0,
(1)求证:不论 k 取何值,直线和圆总相交; (2)求当 k 取何值时,圆被直线 l 截得弦最短,并求最短弦长 的值.
题型一 直线与圆位置关系的判断 [学透用活]
[典例 1] 求实数 m 的取值范围,使直线 x-my+3=0 与圆 x2+y2-6x+5=0 分别满足:
(1)相交;(2)相切;(3)相离.
[解] 圆的方程化为标准形式为(x-3)2+y2=4,
故圆心(3,0)到直线 x-my+3=0 的距离为 d= m62+1,圆
)
A.0 或 2
B.2
C. 2
D.无解
解析:由圆心(0,0)到直线
x+y+m=0
的距离为半径得|m|= 2
m,解得 m=2.
答案:B
4.直线 y=2x+3 被圆 x2+y2-6x-8y=0 所截得方 程 可 化 为 (x - 3)2 + (y - 4)2 = 25. 故 圆 心 为 (3,4),半径 r=5.又直线方程为 2x-y+3=0,所以圆心到 直线的距离为 d=|2×34-+41+3|= 5,所以弦长为 2 r2-d2 =2× 25-5=4 5.
2.[变条件]若将本例中条件“与直线 y=x+2 平行”换为“过 点 P(5,1)”其他条件不变,结论又如何呢?
解:设所求切线方程为 y-1=k(x-5), 即 kx-y-5k+1=0. 由|2k-3k-2+5k1+1|=2 2.得 k=-6±2 10. 故所求切线方程为(-6+2 10)x-y+31-10 10=0 或(-6 -2 10)x-y+31+10 10=0.
[课堂思维激活] 一、综合性——强调融会贯通 1.已知圆 C:(x-3)2+(y-4)2=4 和直线 l:kx-y-4k+3=0,
(1)求证:不论 k 取何值,直线和圆总相交; (2)求当 k 取何值时,圆被直线 l 截得弦最短,并求最短弦长 的值.
直线与圆的位置关系课件(第一课时)(浙教版)
应用:海中有一个小岛P,该岛四周12海里范 围内是一暗礁区.今有货轮自西向东航行,开 始在A点观测P在北偏东600方向, 行驶10海 里后到达B点观测P在北偏东450方向,若货轮 不改变方向继续向东航行.
P
60°
A
45°
B
例题1:已知点P是∠ABC的平分线上的 一点,⊙P与BC相切。求证:⊙P与AB 相切。
并视察发现d与r的不同数量关系对应相应的直 线与圆的位置关系。
把半径r与圆心与直线的距离d作比较,可以判断 直线与圆的位置关系!
直线与圆的位置关系:
r ●O ┐d
相交
• 直线和圆相交 直线和圆相切 直线和圆相离
r ●O
d ┐ 相切
r ●O d ┐ 相离
d < r; d = r; d > r;
(1)课内练习的第1、2题; (2)A组的第3题、第1题。
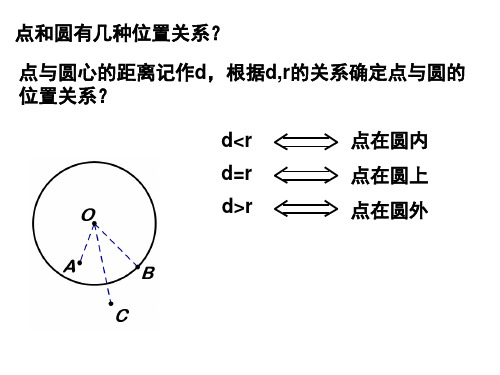
点和圆有几种位置关系?
点与圆心的距离记作d,根据d,r的关系确定点与圆的 位置关系?
d<r
点在圆内
d=r
点在圆上
d>r
点在圆外
千岛湖建兰中学
长大 河漠 落孤 日烟 圆直
天海 涯上 共升 此 时
直线与圆有几种位置关系?
想一想、画一画后填空: 1、过⊙O内一点P作直线l,则直线l与⊙O 的位置关系是 __相__交__ 2、过⊙O外一点P作直线l,则直线l与⊙O 的位置关系是_相__交__、__相__切__或_ 相离 3、过⊙O上一点P作直线l,则直线l与⊙O 的位置关系是 __相__切__或__相__交
4、过⊙O外两点A、B作直线l,则直线l与
⊙O的位置关系是_相__交__、__相_切__或_ 相离
如图,O为直线L外一点,OT⊥L,且OT=d.请以 O为圆心,以任意长为半径画圆.所画的圆与直 线L有什么位置关系?
直线与圆的位置关系 课件

答:支柱A2P2的高度为3.86m.
例5.已知内接于圆的四边形的对角线互相垂直,
求证:圆心到一边的距离等于这条边所对边长的一半.
y
证明:
B
以四边形ABCD互相垂直的对角线
CA、DB所在直线分别为x轴、y轴, C O M
A
建立直角坐标系.
N O′
x
设A(a,0),B(0,b),C(c,0),D(0,d).
E
过四边形ABCD的外接圆的圆心O’分别
D
作AC、BD、AD的垂线,垂足分别为M、N、E,
则M、N、E分别是线段AC、BD、AD的中点.
由线段的中点的坐标公式,得
xo ' xM ac , 2
y y
O'
N
bd , 2
a
d
x ,y E 2E 2所以 |源自O ' E |a 2
c 2
a 2
2
10
所以,直线 l 与圆相交,有两个公共点.
C
A
O
x
由 x2 3x 2 0,解得:x1 2, x2 1
把 x1 2,代x2入方1程①,得 y1 0 ; 2把, x2 1 代入方程① ,得 y2 3 .
直线 l 与圆有两个交点,它们的坐标分别是:A(2,0),B(1,3)
小结:直线与圆的位置关系的判定方法
E 2
D2 E2 4F r
2
问题引入:
一艘轮船在沿直线返回 港口的途中,接到气象台 的台风预报:台风中心位 于轮船正西70km处,受影 响的范围是半径长为30km 的圆形区域。已知港口位 于台风中心正北40km处, 如果这艘轮船不改变航线, 那么它是否会受到台风的 影响?
为解决这个问题,我们以台风中心为原点O,东西方向为x轴,建
例5.已知内接于圆的四边形的对角线互相垂直,
求证:圆心到一边的距离等于这条边所对边长的一半.
y
证明:
B
以四边形ABCD互相垂直的对角线
CA、DB所在直线分别为x轴、y轴, C O M
A
建立直角坐标系.
N O′
x
设A(a,0),B(0,b),C(c,0),D(0,d).
E
过四边形ABCD的外接圆的圆心O’分别
D
作AC、BD、AD的垂线,垂足分别为M、N、E,
则M、N、E分别是线段AC、BD、AD的中点.
由线段的中点的坐标公式,得
xo ' xM ac , 2
y y
O'
N
bd , 2
a
d
x ,y E 2E 2所以 |源自O ' E |a 2
c 2
a 2
2
10
所以,直线 l 与圆相交,有两个公共点.
C
A
O
x
由 x2 3x 2 0,解得:x1 2, x2 1
把 x1 2,代x2入方1程①,得 y1 0 ; 2把, x2 1 代入方程① ,得 y2 3 .
直线 l 与圆有两个交点,它们的坐标分别是:A(2,0),B(1,3)
小结:直线与圆的位置关系的判定方法
E 2
D2 E2 4F r
2
问题引入:
一艘轮船在沿直线返回 港口的途中,接到气象台 的台风预报:台风中心位 于轮船正西70km处,受影 响的范围是半径长为30km 的圆形区域。已知港口位 于台风中心正北40km处, 如果这艘轮船不改变航线, 那么它是否会受到台风的 影响?
为解决这个问题,我们以台风中心为原点O,东西方向为x轴,建
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
∴CD=
AC • BC AB
⋅
3× 4 = =2.4cm 5
即圆心C到AB的距离d=2.4cm
(1)当r=2cm时, d>r 因此⊙C和AB相离 (2)当r=2.4cm时,d=r 因此⊙C和AB相切 (3)当r=3cm时, d<r 因此⊙C和AB相交
风淋室 空 调过滤器
刘雯改
一、复习提问
1、点和圆的位置关系有几种? 、点和圆的位置关系有几种?
(1)d<r ) (2)d=r ) (3)d>r ) 点在圆内 点在圆上 点 在圆外
2、“大漠孤烟直,长河落日圆” 是唐朝诗人王 、 大漠孤烟直,长河落日圆” 维的诗句, 维的诗句,它描述了黄昏日落时分塞外特有的景 如果我们把太阳看成一个圆, 象。如果我们把太阳看成一个圆,地平线看成一 条直线,那你能根据直线与圆的公共点的个数想象 条直线 那你能根据直线与圆的公共点的个数想象 一下,直线和圆的位置关系有几种? 一下,直线和圆的位置关系有几种? 风淋室 空
N
P M
A
Q
风淋室 空 调过滤器
四、课堂小结:
直线和圆的三种位置关系 直线与圆的位置关系 公共点个数 公共点名称 直线名称 数量关系 相交 相切 相离
2
交点 割线
1
切点 切线
0
无 无
d<r
d=r
d>r
风淋室 空 调过滤器
r o d l d>r d=r d<r
r o d
l
风淋室 空 调过滤器
三、练习与例题 1、已知圆的直径为13cm,设直线和圆心的距离为d : 已知圆的直径为13cm,设直线和圆心的距离为d 13cm 2 直线与圆有____个公共点. ____个公共点 1)若 ,则直线与圆 1)若d=4.5cm ,则直线与圆 相交 , 直线与圆有____个公共点. 1 相切 2)若 ,则直线与圆______, 直线与圆有____个公共点. 则直线与圆______ ____个公共点 2)若d=6.5cm ,则直线与圆______ 直线与圆有____个公共点. 0 相离 3)若 ,则直线与圆______, 直线与圆有____个公共点. 则直线与圆______ ____个公共点 3)若d= 8 cm ,则直线与圆______ 直线与圆有____个公共点. 2、已知⊙O的半径为 2、已知⊙O的半径为5cm, 圆心O与直线AB的距离为d, 根据 的半径为5cm, 圆心O与直线 的距离为d, 与直线AB的距离为 条件填写d的范围 的范围: 条件填写 的范围 1)若AB和⊙O相离 则 若 和 相离, 相离
风淋室 空 调过滤器
净化设备 空气过滤器 高效过滤器 KLC超净工作台 KLC传递窗 KLC洁净棚 高效空气过滤器 风淋室 广州金田瑞麟净化设备制造有限公司
(第一课时)
市二中
风淋室 空 调过滤器
A
45°
30°
B
D
风淋室 空 调过滤器
C
思考:如图,公路MN和PQ在P处交汇, 且∠QPN=300 , 点A处 思考:如图, 公路MN和PQ在 处交汇, QPN=30 MN 有一所中学, AP=160 160米 假设拖拉机行使时, 周围100 100米 有一所中学 , AP=160 米 , 假设拖拉机行使时 , 周围 100 米 以内会受到噪音的影响, 已知拖拉机的速度为18千米/ 18千米 以内会受到噪音的影响, 已知拖拉机的速度为18千米/时, 那么学校会受到影响吗? 如果会, 受到影响的时间多长? 那么学校会受到影响吗? 如果会, 受到影响的时间多长?
30° 30°
A
2.5
5
B M
风淋室 空 调过滤器
是一个半径为300m的圆形森林公园的中心, 的圆形森林公园的中心, 例2:如图,点A是一个半径为 :如图, 是一个半径为 的圆形森林公园的中心 在森林公园附近有B, 两村庄 现要在B, 两村庄之间修 两村庄, 在森林公园附近有 ,C两村庄,现要在 ,C两村庄之间修 一条长为1000m的笔直公路将两村连通 现测得∠ABC=45°, 的笔直公路将两村连通, 一条长为 的笔直公路将两村连通 现测得∠ABC=45° 30° 问此公路是否会穿过该森林公园? ∠ACB= 30°.问此公路是否会穿过该森林公园?请通过计 算进行说明. 算进行说明.
B B B D C AD C A CFra bibliotekD A
风淋室 空 调过滤器
解:过C作CD⊥AB,垂足为D, 在Rt△ABC中 AB= AC + BC = 32 + 42 = 5
2 2
1 1 Q S = AC • BC = CD • AB 2 2
练习: 30°,M为OB上一点 上一点, OM=5cm,若以M 3、如图,已知∠AOB= 30°,M为OB上一点,且OM=5cm,若以M 如图,已知∠ 为圆心,r为半径作圆,那么: 为圆心,r为半径作圆,那么: ,r为半径作圆 1)当直线AB与 当直线AB 相离时, 的取值范围是______________; 1)当直线AB与⊙M相离时, r的取值范围是______________; 相离时 r的取值范围是 0cm < r < 2.5cm r = 2.5cm 2)当直线AB与 相切时, 的取值范围是______________; 2)当直线AB与⊙M相切时, r的取值范围是______________; 当直线AB 相切时 r的取值范围是 3)当直线AB与⊙M有公共点时, r的取值范围是___________. 有公共点时, 的取值范围是___________. 3)当直线AB与 当直线AB 有公共点时 r的取值范围是 r≥2.5cm C O
风淋室 空 调过滤器
2、用圆心到直线的距离和圆半径的数量关系,来 圆心到直线的距离和圆半径的数量关系, 圆心到直线的距离和圆半径的数量关系 揭示圆和直线的位置关系。 揭示圆和直线的位置关系。
r o d l (1)直线 和⊙O相离 )直线l 相离 (2)直线 和⊙O相切 )直线l 相切 (3)直线 和⊙O相交 )直线l 相交
调过滤器
二、新授讲解 1、直线与圆相离、相切、相交的定义。 、直线与圆相离、相切、相交的定义。
切点 切线
交点
交点 割线
相离
相切
相交
直线和圆的位置关系是用直线和圆的公共点的个数来 定义的,即直线与圆没有公共点、只有一个公共点 一个公共点、 定义的,即直线与圆没有公共点、只有一个公共点、有两 个公共点时分别叫做直线和圆相离、相切、相交。 个公共点时分别叫做直线和圆相离、相切、相交。 思考:一条直线和一个圆,如果有公共点能不能多于两个呢? 思考:一条直线和一个圆,如果有公共点能不能多于两个呢?
d > 5cm
; ;
2)若AB和⊙O相切 则 d = 5cm 若 和 相切, 相切
3)若AB和⊙O相交 则 0cm≤ d < 5cm. 若 和 相交,则 相交
风淋室 空 调过滤器
90° AC=3cm,BC=4cm, 为圆心, 例1:在Rt△ABC中∠C= 90°,AC=3cm,BC=4cm,以C为圆心, 1:在 r为半径的圆与AB有怎样的关系?为什么? 为半径的圆与AB有怎样的关系? AB有怎样的关系 (1) r=2cm (2) r=2.4cm (3) r=3cm
