高数第九章习题答案

合集下载

第九章习题答案高数下

作业 9—1一.填空:1.已知D 是长方形域：,10;≤≤≤≤y b x a 且⎰⎰=Dd x yf 1)(σ，则⋅=b adx x f )(2 .解：⎰⎰=Dd x yf σ)(⎰⎰⋅=baydy dx x f 1)(21⎰⋅badx x f )( 故⎰⋅=badx x f )( 22.若D 是由1=+y x 和两个坐标轴围成的三角形域,且⎰⎰⎰⋅=Ddx x dxdy x f 1)()(ϕ,那么.=)(x ϕ)()1(x f x -解：⎰⎰=Ddxdy x f )(⎰⎰-⋅=xdy x f xdx 1010)(⎰⋅-10)()1(dx x f x ⎰⋅=1)(dx x ϕ二、单项选择题：1．设1D 是正方形域，2D 是1D 的内切圆，3D 是1D 的外接圆，1D 的中心在（-1，1）处，记1I =⎰⎰---12222D xy x y dxdy e;2I =⎰⎰---22222D xy x y dxdy e;3I =⎰⎰---32222D xy x y dxdy e.则1I ，2I ，3I 大小顺序为（ B ）。

A ．1I ≤2I ≤3I B.2I ≤1I ≤3I C. 3I ≤2I ≤1I D. 3I ≤1I ≤2I解：因为三个被积函数一样，均为正值，213D D D ⊃⊃，故2I ≤1I ≤3I 2. 设D 是第二象限的一个有界闭区域,且10<<y ，记1I =⎰⎰Dd yx σ3;2I =⎰⎰Dd x y σ32;3I =⎰⎰Dd x y σ321.1I ,2I ,3I 的大小顺序是( )。

A ．1I ≤2I ≤3I B.2I ≤1I ≤3I C. 3I ≤1I ≤2I D. 3I ≤2I ≤1I 解：因10<<y ，故212y y y <<，而03<x ，从而323321x y yx x y <<，选（C ）。

三．利用二重积分定义证明： 1．σσ=⎰⎰Dd （其中σ为D 的面积）解：ini iiDf d σηξσλ∑⎰⎰=→∆=⋅10),(lim 1i ni σλ∑=→∆⋅=11limσσσλλ==∆=→=→∑01lim limini故 σσ=⎰⎰Dd （其中λ是各iσ∆的最大直径）2．k d y x kf D=⎰⎰σ),(⎰⎰Dd y x f σ),( （其中k 为常数）解：=⎰⎰Dd y x kf σ),( ini iif σηξλ∑=→∆1),(lim i ni i i f k σηξλ∑=→∆=1),(limi ni i i f k σηξλ∑=→∆=1),(lim ⎰⎰=Dd y x f k σ),( （k 为常数）四．利用二重积分的性质估计下列积分的值： 1．}10,10|),{(,)(⎰⎰≤≤≤≤=+=Dy x y x d y x xy I 其中Ｄσ解： 10,10≤≤≤≤y x∴2)(0≤+≤y x xy∴⎰⎰⎰⎰≤≤+≤DDd d y x xy 22)(0σσ2．}4|),{(,)49(22⎰⎰≤+=++=Dy x d y x I ２２ｙｘ其中Ｄσ 解：中在D ,422ππσ=⋅=,()22222249499yx y x y x ++≤++≤++2549922≤++≤y x∴ σσσ25)49(922≤++≤⎰⎰⎰⎰DDd y x d即 ππ10036≤≤I五．根据二重积分的性质比较下列积分的大小： 1．⎰⎰⎰⎰++DDd y x d y x σσ32)()(与其中积分区域D 是由圆周2)1()2(22=-+-y x 所围成。

华南理工大学高数答案第9章

第九章曲线积分与曲面积分作业13 对弧长的曲线积分1．计算d Lx s ⎰，其中L 为直线y x =及抛物线2y x =所围成的区域的整个边界．解：L 可以分解为[]1:,1,0,1L y x y x '==∈及[]22:,2,0,1L y x y x x '==∈1211d d d LL L x s x s x s x x x x =+=+⎰⎰⎰⎰⎰()()113222001121d 1414883212x x x x =++=+⋅+=+2．4433d L x y s ⎛⎫+ ⎪⎝⎭⎰，其中L 为星形线33cos ,sin x a t y a t = =在第一象限内的弧π02t ⎛⎫≤≤ ⎪⎝⎭．解：L 为33cos ,sin ,0,,2x a t y a t t π⎡⎤= =∈⎢⎥⎣⎦223cos sin ,3sin cos ,3sin cos dx dya t t a t t ds a t tdt dt dt=-== 原式()4722442233031cossin 3sin cos 1sin 2sin 222a t t a t tdt a t tdt ππ⎛⎫=+⋅=- ⎪⎝⎭⎰⎰()7772223333003311cos 2cos 2cos 2cos 2883a t d t a t t a ππ⎛⎫=-+=-+= ⎪⎝⎭⎰ 3．计算d xyz s Γ⎰，其中Γ折线ABC ，这里A ，B ，C 依次为点)3,4,1(),3,2,1(),0,0,0(．解：[]:,,2,3,0,1,123x y zAB x t y t z t t ds =====∈= []:1,3,,2,4,BC x z y t t ds dt ===∈=[]:,,4,3,0,1,143x y zCA x t y t z t t ds =====∈=142d d d 231318ABBCxyz s xyz s xyz s t t t t dt Γ=+=⋅⋅+⋅⋅=⎰⎰⎰⎰⎰4．()22d xy z s Γ+⎰，其中Γ为螺线cos ,sin ,x t t y t t z t = ==上相应于t 从0变到1的一段弧．解：Γ为[]cos ,sin ,,0,1,x t t y t t z t t ds = ==∈=()()112222201d (222x y z s t t t t Γ+=⋅=+-+⎰⎰⎰ ()()1532222122222253t t ⎡⎤=+-⋅+==⎢⎥⎣⎦5．计算22d Lx y s +⎰，其中L ：0,22>=+a ax y x ．解：将L 参数化，22cos ,sin cos ,cos ,cos ,x r t y r t r ar t r a t x a t ==⇒===cos sin ,,,sin 2,cos 2,22y a t t t dx a tdt dy a tdt ds adt ππ⎡⎤=∈-=-==⎢⎥⎣⎦222222222d 2cos 2sin 2Lx y s a tdt a ta ππππ-+====⎰⎰⎰6．计算22ed x y Ls +⎰，其中L 为圆周222a y x =+，直线x y =及x 轴在第一象限内所围成的扇形的整个边界．解：边界曲线需要分段表达，从而需要分段积分[]12:0,0,,;:sin,cos ,0,,;4L y x a ds dx L x a t y a t t ds adt π⎡⎤=∈===∈=⎢⎥⎣⎦2123:,,;L y xx ds L L LL ⎡=∈==++⎢⎣⎦从而22400ed 4aax yxax aLa s e dx e adt e e ππ+=+⋅+=++⎰⎰⎰112244a a a a aa a e e e e e ππ=-++-=+-作业14 对坐标的曲线积分1．计算下列第二型曲线积分：(1) ()()d d L x y x x y y ++-⎰，其中L 为按逆时针方向绕椭圆22221x y a b+=一周；解：L 为cos ,sin ,:02x a t y b t t π==→原式()()20sin cos sin cos cos sin a t a t b t b t a t b t dt π=-++-⎡⎤⎣⎦⎰ 22222200sin 2cos 2sin 2cos 20224a b ab t a b ab t t dt t ππ⎛⎫⎛⎫++=-=+= ⎪ ⎪⎝⎭⎝⎭⎰(2)()d d 1d x x y y x y z Γ+++-⎰，其中Γ是从点()1,1,1到点()2,3,4的一段直线；解：Γ是111,1,12,13,:01213141x y z x t y t z t t ---===+=+=+→--- 原式()()()1121231121t t t t dt =+++++++-⎡⎤⎣⎦⎰()()1126146713t dt t t=+=+=⎰(3)d d d y x x y z Γ-+⎰，其中Γ是圆柱螺线2cos ,2sin , 3 x t y t z t ===从0t =到2πt =的一段弧；解：Γ是2cos ,2sin , 3 ,:02x t y t z t t π===→原式()()202sin 2sin 2cos 2cos 3t t t t dt π=--+⎡⎤⎣⎦⎰ ()()2200432dt t πππ=-+=-=-⎰(4) 计算曲线积分(12e )d (cos e )d y y Lxy x y x y +--⎰,其中L 为由点A (-1, 1)沿抛物线2y x =到点O (0, 0), 再沿x 轴到点B (2, 0)的弧段．解：由于积分曲线是分段表达的，需要分段积分2:,:10AO y x x =-→；:0,:02OB y x =→原式222221(12e )d (cos e )2dx (e )d x x xx x x x x x -=+--+⎰⎰2223221(12e 2cos 2e )d d x x x x x x x x -=+-++⎰⎰()222004211113sin e d de 21sin1sin11xx x x xx x xee ----=-+++=-++=+-⎰⎰2．设力F 的大小等于作用点的横坐标的平方，而方向依y 轴的负方向，求质量为m 的质点沿抛物线21x y -=从点()1,0移动到点()0,1时，力F 所作的功．解：{}{}{}2220,10,,,,:1,:01F x x ds dx dy L x y y =-=-==-→()()11352240028123515L L y y W Fds x dy y y dy y ⎛⎫==-=--+=--+=- ⎪⎝⎭⎰⎰⎰3．把对坐标的曲线积分()(),d ,d LP x y x Q x y y +⎰化成对弧长的曲线积分，其中L为：(1) 在xOy 平面内沿直线从点()0,0到点()1,1； (2) 沿抛物线2y x =从点()0,0到点()1,1．解：（1）:,:01,0;L y x x dx ds =→>==()()()(),,,d ,d ,,d L L P x x Q x x P x y x Q x y y P x x Q x x x +⎡⎤+=+=⎡⎤⎣⎦⎰⎰⎰（2）2:,:01,0;L y x x dx ds =→>=()()()()22,2,,d ,d ,2,d L L P x x xQ x x P x y x Q x y y P x x xQ x x x +⎡⎤⎡⎤+=+=⎣⎦⎰⎰⎰作业15 格林公式及其应用1．填空题(1) 设L 是三顶点(0, 0), (3, 0), (3, 2)的三角形正向边界,(24)d (536)d Lx y x y x y -+++-=⎰12 ．(2) 设曲线L 是以)1,0(),0,1(),1,0(),0,1(--D C B A 为顶点的正方形边界，d d L x yx y ++⎰不能直接用格林公式的理由是_所围区域内部有不可导的点_．（3）相应于曲线积分(,,)d (,,)d (,,)d LP x y z x Q x y z y R x y z z++⎰的第一型的曲线积分是⎰．其中L 为从点(1, 1 ,1)到点(1, 2, 3)的直线段． 2．计算33(e sin )d (ecos )d x xLI y y x y x y =-++⎰,其中L 是沿半圆周x =从点),0(a A -到点),0(a B 的弧．解：L 加上:0,:BA x x a a =→-构成区域边界的负向()3322(e sin )d (e cos )d 3cos axxLDaI y y x y x y x y d ydy σ-=-++=-+-⎰⎰⎰⎰34230233cos 2sin 4a aaa d r dr ydy a πππθ-=-+=-+⎰⎰⎰v3．计算e 31d e 33d xy xy Ly x y x x x y y ⎡⎤⎡⎤+-+++-+⎣⎦⎣⎦⎰,其中L 为椭圆 22221x y a b+=正向一周．解：原式()()e 33e 31xy xyD x x y y x y dxdy x y ⎡⎤∂∂=+-+-+-+⎢⎥∂∂⎣⎦⎰⎰ 44Ddxdy ab π==⎰⎰4．计算曲线积分[]()sin d ()cos πd ,LI f x y x f x y x y '=+-⎰其中)(x f '为连续函数，L 是沿圆周222(1)(π)1πx y -+-=+按逆时针方向由点(2,2π)A 到点)0,0(O 的一段弧．解：令1:,:02L y x x π=→ 则，原式()[]111π()sin d ()cos πd L L L L DI dxdy f x y x f x y x y +'=-=--+-⎰⎰⎰⎰⎰()222π1()sin ()cos ππd 2f x x f x x x x ππππ'⎡⎤=-⋅+-+-⎣⎦⎰ ()()222422223π1()sin ππ1222222x f x x ππππππππ⎡⎤=-⋅+--=-⋅++=-⎢⎥⎣⎦5．计算22d d L x y y xx y -+⎰,其中L 为（1）圆周()()22111x y -+-=（按反时针方向）；解：()()222222222222222x x y x x y x y x x y y x y x y x y ⎛⎫⎛⎫∂+-⋅-∂-=== ⎪ ⎪∂+∂+⎝⎭⎝⎭++，而且原点不在该圆域内部，从而由格林公式，原式0= （2）闭曲线1x y +=（按反时针方向）．解：()()222222222222222x x y x x y x y x x y y x y x y x y ⎛⎫⎛⎫∂+-⋅-∂-=== ⎪ ⎪∂+∂+⎝⎭⎝⎭++，但所围区域内部的原点且仅有该点不满足格林公式条件，从而可作一很小的圆周220.01x y +=（1L 也按反时针方向），在圆环域上用格林公式得，原式()1122d d d d 1001120.01L L Dx y y xx y y xdxdy x y π--===+=+⎰⎰⎰⎰ 6．证明下列曲线积分在xOy 平面内与路径无关,并计算积分值：（1）()()(),0,0e cos d sin d a b x y x y y -⎰；解：由于()()e sin e sin e cos x xx y y y x y∂∂-=-=∂∂在全平面连续，从而该曲线积分在xOy 平面内与路径无关，沿折线()()()0,00,,b a b →→积分即可，原式()()0sin e cos d cos 11cos cos 1bax a ay dy b x b e b e b =-+=-+-=-⎰⎰ （2）()()()()2,14231,023d 4d xy yx x xy y -++-⎰；解：由于()()233442423x xy x y xy y x y∂∂-=-=-+∂∂在全平面连续，从而该曲线积分在xOy 平面内与路径无关，沿直线10,1,:122110x y y x x --==-→--积分也可，原式=()()()24321211341d x x x x x x x ⎡⎤---++--⎣⎦⎰()()243213235141d x x x x x ⎡⎤=-+----⎣⎦⎰()()2543213115x x x x x ⎡⎤=-+----=⎣⎦ （3）()()()()π,20,0ecos d e sin d yy x m x x my y -+-⎰．解：由于()()e sin e cos e cos y y y x my x x m x y∂∂-==-∂∂在全平面连续，从而该曲线积分在xOy 平面内与路径无关，沿折线()()()0,0,0,2ππ→→积分即可，原式()()20cos e sin d y ex m dx my y ππ=-+-⎰⎰()2200sin 2my x mx π⎛⎫=-+- ⎪⎝⎭2m m π=--7．设()f x 在(),-∞+∞上具有连续导数，计算()()2221d 1d L y f xy x x y f xy y y y +⎡⎤+-⎣⎦⎰，其中L 为从点23,3⎛⎫ ⎪⎝⎭到点()1,2的直线段．解：由于()()()()2222111y f xy x y f xy f xy xyf xy x y y y y ⎡⎤+⎧⎫∂∂'⎡⎤-=+-=⎨⎬⎢⎥⎣⎦∂∂⎩⎭⎣⎦在右半平面连续，从而该曲线积分右半平面内与路径无关，沿曲线12:2,,:31L xy y x x==→积分即可，原式()()()()2122232421122d d 22x f f x x x x x x x⎡⎤-+⎢⎥-⎣⎦+⎰13xdx =⎰1232x ⎛⎫= ⎪⎝⎭1942-==- 8．验证下列()(),d ,d P x y x Q x y y +在整个xOy 平面内是某一函数的全微分,并求出它的一个原函数：（1）()()e e d e 1e d x y x yx y x x y ⎡⎤⎡⎤+-+-+⎣⎦⎣⎦；解：由于()()e 1e e e x y x yx y x e e x y x y∂∂⎡⎤⎡⎤-+=-=+-⎣⎦⎣⎦∂∂在全平面连续，从而该曲线积分在xOy 平面内是某一函数的全微分，设这个函数为(),u x y ，则()(),e 1e ,e e x y x y u u u u du dx dy x x y x y y x∂∂∂∂=+=-+=+-∂∂∂∂ 从而()()()e 1e e 1e x y x yu x dy y x g x ⎡⎤=-+=-++⎣⎦⎰()()()e e e e =e x y x y x ux y y g x g x x x∂''=+-=-+⇒∂ ()=e x x x x x g x xd xe e dx xe e c =-=-+⎰⎰，()()1e 1e x y u x y x c =+--++（2）()()223238d 812e d yx y xy x x x y y y ++++；解：由于()()32222812e 31638y x x y y x xy x y xy x y∂∂++=+=+∂∂在全平面连续，从而该曲线积分在xOy 平面内是某一函数的全微分，设这个函数为(),u x y ，则原式3223224d 412e d yydx y x x dy x dy y y =++++()3322224d 412de yydx x dy y x x dy d y =++++⎰()()()32241212e d yyd yx d x y d ye y =++-⎰()32241212e y y d yxx y ye =++-可取32241212e yyu yx x y ye =++-（3）()()222cos cos d 2sin sin d x y y x x y x x y y ++-解：可取折线()()()0,0,0,x x y →→作曲线积分()()22202d 2sin sin d sin cos yx u x x y x x y y y x x y =+-=+⎰⎰9．设有一变力在坐标轴上的投影为2,28X x y Y xy =+=-,这变力确定了一个力场,证明质点在此场内移动时,场力所作的功与路径无关．证：{}2,28F x y xy =+-，质点在此场内任意曲线L 移动时，场力所作的功为()()228Lw x y dx xy dy =++-⎰由于()2282xy y x y x y∂∂⎡⎤-==+⎣⎦∂∂在全平面连续，从而质点在此场内移动时，场力所作的功与路径无关．作业16 对面积的曲面积分1．计算下列对面积的曲面积分： (1)()d xy yz zx S ∑++⎰⎰,其中∑为锥面z =被柱面222x y ax +=所截得的有限部分；解：∑为x y z z z ===dS ==，:02cos ,22D r a ππθθ≤≤-≤≤原式2cos 2302d d cos a Dzx S x y d r dr πθπθθ∑-==⎰⎰⎰⎰⎰⎰()()42242422cos cos 12sin sin sin 4a d d πππθθθθθθ--+=⎰⎰ （2）()222d xy z S ∑++⎰⎰,其中∑为球面2222x y z ax ++=．解：∑为两块y y x a x x =±==dS ==，:0,02D r a θπ≤≤≤≤原式12222d 2d Da a ax S ax S ∑∑+=+=⎰⎰⎰⎰22Da a +2334aDaad πθ=⎰223340=888a d a r aa a πππ--=-=2．计算d y S ∑⎰⎰，∑是平面4=++z y x 被圆柱面122=+y x截出的有限部分．解：∑为两块4,1,1x y z x y z z =--=-=-，dS =，:01,02D r θπ≤≤≤≤原式D=13220sin 03ar d r dr ππθθθ==⋅=⎰ （或由()(),,,,x y z x y z ∈∑⇒-∈∑，而积分微元反号推出）3．求球面2222a z y x =++含在圆柱面ax y x =+22内部的那部分面积．解：∑为两块x y z z z ===dS ==，:0,02D r a θπ≤≤≤≤原式12d 2DS dS ∑∑=+=⎰⎰⎰⎰cos 22=2a ad πθπθ-⎰⎰()()cos 222202=2sin 41242a ad a a a d a a ππθππθθθπ-⎛⎫-=-=- ⎪⎝⎭⎰⎰⎰4．设圆锥面z =()a h 为圆锥面的底面半径，为高,其质量均匀分布,求它的重心位置．解：设密度为单位1，由对称性可设重点坐标为()00,0,zDDzdS ∑==⎰⎰200ad r dr πθ==⎰⎰DDdS dxdy ∑==⎰⎰ad rdr πθπ==⎰⎰023h z ==，故重点坐标为20,0,3h ⎛⎫ ⎪⎝⎭5．求抛物面壳()2212z x y =+()01z ≤≤的质量，此壳的密度按规律z ρ=而变更．解：(2212Dm dS x y ρ∑==+=⎰⎰⎰⎰2012d r π=⎰()()22532200222(1112253515t t t πππ⎛⎫⎡⎤=+-=+-+=- ⎪⎢⎥ ⎪⎣⎦⎝⎭⎰作业17 对坐标的曲面积分1．d d d d d d z x y x y z y z x ∑++⎰⎰，其中∑是柱面221x y +=被平面0z =及3z =所截得的在第一卦限内的部分前侧．解：:01,03,cos 0,0yz y z x D y z x x α=≤≤≤≤>==原式=d d d d d d 0d d yzzxD D z x y x y z y z x y z z x ∑∑∑++=++⎰⎰⎰⎰⎰⎰⎰⎰13100032d 262yz D y z dy π====⎰2．计算曲面积分2()d d d d z x y z z x y ∑+-⎰⎰，其中∑为旋转抛物面221()2z x y =+下侧介于平面0z =及2z =之间的部分．解：22221(),,,:4;2x y xy z x y z x z y D x y =+==+≤:02,yz x D z y =≤≤≤原式=1122()d d ()d d d d zx y z z x y z z x y ∑∑∑+++-⎰⎰⎰⎰⎰⎰((22221d d d d ()d d 2yz yz zxD D D z y z z y z x y z x =-++⎰⎰⎰⎰⎰⎰22222300112d ()d d 222yzzx D D y z x y z x dz d r dr πθ=++=+⎰⎰⎰⎰⎰224232000222824z dz r dr z πππππ=+=+⋅=⎰⎰3．计算d d d d d d xy y z yz z x xz x y ∑++⎰⎰其中∑是平面1,0,0,0=++===z y x z y x 所围成的空间区域的整个边界曲面的外侧．解：分片积分。

高数答案(全集)第九章答案

第九章解答：1、（1）)271,91,31()1,1,1(----或；（2）321+；（3）→→+j i 362、（1）A （2）A3.解：方程两边对x 求导并移项得：⎪⎩⎪⎨⎧=--=+2532322dx dzdx dy x dx dz z dx dy y 由此可解得⎪⎪⎩⎪⎪⎨⎧+-+-=+---=z y y x dxdz z y z x dx dy 61094661015410169)1,1,1(=dx dy ，161)1,1,1(-=dx dz )161,169,1(-∴→＝Ｔ所求切线方程为：1191161--=-=-z y x 法平面方程为：0)1()1(9)1(16=---+-z y x 即024916=--+z y x 4. 将锥面方程变形为： )3(0)3(),,(222≥=---=z y x z z y x F在锥面上任取一点),,(000z y x ，则曲面在该点的法向量))3(2,2,2()),,(),,,(),,,((000000000000---==→z y x z y x F z y x F z y x F n z y x 所以该点的切平面方程为 0))(3()()(000000=----+-z z z y y y x x x将顶点坐标（0,0,3）代入上方程得0)3(202020=-+--z y x 所以过锥面上任一点),,(000z y x 处的切平面都过锥面的顶点（0,0,3）。

→→→→→→+-=-+-+-=-kj i ku j u i u gradu z y x 42)2,1,1()2,1,1()2,1,1()2,1,1(.5解：方向的方向导数最处沿向量在点函数→→→+--=∴k j i P z xy u 42)2,1,1(2211)4(2|)2,1,1(|22=+-+=-grad 其最大值为6.同37.)21,0(0)24(),(0)22(2),(:2222-⎪⎩⎪⎨⎧=+==+++=得唯一驻点解方程组解y e y x f e y y x e y x f xyx x xx yy x xy x xx e f y e f y y x e f 22224),12(4),122(4=+=+++=求二阶导数04,08042)21,0(2>=>=-⨯=--A B AC 又处，在点21)21,0()21,0(-=--∴f 处有极小值，极小值为函数在8. 解：此题为有条件极值问题，在椭圆上任取一点),,(z y x M 则 22222||zy x OM d ++==其中点M 受到两个限制条件：⎩⎨⎧=-++==--=01),,(0),,(2221z y x z y x y x z z y x ϕϕ 作拉格朗日函数 )1()(),,(2221222-+++--+++=z y x y x z z y x z y x L λλ令⎪⎪⎪⎩⎪⎪⎪⎨⎧=-++==--==++==+-==+-=)5(01)4(0)3(02)2(022)1(0222221212121z y x y x z z L y y L x x L z y x ϕϕλλλλλλ由)5()4(,)2()1(及代入知y x =-得： x z x z 21,22-==01222=-+∴x x 故 32,231 =±-==z y x 得两个驻点)32,231,231(±-±-。

高等数学(同济第七版)第九章课后答案

－．《高＂tt雪；＇）( ;r,乞履＞rm习IA全航44， ’ ’i，、、J·．，－一，rr－T令，，、－M－·．‘FEE－’‘．．．．l i··付守年，2－·’、fp····．，．．．、付’创刊令，－2、．四．，。

－H‘．，．JA、。

当”、句，‘－、，．-.----－号ri咱也k fi'l企：，i(r'J ;(,) f尔1’在.i!Iii i ra、2所l'..t全微分r.. l.主R F列的数的全做分：l I ) ：二X)... ...:.. ; (2):=··-:14)u＝‘.， .( 3): sτ兰＝＝：、f叶’.，.I·．·、－= .,ii: ”l' .‘Ez－－－虫”·飞”( I ) I晏为t;_＝（，－干）‘1曹寸、－于）r1r.ii·i i·dz =ι二，I x+ , _ •h，，店，问向f t:l曾il=,l: \－二－.....,..,.h’，：1 2 l I崎＇）.J...＋二二，I‘冉、,1: d‘。

‘1’fr l'..lt、，I‘．“i,)dε =－飞、··．．．．( l、牛＋‘.｝‘ii:_ -J '们飞！－+\1、厅可丁2( 3 > I叫11• , Iv飞＋，－－，－－咱自－－－，电·、，、句’‘‘. t I－－,l:,l 1、·＂l1．．t．．1．．．－F‘｛’. .,..,.,1: ·＝、·,1‘φ. • ,I,A‘.11．，MFa，．’｝iuyt吁《－Itl48 一、o，�舷学’｛第七版）"F筋习忍金’E8ε27.6 一二一一－二I.JO 号i S 2 127. 8 !:, · 12.钊JU 1: l校纷iaF I乎）：内政之佣的地（，j i克i:丁j宫。

高等数学(经济类)课后习题及答案第九章多元函数微分

习题9-1（A ）1．求下列各函数的表达式：（1）设函数22),(y x y x f -=，求(,)f y x --，),(x x f -．解：(,)f y x --22)()(x y -+-=22x y -=，0)(),(22=--=-x x x x f ．（2）设函数)1(3-+=x f y z ，已知1=y 时，x z =，求)(x f 及z 的表达式．解：由1=y 时，x z =，有)1(13-+=x f x ，即，所以1)1()(3-+=x x f ；而1)1(3-+=-+=x y x f y z ．（3）设函数y y x y x f +-=1)1(),(2，求),(xy y x f +．解：2222))(()()(/1)/1()(),(y x y x y x yx y x y x x y x y y x x y y x f -=-+=+-+=+-+=+．（4）设函数xy y x y x f =+-),(，求),(y x f 的表达式．解：（方法1）因为4)()(4)2(244),(222222y x y x y xy x y xy x xy y x y x f --+=+--++==+-，所以),(y x f 422x y -=．（方法2）令v y x u y x =+=-、，则22uv y v u x -=+=、，于是 422),()(22u v u v u v xy y x y x f v u f -=-+==+-=，，所以),(y x f 422x y -=．2．求下列各函数的定义域，并作定义域草图：（1）)ln(x y z -=；（2）221arcsin xy y z -+=；（3）221arcsin yx x x y z --+=；（4）41)16ln(2222-++--=y x y x z ．1]1)1[(1)1(333-+-=-=-x x x f解：（1）由0>-x y 且0≥x ，得定义域}0,),{(≥>=x x y y x D ．（2）由022>-x y 及1≤y ，有1≤<y x ，得定义域}1),{(≤<=y x y x D ．（3）由0100122>--≥≠≤y x x x xy、、、，有0122>≤<+x x y y x 、、，得定义域}0,,1),{(22≠≤<+=x x y y x y x D ．（4）由040162222≥-+>--y x y x 、，有16422<+≤y x ，或4222<+≤y x ，得定义域}42),{(22<+≤=y x y x D ．3．求下列极限：（1）(,)(1,1)2lim2x y x yx y →-+；（2）xxy a y x sin lim ),0(),(→；（3）22)0,0(),(1sinlim y x x y x +→；（4）2)1,0(),(2tan limxy xyy x →；（5）22(,)(1,1)sin()lim x y x y x y →--；（6）231lim )1,1(),(-+-→xy xy y x .解：（1）(,)(1,1)2121lim2213x y x y x y →--==-++．（2）(,)(0,)(,)(0,)sin limlim x y a x y a xy xya x x →→==．（3）因为221sinyx +有界，而0lim )0,0(),(=→x y x ，所以=+→22)0,0(),(1sinlim yx x y x 0．（4）2111211lim tan lim 212tan lim)1,0(),()1,0(),(2)1,0(),(=⨯⨯==→→→y xy xy xy xy y x y x y x ．（5）222222(,)(1,1)(,)(1,1)sin()()sin()limlim 21 2.x y x y x y x y x y x y x y →→-+-==⨯=-- （6）=++=-++-=-+-→→→)23(lim 1)23)(1(lim231lim)1,1(),()1,1(),()1,1(),(xy xy xy xy xy xy y x y x y x 4．4．证明下列极限不存在：（1）(,)(0,0)lim x y x yx y →-+；（2）242)0,0(),(lim y x y x y x +→．证明：（1）沿)1(-≠=k kx y 取极限，则k kkx x kx x y x y x x x kx y +-=+-=+-→→=11lim lim00，当k 取不同值时，该极限值不同，所以极限(,)(0,0)limx y x yx y →-+不存在．（2）沿0=y 取极限，00lim lim 024200==+→→=x x y y x yx ；沿2x y =取极限，212lim lim 44024202==+→→=x x y x y x x x x y ．由于2420242002lim lim y x y x y x y x x x y x y +≠+→=→=，所以极限242)0,0(),(lim y x yx y x +→不存在．习题9-1（B ）1．某厂家生产的一种产品在甲、乙两个市场销售，销售价格分别为y x 、（单位：元），两个市场的销售量21Q Q 、各自是销售价格的均匀递减函数，当售价为10元时，销售量分别为2400、850件，当售价为12元时，销售量分别为2000、700件．如果生产该产品的成本函数是(2012000+=C )21Q Q +，试用y x 、表示该厂生产此产品的利润L ．解：根据已知，设y a b Q x a b Q 222111-=-=、，由10=x 时，24001=Q ；12=x 时，20001=Q ，有⎩⎨⎧=-=-，，2000122400101111a b a b 得、2001=a44001=b ，于是x Q 20044001-=．由10=y 时，8502=Q ；12=y 时，7002=Q ，有⎩⎨⎧=-=-，，70012850102222a b a b 得、752=a16002=b ，于是y Q 7516002-=．两个市场销售该产品的收入为22217516002004400y y x x yQ xQ R -+-=+=，该产品的成本(2012000+=C y x Q Q 15003200040008800012000)21-+-+=+y x 15004000132000--=．根据利润等于收入减去成本，得)15004000132000(751600200440022y x y y x x L ----+-= 132000752003100840022---+=y x y x ．2．求下列极限：（1）y y x xy )11(lim ),2(),(++∞→；（2）22)0,0(),(1e lim 22yx y x y x +-+→；（3）4422),(),(lim y x y x y x ++∞∞→；（4）(,)lim x y →解：（1）==+=++∞→+∞→211),2(),(),2(),(e ])11[(lim )11(lim x xy y x y y x xyxy e ．（2）法1：令t y x =+22，则当)00()(，，→y x 时，+→0t ，所以 =-=+-+→+→t y x t t y x y x 1e lim 1e lim 022)0,0(),(221．法2：因为)00()(，，→y x 时，1e 22-+y x 与22y x +是等价无穷小，所以1lim 1e lim 2222)0,0(),(22)0,0(),(22=++=+-→+→y x y x y x y x y x y x ．（3）因为224424424422110yx y x y y x x y x y x +≤+++=++≤，而00lim ),(),(=∞∞→y x ， 0)11(lim 22),(),(=+∞∞→y x y x ，根据“夹逼准则”得0lim 4422),(),(=++∞∞→yx y x y x ．（4）令θρθρsin cos ==y x 、，则当)00()(，，→y x 时，0→ρ（其中θ在区间)20[π，内任意变化），所以==+<≤→→θθρπθρsin cos lim lim20022)0,0(),(yx xy y x 0．3．证明极限22222)0,0(),()(lim x y y x y x y x -+→不存在．证明：沿0=y 取极限，00lim )(lim 202222200==-+→→=x x y y x y x x x y ；沿x y =取极限，11lim )(lim 0222220==-+→→=x x x y x y y x y x ．因此，极限22222)0,0(),()(lim x y y x y x y x -+→不存在．4．讨论函数⎪⎩⎪⎨⎧=+≠++=0002)(222222y x y x yx xy y x f ，，，，在点），（00处的连续性．解：沿x y =取极限，由)00(11lim 2lim)(lim 0220，，f yx xyy x f x x x y x x y ≠==+=→→=→=，有 )00()(lim )0,0(),(，，f y x f y x ≠→，所以函数)(y x f ，在点），（00处不连续．习题9-2（A ）1. 求下列函数的偏导数：（1）2z xy =；（2）2cos sin()z xy x y =++；（3）z = （4）2ln(ln )z x y =+；（5）yz x=（0>x ）；（6）z = （7）22y x xyz +=；（8）arctanx yz x y+=-；（9）yx z u =；（10）zy x u )tan(22-=．解：（1）2z y x ∂=+∂2z xy y ∂=∂．（2）2sin cos cos()sin 2cos()zxy xy y x y y xy x y x∂=-⋅++=-++∂， 2sin cos cos()sin 2cos()zxy xy x x y x xy x y y∂=-⋅++=-++∂．（3）12z x x y ∂==∂+ 122z y x y ∂=⋅=∂+．（4）22122ln ln z x x x x y x y ∂=⋅=∂++，22111ln (ln )z y y x y y x y ∂=⋅=∂++．（5）x yxy xyx y xy x y xy x y xy y x z sin cos 21)(sin cos 2332+=-⋅-=∂∂， xyx y x yy x x x y xy x y xy x y z sin cos 211sin cos 2-=⋅-=∂∂．（6）)1(212)1(11xy xy yxy y xy x z --=--⋅--=∂∂，)1(212)1(11xy xy x xy x xy y z --=--⋅--=∂∂．（7）2/3223222222)(y x y y x y x x xy y x y xz+=++⋅-+=∂∂，由变量y x 、的对称性，得2/3223)(y x x y z +==∂∂．（8）222211()1()()1()z x y x y yx y x x y x yx y∂⋅--⋅+-==+∂-++-， ()22221()1()1()1()x y x y z xx y y x y x y x y⋅---⋅+∂==+∂-++-．（9）z z yy z z x u y x y x ln 11ln =⋅=∂∂，z z y x y x z z y u y xy x ln )(ln 22-=-⋅=∂∂， yyx y xz yxz y x z u --==∂∂1．（10）zy x x z x y x x u )(sec 22)(sec 222222-=⋅-=∂∂， z y x y z y y x y u )(sec 2)2()(sec 222222--=-⋅-=∂∂，222)tan(z y x z u --=∂∂． 2. 求曲线⎪⎩⎪⎨⎧=+++=1,2122x y x z 在点)3,1,1(M 处的切线与x 轴正向的夹角．解：z x ∂=∂，111112x x y y z x ====∂==∂，用α表示曲线⎪⎩⎪⎨⎧=+++=1,2122x y x z 在点)3,1,1(M 处的切线与y 轴正向的夹角，则21tan =α，所以432621arctan '≈=α． 3. 设xy x y x z xsec)1(e 2-++=，求)0,1(x z 及)0,1(y z ．解：因为1e )0(-+=x x z x ，，所以=11d (1,0)(e 1)(e 1)d xx x x x z x x-=+-=+=e 1+，因为e )1(+=y y z ，，所以1)e (d d)0,1(0=+==y y y yz ．4. 求下列函数的高阶导数：（1）设13323+--=xy xy y x z ，求22223223,,,,z z z z zy x x y x y x∂∂∂∂∂∂∂∂∂∂∂∂.解：xz ∂∂ ,33322y y y x --= y z ∂∂ ;9223x xy y x --=22x z ∂∂ ,62xy = 33xz ∂∂ ,62y = 22y z ∂∂ ;1823xy x -= y x z ∂∂∂2 ,19622--=y y x xy z ∂∂∂2 .19622--=y y x （2）设xy x z ln =，求22x z ∂∂，22y z ∂∂和23yx z ∂∂∂；解：1ln ln +=⋅+=∂∂xy xy y x xy x z ，yxxy x x y z =⋅=∂∂， x xy y x z 122==∂∂，222y x y z -=∂∂，y xy x y x z 12==∂∂∂，2231yy x z -=∂∂∂． 5. 验证：（1）设函数x yz u arctan =，证明0222222=∂∂+∂∂+∂∂zu y u x u ．证：因为2222)()/(1y x yzx y x y z x u +-=-⋅+=∂∂，22222)(y x xyz x u +=∂∂， 2221)/(1y x xzx x y z y u +=⋅+=∂∂，22222)(y x xyz y u +-=∂∂，x y z u arctan =∂∂，022=∂∂zu，所以，00)()(222222222222=++-+=∂∂+∂∂+∂∂y x xyzy x xyz z u y u x u ．（2）设y x z =)1,0(≠>x x ，求证z yzx x z y x 2ln 1=∂∂+∂∂.证明：=∂∂xz ,1-y yx =∂∂y z ,ln x x yy z x x z y x ∂∂+∂∂ln 1 x x xyx y x yy ln ln 11+=-y y x x += .2z =原结论成立．习题9-2（B ）1．设一种商品的需求量Q 是其价格1p 及某相关商品价格2p 的函数，如果该函数存在偏导数，称Q p p Q E 111∂∂-=为需求对价格1p 的弹性、Qp p Q E 222∂∂-=为需求对价格2p 的交叉弹性．如果某种数码相机的销售量Q 与其价格1p 及彩色喷墨打印机的价格2p 有关，为 222110250120p p p Q --+=，当501=p ，52=p 时，求需求对价格1p 的弹性、需求对价格2p 的交叉弹性．解：由211250p p Q -=∂∂，22210p p Q--=∂∂，有1111250Qp Q p p Q E =∂∂-=，Qp p Q p p Q E 222222210+=∂∂-=，当501=p ，52=p 时，50255050250120=--+=Q 需求对价格1p 的弹性：1.0250505015501121======Q p p p Qp E 、、，需求对价格2p 的交叉弹性：=+=====5052225502221210Q p p p Qp p E 、、2．2. 设22arcsiny x x z +=，求x z ∂∂，yz ∂∂.解： =∂∂xz '⎪⎪⎭⎫⎝⎛+⋅+-xy x x y x x 2222211322222)(||y x y y y x +⋅+=.||22y x y += =∂∂yz'⎪⎪⎭⎫⎝⎛+⋅+-yy x x y x x 2222211=y y x x 1sgn 22+-=. 3. 设函数⎪⎩⎪⎨⎧=≠-+=，，，，，x y x y y x yx y x f 0)(证明在)00(，点处),(y x f 的两个偏导数都不存在．证：因为极限x xf x f x x ∆=∆-∆→∆→∆1lim )00()0(lim00，，不存在，极限yf y f y ∆-∆→∆)00()0(lim0，，xx ∆-=→∆1lim0不存在，所以在)00(，点处),(y x f 的两个偏导数都不存在． 4. 设y x yx z -+=arctan ，求22x z ∂∂，22y z ∂∂和y x z ∂∂∂2．解：2222)()()()(11y x yy x y x y x y x y x xz+-=-+---++=∂∂，22222)(2y x xy x z +=∂∂， 2222)()()()(11y x xy x y x y x yx y x yz +=-++--++=∂∂，22222)(2y x xy y z +-=∂∂， 22222222222(2)()()z x y y y y x x y x y x y ∂+--=-=∂∂++．5. 设函数222ln z y x u ++=，证明2222222221z y x z u y u x u ++=∂∂+∂∂+∂∂．证明：将函数改写为)ln(21222z y x u ++=，则 222z y x xx u ++=∂∂，2222222222222222)()(2z y x x z y z y x x x z y x x u ++-+=++⋅-++=∂∂，由变量的对称性，有222222222)(z y x y z x y u ++-+=∂∂，222222222)(z y x z y x z u ++-+=∂∂，所以2222222222222222222)()()()(z y x z y x y z x x z y z u y u x u ++-++-++-+=∂∂+∂∂+∂∂ 22222222221)(zy x z y x z y x ++=++++=．习题9-3（A ）1．求下列函数的全微分：（1）1sin()z x y=+；（2）22z x y =+；（3）xyz e =；（4）yxz tanln =；（5）22y x z u +=；（6）ln(32)u x y z =-+.解：（1）因为1cos()z x x y ∂=+∂，221111cos()()cos()z x x y y y y y ∂=+⋅-=-+∂，所以2211111d cos()d cos()d cos()(d d )z x x x y x x y y y y y y=+-+=+⋅-．（2）因为2z xyx ∂=+∂，2z x y ∂=+∂22(dz xydx x dy =++．（3）因为x yx yx z e 2-=∂∂，x yxy z e 1=∂∂，所以 )d d (e 1d e 1d e d 22x y y x xy x x x y z x yx yx y-=+-=．（4）因为2122cot sec cs c z x x x x y y y y y ∂=⋅=∂，22222cot sec ()csc z x x x x x y y y y y y ∂=⋅-=-∂，所以)d d (2csc 2d 2csc 2d 2csc 2d 22y x x y y xyy y x y x x y x y z -⋅=-=（5）因为z xz x u y x ln 222+=∂∂，z yz y u y x ln 222+=∂∂，12222)(-++=∂∂y x z y x zu ，所以z z y x y z yz x z xz u y xy xy xd )(d ln 2d ln 2d 122222222-+++++⋅+⋅=]d )d d (ln 2[2222z zy x y y x x z zy x +++⋅=+．（6）因为132u x x y z ∂=∂-+，332u y x y z ∂-=∂-+，232u z x y z∂=∂-+，所以 d 3d 2d d 3d 2d d 32323232x y z x y zu x y z x y z x y z x y z--+=++=-+-+-+-+．2.求函数zxyu )(=在点)1,2,1(-处的全微分．解:).ln()( ,1)( ),()(121x y x y y u x x y z y u xy x y z x u z z z ⋅=∂∂⋅=∂∂-⋅=∂∂-- 在点)1,2,1(-处，分别有.2ln 21,41 ,21)1,2,1()1,2,1()1,2,1(=∂∂-=∂∂=∂∂---zuyu xu因此，我们有.2ln 21d 41 21dz y dx dz +-=3.求函数)41ln(22y x z -+=当1=x ，2=y 时的全微分．解因为22418y x x x z -+=∂∂，22412y x yy z -+-=∂∂，821=∂∂==y x xz ，421-=∂∂==y x yz ，所以y x z d 4d 8d )2,1(-=，4.求函数xy e z =在点()2,1处当2.0,1.0=∆=∆y x 时的全微分．解由于,2,,,212212e yz e xz xe y z ye x z y x y x xy xy =∂∂=∂∂=∂∂=∂∂====所以，当2.0,1.0=∆=∆y x 时，函数xye z =在点（2，1）处的全微分为.5.02.021.0222e e e dz =⋅+⋅=习题9-3（B ）1. 计算()2.021.04的近似值．解：设函数(,)yz f x y x ==．显然，要计算的值是函数在 1.04, 2.02x y ==时的函数值()1.04,2.02.f取1,2,0.04,0.02.x y x y ==∆=∆=因为 ,),(1-=y x yx y x f ,ln ),(x x y x f y y =(1,2)1,f =(1,2)2,x f =(1,2)0,y f =所以由公式得 2.02(1.04)120.0400.02 1.08≈+⨯+⨯=． 2．计算3397.102.1+的近似值．解：考虑函数33y x z +=，取03.002.02100-=∆=∆==y x y x 、、、，而33223yx x z x +='，33223yx y z y +='，3)21(=，z 、2/1)21(='，x z 、2)21(='，y z ，则)(97.102.10033y y x x z ∆+∆+=+，y y x z x y x z y x z y x ∆'+∆'+≈)()()(000000，，，95.206.001.03)03.0(202.05.03=-+=-⨯+⨯+=．3. 设函数⎪⎩⎪⎨⎧=+≠++=,0,0,0,),(2222222y x y x y x y x y x f 在点)0,0(O 点处讨论偏导数的存在性、偏导数的连续性以及函数),(y x f 的可微性．解：因为00lim )00()0(lim==∆-∆→∆→∆x x xf x f ，，，00lim )00()0(lim==∆-∆→∆→∆x y yf y f ，，，所以在)0,0(O 点处函数)(y x f ，的两个偏导数都存在，且0)10(0)00(==，、，y x f f ．再讨论可微性，函数在)0,0(O 处的全增量用z ∆表示，则222)()()()00()00(y x yx z y f x f z y x ∆+∆∆⋅∆=∆=∆-∆-∆，，，记22)()(y x ∆+∆=ρ，则2/3222)0,0(),(0])()[()(lim )00()00(limy x yx yf x f z y x y x ∆+∆∆∆=∆-∆-∆→∆∆→ρρ，，不存在（沿0=∆x 取极限，其值为0；沿x y ∆=∆取极限，其值为22/1），所以函数)(y x f ，在)0,0(O 点处不可微．进而得偏导（函）数在)0,0(O 点处不连续（若偏导（函）数在)0,0(O 点处连续，根据可微的充分条件，则函数在点)0,0(O 可微，与函数不可微矛盾）．习题9-4（A ）1.求下列函数的全导数：（1）设函数 32,sin ,t v t u ez vu ===-，求dtdz ；（2）设函数t uv z sin +=，而t e u =，t v cos =，求全导数dtdz ；（3）设函数y x z cos 2=而)(x y y =是x 的可微函数，求xzd d ．解：（1）dtdv v z dt du u z dt dz ∂∂+∂∂==)6(cos 3)2(cos 22sin 2223t t e t e t e t t v u vu -=⋅-+---. （2）tzdt dv v z dt du u z dt dz ∂∂+⋅∂∂+⋅∂∂=t t u ve t cos sin +-= t t e t e t t cos sin cos +-=.cos )sin (cos t t t e t+-= （3）=⋅-=∂∂+∂∂=xy y x y x x y y z x z x z d d sin cos 2d d d d 222cos sin ().x y x y y x '-⋅ 2.求下列函数的一阶偏导数：（1）设函数v uz e =，而y x u +=，y x v -=，求x z ∂∂和yz∂∂；（2）设函数122)(++=xy y x z ，求x z ∂∂和yz ∂∂．解：（1）1e 1e 12⋅-⋅=∂∂∂∂+∂∂∂∂=∂∂v uv uvu v x v v z x u u z x z =-=v uv u v e 2yx yx y x y -+--e )(22， 21e 1e (1)u uv vz z u z v u y u y v y vv ∂∂∂∂∂=+=⋅-⋅-∂∂∂∂∂2+e u v v u v ==22e ()x yx y x x y +--，（2）这是幂指函数求导，为方便求导，将它写作复合函数，为此令122+=+=xy v y x u 、，则vu z ==⋅+=∂∂∂∂+∂∂∂∂=∂∂-y u u x vu xv v z x u u z x z v v ln 21)]ln()1(2[)(2222122y x y y x xy x y x xy ++++++，=⋅+=∂∂∂∂+∂∂∂∂=∂∂-x u u y vu y v v z y u u z y z v v ln 21)]ln()1(2[)(2222122y x x yx xy y y x xy ++++++． 3. 求下列函数的一阶偏导数（其中函数f 具有一阶连续的偏导数或导数）：（1）(e )xyx z f y=，；（2）)(22y x xy f z -=，；（3）)(22y x xf z +=；（4）(,,)u f x xy xyz =．解：（1）121e xy z f f y x y ∂''=⋅+⋅=∂121e xyf y f y''+， 122()e xy z x f f x y y ∂''=⋅-+⋅=∂122e xy xf x f y''-+．（2）212122f x f y x f y f xz '+'=⋅'+⋅'=∂∂，21212)2(f y f x y f x f y z'-'=-⋅'+⋅'=∂∂．（3）=+⋅'+=∂∂2222yx xf x f x z f y x x f '++222，12y z xf y ⨯∂'==∂f yx xy '+22．（4）1231231uf f y f yz f yf yzf x∂''''''=⋅+⋅+⋅=++∂， 123230uf f x f xz xf xzf y∂'''''=⋅+⋅+⋅=+∂， 123300uf f f xy xyf z∂''''=⋅+⋅+⋅=∂． 4. 设函数)(22y x f y z -=，其中)(u f 是可微函数，证明211y zy z y x z x =∂∂+∂∂．证：因为)()(22)()(2222222222y x f y x f xy x y x f y x f y x z --'-=⋅--'-=∂∂， )()(2)(1)()2()()(222222222222222y x f y x f y y x f y x f y y x f y y x f y z --'+-=--⋅-'--=∂∂，所以222222222222112()12().()()()z z yf x y yf x y x x y y f x y yf x y f x y ''∂∂--+=-++∂∂---2222)(yzy x f y y =-=． 5.设函数)(x y xyf z =，其中)(u f 是可微函数，证明z yz y x z x2=∂∂+∂∂．证：因为)()()()()(22x yf x y x y yf xy x y f xy x y yf x z '-=-⋅'+=∂∂，)()(1)()(xyf y x y xf x x y f xy x y xf y z '+=⋅'+=∂∂，所以 z xy xyf x y f y x y xyf x y f y x y xyf y z y x z x2)(2)()()()(22=='++'-=∂∂+∂∂． 6.利用全微分形式的不变性求函数)cos(222z y x eu zy +++=+ 的全微分．解令=+=w z y v ,222z y x ++，由一阶全微分形式的不变性，我们有dw w dv e dw wudv v u du v )sin (-+=∂∂+∂∂=，注意到w v ,又都是z y x ,,的函数，并且,v vdv dy dz dy dz y z∂∂=+=+∂∂ 222.w w w dw dx dy dz xdx ydy zdz x y z∂∂∂=++=++∂∂∂ 将它们带入上式，得.)]sin(2[ )]sin(2[)sin(2 )(2)sin()( )sin (222222222222dz z y x z e dyz y x y edx z y x x zdz ydy xdx z y x dz dy e dww dv e du z y zy z y v ++-+++-+++-=++⋅++-+=-+=+++习题9-4（B ）1.求下列函数的二阶偏导数（其中函数f 具有二阶连续偏导数）：（1）),(y x xy f z +=；（2）)(22y x x f z +=，；解：（1）21f f y xz '+'=∂∂，21f f x y z'+'=∂∂，221211222211211222)()(f f y f y f f y f f y y xz ''+''+''=''+''+''+''=∂∂， 221211222211211222)()(f f x f x f f x f f x x yz''+''+''=''+''+''+''=∂∂， 221211122211211122)()()(f f y x f xy f f f x f f x y f xy zy x z ''+''++''+'=''+''+''+''+'=∂∂∂=∂∂∂．（2）212f x f xz '+'=∂∂，221220f y f y f y z'='+⋅'=∂∂，2221211222212121122442)2(22)2(f x f x f f f x f x f f x f xz''+''+''+'=''+''+'+''+''=∂∂， 2222222122242)20(22f y f f y f y f yz''+'=''+⋅''+'=∂∂， 221222212242)2(2f xy f y f x f y xy zy x z ''+''=''+''=∂∂∂=∂∂∂． 2. 设函数)(3x yxy f x z ，=，其中函数)(v u f ，有二阶连续偏导数，求yx z y z y z ∂∂∂∂∂∂∂222、、．解：2214213)1(f x f x f xf x x y z '+'='+'=∂∂， 24253111221*********11()()2z x xf f x xf f x f x f xf y x x∂''''''''''''''=+++=++∂， )(2)(422221221221141322f x yf y x f x f x y f y x f x x y z y x z ''-''+'+''-''+'=∂∂∂=∂∂∂ 2211421324f y f y x f x f x ''-''+'+'=． 3.设),(y x f z =有连续的一阶偏导数，且θθsin ,cos r y r x ==.求θ∂∂∂∂zr z ,，并证明 .)()()(1)(22222y z x z z r r z ∂∂+∂∂=∂∂+∂∂θ解由链式法则，得cos sin ,sin cos .z z x z y z z r x r y r x yz z x z y z z r r x y x yθθθθθθθ∂∂∂∂∂∂∂=+=⋅+⋅∂∂∂∂∂∂∂∂∂∂∂∂∂∂=+=-⋅+⋅∂∂∂∂∂∂∂于是有222)(1)(θ∂∂+∂∂z r r z 222)cos sin (1)sin (cos y zr x z r r y z x z ∂∂⋅+∂∂⋅-+∂∂⋅+∂∂⋅=θθθθ.)()(22yz x z ∂∂+∂∂=习题9-5（A ）1.若函数)(x y y =分别由下列方程确定，分别求xy d d ：（1）1cos y x y =+；（2）yx y e 2+=；（3）xyy x arctan ln22=+；解（1）法1：设()1cos F x y y x y =--，，则cos 1sin x y F y F x y =-=+、，所以d cos .d 1sin x y F y y x F x y=-=+ 法2：方程1cos y x y =+两边同时对x 求导，有d d cos sin d d y yy x y x x=-，解得d cos d 1sin y yx x y=+．（2）方程yx y e 2+=两边同时对x 求导，有xy x y yy d d e 1d d 2+=，解得yy x y e 21d d -=．（3）令()221(,)arctanln arctan ,2y yF x y x y x x==+- 则 ,),(22y x y x y x F x ++=,),(22yx xy y x F y +-= y x F F dx dy -= .xy yx -+-= 2. 设()y y x =由方程 1yy xe =+所确定的隐函数，求 202.x d ydx=解令 (.)1; 1yyy dy e F x y xe y dx xe =+-=--，当0x =时01y =+，此时x dy e dx==，所以222(1)()(1)yy y y y y dy dy e xe e e xe d ydx dx dx xe --+=--，222022(01)(0)2(01)x d y e e e e dx =--+=-=-. 3.设函数y x z =，而函数)(x y y =由方程yy x e +=确定，求全导数xz d d ．解：方程yy x e +=两边同时对x 求导，有x y x y y d d e d d 1+=，得yx y e 11d d +=， =+=∂∂+∂∂=-x y x x yx x y y z x z x z yy d d ln d d d d 1y y y x x yx e1ln 1++-． 4. 若函数),(y x z z =分别由下列方程确定，求x z ∂∂及yz∂∂．（1）21z y xz -=；（2）xyz z y x 2222=-+；（3）22)sin(xyz xyz =；（4）yz z x ln =．解：（1）法1：设1)(2--=xz y z z y x F ，，，则x yz F z F z F z y x -==-=22、、，所以xyz z F F y z x yz z F F x z z y z x --=-=∂∂-=-=∂∂222，．法2：方程21z y xz -=两边对x 求导，有20z zyzz x x x∂∂--=∂∂，得x yz z x z -=∂∂2，方程21z y xz -=两边对y 求导，有022=∂∂-+∂∂y z x z y z yz ，得xyz z y z --=∂∂22．（以下都按方法2作）（2）方程xyz z y x 2222=-+两边同时对x 求导，有xzxy yz x z zx ∂∂+=∂∂-2222，得 xyz yzx x z +-=∂∂，方程xyz z y x 2222=-+两边同时对y 求导，有yzxy xz y z zy ∂∂+=∂∂-2222，得 xy z xz y y z +-=∂∂（或由变量y x 、的对称性，得xyz xzy y z +-=∂∂）．（3）方程22)sin(xyz xyz =两边对x 求导，有xz xyz yz x z xyz yz xyz ∂∂+=∂∂+⋅2)2()cos(222，即0)2](1)[cos(22=∂∂+-x z xyzyz xyz ，而01)cos(2≠-xyz ，所以022=∂∂+xzxyz yz ，得x z xyz yz x z 222-=-=∂∂，由变量y x 、对称性有yzy z 2-=∂∂．（4）方程yzz x ln =改写为)ln (ln y z z x -=，方程)ln (ln y z z x -=两边对x 求导，有x zz x x z z z y z x z ∂∂+=∂∂+∂∂=)1(1ln 1，得zx z x z +=∂∂，方程)ln (ln y z z x -=两边对y 求导，有)11(ln 0y y z z z y z y z -∂∂+∂∂=，得)(2z x y z y z +=∂∂． 5.设04222=-++z z y x ，求22xz∂∂.解：令,4),,(222z z y x z y x F -++=则 ,2x F x = ,42-=z F z,2zx F F x z z x -=-=∂∂222(2)(2)z z xz x x z ∂-+∂∂=∂- 2)2(2)2(z z xx z --⋅+-=.)2()2(322z x z -+-=6.若函数),(z y x x =，),(z x y y =，),(y x z z =都是由方程0),,(=z y x F 确定的隐函数，其中),,(z y x F 有一阶连续非零的偏导数，证明1-=∂∂⋅∂∂⋅∂∂xzz y y x ．证：因为zx y z x y F F x zF F z y F F y x -=∂∂-=∂∂-=∂∂、、，所以1)()()(-=-⋅-⋅-=∂∂⋅∂∂⋅∂∂zx y z x y F F F F F F x z z y y x ． 7.若z 是,x y 的函数，并由 222()zx y z yf y ++=确定，求,z z x y∂∂∂∂.解：令 222(,,)()z F x y z x y z yf y =++-22()+()12()2()x y z F x z z zF y f f y y y z zF z yf z f y y y='=-''=-=-，，，因此，2212()()2x zF z x x z z x F z yf f zy y y∂=-=-=∂''-⋅-，2()()()2()().1()()2y zz z z z z zy f yf y f f F z y y y y y y z z y F z yf f zy y y ''----+∂=-=-=∂''-22-习题9-5（B ）1.设函数xyz u e =，而函数)(x y y =、)(x z z =分别由方程xyy e =及z xz e =确定，求全导数xud d ．解：方程xyy e =两边同时对x 求导，有)d d ()d d (e d d xy x y y x y x y x y xy+=+=，得xy y x y -=1d d 2，方程z xz e =两边同时对x 求导，有x z xz x z x z xz z d d d d e d d ==+，得xxz zx z -=d d ，所以 xxz z xy xy y xz yz x z z u x y y u x u x u xyz xyzxyz -+-+=∂∂+∂∂+∂∂=e 1e e d d d d d d 2 )11(e2-+-+=z yzxy z xy yz xyz．2．设函数32yz x u =，而),(y x z z =由方程xyz z y x 3222=++确定，求)1,1,1(xu ∂∂．解：方程xyz z y x 3222=++两边同时对x 求导，有)(322xzxy yz x z zx ∂∂+=∂∂+，用1=x 、11==z y 、代入，有 (1,1,1)(1,1,1)223(1)zz xx∂∂+=+∂∂，得1)1,1,1(-=∂∂xz ．于是x z yz x xyz x u ∂∂+=∂∂22232，所以13232)1,1,1()1,1,1(-=-=∂∂+=∂∂xzxu ．3．设),(xyz z y x f z ++=，求x z ∂∂，y x ∂∂，zy ∂∂. 解：令,z y x u ++= ,xyz v = 则 ),,(v u f z = 把z 看成y x ,的函数对x 求偏导数得xz∂∂ )1(x z f u ∂∂+⋅= ),(x z xy yz f v ∂∂+⋅+整理得xz ∂∂ ,1v u vu xyf f yzf f --+=把x 看成y z ,的函数对y 求偏导数得)1(0+∂∂⋅=yx f u ),(y xyz xz f v ∂∂+⋅+整理得yx ∂∂ ,v u vuyzf f xzf f ++-= 把y 看成z x ,的函数对z 求偏导数得)1(1+∂∂⋅=z y f u ),(zyxz xy f v ∂∂+⋅+ 整理得zy ∂∂ .1v u vu xzf f xyf f +--=4.若函数),(y x z z =由方程133=-xyz z 确定，求yx z∂∂∂2．解：方程133=-xyz z 两边对x 求导，有0)(332=∂∂+-∂∂xz xy yz x z z，得xy z yz x z -=∂∂2，由变量y x 、的对称性，得xyz xzy z -=∂∂2．法１：等式0)(2=∂∂+-∂∂xzxy yz x z z两边同时对y 求导，有 0)(2222=∂∂∂+∂∂+∂∂+-∂∂∂+∂∂∂∂yx z xy x z x y z y z y x z z x z y z z，即2222242222222)()2()(2)(xy z y x xyz z z xy z xyz z xy z yz x xy z xz y z y x z xy z ---=---+-+=∂∂∂- 所以=∂∂∂y x z 2322224)()2(xy z y x xyz z z ---．法２：)(22xyz yz y y x z -∂∂=∂∂∂ 322224222)()2()()2())((xy z y x xyz z z xy z x yz z yz xy z y z y z ---=--∂∂--∂∂+=．5.设 (,)F u v 具有连续的偏导数，方程 [(),()]0F a x z b y z --=（其中,a b 是非零常数）确定z 是,x y 的隐函数，且0aFu bFv +≠，求z zx y∂∂+∂∂. 解：令 (),()u a x z v b y z =-=-因此,x u u z u v u vF aF aF zx F aF bF aF bF ∂=-=-=∂--+y v v z u v u vF bF bF zy F aF bF aF bF ∂=-=-=∂--+，1u v u v u vaF bF z z x y aF bF aF bF ∂∂+=+=∂∂++. 6. 求由下列方程组所确定函数的导数或偏导数：（1）⎩⎨⎧=++=++，，41222z y x z y x 求x y d d 和xzd d ．（2）⎩⎨⎧-=+=，，v u y v u x uu cos e sin e 求x v y u x u ∂∂∂∂∂∂、、及y v∂∂．解：（1）方程组⎩⎨⎧=++=++41222z y x z y x ，两边同时对x 求导，有⎪⎩⎪⎨⎧=++=++，，0d d 2d d 220d d d d 1x z z x y y x x zx y 消去xz d d ，有0)d d 1(d d =+-+x y z x y y x ，得z y x z x y --=d d ，而z y yx x y x z --=--=d d 1d d ．（2）方程组⎩⎨⎧-=+=vu y v u x uu cos e sin e ，两边同时对x 求导，有⎪⎩⎪⎨⎧∂∂+∂∂-∂∂=∂∂+∂∂+∂∂=)2(.sin cos e 0)1(cos sin e 1x vv u v x u x u x v v u v x u x u u u ，（1）sin v ⨯-（2）cos v ⨯，有xux u v v v u∂∂+∂∂-=)cos (sin e sin ，得)cos (sin e 1sin v v vx u u -+=∂∂，再代入到（2）之中得)]cos (sin e 1[e cos v v u v x v uu -+-=∂∂．方程组⎩⎨⎧-=+=v u y v u x u u cos e sin e ，两边同时对y 求导，有⎪⎪⎩⎪⎪⎨⎧∂∂+∂∂-∂∂=∂∂+∂∂+∂∂=.sin cos e 1cos sin e 0y vv u v y u y u y v v u v y u y u u u ，与前面解法类似，得)cos (sin e 1cos v v vy u u -+-=∂∂，)]cos (sin e 1[e in v v u v s y v u u -++=∂∂．习题9-6（A ）1.求下列函数的极值：（1）222),(y x x y x f --=；（2）x y x y x y x f 936),(2233+++-=；（3）)2(e ),(2y y x y x f x++=；（4）2/322)(1),(y x y x f +-=．解：（1）定义域为全平面，并且函数处处可微．由⎩⎨⎧=-==-=，，，，02)(022)(y y x f x y x f y x 得唯一驻点)01(，．2)01(0)01(02)01(-====<-==，、，、，yy xy xx f C f B f A ，042>=-B AC ，根据二元函数极值的充分条件，点)01(，是函数的极大值点，极大值为1)0,1(=f ，该函数无极小值．（2）定义域为全平面，并且函数处处可微．由⎪⎩⎪⎨⎧=+-==++=，，，，063)(09123)(22y y y x f x x y x f y x 即⎩⎨⎧=-=++，，0)2(0)3)(1(y y x x 得函数的所有驻点是)23()03()21()01(4321，、，、，、，----P P P P ． 66)(0)(126)(+-====+==y y x f C y x f B x y x f A yy xy xx ，、，、，，对上述诸点列表判定：所以函数的极大值为4)2,3(=-f ，极小值为4)0,1(-=-f ．（3）定义域为全平面，并且函数处处可微．由⎪⎩⎪⎨⎧=+==+++=，，，，0)22(e )(0)21(e )(2y y x f y y x y x f xyx x 得唯一驻点(01)-，．x yy x xy x xx y x f y y x f y y x y x f e 2)()22(e )()22(e )(2=+=+++=，、，、，， 01>=A 、0=B 、2=C ，022>=-B AC ，根据二元函数极值的充分条件，点)10(-，是函数的极小值点，极小值1)1,0(-=-f ，该函数无极大值．（4）定义域为全平面，函数处处可微．由⎪⎩⎪⎨⎧=+-==+-=，，，，03)(03)(2222y x y y x f y x x y x f y x 得唯一驻点)00(，．由于在)00(，点处函数的二阶偏导数不存在，不能用定理8.2判定，为此根据极值的定义，当022≠+y x （即非)00(，点）时)00(1)(1),(2/322，f y x y x f =<+-=，所以点)00(，是该函数的极大值点，极大值为1)0,0(=f ，该函数无极小值． 2.求函数 5020(0,0)z xy x y x y=++>> 的极值．解：由 22500200z y xx z x yy ∂⎧=-=⎪∂⎪⎨∂⎪=-=∂⎪⎩，解出 52.x y ⎧⎨=⎩＝，222232310040, 1, z z z x y x x y y∂∂∂===∂∂∂∂ 在点(5,2)处，233100404130, 0552AC B A -=⋅-=>=>所以函数在(5,2)处由极小值 (5.2)30z=.3.求曲面 21 (0)z xy z -=>上到原点距离最近的点．解：设 222F,,,(1)x y z x y z z xy λλ+++--2()=，则 2202022010Fx y x F y x y F z z z z xy λλλ∂⎧=-=⎪∂⎪∂⎪=-=⎪∂⎨⎪∂=+=⎪∂⎪⎪--=⎩，解出 0011.x y z λ=⎧⎪=⎪⎨=⎪⎪=-⎩，，，因为(0,0,1)是 2222d x y z =++在0z >时的唯一驻点，由题意可知在0z >的曲面上存在与原点距离最小的点，所以(0,0,1)即为所求的点． 4. 将正数12分成三个正数z y x ,,之和使得z y x u 23=为最大. 解令 )12(),,(23-+++=z y x z y x z y x F λ,则223323020012x y z F x y z F x yz F x y x y z λλλ'⎧=+=⎪'=+=⎪⎨'=+=⎪⎪++=⎩，，，，解得唯一驻点)2,4,6(，故最大值为.691224623max =⋅⋅=u5. 用面积为12（m 2）铁板做一个长方体无盖水箱，问如何设计容积最大？解设水箱的长、宽、高分别为z y x 、、，体积为V ，则目标函数为xyz V =（，0>x ，0>y 0>z ），附加条件是1222=++yz xz xy ．设)1222()(-+++=yz xz xy xyz z y x L λ，，（000>>>z y x ，，），由(2)0(2)02()02212x yz L yz y z L xz x z L xy x y xy xz yz λλλ=++=⎧⎪=++=⎪⎨=++=⎪⎪++=⎩，，，，得唯一可能极值点12===z y x 、，根据实际意义，当长方体表面积一定是其体积有最大值，所以当长、宽都为2（m ），高为1（m ）时无盖长方体水箱容积最大(此时体积为4（m 3）)． 6.在斜边长为l 的直角三角形中，求周长最大的三角形及其周长．解：设两直角边长分别为y x 、，三角形周长为L ，则目标函数是l y x L ++=（00>>y x ，），附加条件为222l y x =+．设)()(222l y x l y x y x F -++++=λ，，由⎪⎩⎪⎨⎧=+=+==+=，，，222021021l y x y F x F y x λλ在00>>y x ，时得唯一可能极值点2l y x ==，由实际意义，斜边长为一定的直角三角形中，周长有最大值，所以当两直角边长都为2l （即等腰直角三角形）时，其周长最大，且最大周长为l )21(+．7.有一宽为24cm 的长方形铁板，把它折起来做成一断面为等腰梯形的水槽．问怎么折才能使断面的面积最大．解设折起来的边长为xcm ，倾角为α（图8-17），那么梯形的下底长为242x -，上底长为2422cos x x α-+，高为sin x α，所以断面的面积为1[(2422cos )242]sin 2=-++-⋅A x x x x αα，即2224sin 2sin cos sin (012,0)2A x x x x πααααα=-+<<<≤.为求其最大值，我们先来解方程组222224sin 4sin 2sin cos 0,24cos 2cos +(sin cos )0.x A x x A x x x ααααααααα=-+=⎧⎨=--=⎩ 由于sin 0,0x α≠≠，将上述方程组两边约分，得122cos 0,24cos 2cos cos 20.=-+=⎧⎨=-+=⎩x A x x A x x ααααα 解这个方程组，得,8().3x cm πα==根据题意，断面面积的最大值一定存在，又由A 的定义，0,12;0.x α≠≠因此最大值点只可能在区域的内部或开边界2πα=上取到．但当2πα=时，2242A x x =-的最大值为72．因此，该函数的最大值只能在区域的内点处取得，而它只有一个稳定点，因此可以断定(8,)=483723A π>是其最大值．即将铁板折起8cm ，并使其与水平线成3π角时所得断面面积最大．24242x-ax a。

高等数学课后习题答案--第九章

9. 设 x n ＞0，
10. 讨论下列级数的收敛性(包括条件收敛与绝对收敛)
182
⑴ ⑶ ⑸ ⑺ ⑼
x sin ; n n =1 ∞ n (−1) n −1 n −1 ; ∑ 3 n =1 n +1 ∞ (−1) ( x > 0 ); ∑ n =1 n + x
∑ (−1)
∞
n +1
⑵ ⑷ ⑹ ⑻ ⑽
180
(4) (6)
∑
∞
∞
n =1 ∞
∑
n =1
ln n ln n 1 ln n 1 n 1 , = = 3 . 收敛; < 2 2 n n n n n n n2 1 1 1 , < , 收敛; n ln (n + 2) ln(n + 2) 2
n
(5)
收敛;
(7) (8) (13) (14)
∑ (
n =1
n −1
)
n
发散
由于 lim (10
a −1
1 n
n →∞
= ln a , 而 n n − 1 > n a − 1 ;
(11)
发散;
∑
n =1
∞
∞
∑
n =1
( n + 1 − n − 1 ), ( n + 1 − (2n − n + 1 − n − 1) = (n −
2 2 2 2 2
(9) 收敛;
收敛;
5.利用级数收敛的必要条件，证明： nn (1) lim = 0， (2) n →∞ ( n !) 2
∞
n →∞
lim
( 2 n) ! = 0. 2 n ( n +1)

《高等数学》同济第六版第9章答案

1 得C = 0 ， 9 1 1 故所求的特解为: y = x ln x − x 3 9
代入初始条件 y (1) = − 11．求下列微分方程的通解（1） y′′ − 4 y′ + 3 y = 0 （3） y′′ − 4 y′ + 4 y = 0 解：（1）特征方程为（2） y′′ − 4 y′ = 0 （4） y′′ − 4 y′ + 5 y = 0
x )dy = 0 y
解：（1）原方程可化为: 3
dy x 2 y = + , 这是齐次方程. dx y 2 x
设u
=
y dy du ,由 y = xu 得 =u + x⋅ dx dx x
3u 2 1 du = dx 代入原方程并分离变量得： 3 x 1 − 2u
两边积分得： −
3
1 ln 1 − 2u 3 = ln x + ln C1 2 1 C 3 ，即 1 − 2u = 2 ， 2 2 C1 x x
3 3 ⎤ ∫ y dy ⎡ y − ∫ y dy x=e dy + C ⎥ ⎢∫ − e ⎢ ⎥ ⎣ 2 ⎦
y 1 1 y2 = y 3 ( ∫ − ⋅ 3 dy + C ) = y 3 ( + C ) = Cy 3 + 2 2 y 2y
10．求微分方程 xy′ + 2 y = x ln x 满足 y (1) = − 解：原方程化为将 P ( x) =
有⎨
⎧ C1 = 0 解得 C1 = 0, C2 = 1 . C + 2 C = 1 ⎩ 2 1
写出由下列条件确定的曲线所满足的微分方程．
4
（1）曲线在点 ( x, y ) 处的切线斜率等于该点横坐标的 5 倍. (2) 曲线在点 ( x, y ) 处的切线斜率等于该点横坐标与纵坐标乘积的倒数. 答案．(1) y ′ = 5 x (2) y ′ =

高等数学第九章多元函数微分学试题及答案

第九章多元函数微分学§9.1 多元函数的概念、极限与连续性一、多元函数的概念1．二元函数的定义及其几何意义设D 是平面上的一个点集，如果对每个点()D y x P ∈,，按照某一对应规则f ，变量z 都有一个值与之对应，则称z 是变量x ，y 的二元函数，记以()y x f z ,=，D 称为定义域。

二元函数()y x f z ,=的图形为空间一卦曲面，它在xy 平面上的投影区域就是定义域D 。

例如 221y x z --=，1:22≤+y x D ，此二元函数的图形为以原点为球心，半径为1的上半球面，其定义域D 就是 xy 平面上以原点为圆心，半径为1的闭圆。

2．三元函数与n 元函数()z y x f u ,,= ()Ω∈z y x ,,空间一个点集称为三元函数()n x x x f u ,,21 = 称为n 元函数它们的几何意义不再讨论，在偏导数和全微分中会用到三元函数。

条件极值中，可能会遇到超过三个自变量的多元函数。

二、二元函数的极限设函数),(y x f 在区域D 内有定义，),(000y x P 是D 的聚点，如果存在常数A ，对于任意给定的0>ε，总存在0>δ，当),(y x P 满足δ<-+-=<20200)()(0y y x x PP 时，恒有ε<-A y x f ),(成立。

则记以()A y x f y y x x =→→,lim 0或()()()A y x f y x y x =→,lim00,,。

称当()y x ,趋于()00,y x 时，()y x f ,的极限存在，极限值A ，否则称为极限不存在。

值得注意：这里()y x ,趋于()00,y x 是在平面范围内，可以按任何方式沿任意曲线趋于()00,y x ，所以二元函数的极限比一元函数的极限复杂；但考试大纲只要求知道基本概念和简单的讨论极限存在性和计算极限值，不像一元函数求极限要求掌握各种方法和技巧。

高数答案第9章

第9章（之1）（总第44次）*1．微分方程7359)(2xy y y y =''''-''的阶数是（）（A ）3；（B ）4；（C ）6；（D ）7．答案（A ）解微分方程的阶数是未知函数导数的最高阶的阶数．*2．下列函数中的C 、α、λ及k 都是任意常数，这些函数中是微分方程04=+''y y 的通解的函数是（）（A ）x C x C y 2sin )2912(2cos 3-+=；（B ）)2sin 1(2cos x x C y λ+=；（C ）x C k x kC y 2sin 12cos 22++=；（D ）)2cos(α+=x C y ．答案（D ）解二阶微分方程的通解中应该有两个独立的任意常数．（A ）中的函数只有一个任意常数C ；（B ）中的函数虽然有两个独立的任意常数，但经验算它不是方程的解；（C ）中的函数从表面上看来也有两个任意常数C 及k ，但当令kC C =时，函数就变成了x C x C y 2sin 12cos 2++=，实质上只有一个任意常数；（D ）中的函数确实有两个独立的任意常数，而且经验算它也确实是方程的解．*3．在曲线族 xxec e c y -+=21中，求出与直线x y =相切于坐标原点的曲线．解根据题意条件可归结出条件1)0(,0)0(='=y y ，由xxe c e c y -+=21， xx ec e c y --='21，可得1,02121=-=+c c c c ，故21,2121-==c c ，这样就得到所求曲线为)(21x x e e y --=，即x y sinh =．*4．证明：函数y e x x =-2333212sin 是初值问题⎪⎪⎩⎪⎪⎨⎧===++==1d d ,00d d d d 0022x x x y y y x yx y 的解．证明 '=-+--y e x e x x x 3332321212sin cos ，''=----y e x e x x x 3332321212sin cos ，代入方程得 ''+'+=y y y 0，此外，，1)0(0)0(='=y y 故y e x x =-2333212sin 是初始值问题的解．*5．验证y e e t Ce x t xx=+⎰20d （其中C 为任意常数）是方程'-=+y ye x x 2的通解．证明 '=+⋅+⎰y ee t e e Ce xt xx x x 220d =++ye x x 2，即 2x x e y y +=-'，说明函数确实给定方程的解．另一方面函数y ee t Ce xt x x=+⎰2d 含有一任意常数C ，所以它是方程的通解．**6．求以下列函数为通解的微分方程：（1）31+=Cx y ；解将等式31+=Cx y 改写为13+=Cx y ，再在其两边同时对x 求导，得C y y ='23，代入上式，即可得到所求之微分方程为1332-='y y xy ．（2）xC x C y 21+=．解因为给定通解的函数式中有两个独立的任意常数，所以所求方程一定是二阶方程，在方程等式两边同时对x 求两次导数，得221x C C y -='，322xC y =''．从以上三个式子中消去任意常数1C 和2C ，即可得到所求之微分方程为02=-'+''y y x y x ．**7．建立共焦抛物线族)(42C x C y +=（其中C 为任意常数）所满足的微分方程［这里的共焦抛物线族是以x 轴为对称轴，坐标原点为焦点的抛物线］．解在方程)(42C x C y +=两边对x 求导有C y y 42='，从这两式中消去常数所求方程为)2(y y x y y '+'=．**8．求微分方程，使它的积分曲线族中的每一条曲线)(x y y =上任一点处的法线都经过坐标原点．解任取)(x y y =上的点 ),(y x ，曲线在该点处的切线斜率为 y '=dxdy ．所以过点),(y x 的法线斜率为y '-1，法线方程为y Y -=y '-1)(x X -，因为法线过原点，所以=-y 0y '-1)0(x -从而可得所求微分方程为0='+y y x ．第9章（之2）（总第45次）教学容：§9.2 .1可分离变量的方程； §9.2 .2一阶线性方程**1．求下列微分方程的通解：（1）21)1(x y x y +-='；解：分离变量21d 1d x x x y y +=-，两边积分⎰⎰+=-21d 1d x xx y y ，得C x y ln )1ln(21)1ln(2-+=--，即211xC y +-=．（2）222y x e yx y -='；解：分离变量x xe y ye x y d d 222=，两边积分就得到了通解)d (21222x e xe e x x y ⎰-=c e xe x x +-=)21(2122．（3）042)12(=-+'+y y e y e x ．解： 12d 42d +-=-x xe y e y y ，C x e y ln 21)12ln(21)2ln(21++-=-，即 ()()e x C y-+=221．**2．试用两种不同的解法求微分方程xy y x y +--='1的通解．解法一（可分离变量方程的分离变量法）这是一个一阶可分离变量方程，同时也是一个一阶线性非齐次方程，这时一般作为可分离变量方程求解较为容易．分离变量，)1)(1(y x y --='，x x y y d )1(1d -=-，并积分 x x y yd )1(1d -=-⎰⎰ 得c x x y +-=--221)1ln(，所求通解为 x x ce y -+=2211．解法二（线性方程的常数变易法）将原方程改写为x y x y -=-+'1)1(，这是一个一阶线性非齐次方程．对应的齐次方程为0)1(=-+'y x y ，其通解为○1x x e C y -=221．代入原非齐次方程得x e C x x -='-1221，解得○2C eC x x +=-221，○2代入○1即可得原方程的通解xx Cey -+=2211．*3．求解下列初值问题：（1）21x yy -='，6)21(πe y -=．解：Θy '=21xy -，∴21d d xx y y -= (0≠y )， 21d d xx y y -=⎰⎰，∴C x y +=arcsin ln ， ∴ x Ce y arcsin =，Θπ6)21(e y -=，∴21arcsin 6Ce e =-π，∴1-=C ， ∴ x e y arcsin -=．（2）22x e xy y -=+'，1)0(=y ；解: Θ22x e xy y -=+'， x x p 2)(=∴，2)(x e x q -=，=∴)(x y ⎰-xx ed 2⎥⎦⎤⎢⎣⎡+⎰⎰-C dx e e x x x d 222x e -=⎥⎦⎤⎢⎣⎡+⎰⎰-C dx e e x x x d 2222x x Ce xe --+=， Θ 1)0(=y ， 101=⇒+=∴c c ， 2)1(x e x y -+=∴．（3）xex y y cos cot =+'，1)2(=πy ；解： Θ xex y y cos cot =+'， ∴x x P cot )(=，xex Q cos )(=．∴ ⎥⎦⎤⎢⎣⎡⎰+⎰=⎰-x C y xx x x x d e e e d cot cos d cot )d e e (e sin ln cos sin ln ⎰+=-x C x x x)d sin e (csc cos ⎰+=x x C x x x C xcsc )e(cos -=，由1)2(=πy ，可确定 2=C ，所以x y x csc )e 2(cos -=．（4）0d )12(d 2=+-+x x xy y x ，01==x y ．解：方程变形为 2112xx y x y -=+'，是一阶线性非齐次方程，其通解为⎥⎦⎤⎢⎣⎡⎰-+⎰=⎰-dx ex x c e y dx x dx x 222)11( ⎥⎦⎤⎢⎣⎡-+=⎰dx x x x c x 222)11(1⎥⎦⎤⎢⎣⎡-+=x x c x22211x xc 1212-+= 由 0)1(=y ，得 21=c ，所以特解为：x xy 121212-+=．**4．求微分方程 0d )ln (d ln =-+y y x x y y 的通解（提示将x 看作是y 的函数）．解：将x 看作是y 的函数，原方程可化为yx y y dy dx 1ln 1=+，这是一阶线性方程，将其中yy Q y y y P 1)( ,ln 1)(==代入一阶线性方程求解公式，得通解 1e 1)ln(ln )ln(ln ln 1ln 1⎥⎦⎤⎢⎣⎡+=⎥⎥⎦⎤⎢⎢⎣⎡⎰+⎰=⎰⎰--dy e y c dy ey c e x y y dy y y dy y y y y c dy y y c y ln 21ln ln ln 1+=⎥⎦⎤⎢⎣⎡+=⎰．**5．求满足关系式)(d )(22x y x u u uy x +=⎰的可导函数)(x y ．解：这是一个积分方程，在方程等式两边同对x 求导，可得微分方程xy x x y x()d d =+2，即d d yxxy x -=-2，分离变量得d d y y x x -=2，积分得y Ce x =+222，在原方程两边以2=x 代入，可得初试条件22-==x y．据此可得14--=e C ，所以原方程的解为 24122+-=-x e y ．**6．设降落伞自塔顶自由下落，已知阻力与速度成正比（比例系数为k ），求降落伞的下落速度与时间的函数关系．解：根据牛顿运动第二定理有kv mg tvm -=d d ．这是一个可分离变量方程，分离变量并积分得--=+1k mg kv tmC ln()．由初始条件0)0(=v ，得)ln(1mg k C -=，即得 v mg k e kmt =-⎛⎝ ⎫⎭⎪-1．**7．求一曲线，已知曲线过点)1,0(，且其上任一点),(y x 的法线在x 轴上的截距为kx ．解：曲线在点(,)x y 处的法线斜率为y '-1，所以法线方程为Y y y X x -=-'-1()．只要令0=Y ，就可以得到法线在x 轴上的截距为 y y x X '+= ．据题意可得微分方程x yy kx +'=，即x k y y )1(-='．这是一个可分离变量方程，分离变量并积分得所求曲线C x k y =-+22)1(，由于曲线过点)1,0(，所以1=C ，所以所求曲线方程为 y k x 2211+-=()．***8．求与抛物线族2Cx y =（C 是常数）中任一抛物线都正交的曲线（族）的方程．解：在给定曲线2cx y =上任意一点),(y x 处切线斜率为cx y k 20='=，从上面两式中消去c 得x y y k 20='=，这样就得到了给定曲线族所满足的微分方程xyy 2='．设所求曲线方程为 )(x y y =，在同一点),(y x 处切线斜率为y k '=，则根据正交要求有10-=k k ，这样就得到了所求曲线族应该满足的微分方程yx y 2-='．这是一个可分离变量方程，分离变量xdx ydy -=2，积分得所求曲线族c x y +-=2221，即椭圆族c x y =+2221． ***9．作适当变换，求微分方程 1224+-='-x e y y的通解．解原方程可化为4122=++'y ye x y e ，在换元y e z =下方程可化为4122=++'x zz ，这是一个一阶线性方程，其通解为⎭⎬⎫⎩⎨⎧+=⎰+⎰+-⎰x eC ez x xx xd 412d 212d 2}44{1212x x C x +++=．***10．作适当变换，求微分方程 d d tan y x y x y y x =+⎛⎝ ⎫⎭⎪2122的通解．解：令ux y =2，代入方程整理得 xxu u d tan d =，积分得 Cx u =sin ，以 x y u 2= 代入上式，即得原方程的通解： Cx xy =2sin ．第9章（之3）（总第46次）教学容：§9.2 .3齐次型方程；9.2.4伯努利方程．**1．求下列微分方程的通解：(1) )ln ln 1(d d x y xyx y -+=；解： Θ )ln ln 1(d d x y x y x y -+=， ∴ dx dy =x y (1+xyln )，这是一个一阶齐次型方程．令 xyu =，则 ux y =，即u x u y '+='，于是原方程可化为u u u x ln ='．这是一个可分离变量方程．分离变量x dx u u du =ln ，并积分⎰⎰=xdxu u du ln ，得c x u ln ln ln ln +=，即cx e u =．以 xy u =代入，得所求的通解为cxxe y =．（2）()arctan xy y yxx '-=．解：方程可化为xy xy y arctan1+='，这是一个一阶齐次型方程．令 x y u =，则 ux y =，即u x u y '+='，于是原方程可化为ux u x arctan 1d d =，这是一个可分离变量方程．分离变量后积分得 x u Ce u u 12+=arctan ．以 xy u =代入上式得原方程的通解：x y Cey x yx 22+=arctan ． **2．求解下列初值问题：（1）0d )2(d 22=+-y y x x xy 满足初始条件 1)2(=y 的特解．解: Θ 0d )2(d 22=+-y y x x xy ，dy dx =x y y x +2，令 yxu = ，则 u u dy du yu 12+=+， u u du 1+=y dy ， ∴⎰+uu du 1=⎰y dy，c y u ln ln )1ln(212+=+∴， cy u =+∴12，即 2221y c u =+ ，代回即得22y x +1=22y c ， 1)2(=y Θ， ∴52=c ，因此 22y x +=54y ．（2）⎩⎨⎧==-++=.0,0d )(d )(0x y y y x x y x解：原方程可表为11d d -+=-+=x y x yx y y x x y ，令 x y u =，u x u y '+='，代入方程，有 11-+='+u uu x u ，即 121d d 2--+=u u u x u x ，分离变量x x u uu u d 1d 2112=-+-，积分得 C x u u ln ln )21ln(212-=-+- ⇒通解 C y xy x =-+222，令 0,0==y x ，得 0=C ．所以初值问题的解为 0222=-+y xy x ．***3．试证明：当1221b a b a ≠时，总能找到适当的常数h ，k ，使一阶微分方程)(222111c y b x a c y b x a f y ++++='在变换k y s -=，h x t -=之下，可化为一阶齐次型方程)(d d 2211sb t a s b t a f t s++=．并求方程 0d )32(d )12(=++++y y x x y x 的解．证明：令⎩⎨⎧+=+++=++s b t a c y b x a sb t ac y b x a 2222211111 1221b a b a ≠Θ，∴可解得：⎪⎪⎩⎪⎪⎨⎧---=---=1221122112212112b a b a c b c b x t b a b a c a c a y s 因此可取：⎪⎪⎩⎪⎪⎨⎧--=--=1221122112212112b a b a c b c b h b a b a c a c a k解：0)32()12(=++++dy y x dx y x Θ，令⎩⎨⎧-=+=32x t y s ⎩⎨⎧==⇒x t ys d d d d[][]0)2(3)3(21)2(23=-++++-++∴ds s t dt s t ，()0)32(2=+++ds s t dt s t ，ts t sdt ds dtdst s t s 32210)32(21++-=⇒=+++⇒，令dt dutu dt ds t s u +=⇒=， 23)1)(13(3221+++-=⇒++-=+∴u u u dt du t u u dt du t u ， ⎰⎰-=⎥⎦⎤⎢⎣⎡+++∴-=+++⇒t dtdu u u t dt du u u u )13(23)1(21,)1)(13()23(， c t u u ln ln )13)(1ln(21+-=++即，c tst s t ct u u =++⇒=⋅++∴)13)(1()13)(1(，c x xy x y c x y x y x 243)3631)(321()3(22=+++⇒=-++-++-∴．**4．求下列微分方程的通解（1）0ln 2=+-'x y y y x ；解： 0ln '2=+-x y y xy Θ xxy x y y ln 1'12-=-∴-- 令x x t x dx dt y t ln 11=+⇒=-， ,ln )Q( ,1)(xx x x x P ==∴ln 1 d ln )(d 1d 1⎥⎦⎤⎢⎣⎡⋅+=⎥⎦⎤⎢⎣⎡⎰+⎰=∴⎰⎰-xdx x x C x x e x x C e x t x x x x1ln C )ln (C 11-+=-+=---x x x x x x x x ， 111ln --+-=Cx x y ．（2）0d d )2(=+-y x x xy y ．解： Θ 0d d )2(=+-y x x xy y ， x y d d +y x 1=212y x， y y '-21+211y x =x 2， 21y u =，x u d d +x 21x u 1=， ∴x x P 21)(=，xx Q 1)(．∴⎥⎦⎤⎢⎣⎡⎰+⎰=⎰-x e x C e x u x x x x d 1)(d 21d 2121-=x ⎥⎦⎤⎢⎣⎡+⎰x x x C d 121[]x C x +=-21， ∴ []x C xy +=-2121， ∴xC x y +=．（3）'=-y y xy x 3222()解一：令u y =2，原方程化为： d d u x u x u x =⎛⎝ ⎫⎭⎪⎛⎝ ⎫⎭⎪-21，解此方程得 u Ce u x =，以u y =2代入上式，原方程通解为 y Ce y x22=．解二：原方程写成d d x y y x yx -=-2232，令x z -=1，则方程化为：322d d yz y y z =+，则通解 z eC y e y yy y y =+⎡⎣⎢⎢⎤⎦⎥⎥-⎰⎰⎰2322d d d ]ln 2[12y C y+= ，故原方程通解：1122x yC y =+[ln ]． **5．求下列伯努力方程满足初始条件的特解：yxy y 2-='，1)0(=y ．解：x y yy', xy y y 22'21-=-∴-=-Θ，令 x t dxdty t 42 2-=-⇒=， x x Q x P 4)( ,2)(-=-=∴， []12010211)0(1212 )]2[ d 4 d )4()(2022222222d 2d 2+=∴=⇒++⨯=∴=++=∴++=++=-=⎥⎦⎤⎢⎣⎡⎰-+⎰=∴----⎰⎰x y C Ce y Ce x y x Ce e xe C e xxe C e x e x C e x t xx x x x x x x x，Θ****6．作适当的变换求方程 12222212+⋅'=++x y y x y e x sin sin 的通解．解：原方程化为：12222212+=++x yxx y e x d sin d sin ，令z y =sin 2，得d d z x x x ze x x -+=++21122122，故 ⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧++=⎰⎰+-+⎰+x exeC ez xx x x x x x d 1d 12212d 12222)1ln(2121222x x eCex x +++=++原方程的通解为 sin ln()221212221y Ce e x x x x =+++++．***7．已知)(2d )(1)(2202x y x y y x+='+⎰ξξξ，求y x ()．解：两边关于x 求导得212yy y '-=-，解得 y Ce x 21=+，由yx ==00，求得C =-1，故原方程的解为：y e x21=-．***8．曲线过点(,)11，其上任一点与原点的距离平方等于该点横坐标与该点的曲线的法线在x 轴上的截距乘积的两倍，求曲线方程．解：x y x x yy y 22211+=+'=(),(), 212yy xy x '-=- 令y z 2=，解得z y x C x ==-2()由y ()11=，得 C =2，曲线方程为： x y x 222+=．***9．根据托里斥利定律，液体从容器小孔中流出的速度为 gh A v 2α=，其中 g 为重力加速度，h 为液面与底部孔口之间的距离，A 为孔口面积，α为孔口收缩系数，实验确定其取值为 62.0=α．现有一直径为1m ，高为2m 的直立圆柱形容器，其中盛满的水从底部直径为1=d cm 的圆孔流出，要多长时间容器的水才会完全流尽？解：设在时刻t 时，容器中液面高度)(t h ，则经过t ∆后液面高度为)(t t h ∆+，于是有t t gh A t t h t h r ∆=∆+-)(2))()((2απ，即 22)()(rghA t t h t t h πα=∆-∆+-，令0→∆t ，得⎪⎩⎪⎨⎧==-200)0(2d d 2h gh r At h πα解得 200222+=t g rAh πα，代入0=h ， 980=g ， 50=r ， 4π=A ， 62.0=α，得10304=t （秒）．第9章（之4）（总第47次）教学容：§9.3可降阶的高阶微分方程**1．解下列问题：（1）．微分方程'+''=''y y xy 满足条件'==y y (),()2121的解是（）（A ）y x =-()12（B ）y x =+-()122142（C ）y x =-+121122() （D ）y x =--()12542解：（C ）（2）．微分方程''-'=y yy 203满足条件'=-=y y (),()0101的解是（）（A ）y x 3313=+（B ）x y 331=- （C ）y x 3313=-+（D ）x y 331=-+ 解：（C ）**2．求下列微分方程的通解．（1）0='+''y y x ；解： Θ 0='+''y y x 是一不显含因变量y 的二阶方程，令 y p '= ⇒ y ''x p d d =∴0=+'p p x ， ⇒p p d =xxd -，⇒⎰⎰-=x xp p d d ⇒ 1ln ln ln C x p +-= ⇒xC p 1=， ∴=xy d d x C 1， x x C y d d 1=， ⎰⎰=x x C y d d 1 ，21ln C x C y +=．（2）()1212+''+'=x y xy ；解：''++'=+y x x y x 211122， '=++y x x C 1121()， y x C x C =+++121212ln()arctan．（3）()02='+''y y y ；解：∵()02='+''y y y ，令 y p '=，则 yppy d d =''，代入方程有 0d d 2=+⋅⋅p ypp y ， 0)d d (=+⋅⇒p ypy p ，因为求通解，所以 p 满足 0d d =+⋅p ypy ．由⎰⎰-=⇒-=y yp p y y p p d d d d ， y C p C y p 11ln ln ln '=⇒+-=⇒， ⎰⎰'=⇒'=⇒'=⇒x C y y x C y y yC x y d d d d d d 111 212C x C y +=⇒． ∴ 通解：212C x C y +=．（4）()1222+''='y y yy解：令：'=''='y p y y pp (),，得()1222+⋅'=y p p p y ，即d d p p yy y =+212，得 p C y =+121()，所以 d d yyC x 121+=，通解为：arctan y C x C =+12．第9章（之5）（总第48次）教学容：§9 .4 .1二阶线性方程和解的存在性；§9 .4 .2二阶线性方程解的结构**1．若21,y y 是方程)()()(x R y x Q y x P y =+'+''的两个解，试证12y y - 必是其对应齐次方程0)()(=+'+''y x Q y x P y 的解．证明：因为21,y y 是方程)()()(x R y x Q y x P y =+'+''的解．所以成立下式：)2()()()()1()()()(222111x R y x Q y x P y x R y x Q y x P y =+'+''=+'+''将 (1)、(2) 两式相减，得)3(0))(())(()(212121=-+'-'+''-''y y x Q y y x P y y(2) 式可写为0))(())(()(212121=-+'-+''-y y x Q y y x P y y ，所以 21y y - 是齐次方程 0)()(=+'+''y x Q y x P y 的解．***2．已知23211,1,1x y x y y +=+==是方程22222xy x y x y =+'-''的三个特解，问能否求出该方程得通解？若能则求出通解来．解：按（1）证明可知 21312,x y y x y y =-=- 分别是其对应齐次方程0222=+'-''y xy x y 的解，并且线性无关，所以221x C x C + 为齐次方程的通解．所以原方程的通解可以表示为：1221++=x C x C y ．*3．验证：22,t t e e -是微分方程''-'-=x tx t x 1402的两个线性无关特解，并求此方程的通解．证明：因为()()222241t t t e t e t e -'-"0421********=-⨯-+=t t t t e t te te t e ，()()2222"41t t t e t e t e ----'-=-+-⨯--=--241240222222e t e tte t e t t t t ()，故22,t t e e -是方程的解，且≠=-2222t t t e ee 常数．于是22,t t e e -是方程线性无关的解（构成基本解组），故方程的通解为2221t t e C e C x -+=，其中21,C C 为任意常数．*4．已知函数 x y e y x==21, 是方程 0)1(=-'+''-y y x y x 的两解，试求该方程满足初始条件 0)0(,1)0(='=y y 的特解．解：方程的通解为 x c e c y x21+=，将初始条件代入，有：，，0)0('1)0(21211=+=+===c c c e c y c y x解得21,c c 为： 1,121-==c c ，所以特解为：x e y x -=．**5．设x t 1()是非齐次线性方程''+'+=x t a t x t a t x t f t ()()()()()()()1211的解．x t 2()是方程''+'+=x t a t x t a t x t f t ()()()()()()()1222的解．试证明 x x t x t =+12()()是方程''+'+=+x t a t x t a t x t f t f t ()()()()()()()()12123的解．解：因为)(2),(1t x t x 分别为方程（1）和方程（2）的解，所以)1()()()()()()(112111'≡+'+''t f t x t a t x t a t x''+'+≡'x t a t x t a t x t f t 2122222()()()()()()()()()12'+'得：()()())()()()()()()()()()(2121221121t f t f t x t x t a t x t x t a t x t x +='++'++"+即 x x t x t =+12()() 是方程（3）的解．第9章（之6）（总第49次）教学容：§9 .4 .3二阶线性常系数方程的解法**1．解下列问题：（1）方程08=+''y y 的通解为=y _______________．解：x c x c y 22sin 22cos 21+=．（2）方程025'6"=++y y y 的通解为=y _______________．解：)4sin 4cos (213x c x c e y x+=-．（3）方程0158=+'-''y y y 的通解为=y _______________．解：x xC C y 5231e e +=．（4）方程031525=+'+''y y y 的通解为=y _______________．解：)(21515C x C e y x +=-．（3）方程06=+'+''py y y 的通解为)2sin 2cos (e 21x C x C y kx+=，则=p ___，=k _____．解：11，3-．**2．求解下列初值问题：（1）0)1(,)1(,01684='==+'-''y e y y y y ；解：∵0)4(16822=-=+-λλλ， ∴421=，λ，通解为：xe x c c y 421)(+=．将初始条件代入，有 4421)()1(e e c c y =+=，04)(4)(4)1('4424214242142=+=++=++=e e c e c c e c e x c c e c y x x得到：4521-==c c ，所以特解为：x e x y 4)45(-=．（2）3)2(,1)2(,0294='==+'+''ππy y y y y ；解：02942=++λλ， i i5221042116164±-=±-=-±-=λ，通解为：)5sin 5cos (212x c x c ey x+=-．代入初始条件有： πππe c c ey =⇒=+=-221)0()2(，)5cos 55sin 5()5sin 5cos (2)2(212212x c x c e x c x c ey x x+-++-='--π，得：πe c -=1．特解为：)5sin 5cos (2x x e y x+-=-π．（3）10)0(,6)0(,034='==+'+''y y y y y ；解： 0342=++λλ， 0)3)(1(=++λλ，所以通解为 x xe c e c y 321--+=．代入初始条件有：6)0(21=+=c c y ，1033)0('21321=--=--=--c c e c e c y x x ，特解为：x xe ey 3814---=．**3．求解初值问题'++==⎧⎨⎪⎩⎪≥⎰y y y x y x x210100d ()解：将原方程对x 求导得 ''+'+=y y y 201()且有'=-=-y y ()()01201微分方程（1）的通解为：y e C x C x =+-()12，代入初始条件1)0(,1)0(-='=y y ，得1,021==C C ，故所求问题的解为：xe y -=．***4．设函数)(x ϕ二阶连续可微，且满足方程⎰-+=xu u u x x 0d )()(1)(ϕϕ，求函数ϕ()x ．解：原方程关于x 求导得⎰⎰=-+='xxu u x x x x u u x 0d )()()(d )()(ϕϕϕϕϕ,0)0(='ϕ，再求导得： )()(x x ϕϕ=''，且由原方程还有：1)0(=ϕ，微分方程的通解为： xxeC e C x -+=21)(ϕ，代入条件0)0(,1)0(='=ϕϕ，得2121==C C ，故所求函数为：x e e x x x ch )(21)(=+=-ϕ．***5．长为100cm 的链条从桌面上由静止状态开始无摩擦地沿桌子边缘下滑．设运动开始时，链条已有20cm 垂于桌面下，试求链条全部从桌子边缘滑下需多少时间．解：设链条单位长度的质量为ρ，则链条的质量为ρ100．再设当时刻 t 时，链条的下端距桌面的距离为)(t x ，则根据牛顿第二定律有：gx dt x d ρρ=22100，即 010022=-x gdtx d ．又据题意知：20)0(=x ， 0)0(='x ，所以 )(t x 满足下列初值问题：⎪⎩⎪⎨⎧='==-0)0(20)0(010022x x x gdt x d ，解得方程的通解为：tg tgec ec x 102101-+=．又因为有初始条件： ()()⎩⎨⎧==⇒⎩⎨⎧==1010020021'c c x x 所以 tg t gee x 10101010-+=．又当链条全部从桌子边缘滑下时，100=x ，求解t ，得：tg tg e e 10101010100-+=，即： 510=t gch， 510arch gt =．***6．设弹簧的上端固定，下端挂一个质量为2千克的物体，使弹簧伸长2厘米达到平衡，现将物体稍下拉，然后放手使弹簧由静止开始运动，试求由此所产生的振动的周期．解：取物体的平衡位置为坐标原点，x 轴竖直向下，设t 时刻物体m 位于x t ()处，由牛顿第二定律：22222d d ()xtg g x gx =-+=- ，其中g =980厘米/秒2其解为：x C g t C g t =+1222cossin ，振动周期为 T g ==≈222490028ππ.．第9章（之7）（总第50次）教学容：§9.4.3二阶线性常系数方程的解法； §9.4.4高阶线性常系数微分方程 **1．微分方程x x y y sin =+''的一个特解应具有形式（）（A ）()sin Ax B x +（B ）x Ax B x x Cx D x ()sin ()cos +++ （C ）x Ax B x x ()(cos sin )++ （D ）x Ax B C x D x ()(sin cos )++ 解：（B ）**2．设A B C D ,,,是待定常数，则微分方程''+=+y y x x cos 的一个特解应具有形式（）（A ）Ax B C x ++cos（B ）Ax B C x D x +++cos sin（C ）Ax B x C x D x +++(cos sin ) （D ）Ax B Cx x ++cos 答：（C ）**3．求下列非齐次方程的一个解（1）122+=-'-''x y y y ；解：∵ 022=--λλ， ∴1,22,1-=λ， 0Θ不是特征根．设 01b x b y p +=，代入原方程，得：1222011+=---x b x b b ，有：1,010-=b b ，特解为：x y -=．（2）xey y y -=+'+''2．解： ∵ 1- 是二重特征根， ∴ 设 02b e x y xp -=， 0202b e x b xe y xxp ---='，02002022b e x b xe b e x b e y x x x x p----+--=''，代入 xe y y y -=++'2''，解得：210=b ，特解为：xe x y -=221．**4．求微分方程''-'+=y y y xe x32满足条件y y ()()000='=的特解．解：特征方程0232=+-r r 的根为2,121==r r ，相应齐次方程的通解为x x h e C e C y 221+=，设特解为x p e B Ax x y )(+=，代入方程得： 1,21-=-=B A ．故方程的通解为xxx e x x eC e C y ⎪⎪⎭⎫ ⎝⎛+-+=22221，代入条件0)0()0(='=y y ，得1,121=-=C C ，因此所求特解为 x xe x x ey ⎪⎪⎭⎫ ⎝⎛++-=1222．**5．求下列非齐次方程的通解：)(2x f y y ='+''x x f e x f x x f x cos )()3,)()2,14)()12==+=；解：特征方程：022=+λλ，特征根： 2,021-==λλ，所以方程0'2=+''y y 的通解为 xh e c c y 221-+=．1）对于方程14'2+=+''x y y ，由于0是特征方程的单根，故设其特解为：x b x b y p )(10+=，代入方程有：14242100+=++x b x b b ，解得 21110-==b b ，所以特解为：x x y p 212-=．所以方程的通解为：x x e c c y y y xp h 212221-++=+=-．2）对于方程xe y y 2'2=+'''，由于2不是特征方程的根，故设其特解为：02b e y xp =，代入方程有：810=b ， xp e y 281=，所以方程的通解为：x xp h e ec c y y y 222181++=+=-．3）对于方程：x y y cos '2=+'''，由于i ±不是特征方程的根，故设其特解为： x b x b y p sin cos 10+=，代入方程有：x b x b y p cos sin '10+-=， x b x b y p sin cos "10--=，x x b x b x b x b cos cos sin 2sin cos 1010=+---，得：525120=-=b b ， x x y p sin 52cos 51+-=，所以方程的通解为：x x e c c y y y xp h sin 52cos 51221+-+=+=-．**6．求微分方程''-'+=y y y e x x6925sin 的通解．解：特征方程r r 2690-+=的根为r 123,=，相应齐次方程的通解为xh e x C C y 321)(+=设特解为y e A x B x p x=+(cos sin )，代入方程得：A B ==43,故方程的通解为 y C C x e e x x x x =+++()(cos sin )12343***7．已知曲线y y x x =≥()()0过原点，位于x 轴上方，且曲线上任一点),(00y x M =处切线斜率数值上等于此曲线与x 轴，直线x x =0所围成的面积与该点横坐标的和，求此曲线方程．解：由已知y ()00=，且'=+'=⎰y y x x y xd ,()000，将此方程关于x 求导得''=+y y 1其通解为： y C e C exx=+--121 ，代入初始条件y y (),()0000='=，得 C C 1212==，故所求曲线方程为：y e e x xx =+-=--1211()ch ．***8．设一物体质量为m ，以初速v 0从一斜面滑下，若斜面与水平面成θ角，斜面摩擦系数为μμθ(tan )0<<，试求物体滑下的距离与时间的关系．解：设t 时刻物体滑过的距离为S ，由牛顿第二定律m Stmg mg d d sin cos 22=-θμθ 且 S S v (),()0000='=方程的通解为S gt C t C =-++12212(sin cos )θμθ 代入初始条件得C v C 1020==,，故物体滑下的距离与时间的关系为S gt v t =-+1220(sin cos )θμθ***9．设弹簧的上端固定，下端挂一质量为m 的物体，开始时用手托住重物，使弹簧既不伸长也不缩短，然后突然放手使物体开始运动，弹簧的弹性系数为k ，求物体的运动规律．解：取物体未发生运动时的位置为坐标原点，x 轴垂直向下，设t 时刻物体位于x t ()处，由牛顿第二定律： m xtkx mg d d 22+=，且 0)0(0)0(='=x x ，．方程的通解为： x C k m t C k m t m kg =++12cos sin ，代入初始条件得C mkg C 120=-=,，故物体的运动规律为x mg k k m t =-⎛⎝ ⎫⎭⎪1cos．***10．求下列方程的通解：（1）02)4(=''+'''-y y y；解： 02234=+-λλλ， 0)12(22=+-λλλ， 0)1(22=-λλ，所以通解为 x e x c c x c c y ）（4321+++=．（2）0365)4(=-''+y y y．解：036524=-+λλ， 0)9)(2)(2(2=++-λλλ，所以通解为 x c x c ec e c y xx 3sin 3cos 432221+++=-．****11* 试证明，当以 x t ln =为新的自变量时，变系数线性方程（其中a,b,c 为常数，这是欧拉方程）)('"2x f cy bxy y ax =++可化为常系数线性方程)()(22t e f cy dt dya b dty d a =+-+并求下列方程通解：（1）022=-''y y x ；（2）x x y y x y x ln 22=+'-''．证明：令 x t ln =， t e x =，dtdyx dx dt dt dy dx dy 1==，⎪⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛+-=dt dy dt y d x dt dy dx d x dt dy x dx y d 222222111，将y y ''',代入方程有：()()te f cy dt dy a b dt y d a cy dt dy b dt dy dt y d a cy y bx y ax =+-+=++⎪⎪⎭⎫ ⎝⎛-=+'+''22222，得证．（1）令 x t ln =， te x =，原方程化为：0222=--y dt dydty d ．其通解为t t e c e c y -+=221．将x 代入，得：xc x c y 221+=．（2）令 x t ln =， te x =，原方程化为：tte y dt dy dty d =+-2222，上述方程的相应其次方程的通解为：()t c t c e y t h sin cos 21+=．令上述方程一个特解为：()10b t b e y t p +=，代入方程得：0,110==b b ，即：t e y t p =．原方程得通解为：()t t c t c e y t ++=sin cos 21，即：()()[]x x c x c x y ln ln sin ln cos 21++=．***12．一质量为m 的潜水艇在水面从静止状态开始下降，所受阻力与下降速度成正比（比例系数为k >0），浮力为常数B ，求潜水艇下降深度x 与时间t 之间的函数关系．解： ma B F F =--阻重， a 为加速度， ma B kv mg =--， v 为下降速度，因为 22,dt x d dt dv a dt dx v ===，所以 22dt xd m B dt dx k mg =--，即 m Bg dt dx m k dtx d -=+22 ，其特征方程为： 02=+λλmk ，解得特征根为 m k-==21,0λλ．所以对应的齐次方程的通解为：21c e c x t mkh +=-．由于0是特征方程的单根，故设其特解为：t b x 01=，代入方程有：m B g b m k -=0，得 kBmg b -=0．所以微分方程的通解为：t kBmg c e c x t mk-++=-21，因为初始位置为０，初始速度为０，所以有初始条件 ()()00,00'==x x ，代入微分方程有： ⎪⎩⎪⎨⎧=-+-=++000121k Bmg c mk c c 求得：222221,kgm Bm c k Bm g m c -=-=，所以x 与t 的关系可表示为： t k B mg e k g m Bm x t m k-+⎪⎪⎭⎫ ⎝⎛--=-122．***13．证明：若有方程'=-f x f x ()()1，则必有''+=f x f x ()()0，并求解此方程．证明：由于'=-f x f x ()()1，两边关于x 求导得''=-'-=---=-f x f x f x f x ()()[()]()111故得''+=f x f x ()()0（1）解方程（1）得通解为 f x C x C x ()cos sin =+12（2）'=-+f x C x C x ()sin cos 12 （3）'='=f f f f ()(),()()0110，将此代入(2),(3)得C C C C C C 1221211111cos sin sin cos +=-+=⎧⎨⎩ 解得：C C 21111=+sin cos所以原方程的解为： f x C x x ()cos sin cos sin =++⎛⎝⎫⎭⎪1111．第9章（之8）（总第51次）教学容：§9.6 微分方程应用举例 (机动)第9章（之9）（总第52次）教学容：§9.7 差分方程1. 已知t t e y 3=是二阶差分方程tt t e ay y =+-+11的一个特解，求a ．解： )31(3e ea -=．2. 求下列差分方程的一般解： (1) 0721=+-t t y y ；解：tt C y )27(-=(2) 431-=--t t y y ；解：23+=tt C y(3) 051021=-++t y y t t ；解：)61(125)5(-+-=t C y tt (4) tt t y y 2124=-+；解：144-+=t t t t C y (5) tt t t y y 21⋅=-+．解：tt t C y 2)2(-+=3. 写出下列差分方程的一个特解形式： (1) t y y t t sin 1=-+；解：t B t B Y t cos sin 21+=(2) t y y t t πcos 31-=++．解：)sin cos (21t B t B t Y t ππ+=4. 设t y 为第t 期国民收入，t C 为第t 期消费，I 为每期投资（I 为常数）．已知t y ，t C ，I 之间有关系 I C y t t +=，βα+=-1t t y C ，其中10<<α，0>β，试求t y ，t C ．解：t y 满足：βα+=--I y y t t 1，解得 αβα-++=1I C y tt ，从而 =-=I y C t t ααβα-++1I C t．5. 已知差分方程t t t cy y by a =++1)(，其中a ，b ，c 为正的常数．设初始条件0)0(0>=y y ，证明：(1) 对任意Λ,2,1=t ，有0>t y ；(2) 在变换tt y u 1=之下，原差分方程可化为有关t u 的线性差分方程，写出该线性差分方程并求其一般解；(3) 求方程t t t y y y =++1)21(的满足初始条件20=y 的解．解：（1）归纳法证明．（2）令 t t y u 1=，即t t u y 1=，111++=t t u y ，则原方程化为线性差分方程 b au cu t t =-+1，其一般解为 a c ≠时， ac bcaC u tt -+=)( ； a c =时， b C u t +=．（3）令 tt y u 1=，原方程化为 21=-+t t u u ，一般解为 2+=C u t ，所以原方程的一般解为 t t u y 1=21+=C ，代入 20=y ，得 23-=C ，所以特解为 2=t y ．。

高等数学第9章参考答案

第八章多元函数的微分法及其应用§ 1 多元函数概念一、设]),,([:,),(,),(22222y y x f y x y x y x y x f ϕϕ求-=+=.二、求下列函数的定义域：1、2221)1(),(y x y x y x f ---= 222{(,)|(,)R ,1};x y x y y x ∈+≠ 2、xyz arcsin = };0,|),{(≠≤x x y y x三、求下列极限：1、222)0,0(),(sin lim y x yx y x +→ （0） 2、x y x x y3)2,(),()1(lim+∞→ (6e )四、证明极限 242)0,0(),(lim yx yx y x +→不存在. 证明：当沿着x 轴趋于（0，0）时，极限为零，当沿着2x y =趋于（0，0）时，极限为21, 二者不相等，所以极限不存在五、证明函数⎪⎩⎪⎨⎧=≠+=)0,0(),(,0)0,0(),(,1sin ),(22y x y x yx xy y x f 在整个xoy 面上连续。

证明：当)0,0(),(≠y x 时，为初等函数，连续),(y x f 。

当)0,0(),(=y x 时，)0,0(01sin lim 22)0,0(),(f yx xy y x ==+→，所以函数在（0，0）也连续。

所以函数在整个xoy 面上连续。

六、设)(2y x f y x z +++=且当y=0时2x z =，求f(x)及z 的表达式. 解：f(x)=x x -2，z y xy y x -++=2222 § 2 偏导数1、设z=x yx e x y + ,验证 z xy +=∂∂+∂∂yzyx z x 证明：x yx yx ye x ,e x y e y +=∂∂-+=∂∂y z x z ，∴z xy xe xy xy x y+=++=∂∂+∂∂yzy x z x 42244222222)()),,((y y x x y y x y y x f +-=+-=ϕ答案：2、求空间曲线⎪⎩⎪⎨⎧=+=Γ21:22y y x z 在点（1,21,23）处切线与y 轴正向夹角(4π) 3、设yx y xy y x f arcsin )1(),(2-+=, 求)1,(x f x ( 1)4、设yz x u =, 求x u ∂∂ ，y u ∂∂ ，zu ∂∂ 解：1-=∂∂y zx y z x u ，x x yz y u y zln 2-=∂∂ x x y z u y zln 1=∂∂ 5、设222z y x u ++=，证明 : u zu y u x u 2222222=∂∂+∂∂+∂∂6、判断下面的函数在(0,0) 处是否连续？是否可导（偏导）？说明理由⎪⎩⎪⎨⎧≠+≠++=0,00,1sin ),(222222y x y x yx x y x f )0,0(0),(lim 00f y x f y x ==→→ 连续； 201sin lim )0,0(xf x x →= 不存在， 0000lim )0,0(0=--=→y f y y7、设函数 f(x,y)在点（a,b ）处的偏导数存在，求 xb x a f b x a f x ),(),(lim--+→（2f x (a,b)） § 3 全微分 1、单选题（1）二元函数f(x,y)在点(x,y)处连续是它在该点处偏导数存在的 __________(A) 必要条件而非充分条件（B ）充分条件而非必要条件（C ）充分必要条件（D ）既非充分又非必要条件（2）对于二元函数f(x,y)，下列有关偏导数与全微分关系中正确的是___(A) 偏导数不连续，则全微分必不存在（B ）偏导数连续，则全微分必存在（C ）全微分存在，则偏导数必连续（D ）全微分存在，而偏导数不一定存在 2、求下列函数的全微分：1）x y e z = )1(2dy x dx xy e dz x y+-=2）)sin(2xy z = 解：)2()cos(22xydy dx y xy dz +=3）zyx u = 解：xdz x zyxdy x z dx x z y du z yz yz yln ln 121-+=-3、设)2cos(y x y z -=，求)4,0(πdz解：dy y x y y x dx y x y dz ))2sin(2)2(cos()2sin(-+-+--= ∴)4,0(|πdz =dy dx 24ππ-4、设22),,(yx z z y x f += 求：)1,2,1(df )542(251dz dy dx +--5、讨论函数⎪⎩⎪⎨⎧=≠++=)0,0(),(,0)0,0(),(,1sin )(),(2222y x y x y x y x y x f 在（0，0）点处的连续性、偏导数、可微性解：)0,0(01sin )(lim 2222)0,0(),(f y x y x y x ==++→ 所以),(y x f 在（0，0）点处连续。

高数课后习题九详细答案

第9章课后习题详解重积分课后习题全解习题9-1★1.设有一平面薄板（不计其厚度），占有xOy 面上的闭区域D ，薄板上分布着面密度为),(y x μμ=的电荷，且),(y x μ在D 上连续，试用二重积分表达该板上的全部电荷Q .解：将D 任意分割成n 个小区域{}i σ∆，在第i 个小区域上任取一点),(i i ηξ，由于),(y x μ在D 上连续和i σ∆很小，所以用),(i i ηξμ作为i σ∆上各点函数值的近似值，则i σ∆上的电荷i i i i Q σηξμ∆≈∆),(从而该板上的全部电荷⎰⎰∑=∆==→Dni i i i d y x Q σμσηξμλ),(),(lim 1其中λ是各i σ∆中的最大直径。

★★2.利用二重积分定义证明：（1）σσ=⎰⎰Dd （σ为区域D 的面积）；（2）⎰⎰⎰⎰=DDd y x f k d y x kf σσ),(),(（其中k 为常数）；（3）⎰⎰⎰⎰⎰⎰+=21),(),(),(D D Dd y x f d y x f d y x f σσσ，其中21D D D=, 21,D D 为两个无公共内点的闭区域。

证明：（1）这里，被积函数1),(≡y x f ，由二重积分的定义，对任意分割和取点法，=∙⎰⎰Dd σ1∑∑=→=→∆∙=∆n i i ni iiif 111lim ),(lim σσηξλλ∑=→∆=ni i 1lim σλσσλ==→0lim ，∴σσ=⎰⎰Dd ，其中λ是各iσ∆中的最大直径。

（2）=⎰⎰Dd y x kf σ),(∑∑=→=→∆=∆ni i i i ni iiif k kf 101),(lim ),(lim σηξσηξλλ∑=→∆=ni i i i f k 1),(lim σηξλ⎰⎰=Dd y x f k σ),(（3）将1D 任意分割成1n 个小区域{}1i σ∆，1λ是其各小区域的最大直径，将2D 任意分割成2n 个小区域{}2i σ∆，2λ有类似的意义。

高数第九章解答_khdaw

孑毖 ?、阜
9,t9’ o厶
Ⅱ 【秃
留饪 ∵私19`铞
g℃ 1亠 -孓 c关
∠
q亻△ˇ留'仉 ~幻 f丬丿o吖'饫 ′+留吖 ′-q'皈 -叨绽 ′
`=留
〃-留〃 =ˉ Tru丿 9?g△ 十
,恭喉厶拶句″ `V午钉 ,,勹切
`J扌颐
`为 Gqt以 9干 C,刁巳f∝ 丿
宀耐饪 J、'廷
亻⑷ 辶泓以吧
以十6)s以》伽大十 2扬呒从 $丿 +CI△ 丈干 r,s义
△ G宀大 fC,⒐
⊥
#孛
一
ˉ ct铴众十 r冫
歹、 X)矽 ″-4爿
9'洋
^一
6u。
口
天·et
/ 贾
sF乡亻
G9f=r匕匕~匕/)去
)舞砝 %Ξ {∶I讠{l丨
E-彳一繁
课后答案网幻r~吆 .′ -4勹 /十 ‘ °f‘ 0o
冫l
◇σ 干 ε,乙圹叶C、 ⒐跷十兽
1细 (‰ 9· 9十 O。 str‰
f
'冫巩轻甲tJ
www.khd课后a答w案.网com
U孔 , , r。 f丿
亻 ′-⒊ V′ 十冫
(3,灼孓‘叼'彳 ?V=o
占沟 △亻子刀 Ⅱ
入△ ;入 f亠 =。 .^=(、 λ ⒓ . C‘ g丬千 C亠 e2x
递乙甲‘2 课后答案网
C /Ⅱ f∫
°/U二万锈丐 .告监亻l+圹卜 rl劳一席轩 ,。f丬 =荔 ″卜些厶Cl+犭勹十
`斋 y~lr.疒丿-荔犭L茂 ‘rf9·丿千C讠

高等数学第九章练习题答案

第九章练习题一、填空第一节1、 22222)1ln(),(y x y x y x f --+-+=的定义域是2122≤+<y x ．2、 2222911),(y x y x y x f --+-+=的定义域是9122≤+<y x ．3、 2222001sin)(lim yx y x y x ++→→＝ 0 ． 4、=+-→→xyxy y x 93lim0 16- ．5、、函数y x z -=的定义域是 (){}y x y x y x ≥≥≥2,0,0/,6、函数()12ln 2+-=x y z 的定义域是 0122>+-x y7、()()=+-→11lim0,0,xy xy y x 2-. 19. ()()=-+→xyxy y x 24lim0,0,41. 8、求极限()()()yxy y x tan lim0,2,→= 29、 2210ln()lim y x y x e x y →→++= ln 2 . 第二节1、设z =zx ∂∂2、设z arctan(xy )=，则zx∂=∂ ，z y ∂=∂ ．22,1()1()y x xy xy ++ 3、设223z x xy y =++，则(1,2)zx ∂∂= 8 ，(1,2)z y ∂∂= 7 .4、设y x e z 2-=，而t x sin =，3t y =，则=dtdz()22sin 6cos 3t t e t t -- 5、设y x z =，而te x =，12-=t e y ，则=dt dz ()2231-+-t t t e e e6、设(1)y z xy =+，则zx∂∂= 21(1)y y xy -+ 7、设(1)xy z x =+，则zy∂∂=(1)ln(1)xy x x x ++ 8、设y x z y3⋅=，求=∂∂∂y x z 2 ⎪⎪⎭⎫ ⎝⎛-y y y 13ln 3 。

9、函数222234x y z x ++=，则z x ∂=∂ 23z x x z∂-=∂，z y ∂=∂ 。

高等数学课后习题答案第九章1

第九章习题解答（2）习题9.31、求上半球面222y x a z含在柱面ax y x 22内部的曲面面积解：被积函数为222y x a z 22222)(y x a x z x 22222)(yx a y z y --= 所以 dxdy yx a a dS 222--=积分区域为：:D ax y x =+22，化成极坐标：设θcos r x =，θsin r y = dr rd dxdy θ=θπθπc o s 0,22a r ≤≤≤≤-⎰⎰-=-θππθcos 02222a ra ardr d S cos 0222222)(2a r a r a d d a ⎰---=22cos 022ππθθd r a a a)2(222)sin (222220-=⋅+-=--=⎰ππθθπa a a d a a a2、求圆锥面22y x z +=被柱面x z 22=所截下的曲面面积解：被积函数为22y x z += 2222)(y x x z x += ， 2222)(yx y z y += 所以 dxdy dS 2=积分区域为：:D x y x 222=+，设θcos r x =，θsin r y = dr rd dxdy θ=θπθπc o s 20,22≤≤≤≤-r⎰⎰-=θππθcos 20222rdr d S ππθθππ222124cos 22222=⋅⋅==⎰-d3、求抛物柱面221x z =含在由平面x y y x ===,0,1所围的柱体内的面积解：被积函数为221x z = 22)(x z x = ， 0)(2=y z所以 dxdy x dS 21+=积分区域为：:D x y y x ===,0,1，0=z 围成的闭区域=+=⎰⎰x xdy x dx S 021⎰+xdx x x 0213122)1(3121)1(1211232022-=+⋅=++=⎰x x d x x 。

4、求下列图形的形心（1）、:D 1,0,2===x y x y ，围成的闭区域解：将密度看成1；⎰⎰⎰⎰=xDdy dx dxdy 201032221==⎰dx x 522210232010===⎰⎰⎰⎰⎰dx x dy xdx xdxdy xD2112010===⎰⎰⎰⎰⎰dx x ydy dx ydxdy xD于是得形心坐标为：53322522~==x 82332221~==y 形心为)82353( （2）、:D θρco s 1+=，围成的闭区域解：将密度看成1；πθ23=⎰⎰Ddr rd （前面求出的结果） dr r d rdrd r xdxdy D D⎰⎰⎰⎰⎰⎰+'==θπθθθθcos 10220cos cos⎰+=πθθθ203)cos 1(cos 31d +⎰πθθ20cos 31d +⎰πθθ202cos d +⎰πθθ203cos d ⎰πθθ204cos 31d +=0++⎰πθθ20)2cos 1(21d +0⎰++πθθθ20242cos 2cos 2131d=π1215242122πππ=++65231215~==ππx 由图形关于x 轴的对称性得0~=y 形心为)065(（3）、:D 0,12222≥=+x by a x ，围成的闭区域解：面积ab 2π=⎰⎰⎰⎰---=2222110a xb a x b a Dxdy dx xdxdy ⎰-=adx ax x b 0221232)1(32)2(22123222ba a x ab =--= ππ34232~2a ab ba x == 由图形关于x 轴的对称性得0~=y 形心为)034(πa5、圆盘)0(222>≤+a ax y x 内各点处的密度=),(y x μ22y x +，求此圆盘的质心解：=M =⎰⎰Ddxdy y x ),(μ=+⎰⎰Ddxdy y x 22⎰⎰-θππθcos 20222a dr r d3203332316cos 316a d a ⋅==⎰πθθ3932a ==y M =⎰⎰Ddxdy y x x ),(μ=+⎰⎰Ddxdy y x x 22⎰⎰-θππθθcos 20322cos a dr r d15641588cos 1641442254a a d a =⋅==⎰-ππθθ 56~a M M x y ==，由对称性得0~=y 所求质心为)056(a6、设有一个等腰直角三角形薄片，各点处的密度等于该点到直角顶点距离的平方，求此圆薄片质心解：设等腰直角三角形的顶点为),0(),0,(),0,0(a a 则22),(y x y x +=μ=M =⎰⎰D dxdy y x ),(μ=+⎰⎰Ddxdy y x )(22⎰⎰-+xa a dy y x dx 0220)( ⎰-+-=a dx x a x a x 032])(31)([⎰-+-=a dx x a x a ax 03322]31312[ 62132444a a a =-= =y M =⎰⎰Ddxdy y x x ),(μ=+⎰⎰Ddxdy xy x)(23⎰⎰-+xa a dy xy x dx 0230)(⎰-+-=adx x a x x a x 033])(31)([⎰-+-=a dx x x a x a ax 043223]34312[ 5555515115463121a a a a a =-+-= 由对称性得=x M =⎰⎰Ddxdy y x y ),(μ=+⎰⎰Ddxdy y y x)(32⎰⎰-+ya a dx y y x dy 032)(155a = 52~a M M x y ==，52~a M M x x == 所求质心为)5252(aa 7、设有顶角为α2，半径为R 的扇形薄片，各点处的密度等于该点到扇形顶点距离的平方，求此薄片质心解：设扇形顶点为)0,0(关于x 轴对称则22),(y x y x +=μ=M =⎰⎰Ddxdy y x ),(μ=+⎰⎰Ddxdy y x)(22⎰⎰-Rdr r d 03ααθ24R α==y M =⎰⎰Ddxdy y x x ),(μ=+⎰⎰Ddxdy y x x )(22⎰⎰-Rdr r d 04cos θθαα5sin 2αR =5sin 4~αR M M x y == 由对称性得0~=y ，所求质心为)05sin 4(αR8、设均匀薄片（面密度为常数)ρ，战局的区域如下，求指定的转动惯量（1）、⎭⎬⎫⎩⎨⎧≤+=1),(2222b y a x y x D 求y I ，l I ，其中是过原点切倾斜角为α的直线解：ab M ρπ=y I ρμ==⎰⎰Ddxdy y x x ),(2ρ=⎰⎰Ddxdy x 2⎰⎰123203cos dr r d b a θθπ ===⎰4cos 43202ba d abρθθρπ42Ma由题设可知薄片上任意点到直线l 的距离为αα2tan 1tan +-=y x dl I ==⎰⎰Ddxdy y x d ),(2μ⎰⎰++Ddxdy xy y x )tan 2tan (tan12222αααρ⎰⎰+=Ddxdyx 222tan 1tan ααρ⎰⎰++Ddxdy y 22tan 1αρ⎰⎰+-Dxydxdy ααρ2tan 1tan 24tan 1tan 222Ma ⋅+=ααρdr r d ab ⎰⎰++1322023sin tan 1ϑθαρπdr r d b a θθθαρπ⎰⎰+-1320222sin cos tan 14tan 1tan 222Ma ⋅+=αα2tan 123παρ⋅++ab 4tan 1tan 222Ma ⋅+=αα4tan 1122Mb ⋅++ααα2222tan 1tan 4++⋅=a b M （2）、{}b y a x y x D ≤≤≤≤=0,0),(求y I ，l I ，其中是过原点与点),(b a 的对角线ab M ρ=y I ρμ==⎰⎰Ddxdy y x x ),(2ρ=⎰⎰Ddxdy x 2⎰⎰bady dx x 023323Ma ba ==ρx I ρμ==⎰⎰Ddxdy y x y ),(2ρ=⎰⎰Ddxdy y2⎰⎰bady y dx 0232Mb =由题设可知薄片上任意点到直线l 的距离为22ba ay bx d +-=l I ==⎰⎰Ddxdy y x d ),(2μ⎰⎰-++Ddxdy abxy y a x b b a )2(222222ρ=⎰⎰+Ddxdy x ba b 2222ρ⎰⎰++Ddxdy y ba a 2222ρ⎰⎰+-Dxydxdy ba ab222ρ22223b a b Ma +=22223b a a Mb ++22222b a b a M +-)(62222b a b Ma += 习题9.41、化三重积分⎰⎰⎰Ωdv z y x F ),,(为三次积分（只须先,z 次对,y 后对x 一种次序）（1）、由三个坐标面与平面06236=-++z y x 围成解：23230yx z --≤≤，,220x y -≤≤10≤≤x ⎰⎰⎰Ωdv z y x f ),,(⎰⎰⎰---=yx x dz z y x f dy dx 32302201),,(（2）、由旋转抛物面22y x z +=与平面1=z 围成解：122≤≤+z y x ，,1122x y x -≤≤--11≤≤-x⎰⎰⎰Ωdv z y x f ),,(⎰⎰⎰+-+---=111112222),,(y x x x dz z y x f dy dx（3）、由圆锥面22y x z +=与上半球面222y x z --=围成解：22222y x z y x --≤≤+，,2222x y x -≤≤--22≤≤-x⎰⎰⎰Ωdv z y x f ),,(⎰⎰⎰--+-+---=22222222222),,(y x y x x x dz z y x f dy dx（4）、由双曲抛物面xy z =与平面0,1==+z y x 围成解：xy z ≤≤0，,10x y -≤≤10≤≤x⎰⎰⎰Ωdv z y x f ),,(⎰⎰⎰-=xyxdz z y x f dy dx 01010),,(2、设有一物体，点据空间闭区域{}10,10,10),,(≤≤≤≤≤≤=Ωz y x z y x 密度函数为z y x z y x ++=),,(μ，求该物体的质量解：=++=⎰⎰⎰Ωdv z y x M )(=⎰⎰⎰Ωxdv ++⎰⎰⎰Ωydv =⎰⎰⎰Ωzdv =⎰⎰⎰Ωzdv 32331011==⎰⎰⎰zdz dy dx 3、计算三重积分（1）、⎰Ωx y d v⎭⎬⎫⎩⎨⎧=++====Ω132,0,0,0),,(z y x z y x z y x ⎰⎰⎰Ωxydv ⎰⎰⎰---=)21(30)1(2010yx x xydz dy dx ⎰⎰---=)1(202210)2333(x dy xy y x xy dx ⎰⎰---=)1(202210)2333(x dy xy y x xy dx⎰-----=103222])22(21)22(33)22(23[dx x x x x x x ⎰-----=103222])22(21)22(33)22(23[dx x x x x x x 101512215105]12303010[10432=-+-=-+-=⎰dx x x x x （2）、⎰⎰⎰Ωzdv y x 22 {}x z z x y x y x z y x ==-====Ω.0,,,1),,( ⎰⎰⎰Ωxyzdv ⎰⎰⎰-=xxx zdz y x dy dx 02210⎰⎰-=x x dy y x dx 24102124131107==⎰dx x （3）、⎰Ωx y z d v{}0,1,,),,(=====Ωz x x y xy z z y x⎰⎰⎰Ωxyzdv ⎰⎰⎰=xyxxyzdz dy dx 01264181107==⎰dx x （4）、⎰Ωdv z 2 {}0,1),,(22=--==Ωz y x z z y x⎰⎰⎰Ωxyzdv ⎰⎰⎰------=22221021111y x x x dz z dy dx ⎰⎰--=x dy y x dx 0232210)1(311525132)1(311023220ππθπ=⋅=-=⎰⎰rdr r d （5）、⎰Ωdv z 2 {}z x y z z y x 2),,(222≤++=Ω解；积分区域是1)1(222=-++z y x ，22221111y x z y x --+≤≤---2211x y x -≤≤--111≤≤-x这样计算很繁琐，改为下面的方法（是很高的技巧）任意取一点,z 则截口面积为)2(2z z dxdy -=π⎰⎰⎰⎰⎰⎰=ΩDdxdy dz z dv z2022dz z z )2(243⎰-=π58)542(2054ππ=-=z z4、利用柱坐标计算（1）⎰⎰⎰Ωzdv 其中Ω是由上半球面222y x z --=与旋转抛物面22y x z +=围成的闭区域解：先确定该区域在xoy 面的投影区域⎪⎩⎪⎨⎧+=--=22222y x z y x z 为⎩⎨⎧==+0122z y x 就是{}1),(22≤+=y x y x D 设：θθsin ,cos ,r y r x z z ===，有rdxdydz dv =，222r z r -≤≤ 10,20≤≤≤≤r πθ⎰⎰⎰Ωzdv ⎰⎰⎰-=222120r rzdz rdr d πθ⎰⎰--=104220]2[21dr r r r d πθ 127)61411(]2[21105320ππθπ=--=--=⎰⎰dr r r r d （2）⎰⎰⎰Ω+dv y x z22 其中Ω是由旋转抛物面22y x z +=与平面1=z 围成的闭区域解：先确定该区域在xoy 面的投影区域⎩⎨⎧+==221yx z z 为⎩⎨⎧==+0122z y x 就是{}1),(22≤+=y x y x D 设：θθsin ,cos ,r y r x z z ===，有rdxdydz dv =，12≤≤z r 10,20≤≤≤≤r πθ⎰⎰⎰Ωzdv ⎰⎰⎰=112202rzdz dr r d πθ⎰⎰-=104220]1[21dr r r d πθ 214)7131(][21106220ππθπ=-=-=⎰⎰dr r r d5、设密度为常量μ的均匀物体占据由223y x z --=与0,1,1=±=±=z y x 围成的闭区域，求（1）、物体的质量（2）、物体的重心（3）、物体对于z 轴的转动惯量解：先确定该区域在xoy 面的投影区域就是{}11,11),(≤≤-≤≤-=y x y x D （1）、=M ⎰Ωdv μ ⎰⎰⎰----=22301111y x dz dy dx μ⎰⎰--=-12211)3(2dy y x dx μμμμ328)3138(4)38(4102=-=-=⎰dx x（2）、由对称性得0~,0~==y x=z M =⎰⎰⎰Ωzdv μ⎰⎰⎰----22301111y x zdz dy dx μ⎰⎰--=-122211)3(dy y x dx μμμ45506)316536(2142=+-=⎰dx x x ==MM z z ~210253，所以物体的重心是)210253,0,0( （3）=z I ⎰⎰⎰Ω+dv y x )(22μ⎰⎰⎰----+=2230112211)(y x dz dy y x dx μ⎰⎰--+=122221)3)((4dy y x y x dx μ⎰⎰---+=14422221)233(4dy y x y x y x dx μM dx x x 1056245248)519754(4)3754(41042==-+=-+=⎰μμμ6、设密度为常量1的均匀物体占据由上半球面222y x z --=与圆锥面22y x z +=围成的闭区域，求（1）、物体的质量（2）、物体的重心（3）、物体对于z 轴的转动惯量解：先确定该区域在xoy 面的投影区域⎪⎩⎪⎨⎧+=--=22222y x z y x z 为⎩⎨⎧==+0122z y x 就是{}1),(22≤+=y x y x D 设：θθsin ,cos ,r y r x z z ===，有rdxdydz dv =，22r z r -≤≤ 10,20≤≤≤≤r πθ，于是（1）、=M ⎰⎰⎰Ωdv ⎰⎰⎰-=22120r rdz rdr d πθ⎰⎰--=1220]2[dr r r r d πθ=--=⎰⎰102220]2[dr r r r d πθ)12(34)12(3220-=-=⎰πθπd （2）、由对称性得0~,0~==y x =z M ⎰⎰⎰Ωzdv ⎰⎰⎰-=22120r rzdz rdr d πθ⎰⎰--=102220]2[21dr r r r d πθ=-=⎰⎰10320][dr r r d πθ24120πθπ==⎰d==MM z z ~)12(83+，所以物体的重心是))12(83,0,0(+（3）、=z I ⎰⎰⎰Ω+dv y x )(22 ⎰⎰⎰-=221320r rdz dr r d πθ⎰⎰--=12320]2[dr r r r d πθ=--=⎰⎰1042320]2[dr r r r d πθ)51(2-A π =A dt t t dr r r)(cos sin 242223123⎰⎰=-πdt t t )sin (sin 245203-=⎰π1528)15832(24=-= 所以=z I )328(152)511528(2-=-=ππ （B ）的习题 1、⎰⎰⎰Ω+dv z x y )cos( ⎭⎬⎫⎩⎨⎧==+====Ω0.2,,0,2),,(z z x x y y x z y x ππ ⎰⎰⎰Ωxyzdv ⎰⎰⎰-+=xxdz z x y dy dx 202)cos(ππ=⎰⎰-xdy x y dx 020)sin 1(π⎰-=20)sin 1(21πdx x x 202]cos [sin 2116ππx x x --=21162-=π2、⎰⎰⎰Ωzdv {}z z y x z y xz y x 2,1),,(222222=++=++=Ω皆7：先确定该区域在xoy 面的投影区域⎩⎨⎧=++=++z z y x z y x 21222222为⎪⎩⎪⎨⎧==+04322z y x 就是⎭⎬⎫⎩⎨⎧≤+=43),(22y x y x D 设：θθsin ,cos ,r y r x z z ===，有rdxdydz dv =，22111r z r -≤≤-- 230,20≤≤≤≤r πθ，于是 ⎰⎰⎰Ωzdv ⎰⎰⎰---=221112320r r zdz rdr d πθ=⎰⎰--230220)112(21dr r r d πθ245]21)1(32[2302232ππ=---=r r习题9.51、计算下列对弧长曲线积分（1）、ds y x nl⎰+)(22，其中l 为圆周222a y x =+解：设t a y t a x sin ,cos ==，adt ds =ds y xn l⎰+)(22⎰++==ππ2012122n n a dt a（2）、⎰l yds x sin 其中l 是连接点)0,0(，),3(ππ的直线段解：l 的方程为x y 31=π30≤≤x dx dx ds 310911=+=⎰lyds x sin dx xx ⎰=π303sin 310dt t t ⎰=π0sin 103π103= （3）、⎰l y ds 其中l 是连接点x y 42=上点)0,0(，)2,1(的一段弧解：l 的方程为x y 42= 10≤≤x dx xds 11+= ⎰lyds )122(34)1(34121231-=+=+=⎰x dx x （4）、⎰+l ds y x )( 其中l 是连接点)0,1(，)1,0(的直线段解：l 的方程为x y -=1 ， 10≤≤x ， dx ds 2=⎰+lds y x )(dx ⎰=122=（5）、ds x l⎰，其中l 为x y =与2x y =所围区域的边界解：l 的方程为x y = ， 10≤≤x dx ds 2=l 的方程为2x y = ， 10≤≤x dx x ds 241+=ds x l ⎰dx x x dx x ⎰⎰++=1210412)12655(121)41(32812210232-+=+⋅+x （5）、ds x l⎰，其中l 为x y =与2x y =所围区域的边界解：l 的方程为x y = ， 10≤≤x dx ds 2=l 的方程为2x y = ， 10≤≤x dx x ds 241+=ds x l ⎰dx x x dx x ⎰⎰++=1210412)12655(121)41(32812210232-+=+⋅+x （6）、ds y l⎰，其中l 为圆周122=+y x解：设t y t x sin ,cos ==，dtds =ds y l⎰⎰=πsin tdt ⎰-ππ2sin tdt πππ20cos cos x x +-=422=+= （7）、ds el y x ⎰+22，其中l 为圆周0,,422===+y x y y x 在第一象限的区域的边界解：在直线0=y 上 20≤≤x dx ds =ds ely x ⎰+122122-==⎰e dx e x在弧422=+y x 上设t y t x sin 2,cos 2==，dt ds 2=40π≤≤tds el y x ⎰+222222402ππ⋅==⎰e dt e在直线x y =上 20≤≤x dx ds 2=ds el y x ⎰+32212220222-===⎰e edx exxds ely x ⎰+22+-=)1(2e +⋅22πe )1(2-e )22(2+=πe 2-（8）、⎰l x y ds 其中l 是2,4,0,0====y x y x 围成的矩形的边界解：4321l l l l l +++=1l 的方程为0=y =⎰1l x y d s 001=⎰dx l ，4l 的方程为0=x=⎰4l xyds 004=⎰dy l2l 的方程为4=x=⎰2l x y d s 842==⎰y d y， 3l 的方程为2=y=⎰3l x y d s1624=⎰xdx24=⎰lxyds（9）、⎰l ds y 2其中l 是摆线)cos 1(),sin (t a y t t a x -=-=的一拱解：dt t a t a ds 2222sin )cos 1(+-=dt ta 2sin 22= ⎰l ds y 232022282sin 2)cos 1(a dt t a t a =-=⎰π=⎰π2052sin dt t ⎰π053sin 16udu a1525615832sin 32332053aa udu a =⋅==⎰π（10）、⎰+lds y x 22 其中l 是上半圆周x y x 222=+与x 轴围域的边界解：21l l l +=，1l ：x y x 222=+化为1)1(22=+-y x 设t y t x sin ,cos 1==-，dt ds =⎰+122l ds y x =++=⎰π22sin )cos 1(dt t t =⎰π2cos dt t4cos 420=⎰πudu2l ：0=y ，dx ds =⎰+222l ds y x 22==⎰xdx62422=+=+⎰lds y x2、求半径为,R 中心角为α2的扇形圆弧的质心（密度均匀)1=μ解：选择与书上168页图9-34一样的坐标系，于是根据对x 轴的对称性得0~=y 设1=μ，t R y t R x sin ,.cos ==Rdt ds =R M α2=⎰=lyds M x 1~==⎰-ααtdt R M cos 12==⎰α2cos 2tdt R Mαααsin sin 22R M R ==所求质心为)0sin (ααR3、计算下列关于坐标的曲线积分（1）、⎰+ldx y x )(22，L 是抛物线2x y =上)0,0(O 到)4,2(A 一段弧解：⎰+l dx y x )(221556]53[)(20532042-=+=+=⎰x x dx x x（2）、⎰l y dx ，L 是 2,4,0,0====y x y x 矩形的边界按照逆时针方向解：A O ：0=y ，4:=x B A0=dx ，2:=y C A ，0:=x O C0=dx ，⎰lydx ⎰⎰⋅+=ABOAy dx 00⎰⎰⋅++COBCy dx 028204-==⎰dx（3）、⎰+l x d y y dx ，L 是 20,sin ,cos π≤≤==t t R y t R x 一段针方向的弧解：⎰+l xdy ydx dt x x dt t tR R t R t R )(]cos cos )sin (sin [242⎰++-=π02sin 22cos 202202===⎰ππtR dt t R（4）、⎰+-++lyx dyx y dx y x 22)()(，L 是圆周 222a y x =+沿逆时针方向解：t a y t a x sin ,cos ==，⎰+-++l y x dy x y dx y x 22)()(⎰-+-+=π2022]cos )sin (cos )sin )(sin [(cos a dt t t t t t t a ππ2120-=-=⎰dt（5）、⎰++l x dy dx y x )(，L 是折线 x y --=11从)0,0(到)0,2(一段解：⎩⎨⎧>-≤=121x x x xy ，弧dx dy x y A O ==,: ，dx dy x y B A -=-=,2:⎰++lxydy dx y x )(⎰⎰+=OAAB383732311)22()2(212102=+-++=+-++=⎰⎰dx x x dx x x （6）、⎰---l dy y a dx y a )()2(，L 是 )cos 1(),sin (t a y t t a x -=-=摆线的一拱，从)0,0(到)0,2(a π解：⎰---ldy y a dx y a )()2(dt t a t a a ⎰---=π20)cos 1()]cos 1(2[dt t a t a a ⎰---π20sin )]cos 1([dt t t t a ⎰+=π2022)cos sin (sin220222sin 2cos 1(a dt tt a ππ=+-=⎰4、计算⎰-++l dy x y dx y x )()(，其中L 分别是（1）、x y =2上点)1,1(到)2,4( （2）、点)1,1(到)2,4(的直线段解：（1）、在x y =2上点)1,1(到)2,4(，dx xdy 21=⎰-++ldy x y dx y x )()(dx x x xx x )](21[41-++=⎰3342153723)2121(41=++=++=⎰dx x x （2）、点)1,1(到)2,4(的直线段，3231+=x y ，dx dy 31=⎰-++ldy x y dx y x )()(dx x x x x )]3231(313231[41-++++=⎰ 11398215910)98910(41=⋅+⋅=+=⎰dx x 5、计算⎰+++l dy y x dx y x )2()2(，其中L 分别是（1）、2x y =上点)0,0(到)1,1(的一段弧（2）、3x y =点)0,0(到)1,1(的一段弧（3）、点)0,0(到点)0,1(再到点)1,1(的折线解：（1）、2x y =上点)0,0(到)1,1(，xdx dy 2=⎰+++ldy y x dx y x )2()2(dx x x x xx ])2(22[122⎰+++=3111)432(132=++=++=⎰dx x x x（2）、3x y =点)0,0(到)1,1(的一段弧，dx x dy 23=⎰+++ldy y x dx y x )2()2(dx x xx ])642[153⎰++=3111=++=（3）、点)0,0(到点)0,1(再到点)1,1(的折线⎰+++ldy y x dx y x )2()2(+=⎰dx x 102⎰+1)21(dy y 3=6、一力场由沿x 轴正向的常力→F 构成，求将一个质量为m 的质点沿222R y x =+按逆时针方向移动过第一象限那段弧所做的功解：→F →=i F dx F W l⎰=F R tdt R F -=-=⎰2sin π节9.6习题处理1、计算下列关于坐标的曲线积分，并验证格林公式的正确性（1）dy y x dx y x l )()(22--+⎰，L 是椭圆12222=+by a x 沿逆时针方向解：设t b dy t b y t a dx t a x cos ,sin ,sin ,cos ==-==dy y x dx y xl)()(22--+⎰⎰⎰⎰-+-=πππ2023202320sin cos cos sin tdt t atdt t bdt abab π2-=用格林公式y x y x P +=2),( 2),(y x y x Q +-=1),(-=y x Q x 1),(=y x P ydy y x dx y x l)()(22--+⎰ab dxdy Dπ22-=-=⎰⎰ （2）、dy y x dx y x l )()(222+-+⎰)0,0()1,0()0,1()0,0(:→→→L 直线段围成的闭路解：0),0,1()0,0(:1=→y L ； x y L -=→1),1,0()0,1:2；0),0,0()1,0(:3=→x Ldy y x dx y x l)()(222+-+⎰1])1([012012210-=--+-=⎰⎰⎰dy y dx x x xdx 用格林公式2)(),(y x y x P += 22),(y x y x Q --=x y x Q x 2),(-= )(2),(y x y x P y +=dy y x dx y x l)()(222+-+⎰=+-=⎰⎰Ddxdy y x )2(2⎰⎰-+-xdy y x dx 1010)2(21)2321(210-=-+-=⎰dx x x2、求星形线t a y t a x 33sin ,cos ==所围的面积解：dt t t a ydx xdy A l ⎰⎰=-=π20222sin cos 232183)4cos 1(1632202a dt t t a ππ=-=⎰3、用格林公式计算（1）、dy y x dx y x l)653()42(-+++-⎰)0,0()2,3()0,3()0,0(:→→→L 直线段围成的三角形边界解：653),(-+=y x y x Q 42),(+-=y x y x P3),(=y x Q x y y x P y -=),(dy y x dx y x l)653()42(-+++-⎰12212344=⨯⨯⨯==⎰⎰Ddxdy ⎰⎰-+-x dy y x dx 1010)2(2（2）、dy y y x dx xe xy l x)cos ()32(2-++⎰1:2222=+by a x L 逆时针方向解：x xe xy y x P 32),(+= y y x y x Q c o s ),(2-=x y x Q x 2),(= x y x P y 2),(=dy y x dx y x l)653()42(-+++-⎰00==⎰⎰Ddxdy（3）、⎰+++l y ydy e x dx xey )1()(22224:x x y l -=由)0,4()0,0(→的弧解：先补足成闭路1-+=l OA Ly xe y y x P 2),(+= 1),(22+=y e x y x Qy x xe y x Q 22),(= y y xe y x P 221),(+=⎰+++L y y dy e x dx xe y )1()(222ππ2)2(212-=-=-=⎰⎰Ddxdy 于是⎰+++ly ydy e x dx xey )1()(222-+++=⎰dy e x dx xe y y OA y )1()(22(2⎰+++Ly ydy e x dx xey )1()(222ππ2824+=+=⎰xdx（4）、⎰---l dy y y x dx y )sin ()cos 1(x y l s i n:=上由)0,()0,0(π→的弧解：先补足成闭路1-+=l OA Ly y x P cos 1),(-= )s i n (),(y y x y x Q --=y y y x Q x sin ),(+-= y y x P y s i n ),(=⎰-+---1)sin ()cos 1(l OA dy y y x dx y ⎰⎰⎰⎰-=-=xDydy dxydxdy sin 0π4)12((cos 41sin 21002πππ-=-=-=⎰⎰x xdx于是⎰---ldy y y x dx y )sin ()cos 1(----=⎰dy y y x dx y OA )sin ()cos 1((⎰-+---1)sin ()cos 1(l OA dy y y x dx y4400πππ=+=⎰dx（5）、⎰+--l dy y x dx y x )sin ()(2222:x x y l -=上由)1,1()0,0(→的弧解：先补足成闭路1-++=l AB OA Ly x y x P -=2),( )s i n ),(2y x y x Q --=-=),(y x Q x 1),(-=y x P y⎰-+++--1)sin ()(22lAB OA dy y x x dx y x 0=于是⎰+--l dy y x dx y x )sin ()(22+--=⎰dy y x dx y x OA)sin ()(22dy y x dx y x AB)sin ()(22--=⎰+=⎰102dx x ⎰--12)sin 1(dy y⎰---=10)2cos 1(21131dy y 672sin 41-= （6）、⎰+++l xxdy e x dx ye )()1( 1:2222=+by a x L 上由)0,()0,(a a →-的上半椭圆解：先补足成闭路1),(-++-=l a a Lx ye y x P +=1),( x e x y x Q +=),(x x e y x Q +=1),( x y e y x P =),(ab dxdy dy e x dx ye Dl a a x x π21)()1(1),(==+++⎰⎰⎰-++- 于是⎰+++lxx dy e x dx ye )()1(ab dy e x dx ye a a x x π21)()1(),(-+++=⎰+- ab dx a a π21-=⎰-ab a π212-= 4、证明下列曲线积分在xoy 面内与路径无关，并计算积分值（1）、⎰-++)3,2()1,1()()(dy y x dx y xy x y x P +=),( y x y x Q -=),( 都是初等函数，因此在xoy 面内有连续的偏导数1),(=y x Q x 1),(=y x P y 得 =),(y x Q x ),(y x P y 所以曲线积分在xoy 面内与路径无关⎰-++)3,2()1,1()()(dy y x dx y x ⎰+=21)1(dx x ⎰-+31)2(dy y=--+-+=)19(214)14(21125 （2）、⎰-++-)1,2()0,1(324)4()32(dy xy x dx y xy32),(4+-=y xy y x P 324),(xy x y x Q -= 都是初等函数，因此在xoy 面内有连续的偏导数342),(y x y x Q x -= 342),(y x y x P y -= 得 =),(y x Q x ),(y x P y 所以曲线积分在xoy 面内与路径无关⎰-++-)1,2()0,1(324)4()32(dy xy x dx y xy ⎰+=21)22(dx x ⎰-+13)164(dy y544)14(2=-+-+=25（3）、⎰-++),()0,0()c o s ()s i n (ππdy y xe dx x e y yx e y x P y sin ),(+= y xe y x Q y cos ),(-= 都是初等函数，因此在xoy 面内有连续的偏导数y x e y x Q =),( yy e y x P =),( 得 =),(y x Q x ),(y x P y 所以曲线积分在xoy 面内与路径无关⎰-++),()0,0()cos ()sin (ππdy y xe dx x e yy⎰+=π0)sin 1(dx x ⎰-+ππ0)cos (dy y e y=--++=0)1(2πππe 252+=ππe 5、验证下列dy y x Q dx y x P ),(),(+在整个xoy 面内是某一个函数),(y x u 的全微分，并且求这样的函数),(y x u（1）、dy y x dx y x )2()2(+++解答：y x y x P 2),(+= y x y x Q +=2),( 都是初等函数，因此在xoy 面内有连续的偏导数2),(=y x Q x 2),(=y x P y 得 =),(y x Q x ),(y x P y所以曲线积分在xoy 面内存在),(y x u ，使dy y x dx y x y x du )2()2(),(+++=⎰+++=),()0,0()2()2(),(y x dy y x dx y x y x u ⎰=x xdx 0⎰++ydy y x 0)2(2221221y xy x ++=（2）、dy y xe dx e x y y )2()2(-++解答：y e x y x P +=2),( y xe y x Q y 2),(-= 都是初等函数，因此在xoy 面内有连续的偏导数y x e y x Q =),( y y e y x P =),( 得 =),(y x Q x ),(y x P y所以曲线积分在xoy 面内存在),(y x u ，使=),(y x du dy y xe dx e x y y )2()2(-++⎰-++=),()0,0()2()2(),(y x yydy y xe dx e x y x u ⎰+=x dx x 0)12(⎰-+yy dy y xe 0)2(=-+-+=x xe y x x y 22y xe y x +-22（3）、y d y x y d x x 3c o s 2c o s 33s i n 2s i n2-解答：y x y x P 3sin 2sin 2),(= y x y x Q 3c o s 2c o s 3),(-= 都是初等函数，因此在xoy面内有连续的偏导数y x y x Q x 3c o s 2s i n 6),(= y x y x P y 3c o s 2s i n 6),(= 得 =),(y x Q x ),(y x P y所以曲线积分在xoy 面内存在),(y x u ，使=),(y x du dy y x Q dx y x P ),(),(+⎰-=),()0,0(3cos 2cos 33sin 2sin 2),(y x ydy x ydx x y x uy x ydy x y 3sin 2cos 3cos 2cos 30-=-=⎰（4）、dy ye y x y x dx xy y x y)122()3(223322++++解答：32283),(xy y x y x P += yye y x y x y x Q ++=223122),( 都是初等函数，因此在xoy 面内有连续的偏导数22246),(xy y x y x Q x += =),(y x P y 22246xy y x + 得 =),(y x Q x ),(y x P y 所以曲线积分在xoy 面内存在),(y x u ，使=),(y x du dy y x Q dx y x P ),(),(+⎰++++=),()0,0(223322)122()83(),(y x y dy ye y x y x dx xy y x y x u31 ⎰++=yy dy ye y x y x y x u 0223)122(),(y y e ye y x y x -++=322346、设→→→-++=j xy i y x F )12()(2试证：在在xoy 面内，→F 作的功与路径无关证明：⎰-++=l dy xy dx y x W )12()(22),(y x y x P += 12),(-=xy y x Q 都是初等函数，因此在xoy 面内有连续的偏导数 y y x Q x 2),(= y y x P y 2),(= 得 =),(y x Q x ),(y x P y所以曲线积分在xoy 面内积分与路径无关，所以在在xoy 面内， →F 作的功与路径无关。

高等数学课后习题答案第九章2

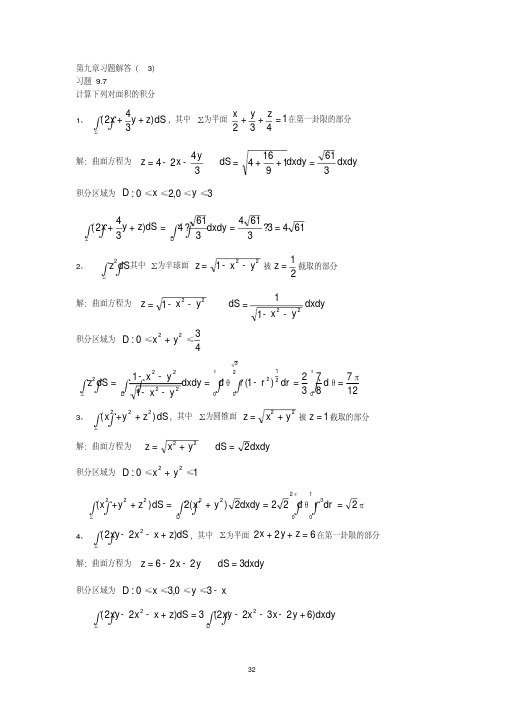
第九章习题解答（3）习题9.7计算下列对面积的积分1、dS z y x )342(++∫∫Σ，其中Σ为平面1432=++zy x 在第一卦限的部分解：曲面方程为3424y x z --=dxdydxdy dS 36119164=++=积分区域为30,20:≤≤≤≤y x D dS z y x )342(++∫∫Σdxdy D∫∫?=361461433614=?=2、∫∫ΣdS z2其中Σ为半球面221y x z --=被21=z 截取的部分解：曲面方程为221yx z --=dxdyyx dS 2211--=积分区域为430:22≤+≤y x D dS z ∫∫Σ2dxdy y x yx D ∫∫----=222211∫∫-=πθ0230212)1(dr r r d 12787320πθπ==∫d 3、dS z y x )(222++∫∫Σ，其中Σ为圆锥面22y x z +=被1=z 截取的部分解：曲面方程为22yx z +=dxdydS 2=积分区域为10:22≤+≤y x D dS z yx )(222++∫∫Σdxdy y x D∫∫+=2)(222∫∫=πθ201322dr r d π2=4、dS z x x xy ∫∫Σ+--)22(2，其中Σ为平面622=++z y x 在第一卦限的部分解：曲面方程为y x z 226--=dxdydS 3=积分区域为xy x D -≤≤≤≤30,30:dS z x x xy ∫∫Σ+--)22(2dxdyy x x xy D∫∫+---=)62322(32∫∫-+---=3302)62322(3xdy y x x xy dx ∫-+-------=30222)]3(6)3()3(3)3(2)3([3dxx x x x x x x x ∫+-=323]9103[3dx x x 4278127108149-=+×-×=5、dS y x )(22∫∫Σ+，其中Σ为旋转抛物面222y x z --=在xoy 面上方的部分解：曲面方程为222yx z --=dxdyy x dS )(4122++=积分区域为20:22≤+≤y x D dS y x )(22∫∫Σ+dxdy y x y x D∫∫+++=)(41)(2222∫∫+=πθ2022341drr r d ∫∫+=πθ20220231161duu u d 其中du u u222031+∫单独计算为设tdt du t u 2sec ,tan ==，du u u 222031+∫==∫dt tt22arctan 063cos sin ∫-22arctan 062cos )(cos )1(cos tt d t 15596151307263265242)11(41316=-=-=-=∫dv v vdS y x )(22∫∫Σ+3014915596162ππ=×=（6）、dS xz z y y x )(222222++∫∫Σ，其中Σ为圆锥面22y x z +=被圆柱面xy x 222=+所截取的部分解：曲面方程为22yx z +=dxdydS 2=积分区域为：θπθcos 20,20:≤≤≤≤r DdS x z z y y x )(222222++∫∫Σdrr d )1sin (cos 2222cos 2052+=∫∫θθθθπθθθθπd )cos cos (cos 6222621086+-×=∫8229)2047(322)!!6!!5!!10!!9!!8!!7(62226πππ=+=×+-×=2、求抛物面)10)((2122≤≤+=z y x z 的质量，此壳的密度z=μ解：dSz M ∫∫Σ=dxdyy x dS 221++=积分区域为：20,20:≤≤≤≤r D πθdS z M ∫∫Σ=dr r rd 223212+=∫∫πθ∫∫--=2arctan 06220cos cos )cos 1(2t td t d πθdu u u d )11(24131620-=∫∫πθdu u u d )11(2413162-=∫∫πθ)33315139(-+-=π)136(152+=π3、求均匀抛物面壳)410(22≤≤+=z y x z 的重心解：∫∫Σ=dSM dxdyy x dS )(4122++=积分区域为：210,20:≤≤≤≤r D πθ∫∫Σ=dS M dr r r d 22102414+=∫∫πθ)2()2(1)2(22102r d r r d +=∫∫πθdu u u d 21020)(1+=∫∫πθ)122(6)1(322121232-=+??=ππu 由对称性得~~==y xMz 1~=∫∫ΣzdS ∫∫+=πθ2021023411dr r rd M ∫∫+=πθ201231161duu ud M∫∫--=ππθ204062cos cos )cos 1(161t t d t d Mdv v v d M )11(1612012146∫∫-=πθ×=M 8π=-+-)32215124()12(1528+?M π70235+=所以重心为?????+70235004、设稳定不可压缩的流体速度场为→→→→++=k z y j y x i xz V 22，Σ是圆柱面122=+y x 的外侧被平面1,0==z z 截取的位于第一、第四卦限部分，求流体流向Σ指定一侧的流量Φ解：Φzdxdyy ydzdx x xzdydz 22++=∫∫Σ设;0:1=Σz ;0:2=Σy ;1:3=Σz 于是-Σ-Σ12Σ3Σ+构成封闭的曲面∫∫∫∫∫?Σ+Σ-Σ-Σ++=++=dv z yx zdxdy y ydzdx x xzdydz )(2222321dz z r rdr d ][21010220+=∫∫∫πθ2)21(21320πθπ=+=∫∫dr r r d =++∫∫Σ+Σ-Σ-zdxdy y ydzdx x xzdydz 22321+∫∫Σ-310dxdy ∫∫Σ-20dzdx ∫∫Σ+32dxdy y 8sin 210322πθθπ==∫∫dr r d 所以838222πππ=-=++=Φ∫∫Σzdxdy y ydzdx x xzdydz 5、计算下列对坐标的曲面积分（1）、∫∫Σdxdy yx 22，其中是球面2222a z y x =++下半部分的下侧解：球面方程为222y x a z ---=，积分区域为ar ≤≤≤≤0,20:πθ取外法线方向为正∫∫Σdxdy y x 22dxdy y x a y x D)(22222----=∫∫dxdyy x a yx D22222--=∫∫drr a r∫∫-=102252022cos sinθθπ1052)!!7!!5!!5!!3(4)sin (sin 84cos 1220752022a a dr t t d a ππθθππ=-=--=∫∫（2）、∫∫Σ+dydz y 2)1(，其中是球面1222=++z y x 的外侧在0≥x 的部分解：球面方程为221y x x --=，积分区域为10,20:≤≤≤≤r πθ取外法线方向为正∫∫Σ+dydz y 2)1(dr r r d ∫∫+=1220)1sin (θθπdrr r r d ∫∫++=122320)sin 2sin (θθθπ∫++=πθθθ202)21sin 32sin 41(d 45)82cos 1(20ππθθπ=+-=∫d （3）、∫∫Σdxdy z2，其中是圆锥面22y x z +=被平面1=z 截取的有限部分的下侧解：积分区域为10,20:≤≤≤≤r πθ取外法线方向为正∫∫Σdxdy z 2∫∫+-=Ddxdyy x )(22dr r d ∫∫-=10320πθ2412ππ-=×-=（4）、xdxdyydzdx xdydz ++∫∫ΣΣ是圆柱面122=+y x 的外侧被平面3,0==z z 截取的位于第一限部分解：=++∫∫Σxdxdy ydzdx xdydz C B A ++∫∫Σ=xdydz A ，∫∫Σ=ydzdx B ，∫∫Σ=zdxdy C 由于Σ在xoy 面的投影区域面积为零，所以0==∫∫Σzdxdy C ∫∫Σ=xdydz A dy y dz dydz y yzD∫∫∫∫-=-=1023021143cos 3202ππ==∫tdt ∫∫Σ=ydzdx B dy x dz dydz x zxD∫∫∫∫-=-=1023021143cos 3202ππ==∫tdt 所以=++∫∫Σxdxdy ydzdx xdydz 2304343πππ=++=++C B A（5）、∫∫Σ-+-+-dxdy x z dzdx z y dydz y x )()()(Σ{}c z b y a x z y x ≤≤≤≤≤≤=0,0,0),,(解：用高斯公式、∫∫Σ-+-+-dxdy x z dzdx z y dydz y x )()()(abcdv 3==∫∫∫（6）、∫∫Σ++zxdxdyyzdzdx xydydz Σ{}1,0,0,0),,(=++====z y x z y x z y x 的外侧解：用高斯公式、∫∫Σ++zxdxdyyzdzdx xydydz =++=∫∫∫dv z y x )(∫∫∫---++yx xdzz y x dydx101010)(∫∫---+--+=xdy y x y x y x dx 10210])1(21)1)([(∫∫----=xdy y xy x dx 102210]21[21∫------=10322])1(31)1()1)(1[(21dx x x x x x 81)3132(21103=+-=∫dx x x 习题9.81、利用高斯公式计算（1）、∫∫Σ++dxdyz dzdx y dydz x 222Σ{}a z a y a x z y x ≤≤≤≤≤≤=0,0,0),,(的表面的外侧解：∫∫Σ++dxdy z dzdx y dydz x 222=++=∫∫∫dv z y x )(2∫∫∫?zdv 64236azdz aa ==∫（2）、∫∫Σ-+dxdyy x dzdx y xydydz 4223Σ)1,0,0(),0,01(),0,0,1(),0,0,0(:为顶点的四面体的表面的外侧解：∫∫Σ-+dxdy y x dzdx y xydydz 4223=+=∫∫∫dv y y )23(∫∫∫?ydv5任取一点y 得到与四面体的截面面积为2)1(21y dzdx yD-=∫∫于是245)413221(25)1(255102=+-=-=∫∫∫∫dy y y ydv （3）、zdxdy ydzdx xdydz ++∫∫Σ，222:y x a z --=Σ的上侧解：加一个底面1Σ0=z ，则1Σ+Σ=Σ′3326433a a dv zdxdy ydzdx xdydz ππ=×==++∫∫∫∫∫?Σ′而：001=-=++∫∫∫∫ΣxyD dxdy zdxdy ydzdx xdydz 所以32azdxdy ydzdx xdydz π=++∫∫Σ（4）、dxdy z x dzdx y z dydz x y )()()(222-+-+-∫∫Σ，221:y x z --=Σ在xoy 面上方的上侧解：加一个底面1Σ0=z ，则1Σ-Σ=Σ′dxdy z x dzdx y z dydz x y )()()(2221-+-+-∫∫Σ-Σππ23)1(3310-=-×-=-=∫∫∫∫dz z dv 而：dxdyz x dzdx y z dydz x y )()()(2221-+-+-∫∫Σ4cos 1023202πθθπ-=-=-=∫∫∫∫dr r d dxdy x xyD45423)()()(222πππ-=+-=-+-+-∫∫Σdxdy z x dzdx y z dydz x y 2、设稳定的、不可压缩的流体的速度场为→→→→++=k z j y i x V 222，Σ是球面2222a z y x =++的外侧位于第一卦限部分，求流体流向Σ指定一侧的流量Φ解：Φdxdy z dzdx y dydz x 222++=∫∫Σ设;0:1=Σx ;0:2=Σy ;0:3=Σz 于是-Σ-Σ12Σ3Σ-构成封闭的曲面∫∫∫∫∫?Σ+Σ+Σ+Σ++=++dv z y x dxdy z dzdx y dydz x )(2222321dzz r rdr d ar a ])sin (cos [2002022++=∫∫∫-θθθπ∫∫-+=adr r a r d 022220)sin (cos 2πθθθ∫∫-+adrr a r d 02220)(πθ∫-=20424)sin (sin 4πdt t t a )42(244a a -+π8384444aa a πππ=+=而222321=++∫∫Σ+Σ+Σdxdy z dzdx y dydz x 所以dxdy z dzdx y dydz x 222++=∫∫Σ834aπ=三重积分也可以另解为：任取一点z ，得到截面z D 的面积为)(422z a dxdy zD -=∫∫π根据对称性有∫∫∫++dv z y x )(24032083)(466a dz z z a dxdy zdz a D azππ=-==∫∫∫∫第九章习题解答完毕2008-5-11于利民开发区宏信广场。

上海财经大学《高等数学》第九章习题及解答

第九章习题解答1.设xoy 平面上的一块平面薄片D ，薄片上分布有密度为),(y x u 的电荷，且),(y x u 在D 上连续，请给出薄片上电荷Q 的二重积分表达式．[解] 板上的全部电荷应等于电荷的面密度(,)u x y 在该板所占闭区域D 上的二重积分, 即=(,)DQ u x y d σ⎰⎰.2.由平面1342=++z y x ，0=x ， 0=y ，0=z 围成的四面体的体积为V ，试用二重积分表示V ． [解] 4(1)23Dx yV dxdy =--⎰⎰. 3．比较大小 (1) σ⎰⎰+D d y x 2)( 与σ⎰⎰+Dd y x 3)(，其中D 是x 轴、y 轴与直线1=+y x 所围成．(2)σ⎰⎰+Dd y x 2)(与σ⎰⎰+Dd y x 3)(，其中D 是由圆2)1()2(22=-+-y x 所围成． [解] (1) 由0x 1y ≤+≤，得32()x y ≤+(x+y), 由二重积分的性质可得23()()DDx y d x y d σσ+≥+⎰⎰⎰⎰.(2) 由积分区域D 位于+1x y ≥的半平面内，所以D 内有23()()x y x y +≤+，由二重积分的性质可得23()()DDx y d x y d σσ+≤+⎰⎰⎰⎰. 4．估计： (1) I=σ⎰⎰+Dd y x xy )(，其中D 是矩形区域：0≤x ≤1，0≤y ≤1；(2) I=σ⎰⎰++Dd y x )1(，其中D 是矩形区域：0≤x ≤1，0≤y ≤2；(3) I=σ⎰⎰++Dd y x )9(22，其中D 是圆形区域：422≤+y x ． [解] (1) 因为在区域D 上有01,0y 1x ≤≤≤≤，所以01,02,xy x y ≤≤≤+≤故0()2xy x y ≤+≤，所以0()22,DDDd xy x y d d D σσσ≤+≤=⎰⎰⎰⎰⎰⎰上海财经大学《高等数学》第九章习题及解答即()2Dxy x y d σ≤+≤⎰⎰0.（2）因为在区域D 上01,02x y ≤≤≤≤，所以114x y ≤++≤，故()=x 14=4DDDD d y d d D σσσ≤++≤⎰⎰⎰⎰⎰⎰，即()218Dx y d σ≤++≤⎰⎰.(3) 因为2222x 494()925,y x y ≤++≤++≤9，所以25D I D ≤≤9，即36100I ππ≤≤.5．由二重积分的几何意义计算⎰⎰--Dd y x R σ222，222:R y x D ≤+．[解] 令2222z x y z R =++=，所以z Dd σ⎰⎰为上半球体的体积, 于是有314=23DR σπ⋅⎰⎰.6．求下列二重积分 1)σ⎰⎰+D d y x)(22，其中D 是矩形区域：|x|≤1， |y|≤1；2)σ⎰⎰+Dd y x )23(，其中D 是x 轴、y 轴与直线2=+y x 所围成闭区域;3)σ⎰⎰++Dd y y x x )3(322，其中D 是矩形闭区域：0≤x ≤1，0≤y ≤1； 4)σ⎰⎰+Dd y x x )cos(, 其中D 是顶点分别为（0，0），（π,0）和(π,π)的三角形闭区域; 5）σ⎰⎰Dy x d e),max{22，其中D 是矩形闭区域：0≤x ≤1，0≤y ≤1.[解] (1) 1112222211128233Dx y d x y dxdy x dx σ---+=+=+=⎰⎰⎰⎰⎰（）（）（）. （2）22-003232xDx y d dx x y dy σ+=+⎰⎰⎰⎰（）（）22224)xx dx =++⎰(-3220220(4)33x x x =-++=.(3) 11323323033Dx x y y d dy xx y y dx σ++=++⎰⎰⎰⎰（）（）42131001()()14424y y y y y dy =++=++=⎰.(4)coscos()xDx x y d xdx x y dy πσ+=+⎰⎰⎰⎰（）001(sin 2sin )(cos 2cos )2x x x dx xd x x ππ=-=--⎰⎰00113(cos 2-cos )cos 2-cos 222x x x x x dx πππ=-+=-⎰（）. (5) 因{}222222111max ,100001111(1)2222x x y x x x xD e d dx e dy e xdx e dx e e σ=====-⎰⎰⎰⎰⎰⎰, 所以 {}22max ,(1)x y Ded e σ=-⎰⎰.7. 画出积分区域，计算积分： 1) σ⎰⎰Dd y x ，其中D 是由两条抛物线2x y =, x y =所围成闭区域， 2) σ⎰⎰Dd xy2，其中D 是由圆周422=+y x 及y 轴所围成右半闭区域，3) σ⎰⎰+D yx d e, 其中D 是由1≤+y x 所确定的闭区域，4)σ⎰⎰-+Dd x y x )(22，其中D 是由直线x y y ==,2 及x y 2=所围成的闭区域． [解] （1）图略.27114400226()3355xDdx x x dx σ==-=⎰⎰⎰⎰（2）图略.222352222164();31015Dxy d dy dx y y σ--==-=⎰⎰⎰ （3）图略.1111101x x x y x y x y x x De d e dx e dy e dx e dy σ+-++----=+⎰⎰⎰⎰⎰⎰1211211()()x x ee dx e e dx +---=-+-⎰⎰21021111111()()22x x e x ex e e e e +---=-+-=-.(4) 图略.2222202()()yy Dxy x dy x y x dx +-=+-⎰⎰⎰⎰2330193()248y y dy =-⎰ 4321911()2448y y =⋅- 136=. 8. 交换下列的积分顺序 1) ⎰⎰--22221),(x x xdy y x f dx ,2) ⎰⎰--aax a dy y x f dx 220),(3）⎰⎰-xx dy y x f dx sin 2sin 0),(π；4）⎰⎰--2ln 1),(2y e dx y x f dy ⎰⎰-++2)1(2112),(y dx y x f dy ;5)⎰⎰⎰⎰-+31301020),(),(yy dx y x f dy dx y x f dy ;6)⎰⎰--2ln 1),(2ye dx y xf dy ⎰⎰-++2)1(2112),(y dx y x f dy .[解] (1) 图略.2111202(,)(,)xydx f x y dy dy f x y dx--=⎰⎰⎰(2) 图略.(,)(,)aaadx f x y dy dy f x y dx-=⎰⎰(3) 图略.sin 01arcsin 0sin12arcsin 0arcsin 2(,)(,)(,)xyx yydx f x y dy dy f x y dx dy f x y dxπππ----=+⎰⎰⎰⎰⎰⎰(4) 图略. 因{}{}22ln =1,2(,)111)2D y e y x x y y y x -≤≤-≤≤⋃≤≤-≤≤（x,y ）,因此积分区域还可以表示为212,02,1x D x y x e y x -⎧⎫⎪⎪=≤≤≤≤+⎨⎬⎪⎪⎩⎭（）,所以 1222212221(101)1 (,)(,)(,)x x eIn y yedy f x y dx f x y dx dx f x y dy --+--+=⎰⎰⎰⎰⎰⎰.(5) 图略. 由3x y =-和=2=1x y ,，得123323012(,)(,)=(,)yyxxdy f x y dx dy f x y dx dx f x y dy --+⎰⎰⎰⎰⎰⎰.9．计算下列二重积分： ⑴⎰⎰+Dy x d e σ23．2||,2||:≤≤y x D ⑵⎰⎰+Dd y xσ)(22．1||||:≤+y x D ．⑶⎰⎰+Ddxdy y x 221．10,10:≤≤≤≤y x D . ⑷⎰⎰--Ddxdy y x )2(21．2,:x y x y D ==． [解] 223232322266442222111(1)()()326x y x y x y De d e dx e dy e e e e e e σ+------==+=--⎰⎰⎰⎰. (2)3111222100()()3xxy dx x y dy dx x y --+=+⎰⎰⎰3120(1)(1)3x x x dx ⎡⎤-=-+⎢⎥⎣⎦⎰ 12463=⨯=. (3) 23112110220011arctan 1133412Dx x dxdy x dx dy yy y ππ===⋅=++⎰⎰⎰⎰. (4)21011(2)(2)22x x Dx y dxdy dx x y --=--⎰⎰⎰⎰ 22101(2)22xx y dx y xy =--⎰2412230122222x x x x x x dx ⎡⎤⎛⎫⎛⎫=-----⎢⎥ ⎪ ⎪⎝⎭⎝⎭⎣⎦⎰1711(1)26410=-++ 11120=.10．利用极坐标求下列积分 1）⎰⎰+Dd y x σ)(22其中D 是由直线x y =, )0(3,,>==+=a a y a y a x y 所围成的区域. 2)⎰⎰+Ddxdy y x 22．1:22≤+y x D ．3）⎰⎰--D d y x R σ222,其中D 是由圆周Rx y x =+22所围成的区域.4) ⎰⎰+Ddxdy y x)(22．y y x D 6:22≤+．5）⎰⎰-+Dd y x σ222,其中D :322≤+y x . 6)σ⎰⎰++Dd y x )1ln(22,其中D 是由圆周122=+y x 及坐标轴所围成的第一象限内的闭区域； 7)计算dxdy y x D)(22⎰⎰+，其 D 为由圆 y y x 222=+，y y x 422=+及直线y x 3-0=， 03=-x y 所围成的平面闭区域8) 计算二重积分⎰⎰++Ddxdyyx y x 2222)sin(π,其中积分区域为22{(,)|14}D x y x y =≤+≤；9)σ⎰⎰++--Dd yx y x 222211，其中D 是由圆周122=+y x 及坐标轴所围成的第一象限内的闭区域． 10)⎰⎰++Dd y xσ)1ln(22．4:22≤+y x D ，0≥x ，0≥y ．[解] (1) 32222414ayay a Dx y d dy x y dx a σ-+=+=⎰⎰⎰⎰（）（）.（2）2120012233Dd r dr πθππ==⋅=⎰⎰.（3）cos 202R Dd rdr πθπθ-=⎰⎰cos 202R d rdr πθθ=⎰⎰33320112(sin )33R R d πθθ=-⎰34()33R π=-. （4）设cos ,sin x r y r θθ==, 则006sin r θπθ≤≤≤≤，.22=Dx y dxdy +⎰⎰原式（）6sin 3444000136sin 6432d r dr d πθπθθθπ==⨯=⎰⎰⎰.2222222000442230(5)22)2)55((24442D x y d d rdr d r rdr r rdr r r d r r πππσθθθππ⎡⎤+-=-=-+-⎢⎥⎣⎦⎡=--=⋅=⎢⎣⎰⎰⎰⎰⎰（6）积分区域D 的极坐标表达式0,012r πθ≤≤≤≤，则12222+x (1)(221)4DInd In r rdr In ππσ=+=-⎰⎰⎰⎰（1+y ）.（7）内边界22sin 2sin r r r θθ=⇒=, 外边界24sin 4sin r r r θθ=⇒=,则,2sin 4sin 63r ππθθθ≤≤≤≤，所以原式=4sin 2224332sin 6660sin 15(48Ddxdy d r rdr d ππθππθπθθθ=⋅==-⎰⎰⎰⎰⎰（x +y ）（8）cos ,sin x r y r θθ==，则02,12r θπ≤≤≤≤，原式221=sin 4Dd rdr πθπ==-⎰⎰.（9）采用极坐标计算200(2)8Dd ππθπ==-⎰⎰. (10) 积分区域D 的极坐标表达式为022r πθ≤≤≤≤0，，则22222+(1)(554)4DInd d In r rdr In ππσθ=+=-⎰⎰⎰⎰（1x +y ）.11. 将三次积分⎰⎰⎰yxxdz z y x f dy dx ),,(110改换积分次序为z y x →→.[解] 110(,,)(,,)xy yy x xxD I dx dy f x y z dz d f x y z dz σ==⎰⎰⎰⎰⎰⎰，现改为先y 后x 的顺序：11(,,)(,,)yyxDxzI dy dx f x y z dz dy f x y z d σ==⎰⎰⎰⎰⎰⎰现改为先x 后z 的顺序:10(,,)(,,)yzy z zD I dy dz f x y z dx d f x y z dx σ==⎰⎰⎰⎰⎰⎰现改为先y 后z 的顺序:110(,,)zzI dz dy f x y z dx =⎰⎰⎰.12．将三次积分⎰⎰⎰+10122),,(y x dz z y x f dy dx 改变成按x z y ,,的次序积分.[解] 1()(,,)(,,)D x I f x y z dV dx f x y z Ω==⎰⎰⎰⎰⎰⎰,其中22.Dy ≤≤≤≤+（x ）：0y 1,0z x 现改为先y 后z 的顺序，将D （x ）分成两部分: 2,01;y ≤≤≤≤0z x2211x z x y ≤≤+≤≤,所以：222111110=x x xI dx dz dy dx dz ++⎰⎰⎰⎰⎰.13．.求下列给定区域的体积 1)求由曲面222y xz +=及2226y x z --=,所围成的立体的体积;2）求由下列曲面所围成的立体体积，y x z+=，xy z =，1=+y x ，0=x ，0=y .[解] 1) 222226(2)z x y x y =+=-+, {22(,)|2},D x y x y =+≤ 于是2222(62)(2)DV z y x y dxdy =---+⎰⎰2263()D xy dxdy =-+⎰⎰2203)6r rdrd πθπ=-=⎰. 2) []111107()24xx y xx y z x xyV d d d d x y xydy -+-==+-=⎰⎰⎰⎰⎰. 14．作适当的变换,计算下列二重积分:1）⎰⎰Ddxdy y x22,其中D 是由两条双曲线1=xy 和2=xy ,直线x y =和xy 4=所围成的在第Ⅰ象限的闭区域. 2）⎰⎰+Ddxdy y x )(22,其中D 是椭圆区域:1422≤+y x . [解] 1) (,)(,)1,2,(,)(,)22u xyu v x y v yx y u v v v =⎧∂∂⎪==⎨∂∂=⎪⎩, {}'(,)|12,14D u v u v =≤≤≤≤, 于是,2422221117ln 2223x y u v u v D D u x y d d u d d d d v v =⋅==⎰⎰⎰⎰⎰⎰. 2) cos 1sin 2x r y r θθ=⎧⎪⎨=⎪⎩, {}'(,)|01,02D r r θθπ=≤≤≤≤, 于是 ,,222221()(cos sin )42D Dr x y dxdy r drd θθθ+=+⎰⎰⎰⎰ 123001535(cos 2)28832r drd πθθπ=+=⎰⎰.15. 计算dxdydz z xy V42⎰⎰⎰．31,20,10:≤≤≤≤≤≤z y x V ．[解]1232424213230010111196823515Vxy z dxdydz xdx y dy z dz x y z ==⋅⋅=⎰⎰⎰⎰⎰⎰. 16．计算dxdydz z y x V⎰⎰⎰++)sin(．V 由平面0=x ，0=y ，0=z ，2π=++z y x 围成．[解]222sin()sin()x yx y z dxdydz dx dy x y z dz πππ--Ω++=++⎰⎰⎰⎰⎰⎰22200cos()|x ydx x y z dy πππ--=-++⎰⎰22sin()|xx y dx ππ-=+⎰12π=-.17．在柱面坐标系下计算三重积分dxdydz y xV⎰⎰⎰+)(22，其中V 由旋转抛物面)(2122y x z +=及平面2=z 所围成的立体． [解] 令cos sin x r y r θθ=⎧⎨=⎩, {}'02,02V r z θπ=≤≤≤≤≤≤, 于是,222223016()3x y z r z r z VVx y d d d r rd d d d d d πθθπ+=⋅==⎰⎰⎰⎰⎰⎰⎰⎰. 18．设有物体占有空间V: 0≤x ≤1, 0≤y ≤1,0≤z ≤1,在点()z y x ,,的密度是()z y x z y x ++=,,ρ,求该物质量.[解] (,,)()M x y z dxdydz x y z dxdydz ρΩΩ==++⎰⎰⎰⎰⎰⎰1113()2dx dy x y z dz =++=⎰⎰⎰. 19.计算⎰⎰⎰Vdxdydz z xy32,其中V 是曲面xy z =与平面1,==x x y 和0=z 所围成的闭区域．[解] Ω在xOy 面上的投影区域Dxy 由,1,0y x x y ===所围成，则11232312001128364xxyxyz dxdydz xdx y dy z dz x dx Ω===⎰⎰⎰⎰⎰⎰⎰. 20.计算⎰⎰⎰+++Vz y x dxdydz3)1(, 其中V 是平面1,0,0,0=++===z y x z y x 所围成的四面体．[解] 令1x y z ++=中的0z =，得1x y +=，Ω在xOy 面上的投影区域Dxy 由0,0,1x y x y ==+=所围成, 所以111330001(1)(1)x x y dxdydz dx dy dz x y z x y z ---Ω=++++++⎰⎰⎰⎰⎰⎰ 1120011115()(ln 2)24(1)28x x y d d x y -=--=--++⎰⎰. 21. 计算⎰⎰⎰Vxyzdxdydz ,其中V 是球面1222=++z y x 及坐标面所围成的第一卦限内的闭区域．[解] 令2221x y z ++=中z=0得221y +=x ，故Ω在xOy 面上的投影区域Dxy 由221,0,0x y x y +===所围成，故1xyzdxdydz dx xyzdz Ω=⎰⎰⎰⎰1122220001111(1)(1)22448xdx y x y dy x x dx ⎡⎤=--=-=⎢⎥⎣⎦⎰⎰. 22. 计算⎰⎰⎰Vxyzdxdydz ,其中V 是平面1,,0===y y z z 以及抛物柱面2x y =所围成的闭区域．[解] （1）故Ω在xOy 面上的投影区域Dxy 由1y =，2y x =所围成, 所以2111yxxzdxdydz dx dy xzdz -Ω=⎰⎰⎰⎰⎰⎰21121102x xdx y dy -==⎰⎰. （2）Ω在z 轴上的投影区域为[]0,h ，过[]0h ，内的任一点做垂直于z 轴的平面截Ω得截面为一圆域Dz ，其半径为R z h，所以Dz 为：22222R x y z h +=，面积为222R z h π，所以222224hhDzR R h zdxdydz zdz dxdy zz dz h ππΩ===⎰⎰⎰⎰⎰⎰⎰.23. 计算⎰⎰⎰Vzdxdydz , 其中V 是曲面222y x z --=及22y x z +=所围成的闭区域． [解]联立z =及22z x y =+，22=1x y +，故Ω在xOy 面上的投影区域为221x y +≤ ，用柱坐标得2242121027()2212rr r zdv d rdr d r dr ππθπθΩ-==-=⎰⎰⎰⎰⎰⎰⎰.24. 计算⎰⎰⎰+Vdv y x )(22,其中V 是z y x 222=+及平面2=z 所围成的闭区域． [解] 联立222x y z +=及2z =得224x y +=，故Ω在xOy 面上的投影区域为224x y +≤，所以2222223216()3r x y dv d r dr dz ππθΩ+==⎰⎰⎰⎰⎰⎰. 25. 计算⎰⎰⎰++Vdv z y x )(222,其中V 是球面1222=++z y x 所围成的闭区域． [解]2122240004()sin 5x y z dv d d r dr ππϕπθϕΩ++==⎰⎰⎰⎰⎰⎰. 26. 计算⎰⎰⎰Vzdv ,其中V 是由不等式()2222a a z y x ≤-++, 222z y x ≤+所围成的闭区域．[解] 在球面坐标系中，2222()y z a a ++-≤x ，即为2222cos ,r a x y z ϕ≤+≤，即4πϕ≤，所以22cos 2344440sin cos 2sin 2cos a zdv d d r dr ad d πππϕπϕϕϕϕϕθϕθΩ==⎰⎰⎰⎰⎰⎰⎰⎰245440074cos (cos )6ad d a ππθϕϕπ=-=⎰⎰.27. 用三重积分计算下面所围体的体积:(1) 226y x z --=及22y x z +=(2) az z y x 2222=++及222z y x =+(含z 轴部分).[解] (1) 226z x y =--可变为26z r =-, z =变为z r =, 则22262230322(6)3r rV dv rdrd dz d rdr dz r r r dr r πθθπ-ΩΩ====--=⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰. (2) 222x y z +=的球面坐标方程为=4πϕ, 2222x y z az ++=的球面坐标方程为2cos r a ϕ=, 则22cos 22340sin sin a V dv r drd d d d r dr a ππϕϕϕϕθπθϕΩΩ====⎰⎰⎰⎰⎰⎰⎰⎰⎰.28. 求球面2222a z y x=++，含在圆柱体ax y x =+22内部的那部分面积.[解]上半球面方程为1D 为曲面在第一象限的投影：22,0x y ax y +≤≥，14D A =14D =cos 204a d πθθ=⎰⎰204(sin )a a a d πθθ=-⎰22(2)a π=-.29. 求锥面22y x z +=被柱面x z 22=所截得部分的曲面面积.[解] 由2222,2z x y z x =+=得222x y x +=，故所求曲面在xOy 的投影区域D 为222y x +≤x ，于是DA =D=⎰⎰Ddxdy ==.30. 求圆柱面222x y R +=将球面22224x y z R ++=截下部分的面积.[解] 由对称性,只考虑z =D :222x y R +≤, 于是x z =，y z =,==.因此，2S σ=⎰⎰4R d σ=⎰⎰4R θ=⎰⎰204R Rd πθ=⎰⎰0142(2RR π=⋅⋅-⋅28(2R π=.31. 求圆柱面222x y R +=，222x z R +=所围成的立体的表面积.[解] 由对称性,只考虑z =，D ：222x y R +≤. 于是，==, 因此所求的表面积为16S σ=⎰⎰16σ=⎰⎰16R Rdx =⎰201616RR dx R ==⎰.32. 已知A 球的半径为R , B 球的半径为h 且球心在A 球的表面上, 求夹在A 球内部的B球的部分面积(02h R ≤≤).[解] 建立坐标系可设球A ：2222x y z R ++=，球B ：2222()x y z R h ++-=，则两球面的交线在xOy 面的投影区域为D ：222222(4)4h x y R h R+=-，在A 球内部的B球面为：z R =A 球内部的B 球的表面积()S h σ=⎰⎰σ=⎰⎰θ=⎰⎰20hd πθ=⎰322h h Rππ=-.33. 求均匀半球体0,2222≥≤++z r z y x 的质心.[解]),0,0(r34. 求下列均匀的平面薄板重心：(1) 半椭圆;0,12222≥≤+y by a x (2) 高为h ，底分别为a 和b 的等腰梯形.[解] (1)设重心位置在),(y x ,由对称性0=x ,现求y .⎰⎰⎰⎰⎰⎰==DDDydxdy ab dxdyydxdyy πμμ2dr r ab d ab θθππsin 22120⎰⎰=π34b =. (2)设等腰梯形在直角坐标系中位置如图,其重心位置为),(y x , 对称性可得0=x ，并且有⎰⎰⎰⎰⎰⎰+==D DD ydxdy h b a dxdy ydxdyy )(2μμ⎰⎰--+=h y L y L dx ydy h b a 0)()(1211)(2 =⎰+--+h ydy a h y h b a h b a 0])([)(2=h b a ab )(32++，其中，12():()2h a L x y x h b a =++-, 22():()2h aL x y x h a b =-+-. 35. 由直线2,2,2===+y x y x 所围成的质量分布均匀 (设面密度为μ)的平面薄板,关于x 轴的转动惯量xI .[解] 2222024x y x yDI y d y d d σμμμ-===⎰⎰⎰⎰.36. 求边长为密度均匀的立方体关于其任一棱边的转动惯量.[解] 设方体的密度为ρ, 则22()z VI x y dxdydz ρ=+⎰⎰⎰2250002()3aaadx dy x y dz a ρρ=+=⎰⎰⎰.37. 求半径为a ，高为h 的圆柱体对于过其中心并且平行于母线的轴的转动惯量(假设密度1ρ=).[解] 建立坐标系，过中心且平行于母线的轴即为z 轴, 于是 22()(,,)z I x y x y z dv ρΩ=+⎰⎰⎰22()x y dv Ω=+⎰⎰⎰3r drd dz θΩ=⎰⎰⎰23ahd r dr dz πθ=⎰⎰⎰424a h π=⋅⋅412a h π=.38. 求抛物线2y x =，直线1y =所围成的均匀薄片对于直线1y =-的转动惯量.[解] 21(1)y DI y d ρσ=-=+⎰⎰21121(1)xdx y dy ρ-=+⎰⎰1231{8(1)}3x dx ρ-=-+⎰12302{8(1)}3x dx ρ=-+⎰164202{733}3x x x dx ρ=---⎰ 213368{71}375105ρρ=---=. 39. 求密度为ρ的均匀半球体对于在其中心的一单位质量的质点的引力.[解] 设球半径为R ，建立坐标系如图，由对称性，0x y F F ==；02222dv mdMdF kk r x y zρ==++， cos z dF dF γ={,,}n x y z =，02211,,}||n n x y z n x y ==+，故cos γ=；cos z dF dF γ=320222()zk dv x y z ρ=++，从而32222()z zdvF k x y z ρΩ=++⎰⎰⎰203cos sin r k r drd d rϕρϕθϕΩ=⎰⎰⎰0cos sin k drd d ρϕϕθϕΩ=⎰⎰⎰220000cos sin Rk d d dr ππρθϕϕϕ=⎰⎰⎰001{2}2k R k R ρπρπ=⋅⋅=.40. 求均匀薄片R y x ≤+22,0=z 对于轴上一点),0,0(c )0(>c 处的单位质量的引力;[解] 由对称性，引力方向必在z 轴方向上，因此0=x F ，0=y F ，且dxdy z y x ck F R y x x ⎰⎰≤+++=22223222)(μdr c r r d c k R⎰⎰+=0232220)(πθμ]1[222cR c k +-=πμ.故},0,0{Z F F =.41．求均匀柱体222a y x ≤+,h z ≤≤0对于点),0,0(c P )(h c >处的单位质量的引力.[解] 设物体密度为μ,由对称性0=x F ，0=y F . 进一步32222[()]z Vz cF k dxdydz x y z c μ-=++-⎰⎰⎰dz c z r c z dr r d k ha ⎰⎰⎰-+-=032220]])([[πθμ2]h k πμ=，故{0,0,2]}F h k πμ=, 其中k 为引力系数.。

高等数学(本科)第九章课后习题解答

习题9.11.二元函数()y x f ,在有界闭区域D 可积的充分与必要条件是什么？它的几何意义和物理意义是什么？【答】几何意义表曲顶柱体的体积的代数和；物理意义表平面薄片的质量. 2.设()(){}11|,22≤+-=y x y x D ，则二重积分⎰⎰=Ddxdy π.【解】根据二重积分的性质，⎰⎰Ddxdy 等于积分区域D 的面积.而此处积分区域D 是半径为1的圆域，因此其面积为π. 3.求⎰⎰Ddxdy 4，其中(){}1|,≤+=y x y x D .【解】⎰⎰Ddxdy 4()()824442=⨯===⎰⎰D S dxdy D.4.如果闭区域D 被分成区域1D 、2D 且()5,1⎰⎰=D dxdy y x f ，()1,2⎰⎰=D dxdy y x f ，求()⎰⎰Ddxdy y x f ,.【解】根据二重积分的性质()⎰⎰Ddxdy y x f ,()⎰⎰+=1,D dxdy y x f ()615,2=+=⎰⎰D dxdy y x f .5.设()⎰⎰+=13221D d y x I σ， (){}22,11|,1≤≤-≤≤-=y x y x D ；()⎰⎰+=23222D d y x I σ，其中(){}20,10|,2≤≤≤≤=y x y x D .试利用二重积分的几何意义说明1I 与2I 之间的关系.【解】因为积分区域2D 关于x 轴及y 轴均对称，且被积函数()()322,y x y x f +=为偶函数，故根据二重积分的对称性知214I I =. 6.估计下列积分的值. （1）⎰⎰+=Dy xd e I σ22，其中(){}41|,22≤+≤=y x y x D ；【解】积分区域D 的面积πσ3=.显然被积函数()32,y x e y x f +=在积分区域D 内有最小值e e m ==1及最大值4e M =，因此由估值定理知 433e I e ππ≤≤.（2）⎰⎰=Dyd x I σ22sin sin ，其中(){}ππ≤≤≤≤=y x y x D 0,0|,.【解】积分区域D 的面积2πσ=.显然被积函数()x x y x f 22sin sin ,=在积分区域D 内有最小值()00,0==f m 及最大值12,2=⎪⎭⎫⎝⎛=ππf M ，因此由估值定理知20π≤≤I .7.设函数()y x f ,在点()b a ,的某个邻域内连续，D 表示以点()b a ,为圆心且完全含在上述邻域内的圆域（半径为R ）.求极限 ()⎰⎰→DR d y x f R σπ,1lim20.【解】积分区域D 的面积2R πσ=.由积分中值定理知 ()⎰⎰Dd y x f σ,()()ηξπσηξ,.,2f R f ==.显然当0→R 时，()()b a ,,→ηξ，所以 ()⎰⎰→DR d y x f R σπ,1lim20()()b a f f R ,,lim 0==→ηξ.8.设区域(){}1|,22≤+=y x y x D ，()y x f ,为区域D 上的连续函数，且 ()()dxdy y x f y x y x f D⎰⎰---=,11,22π. ① 求()y x f ,.【解】记 ()dxdy y x f a D⎰⎰=,. ②则①成为()πay x y x f ---=221,. ③由③得()⎰⎰⎰⎰⎰⎰---=DDDdxdy adxdy y x dxdy y x f π221,. ④其中，根据几何意义及性质可知32134211322ππ=⎪⎭⎫ ⎝⎛⨯=--⎰⎰dxdy y x D.π=⎰⎰Ddxdy .所以由④式得到 3.32ππππ=⇒-=a a a . 将3π=a 代入③即得到()311,22---=y x y x f .习题9.21.在化二重积分时，选择坐标系的原则是什么？【解】选择坐标系的原则主要是根据积分区域的形状，具体地讲，积分区域的边界曲线是用直角坐标方程表示方便还是用极坐标方程表示简洁.当然，被积函数的特征也要考虑，如形如()22y xf+的积分就首选极坐标系来计算.2.先画出积分区域，再计算二重积分.（1）()⎰⎰+Dd y x σ22，其中D 是矩形区域：1,1≤≤y x ；【解】记(){}10,10|,1≤≤≤≤=y x y x D .由对称性知()⎰⎰+Dd y xσ22()⎰⎰+=1224D d y x σ()dy y x dx ⎰⎰+=101224⎰⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛+=101032|314dx y y x 3831314314101032|=⎪⎭⎫ ⎝⎛+=⎪⎭⎫ ⎝⎛+=⎰x x dx x .（2）()⎰⎰++Dd y y x x σ3233，其中D 是矩形区域：10,10≤≤≤≤y x ；【解】()⎰⎰+Dd y xσ22()dy y y x x dx ⎰⎰++=10103233⎰⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛++=10104223|4123dx y y x y x1412141412310103423|=⎪⎭⎫ ⎝⎛++=⎪⎭⎫ ⎝⎛++=⎰x x x dx x x .（3）()⎰⎰+Dd y x σ23，其中D 是由两坐标轴及直线2=+y x 所围成的区域；【解】()⎰⎰+Dd y x σ23()dy y x dx x⎰⎰-+=202023()⎰⎥⎦⎤⎢⎣⎡+=-20202|3dx y xy x()()[]()3204324222232020232022|=⎪⎭⎫ ⎝⎛++-=++-=-+-=⎰⎰x x x dx x x dx x x x .（4）()⎰⎰+Dd y x x σcos ，其中D 是顶点分别为()0,0，()0,π，()ππ,的三角形区域；【解】()⎰⎰+Dd y x x σcos ()dy y x x dx x ⎰⎰+=π00cos ()⎰⎥⎦⎤⎢⎣⎡+=π00|sin dx y x x x()⎰⎰⎰-=-=πππ0sin 2sin sin 2sin xdx x xdx x dx x x x()()⎰⎰+-=ππ00cos 2cos 21x xd x xd 【分部】()⎥⎦⎤⎢⎣⎡-+⎥⎦⎤⎢⎣⎡--=⎰⎰ππππ0000cos cos 22cos 212cos 21||xdx x x x xd x xπππππππ2321sin 2sin 2121||00-=--=⎥⎦⎤⎢⎣⎡--+⎥⎦⎤⎢⎣⎡--=x x .（5）⎰⎰Dxy dxdy ye ，其中D 是由曲线2,2,1===y x xy 所围成的区域；【解】⎰⎰Dxydxdy ye dy ye dx x xy⎰⎰=22121()x d e yd x x xy ⎰⎰⎥⎦⎤⎢⎣⎡=221211x d dy e ye x x xy x xy ⎰⎰⎪⎪⎭⎫ ⎝⎛-=2212121|1x d e x x e e x x xy x⎰⎪⎪⎭⎫ ⎝⎛--=221212|1121 x d e x e x x x ⎰⎪⎭⎫ ⎝⎛-=22122212x d e x x⎰=221212x d e xx ⎰-221221其中=⎰x d e x x 221221⎪⎭⎫ ⎝⎛-⎰x d e x 12212【分部】()⎥⎦⎤⎢⎣⎡--=⎰2212221211|x x e d x e x ++-=e e 2214x d e xx ⎰221212.所以⎰⎰Dxydxdy ye -=⎰x d e x x 221212e e dx e x e e x22112221422214-=⎥⎦⎤⎢⎣⎡++-⎰. （6）()⎰⎰+Ddxdy y x sin ，其中D 是矩形区域：ππ20,0≤≤≤≤y x .【解】以直线π=+y x 及π2=+y x 将区域D 分成三个子区域：321D D D D ⋃⋃=.其中，⎩⎨⎧≤≤-≤≤,0,0:1ππx x y D ， ⎩⎨⎧≤≤-≤≤-,0,2:2πππx x y x D ，⎩⎨⎧≤≤≤≤-,0,22:3πππx y x D ()dy y x dx I x⎰⎰-+=ππ0sin ()dy y x dx x x ⎰⎰--+-+πππ02sin ()dy y x dx x⎰⎰-++πππ022sin其中()dy y x dx x⎰⎰-+ππ0sin ()dx y x x ⎰⎥⎦⎤⎢⎣⎡+-=-ππ00|cos ()()πππ=+=+=⎰|0sin cos 1x x dx x ；()dy y x dx xx⎰⎰--+-πππ02sin ()dx y x xx ⎰⎥⎦⎤⎢⎣⎡+=--πππ02|cosππ220==⎰dx ；()dy y x dx x ⎰⎰-+πππ022sin ()dx y x x ⎰⎥⎦⎤⎢⎣⎡+-=-πππ022|cos ()()πππ=-=-=⎰|0sin cos 1x x dx x .所以 .42ππππ=++=I3.化二重积分()⎰⎰Dd y x f σ,为二次积分，且二次积分的两个变量的积分次序不同，其中积分区域D 为：（1）由直线x y =及抛物线x y 42=所围成的区域；【解】联立⎩⎨⎧==,4,2x y x y 解得⎩⎨⎧==,0,0y x 或⎩⎨⎧==.4,4y x 所以直线x y =及抛物线x y 42=的交点为()0,0及()4,4.（i ）若视区域D 为-X 型区域，则⎩⎨⎧≤≤≤≤.40,2:x x y x D()⎰⎰Dd y x f σ,()⎰⎰=402,xxdy y x f dx .（ii ）若视区域D 为-Y 型区域，则⎪⎩⎪⎨⎧≤≤≤≤.40,41:2y y x y D()⎰⎰Dd y x f σ,()⎰⎰=40412,y y dx y x f dy .（2）半圆形区域222r y x ≤+，0≥y .（i ）若视区域D 为-X 型区域，则⎪⎩⎪⎨⎧≤≤--≤≤.,0:22r x r x r y D()⎰⎰Dd y x f σ,()⎰⎰--=rrx r dy y x f dx 320,.（ii ）若视区域D 为-Y 型区域，则⎪⎩⎪⎨⎧≤≤-≤≤--.0,:3222r y y r x y r D()⎰⎰Dd y x f σ,()⎰⎰---=ry r y r dx y x f dy 03222,.4．交换下列积分次序（1）()⎰⎰--21222,x x xdy y x f dx ；【解】D 是由圆周曲线()1122=+-y x ，2=+y x 【两曲线交于点()1,1】所围成的区域.故()⎰⎰--21222,x x xdy y x f dx ().,11122⎰⎰-+-=y ydy y x f dy（2）()⎰⎰e xdy y x f dx 1ln 0,；【解】积分区域D 由曲线x y ln =，及x 轴和直线e x =所围成. 若改变积分次序，即将区域D 视为-Y 型区域，则⎩⎨⎧≤≤≤≤,10:1y ex e D y ，所以()⎰⎰e xdy y x f dx 1ln 0,().,10⎰⎰=eey dx y x f dy（3）()⎰⎰102,x xdy y x f dx ；【解】积分区域D 由抛物线x y 42=及两直线x y =和直线1=x 所围成.若改变积分次序，即将区域D 视为-Y 型区域，则需要将D 分块： 21D D D ⋃=.其中⎪⎩⎪⎨⎧≤≤≤≤,1041:21y yx y D ，⎪⎩⎪⎨⎧≤≤≤≤,21141:22y x y D .所以 ()⎰⎰102,xxdy y x f dx()⎰⎰=10412,y y dx y x f dy ()⎰⎰+211412,y dx y x f dy .（4）()⎰⎰--0121,ydx y x f dy ()⎰⎰++1021,ydx y x f dy .【解】积分区域21D D D ⋃=.其中⎩⎨⎧≤≤-≤≤-,0121:1y x y D ，⎩⎨⎧≤≤≤≤+,1021:2y x y D 因此积分区域D 是由三直线1,1=-=+y x y x 及2=x 所围成的三角形区域.若改变积分次序，即将区域D 视为-X 型区域，则⎩⎨⎧≤≤-≤≤-21,11:x x y x D所以 ()⎰⎰--0121,y dx y x f dy ()⎰⎰++1021,ydx y x f dy ()⎰⎰--=2111,x x dy y x f dx .5.计算⎰⎰-10122xy dy e dx x .【解】积分区域D 是由直线x y =、1=y 及y 轴所围成的三角形区域. 改变积分次序得⎰⎰-10122x y dy e dx x ⎰⎰-=10022y y dx x dy e ⎰⎪⎭⎫ ⎝⎛=-1003|312dy x e y y⎰-=103231dy e y y ()⎰--=102261y ed y 【分部】 ()⎥⎦⎤⎢⎣⎡-+-=⎰--10210222|61y d e e y y y ⎥⎦⎤⎢⎣⎡+-=--|101261y e e 6131+-=e .6.求由平面0,0==y x 及1=+y x 所围成的柱体被平面0=z 及抛物面z y x -=+622截得的立体的体积.【解】根据二重积分的几何意义知()⎰⎰--=Ddxdy y x V 226.其中积分区域D 是xoy 面内由直线1=+y x 及x 轴、y 轴所围成的平面区域.V ()dy y x dx x⎰⎰---=1010226⎰⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛--=-101032|316dx y y x y x()()()⎰⎰⎪⎭⎫ ⎝⎛+--=⎥⎦⎤⎢⎣⎡-----=101023323175234131116dx x x x dx x x x x .617317253231|10234=⎪⎭⎫ ⎝⎛+--=x x x x . 7.利用极坐标计算下列各题. （1）⎰⎰+Dy xd e σ22，其中D 是圆形区域：422≤+y x ；【解】⎰⎰+Dy xd e σ22⎰⎰+=1224D y xd e σ【极坐标】()121244202020|22-=⎪⎭⎫⎝⎛==⎰⎰e e rdr e d r r ππθπ.（2）()⎰⎰++Dd y x σ221ln ，其中D 是圆周122=+y x 及坐标轴在第一象限内所围成的区域；【解】()⎰⎰++Dd y x σ221ln 【极坐标】()=+=⎰⎰rdr r d 20121ln πθ【令t r =2】()dt t ⎰+=11ln 4π【分部】()⎥⎦⎤⎢⎣⎡+-+=⎰dt t t t t 101011ln 4|π()⎥⎦⎤⎢⎣⎡+-+-=⎰dt t t 101112ln 4π []()12ln 241ln 42ln 4|10-=+--=πππt t .（3）σd x yD⎰⎰arctan ，其中D 是由圆周122=+y x ，422=+y x 及直线xy y ==,0在第一象限内所围成的区域；【解】rdr r r d dxdy x y I D.cos sin arctan arctan 4021⎰⎰⎰⎰==πθθθ==⎰⎰rdr d .421πθθ .64321.21.22124024021||πθθθππ=⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡=⎰⎰r dr r d（4）⎰⎰Dxdxdy ，(){}x y x y x D 22|,22≤+≤=；【解】⎰⎰Dxdxdy ⎰⎰=12D xdxdy 【极坐标】⎥⎦⎤⎢⎣⎡+=⎰⎰⎰⎰24cos 204020.cos .cos 2ππθπθθθθrdr r d rdr r d⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛+=⎰⎰⎰24cos 20340202|31cos .cos 2ππθπθθθθd r dr r d ⎥⎥⎦⎤⎢⎢⎣⎡+⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛=⎰24420340cos 3831sin 2||πππθθθd r θθππd ⎰+=244cos 3163424132331634ππ=⎥⎦⎤⎢⎣⎡-+=.【其中θθππd ⎰244cos θθππd 22422cos 1⎰⎪⎭⎫ ⎝⎛+=()θθθππd ⎰++=2422cos 2cos 2141⎰=2441ππθd ()⎰+2422cos 41ππθθd ＋⎰+2424cos 141ππθθd 413234sin 3214812sin 41441||2424-=⎥⎦⎤⎢⎣⎡+⨯++⨯=πθπθπππππ】. 【注意：此题书中答案有误】.（5）⎰⎰-Ddxdy y x ，(){}0,0,1|,22≥≥≤+=y x y x y x D ；【解】以直线x y =将积分区域D 分块：21D D D ⋃=其中1D 由圆周()0,0122≥≥=+y x y x 及x 轴和直线x y =所围成；其中2D 由圆周()0,0122≥≥=+y x y x 及y 轴和直线x y =所围成.⎰⎰-Ddxdy y x ()+-=⎰⎰1D dxdy y x ()⎰⎰-2D dxdy x y 【极坐标】()rdr r r d ⎰⎰-=14sin cos θθθπ()rdr r r d ⎰⎰-+124cos sin θθθππ()dr r d ⎰⎰-=1240sin cos πθθθ()dr r d ⎰⎰-+1224cos sin ππθθθ()⎪⎭⎫ ⎝⎛⎥⎦⎤⎢⎣⎡+=||1034031.cos sin r πθθ()⎪⎭⎫ ⎝⎛⎥⎦⎤⎢⎣⎡+-+||1032431.sin cos r ππθθ ()()12311231-+-=()1232-=. （6）()⎰⎰+Ddxdy y x y 23，(){}0,4|,22≥≤+=y y x y x D .【解】()⎰⎰+Ddxdy y x y 23⎰⎰=Dydxdy ⎰⎰+Ddxdy y x 230+=⎰⎰Dydxdy【极坐标】rdr r d ⎰⎰=20.sin θθπdr r d ⎰⎰=220sin πθθ31631cos ||2030=⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡-=r πθ. 8.把()⎰⎰+=Ddxdy y xfI 22化为单重积分，其中(){}1|,22≤+=y x y x D .【解】()⎰⎰+=Ddxdy y xfI 22【极坐标】()⎰⎰=1204rdr r f d πθ()⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛=⎰⎰1020.4rdr r f d πθ()⎰=102rdr r f π.9.把下列积分化为极坐标形式，并计算其积分值. （1）()⎰⎰-+ay a dx y xdy 002222；【解】()⎰⎰-+ay a dx y xdy 02222【极坐标】404228412|a r rdr r d aaππθπ=⎪⎭⎫ ⎝⎛==⎰⎰. （2）()⎰⎰-+ax ax dy y xdx 2020222；【解】()⎰⎰-+ax ax dy y xdx 2020222【极坐标】==⎰⎰rdr r d a 20cos 202πθθ⎰⎪⎭⎫ ⎝⎛20cos 204|41πθθd r a . 44244432.!!4!!34cos 4a a d a ππθθπ=⎪⎭⎫ ⎝⎛==⎰.（3）⎰⎰+axdy y x dx 022；【解】⎰⎰+axdy y x dx 022【极坐标】==⎰⎰rdr r d a 40sec 0.πθθ⎰⎪⎭⎫ ⎝⎛40sec 03|31πθθd r a ⎰=4033sec 31πθθd a []|403tan sec ln tan .sec 61πθθθθ++=a()[]21ln 2613++=a【其中，()⎰⎰==θθθθtan sec sec 3d d I 【分部】()⎰-=θθθθsec tan tan .sec d⎰-=θθθθθd 2tan sec tan .sec ()⎰--=θθθθθd 1sec sec tan .sec 2 I d d -++=+-=⎰⎰θθθθθθθθθθtan sec ln tan .sec sec sec tan .sec 3所以，[]C I +++=θθθθtan sec ln tan .sec 21.】（4）⎰⎰+1222xxdx y x dx .【解】⎰⎰+10222xxdx y x dx 【极坐标】==⎰⎰rdr r d a 40sec tan 0.πθθθ⎰⎪⎭⎫ ⎝⎛40tan sec 03|31πθθθd r a ⎰=40333tan sec 31πθθθd a ()()⎰-=40223sec 1sec sec 31πθθθd a()12452sec 31sec 5131|40353+=⎥⎦⎤⎢⎣⎡-=πθθa .10.设()x f 为连续函数，且()()⎰⎰+=Ddxdy y x f t F 22，其中(){}222|,t y x y x D ≤+=，求极限()tt F t '→0lim.【解】()()⎰⎰+=Ddxdy y x f t F 22【极坐标】()rdr r f d t⎰⎰=πθ202()r dr r f t⎰=022π.故 ()()22t tf t F π='. ① 所以()t t F t '→0lim【代入 ①】()()022lim 0f t t tf t ππ==→. 【注意：怀疑此题本身有问题，故对题目本身作了合理修正】11*.设()x f 在[]1,0上连续，并设()A dx x f =⎰10，求()()⎰⎰101xdy y f x f dx .【解】记⎩⎨⎧≤≤≤≤,10,1:1x y x D ⎩⎨⎧≤≤≤≤,10,0:2x x y D ，21D D D ⋃=.则 ()()()()dxdy y f x f dy y f x f dx I D x⎰⎰⎰⎰==1111. ①()()()()dxdy y f x f dy y f x f dx I D x⎰⎰⎰⎰==2102. ②又交换积分次序后()()==⎰⎰111x dy y f x f dx I ()()⎰⎰10y dx y f x f dy ()()⎰⎰=10xdy y f x f dx ，即21I I =.所以有 ()()()dxdy y f x f I I I D⎰⎰=+=2121211 ()()210102121A dy y f dx x f ==⎰⎰. 12*.设()x ϕ为[]1,0上的正值连续函数，证明：()()()()()b a dxdy x y x b y a D+=++⎰⎰21ϕϕϕϕ，其中b a ,为常数，(){}10,10|,≤≤≤≤=y x y x D . 【证明】因为积分区域D 关于直线x y =对称，则 ()()()=+=⎰⎰Ddxdy y x x I ϕϕϕ()()()⎰⎰+Ddxdy y x y ϕϕϕ. ① 故有()()()()212121==⎥⎦⎤⎢⎣⎡++=⎰⎰⎰⎰DD dxdy dxdy y x y x I ϕϕϕϕ. ② 所以有()()()()=++⎰⎰D dxdy x y x b y a ϕϕϕϕ()()()b dxdy y x y a D++⎰⎰ϕϕϕ()()()⎰⎰+Ddxdy y x x ϕϕϕ ).(21b a bI aI +=+= 13*.设闭区间[]b a ,上()x f 连续且恒大于零，试利用二重积分证明不等式()()()21a b dx x f dx x f baba-≥⎰⎰. 【证法一】考虑到定积分与变量的记号无关.故有： ()()⎰⎰=b a bay f dy x f dx. ① 以及()().dy y f dx x f baba⎰⎰= ②所以有()()()()..⎰⎰⎰⎰=⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡D b a b a dxdy y f x f x f dx dx x f ③其中，⎩⎨⎧≤≤≤≤.,:b y a b x a D 同时()()()()..⎰⎰⎰⎰=⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡D b a b a dxdy x f y f x f dx dx x f ④ ③+④，得()()()()()()()()()().2.2⎰⎰⎰⎰⎰⎰≥⎥⎦⎤⎢⎣⎡+=⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡D Db a b a dxdy y f x f x f y f dxdy y f x f x f y f x f dx dx x f ()222.Ddxdy b a ==-⎰⎰即： ()()()2..b b a a dx f x dx b a f x ⎡⎤⎡⎤≥-⎢⎥⎢⎥⎣⎦⎣⎦⎰⎰ 【证法二】：因为()0≥x f ，所以有20b a dx ⎡⎤⎢≥⎢⎣⎰，即 ()()()220.bbaadxf x dx b a f x λλ⎡⎤+-+≥⎢⎥⎣⎦⎰⎰① ①式左边是λ的非负二次三项式，因此必有判别式()()()20b b a a dx b a f x dx f x ⎡⎤⎡⎤∆=--≤⎢⎥⎢⎥⎣⎦⎣⎦⎰⎰. ② 故由②得到()()()2..b b a a dx f x dx b a f x ⎡⎤⎡⎤≥-⎢⎥⎢⎥⎣⎦⎣⎦⎰⎰14*.设()x f 在闭区间[]b a ,上连续.试利用二重积分证明不等式()()()dx x fa b dx x f ba ba ⎰⎰-≤⎥⎦⎤⎢⎣⎡22.【证明】由于()2⎥⎦⎤⎢⎣⎡⎰dx x f b a ()()⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡=⎰⎰dx x f dx x f b a b a ()()⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡=⎰⎰dy y f dx x f ba b a . ① 令 ⎩⎨⎧≤≤≤≤.,:b y a b x a D 则由①得到()()()dxdy y f x f dx x f Dba ⎰⎰⎰=⎥⎦⎤⎢⎣⎡2. ②又 ()()()()222y fx fy f x f +≤.③故()()()dxdy y fx f dx x f Db a ][21222+≤⎥⎦⎤⎢⎣⎡⎰⎰⎰()()⎥⎦⎤⎢⎣⎡+=⎰⎰⎰⎰b a b a b a b a dy y f dx dx x f dy 2221 ()()dx x f a b b a ⎰-=221()()dy y f a b b a ⎰-+221【定积分与变量记号无关()()dx x fa b ba⎰-=2.15*.设区域(){}0,1|,22≥≤+=x y x y x D ，求二重积分⎰⎰+++Ddxdy y x xy2211.【解】⎰⎰+++Ddxdy y x xy 2211⎰⎰++=D dxdy y x 2211⎰⎰+++D dxdy yx xy221 0112122+++=⎰⎰D dxdy y x 【极坐标】rdr r d ⎰⎰+=2102112πθ ()().2ln 21ln 21112|1022102πππ=+=++=⎰rr d r习题9.３1.利用定积分、二重积分和三重积分计算空间立体体积时，被积函数和积分区域各有什么不同？【解】略.2.将三重积分()dxdydz z y x f I ⎰⎰⎰Ω=,,化为三次积分，其中空间区域分别为：（1）由曲面22y x z +=，0=x ，0=y ，1=z 所围成且在第一卦限内的区域；【解】⎪⎪⎩⎪⎪⎨⎧≤≤-≤≤≤≤+Ω.10,10,1:222x x y z y x Ω向xoy 面上投影区域为⎪⎩⎪⎨⎧≤≤-≤≤.10,10:2x x y D xy ，所以()dz z y x f dy dx I y x x ⎰⎰⎰+-=1101222,,.（2）由双曲抛物面xy z =及平面01=-+y x ，1=z 所围成的区域；【解】⎪⎩⎪⎨⎧≤≤-≤≤≤≤Ω.10,10,0:x x y xy z Ω向xoy 面上投影区域为⎩⎨⎧≤≤-≤≤.10,10:x x y D xy ，所以()dz z y x f dy dx I xyx⎰⎰⎰-=01010,,.（3）由曲面222y x z +=及22x z -=所围成的区域. 【解】联立⎪⎩⎪⎨⎧-=+=,2,2222x z y x z 消去z ，得 Ω向xoy 面上的投影区域为 1:22≤+y x D xy . 故⎪⎪⎩⎪⎪⎨⎧≤≤--≤≤---≤≤+Ω.11,11,22:22222x x y x x z y x所以()dz z y x f dy dx I x y x x x ⎰⎰⎰-+----=22222221111,,.3.利用直角坐标系计算下列三重积分.（1）dV z xy ⎰⎰⎰Ω32，其中Ω是由平面x y =，1=x ，0=z 及曲面xy z =所围区域.【解】Ω在xoy 坐标面上的投影区域为三角形区域.10,0:⎩⎨⎧≤≤≤≤x x y D 故dz z dy y xdx dV z xy xyx⎰⎰⎰⎰⎰⎰=Ω03021032⎰⎰⎥⎦⎤⎢⎣⎡=xxy dy z y xdx 004210|41⎰⎰=x dy y dx x 0610541⎰⎥⎦⎤⎢⎣⎡=10075|7141dx y x x 3641131281281|10131012=⨯==⎰x dx x . （2）()⎰⎰⎰Ω+++31z y x dV，其中Ω是由平面0=x ，0=y ，0=z 及1=++z y x 所围成的四面体；【解】Ω在xoy 坐标面上的投影区域为三角形区域.10,10:⎩⎨⎧≤≤-≤≤x x y D 故()dxdydz z y x ⎰⎰⎰Ω+++311=()dz z y x dy dx x y x ⎰⎰⎰---+++101010311()()z y x d z y x dy dx xyx ++++++=⎰⎰⎰---1111010103()⎰⎰---⎥⎦⎤⎢⎣⎡+++-=1010102|11.21xy x dy z y x dx ()⎰⎰-⎥⎦⎤⎢⎣⎡-++=10102411121xdy y x dx ⎰-⎪⎪⎭⎫ ⎝⎛-++-=1010|411121dx y y x x⎰⎪⎭⎫⎝⎛+++-=101144321dx x x ().1652ln 21811ln 4321|102-=⎪⎭⎫ ⎝⎛+++-=x x x （3）()dxdydz z x y ⎰⎰⎰Ω+cos ，其中Ω是由抛物柱面x y =以及平面0=y ，0=z ，2π=+z x 所围成区域.【解】Ω在xoy 坐标面上的投影区域为.20,0:⎪⎩⎪⎨⎧≤≤≤≤πx x y D 故()dxdydz z x y ⎰⎰⎰Ω+cos =()dz z x ydy dx xx⎰⎰⎰-+2020cos ππ()⎰⎰⎥⎦⎤⎢⎣⎡+=-200|2sin ππxxdy z x y dx ()⎰⎰-=200sin 1πx ydy x dx ()⎰⎥⎦⎤⎢⎣⎡-=2002|21sin 1πdx y x x ()⎰-=20sin 121πdx x x⎰=2021πxdx 21161sin 21220-=-⎰ππxdx x .【其中2202201614121|πππ==⎰x xdx ；()⎰⎰=-2020cos 21sin 21ππx xd xdx x 【分部】⎥⎦⎤⎢⎣⎡-=⎰2020cos cos 21|ππxdx x x 21sin 21|20-=-=πx .】4.利用柱面坐标计算三重积分.（1）()d V y x ⎰⎰⎰Ω+22，其中Ω是由曲面z y x 222=+及平面2=z 所围成的区域；【解】本题宜采用“切片法”计算()()dxdy y x dz dz dxdy y xzD ⎰⎰⎰⎰⎰⎰+=+Ω22222.3163242.||20320202422020πππθπ====⎰⎰⎰⎰z dz r rdr r d dz z z如采用柱面坐标系：()dz dxdy y x⎰⎰⎰Ω+22.3166.2142222.2|206420223222202πππθπ=⎥⎦⎤⎢⎣⎡-=⎪⎪⎭⎫⎝⎛-==⎰⎰⎰⎰r r dr r r dz r rdr d r （2）()d V y x ⎰⎰⎰Ω+22，其中Ω是由曲面()222254y x z +=及平面5=z 所围成的区域；【解】（柱面坐标法）Ω在xoy 坐标面上的投影区域为.4:22≤+y x D()V d y x⎰⎰⎰Ω+22dr z r dz r rdr d r r ⎰⎰⎰⎰⎪⎪⎭⎫⎝⎛==20205253525220|.2πθπ dr r r ⎪⎭⎫ ⎝⎛-=⎰255223πππ82452|2054=⎥⎦⎤⎢⎣⎡-=r r .（3）dV xyz ⎰⎰⎰Ω，其中Ω是由球面1222=++z y x 及三个坐标面所围且在第一卦限内的区域.【解】（球面坐标法）Ω在xoy 坐标面上的投影区域为V xyzd ⎰⎰⎰Ω⎰⎰⎰=2015320cos sin cos sin ππρρϕϕϕθθθd d d48161.sin 41.sin 21|||106204202=⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡=ρϕθππ.5.利用球面坐标计算三重积分.（1）()d V z y x ⎰⎰⎰Ω++222，其中()(){}222223,|,,y x z z z y x z y x +≥≤++=Ω；【解】（球面坐标法）()d V z y x⎰⎰⎰Ω++222⎰⎰⎰=60cos 02220.sin πϕπρρρϕϕθd d dϕρϕππϕd ⎰⎥⎦⎤⎢⎣⎡=6cos 05|51sin 2ϕϕϕππd ⎰=605sin cos 52()ϕϕππcos cos 52605d ⎰-=πϕππ96037cos 6152|606=⎥⎦⎤⎢⎣⎡-=.（2）dxdydz z ⎰⎰⎰Ω2，其中Ω是由抛物面22y x z +=之上，球面2222=++z y x 之内的部分围成；【解】（柱面坐标法）联立⎩⎨⎧+==++22222,2y x z z y x 消z ,得Ω在xoy 坐标面上投影区域.1:22≤+y x D 所以dz dxdy z⎰⎰⎰Ω2⎰⎰⎰-=1222022r rdz z rdr d πθ⎰⎥⎦⎤⎢⎣⎡=-123|22312r r z r π()⎰⎥⎦⎤⎢⎣⎡--=10632232dr r r r π()⎰-=1032232dr r r π()πππππ121228151121232107--=-=-⎰dr r ()1323260-=π.【其中()⎰-1032232dr r r π【令t r sin 2=】⎰=404cos .sin 328ππtdt t ()()πππππ228151cos 51328cos cos 328|405404-=⎥⎦⎤⎢⎣⎡-=-=⎰t t td ； .121813232|108107πππ-=⎥⎦⎤⎢⎣⎡-=-⎰r dr r 】（3）dxdydz x ⎰⎰⎰Ω，其中()(){}0,0,0|,,2222≥≥>≤++=Ωy x a a z y x z y x .【解】（球面坐标法）⎰⎰⎰Ωxdxdydz ⎰⎰⎰=ππρρθϕρϕϕθ00220.cos sin sin ad d d ⎰⎰⎰=ππρρρϕϕθθ0222.sin cos ad d d404020841.2sin 4121.sin |||a a πρϕϕθππ=⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛-⎥⎦⎤⎢⎣⎡=.6.采用三种坐标计算三重积分dxdydz z ⎰⎰⎰Ω2，其中()2222|,,{R z y x z y x ≤++=Ω()}2,0222Rz z y x R ≤++>.【解法一】（柱面坐标法）联立⎩⎨⎧=++=++,2,222222Rz z y x R z y x 消z ,得Ω在xoy 坐标面上的投影区域为 .43:222R y x D ≤+dz dxdy z ⎰⎰⎰Ω2 dr z r dz z rdr d R R r R r R R r R r R R ⎰⎰⎰⎰⎪⎪⎭⎫ ⎝⎛==------232303220|222222223.2πθπ()()⎰⎥⎦⎤⎢⎣⎡----=R dr rR R r R r 23032232232π（令t R r sin =）()[]⎰--=30333cos .cos cos sin 32ππtdt R t R R t R t R[]⎰-+-=30235cos sin cos 3cos 31cos 232ππtdt t t t t R⎰=3045sin cos 34ππtdt t R ⎰-305sin cos 32ππtdt t R⎰+3025sin cos 2ππtdt t R⎰-3035sin cos 2ππtdt t R|30555cos 34ππt R -=|30252cos 32ππt R +|30353cos 2ππt R -|30454cos 2ππt R + ⎪⎭⎫ ⎝⎛--=32311545R π⎪⎭⎫ ⎝⎛-+4335R π⎪⎭⎫ ⎝⎛--87325R π⎪⎭⎫ ⎝⎛-+161525R π .480595R π=【解法二】（球面坐标法）球面坐标计算：这时首先要把积分区域Ω分成两个子区域： .21Ω⋃Ω=Ω 其中⎪⎩⎪⎨⎧≤≤≤≤≤≤Ω,0,30,20:1R ρπϕπθ ⎪⎩⎪⎨⎧≤≤≤≤≤≤Ω,cos 20,232,20:2ϕρπϕππθR则dz dxdy z ⎰⎰⎰Ω2=dz dxdy z ⎰⎰⎰Ω12dz dxdy z ⎰⎰⎰Ω+22ρρϕρϕϕθππd d d R⎰⎰⎰=2030222.cos sinρρϕρϕϕθπππϕd d d R ⎰⎰⎰+2023cos 20222.cos sin⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛=⎰⎰R d d 04302cos .sin 2ρρϕϕϕππ ⎪⎪⎭⎫ ⎝⎛+⎰⎰ϕππρρϕϕϕπcos 204232cos .sin 2R d d ⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛-=||0530351cos 312R ρϕππ⎪⎪⎭⎫ ⎝⎛+⎰2375cos .sin 32512ππϕϕϕπd R 551.247.2R π=⎪⎪⎭⎫ ⎝⎛-+|2385cos 81564ππϕπR 5607R π=⎪⎭⎫ ⎝⎛+81.25615645R π5607R π=5160R π+.480595R π= 【解法三】（直角坐标系之“切片法”）将Ω分块为21Ω⋃Ω=Ω.其中()()⎪⎩⎪⎨⎧∈≤≤Ω11,,20z D y x R z ：，()22212:z Rz y x D z -≤+； ()()⎪⎩⎪⎨⎧∈≤≤Ω22,,2z D y x R z R：，()22222:z R y x D z -≤+. ()()()()[]dz z Rz z dz D S z dxdy dz z dz dxdy zR z D R R z220212022022211-===⎰⎰⎰⎰⎰⎰⎰⎰Ωπ5205440151412|R z z R Rππ=⎥⎦⎤⎢⎣⎡-=；()()()()[]dz z R z dz D S z dxdy dz z dz dxdy z RR z D RR R R z222222222222-===⎰⎰⎰⎰⎰⎰⎰⎰Ωπ 52532480475131|R z z R R R ππ=⎥⎦⎤⎢⎣⎡-=. 所以dz dxdy z ⎰⎰⎰Ω2=dz dxdy z ⎰⎰⎰Ω12dz dxdy z ⎰⎰⎰Ω+225554805948047401R R R πππ=+=. 7.若柱面122=+y x 与平面0=z ，1=z 所围成的柱体内任一点()z y x ,,处的密度22y x z --=μ，试计算该柱体的质量.【解】()()⎪⎩⎪⎨⎧Ω∈-+Ω∈--=--=.,,,,,22212222y x z y x y x y x z y x z μ 其中()⎩⎨⎧∈≤≤+ΩD y x z y x ,,1221：；()⎩⎨⎧∈+≤≤ΩD y x y x z ,,0222：；1:22≤+y x D . 所以 =M ()dz dxdy y xz ⎰⎰⎰Ω--122()πππ316161222=+=-++⎰⎰⎰Ωdz dxdy z y x .【其中()dz dxdy y xz ⎰⎰⎰Ω--122【柱面坐标】()dr z r z r dz r z rdr d r r ⎰⎰⎰⎰⎪⎪⎭⎫ ⎝⎛-=-=10101221220|222.2πθπ()πππ6161222|10642153=⎪⎪⎭⎫ ⎝⎛+-=+-=⎰r r r dr r r r ；()dz dxdy z y x⎰⎰⎰Ω-+222【柱面坐标】()dr z z r r dz z r rdr d r r ⎰⎰⎰⎰⎪⎭⎫ ⎝⎛-=-=110022220|2221.2πθππππ6161|10615=⎪⎭⎫ ⎝⎛==⎰r dr r .】8.分别用定积分、二重积分和三重积分求由22y x z +=和22y x z +=所围成的立体Ω的体积.【解】联立⎪⎩⎪⎨⎧+=+=,,2222y x z y x z 消z ,得Ω在xoy 坐标面上的投影区域为 .1:22≤+y x D（一）定积分过z 轴上任意一点z 作Ω的截面，则该截面的面积为 ()()()[]1,0,222∈-=-=z z z z z z A πππ所以Ω的体积为()()πππ613121|103210210=⎪⎭⎫ ⎝⎛-=-==⎰⎰z z dz z z dz z A V .（二）二重积分 ()[]d xdy y x y xV D⎰⎰+-+=2222【极坐标】()ππθπ61432|10432012=⎪⎪⎭⎫ ⎝⎛-=-=⎰⎰r r rdr r r d . （三）三重积分⎰⎰⎰Ω=dV V 【球面坐标】ρρϕϕθπϕϕππd d d ⎰⎰⎰=20sin cos 02242sin()ϕϕπϕϕϕπϕρϕπππππππϕϕcot cot 32sin cos 3231sin 2243245324sin cos 03|2d d d ⎰⎰⎰-==⎥⎦⎤⎢⎣⎡=πϕπππ61cot 4132|244=⎥⎦⎤⎢⎣⎡-=. 9.设()x f 在0=x 处可导，且()00=f ，求极限()d xdydz z y x f t t ⎰⎰⎰Ω→++22241lim，其中(){}2222|,,t z y x z y x ≤++=Ω.【解】()d xdydz z y x f tt ⎰⎰⎰Ω→++222401lim ()⎰⎰⎰=ππρρρϕϕθ00220.sin ad f d d()ρρρϕππd f a 200.cos 2|⎰⎥⎦⎤⎢⎣⎡-=()ρρρπd f a 20.4⎰=. ①所以()d xdydz z y x ft t ⎰⎰⎰Ω→++22241lim【由①】()4204lim t f tt ⎰→=ρρπ【洛必达法则】()32044lim t t t f t π→=()t t f t 0lim →=π()()00lim 0--=→t f t f t π()0f '=π. 习题9.４1.求由曲线()xy y x C =+222:所围平面图形D 的面积.【解】化曲线C 为极坐标表示：θθsin cos 2=r ，⎥⎦⎤⎢⎣⎡⋃⎥⎦⎤⎢⎣⎡∈πππθ23,2,0.由对称性知()⎰⎰=12D d D S σ【极坐标】θθπθθπθθd r dr r d ⎰⎰⎰⎥⎦⎤⎢⎣⎡==20cos sin 0220cos sin 0|2122()21sin 21sin sin cos sin |2022020====⎰⎰πππθθθθθθθd d d .2.求由曲面222y x z +=及2226y x z --=所围成的立体Ω的体积. 【解】联立⎪⎩⎪⎨⎧--=+=,26,22222y x z y x z 消去z ，得 Ω向xoy 面上的投影区域为 2:22≤+y x D xy .所以Ω的体积为 ()()[]d xdy y x y xV xyD ⎰⎰+---=2222226()d xdy y xxyD ⎰⎰--=22336()ππθπ6433236|2422022=⎥⎦⎤⎢⎣⎡-=-=⎰⎰r rrdr r d . 3.求由曲面()xyz a z y x S 332223:=++所围立体的体积.【解】做球坐标变换：⎪⎩⎪⎨⎧===,cos ,sin sin ,cos sin ϕρθϕρθϕρz y x 则S 在球坐标下的方程为θθϕϕρsin cos cos sin 3233a =ρρϕϕθθθϕϕππd d d dV V a ⎰⎰⎰⎰⎰⎰Ω==3231cos sin cos sin 3022020sin 44⎰⎰⎥⎦⎤⎢⎣⎡=2020cos sin cos sin 303|32331sin 4ππθθϕϕϕρϕθd d a ⎰⎰=22033cos sin cos sin 4ππϕϕϕθθθd d a.21sin 41sin 21432042023||a a =⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡=ππϕθ4.证明：曲面2214:y x z S ++= ① 任一点处的切平面与曲面22:2y x z S +=所围立体图形Ω的体积为定值.【证明】任取曲面1S 上一点()0000,,z y x M .令 ()z y x z y x F -++=224,,.则1S 在点()0000,,z y x M 处的切平面的法向量为 ()()(){}{}1,2,2,,00000-='''=y x M F M F M F z y x .1S 在点()0000,,z y x M 处的切平面π的法平面为()()()02200000=---+-z z y y y x x x .即 ()0222:02020000=-+---+z y x z z y y x x π. ②又由于()10000,,S z y x M ∈，故402020-=-+z y x . ③ 将③式代入②式得0822:000=+--+z z y y x x π. ④ 联立⎩⎨⎧+==+--+,,082222000y x z z z y y x x 消去z ，得 ()()8020202020+-+=-+-z y x y y x x 【由③】4=，故Ω向xoy 面上的投影区域为()()4:2020≤-+-y y x x D xy . ⑤所以，Ω的体积为 ()()[]d xdy y x z y yx x V xyD ⎰⎰+-+-+=2200822()()()[]d xdy y y x x z y xxyD ⎰⎰----+-+=202002028【由③】()()[]d xdy y y x x xyD ⎰⎰----=2024令⎩⎨⎧+=+=.sin ,cos 00θθr y y r x x 则()()r r r y r y xrxr y x J =-=∂∂∂∂∂∂∂∂=∂∂=θθθθθθθcos sin sin cos ,,所以()dr d r r V r D θθ⎰⎰-=24()ππθπ841224|20422022=⎥⎦⎤⎢⎣⎡-=-=⎰⎰r r rdr r d .从而:2S 与π所围立体图形Ω的体积为定值π8.5.形状如22y x z +=，100≤≤z （单位：米）的“碗”，计划在其上刻上刻度使其成为一个容器.求对应于容积为１立方米的液体在该容器内的高度是多少？【解】设对应于容积为１立方米的液体在该容器内的高度是h （米）. 由题意知()()σπd y xh h D⎰⎰+-⨯=222.1. ①其中222:h y x D ≤+.()⎰⎰⎰⎰=+πθσ200222.h Drdr r d d y x20421412|h r h ππ=⎥⎦⎤⎢⎣⎡=. ②将②式代入①式得2221.1h h ππ-=，即 2211h π=，解之得π2=h （米）.6.求均匀密度的半椭圆平面薄片()01:2222≥≤+y by a x D 的质心.【解】设D 的质心坐标为()y x ,.由质心坐标公式得⎰⎰⎰⎰=DDxd d x σσ1； ①⎰⎰⎰⎰=DDyd d y σσ1②【其中令⎩⎨⎧==,sin ,cos θθbr y ar x 则()()abrbr b ar a y ry xrxr y x J =-=∂∂∂∂∂∂∂∂=∂∂=θθθθθθθcos sin sin cos ,,由对称性知0=⎰⎰σd x D；()⎰⎰⎰⎰⎰⎰==πθθθθσθ0102.sin sin rdr r d ab drd J br d y r D D⎰⎥⎦⎤⎢⎣⎡=πθθ01032|31sin d r ab2020232cos 31sin 31|ab ab d ab =-==⎰ππθθθ；又 ()ab D S d Dπσ2121==⎰⎰. 故⎰⎰⎰⎰==DDxd d x 01σσ；ππσσ34213212bab ab yd d y DD===⎰⎰⎰⎰. 所以，平面薄片()01:2222≥≤+y b y a x D 的质心为⎪⎭⎫⎝⎛π34,0b .7.社平面薄片所占的区域D 由抛物线2x y =及直线x y =所围成，它在点()y x ,处的面密度()y x y x 2,=ρ，求此薄片的质心.【解】设D 的质心坐标为()y x ,.由质心坐标公式得()()⎰⎰⎰⎰=DDd y x x d y x x σρσρ,,1σσ⎰⎰⎰⎰=DDyd x yd x 321； ① ()()⎰⎰⎰⎰=D D d y x y d y x y σρσρ,,1⎰⎰⎰⎰=DDd y x yd xσσ2221②ydy x dx yd x xx D⎰⎰⎰⎰=10222σ⎰⎪⎭⎫ ⎝⎛=1022|221dx y x x x ()⎰-=106421dx x x 351715121|1075=⎪⎭⎫ ⎝⎛-=x x ； ③ydy x dx yd x x x D⎰⎰⎰⎰=10332σ⎰⎪⎭⎫ ⎝⎛=1023|221dx y x x x ()⎰-=107521dx x x 481816121|1086=⎪⎭⎫ ⎝⎛-=x x ； ④ dy y x dx d y x xx D2102222⎰⎰⎰⎰=σ⎰⎪⎭⎫⎝⎛=1032|231dx y x x x ()⎰-=108531dx x x 541916131|1096=⎪⎭⎫ ⎝⎛-=x x . ⑤故 4835351481==x ；5435351541==y .所以此薄片的质心为⎪⎭⎫⎝⎛5435,4835.8.平面薄片D 由ax y x ≥+22，222a y x ≤+确定，其上任一点处的面密度与离原点的距离成正比，求此薄片的质心.【解】由题意知，面密度()22,y x k y x +=ρ)0(>k .。