极小曲面的凸水平集的曲率关于函数高度的凸性
凸集和凸函数

凸集和凸函数凸集和凸函数是数学中一些重要的概念。
它们的应用范围广泛,涉及到诸如优化、几何学、经济学、物理学等领域。
本文将分步骤阐述凸集和凸函数的定义、性质及应用。
一、凸集的定义和性质凸集是指在欧几里得空间中,对于其中的任意两点,它们之间的连线都落在该集合内。
换句话说,凸集中的任何一条线段都是完全落在凸集内的。
要说明集合是凸的,需要证明其满足如下两个条件:①对于其中的任意两点x和y,它们之间的任意一个点z,都应该满足z=λx+(1-λ)y(其中0≤λ≤1);②该集合是一个凸组合的闭包。
凸集有以下性质:1. 任意两个凸集的交集也是凸集;2. 凸集的闭包是凸集;3. 凸集的凸壳是凸集;4. 凸集的极小凸包是凸集;5. 凸集是连通的。
二、凸函数的定义和性质凸函数是指在函数图像下方的区域是凸集。
凸函数有以下几个特征:1. 任意两个点的线段都落在函数图像下方;2. 函数的一阶导数递增或数值非负;3. 函数的二阶导数数值非负。
凸函数具有以下性质:1. 任意两个凸函数的和是一个凸函数;2. 凸函数的下凸包是凸函数;3. 凸函数的上凸包是凸函数;4. 若函数f在定义域D内是凸的,那么其上任意一点的全体支撑线构成的集合是非空凸集。
在实际应用中,凸函数可用于优化问题、光学物理等方面。
因为凸函数有唯一的最小值和全局最小值,这种性质对于优化问题非常重要。
光学物理中,利用凸函数可对某些照明系统进行设计。
三、凸集和凸函数的应用凸集和凸函数的应用非常广泛。
它们在很多领域都得到了充分的应用,下面将简单介绍一些常见应用:1. 最优化问题。
凸函数有唯一的最小值和全局最小值,因此可以用于优化问题中,如线性规划、非线性规划等。
2. 几何形状分析。
凸集的定义是指一个区域内的两点连线都在该区域内,因此凸集可以用于分析几何形状。
3. 光学物理。
利用凸函数可以对光学系统进行设计,尤其是在非均匀照明下平均照度问题的解决中可以应用到凸函数。
4. 机器学习。
函数的凸性曲线的曲率

第7章 函数的凸性·曲线的曲率①凸函数 函数的“凸性”概念最初来自曲线的弯曲方向。
例如,曲线3x y =(图1)在Oy 轴左边是向下弯曲的(称为上凸)而在Oy 轴右边是向上弯曲的(称为下凸)。
虽然说“弯曲方向” 或“凸性”这些名称是几何上的术语,但经过抽象后的凸函数 理论在其它数学分支中也是很有用的。
从图2中看出,向上弯曲(下凸)的曲线上任何两点的连线(AB 的中点C 在弧AB 的上方;而从图3中看出,向下弯曲(上凸)的曲线上任何两点的连线(弦)AB 的中点C 在弧AB 的下方。
【注1】在国内早期的一些教科书(包括翻译前苏联的一些教科书)中,都把下凸函数称为“凹函数”,而把上凸函数称为“凸函数”。
这里的称呼与新近一些教科书或论文中的称呼是一致的。
请读者注意到这些区别。
【注2】还请读者注意,通常说“函数()f x 在区间(,)a b 内是下(上)凸函数”,若对于(,)a b 内任意两点1x 和2x 12()x x ≠与任意(0,1)t ∈,都满足琴生(Jesen)不等式[]1212()(1)()(1)()f t x t x t f x t f x >+-<+-它等价于不等式()11221122()()()f t x t x t f x t f x >+<+(其中1t 和2t 为正数且121t t +=)显然,不等式(※)是琴生不等式的特殊情形。
不过,对于连续函数来说,不等式(※)与琴生不等式是等价的。
因此,我们就用简单的不等式(※)定义函数的凸性。
关于连续函数情形下两者等价性的证明,有兴趣的读者可去看本网站上的专题选讲。
【注3】若函数)(x f 在区间),(b a 内可微分,则从下图4看出,下凸(上凸)函数的图形上,每一点处图2O x 1 (x 1+x 2 )/2 x 2图3112108 的切线都在图形的下面(上面),而且导函数)(x f '(切线的斜率)是增大(减小)的。
凸集和凸函数的性质和应用

凸集和凸函数的性质和应用凸集和凸函数是数学领域中的两个重要概念,分别在几何、优化、概率等领域中都有广泛的应用。
在这篇文章中,我们将会详细讨论凸集和凸函数的性质以及它们的应用。
一、凸集凸集是指满足任意两个点之间的线段都在集合内的集合。
换句话说,如果有一个集合S,那么S是凸集当且仅当对于S中的任意两个点x和y,x和y之间的线段上的所有点都在S内。
对于凸集,我们可以根据其性质进行分类。
首先,全空间和空集都是凸集,这两个极端情况被称为平凸集和空凸集。
而对于非平凸集来说,则可以有以下几种情况。
1.开凸集:对于某个凸集,如果它不包含任何边界点,则被称为开凸集。
2.闭凸集:对于某个凸集,如果它包含所有边界点,则被称为闭凸集。
3.紧凸集:对于某个凸集,如果它是有限的并且紧致的,则被称为紧凸集。
4.凸包:对于一组点,包含这些点的最小凸集,被称为凸包。
凸集不仅仅在数学中有着广泛的应用,还在计算机科学、优化问题等领域中得到广泛的应用。
例如,在计算机图形学中,我们可以使用凸集来进行边界的处理和剪裁等;在优化问题中,我们可以使用凸集来化简复杂问题,以便更好地对其求解。
二、凸函数凸函数是指函数图像上任意两点的连线不在函数图像下方的函数。
更具体地说,如果一个函数f(x)满足以下不等式:f(λx+(1−λ)y)≤λf(x)+(1−λ)f(y),其中0≤λ≤1则f(x)是凸函数。
这个不等式的意义是,对于函数图像上的任意两点x和y,它们之间线段上的所有点都在函数图像上方,即满足上述不等式。
凸函数的常见形式包括线性函数、指数函数、幂函数、对数函数等。
此外,两个凸函数的和、积和复合函数也都是凸函数。
凸函数的定义和凸集的定义类似,都是指在某一区间(或者全空间)内,满足一定的条件(凸性)。
凸函数的性质包括以下几个方面。
1.凸函数的上确界在左连续下降。
2.凸函数的导函数单调不减,且导函数的左导数和右导数存在并相等。
3.凸函数的一阶导数是凸函数。
极小曲面方程及其解法

极小曲面方程及其解法曲面是三维空间中常见的数学物体,由于其具有良好的几何性质和广泛的应用场景,在数学、自然科学、物理学等领域都受到了广泛关注。
在曲面的研究中,曲面的形状和能量密度是两个重要的研究方向,其中极小曲面是一类非常特殊的曲面,极小曲面方程成为了极小曲面研究的重要数学工具。
一、极小曲面的定义与性质极小曲面指的是在某一区域内的曲面,其表面积相对于该区域内其他曲面的表面积是最小的。
极小曲面在几何学中具备了许多重要的性质,其中最重要的一条是它的高斯曲率恒为零,即该曲面上任意一点的曲率只有沿垂直于该曲面的切平面方向存在,垂直于该曲面的方向上的曲率均为零。
此外,极小曲面还具备其他一些好的性质,比如对称性和稳定性,这些性质在曲面的研究中都有广泛的应用。
二、极小曲面方程的基本形式极小曲面方程是研究极小曲面的一个非常重要的数学工具,它的基本形式可以表示为如下的泊松方程:$$\Delta f=2Hf$$其中,$\Delta$表示拉普拉斯算子,$H$表示曲面上某一点处的平均曲率,$f$表示曲面的高度函数。
其中泊松方程的解可以使用各种数学方法求解,比如分离变量法、格林函数法、有限元方法等,但是这些方法都存在着一些问题,比如求解困难、计算量大等。
为了克服这些问题,后来的研究者提出了一系列新的求解方法和数学工具。
三、极小曲面方程的求解方法根据极小曲面方程的基本形式,可以采用不同的数学方法求解,其中最常用的方法是能量方法和最小曲面面积方法。
这些方法都主要基于曲面的微分几何性质和函数分析理论来计算方程的解。
1. 能量方法:能量方法主要利用了曲面的形状和能量密度之间的关系,可以采用最小化能量密度的方式来求解极小曲面方程。
其中最常用的能量密度为:$$E(f)=\frac{1}{2}\int_{\Omega} (\vertdf\vert^2+2Hf^2)d\Omega$$其中,$\vert df\vert^2$表示高度函数的梯度大小的平方,$H$表示曲面上任意一点处的平均曲率,$\Omega$表示曲面所在的区域。
函数的曲率与曲线的凹凸性

函数的曲率与曲线的凹凸性曲率和凹凸性是微积分中研究曲线性质的重要概念。
在数学中,曲率描述了曲线的弯曲程度,而凹凸性则揭示了曲线的凸起和凹陷特征。
本文将探讨曲率和凹凸性之间的关系,并介绍如何通过曲率来分析曲线的凹凸性。
一、曲线的曲率曲率是曲线在每一点上的弯曲程度的度量。
对于平面曲线,我们可以通过曲率来衡量曲线弯曲得有多“急促”。
曲率的定义如下:设曲线上一点P,P点处的切线方程为L,过该点的圆的半径为r,则曲率k为曲线在P点的曲率半径r的倒数。
曲率可以用数学表达式表示为:k = |dr/ds| / |ds/dt|其中|dr/ds|表示切线上的速率,即切线在曲线上的变化率;|ds/dt|表示弧长在t上的变化率,即曲线的弧长参数。
曲率越大,曲线的弯曲程度越大。
二、曲线的凹凸性在微积分中,凹凸性是研究函数曲线的形状特征的重要概念。
一条曲线可以是凸的、凹的或是既非凸也非凹的。
为了确定曲线的凹凸性,我们需要根据曲线的二阶导数来判断。
设函数f(x)在区间I上连续,并且具有二阶导数。
如果在I上对于任意的x,f''(x)≥0,那么函数f(x)在I上是凹的;如果f''(x)≤0,那么函数f(x)在I上是凸的;如果f''(x)既不大于0也不小于0,那么函数f(x)在I 上既不是凹的也不是凸的。
三、曲率与凹凸性的关系曲率与凹凸性之间存在一定的联系。
在曲线的凹凸点上,曲率取得极值或者改变符号。
具体而言,如果曲率k在某点是正值,那么曲线在该点是凸的;如果曲率k在某点是负值,那么曲线在该点是凹的。
通过曲率可以进一步判断曲线的凹凸性:如果曲线的曲率函数k(x)在定义域上始终非负(或始终非正),那么曲线在整个区间上是凸的(或凹的);如果曲率函数k(x)在某一区间上既非正也非负,那么曲线在该区间上既非凸也非凹。
综上所述,曲率和凹凸性是密切相关的。
曲率描述了曲线的弯曲程度,而凹凸性则揭示了曲线的凸起和凹陷特征。
函数的凸性曲线的曲率资料

第7章 函数的凸性·曲线的曲率①凸函数 函数的“凸性”概念最初来自曲线的弯曲方向。
例如,曲线3x y =(图1)在Oy 轴左边是向下弯曲的(称为上凸)而在Oy 轴右边是向上弯曲的(称为下凸)。
虽然说“弯曲方向” 或“凸性”这些名称是几何上的术语,但经过抽象后的凸函数 理论在其它数学分支中也是很有用的。
从图2中看出,向上弯曲(下凸)的曲线上任何两点的连线(AB 的中点C 在弧AB 的上方;而从图3中看出,向下弯曲(上凸)的曲线上任何两点的连线(弦)AB 的中点C 在弧AB 的下方。
【注1】在国内早期的一些教科书(包括翻译前苏联的一些教科书)中,都把下凸函数称为“凹函数”,而把上凸函数称为“凸函数”。
这里的称呼与新近一些教科书或论文中的称呼是一致的。
请读者注意到这些区别。
【注2】还请读者注意,通常说“函数()f x 在区间(,)a b 内是下(上)凸函数”,若对于(,)a b 内任意两点1x 和2x 12()x x ≠与任意(0,1)t ∈,都满足琴生(Jesen)不等式[]1212()(1)()(1)()f t x t x t f x t f x >+-<+-它等价于不等式()11221122()()()f t x t x t f x t f x >+<+(其中1t 和2t 为正数且121t t +=)显然,不等式(※)是琴生不等式的特殊情形。
不过,对于连续函数来说,不等式(※)与琴生不等式是等价的。
因此,我们就用简单的不等式(※)定义函数的凸性。
关于连续函数情形下两者等价性的证明,有兴趣的读者图2O x 1 (x 1+x 2 )/2 x 2图3可去看本网站上的专题选讲。
【注3】若函数)(x f 在区间),(b a 内可微分,则从下图4看出,下凸(上凸)函数的图形上,每一点处的切线都在图形的下面(上面),而且导函数)(x f '(切线的斜率)是增大(减小)的。
椭圆偏微分方程解的水平集的凸性

椭圆偏微分方程解的水平集的凸性【摘要】:凹凸性是几何对象的一种基本特性,在光滑情形也是一种可以通过微分来描述的特性,因而凸性的研究既是几何研究的需要,也使得它跟分析产生自然的联系,从而凸性也成为分析研究的重要内容;不仅如此,随着对偏微分方程研究的深入,人们发现有时凸性亦是研究方程本身的需要,例如自由边界问题(见后文)。
因此,凸性研究不仅有着长久的历史,也越来越成为人们感兴趣的问题。
在研究微分方程的凸性时,通常可分为研究方程解本身的凸性和解的水平集的凸性,解的凸性可导出水平集的凸性,从这一角度来说,水平集的凸性是更精细的问题。
本文对偏微分方程中研究凸性的历史做一些总结,利用经典的极值原理,首先给出一类低维p-调和函数的水平集凸性的定量估计。
同时,常秩定理是处理关于凸性问题的一个强有力工具,它在偏微分方程解的几何性质及微分几何中的应用有着深刻意义。
本文亦对预定平均曲率超曲面的水平集的常秩定理作了尝试。
另外,我们对低维极小超曲面的水平集凸性亦作了估计,并发现了与二维极小超曲面水平线有关的一些调和或下调和函数,由此可同时得到其水平集严格凸性的新证明。
最后,我们用分部积分法研究完全非线性问题,给出了一类Hessian不等式不存在性结果的新证明。
主要结果如下:定理0.0.1.设u为R~2中区域Ω上的p-调和函数,即满足方程且|▽u|≠0,u的水平集凸,则当3/2≤p≤3时,u的水平集的高斯曲率不能在Ω内部取到最小值,除非是常数。
定理0.0.2.设u为R~3中区域Ω上的p-调和函数,即满足方程且|▽u|≠0,u的水平集严格凸,则当p≥2时,u的水平集的高斯曲率不能在Ω内部取到最小值,除非是常数。
定理0.0.3.(相关术语见后文)设M~2为R~3中极小曲面,若M~2的相对于ξ方向的高度函数u无临界点,即|▽u|≠0,相应水平线的曲率为K,最速下降线的曲率为G,则(i)|▽u|~(-1)K、|▽u|~(-1)G是M~2上的调和函数。
清华微积分(高等数学)课件第十讲极值与凸性

如果对于函数$f(x)$在区间$I$上的任意三点$x_1, x_2, x_3$,都有$frac{f(x_2) - f(x_1)}{x_2 - x_1} geq frac{f(x_3) - f(x_1)}{x_3 - x_1}$,则函数$f(x)$在区间$I$上是凸的。
04
极值与凸性的关系
和精度。
06
总结与展望
本讲内容的总结
极值的基本概念
本讲介绍了极值的概念,包括局部极 值和全局极值,以及极值的必要条件 和充分条件。
凸性的定义与性质
凸性是微积分中的一个重要概念,本 讲详细介绍了凸函数的定义、性质以 及凸函数的判别方法。
极值与凸性的关系
本讲通过实例说明了极值与凸性的关 系,如函数在凸区间上的极值点一定 是函数的拐点。
几何意义
在二维空间中,凸函数对应的曲线位于其任意两点连线的下方,即对于任意两 点$x_1$和$x_2$,曲线上的点位于这两点连线的下方或恰好在这条直线上。
凸函数的性质
凸函数的导数性质
如果函数$f(x)$在区间$I$上可导,且 为凸函数,那么其导数$f'(x)$在区间 $I$上单调递增。
凸函数的二阶导数性质
极值与最优化问题
本讲还介绍了极值在解决最优化问题 中的应用,如利用极值条件求解最优 化问题的方法。
未来研究方向的展望
极值理论的进一步
研究
虽然极值的基本理论已经比较完 善,但仍有许多值得进一步研究 的问题,如多变量函数的极值问 题、无穷维空间的极值问题等。
凸性理论的深化
凸性理论在数学和工程领域有着 广泛的应用,未来可以进一步研 究凸性的性质、凸函数的分类等 问题。
极值点一定是凸点
极值点是函数在某点的取值达到局部最大或最小的点,而凸 点是函数图像上凸起的部分,因此极值点一定是凸点。
凸函数在物理学中的应用

凸函数在物理学中的应用凸函数是一个在高等数学中十分重要的概念,它在数学、物理学等学科中有着广泛的应用。
这篇文章主要探讨凸函数在物理学中的应用。
1. 堆积论堆积论是物理学中的重要分支,它研究的是大量粒子在被堆积时所形成的几何形状和物理性质。
堆积论中常常涉及到密度、体积、分布函数等概念,而这些概念往往可以通过凸函数来描述。
例如,假设存在一个连续聚堆充满了一个方形容器。
容器底部的压力可以用连续聚堆的密度分布来描述,而密度分布可以通过凸函数来刻画。
具体而言,假设连续聚堆的密度分布函数为f(r),其中r表示离堆心的距离,则f(r)应该具有凸性。
这是因为,在离堆心较远的地方,密度分布应该随着距离的增加而减小;而在离堆心较近的地方,密度分布应该随着距离的减小而增加。
因此,密度分布函数f(r)应该具有单峰形状,且这个峰应该位于堆心,这也被称作“平衡态”。
2. 能量最小化问题在物理学中,许多问题可以归结为能量最小化问题。
例如,对于一个弹性体,在经历了一定的变形后,它所存储的弹性能就代表了它的总能量。
因此,弹性体的形状在一定程度上影响了它所存储的能量大小。
假设弹性体的形状可以用曲面z=f(x,y)来描述。
如果我们希望找到一个能够存储最小能量的曲面,则可以将问题归结为对能量函数的最小化。
具体而言,假设弹性体的弹性函数为E(z),则弹性能可以用积分形式表示:U=\int E(f(x,y))dxdy为了使U最小化,需要找到一个满足约束条件的$f(x,y)$,即满足体积守恒和边界条件的情况下能够最小化弹性能。
这个问题可以通过约束优化问题来解决。
其中,约束条件可以使用拉格朗日乘子法表示。
通过求解拉格朗日函数的梯度,可以得到一个关于$f(x,y)$的偏微分方程。
如果这个方程形如一个椭圆型方程,则交替方向乘子法可以用来求解这个方程。
3. 统计力学在统计力学中,凸函数也有着广泛的应用。
例如,假设我们希望研究一组粒子在热力学平衡时的分布情况。
极小曲面发展历程

极小曲面发展历程极小曲面是微分几何学中的一个重要概念,它代表了曲面上的每一点都是极小曲率的曲面。
极小曲面的研究历程可以追溯到18世纪,一直到今天,它在数学领域中有着广泛的应用和深远的理论意义。
极小曲面的研究始于欧拉在18世纪的工作。
他首次提出了对曲面上每一点的曲率进行极小化的概念。
随后,拉格朗日、拉普拉斯等数学家陆续对欧拉的研究进行了拓展,提出了不同的极小曲面模型,并给出了一些重要的性质与定理。
然而,在这个阶段,对极小曲面的研究还相对较少,也没有形成完整的理论体系。
进入19世纪,极小曲面的研究逐渐得到了更多人的关注。
高斯在1827年发表了《平面弯曲论》一书,详细地探讨了曲面上的曲率理论,并首次将极小曲面的概念引入其中。
他给出了极小曲面的重要性质——极小曲面的高斯曲率为负。
这个发现对极小曲面的研究产生了重要的影响,并为后续的研究奠定了基础。
随后的几十年里,极小曲面的研究日渐成熟。
黎曼在19世纪中叶提出了黎曼曲面的概念,并在其上进行了广泛的研究。
他提出了极小曲面的黎曼映射问题,即寻找一种变换将给定曲面变为一极小曲面,并成功解决了这个问题。
这一成果使得极小曲面的研究迈入了一个新的阶段,为后来的数学家提供了新的思路与方法。
20世纪初,极小曲面的研究迎来了重大突破。
福柯斯首次提出了极小曲面的存在性问题,并证明了任意有限面积的边界闭曲面都存在极小曲面。
同时,他给出了极小曲面的一个重要性质——调焦不变性,即极小曲面在均匀缩放下具有不变性。
这个性质使得极小曲面在物理学领域中有着广泛的应用,如油膜的形成与液滴的稳定性等。
近年来,随着计算机的发展,极小曲面的研究进入了一个新的时期。
研究者们开始利用计算机来模拟和分析极小曲面的形态和性质,取得了一系列重要的成果。
同时,利用计算机进行数值计算和模拟还提供了一种新的方法来研究极小曲面的变形与演化,从而为曲面设计、形态优化等应用提供了新的理论和技术支持。
极小曲面的研究历程可谓是一个不断发展、不断创新的过程。
极小曲面方程黎曼几何

极小曲面方程黎曼几何全文共四篇示例,供读者参考第一篇示例:极小曲面方程是黎曼几何中一个重要的概念,它研究的是曲面上的特殊曲面,这些曲面在曲率非常小的情况下表现出特殊的几何性质。
在黎曼几何中,曲面的曲率是一个重要的性质,它描述了曲面的变曲性,即在曲面上任意一点处的曲线的曲率。
极小曲面是指曲率几乎为零的曲面,它们在曲率几乎为零的情况下表现出来的性质是非常特殊的。
我们来看极小曲面的定义。
一个曲面被称为极小曲面,如果它的高斯曲率等于零,即K = 0。
在曲面的参数化表示下,极小曲面的方程通常是一个非线性偏微分方程,其解可能是很复杂的。
极小曲面的权力意味着其具有一些特殊的性质,比如在其上的曲线的长度最小等。
那么极小曲面在黎曼几何中有什么重要性呢?极小曲面的研究在几何学和拓扑学中占有重要地位。
极小曲面的研究可以帮助我们理解曲面的局部结构。
极小曲面存在的条件对于拓扑学中的一些问题具有重要的应用价值。
在黎曼几何中常常用极小曲面来研究拓扑空间的不变量,比如欧拉数等。
极小曲面方程在黎曼几何中的研究是一个重要的课题,它不仅有着深刻的理论意义,还具有广泛的应用价值。
通过研究极小曲面方程,我们可以更深入地理解曲面的几何性质,进而推动几何学和拓扑学等领域的发展。
希望未来能有更多的学者投入到极小曲面方程的研究中,为这一领域的发展带来更多的新的突破和进展。
第二篇示例:极小曲面方程是黎曼几何中一个非常重要的概念。
在黎曼几何中,我们研究的对象是曲面和流形,而极小曲面则是其中的一类特殊的曲面。
极小曲面在数学和物理领域都具有重要的应用价值,它们在微分几何、微分方程、拓扑学等领域都有着广泛的应用。
我们来介绍一下什么是极小曲面。
在黎曼几何中,给定一个曲面,我们可以通过测量曲面上的长度、角度等几何量来描述这个曲面。
极小曲面是指在给定度量下表面积最小的曲面。
具体来说,对于一个曲面上的曲线,我们可以通过积分来计算这个曲线的长度,而曲面上的面积则可以通过这些曲线的长度来计算。
函数的凸性曲线的曲率

第7章 函数的凸性·曲线的曲率①凸函数 函数的“凸性”概念最初来自曲线的弯曲方向。
例如,曲线3x y =(图1)在Oy 轴左边是向下弯曲的(称为上凸)而在Oy 轴右边是向上弯曲的(称为下凸)。
虽然说“弯曲方向” 或“凸性”这些名称是几何上的术语,但经过抽象后的凸函数 理论在其它数学分支中也是很有用的。
从图2中看出,向上弯曲(下凸)的曲线上任何两点的连线(AB 的中点C 在弧AB 的上方;而从图3中看出,向下弯曲(上凸)的曲线上任何两点的连线(弦)AB 的中点C 在弧AB 的下方。
【注1】在国内早期的一些教科书(包括翻译前苏联的一些教科书)中,都把下凸函数称为“凹函数”,而把上凸函数称为“凸函数”。
这里的称呼与新近一些教科书或论文中的称呼是一致的。
请读者注意到这些区别。
【注2】还请读者注意,通常说“函数()f x 在区间(,)a b 内是下(上)凸函数”,若对于(,)a b 内任意两点1x 和2x 12()x x ≠与任意(0,1)t ∈,都满足琴生(Jesen)不等式[]1212()(1)()(1)()f t x t x t f x t f x >+-<+-它等价于不等式()11221122()()()f t x t x t f x t f x >+<+(其中1t 和2t 为正数且121t t +=)显然,不等式(※)是琴生不等式的特殊情形。
不过,对于连续函数来说,不等式(※)与琴生不等式是等价的。
因此,我们就用简单的不等式(※)定义函数的凸性。
关于连续函数情形下两者等价性的证明,有兴趣的读者图2O x 1 (x 1+x 2 )/2 x 2图3可去看本网站上的专题选讲。
【注3】若函数)(x f 在区间),(b a 内可微分,则从下图4看出,下凸(上凸)函数的图形上,每一点处的切线都在图形的下面(上面),而且导函数)(x f '(切线的斜率)是增大(减小)的。
清华微积分课件第十讲极值与凸性

f x
(x) x0
0
5
由极, 限 0 ,使 性(x 在 质 0, x0)
中有 f ( x) 0
x x0
在 ( x 0 ,x 0 ) 内 ,有 f( x ) 0
在 (x 0 ,x 0 ) 内 ,有 f(x ) 0
根据定 1知 ,理 f在x0取得极. 小值
设 f (x)有二阶导数, 若(x0, f (x0 ))为 f (x)的 拐点,则有f (x0 ) 0.
性,有
lim f(x)f(x1)lim f(x)f(x2)
x x1 xx1
x x1 xx2
2019/9/23
即 f(x1)f(xx11 ) xf2(x2)
22
也l有 im f(x )f(x 1)lim f(x )f(x 2) x x 2 xx 1 x x 2 xx 2
间(a, b)可导,则f 在[a, b]为下凸函数的充
分必要条件:是 x0 [a, b], 有 切线位于
2019/9/23
f (x)
f (x0)
f (x0)(x x0)
曲线下方
25
[证] 必要性
假设f 为下凸函数
x 0 ,x 1 ,x [a ,b ]且 , x 0 x 1 x ,有
2019/9/23 ma f(ax ),f(b),f(xi)i,1,2, ,n 11
( B ) 最大、最小值应用问题
(1) 如果在 (a,b)内f(x)有唯一的x驻 0, 点 而 且 是 极.值 则f点 (x0)就 是 所 要 求 最大值或最. 小值
(2)如果在(a,b)内f (x)有唯一的驻x0点 , 又从实际问题本身知可道以 , f (x)的
当a 0时,
函数的凸性曲线的曲率

第7章 函数的凸性·曲线的曲率①凸函数 函数的“凸性”概念最初来自曲线的弯曲方向。
例如,曲线3x y =(图1)在Oy 轴左边是向下弯曲的(称为上凸)而在Oy 轴右边是向上弯曲的(称为下凸)。
虽然说“弯曲方向” 或“凸性”这些名称是几何上的术语,但经过抽象后的凸函数 理论在其它数学分支中也是很有用的。
从图2中看出,向上弯曲(下凸)的曲线上任何两点的连线(AB 的中点C 在弧AB 的上方;而从图3中看出,向下弯曲(上凸)的曲线上任何两点的连线(弦)AB 的中点C 在弧AB 的下方。
【注1】在国内早期的一些教科书(包括翻译前苏联的一些教科书)中,都把下凸函数称为“凹函数”,而把上凸函数称为“凸函数”。
这里的称呼与新近一些教科书或论文中的称呼是一致的。
请读者注意到这些区别。
【注2】还请读者注意,通常说“函数()f x 在区间(,)a b 内是下(上)凸函数”,若对于(,)a b 内任意两点1x 和2x 12()x x ≠与任意(0,1)t ∈,都满足琴生(Jesen)不等式[]1212()(1)()(1)()f t x t x t f x t f x >+-<+-它等价于不等式()11221122()()()f t x t x t f x t f x >+<+(其中1t 和2t 为正数且121t t +=)显然,不等式(※)是琴生不等式的特殊情形。
不过,对于连续函数来说,不等式(※)与琴生不等式是等价的。
因此,我们就用简单的不等式(※)定义函数的凸性。
关于连续函数情形下两者等价性的证明,有兴趣的读者可去看本网站上的专题选讲。
【注3】若函数)(x f 在区间),(b a 内可微分,则从下图4看出,下凸(上凸)函数的图形上,每一点处图2O x 1 (x 1+x 2 )/2 x 2图3112108 的切线都在图形的下面(上面),而且导函数)(x f '(切线的斜率)是增大(减小)的。
函数的凸性曲线的曲率

第7章 函数的凸性·曲线的曲率①凸函数 函数的“凸性”概念最初来自曲线的弯曲方向。
例如,曲线3x y =(图1)在Oy 轴左边是向下弯曲的(称为上凸)而在Oy 轴右边是向上弯曲的(称为下凸)。
虽然说“弯曲方向”或“凸性”这些名称是几何上的术语,但经过抽象后的凸函数理论在其它数学分支中也是很有用的。
从图2中看出,向上弯曲(下凸)的曲线上任何两点的连线(AB 的中点C 在弧AB 的上方;而从图3中看出,向下弯曲(上凸)的曲线上任何两点的连线(弦)AB 的中点C 在弧AB 的下方。
【注1】在国内早期的一些教科书(包括翻译前苏联的一些教科书)中,都把下凸函数称为“凹函数”,而把上凸函数称为“凸函数”。
这里的称呼与新近一些教科书或论文中的称呼是一致的。
请读者注意到这些区别。
【注2】还请读者注意,通常说“函数()f x 在区间(,)a b 内是下(上)凸函数”,若对于(,)a b 内任意两点1x 和2x 12()x x ≠与任意(0,1)t ∈,都满足琴生(Jesen)不等式[]1212()(1)()(1)()f t x t x t f x t f x >+-<+-它等价于不等式()11221122()()()f t x t x t f x t f x >+<+ (其中1t 和2t 为正数且121t t +=)显然,不等式(※)是琴生不等式的特殊情形。
不过,对于连续函数来说,不等式(※)与琴生不等式是等价的。
因此,我们就用简单的不等式(※)定义函数的凸性。
关于连续函数情形下两者等价性的证明,有兴趣的读者图2O x 1 (x 1+x 2 )/2 x 2图3108 可去看本网站上的专题选讲。
【注3】若函数)(x f 在区间),(b a 内可微分,则从下图4看出,下凸(上凸)函数的图形上,每一点处的切线都在图形的下面(上面),而且导函数)(x f '(切线的斜率)是增大(减小)的。
凸函数为什么如此重要?

凸函数为什么如此重要?凸函数是在数学中经常出现的概念,它在极为宽广的数学以及相关领域内发挥了巨大的作用。
凸函数的定义非常简洁直观,但仅仅做了这样一个“小小”的要求后,我们往往会发现之后的事情会变得非常不一样,有些时候可谓“化腐朽为神奇”。
那么,凸函数到底有什么神奇的力量呢?首先我们从凸函数的定义说起。
一般而言,欧式空间Rⁿ上的凸函数f(x)如下定义:为了下文讨论的方便,我们所说的凸函数一般都是定义在Rⁿ上的。
关于凸函数的定义我们必须要多说几句。
对凸函数比较熟悉的同学可能常常会疑惑,为什么不同的地方对凸函数的定义和称呼不一样?有时候不仅定义有差别,甚至有时候连名称都不一样。
目前学界对凸函数的定义和称呼没有同一的规定,有时候我们称凸函数为“上凸”,但有的时候会发现“上凸”指的是“凹”,但有的时候又指的是“凸”,所以在不同的文献中要仔细识别“凸”的含义。
相对于凸函数,我们还有凹函数的概念,一个函数f(x)被称为凹函数如果-f(x)是凸函数。
这里我们给出的凸函数是定义在n维实数空间上的,实际上,凸函数可以定义在Rⁿ的任何凸子集上,而凸子集的定义与凸函数类似,指的就是那些任意两点连线都在自身里的集合。
更一般的,凸函数可以定义在向量空间上,例如泛函分析中的巴拿赫空间,这种向量空间甚至可以是无限维的。
我们都知道,凸函数具有强烈的几何直观意义,也就是说,它的图像围成的区域是个凸集。
接下来我们就来看看凸函数的一些良好性质,借此我们就可以看出凸函数为什么在数学中如此重要。
可微性首先我们注意到,在凸函数的一般定义中,我们没有要求函数的连续性,更没有要求可导性。
但令人吃惊的是,连续性是Rⁿ中凸函数的内在性质!也就是说:Rⁿ中的凸函数f(x)一定是连续的!更一般的,f(x)是局部利普希茨连续的。
不过很可惜的是,这样美妙的性质对于无限维空间而言是不正确的。
应该说,我们都习惯于接受可以求导,尤其是二次求导的凸函数,因为这样我们可以直接利用函数的二阶导数(高维情形是Hessian矩阵)来判断它的凹凸性,也就是说,可以利用凸函数的定义证明:但在一般定义中,我们没有要求函数的可导可微性,因为实际上,可导可微性是非常强的数学性质,数学中很多函数没有这样良好的性质,很多凸函数也是如此。
极小曲面公式

极小曲面公式“极小曲面公式”有着漫长的历史,始于17世纪时,几何学家米歇尔贝叶斯(René Descartes)和白瑞森(Isaac Barrow)提出的第一个曲面公式。
历经数百年,极小曲面公式已经成为数学家解决几何问题最为重要的工具之一。
极小曲面公式描述了一种特殊几何形状,通常被称为“极小曲面”,它是一种有限几何体,可以用多面体覆盖,但它却有更复杂的结构,比如圆柱面和椭圆曲面。
比如,一个以椭圆曲面为表面的玻璃球,可以用17个四面体来覆盖,但这17个四面体的公式就叫做“极小曲面公式”。
二、极小曲面公式及其原理极小曲面公式是一个多项式,它包含着多个变量,可以描述和表示覆盖体积最小的几何体。
极小曲面公式的原理是,它将任意几何体的多面体覆盖表示为有依次降低的阶数的多项式,这样可以得到一个最小的覆盖体积,也就是极小曲面公式。
所以,数学家用极小曲面公式进行几何表示,可以将曲面的复杂结构表示为简单的多项式,而这个多项式的阶数越低,说明曲面越平滑,也就等于说覆盖体积越小。
三、极小曲面公式的应用极小曲面公式用于几何学中对曲面表示和分析,这是数学家用来描述几何体结构的最好方法。
它可以用于分析和描述曲面,以便更准确地分析几何体结构,比如表面和边界,从而更好地了解物理空间和几何形状之间的关系。
此外,极小曲面公式也用于解决经典的几何问题,如“四色定理”,它表明地球的表面上不能用四种颜色将所有的国家划分为独立的区域,或者比如“正方体填充问题”,它证明正方体空间的每一点都可以用8个球体覆盖,而且这8个球体的半径之和最小,即它们都是最小的覆盖体积。
四、结语极小曲面公式是数学家运用多项式对几何曲面进行表示和分析的最有效的方法。
它能够把几何图形中的复杂结构表示为简单的多项式,并且多项式的阶数越小,说明几何体的覆盖体积越小,也就是说,极小曲面公式可以有效地描述曲面结构,并用于求解各种几何问题,是探索几何上的奥秘的重要工具之一。
函数的凸性曲线的曲率资料

第7章 函数的凸性·曲线的曲率①凸函数 函数的“凸性”概念最初来自曲线的弯曲方向。
例如,曲线3x y =(图1)在Oy 轴左边是向下弯曲的(称为上凸)而在Oy 轴右边是向上弯曲的(称为下凸)。
虽然说“弯曲方向” 或“凸性”这些名称是几何上的术语,但经过抽象后的凸函数 理论在其它数学分支中也是很有用的。
从图2中看出,向上弯曲(下凸)的曲线上任何两点的连线(AB 的中点C 在弧AB 的上方;而从图3中看出,向下弯曲(上凸)的曲线上任何两点的连线(弦)AB 的中点C 在弧AB 的下方。
【注1】在国内早期的一些教科书(包括翻译前苏联的一些教科书)中,都把下凸函数称为“凹函数”,而把上凸函数称为“凸函数”。
这里的称呼与新近一些教科书或论文中的称呼是一致的。
请读者注意到这些区别。
【注2】还请读者注意,通常说“函数()f x 在区间(,)a b 内是下(上)凸函数”,若对于(,)a b 内任意两点1x 和2x 12()x x ≠与任意(0,1)t ∈,都满足琴生(Jesen)不等式[]1212()(1)()(1)()f t x t x t f x t f x >+-<+-它等价于不等式()11221122()()()f t x t x t f x t f x >+<+(其中1t 和2t 为正数且121t t +=)显然,不等式(※)是琴生不等式的特殊情形。
不过,对于连续函数来说,不等式(※)与琴生不等式是等价的。
因此,我们就用简单的不等式(※)定义函数的凸性。
关于连续函数情形下两者等价性的证明,有兴趣的读者图2O x 1 (x 1+x 2 )/2 x 2图3可去看本网站上的专题选讲。
【注3】若函数)(x f 在区间),(b a 内可微分,则从下图4看出,下凸(上凸)函数的图形上,每一点处的切线都在图形的下面(上面),而且导函数)(x f '(切线的斜率)是增大(减小)的。
极小曲面浅谈
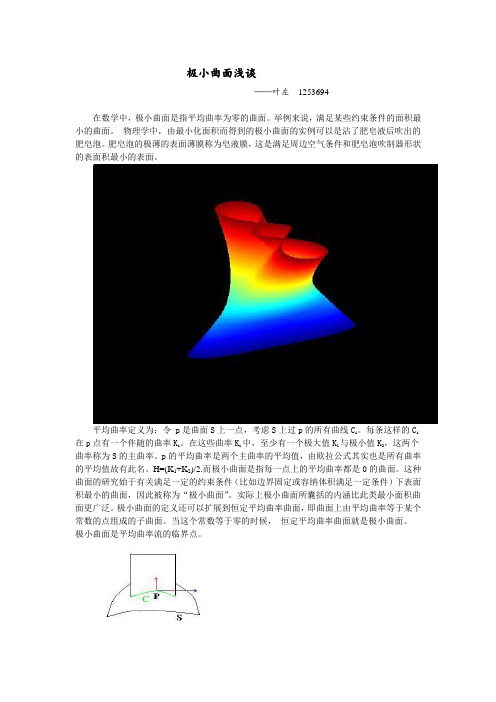
极小曲面浅谈——叶左1253694在数学中,极小曲面是指平均曲率为零的曲面。
举例来说,满足某些约束条件的面积最小的曲面。
物理学中,由最小化面积而得到的极小曲面的实例可以是沾了肥皂液后吹出的肥皂泡。
肥皂泡的极薄的表面薄膜称为皂液膜,这是满足周边空气条件和肥皂泡吹制器形状的表面积最小的表面。
平均曲率定义为:令 p是曲面S上一点,考虑S上过p的所有曲线C i。
每条这样的C i 在p点有一个伴随的曲率K i。
在这些曲率K i中,至少有一个极大值K1与极小值K2,这两个曲率称为S的主曲率。
p的平均曲率是两个主曲率的平均值,由欧拉公式其实也是所有曲率的平均值故有此名。
H=(K1+K2)/2.而极小曲面是指每一点上的平均曲率都是0的曲面。
这种曲面的研究始于有关满足一定的约束条件(比如边界固定或容纳体积满足一定条件)下表面积最小的曲面,因此被称为“极小曲面”。
实际上极小曲面所囊括的内涵比此类最小面积曲面更广泛。
极小曲面的定义还可以扩展到恒定平均曲率曲面,即曲面上由平均曲率等于某个常数的点组成的子曲面。
当这个常数等于零的时候,恒定平均曲率曲面就是极小曲面。
极小曲面是平均曲率流的临界点。
极小曲面的经典例子包括:1).欧几里得平面,无特别约束条件下最平常的极小曲面;2).悬链面:由悬链线围绕其水平准线旋转而得到的曲面。
这是最早发现的“不寻常”的极小曲面。
3).正螺面:一个线段沿着垂直于其中点的直线匀速螺旋上升时扫过的曲面。
这是继悬链曲面后发现的第二种不寻常的极小曲面;4).Enneper曲面。
4).Scheck曲面;5).Costa —Hoffman—Meeks曲面。
悬链面悬链曲面状的皂液膜可以由将两个等大的圆环紧贴放入肥皂水中,拿出后再缓慢分开得到.方程:z=cosh-1错误!.正螺面就是让一条直线l的初始位置与x轴重合,然后让直线l一边绕z轴作匀速转动,一边沿z轴方向作匀速运动,则直线在这两种运动的合成下扫出的曲面就是正螺旋面,它的方程为:z=arctan(y/x).显然正螺旋面可以看做是由直线形成的,即它是一个直纹面Costa面在三维欧氏空间E3中,若一张曲面可用方程z=z(x,y)来表示,则称它为图,或非参数化曲面。
函数凹凸性方面应用

§6.5 微分中值定理在研究函数的凹凸性方面的应用教学目标: 掌握讨论函数的凹凸性和方法.教学要求: 弄清函数凸性的概念,掌握函数凸性的几个等价论断,会求曲线的拐点,能应用函数的凸性证明某些有关的命题.教学重点: 利用导数研究函数的凸性教学难点: 利用凸性证明相关命题教学方法: 系统讲授法+演例如题教学过程:引言上面已经讨论了函数的升降与极值,这对函数性状的了解是有很大作用的.为了更深入和较准确地掌握函数的性状,我们在这里再讲述一下有关函数凸性的概念及其与函数二阶导数的关系.什么叫函数的凸性呢?我们先以两个具体函数为例,从直观上看一看何谓函数的凸性.如函数y x=所表示的曲线是向上凸的,而2=所表示的曲线是向下凸的,这与我们日常习惯上的y x称呼是相类似的.或更准确地说:从几何上看,假设y=f(x)的图形在区间I上是凸的,那么连接曲线上任意两点所得的弦在曲线的上方;假设y=f(x)的图形在区间I上是凹的,那么连接曲线上任意两点所得的弦在曲线的下方.如何把此直观的想法用数量关系表示出来呢?设函数()f x 在区间I 上是凸的〔向下凸〕,任意1x ,2x I ∈〔12x x <〕.曲线()y f x =上任意两点11(,())A x f x ,11(,())B x f x 之间的图象位于弦AB 的下方,即任意12(,)x x x ∈,()f x 的值小于或等于弦AB 在x 点的函数值,弦AB 的方程211121()()()()f x f x y x x f x x x -=-+-.对任意12(,)x x x ∈有211121()()()()()f x f x f x x x f x x x -≤-+-,整理得21122121()()()x x x x f x f x f x x x x x --≤+--.令221()x x t x x -=-,那么有01t <<,且12(1)x tx t x =+-,易得1211x x tx x -=--,上式可写成1212[(1)]()(1)()f tx t x tf x t f x +-≤+-.一、凸函数定义以及与连续性的关系 (一) 凸〔凹〕函数的定义定义1 设函数f 为定义在区间I 上的函数,假设对I 上任意两点1x 、2x 和任意实数(0,1)λ∈总有1212((1))()(1)()f x x f x f x λλλλ+-≤+-,那么称f 为I 上的凸函数.反之,如果总有1212((1))()(1)()f x x f x f x λλλλ+-≥+-,那么称f 为I 上的凹函数.注 易证:假设一f 为区间I 上的凸函数,那么f 为区间I 上的凹函数,因此,今后只讨论凸函数的性质即可.定义2 设曲线y =f(x)在点(00,()x f x )处有穿过曲线的切线,且在切点近旁,曲线在切线的两侧分别是严格凸或严格凹的,这时称(00,()x f x )为曲线y =f(x)的拐点.必须指出;假设(00,()x f x )是曲线y=f 〔x)的一个拐点,y =f(x)在点0x 的导数不一定存在,如3y x =在x =0的情形. (二) 凸函数的特征引理 f 为I 上的凸函数⇔对于I 上任意三点123x x x <<总有:32212132()()()()f x f x f x f x x x x x --≤-- (3) ()f x 严格凸函数⇔上式严格不等式成立.证⇒记3231x x x x λ-=-,那么01λ<<及213(1)x x x λλ=+-, 由f 的凸性知213()()(1)()f x f x f x λλ≤+-3221133131()()x x x xf x f x x x x x --=+-- (4) 从而有312321213()()()()()()x x f x x x f x x x f x -≤-+-即 322212321213()()()()()()()()x x f x x x f x x x f x x x f x -+-≤-+- 整理即得(3)式.⇐13,x x I ∀∈13()x x <,(0,1)λ∀∈记213(1)x x x λλ=+-,那么123x x x <<,3221x x x x λ-=-由必要性的推导步骤可逆,从(3)式便得(4)式.故f 为凸函数.同理便知,曲线上首尾相连的线,其斜率是递增的,即123,,x x x I ∀∈,123x x x <<,有31212131()()()()f x f x f x f x x x x x --≤--()f x 严格凸函数⇔上式严格不等式成立.定理 设为开区间上的凸函数.假设那么在上满足利普希茨条件,且在上连续.证明(证明开区间上的凸函数必为连续函数) 当取定后,由为开区间,必可选取中的四点满足:.如下图,再在中任取两点. 应用引理得到.令,那么,.显然,上述 L 与中的点无关, 故在上的每个闭区间上满足利普希茨条件.由此容易推知在上连续,再由在上的任意性,又可推知在上处处连续.如果f 是I 上的可导函数,那么进一步有: 二、凸函数与导数的关系定理1〔可导函数为凸函数的等价命题〕 设f 为区间I 上的可导函数,那么下述论断互相等价:〔1〕f 为I 上的凸函数;〔2〕f '为I 上的增函数;〔3〕对I 上的任意两点12,x x 总有21121()()()()f x f x f x x x '≥+-证(i)(ii),并取,使据定理3.12,有由可微,当时,对上述不等式取极限后,得到.所以是上的递增函数.(ii)(iii)由微分中值定理和递增,便可证得当时,也有一样结论.(iii)(i),并记,那么有,由(iii)可得.注定理中(iii)的几何意义如下列图所示:曲线上任意一点处的切线恒位于曲线的下方在为可微的前提条件下,常用上述切线与曲线的位置关系(iii)来表述凸函数.但是在没有可微条件假设时,凸函数只能用曲线与其任一弦的位置关系(定义1)来定义.如果f 在I 上二阶可导,那么进一步有:定理2〔凸函数与二阶导数的关系〕 设f 为I 上的二阶可导函数,那么在I 上f 为凸〔凹〕函数⇔()0f x ''>〔()0f x ''<〕,x I ∈.f 为严格凸⇔1〕()0f x ''≥;2〕()f x ''不在I 上的任一子区间上恒为零.此定理说明:f 为严格凸,那么曲线中不含有直线段〔()0f x ''=〕.对于凹函数情形,也有类似的定理〔因为f 凸,那么f -凹〕. 可导函数f 有如下相互等价的论断:1〕f 为I 上凹函数.2〕123,,x x x I ∀∈,123x x x <<有32212132()()()()f x f x f x f x x x x x --≥--.即割线斜率递减.3〕()f x '为I 上递减函数.4〕0x I ∀∈,有000()()()()f x f x f x x x '≤+-,x I ∈.当f 在I 上二阶可导时,下述论断与1〕,2〕,3〕,4〕相等价. 5〕在I 上()0f x ''≤.对严格凹的情形可类似得出等价论断. 二、拐点定义2 设曲线y =f(x)在点(00,()x f x )处有穿过曲线的切线,且在切点近旁,曲线在切线的两侧分别是严格凸或严格凹的,这时称(00,()x f x )为曲线y =f(x)的拐点.〔即为曲线凹凸局部的分界点〕必须指出;假设(00,()x f x )是曲线y=f 〔x)的一个拐点,y =f(x)在点0x 的导数不一定存在,如3y x =x =0的情形.定理3〔拐点必要条件〕 假设f 在0x 二阶可导,那么(00,()x f x )为曲线y =f(x)的拐点的必要条件是0()0f x ''=.综上知:(00,()x f x )的拐点,那么要么〔1〕0()0f x ''=;要么〔2〕f 在0x 点不可导.定理4 设f 在点0x 可导,在某邻域0()U x 二阶可导,假设在0()U x +和0()U x -上()f x ''的符号相反,那么(00,()x f x )为曲线y =f(x)的拐点.例1 讨论函数()arctan f x x =的凸性与拐点.解222()(1)xf x x ''=-+,因而当0x ≤时,()0f x ''≥;当0x ≥时,()0f x ''≤,从而函数f 为(,0]-∞上的凸函数,在[0,)+∞上为凹函数.而()f x 在原点连续,故原点为曲线()y f x =的拐点例2 假设f 在(,)a b 可导、凸〔凹〕函数,那么0(,)x a b ∈为f 的极小〔大〕值点⇔0()0f x '=.即0x 为f 的稳定点.证 ⇒〕费马定理.⇐〕因f 凸,故(,)x a b ∀∈有000()()()()f x f x f x x x '≥+-.因0()0f x '=,故(,)x a b ∀∈总有0()()f x f x ≥.即0x 为f 的极小值点.例3 设f 在开区间I 上为凸〔凹〕函数,证明f 在开区间I 任一点0x 都存在左、右导数. 证 只证凸函数f 在0x 存在右导数,其它情形同理可证.令120h h <<,记101x x h =+,202x x h =+,那么012x x x <<〔取2||h 充分小使02x h I +∈〕, 由(3)'式得:01002012()()()()f x h f x f x h f x h h +-+-≤记00()()()f x h f x F h h +-=(0)h >那么有21()()F h F h ≤即()F h 为单调递增函数.取4x I ∈且40x x ≤,那么040004()()()()f x f x f x h f x x x h -+-≤-,从而()F h 递增有下界,从而0lim ()h F h +→存在,即0()f x +'存在.注 对区间端点,左、右导数可能存在,也可能为∞.由第五章§1习题10知〔假设f 在0x 的左、右导数都存在,那么f 在0x 连续〕,假设f 在为开区间(,)a b 的凸〔凹〕函数,那么f 为(,)a b 的连续函数.〔但不一定可导,如()||f x x =〕 三、 詹森(Jensen)不等式定理(詹森(Jensen)不等式) 设f 为[,]a b 上的凸函数,[,]i x a b ∈,0i λ>(1,2,,)i n =且11nii λ==∑,那么有11()()nni i i i i i f x f x λλ==≤∑∑ 〔6〕成立.假设f 为严格凸函数,(1,2,,)i x i n =不全相等,那么上式严格不等式成立.证 用归纳法:2n =时命题由凸函数定义显然成立.假设n k =时命题成立,即0i λ>(1,2,,)i k =,11ki i λ==∑,那么有11()()kki i i i i i f x f x λλ==≤∑∑. 要证1n k =+时命题成立.设0i λ>(1,2,,,1)i k k =+,111k i i λ+==∑1111111111()()[(1)]1k k ki ii i i i k k k k k i i i k x f x f x x f x λλλλλλλ++++++===+=+=-+-∑∑∑〔由归纳法可知,当11nii λ==∑,(,)i x a b ∈时1ni ii x λ=∑(,)a b ∈,因为111kii k λλ==-∑,故111ki i i k x λλ=+-∑(,)a b ∈ 〕11111(1)()()1ki k i k k i k f x f x λλλλ+++=+≤-+-∑11111(1)()()1kik i k k i k f x f x λλλλ+++=+≤-+-∑11()k i i i f x λ+==∑⇒结论成立.注 由于(6)式中当时即为凸函数的定义式(1),所以詹森不等式(6)也可用来作为凸函数的定义,而詹森不等式的应用也就是凸函数的应用.对具体的函数套用Jensen 不等式的结果, 可以证明一些较复杂的不等式. 这种证明不等式的方法称为Jensen 不等式法或凸函数法. 具体应用时, 往往还用到所选函数的严格单调性.例4 证明: 对,,R ∈∀y x 有不等式 )(212y xyx e e e +≤+. 例5 设0i x >(1,2,,)i n =,那么121212111nn n nx x x n x x x nx x x +++≤≤+++当且仅当所有i x 全相等时等号成立.证 所有i x 全相等时,等号显然成立.只须证i x 不全等时,有严格不等号成立即可. 取()ln f x x =-,那么f 在(0,)+∞上严格凸,由例4知1121211ln (ln )ln()nni n i x x x x x x x nn-=+++-<-=-∑即 1212ln nn nx x x x x x n+++>因ln x 严格增,故有1212nn nx x x x x x n+++>又i x 不全等⇒1i x 不全等,故1121111ln (ln )nni ii i n x n n x x ==-<-=-∑∑所以 211nni inx x =<∑例6 在⊿ABC 中, 求证 233sin sin sin ≤++C B A . 解 考虑函数x x x f x x x f sin . 0 , 0 sin .0 ,sin )(⇒<<-=''≤≤=ππ在 区间) , 0 (π凹, 由Jensen 不等式, 有233sin 33)()()(3sinC sinB sinA ==⎪⎭⎫⎝⎛++≤++=++∴πC B A f C f B f A f . 233sinC sinB sinA ≤++⇒. 例7 1 ,,,=++∈+c b a c b a R . 求证6737373333≤+++++c b a .解 考虑函数3)(x x f =, )(x f 在) , 0 (∞+严格上凸. 由Jensen 不等式, 有≤+++++=+++++3)73()73()73(3737373333c f b f a f c b a28)8()7(37373733===+++=⎪⎭⎫⎝⎛+++++≤f c b a f c b a f . ⇒6737373333≤+++++c b a .例8 .2 , 0 , 033≤+>>βαβα 求证 2≤+βα. ( 留为作业 )(解 函数3)(x x f =在) , 0 (∞+严格下凸. 由Jensen 不等式, 有=+≤⎪⎭⎫ ⎝⎛+=⎪⎭⎫ ⎝⎛+=+2)()(228)(33βαβαβαβαf f f ⇒=≤+ ,122233βα- -- word.zl 2 , 8)(3≤+⇒≤+βαβα. )作业 P153 3⑶,5,8⑴; P158—159 17,18,19.。
