矢量分析
合集下载
第1章(矢量分析)
矢量分析与张量初步第一章矢量分析U STU STU ST标量（数量）：有大小，没方向的物理量。
矢量：既具有大小又具有方向的物理量，矢量又称为向量。
矢量与标量的根本区别是：有没有方向性。
如：温度、质量、角度、长度等。
如：力、速度、电场强度、力矩等。
矢量的模：矢量的大小。
矢量的模记为：或。
A K A ||A KU STU STU ST自由矢量：矢量平移后，其作用效果不变。
即自由矢量就是具有平移不变性的矢量。
FK 只考虑刚体的质心运动，作用力可以平移。
能不能平移？下面只讨论自由矢量。
如果要考虑刚体的转动，则作用力不能平移。
U STU STU ST始端在坐标原点的矢量常称为矢径，显然矢径的末端与直角坐标系中的三个坐标分量之间具有一一对应的关系，则矢径可用其末端的空间坐标来表示：①在直角坐标中的表示对矢量，始端平移到坐标原点，表示为：A Kr xi yj zk=++KK K K、、：单位矢量，分别指向三个坐标轴的正向。
i K j K k K x y z A A i A j A k=++K K K KU STU STU ST其中：为矢量的模，为指向矢量方向上的单位矢量。
R A A e A 三个：、和。
R βαcos cos cos A e i j kαβγ=++K K K KAKRxy zO因为222cos cos cos 1αβγ++=的直角坐标表示为A e K有几个独立坐标量？A Kr e =KU STU STU STOxe ρρK zA kK A K cos sin e i j ρϕϕ=+K K K三个：、和。
ρϕz 的直角坐标表示为e ρK在矢量的球坐标及柱坐标表示中，只要分别把单位矢量和的直角坐标表示代入，即得到矢量的直角坐标表示。
e ρKr e K 有几个独立坐标量？A K第一章矢量分析U STU ST U ST U STU STcos xA Aα=cos yA Aβ=cos zA A γ=(cos cos cos )A A i j k αβγ=++K K K K④方向余弦表示：设矢量与直角坐标三个坐标轴正向的夹角分别为、和，则：αγβA K用方向余弦（）表示矢量：A Kcos ,cos ,cos αβγcos x A A α=这实际上就是直角坐标表示，因为：cos y A A β=cos z A A γ=U STU STU ST不能按大小排列）。
矢量分析
性质
∇ × ∇ϕ = 0
梯度
三、矢量场的通量、散度
1、通量
r 定义：若矢量场 A 分布于空间中，在空间中存在任意曲面 S
r 上。定义 A 在曲面上的积分为通量。
r r Ψ = ∫ A ⋅ dS
s
曲面 S 的方向 开表面： 作一封闭线圈，选定绕行方向后，沿绕行方向 按右手螺旋法则，拇指方向为开表面方向 闭合面：外法线方向
s l
无旋场 性质
r ∇× A = 0
r ∇ ⋅ (∇ × A) = 0
旋度
例题讲解（课本） 例题1-8 例题1-9 例题1-10
例题
五、亥姆霍兹定理
内容：位于空间有限区域内的矢量场，当它的散度，旋度 以及它在区域边界上的场分布给定之后，该矢量场就被唯 一确定；对于无限大空间，如果矢量在无限远处减少至零 则该矢量由其散度和旋度唯一确定。
基础
矢量表示式
r r r r A = er Ar + eϕ Aϕ + e z Az
微分长度
r r r r dl = er dr + eϕ rdϕ + e z dz
微分面积
r r dS r = er rdϕdz r r dS ϕ = eϕ drdz r r dS z = e z rdrdϕ
微分体积
dV = rdrd ϕdz
只改变大小，不改变方向 矢量与矢量点乘
s r r r A ⋅ B = A B cosθ AB = Ax Bx + Ay B y + Az Bz
r r r r A⋅B = B⋅A
基础
说明： 1、两个矢量的标量积或点积，是一个标量 。 2、Θ是A、B之间较小的夹角，小于Π弧度。 3、其结果表示一个矢量的模和另一个矢量在该矢量 上的投影和乘积。 矢量与矢量叉乘
∇ × ∇ϕ = 0
梯度
三、矢量场的通量、散度
1、通量
r 定义：若矢量场 A 分布于空间中，在空间中存在任意曲面 S
r 上。定义 A 在曲面上的积分为通量。
r r Ψ = ∫ A ⋅ dS
s
曲面 S 的方向 开表面： 作一封闭线圈，选定绕行方向后，沿绕行方向 按右手螺旋法则，拇指方向为开表面方向 闭合面：外法线方向
s l
无旋场 性质
r ∇× A = 0
r ∇ ⋅ (∇ × A) = 0
旋度
例题讲解（课本） 例题1-8 例题1-9 例题1-10
例题
五、亥姆霍兹定理
内容：位于空间有限区域内的矢量场，当它的散度，旋度 以及它在区域边界上的场分布给定之后，该矢量场就被唯 一确定；对于无限大空间，如果矢量在无限远处减少至零 则该矢量由其散度和旋度唯一确定。
基础
矢量表示式
r r r r A = er Ar + eϕ Aϕ + e z Az
微分长度
r r r r dl = er dr + eϕ rdϕ + e z dz
微分面积
r r dS r = er rdϕdz r r dS ϕ = eϕ drdz r r dS z = e z rdrdϕ
微分体积
dV = rdrd ϕdz
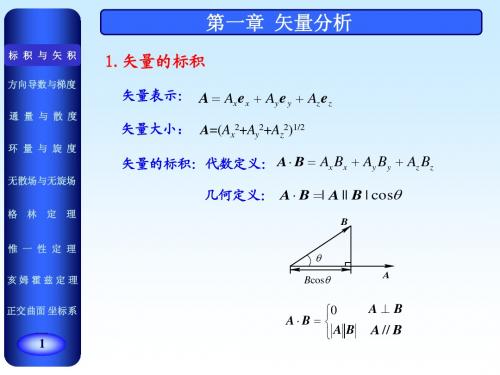
只改变大小，不改变方向 矢量与矢量点乘
s r r r A ⋅ B = A B cosθ AB = Ax Bx + Ay B y + Az Bz
r r r r A⋅B = B⋅A
基础
说明： 1、两个矢量的标量积或点积，是一个标量 。 2、Θ是A、B之间较小的夹角，小于Π弧度。 3、其结果表示一个矢量的模和另一个矢量在该矢量 上的投影和乘积。 矢量与矢量叉乘
矢量分析
矢 量 分 析一：定义标量：只有大小，没有方向的物理量。
如质量，时间，温度等矢量：即有大小，又有方向的物理量。
如力，位移，速度等 二：矢量表示法线段的长度表示矢量的大小箭头的指向表示矢量的方向 记为：A或x o三：矢量的模和单位矢量模： 矢量的大小，记为A单位矢量：若矢量0A的模为1，且方向与 A 相同,则称0A 为A方向上的单位矢量。
有A =A0A----大小和方向分离表示四：矢量运算相等：两个大小相等且方向相同的矢量相等。
平移：矢量平移后，大小和方向均保持不变。
负矢量：大小相等，方向相反的矢量，记为-A加法：既矢量合成，服从平行四边形法则=A+ BA可演化成三角形法则多矢量合成服从多边形法则减法：既矢量的分解，是加法的逆运算)(BABAC-+=-=大小Am数乘：AmAm=⨯方向: m＞0 与A同向m＜0 与A反向五：矢量的坐标表示222ZY X Z Y X A A A A kA j A i A A ++=++= 令 两矢量kB j B i B B kA j A i A A Z Y X Z Y X++=++=则有kmA j mA i mA k A j A i A m A m k B A j B A i B A B A z y x z y x z z y y x x ++=++=±+±+±=±)()()()( B A = 当且仅当 z z y y x x B A B A B A===六：标积（点积）两矢量相乘得到一个标量A B Cos B A B A C⋅==⋅=θ c由定义可知当θ=0时 C οS θ=1 BA B A=⋅ B当θ=π/2时 C οS θ=00=⋅B A七：矢积（叉积）A两矢量相乘得到一个矢量B A C⨯= 大小: ),(B A Sin B A Sin B A =θ方向: 右手系由定义可知当θ=0时 Sin θ=0 0=⨯B A当θ=π/2时 Sin θ=1 B A B A=⨯)(A B B A⨯-=⨯ 不服从交换律八：矢量的求导令存在矢量 k t A j t A i t A t A z y x )()()()(++=则有:k dtt dA j dt t dA i dt t dA dt t A d z y x)()()()(++=例： 一人字原点出发，先向东走了30米，又向南走了10米，再向西北走了18米，求合位移的大小和方向。
第一章 矢量分析
格 林 定 理
立了面积分和线积分的关系。从物理角度可以理解为斯托克 立了面积分和线积分的关系。从物理角度可以理解为斯托克 斯定理建立了区域 S 中的场和包围区域 S 的闭合曲线 l 上的 场之间的关系。因此， 中的场， 场之间的关系。因此，如果已知区域 S 中的场，根据斯托克 上的场，反之亦然。 斯定理即可求出边界 l 上的场，反之亦然。
Ψ = ∫ A ⋅ dS
S
通量可为正、或为负、或为零 当矢量穿出某个闭合面时， 通量可为正、或为负、或为零。当矢量穿出某个闭合面时， 认为该闭合面中存在产生该矢量场的源 认为该闭合面中存在产生该矢量场的源；当矢量进入这个闭合 面时，认为该闭合面中存在汇聚该矢量场的洞 ）。闭合 面时，认为该闭合面中存在汇聚该矢量场的洞（或汇）。闭合
惟 一 性 定 理 亥姆霍兹定理 正交曲面 坐标系
10
第一章 矢量分析
标 积 与 矢 积 方向导数与梯度 通 量 与 散 度 环 量 与 旋 度 环 量 与 旋 度 无散场与无旋场 格 林 定 理
2. 旋度：旋度是一个矢量。若以符号 rot A 表示矢量 A 的旋 旋度：旋度是一个矢量。 具有最大环量强度的方向， 度, 则其方向是使矢量 A 具有最大环量强度的方向， 其大小等于对该矢量方向的最大环量强度， 其大小等于对该矢量方向的最大环量强度，即
惟 一 性 定 理 亥姆霍兹定理 正交曲面 坐标系
1
0 A⋅ B = A B
A⊥B
A // B
第一章 矢量分析
标 积 与 矢 积 方向导数与梯度
2.矢量的失积 2.矢量的失积
矢量的失积：代数定义： 矢量的失积：代数定义：
ex A × B = Ax Bx ey Ay By ez Az Bz
立了面积分和线积分的关系。从物理角度可以理解为斯托克 立了面积分和线积分的关系。从物理角度可以理解为斯托克 斯定理建立了区域 S 中的场和包围区域 S 的闭合曲线 l 上的 场之间的关系。因此， 中的场， 场之间的关系。因此，如果已知区域 S 中的场，根据斯托克 上的场，反之亦然。 斯定理即可求出边界 l 上的场，反之亦然。
Ψ = ∫ A ⋅ dS
S
通量可为正、或为负、或为零 当矢量穿出某个闭合面时， 通量可为正、或为负、或为零。当矢量穿出某个闭合面时， 认为该闭合面中存在产生该矢量场的源 认为该闭合面中存在产生该矢量场的源；当矢量进入这个闭合 面时，认为该闭合面中存在汇聚该矢量场的洞 ）。闭合 面时，认为该闭合面中存在汇聚该矢量场的洞（或汇）。闭合
惟 一 性 定 理 亥姆霍兹定理 正交曲面 坐标系
10
第一章 矢量分析
标 积 与 矢 积 方向导数与梯度 通 量 与 散 度 环 量 与 旋 度 环 量 与 旋 度 无散场与无旋场 格 林 定 理
2. 旋度：旋度是一个矢量。若以符号 rot A 表示矢量 A 的旋 旋度：旋度是一个矢量。 具有最大环量强度的方向， 度, 则其方向是使矢量 A 具有最大环量强度的方向， 其大小等于对该矢量方向的最大环量强度， 其大小等于对该矢量方向的最大环量强度，即
惟 一 性 定 理 亥姆霍兹定理 正交曲面 坐标系
1
0 A⋅ B = A B
A⊥B
A // B
第一章 矢量分析
标 积 与 矢 积 方向导数与梯度
2.矢量的失积 2.矢量的失积
矢量的失积：代数定义： 矢量的失积：代数定义：
ex A × B = Ax Bx ey Ay By ez Az Bz
矢量分析
二、方向导数 在实际应用中，不仅需要宏观上了解场在空间的数值，还要知道在不同 方向上场变化的情况。方向导数表征标量场空间中，某点处场沿各个方向变 化的规律。
取等位面 u 1、定义：
x, y , z
增加的方向，相互垂直且满足右手螺旋法则
v ˆ ˆ ˆ 矢量表示： A = e x Ax + e y Ay + e z Az
v 位置矢量： r = e x x + e y y + e z z ˆ ˆ ˆ
v ˆ ˆ ˆ dr = e x dx + e y dy + e z dz 微分长度元：
（2）球面坐标系下矢量运算
v ˆ ˆ ˆ A = er Ar + eθ Aθ + eϕ Aϕ v ˆ ˆ ˆ B = er Br + eθ Bθ + eϕ Bϕ
v v ˆ ˆ ˆ A ± B = er ( Ar ± Br ) + eθ ( Aθ ± Bθ ) + eϕ ( Aϕ ± Bϕ )
v v A• B = Ar Br + Aθ Bθ + Aϕ Bϕ
e 单位矢量：ˆ ρ
ρ
,φ
ˆ , eφ
,z
ˆ , ez
0 ≤ ρ < ∞ , 0 ≤ φ ≤ 2π , − ∞ < z < ∞
ˆ ˆ ˆ e z = e ρ × eφ ˆ ˆ ˆ e ρ = eφ × e z ˆ ˆ ˆ eφ = e z × e ρ
ˆ ˆ ˆ ↑ e ρ 、eφ 、e z
分别代表ρ、φ、z 增加的方向，相互垂直且满足右手螺旋法则
ˆ 由于 θ、ϕ 不是常矢量，与 er
ˆ ∂er ˆ =eθ ∂θ ˆ ∂ eθ ˆ = −er ∂θ ˆ ∂ eϕ = 0 ∂θ
矢量分析
对于矢量也存在相应的函数，称为矢性函数
例如：卫星的速度是时间 t 的矢性函数
V V t
第一章
矢量分析
场的定义：
如果在某一空间区域内的每一点，都对应着某 个物理量的一个确定的值，则称在此区域内确定了 该物理量的一个场。
若该物理量为标量，则称标量场,
可用标量函数表示f(x,y,z)；
x
证明：M点的坐标为M(x0+Δx, y0+Δy, z0+Δz)，由于函数φ在 M0处可微，故
( M ) ( M 0 ) x y z x y z
第一章
矢量分析
z
两边除以ρ，可得
x y z x y z cos cos cos x y z
x 2 y 2 c2 解之即得矢量方程 z c1 x
c1和c2是积分常数。
第一章
矢量分析
1.2 标量场的方向导数和梯度
1.2.1 标量场的方向导数
方向导数表征标量 场空间中，某点处场值沿
各个方向变化的规律。
方向导数的定义：
图 1-2 方向导数的定义
第一章
矢量分析
设M0是标量场φ=φ(M)中的一个已知点，从M0出发沿某一方
A B
矢量的加法运算
A B B A
A B
A B
A B A ( B)
矢量的减法运算
A B
第一章
矢量分析
两个矢量的乘积
两个矢量的乘积有两个定义： 点积
运算结果 运算结果
标量 矢量
标积 矢积
第1章-矢量分析
⎝
2⎠
⎝
2⎠
Ay
⎜⎛ x,y+Δy,z ⎟⎞ ⎝ 2⎠
=
Ay
(x,y,z)
+
∂Ay ∂y
(x,y,z)
Δy 2
+
1 2!
∂2 Ay ∂y2
( Δy )2 2
+ ...
得
ΔΨr
=
( Ay
+
∂Ay ∂y
Δy 2
+ .........) ΔxΔz
divA 直角坐标表示式的推导
11
§1.2通量、散度、散度定理
8
§1.2通量、散度、散度定理
作业：1.1-1,1.1-3,1.1-5
S为封闭面时： 若Ψ > 0， 有净通量流出，说明S内有源； 若Ψ < 0， 有净通量流入，说明S内有洞(负源); 若Ψ = 0， 则净通量为零，说明S内无源。
举例：
由《大学物理》知，电通量 Ψe = ∫sD ⋅ ds = Q（高斯定理） 水流的单位时间流量（米3/秒）＝ v ⋅ d s
A 矢量的模：
γ
β o
Ay
α Ax
y
A = A = Ax2 + Ay 2 + Az 2
x
A 的单位矢量：
Aˆ = A = xˆ Ax + yˆ A y + zˆ Az AA AA
= xˆ cosα + yˆ cos β + zˆ cosγ
2
§1.1矢量代数
二、标量积和矢量积
a) 标量积（点乘）
加减乘除
∂y 4π r 5
∂Dz = q r 2 − 3z 2
∂z 4π r 5
第1章矢量分析
F dS S
S1 F dS1
S2 F dS2
S3 F dS3
S4 F dS4
S5 F dS5
S6 F dS6
aˆx aˆz 0, aˆy aˆy 1,
aˆy aˆz 0 aˆz aˆz 1
A B (Axaˆx Ayaˆy Azaˆz ) (Bxaˆx Byaˆy Bzaˆz )
Ax Bx Ay By Az Bz
•结论: 两矢量点积等于对应分量的乘积之和。
电磁场与电磁波
第1章 矢量分析
其中：dl ,dS 和 dV 称为微分元。
dS
dl
1. 直角坐标系
在直角坐标系中，坐标变量为(x,y,z)，如图，做一微分体元。
线元：dlx dxaˆx
dly dyaˆy
面元： dSx dydzaˆx dSy dxdzaˆy
dlz dzaˆz dl dxaˆx dyaˆy dzaˆz
电磁场与电磁波
第1章 矢量分析
3.乘法：
（1）标量与矢量的乘积：
k 0 方向不变，大小为|k|倍
kA k | A | aˆ
k
0
k 0 方向相反，大小为|k|倍
（2）矢量与矢量乘积分两种定义
a. 标量积（点积）：
B
A B | A| | B | cos
A
两矢量的点积含义： 一矢量在另一矢量方向上的投影与另一矢量模的乘积，
定义： A BC | A|| B || C | sin cos
含义： 标量三重积结果为三矢量构成
的平行六面体的体积 。
h BC
A C
B
电磁场与电磁波
第1章 矢量分析
V A (BC) C (A B) B (C A)
第一章矢量分析
r u ( x, y , z , t ) 、 F ( x , y , z , t )
r u ( x, y, z )、 F ( x, y, z )
第一章 矢量分析
1.1.1 标量场的等值面
标量场空间中，由所有场值相等的点所构成的面，即为等值面。 即若标量函数为 u u( x, y, z) ，则等值面方程为：
第一章 矢量分析
第一章
主 要
矢量分析
内 容
梯度、散度、旋度、亥姆霍兹定理 1. 标量场的方向导数与梯度
2. 矢量场的通量与散度 3. 矢量场的环量与旋度 4. 无散场和无旋场 5. 格林定理
6. 矢量场的惟一性定理
7. 亥姆霍兹定理 8. 正交曲面坐标系
第一章 矢量分析
1.1 矢量代数
1.1.1 标量和矢量
空间中存在任意曲面S，则定义：
v v S A(r ) dS
为矢量 A(r ) 沿有向曲面 S 的通量。
矢量场的通量
第一章 矢量分析
若S 为闭合曲面
s
v v v Ñ A ( r ) dS
物理意义：表示穿入和穿出闭合面S的通量的代数和。 说明：1) 面元矢量 dS 定义：面积很小的有向曲面。
s
第一章 矢量分析
通过闭合面S的通量的物理意义：
0
0
若 0 ，通过闭合曲面有净的矢量线穿出，闭合面内有发 出矢量线的正源； 若 0 ，有净的矢量线进入，闭合面内有汇集矢量线的负源； 若 0 ，进入与穿出闭合曲面的矢量线相等，闭合面内无 源，或正源负源代数和为0。 局限：只能判断闭合曲面中源的正负特性，不能显示源的特 性。如果令包围某点的闭合面无限收缩，那么该点就可以通量 可以表示源的特性。
电磁场与电磁波第1章矢量分析
例：已知一矢量场F=axxy-ayzx, 试求：
（1） 该矢量场的旋度;
（2） 该矢量沿半径为3的四分 之一圆盘的线积分， 如图所 示， 验证斯托克斯定理。
y B
r＝ 3
O
Ax
四分之一圆盘
第 7、8 学时 1.4 标量的方向导数和梯度
1.4.1标量的方向导数和梯度
一个标量场u可以用一个标量函数来表示。在直角坐标 系中， 可将u表示为
lim l A dl
SP S
称固定矢量R为矢量A的 旋度，记作
rotA=R
上式为旋度矢量在n方 向的投影，如图所示， 即
A dl
lim l
SP S
rotn A
ro tA
n
旋涡面
P l
旋度及其投影
矢量场的旋度仍为矢量。在直角坐标系中，旋度的表达式为
rotA
ax
Az y
Ay z
a
y
Ax z
Az x
z
l
式 中 ， 当 Δl→0 时 δ→0 。 将 上 式 两 边 同 除 以 Δl 并 取 极限得到方向导数的计算公式：
u u cos u cos u cos
l x
y
z
ห้องสมุดไป่ตู้
其中，cosα, cosβ, cosγ为l方向的方向余弦。
1.4.4 标量场的梯度
1. 梯度的定义
方向导数为我们解决了函数u(P)在给定点处沿某个方向的 变化率问题。然而从场中的给定点P出发，标量场u在不 同方向上的变化率一般说来是不同的，那么，可以设想，
▽ ·(▽ ×A)≡0
即如果有一个矢量场B的散度等于零，则该矢量B就可 以用另一个矢量A的旋度来表示，即当 ▽ ·B=0 则有
矢量分析
关于散度的一些计算
r r r r ∇ ⋅ ( A ± B) = ∇ ⋅ A ± ∇ ⋅ B r r r ∇ ⋅ (ϕ A) = ϕ∇ ⋅ A ± A ⋅∇ϕ
3)、散度定理（奥——高定理） 、散度定理（ 高定理） 高定理
∫
V
r r r ∇ ⋅ AdV = A ⋅ dS ∫
S
它将矢量散度的体积分变换成该矢量的面积分， 它将矢量散度的体积分变换成该矢量的面积分，或将矢量 的面积分转换为该矢量散度的体积分。 的面积分转换为该矢量散度的体积分。
第一章 矢量分析
场的几何描述 r 矢量场 A( x, y, z ) 的场线及场线方程
dx dy dz = = Ax Ay Az
标量场
ϕ (x, y, z) 的等值面方程为
ϕ ( x, y , z ) = const.
第一章 矢量分析
2 通过点M 的等值面方程。 例1、 求标量场 ϕ = ( x + y ) − z 通过点 (1, 0, 1)的等值面方程。 、 的等值面方程
第一章 矢量分析
4、 矢量场的环量和旋度
1）、环流（环量 ） 环流（
r r 沿曲线c关于 在矢量场 A 中，沿曲线 关于 的线积分称为该矢量场 A
的环流 。
∫
c
r r A ⋅ dl = A cos θ dl ∫
c
环流表示闭合曲线内存在另 一种源——涡旋源 一种源 涡旋源
第一章 矢量分析
2）、 矢量场的旋度 ）、
max
r ∂ϕ r ∂ϕ r ∂ϕ r = G =| ex + ey + ez | ∂x ∂y ∂z
第一章 矢量分析
中的一点M处有一矢量 处有一矢量， 定义：在标量场 ϕ ( x, y , z )中的一点 处有一矢量，其方向取函 r 点处变化率最大的方向， 数 ϕ 在M点处变化率最大的方向，其模等于 | G | ，该矢量称为标 点处变化率最大的方向 点处的梯度 表示。 量场 ϕ 在M点处的梯度，用grad ϕ 表示。 点处的梯度， 在直角坐标系中， 梯度的表达式为 直角坐标系中
第1章 矢量分析
体积元
dV dxdydz
z
z
z0
（ 平面） ez
P
ey
ex
o
点P(x0,y0,z0)
y
y y0（平面） x x x0 （平面）
直角坐标系
z dSz ezdxdy
dz
dSy eydxdz
o
dy
dx dSx exdydz
y
x
直角坐标系的长度元、面积元、体积元
第一章 矢量分析
A Axex Ayey Azez
sin cos
0
0 ex
0
e y
1 ez
ex cos
ey
sin
ez 0
sin cos
0
0 e
0
e
1 ez
第一章 矢量分析
2、直角坐标系与球坐标系的关系
er ex sin cos ey sin sin ez cos e cos cos ex cos sin ey sin ez e ex sin ey cos
坐标变量 坐标单位矢量 位置矢量 线元矢量 面元矢量
x, y, z,( x, y, z )
ex , ey , ez
r ex x ey y ez z
dl
exdx
ey
dy
ezdz
dSx exdlydlz exdydz
dSy eydlxdlz eydxdz
dSz ezdlxdly ezdxdy
A B AxBx Ay By Az Bz
ex ey ez
A B Ax Ay Az Bx By Bz
ex
Ay By
Az Bz
ey
Ax Bx
第一章 矢量分析
第一章 矢量分析§1 场的概念 一. 矢量与标量1.概念标量 实数域内只有大小的量。
如：电压、温度、时间、电荷等。
矢量 实数域内既有大小又有方向的量，且加法运算遵循平行四边形法则。
如：力F 、电场强度E 、磁场强度H、速度等。
常矢：矢量的模和方向都不变。
如：x e 、y e 、z e。
变矢：模和方向或两者之一变化的矢量(在实际问题中遇到的更多)。
如：r e 、θe 、ϕe 、ρe。
物理量 标量或矢量被赋予物理单位，成为有物理意义的量。
2.矢量的表示印刷 黑体 A ；A(白体)表示A的模。
手写 模和方向均表示出。
表示A 的方向(模为1)。
A 表示矢量A 的模。
▪ 零矢（空矢）：模为零的矢量。
0▪单位矢量：模为1的矢量。
如直角坐标系坐标轴方向x e 、y e 、z e （参考书）。
也有用x a、y a 、z a或i 、j 、k 或 x ˆ、y ˆ、z ˆ 等表示。
若三个相互垂直的坐标轴上的分量已知，一个矢量就确定了。
如直角坐标系中，矢量A的三个分量模值分别是A x , A y , A z ，则直角坐标系： A的模为 A的单位矢量为判断以下手写表示是否正确：（矢量≠标量） （标量≠矢量） ☹ 常见手写表示错误： Aa A 0=A A a=0zz y y x x A e A e A e A ++=222z y x A A A A ++=γβcos cos cos ˆ0z y x zz y y x x A e e a e A A e A A e A A e A A a A++=++===5=E 5x e E=5x e E =765zy x e e e E ++= 765z y x e e e E++=二. 矢量的代数运算1.矢量的加减法2.矢量的乘法a.标量积(点乘) 结果为标量！b.矢量积(叉乘) 结果为矢量！直角坐标系：∙ 点乘 垂直 平行点乘符合交换律： ∙ 叉乘平行 垂直注意：z x y e e e-=⨯ 叉乘不符合交换律： 三.矢量场与标量场1.场在某一空间区域内的每一点，都对应着某个物理量的一个确定的值，则称在此区域内确定了该物理量的一个场。
矢量分析
运 算 规律： A B B A （交换律）
A (B C) A B AC （分配律）
AB
AB 0
A// B
A B AB
ex ey ey ez ez ex 0
ex ex ey ey ez ez 1
第一章 矢量分析
（4）矢量的矢量积（叉积）
A B
A B en ABsin
C=A+B
A
AB
B
C2 C C (A B) (A B)
A A B B 2A B
A2 B2 2 ABcosAB A2 B2 2 ABcos
第一章 矢量分析
1.2 三种常用的正交曲线坐标系
三维空间任一点的位置可通过三条相互正交曲线的交点来确定。 三条正交曲线组成的确定三维空间任意点位置且满足右手螺旋 规则的体系，称为正交曲线坐标系；三条正交曲线称为坐标轴； 描述坐标轴的量称为坐标变量。 在电磁场与波理论中，三种常用的正交曲线坐标系为：直角坐 标系、圆柱坐标系和球坐标系。
B
推论：任意多个矢量首尾相连组成闭合多边
矢量的减法
形，矢量和必为零。
第一章 矢量分析
（2）标量乘矢量（数乘）
kA exkAx eykAy ezkAz
（3）矢 量 的标量积（点积）
A B AB cos AxBx Ay By Az Bz
两矢量点积含义：矢量在另一矢量方向上的投影与另一
矢量模的乘积，其结果是一标量。
0
坐标变量
,, z 0 2
坐标单位矢量
e , e , ez
z
位置矢量
r e ez z
线元矢量
dl ed e d ezdz
面元矢量
dS
e dldlz
矢量分析
A
24
1.2.4 散度定理 (高斯公式)
由散度定义： 1 divA lim
0
A dS
s
divA A ds
s
该式只对微小体积
0 成立。
1 , 2 , 3
对于有限大体积V，分为许多小体积
x
γ α
Az
β
y Ax Ay
ex , ey , ez 单位矢量，长度为1 方向分别为x,y,z方向
NOTE: 在直角坐标系下为常矢量（大小，方向固定）
并不是所有单位矢量是常矢量（如圆柱、直角坐标系）
Ax , Ay , Az 标量（数值）
可以看出，一个矢量场对应三个标量场。
4
源点、场点、位置矢量（矢径）、距离矢量
大小：疏密定性
17
一个矢量场可以用一个矢量函数表示
A(r ) A( x, y, z) ex Ax ( x, y, z) ey Ay ( x, y, z) e z Az ( x, y, z)
矢量线上任意点的矢径的微分即为该点处的切向矢量
dr ex d x ey d y ez d z
第1章 矢量分析
主要内容： 矢量代数 散度及散度定理（重点） 旋度及旋度定理 （重点） 梯度（重点） 亥姆霍兹定理（理解） 常用坐标系（了解）
1
标量场与矢量场
它把物理量用空间和时间的数学函数来描述
标量场：只有大小，没有方向 T ( x, y, z, t ) F ( x, y, z, t ) 矢量场：有大小，有方向
ex ey Ay By ez Az Bz
A B Ax Bx
= ex(4×7－2×4) + ey(2×2 － 3×7) + ez(3×4 － 4×2) = ex20 － ey17 + ez4
24
1.2.4 散度定理 (高斯公式)
由散度定义： 1 divA lim
0
A dS
s
divA A ds
s
该式只对微小体积
0 成立。
1 , 2 , 3
对于有限大体积V，分为许多小体积
x
γ α
Az
β
y Ax Ay
ex , ey , ez 单位矢量，长度为1 方向分别为x,y,z方向
NOTE: 在直角坐标系下为常矢量（大小，方向固定）
并不是所有单位矢量是常矢量（如圆柱、直角坐标系）
Ax , Ay , Az 标量（数值）
可以看出，一个矢量场对应三个标量场。
4
源点、场点、位置矢量（矢径）、距离矢量
大小：疏密定性
17
一个矢量场可以用一个矢量函数表示
A(r ) A( x, y, z) ex Ax ( x, y, z) ey Ay ( x, y, z) e z Az ( x, y, z)
矢量线上任意点的矢径的微分即为该点处的切向矢量
dr ex d x ey d y ez d z
第1章 矢量分析
主要内容： 矢量代数 散度及散度定理（重点） 旋度及旋度定理 （重点） 梯度（重点） 亥姆霍兹定理（理解） 常用坐标系（了解）
1
标量场与矢量场
它把物理量用空间和时间的数学函数来描述
标量场：只有大小，没有方向 T ( x, y, z, t ) F ( x, y, z, t ) 矢量场：有大小，有方向
ex ey Ay By ez Az Bz
A B Ax Bx
= ex(4×7－2×4) + ey(2×2 － 3×7) + ez(3×4 － 4×2) = ex20 － ey17 + ez4
第一章 矢量分析
(
)
( )
( )
(
)
(
)
16
导矢的物理意义 M0
z
s
M
dr dr ds 导矢： 导矢： = ⋅ l dt ds dt o y dr : 点M 处的单位切向矢量τ x ds ds 处质点的速度大小， : 点M 处质点的速度大小，用v 表示 dt dr 质点M 质点M 的速度矢量 = vτ = v dt dv d 2 r w= = 2 质点M 质点M 的加速度矢量 dt dt
d dA dB d A± B = ± C = 0, C为常矢 dt dt dt dt d dA d du dA kA = k , k为常数 uA = A+u dt dt dt dt dt d dB dA d 2 dA A⋅ B = A⋅ + ⋅B 特例： A = 2 A ⋅ dt dt dt dt dt d dB dA A× B = A× + ×B dt dt dt dA dA du = ⋅ 若有复合函数 A＝A ( u ) dt du dt
7
第一章
第二节 矢性函数的导数与微分
1. 矢性函数的导数 定义 设矢性函数 A ( t )在点 t的某一邻 的某一邻 域内有定义， 域内有定义，并设 t +△t 也在这邻域内。 △ 也在这邻域内。 若
M
A (t ) A′ ( t )
∆A
N l
其极限存在， 在 ∆t → 0 时，其极限存在，则称此极限 ∆A=A ( t +∆t ) -A ( t ) 为矢性函数 A ( t ) 在点 处的导数（简称 导数（ 在点t 处的导数 导矢）， ），记作 导矢），记作 dA/dt 或 A′ ( t ) 。
13
矢量分析-PPT
0
2 2 2 2
x2 y2 z2
1 .4 .2 格林定理
将散度定理中矢量A表示为某标量函数的梯度 ψ与另一标 量函数 φ的乘积, 则有
A ( ) 2
取上式在体积V内的积分, 并应用散度定理, 得
(2 )dv
V
s( ) nˆds
s
n
ds
(1 -49)
式中S是包围体积V的封闭面, nˆ 是封闭面S的外法线方向单位矢
量。此式对于在体积V内具有连续二阶偏导数的标量函数φ和ψ都 成立, 称为格林( G .Green)第一定理。
divA A
A
xˆ
x
yˆ
y
zˆ
z
(xˆAx
yˆAy
zˆAz
)
Ax Ay Az x y z
利用哈密顿算子, 读者可以证明, 散度运算符合下列规则:
(A B) A B
(A) A A
1 .2 .3 散度定理
既然矢量的散度代表的是其通量的体密度, 因此直观地可知, 矢量场散度的体积分等于该矢量穿过包围该体积的封闭面的总 通量, 即
ds nˆds
nˆ 是面元的法线方向单位矢量。nˆ 的取法(指向)有两种情形: 对
开曲面上的面元, 设这个开曲面是由封闭曲线l所围成的, 则当选
定绕行l的方向后, 沿绕行方向按右手螺旋的姆指方向就是 nˆ 的方 向, 如图1 -4所示; 对封闭曲面上的面元, nˆ 取为封闭面的外法线方
向。
图 1 -4 开曲面上的面元
为A , B崐所在平面的右手法向 n:ˆ
A B nˆAB sin aAB
它不符合交换律。 由定义知,
A B (B A)
并有
xˆ xˆ yˆ yˆ zˆ zˆ 0 xˆ yˆ zˆ, yˆ zˆ xˆ, zˆ xˆ yˆ
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
利用哈密顿算子, 读者可以证明, 散度运算符合下列规则:
( A B) A B (A) A A
第一章 矢 量 分 析
1 .2 .3 散度定理
既然矢量的散度代表的是其通量的体密度, 因此直观地可知, 矢量场散度的体积分等于该矢量穿过包围该体积的封闭面的总 通量, 即
[ A dl]max
l
S 0
S
可见, 矢量A的旋度是一个矢量, 其大小是矢量A在给定点处的最 大环量面密度, 其方向就是当面元的取向使环量面密度最大时, 该面元矢量的方向
ˆ 。 它描述A在该点处的旋涡源强度。 若 n
某区域中各点rot A=0, 称A为无旋场或保守场。
第一章 矢 量 分 析 矢量A的旋度可表示为算子与A的矢量积, 即
q ˆds e D ds r r 3 s 4r s q q 2 ds 4 r q 2 s 2 4r 4r
这证明在此球面上所穿过的电通量
e 的源正是点电荷q。
第一章 矢 量 分 析 例1 .2 球面S上任意点的位置矢量为 r 试利用散度定理计算 r ds
图 1 -2 矢量的相加和相减
第一章 矢 量 分 析
1 .1 .2 标量积和矢量积
矢量的相乘有两种定义: 标量积(点乘)和矢量积(叉乘)。 标量
积A· B是一标量, 其大小等于两个矢量模值相乘, 再乘以它们夹角
αAB(取小角, 即αAB≤π)的余弦:
A B AB cosaAB
它符合交换律:
Dy
q r 3y , 5 y 4 r
2 2 2 2
Dz q r 3z 5 z 4 r
第一章 矢 量 分 析
Dx Dy Dz q 3r 2 3( x 2 y 2 z 2 ) D 0 5 x y z 4 r
可见，除点电荷所在源点（r=0）外，空间各点的电通量密 度散度均为零。它是管形场。
求任意点处(r≠0)电场强度的旋度▽×E。
第一章 矢 量 分 析
[解 ]
ˆ x q
ˆ y
ˆ z
E 4 0 x y z x r3 y r3 z r3
S
ˆx y ˆy z ˆr, ˆz r x
［解］
x y z r 3 x y z
4 3 3 S rds V rdv 3V dv 3 3 r 4r
第一章 矢 量 分 析
§1 .3 环量与旋度, 斯托克斯定理
1 .3 .1 环量
球面的电通量 e [解 ] 求任意点处电通量密度的散度▽· D，并求穿出r为半径的
ˆx y ˆy z ˆz q x ˆDx y ˆ Dy z ˆDz D x 2 2 2 3/ 2 4 ( x y z )
第一章 矢 量 分 析
Dx q x 2 2 2 3/ 2 x 4 x ( x y z ) 1 3x 2 2 2 2 2 3/ 2 2 2 5/ 2 ( x y z ) ( x y z ) q r 2 3x 2 4 r5 q 4
A ( B C ) B (C A) C ( A B)
矢量三重积为
A ( B C ) B( A C ) C( A B)
公式右边为“BAC-CAB”, 故称为“Back -Cab”法则, 以便记忆。
第一章 矢 量 分 析
图 1 -3 矢量乘积的说明
第一章 矢 量 分 析 A×B各分量的下标次序具有规律性。例如,
ˆ 分量第一项是y→z, x
其第二项下标则次序对调: z→y, 依次类推。并有
ˆ x
ˆ y
ˆ z
A B Ax Ay Az Bx B y Bz
第一章 矢 量 分 析 1 .1 .3 三重积 ; 矢量的三连乘也有两种。 标量三重积为
A B B A
并有
ˆ y ˆy ˆz ˆ0 ˆz ˆx x ˆx ˆy ˆy ˆz ˆz ˆ 1 x
第一章 矢 量 分 析 因而得
A B Ax Bx Ay By Az Bz A A A A A A
2 x 2 y 2 z 2
矢量积A×B是一个矢量, 其大小等于两个矢量的模值相乘, 再乘以它们夹角αAB(≤π)的正弦, 其方向与A , B成右手螺旋关系, 为A , B崐所在平面的右手法向 : ˆ n
也称为A在曲面S上的面积分:
ˆ ds A ds A n
s s
如果S是一个封闭面, 则
A ds
S
表示A穿过封闭面的通量。 若Φ＞0, 表示有净通量流出, 这说明S 内必定有矢量场的源; 若Φ ＜0, 表示有净通量流入, 说明S内有洞 (负的源)。 通过封闭面的电通量Φ等于该封闭面所包围的自由电荷
A dl
l
S 0
S
这个极限的意义就是环量的面密度, 或称环量强度。 由于面 元是有方向的, 它与封闭曲线l的绕行方向成右手螺旋关系, 因此 在给定点处, 上述极限值对于不同的面元是不同的。 为此, 引入
如下定义, 称为旋度(rotation):
第一章 矢 量 分 析
ˆ lim rotA n
开曲面上的面元, 设这个开曲面是由封闭曲线l所围成的, 则当选 定绕行l的方向后, 沿绕行方向按右手螺旋的姆指方向就是 n ˆ 的方 向, 如图1 -4所示; 对封闭曲面上的面元, 向。
第一章 矢 量 分 析
图 1 -4 开曲面上的面元
第一章 矢 量 分 析
将曲面S各面元上的A· ds相加, 它表示A穿过整个曲面S的通量,
把两个矢量的对应分量相加或相减, 就得到它们的和或差。 设
ˆBx y ˆBy z ˆBz Bx
则
ˆ( Ax Bx ) y ˆ ( Ay By ) z ˆ( Az Bz ) A B x
第一章 矢 量 分 析
图 1 -1 直角坐标系中矢量的分解
第一章 矢 量 分 析
是标量, 它是A通过某点处单位体积的通量(即通量体密度)。 它 反映A在该点的通量源强度。 显然, 在无源区中, A在各点的散度 为零。 这个区域中的矢量场称为无散场或管形场。
第一章 矢 量 分 析 哈密顿(W .R .Hamilton)引入倒三角算符(读作“del (德尔)”或“nabla(那勃拉)”)表示下述矢量形式的微分算子:
rotA A
计算▽×A时, 先按矢量积规则展开, 然后再作微分运算, 得
ˆ ˆ ˆ ˆ ˆ ˆAz ) A x y z ( x A y Ay z x x y z Az Ay Ax Az Ay Ax ˆ ˆ ˆ x z y z y z x x y
第一章 矢 量 分 析
第一章 矢 量 分 析
§1.1 矢量表示法和代数运算 §1.2 通量与散度,散度定理 §1.3 环量与旋度,斯托克斯定理
§1.4 方向导数与梯度,格林定理
§1.5 曲面坐标系
§1.6 亥姆霍兹定理
第一章 矢 量 分 析
§1 .1 矢量表示法和代数运算
1 .1 .1 矢量表示法及其和差
第一章 矢 量 分 析 即
ˆ x
ˆ y
ˆ z
A x y z Ax Ay Az
第一章 矢 量 分 析 旋度运算符合如下规则:
( A B) A B (A) A A ( A B) B A A B ( A) 0 A ( A) A
第一章 矢 量 分 析
§1 .2 通量与散度, 散度定理
在描绘矢量场的特性时, 矢量场穿过一个曲面的通量是一个 很有用的概念。 在矢量分析中, 将曲面的一个面元用矢量ds来表 示, 其方向取为面元的法线方向, 其大小为ds, 即
ˆds ds n
ˆ n ˆ 的取法(指向)有两种情形: 对 是面元的法线方向单位矢量。n ˆ 取为封闭面的外法线方 n
AdV A dS
V S
上式称为散度定理, 也称为高斯公式。 利用散度定理可将矢量 散度的体积分化为该矢量的封闭面积分, 或反之。
第一章 矢 量 分 析 例1 .1 点电荷q在离其r处产生的电通量密度为
q 2 2 2 1/ 2 ˆ ˆ ˆ D r , r xx yy zz , r ( x y z ) 3 4r
ˆ y ˆ ˆ x z x y z
它兼有矢量和微分运算双重作用, 因而与普通矢量有所不同:
A A ; A A ;
A的散度可表示为算子与矢量A的标量积, 即
divA A
第一章 矢 量 分 析
ˆ y ˆ ˆAx y ˆ Ay z ˆ ˆAz ) A z (x x y z x Ax Ay Az x y z
Q。 若Q为正电荷, Φ为正, 有电通量流出; 反之, 若Q为负电荷, 则Φ
为负, 有电通量流入。
第一章 矢 量 分 析
1 .2 .2 散度, 哈密顿算子 ;
定义如下极限为矢量A在某点的散度(divergence), 记为divA:
A ds divA lim
S V 0
V
式中ΔV为封闭面S所包围的体积。 此式表明, 矢量A的散度
s l
此式称为斯托克斯(Stokes)定理或斯托克斯公式。 它可将矢量 旋度的面积分变换为该矢量的线积分, 或反之。
第一章 矢 量 分 析 例1 .3 自由空间中的点电荷q所产生的电场强度为
ˆx y ˆy z ˆz x E r 3 4 0r 4 0 ( x 2 y 2 z 2 )3 / 2 q q
( A B) A B (A) A A
第一章 矢 量 分 析
1 .2 .3 散度定理
既然矢量的散度代表的是其通量的体密度, 因此直观地可知, 矢量场散度的体积分等于该矢量穿过包围该体积的封闭面的总 通量, 即
[ A dl]max
l
S 0
S
可见, 矢量A的旋度是一个矢量, 其大小是矢量A在给定点处的最 大环量面密度, 其方向就是当面元的取向使环量面密度最大时, 该面元矢量的方向
ˆ 。 它描述A在该点处的旋涡源强度。 若 n
某区域中各点rot A=0, 称A为无旋场或保守场。
第一章 矢 量 分 析 矢量A的旋度可表示为算子与A的矢量积, 即
q ˆds e D ds r r 3 s 4r s q q 2 ds 4 r q 2 s 2 4r 4r
这证明在此球面上所穿过的电通量
e 的源正是点电荷q。
第一章 矢 量 分 析 例1 .2 球面S上任意点的位置矢量为 r 试利用散度定理计算 r ds
图 1 -2 矢量的相加和相减
第一章 矢 量 分 析
1 .1 .2 标量积和矢量积
矢量的相乘有两种定义: 标量积(点乘)和矢量积(叉乘)。 标量
积A· B是一标量, 其大小等于两个矢量模值相乘, 再乘以它们夹角
αAB(取小角, 即αAB≤π)的余弦:
A B AB cosaAB
它符合交换律:
Dy
q r 3y , 5 y 4 r
2 2 2 2
Dz q r 3z 5 z 4 r
第一章 矢 量 分 析
Dx Dy Dz q 3r 2 3( x 2 y 2 z 2 ) D 0 5 x y z 4 r
可见，除点电荷所在源点（r=0）外，空间各点的电通量密 度散度均为零。它是管形场。
求任意点处(r≠0)电场强度的旋度▽×E。
第一章 矢 量 分 析
[解 ]
ˆ x q
ˆ y
ˆ z
E 4 0 x y z x r3 y r3 z r3
S
ˆx y ˆy z ˆr, ˆz r x
［解］
x y z r 3 x y z
4 3 3 S rds V rdv 3V dv 3 3 r 4r
第一章 矢 量 分 析
§1 .3 环量与旋度, 斯托克斯定理
1 .3 .1 环量
球面的电通量 e [解 ] 求任意点处电通量密度的散度▽· D，并求穿出r为半径的
ˆx y ˆy z ˆz q x ˆDx y ˆ Dy z ˆDz D x 2 2 2 3/ 2 4 ( x y z )
第一章 矢 量 分 析
Dx q x 2 2 2 3/ 2 x 4 x ( x y z ) 1 3x 2 2 2 2 2 3/ 2 2 2 5/ 2 ( x y z ) ( x y z ) q r 2 3x 2 4 r5 q 4
A ( B C ) B (C A) C ( A B)
矢量三重积为
A ( B C ) B( A C ) C( A B)
公式右边为“BAC-CAB”, 故称为“Back -Cab”法则, 以便记忆。
第一章 矢 量 分 析
图 1 -3 矢量乘积的说明
第一章 矢 量 分 析 A×B各分量的下标次序具有规律性。例如,
ˆ 分量第一项是y→z, x
其第二项下标则次序对调: z→y, 依次类推。并有
ˆ x
ˆ y
ˆ z
A B Ax Ay Az Bx B y Bz
第一章 矢 量 分 析 1 .1 .3 三重积 ; 矢量的三连乘也有两种。 标量三重积为
A B B A
并有
ˆ y ˆy ˆz ˆ0 ˆz ˆx x ˆx ˆy ˆy ˆz ˆz ˆ 1 x
第一章 矢 量 分 析 因而得
A B Ax Bx Ay By Az Bz A A A A A A
2 x 2 y 2 z 2
矢量积A×B是一个矢量, 其大小等于两个矢量的模值相乘, 再乘以它们夹角αAB(≤π)的正弦, 其方向与A , B成右手螺旋关系, 为A , B崐所在平面的右手法向 : ˆ n
也称为A在曲面S上的面积分:
ˆ ds A ds A n
s s
如果S是一个封闭面, 则
A ds
S
表示A穿过封闭面的通量。 若Φ＞0, 表示有净通量流出, 这说明S 内必定有矢量场的源; 若Φ ＜0, 表示有净通量流入, 说明S内有洞 (负的源)。 通过封闭面的电通量Φ等于该封闭面所包围的自由电荷
A dl
l
S 0
S
这个极限的意义就是环量的面密度, 或称环量强度。 由于面 元是有方向的, 它与封闭曲线l的绕行方向成右手螺旋关系, 因此 在给定点处, 上述极限值对于不同的面元是不同的。 为此, 引入
如下定义, 称为旋度(rotation):
第一章 矢 量 分 析
ˆ lim rotA n
开曲面上的面元, 设这个开曲面是由封闭曲线l所围成的, 则当选 定绕行l的方向后, 沿绕行方向按右手螺旋的姆指方向就是 n ˆ 的方 向, 如图1 -4所示; 对封闭曲面上的面元, 向。
第一章 矢 量 分 析
图 1 -4 开曲面上的面元
第一章 矢 量 分 析
将曲面S各面元上的A· ds相加, 它表示A穿过整个曲面S的通量,
把两个矢量的对应分量相加或相减, 就得到它们的和或差。 设
ˆBx y ˆBy z ˆBz Bx
则
ˆ( Ax Bx ) y ˆ ( Ay By ) z ˆ( Az Bz ) A B x
第一章 矢 量 分 析
图 1 -1 直角坐标系中矢量的分解
第一章 矢 量 分 析
是标量, 它是A通过某点处单位体积的通量(即通量体密度)。 它 反映A在该点的通量源强度。 显然, 在无源区中, A在各点的散度 为零。 这个区域中的矢量场称为无散场或管形场。
第一章 矢 量 分 析 哈密顿(W .R .Hamilton)引入倒三角算符(读作“del (德尔)”或“nabla(那勃拉)”)表示下述矢量形式的微分算子:
rotA A
计算▽×A时, 先按矢量积规则展开, 然后再作微分运算, 得
ˆ ˆ ˆ ˆ ˆ ˆAz ) A x y z ( x A y Ay z x x y z Az Ay Ax Az Ay Ax ˆ ˆ ˆ x z y z y z x x y
第一章 矢 量 分 析
第一章 矢 量 分 析
§1.1 矢量表示法和代数运算 §1.2 通量与散度,散度定理 §1.3 环量与旋度,斯托克斯定理
§1.4 方向导数与梯度,格林定理
§1.5 曲面坐标系
§1.6 亥姆霍兹定理
第一章 矢 量 分 析
§1 .1 矢量表示法和代数运算
1 .1 .1 矢量表示法及其和差
第一章 矢 量 分 析 即
ˆ x
ˆ y
ˆ z
A x y z Ax Ay Az
第一章 矢 量 分 析 旋度运算符合如下规则:
( A B) A B (A) A A ( A B) B A A B ( A) 0 A ( A) A
第一章 矢 量 分 析
§1 .2 通量与散度, 散度定理
在描绘矢量场的特性时, 矢量场穿过一个曲面的通量是一个 很有用的概念。 在矢量分析中, 将曲面的一个面元用矢量ds来表 示, 其方向取为面元的法线方向, 其大小为ds, 即
ˆds ds n
ˆ n ˆ 的取法(指向)有两种情形: 对 是面元的法线方向单位矢量。n ˆ 取为封闭面的外法线方 n
AdV A dS
V S
上式称为散度定理, 也称为高斯公式。 利用散度定理可将矢量 散度的体积分化为该矢量的封闭面积分, 或反之。
第一章 矢 量 分 析 例1 .1 点电荷q在离其r处产生的电通量密度为
q 2 2 2 1/ 2 ˆ ˆ ˆ D r , r xx yy zz , r ( x y z ) 3 4r
ˆ y ˆ ˆ x z x y z
它兼有矢量和微分运算双重作用, 因而与普通矢量有所不同:
A A ; A A ;
A的散度可表示为算子与矢量A的标量积, 即
divA A
第一章 矢 量 分 析
ˆ y ˆ ˆAx y ˆ Ay z ˆ ˆAz ) A z (x x y z x Ax Ay Az x y z
Q。 若Q为正电荷, Φ为正, 有电通量流出; 反之, 若Q为负电荷, 则Φ
为负, 有电通量流入。
第一章 矢 量 分 析
1 .2 .2 散度, 哈密顿算子 ;
定义如下极限为矢量A在某点的散度(divergence), 记为divA:
A ds divA lim
S V 0
V
式中ΔV为封闭面S所包围的体积。 此式表明, 矢量A的散度
s l
此式称为斯托克斯(Stokes)定理或斯托克斯公式。 它可将矢量 旋度的面积分变换为该矢量的线积分, 或反之。
第一章 矢 量 分 析 例1 .3 自由空间中的点电荷q所产生的电场强度为
ˆx y ˆy z ˆz x E r 3 4 0r 4 0 ( x 2 y 2 z 2 )3 / 2 q q