八年级数学证明题
初二数学证明题

ABDC1)如图,在等腰ΔABC 中,CH 是底边上的高线,点P 是线段CH 上不与端点重合的任意一点,连结AP 交BC 于点E ,连结BP 交AC 于点F 。
(1)证明:∠CAE=∠CBF ; (2)证明:AE=BF ;2)如图,在四边形ABCD 中,AB=BC ,BF 是∠ABC 的平分线,AF ∥DC,连接AC 、CF ,求证:CA 是∠DCF 的平分线。
3)已知:如图,在三角形ABC 中AB = AC ,O 是三角形ABC 内一点,且OB = OC , 求证:AO ⊥ BC4)如图,在∆ABC 中,AB = AC, ∠BAC =120︒,且BD = AD,求证:CD = 2BD5)如图所示。
在△ABC 中,D 、E 分别是AC 和AB 上 的一点,BD 与CE 交于点O ,给出下列四个条件: ①DCO EBO ∠=∠; ②CDO BEO ∠=∠;③CD BE =;④OC OB =。
(1) 上述四个条件中,哪两个条件可以判定△ABC 是等腰三角形(用序号写出所有的情形))2(选择)1(小题中的一种情形,证明△ABC 是等腰三角形。
6)已知:如图,在□ABCD 中,BE 、CE 分别平分∠ABC 、∠BCD , E 在AD 上,BE =12 cm ,CE =5 cm .求□ABCD 的周长和面积. 7)如图,AB=CD ,AD=BC ,EF 经过AC 的中点O ,分别交AB 、CD 于E 、F 。
求证:OE=OF.A E D C B8)已知:如图12,AB =CD ,DE ⊥AC ,BF ⊥AC ,E ,F 是垂 足,DE BF =.求证:(1)AF CE =;(2)AB CD ∥.9)如图13,工人师傅要检查人字梁的∠B 和∠C 是否相等,但他手边没有量角器,只有一个刻度尺.他是这样操作的: ①分别在BA 和CA 上取BE CG =; ②在BC 上取BD CF =;③量出DE 的长a 米,FG 的长b 米.如果a b =,则说明∠B 和∠C 是相等的.他的这种 做法合理吗?为什么?10) 如图14,ABC △中,∠B =∠C ,D ,E ,F 分别在AB ,BC ,AC 上,且BD CE =,=DEF B ∠∠ 求证:=ED EF .11)如图15,O 为码头,A ,B 两个灯塔与码头的距离相等,OA ,OB 为海岸线,一轮船从码头开出,计划沿∠AOB 的平分线航行,航行途中,测得轮船与灯塔A ,B 的距离相等,此时轮船有没有偏离航线?画出图形并说明你的理由.12)如图16,把△ABC 纸片沿DE 折叠,当点A 落在四边形BCDE (1)写出图中一对全等的三角形,并写出它们的所有对应角; (2)设AED ∠的度数为x ,∠ADE 的度数为y ,那么∠1,∠2的度数分别是多少?(用含有x 或y 的代数式表示) (3)∠A 与∠1+∠2之间有一种数量关系始终保持不变, 请找出这个规律.13)如图,已知点M 、N 分别是边BC 、CA 的中点,BN=QN ,AM=PM 。
初二数学图形与证明试题

初二数学图形与证明试题1.如图,在△ABC中,∠A=36°,AB=AC,BD是△ABC的角平分线,若在边AB上截取BE=BC,连接DE,则图中等腰三角形共有()A.2个B.3个C.4个D.5个【答案】D【解析】在△ABC中,∠A=36°,AB=AC,求得∠ABC=∠C=72°,且△ABC是等腰三角形.因为BD是△ABC的角平分线所以∠ABD=∠DBC=36°所以△ABD是等腰三角形.在△BDC中有三角形的内角和求出∠BDC=72°所以△BDC是等腰三角形.所以BD=BC=BE 所以△BDE是等腰三角形.所以∠BDE=72°, 所以∠ADE=36°, 所以△ADE是等腰三角形.共5个.故选D.【考点】角平分线的定义,三角形内角和、外角和,平角的定义.2.(本题满分8分)如图,已知□ABCD的对角线AC、BD相交于点O,四边形OCED为菱形.(1)求证:□ABCD是矩形;(2)连接AE、BE,AE与BE相等吗?请说明理由.【答案】(1)参见解析;(2)相等,理由参见解析.【解析】(1)利用对角线相等的平行四边形是矩形证得结论.(2)证明AE,BE,所在的三角形:△ADE≌△BCE,证得结论.试题解析:(1)∵四边形ABCD为平行四边形∴ AC=2OC,BD=2OD,∵四边形OCED是菱形∴OC=OD∴AC=BD又∵四边形ABCD为平行四边形,∴四边形ABCD是矩形.(2)∵四边形ABCD是矩形,∴AD=BC,∠ADC=∠BCD=90º,∵四边形OCED是菱形,∴ DE=CE,∴∠EDC=∠ECD,∴∠EDC+∠ADC =∠ECD+∠BCD,∴∠ADE=∠BCE,∴△ADE≌△BCE (SAS),∴AE=BE.【考点】1.矩形性质与判定;2.菱形性质的应用;3.证线段相等的方法.3.如图,已知△ABC的面积为24,点D在线段AC上,点F在线段BC的延长线上,且,四边形DCFE是平行四边形,则图中阴影部分的面积为().A.8B.6C.4D.3【答案】A.【解析】如图,过点A作AM⊥BC于点M,根据三角形的面积公式可得图中阴影部分的面积为,,由四边形DCFE是平行四边形可得DE=CF,又因,DE=CF可得BC=3DE,所以,即.所以图中阴影部分的面积为=8.故答案选A.【考点】平行四边形的性质;三角形的面积公式.4.如图,在□ABCD中,AD=6,AB=4,DE平分∠ADC交BC于点E,则BE的长是()A.2B.3C.4D.5【答案】A.【解析】由平行四边形的性质可得AD=BC=6,AB=CD=4,再由平行线的性质和角平分线的定义可证得∠CED=∠CDE,所以CE=CD=4,即可得BE=BC-CE=6-4=2.故答案选A.【考点】平行四边形的性质;平行线的性质;等腰三角形的性质.5.如图,四边形ABCD的对角线交于点O,从下列条件:①AD∥BC,②AB=CD,③AO=CO,④∠ABC=∠ADC中选出两个可使四边形ABCD是平行四边形,则你选的两个条件是.(填写一组序号即可)【答案】①③【解析】根据AD∥BC可得∠DAO=∠OCB,∠ADO=∠CBO,再根据AO=CO得出△AOD≌△COB,从而得出BO=DO,最后根据对角线互相平分的四边形是平行四边形可得答案.【考点】平行四边形的判定6.(3分)如图,在正方形ABCD的内部作等边△ADE,连接BE,CE,则∠BEC的度数为.【答案】150°.【解析】由等边三角形的性质可得AD=DE,∠ADE=60°,由正方形的性质可得AD=DC,∠ADC=90°,所以DE=DC,CDE=∠ADC﹣∠ADE=90°﹣60°=30°,再根据等边对等角和三角形的内角和定理可得∠CED=∠ECD=(180°﹣30°)=75°,同理可得∠AEB=75°,所以∠BEC=360°﹣75°×2﹣60°=150°.【考点】正方形的性质;等边三角形的性质.7.若一个正方形的面积为8,则这个正方形的边长为()A.4B.2C.D.8【答案】B【解析】正方形的面积等于正方形边长的平方,设正方形的边长为x,根据题意可得:=8,则x==2.【考点】正方形的性质8.(3分)下列各组数据中,不可以构成直角三角形的是()A.7,24,25B.1.5,2,2.5C.,1,D.40,50,60【答案】D【解析】本题考查勾股定理的逆定理的应用.判断三角形是否为直角三角形,已知三角形三边的长,只要利用勾股定理的逆定理加以判断即可.由勾股定理的逆定理,只要验证两小边的平方和是否等于最长边的平方即可.解:A、72+242=625=252,故是直角三角形,不符合题意;B、1.52+22=6.25=2.52,故是直角三角形,不符合题意;C、12+()2==()2,故是直角三角形,不符合题意;D、402+502=4100≠602,故不是直角三角形,符合题意.故选:D.【考点】勾股定理的逆定理.9.已知E为平行四边形ABCD外一点,AE⊥CE,BE⊥DE,求证:平行四边形ABCD是矩形.【答案】详见解析.【解析】如图,连接AC、BD交于点O,连接OE,已知AE⊥CE,BE⊥DE,根据直角三角形斜边上的中线等于斜边的一半得到OE=AC=BD,进而得到AC=BD,根据对角线相等的平行四边形是矩形即可判定平行四边形ABCD是矩形..试题解析:证明:连接AC、BD交于点O,连接OE,∵AE⊥CE,BE⊥DE,∴OE=AC=BD,∴AC=BD,∵四边形ABCD是平行四边形,∴平行四边形ABCD为矩形.【考点】平行四边形的性质;矩形的判定.10.如图,▱ABCD的对角线AC与BD相交于点O,AB⊥AC,若AB=4,AC=6,则BD的长是()A.8B.9C.10D.11【答案】C.【解析】∵▱ABCD的对角线AC与BD相交于点O,∴BO=DO,AO=CO,∵AB⊥AC,AB=4,AC=6,∴BO=,∴BD=2BO=10,故选C.【考点】1.平行四边形的性质;2.勾股定理.11.(8分)如图,已知平行四边形ABCD,延长BC至E,使CE=BC,连接AC,DE,求证:AC=DE.【答案】见试题解析【解析】根据平行四边形的判定和性质定理即可得到结论.试题解析:证明:∵四边形ABCD 是平行四边形,∴AD=BC,AD∥BC,∵CE=BC,∴AD∥CE,AD=CE,∴四边形ACED是平行四边形,∴AC=DE.【考点】平行四边形的判定与性质.12.长方形纸片ABCD中,AD=4cm,AB=10cm,按如图方式折叠,使点B与点D重合,折痕为EF,求DE的长.【答案】【解析】设DE=xcm,在折叠的过程中,BE=DE=x,AE=AB﹣BE=10﹣x,△ADE中,DE2=AE2+AD2,即x2=(10﹣x)2+16.∴x=(cm).【考点】勾股定理;翻折变换(折叠问题).13.如图,在平四边形ABCD中,对角线AC与BD相交于点O,P为线段BC上一点(除端点外),连接PO并延长交AD于点Q,延长BC到点E,使CE=BC,连接DE.(1)求证:BP=DQ;(2)已知AB=5,AC=6,若CD=BE,求△BDE的周长.【答案】见试题解析【解析】(1)由平行四边形的性质得出AD∥BC,OB=OD,AD=BC,CD=AB,得出∠OBP=∠ODQ,由ASA证明△BOP≌△DOQ,得出对应边相等即可;(2)先证明四边形ACED是平行四边形,得出DE=AC=6,再证明△BDE是直角三角形,根据勾股定理求出BD,即可得出结果.试题解析:(1)证明:∵四边形ABCD是平行四边形,∴AD∥BC,OB=OD,AD=BC,CD=AB,∴∠OBP=∠ODQ,在△BOP和△DOQ中,,∴△BOP≌△DOQ(ASA),∴BP=DQ;(2)解:∵AD=BC,CE=BC,∴AD=CE=BC,∵AD∥BC,∴AD∥CE,∴四边形ACED是平行四边形,∴DE=AC=6,∵CD=BE,∴∠BDE=90°,BE=2CD=2AB=10,∴BD===8,∴△BDE的周长=BD+BE+DE=8+10+6=24.【考点】平行四边形的性质;全等三角形的判定与性质;勾股定理.14.如图,在直角三角形ABC中,∠ACB=90°,CD是AB边上的高,AB=13cm,BC=12cm,AC=5cm,求:(1)CD的长;(2)作出△ABC的边AC上的中线BE,并求出△ABE的面积.(10分)【答案】(1)cm;(2)15cm2.【解析】(1)由勾股定理求得AB==13cm,再由S△ABC=×BC×AC=AB•CD即可求得CD的长;(2)已知BE为△ABC的边AC上的中线,根据S△ABE =S△ABC即可得△ABE的面积.试题解析:解:∵∠ACB=90°,BC=12cm,AC=5cm,∴AB==13cm,∵S△ABC=×BC×AC=30cm2,∴AB•CD=30,∴CD=cm;如图∵E为AC的中点,∴S△ABE =S△ABC=×30=15cm2.【考点】勾股定理;直角三角形面积的两种表示法;三角形的中线的性质.15.如图所示,折叠长方形一边AD,点D落在BC边的点F处,已知BC=10厘米,AB=8厘米,求EC的长。
人教版八年级数学上册几何证明习题集

C八年级上册几何证明题题集1、 已知:在⊿ABC 中,AB=AC ,延长AB 到D ,使AB=BD ,E 是AB 的中点。
求证:CD=2CE 。
2、 已知:在⊿ABC 中,作∠FBC=∠ECB=21∠A 。
求证:BE=CF 。
B3、 已知:在⊿ABC 中,∠A=900,AB=AC ,在BC 上任取一点P ,作PQ ∥AB 交AC 于Q ,作PR∥CA 交BA 于R ,D 是BC 的中点,求证:⊿RDQ 是等腰直角三角形。
CB4、 已知:在⊿ABC 中,∠A=900,AB=AC ,D 是AC 的中点,AE ⊥BD ,AE 延长线交BC 于F ,求证:∠ADB=∠FDC 。
ABB DCA B C DE P 图 ⑴5、如图甲,Rt ∆ABC 中,AB=AC ,点D 、E 是线段AC 上两动点,且AD=EC ,AM ⊥BD ,垂足为M ,AM 的延长线交BC 于点N ,直线BD 与直线NE 相交于点F 。
(1)试判断∆DEF 的形状,并加以证明。
(2)如图乙,若点D 、E 是直线AC 上两动点,其他条件不变,试判断∆DEF 的形状,并加以证明。
6、已知:在⊿ABC 中BD 、CE 是高,在BD 、CE 或其延长线上分别截取BM=AC 、CN=AB ,求证:MA ⊥NA 。
7、已知:如图(1),在△ABC 中,BP 、CP 分别平分∠ABC 和∠ACB ,DE 过点P 交AB 于D ,交AC 于E ,且DE ∥BC .求证:DE -DB=EC .①②③图88、△ABC为正三角形,点M是射线BC上任意一点,点N是射线CA上任意一点,且BM=CN,直线BN与AM相交于Q点,就下面给出的三种情况,如图8中的①②③,先用量角器分别测量∠BQM的大小,然后猜测∠BQM等于多少度.并利用图③证明你的结论.9、在Rt△ABC中,AB=AC,∠BAC=90°,O为BC的中点。
(1)写出点O到△ABC的三个顶点A、B、C的距离的大小关系(不要求证明);(2)如果点M、N分别在线段AB、AC上移动,在移动中保持AN=BM,请判断△OMN的形状,并证明你的结论。
八年级上册数学全等三角形证明题

八年级上册数学全等三角形证明题一、全等三角形证明题1 20题及解析。
(一)题目1。
1. 题目。
已知:如图,在△ABC中,AD是BC边上的中线,E是AD上一点,且BE = AC,延长BE交AC于F。
求证:AF = EF。
2. 解析。
证明:延长AD到G,使DG = AD,连接BG。
因为AD是BC边上的中线,所以BD = CD。
在△BDG和△CDA中,BD = CD,∠BDG = ∠CDA(对顶角相等),DG = DA。
根据SAS(边角边)全等判定定理,可得△BDG≌△CDA。
所以BG = AC,∠G = ∠CAD。
又因为BE = AC,所以BG = BE。
所以∠G = ∠BEG。
因为∠BEG = ∠AEF(对顶角相等),所以∠AEF = ∠CAD。
所以AF = EF。
(二)题目2。
1. 题目。
如图,在△ABC和△DEF中,AB = DE,BE = CF,∠B = ∠DEF。
求证:AC = DF。
2. 解析。
因为BE = CF,所以BE + EC = CF+EC,即BC = EF。
在△ABC和△DEF中,AB = DE,∠B = ∠DEF,BC = EF。
根据SAS全等判定定理,可得△ABC≌△DEF。
所以AC = DF。
(三)题目3。
1. 题目。
已知:如图,AB = CD,AE = DF,CE = FB。
求证:AF = DE。
2. 解析。
因为CE = FB,所以CE + EF = FB + EF,即CF = BE。
在△AEB和△DFC中,AB = CD,AE = DF,BE = CF。
根据SSS(边边边)全等判定定理,可得△AEB≌△DFC。
所以∠B = ∠C。
在△ABF和△DCE中,AB = CD,∠B = ∠C,BF = CE。
根据SAS全等判定定理,可得△ABF≌△DCE。
所以AF = DE。
(四)题目4。
1. 题目。
如图,在Rt△ABC中,∠ACB = 90°,CA = CB,D是AC上一点,E在BC的延长线上,且AE = BD,BD的延长线与AE交于点F。
初中数学证明题练习5套(含答案)
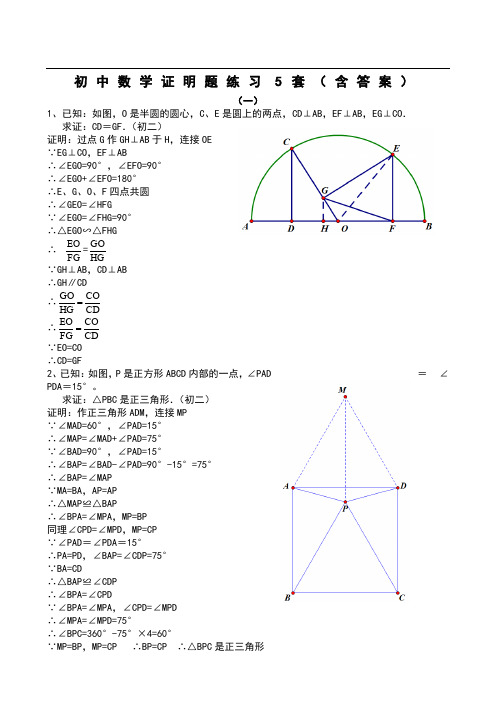
初中数学证明题练习5套(含答案)(一)1、已知:如图,O 是半圆的圆心,C 、E 是圆上的两点,CD ⊥AB ,EF ⊥AB ,EG ⊥CO .求证:CD =GF .(初二)证明:过点G 作GH ⊥AB 于H ,连接OE ∵EG ⊥CO ,EF ⊥AB∴∠EGO=90°,∠EFO=90° ∴∠EGO+∠EFO=180° ∴E 、G 、O 、F 四点共圆 ∴∠GEO=∠HFG∵∠EGO=∠FHG=90° ∴△EGO ∽△FHG∴FG EO =HGGO∵GH ⊥AB ,CD ⊥AB ∴GH ∥CD ∴CD CO HG GO = ∴CD CO FG EO = ∵EO=CO ∴CD=GF 2、已知:如图,P 是正方形ABCD 内部的一点,∠PAD =∠PDA =15°。
求证:△PBC 是正三角形.(初二) 证明:作正三角形ADM ,连接MP ∵∠MAD=60°,∠PAD=15° ∴∠MAP=∠MAD+∠PAD=75° ∵∠BAD=90°,∠PAD=15°∴∠BAP=∠BAD-∠PAD=90°-15°=75° ∴∠BAP=∠MAP ∵MA=BA ,AP=AP ∴△MAP ≌△BAP∴∠BPA=∠MPA ,MP=BP 同理∠CPD=∠MPD ,MP=CP ∵∠PAD =∠PDA =15°∴PA=PD ,∠BAP=∠CDP=75° ∵BA=CD∴△BAP ≌∠CDP ∴∠BPA=∠CPD∵∠BPA=∠MPA ,∠CPD=∠MPD ∴∠MPA=∠MPD=75°∴∠BPC=360°-75°×4=60°∵MP=BP ,MP=CP ∴BP=CP ∴△BPC 是正三角形3、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC 的延长线交MN 于E 、F .求证:∠DEN =∠F .证明:连接AC ,取AC 的中点G,连接NG 、MG ∵CN=DN ,CG=DG∴GN ∥AD ,GN=21AD∴∠DEN=∠GNM ∵AM=BM ,AG=CG∴GM ∥BC ,GM=21BC∴∠F=∠GMN ∵AD=BC ∴GN=GM∴∠GMN=∠GNM ∴∠DEN=∠F(二)1、已知:△ABC 中,H 为垂心(各边高线的交点),O 为外心,且OM ⊥BC 于M . (1)求证:AH =2OM ;(2)若∠BAC =600,求证:AH =AO .(初二)证明:(1)延长AD 交圆于F ,连接BF ,过点O 作OG ⊥AD 于G∵OG ⊥AF ∴AG=FG ∵AB ⌒ =AB⌒ ∴∠F=∠ACB又AD ⊥BC ,BE ⊥AC ∴∠BHD+∠DBH=90° ∠ACB+∠DBH=90° ∴∠ACB=∠BHD ∴∠F=∠BHD∴BH=BF 又AD ⊥BC ∴DH=DF∴AH=AG+GH=FG+GH=GH+DH+DF+GH=2GH+2DH=2(GH+DH )=2GD 又AD ⊥BC ,OM ⊥BC ,OG ⊥AD ∴四边形OMDG 是矩形 ∴OM=GD ∴AH=2OM (2)连接OB 、OC∵∠BAC=60∴∠BOC=120° ∵OB=OC ,OM ⊥BC∴∠BOM=21∠BOC=60°∴∠OBM=30°∴BO=2OM由(1)知AH=2OM ∴AH=BO=AO2、设MN 是圆O 外一条直线,过O 作OA ⊥MN 于A ,自A 引圆的两条割线交圆O 于B 、C 及D 、E ,连接CD 并延长交MN 于Q ,连接EB 并延长交MN 于P. 求证:AP =AQ .证明:作点E 关于AG 的对称点F ,连接AF 、CF 、QF ∵AG ⊥PQ ∴∠PAG=∠QAG=90°又∠GAE=∠GAF ∴∠PAG+∠GAE=∠QAG+∠GAF 即∠PAE=∠QAF∵E 、F 、C 、D 四点共圆 ∴∠AEF+∠FCQ=180° ∵EF ⊥AG ,PQ ⊥AG ∴EF ∥PQ∴∠PAF=∠AFE ∵AF=AE∴∠AFE=∠AEF ∴∠AEF=∠PAF ∵∠PAF+∠QAF=180° ∴∠FCQ=∠QAF ∴F 、C 、A 、Q 四点共圆 ∴∠AFQ=∠ACQ 又∠AEP=∠ACQ ∴∠AFQ=∠AEP3、设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE ,设CD 、EB 分别交MN 于P 、Q . 求证:AP =AQ .(初二)证明:作OF ⊥CD 于F ,OG ⊥BE 于G ,连接OP 、OQ 、OA 、AF 、AG ∵C 、D 、B 、E 四点共圆 ∴∠B=∠D ,∠E=∠C ∴△ABE ∽△ADC∴DF BG FD 2BG 2DC BE AD AB === ∴△ABG ∽△ADF ∴∠AGB=∠AFD ∴∠AGE=∠AFC ∵AM=AN , ∴OA ⊥MN 又OG ⊥BE ,∴∠OAQ+∠OGQ=180° ∴O 、A 、Q 、E 四点共圆 ∴∠AOQ=∠AGE 同理∠AOP=∠AFC ∴∠AOQ=∠AOP在△AEP 和△AFQ 中 ∠AFQ=∠AEP AF=AE ∠QAF=∠PAE ∴△AEP ≌△AFQ ∴AP=AQ又∠OAQ=∠OAP=90°,OA=OA ∴△OAQ ≌△OAP ∴AP=AQ4、如图,分别以△ABC 的AB 和AC 为一边,在△ABC 的外侧作正方形ABFG 和正方形ACDE ,点O 是DF 的中点,OP ⊥BC 求证:BC=2OP (初二)证明:分别过F 、A 、D 作直线BC 的垂线,垂足分别是L 、M 、N ∵OF=OD ,DN ∥OP ∥FL∴PN=PL∴OP 是梯形DFLN 的中位线 ∴DN+FL=2OP ∵ABFG 是正方形 ∴∠ABM+∠FBL=90° 又∠BFL+∠FBL=90° ∴∠ABM=∠BFL又∠FLB=∠BMA=90°,BF=AB ∴△BFL ≌△ABM ∴FL=BM同理△AMC ≌△CND ∴CM=DN∴BM+CN=FL+DN ∴BC=FL+DN=2OP(三)1、如图,四边形ABCD 为正方形,DE ∥AC ,AE =AC ,AE 与CD 相交于F .求证:CE =CF .(初二)证明:连接BD 交AC 于O 。
八年级全等三角形证明经典50题(含答案)

1. 已知:AB=4,AC=2,D 是BC 中点,AD 是整数,求AD解:延长AD 到E,使AD=DE∵D 是BC 中点∴BD=DC在△ACD 和△BDE 中AD=DE∠BDE=∠ADCBD=DC∴△ACD ≌△BDE∴AC=BE=2∵在△ABE 中AB-BE <AE <AB+BE∵AB=4即4-2<2AD <4+21<AD <3∴AD=22. 已知:D 是AB 中点,∠ACB=90°,求证:12CD AB延长CD 与P ,使D 为CP 中点。
连接AP,BP∵DP=DC,DA=DB∴ACBP 为平行四边形又∠ACB=90∴平行四边形ACBP 为矩形∴AB=CP=1/2AB3. 已知:BC=DE ,∠B=∠E ,∠C=∠D ,F 是CD 中点,求证:∠1=∠2AD BC证明:连接BF 和EF∵ BC=ED,CF=DF,∠BCF=∠EDF∴ 三角形BCF 全等于三角形EDF(边角边)∴ BF=EF,∠CBF=∠DEF连接BE在三角形BEF 中,BF=EF∴ ∠EBF=∠BEF 。
∵ ∠ABC=∠AED 。
∴ ∠ABE=∠AEB 。
∴ AB=AE 。
在三角形ABF 和三角形AEF 中AB=AE,BF=EF,∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF∴ 三角形ABF 和三角形AEF 全等。
∴ ∠BAF=∠EAF (∠1=∠2)。
4. 已知:∠1=∠2,CD=DE ,EF//AB ,求证:EF=AC过C 作CG ∥EF 交AD 的延长线于点GCG ∥EF ,可得,∠EFD =CGDDE =DC∠FDE =∠GDC (对顶角)∴△EFD ≌△CGDEF =CGB ACDF21E∠CGD=∠EFD又,EF∥AB∴,∠EFD=∠1∠1=∠2∴∠CGD=∠2∴△AGC为等腰三角形,AC=CG又EF=CG∴EF=AC5.已知:AD平分∠BAC,AC=AB+BD,求证:∠B=2∠CA证明:延长AB取点E,使AE=AC,连接DE∵AD平分∠BAC∴∠EAD=∠CAD∵AE=AC,AD=AD∴△AED≌△ACD (SAS)∴∠E=∠C∵AC=AB+BD∴AE=AB+BD∵AE=AB+BE∴BD=BE∴∠BDE=∠E∵∠ABC=∠E+∠BDE∴∠ABC=2∠E∴∠ABC=2∠C6.已知:AC平分∠BAD,CE⊥AB,∠B+∠D=180°,求证:AE=AD+BE证明:在AE 上取F ,使EF =EB ,连接CF∵CE ⊥AB∴∠CEB =∠CEF =90°∵EB =EF ,CE =CE ,∴△CEB ≌△CEF∴∠B =∠CFE∵∠B +∠D =180°,∠CFE +∠CFA =180°∴∠D =∠CFA∵AC 平分∠BAD∴∠DAC =∠FAC∵AC =AC∴△ADC ≌△AFC (SAS )∴AD =AF∴AE =AF +FE =AD +BE7. 已知:AB=4,AC=2,D 是BC 中点,AD 是整数,求AD解:延长AD 到E,使AD=DE ∵D 是BC 中点∴BD=DC在△ACD 和△BDE 中AD=DE∠BDE=∠ADCAD BCBD=DC∴△ACD≌△BDE∴AC=BE=2∵在△ABE中AB-BE<AE<AB+BE ∵AB=4即4-2<2AD<4+2 1<AD<3∴AD=28.已知:D是AB中点,∠ACB=90°,求证:12 CD AB9.已知:BC=DE,∠B=∠E,∠C=∠D,F是CD中点,求证:∠1=∠2证明:连接BF 和EF 。
初二数学几何证明题(5篇可选)

初二数学几何证明题(5篇可选)第一篇:初二数学几何证明题1.在△ABC中,AB=AC,D在AB上,E在AC的延长线上,且BD=CE,线段DE交BC于点F,说明:DF=EF。
2.已知:在正方形ABCD中,M是AB的中点,E是AB延长线上的一点,MN垂直DM于点M,且交∠CBE的平分线于点N.(1)求证:MD=MN.(2)若将上述条件中的“M是AB的中点”改为“M 是AB上任意一点”其余条件不变,则(1)的结论还成立吗?如果成立,请证明,如果不成立,请说明理由。
3.。
如图,点E,F分别是菱形ABCD的边CD和CB延长线上的点,且DE=BF,求证∠E=∠F。
4,如图,在△ABC中,D,E,F,分别为边AB,BC,CA,的中点,求证四边形DECF为平行四边形。
5.如图,在菱形ABCD中,∠DAB=60度,过点C作CE垂直AC 且与AB的延长线交与点E,求证四边形AECD是等腰梯形?6.如图,已知平行四边形ABCD中,对角线AC,BD,相交与点0,E是BD延长线上的点,且三角形ACE是等边三角形。
1.求证四边形ABCD是菱形。
2.若∠AED=2∠EAD,求证四边形ABCD是正方形。
7.已知正方形ABCD中,角EAF=45度,F点在CD边上,E点在BC边上。
求证:EF=BE+DF第二篇:初二几何证明题1如图,在△ABC中,D是BC边上的一点,E是AD的中点,过点A作BC的平行线交BE的延长线于F,且AF=DCCF.(1)求证:D是BC的中点;(2)如果AB=ACADCF的形状,并证明你的结论AEB第三篇:初二几何证明题初二几何证明题1.已知:如图,在△ABC中,AD⊥BC,垂足为D,BE⊥AC,垂足为E。
M为AB中点,联结ME,MD、ED求证:角EMD=2角DAC证明:∵M为AB边的中点,AD⊥BC,BE⊥AC,∴MD=ME=MA=MB(斜边上的中线=斜边的一半)∴△MED为等腰三角形∵ME=MA∴∠MAE=∠MEA∴∠BME=2∠MAE∵MD=MA∴∠MAD=∠MDA,∴∠BMD=2∠MAD,∵∠EMD=∠BME-∠BMD=2∠MAE-2∠MAD=2∠DAC2.如图,已知四边形ABCD中,AD=BC,E、F分别是AB、CD中点,AD、BC的延长线与EF的延长线交于点H、D求证:∠AHE=∠BGE证明:连接AC,作EM‖AD交AC于M,连接MF.如下图:∵E是CD的中点,且EM‖AD,∴EM=1/2AD,M是AC的中点,又因为F是AB的中点∴MF‖BC,且MF=1/2BC.∵AD=BC,∴EM=MF,三角形MEF为等腰三角形,即∠MEF=∠MFE.∵EM‖AH,∴∠MEF=∠AHF ∵FM‖BG,∴∠MFE=∠BGF∴∠AHF=∠BGF.3.写出“等腰三角形两底角的平分线相等”的逆命题,并证明它是一个真命题这是经典问题,证明方法有很多种,对于初二而言,下面的反证法应该可以接受如图,已知BD平分∠ABC,CE平分∠ACB,BD=CE,求证:AB=AC证明:BD平分∠ABC==>BE/AE=BC/AC==>BE/AB=BC/(BC+AC)==>BE=AB*BC/(BC+AC)同理:CD=AC*BC/(BC+AB)假设AB≠AC,不妨设AB>AC.....(*)AB>AC==>BC+ACAC*BC==>AB*AB/(BC+AC)>AC*BC/(BC+AB)==>BE>CDAB>AC==>∠ACB>∠ABC∠BEC=∠A+∠ACB/2,∠BDC=∠A+∠ABC/2==>∠BEC>∠BDC过B作CE平行线,过C作AB平行线,交于F,连DF则BECF为平行四边形==>∠BFC=∠BEC>∠BDC (1)BF=CE=BD==>∠BDF=∠BFDCF=BE>CD==>∠CDF>∠CFD==>∠BDF+∠CDF>∠BFD+∠CFD==>∠BDC>∠BFC (2)(1)(2)矛盾,从而假设(*)不成立所以AB=AC。
初二数学-全等三角形证明经典50题
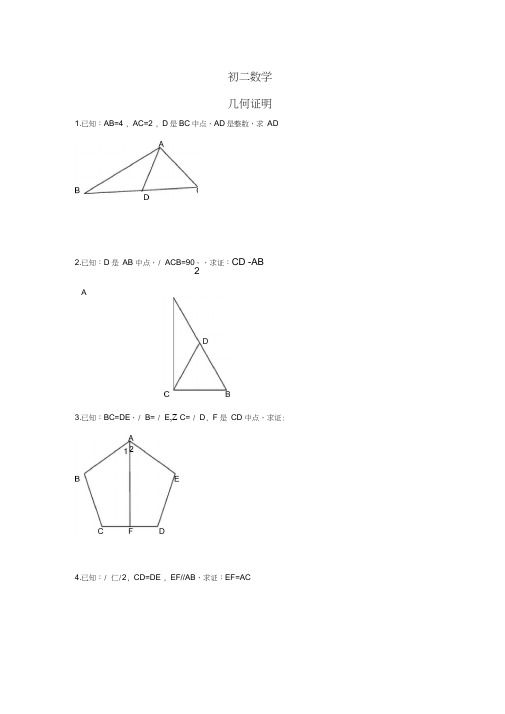
初二数学几何证明1.已知:AB=4 , AC=2 , D是BC中点,AD是整数,求AD2.已知:D 是AB 中点,/ ACB=90。
,求证:CD -AB2A3.已知:BC=DE,/ B= / E,Z C= / D, F 是CD 中点,求证:4.已知:/ 仁/2, CD=DE , EF//AB,求证:EF=AC已知:AD 平分/ BAC , AC=AB+BD ,求证:/ B=2 / C7.已知:AB=4 , AC=2 , D 是BC 中点,AD 是整数,求 ADD5. AE=AD+BE,求证: O6.8.已知:D 是AB 中点,/ ACB=90 °,求证:CD 1 AB29.已知:BC=DE,/ B= / E,/ C= / D, F 是CD 中点,求证:12.已知:AC 平分/ BAD , CE丄AB , / B+ / D=180 °,求证:AE=AD+BECD=DE , EF//AB,求证:EF=AC10.已知:/ 1 = / 2,c12.如图,四边形ABCD中,AB // DC, BE、CE分别平分/ ABC、/ BCD,且点E在AD 上。
求证:BC=AB+DC。
D14.已知:AB=CD,/ A= / D,求证:/ B= / CB15. P 是/ BAC 平分线 AD 上一点,AC>AB ,求证:PC-PB<AC-AB17.已知,E 是 AB 中点,AF=BD , BD=5 , AC=7,求 DC18. ( 5 分)如图,在△ ABC 中,BD=DC ,/ 仁/2,求证:AD 丄 BC .19. ( 5分)如图,0M 平分/ POQ , MA 丄OP,MB 丄OQ , A 、B 为垂足,AB 交0M 于点N . 求证:/ OAB= /OBA16.已知/ ABC=3 / C ,Z 1 = / 2, BE 丄 AE ,求证:AC-AB=2BE20. ( 5分)如图,已知 AD // BC ,/ PAB 的平分线与/ CBA 的平分线相交于 E , CE 的连线 交 AP 于D .求证:AD+BC=AB .(6分)如图,△ ABC 中,AD 是/ CAB 的平分线,且 AB=AC+CD ,求证:/ C=2/ B22. (6分)如图①,E 、F 分别为线段 AC 上的两个动点,且 DE 丄AC 于E , BF 丄AC 于F , 若AB=CD , AF=CE , BD 交 AC 于点 M .(1) 求证:MB = MD , ME=MF(2) 当E 、F 两点移动到如图②的位置时,其余条件不变,上述结论能否成立?若成立 请给予证明;若不成立请说明理由.23. ( 7分)已知:如图, DC // AB ,且DC =AE , E 为AB 的中点,(1)求证:△ AEDEBC.21.(2)观看图前,在不添辅助线的情况下,除△EBC夕卜,请再写出两个与△ AED的面积相等的三角形.(直接写出结果,不要求证明):24. (7分)如图,△ ABC中,/ BAC=90度,AB=AC, BD是/ ABC的平分线,BD的延长线垂直于过C点的直线于E,直线CE交BA的延长线于F .求证:BD=2CE.25、(10分)如图: DF=CE AD=BC/ D=Z G 求证:△26、(10分)如图:AE、BC交于点M F点在AM上,求证:AM>^ ABC的中线。
八年级数学几何证明题

特殊方法:在求有关三角形的定值一类的问题时,常把某点到原三角形各顶点的线段连接起来,利用三角形面积的知识解
∵△ECD为等边三角形 ∴△ECB≌△DCA( HL )
∴∠ECD=60° CD=EC ∴BC=AC
即ACB==60° ∵∠ACB=60°
—
∴△ 是等边三角形
[例2】、如图,已知BC > AB,AD=DC。BD平分∠ABC。求证:∠A+∠C=180°.
证明:在BC上截取BE=BA,连接DE, ∴∠A=∠BED AD= DE
)
∵BC = DC∴△ABD ≌ △EBD (ASA)
∠CBD=∠CDB ∴AD = DE
]
【课堂练习】
1.如图,已知AE平分∠BAC,BE上AE于E,ED∥AC,∠BAE=36°,那么∠BED=126°
延长AE交AC于F
2.如图:BE⊥AC,CF⊥AB,BM=AC,CN=AB。求证:(1)AM=AN;(2)AM⊥AN。
【变式练习】、如图,△ABC中,BD=DC=AC,E是DC的中点,求证:AD平分∠BAE.
证明:延长AE到点F,使得EF=AE 联结DF
—
在△ACE和△FDE中 ∴∠ADB=∠ACD+∠CDA
CE =DE ∵∠ACE=∠FDE
∠AEC=∠FED ∴∠ADB=∠ADC+∠FDE
AE=FE 即 ∠ADB = ∠ADF
在△ADC和△GDB中 ∴BG= BF
AD=GD ∴ ∠BFG=∠BGF
初中八年级数学上册的第12章全等三角形证明经典50题含答案

1.已知:AB=4,AC=2,D是BC中点,111749AD是整数,求ADABCD解:延伸AD到E,使AD=DE∵D是BC中点∴BD=DC在△ACD和△BDE中AD=DE∠BDE=∠ADCBD=DC∴△ACD≌△BDE∴AC=BE=2∵在△ABE中AB-BE<AE<AB+BE∵AB=4即4-2<2AD<4+21<AD<3∴AD=22.已知:D是AB中点,∠ACB=90°,求证:1CDAB2 ADA21EBCFD证明:连结BF和EF∵BC=ED,CF=DF,∠BCF=∠EDF∴三角形BCF全等于三角形EDF(边角边)∴BF=EF,∠CBF=∠DEF连结BE在三角形BEF中,BF=EF∴∠EBF=∠BEF。
∵∠ABC=∠AED。
∴∠ABE=∠AEB。
∴AB=AE。
在三角形ABF和三角形AEF中AB=AE,BF=EF,∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF∴三角形ABF和三角形AEF全等。
∴∠BAF=∠EAF(∠1=∠2)。
4.已知:∠1=∠2,CD=DE,EF//AB,求证:EF=ACA21F∠CGD=∠EFD又,EF∥AB∴,∠EFD=∠1∠1=∠2∴∠CGD=∠2∴△AGC为等腰三角形,AC=CG又EF=CG∴EF=AC5.已知:AD均分∠BAC,AC=AB+BD,求证:∠B=2∠CA证明:延伸AB取点E,使AE=AC,连结DE∵AD均分∠BAC∴∠EAD=∠CAD∵AE=AC,AD=AD证明:在AE上取F,使EF=EB,连结CF∵CE⊥AB∴∠CEB=∠CEF=90°∵EB=EF,CE=CE,∴△CEB≌△CEF∴∠B=∠CFE∵∠B+∠D=180°,∠CFE+∠CFA=180°∴∠D=∠CFA∵AC均分∠BAD∴∠DAC=∠FAC∵AC=AC∴△ADC≌△AFC(SAS)∴AD=AF∴AE=AF+FE=AD+BE7.已知:AB=4,AC=2,D是BC中点,AD是整数,求AD ABD=DC∴△ACD≌△BDE∴AC=BE=2∵在△ABE中AB-BE<AE<AB+BE∵AB=4即4-2<2AD<4+21<AD<3∴AD=28.已知:D是AB中点,∠ACB=90°,求证:1CDAB2 ADCB解:延伸AD到E,使AD=DE∵D是BC中点∴BD=DC在△ACD和△BDE中AD=DEA21EBCFD证明:连结BF和EF。
初二数学证明试题

初二数学证明试题1.老李到办公室后,他总要完成以下事情:烧开水10分钟,洗茶杯1分钟,准备茶叶和冲茶1分钟,打扫办公室9分钟,收听新闻10分钟,问老李做好以上事情至少需要分钟时间.【答案】11分钟【解析】可以同时进行的项目为:烧开水10分钟,洗茶杯1分钟,打扫办公室9分钟,收听新闻10分钟,用时10分;再加上准备茶叶和冲茶1分钟,至少需要11分钟.解:在烧水的过程种,可以同时收听新闻,洗茶杯,打扫办公室,这个过程需要10分钟;然后再准备茶叶和冲茶需1分钟;因此至少需要10+1=11分钟.点评:解决本题的关键是找到可以同时进行的项目及所用时间.2. A、B、C、D四人参加某一期的体育彩票兑奖活动,现已知:如果A中奖,那么B也中奖;如果B中奖,那么C中奖或A不中奖;如果D不中奖,那么A中奖,C不中奖;如果D中奖,那么A也中奖,则这四个人中,中奖的人数是人.【答案】4【解析】从最后一句话出发:如果D中奖,那么A也中奖;返回到第一句,如果A中奖,那么B 也中奖;继续判断,A已经中奖,那么“如果B中奖,那么C中奖或A不中奖”的条件中,应只考虑C中将的情况.可得到如果B中奖,那么C中奖.所以一共有4个人中奖.解:根据题意,可将已知条件大致分为三类:(为叙述方便,将中奖简写为“中”)①如果A中,则B中;②如果B中,则C中或A不中;③如果D不中,则A中且C不中;已知了A中且D中,当A中时,由①知:B也中;当B中时,由②知C也中(由于A已中奖,因此A不中的条件可以舍去);因此A、B、C、D四人都中奖了,由此可得出中奖的人数为4人.故答案为:4.点评:此题主要考查了推理论证,解决本题应从所给的假设入手,然后依据题目所给的条件逐步分析判断.3.甲、乙、丙、丁和小强五位同学单循环比赛象棋,到现在为止甲已经赛了四盘,乙赛了三盘,丙赛了二盘,丁赛了一盘,则小强赛了盘.【答案】2【解析】根据甲赛的盘数,可知甲与乙、丙、丁和小强4人各赛了一盘.然后探究乙、丙、丁和小强4人之间赛的盘数(设小强赛的盘数为x),进而得到小强赛的总盘数.解:乙、丙、丁和小强除去与甲赛的一盘后,在他们之间赛的盘数分别是:2、1、0、x.即丁只和甲赛了一盘,没与乙、丙、小强比赛,则乙、丙、小强之间赛的盘数分别为2、1、x,假设丙与小强赛了一盘,那么乙赛的两盘都是与小强赛的,这与单循环比赛相矛盾,是不可能的,所以丙与乙赛了一场,乙又与小强赛了一盘,小强与甲也赛了一盘,故小强共赛了2盘.故填2.点评:解决问题的关键是读懂题意,将实际问题转化为数学问题,利用数学知识进行探讨、解答实际问题.4.有12名游客要赶往离住地40千米的一个火车站去乘火车,离开车时间只有3小时了,他们步行的速度为每小时6千米,靠走路是来不及了,唯一可以利用的交通工具只有一辆小汽车,但这辆小汽车连司机在内最多能乘5人,汽车的速度为每小时60千米.(1)甲游客说:我们肯定赶不上火车;(2)乙游客说:只要我们肯吃苦,一定能赶上火车;(3)丙游客说:赶上或赶不上火车,关键取决于我们自己.亲爱的同学,当你身处其境,一定也有自己的想法,请你就某位游客的说法,用数学知识以理其人,由于难度不同,请你慎重选择.选择(1)答对只能给3分,选择(2)答对可以给4分,选择(3)答对我们奖赏你满分6分.【答案】见解析【解析】(1)因为共有12人,这辆小汽车连司机在内最多能乘5人.所以当汽车首先载4位乘客时,其余乘客在原地不动,12位乘客分3批,计算所需要的时间和3小时进行比较即可;(2)在汽车每接送一批顾客的时候,剩下的顾客也要同时往前赶,计算所需的时间和3小时进行比较即可.解:选择(1)当汽车首先载4位乘客时,其余乘客在原地不动,12位乘客分3批,汽车共需时间:40×5=200千米,200÷60=>3,故肯定赶不上火车;选择(2)当汽车首先载4位乘客时,其余乘客以每小时6千米的速度前进,当汽车接第二批4位乘客,共需时:(40+40)÷(60+6)=,此时,乘客已走6×==≈7.7千米,当司机接走第二批4位乘客时,余下4位乘客在原地不动,汽车共走4×(40﹣7.7)+40=169.2千米<3小时×60千米/小时=180千米,说明能赶上火车.当司机接走第二批4位乘客时,余下4位乘客以每小时6千米的速度前进,由上可知,汽车走更少的路,说明更能赶上火车;选择(3):将选择(1)和选择(2)综合即可.点评:此题的难点在于计算第二种选择,注意在汽车所走的时间内,剩下的顾客一直在走,从而得到每一次汽车接送顾客时所走的路程.5.甲,乙,丙,丁,戊与小强六位同学参加乒乓球比赛,每两人都要比赛一场,到现在为止,甲已经赛了5场,乙已经赛了4场,丙已经赛了3场,丁已经赛了2场,戊已经赛了1场,小强已经赛了()A.1场B.2场C.3场D.4场【答案】C【解析】根据甲参赛了5场,则甲和每人参赛了一场,所以根据戊已经赛了1场,戊只和甲比赛了一场;再根据乙已经赛了4场,则乙和甲、丙、丁、小强各参赛了一场.根据丁已经赛了2场,则丁只和甲、乙进行了比赛;再根据丙已经赛了3场,则丙和甲、乙、小强各比赛了一场.所以小强比赛了3场.解:由于每两人比赛一场,因此每个人最多比5场.甲已经赛了5场,则说明甲和其他5人都比了一场;由此可知:甲与小强比了一场,戊只和甲赛了一场;乙赛了4场,除去和甲赛的一场外,还和其他三人各赛一场,因此这三人必为:丙、丁和小强;丁赛了2场,由上面两个人的比赛情况可知:丁只与甲、乙进行了比赛;丙赛了3场,除去和甲、丁的两场比赛,还剩下一场,而丁和戊都没有和丙比赛,因此丙剩下的一场比赛必为和小强的比赛.因此小强赛了三场,且对手为甲、乙、丙.故选C.点评:本题要首尾结合进行逐步推理.6.在一次1500米比赛中,有如下的判断:甲说:丙第一,我第三;乙说:我第一,丁第四;丙说:丁第二,我第三.结果是每人的两句话中都只说对了一句,则可判断第一名是()A.甲B.乙C.丙D.丁【答案】B【解析】假设甲说的前半句话是正确的,即丙第一,则乙的后半句是正确的,即丁第四,则丙说的后半句应是正确的,出现矛盾,所以必须是甲说的后半句是正确的,即甲第三,所以丙说的前半句是正确的,即丁第二,所以乙说的前半句是正确的,即乙第一.解:根据分析,知第一名应是乙.故选B.点评:此类题应从假设出发,经过推理,如果得到矛盾,则假设错误,再进一步推理即可.7.已知4个矿泉水空瓶可以换矿泉水一瓶,现有12个矿泉水空瓶,若不交钱,最多可以喝矿泉水瓶()A.2瓶B.3瓶C.4瓶D.5瓶【答案】C【解析】4个矿泉水空瓶可以换矿泉水一瓶,12个矿泉水空瓶可换3瓶矿泉水,喝完后借1个空矿泉水瓶又得4个空矿泉水瓶,又可换一瓶,喝完后得一空瓶归还.所以最多可以喝矿泉水4瓶.解:12个空瓶可换12÷4=3瓶矿泉水;3瓶矿泉水喝完后借1个空矿泉水瓶又可得到4个空瓶子,可换4÷4=1瓶矿泉水,喝完后得一空瓶归还;因此最多可以喝矿泉水3+1=4瓶.故选C.点评:考查了推理与论证,本题需注意喝完3瓶矿泉水后,借1个空矿泉水瓶又可得到4个空瓶即1瓶矿泉水.8.甲、乙、丙3人从图书馆各借了一本书,他们相约在每个星期天相互交换读完的书.经过数次交换后,他们都读完了这3本书.若乙读的第三本书是丙读的第二本书,则乙读的第一本书是甲读的()A.第一本书B.第二本书C.第三本书D.不能确定【答案】B【解析】根据甲、乙、丙3人从图书馆各借了一本书,在每个星期天相互交换读完的书,得出3人交换书的所有情况,进而得出乙读的第一本书是甲读的第二本书.解:设3人分别读了a,b,c三本书,则甲:a b c乙:b c a丙:c a b,∵乙读的第三本书是丙读的第二本书,∴乙读的第一本书是甲读的第二本书.故选:B.点评:此题主要考查了推理与论证,根据已知得出交换书的所有情况是解题关键.9.你们曾经玩过“两人‘抢30’游戏”(游戏规则中规定每次每人只能说一个或两个数,谁先抢到30,谁得胜),若将“抢30”换成“抢20”.下列说法正确的个数是()(1)“抢20”游戏不公平;(2)第一个报数人一开始报“1”,就掌握获胜的主动权;(3)第一个报数人,一定能抢到20;(4)第二个报数人,一定能抢到20.A.1B.2C.3D.4【答案】A【解析】因为两人都可以说1个数或2个数,所以,甲只要保证从第二次开始所说的数与乙的数的个数的和是3,第一次所说的数的个数是20除以3的余数,即可一定抢到20.解:∵20÷3=6…2,∴只要是第一个人先说2个数,然后保证下一次所说的数的个数与第二个人所说的数的个数的和是3,就一定能抢到20;所以,游戏不公平,偏向第一个人;故选:A.点评:本题考查了游戏的公平性,读懂题意,确定出甲从第二次开始保证与乙所说的数的个数的和是3是确定出第一次所说的数的关键.10.甲、乙、丙、丁四个小朋友正在教室里玩耍,忽听“砰”的一声,讲台上的花盆被打破了.甲说:“是乙不小心闯的祸.”乙说:“是丙闯的祸.”丙说:“乙说的不是实话.”丁说:“反正不是我闯的祸.”如果刚才四个小朋友中只有一个人说了实话,那么这个小朋友是()A.甲B.乙C.丙D.丁【答案】C【解析】运用反证法的方法先分别假设甲说的是实话、乙说的是实话、丁说的是实话,然后推理都得出与题设相矛盾的结论,则只有丙只有一个人说了实话.解:假设甲说的是实话,“是乙不小心闯的祸.”,则丁说的也应该是实说,这与四个小朋友中只有一个人说了实话相矛盾;假设乙说的是实话,则丁说的也应该是实说,这与四个小朋友中只有一个人说了实话相矛盾;假设丁说的是实话,乙说的是假话,则丙说:“乙说的不是实话.”应该是实话,这与四个小朋友中只有一个人说了实话相矛盾;所以四个小朋友中只有一个人说了实话,这个小朋友是丙.故选C.点评:本题考查了运用反证法的方法进行推理与论证.。
初二数学证明(含答案_证明题有过程)

18-9AB E FC D23.(本题8分).如图,已知:△ABC 中,AD 是∠BAC 的平分线,AD 的垂直平分线交AD 于E,交BC 的延长线于F.求证:FD 2=FB.FC.24.(本题8分)已知ABC △,延长BC 到D ,使CD BC =.取AB 的中点F ,连结FD 交AC 于点E .(1)求AE AC的值; (2)若AB a FB EC ==,,求AC 的长.25.(本题8分)如图:已知△ABC 中,AB=5,BC=3,AC=4,PQ ∥AB ,P 点在AC 上(与A 、C 不重合),Q 在BC 上.(1) 当△PQC 的面积等于四边形PABQ 面积的31,求CP 的长. (2)当△PQC 的周长与四边形PABQ 的周长相等时,求CP 的长.(3)试问:在AB 上是否存在一点M ,使得△PQM 为等腰直角三角形,若不存在,请简要说明理由:若存在,请求出PQ 的长.23、连接FA,证明FAC Δ∽FBA Δ,由于FD FA ,命题获证。
24、法一:连接AD FC ,;法二:过F E 或者 做平行线,命题获证,在命题获证的基础上第二问求出。
25、(1)用相似CPQ Δ∽CAB Δ(2)设出x PC 表示出CQ ,利用周长列出方程,求出PC(3)当∠PQM=90°时(画图)过P 作PN ⊥AB 于N设PQ=QM=PN=MN=a∠QMB=∠ANP=90°∠B=90°-∠A=∠APN∴△MQB ∽△NAP ∽△CAB∴AN:PN=AC:BC ,BM:QM=BC:BC∴MB=3/4a ,AN=4/3a∵AB=AN+NM+MB∴3/4a+4/3a+a=5∴PQ=a=60/37当∠QPM=90°时同理有PQ=60/37当∠PMQ=90°时过P 作PN ⊥AB 于N,过Q 作QR ⊥AB 于R,过M 作MS ⊥PQ 于S设PN=QR=a则PQ=MN=2a类似前两种情况可得△RQB ∽△NAP ∽△CAB∴RB=3/4a,AN=4/3a∵AB=AN+NM+MB∴3/4a+4/3a+2a=5∴a=60/49 ∴PQ=2a=120/4926、(1)1 ::0.8=X :4.08 求出甲树高X=5.1米(2)先求墙壁上的影长展开在地上的距离 1 :0.8=1.2:X 求出X=0.96米得出落在地面上的影长一共为0.96+2.4=3.36米则 1:0.8=X:3.36 求出乙树高X=4.2米(3)台阶高0.3米投影到地面则影长为1:0.8=0.3:X 求出X=0.24 则在水平面上的总影长为0.24+0.2+4.4=4.84米则1:0.8=X:4.84求出丙树高X=6.05米(4)1.6:2=X:3.2求出X=2.56米则1:0.8=2.56:X 求出斜面上的影子落在水平面上的影长X=2.048米则丁树在水平面上的总影长为2.048+2.4=4.448 则1:0.8=X:4.448 求出丁树高X=5.56米。
期中真题几何证明40题专练—2023-2024学年八年级数学上册(沪教版)(解析版)

期中真题几何证明40题专练一.解答题(共40小题)1.(2022秋•宝山区校级期中)五边形ABCDE中,AB=AE,AD平分∠CDE,∠B+∠E=180°,求证:BC+DE=CD.【分析】在DC上截取DF=DE,连接AF,先证△ADF≌△ADE,再证△ACF≌△ACB,即可得证结果.【解答】证明:如图,在DC上截取DF=DE,连接AF,∵AD平分∠CDE,∴∠ADF=∠ADE,在△ADF和△ADE中,,∴△ADF≌△ADE(SAS),∴AF=AE,∠FAD=∠EAD,∵AB=AE,∠BAE=∠CAD,∴AB=AF,∠BAC=∠FAC,在△ACF和△ACB中,,∴△ACF≌△ACB(SAS)∴BC=CF,∵CD=CF+DF,∴CD=BC+DE.【点评】本题考查了全等三角形的判定与性质,角平分线的定义,解题的关键是准确作出辅助线构造全等三角形.2.(2022秋•虹口区校级期中)如图,△ABC和△DBC中,∠ACB=∠DBC=90°,E是BC的中点,且ED ⊥AB于点F,且AB=DE.(1)求证:BD=2EC;(2)若BD=10cm,求AC的长.【分析】(1)根据AAS证明△ABC≌△EDB得BD=BC,再根据E是BC的中点,即可得出结论;(2)根据(1)的结论,结合BD=10,即可求出AC的长.【解答】(1)证明:∵ED⊥AB,∠ACB=∠DBC=90°,∴∠BFE=∠DBC=90°,∴∠BEF+∠ABC=∠BDE+∠BEF=90°,∴∠ABC=∠BDE,在△ABC和△EDB中,,∴△ABC≌△EDB(AAS),∴BD=BC,∵E是BC的中点,∴BC=2CE,∴BD=2EC;(2)解:由(1)知,△ABC≌△EDB,∴BE=AC,∵BD=2CE,即BD=2BE,∵BD=10,∴AC=BE=5cm.【点评】本题考查了全等三角形的判定与性质,证明△ABC≌△EDB是解题的关键.3.(2022秋•静安区校级期中)如图,AD是△ABC的高,∠B=2∠C,BD=5,BC=25,求AB的长.【分析】在线段DC上截取DE=BD,连接AE,根据线段垂直平分线的性质得到AB=AE,求得∠B=∠AEB,根据三角形外角的性质得到∠AEB=∠CAE+∠C,求得AE=CE,于是得到结论.【解答】解:如图:在线段DC上截取DE=BD,连接AE,∵AD⊥BC,∴AB=AE,∴∠B=∠AEB,∵∠B=2∠C,∴∠AEB=2∠C,∵∠AEB=∠CAE+∠C,∴∠C=∠CAE,∴AE=CE,∵BD=5,BC=25,∴DE=BD=5,∴AB=AE=CE=BC﹣BD﹣DE=15.【点评】此题主要考查的是等腰三角形的判定和性质,作出辅助线正确构建出等腰三角形是解答此题的关键.4.(2020秋•杨浦区校级期中)如图,在△ABC中,∠ACB=90°,D是AB上一点,且BD=AD=CD,过B作BE⊥CD,分别交AC于点E、交CD于点F.(1)求证:∠A=∠EBC;(2)如果AC=2BC,请猜想BE和CD的数量关系,并证明你的猜想.【分析】(1)证得∠EBC=∠ACD,∠A=∠ACD,则结论可得出;(2)过点D作DG⊥AC于点G,根据ASA证明△DCG≌△EBC,可得出结论.【解答】(1)证明:∵BE⊥CD,∴∠BFC=90°,∴∠EBC+∠BCF=180°﹣∠BFC=90°,∵∠ACB=∠BCF+∠ACD=90°,∴∠EBC=∠ACD,∵AD=CD,∴∠A=∠ACD,∴∠A=∠EBC;(2)解:CD=BE.过点D作DG⊥AC于点G,∵DA=DC,DG⊥AC,∴AC=2CG,∵AC=2BC,∴CG=BC,∵∠DGC=90°,∠ECB=90°,∴∠DGC=∠ECB,在△DGC和△ECB中,,∴△DCG≌△EBC(ASA),∴CD=BE.【点评】此题主要考查了全等三角形的判定与性质,等腰三角形的性质,关键是掌握全等三角形的判定定理.5.(2020秋•徐汇区校级期中)如图,AD∥BC,点E是AB的中点,联结DE并延长交CB的延长线于点F,点G在边BC上,且∠GDF=∠ADF.(1)求证:AD=BF;(2)当点G是FC的中点时,判断△FDC的形状.【分析】(1)由AD与BC平行,利用两直线平行内错角相等,得到一对角相等,再由一对对顶角相等及E 为AB中点得到一对边相等,利用AAS即可得出△ADE≌△BFE,根据全等三角形的性质即可得解;(2)连接EG,根据题意,结合全等三角形的性质得到GE⊥DF,GE是△FDC的中位线,根据三角形中位线的性质即可得出△FDC是直角三角形.【解答】(1)证明:∵AD∥BC,∴∠ADE=∠BFE,∵E为AB的中点,∴AE=BE,在△ADE和△BFE中,,∴△ADE≌△BFE(AAS),∴AD=BF;(2)解:△FDC是直角三角形,理由如下:连接EG,∵∠GDF=∠ADE,∠ADE=∠BFE,∴∠GDF=∠BFE,由(1)△ADE≌△BFE得:DE=FE,即GE为DF上的中线,∴GE⊥DF,∵点G是FC的中点,DE=FE,∴GE∥CD,∴CD⊥DF,∴△FDC是直角三角形.【点评】此题考查了全等三角形的判定与性质,平行线的性质,以及等腰三角形的判定与性质,利用AAS证明△ADE≌△BFE是解本题的关键.6.(2022秋•静安区校级期中)如图,AB=AC,AD=AE,∠BAD=∠CAE,BE与CD相交于点F.求证:(1)∠ADC=∠AEB;(2)FD=FE.【分析】(1)利用AAS证明△ABD≌△ACE即可;(2)连接DE,利用等腰三角形的性质和判定即可证明结论.【解答】证明:(1)∵∠BAD=∠CAE,∴∠BAD+∠EAD=∠CAE+∠DAE,∴∠BAE=∠CAD,在△ABE与△ACD中,,∴△ABE≌△ACD(SAS),∴∠ADC=∠AEB;(2)连接DE,∵AD=AE,∴∠ADE=∠AED,∵∠ADC=∠AEB,∴∠ADC﹣∠ADE=∠AEB﹣∠AED,∴∠FDE=∠FED,∴FD=FE.【点评】本题主要考查了全等三角形的判定与性质,等腰三角形的判定与性质,熟练掌握等腰三角形的性质和判定是解题的关键.7.(2022秋•杨浦区期中)如图,已知AB=AC,∠BEF=∠CFH,BE=CF,M是EH的中点.求证:FM⊥EH.【分析】根据等腰三角形的性质可求∠B=∠C,根据ASA可证△BEF≌△CFH,根据全等三角形的性质可求EF=FH,再根据等腰三角形的性质可证FM⊥EH.【解答】证明:∵AB=AC,∴∠B=∠C,在△BEF与△CFH中,,∴△BEF≌△CFH(ASA),∴EF=FH,∵M是EH的中点,∴FM⊥EH.ASA证明△BEF≌△CFH.8.(2021秋•浦东新区期中)如图,在△ABC中,BD平分∠ABC,∠A=2∠C,求证:BC=AB+AD.【分析】在BC上截取BE=BA,由“SAS”可证△ABD≌△EBD,可得∠BED=∠A,AB=BE,AD=DE,由外角的性质可得∠C=∠EDC,可证EC=ED,即可得结论.【解答】证明:如图,在BC上截取BE=BA,连接DE,∵BD平分∠ABC,∴∠ABD=∠CBD,在△ABD和△EBD中,,∴△ABD≌△EBD(SAS),∴∠BED=∠A,AB=BE,AD=DE,∵∠A=2∠C,∴∠BED=2∠C,∵∠BED=∠C+∠EDC,∴∠C=∠EDC,∴EC=ED,∴BC=BE+EC=AB+AD.【点评】本题考查了全等三角形的判定和性质,添加恰当辅助线构造全等三角形是解题的关键.9.(2021秋•徐汇区校级期中)已知在△ABC中,AB=AC,在边AC上取一点D,以D为顶点,DB为一条边作∠BDF=∠A,点E在AC的延长线上,∠ECF=∠ACB.求证:(1)∠FDC=∠ABD;(2)DB=DF;(3)当点D在AC延长线上时,DB=DF是否依然成立?在备用图中画出图形,并说明理由.【分析】(1)根据角的和差即可得到结论;(2)过D作DG∥BC交AB于G,根据等腰三角形的性质和全等三角形的判定和性质定理即可得到结论;(3)过D作DG∥BC交AB于G,根据平行线的性质得到∠ADG=∠ACB,∠AGD=∠ABC,根据等腰三角形的性质得到∠ABC=∠ACB,根据全等三角形的判定和性质即可得到结论.【解答】(1)证明:∵∠BDC=∠A+∠ABD,即∠BDF+∠FDC=∠A+∠ABD,∵∠BDF=∠A,∴∠FDC=∠ABD;(2)过D作DG∥BC交AB于G,∴∠ADG=∠ACB,∠AGD=∠ABC,∵AB=AC,∴∠ABC=∠ACB,∴∠AGD=∠ADG,∴AD=AG,∴AB﹣AG=AC﹣AD,即BG=DC,∵∠ECF=∠ACB=∠AGD,∴∠DGB=∠FCD,在△GDB与△CFD中,,∴△GDB≌△CFD(ASA),∴DB=DF;(3)仍然成立,如图2,过D作DG∥BC交AB于G,∴∠ADG=∠ACB,∠AGD=∠ABC,∵AB=AC,∴∠ABC=∠ACB,∴∠AGD=∠ADG,∴AD=AG,∴AG﹣AB=AD﹣AC,即BG=DC,∵∠ECF=∠ACB=∠AGD,∴∠DGB=∠FCD,∵∠ACB+∠BCF+∠FCD=180°,∴∠ACB+∠BCF+∠DGB=180°,∵∠DGB=∠ABC.∴∠ACB+∠BCF∠ABC=180°,∵∠A+∠ABC+∠ACB=180°,∴∠A=∠BCF,∵∠BDF=∠A,∴∠BCF=∠BDF,∴∠CBD=∠CFD,∵∠GBD=180°﹣∠ABC﹣∠CBD=180°﹣∠FCD﹣∠CFD=∠FDC,∴∠GBD=∠FDC,在△GDB与△CFD中,,∴△GDB≌△CFD(ASA),∴DB=DF.【点评】本题考查了全等三角形的判定和性质,等腰三角形的判定和性质,平行线的性质,正确的作出辅助线是解题的关键.10.(2022秋•浦东新区期中)如图,已知在△ABC中,AB=AC,点D、E分别在AC、AB上,且AD=AE,点F在BC的延长线上,DB=DF.(1)求证:∠ABD=∠ACE.(2)求证:CE∥DF.【分析】(1)由“SAS”可证△ADB≌△AEC,可得∠ABD=∠ACE;(2)由等腰三角形的性质可得∠=∠F,由外角的性质可得∠ACE=∠CDF,可得结论.【解答】证明:(1)∵△ABC是等边三角形,∴AB=AC,∠ABC=∠ACB=60°,在△ADB和△AEC中,,∴△ADB≌△AEC(SAS),∴∠ABD=∠ACE;(2)∵DB=DF,∴∠DBF=∠F,∵∠ABC=∠ABD+∠DBC,∠ACB=∠F+∠CDF,∴∠ABD=∠CDF,∴∠ACE=∠CDF,∴CE∥DF.【点评】本题考查了全等三角形的判定和性质,等腰三角形的性质,等边三角形的性质,掌握全等三角形的判定方法是本题的关键.11.(2020秋•浦东新区校级期中)已知:如图,点B、F、C、E在同一条直线上,AC∥DF,AC=DF,BF =CE.求证:AB∥DE.【分析】根据线段的和差求出BC=EF,由平行线的性质证得∠ACB=∠DFE,根据SAS定理推出△BAC≌△EDF,根据全等三角形的性质得出∠B=∠E,根据平行线的判定即可证得AB∥DE.【解答】证明:∵BF=CE,∴BF+FC=CE+FC,∴BC=EF,∵AC∥DF,∴∠ACB=∠DFE,在△BAC和△EDF中,,∴△BAC≌△EDF(SAS),∴∠B=∠E,∴AB∥DE.【点评】本题考查了全等三角形的性质和判定,平行线的判定的应用,能推出△BAC和△EDF全等是解此题的关键.12.(2022秋•长宁区校级期中)已知:如图,△ABC中,AD平分∠BAC交BC于点D,CF∥AB且CD平分∠FCA,联结FD并延长交边AB于点E,说明CF=AC﹣AE的理由.【分析】由CF∥AB得∠FCB=∠ABC,由CD平分∠FCA得∠FCB=∠ACB,可得∠ACB=∠ABC,从而得AB =AC,由AD平分∠BAC可得CD=BD,再根据ASA证明△FCD≌△EBD,可得FC=BE,从而可得结论.【解答】解:∵CF∥AB,∴∠FCB=∠ABC,∵CD平分∠FCA,∴∠FCB=∠ACB,∴∠ACB=∠ABC,∴AB=AC,∵AD平分∠BAC,∴CD=BD,在△FCD和△EBD中,,∴△FCD≌△EBD(ASA),∴FC=BE,∵AC=AB=AE+EB=AE+CF,∴CF=AC﹣AE.【点评】本题主要考查了等腰三角形的判定与性质,全等三角形的判定与性质,角平分线的意义等知识,运用ASA证明△FCD≌△EBD是解答本题的关键.13.(2022秋•杨浦区期中)如图1所示,已知点E在直线AB上,点F,G在直线CD上且∠EFG=∠FEG,EF平分∠AEG,如图2所示,H是AB上点E右侧一动点,∠EGH的平分线GQ交FE的延长线于点Q,设∠Q=α,∠EHG=β,(1)若∠HEG=40°,∠QGH=20°,求∠Q的度数;(2)判断:点H在运动过程中,α和β的数量关系是否发生变化?若不变,求出α和β的数量关系;若变化,请说明理由.【分析】(1)先证明,再依据∠HEG=40°,即可得到∠FEG=70°,依据QG平分∠EGH,即可得到∠QGH=∠QGE=20°,根据∠Q=∠FEG﹣∠EGQ进行计算即可;(2)根据∠FEG是△EGQ的外角,∠AEG是△EGH的外角,即可得到∠Q=∠FEG﹣∠EGQ,∠EHG=∠AEG ﹣∠EGH,再根据FE平分∠AEG,GQ平分∠EGH,即可得出,,最后依据∠Q=∠FEG﹣∠EGQ进行计算,即可得到.【解答】解:(1)∵EF平分∠AEG,∴∠AEF=∠GEF,∵∠EFG=∠FEG,∴∠AEF=∠GFE,∴AB∥CD,∵∠HEG=40°,∴,∵QG平分∠EGH,∴∠QGH=∠QGE=20°,∴∠Q=∠FEG﹣∠EGQ=70°﹣20°=50°;(2)点H在运动过程中,α和β的数量关系不发生变化,∵∠FEG是△EGQ的外角,∠AEG是△EGH的外角,∴∠Q=∠FEG﹣∠EGQ,∠EHG=∠AEG﹣∠EGH,又∵FE平分∠AEG,GQ平分∠EGH,∴,,∴∠Q=∠FEG﹣∠EGQ==,即.【点评】本题主要考查了平行线的判定与性质,三角形外角性质的运用,解题的关键是利用三角形的外角性质:三角形的外角等于与它不相邻的两个内角的和.14.(2022秋•宝山区校级期中)如图,在五边形ABCDE中,(1)已知AB=AE,BC=ED,∠B=∠E,F是CD中点,求证:AF⊥CD.(2)已知AB=AE,BC=ED,∠C=∠D,F是CD中点,求证:AF⊥CD.(3)已知∠B=∠E,BC=ED,∠C=∠D,F是CD中点,求证;AF⊥CD.【分析】(1)连接AC,AD,根据全等三角形的判定和性质得出△ABC≌△AED,AC=AD,再由等腰三角形三线合一即可证明;(2)连接BF,EF,BCF≌△EDF,△ABF≌△AEF,∠CFB=∠DFE,∠AFB =∠AFE,结合图形得出∠AFC=∠AFD,即可证明;(3)连接BD,CE交于点G,根据全等三角形的判定和性质得出△BCD≌△EDC,△CGF≌△DGF,∠AFC=∠AFD,结合图形即可证明.【解答】解:(1)如图所示,连接AC,AD,在△ABC与△AED中,,∴△ABC≌△AED(SAS),∴AC=AD,∵F是CD中点,∴AF⊥CD;(2)如图所示,连接BF,EF,∵F是CD中点,∴CF=FD,在△BCF与△EDF中,,∴△BCF≌△EDF(SAS),∴BF=EF,∠CFB=∠DFE在△ABF与△AEF中,,∴△ABF≌△AEF(SSS),∴∠AFB=∠AFE,∴∠AFB+∠CFB=∠DFE+∠AFE,即∠AFC=∠AFD,∵∠AFC+∠AFD=180°,∴∠AFD=90°,∴AF⊥CD;(3)如图所示,连接BD,CE交于点G,∵F是CD中点,∴CF=FD,在△BCD与△EDC中,,∴△BCD≌△EDC(SAS),∴∠CDB=∠DCE,∴CG=DG,在△CGF与△DGF中,,∴△CGF≌△DGF(SAS),∴∠AFC=∠AFD,∵∠AFC+∠AFD=180°,∴∠AFD=90°,∴AF⊥CD.【点评】题目主要考查全等三角形的判定和性质,线段中点的性质及等腰三角形的判定和性质等,理解题15.(2022秋•宝山区校级期中)如图,△ABC和△ABD,AB=AD,点E、F在边BC上,点A、F、D共线,∠BAC=∠AFC,∠EAC=∠FCD,求证:AE=CD.【分析】根据三角形内角和定理得出∠CAD=∠ABC,再由三角形外角的性质及全等三角形的判定和性质即可证明.【解答】证明:∵∠BAC=∠AFC,∴180°﹣∠BAC﹣∠ACB=180°﹣∠AFC﹣∠ACB,即∠CAD=∠ABC,∵∠EAC=∠FCD,∴∠EAC+∠ACB=∠FCD+∠ACB,即∠AEB=∠ACD,在△AEB与△DCA中,,∴△AEB≌△DCA(AAS),∴AE=CD.【点评】题目主要考查全等三角形的判定和性质,三角形内角和定理及外角的性质,熟练掌握全等三角形的判定和性质是解题关键.16.(2022秋•虹口区校级期中)如图,△ABC和△BDE都是等边三角形,且点A、D、E在同一直线上,证明AE=BE+CE.【分析】根据等边三角形的性质,得出∠ABC=∠DBE=60°,AB=CB,BD=BE=DE,再根据角之间的数量关系,得出∠ABD=∠CBE,再根据“边角边”,得出△ABD≌△CBE,再根据全等三角形的性质,得出AD=CE,再根据等量代换,即可得出结论.【解答】证明:∵△ABC和△BDE都是等边三角形,∴∠ABC=∠DBE=60°,AB=CB,BD=BE=DE,∴∠ABC=∠ABD+∠DBC,∠DBE=∠DBC+∠CBE,∴∠ABD=∠CBE,在△ABD和△CBE中,,∴△ABD≌△CBE(SAS),∴AD=CE,∴AE=DE+AD=BE+CE.【点评】本题考查了等边三角形的性质、全等三角形的判定与性质,解本题的关键在熟练掌握相关的性质定理.17.(2022秋•普陀区校级期中)如图,在△ABC中,AD平分∠BAC,E是BC的中点,过点E作FG⊥AD 交AD的延长线于H,交AB于F,交AC的延长线于G.求证:(1)AF=AG;(2)BF=CG.【分析】(1)由FG⊥AD交AD的延长线于H,∠AHF=∠AHG=90°,可根据全等三角形的判定定理“ASA”证明△AHF≌△AHG,得AF=AG;(2)作CL∥AB交FG于点L,则∠AFG=∠CLG,由AF=AG,得∠AFG=∠G,则∠CLG=∠G,得CL=CG,再证明△BEF≌△CEL,得BF=CL,所以BF=CG.【解答】证明:(1)∵AD平分∠BAC,∴∠FAH=∠GAH,∵FG⊥AD交AD的延长线于H,∴∠AHF=∠AHG=90°,在△AHF和△AHG中,,∴△AHF≌△AHG(ASA),∴AF=AG.(2)作CL∥AB交FG于点L,则∠B=∠ECL,∠AFG=∠CLG,∵AF=AG,∴∠AFG=∠G,∴∠CLG=∠G,∴CL=CG,∵E是BC的中点,∴BE=CE,在△BEF和△CEL中,,∴△BEF≌△CEL(ASA),∴BF=CL,∴BF=CG.【点评】此题重点考查全等三角形的判定与性质、等腰三角形的判定与性质、平行线的性质等知识,正确地作出所需要的辅助线构造全等三角形是解题的关键.18.(2022秋•浦东新区期中)如图,已知AB=AC,∠BEF=∠CFH,BE=CF,M是EH的中点.求证:∠EFM=∠HFM.【分析】证明△BEF≌△CFH(ASA),△EFM≌△HFM(SSS)即可求解.【解答】证明:∵AB=AC,∠BEF=∠CFH,BE=CF,∴∠B=∠C,在△BEF和△CFH中,,∴△BEF≌△CFH(ASA),∴EF=FH,∵M是EH的中点,∴EM=HM,FM为公共边,∴△EFM≌△HFM(SSS),∴∠EFM=∠HFM.【点评】本题主要考查全等三角形的判定和性质,掌握三角形全等的判定方法和性质是解题的关键.19.(2017秋•上海期中)如图,在△ABC中,AB=AC,点D、E、F分别在BC、AB、AC边上,且BE=CF,BD=CE.(1)求证:△DEF是等腰三角形;(2)当∠A=40°时,求∠DEF的度数.【分析】(1)首先根据条件证明△DBE≌△ECF,根据全等三角形的性质可得DE=FE,进而可得到△DEF是等腰三角形;(2)根据△BDE≌△CEF,可知∠FEC=∠BDE,∠DEF=180°﹣∠BED﹣∠FEC=180°﹣∠DEB﹣∠EDB=∠B即可得出结论,再根据等腰三角形的性质即可得出∠DEF的度数.【解答】(1)证明:∵AB=AC∴∠B=∠C,在△BDE与△CEF中,,∴△BDE≌△CEF(SAS).∴DE=EF,即△DEF是等腰三角形.(2)解:由(1)知△BDE≌△CEF,∴∠BDE=∠CEF∵∠CEF+∠DEF=∠BDE+∠B∴∠DEF=∠B∵AB=AC,∠A=40°∴∠DEF=∠B=70°.【点评】本题考查了全等三角形的判定与性质,等腰三角形的判定与性质,熟知等腰三角形的两个底角相等是解答此题的关键.20.(2022秋•静安区校级期中)已知:如图,AD∥CF,∠A=∠C=90°,DB平分∠ADF,AD+CF=DF.求证:FB平分∠CFD.【分析】在DF上取一点E,使DE=AD,进而利用SAS证明△ADB与△EDB全等,进而证明△FCB与△FEB 全等,进而解答即可.【解答】证明:在DF上取一点E,使DE=AD,∵DB平分∠ADF,∴∠ADB=∠EDB,在△ADB与△EDB中,,∴△ADB≌△EDB(SAS),∴AB=BE,∠BAD=∠BED,AD=DE,∴∠BAD=∠BED=90°,∵AD∥CF,∴∠C=∠A=90°,∵DF=AD+CF,∴EF=DF﹣DE=DF﹣AD=CF,在Rt△BEF与Rt△BCF中,,∴Rt△BEF≌Rt△BCF(HL),∴∠EFB=∠CFB,即FB平分∠CFD.【点评】本题考查了全等三角形的判定与性质,熟练掌握全等三角形的判定与性质是解题的关键.21.(2022秋•静安区校级期中)已知如图,AB=AC,AD=AE,∠BAE=∠CAD,BD与CE相交于点F,求证:FB=FC.【分析】由已知条件证得△ABD≌△ACE,连接BC,要证FB=FC,可利用等式性质来证得.【解答】证明:∵∠BAE=∠CAD(已知),∴∠BAE+∠EAD=∠CAD+∠DAE(等式性质),即∠BAD=∠CAE.在△ABD和△ACE中,,∴△ABD≌△ACE(SAS).∴∠ABD=∠ACE(全等三角形对应角相等),连接BC.∵AB=AC(已知),∴∠ABC=∠ACB(等边对等角).∵∠ABD=∠ACE(已证),∴∠ABC﹣∠ABD=∠ACB﹣∠ACE(等式性质),即∠FBC=∠FCB.∴FB=FC(等角对等边).【点评】本题主要考查了两个三角形的判定和性质,关键是根据SAS证得△ABD≌△ACE.22.(2022秋•闵行区校级期中)如图,已知点A、F、C、D在同一直线上,AB∥DE,AB=DE,AF=CD,求证:BC∥EF.【分析】证△ABC≌△DEF(SAS),得∠BCA=∠EFD,再由平行线的判定即可得出结论.【解答】证明:∵AB∥DE,∴∠A=∠D,∵AF=CD,∴AF+CF=CD+CF,即AC=DF,在△ABC与△DEF中,,∴△ABC≌△DEF(SAS),∴∠BCA=∠EFD,∴BC∥EF.【点评】考查了全等三角形的判定与性质、平行线的判定与性质等知识,熟练掌握平行线的判定与性质,证明三角形全等是解题的关键.23.(2022秋•杨浦区期中)如图,已知△ABC和△CDE都是等边三角形,点D、A、C在同一直线上,延长BA交边DE于点F,联结AE、BD.(1)试说明△ADB≌△F AE的理由;(2)延长EA交BD于点H,求∠DHE的度数.【分析】(1)证△ADF是等边三角形,得AD=FA=DF,∠DFA=60°,再证CD=BF,则AB=FE,然后证∠BAD=∠EFA,进而证△ADB≌△FAE(SAS);(2)由全等三角形的性质得∠ABD=∠FEA,再证∠DHE=∠FEA+∠FAE,即可得出结论.【解答】(1)证明:∵△ABC和△CDE都是等边三角形,∴AB=AC,∠DAF=∠BAC=60CDE=60°,CD=DE,∴△ADF是等边三角形,∴AD=FA=DF,∠DFA=60°,∴AC+AD=AB+FA,即CD=BF,∴BF﹣FA=DE﹣DF,即AB=FE,∵∠BAD=180°﹣∠DAF=180°﹣60°=120°,∠EFA=180°﹣∠DFA=180°﹣60°=120°,∴∠BAD=∠EFA,在△ADB和△FAE中,,∴△ADB≌△FAE(SAS);(2)解:由(1)得:△ADB≌△FAE,∴∠ABD=∠FEA,∵∠DHE=∠ABD+∠BAH,∠FAE=∠BAH,∴∠DHE=∠FEA+∠FAE,∵∠DFA=∠FEA+∠FAE,∴∠DHE=∠DFA=60°.【点评】本题考查了全等三角形的判定与性质、等边三角形的判定与性质等知识,熟练掌握等边三角形的判定与性质,证明三角形全等是解题的关键.24.(2022秋•闵行区期中)如图,点D,E在△ABC的边BC上,AD=AE,BD=CE,求证:∠B=∠C.【分析】方法一:利用全等三角形的性质证明即可.方法二:作AM⊥BC于M.证明AN垂直平分线段BC 即可;【解答】证明方法一:∵AD=AE,∴∠ADE=∠AED,∵∠ADE+∠ADB=∠AED+∠AEC=°,∴∠ADB=∠AEC,在△ABD和△ACE中,∴△ABD≌△ACE(SAS),∴∠B=∠C.证明方法二:作AM⊥BC于M.∵AD=AE,∴DM=EM,∵BD=CE,∴DM+BD=EM+CE,即:BM=CM,又∵AM⊥BC,即AM为BC的垂直平分线,∴AB=AC,∴∠B=∠C.【点评】本题考查全等三角形的判定和性质,等腰三角形的判定和性质,线段的垂直平分线的性质等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.25.(2022秋•普陀区期中)已知:如图,在四边形ABCD中,BC=DC,点E在边AB上,∠EBC=∠EDC.(1)求证:EB=ED.(2)当∠A=90°,求证:∠BED=2∠BDA.【分析】(1)由BC=DC,得出∠CBD=∠CDB,再由∠EBC=∠EDC,推出∠EBD=∠EDB,即可得出结论;(2)由三角形内角和定理得出∠BDA+∠ABD=90°=∠A,再由(1)得∠EBD=∠EDB,则∠BDA+∠EDB=∠A,然后由三角形的外角性质即可得出结论.【解答】证明:(1)∵BC=DC,∴∠CBD=∠CDB,∵∠EBC=∠EDC,∴∠EBC﹣∠CBD=∠EDC﹣∠CDB,即∠EBD=∠EDB,∴EB=ED;(2)∵∠A=90°,∴∠BDA+∠ABD=90°=∠A,由(1)得:∠EBD=∠EDB,∴∠BDA+∠ABD=∠BDA+∠EDB=∠A,∴∠BED=∠A+∠ADE=∠BDA+∠EDB+∠ADE=∠BDA+∠BDA=2∠BDA.【点评】本题考查了等腰三角形的判定与性质、三角形内角和定理、三角形外角的性质等知识,熟练掌握等腰三角形的判定与性质是解题的关键.26.(2021秋•奉贤区校级期中)在△ABC中,AB=AC,点D是直线BC上的一点(不与点B、C重合),以AD为腰右侧作等腰三角形△ADE,且AD=AE,∠BAC=∠DAE,连接CE.(1)如图1,当点D在线段BC上,如果∠BAC=90°,则∠BCE=度.(2)设∠BAC=α,∠BCE=β.①点D是在线段BC上移动时,如图2,则α、β之间有怎样的数量关系?试说明理由.②点D是在射线CB上移动时,则α、β之间有怎样的数量关系?试直接写出结论.【分析】(1)证明△BAD≌△CAE,得∠B=∠ACE,即可证明;(2)①与(1)同理证明△BAD≌△CAE,得∠ABD=∠ACE,则∠BAC+∠BCE=∠BAC+∠BCA+∠ACE=∠BAC+∠BCA+∠B=180°;②同理证明△ADB≌△AEC,得∠ABD=∠ACE,由∠ABD=∠BAC+∠ACB,则∠BAC=∠BCE.【解答】解:(1)∵∠BAC=∠DAE,∴∠BAD=∠CAE,在△BAD与△CAE中,,∴△BAD≌△CAE(SAS),∴∠B=∠ACE,∴∠BCE=∠ACB+∠ACE=90°,故答案为:90;(2)①α+β=180°,理由如下:∵∠BAC=∠DAE,∴∠BAD=∠CAE,在△BAD与△CAE中,,∴△BAD≌△CAE(SAS),∴∠ABD=∠ACE,∵∠BAC+∠ABD+∠BCA=180°,∴∠BAC+∠BCE=∠BAC+∠BCA+∠ACE=∠BAC+∠BCA+∠B=180°,∴α+β=180°;②α=β,理由如下:∵∠DAE=∠BAC,∴∠DAB=∠EAC,在△ADB与△AEC中,,∴△ADB≌△AEC(SAS),∴∠ABD=∠ACE,∵∠ABD=∠BAC+∠ACB,∴∠BAC=∠BCE,∴α=β.【点评】本题主要考查了等腰三角形的性质,全等三角形的判定与性质,三角形外角的性质等知识,证明△ADB≌△AEC是解题的关键.27.(2021秋•浦东新区期中)如图,在△ABC中,AD平分∠BAC,DE∥AC,过点E作EF⊥AD于点O,交BC的延长线于F,连接AF,求证:AF=DF.【分析】根据平行线的性质和等腰三角形的判定和性质解答即可.【解答】证明:∵DE∥AC,∴∠EDA=∠DAC,∵AD平分∠BAC,∴∠EAD=∠DAC,∴∠EAD=∠EDA,∴AE=DE,∵EF⊥AD,∴EF垂直且平分AD,∴F在AD的垂直平分线上,∴AF=DF.【点评】此题考查等腰三角形的判定和性质,关键是根据平行线的性质和等腰三角形的判定和性质解答.28.(2020秋•浦东新区期中)如图,已知在△ABC中,AB=AC,D是AB上一点,延长AC至点E,使CE =BD.联结DE交BC于点F,求证:DF=EF.【分析】过点D作DG∥AC交BC于点G,由“AAS”可证△DFG≌△ECF,可得DF=EF.【解答】证明:如图,过点D作DG∥AC交BC于点G,∵AB=AC,∵DG∥AC,∴∠ACB=∠DGB,∠DGF=∠ECF,∴∠ACB=∠DGB=∠B,∴DG=DB,∵CE=BD,∴DG=CE,在△DFG和△EFC中,,∴△DFG≌△EFC(AAS)∴DF=EF.【点评】本题考查了全等三角形的判定和性质、等腰三角形的判定与性质等知识,添加恰当辅助线构造全等三角形是解题的关键.29.(2022秋•奉贤区校级期中)如图,点A、B、C、D在同一直线上,BE∥DF,∠A=∠F,AB=FD.求证:AE=FC.【分析】根据BE∥DF,可得∠ABE=∠D,再利用ASA求证△ABC和△FDC全等即可.【解答】证明:∵BE∥DF,在△ABE和△FDC中,,∴△ABE≌△FDC(ASA),∴AE=FC.【点评】此题主要考查全等三角形的判定与性质和平行线的性质等知识点的理解和掌握,此题的关键是利用平行线的性质求证△ABC和△FDC全等.30.(2020秋•普陀区期中)如图,已知AB=AC,BD=CD,过点D作DE⊥AB交AB的延长线于点E、DF ⊥AC交AC的延长线于点F,垂足分别为点E、F.(1)求证:∠DBE=∠DCF.(2)求证:BE=CF.【分析】(1)连接AD,证△ABD≌△ACD(SSS),得∠ABD=∠ACD,即可得出结论;(2)证△BDE≌△CDF(AAS),即可得出结论.【解答】证明:(1)连接AD,如图:在△ABD和△ACD中,,∴△ABD≌△ACD(SSS),∴∠ABD=∠ACD,∴∠DBE=∠DCF.(2)∵DE⊥AB,DF⊥AC,∴∠E=∠F=90°,由(1)得:∠DBE=∠DCF,在△BDE和△CDF中,,∴△BDE≌△CDF(AAS),∴BE=CF.【点评】本题考查了全等三角形的判定和性质等知识;熟练掌握全等三角形的判定与性质是解题的关键.31.(2017秋•静安区期中)如图,在△ABC中,D为AB的中点,F为BC上一点,DF∥AC,延长FD至E,且DE=DF,联结AE、AF.(1)求证:∠E=∠C;(2)如果DF平分∠AFB,求证:AC⊥AB.【分析】(1)根据SAS证明△AED与△BFD全等,再利用等量代换证明即可;(2)根据角平分线的定义和等腰三角形的性质进行证明即可.【解答】证明:(1)∵D为AB的中点,∴BD=AD,在△AED与△BFD中,,∴△AED≌△BFD(SAS),∴∠E=∠DFB,∵DF∥AC,∴∠C=∠DFB,∴∠C=∠E;(2)∵DF平分∠AFB,∴∠AFD=∠DFB,∵∠E=∠DFB,∴∠AFD=∠AED,∵ED=DF,∴∠DAF+∠AFD=90°,∵EF∥AC,∴∠AFD=∠FAC,∴∠DAF+∠FAC=90°,∴AC⊥AB.【点评】本题考查了全等三角形的判定与性质,关键是根据平行线的性质、全等三角形的判定与性质等知识进行解答.32.(2021秋•浦东新区期中)如图1,在△ABC中,∠A=120°,∠C=20°,BD平分∠ABC,交AC于点D.(1)求证:BD=CD.(2)如图2,若∠BAC的角平分线AE交BC于点E,求证:AB+BE=AC.(3)如图3,若∠BAC的外角平分线AE交CB的延长线于点E,则(2)中的结论是否成立?若成立,给出证明,若不成立,写出正确的结论.【分析】(1)根据∠A=120°,∠C=20°,可得∠ABC的度数,再根据BD平分∠ABC,可得∠DBC=∠C=20°,进而可得结论;(2)如图2,过点E作EF∥BD交AC于点F,证明△ABE≌△AFE,可得BE=EF=FC,进而可得AB+BE=AC;(3)如图3,过点A作AF∥BD交BE于点F,结合(1)和AE是∠BAC的外角平分线,可得FE=AF=AC,进而可得结论BE﹣AB=AC.【解答】(1)证明:∵∠A=120°,∠C=20°,∴∠ABC=180°﹣120°﹣20°=40°,∵BD平分∠ABC,∴∠ABD=∠DBC=ABC=20°,∴∠DBC=∠C=20°,∴BD=CD;(2)证明:如图2,过点E作EF∥BD交AC于点F,∴∠FEC=∠DBC=20°,∴∠FEC=∠C=20°,∴∠AFE=40°,FE=FC,∴∠AFE=∠ABC,∵AE是∠BAC的平分线,∴∠BAE=∠FAE,在△ABE和△AFE中,,∴△ABE≌△AFE(AAS),∴BE=EF,∴BE=EF=FC,∴AB+BE=AF+FC=AC;(3)(2)中的结论不成立,正确的结论是BE﹣AB=AC.理由如下:如图3,过点A作AF∥BD交BE于点F,∴∠AFC=∠DBC=20°,∴∠AFC=∠C=20°,∴AF=AC,∵AE是∠BAC的外角平分线,∴∠EAB=(180°﹣∠ABC)=30°,∵∠ABC=40°,∴∠E=∠ABC﹣∠EAB=10°,∴∠E=∠FAE=10°,∴FE=AF,∴FE=AF=AC,∴BE﹣AB=BE﹣BF=EF=AC.【点评】本题考查了全等三角形的判定与性质,解决本题的关键是掌握全等三角形的判定与性质.33.(2022秋•奉贤区校级期中)(1)已知:如图①,△ABC是等边三角形,AD、CE分别平分∠BAC、∠ACB,AD、CE相交于点F,猜想:线段EF、DF之间有怎样的数量关系?并证明你的猜想.(2)已知:如图②,在△ABC中,∠B=60°,AD、CE分别平分∠BAC、∠ACB,AD、CE相交于点F,猜想:上述(1【分析】(1)证明△EAC≌△DCA(ASA),可得EC=DA,然后根据线段的和差即可得结论;(2)在CA上截取CG=CD,证明△CDF≌△CGF(SAS),可得DF=GF,∠DFC=∠GFC,再证明△AEF≌△AGF(ASA),可得EF=GF,进而可得结论.【解答】解:(1)EF=DF,证明:∵△ABC是等边三角形,∴∠BAC=∠BCA=60°,∵AD、CE分别平分∠BAC、∠ACB,∴∠FAC=BAC,∠FCA=BCA,∴∠FAC=∠FCA,∴FA=FC,在△EAC和△DCA中,,∴△EAC≌△DCA(ASA),∴EC=DA,∵FA=FC,∴EF=DF;(2)EF=DF仍成立,理由如下:如图,在CA上截取CG=CD,在△CDF和△CGF中,,∴△CDF≌△CGF(SAS),∴DF=GF,∠DFC=∠GFC,∵∠DFC=∠FAC+∠FCA=BAC+BCA=60°,∴∠GFC=60°,∠AFE=60°,∴∠AFC=180°﹣(∠FAC+∠FCA)=180°﹣(BAC+BCA)=180°﹣60°=120°,∴∠AFG=120°﹣60°=60°,∴∠AFE=∠AFG,在△AEF和△AGF中,,∴△AEF≌△AGF(ASA),∴EF=GF,∴EF=DF.【点评】本题考查了角平分线的性质,全等三角形的判定与性质,三角形的内角和定理,遇到角平分线,作角平分线上的点到两边的距离构造出全等三角形是解题的关键.34.(2021秋•台江区期中)如图,在△ABE中,AB=AE,AD=AC,∠BAD=∠EAC,BC、DE交于点O.求证:(1)△ABC≌△AED;(2)OB=OE.【分析】(1)利用SAS ABC≌△AED;(2)根据全等三角形的性质得到∠ABC=∠AED,根据等腰三角形的性质得到∠ABE=∠AEB,得到∠OBE=∠OEB,根据等腰三角形的判定定理证明.【解答】证明:(1)∵∠BAD=∠EAC,∴∠BAD+∠DAC=∠EAC+∠DAC,即∠BAC=∠EAD,在△BAC和△EAD中,,∴△BAC和≌EAD;(2)∵△BAC≌△EAD,∴∠ABC=∠AED,∵AB=AE,∴∠ABE=∠AEB,∴∠OBE=∠OEB,∴OB=OE.【点评】本题考查的是全等三角形的判定和性质、等腰三角形的性质,掌握全等三角形的判定定理和性质定理是解题的关键.35.(2022秋•宝山区校级期中)如图,已知在△ABC中,AB=AC,点D、E分别在边AB、AC上,且AD =AE.(1)求证:DE∥BC;(2)如果F是BC延长线上一点,且∠EBC=∠EFC,求证:DE=CF.【分析】(1)根据等腰三角形的性质和三角形内角和证明即可;(2)根据AAS证明△BDE与△EFC全等即可.【解答】证明:(1)∵AB=AC,∴∠ABC=∠ACB,∵AD=AE,∴∠ADE=∠AED,∵∠A=∠A,∴∠ADE=∠ABC,∴DE∥BC;(2)∵∠EBC=∠EFC,∠ABC=∠ACB,∴∠DBE+∠EBC=∠CEF+∠EFC,∴∠DBE=∠CEF,∠DEB=∠EFC,在△BDE与△EFC中,,∴△BDE≌△EFC(AAS),∴DE=CF.【点评】本题考查了等腰三角形的性质的运用,平行线的性质的运用,全等三角形的判定语言性质的运用,解答时证明三角形全等是关键.36.(2022秋•浦东新区期中)已知:如图,AB=DC,AC=BD.求证:∠B=∠C.【分析】连接AD,利用SSS判定△ABD≌△DCA,根据全等三角形的对应角相等即证.【解答】解:如图,连接AD,在△ABD和△DCA中,,∴△ABD≌△DCA(SSS),∴∠B=∠C.【点评】本题考查三角形全等的判定方法和三角形全等的性质,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.37.(2022秋•徐汇区校级期中)已知:如图,在△ABC中,∠ACB=90°,AD为△ABC的外角平分线,交BC的延长线于点D,且∠B=2∠D.求证:AB+AC=CD.【分析】过点D作DE⊥AB,垂足为点E,由“在角的平分线上的点到这个角的两边的距离相等”可知DE=DC,再证明Rt△ACD≌Rt△AED,由此可得AC=AE,在证明BE=DE即可.【解答】证明:过点D作DE⊥AB,垂足为点E,又∵∠ACB=90°(已知),∴DE=DC(在角的平分线上的点到这个角的两边的距离相等).在Rt△ACD和Rt△AED中∴Rt△ACD≌Rt△AED(H.L).∴AC=AE,∠CDA=∠EDA.∵∠B=2∠D(已知),∴∠B=∠BDE.∴BE=DE.又∵AB+AE=BE,∴AB+AC=CD.【点评】本题考查了全等三角形的判定与性质,关键是作辅助线使得AB与AC在同一条直线上才好证AB+AC =CD.38.(2021秋•徐汇区校级期中)如图,AB⊥BC,DC⊥BC,垂足分别是点B、C,点E是线段BC上一点,且AE⊥DE,AE=ED,如果BE=3,AB+BC=11,求AB的长.【分析】求出∠A=∠DEC,∠B=∠C=90°,根据AAS证△ABE≌△ECD,推出AB=CE,求出AB+BC=2AB+BE =11,把BE=3代入求出AB即可.【解答】解:∵AB⊥BC,DC⊥BC,垂足分别是点B、C,∴∠B=∠C=90°.∴∠A+∠AEB=90°,∵AE⊥DE,∴∠AED=90°,∵∠AEB+∠AED+∠DEC=180°,∴∠AEB+∠DEC=90°,∴∠A=∠DEC,∵在△ABE和△ECD中,,∴△ABE≌△ECD(AAS),∴AB=CE,∵BC=BE+CE=BE+AB,∴AB+BC=2AB+BE=11,∵BE=3,∴AB=4.【点评】本题考查了全等三角形的性质和判定,三角形的内角和定理,注意:全等三角形的对应边相等,全等三角形的判定定理有SAS,ASA,AAS,SSS.39.(2022秋•奉贤区校级期中)△ABC为等边三角形,D为AB边上的任意一点.连接CD.(1)在BD的左侧,以BD为一边作等边三角形BDE(尺规作图,保留作图痕迹,不写作法);(2)连接AE,试说明:CD=AE.【分析】(1)可以分别以B、D为圆心,以BD为半径作弧,相交于E;(2)由已知条件,证明△BCD≌△EAB即可.【解答】(1)解:如图:(2)证明:连接AE,如图,∵在△BCD与△BAE中,,∴△BCD≌△BAE(SAS)∴CD=AE.【点评】此题主要考查等边三角形的作法以及性质的运用,还涉及到全等三角形的判定,综合性强.求得三角形全等是正确解答本题的关键.40.(2022秋•静安区校级期中)如图①,点M为锐角三角形ABC内任意一点,连接AM、BM、CM.以AB 为一边向外作等边三角形△ABE,将BM绕点B逆时针旋转60°得到BN,连接EN.(1)求证:△AMB≌△ENB;。
初中数学-几何证明经典试题(含答案)
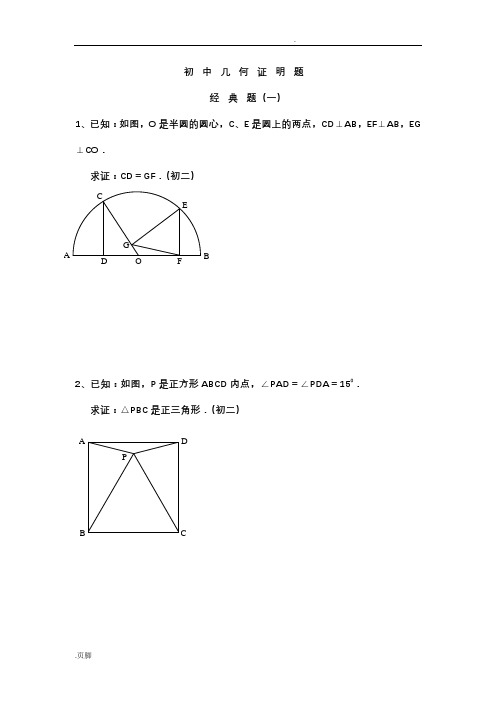
初中几何证明题经典题(一)1、已知:如图,O 是半圆的圆心,C 、E 是圆上的两点,CD ⊥AB ,EF ⊥AB ,EG ⊥CO .求证:CD =GF .(初二)2、已知:如图,P 是正方形ABCD 内点,∠PAD =∠PDA =150.求证:△PBC 是正三角形.(初二)AP C DB A F GC EB O D3、如图,已知四边形ABCD 、A 1B 1C 1D 1都是正方形,A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点.求证:四边形A 2B 2C 2D 2是正方形.(初二)D 2C 2 B 2 A 2D 1 C 1 B 1 C BD A A 14、已知:如图,在四边形ABCD中,AD=BC,M、N分别是AB、CD的中点,AD、BC的延长线交MN于E、F.求证:∠DEN=∠F.经典题(二)1、已知:△ABC中,H为垂心(各边高线的交点),O为外心,且OM⊥BC于M.(1)求证:AH=2OM;(2)若∠BAC=600,求证:AH=AO.(初二)2、设MN是圆O外一直线,过O作OA⊥MN于A,自A引圆的两条直线,交圆于B、C及D、E,直线EB及CD分别交MN于P、Q.F3、如果上题把直线MN 由圆外平移至圆内,则由此可得以下命题:设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE ,设CD 、EB 分别交MN 于P 、Q .(初二)4、如图,分别以△ABC 的AC 和BC 为一边,在△ABC 的外侧作正方形ACDE 和正方形CBFG ,点P 是EF 的中点.求证:点P 到边AB 的距离等于AB 的一半.(初二)经典题(三)1、如图,四边形ABCD为正方形,DE∥AC,AE=AC,AE与CD相交于F.2、如图,四边形ABCD 为正方形,DE ∥AC ,且CE =CA ,直线EC 交DA 延长线于F .求证:AE =AF .(初二)3、设P 是正方形ABCD 一边BC 上的任一点,PF⊥AP ,CF 平分∠DCE . 求证:PA =PF .(初二)D4、如图,PC切圆O于C,AC为圆的直径,PEF为圆的割线,AE、AF与直线PO相交于B、D.求证:AB=DC,BC=AD.(初三)经典题(四)1、已知:△ABC是正三角形,P是三角形内一点,PA=3,PB=4,PC=5.求:∠APB的度数.(初二)2、设P是平行四边形ABCD内部的一点,且∠PBA=∠PDA.求证:∠PAB=∠PCB.(初二)3、设ABCD为圆内接凸四边形,求证:AB·CD+AD·BC=AC·BD.(初三)4、平行四边形ABCD中,设E、F分别是BC、AB上的一点,AE与CF相交于P,且AE=CF.求证:∠DPA=∠DPC.(初二)经典难题(五)1、 设P 是边长为1的正△ABC 内任一点,L =PA +PB +PC , 求证:≤L <2.1的正方形ABCD 内的一点,求PA +PB +PC 的最小值.、P 为正方形ABCD 内的一点,并且PA =a ,PB =2a ,PC =3a ,求正方形的边长.APCBACBP D A CBPD4中,∠ABC=∠ACB=800,D、E分别是AB、AC上的点,∠=200,求∠BED的度数.参考答案经典题(一)1.如下图做GH⊥AB,连接EO。
人教版初二数学8年级下册 第18章(平行四边形)证明题专题训练(含答案)

人教版八年级下册数学第十八章平行四边形证明题专题训练1.如图,在平行四边形ABCD中,E、F是对角线AC所在直线上的两点,且AE=CF.求证:四边形EBFD 是平行四边形.2.如图,在△ABC中,点D,E分别是BC,AC的中点,延长BA至点F,使得AF= 1AB,连接DE,AD,EF,DF.2(1)求证:四边形ADEF是平行四边形;(2)若AB=6,AC=8,BC=10,求EF的长.的对角线AC的垂直平分线与边AD,BC分别相交于点E,3.如图所示,ABCDF.求证:四边形AFCE是菱形.AC BD交于点,O过点O任作直线分别交4.如图,在平行四边形ABCD中,对角线,AB CD于点E F,、.求证:OE OF =.5.已知:如图,在ABCD 中,,E F 是对角线BD 上两个点,且BE DF =.求证:.AE CF =6.已知:如图,矩形ABCD 中,O 是AC 与BD 的交点,过O 点的直线EF 与AB 、CD 的延长线分别相交于点E 、F .(1)求证:△BOE ≌△DOF ;(2)当EF 与AC 满足什么关系时,以A 、E 、C 、F 为顶点的四边形是菱形?并给出证明.7.如图,菱形ABCD 的对角线AC 、BD 相交于点O ,//BE AC ,//AE BD ,OE 与AB 交于点F .(1)求证:四边形AEBO 的为矩形;(2)若OE =10,AC =16,求菱形ABCD 的面积.8.已知:如图,在ABC 中,中线,BE CD 交于点,,O F G 分别是,OB OC 的中点.求证:(1)//DE FG ;(2)DG 和EF 互相平分.9.如图,在平行四边形ABCD 中,AC 是对角线,且AB =AC ,CF 是∠ACB 的角平分线交AB 于点F ,在AD 上取一点E ,使AB =AE ,连接BE 交CF 于点P .(1)求证:BP =CP ;(2)若BC =4,∠ABC =45°,求平行四边形ABCD 的面积.10.如图,AB,CD相交于点O,AC∥DB,OA=OB,E、F分别是OC,OD中点.(1)求证:OD=OC.(2) 求证:四边形AFBE平行四边形.11.如图所示,在菱形ABCD中,E、F分别为AB、AD上两点,AE=AF.(1)求证:CE=CF;(2)若∠ECF=60°,∠B=80°,试问BC=CE吗?请说明理由.12.已知:如图,在矩形ABCD中,M、N分别是边AD、BC的中点,E、F分别是线段BM、CM的中点.(1)求证:△ABM≌△DCM;(2)当AB:AD的值为多少时,四边形MENF是正方形?请说明理由.13.如图,在矩形ABCD中,过对角线AC的中点O作AC的垂线,分别交射线AD 和CB于点E,F连接AF,CE.(1)求证:OE=OF;(2)求证:四边形AFCE是菱形.14.如图,BD是△ABC的角平分线,过点作DE//BC交AB于点E,DF//AB交BC 于点F.(1)求证:四边形BEDF是菱形;(2)若∠ABC=60°,∠ACB=45°,CD=6,求菱形BEDF的边长.15.如图,在边长为6的正方形ABCD中,E是边CD的中点,将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG.(1)求证:△ABG≌△AFG;(2)求∠EAG的度数;(3)求BG的长.16.如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D在AB边上一点.过点D作DE⊥BC,交直线MN于E,垂足为F,连接CD、BE.(1)求证:CE=AD;(2)当点D在AB中点时,四边形BECD是什么特殊四边形?说明你的理由.17.如图,在△ABC中,AB=AC,点D为边BC上一点,以AB,BD为邻边作▱ABDE,连接AD、EC.(1)求证:△ADC≌△ECD; (2)若BD=CD,求证:四边形ADCE是矩形.18.如图,在四边形ABCD中,AB=CD,BF=DE,AE⊥BD,CF⊥BD,垂足分别为E、F.(1)求证:△ABE≌△CDF;(2)若AC与BD交于点O,求证:AO=CO.19.在平行四边形ABCD中,点E在AD边上,连接BE、CE,EB平分∠AEC,(1)如图1,判断△BCE的形状,并说明理由;(2)如图2,若∠A=90°,BC=5,AE=1,求线段BE的长.20.如图,在四边形ABCD中,AB=AD,CB=CD,E是CD上一点,BE交AC于点F,连接DF.(1)求证:∠BAC=∠DAC,∠AFD=∠CFE;(2)若AB∥CD,试证明四边形ABCD是菱形;(3)在(2)的条件下,试确定E点的位置,使∠EFD=∠BCD,并说明理由.参考答案:1.解:证明:如图,连接BD交AC于点O,∵四边形ABCD是平行四边形,∴OA=OC,OB=OD,又∵AE=CF,∴OA-AE=OC-CF,即OE=OF,∴四边形EBFD是平行四边形.2.(1)证明:∵点D,E分别是BC,AC的中点,∴DE是△ABC的中位线,∴DE∥AB,DE=12 AB,∵AF=12 AB,∴DE=AF,DE∥AF,∴四边形ADEF是平行四边形;(2)解:由(1)得:四边形ADEF是平行四边形,∴EF=AD,∵AB=6,AC=8,BC=10,∴AB2+AC2=BC2,∴△ABC是直角三角形,∠BAC=90°,∵点D是BC的中点,∴AD=12BC=5,∴EF=AD=5.3.证明:∵四边形ABCD 是平行四边形∴//AE FC ,AO CO =,∴EAC FCA ∠=∠,∵EF 是AC 的垂直平分线,∴EF AC ⊥,在AOE △与COF 中,EAO FCO AO COAOE COF ∠=∠⎧⎪=⎨⎪∠=∠⎩∴()ASA AOE COF ≌△△,∴EO FO =,∴四边形AFCE 为平行四边形,又∵EF AC ⊥,∴四边形AFCE 为菱形.4.解:证明:∵四边形ABCD 是平行四边形,∴AD ∥BC ,OA =OC ,∴∠EAO =∠FCO ,在△AEO 和△CFO 中,OAE OCF OA OCAOE COF ∠=∠⎧⎪=⎨⎪∠=∠⎩,∴△AEO ≌△CFO (ASA ),∴OE =OF .5.证明:∵四边形ABCD 是平行四边形,∴AB =CD ,AB ∥CD .∴∠ABE =∠CDF .在△ABE 和△CDF 中AB CD ABE CDF BE DF =⎧⎪∠=∠⎨⎪=⎩∴△ABE ≌△CDF (SAS )∴AE =CF .6.(1)证明:∵四边形ABCD 是矩形,∴OB =OD ,∵AE //CF ,∴∠E =∠F ,∠OBE =∠ODF ,在△BOE 与△DOF 中,E F OBE ODF OB OD ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△BOE ≌△DOF (AAS );(2)当EF ⊥AC 时,四边形AECF 是菱形. 证明:∵△BOE ≌△DOF ,∴OE =OF ,∵四边形ABCD 是矩形,∴OA =OC ,∴四边形AECF 是平行四边形,∵EF ⊥AC ,∴四边形AECF 是菱形.7.解:(1)证明:∵//BE AC ,//AE BD ,∴四边形AEBO 为平行四边形,又∵四边形ABCD 为菱形,∴BD AC ⊥,∴90AOB ∠=︒,∴平行四边形AEBO 为矩形;(2)∵四边形AEBO 为矩形,∴AB =OE =10,又∵四边形ABCD 为菱形,∴AO =12AC =8,∴90AOB ∠=︒,∴6BO ==,∴BD =2BO =12,∴菱形ABCD 的面积=12121696⨯⨯=.8.(1)在△ABC 中,∵BE 、CD 为中线∴AD =BD ,AE =CE ,∴DE ∥BC 且DE =12BC .在△OBC 中,∵OF =FB ,OG =GC ,∴FG ∥BC 且FG =12BC .∴DE ∥FG(2)由(1)知:DE ∥FG ,DE =FG .∴四边形DFGE 为平行四边形.∴DG 和EF 互相平分9.解:(1)设AP 与BC 交于H ,∵在平行四边形ABCD 中,AD ∥BC ,∴∠AEB=∠CBE,∵AB=AE,∴∠ABE=∠AEB,∴∠ABE=∠CBE,∴BE平分∠ABC,∵CF是∠ACB的角平分线,BE交CF于点P,∴AP平分∠BAC,∵AB=AC,∴AH垂直平分BC,∴PB=PC;(2)∵AH垂直平分BC,∴AH⊥BC,BH=CH=12BC=2,∵∠ABH=45°,∴AH=BH=2,∴平行四边形ABCD的面积=4×2=8.10.证明:(1)∵AC∥DB,∴∠CAO=∠DBO,∵∠AOC=∠BOD,OA=OB,∴△AOC≌△BOD,∴OC=OD;(2)∵E是OC中点,F是OD中点,∴OE=12OC,OF=12OD,∵OC=OD,∴OE=OF,又∵OA=OB,∴四边形AFBE是平行四边形.11.(1)证明:∵ABCD是菱形,∴AB =AD ,BC =CD ,∠B =∠D ,∵AE =AF ,∴AB ﹣AE =AD ﹣AF ,∴BE =DF ,在△BCE 与△DCF 中,∵BE DF B D BC CD =⎧⎪∠=∠⎨⎪=⎩,∴△BCE ≌△DCF ,∴CE =CF ;(2)结论是:BC =CE .理由如下:∵ABCD 是菱形,∠B =80°,∴∠A =100°,∵AE =AF ,∴180100402AEF AFE ︒-︒∠=∠==︒由(1)知CE =CF ,∠ECF =60°,∴△CEF 是等边三角形,∴∠CEF =60°,∴∠CEB =180°﹣60°﹣40°=80°,∴∠B =∠CEB ,∴BC =CE .12.(1)证明:∵四边形ABCD 是矩形,∴AB =DC ,∠A =∠D =90°,∵M 为AD 中点,∴AM =DM ,在△ABM 和△DCM ,AM DM A D AB CD =⎧⎪∠=∠⎨⎪=⎩,∴△ABM ≌△DCM (SAS );(2)解:当AB :AD =1:2时,四边形MENF 是正方形,理由:当四边形MENF 是正方形时,则∠EMF =90°,∵△ABM ≌△DCM ,∴∠AMB =∠DMC =45°,∴△ABM 、△DCM 为等腰直角三角形,∴AM =DM =AB ,∴AD =2AB ,即当AB :AD =1:2时,四边形MENF 是正方形.13.解:(1)∵四边形ABCD 是矩形,∴//AD BC ,∴∠EAO =∠FCO ,∵AC 的中点是O ,∴OA =OC ,在EOA △和FOC 中,AOE COF AO COEAO FCO ∠=∠⎧⎪=⎨⎪∠=∠⎩,()EOA FOC ASA ∴ ≌,∴OE =OF ;(2)∵OE =OF ,AO =CO ,∴四边形AFCE 是平行四边形,∵EF ⊥AC ,∴四边形AFCE 是菱形.14.证明:(1)∵DE ∥BC ,DF ∥AB ,∴四边形DEBF 是平行四边形,∵DE ∥BC ,∴∠EDB =∠DBF ,∵BD平分∠ABC,∠ABC,∴∠ABD=∠DBF=12∴∠ABD=∠EDB,∴DE=BE,又∵四边形BEDF为平行四边形,∴四边形BEDF是菱形;(2)如图,过点D作DH⊥BC于H,∵DF∥AB,∴∠ABC=∠DFC=60°,∵DH⊥BC,∴∠FDH=30°,DF,DH,∴FH=12∵∠C=45°,DH⊥BC,∴∠C=∠HDC=45°,∴DC DH=6,∴DF=,∴菱形BEDF的边长为15.(1)证明;在正方形ABCD中,AD=AB=BC=CD,∠D=∠B=∠BCD=90°,∵将△ADE沿AE对折至△AFE,∴AD=AF,DE=EF,∠D=∠AFE=90°,∴AB=AF,∠B=∠AFG=90°,又∵AG=AG,在Rt △ABG 和Rt △AFG 中,AG=AG AB=AF ⎧⎨⎩,∴△ABG ≌△AFG (HL );(2)∵△ABG ≌△AFG ,∴∠BAG =∠FAG ,∴∠FAG =12∠BAF ,由折叠的性质可得:∠EAF =∠DAE ,∴∠EAF =12∠DAF ,∴∠EAG =∠EAF +∠FAG =12(∠DAF +∠BAF )=12∠DAB =12×90°=45°;(3)∵E 是CD 的中点,∴DE =CE =12CD =12×6=3,设BG =x ,则CG =6﹣x ,GE =EF +FG =x +3,∵GE 2=CG 2+CE 2∴(x +3)2=(6﹣x )2+32,解得:x =2,∴BG =2.16.(1)证明:∵DE ⊥BC ,∴∠DFB =90°,∵∠ACB =90°,∴∠ACB =∠DFB ,∴AC ∥DE ,∵MN ∥AB ,即CE ∥AD ,∴四边形ADEC 是平行四边形,∴CE =AD ;(2)解:四边形BECD 是菱形,理由是:∵D 为AB 中点,∴AD =BD ,∵CE =AD ,∴BD =CE ,∵BD ∥CE ,∴四边形BECD 是平行四边形,∵∠ACB =90°,D 为AB 中点,∴CD =BD ,∴四边形BECD 是菱形.17.(证明:(1)∵四边形ABDE 是平行四边形(已知),∴AB ∥DE ,AB =DE (平行四边形的对边平行且相等);∴∠B =∠EDC (两直线平行,同位角相等);又∵AB =AC (已知),∴AC =DE (等量代换),∠B =∠ACB (等边对等角),∴∠EDC =∠ACD (等量代换);∵在△ADC 和△ECD 中,AC ED ACD EDC DC CD =⎧⎪∠=∠⎨⎪=⎩,∴△ADC ≌△ECD (SAS );(2)∵四边形ABDE 是平行四边形(已知),∴BD ∥AE ,BD =AE (平行四边形的对边平行且相等),∴AE ∥CD ;又∵BD =CD ,∴AE =CD (等量代换),∴四边形ADCE 是平行四边形(对边平行且相等的四边形是平行四边形);在△ABC 中,AB =AC ,BD =CD ,∴AD ⊥BC (等腰三角形的“三合一”性质),∴∠ADC =90°,∴▱ADCE 是矩形.18.证明:(1)∵BF=DE ,∴BF EF DE EF -=-,即BE=DF ,∵AE ⊥BD ,CF ⊥BD ,∴∠AEB=∠CFD=90°,在Rt △ABE 与Rt △CDF 中,AB CD BE DF =⎧⎨=⎩,∴Rt ABE Rt CDF ∆∆≌(HL );(2)如图,连接AC 交BD 于O ,∵Rt ABE Rt CDF ∆∆≌,∴ABE CDF ∠=∠,∴//D AB C ,∵=D AB C ,∴四边形ABCD 是平行四边形,∴AO CO =.19.证明:∵四边形ABCD 是平行四边形,∴BC ∥AD ,∴∠CBE=∠AEB ,∵EB 平分∠AEC ,∴∠CBE=∠BEC ,∴CB=CE ,∴△CBE 是等腰三角形;(2)如图2中,∵四边形ABCD 是平行四边形,∠A=90°,∴四边形ABCD 是矩形,∴∠A=∠D=90°,BC=AD=5,在Rt △ECD 中,∵∠D=90°,ED=AD-AE=4,EC=BC=5,3AB CD ∴====,在Rt AEB 中,∵∠A=90°,AB=3.AE=1,BE ∴===20.(1)证明:在△ABC 和△ADC 中,AB AD CB CD AC AC =⎧⎪=⎨⎪=⎩∴△ABC ≌△ADC(SSS),∴∠BAC=∠DAC ,在△ABF 和△ADF 中,AB AD BAF DAF AF AF =⎧⎪∠=∠⎨⎪=⎩∴△ABF ≌△ADF(SAS),∴∠AFB=∠AFD ,∵∠CFE=∠AFB ,∴∠AFD=∠CFE ,∴∠BAC=∠DAC ,∠AFD=∠CFE ;(2)证明:∵AB ∥CD ,∴∠BAC=∠ACD ,∵∠BAC=∠DAC ,∴∠DAC=∠ACD,∴AD=CD,∵AB=AD,CB=CD,∴AB=CB=CD=AD,∴四边形ABCD是菱形;(3)BE⊥CD时,∠BCD=∠EFD;理由如下:∵四边形ABCD是菱形,∴BC=CD,∠BCF=∠DCF,∵CF=CF,∴△BCF≌△DCF,∴∠CBF=∠CDF,∵BE⊥CD,∴∠BEC=∠DEF=90°,∴∠BCD=∠EFD.。
八年级全等三角形简单证明题及解答(5道)

汇报人:XX
目 录
• 题目一:基本的全等三角形证明 • 题目二:利用角平分线性质证明 • 题目三:通过边边边条件证明 • 题目四:结合中线性质进行证明 • 题目五:综合应用多种性质证明 • 总结与拓展
01
题目一:基本的全等三角形证明
题目描述
• 已知三角形$ABC$和三角形$DEF$,其中$AB = DE$,$AC = DF$,$\angle BAC = \angle EDF$。求证:$\triangle ABC \cong \triangle DEF$。
由第二步可知,△BDE∽△CFD。
详细解答
4. 第四步,根据相似三角形的性质,对应边成比例,所以BD/CF=DE/DF。
5. 第五步,因为BD=AD(已知),所以AD/CF=DE/DF。又因为AE/EC=DE/EF(已知), 所以AD/CF=AE/EC。
6. 第六步,交叉相乘得AD*EC=AE*CF,即AE/AD=EC/CF。又因为∠A=∠ACF(对顶角相 等),所以△ADE∽△ACF。
第三步,根据相似三 角形的性质,有 AB/AC = BD/DC。
综上,我们证明了 AB/AC = BD/DC。
03
题目三:通过边边边条件证明
题目描述
已知
△ABC和△DEF中,AB = DE,BC = EF,AC = DF。
求证
△ABC ≌ △DEF。
题目描述
【分析】
本题主要考察全等三角形的判定方法——边边边条件。根据已知条件,我们可以 直接应用边边边定理来证明两个三角形全等。
题目描述
01
【解答】
02
证明
03
04
∵ 在△ABC和△DEF中,AB = DE,BC = EF,AC = DF(已
八年级数学证明题

A B F CD E A B E C F D A BF O CD E 平行四边形 1. 已知:如图,AB=CD ,BC=DA ,AE=CF . 求证:BF=DE .2、在ABCD 中,E 、F 分别在DC 、AB 上,且DE =BF 。
求证:四边形AFCE 是平行四边形。
3、 如图所示,四边形ABCD 是平行四边形,且∠EAD =∠BAF 。
① 求证:ΔCEF 是等腰三角形;②观察图形,ΔCEF 的哪两边之和恰好等于ABCD 的周长?并说明理由。
4、如图所示,ABCD 中的对角线AC 、BD 相交于O ,EF 经过点O 与AD 延长线交于E ,与CB 延长线交于F 。
求证:OE=OF5、如图, ABCD 中,G 是CD 上一点,BG 交AD 延长线于E ,AF=CG , 100=∠DGE .(1) 求证:DF=BG ; (2)求AFD ∠的度数.6、如图,在□ABCD 中,E 、F 、G 、H 分别是四条边上的点,且满足BE=DF,CG=AH,连接EF 、GH 。
求证:EF 与GH 互相平分。
A B C D F E GAB C D E F OG H7、 如图,在▱ABCD 中,对角线AC,BD 相交于点O ,MN 是过O 点的直线,交BC 于M ,交AD 于N ,BM=2,AN=2.8,则BC= ,AD=8、 如图,在ABCD 中,点E 、F 分别为DC 、AB 边上的点,且DE =BF.试说明四边形AFCE 是平行四边形.菱形:1. 已知:如图,在△ABC 中,∠BAC=90°,AD ⊥BC 于D ,CE 平分∠ACB ,交AD 于G ,交AB 与E ,EF ⊥BC 于F 。
求证:四边形AEFG 为菱形。
2. 已知:如图,在平行四边形ABCD 中,AE 是BC 边上的高,将△ABE 沿BC 方向平移,使点E 与点C 重合,得△GCF .求证:BE=DG .3. 将平行四边形纸片ABCD 按如图方式折叠,使点C 与A 重合,点D 落到D ′ 处,折痕为EF .DE C BF A 图19(1)求证:△ABE ≌△AD ′F ;(2)连接CF ,判断四边形AECF 是什么特殊四边形?证明你的结论.4. 两个完全相同的矩形纸片ABCD 、BFDE 如图7放置,AB BF =,求证:四边形BNDM 为菱形.5. 如图,在△ABC 中,AB =AC ,D 是BC 的中点,连结AD ,在AD 的延长线上取一点E ,连结BE ,CE.(1)求证:△ABE ≌△ACE(2)当AE 与AD 满足什么数量关系时,四边形ABEC 是菱形?并说明理由.6. 在菱形ABCD 中,对角线AC 与BD 相交于点O ,56AB AC ==,.点D 作DE AC ∥交BC 的延长线于点E .(1)求BDE △的周长;(2)点P 为线段BC 上的点,连接PO 并延长交AD 于点Q .求证:BP DQ =. A QDE BP C OC D E M ABFN A B C DE F D ′7.如图,四边形ABCD 中,AB CD ∥,AC 平分BAD ∠,CE AD ∥交AB 于E .(1)求证:四边形AECD 是菱形;(2)若点E 是AB 的中点,试判断ABC △的形状,并说明理由.8.如图,在平行四边形ABCD 中,E F ,分别为边AB CD ,的中点,连接DE BF BD ,,.(1)求证:ADE CBF △≌△.(2)若AD BD ⊥,则四边形BFDE 是什么特殊四边形?请证明你的结论.矩形:1. 已知:如图,在平行四边形ABCD 中,AE 、BF 、CH 、DG 分别为内角平分线,这四条角平分线分别交于点M 、N 、P 、Q 求证:四边形MNPQ 是矩形AB CD E F 2.如图,将矩形ABCD 沿直线EF 对折,点D 恰好与BC 边上的点H 重合,∠GFP=62°,那么∠EHF 的度数等于——3. .如图,△ABC 中,AB =AC ,AD 、AE 分别是∠BAC 和∠BAC 和外角的平分线,BE ⊥AE .(1)求证:DA ⊥AE ;(2)试判断AB 与DE 是否相等?并证明你的结论. . 4.如图,Rt △ABC 中,∠C=90°,AC=3,BC=4,点P 为AB 边上任一点,过P 分别作PE ⊥AC 于E ,PF ⊥BC 于F ,则线段EF 的最小值是5.如图,矩形ABCD 中,点E 是BC 上一点,AE =AD ,DF ⊥AE 于F ,连结DE ,求证:DF =DC .6. 如图,O 为△ABC 内一点,把AB 、OB 、OC 、AC 的中点D 、E 、F 、G 依次连接形成四边形DEFG . 四边形DEFG 是什么四边形,请说明理由;7. 如图,四边形ABCD 是矩形,△PBC 和△QCD 都是等边三角形,且点P 在矩形上方,点Q 在矩形内.求证:(1)∠PBA =∠PCQ =30°;(2)P A =PQ .DA BC DE F8.如图,已知Rt △ABC 中,∠BAC=90°,AB=AC ,P 是BC 延长线上一点,PE ⊥AB 交BA 延长线于E ,PF ⊥AC 交AC 延长线于F ,D 为BC 中点,连接DE ,DF .求证:DE=DF .正方形:1.四边形ABCD 、DEFG 都是正方形,连接AE 、CG .(1)求证:AE =CG ;(2)观察图形,猜想AE 与CG 之间的位置关系,并证明你的猜想.2. 如图:已知在ABC △中,A B A C =,D 为BC 边的中点,过点D 作DE AB DF AC ⊥,⊥,垂足分别为E F ,.(1) 求证:BED CFD △≌△;(2)若90A ∠=°,求证:四边形DFAE 是正方形.3. 、已知:如图,在正方形ABCD 中,G 是CD 上一点,延长BC 到E ,使CE =CG ,连接BG 并延长交DE 于F . ACBD P QD CB EAF(1)求证:△BCG ≌△DCE ;(2)将△DCE 绕点D 顺时针旋转90°得到△DAE ′,判断四边形E ′BGD 是什么特殊四边形?并说明理由.4.如图 ,ABCD 是正方形.G 是 BC 上的一点,DE ⊥AG 于 E ,BF ⊥AG 于 F .(1)求证:ABF DAE △≌△;(2)求证:DE EF FB =+.5. 、如图8-1,已知P 为正方形ABCD 的对角线AC 上一点(不与A 、C 重合),PE ⊥BC 于点E ,PF ⊥CD 于点F .(1) 求证:BP =DP ;(2) 如图8-2,若四边形PECF 绕点C 按逆时针方向旋转,在旋转过程中是否总有BP =DP ?若是,请给予证明;若不是,请用反例加以说明;6. 把正方形ABCD 绕着点A ,按顺时针方向旋转得到正方形AEFG ,边FG 与BC 交于点H (如图).试问线段HG 与线段HB 相等吗?请先观察猜想,然后再证明你的猜想.7. E 、F 、M 、N 分别是正方形ABCD 四条边上的点,AE=BF=CM=DN ,四边形EFMN 是什么图形?证明你的结论. AD EF C BA B C DE F E ' GD C A BGH F E8.如图,已知平行四边形ABCD 中,对角线AC BD ,交于点O ,E 是BD 延长线上的点,且ACE △是等边三角形.(1)求证:四边形ABCD 是菱形;(2)若2AED EAD ∠=∠,求证:四边形ABCD 是正方形.梯形:1. 已知:如图,D 、E 、F 分别是△ABC 各边的中点,AH 是BC 边上的高,求证:四边形DEFH 是等腰梯形2. .如图,在等腰梯形ABCD 中,∠C =60°,AD ∥BC ,且AD =DC ,E 、F 分别在AD 、DC 的延长线上,且DE =CF ,AF 、BE 交于点P .(1)求证:AF =BE ;3.如图,在梯形ABCD 中,AD BC ∥,AB AD DC ==,AC AB ⊥,将CB 延长至点F ,使BF CD =.(1)求ABC ∠的度数;(2)求证:CAF △为等腰三角形.EB AD E PBAC4.如图9,梯形ABCD 中,AD BC ∥,AB DC =,P 为梯形ABCD 外一点,PA PD 、分别交线段BC 于点E F 、,且PA PD =. 求证:ABE DCF △≌△.5.如图,在梯形ABCD 中,AD ∥BC ,AD=2,BC=8,AC=6,BD=8,则此梯形的面积是___6.已知:如图,梯形ABCD 中,AB ∥DC ,E 是BC 的中点,AE 、DC 的延长线相交于点F ,连接AC .BF .(1)求证:AB=CF ;(2)四边形ABFC 是什么四边形,并说明你的理由.7.如图,在梯形ABCD 中,已知AD ∥BC ,BC=BD ,AD=AB=4cm ,∠A=120°,求梯形ABCD 的面积.8.如图,在等腰梯形ABCD 中,AD ∥BC ,AB=CD ,∠DBC=45°,点F 在AB 边上,点E 在BC 边上,将△BFE 沿折痕EF 翻折,使点B 落在点D 处.若AD=1,BC=5。
初二数学证明题(精选多篇)

初二数学证明题(精选多篇)第一篇:初二数学证明题初二数学证明题1、如图,ab=ac,∠bac=90°,bd⊥ae于d,ce⊥ae于e.且bd>ce,证明bd=ec+ed.解答:证明:∵∠bac=90°,ce⊥ae,bd⊥ae,∴∠abd+∠bad=90°,∠bad+∠dac=90°,∠adb=∠aec=90°.∴∠abd=∠dac.又∵ab=ac,∴△abd≌△cae(aas).∴bd=ae,ec=ad.∵ae=ad+de,∴bd=ec+ed.2、△abc是等要直角三角形。
∠acb=90°,ad是bc边上的中线,过c 做ad的垂线,交ab于点e,交ad于点f,求证∠adc=∠bde解:作ch⊥ab于h交ad于p,∵在rt△abc中ac=cb,∠acb=90°,∴∠cab=∠cba=45°.∴∠hcb=90°-∠cba=45°=∠cba.又∵中点d,∴cd=bd.又∵ch⊥ab,∴ch=ah=bh.又∵∠pah+∠aph=90°,∠pcf+∠cpf=90°,∠aph=∠cpf,∴∠pah=∠pcf.又∵∠aph=∠ceh,在△aph与△ceh中∠pah=∠ech,ah=ch,∠pha=∠ehc,∴△aph≌△ceh(asa).∴ph=eh,又∵pc=ch-ph,be=bh-he,∴cp=eb.在△pdc与△edb中pc=eb,∠pcd=∠ebd,dc=db,∴△pdc≌△edb(sas).∴∠adc=∠bde.2证明:作oe⊥ab于e,of⊥ac于f,∵∠3=∠4,∴oe=of.(问题在这里。
理由是什么埃我有点不懂)∵∠1=∠2,∴ob=oc.∴rt△obe≌rt△ocf(hl).∴∠5=∠6.∴∠1+∠5=∠2+∠6.即∠abc=∠acb.∴ab=ac.∴△abc是等腰三角形过点o作od⊥ab于d过点o作oe⊥ac于e再证rt△aod≌rt△aoe(aas)得出od=oe就可以再证rt△dob≌rt△eoc(hl)得出∠abo=∠aco再因为∠obc=∠ocb得出∠abc=∠abc得出等腰△abc41.e是射线ab的一点,正方形abcd、正方形defg有公共顶点d,问当e在移动时,∠fbh的大小是一个定值吗?并验证(过f作fm⊥ah于m,△ade全等于△mef证好了)2.三角形abc,以ab、ac为边作正方形abmn、正方形acpq1)若de⊥bc,求证:e是nq的中点2)若d是bc的中点,∠bac=90°,求证:ae⊥nq3)若f是mp的中点,fg⊥bc于g,求证:2fg=bc3.已知ad是bc边上的高,be是∠abc的平分线,ef⊥bc于f,ad与be交于g求证:1)ae=ag(这个证好了)2)四边形aefg是菱形第二篇:初二数学证明题测试例1、如图,ab∥cd,且∠abe=120°,∠cde=110°,求∠bed的度数。
初二数学证明试题

初二数学证明试题1.如图,电路中有4个电阻和一个电流表A,若没有电流通过电流表A,问电阻器断路的可能情况共有种.【答案】8+3=11种【解析】要使没有电流通过电流表A,则若总路上的电阻是断开的,其它的三个电阻无论是断开,还是通的都可以,共有23=8种情况;若总路上的电阻是通的,则每一个支路都不能是通的,所以下面的电阻一定是断开的,上面的两个电阻只要有一个是断开的即可,有3种情况.故共有11种情况.解:本题分两种情况:①若主路的电阻不通,那么这个电路必为断路.因此共有2×2×2=8种可能;②若主路的电阻通电,那么两条支路必须同时为断路,因此共有3种可能.故电阻器断路的可能情况共有8+3=11种.点评:此题的学科综合性较强,能够结合物理中的知识进行分析求解是解答本题的关键.2.有一地球同步卫星A与地面四个科研机构B、C、D、E,它们两两之间可以互相接发信息,由于功率有限,卫星及每个科研机构都不能同时向两处发送信息(如A不能同时给B、C发信息,它可先发给B,再发给C),它们彼此之间一次接发信息的所需时间如右图所示.则一个信息由卫星发出到四个科研机构都接到该信息时所需的最短时间为.【答案】4【解析】首先卫星A传递信息给B用时1(秒),然后B传给C(3秒);同时卫星传给E(1秒),信息传给D和C的时候同时进行,所有动作在4秒钟内结束.解:开始的时候,时间0秒,卫星传给B(1秒)第1秒钟时候,B传给C(3秒);同时卫星传给E(1秒),第2秒钟的时候,E传给D,所有动作在4秒钟内结束,故接到该信息时所需的最短时间为4秒,故答案为4.点评:本题主要考查推理与论证的知识点,解答本题的关键是注意卫星传递信息的同时性,此题难度不大.3.暑假期间,小丽、小杰决定定期到敬老院打扫卫生,小丽每4天去一次,小杰每6天去一次,如果8月1日他们俩都在敬老院打扫卫生,那么,他们下一次同时在敬老院打扫卫生的时间是几月几日?【答案】8月13日【解析】根据4、6的最小公倍数是12,则他们每隔12天相遇一次,所以他们应在12天以后,即第13日再相遇.解:4、6的最小公倍数是12,所以他们应在12天以后,即第13日再相遇.答:他们下一次同时在敬老院打扫卫生的时间是8月13日.点评:本题主要是利用最小公倍数进行求解.4.有人认为数学没有多少使用价值,我们只要能数得清钞票,到菜场算得出价钱这点数学知识就够了.根据你学习数学的体会,谈谈你对数学这门学科的看法.【答案】见解析【解析】可以从数学的基础性,应用的广泛性,培养严密的逻辑思维能力,人文素养,科学精神等各方面价值作简单说明.解:答案不唯一,如:数学是思维的体操,可以培养自己的逻辑思维能力、发散思维能力等. 点评:此题为开放性试题,主要是考查学生对数学的认识.5. 推理能力都很强的甲、乙、丙站成一列,丙可以看见甲、乙,乙可以看见甲但看不见丙,甲看不见乙、丙.现有5顶帽子,3顶白色,2顶黑色.老师分别给每人戴上一顶帽子(在各自不知道的情况下).老师先问丙是否知道头上的帽子颜色,丙回答说不知道;老师再问乙是否知道头上的帽子颜色,乙也回答说不知道;老师最后问甲是否知道头上的帽子颜色,甲回答说知道.请你说出甲戴了什么颜色的帽子,并写出推理过程. 【答案】见解析【解析】如果甲、乙都戴黑帽子,丙马上知道自己戴的是白帽子,如果甲戴黑帽子,甲、乙中至少有一个人戴白帽子,则乙马上知道自己戴的是白帽子. 解:甲戴的是白帽子.理由如下:因为丙说不知道,说明甲、乙中至少有一个人戴白帽子(如果甲、乙都戴黑帽子,丙马上知道自己戴的是白帽子).因为乙也说不知道,说明甲戴的是白帽子(如果甲戴黑帽子,甲、乙中至少有一个人戴白帽子,则乙马上知道自己戴的是白帽子).点评:本题主要考查了论证与推理的一些基础知识,能够找出题中的内在联系,从而求解.6. 10名棋手参加比赛,规定:每两名棋手间都要比赛一次,胜者得2分,下和各得1分,输者得0分.比赛结果表明:棋手们所得分数各不相同,前两名棋手没输过,前两名的总分之和比第三名多20分,第四名得分与后四名得分总和相等,那么前六名得分分别是多少? 【答案】17,16,13,12,11,9【解析】先设第k 名选手的得分为a k (1≤k≤10),得出a 1、a 2的值,再根据得出a 4≥12,求出a 3,再根据a 1≤a 3﹣1=12,求出a 4,最后根据a 1+a 2+a 3+…a 8+a 9+a 10=90分别求出a 5、a 6的值.解:设第k 名选手的得分为a k (1≤k≤10),依题意得:a 1>a 2>a 3>…a 9>a 10a 1≤1+2×(9﹣1)=17,a 2≤a 1﹣1=16,a 3+20=a 1+a 2,∴a 3≤13 ①,又后四名棋手相互之间要比赛=6场,每场比赛双方的得分总和为2分,∴a 7+a 8+a 9+a 10≥12,∴a 4≥12而a 3≥a 4+1≥13,②∴由①②得:a 3=13,∴a 1+a 2=33,∴a 1=17,a 2=16,又∵a 1≤a 3﹣1=12,∴a 4=12, ∵a 1+a 2+a 3+…a 8+a 9+a 10=×2=90,∴17+16+13+12+a 5+a 6+12=90,而a 5+a 6≤a 5+a 5﹣1,即:a 5≥10\frac{1}{2},又a5<a 4=12, ∴a 5=11,a 6=9,故前六名得分分别是:17,16,13,12,11,9.点评:本题考查了推理与论证;解决问题的关键是读懂题意,找到所求的量的等量关系是解题的关键.7. 图中小圆圈表示网络的结点,结点之间的连接表示它们有网线相连,相连标注的数字表示该段网线单位时间内可以通过的最大信息量.现从结点A 向结点B 传递信息,若信息可以分开沿不同路线同时传递,则单位时间内传递的最大信息量为( )A .11B .10C .8D .7【答案】C【解析】先找出从结点A 向结点B 传递信息可沿A ﹣C ﹣B 和A ﹣D ﹣B 路线同时传递,再找出每条路线通过的最大信息量,然后相加即可得到答案.解:由于信息可以分开沿不同路线同时传递,所以从结点A 向结点B 传递信息可经过结点D 和结点B ;又因为从结点A 到结点D 的最大信息量为5,从结点C 到结点B 的最大信息量为3,所以从结点A 向结点B 传递信息,若信息可以分开沿不同路线同时传递,则单位时间内传递的最大信息量为5+3=8. 故选C .点评:本题考查了推理与论证的方法:先分析题目所给的条件或要求,然后通过推理得到相关的结论.8. 如果甲的身高或体重数至少有一项比乙大,则称甲不亚于乙.在100个小伙子中,若某人不亚于其他99人,我们就称他为棒小伙子,那么100个小伙子中,棒小伙子最多可能有( ) A .1个 B .2个 C .50个 D .100个【答案】D【解析】因为求得最多是多少人,且如果甲的身高或体重数至少有一项比乙大,我们可把这一百个小伙子用A 1~A 100来表示,然后根据体重和身高两个条件找出答案. 解:先退到两个小伙子的情形,如果 甲的身高数>乙的身高数,且 乙的体重数>甲的体重数 可知棒小伙子最多有2人. 再考虑三个小伙子的情形,如果甲的身高数>乙的身高数>丙的身高数,且 丙的体重数>乙的体重数>甲的体重数 可知棒小伙子最多有3人.这时就会体会出小伙子中的豆芽菜与胖墩现象.由此可以设想,当有100个小伙子时,设每个小伙子为A i ,(i=1,2,…,100),其身高数为x i ,体重数为y i ,当y 100>y 99>…>y i >y i ﹣1>…>y 1且 x 1>x 2>…>x i >x i+1>…>x 100时,由身高看,A i 不亚于A i+1,A i+2,…,A 100; 由体重看,A i 不亚于A i ﹣1,A i ﹣2,…,A 1所以,A i 不亚于其他99人(i=1,2,...,100) 所以,A i 为棒小伙子(i=1,2, (100)因此,100个小伙子中的棒小伙子最多可能有 100个. 故选D .点评:本题考查推理和论证,关键注意本题有身高和体重两种情况,少有一项大,就称作不亚于,从而可求出解.9. 用1,2,3,4共可以写成不同的四位数( ) A .4个 B .12个 C .18个 D .24个【答案】D【解析】当1作千位时,可得1234,1243,1324,1342,1423,1432,6个不同的四位数.同理可得其余3个数字当千位上的数字也会有6个不同的四位数,那么可以写成24个不同的四位数.解:当1作千位上的数字时,四位数可写成1234,1243,1324,1342,1423,1432共6个; 同理,当2、3、4作千位上的数字时,也分别可写成6个不同的四位数. 因此用1、2、3、4共可写成的不同四位数的个数为4×6=24.故选D . 点评:解决本题应先找到确定一个数位上数的四位数的情况,进而得解.10.用锯锯木,锯会发热;用锉锉物,锉会发热;在石头上磨刀,刀会发热,所以物体摩擦会发热.此结论的得出运用的方法是()A.观察B.实验C.归纳D.类比【答案】C【解析】由多种现象得到一个规律属于归纳.解:由多种现象得到一个规律属于归纳.故选C.点评:本题考查归纳的形成.所谓归纳,是指通过对特例的分析来引出普遍结论的一种推理形式.它由推理的前提和结论两部分构成:前提是若干已知的个别事实,是个别或特殊的判断、陈述,结论是从前提中通过推理而获得的猜想,是普遍性的陈述、判断.。
初二数学证明试题

初二数学证明试题1.要判定一个命题是真命题,往往需要从命题的条件出发,根据已知的定义、公理、定理一步一步推得结论成立.这样的推理过程叫做_______.【答案】证明【解析】根据证明的概念直接填空即可。
要判定一个命题是真命题,往往需要从命题的条件出发,根据已知的定义、公理、定理一步一步推得结论成立.这样的推理过程叫做证明.【考点】本题考查的是证明的概念点评:解答本题的关键是熟练掌握证明的概念:要判定一个命题是真命题,往往需要从命题的条件出发,根据已知的定义、公理、定理一步一步推得结论成立.这样的推理过程叫做证明.2.证明几何命题时,表述要按照一定的格式,一般为:(1)按题意________;(2)分清命题的________,结合图形,在“已知”中写出______,在“求证”中写出______;(3)在“证明”中写出______.【答案】画出图形,条件和结论,条件,结论,推理过程【解析】根据证明几何命题的格式直接填空即可。
证明几何命题时,表述要按照一定的格式,一般为:(1)按题意画出图形;(2)分清命题的条件和结论,结合图形,在“已知”中写出条件,在“求证”中写出结论;(3)在“证明”中写出推理过程.【考点】本题考查的是证明几何命题的格式点评:解答本题的关键是熟练掌握证明几何命题的格式:(1)按题意画出图形;(2)分清命题的条件和结论,结合图形,在“已知”中写出条件,在“求证”中写出结论;(3)在“证明”中写出推理过程.3.在△ABC中,∠A+∠B=110°,∠C=2∠A,则∠A=______,∠B=_______.【答案】∠A=35°,∠B=75°【解析】根据∠A+∠B=110°,三角形的内角和为180°,即可求得∠C的度数,再根据∠C=2∠A 求得∠A的度数,从而得到∠B的度数。
∵∠A+∠B=110°,∴∠C=180°-(∠A+∠B)=70°,∵∠C=2∠A,∴∠A=35°,∴∠B=180°-∠A-∠C=75°.【考点】本题考查的是三角形的内角和定理点评:解答本题的关键是熟练掌握三角形的内角和为180°.4.如图所示,AB∥CD,CE平分∠ACD并交AB于E,∠A=118°,则______.【答案】31°【解析】由AB∥CD,∠A=118°,根据平行线的性质可求得∠ACD的度数,再由CE平分∠ACD可求得∠ECD的度数,再根据平行线的性质即可得到结果。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(2)观察图形,猜想AE与CG之间的位置关系,并证明你的猜想.
2.如图:已知在 中, , 为 边的中点,过点 作 ,垂足分别为 .
(1)求证: ;
(2)若 ,求证:四边形 是正方形.
3.、已知:如图,在正方形ABCD中,G是CD上一点,延长BC到E,使CE=CG,连接BG并延长交DE于F.
5.如图,矩形ABCD中,点E是BC上一点,AE=AD,DF⊥AE于F,连结DE,求证:DF=DC.
6.如图,O为△ABC内一点,把AB、OB、OC、AC的中点D、E、F、G依次连接形成四边形DEFG.
四边形DEFG是什么四边形,请说明理由;
7.如图,四边形ABCD是矩形,△PBC和△QCD都是等边三角形,且点P在矩形上方,点Q在矩形内.
(1)求证:BP=DP;
(2)如图8-2,若四边形PECF绕点C按逆时针方向旋转,在旋转过程中是否总有BP=DP?若是,请给予证明;若不是,请用反例加以说明;
6.把正方形 绕着点 ,按顺时针方向旋转得到正方形 ,边 与 交于点 (如图).试问线段 与线段 相等吗?请先观察猜想,然后再证明你的猜想.
7.E、F、M、N分别是正方形ABCD四条边上的点,AE=BF=CM=DN,四边形EFMN是什么图形?证明你的结论.
(1)求证:△BCG≌△DCE;
(2)将△DCE绕点D顺时针旋转90°得到△DAE′,判断四边形E′BGD是什么特殊四边形?并说明理由.
4.如图,ABCD是正方形.G是BC上的一点,DE⊥AG于E,BF⊥AG于F.
(1)求证: ;
(2)求证: .
5.、如图8-1,已知P为正方形ABCD的对角线AC上一点(不与A、C重合),PE⊥BC于点E,PF⊥CD于点F.
3.将平行四边形纸片ABCD按如图方式折叠,使点C与A重合,点D落到D′处,折痕为EF.
(1)求证:△ABE≌△AD′F;
(2)连接CF,判断四边形AECF是什么特殊四边形?证明你的结论.
4.两个完全相同的矩形纸片 、 如图7放置, ,求证:四边形 为菱形.
5.如图,在△ABC中,AB=AC,D是BC的中点,连结AD,在AD的延长线上取一点E,连结BE,CE.
(1)求证:△ABE≌△ACE
(2)当AE与AD满足什么数量关系时,四边形ABEC是菱形?并说明理由.
6.在菱形 中,对角线 与 相交于点 , .点 作 交 的延长线于点 .
(1)求 的周长;
(2)点 为线段 上的点,连接 并延长交 于点 .求证: .
7.如图,四边形 中, , 平分 , 交 于 .
5.如图所示, ABCD中的对角线AC、BD相交于O,EF经过点O与AD延长线交于E,与CB延长线交于F。求证:OE=OF
6.如图, ABCD 中,G是CD上一点,BG交AD延长线于E,AF=CG, .
(1) 求证:DF=BG; (2)求 的度数.
7.如图,在□ABCD中,E、F、G、H分别是四条边上的点,且满足BE=DF,CG=AH,连接EF、GH。求证:EF与GH互相平分。
8.如图,在▱ABCD中,对角线AC,BD相交于点O,MN是过O点的直线,交BC于M,交AD于N,BM=2,AN=2.8,则BC=,AD=
菱形:
1. 已知:如图,在△ABC中,∠BAC=90°,AD⊥BC于D,CE平分∠ACB,交AD于G,交AB与E,EF⊥BC于F。求证:四边形AEFG为菱形。
2.已知:如沿BC方向平移,使点E与点C重合,得△GCF.求证:BE=DG.
(1)求证:AF=BE;
3.如图,在梯形 中, , , ,将 延长至点 ,使 .
(1)求 的度数;
(2)求证: 为等腰三角形.
4.如图9,梯形 中, , , 为梯形 外一点, 分别交线段 于点 ,且 .求证: .
5.如图,在梯形ABCD中,AD∥BC,AD=2,BC=8,AC=6,BD=8,则此梯形的面积是___
3..如图,△ABC中,AB=AC,AD、AE分别是∠BAC和∠BAC和外角的平分线,BE⊥AE.
(1)求证:DA⊥AE;
(2)试判断AB与DE是否相等?并证明你的结论.
.4.如图,Rt△ABC中,∠C=90°,AC=3,BC=4,点P为AB边上任一点,过P分别作PE⊥AC于E,PF⊥BC于F,则线段EF的最小值是
平行四边形
2.已知:如图,AB=CD,BC=DA,AE=CF.求证:BF=DE.
3.在 ABCD中,E、F分别在DC、AB上,且DE=BF。求证:四边形AFCE是平行四边形。
4.如图所示,四边形ABCD是平行四边形,且∠EAD=∠BAF。
1 求证:ΔCEF是等腰三角形;
②观察图形,ΔCEF的哪两边之和恰好等于 ABCD的周长?并说明理由。
6.已知:如图,梯形ABCD中,AB∥DC,E是BC的中点,AE、DC的延长线相交于点F,连接AC.BF.
(1)求证:AB=CF;
(2)四边形ABFC是什么四边形,并说明你的理由.
7.如图,在梯形ABCD中,已知AD∥BC,BC=BD,AD=AB=4cm,∠A=120°,求梯形ABCD的面积.
8.如图,在等腰梯形ABCD中,AD∥BC,AB=CD,∠DBC=45°,点F在AB边上,点E在BC边上,将△BFE沿折痕EF翻折,使点B落在点D处.若AD=1,BC=5。则BD的长为多少?
求证:(1)∠PBA=∠PCQ=30°;(2)PA=PQ.
8.如图,已知Rt△ABC中,∠BAC=90°,AB=AC,P是BC延长线上一点,PE⊥AB交BA延长线于E,PF⊥AC交AC延长线于F,D为BC中点,连接DE,DF.求证:DE=DF.
正方形:
1.四边形ABCD、DEFG都是正方形,连接AE、CG.
(1)求证:四边形 是菱形;
(2)若点 是 的中点,试判断 的形状,并说明理由.
8.如图,在平行四边形ABCD中, 分别为边 的中点,连接 .
(1)求证: .
(2)若 ,则四边形 是什么特殊四边形?请证明你的结论.
矩形:
1.已知:如图,在平行四边形ABCD中,AE、BF、CH、DG分别为内角平分线,这四条角平分线分别交于点M、N、P、Q求证:四边形MNPQ是矩形
8.如图,已知平行四边形 中,对角线 交于点 , 是 延长线上的点,且 是等边三角形.
(1)求证:四边形 是菱形;
(2)若 ,求证:四边形 是正方形.
梯形:
1.已知:如图,D、E、F分别是△ABC各边的中点,AH是BC边上的高,
求证:四边形DEFH是等腰梯形
2..如图,在等腰梯形ABCD中,∠C=60°,AD∥BC,且AD=DC,E、F分别在AD、DC的延长线上,且DE=CF,AF、BE交于点P.
