江苏省赣榆县海头高级中学高一上学期期中考试数学试题
江苏省赣榆高级中学2016_2017学年高一数学上学期期中试题

江苏省赣榆高级中学2016-2017学年度第一学期期中考试高一数学试题一、填空题:本大题共14小题,每小题5分,共70分.请把答案直接填写在答题卡相应位置上......... 1.已知集合{},,,A =-2136,{}|B x x =-<<24,则A ∩B = ▲ . 2.式子a 2a >0)用分数指数幂表示为 ▲ . 3.函数y x-12的定义域是 ▲ . 4.计算(lg lg )-⨯=121251004▲ .5.设.a =032,.b =203,c =,将,,a b c 按从小到大....的顺序用不等号连接为 ▲ . 6.已知函数()f x x ax bx =++-533,若()f -=-25,则()f =2 ▲ . 7.函数()log ()f x x =-221的单调减区间为 ▲ .8.已知函数log ,,(),,x x x f x x >⎧⎪=⎨⎛⎫≤ ⎪⎪⎝⎭⎩20102 则满足方程()f a =1的所有a 的取值构成的集合为 ▲ .9.已知幂函数()()()kkf x k k x k Z -=+-∈2231的图象关于y 轴对称,且在(0,+∞)上是减函数,则k 的值为 ▲ .10.已知()f x 是定义在R 上的偶函数,且在(],-∞0上为减函数,f ⎛⎫= ⎪⎝⎭102,则不等式(log )f x >40的解集为 ▲ .11.已知函数()lg()f x mx =-1在[,)+∞2上单调递增,则实数m 的取值范围为 ▲ .12.已知集合{}||(,)|x A x y y -==+131,{}(,)|B x y y k ==,若集合A ∩B 只有一个真子集,则实数k的取值集合是 ▲ .13.已知函数,,(),,xx x x f x x a ⎧---≤≤=⎨-<≤⎩224020的值域是[-8,1],则实数a 的取值范围是 ▲ . 14.已知函数()f x 满足()f x f x ⎛⎫= ⎪⎝⎭12,当[,]x ∈13时,()ln f x x =,若在区间,⎡⎤⎢⎥⎣⎦133内,存在互不相等的实数,a b 使()()f a f b =,则ab 的取值范围为 ▲ .二、解答题:本大题共6小题,共90分.请在答题卡指定区域.......内作答. 解答时应写出文字说明、证明过程或演算步骤. 15.(本小题满分14分)已知集合{}|A x x =≤<15,{}|B x a x a =-<≤+3. (1)若a =1,U R =,求U C A ∩B ; (2)若B ∩A =B ,求实数a 的取值范围.16.(本小题满分14分)已知函数()()f x ax ax b a =-++≠2220在区间[2,3]上有最大值5,最小值2. (1)求,a b 的值;(2)若b <1,且()()m g x f x x =-2在[2,3]上单调,求实数m 的取值范围.赣榆区自行车主题景观大道引进50辆自行车供游客租赁使用,管理这些自行车的费用是每日125元.根据经验,若每辆自行车的日租金不超过6元,则自行车可以全部租出;若超过6元,则每提高1元,租不出去的自行车就增加3辆.规定:每辆自行车的日租金不超过20元,每辆自行车的日租金x 元只取整数,并要求出租所有自行车一日的总收入必须超过一日的管理费用,用y 表示出租所有自行车的日净收入(即一日中出租所有自行车的总收入减去管理费后的所得). (1)求函数)(x f y =的解析式及定义域;(2)试问日净收入最多时每辆自行车的日租金应定为多少元? 日净收入最多为多少元?18.(本小题满分16分)已知函数()||f x ax x =-+1(x ∈R ).(1)设函数()g x 为定义在R 上的奇函数,且当x >0时,()()g x f x =,求()g x 的解析式; (2)若函数()f x 有最大值,求实数a 的取值范围.设函数()x x f x ka a -=-(a >0且a ≠1)是奇函数. (1)求k 的值;(2)若()f >10,解关于x 的不等式()()f x f x ++->240; (3)若()f =312,且对任意的[,)x ∈+∞1,不等式()x x a a mf x -+-+≥22220恒成立,求实数m 取值范围.20.(本小题满分16分)设函数()()f x ax a c x c =-++232(,,)a a c >∈R 0.(1)若a =1,函数()f x 在区间(,)01和(,)+∞1上各有一个零点,求实数c 的取值范围; (2)设a >0,若()f x cx a >-+2对任意[,)x ∈+∞1恒成立,求实数c 的取值范围; (3)函数()f x 在区间(,)01内是否有零点,如果有,请确定零点的个数,并说明理由.江苏省赣榆高级中学2016-2017学年度第一学期期中考试高一数学试题一、填空题:本大题共14小题,每小题5分,共70分.请把答案直接填写在答题卡相应位置上......... 1 {1,3} 2. a 523. {}3,2x x x ≥-≠且 4. 20- 5. b a c << 6. -17. (-∞,-1) 8. {2,0} 9. 1 10.⎝ ⎛⎭⎪⎫0,12∪(2,+∞) 11. ,⎛⎫∞ ⎪⎝⎭12+12. {2} 13.](,03 14. (1二、解答题:本大题共6小题,共90分.请在答题卡指定区域.......内作答. 解答时应写出文字说明、证明过程或演算步骤. 15.(本小题满分14分)解:(1){}|A x x =≤<15,{}|U C A x x x =<≥或15…………………………………………2分 当a =1时,{}|B x x =-<≤14 ………………………………………4分故U C A ∩B ={}|x x -<<11 …………………………………………6分 (2)因为B ∩A =B ,所以B ⊆A .①当B =∅时,满足B ⊆A ,此时-a ≥a +3,得a ≤-32; ……………………………………8分②当B ≠∅时,要使B ⊆A ,则⎩⎪⎨⎪⎧-a <a +3,-a ≥1,a +3<5,解得-32<a ≤-1. (12)分综上,a 的取值范围是(-∞,-1]. ………………………………14分 16.(本小题满分14分)解:(1)f (x )=a (x -1)2+2+b -a . ① 当a >0时,f (x )在[2,3]上为增函数, 故⎩⎪⎨⎪⎧f =5,f=2⇒⎩⎪⎨⎪⎧9a -6a +2+b =5,4a -4a +2+b =2⇒⎩⎪⎨⎪⎧a =1,b =0.……………………………………2分② 当a <0时,f (x )在[2,3]上为减函数,故⎩⎪⎨⎪⎧f =2,f=5⇒⎩⎪⎨⎪⎧9a -6a +2+b =2,4a -4a +2+b =5⇒⎩⎪⎨⎪⎧a =-1,b =3.…………………………………4分故a =1,b =0或a =-1,b =3. ………………………………………6分 (2)∵b <1,∴a =1,b =0,即f (x )=x 2-2x +2, ………………………………………8分g (x )=x 2-2x +2-2m x =x 2-(2+2m )x +2.若g (x )在[2,3]上单调,则2+2m2≤2或2m+22≥3, (结果正确每个 2分)∴2m≤2或2m≥4,即m ≤1或m ≥2. ……………………………………12分 故m 的取值范围是(-∞,1]∪[2,+∞) ……………………………………14分17.(本小题满分14分)解:当x ≤6时,y x =-50125,令x ->501250,计算得出.x >25,x N ∈,36,x x N ∴≤≤∈.……………………2分当x <≤620时,[()]y x x x x =---=-+-25036125368125; ………………………4分 综上所述,250125, 36,368125, 620,x x x N y x x x x N-≤≤∈⎧=⎨-+-<≤∈⎩. ………………………………6分当36x ≤≤且x N ∈时,y x =-50125是增函数,∴当x 6=时,max y =175元 ………8分当x <≤620且x N ∈时,()y x x x =-+---+2234781368125333=,所以x =11时,max y =260元. ………………………………12分综上所述,当每辆自行车日租金定在11元时才能使得日净收入最多,为260元. ………14分 18.(本小题满分16分)解 (1)(),,()(),,a x x f x a x x --≥-⎧=⎨++<-⎩111111 注:范围中的“=”两段中均可以,但不能漏掉! (2)分要使函数f (x )有最大值,需,,a a -≤⎧⎨+≥⎩1010∴-1≤a ≤1. (4)分即当a ∈[-1,1]时,f (x )有最大值.故a 的取值范围为[-1,1]. ………………………6分(2)∵g (x )为定义在R 上的奇函数,∴g (-0)=-g (0),∴g (0)=0. ……………………8分当x >0时,()()g x f x ==()a x --11 ………………………10分 设x<0,则-x >0.∴g (x )=-g (-x )=()()()a x a x ---+=-+1111, ………………………14分∴(),(),(),a x x g x x a x x -->⎧⎪==⎨⎪-+<⎩11000110 ………………………16分19.(本小题满分16分)解 (1)因为f (x )是奇函数,且f (0)有意义,所以f (0)=0,所以k -1=0,k =1. (2)分(2)因为f (1)>0,所以a -1a>0,∴a >1,∴f (x )=a x -a -x是R 上的单调增函数. (4)分于是由f (x +2)>-f (x -4)=f (4-x ),得x +2>4-x ,解得x >1. ………………6分所以不等式的解集是{}1x x >. ………………8分 (3)因为f (1)=32,所以a -1a =32,解得a =2(a >0), (10)分设g (x )=22x+2-2x-2m (2x -2-x )+2=(2x -2-x )2-2m (2x -2-x)+4.设t =f (x )=2x -2-x,则由x ≥1,得t ≥f (1)=32, ………………12分g (t )=t 2-2mt +4=(t -m )2+4-m 2.若m ≥32,则当t =m 时,y min =4-m 2≥0,解得m ≤≤322.若m <32,则当t =32时,y min =m -≥25304,解得m <32. ………………14分综上得m ≤2 …………………………16分20.(本小题满分16分).解 (1)将a =1代入()()f x ax a c x c =-++232得()()f x x c x c =-++2321,由函数()f x 在区间(,)01和(,)+∞1上各有一个零点,且函数开口向上,知()f <10, 即()c c -++<3210,解得c >1. ………………4分(2) 由()f x cx a >-+2,将()()f x ax a c x c =-++232代入得()ax a c x c cx a -++>-+2322;c ax ax a >-+232+,令()g x ax ax a =-+232+,a >0 ………………6分 ()f x cx a >-+2对任意[,)x ∈+∞1恒成立,即max ()c g x >, ………………8分()()g x ax ax a a x a =-+--+221432333+=,由()g x 在[,)x ∈+∞1上单调递减,max ()()g x g =10= c ∴>0.故实数c 的取值范围是c >0. ………………10分(2)①若f (0)·f (1)=c ·(a -c )<0,则c <0,或a <c ,二次函数f (x )在(0,1)内只有一个零点. ………………12分 ②若f (0)=c >0,f (1)=a -c >0,则a >c >0.因为二次函数f (x )=3ax 2-2(a +c )x +c 的图象的对称轴是x =a +c 3a .而f ⎝ ⎛⎭⎪⎫a +c 3a =-a 2+c 2-ac 3a <0,所以函数f (x )在区间⎝⎛⎭⎪⎫0,a +c 3a 和⎝ ⎛⎭⎪⎫a +c 3a ,1内各有一个零点,故函数f (x )在区间(0,1)内有两个零点. ………………16分。
江苏省海头高级中学高一上学期数学综合训练(4).pdf

一、填空题:本大题共14小题,每小题5分,共计70分.请把答案填写在答题纸的相应位置上.1.已知集合,集合,,则=▲ .2.已知,则实数=▲ . 3.函数的定义域是 ▲ . 4.设是定义在R上的奇函数,且,则 ▲ . 5.二次函数()的最大值为 ▲ . 6. 函数(且)的图象所经过的定点坐标为 ▲ . 7.已知,则 ▲ . 8.若函数与函数的图象有两个公共点,则的取值范围是 ▲ . 9.已知幂函数的图象不经过原点,则实数的值为 ▲ . 10.已知函数有两个不同的零点,且,则实数的取值范围为 ▲ . 11.已知函数在定义域上是单调减函数,且对任意,恒成立,则实数的取值范围是 ▲ . 12.设,函数,且,则=▲ . 13.函数的单调递增区间为 ▲ . 14.已知函数若在区间上是减函数,则实数a的取值范围是 ▲ . 二、解答题:本大题共6小题,共计90分.请在答题纸指定区域内作答,解答时应写出文字说明、证明过程或演算步骤. 15. (本小题满分14分) (1)求值: (2)求值:的定义域为A,指数函数(>0且≠1)()的值域为B. (1)若,求; (2)若=(,2),求的值. 17、(本小题满分15分) 已知函数. (1)判断函数的奇偶性,并说明理由; (2)指出函数在区间,上的单调性,并加以证明. 18. (本小题满分15分) 声音通过空气的振动所产生的压强叫声压强,简称声压,单位为帕(Pa).把声压的有效值取对数来表示声音的强弱,这种表示声音强弱的数值叫声压级.声压级以符号表示,单位为分贝(dB),公式为:(声压级)(dB),式中为待测声压的有效值,为参考声压,在空气中参考声压一般取值Pa.根据上述材料,回答下列问题. (1)若某两人小声交谈时的声压有效值Pa,求其声压级; (2)已知某班开主题班会,测量到教室内最高声压级达到90 dB,求此时该班教室内声压的有效值. 19. (本小题满分16分) 已知函数是定义在上的奇函数,当时,. (1)当时,求函数的表达式; (2)若,集合,,试判断集合A和B的关系; (3)已知对于任意的,不等式恒成立,求证:函数的图象与直线没有交点.。
江苏省海头高级中学2021-2022高一数学上学期第三次月考试题

江苏省海头高级中学2021-2022高一数学上学期第三次月考试题(考试时间:120分钟 试卷满分:150分)一、单项选择题:本大题共8小题,每小题5分,共计40分.1.已知集合{}{}|31,1,0,1A x x B =-<<=-,则A B = ( )A. {}2,1,0,1--B. {}2,1,0--C. {}1,0,1-D. {}1,0-2.若(5,3),(1,2),m n →→=-=-且m n λ→→+与2n m →→+互相垂直,则实数λ的值等于( )A .B .C .D . 3.函数6()12log f x x =-的定义域为 ( ) A .),0(+∞ B. )6,(-∞C. ]6,0(D. ]6,(-∞4.方程3log 3x x +=的解是0x ,若()0,1,x n n n N ∈+∈,则n = ( )A .0B .1C .2D .35.已知51cos sin ),,0(=+∈ααπα ,则=αtan ( )A .43-B .34C .34- D .436.为了得到函数x y 2sin =的图象,可以将函数)32sin(π+=x y 的图象( )A .向左平移6π个单位 B .向右平移6π个单位C .向左平移3π个单位 D .向右平移3π个单位7.若c b a ,,满足0=++c b a ,且,4||,1||,3||===c b a 则a c c b b a ⋅+⋅+⋅=( )A .-11B .-12C .-13D .-148.函数()2xx f x x ⋅=的图象大致为 ( )83-38-3883二、多项选择题:本大题共4小题,每小题5分,共计20分.9.下列函数中,既是偶函数又是0+∞(,)上的减函数的是( ) A. 1y x= B. x y e -= C. 21y x =-+ D. 12log ||y x = 10.在平面上的点(2,1)A ,(0,2)B ,(2,1)C -,(0,0)O ,下面结论正确的是( ) A.=- B. =+ C.2-= D. 2OA OB OC +=11.已知单位向量→a 、→b ,则下面正确的式子是( )A. →a ·→b =1B.22a b =C. →a =→bD. |→a |-|→b |=012.对于函数),,(sin )(3Z c R b a c x b ax x f ∈∈++=,选取c b a ,,的一组值去计算)1(-f 和)1(f ,所得出的正确结果可能是( )A .2和6B .3和9C .4和11D .5和13三、填空题:本大题共4小题,每小题5分,共计20分.13.已知幂函数()f x 的图象过点()4,2,则()8f = .14.已知,满足1||||==a 且3|23|=-,则=+|3|_________15.已知函数2sin()y x ωϕ=+为偶函数,其中πϕω<<>0,0,若此函数的最小正周期为π,则=+)3tan(πωϕ____________. 16. 若15sin(),sin()646x x ππ+=-=则__________.2sin ()=3x π-_________.四、解答题:17题10分,18,19,20,21,21,22每题12分,共计70分.17.已知向量(2,1),(3,2),(3,4)a b c =-=-=,(1)求()a b c ⋅+;(2)若()a b c λ+,求实数λ的值。
【数学】江苏省海头高级中学2013-2014学年高一上学期期中9

江苏省海头高级中学2013--2014学年度高一第一学期期中考试数学试题一、填空题(本大题共14小题,每小题5分,共计70分.) 1.将指数式3mn =转化为对数式为 ; 2.函数lg y x =的定义域为 ; 3.不等式lg(1)1x -<的解集为 ;4.已知全集{0,1,2,3,4}U =,{0,1,2}M =,{2,3}N =,则()U C M N = ;5.已知2()26f x x mx =-+在(]1-∞-,为减函数,则m 的范围为 ; 6.已知23.0=a ,3.0log2=b ,3.02=c ,则a b c ,,的大小关系是 ;7.已知函数x y a b =+的图像如右图所示,则a b += ; 8.方程2|log |20x x +-=解的个数为 ;9.设1{212}2a ∈---,,,,若幂函数ay x =为偶函数且在(0)+∞,上单调递减,则a = ;10.对应:f A B →是集合A 到集合B 的映射,若集合{10}A =-,,{12}B =,,则这样的映射有 个;11.用二分法求函数)(x f y =在区间[24],上零点的近似解,经验证有0)4()2(<⋅f f .取区间的中点为1=3x ,计算得0)()2(1<⋅x f f ,则此时零点∈0x ;(填区间)12.下列推理中,①A l A l B l B ααα∈∈⎫⇒⊂⎬∈∈⎭,,; ②A A AB B B αβαβαβ∈∈⎫⇒=⎬∈∈⎭,,;③a A A a αα⊂⎫⇒∈⎬∈⎭; ④a A A a αα⊄⎫⇒∉⎬∈⎭.其中正确的序号是 ;13.设函数22460()6log (1)0x x x f x x x ⎧-+≥=⎨--<⎩,,,若互不相同的三个实数123x x x ,,满足123()()()f x f x f x ==,则123x x x ++的取值范围是 ;14.设()f x 是定义在R 上的奇函数,且当0≥x 时,2)(x x f =,若对任意的[2]x t t ∈+,,不等式(2)4()f x t f x +≥恒成立,则实数t 的取值范围是 .二、解答题(本大题共6小题,共计90分.请在答题卡指定区域.......内作答,解答时应写出必要的文字说明、证明过程或演算步骤.) 15.(本题满分14分)设全集U R =,记函数25()22f x x x =-+的值域为M ,集合(1][3+)N =-∞∞,,. (1)求集合M ; (2)若集合M N 和()U C MN .16.(本题满分14分)(1)已知a =,b =,求231212322[()()]a b ab a -----的值;(2)计算22lg8lg 5lg 2lg 50lg 253++⋅+的值.17.(本题满分14分)已知函数22()21x xa a f x ⋅-+=+(a R ∈). (1)试判断)(x f 的单调性,并证明你的结论; (2)若)(x f 为定义域上的奇函数,① 当[11]x ∈-,时,求函数()f x 的值域; ② 求满足()(2)f ax f a x ≤-的x 的取值范围.18.(本题满分16分)某校高一(2)班共有学生51人,据统计原来每人每年用于购买饮料的平均支出是a 元,若该班全体学生改饮某品牌的桶装纯净水,经测算和市场调查,其年总费用由两部分组成,一部分是购买纯净水的费用,另一部分是其它费用228元,其中,纯净水的销售价x (元/桶)与年购买总量y (桶)之间满足如图所示关系.(1)求y 关于x 的函数关系式;(2)当120=a 时,若该班每年需要纯净水380桶,请你根据提供的信息比较,该班全体学生改饮桶装纯净水的年总费用与该班全体学生购买饮料的年总费用,哪一种更少?说明你的理由;(3)当a 至少为多少时,该班学生集体改饮桶装纯净水的年总费用一定比该班全体学生购买饮料的年总费用少?19.(本题满分16分)已知函数1)(2++=bx ax x f (a b R ∈,且0≠a ),⎩⎨⎧<->=0),(0),()(x x f x x f x F .(1)若0)1(=-f ,且函数)(x f 的值域为[0)+∞,,求)(x F 的解析式; (2)在(1)的条件下,当[22]x ∈-,时,kx x f x g -=)()(是单调函数,求实数k 的取值范围;(3)设0<mn ,0,0>>+a n m , 且)(x f 是偶函数,判断)()(n F m F +是否大于零?/桶)20.(本题满分16分)若函数()f x 满足下列条件:在定义域内存在,0x 使得00(1)()(1)f x f x f +=+成立,则称函数()f x 具有性质M ;反之,若0x 不存在,则称函数()f x 不具有性质M . (1)证明:函数()2xf x =具有性质M ,并求出对应的0x 的值; (2)已知函数2()lg1ah x x =+具有性质M ,求a 的取值范围; (3)试探究形如:①(0)y kx b k =+≠,②2(0)y ax bx c a =++≠,③(0)ky k x=≠,④x y a =(01)xy a a a =>≠且,⑤log (01)a y x a a =>≠且的函数,指出哪些函数一定具有性质M ?并说明理由.1.3log m n = 2.(0,1] 3.(1,11) 4.{3} 5.1m ≥- 6.c a b >> 7.0 8.2 9.2- 10.4 11.(2,3) 12.①②③13.(11,4)- 14.[2,+∞)(3)设该班每年购买纯净水的费用为P 元,则,3240)9(40)72040(2+--=+-==x x x xy P 32409max ==∴P x 时,当要使饮用桶装纯净水的年总费用一定比该班全体学生购买饮料的年总费用少,则,22851max +≥P a 解得68≥a ,故a 至少为68元时全班饮用桶装纯净水的年总费用一定比该班全体学生购买饮料的年总费用少。
2019-2020学年江苏省连云港市海头高级中学高一上学期期中数学试题(解析版)

2019-2020学年江苏省连云港市海头高级中学高一上学期期中数学试题一、单选题1.已知集合{1,2,3,6}A =-,{|23}B x x =-<<,则A B =I ( ) A .{|23}x x -<< B .{3,6} C .{1,2}-D .{1,2,3}-【答案】C【解析】根据已知中集合{1,2,3,6}A =-,{|23}B x x =-<<,结合集合交集的定义可得答案. 【详解】解:Q 集合{1,2,3,6}A =-,{|23}B x x =-<<,{}1,2A B ∴=-I ,故选:C . 【点睛】本题考查的知识点是集合的交集及其运算,难度不大,属于基础题. 2.函数()2log (1)a f x x =++(0a >,且1a ≠)恒过定点( ) A .(0,1) B .(1,2)C .(1,3)D .(0,2)【答案】D【解析】令()2log (1)a f x x =++的真数值为1,求得自变量x 的值即可求得答案. 【详解】解:()2log (1)a f x x =++Q 令11x +=,得0x =,()()02log 012a f =++=Q ,∴函数()2log (1)a f x x =++的图象经过定点()0,2.故选:D . 【点睛】本题考查对数函数的单调性与特殊点,属于基础题.3.已知幂函数图像经过点(2,8),则该幂函数的解析式是( )A .3x y =B .x y =C .3y x =D .y x =【答案】C【解析】设出幂函数的解析式,代入点的坐标,求出函数的解析式即可. 【详解】解:设幂函数为()f x x α=,因为图象经过点(2,8), ()228f α∴==,解得3α=,函数的解析式3()f x x =, 故选:C . 【点睛】本题考查了求幂函数的解析式问题,待定系数法是常用方法之一,属于基础题. 4.设()338xf x x =+-,用二分法求方程3380x x +-=在()1,2x ∈内近似解的过程中得()()()10, 1.50, 1.250,f f f <><则方程的根落在区间( ) A .()1,1.25 B .()1.25,1.5C .()1.5,2D .不能确定【答案】B【解析】根据二分法求根的方法判断即可. 【详解】由()()1.50, 1.250,f f ><可知方程的根落在()1.25,1.5内. 故选:B 【点睛】本题主要考查了二分法求根的方法等,属于基础题型.5.已知()f x 是奇函数,当0x >时()(1)f x x x =-+,当0x <时,()f x 等于( ) A .(1)x x -- B .(1)x x -C .(1)x x -+D .(1)x x +【答案】B【解析】由0x <时,0x ->,则()(1)f x x x -=-,根据函数的奇偶性,即可得到函数的解析式;【详解】当x 0<时,x 0->,则()()f x x 1x -=-.又()f x 是R 上的奇函数,所以当x 0<时()()()f x f x x 1x =--=--. 故选项A 正确. 【点睛】本题主要考查了利用函数的奇偶性求解函数的解析式,其中解答中合理利用函数的奇偶性转化求解是解答的关键,着重考查了推理与计算能力,属于基础题. 6.函数()f x 的增区间是(2,3)-,则(5)y f x =+的单调增区间是( ) A .(3,8) B .(7,2)--C .(2,8)-D .(2,3)-【答案】B【解析】函数(5)y f x =+是函数()f x 向左平移5个单位,利用函数()f x 在区间(2,3)-是增函,即可得到结论. 【详解】解:函数(5)y f x =+是函数()f x 向左平移5个单位Q 函数()f x 在区间(2,3)-是增函数(5)y f x ∴=+增区间为(2,3)-向左平移5个单位,即增区间为(7,2)--,故选:B . 【点睛】本题考查图象的变换,及函数的单调性,属于基础题.7.设13log 5a =,153b =,0.315c ⎛⎫= ⎪⎝⎭,则有( ) A .a b c << B .c b a << C .c a b << D .a c b <<【答案】D【解析】根据对数函数的单调性,可以判断出a <0,b >1,根据指数函数的值域及单调性可判断出0<c <1,进而得到a 、b 、c 的大小顺序. 【详解】∵y=13log x 在定义域上单调递减函数,∴a 13log =5<13log 1=0,y=3x 在定义域上单调递增函数,b10533==>1,y=(15)x在定义域上单调递减函数,0<c =(15)0.3<(15)0=1, ∴a <c <b 故选D . 【点睛】本题考查的知识点是利用函数的单调性比较数的大小,熟练掌握指数函数和对数函数的单调性是解答的关键. 8.若2log 13a<,则实数a 的取值范围是( ) A .203a << B .23a >C .203a <<或1a > D .213a <<【答案】C【解析】讨论底数与1的关系,确定函数的单调性,根据函数的单调性整理出关于a 的不等式,得到结果,把两种情况求并集得到结果. 【详解】∵log a 23<1=log a a ,当a >1时,函数是一个增函数,不等式成立,当0<a <1时,函数是一个减函数,根据函数的单调性有a 23<, 综上可知a 的取值范围是203a <<或1a >, 故选C. 【点睛】本题主要考查对数函数单调性的应用、不等式的解法等基础知识,本题解题的关键是讨论底数与1的关系,属于基础题.9.函数()221f x ax x =-+在区间()1,1-和区间()1,2上分别有一个零点,则实数a 的取值范围是 ( ) A .()3,1--B .3,14⎛⎫⎪⎝⎭C .33,4⎛⎫- ⎪⎝⎭D .()3,3,4⎛⎫-∞-⋃+∞⎪⎝⎭【答案】B【解析】利用排除法:当1a =时,()()22211f x x x x =-+=-,此时函数只有一个零点,不合题意,排除D 选项,当0a =时,()21f x x =-+,此时函数只有一个零点,不合题意,排除AC 选项,本题选择B 选项.10.已知函数3())8f x x x =+-,且(2)10f -=,那么(2)f =( ) A .10 B .10-C .18-D .26-【答案】D【解析】令g (x)=)lnx ,由函数奇偶性的定义得其为奇函数,根据题意和奇函数的性质求出f (2)的值. 【详解】 令g (x)=)lnx ,则g (-x)=)lnx ,g (x )+ g (-x )=))ln ?ln10x x ln +==,可得其为奇函数,又y=3x 为奇函数,则f (x )+8为奇函数,所以f (﹣2)+8+f(2)+8=0,即10+8+ ()280f +=, 则f (2)=﹣26, 故选:D . 【点睛】本题考查函数奇偶性的判定及应用,以及整体代换求函数值的方法,属于中档题.11.已知()243,1log 2,1a x ax x f x x a x ⎧-+<=⎨+≥⎩满足对任意12x x ≠,都有()()12120f x f x x x -<-成立,那么a 的取值范围是( ) A .10,2⎛⎤ ⎥⎝⎦B .1,12⎡⎫⎪⎢⎣⎭C .12,23⎡⎤⎢⎥⎣⎦D .2,13⎡⎫⎪⎢⎣⎭【答案】C【解析】判断函数的单调性.利用分段函数解析式,结合单调性列出不等式组求解即可. 【详解】解:243,1log 2,1a x ax x f x x a x ⎧-+<=⎨+≥⎩()满足对任意12x x ≠,都有()()12120f x f x x x --<成立, 所以分段函数是减函数,所以:0121442aaa a<<⎧⎪≥⎨⎪-≥⎩,解得12,23a⎡⎤∈⎢⎥⎣⎦.故选:C.【点睛】本题考查分段函数的单调性的应用,函数的单调性的定义的理解,考查转化思想以及计算能力.12.设函数3log,03()4,3x xf xx x⎧<≤=⎨-+>⎩,若实数,,a b c满足a b c<<,且()()()f a f b f c==,则(2)cab+的取值范围是()A.(3,4)B.(3,27)C.(9,27)D.(27,81)【答案】D【解析】根据函数解析式作出函数图象,由a b c<<,且()()()f a f b f c==,可得1ab=,34c<<,根据指数函数的单调性即可求出(2)cab+的取值范围.【详解】解:3log,03()4,3x xf xx x⎧<≤=⎨-+>⎩Q可作函数图象如下所示:因为实数,,a b c满足a b c<<,且()()()f a f b f c==,由图可知11343a b c ∴<<<<<< 33log log a b ∴=33log log a b ∴-=即1a b -=1ab ∴=(2)3c c ab ∴+=3x y =Q 在定义域上单调递增,且()3,4c ∈()327,81c ∴∈即()(2)27,81c ab ∴+∈故选:D 【点睛】本题考查数形结合思想,函数单调性的应用,以及对数的运算,属于难题.二、填空题13.已知函数()f x 满足()x f e x =,则(5)f =________. 【答案】ln 5【解析】由已知,()xf e x =,将5写成e α形式,则实数α为所求.【详解】解:由于()xf e x =,令5x e =,转化为对数式得出,log 55e x ln ==,即有()55()5ln f f e ln ==故答案为:5ln . 【点睛】本题考查函数的解析式表示法,函数值求解.根据函数的解析式构造出()()55ln f f e =是关键,属于基础题. 14.已知集合1|22xA x ⎧⎫=≤⎨⎬⎩⎭,(,)B a =-∞,若A B ⊆,则实数a 的取值范围是(,)c +∞,其中c =________.【答案】-1【解析】由题意解出集合A ,根据集合的包含关系求出参数a 的取值范围,即可得到c 的值.解:1|22xA x ⎧⎫=≤⎨⎬⎩⎭Q {}(]|1,1A x x ∴=≤-=-∞-(,)B a =-∞Q 且A B ⊆1a ∴>-即()1,a ∈-+∞又a Q 的取值范围是(,)c +∞1c ∴=-故答案为:1- 【点睛】本题考查根据集合的包含关系求参数的取值范围问题,属于基础题.15.定义域{|0}x x >为的函数()f x 满足()()()f xy f x f y =+且(8)3f =,则(2)f =_______.【答案】1【解析】根据题意可得()()832f f =,从而求得()2f 的值. 【详解】解:Q 函数()f x 满足()()()f xy f x f y =+,()(),0,x y ∈+∞且(8)3f =,()()()()842323f f f f ∴=+==∴()21f =,故答案为:1. 【点睛】本题考查根据函数的性质求函数的值,属于基础题.16.函数()y f x =是定义域为R 的增函数,且()y f x =的图像经过点(2,3)A --和()1,3B ,则不等式()3f x <的解集为________.【答案】(2,1)-【解析】由题意()3f x <等价于3()3f x -<<根据函数的单调性与特殊点的函数值,将函数不等式转化为自变量的不等式,即可求解.解: ()3f x <Q3()3f x ∴-<<()y f x =Q 的图像经过点(2,3)A --和()1,3B()23f ∴-=-,()13f =又因为()y f x =是定义域为R 的增函数,()()()21f f x f ∴-<<21x ∴-<<故答案为: ()2,1- 【点睛】本题考查函数的单调性,属于基础题.三、解答题17.计算:(1)22333(0.9)()(3)28--+⋅(2)7log 23log lg25lg47++-.【答案】(11 ; (2)32. 【解析】根据实数指数幂的运算公式和对数的运算公式,即可求解的结果. 【详解】由题意,(1)原式4911)194=+⨯+=; (2)原式3133log 27(lg 25lg 4)222222=++-=+-=.【点睛】本题主要考查了指数幂的化简,运算求值和对数的运算求值问题,其中熟记实数指数幂的运算公式和对数的运算公式是解答此类问题的关键,着重考查了推理与运算能力,属于基础题.18.已知函数1()lg 33x f x ⎛⎫=- ⎪⎝⎭的定义域为M .(1)求M ;(2)当x M ∈时,求111()242xx g x -⎛⎫⎛⎫=-+ ⎪ ⎪⎝⎭⎝⎭的值域.【答案】(1)(1,2]M =-(2)[1,2)【解析】(1)根据偶次方根的被开方数大于等于零,对数函数的真数大于零,得到不等式组,解得;(2)令12xt ⎛⎫= ⎪⎝⎭将函数转化为关于t 的二次函数,结合t 的取值范围求出函数的值域.【详解】 解:(1)1()2lg 33x f x x ⎛⎫=-+- ⎪⎝⎭Q201303x x -≥⎧⎪∴⎨->⎪⎩,解得12x -<≤,即(1,2]x ∈-,即函数的定义域(1,2]M =-. (2)因为(1,2]M =-,令12xt ⎛⎫= ⎪⎝⎭,1,24t ⎡⎫∈⎪⎢⎣⎭, 则22()22(1)1g t t t t =-+=-+,而()g t 在1,14⎡⎤⎢⎥⎣⎦上单调递减,[1,2)上单调递增, 所以()[(1),(2))g t g g ∈,即()[1,2)g t ∈, 所以值域为[1,2). 【点睛】本题考查函数的定义域值域的求解,利用换元法求函数的值域,属于基础题.19.某企业拟用10万元投资甲、乙两种商品.已知各投入x 万元,甲、乙两种商品分别可获得12,y y 万元的利润,利润曲线11:nP y ax =,22:P y bx c =+,如图所示.(1)求函数12,y y 的解析式;(2)应怎样分配投资资金,才能使投资获得的利润最大? 【答案】(1)1y =214y x =;(2)当投资甲商品6.25万元,乙商品3.75万元时,所获得的利润最大值为6516万元. 【解析】【详解】试题分析:(1)由图可知,点()()1,1.25,4,2.5在曲线1P 上,将两点的坐标代入曲线的方程,列方程组可求得1y =同理()4,1在曲线2P 上,将其代入曲线的方程可求得214y x =.(2)设投资甲商品x 万元,乙商品10x -万元,则利润表达式为1542y x =+,利用换元法和配方法,可求得当投资甲商品6.25万元,乙商品3.75万元时,所获得的利润最大值为6512万元. 试题解析:(1)由题知()1,1.25,()4,2.5在曲线1P 上,则 1.2512.54n na a ⎧=⋅⎨=⋅⎩, 解得54{12a n ==,即1y =又()4,1在曲线2P 上,且0c =,则14b =, 则14b =,所以214y x =. (2)设甲投资x 万元,则乙投资为()10x -万元, 投资获得的利润为y 万元,则()1104y x =-1542x =+,t ⎡=∈⎣,则2215515654424216y t t t ⎛⎫=-++=--+⎪⎝⎭. 当52t =,即25 6.254x ==(万元)时,利润最大为6516万元,此时10 3.75x -=(万元),答:当投资甲商品6.25万元,乙商品3.75万元时,所获得的利润最大值为6516万元. 20.已知函数13()log 1a xf x x-=+是定义在(1,1)-上的奇函数. (1)求a 的值;(2)判断函数()f x 在(1,1)-区间上的单调性,并证明; (3)求不等式(2)(1)0f x f x +->的解集.【答案】(1)1a =(2)函数()f x 在区间(1,1)-上的单调递增,证明见解析(3)10,2x ⎛⎫∈ ⎪⎝⎭【解析】(1)根据函数为在(1,1)-上的奇函数,则()00f =,得到关于a 的方程,求解可得,需注意检验;(2)利用定义法证明函数的单调性,按照“设元,作差,变形,判断符号,下结论”五步来完成即可;(3)根据函数的单调性奇偶性,将函数不等式转化为自变量的不等式,需注意函数的定义域,得到不等式组,解得; 【详解】解:(1)因为函数13()log 1a xf x x-=+是定义在(1,1)-上的奇函数, 所以13(0)log 0f a ==,解得1a =,此时131()log 1x f x x -=+,由101xx ->+,得定义域为(1,1)-, 而131()log 1x f x x +-=-131log 1xx -=-+()f x =-, 则函数13()log 1a xf x x-=+是奇函数, 所以1a =满足题意.(2)函数()f x 在区间(1,1)-上的单调递增, 下面证明:任取12,(1,1)x x ∈-,且12x x <, 则()()121211123311log log 11x x f x f x x x ---=-++()()()()12112311log 11x x x x -+=+-, 而()()()()()()()1221121211211111x x x x x x x x -+--=+-+-,因为12,(1,1)x x ∈-,且12x x <, 所以210x x ->,1210,0x x +>->,所以()()()()()()()12211212112101111x x x x x x x x -+--=>+-+-,所以()()()()121211111x x x x -+>+-,所以()()()()()()1212112311log 011x x f x f x x x -+-=<+-,所以()()120f x f x -<, 所以()()12f x f x <,所以函数()f x 在区间(1,1)-上的单调递增. (3)因为函数()f x 是定义在(1,1)-上的奇函数, 所以不等式(2)(1)0f x f x +->可化为(2)(1)f x f x >-, 又因为函数()f x 在区间(1,1)-上的单调递增,所以12111121x x x x -<<⎧⎪-<-<⎨⎪>-⎩,解得10,2x ⎛⎫∈ ⎪⎝⎭.【点睛】本题考查利用函数的奇偶性求函数解析式,函数单调性的证明,利用函数的单调性解不等式,属于综合题.21.已知f(x)=ax2+bx+c(a≠0),满足条件f(x+1)-f(x)=2x(x∈R),且f(0)=1.(Ⅰ)求f(x)的解析式;(Ⅱ)当x≥0时,f(x)≥mx-3恒成立,求实数m的取值范围.【答案】(Ⅰ)f(x)=x2-x+1;(Ⅱ)(-∞,3].【解析】(Ⅰ)根据f(0)=1及f(x+1)-f(x)=2x,代入解析式,根据对应位置系数相等,即可求得a、b、c的值,得到f(x)的解析式。
江苏省连云港市赣榆县海头高级中学高三数学上学期期中

海州高级中学2014--2015学年度第一学期期中学情调查考试高三数学试题填空题:本大题共14小题,每小题5分,共计70分.1. 已知集合A={-2,-1,3,4},B={x| x > 0}, 则=B A I2. 若复数()是虚数单位)i i z (432+=, 则z 的虚部为3. 执行如图所示的程序框图,如果输入a=2, b=2,那么输出的a 值为4. 从1,2,3,4这4个数中一次随机地取2个数,则所取2个数和为5的概率是5. 已知函数x y 2sin =与()()πϕϕ<≤+=0cos x y , 它们的图象有一个横坐标为12π的交点, 则ϕ的值是6. 随机抽取100名年龄在[)[)[)60,50,,30,20,20,10ΛΛ年龄段的市民进行问卷调查,由此得到样本的频率分布直方图如图所示,从不小于40岁的人中按年龄段分层抽样的方法随机抽取8人,则在[)60,50年龄段抽取的人数为 .7. 已知等比数列{a n }中, a 3+a 5=8, a 1a 5=4, 则=913a a 8. 已知直线y=kx+3与圆()()43222=-+-y x 相交与M,N 点,若|MN|≥23,则k 的取值范围是9. 平面直角坐标系xoy 中,若曲线axe y =在点(0,1)处的切线为m x y +=2,则a+m 的值是10. 不共线的四点O,A,B,C 满足=+=BCAB OC OA OB 则,3231 开始 输入a ,blog 3a >4aa b否 是输出a 结束(第3题)(第6题)A B P 11.已知函数122++=ax ax y 的值域为[)+∞,0, 则实数a 的取值范围是12. 在⊿ABC 中,若AB=2,AC+BC=3,则cosC 的最小值是 13.某公园的摩天轮观览车主架示意图如图所示,其中O 为轮轴中心,距地面32m (即OM 长),巨轮半径为30m ,AM=BP=2m ,巨轮逆时针旋转且12分钟转动一圈. 若点M 为P 的初始位置(O,A,M 共线),经过t 分钟,该吊舱P 距地面的高度为h(t),则h(t)=14.已知()x f 是定义在R 上且周期为2的函数,当[)2,0∈x 时,()112--=x x f ,若函数()a x f y -=在区间上有8个零点(互不相同),则实数a 的取值范围是一、解答题: 本大题共6小题,共计90分. 解答时应写出文字说明、证明过程或演算步骤.15.(本小题满分14分) 已知αα,135sin -=是第四象限角 (1) 求⎪⎭⎫⎝⎛-απ3sin 的值; (2) 求⎪⎭⎫⎝⎛-απ265cos 的值.16. (本小题满分14分)如图, 在等腰直角⊿ABC 中, ∠ABC=900,腰长为2, P 为⊿ABC 外一点, ∠BPC=900. (1) 若PC=3,求PA 长;(2) 若∠APB=300, 求tan ∠PBA.17. (本小题满分14分)如图,某山区的两个工厂A 、B 直线距离14km ,工厂C 距A 、B 直线距离都是25km ,E 为线段AB 的中点,在线段CE 上选建变电站D, 并从点D 处铺设到工厂A,B,C 的输电线DA,DB,DC. (1) 变电站D 建在何处,可使铺设的总输电线长最短?(2) 因山区复杂条件, 希望铺设的三段输电线中最远一段的长度为最小, 那么变电站D 建在何处?18. (本小题满分16分)如图,已知椭圆E: 23)0(12222的离心率为>>=+b a b y a x , 过左焦点F ()03,-且斜率为k 的直线交椭圆于A,B 两点,线段AB 的中点为M, 直线04:=+ky x l(1) 求椭圆E 的方程;(2) 求证:点M 在直线l 上;(3) 若⊿BDM 的面积是⊿ACM 面积的3倍, 求斜率k 的值.19. (本小题满分16分)设函数())(ln 2R a x ax x x f ∈-+=(1) 若a=1, 求函数()x f 的单调区间;(2) 设函数()()2x x f x g -=,若()x g 在区间(]1,0上是减函数, 求实数a 的取值范围;(3) 过坐标原点O 作曲线()x f y =的切线,证明:切点的横坐标为1.20. (本小题满分16分)设数列{a n }是等差数列,首项为a 1, 公差为d, 前n 项和为S n , 若数列{a n }中任意不同两项之和仍是该数列中的一项,则称该数列为“F 数列”. (1)若a 1=4, d=2, 判断该数列是否为“F 数列”.(2)若a 1,d N ∈,是否存在这样的“F 数列”, 使S 10 ≤70? 若存在,求出所有满足条件的数列的通项公式;若不存在,请说明理由.(3)试问:数列{a n }为“F 数列”的充要条件是什么?给出你的结论并加以证明.高三数学参考答案 一、填空题:1.、{3,4} 2、 24 3、 256 4、31 5.、 4π6、 27、 98、 ⎥⎦⎤⎢⎣⎡-33,33 9.、 3 10、 2 11、 __ [)+∞,1 12、91 13、h (t )=3026sin 30+⎪⎭⎫ ⎝⎛-ππt 14、 (0,1)二、解答题15..解 (1)由题意得13121351sin 1cos 22=⎪⎭⎫⎝⎛--=-=αα所以,26312513521131223sin 3cos cos 3sin 3sin +=⎪⎭⎫ ⎝⎛-⋅-⋅=-=⎪⎭⎫⎝⎛-απαπαπ----7分 (2)由(1)得1691191cos 22cos ,169120cos sin 22sin 2=-=-==ααααα,所以, 3383119120)169120(21169119232sin 65sin 2cos 65cos 265cos +-=-⋅+⋅-=+=⎪⎭⎫⎝⎛-απαπαπ------------------------------------------------------------------------------------------------------------14分16.解 (1)在直角⊿BPC 中,∠BPC=900,BC=2,PC=3,所以,∠BC P=300又等腰直角⊿ABC 中, ∠ABC=900,所以在⊿PCA 中,∠PCA=750,AC=22根据余弦定理,0222752COS AC PC AC PC PA ⋅⋅-+= 因()42630sin 45sin 30cos 45cos 3045cos 75cos 000000-=-=+= 所以325426223283+=-⨯⨯⨯-+=PA --------------------------7分 (2)设∠PBA= x 则∠PBC= x-900,∠PAB=1500-x在直角⊿BPC 中,BP=2()x -090cos在⊿PAB 中,根据正弦定理 ()()xx --=000150sin 90cos 230sin 2,即()x x sin 21150sin 0=- 化简得213tan +-=x ,于是得 t an ∠PBA=213+-=-------------14分 17.解:(1)设DE=xkm ,铺设的总输电线长为l km ,根据题意 ()x l =24-x+2492+x (0≤x ≤24) ()49212'++-=x x x l ,令()0'=x l 得337=x 因)337,0(∈x 时()0'<x l ,()x l 单调递减 )24,337(∈x 时()0'>x l ,()x l 单调递增, 所以当337=x ()x l 最小 于是,变电站D 建在线段CE 上距点Ekm 337,可使铺设的总输电线长最短-----7分 (2)设DE=xkm ,铺设的三段输电线中最远一段的长度为)(x d km ,则有 {}49,24max )(2+-=x x x d (0≤x ≤24)⎪⎩⎪⎨⎧+<-++≥--=4924,494924,24)(222x x x x x x x d=⎪⎩⎪⎨⎧≤<+≤≤-2448569,49485690,242x x x x 因()x x d x -=⎥⎦⎤⎢⎣⎡∈24,48569,0单调递减,⎥⎦⎤ ⎝⎛∈24,48569x ,49)(2+=x x d 单调递增 所以48569=x 时,)(x d 取得最小值于是变电站D 建在线段CE 上距点E km 48569处,可使铺设的三段输电线中最远一段的长度为最小.------------------------------------------------------------------------------------------------14分 18.解:(1)椭圆方程1422=+y x --------------------------4分(2)证明:设A(x 1,y 1),B(x 2,y 2),M(x 0,y 0)⎪⎩⎪⎨⎧=++=14)3(22y x x k y 即041238)14(2222=-+++k x k x k 所以14342,1438222102221+-=+=+-=+k k x x x k k x x ,143)3(200+=+=k kx k y 因为014341434222=+⋅++-k k k k k ,所以D 点M 在直线l 上.----------------8分 (3)由(2)知点A 到直线CD 的距离与点B 到直线CD 的距离相等,因⊿BDM 的面积是⊿ACM 面积的3倍,所以DM=3CM, 又|OD|=|OC|, 于是M 是OC 的中点----10分设点C 的坐标为(x 3,y 3) 则y 0=23y 因为⎪⎩⎪⎨⎧=+-=14422y x ky x ,解得14123+=k y ,于是143142122+=+k k k ,解得812=k 所以42±=k -----------------------------------------------------------------------16分19.解:(1)当a=1时, ())0(ln 2>-+=x x x x x f()()xx x x x x f )1(12112'+-=-+= 当⎪⎭⎫ ⎝⎛∈21,0x 时, ()0'>x f , 当⎪⎭⎫ ⎝⎛+∞∈,21x 时, ()0'<x f ,所以()x f 单调递减区间⎪⎭⎫ ⎝⎛21,0,()x f 单调递增区间⎪⎭⎫ ⎝⎛+∞,21-----------4分(3) ()())0(ln 2>-=-=x x ax x x f x g , ()xax x a x g 11'-=-= 当a ≤0时,()0'<x g , ()x g 在区间(]1,0上是减函数当a>0时, ()xa x a x ax x a x g )1(11'-=-=-= 当⎪⎭⎫ ⎝⎛∈a x 1,0时, ()0'<x g , 当⎪⎭⎫ ⎝⎛+∞∈,1a x 时, ()0'>x g 此时函数()x g 的单调减区间为⎪⎭⎫ ⎝⎛a 1,0因()x g 在区间(]1,0上是减函数, 所以(]⎥⎦⎤ ⎝⎛⊆a1,01,0于是有11≥a即0<1≤a . 综上, 实数a 的取值范围(]1,∞------------10分 (3) 证明: 设切点为M ()()t f t ,, ()x a x x f 12'-+= 切线的斜率ta t k 12-+=, 又切线过原点, 所以()t t f k = ,()ta t t t f 12-+=, 即12ln 22-+=-+at t t at t所以0ln 12=+-t t存在性: t=1满足方程0ln 12=+-t t唯一性: 设 t t t h ln 1)(2+-=, ()012'>+=tt t h ,)(t h 在(0,+∞)单调递增,且0)1(=h 所以0ln 12=+-t t 有唯一解.综上, 切点的横坐标为1.---------------------------------------------------------------------16分20.(本小题满分16分)解 (1)由题意,a n =2n+2, 对于任意m,n 有a m +a n =2(m+n+1)+2, 因m+n+1*N ∈ ,于是令 P=m+n+1,则有a p =2p+2{}n a ∈,所以数列{a n }为“F 数列”.------------ 4分 (2)假设存在数列{a n }满足条件,即10a 1+45d ≤70, 则a 1和d 的可能值 ①d=0, a 1=0,1,2,3,4,5,6,7, 此时a n =0是“F 数列” ②d=1, a 1=0,1,2 此时a n =n-1,a n =n, a n =n+1均为“F 数列所以满足条件的数列通项公式为a n =0, a n =n-1, a n =n, a n =n+1-------------- ---8分 (3)结论: 数列{a n }为“F 数列”的充要条件是存在整数m ≥-1使a 1=md ------10分 证明:ⅰ) 充分性 若存在整数m ≥-1使a 1=md,则任取等差数列的两项a s , a t (s ≠t) 因s+t ≥3, m ≥-1所以s+t+m-1为≥1的正整数,于是a s +a t =a 1+(s-1)d+md+(t-1)d=a 1+(s+t+m-2)d=a m+s+t-1{}n a ∈-------12分 ⅱ) 必要性 任取等差数列的两项a s , a t (s ≠t),若存在a k 使得a s +a t =a k则2a1+(s+t-2)d=a1+(k-1)d, 于是a1=(k-s-t+1)d,故存在m=k-s-t+1∈Z使a1=md,下面证明m≥-1.当d=0,显然成立当d≠0,若m<-1, 则取p=-m≥-2,对不同的两项a1, a p,存在a q使a1+a p=a q.即2md+(-m-1)d=md+(q-1)d, 可得qd=0,这与q>0,d≠0矛盾故存在整数m≥-1使a1=md-----------------------------------------16分。
江苏省连云港市高一上学期数学期中考试试卷

江苏省连云港市高一上学期数学期中考试试卷姓名:________ 班级:________ 成绩:________一、单选题 (共10题;共20分)1. (2分) (2016高二上·宾阳期中) 已知A={x|x2﹣2x﹣3<0},B={x|ax2﹣x+b≥0},若A∩B=∅,A∪B=R,则a+b等于()A . 1B . ﹣1C . 2D . 42. (2分)下列四组中表示相等函数的是()A .B .C .D .3. (2分) (2017高一上·中山月考) 已知集合,且,则等于()A . -1B .C .D . 或-14. (2分) (2018高一上·吉林期末) 函数的值域是()A .B .C .D .5. (2分) (2018高一上·苏州期中) 不等式log2x<的解集是()A . {x|0<x< }B . {x|0<x< }C . {x|x> }D . {x|x> }6. (2分)已知函数f(x)的图象是连续不间断的,且有如下的x,f(x)对应值表:x123456f(x)11.88.6﹣6.4 4.5﹣26.8﹣86.2则函数f(x)在区间[1,6]上的零点有()A . 2个B . 3个C . 至少3个D . 至多2个7. (2分)设是连续的偶函数,且当时是单调函数,则满足的所有x之和为()A .B . 3C . -8D . 88. (2分)下列函数中既是奇函数,又是在上为增函数的是()A .B .C .D .9. (2分)函数的图象()A . 关于y轴对称B . 关于x轴对称C . 关于原点对称D . 关于直线y=x对称10. (2分) (2015高三上·平邑期末) 设函数y=f(x)满足f(﹣x)+f(x)=0且f(x+1)=f(x﹣1),若x∈(0,1)时,f(x)=log2 ,则y=f(x)在(1,2)内是()A . 单调增函数,且f(x)<0B . 单调减函数,且f(x)<0C . 单调增函数,且f(x)>0D . 单调减函数,且f(x)>0二、填空题 (共7题;共8分)11. (1分) (2016高一上·铜仁期中) 函数的定义域是________12. (1分) (2017高一上·吉林期末) 已知定义在R上的函数f(x)满足f(x+2)﹣f(x)=0,当x∈(0,2]时,f(x)=log4x,则f(2016)=________.13. (1分)已知幂函数y=f(x)的图象过点(3,),则log4f(2)=________14. (2分)甲、乙、丙、丁四个物体同时从某一点出发向同一个方向运动,其路程关于时间的函数关系式分别为,,,,有以下结论:①当时,甲走在最前面;②当时,乙走在最前面;③当时,丁走在最前面,当时,丁走在最后面;④丙不可能走在最前面,也不可能走在最后面;⑤如果它们一直运动下去,最终走在最前面的是甲.其中,正确结论的序号为________(把正确结论的序号都填上,多填或少填均不得分).15. (1分)若二次函数f(x)=ax2+bx+c(a≠0)的图象与直线y=x无交点,现有下列结论:①若a=1,b=2,则c>②若a+b+c=0,则不等式f(x)>x对一切实数x都成立③函数g(x)=ax2﹣bx+c的图象与直线y=﹣x也一定没有交点④若a>0,则不等式f[f(x)]>x对一切实数x都成立⑤方程f[f(x)]=x一定没有实数根其中正确的结论是________ (写出所有正确结论的编号)16. (1分) (2016高一上·辽宁期中) 设x∈R,[x]表示不超过x的最大整数,若存在实数t,使得[t]=1,[t2]=2,…,[tn]=n同时成立,则正整数n的最大值是________17. (1分) (2017高一上·张家港期中) 对实数a和b,定义运算“⊗”:a⊗b= ,设函数f(x)=(x2﹣2)⊗(x﹣x2),x∈R,若函数y=f(x)+c的图象与x轴恰有两个公共点,则实数c的取值范围是________.三、解答题 (共5题;共50分)18. (10分) (2016高一上·河北期中) 化简求值(1) 2 × ×(2)(log43﹣log83)(log32+log92)19. (10分) (2019高一上·沈阳月考) 已知集合,或.(1)若,求.(2)若,求的取值范围.20. (15分) (2019高二上·辽宁月考) 在等比数列中,公比,且满足,.(1)求数列的通项公式;(2)设,数列的前项和为,当取最大值时,求的值.21. (10分)已知二次函数f(x)=ax2+x+1,a∈R,a≠0).(1)若不等式f(x)>0的解集为,求实数a的值;(2)当a∈[﹣2,0]时,不等式f(x)>0恒成立,求实数x的取值范围;(3)对x∈[0,2]时,不等式f(x)>0恒成立,求实数a的取值范围.22. (5分) (2016高一上·荆州期中) 已知函数f(x)= (x∈R)(1)用定义证明f(x)是增函数;(2)若g(x)=f(x)﹣a是奇函数,求g(x)在(﹣∞,a]上的取值集合.参考答案一、单选题 (共10题;共20分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、二、填空题 (共7题;共8分)11-1、12-1、13-1、14-1、15-1、16-1、17-1、三、解答题 (共5题;共50分) 18-1、18-2、19-1、19-2、20-1、20-2、21-1、21-2、21-3、22-1、22-2、。
2023—2024学年江苏省连云港市赣榆区高一上学期11月期中数学试卷

2023—2024学年江苏省连云港市赣榆区高一上学期11月期中数学试卷一、单选题1. 已知集合,则()A.B.C.D.2. 命题“”的否定是()A.B.C.D.3. “”是“”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件4. 已知函数,则的值为()A.1B.2C.3D.45. 已知函数在上单调递减,则实数的取值范围是()A.B.C.D.6. 函数的值域是()A.B.C.D.7. 下棋可以锻炼脑部,促进脑细胞新陈代谢,锻炼脑力发育,开发智力.围棋拥有的超大棋盘,成为状态空间复杂度最高的棋类运动,其状态空间复杂度上限约为,而中国象棋的状态空间复杂度上限为,则下列各数中与最接近的是()A.B.C.D.8. 已知对任意两个实数,定义,设函数,设函数,若存在使得成立,则实数的取值范围为()A.B.C.D.二、多选题9. 已知,且,则下列结论正确的有()A.B.C.D.10. 设,若,则实数的值可以是()A.0B.C.D.211. “若对任意的都成立,则在上是增函数”为假命题,则下列函数中符合上述条件的是()A.B.C.D.12. 已知函数,且对任意的,当时,,且,则下列说法正确的是()A.B.C.在上是减函数D.在上的最小值为三、填空题13. 已知,则 __________ .14. 函数的单调递减区间是 ________ .15. 若不等式的一个必要条件为,则实数的取值范围是__________ .16. 设函数的定义域为,满足,且当时,.若对任意,都有,则实数的取值范围是 __________ .四、解答题17. 计算下列各式的值.(1) ;(2) .18. 已知函数.(1)画出函数的图像,并写出单调区间;(2)求函数的值域.19. 已知命题:关于的方程有实数根,命题.(1)若命题是真命题,求实数的取值范围;(2)若是的充分条件,求实数的取值范围.20. 已知函数.(1)判断函数在上的单调性,并利用定义证明;(2)若,求实数的取值范围.21. 设矩形的周长为,把沿向折叠,折过去后交于点.当矩形的宽为多少时,的面积最大?并求出这个最大值.22. 设函数,其中.(1)若,解关于的不等式;(2)当时,的最大值记为,最小值记为,求的解析式.。
江苏省赣榆县海头高级中学高一数学 综合测试 (3)

江苏省赣榆县海头高级中学高一数学综合测试(3)1、下列说法正确的是A、需要加热才能发生的反应一定是吸热反应B、化学反应中的能量变化都表现为热量变化C、任何放热反应在常温下一定能发生反应D、反应物和生成物所具有的总能量决定了反应是放热还是吸热2、已知:H+(aq)+OH-(aq)===H2O(l) △H=-57.3 kJ·mol-1。
现将一定量的稀盐酸、浓硫酸、稀醋酸分别和1L 1mol·L-1的NaOH溶液恰好完全反应,其反应热分别为△H1、△H2、△H3,则△H1、△H2和△H3的大小关系为A、△H1=△H2>△H3B、△H3>△H2>△H1C、△H3>△H1>△H2D、△H2>△H1>△H33、已知蓄电池在充电时作电解池,放电时作原电池。
铅蓄电池上有两个接线柱,一个接线柱旁标有“+”,另一个接线柱旁标有“—”。
关于标有“+”的接线柱,下列说法中正确..的是A.充电时作阳极,放电时作负极B.充电时作阳极,放电时作正极C.充电时作阴极,放电时作负极D.充电时作阴极,放电时作正极4、某混合溶液中只含有两种溶质NaCl和H2SO4,且n(NaCl): n(H2SO4)=3:1。
若以石墨电极电解该溶液,下列推断中不正确的是A.阴极产物为H2B.阳极先析出Cl2,后析出O2C.电解液的pH不断增大,最终大于7 D.整个电解的过程实质是电解水5、已知H—H键能为436 KJ/mol,H—N键能为391KJ/mol,根据化学方程式:N2 + 3H2 = 2NH3ΔH=—92.4 KJ/mol,则N≡N键的键能是 ( )A.431 KJ/mol B.946 KJ/mol C.649 KJ/mol D.869 KJ/mol6、已知充分燃烧a g 乙炔气体时生成1mol二氧化碳气体和液态水,并放出热量b kJ,则乙炔燃烧的热化学方程式正确的是A.2C2H2(g) + 5O2 (g) == 4CO2(g) + 2H2O(l);△H = -4b KJ/molB.C2H2(g) + 5/2O2(g) == 2CO2(g) + H2O(l);△H = 2b KJ/molC.2C2H2(g) + 5O2(g) == 4CO2(g) + 2H2O(l);△H = -2b KJ/molD.2C2H2(g) + 5O2(g) == 4CO2(g) + 2H2O(l);△H = b KJ/mol7、在一2L密闭容器中,盛有2molX和2molY物质进行如下反应:X(s)+3Y(g,当反应进行10s后,测得生成0.5molZ,则平均反应速率正确的为()A.v Z=0.05 mol·L-1·s-1B.v X.=0.025 mol·L-1·s-1C.v Y=0.05 mol·L-1·s-1D.v Y=0.075 mol·L-1·s-18、在500K,相同体积的甲、乙容器,甲容器中充入m g SO2和m g O2,乙容器中充入n g SO2和n g O2 (n>m),则下列叙述错误的是:()A.化学反应速率:乙>甲B.平衡时O2的浓度:乙>甲C.SO2的转化率:甲>乙D.平衡时SO2的体积分数:甲<乙9、一定条件下,在密闭容器中,能表示反应X(气)+ 2Y(气)2Z(气)一定达到化学平衡状态的是()①X、Y、Z的物质的量之比为1:2:2 ②X、Y、Z的浓度不再发生变化③容器中的压强不再发生变化④单位时间内生成n molZ,同时生成2n molYA.①②B.①④C.②③D.③④10、下列化学反应的混乱度(△S)增大的是()A、S(s)+3C(s)+2KNO3(s)=N2(g)+3CO2(g)+K2S(s)B、2NO(g)+O2(g)=2NO2(g)C、2CO(g)=C(s)+CO2(g)D、2SO2(g)+O2(g)=2SO3(g)11、在容积一定的密闭容器中,反应2A B(g)+C(g)达到平衡后,升高温度容器内气体的密度增大,则下列叙述正确的是()A.正反应是吸热反应,且A不是气态B.正反应是放热反应,且A是气态C.其他条件不变,加入少量A,该平衡向正反应方向移动D.12、对于反应2Z(g)不同温度(T1和T2)及压强(p1和p2)下产物Z的物质的量n(Z)和反应时间t的关系如右图所示,下列判断正确的是()A.T1<T2,p1<p2,△H<0B.T1<T2,p1>p2,△H>0C.T1>T2,p1>p2,△H<0D.T1>T2,p1<p2,△H>013、下列溶液,一定呈中性的是A. c(H+)=1×10-7mol/L的溶液B. pH=pOH 的溶液C. pH=14-pOH 的溶液D. 由等体积、等物质的量浓度的一元酸跟氢氧化钠溶液混合后所形成的溶液14、可逆反应:N2+3H2 2NH3的正、逆反应速度可用各反应物或生成物浓度变化来表示。
江苏省海头高级中学2021-2022高一数学上学期期中试题

江苏省海头高级中学2021-2022高一数学上学期期中试题(考试时间:120分钟 试卷满分:150分)一、选择题:本大题共12小题,每小题5分,共计60分.请把答案填写在答题卡相应位置. 1.已知集合A ={-1,2,3,6},B ={x |-2<x <3},则A ∩B =( )A .{x |-2<x <3}B .{3,6}C .{-1,2}D .{-1,2,3} 2.函数)1(log 2)(++=x x f a (0>a ,且1≠a )恒过定点( ) A.()0,1B.()1,2C.()1,3D.()0,23.已知幂函数图像经过点(2,8),则该幂函数的解析式是( ) A .xy 3= B .()xy 22= C .3x y =D .22x y =4.已知函数833)(-+=x x f x,在用二分法求方程0833=-+x x 在)2,1(内近似根的过程中,已经得到0)1(<f ,0)5.1(>f ,0)25.1(<f ,则方程的根落在区间( ) A .()1,1.25 B .()1.25,1.5C .()1.5,2D .不能确定5.已知()f x 是奇函数,当0x >时()(1)f x x x =-+,当0x <时,()f x 等于( ) A .(1)x x -- B .(1)x x - C .(1)x x -+D .(1)x x +6.函数f (x )在区间(-2,3)上是增函数,则y =f (x +5)的单调增区间是( ) A .(3,8) B .(-7,-2) C .(-2,8) D .(-2,3)7.设13log 5a =,153b =,0.315c ⎛⎫= ⎪⎝⎭,则有( ) A .a b c << B .c b a << C .c a b<< D .a c b <<8.若2log 13a<,则实数a 的取值范围是( ) A .203a <<B .23a >C .203a <<或1a >D .213a << 9.函数12)(2+-=x ax x f 在区间)1,1(-和区间)2,1(上分别有一个零点,则实数a 的取值范围是 ( )A .)1,3(--B .)1,43(C .)43,3(-D .),43()3,(+∞--∞U 10.已知函数3())8f x x x =+-,且(2)10f -=,那么(2)f =( ) A .10B .10-C .18-D .26-11.已知()243,1log 2,1a x ax x f x x a x ⎧-+<=⎨+≥⎩满足对任意12x x ≠,都有()()12120f x f x x x -<-成立,那么a 的取值范围是( ) A. 10,2⎛⎤ ⎥⎝⎦B. 1,12⎡⎫⎪⎢⎣⎭C. 12,23⎡⎤⎢⎥⎣⎦D. 2,13⎡⎫⎪⎢⎣⎭12. 设函数⎩⎨⎧>+-≤<=3,430,log )(3x x x x x f ,若实数c b a ,,满足c b a <<,且)()()(c f b f a f ==,则cab )2(+的取值范围是( ) A.(3,4) B.(3,27) C.(9,27) D. (27,81)二、填空题:本大题共4小题,每小题5分,共计20分.请把答案填写在答题卡相应位置.13.已知函数)(x f 满足x e f x=)(,则=)5(f .14.已知集合⎭⎬⎫⎩⎨⎧≤=212|xx A ,(),Ba =-∞,若A B ⊆,则实数a 的取值范围是(),c +∞,其中c = . 15.定义域为{}0x x >的函数()f x 满足()()()f xy f x f y =+且(8)3f =,则=)2(f _______.16.函数)(x f y =是定义域为R 的增函数,且)(x f y =的图像经过点)3,2(--A 和)3,1(B ,则不等式3)(<x f 的解集为 .三、解答题:请把答案填写在答题卡相应位置. 17.(本小题满分10分)计算:(1)222333(0.9)()(3)(12)28--+⋅+-;(2)7log 23log 27lg25lg47++-.18.(本小题满分12分) 已知函数)313lg(2)(-+-=x x x f 的定义域为M .(1)求M ;(2)当M x ∈时,求22141)(1+⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛=-x x x g 的值域.19.(本小题满分12分)某企业拟共用10万元投资甲、乙两种商品.已知各投入x 万元时,甲、乙两种商品可分别获得y 1,y 2万元的利润,利润曲线P 1:y 1=ax n ,P 2:y 2=bx +c 如图所示.(1)求函数y 1,y 2的解析式;(2)为使投资获得最大利润,应怎样分配投资?20.(本小题满分12分) 已知函数xxa x f +-=1log )(31是定义在)1,1(-上的奇函数. (1)求a 的值;(2)判断函数)(x f 在区间)1,1(-上的单调性,并证明; (3)求不等式0)1()2(>-+x f x f 的解集.21.(本小题满分12分)已知c bx ax x f ++=2)()0(≠a ,满足条件x x f x f 2)()1(=-+)(R x ∈,且1)0(=f .(1)求)(x f 的解析式;(2)当0≥x 时,3)(-≥mx x f 恒成立,求实数m 的取值范围.22.(本小题满分12分)已知二次函数2()fx x b xc =++的图像经过点(1,13),且函数1()2y f x =-是偶函数. (1)求函数()f x 的解析式;(2)已知2t <,2()()13g x fx x x ⎡⎤=--⋅⎣⎦,求函数()g x 在[],2t 上的最大值和最小值; (3)函数()y f x =的图像上是否存在这样的点,其横坐标是正整数,纵坐标是一个完全平方数?如果存在,求出这样点的坐标;如果不存在,请说明理由.海头高级中学2021—2010第一学期期中考试高一数学答案1-5 CDCBA 6-10 BDCBD 11-12 CD 13. 5ln 14. 1- 15. 1 16. )1,2(- 17. 解:(1)12-. ---------------5分 (2)23.---------------10分 18. 解:(1)由⎪⎩⎪⎨⎧>-≥-031302x x ,---------------2分解得(]2,1-∈x ,即(]2,1-=M .---------------5分 (2)因为(]2,1-=M ,令xt ⎪⎭⎫ ⎝⎛=21,⎪⎭⎫⎢⎣⎡∈2,41t ,---------------7分 则1)1(22)(22+-=+-=t t t t g ,---------------8分而)(t g 在⎥⎦⎤⎢⎣⎡1,41上单调递减,[)2,1上单调递增,---------------10分所以[))2(),1()(g g t g ∈,即[)2,1)(∈t g , 所以值域为[)2,1.---------------12分19.解:(1)由题图知P 1:y 1=ax n过点⎝ ⎛⎭⎪⎫1,54,⎝ ⎛⎭⎪⎫4,52,∴⎩⎪⎨⎪⎧ 54=a ·1n ,52=a ·4n,∴⎩⎪⎨⎪⎧a =54,n =12,∴y 1=54x 12,x ∈[0,+∞).---------------3分P 2:y 2=bx +c 过点(0,0),(4,1),∴⎩⎪⎨⎪⎧0=0+c ,1=4b +c ,∴⎩⎪⎨⎪⎧c =0,b =14,∴y 2=14x ,x ∈[0,+∞).---------------6分(2)设用x 万元投资甲商品,那么投资乙商品为(10-x )万元,---------------7分 则y =54x +14(10-x )=-14x +54 x +52=-14⎝ ⎛⎭⎪⎫x -522+6516(0≤x ≤10),---------------9分当且仅当x =52即x =254=6.25时,y max =6516,此时投资乙商品为10-x =10-6.25=3.75万元,---------------11分答:用6.25万元投资甲商品,3.75万元投资乙商品,才能获得最大利润.---------------12分(说明:利用换元法求最值,只要答案对,可得满分.)20.解:(1)因为函数xxa x f +-=1log )(31是定义在)1,1(-上的奇函数, 所以0log )0(31==a f ,解得1=a ,---------------2分此时x x x f +-=11log )(31,由011>+-x x,得定义域为)1,1(-, 而)(11log 11log )(3131x f x x x x x f -=+--=-+=-,则函数x xa x f +-=1log )(31是奇函数,所以1=a 满足题意. ---------------3分(2)函数)(x f 在区间)1,1(-上的单调递增,---------------4分 下面证明:任取)1,1(,21-∈x x ,且21x x <, 则)1)(1()1)(1(log 11log 11log )()(2121312231113121x x x x x x x x x f x f -++-=+--+-=-, 而)1)(1()(21)1)(1()1)(1(21122121x x x x x x x x -+-=--++-,因为)1,1(,21-∈x x ,且21x x <, 所以0,01,02112>->+>-x x x x ,所以0)1)(1()(21)1)(1()1)(1(21122121>-+-=--++-x x x x x x x x , 所以1)1)(1()1)(1(2121>-++-x x x x ,所以0)1)(1()1)(1(log )()(21213121<-++-=-x x x x x f x f ,所以0)()(21<-x f x f ,所以)()(21x f x f <,所以函数)(x f 在区间)1,1(-上的单调递增. ---------------8分 (3)因为函数)(x f 是定义在)1,1(-上的奇函数,所以不等式0)1()2(>-+x f x f 可化为)1()2(->x f x f ,---------------9分 又因为函数)(x f 在区间)1,1(-上的单调递增,所以⎪⎩⎪⎨⎧-><-<-<<-12111121x x x x ,---------------11分解得)21,0(∈x .---------------12分 (说明:单调性证明只要能判断即可得满分.)21. 解:(1)因为c bx ax x f ++=2)(且x x f x f 2)()1(=-+,所以x c bx ax c bx x a 2)()1(22=++-+++,即x b a ax 22=++,所以⎩⎨⎧=+=022b a a ,解得1,1-==b a ,---------------2分又1)0(=f ,得1=c ,---------------3分 所以1)(2+-=x x x f .---------------4分 (2)法一:因为当0≥x 时,3)(-≥mx x f 恒成立, 所以当0≥x 时,04)1(2≥++-x m x 恒成立, 令4)1()(2++-=x m x x g ,[)+∞∈,0x所以021≤+m ,---------------7分 或⎪⎩⎪⎨⎧≤∆>+0021m ,---------------10分 解得3≤m .---------------12分 法二:因为当0≥x 时,3)(-≥mx x f 恒成立, 所以当0≥x 时, 04)1(2≥++-x m x 恒成立, 令4)1()(2++-=x m x x g ,[)+∞∈,0x ,所以①当021≤+m ,即1-≤m 时,)(x g 在[)+∞,0上单调递增, 所以04)0()(min >==g x g 恒成立,---------------7分 ②当021>+m ,即1->m 时,)(x g 在⎪⎭⎫⎢⎣⎡+21,0m 上单调递减,⎪⎭⎫⎢⎣⎡+∞+,21m 上单调递增, 所以0)21()(min ≥+=m g x g ,解得3≤m ,所以31≤<-m ,---------------10分 综上,3≤m .---------------12分 法三:因为当0≥x 时,3)(-≥mx x f 恒成立, 所以当0≥x 时,42+-≤x x mx 恒成立,①当0=x 时,即40≤恒成立,即R m ∈,---------------6分 ②当0>x 时,则14-+≤xx m 恒成立, 令14)(-+=xx x g ,),0(+∞∈x , 任取),0(,21+∞∈x x ,且21x x <, 则2121212211214)()14()14()()(x x x x x x x x x x x g x g -⋅-=-+--+=-, 当]2,0(,21∈x x 时,因为21x x <,所以4,02121<<-x x x x ,所以0421<-x x , 所以0)()(21>-x g x g ,所以)()(21x g x g >, 所以函数)(x g 在]2,0(上单调递减, 当),2[,21+∞∈x x 时,因为21x x <,所以4,02121><-x x x x ,所以0421>-x x , 所以0)()(21<-x g x g ,所以)()(21x g x g <,所以函数)(x g 在),2[+∞上单调递增,---------------10分 所以3)2()(min ==g x g ,---------------11分 所以3≤m .---------------12分22. 解:(1)因为函数1()2y f x =-是偶函数,所以1()2y f x =-图像的对称轴为y 轴,因而二次函数2()fx x b xc =++的图像的对称轴方程为12x =-,即122b -=-,所以1b =-------------1分 又二次函数2()fx x b xc =++的图像经过点(1,13),所以113b c ++=,解得11c = 所以函数()f x 的解析式为2()11fx x x =++---------------------3分 (2)由(1)知,2()11fx x x =++ 则222(1)1,0()()13(2)(1)1,0x x g x f x x x x x x x ⎧--+≤⎪⎡⎤=--⋅=-⋅=⎨⎣⎦-->⎪⎩画出函数的图像可知当[],2x t ∈时,m a x ()0gx =------------------4分 当12t ≤<时,2m i n()()2g x g t t t ==---------------------5分 当121t -≤<时,m i n ()1gx =-----------------------6分 当12t <-时,2m i n()()2g x g t t t ==-+---------------------7分(3)假设函数()y f x =的图像上是否存在这样的点2(,),,P m n m N n N*∈∈符合要求, 则2211m m n++=,从而224(21)43n m -+= 即[2(21)][2(21)]43n m n m ++-+=----------------9分注意到43是质数,且2(21)2(21),2(21)0n m n m n m ++>-+++>所以2(21)432(21)1n m n m ++=⎧⎨-+=⎩,解得1011m n =⎧⎨=⎩,---------------------------11分所以函数()y f x =的图像上存在符合题意得点,其坐标为(10,121). ---------------12分。
江苏省海头高级中学高三数学上学期期中考试试卷
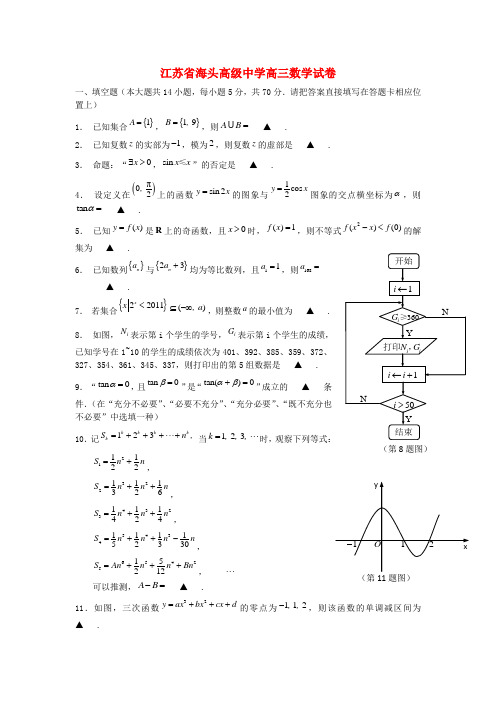
江苏省海头高级中学高三数学试卷一、填空题(本大题共14小题,每小题5分,共70分.请把答案直接填写在答题卡相应位置上) 1. 已知集合{}1A =,{}19B =, ,则A B =U ▲ .2. 已知复数z 的实部为1-,模为2,则复数z 的虚部是 ▲ . 3. 命题:“0x ∃>,sin x x ≤”的否定是 ▲ .4. 设定义在()π02, 上的函数sin 2y x =的图象与1cos 2y x =图象的交点横坐标为α,则tan α= ▲ .5. 已知()y f x =是R 上的奇函数,且0x >时,()1f x =,则不等式2()(0)f x x f -<的解集为 ▲ .6. 已知数列{}n a 与{}23n a +均为等比数列,且11a =,则168a =▲ .7. 若集合{}22011xx <()a ⊆-∞, ,则整数a 的最小值为 ▲ .8. 如图,i N 表示第i 个学生的学号,i G 表示第i 个学生的成绩,已知学号在1~10的学生的成绩依次为401、392、385、359、372、327、354、361、345、337,则打印出的第5组数据是 ▲ . 9. “tan 0α=,且t a n 0β=”是“t a n ()0αβ+=”成立的 ▲ 条件.(在“充分不必要”、“必要不充分”、“充分必要”、“既不充分也不必要”中选填一种)10.记123k k k kk S n =+++⋅⋅⋅+, 当123k =⋅⋅⋅, , , 时,观察下列等式:211122S n n =+,322111326S n n n =++,4323111424S n n n =++,5434111152330S n n n n =++-, 6542515212S An n n Bn =+++, ⋅⋅⋅可以推测,A B -= ▲ .11.如图,三次函数32y ax bx cx d =+++的零点为112-, , ,则该函数的单调减区间为 ▲ .(第11题图)12.已知函数e xy =的图象在点(e )k a k a , 处的切线与x 轴的交点的横坐标为1k a +,其中*k ∈N ,10a =,则135a a a ++= ▲ .13.已知中心为O 的正方形ABCD 的边长为2,点M 、N 分别为线段BC 、CD 上的两个不同点,且1MN ≤,则OM ON ⋅的取值范围是 ▲ .14.已知偶函数f :→Z Z 满足(1)1f =,(2011)1f ≠,对任意的a b ∈Z 、,都有()f a b +≤{}max ()()f a f b , ,(注:{}max x y , 表示x y , 中较大的数),则(2012)f 的可能值是▲ .二、解答题(本大题共6小题,共90分.解答时应写出文字说明、证明过程或演算步骤) 15.(本小题满分14分)平面直角坐标系xOy 中,已知向量()()()6123AB BC x y CD ===--, , , , , ,且//AD BC .(1)求x 与y 之间的关系式;(2)若AC BD ⊥,求四边形ABCD 的面积.16.(本小题满分14分)如图甲,在直角梯形PBCD 中,//PB CD ,CD BC ⊥,2BC PB CD ==,A 是PB 的中点. 现沿AD 把平面PAD 折起,使得PA AB ⊥(如图乙所示),E 、F 分别为BC 、AB 边的中点.(Ⅰ)求证:PA ⊥平面ABCD ; (Ⅱ)求证:平面PAE ⊥平面PDE ;(Ⅲ)在PA 上找一点G ,使得//FG 平面PDE .17.(本小题满分14分)如图,某兴趣小组测得菱形养殖区ABCD 的固定投食点A 到两条平行河岸线12l l 、的距离分别为4m 、8m ,河岸线1l 与该养殖区的最近点D 的距离为1m ,2l 与该养殖区的最近点B 的距离为2m .(1)如图甲,养殖区在投食点A 的右侧,若该小组测得60BAD ∠=,请据此算出养殖区的面积;(2)如图乙,养殖区在投食点A 的两侧,试在该小组未测得BAD ∠的大小的情况下,估算出养殖区的最小面积.18.(本小题满分16分)若椭圆22221x y a b += (0a b >>)过点(32)-,,离心率为3 ,O ⊙的圆心为原点,直径为椭圆的短轴,M ⊙的方程为22(8)(6)4x y -+-=,过M ⊙上任一点P 作O ⊙的第16题图甲图乙1l2l D A BC 1l 2lD A B C(图甲) (图乙)切线PA ,PB ,切点为A ,B 。
江苏省海头高级中学高一上学期数学综合训练(8).pdf

一、填空题本大题共每小题分,共分化简后等于 . 2.已知幂函数的图象过点 . 3.若,则的值为 . 4.已知函数,则函数=. 5.函数的定义域是 .函数 零点的个数为 个.斜二测直观图如右图所示,已知, ,则中边上中线的实际长度为 . 8.已知函数,则的值是 . 9.若,,且,则实数的值为 . 10.定义在上的偶函数当时单调递减,则的取值范围是,设函数是三个函数中的最小值,则函数的最大值是 . 12.在上有意义,则实数的取值范围是 . 13.函数,的是序号 ①当=0时,是偶;一定存在零点;在区间上单调递减;当0<<1时,的最小值为.在定义域上是单调函数.若对任意都有则 . 二、解答题(6大题共90分,将答案写到答题纸规定的位置,要求有必要的文字说明和步骤) 15.(本题满分1分) (1)求A∪B; (2)如果A∩C≠,求实数的取值范围. 16.(本题满分1分)为奇函数(为常数). 求的值; 用函数单调性定义证明函数在区间(1,+∞)上单调递增. 17.(本题满分1分)(a>0,a≠1,a为常数,x∈R). (1)若f(m)=8,求f(-m)的值; (2)若f(1)=3,求f(2)及的值 18. (本小题满分16分)某企业为适应市场需求,准备投入资金万生产和型两种产品.经市场预测,生产型产品所获利润(万元)与投入资金(万元)成正比例关系,又估计当投入资金万元时,可获利润万元.生产型产品所获利润(万元)与投入资金(万元)的关系满足,为获得最大利润,问生产型两种产品各应投入资金多少万元?获得的最大利润是多少?(本题满分16分) (1)求的值; (2)若在上无零点,求的取值范围. 20.(本题满分16分)(). (1)当时,函数的值域是,求实数a的值; (2)令函数. 当时,存在最大实数t,使得,有恒成立,请写出与的关系式.。
江苏省海头高级中学高一数学上学期综合训练(5)苏教版.pdf

江苏省海头高级中学高一上学期数学综合训练(5) 一、填空题:本大题共14小题,每小题5分,共70分,请把答案填写在答题纸相应的位置上 1.若,则 ▲ . 2.函数的定义域是 ▲ . .已知幂函数的图象过点,则 ▲ . .设函数满足,则的表达式是 ▲ . .的值域是 ▲ ..若,则按从大到小可排列为 ▲ . .已知,则 ▲ .在区间上的最大值与最小值之和为,则a的值为 ▲ ..,②,③,④,其中在区间上是单调是 ▲ ..已知方程的解所在区间为,则=▲ . .已知函数在上是减函数,则的取值范围是 ▲ . 1.定义在R上的奇函数满足:①在内单调递增②,则不等式的解集为 ▲ .13.已知,当时,恒成立,则实数的取值范围是 ▲ .14.已知函数,现给出下列命题: ① 当其图象是一条连续不断的曲线时则=; ② 当其图象是一条连续不断的曲线时能找到一个非零实数使在上是增函数; ③ 当时,不等式恒成立; ④ 函数是偶函数. 其中正确命题的序号是 ▲ .(填上所有你认为正确的命题的序号) 15.(本小题满分14分) 设全集R,集合,. (1)求; (2)若集合,满足,求实数的取值范围 16.(本小题满分14分) (1)计算的值; (),求和的值.17.(本小题满分15分) 已知为定义在R上的奇函数,当时为二次函数,在上的两个零点为和. (1)求函数在R上的解析式; (2)作出的图象并根据图象讨论关于的方程根的个数. .(本小题满分15分) 已知函数,其中,的定义域. ()求函数的定义域; ()若函数的最小值为,求的值; (),不等式<恒成立,求实数的取值范围. ()若为奇函数,求函数的值域求满足的的取值范围. 20.(本小题满分16分) 若函数满足下列条件:在定义域内存在使得成立,则称函数具有性质;反之,若不存在,则称函数不具有性质. (1)证明:函数具有性质,并求出对应的的值; (2)已知函数具有性质,求的取值范围; ()试探究①,②,③,④ ,⑤的函数,指出哪些函数一定具有性质?并明.。
江苏省海头高级中学高一数学上学期综合训练(5)苏教版

江苏省海头高级中学高一上学期数学综合训练(5)一、填空题:本大题共14小题,每小题5分,共70分,请把答案填写在答题纸相应的位置上.........1.若21{,x x ∈},则x = ▲ . 2.函数1x y x=-的定义域是 ▲ . 3.已知幂函数...)(x f y =的图象过点1(2,)4,则1()3f = ▲ . 4.设函数()f x 满足2(21)4f x x -=,则()f x 的表达式是 ▲ .5.函数2(),[2,1]f x x x x =- ∈-的值域是 ▲ .6.若(1,2)m ∈,0.30.30.3,log ,m a b m c m = = =,则用“>”将,,a b c 按从大到小可排列为 ▲ . 7.已知函数2,0()(1),x x f x f x x >⎧=⎨+ 0⎩≤,则55()()33f f +-= ▲ . 8.若函数()log (1)x a f x a x =++(01)x y a a a =>≠且在区间[0,2]上的最大值与最小值之和为2a ,则a 的值为 ▲ .9.给定函数:①y x =,②12log (1)y x =+,③12x y -=,④|2|y x x =--,其中在区间(0,1)上是单调减函数的序号是 ▲ .(填上所有你认为正确的结论的序号)10.已知方程3log 6x x =-的解所在区间为(,1)()k k k N *+ ∈,则k = ▲ .11.已知函数2()23f x ax x =-+在区间(1,2)上是减函数,则a 的取值范围是 ▲ .12.定义在实数集R 上的奇函数()f x 满足:①()f x 在(0,)+∞内单调递增,②(1)0f -=,则不 等式(1)()x f x +>0的解集..为 ▲ . 13.已知函数2()x f x x a =-(01)x y a a a =>≠且,当(1,1)x ∈-时,1()2f x <恒成立,则实数a 的取值范围是 ▲ .14.已知函数(31)5,1()log ,1a a x a x f x x x -+ <⎧=⎨ ⎩≥(01)x y a a a =>≠且,现给出下列命题: ① 当其图象是一条连续不断的曲线时,则a =81; ② 当其图象是一条连续不断的曲线时,能找到一个非零实数a 使()f x 在(,)-∞+∞上是增函数;③ 当11(,)83a ∈时,不等式(1)(1)0f a f a +⋅-<恒成立;④ 函数(|1|)y f x =+是偶函数. 其中正确命题的序号是 ▲ .(填上所有你认为正确的命题的序号)二、解答题:本大题共6小题,共计90分,请在答题纸相应的位置上.........作答,解答时应写出文字说明、证明或演算步骤15.(本小题满分14分)设全集U =R ,集合{}|13A x x =-<≤,{}|242B x x x =--≥.(1)求U Mð()A B I ; (2)若集合{|20}C x x a =+>,满足B C C =U ,求实数a 的取值范围16.(本小题满分14分)(1)计算22lg8lg 5lg 2lg50lg 253++⋅+的值; (2)已知15a a-+=,求22a a -+和1122a a -+的值.17.(本小题满分15分)已知()f x 为定义在R 上的奇函数,当0x >时,()f x 为二次函数,且满足(2)1f =,()f x 在(0,)+∞上的两个零点为1和3.(1)求函数()f x 在R 上的解析式;(2)作出()f x 的图象,并根据图象讨论关于x 的方程()0f x c -=()c R ∈根的个数.18.(本小题满分15分)已知函数()log (1)log (3)a a f x x x =-++,其中01a <<,记函数)(x f 的定义域为D .(1)求函数)(x f 的定义域D ;(2)若函数()f x 的最小值为4-,求a 的值;(3)若对于D 内的任意实数x ,不等式2222x mx m m -+-+<1恒成立,求实数m 的取值范围.(2)若)(x f 为定义域上的奇函数,① 求函数()f x 的值域;② 求满足2()(2)f ax f a x <-的x 的取值范围.20.(本小题满分16分)若函数()f x 满足下列条件:在定义域内存在,0x 使得00(1)()(1)f x f x f +=+成立,则称函数()f x 具有性质M ;反之,若0x 不存在,则称函数()f x 不具有性质M .(1)证明:函数()2x f x =具有性质M ,并求出对应的0x 的值;(2)已知函数2()lg 1a h x x =+具有性质M ,求a 的取值范围; (3)试探究形如:①(0)y kxb k =+≠,②2(0)y ax bxc a =++≠,③(0)k y k x=≠,④x y a = (01)x y a a a =>≠且,⑤log (01)a y x a a =>≠且的函数,指出哪些函数一定具有性质M ?并说明理由.。
江苏省海头高级中学高一上学期数学综合训练(10).pdf

一、题:本大题共1小题,每小题5分,共0分. 1.>1的解集为_____________ 2.设集合,,则=。
函数f(x)=的最大值为f(x)的图象经过点,则的值等于 5.已知(a>0) ,则 若函数是定义在R上的奇函数,且当时,,那么当时,=________..函数的单调增区间为____________。
8.若函数是奇函数,则a=9.已知均为R上的奇函数且解为(4,10),解为(2,5),则的解集为 .设二次函数f(x)=ax2+bx(a≠0)若f(x1)=f(x2+1) (x1-x2≠2),则f(x)=11.由等式定义映射,则_____________ 12.的长度为.已知函数的定义域为,值域为,则区间的长度的最大值与最小值的差为_________. 14.,86,-75,,-1}每一个非空子集的元素乘积(单元素集取元素本身)之和为__________ 二、解答题:本大题共6小题,共0分.解答应写出文字说明,证明过程或演算步骤. 15. x≥0时,f(x)=x+x2. (1)求x0f(x)=是R上的偶函数. (1)求a的值; (2)求证:f(x)在(0,+∞)上是增函数. .定义在R上的函数f(x)满足:任意x,x∈R,都有f()≤,则称函数f(x)是R上的凹函数. 已知二次函数f(x)=x+x(∈R, ≠0). (1)求证:当>0时,函数f(x)是凹函数. (2)如果x∈[0,1]时,|f(x)|≤1,试求实数的范围.19.用水清洗一堆蔬菜上残留的农药,对用一定量的水清洗一次的效果作如下假定:用1个单位量的水可洗掉蔬菜上残留农药用量的,用水越多洗掉的农药量也越多,但总还有农药残留在蔬菜上.设用x单位量的水清洗一次以后,蔬菜上残留的农药与本次清洗前残留有农药量之比为函数f(x). (1)试规定f(0)的值,并解释其实际意义; (2)试根据假定写出函数f(x)应该满足的条件和具有的性质; (3)设f(x)=,现有a(a>0)单位量的水,可以清洗一次,也可以把水平均分成2份后清洗两次.试问用哪种方案清洗后蔬菜上的农药量比较少?说明理由. ,对于给定的负数a,有一个最大的正数,使得[0,],时,恒有||5, (1)求关于a的表达式; (2)求的最大值及相应的a的值。
