高中数学第一章集合与函数概念单元测评3新人教A版1!
人教新课标A版必修一第一章集合与函数的概念单元测试(带答案)

新课标人教A 版第一章集合与函数的概念单元测试一、单选题(每小题5分)1. 已知集合和集合2{}B y y x ==,则A B 等于( )A.(0,1)B.[0,1]C.(0,+∞)D.{(0,1),(1,0)}2.函数()f x =的定义域为( ) A.[3,+∞) B.[3,4)∪(4,+∞) C.(3,+∞) D.[3,4)3. (2018•卷Ⅰ)已知集合2{20}A x x x =-->,则∁R A=( ) A.{12}x x -<< B.{12}x x -≤≤ C.{1}{2}x x x x <-> D.{1}{2}x x x x ≤-≥4. 函数f (x )=|x 2﹣6x+8|的单调递增区间为( )A.[3,+∞) B.(﹣∞,2)(4,+∞) C.(2,3)(4,+∞) D.(﹣∞,2][3,4]5. (2018•卷Ⅰ)已知集合A={0,2},B={-2,-1,0,1,2},则A ∩B=( )A.{0,2}B.{1,2}C.{0}D.{-2,-1,0,1,2}6. 已知全集U={1,2,3,4,5,6},A={1,2,6},B={2,4,5},则(∁UA )∩B=( )A.{4,5}B.{1,2,3,4,5,6}C.{2,4,5}D.{3,4,5}7. 若函数f (x )对于任意实数x 恒有f (x )﹣2f (﹣x )=3x ﹣1,则f (x )等于( ) A.x+1 B.x ﹣1 C.2x+1 D.3x+38. 已知函数21,2()22,2x x f x x x x ⎧+>⎪=-⎨⎪+≤⎩,则f[f (1)]=( ) A.12- B.2 C.4 D.11 9. 已知集合A={x ∈N *|x ﹣3<0},则满足条件B ⊆A 的集合B 的个数为( )A.2B.3C.4D.810. 函数2()23f x x mx =-+,当[2,)x ∈-+∞时是增函数,当(,2]x ∈-∞-时是减函数,则(1)f 等于( )A.-3B.13C.7D.511. 已知函数22,1()2,1a x f x x x x x ⎧+>⎪=⎨⎪-+≤⎩在R 上单调递增,则实数a 的取值范围是( )A.[﹣1,+∞)B.(﹣1,+∞) .[﹣1,0) D.(﹣1,0)12. 下列有关集合的写法正确的是( )A.{0}{0,1,2}∈B.{0}∅=C.0∈∅D.{}∅∈∅二、填空题(每题5分)13. 非空数集A 与B 之间定义长度(,)d x y ,使得()1212d y y y y -=-,其中1y A ∈,2y B ∈,若所有的(,)d x y 中存在最小值()12','d y y ,则称()12','d y y 为集合A 与B 之间的距离,现已知集合11{21}A y a y a =≤≤-,222111{1,}B y y y y y A ==++∈,且()12','d y y =4,则a 的值为_______.14. 已知f(x)为奇函数,()()9,(2)3g x f x g =+-=,则f(2)=__________.15. 设集合A ={x|-1<x<2},集合B ={x|1<x<3},则A ∪B 等于________16. 若集合{12}M x x =-<<,2{1,}N y y x x R ==+∈,则集合M N =___三、解答题(17-22题,12分+12分+12分+12分+12分+12分+10分)17. 设集合2{40,}A x x x x R =+=∈,22{2(1)10,}B x x a x a x R =+++-=∈.(1)若A B B =,求实数a 的值;(2)若A B B =,求实数a 的范围.18. 已知函数239,2()1,211,1x x f x x x x x +≤-⎧⎪=--<<⎨⎪-+>⎩.(1)做出函数图象;(2)说明函数()f x 的单调区间(不需要证明);(3)若函数()y f x =的图象与函数y m =的图象有四个交点,求实数m 的取值范围.19. 已知函数21 ()1xf xx+=+.(1)判断函数()f x在区间[1,+)∞上的单调性,并用定义证明你的结论;(2)求该函数在区间[1,4]上的最大值与最小值.20. 已知函数f(x)对任意的实数m,n都有:f(m+n)=f(m)+f(n)-1,且当x >0时,有f(x)>1.(1)求f(0).(2)求证:f(x)在R上为增函数.(3)若f(1)=2,且关于x的不等式f(ax-2)+f(x-x2)<3对任意的x∈[1,+∞)恒成立,求实数a的取值范围.21. 已知二次函数f(x)的图象过点(0,4),对任意x满足f(3﹣x)=f(x),且f(1)=2.(1)若f(x)在(a,2a﹣1)上单调递减,求实数a的取值范围.(2)设函数h(x)=f(x)﹣(2t﹣3)x,其中t∈R,求h(x)在区间[0,1]上的最小值g (t).22. 若集合A={x|x2+5x﹣6=0},B={x|x2+2(m+1)x+m2﹣3=0}.(1)若m=0,写出A∪B的子集;(2)若A∩B=B,求实数m的取值范围.答案:1-5.BBBCA 6-10.AACCB 11-12.CD13. a=214. 615. {x|-1<x <3}16. [1,3)17. (1)a=1 (2)a=1或a ≤-118. (2)单调增区间(-∞,-2)和(0,1)单调减区间(-2,0)和(1,+∞) (3)(1,0)m ∈-19. (1)函数f(x)在[1,+∞)上是增函数 (2)最小值f(1)=32 最大值9(4)5f =20. (1)f(0)=1(2)略 (3)(1)-∞21. (1)5(1,]4a ∈ (2) 0(5)4t g ≤=时, 201()4t g t t<<=-时, 1()52t g t t ≥=-时, 22. (1){6,3,1}A B =--{-6}{-3}{1}{-6-3}{-6,1}{-3,A B ∅的子集:,,,,,,,,, (2)∞(-,-2]。
高中人教A版数学必修1单元测试:第一章 集合与函数概念Word版含解析

高中人教A版数学必修1单元测试第一章集合与函数概念(一)(集合)第Ⅰ卷(选择题共60分)一、选择题(本大题共12个小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.下列四个集合中,是空集的是()A.{x|x+3=3} B.{(x,y)|y=-x2,x,y∈R}C.{x|x2≤0} D.{x|x2-x+1=0,x∈R}2.已知集合A={x∈N|x<6},则下列关系式错误的是()A.0∈A B.1.5∉A C.-1∉A D.6∈A3.已知集合U={1,3,5,7,9},A={1,5,7},则∁U A=()A.{1,3} B.{3,7,9} C.{3,5,9} D.{3,9}4.设集合A={1,2},B={1,2,3},C={2,3,4},则(A∩B)∪C=()A.{1,2,3} B.{1,2,4} C.{2,3,4} D.{1,2,3,4}5.满足条件{1,2}∪A={1,2}的所有非空集合A的个数是()A.1个B.2个C.3个D.4个6.若集合A={1,4,x},B={1,x2},A∪B={1,4,x},则满足条件的实数x有()A.1个B.2个C.3个D.4个7.已知集合M={y|x+y=2},N={(x,y)|x-y=4},那么集合M∩N为() A.{x=3,y=-1} B.{(x,y)|x=3或y=-1}C.∅D.{(3,-1)}8.已知集合A={0,1,2,3},B={1,3,4},则A∩B的子集个数为()A.2 B.3 C.4 D.169.设全集U 是实数集R ,M ={x |x >2或x <-2},N ={x |x ≥3或x <1}都是U 的子集,则图中阴影部分所表示的集合是( )A .{x |-2≤x <1}B .{x |-2≤x ≤2}C .{x |1<x ≤2}D .{x |x <2}10.如果集合A ={x |ax 2+2x +1=0}中只有一个元素,则a 的值是( ) A .0 B .0或1 C .1 D .不能确定11.集合⎩⎨⎧⎭⎬⎫x ∈N *⎪⎪⎪12x ∈Z 中含有的元素个数为( )A .4B .6C .8D .1212.设a ,b 都是非零实数,则y =a |a |+b |b |+ab|ab |可能取的值组成的集合为( ) A .{3} B .{3,2,1} C .{3,-2,1}D .{3,-1}第Ⅱ卷 (非选择题 共90分)二、填空题(本大题共4个小题,每小题5分,共20分,请把正确答案填在题中横线上)13.若集合A ={x |-1≤x <2},B ={x |x ≤a },若A ∩B ≠∅,则实数a 的取值范围是________.14.已知集合A =⎩⎨⎧⎭⎬⎫x ⎪⎪⎪ x =a +16,a ∈Z ,B =⎩⎨⎧⎭⎬⎫x ⎪⎪⎪x =b 2-13,b ∈Z ,C =⎩⎨⎧⎭⎬⎫x ⎪⎪⎪x =c 2+16,c ∈Z ,则A ,B ,C 之间的关系是________.15.若集合A ={x |x 2+x -6=0},B ={x |mx +1=0},且B ⊆A ,则m 的取值集合为________.16.若三个非零且互不相等的实数a ,b ,c ,满足1a +1b =2c ,则称a ,b ,c 是调和的;若满足a +c =2b ,则称a ,b ,c 是等差的.若集合P 中元素a ,b ,c 既是调和的,又是等差的,则称集合P 为“好集”.若集合M ={x ||x |≤2014,x ∈Z },集合P ={a ,b ,c }⊆M ,则“好集”P 的个数为________.三、解答题(本大题共6个小题,共70分,解答时应写出必要的文字说明、证明过程或演算步骤)17.(本小题满分10分)设全集为R ,A ={x |3≤x <7},B ={x |2<x <10}. 求:A ∪B ,∁R (A ∩B ),(∁R A )∩B .18.(本小题满分12分)(1)已知全集U =R ,集合M ={x |x +3≤0},N ={x |x 2=x +12},求(∁U M )∩N ; (2)已知全集U =R ,集合A ={x |x <-1或x >1},B ={x |-1≤x <0},求A ∪(∁U B ).19.(本小题满分12分)已知集合A={x|-2<x<-1或x>1},B={x|a≤x<b},A∪B={x|x>-2},A∩B={x|1<x<3},求实数a,b的值.20.(本小题满分12分)已知集合A={x|x≤a+3},B={x|x<-1或x>5}.(1)若a=-2,求A∩∁R B;(2)若A⊆B,求a的取值范围.21.(本小题满分12分)设集合A ={x |x 2-8x +15=0},B ={x |ax -1=0}. (1)若a =15,判断集合A 与B 的关系; (2)若A ∩B =B ,求实数a 组成的集合C .22.(本小题满分12分)已知集合A ={x |(a -1)x 2+3x -2=0},B ={x |x 2-3x +2=0}. (1)若A ≠∅,求实数a 的取值范围; (2)若A ∩B =A ,求实数a 的取值范围.详解答案第一章 集合与函数概念(一)(集 合)1.D 解析:选项D 中Δ=(-1)2-4×1×1=-3<0,所以方程x 2-x +1=0无实数根.2.D 解析:∵集合A ={x ∈N |x <6}={0,1,2,3,4,5},∴6∉A .故选D. 3.D 解析:∵U ={1,3,5,7,9},A ={1,5,7},∴∁U A ={3,9}.故选D. 4.D 解析:∵A ∩B ={1,2},C ={2,3,4},∴(A ∩B )∪C ={1,2,3,4}. 5.C 解析:∵{1,2}∪A ={1,2}∴集合A 可取集合{1,2}的非空子集.∴集合A 有3个.故选C.6.C 解析:∵A ∪B ={1,4,x },∴x 2=4或x 2=x .解得x =±2或x =1或x=0.检验当x =1时,A ={1,4,1}不符合集合的性质,∴x =2或x =-2或x =0.故选C.7.C 解析:∵集合M 的代表元素是实数,集合N 的代表元素是点,∴M ∩N =∅.故选C.8.C 解析:∵A ∩B ={1,3},∴A ∩B 的子集分别是∅,{1},{3},{1,3}.故选C.解题技巧:本题主要考查了列举法表示两个集合的交集,考查了子集的求法,解决本题的关键是确定出A ∩B 所含元素的个数n ,因此所有子集的个数为2n 个.9.A 解析:∵图中阴影部分表示:x ∈N 且x ∉M ,∴x ∈N ∩∁U M .∴∁U M ={x |-2≤x ≤2},∴N ∩∁U M ={x |-2≤x <1}.故选A.10.B 解析:∵集合A ={x |ax 2+2x +1=0}中只有一个元素,∴①当a =0时,集合A ={x |2x +1=0}只有一个元素,符合题意;②当a ≠0时,一元二次方程ax 2+2x +1=0只有一解,∴Δ=0,即4-4a =0,∴a =1.故选B.11.B 解析:∵x ∈N *,12x ∈Z ,∴x =1时,12x =12∈Z ;x =2时,12x =6∈Z ;x =3时,12x =4∈Z ;x =4时,12x =3∈Z ;x =6时,12x =2∈Z ;x =12时,12x =1∈Z .12.D 解析:①当a >0,b >0时,y =3;②当a >0,b <0时,y =-1;③当a <0,b >0时,y =-1;④当a <0,b <0时,y =-1.13.a ≥-1 解析:如图:∵A ∩B ≠∅,且A ={x |-1≤x <2},B ={x |x ≤a },∴a ≥-1. 14.AB =C 解析:A =⎩⎨⎧⎭⎬⎫x ⎪⎪⎪x =a +16,a ∈Z=⎩⎨⎧⎭⎬⎫x ⎪⎪⎪ x =16(6a +1),a ∈Z ,B =⎩⎨⎧⎭⎬⎫x ⎪⎪⎪ x =b 2-13,b ∈Z =⎩⎨⎧⎭⎬⎫x ⎪⎪⎪ x =16(3b -2),b ∈Z =⎩⎨⎧⎭⎬⎫x ⎪⎪⎪ x =16[3(b +1)-2],b ∈Z ,C =⎩⎨⎧⎭⎬⎫x ⎪⎪⎪ x =c 2+16,c ∈Z =⎩⎨⎧⎭⎬⎫x ⎪⎪⎪ x =16(3c +1),c ∈Z .∴A B =C .15.m =⎩⎨⎧⎭⎬⎫0,-12,13 解析:集合A ={2,-3},又∵B ⊆A ,∴B =∅,{-3},{2}.∴m =0或m =-12或m =13.16.1 006 解析:因为若集合P 中元素a ,b ,c 既是调和的,又是等差的,则1a +1b =2c 且a +c =2b ,则a =-2b ,c =4b ,因此满足条件的“好集”为形如{-2b ,b,4b }(b ≠0)的形式,则-2 014≤4b ≤2 014,解得-503≤b ≤503,且b ≠0,符合条件的b 的值可取1 006个,故“好集”P 的个数为1 006个.解题技巧:本题主要考查了以集合为背景的新概念题,解决本题的关键是弄清楚新概念、新运算、新方法的含义,转化为集合问题求解.17.解:∵全集为R ,A ={x |3≤x <7},B ={x |2<x <10}, ∴A ∪B ={x |2<x <10},A ∩B ={x |3≤x <7}, ∴∁R (A ∩B )={x |x ≥7或x <3}. ∵∁R A ={x |x ≥7或x <3},∴(∁R A )∩B ={x |2<x <3或7≤x <10}.18.解:(1)M ={x |x +3=0}={-3},N ={x |x 2=x +12}={-3,4}, ∴(∁U M )∩N ={4}.(2)∵A ={x |x <-1或x >1},B ={x |-1≤x <0}, ∴∁U B ={x |x <-1或x ≥0}. ∴A ∪(∁U B )={x |x <-1或x ≥0}.19.解:∵A ∩B ={x |1<x <3},∴b =3, 又A ∪B ={x |x >-2}, ∴-2<a ≤-1, 又A ∩B ={x |1<x <3}, ∴-1≤a <1, ∴a =-1.20.解:(1)当a =-2时,集合A ={x |x ≤1},∁R B ={x |-1≤x ≤5}, ∴A ∩∁R B ={x |-1≤x ≤1}.(2)∵A ={x |x ≤a +3},B ={x |x <-1或x >5},A ⊆B , ∴a +3<-1,∴ a <-4.解题技巧:本题主要考查了描述法表示的集合的运算,集合间的关系,解决本题的关键是借助于数轴求出符合题意的值.在解决(2)时,特别注意参数a 是否取到不等式的端点值.21.解:A ={x |x 2-8x +15=0}={3,5}. (1)若a =15,则B ={5},所以B A . (2)若A ∩B =B ,则B ⊆A . 当a =0时,B =∅,满足B ⊆A ;当a ≠0时,B =⎩⎨⎧⎭⎬⎫1a ,因为B ⊆A ,所以1a =3或1a =5,即a =13或a =15;综上所述,实数a 组成的集合C 为⎩⎨⎧⎭⎬⎫0,13,15.22.解:(1)①当a =1时,A =⎩⎨⎧⎭⎬⎫23≠∅;②当a ≠1时,Δ≥0,即a ≥-18且a ≠1,综上,a ≥-18;(2)∵B ={1,2},A ∩B =A ,∴A =∅或{1}或{2}或{1,2}. ①A =∅,Δ<0,即a <-18;②当A ={1}或{2}时,Δ=0,即a =0且a =-18,不存在这样的实数; ③当A ={1,2},Δ>0,即a >-18且a ≠1,解得a =0. 综上,a <-18或a =0.第一章集合与函数概念(二)(函数的概念与基本性质)第Ⅰ卷(选择题共60分)一、选择题(本大题共12个小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.下列四组函数中,表示同一函数的是()A.y=x-1与y=(x-1)2B.y=x-1与y=x-1 x-1C.y=4lg x与y=2lg x2D.y=lg x-2与y=lgx 1002.已知f:x→x2是集合A到集合B={0,1,4}的一个映射,则集合A中的元素个数最多有()A.3个B.4个C.5个D.6个3.函数f(x)=x+1x-1的定义域是()A.-1,1) B.-1,1)∪(1,+∞) C.-1,+∞) D.(1,+∞)4.函数y=2--x2+4x的值域是()A.-2,2] B.1,2]C.0,2] D.-2, 2 ] 5.已知f(x)的图象如图,则f(x)的解析式为()A .f (x )=⎩⎪⎨⎪⎧1,0≤x ≤1-x -2,1<x ≤2B .f (x )=⎩⎪⎨⎪⎧-1,0≤x ≤1x +2,1<x ≤2C .f (x )=⎩⎪⎨⎪⎧-1,0≤x ≤1x -2,1<x ≤2D .f (x )=⎩⎪⎨⎪⎧-1,0≤x ≤1-x +2,1<x ≤26.定义两种运算:a ⊕b =a 2-b 2,a b =(a -b )2,则函数f (x )=2⊕x (x2)-2的解析式为( )A .f (x )=4-x 2x ,x ∈-2,0)∪(0,2]B .f (x )=x 2-4x ,x ∈(-∞,-2]∪2,+∞) C .f (x )=-x 2-4x ,x ∈(-∞,-2]∪2,+∞) D .f (x )=-4-x 2x ,x ∈-2,0)∪(0,2]7.函数f (x )=1x -x 的图象关于( ) A .坐标原点对称 B .x 轴对称 C .y 轴对称D .直线y =x 对称8.设f (x )是定义在-6,6]上的偶函数,且f (4)>f (1),则下列各式一定成立的是( )A .f (0)<f (6)B .f (4)>f (3)C .f (2)>f (0)D .f (-1)<f (4)9.若奇函数f (x )在1,3]上为增函数,且有最小值0,则它在-3,-1]上( ) A .是减函数,有最小值0 B .是增函数,有最小值0 C .是减函数,有最大值0D .是增函数,有最大值010.已知函数f (x )=⎩⎪⎨⎪⎧a x (x <0),(a -3)x +4a (x ≥0),满足对任意x 1≠x 2,都有f (x 1)-f (x 2)x 1-x 2<0成立,则a 的取值范围是( )A.⎝ ⎛⎦⎥⎤0,14 B .(0,1) C.⎣⎢⎡⎭⎪⎫14,1 D .(0,3)11.若f (x )是R 上的减函数,且f (x )的图象经过点A (0,4)和点B (3,-2),则当不等式|f (x +t )-1|<3的解集为(-1,2)时,t 的值为( )A .0B .-1C .1D .212.已知函数y =f (x )满足:①y =f (x +1)是偶函数;②在1,+∞)上为增函数.若x 1<0,x 2>0,且x 1+x 2<-2,则f (-x 1)与f (-x 2)的大小关系是( )A .f (-x 1)>f (-x 2)B .f (-x 1)<f (-x 2)C .f (-x 1)=f (-x 2)D .无法确定第Ⅱ卷 (非选择题 共90分)二、填空题(本大题共4个小题,每小题5分,共20分,请把正确答案填在题中横线上)13.若函数f (x )=ax 7+bx -2,且f (2 014)=10,则f (-2 014)的值为________. 14.若函数f (x )=ax +1x +2在x ∈(-2,+∞)上单调递减,则实数a 的取值范围是________.15.已知函数f (x )=x +3x +1,记f (1)+f (2)+f (4)+f (8)+f (16)=m ,f ⎝ ⎛⎭⎪⎫12+f ⎝ ⎛⎭⎪⎫14+f ⎝ ⎛⎭⎪⎫18+f ⎝ ⎛⎭⎪⎫116=n ,则m +n =________. 16.设a 为常数且a <0,y =f (x )是定义在R 上的奇函数,当x <0时,f (x )=x +a 2x -2.若f (x )≥a 2-1对一切x ≥0都成立,则a 的取值范围为________.三、解答题(本大题共6个小题,共70分,解答时应写出必要的文字说明、证明过程或演算步骤)17.(本小题满分10分)(1)已知f (x -2)=3x -5,求f (x );(2)若f (f (f (x )))=27x +26,求一次函数f (x )的解析式.18.(本小题满分12分) 已知f (x )=1x -1,x ∈2,6].(1)证明:f (x )是定义域上的减函数; (2)求f (x )的最大值和最小值.19.(本小题满分12分)某公司生产一种电子仪器的固定成本为20 000元,每生产一台仪器需增加投入100元,已知总收益满足函数:R (x )=⎩⎨⎧400x -12x 2,0≤x ≤400,80 000,x >400,其中x 是仪器的月产量.(1)将利润f (x )表示为月产量x 的函数;(2)当月产量x 为何值时,公司所获利润最大?最大利润是多少元?(总收益=总成本+利润)20.(本小题满分12分)已知函数f(x)=x2+2ax+2,x∈-5,5].(1)当a=-1时,求函数的最大值和最小值;(2)若y=f(x)在区间-5,5]上是单调函数,求实数a的取值范围.21.(本小题满分12分)已知二次函数f(x)=ax2+bx(a,b∈R),若f(1)=-1且函数f(x)的图象关于直线x=1对称.(1)求a,b的值;(2)若函数f(x)在k,k+1](k≥1)上的最大值为8,求实数k的值.22.(本小题满分12分)已知二次函数f(x)的图象过点(0,4),对任意x满足f(3-x)=f(x),且有最小值74.(1)求f(x)的解析式;(2)求函数h(x)=f(x)-(2t-3)x在区间0,1]上的最小值,其中t∈R;(3)在区间-1,3]上,y=f(x)的图象恒在函数y=2x+m的图象上方,试确定实数m的范围.详解答案第一章集合与函数概念(二)(函数的概念与基本性质)1.D解析:∵y=x-1与y=(x-1)2=|x-1|的对应关系不同,∴它们不是同一函数;y=x-1(x≥1)与y=x-1x-1(x>1)的定义域不同,∴它们不是同一函数;又y=4lg x(x>0)与y=2lg x2(x≠0)的定义域不同,因此它们也不是同一函数,而y=lg x-2(x>0)与y=lg x100=lg x-2(x>0)有相同的定义域、值域与对应关系,因此它们是同一函数.2.C解析:令x2=0,1,4,解得x=0,±1,±2.故选C.3.B 解析:由⎩⎪⎨⎪⎧x +1≥0,x -1≠0,解得x ≥-1,且x ≠1.4.C 解析:令t =-x 2+4x ,x ∈0,4],∴t ∈0,4].又∵y 1=x ,x ∈0,+∞)是增函数∴ t ∈0,2],-t ∈-2,0],∴y ∈0,2].故选C.5.C 解析:当0≤x ≤1时,f (x )=-1;当1<x ≤2时,设f (x )=kx +b (k ≠0),把点(1,-1),(2,0)代入f (x )=kx +b (k ≠0),则f (x )=x -2.所以f (x )=⎩⎪⎨⎪⎧-1,0≤x ≤1,x -2,1<x ≤2.故选C. 6.D 解析:f (x )=2⊕x (x2)-2=22-x 2(x -2)2-2=4-x 2|x -2|-2.由⎩⎪⎨⎪⎧4-x 2≥0,|x -2|-2≠0,得-2≤x ≤2且x ≠0.∴f (x )=-4-x 2x .7.A 解析:函数f (x )的定义域关于原点对称,又∵f (-x )=1-x+x =-⎝ ⎛⎭⎪⎫1x -x =-f (x ),∴f (x )为奇函数,其图象关于坐标原点对称.8.D 解析:∵f (x )是定义在-6,6]上的偶函数,∴f (-1)=f (1).又f (4)>f (1),f (4)>f (-1).9.D 解析:因为奇函数f (x )在1,3]上为增函数,且有最小值0,所以f (x )在-3,-1]上是增函数,且有最大值0.10.A 解析:由于函数f (x )=⎩⎪⎨⎪⎧a x (x <0),(a -3)x +4a (x ≥0)满足对任意x 1≠x 2,都有f (x 1)-f (x 2)x 1-x 2<0成立,所以该函数为R 上的减函数,所以⎩⎪⎨⎪⎧0<a <1,a -3<0,4a ≤a 0,解得0<a ≤14.解题技巧:本题主要考查了分段函数的单调性,解决本题的关键是利用好该函数为R 上的减函数这一条件.应特别注意隐含条件“a 0≥4a ”.11.C 解析:由不等式|f (x +t )-1|<3,得-3<f (x +t )-1<3,即-2<f (x +t )<4.又因为f (x )的图象经过点A (0,4)和点B (3,-2),所以f (0)=4,f (3)=-2,所以f (3)<f (x +t )<f (0).又f (x )在R 上为减函数,则3>x +t >0,即-t <x <3-t ,解集为(-t,3-t ).∵不等式的解集为(-1,2),∴-t =-1,3-t =2,解得t =1.故选C.12.A 解析:由y =f (x +1)是偶函数且把y =f (x +1)的图象向右平移1个单位可得函数y =f (x )的图象,所以函数y =f (x )的图象关于x =1对称,即f (2+x )=f (-x ).因为x 1<0,x 2>0,且x 1+x 2<-2,所以2<2+x 2<-x 1.因为函数在1,+∞)上为增函数,所以f (2+x 2)<f (-x 1),即f (-x 1)>f (-x 2),故选A.13.-14 解析:设g (x )=ax 7+bx ,则g (x )是奇函数,g (-2 014)=-g (2 014).∵f (2 014)=10且f (2 014)=g (2 014)-2,∴g (2 014)=12,∴g (-2 014)=-12,∴f (-2 014)=g (-2 014)-2,∴f (-2 014)=-14.14.a <12 解析:f (x )=ax +1x +2=a +1-2a x +2.∵y =1x +2在x ∈(-2,+∞)上是减函数,∴1-2a >0,∴a <12.15.18 解析:因为函数f (x )=x +3x +1,所以f ⎝ ⎛⎭⎪⎫1x =1+3xx +1.又因为f (x )+f ⎝ ⎛⎭⎪⎫1x =4(x +1)x +1=4,f (1)+f (2)+f (4)+f (8)+f (16)+f ⎝ ⎛⎭⎪⎫12+f ⎝ ⎛⎭⎪⎫14+f ⎝ ⎛⎭⎪⎫18+f ⎝ ⎛⎭⎪⎫116 =f (1)+f (2)+f ⎝ ⎛⎭⎪⎫12+f (4)+f ⎝ ⎛⎭⎪⎫14+f (8)+f ⎝ ⎛⎭⎪⎫18+f (16)+f ⎝ ⎛⎭⎪⎫116=f (1)+4×4=18, 所以m +n =18.解题技巧:本题主要考查了学生的观察、归纳、推理的能力,解决本题的关键是挖掘出题目中隐含的规律f (x )+f ⎝ ⎛⎭⎪⎫1x =4.16.-1≤a <0 解析:当x =0时,f (x )=0,则0≥a 2-1,解得-1≤a ≤1,所以-1≤a <0.当x >0时,-x <0,f (-x )=-x +a 2-x -2,则f (x )=-f (-x )=x +a 2x +2.由对数函数的图象可知,当x =a 2=|a |=-a 时,有f (x )min =-2a +2, 所以-2a +2≥a 2-1,即a 2+2a -3≤0,解得-3≤a ≤1.又a <0, 所以-3≤a <0. 综上所述,-1≤a <0.17.解:(1)令t =x -2,则x =t +2,t ∈R ,由已知有f (t )=3(t +2)-5=3t +1,故f (x )=3x +1.(2)设f (x )=ax +b (a ≠0),f (f (x ))=a 2x +ab +b , f (f (f (x )))=a (a 2x +ab +b )+b =a 3x +a 2b +ab +b ,∴⎩⎪⎨⎪⎧a 3=27,a 2b +ab +b =26,解得a =3,b =2.则f (x )=3x +2.18.(1)证明:设2≤x 1<x 2≤6,则f (x 1)-f (x 2)=1x 1-1-1x 2-1=x 2-x 1(x 1-1)(x 2-1),因为x 1-1>0,x 2-1>0,x 2-x 1>0,所以f (x 1)-f (x 2)>0, 即f (x 1)>f (x 2).所以f (x )是定义域上的减函数.(2)由(1)的结论可得,f (x )min =f (6)=15,f (x )max =f (2)=1. 19.解:(1)当0≤x ≤400时,f (x )=400x -12x 2-100x -20 000=-12x 2+300x -20 000. 当x >400时,f (x )=80 000-100x -20 000=60 000-100x ,所以f (x )=⎩⎨⎧-12x 2+300x -20 000,0≤x ≤400,60 000-100x ,x >400.(2)当0≤x ≤400时,f (x )=-12x 2+300x -20 000=-12(x -300)2+25 000; 当x =300时,f (x )max =25 000; 当x >400时,f (x )=60 000-100x <f (400)=20 000<25 000; 所以当x =300时,f (x )max =25 000.故当月产量x 为300台时,公司获利润最大,最大利润为25 000元. 20.解:(1)当a =-1时,f (x )=x 2-2x +2=(x -1)2+1. 又因为x ∈-5,5].所以函数的最大值为37,最小值为1. (2)若y =f (x )在区间-5,5]上是单调函数, 则有-a ≤-5或-a ≥5解得a ≤-5或a ≥5.解题技巧:本题主要考查了二次函数在给定区间上的最值与单调性.解决本题的关键是确定对称轴和区间端点的关系.注意分类讨论.21.解:(1)由题意可得f (1)=a +b =-1且-b2a =1, 解得a =1,b =-2. (2)f (x )=x 2-2x =(x -1)2-1.因为k ≥1,所以f (x )在k ,k +1]上单调递增, 所以f (x )max =f (k +1)=(k +1)2-2(k +1)=8, 解得k =±3. 又k ≥1,所以k =3.22.解:(1)由题知二次函数图象的对称轴为x =32,又最小值是74,则可设f (x )=a ⎝ ⎛⎭⎪⎫x -322+74(a ≠0), 又图象过点(0,4),则a ⎝ ⎛⎭⎪⎫0-322+74=4,解得a =1. ∴f (x )=⎝ ⎛⎭⎪⎫x -322+74=x 2-3x +4. (2)h (x )=f (x )-(2t -3)x =x 2-2tx +4=(x -t )2+4-t 2,其对称轴x =t . ①t ≤0时,函数h (x )在0,1]上单调递增,最小值为h (0)=4;②当0<t <1时,函数h (x )的最小值为h (t )=4-t 2;③当t ≥1时,函数h (x )在0,1]上单调递减,最小值为h (1)=5-2t ,所以h (x )min =⎩⎪⎨⎪⎧ 4,t ≤0,4-t 2,0<t <1,5-2t ,t ≥1.(3)由已知:f (x )>2x +m 对x ∈-1,3]恒成立,∴m <x 2-5x +4对x ∈-1,3]恒成立.∴m <(x 2-5x +4)min (x ∈-1,3]).∵g (x )=x 2-5x +4在x ∈-1,3]上的最小值为-94, ∴m <-94.。
【师说】高中数学 第一章 集合与函数概念质量评估检测 新人教A版必修1

【师说】2015-2016学年高中数学第一章集合与函数概念质量评估检测新人教A版必修1时间:120分钟满分:150分一、选择题:本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.若集合A={x∈R|ax2+ax+1=0}中只有一个元素,则a=( )A.4 B.2C.0 D.0或4解析:当a=0时,方程化为1=0,无解,集合A为空集,不符合题意;当a≠0时,由Δ=a2-4a=0,解得a=4.答案:A2.已知集合A,B均为全集U={1,2,3,4}的子集,且∁U(A∪B)={4},B={1,2},则A∩∁U B=( )A.{3} B.{4}C.{3,4} D.∅解析:∵U={1,2,3,4},∁U(A∪B)={4},∴A∪B={1,2,3}.又∵B={1,2},∴{3}⊆A⊆{1,2,3}.又∁U B={3,4},∴A∩∁U B={3}.答案:A3.衡水高一检测下列各组中的两个函数是同一函数的为( )(1)y=x+x-x+3,y=x-5.(2)y=x+1x-1,y=x+x-.(3)y=x,y=x2.(4)y=x,y=3x3.(5)y=(2x-5)2,y=2x-5. A.(1),(2) B.(2),(3) C.(3),(5) D.(4)解析:(1)中的y=x+x-x+3与y=x-5定义域不同.(2)中两个函数的定义域不同.(3)中第1个函数的定义域、值域都为R,而第2个函数的定义域是R,但值域是{y|y≥0}.(5)中两个函数的定义域不同,值域也不同.(4)中显然是同一函数.答案:D4.福州高一检测下列函数是偶函数的是( )A.y=2x2-3 B.y=x3C.y=x2,x∈[0,1] D.y=x解析:由函数奇偶性定义可知B、D均为奇函数,C定义域不关于原点对称,为非奇非偶函数,A为偶函数.答案:A5.洛阳高一检测若函数f(x)满足f(3x+2)=9x+8,则f(x)的解析式是( )A.f(x)=9x+8B.f(x)=3x+2C.f(x)=-3x-4D.f(x)=3x+2或f(x)=-3x-4解析:令3x+2=t,则3x=t-2,故f(t)=3(t-2)+8=3t+2.答案:B 6.大庆高一检测设f (x )是定义在R 上的奇函数,当x ≤0时,f (x )=2x 2-x ,则f (1)=( )A .-3B .-1C .1D .3解析:∵x ≤0时,f (x )=2x 2-x ,∴f (-1)=2-(-1)=3.又f (x )为R 上的奇函数,故f (-1)=-f (1),所以f (1)=-3.答案:A7.设集合S ={x |x >-2},T ={x |-4≤x ≤1},则S ∩T =( )A .[-4,+∞) B.(-2,+∞)C .[-4,1]D .(-2,1]解析:S ∩T ={x |x >-2}∩{x |-4≤x ≤1}={x |-2<x ≤1}.答案:D8.函数f (x )=1+x +1x的定义域是( ) A .[-1,∞)B .(-∞,0)∪(0,+∞)C .[-1,0)∪(0,+∞)D .R解析:要使函数有意义,需满足⎩⎪⎨⎪⎧ 1+x ≥0,x ≠0,即x ≥-1且x ≠0,故选C.答案:C9.已知f (x )是奇函数,g (x )是偶函数,且f (-1)+g (1)=2,f (1)+g (-1)=4,则g (1)等于( )A .4B .3C .2D .1解析:∵f (x )是奇函数,∴f (-1)=-f (1).又g (x )是偶函数,∴g (-1)=g (1).∵f (-1)+g (1)=2,∴g (1)-f (1)=2.①又f (1)+g (-1)=4,∴f (1)+g (1)=4.②由①②,得g (1)=3.答案:B 10.浏阳高一检测已知偶函数y =f (x )在[0,4]上是增函数,则一定有( )A .f (-3)>f (π)B .f (-3)<f (π)C .f (3)>f (-π)D .f (-3)>f (-π)解析:∵f (x )是偶函数,∴f (-3)=f (3),f (-π)=f (π).又f (x )在[0,4]上是增函数,∴f (3)<f (π).∴f (-3)<f (π).答案:B11.(2014·昆明高一检测)已知f (x )是定义在R 上的奇函数,当x <0时,f (x )=x -x 2,则当x >0时,f (x )=( )A .x -x 2B .-x -x 2C .-x +x 2D .x +x 2解析:当x >0时,-x <0,∴f (-x )=-x -(-x )2=-x -x 2,又f (-x )=-f (x ),故f (x )=x +x 2.答案:D 12.安阳高一检测一个偶函数定义在[-7,7]上,它在[0,7]上的图象如图所示,下列说法正确的是( )A .这个函数仅有一个单调增区间B .这个函数有两个单调减区间C .这个函数在其定义域内有最大值是7D .这个函数在其定义域内有最小值是-7解析:结合偶函数图象关于y 轴对称可知,这个函数在[-7,7]上有三个单调递增区间,三个单调递减区间,且定义域内有最大值7,无法判断最小值是多少.答案:C二、填空题:本大题共4小题,每小题5分,共20分.13.已知函数f (x )=x -1.若f (a )=3,则实数a =__________.解析:因为f (a )=a -1=3,所以a -1=9,即a =10.答案:1014.用列举法表示集合:A ={x |2x +1∈Z ,x ∈Z }=__________. 解析:因为x ∈Z ,所以当x =-3时,有-1∈Z ;当x =-2时,有-2∈Z ;当x =0时,有2∈Z ;当x =1时,有1∈Z ,所以A ={-3,-2,0,1}.答案:{-3,-2,0,1}15.函数f (x )=-x 2+b 在[-3,-1]上的最大值是4,则它的最小值是__________.解析:函数f (x )=-x 2+b 在[-3,-1]上是增函数,当x =-1时取最大值,所以b=5,当x =-3时,取最小值f (-3)=-9+5=-4.答案:-416.已知函数y =f (x )在(-∞,0)∪(0,+∞)上为奇函数,且在(0,+∞)上为增函数,f (-2)=0,则不等式x ·f (x )<0的解集为________.解析:根据题意画出f (x )由图象可知-2<x <0或0<x 答案:(-2,0)∪(0,2)三、解答题:本大题共6小题,共70分,解答应写出文字说明,证明过程或演算步骤.17.2014·武昌高一检测,10分已知函数f (x )=x +m x ,且f (1)=3.(1)求m ;(2)判断函数f (x )的奇偶性.解析:(1)∵f (1)=3,即1+m =3,∴m =2.4分(2)由(1)知,f (x )=x +2x,其定义域是{x |x ≠0},关于原点对称,7分 又f (-x )=-x +2-x =-⎝ ⎛⎭⎪⎫x +2x =-f (x ),所以此函数是奇函数.10分 18.杭州高一检测,12分已知集合A ={x |3≤x <6},B ={x |2<x <9}. (1)分别求∁R (A ∩B ),(∁R B )∪A ;(2)已知C ={x |a <x <a +1},若C ⊆B ,求实数a 的取值范围.解析:(1)∵A ∩B ={x |3≤x <6},∴∁R (A ∩B )={x |x <3或x ≥6},∵∁R B ={x |x ≤2或x ≥9},∴(∁R B )∪A ={x |x ≤2或3≤x <6或x ≥9}.6分(2)∵C ⊆B ,∴⎩⎪⎨⎪⎧ a ≥2,a +1≤9,∴2≤a ≤8.∴实数a 的取值范围为:2≤a ≤8.12分 19.郑州高一检测,12分已知函数f (x )=x 2+2ax +2,x ∈[-5,5]. (1)当a =-1时,求函数f (x )的最大值和最小值;(2)求实数a 的取值范围,使y =f (x )在区间[-5,5]上是单调函数.解析:(1)当a =-1时,f (x )=x 2-2x +2=(x -1)2+1.∵x ∈[-5,5],故当x =1时,f (x )的最小值为1,当x =-5时,f (x )的最大值为37.6分(2)函数f (x )=(x +a )2+2-a 2的图象的对称轴为x =-a .∵f (x )在[-5,5]上是单调的,∴-a ≤-5或-a ≥5.即实数a 的取值范围是a ≤-5或a ≥5.12分 20.德州高一检测,12分设函数f (x )=x 2-2|x |-1(-3≤x ≤3), (1)证明:f (x )是偶函数;(2)画出这个函数的图象;(3)指出函数f (x )的单调区间,并说明在各个单调区间上f (x )是增函数还是减函数;(4)求函数的值域.解析:(1)∵f (-x )=(-x )2-2|-x |-1=x 2-2|x |-1=f (x ),即f (-x )=f (x ),∴f (x )是偶函数.3分(2)当x ≥0时,f (x )=x 2-2x -1=(x -1)2-2,当x <0时,f (x )=x 2+2x -1=(x +1)2-2,即f (x )=⎩⎪⎨⎪⎧x -2-2,0≤x ≤3,x +2-2,-3≤x <0. 根据二次函数的作图方法,可得函数图象如图.6分(3)函数f (x )的单调区间为[-3,-1),[-1,0),[0,1),[1,3].f (x )在区间[-3,-1),[0,1)上为减函数,在区间[-1,0),[1,3]上为增函数.9分(4)当x ≥0时,函数f (x )=(x -1)2-2的最小值为-2,最大值f (3)=2;当x <0时,函数f (x )=(x +1)2-2的最小值为-2,最大值f (-3)=2.故函数f (x )的值域为[-2,2].12分 21.临沂高一检测,12分已知函数f (x )=mx 2+23x +n 是奇函数,且f (2)=53. (1)求实数m 和n 的值;(2)判断函数f (x )在(-∞,-1]上的单调性,并加以证明.解析:(1)∵f (x )是奇函数,∴f (-x )=-f (x ).即mx 2+2-3x +n =-mx 2+23x +n =mx 2+2-3x -n, 比较得n =-n ,n =0,又f (2)=53,∴4m +26=53,m =2, 即实数m 和n 的值分别是2和0.6分(2)函数f (x )在(-∞,-1]上为增函数.证明如下:由(1)知f (x )=2x 2+23x =2x 3+23x, 设x 1<x 2≤-1,则f (x 1)-f (x 2)=23(x 1-x 2)⎝ ⎛⎭⎪⎫1-1x 1x 2 =23(x 1-x 2)·x 1x 2-1x 1x 2, 23(x 1-x 2)<0,x 1x 2>0,x 1x 2-1>0, ∴f (x 1)-f (x 2)<0,∴f (x 1)<f (x 2),即函数f (x )在(-∞,-1]上为增函数.12分 22.济宁高一检测,12分函数f (x )=ax +b 1+x 2是定义在(-1,1)上的奇函数,且f ⎝ ⎛⎭⎪⎫12=25. (1)确定函数f (x )的解析式;(2)用定义证明:f (x )在(-1,1)上是增函数;(3)解不等式f (t -1)+f (t )<0.解析:(1)∵f (x )是定义在(-1,1)上的奇函数,∴f (-x )=-f (x ),即-ax +b 1+x 2=-ax -b 1+x 2. ∴b =-b ,b =0.∵f ⎝ ⎛⎭⎪⎫12=25,∴12a 1+14=25, ∴a =1.3分∴函数解析式为f (x )=x1+x 2(-1<x <1). (2)证明:任取x 1,x 2∈(-1,1),且x 1<x 2, f (x 1)-f (x 2)=x 11+x 21-x 21+x 22=x 1-x 2-x 1x 2+x 21+x 22, ∵-1<x 1<x 2<1,∴x 1-x 2<0,1-x 1x 2>0,(1+x 21)(1+x 22)>0,∴f (x 1)-f (x 2)<0,即f (x 1)<f (x 2).∴f (x )在(-1,1)上为增函数.6分(3)∵f (t -1)+f (t )<0,∴f (t -1)<-f (t ).∵f (-t )=-f (t ),∴f (t -1)<f (-t ).∴f (x )为(-1,1)上的增函数. ∴⎩⎪⎨⎪⎧ -1<t -1<1,-1<-t <1,t -1<-t .解得0<t <12.∴不等式的解集为{t |0<t <12}.12分。
高中数学第一章集合与函数概念本章测评4新人教A版必修1

第一章集合与函数概念自主建构本章测评1. 下列几组对象可以构成集合的是( )A.充分接近π的实数的全体B.善良的人C. A校高一(1)班所有聪明的学生D. B单位所有身高在1.75 cm以上的人思路解析:因A、B、C不具备元素的确定性.答案:D2. 集合{1,2,3}的真子集共有( )A. 5个B. 6个C. 7个D. 8个思路解析:可使用穷举法,注意到不含集合本身.或使用所总结的规律n=23-1=7.答案:C3. 设A、B是全集U的两个子集,且A⊆B,则下列式子成立的是( )A. U A⊆U BB. U A∪U B=UC. A∩U B=∅D. U A∩B=∅思路解析:使用韦恩图.答案:C4. 如果集合A={x|ax2+2x+1=0}中只有一个元素,那么a的值是( )A.0B.0或1C.1D.不能确定思路解析:注意到a=0满足题意,此时x=-21;而当a ≠0时,要使得此二次方程的判别式为零,即4-4a=0,可解出a=1.答案:B5. 对于定义在R 上的任何奇函数f(x),下列结论不正确的是( )A. f(x)+f(-x)=0B. f(x)-f(-x)=2f(x)C. f(x)·f(-x)≤0D. )()(x f x f -=-1思路解析:利用奇函数定义f(-x)=-f(x)容易证明A 、B 、C ;而常函数f(x)=0,既是奇函数又是偶函数,但其不符合D.答案:D6. 已知A={1,2,a 2-3a-1},B={1,3},A ∩B={3,1},则a 等于( )A .-4或1B .-1或4C .-1D .4思路解析:因为A ∩B={3,1},所以a 2-3a-1=3,解得a=-1或4.答案:B7. 已知I 为全集,集合M 、N I ,若M ∩N=N ,则 …( )A. M ⊇NB. N ⊆MC. M ⊆ND. M ⊇N思路解析:由M ∩N ⊆M 及已知M ∩N=N 知N ⊆M ,从而有M ⊆N .故选C.答案:C8. 若y=f(a)为偶函数,则下列点的坐标在函数图象上的是( )A. (-a,-f(a))B. (a,-f(a))C. (-a, f(a))D. (-a,-f(-a))思路解析:考查偶函数定义:f(-a)=f(a).答案:C9. 偶函数y=f(x)在区间[0,4]上单调递减,则有( )A. f(-1)>f(3π)>f(-π)B. f(3π)>f(-1)>f(-π)C. f(-π)>f(-1)>f(3π) D. f(-1)>f(-π)>f(3π) 答案:A10.设U={1,2,3,4,5},A 、B 为U 的子集,若A ∩B={2},(U A )∩B={4},(U A )∩(U B )={1,5},则下列结论正确的是( )A. 3∉A, 3∉BB. 3∉A, 3∈BC. 3∈A, 3∉BD. 3∈A, 3∈B思路解析:可结合韦恩图法.答案: C11. 设A={x ∈Z|x 2-px+15=0},B={x ∈Z|x 2-5x+q=0},若A ∪B={2,3,5},A 、B 分别为( )A . {3,5}、{2,3}B . {2,3}、{3,5}C . {2,5}、{3,5}D . {3,5}、{2,5}思路解析:验证可知当3∈A 时,可解出p=8,此时A={3,5},则2∈B,可解出q=6,此时,集合B={2,3}.答案:A12. 设※是集合A 中元素的一种运算,如果对于任意的x 、y ∈A,都有x ※y ∈A,则称运算※对集合A 是封闭的,若M={x|x=a+2b,a 、b ∈Z),则对集合M 不封闭的运算是…( )A .加法B .减法C .乘法D .除法思路解析:设x 1=a 1+2b 1,x 2=a 2+2b 2,有a 1+2b 1+a 2+2b 2=(a 1+a 2)+(a 1+a 2)2满足上述定义,同理可知对减法、乘法也是封闭的.答案:D13. 若f(x)为定义在区间[-6,6]上的偶函数,且f(3)>f(1),下列各式中一定成立的是( )A. f(-1)<f(3)B. f(0)<f(6)C. f(3)>f(2)D. f(2)>f(0)思路解析:考查数形结合思想或转化思想,画图观察,或由f(-1)=f(1)<f(3).答案:A14. 若一数集中的任一元素的倒数仍在该集合中,则称该集合为“可倒数集”,试写出一个含三个元素的可倒数集 .(只需写出一个集合) 思路解析:因为是三个元素,显然有1,在其中另一个数可选择非零的整数.答案:{1,2,21}(答案不唯一) 15. 设f (x )是R 上的偶函数,且在(0,+∞)上是减函数,若x 1<0且x 1+x 2>0,则( )A . f (-x 1)>f (-x 2)B . f (-x 1)=f (-x 2)C . f (-x 1)<f (-x 2)D . f (-x 1)与f (-x 2)大小不确定思路解析:x 2>-x 1>0,f (x )是R 上的偶函数,∴f (-x 1)=f (x 1).又f (x )在(0,+∞)上是减函数,∴f (-x 2)=f (x 2)<f (-x 1). 答案:A16. 设全集为U ,用集合A 、B 、C 的交、并、补集符号表示图中的阴影部分.(1) ;(2) ;(3) .思路解析:利用韦恩图这个重要工具,体现了数形结合思想,要认真领会,熟练应用. 答案:(1)(A ∪B )∩U (A ∩B)(2)[(U A )∪(U B )]∩C(3)(A ∩B )∩(U C )17. 若f(x 1)=xx -1,则f(x)= . 思路解析:求函数的解析式,要从观察题目的特点入手,此题的特点是“分式”,所以联想到换元法.但是所给的“解析式”并不能直接换元,所以还要做适当的变形. (换元法)令t=x 1,则x=t1(t ≠0). ∴f(t)=tt 111-=11-t . ∴f(x)= 11-x (x ≠0且x ≠1).答案:11-x (x ≠0且x ≠1) 18. 已知函数y=f(x)是奇函数,在(0,+∞)内是减函数,且f(x)<0,试问F(x)=)(1x f 在(-∞,0)内是增函数还是减函数?并证明之.思路解析:设x 1<x 2<0,则-x 1>-x 2>0.而f(x)为奇函数,则f(-x 1)=-f(x 1),f(-x 2)=-f(x 2). 又∵f(x)在(0,+∞)内为减函数,∴f(-x 1)<f(-x 2).∴f(x 2)-f(x 1)<0.由已知f(x)<0,得f(-x 1)<0,f(-x 2)<0.∴f(x 1)f(x 2)=f(-x 1)f(-x 2)>0.∴F(x 1)-F(x 2)=)()()()(2112x f x f x f x f -<0. ∴F(x)在(-∞,0)上是增函数.答案:F(x)在(-∞,0)上是增函数.19. 已知f(x)是定义在R 上的偶函数,且在[0,+∞)上为减函数,若f(22--a a )>f(2a-1),求实数a 的取值范围.思路解析:本题的解题关键是如何使用已知条件f(22--a a )>f(2a-1),即如何把这个已知条件转化成关于a 的不等式,也就是把自变量“部分”化到一个单调区间内,才能根据函数的单调性达到转化的目的.这时我们想到了“若f(x)是偶函数,那么f(x)=f(-x)=f(|x|).”于是f(2a-1)=f(|2a-1|).解:由f(x)是偶函数,且f(22--a a )>f(2a-1)等价于f(22--a a )>f(|2a-1|). 又f(x)在[0,+∞)上是减函数,∴⎪⎩⎪⎨⎧-<--≥--22)12(2202a a a a a 解之,得a ≤-1或a ≥2.20. 已知集合A={x|x 2+4x=0,x ∈R},B={x|x 2+2(a +1)x +a 2-1=0,x ∈R},若A ∪B=A ,求实数a 的取值范围.思路解析:本题主要考查集合的运算和包含关系,解题过程中运用了分类讨论思想,分类时易漏掉B 为空集的情况,应引起重视.解:因为A={x|x(x +4)=0}={0,-4},B={x|x 2+2(a +1)x +a 2-1=0,x ∈R},且B ⊆A ,所以B=∅,或{0},或{-4},或{0,-4}.(1)当B=∅时,方程x 2+2(a +1)x +a 2-1=0无实根,即Δ<0,解得a <-1.(2)当B={0}时,方程x 2+2(a +1)x +a 2-1=0有唯一根0,所以⎩⎨⎧=∆=-002a a 解得a=-1.(3)当B={-4}时,方程x 2+2(a +1)x +a 2-1=0有唯一根-4,所以⎩⎨⎧=∆=-++-001)1(8162a a .解得a 无解. (4)当B={0,-4}时,方程x 2+2(a +1)x +a 2-1=0有两根0,-4,所以⎪⎩⎪⎨⎧=-+-=->∆01)1(2402a a .解之,得a=1.综合(1)(2)(3)(4),可知a ≤-1或a=1.21. 已知函数f(x)=ax 2+a 2x+2b-a 3,(1)当x ∈(-2,6)时,其值为正;x ∈(-∞,-2)∪(6,+∞)时,其值为负,求a 、b 的值及f(x)的表达式;(2)设F(x)=-x k f(x)+4(k+1)x+2(6k-1),k 为何值时,函数F(x)的值恒为负值. 思路解析:(1)由已知⎪⎩⎪⎨⎧=-++==-+-=-02636)6(0224)2(3222a b a a f a b a a f . 解得32a+8a 2=0(a<0).∴a=-4.从而b=-8.∴f(x)=-4x 2+16x+48.(2)F(x)=-4k (-4x 2+16x+48)+4(k+1)x+2(6k-1)=kx 2+4x-2. 欲F(x)<0,则⎩⎨⎧<+=∆<,0816,0k k 即k<-2.答案:(1)a=-4,b=-8,f(x)=-4x 2+16x+48.(2)k<-2.22. 已知函数f(x)=x 2+2ax+1在区间[-1,2]上的最大值是4,求a 的值.思路解析:考查分类讨论的数学思想. 若是已知最小值,此种分类同样适用,也可分-a 在(-∞,-1],(-1,2],(2,+∞)三个区间.但本题亦可将1°、2°和3°、4°分别合并成两个区间讨论.抛物线对称轴为x=-a,区间[-1,2]中点为21. 解:(1)当2≥-a,即a ≤-2时,由题设:f(-1)=4,即1-2a+1=4,a=-1(不合).(2)当21≤-a<2,即-2<a ≤1时,由题设f(-1)=4,即a=-1. (3)当-1≤-a<21,即-21<a ≤1时,由题设f(2)=4,即4+4a+1=4,a=-41. (4)当-a<-1,即a>1时,由题设f(2)=4,即4+4a+1=4,a=-41(不合题意). 23. 已知函数f(x),当x,y ∈R 时,恒有f(x+y)=f(x)+f(y),(1)求证:f(x)是奇函数.(2)若f(-3)=a ,试用a 表示f(24).(3)如果x>0时,f(x)>0且f(1)<0,试求f(x)在区间[-2,6]上的最大值与最小值.思路解析:(1)令x=y=0,得f(0)=0,再令y=-x ,得f(0)=f(x)+f(-x). ∴f(x)=f(-x).∴f(x)为奇函数.(2)由f(-3)=a,得f(3)=-f(-3)=-a.f(24)=f( 38333个+++)=8f(3)=-8f(-3)=-8a.(3)设x 1<x 2,则f(x 2)=f(x 1+x 2-x 1)=f(x 1)+f(x 2-x 1)<f(x 1),∵x 2-x 1>0,f(x 2-x 1)<0,∴f(x)在区间[-2,6]上是减函数.∴f(x) max =f(-2)=-f(2)=-2f(1)=1,f(x) min =f(6)=6f(1)=-3.答案:(1)f(x)=f(-x),∴f(x)为奇函数.(2)-8a.(3)f(x) max =1,f(x) min =-3.。
高中数学 第1章 集合与函数概念单元测试 新人教A版必

第1章 集合与函数概念章末检测(考试时间:120分钟 试卷满分:150分)注意事项:1.本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答第Ⅰ卷时,选出每小题答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
写在本试卷上无效。
3.回答第Ⅱ卷时,将答案写在答题卡上。
写在本试卷上无效。
4.考试结束后,将本试卷和答题卡一并交回。
第Ⅰ卷一、选择题(本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.已知2{|4,},{|24}M y y x x P x x ==-∈=≤≤R ,则M 与P 的关系是A .M P =B .M P ∈C .M P =∅ID .M P ⊇2.下列函数中,在定义域内既是奇函数又是增函数的为A .1y x =+B .3y x =-C .1y x =D .y x x = 3.已知全集U 和集合A ,B 如图所示,则()U A B =I ðA .{}5,6B .{}3,5,6C .{}3D .{}0,4,5,6,7,84.已知集合{}|1A x x =∈≤N ,{}|B x x A =⊆,{}|C x x B =⊆,则集合C 中元素的个数为A .4B .8C .16D .205.若函数()f x 满足()1+2()3f x f x x =,则()2f =A .0B .1C .1-D .26.下列四组中表示相等函数的是A .x x x g t t t f -+=-+=11)(11)(与C 7.设函数3,10()((5)),10x x f x f f x x -≥⎧=⎨+<⎩,则(6)f 的值为A .5B .6C .7D .88.已知函数21()1x f x x +=-,其定义域是 [8,4)--,则下列说法正确的是 A .()f x 有最大值53,无最小值 B .()f x 有最大值53,最小值75C .()f x 有最大值75,无最小值D .()f x 有最大值2,最小值759.已知函数(2)f x +的定义域为[2,2]-,则(1)(1)f x f x -++的定义域为A .[1,1]-B .[1,5]-C .[1,3]D .[1,5]10.若()f x 是偶函数,其定义域为(),-∞+∞,且在[)0,+∞上是减函数,则32f ⎛⎫- ⎪⎝⎭与2522f a a ⎛⎫++ ⎪⎝⎭的大小关系是 A .235222f f a a ⎛⎫⎛⎫->++ ⎪ ⎪⎝⎭⎝⎭ B .235222f f a a ⎛⎫⎛⎫-<++ ⎪ ⎪⎝⎭⎝⎭ C .235222f f a a ⎛⎫⎛⎫-≥++ ⎪ ⎪⎝⎭⎝⎭ D .235222f f a a ⎛⎫⎛⎫-≤++ ⎪ ⎪⎝⎭⎝⎭11.已知奇函数()f x 在(,0)-∞上是单调减函数,且(2)0f =,则不等式(1)(1)0x f x -->的解集为A .{|31}x x -<<-B .{|1113}x x x -<<<<或C .{|3013}x x x -<<<<或D .{|312}x x x -<<>或12.已知函数()a f x x x=+(0a >)在(上是减函数,在)+∞上是增函数,若函数()25f x x x =+在[),m +∞(0m >)上的最小值为10,则m 的取值范围是 A .(]0,5 B .()0,5C .[)5,+∞D .()5,+∞第Ⅱ卷二、填空题(本题共4小题,每小题5分,共20分)13.函数y =的定义域是____________.(用区间形式表示) 14.若函数2(),(,)(2,)21x a f x x b b x +=∈-∞++∞-U 是奇函数,则a b +=____________. 15.已知集合2{20|}A x x px =--=,2{0}|B x x qx r =++=,且{2,1,5}A B =-U ,{2}A B =-I ,则p q r ++=____________.16.已知函数2()1f x x x =-+,若在区间[]1,1-上,不等式()2f x x m >+恒成立,则实数m 的取值范围是____________.三、解答题(本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤)17.(本小题满分10分)已知全集为R ,集合{|24}A x x =≤<,{|3782}B x x x =-≥-,{|}C x x a =<.(1)求A B I ;(2)求()A B R U ð;(3)若A C ⊆,求a 的取值范围.18.(本小题满分12分)已知()f x 是定义在R 上的奇函数,且当0x ≥时,2()2f x x x =-.(1)画出函数()f x 的图象,写出它的单调区间;(2)当12x -<<时,求()f x 的取值范围.19.(本小题满分12分)已知一次函数()f x 是R 上的增函数,()()()x x g f x m =+,且(())165f f x x =+.(1)求()f x 的解析式;(2)若()g x 在(1,)+∞上单调递增,求实数m 的取值范围.20.(本小题满分12分)若非零函数()f x 对任意实数,a b 均有()()()f a b f a f b +=,且当0x <时,()1f x >.(1)求证:()0f x >;(2)求证:()f x 为减函数;(321.(本小题满分12分)某企业生产A 、B 两种产品,根据市场调查,A 产品的利润与投资成正比,其关系如图1,B 产品的利润与投资的算术平方根成正比,其关系如图2(注:单位是万元).图1 图2(1)分别将A 、B 两种产品的利润表示为投资的函数,写出它们的函数关系式;(2)现企业有20万元资金全部投入A 、B 两种产品的生产,问:怎样分配这20万元资金,能使获得的利润最大,其最大利润是多少万元?22.(本小题满分12分) 已知()3,[]1,2f x xx b x =∈-+. (1)当2b =时,求()f x 的值域;(2)若b 为正实数,()f x 的最大值为M ,最小值为m ,且满足4M m -≥,求b 的取值范围.。
高一数学人教A版必修1单元测评第一章集合与函数的概念

B 卷本试卷满分:100分;考试时间:90分钟一、选择题(本大题共10小题,每小题4分,共40分,在每小题给出的四个选项中,只有一项是符合要求的)1.下列函数中与函数y =x -1相同的是( ) A .y =(1-x )2 B .y =2)1(-xC .y =1123++-x x xD .y =112+-x x2.下列函数表示偶函数的是( ) A .y =2x B .y =x 3 C .y =x +1D .y =x 2(-1<x ≤1)3.函数y =242x x ---的定义域是( ) A .{2} B .{1,2} C .{x |x ≤-2} D .∅4.已知符号函数:sgn (x )=⎪⎩⎪⎨⎧<-=>).0(1),0(0),0(1x x x 不等式sgn (x -2)<1的解集是( )A .x ≤2B .x <2C .x ≥2D .x <3 5.已知f (x )是奇函数,且当x >0时,f (x )=x (1-x ),则x <0时,f (x )为( ) A .-x (1-x ) B .x (1-x ) C .x (1+x ) D .-x (1+x )6.已知集合A ={(x ,y )|2x -y =0},集合B ={(x ,y )|x -y =3},则集合A ∩B 是( ) A .{-6,-3} B .{(-3,-6)} C .{3,6} D .(-3,-6)7.函数f (x )=xx x -+-||1212的定义域是( ) A .{x |x ≤0}B .{x |x ≤-1)C .{x |x ≥1)D .{x |x ≤-1或x ≥1)8.已知狄利克雷函数的定义为:则D (x )的图象是( )A .两条平行直线B .两条平行直线上稠密的点C .两条相交直线D .两条相交直线上稠密的点 9.函数y =2x +x1(x ≥1)的值域是( ) A .{y |y ≥3} B .{y |y ≥22} C .{y |y ≥4} D .{y |22≤y ≤3} 10.函数y =x1-x 的大致图象是( )答案:1.C 2.A 3.A 4.A 5.C 6.B 7.B 8.B 9.A 10.B二、填空题(本大题共4小题,每小题5分,共20分,把答案填在题中横线上) 11.在给定A →B 的映射f :(x ,y )→(x +y ,x -y )下,集合A 中的元素(2,1)对应着B 中的元素__________. 答案:(3,1)12.函数y -||x -3|的递减区间是__________. 答案:(-∞,3] 13.函数f (x )对于任意的x 1,x 2∈R +恒有f (x 1+x 2)=f (x 1)+f (x 2)成立,且f (1)=41,则f (2 008)=__________. 答案:50214.要修一个面积为800 m 2的长方形的网球场,并且四周修前后l m ,左右2 m 的小路(如图),则占地面积的最小值是__________m 2.答案:968三、解答题(本大题共5小题,每小题8分,共40分,解答应写出文字说明、证明过程或 演算步骤)15.甲、乙两地相距s km ,汽车从甲地匀速行驶到乙地:速率不超过c km /h .已知汽车每小时的运输成本(单位:元)由可变部分和固定部分组成.可变部分与速率钞km /h 的平方成正比,比例系数为b ,固定部分为a 元.(1)把全部运输成本y 元表示成速率v km /h 的函数,指出函数的定义域; (2)为了使全程运输成本最小,汽车应以多大的速率行驶? 答案:(1)y =v s (bv 2+a )=bsv +vsa(0<a ≤c ) (2)(i )若c b a ≤,即a ≤c 2b ,当v =b a 时,y m in =2s ab ;(ii )若c ba >,即a > c 2b ,当v =c 时,y m in =csa+bsc 16.函数y =f (x )的图象如图所示.(1)函数y =f (x )的定义域可能是什么? (2)函数y =f (x )的值域可能是什么? (3)y 的哪些值只与x 的一个值对应?答案:(1)定义域{x |-7≤x ≤0或2<x <6} (2)值域{y |0<y <+∞}(3){y |0<y <2或5<y <+∞) 17.先用定义判断函数f (x )=1+12-x 在区间[2,6]上的单调性,再求函数f (x )在区间[2,6]上的最大值和最小值.答案:易证f (x )在[2,6]上是减函数,∴f (x )max =3,f (x )max =57 18.(1)求下列函数的定义域: ①1231)(2-++-=x x x x f ;②03)1(1312)(-+++-=x x x x f .(2)已知函数f (x )= 213+++x x . ①求f (-3)、f (32)的值; ②当m >0时,求f (m -1)的值. 答案:(1)①{x |x >1且x ≠2};②{x |x ≥21且x ≠1) (2)①f (-3)=-1,f (32)=333+83;②f (m -1)=112+++m m19.设某公民的月所得(工资、薪金所得)x 元,每月纳所得税f (x )元是x 的函数.当前国家制定的《个人所得税率表》如下:(1)在表中填写函数f (x )表达式;(2)某人在某月缴纳个人所得税是240元,他那个月的工资、薪金收入是多少元?(结果保留整数)答案:(1)⎪⎪⎩⎪⎪⎨⎧≤<-≤<-≤<-≤<-216006600,6952.0,66003600,36515.0,36002100,1851.0,21001600,8005.0)(x x x x x x x x x f(2)0.15x -365=240,解之得x ≈4033页。
(新课程)高中数学《第一章 集合与函数的概念》素质测评 新人教A版必修1

第一章 素质测评一、选择题1.下列关系式中,正确的是( )A .Ø∈{0}B .0⊆{0}C .0∈{0}D .0{0} 答案:C2.满足A ∪{-1,1}={-1,0,1}的集合A 共有( )A .2个B .4个C .8个D .16个解析:由题意知A ={0}或A ={0,-1}或A ={0,1}或A ={-1,0,1},共4个.故选B. 答案:B3.如下图所示,阴影部分表示的集合是( )A .(∁UB )∩A B .(∁U A )∩BC .∁U (A ∩B )D .∁U (A ∪B )解析:因为阴影部分在集合∁U B 中又在集合A 中,所以阴影部分是(∁U B )∩A .故选A. 答案:A4.如下图所示,对应关系f 是从A 到B 的映射的是( )解析:B 、C 中的集合A 中都有剩余元素,故B 、C 不是映射;A 中有一对多的情况,故A 不是映射.故选D.答案:D5.设集合M ={x |x >1},P ={x |x 2-6x +9=0},则下列关系中正确的是( )A .M =PB .P MC .M PD .M ∪P =R解析:P ={3},∵3>1,∴3∈M .∴P ⊆M .但是2∈M,2∉P ,∴P M . 答案:B6.已知f (x )=⎩⎪⎨⎪⎧x 2(x >0)2(x =0)0 (x <0),则f {f [f (-2)]}的值为( )A .0B .2C .4D .8 解析:∵-2<0, ∴f (-2)=0,∴f [f (-2)]=f (0)=2>0,f {f [f (-2)]}=f (2)=4.故选C. 答案:C7.对任意两个实数对(a ,b )和(c ,d ),规定:(a ,b )=(c ,d ),当且仅当a =c ,b =d ;运算“”为:(a ,b )(c ,d )=(ac -bd ,bc +ad );运算“”为:(a ,b )(c ,d )=(a +c ,b +d ).设p 、q ∈R,若(1,2)(p ,q )=(5,0),则(1,2)(p ,q )=( )A .(0,-4)B .(0,2)C .(4,0)D .(2,0)解析:∵(1,2)(p ,q )=(p -2q,2p +q )=(5,0),∴⎩⎪⎨⎪⎧p -2q =5,2p +q =0,解得⎩⎪⎨⎪⎧p =1,q =-2.∴(1,2) (p ,q )=(1+p,2+q )=(2,0),故选D.答案:D8.函数y =x 2-2x +3,-1≤x ≤2的值域是( )A .RB .[3,6]C .[2,6]D .[2,+∞) 解析:画出函数的图象,如右图所示,观察函数的图象可得图象上所有点的纵坐标的取值范围是[2,6], 所以值域是[2,6]. 答案:C9.函数f (x )=x 2-2ax ,x ∈[1,+∞)是增函数,则实数a 的取值范围是( )A .RB .[1,+∞)C .(-∞,1]D .[2,+∞)解析:f (x )=x 2-2ax 的对称轴是直线x =a ,则a ≤1. 答案:C10.定义在R 上的偶函数在[0,7]上是增函数,在[7,+∞)上是减函数,又f (7)=6,则f (x )( )A .在[-7,0]上是增函数,且最大值是6B .在[-7,0]上是减函数,且最大值是6C .在[-7,0]上是增函数,且最小值是6D .在[-7,0]上是减函数,且最小值是6解析:由f (x )是偶函数,得f (x )关于y 轴对称,其图象可以用下图简单地表示,则f (x )在[-7,0]上是减函数,且最大值为6. 答案:B11.已知函数f (x )是(-∞,0)∪(0,+∞)上的奇函数,且当x <0时,函数的部分图象如右图所示,则不等式xf (x )<0的解集是( )A .(-2,-1)∪(1,2)B .(-2,-1)∪(0,1)∪(2,+∞)C .(-∞,-2)∪(-1,0)∪(1,2)D .(-∞,-2)∪(-1,0)∪(0,1)∪(2,+∞)解析:根据奇函数图象关于原点对称,作出函数图象,则不等式xf (x )<0的解为 ⎩⎪⎨⎪⎧ x <0,f (x )>0,或⎩⎪⎨⎪⎧x >0,f (x )<0.故选D.答案:D12.已知函数f (x )在[-1,2]上是减函数,且点A (-1,3)和点B (2,-1)在函数f (x )的图象上,则满足条件-1≤f (x -2)≤3的x 的集合是( )A .{x |1≤x ≤4}B .{x |-3≤x ≤0}C .{x |x ∈R}D .{x |x ∈Ø} 解析:∵f (-1)=3,f (2)=-1, 又∵-1≤f (x -2)≤3, ∴f (2)≤f (x -2)≤f (-1). 又∵f (x )在[-1,2]上单调递减, ∴-1≤x -2≤2, ∴1≤x ≤4.故选A. 答案:A 二、填空题13.已知集合A ={x |x 2+ax +b =0}中仅有一个元素1,则a =________,b =________. 答案:-2 114.函数f (x )=5+4x -x 2的值域是________.解析:∵y =5+4x -x 2=-(x -2)2+9,且0≤-(x -2)2+9≤9,∴函数y =5+4x -x 2的值域为[0,3].答案:[0,3]15.某粮店销售大米,若一次购买大米不超过50 kg 时,单价为m 元;若一次购买大米超过50 kg 时,其超出部分按原价的90%计算,某人一次购买了x kg 大米,其费用为y 元,则y 与x 的函数关系式y =________.解析:当0≤x ≤50时,y =mx ;当x >50时,y =50m +(x -50)×90%·m =0.9mx +5m .答案:⎩⎪⎨⎪⎧mx ,0≤x ≤50,0.9mx +5m ,x >5016.设函数f (x )=⎩⎪⎨⎪⎧|x -1|(0<x <2),2-|x -1|(x ≤0或x ≥2),则函数y =f (x )与y =12的交点个数是________.解析:函数y =f (x )的图象如下图所示,则两函数y =f (x )与y =12的交点个数是4.答案:4 三、解答题 17.已知全集U =R ,集合M ={x |x ≤3},N ={x |x <1},求M ∪N ,(∁U M )∩N ,(∁U M )∪(∁U N ). 解:由题意得M ∪N ={x |x ≤3},∁U M ={x |x >3},∁U N ={x |x ≥1}, 则(∁U M )∩N ={x |x >3}∩{x |x <1}=Ø,(∁U M )∪(∁U N )={x |x >3}∪{x |x ≥1}={x |x ≥1}.18.已知a 、x ∈R,集合A ={2,4,x 2-5x +9},B ={3,x 2+ax +a },C ={x 2+(a +1)x -3,1}.(1)使A ={2,3,4}的x 的值; (2)使2∈B ,B A 的a 、x 的值.解:(1)由集合相等的定义知x 2-5x +9=3,解之得x 2-5x +6=0,x =2或x =3. 经检验,x =2或3都符合题意. (2)∵2∈B ,B A ,∴⎩⎪⎨⎪⎧2=x 2+ax +a ,①x 2-5x +9=3,②解②得x =2或x =3. 把x =2代入①得a =-23;把x =3代入①得a =-74.经检验⎩⎪⎨⎪⎧a =-23,x =2,或⎩⎪⎨⎪⎧a =-74,x =3.都适合题意.19.已知函数f (x )是正比例函数,函数g (x )是反比例函数,且f (1)=1,g (1)=2.(1)求函数f (x )和g (x );(2)判断函数f (x )+g (x )的奇偶性.解:(1)设f (x )=k 1x ,g (x )=k 2x,其中k 1k 2≠0,则k 1×1=1,k 21=2,∴k 1=1,k 2=2.则f (x )=x ,g (x )=2x. (2)设h (x )=f (x )+g (x ),则h (x )=x +2x,∴函数h (x )的定义域是(-∞,0)∪(0,+∞).h (-x )=-x +2-x =-(x +2x)=-h (x ),∴函数h (x )是奇函数,即函数f (x )+g (x )是奇函数.20.已知f ⎝ ⎛⎭⎪⎫x -1x +1=-x -1.(1)求f (x );(2)求f (x )在区间[2,6]上的最大值和最小值.解:(1)令t =x -1x +1,则x =-t -1t -1,∴f (t )=2t -1,∴f (x )=2x -1(x ≠1).(2)任取x 1,x 2∈[2,6],且x 1<x 2,f (x 1)-f (x 2)=2x 1-1-2x 2-1=2(x 2-x 1)(x 1-1)(x 2-1),∵2≤x 1<x 2≤6,∴(x 1-1)(x 2-1)>0,2(x 2-x 1)>0, ∴f (x 1)-f (x 2)>0,∴f (x )在[2,6]上单调递减, ∴当x =2时,f (x )max =2,当x =6时,f (x )min =25.21.扬州某公司生产的新产品的成本是2元/件,售价是3元/件,年销售量为10万件,为了获得更好的效益,公司准备拿出一定的资金做广告.根据经验,每年投入的广告费是x (万元)时,它们的关系如下表:(1)求y 与x (2)如果利润=销售总额-成本费-广告费,试写出年利润S (万元)与广告费x (万元)的函数关系式;并求出当广告费x 为多少万元时,年利润S 最大.解:(1)由于y 是x 的二次函数,所以可设函数的解析式为y =ax 2+bx +c (a ≠0)(x ≥0);由于点(1,1.5)、(2,1.8)、(5,1.5)在函数图象上,所以⎩⎪⎨⎪⎧1.5=a +b +c ,1.8=4a +2b +c ,1.5=25a +5b +c ,解得⎩⎪⎨⎪⎧a =-110,b =35,c =1.所以所求函数的解析式为y =-110x 2+35x +1,(x ≥0).(2)当投入广告费x 万元时,产品的销量是10y 万件,成本2元/件,售价3元/件,每件获得利润1元,共获利10y (3-2)=10y 万元,由题意得S =10y (3-2)-x =10(-110x 2+35x +1)-x=-x 2+5x +10=-(x -52)2+654(x ≥0).当x =52时,S max =654.即当投入2.5万元广告费时,年利润最大.22.函数f (x )=ax +b x 2+1是定义在(-∞,+∞)上的奇函数,且f (12)=25.(1)求实数a 、b ,并确定函数f (x )的解析式;(2)判断f (x )在(-1,1)上的单调性,并用定义证明你的结论. 解:(1)∵f (x )是奇函数, ∴f (-x )=-f (x ), 即-ax +b x 2+1=-ax +b x 2+1,-ax +b =-ax -b ,∴b =0,∴f (x )=ax x 2+1,又f (12)=25,∴12a 14+1=25,∴a =1,∴f (x )=x x 2+1. (2)f (x )在(-1,1)上是增函数.证明如下:任取x 1,x 2∈(-1,1),且x 1<x 2,f (x 1)-f (x 2)=x 1x 21+1-x 2x 22+1=(x 1-x 2)(1-x 1x 2)(x 21+1)(x 22+1) ∵-1<x 1<x 2<1,∴-1<x 1x 2<1,x 1-x 2<0,1-x 1x 2>0,x 21+1>0,x 22+1>0, ∴f (x 1)-f (x 2)<0,即f (x 1)<f (x 2), ∴f (x )在(-1,1)上是增函数.。
人教新课标版数学高一A版必修1单元检测 第一章集合与函数概念

数学人教A 必修1第一章 集合与函数概念单元检测(时间:90分钟 满分:100分) 第Ⅰ卷(选择题 共50分)一、选择题(本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.已知集合A ={1,2},B ={2,4},则A ∪B =( ).A .{2}B .{1,2,2,4}C .{1,2,4}D .∅2.2010年11月,第16届亚运会在广州举行,在这次亚运会中,下列能构成集合的是( ).A .所有著名运动员B .所有志愿者C .所有喜欢中国的运动员D .参加开幕式表演的所有高个子演员 3.给出下列集合A 到集合B 的几种对应:其中,是从A 到B 的映射的有( ).A .(1)(2)B .(1)(2)(3)C .(1)(2)(4)D .(1)(2)(3)(4) 4.已知全集U =R ,集合A ={x |2x 2-3x -2=0},集合B ={x |x >1},则A ∩(∁U B )=( ). A .{2} B .{x |x ≤1}C.12⎧⎫-⎨⎬⎩⎭D .{x |x ≤1,或x =2}5.函数f (x )( ). A .[-1,+∞) B .(-∞,0)∪(0,+∞) C .[-1,0)∪(0,+∞) D .R6.已知全集U =R ,集合P ={x ∈N *|x <7},Q ={x |x -3>0},那么图中阴影表示的集合是( ).A .{1,2,3,4,5,6}B .{x |x >3}C .{4,5,6}D .{x |3<x <7}7.设集合M ={x |x >1},P ={x |x 2-6x +9=0},则下列关系中正确的是( ). A .M =P B .P M C .M P D .M ∪P =R8.函数y =x 2-2x +3,-1≤x ≤2的值域是( ). A .R B .[3,6]C .[2,6]D .[2,+∞)9.定义在R 上的偶函数f (x )在[0,7]上是增函数,在[7,+∞)上是减函数,f (7)=6,则f (x )( ).A .在[-7,0]上是增函数,且最大值是6B .在[-7,0]上是减函数,且最大值是6C .在[-7,0]上是增函数,且最小值是6D .在[-7,0]上是减函数,且最小值是610.定义在R 上的偶函数f (x )满足:对任意x 1,x 2∈(-∞,0](x 1≠x 2),都有2121()()x x f x f x -->0,则( ).A .f (-5)<f (4)<f (6)B .f (4)<f (-5)<f (6)C .f (6)<f (-5)<f (4)D .f (6)<f (4)<f (-5)第Ⅱ卷(非选择题 共50分)二、填空题(本大题共5小题,每小题5分,共25分.把答案填在题中的横线上) 11.定义在[-2,4]上的函数f (x )的图象如图所示,则函数f (x )的单调递增区间是__________,单调递减区间是__________.12.已知函数f (x )=31,3,,3,x x x x +<⎧⎪⎨>⎪⎩则f [f (1)]=__________.13.已知集合A ={x |x 2+x -6=0},B ={x |mx +1=0},A ∩B =B ,设实数m 所能取的一切值构成的集合为P ,则用列举法表示P =__________.14.已知函数f (x )=2x +3,g (x )=3x -5,如果f [g (x 0)]=1,则x 0=__________. 15.如图是偶函数y =f (x )的局部图象,根据图象所给信息,有以下结论:①函数一定有最小值; ②f (-1)-f (2)>0;③f (-1)-f (2)=0; ④f (-1)-f (2)<0; ⑤f (-1)+f (2)>0.其中正确的结论有__________.(填序号)三、解答题(本大题共2小题,共25分.解答时应写出文字说明、证明过程或演算步骤) 16.(10分)已知函数f (x )=-2x +m ,其中m 为常数. (1)求证:函数f (x )在R 上是减函数;(2)当函数f (x )是奇函数时,求实数m 的值.17.(15分)已知函数f (x )是正比例函数,函数g (x )是反比例函数,且f (1)=1,g (1)=2, (1)求函数f (x )和g (x );(2)判断函数f (x )+g (x )的奇偶性.(3)求函数f (x )+g (x )在(0,2]上的最小值.参考答案1. 答案:C2. 答案:B3. 答案:A 根据映射的定义知,(3)中集合A 中的元素a 对应集合B 中的两个元素x ,y ,则此对应不是映射;(4)中集合A 中的元素b 在集合B 中没有对应元素,则此对应也不是映射.仅有(1)(2)符合映射的定义,则(1)(2)是映射.4. 答案:C A =1,22⎧⎫-⎨⎬⎩⎭,B ={x |x ≤1}, 则A (B )=12⎧⎫-⎨⎬⎩⎭.5. 答案:C 要使函数有意义,x 的取值需满足10,0,x x +≥⎧⎨≠⎩解得x ≥-1,且x ≠0,则函数的定义域是[-1,0)(0,+).6. 答案:C P ={1,2,3,4,5,6},Q ={x |x >3},则阴影表示的集合是P Q ={4,5,6}.7. 答案:B ∵P ={3},∴PM .8. 答案:C 画出函数y =x 2-2x +3,-1≤x ≤2的图象,如图所示,观察函数的图象可得图象上所有点的纵坐标的取值范围是[2,6],所以值域是[2,6].9. 答案:B ∵f (x )是偶函数,∴f (x )的图象关于y 轴对称.∴f (x )在[-7,0]上是减函数,且最大值为6.10. 答案:C ∵对任意x 1,x 2(-,0](x 1≠x 2),都有2121()()x x f x f x -->0,∴对任意x 1,x 2∈(-,0],若x 1<x 2,总有f (x 1)<f (x 2),∴f (x )在(-,0]上是增函数.∴f (-4)>f (-5)>f (-6). 又∵函数f (x )是偶函数, ∴f (-6)=f (6),f (-4)=f (4), ∴f (6)<f (-5)<f (4).11. 答案:(-1,1) [-2,-1],[1,4]12. 答案:2 f (1)=3+1=4,f [f (1)]=f (4)=4=2. 13. 答案:11,0,23⎧⎫-⎨⎬⎩⎭由题意得A ={-3,2},集合B 是关于x 的方程mx +1=0的解集.由A B =B 得BA ,∴B =或B ≠.当B =时,m =0;当B ≠时,m ≠0,则x =1m-A ,则1m-=-3或1m -=2,解得m =13或12-.综上,m =0或13或12-,则P =11,0,23⎧⎫-⎨⎬⎩⎭. 14. 答案:43因为g (x 0)=3x 0-5,所以f [g (x 0)]=f (3x 0-5)=2(3x 0-5)+3=6x 0-7=1,解得x 0=43.15. 答案:④⑤ ∵所给图象为函数的局部图象,∴不能确定函数一定有最小值;由图象知函数y =f (x )在区间[1,3]上是增函数,则f (1)-f (2)<0,又函数y =f (x )是偶函数,则f (-1)=f (1),则f (-1)-f (2)<0.∵f (-1)=f (1)>0,f (2)>0, ∴f (-1)+f (2)>0.16. 答案:(1)证明:设x 1,x 2是R 上的任意两个实数,且x 1<x 2, 则f (x 1)-f (x 2)=(-2x 1+m )-(-2x 2+m )=2(x 2-x 1), ∵x 1<x 2,∴x 2-x 1>0.∴f (x 1)>f (x 2). ∴函数f (x )在R 上是减函数. (2)解:∵函数f (x )是奇函数, ∴对任意x ∈R ,有f (-x )=-f (x ). ∴2x +m =-(-2x +m ).∴m =0. 17. 答案:解:(1)设f (x )=k 1x ,g (x )=2k x,其中k 1k 2≠0. ∵f (1)=1,g (1)=2,∴k 1×1=1,2k x=2, ∴k 1=1,k 2=2.∴f (x )=x ,g (x )=2x . (2)设h (x )=f (x )+g (x ),则h (x )=x +2x, ∴函数h (x )的定义域是(-∞,0)∪(0,+∞). ∵h (-x )=-x +22x x x ⎛⎫=-+ ⎪-⎝⎭=-h (x ), ∴函数h (x )是奇函数,即函数f (x )+g (x )是奇函数. (3)由(2)知h (x )=x +2x,设x 1,x 2是(0]上的任意两个实数,且x 1<x 2,则h (x 1)-h (x 2)=121222x x x x ⎛⎫⎛⎫+-+ ⎪ ⎪⎝⎭⎝⎭=(x 1-x 2)+1222x x ⎛⎫- ⎪⎝⎭=(x 1-x 2)12121212()(2)21x x x x x x x x ⎛⎫---=⎪⎝⎭, ∵x 1,x 2(02,且x 1<x 2, ∴x 1-x 2<0,0<x 1x 2<2.∴x 1x 2-2<0,(x 1-x 2)(x 1x 2-2)>0. ∴h (x 1)>h (x 2).∴函数h (x )在(02]上是减函数,函数h (x )在(02]上的最小值是h 2)=22 即函数f (x )+g (x )在(02]上的最小值是22.。
高中数学人教版必修1第一章集合与函数概念单元测试卷(A)(含答案)
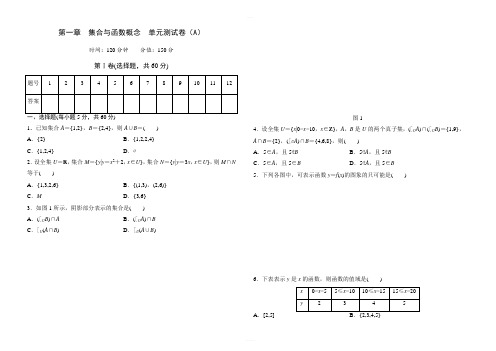
第一章 集合与函数概念 单元测试卷(A )时间:120分钟 分值:150分第Ⅰ卷(选择题,共60分)1.已知集合A ={1,2},B ={2,4},则A ∪B =( ) A .{2} B .{1,2,2,4} C .{1,2,4}D .∅2.设全集U =R ,集合M ={y |y =x 2+2,x ∈U },集合N ={y |y =3x ,x ∈U },则M ∩N 等于( ) A .{1,3,2,6} B .{(1,3),(2,6)} C .MD .{3,6}3.如图1所示,阴影部分表示的集合是( ) A .(∁U B )∩A B .(∁U A )∩B C .∁U (A ∩B )D .∁U (A ∪B )图14.设全集U ={x |0<x <10,x ∈Z },A ,B 是U 的两个真子集,(∁U A )∩(∁U B )={1,9},A ∩B ={2},(∁U A )∩B ={4,6,8},则( )A .5∈A ,且5∉B B .5∉A ,且5∉B C .5∈A ,且5∈BD .5∉A ,且5∈B5.下列各图中,可表示函数y =f (x )的图象的只可能是( )6.下表表示y 是x 的函数,则函数的值域是( )A .[2,5] C .(0,20)D .N7.图中给出的对应是从A 到B 的映射的是( )8.已知函数f (x )=⎩⎪⎨⎪⎧x ,x ≥0,x 2,x <0,则f [f (-2)]的值是( )A .2B .-2C .4D .-49.函数y =x 2-2x +3,-1≤x ≤2的值域是( )A .RB .[3,6]C .[2,6]D .[2,+∞)10.已知函数f (x )是(-∞,0)∪(0,+∞)上的奇函数,且当x <0时,函数的部分图象如图4所示,则不等式xf (x )<0的解集是( )图4A .(-2,-1)∪(1,2)B .(-2,-1)∪(0,1)∪(2,+∞)C .(-∞,-2)∪(-1,0)∪(1,2)D .(-∞,-2)∪(-1,0)∪(0,1)∪(2,+∞)11.定义在R 上的偶函数f (x )在[0,7]上是增函数,在[7,+∞)上是减函数,f (7)=6,则f (x )( )A .在[-7,0]上是增函数,且最大值是6B .在[-7,0]上是减函数,且最大值是6C .在[-7,0]上是增函数,且最小值是6D .在[-7,0]上是减函数,且最小值是612.定义在R 上的偶函数f (x )满足:对任意x 1,x 2∈(-∞,0](x 1≠x 2),都有x 2-x 1f (x 2)-f (x 1)>0,则( )A .f (-5)<f (4)<f (6)B .f (4)<f (-5)<f (6)C .f (6)<f (-5)<f (4)D .f (6)<f (4)<f (-5)第Ⅱ卷(非选择题,共90分)二、填空题(每小题5分,共20分)13.设P 和Q 是两个集合,定义集合P -Q ={x |x ∈P ,且x ∉Q },若P ={1,2,3,4},Q ={x |x +12<2,x ∈R },则P -Q =________.14.函数y =x 2+2x -3的单调递减区间是________.15.若函数f (x )=kx 2+(k -1)x +2是偶函数,则f (x )的递减区间是________.16.设函数f (x )=⎩⎪⎨⎪⎧|x -1|(0<x <2),2-|x -1|(x ≤0,或x ≥2),则函数y =f (x )与y =12的图象的交点个数是________.三、解答题(写出必要的计算步骤,只写最后结果不得分,共70分)17.(10分)已知集合A ={x |2≤x ≤8},B ={x |1<x <6},C ={x |x >a },U =R . (1)求A ∪B ,(∁U A )∩B ;(2)若A ∩C ≠∅,求a 的取值范围.18.(12分)设A ={x |x 2+2(a +1)x +a 2-1=0},B ={x |x (x +4)(x -12)=0,x ∈Z }.若A ∩B =A ,求a 的取值范围.19.(12分)已知函数f (x )=-2x +m ,其中m 为常数. (1)求证:函数f (x )在R 上是减函数; (2)当函数f (x )是奇函数时,求实数m 的值.20.(12分)某公司生产的水笔上年度销售单价为0.8元,年销售量为1亿支.本年度计划将销售单价调至0.55~0.75元(含端点值),经调查,若销售单价调至x元,则本年度新增销售量y(亿支)与x-0.4成反比,且当x=0.65时,y=0.8.(1)求y与x的函数关系式;(2)若每支水笔的成本价为0.3元,则水笔销售单价调至多少时,本年度该公司的收益比上年度增加20%?21.(12分)已知函数f(x)是正比例函数,函数g(x)是反比例函数,且f(1)=1,g(1)=2,(1)求函数f(x)和g(x);(2)判断函数f(x)+g(x)的奇偶性.(3)求函数f(x)+g(x)在(0,2]上的最小值.22.(12分)函数f(x)=ax+b1+x2是定义在(-1,1)上的奇函数,且f(12)=25.(1)求f(x)的解析式;(2)证明f(x)在(-1,1)上为增函数;(3)解不等式f(t-1)+f(t)<0.第一章集合与函数概念单元综合测试一答案第Ⅰ卷(选择题,共60分)一、选择题(每小题5分,共60分)1.答案:C2.解析:M=[2,+∞),N=R.答案:C3.解析:因为阴影部分既在集合∁U B中又在集合A中,所以阴影部分为(∁B)∩A.U答案:A4.解析:可借助V enn图(如图2)解决,数形结合.图2答案:A5.解析:根据函数的概念知,只有“一对一”或“多对一”对应才能构成函数关系.答案:A6.答案:B7.解析:根据映射定义,A中每一个元素在B中仅有1个元素与之对应,仅D适合.答案:D8.解析:∵x =-2,而-2<0, ∴f (-2)=(-2)2=4. 又4>0,∴f [f (-2)]=f (4)=4. 答案:C9.解析:画出函数y =x 2-2x +3,-1≤x ≤2的图象,如图3所示,观察函数的图象可得图象上所有点的纵坐标的取值范围是[2,6],所以值域是[2,6].图3答案:C10.解析:xf (x )<0⇔x 与f (x )异号,由函数图象及奇偶性易得结论. 答案:D11.解析:∵f (x )是偶函数,∴f (x )的图象关于y 轴对称.∴f (x )在[-7,0]上是减函数,且最大值为6. 答案:B12.解析:∵对任意x 1,x 2∈(-∞,0](x 1≠x 2),都有x 2-x 1f (x 2)-f (x 1)>0,∴对任意x 1,x 2∈(-∞,0],若x 1<x 2,总有f (x 1)<f (x 2),∴f (x )在(-∞,0]上是增函数.∴f (-4)>f (-5)>f (-6).又∵函数f (x )是偶函数,∴f (-6)=f (6), f (-4)=f (4),∴f (6)<f (-5)<f (4). 答案:C第Ⅱ卷(非选择题,共90分)二、填空题(每小题5分,共20分)13.解析:因为x ∉Q ,所以x ∈∁R Q ,又Q ={x |-12≤x <72}, 故∁R Q ={x |x <-12,或x ≥72},故P -Q ={4}. 答案:{4}14.解析:由x 2+2x -3≥0,得x ≥1或x ≤-3, ∴函数减区间为(-∞,-3]. 答案:(-∞,-3]15.解析:∵f (x )是偶函数,∴f (-x )=kx 2-(k -1)x +2=kx 2+(k -1)x +2=f (x ). ∴k =1.∴f (x )=x 2+2,其递减区间为(-∞,0]. 答案:(-∞,0]16.解析:函数y =f (x )的图象如图5所示,则函数y =f (x )与y =12的图象的交点个数是4.图5答案:4三、解答题(写出必要的计算步骤,只写最后结果不得分,共70分) 17.解:(1)A ∪B ={x |2≤x ≤8}∪{x |1<x <6}={x |1<x ≤8}. ∁U A ={x |x <2或x >8}. ∴(∁U A )∩B ={x |1<x <2}. (2)∵A ∩C ≠∅,∴a <8.18.解:由B ={x |x (x +4)(x -12)=0,x ∈Z },得B ={-4,0}.由A ∩B =A ,得A ⊆B .于是,A 有四种可能,即A =∅,A ={-4},A ={0},A ={-4,0}.以下对A 分类讨论:(1)若A =∅,则Δ=4(a +1)2-4a 2+4=8a +8<0,解得a <-1; (2)若A ={-4},则Δ=8a +8=0,解得a =-1.此时x 2+2(a +1)x +a 2-1=0可化为x 2=0,所以x =0,这与x =-4是矛盾的;(3)若A ={0},则由(2)可知,a =-1; (4)若A ={-4,0},则⎩⎪⎨⎪⎧Δ=8a +8>0,-2(a +1)=-4,a 2-1=0,解得a =1.综上可知,a 的取值范围是{a |a ≤-1,或a =1}.19.解:(1)证明:设x 1,x 2是R 上的任意两个实数,且x 1<x 2,则f (x 1)-f (x 2)=(-2x 1+m )-(-2x 2+m )=2(x 2-x 1),∵x 1<x 2,∴x 2-x 1>0. ∴f (x 1)>f (x 2).∴函数f (x )在R 上是减函数. (2)∵函数f (x )是奇函数,∴对任意x ∈R ,有f (-x )=-f (x ). ∴2x +m =-(-2x +m ).∴m =0.20.解:(1)设y =kx -0.4,由x =0.65,y =0.8,得k =0.2,所以y =15x -2(0.55≤x ≤0.75).(2)依题意,(1+15x -2)·(x -0.3)=1×(0.8-0.3)×(1+20%),解得x =0.6或x =0.5(舍去),所以水笔销售单价应调至0.6元. 21.解:(1)设f (x )=k 1x ,g (x )=k 2x ,其中k 1k 2≠0. ∵f (1)=1,g (1)=2,∴k 1×1=1,k 21=2. ∴k 1=1,k 2=2.∴f (x )=x ,g (x )=2x . (2)设h (x )=f (x )+g (x ),则h (x )=x +2x , ∴函数h (x )的定义域是(-∞,0)∪(0,+∞). ∵h (-x )=-x +2-x=-(x +2x )=-h (x ),∴函数h (x )是奇函数,即函数f (x )+g (x )是奇函数.(3)由(2)知h (x )=x +2x ,设x 1,x 2是(0,2]上的任意两个实数,且x 1<x 2, 则h (x 1)-h (x 2)=(x 1+2x 1)-(x 2+2x 2)=(x 1-x 2)+(2x 1-2x 2)=(x 1-x 2)(1-2x 1x 2)=(x 1-x 2)(x 1x 2-2)x 1x 2,∵x 1,x 2∈(0,2],且x 1<x 2,∴x 1-x 2<0,0<x 1x 2<2. ∴x 1x 2-2<0,(x 1-x 2)(x 1x 2-2)>0. ∴h (x 1)>h (x 2).∴函数h (x )在(0,2]上是减函数,函数h (x )在(0,2]上的最小值是h (2)=2 2.即函数f (x )+g (x )在(0,2]上的最小值是2 2.22.解:(1)由题意得⎩⎨⎧f (0)=0,f (12)=25,解得⎩⎪⎨⎪⎧a =1,b =0.所以f (x )=x 1+x 2. (2)证明:任取两数x 1,x 2,且-1<x 1<x 2<1,则f (x 1)-f (x 2)=x 11+x 21-x 21+x 22=(x 1-x 2)(1-x 1x 2)(1+x 21)(1+x 22).因为-1<x 1<x 2<1,所以x 1-x 2<0,x 1x 2<1,故1-x 1x 2>0,所以f (x 1)-f (x 2)<0,故f (x )在(-1,1)上是增函数.(3)因为f (x )是奇函数,所以由f (t -1)+f (t )<0,得f (t -1)<-f (t )=f (-t ).由(2)知, f (x )在(-1,1)上是增函数,所以-1<t -1<-t <1,解得0<t <12,所以原不等式的解集为{t |0<t <12}.。
2021年高中数学 第一章 集合与函数概念单元检测(3)新人教A版必修1

2021年高中数学 第一章 集合与函数概念单元检测(3)新人教A 版必修1班级 姓名 分数一、选择题:(每小题5分,共30分)。
1.在“①高一数学课本中的难题;②所有的正三角形; ③方程的实数解”中,能够表示成集合的是( )(A )② (B )③ (C )②③ (D )①②③2.若,则( )(A ) (B ) (C ) (D )3.设M={菱形},N={平行四边形},P={四边形},Q={正方形},则这些集合之间的关系为()(A ) (B )(C ) (D )4.3.设,给出的4个图形中能表示集合到集合的映射的是( )5.有下列函数:①;②;③;④,其中是偶函数的有:( )(A )① (B )①③ (C )①② (D )②④6.f(x)是定义在(0,+∞)上的增函数,则不等式f(x)>f[8(x-2)]的解集是( )(A)(0 ,+∞) (B)(0 , 2) (C) (2 ,+∞) (D) (2 ,)二、填空题:请把答案填在题中横线上(每小题5分,共20分).7.若,则 .8.已知集合,则集合A 的真子集的个数是9.,的最大值是10.已知一次函数满足关系式,则___________.三、解答题:解答应写出文字说明、证明过程或演算步骤(共50分).11.(16分)设A={x ∈Z| ,,求:(1);(2)B.12.(16分)已知函数f(x)=x+,且f(1)=2.(1)求m;(2)判断f(x)的奇偶性;13.(18分)已知函数.(1)证明:在上是减函数;(2)当时,求的最大值和最小值.集合与函数概念单元检测(B卷)班级姓名分数一、选择题:(每小题5分,共30分)。
1.若,则 ( )(A)(B)(C)(D)2.已知,则()A.5 B.-1 C.-7D.23.函数y==x2-6x+10在区间(2,4)上是()A.递减函数B.递增函数 C.先递减再递增D.先递增再递减.4.函数f(x)=-x2+2(a-1)x+2在(-∞,4)上是增函数,则a的范围是()A.a≥5 B.a≥3 C.a≤3 D.a≤-55.若,则的值为 ( )(A)0 (B)1 (C)(D)1或6.已知定义在R上的奇函数满足,则的值为()(A)1 (B)0 (C)1 (D)2二、填空题:请把答案填在题中横线上(每小题5分,共20分)7.函数的定义域是8.已知,则9.已知函数是偶函数,的图象与x 轴有四个交点,则的所有实根之和为________10.函数对于任意实数满足条件,若 则f ( 5 ) = ___三、解答题:解答应写出文字说明、证明过程或演算步骤(共50分).11.(16分)若集合{}{}2|60,|(2)()0M x x x N x x x a =+-==--=,且,求实数的值。
高中数学 第一章 集合与函数概念单元检测3 新人教A版

第一章 集合与函数概念单元检测参考完成时间:120分钟 实际完成时间:_____分钟 总分:150分 得分:______一、选择题(本大题共12小题,每小题5分,共60分)1.给出以下五个对象,其中能构成集合的个数为( )①你所在班中身高超过1.75 m 的同学;②所有平行四边形;③某数学教辅书中的所有习题;④所有有理数;⑤2012年高考试卷中的所有难题.A .1B .2C .3D .42.设全集U =Z ,集合A ={1,3,5,7,9},B ={1,2,3,4,5},则图中阴影部分表示的集合是( )A .{1,3,5}B .{1,2,3,4,5}C .{7,9}D .{2,4}3.如果全集U ={x |x 是小于9的正整数},集合A ={1,2,3,4},B ={3,4,5,6},则(U A )I (U B )为( )A .{1,2}B .{3,4}C .{5,6}D .{7,8}4.下列各组函数表示同一函数的是( )A .f (x )2x g (x )=x 2B .f (x )=1,g (x )=x 0C .,0,(),0,x x f x x x ≥⎧=⎨-<⎩g (t )=|t | D .f (x )=x +1,g (x )=211x x -- 5.已知函数221,2,()3,2,x x f x x x x -≥⎧=⎨-+<⎩则f (-1)+f (4)的值为( ) A .-7 B .3C .-8D .46.已知函数2211f x x x x ⎛⎫-=+ ⎪⎝⎭,则f (3)=( ) A .8 B .9C .11D .107.下列函数中,值域是(0,+∞)的是( )A .221y x x =-+B .21x y x +=+(x ∈(0,+∞))C .2121y x x =++(x ∈N )D .1|1|y x =+ 8.函数f (x )=2911x x-++是( ) A .奇函数B .偶函数C .既是奇函数又是偶函数D .非奇非偶函数9.已知集合A ={0,2,a 2},B ={1,a },若A I B ={1},则a 的值为( )A .0B .1C .-1D .±110.已知函数f (x )=x 2+mx +1在区间(-∞,-1]上是减函数,在区间[1,+∞)上是增函数,则实数m 的取值范围是( )A .[-2,2]B .(-∞,-2]C .[2,+∞)D .R11.若函数f (x )和g (x )都是奇函数,且F (x )=af (x )+bg (x )+2在区间(0,+∞)上有最大值5,则F (x )在区间(-∞,0)上( )A .有最小值-5B .有最大值-5C .有最小值-1D .有最大值-312.函数f (x )对于任意实数x 满足f (x +2)=1()f x ,若f (1)=-5,则f (f (5))等于( )A .2B .5C .-5D .15- 二、填空题(本大题共4小题,每小题5分,共20分.把答案填在题中的横线上)13.函数4x y -=的定义域为__________(用区间表示). 14.若函数f (x )=(1)(2)x x x a +-为奇函数,则a =__________. 15.设函数221,1,()22,1,x x f x x x x +≥⎧=⎨--<⎩若f (x 0)>1,则x 0的取值范围为__________. 16.若一系列函数的解析式相同,值域相同,但定义域不同,则称这些函数为“孪生函数”,则解析式为y =2x 2+1,值域为{5,19}的“孪生函数”共有__________个.三、解答题(本大题共6小题,共70分.解答时应写出文字说明、证明过程或演算步骤)17.(10分)已知全集U =R ,若集合A ={}310x x ≤<,B ={x |2<x ≤7}.(1)求A I B ,A U B ,(U A )I (U B );(2)若集合C ={x |x >a },A ⊆C ,求a 的取值范围.(结果用区间或集合表示)18.(12分)已知函数35,0,()5,01,28, 1.x x f x x x x x +≤⎧⎪=+<≤⎨⎪-+>⎩(1)求32f ⎛⎫ ⎪⎝⎭,1πf ⎛⎫ ⎪⎝⎭,f (-1)的值; (2)画出这个函数的图象;(3)求f (x )的最大值.19.(12分)奇函数f (x )是定义在区间(-2,2)上的减函数,且满足f (m -1)+f (2m -1)>0,求实数m 的取值范围.20.(12分)利用函数的单调性定义证明函数f (x )=1x x -,x ∈[2,4]是单调递减函数,并求该函数的值域.21.(12分)已知函数f (x )=x +1x, (1)判断函数f (x )的奇偶性; (2)判断函数f (x )在区间(0,1)和(1,+∞)上的单调性,并用定义证明; (3)当x ∈(-∞,0)时,写出函数f (x )=x +1x 的单调区间(不必证明). 22.(12分)已知二次函数f (x )的最小值为1,且f (0)=f (2)=3.(1)求f (x )的解析式;(2)若f (x )在区间[2a ,a +1]上不单调,求实数a 的取值范围;(3)在区间[-1,1]上,y =f (x )的图象恒在y =2x +2m +1的图象上方,试确定实数m 的取值范围.参考答案1.D 点拨:由于①②③④项中的对象具备确定性,故①②③④能构成集合.⑤项不符合集合中元素的确定性,故不能构成集合.2.D 点拨:题图中所示阴影表示的集合是(U A )I B ={2,4}.3.D 点拨:U ={1,2,3,4,5,6,7,8},U A ={5,6,7,8},U B ={1,2,7,8},故(U A )I (U B )={5,6,7,8}I {1,2,7,8}={7,8}.4.C 点拨:选项A ,B ,D 中两函数定义域不同,只有C 项符合.5.B 点拨:f (-1)+f (4)=-(-1)2+3×(-1)+2×4-1=3.6.C 点拨:∵2112f x x x x ⎛⎫⎛⎫-=-+ ⎪ ⎪⎝⎭⎝⎭, ∴f (3)=9+2=11.7.D 点拨:在选项A 中y 可等于零,选项B 中y 显然大于1,选项C 中x ∈N ,值域不是(0,+∞),选项D 中|x +1|>0,即y >0.8.B 点拨:∵函数f (x )的定义域是[-1,1],且f (-x )=f (x ),∴该函数为偶函数.9.C 点拨:由A I B ={1},知1∈A ,则a 2=1,解得a =±1,由于当a =1时,B ={1,1},与元素的互异性不符,故a =1不合题意舍去.因此a =-1.10.A 点拨:二次函数的对称轴是直线2m x =-,则由题意可得-1≤2m ≤1,所以-2≤m ≤2. 11.C 点拨:∵当x >0时,F (x )≤5,即af (x )+bg (x )+2≤5,∴af (x )+bg (x )≤3. 设x <0,则-x >0,∴af (-x )+bg (-x )≤3,即af (x )+bg (x )≥-3.∴F (x )=af (x )+bg (x )+2≥-1.12.D 点拨:f (5)=1(3)f =f (1)=-5, f (-5)=1(3)f -=f (-1)=1(1)f =15-. 13.[4,5)U (5,+∞) 点拨:由4050x x -≥⎧⎪⎨-≠⎪⎩,,解得x ≥4且x ≠5. 14.2 点拨:由题意知x ≠-1且x ≠2a .因为函数f (x )为奇函数,所以其定义域应关于原点对称.故x ≠1,即2a =1,a =2. 15.(-∞,-1)U [1,+∞) 点拨:f (x 0)>1⇒001211x x ≥⎧⎨+>⎩,或02001221x x x <⎧⎪⎨-->⎪⎩,⇒x 0≥1或x 0<-1.16.9 点拨:令2x 2+1=5,解得x =2±,令2x 2+1=19,解得x =±3.如果函数f (x )=2x 2+1的值域为{5,19},则函数f (x )的定义域中最多含有4个元素2±和±3,且至少含有一个绝对值为2的实数,和至少含有一个绝对值为3的实数,所以函数f (x )的定义域可能是{2-,-3},{2-,3},{2,-3},{2,3},{2-,2,-3},{2-,2,3},{-3,3,2-},{-3,3,2},{-3,2-,2,3}.故所求“孪生函数”共有9个.17.解:(1)A I B =[3,7],A U B =(2,10),(U A )I (U B )=(-∞,2]U [10,+∞).(2){a |a <3}.18.解:(1)32f ⎛⎫ ⎪⎝⎭=(-2)×32+8=5,11ππf ⎛⎫= ⎪⎝⎭+5=5π1π+,f (-1)=-3+5=2.(2)作出函数f (x )的图象如图所示.(3)由函数图象可知,当x =1时,f (x )的最大值为6.19.解:∵f (x )是奇函数,∴f (-x )=-f (x ),由f (m -1)+f (2m -1)>0,得f (m -1)>-f (2m -1),即f (m -1)>f (1-2m ).∵f (x )是定义在区间(-2,2)上的减函数, ∴2122122112m m m m -<-<⎧⎪-<-<⎨⎪-<-⎩,,,解得12-<m <23. 20.证明:在区间[2,4]上任取x 1,x 2且x 1<x 2,则f (x 1)-f (x 2)=1221121211()(1)x x x x x x x x x --=----. ∵2≤x 1<x 2≤4,∴x 2-x 1>0,x 1-1>0,x 2-1>0.∴f (x 1)-f (x 2)>0.∴f (x 1)>f (x 2).∴函数f (x )在区间[2,4]上是减函数.∴f (x )min =f (4)=43,f (x )max =f (2)=2. 因此,所求函数的值域为4,23⎡⎤⎢⎥⎣⎦. 21.解:(1)∵函数f (x )=x +1x的定义域是(-∞,0)U (0,+∞),关于原点对称, 又f (-x )=-x -1x=-f (x ), ∴函数f (x )=x +1x 为奇函数. (2)证明:在区间(0,1)上任取两个数x 1和x 2,且设x 1<x 2,则f (x 1)-f (x 2)=(x 1-x 2)12121x x x x ⎛⎫- ⎪⎝⎭.∵0<x 1<x 2<1,∴0<x 1x 2<1,x 1-x 2<0.∴f (x 1)-f (x 2)>0.∴f (x 1)>f (x 2).∴函数f (x )在区间(0,1)上是减函数.同理,在区间(1,+∞)上任取两个数x 1和x 2,且设x 1<x 2,则x 1x 2>0,x 1x 2>1,x 1-x2<0.∴f(x1)<f(x2).因此函数f(x)在区间(1,+∞)上是增函数.(3)由(1)(2)知当x∈(-∞,0)时,函数f(x)=x+1x在区间(-∞,-1)上是增函数,在区间(-1,0)上是减函数.22.解:(1)由f(0)=f(2)知二次函数f(x)关于直线x=1对称,又函数f(x)的最小值为1,故可设f(x)=a(x-1)2+1,由f(0)=3,得a=2.故f(x)=2x2-4x+3.(2)要使函数不单调,则2a<1<a+1,则0<a<12.(3)由已知,即2x2-4x+3>2x+2m+1,化简得x2-3x+1-m>0,设g(x)=x2-3x+1-m,则只要g(x)min>0,∵x∈[-1,1],∴g(x)min=g(1)=-1-m,得m<-1.。
2021年高中数学 第一章 集合与函数概念单元测试 新人教A版必修1

2021年高中数学第一章集合与函数概念单元测试新人教A版必修1一、选择题(本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.设集合M={x|x2+2x=0,x∈R},N={x|x2-2x=0,x∈R},则M∪N=( )A.{0} B.{0,2}C.{-2,0} D.{-2,0,2}解析M={x|x(x+2)=0.,x∈R}={0,-2},N={x|x(x-2)=0,x∈R}={0,2},所以M∪N={-2,0,2}.答案D2.设f:x→|x|是集合A到集合B的映射,若A={-2,0,2},则A∩B=( )A.{0} B.{2}C.{0,2} D.{-2,0}解析依题意,得B={0,2},∴A∩B={0,2}.答案 C3.f(x)是定义在R上的奇函数,f(-3)=2,则下列各点在函数f(x)图象上的是( ) A.(3,-2) B.(3,2)C.(-3,-2) D.(2,-3)解析∵f(x)是奇函数,∴f(-3)=-f(3).又f(-3)=2,∴f(3)=-2,∴点(3,-2)在函数f(x)的图象上.答案 A4.已知集合A={0,1,2},则集合B={x-y|x∈A,y∈A}中元素的个数是( )A.1 B.3C.5 D.9解析逐个列举可得.x=0,y=0,1,2时,x-y=0,-1,-2;x=1,y=0,1,2时,x -y =1,0,-1;x =2,y =0,1,2时,x -y =2,1,0.根据集合中元素的互异性可知集合B的元素为-2,-1,0,1,2.共5个.答案 C5.若函数f (x )满足f (3x +2)=9x +8,则f (x )的解析式是( ) A .f (x )=9x +8 B .f (x )=3x +2 C .f (x )=-3x -4D .f (x )=3x +2或f (x )=-3x -4解析 ∵f (3x +2)=9x +8=3(3x +2)+2,∴f (x )=3x +2. 答案 B 6.设f (x )=⎩⎪⎨⎪⎧x +3 x >10,fx +5 x ≤10,则f (5)的值为( ) A .16 B .18 C .21D .24解析 f (5)=f (5+5)=f (10)=f (15)=15+3=18. 答案 B7.设T ={(x ,y )|ax +y -3=0},S ={(x ,y )|x -y -b =0},若S ∩T ={(2,1)},则a ,b 的值为( )A .a =1,b =-1B .a =-1,b =1C .a =1,b =1D .a =-1,b =-1解析 依题意可得方程组⎩⎪⎨⎪⎧2a +1-3=0,2-1-b =0,⇒⎩⎪⎨⎪⎧a =1,b =1.答案 C8.已知函数f (x )的定义域为(-1,0),则函数f (2x +1)的定义域为( ) A .(-1,1) B.⎝⎛⎭⎪⎫-1,-12C .(-1,0) D.⎝ ⎛⎭⎪⎫12,1解析 由-1<2x +1<0,解得-1<x <-12,故函数f (2x +1)的定义域为⎝ ⎛⎭⎪⎫-1,-12. 答案 B9.已知A ={0,1},B ={-1,0,1},f 是从A 到B 映射的对应关系,则满足f (0)>f (1)的映射有( )A .3个B .4个C .5个D .6个解析 当f (0)=1时,f (1)的值为0或-1都能满足f (0)>f (1);当f (0)=0时,只有f (1)=-1满足f (0)>f (1);当f (0)=-1时,没有f (1)的值满足f (0)>f (1),故有3个.答案 A10.定义在R 上的偶函数f (x )满足:对任意的x 1,x 2∈(-∞,0](x 1≠x 2),有(x 2-x 1)[f (x 2)-f (x 1)]>0,则当n ∈N *时,有( )A .f (-n )<f (n -1)<f (n +1)B .f (n -1)<f (-n )<f (n +1)C .f (n +1)<f (-n )<f (n -1)D .f (n +1)<f (n -1)<f (-n )解析 由题设知,f (x )在(-∞,0]上是增函数,又f (x )为偶函数, ∴f (x )在[0,+∞)上为减函数. ∴f (n +1)<f (n )<f (n -1). 又f (-n )=f (n ),∴f (n +1)<f (-n )<f (n -1). 答案 C11.函数f (x )是定义在R 上的奇函数,下列说法:①f (0)=0; ②若f (x )在[0,+∞)上有最小值为-1,则f (x )在(-∞,0]上有最大值为1;③若f (x )在[1,+∞)上为增函数,则f (x )在(-∞,-1]上为减函数;④若x >0时,f (x )=x 2-2x ,则x <0时,f (x )=-x 2-2x .其中正确说法的个数是( )A .1个B .2个C .3个D .4个解析 ①f (0)=0正确;②也正确;③不正确,奇函数在对称区间上具有相同的单调性;④正确.答案 C12.f (x )满足对任意的实数a ,b 都有f (a +b )=f (a )·f (b )且f (1)=2,则f 2f 1+f 4f 3+f 6f 5+…+f 2014f 2013=( ) A .1006 B .xx C .xxD .1007解析 因为对任意的实数a ,b 都有f (a +b )=f (a )·f (b )且f (1)=2,由f (2)=f (1)·f (1),得f 2f 1=f (1)=2,由f (4)=f (3)·f (1),得f 4f 3=f (1)=2,……由f (xx)=f (xx)·f (1), 得f 2014f 2013=f (1)=2,∴f 2f 1+f 4f 3+f 6f 5+…+f 2014f 2013=1007×2=xx. 答案 B二、填空题(本大题共4小题,每小题5分,共20分.把答案填在题中横线上) 13.函数y =x +1x的定义域为________. 解析 由⎩⎪⎨⎪⎧x +1≥1,x ≠0得函数的定义域为{x |x ≥-1,且x ≠0}.答案 {x |x ≥-1,且x ≠0}14.f (x )=⎩⎪⎨⎪⎧x 2+1x ≤0,-2x x >0,若f (x )=10,则x =________.解析 当x ≤0时,x 2+1=10,∴x 2=9,∴x =-3. 当x >0时,-2x =10,x =-5(不合题意,舍去). ∴x =-3. 答案 -315.若函数f (x )=(x +a )(bx +2a )(常数a ,b ∈R )是偶函数,且它的值域为(-∞,4],则该函数的解析式f (x )=________.解析 f (x )=(x +a )(bx +2a )=bx 2+(2a +ab )x +2a 2为偶函数,则2a +ab =0,∴a =0,或b =-2.又f (x )的值域为(-∞,4],∴a ≠0,b =-2,∴2a 2=4. ∴f (x )=-2x 2+4. 答案 -2x 2+416.在一定范围内,某种产品的购买量y 吨与单价x 元之间满足一次函数关系,如果购买1000吨,每吨为800元,购买xx 吨,每吨为700元,那么客户购买400吨,单价应该是________元.解析 设一次函数y =ax +b (a ≠0),把⎩⎪⎨⎪⎧x =800,y =1000,和⎩⎪⎨⎪⎧x =700,y =2000,代入求得⎩⎪⎨⎪⎧a =-10,b =9000.∴y =-10x +9000,于是当y =400时,x =860. 答案 860三、解答题(本大题共6小题,共70分.解答应写出必要的文字说明、证明过程或演算步骤)17.(本小题满分10分)已知集合A ={x |2≤x ≤8},B ={x |1<x <6},C ={x |x >a },U =R .(1)求A ∪B ,(∁U A )∩B ;(2)若A ∩C ≠∅,求a 的取值范围. 解 (1)A ∪B ={x |2≤x ≤8}∪{x |1<x <6} ={x |1<x ≤8}. ∁U A ={x |x <2,或x >8}. ∴(∁U A )∩B ={x |1<x <2}. (2)∵A ∩C ≠∅,∴a <8.18.(本小题满分12分)设函数f (x )=1+x21-x 2.(1)求f (x )的定义域; (2)判断f (x )的奇偶性;(3)求证:f ⎝ ⎛⎭⎪⎫1x +f (x )=0.解 (1)由解析式知,函数应满足1-x 2≠0,即x ≠±1. ∴函数f (x )的定义域为{x ∈R |x ≠±1}. (2)由(1)知定义域关于原点对称, f (-x )=1+-x 21--x2=1+x 21-x2=f (x ). ∴f (x )为偶函数.(3)证明:∵f ⎝ ⎛⎭⎪⎫1x =1+⎝ ⎛⎭⎪⎫1x 21-⎝ ⎛⎭⎪⎫1x 2=x 2+1x 2-1, f (x )=1+x 21-x2,∴f ⎝ ⎛⎭⎪⎫1x +f (x )=x 2+1x 2-1+1+x 21-x 2 =x 2+1x 2-1-x 2+1x 2-1=0. 19.(本小题满分12分)已知y =f (x )是定义在R 上的偶函数,当x ≥0时,f (x )=x 2-2x .(1)求当x <0时,f (x )的解析式;(2)作出函数f (x )的图象,并指出其单调区间. 解 (1)当x <0时,-x >0,∴f (-x )=(-x )2-2(-x )=x 2+2x . 又f (x )是定义在R 上的偶函数, ∴f (-x )=f (x ).∴当x <0时,f (x )=x 2+2x .(2)由(1)知,f (x )=⎩⎪⎨⎪⎧x 2-2xx ≥0,x 2+2xx <0.作出f (x )的图象如图所示:由图得函数f (x )的递减区间是(-∞,-1],[0,1].f (x )的递增区间是[-1,0],[1,+∞).20.(本小题满分12分)已知函数f (x )=2x +1x +1, (1)判断函数在区间[1,+∞)上的单调性,并用定义证明你的结论. (2)求该函数在区间[1,4]上的最大值与最小值. 解 (1)函数f (x )在[1,+∞)上是增函数.证明如下: 任取x 1,x 2∈[1,+∞),且x 1<x 2,f (x 1)-f (x 2)=2x 1+1x 1+1-2x 2+1x 2+1=x 1-x 2x 1+1x 2+1,∵x 1-x 2<0,(x 1+1)(x 2+1)>0, 所以f (x 1)-f (x 2)<0,即f (x 1)<f (x 2), 所以函数f (x )在[1,+∞)上是增函数.(2)由(1)知函数f (x )在[1,4]上是增函数,最大值f (4)=95,最小值f (1)=32.21.(本小题满分12分)已知函数f (x )的定义域为(0,+∞),且f (x )为增函数,f (x ·y )=f (x )+f (y ).(1)求证:f ⎝ ⎛⎭⎪⎫x y=f (x )-f (y );(2)若f (3)=1,且f (a )>f (a -1)+2,求a 的取值范围.解 (1)证明:∵f (x )=f ⎝⎛⎭⎪⎫x y ·y =f ⎝ ⎛⎭⎪⎫xy+f (y ),(y ≠0) ∴f ⎝ ⎛⎭⎪⎫x y=f (x )-f (y ).(2)∵f (3)=1,∴f (9)=f (3·3)=f (3)+f (3)=2.∴f (a )>f (a -1)+2=f (a -1)+f (9)=f [9(a -1)]. 又f (x )在定义域(0,+∞)上为增函数,∴⎩⎪⎨⎪⎧a >0,a -1>0,a >9a -1,∴1<a <98.22.(本小题满分12分)某商场经销一批进价为每件30元的商品,在市场试销中发现,此商品的销售单价x (元)与日销售量y (件)之间有如下表所示的关系:x 30 40 45 50 y603015(1)(x ,y )的对应点,并确定y 与x 的一个函数关系式.(2)设经营此商品的日销售利润为P 元,根据上述关系,写出P 关于x 的函数关系式,并指出销售单价x 为多少元时,才能获得最大日销售利润?解 (1)由题表作出(30,60),(40,30),(45,15),(50,0)的对应点,它们近似地分布在一条直线上,如图所示.设它们共线于直线y =kx +b ,则⎩⎪⎨⎪⎧50k +b =0,45k +b =15,⇒⎩⎪⎨⎪⎧k =-3,b =150.∴y =-3x +150(0≤x ≤50,且x ∈N *),经检验(30,60),(40,30)也在此直线上. ∴所求函数解析式为y =-3x +150(0≤x ≤50,且x ∈N *). (2)依题意P =y (x -30)=(-3x +150)(x -30)=-3(x -40)2+300.∴当x =40时,P 有最大值300,故销售单价为40元时,才能获得最大日销售利润.€L3502788D3 裓33856 8440 葀)z33241 81D9 臙38683 971B 霛26266 669A 暚30115 75A3 疣^}37706 934A 鍊21716 54D4 哔29669 73E5 珥。
人教A版数学必修一第一章 《集合与函数概念》单元测试题.doc

高中数学学习材料马鸣风萧萧*整理制作第一章 《集合与函数概念》单元测试题姓名: 班别: 学号:一、选择题:每小题4分,共40分1、在“①高一数学课本中的难题;②所有的正三角形; ③方程220x +=的实数解”中,能够表示成集合的是( )(A )② (B )③(C )②③ (D )①②③2、若{}{}|02,|12A x x B x x =<<=≤<,则A B ⋃= ( ) (A ){}|0x x ≤ (B ){}|2x x ≥(C ){}02x ≤≤ (D ){}|02x x << 3、若{}{}0,1,2,3,|3,A B x x a a A ===∈,则A B ⋂= ( )(A ){}1,2 (B ){}0,1(C ){}0,3 (D ){}34、在映射中B A f →:,},|),{(R y x y x B A ∈==,且),(),(:y x y x y x f +-→,则与A 中的元素)2,1(-对应的B 中的元素为() (A ))1,3(- (B ))3,1( (C ))3,1(-- (D ))1,3(5、下列各组函数)()(x g x f 与的图象相同的是( )(A )2)()(,)(x x g x x f == (B )22)1()(,)(+==x x g x x f(C )0)(,1)(x x g x f == (D )⎩⎨⎧-==xx x g x x f )(|,|)( )0()0(<≥x x 6、是定义在上的增函数,则不等式的解集是( )(A)(0 ,+∞) (B)(0 , 2) (C) (2 ,+∞) (D) (2 ,716) 7、若奇函数()x f 在[]3,1上为增函数,且有最小值0,则它在[]1,3--上( )A .是减函数,有最小值0B .是增函数,有最小值0C .是减函数,有最大值0D .是增函数,有最大值08、如图所示,阴影部分的面积S 是h 的函数()H h ≤≤0。
高中数学人教a版高一必修一_第一章_集合与函数概念_学业分层测评3

学业分层测评(三) 集合间的基本关系(建议用时:45分钟)[学业达标]一、选择题1.(2016·漳州高一检测)已知集合A ={x |x 2-1=0},则有( )A .1∉AB .0⊆AC .∅⊆AD .{0}⊆A【解析】 由已知,A ={1,-1},所以选项A ,B ,D 都错误,因为∅是任何非空集合的真子集,所以C 正确.【答案】 C2.(2016·普洱高一检测)已知集合N ={1,3,5},则集合N 的真子集个数为( )A .5B .6C .7D .8【解析】 ∵集合N ={1,3,5},∴集合N 的真子集个数是23-1=7个,故选C.【答案】 C3.集合A ={2,-1},B ={m 2-m ,-1},且A =B ,则实数m =( )A .2B .-1C .2或-1D .4【解析】 ∵A =B ,∴m 2-m =2,即m 2-m -2=0,∴m =2或-1.【答案】 C4.已知集合P ={x |x 2=1},Q ={x |ax =1},若Q ⊆P ,则a 的值是( )A .1B .-1C .1或-1D .0,1或-1【解析】 由题意,当Q 为空集时,a =0;当Q 不是空集时,由Q ⊆P ,a =1或a =-1.【答案】 D5.(2016·南阳高一检测)集合M =x ⎪⎪⎪ x =k 2+13,k ∈Z ,N =x ⎪⎪⎪x =k +13,k ∈Z ,则( ) 【导学号:97030012】A .M =NB .M ⊆NC .N ⊆MD .M ∩N ∅ 【解析】 ∵M 中:x =k 2+13=⎩⎪⎨⎪⎧ n +13,k =2n ,n ∈Z n +56,k =2n +1,n ∈Z .N 中:x =k +13=n +13,k =n ∈Z ,∴N ⊆M .【答案】 C二、填空题6.设a ,b ∈R ,集合⎩⎨⎧⎭⎬⎫0,b ,b a ={1,a ,a +b },则a +2b =________. 【解析】∵⎩⎨⎧⎭⎬⎫0,b ,b a ={1,a ,a +b },而a ≠0,∴a +b =0,b a =-1,从而b =1,a =-1, 可得a +2b =1.【答案】 17.已知集合A ={x |1<x -1≤4},B =(-∞,a ),若A ⊆B ,则实数a 的取值范围是(c ,+∞),其中c =________.【解析】 ∵A =(2,5],A ⊆B ,∴5<a ,又a ∈(c ,+∞),∴c =5.【答案】 58.(2016·保定高一检测)设集合A ={x |x 2+x -6=0},B ={x |mx +1=0},则满足B ⊆A 的实数m 的取值集合为________.【解析】 ∵A ={x |x 2+x -6=0}={-3,2},又∵B ⊆A ,当m =0,mx +1=0无解,故B=∅,满足条件,若B ≠∅,则B ={-3},或B ={2},即m =13,或m =-12,故满足条件的实数m ∈⎩⎨⎧⎭⎬⎫0,13,-12. 【答案】 ⎩⎨⎧⎭⎬⎫0,13,-12 三、解答题9.(2016·菏泽高一检测)已知A ={x |x <3},B ={x |x <a }.(1)若B ⊆A ,求a 的取值范围;(2)若A ⊆B ,求a 的取值范围.【解】 (1)因为B ⊆A ,B 是A 的子集,由图(1)得a ≤3.(1)(2)因为A ⊆B ,A 是B 的子集,由图(2)得a ≥3.(2)10.已知集合A ={x |x 2+4x =0},B ={x |x 2+2(a +1)x +a 2-1=0,a ∈R },若B ⊆A ,求实数a 的取值范围.【解】 A ={x |x 2+4x =0}={0,-4},∵B ⊆A ,∴B =∅或B ={0}或B ={-4}或B ={0,-4}.(1)当B =∅时,方程x 2+2(a +1)x +a 2-1=0无实根,则Δ<0,即4(a +1)2-4(a 2-1)<0.∴a <-1.(2)当B ={0}时,有⎩⎨⎧ Δ=0a 2-1=0,∴a =-1. (3)当B ={-4}时,有⎩⎨⎧Δ=0a 2-8a +7=0,无解. (4)当B ={0,-4}时,由韦达定理得a =1.综上所述,a =1或a ≤-1.[能力提升]1.(2016·石家庄高一检测)已知集合A 满足{1,2}⊆A ⊆{1,2,3,4},则集合A 的个数为( )A .8B .2C .3D .4 【解析】 由题意,集合A 可以为:{1,2},{1,2,3},{1,2,4},{1,2,3,4}.故选D.【答案】 D2.(2016·达州高一检测)下列四个集合中,是空集的是( )A .{x |x +3=3}B .{(x ,y )|y 2=-x 2,x ,y ∈R }C .{x |x 2≤0}D .{x |x 2-x +1=0,x ∈R }【解析】 根据题意,由于空集中没有任何元素,对于选项A ,x =0;对于选项B ,(0,0)是集合中的元素;对于选项C ,由于x =0成立;对于选项D ,方程无解.故选D.【答案】 D3.(2016·衡水高一检测)若三个非零且互不相等的实数a 、b 、c 满足1a +1b =2c ,则称a 、b 、c 是调和的;若满足a +c =2b ,则称a 、b 、c 是等差的.若集合P 中元素a 、b 、c 既是调和的,又是等差的,则称集合P 为“好集”.若集合M ={x ||x |≤2 016,x ∈Z },集合P ={a ,b ,c }⊆M .则:(1)“好集”P 中的元素最大值为__________________;(2)“好集”P 的个数为______________________.【解析】 (1)∵1a +1b =2c ,且a +c =2b ,∴(a -b )(a +2b )=0,∴a =b (舍),或a =-2b ,∴c =4b ,令-2 016≤4b ≤2 016,得-504≤b ≤504,∴P 中最大元素为4b =4×504=2 016.(2)由(1)知P ={-2b ,b,4b }且-504≤b ≤504,∴“好集”P 的个数为2×504=1 008.【答案】 (1)2 016 (2)1 0084.已知集合A ={x |-3≤x ≤5},B ={x |m -2<x <2m -3},且B ⊆A ,求实数m 的取值范围.【导学号:97030013】【解】 ∵集合A ={x |-3≤x ≤5},B ={x |m -2<x <2m -3},且B ⊆A ,∴当B ≠∅时,应有⎩⎨⎧ m -2≥-32m -3≤5m -2<2m -3,解得1<m ≤4. 当B =∅时,应有m -2≥2m -3,解得m ≤1.综上可得,实数m 的取值范围为(-∞,4].。
高中数学 第一章 集合与函数概念本章测评 新人教A版必修1

第一章测评(时间:120分钟满分:150分)一、选择题(本大题共12小题,每小题5分,共60分)1.已知全集U={1,2,3,4,5,6},集合A={2,3,5},集合B={1,3,4,6},则集合A∩(∁U B)=()A.{3}B.{2,5}C.{1,4,6}D.{2,3,5}解析:∵∁U B={2,5},A={2,3,5},∴A∩(∁U B)={2,5}.故选B.答案:B2.(2016·福建福州长乐一中高一月考)在映射f:A→B中,A=B={(x,y)|x,y∈R},且f:(x,y)→(x-y,x+y),则与A中的元素(-1,2)对应的B中的元素为()A.(-3,1)B.(1,3)C.(-1,-3)D.(3,1)解析:∵x-y=-1-2=-3,x+y=-1+2=1,∴与A中的元素(-1,2)对应的B中的元素为(-3,1).答案:A3.已知全集U=R,集合P={x∈N*|x<7},Q={x|x-3>0},则图中阴影部分表示的集合是()A.{1,2,3,4,5,6}B.{x|x>3}C.{4,5,6}D.{x|3<x<7}解析:由题意知P={1,2,3,4,5,6},Q={x|x>3},则阴影部分表示的集合是P∩Q={4,5,6}.答案:C4.函数f(x)=的图象是()解析:由于f(x)=故选C.答案:C5.函数f(x)=的定义域为()A.[-1,2)∪(2,+∞)B.(-1,+∞)C.[-1,2)D.[-1,+∞)解析:由解得x≥-1,且x≠2.答案:A6.若函数f(x)=x2-x-3,则f(f(2))的值为()A.-1B.-3C.0D.-8解析:f(2)=22-2-3=-1,f(f(2))=f(-1)=(-1)2-(-1)-3=1+1-3=-1.答案:A7.若函数f(x)(x∈R)是奇函数,则()A.函数f(x2)是奇函数B.函数[f(x)]2是奇函数C.函数f(x)·x2是奇函数D.函数f(x)+x2是奇函数解析:f((-x)2)=f(x2),则函数f(x2)是偶函数,故A错误;[f(-x)]2=[-f(x)]2=[f(x)]2,则函数[f(x)]2是偶函数,故B错误;函数f(-x)·(-x)2=-f(x)·x2,则函数f(x)·x2是奇函数,故C正确;f(-x)+(-x)2≠f(x)+x2,且f(-x)+(-x)2≠-f(x)-x2,则函数f(x)+x2既不是奇函数又不是偶函数,故D错误.答案:C8.(2016·湖南岳阳一中高一月考)已知偶函数f(x)在区间[0,+∞)上单调递增,则满足f(2x-1)<f 的x的取值范围是()A. B.C. D.解析:∵函数f(x)是偶函数,∴f(2x-1)<f等价于f(|2x-1|)<f.又f(x)在区间[0,+∞)上单调递增,∴|2x-1|<,解得<x<.答案:A9.若函数f(x)=满足f(f(x))=x,则常数c等于()A.3B.-3C.3或-3D.5或-3解析:f(f(x))==x,即x[(2c+6)x+9-c2]=0,所以解得c=-3.故选B.答案:B10.已知函数f(x)=ax3+bx+7(其中a,b为常数),若f(-7)=-17,则f(7)的值为()A.31B.17C.-17D.15解析:令g(x)=ax3+bx,则g(x)为奇函数.因为f(-7)=g(-7)+7=-17,所以g(-7)=-17-7=-24,g(7)=24,f(7)=g(7)+7=31.答案:A11.若f(x)=是定义在(-∞,+∞)上的减函数,则a的取值范围是()A. B.C. D.解析:由题意可得解得≤a<,故选A.答案:A12.导学号29900060定义运算a b=则函数f(x)=x2 |x|的图象是()解析:根据运算a b=得f(x)=x2 |x|=由此可得图象如图所示.答案:B二、填空题(本大题共4小题,每小题5分,共20分)13.若函数f(x)=则f(f(1))的值为.解析:f(1)=5-1=4,f(f(1))=f(4)=42+7×4=44.答案:4414.若函数f(x)=在区间(-2,+∞)上单调递减,则实数a的取值范围是.解析:f(x)==a+.∵y=在区间(-2,+∞)上是减函数,∴1-2a>0,∴a<.答案:a<15.已知集合A={x|0≤x≤4},集合B={y|0≤y≤2},从A到B的对应关系f分别为:①f:x→x;②f:x→x-2;③f:x→;④f:x→|x-2|.其中表示函数关系的是.(只填序号)解析:由函数的定义可判定①③④正确.对于②,由于当0≤x≤4时,-2≤x-2≤2.显然不满足函数的定义.答案:①③④16.导学号29900061已知函数f(x)同时满足:①对于定义域上的任意x,恒有f(x)+f(-x)=0;②对于定义域上的任意x1,x2.当x1≠x2时,恒有<0,则称函数f(x)为“理想函数”.在下列三个函数中:(1)f(x)=,(2)f(x)=x2,(3)f(x)=“理想函数”有(只填序号).解析:由题意知“理想函数”为定义域上的奇函数且在定义域上是减函数.函数f(x)=是奇函数,其虽然在区间(-∞,0)和(0,+∞)上是减函数,但不能说其在定义域(-∞,0)∪(0,+∞)上是减函数,所以f(x)=不是“理想函数”;函数f(x)=x2是偶函数,且其在定义域R上先减后增,也不是“理想函数”;函数f(x)=是“理想函数”.答案:(3)三、解答题(本大题共6小题,共70分.解答时应写出文字说明、证明过程或演算步骤)17.(本小题满分10分)已知A={1,2,x},B={1,x2},且A∩B=B,求x的值.解:∵A∩B=B,∴x2=2或x2=x,即x=±或x=0或x=1.当x=时,A={1,2,},B={1,2},符合题意;当x=-时,A={1,2,-},B={1,2},符合题意;当x=0时,A={1,2,0},B={1,0},符合题意;当x=1时,A={1,2,1},B={1,1},由集合中元素的互异性知x=1不符合题意,应舍去.故x=±或x=0.18.(本小题满分12分)已知f(x)=,x∈[2,6].(1)证明f(x)是定义域上的减函数;(2)求f(x)的最大值和最小值.解:(1)设2≤x1<x2≤6,则f(x1)-f(x2)=.因为x1-1>0,x2-1>0,x2-x1>0,所以f(x1)-f(x2)>0,即f(x1)>f(x2).所以f(x)是定义域上的减函数.(2)由(1)的结论可得,f(x)min=f(6)=,f(x)max=f(2)=1.19.(本小题满分12分)(2016·河北正定中学高一月考)已知函数f(x)=ax2+bx+1(a,b为实数),设F(x)=(1)若f(-1)=0,且对任意实数x均有f(x)≥0成立,求F(x)的表达式;(2)在(1)的条件下,当x∈[-2,2]时,g(x)=f(x)-kx是单调函数,求实数k的取值范围;(3)设mn<0,m+n>0,a>0,且f(x)满足f(-x)=f(x),试比较F(m)+F(n)的值与0的大小.解:(1)∵f(-1)=0,∴b=a+1.由f(x)≥0恒成立知,a>0,且Δ=b2-4a=(a+1)2-4a=(a-1)2≤0,∴a=1.从而f(x)=x2+2x+1.故F(x)=(2)由(1)知,f(x)=x2+2x+1,∴g(x)=f(x)-kx=x2+(2-k)x+1.由g(x)在区间[-2,2]上是单调函数,知-≤-2或-≥2,得k≤-2或k≥6.故k的取值范围为k≤-2或k≥6.(3)∵f(-x)=f(x),∴f(x)为偶函数,b=0.∵a>0,∴f(x)在区间[0,+∞)为增函数.对于F(x),当x>0时,-x<0,F(-x)=-f(-x)=-f(x)=-F(x);当x<0时,-x>0,F(-x)=f(-x)=f(x)=-F(x),∴F(-x)=-F(x),且F(x)在区间[0,+∞)上为增函数.由mn<0,知m,n异号,不妨设m>0,n<0,由m>-n>0,知F(m)>F(-n)=-F(n),∴F(m)+F(n)>0.20.(本小题满分12分)已知函数f(x)=mx+(m,n是常数),且f(1)=2,f(2)=.(1)求m,n的值;(2)当x∈[1,+∞)时,判断f(x)的单调性并证明;(3)若不等式f(1+2x2)>f(x2-2x+4)成立,求实数x的取值范围.解:(1)由题意知f(1)=m+=2,f(2)=2m+,∴将上式联立方程组解得(2)f(x)在区间[1,+∞)上是增函数.证明如下:设1≤x1<x2,则f(x1)-f(x2)=x1+=(x1-x2)=(x1-x2).∵1≤x1<x2,∴x1-x2<0,x1x2>1,∴2x1x2>2>1,∴f(x1)-f(x2)<0,即f(x1)<f(x2),∴f(x)在区间[1,+∞)上是增函数.(3)∵1+2x2≥1,x2-2x+4=(x-1)2+3≥3,∴1+2x2>x2-2x+4,∴x2+2x-3>0,解得x<-3或x>1.故x的取值范围是(-∞,-3)∪(1,+∞).21本小题满分12分)已知f(x)对任意的实数m,n都有f(m+n)=f(m)+f(n)-1,且当x>0时,有f(x)>1.(1)求f(0);(2)求证:f(x)在R上为增函数;(3)若f(1)=2,且关于x的不等式f(ax-2)+f(x-x2)<3对任意的x∈[1,+∞)恒成立,求实数a的取值范围.(1)解:令m=n=0,则f(0)=2f(0)-1,∴f(0)=1.(2)证明:任取x1,x2∈R,且x1<x2,则x2-x1>0,f(x2-x1)>1.∵f(m+n)=f(m)+f(n)-1,∴f(x2)=f[(x2-x1)+x1]=f(x2-x1)+f(x1)-1>1+f(x1)-1=f(x1),∴f(x2)>f(x1).故f(x)在R上为增函数.(3)解:∵f(ax-2)+f(x-x2)<3,即f(ax-2)+f(x-x2)-1<2,∴f(ax-2+x-x2)<2.∵f(1)=2,∴f(ax-2+x-x2)<f(1).又f(x)在R上为增函数,∴ax-2+x-x2<1.∴x2-(a+1)x+3>0对任意的x∈[1,+∞)恒成立.令g(x)=x2-(a+1)x+3,当≤1,即a≤1时,由g(1)>0,得a<3,∴a≤1;当>1,即a>1时,由Δ<0,即(a+1)2-3×4<0,得-2-1<a<2-1,∴1<a<2-1.综上,实数a的取值范围为(-∞,2-1).22本小题满分12分)已知二次函数f(x)的图象过点(0,4),对任意x满足f(3-x)=f(x),且有最小值.(1)求f(x)的解析式;(2)求函数h(x)=f(x)-(2t-3)x在区间[0,1]上的最小值,其中t∈R;(3)在区间[-1,3]上,y=f(x)的图象恒在函数y=2x+m的图象上方,试确定实数m的取值范围.解:(1)由题意知二次函数图象的对称轴为x=,最小值为,可设f(x)=a(a≠0).因为f(x)的图象过点(0,4),则a=4,解得a=1,所以f(x)==x2-3x+4.(2)h(x)=f(x)-(2t-3)x=x2-2tx+4=(x-t)2+4-t2,其图象的对称轴为x=t.当t≤0时,函数h(x)在区间[0,1]上是增函数,所以h(x)的最小值为h(0)=4;当0<t<1时,函数h(x)的最小值为h(t)=4-t2;当t≥1时,函数h(x)在区间[0,1]上是减函数,所以h(x)的最小值为h(1)=5-2t.所以h(x)min=(3)由已知得f(x)>2x+m在区间[-1,3]上恒成立,∴m<x2-5x+4在区间[-1,3]上恒成立,∴m<(x2-5x+4)min(x∈[-1,3]).令g(x)=x2-5x+4,∵g(x)=x2-5x+4在区间[-1,3]上的最小值为-,∴m<-.故实数m的取值范围为m<-.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第一章 集合与函数概念本章知识结构本章测试1.下列四个命题:其中正确的有( )①∅={0} ②空集没有子集 ③任何一个集合必有两个或两个以上的子集 ④空集是任何一个集合的子集.A.0个B.1个C.2个D.3个思路解析:∅是不含有任何元素的集合,而{0}是含有元素0的集合,所以①是错误的;任何一个集合都是它本身的子集,空集只有它本身一个子集,同时空集也是任何一个集合的子集,因此②③是错误的,④是正确的.故答案应选B. 答案:B2.在下列四组函数中,f (x )与g (x )表示同一函数的是( )A.f (x )=x-1,g (x )=112+-x xB.f (x )=|x+1|,g (x )=⎩⎨⎧-<---≥+.1,1,1,1x x x xC.f (x )=x+1,x ∈R ,g (x )=x+1,x ∈ZD.f (x )=x ,g (x )=(x )2思路解析:选项A 、C 、D 两个函数的定义域不同,所以不是同一个函数,应选B. 答案:B3.已知M={x 2,2x-1,-x-1},N={x 2+1,-3,x+1},且M ∩N={0,-3},则x 的值为( ) A.-1 B.1 C.-2 D.2思路解析:∵M ∩N={0,-3},可知N 中有元素0,由于x 2+1≠0,故只能是x+1=0,解得x=-1,此时M={1,-3,0},N={2,-3,0},符合题意.应选A. 答案:A 4.y=f (x )(x ∈R )是奇函数,则它的图象必经过点( ) A.(-a ,-f (-a )) B.(a ,-f (a )) C.(a ,f (1a )) D.(-a ,-f (a ))思路解析:由函数解析式的含义可知函数f (x )的图象经过点(a ,f (a )),又因为y=f (x )(x ∈R )是奇函数,所以有f (-a )=-f (a ),即函数图象经过点 (-a ,-f (a )),应选D. 答案:D5.拟定从甲地到乙地通话m 分钟的电话费由f (m )=1.06×(0.5·[m ]+1)(元)决定,其中m >0,[m ]是小于或等于m 的最大整数,则从甲地到乙地通话时间为6.5分钟的电话费为( )A.3.71元B.3.97元C.4.24元D.4.77元 思路解析:根据题意知m=6.5,[m ]=6, 所以f (m )=1.06×(0.5·[m ]+1)=1.06×4=4.24元,应选C. 答案:C6.已知集合M 、P 、S ,满足M ∪P=M ∪S ,则( ) A.P=S B.M ∩P=M ∩SC.M ∩(P ∪S )=M ∩(P ∩S )D.(S ∪M )∩P=(P ∪M )∩S思路解析:特例法,举M={1,2},P={3},S={1,2,3},满足M ∪P=M ∪S ,而P ≠S ,M ∩P ≠M ∩S ,M ∩(P ∪S )={1,2},M ∩(P ∩S )=∅,所以A 、B 、C 均是错误的,故正确答案应该为D.答案:D7.已知集合P={x ∈N |1≤x ≤10},集合Q={x ∈R |x 2+x-6≤0},则P ∩Q 等于( )A.{2}B.{1,2}C.{2,3}D.{1,2,3} 思路解析:P={1,2,3,4,5,6,7,8,9,10},Q={-3,2},P ∩Q={2}. 答案:A8.函数y=ax 2+a 与y=xa(a ≠0)在同一坐标系中的图象可能是( )思路解析:从A 中的反比例图象可以看出a>0,此时y=ax 2+a 应是开口向上,且与x 轴没有交点的抛物线,故A 、B 、C 均是错误的;而对于D 可知a <0,y=ax 2+a 应是开口向下,且与x 轴没有交点的抛物线,所以D 是正确的. 答案:D9.已知集合M={x |x ≥2或x ≤-1},N={x |x —a ≤0},若M ∩N ≠∅,则a 的取值范围是( )A.(-∞,2)B.(-1,+∞)C.(-∞,1) D(-∞,1] 思路解析:由题意知M={x |-1<x <2=,N={x |x ≤-a},若M ∩N ≠∅,根据数轴,可得-a>-1即a <1,故选C. 答案:C 10.函数y=2)1(20++--x x x 的定义域为( )A.(-1, 2)B.(-1,1)∪(1,2)C.(-∞,1)∪(1,+∞)D.[-1,1]∪(1,2] 思路解析:要使函数有意义,则⎩⎨⎧>++-≠.02,12x x x 解得(-1,1)∪(1,2).答案:B11.函数f (x )=-x 2+2(a-1)x+3在(-∞,4)上是增函数,则a 的范围是( ) A.a ≥5 B.a ≥3 C.a ≤3 D.a ≤-5思路解析:本题作出函数f (x )=-x 2+2(a-1)x+3的图象,可知此函数图象的对称轴是x=a-1,由图象可知,当a-1≥4,即当a ≥5时,函数f (x )=-x 2+2(a-1)x+2在(-∞,4)上是增函数. 答案:A12.已知集合A={x |y=x 2-2x-3,x ∈R },B={y |y=x 2-2x+2,x ∈R },则A ∩B=_________.思路解析:集合A={x |y=x 2-2x-3,x ∈R }表示函数y=x 2?x-3的定义域,所以A=R ;而B={y |y=x 2-2x+2,x ∈R }表示函数y=x 2-2x+2的值域,应有B={y |y ≥1},因此A ∩B={y |y ≥1}. 答案:{y |y ≥1}13.如右图,有一块边长为a 的正方形铁皮,将其四个角各截去一个边长为x 的小正方形,然后折成一个无盖的盒子,写出体积V 以x 为自变量的函数式是_____________,这个函数的定义域为___________________.思路解析:围成的几何体是一个长方体,它的底面积为(a-2x)2,高为x ,所以体积V=x(a-2x)2,而x 满足a-2x >0且x >0,所以0<x <2a. 答案:V=x (a-2x )2{x|0<x <2a } 14.给定映射f :(x ,y )→(x ,x+y ),在映射f 下象(2,12)的原象是(a ,b ),则函数f (x )=ax 2+bx 的顶点坐标是____________________. 思路解析:根据题意有a=2,a+b=12,解得a=4,b=8,所以函数f(x)=4x 2+8x=4(x+1)2-4,其顶点坐标为(-1,-4). 答案:(-1,-4)15.函数f (x )=x 2-2|x |的单调减区间是____________________.思路解析:因为f (-x )=x 2-2|x |=f (x ),所以f(x)是偶函数,我们可先考虑x >0的情况,当x >0时,f(x)=x 2-2x ,函数在(0,1)上为减函数,在[1,+∞)上为增函数;由于偶函数的图象关于y 轴对称,故函数在(-1,0)上为增函数,在(-∞,-1)上为减函数. 答案:(0,1)和(-∞,-1]16.设A={x|x 2-x-12=0} ,B={x|x 2-2ax+b=0},若B ≠∅,且A ∪B=A,求a 、b 的值. 思路解析:分别将每一个集合化简,再利用集合的运算进行求解.解:∵A={x|x 2-x-12=0}={-3,4}, 若B ≠∅,且A ∪B=A ,则B ⊆A, 当A=B 时,a=21,b=-12; 当B={-3}时,a=-3,b=9; 当B={4}时,a=4,b=16. 因此,a=21,b=-12或A=-3,b=9或 a=4,b=16. 17.设g(x)=⎩⎨⎧>≤,0,ln ,0,x x x e x 则g [g(21)]=__________________.解:依题可知g(21)=ln 21=-ln2<0 所以,g [g (21)]=g(-ln2)=21ln e =21.18.已知函数f(x)=ax 2+2ax+4(0<a <3=,若x 1<x 2,x 1+x 2=1-a,则( )A.f(x 1)<f(x 2)B.f(x 1)=f(x 2)C.f(x 1)>f(x 2)D.f(x 1)与f(x 2)的大小不能确定思路解析:由f(x)=ax 2+2ax+4(0<a <3=,得f(x)为二次函数,且对称轴为x 0=-1, ∵x 1+x 2=1-a,∴221x x +=21a -,即x 1,x 2中点横坐标为21a -,又∵0<a <3,∴21a->-1.∵x 1<x 2, 如右图∴x 1离对称轴的距离小于x 2离对称轴的距离,∴f(x 1)<f(x 2). 答案:A19.快艇和轮船分别从A 地和C 地同时开出,各沿箭头方向航行,如右图所示,快艇和轮船的速度分别是45千米/时和15千米/时,已知AC=150千米,经过多少时间后,快艇和轮船之间的距离最短?思路解析:解决有关函数的应用题,关键在于审清题意,正确列出函数模型. 解:设经过x 小时后快艇和轮船之间的距离最短,距离设为y ,y=22)15()45150(x x +-(0<x ≤310), 可求得当x=3时,y 有最小值.答:经过3小时后,快艇和轮船之间的距离最短.20.设f (x )是定义在R 上的增函数,f (xy )=f (x )+f (y ),f (3)=1,求解不等式f (x )+f (x-2)>1.思路解析:对抽象不等式,常把常数看成某些变量的函数值,再利用函数的性质去“外层包装”,取出x ,化成一元一次或二次不等式求解. 解:由条件可得f (x )+f (x-2)=f [x (x-2)],1=f (3). 所以f [x (x-2)]>f (3),又f (x )是定义在R 上的增函数, 所以有x (x-2)>3,可解得x >3或x <-1. 答案:x >3或x <-1 21.已知函数f (x )=x+xm,且f (1)=2. (1)求m ;(2)判断f (x )的奇偶性;(3)判断函数f (x )在[1,2]上的单调性,并求函数f (x )在[1,2]上的最值. 思路解析:判断函数的奇偶性,首先观察函数的定义域是否关于原点对称,然后判断 f (-x )与f(x)的关系;而证明在某一区间上的单调性,常用定义进行证明,由于单调函数在闭区间内肯定有最值,可根据单调性求出最值. 解:(1)f (1)=1+m=2,解得m=1. (2)f (x )=x+x 1,f (-x )=-x-x1=-f (x ), ∴f (x )是奇函数.(3)设x 1、x 2是[1,2]上的任意两个实数,且x 1<x 2,则 f (x 1)-f (x 2)=x 1+11x -(x 2+21x )=x 1-x 2+(11x -21x )=x 1-x 2-2121x x x x -=(x 1-x 2)21211x x x x -. 当1≤x 1<x 2≤2时,x 1x 2>1,x 1x 2-1>0,从而f (x 1)-f (x 2)<0,即f (x 1)<f (x 2). ∴函数f (x )=x 1+x 在[1,2]上为增函数,其最小值为 f (1)=2,最大值为f (2)=25.。
