第10章 齿轮机构及设计03
机械原理第10章齿轮机构及其设计

2、具有标准顶隙:c = c *m
2.1.2 标准中心距
a=ra1+c+rf2 =r1+h*am+c*m+r2-( h*am+c*m)
=r1+r2=m(z1+z2) / 2
两轮的中心距a应等于两轮分度 圆半径之和,我们把这种中心距称为 标准中心距a
实际中心距a’
2.1.3 啮合角
啮合角α’——两轮传动时其节点P的圆周速度方向与啮合线 N1N2之间所夹的锐角,其值等于节圆压力角。 压力角α和啮合角α’的区别
2、对于按标准中心距安装的标准齿轮传动,当两轮的 齿数趋于无穷大时的极限重合度εαmax=1.981。
3、重合度εα还随啮合角α’的减小和齿顶高系数ha*的增 大而增大。
4、重合度是衡量齿轮传动质量的指标。 重合度承载能力传动平稳性
[例] 已知 z1=19、z2=52、=20、m =5mm、ha*=1。求 。
rb1+rb2=(r1+r2)cosα=(r1’+r2’)cos α’
齿轮的中心距与啮合角的关系为: a’cos α’=acos α
r1 =r1
O1
ω1 rb1 N1
=
r1 r1
O1
ω1 rb1 N1
N2
P
rb2 r2 =r2
P
N2 a
rb2
r2
r2
a
ω2
ω2
O2
O2
2.2 齿轮与齿条啮合传动 齿轮与齿条标准安装:齿轮的分度圆和齿条的分度线相切。
2.齿轮传动的中心距和啮合角
2.1 外啮合传动
2.1.1 齿轮正确安装的条件: 1、齿侧间隙为零:
即 s'1 e'2 及s'2 e'1
10第十章 齿轮机构及其设计19页word文档

第十章 齿轮机构及其设计第一节 齿轮机构的应用和分类一、齿轮机构的应用1、功用:齿轮机构可用于传递空间任意两轴(平行、相交、交错)的旋转运动,或将转动转换为移动。
图10—1 图10—2 图10—32、优点:①传动比准确、传动平稳。
②圆周速度大,高达300 m/s 。
③传动功率范围大,从几瓦到10万千瓦。
④效率高(η→0.99)、使用寿命长、工作安全可靠。
3、缺点:加工成本高、不适宜远距离传动。
二、齿轮机构的分类图10—4非圆齿轮 图10—5斜齿圆锥齿轮图10—6曲线齿圆锥齿轮 图10—7准双曲面齿轮第二节 齿轮的齿廓曲线共轭齿廓:一对能实现预定传动比(i12=ω1/ω2)规律的啮合齿廓。
1、齿廓啮合基本定律如图10—8所示,一对齿廓在K 点接触时,速度不相等:vk1≠vk2,但法向速度应相等:vkn1=vkn2,根据三心定律,P 点为相对瞬心:i12=ω1/ω2=O2P/O1P齿廓啮合基本定律:互相啮合的一对齿轮在任一位置啮合时的传动比,都与连心线O1O2被其啮合齿廓在接触点的公法线所分成的两线段成反比。
分点P 称为节点。
P 点分别在与两齿轮固定的平面内的轨迹称为节线。
显然一对齿轮的啮合相当于两齿轮的节线在作纯滚动。
如果要求传动比为常数,则O2P/O1P 为常数,P 必为一个定点。
两节线为节圆,相切于P 点,两节圆作纯滚动。
如果传动比不恒定,则O2P/O1P 为不是常数,节线为非圆曲线。
2、齿廓曲线的选择常见齿廓曲线有渐开线、摆线、变态摆线、圆弧、抛物线等,其中渐开线具有很好的传动性能,而且便于制造、安装、测量和互换使用等优点,因此应用最广。
第三节 渐开线的形成及其特性1、渐开线的形成如图10—9所示,―条直线在圆上作纯滚动时,直线上任一点的轨迹即为渐开线。
BK -发生线, 图7—8基圆-rb,θk-AK段的展角。
2、渐开线的特性①AB =BK;如图7—10所示,发生线滚过基圆的长度等于基圆上被滚过的弧长。
机械原理(PDF)孙桓复习笔记chapter10

齿顶高 ha:分圆到顶圆的经向距离。 齿根高 hf: 根圆到分圆的经向距离。
全齿高 h: 根圆到顶圆的经向距离。即 h = h a + hf 任意圆 ri: 以任意半径所作的圆;其齿厚、齿槽宽、齿距分别以
注: 单个齿轮无节圆。
si、ei、pi表示
基 节 pb: 相邻两齿同侧齿廓沿基圆的弧长。
pb = pcos α
2 .刀具标准位置: 齿条型刀具的分度线与被切齿轮的分度圆相切并纯滚。
注: 因刀具在分度线上的齿厚等于齿槽宽,所以被加工齿轮的分度圆的
齿厚也等于齿槽宽,即切制成的齿轮为标准齿轮。
三.渐开线齿郭的根切现象和标准齿轮不发生根切的最少齿数
1.根切现象: 用范成法加工齿轮时,轮齿根部的部分渐开线齿廓
被切去的现象。(图 8-12 )
α
P
se
p
1
ha hf α
才能使齿顶部分的齿廓均为渐开线)
63
《机械原理》 (第七版)孙桓主编
§10—5 渐开线直 齿圆柱齿轮的 啮合传动 一.一对渐开线齿轮正确啮合的条件
由于渐开线齿轮副的接触点都在线
1 2上
所以各齿对要在 1 2上同时啮合,两轮的法节应相等:
pn1=p b1=πmc1os α =K1 K′=πm cos2α =p b22=p n2
5 )基圆内与渐开线(∵ nn 总与基圆相切)
二.渐开线方程方 方 程 程 式 式 及 及 渐 渐 开 开 线 线 函 函 数 数 当齿轮绕轴心 O 转动时,渐开线齿廓 AK 上 K 点的速度 vk⊥rk,又该齿廓与另一 轮的齿廓在 K 接触时,所受法向力 F n必沿 nn。
60
《机械原理》 (第七版)孙桓主编
*
第十章齿轮机构及其设计

第十章齿轮机构及其设计第十章齿轮机构及其设计基本要求了解齿轮机构的应用及其分类以及齿廓啮合的基本定律、共轭齿廓等概念。
熟练掌握渐开线直齿圆柱齿轮几何尺寸的计算以及一对轮齿的啮合过程、正确啮合条件、连续传动条件、渐开线齿轮传动的特点等。
了解渐开线齿轮的切制原理。
掌握标准齿轮不发生根切的最少齿数以及最小变位系数的计算和变位齿轮几何尺寸的计算。
了解斜齿圆柱齿轮传动的特点、齿廓的形成。
掌握端面和法面参数之间的关系转换及基本尺寸的计算。
了解圆锥齿轮和蜗轮蜗杆传动的特点以及主要几何尺寸的计算。
基本概念题和答案1.什么是齿廓啮合基本定律,什么是定传动比的齿廓啮合基本定律?齿廓啮合基本定律的作用是什么?答:一对齿轮啮合传动,齿廓在任意一点接触,传动比等于两轮连心线被接触点的公法线所分两线段的反比,这一规律称为齿廓啮合基本定律。
若所有齿廓接触点的公法线交连心线于固定点,则为定传动比齿廓啮合基本定律。
作用;用传动比是否恒定对齿廓曲线提出要求。
2.什么是节点、节线、节圆?节点在齿轮上的轨迹是圆形的称为什么齿轮?答:齿廓接触点的公法线与连心线的交点称为节点,一对齿廓啮合过程中节点在齿轮上的轨迹称为节线,节线是圆形的称为节圆。
具有节圆的齿轮为圆形齿轮,否则为非圆形齿轮。
3.什么是共轭齿廊?答:满足齿廓啮合基本定律的一对齿廓称为共轭齿廓。
4.渐开线是如何形成的?有什么性质?答:发生线在基圆上纯滚动,发生线上任一点的轨迹称为渐开线。
性质:(1)发生线滚过的直线长度等于基圆上被滚过的弧长。
(2)渐开线上任一点的法线必切于基圆。
(3)渐开线上愈接近基圆的点曲率半径愈小,反之则大,渐开线愈平直。
(4)同一基圆上的两条渐开线的法线方向的距离相等。
(5)渐开线的形状取决于基圆的大小,在展角相同时基圆愈小,渐开线曲率愈大,基圆愈大,曲率愈小,基圆无穷大,渐开线变成直线。
(6)基圆内无渐开线。
5.请写出渐开线极坐标方程。
答:r k = r b/ cos αk θk= inv αk= tgαk一αk6.渐开线齿廓满足齿廓啮合基本定律的原因是什么?答;(1)由渐开线性质中,渐开线任一点的法线必切于基圆(2)两圆的同侧内公切线只有一条,并且两轮齿廓渐开线接触点公法线必切于两基圆,因此节点只有一个,即i12=ω1/ ω2=O2P / O1P =r2′/ r1′= r b2/ r b1= 常数7.什么是啮合线?答:两轮齿廓接触点的轨迹。
机械原理课件:第10章 齿轮机构及其设计[优选内容]
![机械原理课件:第10章 齿轮机构及其设计[优选内容]](https://img.taocdn.com/s3/m/982da12365ce0508763213ed.png)
行业借鉴#
11
§10-3 渐开线齿廓及其啮合特性
一、渐开线及其特性
1、渐开线的形成
K
rK
发生线
一发生线在基圆
要上素相:切基纯圆滚,发动生,线发生。
渐A 开
K
K
o rb
B
线
基圆
线平rb 上面任内一走基点过圆K的半在轨径基迹圆Ak
即 K为渐开渐线开。线展角
行业借鉴#
12
2、渐开线特性
渐
K
1)BK AB
1)、模数m
当齿数为Z,计算ri圆上周长为:
2ri pi Z , d i
人为规定:
pi
mi
pi Z
规定m:i —分度完圆整上有理的数模称数为为模标数 准值。
式中m可见:
d
p
i
mi Z
, d
mZ
当Z一定时,不同圆上的模数不等。
行业借鉴#
21
2)、压力角
cos i
rb ri
当rb一定时,不同圆上的压力角不等。
标准齿轮:
具有标准齿廓参数
(
m,
,
h a
,
c
)
且分度圆上s e的齿轮。
标准齿轮的基本参数:
Z,
m, ,
h* a
,
c* .
d mZ
ha
h a
m
da d 2ha
hf
(
h a
c
)
m
d f d 2hf
h ha hf
db d cos
p 行业借鉴# m ; s e m26 2
根据渐开线特性可导出:法节=基节 则 pb p cos m cos
齿轮机构及其设计

齿轮机构及其设计齿轮机构是现代机械中应用最广泛的一种传动机构。
与其它传动机构相比,齿轮机构的优点是结构紧凑,工作可靠,效率高,寿命长,能保证恒定的传动比,而且其传动的功率与适用的速度范围达。
但是,其制造安装费用较高,及精度齿轮传动的振动噪声较大。
齿轮机构根据实现传动比的情况,分为定传动比和变传动比齿轮机构。
定传动比的圆形齿轮机构根据两传动轴线的相对位置,可分三类:平行轴齿轮机构(两齿轮的传动轴线平行)、相交轴齿轮机构(两齿轮的传动轴线相较于一点)、交错轴齿轮机构(两齿轮的传动轴线为空间任意交错位置)。
1.瞬时传动比两齿轮的传动比总等于齿数的反比,即n1/n2=z2/z1,但其瞬时传动比却与齿廓的形状有关。
按三心定理,公法线n-n与二齿轮连心线的交点C为二齿轮的相对速度瞬心,即二齿轮在C点的线速度应相等:ω1 O1C=ω2 O2C,由此得瞬时传动比і12:і12= ω1/ω2= O2C/ O1C=r2/r1该式说明,具有任意齿廓的二齿轮啮合时,其瞬时角速度的比值等于齿廓接触点公法线将其中心距分成两段长度的反比。
这就是齿廓啮合基本定律。
满足齿廓啮合基本定律的传动比为常数或按一定规律变化的一对齿廓称为共轭齿廓。
在齿轮机构中,相对速度瞬心C称为啮合节点,简称节点。
为实现定传动比传动,要求两齿廓在任何位置啮合时,其节点C都为中心线上的一个固定点,分别以O1、O2为圆心、以O1C 和O2C为半径的圆C1和C2,称为齿轮的节圆(注意非分度圆)。
故节圆是齿轮的相对瞬心线,齿轮的啮合传动相当于其两节圆作无滑动的纯滚动。
2.渐开线圆柱齿轮及其基本齿廓1)齿轮的各部分名称•齿顶圆(直径d a)•齿根圆(直径d f)•齿厚(分度圆处s,任意圆周处sі)•齿槽宽(分度圆处e,任意圆周处eі)•齿距(分度圆处p,任意圆周处pі=sі+eі)•分度圆(直径d,规定标准齿轮分度圆上的齿厚s与齿槽宽e相等,即s=e=1/2 p)•齿顶高(齿顶部分的径向高度h a)•齿根高(齿根部分的径向高度h f)•全齿高(齿顶圆与齿根圆之间的径向距离,h=h a+h f)。
机械原理第十章齿轮机构及其设计

齿轮机构在实际应用中的案例分析和优 化建议
1
案例分析
以汽车变速器齿轮机构为例,分析设计难点和优化方案。
2
优化建议
增加齿轮配对的精度和硬度,增强齿面润滑和冷却,改善齿轮啮合性能。
3
ห้องสมุดไป่ตู้
结论
齿轮机构的优化设计可以提高传动效率和使用性能,减少噪音和故障,从而为工业生产 带来更多的价值。
1
齿轮的传动原理
齿轮的传动是通过齿的啮合转动相互连接,实现旋转和转矩的传递。
2
齿轮的计算方法
齿轮的计算需要考虑齿轮啮合角度、模数、齿数等因素,以确保其传动性能。
3
齿轮的应用
齿轮广泛应用于各种机械设备和装置,例如汽车、工厂机器、重型设备等。
齿轮机构的设计要点和步骤
要点
• 合理选择齿轮类型和规格; • 确定齿轮的啮合方式和传动参数; • 考虑齿轮的制造和安装工艺; • 考虑齿轮的润滑和保养。
齿轮的基本概念和组成部分
基本概念
齿轮由齿、齿宽、齿高、模数等组成。
组成部分
齿轮一般由轮毂、齿、齿面和齿槽等组成。
不同类型的齿轮机构
平面齿轮机构
齿轮平面呈直线排列,适 用于同轴传动。
锥齿轮机构
齿轮锥面呈锥形,适用于 斜轴传动。
蜗杆齿轮机构
由蜗杆和蜗轮组成,适用 于大减速比传动。
齿轮的传动原理和计算方法
步骤
1. 确定传递功率和转速比; 2. 计算齿轮的模数、齿数和啮合角度; 3. 选择齿轮的材料和硬度; 4. 进行齿轮的传动计算和强度校核; 5. 进行齿轮的制造和安装; 6. 进行试车和试运转。
常见的齿轮设计问题和解决方法
问题
齿轮的使用寿命较短、传动效率低、噪音大等。
机械原理课件10 齿轮机构及其设计

§ 10-4 渐开线标准齿轮的基本参数和几何尺寸
1 齿轮各部分的名称和符号
基圆(db,rb);
ei
齿顶圆(da,ra);
齿根圆(df,rf);
任意圆(di,ri); 任意圆齿距pi ; 任意圆齿厚si;
ra rf
ri rb
任意圆齿槽ei;
pi(= si+ ei)
O
分度圆―设计基准圆(d,r);
分度圆齿距p, 分度圆齿厚s; 分度圆齿槽e,
O1 1
n
C1
1
C2 K
P
2
VP O1P 1 O2P 2
故两轮的传动比为:
i12
1 2
O2 P O1 P
2
O2
齿轮传动满足定传动比要求的条件是:P 在 连心线上为一定点。
i12
1 2
O2 P O1 P
齿廓啮合基本定律―两相互啮合传动的一
对齿轮,在任一位置时的角速度ω1/ω2
都等于节点P所分连心线 O1O的2 两段线段 r1’
(p = s+e)
齿顶高ha, , 齿根高hf 全齿高h;
rf ra
齿顶圆直径: da = d+2ha
齿根圆直径: df = d-2 hf
S=e
s e ha
hf h
r
rb
O
2 渐开线齿轮的基本参数 1)齿数:z
2)模数:m 分度圆圆周为:d = ZP
分度圆直径为:d zP
令: m P
则: d zm
齿轮机构的分类
1)按相对 运动形式分
平面齿轮 机构
空间齿轮 机构
外啮合齿轮传动
直齿轮
内啮合齿轮传动
齿轮齿条传动 平行轴斜齿轮
第十章齿轮机构及其设计一、齿轮的...

第十章 齿轮机构及其设计一、齿轮的齿廓曲线1.共轭齿廓:一对能实现预定传动比(i 12=ω1/ω2)规律的啮合齿廓。
2.齿廓啮合基本定律齿廓啮合基本定律:互相啮合的一对齿轮在任一位置啮合时的传动比,都与连心线O 1O 2被其啮合齿廓在接触点的公法线所分成的两线段长成反比。
二、渐开线 1.特性:①发生线滚过基圆的长度等于基圆上被滚过的弧长。
②渐开线上任意点的法线切于基圆,渐开线上任意点的法线即渐开线的发生线。
③B 点为曲率中心,BK 为曲率半径。
渐开线起始点A 处曲率半径为0。
④渐开线形状取决于基圆,基圆越大,渐开线越平缓,当r b →∞,渐开线变成直线,齿轮变为齿条。
⑤基圆内无渐开线。
⑥同一基圆上任意两条渐开线公法线处处相等。
2.渐开线方程式压力角:啮合时K 点正压力方向与绝对速度方向所夹锐角为渐开线上该点之压力角αk 。
αk r b =r k cos αkcos αk= r b/ r k (渐开线离基圆愈远,其压力角越大)极坐标方程:tg αk = BK/r b =AB/r b = r b (θk +αk )/r bθk = tg αk -αk上式称为渐开线函数,用inv αk 表示:θk =inv αk =tg αk -αk由tg αk = BK/r b- ------得渐开线任一点的曲率半径 ρ=BK= r b tg αk ,则分度园上的曲率半径(*会计算)ρ=BK= r b tg α3、渐开线齿廓的啮合特性1)渐开线齿廓能保证定传动比传动两齿廓在任意点K 啮合时,过K 作两齿廓的法线N 1N 2,是基圆的切线,且为定直线;两轮中心连线也为定直线,故交点P 必为定点 i 12=ω1/ω2=O 2P/ O 1P=const2)齿廓间正压力方向不变N 1N 2是啮合点的轨迹,称为啮合线,该线又是接触点的法线,正压力总是沿法线方向,故正压力方向不变。
该特性对传动的平稳性有利。
3)运动可分性7—14传动比写成:i 12=ω1/ω2=O 2P/ O 1P = r b2 /r b1= r 2’ /r 1’传动比为基圆半径之反比。
第十章齿轮机构及其设计(精)
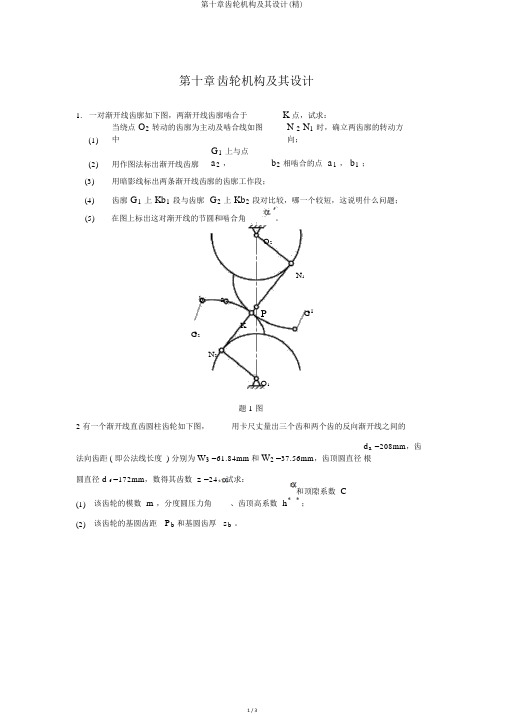
第十章齿轮机构及其设计1. 一对渐开线齿廓如下图,两渐开线齿廓啮合于K 点,试求:(1) 当绕点 O2转动的齿廓为主动及啮合线如图中N 2 N1时,确立两齿廓的转动方向;(2) 用作图法标出渐开线齿廓G1上与点a2,b2相啮合的点 a1, b1;(3)用暗影线标出两条渐开线齿廓的齿廓工作段;(4)齿廓 G1上 Kb1段与齿廓 G2上 Kb2段对比较,哪一个较短,这说明什么问题;(5)在图上标出这对渐开线的节圆和啮合角。
O2N1b2a2P G1KG2N2O1题 1 图2 有一个渐开线直齿圆柱齿轮如下图,用卡尺丈量出三个齿和两个齿的反向渐开线之间的法向齿距 ( 即公法线长度 ) 分别为W3 =61.84mm和W2 =37.56mm,齿顶圆直径d a=208mm,齿根圆直径 d f=172mm,数得其齿数 z =24,试求:(1) 该齿轮的模数 m ,分度圆压力角、齿顶高系数 h* 和顶隙系数 C *;(2) 该齿轮的基圆齿距 P b和基圆齿厚s b。
W3W2D BA Cr bO题 2 图3 已知一对渐开线外啮合标准直齿圆柱齿轮机构,=20°,h* =1,m =4mm,z1 =18,z2 =41。
试求:(1) 标准安装时的重合度;(2) 用作图法画出理论啮合线N1 N 2,在其上标出实质啮合线段B1B2,并标出单齿啮合区和双齿啮合区,以及节点P 的地点。
O1r a1r b1p b p b 1NB1 B2 N2 P8p b 2p b0.3 0.662p b b. p.6231r b2 r a2O2题3解图4丈量齿轮的公法线长度是查验齿轮精度的常用方法之一,试用图证明渐开线齿轮公法线长度 W 和卡尺跨的齿数 k 的计算公式:W m cos (k 0.5) zinv a 2xmsin ak ( z 0.5) z( tg x tg ) 2x tg式中 z 为被测齿轮的齿数,k 为卡尺跨的齿数,目的是为了卡尺一定卡在渐开线齿廓上。
第十章齿轮机构及其设计(10-1、2、3)

§10—3 渐开线齿廓及啮合特点
一、渐开线的形成及特征
1、形成
渐开线是发生线在基圆上作纯
滚动时,发生线上任意点K所走的
轨迹AK。
2、特性
1) BK= AB。
2)渐开线上任一点的法线是基圆 的切线。
3)线段BK是渐开线在K点的曲率半 径,
B点是渐开线在K点的曲率中心。
图10-6
4)渐开线的形状取决于基圆的大小。
图10-4
ω1 /ω2= O2P/ O1P=i12 ——齿廓啮合基本定律 若 两轮的传动比为常数 O2P/ O1P=常数
P在O1O2上必须是定点 要使两齿轮作定传动比传动,则不论 两齿廓在何处接触,过接触点所作的 公法线必须与连心线交于一定点。
——定比传动齿轮的齿廓啮合 基本定律
P: 节点 (对定比传动:P为定点) P点在齿轮运动平面上的轨迹: 节线 (对定比传动:节线为节圆r1′、r2′)
a)
b)
c)
图10-1
§10—2 齿轮的齿廓曲线
一、齿廓啮合基本定律 研究传动比与齿廓曲线பைடு நூலகம்间 的关系
分析: P点为速度瞬心. V1P=V2P → ω1·O1P=ω2·O2P ω1 /ω2= O2P/ O1P=i12 (10-2)
—— 互相啮合的一对齿轮,其 传动比等于其连心线被啮合齿 廓接触点处的公法线所分成的 两段线段的反比。
∵ △O1PN1∽△O2PN2
∴ O2P/O1P= O2N2/ O1N1= rb2 / rb1 ∵ i12=ω1 /ω2= O2P/ O1P= r2′/ r1′ ∴ i12=ω1 /ω2= rb2 / rb1
2、中心距具有可分性
即传动比不因中心距的稍
α′
有变动而变动
机械原理(第七版)优秀课件—第十章 齿轮机构及其设计

Gears and its Design
• 10.1 齿轮机构的特点及分类
• 10.1.1 概述 • 1.什么是齿轮?
• 2.特点:适应范围广(v、p、r);效率
高(0.99);速比稳定、传动精度高;工 作可靠;可实现任意轴间的传动。制造 和安装精度要求高,成本较高;不适于 远距离传动。
• 刀具不标准
2.变位齿轮问题的提出
1)z<zmin时又要不根切; 2)a’≠a;
3)ρ小<ρ大, σ小>σ大, u小>u大,
• 3.刀具的变位 1)正变位 2)负变位 • 4. 变位传动
1)零变位齿轮传动:∑x=0,α’=α, a’=a • x1=x2=0 标准齿轮传动 x1=-x2 等移距变位齿轮传动 • 2)非零变位齿轮传动:∑x≠0,α’≠α, a’≠a
曲齿
交错轴斜齿轮传动
• 3.按齿廓曲线分:渐开线、摆线、圆弧 • 4.按工作条件分: • 1)开式:2)闭式:
• 5.按运动速度分:
• 低速:<1m/s
• 中速:1~25
• 高速:>25m/s • 超高:>100m/s
• 10.1.3 对齿轮传动的基本要求
– 1.传动准确平稳
i 1 d1
2 d 2
α
r
α N1
xm ha m
p
Q
• 2. 变位齿轮的几何计算
• m、a由强度计算确定,α、z、d、db不变化 • h高a和、齿h厚f 、的d变a化、 df、s 、e 、α’都将变化,而关键是齿
• 1)齿顶高、齿根高
hai (ha* xi y)m
hfi (ha* c* xi)m
x的选择:无侧隙、不根
2
c os '
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第七节
渐开线变位齿轮简介
3、变位齿轮传动 、
作业:10-8、10-9、10-10 作业
xm
用改变刀具与轮坯的相对位置来切制齿轮的方法, 用改变刀具与轮坯的相对位置来切制齿轮的方法, 叫:变位修正法。(x称为变位系数) 变位修正法。(x称为变位系数) 。( 第七节 渐开线变位齿轮简介
1、变位齿轮的概念 、
变位加工中仍然保持 =rω,所以节点c位置不变,只 是刀具中线不再同分度圆相切纯滚,而是由另一条平 行中线的线,称为加工节线 加工节线,同分度圆相切纯滚。 加工节线 第七节 渐开线变位齿轮简介
a ′ < a,α ′ < α ,y < 0,∆y > 0
第七节
渐开线变位齿轮简介
3、变位齿轮传动 、 (4) 变位齿轮传动的设计 (a)已知中心距的设计 (b)已知变位系数的设计
第七节
渐开线变位齿轮简介
3、变位齿轮传动 、 (4) 变位齿轮传动的设计
a、已知中心Βιβλιοθήκη 的设计已知条件:z1、z2、m、 a’ ,其设计步骤如下: 其设计步骤如下: 已知条件: 1)计算啮合角:α’=arccos(acosα/ a’) 计算啮合角: arccos(a a’) 2)确定变位系数之和: x1+ x2=(invα’-invα)( z1+ z2)/2tgα 2)确定变位系数之和: 确定变位系数之和 3)确定中心距变动系数: y=(a’-a)/m 3)确定中心距变动系数 y=(a’确定中心距变动系数: 4)确定齿顶高降低系数: △y=(x1+ x2) -y 4)确定齿顶高降低系数 5)分配变位系数。 5)分配变位系数 分配变位系数。 6)按公式表计算两轮的几何尺寸。 按公式表计算两轮的几何尺寸。
a ′′ = ra1 + c ∗m + rf 2
= r1 + (ha + x 1 )m + c m + r2 − (ha + c − x 2 )m
∗ ∗ ∗ ∗
a ′′ = a + (x 1 + x 2 )m
a ′ = a + ym
第七节 渐开线变位齿轮简介
3、变位齿轮传动 、 (2)变位齿轮传动的中心距。 )变位齿轮传动的中心距。 中心距 a)满足无侧隙啮合 得到 )满足无侧隙啮合-->得到 无侧隙啮合 得到a’
推导过程: 推导过程:
第七节 渐开线变位齿轮简介
无侧隙啮合方程式推导: 无侧隙啮合方程式推导: 啮合方程式推导
′ s1′ = e2 ′ p ′ = s1′ + s 2 ′ e1′ = s 2 p ′ = s1′ + e1′ p ′ cos α ′ = p cos α s si′ = ri′ − 2ri′ invαi′ − invα ) ( r
第七节 渐开线变位齿轮简介
1、变位齿轮的概念 、 问题的提出 :标准齿轮有不足 改善 不足 对齿轮进行修正 (变位修正法) 变位修正法)
第七节
渐开线变位齿轮简介
1、变位齿轮的概念 、
α
用范成法加工齿轮时, 用范成法加工齿轮时,当 刀具齿顶线超过啮合极限
α
ha* m
xm
P Q
Ν1
点时,就发生根切。 点时,就发生根切。为避 免根切现象, 免根切现象,可把刀具往 外移动,使刀具齿顶线落 外移动, 在啮合极限点N之下方。 在啮合极限点N之下方。
渐开线变位齿轮简介
2、变位齿轮的几何尺寸 、
标准齿轮
1、模数 有变化吗? 、模数m有变化吗 有变化吗? 2、齿数 有变化吗? 、齿数z有变化吗 有变化吗?
变位齿轮
答案: 答案:不变 答案:不变 答案:
因为加工机床的范成运动未变 。
第七节
渐开线变位齿轮简介
2、变位齿轮的几何尺寸 、
标准齿轮
1、模数 有变化吗? 、模数m有变化吗 有变化吗? 2、齿数 有变化吗? 、齿数z有变化吗 有变化吗? 3、压力角有变化吗? 、压力角有变化吗?
第七节 渐开线变位齿轮简介
2、变位齿轮的几何尺寸 、
标准齿轮
1、模数 有变化吗? 、模数m有变化吗 有变化吗?
变位齿轮
答案: 答案:不变
因为齿条刀上平行于中线的任何一条线 上的齿距都等于中线上齿距P, 上的齿距都等于中线上齿距 ,所以分度 圆上的齿距仍为P, 圆上的齿距仍为 ,故m不变 。 不变
第七节
第七节 渐开线变位齿轮简介
一、变位齿轮的概念 问题的提出 :标准齿轮有不足 1、齿数小于 个齿时,要求无根切 ,怎么办? 、齿数小于17个齿时 个齿时, 怎么办? 2、中心距不等于分度圆半径之和时,怎么办? 、中心距不等于分度圆半径之和时,怎么办? 3、一对标准齿轮啮合中,小齿轮齿廓曲率半径 、一对标准齿轮啮合中, 齿根厚度较薄,参与啮合次数较多, 小,齿根厚度较薄,参与啮合次数较多,强度 较低,影响整个传动承载能力。 较低,影响整个传动承载能力。
补充知识、 补充知识、最小变位系数
α
ha* m
xm
P
α
Ν1
Q
x min
h a ( z min − z ) = z min
*
xm
第七节
渐开线变位齿轮简介
3、变位齿轮传动 、 正确啮合条件及 (1)变位齿轮传动的正确啮合条件及连续 )变位齿轮传动的正确啮合条件 与标准齿轮相同。 传动条件与标准齿轮相同 传动条件与标准齿轮相同。 中心距。 (2)变位齿轮传动的中心距。 )变位齿轮传动的中心距 a)满足无侧隙啮合 得到 )满足无侧隙啮合-->得到 无侧隙啮合 得到a’ b)满足标准顶隙 得到 )满足标准顶隙-->得到 标准顶隙 得到a’’
3、变位齿轮传动 、 (2)变位齿轮传动的中心距。 )变位齿轮传动的中心距。 中心距 a)满足无侧隙啮合 得到 )满足无侧隙啮合-->得到 无侧隙啮合 得到a’
a ′ = a + ym
a ′ cos α ′ = a cos α
a = m(z1 + z2 ) / 2
第七节 渐开线变位齿轮简介
3、变位齿轮传动 、 (2)变位齿轮传动的中心距。 )变位齿轮传动的中心距。 中心距 a)满足无侧隙啮合 得到 )满足无侧隙啮合-->得到 无侧隙啮合 得到a’
齿顶高降低系数 ∆y
= (x 1 + x 2 ) − y
此时,变位齿轮的齿顶高为:
ha = ha m + xm − ∆ym
∗
第七节
渐开线变位齿轮简介
3、变位齿轮传动 、 (3)变位齿轮传动的类型 )
1)标准齿轮传动 ) x1= x2= 0 2)等变位齿轮传动 ) x1= - x2≠0 a ′ = a,α ′ = α ,y = 0,∆y = 0 3)不等变位齿轮传动 x1 + x2 ≠ 0 ) 当x1 + x2 > 0时,为正传动; a ′ > a ,α ′ > α ,y > 0,∆y > 0 当x1 + x2 < 0时,为负传动。
第七节
渐开线变位齿轮简介
3、变位齿轮传动 、 (2)变位齿轮传动的中心距。 )变位齿轮传动的中心距。 中心距 a)满足无侧隙啮合 得到 )满足无侧隙啮合-->得到 无侧隙啮合 得到a’ 无侧隙啮合方程式: 无侧隙啮合方程式: 啮合方程式
invα ′ = 2 tan α(x 1 + x 2 ) /(z1 + z2 ) + invα
变位齿轮
答案: 答案:不变 答案:不变 答案: 答案:不变(分度圆) 答案:不变(分度圆)
因为齿条刀的直线齿廓上各点压力角都一 样,均为刀具角a 。
第七节 渐开线变位齿轮简介
2、变位齿轮的几何尺寸 、
标准齿轮
1、模数 有变化吗? 、模数m有变化吗 有变化吗? 2、齿数 有变化吗? 、齿数z有变化吗 有变化吗? 3、压力角有变化吗? 、压力角有变化吗?
1、变位齿轮的概念 、
Ο1
r
节线
1
刀具远离齿轮中心时加工的齿轮 称正变位齿轮, x > 0 正变位齿轮, 齿轮
Ν1
P
xm
分度线
刀具靠近齿轮中心时加工的齿轮 负变位齿轮 齿轮, 称负变位齿轮, x < 0 第七节 渐开线变位齿轮简介
2、变位齿轮的几何尺寸 、
标准齿轮
变位齿轮
比较: 比较:基本参数与几何尺寸 是否有变化? 是否有变化?
a ′ = a + ym
b)满足标准顶隙 得到 )满足标准顶隙-->得到 标准顶隙 得到a’’
a ′′ = a + (x 1 + x 2 )m
按照无侧隙安装,将两轮齿顶各减短 ∆ym
齿顶高降低系数
∆y = (x 1 + x 2 ) − y
第七节
渐开线变位齿轮简介
3、变位齿轮传动 、 (2)变位齿轮传动的中心距。 )变位齿轮传动的中心距。 中心距 按照无侧隙安装,将两轮齿顶各减短 ∆ym
变位齿轮
答案: 答案:不变 答案:不变 答案: 答案:不变(分度圆) 答案:不变(分度圆)
4、ha* 、c*有变化吗? 答案:不变 、 有变化吗? 答案: 有变化吗
第七节 渐开线变位齿轮简介
2、变位齿轮的几何尺寸 、
标准齿轮
1、模数 有变化吗? 、模数m有变化吗 有变化吗? 2、齿数 有变化吗? 、齿数z有变化吗 有变化吗? 3、压力角有变化吗? 、压力角有变化吗? 4、ha* 、c*有变化吗? 、 有变化吗? 有变化吗
πm/2 + 2xmtanα πm/2 − 2xmtanα
2、变位齿轮的几何尺寸 、
正变位齿轮:
∗ ∗ 齿根高: hf = ha m + c m − xm
