2.建立描述飞机运动特性的全量运动方程
2015飞力实验班典型模态实验指导书

航空科学与工程学院《飞行力学实验班》课程实验飞机典型模态特性仿真实验报告学生姓名:张恺玲学号:12051265专业方向:飞行器设计指导教师:王维军(2015年6月17日)实验名称: 飞机典型模态特性仿真实验实验所属课程编号:实验所属课程名称:飞行力学(Flight Dynamics)开课学期:春季一.实验目的飞机运动模态是比较抽象的概念, 是课程教学中的重点和难点。
本实验针对这一问题,采用计算机动态仿真和在人-机飞行仿真实验平台上的驾驶员在环仿真实验,让学生身临其境地体会飞机响应与模态特性的关系,加深对飞机运动模态特性的理解。
二.实验内容1.纵向摸态特性实验计算某机在某状态下的短周期运动、长周期运动的模态参数;进行时域的非实时或实时仿真实验,操纵升降舵激发长、短周期运动模态,并由结果曲线分析比较模态参数;放宽飞机静稳定性,观察典型操纵响应曲线,并通过驾驶员在环实时仿真体验飞机的模态特性变化。
2.横航向模态特性实验计算某机在某状态下的滚转、荷兰滚、螺旋模态参数;进行时域仿真计算,操纵副翼或方向舵,激发滚转、荷兰滚等运动模态,并由结果曲线分析比较模态参数。
三、要求及考核方式1.要求学生就上述实验教学内容中的模态特性分析和动态仿真,独立在实验平台上编程、操作,并完成计算和分析报告。
2.实验操作与讨论表现、实验报告质量综合评分。
严禁抄袭。
四、实验步骤1.模态特性分析。
按小扰动线化运动方程和给定的某飞机的数据,理论计算飞机运动的典型模态参数,包括纵向短周期模态、长周期模态及横、航向三个典型模态;2.动态仿真。
对上述模态分析结果,分别进行纵向和横航向的实时或非实时动态仿真,观察飞机的动态响应。
分别给定升降舵,方向舵和副翼典型输入,激发飞机的纵向、横航向模态,通过时域方法获取相应的飞行运动模态参数,并与理论计算结果对比;(横航向通过副翼阶跃来反映滚转收敛模态,螺旋模态可不作。
)尝试改变某些气动参数,观察飞机的模态特性变化。
建立飞行器运动方程

一、动力学方程
动力学方程——以动力学为基础, 描述力与力矩平衡关系的方程,亦即 为考虑在体轴系下运动参数与力、力 矩的方程。(由于体轴系为动坐标系, 所以建方程时既要考虑相对运动,又 要考虑绝对运动。
一、动力学方程式
动力学方程式是描述飞机所受力、力矩与飞机运
动参数间关系的方程,显然包括两组方程:
2、线运动方程
用机体系表示绝对参数变化时:
1v
d~v dt
dv dt
Iv
d~v dt
为速度向量 V
v
相对于动坐标系的变化率,
V
为由于动坐标系转动而引起的向量变化率,是牵连
加速度。
dv Iv dt iu jv kw
i jk
v
p
q
r i(wq vr) j(ur wp) k(vp uq)
N rI z pI xz pq(I r I x ) prI xz
力平衡方程式:
F
m
dv dt
Fx
Fy
X
Y
(u wq vr)m (v ur wp)m
Fz Z (w vp up)m
二、运动学方程式
运动学方程——通过体轴系与地轴系的关系, 找出体轴系下角速度、位移量与地面轴系下角速 度、位移量的关系。包括两种方程:
二、 六自由度飞机运动方程
1、飞机运动的自由度:(six-degrees-of freedom)
飞机在空间的运动有六个自由度,即质心沿地 面坐标系的三个移动自由度和绕机体坐标轴系 的三个转动自由度 。
一个角运动 : 俯仰q
纵向两个线运动:高 航度 程HL
侧向两个角运动:滚 偏转 航pr 一个线运动 : 侧偏Y
2.1、飞行器运动方程组
飞行动力学飞机方程

xydm Ixy
表示惯性积
依据假设 Ixy=Izy=0 ,H 的各分量
H
x
H y
pI x qI y
rI xz
代入
dH dt
1H
dH dt
H
H x dt
pI x rI xz
dH y dt
qI y
dH z dt
rI z pI xz
由于
i jk
H p q r i(qH z rH y ) j(rH x pH z ) k ( pH y qH x )
1.地轴系与机体轴系间的方向余弦表
o
xg
x
cos cos
y
cos sin sin- sincos
z
cos sin cos+sinsin-
yg sincos sin sin sin+cos cos sin sin cos-cos sin
zg -sin cos sin cos cos
表中,oxyz为机体轴系, oxgygzg为地轴系
—动坐标系对惯性系的总角速度向量
—表示叉积,向量积
1H —沿动量矩 H 的单位向量
dV , dH dt dt
—对动坐标系的相对导数
1.力方程
F
m
dV dt
dV dt
1V
dV dt
V
V 和 用机体坐标系上的分量(u,v,w;p,q,r)表示
V iu jv kw, ip jq kr
三个力方程 三个力矩方程 飞机六自由 度动力学
线性方程 增量方程
m
d u dt
( X u
)0 u
( X
)0
( X
)0
m
飞行力学第六章-运动方程

ωx
ω y I x ω x I xy
0 I zx
I xy Iy I yz
I zx ω x M x I yz ω y = M y I z ω z M z
飞行器飞行力学2010
得
dω x 2 2 + ( I z I y )ω y ω z + I yz (ω z ω y ) + Ix dt dω y dω z I xy (ω x ω z ) I zx (ω x ω y + ) = Mx dt dt dω y 2 2 + ( I x I z )ω x ω z + I zx (ω x ω z ) + Iy dt dω z dω x I yz (ω x ω y ) I xy (ω y ω z + ) = M y dt dt dω z 2 2 + ( I y I x )ω x ω y + I xy (ω y ω x ) + Iz dt dω y dω x I zx (ω y ω z ) I yz (ω z ω x + ) = Mz dt dt
飞行器飞行力学2010
根据速度之间的关系
u = V cos α cos β v = V sin β w = V sin α cos β
可得
du dV dα dβ V sin α cos β V cos α sin β cos α cos β = dt dt dt dt dv dV dβ V cos β sin β + = dt dt dt dw dV dα dβ sin α cos β + V cos α cos β V sin α sin β = dt dt dt dt
dω z dω x + ( I z I y )ω y ω z I zx (ω x ω y + Ix ) = Mx dt dt 方 程 dω y 2 2 + ( I x I z )ω x ω z + I zx (ω x ω z ) = My 简 Iy dt 化 为 I d ω z + ( I I )ω ω + I (ω ω d ω x ) = M z y x x y zx y z z dt dt
飞机运动动力学建模

至此,飞机的运动方程已经建立起来!
谢谢
飞机绕质心转动的动力学方程
飞机绕质心转动的动力学方程
机体坐标系中 飞机绕质心转动的动力学方程
对于飞机,一般Oxbzb平面为对称平面,有 I xy I yz 0 。 在机体轴系中,角速度投影为
x
x
ωy My
ωz Mz
p
T b
q M
r
T
外力矩的投影为
M
L
T b
N
T k
0 0
T
x y z k
. sin 0 0 . . Lgk 0 . 0 cos
航迹坐标系中 飞机质心运动的动力学方程
飞机运动 动力学建模
常用坐标系
地面坐标系 (g系) 坐标原点 X轴正向 地面选定的 固定点 地平面内任 意选定 铅垂向下
对于飞机,g系 可以看作惯性坐 标系
机体坐标系 (b系) 飞机质心 对称平面内 平行于机身 轴线指向前 气流坐标系 (a系) 飞机质心 空速方向 航迹坐标系 (k系) 飞机质心 地速方向 包含Oxk的铅 垂面内垂直 Oxk向下
航迹坐标系中 飞机质心运动的动力学方程
g x 0 g sin L m 0 m 0 m g y gk gz k g g cos
dV T cos cos D m g sin dt d m V cos T sin sin cos sin cos C cos L sin dt d mV T sin cos cos sin sin C sin L cos m g cos dt m
飞行动力学飞机方程

设方向余弦表为矩阵Mbg,用欧拉角描述:
体轴坐标与地轴坐标可以互相转换
Mbg是复共轭矩阵:
x
y
M bg
xg
yg
z
zg
M 1 bg
MbTg
姿态角变化率与角速度分量间的几何关系
地轴系 Oxgyg平面
飞机三个姿态角变化率的方位
—沿ozg轴的向量,向下为正
—在水平面内与ox轴在水平面上的
u vw
F 按各轴分解,表示为: F iX jY kZ
各轴分量:
X m u wq vr
Y
m v ur
wp
Z
m
w
vp
uq
飞机的力方程
2.力矩方程
M
dH dt
dH dH dt 1H dt H
先考虑第一项
H 是动量矩,单元质量dm因角速度引起的动量矩为
dH r ( r )dm
式中:r 为质心至单元质量dm 的向径。
对飞行器的全部质量积分,可得总的动量矩 H r ( r )dm
式中: r ix jy kz, ip jq kr
依据:
i jk r p q r i(qz r y) j(r x pz) k( p y xq)
xyz
i r ( r ) x
xydm Ixy
表示惯性积
依据假设 Ixy=Izy=0 ,H 的各分量
H
x
H y
pI x qI y
rI xz
代入
dH dt
1H
dH dt
H
H
z
rI z
pI xz
可得
dH x dt
pI x rI xz
dH y dt
qI y
(完整版)飞机动力学模型建立

建立飞机飞行动力学模型飞机的本体飞行动力学模型分为非线性模型和线性模型。
如图所示,线 性模型常用于飞机的飞行品质特性分析和飞行控制律设计,而非线性模型通常 用于飞机稳定性和操纵性特征的精确估计,从而进行各种非线性特征和线性模 型的误差分析。
另外,非线性模型还特别用在一些特殊的飞行任务,例如大迎 角和快速机动飞行等线性模型不适用的场合。
线性模型:主要进行飞机飞行品质 分析歩飞行控制律设计建立全量非线性六自由度运动方程 (1) 刚体飞机运动的假设['3]: ① 飞机为刚体且质量为常数;② 固定于地面的坐标系为惯性坐标系;③ 固定于机体的坐标系以飞机质心为原点;④ 忽略地球曲率,即采用所谓的“平板地球假设”; ⑤ 重力加速度不随飞行高度变化;以上假设是针对几云Jv3,H<30加飞机的。
(2) 坐标系说明:① 地面坐标轴系凡一 Q x:夕。
29:在地面上选一点09,使xg 轴在水平面内 并指向某一方向,z 。
轴垂直于地面并指向地心,yg 轴也在水平面内并 垂直于X 。
轴,其指向按照右手定则确定,如图2 一 3(a)② 机体坐标轴系凡一 d 朴忆:原点O 取在飞机质心处,坐标系与飞机固 连,x 轴在飞机对称面内并平行于飞机的设计轴线指向机头 ,y 轴垂直全董六自由度非蝇性动力学模型非陸模型:主要进行恃奏验证 和非线性分析四阶纵向动 力学模型四外横航向 动力学模型短周期近似模型于飞机对称面指向机身右方 机身下方,如图2 一 3(b)。
oy,:轴在飞机对称面内,与x 轴垂直并指向乩地面坐标轴系氐机体坐标轴系 图2胡常用塑标系说明⑶刚体飞机的全量六自由度非线性运动方程为 力方程组: 力矩方程组: - /)-匚(/十阳)一你3-小)二丄人=A0 二 p + q sin 0 tan 0 十 r cos 0 tan 0W一 心因-几 3 -qJ-钮+v )-4(p —")二览=v 运动方程组: & - i/COS^ 一厂血00 二 ------ (q sin 0 + r cos 0)COS0v - pw一 皿+輕歸讪+ :(F —圖) w — qu —严+心肌0讣(益+导航方程组:ccs^ + 训一sin 妙LOH0 丰cos sin 9 sin 0 + w (sin 肖sin / + cos sin cos y, = sin y/cos0 + r(co$4y cosc* + siny/sin6?sin 0) + ^-cos^sin + sin^ sin Otosd) h --nsin 0 - vcos^sin^ - wcostf cos^符号说明:心飞机质量,重力加速度:2b E机机翼禹税、平均T动茁长和展検:u,v,w速度矢命在分别在体轴条厂八二上的投影;p.q”体轴宗相对于地轴系旋转角速度矢览分别在体轴^x.y.z上的投影;%动力在体耙系各轴上的投勲貝丹押的,丫皿沖.推力在休轴系各细上的投影*飞机的俯仰角、滚转角和偏航角;飞机迎角*侧滑角和绕速度轴矢戟的滚转角;总机速區矢量.飞机航迹倾斜角.荻迹偏转角;飞机体轴系下各轴的转动惯电:匕机体轴系下谷轴的惯性积;飞机所爱升力、胆力、侧力和发动机抵力:合力矩分别在体轴系「丫2上的投影;E机位垃欠_&在炮轴系上的投影柯飞机岛度:飞机升降蛇偏角、亂罠倔角、方向舵偏角和油门位置:建立飞机小扰动线化方程(I)基本假设:①小扰动假设:我们把运动状态与飞机基准运动状态差别很小的扰动运动称为小扰动运动。
飞机六自由度飞行动力学仿真实验
飞机六自由度飞行动力学仿真实验一.实验目的1.本实验将理论力学课程教学内容与航空航天工程应用相结合,分析、研究飞机受力与六自由度运动特性,培养学生分析问题和解决问题的能力,展现理论力学知识在航空航天工程中的应用。
2.通过本实验,使学生更好地学习和理解理论力学的有关内容,如飞机的受力分析、空间力系的简化与合成、刚体的平面运动与一般运动、刚体微分方程的建立与求解等,激发学生对理论力学的学习兴趣,开阔视野,增强工程概念。
二.实验仪器与设备实验在PC 个人计算机、WINDOWS 98以上操作系统环境中进行。
三.实验原理飞机在空中的运动,在一定的假设条件下,可以视为理想刚体的运动,遵循刚体的运动规律,理论力学中介绍的刚体平动和转动基本定律都适用于飞行器的运动分析。
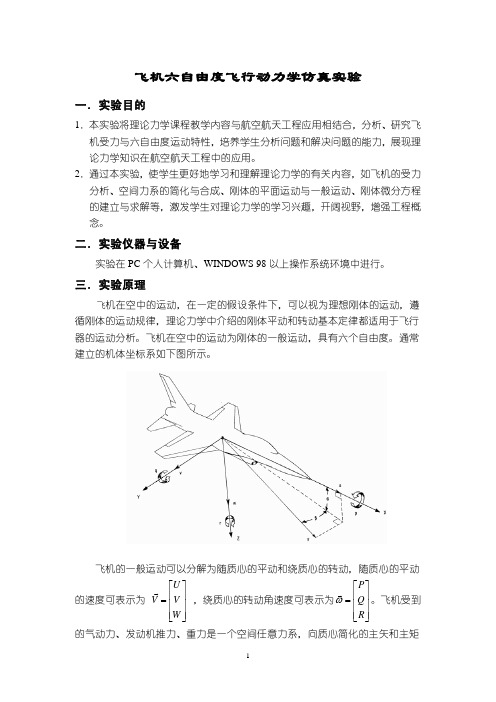
飞机在空中的运动为刚体的一般运动,具有六个自由度。
通常建立的机体坐标系如下图所示。
飞机的一般运动可以分解为随质心的平动和绕质心的转动,随质心的平动的速度可表示为 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=W V U V G ,绕质心的转动角速度可表示为⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=R Q P ωG 。
飞机受到的气动力、发动机推力、重力是一个空间任意力系,向质心简化的主矢和主矩分别为⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=Fz Fy Fx F G 和⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=Mz My Mx M G 。
根据质心运动定理(牛顿方程)和相对于质心的动量矩定理可得飞机的动力学微分方程,一般说来,该方程没有解析解,只能通过数值积分得到数值解。
系统分为“概念演示”与“f16实时仿真”两大模块。
在“概念演示”模块中着重介绍了飞机运动的自由度、单自由度下的操纵与响应特性。
在“f16实时仿真”模块中介绍了飞机定直平飞、盘旋、拉起、起飞、着陆、失速尾旋等的飞行过程及受力情况,学生也可以亲自驾驶这架F16进行实时仿真飞行。
四.实验步骤1.概念演示六自由度演示:点击菜单“概念演示->六自由度演示”,进入六自由度演示状态,如下图所示。
飞行器动力学的数学模型和分析方法

飞行器动力学的数学模型和分析方法飞行器是人类一项重要的创造,其对于人类的交通和工作起到了不可或缺的作用。
要想让飞行器在空中顺利地运作,需要对其动力学进行分析和建模。
本文将介绍飞行器动力学的数学模型和分析方法。
一、飞行器动力学的数学模型飞行器动力学的数学模型是建立在牛顿第二定律的基础之上的,它描述了飞行器在空气中的运动轨迹和受到的力的作用。
在飞行器动力学模型中,需要考虑以下因素:1.飞行器的质量和重心位置:飞行器质量和重心位置是影响其运动的重要因素。
质量越大,飞行器所受到的阻力也越大,需消耗更多的能量才能继续前进。
重心位置影响了飞行器的稳定性和姿态调整能力。
2.气流对飞行器的影响:飞行器在空气中会受到阻力、升力和重力等相互作用的力。
阻力是由于空气的粘滞力和飞行器的速度造成的,如果飞行器速度过快,阻力将随之增大。
升力是由于飞行器的机翼形状和速度产生的,它是支撑飞行器飞行的主要力量。
重力是由于地球的引力引起的,它影响了飞行器的下降速度。
3.飞行器的驱动力:飞行器的驱动力是通过动力系统来提供的。
不同的飞行器有不同的动力系统,如螺旋桨、喷气、火箭等。
动力系统的强弱将直接影响飞行器的速度和高度。
基于以上因素,可以建立飞行器动力学的数学模型。
根据牛顿第二定律,飞行器所受到的合力等于质量乘以加速度,即F=ma。
其中,F为合力,m为质量,a为加速度。
合力可以分解为横向力和纵向力。
横向力由于风向对飞行器横向飞行的影响而产生,其大小与飞行器的侧滑角和速度等因素有关。
纵向力由于飞行器前进时所受到的空气阻力和升力而产生,其大小与飞行器的速度、密度、机翼面积等因素有关。
二、飞行器动力学的分析方法1.离线仿真离线仿真是指在计算机上使用飞行器动力学的数学模型进行模拟。
这种方法的优势在于可以模拟不同场景下的飞行情况,如恶劣天气、机械故障等,从而推测出实际情况下飞行器的运动轨迹和各种指标。
离线仿真还可以对飞行器的设计进行优化和评估。
飞行器动力学特性的数值计算与分析

飞行器动力学特性的数值计算与分析随着科技的不断进步,飞行器在现代化社会中起着至关重要的作用。
飞行器的动力学特性是评估其性能和安全性的关键因素之一。
为了精确地预测飞行器的运行和飞行特性,数值计算与分析方法成为一种可靠的工具。
本文将探讨飞行器动力学特性的数值计算与分析方法。
首先,数值计算是通过将飞行器的运动问题转化为数学模型,利用计算机算法对其进行求解和预测。
数值方法分为两类:迭代法和递推法。
在迭代法中,通过重复应用某一计算公式,逐步逼近所需的解。
常见的数值迭代方法包括欧拉方法、龙格-库塔方法等。
在递推法中,问题的解由前一步的解通过某一递推关系获得。
递推法在求解动力学特性的初值问题中很常见。
数值计算方法的关键是建立准确的数学模型。
飞行器的动力学可以通过运动方程来描述。
运动方程是描述飞行器在不同时间和空间坐标上的动力学行为的方程。
对于刚体飞行器,通常使用牛顿力学的基本定律来描述其运动。
最常见的运动方程是牛顿第二定律:力等于质量乘以加速度。
通过将牛顿第二定律应用到飞行器的自由度上,可以建立动力学模型。
在数值计算中,通常采用数值积分来求解运动方程。
数值积分是将连续的运动方程离散化,将其转化为一系列离散的时间步骤上的代数方程。
最常见的数值积分方法是欧拉方法。
欧拉方法是一种基本的数值积分方法,通过将连续时间上的运动方程离散为离散的时间步长上的代数方程来求解。
除了数值计算方法外,分析方法也是研究飞行器动力学特性的重要手段。
分析方法是通过数学推导和分析来得到精确的解析解。
分析方法通常基于刚体动力学和控制理论,利用数学推导和物理原理来得到飞行器的运动特性。
分析方法的优点是准确性高,可以提供深入的理论洞察,但对于复杂的飞行器模型来说,分析方法的求解过程可能会非常复杂。
在实际应用中,数值计算和分析方法常常结合使用。
数值计算方法可以通过计算机模拟进行大规模的数值实验,获得详细的飞行器运行和运动特性数据。
分析方法则提供了对数值计算结果的解释和验证,从而确保数值计算的准确性和可信度。
《飞行控制系统》第二章 飞行器运动方程(1+2+3)

一、动力学方程
动力学方程——以动力学为基础, 描述力与力矩平衡关系的方程,亦即 为考虑在体轴系下运动参数与力、力 矩的方程。(由于体轴系为动坐标系, 所以建方程时既要考虑相对运动,又 要考虑绝对运动。
一、动力学方程式
动力学方程式是描述飞机所受力、力矩与飞机运 动参数间关系的方程,显然包括两组方程:
dLx dt
pI x
rIxz
dLy dt
qI y
dLz
dt
rIz
pIxz
i jk
L p q r i qLz rLy j rLx pLz k pLy qLx
Lx Ly Lz
(2)、角运动方程式
将合力矩沿机体坐标系分解
q c5 pr c6 ( p2 r2 ) c7M
r (c8 p c2r)q c4L c9 N
式中 ci 定义参见书P55
飞机动力学方程式
取机体座标系作为动座标系 力矩的平衡方程式:
L M
pI x qI r
rI xz pr(I x
qr(I z Iz)
Ir (p
)
2
pqI xz r 2 )I xz
N rI z pI xz pq(I r I x ) prI xz
力平衡方程式:
F
m
dv dt
Fx
Fy
Fz
X
Y
Z
(u wq vr)m (v ur wp)m (w vp up)m
绕 oz 轴转 得到 x1 y1z g
飞行器运动方程

& + ur − wp ) Y = m(v & + vp − uq ) Z = m( w
PDF 文件使用 "pdfFactory Pro" 试用版本创建
2.1.1动力学方程
v
角运动方程:
&Ix − r &I xz + qr ( I z − I y ) − pqI xz L=p &I y + pr ( I x − I z ) + ( p 2 − r 2 ) I xz M =q &I z − p & I xz + pq ( I y − I x ) + qrI xz N =r
PDF 文件使用 "pdfFactory Pro" 试用版本创建
2.1.1动力学方程(本教材)
v
v
在惯性坐标系中应用牛顿第二定律: dV = F m ∑ › 飞机在外合力作用下的线运动方程为: dt dL › 飞机在外合力矩作用下的角运动方程为: ∑ M = dt 选用机体坐标系作为动坐标系,将在地面坐标系中得到的运动速度V及动 量矩L向机体坐标轴系上分解,假设机体坐标系相对于惯性坐标系的速度 & + wq − vr ) 为V,角速度向量为Ω,则上式在动坐标系中表示为: X = m(u
V上的 单位向 量
速 度 标 量
i,J和k分别表示沿机体坐标轴系OX,OY,OZ的单位向量.
2.1.1动力学方程
~ ~ dV du 由此可得: =i + 1V dt dt i j Ω ×V = p q ~ ~ dυ dω & + kω & & + jυ j +k = iu dt dt k r
第一章-6 飞行动力学-飞机的横侧运动+飞机方程

注:上式中大导数与表 中大导数的表达式可能 不完全相同,建模时需 要自行推导验证
二、横侧向扰动运动与三种模态
纵向运动时的同一飞机,以M=0.9.高度h=11000m作定常平飞, 各参数及气动导数如下(对稳定轴系):
由表中表 达式计算: 扰动运动 控制输入为0:a=r=0
拉氏变换后得代数方程:
3、轴对称系统的传递函数特点
三通道交叉影响小 1)侧滑角=0, 只引起升力、俯仰力矩; 只引起侧力、偏航力矩 不引起滚转力矩 2) =0,也不引起滚转力矩 3)只有 0和0,且 时才会引起小量的滚转力矩 荷兰滚运动变成无滚转的振摆运动,与纵向短周期动态过程 相同,传递函数也相同 导弹以法向、侧向过载为控制目标
3.螺旋模态
当Cl较小而Cn较大时,易形成不稳定的螺旋模态。 若t=0有正的滚转角(>0),则升力L右倾斜与重力合力使飞机向右侧滑, 由于Cl小,则使角减小的负滚转力矩小,而Cn较大,使得偏航角速率r 正值大。交叉动导数Clr为正,产生较大的正滚转力矩。 当负滚转力矩小于正滚转力矩时,飞机更向右滚转.于是合力作用使飞机 更向右侧滑。 如此逐渐使角正向增大,升力的垂直分量Lcos则逐渐减小,轨迹向心 力Lsin则逐渐增大,致使形成盘旋 半径愈来愈小,高度不断下降的螺旋 线飞行轨迹,故称为螺旋模态。 螺旋模态的初期发散是很缓慢的 设计时要与荷兰滚模态配合, 为尽量增大荷兰滚模态的阻尼比, 宁可让螺旋模态有稍微的不稳定
P=Pp=Pr=0,经拉氏变换:
特征多项式: 代入数据, 全量系统的精确解:
一阶系统 解得: 误差为:
螺旋摸态的稳定条件:b4>0, 转为小导数:
三、横侧向运动的传递函数
飞机运动方程

co s co s u v (sin sin co s co s sin ) w (co s sin co s sin sin )
dH dt
1H
~ dH dt
H
这里: 1 V 为速度向量的单位向量; 为动坐标系相对惯性系的总的角速度向量,目前表示的是沿机体坐标系测量的角 速度向量; 表示矢量叉积运算符号; 1 H 为动量矩的单位向量; ~ ~ d V , H 表示对动坐标系的相对导数。 d
dt
dt
注意:这里研究的是速度在动坐标系的表示形式。
机体角速度在地面的投影
p sin q cos cos sin
r sin cos cos
p ( r cos q sin ) tan
q cos r sin
牵连运动的加速度合成定理其中分别是动系各轴上的单位矢量如果从动系中观察它们都表示矢量在动系中的导数称为相对矢导数导数符号记为如果从惯性坐标系观察都是变矢量当动系以角速度转动时利用泊桑公式有此为矢量在惯性坐标系中的导数称为绝对矢导数
飞机的六自由度运动方程
1. 牵连运动 2.动力学方程 3.运动学方程
牵连运动
V i u j v k w i ( w q vr ) j ( u r w p ) k ( vp u q )
F
作用在机体坐标系的合外力 根据
dV F m dt
表示为
01_飞机的一般运动方程

0 1 L qh 0 cos s 0 sin s
0 sin s cos s
coscos Ltq sin cos sin
sin cos 0
cos sin sin sin cos
2015/10/7 5
无人驾驶飞机:无人飞机和微型无人飞机
最大尺寸微型飞行器
英国的“Sender”无人机
微型飞行器和小尺寸无人机的尺寸对比
2015/10/7 6
“黑寡妇”微型飞机
“微星”微型飞机
2015/10/7
7
特殊航空器:微型扑翼和旋翼飞机
加州理工大学的“微型蝙蝠” 微型扑翼飞机
美国加州大学:扑翼机(翼展 200mm,总重11.5克,微型电 机驱动
10
三、飞机的主要组成部分及其功能
2015/10/7
11
机翼 :产生升力 ,机翼上一般有用于横向操 纵的副翼和扰流片;机翼前后缘部分还设有各 种形式的襟翼,增加升力 尾翼:水平尾翼和垂直尾翼;V型尾翼;水平尾 翼一般有水平安定面和升降舵组成;垂直尾翼 一般有垂直安定面和方向舵组成;超音速飞行 时通常采用全动水平尾翼(差动);鸭翼 机身:容纳人员、货物或其他载重和设备;要 求流线;飞翼式飞机取消机身。 起落架:起飞降落(机轮、滑撬、浮桶)
2015/10/7
17
半机体坐标系Oxbybzb :O在质心, Oxb沿飞 行速度矢量 V 在飞机对称平面投影方向, Oyb在对称平面内,垂直于Oxb向上(因而与 Oyq重合),Ozb垂直于飞机对称平面(与轴 Ozt重合)。
2015/10/7
18
2015/10/7
图2-2
19
航迹坐标系 Oxhyhzh : O 在质心, Oxh与 Oxq一 致,Oyh在包含飞行速度矢量V的铅垂面内, 指向上, Ozh 垂直于 Oxhyh(因而使水平的), 指向右。
飞行器质心运动方程

内容绪论1.1 作用在飞机上的外力1.3 常用坐标系及其转换1.4 飞机质心运动方程小结本章作业1.1;1.2;1.3;1.4;1.5;1.7;1.8;1.9绪论飞行动力学=飞行性能+飞行品质研究飞机的飞行性能和飞行轨迹特性时,可将飞机视为一可控的质点来处理。
可控:是指飞机的飞行轨迹是可以人为改变的,而轨迹的改变取决于作用于飞机上的外力的改变。
绪论质点运动:通过偏转操纵机构,使飞机的合力矩为零;研究飞机的飞行轨迹和飞行性能时可以把飞机视为质点运动。
力矩平衡作为运动的约束条件。
质点系运动:合力矩不为零。
研究飞机飞行品质时将其视为质点系运动。
1.1.1 升阻特性1.1.2 发动机推力TJ G 从飞行性能的角度,假设操纵面偏转可使力矩平衡,但将其最大平衡能力作为约束。
实际还常忽略操纵面偏转对力平衡的影响。
外力一般不通过质心,它将引起绕质心转动的力矩L J GD JG W JJ G T J G 'L J G 1.1作用在飞机上的外力1.1作用在飞机上的外力在常规飞行性能问题中,假设飞行无侧滑,视侧力为零升力系数阻力系数侧力系数2L L V SC ρ=2D D V SC ρ=2CC V S C ρ=升力和阻力系数主要取决于马赫数、雷诺数、迎角、侧滑角以及飞机的外形马赫数的物理含义?雷诺数的物理含义?迎角的定义?侧滑角的定义?9马赫数:指空气的压缩性效应;低速空气流场不相互影响,高速时则前后相互影响。
9雷诺数:指飞机的尺寸效应;即飞机的尺寸大小会影响飞机的气动特性,一般飞机在真实大气中飞行时,其雷诺数在1000万以上。
这就是研究飞机气动特性时,要建立大尺寸风洞和进行飞行试验研究的原因。
DO1. 升力特性(1)定义升力是飞机上的空气动力的合力在飞机纵向对称平面上垂直于飞行速度方向的分力。
向上为正。
飞机的最大的升力系数约1.2—1.5;采用增升装置后,飞机的最大的升力系数约2.2—3.0。
1. 升力特性0)L L L C αδαα−+升力线斜率,与翼型、机翼平面形状、M 数有关,即~M ,λ, χ零升迎角,取决于机翼有效弯度和M 数,即~M ,f升力部件有翼-身组合体和平尾。
飞机设计的基础:六自由度非线性运动方程的建立过程

飞机设计的基础:六自由度非线性运动方程的建立过程飞机飞行,涉及到力(力矩)平衡、静稳定和静操纵性等一系列的问题。
为了保证飞机的飞行安全和良好的飞行品质,还必须在静品质基础上研究飞机的动态特性。
可以说,飞机的各个系统设计都是围绕着飞机的飞行运动这一基本概念进行的,无论是总体设计、结构设计、气动设计、控制系统设计等等。
今天我们来简单介绍一下飞机运动方程建立的基本思路。
飞行中的歼-20从动力学观点来看,动态特性是研究飞机在外力或外力矩(外界扰动或飞行员操纵)作用下,各个运动参数随时间的变化规律,也就是求解飞机的运动方程,并在此基础上,对动态特性作进一步定量分析。
对于在三维空间运动的刚体飞机,具有6个自由度。
也就是说,如果要完整地描述飞机的运动,需要6个相互独立的微分方程组。
如果再加上空间位置和姿态,完整表征飞机的各个运动参数则需要15个微分方程。
对飞机运动进行受力分析可知,飞机运动要受到重力、发动机推力、空气动力以及三个轴向的滚转力矩作用。
这些力、力矩和运动参数的定义,不在同一坐标系下,因此求解时还需要经过坐标系转换变换到同一坐标系。
六自由度微分方程组加上复杂的坐标系变换,注定了飞机运动方程是复杂的。
飞行中的无人机不过,飞机运动方程能够真实地反映运动过程每一瞬间的情况,是对飞行性能、控制律设计以及运动仿真最基本的依据。
因此,有必要明白运动方程建立的基本方法和具体表现形式。
但是,现代控制理论主要是以传递函数和矩阵形式的状态方程作为分析对象进行研究和设计的。
因此,为了分析飞机稳定性、操纵性、控制律设计的方便,有必要研究建立飞机现行矩阵运动模型的方法。
垂直起降的F-35战机飞机的运动是一个复杂的动力学问题。
如果要全面考虑地球的曲率、燃油的消耗、武器的投射,飞机内部动力系统和操纵系统等机件的相对运动及飞机本身的弹性变形,外力使飞机外形、飞行姿态和运动参数变化等因素,会使飞机运动方程的推导变得极为复杂,并且很难进行解析处理。
飞机运动微分方程2

空气动力矢量A一般 定义在气动坐标系 Oxayaza内:
A = −D ia + C ja − L k a
空气动力A
xb
αβ
xa (阻力D) VC
气动坐标系xa轴沿飞 行速度矢VC方向, za 轴在飞机对称面内垂
直于飞行速度矢VC指 向下, ya轴垂直于
xaza面指向横侧。
对称面
ya (侧力C)
za(升力L)
⎪⎩ r ⎪⎭b
⎪⎩ψ ⎪⎭
⎪⎩0⎪⎭
⎪⎩0⎪⎭
⎪⎩−
Sφθ
+
Cφ
Cθψ
⎪ ⎭
2.2.8 从Euler角速度到机体轴系角速度分量间的变换
如果已知任意时刻机体坐标
系中速度、角速度投影分量 (u, v, w, p, q, r),对右式(2) 可直接积分(例如数值积分) 得到三个Euler角;进一步
Cθ Cψ
Cψ − Cφ
Sψ
⎢⎣Sθ CφCψ + Sφ Sψ
Cθ Sψ Sθ Sφ Sψ + CφCψ Sθ Cφ Sψ − SφCψ
− Sθ Sφ Cθ
⎤ ⎥ ⎥
CφCθ ⎥⎦
2.2.8 从Euler角速度到机体轴系角速度分量间的变换
问 如题变换能否直接通过如下类似于质心速度分量的变换实现?
题
问题封闭!
6个动力学方程,9个运动学变换方程
问题: 上述分析中,我们忽略了什么因素对飞机运动动力学的影响?
常规飞机飞行控制原理图
操纵稳定问题
驾驶杆(盘)
操纵 系统
升降舵偏角
飞机 刚体
α
飞
脚蹬
动力 副翼偏角 学 方向舵偏角
动力 γs 学β
飞行器运动方程

假定飞机有一个对称面xoz(机体坐标系),且飞 行器不仅几何外形对称,而且内部质量分布亦对 称,惯性积
I xy I zy O
;
忽略地面曲率,视地面为平面;
二、 六自由度飞机运动方程
1、飞机运动的自由度:(six-degrees-of freedom)
飞机在空间的运动有六个自由度,即质心沿地 面坐标系的三个移动自由度和绕机体坐标轴系 的三个转动自由度 。
x1 0 sin x1 1 0 y1 C y 1 z g 0 cos z g 得到 xyz 最后绕 ox 轴转
0 0 x x 1 x y 0 cos sin y C y 1 z z 0 sin cos z2
0 求 与 p,q,r 的关系。再将 加上可得: ,
0 0 cos 0 sin 0 p 1 q 0 cos sin 0 1 0 0 0 r 0 sin cos sin 0 cos
dV dV 1V V dt dt
dL dL 1H L dt dt
1、牵连运动
1V :沿 V 的单位向量;
:动坐标系对惯性系的总角速度向量;
1L :沿动量矩 L的单位向量; :表示叉乘 v 是牵连加速度。
dV dt
dV dt
和
dH dt
dH dt
:表示在动坐标系内的相对导数。
一、动力学方程式
动力学方程式是描述飞机所受力、力矩与飞机运 动参数间关系的方程,显然包括两组方程:
