一次函数与二次函数综合(题)
中考数学总复习《二次函数与一次函数的综合应用》练习题及答案
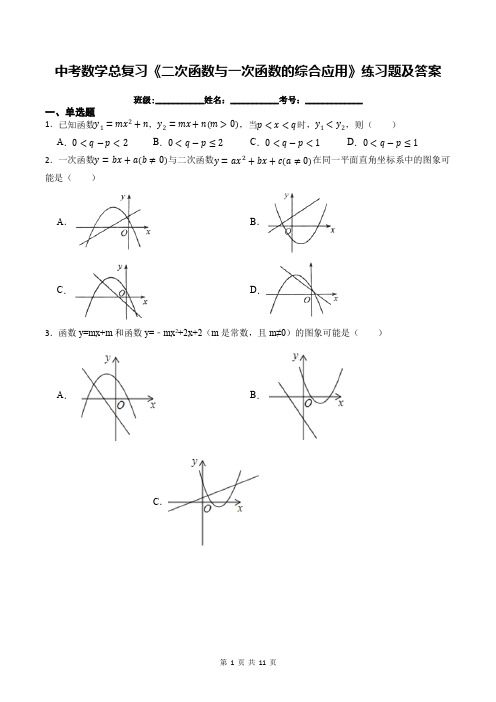
中考数学总复习《二次函数与一次函数的综合应用》练习题及答案班级:___________姓名:___________考号:_____________一、单选题1.已知函数y1=mx2+n,y2=mx+n(m>0),当p<x<q时,y1<y2,则()A.0<q−p<2B.0<q−p≤2C.0<q−p<1D.0<q−p≤12.一次函数y=bx+a(b≠0)与二次函数y=ax2+bx+c(a≠0)在同一平面直角坐标系中的图象可能是()A.B.C.D.3.函数y=mx+m和函数y=﹣mx2+2x+2(m是常数,且m≠0)的图象可能是()A.B.C.D.4.小飞研究二次函数y=-(x-m)2-m+1(m为常数)性质时如下结论:①这个函数图象的顶点始终在直线y=-x+1上;②存在一个m的值,使得函数图象的顶点与x轴的两个交点构成等腰直角三角形;③点A(x1,y1)与点B(x2,y2)在函数图象上,若x1<x2,x1+x2>2m,则y1<y2;④当-1<x<2时,y随x的增大而增大,则m的取值范围为m≥2其中错误结论的序号是()A.①B.②C.③D.④5.将二次函数y=x2﹣5x﹣6在x轴上方的图象沿x轴翻折到x轴下方,图象的其余部分不变,得到一个新图象,若直线y=2x+b与这个新图象有3个公共点,则b的值为()A.﹣734或﹣12B.﹣734或2C.﹣12或2D.﹣694或﹣126.如图,函数y1=|x2﹣m|的图象如图,坐标系中一次函数y2=x+b的图象记为y2,则以下说法中:①当m=1,且y1与y2恰好有三个交点时b有唯一值为1;②当m=4,且y1与y2只有两个交点时,b>174或﹣2<b<2;③当m=﹣b时,y1与y2一定有交点:④当m=b时,y1与y2至少有2个交点,且其中一个为(0,m).正确的有()A.1个B.2个C.3个D.4个7.直线y=ax﹣6与抛物线y=x2﹣4x+3只有一个交点,则a的值为()A.a=2B.a=10C.a=2或a=﹣10D.a=2或a=108.已知一次函数y1=2x−2,二次函数y2=x2,对于x的同一个值,这两个函数所对应的函数值分别为y1和y2,则下列表述正确的是()A.y1>y2B.y1<y2C.y1=y2D.y1,y2的大小关系不确定9.已知一次函数y1=kx+m(k≠0)和二次函数y2=ax2+bx+c(a≠0)部分自变量和对应的函数值如表:x…-10245…y1…01356…y2…0-1059…21A.-1<x<2B.4<x<5C.x<-1或x>5D.x<-1或x>410.对于每个x,函数y是y1=-x+6,y2=-2x2+4x+6这两个函数的较小值,则函数y的最大值是()A.3B.4C.5D.611.如图是王阿姨晚饭后步行的路程s(单位:m)与时间t(单位:min)的函数图象,其中曲线段AB是以B为顶点的抛物线一部分.下列说法不正确的是()A.25min~50min,王阿姨步行的路程为800mB.线段CD的函数解析式为s=32t+400(25≤t≤50)C.5min~20min,王阿姨步行速度由慢到快D.曲线段AB的函数解析式为s=-3(t-20)2+1200(5≤t≤20)12.如图,平面直角坐标系中,点M是直线y=2与x轴之间的一个动点,且点M是抛物线y= 12x2+bx+c的顶点,则抛物线y= 12x2+bx+c与直线y=1交点的个数是()A.0个或1个B.0个或2个C.1个或2个D.0个、1个或2个二、填空题13.抛物线y=2x2+x+a与直线y=−x+3没有交点,则a的取值范围是.14.如图,已知抛物线y1=−2x2+2,直线y2=2x+2,当x任取一值时,x对应的函数值分别为y1,y2,若y1≠y2,取y1,y2中的较小值记为M;若y1=y2,记M=y1=y2,例如:当x=1时,y1=0,y2=4,y1<y2,此时M=0,下列判断:①当x<0时,y1>y2;②当x<0时,x值越大,M值越小;③使得M大于2的x值不存在;④使得M=1的x值是−12或√22.其中正确的是.15.如图,已知直线y=﹣34x+3分别交x轴、y轴于点A、B,P是抛物线y=﹣12x2+2x+5的一个动点,其横坐标为a,过点P且平行于y轴的直线交直线y=﹣34x+3于点Q,则当PQ=BQ时,a的值是.16.已知一次函数y1=kx+m(k≠0)和二次函数y2=ax2+bx+c(a≠0)部分自变量和对应的函数值如表:x…﹣10245…y1…01356…y2…0﹣1059…21的取值范围是.17.如图,在平面直角坐标系中,O为坐标原点,点C为y轴正半轴上的一个动点,过点C的直线与二次函数y=x2的图象交于A、B两点,且CB=3AC,P为CB的中点,设点P的坐标为P(x,y)(x>0),写出y关于x的函数表达式为:.18.直线y=x+2与抛物线y=x2的交点坐标是.三、综合题19.随着互联网的普及,某手机厂商采用先网络预定,然后根据订单量生产手机的方式销售,2015年该厂商将推出一款新手机,根据相关统计数据预测,定价为2200元,日预订量为20000台,若定价每减少100元,则日预订量增加10000台.(1)设定价减少x元,预订量为y台,写出y与x的函数关系式;(2)若每台手机的成本是1200元,求所获的利润w(元)与x(元)的函数关系式,并说明当定价为多少时所获利润最大;(3)若手机加工成每天最多加工50000台,且每批手机会有5%的故障率,通过计算说明每天最多接受的预订量为多少?按最大量接受预订时,每台售价多少元?20.在平面直角坐标系xOy中,抛物线y=ax2+bx+2过B(﹣2,6),C(2,2)两点.(1)试求抛物线的解析式;(2)记抛物线顶点为D,求△BCD的面积;(3)若直线y=﹣12x向上平移b个单位所得的直线与抛物线段BDC(包括端点B、C)部分有两个交点,求b的取值范围.21.如图,已知抛物线 y =−12x 2+bx +c 经过A (2,0)、B (0,-6)两点,其对称轴与轴交于点C(1)求该抛物线和直线BC 的解析式;(2)设抛物线与直线BC 相交于点D ,连结AB 、AD ,求△ABD 的面积.22.某企业研发了一种新产品,已知这种产品的成本为30元/件,且年销售量 y (万件)与售价 x (元/件)的函数关系式为 y ={−2x +140,(40≤x <60)−x +80.(60≤x ≤70)(1)当售价为60元/件时,年销售量为 万件;(2)当售价为多少时,销售该产品的年利润最大?最大利润是多少? (3)若销售该产品的年利润不少于750万元,直接写出 x 的取值范围.23.抛物线y =ax 2与直线y =2x -3交于点A(1,b).(1)求a ,b 的值;(2)求抛物线y =ax 2与直线y =-2的两个交点B ,C 的坐标(B 点在C 点右侧); (3)求△OBC 的面积.24.如图,平面直角坐标系中,抛物线 y =ax 2+bx +c 经过 A(−1,0) , B(3,0) 两点,与 y 轴交于点 C(0,−3) ,点 D 是抛物线的顶点.(1)求抛物线的解析式;(2)设P(m,n)为对称轴上一点,若∠PCD为钝角,求n的取值范围.参考答案1.【答案】D 2.【答案】C 3.【答案】D 4.【答案】C 5.【答案】A 6.【答案】B 7.【答案】C 8.【答案】B 9.【答案】D 10.【答案】D 11.【答案】C 12.【答案】D 13.【答案】a >3.5 14.【答案】③④15.【答案】﹣1,4,4+2 √5 ,4﹣2 √5 16.【答案】x <﹣1或x >4 17.【答案】y =83x 218.【答案】(-1,1)和(2,4)19.【答案】(1)解:根据题意:y =20000+ x 100 ×10000=100x+20000(2)解:设所获的利润w (元) 则W =(2200﹣1200﹣x )(100x+20000) =﹣100(x ﹣400)2+36000000;所以当降价400元,即定价为2200﹣400=1800元时,所获利润最大 (3)解:根据题意每天最多接受50000(1﹣0.05)=47500台 此时47500=100x+20000 解得:x =275.所以最大量接受预订时,每台定价2200﹣275=1925元.20.【答案】(1)解:由题意 {4a −2b +2=64b +2b +2=2 解得 {a =12b =−1∴抛物线解析式为y= 12x 2﹣x+2.(2)解:∵y= 12 x 2﹣x+2= 12 (x ﹣1)2+ 32.∴顶点坐标(1,3 2)∵直线BC为y=﹣x+4,∴对称轴与BC的交点H(1,3)∴S△BDC=S△BDH+S△DHC= 12×32•3+ 12×32•1=3.(3)解:由{y=−12x+by=12x2−x+2消去y得到x2﹣x+4﹣2b=0当△=0时,直线与抛物线相切,1﹣4(4﹣2b)=0∴b= 15 8当直线y=﹣12x+b经过点C时,b=3当直线y=﹣12x+b经过点B时,b=5∵直线y=﹣12x向上平移b个单位所得的直线与抛物线段BDC(包括端点B、C)部分有两个交点∴158<b≤3.21.【答案】(1)解:将A(2,0)、B(0,-6)代入y=−12x2+bx+c中可得{−12×22+2b+c=0c=−6解得:b=4;c=-6∴该抛物线的解析式为y=−12x2+4x−6∴抛物线对称轴为x=−42×(−12)=4∴C(4,0)设直线BC的解析式为y=kx+b(k≠0)将B(0,-6),C(4,0)代入得解得:k=32,b=−6∴直线BC 的解析式为 y =32x −6(2)解:连立方程组可得 {y =32x −6y =−12x 2+4x −6解得 {x =5y =32∴D(5, 32)∴△ABD 的面积为 12×2×(23+6)=15222.【答案】(1)20(2)解:设销售该产品的年利润为 W 万元当 40≤x <60 时, W =(x −30)(−2x +140)=−2(x −50)2+800 . ∵-2<0 ∴当 x =50 时 当 60≤x ≤70 时 ∵−1<0 ∴当 x =60 时 ∵800>600 ∴当 x =50 时∴当售价为50元/件时,年销售利润最大,最大为800万元. (3)解: 45≤x ≤55 理由如下:由题意得(x −30)(−2x +140)≥750解得 45≤x ≤5523.【答案】(1)解:∵点 A(1,b) 在直线 y =2x −3 上∴b =−1∴点 A 坐标 (1,−1)把点 A(1,−1) 代入 y =ax 2 得到 a =−1∴a =b =−1.(2)解:由 {y =−x 2y =−2 解得 {x =√2y =−2 或 {x =−√2y =−2 ∴点 C 坐标 (−√2,−2), 点 B 坐标 (√2,−2). (3)解: S △BOC =12×2√2×2=2√2.24.【答案】(1)解:由已知,设 y =a(x +1)(x −3)把C(0,−3)代入,得−3a=−3∴y=(x+1)(x−3)即y=x2−2x−3.(2)解:由y=x2−2x−3,得y=(x−1)2−4∴顶点D(1,−4).过点D作DH⊥y轴于点H,连结BC交对称轴于点E,连结DC.∵B(3,0),C(0,−3)∴OB=OC=3∴∠BCO=∠DCH=45°∴∠DCE=90°设BC函数表达式为y=kx+b把B(3,0),C(0,−3)两点代入y=kx+b得{k=1b=−3即BC函数表达式为y=x−3∵点E在对称轴上∴点E横坐标为1,代入y=x−3得E(1,−2)由∠PCD为钝角,则点P在点E上方即n>−2.第11页共11页。
二次函数与一次函数的综合题

二次函数与一次函数图像相交的点为方程组的解
相交点的个数取决于方程组的解的个数
垂直关系
二次函数与一次函数的图像垂直关系可以通过求导数的方法来判断。如果两个函数的导数相等,则它们的图像平行;如果一个函数的导数为0,另一个函数的导数不为0,则它们的图像垂直。
二次函数与一次函数的图像垂直关系可以通过代入法来判断。将一次函数的解析式代入二次函数的解析式中,得到一个关于x的二次方程,如果该二次方程的判别式Δ=0,则说明两个函数的图像垂直。
奇偶性的判断方法
代数法:通过代入特殊值或化简函数表达式来判断函数的奇偶性
性质法:利用奇偶函数的性质来判断函数的奇偶性
定义法:根据奇偶性的定义来判断函数的奇偶性
图像法:通过观察函数的图像来判断函数的奇偶性
奇偶性的应用
利用奇偶性判断函数图像的对称性
利用奇偶性简化函数表达式
利用奇偶性求解函数值域
利用奇偶性分析函数的单调性
定义法:利用函数单调性的定义,通过比较自变量取值范围内任意两点处的函数值大小来证明函数的单调性。
导数法:利用导数与函数单调性的关系,通过判断导数的正负来证明函数的单调性。
图像法:利用函数图像的走势来判断函数的单调性,通过观察图像在自变量取值范围内的变化趋势来证明函数的单调性。
05
二次函数与一次函数的奇偶性
相切关系
在切点处,二次函数的导数等于一次函数的斜率,即切线的斜率。
二次函数与一次函数相切时,它们的图像在切点处相切,切线的斜率等于一次函数的斜率。
二次函数与一次函数相切的条件是二次函数的导数等于一次函数的斜率。
当二次函数与一次函数相切时,它们的交点只有一个,即切点。
相交关系
2023年中考苏科版数学一轮复习专题提优练习-一次函数和二次函数综合

2023年中考数学一轮复习专题提优练习一次函数和二次函数综合一、选择题1.二次函数y 1=ax 2+bx +c 与一次函数y 2=mx +n 的图象如图所示,则满足ax 2+bx +c >mx +n 的x 的取值范围是( )A .﹣3<x <0B .x <﹣3或x >0C .x <﹣3D .0<x <3第1题 第2题2.如图,直线y =kx +b 与直线y =mx 相交于点A (﹣1,2),与x 轴相交于点B (﹣3,0),则关于x 的不等式组0<kx +b <mx 的解集为( )A .x >﹣3B .﹣3<x <﹣1C .﹣1<x <0D .﹣3<x <03.已知二次函数y=-(x -h)2(h 为常数),当自变量x 的值满足2≤x≤5时,与其对应的函数值y 的最大值为-1,则h 的值为( )A .3或6B .1或6C .1或3D .4或64.用列表法画二次函数y=x 2+bx+c 的图象时先列一个表,当表中自变量x 的值以相等间隔增加时,函数y 所对应的值依次为:20, 56, 110, 182, 274, 380, 506, 650. 其中有一个值不正确,这个不正确的值是( )A .505B .380C .274D .1825.若平面直角坐标系内的点M 满足横、纵坐标都为整数,则把点M 叫作“整点”. 例如:P (1,0),Q (2,-2)都是“整点”. 抛物线y=mx 2-4mx+4m -2(m>0)与x 轴的交点为A ,B ,若抛物线在点A ,B 之间的部分与线段AB 所围成的区域(包含边界)恰有7个“整点”,则m 的取值范围是( )A .121<≤m B .121≤<m C .1<m ≤2 D .1≤m<26.四位同学在研究函数y=x 2+bx+c (b, c 是常数)时,甲发现当x=1时,函数有最小值;乙发现-1是方程x 2+bx+c=0的一个根;丙发现函数的最小值为3;丁发现当x=2时,y=4. 已知这四位同学中只有一位发现的结论是错误的,则该同学是( )A .甲B .乙C .丙D .丁7.根据关于x 的一元二次方程x 2+px +q =0,可列表如下:则方程x 2+px +q =0的正数解满足( )x 0 0.5 1 1.1 1.2 1.3 x 2+px +q﹣15﹣8.75﹣2﹣0.590.842.29A .解的整数部分是0,十分位是5B .解的整数部分是0,十分位是8C .解的整数部分是1,十分位是1D .解的整数部分是1,十分位是28. 已知二次函数c bx x y ++=2中,函数y 与自变量x 之间的部分对应值如下表所示:X … 0 1 2 3 … y…5212…点A (x 1,y 1),B (x 2,y 2)在函数图象上,则当0<x 1<1,2<x 2<3时,y 1与y 2的大小关系正确性是( )A .y 1≥y 2B .y 1>y 2C .y 1<y 2D .y 1≤y 2二、填空题9.已知二次函数y =ax 2+bx +c (a ≠0)的顶点坐标(﹣1,﹣3.2)及部分图象(如图),由图象可知关于x 的方程ax 2+bx +c =0的两个根分别是x 1=1.3和x 2= .10.如图,在抛物线y 1=ax 2(a >0)和和y 2=mx 2+nx (m <0)中,抛物线y 2的顶点在抛物线y 1上,且与x 轴的交点分别为(0,0)(4,0),则不等式(a ﹣m )x 2﹣nx <0的解集是 .第9题 第10题 第11题 第12题11.如图,二次函数y 1=ax 2+bx +c 与一次函数y 2=kx 的图象交于点A 和原点O ,点A 的横坐标为﹣4,点A 和点B 关于抛物线的对称轴对称,点B 的横坐标为1,则满足0<y 1<y 2的x 的取值范围是 .12. 如图是抛物线y=c bx ax ++2(0≠a )的一部分,其对称轴为直线x=2,若其与x 轴的一个交点为B (5,0),则由图像可知,不等式02>++c bx ax 的解集是________. 13. 如图,抛物线y =ax 2与直线y =bx +c 的两个交点坐标分别为A (﹣2,4),B (1,1),则方程ax 2=bx +c 的解是__________________.第13题 第14题14.已知点A (﹣2,0),点P 是直线y =x 上的一个动点,当以A ,O ,P 为顶点的三角形面积是3时,点P 的坐标为 .15. 对于二次函数322-==mx x y ,有下列说法:①它的图像与x 轴有两个公共点;②如果当x≤1时,y 随x 的增大而减小,则m=1;③如果将它的图象向左平移3个单位后过原点,则m=-1;④如果当x=4时的函数值与x=2008时的函数值相等,则当x=2012时的函数值为-3. 其中正确的说法是___________(把你认为正确说法的序号都填上). 三、解答题16.如图,二次函数y =ax 2+bx +c 的图象与x 轴交于A ,B 两点,其中点A (﹣1,0),点C (0,5),点D (1,8)都在抛物线上,M 为抛物线的顶点.(1)求抛物线的函数解析式; (2)求△MCB 的面积;(3)根据图形直接写出使一次函数值大于二次函数值的x 的取值范围.17.如图①,将抛物线y =ax 2(﹣1<a <0)平移到顶点恰好落在直线y =x ﹣3上,并设此时抛物线顶点的横坐标为m .(1)求抛物线的解析式(用含a 、m 的代数式表示)(2)如图②,Rt △ABC 与抛物线交于A 、D 、C 三点,∠B =90°,AB ∥x 轴,AD =2,BD :BC =1:2.①求△ADC 的面积(用含a 的代数式表示)②若△ADC 的面积为1,当2m ﹣1≤x ≤2m +1时,y 的最大值为﹣3,求m 的值.18.如图1,平面直角坐标系xOy 中,已知抛物线y =ax 2+4x 与x 轴交于O 、A 两点.直线y =kx +m 经过抛物线的顶点B 及另一点D (D 与A 不重合),交y 轴于点C .(1)当OA =4,OC =3时.①分别求该抛物线与直线BC 相应的函数表达式;②连结AC ,分别求出tan ∠CAO 、tan ∠BAC 的值,并说明∠CAO 与∠BAC 的大小关系; (2)如图2,过点D 作DE ⊥x 轴于点E ,连接CE .当a 为任意负数时,试探究AB 与CE 的位置关系?19.如图,在平面直角坐标系xOy 中,已知二次函数y =ax 2+bx +c (a ≠0)的图象与x 轴交于A ,B 两点(点A 在点B 的左边),与y 轴交于点C ,其顶点的横坐标为1,且过点(2,3)和(﹣3,﹣12).(1)求此二次函数的表达式;(2)若点P 是位于该二次函数对称轴右边图象上不与顶点重合的任意一点,若锐角∠PCO =∠ACO ,写出此时点P 的坐标;(3)若直线l :y =kx (k ≠0)与线段BC 交于点D (不与点B ,C 重合),则是否存在这样的直线l ,使得以B ,O ,D 为顶点的三角形与△BAC 相似?若存在,求出该直线的函数表达式及点D 的坐标;若不存在,请说明理由.20. 如图,抛物线y=ax ax 22(a<0)位于x 轴上方的图象记为F 1,它与x 轴交于P 1,O 两点,图象F 2与F 1关于原点O 对称,F 2与x 轴的另一个交点为P 2,将F 1与F 2同时沿x 轴向右平移P 1P 2的长度即可得F 5与F 6;……;按这样的方式一直平移下去即可得到一系列图象F 1,F 2,…,F n ,我们把这组图象称为“波浪抛物线”.(1)当a=-1时, ①求图象F 1的顶点坐标.②点H (2014,-3)________(填“在”或“不在”)该“波浪抛物线”上;若图象F n 的顶点T n 的横坐标为201,则图象F n 对应的解析式为__________,其自变量x 的取值范围为_________.(2)设图象F m ,F m+1的顶点分别为T m ,T m+1(m 为正整数),x 轴上一点Q 的坐标为(12,0).试探究:当a 为何值时,以O ,T m ,T m+1,Q 四点为顶点的四边形为矩形?并直接写出此时m 的值.21. 设二次函数)(2b a bx ax y +-+=(a ,b 是常数,a≠0).(1)判断该二次函数图象与x 轴的交点的个数,说明理由.(2)若该二次函数图象经过A (-1,4),B (0,-1),C (1,1)三个点中的其中两个点,求该二次函数的表达式.(3)若a+b<0,点P (2,m )(m>0)在该二次函数图象上,求证:a>0.22. 如图所示,已知二次函数c bx x y ++-=2的图像经过点C (0,3),与x 轴分别交于点A.点B (3,0).点D (n, y 1).E (n+t ,y 2).F (n+4,y 3)都在这个二次函数的图像上,其中0<t<4,连接DE.DF.EF ,记ΔDEF 的面积为S.(1)求二次函数c bx x y ++-=2的表达式; (2)若n=0,求S 的最大值,并求此时t 的值;(3)若t=2,当n 取不同数值时,S 的值是否变化?如不变,求该定值;如变化,试用含n 的代数式表示S.23.如图,Rt△OAB如图所示放置在平面直角坐标系中,直角边OA与x轴重合,∠OAB=90°,OA=4,AB=2,把Rt△OAB绕点O逆时针旋转90°,点B旋转到点C的位置,一条抛物线正好经过点O,C,A三点.(1)求该抛物线的解析式;(2)在x轴上方的抛物线上有一动点P,过点P作x轴的平行线交抛物线于点M,分别过点P,点M作x轴的垂线,交x轴于E,F两点,问:四边形PEFM的周长是否有最大值?如果有,请求出最值,并写出解答过程;如果没有,请说明理由.(3)如果x轴上有一动点H,在抛物线上是否存在点N,使O(原点).C.H.N四点构成以OC为一边的平行四边形?若存在,求出N点的坐标;若不存在,请说明理由.。
一次函数、反比例函数、二次函数综合题

一次函数、反比例函数、二次函数的综合题一、选择题1.(09莆田)如图1,在矩形MNPQ 中,动点R 从点N 出发, 沿N →P →Q →M 方向运动至点M 处停止.设点R 运动的路程为x ,MNR △的面积为y ,如果y 关于x 的函数图象如图2 所示,则当9x =时,点R 应运动到( ) A .N 处B .P 处C .Q 处D .M 处2.(09遂宁)已知整数x 满足-5≤x≤5,y 1=x+1,y 2=-2x+4对任意一个x ,m 都取y 1,y 2中的较小值,则m 的最大值是 ( )A.1B.2C.24D.-93.3.(09凉山)若0ab <,则正比例函数y ax =与反比例函数by x=在同一坐标系中的大致图象可能是( )4.(06威海)如图,过原点的一条直线与反比例函数y =kx(k<0)的图像分别交于A 、B 两点,若A 点的坐标为(a ,b ),则B 点的坐标为( ) A .(a ,b ) B .(b ,a ) C .(-b ,-a ) D .(-a ,-b )5.下列图中阴影部分的面积与算式122)21(|43|-++-的结果相同的是( )6. 已知一次函数y=kx+b 的图象如图所示,则k ,b 的符号是( )(A) k>0,b>0 (B) k>0,b<0 (C) k<0,b>0 (D) k<0,b<07. 函数y=(m+1)x-(4m-3)的图象在第一、二、四象限,那么m 的取值范围是( )(图1)xxxxB .8. 下图中表示一次函数y =mx+n 与正比例函数y =m nx(m ,n 是常数,且mn<0)图像的是( ).9. 一次函数y =ax +1与y =bx -2的图象交于x 轴上一点,那么a :b 等于A.21B.21-C.23D.以上答案都不对二、填空题10.直线y kx b =+经过(21)A ,,(12)B --,两点,则不等式122x kx b >+>-的解集为 . 11. 反比例函数x k y =的图像经过A (-23,5)点、B (a ,-3),则k = ,a = .12.(06旅顺)如图是一次函数y 1=kx +b 和反比例函数y 2==mx的图象,•观察图象写出y 1>y 2时,x 的取值范围是_________.14. 已知∆ABC 中,BC=8,BC 上的高h =4,D 为BC 上一点,EF BC //,交AB 于点E ,交AC 于点F (EF 不过A 、B ),设E 到BC 的距离为x ,则∆DEF 的面积y 关于x 的函数__________________15. 若函数y= -2x m+2是正比例函数,则m 的值是 。
中考数学专题专练--二次函数与一次函数的综合

中考数学专题专练--二次函数与一次函数的综合1.如图,二次函数y=- 34x2+94x+3的图象与x轴交于点A、B(B在A右侧),与y轴交于点C.(1)求点A、B、C的坐标;(2)求△ABC的面积.2.如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣1,且抛物线经过A (1,0),C(0,3)两点,与x轴相交于点B.(1)求抛物线的解析式;(2)在抛物线的对称轴x=﹣1上找一点M,使点M到点A的距离与到点C的距离之和最小,求出点M的坐标;(3)设点P为抛物线的对称轴x=﹣1上的一个动点,求使△BPC为直角三角形的点P的坐标.3.如图,抛物线y=x2 +bx+c与x轴交于A(﹣1,0),B(2,0)两点.(1)求该抛物线的解析式;(2)设(1)中的抛物线上有一个动点P,当点P在该抛物线上滑动到什么位置时,满足S△P AB=6,并求出此时P点的坐标.4.如图,抛物线y1=a(x-1)2+4与x轴交于A(-1,0)。
(1)求该抛物线所表示的二次函数的表达式;(2)一次函数y2=x+1的图象与抛物线相交于A,C两点,过点C作CB垂直于x 轴于点B,求△ABC的面积。
5.如图,已知直线y=-3x+3与x轴交于点A,与y轴交于点C,抛物线y=ax2+bx+c经过点A和点C,对称轴为直线I:x=-1,该抛物线与x轴的另一个交点为B。
(1)求此抛物线的解析式;(2)点P在抛物线上且位于第二象限,求△PBC的面积最大值及点P的坐标。
(3)点M在此抛物线上,点N在对称轴上,以B、C、M、N为顶点的四边形能否为平行四边形?若能,写出所有满足要求的点M 的坐标;若不能,请说明理由。
6.如图,直线y=-x+2与抛物线y=ax 2交于A ,B 两点,点A 坐标为(1,1)。
(1)水抛物线的函数表达式:(2)连结OA ,OB ,求△AOB 的面积。
7.已知抛物线y=ax 2+bx+c 的顶点P(1,-1),且过Q(5,3)。
一次函数与二次函数的综合应用题

一次函数与二次函数的综合应用题一、引言在数学中,一次函数和二次函数是我们经常遇到的两种函数类型。
一次函数以y = ax + b的形式呈现,其中a和b是常数,而x是自变量。
二次函数则以y = ax^2 + bx + c的形式表达,其中a、b和c都是常数,而x依然是自变量。
本文将基于一次函数和二次函数,介绍它们在实际问题中的综合应用。
二、一次函数的综合应用1. 直线的运动一次函数可以应用于描述直线的运动情况。
假设有一个小车匀速地沿直线前进,设x表示时间(单位:秒),y表示小车距离起点的距离(单位:米),小车的速度为v(单位:米/秒)。
则可以建立起以下一次函数表示小车的位置:y = vx通过该函数,我们可以轻松计算在不同时间点小车的位置,并预测未来的移动情况。
2. 商品价格和销量的关系一次函数还可以应用于描述商品价格和销量之间的关系。
假设某商品的售价为p(单位:元),销量为s(单位:件),根据市场调研,得到以下一次函数表达式:s = -ap + b通过该函数,我们可以研究价格对销量的影响,并进行销售策略的调整。
三、二次函数的综合应用1. 抛体运动二次函数常用于描述抛体在空中的轨迹。
假设有一个物体以初速度v0竖直向上抛出,设x表示时间(单位:秒),y表示物体的高度(单位:米),加速度为g(单位:米/秒^2)。
则可以建立起以下二次函数表示物体的高度:y = -0.5gt^2 + v0t通过该函数,可以计算物体在不同时间点的高度,并分析物体的抛体运动规律。
2. 二次方程的解析二次函数也可以用于解决实际问题中的二次方程。
一个经典的例子是求解一个矩形地块的最大面积。
假设矩形地块的长度为x米,宽度为y米,已知周长为p米。
可以建立以下方程:2x + 2y = p根据周长的限制条件,我们可以得出以下表达式:x = (p-2y)/2,进而得到矩形地块的面积表达式:A = xy = (p-2y)y通过求解该二次函数的极值,即可得到矩形地块的最大面积。
综合题:一次函数二次函数反比例函数中考综合题复习

第一部分:一次函数考点归纳:一次函数:若y=kx+b(k,b 是常数,k ≠0),那么y 叫做x 的一次函数,特别的,当b=0时,一次函数就成为y=kx(k 是常数,k ≠0),这时,y 叫做x 的正比例函数,当k=0时,一次函数就成为若y=b ,这时,y 叫做常函数。
☆A 与B 成正比例 A=kB(k ≠0)直线位置与k ,b 的关系:(1)k >0直线向上的方向与x 轴的正方向所形成的夹角为锐角; (2)k <0直线向上的方向与x 轴的正方向所形成的夹角为钝角; (3)b >0直线与y 轴交点在x 轴的上方; (4)b =0直线过原点;(5)b <0直线与y 轴交点在x 轴的下方;平移1,直线x y 31=向上平移1个单位,再向右平移1个单位得到直线 。
2, 直线143+-=x y 向下平移2个单位,再向左平移1个单位得到直线________方法:直线y=kx+b ,平移不改变斜率k ,则将平移后的点代入解析式求出b 即可。
直线y=kx+b 向左平移2向上平移3 <=> y=k(x+2)+b+3;(“左加右减,上加下减”)。
练习:直线m:y=2x+2是直线n 向右平移2个单位再向下平移5个单位得到的,而(2a,7)在直线n 上,则a=____________;函数图形的性质例题:1.下列函数中,y 是x 的正比例函数的是( )A.y=2x-1 B.y=3xC.y=2x2 D.y=-2x+12,一次函数y=-5x+3的图象经过的象限是()A.一、二、三 B.二、三、四C.一、二、四 D.一、三、四3,若函数y=(2m+1)x2+(1-2m)x(m为常数)是正比例函数,则m的值为()A.m>12B.m=12C.m<12D.m=-124、直线y kx b=+经过一、二、四象限,则直线y bx k=-的图象只能是图4中的()5,若一次函数y=(3-k)x-k的图象经过第二、三、四象限,则k的取值范围是()A.k>3 B.0<k≤3 C.0≤k<3 D.0<k<36,已知一次函数的图象与直线y=-x+1平行,且过点(8,2),那么此一次函数的解析式为()A.y=-x-2 B.y=-x-6 C.y=-x+10 D.y=-x-17,已知关于x的一次函数27y mx m=+-在15x-≤≤上的函数值总是正数,则m的取值范围是()A.7m>B.1m>C.17m≤≤D.都不对8、如图,两直线1y kx b=+和2y bx k=+在同一坐标系内图象的位置可能是()9,一次函数y=ax+b与y=ax+c(a>0)在同一坐标系中的图象可能是()xyo xyoxyoxyoA B C D10,,已知一次函数(1)当m 取何值时,y 随x 的增大而减小? (2)当m 取何值时,函数的图象过原点?函数解析式的求法:正比例函数设解析式为: ,一个点的坐标带入求k. 一次函数设解析式为: ;两点带入求k,b1,已知一个正比例函数与一个一次函数的图象交于点A (3,4),且OA=OB(1) 求两个函数的解析式;(2)求△AOB 的面积;第二部分:二次函数(待讲)课前小测:1,抛物线3)2x (y 2-+=的对称轴是( )。
人教版数学九年级上学期课时练习-二次函数与一次函数综合(基础篇)(人教版)

专题22.19 二次函数与一次函数综合专题(基础篇)(专项练习)一、单选题1.已知函数y=2x与y=x2﹣c(c为常数,﹣1≤x≤2)的图象有且仅有一个公共点,则常数c的值为()A.0<c≤3或c=﹣1B.﹣l≤c<0或c=3C.﹣1≤c≤3D.﹣1<c≤3且c≠02.函数y=kx﹣k与y=kx2的图象大致是()A.B.C.D.3.在同一直角坐标系中,a≠0,函数y=ax与y=ax2的图象可能正确的有()A.0B.1C.2D.34.二次函数y=ax2+bx+c的图象如图所示,则一次函数y=bx+ac的图象不经过()A.第一象限B.第二象限C.第三象限D.第四象限5.已知一次函数y=bax+c的图象如图,则二次函数y=ax2+bx+c在平面直角坐标系中的图象可能是()A .B .C .D .6.如图,二次函数y =ax 2+bx 的图象开口向下,且经过第三象限的点P .若点P 的横坐标为﹣1,则一次函数y =(a ﹣b )x +b 的图象大致是( )A .B .C .D .7.已知二次函数2(0)y ax bx c a =++≠的图象如图所示,对称轴为12x =-,下列结论中,正确的是( )A .abc >0B .a +b =0C .b +c >aD .a +c <b8.已知,在同一平面直角坐标系中,二次函数2y ax =与一次函数y bx c =+的图象如图所示,则二次函数2y ax bx c =++的图象可能是( )A .B .C .D .9.如图,一次函数1y x =与二次函数22y x bx c =++的图像相交于P 、Q 两点,则函数()21y x b x c =+-+的图像可能是( )A .B .C .D .10.二次函数2441y ax bx =++与一次函数y =2ax +b 在同一平面直角坐标系中的图象可能是( )A .B .C .D .11.二次函数y =a (x ﹣2)2+c 与一次函数y =cx +a 在同一坐标系中的大致图象是( )A .B .C .D .12.已知在同一直角坐标系中,二次函数2y ax bx =-和反比例函数cy x=的图象如图所示,则一次函数y acx b =+的图象可能是( )A .B .C .D .13.在平面直角坐标系xOy 中,对于点(,)P a b ,若0ab >,则称点P 为“同号点”,下列函数的图象上不存在“同号点”的是( )A .23y x =-+B .22y x x =-C .5y x=-D .21y x x=+14.已知直线y ax b =+经过一、二、三象限,则抛物线2y ax bx =+大致是( )A .B .C .D .15.已知一次函数y bx c =-与二次函数2y ax bx c =++,它们在同一坐标系内的大致图象可能是( )A .B .C .D .16.已知二次函数y=a(x−1)2−c的图象如图所示,则一次函数y=ax+c的大致图象可能是()A.B.C.D.二、填空题17.二次函数y=a(x﹣m)2+n的图象如图,则一次函数y=mx+n的图象不经过第___象限.=+的图象不经过第18.已知二次函数2=++的图象如图所示,则一次函数y ax bcy ax bx c____________象限19.函数y=x2+bx+c与y=x的图象如图所示,有以下结论:①bc>0;①b2﹣4c>0;①b+c+1=0;①3b+c+6=0;①当1<x<3时,x2+(b﹣1)x+c<0.其中正确的是_____.20.如图已知二次函数y 1=x 2+c 与一次函数y 2=x+c 的图象如图所示,则当y 1<y 2时x 的取值范围_____.21.已知直线y 2x 1=-与抛物线2y 5x k =+交点的横坐标为2,则k =________,交点坐标为________.三、解答题22.如图,正比例函数y 1=x 与二次函数y 2=x 2-bx 的图象相交于O (0,0),A (4,4)两点. (1)求 b 的值;(2)当 y 1< y 2 时,直接写出 x 的取值范围.23.如图,二次函数的图像与x 轴交于()30A -,和()10B ,两点,交y 轴于点()0,3C ,点C 、D是二次函数图像上的一对对称点,一次函数的图像过点B、D(1)求D点坐标;(2)根据图像直接写出使一次函数值大于二次函数值的x的取值范围.24.抛物线y1=ax2+bx+c与直线y2=kx+m的图象如图所示,根据图象回答下列问题:(1)指出b,b2﹣4ac,a﹣b+c的符号;(2)若y1<0,指出x的取值范围;(3)若y1>y2,指出x的取值范围.25.设k≠0,若函数y1=kx+3,y2=(x﹣k)2+k和y3=(x+k)2﹣k的图象与y轴依次交于A,B和C三点,设函数y2,y3的图象的顶点分别为D,E.(1)当k=1时,请在直角坐标系中,分别画出函数y1,y2,y3的草图,并根据图象,写出你发现的两条结论;(2)BC长与k之间是正比例函数关系吗?请作出判断,并说明理由;(3)若①ADE的面积等于9,求y2随x的增大而减小时,x的取值范围.参考答案1.A【分析】利用直线y=2x与y=x2﹣c(c为常数,﹣1≤x≤2)的图象有且仅有一个公共点,由根的判别式求出c的值,即可求得直线的解析式.解:把y=2x代入y=x2﹣c,整理得x2﹣2x﹣c=0,根据题意△=(﹣2)2+4c=0,解得c=﹣1,把x=﹣1代入y=2x与y=x2﹣c得,c=3,把x=2代入y=2x与y=x2﹣c得,c=0,①当0<c≤3或c=﹣1时,函数y=2x与y=x2﹣c(c为常数,﹣1≤x≤2)的图象有且仅有一个公共点,故选A.【点拨】本题考查一次函数和二次函数的交点坐标,根的判别式.2.B【分析】由选项中的二次函数图象可得k>0,可判定出一次函数的正确图象.解:由选项中的二次函数图象可得k>0,所以y=kx﹣k过一,三,四象限.故选B.【点拨】本题主要考查了二次函数及一次函数的图象,解题的关键是熟记二次函数及一次函数的图象的特征.3.C【分析】分a>0和a<0时,分别判断两函数的图象即可求得答案.解:当a>0时,则函数y=ax中,y随x的增大而增大,函数y=ax2开口向上,故①正确,①错误;当a<0时,则函数y=ax中,y随x的增大而减小,函数y=ax2开口向下,故①不正确,①正确;①两函数图象可能是①①,故选:C.【点拨】本题主要考查了一次函数的图象和二次函数的图象,掌握一次函数的图象和二次函数的图象是解题的关键.4.D【分析】根据二次函数y=ax2+bx+c的图象可以判断a、b、c的正负,从而可以判断一次函数y=bx+ac的图象经过哪几个象限即可.解:由二次函数y=ax2+bx+c的图象可得:a>0,b>0,c>0,①ac>0,①一次函数y=bx+ac的图象经过第一、二、三象限,不经过第四象限.故选:D.【点拨】考查了二次函数的图象与系数的关系,解题关键是根据函数的图象得到a>0,b>0,c>0,由此再判断一次函数的图象.5.C【分析】由一次函数的图象判断出ba>0、c>0,再判断二次函数的图象特征,进而求解.解:观察函数图象可知:ba>0、c>0,①二次函数y=ax2+bx+c的图象对称轴x=-2ba<0,与y轴的交点在y轴正半轴.故选:C.【点拨】本题考查了二次函数图象与一次函数的图象,解题的关键是根据一次函数的图象判断出ba>0、c>0.6.D【分析】根据二次函数的图象可以判断a、b、a-b的正负情况,从而可以得到一次函数经过哪几个象限,本题得以解决.解:由二次函数的图象可知,a<0,b<0,当x=-1时,y=a-b<0,①y=(a-b)x+b的图象在第二、三、四象限,故选:D.【点拨】本题考查二次函数的性质、一次函数的性质,解答本题的关键是明确题意,利用函数的思想解答.7.D【分析】由抛物线开口方向得到a >0,由对称轴得到b =a >0,由抛物线与y 轴的交点得到c <0,则abc <0;a +b >0,据此来进行一一判断即可.解:①抛物线开口向上,①a >0,①抛物线的对称轴为直线x =122b a -=-, ①b =a >0,①抛物线与y 轴的交点在x 轴下方,①c <0,①abc <0;a +b >0;故选项A 、B 错误;①b =a >0,c <0,①b +c <a ,a +c <b ,故选项C 错误,选项D 正确,故选:D .【点拨】此题考查了二次函数图象与系数的关系.此题难度适中,解题的关键是掌握数形结合思想的应用,注意掌握二次函数图象与系数的关系,掌握二次函数的对称性.8.B【分析】题干中二次函数2y ax =的图象开口向下,可以判断出a 的符号为负,一次函数y bx c =+的图象与x 轴正方向夹角小于90°,且与y 轴交点在y 轴的正半轴,可以据此判断出b 、c 的符号皆为正,再去判断各选项哪个符合二次函数2y ax bx c =++的图象.解:①二次函数2y ax =的图象开口向下,①a <0,又①一次函数y bx c =+的图象与x 轴正方向夹角小于90°,且与y 轴交点在y 轴的正半轴,①b >0,c >0, 则2b a ->0,可知二次函数2y ax bx c =++开口方向向下,对称轴在y 轴右侧,且与y 轴交点在y 的正半轴,选项B 图象符合,故选:B .【点拨】本题考查了一次函数、二次函数图象与系数的关系,题目比较简单,解决题目需要熟练掌握图象与系数的关系.9.A【分析】根据函数图象和二次函数的性质判断即可.解: 由2y =x 2+bx +c 图象可知,对称轴x =2b ->0,0c <, 0b ∴<,抛物线21y x b x c =+-+()与y 轴的交点在x 轴下方,故选项B ,C 错误, 抛物线21y x b x c =+-+()的对称轴为1122b b x --=-=, ①102b ->, ①抛物线y =x 2+(b -1)x +c 的对称轴在y 轴的右侧,故选项D 错误,故选:A .【点拨】本题考查二次函数图像和性质,明确二次函数2y ax bx c =++ 中各项系数的意义及利用数形结合的思想是解答本题的关键.10.D【分析】 根据题意可得由抛物线的对称轴为直线4242b b x a a=-=-⨯;一次函数y =2ax +b 的图象与x 轴交于点,02⎛⎫- ⎪⎝⎭b a ,再逐项判断即可求解. 解:抛物线的对称轴为直线4242b b x a a=-=-⨯;一次函数y =2ax +b 的图象与x 轴交于点,02⎛⎫- ⎪⎝⎭b a , A 、此时一次函数y =2ax +b 的图象没有过点,02⎛⎫- ⎪⎝⎭b a ,故本选项不符合题意; B 、此时一次函数y =2ax +b 的图象没有过点,02⎛⎫- ⎪⎝⎭b a ,故本选项不符合题意; C 、此时一次函数y =2ax +b 的图象没有过点,02⎛⎫- ⎪⎝⎭b a ,故本选项不符合题意;D 、此时一次函数y =2ax +b 的图象过点,02⎛⎫- ⎪⎝⎭b a ,故本选项符合题意; 故选:D【点拨】本题主要考查了二次函数和一次函数的图象和性质,熟练掌握二次函数和一次函数的图象和性质是解题的关键.11.B【分析】可先根据一次函数的图像判断a 、b 的符号,再看二次函数图像开口方向与最值与实际是否相符,判断正误.解:A 、由一次函数y =cx +a 的图像可得0a <,0c <,此时二次函数的图像应该开口向下,故A 错误;B 、由一次函数y =cx +a 的图像可得0a >,0c <,此时二次函数的图像应该开口向上,图像顶点应在x 轴下方,故B 正确;C 、由一次函数y =cx +a 的图像可得0a <,0c >,此时二次函数的图像应该开口向下,x =2时二次函数取最大值,故C 错误;D 、由一次函数y =cx +a 的图像可得0a >,0c >,此时二次函数的图像应该开口向上,图像顶点应在x 轴上方,故D 错误;【点拨】本题主要考查一次函数和二次函数的图象,解题的关键是熟练掌握二次函数y =a (x ﹣2)2+c 的图象和一次函数的图象与系数之间的关系.12.B【分析】根据反比例函数图象和二次函数图象位置可得出:a ﹤0,b ﹤0,c ﹥0,由此可得出0ac <,一次函数图象与y 轴的交点在y 轴的负半轴,对照四个选项即可解答.解:由二次函数图象开口向下可知:a ﹤0, 对称轴02b x a-=-> 0b ∴<, 由反比例函数图象分别在第一、三象限知:c ﹥0,0ac ∴<,∴一次函数y acx b =+的图象经过二,三,四象限,与y 轴的交点在y 轴的负半轴,对照四个选项,只有B 选项符合一次函数y acx b =+的图象特征,故选:B .【点拨】本题考查反比例函数的图象、二次函数的图象、一次函数的图象,熟练掌握函数图象与系数之间的关系是解答的关键.13.C【分析】由题意,图象经过第一和第三象限的函数都是满足条件的,由此判断即可.解:由题意,图象经过第一和第三象限的函数都是满足条件的, 函数5y x=-的图象在二、四象限,不满足条件, 故选:C .【点拨】本题考查了反比函数的性质,一次函数的性质,二次函数的性质.可以用特值法进行快速的排除.14.A【分析】由直线y ax b =+经过一、二、三象限,可确定00a b >>,,由0a >,抛物线开口向上,可判断D 不正确,由00a b >>,抛物线的对称轴x≠0,可判断C 不正确,由x=02b a-<抛物线对称轴在y 轴左侧可判断D 不正确,A 正确.解:①直线y ax b =+经过一、二、三象限,①00a b >>,,①0a >,抛物线开口向上,则D 不正确,①00a b >>,,①抛物线的对称轴x≠0,则C 不正确,由x=02b a -<, 抛物线对称轴在y 轴左侧,则D 不正确,A 正确,故选择:A .【点拨】本题考查一次函数经过象限确定抛物线的位置,掌握抛物线的性质,特别是抛物线的性质与系数a b ,的关系是解题关键.15.D【分析】先根据各项中一次函数与二次函数的图象判断a 、b 、c 的正负,二者一致的即为正确答案.解:A 、由一次函数图象得:0b >,0c <,由二次函数图象得:0a <,0b <,0c >,矛盾,故本选项不符合题意;B 、由一次函数图象得:0b >,0c >,由二次函数图象得:0a <,0b <,0c >,矛盾,故本选项不符合题意;C 、由一次函数图象得:0b >,0c <,由二次函数图象得:0a >,0b >,0c >,矛盾,故本选项不符合题意;D 、由一次函数图象得:0b >,0c <,由二次函数图象得:0a >,0b >,0c <,本选项符合题意;故选:D .【点拨】本题考查一次函数与二次函数图象与系数之间的关系,理解基本性质,并灵活根据图象分析是解题关键.16.C【分析】首先根据二次函数图象得出a ,c 的值,进而利用一次函数性质得出图象经过的象限. 解:根据二次函数开口向上则a >0,根据−c 是二次函数顶点坐标的纵坐标,得出c >0,故一次函数y =ax +c 的大致图象经过一、二、三象限,故选:C .【点拨】此题主要考查了二次函数的图象以及一次函数的性质,根据已知得出a ,c 的值是解题关键.17.二##2【分析】由二次函数解析式表示出顶点坐标,根据图形得到顶点在第四象限,求出m 与n 的正负,即可作出判断.解:根据题意得:抛物线的顶点坐标为(m ,n ),且在第四象限,①m >0,n <0,即m >0,n <0,则一次函数y =mx +n 经过一、三、四象限,不经过第二象限.故答案为:二.【点拨】此题考查了二次函数与一次函数图象与系数的关系,熟练掌握二次函数及一次函数的图象与性质是解本题的关键.18.二##2【分析】由抛物线的开口方向、与y 轴的交点以及对称轴,可确定a ,b ,c 的符号,继而可判定一次函数y ax bc =+的图象不经过哪个象限即可. 解:开口向上,0a ∴>,与y 轴交于负半轴,0c ∴<,对称轴在y 轴左侧,02b a∴-<, 又①0a >,0b ∴>,0bc ∴<,∴一次函数y ax bc =+的图象经过一、三、四象限,不经过第二象限.故答案为:二.【点拨】主要考查二次函数图象与二次函数系数之间的关系.注意二次函数2y ax bx c =++系数符号由抛物线开口方向、对称轴、抛物线与y 轴的交点确定,也考查了一次函数图象的性质.19.①①【分析】根据函数y =x 2+bx +c 的图象得出a 、b 、c 的符号,对①进行判断;利用判别式的意义对①进行判断;利用x =1,y =1可对①进行判断;利用x =3,y =3对①进行判断;根据1<x <3时,x 2+bx +c <x 可对①进行判断.解:由图象开口向上,则a >0,对称轴在y 轴右侧,则a ,b 异号,故b <0,图象与y 轴交在正半轴,故c >0,则bc <0,故①错误;①抛物线与x 轴没有公共点,①①=b 2﹣4c <0,所以①错误;①x =1,y =1,①1+b +c =1,即b +c =0,所以①错误;①x=3,y=3,①9+3b+c=3,①3b+c+6=0,所以①正确;①1<x<3时,x2+bx+c<x,①x2+(b﹣1)x+c<0的解集为1<x<3,所以①正确.故答案为:①①.【点拨】本题考查二次函数图象与系数的关系,二次函数与不等式(组):利用两个函数图象在直角坐标系中的上下位置关系求自变量的取值范围,可作图利用交点直观求解,也可把两个函数解析式列成不等式求解.20.0<x<1.【分析】首先将两函数解析式联立得出其交点横坐标,进而得出当y1<y2时x的取值范围.解:由题意可得:x2+c=x+c,解得:x1=0,x2=1,则当y1<y2时x的取值范围:0<x<1.故答案为0<x<1.【点拨】此题主要考查了二次函数与一次函数,正确得出两函数的交点横坐标是解题关键.21.-17(2,3)【分析】根据交点的横坐标,代入直线解析式,可得交点的纵坐标,把交点的坐标代入抛物线的解析式,利用待定系数法,可得k的值.解:将x=2代入直线y=2x﹣1得,y=2×2﹣1=3,则交点坐标为(2,3),将(2,3)代入y=5x2+k得,3=5×22+k,解得k=﹣17,故答案为﹣17,(2,3).【点拨】考查了二次函数和一次函数的交点坐标,掌握待定系数法求二次函数解析式是解题的关键.x>22.(1)3b=(2)0x<或4【分析】(1)将点A (4,4)代入22y x bx =-进行解答即可得;(2)由图像即可得.(1)解:将点A (4,4)代入22y x bx =-得,1644b -=412b =解得3b =.(2)解:由图像可知,当0x <或4x >时,12y y <.【点拨】本题考查了正比函数,二次函数,解题的关键是掌握正比函数的性质和二次函数的性质.23.(1)D (-2,3);(2)x <-2或x >1【分析】(1)根据点A 和点B 的坐标即可求出抛物线的对称轴,然后利用C 、D 的对称性即可求出点D 的坐标;(2)根据图象即可得出结论.解:(1)①如图,二次函数的图象与x 轴交于A (-3,0)和B (1,0)两点,①该抛物线的对称轴是直线x=312-+=-1. 又点C (0,3),点C 、D 是二次函数图象上的一对对称点,①D (-2,3);(2)由图象可知:在点D 左侧和点B 右侧,一次函数的图象在二次函数的上方,即一次函数值大于二次函数值一次函数值大于二次函数值时,x <-2或x >1.【点拨】本题考查了二次函数的图象及性质以及二次函数与一次函数的综合,解题时,要注意数形结合数学思想的应用.24.(1)b <0,b 2﹣4ac >0,a ﹣b+c >0;(2)1<x <4;(3)x <1或x >5.【分析】(1)根据二次函数开口向上a >0,﹣2b a>0,得出b 的符号,再利用二次函数与坐标轴的交点个数得出b 2﹣4ac 符号,再利用x=﹣1时求出a ﹣b+c 的符号;(2)根据图象即可得出y 1=ax 2+bx+c 小于0的解集;(3)利用两函数图象结合自变量的取值范围得出函数大小关系.解:(1)①二次函数开口向上a >0,﹣2b a>0,得出b <0, ①b <0,①二次函数与坐标轴的交点个数为2,①b 2﹣4ac >0,①x=﹣1时,y=a ﹣b+c ,结合图象可知,①a ﹣b+c >0;(2)结合图象可知,当1<x <4 时,y 1<0;(3)结合图象可知,当x <1或x >5时,y 1>y 2.【点拨】此题主要考查了二次函数图象与系数的关系以及一次函数的图象性质,结合图象比较函数的大小关系是初中阶段难点,同学们应重点掌握.25.(1)见分析,直线与两抛物线始终有两个交点;B 点在C 点上方;(2)BC 长与k 之间是正比例函数关系,见分析;(3)x≤3.【分析】(1)当k=1时,分别求出它们的解析式,画出图象;(2)求出B 与C 的坐标,求出BC=2k ,可知BC 与k 是正比例函数;(3)构造矩形求①BDE 的面积,利用面积求k 的值,进而求出y 2的函数解析式,从而求解. 解:(1)当k =1时,y 1=x+3,y 2=(x ﹣1)2+1和y 3=(x+1)2﹣1.如图,直线与两抛物线始终有两个交点;B 点在C 点上方;(2)B (0,k 2+k ),C (0,k 2﹣k ),①BC =(k 2+k )﹣(k 2﹣k )=2k ,①BC 长与k 之间是正比例函数关系;(3)由表达式可知:D(k,k),E(﹣k,﹣k),过D,E分别向x轴作垂线,过A,E分别向y轴作垂线,交点为O,P,E,N,则由OPEN构造长方形,①S△ADE=S PONE﹣S△APE﹣S△AOD﹣S△EDN=2k(3+k)﹣12k•(3+k)﹣122k•2k﹣12k•(3﹣k)=3k,①①ADE的面积等于9,①3k=9,①k=3,①y2=(x﹣k)2+k=(x﹣3)2+3,①对称轴是x=3,当y2随x的增大而减小时,x≤3.故答案为(1)见分析,直线与两抛物线始终有两个交点;B点在C点上方;(2)BC长与k 之间是正比例函数关系,见分析;(3)x≤3.【点拨】本题考查二次函数与一次函数的图象;正比例函数的判别;二次函数顶点,对称轴;三角形面积.能够将一次函数,正比例函数,二次函数三个函数的图象与解析式结合解题,同时数形结合思想的运用起到关键作用.。
中考数学总复习《二次函数与一次函数的综合应用》练习题附有答案
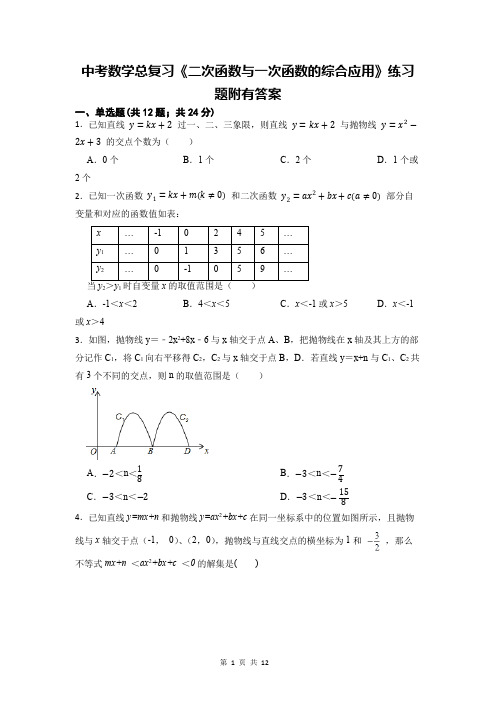
中考数学总复习《二次函数与一次函数的综合应用》练习题附有答案一、单选题(共12题;共24分)1.已知直线y=kx+2过一、二、三象限,则直线y=kx+2与抛物线y=x2−2x+3的交点个数为()A.0个B.1个C.2个D.1个或2个2.已知一次函数y1=kx+m(k≠0)和二次函数y2=ax2+bx+c(a≠0)部分自变量和对应的函数值如表:x…-10245…y1…01356…y2…0-1059…21A.-1<x<2B.4<x<5C.x<-1或x>5D.x<-1或x>43.如图,抛物线y=﹣2x2+8x﹣6与x轴交于点A、B,把抛物线在x轴及其上方的部分记作C1,将C1向右平移得C2,C2与x轴交于点B,D.若直线y=x+n与C1、C2共有3个不同的交点,则n的取值范围是()A.−2<n<18B.−3<n<−74C.−3<n<−2D.−3<n<−1584.已知直线y=mx+n和抛物线y=ax2+bx+c在同一坐标系中的位置如图所示,且抛物线与x轴交于点(-1,0)、(2,0),抛物线与直线交点的横坐标为1和,那么不等式mx+n <ax2+bx+c <0的解集是()A.1<x<2B.x<或x>1C.<x<2D.-1<x<25.若min{a,b,c}表示a,b,c三个数中的最小值,当y=min{x2,x+2,8−x}时(x≥0),则y的最大值是()A.4B.5C.6D.7 6.新定义:若一个点的纵坐标是横坐标的2倍,则称这个点为二倍点.若二次函数y= x2−x+c(c为常数)在−2<x<4的图象上存在两个二倍点,则c的取值范围是()A.−2<c<14B.−4<c<94C.−4<c<14D.−10<c<947.二次函数y1=x2+bx+c与一次函数y2=kx−9的图象交于点A(2,5)和点B(3,m),要使y1<y2,则x的取值范围是()A.2<x<3B.x>2C.x<3D.x<2或x>38.将二次函数y=−x2+2x+3的图象在x轴上方的部分沿x轴翻折后,所得新函数的图象如图所示.当直线y=x+b与新函数的图象恰有3个公共点时b的值为()A.−214或−3B.−134或−3C.214或−3D.134或−39.如图,平面直角坐标系中,点M是直线y=2与x轴之间的一个动点,且点M是抛物线y=12x2+bx+c的顶点,则方程12x2+bx+c=1的解的个数是()A.0或2B.0或1C.1或2D.0,1或210.如图①,在正方形ABCD中,点P沿边DA从点D开始向点A以1cm/s的速度移动,同时点Q沿边AB,BC从点A开始向点C以2cm/s的速度移动,当点P移动到点A时P、Q同时停止移动。
一次函数与二次函数的综合练习题

一次函数与二次函数的综合练习题在数学学科中,一次函数和二次函数是我们经常接触到的两种函数类型。
它们在图像特点、方程性质以及实际问题应用等方面具有一定的差异。
为了加深对这两类函数的理解和掌握,下面将提供一些综合练习题来进行实践。
练习题1:已知函数y = 3x - 2和y = x^2 + 1,求二者的交点坐标。
解析:设两个函数相交时的x值为a,则有:3a - 2 = a^2 + 1将方程化为一般形式:a^2 - 3a + 3 = 0根据一元二次方程的求根公式,得到:a = (3 ± √5) / 2因此,交点的坐标为((3 + √5) / 2,(3(3 + √5) / 2) - 2)和((3 - √5) / 2,(3(3 - √5) / 2) - 2)。
练习题2:对于函数y = -2x + 3和y = 2x^2 - 1,求二者的交点坐标。
解析:设两个函数相交时的x值为b,则有:-2b + 3 = 2b^2 - 1将方程化为一般形式:2b^2 + 2b - 4 = 0将方程化简得:b^2 + b - 2 = 0根据一元二次方程的求根公式,得到:b = -2 或 b = 1因此,交点的坐标为(-2,-2)和(1,1)。
练习题3:已知函数y = 4x + 7和y = -x^2 + 3x,求二者的交点坐标。
解析:设两个函数相交时的x值为c,则有:4c + 7 = -c^2 + 3c将方程化为一般形式:c^2 - c + 7 = 0但这个方程没有实数解,说明两个函数在平面上没有交点。
练习题4:已知函数y = 5x和y = x^2 - 4,求二者的交点坐标。
解析:设两个函数相交时的x值为d,则有:5d = d^2 - 4将方程化为一般形式:d^2 - 5d - 4 = 0根据一元二次方程的求根公式,得到:d = 5 或 d = -1因此,交点的坐标为(5,25)和(-1,-5)。
练习题5:已知函数y = -3x和y = 2x^2 + 2,求二者的交点坐标。
专题:一次函数与二次函数综合

一次函数与二次函数综合【课前热身】1.抛物线与x 轴分别交于A 、B 两点,则AB 的长为________.322--=x x y 2.已知函数:(1)图象不经过第二象限;(2)图象经过(2,-5),请你写出一个同时满足(1)和(2)的函数_________________3.如图,用一段长为30米的篱笆围成一个一边靠墙(墙的长度不限)的矩形菜园,ABCD 设边长为米,则AB x 菜园的面积(单位:米)与(单位:米)的函数关系式为 .(不y 2x 要求写出自变量的取值范围)x 4.当路程一定时,速度与时间之间的函数关系是( )s v t A .正比例函数 B .反比例函数 C .一次函数 D .二次函数5.函数与(k≠0)在同一坐标系内的图象可能是( )2y kx =-k y x =6.(甘肃)如图是某种蜡烛在燃烧过程中高度与时间之间关系的图像,由图像解答下列问题:⑴ 此蜡烛燃烧1小时后,高度为 cm ;经过 小时燃烧完毕;⑵ 这个蜡烛在燃烧过程中高度与时间之间关系的解析式是 .7. 如图,已知中,BC=8,BC 上的高,D 为BC 上一点,,交AB 于∆ABC h =4EF BC //点E ,交AC 于点F (EF 不过A 、B ),设E 到BC 的距离为,则的面积关于x ∆DEF y 的函数的图像大致为( )x 8.(贵阳) 某商场购进一种单价为元的篮球,如果以单价元售出,那么每月可售出4050 个.根据销售经验,售价每提高元,销售量相应减少个.500110⑴ 假设销售单价提高元,那么销售每个篮球所获得的利润是___________元;这种x 篮球每月的销售量是___________个.(用含的代数式表示)x ⑵ 当篮球的售价应定为 元时,每月销售这种篮球的最大利润,此时最大利润是 元.A D (第3题)菜园墙【考点链接】1.点A 在函数的图像上.则有 .()o y x ,0c bx ax y ++=22. 求函数与轴的交点横坐标,即令 ,解方程 ;b kx y +=x 与y 轴的交点纵坐标,即令 ,求y 值3. 求一次函数的图像与二次函数的图像的交()0≠+=k n kx y l ()02≠++=a c bx ax y 点,解方程组 .4.二次函数通过配方可得,c bx ax y ++=2224(24b ac b y a x a a -=++⑴ 当时,抛物线开口向 ,有最 (填“高”或“低”)点, 当0a > 时,有最 (“大”或“小”)值是 ;x =y ⑵ 当时,抛物线开口向 ,有最 (填“高”或“低”)点, 当0a < 时,有最 (“大”或“小”)值是 .x =y 5. 每件商品的利润P = - ;商品的总利润Q = × .【典例精析】例1(烟台)如图(单位:m ),等腰三角形ABC 以2米/秒的速度沿直线L 向正方形移动,直到AB 与CD 重合.设x 秒时,三角形与正方形重叠部分的面积为ym 2.⑴ 写出y 与x 的关系式;⑵ 当x=2,3.5时,y 分别是多少?⑶ 当重叠部分的面积是正方形面积的一半时,三角形移动了多长时间?求抛物线顶点坐标、对称轴.例2 如右图,抛物线经过点,与y 轴交于点B.n x x y ++-=52)0,1(A (1)求抛物线的解析式;(2)P 是y 轴正半轴上一点,且△PAB 是等腰三角形,试求点P 的坐标.例3、近年来,“宝胜”集团根据市场变化情况,采用灵活多样的营销策略,产值、利税逐年大幅度增长.第六销售公司2004年销售某型号电缆线达数万米,这得益于他们较好地把握了电缆售价与销售数量之间的关系.经市场调研,他们发现:这种电缆线一天的销量y (米)与售价x (元/米)之间存在着如图所示的一次函数关系,且40≤x≤70.(1) 根据图象,求y与x之间的函数解析式;(2) 设该销售公司一天销售这种型号电缆线的收入为w元.① 试用含x 的代数式表示w;② 试问当售价定为每米多少元时,该销售公司一天销售该型号电缆的收入最高?最高是多少元?例4 (南宁)随着绿城南宁近几年城市建设的快速发展,对花木的需求量逐年提高.某园林专业户计划投资种植花卉及树木,根据市场调查与预测,种植树木的利润与投资量1y 成正比例关系,如图(1)所示;种植花卉的利润与投资量成二次函数关系,x 2y x 如图(2)所示(注:利润与投资量的单位:万元)⑴ 分别求出利润与关于投资量的函数关系式;1y 2y x ⑵ 如果这位专业户以8万元资金投入种植花卉和树木,他至少获得多少利润?他能获取的最大利润是多少?【中考演练】1. 反比例函数的图像经过A (-,5)点、B (,-3),则= ,=x k y23a k a .2.(06旅顺)如图是一次函数y 1=kx +b 和反比例函数y 2==的图象, 观察图象写出y 1>y 2时,x 的取值范m x围是_________.3.根据右图所示的程序计算变量y 的值,若输入自变量x 的值为,则输出32的结果是_______.4.(06威海)如图,过原点的一条直线与反比例函数y =(k<0)k x 的图像分别交于A 、B 两点,若A 点的坐标为(a ,b ),则B 点的坐标为( ) A .(a ,b ) B .(b ,a ) C .(-b ,-a ) D .(-a ,-b )5. 二次函数y =x 2+2x -7的函数值是8,那么对应的x 的值是( ) A .3 B .5 C .-3和5 D .3和-5 6.下列图中阴影部分的面积与算式的结果相同的是( )12221(|43|-++-7. 如图,方格纸上一圆经过(2,5),(-2,1),(2,-3),(6,1) 四点,则该圆圆心的坐标为( )A.(2,-1)B.(2,2)C.(2,1)D.(3,1)三、解答题8. 已知点的坐标为,点的坐标为.A (13),B (31),⑴ 写出一个图象经过两点的函数表达式;A B ,⑵指出该函数的两个性质.xx B F A C D E x G 9. 反比例函数y =的图象在第一象限的分支上有一点A (3,4),P 为x 轴正半轴上的xk 一个动点,(1)求反比例函数解析式.(2)当P 在什么位置时,△OPA 为直角三角形,求出此时P 点的坐标.10.(枣庄)如图,在直角坐标系中放入一个边长OC 为9的矩形纸片ABCO .将纸片翻折后,点B 恰好落在x 轴上,记为B′,折痕为CE ,已知tan∠OB′C=34.(1)求B′点的坐标;(2)求折痕CE 所在直线的解析式.11. 如图所示,在直角梯形ABCD 中,∠A =∠D =90°,截取AE =BF =DG =x.已知AB =6,CD =3,AD =4;求四边形CGEF 的面积S 关于x 的函数表达式和x 的取值范围.12. (06沈阳) 某企业信息部进行市场调研发现:信息一:如果单独投资A 种产品,则所获利润(万元)与投资金额(万元)之间存在A y x 正比例函数关系:,并且当投资5万元时,可获利润2万元;A y kx 信息二:如果单独投资B 种产品,则所获利润(万元)与投资金额(万元)之间存在B y x二次函数关系:,并且当投资2万元时,可获利润2.4万元;2B y ax bx =+当投资4万元,可获利润3.2万元.(1) 请分别求出上述的正比例函数表达式与二次函数表达式;(2) 如果企业同时对A 、B 两种产品共投资10万元,请你设计一个能获得最大利润的投资方案,并求出按此方案能获得的最大利润是多少.13. 如图,已知矩形OABC 的长OA ,宽OC =1,将△AOC 沿AC 翻折得△APC.(1)填空:∠PCB= 度,P 点坐标为 ;(2)若P 、A 两点在抛物线y =-x 2+bx +c 上,求b 、c 的值,并说明点C 在此抛43物线上;﹡(3)在(2)中的抛物线CP 段(不包括C ,P 点)上,是否存在一点M ,使得四边形MCAP 的面积最大?若存在,求出这个最大值及此时M 点的坐标;若不存在,请说明理由.二次函数与一次函数结合常见考题(含答案)1,(2010•密云县)附加题:已知:如图,正比例函数y=ax 的图象与反比例函数y=的图象交于点A (3,2)(1)试确定上述正比例函数和反比例函数的表达式;(2)根据图象回答,在第一象限内,当x 取何值时,反比例函数的值大于正比例函数的值;(3)M (m ,n )是反比例函数图象上的一动点,其中0<m <3,过点M 作直线MN ∥x 轴,交y 轴于点B ;过点A 作直线AC ∥y 轴交x 轴于点C ,交直线MB 于点D .当四边形OADM 的面积为6时,请判断线段BM 与DM 的大小关系,并说明理由.,2,(2011•雅安)如图,过y轴上点A的一次函数与反比例函数相交于B、D两点,B(﹣2,3),BC⊥x轴于C,四边形OABC面积为4.(1)求反比例函数和一次函数的解析式;(2)求点D的坐标;(3)当x在什么取值范围内,一次函数的值大于反比例函数的值.(直接写出结果)3.(2009•吉林)如图,反比例函数y=的图象与直线y=x+m在第一象限交于点P(6,2),A、B为直线上的两点,点A的坐标为2,点B的横坐标为3.D、C为反比例函数图象上的两点,且AD、BC平行于y轴.(1)直接写出k,m的值;(2)求梯形ABCD的面积.4.(2009•达州)如图,直线y=kx+b与反比例函数y=(x<0)的图象相交于点A、点B,与x轴交于点C,其中点A的坐标为(﹣2,4),点B的横坐标为﹣4.(1)试确定反比例函数的关系式;(2)求△AOC的面积.5.(2009•河池)为了预防流感,某学校在休息天用药熏消毒法对教室进行消毒.已知药物释放过程中,室内每立方米空气中的含药量y(毫克)与时间x(分钟)成正比例;药物释放完毕后,y与x成反比例,如图所示.根据图中提供的信息,解答下列问题:(1)写出从药物释放开始,y与x之间的两个函数关系式及相应的自变量取值范围;(2)据测定,当空气中每立方米的含药量降低到0.45毫克以下时,学生方可进入教室,那么从药物释放开始,至少需要经过多少小时后,学生才能进入教室?。
一次函数和二次函数的综合练习(相交识大小,形成图形面积等问题)附一次与反比例的综合问题(看图识大小)

一次函数和二次函数的综合练习(相交产生大小,形成图形面积等问题)类型一:已知一次函数和二次函数解析式求交点坐标并比较大小类型二:已知相关点的坐标求解一次函数和二次函数的解析式并比较大小如图,二次函数y=(x-2)2+m 的图象与y 轴交于点C ,点B 是点C 关于该二次函数图象的对称轴对称的点.已知一次函数y=kx+b 的图象经过该二次函数图象上点A (1,0)及点B . (1)求一次函数与二次函数的解析式;(2)根据图象,写出满足kx+b≥(x-2)2+m 的x 的取值范围.练习1:如图所示,二次函数的图象与x 轴相交于A 、B 两点,与y 轴相交于点C ,点C 、D 是二次函数图象上的一对对称点,一次函数的图象过点B 、D .(1)求D 点的坐标和一次函数、二次函数的解析式;(2)根据图象写出使一次函数值大于二次函数值的x 的取值范围.练习2:在同一直角坐标系,开口向上的抛物线与坐标轴分别交于A (-1,0),B (3,0),C (0,-3),一次函数图象与二次函数图象交于B 、C 两点. (1)求一次函数和二次函数的解析式.(2)当自变量x 为何值时,两函数的函数值都随x 的增大而增大? (3)当自变量x 为何值时,一次函数值大于二次函数值. (4)当自变量x 为何值时,两函数的函数值的积小于0.类型三:与一次函数和二次函数的交点有关的面积类问题。
练习1:如图,A (-1,0)、B (2,-3)两点在一次函数y 1=-x+m 与二次函数y 2=ax 2+bx-3的图象上.(1)求m 的值和二次函数的解析式.(2)二次函数交y 轴于C ,求△ABC 的面积.变式:已知一次函数y 1=-x+m 与二次函数y 2=ax 2+bx-3的图象交于两点A (-1,0)、B (2,-3),且二次函数与y 轴交于点C ,P 为抛物线顶点.求△ABP 的面积.练习2:如图,一次函数的图象与x 轴交于点A ,与y 轴交于点B ;二次函数y=21x 2+bx+c 的图象与一次函数y=21x+1的图象交于B ,C 两点,与x 轴交于D ,E 两点,且D 点坐标为(1,0).(1)求二次函数的解析式;(2)求线段BC 的长及四边形BDEC 的面积S ;附加一次与反比例的综合问题(看图识大小)1.:已知:如图,正比例函数y=ax 的图象与反比例函数y=的图象交于点A (3,2)(1)试确定上述正比例函数和反比例函数的表达式;(2)根据图象回答,在第一象限内,当x 取何值时,反比例函数的值大于正比例函数的值;(3)M (m ,n )是反比例函数图象上的一动点,其中0<m <3,过点M 作直线MN ∥x 轴,交y 轴于点B ;过点A 作直线AC ∥y 轴交x 轴于点C ,交直线MB 于点D .当四边形OADM 的面积为6时,请判断线段BM 与DM 的大小关系,并说明理由.,2.如图,过y 轴上点A 的一次函数与反比例函数相交于B 、D 两点,B (﹣2,3),BC ⊥x 轴于C ,四边形OABC 面积为4.(1)求反比例函数和一次函数的解析式; (2)求点D 的坐标;(3)当x 在什么取值范围内,一次函数的值大于反比例函数的值.(直接写出结果)3.如图,反比例函数y=的图象与直线y=x+m在第一象限交于点P(6,2),A、B为直线上的两点,点A的坐标为2,点B的横坐标为3.D、C为反比例函数图象上的两点,且AD、BC平行于y轴.(1)直接写出k,m的值;(2)求梯形ABCD的面积.4.如图,直线y=kx+b与反比例函数y=(x<0)的图象相交于点A、点B,与x轴交于点C,其中点A的坐标为(﹣2,4),点B的横坐标为﹣4.(1)试确定反比例函数的关系式;(2)求△AOC的面积.。
初中数学二次函数综合题及答案(经典题型)

二次函数综合题1、已知一次函数y= ax+c与二次函数y=ax2+bx+c(a≠0),它们在同一坐标系内的大致图象是图中的()二填空题:2、无论m为任何实数,总在抛物线y=x2+2mx+m上的点的坐标是————————————。
3、若抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=2,最小值为-2,则关于方程ax2+bx+c=-2的根为————————————。
4、抛物线y=(k+1)x2+k2-9开口向下,且经过原点,则k=—————————解答题:(二次函数与三角形)5、已知:二次函数y=x2+bx+c,其图象对称轴为直线x=1,且经过点(2,﹣).(1)求此二次函数的解析式.(2)设该图象与x轴交于B、C两点(B点在C点的左侧),请在此二次函数x轴下方的图象上确定一点E,使△EBC 的面积最大,并求出最大面积.6、如图,在平面直角坐标系中,抛物线与x轴交于A、B两点(A在B的左侧),与y轴交于点C (0,4),顶点为(1,92).(1)求抛物线的函数表达式;(2)设抛物线的对称轴与轴交于点D,试在对称轴上找出点P,使△CDP为等腰三角形,请直接写出满足条件的所有点P的坐标.(3)若点E是线段AB上的一个动点(与A、B不重合),分别连接AC、BC,过点E作EF∥AC交线段BC于点F,连接CE,记△CEF的面积为S,S是否存在最大值?若存在,求出S的最大值及此时E点的坐标;若不存在,请说明理由.7、如图,一次函数y =-4x -4的图象与x 轴、y 轴分别交于A 、C 两点,抛物线y =43x 2+bx +c 的图象经过A 、C 两点,且与x 轴交于点B . (1)求抛物线的函数表达式;(2)设抛物线的顶点为D ,求四边形ABDC 的面积;(3)作直线MN 平行于x 轴,分别交线段AC 、BC 于点M 、N .问在x 轴上是否存在点P ,使得△PMN 是等腰直角三角形?如果存在,求出所有满足条件的P 点的坐标;如果不存在,请说明理由.(二次函数与四边形)8、已知抛物线217222y x mx m =-+-. (1)试说明:无论m 为何实数,该抛物线与x 轴总有两个不同的交点;(2)如图,当该抛物线的对称轴为直线x =3时,抛物线的顶点为点C ,直线y =x -1与抛物线交于A 、B 两点,并与它的对称轴交于点D .①抛物线上是否存在一点P 使得四边形ACPD 是正方形?若存在,求出点P 的坐标;若不存在,说明理由; ②平移直线CD ,交直线AB 于点M ,交抛物线于点N ,通过怎样的平移能使得C 、D 、M 、N 为顶点的四边形是平行四边形.9、已知抛物线y=ax 2+bx+c 的对称轴为直线x=2,且与x 轴交于A 、B 两点.与y 轴交于点C .其中AI(1,0),C(0,—3).(1)求抛物线的解析式;(2)若点P 在抛物线上运动(点P 异于点A ).①如图l .当△PBC 面积与△ABC 面积相等时.求点P 的坐标;②如图2.当∠PCB=∠BCA 时,求直线CP 的解析式。
专题13 函数之一次函数、反比例函数和二次函数综合问题(压轴题)

《中考压轴题》专题13:函数之一次函数、反比例函数和二次函数问题一、选择题1.函数y=ax 2+1与a y x =(a≠0)在同一平面直角坐标系中的图象可能是【】A .B .C .D .2.二次函数2y ax b =+(b >0)与反比例函数a y x=在同一坐标系中的图象可能是【】A. B. C. D.3.函数a y x=与y=ax 2(a≠0)在同一平面直角坐标系中的图象可能是【】A. B. C. D.4.已知反比例函数k y x =的图像如图所示,则二次函数22y 2kx 4x k =-+的图像大致为【】A. B. C. D.5.已知反比例函数k y x =的图像如图所示,则二次函数22y 2kx 4x k =-+的图像大致为【】A. B. C. D.6.在平面直角坐标系中,函数y=x 2﹣2x (x≥0)的图象为C 1,C 1关于原点对称的图象为C 2,则直线y=a (a 为常数)与C 1、C 2的交点共有【】A.1个B.1个或2个C.个或2个或3个D.1个或2个或3个或4个7.函数k y x=与y=﹣kx 2+k (k≠0)在同一直角坐标系中的图象可能是【】A. B. C.D.8.已知a ≠0,在同一直角坐标系中,函数y ax =与2y ax =的图象有可能是【】A. B. C. D.9.一次函数()y ax b a 0=+≠、二次函数2y ax bx =+和反比例函数()k y k 0x=≠在同一直角坐标系中图象如图,A 点为(-2,0)。
则下列结论中,正确的是【】A .b 2a k =+B .a b k =+C .a b 0>>D .a k 0>>10.若正比例函数y=mx (m ≠0),y 随x 的增大而减小,则它和二次函数y=mx 2+m 的图象大致是【】11.如图,已知抛物线21y x 4x =-+和直线2y 2x =.我们约定:当x 任取一值时,x 对应的函数值分别为y 1、y 2,若y 1≠y 2,取y 1、y 2中的较小值记为M ;若y 1=y 2,记M=y 1=y 2.下列判断:①当x >2时,M=y 2;②当x <0时,x 值越大,M 值越大;③使得M 大于4的x 值不存在;④若M=2,则x=1.其中正确的有【】A .1个B .2个C .3个D .4个12.二次函数的图象如图所示,反比例函数与一次函数在同一平面直角坐标系中的大致图象是【】A .B .C .D .13.二次函数y=ax 2+bx+c (a ≠0)的图象如图所示,则函数a y x=与y=bx+c 在同一直角坐标系内的大致图象是【】A .B .C .D .二解答题1.如图①,双曲线kyx(k≠0)和抛物线y=ax2+bx(a≠0)交于A、B、C三点,其中B(3,1),C(﹣1,﹣3),直线CO交双曲线于另一点D,抛物线与x轴交于另一点E.(1)求双曲线和抛物线的解析式;(2)抛物线在第一象限部分是否存在点P,使得∠POE+∠BCD=90°?若存在,请求出满足条件的点P的坐标;若不存在,请说明理由;(3)如图②,过B作直线l⊥OB,过点D作DF⊥l于点F,BD与OF交于点N,求DNNB的值.2.已知抛物线l:y=ax2+bx+c(a,b,c均不为0)的顶点为M,与y轴的交点为N,我们称以N为顶点,对称轴是y轴且过点M的抛物线为抛物线l的衍生抛物线,直线MN为抛物线l的衍生直线.(1)如图,抛物线y=x2﹣2x﹣3的衍生抛物线的解析式是,衍生直线的解析式是;(2)若一条抛物线的衍生抛物线和衍生直线分别是y=﹣2x2+1和y=﹣2x+1,求这条抛物线的解析式;(3)如图,设(1)中的抛物线y=x2﹣2x﹣3的顶点为M,与y轴交点为N,将它的衍生直线MN先绕点N旋转到与x轴平行,再沿y轴向上平移1个单位得直线n,P是直线n上的动点,是否存在点P,使△POM 为直角三角形?若存在,求出所有点P的坐标;若不存在,请说明理由.3.在平面直角坐标系中,一次函数y=kx+b 的图象与x 轴、y 轴分别相交于A (﹣3,0),B (0,﹣3)两点,二次函数y=x 2+mx+n 的图象经过点A .(1)求一次函数y=kx+b 的解析式;(2)若二次函数y=x 2+mx+n 图象的顶点在直线AB 上,求m ,n 的值;(3)当﹣3≤x≤0时,二次函数y=x 2+mx+n 的最小值为﹣4,求m ,n 的值.4.在平面直角坐标系中,抛物线()2y x k 1x k =+--与直线y kx 1=+交于A,B 两点,点A 在点B 的左侧.(1)如图1,当k 1=时,直接写出....A ,B 两点的坐标;(2)在(1)的条件下,点P 为抛物线上的一个动点,且在直线AB 下方,试求出△ABP 面积的最大值及此时点P 的坐标;(3)如图2,抛物线()()2y x k 1x k k >0=+--与x 轴交于C ,D 两点(点C 在点D 的左侧).在直线y kx 1=+上是否存在唯一一点Q ,使得∠OQC=90°?若存在,请求出此时k 的值;若不存在,请说明理由.5.给定直线l :y=kx ,抛物线C :y=ax 2+bx+1.(1)当b=1时,l 与C 相交于A ,B 两点,其中A 为C 的顶点,B 与A 关于原点对称,求a 的值;(2)若把直线l 向上平移k 2+1个单位长度得到直线r ,则无论非零实数k 取何值,直线r 与抛物线C 都只有一个交点.①求此抛物线的解析式;②若P 是此抛物线上任一点,过P 作PQ ∥y 轴且与直线y=2交于Q 点,O 为原点.求证:OP=PQ .6.已知:直线y=ax+b 与抛物线2y ax bx c =-+的一个交点为A (0,2),同时这条直线与x 轴相交于点B ,且相交所成的角β为45°.(1)求点B 的坐标;(2)求抛物线2y ax bx c =-+的解析式;(3)判断抛物线2y ax bx c =-+与x 轴是否有交点,并说明理由.若有交点设为M ,N (点M 在点N 左边),将此抛物线关于y 轴作轴反射得到M 的对应点为E ,轴反射后的像与原像相交于点F ,连接NF ,EF 得△DEF ,在原像上是否存在点P ,使得△NEP 的面积与△NEF 的面积相等?若存在,请求出点P 的坐标;若不存在,请说明理由.7.如图,在△ABC中,4AB=5AC,AD为△ABC的角平分线,点E在BC的延长线上,EF⊥AD于点F,点G在AF上,FG=FD,连接EG交AC于点H.若点H是AC的中点,则AGFD的值为.8.某体育用品商店试销一款成本为50元的排球,规定试销期间单价不低于成本价,且获利不得高于40%.经试销发现,销售量y(个)与销售单价x(元)之间满足如图所示的一次函数关系.(1)试确定y与x之间的函数关系式;(2)若该体育用品商店试销的这款排球所获得的利润Q元,试写出利润Q(元)与销售单价x(元)之间的函数关系式;当试销单价定为多少元时,该商店可获最大利润?最大利润是多少元?(3)若该商店试销这款排球所获得的利润不低于600元,请确定销售单价x的取值范围.9.大学生小张利用暑假50天在一超市勤工俭学,被安排销售一款成本为40元/件的新型商品,此类新型商品在第x 天的销售量p 件与销售的天数x 的关系如下表:x (天)123...50p (件)118116114 (20)销售单价q (元/件)与x 满足:当1≤x <25时q=x+60;当25≤x≤50时1125q 40x=+.(1)请分析表格中销售量p 与x 的关系,求出销售量p 与x 的函数关系.(2)求该超市销售该新商品第x 天获得的利润y 元关于x 的函数关系式.(3)这50天中,该超市第几天获得利润最大?最大利润为多少?10.如图,已知直线AB :y kx 2k 4=++与抛物线21y x 2=交于A 、B 两点,(1)直线AB 总经过一个定点C ,请直接写出点C 坐标;(2)当1k 2=-时,在直线AB 下方的抛物线上求点P ,使△ABP 的面积等于5;(3)若在抛物线上存在定点D 使∠ADB =90°,求点D 到直线AB 的最大距离.11.某校八年级学生小丽、小强和小红到某超市参加了社会实践活动,在活动中他们参与了某种水果的销售工作.已知该水果的进价为8元/千克,下面是他们在活动结束后的对话.小丽:如果以10元/千克的价格销售,那么每天可售出300千克.小强:如果每千克的利润为3元,那么每天可售出250千克.小红:如果以13元/千克的价格销售,那么每天可获取利润750元.【利润=(销售价-进价) 销售量】(1)请根据他们的对话填写下表:销售单价x(元/kg)101113销售量y(kg)(2)请你根据表格中的信息判断每天的销售量y(千克)与销售单价x(元)之间存在怎样的函数关系.并求y(千克)与x(元)(x>0)的函数关系式;(3)设该超市销售这种水果每天获取的利润为W元,求W与x的函数关系式.当销售单价为何值时,每天可获得的利润最大?最大利润是多少元?12.如图,抛物线y=ax 2+bx+c 关于y 轴对称,它的顶点在坐标原点O ,点B (2,43-)和点C (﹣3,﹣3)两点均在抛物线上,点F (0,34-)在y 轴上,过点(0,34)作直线l 与x 轴平行.(1)求抛物线的解析式和直线BC 的解析式.(2)设点D (x ,y )是线段BC 上的一个动点(点D 不与B ,C 重合),过点D 作x 轴的垂线,与抛物线交于点G .设线段GD 的长度为h ,求h 与x 之间的函数关系式,并求出当x 为何值时,线段GD 的长度h 最大,最大长度h 的值是多少?(3)若点P (m ,n )是抛物线上位于第三象限的一个动点,连接PF 并延长,交抛物线于另一点Q ,过点Q 作QS ⊥l ,垂足为点S ,过点P 作PN ⊥l ,垂足为点N ,试判断△FNS 的形状,并说明理由;(4)若点A (﹣2,t )在线段BC 上,点M 为抛物线上的一个动点,连接AF ,当点M 在何位置时,MF+MA 的值最小,请直接写出此时点M 的坐标与MF+MA 的最小值.13.如图,直线y=﹣3x+3与x 轴、y 轴分别交于点A 、B ,抛物线()2y a x 2k =-+经过点A 、B ,并与x 轴交于另一点C ,其顶点为P .(1)求a ,k 的值;(2)抛物线的对称轴上有一点Q ,使△ABQ 是以AB 为底边的等腰三角形,求Q 点的坐标;(3)在抛物线及其对称轴上分别取点M 、N ,使以A ,C ,M ,N 为顶点的四边形为正方形,求此正方形的边长.14.如图,在平面直角坐标系中,O 为坐标原点,抛物线过2y ax bx c(a 0)=++≠过O 、B 、C 三点,B 、C 坐标分别为(10,0)和(185,245-),以OB 为直径的⊙A 经过C 点,直线l 垂直于x 轴于点B.(1)求直线BC 的解析;(2)求抛物线解析式及顶点坐标;(3)点M 是⊙A 上一动点(不同于O ,B ),过点M 作⊙A 的切线,交y 轴于点E ,交直线l 于点F ,设线段ME 长为m ,MF 长为n ,请猜想m n ⋅的值,并证明你的结论;(4)点P 从O 出发,以每秒1个单位速度向点B 作直线运动,点Q 同时从B 出发,以相同速度向点C 作直线运动,经过t(0<t)秒时恰好使△BPQ 为等腰三角形,请求出满足条件的t 值.15.在平面直角坐标系中,我们不妨把横坐标与纵坐标相等的点称为“梦之点”,例如点(﹣1,﹣1),(0,0),),…都是“梦之点”,显然,这样的“梦之点”有无数个.(1)若点P (2,m )是反比例函数ny x=(n 为常数,n≠0)的图象上的“梦之点”,求这个反比例函数的解析式;(2)函数y=3kx+s ﹣1(k ,s 是常数)的图象上存在“梦之点”吗?若存在,请求出“梦之点”的坐标;若不存在,请说明理由;(3)若二次函数y=ax 2+bx+1(a ,b 是常数,a >0)的图象上存在两个不同的“梦之点”A (x 1,x 1),B (x 2,x 2),且满足﹣2<x 1<2,|x 1﹣x 2|=2,令t=b 2﹣2b+15748,试求出t 的取值范围.16.已知抛物线()25k 2y x k 2x 4+=-++和直线()()2y k 1x k 1=+++.(1)求证:无论k 取何实数值,抛物线总与x 轴有两个不同的交点;(2)抛物线于x 轴交于点A 、B ,直线与x 轴交于点C ,设A 、B 、C 三点的横坐标分别是x 1、x 2、x 3,求x 1•x 2•x 3的最大值;(3)如果抛物线与x 轴的交点A 、B 在原点的右边,直线与x 轴的交点C 在原点的左边,又抛物线、直线分别交y 轴于点D 、E ,直线AD 交直线CE 于点G (如图),且CA•GE=CG•AB ,求抛物线的解析式.17.如图①,直线l :y=mx+n (m >0,n <0)与x ,y 轴分别相交于A ,B 两点,将△AOB 绕点O 逆时针旋转90°,得到△COD ,过点A ,B ,D 的抛物线P 叫做l 的关联抛物线,而l 叫做P 的关联直线.(1)若l :y=﹣2x+2,则P 表示的函数解析式为;若P :y=﹣x 2﹣3x+4,则l 表示的函数解析式为.(2)求P 的对称轴(用含m ,n 的代数式表示);(3)如图②,若l :y=﹣2x+4,P 的对称轴与CD 相交于点E ,点F 在l 上,点Q 在P 的对称轴上.当以点C ,E ,Q ,F 为顶点的四边形是以CE 为一边的平行四边形时,求点Q 的坐标;(4)如图③,若l :y=mx ﹣4m ,G 为AB 中点,H 为CD 中点,连接GH ,M 为GH 中点,连接OM .若OM=,直接写出l ,P 表示的函数解析式.18.如图,直线y=x ﹣4与x 轴、y 轴分别交于A 、B 两点,抛物线21y x bx c 3=++经过A 、B 两点,与x 轴的另一个交点为C ,连接BC .(1)求抛物线的解析式及点C 的坐标;(2)点M 在抛物线上,连接MB ,当∠MBA+∠CBO=45°时,求点M 的坐标;(3)点P 从点C 出发,沿线段CA 由C 向A 运动,同时点Q 从点B 出发,沿线段BC 由B 向C 运动,P 、Q 的运动速度都是每秒1个单位长度,当Q 点到达C 点时,P 、Q 同时停止运动,试问在坐标平面内是否存在点D ,使P 、Q 运动过程中的某一时刻,以C 、D 、P 、Q 为顶点的四边形为菱形?若存在,直接写出点D 的坐标;若不存在,说明理由.19.如图,抛物线y=-x2+bx+c交x轴于点A,交y轴于点B,已知经过点A,B的直线的表达式为y=x+3.(1)求抛物线的函数表达式及其顶点C的坐标;(2)如图①,点P(m,0)是线段AO上的一个动点,其中-3<m<0,作直线DP⊥x轴,交直线AB于D,交抛物线于E,作EF∥x轴,交直线AB于点F,四边形DEFG为矩形.设矩形DEFG的周长为L,写出L 与m的函数关系式,并求m为何值时周长L最大;(3)如图②,在抛物线的对称轴上是否存在点Q,使点A,B,Q构成的三角形是以AB为腰的等腰三角形?若存在,直接写出所有符合条件的点Q的坐标;若不存在,请说明理由.20.如图,已知直线l的解析式为1y x12=-,抛物线y=ax2+bx+2经过点A(m,0),B(2,0),D51,4⎛⎫⎪⎝⎭三点.(1)求抛物线的解析式及A点的坐标,并在图示坐标系中画出抛物线的大致图象;(2)已知点P(x,y)为抛物线在第二象限部分上的一个动点,过点P作PE垂直x轴于点E,延长PE与直线l交于点F,请你将四边形PAFB的面积S表示为点P的横坐标x的函数,并求出S的最大值及S最大时点P的坐标;(3)将(2)中S最大时的点P与点B相连,求证:直线l上的任意一点关于x轴的对称点一定在PB所在直线上.21.今年5月1日起实施《青海省保障性住房准入分配退出和运营管理实施细则》规定:公共租赁住房和廉租住房并轨运行(以下简称并轨房),计划10年内解决低收入人群住房问题.已知第x年(x为正整数)投入使用的并轨房面积为y百万平方米,且y与x的函数关系式为1y x56=-+.由于物价上涨等因素的影响,每年单位面积租金也随之上调.假设每年的并轨房全部出租完,预计第x年投入使用的并轨房的单位面积租金z与时间x满足一次函数关系如下表:时间x(单位:年,x为正整数)12345…单位面积租金z(单位:元/平方米)5052545658…(1)求出z与x的函数关系式;(2)设第x年政府投入使用的并轨房收取的租金为W百万元,请问政府在第几年投入使用的并轨房收取的租金最多,最多为多少百万元?22.如图,抛物线y=14x2+bx+c与x轴交于A(5,0)、B(﹣1,0)两点,过点A作直线AC⊥x轴,交直线y=2x于点C;(1)求该抛物线的解析式;(2)求点A关于直线y=2x的对称点A′的坐标,判定点A′是否在抛物线上,并说明理由;(3)点P是抛物线上一动点,过点P作y轴的平行线,交线段CA′于点M,是否存在这样的点P,使四边形PACM是平行四边形?若存在,求出点P的坐标;若不存在,请说明理由.23.如图,过A(1,0)、B(3,0)作x轴的垂线,分别交直线y=4﹣x于C、D两点.抛物线y=ax2+bx+c经过O、C、D三点.(1)求抛物线的表达式;(2)点M为直线OD上的一个动点,过M作x轴的垂线交抛物线于点N,问是否存在这样的点M,使得以A、C、M、N为顶点的四边形为平行四边形?若存在,求此时点M的横坐标;若不存在,请说明理由;(3)若△AOC沿CD方向平移(点C在线段CD上,且不与点D重合),在平移的过程中△AOC与△OBD 重叠部分的面积记为S,试求S的最大值.24.如图,在平面直角坐标系中,抛物线与x轴交于点A(﹣1,0)和点B(1,0),直线y=2x﹣1与y轴交于点C,与抛物线交于点C、D.(1)求抛物线的解析式;(2)求点A到直线CD的距离;(3)平移抛物线,使抛物线的顶点P在直线CD上,抛物线与直线CD的另一个交点为Q,点G在y轴正半轴上,当以G、P、Q三点为顶点的三角形为等腰直角三角形时,求出所有符合条件的G点的坐标.25.二次函数y=ax2+bx+c的图象经过点(﹣1,4),且与直线1y x12=-+相交于A、B两点(如图),A点在y轴上,过点B作BC⊥x轴,垂足为点C(﹣3,0).(1)求二次函数的表达式;(2)点N是二次函数图象上一点(点N在AB上方),过N作NP⊥x轴,垂足为点P,交AB于点M,求MN的最大值;(3)在(2)的条件下,点N在何位置时,BM与NC相互垂直平分?并求出所有满足条件的N点的坐标.26.如图,在平面直角坐标系中,抛物线2y ax bx 3=++与x 轴交于点A (﹣4,0),B (﹣1,0)两点.(1)求抛物线的解析式;(2)在第三象限的抛物线上有一动点D .①如图(1),若四边形ODAE 是以OA 为对角线的平行四边形,当平行四边形ODAE 的面积为6时,请判断平行四边形ODAE 是否为菱形?说明理由.②如图(2),直线1y x 32=+与抛物线交于点Q 、C 两点,过点D 作直线DF ⊥x 轴于点H ,交QC 于点F .请问是否存在这样的点D ,使点D 到直线CQ 的距离与点C 到直线DF :2?若存在,请求出点D 的坐标;若不存在,请说明理由.27.如图,已知一次函数11y x b 2=+的图象l 与二次函数22y x mx b =-++的图象'C 都经过点B (0,1)和点C ,且图象'C 过点A (52-,0).(1)求二次函数的最大值;(2)设使21y y >成立的x 取值的所有整数和为s ,若s 是关于x 的方程131x 0a 1x 3⎛⎫++= ⎪--⎝⎭的根,求a 的值;(3)若点F 、G 在图象'C 上,长度为5的线段DE 在线段BC 上移动,EF 与DG 始终平行于y 轴,当四边形DEFG 的面积最大时,在x 轴上求点P ,使PD+PE 最小,求出点P 的坐标.28.如图,已知直线y 3x 3=-+与x 轴交于点A ,与y 轴交于点C ,抛物线2y ax bx c =++经过点A 和点C ,对称轴为直线l :x 1=-,该抛物线与x 轴的另一个交点为B .(1)求此抛物线的解析式;(2)点P 在直线l 上,求出使△PAC 的周长最小的点P 的坐标;(3)点M 在此抛物线上,点N 在y 轴上,以A 、B 、M 、N 为顶点的四边形能否为平行四边形?若能,直接写出所有满足要求的点M 的坐标;若不能,请说明理由.29.如图,抛物线y=x2+bx+c与直线y=x﹣1交于A、B两点.点A的横坐标为﹣3,点B在y轴上,点P是y轴左侧抛物线上的一动点,横坐标为m,过点P作PC⊥x轴于C,交直线AB于D.(1)求抛物线的解析式;=2S△BPD;(2)当m为何值时,S四边形OBDC(3)是否存在点P,使△PAD是直角三角形?若存在,求出点P的坐标;若不存在,说明理由.30.已知:直线l:y=﹣2,抛物线y=ax2+bx+c的对称轴是y轴,且经过点(0,﹣1),(2,0).(1)求该抛物线的解析式;(2)如图①,点P是抛物线上任意一点,过点P作直线l的垂线,垂足为Q,求证:PO=PQ.(3)请你参考(2)中结论解决下列问题:(i)如图②,过原点作任意直线AB,交抛物线y=ax2+bx+c于点A、B,分别过A、B两点作直线l的垂线,垂足分别是点M、N,连结ON、OM,求证:ON⊥OM.(ii)已知:如图③,点D(1,1),试探究在该抛物线上是否存在点F,使得FD+FO取得最小值?若存在,求出点F的坐标;若不存在,请说明理由.31.如图,已知抛物线23y ax x c 2=-+与x 轴相交于A 、B 两点,并与直线1y x 22=-交于B 、C 两点,其中点C 是直线1y x 22=-与y 轴的交点,连接AC .(1)求抛物线的解析式;(2)证明:△ABC 为直角三角形;(3)△ABC 内部能否截出面积最大的矩形DEFG ?(顶点D 、E 、F 、G 在△ABC 各边上)若能,求出最大面积;若不能,请说明理由.32.对某一个函数给出如下定义:若存在实数M 0>,对于任意的函数值y ,都满足M y M -≤≤,则称这个函数是有界函数,在所有满足条件的M 中,其最小值称为这个函数的边界值.例如,下图中的函数是有界函数,其边界值是1.(1)分别判断函数()1y x 0x=>和()y x 14x 2=+-<≤是不是有界函数?若是有界函数,求其边界值;(2)若函数()y x 1a x b b a =-+≤≤>,的边界值是2,且这个函数的最大值也是2,求b 的取值范围;(3)将函数()2y x 1x m m 0=-≤≤≥,的图象向下平移m 个单位,得到的函数的边界值是t ,当m 在什么范围时,满足3t 14≤≤33.如图,抛物线2y x bx c =-++与x 轴交于A(-1,0),B(5,0)两点,直线3y x 34=-+与y 轴交于点C ,,与x 轴交于点D.点P 是x 轴上方的抛物线上一动点,过点P 作PF ⊥x 轴于点F ,交直线CD 于点E.设点P 的横坐标为m.(1)求抛物线的解析式;(2)若PE =5EF ,求m 的值;(3)若点E /是点E 关于直线PC 的对称点、是否存在点P ,使点E /落在y 轴上?若存在,请直接写出相应的点P 的坐标;若不存在,请说明理由.34.某公司销售一种进价为20元/个的计算机,其销售量y (万个)与销售价格x (元/个)的变化如下表:价格x (元/个)…30405060…销售量y (万个)…5432…同时,销售过程中的其他开支(不含造价)总计40万元.(1)观察并分析表中的y 与x 之间的对应关系,用所学过的一次函数,反比例函数或二次函数的有关知识写出y (万个)与x (元/个)的函数解析式.(2)求出该公司销售这种计算器的净得利润z (万个)与销售价格x (元/个)的函数解析式,销售价格定为多少元时净得利润最大,最大值是多少?(3)该公司要求净得利润不能低于40万元,请写出销售价格x (元/个)的取值范围,若还需考虑销售量尽可能大,销售价格应定为多少元?35.如图,直角梯形ABCO的两边OA,OC在坐标轴的正半轴上,BC∥x轴,OA=OC=4,以直线x=1为对称轴的抛物线过A,B,C三点.(1)求该抛物线线的函数解析式.=+,它与x轴的交于点G,在梯形ABCO的一边上取点P.(2)已知直线l的解析式为y x m①当m=0时,如图1,点P是抛物线对称轴与BC的交点,过点P作PH⊥直线l于点H,连结OP,试求△OPH的面积.=-时,过P点分别作x轴、直线l的垂线,垂足为点E,F.是否存在这样的点P,使以P,E,F ②当m3为顶点的三角形是等腰三角形?若存在,求出点P的坐标;若不存在,请说明理由.36.某公司经营杨梅业务,以3万元/吨的价格向农户收购杨梅后,分拣成A、B两类,A类杨梅包装后直接销售,B类杨梅深加工再销售.A类杨梅的包装成本为1万元/吨,根据市场调查,它的平均销售价格y (单位∶万元/吨)与销售数量x(x≥2)(单位∶吨)之间的函数关系式如图,B类杨梅深加工总费用s(单位:万元)与加工数量t(单位∶吨)之间的函数关系是s=12+3t,平均销售价格为9万元/吨.(1)直接写出A类杨梅平均销售价格y与销售量x这间的函数关系式;(2)第一次,该公司收购了20吨杨梅,其中A类杨梅x吨,经营这批杨梅所获得的毛利润为w万元(毛利润=销售总收人-经营总成本).①求w关于x的函数关系式;②若该公司获得了30万元毛利润,问∶用于直销的A类杨梅有多少吨?(3)第二次该公司准备投人132万元资金,请设计-种经营方案,使公司获得最大毛利润,并求出最大毛利润.37.如图,直角梯形ABCO的两边OA,OC在坐标轴的正半轴上,BC∥x轴,OA=OC=4,以直线x=1为对称轴的抛物线过A,B,C三点.(1)求该抛物线线的函数解析式.=+,它与x轴的交于点G,在梯形ABCO的一边上取点P.(2)已知直线l的解析式为y x m①当m=0时,如图1,点P是抛物线对称轴与BC的交点,过点P作PH⊥直线l于点H,连结OP,试求△OPH的面积.=-时,过P点分别作x轴、直线l的垂线,垂足为点E,F.是否存在这样的点P,使以P,E,F ②当m3为顶点的三角形是等腰三角形?若存在,求出点P的坐标;若不存在,请说明理由.38.已知函数23y kx 2x 2=-+(k 是常数)(1)若该函数的图像与x 轴只有一个交点,求k 的值;(2)若点()M 1,k 在某反比例函数的图像上,要使该反比例函数和二次函数23y kx 2x 2=-+都是y 随x 的增大而增大,求k 应满足的条件以及x 的取值范围;(3)设抛物线23y kx 2x 2=-+与x 轴交于()()12x ,0,B x A ,0两点,且12x x <,2212x x 1+=,在y 轴上,是否存在点P ,使△ABP 是直角三角形?若存在,求出点P 及△ABP 的面积;若不存在,请说明理由。
中考数学总复习《二次函数与一次函数的综合应用》练习题附带答案
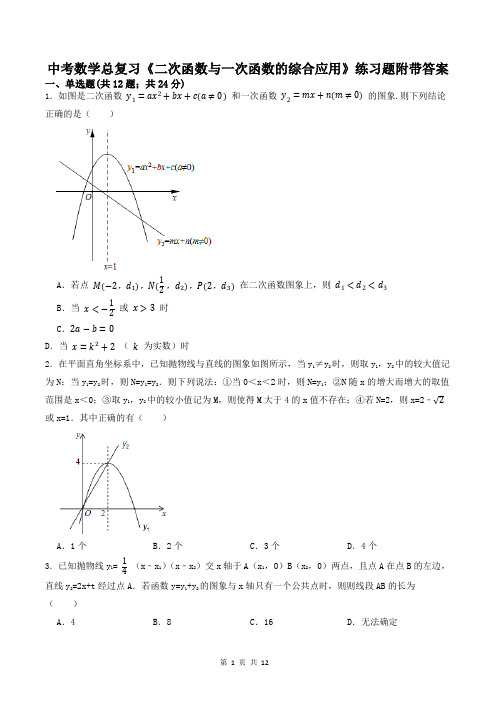
中考数学总复习《二次函数与一次函数的综合应用》练习题附带答案一、单选题(共12题;共24分)1.如图是二次函数 y 1=ax 2+bx +c(a ≠0) 和一次函数 y 2=mx +n(m ≠0) 的图象.则下列结论正确的是( )A .若点 M(−2,d 1),N(12,d 2),P(2,d 3) 在二次函数图象上,则 d 1<d 2<d 3B .当 x <−12或 x >3 时C .2a −b =0D .当 x =k 2+2 ( k 为实数)时2.在平面直角坐标系中,已知抛物线与直线的图象如图所示,当y 1≠y 2时,则取y 1,y 2中的较大值记为N ;当y 1=y 2时,则N=y 1=y 2.则下列说法:①当0<x <2时,则N=y 1;②N 随x 的增大而增大的取值范围是x <0;③取y 1,y 2中的较小值记为M ,则使得M 大于4的x 值不存在;④若N=2,则x=2﹣√2或x=1.其中正确的有( )A .1个B .2个C .3个D .4个3.已知抛物线y 1= 14(x ﹣x 1)(x ﹣x 2)交x 轴于A (x 1,0)B (x 2,0)两点,且点A 在点B 的左边,直线y 2=2x+t 经过点A .若函数y=y 1+y 2的图象与x 轴只有一个公共点时,则则线段AB 的长为( ) A .4B .8C .16D .无法确定4.如图,抛物线y =ax 2+bx +c 和直线y =kx +b 都经过点(﹣1,0),抛物线的对称轴为x =1,那么下列说法正确的是( )A .ac >0B .b 2﹣4ac <0C .k =2a +cD .x =4是ax 2+(b ﹣k )x +c <b 的解5.直线y=ax ﹣6与抛物线y=x 2﹣4x+3只有一个交点,则a 的值为( )A .a=2B .a=10C .a=2或a=﹣10D .a=2或a=106.如图是函数y =x 2+bx+c 与y =x 的图象,有下列结论:(1)b 2﹣4c >0;(2)b+c+1=0;(3)方程x 2+(b ﹣1)x+c =0的解为x 1=1,x 2=3;(4)当1<x <3时,则x 2+(b ﹣1)x+c <0.其中正确结论的个数为( ) A .1B .2C .3D .47.在直角坐标系中,直线y=x+2和抛物线y=x 2-x+1的若干组函数值如下表所示:x … 1 1.5 2 2.5 3 … y=x+2 … 3 3.5 4 4.5 6 … y=x 2-x+1…11.7534.7513…A .1<x<1.5B .1.5<Xx2C .2<x<2.5D .2.5<x<38.割圆术是我国古代数学家刘徽创造的一种求周长和面积的方法:随着圆内接正多边形边数的增加,它的周长和面积越来越接近圆周长和圆面积,“割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体而无所失矣”.刘徽就是大胆地应用了以直代曲、无限趋近的思想方法求出了圆周率.请你也用这个方法求出二次函数 y=14(x −4)2的图象与两坐标轴所围成的图形最接近的面积是( )A .5B .225C .4D .17﹣4π9.如图,“心”形是由抛物线 y =−x 2+6和它绕着原点O ,顺时针旋转60°的图形经过取舍而成的,其中顶点C 的对应点为D ,点A ,B 是两条抛物线的两个交点,直线AB 为“心”形对称轴,点E ,F ,G 是抛物线与坐标轴的交点,则AB=( )A .6√3B .8C .10D .10√310.已知一次函数y=ax+c 与二次函数y=ax 2+bx+c ,它们在同一坐标系内的大致图象是( )A .B .C .D .11.如图,抛物线y =﹣x 2+4x ﹣3与x 轴交于点A 、B ,把抛物线在x 轴及其上方的部分记作C 1,将C 1向右平移得到C 2,C 2与x 轴交于B 、D 两点.若直线y =kx ﹣k 与C 1、C 2共有3个不同的交点,则k 的最大值是( )A .12B .2 √5 ﹣6C .6+4 √2D .6﹣4 √212.在平面直角坐标系中,已知点 A(−1,4) , B(2,1) 直线 AB 与 x 轴和 y 轴分别交于点 M ,N 若抛物线 y =x 2−bx +2 与直线 AB 有两个不同的交点,其中一个交点在线段 AN 上(包含 A , N 两个端点),另一个交点在线段 BM 上(包含 B , M 两个端点),则 b 的取值范围是( )A.1≤b≤52B.b≤1或b≥52C.52≤b≤113D.b≤52或b≥113二、填空题(共6题;共6分)13.如图,抛物线y=ax2﹣2与y轴交于点A,过点A与x轴平行的直线交抛物线y=﹣12 x2于点B,C,则S△BOC= .14.在平面直角坐标系xOy中,函数y1=x(x<m)的图象与函数y2=x2(x≥m)的图象组成图形G.对于任意实数n,过点P(0,n)且与x轴平行的直线总与图形G有公共点,写出一个满足条件的实数m的值为(写出一个即可).15.如图,抛物线y=ax2+bx+1的顶点在直线y=kx+1上,对称轴为直线x=1,以下四个结论:①ab<0;②b<13;③a=−k;④当0<x<1其中正确的是.(填序号)16.如图,抛物线y=x2﹣2x+k与x轴交于A、B两点,与y轴交于点C(0,﹣3).若抛物线y=x2﹣2x+k上有点Q,使△BCQ是以BC为直角边的直角三角形,则点Q的坐标为.17.已知抛物线p :y=ax 2+bx+c 的顶点为C ,与x 轴相交于A 、B 两点(点A 在点B 左侧),点C 关于x轴的对称点为C ′,我们称以A 为顶点且过点C ′,对称轴与y 轴平行的抛物线为抛物线p 的“梦之星”抛物线,直线AC ′为抛物线p 的“梦之星”直线.若一条抛物线的“梦之星”抛物线和“梦之星”直线分别是y=x 2+2x+1和y=2x+2,则这条抛物线的解析式为 .18.如图,抛物线y=13x 2﹣4√33x+3与x 轴交于A ,B 两点,与y 轴交于点C ,点M 的坐标为(2√3,1).以M 为圆心,2为半径作⊙M .则下列说法正确的是 (填序号). ①tan ∠OAC=√3; ②直线AC 是⊙M 的切线; ③⊙M 过抛物线的顶点; ④点C 到⊙M 的最远距离为6;⑤连接MC ,MA ,则△AOC 与△AMC 关于直线AC 对称.三、综合题(共6题;共73分)19.在平面直角坐标系中,已知A ,B 是抛物线y=ax 2(a >0)上两个不同的点,其中A 在第二象限,B 在第一象限.(1)如图1所示,当直线AB 与x 轴平行,∠AOB=90°,且AB=2时,则求此抛物线的解析式和A ,B 两点的横坐标的乘积;(2)如图2所示,在(1)所求得的抛物线上,当直线AB 与x 轴不平行,∠AOB 仍为90°时,则求证:A、B两点横坐标的乘积是一个定值;(3)在(2)的条件下,如果直线AB与x轴、y轴分别交于点P、D,且点B的横坐标为1 2.那么在x轴上是否存在一点Q,使△QDP为等腰三角形?若存在,请直接写出点Q的坐标;若不存在,请说明理由.20.某公司成功开发出一种产品,正式投产后,生产成本为5元/件.公司按订单生产该产品(销售量=产量),年销售量y(万件)与售价x(元/件)之间满足如图1所示的函数关系,公司规定产品售价不超过15元/件,受产能限制,年销售量不超过30万件;为了提高该产品竞争力,投入研发费用P 万元(P万元计入成本),P与x之间的函数关系式如图2所示,当10≤x≤15时可看成抛物线P= 14x2−4x+m.(1)求y与x之间的函数关系式.(2)求这种产品年利润W(万元)与售价x(元/件)满足的函数关系式.(3)当售价x为多少元时,则年利润W最大,并求出这个最大值.21.如图,抛物线y=ax2+32 x+c(a≠0)与x轴交于点A,B两点,其中A(-1,0),与y轴交于点C(0,2).(1)求抛物线的表达式及点B坐标;(2)点E是线段BC上的任意一点(点E与B、C不重合),过点E作平行于y轴的直线交抛物线于点F,交x轴于点G.①设点E的横坐标为m,用含有m的代数式表示线段EF的长;②线段EF长的最大值是.22.已经二次函数y=ax2+bx+1 .(1)如图,其图象与x轴交于点A(−1,0)和点B,与y轴交于点C,对称轴为直线x=1 .①求二次函数解析式;②F为线段BC上一点,过F分别作x轴,y轴垂线,垂足分别为E、F,当四边形OEFG为正方形时,则求点F坐标;(2)其图象上仅有一个点的横坐标、纵坐标互为相反数,且二次函数y=ax2+bx+1函数值存在负数,求b的取值范围.23.定义符号min{a,b}的含义为:当a≥b时,则min{a,b}=b;当a<b时,则min{a,b}=a.如:min{1,﹣2}=﹣2,min{﹣1,2}=﹣1.(1)求min{x2﹣1,﹣2};(2)已知min{x2﹣2x+k,﹣3}=﹣3,求实数k的取值范围;(3)已知当﹣2≤x≤3时,则min{x2﹣2x﹣15,m(x+1)}=x2﹣2x﹣15.直接写出实数m的取值范围.24.某企业研发了一种新产品,已知这种产品的成本为30元/件,且年销售量y(万件)与售价x(元/件)的函数关系式为y={−2x+140,(40≤x<60)−x+80.(60≤x≤70)(1)当售价为60元/件时,则年销售量为万件;(2)当售价为多少时,则销售该产品的年利润最大?最大利润是多少?(3)若销售该产品的年利润不少于750万元,直接写出x的取值范围.参考答案1.【答案】D 2.【答案】B 3.【答案】B 4.【答案】D 5.【答案】C 6.【答案】B 7.【答案】C 8.【答案】A 9.【答案】A 10.【答案】C 11.【答案】C 12.【答案】C 13.【答案】414.【答案】1(答案不唯一) 15.【答案】①③④16.【答案】(1,﹣4)和(﹣2,5) 17.【答案】y=x 2﹣2x ﹣3 18.【答案】①②③④ 19.【答案】(1)解:如图1作BE ⊥x 轴∴△AOB 是等腰直角三角形 ∴BE=OE= 12AB=1∴A (﹣1,1),B (1,1)∴A ,B 两点的横坐标的乘积为﹣1×1=﹣1∵抛物线y=ax 2(a >0)过A ,B ∴a=1 ∴抛物线y=x 2 (2)解:如图2作BN ⊥x 轴,作AM ⊥x 轴 ∴∠AOB=AMO=∠BNO=90° ∴∠MAO=∠BON ∴△AMO ∽△ONB ∴AM ON =OM BN ∴AM ×BN=OM ×ON设A (x 1,y 1),B (x 2,y 2)在抛物线上 ∴AM=y 1=x 12,BN=y 2=x 22,OM=﹣x 1,ON=x 2 ∴x 12×x 22=﹣x 1×x 2 ∴x 1×x 2=﹣1∴A ,B 两点横坐标的乘积是一个定值;(3)解:由(2)得,A ,B 两点横坐标的乘积是一个定值为﹣1,∵点B 的横坐标为 12,∴点A 的横坐标为﹣2,∵A ,B 在抛物线上,∴A (﹣2,4),B ( 12 , 14 ),∴直线AB 解析式为y=﹣ 32x+1,∴P ( 23 ,0),D (0,1)设Q (n ,0),∴DP 2= 139 ,PQ 2=(n ﹣ 23)2,DQ 2=n 2+1∵△QDP 为等腰三角形∴①DP=PQ ,∴DP 2=PQ 2,∴139 =(n ﹣ 23 )2,∴n= 2±√133 ,∴Q 1( 2+√133 ,0),Q 2( 2−√133 ,0)②DP=DQ ,∴DP 2=DQ 2,∴139 =n 2+1,∴n= 23 (舍)或n=﹣ 23 ,Q 3(﹣ 23 ,0)③PQ=DQ ,∴PQ 2=DQ 2,∴(n ﹣ 23 )2=n 2+1∴n=﹣ 512 ,∴Q4(﹣ 512 ,0),∴存在点Q 坐标为Q 1( 2+√133 ,0),Q 2(2−√133 ,0),Q 3(﹣ 23 ,0),Q4(﹣ 512 ,0)20.【答案】(1)解:设y 与x 的函数关系式为:y=kx+b将点(5,30),(15,10)代入可得:{30=5k +b 10=15k +b解得:{b =40k =−2∴y 与x 的函数关系式为:y=-2x+40(5≤x ≤15); (2)解:当5≤x ≤10时,则根据图像可得:P=60 ∴W=(x-5)y-P=(x-5)(-2x+40)-60=-2x 2+50x-260;当10≤x ≤15时,则P =14x 2−4x +m由图可得经过点(10,60),将其代入可得:60=14×102−4×10+m 解得:m=75∴P =14x 2−4x +75;∴W=(x-5)y-P=(x-5)(-2x+40)-(14x 2−4x +75)=−94x 2+54x −275;综上:W ={−2x 2+50x −260(5≤x ≤10)−94x 2+54x −275(10≤x ≤15);(3)解:由(2)可得:当5≤x ≤10时W=-2x 2+50x-260=-2(x −252)2+1052∴x =252不在5≤x <10,由于开口向下在5≤x <10内随x 增大而增大 在x=10时,则取得最大值为W=40; 当10≤x ≤15时W=−94x 2+54x −275对称轴为x=−b2a=12 由于函数开口向下 ∴当x=12时,则W=49∴当x=12时,则W 取得最大值为49;综上可得:当售价为12元时,则年利润最大,最大为49万元.21.【答案】(1)解:将A(-1,0)、 C(0,2)代入y =ax 2+ 32x +c (a ≠0)得:a =- 12, c =2y =- 12 x 2+ 32x +2 当y =0时,则x 1=-1,x 2=4,故B(4,0)(2)解:设直线BC 的函数表达式为y =kx +b ,将B(4,0)、 C(0,2)代入 得:y =- x +2,EF =FG -GE =- m 2+ m +2-(- m +2) =- m 2+2m ;2 22.【答案】(1)解:①由题: {a −b +1=0−b 2a =1 解得 {a =−13b =23∴ 二次函数解析式为: y =−13x 2+23x +1 ; ②设BC 解析式为: y =kx +b 对称轴为直线 x =1 .∵ 图象与x 轴交于点 A(−1,0) 和点B ,对称轴为直线 x =1 .∴ 点 B(3,0)将 B(3,0) , C(0,1) 代入得: {3k +b =0b =1解得: {a =−13b =1∴BC 解析式为: y =−13x +1 设点 F(m,−13m +1) ∵ 四边形 OEFG 是正方形∴EF =GF∴m =−13m +1解得 m =34∴F(34,34) (2)解:二次函数的图象其有且只有一个点横、纵坐标之和互为相反数∴−x =ax 2+bx +1 有两相等实根,即 ax 2+(b +1)x +1=0 有两相等实根 ∴{a ≠0(b +1)2−4a =0解得: a =(b+1)24>0 ,且 b ≠−1 ∵y =ax 2+bx +1 存在负值∴b 2−4a =b 2−(b +1)2>0 ,解得 b <−12综上: b <−12且 b ≠−123.【答案】(1)解:∵x2≥0∴x2﹣1≥﹣1∴x2﹣1>﹣2.∴min{x2﹣1,﹣2}=﹣2(2)解:∵x2﹣2x+k=(x﹣1)2+k﹣1∴(x﹣1)2+k﹣1≥k﹣1.∵min{x2﹣2x+k,﹣3}=﹣3∴k﹣1≥﹣3.∴k≥﹣2(3)解:对于y=x2﹣2x﹣15,当x=﹣2时,则y=﹣7当x=3时,则y=﹣12由题意可知抛物线y=x2﹣2x﹣15与直线y=m(x+1)的交点坐标为(﹣2,﹣7),(3,﹣12)所以m的范围是:﹣3≤m≤7.24.【答案】(1)20(2)解:设销售该产品的年利润为W万元当40≤x<60时W=(x−30)(−2x+140)=−2(x−50)2+800 .∵-2<0∴当x=50时W最大=800当60≤x≤70时W=(x−30)(−x+80)=−(x−55)2+625∵−1<0∴当x=60时W最大=600∵800>600∴当x=50时W最大=800∴当售价为50元/件时,则年销售利润最大,最大为800万元.(3)解:45≤x≤55理由如下:由题意得(x−30)(−2x+140)≥750解得45≤x≤55。
2023年中考数学专题复习——二次函数与一次函数的综合

2023年中考数学专题——二次函数与一次函数的综合一、综合题1.如图,二次函数的图象与x 轴交于A (-3,0)和B (1,0)两点,交y 轴于点C (0,3),点C 、D 是二次函数图象上的一对对称点,一次函数的图象过点B 、D .(1)求二次函数的解析式;(2)根据图象直接写出使一次函数值大于二次函数值的x 的取值范围;2.已知一次函数y=x+4的图象与二次函数y=ax (x ﹣2)的图象相交于A (﹣1,b )和B ,点P 是线段AB 上的动点(不与A 、B 重合),过点P 作PC⊥x 轴,与二次函数y=ax (x ﹣2)的图象交于点C .(1)求a 、b 的值(2)求线段PC 长的最大值;(3)若⊥PAC 为直角三角形,请直接写出点P 的坐标.3.如图,已知一次函数 3y kx =+ 的图象与 x 轴交于 ()30A ,,与 y 轴交于点 B .(1)求一次函数的解析式和点 B 的坐标;(2)若二次函数 2---y x bx c = 的图象经过点 A , B ,结合函数的图象,直接写出不等式2---3x bx c kx >+ 的解集.4.如图,二次函数 26y x x n =++ 的图象与y 轴交于点C ,点B 在抛物线上,且与点C 关于抛物线的对称轴对称,已知一次函数y=kx+b 的图象经过该二次函数图象上的点A (﹣2,0)及点B .(1)求二次函数与一次函数的解析式;(2)根据图象,写出满足 26x x n ++ ≤kx+b 的x 的取值范围.5.如图,二次函数的图象与x 轴交于A (-3,0)和B (1,0)两点,交y 轴于点C(,3),点C 、D 是二次函数图象上的一对对称点,一次函数的图象过点B 、D .(1)请直接写出D 点的坐标; (2)求二次函数的解析式;(3)根据图象直接写出使一次函数值大于二次函数值的x 的取值范围.6.如图,已知抛物线y=x 2﹣(m+3)x+9的顶点C 在x 轴正半轴上,一次函数y=x+3与抛物线交于A 、B 两点,与x 、y 轴交于D 、E 两点.(1)求m 的值.(2)求A 、B 两点的坐标.(3)点P (a ,b )(﹣3<a <1)是抛物线上一点,当⊥PAB 的面积是⊥ABC 面积的2倍时,求a ,b 的值.7.如图,一次函数y=﹣12x+2分别交y 轴、x 轴于A ,B 两点,抛物线y=﹣x 2+bx+c 过A ,B 两点.(1)求这个抛物线的解析式;(2)作垂直于x 轴的直线x=t ,在第一象限交直线AB 于M ,交这个抛物线于N .求当t 取何值时,⊥NAB 的面积有最大值?最大值是多少?(3)在(2)的情况下,以A 、M 、N 、D 为顶点作平行四边形,求第四个顶点D 的坐标.8.如图,二次函数y=(x-2)2+m 的图象与y 轴交于点C ,点B 是点C 关于该二次函数图象的对称轴对称的点,已知一次函数y=kx+b 的图象上的点A (1,0)及B.(1)求二次函数与一次函数的解析式;(2)根据图象,写出满足kx+b≤(x-2)2+m 的x 的取值范围.9.如图,二次函数y=x 2+bx+c (a≠0)的图象经过点A (1,0)且与y 轴交卡点C,点B和点C 关于该二次函数图象的对称轴直线x=2对称,一次函数y=kx+b 的图象经过点A 及点B.(1)求二次函数与一次函数的解析式;(2)根据图象,直接写出不等式kx+b≤x 2+bx+c 的解集.10.如图,二次函数y=(x+2)2+m 的图象与y 轴交于点C ,点B 在抛物线上,且与点C 关于抛物线的对称轴对称,已知一次函数y=kx+b 的图象经过该二次函数图象上的点A (﹣1,0)及点B .(1)求二次函数与一次函数的解析式;(2)根据图象,写出满足(x+2)2+m≥kx+b 的x 的取值范围.11.如图,二次函数的图象与 x 轴交于点 ()30A -,, ()10B , ,交 y 轴于点 ()03C , ,点 C , D 是二次函数图象上关于抛物线对称轴的一对对称点,一次函数的图象过点 B , D .(1)请直接写出点 D 的坐标; (2)求二次函数的解析式;(3)根据图象直接写出一次函数值大于二次函数值的 x 的取值范围.12.如图,已知抛物线 2y x bx c =++ 的顶点坐标为(2,-1),与x 轴交于A ,B 两点(点A 在点B 的左边).与y 轴交于点C ,一次函数y=kx+c 经过点B 和点C .(1)求点B 的坐标·(2)根据图象,直接写出不等式kx+c≤x 2+bx+c 的解集.13.如图,二次函数y 2=ax 2+bx+3的图象与x 轴相交于点A(−3,0)、B(1,0),交y 轴于点C,C 、D 是二次函数图象上的一对对称点,一次函数y 1=mx+n 的图象经过B.D 两点.(1)求a 、b 的值及点D 的坐标;(2)根据图象写出y 2>y 1时,x 的取值范围.14.如图,二次函数 2y=(x+2)+m 的图象与y 轴交于点C,点B在抛物线上,且与点C关于抛物线的对称轴对称,已知一次函数y=kx+b 的图象经过该二次函数图象上的点A(−1,0)及点B.(2)根据图象,写出满足 2(x+2)+m kx+b ≥ 的x 的取值范围。
2023年中考高频数学专题练习--二次函数与一次函数的综合

2023年中考高频数学专题练习--二次函数与一次函数的综合1.平面直角坐标系 xOy 中, O 是坐标原点。
已知A(0, 52 ),B(1,0),C (6, 52),有一抛物线恰好经过这三点.(1)求该抛物线解析式;(2)若抛物线交 x 轴的另一交点为D ,那么抛物线上是否存在一点P ,使得POB CBD ∠=∠ ,若存在,求出P 的坐标,若不存在,请说明理由。
2.如图, 21y ax bx =+ 的图像交x 轴于O 点和A 点,将此抛物线绕原点旋转180°得图像y 2,y 2与x 轴交于O 点和B 点.(1)若y 1=2x 2-3x ,则y 2= .(2)设 y 1 的顶点为C ,则当△ABC 为直角三角形时,请你任写一个符合此条件的 y 1 的表达式 .3.如图,抛物线 28(0)y ax bx a =++≠ 与x 轴交于点 (2,0)A - 和点 (8,0)B ,与y 轴交于点C ,顶点为D ,连接AC ,BC ,BC 与抛物线的对称轴l 交于点E .(1)求抛物线的表达式;(2)点P是第一象限内抛物线上的动点,连接PB,PC,当35PBC ABCS S∆∆=时,求点P的坐标.4.已知:如图,抛物线y=ax2+4x+c经过原点O(0,0)和点A (3,3),P为拋物线上的一个动点,过点P作x轴的垂线,垂足为B(m,0),并与直线OA交于点C。
(1)求抛物线的解析式;(2)当点P在直线OA上方时,求线段PC的最大值。
5.如图所示,已知抛物线y= 13x2+bx+c经过点A(-1,0),B(5,0).(1)求抛物线的解析式并写出顶点M的坐标;(2)若点C在抛物线上,且点C的横坐标为8,求四边形AMBC的面积.6.如图,已知二次函数y=﹣x2+bx+c的图象经过点A(﹣2,0),B(6,0),与y轴交于点C.(1)求抛物线的解析式;(2)抛物线的对称轴上是否存在点P,使△PAB=△ABC,若存在请直接写出点P的坐标,若不存在,请说明理由.7.如图,抛物线y=ax2+bx﹣4(a≠0)与x轴交于A(4,0),B(﹣1,0)两点,过点A的直线y=﹣x+4交抛物线于点C.(1)求此抛物线的解析式;(2)在直线AC上有一动点E,当点E在某个位置时,使△BDE的周长最小,求此时E点坐标.8.如图,二次函数y=ax2+bx+c的图象与x轴交于A、B两点,其中A点坐标为(-1,0),点C(0,5),另抛物线经过点(1,8),M为它的顶点.(1)求抛物线的解析式(2)求△MCB的面积S△MCB.9.如图,抛物线y=-x2+bx+c的顶点为C(3,4),交x轴于点A,B(点B在点A的右侧),点P在第一象限,且在抛物线AC 部分上,PD△PC 交x 轴于点D 。
精品中考数学 一次函数与二次函数综合练习题

三 函数3.1 一次函数例1.已知一次函数物图象经过A(-2,-3),B(1,3)两点.(1)求这个一次函数的解析式;(2)试判断点P(-1,1)是否在这个一次函数的图象上;(3)求此函数与x 轴、y 轴围成的三角形的面积.例2.已知21y y y +=,y 1与 x 成正比例,y 2与x 成反比例,并且当x=2时,y=6;当 x=3时,y=5,求y 与x 的函数关系式。
课堂练习:1.点P 在第二象限内,P 到x 轴的距离是4,到y 轴的距离是3,那么点P 的坐标为( ) A.(-4,3) B.(-3,-4) C.(-3,4) D.(3,-4)2.已知函数y kx b =+的图象如图,则2y kx b =+的图象可能是( )3.如图,点A 的坐标为(-1,0),点B 在直线y=x 上运动,当线段AB 最短时,点B 的坐标为 ( )A.(0,0)B.(22,22-) C.(-21,-21) D.(-22,-22) 4.已知整数x 满足-5≤x ≤5,y 1=x+1,y 2=-2x+4对任意一个x ,m 都取y 1,y 2中的较小值,则m 的最大值是( )A.1B.2C.24D.-95.将点P(5,3)向左平移4个单位,再向下平移1个单位后,落在函数y=kx-2的图象上,则k 的值为( ) A.k=2 B.k=4 C.k=15 D.k=366.如图(1),在直角梯形ABCD 中,动点P 从点B 出发,沿BC ,CD 运动至点D 停止.设点P 运动的路程为x ,△ABP 的面积为y ,如果y 关于x 的函数图象如图(2)所示,则△BCD 的面积是( )A.3B.4C.5D.67.如图,在中学生耐力测试比赛中,甲、乙两学生测试的路程s (米)与时间t (秒)之间的函数关系的图象分别为折线OABC 和线段OD ,下列说法正确的是( )A.乙比甲先到终点B.乙测试的速度随时间增加而增大C.比赛到29.4秒时,两人出发后第一次相遇D.比赛全程甲测试速度始终比乙测试速度快8.如图,已知点F 的坐标为(3,0),点A 、B 分别是某函数图象与x 轴、y 轴的交点,点P 是此图象上的一动点,设点P 的横坐标为x,PF 的长为d,且d 与x 之间满足关系:)50(535≤≤-=x x d ,则结论: (1)AF=2;(2)BF=4;(3)OA=5;(4)OB=3,正确结论的序号是( )A.(1)(2)(3)B. (1)(3)C.(1)(2)(4)D.(3)(4)9.一电工沿着如图所示的梯子NL 往上爬,当他爬到中点M 处时,由于地面太滑,梯子沿墙面与地面滑下,设点M 的坐标为(x ,y )(x>0),则y 与x 之间的函数关系用图象表示大致是( )10.如果直线方程ax+by+c=0中,a <0,b <0且bc <0,则此直线经过第________象限.11.如图,一个正比例函数的图象和一个一次函数的图象交于点 A (-1,2),且△ABO 的面积为 5,求这两个函数的解析式。
