习题word版:第26章 二次函数
初四数学第26章二次函数测试

初四数学第26章(二次函数)检测卷一、选择题:1、已知二次函数c bx ax y ++=2的图象如右图所示,则a、b、c满足( ) A 、a <0,b <0,c >0 B 、 a <0,b <0, c <0 C 、 a <0,b >0,c >0 D 、a >0,b <0,c >02、下列抛物线,对称轴是直线x=12 的是( )A 、y=12x2 B 、y=x2+2xC 、y=x2+x+2 D 、y=x2-x-23、如图,如果函数y =kx +b 的图像在第一、二、三象限内,那么函数y =kx 2+bx -1的图像大致是( )4、如图所示,二次函数y=x 2-4x+3的图象交x轴于A 、B 两点,交y 轴于点C, 则△ABC 的面积为( ) A 、6 B 、4 C 、3 D 、15、二次函数221y x x =-+与x 轴的交点个数是( )A 、0B 、1C 、2D 、36、在同一坐标系中一次函数y ax b =+和二次函数2y ax bx =+的图象可能为( )二、填空题:7、如图所示的抛物线是二次函数2231y ax x a =-+-的图象,那么a 的值是 ;8、已知二次函数22y x x m =-++的部分图象如图所示,则关于x 的一元二次方程220x x m -++=的解xBAC y O题9题8为 ;9、已知二次函数2y ax bx c =++的图象如图所示,则点()P a bc ,在第 象限; 10、小敏在某次投篮中,球的运动路线是抛物线 y=-51x 2+3.5的一部分(如图),若命中篮圈中心, 则他与篮底的距离l 是 。
三、解答题:11、已知一抛物线与x 轴的交点是)0,2(-A 、B (1,0),且经过点C (2,8)。
(1)求该抛物线的解析式;(2)求该抛物线的顶点坐标。
12、在直角坐标平面内,二次函数图象的顶点为(14)A -,,且过点(30)B ,. (1)求该二次函数的解析式;(2)将该二次函数图象向右平移几个单位,可使平移后所得图象经过坐标原点?并直接写出平移后所得图象与x 轴的另一个交点的坐标.13、二次函数2(0)y ax bx c a =++≠的图象如图所示,根据图象解答下列问题: (1)写出方程20ax bx c ++=的两个根.(2分) (2)写出不等式20ax bx c ++>的解集.(2分)(3)写出y 随x 的增大而减小的自变量x 的取值范围.(2分)(4)若方程2ax bx c k ++=有两个不相等的实数根,求k 的取值范围.(4分)x)14、某商场销售一批名牌衬衫,平均每天可售出20件,每件盈利40元,为了扩大销售,增加盈利,尽快减少库存,商场决定采取适当的降价措施.经调查发现每件衬衫降价1元, 商场平均每天可多售出2件: (1)若商场平均每天要盈利1200元,每件衬衫要降价多少元, (2)每件衬衫降价多少元时,商场平均每天盈利最多?15、如图,一元二次方程2230x x +-=的二根12x x ,(12x x <)是抛物线2y ax bx c =++与x 轴的两个交点B C ,的横坐标,且此抛物线过点(36)A ,. (1)求此二次函数的解析式.(2)设此抛物线的顶点为P ,对称轴与线段AC 相交于点Q ,求点P 和点Q 的坐标. (3)在x 轴上有一动点M ,当MQ MA +取得最小值时,求M 点的坐标.。
初三数学26章二次函数小题训练练习测试
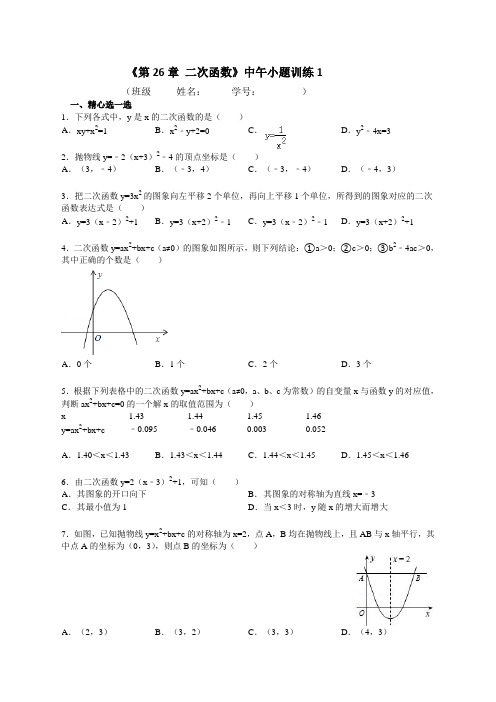
《第26章二次函数》中午小题训练1(班级姓名:学号:)一、精心选一选3.把二次函数y=3x2的图象向左平移2个单位,再向上平移1个单位,所得到的图象对应的二次4.二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论:①a>0;②c>0;③b2﹣4ac>0,其中正确的个数是()5.根据下列表格中的二次函数y=ax2+bx+c(a≠0,a、b、c为常数)的自变量x与函数y的对应值,227.如图,已知抛物线y=x2+bx+c的对称轴为x=2,点A,B均在抛物线上,且AB与x轴平行,其中点A的坐标为(0,3),则点B的坐标为()二、细心填一填(2,3,4,5写过程)1.如图,是二次函数y=ax2+bx+c图象的一部分,其对称轴为直线x=1,若其与x轴一交点为A(3,0),则由图象可知,不等式ax2+bx+c<0的解集是_________.2.将抛物线:y=x2﹣2x向上平移3个单位,再向右平移4个单位得到的抛物线是_________.3.将抛物线y=2x2﹣12x+10绕它的顶点旋转180°,所得抛物线的解析式是_________..已知函数y=(k﹣3)x2+2x+1的图象与x轴有交点,则k的取值范围是?5.y=﹣2x2﹣bx+3的对称轴是直线x=1,则b的值为_________.三、解答题1.已知二次函数y=﹣x2+bx+c的图象如图所示,它与x轴的一个交点坐标为(﹣1,0),与y轴的交点坐标为(0,3).(1)求出b,c的值,并写出此二次函数的解析式;(2)根据图象,写出函数值y为正数时,自变量x的取值范围.2.如图,已知二次函数y=ax2﹣4x+c的图象与坐标轴交于点A(﹣1,0)和点B(0,﹣5).(1)求该二次函数的解析式;(2)已知该函数图象的对称轴上存在一点P,使得△ABP的周长最小.请求出点P的坐标.3.随着近几年城市建设的快速发展,对花木的需求量逐年提高.某园林专业户计划投资种植花卉及树木,根据市场调查与预测,种植树木的利润y1与投资量x成正比例关系,如图①所示;种植花卉的利润y2与投资量x成二次函数关系,如图②所示(注:利润与投资量的单位:万元)(1)分别求出利润y1与y2关于投资量x的函数关系式;(2)如果这位专业户以8万元资金投入种植花卉和树木,他至少获得多少利润,他能获取的最大利润是多少?4.如图,在平面直角坐标系中,O是坐标原点,点A的坐标是(﹣2,4),过点A作AB⊥y轴,垂足为B,连接OA.(1)求△OAB的面积;(2)若抛物线y=﹣x2﹣2x+c经过点A.①求c的值;②将抛物线向下平移m个单位,使平移后得到的抛物线顶点落在△OAB的内部(不包括△OAB的边界),求m的取值范围.。
华东师大版九年级数学下册第26章 二次函数 单元测试题-word文档资料

第26章 二次函数一、选择题(本大题共6小题,每小题4分,共24分) 1.下面的函数是二次函数的是( )A .y =3x +1B .y =x 2+2xC .y =x 2D .y =2x2.对于函数y =5x 2,下列结论正确的是( ) A .y 随x 的增大而增大 B .图象开口向下 C .图象关于y 轴对称D .无论x 取何值,y 的值总是正的3.在同一平面直角坐标系内,将函数y =2x 2+4x -3的图象向右平移2个单位,再向下平移1个单位,得到的新图象的顶点坐标是( )A.()-3,-6B.()1,-4C.()1,-6D.()-3,-44.一个网球发射器向空中发射网球,网球飞行的路线呈一条抛物线,如果网球距离地面的高度h (米)关于运行时间t (秒)的函数关系式为h =-180t 2+15t +1(0≤t ≤20),那么网球到达最高点时距离地面的高度是( )A .1米B .1.5米C .1.6米D .1.8米 5.二次函数的图象如图26-Z -1所示,则其表达式是( )图26-Z -1A .y =-x 2+2x +3 B .y =x 2-2x -3 C .y =-x 2-2x +3 D .y =-x 2-2x -36.如图26-Z -2,边长为4个单位的正方形ABCD 的边AB 与等腰直角三角形EFG 的斜边FG 重合,△EFG 以每秒1个单位的速度沿BC 向右匀速运动(保持FG ⊥BC ),当点E 运动到CD 边上时△EFG 停止运动.设△EFG 的运动时间为t 秒,△EFG 与正方形ABCD 重叠部分的面积为S ,则S 关于t 的函数图象大致为( )图26-Z-2 图26-Z-3二、填空题(本大题共6小题,每小题4分,共24分)7.已知A(0,3),B(2,3)是抛物线y=-x2+bx+c上的两点,该抛物线的顶点坐标是________.8.如图26-Z-4,抛物线y=-x2+2x+3与y轴交于点C,点D(0,1),P是抛物线上的动点.若△PCD是以CD为底的等腰三角形,则点P的坐标为________.图26-Z-49.如图26-Z-5所示,二次函数y1=ax2+bx+c与一次函数y2=kx+m(k≠0)的图象相交于点A(-2,4),B(8,2),则能使y1>y2成立的x的取值范围是____________.图26-Z-510.汽车刹车距离s(m)与速度v(km/h)之间的函数关系式是s=1100v2,在一辆车速为100 km/h 的汽车前方80 m处,发现停放着一辆故障车,此时刹车________有危险(填“会”或“不会”).11.已知二次函数y=-x2+2x+m的部分图象如图26-Z-6所示,则关于x的一元二次方程-x2+2x+m=0的解为____________.图26-Z-612.如图26-Z-7是抛物线y1=ax2+bx+c的一部分,抛物线的顶点坐标是A(1,3),与x 轴的一个交点是B(4,0),直线y2=mx+n(m≠0)与抛物线交于A,B两点,下列结论:①abc>0;②方程ax2+bx+c=3有两个相等的实数根;③抛物线与x轴的另一个交点是(-1,0);④当1<x<4时,有y2>y1;⑤x(ax+b)≤a+b.其中正确的结论是________.(只填写序号)图26-Z-7三、解答题(本大题共4小题,共52分)13.(12分)如图26-Z-8,已知二次函数y=ax2+bx+c的图象经过点A(-1,-1),B(0,2),C(1,3).(1)求该二次函数的关系式;(2)画出该二次函数的图象.图26-Z-814.(12分)已知二次函数y=x2-2mx+m2+3(m是常数).(1)求证:不论m为何值,该函数的图象与x轴没有公共点;(2)把该函数的图象沿y轴向下平移多少个单位后,得到的函数的图象与x轴只有一个公共点?15.(14分)九年级(3)班数学兴趣小组经过市场调查整理出某种商品在第x天(0<x≤90,且x 为整数)的售价与销售量的相关信息分别如图26-Z-9和下表,已知每件商品的进价为30元,设该商品每件的售价为y(单位:元),每天的销售量为p(单位:件),每天的销售利润为w(单位:元).(1)求出w与x之间的函数关系式.(2)销售该商品第几天时,当天的销售利润最大?并求出最大利润.(3)该商品在销售过程中,共有多少天每天的销售利润不低于5600元?请直接写出结果.16.(14分)如图26-Z-10所示,在平面直角坐标系中,抛物线y=ax2+bx+c经过A(-3,0),B(1,0),C(0,3)三点,其顶点为D,连结AD,P是线段AD上的一个动点(不与点A,D 重合).经过点P作y轴的垂线,垂足为E,连结AE.(1)求抛物线所对应的函数关系式,并写出顶点D的坐标;(2)如果点P的坐标为(x,y),△PAE的面积为S,求S与x之间的函数关系式,直接写出自变量x的取值范围,并求S的最大值;(3)在(2)的条件下,当S取到最大值时,过点P作x轴的垂线,垂足为F,连结EF,把△FPE 沿直线EF折叠,点P的对应点为点P′,求出点P′的坐标,并判断点P′是否在该抛物线上.图26-Z-10教师详解详析作者说卷1.[解析] B A 项,y =3x +1是一次函数,故本选项不符合题意; B 项,y =x 2+2x ,符合二次函数的定义,故本选项符合题意; C 项,y =x2是一次函数,故本选项不符合题意;D 项,y =2x是反比例函数,故本选项不符合题意.故选B.2.[解析] C ∵二次函数y =5x 2中a >0,∴二次函数图象开口向上,当x <0时,y 随x 的增大而减小,当x >0时,y 随x 的增大而增大,对称轴为y 轴,无论x 取何值,y 的值总是非负数.故选C.3.[解析] C 二次函数y =2x 2+4x -3配方得y =2(x 2+2x )-3=2(x 2+2x +1-1)-3=2(x +1)2-5,将抛物线y =2(x +1)2-5向右平移2个单位所得抛物线的表达式为y =2(x +1-2)2-5=2(x -1)2-5,将抛物线y =2(x -1)2-5向下平移1个单位所得抛物线的表达式为y =2(x -1)2-5-1=2(x -1)2-6,此时的二次函数图象的顶点坐标为(1,-6).4.[解析] D h =-180t 2+15t +1=-180(t 2-16t +64-64)+1=-180(t -8)2+1.8.故选D.5.[解析] A 设抛物线的表达式为y =a (x +1)(x -3),把(0,3)代入,得a ·1·(-3)=3,解得a =-1,所以抛物线的表达式为y =-(x +1)(x -3),即y =-x 2+2x +3.故选A. 6.[解析] B 如图①,当0≤t <2时,等腰直角三角形EFG 与正方形ABCD 重叠部分为梯形MNGF ,其下底FG =4,高PQ =t ,∴EP =EQ -PQ =2-t ,∴上底MN =2(2-t ),∴S =12[2(2-t )+4]·t =-t 2+4t =-(t -2)2+4(0≤t <2),其图象为开口向下的抛物线对称轴(直线t =2)左侧的一部分;如图②,当2≤t ≤4时,等腰直角三角形EFG 与正方形ABCD 重叠部分为等腰直角三角形EFG 本身,其面积S =12×4×2=4(2≤t ≤4),其图象为平行于x 轴的一条线段;如图③,当4<t ≤6时,等腰直角三角形EFG 与正方形ABCD 重叠部分为等腰直角三角形EMN ,此时PQ =HQ -HP =t -4,EP =EQ -PQ =2-(t -4)=6-t ,MN =2EP =2(6-t ),∴S =12×2(6-t )·(6-t )=(t -6)2(4<t ≤6),其图象为开口向上的抛物线对称轴(直线t =6)左侧的一部分.故选B. 7.[答案] (1,4)[解析] 方法一:把A (0,3)和B (2,3)的坐标代入函数关系式,得c =3和3=-22+2b +3,解得b =2,c =3,∴抛物线的函数关系式为y =-x 2+2x +3=-(x -1)2+4,∴该抛物线的顶点坐标为(1,4). 方法二:把A (0,3)和B (2,3)的坐标代入函数关系式,得c =3和3=-22+2b +3,解得b =2,c =3,∴抛物线的函数关系式为y =-x 2+2x +3,由顶点坐标公式⎝ ⎛⎭⎪⎫-b 2a ,4ac -b 24a , 可得顶点坐标为(1,4).方法三:由点A 与点B 的纵坐标相同,可知抛物线的对称轴为直线x =0+22=1,故-b2×(-1)=1,∴b =2.又∵c =3,故抛物线的函数关系式为y =-x 2+2x +3,当x =1时,y =-1+2+3=4,故顶点坐标为(1,4).8.[答案] (1+2,2)或(1-2,2)[解析] ∵抛物线y =-x 2+2x +3与y 轴交于点C ,把x =0代入 y =-x 2+2x +3得y =3,点C 的坐标为(0,3).∵点D (0,1),线段CD 的中点的坐标为(0,2),把y =2代入y =-x2+2x +3,得 -x 2+2x +3=2,解这个一元二次方程得x 1=1+2,x 2=1-2,则点P 的坐标为(1+2,2)或(1-2,2).9.[答案] x <-2或x >8[解析] 通过观察图象可以看出,y 1>y 2的图象分为两部分,即当x <-2时或x >8时.同样我们也可以看出当y 1<y 2时-2<x <8. 10.[答案] 会[解析] 把v =100代入s =1100v 2,得汽车刹车距离s =100>80,因此会有危险. 11.[答案] x 1=-1,x 2=3[解析] 由图象可知抛物线过点(3,0),将其坐标代入函数关系式,得m =3,解方程-x 2+2x +3=0可得另一个交点的坐标为(-1,0). 12.[答案] ②⑤[解析] ①根据函数图象开口方向、对称轴、与y 轴交点的位置可知a <0,b >0,c >0,故abc <0;②根据函数图象的顶点坐标,得方程ax 2+bx +c =3有两个相等的实数根x 1=x 2=1;③根据抛物线的对称性知,抛物线与x 轴的另一个交点是(-2,0);④根据函数图象知,当1<x <4时,有y 2<y 1;⑤当x =1时,y =a +b +c =3,而x (ax +b )+c =ax 2+bx +c ≤3, ∴x (ax +b )≤a +b .故正确的结论是②⑤. 13.解:(1)根据题意,得⎩⎪⎨⎪⎧c =2,a -b +c =-1,a +b +c =3,解得⎩⎪⎨⎪⎧a =-1,b =2,c =2,所以该二次函数的关系式为y =-x 2+2x +2. (2)略.14.解:(1)证明:证法一:因为()-2m 2-4(m 2+3)=-12<0,所以方程x 2-2mx +m 2+3=0没有实数根,所以不论m 为何值,函数y =x 2-2mx +m 2+3的图象与x 轴没有公共点. 证法二:因为a =1>0, 所以该函数的图象开口向上.又因为y =x 2-2mx +m 2+3=(x -m )2+3≥3,所以该函数的图象在x 轴的上方, 所以不论m 为何值,函数y =x 2-2mx +m 2+3的图象与x 轴没有公共点. (2)y =x 2-2mx +m 2+3=(x -m )2+3.把函数y =(x -m )2+3的图象沿y 轴向下平移3个单位后,得到函数y =(x -m )2的图象,它的顶点坐标是(m ,0),因此,这个函数的图象与x 轴只有一个公共点.所以把函数y =x 2-2mx +m 2+3的图象沿y 轴向下平移3个单位后,得到的函数的图象与x 轴只有一个公共点.15.解:(1)当0<x <50时,设每件商品的售价y 与时间x 之间的函数关系式为y =kx +b (k ,b 为常数,且k ≠0).∵直线y =kx +b 经过点(0,40),(50,90),∴⎩⎪⎨⎪⎧b =40,50k +b =90,解得⎩⎪⎨⎪⎧k =1,b =40,∴y 与x 之间的函数关系式为y =x +40(0<x <50,且x 为整数),∴y =⎩⎪⎨⎪⎧x +40(0<x <50,且x 为整数),90(50≤x ≤90,且x 为整数).由数据可知每天的销售量p 与时间x 成一次函数关系,设每天的销售量p 与时间x 之间的函数关系式为p =mx +n (m ,n 为常数,且m ≠0). ∵直线p =mx +n 过点(60,80),(30,140),∴⎩⎪⎨⎪⎧60m +n =80,30m +n =140,解得⎩⎪⎨⎪⎧m =-2,n =200, ∴p =-2x +200.将(1,198),(90,20)分别代入上式均成立, ∴p =-2x +200(0<x ≤90,且x 为整数).当0<x <50时,w =(y -30)p =(x +40-30)(-2x +200)=-2x 2+180x +2019, 当50≤x ≤90时,w =(90-30)(-2x +200)=-120x +12019. 综上所述,每天的销售利润w 与时间x 之间的函数关系式为w =⎩⎪⎨⎪⎧-2x 2+180x +2000(0<x <50,且x 为整数),-120x +12000(50≤x ≤90,且x 为整数). (2)当0<x <50时,w =-2x 2+180x +2019=-2(x -45)2+6050. ∵a =-2<0且0<x <50, ∴当x =45时,w 最大值=6050. 当50≤x ≤90时,w =-120x +12019. ∵k =-120<0,∴w 随x 的增大而减小, ∴当x =50时,w 最大值=6000. ∵6050>6000,∴销售该商品第45天时,当天的销售利润最大,最大利润为6050元. (3)24天.16.解:(1)∵抛物线过点A (-3,0),B (1,0), ∴设其函数关系式为y =a (x +3)(x -1). 将点C 的坐标代入关系式,得a =-1,即抛物线所对应的函数关系式为y =-(x +3)(x -1)=-x 2-2x +3,顶点D 的坐标为(-1,4).(2)如图①,过点A 作AH ⊥EP 交EP 的延长线于点H . ∵A (-3,0),D (-1,4),∴直线AD 所对应的函数关系式为y =2x +6,∴S =12AH ·EP =-12xy =-x (x +3)=-(x +32)2+94,自变量x 的取值范围是-3<x <-1.当x =-32时,S 取得最大值,最大值为94.(3)当S 取到最大值时,点P 的坐标为(-32,3),且点E 与点C 重合.如图②所示,过点P ′作x 轴的垂线交x 轴于点N ,交PE 的延长线于点M . ∵PE =1.5,PF =3,且△FPE ≌△FP ′E ,∴P′F=PF=3,P′E=PE=1.5.设点P′的坐标为(m,n),可得ME=m,MP′=3-n,NP′=n,NF=m+1.5. 易证△MEP′∽△NP′F,∴MENP′=MP′NF=EP′P′F=1.53,即mn=3-nm+1.5=12,解得m=0.9,n=1.8,∴P′(0.9,1.8).当x=0.9时,y=-x2-2x+3=-0.81-1.8+3=0.39≠1.8,∴点P′不在抛物线y=-x2-2x+3上.。
第26章 二次函数 华东师大版九年级数学下册达标测试卷(含答案)

第26章二次函数达标测试卷一、选择题(每题3分,共24分)1.下列函数中,是二次函数的是()A.y=5x2B.y=22-2x C.y=2x2-3x3+1 D.y=1 x22.抛物线y=3(x-1)2+8的顶点坐标为()A.(1,8) B.(-1,8) C.(-1,-8) D.(1,-8) 3.某商场第1年销售计算机5 000台,设平均每年的销售量增长率为x,第3年的销售量为y台,则y关于x的函数表达式为()A y=5 000(1+2x)B y=5 000(1+x)2C y=5 000(1-2x)D y=5 000(1-x)2 4.在平面直角坐标系中,抛物线y=2x2保持不动,将x轴向上平移1个单位(y轴不动),则在新坐标系下抛物线的表达式是()A.y=2x2+1 B.y=2x2-1 C.y=2(x-1)2D.y=2(x+1)2 5.已知点A(2,y1)、B(3,y2)、C(-1,y3)均在抛物线y=ax2-4ax+c(a >0)上,则y1、y2、y3的大小关系为()A.y1<y2<y3B.y1<y3<y2 C.y2<y1<y3D.y2<y3<y1 6.二次函数y=ax2与一次函数y=ax+a在同一坐标系中的大致图象为()7.若二次函数y=-x2+mx在-2≤x≤1时的最大值为5,则m的值是()A.-2 5或6 B.2 5或6 C.-92或6 D.-92或-2 5 8.如图,在平面直角坐标系中,抛物线y=13x2经过平移得到抛物线y=ax2+bx,其对称轴与两段抛物线所围成的阴影部分的面积为83,则a,b的值分别为()A.13,43 B.13,-23 C.13,-43D.-13,43(第8题) (第13题) (第14题)二、填空题(每题3分,共18分)9.已知点P⎝ ⎛⎭⎪⎫a,12在抛物线y=2x2上,则a等于________.10.抛物线y=x2+6x+c与x轴有且只有1个公共点,则c=________.11.某小型无人机着陆后滑行的距离s(米)关于滑行的时间t(秒)的函数表达式是s=-0.25t2+10t,那么无人机着陆后滑行__ _秒才能停下来.12.已知二次函数y=ax2+bx+c,x与y的部分对应值如下表:则不等式ax2+bx+c>-3的解集为________.13.如图,过点A(0,4)作平行于x轴的直线AC,分别交抛物线y1=x2(x≥0)与y2=14x2(x≥0)于点B、C,则BC的长是________.14.二次函数y=ax2+bx+c的图象如图所示,则下列结论:①ac<0;②a+b=0;③a+b+c>0;④b2-4ac<0.其中正确的是___(填序号)三、解答题(第15,16题每题5分,第17~19题每题6分,第20,21题每题8分,第22题10分,其余每题12分,共78分)15.一抛物线以(-1,9)为顶点,且经过x轴上一点(-4,0),求该抛物线的表达式及抛物线与y轴的交点坐标.16.如图,二次函数y=-x2+bx+c的图象经过坐标原点,且与x轴交于点A(-2,0).(1)求此二次函数的表达式;(2)结合图象,直接写出满足y>0的x的取值范围.(第16题)17.一名男生推铅球,铅球行进高度y(m)与水平距离x(m)之间满足关系式y=-112x2+23x+53.(1)求铅球离手时的高度;(2)求铅球推出的最大距离.18.在平面直角坐标系中,二次函数y=-2x2+bx+c的图象经过点A(-2,4)和点B(1,-2).(1)求这个二次函数的表达式及其图象的顶点坐标;(2)平移该二次函数的图象,使其顶点恰好落在原点的位置上,请直接写出平移方法.19.某网店正在热销一款电子产品,其成本为每件10元,销售过程中发现,该商品每天的销量y(件)与销售单价x(元)之间存在如图所示的函数关系.(1)求y与x之间的函数关系式;(2)该款电子产品的销售单价为多少时,每天的销售利润最大?最大利润是多少?(第19题)20.如图,已知抛物线y=ax2+(a-1)x+3(a≠0)与x轴交于A、B(1,0)两点,与y轴交于点C.(1)点C的坐标为________;(2)将抛物线y=ax2+(a-1)x+3平移,使平移后的抛物线仍经过点B,与x轴的另一个交点为B′,且点B′的坐标为(3,0),求平移后的抛物线的表达式.(第20题) 21.现有一面12米长的墙,某农户计划用28米长的篱笆靠墙围成一个如图所示的矩形养鸡场ABCD.(1)若矩形养鸡场的面积为90平方米,求所用的墙长AD;(2)求矩形养鸡场的最大面积.(第21题)22.如图,矩形OABC的顶点A、C的坐标为A(2 3,0)、C(0,2),抛物线y=-x2+bx+c经过点B、C.(1)求该抛物线的表达式;(2)将矩形OABC绕原点O顺时针旋转一个角度α(0°<α<90°),在旋转过程中,当矩形的顶点A的对应点A′落在抛物线的对称轴上时,求此时点A′的坐标.(第22题)23.某班数学兴趣小组对函数y =x 2-2|x |的图象和性质进行了探究,探究过程如下,请补充完整.(1)自变量x 的取值范围是全体实数,x 与y 的几组对应值如下表:其中m =__________;(2)根据表中数据,在如图所示的平面直角坐标系中描点,并画出了函数图象的一部分,请画出该函数图象的另一部分;(3)(3)观察函数图象,写出两条函数的性质;(4)进一步探究函数图象发现:①函数图象与x 轴有__________个交点,对应的方程x 2-2|x |=0有__________个实数根;②方程x 2-2|x |=2有__________个实数根;③关于x 的方程x 2-2|x |=a 有4个实数根时,a 的取值范围是__________.(第23题)答案一、1.A 2.A 3.B 4.B5.A 【点拨】∵y =ax 2-4ax +c ,且a >0, ∴图象开口向上,对称轴是直线x =--4a2a =2, ∴x ≥2时,y 随x 的增大而增大,∵C (-1,y 3)关于直线x =2的对称点是(5,y 3),2<3<5,∴y 1<y 2<y 3. 6.C7.C 【点拨】∵y =-x 2+mx ,∴图象开口向下,对称轴为直线x =-m 2×(-1)=m2.①当m 2≤-2,即m ≤-4时,函数在x =-2时取得最大值5,∴-4-2m =5,解得m =-92;②当m2≥1,即m ≥2时,函数在x =1时取得最大值5, ∴-1+m =5,解得m =6.③当-2<m 2<1,即-4<m <2时,函数在x =m 2时取得最大值5,∴-m 24+m 22=5,解得m =2 5(舍去)或m =-2 5(舍去).综上所述,m 的值为-92或6.8.C 【点拨】如图,设平移后所得新抛物线的对称轴和两抛物线分别相交于点A 和点B ,连结OA 、OB ,(第8题)∴S 阴影=S △OAB .由题意得a =13,∴y =ax 2+bx =13x 2+bx =13⎝ ⎛⎭⎪⎫x +3b 22-3b 24,∴点A 的坐标为⎝ ⎛⎭⎪⎫-3b 2,-3b 24,∴点B 的坐标为 ⎝ ⎛⎭⎪⎫-3b 2,3b 24,∴AB =3b 22,点O 到AB 的距离为-3b2,∴S △AOB =12×3b 22×⎝ ⎛⎭⎪⎫-3b 2=83,解得b =-43.二、9.12或-12 10.9 11.2012.0<x <2 13.2 14.①②③三、15.解:设抛物线的表达式为y =a (x +1)2+9,将(-4,0)代入y =a (x +1)2+9, 得0=9a +9,解得a =-1, ∴抛物线的表达式为y =-(x +1)2+9.令x =0,则y =8,∴抛物线与y 轴的交点坐标为(0,8).16.解:(1)把(0,0)和(-2,0)分别代入y =-x 2+bx +c ,得⎩⎨⎧c =0,-4-2b +c =0,解得⎩⎨⎧b =-2,c =0,∴二次函数的表达式为y =-x 2-2x . (2)-2<x <0.17.解:(1)令x =0,则y =53.∴铅球离手时的高度为53 m.(2)当y =0时,-112x 2+23x +53=0, 解得x 1=10,x 2=-2(不合题意,舍去), ∴铅球推出的最大距离是10 m.18.解:(1)∵二次函数y =-2x 2+bx +c 的图象经过点A (-2,4)和点B (1,-2).∴⎩⎨⎧-2×4-2b +c =4,-2×1+b +c =-2,解得⎩⎨⎧b =-4,c =4, ∴这个二次函数的表达式为y =-2x 2-4x +4. ∵y =-2x 2-4x +4=-2(x +1)2+6, ∴顶点坐标为(-1,6).(2)(答案不唯一)将该二次函数图象先向右平移1个单位,再向下平移6个单位. 19.解:(1)设y 与x 之间的函数关系式为y =kx +b ,将(20,100),(25,50)代入,得 ⎩⎨⎧20k +b =100,25k +b =50,解得⎩⎨⎧k =-10,b =300, ∴y 与x 之间的函数关系式为y =-10x +300. (2)设该款电子产品的销售利润为w 元,根据题意得w =(x -10)(-10x +300)=-10x 2+400x -3 000=-10(x -20)2+1 000, ∵-10<0,∴x =20时,w 最大,为1 000.答:该款电子产品的销售单价为20元时,每天销售利润最大,最大利润是1 000元. 20.解:(1)(0,3)(2)∵抛物线y =ax 2+(a -1)x +3与x 轴交于点B (1,0),∴a +a -1+3=0,∴a =-1,∴y =-x 2-2x +3.设平移后的抛物线表达式为y =-(x +h )2+k , ∵平移后的抛物线经过点B (1,0)和点B ′(3,0), ∴⎩⎨⎧-(1+h )2+k =0,-(3+h )2+k =0,解得⎩⎨⎧h =-2,k =1, ∴平移后的抛物线表达式为y =-(x -2)2+1.21.解:(1)设所用的墙长AD 为x 米,则AB 的长为28-x2米,由题意可得x ·28-x2=90,解得x 1=18(舍去),x 2=10.答:所用的墙长AD 为10米. (2)设AB 为a 米,面积为S 平方米, 则S =a (28-2a )=-2(a -7)2+98, ∵0<28-2a ≤12,∴8≤a <14,∴当a =8时,S 取得最大值,此时S =96, 答:矩形养鸡场的最大面积是96平方米.22.解:(1)∵A (2 3,0),C (0,2),∴易得B (2 3,2). 把点C 和点B 的坐标代入y =-x 2+bx +c , 得⎩⎨⎧c =2,-12+2 3b +c =2,解得⎩⎨⎧b =2 3,c =2, ∴该抛物线的表达式为y =-x 2+2 3x +2. (2)设对称轴与x 轴交于点D ,∴易得OD =3, 又∵OA ′=OA =2 3,∴A ′D =(2 3)2-(3)2=3,∴A ′(3,-3). 23.解:(1)0 (2)如图.(3)①函数y =x 2-2|x |的图象关于y 轴对称;②当x >1时,y 随x 的增大而增大. (4)①3;3 ②2 ③-1<a <0(第23题)【点拨】(3)题答案不唯一.24. 解:(1)由题意得⎩⎨⎧a -b +c =0,16a +4b +c =0c =3,,解得⎩⎪⎨⎪⎧a =-34,b =94,c =3,∴抛物线对应的函数表达式为y =-34x 2+94x +3.(2)设直线BC 对应的函数表达式为y =kx +d ,则⎩⎨⎧4k +d =0,d =3,解得⎩⎪⎨⎪⎧k =-34,d =3,∴y =-34x +3.设D (m ,-34m 2+94m +3)(0<m <4).过点D 作DM ⊥x 轴交BC 于点M ,则M ⎝ ⎛⎭⎪⎫m ,-34m +3,DM ∥OC ,∴DM =⎝ ⎛⎭⎪⎫-34m 2+94m +3-⎝ ⎛⎭⎪⎫-34m +3=-34m 2+3m ,∠DME =∠OCB ,又∵∠DEM =∠BOC =90°,∴△DEM ∽△BOC , ∴DE OB =DMBC .∵OB =4,OC =3,∴BC =5,∴DE =45DM ,∴DE =-35m 2+125m =-35(m -2)2+125(0<m <4).当m =2时,DE 取得最大值,最大值是125. (3)存在.∵F 为AB 的中点, ∴OF =32,∴tan ∠CFO =OCOF =2.如图,过点B 作BG ⊥BC ,交CD 的延长线于点G ,过点G 作GH ⊥x 轴,垂足为H .(第24题)①若∠DCE =∠CFO ,则tan ∠DCE =GBBC =2, ∴BG =10.易得△GBH ∽△BCO ,∴GH BO =HB OC =GBBC ,∴GH =8,BH =6,∴G (10,8). 设直线CG 对应的函数表达式为y =px +n ,11∴⎩⎨⎧n =3,10p +n =8,解得⎩⎪⎨⎪⎧p =12,n =3,∴直线CG 对应的函数表达式为y =12x +3,令12x +3=-34x 2+94x +3,解得x =73或x =0(舍去). ②若∠CDE =∠CFO ,同理可得BG =52,GH =2,BH =32,∴G ⎝ ⎛⎭⎪⎫112,2.易得直线CG 对应的函数表达式为y =-211x +3,令-211x +3=-34x 2+94x +3,解得x =10733或x =0(舍去).综上所述,点D 的横坐标为73或10733.12。
华师大九年级下《第26章二次函数》检测题含答案

二次函数单元练习题一、选择题1.下列函数中是二次函数的是( B )A .y =3x -1B .y =3x 2-1 C.y =(x +1)2-x 2 D .y =x 3+2x -32.将抛物线y =3x 2向右平移两个单位,再向下平移4个单位,所得抛物线是( )(A)y =3(x +2)2+4 (B) y =3(x -2)2+4 (C) y =3(x -2)2-4 (D)y =3(x +2)2-43.二次函数y =ax 2+bx +c(a ≠0)的图象如图所示,则下列结论中正确的是( B )A .a >0B .当-1<x <3时,y >0C .c <0D .当x ≥1时,y 随x 的增大而增大4.二次函数y =x 2-8x +c 的最小值是0,那么c 的值等于( )(A)4 (B)8 (C)-4 (D)165.抛物线y =-2x 2+4x +3的顶点坐标是( )(A)(-1,-5) (B)(1,-5) (C)(-1,-4) (D) (-2,-7)6. 若二次函数=ax 2+c ,当x 取x 1,x 2(x 1≠x 2)时,函数值相等,则当x 取x 1+x 2时,函数值为( )(A)a +c (B)a -c (C)-c (D)c7.如图,已知:正方形ABCD 边长为1,E 、F 、G 、H 分别为各边上的点, 且AE =BF =CG =DH , 设小正方形EFGH 的面积为s ,AE 为x ,则s 关于x 的函数图象大致是( )(A) (B) (C) (D)8.抛物线y =ax 2+bx +c 的顶点为D(-1,2),与x 轴的一个交点A 在点(-3,0)和(-2,0)之间,其部分图象如图,则以下结论:①b 2-4ac <0;②a +b +c <0;③c -a =2;④方程ax 2+bx +c -2=0有两个相等的实数根.其中正确的结论的个数为( C )A .1个B .2个C .3个D .4个二、填空题9.已知函数y =ax 2+bx +c ,当x =3时,函数的最大值为4,当x =0时,y =-14,则函数关系式____.10.若二次函数y =-x 2+4x +k 的最大值等于3,则k 的值等于____. .11.函数42-=x y 的图象与y 轴的交点坐标是________. 12.已知抛物线的顶点是(0,1),对称轴是y 轴,且经过(-3,2),则此抛物线的函数关系式为_________,当x >0时,y 随x 的增大而____.13.已知抛物线y =ax 2+bx +c(a≠0)与x 轴的两个交点的坐标是(5,0),(-2,0),则方程ax 2+bx+c=0(a≠0)的解是_______.14.抛物线y=(m-4)x2-2mx-m-6的顶点在x轴上,则m=______.15.若函数y=a(x-h)2+k的图象经过原点,最大值为8,且形状与抛物线y=-2x2-2x+3相同,则此函数关系式______.16.已知二次函数y1=ax2+bx+c(a≠0)与一次函数y2=kx+m(k≠0)的图象相交于点A(-2,4),B(8,2),如图所示,则使y1>y2成立的x的取值范围是______ __三、解答题17.(8分)已知抛物线y=a(x-h)2-4经过点(1,-3),且与抛物线y=x2的开口方向相同,形状也相同.(1)求a,h的值;(2)求它与x轴的交点,并画出这个二次函数图象的草图;(3)若点A(m,y1),B(n,y2)(m<n<0)都在该抛物线上,试比较y1与y2的大小.y x mx m.18、已知抛物线22(1)求证此抛物线与x轴有两个不同的交点;y x mx m与x轴交于整数点,求m的值;(2)若m是整数,抛物线22(3)在(2)的条件下,设抛物线顶点为A,抛物线与x轴的两个交点中右侧交点为B.若M为坐标轴上一点,且MA=MB,求点M的坐标.19.(8分)如图,已知二次函数y=-x2+bx+c的图象与x轴交于A(-1,0),B(3,0)两点,与y轴交于点C,顶点D.(1)求这个二次函数的关系式;(2)求四边形ABDC的面积.20.(12分)(2011·聊城)如图,已知抛物线y =ax 2+bx +c(a ≠0)的对称轴为x =1,且抛物线经过A(-1,0)、C(0,-3)两点,与x 轴交于另一点B.(1)求这条抛物线所对应的函数解析式;(2)在抛物线的对称轴x =1上求一点M ,使点M 到点A 的距离与到点C 的距离之和最小,并求出此时点M 的坐标;(3)设点P 为抛物线的对称轴x =1上的一动点,求使∠PCB =90°的点P 的坐标.参考答案:一、1-5 BCBDB 6-8 DBC .二、9.y =-2(x -3)2+4; 10.-1 ;11.(0.-4) ; 12.y =19x 2+1 ;增大. 13.向上,x =41,(825,41-);14.略. 15.y =-2x 2+8x 或y =-2x 2-8x ; 16.x <-2或x >8; 三、17.解:(1)a =1,h =2 (2)它与x 轴的交点坐标为(0,0),(4,0),图象略 (3)y 1>y 218.由已知,得30423c a b c a b c =-⎧⎪-+=⎨⎪++=-⎩,,解得a =1,b =-2,c =-3.所以y =x 2-2x -3.(2)开口向上,对称轴x =1,顶点(1,-4).19、解:(1)y =-x 2+2x +3 (2)连结OD ,可求得C (0,3),D (1,4),则S 四边形ABDC =S △AOC+S △COD +S △BOD =12×1×3+12×3×1+12×3×4=920、解:(1)根据题意,y =ax 2+bx +c 的对称轴为x =1,且过A(-1,0),C(0,-3),可得⎩⎪⎨⎪⎧ -b 2a =1a -b +c =0,c =-3解得⎩⎨⎧ a =1,b =-2,c =-3.∴抛物线所对应的函数解析式为y =x 2-2x -3.(2)由y =x 2-2x -3可得,抛物线与x 轴的另一交点B(3,0)如图①,连结BC ,交对称轴x =1于点M.因为点M 在对称轴上,MA =MB.所以直线BC 与对称轴x =1的交点即为所求的M 点.设直线BC 的函数关系式为y =kx +b ,由B(3,0),C(0,-3),解得y =x -3,由x =1,解得y =-2.故当点M 的坐标为(1,-2)时,点M 到点A 的距离与到点C 的距离之和最小.(3)如图②,设此时点P 的坐标为(1,m),抛物线的对称轴交x 轴于点F(1,0).连结PC 、PB ,作PD 垂直y 轴于点D ,则D(0,m).。
2013新人教版九下第26章《二次函数》word期末复习测试

一、选择题1.抛物线3)2(2+-=x y 的对称轴是直线( ) A .2-=xB .2=xC .3=xD .3-=x2)A .开口向下,顶点坐标B .开口向上,顶点坐标C .开口向下,顶点坐标D .开口向上,顶点坐标3.二次函数222+-=x x y 与坐标轴的交点个数是( ) A .0个B .1个C .2个D .3个4.将抛物线22y x =的图象向上平移1个单位,则平移后的抛物线的解析式为( ) A .22(1)y x =+ B .22(1)y x =- C .221y x =+ D .221y x =-5.已知:抛物线的顶点在x 轴上,则 b 的值一定是( )A 1B 2C -2D 2或-2 6.如图是二次函数2y ax bx c =++的部分图象,由图象可知不等式20ax bx c ++<的解集是A .15x -<<B .5x >C .15x x <->且D .15x x <->或7.下列各图中有可能是函数y =ax 2+c )8.若二次函数2()1y x m =--.当x ≤l 时,y 随x 的增大而减小,则m 的取值范围是(53),(53),(53)-,(53)-,yx( )A .m =lB .m >lC .m ≥lD .m ≤l 9.将抛物线y =2x 2-12x +16绕它的顶点旋转180°,所得的解析式是( ) A. y =-2x 2-12x +16 B. y =-2x 2+12x -16 C. y =-2x 2+12x -19 D. y =-2x 2+12x -2010.抛物线y =ax 2+bx +c 的图角如图,则下列结论:①abc >0;②a +b +c =2;③a ④b <1.其中正确的结论是( )(A )①② (B )②④ (C )②③ (D )③④二、填空题11.已知函数()x x m y m3112+-=+,当=m 时,它是二次函数.12.二次函数错误!未找到引用源。
二次函数的图象和性质练习题(含参考答案)

新华师大版九年级下册数学第26章 二次函数的图象和性质部分练习题姓名____________ 时间: 90分钟 满分:120分 总分____________一、选择题(每小题10分,共30分)1. 将抛物线2x y =向右平移2个单位,再向上平移1个单位,所得新抛物线对应的函数表达式为 【 】 (A )()122++=x y (B )()122-+=x y(C )()122+-=x y (D )()122--=x y2. 将抛物线()312+-=x y 向左平移1个单位,得到的抛物线与y 轴的交点坐标是 【 】(A )(0 , 2) (B )(0 , 3) (C )(0 , 4) (D )(0 , 7)3. 抛物线321532-⎪⎭⎫⎝⎛+-=x y 的顶点坐标是 【 】(A )⎪⎭⎫ ⎝⎛-3,21 (B )⎪⎭⎫ ⎝⎛--3,21 (C )⎪⎭⎫ ⎝⎛3,21 (D )⎪⎭⎫⎝⎛-3,214. 抛物线322++=x x y 的对称轴是 【 】 (A )直线1=x (B )直线1-=x (C )直线2-=x (D )直线2=x5. 在平面直角坐标系中,将抛物线221x y -=先向下平移1个单位长度,再向左平移1个单位长度,得到的抛物线的解析式为 【 】(A )23212---=x x y (B )21212-+-=x x y (C )23212-+-=x x y (D )21212---=x x y6. 关于抛物线()212--=x y ,下列说法错误的是 【 】(A )顶点坐标为()2,1- (B )对称轴是直线1=x(C )开口向上 (D )当1>x 时,y 随x 的增大而减小7. 如图所示,把抛物线2x y =沿直线x y =向右平移2个单位后,其顶点在直线上的A 处,平移后的抛物线解析式是 【 】(A )()112-+=x y (B )()112++=x y(C )()112+-=x y (D )()112--=x y第 7 题图8. 关于二次函数1422-+=x x y ,下列说法正确的是 【 】 (A )图象与y 轴的交点坐标为(0 , 1) (B )图象的对称轴在y 轴的右侧 (C )当0<x 时,y 的值随x 值的增大而减小 (D )y 的最小值为3-9. 抛物线1822-+-=x x y 的顶点坐标为 【 】 (A )(7,2-) (B )(2 , 7) (C )(2 ,25-) (D )(2 ,9-)10. 已知二次函数()12+-=h x y ,在自变量x 的值满足1≤x ≤3的情况下,与其对应的函数值y 的最小值为5,则h 的值为 【 】 (A )1或5- (B )1-或5 (C )1或3- (D )1或3 二、填空题(每小题3分,共30分)11. 抛物线()5232+-=x y 的顶点坐标为_________.12. 将抛物线2x y =向左平移2个单位,再向下平移5个单位,平移后所得新抛物线的表达式为________________.13. 用配方法将二次函数982--=x x y 化为()k h x a y +-=2的形式为________________.14. 抛物线132+-=x x y 的顶点坐标为_________. 15. 抛物线x x y 92+-=的最大值为_________.16. 将抛物线()2432+-=x y 向右平移1个单位,再向下平移3个单位,平移后抛物线的解析式是________________. 17. 已知点()1,4y A ,()2,2y B,()3,2y C -都在二次函数()122--=x y 的图象上,则321,,y y y 的大小关系是__________.18. 抛物线m x x y +-=22与x 轴只有一个交点,则m 的值为_________.19. 已知点()11,y x A ,()22,y x B 为函数()3122+--=x y 图象上的两点,若121>>x x ,则21,y y 的大小关系是__________.20. 如图,把抛物线221x y =平移得到抛物线m ,抛物线m 经过点()0,8-A 和原点O (0 , 0),它的顶点为P ,它的对称轴与抛物线221x y =交于点Q ,则图中阴影部分的面积为_________.三、解答题(共60分) 21.(10分)已知抛物线()31432--=x y . (1)写出抛物线的开口方向、对称轴;(2)函数y 有最大值还是最小值?并求出这个最值;(3)设抛物线与y 轴的交点为P ,与x 轴的交点为Q ,求直线PQ 的函数表达式.22.(10分)已知二次函数的图象以()4,1-A 为顶点,且过点()5,2-B . (1)求该函数的关系式;(2)求该函数的图象与坐标轴的交点坐标.23.(10分)已知抛物线c bx ax y ++=2的顶点坐标为()1,4-,与y 轴交于点(0 , 3),求这条抛物线的函数表达式.24.(10分)如图,在平面直角坐标系中,把抛物线2x y =向左平移1个单位,再向下平移4个单位,得到抛物线()k h x y +-=2.所得抛物线与x 轴交于A 、B 两点(点A 在点B 的左边),与y轴交于点C ,顶点为D . (1)求k h ,的值; (2)判断△ACD 的形状.yxDC BA O25.(10分)已知抛物线22212-+-=x x y . (1)写出此抛物线的开口方向、对称轴和顶点坐标; (2)求出抛物线与x 轴、y 轴的交点坐标;(3)在(2)中,设抛物线与y 轴交于点A ,与x 轴交于点B ,若以点A 为顶点的抛物线经过点B ,请你求出这条抛物线的解析式,并指出其开口方向和函数的最值.26.(10分)已知二次函数m x x y ++=22的图象1C 与x 轴有且只有一个公共点. (1)求1C 的顶点坐标;(2)将1C 向下平移若干个单位后,得抛物线2C ,如果2C 与x 轴的一个交点为()0,3-A ,求2C 的函数关系式,并求2C 与x 轴的另一个交点坐标;(3)若()1,y n P ,()2,2y Q 是1C 上的两点,且21y y >,求实数n 的取值范围.新华师大版九年级下册数学第26章 二次函数的图象和性质练习题参考答案一、选择题(每小题3分,共30分)二、填空题(每小题3分,共30分)11. (2 , 5) 12. ()522-+=x y 13. ()2542--=x y 14. ⎪⎭⎫⎝⎛-45,2315.481 16. ()1532--=x y 17. 312y y y << 18. 1 19. 21y y < 20. 32三、解答题(共60分) 21.(10分)已知抛物线()31432--=x y . (1)写出抛物线的开口方向、对称轴; (2)函数y 有最大值还是最小值?并求出这个最值;(3)设抛物线与y 轴的交点为P ,与x 轴的交点为Q ,求直线PQ 的函数表达式. 解:(1)开口向上,对称轴为直线1=x ; ……………………………………………2分 (2)函数y 有最小值,最小值为3-=y ; ……………………………………………4分 (3)令0=x ,则()49310432-=--⨯=y ∴⎪⎭⎫ ⎝⎛-49,0P ……………………………5分令0=y ,则()031432=--x 解之得:3,121=-=x x∴()0,1-Q 或Q (3 , 0)……………………………………………6分 设直线PQ 的函数表达式为b kx y +=当⎪⎭⎫ ⎝⎛-49,0P ,()0,1-Q 时⎪⎩⎪⎨⎧=+--=049b k b 解之得:⎪⎪⎩⎪⎪⎨⎧-=-=4949b k∴直线PQ 的函数表达式为4949--=x y ; ……………………………………………8分当⎪⎭⎫ ⎝⎛-49,0P , Q (3 , 0)时⎪⎩⎪⎨⎧=+-=0349b k b 解之得:⎪⎪⎩⎪⎪⎨⎧-==4943b k∴直线PQ 的函数表达式为4943-=x y …………………………………………10分 综上所述,直线PQ 的函数表达式为4949--=x y 或4943-=x y . 22.(10分)已知二次函数的图象以()4,1-A 为顶点,且过点()5,2-B . (1)求该函数的关系式;(2)求该函数的图象与坐标轴的交点坐标. 解:(1)由题意可设该函数的关系式为()k h x a y +-=2∵其顶点为()4,1-A ∴4,1-==k h……………………………………………2分 ∴()412--=x a y把()5,2-B 代入()412--=x a y 得:()54122-=--⨯a解之得:1-=a……………………………………………4分 ∴该函数的关系式为()412---=x y ;(2)令0=x ,则()54102-=---=y∴该函数的图象与y 轴的交点为()5,0-;……………………………………………7分 令0=y ,则()0412=---x∴()412-=-x∴方程无实数解∴该函数的图象与x 轴无交点.…………………………………………10分 23.(10分)已知抛物线c bx ax y ++=2的顶点坐标为()1,4-,与y 轴交于点(0 , 3),求这条抛物线的函数表达式.解:由题意可设该抛物线为()k h x a y +-=2∵其顶点坐标为()1,4- ∴1,4-==k h……………………………………………4分 ∴()142--=x a y把(0 , 3)代入()142--=x a y 得:()31402=--⨯a……………………………………………6分 解之得:41=a …………………………………………10分 ∴这条抛物线的函数表达式为()14412--=x y . 24.(10分)如图,在平面直角坐标系中,把抛物线2x y =向左平移1个单位,再向下平移4个单位,得到抛物线()k h x y +-=2.所得抛物线与x 轴交于A 、B 两点(点A 在点B 的左边),与y 轴交于点C ,顶点为D . (1)求k h ,的值; (2)判断△ACD 的形状.解:(1)平移后,抛物线的解析式为()412-+=x y……………………………………………3分 ∴4,1-=-=k h ;……………………………………………5分 (2)令0=y ,则()0412=-+x解之得:1,321=-=x x ∵点A 在点B 的左边 ∴()0,3-A ,B (1 , 0)……………………………………………6分 ∴3=OA令0=x ,则()34102-=-+=y∴()3,0-C……………………………………………7分 ∴3=OC∴OC OA =∴△AOC 为等腰直角三角形∴︒=∠45ACO∵点D 为抛物线()412-+=x y 的顶点∴()4,1--D……………………………………………8分 过点D 作y DE ⊥轴 ∴4,1==OE DE∴134=-=-=OC OE CE ∴CE DE =∴△DCE 为等腰直角三角形∴︒=∠45DCE∴︒=︒-︒-︒=∠904545180ACD ∴△ACD 为直角三角形.…………………………………………10分 25.(10分)已知抛物线22212-+-=x x y . (1)写出此抛物线的开口方向、对称轴和顶点坐标;(2)求出抛物线与x 轴、y 轴的交点坐标; (3)在(2)中,设抛物线与y 轴交于点A ,与x 轴交于点B ,若以点A 为顶点的抛物线经过点B ,请你求出这条抛物线的解析式,并指出其开口方向和函数的最值. 解:(1)()222212221--=-+-=x x x y ……………………………………………1分 开口向下,对称轴为直线2=x ,顶点坐标为(2 , 0);……………………………………………4分 (2)令0=y ,则()02212=--x 解之得:2=x∴抛物线与x 轴的交点为(2 , 0)……………………………………………5分 令0=x ,则()220212-=-⨯-=y ∴抛物线与y 轴的交点为()2,0-;……………………………………………6分 (3)由题意可设抛物线的解析式为k ax y +=2∵其顶点为A ()2,0- ∴2-=k……………………………………………7分 ∴22-=ax y把B (2 , 0)代入22-=ax y 得:024=-a 解之得:21=a……………………………………………8分∴2212-=x y开口向上,函数的最小值为2-.…………………………………………10分 26.(10分)已知二次函数m x x y ++=22的图象1C 与x 轴有且只有一个公共点. (1)求1C 的顶点坐标;(2)将1C 向下平移若干个单位后,得抛物线2C ,如果2C 与x 轴的一个交点为()0,3-A ,求2C 的函数关系式,并求2C 与x 轴的另一个交点坐标;(3)若()1,y n P ,()2,2y Q 是1C 上的两点,且21y y >,求实数n 的取值范围.解:(1)()11222-++=++=m x m x x y∵其图象1C 与x 轴有且只有一个公共点 ∴01=-m ∴1=m……………………………………………3分∴()21+=x y∴1C 的顶点坐标为()0,1-;……………………………………………4分(2)设2C 的函数关系式为()k x y ++=21把()0,3-A 代入()k x y ++=21得:()0132=++-k解之得:4-=k∴2C 的函数关系式为()412-+=x y……………………………………………7分 令0=y ,则()0412=-+x解之得:1,321=-=x x∴2C 与x 轴的另一个交点坐标为(1 , 0); ……………………………………………8分 (3)2>n 或4-<n .…………………………………………10分。
《二次函数y=ax2的图象与性质》练习题

1 2 1 2 8.如图,⊙O的半径为2,C1是函数y= 2 x 的图象,C2是函数y=- 2 x 2π 的图象,则阴影部分的面积是________.
9.定义:给定关于x的函数y,对于该函数图象上任意两点(x1,y1), (x2,y2),当x1<x2时,都有y1<y2,称该函数为增函数,根据以上定义,可 ①③ 填上所有正确答案的序 以判断下面所给的函数中,是增函数的有________( 号). 1 ①y=2x;②y=-x+1;③y=x2(x>0);④y=- . x
5.二次函数y=mxm2-1在其图象对称轴的左侧,y随x的增大而增大,则m=
- 3 ________.
a 6.已知反比例函数y= (a≠0),当x<0时,y随x的增大而减小,则函 x 数y=ax2的图象经过的象限是( B ) A.第三、四象限 B.第一、二象限 C.第二、四象限 D.第一、三象限 7.如图,若抛物线y=ax2(a<0)的图象经过点A(-1,y1),B(2,y2), C(3,y3),则( A ) A.y1>y2>y3 B.y1<y2<y3 C.y2<y1<y3 D.y3<y1<y2
1 2 3.抛物线 y=2x ,y=-2x ,y=2x 共有的性质是(B
2 2
பைடு நூலகம்
)
A.开口向下 B.对称轴是 y 轴 C.都有最低点 D.y 随 x 的增大而减小 4.如图,根据图形写出一个符合图象的二次函数关系式: 1 2 y=-2x (答案不唯一) __________________________.
10.函数y=ax2(a≠0)与直线y=2x-3交于点(1,b). (1)求a、b的值; (2)求抛物线y=ax2的顶点坐标和对称轴;
(3)x取何值时,函数y=ax2中,y随x的增大而增大?
《二次函数》练习题

C.S是r的二次函数 D.以上答案都不对
3.若函数y=(m-1)x2+3x+1是二次函数,则有( B )
A.m≠0 B.m≠1 C.x≠0 D.x≠1
4.对于任意实数m,下列函数一定是二次函数的是( C )
A.y=(m-1)2x2 B.y=(m+1)2x2
C.y=(m2+1)x2 D.y=(m2-1)x2 5.已知两个变量x,y之间的关系式为y=(a-2)x2+(b+2)x-3. a≠2 时,x,y之间是二次函数关系; (1)当_______ a=2,b≠-2 时,x,y之间是一次函数关系. (2)当_______________
③实际出厂单价不能低于51元.
根据以上信息,解答下列问题: (1)当一次订购量为_____ 550 个时,零件的实际出厂单价降为51元. (2)设一次订购量为 x 个时,零件的实际出厂单价为 P 元,写出P 与x的 函数关系式. (3)当销售商一次订购500个零件时,该厂获得的利润是多少元?如果
订购1 000个,利润又是多少元?(工厂售出一个零件的利润=实际出
九年级下册数学(华师版)
第26章 二次函数
26.1 二次函数
知识点 1:二次函数的概念 1.在下列 y 关于 x 的函数中,一定是二次函数的是( A ) A.y=2x2 C.y=ax
2
B.y=2x-2 a D.y= 2 x
2.圆的面积公式S=πr2中,S与r之间的关系是( C ) A.S是r的正比例函数 B.S是r的一次函数
(1)写出y与x的函数关系式 ;
(2)求出W与x的函数关系式.(不必写出x的取值范围)
解:(1)y=300+20x.
(2)由题意可得,W与x的函数关系式为: W=(300+20x)(60-40-x)=-20x2+100x+6 000.
第26章《二次函数》单元测试(2)

第26章《二次函数》单元测试一、选择题(每题3分,共30分)1.若直线y =3x +m 经过第一、三、四象限,则抛物线y =(x -m )2+1的顶点必在( )(A )第一象限 (B )第二象限 (C )第三象限 (D )第四象限2.抛物线的顶点为(1,9),它与x 轴交于A (-2,0),B 两点,则B 点坐标为( )(A )(1,0) (B )(2,0) (C )(3,0) (D )(4,0)3.抛物线y =2(x +3) (x -1)的对称轴是( )(A )x =1 (B )x =-1 (C )x =12(D )x =-2 4.函数y =(m -n ) x 2+mx +n 是二次函数的条件是( )(A) m 、n 是常数,且m ≠0 (B) m 、n 是常数,且m ≠n(C) m 、n 是常数,且n ≠0 (D) m 、n 可以为任意实数5.直线y =mx +1与抛物线y =2x 2-8x +k +8相交于点(3,4),则m 、k 值为( )(A) ⎩⎨⎧m =1k =3 (B)⎩⎨⎧m =-1k =2 (C) ⎩⎨⎧m =1k =2 (D) ⎩⎨⎧m =2k =16.抛物线y =2x 2如何平移可得到抛物线y =2(x -4)2-1( )(A )向左平移4个单位,再向上平移1个单位(B )向左平移4个单位,再向下平移1个单位(C )向右平移4个单位,再向上平移1个单位(D )向右平移4个单位,再向下平移1个单位7.烟花厂为扬州三月经贸旅游节特别设计制作一种新型礼炮,这种礼炮的升空高度h (m )与飞行时间t (s )的关系式是h =-52t 2+20x +1,若这种礼炮在点火升空到最高点处引爆,则从点火升空到引爆需要的时间为( ) (A )3s (B )4s (C )5s (D )6s8.如图所示是二次函数y =-12x 2+2的图象在x 轴上方的一部分,对于这段图象与x 轴所围成的阴影部分的面积,你认为与其最.接近的值是( ) (A )4 (B )163(C )2π (D )8 9.如图,某厂有许多形状为直角梯形的铁皮边角料,为节约资源,现要按图中所示的方法从这些边角料上截取矩形(阴影部分)铁皮备用,当截取的矩形面积最大时,矩形两边长x ,y 应分别为( ) (A )x =10,y =14 (B )x =14,y =10 (C )x =12,y =15 (D )x =15,y =1210.若A (-134,y 1),B (-54,y 2),C (14,y 3)为二次函数y =x 2+4x -5的图象上的三点,则y 1,y 2,y 3的大小关系是( )(A )y 1<y 2<y 3 (B )y 2<y 1<y 3 (C )y 3<y 1<y 2 (D )y 1<y 3<y 2(第18题)(第19题)二、填空题(每题3分,共30分)1.若抛物线y =x 2+(m -1)x +(m +3)的顶点在y 轴上,则m = .2.不论x 取何值y =-x 2+6x +c 的函数值总为负数,•则c 的取值范围为 .3.抛物线y =x 2-4x +3•的顶点及它与x 轴的交点三点连线所围成的三角形面积是 .4.已知二次函数y =x 2-4x -3,若-1≤x ≤6,则y 的取值范围为_______.5.行驶中的汽车刹车后,由于惯性的作用,还会继续向前滑行一段距离,这段距离称为“刹车距离”.某车的刹车距离S (m )与车速x (km/h )•之间有下述的函数关系式:S =0.01x +0.002x 2,现该车在限速140km/h 的高速公路上出了交通事故,事后测得刹车距离为46.5m ,请推测:刹车时,汽车 超速(填“是”或“否”)6.已知二次函数y =x 2-2x -3与x 轴交于A 、B 两点,在x 轴上方的抛物线上有一点C ,且△ABC 的面积等于10,则C 点坐标为 .7.直线y =2x +2与抛物线y =x 2+3x 的交点坐标为________. 8.已知二次函数y =ax 2+bx +c (a ≠0)的顶点坐标(-1,-3.2)及部分图象,由图象可知关于x 的一元二次方程ax 2+bx +c =0的两个根分别是x 1=1.3和x 2= . 9.如图,半圆A 和半圆B 均与y 轴相切于点O ,其直径CD 、EF 均和x 轴垂直,以O 为顶点的两条抛物线分别经过点C 、E 和点D 、F ,则图中阴影部分的面积是 .10.老师给出一个二次函数,甲、乙、丙三位同学各指出这个函数的一个性质:甲:函数的图象经过第一、二、四象限; 乙:当x <2时,y 随x 的增大而减小;丙:函数的图象与坐标轴...只有两个交点. 已知这三位同学叙述都正确,请构造出满足上述所有性质的一个函数__________________.三、解答题(共60分)1.已知一抛物线与x 轴的交点是A(-2,0)、B (1,0),且经过点C (2,8)。
二次函数的图象和性质练习题(含参考答案)

新华师大版九年级下册数学第26章 二次函数的图象和性质练习题姓名____________ 时间: 90分钟 满分:120分 总分____________一、选择题(每小题3分,共30分)1. 在二次函数122++-=x x y 的图象中,若y 随x 的增大而增大,则x 的取值范围是 【 】 (A )1<x (B )1>x (C )1-<x (D )1->x2. 若二次函数142-++=m x mx y 的最小值是2,则m 的值是 【 】 (A )4 (B )3 (C )1- (D )4或1-3. 已知二次函数m x x y +-=32(m 为常数)的图象与x 轴的一个交点为(1 , 0),则关于x 的一元二次方程032=+-m x x 的两个实数根是 【 】 (A )1,121-==x x (B )2,121==x x (C )0,121==x x (D )3,121==x x4. 如图,由二次函数c bx ax y ++=2的图象可知,不等式02<++c bx ax 的解集是 【 】 (A )13<<-x (B )1>x (C )3-<x 或1>x (D )3-<x第 4 题图第 5 题图5. 如图是抛物线c bx ax y ++=2的一部分,它的对称轴是直线1=x ,若抛物线x 轴的一个交点为A (3 , 0),则不等式02<++c bx ax 的解集是 【 】 (A )3>x (B )3<x (C )30<<x (D )31<<-x6. 若一次函数()a x a y ++=1的图象过第一、三、四象限,则二次函数ax ax y -=2 【 】(A )有最大值4a (B )有最大值4a - (C )有最小值4a (D )有最小值4a-7. 将抛物线216212+-=x x y 向左平移2个单位后,所得新抛物线的解析式为 【 】(A )()58212+-=x y (B )()54212+-=x y(C )()38212+-=x y (D )()34212+-=x y8. 二次函数的部分图象如图所示,对称轴是直线1-=x ,则这个二次函数的表达式为 【 】 (A )322++-=x x y (B )322++=x x y (C )322-+-=x x y (D )322+--=x x y第 8 题图第 9 题图9. 如图,若二次函数c bx ax y ++=2(0≠a )图象的对称轴为直线1=x ,与y 轴交于点C ,与x 轴交于点A 、点B ()0,1-,则①二次函数的最大值为c b a ++; ②0<+-c b a ;③042<-ac b ; ④当0>y 时,31<<-x .其中正确的个数是 【 】 (A )1 (B )2 (C )3 (D )410. 若二次函数12+=ax y 的图象经过点()0,2-,则关于x 的方程()0122=+-x a 的实数根为 【 】 (A )4,021==x x (B )6,221=-=x x (C )25,2321==x x (D )0,421=-=x x 二、填空题(每小题3分,共30分)11. 若抛物线()12-++=m m x y 的对称轴是直线1=x ,则它的顶点坐标是_________.12. 若抛物线c bx ax y ++=2(0≠a )与抛物线342+-=x x y 关于y 轴对称,则函数c bx ax y ++=2的关系式为________________.13. 已知二次函数c bx ax y ++=2(0≠a ),其中c b a ,,满足0=++c b a 和039=+-c b a ,则该二次函数图象的对称轴是直线_________.14. 若二次函数n x x y +-=42的图象与x 轴只有一个公共点,则实数n 的值为_________. 15. 二次函数542++=x x y ,当3-≤x ≤0的最小值为_________.16. 如果将抛物线122-+=x x y 向上平移,使它经过点()3,0A ,那么所得新抛物线的表达式为________________.17. 经过A (4 , 0),)0,2(-B ,C (0 , 3)三点的抛物线的解析式是___________.18. 若二次函数c bx ax y ++=2(0<a )的图象经过点(2 , 0),且其对称轴为直线1-=x ,则使函数值0>y 成立的x 的取值范围是__________.19. 将一条抛物线向上平移4个单位,再向左平移2个单位后,得到新的抛物线为442++=x x y ,则原抛物线的解析式为________________.20. 已知抛物线c bx ax y ++=2(0≠a )与x 轴交于A 、B 两点,若点A 为()0,2-,抛物线的对称轴为直线2=x ,则线段AB 的长为_________. 三、解答题(共60分)21.(10分)如图,抛物线122++=ax ax y 与x 轴仅有一个公共点A ,经过点A 的直线交该抛物线于点B ,交y 轴交于点C ,且点C 是线段AB 的中点. (1)求这条抛物线的函数解析式; (2)求直线AB 的函数解析式.yxCA BO22.(10分)如图所示,二次函数m x x y ++-=22的图象与x 轴的一个交点为A (3 , 0),另一个交点为B ,且与y 轴交于点C . (1)求m 的值; (2)求点B 的坐标;(3)若点D 为x 轴上方该函数图象上的一点,且ABC ABD S S ∆∆=,求点D 的坐标.yxCBAO23.(10分)如图,一次函数b kx y +=的图象与x 轴和y 轴分别交于A (6 , 0)和()32,0B ,线段AB 的垂直平分线交x 轴于点C ,交AB 于点D . (1)求一次函数的关系式;(2)求过A、B 、C 三点的抛物线的函数关系式.x24.(10分)如图,二次函数c bx ax y ++=2的图象与x 轴交于A 、B 两点,其中点A 的坐标为()0,1-,与y 轴交于点C (0 , 5),另抛物线经过点(1 , 8),点M 是抛物线的顶点.(1)求抛物线的解析式; (2)求△MCB 的面积.y xMCBA O25.(10分)已知二次函数c bx x y ++=2的图象与x 轴交于A 、B 两点,其中点A 的坐标为()0,3-,与y 轴交于点C ,点()3,2--D .(1)求抛物线的解析式;(2)抛物线的对称轴上有一动点P ,求出PD PA +的最小值.yxD C AB OFPyx备用图D C AB O FP 26.(10分)如图所示,抛物线c bx x y ++=2与直线1-=x y 交于A 、B 两点,点A 的纵坐标为4-,点B 在y 轴上,直线AB 与x 轴交于点F ,点P 是线段AB 下方的抛物线上一动点,横坐标为m ,过点P 作PC x ⊥轴于C ,交直线AB 于D .(1)求抛物线的解析式;(2)当m 取何值时,线段PD 的长度取得最大值,其最大值是多少?(3)是否存在点P ,使△P AD 是直角三角形?若存在,求出点P 的坐标;若不存在,说明理由.新华师大版九年级下册数学第26章 二次函数的图象和性质练习题参考答案一、选择题(每小题3分,共30分)二、填空题(每小题3分,共30分)11. ()2,1- 12. 342++=x x y 13. 1-=x 14. 4 15. 1 16. 322++=x x y 17. ()()4283-+-=x x y 18. 24<<-x 19. 42-=x y 20. 8三、解答题(共60分)21.(10分)如图,抛物线122++=ax ax y 与x 轴仅有一个公共点A ,经过点A 的直线交该抛物线于点B ,交y 轴交于点C ,且点C 是线段AB 的中点.(1)求这条抛物线的函数解析式; (2)求直线AB 的函数解析式.yxCA BO解:(1) ∵抛物线122++=ax ax y 与x 轴仅有一个公共点A∴()0422=-=∆a a……………………………………………2分 ∴02=-a a 解之得:1,021==a a……………………………………………4分 ∵0≠a ∴1=a……………………………………………5分 ∴这条抛物线的函数解析式为()22112+=++=x x x y ;(2)∵点A 为抛物线()21+=x y 的顶点∴()0,1-A……………………………………………6分 ∵点C 是线段AB 的中点∴点B 的横坐标为1对于()21+=x y ,当1=x 时,4=y∴B (1 , 4)……………………………………………7分 设直线AB 的函数解析式为b kx y += 把()0,1-A , B (1 , 4)分别代入b kx y +=得:⎩⎨⎧=+=+-40b k b k 解之得:⎩⎨⎧==22b k∴直线AB 的函数解析式为22+=x y . 附 中点坐标公式中点坐标公式在平面直角坐标系中,如果线段AB 的端点A 、B 的坐标分别为A ),(11y x 、B ),(22y x ,则其中点P ),(n m 的坐标为⎪⎪⎩⎪⎪⎨⎧+=+=222121y y n x x m 图形说明如图(1)所示.图(1)22.(10分)如图所示,二次函数m x x y ++-=22的图象与x 轴的一个交点为A (3 , 0),另一个交点为B ,且与y 轴交于点C .(1)求m 的值; (2)求点B 的坐标;(3)若点D 为x 轴上方该函数图象上的一点,且ABC ABD S S ∆∆=,求点D 的坐标.yxCBAO解:(1)把A (3 , 0)代入m x x y ++-=22得:069=++-m解之得:3=m……………………………………………3分 ∴该抛物线的解析式为322++-=x x y ; (2)令0=x ,则0322=++-x x 解之得:3,121=-=x x ∴点B 的坐标为()0,1-;……………………………………………6分 (3)令0=x ,则3=y∴C (0 , 3)……………………………………………7分∵ABC ABD S S ∆∆=∴点C 与点D 的纵坐标相等 令3=y ,则3322=++-x x 解之得:2,021==x x ∴点D 的坐标为(2 , 3).…………………………………………10分 23.(10分)如图,一次函数b kx y +=的图象与x 轴和y 轴分别交于A (6 , 0)和()32,0B ,线段AB 的垂直平分线交x 轴于点C ,交AB 于点D .(1)求一次函数的关系式;(2)求过A 、B 、C 三点的抛物线的函数关系式.解:(1)把A (6 , 0)和()32,0B 分别代入b kx y +=得:⎩⎨⎧==+3206b b k 解之得:⎪⎩⎪⎨⎧=-=3233b k∴一次函数的关系式为3233+-=x y ; ……………………………………………4分 (2)连结BC.∵直线CD 是线段AB 的垂直平分线 ∴BC AC =∵A (6 , 0)()32,0B ∴32,6==OB OA设x BC AC ==,则x AC OA OC -=-=6 在Rt △BOC 中,由勾股定理得:222BC OC OB =+∴()()222632x x =-+解之得:4=x ∴4=AC∴246=-=-=AC OA OC ∴C (2 , 0)……………………………………………7分设过A 、B 、C 三点的抛物线的函数关系式为()()62--=x x a y把()32,0B 代入()()62--=x x a y 得:()()326020=--⨯a解之得:63=a ∴抛物线的解析式为()()6263--=x x y . …………………………………………10分x第(2)问另解: ∵A (6 , 0)()32,0B ∴32,6==OB OA 在Rt △AOB 中 ∵33632tan ===∠OA OB BAO ∴︒=∠30BAO……………………………………………5分 ∴342==OB AB∵直线CD 是线段AB 的垂直平分线 ∴3221==AB AD 在Rt △ACD 中 ∵233230cos ===︒AC AC AD ∴4=AC∴246=-=-=AC OA OC ∴C (2 , 0)……………………………………………7分 设过A 、B 、C 三点的抛物线的函数关系式为()()62--=x x a y把()32,0B 代入()()62--=x x a y 得:()()326020=--⨯a解之得:63=a ∴抛物线的解析式为()()6263--=x x y . …………………………………………10分 注意:若抛物线与x 轴交于A )0,(1x 、B )0,(2x 两点,则可设抛物线的解析式为:()()21x x x x a y --=.24.(10分)如图,二次函数c bx ax y ++=2的图象与x 轴交于A 、B 两点,其中点A 的坐标为()0,1-,与y 轴交于点C (0 , 5),另抛物线经过点(1 , 8),点M 是抛物线的顶点. (1)求抛物线的解析式; (2)求△MCB 的面积.解:(1)把()0,1-,(0 , 5),(1 , 8)分别代入c bx ax y ++=2得:⎪⎩⎪⎨⎧=++==+-85c b a c c b a 解之得:⎪⎩⎪⎨⎧==-=541c b a∴该抛物线的解析式为542++-=x x y ;……………………………………………4分 (2)∵542++-=x x y ∴()922+--=x y……………………………………………5分∵点M 是抛物线()922+--=x y 的顶点∴M (2 , 9)……………………………………………6分 令0=y ,则()0922=+--x解之得:5,121=-=x x ∴B (5 , 0)……………………………………………7分 作y ME ⊥轴 ∴9,2==OE ME∴459=-=-=OC OE CE ∴BOC MCE MEOB MCB S S S S ∆∆∆--=梯形()552124212529⨯⨯-⨯⨯-+⨯=15=…………………………………………10分 25.(10分)已知二次函数c bx x y ++=2的图象与x 轴交于A 、B 两点,其中点A 的坐标为()0,3-,与y 轴交于点C ,点()3,2--D . (1)求抛物线的解析式;(2)抛物线的对称轴上有一动点P ,求出PD PA +的最小值.解:(1)把A ()0,3-、()3,2--D 分别代入c bx x y ++=2得:⎩⎨⎧-=+-=+-324039c b c b 解之得:⎩⎨⎧-==32c b∴抛物线的解析式为322-+=x x y ; ……………………………………………4分 (2)令0=y ,则0322=-+x x 解之得:3,121-==x x ∴B (1 , 0),1=OB……………………………………………6分 ∵A 、B 两点是抛物线322-+=x x y 与x 轴的两个交点∴A 、B 两点关于直线1-=x 对称如图,连结BD ,与直线1-=x 的交点即为PD PA +的值最小时,点P 的位置,作x DE ⊥轴,并连结P A .∴PB PA =∴BD PD PB PD PA =+=+……………………………………………7分∵()3,2--D ∴2,3==OE DE∴321=+=+=OE OB BE 在Rt △BDE 中,由勾股定理得:23332222=+=+=DE BE BD∴PD PA +的最小值为23.…………………………………………10分关于两条线段之和取得最小值的问题有许多几何问题都涉及到两条线段之和最小的问题,解决这类问题的主要方法是依据“两点之间线段最短”,将两条线段的和转化为一条线段,该线段的长度即为两条线段之和的最小值.怎么转化是解决问题的关键-----借助于图形变换中的轴对称可以实现转化.另外还要用到线段垂直平分线的性质定理、勾股定理等知识,有些题目还与函数知识相结合,难度较高.也有部分几何问题涉及到三条线段之和最小,情形比较复杂,但解决问题的依据和思路基本上是不变的.要求:(1)会作出一个点关于某条直线的对称点. (2)熟悉并掌握线段垂直平分线的性质定理.(3)通过合理添加辅助线构造直角三角形,使用勾股定理求解线段(边)的长度. (4)掌握两点关于坐标轴对称时坐标之间的关系,如两点关于y轴对称时,它们的横坐标互为相反数,纵坐标相等.(5)学会并掌握用待定系数法求一次函数的关系式.26.(10分)如图所示,抛物线cbxxy++=2与直线1-=xy交于A、B两点,点A的纵坐标为4-,点B在y轴上,直线AB与x轴交于点F,点P是线段AB下方的抛物线上一动点,横坐标为m,过点P作PC x⊥轴于C,交直线AB于D.(1)求抛物线的解析式;(2)当m取何值时,线段PD的长度取得最大值,其最大值是多少?(3)是否存在点P,使△P AD是直角三角形?若存在,求出点P的坐标;若不存在,说明理由.yxDC FABOP解:(1)对于1-=xy令4-=y,则41-=-x,解之得:3-=x∴()4,3--A令0=x,则1-=y∴()1,0-B把()4,3--A 和()1,0-B 分别代入c bx x y ++=2得:⎩⎨⎧-=-=+-1439c c b 解之得:⎩⎨⎧-==14c b∴抛物线的解析式为142-+=x x y ; ……………………………………………3分 (2)∵点P 是线段AB 下方的抛物线上一动点,横坐标为m∴()14,2-+m m m P (03<<-m ) ∵PC x ⊥轴,点D 在直线1-=x y ∴()1,-m m D ∵点D 在点P 的上方∴()m m m m m PD 314122--=-+--=∴49232+⎪⎭⎫ ⎝⎛+-=m PD……………………………………………5分∴当23-=m 时,线段PD 的长度取得最大值,最大值为49;……………………………………………6分 (3)存在点P ,使△P AD 是直角三角形. 对于1-=x y 令0=y ,则01=-x 解之得:1=x ∴F (1 , 0)∴1==OF OB∴△BOF 和△DCF 都是等腰直角三角形 ∴︒=∠=∠45ADP CDF分为两种情况:①当︒=∠90PAD 时,△P AD 是等腰直角三角形 作PC AE ⊥ ∴()m m PD AE 321212--==∵()4,3--A ,()0,m C ∴()m m AE +=--=33 ∴()m m m +=--33212 整理得:0652=++m m 解之得:3,221-=-=m m ∵03<<-m ∴2-=m∴()()512421422-=--⨯+-=-+m m∴()5,2--P ;……………………………………………8分 ②当︒=∠90APD 时,PD PA =∴()m m m 332--=-- 整理得:0342=++m m 解之得:3,121-=-=m m ∵03<<-m ∴1-=m∴()()411411422-=--⨯+-=-+m m∴()4,1--P ;…………………………………………10分 综上所述,存在点P ,使△P AD 是直角三角形,点P 的坐标为()5,2--或()4,1--.yxDCFABO P注意:对于讨论的第①种情况,我们还可以用下面的方法予以求解,希望借此拓宽大家的视野.先补充知识点: 对于两条直线:222111::b x k y l b x k y l +=+=若21l l ⊥,则121-=k k .注意 此结论通常用来求一次函数的解析式.例如:直线1l 的解析式为2+-=x y ,直线2l 与1l 垂直,且直线2l 经过点)2,1(-,求直线2l 的解析式.解:由题意可设直线2l 为:b x y +=∵其图象经过点)2,1(- ∴3,21-=-=+b b∴直线2l 的解析式为3-=x y . 回到本题:①当︒=∠90PAD 时,AB AP ⊥ 设直线AP 为n mx y += ∵直线AB 为1-=x y ∴1-=m∴n x y +-= 把()4,3--A 代入n x y +-=得:43-=+n∴7-=n∴直线AP 为7--=x y 解方程7342--=-+x x x 得:3,221-=-=x x (不合题意,舍去)∴()5,2--P .学生整理用图。
第26章二次函数单元测试(人教版九年级)!.docx

第二十六章检测 二次函数时间:90分钟满分:100分一、选择题(每小题3分,共30分)(2010,金华中考)已知抛物线),=0?+加的开口向下,顶点坐标为(2,宁夏中考)把抛物线j = -^2向左平移1个单位,然后向上平移3个单位,则平移后抛物线的表达式( ) -3),那么该抛物线有( A.最小值一3 )B.最大值一3C.最小值2D.最大值22、(2010,安徽中考) 若二次函数y =川+加+ 5配方后为〉,=(兀_ 2尸+ R ,则b 、 比的值分别为( A 、0. 5 0. 13、 (2010,河北中考)如图5,已知抛物线y = x 2+bx + c 的对称轴为"2,点力, 2均在抛物线上,且〃〃与x 轴平行,其中点力的坐 标为(0, 3),则点〃的坐标为A. (2, 3)B. (3, 2)C. (3, 3)D. (4, 3)4、 (2010,芜湖中考)二次函数y 二曰#+bx+c 的图象如图 所示,反比例函数尸纟与正比例函数y 二(b+c )x 在同一坐 )C 、一4. 5D 、一4. 12y 万元,则y 与x Z 间的函数表达式为()A. y 二60 (1-x ) 2B. y=60 (1一x )C. y=60-x 2D. y=60 (1 + 7、某幢建筑物,从10m 高的窗口 A 用水管向外喷水,喷出的水 成抛物线状(抛物线所在平面与地面垂直)。
如果抛物线的最高40 lm ,离地面—则水流落地点离墙的距离0B 为 3 点M 离墙 ( )A. 2mB. 3mC. 4mD. 5m x) 21、 8、 (2010,B A I I y :x = 2 O 图5是()A. y=^2x +x+2B. y^x +3x+2C. y^x~2x+3D. y=x~3x+2.6、一台机器原价为60万元,如果每年的折旧率为x,两年后这台机器的价位为A. y = —(x_l)_+3B. y =—(兀 + 1)_+3C. y = _(无一1)~—3D. y = —(x +1)~ ~ 39、已知二次函数y = x 2 - 2twc + m- 1的图象经过原点,与兀轴的另一个交点A,抛物线的顶点为B,则AOAB 的面积为( )3 1A 、 一B 、 2C 、 1D 、 一 2 210、已知函数尸2x — 2的图象如图示,根据其中提供的 信息,可求得使成立的x 的取值范围是()A 、一1W/W3B 、一3MW1C 、心一3D 、穴一1 或 心3.二、填空题(每题3分,共30分)11 > 把y=£-4x-4转化成 y = a(x- h)2 + k 形式 _________12、 ____________________________________________________ 抛物线y = x 2-4x + m 与x 轴只有一个交点,则in 二 __________________________ 。
新人教版26章 二次函数试题(含参考答案及评析)

新人教版九年级下第26章《二次函数》试题班级姓名得分一.选择题(共10小题)1.(2013•遵义)二次函数y=ax2+bx+c(a≠0)的图象如图如图所示,若M=a+b﹣c,N=4a﹣2b+c,P=2a﹣b.则M,N,P中,值小于0的数有()23.(2013•岳阳)二次函数y=ax2+bx+c的图象如图所示,对于下列结论:①a<0;②b<0;③c>0;④b+2a=0;⑤a+b+c <0.其中正确的个数是()4.(2013•烟台)如图是二次函数y=ax2+bx+c图象的一部分,其对称轴为x=﹣1,且过点(﹣3,0).下列说法:①abc<0;②2a﹣b=0;③4a+2b+c<0;④若(﹣5,y1),(,y2)是抛物线上两点,则y1>y2.其中说法正确的是()26.(2013•攀枝花)二次函数y=ax 2+bx+c (a ≠0)的图象如图所示,则函数y=与y=bx+c 在同一直角坐标系内的大致图象是( ).C D .7.(2013•南昌)若二次函数y=ax 2+bx+c (a ≠0)的图象与x 轴有两个交点,坐标分别为(x 1,0),(x 2,0),且x 18.(2013•牡丹江)抛物线y=ax 2+bx+c (a <0)如图所示,则关于x 的不等式ax 2+bx+c >0的解集是( )210.(2012•泰安)设A (﹣2,y 1),B (1,y 2),C (2,y 3)是抛物线y=﹣(x+1)2+a 上的三点,则y 1,y 2,y 3的二.填空题(共10小题)11.(2013•宿迁)若函数y=mx 2+2x+1的图象与x 轴只有一个公共点,则常数m 的值是 _________ .12.(2013•牡丹江)抛物线y=ax 2+bx+c (a ≠0)经过点(1,2)和(﹣1,﹣6)两点,则a+c= _________ .13.(2012•扬州)如图,线段AB 的长为2,C 为AB 上一个动点,分别以AC 、BC 为斜边在AB 的同侧作两个等腰直角三角形△ACD 和△BCE ,那么DE 长的最小值是 _________ .14.(2012•新疆)当x= _________ 时,二次函数y=x 2+2x ﹣2有最小值.15.(2011•资阳)将抛物线y=2x2﹣1沿x轴向右平移3个单位后,与原抛物线交点的坐标为_________.16.(2010•镇江)已知实数x,y满足x2+3x+y﹣3=0,则x+y的最大值为_________.17.(2010•扬州)抛物线y=2x2﹣bx+3的对称轴是直线x=1,则b的值为_________.18.(2008•青海)二次函数y=ax2+bx+c图象如图所示,则点A(b2﹣4ac,﹣)在第_________象限.19.(2007•眉山)如图,已知等腰直角△ABC的直角边长与正方形MNPQ的边长均为20厘米,AC与MN在同一直线上,开始时点A与点N重合,让△ABC以每秒2厘米的速度向左运动,最终点A与点M重合,则重叠部分面积y(厘米2)与时间t(秒)之间的函数关系式为_________.20.(2007•黄石)二次函数y=a(x﹣1)2+bx+c(a≠0)的图象经过原点的条件是_________.三.解答题(共5小题)21.(2010•双鸭山)已知二次函数的图象经过点(0,3),(﹣3,0),(2,﹣5),且与x轴交于A、B两点.(1)试确定此二次函数的解析式;(2)判断点P(﹣2,3)是否在这个二次函数的图象上?如果在,请求出△PAB的面积;如果不在,试说明理由.22.(2013•泉州)已知抛物线y=a(x﹣3)2+2经过点(1,﹣2).(1)求a的值;(2)若点A(m,y1)、B(n,y2)(m<n<3)都在该抛物线上,试比较y1与y2的大小.23.(2013•牡丹江)如图,已知二次函数y=x2+bx+c过点A(1,0),C(0,﹣3)(1)求此二次函数的解析式;(2)在抛物线上存在一点P使△ABP的面积为10,请直接写出点P的坐标.24.已知:二次函数的图象与一次函数y=4x﹣8的图象有两个公共点P(2,m)、Q(n,﹣8).如果抛物线的对称轴是x=﹣1,(1)求二次函数的解析式;(2)当x为何值时,y随x增大而增大,当x为何值时,抛物线在x轴上方.25.(2012•新疆)如图1,在直角坐标系中,已知△AOC的两个顶点坐标分别为A(2,0),C(0,2).(1)请你以AC的中点为对称中心,画出△AOC的中心对称图形△ABC,此图与原图组成的四边形OABC的形状是_________,请说明理由;(2)如图2,已知D(,0),过A,C,D的抛物线与(1)所得的四边形OABC的边BC交于点E,求抛物线的解析式及点E的坐标;(3)在问题(2)的图形中,一动点P由抛物线上的点A开始,沿四边形OABC的边从A﹣B﹣C向终点C运动,连接OP交AC于N,若P运动所经过的路程为x,试问:当x为何值时,△AON为等腰三角形(只写出判断的条件与对应的结果)?新人教版九年级下第26章《二次函数》试题参考答案与试题解析一.选择题(共10小题)1.(2013•遵义)二次函数y=ax2+bx+c(a≠0)的图象如图如图所示,若M=a+b﹣c,N=4a﹣2b+c,P=2a﹣b.则M,N,P中,值小于0的数有()>﹣23.(2013•岳阳)二次函数y=ax2+bx+c的图象如图所示,对于下列结论:①a<0;②b<0;③c>0;④b+2a=0;⑤a+b+c <0.其中正确的个数是()=1=14.(2013•烟台)如图是二次函数y=ax2+bx+c图象的一部分,其对称轴为x=﹣1,且过点(﹣3,0).下列说法:①abc <0;②2a﹣b=0;③4a+2b+c<0;④若(﹣5,y1),(,y2)是抛物线上两点,则y1>y2.其中说法正确的是()=26.(2013•攀枝花)二次函数y=ax2+bx+c(a≠0)的图象如图所示,则函数y=与y=bx+c在同一直角坐标系内的大致图象是().C D.y=(2013•南昌)若二次函数y=ax2+bx+c(a≠0)的图象与x轴有两个交点,坐标分别为(x1,0),(x2,0),且x17.8.(2013•牡丹江)抛物线y=ax2+bx+c(a<0)如图所示,则关于x的不等式ax2+bx+c>0的解集是()2,在对10.(2012•泰安)设A(﹣2,y1),B(1,y2),C(2,y3)是抛物线y=﹣(x+1)2+a上的三点,则y1,y2,y3的二.填空题(共10小题)11.(2013•宿迁)若函数y=mx2+2x+1的图象与x轴只有一个公共点,则常数m的值是0或1.12.(2013•牡丹江)抛物线y=ax2+bx+c(a≠0)经过点(1,2)和(﹣1,﹣6)两点,则a+c=﹣2.13.(2012•扬州)如图,线段AB的长为2,C为AB上一个动点,分别以AC、BC为斜边在AB的同侧作两个等腰直角三角形△ACD和△BCE,那么DE长的最小值是1.CE=x(14.(2012•新疆)当x=﹣1时,二次函数y=x2+2x﹣2有最小值.15.(2011•资阳)将抛物线y=2x2﹣1沿x轴向右平移3个单位后,与原抛物线交点的坐标为(,).,解得,16.(2010•镇江)已知实数x,y满足x2+3x+y﹣3=0,则x+y的最大值为4.17.(2010•扬州)抛物线y=2x2﹣bx+3的对称轴是直线x=1,则b的值为4.,即﹣=1,.18.(2008•青海)二次函数y=ax2+bx+c图象如图所示,则点A(b2﹣4ac,﹣)在第四象限.x=<,﹣)在第四象限.19.(2007•眉山)如图,已知等腰直角△ABC的直角边长与正方形MNPQ的边长均为20厘米,AC与MN在同一直线上,开始时点A与点N重合,让△ABC以每秒2厘米的速度向左运动,最终点A与点M重合,则重叠部分面积y(厘米2)与时间t(秒)之间的函数关系式为y=(20﹣2t)2.y=(20.(2007•黄石)二次函数y=a(x﹣1)2+bx+c(a≠0)的图象经过原点的条件是a+c=0.三.解答题(共5小题)21.(2010•双鸭山)已知二次函数的图象经过点(0,3),(﹣3,0),(2,﹣5),且与x轴交于A、B两点.(1)试确定此二次函数的解析式;(2)判断点P(﹣2,3)是否在这个二次函数的图象上?如果在,请求出△PAB的面积;如果不在,试说明理由.;×22.(2013•泉州)已知抛物线y=a(x﹣3)2+2经过点(1,﹣2).(1)求a的值;(2)若点A(m,y1)、B(n,y2)(m<n<3)都在该抛物线上,试比较y1与y2的大小.23.(2013•牡丹江)如图,已知二次函数y=x2+bx+c过点A(1,0),C(0,﹣3)(1)求此二次函数的解析式;(2)在抛物线上存在一点P使△ABP的面积为10,请直接写出点P的坐标.,24.已知:二次函数的图象与一次函数y=4x﹣8的图象有两个公共点P(2,m)、Q(n,﹣8).如果抛物线的对称轴是x=﹣1,(1)求二次函数的解析式;(2)当x为何值时,y随x增大而增大,当x为何值时,抛物线在x轴上方.,得到﹣25.(2012•新疆)如图1,在直角坐标系中,已知△AOC的两个顶点坐标分别为A(2,0),C(0,2).(1)请你以AC的中点为对称中心,画出△AOC的中心对称图形△ABC,此图与原图组成的四边形OABC的形状是正方形,请说明理由;(2)如图2,已知D(,0),过A,C,D的抛物线与(1)所得的四边形OABC的边BC交于点E,求抛物线的解析式及点E的坐标;(3)在问题(2)的图形中,一动点P由抛物线上的点A开始,沿四边形OABC的边从A﹣B﹣C向终点C运动,连接OP交AC于N,若P运动所经过的路程为x,试问:当x为何值时,△AON为等腰三角形(只写出判断的条件与对应的结果)?,的坐标为(,﹣﹣2或。
新人教版九年级上册第26章二次函数测试题.doc

二次函数测试题班级 姓名 成绩一、选择题(每小题3分,共30分) 1、二次函数()212+-=x y 的最小值是( )。
A 、-2B 、2C 、-1D 、12、已知抛物线的解析式为()122++=x y ,则抛物线的顶点坐标是( )。
A 、(-2,1) B 、(2,1)C 、(2,-1)D 、(1,2) 3、函数2y ax b y ax bx c =+=++和在同一直角坐标系内的图象大致是( )。
4、已知二次函数c bx ax y ++=2的图象如图所示,则下列结论正确的是( )。
A 、ab >0,c >0B 、ab >0,c <0C 、ab <0,c >0D 、ab <0,c <05、对于2)3(22+-=x y 的图象下列叙述正确的是( )。
A 、顶点坐标为(-3,2)B 、当3≥x 时y 随x 增大而增大C 、对称轴为y=3D 、当3≥x 时y 随x 增大而减小6、把二次函数213212---=x x y 的图象向上平移3个单位,再向右平 移4个单位,则两次平移后的图象的解析式是( )。
A 、x y (21-=- 1)2 +7 B 、x y (21-=+7)2 +7 C 、x y (21-=+3)2 +4 D 、x y (21-=-1)2 +1 7、已知二次函数772--=x kx y 的图象和x 轴有交点,则k 的取值范围是( )。
A 、47->kB 、k ≥47-且0≠kC 、k ≥47- D 、47->k 且0≠k 8、在一定条件下,若物体运动的路程s (米)与时间t (秒)的关系式为t t s 252+=,则当t =4时,该物体所经过的路程为( )。
A 、28米B 、48米C 、68米D 、88米9、若点(2,5),(4,5)在抛物线c bx ax y ++=2上,则它的对称轴是( )A 、3=xB 、1=xC 、2=xD 、a b x -= 10、已知二次函数7522++=x x y 的图象上有有点A 1(2)y -,,B 21(5)3y -,,C 31(1)5y -,,则321,,y y y 的大小关系为( )。
第26章二次函数同步练习(一)及答案

第26章二次函数 同步学习检测(一)班级 _______________座号 姓名 ___ 得分_____一、填空题:(每小题2分,共80分)1、(2009年北京市)若把代数式223x x --化为()2x m k -+的形式,其中,m k 为常数,则m+k= __________ .2、(2009年安徽)已知二次函数的图象经过原点及点(12-,14-),且图象与x 轴的另一交点到原点的距离为1,则该二次函数的解析式为3、(2009 黑龙江大兴安岭)当=x 时,二次函数222-+=x x y 有最小值.4、(2009年郴州市)抛物线23(1)5y x =--+的顶点坐标为_______________________. 5、(2009年上海市)将抛物线22y x =-向上平移一个单位后,得以新的抛物线,那么新的抛物线的表达式是 ______________ .6、(2009年内蒙古包头)已知二次函数2y ax bx c =++的图象与x 轴交于点(20)-,、1(0)x ,,且112x <<,与y 轴的正半轴的交点在(02),的下方.下列结论:①420a b c -+=;②0a b <<;③20a c +>;④210a b -+>.其中正确结论的个数是 ____ 个. 7、(2009湖北省荆门市)函数(2)(3)y x x =--取得最大值时,x =____________. 8、(2009年齐齐哈尔市)当x =_____________时,二次函数222y x x =+-有最小值. 9、(2009年贵州省黔东南州)二次函数322--=x x y 的图象关于原点O (0, 0)对称的图象的解析式是_________________。
10、已知二次函数2122y x x =-+, 当x______________时,y 随x 的增大而增大. 11、(2009襄樊市)抛物线2y x bx c =-++的图象如图所示,则此抛物线的解析式为 .12、(2009年娄底)如图,⊙O 的半径为2,C 1是函数y =12x 2的图象,C 2是函数y =-12x 2的图象,则阴影部分的面积是 .13、(2009年甘肃庆阳)如图为二次函数2y ax bx c =++的图象,给出下列说法: ①0ab <;②方程20ax bx c ++=的根为1213x x =-=,;③0a b c ++>;④当1x >时,y 随x 值的增大而增大;⑤当0y >时,13x -<<.其中,正确的说法有 .(请写出所有正确说法的序号)14、(2009年甘肃定西)抛物线2y x bx c =-++的部分图象如图所示,请写出与其关系式、图象相关的2个正确结论: , .(对称轴方程,图象与x 正半轴、y 轴交点坐标例外)15、(2009年鄂州)把抛物线y =ax+bx+c 的图象先向右平移3个单位,再向下平移2个单位,所得的图象的解析式是y =x -3x+5,则a+b+c=__________16、(2009年包头)将一条长为20cm 的铁丝剪成两段,并以每一段铁丝的长度为周长各做成一个正方形,则这两个正方形面积之和的最小值是 cm 2.17、(2009年黄石市)若抛物线23y ax bx =++与232y x x =-++的两交点关于原点对称,则a b 、分别为 .18.某商场销售一批名牌衬衫,平均每天可售出20件,每件盈利40元。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第26章 二次函数 26.1 二次函数01 基础题知识点1 二次函数的定义1.下列各式中,y 是x 的二次函数的是(B )A .y =ax 2+bx +cB .x 2+y -2=0C .y 2-ax =-2D .x 2-y 2+1=02.在自由落体公式h =12gt 2(g 为常量)中,h 与t 之间的关系是(C )A .正比例函数B .一次函数C .二次函数D .以上答案都不对3.下列函数中,是二次函数的是①④⑥.(填序号)①y =13x 2-5x +612;②y =3x 2+1;③y =(x -1)2-x 2;④y =x(x -1);⑤y =13x +32;⑥y =12-12m +m 2.4.已知两个变量x ,y 之间的关系式为y =(a -2)x 2+(b +2)x -3.(1)当a ≠2时,x ,y 之间是二次函数关系;(2)当a =2且b ≠-2时,x ,y 之间是一次函数关系. 知识点2 实际问题中二次函数关系式5.在一个边长为2的正方形中挖去一个边长为x(0<x <2)的小正方形,如果设剩余部分的面积为y ,那么y 与x 的函数关系式是(B )A .y =x 2B .y =4-x 2C .y =x 2-4D .y =4-2x6.某商店从厂家以每件21元的价格购进一批商品,该商店可以自行定价.若每件商品售价为x 元,则可卖出(350-10x)件商品,则该商品的销售利润y 元与售价x 元的函数关系式为(B )A .y =-10x 2-560x +7 350B .y =-10x 2+560x -7 350C .y =-10x 2+350xD .y =-10x 2+350x -7 3507.某车的刹车距离y(m )与开始刹车时的速度x(m /s )之间的关系满足二次函数y =120x 2(x>0).若该车某次的刹车距离为5 m ,则开始刹车时的速度为(C )A .40 m /sB .20 m /sC .10 m /sD .5 m /s8.菱形的两条对角线的长度之和为26 cm ,则菱形的面积S(cm 2)与其中一条对角线的长x(cm )之间的函数关系式为S =-12x 2+13x ,自变量x 的取值范围是0<x<26.9.如图所示,长方体的底面是边长为x 的正方形,高为6,请你用含x 的代数式表示:这个长方体的侧面展开图的面积S =24x ,长方体的体积V =6x 2,各边长的和L =8x +24,在上面的三个函数中,V =6x 2是关于x 的二次函数.10.(教材P 4习题T 4变式)如图,有一个长为24米的篱笆,一面利用墙(墙的最大长度a 为10米)围成中间隔有一道篱笆的长方形花圃.设花圃的宽AB 为x 米,面积为S 平方米.(1)求S 与x 之间的函数关系式;(2)如果要围成面积为45平方米的花圃,那么AB 的长为多少米?解:(1)S =x(24-3x), 即S =-3x 2+24x. (2)当S =45时, -3x 2+24x =45. 解得x 1=3,x 2=5.又∵当x =3时,BC =24-3x =15>10(舍去), ∴x =5,即AB 的长为5米.易错点 忽视二次函数表达式中二次项系数不为零11.已知两个变量x ,y 之间的关系式为y =(m -2)xm 2-2+x -1.若x ,y 之间是二次函数关系,则m =-2.【变式】 若y =(a +1)x |a|+1是关于x 的二次函数,则a 的值是1.02 中档题12.对于任意实数m ,下列一定是二次函数的是(C )A .y =(m -2)2x 2B .y =(m +2)x 2C .y =(m 2+1)x 2D .y =(m 2-1)x 213.(2019·郑州实验外国语中学模拟)下列函数关系中,是二次函数的是(D )A .在弹性限度内,弹簧的长度y 与所挂物体质量x 之间的关系B .当距离一定时,火车行驶的时间t 与速度v 之间的关系C .等边三角形的周长C 与边长a 之间的关系D .半圆面积S 与半径R 之间的关系14.如图,正方形ABCD 的边长为5,点E 是AB 上一点,点F 是AD 延长线上一点,且BE =DF.四边形AEGF 是矩形,则矩形AEGF 的面积y 与BE 的长x 之间的函数关系式为(D )A .y =5-xB .y =5-x 2C .y =25-xD .y =25-x 215.如图,在正方形ABCD 中,AB =2,点M 为正方形ABCD 的边CD 上的动点(与点C ,D 不重合),连结BM ,作MF ⊥BM ,与正方形ABCD 的外角∠ADE 的平分线交于点F.设CM =x ,△DFM 的面积为y ,则y 与x 之间的函数关系式为y =-12x 2+x .16.某工厂生产的某种产品按质量分为10个档次,第1档次(最低档次)的产品一天能生产95件,每件利润6元.每提高一个档次,每件利润增加2元,但一天产量减少5件.(1)若生产第x 档次的产品一天的总利润为y 元(其中x 为正整数,且1≤x ≤10),求出y 关于x 的函数关系式; (2)若生产第x 档次的产品一天的总利润为1 120元,求该产品的质量档次. 解:(1)∵第x 档次的产品提高的档次是(x -1)档, ∴y =[6+2(x -1)][95-5(x -1)],即y =-10x 2+180x +400(其中x 是正整数,且1≤x ≤10). (2)由题意,得-10x 2+180x +400=1 120. 整理,得x 2-18x +72=0. 解得x 1=6,x 2=12(舍去). 答:该产品的质量档次为第6档.03 综合题17.如图,在△ABC 中,∠B =90°,AB =12 mm ,BC =24 mm ,动点P 从点A 开始沿边AB 向B 以2 mm /s 的速度移动(不与点B 重合),动点Q 从点B 开始沿边BC 向C 以4 mm /s 的速度移动(不与点C 重合).如果P ,Q 分别从A ,B 同时出发,设运动的时间为x s ,四边形APQC 的面积为y mm 2.(1)求y 与x 之间的函数关系式; (2)求自变量x 的取值范围;(3)四边形APQC 的面积能否等于172 mm 2?若能,求出运动的时间;若不能,说明理由.解:(1)由题意可知,AP =2x ,BQ =4x ,则 y =12BC ·AB -12BQ ·BP =12×24×12-12·4x ·(12-2x), 即y =4x 2-24x +144. (2)∵0<AP <AB ,0<BQ <BC , ∴0<2x <12,0<4x <24. ∴0<x<6.(3)不能.理由如下:当y =172时,4x 2-24x +144=172. 解得x 1=7,x 2=-1. 又∵0<x<6,∴四边形APQC 的面积不能等于172 mm 2.26.2 二次函数的图象与性质26.2.1 二次函数y =ax 2的图象与性质01 基础题知识点1 二次函数y =ax 2的图象 1.二次函数y =x 2的图象是(C )A .线段B .直线C .抛物线D .双曲线2.如图,函数y =-2x 2的图象是(C )A .①B .②C .③D .④3.(2020·南阳南召县模拟)如果抛物线y =(a +2)x 2的开口向下,那么a 的取值范围为(D )A .a >2B .a <2C .a >-2D .a <-24.抛物线y =-x 2的开口向下,顶点坐标是(0,0),对称轴是y 轴.5.下列各点:(-1,2),(-1,-2),(-2,-4),(-2,4),其中在二次函数y =-2x 2的图象上的是(-1,-2).6.(教材P 7练习T 1变式)在同一平面直角坐标系中,画出下列函数的图象.(1)y =2x 2;(2)y =12x 2.解:列表:x … -2 -1 0 1 2 … y =2x 2… 8 2 0 2 8 … y =12x 2 …212122…描点、连线可得图象如图.知识点2 二次函数y =ax 2的性质7.对于函数y =4x 2,下列说法正确的是(B )A .当x>0时,y 随x 的增大而减小B .当x<0时,y 随x 的增大而减小C .y 随x 的增大而减小D .y 随x 的增大而增大8.已知原点是抛物线y =(m -2)x 2的最低点,则m 的取值范围是(A )A .m>2B .m>-2C .m<2D .m<09.已知抛物线y =-x 2过A(-2,y 1),B(-1,y 2)两点,则下列关系式一定正确的是(C )A .y 1<0<y 2B .y 2<0<y 1C .y 1<y 2<0D .y 2<y 1<010.抛物线y =2x 2,y =-2x 2,y =12x 2共有的性质是(B )A .开口向下B .图象对称轴是y 轴C .都有最低点D .y 随x 的增大而减小11.已知二次函数y =x 2,当x >0时,y 随x 的增大而增大(填“增大”或“减小”). 12.二次函数y =ax 2(a >0)的图象经过点(1,y 1),(2,y 2),则y 1<y 2(填“>”或“<”). 13.已知抛物线y =ax 2经过点(1,3).(1)求a 的值;(2)当x =3时,求y 的值; (3)说出此二次函数的三条性质.解:(1)∵抛物线y =ax 2经过点(1,3),∴a =3. (2)把x =3代入抛物线y =3x 2,得y =3×32=27.(3)答案不唯一,如:抛物线的开口向上;坐标原点是抛物线的顶点;当x >0时,y 随着x 的增大而增大;抛物线有最低点;当x =0时,y 有最小值,最小值是0等.02 中档题14.(2019·咸宁)已知点A(-1,m),B(1,m),C(2,m -n)(n >0)在同一个函数的图象上,这个函数可能是(D )A .y =xB .y =-2xC .y =x 2D .y =-x 215.如图,A ,B 为抛物线y =x 2上两点,且线段AB ⊥y 轴.若AB =6,则点A 的坐标为(D )A .(3,3)B .(3,9)C .(-3,3)D .(-3,9)16.(2019·呼和浩特)二次函数y =ax 2与一次函数y =ax +a 在同一坐标系中的大致图象可能是(D )A. B.C. D.17.定义运算“※”为:a ※b =⎩⎪⎨⎪⎧ab 2(b>0),-ab 2(b ≤0),如1※(-2)=-1×(-2)2=-4,则函数y =2※x 的图象大致是(C )18.已知二次函数y =mxm 2-1,在其图象对称轴的左侧y 随x 的增大而增大,则m =-3.19.【易错】下列四个二次函数:①y =x 2;②y =-2x 2;③y =12x 2;④y =3x 2,其中抛物线开口从大到小的排列顺序是③①②④.【变式】 如图,各抛物线所对应的函数表达式分别为:①y =ax 2;②y =bx 2;③y =cx 2;④y =dx 2.比较a ,b ,c ,d 的大小,用“>”连结为a >b >d >c .抛物线的开口方向决定了a 的正负性,抛物线的开口大小决定了a 的绝对值的大小,即开口越大,|a|越小,开口越小,|a|越大.20.根据下列条件求m 的取值范围.(1)函数y =(m +3)x 2,当x >0时,y 随x 的增大而减小,当x <0时,y 随x 的增大而增大; (2)函数y =(2m -1)x 2有最小值;(3)抛物线y =(m +2)x 2与抛物线y =-12x 2的形状相同.解:(1)∵函数y =(m +3)x 2,当x >0时,y 随x 的增大而减小,当x <0时,y 随x 的增大而增大, ∴m +3<0. ∴m <-3.(2)∵函数y =(2m -1)x 2有最小值, ∴2m -1>0. ∴m >12.(3)∵抛物线y =(m +2)x 2与抛物线y =-12x 2的形状相同,∴m +2=±12.解得m =-52或-32.03 综合题21.(2020·南充)如图,正方形四个顶点的坐标依次为(1,1),(3,1),(3,3),(1,3).若抛物线y =ax 2的图象与正方形有公共点,则实数a 的取值范围是(A )A .19≤a ≤3B .19≤a ≤1 C .13≤a ≤3 D .13≤a ≤126.2.2 二次函数y =ax 2+bx +c 的图象与性质 第1课时 二次函数y =ax 2+k 的图象与性质01 基础题知识点1 二次函数y =ax 2+k 与y =ax 2的图象之间的关系1.如图,将抛物线y =13x 2向上平移2个单位长度得到抛物线y =13x 2+2;将抛物线y =13x 2向下平移2个单位长度得到抛物线y =13x 2-2.2.将二次函数y =x 2-1的图象向上平移3个单位长度,得到的图象所对应的函数表达式是y =x 2+2. 3.将二次函数y =x 2的图象向下平移1个单位长度,则平移后的二次函数的关系式为(A )A .y =x 2-1B .y =x 2+1C .y =(x -1)2D .y =(x +1)24.函数y =x 2+1与y =x 2的图象的不同之处是(C )A .对称轴B .开口方向C .顶点D .形状知识点2 二次函数y =ax 2+k 的图象与性质 5.抛物线y =-12x 2-3的顶点坐标是(C )A .(12,-3) B .(-3,0) C .(0,-3) D .(0,3)6.函数y =-x 2+1的图象大致为(B )7.(2020·南阳南召县模拟)抛物线y =2x 2+4与y 轴的交点坐标是(C )A .(0,2)B .(0,-2)C .(0,4)D .(0,-4)8.下列函数中,当x <0时,y 随x 的增大而增大的是(D )A .y =-2xB .y =-x +2C .y =1xD .y =-x 2-39.与抛物线y =-45x 2-1顶点相同,形状也相同,而开口方向相反的抛物线所对应的函数表达式是(B )A .y =-45x 2-1B .y =45x 2-1C .y =-45x 2+1 D .y =45x 2+110.已知点(x 1,y 1),(x 2,y 2)均在抛物线y =x 2-1上,下列说法中正确的是(D )A .若y 1=y 2,则x 1=x 2B .若x 1=-x 2,则y 1=-y 2C .若0<x 1<x 2,则y 1>y 2D .若x 1<x 2<0,则y 1>y 211.二次函数y =3x 2-3的图象开口向上,顶点坐标为(0,-3),对称轴为y 轴,当x>0时,y 随x 的增大而增大;当x<0时,y 随x 的增大而减小.因为a =3>0,所以y 有最小值,当x =0时,y 的最小值是-3. 12.(教材P 10练习T 1变式)在同一个平面直角坐标系中,作出y =12x 2,y =12x 2-1的图象.(1)分别指出它们的开口方向、对称轴以及顶点坐标; (2)抛物线y =12x 2-1与抛物线y =12x 2有什么关系?解:如图所示.(1)y =12x 2开口向上,对称轴为y 轴,顶点坐标为(0,0);y =12x 2-1开口向上,对称轴为y 轴,顶点坐标为(0,-1).(2)抛物线y =12x 2-1可由抛物线y =12x 2向下平移1个单位长度得到.易错点 求函数值的取值范围时忽视顶点处的取值13.对于二次函数y =-2x 2+4,当-2<x ≤1时,y 的取值范围是-4<y ≤4. 02 中档题14.(2019·河南实验中学模拟)二次函数y =ax 2+c 的图象与y =2x 2的图象形状相同,开口方向相反,且经过点(1,1),则该二次函数的表达式为(D )A .y =2x 2-1B .y =2x 2+3C .y =-2x 2-1D .y =-2x 2+315.已知y =ax 2+k 的图象上有三点A(-3,y 1),B(1,y 2),C(2,y 3),且y 2<y 3<y 1,则a 的取值范围是(A )A .a>0B .a<0C .a ≥0D .a ≤016.在同一平面直角坐标系中,函数y =ax 2+b 与y =ax +b(a ,b 都不为0)的图象的相对位置可以是(A )17.【易错】已知y =(m +2)xm 2+m -4-3是二次函数,且当x >0时,y 随x 的增大而减小,则m =-3. 18.已知二次函数y =ax 2+c ,当x 取x 1,x 2(x 1≠x 2)时,函数值相等,则当x =x 1+x 2时,函数值为c . 19.把二次函数y =-12x 2的图象向上平移2个单位长度.(1)求新图象的表达式、顶点坐标和对称轴; (2)画出平移后的函数图象;(3)求平移后的函数的最大值或最小值,并求对应的x 的值. 解:(1)y =-12x 2+2,顶点坐标是(0,2),对称轴是y 轴.(2)略.(3)x =0时,y 有最大值,最大值为2.20.已知函数y =2x 的图象和抛物线y =ax 2+3相交于点(2,b).(1)求a ,b 的值;(2)若函数y =2x 的图象上纵坐标为2的点为A ,抛物线y =ax 2+3的顶点为B ,求S △AOB 的值. 解:(1)∵点(2,b)在直线y =2x 上,∴b =4. 又∵(2,b)即(2,4)在抛物线y =ax 2+3上, ∴4a +3=4.∴a =14.(2)在y =2x 中,令y =2,则x =1, ∴A(1,2).∵抛物线y =14x 2+3的顶点B 为(0,3),∴S △AOB =12OB ·|x A |=12×3×1=32.03 综合题21.已知抛物线y =14x 2+1具有如下性质:该抛物线上任意一点到定点F(0,2)的距离与到x 轴的距离始终相等.如图,点M 的坐标为(3,3),P 是抛物线y =14x 2+1上一个动点.(1)若PF =5,求该点P 的坐标; (2)求△PMF 周长的最小值.解:(1)∵PF =5,∴根据题意知点P 的纵坐标为5. 当y =5时,14x 2+1=5,x =±4.∴点P 的坐标为(4,5)或(-4,5).(2)过点M 作ME ⊥x 轴,交抛物线于点P ′,此时△P ′MF 周长最小. ∵F(0,2),M(3,3),∴ME =3,FM =(3-0)2+(3-2)2=2. ∴△PMF 周长的最小值为ME +MF =3+2=5.第2课时 二次函数y =a(x -h)2的图象与性质01 基础题知识点1 二次函数y =a (x -h )2与y =ax 2的图象之间的关系1.将抛物线y =x 2向左平移5个单位长度得到抛物线y =(x +5)2;将抛物线y =x 2向右平移5个单位长度得到抛物线y =(x -5)2.2.如果将抛物线y =x 2向右平移1个单位长度,那么所得新抛物线的函数关系式是(C )A .y =x 2-1B .y =x 2+1C .y =(x -1)2D .y =(x +1)23.下列方法可以得到抛物线y =25(x -2)2的是(A )A .将抛物线y =25x 2向右平移2个单位长度B .将抛物线y =25x 2向左平移2个单位长度C .将抛物线y =25x 2向上平移2个单位长度D .将抛物线y =25x 2向下平移2个单位长度知识点2 二次函数y =a (x -h )2的图象与性质 4.抛物线y =(x +1)2的顶点坐标是(A )A .(-1,0)B .(-1,1)C .(0,-1)D .(1,0)5.在平面直角坐标系中,二次函数y =a(x -h)2(a ≠0)的图象可能是(D )6.已知二次函数y =a(x -5)2,当x <5时,y 随x 的增大而增大,则a 的取值范围是(D )A .a ≥0B .a ≤0C .a >0D .a <07.关于抛物线y =(x -1)2,下列说法错误的是(D )A .开口向上B .与x 轴有一个交点C .对称轴是直线x =1D .当x >1时,y 随x 的增大而减小8.二次函数y =3(x +4)2的图象开口向上,对称轴是直线x =-4,当x>-4时,y 随x 的增大而增大,当x<-4时,y 随x 的增大而减小,当x =-4时,y 的最小值是0.9.已知函数y =-(x -1)2图象上的两点A(2,y 1),B(a ,y 2),其中a >2,则y 1与y 2的大小关系是y 1>y 2(填“<”“>”或“=”).10.(教材P 13练习T 1变式)在同一平面直角坐标系中,画出函数y =x 2,y =(x +2)2,y =(x -2)2的图象,并写出对称轴及顶点坐标.解:图象如图.抛物线y =x 2的对称轴是直线x =0,顶点坐标为(0,0).抛物线y =(x +2)2的对称轴是直线x =-2,顶点坐标为(-2,0). 抛物线y =(x -2)2的对称轴是直线x =2,顶点坐标为(2,0).易错点 二次函数增减性相关的易错11.已知在二次函数y =2(x -h)2的图象上,当x >3时,y 随x 的增大而增大,则h 的取值范围是h ≤3. 02 中档题12.(2019·河南模拟)如图,在平面直角坐标系中,过点A 且与x 轴平行的直线交抛物线y =13(x +1)2于B ,C 两点.若线段BC 的长为6,则点A 的坐标为(C )A .(0,1)B .(0,4.5)C .(0,3)D .(0,6)13.在同一平面直角坐标系中,一次函数y =ax +c 和二次函数y =a(x +c)2的图象大致为(B )14.(2020·焦作一模)若抛物线y =2(x -1)2经过(m ,n)和(m +3,n)两点,则n 的值为(A )A .92B .-92C .1D .1215.已知二次函数y =-(x -h)2(h 为常数),当自变量x 的取值范围是2≤x ≤5时,与其对应的函数值y 的最大值为-1,则h 的值为(B )A .3或6B .1或6C .1或3D .4或616.把抛物线y =a(x -4)2向左平移6个单位长度后得到抛物线y =-3(x -h)2.若抛物线y =a(x -4)2的顶点是A ,且与y 轴交于点B ,抛物线y =-3(x -h)2的顶点是M ,求:(1)a ,h 的值; (2)S △MAB 的值.解:(1)∵抛物线y =a(x -4)2向左平移6个单位长度后得到抛物线y =-3(x -h)2, ∴a =-3,4-6=h ,解得h =-2.(2)∵抛物线y =a(x -4)2即y =-3(x -4)2的顶点是A ,且与y 轴交于点B , ∴A(4,0),B(0,-48).∵抛物线y =-3(x -h)2即y =-3(x +2)2的顶点是M ,∴M(-2,0). ∴S △MAB =12×|4-(-2)|×|-48|=144.03 综合题17.如图,已知二次函数y =(x +2)2的图象与x 轴交于点A ,与y 轴交于点B ,连结AB.(1)求点A ,点B 的坐标; (2)求S △AOB ;(3)在对称轴上是否存在一点P ,使以P ,A ,O ,B 四点为顶点的四边形为平行四边形?若存在,求出P 点的坐标;若不存在,请说明理由.解:(1)∵二次函数y =(x +2)2的图象与y 轴交于点B , ∴令x =0,则y =4. ∴B(0,4).∵二次函数y =(x +2)2的图象与x 轴交于点A , ∴令y =0,则(x +2)2=0. 解得x =-2. ∴A(-2,0).(2)S △AOB =12|AO|·|BO|=12×|-2|×|4|=4.(3)对称轴上存在一点P ,使以P ,A ,O ,B 为顶点的四边形为平行四边形. 理由:当P 点坐标是(-2,4)时,AP ∥OB ,AP =OB ,四边形PAOB 是平行四边形; 当P 点坐标是(-2,-4)时,AP ∥OB ,AP =OB ,四边形PABO 是平行四边形.综上所述,点P 的坐标为(-2,4)或(-2,4)时,以P ,A ,O ,B 为顶点的四边形是平行四边形.第3课时二次函数y=a(x-h)2+k的图象与性质01基础题知识点1二次函数y=a(x-h)2+k与y=ax2的图象之间的关系1.二次函数y=-3(x-4)2+2的图象是由抛物线y=-3x2先向右(填“左”或“右”)平移4个单位长度,再向上(填“上”或“下”)平移2个单位长度得到的.2.(2020·哈尔滨)将抛物线y=x2向上平移3个单位长度,再向右平移5个单位长度,所得到的抛物线为(D) A.y=(x+3)2+5 B.y=(x-3)2+5C.y=(x+5)2+3 D.y=(x-5)2+33.抛物线y=(x+2)2-3可以由抛物线y=x2平移得到,则下列平移过程正确的是(B)A.先向左平移2个单位长度,再向上平移3个单位长度B.先向左平移2个单位长度,再向下平移3个单位长度C.先向右平移2个单位长度,再向上平移3个单位长度D.先向右平移2个单位长度,再向下平移3个单位长度4.在同一平面直角坐标系内,将抛物线y=(x-2)2+5先向左平移2个单位长度,再向下平移1个单位长度后,所得抛物线的顶点坐标为(D)A.(4,4) B.(4,6)C.(0,6) D.(0,4)知识点2 二次函数y=a(x-h)2+k的图象与性质5.(2020·南阳南召县期末)抛物线y=-(x+2)2+5的顶点坐标是(B)A.(2,5) B.(-2,5)C.(-2,-5) D.(2,-5)6.二次函数y=(x+2)2-1的图象大致为(D)7.设二次函数y=(x-3)2-4图象的对称轴为直线l,若点M在直线l上,则点M的坐标可能是(B) A.(1,0) B.(3,0)C.(-3,0) D.(0,-4)8.(2020·甘孜州)如图,二次函数y =a(x +1)2+k 的图象与x 轴交于A(-3,0),B 两点,下列说法错误的是(D )A .a<0B .图象的对称轴为直线x =-1C .点B 的坐标为(1,0)D .当x<0时,y 随x 的增大而增大9.(2020·南阳南召县模拟)如果点A(-5,y 1)与点B(-2,y 2)都在抛物线y =(x +1)2+1上,那么y 1>y 2.(填“>”“<”或“=”)易错点 将图象平移与坐标轴平移混淆10.在平面直角坐标系中,若抛物线y =3x 2不动,而把x 轴、y 轴分别向上、向右平移1个单位长度,则在新的平面直角坐标系中,抛物线的函数表达式为y =3(x +1)2-1. 02 中档题11.若抛物线y =(x -a)2+(a -1)的顶点在第一象限,则a 的取值范围为(A )A .a >1B .a >0C .a >-1D .-1<a <012.函数y =(x -1)2+k 与y =k x(k 是不为0的常数)在同一平面直角坐标系中的图象大致为(B )13.(2020·衢州)二次函数y =x 2的图象平移后经过点(2,0),则下列平移方法正确的是(C )A .向左平移2个单位长度,向下平移2个单位长度B .向左平移1个单位长度,向上平移2个单位长度C .向右平移1个单位长度,向下平移1个单位长度D .向右平移2个单位长度,向上平移1个单位长度14.(2020·南京)下列关于二次函数y =-(x -m)2+m 2+1(m 为常数)的结论:①该函数的图象与函数y =-x 2的图象形状相同;②该函数的图象一定经过点(0,1);③当x>0时,y 随x 的增大而减小;④该函数的图象的顶点在函数y =x 2+1的图象上,其中所有正确结论的序号是①②④.15.如图,7×8网格的每个小正方形边长均为1,将抛物线y 1=x 2-1的图象向右平移2个单位长度得到抛物线y 2.(1)请直接写出抛物线y 2的函数表达式y 2=(x -2)2-1; (2)求图中阴影部分的面积;(3)若将抛物线y 2沿x 轴翻折,求翻折后的抛物线表达式. 解:(2)图中阴影部分的面积为2×4=8.(3)将抛物线y 2沿x 轴翻折,翻折后的抛物线表达式为-y =(x -2)2-1,即y =-(x -2)2+1. 03 综合题16.如图,已知抛物线y =a(x -1)2-3(a ≠0)与y 轴交于点A(0,-2),顶点为B.(1)试确定a 的值,并写出B 点的坐标;(2)若一次函数的图象经过A ,B 两点,试写出一次函数的表达式; (3)试在x 轴上求一点P ,使得△PAB 的周长取最小值.解:(1)将A(0,-2)代入y =a(x -1)2-3,得-2=a -3, 解得a =1.∴抛物线的表达式为y =(x -1)2-3. ∴顶点B 的坐标是(1,-3). (2)设直线AB 的表达式为y =kx +b.将点A(0,-2)和B(1,-3)代入y =kx +b ,得⎩⎪⎨⎪⎧-2=b ,-3=k +b ,解得⎩⎪⎨⎪⎧k =-1,b =-2. ∴直线AB 的表达式为y =-x -2. (3)设点A 关于x 轴对称的点为C. ∴C(0,2).设直线CB 的表达式为y =mx +n.直线CB 与x 轴交于点P ,此时△PAB 的周长取最小值. 把C(0,2)和B(1,-3)代入y =mx +n ,得⎩⎪⎨⎪⎧2=n ,-3=m +n ,解得⎩⎪⎨⎪⎧m =-5,n =2. ∴直线CB 的表达式为y =-5x +2. 令y =0,则-5x +2=0.解得x =25.∴点P 的坐标为(25,0).在同一平面直角坐标系中判断函数的图象1.【数形结合思想】将函数y =kx 2与y =kx +k 的图象画在同一个平面直角坐标系中,可能的是(C ),A B C D【方法指导】 假设函数表达式的参数为正或负,选出符合条件的图象.如本题中,假设k >0或k <0,选出符合题意的选项.2.【数形结合思想】在同一平面直角坐标系中,一次函数y =ax +c 和二次函数y =a(x +c)2的图象大致为(B )A B C D【方法指导】 分别判断每个选项中,两个函数的所有参数的正负性,其中同一参数的正负性一致的为正确选项.如本题中,分别判断A ,B ,C ,D 四个选项中,两个函数的参数a ,c 的符号,其中两个函数中a ,c 的符号分别一致的为正确选项.周测(26.1~26.2.2第3课时)(时间:40分钟 满分:100分)一、选择题(每小题4分,共32分) 1.下列函数中,属于二次函数的是(B )A .y =2xB .y =2(x +1)(x -3)C .y =3x -2D .y =x 2+1x2.二次函数y =(x -1)2+2的图象的对称轴是(D )A .直线x =-2B .直线x =2C .直线x =-1D .直线x =13.长方形的周长为24 cm ,其中一边为x cm (x >0),面积为y cm 2,则y 与x 之间的函数关系式为(C )A .y =x 2B .y =12-x 2C .y =(12-x)xD .y =2(12-x)4.若抛物线y =x 2+b 与抛物线y =ax 2-2的形状相同,只是位置不同,则a ,b 的值分别是(A )A .a =1,b ≠-2B .a =-2,b ≠2C .a =1,b ≠2D .a =2,b ≠25.将抛物线y =2(x -3)2+2向左平移3个单位长度,再向下平移2个单位长度,得到抛物线的表达式是(C )A .y =2(x -6)2B .y =2(x -6)2+4C .y =2x 2D .y =2x 2+46.平行于x 轴的直线与抛物线y =a(x -2)2的一个交点坐标为(-1,2),则另一个交点坐标为(C )A .(1,2)B .(1,-2)C .(5,2)D .(-1,4)7.对于抛物线y =-2(x +1)2+3,下列结论:①抛物线的开口向下;②对称轴为直线x =1;③顶点坐标为(-1,3);④当x >-1时,y 随x 的增大而减小,其中正确结论的个数为(C )A .1B .2C .3D .48.已知二次函数y =-2(x -m)2+4,当x <-2时,y 随x 增大而增大,当x >0时,y 随增大而减小,且m 满足m 2-2m -3=0,则当x =0时,y 的值为(A )A .2B .4C .1+ 2D .1± 2二、填空题(每小题4分,共20分)9.二次函数y =-(x -6)2+8的最大值是8.10.若y=(m-1)xm2+m是关于x的二次函数,则m的值为-2.11.如果抛物线y=(a-3)x2-2有最低点,那么a的取值范围是a>3.12.已知抛物线y=3(x+2)2的图象上有两点(x1,y1)和(x2,y2),且x1<x2<-2,则y1与y2的大小关系是y1>y2.13.如图,已知正方形ABCD中,A(1,1),B(1,2),C(2,2),D(2,1),有一抛物线y=-(x+1)2向上平移m个单位长度(m>0)与正方形ABCD的边(包括四个顶点)有交点,则m的取值范围是5≤m≤11.三、解答题(共48分)14.(10分)在同一平面直角坐标系中画出二次函数y=-2x2,y=-2x2+3的图象.(1)分别指出它们的开口方向、对称轴以及顶点坐标;(2)抛物线y=-2x2+3可由抛物线y=-2x2向上平移3个单位长度得到.解:如图所示.抛物线y=-2x2开口方向向下,对称轴为y轴,顶点坐标为(0,0).抛物线y=-2x2+3开口方向向下,对称轴为y轴,顶点坐标为(0,3).15.(12分)分别根据下列条件,列出函数关系式.(1)某企业因生产转型,二月份产值比一月份下降20%,转型成功后生产呈现良好上升势头,三、四月份稳步增长,月平均增长率为x,设该企业一月份产值为a,四月份产值为y,y是x的函数;(2)已知⊙A的半径为10 m,当半径减小x(m)时,圆的面积就减小y(m2),y是x的函数.解:(1)y=a(1-20%)(1+x)2.(2)y=π·102-π·(10-x)2=-πx2+20πx(0≤x<10).16.(12分)如图,已知二次函数y =(x -1)2图象的顶点为C ,图象与直线y =x +m 交于A ,B 两点,其中点A 的坐标为(3,4),点B 在y 轴上.(1)求m 的值;(2)P 为线段AB 上的一个动点(点P 与点A ,B 不重合),过点P 作x 轴的垂线与这个二次函数的图象交于点E ,设线段PE 的长为h ,点P 的横坐标为x ,求h 与x 之间的函数关系式,并写出自变量x 的取值范围.解:(1)∵点A(3,4)在直线y =x +m 上,∴4=3+m.∴m =1. (2)∵PE 与x 轴垂直,∴点P ,E 的横坐标相同,均为x. 设P ,E 两点的纵坐标分别为y P 和y E ,则PE =h =y P -y E =(x +1)-(x -1)2=-x 2+3x , 即h =-x 2+3x(0<x <3).17.(14分)如图是二次函数y =(x +m)2+k 的图象,其顶点坐标为M(1,-4).(1)求出图象与x 轴的交点A ,B 的坐标;(2)在二次函数的图象上是否存在点P ,使S △PAB =54S △MAB ?若存在,求出点P 的坐标;若不存在,请说明理由.解:(1)∵抛物线y =(x +m)2+k 的顶点坐标为M(1,-4), ∴y =(x -1)2-4.令y =0,即(x -1)2-4=0. 解得x 1=3,x 2=-1.∴A(-1,0),B(3,0).(2)∵△PAB 与△MAB 同底,且S △PAB =54S △MAB ,∴|y P |=54|y M |=54×4=5,即y P =±5.又∵点P 在二次函数y =(x -1)2-4的图象上, ∴y P ≥-4.∴y P =5.令(x -1)2-4=5,解得x 1=4,x 2=-2, ∴存在这样的点P ,其坐标为(4,5)或(-2,5).第4课时 二次函数y =ax 2+bx +c 的图象与性质01 基础题知识点1 将二次函数y =ax 2+bx +c 化为y =a(x -h)2+k 的形式 1.用配方法将二次函数y =x 2-8x -9化为y =a(x -h)2+k 的形式为(B )A .y =(x -4)2+7B .y =(x -4)2-25C .y =(x +4)2+7D .y =(x +4)2-252.(2020·南阳南召县模拟)二次函数y =-3x 2+6x 变形为y =a(x +m)2+n 的形式,正确的是(D )A .y =-3(x +1)2-3B .y =-3(x -1)2-3C .y =-3(x +1)2+3D .y =-3(x -1)2+3知识点2 二次函数y =ax 2+bx +c 的图象与性质3.(2020·驻马店上蔡县期末)二次函数y =x 2+2x +4的图象的顶点坐标是(B )A .(1,3)B .(-1,3)C .(1,-3)D .(-1,-3)4.(2019·重庆B 卷)抛物线y =-3x 2+6x +2的对称轴是(C )A .直线x =2B .直线x =-2C .直线x =1D .直线x =-15.(2020·成都)关于二次函数y =x 2+2x -8,下列说法正确的是(D )A .图象的对称轴在y 轴的右侧B .图象与y 轴的交点坐标为(0,8)C .图象与x 轴的交点坐标为(-2,0)和(4,0)D .y 的最小值为-96.在二次函数y =ax 2+bx +c(a ≠0)中,函数值y 与自变量x 的部分对应值如下表:x … -2 -1 1 2 3 … y…83-13…则该函数图象的对称轴是直线(B )A .x =2B .x =1C .x =32D .x =-127.(2020·南阳镇平县一模)已知函数y =-x 2+bx +c ,其中b >0,c <0,此函数的图象可以是(D )8.(2019·济宁)将抛物线y =x 2-6x +5向上平移2个单位长度,再向右平移1个单位长度后,得到的抛物线表达式是(D )A .y =(x -4)2-6B .y =(x -1)2-3C .y =(x -2)2-2D .y =(x -4)2-2①将二次函数y =ax 2+bx +c 的图象向上或向下平移m(m >0)个单位长度,得到抛物线的表达式为y =ax 2+bx +c +m 或y =ax 2+bx +c -m ;②将二次函数y =ax 2+bx +c 的图象向左或向右平移n(n >0)个单位长度,得到抛物线的表达式为y =a(x +n)2+b(x +n)+c 或y =a(x -n)2+b(x -n)+c. 9.(2020·温州)已知抛物线y =ax 2+bx +1经过点(1,-2),(-2,13).(1)求a ,b 的值;(2)若(5,y 1),(m ,y 2)是抛物线上不同的两点,且y 2=12-y 1,求m 的值. 解:(1)把点(1,-2),(-2,13)代入y =ax 2+bx +1,得⎩⎪⎨⎪⎧-2=a +b +1,13=4a -2b +1,解得⎩⎪⎨⎪⎧a =1,b =-4. (2)由(1)得函数表达式为y =x 2-4x +1, 把x =5代入y =x 2-4x +1,得y 1=6, ∴y 2=12-y 1=6. ∴y 1=y 2.∵对称轴为x =--42×1=2,∴m =2×2-5=-1.易错点 化二次函数为y =a(x -h)2+k 形式时,漏掉二次项系数10.把二次函数y =12x 2-3x +1化成y =a(x -h)2+k 的形式为y =12(x -3)2-72.02 中档题11.(2020·陕西)在平面直角坐标系中,将抛物线y =x 2-(m -1)x +m(m>1)沿y 轴向下平移3个单位长度,则平移后得到的抛物线的顶点一定在(D )A .第一象限B .第二象限C .第三象限D .第四象限12.(2020·开封二模)二次函数y =-ax 2+bx +c(a ≠0)的图象如图所示,则下列结论中,正确的是(D )A .a <0B .b >0C .c >-1D .4a +c >2b13.(2020·天水)若函数y =ax 2+bx +c(a ≠0)的图象如图所示,则函数y =ax +b 和y =c x 在同一平面直角坐标系中的图象大致是(B )14.抛物线y =ax 2+bx +c(a ≠0)向右平移2个单位长度得到抛物线y =a(x -3)2-1,且平移后的抛物线经过点A(2,1).(1)求平移后的抛物线表达式;(2)设原抛物线与y 轴的交点为B ,顶点为P ,平移后抛物线的对称轴与x 轴交于点M ,求△BPM 的面积. 解:(1)把点A(2,1)代入y =a(x -3)2-1,得 1=a(2-3)2-1. 解得a =2.则平移后的抛物线表达式为y =2(x -3)2-1.(2)由(1)知,平移后的抛物线表达式为y =2(x -3)2-1,则M(3,0).∵抛物线y =ax 2+bx +c(a ≠0)向右平移2个单位长度得到抛物线y =2(x -3)2-1, ∴平移前的抛物线表达式为y =2(x -1)2-1. ∴P(1,-1). 令x =0,则y =1.故B(0,1),∴BM =10,BP =5,PM = 5. ∴BM 2=BP 2+PM 2,即△BPM 为直角三角形. ∴S △BPM =12BP ·PM =12×5×5=52.03 综合题15.如图,已知二次函数y =-12x 2+bx +c 的图象经过A(2,0),B(0,-6)两点.(1)求这个二次函数的表达式;(2)设该二次函数图象的对称轴与x 轴交于点C ,连结BA ,BC ,求△ABC 的面积;(3)若抛物线的顶点为D ,在y 轴上是否存在一点P ,使得△PAD 的周长最小?若存在,求出点P 的坐标;若不存在,请说明理由.解:(1)将点A(2,0),B(0,-6)代入y =-12x 2+bx +c ,得⎩⎪⎨⎪⎧-2+2b +c =0,c =-6,解得⎩⎪⎨⎪⎧b =4,c =-6.∴这个二次函数的表达式为y =-12x 2+4x -6.(2)∵二次函数的表达式为y =-12x 2+4x -6,∴二次函数的对称轴为直线x =4,即OC =4. ∴AC =2.故S △ABC =12AC ·BO =6.(3)存在,点P 的坐标为(0,23).理由如下:作点A 关于y 轴的对称点A ′,连结A ′D ,则A ′D 与y 轴的交点即是点P 的位置. ∵点A ′与点A 关于y 轴对称, ∴点A ′的坐标为(-2,0). 又∵顶点D 的坐标为(4,2), ∴直线A ′D 的表达式为y =13x +23.令x =0,则y =23.∴点P 的坐标为(0,23).函数值的大小比较【例】 已知A(-4,y 1),B(1,y 2)两点都在二次函数y =-3(x +1)2+2的图象上,求y 1与y 2的大小关系.方法1(代入法):把A(-4,y1),B(1,y2)分别代入y=-3(x+1)2+2中,得y1=-25,y2=-10,所以y1<y2.,方法2(增减性法):∵二次函数的对称轴为直线x=-1,∴点B关于对称轴对称的点为(-3,y2).∵抛物线开口向下,∴在对称轴的左侧,y随x的增大而增大.又∵-4<-3,∴y1<y2.方法3(距离比较法):∵抛物线开口向下,且对称轴是直线x=-1,∴抛物线上的点离对称轴越远,对应的函数值就越小.又∵点A(-4,y1)到对称轴的距离比点B(1,y2)到对称轴的距离远(填“近”或“远”),∴y1<y2. 【变式1】若A(-3,y1),B(-\r(2),y2),C(2,y3)为二次函数y=x2+2x-5图象上的三点,则y1,y2,y3的大小关系是y2<y1<y3.【变式2】已知二次函数y=a(x-2)2+k(a>0),当自变量x分别取3,-1时,对应的函数值分别为y1,y2,则y1<y2(填“<”“>”或“=”) .【变式3】已知a,b,c是实数,点A(a-1,b),B(a-2,c)在二次函数y=x2-2ax+1的图象上,则b,c的大小关系是b<c(填“>”或“<”).第5课时 二次函数最值的应用01 基础题知识点1 求二次函数的最值1.已知抛物线y =ax 2+bx +c 的开口向上,顶点坐标为(3,-2),那么该抛物线有(A )A .最小值-2B .最大值-2C .最小值3D .最大值32.(2020·驻马店新蔡县模拟)二次函数y =x 2-4x +7的最小值为(C )A .2B .-2C .3D .-33.若关于x 的一次函数y =(a +1)x +a 的图象过第一、三、四象限,则二次函数y =ax 2-ax(B )A .有最大值a 4B .有最大值-a 4C .有最小值a 4D .有最小值-a 4知识点2 几何图形的面积最值问题4.如图,假设篱笆(虚线部分)的长度为16 m ,则所围成矩形ABCD 的最大面积是(C )A .60 m 2B .63 m 2C .64 m 2D .66 m 25.为搞好环保,某公司准备修建一个长方体的污水处理池,池底矩形的周长为100 m ,则池底的最大面积是(B )A .600 m 2B .625 m 2C .650 m 2D .675 m 26.(2019·连云港)如图,利用一个直角墙角修建一个梯形储料场ABCD ,其中∠C =120°.若新建墙BC 与CD 总长为12 m ,则该梯形储料场ABCD 的最大面积是(C )A .18 m 2B .18 3 m 2C .24 3 m 2D .4532m 27.已知一个直角三角形两直角边的和为20 cm ,则这个直角三角形的最大面积为50cm 2. 8.如图,已知▱ABCD 的周长为8 cm ,∠B =30°,若边长AB =x cm .。
