2019年中国数学奥林匹克希望联盟夏令营
2019年高中数学夏令营获奖名单
赵奕杰
历城二中
胡玉帅
临邑一中
解文浩
五莲一中
李青天
广饶一中
宋佳昕 济宁孔子国际学校
谭金生
烟台二中
王圣远 烟台开发区高级中学
王仝
东平高级中学
王子豪
泰安一中
吴明轩
郓城一中
袁朔星 烟台开发区高级中学
张瑞哲
山东省实验
张阳
山师附中
赵嘉宁
日照一中
邹清源
威海二中
董保国
庆云一中
郝钰涵
禹城一中
焦方亮
临沂一中
刘福龙
城阳一中
201919779 201919176 201919206 201919247 201919426 201919470 201919527 201919532 201919555 201919569 201919676 201919729 201919747 201919768 201919817 201919077 201919160 201919202 201919292 201919323 201919520 201919062 201919209 201919353 201919371 201919382 201919384 201919414 201919425 201919447 201919498 201919559 201919579 201919605
潍坊 青岛 临沂 枣庄 济南 临沂 济南 青岛 临沂 东营 济南 临沂 东营 烟台 济南 枣庄 临沂 临沂 德州 青岛 济南 济南 菏泽 烟台 烟台 济南 东营 济南 枣庄 青岛 青岛 临沂 泰安 烟台
201919637 201919005 201919172 201919295 201919409 201919652 201919686 201919778 201919108 201919751 201919002 201919238 201919322 201919505 201919576 201919121 201919141 201919318 201919418 201919509 201919538 201919561 201919774 201919663 201919026 201919074 201919102 201919152 201919531 201919698 201919785 201919117 201919213 201919217
这八大赛事数竞党必须了解

常有学生问:学竞赛有没有什么秘诀?当然有,秘诀就4个字,勤思多练。
这可不是灌鸡汤,至少在CMO之前,还远没有到需要拼智商或天赋的程度,学好每一个知识点,打牢基础,多刷题,常总结,想不获奖都很难呐。
此外,学竞赛闭门造车是行不通的,多和大佬切磋交流,多见识不同题型,非常非常重要,所以,今天要给大家介绍八大不可错过的赛事,那里高手云集,任思想激扬碰撞,那里好题无数,亦是高联前练兵的好机会。
下面进入正题,首先隆重推出今天要聊的八大赛事:1、中国女子数学奥林匹克2、中国西部数学奥林匹克3、中国东南地区数学奥林匹克4、北方希望之星数学邀请赛5、中国数学奥林匹克协作体夏令营6、中国数学奥林匹克希望联盟数学夏令营7、陈省身杯全国高中数学奥林匹克夏令营8、爱尖子数学能力测评如果你对以上赛事如数家珍,欢迎跳到文末,有历届试题可以下载哦(超级福利);如果你是萌新,请仔细往下阅读,下面将逐一详细介绍每项赛事的时间、参赛对象、考试形式、奖项等。
(点击可查看大图)中国女子数学奥林匹克简称女奥(CGMO),这是一项专门为女生而设的数学竞赛,参赛对象是高一、高二女生(也有人称之为“妹赛”)。
自首届女奥在珠海举办,迄今已成功举办了16届,比赛时间一般在每年8月中旬。
由全国各省市、港澳台及部分国外代表队各组织一个代表队参赛,另外会邀请近3年承办过女奥的学校各派一个代表队参赛。
每支代表队最多由4名高中女学生和1名领队教师组成。
竞赛分两天,每天4道题,共8道题,每题15分,满分120分,考试时间均为8:00~12:00,试题难度介于全国高中数学联赛和中国数学奥林匹克之间,最终根据成绩评出团体总分第1名和个人金、银、铜牌。
其奖项对高校自主招生及清北学科营有一定参考意义,个人总分前12名的同学可直接进入中国数学奥林匹克(CMO)。
此外,和其他数学竞赛相比,女奥还别具一格地设有健美操团体比赛。
中国西部数学奥林匹克中国西部数学奥林匹克(CWMO),是由中国数学会奥林匹克委员会创办,主要面向中国中西部地区及亚洲地区高一、高二年级学生的数学探究活动。
2019协作体数学奥林匹克夏令营
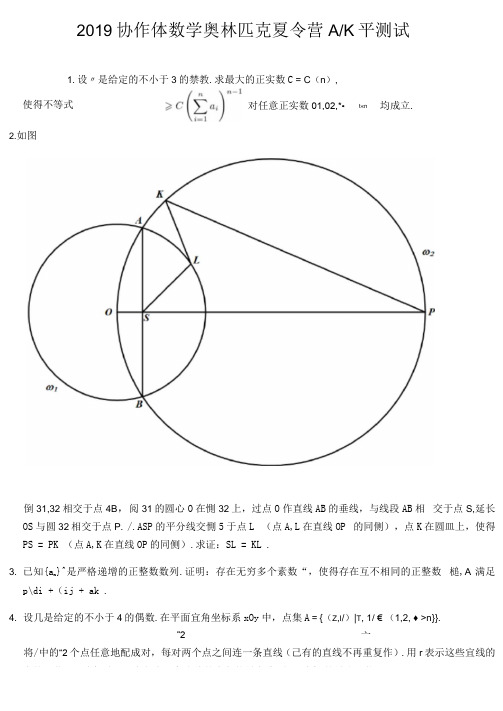
2019协作体数学奥林匹克夏令营A/K平测试1.设〃是给定的不小于3的禁教.求最大的正实数C = C(n),使得不等式对任意正实数01,02,*•t«n 均成立.2.如图倒31,32相交于点4B,阅31的圆心O在惻32上,过点O作直线AB的垂线,与线段AB相交于点S,延长OS与圆32相交于点P. /.ASP的平分线交惻5于点L (点A,L在直线OP 的同侧),点K在圆皿上,使得PS = PK (点A,K在直线OP的同侧).求证:SL = KL .3. 已知{a n}^是严格递增的正整数数列.证明:存在无穷多个素数“,使得存在互不相同的正整数槌,A 满足p\di +(ij + ak .4. 设几是给定的不小于4的偶数.在平面宜角坐标系xOy中,点集A={(Z,I/)|T, 1/ € (1,2, ♦ >n}}.”2亠将/中的“2个点任意地配成对,每对两个点之间连一条直线(己有的直线不再重复作).用r 表示这些宜线的全体,井用«(r)表示r中任意两条直线的夹角的最大偵.求a(r)的最小正位.2019协作体数学奥林匹克夏令营O水平测试1. 己知"佔是不同的实数,使得关于X的一元二次方程F + a + 3b = 0 与x2 + bx + 3〃= 0有一个公共根,则〃 +力=・2. 函数/(%) = (x + a)(|x-a| + |x- 2019|)的图像为中心对称图形.则实数a的值为・3. 己知肩,亓是两个非零向量.且同=2,|尻+ 2吊=4,则肺+亓| +间的最大值为・4. 方程4sinx + 2sin2x = 3 V5的解集是・5. 数列0}定义如下:们=1, a n = 5外_] + 3”一\〃 = 2,3,…,则血卬除以3所得的余数是.6. 设非负实数a,b,c满足o + b + c=l.则V2«+ + V6c的最小值为.最大值为是.7. 全国高中数学联赛一试由8道填空题和3道解答题组成.其中填空题每题8分;解答题分步给分,第1道解答题16分-分4步-每步4分; 第2和第3道解答题均为20分.分四步每步5分.批阅解答题时规定-若第〃步不得分则第m步(m >n)也不得分.现知某生恰好考了10。
2014年中国数学奥林匹克希望联盟夏令营讲义(教师版含答案)

2014年中国数学奥林匹克希望联盟夏令营讲义(一)平面解析几何讲义一、平面几何背景下的解析几何问题 (一)解法思想:充分利用平面几何中的几何性质,合理而恰当地把几何特征表示为代数形式,以几何直观为导向,运用代数工具和相应的方法进行推理或论证,达到解题目的.(二)例题选讲:例1.在周长为定值的△ABC 中,已知|AB|=6,且当顶点C 位于定点P 时,cos C 有最小值为257. (I )建立适当的坐标系,求顶点C 的轨迹方程.(II )过点A 作直线与(1)中的曲线交于M 、N 两点,求||||BN BM ⋅的最小值.解析(I )设||,||CA m CB n ==,则222236()236()36cos 1222m n m n mn m n C mn mn mn+-+--+-===-.设定值m n d +=,则222222363627272cos 111122()2d d d C m n mn d d ---=-≥-=-=-+,所以2727125d -=,解得10d =. 把,A B 两点放在x 轴上(点A 在左),线段AB 的垂直平分线为y 轴,建立平面直角坐标系.则据椭圆定义可得顶点C 的轨迹方程为2212516x y +=. (II )设点,M N 的坐标分别为11(,)x y 和22(,)x y ,则22121212||||()()()BM BN a ex a ex a c x x e x x ⋅=--=-++.当直线MN 的斜率不存在时,12x x c ==-,此时22221156||||225BM BN a c c e ⋅=++=; 当直线MN 的斜率存在时,设其方程为()y k x c =+,代入椭圆方程中得 22222222222()20b a k x ca k x a k c a b +++-=可得222222212122222222,ca k a k c a b x x x x b a k b a k-+=-=++,所以 22224222222422222222222()||||c a k k c c b k a c b BM BN a b a k b a k b a k -++⋅=++=+++令222b a k t +=,则2222222242()()||||a c t b a c a b BM BN a t+-++⋅= 222222222222()()34167562525a c b a b a c a a t t+-+=+⋅=-⋅.因为2222162516t b a k k =+=+≥,所以2341675640016252525t -⋅≥=,即得||||BN BM ⋅的最小值为16,此时0k =.例2.设F 是椭圆2212516x y +=的一个焦点,A 是椭圆上距离点F 最远的一个顶点,在椭圆的短轴BC 上取互异的2013个点(1,2,,2013)i P i =,设直线i FP 交线段或于点M ,直线AP 交线段或于点i N .试问:直线(1,2,,2013)i i M N i =解析:如图示,设点m P 的坐标为(0,)m y ,||||||1||||||m m m m BP AM OF P O FA M B ⋅⋅=,可得||8||3(4)m mm m AM y M B y =-,坐标为15(4)32(,)512512m mm m y y y y -++.同理可得点m N 的坐标为15(4)32(,)320320m m m m y y y y --++,所以直线m M m N 的斜率为815(4)mm y y -+,可得其直线方程为32815(4)()32015(4)320m m m m m m y y y y x y y y ---=++++.令0y =,则4530015(320)15320320m m m m y y x y y ++===++,这说明直线m M m N 经过定点(15,0),而定点(15,0)在椭圆外部,可见任意两条直线(1,2,,2013)i i M N i =都相交,且交点均为(15,0),说明这2013条直线任两条直线在椭圆内部均不可能相交,于是它们把椭圆可分成2014块.例3.作斜率为13的直线l 与椭圆C :143622=+y x 交于,A B 两点(如图所示),且)2,23(P 在直线l 的上方.(I )证明:△PAB 的内切圆的圆心在一条定直线上;(II )若︒=∠60APB ,求△PAB 的面积.解析(I )分析:易计算出以点P 为切点的椭圆的切线的斜率为13-,由此可知以点P 关于x 轴的对称点为切点的椭圆的切线的斜率为13.可见斜率为13的直线l 在平移过程中与椭圆相切时恰好是上面的切线,由此可猜想直线PA 与直线PB 的斜率互为相反数,下面给予验证:设直线l 的方程为13y x b =+,点,A B 的坐标分别为11(,)x y 和22(,)x y .把直线方程代入椭圆方程中可得22269360x bx b++-=,即得212129363,2bx x b x x-+=-=.因为PAk=PBk=两式相加=因为11221133y x b y x b=+=+,所以12121((3y x x b x-=+-12121(3x x b x b=+-,21211((3y x x b x-=+-12211(3x x b x b=+-,于是122112122((()3y x y x x x b x x b-+--=+-+-23123(0b b b b=----=.所以0PA PBk k+=.于是PAB∆的内切圆的圆心一定在直线x=(II)因为︒=∠60APB,所以直线PA,可得直线PA的方程为y x=-+代入椭圆方程中得2142340x x-+-=,由韦达定理可得点A.故由弦长公式可得|||1477PA-+=-==.同理可求得1)||7PB=.所以,△PAB的面积为111826||||sin602249PA PB⋅⋅︒=⋅=例4.在平面直角坐标系xOy中,椭圆的方程为22221(0)x ya ba b+=>>,12,A A分别为椭圆的左、右顶点,12,F F分别为椭圆的左、右焦点,P 为椭圆上不同于1A 和2A 的任意一点.若平面中两个点Q 、R 满足11221122,,,QA PA QA PA RF PF RF PF ⊥⊥⊥⊥,试确定线段QR 的长度与b 的大小关系,并给予证明.解析:如右图示,据题意可知12,,,P A Q A 四点共圆,又原点O 为该圆的弦12A A 的中点,则据圆的性质可得该圆的圆心在y 轴上;又PQ 为该圆的直径,所以线段PQ 的中点在y 轴上.同理,线段PR 的中点也在y 轴上.所以,点,Q R 的横坐标相等,且为点P 的横坐标的相反数.设点P 的坐标为00(,)x y ,则可设点,Q R 的坐标分别为01(,)x y -和02(,)x y -,且12||||QR y y =-. 据题设,1212tan tan A PA AQA ∠=-∠,则据直线的到角公式有001100000011000011y y y yx a x a x a x ay y y y x a x a x a x a---+-+=+⋅+⋅-+-+,即012222220001y y x y a x y a =+-+-,整理得22010x a y y -=.同理可推得22020x c y y -=.于是222220021000||||||x c x a b y y y y y ---=-=.由于00||y b <≤,所以20||b b y ≥,即得线段QR 的长度不小于b .又解:设点P 的坐标为00(,)x y ,则可得直线1A Q 的方程为00()x ay x a y +=-+;同理可得直线2A Q 的方程为00()x a y x a y -=--,两方程联立可得点Q 的坐标为22000(,)x a x y --. 同理可得点R 的坐标为22000(,)x c x y --.于是得20||||b QR y =. 因为00||y b <≤,所以20||||b QR b y =≥,可得线段QR 的长度不小于b .二、向量条件下的曲线的弦问题 (一)题型特点及解法思想:当直线与曲线相交但不相切,此时将产生曲线的一条弦,围绕着这条线弦展开的问题,我们把它称为曲线的“弦问题”.解决这类问题的基本思想是联立方程组,运用二次方程的有关知识加以解决.在曲线的“弦问题”中,时常把题中的条件通过向量的形式给出,或以向量为背景来设置问题.解决这种问题时,可以从两个方面来考虑向量知识的运用,一是运用向量的坐标表示形式解题,这与解析法一脉相承;二是运用向量的几何意义解题,即通过向量来揭示所研几何图像的几何性质,再运用数形结合的思想解题.(二)例题选讲:例5.点A 在直线y kx =上,点B 在直线y kx =-上(0)k >,且A 、B 两点在y 轴同侧,并满足2||||1OA OB k ⋅=+.(I )求AB 中点M 的轨迹C ;(II )若曲线C 与抛物线22(0)x py p =>相切于两点,求证这两个切点分别在定直线上,并求切线方程. 解(I )设点A 的坐标为11(,)t kt ,点B 的坐标为22(,)t kt -,则1||||OA t →=2||||OB t →=所以有12||1t t =,由于A 、B 两点在y 轴同侧,所以121t t =.设AB 的中点M 的坐标为(,)x y ,则12122()2t t x k t t y +⎧=⎪⎪⎨-⎪=⎪⎩,整理得22122y x t t k -=,即得2221y x k -=.所以点M 的轨迹C 的方程为2221y x k-=,可知轨迹C 是以直线y kx =和y kx =-为渐近线的双曲线.(II )联立22x py =与2221y x k -=,得2221y py k-=,即22220y pk y k -+=,可知该关于y 的二次方程有两个相同的正根,即得242440p k k -=,即221p k =,即得1pk =.此时切点的纵坐标为2pk ,可得两切点坐标为2(,)pk ,即()k.由此可知两个切点分别在定直线x =x =当切点坐标为)k 时,切线的斜率为p,切线方程为y k x p -=,10py --=;当切点坐标为()k 时,切线的斜率为p -,切线方程为(y k x p-=-+,10py ++=. 例6.设直线:l y kx m =+(其中,k m 为整数)与椭圆2211612x y +=交于不同两点,A B ,与双曲线221412x y -=交于不同两点,C D ,问是否存在直线l ,使得向量0AC BD +=,若存在,指出这样的直线有多少条?若不存在,请说明理由.解析 设,A B 两点的坐标分别为11(,)x y 和22(,)x y ,,C D 两点的坐标分别为33(,)x y 和44(,)x y ,则由0AC BD +=可得1234x x x x +=+.把直线l 的方程代入椭圆方程中可得222(34)84480k x kmx m +++-=,于是122834kmx x k+=-+,且2212160k m +->. 把直线l 的方程代入双曲线方程中可得222(3)2120k x kmx m ----=.因为k 为整数,所以230k -≠,于是34223km x x k+=-,且221240m k +->. 由1234x x x x +=+可得2282343km kmk k -=+-,于是当0k =时,需2120m ->且2120m +>,即m -<<,这样的有序整数对(,)k m 共有7个,此时,共有7条满足题设的直线;当0m =,0k ≠时,需212160k +>,且21240k ->,即k <<这样的直线共有2条;当0m ≠且0k ≠时,2282343km kmk k -=+-即123-=,不能成立,此时没有满足题设的直线.综上,存在直线l ,这样的直线有9条.例7.已知椭圆1222=+y x ,过定点(1,0)C 两条互相垂直的动直线分别交椭圆于Q P ,两点.21,F F 分别为左右焦点,O 为坐标原点.(I )求||21PF PF +的最小值;(II )当向量21PF PF +与21QF QF +互相垂直时,求Q P ,两点所在直线的斜率.解析(I )因为122PF PF PO +=,所以只需求||PO 的最小值.显然min ||1PO b ==,所以||21PF PF +的最小值为2.(II )由21PF PF +与21QF QF +互相垂直可知OP OQ ⊥.又CP CQ ⊥,所以PQ 是两个直角三角形POQ 和PCQ 的公共斜边,即得线段PQ 的中点到,O C 两点的距离相等,即线段PQ 中点的横坐标为12. 法1:设Q P ,两点所在直线的斜率k ,线段PQ 的中点坐标为01(,)2y ,则有2020014b x k a y y =-=-.故可设直线PQ 的方程为01()2y y k x -=-,即11()42y k x k +=-,代入椭圆方程中可得2212()2024k x kx k+---=,即2222213(12)(21)()0282k k x k x k +-+++-=.设1122(,),(,)P x y Q x y ,则42122241218(12)k k x x k k -+=+,而121x x +=,所以424221212122211412114()()()24248(12)16k k k k k y y k x x k x x k k k k-+-=-++++=++ 4222284116(12)k k k k -++=+. 因为12120x x y y +=,所以424222224121284108(12)16(12)k k k k k k k k -+-+++=++,可得42202030k k --+=,即得2510k -+=,即k =法2:设直线PQ 的方程为y kx b =+,代入椭圆方程中得222(12)4220k x kbx b +++-=. 设1122(,),(,)P x y Q x y ,则122412kb x x k+=-+.而121x x +=,所以2124k kb +=-——(1) 另一方面,21222212b x x k -=+,于是222222121212222()12k b k y y k x x kb x x b kb b k -=+++=+++. 因为12120x x y y +=,所以2222222222201212b k b k kb b k k--+++=++,即得 22322422320k b k b k b kb +-++-=——(2)由(1)(2)消去b 可得42202030k k --+=,于是k =法3:设直线PQ 的方程为y kx b =+,代入椭圆方程中得222(12)4220k x kbx b +++-=.设1122(,),(,)P x y Q x y ,则122412kbx x k+=-+,21222212b x x k -=+. 一方面,由12120x x y y +=,因222212121222()12k b y y k x x kb x x b k -+=+++=+,故得2222222201212b k b k k--++=++即223220b k --=——(1) 另一方面,由1122(1,)(1,)0x y x y -⋅-=可得121212()10x x x x y y -+++=,因此有222222224210121212b kb k b k k k--++++=+++即23410b kb +-=——(2)由(1)(2)消去b 可得42202030k k --+=,于是k =法4:设||,||OP m OQ n ==,则有2222111132m n a b +=+=,即得222232m n m n +=,可知原点O 到直线PO 的距离为3.故设直线PQ 的方程为cos sin 3x y θθ+=,代入椭圆方程可得22224(sin 2cos )cos 2sin 03x θθθθ++-=.设1122(,),(,)P x y Q x y ,则122243sin 2cos x x θθθ+=⋅+,而121x x +=,所以223sin 2cos θθθ=+,即23cos 30θθ-+=,解得cos θ=,于是得cot =,即斜率为k =三、曲线的切线问题(一)题型特点及解法思想:这里的曲线通常是二次曲线,其切线是指与曲线有两个相同的交点的直线,解题的基本思路是联立方程组,运用判别式等于0来体现切线特点.当然,还可以从导数的角度来分析切线,并运用导数工具研究切线.(二)例题选讲:例8.过直线l :57700x y --=上点P 作椭圆221259x y +=的切线PM 、PN ,切点分别为M 、N ,联结MN .(I )当点P 在直线l 上运动时,证明:直线MN 经过定点Q ; (II )当//MN l 时,证明:定点Q 平分线段MN .解析(I )设点P 的坐标为00(,)x y ,切点M 、N 的坐标分别为11(,)x y 和22(,)x y ,则两条切线的方程分别为111259x x y y +=和221259x x y y +=.因为点P 在这两条切线上,所以有 10101259x x y y +=且20201259x x y y+=. 这说明过切点M 、N 的切点弦所在直线MN 的方程为001259x x y y+=.因为0057700x y --=,即007145x y =+,所以直线MN 的方程为0147()1x y x y ++=. 令709125y x +=,则14125x =,解得2514x =,所以,直线MN 经过定点Q ,其坐标为25(,14(II )若//MN l ,则直线MN 的方程为y 要证明此时定点Q 平分线段MN ,弦所在直线的方程就是9525()10714y x +=-此时可设,M N 两点的坐标分别为11(,x y 得1212121211()()()()0259x x x x y y y y -++-+=,因为1212,75x x y y +=+=-,所以 121211()()075x x y y ---=,即121257y y x x -=-,所以,此时直线MN 的斜率为57,其方程就是9525()10714y x +=-,这就是说,定点Q 平分线段MN . 例9.过点)3,2(作动直线l 交椭圆1422=+y x 于两个不同的点Q P ,,过Q P ,作椭圆的切线,两切线的交点为M .(I )求点M 的轨迹方程;(II )设O 为坐标原点,当四边形POQM 的面积为4时,求直线l 的方程.解析(I )设直线l 的方程为sin (2)cos (3)x y θθ-=-,即sin cos 3cos 2sin 0x y θθθθ-+-=.设交点M 的坐标为00(,)x y ,则直线PQ 的方程为0014x xy y +=,即00440x x y y +-=. 于是有0044sin cos 3cos 2sin x y θθθθ-==--,即得动点M 的参数方程为(II 2(14)k +2sin α=.所以,四边形POQM 的面积为1||||sin 2S PQ OM α=⋅ 22|23|14k k =-+=. 所以,4|23|k =-,解得1k =或11k =,得直线l 的方程为10x y -+=或114100x y --=.例10.已知111222(,),(,),A x y A x y 在的直线与抛物线22(0)x qy q =>证明:对不同的{},1,2,3i j ∈,i y y 证 如图,不妨设边13A A 和23A A相切,切点分别为1T 和2T .那么切点弦1T 2T 所在直线方程为33()x x q y y =+.设切点1T 和2T 的坐标分别为211(,)2t t q 和222(,)2t t q ,则切线13A A 的斜率为1t q ,于是有31131y y t x x q -=-,即1312t py y q=+.把切点1T 的坐标代入直线方程33()x x q y y =+中,可得21313()2t x t q y q =+,整理即223113()22y t t q y p q=+,再把1312t py y q=+中的1t 代入该式,可得22332313122[]2()y pq p q q y p y y y y ⋅=+++,即2233231312()y p q y y y y y =+++, 即213231312()y y p q y y y y -=++,即得21313()2y y y y p q +=-. 同理,利用切点2T 可以推得22323()2y y y y p q +=-.上面两式相减可得123y y y +=-;上面两式相加可得2222312312()()4y y y y y y p q +++=-,即得 232312123[()2]4y y y y y y p q +--=-,即23233123(2)4y y y y y p q --=-,即得21232y y y p q =. 所以21212123()2y y y y y y y p q +=-=-.综上,对不同的{},1,2,3i j ∈,()i j i j y y y y +为定值,定值为22p q -.四、焦点问题(一)题型特点及解法思想:此类题目总是围绕圆锥曲线的焦点展开,它紧扣圆锥曲线的定义,能更直接地揭示圆锥曲线的本质.解决这类问题时,一要抓住圆锥曲线的定义,包括椭圆、双曲线的第一、第二定义;二要抓住焦点与对应准线之间的关系;三要用好焦半径.(二)例题选讲:例11.如图,MN 为过椭圆22221(0)x y a b a b+=>>右焦点F 的弦,,A B 分别为椭圆的左、右顶点,直线AM 与BN 交于点P ,求点P 的横坐标.解析 如图,设点,M N 的坐标分别为(cos ,sin )a b αα和(cos ,sin )a b ββ,设点P 的坐标为00(,)x y ,则一方面有00sin sin cos cos 1y b b x a a a a αααα==⋅+++, 00sin sin cos cos 1y b b x a a a a ββββ==⋅---, 两式相除可得00sin cos 1sin cos 1x a x a αββα--=⋅++ ————(1) 另一方面,有sin sin cos cos b b a c a c αβαβ=--,即sin sin cos cos e eαβαβ=-- ————(2)由(1)得0[sin()sin sin ][sin()sin sin ]x a βααββαβα-++=++- ————(3) 由(2)得sin()(sin sin )e αβαβ-=- ————(4) 又(3)式左边为00[sin()sin sin ]2cos(sinsin)222x x βαβααββααβ--+-++=+04cossincos222x βαβα-=.(3)式右边为[sin()sin sin ]2cos(sinsin)222a a αβαββαβαβα++-++-=+4cossincos222a αββα+=.所以有0cos2cos2a x βαβα+=- ————(5)由(4)式可得2sin cos 2cos sin 2222e αβαβαβαβ--+-=,即cos cos22e αβαβ-+=,即cos12cos2e αβαβ+=-,代入(5)式中可得20a x c =.所以,点P 的横坐标为2a c .例12.如图,在平面直角坐标系xOy 中,椭圆的左、右焦点分别为,.已知和都在椭圆上,其中e 为椭圆的离心率.(I )求椭圆的方程;(II )设是椭圆上位于轴上方的两点,且直线与直线平行,与交于点P . 求证:是定值.解析(I )易求得椭圆方程为2212x y +=; (II )设12||,||AF m BF n ==,则2||||m AP PF n =,1||||nBP PF m=. 因为1212||||||||2AF AF BF BF a +=+=,所以21(1)||(1)||2m nm PF n PF a n m ++=++=, 即得2122||,||an mn am mn PF PF m n m n --==++,于是212||||2mnPF PF a m n+=-+. 设12AF F θ∠=,则2BF x θ∠=,于是,1cos 1cos ep epm n e e θθ==+-,所以 2222222,1cos 1cos e p epmn m n e e θθ=+=--, 可得222mn c b b ep m n a c a==⋅=+.所以221||||22b PF PF a a +=-==,可见是定值. 例13.已知椭圆Γ的方程为),0(12222>>=+b a b y a x 离心率12e =,1F 是椭圆Γ的左焦点,直线l 过点M()0,2a -交椭圆Γ于A 、B 两点,且,121||1||111=+BF AF 当△1ABF 的面积最大时,求直线l 的方程. 22221(0)x y a b a b+=>>1(0)F c -,2(0)F c ,(1)e,e ⎛ ⎝⎭,A B x 1AF 2BF 2AF 1BF 12PF PF +12PF PF +解析 如图,因为12e =,所以12c a =,可得2a c =.于是,2222a a a c a==,可知直线2x a =-是该椭圆的左准线,即得点M 落在左准线上.假设,A B 两点在x 轴的上方,并设它们的坐标分别为11221212(,),(,)(,)x y x y x x y y <<. 则1212113(2)()()22ABF S a c y y c y y ∆=--=-. 设直线AB 的方程为4x my c =-,代入椭圆方程2222434120c x c y c +-=中可得222(34)24360m y cmy c +-+=.所以21y y -==. 令234m t +=,则21348m t ==≤+,于是212y y -≤,可知124ABF S c ∆≤,且当23432m +=即2283m =时等号成立. 另一方面,分别过,A B 作左准线的垂线,垂线段长分别为12,d d ,则111211||,||22AF d BF d ==,而1122,y m d y m d ==,可得1212()y y m d d +=+. 因为1222434cmy y m +=+,所以21222434cm d d m +=+.所以211122112||||()234cm AF BF d d m +=+=+. 又因为21223634c y y m =+,即222121223634c m d d m y y m ==+,即221129||||34c m AF BF m =+.而条件有11111||||12AF BF +=,即111112(||||)||||AF BF AF BF +=,即得22222129123434cm c m m m ⋅=++,解得16c =,所以264a =.可得直线l的方程为64)14y x =±+. 例14.在双曲线C :22145x y -=中,12,F F 分别为双曲线C 的左右两个焦点,P 为双曲线上且在第一象限内的点,12PF F ∆的重心为G ,内心为(I )是否存在一点P ,使得IG //(II )已知A 为双曲线C 的左顶点,足1212k k +=-,求直线l 的方程. 解析(I )设点P 的坐标为00(,)(x y 面积为03y 001(6)2ex a ex a r ++-+,即0(ex +0(2)32x r +,即得00(2)332x ry +=,因为IG //12F F ,所以013r y =,可求得0y =.综上,存在一点P ,其坐标为,使得IG //12F F .(II )可设直线l 的方程为3x my =+,设,M N 两点的坐标为分别为11(,)x y 和22(,)x y .把直线方程代入双曲线方程中,得22(54)30250m y my -++=.于是有1223045m y y m +=-,1222545y y m=-- ————(1) 另一方面,因为121212,22y y k k x x ==++,而1212k k +=-,所以有12121222y y x x +=-++, 即得12121552y y my my +=-++,整理得21212(4)(105)()250m m y y m y y +++++=——(2)由(1),(2)可得:2222530(4)(105)2504545m m m m m m -+⋅++⋅+=--,解得12m =-. 所以,直线l 的方程为132x y =-+,即26y x =-+. 五、曲线组问题 (一)题型特点:这是一类典型的曲线性质探究问题,其曲线背景是由两条以上曲线组合而成,它使得问题更为复杂,体现出的综合性更强,更能突出曲线之间的自然联系.求解时,图形复杂,变量多,联系多,式子多,能很好地考查综合运用知识分析问题和解决问题的能力,更能考查思维素质.(二)例题选讲:例15.如图,曲线C 由上半椭圆1C :22221(0,0)y x a b y a b+=>>≥和部分抛物线2C :21(0)y x y =-+≤连接而成,12,C C 的公共点为,A B ,其中1C 的离心率为32. (I )求,a b 的值;(II )过点B 的直线l 与12,C C 分别交于,P Q (均异于点,A B ),若AP AQ ⊥,求直线l 的方程.解析(I )易知曲线12,C C 的结合点,A B 的坐标分别为(1,0)-和(1,0),于是可得1b =,再由1C 的离心率为32可得2a =. 所以,2a =,1b =.(II )显然直线l 的斜率存在,故设其方程为(1)y k x =-,将其代入曲线2C 的方程中可得210x kx k +--=,知该方程的一个根为1,由韦达定理可得点Q 的横坐标为1k --,于是点Q 的坐标为2(1,2)k k k ----;把直线l 的方程代入曲线1C 的方程中,可得2222(4)240k x k x k +-+-=,知该方程的一个根为1,由韦达定理可得点P 的横坐标为2244k k -+,于是点P 的坐标为22248(,)44k k k k --++. 由AP AQ ⊥可得:4(2)1k k -⋅+=-,解得83k =-. 所以,直线l 的方程为8(1)3y x =--,即8380x y +-=.例16.如图,设P 是抛物线1C :2x y =上的动点.过点P 做圆2C 1)3(:22=++y x 的两条切线,交直线l :3y =-于,A B 两点.(Ⅰ)求2C 的圆心M 到抛物线1C 准线的距离.(Ⅱ)是否存在点P ,使线段AB 被抛物线1C 在点P 处的切线平分,若存在,求出点P 的坐标;若不存在,请说明理由.解析(Ⅰ)抛物线1C 的准线方程为14y =-,所以2C 的圆心M 到抛物线 1C 准线的距离114. (Ⅱ)设点P 的坐标为200(,)x x ,切线方程可设为200()y x k x x -=-,则有2002|3|11kx x k--=+,即2234200000(1)(26)680x k x x k x x--++++=.于是3420000121222002668,11x x x xk k k kx x++++==--————(1)同时可得,A B两点的坐标分别为213(,3)xxk+--和223(,3)xxk+--,那么线段AB的中点坐标为22001233(,3)22x xxk k++---.以点P为切点的抛物线的切线方程为20002()y x x x x-=-,即2002y x x x=-,所以22200000123332()22x xx x xk k++-=---,整理得2120012(3)(1)0k kx xk k++-=,即1212k kxk k=+————(2)由(1)可得420012312006826x xk kk k x x++=++,代入到(2)中可得48x=,解得x=,此时点P的坐标为(,关于k的方程为21)3)160k k±++=,其判别式为23)1)(4640∆=-+=+>,可见这样的切线是存在的.综上,存在点P,其坐标为(.例17.设m R∈,在平面直角坐标系中,(,1)a mx y→=+,(,1)b x y→=-,a b→→⊥,动点(,)M x y的轨迹为E.(I)求轨迹E的方程,并说明该方程所表示的曲线的形状;(II)已知14m=,证明:存在圆心在原点的圆,使得该圆的任意一条切线与轨迹E恒有两个交点A,B,且OA OB⊥(O为坐标原点),并求该圆的方程;(III)已知14m=.设直线l与圆C:222(12)x y R R+=<<相切于A1,且l与轨迹E只有一个公共点B1.当R为何值时,|A1B1|取得最大值?并求最大值.解析(I)由a b→→⊥得221mx y+=,即为轨迹E的方程.当0m<时,方程表示焦点在y轴上的双曲线;当0m=时,方程表示两条互相平行的直线;当01m<<时,方程表示焦点在x轴上的椭圆;当1m=时,方程表示圆心在原点的单位圆;当1m>时,方程表示焦点在y轴上的椭圆.(II)此时方程为2214xy+=,如图.设|OA| = m,|OB| = n,则可设点A、B的坐标分别为(cos ,sin )m m θθ和(cos(),sin())22m m ππθθ++,代入椭圆方程中得 22222222cos sin 14sin cos 14m m n n θθθθ⎧+=⎪⎪⎨⎪+=⎪⎩,即 222222cos 1sin 4sin 1cos 4m n θθθθ⎧+=⎪⎪⎨⎪+=⎪⎩, 两式相加可得221115144n m +=+=.(注:形成公式22221111n m a b+=+)=O 到直线AB 的距离为d ,则据面积法有mn =所以d =.这说明存在圆2245x y +=,使得该圆的任意一条切线与轨迹E 恒有两个交点A,B,且OA OB ⊥(O 为坐标原点). (III )设点11,A B 的坐标分别为11(,)x y 和22(,)x y .由于直线l 与圆O 和椭圆E 均相切,所以直线l 的方程既是211x x y y R +=,也是2214x xy y +=,所以有 211224x y R x y ==,即2212124,x R x y R y == ————(※) 因为222111||||A B OB R =-,而222122||OB x y =+,又 222214x y +=,22211x y R +=,结合(※)有222222116R x R y +=, 可得222216(1)3R x R -=,222243R y R -=.所以2222122216(1)454||33R R R OB R R R---=+=, 得 22221122544||5()1R A B R R R R-=-=-+≤,且当R = 所以,当R =,|A 1B 1|取得最大值,最大值为1.五、综合问题例18.给定整数(2)n ≥,设000(,)M x y 是抛物线21y nx =-与直线y x =的一个交点,试证明:对于任意整数m ,必存在整数2k ≥,使得点00(,)m mx y 为抛物线21y kx =-与直线y x =的一个交点.解析 据题设,有2001x nx =-,2001m mx kx =-,整理得001n x x =+,001mm k x x =+.注意到211000000211000000111111()()()()()m m m m m m m m m m x x x x n x x x x x x x x +++++++=++-+=+-+. 当1m =时,001k x n x =+=显然是存在的;当2m =时,22001()222k x n x =+-=->显然也是存在的;假设,1()m s m s s N +==+∈时,k 存在,即001m mx x +和1101m m x x +++均为不小于2的整数,那么当2m s =+时,101011()()m mm m k n x x x x ++=+-+,其显然也是一个整数,又202012m m k x x ++=+≥,所以此时的k 为不小于2的整数.综上,对任意正整数m ,都存在不小于2的整数k .若0m =,则2k =,显然存在;若m 为负整数,可令m p =-,那么001,pp k x p N x +=+∈,由上面证明可知依然存在不小于2的整数k .综上,命题获证. 六、练习题1.已知ABC ∆边上作匀速运动的点,,D E F ,在0t =时分别从,,A B C 出发,各以一定速度向,,B C A 前进,当时刻1t =时,分别到达,,B C A .(1)证明:运动过程中DEF ∆的重心不变;(2)当DEF ∆面积取得最小值时,其值是ABC ∆面积的多少倍?2.已知抛物线x y 62=上的两个动点1122(,)(,)A x y B x y 和,其中21x x ≠且421=+x x .线段AB 的垂直平分线与x 轴交于点C ,求ABC ∆面积的最大值.3.已知抛物线y 2 = 4px ( p > 0 ),过顶点O 作两条直线分别交抛物线于A 、B 两点,若OA ⊥OB,求O 在弦AB 上的射影M 的轨迹.4.已知梯形ABCD 中,AB = 2CD,点E 分有向线段→AC 所成的比为λ,双曲线过C 、D 、E 三点,且以A 、B 为焦点.当4332≤≤λ时,求双曲线离心率e 的取值范围. 5.是否存在无穷多条直线(1,2,,,)n l n m =形成的直线族,满足条件:(1)点(1,1)在直线(1,2,,,)n l n m =上;(2)1n n n k a b +=-,这里1n k +表示直线1(1,2,,,)n l n m +=的斜率,n a 、n b 分别表示直线(1,2,,,)n l n m =的横截距和纵截距;(3)10(1,2,,,)n n k k n m +>=.6.对于曲线C 1:3 ( x 2 + 2y 2 ) 2 = 2 ( x 2 + 4y 2 )上除原点外的每一点P,求证:存在过P 的直线与椭圆C 2:x 2 + 2y 2 = 2相交于两点A 、B,使∆AOP 与∆BOP 均为等腰三角形(O 为坐标原点).七、练习题解答1.解析(1)如图,据题可令||||||||||||AD BE CF k AB BC CA ===, 则 ,,AD k AB BE k BC CF kCA ===.建立平面直角坐标系如图,设点B 的坐标为(,0)m ,点C 的坐标为(,)t s ,则点D 的坐标为(,0)km ,点E 的坐标为(,)m km kt ks -+,点F的坐标为(,)t kt s ks --.所以DEF ∆的重心坐标为(,)33m t s +,而ABC ∆的重心坐标也是(,)33m t s+,所以DEF ∆的重心不变. (2)因为(1)ADF ABC S k k S ∆∆=-,(1)BDE ABC S k k S ∆∆=-,(1)ECF ABC S k k S ∆∆=-,所以2[13(1)](331)DEF ABC ABC S k k S k k S ∆∆∆=--=-+,其最小值为14ABC S ∆,且当12k =时取到. 所以,当DEF ∆面积取得最小值时,其值是ABC ∆面积的14倍. 2.解析:设AB 的中点D 的坐标为0(2,)y ,则由21122266y x y x ⎧=⎪⎨=⎪⎩可得1212126y y x x y y -=-+,即03AB k y =.设点C 的坐标为(,0)t ,则00312y t y ⋅=--,可得5t =,所以点C 的坐标为(5,0). 设直线AB 的方程为003(2)y y x y -=-,与抛物线x y 62=联立可得220022120y y y y -+-=,于是可得||AB ==而||CD =所以20(9)ABC S y ∆=+.因为20(9)y +=当且仅当22002429y y -=+,即205y =时,20(9)ABC S y ∆=+取到最大,. 所以,ABC ∆此时直线AB的斜率为.3.解析 设OA 直线方程为y = kx ,与抛物线方程y 2 = 4px 联立后得点A 的坐标为)442k pk p ,(.进而由OA ⊥OB 容易得到点B 的坐标(4pk 2,– 4pk ). 所以,直线AB 的方程为( 1 – k 2 ) y = k ( x – 4p ) -------- ( 1 )由此易得直线OM 的方程为)0(12≠-=k x kk y ------ ( 2 )由(1)(2)消参数k 后得:( x – 2p ) 2 + y 2 = 4p 2.经检验点M 不可能在原点,故x ≠0.所以,点M 的轨迹是以(2p ,0)为圆心,2 p 为半径的圆,还需除去原点.4.解析 据双曲线的对称性可知梯形ABCD 为等腰梯形,且AD = BC .以直线AB 为x 轴,线段AB 的垂直平分线为y 轴建立平面直角坐标系,如图. 则可设双曲线的方程为22221(,0)x y a b a b-=>.由AB = 2CD可得|CD| = c ,可知点C 的横坐标为2c,代入双曲线方程中可得点C的纵坐标为2a ,即得C点坐标为(,22c a. 由1AE AC λλ→→=+得点E的坐标为2(,12(1)cc a λλλλ-++,而E 点在双曲线上,所以有222222222(2)(4)14(1)4(1)c c a a a λλλλ---=++, 整理得 2222(2)a c c a λ+=-,同除2a 可得22(2)1e e λ+=-,即得2212e eλ-=+. 因为4332≤≤λ,所以22213324e e -≤≤+,解得双曲线离心率e的取值范围是. 5.解析 据题设可设直线(1,2,,,)n l n m =的方程为1(1)n y k x -=-,则11n n a k =-,1n n b k =-,可得11n n nk k k +=-. 由于10(1,2,,,)n n k k n m +>=,所以所有的直线的斜率同号,不妨设0(1,2,,,)n k n m >=,则有110n n nk k k +-=-<,可知数列{}n k 是递减数列. XYOABM因为1112111()n n k k k k k +-=-+++,即1112111()n n k k k k k +=-+++,又因为121111n nk k k k +++>,所以111121111()n n n k k k k k k k +=-+++<-. 令110n k k -<,得21n k >,故取21[]1N k >+,则1110N Nk k k +<-<,可知从第N+1项开始,数列{}n k 的每一项都是负值,与题设矛盾.同理,若0(1,2,,,)n k n m <=也矛盾.综上,不存在这样无穷多条直线.6.先分析:逆着思考这个问题,曲线C 1应该是点P 走出的轨迹,那么这样的点应该满足题中“使∆AOP 与∆BOP 均为等腰三角形”的条件.可以判断曲线C 1上的所有点都在椭圆的内部,所以点P 一定在椭圆的内部,如图.因此猜想当OA ⊥OB,且点P是弦AB 的中点时,可以使条件“使∆AOP 与∆BOP 均为等腰三角形”解析:变形方程3 ( x 2 + 2y 2 ) 2 = 2 ( x 2 + 4y 2 )得 22222223(2)6(2)4()0x y x y x y +-+++= 因为点P 不是坐标原点,所以x ,y 不可能同时为零,即得224()0x y +>,则有 222223(2)6(2)0x y x y +-+<,可得 22022x y <+<,即点P 在椭圆2222x y +=的内部.若OA ⊥OB,且点P 是弦AB 的中点,现求点P 的轨迹方程: 如果直线AB 垂直于x 轴,则易求得点P 的坐标为(,0)3±,显然满足方程 222223(2)2(4)x y x y +=+; 如果直线AB 不垂直于x 轴,可设其斜率为k ,A 、B 两点的坐标为11(,)x y 和22(,)x y ,线段AB 的中点P 的坐标为00(,)x y .由点差法可得2002002b x xk a y y =-=- ————(1)设直线AB 的方程为00()y y k x x -=-,又设|OA| = m ,|OB| = n ,则2222111113122m n a b +=+=+=. 因为点O 到直线AB ,故据直角三角形的等面积法有mn =,即222200111()k m n y kx ++=-.所以有220013()2ky kx+=-————(2)把(1)代入(2)中得22221432()2xyxyy+=+,整理得2200222002(4)3(2)x yx y+=+,即得 2222200003(2)2(4)x y x y+=+.综上,点P的轨迹方程为 222223(2)2(4)x y x y+=+.由于点P的轨迹方程 222223(2)2(4)x y x y+=+与点P满足的几何条件是充分必要的,所以满足方程 222223(2)2(4)x y x y+=+的点P,也一定能使“OA⊥OB,且点P是弦AB的中点”成立.那么,∆AOP与∆BOP 均为等腰三角形.2014年中国数学奥林匹克希望联盟夏令营讲义(二)函数与导数江苏南菁高级中学【知识要点概述】一、函数值域与最值问题:(1) 解决一切函数问题必须认真确定该函数的定义域,定义域含三种:①自然型:②限制型:③实际型:(2) 求函数的值域是比较困难的数学问题,求函数值域方法一般有:①配方法(将函数转化为二次函数); ②判别式法(将函数转化为二次方程); ③不等式法(运用不等式的各种性质); ④函数法(运用基本函数性质,或抓住函数的单调性、函数图象等);⑤换元法; ⑥反解法; ⑦几何法; ⑧导数法.(3) 恒成立问题:①不等式f (x )>k 恒成立⇔f (x )min >k ;②不等式f (x )<k 恒成立⇔f (x )max <k③f (x )≥g (x )恒成立⇔ f (x )−g (x )≥0恒成立⇔[f (x )−g (x )]min ≥0 (典型错误min max ()()f x g x ⇔≥) (4) 有解问题:①方程f (x )=k 有解⇔k 的取值范围即为f (x )的值域;②不等式f (x )>k 有解⇔f (x )max >k ;③不等式f (x )<k 有解⇔f (x )min <k .(5) 最值存在定理:f (x )在闭区间[a , b ]内连续, 则f (x )必有最大值与最小值.二、函数基本性质:1.奇偶性定义:定义域关于原点对称, 且对∨−x ∈D ,f (−x )=f (x ) (偶函数) 或f (−x )=-f (x ) (奇函数) ①奇函数的图象关于原点对称;②偶函数的图象关于y 轴对称;③若奇函数的定义域包含0,则f (0)=0. 2.单调性定义:对∨−x 1, x 2∈I 且x 1<x 2⇒ f (x 1)<f (x 2) (增函数) 或f (x )>f (x 2) (减函数). 3.研究函数的单调性,常用以下方法:(1)定义法:利用定义严格判断. 步骤为:①取值;②作差;③判断符号;④下结论.(2)直接利用已知基本初等函数的单调性. 例如若f (x )、g (x )为增函数,则 ①f (x )+g (x )为 函数;②1f (x )为 函数(f (x )>0);③f (x )为 函数(f (x )≥0);④-f (x )为 函数. (3)利用复合函数y = f [g (x )]的单调性(其中y =f (u ), u =g (x )):判断的法则是“同增异减”具体步骤为:①求定义域;②找分界点,确定单调区间;③分析函数在每个区间上的单调性得出结论. (4)图象法:若一个函数的图象可画出来,则由图象可得单调区间.(5)利用奇偶函数的性质:①奇函数在对称区间上的单调性相同;②偶函数在对称区间上的单调性相反.(6)单调函数必存在反函数,且反函数的单调性与原函数的单调性相同.4.周期函数定义:若存在常数T (T ≠0),使得f (x +T )=f (x )对定义域内任意x 恒成立,则称f (x )为周期函数,T 称为这个函数的周期,f (x+T )=f (x )常常写作f (x +T 2)=f (x -T2), 周期函数的定义域一定是无限集.①若T 是y =f (x )的周期,那么kT (k ∈N *)也是它的周期.②若y =f (x )是周期为T 的函数,则y =f (ax +b )(a ≠0)是周期为Ta的周期函数.③若u =g (x )是周期函数, f (u )是任意函数, 则f [g (x )]也是周期函数. 5.周期的常用结论:设a 为非零常数,若对f (x )定义域内的任意x 恒有下列条件之一成立, 则f (x )的周期为2a①()()f x a f x a +=-;②()()f x a f x +=-;③1()()f x a f x +=;④1()()f x a f x +=-;⑤()1()()1f x f x a f x ++=-;⑥1()()1()f x f x a f x -+=+. 上述结论可以通过反复运用已知条件来证明.另外:()1()()1f x f x a f x -+=+或1()()1()f x f x a f x ++=-,则f (x )的周期为4a .证明:由已知f (x +2a )=()11()11()1()1()1()1()1f x f x a f x f x f x a f x f x --+-+===--++++, 于是f (x +4a )=-1(2)f x a +=f (x ) 6.周期性与对称性有如下关系:①若函数f (x )图象关于直线x =a 与x =b 对称,则它一定是周期函数,且2|a −b |是它的周期. ②若函数f (x )图象关于点(a , 0)和(b , 0)对称,则它一定是周期函数,且2|a −b |是它的周期. ③若函数f (x )图象关于直线x =a 及点(b , 0)对称,则它一定是周期函数,且4|a −b |是它的周期.证明①:不妨设a >b ,于是f [x +2(a -b )]=f [2a -(2b -x )]=f (2b -x )=f (x ), ∴ 2(a -b )是f (x )的一个周期.已知函数f (x )对任意实数x , 都有f (m +x )=f (m -x ),且f (x )是偶函数, 则f (x )的周期为_________ 已知函数f (x )对任意实数x , 都有f (m +x )=f (m -x ),且f (x )是奇函数, 则f (x )的周期为_________ 三、基本初等函数:1. 指数函数及其性质:形如y =a x (a >0, a ≠1)的函数叫做指数函数,其性质有:①定义域为R ,值域为(0,+∞); ②当0<a <1时为减函数,当a >1时为增函数;③图象有两个特殊点:定点(0,1),不变点(1,a ); ④非奇非偶,但xy a =与xy a -=的图象关于y 轴对称;xy a =与xy a =-的图象关于x 轴对称;x y a =与log a y x =的图象关于直线y =x 对称;⑤对应关系为一一映射,从而存在反函数--对数函数;⑥抽象性质:()(01)xf x a a a =>≠且⇒()()()(),()()f x f x y f x f y f x y f y +=⋅-=2. 对数函数及其性质:形如y =log a x (a >0, a ≠1)的函数叫做对数函数,其性质:①定义域为(0, +∞), 值域为R ;②图象有两个特殊点:定点(1,0), 不变点(a , 1);③当0<a <1时为减函数,当a >1时为增函数; ④非奇非偶,但-1log log a a y x y x ==与关于x 轴对称,log log ()a a y x y x ==-与图象关于y 轴对称,log x a y x y a ==与图象关于直线y x =对称;⑤对应关系为一一映射,因而有反函数——指数函数.3. 幂函数:形如y =x α的函数叫做幂函数,幂函数有如下性质:⑴它的图象都过(1,1)点,都不过第四象限,且除原点外与坐标轴都不相交;⑵定义域为R 或(−∞, 0)∪(0, +∞)的幂函数都具有奇偶性,定义域为(0, +∞)或[0, +∞)的幂函数都不具有奇偶性; ⑶幂函数y =x α都是无界函数;在第一象限中,当α<0时为减函数,当α>0时为增函数; ⑷任意两个幂函数的图象至少有一个公共点(1,1),至多有三个公共点;4. 画幂函数y =x α(α=mn , m 、n 是互质的整数)草图的一般步骤是:(1)根据指数α的大小判断函数图象在第一象限的情形如图: (2)判断函数的奇偶性并确定函数图像在其他象限的情况:①m , n 均为奇数时,y =x α为奇函数,图象在一、三象限内关于原点中心对称. ②m 为偶数,n 为奇数时y =x α为偶函数,图象在一、二象限内关于y 轴对称. ③m 为奇数,n 为偶数时,y =x α既不是奇函数也不是偶函数,函数只在第一象限有图像.5.二次函数的图像和性质:二次函数是初等数学中遇到比较多的函数之一,它的图象简单,性质易于掌握,又与二次方程、二次不等式有联系,与之相关的理论如判别式,韦达定理,求根公式等又是中学教材的重点内容,因此有必要进一步认识二次函数的性质,研究与二次函数有关的解题规律、方法与技巧.(1) 二次函数的解析式:①一般式:2()(0)f x ax bx c a =++≠ ②顶点式:2()()f x a x h k =-+,顶点为(,)h k ③两根式:12()()()f x a x x x x =-- ④三点式:132312321313221231213()()()()()()()()()()()()()()()()x x x x x x x x x x x x f x f x f x f x x x x x x x x x x x x x ------=++------(2)2()(0)f x ax bx c a =++≠的图像是抛物线,顶点坐标24(,)24b ac b a a --,对称轴方程为2bx a=-,开口与。
中国数学奥林匹克介绍

中国数学奥林匹克◇考试介绍中国数学奥林匹克又称全国中学生数学冬令营,是在全国高中数学联赛的基础上进行的一次较高层次的数学竞赛。
1985年,由北京大学、南开大学、复旦大学和中国科技大学四所大学倡议,中国数学会决定,自1986年起每年一月份举行全国中学生数学冬令营,后又名中国数学奥林匹克(ChineseMathematicalOlympiad,简称CMO)。
冬令营邀请各省、市、自治区在全国高中数学联赛中的优胜者参加,人数100多人,分配原则是每省市区至少一人,然后设立分数线择优选取。
冬令营为期5天,第一天为开幕式,第二、第三天考试,第四天学术报告或参观游览,第五天闭幕式,宣布考试成绩和颁奖。
中国数学奥林匹克考试完全模拟国际数学奥林匹克进行,每天3道题,限四个半小时完成。
每题21分(为IMO试题的3倍),6个题满分为126分。
题目难度接近IMO,颁奖也与IMO类似,设立一、二、三等奖,分数最高的前20至30名选手将组成参加当年国际数学奥林匹克(InternationalMathematicalOlympiad,简称IMO)的中国国家集训队。
从1990年开始,全国中学生数学冬令营设立了陈省身杯团体赛。
从1991年起,全国中学生数学冬令营被正式命名为中国数学奥林匹克,它成为中国中学生最高级别、最具规模、最有影响的数学竞赛。
附:中国数学奥林匹克相关制度条例1.《全国中学生数学竞赛条例(试行)》2.《中国数学奥林匹克实施细则(试行)》◇报名条件根据《中国数学奥林匹克实施细则(试行)》规定,参加中国数学奥林匹克的选手必须是本年度全国高中数学联赛一等奖获得者或上一年度国家集训队中尚未高中毕业的队员。
◇报名时间中国数学会奥林匹克委员会确定参赛选手总人数;中国数学会普及工作委员会根据当年全国高中数学联赛成绩确定各省、自治区、直辖市代表队队员名单;各省、自治区、直辖市数学会确定各代表队领队(壹人)名单;以上两名单于11月15日前报数学奥林匹克委员会。
2019中国数学奥林匹克希望联盟夏令营(一)

=> (A +/2)2
一竽
当且仅当AB =4C时,上式等号成立.
2020年第1期
因此,入+ “的最小值为
由 3 >0,知 ®min =y •
4.15°. 利用双曲线的第二定义知 CA = FA CB = FB => FC为“ABF的外角平分线
=> z CK4 =y(50° +20°) = 35°
Q]=血=1 , +5
问:是否存在实数%、y(%M0),使得 +'"}(其中,力=(nx +y)a„,n G Z+ ) 为常着数列?
2
2
11. (20 分)设椭圆 C:务 +§=l(a >b >0)
ab
的左、右焦点分别为Fl、耳,过点八且倾斜角
为a的,且点乙到直线AB
31
■ a2 +fe3 +c4 +2 019 田 106 +123c+26
a2 +42 +b3 +43 +43 +c4 +54 +54 +54 2a+126 +125c
>8a+486j1500c =4 2a+ 126+125c
当且仅当a=b=4,c=5时,上式等号成立. 故所求最小值为4.
»=令+学仏e z).
中国数学奥林匹克希望联盟夏令营第一天考试答案

中国数学奥林匹克希望联盟夏令营试卷(第一天)一、填空题(每题7分,共70分)1. 已知*N k ∈,且3≥k ,若一元二次方程2(1)20k x px k --+=的两个根都是正整数,则212()51()3p k p k +++-的值等于 。
【解析】设方程2(1)20k x px k --+=的两个根12,x x 都是正整数,由韦达定理,得121p x x k +=-,① 12x x 21k k =-,② 由②,12x x 21k k =-22,1k =+-又因为*N k ∈,且3≥k ,所以12,3,k k -==即于是12x x 3=,所以124x x +=,代入①得8p =, 故212()51()3p k p k +++-2121151=⨯+113⨯-=2019.2. 若等腰直角三角形的三个顶点均在边长为1的正方形的边上,且不与正方形的顶点重合,则该等腰直角三角形面积的取值范围为______________。
【解析】)21,41[3.2019年全国高中数学联赛一试试卷由8道填空题和3道解答题组成,其中填空题每小题7分;解答题分步给分,第一道解答题14分,分三步各自分数为4,4,6分;第二和第三道解答题均为15分,分三步每步5分,解答题中若第n 步不得分则第m 步(n m >)也不得分; 那么共有______种得分方式恰好能够得到80分。
(用数字作答)【解析】由于填空题每题7分,解答题第二题和解答题第三题均为每步5分,所以我们优先考虑解答题第一题的得分(1)解答题第一题得14分时 由于总分被扣掉20分,因此只能是被扣掉4个5分,填空题满分,这4个5分的扣分情况有3种(第二题扣15第三题扣5,第二题扣10第三题扣10,第二题扣5第三题扣15)(2)解答题第一题得8分时 由于余下题目被扣掉14分,因此只能是余下题目中恰只有两个填空题被扣分,共有C 82 =28种情况 (3)解答题第一题得4分时 由于余下题目被扣掉10分,因此只能是被恰被扣掉2个5分,讨论知这样的情况共有3种(4)解答题第一题得10分或0分时,易知没有得80分的情况 综上知共有 3+28+3+0=34种情况4.若关于x 的方程0)368lg()20lg(2=---+a x x x 有唯一解,则实数a 的取值范围是____________________。
《中等数学》2020年总目次

2020年第12期49《中等数学》2020年总目次I M O快讯(10.封底)数学活动课程讲座.初中.初中数学竞赛中的组合最值问题解法举例(钟志强6-2)完全平方数的性质及其应用(李昌勇刘应成6-7)•高中•一些关于无穷多个素因子的问题(吴宇培丨*2) “线性化”在多元不等式证明与最值求解中的应用(唐智逸茹双林2-2)数学竞赛中两种不等式基本思想的应用(缠祥瑞3*2)数学竞赛中的复数问题(唐立华 4.27-2)数学竞赛中组合几何问题的常见解法(程振峰李宝毅5-2)递归计数的六种方式(冯跃峰8-2)圆锥曲线几个结论的证明与应用(金荣生9-2)数学竞赛中数列不等式的常见解法举例(王逸凡王彬瑶10-2)数论中的升幂引理及其应用(王永喜丨卜2)对应思想在组合问题中的应用(缠祥瑞12-2)命题与解题数学命题中的“抱残守缺”(陶平生I*7)例谈不等式题的命制方法(张端阳卜1丨)两道赛题的创作思路、答题情况及启示(林天齐何忆捷熊斌2-8)开世定理的推广与应用(李庆圣2,12)老题新芽别样趣味(肖恩利陈博文3-6) 2019年全国高中数学联赛加试第三题的改进(晏兵川赵凌燕3*13)一道罗马尼亚竞赛题的分析与推广(朱华伟邱际春4‘7)一道高中数学竞赛题的探讨(邱慎海沈家书4’11)一道集训队选拔考试题的推广(李伟健4*14)一道不等式赛题的演变与推广(邱际春朱华伟郑焕5-9)利用抽屉原理证明三道竞赛题(隋婷婷5*11)一道数学竞赛题的推广(林根 5 •13)一道中国北方数学奥林匹克试题的引申(赵凌燕隋世友6‘11)判别式在不定方程中的应用(雷勇7-9)三道国外竞赛题的简解(姚先伟于娟7 •12)两道数学竞赛题的分析与推广(邱际春朱华伟8‘12)与三角形的内切圆有关的一个性质及相关性质和命题(李庆圣一道印度赛题的解题思考(李明谈谈数学竞赛中的数学期望(吴宇培关于一道数论题的思考(李彬解题小品—投石问路(陶平生利用复数证明竞赛题(刘东华华洁一道东南赛题与2020年高中联赛数论题的渊源(陶平生一道高中联赛题的推广与变形(王若飞9.9)9.16)10.11)10-13)11.7)11-11)12.7)12.9)赛题另解(1-154-155-157-1310-15)2020年全年高中数学联赛加试题另解(李庆圣杨续亮刘晓理等12-13)专题写作一类麦比乌斯反演问题及其应用(刘志乐2•15)多项式根的倒数和问题求解(梅述恩 3 •17)一个与多项式相关的不等式(刘亮赵斌5*18)高斯整数在数学竞赛中的应用(古德麟 7_15)一道北方希望之星数学夏令营试题的拓展第29届南美洲数学奥林匹克(8.36) (贾秀平段敏敏11-14)2020年全国高中数学联赛浙江赛区预赛(9-20)学生习作2020年全国高中数学联赛重庆赛区预赛(9-25)2018中国香港代表队选拔考试(9-28)论局部调整法的妙用(阮书镐4-17)2018中美洲及加勒比地区数学奥林匹克(9-32)构造表格探究一类数的分布(徐博润6-18)第61届I M O试题(10-16)一种证明三元齐次不等式的方法(王一鹏8.16)2020年全国高中数学联合竞赛(10-17)两道罗马尼亚大师杯赛题的另解(严彬玮9-18)第17届中国东南地区数学奥林匹克(10-25)竞赛之窗第61届I M O试题解答(11-18)第16届中国东南地区数学奥林匹克2019中国数学奥林匹克希望联盟夏令营(1.29 2.30第30届亚太地区数学奥林匹克第35届中国数学奥林匹克2019年全国高中数学联赛四川赛区预赛第三届中国北方希望之星数学夏令营2019青少年数学国际城市邀请赛2019年全国高中数学联赛江苏赛区预赛2019美国数学竞赛(八年级)2019年北京市中学生数学竞赛复赛(高一)2019年全国高中数学联赛吉林赛区预赛第六届伊朗几何奥林匹克2019年全国高中数学联赛甘肃赛区预赛第12届罗马尼亚大师杯数学邀请赛2020美国数学竞赛(十、十二年级)2018爱沙尼亚国家队选拔考试(初中)2018荷兰数学奥林匹克(初中)2019马其顿数学奥林匹克(初中)2019巴尔干地区数学奥林匹克(初中)2〇19希腊数学奥林匹克(初中)2019希腊国家队选拔考试(初中)2019年全国高中数学联赛贵州赛区预赛2019年全国高中数学联赛重庆赛区预赛第83届莫斯科数学奥林匹克(7,29 2020欧洲女子数学奥林匹克2019年全国高中数学联赛广西赛区预赛2019美国国家队选拔考试第60届I M O预选题(11-2212-20) 0-17)2019亚太地区数学奥林匹克(11-32) 3-33)第19届中国女子数学奥林匹克(11-36)首届百年老校数学竞赛(12-30) (1*35)(2.18)2019瑞士数学奥林匹克(初赛)(12-37) (2.25)再品佳题(2-36)(3.20)第二届国际大都市竞赛(数学)(1-38) (3-27)第32届北欧数学竞赛(2-39) (4.21)2018瑞士数学奥林匹克(预赛)(3-39)(4.26)课外训练(4-29)(4.34).初中.(5.20)(186罗家亮 6.34187 李铁汉汪波 6 •(5.27)39 188 谢文晓9.34189 陈迁赵手志(5-32)王祥10.38)(6.20).高中■(6.23)(247 巢中俊 1.41 248王永中2•41 249 (6.28)于现峰 3.41250王永喜4■41251 刘(6-30)小杰宛昭勋5‘42252杨运新6•42 253 (6.31)李潜7 41254徐节槟龙崎钢8-40(6.33)255何忆捷9.39256李培臣谭祖春郝(7.20)泽来10.42 257 胡满11.42258褚小光(7-26)田开斌12.39)8.29)(7.36)(8.20)(8.24)数学奥林匹克问题(1-48 2-47 3.474-475-48 6.477.488.469-4610-48 11-48 12-46)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
( 3. 已知函数 f (x) = A sin(ωx + ϕ) A ̸= 0,
____ .
)
()
ω
>
0, 0
<
ϕ
<
π 2
.若 f
5π 6
+ f (0) = 0 ,则 ω 的最小值为
4.
已知双曲线
x2 y2 Γ : a2 − b2
= 1(a, b > 0) , F
为
Γ
的右焦点,不过
F
的直线
l
与
Γ
的右准线及
9. 已知 f (x) = loga x(a > 0, a ̸= 1), g(x) = x2 − 6x + 9 ,若存在唯一实数 x 使得 f(g(x)) = g(f (x)) = 0 , 求实数 a 的值.
10. 已知抛物线 Γ : y2 = 2px(p > 0) ,焦点为 F ,过 Γ 外一点 Q(不在 x 轴上)作 Γ 的两条切线,切点分 别为 A, B ,直线 QA, QB 分别交 y 轴于 C, D 两点, △QAB 的外心为 M .证明: F M 为 △F CD 外接圆的切线.
.
ab
3. 已知椭圆
x2 y2 + =1
的右焦点为
F ,上顶点为
A,P
是椭圆上位于第一象限内的动点,则
△AP F
54
面积的最大值为
.
4. 正四面体 ABCD 的棱长为 2 ,则与此正四面体的四个顶点距离相等的所有平面截这个四面体的外接球
所得截面面积的总和为
.
5. 已知
sin α + 2 cos β = 2 ,则 y = sin
2019年中国数学奥林匹克希望联盟夏令营试题(一)
一、填空题(本大题共8道小题,每小题8分)
1. 已知集合 A = {x| loga(ax − 1) > 1} ,若 3 ∈ A ,则 a 的取值范围是________.
2. 在 △ABC 中, A = 30◦ ,O 为 △ABC 的外心,且 O# A» = λO# B» + µO# C» ,则 λ + µ 的最小值为______.
10. 已知抛物线 C : y2 = 4x 的焦点为 F ,点 A(x1, y1), B(x2, y2) 在 C 上,且 x1 +x2 = 4 ,分别以 AF, BF 为直径的两个圆的公共弦所在直线为 l , l 交 C 于 M, N 两点,求 | M N | 的取值范围.
11. 已知正实数 x, y, z 满足 (x + y + z)xyz = 4 ,求 (x + y)2 + 2(y + z)2 + 3(z + x)2 的最小值.
2019年中国数学奥林匹克希望联盟夏令营试题(一)
一、(本题满分40分)
给定正整数
n ,设实数
a1, a2, · · · , an
与正实数
22
b1, b2, · · · , bn
使
∑n
i=1
ai
∏n (max{0, ai })2
e
bi
的最小值.
i=1
8
且
∑n
i=1
b
4 ,求
二、(本题满分40分)
如图,点 O, I 分别为 △ABC 外心及内心, N 为弧 BùAC 中点,直线 N I 交 BC 于点 K ,直线
N O 交 BC 与点 M ,交 ⊙O 于点 S ,直线 IO 交 ⊙O 于 D, T 两点.证明:若 AD 平分 N I ,则 S, K, T 三点共线.
三、(本题满分50分) 考虑正六十边形的 60 个顶点,将其中 10 个染红色,另外 20 个染黄色,其余 30 个染蓝色.求最小的 正整数 m ,使得总能找到 m 条直线将平面分成若干区域,满足每个区域中所有点的颜色相同.
Γ
的
右支依次交于点 C, A, B .若 ∠F AB = 50◦, ∠F BA = 20◦ .则 ∠F CA = ______.
¨
5. 集合 A = (x, y)|(x − t)2 + y2
( t )2 1 − , |t| 2
«
2 所表示平面区域的面积为 ______.
6. 已知正数 a, b, c 满足 a + b + c = 13 ,则 a2 + b3 + c4 + 2019 的最小值为 ______. 10b + 123c + 26
二、(本题满分40分)
给定正整数 n ,求最小的实数 λ ,使得存在区间 [0, 1] 内的实数 a1, a2, · · · , an ,对于满足 0 x1 x2 · · · xn 1 的任意实数 xi(i = 1, 2, · · · , n) ,都有 min1 i n |xi − ai || λ .
长春嘉年华 G 共有 1栈道恰连接两个 景点,每两个景点之间至多有一条栈道.如果从某个景点出发,沿一系列不同栈道经过不同景点之后回到 了该景点,那么我们把这样的一系列栈道称为” 环线”,并将环线中所含的栈道条数定义为环线的“长度”. 若该嘉年华 G 的每条栈道都落在一个长度至多为 c(G) 的环线上,且栈道总数为 e(G) .求 c(G) + e(G) 的最小可能值.
三、(本题满分50分) 已知圆 Γ1 和圆 Γ2 交于 A, B 两点,点 C, D 分别在 Γ1, Γ2 上且线段 CD 交 Γ1 于点 E (异于点 C ),直线 BC 交 Γ2 于点 F (异于点 B ),直线 DF 与直线 EB 交于点 G ,直线 CG 与直线 AB 交于点 P .证明:若 E 为 CD 中点,则直线 P F 与直线 CA 的交点 Q 在 Γ2 上.
.
4.
有一个圆柱形水杯(厚度忽略不计),其底面直径为
8 ,高为
√ 83
,水杯中有适量水,缓慢倾斜水杯至水
恰好溢出,此时水杯的母线与水平面的夹角为 π .继续缓慢倾斜水杯,停止倒水时水杯的母线与水平面
的夹角为 π ,则所倒出的水的体积为
3 .
6
5.
已知数列
{(−1)n
·
3n n(n +
+2 1)2n+1 }
.
1 − x2 + 1
2.
已知
1 − 4sin α tan α
= √ 3 ,其中
α
∈
(0,
π 2
)
,则
α=
.
3. 已知双曲线
C
:
x2 a2
−
y2 b2
=
1 , A1 , A2
是
C
的左右顶点, F
是
C
的焦点.以坐标原点
O 为圆心,
| OF | 为半径的圆与 C 的渐近线的一个交点为 B .若 ∠A1 BA2 = 60◦ ,则 C 的离心率为
a2 = 1,
an+1
=
n2 a2n + 5 (n 2 − 1) an− 1
(n
>
1) ,问是否存在实数
x, y(x ≠ 0)
使
得
bn+2 + bn bn+1
为常值数列,其中
bn = (nx + y)an .
11.
设椭圆
C
:
x2 a2
+
y2 b2
= 1(a > b > 0)
的左右焦点分别为
F1, F2 ,过
倍数的概率为 ______.
二、解答题(本大题共3道小题,第9题16分,第10题20分,第11题20分) 9. 若复数 z1 , z2 满足 |z1 | < 1,|z2| < 1, z1 + z2 为实数,且 z1 + z2 + z1z2 = 0 .求 z1z2 的取值范围.
10. 已知数列 {an} 满足 a1 = 1,
11. 已知数列 {an}, {bn} 满足 a1 = 1, b1 = 2 ,且 an+1bn = 1 + an + anbn, bn+1an = 1 + bn + anbn .求证: 数列 {[an]} 从某一项起一定是常数数列.( [x] 表示不超过 x 的最大整数)
2019年中国数学奥林匹克希望联盟夏令营试题(三)
四、(本题满分50分) 数列 {an} 满足: a1 = 1 ,且对任意的正整数 k ,都有 ak, ak+1, ak+2 能构成某个三角形的三边长.若
7. 在正四面体 P—− ABC 中,点 D, E, F 分别在棱 P A, P B, P C 上,若 P E ≠ P F ,且 DE = DF = √ 7, EF = 2 ,则四面体 P − DEF 的体积为 ______.
{
}
8. 已知集合 T = n|n = 5a + 5b, 0 a b 30, a, b ∈ Z ,若从集合 T 中随机出一个数,则该数是 9 的
四、(本题满分50分) 是否存在全体正整数的一个排列,使得对任意的整数 l(l 2) ,排列中任意连续 l 个数的和都不能写成 形如 ab 的数,其中 a, b 均是不小于 2 的正整数?
2019年中国数学奥林匹克希望联盟夏令营试题(二)
一、填空题(本大题共8道小题,每小题8分)
√
√
1. 函数 y = 1√+ x + 1 − x 的值域为
|
#b»|
=
|
#c»|
=
2,
#» b
·
#c»
=
0,
λ
∈
