第16章a二端口网络共50页文档
第十六章二端口网络

第十六章二端口网络16二端网络口1-61二端口网络16-2 二口端方的程和参数1-6 二3端的等口电路1效6-4 端口二的移转数函61-5二端的连接口166 -转回和器负抗变阻换器16- 二端口网1一、络一口端网络+ iI+u- UiN I U +-U OC+-Z-Y I S二C、二端网口络a. 1i= i1’i2= i’21b 不.含包任独立何电c.源零状+ 态1u1ii ’11 -二口端网络i2i ’2+ u22- 2由线性RL、C及、线性受控源组成在复,频域是络工程实际题问常要常研究一网个的络对端钮之间的两系关16- 二2口的端方程和数参1+u111i-二端口络网i2+u2 2- 2电压、电关系流描述的用(量描述相) I 1 , I2 U1 , U2 U1 ,U 2 I , 1I2 U1I , 1U 2 , I 2 1I U 1 = Y Y 数参矩阵I U 22 U1 I1 = Z Z数矩参阵U I 2 2 U1 U 2 =T 参数矩T 阵I -I 1 2 , I I U, 1 U = H I 1 U 12 参数矩阵H 1 2 I 2 2 Uii1bi βibi o+ uo-+ u 1i11-二端口网络i2+2u2- 2+ iu-一Y参数方、(导纳程数参矩)阵1 方、程导的出11 LTII+ U1I 2 20N U 2 1I = 1Y U1 +1Y1 2 U 2 I 2 =Y 211U +Y 22U 2 I1 Y11 Y1 2 U 1 = I 2Y Y12 2 2 U 2- 1 2、参2的数义含(路导纳参短数) I 2 12I 1LT I+ U1-N021IY 1 1= U1 U 20=1端2-2口短路,端口11-的入端导纳端2-口2 短路正,向移导转纳I2 2Y1= 1U2 =01UI1 TIL 0NI2 2+- 2U I1 = Y11 U1 + Y12U 2 I =2Y 1U12 +22 U 21Y2 I2Y22 = 2U I 1Y1 =2 U 2 U =01口1-1 端路,短端2口2 的-端入纳端导口11 短-路,反转向移导U1 纳0=例1Y求数。
第十六章 二端口网络

1、一般情况
+
I1 z11–z12 z22–z12
-
I2
++
U1
z12
(z21–z12)I1 U2
-
-
2、如果二端口网络满足互易条件,即z12= z21
z11–z12 z22–z12
+
I1
U1
z12
I2
+
U2
-
-
二、用Y参数表示的等效电路 1、一般情况
+ I1
-Y12
I2
+
U1
U2
-
- ( Y21-Y12 )U1
. 1 I1
+.
-U1
1
.
I2
+. 2
NIC
-U2
2
T参数
电流反向型
. U. 1 = 1 I1 0
. 0 U. 2 -k -I2
电压反向型
. U. 1 = -k I1 0
0 U.. 2 1 -I2
1、负阻抗变换器应用
电路设计中,实现负阻抗——负R、L、C
.
.
I1 1
- Z1
+. U1
I2
2
.+
例1 求Y 参数。
I1
Yb
I2
I1 Y11U 1 Y12U 2 +
+
I2
Y21U 1
Y22U 2
U1
Ya
Yc
U2
解:
I1
+
U1
U1 0
第016章二端口网络共57页文档

Z22
U2 I2
I10
其中 =Y11Y22 –Y12Y21
Z参数又称开路阻抗参数
U1 Z11I1 Z12I2 U2 Z21I1 Z22I2
Z
Z11 Z21
Z12
Z22
称为 Z 参数矩阵
(16-2)
互易二端口 Z12Z21
对称二端口 Z11Z22(Z12Z21)
UI22B B1211 BB1222UI11 19
四、H 参数和方程:
1、H 参数方程
U1 H11I1 H12U2
I1
+ U- 1
线性 无源
I2 H21I1 H22U2
矩阵形式:
UI21H H1211 H H1222UI12
i2
3、二端口网络与四端网络:
i2
+
u2 –
i1
i3
四端网络
i4
4
例
1 +
i1
i 3
R
4 i2 2 +
u1
i1
i2
u2
–
–
1 i1 3
4 i2 2
1-1、 2-2是二端口。
3-3 、4-4是不是二端口?
当i≠ 0时, i1' i1 i i1
i
' 2
i2
i
i2
不满足端口条件
注意: 量纲和双下标。
9
例16-1 求Y 参数。
解:
II12
Y11U1 Y12U2 Y21U1 Y22U2
I1
Yb
I 2
+
U 1
Ya
Yc
第16章 二端口网络

+ & U
2
−
Y’ C
Y’’ − C
Y C = Y’ + Y’’ C C
章目录 返回 上一页 下一页
例2: + : & U
& I11 YB
2
1
YA
YC
−
+ & & U2 gU1
& I2
−
总结: 1)线性无源(包含受控源)二端口,Y12=Y21不再成立,需要 四个独立的参数来表示这个二端口网络。 章目录 返回 上一页 下一页
2、已知Z参数方程确定T型电路 、已知Z参数方程确定T
①画等效电路 ③对照系数
②根据电路建立方程
& & & ( Za + Zb ) I1 + Zb I 2 = U 1 & & & Zb I1 + ( Zb + Zc ) I 2 = U 2
章目录 返回 上一页 下一页
已知[Y],求等效电路。 例 已知 ,求等效电路。
二、 Z参数及方程 参数及方程 N 1、方程的建立 、 1) 由Y参数方程导出 参数方程导出 (已知 求 )
Z参数方程 参数方程
章目录 返回 上一页 下一页
2)应用迭加原理 ) 单独作用
−
单独作用
& " U1
" 2
& U
迭加 方程
章目录 返回 上一页 下一页
矩阵形式
2. Z参数的意义和性质 参数的意义和性质 1)意义 意义
章目录 返回 上一页 下一页
二、四端网络 在工程实际中, 在工程实际中,网络中伸出四个端子与外电路 相连。称为为四端网络 四端网络。 相连。称为为四端网络。
十六章 二端口网络
U 2
11
二端口网络的Y、Z参数特性:
1、对于线性R、L(M)、C元件构成的 任何无源二端口,Z12=Z21,Y12=Y21
2、对于对称的二端口,Z11=Z22,Y11=Y22 3、Z=Y-1参数
I 1 I 2
方法一:分别求Z四个 参数
+ -
+
-
U 1
第十六章 二端口网络(369)
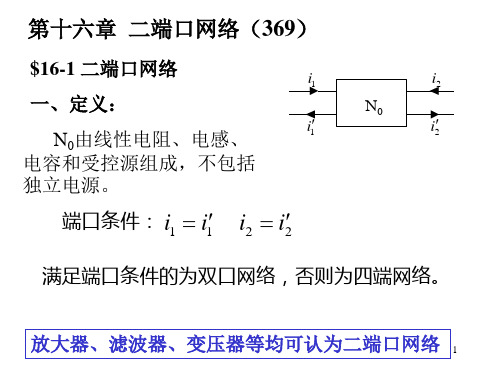
$16-1 二端口网络 一、定义: N0由线性电阻、电感、 电容和受控源组成,不包括 独立电源。 端口条件: i1
i1
i1
i2
N0
i2
i1
i2 i2
满足端口条件的为双口网络,否则为四端网络。 放大器、滤波器、变压器等均可认为二端口网络
1
二端口网络分析特性: 1、对于二端口网络,主要分析端口的电流和电压, 不涉及内部电路的工作状况。因此,本章主要讨论 端口u、i为变量的电路方程(二端口VAR约束方程) 2、二端口网络端口有四个物理量(u1、i1、u2、i2), 若其中两个为自变量,另两个为应变量,可有六组 表征网络特性的独立方程:
4
方法二:分别求出四个Y参数,从而得出Y矩阵
根据方程
1 Y1 1U 1 Y1 2U 2 I 2 Y2 1U 1 Y2 2U 2 I
0 ,U 1V,则如图 1、令 U 1 2
I Y1 2 1 U2
I 1 U 1
0 U 1
I 1
二、电流控制型二端口VAR方程
+
I 1
U 1 -
No
+
i2 ) u1 f(i1 , i2 ) u 2 f(i1 , 结构电 路 如 图
第16章 二端口网络

Ya
Yc
有 Y12=Y21 且Y11=Y22 称为对称二端口。
对称二端口只有两个参数是独立的。
I2 U+ 2 -
对称二端口是指两个端口电气特性上对称。电路结构 左右对称的,端口电气特性对称;电路结构不对称的二端 口,其电气特性也可能是对称的。这样的二端口也是对称 二端口。
例
I1 2
10
I2
+
U1 5
U 2 0
I2
U+ 2 -
Y11 Y21
I1 UI21 U 1
U 2 0 Ya Yb U2 0 Yb
Y12
I1 U 2
U1 0 Yb
Y22
I2 U 2
U 2 0 Yb Yc
互易二端口
Y
Ya Yb
Yb
Yb
Yb
Yc
若 Ya=Yc,则Y11=Y22 。
I1
+ U 1 -
Yb
2
经比较,得
T11
Y22 Y21
1 T12 Y21
T21
Y12Y21 Y11Y22 Y21
其矩阵形式
T22
Y11 Y21
UI11
T11 T21
T12
T22
U 2 I2
(注意负号)
T
T11 T21
T12
T22
称为T 参数矩阵。
互易二端口、对称二端口T 参数之间关系:
互易二端口
I2 ( g Yb )U1 YbU 2
Y
Ya Yb g Yb
Yb
Yb
非互易二端口网络(网络内部有受控源)四个独立参数。
二、Z 参数(impedance parameters)和方程
第十六章-二端口网络解析精选课件PPT

对一个端口来说,从其一个端子流 1 i 入的电流一定等于从另一个端子流出的
电流,这种具有向外引出一对端子的电
路或网络称为一端口网络或二端网络。
i
1'
二、二端口网络
反馈网络
2021/3/2
制作群
放大器
4
主 页 总目录 章目录 上一页 下一页 退 出
§16-1 二端口网络
二端口的端口条件:
对于所有时间 t ,从端子1流入方 1 i1
§16-2 二端口的方程和参数
例2:求图示二端口的Y参数。
解: Y Y Y a a b U Y Y 1 b b U U Y 1 1 b Y Y Y b b U U c U 2 2 2 I I 1 1 I 2 g U 1 U-+11I1 Y b g U 1 Y b Y c U 2 I 2 1'
解:
方法一
1
Yb
2
Ya
Yc
I1 U 1Y a Y b I2 U1Yb
Y11UI11 U20 Ya Yb Y21UI21 U20 Yb
I2 U 2Y b Y c I1U2Yb
Y22UI22 U10 YbYc
Y12
2021/3/2
UI12
U10
Yb
制作群
ห้องสมุดไป่ตู้1'
2'
1 I1
Yb
I2 2
+
U1 Y a
Yc
-
1'
本章介绍的二端口:由线性电阻、电感(耦合电感)、 电容和线性受控源组成,并规定不含任何独立电源(如 用运算法分析时,其独立初始条件为零)。
2021/3/2
制作群
6
电路原理 第16章 二端口(网络)

口网络,短路参数为Y
3 80
1 40
1 40
1 20
,求支路电流I1和I2。
解:列写回路方程为
R1I1 R2 I2
+U1 +U2
= Us =0
R1 I 1
US U1
I2
N U2
R2
II12
Y11U1 Y12U2 Y21U1 Y22U2
(R12YR211UY111)U(11RR21YY2122)UU22U0s
即:
I1 I2
Y11U 1 Y12U 2 Y21U 1 Y22U 2
Y 参数方程
写成矩阵形式为:
I1 I2
Y11 Y21
Y12
Y22
UU 12
[Y
]
Y11 Y21
Y12
Y22
Y参数值由内部参数及连接关系决定。
Y 参数矩阵.
(2) Y参数的物理意义及计算和测定
Y11 UI11 U 2 0 自导纳
端口电压电流有六种不同的方程来表示,即可用六套 参数描述二端口网络。
i1 u1 i2 u2
u1 u2 i1 i2
u1 i1 i2 u2
1. Y 参数和方程
•
(1)Y参数方程
I1
+
•
U1
N
•
I2
+ • U2
采用相量形式(正弦稳态)。将两个端口各施加一电压
源,则端口电流可视为这些电压源的叠加作用产生。
互易二端口: 对称二端口:
H12 H21 H11H22 H12H21 1
例3
•
I1
+
•
U1
R1
•
I2
Chapter16二端口网络..

Chapter 16 二端口网络主要内容1. 二端口网络及其方程;2. 二端口的Y,Z, T (A), H参数矩阵及其相互关系;3. 转移函数,T型和型等效电路;4. 二端口的连接;§ 16-1二端口网络端口:从端子1流入的电流等于从端子1'流出的电流,则1-1'两个端子构成一个端口。
二端口网络(双口网络):1-1' 一对端子为输入端子,2- 2' 一对端子为输出端子,以便与其他设备相联接。
变压器、滤波器、运算放大器等均属于双口网络。
本章所研究的二端口网络,由线性元件R,L(M互感),C及受控源组成不含有独立电源和初始值构成的附加电源,当网络不含受控源时,成为无源线性双口网络。
§ 16-2二端口网络的方程及参数用二端口概念分析电路,仅对二个端口处的电流、电压之间的关系感兴趣。
12;A双口网络r、Y参数方程(短路参数);「1 =丫1山1 +Y2U 2 -丫11 ¥2「U I L Y_U j12 =Y21U1 +%2U2 ] 2 - ]丫21 2 - ^U 21双口2----- ■------- 尸---------- A +网络u2 =0 r2H双口网络.2'+礙)2H Y参数矩阵,短路导纳矩阵1. 短路导纳参数的测定I2 U1I2 ---- 1—U2r 2「丫U2 丫=0 2 丫U1 =0例16- 1:求下图所示二端口的Y参数解:①把端口2- 2'短路,则② 对称二端口,丫1 =丫22,则此二端口的二个端口 1- 1'和2- 2'互换位置 后,其外部特性不会有任何变化;对称二端口中,因丫1 =Y 22,丫12 =丫21故其丫参数中只有两个是独立的11 二U l Y a Y b -I 2 二U i Y b②把端口 1-1'短路,12Y c Y b-l i 二U z Y b2. 丫参数的特点 ①根据互易定理,由线性丫11 11=U~ U2=0=Ya +Yb丫21I 2=------- —U 1U 2兰 =-Y b则Y22I2一 U ; U ;=0=Yc+Y bY 12~U~U;空=-Y bR, L(M ), C 构成的任何无源二端口,故一个无源线性二端口,只要 3个独立的参数足以表征其性能;U1=Z 11I 1Z 12I 2U 2 二 Z 21I 1 Z 22 丨2U 1 丨 Zu • = I [U2 一 721乙2〕[|1【 Z22 - U 2 _V 1I Ldef ZuIL Z21参数矩阵,开路阻抗矩阵乙2【 Z1.开路阻抗参数的测定IVU i •I I 2」,11 Z 21U 2Z 12U iI2 Z 22U 2 I 22.Z 参数的特点 ①无源二端口(线性R ,L (M ), C 元件构成),Z 12 =Z 21 , Z 参数只有3个 是独立的; ② 对称二端口,乙1 =Z 22,乙2二Z 21,Z 参数只有二个是独立的; ③ Z 川,丫二Z ,; ④ 含有受控源的线性R,L (M ), C 二端口,丫2式丫21,乙2^Z 21,互易定理不 再成立。
第16章a二端口网络

•+ U1
-
线性 无源
•
I2 +
•
-U 2
UU12
Z11 Z 21
Z12 Z 22
II12
Z参数的实验测定
入端阻抗 转移阻抗
Z11
U1 I1
I2 0
Z12
U1 I2
I1 0
Z
Z11
Z
21
Z12
Z
22
称为Z参数矩阵
Z21
U2 I1
I2 0
转移阻抗
Z22
U2 I2
I1 0
出端阻抗
BACK NEXT
4. 互易二端口有三个独立参数,对称时只有二个独立参数
Y
Z
T
H
互易 Y12=Y21 Z12=Z21 detT=1 H12= -H21 对称 Y11=Y22 Z11=Z22 A=D detH=1
detT AD BC
det H H11H22 H12 H21
5 .含有受控源的电路四个独立参数。
i1
n 0
0 1 n
u2 i2
i2
+ u2
n 0
则
T
0
1
n
BACK NEXT
例2
I1 1
求T参数 +
U1
2 I2
+
2
U2
I1 1
+ U1
2
+ 2 U2
UI11
A C
B
D
U2 I2
I1 1
+ U1
2 I2 2
A U1 U2
I2 0
12 2
1.5
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
C I1 U2
I20 0.5 S
B U I1 2U 2 0I1[1 0 .5 (2 I1 /2 /) ]4Ω
D I1 I2
U20
I1 0.5I1
2
BACK NEXT
四、H 参数和方程
H 参数也称为混合参数,常用于晶体管等效电路。
U2
U1
I1
I2
H 参数方程
BACK NEXT
§16-2 二端口的方程和参数
+ i1 u1 -
i2 + u2 -
端口物理量4个 i1 i2 u1 u2
端口电压电流有六种不同的方程来表示,即可用六套 参数描述二端口网络。
我们采用相量形式(正弦稳态)来讨论。
I1
U1
I2 U 2
U
1
U
2
I1 I2
U
1
I1
H H1222U I12
I1 + U1
-
线性 无源
I2 +
-U 2
H 参数的实验测定
H1 1
U1 I1
U2 0
H2 1
I2 I1
U2 0
互易二端口
短路参数
H1 2
U1 U 2
I1 0
H22
I2 U2
I1 0
开路参数
H12H21
无源
-U 2
Y 短路导纳参数
BACK NEXT
例1. 求Y 参数。
I1
Yb
I2
+
U1
Ya
Yc
U2 0
解: Y11UI11 U20 Ya Yb
I1
U1 0
Yb Ya Yc
I2
+
U2
Y21UI21 U20 Yb
Y12
I1 U 2
U 1 0 Yb
产生响应,当激励和响应互换
I1
I2
位置时,其比值保持不变。
+
U1
.
.
-
线性 无源
U1 I2
.
.
U2 I1
I1
I2
线性
+
.
.
I2 I1
无源
-U 2
.
.
.
.
.
.
U 1 U 2 当 U1U2时I1, I2
BACK NEXT
Y参数的实验测定
Y11
I1 U 1
U 2 0
-U 2
由Y 参数方程
II12
Y11U1 Y21U1
Y12U2 Y22U2
可解 U 1出 ,U 2.
Z11
Z12
即:
U1
Y22 Δ
I1
Y12 Δ
I2
Z11 I1Z12 I2
U2
Y21 Δ
I1
Y11 Δ
I2
Z 2I 1 1Z 2I 2
Y21
I2 U 1
U 2 0
I1 Y11U 1 Y12U 2 I2 Y21U 1 Y22U 2
自导纳 (驱动点导纳)
+
I1
U1
-
转移导纳
线性 无源
I2
Y12
I1 U 2
U1 0
转移导纳
I1
线性
I2 +
Y22
I2 U 2
U1 0
自导纳
则
T
0
1
n
BACK NEXT
例2
I1 1
求T参数 +
U1
2 I2
+
2
U2
I1 1
+ U1
2
+ 2 U2
UI11CA
B D
U I22
I1 1
+ U1
2 I2 2
AU U1 2 I201 221.5
Zc
+
U1
Zb
r I1
+
I2
+
U2
U 1Z aI 1Z b(I 1I 2) U 2 r I 1 Z cI 2 Z b (I 1 I 2 )
ZZraZZbb
Zb ZbZc
BACK NEXT
三、T 参数 (传输参数) 和方程
U2
I1
+ U1
-
线性 无源
I2 +
-U 2
UI21
H11I1 H21I1
H12U 2 H22U 2
矩阵形式
U I21H H1211 H H1222U I12
BACK NEXT
U I21H H1211
Z
Z11 Z21
Z12
Z2
2
称为Z参数矩阵
Z21U I12 I20 转移阻抗 Z22U I22 I10 出端阻抗
Z参数又称开路阻抗参数
BACK NEXT
互易二端口 对称二端口
Z12Z21 Z11Z22 (Z12Z21)
则 例
YZ1 ZY 1
I1
Za
约定
1. 讨论范围
线性 R、L、C、M与线性受控源
不含独立源 应用运算法分析电路时,规定独立初始条件均为零, 即不存在附加电源。
2. 参考方向(对于端口来说为关联参考方向)
+
i1
u1 –
i1
线性RLCM 受控源
i2
+
u2 – i2
BACK NEXT
分析方法 1. 确定二端口处电压、电流之间的关系,写出参数矩阵。 2. 利用端口参数比较不同的二端口的性能和作用。 3. 对于给定的一种二端口参数矩阵,会求其它的参数矩阵。 4. 对于复杂的二端口,可以看作由若干简单的二端口组 成。由各简单的二端口参数推导出复杂的二端口参数。
I1
U1 0
Yb
Ya g U 1
I2
+
U2
Y12UI12 U10 Yb
Y22
I2 U2
U10 Yb
BACK NEXT
解二
I1
+
U1
Yb
Ya g U 1
I2
+
U2
I 1Y aU 1Y b(U 1U 2) I2Y b(U 2U 1)gU 1
第十六章 二端口网络
161 二端口网络 16-2 二端口的参数和方程 16-3 二端口的等效电路 16-4 二端口的转移函数 16-5 二端口的联接 16-6 回转器与负阻抗变换器
BACK NEXT
第十六章 二端口网络
§16-1 二端口网络
一. 二端口网络
+
i
us
P
-
i
i
A
R
i
端口条件
i入i出
–
–
1 i1 3
4 i2 2
1-1’ 2-2’是二端口
3-3’ 4-4’不是二端口,是四端网络
i1' i1 i i1 i2' i2 i i2
端口条件破坏
BACK NEXT
二. 二端口网络研究的问题
+
i1
u1 –
i1
线性RLCM 受控源
例:
E
i2
+
u2 – i2
BACK NEXT
3s 16
Y11
Y22
3s 16
电气对称
BACK NEXT
例2
解一
I1 +
U1
I1
Yb
I2
+
U1
Ya g U 1
+
求Y参数
U2
Yb
Ya g U 1
I2
Y11UI11 U20 Ya Yb
U 2 0 Y21U I21 U20 Ybg
U1
I2
I1
I1
+ U1
-
UI11CAUU22DB((II22))
线性 无源
I2 +
-U 2
(注意负号)
其矩阵形式
U I11CA
B D
U I22
T
A C
B D
称为T 参数矩阵
BACK NEXT
当一个电路与外部电路通过两个端口连接时称 此电路为二端口网络。
i1
i2
i1
i2
i1
i2
二端口
i2 i1
i3
i4
四端网络
i1
i2
具有公共端的二端口
三端口或六端网络
BACK NEXT
3. 二端口的两个端口间若有外部连接,则会破坏原二端 口的端口条件。
1 +
