(整理)利用导数讨论函数性质
导数与原函数若干性质的讨论

导数与原函数若干性质的讨论摘要:我们知道奇函数与偶函数及周期函数在一些分析计算中会带来许多方便对于原函数及导函数自身之间的奇偶性及周期性有无一定的联系一般文献中涉及较少大都没有给出一个较完整的讨论和总结本文对及其导函数之间奇偶性及周期性分别作了一些初步的探讨和总结获及到一些原函数导数它们的奇偶性及周期性之间一些有益的结论该结论对于研究函数的内在性质及在一些分析运算中会带来一些简化和帮助关键词:导函数;原函数;奇偶性;周期性一、引言对于原函数及导函数以及其函数自身之间的奇偶性都没有给出一个较完整的讨论和总结另外原函数及导函数的周期性有无联系为此本文对原函数与导函数的奇偶性和周期性分别加以总结和探讨并给出相关命题和结论使得导函数与原函数之间有了一定的内在联系为后面讨论方便起见对有关性质概念作以陈述(一)奇偶性设函数f(x)在区间X上有定义且x关于原点o对称,如果对于恒有则称f(x)为偶函数(或f(x)为奇函数).奇偶函数的运算性质(1)奇函数的代数和仍为奇函数偶函数的代数和仍为偶函数.(2)偶数个奇(或偶)函数之积为偶函数奇数个奇函数的积为奇函数.(3)奇函数与偶函数的乘积为奇函数(二)周期性设函数f(x)在区间X上有定义,若存在一个与x无关的正数T,使对于任一恒有则称f(x)是以T为周期的周期函数周期函数的运算性质:二、相关结果(一)奇偶性的讨论三、结束语本文对导数与原函数的几个性质进行了研究讨论了这些性质之间的联系对导数与原函数奇偶性和周期性分别给予重点总结和探讨其结果使得导数与原函数的奇偶性和周期性之间有了一定的内在联系利用导函数与原函数的简单推倒得出的可微函数的导函数与原函数的奇偶性和周期性的特点应用这些结论对研究函数的极值函数的性态有深刻的意义参考文献:[1]张文忠周期函数集萃重庆西南师范大学出版社 1991年8月9-10;[2]张奠宙现代数学与中学数学上海上海教育出版社 1986年5月4-5;[3]刘永根评述函数奇偶性的一个命题抚顺师专学报 1995年1期;[4]刘爱德孙盛杰高存臣奇偶函数及其性质研究烟台师范学院学报(自然科学版)1999年4期。
2024北京高三一模数学题目(含答案)利用导数研究函数的性质

一、单选2024北京高三一模数学题目(含答案)利用导数研究函数的性质题1.(2024北京朝阳高三一模)已知n 个大于2的实数12,,,n x x x ⋅⋅⋅,对任意()1,2,,i x i n =⋅⋅⋅,存在2i y ≥满足i i y x <,且i i y xi i x y =,则使得12115n n x x x x -++⋅⋅⋅+≤成立的最大正整数n 为()A .14B .16C .21D .232.(2024北京海淀高三一模)函数()f x 是定义在(4,4)-上的偶函数,其图象如图所示,(3)0f =.设()f x '是()f x 的导函数,则关于x 的不等式(1)()0f x f x '+⋅≥的解集是()A .[0,2]B .[3,0][3,4)-C .(5,0][2,4)-D .(4,0][2,3)- 3.(2024北京海淀高三一模)已知()()3,0lg 1,0x x f x x x ⎧≤⎪=⎨+>⎪⎩,函数()f x 的零点个数为m ,过点(0,2)与曲线()y f x =相切的直线的条数为n ,则,m n 的值分别为()A .1,1B .1,2C .2,1D .2,24.(2024北京房山高三一模)若函数(]()ln ln(1),,0()1,0,exx x x x ∞∞⎧-∈-⎪=⎨∈+⎪⎩,则函数()()g x f x x c =++零点的个数为()A .1B .2C .1或2D .1或35.(2024北京延庆高三一模)已知函数()321x f x x =--,则不等式()0f x <的解集是()A .()0,1B .()0,∞+C .(),0∞-D .()(),01,∞∞-⋃+二、填空题6.(2024北京顺义·二模)已知函数()()213f x kx b x =-++,给出下列四个结论:①当0k =时,对任意b ∈R ,()f x 有1个极值点;②当18k >时,存在b ∈R ,使得()f x 存在极值点;③当0b =时,对任意k ∈R ,()f x 有一个零点;④当103b <<时,存在k ∈R ,使得()f x 有3个零点.其中所有正确结论的序号是.7.(2024北京海淀高三一模)已知函数()f x =①函数()f x 是奇函数;②R k ∀∈,且0k ≠,关于x 的方程0()f x kx -=恰有两个不相等的实数根;③已知P 是曲线()y f x =上任意一点,1,02A ⎛⎫- ⎪⎝⎭,则12AP ≥;④设()11,M x y 为曲线()y f x =上一点,()22,N x y 为曲线()y f x =-上一点.若121x x +=,则1MN ≥.其中所有正确结论的序号是.8.(2024北京石景山高三一模)黎曼函数在高等数学中有着广泛应用,其一种定义为:[]0,1x ∈时,()()*1,,N ,0,0,10,1p p x p q q q q R x x ⎧⎛⎫=∈⎪ ⎪=⎨⎝⎭⎪=⎩为既约真分数和内的无理数.若数列*1,n n a R n n -⎛⎫=∈ ⎪⎝⎭N ,给出下列四个结论:①1n a n =;②21n n a a ++<;③1112n i i i a a +=<∑;④11ln 2ni i n a =+≥∑.其中所有正确结论的序号是.9.(2024北京石景山高三一模)设函数()323,13,1x ax x f x x a x ⎧+≤=⎨+>⎩,①若()f x 有两个零点,则实数a 的一个取值可以是;②若()f x 是R 上的增函数,则实数a 的取值范围是.10.(2024北京延庆高三一模)已知函数()221ln 1.x ax x f x a x x x⎧+<⎪=⎨≥⎪⎩,,,给出下列四个结论:①存在实数a ,使得函数()f x 的最小值为0;②存在实数0a <,使得函数()f x 的最小值为1-;③存在实数a ,使得函数()f x 恰有2个零点;④存在实数a ,使得函数()f x 恰有4个零点.其中所有正确结论的序号是.三、解答题11.(2024北京东城高三一模)已知函数()()ln 1f x x x =-.(1)求曲线()y f x =在2x =处的切线方程;(2)设()()g x f x '=,求函数()g x 的最小值;(3)若()2f x x a>-,求实数a 的值.12.(2024北京朝阳高三一模)已知函数()()()1e R xf x ax a =-∈.(1)讨论()f x 的单调性;(2)若关于x 的不等式()()1f x a x >-无整数解,求a 的取值范围.13.(2024北京顺义·二模)设函数()e cos xf x a x =+,a ∈R .曲线()y f x =在点()()0,0f 处的切线方程为2y x =+.(1)求a 的值;(2)求证:方程()2f x =仅有一个实根;(3)对任意()0,x ∈+∞,有()sin 2f x k x >+,求正数k 的取值范围.14.(2024北京房山高三一模)已知函数1()e axf x x=+.(1)当0a =时,求曲线()y f x =在点(1,(1))f 处的切线方程;(2)设2()()g x f x x '=⋅,求函数()g x 的极大值;(3)若e a <-,求函数()f x 的零点个数.15.(2024北京西城高三一模)已知函数()()1ln e xf x x ax x a=++.(1)当1a =时,求曲线()y f x =在点()()1,1f 处切线的斜率;(2)当1a =-时,讨论()f x 的单调性;(3)若集合(){}1xf x ≥-∣有且只有一个元素,求a 的值.16.(2024北京海淀高三一模)已知函数12()e a x f x x -=.(1)求()f x 的单调区间;(2)若函数2()()e ,(0,)g x f x a x -=+∈+∞存在最大值,求a 的取值范围.17.(2024北京门头沟高三一模)已知函数()()21ln 12f x ax x x a x =-+-.(1)当1a =时,求曲线()y f x =在点())1,1f 处的切线方程;(2)当a<0时,求()f x 的极值;(3)当112a ≤≤时,判断()f x 零点个数,并说明理由.18.(2024北京石景山高三一模)已知函数()()e 0axf x x a =>.(1)求曲线()y f x =在点()()0,0f 处的切线方程;(2)求()f x 在区间[]1,1-上的最大值与最小值;(3)当1a =时,求证:()ln 1f x x x ≥++.19.(2024北京丰台高三一模)已知函数()()e ln 1xf x x x =++-,曲线():C y f x =在点()()00,x f x 处的切线为():l yg x =,记()()()h x f x g x =-.(1)当00x =时,求切线l 的方程;(2)在(1)的条件下,求函数()h x 的零点并证明()0xh x ≥;(3)当00x ≠时,直接写出函数()h x 的零点个数.(结论不要求证明)20.(2024北京延庆高三一模)已知函数()()ln 22f x x a x =-++-.(1)若曲线()y f x =的一条切线方程为1y x =-,求a 的值;(2)若函数()f x 在区间()1,2上为增函数,求a 的取值范围;(3)若21,e x ∀∈+∞⎛⎫⎪⎝⎭,()f x 无零点,求a 的取值范围.参考答案1.D【分析】构造函数()()ln 2xf x x x=≥,结合函数单调性可得e 4ix <≤,则有()1211e 154n n x x x x n -++⋅≥⋅-⋅≥+,即可得解.【详解】由i i y xi i x y =,且2i y ≥,2i x >,故ln ln i i i i y x x y =,即ln ln i ii ix y x y =,令()()ln 2xf x x x=≥,()21ln x f x x -'=,故当()2,e x ∈时,()0f x ¢>,当()e,+x ∈∞时,()0f x '<,即()f x 在()2,e 上单调递增,在()e,+∞上单调递减,由ln ln i ii ix y x y =,即()()i i f x f y =,故e i x >,2e i y ≤<,又()()ln 2ln 42424f f ===,故4i x ≤,即e 4i x <≤,若12115n n x x x x -++⋅⋅⋅+≤,则有()1211e154n n x x x x n -++⋅≥⋅-⋅≥+,即601en ≤+,由e 2.72≈,故60122.06123.07e +≈+=.故最大正整数n 为23.故选:D.【点睛】关键点点睛:本题关键点在于借助函数()ln xf x x=的性质,结合其单调性得到2e i y ≤<,从而得到e 4i x <≤,则有()1211e154n n x x x x n -++⋅≥⋅-⋅≥+,即可得解.2.D【分析】借助函数图象与导数的关系计算即可得.【详解】由(3)0f =,且()f x 为偶函数,故(3)0f -=,由导数性质结合图象可得当()4,0x ∈-时,()0f x '<,当()0,4x ∈时,()0f x '>,当0x =时,即()00f '=,则由(1)()0f x f x '+⋅≥,有41444x x -<+<⎧⎨-<<⎩,解得43x -<<,亦可得()()100f x f x ⎧+>>'⎪⎨⎪⎩,或()()100f x f x ⎧+<<'⎪⎨⎪⎩,或()10f x +=,或()0f x '=,由()()100f x f x ⎧+>>'⎪⎨⎪⎩可得41304x x -<+<-⎧⎨<<⎩或31404x x <+<⎧⎨<<⎩,即23x <<,由()()100f x f x ⎧+<<'⎪⎨⎪⎩可得31340x x -<+<⎧⎨-<<⎩,即40x -<<,由()10f x +=,可得13x +=±,即2x =或4x =-(舍去,不在定义域内),由()0f x '=,可得0x =,综上所述,关于x 的不等式(1)()0f x f x '+⋅≥的解集为(4,0][2,3)- .故选:D.3.B【分析】借助分段函数性质计算可得m ,借助导数的几何意义及零点的存在性定理可得n .【详解】令()0f x =,即0x ≤时,30x =,解得0x =,0x >时,()lg 10x +=,无解,故1m =,设过点(0,2)与曲线()y f x =相切的直线的切点为()00,x y ,当0x <时,()23f x x '=,则有()320003y x x x x -=-,有()3200023x x x -=-,整理可得301x =-,即01x =-,即当00x <时,有一条切线,当0x >时,()lg e1f x x '=+,则有()()000lg 1e lg 1y x x x x -=-++,有()()000l 2g elg 11x x x -+=-+,整理可得()()()000221lg 10lg e x x x ++-++=,令()()()()()2l 0g 2l 1e 1g g x x x x x =++-++>,则()()2lg 1g x x '=-+,令()0g x '=,可得99x =,故当()0,99x ∈时,()0g x '>,即()g x 在()0,99上单调递增,当()99,x ∈+∞时,()0g x '<,即()g x 在()99,∞+上单调递减,由()()992lg e 99220099lg e 0g =+⨯+-=>,()02020g =-=>,故()g x 在()0,99x ∈上没有零点,又()()9992lg e 999210003999lg e 10000g =+⨯+-⨯=-<,故()g x 在()99,999上必有唯一零点,即当00x >时,亦可有一条切线符合要求,故2n =.故选:B.4.A【分析】令()()0g x f x x c =++=,则()f x x c +=-,则函数()g x 零点的个数即为函数(),y f x x y c =+=-图象交点的个数,构造函数()()h x f x x =+,利用导数求出函数()h x 的单调区间,作出其大致图象,结合图象即可得解.【详解】(]()(]()[)ln ln(1),,0ln(1),,0(),0,11,0,1e ,1,x x x x x f x x x x x x∞∞∞∞⎧⎪-∈-⎧-∈-⎪⎪==∈⎨⎨∈+⎪⎪⎩⎪∈+⎩,令()()0g x f x x c =++=,则()f x x c +=-,则函数()g x 零点的个数即为函数(),y f x x y c =+=-图象交点的个数,令()()(]()[)ln(1),,02,0,11,1,x x x h x f x x x x x x x∞∞⎧⎪-+∈-⎪=+=∈⎨⎪⎪+∈+⎩,当(],0x ∈-∞时,()()ln 1h x x x =-+,则()11011x h x x x =+=-'≥-,所以函数()h x 在(],0-∞上单调递增,且()00h =,当()0,1x ∈时,()()20,2h x x =∈,当[)1,x ∞∈+时,()1h x x x =+,则()2221110x h x x x-=='-+≥,所以函数()h x 在[)1,+∞上单调递增,且()12h =,又当x →-∞时()h x ∞→-,当x →时,()h x ∞→+,作出函数()h x的大致图象如图所示,由图可知函数(),y f x x y c =+=-的图象有且仅有一个交点,所以函数()()g x f x x c =++零点的个数为1个.故选:A.【点睛】方法点睛:利用导数解决函数零点问题的方法:(1)直接法:先对函数求导,根据导数的方法求出函数的单调区间与极值,根据函数的基本性质作出图象,然后将问题转化为函数图象与x 轴的交点问题,突出导数的工具作用,体现了转化与化归思想、数形结合思想和分类讨论思想的应用;(2)构造新函数法:将问题转化为研究两函数图象的交点问题;(3)参变量分离法:由()0f x =分离变量得出()a g x =,将问题等价转化为直线y a =与函数()y g x =的图象的交点问题.5.A【分析】利用导数及导函数的单调性判断极小值点在001x <<,再由函数的单调性及(0)(1)0f f ==可得不等式的解集.【详解】因为()32ln 3x f x '=-单调递增,且(0)ln 320f '=-<,(1)3ln 320f '=->,所以存在唯一0(0,1)x ∈,使得0()0f x '=,所以当0x x <时,()0f x '<,当0x x >时,()0f x '>,所以函数()f x 在()0,x -∞上单调递减,在()0,x +∞上单调递增,又(0)(1)0f f ==,且001x <<,所以由()0f x <可得01x <<,故选:A 6.①④【分析】对①:借助导数研究函数的单调性即可得极值点个数;对②:借助导函数的导函数研究导函数可得导函数无零点,故函数不存在极值点;对③:举出反例即可得;对④:将零点个数转化为直线y kx b =+与曲线213y x =+的交点个数,从而可通过研究过()0,b 的曲线213y x =+的切线,结合零点的存在性定理得到直线y kx b =+与曲线213y x =+的关系.【详解】对①:当0k =时,()213f x b x =,()()2232x f x x -'=+,则(),0x ∈-∞时,()0f x ¢>,当()0,x ∈+∞时,()0f x '<,故()f x 在(),0∞-上单调递增,在()0,∞+上单调递减,故对任意b ∈R ,()f x 有1个极大值点0x =,故①正确;对②:当18k >时,()()2232f x k x x +-'=-,若()f x 存在极值点,则()f x '有变号零点,则()2232xk x -=+必须有解,令()()2232xx g x -=+,则()()()()()()()()2222224332222611238386333x x x x x x g x x x x x +'+=--+++-=++-+=,故当()(),11,x ∈-∞-⋃+∞时,()0g x '>,当()1,1x ∈-时,()0g x '<,故()g x 在(),1-∞-、()1,+∞上单调递增,在()1,1-上单调递减,又0x ≥时,()0g x ≤,()()()28211131g =+-⨯--=,即()18g x ≤恒成立,故当18k >时,()2232x k x -=+无解,故②错误;对③:当0b =时,()213f x kx x =-+,当0k =时,()2103f x x =>+,此时函数()f x 无零点,故③错误;对④:当103b <<时,若存在k ∈R ,使得()f x 有3个零点,则直线y kx b =+与曲线213y x =+有三个不同交点,由直线y kx b =+过点()0,b ,曲线213y x =+过点10,3⎛⎫⎪⎝⎭,又103b <<,213y x =+是偶函数,且在()0,∞+上单调递减,故当0k <时,直线y kx b =+与曲线213y x =+在第二象限必有一交点,同理,当0k >时,直线y kx b =+与曲线213y x =+在第一象限必有一交点,过点()0,b 作曲线213y x =+0201,3x x ⎛⎫ ⎪+⎝⎭,则切线方程为()()00020222133x y x x x x --+-=+,即()()00020222133x b x x x --+⨯-=+,则()()22020313x b x +=+,由103b <<,则()()0220231133x x +<+,即()()2220011540x x +-++>,即()()()22220000141130x x x x +-+-=->,即203x ≥,故当103b <<时,存在()0,x ∈-∞+∞ ,使曲线213y x =+有过点()0,b 的切线,且切点为021,3x x ⎛⎫ ⎪+⎝⎭,当0x >时,切线斜率为()22230x x +<-,则当()02022,03x k x ⎛⎫- ⎪∈ ⎪+⎝⎭时,有()00f x <,又()1030b f =->,则存在()100,x x ∈,使()10f x =,此时函数y kx b =+单调递减,而2103y x =>+恒成立,故存在()20,x x ∈+∞,使()20f x =,即当0x >时,存在()02022,03x k x ⎛⎫- ⎪∈ ⎪+⎝⎭,使得()f x 有3个零点,同理可得,当0x <()02020,23x k x ⎛⎫- ∈ ⎪+⎝⎭,使得()f x 有3个零点,故④正确.故答案为:①④.【点睛】关键点点睛:第④个结论关键点在于将零点个数转化为直线y kx b =+与曲线213y x =+的交点个数,从而可通过研究过()0,b 的曲线213y x=+的切线,结合零点的存在性定理去得到直线y kx b =+与曲线213y x =+的关系.7.②③④【分析】对①:计算定义域即可得;对②:对0k >与0k <分类讨论,结合二次函数求根公式计算即可得;对③:借助两点间的距离公式与导数求取最值计算即可得;对④:结合函数性质与③中所得结论即可得.【详解】对①:令30x x -≥,即有()()110x x x +-≥,即[][]1,01,x ∞∈-⋃+,故函数()f x 不是奇函数,故①错误;对②:0()f x kx kx -==kx =,当0x =00-=,故0是该方程的一个根;当0x ≠,0k >kx =,故0x >,结合定义域可得[]1,x ∞∈+,有322x x k x -=,即()2210x x k x --=,令2210x k x --=,440k ∆=+>,有22k x =或22k x =(负值舍去),则20122k x +=,故2210x k x --=必有一个大于1的正根,即0()f x kx -=必有一个大于1的正根;当0x ≠,0k <kx =,故0x <,结合定义域有[)1,0∈-x ,有322x x k x -=,即()2210x x k x --=,令2210x k x --=,440k ∆=+>,有22k k x =或22k k x =(正值舍去),令244k t +=>,即24k t =-,则2221171174242412222k t x ⎫⎛⎫--⎪ ⎪--⎝⎭⎝⎭==>=-,即1x =-,故2210x k x --=在定义域内亦必有一根,综上所述,R k ∀∈,且0k ≠,关于x 的方程0()f x kx -=恰有两个不相等的实数根,故②正确;对③:令(),P x y,则有y =222321124AP x x x⎛⎫=++=++⎪⎝⎭,令()3214g x x x =++,[][]1,01,x ∞∈-⋃+,()()23232g x x x x x =='++,当()21,1,3x ∞⎛⎫∈--⋃+ ⎪⎝⎭时,()0g x '>,当2,03x ⎛⎫∈- ⎪⎝⎭时,()0g x '<,故()g x 在21,3⎛⎫-- ⎪⎝⎭、()1,∞+上单调递增,在2,03⎛⎫- ⎪⎝⎭上单调递减,又()1111144g -=-++=,()110044g =+=,故()14g x ≥恒成立,即214AP ≥,故12AP ≥,故③正确;对④:当12x x =时,由[][]1,01,x ∞∈-⋃+,121x x +=,故1212x x ==-,此时,124y y =-==,则12MN =≥,当12x x ≠时,由()y f x =与()y f x =-关于x 轴对称,不妨设12x x <,则有1210x x -≤<≤或121012x x -≤≤<≤≤,当121012x x -≤≤<≤≤时,由2121x x x -≥≥,有121MN x x =≥-≥,故成立;当1210x x -≤<≤时,即有211x x =-,由③知,点M 与点N 在圆2211:24A x y ⎛⎫++= ⎪⎝⎭上或圆外,设点()1,M x m '与点()2,N x n '在圆上且位于x 轴两侧,则1M N ''=,故1MN M N ''≥=;综上所述,1MN ≥恒成立,故④正确.故答案为:②③④.【点睛】关键点点睛:结论④中的关键点在于借助结论③,结合函数的对称性,从而得到当1x 、2x 都小于零时,MN 的情况.8.②③④【分析】根据黎曼函数的定义和性质逐项分析.【详解】对于①,N ,1n n +∈∴= 时,()11001a R ==≠,故①错误;对于②,111n a n +=+,212n a n +=+,+12n n a a +∴>,故②正确;对于③,11223341111111123341ni i n n i a a a a a a a a a a n n ++==++++=⨯+⨯++⋅+∑ 11111111123341212n n n =-+-++--<++ ,故③正确;对于④,123111123ni n i a a a a a n==++++=+++∑ ,()2n ≥,构造函数()e 1xg x x =--,()0x >,则()e 10xg x ='->,()g x 单调递增,()(0)0g x g ∴>=,即当0x >时e 1x x >+,11132111e 1,e 1,,e 123n n>+>+>+ ,11123345111111eln 2342232nn n n n n +++++⎛⎫>⨯⨯⨯⨯=∴+++> ⎪⎝⎭,当1n =时,110ni i a a ===∑,11ln 02+=,11ln 2ni i n a =+⎛⎫∴≥ ⎪⎝⎭∑,故④正确.故选:②③④.【点睛】方法点睛:新定义题型的特点是:通过给出一个新概念,或约定一种新运算,或给出几个新模型来创设全新的问题情景,要求考生在阅读理解的基础上,依据题目提供的信息,联系所学的知识和方法,实现信息的迁移,达到灵活解题的目的:遇到新定义问题,应耐心读题,分析新定义的特点,弄清新定义的性质,按新定义的要求,“照章办事”,逐条分析、验证、运算,使问题得以解决.9.1-(13a <-内的值都可以)01a ≤≤或2a ≥【分析】①分析函数的性质,确定零点所在的区间,通过解方程的方法,即可求解;②根据分段函数的形式,确定两段函数都是单调递增,并根据分界点处函数值的关系不等式,即可求解.【详解】①函数()23f x x a =+在()1,+∞上单调递增,()2130f a =+>,所以函数()f x 在区间()1,+∞上无零点,则函数()33f x x ax =+在(],1-∞上有2个零点,即330x ax +=,()230x x a +=,则0x =,或x =或x =,a<0,1>,解得:13a <-,所以a 的一个值是1-;②函数()23f x x a =+在()1,+∞上单调递增,则在(],1-∞上,()33f x x ax =+也单调递增,且321331a a +≤⨯+,若函数在()33f x x ax =+在区间(],1-∞单调递增,则()2330f x x a '=+≥,即2≥-a x 在区间(],1-∞上恒成立,即()2maxa x≥-,即0a ≥,不等式321331a a +≤⨯+,解得:2a ≥或1a ≤,综上可知,01a ≤≤或2a ≥.故答案为:1-(13a <-内的值都可以);01a ≤≤或2a ≥10.①③【分析】取特殊值判断①,当0a <时,分别分析分段函数两部分的最值判断②,根据分段函数每部分的零点确定函数的零点可判断③④.【详解】当0a =时,()210 1.x x f x x ⎧<=⎨≥⎩,,,,显然函数的最小值为0,故①正确;当0a <时,ln ()(1)a xf x x x =≥,()21ln ()a x f x x-'=,当1e x <<时,()0f x '<,当e x <时,()0f x '>,所以()f x 在[)1,e 上单调递减,在[)e,+∞上单调递增,所以e x =时,()f x 有最小值(e)eaf =,由1e a =-可得a e =-,此时,1x <时,2()2e f x x x =-,()f x 在(,1)-∞上单调递减,所以()(1)12e f x f >=-,与最小值为1-矛盾,若1x <时,2()2f x x ax =+的对称轴方程为0x a =->,当1x a =-<时,即1a >-时,2min ()()f x f a a =-=-,若21a -=-,则1a =-与1a >-矛盾,当1x a =-≥时,()f x 在(,1)-∞上单调递减,无最小值,综上,当0a <时,函数()f x 的最小值不为1-,故②错误;由②知,1a <-时,1x <时,()f x 单调递减且(0)0f =,当1x ≥时,()0f x ≤且(1)0f =,所以函数恰有2个零点,故③正确;当0a >时,ln ()0(1)a xf x x x=≥≥且仅有(1)0f =,即ln ()(1)a x f x x x =≥有且只有1个零点,当0a <时,ln ()0(1)a xf x x x=≤≥且仅有(1)0f =,即ln ()(1)a x f x x x =≥有且只有1个零点,综上0a ≠时,ln ()(1)a xf x x x=≥有且只有1个零点,而2()2(2)f x x ax x x a =+=+在1x <上至多有2个零点,所以0a ≠时,函数没有4个零点,当0a =时,函数有无数个零点,故④错误.故答案为:①③【点睛】关键点点睛:本题的关键是对a 分类讨论,利用导数研究[)1,+∞上的函数性质,结合二次函数性质研究另一段函数.11.(1)24y x =-(2)2(3)2a =【分析】(1)求导,再根据导数的几何意义即可得解;(2)利用导数求出函数()g x 的单调区间,进而可求出最小值;(3)分1a ≤和1a >两种情况讨论,在1a >时,再分x a >和1x a <<两种情况讨论,分离参数,构造函数并求出其最值,即可得解.【详解】(1)()()()ln 111xf x x x x '=-+>-,则()()22,20f f '==,所以曲线()y f x =在2x =处的切线方程为()22y x =-,即24y x =-;(2)()()()()ln 111xg x f x x x x '==-+>-,()()()22112111x x x g x x x x ---'=+=---,当12x <<时,()0g x '<,当2x >时,()0g x '>,所以函数()g x 在()1,2上单调递减,在()2,+∞上单调递增,所以()()min 22g x g ==;(3)函数()f x 的定义域为()1,+∞,当1a ≤时,0x a ->,则()2f x x a>-,即()()2f x x a >-,即()22a f x x -<-,由(2)得()2f x '≥,令()()2h x f x x =-,则()()()201h x f x x ''=-≥>,所以()h x 在()1,+∞上单调递增,又当1x →时,()h x →-∞,因为1a ≤,所以22a -≥-,此时()22a f x x -<-不恒成立,故1a ≤不符题意;当1a >时,若x a >,则0x a ->,则()2f x x a>-,即()()2f x x a >-,即()22a f x x -<-,由上可知函数()()2h x f x x =-在(),a +∞上单调递增,所以()()()()ln 12h x h a a a a x a >=-->,所以()2ln 12a a a a -≤--,解得2a ≥①,若1x a <<,则()2f x x a>-,即()()2f x x a <-,即()22a f x x ->-,由上可知函数()()2h x f x x =-在()1,a 上单调递增,所以()()()()ln 1211h x h a a a a a <=--<<,所以()2ln 12a a a a -≥--,解得2a ≤②,由①②可得2a =,综上所述,2a =.【点睛】方法点睛:对于利用导数研究不等式的恒成立与有解问题的求解策略:(1)通常要构造新函数,利用导数研究函数的单调性,求出最值,从而求出参数的取值范围;(2)利用可分离变量,构造新函数,直接把问题转化为函数的最值问题.(3)根据恒成立或有解求解参数的取值时,一般涉及分离参数法,但压轴试题中很少碰到分离参数后构造的新函数能直接求出最值点的情况,进行求解,若参变分离不易求解问题,就要考虑利用分类讨论法和放缩法,注意恒成立与存在性问题的区别.12.(1)答案见解析(2)1a ≥【分析】(1)首先求函数的导数,再分0,0,0a a a ><=三种情况讨论()f x 的单调性;(2)不等式转化为11e x x a x -⎛⎫-< ⎪⎝⎭,设函数()1e x x h x x -=-,利用导数求函数的取值范围,再结合不等式,讨论a 的取值,即可求解.【详解】(1)()()1e xf x a ax '=--,当()0f x '=,得1ax a-=,当0a >时,1,a x a -⎛⎫∈-∞ ⎪⎝⎭时,()0f x ¢>,()f x 单调递增,1,-⎛⎫∈+∞ ⎪⎝⎭a x a 时,()0f x '<,()f x 单调递减,当0a <时,1,a x a -⎛⎫∈-∞ ⎪⎝⎭时,()0f x '<,()f x 单调递减,1,-⎛⎫∈+∞ ⎪⎝⎭a x a 时,()0f x ¢>,()f x 单调递增,当0a =时,()e xf x =,函数()f x 在R 上单调递增,综上可知,0a >时,函数()f x 的单调递增区间是1,a a -⎛⎫-∞ ⎝⎭,单调递减区间是1,a a -⎛⎫+∞⎪⎝⎭,0a <时,函数()f x 的单调递减区间是1,a a -⎛⎫-∞ ⎪⎝⎭,单调递增区间是1,a a -⎛⎫+∞⎪⎝⎭,0a =时,函数()f x 的增区间是(),-∞+∞,无减区间.(2)不等式()()1e 1xax a x ->-,即11e x x a x -⎛⎫-< ⎪⎝⎭,设()1e x x h x x -=-,()2e 21e ex x xx x h x -+-'=-=,设()e 2xt x x =+-,()e 10x t x '=+>,所以()t x 单调递增,且()01t =-,()1e 20t =->,所以存在()00,1x ∈,使()00t x =,即()00h x '=,当()0,x x ∈-∞时,()0h x '<,()h x 单调递减,当()0,x x ∈+∞时,()0h x '>,()h x 单调递增,所以()()00000e 1e x x x x h x h x -+≥=,因为e 1xx ≥+,所以()()()00002000000011e 110e e e x x x x x x x x x x h x h x +-+-++≥=≥=>,当0x ≤时,()()01h x h ≥=,当1x ≥时,()()11h x h ≥=,不等式()()1e 1xax a x ->-无整数解,即11e x x a x -⎛⎫-< ⎪⎝⎭无整数解,若0a ≤时,不等式恒成立,有无穷多个整数解,不符合题意,若1a ≥时,即11a≤,因为函数()h x 在(],0-∞上单调递减,在[)1,+∞上单调递增,所以Z x ∈时,()()(){}1min 0,11h x h h a ≥=≥,所以()1h x a<无整数解,符合题意,当01a <<时,因为()()1011h h a==<,显然0,1是()1a h x ⋅<的两个整数解,不符合题意,综上可知,1a ≥.【点睛】关键点点睛:本题第二问的关键1是不等式的变形11e x x a x -⎛⎫-< ⎪⎝⎭,第二个关键是确定函数()1ex x h x x -=-的单调性,以及确定()()011h h ==.13.(1)1a =;(2)证明见解析;(3)01k <≤.【分析】(1)根据切点在曲线和切线上可得;(2)分0x >,0x =,0x <,利用导数讨论单调性,通过单调性讨论即可得证;(3)令()e cos sin 2xF x x k x =+--,分01k <≤,1k >两种情况,利用导数讨论最值即可得解.【详解】(1)解:因为()e cos x f x a x =+,所以()00e 1f a a =+=+,又点()()0,0f 在切线2y x =+上,所以()02f =,所以12a +=,即1a =.(2)证明:欲证方程()2f x =仅有一个实根,只需证明e cos 20x x +-=仅有一个零点,令()e cos 2x g x x =+-,则()e sin xg x x '=-,令()()e sin xh x g x x =-'=,则()e cos x h x x '=-,讨论:(1)当0x >时,()0e cos e cos 1cos 0x h x x x x =->-=-≥',所以()h x 在()0,∞+上单调递增,所以()()01h x h >=,即()e sin 10xg x x =>'->,所以()g x 在()0,∞+上单调递增,()()00g x g >=,即此时无零点;(2)当0x =时,()00g =,即此时有一个零点;(3)当0x <时,()0e cos 2e cos 21cos 0x g x x x x =+-<+-=-+≤所以,当0x <时,()0g x <,即此时无零点综上可得,()e cos 2xg x x =+-仅有一个零点,得证.(3)当()0,x ∞∈+时,e cos sin 2x x k x +>+,即e cos sin 20x x k x +-->恒成立,令()e cos sin 2xF x x k x =+--,则()e sin cos xF x x k x =-'-,由(Ⅱ)可知,()0,x ∞∈+时e sin 1x x ->,所以()e sin cos 1cos xF x x k x k x '=-->-,讨论:(1)当01k <≤时,因为1cos 1x -≤≤,所以cos k k x k -≤≤,即11cos 1k k x k -≤-≤+,所以()1cos 10F x k x k >≥'--≥,即当01k <≤时,()0F x '>,所以()e cos sin 2xF x x k x =+--在()0,x ∞∈+时单调递增,所以()()00F x F >=恒成立,即满足条件e cos sin 20x x k x +-->,(2)当1k >时,由()e sin cos xF x x k x =-'-可知()010F k ='-<,又()ππe 0F k '=+>,所以存在()00,πx ∈,使得()00F x '=,所以,当()00,x x ∈时,()0F x '<,()F x 单调递减,当()0,x x ∞∈+时,()0F x '>,()F x 单调递增,所以()()000F x F <=,即不能保证e cos sin 20x x k x +-->恒成立,综上可知,正数k 的取值范围是01k <≤.【点睛】思路点睛:根据不等式恒成立求参数范围常用方法:(1)参变分离,将问题转化为函数最值问题;(2)根据参数分类讨论,利用导数求函数最值即可求解.14.(1)3y x =-+(2)答案见解析(3)1【分析】(1)求导,再根据导数的几何意义即可得解;(2)求导,分0a =,0a >和a<0三种情况讨论,再结合极大值的定义即可得解;(3)令1()e 0ax f x x =+=,则1e ax x =-,再分x 的正负讨论,当0x <时,分离参数可得()ln x a x-=-,则函数()f x 零点的个数即为函数()ln ,x y a y x -==-图象交点的个数,构造函数()()()ln 0x h x x x-=-<,利用导数求出其单调区间和极值,作出函数的大致图象,结合图象即可得解.【详解】(1)当0a =时,1()1f x x=+,()21f x x '=-,则()()11,12f f =-'=,所以曲线()y f x =在点(1,(1))f 处的切线方程为()21y x -=--,即3y x =-+;(2)21()e ax f x a x'=-,则()22()()e 10ax g x f x x ax x =⋅=-≠',则()()()222e e 2e 0ax ax axg x ax a x ax ax x =+=+≠',当0a =时,()1g x =-,此时函数()g x 无极值;当0a >时,令()0g x '<,则0x >或2x a <-,令()0g x '<,则20x a -<<,所以函数()g x 在(2,,0,a ∞∞⎛⎫--+ ⎪⎝⎭上单调递增,在2,0a ⎛⎫- ⎪⎝⎭上单调递减,所以()g x 的极大值为2241eg a a ⎛⎫-=- ⎪⎝⎭;当a<0时,令()0g x '<,则0x <或2x a>-,令()0g x '<,则20x a <<-,所以函数()g x 在()2,0,,a ∞∞⎛⎫--+ ⎪⎝⎭上单调递增,在20,a ⎛⎫- ⎪⎝⎭上单调递减,而函数()g x 的定义域为()(),00,∞∞-⋃+,所以此时函数()g x 无极值.综上所述,当0a ≤时,函数()g x 无极大值;当0a >时,()g x 的极大值为241ea -;(3)令1()e 0axf x x =+=,则1e ax x =-,当0x >时,1e ,00axx>-<,所以0x >时,函数()f x 无零点;当0x <时,由1e axx =-,得1ln ax x ⎛⎫=- ⎪⎝⎭,所以()ln x a x-=-,则0x <时,函数()f x 零点的个数即为函数()ln ,x y a y x-==-图象交点的个数,令()()()ln 0x h x x x -=-<,则()()2ln 1x h x x --'=,当e x <-时,()0h x '>,当e 0x -<<时,()0h x '<,所以函数()h x 在(),e ∞--上单调递增,在()e,0-上单调递减,所以()()max 1e eh x h =-=,又当x →-∞时,()0h x >且()0h x →,当0x →时,()h x ∞→-,如图,作出函数()h x 的大致图象,又e a <-,由图可知,所以函数()()ln ,x y a h x x-==-的图象只有1个交点,即当0x <时,函数()f x 只有1个零点;综上所述,若e a <-,函数()f x 有1个零点.【点睛】方法点睛:利用导数解决函数零点问题的方法:(1)直接法:先对函数求导,根据导数的方法求出函数的单调区间与极值,根据函数的基本性质作出图象,然后将问题转化为函数图象与x 轴的交点问题,突出导数的工具作用,体现了转化与化归思想、数形结合思想和分类讨论思想的应用;(2)构造新函数法:将问题转化为研究两函数图象的交点问题;(3)参变量分离法:由()0f x =分离变量得出()a g x =,将问题等价转化为直线y a =与函数()y g x =的图象的交点问题.15.(1)2e 2+(2)单调递增区间为(),1-∞-;单调递减区间为()1,0-(3)1a e=-【分析】(1)根据条件,利用导数的几何意义,即可求出结果;(2)对函数求导得到()()11e x f x x x ⎛⎫=+- ⎪⎝⎭',由函数()f x 定义域知1e 0x x -<,再利用导数与函数单调性间的关系,即可求出结果;(3)对函数求导得到()()1e 1x f x x x a ⎛⎫=++ ⎪⎝⎭',再分0a >和a<0两种情况讨论,利用导数与函数单调性间的关系,求出函数的单调区间,结合条件,即可求出结果.【详解】(1)当1a =时,()ln e xf x x x x =++,所以()()111e x f x x x=+++',得到()12e 2f '=+,所以曲线()y f x =在点()(1,)1f 处切线的斜率为2e 2+.(2)当1a =-时,()()ln e xf x x x x =+--,易知()f x 的定义域为(),0∞-,又()()()1111e 1e x x f x x x x x ⎛⎫=+-+=+- ⎪⎝⎭',因为(),0x ∈-∞,所以1e 0xx-<,所以(),1x ∈-∞-时,()0f x ¢>,()1,0x ∈-时,()0f x '<所以()f x 的单调递增区间为(),1-∞-;单调递减区间为()1,0-.(3)因为()()1ln e xf x x ax x a =++,所以()()1e 1x f x x x a ⎛⎫=++ ⎪⎝⎭',易知0a ≠,当0a >时,()f x 的定义域为()0,∞+,所以()0f x ¢>恒成立,故()f x 在)∞+上单调递增,又12111e 0af a a a⎛⎫=+> ⎪⎝⎭,所以0a >不合题意,当0a <时,()f x 的定义域为(),0∞-,此时1e0xx a+<,所以(),1x ∈-∞-时,()0f x ¢>,()1,0x ∈-时,()0f x '<,故()f x 的单调递增区间为(),1-∞-,单调递减区间为()1,0-,所以()()max 1()11ln ef x f a a =-=-+--.设()()11ln (0)e g x x x x=-+--<,则()2211e 1e e x g x x x x +=+=',当1,e x ∞⎛⎫∈-- ⎪⎝⎭时,()0g x '<,1,0e x ⎛⎫∈- ⎪⎝⎭时,()0g x '>,所以()g x 的单调递减区间为1,e ⎛⎫-∞- ⎪⎝⎭;单调递增区间为1,0e ⎛⎫- ⎪⎝⎭.所以min 1()1e g x g ⎛⎫=-=- ⎪⎝⎭,所以集合(){}1xf x ≥-∣有且只有一个元素时1a e=-.【点睛】方法点睛:对于求不等式成立时的参数范围问题,一般有三个方法:一是分离参数法,使不等式一端是含有参数的式子,另一端是一个区间上具体的函数,通过对具体函数的研究确定含参式子满足的条件;二是讨论分析法,根据参数取值情况分类讨论;三是数形结合法,将不等式转化为两个函数,通过两个函数图像确定条件.16.(1)()f x 的增区间为(),2∞-,减区间为(2,)+∞(2)1a ≥-【分析】(1)对函数求导,得到121(1))e 2(a x f x x -=-',再求出()0f x '>和()0f x '<对应的x 取值,即可求出结果;(2)令2()()e h x f x a -=+,对()h x 求导,利用导数与函数单调性间的关系,求出()h x 的单调区间,进而得出()h x 在(0,)+∞上取值范围,从而将问题转化成1222e e e a a a ---+≥成立,构造函数12()e e x m x x --=+,再利用()m x 的单调性,即可求出结果.【详解】(1)易知定义域为R ,因为12()ea x f x x -=,所以11122211(1)()e2e e 2a x a x a x x x x f ----=-'=,由()0f x '=,得到2x =,当2x <时,()0f x '>,当2x >时,()0f x '<,所以,函数()f x (),2∞,单调递减区间为()2,∞+.(2)令2()()e h x f x a -=+,则()()h x f x ''=,由(1)知,函数()f x 的单调递增区间为(),2∞-,单调递减区间为()2,∞+,所以()h x 在2x =时取得最大值12(2)2e e a h a --=+,所以当2x >时,1222()e e e (0)a x h x x a a h ---=+>=,当02x <<时,()(0)h x h >,即当,()0x ∈+∞时,(]()(0),(2)h x h h ∈,所以函数122()ee a x g x x a --=+在(0,)+∞存在最大值的充要条件是1222e e e a a a ---+≥,即122122e e e e +e 02a a a a a -----++=≥,令12()e e x m x x --=+,则12()e e 0x m x --'=+>恒成立,所以12()e e x m x x --=+是增函数,又因为22(1)e e 0m ---=-=,所以12()e e 0a m a a --=+≥的充要条件是1a ≥-,所以a 的取值范围为[)1,-+∞.【点睛】关键点点晴:本题的关键在于第(2)问,构造函数122()e e a x h x x a --=+,利用函数单调性得到,()0x ∈+∞时,(]()(0),(2)h x h h ∈,从而将问题转化成1222e e e a a a ---+≥,构造函数12()e e x m x x --=+,再利用()m x 的单调性来解决问题.17.(1)12y =-(2)()12f x a =-极大值,无极小值(3)当12a =时()f x 有一个零点,当112a <≤时()f x 无零点【分析】(1)求出函数的导函数,即可求出切线的斜率,从而求出切线方程;(2)求出函数的定义域与导函数,即可求出函数的单调区间,从而求出极值;(3)依题意可得()1ln 102a x x a -+-=,令()()1ln 12F x a x x a =-+-,则判断()f x 的零点个数,即判断()F x 的零点个数,利用导数说明()F x 的单调性,求出()()max ln 221F x a a a =-+,再令()ln 12xH x x x =-+,[]1,2x ∈,利用导数说明()H x 的单调性,即可求出()max H x ,从而得解.【详解】(1)当1a =时()21ln 2f x x x x =-,则()112f =-,()ln 1f x x x '=+-,所以()10f '=,所以曲线()y f x =在点()()1,1f 处的切线方程为12y =-.(2)函数()f x 的定义域为(0,∞+,且()()ln 1ln 1f x a x a x a a x x '=+-+-=-+,令()()ln 1g x f x a x x '==-+,则()1a a xg x x x-'=-=,因为a<0,所以()0g x '<恒成立,所以()g x 在()0,∞+上单调递减,即()f x '在()0,∞+上单调递减,又()10f '=,所以当01x <<时()0f x ¢>,当1x >时()0f x '<,则()f x 在()0,1上单调递增,在()1,+∞上单调递减,所以()f x 在1x =处取得极大值()12f x a =-极大值,无极小值.(3)令()0f x =,即()21ln 102ax x x a x -+-=,因为0x >,所以()1ln 102a x x a -+-=,令()()1ln 12F x a x x a =-+-,所以判断()f x 的零点个数,即判断()F x 的零点个数,又()1222a a x F x x x -'=-=,112a ≤≤,所以当02x a <<时()0F x '>,当2x a >时()0F x '<,所以()F x 在()0,2a 上单调递增,在()2,a +∞上单调递减,所以()()()max 2ln 221F x F a a a a ==-+,令()ln 12xH x x x =-+,[]1,2x ∈,则()11ln 22H x x '=-,因为[]1,2x ∈,所以()()111ln 2ln 210222H x '≤-=-<,所以()H x 在[]1,2上单调递减,所以()()10H x H ≤=,所以()20F a ≤,当且仅当12a =时等号成立,所以当12a =时()F x 有一个零点,即()f x 有一个零点,当112a <≤时()F x 无零点,即()f x 无零点,综上可得当12a =时()f x 有一个零点,当112a <≤时()f x 无零点.【点睛】关键点点睛:第三问的关键是首先将问题转化为()1ln 102a x x a -+-=,利用导数求出()()max ln 221F x a a a =-+,再构造函数()ln 12xH x x x =-+,[]1,2x ∈.18.(1)y x =(2)见解析(3)证明见解析【分析】(1)根据导数的几何意义,求切线方程;(2)首先求函数的导数,再讨论01a <≤和1a >两种情况求函数的单调性,求函数的最值;(3)首先根据不等式构造函数()e ln 1xg x x x x =---,再利用导数求函数的最小值,即可证明.【详解】(1)()()1e axf x ax '=+,()01f '=,()00f =,所以曲线()y f x =在点()()0,0f 处的切线方程为y x =;(2)()()1e axf x ax '=+,0a >当01a <≤时,()0f x '≥在区间[]1,1-上恒成立,()f x 在区间[]1,1-上单调递增,所以函数()f x 的最小值为()1e axf --=-,最大值为()1e a f =,当1a >时,()0f x '=,得()11,0x a=-∈-,()f x '在区间11,a ⎡⎫--⎪⎢⎣⎭小于0,函数()f x 单调递减,()f x '在区间1,1a ⎡⎤-⎢⎥⎣⎦大于0,函数()f x 单调递增,所以函数()f x 的最小值为11e f a a ⎛⎫-=- ⎪⎝⎭,()1e ax f --=-,()1e a f =,显然()()11f f >-,所以函数()f x 的最大值为()1e a f =,综上可知,当01a <≤时,函数()f x 的最小值为()1e ax f --=-,最大值为()1e af =,当1a >时,函数()f x 的最小值为11e f a a ⎛⎫-=- ⎪⎝⎭,最大值为()1e af =;(3)当1a =时,()e xf x x =,即证明不等式e ln 1x x x x ≥++,设()e ln 1xg x x x x =---,0x >,()()11e ⎛⎫'=+- ⎪⎝⎭x g x x x ,设()1e xh x x =-,0x >,()21e 0xh x x'=+>,所以()h x 在()0,∞+单调递增,并且1202h ⎛⎫=< ⎪⎝⎭,()1e 10h =->,所以函数()h x 在1,12⎛⎫⎪⎝⎭上存在唯一零点0x ,使()0001e 0x h x x =-=,即()00g x '=,则在区间()00,x ,()0x '<,()g x 单调递减,在区间()0,x +∞,()0g x '>,()g x 单调递增,所以()g x 的最小值为()00000e ln 1xg x x x x =---,由()0001e 0xh x x =-=,得001x x e =,且00ln x x =-,所以()00g x =,所以()e ln 10xg x x x x =---≥,即()ln 1f x x x ≥++.19.(1)1y x =+(2)函数()h x 有唯一零点0x =,证明过程见解析(3)2【分析】(1)只需分别求出()()0,0f f '即可得解;(2)首先有()()e ln 121xh x x x =++--,()()1e 211x x x h x x +--'=+,令()()()1e 21,1x m x x x x =+-->-,我们可以通过构造导数来说明()0m x >,即()0h x '>,这表明了()h x 单调递增,注意到()00h =,由此即可进一步得证;(3)首先我们可以连续求导说明函数()f x '在(]1,0-上递减,在[)0,∞+上递增.其次()()()()()000h x f x f x x x f x =---',故()()()0h x f x f x ''-'=.进一步有()()000h x h x '==,然后分000,10x x >-<<两种情况分类讨论即可求解.【详解】(1)当00x =时,()()001f x f ==,而()1e 11x f x x =+-+',所以()01f '=,从而切线方程为10y x -=-,也就是1y x =+.(2)由题意()()()()()()e ln 11e ln 121x xh x f x h x x x x x x =-=++--+=++--,所以()()1e 211e 211x xx x h x x x +--=+-='++,令()()1e 21x m x x x =+--,则()()2e 2xm x x =+-',当10x -<<时,122x <+<,0e 1x <<,所以()2e 2e 212x xx +<<⨯=,即()0m x '<,所以当10x -<<时,()m x 单调递减,()()00m x m >=,当0x >时,22x +>,e 1x >,所以()2e 2e 212x xx +>>⨯=,即()0m x '>,所以当0x >时,()m x 单调递增,()()00m x m >=,综上,()0m x ≥恒成立,也就是()0h x '≥恒成立,所以()h x 在()1,∞-+又因为()00h =,故函数()h x 有唯一零点0x =,且当10x -<<时,()0h x <,当0x >时,()0h x >;因此当10x -<<时,()0xh x >,当0x >时,()0xh x >,故()0xh x ≥;(3)对n 个实数12,,...,n a a a ,定义()12max ,,...,n a a a 和()12min ,,...,n a a a 分别为12,,...,n a a a 中最大的一个和最小的一个.现在,()()e ln 1x f x x x =++-,故()1e 11xf x x =+-+',令()()f x x ϕ'=,再对()x ϕ求导一次得到()()21e 1xx x ϕ=-+'.当10x -<<时,()()()02211e e 110101xx x ϕ=-<-='-=++,()x ϕ单调递减;当0x >时,()()()02211e e 110101xx x ϕ=->-='-=++,()x ϕ单调递增.。
第21讲 利用导数研究函数的单调性(解析版)

第21讲 利用导数研究函数的单调性【基础知识回顾】1. 利用导数研究函数的单调性在某个区间(a ,b)内,如果f′(x)≥0且在(a ,b)的任意子区间上不恒为0,那么函数y =f(x)在这个区间内单调递增;如果f′(x)≤0且在(a ,b)的任意子区间上不恒为0,那么函数y =f(x)在这个区间内单调递减.2. 判定函数单调性的一般步骤 (1)确定函数y =f(x)的定义域; (2)求导数f′(x);(3)在函数f(x)的定义域内解不等式f′(x)>0或f′(x)<0; (4)根据(3)的结果确定函数的单调区间. 3. 已知函数单调性求参数的值或参数的范围 (1)函数y =f(x)在区间(a ,b)上单调递增,可转化为f ′(x)≥0在(a ,b)上恒成立,且在(a ,b)的任意子区间上不恒为_0;也可转化为(a ,b)⊆增区间.函数y =f(x)在区间(a ,b)上单调递减,可转化为f′(x)≤0在(a ,b)上恒成立,且在(a ,b)的任意子区间上不恒为_0;也可转化为(a ,b)⊆减区间.(2)函数y =f(x)的增区间是(a ,b),可转化为(a ,b)=增区间,也可转化为f′(x)>0的解集是(a ,b);函数y =f(x)的减区间是(a ,b),可转化为(a ,b)=减区间,也可转化为a ,b 是f′(x)=0的两根.1、.函数f (x )=3+x ln x 的单调递减区间是( ) A.⎝⎛⎭⎫1e ,e B.⎝⎛⎭⎫0,1e C.⎝⎛⎭⎫-∞,1eD.⎝⎛⎭⎫1e ,+∞【答案】 B【解析】因为函数f (x )的定义域为(0,+∞),且f ′(x )=ln x +x ·1x =ln x +1,令f ′(x )<0,解得0<x <1e,故f (x )的单调递减区间是⎝⎛⎭⎫0,1e . 2、函数f(x)=ax 3+bx 2+cx +d 的图像如图,则函数y =ax 2+32bx +c3的单调递增区间是( )第2题图A . (-∞,-2]B . ⎣⎡⎭⎫12,+∞ C . [)-2,3 D . ⎣⎡⎭⎫98,+∞【答案】D【解析】 由题图可知d =0. 不妨取a =1,∵f(x)=x 3+bx 2+cx ,∴f ′(x)=3x 2+2bx +c. 由图可知f′(-2)=0,f ′(3)=0,∴12-4b +c =0,27+6b +c =0,∴b =-32,c =-18. ∴y =x 2-94x -6,y ′=2x -94. 当x >98时,y ′>0,∴y =x 2-94x -6的单调递增区间为[98,+∞).故选D .3、函数f (x )=ln x -ax (a >0)的单调递增区间为( ) A.⎝⎛⎭⎫0,1a B.⎝⎛⎭⎫1a ,+∞ C.⎝⎛⎭⎫-∞,1a D .(-∞,a )【答案】A【解析】 由f ′(x )=1x -a >0,x >0,得0<x <1a .∴f (x )的单调递增区间为⎝⎛⎭⎫0,1a . 4、若函数f (x )=x 2-e x -ax 在R 上存在单调递增区间,则实数a 的取值范围是________. 【答案】 (-∞,2ln 2-2)【解析】 ∵函数f (x )=x 2-e x -ax 在R 上存在单调递增区间,∴f ′(x )=2x -e x -a >0,即a <2x -e x 有解.设g (x )=2x -e x ,则g ′(x )=2-e x ,令g ′(x )=0,得x =ln 2,则当x <ln 2时,g ′(x )>0,g (x )单调递增,当x >ln 2时,g ′(x )<0,g (x )单调递减,∴当x =ln 2时,g (x )取得极大值也是最大值,且g (x )max =g (ln 2)=2ln 2-2,∴a <2ln 2-2.考向一 求函数的单调区间例1、求下列函数的单调区间:(1)f(x)=x 3-12x 2-2x +3;(2)g(x)=x 2-2ln x.【解析】 (1)∵f′(x)=3x 2-x -2=(3x +2)(x -1),定义域为R ,∴当f ′(x )>0时,x ∈⎝⎛⎭⎫-∞,-23∪(1,+∞);当f ′(x )<0时,x ∈⎝⎛⎭⎫-23,1. ∴函数的单调增区间为⎝⎛⎭⎫-∞,-23和(1,+∞),单调减区间为⎝⎛⎭⎫-23,1. (2)g ′(x )=2x -2x =2(x +1)(x -1)x,定义域为(0,+∞),令g ′(x )=0,解得:x =1或x =-1(舍去),列表:x (0,1) 1 (1,+∞) g ′(x ) - 0+ g (x ) 减 极小值 增变式1、(1)下列函数中,在(0,+∞)内为增函数的是( ) A.f (x )=sin 2x B.f (x )=x e x C.f (x )=x 3-xD.f (x )=-x +ln x【答案】 B【解析】 由于x >0,对于A ,f ′(x )=2cos 2x ,f ′⎝⎛⎭⎫π3=-1<0,不符合题意; 对于B ,f ′(x )=(x +1)e x >0,符合题意;对于C ,f ′(x )=3x 2-1,f ′⎝⎛⎭⎫13=-23<0,不符合题意; 对于D ,f ′(x )=-1+1x ,f ′(2)=-12<0,不符合题意.(2)函数f (x )=2x 2-ln x 的单调递减区间是( ) A.⎝⎛⎭⎫-12,12 B.⎝⎛⎭⎫12,+∞ C.⎝⎛⎭⎫0,12 D.⎝⎛⎭⎫-∞,-12∪⎝⎛⎭⎫12,+∞ 【答案】 C【解析】 ∵函数f (x )=2x 2-ln x ,∴f ′(x )=4x -1x =4x 2-1x=4⎝⎛⎭⎫x -12⎝⎛⎭⎫x +12x.由f ′(x )<0,解得0<x <12,∴函数的单调递减区间是⎝⎛⎭⎫0,12. (3).已知定义在区间(-π,π)上的函数f (x )=x sin x +cos x ,则f (x )的递增区间是________. 【答案】 ⎝⎛⎭⎫-π,-π2和⎝⎛⎭⎫0,π2 【解析】 f ′(x )=sin x +x cos x -sin x =x cos x . 令f ′(x )=x cos x >0,则其在区间(-π,π)上的解集为⎝⎛⎭⎫-π,-π2∪⎝⎛⎭⎫0,π2,即f (x )的单调递增区间为⎝⎛⎭⎫-π,-π2和⎝⎛⎭⎫0,π2.变式2、(1)函数f(x)=x 3-15x 2-33x +6的单调减区间为__ __.(2) 函数f(x)=1+x -sin x 在(0,2π)上的单调情况是__ __.(3)已知a<0,函数f(x)=x 3+ax 2-a 2x +2的单调递减区间是__ .【解析】(1)由f(x)=x 3-15x 2-33x +6得f ′(x)=3x 2-30x -33,令f′(x)<0,即3(x -11)(x +1)<0,解得-1<x<11,∴函数f(x)的单调减区间为(-1,11). (2) f′(x)=1-cos x>0在(0,2π)上恒成立,∴f(x)单调递增.(3)f′(x)=3x 2+2ax -a 2=(3x -a)(x +a),令f′(x)<0,得a3<x<-a ,∴减区间为⎝⎛⎭⎫a3,-a . 方法总结:1. 利用导数求函数f(x)的单调区间的一般步骤为:(1)确定函数f(x)的定义域;(2)求导函数f ′(x);(3)在函数f(x)的定义域内解不等式f′(x)>0和f′(x)<0;(4)根据(3)的结果确定函数f(x)的单调区间. 2. 利用导数求函数单调性,在对函数求导以后要对导函数进行整理并因式分解,方便后面求根和判断导函数的符号.考向二 给定区间求参数的范围例2、设函数()32132a f x x x bx c =-++,曲线()y f x =在点()()0,0f 处的切线方程为1y =. (1)求,bc 的值;(2)若0a >,求函数()f x 的单调区间;(3)设函数()()2g x f x x =+,且()g x 在区间(2,1)--内存在单调递减区间,求实数a 的取值范围.【解析】:(1)f ′(x )=x 2-ax +b ,由题意得⎩⎪⎨⎪⎧ f 0=1,f ′0=0,即⎩⎪⎨⎪⎧c =1,b =0.(2)由(1)得,f ′(x )=x 2-ax =x (x -a )(a >0),当x ∈(-∞,0)时,f ′(x )>0;当x ∈(0,a )时,f ′(x )<0;当x ∈(a ,+∞)时,f ′(x )>0. 所以函数f (x )的单调递增区间为(-∞,0),(a ,+∞),单调递减区间为(0,a ). (3)g ′(x )=x 2-ax +2,依题意,存在x ∈(-2,-1),使不等式g ′(x )=x 2-ax +2<0成立,即x ∈(-2,-1)时,a <(x +2x )max =-22,当且仅当x =2x 即x =-2时等号成立.所以满足要求的a 的取值范围是(-∞,-22).变式1、已知g (x )=2x +ln x -ax .(1)若函数g (x )在区间[1,2]内单调递增,求实数a 的取值范围; (2)若g (x )在区间[1,2]上存在单调递增区间,求实数a 的取值范围.【解析】(1)g (x )=2x +ln x -ax (x >0),g ′(x )=2+1x +ax2(x >0).∵函数g (x )在[1,2]上单调递增, ∴g ′(x )≥0在[1,2]上恒成立, 即2+1x +ax 2≥0在[1,2]上恒成立,∴a ≥-2x 2-x 在[1,2]上恒成立, ∴a ≥(-2x 2-x )max ,x ∈[1,2]. 在[1,2]上,(-2x 2-x )max =-3, 所以a ≥-3.∴实数a 的取值范围是[-3,+∞). (2)g (x )在[1,2]上存在单调递增区间, 则g ′(x )>0在[1,2]上有解, 即a >-2x 2-x 在[1,2]上有解, ∴a >(-2x 2-x )min ,又(-2x 2-x )min =-10,∴a >-10.变式2、若函数f (x )=x -13sin 2x +a sin x 在(-∞,+∞)上单调递增,则a 的取值范围是( )A.[-1,1]B.⎣⎡⎦⎤-1,13C.⎣⎡⎦⎤-13,13D.⎣⎡⎦⎤-1,-13 【答案】 C【解析】 ∵f (x )=x -13sin 2x +a sin x ,∴f ′(x )=1-23cos 2x +a cos x =-43cos 2x +a cos x +53.由f (x )在R 上单调递增,则f ′(x )≥0在R 上恒成立. 令t =cos x ,t ∈[-1,1], 则-43t 2+at +53≥0,在t ∈[-1,1]上恒成立.∴4t 2-3at -5≤0在t ∈[-1,1]上恒成立. 令g (t )=4t 2-3at -5,则⎩⎪⎨⎪⎧g (1)=-3a -1≤0,g (-1)=3a -1≤0.解之得-13≤a ≤13方法总结: 1.明晰导数概念及其几何意义在解题中的应用,强化方程的思想,培养基本运算能力.2. 辨析区间上单调和区间上存在单调区间的本质区别和处理策略的不同,提升参变分离和构造函数等解决问题的方法和技巧,感悟数学解题背后的思维和内涵.考向三 函数单调区间的讨论例3、已知函数.当时,讨论的单调性; 【解析】函数的定义域为., 因为,所以, ①当,即时,由得或,由得, 所以在,上是增函数, 在上是减函数; ②当,即时,所以在上是增函数;③当,即时,由得或,由得,所以在,.上是增函数,在.上是减函 综上可知:当时在,上是单调递增,在上是单调递减; 当时,在.上是单调递增;当时在,上是单调递增,在上是单调递减. 变式1、讨论下列函数的单调性. (1)f (x )=x -a ln x ; (2)g (x )=13x 3+ax 2-3a 2x .【解析】 (1)f (x )的定义域为(0,+∞), f ′(x )=1-a x =x -ax ,令f ′(x )=0,得x =a ,①当a ≤0时,f ′(x )>0在(0,+∞)上恒成立, ∴f (x )在(0,+∞)上单调递增. ②当a >0时,x ∈(0,a )时,f ′(x )<0,()()11ln f x x m x m R x x ⎛⎫=+-+∈ ⎪⎝⎭1m ()f x ()f x (0,)+∞'21()1m m f x x x -=+-2221(1)[(1)]x mx m x x m x x -+----==1m 10m ->011m <-<12m <<()0f x '>1x >1x m <-()0f x '<11m x -<<()f x ()0,1m -()1,+∞()1,1m -11m -=2m =()0f x '≥()f x ()0,∞+11m ->2m >()0f x '>1x m >-1x <()0f x '<11x m <<-()f x ()0,1()1,m -+∞()1,1m -12m <<()f x ()0,1m -()1,+∞()1,1m -2m =()f x ()0,∞+2m >()f x ()0,1()1,m -+∞()1,1m -x ∈(a ,+∞)时,f ′(x )>0,∴f (x )在(0,a )上单调递减,在(a ,+∞)上单调递增. 综上,当a ≤0时,f (x )在(0,+∞)上单调递增,当a >0时,f (x )在(0,a )上单调递减,在(a ,+∞)上单调递增. (2)g (x )的定义域为R ,g ′(x )=x 2+2ax -3a 2=(x +3a )(x -a ), 当a =0时,g ′(x )≥0, ∴g (x )在R 上单调递增. 当a >0时,x ∈(-∞,-3a )∪(a ,+∞)时,g ′(x )>0,g (x )单调递增, x ∈(-3a ,a )时,g ′(x )<0,g (x )单调递减. 当a <0时,x ∈(-∞,a )∪(-3a ,+∞)时,g ′(x )>0,g (x )单调递增, x ∈(a ,-3a )时,g ′(x )<0,g (x )单调递减, 综上有a =0时,g (x )在R 上单调递增;a <0时,g (x )在(-∞,a ),(-3a ,+∞)上单调递增,在(a ,-3a )上单调递减; a >0时,g (x )在(-∞,-3a ),(a ,+∞)上单调递增,在(-3a ,a )上单调递减. 变式2、已知函数f (x )=x -2x +a (2-ln x ),a >0.讨论f (x )的单调性.【解析】 由题知,f (x )的定义域是(0,+∞), f ′(x )=1+2x 2-a x =x 2-ax +2x 2,设g (x )=x 2-ax +2, g (x )=0的判别式Δ=a 2-8.①当Δ<0,即0<a <22时,对一切x >0都有f ′(x )>0.此时f (x )在(0,+∞)上单调递增. ②当Δ=0,即a =22时,仅对x =2, 有f ′(x )=0,对其余的x >0都有f ′(x )>0. 此时f (x )在(0,+∞)上单调递增.③当Δ>0,即a >22时,方程g (x )=0有两个不同的实根, x 1=a -a 2-82,x 2=a +a 2-82,0<x 1<x 2.当x 变化时,f ′(x ),f (x )的变化情况如下表:x (0,x 1) x 1 (x 1,x 2) x 2 (x 2,+∞)f ′(x )+-+f (x )单调递增 极大值 单调递减 极小值 单调递增此时f (x )在⎝ ⎛⎭⎪⎫0,a -a 2-82上单调递增,在⎝ ⎛⎭⎪⎫a -a 2-82,a +a 2-82上单调递减, 在⎝ ⎛⎭⎪⎫a +a 2-82,+∞上单调递增.方法总结: 对含参函数的合理分类,关键是找到引起分类讨论的原因.2. 会对函数进行准确求导,求导以后进行整理并因式分解,其中能否因式分解、每个因式系数的正负、根的大小等都是引起分类讨论的原因.考向四 构造函数研究单调性例4、(1)设函数f (x )在R 上的导函数为f ′(x ),且2f (x )+xf ′(x )>x 2,则下列不等式在R 上恒成立的是( )A .f (x )>0B .f (x )<0C .f (x )>xD .f (x )<x(2)已知定义域为{x |x ≠0}的偶函数f (x ),其导函数为f ′(x ),对任意正实数x 满足xf ′(x )>-2f (x ),若g (x )=x 2f (x ),则不等式g (x )<g (1)的解集是( )A .(-∞,1)B .(-1,1)C .(-∞,0)∪(0,1)D .(-1,0)∪(0,1)【答案】 (1)A (2)D【解析】(1)法一:令g (x )=x 2f (x )-14x 4,则g ′(x )=2xf (x )+x 2f ′(x )-x 3=x [2f (x )+xf ′(x )-x 2],当x >0时,g ′(x )>0,∴g (x )>g (0), 即x 2f (x )-14x 4>0,从而f (x )>14x 2>0;当x <0时,g ′(x )<0,∴g (x )>g (0), 即x 2f (x )-14x 4>0,从而f (x )>14x 2>0;当x =0时,由题意可得2f (0)>0,∴f (0)>0. 综上可知,f (x )>0.法二:∵2f (x )+xf ′(x )>x 2,∴令x =0,则f (0)>0,故可排除B 、D ,不妨令f (x )=x 2+0.1,则已知条件2f (x )+xf ′(x )>x 2成立,但f (x )>x 不一定成立,故C 也是错误的,故选A.(2)∵f (x )是定义域为{x |x ≠0}的偶函数, ∴f (-x )=f (x ).对任意正实数x 满足xf ′(x )>-2f (x ), ∴xf ′(x )+2f (x )>0. ∵g (x )=x 2f (x ),∴g (x )也是偶函数,当x ∈(0,+∞)时,g ′(x )=2xf (x )+x 2f ′(x )>0. ∵g (x )在(0,+∞)上单调递增, ∴g (x )在(-∞,0)递减. 若g (x )<g (1),则|x |<1(x ≠0), 解得0<x <1或-1<x <0.故g (x )<g (1)的解集是(-1,0)∪(0,1). 变式1、已知定义在上的函数的导函数为,且,,则下列判断中正确的是( )A .B .C .D . 【答案】CD 【解析】令,,则, 因为, 所以在上恒成立, 因此函数在上单调递减, 因此,即,即,故A 错;又,所以,所以在上恒成立, 0,2π⎡⎫⎪⎢⎣⎭()f x ()f x '()00f =()cos ()sin 0f x x f x x '+<6624f f ππ⎛⎫⎛⎫< ⎪ ⎪⎝⎭⎝⎭ln 03f π⎛⎫> ⎪⎝⎭363f ππ⎛⎫⎛⎫> ⎪ ⎪⎝⎭⎝⎭243f ππ⎛⎫⎛⎫> ⎪ ⎪⎝⎭⎝⎭()()cos f x g x x =0,2x π⎡⎫∈⎪⎢⎣⎭2()cos ()sin ()cos f x x f x x g x x '+'=()cos ()sin 0f x x f x x '+<2()cos ()sin ()0cos f x x f x x g x x '+'=<0,2π⎡⎫⎪⎢⎣⎭()()cos f x g x x =0,2π⎡⎫⎪⎢⎣⎭64g g ππ⎛⎫⎛⎫> ⎪ ⎪⎝⎭⎝⎭64cos cos64f f ππππ⎛⎫⎛⎫ ⎪ ⎪⎝⎭⎝⎭>664f f ππ⎛⎫⎛⎫> ⎪ ⎪⎝⎭⎝⎭()00f =(0)(0)0cos0f g ==()()0cos f x g x x =≤0,2π⎡⎫⎪⎢⎣⎭因为,所以,故B 错; 又,所以,即,故C 正确;又,所以,即,故D 正确;故选:CD.变式2、设函数f ′(x )是奇函数f (x )(x ∈R )的导函数,f (-1)=0,当x >0时,xf ′(x )-f (x )<0,则使得f (x )>0成立的x 的取值范围是________. 【答案】 (-∞,-1)∪(0,1)【解析】 因为f (x )(x ∈R )为奇函数,f (-1)=0, 所以f (1)=-f (-1)=0. 当x ≠0时,令g (x )=f (x )x ,则g (x )为偶函数,g (1)=g (-1)=0. 则当x >0时,g ′(x )=⎣⎡⎦⎤f (x )x ′=xf ′(x )-f (x )x 2<0,故g (x )在(0,+∞)上单减,在(-∞,0)上单增.所以在(0,+∞)上,当0<x <1时,g (x )>g (1)=0,得f (x )x >0,所以f (x )>0;在(-∞,0)上,当x <-1时,由g (x )<g (-1)=0,得f (x )x<0,所以f (x )>0. 综上知,使得f (x )>0成立的x 的取值范围是(-∞,-1)∪(0,1).变式3、设f (x ),g (x )分别是定义在R 上的奇函数和偶函数,当x <0时,f ′(x )g (x )+f (x )g ′(x )>0,且g (-3)=0,则不等式f (x )g (x )<0的解集为________. 【答案】 (-∞,-3)∪(0,3) 【解析】 f ′(x )g (x )+f (x )g ′(x )>0⇔ [f (x )g (x )]′>0,所以函数y =f (x )g (x )在(-∞,0)上单调递增. 又由题意知函数y =f (x )g (x )为奇函数,所以其图象关于原点对称,且过点(-3,0),(3,0).ln0,32ππ⎡⎫∈⎪⎢⎣⎭ln 03f π⎛⎫< ⎪⎝⎭63g g ππ⎛⎫⎛⎫> ⎪ ⎪⎝⎭⎝⎭63cos cos 63f f ππππ⎛⎫⎛⎫ ⎪ ⎪⎝⎭⎝⎭>363f ππ⎛⎫⎛⎫> ⎪ ⎪⎝⎭⎝⎭43g g ππ⎛⎫⎛⎫> ⎪ ⎪⎝⎭⎝⎭43cos cos43f f ππππ⎛⎫⎛⎫ ⎪ ⎪⎝⎭⎝⎭>243f ππ⎛⎫⎛⎫> ⎪ ⎪⎝⎭⎝⎭数形结合可求得不等式f (x )g (x )<0的解集为(-∞,-3)∪(0,3).方法总结:(1)对于不等式f ′(x )+g ′(x )>0(或<0),构造函数F (x )=f (x )+g (x );(2)对于不等式f ′(x )-g ′(x )>0(或<0),构造函数F (x )=f (x )-g (x ); 特别地,对于不等式f ′(x )>k (或<k )(k ≠0),构造函数F (x )=f (x )-kx . (3)对于不等式f ′(x )g (x )+f (x )g ′(x )>0(或<0),构造函数F (x )=f (x )g (x ); (4)对于不等式f ′(x )g (x )-f (x )g ′(x )>0(或<0),构造函数F (x )=f xg x(g (x )≠0);(5)对于不等式xf ′(x )+f (x )>0(或<0),构造函数F (x )=xf (x ); (6)对于不等式xf ′(x )-f (x )>0(或<0),构造函数F (x )=f xx(x ≠0).1、函数y=f (x )的导函数()y f x '=的图象如图所示,则函数y=f (x )的图象可能是【答案】D【解析】原函数先减再增,再减再增,且0x =位于增区间内,因此选D .2、设函数()e e xxf x a -=+(a 为常数).若f (x )为奇函数,则a =________;若f (x )是R 上的增函数,则a 的取值范围是___________. 【答案】(]1,0--∞【解析】首先由奇函数的定义得到关于a 的恒等式,据此可得a 的值,然后利用()0f x '≥可得a 的取值范围.若函数()e e xxf x a -=+为奇函数,则()(),f x f x -=-即()ee e e xx x x a a --+=-+,即()()1e e0xxa -++=对任意的x 恒成立,则10a +=,得1a =-.若函数()e e xxf x a -=+是R 上的增函数,则() e e 0x xf x a -'=-≥在R 上恒成立,即2e x a ≤在R 上恒成立,又2e 0x >,则0a ≤, 即实数a 的取值范围是(],0-∞.3、(2021·深圳市龙岗区龙城高级中学高三月考)已知函数()ln f x x =,()g x x =,则当120x x >>时( ) A .1122|()()||()()|f x g x f x g x -<-|B .1122|()()||()()|f x g x f x g x ->-C .1221|()()||()()|f x g x f x g x -<- D .1221|()()||()()|f x g x f x g x ->-【答案】C【解析】令()ln h x x x =-,则()111xh x x x-'=-=,当()0,1x ∈时,()0h x '>,()h x 单调递增,当()1,x ∈+∞时,()0h x '<,()h x 单调递减, 则()()110h x h ≤=-<,则()h x 在()0,1单调递减,在()1,+∞单调递增,∴()1h x 和()2h x 的大小不确定,故AB 错误;由()0h x <可知221ln x x x <<,即()()210f x g x -<, 令1221|()()||()()|W f x g x f x g x =---, 则1221|()()|()()W f x g x f x g x =-+-,当()()12f x g x ≥时,[][]12211122()()()()()()()()0W f x g x f x g x f x g x f x g x =-+-=-+-<; 当()()12f x g x <,[][]21212211()()()()()()()()W g x f x f x g x f x g x f x g x =-+-=+-+,()()ln y f x g x x x =+=+单调递增,0W ∴<, 综上,1221|()()||()()|f x g x f x g x -<-,故C 正确,D 错误.故选:C.4、(2021·广东高三月考)已知函数()ln f x x ax =+在函数()22g x x x b =-+的递增区间上也单调递增,则实数a 的取值范围是( ) A .(],1-∞- B .[)0,+∞C .(][),10,-∞-+∞ D .(]1,0-【答案】B【解析】因为()g x 的单调递增区间为[)1,+∞, 则由题意()f x 在[)1,+∞递增, 而()1axf x x+'=, 所以当0a ≥时,()0f x '>在 [)1,+∞恒成立,()f x 在区间[)1,+∞单调递增,符合题意; 当0a <时,由()10ax f x x +'=>,解得10x a<<- ()f x 的单调递增区间为10,a ⎛⎫- ⎪⎝⎭,不合题意.综上,0a ≥. 故选:B5、(2021·广东高三月考)若对任意的1x ,()2,x m ∈+∞,且12x x <,都有122121ln ln 2x x x x x x -<-,则m 的最小值是( )(注: 2.71828e =⋅⋅⋅为自然对数的底数) A .1eB .eC .1D .3e【答案】A【解析】由题意知210x x >>,可得210x x ->, 则122121ln ln 2x x x x x x -<-等价于()122121ln ln 2x x x x x x -<-,即121212ln 2ln 2x x x x x x +<+,所以()()1221ln 2ln 2x x x x +<+, 所以2121ln 2ln 2x x x x ++<, 令()ln 2x f x x+=,可得21f x f x ,又由21x x m >>,所以()f x 在(),m +∞上是减函数, 所以()2ln 10x f x x--'=≤,解得1x e ≥,则1m e ≥,即m 的最小值为1e . 故选:A.6、(2021·深圳市第七高级中学高三月考)已知定义在R 上的函数()f x 满足()()()()0,6f x f x f x f x +-=+=-,且对[]12,3,0x x ∀∈-,当12x x ≠时,都有()()()()11221221x f x x f x x f x x f x +<+,则以下判断正确的是( )A .函数()f x 是偶函数B .函数()f x 在[]9,6--单调递增C .3x =是函数()f x 的对称轴D .函数()f x 的最小正周期是12【答案】BCD【解析】由定义域为R , ()()0f x f x +-=,即()()f x f x -=-,则函数为奇函数,故A 错误;因为()()6f x f x +=-,而()()f x f x -=-,所以()()6f x f x +=-,所以函数的对称轴为6032x +==,故C 选项正确; 因为()()6f x f x +=-,所以()()()126f x f x f x +=-+=,所以()f x 的最小正周期是12,故D 选项正确;因为[]12,3,0x x ∀∈-,当12x x ≠时,都有()()()()11221221x f x x f x x f x x f x +<+, 则()()()()12120x x f x f x --<,所以[]3,0x ∈-时,()f x 为减函数. 因为函数为奇函数,所以[]0,3x ∈时,()f x 为减函数,又因为函数()f x 关于3x =对称,所以[]3,6x ∈时,()f x 为增函数.因为()f x 的最小正周期是12,所以[]9,6x ∈--的单调性与[]3,6x ∈时的单调性相同. 故,[]9,6x ∈--时,()f x 单调递增,故B 选项正确. 故选:BCD. 7、()3211232f x x x ax =-++,若()f x 在2,3⎛⎫+∞ ⎪⎝⎭上存在单调递增区间,则a 的取值范围是_______ 【答案】19a >- 【解析】:()'22fx x x a =-++,有已知条件可得:2,+3x ⎛⎫∃∈∞ ⎪⎝⎭,使得()'0f x ≥,即()212a x x ≥-,只需()2min12a x x ⎡⎤≥-⎢⎥⎣⎦,而()221122122339y x x ⎡⎤⎛⎫=->-=-⎢⎥ ⎪⎝⎭⎢⎥⎣⎦,所以19a >-。
高中数学利用导数研究函数单调性基础知识梳理+常考例题汇总

∴(-2)+(-1)=a,即 a=-3. 3.[变条件]本例(2)变为:若 g(x)在(-2,-1)内不单调,其他条件不变,求实数 a 的取值范围. 【解析】由 1 知 g(x)在(-2,-1)内为减函数时,实数 a 的取值范围是(-∞,- 3]. 若 g(x)在(-2,-1)内为增函数,则 a≥x+ 2 在(-2,-1)内恒成立,
2.已知函数 f(x)= x a -ln x- 3 ,其中 a∈R,且曲线 y=f(x)在点(1,f(1))处
4x
2
的切线垂直于直线 y= 1 x.
2
(1)求 a 的值;
(2)求函数 f(x)的单调区间.
【解析】(1)对 f(x)求导得 f′(x)= 1 - a - 1 ,
4 x2 x
由 f(x)在点(1,f(1))处的切线垂直于直线 y= 1 x,
【解析】f′(x)= 1 ·x+ln x-k-1=ln x-k,
x
①当 k≤0 时,因为 x>1,所以 f′(x)=ln x-k>0,
所以函数 f(x)的单调递增区间是(1,+∞),无单调递减区间.
②当 k>0 时,令 ln x-k=0,解得 x=ek,
当 1<x<ek 时,f′(x)<0;当 x>ek 时,f′(x)>0.
x
又∵y=x+ 2 在(-2,- 2 )内单调递增,在(- 2 ,-1)内单调递减,
x
∴y=x+ 2 的值域为(-3,-2 2 ),
x
∴实数 a 的取值范围是[-2 2 ,+∞), ∴函数 g(x)在(-2,-1)内单调时,a 的取值范围是(-∞,-3]∪[-2 2 ,+∞), 故 g(x)在(-2,-1)上不单调时,实数 a 的取值范围是(-3,-2 2 ). [解题技法]由函数的单调性求参数的取值范围的方法 (1)由可导函数 f(x)在 D 上单调递增(或递减)求参数范围问题,可转化为 f′(x)≥ 0(或 f′(x)≤0)对 x∈D 恒成立问题,再参变分离,转化为求最值问题,要注意“=”
利用导数研究函数单调性5种常见题型总结(原卷版)

第10讲 利用导数研究函数单调性5种常见题型总结【考点分析】考点一:利用导数判断函数单调性的方法 ①求函数的定义域(常见的0,ln >x x );①求函数的导数,如果是分式尽量通分,能分解因式要分解因式;①令()0='x f ,求出根 ,,,321x x x ,数轴标根,穿针引线,注意x 系数的正负;④判断()x f '的符号,如果()0f x '>,则()y f x =为增函数;如果()0f x '<,则()y f x =为减函数. 考点二:已知函数的单调性求参数问题①若()f x 在[]b a ,上单调递增,则()0f x '≥在[]b a ,恒成立(但不恒等于0); ①若()f x 在[]b a ,上单调递减,则()0f x '≤在[]b a ,恒成立(但不恒等于0).【题型目录】题型一:利用导数求函数的单调区间题型二:利用导函数与原函数的关系确定原函数图像 题型三:已知含量参函数在区间上单调性求参数范围 题型四:已知含量参函数在区间上不单调求参数范围 题型五:已知含量参函数存在单调区间求参数范围【典型例题】题型一:利用导数求函数的单调区间【例1】(2022·广东·雷州市白沙中学高二阶段练习)函数()()2e x f x x =+的单调递减区间是( )A .(),3-∞-B .()0,3C .()3,0-D .()3,-+∞【例2】(2022·北京市第三十五中学高二阶段练习)函数ln xy x=的单调递增区间是( ) A .1,e ⎛⎫-∞ ⎪⎝⎭B .()e,+∞C .10,e ⎛⎫⎪⎝⎭D .()0,e【例3】(2023·全国·高三专题练习)函数21()ln 2f x x x =-的单调递减区间为( ) A .(1,1)-B .(0,1)C .(1,)+∞D .(0,2)【例4】(2022·黑龙江·铁人中学高三开学考试)函数2()ln 1f x x x =--的单调增区间为_________.【例5】(2022·河南·安阳一中高三阶段练习(理))已知函数()()ln 1f x x x =+,则( ) A .()f x 在()1,-+∞单调递增 B .()f x 有两个零点C .曲线()y f x =在点11,22f⎛⎫⎛⎫-- ⎪ ⎪⎝⎭⎝⎭处切线的斜率为1ln2-- D .()f x 是偶函数【例6】(2022·江苏·盐城市第一中学高三阶段练习)若函数()312f x x x =-在区间()1,1k k -+上不是单调函数,则实数k 的取值范围是( ) A .3k ≤-或11k -≤≤或3k ≥ B .31k -<<-或13k << C .22k -<<D .不存在这样的实数【例7】(2022·全国·高二课时练习多选题)设函数()e ln x f x x =,则下列说法正确的是( )A .()f x 的定义域是()0,∞+B .当()0,1x ∈时,()f x 的图象位于x 轴下方C .()f x 存在单调递增区间D .()f x 有两个单调区间【例8】(2022·河北·石家庄二中模拟预测)已知函数f (x )满足()()()2212e 02x f x f f x x -'=-+,则f (x )的单调递减区间为( ) A .()0,∞- B .(1,+∞)C .()1,∞-D .(0,+∞)【例9】 (2022·全国·高二专题练习)已知函数()1xlnx f x e +=,(其中e =2.71828…是自然对数的底数).求()x f 的单调区间.【例10】【2020年新课标2卷理科】已知函数()x x x f 2sin sin 2=.(1)讨论()x f 在区间()π,0的单调性;【例11】(2022·黑龙江·哈尔滨市第六中学校高二期末)已知函数()ln f x x x x =-. (1)求()f x 的单调区间;【例12】(2022·陕西渭南·高二期末(文))函数()()2e x f x x ax b =++,若曲线()y f x =在点()()0,0f 处的切线方程为:450x y ++=. (1)求,a b 的值;(2)求函数()f x 的单调区间.【例13】【2020年新课标1卷理科】已知函数2()e x f x ax x =+-. (1)当1=a 时,讨论()x f 的单调性;【例14】【2019年新课标2卷理科】已知函数()11ln x f x x x -=-+.(1)讨论()x f 的单调性,并证明()x f 有且仅有两个零点;【题型专练】1.(2022湖南新邵县教研室高二期末(文))函数()4ln f x x x =-的单调递减区间为( ) A .()0,∞+ B .10,4⎛⎫⎪⎝⎭C .1,4⎛⎫-∞ ⎪⎝⎭D .1,4⎛⎫+∞ ⎪⎝⎭2.(2022·广东·东莞四中高三阶段练习)函数()()3e x f x x =-,则()f x 的单调增区间是( )A .(),2-∞B .()2,+∞C .(),3-∞D .()3,+∞3.(2022·四川绵阳·高二期末(文))函数()2ln 2x x x f -=的单调递增区间为( )A .()1,-∞-B .()+∞,1C .()1,1-D .()1,04.(2022·广西桂林·高二期末(文))函数()3213f x x x =-的单调递减区间为( )A .()02,B .()()02∞∞-+,,,C .()2+∞,D .()0-∞,5.(2022·重庆长寿·高二期末)函数()65ln f x x x x=--的单调递减区间为( )A .(0,2)B .(2,3)C .(1,3)D .(3,+∞)6.(2023·全国·高三专题练习)函数21()ln 3f x x x =-的单调减区间为__________.7.(2022·全国·高二专题练习)函数2()2x x f x =的单调递增区间为__________.8.(2022·全国·高二专题练习)函数cos y x x =+的单调增区间为_________.9.(2023·全国·高三专题练习)求下列函数的单调区间(1)()211x f x x +=-;(2)()21ln 2f x x x =-; (3)()3223361f x x x x =+-+;(4)()sin ,0f x x x x π=-<<;(5)()()22e xf x x x -=+;(6)()sin 2cos xf x x=+.10.(2022·全国·高二单元测试)已知函数()()321313x x x f x =-++,求()f x 的单调区间.11.函数()x e x x f -=2的递增区间是( ) A .()0,2B .(),0∞-C .(),0∞-,()2,+∞D .()(),02,-∞+∞12.【2022年新高考2卷】已知函数f(x)=x e ax −e x . (1)当a =1时,讨论f(x)的单调性;13.(2022·四川省绵阳南山中学高二期末(理))已知函数()29ln 3f x x x x =-+在其定义域内的一个子区间()1,1m m -+上不单调,则实数m 的取值范围是( )A .51,2⎡⎫⎪⎢⎣⎭B .31,2⎛⎫ ⎪⎝⎭C .51,2⎛⎫⎪⎝⎭D .31,2⎡⎫⎪⎢⎣⎭14.(2020·河北省石家庄二中高二月考)函数1()ln f x x x=的单调递减区间为____________. 15.(2022·全国·高三专题练习(文))函数(2)e ,0()2,0x x x f x x x ⎧-≥=⎨--<⎩的单调递减区间为__________.题型二:利用导函数与原函数的关系确定原函数图像【例1】(2022·河南·高三阶段练习(文))如图为函数()f x (其定义域为[],m m -)的图象,若()f x 的导函数为()f x ',则()y f x '=的图象可能是( )A .B .C .D .【例2】(2022·四川·遂宁中学外国语实验学校高三开学考试(理))设()f x '是函数()f x 的导函数,()y f x '=的图像如图所示,则()y f x =的图像最有可能的是( )A .B .C .D .【例3】(2022·全国·高二课时练习)已知函数()y f x =在定义域3,32⎛⎫- ⎪⎝⎭内可导,其图象如图所示.记()y f x =的导函数为()y f x '=,则不等式()0xf x '≤的解集为( )A .[][)31,0,12,323⎛⎤--⋃⋃ ⎥⎝⎦B .[]18,01,2,333⎡⎤⎡⎫-⋃⋃⎪⎢⎥⎢⎣⎦⎣⎭C .[)1,12,33⎡⎤-⎢⎥⎣⎦D .31148,,,323233⎛⎫⎡⎤⎡⎫--⋃⋃ ⎪⎪⎢⎥⎢⎝⎭⎣⎦⎣⎭【例4】(2022·全国·高二单元测试)已知函数()f x 的导函数()'f x 图像如图所示,则()f x 的图像是图四个图像中的( ).A .B .C .D .【例5】(2022·广东潮州·高二期末多选题)已知函数()f x 与()f x '的图象如图所示,则下列结论正确的为( )A .曲线m 是()f x 的图象,曲线n 是()f x '的图象B .曲线m 是()f x '的图象,曲线n 是()f x 的图象C .不等式组()()02f x f x x >⎧⎨<<'⎩的解集为()0,1D .不等式组()()02f x f x x >⎧⎨<<'⎩的解集为41,3⎛⎫⎪⎝⎭【题型专练】1.(2022·江苏常州·高三阶段练习)如图是()y f x '=的图像,则函数()y f x =的单调递减区间是( )A .()2,1-B .()()2,0,2,-+∞C .(),1-∞-D .()(),1,1,-∞-+∞2.(2022·吉林·东北师大附中高三开学考试)已知函数()y f x =的部分图象如图所示,且()f x '是()f x 的导函数,则( )A .()()()()12012f f f f ''''-=-<<<B .()()()()21012f f f f ''''<<<-=-C .()()()()02112f f f f ''''>>>-=-D .()()()()21021f f f f ''''<<<-<-3.(2022·福建莆田·高二期末)定义在()1,3-上的函数()y f x =,其导函数()y f x '=图像如图所示,则()y f x =的单调递减区间是( )A .()1,0-B .()1,1-C .()0,2D .()2,34.(2022·广东广州·高二期末)已知函数()y f x =的图象是下列四个图象之一,函数()y f x ='的图象如图所示,则函数()y f x =图象是( )A .B .C .D .5.(2022·北京·牛栏山一中高二阶段练习)设()f x '是函数()f x 的导函数,在同一个直角坐标系中,()y f x =和()y f x '=的图象不可能是( )A .B .C .D .6.(2022·福建宁德·高二期末多选题)设()f x 是定义域为R 的偶函数,其导函数为()f x ',若0x ≥时,()f x 图像如图所示,则可以使()()0f x f x '⋅<成立的x 的取值范围是( )A .(),3-∞-B .()1,0-C .()0,1D .()1,3题型三:已知含量参函数在区间上单调性求参数范围【例1】(2023·全国·高三专题练习)已知函数()ax x x x f ++=2ln 的单调递减区间为1,12⎛⎫ ⎪⎝⎭,则( ).A .(],3a ∈-∞-B .3a =-C .3a =D .(],3a ∈-∞【例2】(2022·全国·高三专题练习)已知函数()32391f x x mx mx =-++在()1,+∞上为单调递增函数,则实数m 的取值范围为( ) A .(),1-∞- B .[]1,1- C .[]1,3 D .[]1,3-【例3】(2022·浙江·高二开学考试)已知函数()sin cos f x x a x =+在区间ππ,42⎛⎫ ⎪⎝⎭上是减函数,则实数a 的取值范围为( )A .1a >B .1a ≥C .1a >D .1a ≥-【例4】(2022·全国·高二课时练习)若函数()2ln f x x ax x =-+在区间()1,e 上单调递增,则实数a 的取值范围是( ) A .[)3,+∞ B .(],3-∞C .23,e 1⎡⎤+⎣⎦ D .(2,e 1⎤-∞+⎦【例5】(2022·河南·荥阳市教育体育局教学研究室高二阶段练习)已知函数()321f x x x ax =+-+在R 上为单调递增函数,则实数a 的取值范围为( ) A .1,3⎛⎤-∞- ⎥⎝⎦B .1,3⎛⎫-∞- ⎪⎝⎭C .1,3⎛⎫-+∞ ⎪⎝⎭D .1,3⎡⎫-+∞⎪⎢⎣⎭【例6】(2023·全国·高三专题练习)若函数1()sin 2cos 2f x x a x =+在区间(0,)π上单调递增,则实数a 的取值范围是( ) A .(,1]-∞-B .[1,)-+∞C .(,1)-∞-D .[1,)+∞【例7】(2022·山东临沂·高二期末)若对任意的()12,,x x m ∈+∞,且当12x x <时,都有121212ln ln 3x x x x x x ->-,则m 的最小值是________.【例8】(2022·全国·高三专题练习(文))已知函数()()0ln 232>+-=a x x axx f ,若函数()x f 在[]2,1上为单调函数,则实数a 的取值范围是________.【题型专练】1.(2023·全国·高三专题练习)若函数2()ln 5f x x ax x =+-在区间11,32⎡⎤⎢⎥⎣⎦内单调递增,则实数a 的取值范围为( ) A .(,3]-∞ B .3,2⎛⎤-∞- ⎥⎝⎦C .253,8⎡⎤⎢⎥⎣⎦D .25,8⎡⎫+∞⎪⎢⎣⎭2.(2022·山西·平遥县第二中学校高三阶段练习)若函数()ln 1f x x x ax =-+在[e,)+∞上单调递增,则实数a 的取值范围是( ) A .(,2)-∞ B .(,2]-∞ C .(2,)+∞ D .[2,)+∞3.(2023·全国·高三专题练习)已知函数()sin 2cos f x a x x =+在ππ,34x ⎡⎤∈--⎢⎥⎣⎦上单调递增,则a 的取值范围为( ) A .0a ≥ B .22a -≤≤ C .2a ≥- D .0a ≥或2a ≤-4.(2022·全国·高三专题练习)若函数()d cx bx x x f +++=23的单调递减区间为()3,1-,则=+c b ( )A .-12B .-10C .8D .105.(2022·全国·高三专题练习)若函数()32236f x x mx x =-+在区间()1,+∞上为增函数,则实数m 的取值范围是_______. 6.函数321()3f x ax x a =-+在[1,2]上单调递增,则实数a 的取值范围是( ) A .1a >B .1a ≥C .2a >D .2a ≥7.对于任意1x ,2[1,)x ∈+∞,当21x x >时,恒有2211ln 2()x a x x x <-成立,则实数a 的取值范围是( ) A .(,0]-∞ B .(,1]-∞C .(,2]-∞D .(,3]-∞8.若函数2()ln f x x x x=++在区间[],2t t +上是单调函数,则t 的取值范围是( ) A .[1,2] B .[1,)+∞C .[2,)+∞D .(1,)+∞题型四:已知含量参函数在区间上不单调,求参数范围【例1】(2022·河南宋基信阳实验中学高三阶段练习(文))已知函数()3212132a g x x x x =-++.若()g x 在()2,1--内不单调,则实数a 的取值范围是______.【例2】(2021·河南·高三阶段练习(文))已知函数()()41xf x ax x e =+-在区间[]1,3上不是单调函数,则实数a 的取值范围是( )A .2,416e e ⎛⎫-- ⎪⎝⎭B .2,416e e ⎛⎤-- ⎥⎝⎦C .32,3616e e ⎛⎫-- ⎪⎝⎭D .3,416e e ⎛⎫-- ⎪⎝⎭【题型专练】 1.函数()()2244xf x e xx =--在区间()1,1k k -+上不单调,实数k 的范围是 .2.(2022·全国·高三专题练习)若函数()324132x a f x x x =-++在区间(1,4)上不单调,则实数a 的取值范围是___________.题型五:已知含量参函数存在单调区间,求参数范围【例1】(2023·全国·高三专题练习)若函数()21()ln 12g x x x b x =+--存在单调递减区间,则实数b 的取值范围是( ) A .[)3,+∞ B .()3,+∞ C .(),3-∞D .(],3-∞【例2】(2022·全国·高三专题练习)若函数()313f x x ax =-+有三个单调区间,则实数a 的取值范围是________.【例3】(2022·河北·高三阶段练习)若函数()2()e xf x x mx =+在1,12⎡⎤-⎢⎥⎣⎦上存在单调递减区间,则m 的取值范围是_________.【例4】(2023·全国·高三专题练习)已知()2ln ag x x x x=+-. (1)若函数()g x 在区间[]1,2内单调递增,求实数a 的取值范围; (2)若()g x 在区间[]1,2上存在单调递增区间,求实数a 的取值范围.【题型专练】1.(2022·全国·高三专题练习(文))若函数()()0221ln 2≠--=a x ax x x h 在[]4,1上存在单调递减区间”,则实数a 的取值范围为________.2.若函数()2ln f x ax x x =+-存在增区间,则实数a 的取值范围为 .3.故函已知函数32()3()f x ax x x x =+-∈R 恰有三个单调区间,则实数a 的取值范围为( ) A .()3,-+∞ B .()()3,00,-+∞C .()(),00,3-∞D .[)3,-+∞4.已知函数()()R a x ax x x f ∈+++=123在⎪⎭⎫⎝⎛--31,32内存在单调递减区间,则实数a 的取值范围是( ) A .(0,√3] B .(−∞,√3]C .(√3,+∞)D .(√3,3)。
利用导数研究函数的性质

利用导数研究函数的性质
知识梳理
1. f′( x)>0 在( a, b)上成立是 f (x)在 (a, b)上单调递增的充分不必要条件. 2. f(x)在 (a, b)上是增函数的充要条件是 f′( x)≥ 0,且 f′ (x) =0 在有限个点处取到. 3.对于可导函数 f(x) ,f′( x0)= 0 并不是 f( x)在 x=x0 处有极值的充分条件
变式 2: 已知 f (x)= x3- ax2- 3x. (1)若 f (x)在 [2,+∞ )上是增函数,求实数 a 的取值范围; (2)若 x= 3 是 f(x)的极值点,求 f(x) 在[1 ,a ]上的最小值和最大值.
例 2: 设函数 f (x)= x(ex- 1)-12x2,求函数 f(x)的单调增区间.
变式 2: 若函数 f (x)= 3x+ln x 在区间 (m, m+ 2)上单调递减,则实数 m 的范围是 ________.
变式 3 :若函数 f(x)=1x3-1ax2+ (a- 1) ·x+ 1 在区间 (1,4)上是减函数,在区间 (6,+∞ )上是 32
增函数,则实数 a 的取值范围是 ________.
变式 4.函数 f ( x) 是定义在 R 上的奇函数, f (3) 0,且 x 0时, xf '( x) f ( x) ,则不等 式 f (x) 0的解集是 变式 5.函数 f (x 1) 是定义在 R 上的偶函数, f ( 2) 1 ,且 f ' (x) f (x) ,则不等式 f ( x) ex 的解集是
2023年高考数学课后精练 第3讲 利用导数研究函数的性质(解析版)

第3讲 利用导数研究函数的性质【题型精练】一、单选题1.(2021·北京交通大学附属中学高三开学考试)已知()f x 是定义在R 上的偶函数,当0x >时,'2()()0xf x f x x ->,且()20f -=,则不等式()0f x x >的解集是( ) A .()()2,00,2- B .()(),22,-∞-+∞ C .()()2,02,-+∞D .()(),20,2-∞-【答案】C 【详解】解:∵()f x 是定义在R 上的偶函数,当0x >时,'2()()0xf x f x x ->, ∴()f x x 为增函数,()f x 为偶函数,()f x x 为奇函数, ∴()f x x在(),0-∞上为增函数, ∵()()220f f -==, 若0x >,()202f =,所以2x >; 若0x <,()202f -=-,()f x x 在(),0-∞上为增函数,可得20x -<<, 综上得,不等式()0f x x>的解集是()()2,02,-+∞.故选:C.2.(2021·河南·高三月考(文))函数()2e 21xf x x x x =---的极大值为( )A .1-B .1e- C .ln 2 D .()2ln 21--【答案】B 【详解】由()2e 21xf x x x x =---可得()()()()1e 221e 2x x f x x x x '=+--=+-,由()0f x '>可得:ln 2x >或1x <-, 由()0f x '<可得1ln 2x -<<,所以()f x 在(),1-∞-单调递增,在()1,ln 2-单调递减,在()ln 2,+∞单调递增,所以1x =-时,()f x 取得极大值为()111121e ef -=--+-=-,故选:B.3.(2021·全国·高三月考(文))函数321()3f x x ax =-在(2,1)--上单调递减则实数a 的取值范围为( )A .(,1)-∞-B .(,1]-∞-C .(1,)+∞D .[1,)-+∞【答案】B 【详解】2()2(2)f x x ax x x a '=-=-,∵()f x 在(2,1)--上单调递减,∴()0f x '≤在(2,1)--上恒成立,由二次函数()(2)f x x x a '=-的图象可知22a ≤-,即1a ≤-. 故选:B4.(2021·北京·潞河中学高三月考)函数()ln f x kx x =-在[1,)+∞单调递增的一个必要不充分条件是( ) A .2k > B .1k C .1k > D .0k >【答案】D 【详解】由题得1()f x k x'=-,函数()ln f x kx x =-在区间(1,)+∞单调递增,()0f x ∴'在区间(1,)+∞上恒成立. 1kx ∴, 而1y x=在区间(1,)+∞上单调递减,1k ∴.选项中只有0k >是1k 的必要不充分条件. 选项AC 是1k 的充分不必要条件,选项B 是充要条件. 故选:D5.(2021·甘肃·嘉峪关市第一中学模拟预测(文))已知函数2()ln 22x f x m x x =+-,()0,x ∈+∞有两个极值点,则实数m 的取值范围是( ) A .(],0-∞ B .(],1-∞C .[)1,-+∞D .()0,1【答案】D 【详解】22()2m x x mf x x x x-+'=+-=,因为()f x 有两个极值点,故()f x '有两个变号零点,故2x 2x m 0-+=在()0,∞+上有两个不同的解,故0440m m >⎧⎨∆=->⎩,所以01m <<, 故选:D.6.(2021·山东·嘉祥县第一中学高三期中)已知函数()x x f x e e -=+(其中e 是自然对数的底数),若 1.5(2)a f =,0.8(4)b f =,21log 5c f ⎛⎫= ⎪⎝⎭,则,,a b c 的大小关系为( )A .a b c <<B .c a b <<C .a c b <<D .b a c <<【答案】B 【详解】函数()x x f x e e -=+是偶函数,()x x f x e e -=-',当0,()0;0,()0x f x x f x ''<<>>, 即函数()f x 在(,0)-∞上单调递减,(0,)+∞上单调递增,因为2222log 5log 25log 325=<=, 2.5 1.55222<==⨯,所以 1.522log 5522<<⨯,则 1.51.60.82log 5224<<=,1.50.82221(log )(log 5)(log 5)(2)(4)5f f f f f =-=<<,即c a b <<. 故选:B .7.(2021·陕西·泾阳县教育局教学研究室高三期中(文))已知函数()f x 的定义域为R ,且()21f =,对任意x ∈R ,()()0f x xf x '+<,则不等式()()112x f x ++>的解集是( ) A .(),1-∞ B .(),2-∞ C .()1,+∞ D .()2,+∞【答案】A 【详解】设()()g x xf x =,则()()()0g x f x xf x =+'<' 所以()g x 在R 上单调递减,又()()2222g f == 由()()112x f x ++>,即()()12g x g +>,所以12x +< 所以1x < 故选:A8.(2021·广东深圳·高三月考)已知函数2ln ,0(),1,0x x x f x x x >⎧=⎨-≤⎩若函数()()=-g x f x k 有三个零点,则( ) A .e 1k -<≤B .11k e-<<C .e 0k -<<D .10ek -<<【答案】D 【详解】要使函数()f x k =有三个解,则()y f x =与y k =有三个交点,当0x >时,()ln f x x x =,则()ln 1f x x '=+,可得()f x 在10,e ⎛⎫⎪⎝⎭上递减,在1,e ⎛⎫+∞ ⎪⎝⎭递增,∴0x >时,()ln f x x x =有最小值11f e e ⎛⎫=- ⎪⎝⎭,且10x e <<时,ln 0x x <;当0x +→时,()0f x →;当x →+∞时,()f x →+∞; 当0x ≤时,2()1f x x =-+单调递增;∴()f x 图象如下,要使函数()g x 有三个零点,则10e k -<<,故选:D .二、多选题9.(2021·湖北·高三月考)已知函数()xf x xe ax =+.则下列说法正确的是( )A .当0a =时,()min 1f x e=-B .当1a =时,直线2y x =与函数()f x 的图象相切C .若函数()f x 在区间[)0,+∞上单调递增,则0a ≥D .若在区间[]0,1上()2f x x ≤恒成立,则1a e ≤-【答案】ABD 【详解】解:对于A :当0a =时,()xf x xe =,则()()'+1+x x x f x xe e e x ==,令'0f x,得1x =-,所以当1x <-时,()'0f x <,函数()f x 单调递减,当>1x -时,()'>0f x ,函数()f x 单调递增,所以()()1111f x f e e-≥-=-=-,所以()min 1f x e =-,故A 正确;对于B :当1a =时,()+x f x xe x =,则()'++1xx f x xe e =,设切点为()00,x y ,则过切点的切线方程为:()()()0000000+++1x xx y x e x e x e x x -=-,因为切线过原点,所以()()()00000000+++01x x x x e x x e x e -=-,解得00x =,此时()'000+0+12f e e =⨯=,所以直线2y x =与函数()f x 的图像相切,故B 正确;对于C :由函数()xf x xe ax =+得()()1+x f x x e a '=+,因为函数()f x 在区间[)0,+∞上单调递增,所以()()1+0xf x x e a '=+≥在区间[)0,+∞上恒成立,即()1x a x e ≥--在区间[)0,+∞上恒成立,令()()1x g x x e =--,则()()'+2x g x x e =-,又令[)0,x ∈+∞,所以,()'0g x <,函数()g x 单调递减, 所以()()000+21g x g e e ≤=-=,所以1a ≥,故C 不正确;对于D :在区间[]0,1上()2f x x ≤恒成立,等价于2x xe ax x +≤在区间[]0,1上恒成立,当0x =时,不等式恒成立;当01x <≤时,x a x e ≤-恒成立,令()xh x x e =-,则()'1x h x e =-,令()'0h x =,得0x =,因为01x <≤,()'0h x <,函数()h x 单调递减,所以()()1111h x h e e ≥=-=-,所以1a e -≤,故D 正确;故选:ABD.10.(2021·辽宁沈阳·高三月考)已知函数()()[)ln ,0,1e44,1,x x f x x x⎧-∈⎪⎪=⎨-⎪+∈+∞⎪⎩(其中e 是自然对数的底数),函数()()g x f x kx =-有三个零点()123123,,x x x x x x <<,则( ) A .实数k 的取值范围为()0,1 B .实数k 的取值范围为()0,e C .123x x x 的取值范围为4,e ⎛+∞⎫⎪⎝⎭D .123x x x 的取值范围为()e,+∞ 【答案】AC 【详解】由图可知,0,k >则方程44kx x-=+,即2440kx x -+=有两个正实数解, 所以16160,k =->解得)1(0k ∈,; 由图可知,12301,x x x <<<<所以234x x k⋅=,且11ln x k ex =-因为11ln 1x k ex =-<,则111x e ⎛⎫∈ ⎪⎝⎭,,所以21112311441,1ln x ex x x x x k x e ⎛⎫⎛⎫⋅⋅==-∈ ⎪ ⎪⎝⎭⎝⎭. 设1)0(1lnx t =∈-,,则()24te e g t t⋅=-, 所以()()22421'0t g tt e e t ⋅-=->,即()g t 单调递增, 又4()1g e -=,且0t ⇒时,()g t →+∞,所以()4,g t e ∈+∞⎛⎫ ⎪⎝⎭. 故选:AC11.(2021·重庆·高三月考)定义域在R 上函数()f x 的导函数为f x ,满足()()2'2f x f x <-,()211f e =-,则下列正确的是( ) A .()00f >B .()421f e >-C .()()()2021202021f ef e ->-D .()()22202120201f e f e ->-【答案】BCD 【详解】由题意,构造函数2()1()x f x g x e +=,则2()2(()1)()xf x f xg x e '-+'=,由()()2'2f x f x <-可知()0g x '>, 所以2()1()x f x g x e +=在R 上单调递增,且2(1)1(1)1f g e +==, 故(0)(1)1g g <=,即(0)11f +<,(0)0f <,A 错误;由(2)(1)1g g >=可得()421f e >-,故B 正确;当1x >时,()(1)1g x g >=,所以2()11xf x e +>,()0f x >, 所以()()()22f x f x f x '<<-,()()02f x f x '-->, 令()()2,1x f x h x x e +=>,则()()()20xf x f x h x e ''--=>, 所以()h x 单调递增,()()20212020h h >,即()()202120202202122020f f e e >++,所以()()2220212020f ef e >++,()()()2021202021f ef e ->-, 故C 正确;由(2021)(2020)g g >可得()()22202120201f e f e ->-,故D 正确;故选:BCD12.(2021·全国·高三专题练习)已知函数()y f x =,0,2x π⎛⎫∈ ⎪⎝⎭,()f x '是其导函数,恒有()()sin cos f x f x x x '>,则( )A .34f ππ⎛⎫⎛⎫> ⎪ ⎪⎝⎭⎝⎭B .46f f ππ⎛⎫⎛⎫ ⎪ ⎪⎝⎭⎝⎭C .()2cos116f f π⎛⎫<⋅ ⎪⎝⎭D .()cos 13f f π⎛⎫>21⋅ ⎪⎝⎭【答案】AD 【详解】因为0,2x π⎛⎫∈ ⎪⎝⎭,所以sin 0x >,cos 0x >,又()()sin cos f x f x x x'>,所以()()cos sin f x x f x x '>. 构造函数()()cos g x f x x =,0,2x π⎛⎫∈ ⎪⎝⎭,则()()()cos sin 0g x f x x f x x -''=>,所以()g x 在0,2π⎛⎫⎪⎝⎭上为增函数,因为34ππ>,所以34g g ππ⎛⎫⎛⎫> ⎪ ⎪⎝⎭⎝⎭,所以cos cos 3344f f ππππ⎛⎫⎛⎫> ⎪ ⎪⎝⎭⎝⎭,即34f ππ⎛⎫⎛⎫> ⎪ ⎪⎝⎭⎝⎭,故A 正确;因为46ππ>,所以46g g ππ⎛⎫⎛⎫> ⎪ ⎪⎝⎭⎝⎭,所以cos cos 4466f f ππππ⎛⎫⎛⎫> ⎪ ⎪⎝⎭⎝⎭,即46f f ππ⎛⎫⎛⎫ ⎪ ⎪⎝⎭⎝⎭,故B 错误; 因为16π<,所以()16g g π⎛⎫< ⎪⎝⎭,所以()cos 1cos166f f ππ⎛⎫< ⎪⎝⎭,即()1cos16f f π⎛⎫< ⎪⎝⎭,故C 错误; 因为13π>,所以()13g g π⎛⎫> ⎪⎝⎭,所以()cos 1cos133f f ππ⎛⎫> ⎪⎝⎭,即()21cos13f f π⎛⎫> ⎪⎝⎭,故D 正确, 故选:AD. 三、填空题13.(2021·江西赣州·高三期中(理))已如函数3()5,(2,2)f x x x x =+∈-,若()2()20f t f t +->.则t 的取值范围为___________. 【答案】(1,0)(0,2)- 【详解】3()5f x x x =+,()3()5f x x x f x -==---,函数为奇函数.2()350f x x '=+>,函数单调递增,()2()20f t f t +->,即()2(2)f t f t ->,故22222222t t t t -<<⎧⎪-<-<⎨⎪>-⎩,解得(1,0)(0,2)t ∈-⋃. 故答案为:(1,0)(0,2)-.14.(2021·陕西·西安中学高三月考(理))已知函数()3()x f x e ax a R =+-∈,若对于任意的12,[1,)x x ∈+∞且12x x <,都有211212()()()x f x x f x a x x -<-成立,则a 的取值范围是________. 【答案】(,3]-∞ 【详解】对于任意的1x ,2[1x ∈,)+∞,且12x x <,都有211212()()()x f x x f x a x x -<-成立, ∴不等式等价为1212()()f x a f x ax x ++<恒成立, 令()()f x ah x x+=,则不等式等价为当12x x <时,12()()h x h x <恒成立, 即函数()h x 在(1,)+∞上为增函数; 3()x e ax a h x x+-+=,则23()0x x xe e ah x x -+-'=在[1,)+∞上恒成立; 30x x xe e a ∴-+-;即3x x a xe e --恒成立,令()x x g x xe e =-,()0x g x xe ∴'=>;()g x ∴在[1,)+∞上为增函数; ()g x g ∴(1)0=; 30a ∴-;3a ∴.a ∴的取值范围是(,3]-∞.故答案:(,3]-∞.15.(2021·宁夏·固原一中高三期中(文))已知函数()f x 是定义在R 上的偶函数,()20f =,()()()0xf x f x x '<>,则不等式()0xf x <的解集为______.【答案】(2,0)(2,)-+∞ 【详解】 令()()f x g x x=,则()2()()xf x f x g x x '-'=,当0x >时.由()()xf x f x '<,得()0g x '<, 所以函数()()f xg x x=在(0,)+∞上是减函数, 函数()f x 是定义在R 上的偶函数,∴()()f x f x -=, ∴()()()f x g x g x x--==--, ∴()g x 是定义在(,0)(0,)-∞+∞上的奇函数, ∴()g x 在(,0)-∞上递减,又(2)0f =,∴(2)(2)02f g ==, 则()g x 的大致图象如图所示:∴02x <<时,()0>g x ,2x >时,()0<g x ,根据函数的奇偶性知,20x -<<时,()0<g x ,2x <-时,()0>g x , 当0x ≠时,()0xf x <等价于()0<g x ,当0x =时,()0xf x <不成立, ∴不等式()0xf x <的解集为(2,0)(2,)-+∞,所以不等式()0xf x <的解集是(2,0)(2,)-+∞. 故答案为:(2,0)(2,)-+∞.16.(2021·陕西·千阳县中学二模(理))已知函数9()(),[1,9]g x x a a R x x=+-∈∈,则()g x 的值域是___________.设函数()|()|f x g x =,若对于任意实数a ,总存在0[1,9]x ∈,使得()0f x t ≥成立,则实数t 的取值范围是___________【答案】[]6,10a a -- (],2-∞ 【详解】 (1)()()()223391x x g x x x +-'=-=, 当[]1,3x ∈,()0g x '<,()g x 单调递减;当[]3,9x ∈,()0g x '>,()g x 单调递增;()()min 36g x g a ∴==-,又()()110,910g a g a =-=-,()max 10g x a ∴=-, 故()g x 的值域是[]6,10a a --; (2)()|()|f x g x =,当610a a -≥-,即8a ≥时,()max 66f x a a t =-=-≥恒成立,则2t ≤, 当610a a -<-,即8a <时,()max 1010f x a a t =-=-≥恒成立,则2t ≤, 综上,实数t 的取值范围是(],2-∞. 故答案为:[]6,10a a --;(],2-∞。
(整理)利用导数研究函数的性质.

(整理)利⽤导数研究函数的性质.专题三利⽤导数研究函数的性质1. f ′(x )>0在(a ,b )上成⽴是f (x )在(a ,b )上单调递增的充分不必要条件.2. f (x )在(a ,b )上是增函数的充要条件是f ′(x )≥0,且f ′(x )=0在有限个点处取到. 3.对于可导函数f (x ),f ′(x 0)=0并不是f (x )在x =x 0处有极值的充分条件对于可导函数f (x ),x =x 0是f (x )的极值点,必须具备①f ′(x 0)=0,②在x 0两侧,f ′(x )的符号为异号.所以f ′(x 0)=0只是f (x )在x 0处有极值的必要条件,但并不充分. 4.如果连续函数f (x )在区间(a ,b )内只有⼀个极值点,那么这个极值点就是最值点.在解决实际问题中经常⽤到这⼀结论.1.已知函数f (x )=ln a +ln xx在[1,+∞)上为减函数,则实数a 的取值范围为__________.答案 [e ,+∞)解析 f ′(x )=1x·x -(ln a +ln x )x 2=1-(ln a +ln x )x 2,因为f (x )在[1,+∞)上为减函数,故f ′(x )≤0在[1,+∞)上恒成⽴,即ln a ≥1-ln x 在[1,+∞)上恒成⽴.设φ(x )=1-ln x ,φ(x )max =1,故ln a ≥1,a ≥e. 2.设函数f (x )=ax 3-3x +1 (x ∈R ),若对于任意x ∈[-1,1],都有f (x )≥0成⽴,则实数a的值为________.答案 4解析若x =0,则不论a 取何值,f (x )≥0显然成⽴;当x >0,即x ∈(0,1]时,f (x )=ax 3-3x +1≥0可化为a ≥3x 2-1x 3.设g (x )=3x 2-1x 3,则g ′(x )=3(1-2x )x 4,所以g (x )在区间0,12上单调递增,在区间12,1上单调递减,因此g (x )max =g 12=4,从⽽a ≥4.当x <0,即x ∈[-1,0)时,同理a ≤3x 2-1x3.g (x )在区间[-1,0)上单调递增,∴g (x )min =g (-1)=4,从⽽a ≤4,综上可知a =4.3.若函数f (x )的导函数为f ′(x )=-x (x +1),则函数g (x )=f (log a x )(0__________.答案1,1a 解析由f ′(x )=-x (x +1)≤0,得x ≤-1或x ≥0,即f (x )的减区间为(-∞,-1],[0,+∞),则f (x )的增区间为[-1,0].∵0a 时,g (x )为减函数,∴g (x )的单调减区间为1,1a . 4.直线l 与函数y =3x +1x的图象相切于点P ,且与直线x =0和y =3x 分别交于A ,B 两点,则APBP=________. 答案 1解析设P x 0,3x 0+1x 0,则在点P 处的切线⽅程为y -3x 0+1x 0=3-1x 20(x -x 0),与y =3x 联⽴解得x B =2x 0,所以AP BP =x P x P -x B =x 0x 0-2x 0=1. 5.函数f (x )=12x 2-ln x 在[1,e]上的最⼤值为________.答案 12解析∵f ′(x )=x -1x ,∴当x ∈(1,e)时,f ′(x )>0,∴f (x )在[1,e]上是增函数,故f (x )min =f (1)=12.题型⼀利⽤导数求函数的单调区间例1 已知函数f (x )=x 3+ax 2-x +c ,且a =f ′23.(1)求a 的值;(2)求函数f (x )的单调区间;(3)设函数g (x )=(f (x )-x 3)·e x ,若函数g (x )在x ∈[-3,2]上单调递增,求实数c 的取值范围.解 (1)由f (x )=x 3+ax 2-x +c ,得f ′(x )=3x 2+2ax -1.当x =23时,得a =f ′23=3×232+2a ×23-1,解之,得a =-1.(2)由(1)可知f (x )=x 3-x 2-x +c .则f ′(x )=3x 2-2x -1=3x +13(x -1),列表如下:所以f (x )的单调增区间是(-∞,-13)和(1,+∞);f (x )的单调减区间是-13,1. (3)函数g (x )=(f (x )-x 3)·e x =(-x 2-x +c )·e x ,有g ′(x )=(-2x -1)e x +(-x 2-x +c )e x =(-x 2-3x +c -1)e x ,因为函数g (x )在x ∈[-3,2]上单调递增,所以h (x )=-x 2-3x +c -1≥0在x ∈[-3,2]上恒成⽴.只要h (2)≥0,解得c ≥11,所以c 的取值范围是[11,+∞).探究提⾼利⽤导数研究函数单调性的⼀般步骤:(1)确定函数的定义域; (2)求导数f ′(x );(3)①若求单调区间(或证明单调性),只需在函数f (x )的定义域内解(或证明)不等式f ′(x )>0或f ′(x )<0.②若已知f (x )的单调性,则转化为不等式f ′(x )≥0或f ′(x )≤0在单调区间上恒成⽴问题求解.设函数f (x )=x (e x -1)-ax 2.(1)若a =12,求f (x )的单调区间;(2)若当x ≥0时,f (x )≥0,求a 的取值范围.解 (1)a =12时,f (x )=x (e x -1)-12x 2,f ′(x )=e x -1+x e x -x =(e x -1)(x +1).当x ∈(-∞,-1)时,f ′(x )>0;当x ∈(-1,0)时,f ′(x )<0;当x ∈(0,+∞)时,f ′(x )>0. 故f (x )在(-∞,-1),(0,+∞)上单调递增,在(-1,0)上单调递减.(2)f (x )=x (e x -1-ax ),令g (x )=e x -1-ax ,g ′(x )=e x -a .若a ≤1,则当x ∈(0,+∞)时,g ′(x )>0,g (x )为增函数,⽽g (0)=0,从⽽当x ≥0时,g (x )≥0,即f (x )≥0. 若a >1,则当x ∈(0,ln a )时,g ′(x )<0,g (x )为减函数,⽽g (0)=0,从⽽当x ∈(0,ln a )时,g (x )<0,即f (x )<0. 综合得a 的取值范围为(-∞,1].题型⼆已知单调区间求参数范围例2 已知a ∈R ,函数f (x )=(-x 2+ax )e x (x ∈R ,e 为⾃然对数的底数).(1)当a =2时,求函数f (x )的单调增区间;(2)若函数f (x )在(-1,1)上单调递增,求a 的取值范围.解 (1)当a =2时,f (x )=(-x 2+2x )e x ,所以f ′(x )=(-2x +2)e x +(-x 2+2x )e x =(-x 2+2)e x .令f ′(x )>0,即(-x 2+2)e x >0,因为e x >0,所以-x 2+2>0,解得-2所以函数f (x )的单调增区间是[-2,2].(2)因为函数f (x )在(-1,1)上单调递增,所以f ′(x )≥0对x ∈(-1,1)都成⽴.因为f ′(x )=(-2x +a )e x +(-x 2+ax )e x =[-x 2+(a -2)x +a ]e x ,所以[-x 2+(a -2)x +a ]e x ≥0对x ∈(-1,1)都成⽴.因为e x >0,所以-x 2+(a -2)x +a ≥0对x ∈(-1,1)都成⽴,即a ≥x 2+2x x +1=(x +1)2-1x +1=(x +1)-1x +1对x ∈(-1,1)都成⽴.令y =(x +1)-1x +1,则y ′=1+1(x +1)2>0. 所以y =(x +1)-1x +1在(-1,1)上单调递增,所以y <(1+1)-11+1=32.即a ≥32.因此a 的取值范围为a ≥32.探究提⾼ (1)根据函数的单调性确定参数范围是⾼考的⼀个热点题型,其根据是函数在某区间上单调递增(减)时,函数的导数在这个区间上⼤(⼩)于或者等于零恒成⽴,转化为不等式恒成⽴问题解决.(2)在形式上的⼆次函数问题中,极易忘却的就是⼆次项系数可能等于零的情况,这样的问题在导数单调性的讨论中是经常遇到的,值得特别注意.已知函数f (x )=axx 2+b在x =1处取得极值2.(1)求函数f (x )的表达式;(2)当m 满⾜什么条件时,函数f (x )在区间(m,2m +1)上单调递增?解 (1)因为f ′(x )=a (x 2+b )-ax (2x )(x 2+b )2,⽽函数f (x )=axx 2+b在x =1处取得极值2,所以f ′(1)=0,f (1)=2,即?a (1+b )-2a =0,a1+b =2,得a =4b =1,所以f (x )=4x1+x 2即为所求.(2)由(1)知f ′(x )=4(x 2+1)-8x 2(x 2+1)2=-4(x -1)(x +1)(1+x 2)2. 令f ′(x )=0得x 1=-1,x 2=1,则f (x )的增减性如下表:可知,f (x )的单调增区间是[-1,1],所以m ≥-12m +1≤1?-1m <2m +1,所以当m ∈(-1,0]时,函数f (x )在区间(m,2m +1)上单调递增.题型三函数的极值、最值应⽤问题例3 设函数f (x )=x 4+ax 3+2x 2+b (x ∈R ),其中a ,b ∈R .(1)当a =-103时,讨论函数f (x )的单调性;(2)若函数f (x )仅在x =0处有极值,求a 的取值范围;(3)若对于任意的a ∈[-2,2],不等式f (x )≤1在[-1,0]上恒成⽴,求b 的取值范围.思维启迪:f (x )≤1在[-1,0]上恒成⽴,转化为f (x )在[-1,0]上的最⼤值f (x )max ≤1. 解 (1)f ′(x )=4x 3+3ax 2+4x =x (4x 2+3ax +4).当a =-103时,f ′(x )=x (4x 2-10x +4)=2x (2x -1)(x -2).令f ′(x )=0,得x 1=0,x 2=12,x 3=2.当x 变化时,f ′(x ),f (x )的变化情况如下表:所以f (x )在0,12和(2,+∞)上是增函数,在(-∞,0)和12,2上是减函数. (2)f ′(x )=x (4x 2+3ax +4),显然x =0不是⽅程4x 2+3ax +4=0的根.由于f (x )仅在x =0处有极值,则⽅程4x 2+3ax +4=0有两个相等的实根或⽆实根, Δ=9a 2-4×16≤0,解此不等式,得-83≤a ≤83.这时,f (0)=b 是唯⼀极值.因此满⾜条件的a 的取值范围是-83,83. (3)由(2)知,当a ∈[-2,2]时,4x 2+3ax +4>0恒成⽴.∴当x <0时,f ′(x )<0,f (x )在区间(-∞,0]上是减函数.因此函数f (x )在[-1,0]上的最⼤值是f (-1).⼜∵对任意的a ∈[-2,2],不等式f (x )≤1在[-1,0]上恒成⽴,∴f (-1)≤1,即3-a +b ≤1. 于是b ≤a -2在a ∈[-2,2]上恒成⽴.∴b ≤-2-2,即b ≤-4.因此满⾜条件的b 的取值范围是(-∞,-4].探究提⾼ (1)对含参函数的极值,要进⾏讨论,注意f ′(x 0)=0只是f (x )在x 0处取到极值的必要条件.(2)利⽤函数的极值、最值,可以解决⼀些不等式的证明、函数零点个数、恒成⽴问题等.已知f (x )=ax 2 (a ∈R ),g (x )=2ln x .(1)讨论函数F (x )=f (x )-g (x )的单调性;(2)若⽅程f (x )=g (x )在区间[2,e]上有两个不等解,求a 的取值范围.解 (1)F (x )=ax 2-2ln x ,其定义域为(0,+∞),∴F ′(x )=2ax -2x =2(ax 2-1)x(x >0).①当a >0时,由ax 2-1>0,得x >1a. 由ax 2-1<0,得01a. 故当a >0时,F (x )的增区间为1a ,+∞,减区间为?0,1a . ②当a ≤0时,F ′(x )<0 (x >0)恒成⽴.故当a ≤0时,F (x )在(0,+∞)上单调递减.(2)原式等价于⽅程a =2ln xx 2=φ(x )在区间[2,e]上有两个不等解.∵φ′(x )=2x (1-2ln x )x 4在(2,e)上为增函数,在(e ,e)上为减函数,则φ(x )max =φ(e)=1e ,⽽φ(e)=2e 2<φ(2)=2ln 24=ln 22=φ(2).∴φ(x )min =φ(e),如图当f (x )=g (x )在[2,e]上有两个不等解时有φ(x )min =ln 22, a 的取值范围为ln 22≤a <1e.导数与函数单调性关系不清致误典例:(14分)已知f (x )=x 3-ax 2-3x .(1)若f (x )在[2,+∞)上是增函数,求实数a 的取值范围;(2)若x =3是f (x )的极值点,求f (x )在[1,a ]上的最⼩值和最⼤值.易错分析求函数的单调增区间就是解导数⼤于零的不等式,受此影响,容易认为函数f (x )的导数在区间[2,+∞)上⼤于零,忽视了函数的导数在[2,+∞)上个别的点处可以等于零,这样的点不影响函数的单调性.规范解答解 (1)由题意,知f ′(x )=3x 2-2ax -3,[1分] 令f ′(x )≥0 (x ≥2),得a ≤32x -1x . 记t (x )=32x -1x ,当x ≥2时,t (x )是增函数,[3分] 所以t (x )min =32×2-12=94,所以a ∈?-∞,94.[6分] (2)由题意,得f ′(3)=0,即27-6a -3=0,所以a =4.[7分] 所以f (x )=x 3-4x 2-3x ,f ′(x )=3x 2-8x -3.[9分] 令f ′(x )=0,得x 1=-13,x 2=3.[10分]⼜因为x ∈[1,4],所以x =-13(舍去),故x =3.当x ∈(1,3)时,f ′(x )<0,所以f (x )在[1,3]上为减函数;[11分] 当x ∈(3,4)时,f ′(x )>0,所以f (x )在[3,4]上为增函数.[12分] 所以x =3时,f (x )有极⼩值.于是,当x ∈[1,4]时,f (x )min =f (3)=-18,⽽f (1)=-6,f (4)=-12,所以f (x )max =f (1)=-6.[14分]温馨提醒 (1)若函数y =f (x )在区间(a ,b )上单调递增,则f ′(x )≥0,其逆命题不成⽴,因为f ′(x )≥0包括f ′(x )>0或f ′(x )=0.当f ′(x )>0时函数y =f (x )在区间(a ,b )上单调递增,当f ′(x )=0时f (x )在这个区间内为常函数;同理,若函数y =f (x )在区间(a ,b )上单调递减,则f ′(x )≤0,其逆命题不成⽴.(2)使f ′(x )=0的离散的点不影响函数的单调。
利用导数探究函数的单调性(共10种题型)

利用导数探究函数的单调性一.求单调区间例1:已知函数2()ln (0,1)x f x a x x a a a =+->≠,求函数)(x f 的单调区间 解:()ln 2ln 2(1)ln x x f x a a x a x a a '=-=-++.则令()()g x f x '=因为当0,1a a >≠ 所以2()2ln 0x g x a a '=+> 所以()f x '在R 上是增函数, 又(0)0f '=,所以不等式()0f x '>的解集为(0,)∞+,故函数()f x 的单调增区间为(0,)∞+ 减区间为:(0)-∞,变式:已知()x f x e ax =-,求()f x 的单调区间解:'()x f x e a =- 当0a ≤时,'()0f x >,()f x 单调递增当0a >时,由'()0x f x e a =->得:ln x a >,()f x 在(ln ,)a +∞单调递增由'()0x f x e a =-<得:ln x a <,()f x 在(ln )a -∞,单调递增 综上所述:当0a ≤时,()f x 的单调递增区间为:-∞+∞(,),无单调递减区间当0a >时,()f x 的单调递增区间为:(ln ,)a +∞,递减区间为:(ln )a -∞,二.函数单调性的判定与逆用例2.已知函数32()25f x x ax x =+-+在1132(,)上既不是单调递增函数,也不是单调递减函数,求正整数a 的取值集合 解:2()322f x x ax '=+-因为函数32()25f x x ax x =+-+在1132(,)上既不是单调递增函数,也不是单调递减函数 所以2()322=0f x x ax '=+-在1132(,)上有解 所以''11()()032f f <又*a N ∈ 解得:5542a << 所以正整数a 的取值集合{2}三.利用单调性求字母取值范围 例3. 已知函数()ln xf x ax x=-,若函数()y f x =在1+?(,)上是减函数,求实数a 的最小值. 解:因为()ln xf x ax x=-在1+?(,)上是减函数 所以'2ln 1()0(ln )x f x a x -=-?在1+?(,)上恒成立 即2ln 1(ln )x a x -³在1+?(,)上恒成立令ln ,(1)t x x =>,则0t >21()(0)t h t t t -=> 则max ()a h t ³因为222111111()=()()24t h t t t t t -=-+=--+ 所以max 1()=(2)4h t h =所以14a ³变式:若函数3211()(1)132f x x ax a x =-+-+在区间1,4()上为减函数,在区间(6,)+?上为增函数,试求实数a 的取值范围. 解:2'()=1f x x ax a -+-因为函数()y f x =在区间1,4()上为减函数,在区间(6,)+?上为增函数 所以''()0(1,4)()0,(6,)f x x f x x ìï??ïíï???ïî,恒成立即2210(1,4)10,(6,)x ax a x x ax a x ì-+-??ïïíï-+-???ïî, 所以2211,(1,4)111,(6,)1x a x x x x a x x x ì-ïï?+"?ïï-íï-ï?+"??ïï-ïî所以4161a a ì?ïïíï?ïî所以57a #四.比较大小例4. 设a 为实数,当ln 210a x >->且时,比较x e 与221x ax -+的大小关系. 解:令2()21(0)x f x e x ax x =-+-> 则'()=22x f x e x a -+ 令'()()g x f x = 则'()e 2x g x =- 令'()0g x =得:ln 2x =当ln 2x >时,'()0g x >;当ln 2x <时,'()0g x <所以ln2min ()()=(ln2)2ln2222ln22g x g x g e a a ==-+=-+极小值 因为ln 21a >- 所以'()()0g x f x =>所以()f x 在0+?(,)上单调递增所以()(0)0f x f >= 即2210x e x ax -+-> 所以221x e x ax >-+变式:对于R 上的可导函数()y f x =,若满足'(3)()0x f x ->,比较(1)(11)f f +与2(3)f 的大小关系.解:因为'(3)()0x f x ->所以当3x >时,'()0f x >,()f x 单调递增,故(11)(3)f f >当3x <时,'()0f x <,()f x 单调递减,故(1)(3)f f > 所以(1)(11)2(3)f f f +> 五.证明不等式例5.已知函数|ln |)(x x f =,()(1)g x k x =- (R)k ∈.证明:当1k <时,存在01x >,使得对任意的0(1,)x x ∈,恒有()()f x g x >. 证明:令()|ln |(1)=ln (1),(1,)G x x k x x k x x =----∈+∞ 则有'11(),(1,)kx G x k x x x-=-=∈+∞ 当01k k ≤≥或时,'()0G x >,故 ()G x 在1+∞(,)上单调递增,()G(1)0G x >=.故任意实数 (1,)x ∈+∞ 均满足题意.当 01k << 时,令'()=0G x ,得11x k=>. 当1(1,)x k ∈时,'()0G x >,故 ()G x 在1(1,)k上单调递增当1()x k∈+∞,时,'()0G x <,故 ()G x 在1()k +∞,上单调递减 取01x k=,对任意0(1,)x x ∈,有'()0G x >,故()G x 在0(1,)x 上单调递增所以()G(1)0G x >= 即()()f x g x >综上所述:当1k <时,存在01x >,使得对任意的0(1,)x x ∈,恒有()()f x g x >.变式:已知关于x 的方程2(1)x x e ax a --=有两个不同的实数根12x x 、.求证:120x x <+ 证明:因为2(1)x x e ax a --=所以2(1)1xx e a x -=+令2(1)()1xx e f x x -=+则222222(23)[(1)2]()11x xx x x e x x e f x x x --+--+'==++()()当0x >时()0f x '<,()f x 单调递减 当0x <时()0f x '>,()f x 单调递增因为关于x 的方程2(1)x x e ax a --=有两个不同的实数根12x x 、所以不妨设12(,0),(0,)x x ∈-∞∈+∞ 要证:120x x <+ 只需证:21x x <-因为210x x -∈+∞(,),且函数()f x 在0+∞(,)上单调递减 所以只需证:21()()f x f x >-,又因为21()=()f x f x 所以只需证:11()()f x f x >-即证:11112211(1)(1)11x x x e x e x x --+>++ 即证:(1)(1)0x x x e x e ---+>对0x ∈-∞(,)恒成立 令g()(1)(1)x x x x e x e -=--+,0x ∈-∞(,)则g ()()x x x x e e -'=-因为0x ∈-∞(,)所以0x x e e -->所以g ()()0x x x x e e -'=-<恒成立所以g()(1)(1)x x x x e x e -=--+在0-∞(,)上单调递减所以g()(0)0x g >= 综上所述:120x x <+ 六.求极值例6.已知函数2()()x f x x ax a e =++,是否存在实数a ,使得函数()f x 的极大值为3?若存在,求出a 的值,若不存在,请说明理由.解:'22()(2)()[(2)2]=()(2)x x x x f x x a e x ax a e x a x a e x a x e =++++=+++++ 令'()=0f x 得:2x a x =-=-或当2a =时,'()0f x ≥恒成立,无极值,舍去当2a <时,2a ->-由表可知:2()=(2)(42)3f x f a a e --=-+=极大值 解得:2432a e =-< 当2a >时,2a -<-由表可知:22()=()()3a f x f a a a a e --=-+=极大值,即3a ae -= 所以:=3a a e 令()3(2)a g a e a a =-> 则'2()31310a g a e e =->->所以()y g a =在2+∞(,)上单调递增又2(2)320g e =->所以函数()y g a =在2+∞(,)上无零点即方程=3a a e 无解综上所述:存在实数a ,使得函数()f x 的极大值为3,此时243a e =- 七.求最值例7. 已知函数2()ln (0,1)x f x a x x a a a =+->≠,若存在]1,1[,21-∈x x ,使得12()()e 1f x f x -≥-(其中e 是自然对数的底数),求实数a 的取值范围. 解:因为存在12,[1,1]x x ∈-,使得12()()e 1f x f x --≥成立, 而当[1,1]x ∈-时,12max min ()()()()f x f x f x f x --≤, 所以只要max min ()()e 1f x f x --≥即可又因为x ,()f x ',()f x 的变化情况如下表所示:所以()f x 在[1,0]-上是减函数,在[0,1]上是增函数,所以当[1,1]x ∈-时,()f x 的最小值()()m i n 01f x f ==,()f x 的最大值()max f x 为()1f -和()1f 中的最大值.因为11(1)(1)(1ln )(1ln )2ln f f a a a a a aa--=--=--+++,令1()2ln (0)g a a a a a =-->,因为22121()1(1)0g a a a a '=-=->+,所以1()2ln g a a a a=--在()0,a ∈+∞上是增函数.而(1)0g =,故当1a >时,()0g a >,即(1)(1)f f >-; 当01a <<时,()0g a <,即(1)(1)f f <-所以,当1a >时,(1)(0)e 1f f --≥,即ln e 1a a --≥,函数ln y a a =-在(1,)a ∈+∞上是增函数,解得e a ≥;当01a <<时,(1)(0)e 1f f ---≥,即1ln e 1a a+-≥,函数1ln y a a=+在(0,1)a ∈上是减函数,解得10ea <≤.综上可知,所求a 的取值范围为1(0,][e,)ea ∈∞+ 我变式:已知函数()ln()(0)x a f x e x a a -=-+>在区间0+∞(,)上的最小值为1,求实数a 的值.解:1()=x a f x e x a-'-+ 令()()g x f x '=则21()=0(x a g x e x a -'+>+)所以()y g x =在区间0+∞(,)单调递增所以存在唯一的00x ∈+∞(,),使得0001()0x a g x e x a-=-=+ 即001=x a e x a-+ 所以当0(0,)x x ∈时,()()0g x f x '=<,()y f x =单调递减当0()x x ∈+∞,时,()()0g x f x '=>,()y f x =单调递增 所以0min 00()()ln()x a f x f x e x a -==-+ 由001=x a e x a-+得:00=ln()x a x a --+ 所以0min 00001()()ln()=x a f x f x e x a x a x a-==-++-+001=()2222x a a x aa a++-+≥=- 当且仅当001=x a x a++即0=1x a +,min 0()()22f x f x a ==- 由22=1a -得12a =,此时01=2x ,满足条件 所以12a =八.解不等式例8. 函数2)0())((=∈f R x x f ,,对任意1)()('>+∈x f x f R x ,,解不等式:1)(+>x x e x f e 解:令()()x x g x e f x e =-则()()()(()()1)x x x x g x e f x e f x e e f x f x '''=+-=+-因为对任意1)()('>+∈x f x f R x , 所以()0g x '>,所以()y g x =为R 上的单调递增函数 又(0)(0)11g f =-=所以当1)(+>x x e x f e 即()1x x e f x e -> 所以()(0)g x g > 所以0x >即不等式:1)(+>x x e x f e 的解集为0+∞(,)变式:已知定义在R 上的可导函数()y f x =满足'()1f x <,若(12)()13f m f m m -->-,求m 的取值范围.解:令()()g x f x x =- 则()()1g x f x ''=- 因为'()1f x <所以()()10g x f x ''=-<所以()()g x f x x =-为R 上递减函数 由(12)()13f m f m m -->- 得:(12)()f m m f m m ---(1-2)> 即(12)()g m g m -> 所以12m m ->即13m <九.函数零点个数(方程根的个数)例9. 已知2()2ln()f x x a x x =+--在0x =处取得极值.若关于x 的方程()0f x b +=在区间[1,1]-上恰有两个不同的实数根,求实数b 的取值范围.解: '2()21f x x x a=--+ 因为2()2ln()f x x a x x =+--在0x =处取得极值 所以'2(0)1=0f a=-, 即2a =,检验知2a =符合题意.令2()()2ln(2)[1,1]g x f x b x x x b x =+=+--+∈-,'52()22()21(11)x x g x x x +=--=--≤≤ 所以()=(0)2ln 2g x g b =+极大值因为方程()0f x b +=在区间[1,1]-上恰有两个不同的实数根所以(1)0(0)0(1)0g g g -≤⎧⎪>⎨⎪≤⎩,即02ln 202ln 320b b b ≤⎧⎪+>⎨⎪-+≤⎩解得:2ln 222ln 3b -<≤-所以实数b 的取值范围是:2ln 222ln3]--(, 变式:已知函数()y f x =是R 上的可导函数,当0x ¹时,有'()()0f x f x x+>,判断函数13()()F x xf x x=+的零点个数解:当0x ¹时,有'()()0f x f x x+> 即'()()0xf x f x x+> 令()()g x xf x =,则'()()()g x xf x f x ¢=+所以当0x >时,'()()()0g x xf x f x ¢=+>,函数()y g x =在0+∞(,)单调递增 且()g(0)=0g x >所以当0x >时,13()()0F x xf x x=+>恒成立,函数()y F x =无零点 当0x <时,'()()()0g x xf x f x ¢=+<,函数()y g x =在0∞(-,)单调递减 且()g(0)=0g x >恒成立 所以13()()F x xf x x=+在0∞(-,)上为单调递减函数 且当0x →时,()0xf x ®,所以13()0F x x? 当x →-∞时,10x®,所以()()0F x xf x ? 所以13()()F x xf x x=+在0∞(-,)上有唯一零点 综上所述:13()()F x xf x x =+在0∞∞(-,)(0,+)上有唯一零点 十.探究函数图像例10.设函数在定义域内可导,()y f x =的图像如图所示,则导函数()y f x '=的图像可能为下列图像的 .解:由()y f x =的图像可判断出:()f x 在(,0)-∞递减,在(0)+∞,上先增后减再增 所以在(,0)-∞上()0f x '<,在(0)+∞,上先有()0f x '>,后有()0f x '<,再有()0f x '>. 所以图(4)符合.变式:已知函数ln(2)()x f x x =,若关于x 的不等式2()()0f x af x +>只有两个整数解,求实数a 的取值范围. 解:21ln(2)()=x f x x -',令()=0f x '得2e x = 所以当02e x <<时,()0,()f x f x '>单调递增 当2e x >时,()0,()f x f x '<单调递减 由当12x <时,()0f x <,当12x >时,()0f x >(1)(2)(3)(4)作出()f x 的大致函数图像如图所示: 因为2()()0f x af x +>(1)若0a =,即2()0f x >,显然不等式有无穷多整数解,不符合题意;(2)若0a >,则()()0f x a f x <->或,由图像可知,()0f x >,有无穷多整数解(舍)(3)若0a <则()0()f x f x a <>-或,由图像可知,()0f x <无整数解, 所以()f x a >-有两个整数解因为(1)(2)ln 2f f ==,且()f x 在(,)2e +∞上单调递减 所以()f x a >-的两个整数解为:1,2x x == 又ln 6(3)3f =所以ln 6ln 23a ≤-< 所以ln 6ln 23a -<≤-。
专题3.3 利用导数研究函数的单调性-重难点题型精讲(新高考地区专用)(解析版)

专题3.3 利用导数研究函数的单调性-重难点题型精讲函数的单调性与导数的关系条件 恒有 结论函数y =f (x )在区间(a ,b )上可导f ′(x )>0 f (x )在(a ,b )内单调递增 f ′(x )<0 f (x )在(a ,b )内单调递减 f ′(x )=0f (x )在(a ,b )内是常数函数【思考】“f(x )在区间(a ,b )上是增函数,则f ′(x )>0在(a ,b )上恒成立”,这种说法是否正确? 提示 不正确,正确的说法是:可导函数f (x )在(a ,b )上是增(减)函数的充要条件是对∀x ∈(a ,b ),都有f ′(x )≥0(f ′(x )≤0)且f ′(x )在(a ,b )上的任一非空子区间内都不恒为零.【题型1 不含参函数的单调性】 【方法点拨】确定函数单调区间的步骤 (1)确定函数f (x )的定义域. (2)求f ′(x ).(3)解不等式f ′(x )>0,解集在定义域内的部分为单调递增区间. (4)解不等式f ′(x )<0,解集在定义域内的部分为单调递减区间.【例1】(2021春•鞍山期末)函数f(x)=xx2+1的单调递减区间为.【解题思路】根据题意,求出函数的导数,解f′(x)≤0,利用导数与函数单调性的关系分析可得答案.【解答过程】解:根据题意,函数f(x)=xx2+1,其导数f′(x)=(x2+1)−x×(2x)(x2+1)2=1−x2(x2+1)2,若f′(x)≤0,即1−x2(x2+1)2≤0,解可得:x≤﹣1或x≥1,即函数f(x)的单调递减区间为(﹣∞,﹣1]、[1,+∞);故答案为:(﹣∞,﹣1]、[1,+∞).【变式1-1】(2021春•资阳期末)函数f(x)=√x•lnx的递增区间为()A.(1e2,+∞)B.(1e,+∞)C.(0,1e2)D.(0,1e)【解题思路】对f(x)求导,令f′(x)>0,即可求得函数的递增区间.【解答过程】解:f(x)=√x•lnx的定义域为(0,+∞),f′(x)=12√x lnx+√xx=1√x(12lnx+1),令f′(x)>0,解得x>1e2,即函数f(x)=√x•lnx的递增区间为(1e2,+∞).故选:A.【变式1-2】(2021春•修水县期末)已知函数f(x)=(x−1)e xx2+1.求函数f(x)的单调区间.【解题思路】对f(x)求导,利用导数与单调性的关系即可求解;【解答过程】解:f′(x)=xe x(x2+1)−(x−1)e x(2x)(x2+1)2=x(x2−2x+3)e x(x2+1)2,令f′(x)>0,可得x>0,令f′(x)<0,可得x<0,∴(x)在(﹣∞,0)上单调递减,在(0,+∞)上单调递增.【变式1-3】(2021•全国四模)已知f(x)=e x.求关于x的函数g(x)=f(x)﹣4f(﹣x)﹣5x的单调区间.【解题思路】依题意,得g(x)=e﹣x(e x﹣1)(e x﹣4),由g′(x)>0可得g(x)的增区间,g′(x)<0可得g(x)的减区间;【解答过程】解:g(x)=e x﹣4e﹣x﹣5x,g′(x)=e x+4e﹣x﹣5=e﹣x(e x﹣1)(e x﹣4),∴g′(x)>0⇔x>ln4或x<0,g(x)的增区间为(﹣∞,0),(ln4,+∞);g′(x)<0⇔x>0<x<ln4,g(x)的减区间为(0,ln4);【题型2 含参函数的单调性】【方法点拨】(1)研究含参数的函数的单调性,要依据参数对不等式解集的影响进行分类讨论.(2)划分函数的单调区间时,要在函数定义域内讨论,还要确定导数为零的点和函数的间断点.【例2】(2021•湖南模拟)已知函数f(x)=x3+3a(x+1)(a∈R).讨论f(x)的单调性.【解题思路】对函数f(x)求导,分a≥0及a<0讨论导函数与0的大小关系,即可求得单调性;【解答过程】解:f′(x)=3x2+3a,①当a≥0时,f′(x)≥0,f(x)在R上单调递增;②当a<0时,令f′(x)>0,解得x<−√−a或x>√−a,令f′(x)<0,解得−√−a<x<√−a,∴f(x)在(−∞,−√−a),(√−a,+∞)上单调递增,在(−√−a,√−a)上单调递减;综上,当a≥0时,f(x)在R上单调递增;当a<0时,f(x)在(−∞,−√−a),(√−a,+∞)上单调递增,在(−√−a,√−a)上单调递减;【变式2-1】(2021•肥城市模拟)已知函数f(x)=ln(x+a)−xx+a,a∈R.讨论f(x)的单调性.【解题思路】求出函数的导数,通过讨论a的范围,求出函数的单调区间即可;【解答过程】解:由已知可得函数f(x)的定义域为(﹣a,+∞),f′(x)=x(x+a)2,当a≤0时,x>﹣a≥0,故f'(x)>0,f(x)在(﹣a,+∞)上单调递增;当a>0时,x∈(﹣a,0)时,f'(x)<0,f(x)在(﹣a,0)上单调递减,x∈(0,+∞)时,f'(x)>0,f(x)在(0,+∞)上单调递增;综上所述,当a≤0时,f(x)的单调递增区间是(﹣a,+∞),无单调递减区间;当a>0时,f(x)的单调递减区间是(﹣a,0),f(x)的单调递增区间是(0,+∞).【变式2-2】(2021•庐阳区校级模拟)已知函数f(x)=a2(x−2)2−x+2lnx(a>0).讨论f(x)的单调性.【解题思路】可得f′(x)=(x−2)(ax−1)x,分a=12,0<a<12,a>12三类讨论,可得f(x)的单调性;【解答过程】解:函数f(x)的定义域为(0,+∞),f′(x)=a(x−2)−1+2x=(x−2)(ax−1)x,令f'(x)=0,则x1=2,x2=1 a.(ⅰ)若a=12,则f'(x)≥0恒成立,所以f(x)在(0,+∞)上是增函数.(ⅱ)若0<a<12,则1a>2,当x∈(0,2)∪(1a,+∞)时,f'(x)>0;当x∈(2,1a)时,f'(x)<0.(ⅲ)若a >12,则0<1a <2,当x ∈(0,1a )∪(2,+∞)时,f '(x )>0;当x ∈(1a,2)时,f '(x )<0. 综上所述;当a =12时,f (x )在(0,+∞)上是增函数;当0<a <12,f (x )在(0,2),(1a,+∞)上是增函数,在(2,1a)上是减函数; 当a >12时,f (x )在(0,1a ),(2,+∞)上是增函数,在(1a ,2)上是减函数. 【变式2-3】(2021•丙卷模拟)已知函数ℎ(x)=a 2x −a −1+lnxx,其中a ∈R ,若函数f (x )=x •h (x ),讨论f (x )的单调性.【解题思路】由条件可得f ′(x )=(2ax+1)(ax−1)x,然后分a =0,a >0,a <0三类讨论,可得f (x )的单调情况;【解答过程】解:由题意,得2221()()()1(0)lnxf x x h x x a x a a x ax lnx x x+=⋅=⋅--=--->, 则222121(21)(1)()2a x ax ax ax f x a x a x x x--+-'=--==①当0a =时,1()0f x x'=-<在(0,)+∞上恒成立,()f x ∴在(0,)+∞上单调递减;②当0a >时,110,02x a a-<<>, 令()0f x '>,即(21)(1)0ax ax x +->,解得1x a >;令()0f x '<,即(21)(1)0ax ax x+-<,解得10x a <<,()f x ∴在1(0,)a 上单调递减,在1(,)a+∞上单调递增;③当0a <时,110,02x a a<<->, 令()0f x '>,即(21)(1)0ax ax x +->,解得12x a >-; 令()0f x '<,即(21)(1)0ax ax x +-<,解得102x a<<-,()f x ∴在1(0,)2a-上单调递减,在1(,)2a -+∞上单调递增.综上,当0a =时,()f x 在(0,)+∞上单调递减;当0a >时,()f x 在1(0,)a 上单调递减,在1(,)a+∞上单调递增;当0a <时,()f x 在1(0,)2a-上单调递减,在1(,)2a -+∞上单调递增.【题型3 利用函数单调性比较大小】【例3】(2021•二模拟)已知a=12ln2+14,b=2e,c=lnπ+1π,则a,b,c之间的大小关系为()A.a<b<c B.a<c<b C.c<a<b D.b<c<a【解题思路】本题不能直接比较大小,所以先将a,b化为与c一样的形式,即a=12ln2+14+14=2ln2+14=ln4+14,b=2e=lne+1e,然后令f(x)=lnx+1x,利用导数求出函数的单调性,比较大小.【解答过程】解:令f(x)=lnx+1x,则f′(x)=−lnxx2,令f′(x)>0,解得:0<x<1,所以f(x)在(0,1)上递增,令f′(x)<0,解得:x>1,所以f(x)在(1,+∞)上递减,由题:a=12ln2+14+14=2ln2+14=ln4+14=f(4),b=2e=lne+1e=f(e),c=lnπ+1π=f(π),因为e<π<4,所以f(e)>f(π)>f(4),即b>c>a,故选:B.【变式3-1】(2021•丙卷模拟)已知函数f(x)+f'(x)=2m x,f(x)﹣f'(x)=2m﹣x(m>1),若a=0.75,b=70.5,c=log51,则()A.f(b)<f(a)<f(c)B.f(c)<f(b)<f(a)C.f(c)<f(a)<f(b)D.f(a)<f(b)<f(c)【解题思路】根据条件得到f(x)=e x+e﹣x,然后判断f(x)的奇偶性和单调性,再结合a=0.75,b=70.5,c=log51,判断a,b,c的大小即可.【解答过程】解:由f(x)+f'(x)=2m x与f(x)﹣f'(x)=2m﹣x,得f(x)=m x+m﹣x,f'(x)=m x﹣m﹣x,所以m=e,所以f(x)=e x+e﹣x,由f(x)=f(﹣x),知函数f(x)为偶函数.又f'(x)=e x﹣e﹣x,当x>0时,f'(x)>0,当x<0时,f'(x)<0,所以函数f(x)在(﹣∞,0)上单调递减,在(0,+∞)上单调递增.因为c=log51=0<a=0.75<1<b=70.5,所以f(c)<f(a)<f(b).故选:C.【变式3-2】(2021•皇姑区校级模拟)已知实数x ,y ,z 满足e y lnx =ye x 且e z ln 1x=ze x ,若y >1,则( )A .x >y >zB .x >z >yC .y >z >xD .y >x >z【解题思路】由选项确定比较x ,y ,z 三个字母的大小,题干中只有两个等式及y >1,所以先考虑到将等式变形,确定除x >1,z <0;在比较x 与y 的大小,构造出x ,y 的一个不等式,然后利用函数的单调性求解.【解答过程】解:因为e y•lnx =y •e x可e y y=e x lnx,∵y >1,e y>0,∴e y y>0,∴e x lnx>0,∴lnx >0, ∴x >1,∵e z⋅ln 1x =z ⋅e x,∴e z z =e x ln1x=−e x lnx <0,∵e z >0, ∴z <0;(下面比较x ,y 的大小)令f (x )=x ﹣lnx ,f′(x)=1−1x =x−1x ,当x >1时,f ′(x )>0,∴f (x )在(1,+∞)上单调递增,∴x >1时,f (x )>f (1),即x ﹣lnx >1,一定有x ﹣lnx >0,∴x >lnx >0,∴e x x<e x lnx①,又∵e xlnx=e x y,①式可化为e x x<e y y,令g(x)=e xx ,则g′(x)=e x (x−1)x 2, 当x >1时,g ′(x )>0,∴g (x )在(1,+∞)上单调递增, ∵x >1,y >1,e x x<e y y,∴x <y ,综上:y >x >z 故选:D .【变式3-3】(2021•渝水区校级模拟)已知x ∈(0,π4),且a =2cos 2x+1e 2cos 2x,b =cosx+1e cosx ,c =sinx+1e sinx ,则a ,b ,c 的大小关系式为( ) A .a <b <cB .a <c <bC .b <c <aD .c <a <b【解题思路】构造函数g (x )=x+1e x ,利用导数可得g (x )在区间(0,+∞)单调递减,进一步分析可得2cos 2x >cos x >sin x >0,从而可得答案. 【解答过程】解:令g (x )=x+1e x , 则g ′(x )=−xe x ,所以当x >0时,g ′(x )<0,g (x )单调递减.① 因为x ∈(0,π4), 所以cos x ∈(√22,1),2cos x ∈(√2,2),且cos x >sin x >0, 又2cos 2x ﹣cos x =cos x (2cos x ﹣1)>0, 所以2cos 2x >cos x >sin x >0, 由①得a <b <c , 故选:A .【题型4 利用函数单调性解不等式】【例4】(2021•大通县一模)已知定义在R 上的函数f (x )满足f (2)=20,且f (x )的导函数f '(x )满足f '(x )>6x 2+2,则不等式f (x )>2x 3+2x 的解集为( ) A .{x |x >﹣2}B .{x |x >2}C .{x |x <2}D .{x |x <﹣2或x >2}【解题思路】令g (x )=f (x )﹣2x 3﹣2x ,结合条件判断g (x )的单调性,将问题转化为g (x )>g (2),然后求出不等式的解集即可.【解答过程】解:令g (x )=f (x )﹣2x 3﹣2x ,则g '(x )=f '(x )﹣6x 2﹣2>0, 所以g (x )在R 上单调递增.因为g (2)=f (2)﹣2×23﹣2×2=0, 故原不等式等价于g (x )>g (2),所以x >2, 所以不等式的解集为{x |x >2}. 故选:B .【变式4-1】(2021•全国卷模拟)f (x )是定义在R 上的奇函数,且f (1)=0,f '(x )为f (x )的导函数,且当x ∈(0,+∞)时f '(x )>0,则不等式f (x ﹣1)>0的解集为( )A.(0,1)∪(2,+∞)B.(﹣∞,1)∪(1,+∞)C.(﹣∞,1)∪(2,+∞)D.(﹣∞,0)∪(1,+∞)【解题思路】依题意,作出y=f(x)的图象,得到f(x)>0的解集,继而可得不等式f(x﹣1)>0的解集.【解答过程】解:∵f(x)是定义在R上的奇函数,且f(1)=0,当x∈(0,+∞)时f'(x)>0,∴f(x)在(﹣∞,0),(0,+∞)上单调递增,图形如下:∴f(x)>0的解集为:(﹣1,0)∪(1,+∞),又y=f(x﹣1)的图象是y=f(x)的图象向右平移一个单位,∴不等式f(x﹣1)>0的解集为(0,1)∪(2,+∞),故选:A.【变式4-2】(2021•长春模拟)已知定义域为R的函数f(x)满足f(x)+xf'(x)>1(f'(x)为函数f(x)的导函数),则不等式(1+x)f(1﹣x2)>f(1﹣x)+x的解集为()A.(0,1)B.(0,1]C.(0,+∞)D.(0,1)∪(1,+∞)【解题思路】构造函数g(x)=xf(x)﹣x,求出函数的导数,根据函数的单调性求出不等式的解集即可.【解答过程】解:由(1+x)f(1﹣x2)>f(1﹣x)+x,当x<1时,可得(1﹣x)(1+x)f(1﹣x2)>(1﹣x)f(1﹣x)+(1﹣x)x,即(1﹣x2)f(1﹣x2)>(1﹣x)f(1﹣x)+x﹣x2,即(1﹣x2)f(1﹣x2)﹣(1﹣x2)>(1﹣x)f(1﹣x)﹣(1﹣x),构造函数g(x)=xf(x)﹣x,g'(x)=f(x)+xf'(x)﹣1>0,所以函数g(x)递增,则1﹣x2>1﹣x,此时0<x<1,即0<x<1满足;当x>1时,可得(1﹣x2)f(1﹣x2)﹣(1﹣x2)<(1﹣x)f(1﹣x)﹣(1﹣x),由函数g(x)递增,则1﹣x2<1﹣x,此时x<0或x>1,即x>1满足;当x=1时,2f(0)>f(0)+1,即f(0)>1满足f(x)+x⋅f'(x)>1.综上,x∈(0,+∞),故选:C.【变式4-3】(2021•香坊区校级三模)设函数f'(x)是奇函数f(x)(x∈R)的导函数,当x>0时,lnxf′(x)<−1x f(x),则使得(x2﹣9)f(x)<0成立的x的取值范围是()A.(﹣3,0)∪(3,+∞)B.(﹣∞,﹣3)∪(3,+∞)C.(﹣3,0)∪(0,3)D.(﹣∞,﹣3)∪(0,3)【解题思路】令g(x)=f(x)lnx(x>0),则当x>0时,g(x)=f(x)lnx单调递减,而g(1)=0,于是可得当x∈(0,1)∪(1,+∞)时,f(x)<0;x∈(﹣1,0)∪(﹣∞,﹣1)时,f(x)>0,从而可求得(x2﹣9)f(x)<0的解.【解答过程】解:令g(x)=f(x)lnx(x>0),则g′(x)=f′(x)lnx+1x f(x)<0,∴当x>0时,g(x)=f(x)lnx单调递减.又g(1)=f(1)ln1=0,∴当x∈(0,1)时,g(x)>0,而此时lnx<0,∴f(x)<0;当x∈(1,+∞)时,g(x)<0,而此时lnx>0,∴f(x)<0;又f(x)是奇函数,∴当x∈(﹣1,0)时,f(x)>0;当x∈(﹣∞,﹣1)时,f(x)>0;∵(x2﹣9)f(x)<0,∴当x<0时,x2﹣9<0,解得﹣3<x<0;①当x>0时,x2﹣9>0,解得x>3;②综合①②,得(x2﹣9)f(x)<0成立的x的取值范围为(﹣3,0)∪(3,+∞),故选:A.【题型5 函数单调性与图像关系】【例5】(2020秋•宝鸡期末)若函数y=f(x)的导函数图象如图所示,则y=f(x)的图象可能为()A.B.C.D.【解题思路】根据f′(x)的图象,分别判断函数的单调性即可.【解答过程】解:设f′(x)=0的两个根分别为a,b,0<a<b,则当x<a时,f′(x)<0,函数f(x)为减函数,排除选项A和D;当a<x<b时,f′(x)>0,函数f(x)为增函数,当x>b时,f′(x)<0,函数f(x)为减函数,∵0<a<b,∴选项B不成立,选项C成立,则对应的图象为C,故选:C.【变式5-1】(2021春•葫芦岛期末)设函数f(x)的图象如图所示,则导函数f′(x)的图象可能为()A.B.C .D . 【解题思路】由原函数的单调性确定导函数的函数值的正负,即可得解【解答过程】解:由f (x )的图象知当x ∈(﹣∞,1)时,f (x )单调递减,f '(x )<0当x ∈(1,4)时,f (x )单调递增,f '(x )>0当x ∈(4,+∞)时,f (x )单调递减,f '(x )<0故选:C .【变式5-2】(2020秋•南昌期末)已知定义在R 上的函数y =f (x ),其导函数y =f '(x )的大致图象如图所示,则下列叙述正确的是( )A .f (b )>f (c )>f (d )B .f (b )>f (a )>f (e )C .f (c )>f (e )>f (d )D .f (c )>f (b )>f (a )【解题思路】根据导函数的图象,求出函数f (x )的单调区间,根据a ,b ,c 的大小以及函数的单调性判断函数值的大小即可.【解答过程】解:显然f (x )(﹣∞,c )递增,在(c ,e )递减,在(e ,+∞)递增,而a <b <c ,故f (a )<f (b )<f (c ),故选:D .【变式5-3】(2020秋•渝中区校级月考)已知函数y =f (x )(x ∈R )的图象如图所示,则不等式f′(x)x−1<0的解集为( )A .(﹣∞,0)∪(12,2)B .(﹣1,1)∪(1,3)C .(﹣∞,12)∪(12,2) D .(﹣∞,12)∪(1,2) 【解题思路】根据条件判断函数的单调性,利用数形结合即可解不等式.【解答过程】解:∵f′(x)x−1<0,即(x ﹣1)•f ′(x )<0,∴不等式等价为x >1时,f ′(x )<0,此时函数单调递减,由图象可知此时解集为:(1,2). 当x <1时,f ′(x )>0,此时函数单调递增,由图象可知x <12,即不等式的解集为(﹣∞,12)∪(1,2). 故选:D .【题型6 利用函数单调性求参数】【方法点拨】根据函数单调性求参数的一般思路(1)利用集合间的包含关系处理:y =f (x )在(a ,b )上单调,则区间(a ,b )是相应单调区间的子集.(2)f (x )为增(减)函数的充要条件是对任意的x ∈(a ,b )都有f ′(x )≥0(f ′(x )≤0)且在(a ,b )内的任一非空子区间上,f ′(x )不恒为零,应注意此时式子中的等号不能省略,否则会漏解.(3)函数在某个区间上存在单调区间可转化为不等式有解问题.【例6】(2021•广东模拟)若函数f(x)=ax 2+1e x(e 为自然对数的底数)是减函数,则实数a 的取值范围是( )A .a ≤0B .a ≤1C .a >0D .0≤a ≤1 【解题思路】对f (x )求导,由f (x )是减函数可得f ′(x )≤0恒成立,令g (x )=2ax ﹣ax 2﹣1,则g (x )≤0恒成立,对a 分类讨论,即可求得a 的取值范围.【解答过程】解:函数f(x)=ax 2+1e x 的定义域为R ,f ′(x )=2ax−ax 2−1e x, 因为函数f (x )是减函数,所以f ′(x )≤0恒成立,令g (x )=2ax ﹣ax 2﹣1,则g (x )≤0恒成立,当a=0时,g(x)=﹣1成立;当a<0时,则g(x)的图象开口向上,g(x)≤0不恒成立,不符合题意;当a>0时,要使g(x)≤0恒成立,则△=4a2﹣4a≤0,解得0≤a≤1,又a>0,所以0<a≤1.综上可得,实数a的取值范围是0≤a≤1.故选:D.【变式6-1】(2021•湖南模拟)若函数f(x)=﹣x3+ax2+4x在区间(0,2)上单调递增,则实数a的取值范围为.【解题思路】问题转化为a≥3x2−2x在(0,2)恒成立,令g(x)=3x2−2x,x∈(0,2),求出函数的导数,根据函数的单调性求出a的取值范围即可.【解答过程】解:f(x)=﹣x3+ax2+4x,则f′(x)=﹣3x2+2ax+4,若f(x)在区间(0,2)上单调递增,则﹣3x2+2ax+4≥0在(0,2)恒成立,即a≥3x2−2x在(0,2)恒成立,令g(x)=3x2−2x,x∈(0,2),则g′(x)=32+2x2>0,g(x)在(0,2)递增,故g(x)<g(2)=2,故a≥2,故实数a的取值范围为[2,+∞),故答案为:[2,+∞).【变式6-2】(2021•南昌二模)若函数f(x)=x2+ax+1在(﹣1,+∞)上单调递增,则实数a的取值范围为.【解题思路】根据题意,求出函数的解析式,由函数的导数与单调性的关系,可得f′(x)=1−a+1(x+1)2≥0,即a+1≤(x+1)2的区间(﹣1,+∞)上恒成立,据此分析可得答案.【解答过程】解:根据题意,f(x)=x2+ax+1=x2−1+a+1x+1=x﹣1+a+1x+1,其导数f′(x)=1−a+1 (x+1)2,若函数f(x)=x2+ax+1在(﹣1,+∞)上单调递增,则f′(x)=1−a+1(x+1)2≥0,即a+1≤(x+1)2的区间(﹣1,+∞)上恒成立,又由x∈(﹣1,+∞),则(x+1)2≥0,必有a +1≤0即a ≤﹣1恒成立,即a ≤﹣1,则a 的取值范围为(﹣∞,﹣1]. 故答案为:(﹣∞,﹣1].【变式6-3】(2021•黔江区校级模拟)函数f (x )=x 2﹣axlnx 在(2e ,2)上不单调,则实数a 的取值范围是 .【解题思路】求出函数的导数,问题转化为方程a =2x lnx+1在(2e ,2)上有根,令g (x )=2x lnx+1,根据函数的单调性求出a 的范围即可.【解答过程】解:f ′(x )=2x ﹣a (lnx +1),若函数f (x )=x 2﹣axlnx 在(2e ,2)上不单调,则方程f ′(x )=0在(2e ,2)上有根即方程a =2x lnx+1在(2e ,2)上有根且方程的根是函数f ′(x )的变号零点, 令g (x )=2x lnx+1,则g ′(x )=2lnx (lnx+1)2, x ∈(2e ,1)时,g ′(x )<0,g (x )递减,x ∈(1,2)时,g ′(x )>0,g (x )递增, 又g (1)=2,g (2e )=4eln2,g (2)=4ln2+1,由g (2)﹣g (2e)=4ln2+1−4eln2>0, 得g (x )∈(2,4ln2+1),故a ∈(2,4ln2+1),故答案为:(2,4ln2+1).。
高中数学函数与导数常考题型整理归纳

高中数学(一)函数与导数常考题型整理归纳 题型一:利用导数研究函数的性质利用导数研究函数的单调性、极值、最值是高考的热点问题之一,每年必考,一般考查两类题型:(1)讨论函数的单调性、极值、最值,(2)利用单调性、极值、最值求参数的取值范围.【例1】已知函数f (x )=ln x +a (1-x ).(1)讨论f (x )的单调性;(2)当f (x )有最大值,且最大值大于2a -2时,求实数a 的取值范围.解 (1)f (x )的定义域为(0,+∞),f ′(x )=1x -a .若a ≤0,则f′(x )>0,所以f (x )在(0,+∞)上单调递增.若a >0,则当x ∈⎝ ⎛⎭⎪⎫0,1a 时,f ′(x )>0; 当x ∈⎝ ⎛⎭⎪⎫1a ,+∞时,f ′(x )<0, 所以f (x )在⎝ ⎛⎭⎪⎫0,1a 上单调递增,在⎝ ⎛⎭⎪⎫1a ,+∞上单调递减. 综上,知当a ≤0时,f (x )在(0,+∞)上单调递增;当a >0时,f (x )在⎝ ⎛⎭⎪⎫0,1a 上单调递增,在⎝ ⎛⎭⎪⎫1a ,+∞上单调递减. (2)由(1)知,当a ≤0时,f (x )在(0,+∞)上无最大值;当a >0时,f (x )在x =1a 处取得最大值,最大值为f ⎝ ⎛⎭⎪⎫1a =ln 1a +a ⎝ ⎛⎭⎪⎫1-1a =-ln a +a -1. 因此f ⎝ ⎛⎭⎪⎫1a >2a -2等价于ln a +a -1<0. 令g (a )=ln a +a -1,则g (a )在(0,+∞)上单调递增,g (1)=0.于是,当0<a <1时,g (a )<0;当a >1时,g (a )>0.因此,实数a 的取值范围是(0,1).【类题通法】(1)研究函数的性质通常转化为对函数单调性的讨论,讨论单调性要先求函数定义域,再讨论导数在定义域内的符号来判断函数的单调性.(2)由函数的性质求参数的取值范围,通常根据函数的性质得到参数的不等式,再解出参数的范围.若不等式是初等的一次、二次、指数或对数不等式,则可以直接解不等式得参数的取值范围;若不等式是一个不能直接解出的超越型不等式时,如求解ln a +a -1<0,则需要构造函数来解.【变式训练】已知a ∈R ,函数f (x )=(-x 2+ax )e x (x ∈R ,e 为自然对数的底数).(1)当a =2时,求函数f (x )的单调递增区间;(2)若函数f (x )在(-1,1)上单调递增,求实数a 的取值范围.解(1)当a =2时,f (x )=(-x 2+2x )e x ,所以f ′(x )=(-2x +2)e x +(-x 2+2x )e x=(-x 2+2)e x .令f ′(x )>0,即(-x 2+2)e x >0,因为e x >0,所以-x 2+2>0,解得-2<x <2.所以函数f (x )的单调递增区间是(-2,2).(2)因为函数f (x )在(-1,1)上单调递增,所以f ′(x )≥0对x ∈(-1,1)都成立,因为f ′(x )=(-2x +a )e x +(-x 2+ax )e x=-x 2+(a -2)x +a ]e x ,所以-x 2+(a -2)x +a ]e x ≥0对x ∈(-1,1)都成立.因为e x >0,所以-x 2+(a -2)x +a ≥0对x ∈(-1,1)都成立,即a ≥x2+2x x +1=(x +1)2-1x +1=(x +1)-1x +1对x ∈(-1,1)都成立.令y =(x +1)-1x +1,则y ′=1+1(x +1)2>0. 所以y =(x +1)-1x +1在(-1,1)上单调递增,所以y <(1+1)-11+1=32.即a ≥32.因此实数a 的取值范围为a ≥32.题型二:利用导数研究函数零点或曲线交点问题函数的零点、方程的根、曲线的交点,这三个问题本质上同属一个问题,它们之间可相互转化,这类问题的考查通常有两类:(1)讨论函数零点或方程根的个数;(2)由函数零点或方程的根求参数的取值范围.【例2】设函数f(x)=ln x +m x ,m ∈R .(1)当m =e(e 为自然对数的底数)时,求f (x )的极小值;(2)讨论函数g (x )=f ′(x )-x 3零点的个数.解 (1)由题设,当m =e 时,f (x )=ln x +e x , 定义域为(0,+∞),则f ′(x )=x -e x2,由f ′(x )=0,得x =e.∴当x ∈(0,e),f ′(x )<0,f (x )在(0,e)上单调递减,当x ∈(e ,+∞),f ′(x )>0,f (x )在(e ,+∞)上单调递增, ∴当x =e 时,f (x )取得极小值f (e)=ln e +e e =2,∴f (x )的极小值为2.(2)由题设g (x )=f ′(x )-x 3=1x -m x2-x 3(x >0),令g (x )=0,得m =-13x 3+x (x >0).设φ(x )=-13x 3+x (x >0),则φ′(x )=-x 2+1=-(x -1)(x +1),当x ∈(0,1)时,φ′(x )>0,φ(x )在(0,1)上单调递增;当x ∈(1,+∞)时,φ′(x )<0,φ(x )在(1,+∞)上单调递减.∴x =1是φ(x )的唯一极值点,且是极大值点,因此x =1也是φ(x )的最大值点.∴φ(x )的最大值为φ(1)=23.又φ(0)=0,结合y =φ(x )的图象(如图),可知①当m >23时,函数g (x )无零点;②当m =23时,函数g (x )有且只有一个零点;③当0<m <23时,函数g (x )有两个零点;④当m ≤0时,函数g (x )有且只有一个零点.综上所述,当m >23时,函数g (x )无零点;当m =23或m ≤0时,函数g (x )有且只有一个零点;当0<m <23时,函数g (x )有两个零点.【类题通法】利用导数研究函数的零点常用两种方法:(1)运用导数研究函数的单调性和极值,利用单调性和极值定位函数图象来解决零点问题;(2)将函数零点问题转化为方程根的问题,利用方程的同解变形转化为两个函数图象的交点问题,利用数形结合来解决.【变式训练】函数f (x )=(ax 2+x )e x ,其中e 是自然对数的底数,a ∈R .(1)当a >0时,解不等式f (x )≤0;(2)当a =0时,求整数t 的所有值,使方程f (x )=x +2在t ,t +1]上有解.解 (1)因为e x >0,(ax 2+x )e x ≤0.∴ax 2+x ≤0.又因为a >0,所以不等式化为x ⎝ ⎛⎭⎪⎫x +1a ≤0. 所以不等式f (x )≤0的解集为⎣⎢⎡⎦⎥⎤-1a ,0. (2)当a =0时,方程即为x e x =x +2,由于e x >0,所以x =0不是方程的解,所以原方程等价于e x -2x -1=0.令h (x )=e x -2x -1,因为h ′(x )=e x +2x2>0对于x ∈(-∞,0)∪(0,+∞)恒成立,所以h (x )在(-∞,0)和(0,+∞)内是单调递增函数,又h (1)=e -3<0,h (2)=e 2-2>0,h (-3)=e -3-13<0,h (-2)=e -2>0,所以方程f (x )=x +2有且只有两个实数根且分别在区间1,2]和-3,-2]上,所以整数t 的所有值为{-3,1}.题型三:利用导数研究不等式问题导数在不等式中的应用是高考的热点,常以解答题的形式考查,以中高档题为主,突出转化思想、函数思想的考查,常见的命题角度:(1)证明简单的不等式;(2)由不等式恒成立求参数范围问题;(3)不等式恒成立、能成立问题.【例3】设函数f (x )=e 2x -a ln x .(1)讨论f(x)的导函数f′(x)零点的个数;(2)证明:当a>0时,f(x)≥2a+a ln 2 a.(1)解f(x)的定义域为(0,+∞),f′(x)=2e2x-ax(x>0).当a≤0时,f′(x)>0,f′(x)没有零点.当a>0时,设u(x)=e2x,v(x)=-a x,因为u(x)=e2x在(0,+∞)上单调递增,v(x)=-ax在(0,+∞)上单调递增,所以f′(x)在(0,+∞)上单调递增.又f′(a)>0,当b满足0<b<a4且b<14时,f′(b)<0(讨论a≥1或a<1来检验),故当a>0时,f′(x)存在唯一零点.(2)证明由(1),可设f′(x)在(0,+∞)上的唯一零点为x0,当x∈(0,x0)时,f′(x)<0;当x∈(x0,+∞)时,f′(x)>0.故f(x)在(0,x0)上单调递减,在(x0,+∞)上单调递增,所以当x=x0时,f(x)取得最小值,最小值为f(x0)由于2e2x0-ax0=0,所以f(x0)=a2x0+2ax0+a ln2a≥2a+a ln2a.故当a>0时,f(x)≥2a+a ln 2 a.【类题通法】1.讨论零点个数的答题模板第一步:求函数的定义域;第二步:分类讨论函数的单调性、极值;第三步:根据零点存在性定理,结合函数图象确定各分类情况的零点个数.2.证明不等式的答题模板第一步:根据不等式合理构造函数;第二步:求函数的最值;第三步:根据最值证明不等式.【变式训练】已知函数f(x)=ax+ln x(a∈R).(1)若a=2,求曲线y=f(x)在x=1处的切线方程;(2)求f (x )的单调区间;(3)设g (x )=x 2-2x +2,若对任意x 1∈(0,+∞),均存在x 2∈0,1]使得f (x 1)<g (x 2),求a 的取值范围.解(1)由已知得f ′(x )=2+1x (x >0),所以f ′(1)=2+1=3,所以斜率k =3.又切点为(1,2),所以切线方程为y -2=3(x -1),即3x -y -1=0,故曲线y =f (x )在x =1处的切线方程为3x -y -1=0.(2)f ′(x )=a +1x =ax +1x (x >0),①当a ≥0时,由于x >0,故ax +1>0,f ′(x )>0,所以f (x )的单调增区间为(0,+∞).②当a <0时,由f ′(x )=0,得x =-1a .在区间⎝ ⎛⎭⎪⎫0,-1a 上,f ′(x )>0,在区间⎝ ⎛⎭⎪⎫-1a ,+∞上,f ′(x )<0,所以函数f (x )的单调递增区间为⎝ ⎛⎭⎪⎫0,-1a ,单调递减区间为⎝ ⎛⎭⎪⎫-1a ,+∞. (3)由已知得所求可转化为f (x )max <g (x )max ,g (x )=(x -1)2+1,x ∈0,1],所以g (x )max =2,由(2)知,当a ≥0时,f (x )在(0,+∞)上单调递增,值域为R ,故不符合题意.当a <0时,f (x )在⎝ ⎛⎭⎪⎫0,-1a 上单调递增,在⎝ ⎛⎭⎪⎫-1a ,+∞上单调递减,故f (x )的极大值即为最大值,是f ⎝ ⎛⎭⎪⎫-1a =-1+ln ⎝ ⎛⎭⎪⎫-1a =-1-ln(-a ), 所以2>-1-ln(-a ),解得a <-1e3.。
第三章 导数及其应用3-2利用导数研究函数的性质

6 (1)若 Δ=12-8a =0,即 a=± . 2
2
当
a x∈-∞,3或
a x∈3,+∞时,f
′(x)>0,
此时 f(x)在(-∞,+∞)为增函数. 6 所以 a=± 满足. 2
(2)若 Δ=12-8a2<0,恒有 f ′(x)>0,f(x)在(-∞,+ 3 ∞)上为增函数.所以 a > , 2
(理)(2010·广东省东莞市模拟)已知函数f(x) 的导函数f ′(x)的图象如图所示,那么函数f(x) 的图象最有可能的是( )
解析:由图可知,当x>0时,f ′(x)<0,∴函 数f(x)的图象在(0,+∞)上是单调递减的; 当x<-2时,f ′(x)<0,∴函数f(x)的图象在 (-∞,-2)上也是单调递减的,所以只有A 符合,故选A. 答案:A
重点难点 重点:1.用导数判定函数单调性的方法 2.函数极值的概念及求法、函数的最值 难点:导函数的图象与函数单调性的关系
知识归纳 1.函数的单调性 (1)设函数y=f(x)在区间(a,b)内可导,如果 f ′(x)>0,则f(x)在区间(a,b)内为增函数; 如果f ′(x)<0,则f(x)在区间(a,b)内为减函 数. (2)①如果在某个区间内恒有f ′(x)=0,则f(x) 等于常数.
答案:3
[例3] 函数f(x)的导函数y=f ′(x)的图象如下 图所示,则y=f(x)的图象最有可能的是 ( )
分析:由导函数f ′(x)的图象位于x轴上方(下 方),确定f(x)的单调性,对比f(x)的图象, 用排除法求解. 解析:由f ′(x)的图象知,x∈(-∞,0)时,f ′(x)>0,f(x)为增函数,x∈(0,2)时,f ′(x)<0, f(x)为减函数,x∈(2,+∞)时,f ′(x)>0,f(x) 为增函数. 只有C符合题意,故选C. 答案:C
利用导数讨论函数的单调性

利用导数讨论函数的单调性广西南宁市第二十六中学(530201)许莉[摘要]导数是研究函数性质的一个重要工具,利用求导研究含参函数的单调性是高考的热点,也是学生感到棘手的一个问题.文章结合实例,分类讨论研究导数与函数的单调性之间的关系.[关键词]导数;函数;单调性[中图分类号]G633.6[文献标识码]A[文章编号]1674-6058(2021)14-0030-02一、利用导数求函数的单调区间利用导数研究函数单调性的依据:若函数y=f(x)在某个区间内可导:若f′(x)>0,则f(x)在这个区间内单调递增;若f′(x)<0,则f(x)在这个区间内单调递减;若f′(x)=0,则f(x)在这个区间内是常数函数[1].[例1](2013年高考天津卷节选)已知函数f(x)=x2ln x.求函数f(x)的单调区间.分析:在对f(x)进行求导之前,应先考虑函数的定义域(因为单调区间必须是在定义域的限定范围内,而这个也是学生容易忽略的问题),再进行求导判断符号.解:函数f(x)的定义域为(0,+∞),f'(x)=2x ln x+x=x()2ln x+1,令f'(x)>0,得x>1e;令f'(x)<0,得0<x<1e,所以函数f(x)的单调递减区间是()0,1e,单调递增区间是()1e,+∞.小结:利用导数判断函数单调性的一般步骤:第一步,求函数的定义域;第二步,求导数f′(x),其中求导后若有分母就考虑通分,若能因式分解就要因式分解,不能因式分解再考虑求根公式或者其他化简;第三步,在函数f(x)的定义域内解不等式f′(x)>0和f′(x)<0;第四步,写出函数f(x)的单调区间.二、利用导数讨论含参数函数的单调性[例2](2015年高考新课标卷2节选)已知函数f(x)=ln x+a(1-x),讨论函数f(x)的单调性.分析:在对f(x)进行求导后,发现求导后的函数不能直接判断符号,而是当a不为0时分子为一个含参的一次函数,这类问题就转化为求解含参的一次函数问题.解:f(x)的定义域为(0,+∞),f'(x)=1x-a=1-axx,若a≤0,则f′(x)>0,所以f(x)在(0,+∞)单调递增.若a>0,则当x∈()0,1a时,f′(x)>0;当x∈()1a,+∞时,f′(x)<0.所以f(x)在()0,1a单调递增,在()1a,+∞单调递减.小结:求导后导函数为含参的一次函数,求解不等式ax+b>0(<0)的步骤:(1)将不等式化为ax>-b;(2)a=0时,不等式不是一元一次不等式,单独讨论;(3)若a>0,则x>-ba;若a<0,则x<-ba,还要注意单调区间必须包含在定义域内.[例3](2016年高考四川卷节选)已知函数f(x)=ax2-a-ln x,其中a∈R,讨论f(x)的单调性.分析:在对f(x)进行求导后,发现求导后的函数不能直接判断符号,而当a不为0时分子为一个含参的二次函数,这类问题就转化为求解含参的二次函数问题.对于含参的二次函数,首先考虑的是二次函数图像的开口方向,其次是是否有根,是否能直接求零点,而这也正是分类讨论的标准.对于学生来说,不重不漏地进行分类是答题的关键点.解:定义域{x|x>}0,f′()x=2ax-1x=2ax2-1x,x>0,当a≤0时,2ax2-1≤0,f′()x≤0,f()x在(0,+∞)上单调递减.当a>0时,令f'(x)=0,得x=当x∈(时,f'(x)<0;当x∈)∞时,f′(x)>0.故f(x)在(上单调递减,在)+∞上单调递增.小结:求导后导函数为含参的二次函数,求解不等式ax2+bx+c>0(<0)的步骤:(1)讨论二次项系数;(2)判断是否有零点;(3)根据对应一元二次方程数学·解题研究根的情况,得到一元二次不等式的解集,从而得到函数的单调性.[例4](2019年高考全国卷Ⅲ理20节选)已知函数f (x )=2x 3-ax 2+b .讨论f (x )的单调性.分析:在对f (x )进行求导后,发现求导后可以因式分解,从而得到二次含参函数的零点,这时二次函数的开口方向已经确定,只需要对得到的两个两点进行分类讨论即可.解:(1)f '(x )=6x 2-2ax =2x (3x -a ),令f ′(x )=0,得x =0或x =a3.若a >0,则当x ∈()-∞,0∪()a3,+∞时,f '(x )>0;当x ∈()0,a3时,f '(x )<0.故f (x )在()-∞,0和()a3,+∞上单调递增,在()0,a3上单调递减;若a =0,f (x )在(-∞,+∞)上单调递增;若a <0,则当x ∈()-∞,a3∪()0,+∞时,f ′(x )>0;当x ∈()a3,0时,f ′(x )<0;故f (x )在()-∞,a3∪()0,+∞上单调递增,在()a3,0上单调递减.综上所述,若a =0,f (x )在()-∞,+∞上单调递增;若a <0,f (x )在()-∞,a3和()0,+∞上单调递增,在()a3,0上单调递减.若a >0时,f (x )在()-∞,0和()a3,+∞上单调递增,在()0,a3上单调递减.小结:求导后导函数为含参的二次函数,但是可以直接求出导函数的零点,只需要判断两根的大小,再根据“大于取两边,小于取中间”,得到f ′(x )>0,则f (x )在这个区间内单调递增;若f ′(x )<0,则f (x )在这个区间内单调递减即可.[例5](2018年高考全国卷Ⅰ节选)已知函数f (x )=1x -x +a ln x .讨论f (x )的单调性.分析:在对f (x )进行求导后,发现求导后的二次函数的开口方向已经确定,但是是否有零点还不能判断,因此分类的标准应该是对判别式进行讨论,进而再对可能存在的零点进行讨论,做到不重不漏.解:f (x )的定义域为()0,+∞,f '(x )=-1x2-1+a x =-x 2-ax +1x 2.(1)若a ≤2,则f '(x )≤0,所以f (x )在()0,+∞单调递减.(2)若a >2,令f '(x )=0,得x =a -a 2-42或x =a +a 2-42.当x ∈()0,a -a 2-42∪()a +a 2-42,+∞时,f '(x )<0;当x ∈()0,a -a 2-42,a +a 2-42时,f ′(x )<0.所以f (x )在()0,a -a 2-42,()a +a 2-42,+∞单调递减,在()0,a -a 2-42,a +a 2-42单调递增.小结:求导后导函数为含参的二次函数,但是不能判断导函数是否有零点,则需要根据判别式的正负从而得到“存在零点”和“不存在零点”的分类标准,当判别式大于零时,还要判断是否可以比较两零点的大小,以及零点与定义域的关系,做到分类有序、不重不漏[2].通过以上例题发现,利用导数研究函数的单调性是一个有效的工具.利用导数求含参函数单调性的分类标准为:(1)求导后若导函数为含参数的一次函数,可以根据含参数的一次函数进行分类讨论.(2)求导后若导函数为含参数的二次函数,若求导后不能判断开口方向的,分类的标准是先讨论二次函数的开口方向,再讨论是否存在零点;若求导后导函数可以直接因式分解得到零点,则分类标准是直接对零点进行分类讨论;若求导后导函数确定了开口方向,但是不能判断是否有零点,则分类标准是直接对判别式进行分类讨论[3].而在分类时要做到不重不漏.[参考文献][1]祝敏芝.利用导数研究函数的单调性问题[J ].中学数学教学参考,2020(Z1):130-133.[2]王历权,范美卿,金雷.利用导数研究函数的单调性问题[J ].中学数学教学参考,2019(7):36-39.[3]陈达辉.利用导数研究函数单调性的几种类型[J ].数学学习与研究,2019(8):97.(责任编辑陈昕)数学·解题研究。
利用导数讨论含参函数的单调性

利用导数讨论含参函数的单调性讨论函数的单调性是研究函数问题的基础,对于函数的最值、极值、零点等性质的研究,都是以函数的单调性为基础展开的。
在此,主要讨论含参函数单调性的讨论方法。
函数的单调性由导函数的正负决定,讨论函数的单调性关键在于研究导函数的正负。
含参函数导函数正负的确定最大的困难在于参数的影响,如何对参数进行分类讨论是问题的关键。
在此,我们将提出三种方法。
一.分离参数、数形结合函数求导后,导函数中的参数可以分离,形如:m x g x f -=)()('的形式,若)(x g 有最小值,则分min )(x g m ≤,min )(x g m >两种情况进行分类讨论。
(1)当min )(x g m ≤时,0)()('≥-=m x g x f ;(2)当min )(x g m >时,若0)()('=-=m x g x f 有一个解,且)(x g 单调,设解为0x ,则0x 将定义域分为两个区间,讨论函数的单调性。
若)(x g 有最大值,则分max )(x g m ≥,max )(x g m <两种情况进行分类讨论。
1.(2012年全国卷文科21题) 设函数2)(--=ax e x f x . (1)求)(x f 的单调区间;解:函数)(x f 的定义域为()+∞∞-,,a e x f x -=)(',①若0≤a ,则0)('>x f ,)(x f 在()+∞∞-,单调递增; ②若0>a ,则由0)('=x f 得a x ln =,当()a x ln ,∞-∈时,0)('<x f ,当()+∞∈,ln a x 时,0)('>x f ; 所以)(x f 的单调减区间是()a ln ,∞-,单调增区间是()+∞,ln a ; 2.(2016年山东文科20题)设x a ax x x x f )12(ln )(2-+-=,R a ∈. (1)令)()('x f x g =,求)(x g 的单调区间. 解:函数)(x f 的定义域为()+∞,0,1221ln )()('-+-+==a ax x x f x g ,a xx g 21)('-=(1)若0≤a ,则0)('>x g ,)(x g 在()+∞,0单调递增;(2)若0>a ,则由0)('=x g 得ax 21=,当⎪⎭⎫ ⎝⎛∈a x 21,0时,0)('>x g ,当⎪⎭⎫ ⎝⎛+∞∈,21a x 时,0)('<x g ,所以)(x f 在⎪⎭⎫ ⎝⎛a 21,0单调递增,在⎪⎭⎫ ⎝⎛+∞,21a 单调递减.3.(2015年北京卷文科19题)设函数x k x x f ln 2)(2-=.(1)求)(x f 的单调区间和极值;解:函数)(x f 的定义域为()+∞,0,xkx x k x x f -=-=2')(,①若0≤k ,则0)('>x f ,)(x f 在()+∞,0单调递增; ②若0>k ,则由0)('=x f 得k x =,当()k x ,0∈时,0)('<x f ,当()+∞∈,k x 时,0)('>x f所以)(x f 的单调减区间是()k ,0,单调增区间是()+∞,k .4.(2015年全国二卷文科21题) 已知函数)1(ln )(x a x x f -+=. (1)讨论)(x f 的单调性;解:函数)(x f 的定义域为()+∞,0,xaxa x x f -=-=11)(', ①若0≤a ,则0)('>x f ,)(x f 在()+∞,0单调递增;②若0>a ,则由0)('=x f 得ax 1=,当⎪⎭⎫ ⎝⎛∈a x 1,0时,0)('>x f ,当⎪⎭⎫ ⎝⎛∈0,1a x 时,0)('<x f ;所以)(x f 在⎪⎭⎫ ⎝⎛a 1,0单调递增,在⎪⎭⎫ ⎝⎛0,1a单调递减; 5.(2016年四川卷文科21题) 设函数x a ax x f ln )(2--=. (1)讨论)(x f 的单调性; 解:函数)(x f 的定义域为()+∞,0,⎪⎭⎫⎝⎛-=-=-=22'121212)(x a x x ax x ax x f ,①若0≤a ,则0)('<x f ,)(x f 在()+∞,0单调递减;②若0>a ,则由0)('=x f 得ax 21=,当⎪⎪⎭⎫ ⎝⎛∈a x 21,0时,0)('<x f ,当⎪⎪⎭⎫ ⎝⎛+∞∈,21a x 时,0)('>x f ;所以)(x f 在⎪⎪⎭⎫ ⎝⎛a 21,0单调递减,在⎪⎪⎭⎫ ⎝⎛+∞,21a 单调递增; 若0)()('=-=m x g x f 有两个解,则可以将定义域分为三个区域进行讨论。
导数的基本概念及性质应用

导数的基本概念及性质应用Document number:NOCG-YUNOO-BUYTT-UU986-1986UT导数的基本概念及性质应用考点:1、掌握导数的基本概念及运算公式,并能灵活应用公式求解 2、能运用导数求解单调区间及极值、最值3、理解并掌握极值及单调性的实质,并能灵活应用其性质解题。
能力:数形结合 方法:讲练结合新授课:一、 知识点总结:导数的基本概念与运算公式1、导数的概念函数y =)(x f 的导数)(x f ',就是当Δx →0时,函数的增量Δy 与自变量的增量Δx 的比x Δ yΔ的极限,即)(x f '=0x Δlim→xΔ yΔ=x Δlim→xΔf(x)-x) Δ(+x f说明:分子和分母中间的变量必须保持一致 2、导函数函数y =)(x f 在区间( a, b )内每一点的导数都存在,就说在区)(x f 间( a, b )内可导,其导数也是(a ,b )内的函数,叫做)(x f 的导函数,记作)(x f '或x y ',函数)(x f 的导函数)(x f '在0x x =时的函数值)(0x f ',就是)(x f 在0x 处的导数。
3、导数的几何意义设函数y =)(x f 在点0x 处可导,那么它在该点的导数等于函数所表示曲线在相应点),(00y x M 处的切线斜率。
4、求导数的方法 (1)基本求导公式0='c )()(1Q m mx x m m ∈='-x x cos )(sin =' x x sin )(cos -=' x x e e =')( a a a x x ln )(=' xx 1)(ln =' ax xa ln 1)(log ='(2)导数的四则运算v u v u '±'='±)( v u v u uv '+'=')()0()(2≠=''-'v v v u v u v u(3)复合函数的导数设)(x g u=在点x 处可导,y =在点)(x f 处可导,则复合函数)]([x g f 在点x 处可导,)()())(('''x u f x f x ϕϕ=导数性质:1、函数的单调性⑴设函数y =)(x f 在某个区间内可导,若)(x f '>0,则)(x f 为增函数;若)(x f '<0则为减函数。
14导数、利用导数研究函数的单调性(含答案)
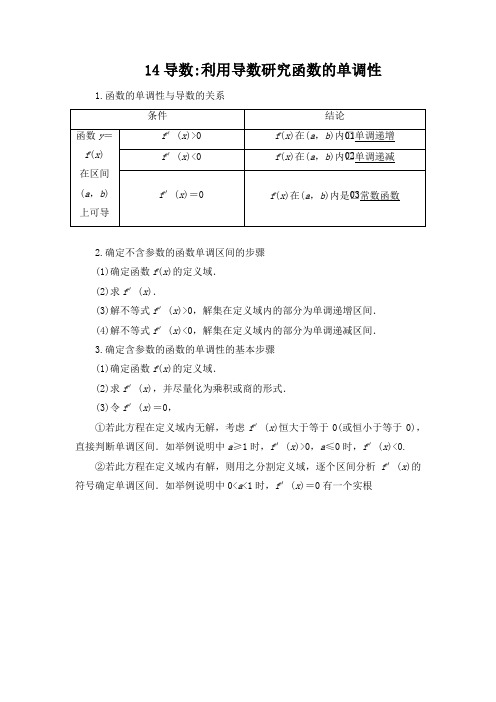
14导数:利用导数研究函数的单调性1.函数的单调性与导数的关系2.确定不含参数的函数单调区间的步骤(1)确定函数f(x)的定义域.(2)求f′(x).(3)解不等式f′(x)>0,解集在定义域内的部分为单调递增区间.(4)解不等式f′(x)<0,解集在定义域内的部分为单调递减区间.3.确定含参数的函数的单调性的基本步骤(1)确定函数f(x)的定义域.(2)求f′(x),并尽量化为乘积或商的形式.(3)令f′(x)=0,①若此方程在定义域内无解,考虑f′(x)恒大于等于0(或恒小于等于0),直接判断单调区间.如举例说明中a≥1时,f′(x)>0,a≤0时,f′(x)<0.②若此方程在定义域内有解,则用之分割定义域,逐个区间分析f′(x)的符号确定单调区间.如举例说明中0<a<1时,f′(x)=0有一个实根练习1.设f′(x)是函数f(x)的导函数,y=f′(x)的图象如图所示,则y=f(x)的图象最有可能的是( )答案 C解析由y=f′(x)的图象易得,当x<0或x>2时,f′(x)>0;当0<x<2时,f′(x)<0.所以函数y=f(x)在(-∞,0)和(2,+∞)上单调递增,在(0,2)上单调递减,故选C.2.f(x)=x3-6x2的单调递减区间为( )A.(0,4) B.(0,2)C.(4,+∞) D.(-∞,0)答案 A解析f′(x)=3x2-12x=3x(x-4),由f′(x)<0得0<x<4,所以f(x)的单调递减区间为(0,4).3.函数f(x)=(x-3)e x的单调递增区间是( )A.(-∞,2) B.(0,3)C.(1,4) D.(2,+∞)答案 D解析函数f(x)=(x-3)e x的导数为f′(x)=[(x-3)e x]′=e x+(x-3)e x =(x-2)e x.由函数导数与函数单调性的关系,得当f′(x)>0时,函数f(x)单调递增,此时由不等式f′(x)=(x-2)e x>0,解得x>2.4.函数f(x)=e x-e x,x∈R的单调递增区间是( )A.(0,+∞) B.(-∞,0)C.(-∞,1) D.(1,+∞)答案 D解析 依题意得f ′(x )=e x -e.由函数导数与函数单调性的关系,得当f ′(x )>0时,函数f (x )单调递增,此时由不等式f ′(x )=e x -e>0,解得x >1.5.函数f (x )=3xx 2+1的单调递增区间是___________. 解析 函数f (x )的定义域为R ,f ′(x )=31-x 2x 2+12=31-x 1+xx 2+12.要使f ′(x )>0,只需(1-x )(1+x )>0,解得x ∈(-1,1).6.已知函数f (x )=x 4+a x -ln x -32,其中a ∈R ,且曲线y =f (x )在点(1,f (1))处的切线垂直于直线y =12x .(1)求a 的值;(2)求函数f (x )的单调区间.解 (1)对f (x )求导得f ′(x )=14-a x 2-1x ,由f (x )在点(1,f (1))处的切线垂直于直线y =12x ,知f ′(1)=-34-a =-2,解得a =54.(2)由(1)知f (x )=x 4+54x -ln x -32(x >0).则f ′(x )=x 2-4x -54x 2.令f ′(x )=0,解得x =-1或x =5. 但-1∉(0,+∞),舍去. 当x ∈(0,5)时,f ′(x )<0; 当x ∈(5,+∞)时,f ′(x )>0.∴f (x )的增区间为(5,+∞),减区间为(0,5).7.已知定义在区间(-π,π)上的函数f (x )=x sin x +cos x ,则f (x )的单调递增区间是.答案 ⎝ ⎛⎭⎪⎫-π,-π2,⎝ ⎛⎭⎪⎫0,π2解析 因为f (x )=x sin x +cos x ,所以f ′(x )=sin x +x cos x -sin x =x cos x . 令f ′(x )>0,得x cos x >0. 又因为-π<x <π,所以-π<x <-π2或0<x <π2, 所以f (x )的单调递增区间是⎝ ⎛⎭⎪⎫-π,-π2,⎝ ⎛⎭⎪⎫0,π2.8.讨论函数f (x )=(a -1)ln x +ax 2+1的单调性. 解 f (x )的定义域为(0,+∞),f ′(x )=a -1x +2ax =2ax 2+a -1x .①当a ≥1时,f ′(x )>0, 故f (x )在(0,+∞)上单调递增;②当a ≤0时,f ′(x )<0,故f (x )在(0,+∞)上单调递减; ③当0<a <1时,令f ′(x )=0,解得x =1-a2a, 则当x ∈⎝ ⎛⎭⎪⎫0,1-a 2a 时,f ′(x )<0; 当x ∈⎝⎛⎭⎪⎫1-a2a ,+∞时,f ′(x )>0, 故f (x )在⎝ ⎛⎭⎪⎫0,1-a 2a 上单调递减, 在⎝⎛⎭⎪⎫1-a2a ,+∞上单调递增. 综上所述,当a ≥1时,f (x )在(0,+∞)上单调递增; 当a ≤0时,f (x )在(0,+∞)上单调递减; 当0<a <1时,f (x )在⎝ ⎛⎭⎪⎫0,1-a 2a 上单调递减, 在⎝ ⎛⎭⎪⎫1-a2a ,+∞上单调递增.9.已知函数f (x )=(x -1)e x -x 2,g (x )=a e x -2ax +a 2-10(a ∈R ).(1)求曲线y=f(x)在点(1,f(1))处的切线方程;(2)讨论函数h(x)=f(x)-g(x)(x>0)的单调性.解(1)由题意,得f′(x)=x e x-2x,则f′(1)=e-2.又f(1)=-1,故所求切线方程为y-(-1)=(e-2)(x-1),即y=(e-2)x+1-e.(2)由已知,得h(x)=f(x)-g(x)=(x-a-1)e x-x2+2ax-a2+10.此函数的定义域为(0,+∞).则h′(x)=e x+(x-a-1)e x-2x+2a=(x-a)(e x-2).①若a≤0,则x-a>0.当0<x<ln 2时,h′(x)<0,当x>ln 2时,h′(x)>0.所以h(x)在(0,ln 2)上单调递减,在(ln 2,+∞)上单调递增.②若0<a<ln 2,则当0<x<a或x>ln 2时,h′(x)>0.当a<x<ln 2时,h′(x)<0.所以h(x)在(0,a)上单调递增,在(a,ln 2)上单调递减,在(ln 2,+∞)上单调递增.③若a=ln 2,则h′(x)≥0,所以h(x)在(0,+∞)上单调递增.④若a>ln 2,则当0<x<ln 2或x>a时,h′(x)>0;当ln 2<x<a时,h′(x)<0.所以h(x)在(0,ln 2)上单调递增,在(ln 2,a)上单调递减,在(a,+∞)上单调递增.10.设函数f(x),g(x)分别是定义在R上的奇函数和偶函数,当x<0时,f′(x)g(x)+f(x)g′(x)>0,且g(3)=0,则不等式f(x)g(x)>0的解集是?解析∵f′(x)g(x)+f(x)g′(x)>0,即[f(x)g(x)]′>0.∴f(x)g(x)在(-∞,0)上单调递增,又f(x),g(x)分别是定义在R上的奇函数和偶函数,∴f(x)g(x)为奇函数,f(0)g(0)=0,∴f(x)g(x)在(0,+∞)上也是增函数.∵f(3)g(3)=0,∴f(-3)g(-3)=0.∴f(x)g(x)>0的解集为(-3,0)∪(3,+∞).11.已知函数f (x )=ln x ,g (x )=12ax 2+2x ,a ≠0.(1)若函数h (x )=f (x )-g (x )存在单调递减区间,求a 的取值范围; (2)若函数h (x )=f (x )-g (x )在[1,4]上单调递减,求a 的取值范围. 解 (1)h (x )=ln x -12ax 2-2x ,x ∈(0,+∞),所以h ′(x )=1x-ax -2,由于h (x )在(0,+∞)上存在单调递减区间, 所以当x ∈(0,+∞)时, 1x-ax -2<0有解,即a >1x 2-2x有解.设G (x )=1x 2-2x,所以只要a >G (x )min 即可.而G (x )=⎝ ⎛⎭⎪⎫1x -12-1,所以G (x )min =-1.所以a >-1. 又因为a ≠0,所以a 的取值范围为(-1,0)∪(0,+∞). (2)因为h (x )在[1,4]上单调递减, 所以当x ∈[1,4]时,h ′(x )=1x -ax -2≤0恒成立,即a ≥1x 2-2x 恒成立.由(1)知G (x )=1x 2-2x,所以a ≥G (x )max , 而G (x )=⎝ ⎛⎭⎪⎫1x -12-1,因为x ∈[1,4],所以1x ∈⎣⎢⎡⎦⎥⎤14,1,所以G (x )max =-716(此时x =4),所以a ≥-716,又因为a ≠0,所以a 的取值范围是 ⎣⎢⎡⎭⎪⎫-716,0∪(0,+∞). 12.已知函数f (x )的导函数f ′(x )=ax 2+bx +c 的图象如图所示,则f (x )的图象可能是( )答案 D解析 当x <0时,由导函数f ′(x )=ax 2+bx +c <0,知相应的函数f (x )在该区间内单调递减;当x >0时,由导函数f ′(x )=ax 2+bx +c 的图象可知,导函数在区间(0,x 1)内的值是大于0的,则在此区间内函数f (x )单调递增.只有D 项符合题意.13.已知函数f (x )=x 3+ax ,则“a >0”是“f (x )在R 上单调递增”的( ) A .充分不必要条件 B .必要不充分条件 C .充要条件 D .既不充分也不必要条件答案 A解析 当a ≥0时,f ′(x )=3x 2+a ≥0,f (x )在R 上单调递增,“a >0”是“f (x )在R 上单调递增”的充分不必要条件.故选A.14.已知函数f (x )=3x +2cos x ,若a =f (32),b =f (2),c =f (log 27),则a ,b ,c 的大小关系是( )A .a <b <cB .c <a <bC .b <a <cD .b <c <a答案 D解析 ∵f (x )=3x +2cos x 的定义域为R ,f ′(x )=3-2sin x >0,∴f (x )为R 上的单调递增函数.又y =log 2x 为(0,+∞)上的单调递增函数,∴2=log 24<log 27<log 28=3.∵y =3x 为R 上的单调递增函数,∴32>31=3,∴2<log 27<3 2.∴f (2)<f (log 27)<f (32),即b <c <a .15.若函数f (x )=e x -(a -1)x +1在(0,1)上单调递减,则a 的取值范围为( )A.(e+1,+∞) B.[e+1,+∞)C.(e-1,+∞) D.[e-1,+∞)答案 B解析由f(x)=e x-(a-1)x+1,得f′(x)=e x-a+1.因为函数f(x)=e x -(a-1)x+1在(0,1)上单调递减,所以f′(x)=e x-a+1≤0在(0,1)上恒成立,即a≥e x+1在(0,1)上恒成立,令g(x)=e x+1,x∈(0,1),则g(x)在(0,1)上单调递增,所以g(x)<g(1)=e+1.所以a≥e+1.所以实数a的取值范围为[e+1,+∞).故选B.16.已知定义在(0,+∞)上的函数f(x)满足xf′(x)-f(x)<0,其中f′(x)是函数f(x)的导函数.若2f(m-2019)>(m-2019)f(2),则实数m的取值范围为( )A.(0,2019) B.(2019,+∞)C.(2021,+∞) D.(2019,2021)答案 D解析令h(x)=f xx,x∈(0,+∞),则h′(x)=xf′x-f xx2.∵xf′(x)-f(x)<0,∴h′(x)<0,∴函数h(x)在(0,+∞)上单调递减,∵2f(m-2019)>(m-2019)f(2),m-2019>0,∴f m-2019m-2019>f22,即h(m-2019)>h(2).∴m-2019<2且m-2019>0,解得2019<m<2021.∴实数m的取值范围为(2019,2021).17.已知f(x)=1+ln x2ax(a≠0,且a为常数),求f(x)的单调区间.解因为f(x)=1+ln x2ax(a≠0,且a为常数),所以f′(x)=-2a ln x2ax2=-ln x2ax2,x>0.所以①若a>0,当0<x<1时,f′(x)>0;当x>1时,f′(x)<0.即a>0时,函数f(x)的单调递增区间为(0,1),单调递减区间为(1,+∞).②若a<0,当0<x<1时,f′(x)<0;当x>1时,f′(x)>0.即a <0时,函数f (x )的单调递增区间为(1,+∞),单调递减区间为(0,1). 18.已知函数f (x )=x 3+ax 2+2x -1.(1)若函数f (x )在区间[1,3]上单调递增,求实数a 的取值范围; (2)若函数f (x )在区间[-2,-1]上单调递减,求实数a 的取值范围. 解 由f (x )=x 3+ax 2+2x -1,得f ′(x )=3x 2+2ax +2.(1)因为函数f (x )在区间[1,3]上单调递增,所以f ′(x )≥0在[1,3]上恒成立.即a ≥-3x 2-22x 在[1,3]上恒成立.令g (x )=-3x 2-22x ,则g ′(x )=-3x 2+22x 2,当x ∈[1,3]时,g ′(x )<0,所以g (x )在[1,3]上单调递减,所以g (x )max =g (1)=-52,所以a ≥-52.(2)因为函数f (x )在区间[-2,-1]上单调递减,所以f ′(x )≤0在[-2,-1]上恒成立,即a ≥-3x 2-22x 在[-2,-1]上恒成立,由(1)易知,g (x )=-3x 2-22x 在[-2,-1]上单调递减,所以a ≥g (-2),即a ≥72.。
专题02 利用导数研究函数单调性问题(含参数讨论) (解析版)

导数及其应用专题二:利用导数研究函数单调性问题(含参数讨论)一、知识储备往往首先考虑是否导数恒大于零或恒小于零,再考虑可能大于零小于零的情况。
常与含参数的一元二次不等式的解法有关,首先讨论二次项系数,再就是根的大小或判别式,能表示出对应一元二次方程的根时讨论根的大小、端点实数的大小,不能时讨论判别式。
二、例题讲解1.(2022·山东莱州一中高三开学考试)已知函数()1ln f x x a x =--(其中a 为参数). (1)求函数()f x 的单调区间; 【答案】(1)答案见解析; 【分析】(1)求导可得()af x x x'-=,分0a ≤和0a >进行讨论即可; 【详解】 (1)()af x x x'-=,(0,)x ∈+∞, 当0a ≤时,()0f x '>,()f x ∴在(0,)+∞上递增, 当0a >时,令()0f x '=,得x a =,()0,x a ∈时,()f x 单调递减, (,)x a ∈+∞时,()f x 单调递增;综上:0a ≤时,()f x 在(0,)+∞上递增,无减区间,当0a >时,()f x 的单调递减区间为()0,a ,单调递增区间为(,)a +∞;2.(2022·宁夏银川一中高三月考(文))已知函数2()(2)ln f x x a x a x =---(a R ∈) (1)求函数()y f x =的单调区间; 【分析】(1)先求出函数的定义域,然后对函数求导,分0a ≤和0a >两种情况判断导数的正负,从而可求得函数的单调区间, 【详解】(1)函数()f x 的定义域是(0,)+∞,(1)(2)()2(2)a x x a f x x a x x'+-=---= 当0a ≤时,()0f x '>对任意(0,)x ∈+∞恒成立, 所以,函数()f x 在区间(0,)+∞单调递增; 当0a >时,由()0f x '>得2a x >,由()0f x '<,得02ax <<, 所以,函数在区间,2a ⎛⎫+∞ ⎪⎝⎭上单调递增,在区间0,2a ⎛⎫ ⎪⎝⎭上单调递减;综上:0a ≤时,()f x 的单调增区间为(0,)+∞,无单调减区间. 0a >时,()f x 的单调增区间为,2a ⎛⎫+∞ ⎪,单调减区间为0,2a ⎛⎫ ⎪.3.(2022·广西高三开学考试(理))函数()322f x x x ax =++,(1)讨论()f x 的单调性;【答案】(1)答案不唯一,具体见解析; 【分析】(1)求得()'f x ,对a 进行分类讨论,由此求得()f x 的单调性.【详解】(1)()'234f x x x a =++,1612a ∆=-①若43a ≥,则0∆≤,()'0f x ≥;()f x 单调递增; ②若43a <则0∆>,当x <x >()'0f x >,()f x 单调递增;x <<,()'0f x <,()f x 单调递减; 【点睛】若函数的导函数含有参数,则需要对参数进行分类讨论,分类讨论要做到不重不漏.三、实战练习1.(2022·全国高三月考)设函数()()()21ln 11f x x x ax x a =++--+-,a R ∈.(1)求()f x '的单调区间 【答案】(1)答案见解析; 【分析】(1)先对函数()f x 进行求导,构造函数再分0a ≤,0a >两种情况进行讨论,利用导数研究函数的单调性即可求解; 【详解】(1)由题意可得()f x 的定义域为{}1x x >-,()()ln 12f x x ax +'=-. 令()()()ln 121g x x ax x =+->-, 则()1122211a axg x a x x --=-='++. 当0a ≤时,当()1,x ∈-+∞时,()0g x '>,函数()g x 单调递增; 当0a >时,当11,12x a ⎛⎫∈-- ⎪⎝⎭时,()0g x '>,函数()g x 单调递增;当11,2x a ⎛⎫∈-+∞ ⎪⎝⎭时,()0g x '<,函数()g x 单调递减,所以当0a ≤时,()f x '的单调递增区间为()1,-+∞; 当0a >时,()f x '的单调递增区间为11,12a ⎛⎫-- ⎪⎝⎭,单调递减区间为11,2a ⎛⎫-+∞ ⎪⎝⎭.2.(2022·浙江舟山中学高三月考)已知函数()22ln (R)f x x x a x a =-+∈(1)当0a >时,求函数()f x 的单调区间; 【答案】(1)当12a ≥时,函数在()0+∞,递增;当102a <<时,函数在()10,x 递增,()12,x x 递减,()2,x +∞递增其中12x x =; 【分析】(1)求()f x ',令()0f x '=可得2220x x a -+=,分别讨论0∆≤和0∆>时,求不等式()0f x '>,()0f x '<的解集,即可求解;【详解】(1)()22ln (R)f x x x a x a =-+∈定义域为()0,∞+, ()22222a x x af x x x x-+'=-+=()0x >, 令()0f x '=可得2220x x a -+=, 当480a ∆=-≤即12a ≥时,()0f x '≥对于()0,x ∈+∞恒成立, 所以()f x 在()0,∞+上单调递增,当480a ∆=->即102a <<时,由2220x x a -+=可得:x =,由()0f x '>可得:0x <<或x >由()0f x '<x <<所以()f x 在⎛ ⎝⎭和⎫+∞⎪⎪⎝⎭上单调递增,在⎝⎭上单调递减, 综上所述:当12a ≥时,()f x 的单调递增区间为()0,∞+;当102a <<时,()f x 的单调递增区间为⎛ ⎝⎭和⎫+∞⎪⎪⎝⎭单调递减区间为⎝⎭. 3.(2022·山东济宁一中)已知函数()ln f x x a x =-,a ∈R . (1)求函数()f x 的单调区间; 【答案】(1)答案见解析; 【分析】(1)对函数求导,进而讨论a 的范围,最后得到函数的单调区间; 【详解】(1)函数()f x 的定义域为{}0x x >,()1a x a f x x x'-=-=0a ≤时,()0f x '>恒成立,函数()f x 在()0,∞+上单调递增;0a >时,令()0f x '=,得x a =.当0x a <<时,()0f x '<,函数()f x 为减函数; 当x a >时,()0f x '>,函数()f x 为增函数.综上所述,当0a ≤时,函数()f x 的单调递增区间为()0,∞+,无单调递减区间; 当0a >时,函数()x 的单调递减区间为()0,a ,单调递增区间为(),a +∞. 4.(2022·仪征市精诚高级中学高三月考)已知函数()()1n f x x ax a =-∈R . (1)讨论函数()f x 的单调性;【答案】(1)答案不唯一,具体见解析;(2)证明见解析. 【分析】(1)求出函数导数,讨论a 的范围结合导数即可得出单调性; 【详解】 (1)11()(0)axf x a x xx-'=-=> 当0a ≤时,()0f x '>,所以()f x 在(0,)+∞上单调递增; 当0a >时,令()0f x '=,得到1x a=, 所以当10,x a ⎛⎫∈ ⎪⎝⎭时,()0f x '>,()f x 单调递增, 当1,x a ⎛⎫∈+∞ ⎪⎝⎭时,()0f x '<,()f x 单调递减.综上所述,当0a ≤时,()f x 在(0,)+∞上单调递增;当0a >时,()f x 在10,a ⎛⎫ ⎪⎝⎭上单调递增,在1,a ⎛⎫+∞ ⎪⎝⎭上单调递减.5.(2022·嘉峪关市第一中学高三模拟预测(理))已知函数()21xf x e ax =--,()()2ln 1g x a x =+,a R ∈.(1)求()f x 的单调区间; 【答案】(1)答案见解析; 【分析】(1)求出函数()f x 的导函数()f x ',按a 分类解不等式()0f x '<、()0f x '>即得;【详解】(1)对函数()21x f x e ax =--求导得,()2xf x e a '=-,当0a ≤时,()0f x '>,()f x 在R 上为增函数,当0a >时,由()20xf x e a '=-=,解得:()ln 2x a =,而()f x '在R 上单调递增,于是得当(,ln(2))∈-∞x a 时,()0f x '<,()f x 在(,ln(2))a -∞上为减函数, 当()()ln 2,x a ∈+∞时,()0f x '>,()f x 在()()ln 2,a +∞上为增函数, 所以,当0a ≤时,()f x 的单调递增区间为R ,当0a >时,()f x 的单调递减区间是(,ln(2))a -∞,单调递增区间是()()ln 2,a +∞;6.(2022·榆林市第十中学高三月考(文))已知函数()2ln f x ax x x =--,0a ≠.(1)试讨论函数()f x 的单调性;【答案】(1)当0a <时,函数()f x 在()0,∞+上单调递减;当0a >时,()f x 在⎛ ⎝⎭上单调递减,在⎫+∞⎪⎪⎝⎭上单调递增. 【分析】(1)求出导函数()212121ax x f x ax x x -'-=--=,设()221g x ax x =--,对a 分类讨论:当0a <时,函数()f x在()0,∞+上单调递减;当0a >时,()f x 在⎛ ⎝⎭上单调递减,在⎫+∞⎪⎪⎝⎭上单调递增. 【详解】函数()2ln f x ax x x =--的定义域为()0+∞,. (1)()212121ax x f x ax x x-'-=--=,设()221g x ax x =--当0a <时,因为函数()g x 图象的对称轴为104x a=<,()01g =-. 所以当0x >时,()0g x <,()0f x '<,函数()f x 在()0,∞+上单调递减;当0a >时,令()0g x =.得1x =2x =当20x x <<时,()0<g x ,()0f x '<,当2x x >时,()0>g x ,()0f x '>.所以函数()f x 在⎛ ⎝⎭上单调递减,在⎫+∞⎪⎪⎝⎭上单调递增. 7.(2022·嘉峪关市第一中学高三三模(理))设函数()2ln f x ax a x =--,其中a ∈R .(1)讨论()f x 的单调性; 【答案】(1)答案见解析; 【分析】(1)求导,当0a ≤时,可得()0f x '<,()f x 为单调递减函数;当0a >时,令()0f x '=,可得极值点,分别讨论在⎛ ⎝和+⎫∞⎪⎭上,()'f x 的正负,可得()f x 的单调区间,即可得答案.【详解】(1)()()212120.ax f x ax x x x-'=-=>当0a ≤时,()0f x '<,()f x 在()0,∞+内单调递减. 当0a >时,由()0f x '=,有x =此时,当x ∈⎛⎝时,()0f x '<,()f x 单调递减;当x ∈+⎫∞⎪⎭时,()0f x '>,()f x 单调递增. 综上:当0a ≤时,()f x 在()0,∞+内单调递减,当0a >时,()f x 在⎛ ⎝内单调递减,在+⎫∞⎪⎭单调递增. 8.(2022·贵州省思南中学高三月考(文))设函数()22ln 1f x x mx =-+.(1)讨论函数()f x 的单调性; 【答案】(1)函数()f x 的单调性见解析; 【分析】(1)求出函数()f x 的定义域及导数,再分类讨论导数值为正、为负的x 取值区间即得; 【详解】(1)依题意,函数()f x 定义域为(0,)+∞,()222(1)2mx f x mx x x-'=-=,当0m ≤时,()0f x '>,()f x 在(0,)+∞上单调递增,当0m >时,由()0f x '=得x =,当0x <<()0f x '>,当x >时,()0f x '<,于是得()f x 在上单调递增,在)+∞上单调递减,所以,当0m ≤时,()f x 在(0,)+∞上单调递增,当0m >时,()f x 在上单调递增,在)+∞上单调递减;9.(2022·河南(理))已知函数()()2ln f x x m x x =--(8m ≥-,且0m ≠).(1)讨论函数()f x 的单调性;【答案】(1)答案不唯一,具体见解析; 【分析】(1)求导得到221()mx mx f x x --'=-,转化为二次函数2()21g x mx mx =--的正负进行讨论,分0∆≤,0∆>两种情况讨论,即得解; 【详解】(1)函数()f x 的定义域为()0,∞+,2121()(21)mx mx f x m x x x--'=--=-, 令2()21g x mx mx =--,()g x 为二次函数,28m m ∆=+, ①当80m -≤<时,0∆≤,()0g x ≤, 所以()0f x '≥,故()f x 在()0,∞+单调递增; ②当0m >时,0∆>, 令()0g x =,得1x =2x =,显然120x x <<,所以当()20,x x ∈,()0g x <, 所以()0f x '>,故()f x 单调递增;当()2,x x ∈+∞时,()0g x >, 所以()0f x '<,()f x 单调递减.综上,当0m >时,()f x 在⎛ ⎝⎭单调递增,在⎫+∞⎪⎪⎝⎭上单调递减; 当80m -≤<时,()f x 在()0,∞+单调递增.10.(2022·河南高三月考(文))已知函数()()2ln f x x m x x =--(8m ≥-,且0m ≠).(1)讨论函数()f x 的单调性;【答案】(1)答案见解析;(2)证明见解析. 【分析】(1)求导2121()(21)mx mx f x m x x x --'=--=-,令2()21g x mx mx =--,然后由0∆≤,0∆>讨论求解;【详解】(1)函数()f x 的定义域为()0,∞+,2121()(21)mx mx f x m x x x--'=--=-, 令2()21g x mx mx =--,()g x 为二次函数,28m m ∆=+, ①当80m -≤<时,0∆≤,()0g x ≤, 所以()0f x '≥,故()f x 在()0,∞+单调递增; ②当0m >时,0∆>,令()0g x =,得1x =2x =,显然120x x <<,所以当()20,x x ∈,()0g x <, 所以()0f x '>,()f x 单调递增; 当()2,x x ∈+∞时,()0g x >, 所以()0f x '<,()f x 单调递减.综上,当80m -≤<时, ()f x 在()0,∞+单调递增;当0m >时,()f x 在⎛ ⎝⎭单调递增,在⎫+∞⎪⎪⎝⎭上单调递减. 11.(2022·湖南高三模拟预测)设函数1()ln ,()3a f x x g x ax x-=+=-. (1)求函数()()()x f x g x ϕ=+的单调递增区间; 【答案】(1)答案见解析;(2)存在符合题意的整数λ,其最小值为0.【分析】(1)求出函数的导数,通过讨论a 的范围,求出函数的单调区间即可;【详解】解:(1)函数()ϕx 的定义域为()0,∞+,函数()ϕx 的导数2(1)(1)()x ax a x x ϕ'++-=, 当0a <时,()ϕx 在10,a a -⎛⎫ ⎪⎝⎭上单调递增,在1,a a -⎛⎫+∞ ⎪⎝⎭上单调递减 当01a 时,()ϕx 在R +上单调递增.当1a >时,()ϕx 在10,a a -⎛⎫ ⎪⎝⎭上单调递减,在1,a a -⎛⎫+∞ ⎪⎝⎭上单调递增. 综上可知,当0a <时,()ϕx 的单调递增区间是10,a a -⎛⎫ ⎪⎝⎭;当01a 时,()ϕx 的单调递增区间是(0,)+∞;当1a >时,()ϕx 的单调递增区间是1,a a -⎛⎫+∞ ⎪⎝⎭. 12.(2022·安徽高三月考(文))已知函数21()ln 2f x x a x =-. (1)讨论()f x 的单调性; 【答案】(1)答案不唯一,具体见解析;(2)12a =. 【分析】 (1)求导函数()'f x ,分类讨论确定()'f x 的正负,得单调区间;【详解】解:(1)由题意,可得0x >且2 ()a x a f x x x x-'=-= ①若0a ≤,()0f x '>恒成立,则()f x 在(0,)+∞上是增函数②0a >,则2()a x a f x x x x -==='-所以当x ∈时,()0f x '<,当)x ∈+∞时,()0f x '>则()f x 在上是减函数,在)+∞上是增函数综上所述,若0a ≤,()y f x =在(0,)+∞上是增函数若0a >,()y f x =在上是减函数,在)+∞上是增函数13.(2022·湖北武汉·高三月考)已知函数2()ln (1),2a f x x x a x a R =+-+∈ (1)讨论函数()f x 的单调区间;【答案】(1)答案见解析;【分析】(1)求得(1)(1)()x ax f x x '--=,分0a ≤,01a <<,1a =和1a >四种情况讨论,结合导数的符号,即可求解; 【详解】(1)由题意,函数2()ln (1)2a f x x x a x =+-+的定义域为(0,)+∞, 且21(1)1(1)(1)()(1)ax a x x ax f x ax a x x x-++--=+-+==', ①当0a ≤时,令()0f x '>,解得01x <<,令()0f x '<,解得1x >,所以()f x 在(0,1)上单调递增,在(1,)+∞上单调递减;②当01a <<时,令()0f x '>,解得01x <<或1x a>, 令()0f x '<,解得11x a <<, 所以()f x 在(0,1),1,a ⎛⎫+∞ ⎪⎝⎭上单调递增,在11,a ⎛⎫ ⎪⎝⎭上单调递减; ③当1a =时,则()0f x '≥,所以在(0,)+∞上()f x 单调递增,④当1a >时,令()0f x '>,解得10x a<<或1x >, 令()0f x '<,解得11x a <<, 所以()f x 在10,a ⎛⎫ ⎪⎝⎭,(1,)+∞上单调递增,在1,1a ⎛⎫ ⎪⎝⎭上单调递减; 综上,当0a ≤时,()f x 在(0,1)上单调递增,在(1,)+∞上单调递减;当01a <<时,()f x 在(0,1),1,a ⎛⎫+∞ ⎪⎝⎭上单调递增,在11,a ⎛⎫ ⎪⎝⎭上单调递减;当1a =时,()f x 在(0,)+∞上单调递增;当1a >时,()f x 在10,a ⎛⎫ ⎪⎝⎭,(1,)+∞上单调递增,在1,1a ⎛⎫ ⎪⎝⎭上单调递减; 14.(2022·双峰县第一中学高三开学考试)已知函数()2()1e x f x x ax =-+.(1)讨论()f x 的单调性;【答案】(1)当0a =时,()f x 在R 上单调递增;当0a <时,()f x 在(),1a -∞-和(1,)-+∞上单调递增,在()1,1a --上单调递减;当0a >时,()f x 在(),1-∞-和(1,)a -+∞上单调递增,在()1,1a --上单调递减;【分析】(1)先对函数求导,然后结合导数与单调性的关系,讨论0a =,0a >和0a <情况下,导数的正负,即可得到()f x 的单调性;【详解】(1)函数()2()1e x f x x ax =-+,求导()()()()21e 11e 2x x f x x a x a x a x '⎡⎤+=⎣+-⎦=-+-+由()0f x '=,得11x a =-,21x =-①当0a =时,()()21e 0x f x x '+≥=,()f x ∴在R 上单调递增;②当0a <时, 在(),1x a ∈-∞-有()0f x '>,故()f x 单调递增;在()1,1x a ∈--有()0f x '<,故()f x 单调递减;在(1,)x ∈-+∞有()0f x '>,故()f x 单调递增;③当0a >时, 在(),1x ∈-∞-有()0f x '>,故()f x 单调递增;在()1,a 1x ∈--有()0f x '<,故()f x 单调递减;在(1,)x a ∈-+∞有()0f x '>,故()f x 单调递增;综上所述,当0a =时,()f x 在R 上单调递增;当0a <时,()f x 在(),1a -∞-和(1,)-+∞上单调递增,在()1,1a --上单调递减;当0a >时,()f x 在(),1-∞-和(1,)a -+∞上单调递增,在()1,1a --上单调递减;。
高考数学一轮复习考点知识专题讲解18---利用导数解决函数的单调性问题

在(a,b)上的任何子区间内都不恒为零.
一、思考辨析(正确的打“√”,错误的打“×”) (1)若函数 f(x)在(a,b)内单调递增,那么一定有 f′(x)>0.( ) (2)如果函数 f(x)在某个区间内恒有 f′(x)=0,则 f(x)在此区间内没有单调性.( ) (3)在(a,b)内 f′(x)≤0 且 f′(x)=0 的根有有限个,则 f(x)在(a,b)内是减函数.( ) [答案] (1)× (2)√ (3)√
考点 2 含参数函数的单调性
研究含参数函数的单调性时,需注意依据参数取值对不等式解集的影响进行分类讨论. (1)讨论分以下四个方面
①二次项系数讨论,②根的有无讨论,③根的大小讨论,
பைடு நூலகம்
④根在不在定义域内讨论.
(2)讨论时要根据上面四种情况,找准参数讨论的分类.
(3)讨论完必须写综述. 已知函数 f(x)=12x2-2a ln x+(a-2)x,当 a<0 时,讨论函数 f(x)的单调性.
-4-/8
(3)函数在某个区间存在单调区间可转化为不等式有解问题.
已知函数 f(x)=ln x,g(x)=12ax2+2x(a≠0).
(1)若函数 h(x)=f(x)-g(x)存在单调递减区间,求 a 的取值范围;
(2)若函数 h(x)=f(x)-g(x)在[1,4]上单调递减,求 a 的取值范围. [解] (1)h(x)=ln x-12ax2-2x,x∈(0,+∞),
考点 4 利用导数比较大小或解不等式
用导数比较大小或解不等式,常常要构造新函数,把比较大小或求解不等式的问题转化
为利用导数研究函数单调性的问题,再由单调性比较大小或解不等式.
常见构造的辅助函数形式有: (1)f(x)>g(x)→F(x)=f(x)-g(x); (2)xf′(x)+f(x)→[xf(x)]′;
利用导数研究函数的单调性专题

利用导数研究函数的单调性1.函数的单调性与导数的关系函数y=f(x)在某个区间内可导,则:(1)若f′(x)>0,则f(x)在这个区间内单调递增;(2)若f′(x)<0,则f(x)在这个区间内单调递减;(3)若f′(x)=0,则f(x)在这个区间内是常数函数.2.函数的极值与导数f′(x0)=0x0附近的左侧f′(x)<0,右侧条件x0附近的左侧f′(x)>0,右侧f′(x)<0f′(x)>0图象形如山峰形如山谷极值f(x0)为极大值f(x0)为极小值极值点x0为极大值点x0为极小值点3.函数的最值与导数(1)函数f(x)在[a,b]上有最值的条件如果在区间[a,b]上函数y=f(x)的图象是一条连续不断的曲线,那么它必有最大值和最小值.(2)求y=f(x)在[a,b]上的最大(小)值的步骤①求函数y=f(x)在(a,b)内的极值;②将函数y=f(x)的各极值与端点处的函数值f(a),f(b)比较,其中最大的一个是最大值,最小的一个是最小值.1.判断下列结论正误(在括号内打“√”或“×”)(1)若函数f(x)在(a,b)内单调递增,那么一定有f′(x)>0.( )(2)如果函数f(x)在某个区间内恒有f′(x)=0,则f(x)在此区间内没有单调性.( )(3)函数的极大值一定大于其极小值.( )(4)对可导函数f(x),f′(x0)=0是x0为极值点的充要条件.( )(5)函数的最大值不一定是极大值,函数的最小值也不一定是极小值.( )2.(选修2-2P32A4 改编)如图是f(x)的导函数f′(x)的图象,则f(x)的极小值点的个数为( )A.1B.2C.3D.43.(选修2-2P32A5(4)改编)函数f(x)=2x-x ln x的极值是( )A.1eB.2eC.eD.e24.(2019·青岛月考)函数f(x)=cos x-x在(0,π)上的单调性是( )A.先增后减B.先减后增C.单调递增D.单调递减5.(2017·浙江卷)函数y=f(x)的导函数y=f′(x)的图象如图所示,则函数y=f(x)的图象可能是( )6.(2019·豫南九校考评)若函数f(x)=x(x-c)2在x=2处有极小值,则常数c的值为( )A.4B.2或6C.2D.6考点一 求函数的单调区间【例1】 已知函数f (x )=ax 3+x 2(a ∈R)在x =-43处取得极值.(1)确定a 的值;(2)若g (x )=f (x )e x,求函数g (x )的单调减区间. 【规律方法】 1.求函数单调区间的步骤:(1)确定函数f (x )的定义域;(2)求f ′(x );(3)在定义域内解不等式f ′(x )>0,得单调递增区间;(4)在定义域内解不等式f ′(x )<0,得单调递减区间.2.若所求函数的单调区间不止一个时,用“,”与“和”连接. 【训练1】 (1)已知函数f (x )=x ln x ,则f (x )( ) A.在(0,+∞)上递增B.在(0,+∞)上递减C.在⎝ ⎛⎭⎪⎫0,1e 上递增D.在⎝ ⎛⎭⎪⎫0,1e 上递减 (2)已知定义在区间(-π,π)上的函数f (x )=x sin x +cos x ,则f (x )的单调递增区间为________.【例2】 (2017·全国Ⅰ卷改编)已知函数f (x )=e x(e x-a )-a 2x ,其中参数a ≤0. (1)讨论f (x )的单调性; (2)若f (x )≥0,求a 的取值范围.【训练2】 已知f (x )=x 22-a ln x ,a ∈R ,求f (x )的单调区间.考点三 函数单调性的简单应用 角度1 比较大小或解不等式【例3-1】 (1)已知函数y =f (x )对于任意的x ∈⎝⎛⎭⎪⎫0,π2满足f ′(x )cos x +f (x )sin x =1+ln x ,其中f ′(x )是函数f (x )的导函数,则下列不等式成立的是( )A.2f ⎝ ⎛⎭⎪⎫π3<f ⎝ ⎛⎭⎪⎫π4B.2f ⎝ ⎛⎭⎪⎫π3>f ⎝ ⎛⎭⎪⎫π4C.2f ⎝ ⎛⎭⎪⎫π6>3f ⎝ ⎛⎭⎪⎫π4D.3f ⎝ ⎛⎭⎪⎫π3>f ⎝ ⎛⎭⎪⎫π6 (2)已知函数f ′(x )是函数f (x )的导函数,f (1)=1e,对任意实数都有f (x )-f ′(x )>0,设F (x )=f (x )ex ,则不等式F (x )<1e2的解集为( )A.(-∞,1)B.(1,+∞)C.(1,e)D.(e ,+∞)角度2 根据函数单调性求参数【例3-2】 (2019·日照质检)已知函数f (x )=ln x ,g (x )=12ax 2+2x .(1)若函数h (x )=f (x )-g (x )存在单调递减区间,求实数a 的取值范围; (2)若函数h (x )=f (x )-g (x )在[1,4]上单调递减,求实数a 的取值范围.【训练3】 (1)已知f (x )是定义在区间(0,+∞)内的函数,其导函数为f ′(x ),且不等式xf ′(x )<2f (x )恒成立,则( )A.4f (1)<f (2)B.4f (1)>f (2)C.f (1)<4f (2)D.f (1)>4f ′(2) (2)(2019·淄博模拟)若函数f (x )=kx -ln x 在区间(2,+∞)上单调递增,则k 的取值范围是( ) A.(-∞,-2] B.⎣⎢⎡⎭⎪⎫12,+∞ C.[2,+∞) D.⎝ ⎛⎦⎥⎤-∞,12【基础巩固题组】(建议用时:40分钟) 一、选择题1.函数y =f (x )的图象如图所示,则y =f ′(x )的图象可能是( )2.函数f (x )=x ·e x -e x +1的单调递增区间是( )A.(-∞,e)B.(1,e)C.(e ,+∞)D.(e -1,+∞)3.(2019·青岛二中调研)若函数f (x )=x 3-12x 在区间(k -1,k +1)上不是单调函数,则实数k 的取值范围是( )A.k ≤-3或-1≤k ≤1或k ≥3B.不存在这样的实数kC.-2<k <2D.-3<k <-1或1<k <34.已知f (x )=ln xx,则( )A.f (2)>f (e)>f (3)B.f (3)>f (e)>f (2)C.f (3)>f (2)>f (e)D.f (e)>f (3)>f (2)5.(2019·济宁一中模拟)函数f (x )的定义域为R ,f (-1)=2,对任意x ∈R ,f ′(x )>2,则f (x )>2x +4的解集为( ) A.(-1,1) B.(-1,+∞) C.(-∞,-1)D.(-∞,+∞)二、填空题6.已知函数f (x )=(-x 2+2x )e x(x ∈R ,e 为自然对数的底数),则函数f (x )的单调递增区间为________.7.若函数f (x )=ax 3+3x 2-x 恰好有三个单调区间,则实数a 的取值范围是________.8.若函数f (x )=-13x 3+12x 2+2ax 在⎣⎢⎡⎭⎪⎫23,+∞上存在单调递增区间,则a 的取值范围是________.三、解答题9.已知函数f (x )=x 4+a x -ln x -32,其中a ∈R ,且曲线y =f (x )在点(1,f (1))处的切线垂直于直线y =12x .(1)求a 的值;(2)求函数f (x )的单调区间.10.(2019·成都七中检测)设函数f (x )=ax 2-a -ln x ,g (x )=1x -e e x ,其中a ∈R ,e =2.718…为自然对数的底数.(1)讨论f (x )的单调性; (2)证明:当x >1时,g (x )>0.【能力提升题组】(建议用时:20分钟)11.(2017·山东卷)若函数e xf (x )(e =2.718 28…是自然对数的底数)在f (x )的定义域上单调递增,则称函数f (x )具有M 性质.下列函数中具有M 性质的是( ) A.f (x )=2-xB.f (x )=x 2C.f (x )=3-xD.f (x )=cos x12.(2019·上海静安区调研)已知函数f (x )=x sin x +cos x +x 2,则不等式f (ln x )+f ⎝⎛⎭⎪⎫ln 1x <2f (1)的解集为( )A.(e ,+∞)B.(0,e)C.⎝ ⎛⎭⎪⎫0,1e ∪(1,e) D.⎝ ⎛⎭⎪⎫1e ,e13.若函数f (x )=x -13sin 2x +a sin x 在(-∞,+∞)单调递增,则a 的取值范围是________.14.已知函数f (x )=a ln x -ax -3(a ∈R). (1)求函数f (x )的单调区间;(2)若函数y =f (x )的图象在点(2,f (2))处的切线的倾斜角为45°,对于任意的t ∈[1,2],函数g (x )=x 3+x 2·⎣⎢⎡⎦⎥⎤f ′(x )+m 2在区间(t ,3)上总不是单调函数,求m 的取值范围.15.(多填题)已知函数f (x )=x 3+mx 2+nx -2的图象过点(-1,-6),函数g (x )=f ′(x )+6x 的图象关于y 轴对称.则m =________,f (x )的单调递减区间为________.答案1.判断下列结论正误(在括号内打“√”或“×”)(1)若函数f(x)在(a,b)内单调递增,那么一定有f′(x)>0.( )(2)如果函数f(x)在某个区间内恒有f′(x)=0,则f(x)在此区间内没有单调性.( )(3)函数的极大值一定大于其极小值.( )(4)对可导函数f(x),f′(x0)=0是x0为极值点的充要条件.( )(5)函数的最大值不一定是极大值,函数的最小值也不一定是极小值.( )【答案】(1)×(2)√(3)×(4)×(5)√【解析】(1)f(x)在(a,b)内单调递增,则有f′(x)≥0.(3)函数的极大值也可能小于极小值.(4)x0为f(x)的极值点的充要条件是f′(x0)=0,且x0两侧导函数异号.【教材衍化】2.(选修2-2P32A4 改编)如图是f(x)的导函数f′(x)的图象,则f(x)的极小值点的个数为( )A.1B.2C.3D.4【答案】 A【解析】由题意知在x=-1处f′(-1)=0,且其两侧导数符号为左负右正.3.(选修2-2P32A5(4)改编)函数f(x)=2x-x ln x的极值是( )A.1eB.2eC.eD.e2【答案】 C【解析】因为f′(x)=2-(ln x+1)=1-ln x,令f′(x)=0,所以x=e,当f′(x)>0时,解得0<x<e;当f′(x)<0时,解得x>e,所以x=e时,f(x)取到极大值,f(x)极大值=f(e)=e.【真题体验】4.(2019·青岛月考)函数f(x)=cos x-x在(0,π)上的单调性是( )A.先增后减B.先减后增C.单调递增D.单调递减【答案】 D【解析】 易知f ′(x )=-sin x -1,x ∈(0,π), 则f ′(x )<0,所以f (x )=cos x -x 在(0,π)上递减.5.(2017·浙江卷)函数y =f (x )的导函数y =f ′(x )的图象如图所示,则函数y =f (x )的图象可能是( )【答案】 D【解析】 设导函数y =f ′(x )与x 轴交点的横坐标从左往右依次为x 1,x 2,x 3,由导函数y =f ′(x )的图象易得当x ∈(-∞,x 1)∪(x 2,x 3)时,f ′(x )<0;当x ∈(x 1,x 2)∪(x 3,+∞)时,f ′(x )>0(其中x 1<0<x 2<x 3),所以函数f (x )在(-∞,x 1),(x 2,x 3)上单调递减,在(x 1,x 2),(x 3,+∞)上单调递增,观察各选项,只有D 选项符合.6.(2019·豫南九校考评)若函数f (x )=x (x -c )2在x =2处有极小值,则常数c 的值为( ) A.4 B.2或6 C.2D.6【答案】 C【解析】 函数f (x )=x (x -c )2的导数为f ′(x )=3x 2-4cx +c 2, 由题意知,在x =2处的导数值为12-8c +c 2=0,解得c =2或6,又函数f (x )=x (x -c )2在x =2处有极小值,故导数在x =2处左侧为负,右侧为正,而当e =6时,f (x )=x (x -6)2在x =2处有极大值,故c =2.【考点聚焦】考点一 求函数的单调区间【例1】 已知函数f (x )=ax 3+x 2(a ∈R)在x =-43处取得极值.(1)确定a 的值;(2)若g (x )=f (x )e x,求函数g (x )的单调减区间. 【答案】见解析【解析】(1)对f (x )求导得f ′(x )=3ax 2+2x , 因为f (x )在x =-43处取得极值,所以f ′⎝ ⎛⎭⎪⎫-43=0, 即3a ·⎝ ⎛⎭⎪⎫-432+2·⎝ ⎛⎭⎪⎫-43=16a 3-83=0,解得a =12.(2)由(1)得g (x )=⎝ ⎛⎭⎪⎫12x 3+x 2e x,故g ′(x )=12x (x +1)(x +4)e x.令g ′(x )<0,即x (x +1)(x +4)<0, 解得-1<x <0或x <-4,所以g (x )的单调减区间为(-1,0),(-∞,-4). 【规律方法】 1.求函数单调区间的步骤:(1)确定函数f (x )的定义域;(2)求f ′(x );(3)在定义域内解不等式f ′(x )>0,得单调递增区间;(4)在定义域内解不等式f ′(x )<0,得单调递减区间.2.若所求函数的单调区间不止一个时,用“,”与“和”连接. 【训练1】 (1)已知函数f (x )=x ln x ,则f (x )( ) A.在(0,+∞)上递增B.在(0,+∞)上递减C.在⎝ ⎛⎭⎪⎫0,1e 上递增D.在⎝ ⎛⎭⎪⎫0,1e 上递减 (2)已知定义在区间(-π,π)上的函数f (x )=x sin x +cos x ,则f (x )的单调递增区间为________. 【答案】 (1)D (2)⎝⎛⎭⎪⎫-π,-π2,⎝ ⎛⎭⎪⎫0,π2 【解析】 (1)因为函数f (x )=x ln x ,定义域为(0,+∞),所以f ′(x )=ln x +1(x >0),当f ′(x )>0时,解得x >1e ,即函数的单调递增区间为⎝ ⎛⎭⎪⎫1e ,+∞;当f ′(x )<0时,解得0<x <1e ,即函数的单调递减区间为⎝ ⎛⎭⎪⎫0,1e .(2)f ′(x )=sin x +x cos x -sin x =x cos x .令f ′(x )=x cos x >0,则其在区间(-π,π)上的解集为⎝ ⎛⎭⎪⎫-π,-π2和⎝ ⎛⎭⎪⎫0,π2,即f (x )的单调递增区间为⎝ ⎛⎭⎪⎫-π,-π2,⎝ ⎛⎭⎪⎫0,π2. 考点二 讨论函数的单调性【例2】 (2017·全国Ⅰ卷改编)已知函数f (x )=e x(e x-a )-a 2x ,其中参数a ≤0. (1)讨论f (x )的单调性;(2)若f (x )≥0,求a 的取值范围. 【答案】见解析【解析】(1)函数f (x )的定义域为(-∞,+∞),且a ≤0.f ′(x )=2e 2x -a e x -a 2=(2e x +a )(e x -a ).①若a =0,则f (x )=e 2x,在(-∞,+∞)上单调递增. ②若a <0,则由f ′(x )=0,得x =ln ⎝ ⎛⎭⎪⎫-a 2.当x ∈⎝ ⎛⎭⎪⎫-∞,ln ⎝ ⎛⎭⎪⎫-a 2时,f ′(x )<0;当x ∈⎝ ⎛⎭⎪⎫ln ⎝ ⎛⎭⎪⎫-a 2,+∞时,f ′(x )>0. 故f (x )在⎝ ⎛⎭⎪⎫-∞,ln ⎝ ⎛⎭⎪⎫-a 2上单调递减, 在区间⎝ ⎛⎭⎪⎫ln ⎝ ⎛⎭⎪⎫-a 2,+∞上单调递增. (2)①当a =0时,f (x )=e 2x ≥0恒成立.②若a <0,则由(1)得,当x =ln ⎝ ⎛⎭⎪⎫-a 2时,f (x )取得最小值,最小值为f ⎝ ⎛⎭⎪⎫ln ⎝ ⎛⎭⎪⎫-a 2=a 2⎣⎢⎡⎦⎥⎤34-ln ⎝ ⎛⎭⎪⎫-a 2,故当且仅当a 2⎣⎢⎡⎦⎥⎤34-ln ⎝ ⎛⎭⎪⎫-a 2≥0,即0>a ≥-2e 34时,f (x )≥0. 综上,a 的取值范围是[-2e 34,0].【规律方法】 1.(1)研究含参数的函数的单调性,要依据参数对不等式解集的影响进行分类讨论. (2)划分函数的单调区间时,要在函数定义域内讨论,还要确定导数为0的点和函数的间断点.2.个别导数为0的点不影响所在区间的单调性,如f (x )=x 3,f ′(x )=3x 2≥0(f ′(x )=0在x =0时取到),f (x )在R 上是增函数.【训练2】 已知f (x )=x 22-a ln x ,a ∈R ,求f (x )的单调区间.【答案】见解析【解析】因为f (x )=x 22-a ln x ,x ∈(0,+∞),所以f ′(x )=x -a x =x 2-ax.(1)当a ≤0时,f ′(x )>0,所以f (x )在(0,+∞)上为单调递增函数. (2)当a >0时,f ′(x )=(x +a )(x -a )x,则有①当x ∈(0,a )时,f ′(x )<0,所以f (x )的单调递减区间为(0,a ). ②当x ∈(a ,+∞)时,f ′(x )>0,所以f (x )的单调递增区间为(a ,+∞). 综上所述,当a ≤0时,f (x )的单调递增区间为(0,+∞),无单调递减区间. 当a >0时,函数f (x )的单调递减区间为(0,a ),单调递增区间为(a ,+∞). 考点三 函数单调性的简单应用 角度1 比较大小或解不等式【例3-1】 (1)已知函数y =f (x )对于任意的x ∈⎝⎛⎭⎪⎫0,π2满足f ′(x )cos x +f (x )sin x =1+ln x ,其中f ′(x )是函数f (x )的导函数,则下列不等式成立的是( )A.2f ⎝ ⎛⎭⎪⎫π3<f ⎝ ⎛⎭⎪⎫π4B.2f ⎝ ⎛⎭⎪⎫π3>f ⎝ ⎛⎭⎪⎫π4C.2f ⎝ ⎛⎭⎪⎫π6>3f ⎝ ⎛⎭⎪⎫π4D.3f ⎝ ⎛⎭⎪⎫π3>f ⎝ ⎛⎭⎪⎫π6 (2)已知函数f ′(x )是函数f (x )的导函数,f (1)=1e,对任意实数都有f (x )-f ′(x )>0,设F (x )=f (x )ex ,则不等式F (x )<1e2的解集为( )A.(-∞,1)B.(1,+∞)C.(1,e)D.(e ,+∞)【答案】 (1)B (2)B【解析】 (1)令g (x )=f (x )cos x ,则g ′(x )=f ′(x )cos x -f (x )(-sin x )cos 2x =1+ln x cos 2x.由⎩⎪⎨⎪⎧0<x <π2,g ′(x )>0,解得1e <x <π2;由⎩⎪⎨⎪⎧0<x <π2,g ′(x )<0,解得0<x <1e .所以函数g (x )在⎝ ⎛⎭⎪⎫0,1e 上单调递减,在⎝ ⎛⎭⎪⎫1e ,π2上单调递增,又π3>π4,所以g ⎝ ⎛⎭⎪⎫π3>g ⎝ ⎛⎭⎪⎫π4,所以f ⎝ ⎛⎭⎪⎫π3cos π3>f ⎝ ⎛⎭⎪⎫π4cosπ4,即2f ⎝ ⎛⎭⎪⎫π3>f ⎝ ⎛⎭⎪⎫π4. (2)F ′(x )=f ′(x )e x -e x f (x )(e x )2=f ′(x )-f (x )ex,又f (x )-f ′(x )>0,知F ′(x )<0, ∴F (x )在R 上单调递减. 由F (x )<1e2=F (1),得x >1,所以不等式F (x )<1e 2的解集为(1,+∞).角度2 根据函数单调性求参数【例3-2】 (2019·日照质检)已知函数f (x )=ln x ,g (x )=12ax 2+2x .(1)若函数h (x )=f (x )-g (x )存在单调递减区间,求实数a 的取值范围; (2)若函数h (x )=f (x )-g (x )在[1,4]上单调递减,求实数a 的取值范围. 【答案】见解析【解析】h (x )=ln x -12ax 2-2x ,x >0.∴h ′(x )=1x-ax -2.(1)若函数h (x )在(0,+∞)上存在单调减区间, 则当x >0时,1x -ax -2<0有解,即a >1x 2-2x有解.设G (x )=1x 2-2x,所以只要a >G (x )min .又G (x )=⎝ ⎛⎭⎪⎫1x -12-1,所以G (x )min =-1. 所以a >-1.即实数a 的取值范围是(-1,+∞). (2)由h (x )在[1,4]上单调递减,∴当x ∈[1,4]时,h ′(x )=1x-ax -2≤0恒成立,则a ≥1x 2-2x 恒成立,设G (x )=1x 2-2x,所以a ≥G (x )max .又G (x )=⎝ ⎛⎭⎪⎫1x -12-1,x ∈[1,4], 因为x ∈[1,4],所以1x ∈⎣⎢⎡⎦⎥⎤14,1,所以G (x )max =-716(此时x =4),所以a ≥-716.又当a =-716时,h ′(x )=1x +716x -2=(7x -4)(x -4)16x ,∵x ∈[1,4],∴h ′(x )=(7x -4)(x -4)16x ≤0,当且仅当x =4时等号成立. ∴h (x )在[1,4]上为减函数.故实数a 的取值范围是⎣⎢⎡⎭⎪⎫-716,+∞.【规律方法】 1.利用导数比较大小,其关键在于利用题目条件构造辅助函数,把比较大小的问题转化为先利用导数研究函数的单调性,进而根据单调性比较大小. 2.根据函数单调性求参数的一般思路(1)利用集合间的包含关系处理:y =f (x )在(a ,b )上单调,则区间(a ,b )是相应单调区间的子集. (2)f (x )是单调递增的充要条件是对任意的x ∈(a ,b )都有f ′(x )≥0且在(a ,b )内的任一非空子区间上,f ′(x )不恒为零,应注意此时式子中的等号不能省略,否则漏解.(3)函数在某个区间存在单调区间可转化为不等式有解问题.【训练3】 (1)已知f (x )是定义在区间(0,+∞)内的函数,其导函数为f ′(x ),且不等式xf ′(x )<2f (x )恒成立,则( ) A.4f (1)<f (2) B.4f (1)>f (2) C.f (1)<4f (2)D.f (1)>4f ′(2)(2)(2019·淄博模拟)若函数f (x )=kx -ln x 在区间(2,+∞)上单调递增,则k 的取值范围是( ) A.(-∞,-2] B.⎣⎢⎡⎭⎪⎫12,+∞C.[2,+∞)D.⎝⎛⎦⎥⎤-∞,12【答案】 (1)B (2)B【解析】 (1)设函数g (x )=f (x )x 2(x >0),则g ′(x )=x 2f ′(x )-2xf (x )x 4=xf ′(x )-2f (x )x 3<0,所以函数g (x )在(0,+∞)内为减函数,所以g (1)>g (2),即f (1)12>f (2)22,所以4f (1)>f (2).(2)由于f ′(x )=k -1x ,f (x )=kx -ln x 在区间(2,+∞)上单调递增,等价于f ′(x )=k -1x≥0在(2,+∞)上恒成立,由于k ≥1x ,而0<1x <12,所以k ≥12.即k 的取值范围是⎣⎢⎡⎭⎪⎫12,+∞. 【反思与感悟】1.已知函数解析式求单调区间,实质上是求f ′(x )>0,f ′(x )<0的解区间,并注意函数f (x )的定义域.2.含参函数的单调性要注意分类讨论,通过确定导数的符号判断函数的单调性.3.已知函数单调性求参数可以利用给定的已知区间和函数单调区间的包含关系或转化为恒成立问题两种思路解决. 【易错防范】1.求单调区间应遵循定义域优先的原则.2.注意两种表述“函数f(x)在(a,b)上为减函数”与“函数f(x)的减区间为(a,b)”的区别.3.在某区间内f′(x)>0(f′(x)<0)是函数f(x)在此区间上为增(减)函数的充分不必要条件.4.可导函数f(x)在(a,b)上是增(减)函数的充要条件是:对∀x∈(a,b),都有f′(x)≥0(f′(x)≤0),且f′(x)在(a,b)的任何子区间内都不恒为零.【分层训练】【基础巩固题组】(建议用时:40分钟)一、选择题1.函数y=f(x)的图象如图所示,则y=f′(x)的图象可能是( )【答案】 D【解析】由函数f(x)的图象可知,f(x)在(-∞,0)上单调递增,f(x)在(0,+∞)上单调递减,所以在(-∞,0)上,f′(x)>0;在(0,+∞)上,f′(x)<0,选项D满足.2.函数f(x)=x·e x-e x+1的单调递增区间是( )A.(-∞,e)B.(1,e)C.(e,+∞)D.(e-1,+∞)【答案】 D【解析】由f(x)=x·e x-e x+1,得f′(x)=(x+1-e)·e x,令f′(x)>0,解得x>e-1,所以函数f(x)的单调递增区间是(e-1,+∞).3.(2019·青岛二中调研)若函数f(x)=x3-12x在区间(k-1,k+1)上不是单调函数,则实数k的取值范围是( )A.k≤-3或-1≤k≤1或k≥3B.不存在这样的实数kC.-2<k <2D.-3<k <-1或1<k <3 【答案】 D【解析】 由f (x )=x 3-12x ,得f ′(x )=3x 2-12, 令f ′(x )=0,解得x =-2或x =2,只要f ′(x )=0的解有一个在区间(k -1,k +1)内,函数f (x )在区间(k -1,k +1)上就不单调,则k -1<-2<k +1或k -1<2<k +1,解得-3<k <-1或1<k <3. 4.已知f (x )=ln xx,则( )A.f (2)>f (e)>f (3)B.f (3)>f (e)>f (2)C.f (3)>f (2)>f (e)D.f (e)>f (3)>f (2)【答案】 D【解析】 f (x )的定义域是(0,+∞),∵f ′(x )=1-ln x x2, ∴x ∈(0,e),f ′(x )>0,x ∈(e ,+∞),f ′(x )<0, 故x =e 时,f (x )max =f (e),又f (2)=ln 22=ln 86,f (3)=ln 33=ln 96,则f (e)>f (3)>f (2).5.(2019·济宁一中模拟)函数f (x )的定义域为R ,f (-1)=2,对任意x ∈R ,f ′(x )>2,则f (x )>2x +4的解集为( ) A.(-1,1) B.(-1,+∞) C.(-∞,-1)D.(-∞,+∞)【答案】 B【解析】 由f (x )>2x +4,得f (x )-2x -4>0,设F (x )=f (x )-2x -4,则F ′(x )=f ′(x )-2, 因为f ′(x )>2,所以F ′(x )>0在R 上恒成立,所以F (x )在R 上单调递增.又F (-1)=f (-1)-2×(-1)-4=2+2-4=0,故不等式f (x )-2x -4>0等价于F (x )>F (-1),所以x >-1. 二、填空题6.已知函数f (x )=(-x 2+2x )e x(x ∈R ,e 为自然对数的底数),则函数f (x )的单调递增区间为________. 【答案】 (-2,2)【解析】 因为f (x )=(-x 2+2x )e x,所以f ′(x )=(-2x +2)e x +(-x 2+2x )e x =(-x 2+2)e x. 令f ′(x )>0,即(-x 2+2)e x>0,因为e x >0,所以-x 2+2>0,解得-2<x <2, 所以函数f (x )的单调递增区间为(-2,2).7.若函数f (x )=ax 3+3x 2-x 恰好有三个单调区间,则实数a 的取值范围是________. 【答案】 (-3,0)∪(0,+∞)【解析】 由题意知f ′(x )=3ax 2+6x -1,由函数f (x )恰好有三个单调区间,得f ′(x )有两个不相等的零点.需满足a ≠0,且Δ=36+12a >0,解得a >-3, 所以实数a 的取值范围是(-3,0)∪(0,+∞).8.若函数f (x )=-13x 3+12x 2+2ax 在⎣⎢⎡⎭⎪⎫23,+∞上存在单调递增区间,则a 的取值范围是________. 【答案】 ⎝ ⎛⎭⎪⎫-19,+∞【解析】 对f (x )求导,得f ′(x )=-x 2+x +2a =-⎝ ⎛⎭⎪⎫x -122+14+2a .当x ∈⎣⎢⎡⎭⎪⎫23,+∞时,f ′(x )的最大值为f ′⎝ ⎛⎭⎪⎫23=29+2a .令29+2a >0,解得a >-19.所以a 的取值范围是⎝ ⎛⎭⎪⎫-19,+∞.三、解答题9.已知函数f (x )=x 4+a x -ln x -32,其中a ∈R ,且曲线y =f (x )在点(1,f (1))处的切线垂直于直线y =12x .(1)求a 的值;(2)求函数f (x )的单调区间. 【答案】见解析【解析】(1)对f (x )求导得f ′(x )=14-a x 2-1x,由f (x )在点(1,f (1))处的切线垂直于直线y =12x 知f ′(1)=-34-a =-2,解得a =54.(2)由(1)知f (x )=x 4+54x -ln x -32(x >0).则f ′(x )=x 2-4x -54x2. 令f ′(x )=0,且x >0, ∴x =5(x =-1舍去).当x ∈(0,5)时,f ′(x )<0;当x >5时,f ′(x )>0.所以函数f (x )的增区间为(5,+∞),减区间为(0,5).10.(2019·成都七中检测)设函数f (x )=ax 2-a -ln x ,g (x )=1x -e e x ,其中a ∈R ,e =2.718…为自然对数的底数.(1)讨论f (x )的单调性; (2)证明:当x >1时,g (x )>0. 【答案】见解析【解析】(1)解:由题意得f ′(x )=2ax -1x =2ax 2-1x(x >0).当a ≤0时,f ′(x )<0,f (x )在(0,+∞)内单调递减. 当a >0时,由f ′(x )=0有x =12a ,当x ∈⎝⎛⎭⎪⎫0,12a 时,f ′(x )<0,f (x )单调递减; 当x ∈⎝ ⎛⎭⎪⎫12a ,+∞时,f ′(x )>0,f (x )单调递增.(2)证明 令s (x )=ex -1-x ,则s ′(x )=ex -1-1. 当x >1时,s ′(x )>0,所以s (x )>s (1),即e x -1>x ,从而g (x )=1x -e e x =e (e x -1-x )x e x >0.【能力提升题组】(建议用时:20分钟)11.(2017·山东卷)若函数e xf (x )(e =2.718 28…是自然对数的底数)在f (x )的定义域上单调递增,则称函数f (x )具有M 性质.下列函数中具有M 性质的是( ) A.f (x )=2-xB.f (x )=x 2C.f (x )=3-xD.f (x )=cos x【答案】 A【解析】 设函数g (x )=e x ·f (x ),对于A ,g (x )=e x ·2-x=⎝ ⎛⎭⎪⎫e 2x,在定义域R 上为增函数,A 正确.对于B ,g (x )=e x ·x 2,则g ′(x )=x (x +2)e x ,由g ′(x )>0得x <-2或x >0,∴g (x )在定义域R 上不是增函数,B不正确.对于C ,g (x )=e x ·3-x =⎝ ⎛⎭⎪⎫e 3x在定义域R 上是减函数,C 不正确.对于D ,g (x )=e x·cos x ,则g ′(x )=2e xcos ⎝⎛⎭⎪⎫x +π4,g ′(x )>0在定义域R 上不恒成立,D 不正确.12.(2019·上海静安区调研)已知函数f (x )=x sin x +cos x +x 2,则不等式f (ln x )+f ⎝⎛⎭⎪⎫ln 1x <2f (1)的解集为( ) A.(e ,+∞)B.(0,e)C.⎝ ⎛⎭⎪⎫0,1e ∪(1,e) D.⎝ ⎛⎭⎪⎫1e ,e 【答案】 D【解析】f (x )=x sin x +cos x +x 2是偶函数,所以f ⎝ ⎛⎭⎪⎫ln 1x =f(-ln x)=f(ln x). 则原不等式可变形为f(ln x)<f(1)⇔f(|ln x|)<f(1). 又f′(x)=xcos x +2x =x(2+cos x), 由2+cos x>0,得x>0时,f′(x)>0. 所以f(x)在(0,+∞)上单调递增. ∴|ln x|<1⇔-1<ln x<1⇔1e<x<e.13.若函数f (x )=x -13sin 2x +a sin x 在(-∞,+∞)单调递增,则a 的取值范围是________.【答案】 ⎣⎢⎡⎦⎥⎤-13,13 【解析】 f ′(x )=1-23cos 2x +a cos x =1-23(2cos 2x -1)+a cos x =-43cos 2x +a cos x +53,f (x )在R上单调递增,则f ′(x )≥0在R 上恒成立.令cos x =t ,t ∈[-1,1],则-43t 2+at +53≥0在[-1,1]上恒成立,即4t 2-3at -5≤0在t ∈[-1,1]上恒成立.令g (t )=4t 2-3at -5,则⎩⎪⎨⎪⎧g (1)=4-3a -5≤0,g (-1)=4+3a -5≤0,解得-13≤a ≤13.14.已知函数f (x )=a ln x -ax -3(a ∈R). (1)求函数f (x )的单调区间;(2)若函数y =f (x )的图象在点(2,f (2))处的切线的倾斜角为45°,对于任意的t ∈[1,2],函数g (x )=x 3+x 2·⎣⎢⎡⎦⎥⎤f ′(x )+m 2在区间(t ,3)上总不是单调函数,求m 的取值范围.【答案】见解析【解析】(1)函数f (x )的定义域为(0,+∞),且f ′(x )=a (1-x )x, 当a >0时,f (x )的递增区间为(0,1), 递减区间为(1,+∞);当a <0时,f (x )的递增区间为(1,+∞),递减区间为(0,1); 当a =0时,f (x )为常函数.(2)由(1)及题意得f ′(2)=-a2=1,即a =-2,∴f (x )=-2ln x +2x -3,f ′(x )=2x -2x.∴g (x )=x 3+⎝ ⎛⎭⎪⎫m2+2x 2-2x ,∴g ′(x )=3x 2+(m +4)x -2.∵g (x )在区间(t ,3)上总不是单调函数, 即g ′(x )在区间(t ,3)上有变号零点.由于g ′(0)=-2,∴⎩⎪⎨⎪⎧g ′(t )<0,g ′(3)>0.当g ′(t )<0时,即3t 2+(m +4)t -2<0对任意t ∈[1,2]恒成立, 由于g ′(0)<0,故只要g ′(1)<0且g ′(2)<0, 即m <-5且m <-9,即m <-9; 由g ′(3)>0,即m >-373.∴-373<m <-9.即实数m 的取值范围是⎝ ⎛⎭⎪⎫-373,-9. 【新高考创新预测】15.(多填题)已知函数f (x )=x 3+mx 2+nx -2的图象过点(-1,-6),函数g (x )=f ′(x )+6x 的图象关于y 轴对称.则m =________,f (x )的单调递减区间为________. 【答案】 -3 (0,2)【解析】 由函数f (x )的图象过点(-1,-6),得m -n =-3.① 由f (x )=x 3+mx 2+nx -2,得f ′(x )=3x 2+2mx +n , 所以g (x )=f ′(x )+6x =3x 2+(2m +6)x +n .21因为g (x )的图象关于y 轴对称,所以-2m +62×3=0, 所以m =-3,代入①得n =0,所以f ′(x )=3x 2-6x =3x (x -2). 由f ′(x )<0,得0<x <2,所以f (x )的单调递减区间是(0,2).。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第二章 一元微分学第六节 利用导数讨论函数性质本节内容包括:利用导数讨论函数的单调性、求函数极值和极值点、最值和最值点及其应用,利用导数讨论函数图形的凹凸性、求曲线的拐点,求曲线切线、法线、渐近线及函数作图等。
这部分内容很重要,事实上前面几节的知识都用到了本节的内容。
在高等数学的各种考试中本节的知识都是重要部分,同学们一定要很熟练。
但由于这部分内容一般不要求很高的技巧(要求熟练、准确及对概念的清楚),所以只简单地举几个例子。
最后举二个例子介绍相关变化率的问题。
例1. 设)(x f 二阶可导,)0()4(>-=ββy y dxdy.若曲线)(x f y =的一个拐点为)3,(0x ,则_______=β.分析:由题设知 ,3|0==x x y 并且0|022==x x dx y d ,而dx dy y y dy d y y dx d dx y d ⋅-=-=])4[(])4[(22ββ =))1(4()4()4(])4([121y y y y y yy y +--=-⋅-+---βββββββ由0||322220====y x x dxyd dx y d ,得3=β 注:本题的解决无需技巧,关键是清楚拐点的概念及复合函数求导.例2:求曲线⎪⎩⎪⎨⎧+==1ln ln t ty tt x 的渐近线 解:先看是否有水平渐近线:易见+∞→t 时1,→+∞→y x ,所以有1lim =+∞→y x ,故有水平渐近线1=y ;再看是否有铅直渐近线:易见0+→t 时∞→→y x ,0,所以有∞=→y x 0lim ,故有铅直渐近线0=x ;再看是否有斜渐近线:易见0lim=+∞→xyx ,故无斜渐近线. 例3.求椭圆12222=+by a x 在第一象限中的切线,使它被两坐标轴所截的线段最短.解法一:椭圆的参数方程为θθsin ,cos b y a x ==,设切点为)20( )sin ,cos (πθθθ<<b a ,那么切线的斜率为θθsin cos a b k -=,切线方程为)cos (sin cos sin θθθθa x a b b y --=-切线在x 轴上的截距为θcos a ,切线在y 轴上的截距为θsin b.从所截线段长为 )20( sin cos )(2222πθθθθ<<+=b a l 求)(θl 的最小值点等价于求)20( sin b cos )(2222πθθθθ<<+=a f 的最小值点. abb a f =⇒=-='θθθθθθtan 0cos sin 2sin cos 2)(3232 从而知)(θf 在)2,0(π有唯一驻点abarctan=θ,由本问题的实际背景我们可以判断)(θf 在)2,0(π内取得最小值,因此a b arctan =θ时)(θf 取得最小值.此时切点坐标为 ba bb y b a a ax +=+= , 所求的切线方程为 )(ba aa xb a abb a b by +--=+-,化简得 1)()(=+++b a b y b a a x解法二:设切点为)0( ),(a x y x <<,那么切线的斜率为ya xb k 22-=,切线方程为)(22x X ya xb y Y --=-切线在x 轴上的截距为xa 2,切线在y 轴上的截距为y b 2.从所截线段长为)0( )(2424a x yb x a x l <<+=求)(x l 的最小值点等价于求)0( )(2424a x y b x a x f <<+=的最小值点.='--='y y b x a x f 343422)(32322234340)(22by a x y a x b y b x a =⇒=---又y x ,满足12222=+by a x联立以上两个方程得:ba b b y ba a a x +=+=,从而知)(x f 在),0(a 有唯一驻点ba a a x +=,由本问题的实际背景我们可以判断)(x f 在),0(a 内取得最小值,因此ba a a x +=时)(x f 取得最小值.此时切点坐标为ba b b y b a a ax +=+= , 所求的切线方程1)()(=+++b a b y b a a x注:利用高等数学知识解决实际问题(即所谓的应用题)几乎是必考的.其中用微分学(一元或多元微分学)知识解决实际应用中的最大值或最小值问题是其中很重要的一部分.解决这种问题的关键是:根据实际背景和问题的要求选好自变量并求出目标函数同时确定该目标函数的定义域I (一般情况下I 是一个区间,可以是开的、闭的或半开半闭,也可是有限的、无限的.) 求出目标函数在I 内的驻点,如果驻点是唯一的,那么可用下面两种方式说明该驻点就是所求的最大值点或最小值点:(1)根据实际问题的背景,可以判定目标函数在区间I 内部取得最大值(或最小值),且在I 内的驻点又是唯一的,则该驻点就是最大值点(最小值点).(2)若目标函数在区间I 内只有唯一驻点,又通过一阶导或二阶导可以判定该驻点为极大值点(或极小值点),则该驻点就是最大值点(最小值点).另外要注意:选择不同的自变量,目标函数的表达式会不一样,计算量及复杂性可能有很大差别,因此选择合适的自变量有时是很关键的. 有的问题既可用一元微分学去解决,也用二元微分学去解决,就看哪个更简便.事实上例3用二元微分学知识去解可能更方便,实际就是求目函数)0,0( ),(2424b y a x yb x a y x f <<<<+=在约束条件12222=+by a x 下的最小值问题,可用拉格朗日乘数法去解决.例4.一长度为m 5的梯子铅直地靠在铅直的墙上,其下端沿地板以s m /3的速度离开墙角而滑动,(1) 当其下端离开墙角m 4.1时,梯子上端下滑的速度是多少? (2) 何时梯子上、下端滑行的速度相同? 解:(1)梯子滑行t 秒时,上、下端距离墙角的距离分别为y 米和x 米,依题意有 225x y -=,3=dtdx,本题欲求4.1|-x dtdy, 对225x y -=两边对时间t 求导得2225325xx dt dx x xdtdy--=--=从而得875.04.1254.11|24.1-=-⨯-=-x dt dy ,即上端下滑速度为s m /875.0.(3) 由32532=-x x ,得225=x ,6253==x t ,即梯子滑行625秒后,其上、下端 滑行的速度相同.注:仔细体会本题的解答,本题中涉及三个变量t y x ,,,任一变量都是任一其它变量的函数,本题中己知y x , 的函数关系,且己知x 对t 的导数,要求y 对t 的导数.这种问题称为相关变化率的问题.在己知y x , 的函数关系0),(=y x F 后,这种问题是简单的,只须两边对t 求导可得0=+dt dy F dt dx F y x,从而求出dtdy .在具体问题中,难点可能是y x , 的函数关系的建立. 例5.溶液自深cm 18顶直径为cm 12的正圆锥漏斗中漏入一直径为cm 10的圆柱形容器中,开始时漏斗盛满水,当溶液在漏斗中深cm 12时,其水平面下落速度为min /1cm ,问此时圆柱形容器中水平面上升的速度为多少?分析:这里涉及三个变量:时刻t ,及时刻t 时漏斗水面深度x 、圆柱形容器中的水面高度y ,y x ,都是t 的函数,y 是x 的函数。
已知1|12-==x dt dx ,欲求12|=x dtdy。
仿上面例题,如能建立y x ,的函数关系,问题就不难了。
那么y x ,的函数关系的建立成为解决本题的关键,这种关系的建立是基于“漏斗漏出的水量和圆柱形容器中的水量相等”。
解:设在t 时刻漏斗水的深度和圆柱形容器中水的深度分别为x 厘米和y 厘米,t 时刻漏斗的水面半径为x r 31=,此时漏斗漏出的水量为 )9186(332x -⨯π,此时圆柱形容器中的水量为y 25π,因此有)9186(3 2532x y -⨯=ππ两边对t 求导得 dt dx dt dy 9125-=,又由min)/(1|12cm dtdxx -==,得 min)/(251625912|212cm dt dy x =⨯==。
练习题:1.设n n x x x x f n(,)!2(!21)(22++++= 为正整数),证明在),(+∞-∞内有正的最小值.(先说明)(x f 有最小值点,记为0x ,那么0)(0='x f ,再利用)!2()()(2000n xx f x f n+'=)2.比较πe 与eπ的大小.(注意变形 取对数变成为比较e ln π与πln e 的大小,它等价于比较e e ln 与ππln 的大小,利用xxx f ln )(=的单调性可解决问题)3.求数列 ,,,3,2,13n n 中的最大项.(数列n a 也是函数)(n f a n =,求其最大值(即最大项)的问题可用单调性解决.这种函数的自变量n 是离散变量,不能对n 求导,于是把n 变成x ,通过讨论)(x f 的单调性进而得到数列n a 随n 增加时(或n1减少时)的变化情况,再求出最大项.本题中x x x f 1)(=,但由于求导不是很方便,可考虑函数xxx g ln )(=)4.求曲线⎪⎩⎪⎨⎧+==323tt y tx 的拐点.(答案:)4,1(),4,1(- ).5.设函数)(x f 的定义域为}1,0|{≠≠=x x x D ,且满足x xx f x f +=-+1)1()(,求)(x f 的表达式并求曲线)(x f y =的渐近线. (由x x x f x f +=-+1)1()(,作换元x x t 1-=得t tt f t f --=-+12)11()(,即 x x x f x f --=-+12)11()(,再作换元t t x 1-=得t t t f t t f 12)11()1(-=--+-即xx x f x x f 12)11()1(-=-+-,由以上三个式子可得)(x f 的表达式,有了表达式后再求渐近线是容易的)6.将10分成n 分n a a a ,,,21 (即10,01=>∑=ni ii aa ),n 为多少且n a a a ,,,21 各是多少时,乘积n a a a 21最大。
(对于固定的n ,n a a a n 1021==== 时乘积n a a a 21最大,最大值为nn)10(,问题转化求n ,使nn)10(最大) 7.(1)求xx x f 1ln )(+=的最小值; (2)设正值序列}{n x 满足11ln 1<++n n x x ,证:}{n x 收敛,并求其极限。
