七年级寒假衔接班讲义第二讲

合集下载

初一七年级下学期历史第2讲讲义解析

寒假初一历史第二讲讲义解析1.汉武帝、唐太宗都是我国历史上杰出的皇帝，他们采取的相同治国措施是A. 重视人才的选拔和培养B. 加强对吐蕃的管理C. 兴建佛寺，传播佛教D. 统一文字和度量衡【解析】A汉武帝与唐太宗都注重人才的选拔和培养。

汉武帝大力推行儒学教育，在长安兴办太学。

唐太宗重视人才的培养和选拔，扩充国学的规模，扩建校舍，增加学员。

故选 A 重视人才的选拔和培养。

2.唐太宗说：“以天下之广，四海之众，千端万绪。

须合变通，皆委百司商量，客相复划，于事稳便，方可奏行。

岂得以一日万机，独断一人之虑也。

” 材料表明他主张A. 发挥宰相等大臣的议政权B. 君权与相权相互制衡C. 中央权力重心应当下移D. 君主不应实行专制统治【解析】A据唐太宗说 “以天下之广，四海之众，千端万绪。

须合变通，皆委百司商量，客相复划，于事稳便，方可奏行。

岂得以一日万机，独断一人之虑也。

” 材料表明他主张发挥宰相等大臣的议政权。

唐朝三省六部制的特点在于分散了丞相及中央机构的权力，把相权 “一分为三”，既有分工，又有合作，互相牵制和监督，提高决策正确性和行政效率；加强了皇权与中央集权、削弱了相权。

故选：A。

3.下列唐朝三省六部制机构设置示意图准确的是A. B.C. D.【解析】A本题考查三省六部制度。

三省六部制是唐朝一种政治制度。

三省指中书省、门下省、尚书省。

六部指尚书省下属的吏部、户部、礼部、兵部、刑部、工部。

每部各辖四司，共为 24 司。

所以，本题的图片A 就是其结构图。

故选 A。

4.有学者认为，唐代前期中央各级行政机关以及地方诸道州府，行政上皆承受于尚书省。

“有事皆申尚书省取裁闻奏，不能径奏君相；诏令制敕亦必先下尚书省详定，然后下百司。

” 由此可见，尚书省A. 剥夺中书与门下省的权力B. 拥有起草诏令制敕的职权C. 阻隔皇帝与各州府的联系D. 成为全国行政运行的枢纽【解析】D依据题干材料 “唐代前期中央各级行政机关以及地方诸道州府，行政上皆承受于尚书省” 可以看出尚书省是中央和地方各级行政机关行政运行的枢纽，故 D 项正确。

七年级上册数学数学预科班资料

前言本资料的编写以《新课程标准》为指南，以知识与技能、过程与方法为指导思想，通过基础、提高、综合的三级训练，每一套资料都是从近几年来新课程教学中和各地区重点中学的试题中提炼出来，既有基础题，也有能力题、综合题、发散题、探究题和开放题，及具代表性，形成有特色的培训资料。

所有资料对疑难问题点拨到位，是学生正确掌握解题方法、避开思维误区，切实能够提高学生的成绩。

学生在老师的辅导下，复习旧知识、巩固新知识，学生对知识的掌握和灵活运用能力、综合运用能力有很大的提高。

教学进度安排如下：第一讲有理数的巧算第二讲有理数及其相关应用第三讲绝对值第四讲一元一次方程第五讲一元一次方程的应用第六讲一次方程综合第七讲线段、角与计数第八讲相交线与平行线第九讲图形的面积第十讲二元一次方程组第十一讲一元一次不等式和一元一次不等式组第十二讲复习 + 考试第十三讲试卷讲评 +含绝对值的一元方程与不等式说明：1. 老师在教学的过程中，根据学生的具体情况和教学进度灵活的处理资料，要求讲清讲透，不能盲目的赶资料的进度。

2. 为了丰富内容，绝大部分资料按120分钟／次编排，老师可以根据学生实际从中选取80分钟内容讲授，余下的部分作为同学们自由练习用。

第一讲有理数的巧算有理数运算是中学数学中一切运算的基础．它要求同学们在理解有理数的有关概念、法则的基础上，能根据法则、公式等正确、迅速地进行运算．不仅如此，还要善于根据题目条件，将推理与计算相结合，灵活巧妙地选择合理的简捷的算法解决问题，从而提高运算能力，发展思维的敏捷性与灵活性．基础训练一、填空题：1、若21()302α-++=b ，则ab = .2、在数量5-，1，3-，5，2-中位数取三个相乘，其中最大的积是，最小的积是 .3、若a ，b 互为相反数，c ，d 互为倒数，则32009()3()--=a +b cd .4、若1=-xyxy，则x 与y 号.（填“同”或“异”） 5、计算1(2)()(2)2---=÷×二、选择题：1、下列计算结果为0的是 . A 、2222-- B 、223(3)-+- C 、22(2)2-+ D 、233--×32、下列各式中正确的是 .A 、22()=-a aB 、33()=-a a C 、22=--a a D 、33=a a3、计算：1110(2)(2)-+-= .A 、2-B 、21(2)-C 、0D 、102-三、计算题： 1、3571()491236--+÷2、27211()9353---÷×(-4)3、23212(10.5)3(3)3⎡⎤⎡⎤--⨯⨯÷-⎣⎦⎢⎥⎣⎦-1-4、如果规定△表示一种运算，且a △b=2a b ab -，求：3△（4△12）的值.拓展训练1．括号的使用在代数运算中，可以根据运算法则和运算律，去掉或者添上括号，以此来改变运算的次序，使复杂的问题变得较简单．例1 计算：例2计算下式的值：211×555+445×789+555×789+211×445．例3计算：S=1-2+3-4+…+(-1)n+1·n．2．用字母表示数（选讲）我们先来计算(100+2)×(100-2)的值：(100+2)×(100-2)=100×100-2×100+2×100-4=1002-22．这是一个对具体数的运算，若用字母a代换100，用字母b代换2，上述运算过程变为(a+b)(a-b)=a2-ab+ab-b2=a2-b2．于是我们得到了一个重要的计算公式:(a+b)(a-b)=a2-b2，①这个公式叫平方差公式，以后应用这个公式计算时，不必重复公式的证明过程，可直接利用该公式计算．例5计算 3001×2999的值．例6计算 103×97×10 009的值．例7计算：(2+1)(22+1)(24+1)(28+1)(216+1)(232+1)．例8 计算：3．观察算式找规律例9计算1+3+5+7+…+1997+1999的值．例10计算 1+5+52+53+…+599+5100的值．（）等比数列的求法错位加减法第二讲有理数及其相关概念一．知识点拨（一）有理数的绝对值 1、绝对值的意义绝对值的定义采用了描述法：正数的绝对值是它的本身，负数的绝对值是它的相反数，零的绝对值是零，有理数a 的绝对值记为|a|。

初一寒假补课讲义(10次)

北京九中初一寒假数学讲义（2011年）第一讲不等式的性质1、填空：(1)当 k______时，-k ≤0；(2)不等式3x- 2＞0与6(x- 2)＞8的解集是否相同．答：______；(3)若a ＞b ，则-2a______-2b ；(4)若a ＜0，b ＜0，c ＜0，则abc 2 ______0；(5)若 a ＞0，b ＜0，c ＞0，则a+c ______5b ；(6)若a ＜0，b ＜0，c ＜0，则|ab|-c______0．2、比较2a 与a 的大小3 、比较a 与2a 的大小4、已知0,10.a b <-<<试将2,,a ab ab 从小到大依次排列.5、若a b >请讨论1a 与1b的大小.6、判断对错，说明理由.（1）如果,a b c d >=那么.ac bd > （）（2）如果22,ac bc >那么.a b > （）（3）如果,ax b <且0a ≠，那么.b x a< （）（4）如果0,ab >那么0.a b> （）7、已知0,10,a b <-<<试将2,,a ab ab 从小到大依次排列，并说明理由.第二讲解一元一次不等式1、解下列不等式（1）（2）（3）2.已知关于x的方程3(32)43(2)+-=++的解是负数，求a的取值范x a x a围.3.已知5(32)8167x x---+--≥-，化简|3|4|25|.x x4.解不等式(1)3->.a x5.若不等式(1)3x x>求a取值范围.a x->的解集为{|3}6解不等式(1)|1|1->+x xx x->-(2)|1|2 1.7、两位搬运工人要将若干箱同样的货物用电梯运到楼上.已知一箱货物的质量是55千克，两位工人的体重之和为160千克，电梯的载重量是1600千克，算一算两位工人一次最多运多少箱货物.专题三不等式组1、解不等式组（1）⎪⎩⎪⎨⎧-<--<-322125223x x x x （2）⎩⎨⎧->-+<-)1(4436265x x x x（3）⎪⎪⎩⎪⎪⎨⎧>+-<-≥+xx x x xx 323254223(4)2(2)8,337,3(2)82x x x x x x +<+⎧⎪-≥-⎨⎪-+>⎩2、求适合不等式-11<2a-5≤3的a 的负整数值3、学校图书馆准备购买定价分别为8元和14元的杂志和小说共80本，计划用钱在750元和850元之间（包括750元和850元），那么14元一本的小说最少可以买多少本？最多可以买多少本？1、若不等式组2113xx a-⎧>⎪⎨⎪>⎩的解集为{|2}x x>，则a的取值范围是_________.2、不等式组230312xmx-≥⎧⎪⎨-≤⎪⎩无解，则m的取值范围是__________.7、七年级（2）班有50名学生，老师安排每人制作一件A型或B的陶艺品，学校现在有甲种制作材料36千克，一种制作材料29千克，制作A、B两类陶（2）请你根据学校现有材料，分别写出七年级（2）班制作A型和B型陶艺制品的件数.专题四二元一次方程组（一）1.满足方程325-=的整数解有_________个;写出其中的三个解x y______________________________;写出使||||x y+的值最小的整数解___________;满足325-=的整数解的规律是_____________________.x y2.解方程组：4．A．a=2，c=14；B．a=2，c≠14；C．a≠2，c=14；D．a≠2，c≠14．5.当x=2和x=3时，二次三项式x2+px+q的值等于零，求p，q的值．6.解方程组：7.已知关于,x y的而原方程组4105x yx my-=⎧⎨-=⎩和3421x y nx my+=⎧⎨+=⎩的解相同，试求,m n的值.专题五二元一次方程组（二）一、选择题1．下列各方程组中，属于二元一次方程组的是（）A 、 ⎩⎨⎧==+5723xy y xB 、⎩⎨⎧=+=+212z x y xC 、⎩⎨⎧=+=2432y x x y D 、⎪⎩⎪⎨⎧=+=+3215y x y 2．下列各对数是二元一次方程2x-5y=3的解的是（）A 、32x y =⎧⎨=⎩B 、21x y =-⎧⎨=-⎩C 、89x y =⎧⎨=⎩D 、93x y =⎧⎨=⎩ 3．已知x 12-m +3y n 24-=-7是关于x 、y 的二元一次方程，则m,n 的值是（）Ａ．⎩⎨⎧==12n m Ｂ．⎩⎨⎧-==231n m Ｃ．⎩⎨⎧==231n m Ｄ．⎩⎨⎧==251n m 4．若方程组⎩⎨⎧==-bxy b x y 2的解x,y 的值都是正数，则b 的值为（）Ａ．b ＞2 B.b=2 C.b ＜2D.b ≠２5．如图，宽为50 cm 的矩形图案由10个全等的小长方形拼成，其中一个小长方形的面积为（）A 、400 cm 2B 、500 cm 2C 、600 cm 2D 、4000 cm 26.小王只带2元和5元两种面值的人民币，他买一件学习用品要支付27元，则付款的方式有（）A 、1种B 、2种C 、3种D 、4种7．某校运动员分组训练，若每组7人，余3人；若每组8人，则缺5人；设运动员人数为x 人，组数为y 组，则列方程组为（）A 、⎩⎨⎧=++=x y x y 5837B 、⎩⎨⎧=-+=x y x y 5837C 、⎩⎨⎧+=-=5837x y x yD 、⎩⎨⎧+=+=5837x y x y二、填空题1．将方程527x y -=变形成用y 的代数式表示x ，则x =___________.2．在432-=x y 中，如果x ＝6，那么y ＝____；如果y ＝-2，那么x =____; 3．若⎩⎨⎧=-=21y x 是方程3x + ay=1的一个解，则a 的值是__________.4．写出一个以23x y =⎧⎨=⎩为解的二元一次方程组__________________ . 5．大数和小数的差为6，这两个数的和为30，则大数是 ___.6．已知二元一次方程x + 3y =10,请写出一组正整数解______________7.若方程组⎩⎨⎧=+=+5231y x y x 的解也是方程3x +ky =10的一个解，则k = ． 8．已知方程组⎩⎨⎧=++=+m y x m y x 32253的解适合x+y =8，则m = .9.已知方程组3,51,ax by x cy +=⎧⎨-=⎩甲正确地解得2,3,x y =⎧⎨=⎩，而乙粗心地把c 看错了，解得3,6,x y =⎧⎨=⎩则a =_________, b=_______, c =_________. 10.陕北的放羊娃隔着沟峁唱着信天游,比他们养的羊数.一个唱到:“你羊没有我羊多,你若给我一只羊,我的是你的两倍”,另一个随声唱到:“没那事,你要给我一只,咱俩的羊儿一样多”.听了他们的对唱,你能知道他们各有多少只羊吗?2.一个老和尚三个小和尚吃１０个桃子，三个小和尚吃一样多，老和尚、小和尚各吃几个？专题六幂的运算(两课时)1. 计算：（1）5633;⨯ （2）312x x ；（3）235;a a a ⋅⋅（4）234x x x x ⋅⋅⋅.2. 计算：（1）24;x x -⋅ （2）3()();m m -⋅- （3）432.x x x x ⋅+⋅3.计算：（1）52(10);（2）56();x （3）210();x （4）23().y y ⋅4.计算：(1)(-3x)3； (2)(-5ab)2； (3)(xy 2)2； (4)(-2xy 3z 2)4 (5)(-5y )3 (6)(2m 2n )4 (7)(-3x 2y 3)25.计算：（1）8851[(6)()];6-⨯ （2）20032000(8)(0.125).-⨯-6.计算：（1）2435232(2)(3)(3);x x x x x +-+-（2）2333332(5)()()(2).x y xy x y x +-+--7.已知23,25,m n ==求322m n -的值.8.比较5040303,4,5的大小.专题七整式的乘法（一）1. 计算：(1)(-5a 2b 3)(-3a)； (2)(2x)3(-5x 2y)；(3)(-3m 3n 2)·(7mn 3) (4))23(3432x y x -⋅ (5);)23(322223xy y x -⋅ (6)(-3ab)(-a 2c)2·6ab(c 2)3 .2. 计算： (1))3()21(222xz yz x xy -⋅-⋅ ; (2)2x 6y 2·x 3y+(-25x 8y 2)(-xy).3.计算： (1)47- x 2yz ·74xy 2z ·(1649-xyz 2)； (2)(21- ab 2c)2·(31-abc 2)3·12a 3b.4. 计算：(1)(-4x)·(2x 2+3x-1)； (2)(32 ab 2-2ab)·21ab; (4) -2xy ·(3x 2+2xy-y 2); (5)(2ab 2-ab+4b)·ab.5. 计算(1)3x 2·(-3xy)2-x 2(x 2y 2-2x)； (2)5x ·(x 2-2x+4)+x 2(x-1)；(3)3ab ·(a 2b-ab 2+ab)-ab 2(2a 2-3ab+2a)；(4)2a ·(a 2+3a-2)-3·(a 3+2a 2-a+1)； (5)21 (m+1)-31 (2m-1)+61(m-5)； (6)t 3-2t ［t 2-2(t-3)］.专题八整式乘法（二）1. 计算：(1)(x+2y)(5a+3b)； (2)(2x-3)(x+4)；(3)(x+3y)(5x+6y) (4) (2a-3b)(a+4b) (5)(x+y)2； (6)(x+y)(x2-xy+y2).2. 计算：(1)(x+2)(x-2)(x2+4)； (2)(1-2x+4x2)(1+2x)；(3)(x-y)(x2+xy+y2)； (4)3x(x2+4x+4)-x(x-3)(3x+4)；(5)5x(x2+2x+1)-(2x+3)(x-5)； (6)(3x-y)(y+3x)-(4x-3y)(4x+3y).3.计算：(1)(x+2)(x+3)； (2)(x-4)(x+1)； (3)(y+4)(y-5)； (4)(y-3)(y-5)；(5)(x-6)(x+7)；(6)(x+6)(x-8)； (7)(y-21)(y+31)； (8)(y+41)(y+51)； (9)(7x+8)(6x-5)；(10)(3x-2)(4x+5)； (11)(2a+3)(23a-5)； (12)(21 x+4)(6x-43).4. 如图，用含有x 的代数式表示槽型刚才的体积.专题九整式的混合运算1.计算：（1）63223ab a b a b a b(3)(4)518.-⋅+⋅a a a-----（2）33224536(2)(3)[2(2)];2.计算：（1）(8)(8)m m+-=（2）(25)(25)+-=a b a b（3）(43)(34)+-=y x x y（4）(41)(41)---=a a3.计算：（1）2a b+=()（2）2-=()a b（3）2(5)x+=（4）2-=m n(32)（5）2++=()a b c4.计算：（1）22(2)(2)y x x y +-（2）2111()()()242x x x --+5.用几何图形演示的方法说明222()2a b a ab b +=++和()()a b a b +-.6.计算：248162481611111(3)(3)(3)(3)(3)33333+++++.。

七年级寒假预科班第二讲

七年级寒假预科班第二讲一、选择题。

1、下列计算正确的是（）A、2a?a?2B、m6?m2?m3C、x2021?x2021?2x2021D、t2?t3?t62、下列语句中错误的是（）A、数字 0 也是单项式B、单项式 a 的系数与次数都是 1C、?2ab3的系数是 ?23D、12x2y2是二次单项式 3、代数式 2021 ,1?，2xy ,1x ,1?2y ，12021(a?b) 中是单项式的个数有（题目虽然简A、2个 B、3个 C、4个 D、5个单，也要仔细噢！ 4、一个整式减去a2?b2等于a2?b2则这个整式为（） A、2b2 B、2a2 C、?2b2 D、?2a25、下列计算正确的是：（）A、2a2+2a3=2a5B、2a-1=1C、(5a3)2=25a5D、(-a22a)2÷a=a3 6、下列计算错误的是：（）①、（2x+y）2=4x2+y2 ②、(3b-a)2=9b2-a2 ③、(-3b-a)(a-3b)=a2-9b2④、（-x-y）2=x2-2xy+y2 ⑤、(x-112 )2=x2-2x+4A、1个B、2个C、3个D、4个7、黎老师做了个长方形教具，其中一边长为2a?b，另一边为a?b，则该长方形周长为( )A、6a?bB、6aC、3aD、10a?b8、下列多项式中是完全平方式的是 ( )A、x2?4x?1B、x2?2y2?1C、x2y2?2xy?y2D、9a2?12a?4 9、饶老师给出：a?b?1 ，a2?b2?2 ，你能计算出 ab 的值为（）A、?1B、3C、?32D、?12 10、已知a?255 ，b?344 ，c?433 ，则a、b、c、的大小关系为：（）A、a?b?cB、a?c?bC、b?a?cD、b?c?a第 1 页共 4 页）二、填空题。

（2分×10=20分）11、单项式 ??ab的系数是，次数是次。

324112、代数式 a3x?a2x3?x 是＿＿＿＿＿＿项式，次数是＿＿＿＿＿次。

人教版七年级数学寒假高分班讲义

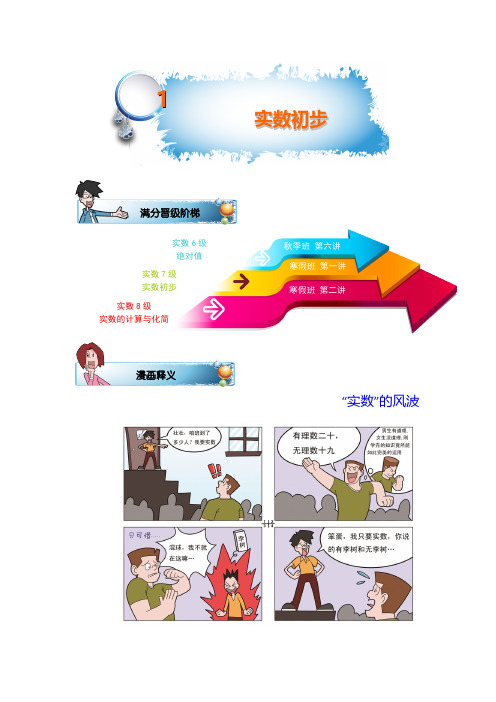
⑤ 16 .
⑵ 求下列各式的值：
① 25 ；
② 0.01 ；
③ 169 ；
2
④ 2 ；
⑤ 62 ；
⑥
16a4 ⑶ 解关于 x 的方程：
① 4x2 49 ； ② 3x2 108 0 ；③ 25 x 12 36
⑷ 比较下列各数大小：
① 2 ___ 3
② 2 ___ 3
③ 140 ___12
2
3
中，无理数有_________个. ⑶ 求下列各数的相反数及绝对值：
① 6 ；② 3.14 ；③1 3 2 ；④ 3 2
⑷ 已知 x 是 4 的平方根， 3 y 2 ， 25 z ，求 x 2 y z 的值.
能力提升
实数与数轴的一一对应关系【例7】 ⑴如图所示，在点 A 和点 B 之间表示整数的点共有_________个.
5 的平方根可表示为 5
用符号表示为“ a ”．
总结：一个正数有两个平方根，且互为相反数；零的平方根是零；负数没有平方
根.
算术平方根的概念：
4 的平方根是 2 ，其中 2 叫做 4 的算
一般地，如果一个正数 x 的平方等于 a ，术平方根. 即 x2 a ，那么这个正数 x 叫做 a 的算术
平方根计算：求一个数的平方根的运算，叫做开平方（开方），开方运算和平方运算互为逆运算.
a (a 0)
a 2 a a ≥ 0, a2 | a | 0 a 0 a (a 0)
夯实基础
对新概念的理解能力
【例1】 ⑴ 求下列各数的平方根与算术平方根：
① 49 ； 64
② 0.0001；
③5；
④ 32 ；
夯实基础
对新概念的运用能力

71初一衔接第2讲

（5）
0
必考题！童鞋们请完成第 25、27题拓展延伸 ——应用题
30．10袋小麦称后记录如图所示（单位：kg）．10袋童鞋们觉得哪种解法比较简单呢？小麦一共多少千克？如果每袋小麦以90kg为标准，10袋哪种解法的计算量比较少呢？小麦总计超过多少千克或不足多少千克？解法2：每袋小麦超过90kg 的千克数记作正数， 91 91 91.5 89 91.2 解法1：不足的千克数记作负数．先计算 10袋小麦一共多少千克： 10袋小麦对应的数分别为：＋＋ 1，＋ 1 ，＋ 1.5 ，－ 1，＋ 1.2＋，＋ 1.3 ，－ 91 91＋ 91.5 ＋ 89 ＋91.2 ＋91.3 88.7 ＋ 88.81.3 ＋，－ 1.2 ，＋ 1.8 ，＋1.1 ．）． 91.8 ＋ 91.1 ＝905.4 （kg 91.3 88.7 88.8 91.8 91.1 1＋1＋1.5＋(－1)＋1.2＋1.3＋(－1.3)＋(－1.2) 再计算总计超过多少千克：＋1.8＋1.1＝5.4（kg）． 905.4－90×10＝5.4（kg）． 90×10＋5.4＝905.4（kg）．超过5.4 ． 905.4 ，总计________kg 答：10袋小麦一共_____kg
1 2 3 4
应用题
课堂小测：5min
课后作业T28~30
卓越秘笈
——减法法则
减法法则：减去一个数，等于加这个数的______ ．相反数思考：在小学，只有当a大于或等于b时，我们才会做a－b（即“大减小”），现在，当a小于b时，也可以做a－b了．一般地，较小的数减去较大的数，负号．所得的差的符号是______
．ቤተ መጻሕፍቲ ባይዱ
典型例题 11．计算：
——减法法则

初一数学寒假衔接讲义

初一寒假讲义目录第1讲同底数幂的乘法第2讲幂、积、商的乘方第3讲整式的乘法第4讲平方差公式及其应用第5讲完全平方公式及其应用第6讲乘法公式综合应用第7讲整式的除法第8讲半期复习与测试第9讲平行线与相交线第10讲平行线与相交线第11讲期末复习第12讲期末测试第1讲同底数幂的乘法一、新知探索1．同底数幂的乘法法则：同底数幂相乘，底数不变，指数相加。

即nm nmaa a +=⋅ (m ，n 都是正整数)．注意：① 三个或三个以上同底数幂相乘时，也具有这一性质．如：p n m p n m a a a a ++=⋅⋅ (m ，n ，p 都是正整数)． ② 此性质可以逆用：n m nm a a a⋅=+说明：在幂的运算中，经常会用到以下的一些变形：（－a ）n＝⎪⎩⎪⎨⎧-);(),(为奇数为偶数n a n a n n （b －a ）n＝⎪⎩⎪⎨⎧---).()(),()(为奇数为偶数n b a n b a nn 二、典例剖析1、顺用公式：例1、计算：（1）35aa a （2）35xx- (3) 231mm bb +⋅（4）mn p aa a ⋅⋅ （5）()()7633-⨯- （6）()()57a a a ---变形练习：（1）234aa a a （2）()()48x x x ---2、常用等式： ()()b a a b -=-- ()()22b a a b -=-()()33b a a b -=--()()44b a a b -=-()()2121n n b a a b ++-=-- ()()22nnb a a b -=-例2、（1）()()()38b a b a b a --- （2）()()()21221222n n n x y y x x y +----（3）()()()48x y y x y x --- （4）()()()37x y y x y x ---3、逆用公式：例3、已知：64,65mn== ，求：6m n+的值。

七年级数学寒假班同步讲义

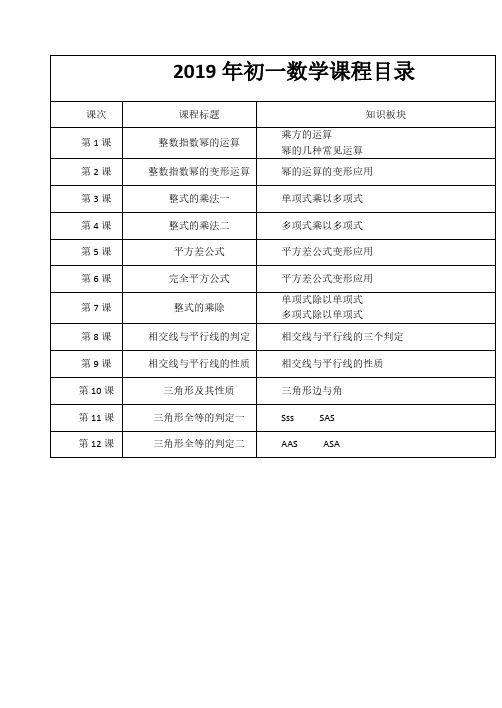
（2）已知10a 5,10ab 25 ，求10b 的值
例 4. 计算下列各式
（1） (x m )3 (x3 )m2 x5m
（2） a 2 (a 4b)3 3
例 5. 试比较 3555 , 4444 , 5333 的大小
【初试锋芒】
1． a a3 a5 =
2． (a2 )3 a5
A． 2100
B． 2100
C．－2
D．2
9．如果单项式 x4ab y2 与 x3 yab 是同类项，则它们的积为（）
A． x6 y4
B． x3 y2
C． 8 x3 y2 3
10．若 a 255, b 344 , c 433 则 a, b, c 的大小关系是（）
D． x6 y4
A．b＞c＞a
第二节同底数幂的除法
【知识要点】
1．同底数幂的除法法则：同底数幂相除，底数不变，指数相减.
即 am an amn （a≠0，m，n 都是正整数且 m＞n） 2．零指数：任何一个不为零的数的 0 次幂都等于 1.即 a0 1(a 0)
3．负整数指数幂：任何不等于零的数的－P（P 是正整数）次幂，等于这个数的 P 次幂的倒数.
A．1
B．2
C．3
D．－3
5．若 1 (a 3)2 b 2 0 ，求 ab 4ba
2
6. 求下列各式中的 m 值
（1） a 2 a 4 a5 a m1
（2） 4.22m 23m 217
7．计算 ( y x)3 (x y)n (x y)n1( y x)2
8．比较 670 与 3535 的大小
例 3. 若 2m 6, 4n 2 ，求 22m2n2 的值.
例 4. 比较大小 218 310与210 315

初一数学寒假衔接班(寒假补课讲义)

初一寒假讲义目录第1讲同底数幂的乘法第2讲幂、积、商的乘方第3讲整式的乘法第4讲平方差公式及其应用第5讲完全平方公式及其应用第6讲乘法公式综合应用第7讲整式的除法第8讲半期复习与测试第9讲平行线与相交线第10讲平行线与相交线第11讲三角形的边角关系第12讲全等三角形的性质和判定第13讲全等三角形的综合应用第14讲期末复习与检测第1讲同底数幂的乘法一、新知探索1．同底数幂的乘法法则：同底数幂相乘，底数不变，指数相加。

即nm nmaa a +=⋅ (m ，n 都是正整数)．注意：① 三个或三个以上同底数幂相乘时，也具有这一性质．如：p n m p n m a a a a ++=⋅⋅ (m ，n ，p 都是正整数)． ② 此性质可以逆用：n m nm a a a⋅=+说明：在幂的运算中，经常会用到以下的一些变形：（－a ）n＝⎪⎩⎪⎨⎧-);(),(为奇数为偶数n a n a n n （b －a ）n＝⎪⎩⎪⎨⎧---).()(),()(为奇数为偶数n b a n b a n n二、典例剖析1、顺用公式：例1、计算：（1）35aa a （2）35xx- (3) 231mm bb +⋅（4）m n p a a a ⋅⋅ （5）()()7633-⨯- （6）()()57a a a ---变形练习：（1）234aa a a （2）()()48x x x ---2、常用等式： ()()b a a b -=-- ()()22b a a b -=-()()33b a a b -=--()()44b a a b -=-()()2121n n b a a b ++-=--()()22nnb a a b -=-例2、（1）()()()38b a b a b a --- （2）()()()21221222n n n x y y x x y +----（3）()()()48x y y x y x --- （4）()()()37x y y x y x ---3、逆用公式：例3、已知：64,65mn== ，求：6m n+的值。

初一数学寒假讲义

练 2-1.如图，直线 AB、CD 相交于点 O，且∠AOD＋∠BOC＝220°，
则∠AOC＝
。
（★）答案:70°
练 2-2.已知∠AOB＝60°，作射线 OC，使∠AOC＝40°OD 是∠BOC 的平分线，那么∠BOD 的度数是（）
A.100° B.100°或 20°
C.50°
D.50°或 10°
练习 1.∠1 和∠2 是对顶角的图形是（）
注意：识别对顶角同时满足的条件：
①有公共顶点
②两个角的两边互为反向延长线.
练习 2.如图直线 AB、CD 相较于 O，则∠COB 的邻补角是（）
A. ∠AOD
B. ∠BOD
C.∠AOC 和∠BOD D.∠AOC
注意：识别邻补角同时满足三条：
①有公共顶点
目录第一讲相交线 ...................................................................................................................................................................................1 第二讲平行线的判断 .....................................................................................................................................................................10 第三讲平行线的性质与判断综合 .................................................................................................................................................17 第四讲平方根和算术平方根 .........................................................................................................................................................25 第五讲立方根与实数 .....................................................................................................................................................................30 第六讲平面直角坐标系 .................................................................................................................................................................36 第七讲阶段自检 .............................................................................................................................................................................43

学而思初一数学寒假班第2讲.二元一次方程组的特殊解法.教师版

方程7级二元一次方程的实际应用方程6级方程组巅峰突破含参方程组方程5级二元一次方程组的特殊解法五百只鸭子漫画释义满分晋级阶梯2二元一次方程组的特殊解法题型切片（两个）对应题目题型目标方程组的基本解法例1；例2；例3；例4；解复杂、特殊的方程组例5；例6；例7；例8；考点一:知道代入、加减消元法的意义1、解方程组：4316x y x y -=⋅⋅⋅⋅⋅⋅⎧⎨+=⋅⋅⋅⋅⎩①②．【解析】①+②得，420x =，解得5x =，把5x =代入①得，54y -=，解得1y =，故此方程组的解为：51x y =⎧⎨=⎩．考点二:选择适当方法解方程组2、已知24328a b a b +=⎧⎨+=⎩，则a b +等于（）A 、3B 、83C 、2D 、1考点剖析知识互联网题型切片【解析】24328a b a b +=⎧⎨+=⎩①②∵①＋②得：4412a b +=，∴3a b +=故选A【点评】本题考察了解二元一次方程组的应用，关键是检查学生能否运用巧妙的方法求出答案，题目比较典型，是一道比较好的题目.【例1】二元一次方程及二元一次方程的解概念【例2】基本的代入、加减消元法解二元一次方程组【例3】解复杂的二元一次方程组【例4】含有字母系数的二元一次方程组，先理解题意再进行计算【例5】叠加叠减法【例6】换元法【例7】倒数法【例8】探索方程组中未知数满足的关系式.定义示例剖析二元一次方程定义：通过化简后，只有两个未知数，并且未知数的项的次数都是1，系数都不是0的整式方程.23x y =，5x y +=，1a b -=，35m n=；二元一次方程的解：使二元一次方程左右两边的值相等的一对未知数的值，叫做这个二元一次方程的一个解．14x y =⎧⎨=⎩是方程5x y +=的一个解；二元一次方程组定义：一般地，含有相同的未知数的两个二元一次方程合在一起，就组成一个二元一次方程组．41x y x y +=⎧⎨-=⎩二元一次方程组的解：使二元一次方程组的两个方程左右两边的值都相等的两个未知数的值（即两个方程的公共解），叫做二元一次方程组的解．31x y =⎧⎨=⎩是二元一次方程组41x y x y +=⎧⎨-=⎩的解.基本方法：⑴ 代入消元法：把方程组中的一个方程进行变形，写出用一个未知数x （或y ）编写思路模块一方程组的基本解法知识导航表示另一个未知数y （或x ）的代数式，然后把它代入另一个方程中，消去未知数y （或x ），得到关于x （或y ）的一元一次方程，通过解这个一元一次方程，再来求二元一次方程组的解．我们把这种通过“代入”消去一个未知数，从而求出方程组的解的方法叫做代入消元法．⑵ 加减消元法：当二元一次方程组中两个方程的某个未知数的系数互为相反数或相等时，可以把方程的两边分别相加（当某个未知数的系数互为相反数时）或相减（当某个未知数的系数相等时）来消去这个未知数，得到一个一元一次方程，进而求得二元一次方程组的解．像上面这种解二元一次方程组的方法叫做加减消元法，简称加减法．易错点：二元一次方程有无数组解，二元一次方程组只有唯一一组解或无数组解.【例1】 ⑴ 已知关于x 、y 的方程()12mm x y ++=是二元一次方程，则m =______.⑵ 当m =_____时，方程220x my +=是关于x 的一元一次方程. ⑶ 写出方程342x y -=的三组解.【解析】 ⑴1；⑵ 0；⑶ 2610147，，x x x y y y ===⎧⎧⎧⎨⎨⎨===⎩⎩⎩等.【例2】解方程组 ⑴2127y x x y =-⎧⎨+=-⎩（北京五中期中）⑵233511x y x y +=⎧⎨-=⎩【解析】 ⑴ 13x y =-⎧⎨=-⎩；⑵21x y =⎧⎨=-⎩【例3】 ⑴ 解方程组121232132x y y x -+⎧-=⎪⎪⎨⎪+=⎪⎩⑵ 若关于x ，y 的方程组18mx ny nx my -=⎧⎨+=⎩的解是21x y =⎧⎨=⎩，则m n -为．【解析】 ⑴ 32x y =⎧⎨=-⎩；⑵ 1.夯实基础能力提升【例4】 ⑴ m 为何值时，方程组522312x y mx y m -=⎧⎨+=-⎩的解x y 、互为相反数？⑵ 已知方程组2420x my x y +=⎧⎨-=⎩有解1x ny n =⎧⎨=+⎩，求m n 、的值.【解析】 ⑴ 9m =；⑵ 将1x n y n =⎧⎨=+⎩代入20x y -=中，即2(1)0n n -+=，解得2n =-，故有21x y =-⎧⎨=-⎩，代入24x my +=中，即44m --=，解得8m =-.定义示例剖析当二元一次方程组比较复杂时，应先化简，利用去分母、去括号、合并同类项等将其变为简单的二元一次方程组后再选择合适的消元法求解.方程组()110.5142335x y x y +⎧--=⎪⎪⎨++⎪=⎪⎩化简得25531x y x y +=⎧⎨-=-⎩易错点：含绝对值的方程组要分类讨论.【例5】解方程组：⑴ 199519975989199719955987x y x y +=⎧⎨+=⎩⑵ 361463102463361102x y x y +=-⎧⎨+=⎩⑶ 201020092008200820072006x y x y -=⎧⎨-=⎩（北京四中期中）【解析】 ⑴ 12x y =⎧⎨=⎩；⑵ 11x y =⎧⎨=-⎩；⑶ 12x y =-⎧⎨=-⎩.【点评】本题尽管可以用常规方法求解，但未知数的系数较大，无论是代入法还是加减法，运算量都很大.选择方法时要根据方程的特点，具体问题具体分析.仔细观察本题系数的特殊规律，大胆地将两个方程分别相加、相减形成新的方程组，进而求得方程组的解.【例6】运用适当的方法解下列方程组夯实基础知识导航模块二解复杂、特殊的方程组⑴()()()()4513453x y x yx y x y⎧++-=⎪⎨+--=⎪⎩（北京十一学校期中）⑵解关于x、y的二元一次方程组3223232232x a y b ax a y b a+-⎧+=⎪⎪⎨+-⎪-=⎪⎩（北京十二中期中）【解析】⑴3212xy⎧=⎪⎪⎨⎪=⎪⎩；提示：令x y u x y v+=-=，⑵22x ay b=-⎧⎨=⎩；提示：令3223x a y bu v+-==，【点评】此题为整体换元法求解. 【例7】解下列方程组⑴1215b aabb aab+⎧=⎪⎪⎨-⎪=⎪⎩⑵13281237xyx yxyx y⎧=⎪+⎪⎨⎪=⎪+⎩【解析】⑴原式可化简为11121115a ba b⎧+=⎪⎪⎨⎪-=⎪⎩，所以207203ab⎧=⎪⎪⎨⎪=⎪⎩⑵取倒数得328237x yxyx yxy+⎧=⎪⎪⎨+⎪=⎪⎩，化简得238327x yx y⎧+=⎪⎪⎨⎪+=⎪⎩得1112xy⎧=⎪⎪⎨⎪=⎪⎩解得112xy=⎧⎪⎨=⎪⎩.【点评】此题为倒数法求解.【例8】 1.（2011年人大附中期中）已知x、y满足方程组2524x yx y+=⎧⎨+=⎩，则x y-的值为 .能力提升真题赏析2.（2013年一六一中学期中）由方程组213x m y m+=⎧⎨-=⎩可得出x 与y 的关系是 .3.（2013年首师大附中期中）已知关于x 、y 的方程组343x y ax y a +=-⎧⎨-=⎩，给出下列结论：①51x y =⎧⎨=-⎩是方程组的解；②当2a =-时，x ，y 的值互为相反数；③当1a =时，方程组的解也是方程4x y a +=-的解； ④,x y 满足的关系式是23x y +=其中正确的是（）A ．①②B ．②③C ．①③④D ．②③④【解析】1. 1x y -=2. 24x y +=3. D.训练1. 如果2223n m n x y ---=是关于x y 、的二元一次方程，那么m = ，n = ．【解析】根据定义得2121n m n -=⎧⎨-=⎩，解得73m n =⎧⎨=⎩.训练2. 解方程组233119,253323.x y x y -=⎧⎨-=⎩①②【解析】 ②-①，得224x y -=，即2x y =+。

寒假七年级数学辅导复习教材

初一数学寒假专题精讲教材大纲课次十节、专题九讲中考专题精讲第一讲数系（一）——有理数及其运算第二讲数与式（一）——代数式初步第三讲平面几何基本元素（一）——线段与角第四讲方程思想（一）——一元一次方程第五讲方程思想（二）——一元一次方程应用下册衔接预科第六讲代数式中的君子第七讲线与角的亲密关系第八讲图形中的王者第九讲 x 与y 的故事第一讲中考专题精讲之数系（一） ——有理数及其运算一．概念与意义 1.有理数的分类其中分数包括有限小数和无限循环小数2.数轴：规定了原点、正方向和单位长度的直线叫做数轴（画数轴时，要注意上述规定的三要素缺一不可）。

任何一个有理数都可以用数轴上的一个点来表示。

解题时要真正掌握数形结合的思想，并能灵活运用。

3.相反数：（1）几何意义：在数轴上分别位于原点的两旁，到原点的距离相等的两个点所表示的数，叫做互为相反数；（2）代数意义：符号不同但绝对值相等的两个数叫做互为相反数。

0的相反数是0。

4.绝对值：（1）几何意义：数轴上表示a 的点与原点的距离叫做数a 的绝对值，记作|a|；（2）代数意义：一个正数的绝对值是它的本身；一个负数的绝对值是它的相反数；零的绝对值是零。

5.倒数：如果a 与b 互为倒数，则有ab=1，反之亦成立。

倒数等于本身的数是1和-1。

零没有倒数。

6.有理数比较大小：正数大于零，负数小于零，正数大于一切负数；数轴上的两个点所表示的数，右边的总比左边的大；两个负数，绝对值大的反而小。

7.有理数的运算：（1）五种运算：加、减、乘、除、乘方（2）有理数的运算顺序先算乘方，再算乘除，最后算加减，如果有括号，先算括号里面的。

（3）运算律加法交换律 a b b a +=+加法结合律 ()()c b a c b a ++=++ 乘法交换律 ba ab = 乘法结合律 ()()bc a c ab =乘法对加法的分配律 ()ac ab c b a +=+正整数整数 0 有理数负整数正分数负分数分数正整数正分数有理数 0 负整数负分数正数负数二、教与学类型一.关于有理数的相关概念1.已知a,b 互为相反数，c ，d 互为倒数，m 的绝对值是1，求2m cd mba +++的值。

寒假班七年级数学2

图1 图 2§7.1探索直线平行线的条件⑴一．教学目标：1．经历探索直线平行的条件的过程，掌握直线平行的条件，并能解决一些问题； 2．会用三角板过已知直线外一点画这条直线的平行线； 3．几何语言利用定理判断两直线平行说理步骤及其理论依据．二．教学重点和难点：在操作、观察的基础上总结出直线平行的条件，并能用几何语言来说明两直线平行．三．教学过程：回顾旧知：1. 如图1，下列结论不正确的是（）A ．∠1与∠3是内错角B ．∠1与∠2是同位角C ．∠1与∠6是同位角D ∠5与∠6是同旁内角2．如图2，下列判断正确的是（）A ．4对同位角，4对内错角，2对同旁内角B ．4对同位角，4对内错角，4对同旁内角C ．6对同位角，4对内错角，4对同旁内角D ．以上判断都不对. 3. 判断下列语句是否正确，并说明道理： ①如果这两条直线不相交，就叫做平行线； ②过一点与一条直线平行的直线只有一条； ③如果直线a 、b 都和c 平行，那么a 、b 就平行.新知讲解：活动一.动手试一试：3根木条（或硬纸条）相交成∠1、∠2，固定木条b 、c ，转动木条a ，问：①在木条a 的转动过程中，木条a 、b 的位置关系发生了什么变化？∠2与∠1的大小关系发生了什么变化？②改变图中∠1的大小，按照上面的方式再试一试，当∠2与∠1的大小满足什么关系时，木条a 与木条b 平行？通过这个实验你能得到什么结论： .例1.如图，a ⊥c ，b ⊥c ，那么a 与b 有何位置关系？并说明之.一个结论： .例2.如图所示：∠1＝∠C ，∠2＝∠C 请你找出图中互相平行的直线，并说明理由BA21几何语言： ∵∠1＝∠2（已知）∴a ∥b ( )例3. 如图，∠1＝135°，∠Ｄ＝45°，试问图中的AB∥ED吗？请说明理由.变式1：如图直线a、b被c所截∠1＝35°，∠2＝145°.问直线a与b平行吗？变式2：如图，已知∠1＝45°，∠2＝135°，l1∥l2吗？为什么？变式3：如图，直线AB、CD被直线EF所截，∠1＝∠2，直线AB和CD平行吗？为什么？活动二.探索内错角条件：如图，直线a、b被直线c所截，∠2＝∠3，直线a与直线b平行吗？为什么？平行线判定定理2：.例4如图，当∠________＝∠_______时，AD∥BC．理由是.例5如图所示，由∠DCE＝∠D，可判断哪两条直线平行？由∠1＝∠2 ，可判断哪两条直线平行？并说明理由.几何语言：∵∠2＝∠3（已知）∴a∥b( )B例4图例5图例6. 如图，点B在DC上，BE平分∠ABD，∠DBE=∠A，则BE∥AC，请说明理由.课堂小结：平行四边形判定⑴ .平行四边形判定⑵ .课时训练1．若∠1，∠2是同位角，则它们之间的关系是（）A．∠1＝∠2 B．∠1＞∠2 C．∠1＜∠2 D．无法确定2．如图，要使AB∥CD，则（）A.∠A＝∠BB.∠A＝∠DCEC.∠B＝∠ACDD.∠B＝∠DCE3．如图，已知∠ADE＝∠B，则____∥_____，由_____＝______，得DF∥AC.4．如图，(1)∠1＝1200，∠4＝1200，则可判定____∥_____，根据是______________________.(2)∠1＝1200 , 由∠3＝600，得∠4＝______则可判定____∥_____.(3) ∠2＝600 , ∠4＝______ ，可判定a∥b，根据是____________________________________. 5．如左图，若∠1=∠D，则_______∥_______，根据是________________________.当哪两个角相等时？我们可以得到AB∥DE.a bc1 2436. 如图，已知∠1＝∠2，要添加下列哪些条件可使CM∥EN成立.（）①∠DMN＝∠FNB②∠AMD＝∠MNF③∠D M N＋∠FNB＝1800④DM⊥AB FN⊥ABA.①B.①②C.①②③D.①②③④变式：如图，已知直线AB、CD被直线EF所截，如果∠BMN＝∠DNF，∠1＝∠2，那么MQ∥NP，试写出推理过程.7. 如图，直线AB、CD被EF所截，且∠1＝∠2，那么直线AB∥CD吗？请说明你的理由.8. 如图，∠1=45o，∠2=135o，∠D=45o.AB与CD平行吗？为什么？BC与DE呢？§7.1探索直线平行线的条件⑵一．教学目标：1．经历探索直线平行的条件的过程，掌握直线平行的条件，并能解决一些问题；2．使学生掌握平行线的三种判定方法．能运用所学过的平行线的判定方法，进行简单的推理和计算；3．使学生初步理解；“从特殊到一般，又从一般到特殊”是认识客观事物的基本方法．二．教学重点和难点：利用平行线的判定定理进行简单的推理．三．教学过程：回顾旧知：如图，①因为∠A＝∠3，可得_____∥______，理由是；②因为∠2＝______，所以AC∥______，理由是；③因为∠5＝______，所以EF∥______，理由是；④因为∠5＝______，所以BC∥______，理由是.新知讲解：活动一.探索新知：如图，直线a、b被直线c所截，∠2＋∠3＝180o，直线a与直线b平行吗？为什么？（用已学过的知识回答，用∵…，∴…写出解题过程）几何语言：∵∠＋∠＝180°（已知）∴∥( ) 根据活动一的探索、交流，我们可以得出： .例1.如图，一个弯形管道ABCD的拐角∠ABC＝110°，∠BCD＝70°，这时管道AB、CD 平行吗？例2.如图，已知：∠1＝43°，∠D＝137°.试说明：AB∥CD例3.如图，填空：①∵∠1＝∠2，∴// ( )②∵∠2＝，∴AD//BE( )③∵∠1＋∠B＝180o，∴// ( )④∵∠1＋∠＝180o，∴AB//DE( )课堂小结：这样我们用来识别两条直线平行的条件有：课时训练：1. 如图，∠1＝∠2，∠3＋∠4＝180o，图中哪些线互相平行，为什么？解：（1）∵∠1＝∠2（）∴// （）（2）∵∠3＋∠4＝180o（）∴// （）想一想：当∠4＝∠_____时，DE//BC（）；当∠4＝∠时，EF//AB（）当∠4＋∠_____＝180°时，EF//AB（）当∠1＝∠_____时，AB//EF（），两直线平行；，两直线平行；，两直线平行.2. 如图三个相同的三角尺拼接成一个图形，请找出图中的一组平行线，并说明你的理由。

七年级数学寒假班讲义

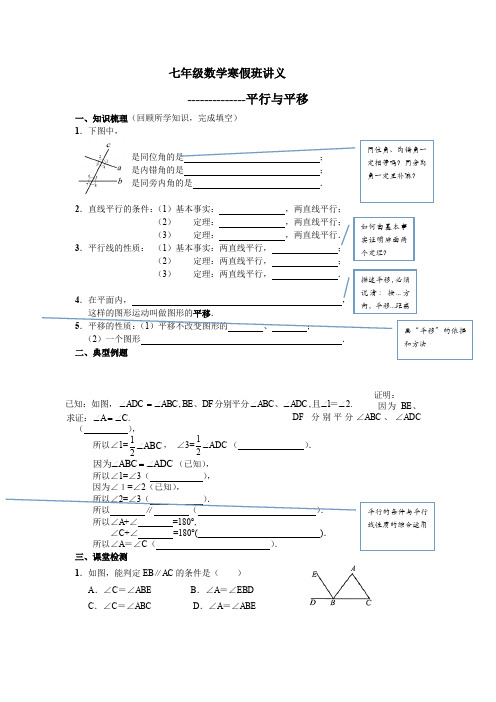
..21,,C A ADC ABC DF BE ABC ADC ∠=∠∠∠∠∠∠=∠求证：＝且、分别平分、已知：如图，七年级数学寒假班讲义--------------平行与平移一、知识梳理（回顾所学知识，完成填空） 1．下图中，是同位角的是；是内错角的是；是同旁内角的是．2．直线平行的条件：（1）基本事实：，两直线平行；（2）定理：，两直线平行；（3）定理：，两直线平行． 3．平行线的性质：（1）基本事实：两直线平行，；（2）定理：两直线平行，；（3）定理：两直线平行，．4．在平面内，，（2）一个图形．二、典型例题证明：因为BE 、DF 分别平分∠ABC 、∠ADC （），所以∠1=，∠3=（）．（已知），所以∠1=∠3（），因为∠１=∠2（已知），所以 ∥ （）所以∠A +∠ =180°, ∠C +∠ =180°( )．所以∠A ＝∠C （）．三、课堂检测 1．如图，能判定EB ∥AC 的条件是（） A ．∠C ＝∠ABE B ．∠A ＝∠EBD C ．∠C ＝∠ABC D ．∠A ＝∠ABEABC ∠21ADC ∠21ADC ABC ∠=∠因为如何由基本事实证明后面两个定理？同位角、内错角一定相等吗？同旁内角一定互补嘛？描述平移，必须说清：按...方向，平移...距离画“平移”的依据和方法平行的条件与平行线性质的综合运用2．如图，直线a ∥b ，∠1＝70°，那么∠2= °．3．如图，将一个长方形纸条折成如图的形状，若已知∠1＝130°，则∠2＝ °．（第2题）（第3题）（第4题）（第5题） 4．如图，把边长为3cm 的正方形ABCD 先向右平移1cm ，再向上平移1cm ，得到正方形 EFGH ，则阴影部分的面积为 cm ²．5．把图中的一个三角形先横向平移x 格，再纵向平移y 格，可以与另一个三角形拼合成一些不同形状的四边形．那么移动的总格数(x +y )的值最小为． 6．如图，点D 在AB 上，直线DG 交AF 于点E ．请从①DG ∥AC ，②AF 平分∠BAC ，③∠ADE ＝∠DEA ．中任选两个作为条件，余下一个作为结论，构造一个真命题，并说明理由．已知：，求证：．（填写序号）证明：7．如图，在△ABC 中，CD ⊥AB ，垂足为D ，点E 在BC 上，EF ⊥AB ，垂足为F ．（1）CD 与EF 平行吗？为什么？（2）如果∠1=∠2，且∠3=115°，求∠ACB 的度数．四：拓展归类1.如图、直线a 、b 被c 所截，所标出的角中有哪些角是同位角？同位角一定相等吗？8765cab 4321b ac 78126543 a bc 56 4 81 23 7 ab122.三类角的位置特征、基本图形、图形结构特征如下表：3.（1）同位角和同旁内角在位置上有什么相同点和不同点？内错角和同旁内角在位置上有什么相同点和不同点？（2）这三类角的共同特征是什么？总结：五、范例点睛例1、如图（1），∠1和∠2是直线_______、_______被直线_______所截得的_______角，∠2和∠3是直线_______、_______被直线_______所截得的_______角；如图（2），∠1和∠2是直线_______、_______被直线_______所截得的_______角，∠4和∠3是直线_______、_______被直线_______所截得的_______角。

初一数学寒假班讲义第02讲-整式及其加减(提高)-学案

初一数学寒假班讲义第02讲-整式及其加减（提高)-学案学科教师辅导讲义学员编号_________年级七年级课时数3学员姓名辅导科目数学学科教师授课主题第02讲---整式及其加减授课类型T同步课堂P实战演练S归纳总结教学目标会用字母表示数；理解代数式的含义，会列代数式并会求值；了解整式的定义，知道单项式多项式的次数及项数；会整式的加减运算，并会化简求值。

授课日期及时段T（Textbook-Based）同步课堂体系搭建一.知识框架二.知识概念（一）代数式1.代数式用运算符号把数和字母连接而成的式子，叫做代数式。

如n-2.0.8a.2n500.abc.2ab2bc2ac（单独一个数或一个字母也是代数式）。

2.列代数式及其求值用具体数值代替代数式中的字母，就可以求出代数式的值。

（三）整式1.整式的分类单项式与多项式单项式只含有数与字母的积，这样的式子叫做单项式，单个字母或者数也是单项式。

单项式的系数单项式中的数字因数叫做单项式的系数。

单项式的次数一个单项式中，所有字母的指数的和叫做这个单项式的次数。

多项式几个单项式的和叫做多项式。

在多项式中，每个单项式叫做多项式的项多项式的次数多项式中，次数最高项的次数，叫做这个多项式的次数。

多项式通常以它的项的次数和项数来命名，称几次几项式。

最高次项的次数是几，就是几次式，项数是几，就是几项式。

比如多项式，可以叫做五次四项式。

（四）合并同类项1.（1）合并同类项的法则是合并同类项时，把同类项的系数相加，字母和字母的指数不变。

（2）合并同类项的步骤准确地找出同类项；利用合并同类项法则合并同类项，把同类项的系数加在一起，字母和字母的指数不变；利用有理数的加减计算出各项系数的和，写出合并后的结果（五）去括号的法则1.括号前是“”号，把括号和它前面的“”号去掉后，原括号里各项的符号都不改变；2.括号前是“-”，把括号和它前面的“-”号去掉后，原括号里各项的符号都要改变。

（六）整式的加减1.整式的加减实质就是将整式中的同类项进行合并，如果有括号应先去括号，再合并同类项2.整式的加减结果注意以下三点结果要是最简，即结果中不再含有同类项；一般按照某一字母的降幂或升幂排列；不能出现带分数，带分数要转化为假分数。