高等数学A(曲线的凹凸拐点渐近线描图)模板
合集下载
高数上凹向、拐点、作图

解
2 y 36 x 24 x 36 x x 3 2 2 0 3 得 x 0 , x 令y 0 1 2 · · 3 x 0时, y 0; 在区间(-∞,0]内曲线是凹的。 2 2 0 x 时, y 0 ; 在区间[0, ]上曲线是凸的。 3 3 2 x 时, y 0. 在区间[ 2 ,+∞)内曲线是凹的。 3 3 2 11 0 , 1、 , 是拐点. 3 27
x2 2
得到曲线上的两个点 (0 ,
1 2
)、( 1,
1
另外f 2
1 , 2 2 e
1
加辅助点 ( 2 ,
2e 1 ). 2 2 e
)
1
2
注:本例特点 (1)利用函数的奇偶性; (2)补充点(0 ,y ( 0 ) ),(2 ,y ( 2 ) ); (3)有水平渐近线。
f ' ( x1 ) f ' ( x2 ) f ' ( x3 ),
f x 递减
f x 0
f x 0
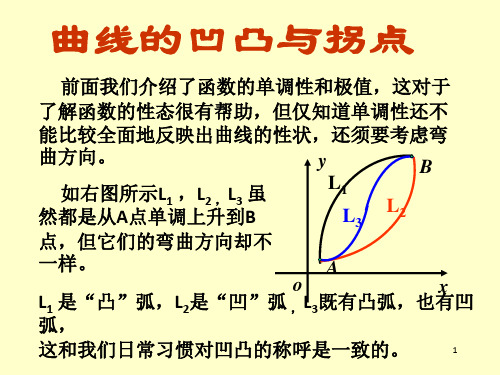
在有些教材中,凹的(曲线)又叫“上凹”,凸的又叫“下凹”。
连续曲线上,不同凹向曲线段的分界点,称为曲线的拐点。 注意:拐点是曲线上的点,应由两个坐标表示:( x0 , f ( x0 ) ). 前面讲过的极值点,是取得极值时自变量的值,记 为 x = xi。 两者不同。 2、曲线凹向的判定 P106定理3.8 函数y = f ( x ) 在闭区间 [ a , b ] 上连续,在开区间内二阶可导, 则当 仍可用“雨水法则” f ”( x ) > 0 时,曲线上凹(凹); 帮助记忆 f ”( x ) < 0 时,曲线下凹(凸)。
2 y 36 x 24 x 36 x x 3 2 2 0 3 得 x 0 , x 令y 0 1 2 · · 3 x 0时, y 0; 在区间(-∞,0]内曲线是凹的。 2 2 0 x 时, y 0 ; 在区间[0, ]上曲线是凸的。 3 3 2 x 时, y 0. 在区间[ 2 ,+∞)内曲线是凹的。 3 3 2 11 0 , 1、 , 是拐点. 3 27
x2 2
得到曲线上的两个点 (0 ,
1 2
)、( 1,
1
另外f 2
1 , 2 2 e
1
加辅助点 ( 2 ,
2e 1 ). 2 2 e
)
1
2
注:本例特点 (1)利用函数的奇偶性; (2)补充点(0 ,y ( 0 ) ),(2 ,y ( 2 ) ); (3)有水平渐近线。
f ' ( x1 ) f ' ( x2 ) f ' ( x3 ),
f x 递减
f x 0
f x 0
在有些教材中,凹的(曲线)又叫“上凹”,凸的又叫“下凹”。
连续曲线上,不同凹向曲线段的分界点,称为曲线的拐点。 注意:拐点是曲线上的点,应由两个坐标表示:( x0 , f ( x0 ) ). 前面讲过的极值点,是取得极值时自变量的值,记 为 x = xi。 两者不同。 2、曲线凹向的判定 P106定理3.8 函数y = f ( x ) 在闭区间 [ a , b ] 上连续,在开区间内二阶可导, 则当 仍可用“雨水法则” f ”( x ) > 0 时,曲线上凹(凹); 帮助记忆 f ”( x ) < 0 时,曲线下凹(凸)。
高数课件-曲线的凹凸性与拐点

4.5 曲线的凹凸性与拐点
4.5.1 曲线的凹凸性 4.5.2 拐点
17-<#>
2021-10-3
前面讨论了函数的单调性和极值.从几何上讲,单调性 反映的是曲线的升降,极值反映的曲线的“峰值”或“谷底”.
单从单调性和极值来研究曲线是不够的.
比如当函数 f x 在某区间单调增加时,其方式是多样的
(见图4-4-6).具体表现在曲线弯曲的方向不同,有凸有凹.曲 线的这种性态称为凹凸性.
设 f ( x)在(a, b)内二阶可导,且 f ( x0 ) 0 , 其中 x0 (a, b),则( x0 , f ( x0 ))是否一定为 曲线 f ( x)的拐点?举例说明.
f
(x0 )
f (1)(x1
x0 )
f (xቤተ መጻሕፍቲ ባይዱ )
1 2
(
x2
x1) f (1) ,
f
(x2 )
f
(x0 )
f
(2 )(x2
x0 )
f
(x0 )
1 2 (x2
x1)
f
(2 ) .
17-1
续证
2021-10-3
两式相加,从而有
f
(x1)
f
( x2 )
2f
(x0)
x2
2
x1 [
故 0,f 0是曲线 y f x的拐点.选(C).
17-1
例
f x x x n 假定 ( )在 = 0處具有直到 階的連續導數,且
f ( x0 ) f ( x0 ) f (n1)( x0 ) 0,但 f (n)( x0 ) 0
n 這裏 為奇數>3,
则( x0 , f ( x0 ))是拐点
4.5.1 曲线的凹凸性 4.5.2 拐点
17-<#>
2021-10-3
前面讨论了函数的单调性和极值.从几何上讲,单调性 反映的是曲线的升降,极值反映的曲线的“峰值”或“谷底”.
单从单调性和极值来研究曲线是不够的.
比如当函数 f x 在某区间单调增加时,其方式是多样的
(见图4-4-6).具体表现在曲线弯曲的方向不同,有凸有凹.曲 线的这种性态称为凹凸性.
设 f ( x)在(a, b)内二阶可导,且 f ( x0 ) 0 , 其中 x0 (a, b),则( x0 , f ( x0 ))是否一定为 曲线 f ( x)的拐点?举例说明.
f
(x0 )
f (1)(x1
x0 )
f (xቤተ መጻሕፍቲ ባይዱ )
1 2
(
x2
x1) f (1) ,
f
(x2 )
f
(x0 )
f
(2 )(x2
x0 )
f
(x0 )
1 2 (x2
x1)
f
(2 ) .
17-1
续证
2021-10-3
两式相加,从而有
f
(x1)
f
( x2 )
2f
(x0)
x2
2
x1 [
故 0,f 0是曲线 y f x的拐点.选(C).
17-1
例
f x x x n 假定 ( )在 = 0處具有直到 階的連續導數,且
f ( x0 ) f ( x0 ) f (n1)( x0 ) 0,但 f (n)( x0 ) 0
n 這裏 為奇數>3,
则( x0 , f ( x0 ))是拐点
函数曲线的凹凸性.ppt

例如 y arctan x,
定义 设f ( x)在区间 I 上连续, 如果对 I 上任意两
点 x1, x2 , 恒有
f ( x1 x2 ) 2
f ( x1 ) 2
f ( x2 ) ,那末称
f ( x) 在 I 上的图形是(向上)凹的(或凹弧);
如果恒有 f ( x1 x2 ) f ( x1) f ( x2 ) ,那末称 f ( x)
定理1 如果 f ( x) 在 [a,b] 上连续,在 (a,b) 内具有
一阶和二阶导数,若在 (a,b)内
(1) f ( x) 0,则 f ( x) 在 [a,b] 上的图形是凹的;
(2) f ( x) 0,则 f ( x) 在 [a,b] 上的图形是凸的.
证 任取x0 (a, b), 泰勒公式
曲线 在(,0]为凸的; 当x 0时, y 0, 曲线 在[0,)为凹的; 注意到, 点(0,0)是曲线由凸变凹的分界点.
三、曲线的拐点及其求法
1、定义 连续曲线上凹凸的分界点称为曲线的拐点. 注意:拐点处的切线必在拐点处穿过曲线. 2、拐点的求法 方法1: 设函数f ( x)在x0的邻域内二阶可导, 且f ( x0 ) 0, (1) x0两近旁f ( x)变号,点( x0, f ( x0 ))即为拐点;
f ( x)
0
0
f ( x) 凹的
拐点 (0,1)
凸的
拐点 (2 3 ,1127)
凹的
凹凸区间为 (,0], [0, 2 3], [2 3 ,).
思考:设 f ( x)在 x0处具有三阶导数, 且 f ''( x0 ) 0 , f ( x0 ) 0 那末 x0是否为 函数 f ( x)的拐点?
曲线的凹凸性与拐点函数图形的描绘模板

是凸的.
(证明从略)
上一页 下一页 返回
例1 判断曲线 y=x3 的凹凸性. 解 因为y 3 x 2,y 6 x,所以
当x (, 0)时,y 0,
此时曲线是凸的;
当x ( 0, )时,y 0,
此时曲线是凹的.
上一页 下一页 返回
定义
连续曲线y=f(x)上凹的曲线弧与凸的曲
2 无限接近于直线y ; (如图所示) 2
y
2
直线y
;当x 时,曲线y arctanx
y = arctan x O
2
x
上一页
下一页
返回
(2) 当x 1 时,曲线 y ln(x 1)无限接近于
直线x 1 (如图所示)
y x=1
y = ln( x-1)
一点x0,使f x0 0. 这样,点( x0 , f ( x0 ))
判定曲线 y=f(x)的拐点的一般步骤:
(1)确定y=f(x)的定义域.
(2)求f (x),f (x),令f (x)=0,求出所有 可能拐点x0.
(3)考察 f (x)在每个可能拐点 x0左右两侧的符 号,如果 f (x)的符号相反,则点(x0 , f(x0))
当x 2时, f ( 2) 0, 因f ( x )在x 2两侧的符号相反,而 f (2) 3
所以点(2, 3)是该曲线的拐点.
上一页 下一页 返回
例3 求曲线 f (x) = (2x-1) 4+ 1 的凹凸性,并
求拐点. 解 (1) 定义域为( , ). (2) f (x) = 8(2x-1)3 , f (x) = 48(2x-1)2 , 令 f (x) = 0,可得 x = 1/2. (3) 因为当x≠1/2时,f (x)>0 ,所以该曲线 在整个定义区间内都是凹的,曲线没有拐 点.
第四节 曲线的凹向,渐近线及图像的描绘-PPT文档资料

(1) f(x)0,则f(x)在[a,b]上的图形是上凹的;
(2) f(x)0,则f(x)在[a,b]上的图形是下凹的.
上一页下一页 返回
例1 判 断 曲 线 y x 3的 凹 向 . DR
解 y3x2, y6x, 当x0时,y 0, 曲 线 在 ( ,0 ] 为 下 凹 的 ; 当x0时,y 0, 曲 线 在 [ 0 , ) 为 上 凹 的 ; 注意到, 点 ( 0 , 0 ) 是 曲 线 由 下 凹 变 上 凹 的 分 界 点 .
上一页下一页 返回
三、作图举例
例5 作函 f(x)数 4(x x 21)2的图 . 形 解 D:x0, 非奇非偶函数,且无对称性.
f(x)4(xx3 2),
f(x)8(xx4 3).
令f(x)0, 得驻 x点 2,
令 f(x)0, 得特殊 x点 3.
lx i m f(x)lx i [m 4(x x 21)2] 2
上一页下一页 返回
上一页下一页 返回
lx i0m f(x)lx i0[m 4(x x 21)2] , 得铅垂渐近x线0.
列表确定函数升降区间,凹向区间及极值点和拐点:
x ( ,3) 3 (3,2)2 (2,0) 0 (0,)
f(x) 0
不存在
f(x)
0
f (x)
拐点
(3, 26) 9
上一页下一页 返回
例2 求 曲 线 y 3 x 4 4 x 3 1 的 拐 点 及 凹 向 .
解 D :(, )
y1x 2 31x 2 2, y36x(x2).
令y0,
得x1
0,
x2
2. 3
3
x (,0)
0
(0, 2 3)
《曲线的凹凸与拐点》课件

《曲线的凹凸与拐点》ppt课件
contents
目录
• 曲线凹凸的定义与性质 • 判断曲线凹凸的方法 • 曲线的拐点及其性质 • 曲线凹凸与拐点的应用 • 总结与思考
01
曲线凹凸的定义与性质
凹凸的定义
凹函数
对于曲线上的任意两点$x_1$和 $x_2$($x_1 < x_2$),如果函 数值$f(x_1) > f(x_2)$,则称该函 数为凹函数。
通过学习更多的函数曲线,加深对 凹凸性和拐点的理解。
探索应用领域
了解曲线凹凸性和拐点在实际问题 中的应用,如物理学、工程学等。
对实际应用的展望
工程设计
在工程设计中,了解曲线的凹凸 性和拐点有助于优化设计,如桥 梁、建筑等结构的稳定性分析。
数据分析
在数据分析中,可以利用曲线凹 凸性和拐点的知识,对数据进行
凸函数
对于曲线上的任意两点$x_1$和 $x_2$($x_1 < x_2$),如果函 数值$f(x_1) < f(x_2)$,则称该函 数为凸函数。
凹凸的性质
01
凹函数的图像呈下凹状,凸函数 的图像呈上凸状。
02
在凹函数中,中点的函数值小于 两端点的函数值;在凸函数中, 中点的函数值大于两端点的函数 值。
凸函数的定义
对于函数$f(x)$在区间$[a,b]$上,如果对任意$x_1, x_2$($x_1 < x_2$)都有 $f(x_1) - f(x_2) > frac{f(x_1) + f(x_2)}{2} (x_1 - x_2)$,则称$f(x)$在区间 $[a,b]$上为凸函数。
凹凸的判断方法
计算二阶导数
拐点的连续性判定
若函数在拐点处的一阶导 数存在且二阶导数改变符 号,则该点为拐点的充分 必要条件是该点连续。
contents
目录
• 曲线凹凸的定义与性质 • 判断曲线凹凸的方法 • 曲线的拐点及其性质 • 曲线凹凸与拐点的应用 • 总结与思考
01
曲线凹凸的定义与性质
凹凸的定义
凹函数
对于曲线上的任意两点$x_1$和 $x_2$($x_1 < x_2$),如果函 数值$f(x_1) > f(x_2)$,则称该函 数为凹函数。
通过学习更多的函数曲线,加深对 凹凸性和拐点的理解。
探索应用领域
了解曲线凹凸性和拐点在实际问题 中的应用,如物理学、工程学等。
对实际应用的展望
工程设计
在工程设计中,了解曲线的凹凸 性和拐点有助于优化设计,如桥 梁、建筑等结构的稳定性分析。
数据分析
在数据分析中,可以利用曲线凹 凸性和拐点的知识,对数据进行
凸函数
对于曲线上的任意两点$x_1$和 $x_2$($x_1 < x_2$),如果函 数值$f(x_1) < f(x_2)$,则称该函 数为凸函数。
凹凸的性质
01
凹函数的图像呈下凹状,凸函数 的图像呈上凸状。
02
在凹函数中,中点的函数值小于 两端点的函数值;在凸函数中, 中点的函数值大于两端点的函数 值。
凸函数的定义
对于函数$f(x)$在区间$[a,b]$上,如果对任意$x_1, x_2$($x_1 < x_2$)都有 $f(x_1) - f(x_2) > frac{f(x_1) + f(x_2)}{2} (x_1 - x_2)$,则称$f(x)$在区间 $[a,b]$上为凸函数。
凹凸的判断方法
计算二阶导数
拐点的连续性判定
若函数在拐点处的一阶导 数存在且二阶导数改变符 号,则该点为拐点的充分 必要条件是该点连续。
《曲线的凹凸与拐点》PPT课件
定理 2 如果 f ( x)在( x0 , x0 )内存在二阶导
数,则点x0 , f ( x0 )是拐点的必要条件是 f "( x0 ) 0 .
证 f ( x) 二阶可导, f ( x) 存在且连续,
7
又( x0 , f ( x0 ) )是拐点, 则 f ( x) [ f ( x)]在x0两边变号, f ( x)在x0取得极值,由可导函数取得极值的条件, f ( x) 0.
13
例4 假定f(x)在x=x0处具有直到n阶的连续导数,且
f ( x0 ) f ( x0 ) f (n1)( x0 ) 0,但 f (n)( x0 ) 0
这里n为奇数≥3, 则( x0 , f ( x0 ))是拐点
证 记 g( x) f ( x) 则 g(n3)( x0 ) f (n)( x0 ) 0 由高阶导数判定极值的方法知
x0 , x2 ]上
x1 x2 x0 分别应用L—定理,得
f ( x0 ) f ( x1 ) f (1 )h ( x1 1 x0 )
f ( x2 ) f ( x0 ) f (2 )h ( x0 2 x2 )
两式相减,得
2 f ( x0 ) [ f ( x1 ) f ( x2 )] [ f (1 ) f (2 )]h
y cos x sin x .
令 y 0,
得
x1
3 4
,
7 x2 4 .
f (3) 2 0,
4
f (7) 2 0,
4
12
在[0,2]内曲线有拐点为 (3 ,0), (7 ,0).
4
4
注意: 若 f ( x0 ) 不存在,点 ( x0 , f ( x0 )) 也可能 是连续曲线 y f ( x)的拐点.
数,则点x0 , f ( x0 )是拐点的必要条件是 f "( x0 ) 0 .
证 f ( x) 二阶可导, f ( x) 存在且连续,
7
又( x0 , f ( x0 ) )是拐点, 则 f ( x) [ f ( x)]在x0两边变号, f ( x)在x0取得极值,由可导函数取得极值的条件, f ( x) 0.
13
例4 假定f(x)在x=x0处具有直到n阶的连续导数,且
f ( x0 ) f ( x0 ) f (n1)( x0 ) 0,但 f (n)( x0 ) 0
这里n为奇数≥3, 则( x0 , f ( x0 ))是拐点
证 记 g( x) f ( x) 则 g(n3)( x0 ) f (n)( x0 ) 0 由高阶导数判定极值的方法知
x0 , x2 ]上
x1 x2 x0 分别应用L—定理,得
f ( x0 ) f ( x1 ) f (1 )h ( x1 1 x0 )
f ( x2 ) f ( x0 ) f (2 )h ( x0 2 x2 )
两式相减,得
2 f ( x0 ) [ f ( x1 ) f ( x2 )] [ f (1 ) f (2 )]h
y cos x sin x .
令 y 0,
得
x1
3 4
,
7 x2 4 .
f (3) 2 0,
4
f (7) 2 0,
4
12
在[0,2]内曲线有拐点为 (3 ,0), (7 ,0).
4
4
注意: 若 f ( x0 ) 不存在,点 ( x0 , f ( x0 )) 也可能 是连续曲线 y f ( x)的拐点.
曲线的凹凸性、渐近线 及函数图形的描绘

3 2 y 3 x 2 x 1 ,讨论曲线的凹凸性. 例1 设
讨论:要解决这个“未知”,需要用什么做“已知”?为了 解 定义域 (, ) , 由y 3 x 3 2 x 2 1 求得, 利用这个“已知”首先应做什么? y 18 x 4 y 9 x 2 4 x
满 足 y 0 的 点 不 一 定 对 应 函 数 曲 线 的 拐 点 , 如
y x 4 (见例 6),如 y 3 x ,当 x 0 时,其二阶导数不存
在, 但(0,0)是其拐点(请自己验证).由此来看,找函数的 拐点时应从二阶导数为零的点及二阶导数不存在的点 处考虑.
上页 目录 下页
定理 1 设函数 y f ( x ) 在区间 ( a , b ) 内二阶可导.
若对任意的 x (a, b) ,都有 f ( x ) 0 ,那么曲线在 ( a , b ) 内是凹的; 若对任意的 x (a, b) ,都有 f ( x ) 0 ,那么曲线在 ( a , b ) 内是凸的.
y 2 xe
x2
, y 2(2 x 1)e
2
x2
,
1 2 ,
解方程 y 0, 得函数的驻点x=0; 解方程 y 0, 得 x
为讨论该函数在 [0, ) 上的单调性、极值及其图像的凹凸 性与拐点,列表分析如下
f ( x ) n(n 1) x n2 0 ,
因此在 (0, ) 上,函数是凹的.
由定义 2,对 x 0, y 0, x y 我们有
x y f ( x) f ( y) f( ) , 2 2
即
1 n x y n ( x yn ) ( ) ( x 0, y 0, x y , n 1) . 2 2
高等数学导数应用二凹凸拐点图形PPT课件

从而, 点 (x0, f (x0 )) 为曲线 y f (x) 的拐点 .
你能由以上的几个定理归纳出 求曲线拐点的步骤吗?
第28页/共56页
求拐点一般步骤
求曲线 y f (x) 拐点的一般步骤 : (1) 求 f (x) 的定义域 (或确定讨论区间 ) ; (2) 计算 f (x) , f (x) , (如需要可求出 f (x)) ; (3) 求拐点可疑点 : 使 f (x) 0 的点和 f (x) 不存在的点 ; (4) 根据定理判别可疑点是 否确为拐点 .
且仅在孤立点处出现 f (x) 0 .
第24页/共56页
于是 f (x) (x0 , x0x ) , f (x) (x0 x, x0 ) , 故 f (x) 在 x x0 处取极小值, 从而必有 f (x0 ) ( f (x)) xx0 0 .
使 f (x) 0 及 f (x) 不存在的点 ,
第26页/共56页
定理 ( 判别拐点的充分条件 )
设 f (x) C( I ) , f (x) 在 U(x0 ) (x0 I )内三阶可导. 若 f (x0 ) 0 , 且 f (x0 ) 0 , 则
点 (x0 , f (x0 )) 为曲线 y f (x) 的拐点 .
第27页/共56页
证 由于 f (x0 ) 0 , 故不妨设 f (x0 ) 0 .
成立 , 则称曲线
y f (x) 在区间 I 上是凹的 ;
第9页/共56页
例1
分析立方抛物线 y x3 的凹凸性.
分析
f ( x1 x2 ) x13 3x12 x2 3x1x22 x23
2
8
1( 2
f
(x1)
f
(x2 ))
高等数学A-第2章-11-10(曲线的凹凸 拐点 渐近线 描图)

x1 ),
若函数为凸函数, 则有
f (x)
f ( x1)
f ( x2 ) x2
f ( x1)( x x1
x1 ),
f (x)
x2 x x2 x1
f ( x1)
x x1 x2 x1
f ( x2 ),
令
x2 x x2 x1
1 ,
x x1 x2 x1
2 ,
则1 2 1, x 1x1 2 x2,
f ( x) f ( y) f ( x y).
2
2
即 1 (xn yn) ( x y)n.
2
2
二. 函数图形的拐点
定义: 连续曲线y=f(x)上凹弧与凸弧的分界点称为拐点.
注意:拐点处的切线必在拐点处穿过曲线.
如y sin x 的拐点有(k ,0), k 0,1,2,.
y
o
x
定理3 (拐点存在的必要条件) 设f ( x)在包含x0的区间I上二阶可导, 若( x0 , f ( x0 ))为拐点,则f ( x0 ) 0.
即当 x1 x2 x3时, f ( x1) f ( x2 ) f ( x3 ). f ( x) 单调递增.
定理1. (1)在区间(a,b)内的可导函数f ( x)为凸函数的 充要条件是导函数f ( x)在(a,b)内递减.
(2)在区间(a,b)内的可导函数f ( x)为凹函数的 充要条件是导函数f ( x)在(a,(
3)( x
x 1)2
1)
,
y
(
x
2 1)3
又因
lim y x x
1, 4
即 k1 4
b lim ( y 1 x) lim [( x 3)2 1 x]
第四节 曲线的凹向,渐近线及图像的描绘

上一页下一页 返回
上一页下一页 返回
lx i0m f(x)lx i0[m 4(x x 21)2] , 得铅垂渐近x线0.
列表确定函数升降区间,凹向区间及极值点和拐点:
x ( ,3) 3 (3,2)2 (2,0) 0 (0,)
f(x) 0
不存在
上一页下一页 返回
思考题
两坐标轴x0,y0是否都是 函数f(x)sinx的渐近线?
x
上一页下一页 返回
思考题解答
limsinx0 x x
y0 是 其 图 象 的 渐 近 线 .
y sin x x
limsinx1 x0 x
x 0 不 是 其 图 象 的 渐 近 线 .
第三章 导数的应用
第四节 曲线的凹凸性与拐点及函数图 形的描绘
在讨论函数图形的时候,仅仅知道函数的单调性 是不够的,如图:
y
y x2
y x 1
0
1
x
上一页下一页 返回
• 学习要求 • 能熟练地求出函数的水平渐近线和铅垂渐近线 • 熟练掌握判断函数的凹向与拐点的方法 • 了解函数图形描绘的步骤
x
x
那么 yb就是 yf(x)的一条水平 . 渐近
例如 yarctxa, n
有水平渐近线两条:
上一页下一页 返回
例 解 1 : : 求 lxi 曲 m 线 fy x x lx2 imx 2 2 x x 21 x23 2的 x1渐 3近 ""线 型 lxim 2 x2x 2
27
拐点
( 1 , 16 ) 3 27
极小值
0
y
B(0,1)
C (3,5) 28
函数的凹凸性,拐点与图形描绘

0
且f ′( x0 ) = 0, 必有f ′( x ) > 0。 不是极值点。 因此 x = x0 不是极值点。
11
第八节 函数图形的描绘
1.一般步骤 1.一般步骤: 一般步骤: (1) 确定 y = f ( x )的定义域,考察函数的 奇偶性;求出 f ′( x )、 f ′′( x ). 的定义域, 奇偶性; (2) 求出 f ′( x ) = 0 , f ′′( x ) = 0的全部实根 , 及 f ′( x ), f ′′( x )不存在 的点 . 并用这些点把定义域划 分为几个部分区间 . (3) 列表讨论 f ( x )的性质 .
4 没有拐点,且它在( + 内是凹的。 即 曲线 y = x 没有拐点,且它在( − ∞, ∞)内是凹的。
9
3 例5 求曲线 y = x 的拐点。 的拐点。 解 定义域:(− ∞ ,+∞ ), 定义域: 1 2 , 当 x ≠ 0 时, y' = 3 2 , y" = − 3 2 3 x 9x x y 当 x = 0 时, ' , y" 都不存在 。
2 2
用拉格朗日中值定理, 对 f ′( x ) 在 [x0 − θ 2 h, x0 + θ 1h] 用拉格朗日中值定理,得
(1)确定函数 y = f (x)的定义域; 的定义域; 的定义域 找出使 不存在的点x (2)求 f ”(x),找出使 f ”(x)=0 和 f ”(x) 不存在的点 i ; 找出 把定义域划分成为小区间, (3)用xi把定义域划分成为小区间,在每个小区间上判定曲线 的凹凸。 的凹凸。 例1. 判断 y = ln x 的凹凸性 . 1 1 解 定义域 (0, ∞ ), Q y ′ = , y ′′ = − 2 < 0. + x x ∴ 曲线是凸的 .
且f ′( x0 ) = 0, 必有f ′( x ) > 0。 不是极值点。 因此 x = x0 不是极值点。
11
第八节 函数图形的描绘
1.一般步骤 1.一般步骤: 一般步骤: (1) 确定 y = f ( x )的定义域,考察函数的 奇偶性;求出 f ′( x )、 f ′′( x ). 的定义域, 奇偶性; (2) 求出 f ′( x ) = 0 , f ′′( x ) = 0的全部实根 , 及 f ′( x ), f ′′( x )不存在 的点 . 并用这些点把定义域划 分为几个部分区间 . (3) 列表讨论 f ( x )的性质 .
4 没有拐点,且它在( + 内是凹的。 即 曲线 y = x 没有拐点,且它在( − ∞, ∞)内是凹的。
9
3 例5 求曲线 y = x 的拐点。 的拐点。 解 定义域:(− ∞ ,+∞ ), 定义域: 1 2 , 当 x ≠ 0 时, y' = 3 2 , y" = − 3 2 3 x 9x x y 当 x = 0 时, ' , y" 都不存在 。
2 2
用拉格朗日中值定理, 对 f ′( x ) 在 [x0 − θ 2 h, x0 + θ 1h] 用拉格朗日中值定理,得
(1)确定函数 y = f (x)的定义域; 的定义域; 的定义域 找出使 不存在的点x (2)求 f ”(x),找出使 f ”(x)=0 和 f ”(x) 不存在的点 i ; 找出 把定义域划分成为小区间, (3)用xi把定义域划分成为小区间,在每个小区间上判定曲线 的凹凸。 的凹凸。 例1. 判断 y = ln x 的凹凸性 . 1 1 解 定义域 (0, ∞ ), Q y ′ = , y ′′ = − 2 < 0. + x x ∴ 曲线是凸的 .
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
解: y 3ax2 2bx, y 6ax 2b.
又(1,3) 是y ax3 bx2的拐点.
y(1) 3 y(1) 0
a b 3 6a 2b
0
a 3,b 9. 22
四. 曲线的渐近线
1. 水平渐近线
若 lim f ( x) A 或 lim f ( x) A 或 lim f ( x) A,
定理1. (1)在区间(a,b)内的可导函数f ( x)为凸函数的 充要条件是导函数f ( x)在(a,b)内递减.
(2)在区间(a,b)内的可导函数f ( x)为凹函数的 充要条件是导函数f ( x)在(a,b)内递增.
定理2. 设 f (x)在(a,b)内有二阶导数, (1) 若x (a,b)时有f ( x) 0, 则 f (x)在(a,b)内的图形是凸的.
1. 定义: 设 f (x)在 I内连续,
x1, x2 I , 1 0,2 0,且1 2 1. (1)若f (1x1 2 x2 ) 1 f ( x1) 2 f ( x2 ),
则 f (x)为区间 I上的凸函数.
(2)若f (1x1 2 x2 ) 1 f ( x1) 2 f ( x2 ),
2
2
例1. 判定下列曲线的凹凸性 (1) f ( x) ln x; (2) f ( x) arctan x.
解: (1) f ( x) ln x 的定义域为 (0,).
f ( x) 1 , x
f
( x)
1 x2
0.
f ( x) ln x 的图形在(0,)上是凸的.
(2)
y
36( (x
3 x 3)3
)
,
令y 0, 得 x 3.
y
72( (x
x
6) 3)4
,
(3)列表讨论如下:
令y 0, 得 x 6.
x (,3) 3 (3,3) 3 (3,6) 6
y 不存在 0
y 不存在
0
y
(6,)
曲线的拐点判别习例 例3. 求y 3x4 4x3 1的凹凸区间与拐点. 例4. 求( y 3)3 x 4的凹凸区间与拐点. 例5. 问a, b为何值时, (1,3)为曲线y ax3 bx2的拐点?
例3.求y 3x4 4x3 1的凹凸区间与拐点.
解: 函数y的定义域为(,).
b lim[ f ( x) kx] lim[
x3
x]
x
x ( x 3)( x 1)
lim
x
2x2 x2 2
x
3
x 3
2,
有斜渐近线 y x 2.
五. 函数图形的描绘
利用函数特性描绘函数图形, 一般步骤如下: (1) 确定函数 f (x)的定义域.
1 o 1
x
函数图形的描绘综合运用 函数性态的研究,是导数应 用的综合考察.
(2) 若x (a,b)时有f ( x) 0, 则 f (x)在(a,b)内的图形是凹的.
曲线的凹凸性习例 例1. 判定下列曲线的凹凸性
(1) f ( x) ln x; (2) f ( x) arctan x.
例2. 证明 1 ( xn yn ) ( x y)n ( x 0, y 0, x y, n 1).
曲线的拐点及判别法
导 数
2.3.5 曲线的拐点及其求法
曲线的拐点判别习例3-5
的 应
曲线的渐近线概念
2.3.6 曲线的渐近线
曲线的渐近线习例6
用
函数图形的描绘方法
2.3.7 函数图形的描绘方法
函数图形的描绘习例7-10
课堂思考与练习
一. 函数图形的凹凸性
y
y
y f (x)
y f (x)
o x1
2
2
拐点有( 3, 3), (0,0), ( 3, 3).
4
4
(5)
lim
x
1
x x
2
0,
y 0 为水平渐近线.
(6) 描图如下: y
1
o1
x
例8.
设
y
1
(
36 x x 3)2
,
描绘图形.
解: (1)函数y的定义域为 (,3) (3,).
则 f (x)为区间 I上的凹函数.
2. 判别法 y
如图所示
y
o x1
x2 x3
xo
x
凹弧的曲线位于各点处切线的上方 凸弧的曲线位于各点处切线的下方
tan tan tan
即当 x1 x2 x3时, f ( x1 ) f ( x2 ) f ( x3 ). f ( x) 单调递增.
y 12x3 12x2, y 36x2 24x 36x( x 2).
3
令
y
0,
得
x1
0,
x2
2 3
.
x (,0)
y
y
0
0 拐点
(0, 2) 3
2 3 0 拐点
(2 ,) 3
(0,1)和 (2 , 11) 是拐点. 3 27
例4. 求( y 3)3 x 4的凹凸区间与拐点.
(2) 求得 f ( x) 0, f ( x) 0的点.
(3)以间断点,不可导点, f ( x) 0 和 f ( x) 0的点把 定义域分成若干个小区间.
(4) 在各小区间上确定f ( x), f ( x) 的符号,从而确定出 图形的升降,凹凸, 极值与拐点.
(5) 求出极值,拐点与坐标轴的交点. (6) 求出渐近线. (7) 描图.
x
x
x
则 y=A 是曲线 y = f(x) 的水平渐近线.
2. 铅直渐近线
若 lim f ( x) 或 lim f ( x) 或 lim f ( x) ,
xa
xa
xa
则 x=a 是曲线 y = f(x) 的铅直渐近线.
3. 斜渐近线
若 lim[ f ( x) (kx b)] 0,
函数图形的描绘习例
例7.
设
y
x 1 x2
, 描绘图形.
例8.
设
y
1
(
36 x x 3)2
, 描绘图形.
例9.
例10.
例7.
设
y
1
x x2
, 描绘图形.
解: (1)函数y的定义域为 (,).
(2)
y
1 (1
x2 x2 )2
,
令y 0, 得x 1.
y
三. 判定函数图形凹凸与拐点的步骤
(1)写出f ( x)的定义域. (2)求f ( x). (3)求出f ( x) 0的点及二阶导数不存在的点xi . (4) xi 将定义区间分成若干个 小区间.
(5)由f ( x)的符号可得凹凸区间; 若在xi左右两侧, f ( x)变号则( xi , f ( xi ))为拐点, 否则不是拐点.
y
o
x
定理3 (拐点存在的必要条件) 设f ( x)在包含x0的区间I上二阶可导, 若( x0 , f ( x0 ))为拐点,则f ( x0 ) 0.
注意:
设f ( x)在U ( x~0 , )内存在,
(1)当x x0时, f ( x) 0;当x x0时, f ( x) 0 则( x0 , f ( x0 ))是曲线y f ( x)的拐点. 或者 (2)当x x0时, f ( x) 0;当x x0时, f ( x) 0 则( x0 , f ( x0 ))是曲线y f ( x)的拐点.
1 ,
x x1 x2 x1
2 ,
则1 2 1, x 1x1 2 x2 ,
f (1x1 2 x2 ) 1 f ( x1) 2 f ( x2 ).
类似地, 若函数为凹函数, 则有
f (1x1 2 x2 ) 1 f ( x1) 2 f ( x2 ).
(4)极大值为 y(3) 4,
拐点有 (6, 11). 3
与坐标轴的交点 : (6 3 3,0), (0,1).
(5)
lim[1
x
(
36 x
x 3)2
]
1,
y 1 是水平渐近线.
lim[1
x3
(
36 x
x 3)2
]
,
x 3 是铅直渐近线.
(6) 描图如下: y
x3
,
x1 x1 ( x 3)( x 1)
lim y lim
x3
,
x3 x3 ( x 3)( x 1)
故有铅直渐近线x 1与 x 3.
又 k lim f ( x) lim
x3
1,
x x x ( x 3)( x 1) x
(2) f ( x) arctan x 的定义域为(,).
f
(
x)
1
1 x
2
,
f
(
x)
(1
2
x x
2
)2
.
令f ( x) 0, 得 x 0.
