外拿破仑三角形的证明
拿破仑 李明波 六芒星
拿破仑 李明波 六芒星郝锡鹏提要 2010年5月25日,李明波发现竟然顺理成章地存在拿破仑三角形的共轭三角形,两者神奇的构成了普通三角形的六芒星。
引理1 两个直接相似三角形对应顶点连线上的等比例分点,是位似中心或是与原三角形直接相似的三角形顶点。
证明 若两个直接相似三角形对应顶点连线交于一点,该点便是位似中心,它分每条对应点连线成比例是人们所熟知的,所以对引理1中三个等比分点合一的情况讨论从略。
下面只讨论此外的情况。
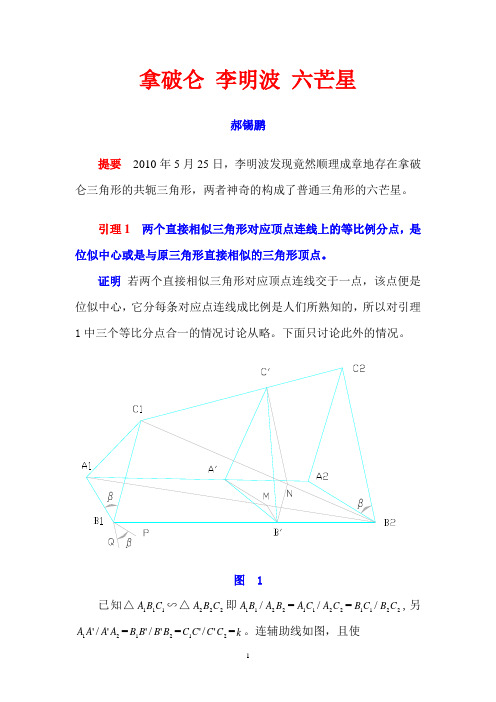
图 1已知△111C B A ∽△222C B A 即11B A /22B A =11C A /22C A =11C B /22C B ,另'1A A /2'A A ='1B B /2'B B ='1C C /2'C C =k 。
连辅助线如图,且使M A 1/2MB =N C 1/2NB =k 。
1、因△M A A '1∽△221B A A ,所以M A '/22B A ='1A A /21A A =k /(k +1);因△N C C '1∽△221B C C ,所以N C '/22C B ='1C C /21C C =k /(k +1)。
得M A '/22B A =N C '/22C B 即M A '/N C '=22B A /22C B (1)2、因△M B B '2∽△112A B B ,所以M B '/11B A ='2B B /12B B =1/(k +1);因△N B B '2∽△112C B B ,所以N B '/11C B ='2B B /12B B =1/(k +1)。
得M B '/11B A =N B '/11C B 即M B '/N B '=11B A /11C B (2)3、由(1)、(2)和已知条件可知M A '/N C '=M B '/N B ' (3)4、作P B 1∥22B A 、Q B 1∥22C B ,则∠''MB A =∠P B A 11、∠''NC B = ∠Q B C 11。
拿破仑定理的简单证明

拿破仑定理的简单证明1. 如图:(外)由余弦定理及面积公式得:)322(31)sin 2132cos (31)3cos(332)3()3(,22222222ABC S c b a A bc A bc c b A c b cbQR AQR ∆+++=+-+=+-+=∆π)322(31,22222ABC S c b a PQ PR CPQ BRP ∆+++==∆∆中,同理,在 所以,结论PQR ∆是等边三角形。
2. 如图:(内)由余弦定理及面积公式得:)322(31)sin 2132cos (31)3cos(332)3()3(,22222222ABC S c b a A bc A bc c b A c b cbQR AQR ∆-++=--+=--+=∆π )322(1,22222ABC S c b a PQ PR CPQ BRP ∆-++==∆∆中,同理,在 所以,结论PQR ∆是等边三角形。
班主任工作心得担任班主任有欢笑,也有苦闷,有欣慰,也有烦恼。
我觉得作为班主任,必须具备“三心”。
1、要有博大的爱心。
每当我踏进教室,面对他们那一张张稚嫩的脸庞和一双双渴望知识的眼神,我深感自己的担子重,责任大。
不但要传授他们知识,还要帮助他们学会如何做人;不仅要关心他们的学习,更要关心他们的生活。
2、要有足够的耐心。
班主任要善于发现、捕捉学生身上的闪光点,哪怕是偶然一瞬闪光点,也要大力表扬鼓励。
3、要有一颗进取心。
人人都要不断努力,争取更大的进步。
我个人在教学上、在班主任工作上,都力争做得更好。
在班级建设上,善于总结方法,运用好的方法。
爱心 耐心 进取心——班 主 任 工 作 心 得[日期:2005-04-22] 来源: 作者:章菲菲 [字体:大 中 小]担任班主任工作已一年有余了,其中有欢笑,也有苦闷,有欣慰,也有烦恼。
有欢笑,是因为我们班被评上校级文明班级,且全班英语三级通过率在96%以上;有苦闷,是因为有时学生成绩下降了,或有学生犯错误了;有欣慰,是因为学生把我看成他们最信赖的人,喜欢把心事向我倾诉;有烦恼,是因为有时在碰到较为棘手的问题时感到手足无措,不知如何解决。
外拿破仑定理的证明

∴∠FBD=∠FGE(∠AGE=∠ABC)
∵在△FBD和△FGE中,
FB=FG,∠FBD=∠FGE,BD=GE
∴△FBD≌△FGE(SAS)
∴FD=FE
同理可证:FD=DE
则△DEF为等边三角形<证毕>
在多边ห้องสมุดไป่ตู้AFBDCE中作一点G,使AG=AF,GE=DC。
连接GF、GA、GE,DE、DF、EF。
∵△ABF、△BCD、△ACE均为底角等于30°的等腰三角形(即∠FAB=∠FBA=∠DBC=∠DCB=∠EAC=∠ECA=30°)
∴△ABF∽△BCD∽△ACE
∴AF/AB = AE/AC = DC/BC
而AG=AF,GE=DC
∴AG/AB = AE/AC = GE/BC,
∴△AGE∽△ABC
∴∠GAE=∠BAC,∠AGE=∠ABC
∴∠FAG =∠EAF-∠GAE =∠EAF-∠BAC =∠FAB+∠EAC = 60°
又∵AG=AF
∴△AGF为等边三角形
∴AG=AF,∠AGF=60°
∵∠FBD =∠ABC+∠FBA+∠DBC =∠ABC+60°
外拿破仑定理的证明
在任意一个三角形的三条边上分别向外做出三个等边三角形,则这三个等边三角形的中心也构成一个等边三角形。这个由三个等边三角形中心构成的三角形称“外拿破仑三角形”。
证明:
设三角形ABC对应边外的正三角形的中心分别为D,E,F,
则:∠FAB=∠FBA=∠DBC=∠DCB=∠EAC=∠ECA=30°
拿破仑定理与拿破仑三角形

拿破仑定理与拿破仑三角形昨天下午一位85岁的老校长(刘梦经)带来他做的数学题--“拿破仑三角形”的证明给我看。
使我夫妇大吃一惊。
他是1963年,我大学毕业首个工作岗位,蚌埠三中的副校长,后来调市计量局,任副局长。
解放前大学毕业,是我们老前辈,退休多年,至今仍然用数学题锻炼思维,身体十分健壮。
他分别用平面几何,解三角形,解析几何三种数学方法证明著名数学问题“拿破仑三角形”,思维清晰,非常值得我们学习。
本文先介绍拿破仑三角形是什么,以后再发表他的解法。
拿破仑定理与拿破仑三角形在任意△ABC的外侧,分别作等边△ABD、△BCE、△CAF,则AE、BF、CD三线共点X,并且AE=BF=CD,如下图。
这个命题称为拿破仑定理。
【定义1】外拿破仑三角形以△ABC的三条边分别向外作等边△ABD、△BCE、△CAF,它们的外接圆⊙P 、⊙Q 、⊙R 的圆心构成的三角形。
如下图可以证明:外拿破仑三角形是一个等边三角形。
还可以证明:点X是外接圆⊙P 、⊙Q 、⊙R 三圆的共点。
【定义2】内拿破仑三角形ABC的三条边分别向△ABC的内侧作等边△ABD、△BCE、△CAF,它们的外接圆⊙P 、⊙Q 、⊙R 的圆心构成的三角形同样可以证明:内拿破仑三角形也是一个等边三角形,外接圆⊙P 、⊙Q 、⊙R共点。
拿破仑三角形还可作如下推广:1、原三角形的面积等于它的外、内拿破仑三角形面积之差。
2、原三角形的重心也是内和外拿破仑三角形的重心。
3、以△ABC的三边为边分别向三角形外侧作三个相似的三角形ABC′、CA′B、B′CA,(相似三角形的顶点对应排列)这三个三角形的外心为 P、Q、R,则△PQR也与这三个三角形相似。
外拿破仑三角形即为此题之特例,这只要让三个相似三角形是正三角形即可。
海伦公式及其证明方法

海伦公式及其证明方法海伦公式是一个三角形的面积与边长之间的关系公式,它由古希腊数学家海伦提出,广泛应用于各种几何问题的求解中。
本文将介绍海伦公式及其证明方法。
首先,我们来看一下海伦公式的表达式:假设有一个三角形,其三边长度分别为a、b、c,海伦公式可以表示为:s=(a+b+c)/2其中s为半周长,即三边长度之和除以2三角形的面积可以用海伦公式表示为:面积=√(s*(s-a)*(s-b)*(s-c))接下来,我们将通过一个简单的证明来验证海伦公式。
证明:假设有一个三角形ABC,边长分别为a、b、c,半周长为s,高为h。
我们知道,三角形的面积可以通过底边和高的乘积的一半来计算,即:面积=1/2*b*h三角形的高可以由海伦公式推导出来,可以用边长表示如下:h=2*(面积/b)将面积代入上式,我们可以得到:h=2*(1/2*b*h/b)=h这是一个平凡的等式,表明三角形的高与边长之间是相等的。
现在我们将这个等式代入到另一个三角形ABC的面积计算公式中:面积=1/2*a*h将h代入,我们得到:面积=1/2*a*(2*(1/2*a*h/a))=a*(1/2*h)同样的,我们可以用边长b代入面积公式:面积=b*(1/2*h)将两个表达式相加面积=a*(1/2*h)+b*(1/2*h)=(1/2*h)*(a+b)=1/2*(a+b+c)*(1/2*h)这里我们可以将a+b+c除以2进行化简,得到:面积=(a+b+c)/2*1/2*h=s*1/2*h=s*r其中r为三角形的内切圆半径。
综上所述,我们可以得出海伦公式:面积=√(s*(s-a)*(s-b)*(s-c))海伦公式的证明就完成了。
它提供了一种方便快捷的方法,通过已知三边长,我们可以计算出任意三角形的面积。
除了上述的几何证明方法外,还有数学分析的证明方法来验证海伦公式,但这种方法相对较为复杂。
这里我们不做详细展开,以保持文章的简洁性。
总结:海伦公式是一个用于计算三角形面积的公式,它通过三角形的边长来计算。
名人与三角形

名人与三角形三角形是平面几何中的基本图形,有关它的性质,研究的也比较多,其中一些有趣内容还是由名人发现的。
下面介绍两个和名人有关的三角形的性质:(一)Napoleon三角形提起拿破仑你能想到什麽?法兰西帝国的辉煌还是滑铁卢战役?大概不会想到他还是一位颇有造诣的数学爱好者,一些有趣的几何题还和他有关联。
下面这个三角形就以他的名字命名:自三角形各边向外作三个正三角形,这三个正三角形的中心构成的三角形叫外拿破仑三角形。
若自三角形各边向内作正三角形还可得到内拿破仑三角形。
拿破仑三角形是一个正三角形。
(二)Euler点、Euler线和Euler圆欧拉是18世纪首屈一指的大数学家,他不但著述量巨大开创性成果多,而且致力于对数学符号的创立和倡导,对数学的统一和发展产生很大的影响,被誉为数学家之英雄。
欧拉在三角形性质的研究方面也是颇有建树的,以下是以他的名字命名的内容:三角形各顶点与其垂心联线的中点叫欧拉点,垂心和外心的联线叫欧拉线,欧拉圆又叫九点圆,是过三角形三边中点、三垂足和三个欧拉点的圆(即这九点共圆)。
九点圆还有一些有趣的性质如:①圆心为欧拉线的中点。
②和三角形的内切圆相切。
③九点圆的直径等于外接圆的半径。
拿破仑定理的证明如图:M 是AD 中点,N 是CE 中点,G、H、I 分别是ΔACF、ΔABD、ΔBCE 的中心。
所以 BM BH 32=,BN BI 32=,MN HI 32=。
在ΔBMN 中,由余弦定理, 有)3cos(2222B BN BM BN BM MN +*-+=π=)sin 3)(cos 23)(23()23()23(22B B a c a c --+ =)sin 3cos (4322B ac B ac a c +-+ ∵ )(21cos 222b a c B ac -+=, 又Rb B 2sin =,这里R 是ΔABC 的外接圆半径。
∴ )232(432222R abc b a c MN +++=, 即2MN 只与ΔABC 的三边a 、b 、c 有关,从而HI 也只与a 、b 、c 有关。
数学定理【圆,三角形】

数学定理【圆,三角形】1. 费马点:定理1等边三角形外接圆上一点,到该三角形较近两顶点距离之和等于到另一顶点的距离;不在等边三角形外接圆上的点,到该三角形两顶点距离之和大于到另一点的距离.定理2 三角形每一内角都小于120°时,在三角形内必存在一点,它对三条边所张的角都是120°,该点到三顶点距离和达到最小,称为“费马点”,当三角形有一内角不小于120°时,此角的顶点即为费马点.2. 拿破仑三角形:在任意△ABC 的外侧,分别作等边△ABD 、△BCE 、△CAF ,则AE 、AB 、CD 三线共点,并且AE=BF =CD ,这个命题称为拿破仑定理. 以△ABC 的三条边分别向外作等边△ABD 、△BCE 、△CAF ,它们的外接圆⊙C 1 、⊙A 1 、⊙B 1的圆心构成的△——外拿破仑的三角形,⊙C 1 、⊙A 1 、⊙B 1三圆共点,外拿破仑三角形是一个等边三角形;△ABC 的三条边分别向△ABC 的内侧作等边△ABD 、△BCE 、△CAF ,它们的外接圆⊙C 2 、⊙A 2 、⊙B 2的圆心构成的△——内拿破仑三角形,⊙C 2 、⊙A 2 、⊙B 2三圆共点,内拿破仑三角形也是一个等边三角形.这两个拿破仑三角形还具有相同的中心.3. 九点圆(Nine point round 或欧拉圆或费尔巴赫圆):三角形中,三边中心、从各顶点向其对边所引垂线的垂足,以及垂心与各顶点连线的中点,这九个点在同一个圆上,九点圆具有许多有趣的性质,例如: (1)三角形的九点圆的半径是三角形的外接圆半径之半; (2)九点圆的圆心在欧拉线上,且恰为垂心与外心连线的中点;(3)三角形的九点圆与三角形的内切圆,三个旁切圆均相切〔费尔巴哈定理〕.4. 欧拉(Euler )线:三角形的外心、重心、九点圆圆心、垂心依次位于同一直线(欧拉线)上.5. 欧拉(Euler )公式:设三角形的外接圆半径为R ,内切圆半径为r ,外心与内心的距离为d ,则d 2=R 2-2Rr . 6. 锐角三角形的外接圆半径与内切圆半径的和等于外心到各边距离的和.7. 重心:三角形的三条中线交于一点,并且各中线被这个点分成2:1的两部分;)3,3(C B A C B A y y y x x x G ++++重心性质:(1)设G 为△ABC 的重心,连结AG 并延长交BC 于D ,则D 为BC 的中点,则1:2:=GD AG ;(2)设G 为△ABC 的重心,则ABC AC G BC G ABGS S S S ∆∆∆∆===31;(3)设G 为△ABC 的重心,过G 作DE ∥BC 交AB 于D ,交AC 于E ,过G 作PF ∥AC 交AB 于P ,交BC于F ,过G 作HK ∥AB 交AC 于K ,交BC 于H ,则2;32=++===ABKHCA FP BC DE AB KH CA FP BC DE ; (4)设G 为△ABC 的重心,则①222222333GC AB GB CA GA BC+=+=+;②)(31222222CA BC AB GC GB GA ++=++;③22222223PG GC GB GA PC PB PA +++=++(P 为△ABC 内任意一点);④到三角形三顶点距离的平方和最小的点是重心,即222GC GB GA ++最小;⑤三角形内到三边距离之积最大的点是重心;反之亦然(即满足上述条件之一,则G 为△ABC 的重心).8. 垂心:三角形的三条高线的交点;)cos cos cos cos cos cos ,cos cos cos cos cos cos (CcB b A a yC cy B b y A a C c B b A a x C c x B b x A a H CB AC B A ++++++++ 垂心性质:(1)三角形任一顶点到垂心的距离,等于外心到对边的距离的2倍;(2)垂心H 关于△ABC 的三边的对称点,均在△ABC 的外接圆上;(3)△ABC 的垂心为H ,则△ABC ,△ABH ,△BCH ,△ACH 的外接圆是等圆;(4)设O ,H 分别为△ABC 的外心和垂心,则HCA BCO ABH CBO HAC BAO ∠=∠∠=∠∠=∠,,.9. 内心:三角形的三条角分线的交点—内接圆圆心,即内心到三角形各边距离相等;),(cb a cy by ayc b a cx bx ax I CB AC B A ++++++++内心性质:(1)设I 为△ABC 的内心,则I 到△ABC 三边的距离相等,反之亦然;(2)设I 为△ABC 的内心,则C AIB B AIC A BIC∠+︒=∠∠+︒=∠∠+︒=∠2190,2190,2190;(3)三角形一内角平分线与其外接圆的交点到另两顶点的距离与到内心的距离相等;反之,若A ∠平分线交△ABC外接圆于点K ,I 为线段AK 上的点且满足KI=KB ,则I 为△ABC 的内心; (4)设I 为△ABC 的内心,,,,c AB b AC a BC ===A ∠平分线交BC 于D ,交△ABC 外接圆于点K ,则acb KD IK KI AK ID AI +===; (5)设I 为△ABC 的内心,,,,c AB b AC a BC ===I 在AB AC BC ,,上的射影分别为F E D ,,,内切圆半径为r ,令)(21c b a p ++=,则①pr S ABC =∆;②c p CD CE b p BF BD a p AF AE -==-==-==;;;③CI BI AI p abcr ⋅⋅⋅=.10. 外心:三角形的三条中垂线的交点——外接圆圆心,即外心到三角形各顶点距离相等;)2sin 2sin 2sin 2sin 2sin 2sin ,2sin 2sin 2sin 2sin 2sin 2sin (CB A Cy By AyC B A Cx Bx Ax O CB AC B A ++++++++外心性质:(1)外心到三角形各顶点距离相等;(2)设O 为△ABC 的外心,则A BOC ∠=∠2或A BOC ∠-︒=∠2360;(3)∆=S abc R 4;(4)锐角三角形的外心到三边的距离之和等于其内切圆与外接圆半径之和.11. 旁心:一内角平分线与两外角平分线交点——旁切圆圆心;设△ABC 的三边,,,c AB b AC a BC ===令)(21c b a p ++=,分别与AB AC BC ,,外侧相切的旁切圆圆心记为C B A I I I ,,,其半径分别记为C B A r r r ,,.旁心性质:(1),21,2190A C BI C BI A C BI C B A ∠=∠=∠∠-︒=∠(对于顶角B ,C 也有类似的式子);(2))(21C A I I I C B A ∠+∠=∠;(3)设A AI 的连线交△ABC 的外接圆于D ,则DC DB DI A ==(对于C B CI BI ,有同样的结论);(4)△ABC 是△I A I B I C 的垂足三角形,且△I A I B I C 的外接圆半径'R 等于△ABC 的直径为2R . 12. 三角形面积公式:C B A R R abc C ab ah S a ABCsin sin sin 24sin 21212====∆)cot cot (cot 4222C B A c b a ++++=))()((c p b p a p p pr ---==,其中a h 表示BC 边上的高,R 为外接圆半径,r 为内切圆半径,)(21c b a p ++=. 13. 三角形中内切圆,旁切圆和外接圆半径的相互关系:;2sin 2cos 2cos 4,2cos 2sin 2cos 4,2cos 2cos 2sin 4;2sin 2sin 2sin4CB A R rC B A R r C B A R r C B A R r c b a ====.1111;2tan2tan ,2tan 2tan ,2tan 2tan r r r r B A r r C A r r C B r r c b a c b a=++===。
关于拿破仑的故事

关于拿破仑的故事拿破仑,十九世纪法国的君主,他的一生有过许多的战役,因而被人们一致认为是一名军事奇才。
拿破仑的一生注定是个天才一样的人物,同时也注定了拿破仑的一生不可能出现任何的平凡。
下面是店铺搜集整理的关于拿破仑的故事,希望对你有帮助。
关于拿破仑的故事拿破仑在许多人心中都是一个非常出色的英雄,他的一生创造了一个伟大的传奇。
但是英雄也是一个男人,而男人自然也会爱上女人的。
拿破仑的爱情还要从他的初恋说起,他的初恋情人是戴斯蕾,一个非常富有的商人家的女儿,当时两个人认识之后很快就相爱了,而拿破仑的爱情也是让他幸福了一段时间,两个人甚至已经约好了以后结婚的事情,但是战争开始之后拿破仑远征离开了,而戴斯蕾始终无法忘记拿破仑,甚至踏上了寻找他的长路。
可是她最后得到的消息却是拿破仑还和别人结婚了,于是伤心失望之下,戴斯蕾嫁给了别人,可是拿破仑的爱情却还在继续,但是当他最后失败的时候,戴斯蕾还曾经劝慰过他,拿破仑的第一次爱情就这样无疾而终。
拿破仑的这一次爱情有些让人惊讶,对方是约瑟芬,一个非常出名的交际花寡妇,是约瑟芬先看上了野心勃勃的拿破仑,而她的美貌也让拿破仑陷入了爱情之中,就算是全家人都非常反对,就算是拿破仑知道了她之前那些不光彩的事情,但是拿破仑的爱情还是无比火热的开始了。
可以说在拿破仑的爱情中,约瑟芬是他最爱的一个女人,他为了她和全家人作对,最后还让约瑟芬成了王后,就算是后来还知道约瑟芬的背叛,但是拿破仑的爱情依旧燃烧着,可是就算是再幸福的爱情也有不甜蜜的时候,约瑟芬无法生育成了拿破仑的心病,最后拿破仑还是和约瑟芬分开了,拿破仑的爱情再一次破碎。
拿破仑的一生成就拿破仑在建立帝国之后开始了军事专权时期,拿破仑的成就在于他积极的鼓励并且帮助工业和商业的发展,在经济上还建立了银行。
同时拿破仑还一直致力于加强中央的统治权和管理权,一切都是以自己为中心的独裁统治。
这些政策都可以算是拿破仑的成就,因为就算是其中包含着拿破仑的野心,但是最终还是被人们所接受了,所以这也是拿破仑的成就之一。
拿破仑与拿破仑三角形_百友数学

数 苑 纵 横
推论 , 例如 : ( 2)在任意三角形的三边上向内作三个正 三角形 , 则这三个正三角形的中心也构成一个 正三角形 — — —N apoleon 内三角形( 拿破仑定理 中的三角形称为 Napoleon 外三角形) ; ( 3)拿破仑外三角形面积与内三角形面积 之差等于原三角形的面积 ; ( 4)拿破仑外三角形与内三角形有相同的 外心 ; ( 5)三角形外侧三个相似三角形的外心是 另一个相似三角形的三个顶点 . 下面笔者先对前 3 个定理给出向量证法 , 第( 4) 个定理在本文第 3 部分证明 , 第( 5) 个定 理的向量证明限于篇幅 , 将另撰文叙述 . 证明 ( 1)记 ■ABC 三边长为 a 、 b 、c , 分 别取 BC 、 CA 、AB 的中点 P 、 Q 、R , 则 : — — ※ — — ※ — — ※ — — ※ 2 1 ——※ 2 2 O 1 O2 = ( O 1 P + B A -O 2 Q) =O1 P + 2 — — ※ — — ※ — — ※ — — ※ — — ※ — — ※ 1 c2 +O 2 2Q + O1 P · B A -O2 Q · B A -2 O1 P 4
若不论 分法如何 ( 或从 某一个顶点 向其他顶点作对角线 , 或从好几个顶点同时作 对角线) , 这些三角 形的内切圆的 半径的和都 相等 .
数 苑 纵 横
亦即 b · d AB + c · d AC =R · a . 同理 c · d BC + a · d AB = R ·b, a · d AC +d BC · b = R ·c . 又 2S ■ABC =2( S ■ABO + S ■BCO S ■CAO ) ,有 c · d AB + a · dBC + b · d AC =r4 ( a+ b +c) , 将前面三式相加后代入此式 , 得 r4 =d AB +d BC +d AC R.
拿破仑三角形的面积公式

拿破仑三角形的面积公式拿破仑三角形是一个受欢迎的数学形状,在许多不同的领域中都有着广泛的应用,尤其是在图形设计和建筑设计中,拿破仑三角形都有着不可忽视的重要性。
而本文旨在介绍拿破仑三角形的面积公式及其相关知识点。
首先,拿破仑三角形的定义是指一个等腰直角三角形(其中两条直角边的长度相同),再加上两个等边直角三角形,这两个直角三角形与等腰直角三角形边长相同。
其次,拿破仑三角形的面积公式是:S = a^2/2 + 2(a^2/8) = 5a^2/8其中,a表示等腰直角三角形的短边,S表示整个拿破仑三角形的面积。
可以看出,拿破仑三角形的面积公式很简洁明了,计算起来也不算太难。
但是,为了更好地理解这个公式,我们需要进一步探讨拿破仑三角形的具体性质。
拿破仑三角形的一个显著特点是:它可以不断分割成更小的拿破仑三角形。
这个性质来源于拿破仑三角形的结构,即三个相似的直角三角形拼凑而成。
将任意一个拿破仑三角形的等腰直角三角形一条直角边加倍,就得到了一个更小的拿破仑三角形。
这个过程可以一直持续下去,直到所得到的拿破仑三角形太小以至于难以识别。
另外,拿破仑三角形还有一个迷人的特点,它的面积是黄金比例的一半。
黄金比例是指一条线段分成两部分的比例为a/b,其中a和b 的比值等于a+b/a,记作φ,其值约为1.6180339887。
拿破仑三角形的面积与黄金比例的联系,可以通过以下公式得到:S/a^2 = 5/8 = 0.625 = φ^2/20通过上述公式可以看出,拿破仑三角形的面积与等腰直角三角形短边平方呈线性关系,而且是一个常数乘以黄金比例的平方。
这个发现对于数学与建筑设计等领域都具有一定的启示意义。
最后,需要注意的是,在实际应用中,拿破仑三角形的面积公式并不是普遍适用的。
对于一些不规则的拿破仑三角形,我们需要通过分割成多个小三角形来计算它们的面积。
此外,拿破仑三角形所存在的一些特殊性质,还可以与其它形状结合,以创造出一些更加优美的图形。
三角形面积与其拿破仑三角形面积关系

三角形面积与其拿破仑三角形面积关系大家好,今天我们来聊聊一个非常有趣的话题:三角形面积与其拿破仑三角形面积关系。
我们得了解一下什么是三角形和拿破仑三角形。
三角形呢,就是由三条线段相互连接的图形。
咱们小时候学过,三角形有三种类型:等边三角形、等腰三角形和普通三角形。
等边三角形的三条边都相等,等腰三角形有两条边相等,普通三角形就更简单了,三条边都不相等。
拿破仑三角形呢,就是将一个普通三角形的顶点沿着一条高线翻折过来形成的图形。
你可能会觉得奇怪,为什么叫拿破仑三角形呢?这是因为拿破仑大元帅曾经发现了一个很有趣的现象:把一个拿破仑三角形剪成两半,然后重新拼接在一起,竟然可以拼成一个完整的三角形!这个发现让人们对三角形的认识有了新的理解。
那么,三角形面积与其拿破仑三角形面积有什么关系呢?别着急,我们先来看看它们的面积是怎么计算的。
三角形的面积可以用底乘以高除以2来计算。
而拿破仑三角形的面积呢,就需要用到一些数学知识了。
我们知道,拿破仑三角形是由一个普通三角形和两个较小的三角形组成的。
这三个三角形的高都是原三角形的高,但是它们的底分别是原三角形底的一半。
所以,拿破仑三角形的面积等于原三角形的面积加上这两个较小三角形的面积之和。
现在我们知道了三角形和拿破仑三角形的面积计算方法,接下来我们就可以探讨它们之间的关系了。
其实,只要我们仔细观察一下,就会发现一个非常有趣的现象:无论是普通三角形还是拿破仑三角形,它们的面积都与底边的长度有关。
具体来说,如果底边的长度增加一倍,那么三角形的面积就会增加四分之一。
这个规律被称为“海伦公式”。
海伦公式是这样的:如果一个三角形的三边长分别为a、b、c,那么它的面积S可以表示为:S = sqrt(p * (p a) * (p b) * (p c)),其中p是半周长,即p = (a + b + c) / 2。
这个公式告诉我们,只要知道一个三角形的三边长和半周长,就可以计算出它的面积。
外拿破仑三角形的证明

外拿破仑三角形的证明第一篇:外拿破仑三角形的证明外拿破仑三角形的证明设△ABC,它向外作的正三角形中心分别为D、E、F设BC=根号3a,AC=根号3b,AB=根号3c则AD=BD=c,AE=CE=b,BF=CF=a易证∠DAE=60+∠BACcos∠DAE=cos(60+∠BAC)=cos60*cos∠BAC-sin60*sin∠BACcos∠BAC=(b^2+c^2-a^2)/2bc,sin∠BAC=根号3a/2R(R为△ABC外接圆的半径)cos∠DAE=(b^2+c^2-a^2)/4bc-3a/4R 由余弦定理得DE^2=AD^2+AE^2-2cos∠DAE*AD*AE=b^2+c^2-(b^2+c^2-a^2)/2+3abc/2R=(a^2+b^2+c^2)/2+3abc/2R同理可得DF^2=EF^2=(a^2+b^2+c^2)/2+3abc/2R…………第二篇:全等三角形证明全等三角形证明1、已知CD∥AB,D F∥EB,DF=EB,问AF=CE吗?说明理由。
CA2、已知∠E=∠F,∠1=∠2,AB=CD,问AE=DF吗?说明理由。
F3、已知,点C是AB的中点,CD∥BE,且CD=BE,问∠D=∠E 吗?说明理由。
4、已知AB=CD,BE=DF,AE=CF,问AB∥CD吗?A BC第三篇:三角形的证明全等三角形的证法1:(SSS或“边边边”)证明三条边相等的两个三角形全等在两个三角形中,若三条边相等,则这两个三角形全等。
几何语言:在三角形中因为ab=AB, ac=AC, bc=BC所以三角形abc全等于三角形ABC2.(SAS或“边角边”)证明有两条边及其夹角对应相等的两个三角形全等在两个三角形中,若有两条边及其夹角对应相等,则这两个三角形全等。
几何语言:在三角形中因为ab=AB,bc=BC, ∠b=∠B,则三角形abc全等于三角形ABC3.(ASA或“角边角”)证明有两角及其夹边对应相等的两个三角形全等在两个三角形中,若有两角及其夹边对应相等的两个三角形全等.几何语言:在三角形中∠a=∠A,∠b=∠B,ab=AB, 则三角形abc全等于三角形ABC4.(AAS或“角角边”)证明有两角及一角的对边对应相等的两个三角形全等在两个三角形中,若两角及一角的对边对应相等的两个三角形全等几何语言:在三角形中∠a=∠A,∠b=∠Bac=AC则三角形abc全等于三角形ABC5.(HL或“斜边,直角边”)证明斜边及一直角边对应相等的两个直角三角形全等在两个直角三角形中,若斜边及一直角边对应相等的两个直角三角形全等几何语言:在三角形中因为ab=AB 直角c=直角C 则三角形abc 全等于三角形ABC所以,SSS,SAS,ASA,AAS,HL均为判定三角形全等的定理。
关于“拿破仑三角形”的探究

数学探索1关于“拿破仑三角形”的探究太白初中 魏兆飞【简历】魏兆飞,男,生于1965年10月。
中共党员,中学高级教师。
1987年毕业于徽州师专生物专业,后在芜湖师专进修数学教育专业,2003年获得双专科学历。
现任教于当涂县太白初中。
工作以来,担任班主任工作十三年、数学教研组长十九年。
多次被评为太白镇先进教师。
1989年被评为县先进教育工作者,2007年被评为市级优秀班主任,2008年荣获县级教学能手称号。
2009年担任市级《初中数学课堂导入策略的案例研究》课题组组长,于2012年课题顺利结题。
教研成果丰硕。
2010年《初中数学课堂导入策略的案例研究初探》论文获市级二等奖;2011年市级课件大赛《多彩的几何图形》获一等奖;2012年市级课件大赛《函数、几何动态问题探究》获一等奖;2013年市级课件大赛《二次函数与反比例函数动态探究》获一等奖,2013年中考所任数学学科位居全县均分第一、及格率第一、优秀率第二的优异成绩;2014年当涂县第四届自然科学优秀学术论文评比《关于“拿破仑三角形”的探究》获三等奖。
【摘要】数学是人们对客观世界定性把握和定量刻画、逐渐抽象概括、形成方法和理论,并进行广泛应用的过程。
本文对古老命题:“拿破仑三角形”进行了深入的探究,引导学生观察发现其中存在“三线共点、三圆共点、费玛点”等相关知识。
以“关联相似”为前提,鼓励学生对拿破仑三角形定理进行猜想、推广与证明;以三角形三边,在三角形的外侧(或内侧)作三个“同向相似”的三角形,研究它们其中对应点组成的三角形与所作 “同向相似”三角形之间的联系,进而将拿破仑三角形定理加以推广,并以其证明了一道国际奥林匹克数学竞赛题,培养了学生的想象能力、创新能力与数学探索精神。
【关键词】拿破仑三角形;三线共点;三圆共点;费玛点;“关联相似”。
一、问题的提出问题还是从一堂数学活动课说起。
我在给学生介绍一些古老的几何命题时,讲到了法国政治家、军事家拿破仑(NapoLeon ),他崇尚几何,曾经研究过一道命题:任意三角形,由它的三边分别向外侧作正三角形,那么这三个正三角形的中心也构成一个正三角形。
拿破仑与圆的四等分法

拿破仑与圆的四等分法
江苏 王佩其
同学们,你大概知道拿破仑是一位有相当造诣的数学爱好者吧!不少几何史上有名的题目还和拿破仑有着关联,例如他曾经研究过的三角形称为“拿破仑三角形”,在任意△ABC 的外侧,分别作等边△ABD ,△BCE ,△CAF ,则AE ,AB ,CD 三线共点,并且AE =BF =CD ,这个命题称为拿破仑定理.你可知道拿破仑还研究过把圆四等分呢!
在戎马倥偬的军旅生涯中,数学书籍是拿破仑手中的得意之物.一次,他曾在马背上哼出了只用圆规四等分圆的妙曲.具体作法为:
(1)在O 上任取一点A ,以R 为关径,自点A 起,顺次截取AB BC CD ==.令O 的半径为R .
(2)分别以A ,D 为圆心,以AC 为半径作弧交于点E .
(3)以A 为圆心,OE 为半径作弧交⊙O 于G ,H 两点.则A ,G ,D ,H 四点即为⊙O 的四等分点. 那么,这种作法合理吗?本文给出如下证明,供同学们参考. 在Rt ACD △
中,可知AC =
,则AE AC ==. 在Rt AOE △
中,算出OE ==,
而AG AH OE ===.
连接AC ,DC 和AE ,OE ,易见AD 是⊙O 的直径,且∠DAC =30°. ∴A ,G ,D ,H 为⊙O 的四等分点.
此法真可谓妙不可言,因为它只用一种作图工具——圆规,就把圆做了四等分.
图1
图2 A A B B C C D D E E O O
H H
G。
海伦公式的几种证明与推广

海伦公式的几种证明与推广高中数学必修⑤第一章在阅读与思考栏目向学生介绍一个非常重要且优美的公式——海伦公式〔Heron's Formula 〕:假设有一个三角形,边长分别为,,,c b a ,三角形的面积S 可由以下公式求得:))()((c p b p a p s ---=,而公式里的)(21c b a p ++=,称为半周长。
图1C海伦公式又译希伦公式,传说是古代的叙拉古国王希伦二世发现的公式,利用三角形的三条边长来求取三角形面积。
但根据Morris Kline 在1908年出版的著作考证,这条公式其实是阿基米德所发现,以托希伦二世的名发表。
由于任何n 边的多边形都可以分割成n-2个三角形,所以海伦公式可以用作求多边形面积的公式。
比如说测量土地的面积的时候,不用测三角形的高,只需测两点间的距离,就可以方便地导出答案。
海伦公式形式漂亮,结构工整,有多种变形,如:S=))()((c p b p a p p ---=))()()((41a c b b c a c b a c b a -+-+-+++=])(][)[(412222b a c c b a ---+ =)]2()[2(41222222ab c b a ab c b a --+-+-+=222222)(441c b a b a -+- =44422222222241c b a c b c a b a ---++ 教课书中并以习题形式出现,给出的参考答案是利用三角形面积计算公式C ab s sin 21=和余弦定理C ab b a c cos 2222-+=的证明过程:C ab s sin 21==C n ab 2cos 121-=2222)2(121abc b a ab -+-下略。
我国南宋著名数学家秦九韶也发现了与海伦公式等价的“三斜求积”公式,中国古代的天元术发展水平非常高,笔者猜想秦九韶在独立推出“三斜求积”公式过程中,利用了解方程的方法,因此海伦公式可以作如下推证,从三角形最基本的面积公式a ABC ah S 21=∆入手,利用勾股定理,布列方程组求高。
拿破仑定理的推广

拿破仑定理的推广拿破仑是十九世纪初(1804—1814)的法国皇帝.他既是政治家和军事家,同时,他还是一位颇有造诣的数学爱好者.下面的定理就是他首先发现并论证的.拿破仑定理若以任意三角形的各边为一边向形外作等边三角形,则它们的中心构成一个等边三角形.这一定理可以等价描述为:若以任意三角形的各边为底边向形外作底角为30°的等腰三角形,则它们的顶点构成一个等边三角形.本文介绍拿破仑定理的两种推广:定理1 如图1,以△ABC的三边为底边各向形外作等腰三角形BCD,CAE和ABF,这三个等腰三角形的底角各为α,β和γ,且α+β+γ=90°,则∠FDE=90°-α,∠DEF=90°-β,∠EFD=90°-γ.证明为方便计,把△ABC的三内角简记为A、B、C.因DC=DB,则可将△DCE绕D点旋转∠BDC至△DBG位置,连FG.∵∠FBG=360°-∠DBF-∠DBG=360°- (α+β+γ) - (α+C+β)=180°-B-C+180°-2(α+β+γ)+β+γ=A+β+γ=∠FAE.又BG=CE=AE,FB=FA,∴△FBG≌△FAE,FG=FE.从而△DGF≌△DEF,∠FDG=∠FDE,同理∠DEF=90°-β,∠EFD=90°-γ.定理2.如图2,在△ABC的外侧作三角形△BCP、△CAQ和△ABR,使∠PBC=∠QAC=α,∠PCB=∠QCA=β,∠RAB=∠RBA=γ,且α+β+γ=90°,则RQ=RP,且∠QRP=2α.证明 RB绕R逆时针旋转2α至RG,连BG、AG、QG.∵∠GBA=∠GBR-γ=90°-α-γ=β又RA=RB=RG,即R为△ABG的外心,∴△ABG∽△ACQ∽△BCP,又∠BAC=∠GAQ,又∠RGQ=∠AGQ+∠AGR=∠ABC+α+γ=∠RBP,∴∠RGQ≌△RBP.∴RQ=RP.又因∠GRQ=∠BRP,∴∠QRP=∠GRB=2α.值得注意的是,两个定理的证明中综合了不少的基础知识和基本方法,学习这些定理的证明,对提高证题能力是很有益的.在第十七届IMO 竞赛中,有一道赛题如下:在△ABC的外侧作三角形△BCD、△CAQ和△ABR,使∠PBC=∠QAC=45°,∠PCB=∠QCA=30°,∠RAB=∠RBA=15°.求证:RQ=RP,且RQ⊥RP.这是本文定理二的特例,可以用定理二的证明方法给出证明.。
一些有名的几何定理.

取材自维基百科-中文版. 没事的时候大家可以证着玩! 答案在这里.1. 阿基米德中点定理说明:圆上有两点A,B,M为弧AB的中点,随意选圆上的一点C,D 为AC上的点使得MD垂直AC。
若M、C在弦AB异侧,则AD=DC+BC;若M、C在弦AB 同侧,则AD=DC-CB。
2. 婆罗摩笈多定理指出:若圆内接四边形的对角线相互垂直,则垂直于一边且过对角线交点的直线将平分对边。
婆罗摩笈多是印度数学家。
3. 凡·奥贝尔定理(van Aubel's theorem)说明:给定一个四边形,在其边外侧构造一个正方形。
将相对的正方形的中心连起,得出两条线段。
线段的长度相等且垂直。
4. 芬斯勒–哈德维格尔定理(Finsler-Hadwiger Theorem)说明:若两个正方形ABCD和AB'C'D'拥有同一个顶点A。
B'D的中点、BD'的中点、ABCD的中心和AB'C'D'的中心将组成一个正方形。
5. 莫雷角三分线定理(Morley's theorem)说明对所有的三角形,其三个内角作角三分线,靠近公共边三分线的三个交点,是一个等边三角形。
此定理由法兰克·莫雷在1899年发现。
对外角作外角三分线,也会有类似的性质,可以再作出4个等边三角形。
此定理有趣的地方是我们没办法用尺规作图作出其等边三角形,因为已经证明出尺规做图无法做出三等分角。
6. 拿破仑定理,是拿破仑发现的平面几何学定理:“以三角形各边为边分别向外侧作等边三角形,则他们的中心构成一个等边三角形。
”该等边三角形称为拿破仑三角形。
如果向内作三角形,结论同样成立。
同时拿破仑留下这样的名言:''一个国家只有数学蓬勃发展,才能表现他的国力强大。
——拿破仑7. 泰博定理是法国几何学家维克多·泰博(Victor Thébault,1882年-1960年))提出的平面几何问题。
