【推荐下载】高二数学暑假作业简答题
高二数学暑假作业最新的高二数学暑假作业试卷练习题

高二数学暑期作业最新的高二数学暑期作业试卷练习题第Ⅰ卷 (选择题:共60 分 )一、选择题 ( 共 12 小题,每题 5 分,每题四个选项中只有一项切合要求。
)1.的值为A. B. C. D.2.已知会合,则 =A. B. C. D.3.若,此中 a、b∈ R, i 是虚数单位,则A. B. C. D.4.命题 r:假如则且.若命题r的否命题为p,命题 r 的否定为 q,则A.P 真 q 假B. P 假 q 真C. p, q 都真D. p,q 都假5.扔掷一枚均匀硬币和一枚均匀骰子各一次,记“硬币正面向上”为事件 A ,“骰子向上的点数是3”为事件 B,则事件A,B 中起码有一件发生的概率是A. B. C. D.6.设,,, (e 是自然对数的底数),则A.B.C.D.7.将名学生疏别安排到甲、乙,丙三地参加社会实践活动,每个地方起码安排一名学生参加,则不一样的安排方案共有A.36 种B.24 种C.18 种D.12 种8. 一个袋子里装有大小同样的 3 个红球和 2 个黄球,从中同时拿出 2 个,则此中含红球个数的数学希望是A. B. C. D.9.设函数,曲线在点处的切线方程为,则曲线在点处切线的斜率为A. B. C. D.10.已知样本 9,10,11,x,y 的均匀数是10,标准差是,则的值为A.100B.98C.96D.9411.现有四个函数:① ;② ;③ ;④的图象 (部分 )以下:则依据从左到右图象对应的函数序号安排正确的一组是A. ①④②③B.①④③②C.④①②③D.③④②①12.若函数在R上可导,且知足,则ABCD第 II 卷 (非选择题,共90 分 )二、填空题 (每题 5 分)13.已知偶函数的定义域为R,知足,若时,,则14.设 a= 则二项式的常数项是15.下边给出的命题中:①已知则与的关系是②已知听从正态散布,且,则③将函数的图象向右平移个单位,获得函数的图象。
此中是真命题的有_____________ 。
参考高二数学暑假作业答案

参考高二数学暑假作业答案自己整理的参考高二数学暑假作业答案相关文档,希望能对大家有所帮助,谢谢阅读![一]1?1变化率和导数1.1.1变化率1 . D2 . D3 . C4-3t-65 .x 26.3?317.(1)0?1(2)0?21(3)2?18.11m/s,10?1m/s 9.25 3t 10.128 a 64 a2 t 11 . f(x)-f(0)x=1x(x0),-1-x(x0)1?1?2导数的概念1 . D2 . C3 . C4-15 . x0,x;x06.67.a=18.a=2 9.-410.(1)2t-6(2)初速度为v0=-6,初位置为x0=1(3)运动开始3秒,在原点向左变化8m (4)x=1,v=611.水面上升速度为0?16m/min,表明 v= h75 15 h ( h) 23,那么 v t= h t 75 15 h ( h) 23,即limt0vt=limt0ht75 15h(h)23=limt0ht25,那就是v’(t)=25h’(t),那么h’(t)=1254=0?16(米/分钟)1?1?三阶导数的几何意义(一)1.C2切线的斜率。
B3。
B4。
f (x)在x0,y-f(x0)=f’(x0)(x-x0)5.36.1357.割线的斜率是3?31,正切的斜率为38.k=-1,x y 2=09.2x-y 4=010.k=14,切点坐标为12,1211.有两个交点,交点的坐标是(1,1),(-2,-8)1?1?3阶导数的几何意义(2)1.C2 a3 . B4 . y=x15。
16.37.y=4x-18.1039.1910.a=3,b=-11,c=9。
提示:首先找出a、b、c之间的关系,即c=3 2a。
B=-3a-2,然后求点(2,-1)处的斜率,得到k=a-2=1,即a=3 11.(1)y=-13x-229(2)125121?导数2的计算1?2?1几种常用函数的导数1.C2。
高二数学暑假作业9附答案

高二数学暑假作业九一、单选题 1.若坐标原点到直线的距离等于,则角的取值集合是( )A.B.C.D.2.已知直线1l : sin 10x y α+-=,直线2l : 3cos 10x y α-+=,若12l l ⊥,则sin2α=( ) A.23 B. 35± C. 35- D. 353.直线分别与轴,轴交于,两点,点在圆上,则面积的取值范围是A.B.C. D.4.若直线l :ax +by +1=0始终平分圆M :x 2+y 2+4x +2y +1=0的周长,则(a -2)2+(b -2)2的最小值为 ( )A. B. 5 C. 2 D. 10 5.已知点是直线上的动点,由点向圆引切线,切点分别为,,且,若满足以上条件的点有且只有一个,则( )A.B.C.D. 6.已知圆,圆,A 、B 分别是圆和圆上的动点,则的最大值为( )A. 5B. 6C. 7D. 8 7.动直线:()与圆:交于点,,则弦最短为( )A.B.C.D.8.直线与圆交于,两点,且,过点,分别作的垂线与轴交于点,,则等于( )A. B. 4C. D. 8 9.已知圆截直线所得线段的长度是,则圆与圆的位置关系是( ) A. 内切 B. 相交 C. 外切 D. 相离 10.已知圆:与圆关于轴对称,为圆上的动点,当到直线的距离最小时,的横坐标为( )A.B.C.D.11.若过点的直线与曲线有公共点,则直线斜率的取值范围为A.B.C.D.12.已知直线20x y a -+=与圆O : 222x y +=相交于A , B 两点(O 为坐标原点),且AOB∆为等腰直角三角形,则实数a 的值为( )A.6或6- B. 5或5- C. 6 D. 513.过点()3,4P 作圆224x y +=的两条切线,切点分别为A , B ,则AB =( )A. 53-B. 52-C.2215 D. 421514.已知圆22C:4630x y x y +---=,点()M 2,0-是圆C 外一点,则过点M 的圆的切线的方程是( )A. 20724140x x y +=+=,-B. 20724140y x y +=++=,C. 20724140x x y +=++=,D. 20724140y x y +=+=,-15.已知直线:3l y x m =+与圆()22:36C x y +-=相交于A 、B 两点,若22AB =,则实数m 的值等于( )A. -7或-1B. 1或7C. -1或7D. -7或116.与直线40x y --=和圆22220x y x y ++-=都相切的半径最小的圆的方程是( ) A. ()()22112x y +++= B. ()()22114x y -++= C. ()()22112x y -++= D. ()()22114x y +++=17.已知直线:3l y x m =+与圆()22:36C x y +-=相交于A , B 两点,若120ACB ∠=︒,则实数m 的值为( )A. 36+或36-B. 326+或326-C. 9或3-D. 8或2-18.过直线23y x =+上的点作圆2246120x y x y +-++=的切线,则切线长的最小值为( ) A.19 B. 25 C.21 D.555 19.圆()()221:131C x y ++-=,圆()()222:554C x y -+-=,M ,N 分别是圆1C , 2C 上的动点,P 为x 轴上的动点,则PM PN +的最小值( ) A. 6 B. 210 C. 7 D. 1020.已知直线0(0)x y k k +-=>与圆224x y +=交于不同的两点,,A B O 是坐标原点,且有43OA OB AB +≥,那么k 的取值范围是 A.()3,+∞ B. )2,⎡+∞⎣ C. )2,22⎡⎣ D. )3,22⎡⎣二、填空题21.过点且与相切的直线方程为__________.22.在平面直角坐标系中,圆与轴的两个交点分别为 ,其中在的右侧,以为直径的圆记为圆,过点作直线与圆,圆分别交于两点.若为线段的中点,则直线的方程为_________. 23.已知直线.若直线与直线平行,则的值为____;动直线被圆截得弦长的最小值为______.24.已知直线于圆交于两点,圆在点处的切线相交于点,则四边形的面积为__________.25.已知点()()3,0,1,2A B ---,若圆()()22220x y r r -+=>上恰有两点,M N ,使得MAB ∆和NAB ∆的面积均为4,则r 的取值范围是____.26.关于x 的方程2444x x kx k -+=+-有两个不等的实数根,则实数k 的取值范围为_______________. 27.已知直线与圆交于两点,,且为等边三角形,则圆的面积为_____________.28.已知AB 为圆22:20C x y y +-=的直径,点P 为直线1y x =-上任意一点,则22||PA PB +的最小值为__________.三、解答题29.已知以点C 2,t t ⎛⎫⎪⎝⎭(t R ∈,且0t ≠)为圆心的圆与x 轴交于点O , A ,与y 轴交于点O ,B ,其中O 为坐标原点.(1)求证: OAB ∆的面积为定值;(2)设直线24y x =-+与圆C 交于点M , N ,若OM ON =,求圆C 的方程.30.已知圆C 的圆心在x 轴正半轴上,且y 轴和直线320x y -+=均与圆C 相切. (1)求圆C 的标准方程;(2)若直线y x m =+与圆C 相交于,M N 两点,点()0,1P ,且MPN ∠为锐角,求实数m 的取值范围.31.已知圆,点,直线. (1)求与圆相切,且与直线垂直的直线方程; (2)在直线上(为坐标原点),存在定点(不同于点),满足:对于圆上任一点,都有为一常数,试求所有满足条件的点的坐标.32.已知. (1)若的切线在轴、轴上截距相等,求切线的方程; (2)从圆外一点向圆引切线为切点,为原点,若,求使最小的点坐标.高二数学暑假作业九答案1.A【解析】分析:先根据点到直线距离公式得角关系式,再解三角方程得结果.详解:因为坐标原点到直线的距离为,所以所以,即,选A.点睛:由求最值,最大值对应自变量满足,最小值对应自变量满足.2.D【解析】因为,所以,所以,所以.故选D.3.A【解析】分析:先求出A,B 两点坐标得到再计算圆心到直线距离,得到点P到直线距离范围,由面积公式计算即可详解:直线分别与轴,轴交于,两点,则点P在圆上圆心为(2,0),则圆心到直线距离故点P 到直线的距离的范围为则故答案选A.点睛:本题主要考查直线与圆,考查了点到直线的距离公式,三角形的面积公式,属于中档题。
高中二年级数学暑假作业答案参考

【导语】⾼⼆⼀年,强⼈将浮出⽔⾯,鸟⼈将沉⼊海底。
⾼⼆重点解决三个问题:⼀,吃透课本;⼆,找寻适合⾃⼰的学习⽅法;三,总结⾃⼰考试技巧,形成习惯。
为了帮助你的学习更上⼀层楼,⾼⼆频道为你准备了《⾼中⼆年级数学暑假作业答案参考》希望可以帮到你! 【⼀】 1?1变化率与导数 1.1.1变化率问题1.D2.D3.C4.-3Δt-65.Δx+26.3?31 7.(1)0?1(2)0?21(3)2?18.11m/s,10?1m/s9.25+3Δt10.128a+64a2t11.f(Δx)-f(0)Δx=1+Δx(Δx>0), -1-Δx(Δx<0) 1?1?2导数的概念1.D2.C3.C4.-15.x0,Δx;x06.67.a=18.a=2 9.-4 10.(1)2t-6(2)初速度为v0=-6,初始位置为x0=1(3)在开始运动后3s,在原点向左8m处改变(4)x=1,v=6 11.⽔⾯上升的速度为0?16m/min.提⽰:Δv=Δh75+15Δh+(Δh)23, 则ΔvΔt=ΔhΔt×75+15Δh+(Δh)23,即limΔt→0ΔvΔt=limΔt→0ΔhΔt×75+15Δh+(Δh)23=limΔt→0ΔhΔt×25, 即v′(t)=25h′(t),所以h′(t)=125×4=0?16(m/min) 1?1?3导数的⼏何意义(⼀)1.C2.B3.B4.f(x)在x0处切线的斜率,y-f(x0)=f′(x0)(x-x0)5.36.135°7.割线的斜率为3?31,切线的斜率为38.k=-1,x+y+2=0 9.2x-y+4=010.k=14,切点坐标为12,12 11.有两个交点,交点坐标为(1,1),(-2,-8) 1?1?3导数的⼏何意义(⼆)1.C2.A3.B4.y=x+15.±16.37.y=4x-18.1039.19 10.a=3,b=-11,c=9.提⽰:先求出a,b,c三者之间的关系,即c=3+2a, b=-3a-2,再求在点(2,-1)处的斜率,得k=a-2=1,即a=3 11.(1)y=-13x-229(2)12512 1?2导数的计算 1?2?1⼏个常⽤函数的导数1.C2.D3.C4.12,05.45°6.S=πr2 7.(1)y=x-14(2)y=-x-148.x0=-3366 9.y=12x+12,y=16x+32.提⽰:注意点P(3,2)不在曲线上10.证明略,⾯积为常数2 11.提⽰:由图可知,点P在x轴下⽅的图象上,所以y=-2x,则y′=-1x,令y′=-12,得x=4,故P(4,-4) 1?2?2基本初等函数的导数公式及导数的运算法则(⼀)1.A2.A3.C4.35.2lg2+2lge6.100! 7.(1)1cos2x(2)2(1-x)2(3)2excosx8.x0=0或x0=2±2 9.(1)π4,π2(2)y=x-11 10.k=2或k=-14.提⽰:设切点为P(x0,x30-3x20+2x0),则斜率为k=3x20-6x0+2,切线⽅程为y-(x30-3x20+2x0)=(3x20-6x0+2)(x-x0),因切线过原点,整理后常数项为零,即2x30-3x20=0,得x0=0或x0=32,代⼊k=3x20-6x0+2,得k=2,或k=-14 11.提⽰:设C1的切点为P(x1,x21+2x1),则切线⽅程为:y=(2x1+2)x-x21;设C2的切点为Q(x2-x22+a),则切线⽅程为:y=-2x2x+x22+a.⼜因为l是过点P,Q的公切线,所以x1+1=-x2, -x21=x22+a,消去x2得⽅程2x21+2x1+1+a=0,因为C1和C2有且仅有⼀条公切线,所以有Δ=0,解得a=-12,此时切线⽅程为y=x-14 2基本初等函数的导数公式及导数的运算法则(⼆)1.D2.A3.C4.50x(2+5x)9-(2+5x)10x25.336.97.a=1 8.y=2x-4,或y=2x+69.π6 10.y′=x2+6x+62x(x+2)(x+3).提⽰:y=lnx(x+2)x+3=12[lnx+ln(x+2)-ln(x+3)] 11.a=2,b=-5,c=2,d=-12 1?3导数在研究函数中的应⽤ 1?3?1函数的单调性与导数1.A2.B3.C4.33,+∞5.单调递减6.①②③ 7.函数在(1,+∞),(-∞,-1)上单调递增,在(-1,0),(0,1)上单调递减 8.在区间(6,+∞),(-∞,-2)上单调递增,在(-2,6)上单调递减9.a≤-3 10.a<0,递增区间为:--13a,-13a,递减区间为:-∞,--13a,-13a,+∞ 11.f′(x)=x2+2ax-3a2,当a<0时,f(x)的递减区间是(a,-3a);当a=0时,f(x)不存在递减区间;当a>0时,f(x)的递减区间是(-3a,a) 1?3?2函数的极值与导数1.B2.B3.A4.55.06.4e27.⽆极值 8.极⼤值为f-13=a+527,极⼩值为f(1)=a-1 9.(1)f(x)=13x3+12x2-2x(2)递增区间:(-∞,-2),(1,+∞),递减区间:(-2,1) 10.a=0,b=-3,c=2 11.依题意有1+a+b+c=-2, 3+2a+b=0,解得a=c, b=-2c-3,从⽽f′(x)=3x2+2cx-(2c+3)=(3x+2c+3)·(x-1).令f′(x)=0,得x=1或x=-2c+33 ①若-2c+33<1,即c>-3,f(x)的单调区间为-∞,-2c+33,[1,+∞);单调减区间为-2c+33,1 ②若-2c+33>1,即c 1?3?3函数的(⼩)值与导数1.B2.C3.A4.x>sinx5.06.[-4,-3]7.最⼩值为-2,值为1 8.a=-29.(1)a=2,b=-12,c=0(2)值是f(3)=18,最⼩值是f(2)=-82 10.值为ln2-14,最⼩值为0 11.(1)h(t)=-t3+t-1(2)m>1.提⽰:令g(t)=h(t)-(-2t+m)=-t3+3t-1-m,则当t∈(0,2)时,函数g(t)<0恒成⽴,即函数g(t)的值⼩于0即可 1?4⽣活中的优化问题举例(⼀)1.B2.C3.D4.32m,16m5.40km/h6.1760元7.115元 8.当q=84时,利润9.2 10.(1)y=kx-12+2000(x-9)(14≤x≤18)(2)当商品价格降低到每件18元时,收益 11.供⽔站建在A,D之间距甲⼚20km处,可使铺设⽔管的费⽤最省 1?4⽣活中的优化问题举例(⼆)1.D2.B3.D4.边长为S的正⽅形5.36.10,196007.2ab 8.4cm 9.当弯成圆的⼀段长为x=100ππ+4cm时,⾯积之和最⼩. 提⽰:设弯成圆的⼀段长为x,另⼀段长为100-x,正⽅形与圆的⾯积之和为S,则S=πx2π2+100-x42(0 10.h=S43,b=2S42711.33a 【⼆】 1.已知集合,,则(C) A.B.C.D. 2.设是定义在上的奇函数,当时,,则(A) A.B.C.1D.3 3.已知向量满⾜,则(D) A.0B.1C.2D. 4.设是等⽐数列,则“”是“数列是递增数列”的(B)A.充分⽽不必要条件B.必要⽽不充分条件C.充分必要条件D.既不充分也不必要条件 5.设m,n是两条不同的直线,、、是三个不同的平⾯,给出下列命题,正确的是(B)A.若,,则B.若,,则C.若,,则D.若,,,则[来 6.函数y=sin(2x+φ)的图象沿x轴向左平移个单位后,得到⼀个偶函数的图象,则φ的⼀个可能的值为(A) A.B.C.D. 7.已知的内⾓A,B,C所对的边分别为a,b,c,若的可能取值为(D) A.B.C.D. 8.设函数,则的值为(A) A.B.2014C.2013D.0 9.已知F是双曲线的左焦点,A为右顶点,上下虚轴端点B、C,若FB交CA于D,且,则此双曲线的离⼼率为(B) A.B.C.D. 【三】 ⼀、填空题(本⼤题共14⼩题,每⼩题5分,共70分) 1.命题:“若a2+b2=0(a,b∈R),则a=b=0”的逆否命题是____________. 解析“且”的否定为“或”,因此逆否命题为若a≠0或b≠0,则a2+b2≠0. 答案若a≠0或b≠0(a,b∈R),则a2+b2≠0 2.命题“ax2-2ax-3>0不成⽴”是真命题,则实数a的取值范围是____________. 解析ax2-2ax-3≤0恒成⽴, 当a=0时,-3≤0成⽴; 当a≠0时,a<0Δ=4a2+12a≤0, 解得-3≤a<0. 故-3≤a≤0. 答案[-3,0] 3.给出下列命题: (1)命题:“若b2-4ac<0,则⽅程ax2+bx+c=0(a≠0)⽆实根”的否命题; (2)命题“△ABC中,AB=BC=CA,那么△ABC为等边三⾓形”的逆命题; (3)命题“若a>b>0,则3a>3b>0”的逆否命题; (4)“若m>1,则mx2-2(m+1)x+(m-3)>0的解集为R”的逆命题. 其中真命题的个数为____________. 解析易知(1)(2)(3)正确;(4)mx2-2(m+1)x+(m-3)>0的解集为R⇒m>0Δ<0⇒m∈∅,故(4) 错误. 答案3 4.如果命题“⾮p或⾮q”是假命题,则在下列各结论中,正确的有____________(填序号). ①命题“p且q”是真命题②命题“p且q”是假命题③命题“p或q”是真命题④ 命题“p或q”是假命题 解析∵“⾮p或⾮q”是假命题,∴⾮p和⾮q都是假命题,∴p和q都是真命题,故 “p且q”和“p或q”都是真命题. 答案①③ 5.在△ABC中,“sin2A=sin2B”是“A=B”的__________条件. 解析由sin2A=sin2B,得:A=B或A+B=π2, ∴sin2A=sin2B⇒/A=B,⽽A=B,可得sin2A=sin2B. 答案必要不充分 6.设有四个命题: ①两条直线⽆公共点,是这两条直线为异⾯直线的充分⽽不必要条件; ②⼀条直线垂直于⼀个平⾯内⽆数条直线是这条直线垂直于这个平⾯的充要条件; ③空间⼀个⾓的两边分别垂直于另⼀个⾓的两边是这两个⾓相等或互补的充要条件; ④a,b是平⾯α外的两条直线,且a∥α,则a∥b是b∥α的必要⽽不充分条件; 其中真命题的个数是______. 解析两条直线⽆公共点,是这两条直线为异⾯直线的必要⽽不充分条件,①错;⼀条 直线垂直于⼀个平⾯内⽆数条直线不能得出这条直线垂直于这个平⾯,②错;空间两个 ⾓相等或互补,它们的边可以什么关系也没有,③错;a,b是平⾯α外的两条直线,且 a∥α,则a∥b是b∥α的充分⽽不必要条件,④错. 答案0 7.条件甲:1+sinθ=12,条件⼄:sinθ2+cosθ2=12,则甲是⼄的____________条件. 解析因为1+sinθ=sin2θ2+cos2θ2+2sinθ2cosθ2=|sinθ2+cosθ2|,所以甲 是⼄的必要不充分条件. 答案必要不充分 8.下列四种说法中,错误的个数是______. ①命题“∃x∈R,x2-x>0”的否定是“∀x∈R,x2-x≤0”; ②“命题p∨q为真”是“命题p∧q为真”的必要不充分条件; ③“若am2 ④若实数x,y∈[0,1],则满⾜:x2+y2>1的概率为π4. 解析③与④错,③中m=0时不成⽴,④的概率应为1-π4. 答案2 9.已知命题p:关于x的⽅程x2-ax+4=0有实根;命题q:关于x的函数y=2x2+ax+4在[3,+∞)上是增函数.若p或q是真命题,p 且q是假命题,则实数a的取值范围是____________. 解析命题p等价于Δ=a2-16≥0,∴a≤-4或a≥4;命题q等价于-a4≤3,∴a≥- 12.p或q是真命题,p且q是假命题,则命题p和q⼀真⼀假.∴实数a的取值范围为(- 4,4)∪(-∞,-12). 答案(-4,4)∪(-∞,-12) 10.若命题p:不等式ax+b>0的解集为{x|x>-ba},命题q:关于x的不等式(x-a)(x-b)<0的解集为{x|a 解析命题p为假命题,命题q为假命题,故只有“⾮p”是真命题. 答案⾮p 11.设函数f(x)=x|x|+bx+c,给出下列四个命题: ①c=0时,f(x)是奇函数;②b=0,c>0时,⽅程f(x)=0只有⼀个实根;③f(x)的图象关 于(0,c)对称;④⽅程f(x)=0⾄多两个实根.其中正确的命题有______(填序号). 解析当c=0时,f(x)是奇函数,①正确;b=0,c>0时,g(x)=x|x|为单调函数,所以⽅ 程f(x)=0只有⼀个实根,②正确;f(x)+f(-x)=2c,所以f(x)的图象关于(0,c)对称,③ 正确;⽅程f(x)=0可能有⼀个、两个、三个、四个实根,④错误. 答案①②③ 12.已知命题p:函数f(x)=(12)x-log13x在区间(0,13)内存在零点,命题q:存在负数x使得(12)x>(13)x,给出下列四个命题①p或q,②p且q,③p的否定,④q的否定,真命题的个数是______. 解析y=log13x在x∈(0,13)为减函数,且log13x>1,y=(12)x在x∈(0,13)为减函数,且 (12)x<1,所以f(x)=(12)x-log13x在x∈(0,13)恒有f(x)<0,即f(x)在x∈(0,13)不存在零点, 命题p错误.当x<0时,(12)x 的否定”是对的. 答案2 13.设p:4x+3y-12>03-x≥0x+3y≤12,(x,y∈R),q:x2+y2>r2(x,y∈R,r>0),若⾮q是⾮p的充分不必要条件,那么p是q______条件,r的取值范围是______. 解析由⾮q是⾮p的充分不必要条件可知,p是q的充分不必要条件;由题意得p对 应的平⾯区域应包含于q对应的平⾯区域,即p表⽰的区域内的所有的点在圆x2+y2= r2(x,y∈R,r>0)外,结合图形可知r的取值范围是(0,125]. 答案充分不必要(0,125] 14.若⾮空集合A、B、C满⾜A∪B=C,且B不是A的⼦集,则下列说法中正确的是______(填序号). ①“x∈C”是“x∈A”的充分条件但不是必要条件 ②“x∈C”是“x∈A”的必要条件但不是充分条件 ③“x∈C”是“x∈A”的充要条件 ④“x∈C”既不是“x∈A”的充分条件也不是“x∈A”的必要条件 解析由题意知,A、B、C的关系⽤图来表⽰.若x∈C,不⼀定有x∈A,⽽x∈A,则 必有x∈C,因此“x∈C”是“x∈A”的必要条件但不是充分条件. 答案② ⼆、解答题(本⼤题共6⼩题,共90分) 15.(14分)已知p:x2-4ax+3a2<0(a<0),q:x2-x-6≤0或x2+2x-8>0.⾮p是⾮q的必要不充分条件,求实数a的取值范围. 解由p:x2-4ax+3a2<0(a<0)得:3a 由q:x2-x-6≤0或x2+2x-8>0得x≥-2或x 因为⾮p是⾮q的必要不充分条件,所以等价于q是p的必要不充分条件,即集合A是 集合B的真⼦集,故a≤-4a<0或3a≥-2a<0,所以a≤-4或-23≤a<0. 16.(14分)设函数f(x)=x2-1,已知对∀x∈[32,+∞),不等式f(xm)-4m2f(x)≤f(x-1)+4f(m)恒成⽴,求实数m的取值范围. 解依据题意得x2m2-1-4m2(x2-1)≤(x-1)2-1+4(m2-1)对∀x∈[32,+∞)恒成⽴, 即1m2-4m2≤-3x2-2x+1对∀x∈[32,+∞)恒成⽴. 因为当x=32时函数y=-3x2-2x+1取得最⼩值-53, 所以1m2-4m2≤-53,即(3m2+1)(4m2-3)≥0,解得m≤-32或m≥32. 17.(14分)已知命题p:⽅程a2x2+ax-2=0在[-1,1]上有解;命题q:只有⼀个实数x满⾜不等式x2+2ax+2a≤0;若命题“p或q”是真命题,⽽命题“p且q”是假命题,且綈q是真命题,求a的取值范围. 解对于命题p:由a2x2+ax-2=0在[-1,1]上有解, 当a=0时,不符合题意; 当a≠0时,⽅程可化为:(ax+2)(ax-1)=0, 解得:x=-2a或x=1a, 因为x∈[-1,1],∴-1≤-2a≤1或-1≤1a≤1, 解得:a≥1或a≤-1, 对于命题q:由只有⼀个实数x满⾜不等式x2+2ax+2a≤0, 得抛物线y=x2+2ax+2a与x轴只有⼀个交点, 所以Δ=4a2-8a=0,∴a=0或2, ⼜因命题“p或q”是真命题,⽽命题“p且q”是假命题,且綈p是真命题, 则命题p是真命题,命题q是假命题,所以a的取值范围为(-∞,-1]∪[1,2)∪(2, +∞). 18.(16分)设命题p:实数x满⾜x2-4ax+3a2<0,其中a>0,命题q:实数x满⾜x2-x-6≤0,x2+2x-8>0. (1)若a=1,且p∧q为真,求实数x的取值范围; (2)若p是q的必要不充分条件,求实数a的取值范围. 解(1)由x2-4ax+3a2<0得(x-3a)(x-a)<0, ⼜a>0,所以a 当a=1时,1 由x2-x-6≤0x2+2x-8>0,得2 若p∧q为真,则p真且q真,所以实数x的取值范围是{x|2 (2)设A={x|x2-4ax+3a2<0,a>0}, B={x|x2-x-6≤0x2+2x-8>0}, 则B?A,⼜A={x|a≤x≤3a},B={x|2 则0 所以实数a的取值范围是{a|1 19.(16分)已知m∈R,命题p:对∀x∈[0,8],不等式log13(x+1)≥m2-3m恒成⽴;命题q:对∀x∈(0,23π),不等式1+sin2x-cos2x≤2mcos(x-π4)恒成⽴. (1)若p为真命题,求m的取值范围; (2)若p且q为假,p或q为真,求m的取值范围. 解(1)令f(x)=log13(x+1),则f(x)在(-1,+∞)上为减函数, 因为x∈[0,8],所以当x=8时,f(x)min=f(8)=-2. 不等式log13(x+1)≥m2-3m恒成⽴,等价于-2≥m2-3m,解得1≤m≤2. (2)不等式1+sin2x-cos2x≤2mcos(x-π4), 即2sinx(sinx+cosx)≤2m(sinx+cosx), 所以m≥2sinx, 因为x∈(0,23π)⇒0 若p且q为假,p或q为真,则p与q有且只有⼀个为真. 若p为真,q为假,那么1≤m≤2,m<2,则1≤m<2; 若p为假,q为真,那么m<1或m>2,m≥2,则m>2. 综上所述,1≤m<2或m>2,即m的取值范围是[1,2)∪(2,+∞). 20.(16分)已知关于x的绝对值⽅程|x2+ax+b|=2,其中a,b∈R. (1)当a,b满⾜什么条件时,⽅程的解集M中恰有3个元素? (2)试求以⽅程解集M中的元素为边长的三⾓形,恰好为直⾓三⾓形的充要条件. 解(1)原⽅程等价于x2+ax+b=2,① 或x2+ax+b=-2,② 由于Δ1=a2-4b+8>a2-4b-8=Δ2, ∴Δ2=0时,原⽅程的解集M中恰有3个元素,即a2-4b=8; (2)必要性:由(1)知⽅程②的根x=-a2,⽅程①的根x1=-a2-2,x2=-a2+2, 如果它们恰为直⾓三⾓形的三边,即(-a2)2+(-a2-2)2=(-a2+2)2, 解得a=-16,b=62. 充分性:如果a=-16,b=62,可得解集M为{6,8,10},以6,8,10为边长的三⾓ 形恰为直⾓三⾓形. ∴a=-16,b=62为所求的充要条件.。
高二数学暑假作业

高二数学暑假作业高二数学暑假作业第一部分选择题 ( 共50分 )一、选择题:本大题共12小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.(1) 下列说法正确的是A. B. C. D.(2)直线的斜率是3,且过点A(1,-2),则直线的方程是A. B.C. D.(3)不等式的解集为A. B.C. D.(4)已知平面向量,,且,则的值为A.-3B.-1C.1D.3(5)若某多面体的三视图(单位:cm)如图所示,则此多面体的体积是A. B. C. D.(6)已知函数的定义域为A. B.C . D.(7)已知函数则该函数的图象②若,则 ;③若,则 ;④若,则14. 若则的最小值是_______________.三、解答题:本大题共6小题,共90分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤.15.(本小题满分12分)已知 , , , .(Ⅰ) 求的值;(Ⅱ) 求的值.16. (本小题满分12分)已知几何体A-BCDE如图所示,其中四边形BCDE为矩形,且BC=2,CD= ,△ABC是边长为2的等边三角形,平面ABC⊥平面BCDE.(1)若F为AC的中点,求证:AE∥平面BDF;(2)求此几何体A-BCDE的体积.17.(本小题满分14分)已知圆经过两点,,且圆心在直线上,直线的方程为 .(1)求圆的方程;(2)证明:直线与恒相交;(3)求直线被圆截得的最短弦长.18. (本小题满分14分)记等差数列{ }的前n项和为,已知, .(Ⅰ)求数列{ }的通项公式;(Ⅱ)令,求数列{ }的前项和 .19.(本题满分14分)设函数的定义域是,对任意正实数恒有,且当时,,(1)求的值;(2)求证:在上是增函数;(3)运用图像法求方程的根的个数.。
【推荐下载】苏教版高中高二数学暑假作业练习及答案

[键入文字]
苏教版高中高二数学暑假作业练习及答案
苏教版高中高二数学暑假作业练习及答案
【摘要】高中学生在学习中或多或少有一些困惑,的编辑为大家总结了苏教版高中高二数学暑假作业练习及答案,各位考生可以参考。
一、填空题(本大题共14小题,每小题5分,共70分)
1.命题:若a2+b2=0(a,b∈R),则a=b=0的逆否命题是____________.
解析 且的否定为或,因此逆否命题为若a≠0或b≠0,则a2+b2≠0.
答案 若a≠0或b≠0(a,b∈R),则a2+b2≠0
2.命题ax2-2ax-30不成立是真命题,则实数a的取值范围是____________.
解析 ax2-2ax-3≤0恒成立,
当a=0时,-3≤0成立;
当a≠0时,a小于0Δ=4a2+12a≤0,
解得-3≤a小于0.
1。
高二数学暑假作业7附答案
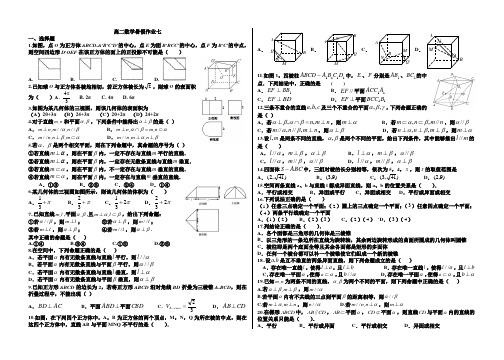
高二数学暑假作业七一、选择题1.如图,点O 为正方体ABCD -A 'B 'C 'D '的中心,点E 为面B 'BCC '的中心,点F 为B 'C '的中点,则空间四边形D 'OEF 在该正方体的面上的正投影不可能是( )A.B.C.D.2.已知球O 与正方体各棱均相切,若正方体棱长为2,则球O 的表面积为( )A.34πB. 2πC. 4πD. 6π 3.如图为某几何体的三视图,则该几何体的表面积为(A )20+3π (B )24+3π (C )20+2π (D )24+2π4.对于直线,m n 和平面,αβ,下列条件中能得出αβ⊥的是( ) A .,//,//m n m n αβ⊥ B .,,m n m n αβα⊥⋂=⊂ C .//,,m n n m βα⊥⊂ D .//,,m n m n αβ⊥⊥5.若αβ、是两个相交平面,则在下列命题中,真命题的序号为( ) ①若直线m α⊥,则在平面β内,一定不存在与直线m 平行的直线. ②若直线m α⊥,则在平面β内,一定存在无数条直线与直线m 垂直. ③若直线m α⊂,则在平面β内,不一定存在与直线m 垂直的直线. ④若直线m α⊂,则在平面β内,一定存在与直线m 垂直的直线. A .①③ B .②③ C .②④ D .①④6.某几何体的三视图如图所示,则该几何体的体积为( ) A .13π+ B .23π+ C .123π+ D .223π+ 7..已知直线,m l ,平面,αβ,且,m l αβ⊥⊂,给出下列命题: ①若//αβ,则m l ⊥; ②若αβ⊥,则//m l ; ③若m l ⊥,则αβ⊥; ④若//m l ,则αβ⊥. 其中正确的命题是( ) A.①④ B.③④ C.①② D.②③ 8.在空间中,下列命题正确的是( )A .若平面α内有无数条直线与直线l 平行,则//l αB .若平面α内有无数条直线与平面β平行,则//αβC .若平面α内有无数条直线与直线l 垂直,则l α⊥D .若平面α内有无数条直线与平面β垂直,则αβ⊥9.已知正方形ABCD 的边长为2,若将正方形ABCD 沿对角线BD 折叠为三棱锥A -BCD ,则在折叠过程中,不能出现( )A .AC BD ⊥B .平面⊥ABD 平面CBD C. 32=-CBD A V D .CD AB ⊥ 10.如图,在下列四个正方体中,A ,B 为正方体的两个顶点,M ,N ,Q 为所在棱的中点,则在这四个正方体中,直线AB 与平面MNQ 不平行的是( ).A .N QBAB .MNQBAC .M NQBAD .MNQBA11.如图1,四棱柱1111D C B A ABCD -中,E 、F 分别是1AB 、1BC 的中点.下列结论中,正确的是 ( ) A .1BB EF ⊥ B .//EF 平面11A ACC C .BD EF ⊥D .⊥EF 平面11B BCC12.三条不重合的直线c b a ,,及三个不重合的平面γβα,,,下列命题正确的是( )A .若n m n ⊥=⋂⊥,,βαβα,则α⊥mB .若n m n m //,,βα⊂⊂,则βα//C .若n m n m ⊥,//,//βα,则βα⊥D .若ββα⊥⊥⊥m n n ,,,则α⊥m 13.设m l ,是两条不同的直线,βα,是两个不同的平面,给出下列条件,其中能够推出m l //的是( )A .α//l ,β⊥m ,βα⊥B .α⊥l ,β⊥m ,βα//C .α//l ,β//m ,βα//D .α//l ,β//m ,βα⊥14.四面体ABC S -中,三组对棱的长分别相等,依次为5,4,x ,则x 的取值范围是 A .)41,2( B .)9,3( C .)41,3( D .)9,2( 15.空间两条直线a 、b 与直线l 都成异面直线,则a 、b 的位置关系是( ). A .平行或相交 B .异面或平行 C .异面或相交 D .平行或异面或相交 16.下列说法正确的是( ) (1)任意三点确定一个平面;(2)圆上的三点确定一个平面;(3)任意四点确定一个平面;(4)两条平行线确定一个平面 A .(1)(2) B .(2)(3) C .(2)(4) `D .(3)(4) 17.列结论正确的是( ).A .各个面都是三角形的几何体是三棱锥B .以三角形的一条边所在直线为旋转轴,其余两边旋转形成的曲面所围成的几何体叫圆锥C .棱柱即是两个底面全等且其余各面都是矩形的多面体D .任何一个棱台都可以补一个棱锥使它们组成一个新的棱锥18..设,a b 是互不垂直的两条异面直线,则下列命题成立的是( )A .存在唯一直线l ,使得l a ⊥,且l b ⊥B .存在唯一直线l ,使得//l a ,且l b ⊥C .存在唯一平面α,使得a α⊂,且//b αD .存在唯一平面α,使得a α⊂,且b α⊥ 19.已知,m n 为两条不同的直线,,αβ为两个不同的平面,则下列命题中正确的是( ) A.若,m αββ⊥⊥,则//m αB.若平面α内有不共线的三点到平面β的距离相等,则//αβC.若,m m n α⊥⊥,则//n αD.若//,m n n α⊥,则m α⊥20.在梯形ABCD 中,AB CD ∥,AB ⊂平面α,CD ⊄平面α,则直线CD 与平面α内的直线的位置关系只能是( ). A .平行 B .平行或异面 C .平行或相交 D .异面或相交二、填空题21. 如图,在一个60°的二面角的棱上有两个点A,B,AC,B D分别是在这个二面角的两个半平面内垂直于AB的线段,且AB=4,AC=6,BD=8,则CD的长为_________。
高二数学上学期暑假作业考试试题(共4页)

一中2021-2021学年高二数学(shùxué)上学期暑假作业考试试题〔满分是:100分时间是:60分钟〕一. 选择题:本大题一一共10小题,每一小题5分,一共50分,在每一小题给出的四个选项里面,只有一项是哪一项符合题目要求的.1.执行如下图的程序框图,输出的s值为A. B. C. D.2.向上抛掷一颗骰子1次,设事件A表示向上的一面出现奇数点,事件B表示向上的一面出现的点数不超过3,事件C表示向上的一面出现的点数不小于4,那么()A. A与B是互斥而非对立事件B. A与B是对立事件C. B与C是互斥而非对立事件D. B与C是对立事件3.,那么〔〕A. 0B.C.D.4.向量,且,那么m=〔A〕−8 〔B〕−6 〔C〕6 〔D〕85.,那么的值是()A. B. C. D.6.将函数(h ánsh ù) 的图象向右平移个单位长度后,得到函数,那么函数的图象的一个对称中心是( )A. B.C. D.7.在△中,为边上的中线,为的中点,那么 A. B. C.D.8.的内角的对边分别为,,,假设的面积为,那么A. B. C. D.9.在△ABC 中,角ABC 的对边分别为a 、b 、c ,假设,那么角B 的值是〔 〕 A .B .C .6π或者 D .3π或者10.函数的局部图象如下图,〔 〕.那么A .B .C .D .二、填空题:本大题一一共4小题,每一小题5分,一共20分. 11.向量(xi àngli àng)夹角为,且;那么12.样本方差,那么样本……的方差为_______.13.在中,假设,,,那么____ . 14.函数的图象与直线y=m的三个交点的横坐标分别为,那么 ____三.解答题:本大题一一共2小题,每一小题15分,一共30分.解容许写出必要的文字说明.32.某城100户居民的月平均用电量(单位:度),以[160,180),[180,200),[200,220),[220,240),[240,260),[260,280),[280,300]分组的频率分布直方图如下图.(1)求直方图中x的值;(2)求月平均用电量的众数和中位数;(3)在月平均用电量为[220,240),[240,260),[260,280),[280,300]的四组用户中,用分层抽样的方法抽取11户居民,那么月平均用电量在[220,240)的用户中应抽取多少户?38.在△ABC中,内角A、B、C的对边分别是a、b、c,且a2=b2+c2+bc.〔1〕求A;〔2〕设a=,S为△ABC的面积(miàn jī),求S+3cosBcosC的最大值,并指出此时B的最值.一、选择题1.二、填空题11. 12.8 13. 14.三、解答15.(1)0.0075;(2)众数是230度.中位数是224度.(3)5户.16.〔1〕由余弦定理得:cosA===﹣,∵A为三角形的内角,∴A=;〔2〕由〔1〕得sinA=,由正弦定理得:b=,csinA=asinC及a=得:S=bcsinA=••asinC=3sinBsinC,那么S+3cosBcosC=3〔sinBsinC+cosBcosC〕=3cos〔B﹣C〕,那么当B﹣C=0,即B=C==时,S+3cosBcosC取最大值3.内容总结。
[高二数学暑假作业简答题]时刻准备着暑假作业高二数学答案
![[高二数学暑假作业简答题]时刻准备着暑假作业高二数学答案](https://img.taocdn.com/s3/m/6f8e2309bb1aa8114431b90d6c85ec3a87c28b31.png)
[高二数学暑假作业简答题]时刻准备着暑假作业高二数
学答案
高二网权威发布高二数学暑假作业简答题,更多高二数学暑假作业简
答题相关信息请访问高二网。
解答题:解答应写出文字说明,证明过程或演算步骤。
17.(本小题满分12分)如图,在△ABC中,已知∠B=45°,D是BC边
上的一点,AD=10,AC=14,DC=6,求AB的长.
18.(本小题满分12分)已知等差数列{an}中,a1=1,a3=-3.
(1)求数列{an}的通项公式;
(2)若数列{an}的前k项和Sk=-35,求k的值.
19.(本小题满分12分)如图,四边形ABCD为正方形,QA⊥平面ABCD,PD∥QA,
QA=AB=12PD.
(1)证明:PQ⊥平面DCQ;
(2)求棱锥QABCD的体积与棱锥PDCQ的体积的比值.
20.(本小题满分12分)从某校随机抽取100名学生,获得了他们一周
课外阅读时间(单位:小时)的数据,整理得到数据分组及频数分布表和频
率分布直方图:
(1)从该校随机选取一名学生,试估计这名学生该周课外阅读时间少
于12小时的概率;
(2)求频率分布直方图中的a,b的值;
(3)假设同一组中的每个数据可用该组区间的中点值代替,试估计样本中的100名学生该周课外阅读时间的平均数在第几组(只需写出结论)
21.(本小题满分12分)设椭圆C∶某2a2+y2b2=1(a>b>0)过点(0,4),离心率为35.
(1)求C的方程;
(2)求过点(3,0)且斜率为45的直线被C所截线段的中点坐标.。
新高二数学暑假练习题

新高二数学暑假练习题【暑假作业】尊敬的高二同学们:暑假将至,作为新高二学生的你们即将面临数学学科的挑战。
为了帮助大家更好地复习与巩固知识,我们为你们准备了一套新高二数学暑假练习题。
本练习题分为四个部分,分别涵盖代数、几何、概率与统计以及数学推理等内容。
请同学们按照要求完成练习并于暑假结束后提交作业。
【第一部分:代数】1. 解方程:求解以下方程组(a) 2x + 3y = 7x - 2y = 1(b) x^2 - 5x + 6 = 02. 算式转化:将指数函数f(x) = 3^(x+1)写成对数函数的形式。
3. 因式分解:将以下多项式进行因式分解(a) x^2 + 5x + 6(b) 2x^3 - 8x^2 +12x【第二部分:几何】1. 直角三角形:已知直角三角形ABC,角A为直角,BC = 8 cm,AC = 6 cm,求AB的长度。
2. 平面几何证明:已知三角形ABC的三边分别为AB = 5 cm,BC = 6 cm,AC = 7 cm,证明该三角形为等腰三角形。
3. 三视图:根据给定的三视图绘制物体的正视图、侧视图和俯视图,并利用三视图还原物体。
【第三部分:概率与统计】1. 抽样调查:设计一个合理的调查问题,并对你的同学进行抽样调查,根据调查结果绘制统计图表。
2. 概率计算:有一批产品,其中20%存在质量问题。
如果从中随机抽取5个产品,计算至少有1个产品存在质量问题的概率。
3. 随机变量:已知某次抛掷一枚硬币,正面朝上的概率为0.6,反面朝上的概率为0.4。
定义随机变量X为连续抛掷硬币直到出现2次反面朝上的次数。
计算X取值为2的概率。
【第四部分:数学推理】1. 证明题:证明在任意一个三角形中,任意两边之差小于第三边,并推导出三角形的两个内角之和等于第三个角的补角。
2. 数列综合:已知数列an的通项公式为an = 2n^2 - 3n + 1,求前n项的和Sn。
3. 数学归纳法证明:证明对于任意正整数n,2n + 1为奇数。
高二数学暑假作业11附答案

高二数学暑假作业十一一、填空题1.已知函数,直线是它的一条对称轴,且是离该轴最近的一个对称中心,则()A.B.C.D.2.,最大值M,最小值N,则()(A).M-N=4 (B).M+N=4 (C). M-N=2 (D). M+N=23.终边在直线上的角的集合是()A.B.C.D.4.在水流速度的自西向东的河中,如果要使船以的速度从河的南岸垂直到达北岸,则船出发时行驶速度的方向和大小为()A. 北偏西,B. 北偏西,C. 北偏东,D. 北偏东,5.已知角θ的终边上有一点P(-4,3) , 则的值是( )A.B.C.D.6.若等边的边长为,平面内一点满足:,A.-1B.-2C.2D.3 ()7.已知向量a、b的夹角为45°,且|a|=1,|2a-b|=,则|b|=()A.3B.2 C. D.18.圆的半径为6,则15的圆心角与圆弧围成的扇形面积为()A. B. C. D.39.(2015秋•商洛月考)在四边形ABCD中,=0,且,则四边形ABCD是()A.平行四边形B.菱形C.矩形D.正方形10.要得到函数y=cos2x的图象,只需将函数y=sin(2x+)的图象沿x轴A.向左平移个单位B.向左平移个单位C.向右平移个单位D.向右平移个单位11.已知平面向量与的夹角等于,如果,那么()A.B.C.D.12.若2cos23sin2cos4θθπθ=⎛⎫+⎪⎝⎭,则sin2θ=A.13B.23- C.23D.13-()13.已知菱形ABCD的边长为2,∠BAD=120°,点E,F分别在边BC,DC上,BEBC= λ,DFDC= μ若AE AF⋅=l,CE CF⋅=23-,则λ+ μ= A.12B.23C.34D.56()14.函数相邻两个对称中心的距离为,以下哪个区间是函数的单调减区间()A. B. C. D.15.在中,则()A.B.C.D.16.已知函数的图像如图所示,则的值是A.B.C.D.()17.若向量=(1,1),=(-1,1),=(4,2),则= ()A.3+B. 3-C.+3D.+318..已知是边长为2的正△边上的动点,则·(+)的A.最大值为8 B.是定值6 C.最小值为2 D.与P的位置有关19.已知,则()(A)(B)(C)(D)20.已知函数()()sin(0,)2f x xπωϕωϕ=+><,其图象相邻两条对称轴之间的距离为2π,且函数12f xπ⎛⎫+⎪⎝⎭是偶函数.下列判断正确的是()A. 函数()f x的最小正周期为2π B. 函数()f x的图象关于点7,012π⎛⎫⎪⎝⎭对称C. ()f x的图象关于直线712xπ=-对称D. ()f x在3,4ππ⎡⎤⎢⎥⎣⎦上单调递增二、填空题21.如图,正方形ABCD中,AB=2,DE=EC,若F是线段BC上的一个动点,则的最大值是 .22.平面向量满足,且,则向量的夹角为 .23.已知向量,,若,则的最小值为_____24.已知,则的值是______.25.=_____26.已知,则__________. 27.若,则__________.28.ABC ∆中, 90,2C CA CB ∠===,点M 在边AB 上,且满足3BM MA =,则CM CB ⋅=__________.三、解答题 29、若的图象关于直线对称,其中(1)求的解析式;(2)将的图象向左平移个单位,再将得到的图象的横坐标变为原来的2倍(纵坐标不变)后得到的图象;若函数的图象与的图象有三个交点且交点的横坐标成等比数列,求的值.30、已知函数f (x )=2sin (ωx +)(ω>0,0<<π)的图象如图所示.(1)求函数f (x )的解析式:(2)已知=,且a ∈(0,),求f (a )的值.31、在ABC ∆中,a 、b 、c 分别是角A 、B 、C 的对边,且cos 2cos C a cB b-=, (Ⅰ)求角B 的大小;(Ⅱ)若3b =,求22ac +的取值范围.32、已知函数的最小值是-2,其图象经过点.(1)求的解析式;(2)已知,且,,求的值.高二数学暑假作业11答案一、填空题1.【答案】B 由直线是它的一条对称轴,且是离该轴最近的一个对称中心,可得,所以,即,又因为直线是它的一条对称轴,且是离该轴最近的一个对称中心,则,所以,故选B.2.【答案】D故函数关于(0,1)对称,则可知其函数最大值和最小值的和为2,故选D.3.【答案】C4.【答案】A如图,船从O点出发,沿OC方向行驶,才能垂直到达河的对岸,则,所以,即船以的速度,向北偏西方向行驶,才能垂直到达对岸.5.【答案】B∵θ的终边上有一点 P(-4,3) ,∴.6. 【答案】B 考点:向量的数量积7.【答案】A【解析】因为a、b的夹角为45°,且|a|=1,|2a-b|=,所以4a2-4a·b+b2=10,即|b|2-2|b|-6=0,解得|b|=3或|b|=-(舍),故选A.8.【答案】B9.【答案】C 由=0,得AB⊥BC ,由,得AB DC,由此能判断四边形ABCD的形状.解:在四边形ABCD中,∵=0,∴AB⊥BC,∵,∴AB DC,∴四边形ABCD是矩形.10.【答案】A11.【答案】C 因,故,应选C.考点:向量的数量积公式及运用.12.【答案】B由条件得,将上式两边分别平方,得,即,解得或(舍去),∴.选B .13.【答案】D==,(1),=,即(2),由(1)(2)可得,故选D.点睛:与平面向量数量积有关的题目的类型及求法:(1)求平面向量数量积有三种方法:一是夹角公式a ·b =|a ||b |cos θ;二是坐标公式a ·b =x 1x 2+y 1y 2;三是利用数量积的几何意义.(2)求较复杂的平面向量数量积的运算时,可先利用平面向量数量积的运算律或相关公式进行化简.14.【答案】C由函数相邻两个对称中心的距离为知:函数的周期满足,故,从而,由得到函数的减区间为:令得:故选C .考点:三角函数的性质. 15.【答案】A在中,,所以,又因为,所以,因为,所以,所以,所以,故选A.考点:平面向量的数量积的运算. 16.【答案】B 根据,结合诱导公式可知,故选B.考点:1.三角函数的图像;2.诱导公式.17.【答案】B 设,则有,解得,所以.18.【答案】B是正三角形,故选B19.【答案】D,得,得.20.【答案】D 由题图象相邻两条对称轴之间的距离为,则;, 又函数是偶函数,可知;则得;A错误,B,图像对称点横坐标为;错误;C,图像的对称直线方程为;,错误;D,函数的增区间为;为它的子集。
高二数学暑假作业1附答案

高二数学暑假作业一一、选择题: 1.的值为A.B.C.D.( )2.已知函数是偶函数,则的值为( )A.B.C.D. 03.若将函数错误!未找到引用源。
的图像向左平移错误!未找到引用源。
个单位长度,则平移后图象的对称轴为A. 错误!未找到引用源。
B. 错误!未找到引用源。
C. 错误!未找到引用源。
D.错误!未找到引用源。
4.已知错误!未找到引用源。
,则错误!未找到引用源。
A. 错误!未找到引用源。
B.错误!未找到引用源。
C. 错误!未找到引用源。
D. 错误!未找到引用源。
( )5.设向量错误!未找到引用源。
,若错误!未找到引用源。
,则错误!未找到引用源。
( )A. 错误!未找到引用源。
B. 错误!未找到引用源。
C. -1D. -36.若错误!未找到引用源。
,错误!未找到引用源。
,则错误!未找到引用源。
的值构成的集合为( )A. 错误!未找到引用源。
B. 错误!未找到引用源。
C. 错误!未找到引用源。
D. 错误!未找到引用源。
7.△ABC 的三边分别为a ,b ,c ,且a=1,B=45°,S △ABC =2,则△ABC 的外接圆的直径为A. 5 B. C. D. ( )8.在错误!未找到引用源。
中,内角错误!未找到引用源。
的对边分别是错误!未找到引用源。
,若错误!未找到引用源。
,则错误!未找到引用源。
一定是( )A. 等边三角形B. 等腰三角形C. 等腰直角三角形D. 直角三角形9.在错误!未找到引用源。
中,错误!未找到引用源。
,则错误!未找到引用源。
边上的高为( )A. 错误!未找到引用源。
B. 错误!未找到引用源。
C. 错误!未找到引用源。
D. 错误!未找到引用源。
10.钝角三角形的三边为,其最大角不超过 ,则的取值范围是( ) A. B. C. D.11.错误!未找到引用源。
的三个内角错误!未找到引用源。
所对的边分别为错误!未找到引用源。
,设向量错误!未找到引用源。
,错误!未找到引用源。
高二数学暑假作业16附答案

高二数学暑假作业十六一、单选题1. 已知集合}9|{},032|{22<=<--=x x B x x x A ,则A.A BB.B AC.A =BD.A ∩B =Φ2. 集合M={ x ∈N*| x (x -3)< 0}的子集个数为 A .1 B .2 C .3 D .43. 0000cos43cos77sin43cos167+的值是( )。
A. 32-B. 12C. 32D. 12-4. 为了得到函数y=3sin 错误!未找到引用源。
的图象,只要把函数y=3sin 错误!未找到引用源。
的图象上所有的点( )A.向右平行移动错误!未找到引用源。
个单位长度B.向左平行移动错误!未找到引用源。
个单位长度C.向右平行移动错误!未找到引用源。
个单位长度D.向左平行移动错误!未找到引用源。
个单位长度5. 已知数列{}n a 的前n 项和为n S ,11a =,12n n S a +=,则n S = ( )A. 12n - B. 21n- C. 13n - D.()1312n- 6. 设a >b >0,x=a -b a +,y=b a -a -,则x 、y 的大小关系为( )A. x >yB. x <yC. x =yD. x 、y 大小关系不定 7. 如图Rt O A B '''∆是一平面图形的直观图,直角边2O B ''=,则这个平面图形的面积是( )A .22B .1C .2D .428. 已知012:,022:21=-+=-+y mx l my x l ,且21l l ⊥,则m 的值为( ) A 、2 B 、1 C 、0 D 、不存在9. 设,m n 是两条不同的直线, αβγ、、是三个不同的平面,给出下列四个命题: ①若,//m n αα⊥,则m n ⊥ ②若//,//,m αββγα⊥,则m γ⊥ ③若//,//m n αα,则//m n ④若,αγβγ⊥⊥,则//αβ其中正确命题的序号是( )A. ①和②B. ②和③C. ③和④D. ①和④ 10. 两圆与总有公共点,则圆半径的取值范围是 A 、[]2,7B 、[]3,7C 、[]2,10D 、[]3,10二、填空题11. 数列{}n a 满足1(1)(1)n n n a a a +--=,82a =,则2017S = . 12. 已知函数()f x 的定义域为[]1,3,则函数()21f x +的定义域为_________13. 如图所示,在平面直角坐标系xOy 中,角α的终边与单位圆交于点A,点A 的纵坐标为4,cos 5α则=_____。 14. 过)0,3(P 做圆1)1()1(22=+++y x 的切线,切点为点,A 则=PA .三、解答题15. 已知在ABC ∆中,角A,B,C,的对边分别为,,a b c ,且222,1b a c ac b =+-=(1)若3tan tan (1tan tan ),3A C A C c -=+求边的值; (2)若2a c =,求ABC ∆的面积.16. 如图,在五棱锥P ABCDE -中,PA ⊥平面ABCDE ,AB ∥CD ,AC ∥ED ,AE ∥BC ,45ABC ︒∠=, 22AB =,24BC AE ==,PAB ∆是等腰三角形.(1)求证:平面PCD ⊥平面PAC ; (2)求侧棱PB 上是否存在点Q ,使得CQ 与平面PCD 所成角大小为30︒,若存在,求出Q 点位置,若不存在,说明理由.高二数学暑假作业十六答案AxOyα1. A 【解析】试题分析:,所以考点:解不等式及集合的子集关系 2. D 【解析】所以集合的子集个数为个,故选D 。
【推荐下载】高中暑假作业:高二数学暑假作业答案解析

[键入文字]
高中暑假作业:高二数学暑假作业答案解析
本文导航
1、首页2、高二数学暑假作业答案解析-23、高二数学暑假作业答案解析-34、高二数学暑假作业答案解析-45、高二数学暑假作业答案解析-5
高中暑假作业:高二数学暑假作业答案解析
【摘要】的编辑就为各位学生带来了高中暑假作业:高二数学暑假作业答案解析
一、选择题(本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有
一项是符合题目要求的)
1.已知集合,,则( C )
A. B. C. D.
2. 设是定义在上的奇函数,当时,,则( A )
A. B. C.1 D.3
3. 已知向量满足,则( D )
1。
【推荐下载】最新的高二数学暑假作业练习题

B. C. D.
[键入文字]
10.已知等差数列 的前 项和 ,满足 ,则 =( ) A.-2015B.-2014C.-2013D.-2012 11.已知 是抛物线 的焦点, 是该抛物线上的两点.若线段 的中点到 轴的距离为 ,则 ( ) A.2B. C.3D.4 12.若函数 满足 ,且 时, ,函数 ,则函数 在区间 内的零点的个数为( ) A.8 B.9 C.10 D.13 第 II 卷(非选择题 共 90 分) 二、填空题:本大题共 4 小题,每小题 5 分,共 20 分。将答案填在答题卡对应题号 的横线上。 13.已知曲线 的极坐标方程是 ,以极点为原点,极轴为 轴的正半轴建立平面直角坐 标系,则曲线 的直角坐标方程为 。 14. 已知 ,且 是第二象限角,那么 。 15.已知等比数列 中, ,若数列 满足 ,则数列 的前 n 项和 =________.
6
4
[键入文字]
(Ⅰ)用分层抽样的方法在患 心肺疾病的人群中抽 3 人,其 中吸烟患者抽到多少人? (Ⅱ)在上述抽取的 3 人中选 2 人,求恰有一名不吸烟患者 的概率; (Ⅲ)是否有 99.5%的把握认为患心肺疾病与吸烟有关? 附: 20. (本小题满分 12 分) 如图,三棱柱 中,侧棱垂直底面, , , 是棱 的中点。 (I) 证明: ⊥平面 (Ⅱ)设 ,求几何体 的体积。
[键入文字]
最新的高二数学暑假作业练习题
这篇最新的高二数学暑假作业练习题是特地为大家整理的,希望对大家有所帮助! 第 I 卷(选择题 共 60 分) 一、选择题:本大题共 12 小题,每小题 5 分,在每小题给出的四个选项中,只有一 项是符合题目要求的。用 2B 铅笔把答题卡上对应题目的答案标号涂黑。 1. 已知集合 , ,则 ( ) A. B. C. D. 2. ( ) A. B. C. D. 3.已知 是定义在 上的奇函数,且 时 的图像 如图所示,则 ( ) A. 4.已知变量 , 满足约束条件 则 的最大值为( )
【推荐下载】最新高二数学暑假作业练习

[键入文字]
最新高二数学暑假作业练习
最新高二数学暑假作业练习
为大家整理了高二数学暑假作业练习,希望对大家有所帮助和练习。
并祝各位同学在暑假中过的快乐!!!。
二、奇偶性、图像及二次函数练习
一、填空题
1.若f(x)=12x-1+a是奇函数,则a= .
2.若f(x)为奇函数,且在(-∞,0)上是减函数,又f(-2)=0,则xf(x)小于0的解集为_______________.
3.如果函数f(x)=x2+bx+c对任意实数t都有f(2+t)=f(2-t),比较f(1),f(2),f(4)的大小关系为____________________.
4.若函数f(x)=x2+3x+p的最小值为-1,则p的值是____________________.
5.若二次函数f(x)=-2x2+4x+t的图象顶点的纵坐标等于1,则t的值是___________.
6.关于x的方程x2-(m+3)x+3m-1=0的两实根一个大于2,一个小于2,则实数m的
1。
【推荐下载】高中高二数学暑假作业答案解析

[键入文字]
由正弦定理知 .8 分 由四点 共圆知, , 所以 10 分 23.解.(I) 的普通方程为 的普通方程为 联立方程组 解得 与 的交点为 , , 则 . (II) 的参数方程为 为参数).故点 的坐标是 ,从而点 到直线 的距离是 , 由此当 时, 取得最小值,且最小值为 . 24.解:(Ⅰ)由 得 ,∴ ,即 , ∴ ,∴ 。┈┈┈┈5 分 (Ⅱ)由(Ⅰ)知 ,令 , 则,
4
[键入文字]
10、已知实数 满足 且 , 不等式 M 恒成立,则 M 的最大值是 ( ) A、 B、 C、 D、 19、 (1)由 得, . ∴ . 又 , ∴ , 即 , ∴ ,∴ . ∴ . (2) 等价于 ,即 , 要使此不等式在 上恒成立, 只需使函数 在 的最小值大于 即可. ∵ 在 上单调递减,
1
[键入文字]
①当 m 小于 时,B={x|2m - ≤m 小于 ; ②当 m= 时,B=Ø,有 B⊆A 成立; ③当 m 时,B={x|1 综上所述,所求 m 的取值范围是- ≤m≤1. (3)∵A={x|-1≤x≤2}, ∴ RA={x|x 小于-1 或 x2}, ①当 m 小于 时,B={x|2m - ≤m 小于-1; ②当 m= 时,不符合题意; ③当 m 时,B={x|1
6
[键入文字]
则 ∵ , , ∴ ,函数 在 上是增函数。当 时,同理函数 在 上是减函数。 ⑵ 当 时, ,则 ; 当 时, ,则 。 22.证明:(I)在 中,由 知: ≌ ,2 分 即 . 所以四点 共圆;5 分 (II)如图,连结 . 在 中, , ,
高二数学下册暑假作业题及答案【推荐下载】

高二数学下册暑假作业题及答案复习部分作业1 直线与圆的方程(一)命题:1.(09年重庆高考)直线与圆的位置关系为()A.相切B.相交但直线不过圆心C.直线过圆心D.相离2.方程x2+y2+2ax-by+c=0表示圆心为C(2,2),半径为2的圆,则a、b、c的值依次为()A.2、4、4;B.-2、4、4;C.2、-4、4;D.2、-4、-43(2011年重庆高考)圆心在轴上,半径为1,且过点(1,2)的圆的方程为()A.B.C.D.4.直线3x-4y-4=0被圆(x-3)2+y2=9截得的弦长为()A.B.4C.D.25. M(x0,y0)为圆x2+y2=a2(a>;0)内异于圆心的一点,则直线x0x+y0y=a2与该圆的位置关系是()A.相切B.相交C.相离D.相切或相交6、圆关于直线对称的圆的方程是().A.B.C.D.7、两圆x2+y2-4x+6y=0和x2+y2-6x=0的连心线方程为().A.x+y+3=0 B.2x-y-5=0C.3x-y-9=0 D.4x-3y+7=08.过点的直线中,被截得最长弦所在的直线方程为()A. B.C. D.9. (2011年四川高考)圆的圆心坐标是10.圆和的公共弦所在直线方程为_ ___.11.(2011年天津高考)已知圆的圆心是直线与轴的交点,且圆与直线相切,则圆的方程为.12(2010山东高考)已知圆过点,且圆心在轴的正半轴上,直线被该圆所截得的弦长为,则圆的标准方程为____________13.求过点P(6,-4)且被圆截得长为的弦所在的直线方程.14、已知圆C的方程为x2+y2=4.(1)直线l过点P(1,2),且与圆C交于A、B两点,若|AB|=23,求直线l的方程;(2)圆C上一动点M(x0,y0),ON→=(0,y0),若向量OQ→=OM→+ON→,求动点Q的轨迹方程“人”的结构就是相互支撑,”众”人的事业需要每个人的参与。
作业2 直线与圆的方程(二)命题:柏庆平1.点的内部,则的取值范围是()A.B.C.D.2.(09年上海高考)点P(4,-2)与圆上任一点连续的中点轨迹方程是()A.B.C.D.3.(09年陕西高考)过原点且倾斜角为的直线被圆所截得的弦长为A. B.2 C. D.24.已知方程x2+y2+4x-2y-4=0,则x2+y2的最大值是( )A.9 B.14 C.14-D.14+5、(09年辽宁高考)已知圆C与直线x-y=0 及x-y-4=0都相切,圆心在直线x+y=0上,则圆C的方程为()A.B.C.D.6、两圆相交于两点(1,3)和(m,1),两圆的圆心都在直线x-y+c2=0上,则m+c的值是()A.-1 B.2 C .3 D.07.(2011安徽)若直线过圆的圆心,则a的值为( )A.1 B.1 C.3 D.38.(09年广东高考)设圆C与圆x2+(y-3)2=1外切,与直线y =0相切,则C的圆心轨迹为( )A.抛物线B.双曲线C.椭圆D.圆9.(09年天津高考)若圆与圆的公共弦长为,则a=________.10.(09年广东高考)以点(2,)为圆心且与直线相切的圆的方程是.11.(09年陕西高考)过原点且倾斜角为的直线被圆所截得的弦长为.12、过点P(-3,-32)且被圆x2+y2=25所截得的弦长为8的直线方程为__________.13、已知圆C的圆心在直线l1:x-y-1=0上,与直线l2:4x+3y+14=0相切,且截得直线l3:3x+4y+10=0所得弦长为6,求圆C的方程.。
高二数学暑假作业21附答案

高二数学暑假作业21一、单选题1.某几何体的三视图如图所示,俯视图右侧是半圆,则该几何体的体积为( ) A.324π+ 错误!未找到引用源。
B. 34π+ 错误!未找到引用源。
C. 322π+ 错误!未找到引用源。
D. 32π+ 错误!未找到引用源。
2.若是两条不同的直线, 是三个不同的平面,则下列结论中正确的是 ( ) A. 若,则 B. 若,则 C. 若,则 D. 若,则 3.用与球心距离为1的平面去截球,所得的截面面积为π, 则球的体积为( )A. 38πB. 328π C. π28 D. 332π4.某三棱锥的三视图如图所示,则该三棱锥的体积为( )A. 16B. 13C. 12D. 15.某几何体的三视图如图所示,则该几何体的体积为( )A. 13π+B. 23π+C. 123π+D. 223π+6.如图在正方体1111ABCD A B C D -中,点O 为线段BD 的中点. 设点P 在线段1CC 上,直线OP 与平面1A BD 所成的角为α,则sin α的取值范围是( )A. 3,13⎡⎤⎢⎥⎣⎦B. 6,13⎡⎤⎢⎥⎣⎦ C. 622,33⎡⎤⎢⎥⎣⎦ D. 22,13⎡⎤⎢⎥⎣⎦7.已知底面边长为1,侧棱长为2的正四棱柱的各顶点均在 同一个球面上,则该球的体积为( )A. 323πB. 4πC. 2πD. 43π8.某几何体的三视图如图所示,则该几何体的体积为( ) A. 12 B. 18 C. 24 D. 309.设m 、n 是两条不同的直线,βα、是两个不同的平面,则( )A. 若,,则B.若,,则C. 若,,,则D. 若,,,则10.正三棱柱111ABC A B C -的底面边长为2,侧棱长为3, D 为BC 中点,则三棱锥11A B DC -的体积为( ) A. 3 B. 32 C. 1D. 3211.设是同一个半径为4的球的球面上四点,为等边三角形且其面积为,则三棱锥体积的最大值为A.B.C.D.12一个三棱锥的三视图是三个直角三角形,如图所示,则该三棱锥的外接球的表面积为( ) A. B. C. D.13已知三棱锥的所有顶点都在球的球面上,,,若三棱锥体积的最大值为2,则球的表面积为( )A. B. C.D. 14.已知球的内接长方体中,,若四棱锥的体积为2,则当球的表面积最小时,球的半径为( )A.B. 2C.D. 115.已知直线、,平面、,给出下列命题: ①若,,且,则②若,,且,则 ③若,,且,则 ④若,,且,则 其中正确的命题是( )A. ②③ B. ①③ C. ①④D.③④16.在边长为2的正方形中,,分别为,的中点,为的中点,沿,,将正方形折起,使,,重合于点,在构成的四面体中,下列结论中错误的是( )A. 平面B. 直线与平面所成角的正切值为C. 异面直线和求所成角为D. 四面体的外接球表面积为 二、填空题17.长方体的长,宽,高分别为3,2,1,其顶点都在球O 的球面上,则球O 的表面积为__________.18.已知一个正方体的所有顶点在一个球面上,若这个正方体的表面积为18,则这个球的体积为____.19.如图,在圆柱O 1 O 2 内有一个球O ,该球与圆柱的上、下底面及母线均相切。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
[键入文字]
高二数学暑假作业简答题
为大家搜集整理了高二数学暑假作业简答题,希望大家可以用心去做,不要只顾着玩耍哦!
解答题:解答应写出文字说明,证明过程或演算步骤。
17.(本小题满分12分)如图,在△ABC中,已知∠B=45°,D是BC边上的一点,AD=10,AC=14,DC=6,求AB的长.
18.(本小题满分12分) 已知等差数列{an}中,a1=1,a3=-3.
(1)求数列{an}的通项公式;
(2)若数列{an}的前k项和Sk=-35,求k的值.
19.(本小题满分12分)如图,四边形ABCD为正方形,QA⊥平面ABCD,PD∥QA,
QA=AB=12PD.
(1)证明:PQ⊥平面DCQ;
(2)求棱锥Q­ABCD的体积与棱锥P­DCQ的体积的比值.
1。
