高三数学球体积
高三数学人教版A版数学(理)高考一轮复习教案空间几何体的表面积与体积

第二节空间几何体的表面积与体积表面积与体积了解球、棱柱、棱锥、台的表面积和体积的计算公式(不要求记忆公式).知识点一空间几何体的表面积1.多面体的表(侧)面积多面体的各个面都是平面,则多面体的侧面积就是所有侧面的面积之和,表面积是侧面积与底面面积之和.2.旋转体的表(侧)面积名称侧面积表面积圆柱(底面半径r,母线长l)2πrl 2πr(l+r)圆锥(底面半径r,母线长l)πrl πr(l+r) 圆台(上、下底面半径r1,r2,母线长l)π(r1+r2)l π(r1+r2)l+π(r21+r22)球(半径为R)4πR2易误提醒(1)几何体的侧面积是指(各个)侧面面积之和,而表面积是侧面积与所有底面面积之和.(2)对侧面积公式的记忆,最好结合几何体的侧面展开图来进行,要特别留意根据几何体侧面展开图的平面图形的特点来求解相关问题.(3)组合体的表面积应注意重合部分的处理.[自测练习]1.正六棱柱的高为6,底面边长为4,则它的表面积为()A.48(3+3)B.48(3+23)C.24(6+2) D.144解析:正六棱柱的侧面积S侧=6×6×4=144,底面面积S底=2×6×34×42=483,S表=144+483=48(3+3).答案:A2.如图所示是一个几何体的三视图,根据图中数据,可得该几何体的表面积是()A .8+4 2B .10πC .11πD .12π解析:由三视图可知几何体是半径为1的球和底面半径为1,高为3的圆柱,故其表面积应为球的表面积与圆柱的表面积面积之和,即S =4π+2π+2π×3=12π,故选D.答案:D知识点二 空间几何体的体积空间几何体的体积(h 为高,S 为下底面积,S ′为上底面积) (1)V 柱体=Sh . (2)V 锥体=13Sh .(3)V 台体=13h (S +SS ′+S ′).(4)V 球=43πR 3(球半径是R ).易误提醒 (1)求一些不规则几何体的体积常用割补的方法将几何体转化成已知体积公式的几何体进行解决.(2)求与三视图有关的体积问题注意几何体还原的准确性及数据的准确性.[自测练习]3.已知某个几何体的三视图如图所示,根据图中标出的尺寸(单位:cm)可得这个几何体的体积是( )A.43 cm 3 B.83 cm 3 C .3 cm 3D .4 cm 3解析:由三视图可知该几何体是一个底面为正方形(边长为2)、高为2的四棱锥,如图所示.由四棱锥的体积公式知所求几何体的体积V =83cm 3.答案:B4.某一容器的三视图如图所示,则该几何体的体积为________.解析:依题意,题中的几何体是从一个棱长为2的正方体中挖去一个圆锥,其中该圆锥的底面半径是1、高是2,因此题中的几何体的体积等于23-13π×12×2=8-2π3.答案:8-2π3考点一 空间几何体的表面积|1.(2015·高考福建卷)某几何体的三视图如图所示,则该几何体的表面积等于( )A .8+2 2B .11+2 2C .14+2 2D .15解析:由题中三视图可知,该几何体是底面为直角梯形、高为2的直四棱柱,所以其表面积为S 表面积=S 侧面积+2S 下底面积=(1+1+2+2)×2+2×12×(1+2)×1=11+22,故选B.答案:B2.(2015·高考课标全国卷Ⅰ)圆柱被一个平面截去一部分后与半球(半径为r )组成一个几何体,该几何体三视图中的正视图和俯视图如图所示.若该几何体的表面积为16+20π,则r =( )A .1B .2C .4D .8解析:由三视图可知,此组合体是由半个圆柱与半个球体组合而成,其表面积为πr 2+2πr 2+4r 2+2πr 2=20π+16,所以r =2.答案:B3.(2016·昆明模拟)一个圆锥过轴的截面为等边三角形,它的顶点和底面圆周在球O 的球面上,则该圆锥的表面积与球O 的表面积的比值为________.解析:设等边三角形的边长为2a ,则S 圆锥表=12·2πa ·2a +πa 2=3πa 2.又R 2=a 2+(3a -R )2(R 为球O 的半径),所以R =233a ,故S 球表=4π·⎝⎛⎭⎫233a 2=16π3a 2,故其表面积比为916. 答案:916(1)由三视图求相关几何体的表面积:,给出三视图时,依据“正视图反映几何体的长和高,侧视图反映几何体的高和宽,俯视图反映几何体的长和宽”来确定表面积公式中涉及的基本量.(2)根据几何体(常规几何体、组合体或旋转体)的特征求表面积:①求多面体的侧面积时,应对每一个侧面分别求解后再相加;求旋转体的侧面积时,一般要将旋转体展开为平面图形后再求面积.②对于组合体,要弄清它是由哪些简单几何体组成的,要注意“表面(和外界直接接触的面)”的定义,以确保不重复、不遗漏.考点二 空间几何体的体积|(1)(2015·高考山东卷)已知等腰直角三角形的直角边的长为2,将该三角形绕其斜边所在的直线旋转一周而形成的曲面所围成的几何体的体积为( )A.22π3B.42π3C .22πD .42π(2)(2015·辽宁五校联考)某几何体的三视图如图所示,则该几何体的体积是________.[解析] (1)由题意,该几何体可以看作是两个底面半径为2、高为2的圆锥的组合体,其体积为2×13×π×(2)2×2=423π.(2)由三视图知,该几何体为长方体去掉一个三棱锥,其体积V =2×2×3-13×⎝⎛⎭⎫12×2×1×3=11.[答案] (1)B (2)11空间几何体体积问题的三种类型及解题策略(1)求简单几何体的体积.若所给的几何体为柱体、锥体或台体,则可直接利用公式求解.(2)求组合体的体积.若所给定的几何体是组合体,不能直接利用公式求解,则常用转换法、分割法、补形法等进行求解.(3)求以三视图为背景的几何体的体积.应先根据三视图得到几何体的直观图,然后根据条件求解.(2015·绵阳模拟)一个机器零件的三视图如图所示,其中俯视图是一个半圆内切于边长为2的正方形,则该机器零件的体积为( )A .8+π3B .8+2π3C .8+8π3D .8+16π3解析:依题意得,该机器零件的形状是在一个正方体的上表面放置了一个14的球体,其中正方体的棱长为2,相应的球半径是1,因此其体积等于23+14×43π×13=8+π3,选A.答案:A考点三 与球有关的切、接问题|与球相关的切、接问题是高考命题的热点,也是考生的难点、易失分点.命题角度多变.归纳起来常见的命题角度有:1.四面体的外接球. 2.四棱锥的外接球. 3.三棱柱的外接球. 4.圆锥的内切球与外接球. 5.四面体的内切球. 探究一 四面体的外接球问题1.(2016·唐山模拟)正三棱锥的高和底面边长都等于6,则其外接球的表面积为( ) A .64π B .32π C .16π D .8π解析:如图,作PM ⊥平面ABC 于点M ,则球心O 在PM 上,PM =6,连接AM ,AO ,则OP =OA =R (R 为外接球半径),在Rt △OAM 中,OM =6-R ,OA =R ,又AB =6,且△ABC 为等边三角形,故AM =2362-32=23,则R 2-(6-R )2=(23)2,则R =4,所以球的表面积S =4πR 2=64π.答案:A探究二 四棱锥的外接球问题2.已知四棱锥P -ABCD 的顶点都在球O 的球面上,底面ABCD 是矩形,平面P AD ⊥底面ABCD ,△P AD 为正三角形,AB =2AD =4,则球O 的表面积为( )A.323π B .32π C .64πD.643π 解析:依题意,AB ⊥平面P AD 且△P AD 是正三角形,过P 点作AB 的平行线,交球面于点E ,连接BE ,CE ,则可得到正三棱柱APD -BEC .因为△P AD 是正三角形,且AD =2,所以△P AD 的外接圆半径是23,球O 的半径R =22+⎝⎛⎭⎫232=43,球O 的表面积S =4πR 2=64π3,故选D.答案:D探究三 三棱柱的外接球问题3.(2016·长春模拟)已知三棱柱ABC -A 1B 1C 1的底面是边长为6的正三角形,侧棱垂直于底面,且该三棱柱的外接球的表面积为12π,则该三棱柱的体积为________.解析:设球半径为R ,上,下底面中心设为M ,N ,由题意,外接球心为MN 的中点,设为O ,则OA =R ,由4πR 2=12π,得R =OA =3,又易得AM =2,由勾股定理可知,OM =1,所以MN =2,即棱柱的高h =2,所以该三棱柱的体积为34×(6)2×2=3 3. 答案:3 3探究四 圆锥的内切球与外接球问题4.(2016·嘉兴模拟)若圆锥的内切球与外接球的球心重合,且内切球的半径为1,则圆锥的体积为________.解析:过圆锥的旋转轴作轴截面,得截面△ABC 及其内切圆⊙O 1和外接圆⊙O 2,且两圆同圆心,即△ABC 的内心与外心重合,易得△ABC 为正三角形,由题意知⊙O 1的半径为r =1,∴△ABC 的边长为23,圆锥的底面半径为3,高为3,∴V =13×π×3×3=3π.答案:3π探究五 四面体的内切球问题5.若一个正四面体的表面积为S 1,其内切球的表面积为S 2,则S 1S 2=________.解析:设正四面体棱长为a ,则正四面体表面积为S 1=4·34·a 2=3a 2,其内切球半径为正四面体高的14,即r =14·63a =612a ,因此内切球表面积为S 2=4πr 2=πa 26,则S 1S 2=3a 2π6a 2=63π. 答案:63π求解与球有关的切、接问题的关键点解决球与其他几何体的切、接问题,关键在于仔细观察、分析,弄清相关元素的关系和数量关系,选准最佳角度作出截面(要使这个截面尽可能多地包含球、几何体的各种元素以及体现这些元素之间的关系),达到空间问题平面化的目的.21.补形法在空间几何体的体积、面积中的应用【典例】 已知某几何体的三视图如图所示,则该几何体的体积为( )A.8π3 B .3π C.10π3D .6π[思维点拨] 可考虑将几何体补完整,再分析求解.[解析] 法一:由三视图可知,此几何体(如图所示)是底面半径为1,高为4的圆柱被从母线的中点处截去了圆柱的14,所以V =34×π×12×4=3π.法二:由三视图可知,此几何体是底面半径为1,高为4的圆柱从母线的中点处截去了圆柱的14,直观图如图(1)所示,我们可用大小与形状完全相同的补成一个半径为1,高为6的圆柱,如图(2)所示,则所求几何体的体积为V =12×π×12×6=3π.[答案] B[方法点评] 某些空间几何体是某一个几何体的一部分,在解题时,把这个几何体通过“补形”补成完整的几何体或置于一个更熟悉的几何体中,巧妙地破解空间几何体的体积问题,这是一种重要的解题策略——补形法.常见的补形法有对称补形、联系补形与还原补形.对于还原补形,主要涉及台体中“还台为锥”问题.[跟踪练习] (2015·沈阳模拟)已知四面体P -ABC 的四个顶点都在球O 的球面上,若PB ⊥平面ABC ,AB ⊥AC ,且BC =1,PB =AB =2,则球O 的表面积为( )A .7πB .8πC .9πD .10π解析:依题意,记题中的球的半径是R ,可将题中的四面体补形成一个长方体,且该长方体的长、宽、高分别是2、1、2,于是有(2R )2=12+22+22=9,4πR 2=9π,所以球O 的表面积为9π,选C.答案:CA 组 考点能力演练1.(2016·长春模拟)如图,网格纸上小正方形的边长为1,粗线画出的是某多面体的三视图,则该多面体的体积为( )A.323 B .64 C.3233 D.643解析:由三视图可知,该多面体是一个四棱锥,且由一个顶点出发的三条棱两两垂直,长度都为4,∴其体积为13×4×4×4=643,故选D.答案:D2.如图是某几何体的三视图,其中正视图是一个正三角形,则这个几何体的外接球的表面积为( )A.16π3B.8π3 C .43π D .23π解析:由对称性可知外接球球心在侧视图中直角三角形的高线上,设外接球的半径为R ,则(3-R )2+12=R 2,R =233,其表面积S =4πR 2=4π⎝⎛⎭⎫2332=16π3.答案:A3.(2016·唐山模拟)某几何体的三视图如图所示,则该几何体的体积为( ) A .8π+16 B .8π-16 C .8π+8 D .16π-8解析:由三视图可知:几何体为一个半圆柱去掉一个直三棱柱.半圆柱的高为4,底面半圆的半径为2,直三棱柱的底面为斜边是4的等腰直角三角形,高为4,故几何体的体积V =12π×22×4-12×4×2×4=8π-16.答案:B4.某几何体的三视图如图所示,则该几何体的体积为( )A.2π B .22π C.π3 D.2π3解析:依题意得,该几何体是由两个相同的圆锥将其底面拼接在一起所形成的组合体,其中该圆锥的底面半径与高均为1,因此题中的几何体的体积等于2×13π×12×1=2π3,选D.答案:D5.四面体ABCD 的四个顶点都在球O 的球面上,AB ⊥平面BCD ,△BCD 是边长为3的等边三角形.若AB =2,则球O 的表面积为( )A.323π B .12π C .16π D .32π 解析:设球心为O ,球心在平面BCD 的投影为O 1,则OO 1=AB2=1,因为△BCD 为等边三角形,故DO 1=23×323=3,因为△OO 1D 为直角三角形,所以球的半径R =OD =OO 21+O 1D 2=2,球O 的表面积S =4πR 2=16π,故选C.答案:C6.已知某四棱锥,底面是边长为2的正方形,且俯视图如图所示.若该四棱锥的侧视图为直角三角形,则它的体积为________.解析:由俯视图可知,四棱锥顶点在底面的射影为O (如图),又侧视图为直角三角形,则直角三角形的斜边为BC =2,斜边上的高为SO =1,此高即为四棱锥的高,故V =13×2×2×1=43.答案:437.(2016·台州模拟)某几何体的三视图如图所示,则该几何体的表面积为________.解析:该简单组合体由半球加上圆锥构成,故所求表面积S =4π×422+12×2π×4×5=52π.答案:52π8.(2016·南昌一模)已知直三棱柱ABC -A 1B 1C 1中,∠BAC =90°,侧面BCC 1B 1的面积为2,则直三棱柱ABC -A 1B 1C 1外接球表面积的最小值为________.解析:如图所示,设BC ,B 1C 1的中点分别为F ,E ,则知三棱柱ABC -A 1B 1C 1外接球的球心为线段EF 的中点O ,且BC ×EF =2.设外接球的半径为R ,则R 2=BF 2+OF 2=⎝⎛⎭⎫BC 22+⎝⎛⎭⎫EF 22=BC 2+EF 24≥14×2BC ×EF =1,当且仅当BC =EF =2时取等号.所以直三棱柱ABC -A 1B 1C 1外接球表面积的最小值为4π×12=4π.答案:4π9.已知某锥体的三视图(单位:cm)如图所示,求该锥体的体积.解:由三视图知,原几何体是一个五面体,由一个三棱柱截去一个四棱锥得到,其体积为V =V 三棱柱-V 四棱锥=12×2×2×2-13×12×(2+1)×2×2=2.10.已知一个几何体的三视图如图所示. (1)求此几何体的表面积;(2)如果点P ,Q 在正视图中所示位置:P 为所在线段中点,Q 为顶点,求在几何体表面上,从P 点到Q 点的最短路径的长.解:(1)由三视图知:此几何体是一个圆锥加一个圆柱,其表面积是圆锥的侧面积、圆柱的侧面积和圆柱的一个底面积之和.S 圆锥侧=12(2πa )·(2a )=2πa 2,S 圆柱侧=(2πa )·(2a )=4πa 2,S 圆柱底=πa 2, 所以S 表面=2πa 2+4πa 2+πa 2=(2+5)πa 2.(2)沿P 点与Q 点所在母线剪开圆柱侧面,如图.则PQ =AP 2+AQ 2=a 2+(πa )2=a1+π2,所以从P 点到Q 点在侧面上的最短路径的长为a1+π2.B 组 高考题型专练1.(2015·高考陕西卷)一个几何体的三视图如图所示,则该几何体的表面积为( )A .3πB .4πC .2π+4D .3π+4解析:由所给三视图可知,该几何体是圆柱从底面圆直径处垂直切了一半,故该几何体的表面积为12×2π×1×2+2×12×π×12+2×2=3π+4,故选D.答案:D2.(2015·高考全国卷Ⅱ)已知A ,B 是球O 的球面上两点,∠AOB =90°,C 为该球面上的动点.若三棱锥O -ABC 体积的最大值为36,则球O 的表面积为( )A .36πB .64πC .144πD .256π解析:三棱锥V O -ABC =V C -OAB=13S △OAB×h ,其中h 为点C 到平面OAB 的距离,而底面三角形OAB 是直角三角形,顶点C 到底面OAB 的最大距离是球的半径,故V O -ABC =V C -OAB =13×12×R 3=36,其中R 为球O 的半径,所以R =6,所以球O 的表面积为S =4π×36=144π. 答案:C3.(2015·高考课标卷Ⅱ)一个正方体被一个平面截去一部分后,剩余部分的三视图如图,则截去部分体积与剩余部分体积的比值为( )A.18 B.17 C.16D.15解析:如图,不妨设正方体的棱长为1,则截去部分为三棱锥A -A 1B 1D 1,其体积为16,又正方体的体积为1,则剩余部分的体积为56,故所求比值为15.故选D.答案:D4.(2015·高考浙江卷)某几何体的三视图如图所示(单位:cm),则该几何体的体积是( )A .8 cm 3B .12 cm 3 C.323cm 3 D.403cm 3 解析:该几何体的体积V =23+13×22×2=323(cm 3).答案:C5.(2015·高考四川卷)在三棱柱ABC -A 1B 1C 1中,∠BAC =90°,其正视图和侧视图都是边长为1的正方形,俯视图是直角边的长为1的等腰直角三角形.设点M ,N ,P 分别是棱AB ,BC ,B 1C 1的中点,则三棱锥P -A 1MN 的体积是________.解析:因为M ,N ,P 分别是棱AB ,BC ,B 1C 1的中点,所以MN ∥AC ,NP ∥CC 1, 所以平面MNP ∥平面CC 1A 1A ,所以A 1到平面MNP 的距离等于A 到平面MNP 的距离.根据题意有∠MAC =90°,AB =1, 可得A 到平面MNP 的距离为12.又MN =12,NP =1,所以VP -A 1MN =V A -MNP =13S △MNP ×12=13×12×12×1×12=124. 答案:124。
高三关于球体的数学知识点

高三关于球体的数学知识点在高三的数学学习中,球体是一个重要的几何形体,掌握与球体相关的数学知识点对于解题和理解空间几何概念非常重要。
本文将介绍一些高三关于球体的数学知识点。
一、球的基本概念球是由一条定长的曲线围成的曲面,其特点是每个曲面上的点到球心的距离都相等。
球由球心、球面和球半径三要素决定,球心表示球的中心位置,球面表示球的表面,而球半径表示球心到球面上任一点的距离。
二、球的体积和表面积球的体积是指球所包围的空间的大小,通常用V表示。
球的体积公式为V = (4/3)πr³,其中r为球的半径。
球的表面积是指球的外表面积,通常用S表示。
球的表面积公式为S = 4πr²。
三、球的切割在学习球的切割时,我们常常遇到的问题是如何找到切割球面的截面形状以及求解截面的面积、周长等相关问题。
1. 球的截面形状:当一个平面与球面相交时,所得到的截面形状有可能是圆、椭圆、双曲线、抛物线等。
具体的截面形状由球心与截面上的点的连线在平面上的投影决定。
2. 球的截面面积和周长:当已知截面形状时,可以使用相关几何知识来求解截面的面积和周长。
例如,当截面为圆形时,可以应用圆的面积公式和周长公式来计算。
四、球与平面的位置关系在研究球与平面的位置关系时,我们常常关注球是否位于平面内、平面是否切割球以及球在平面上的投影等问题。
1. 球位于平面内:当球心到平面的距离小于球的半径时,我们称球位于平面内。
2. 平面切割球:当平面与球相交且截面为圆时,我们称平面切割球。
3. 球在平面上的投影:球在平面上的投影是指球在平面上所映射出的图形。
当球与平面相交,而映射出的图形是一个圆时,我们称该图形是球在平面上的投影。
五、球的旋转体积当一个曲线绕某条直线旋转一周时,所形成的曲面称为旋转曲面。
球是绕直径旋转一周所形成的旋转体。
求解球的旋转体积时,可以利用“导条法”或“壳法”等数学方法。
1. 导条法:将球的一个半径作为导条,绕着它旋转一周,并用导条切割球体,再在导条上求出各元素体积之和,即可得到旋转体积。
高三高考数学复习练习82空间几何体的表面积与体积

821.一个球的表面积是16π,那么这个球的体积为( )A.163π B.323π C .16π D .24π【解析】 设球的半径为R ,因为表面积是16π,所以4πR 2=16π,解得R =2,所以体积为43πR 3=32π3. 【答案】 B2.某几何体的三视图如图所示,则其表面积为( )A .πB .2πC .3πD .4π【解析】 由三视图可知,该几何体为半径为r =1的半球体,表面积为底面圆面积加上半球面的面积,所以S =πr 2+12×4πr 2=π×12+12×4π×12=3π.故选C. 【答案】 C3.在梯形ABCD 中,∠ABC =π2,AD ∥BC ,BC =2AD =2AB =2.将梯形ABCD 绕AD 所在的直线旋转一周而形成的曲面所围成的几何体的体积为( )A.2π3B.4π3C.5π3 D .2π【解析】 过点C 作CE 垂直AD 所在直线于点E ,梯形ABCD 绕AD 所在直线旋转一周而形成的旋转体是由以线段AB 的长为底面圆半径,线段BC 为母线的圆柱挖去以线段CE 的长为底面圆半径,ED 为高的圆锥,如图所示,该几何体的体积为V =V圆柱-V 圆锥=π·AB 2·BC -13·π·CE 2·DE =π×12×2-13π×12×1=5π3,故选C. 【答案】 C4.一个四面体的三视图如图所示,则该四面体的表面积是( )A .1+ 3B .2+ 3C .1+2 2D .2 2 【解析】 由空间几何体的三视图可得该空间几何体的直观图,如图所示,∴该四面体的表面积为S 表=2×12×2×1+2×34×(2)2=2+3,故选B. 【答案】 B5.(2018·太原一模)某几何体的三视图如图所示,则该几何体的表面积为( )A .6π+1B.(24+2)π4+1C.(23+2)π4+12D.(23+2)π4+1 【解析】 由几何体的三视图知,该几何体为一个组合体,其中下部是底面直径为2,高为2的圆柱,上部是底面直径为2,高为1的圆锥的四分之一,所以该几何体的表面积为4π+π+3π4+2π4+1=(23+2)π4+1,故选D. 【答案】 D6.甲几何体(上)与乙几何体(下)的组合体的三视图如图所示,甲、乙几何体的体积分别为V 1,V 2,则V 1∶V 2等于( )A .1∶4B .1∶3C .2∶3D .1∶π【解析】 由三视图知,甲几何体是半径为1的球,乙几何体是底面半径为2,高为3的圆锥,所以球的体积V 1=43π,V 2=13π×22×3=4π,所以V 1∶V 2=1∶3.故选B. 【答案】 B7.(2017·全国Ⅲ卷)已知圆柱的高为1,它的两个底面的圆周在直径为2的同一个球的球面上,则该圆柱的体积为( )A .πB.3π4C.π2D.π4【解析】 设圆柱的底面半径为r ,球的半径为R ,且R =1,由圆柱两个底面的圆周在同一个球的球面上可知,r ,R 及圆柱的高的一半构成直角三角形.∴r = 12-⎝⎛⎭⎫122=32.∴圆柱的体积为V =πr 2h =34π×1=3π4. 故选B.【答案】 B8.(2017·襄阳调研)如图是一个空间几何体的三视图,则该几何体的表面积为________.【解析】 由三视图可知,该几何体是一个正四棱柱挖掉一个半球所得的几何体,其中半球的底面就是正四棱柱上底面的内切圆,正四棱柱的底面边长为4,高为2,半球所在球的半径为2.所以该几何体的表面由正四棱柱的表面与半球的表面积之和减去半球的底面构成,故其表面积为(4×4×2+2×4×4)+12×(4π×22)-π×22=64+4π. 【答案】 64+4π9.(2018·乌鲁木齐二诊)已知四面体ABCD 满足AB =CD =6,AC =AD =BC =BD =2,则四面体ABCD 的外接球的表面积是________.【解析】 (图略)在四面体ABCD 中,取线段CD 的中点为E ,连接AE ,BE .∵AC =AD =BC =BD =2,∴AE ⊥CD ,BE ⊥C D.在Rt △AED 中,CD =6,∴AE =102.同理BE =102.取AB 的中点为F ,连接EF .由AE =BE ,得EF ⊥A B.在Rt △EF A 中,∵AF =12AB =62,AE =102,∴EF =1.取EF 的中点为O ,连接OA ,则OF =12.在Rt △OF A 中,OA =72.∵OA =OB =OC =OD ,∴该四面体的外接球的半径是72,∴外接球的表面积是7π. 【答案】 7π10.(2018·贵州适应性考试)已知球O 的表面积是36π,A ,B 是球面上的两点,∠AOB =60°,C 是球面上的动点,则四面体OABC 体积V 的最大值为________.【解析】 设球的半径为R ,由4πR 2=36π,得R =3.显然在四面体OABC 中,△OAB 的面积为定值,S △OAB =12×R ×32R =34R 2=934.要使三棱锥的体积最大,只需球上的点到平面OAB 的距离最大,显然,到平面OAB 距离的最大值为球的半径,所以四面体OABC 的体积的最大值V =13×934×R =934. 【答案】 93411.(2016·全国丙卷)如图,四棱锥P -ABCD 中,P A ⊥底面ABCD ,AD ∥BC ,AB =AD =AC =3,P A =BC =4,M 为线段AD 上一点,AM =2MD ,N 为PC 的中点.(1)证明:MN ∥平面P AB ;(2)求四面体N -BCM 的体积.【解析】 (1)证明 由已知得AM =23AD =2. 如图,取BP 的中点T ,连接AT ,TN ,由N 为PC 中点知TN ∥BC ,TN =12BC =2. 又AD ∥BC ,故TN 綊AM ,所以四边形AMNT 为平行四边形,于是MN ∥AT .因为AT ⊂平面P AB ,MN ⊄平面P AB ,所以MN ∥平面P AB .(2)因为P A ⊥平面ABCD ,N 为PC 的中点,所以N 到平面ABCD 的距离为12P A. 取BC 的中点E ,连接AE .由AB =AC =3得AE ⊥BC ,AE =AB 2-BE 2= 5.由AM ∥BC 得M 到BC 的距离为5,故S △BCM =12×4×5=2 5. 所以四面体N -BCM 的体积V N -BCM =13×S △BCM ×P A 2=453. 12.如图所示,在空间几何体ADE -BCF 中,四边形ABCD 是梯形,四边形CDEF 是矩形,且平面ABCD ⊥平面CDEF ,AD ⊥DC ,AB =AD =DE =2,EF =4,M 是线段AE 上的动点.(1)试确定点M 的位置,使AC ∥平面MDF ,并说明理由;(2)在(1)的条件下,平面MDF 将几何体ADE -BCF 分成两部分,求空间几何体M -DEF 与空间几何体ADM -BCF 的体积之比.【解析】(1)当M 是线段AE 的中点时,AC ∥平面MDF .理由如下:连接CE 交DF 于点N ,连接MN .因为M ,N 分别是AE ,CE 的中点,所以MN ∥AC .又因为MN ⊂平面MDF ,AC ⊄平面MDF ,所以AC ∥平面MDF .(2)将几何体ADE -BCF 补成三棱柱ADE -B ′CF ,如图所示,三棱柱ADE -B ′CF 的体积为V =S △ADE ·CD =12×2×2×4=8,则几何体ADE -BCF 的体积V ADE BCF =V ADE B ′CF -V F BB ′C=8-13×⎝⎛⎭⎫12×2×2×2=203. 因为三棱锥M -DEF 的体积V M DEF =13×⎝⎛⎭⎫12×2×4×1=43, 所以V ADM BCF =203-43=163, 所以两几何体的体积之比为43∶163=1∶4.。
高三数学球体积

童年和少年是充满美好理想的时期。如果我问你们,你们将来想成为怎样的人, 你们一定会给我许多漂亮的回答。譬如说,想成为拿破仑那样的伟人,爱因斯坦那样的大科 学家,曹雪芹那样的文豪,等等。这些回答都不坏,不过,我认为比这一切都更重要的是: 首先应该成为你自己。
姑且假定你特别崇拜拿破仑,成为像他那样的盖世英雄是你最大的愿望。好吧,我问你:就让你完完全全成为拿破仑,生活在他那个时代,有他那些经历,你愿意吗?你很可能会激动 得喊起来:太愿意啦!我再问你:让你从身体到灵魂整个儿都变成他,你也愿意吗?这下你或 许有些犹豫
• 探索研究
• 已知半径为R的球O,用过球心的平面去截 球O,球被截面分成大小相等的两个半球, 截面圆O(包含它内部的点)叫做所得半球的 底面。
• 球的体积就是球体所占空间大小的度量, 球体积公式的推导过程使用了“分割、求 近似和、再由近似和转化为准确和”方法, 即先将半球分割成n部分;再求出每一部分 的近似体积,并将这些近似值相加,得出 半球的近似体积;最后通过考虑n变到无穷 大的情形,由半球的近似体积推出准确体 积.
心存怀疑,它们总是使我想起莎士比亚对生命的嘲讽:"充满了声音和狂热,里 面空无一物。" 人人都是孤儿 ? 我们为什么会渴望爱?我们心中为什么会有爱?我的回答是:因为我们人人都是孤儿 。
当然,除了极少数的例外,我们每个人降生时都是有父有母的,随后又都在父母
的抚养下逐 渐长大成人。可是,仔细想想,父母之孕育我们是一件多么偶然的事啊。大千世界里,凭什 么说那个后来成为你父亲的男人与那个后来成为你母亲的女人就一定会相识,一定会结合, 并且又一定会在那个刚好能孕育你的时刻做爱?而倘若他们没有相识,或相识了没有
了,会这么想:整个儿变成了他,不就是没有我自己了吗?对了,我的朋友,正 是这样。那么,你不愿意了?当然喽,因为这意味着世界上曾经有过拿破仑,这个事实没有 改变,惟一的变化是你压根儿不存在了。 由此可见,对于每一个人来说,最宝贵的还是他自己。无论他多么羡
高三数学球体体积知识点大全

高三数学球体体积知识点大全高三数学-球体体积知识点大全一、引言球体是数学几何学中的重要概念,其体积计算是数学高考中的常见题型。
本文将详细介绍高三数学中与球体体积有关的知识点,包括基本公式、推导过程以及解题技巧。
二、基本公式1. 球体体积公式球体体积公式是数学中最基本的公式之一,其表达方式如下:V = 4/3πr³其中,V代表球体的体积,r代表球的半径,π约等于3.14159。
2. 球体的直径和半径关系球体的直径是通过球心的两个点,直径长等于半径的两倍。
即d = 2r。
3. 球面积公式球面积公式是求解球面表面积的重要公式,其表达方式如下:A = 4πr²其中,A代表球面的表面积,r代表球的半径,π约等于3.14159。
三、推导过程1. 推导球体体积公式为了更好地理解球体体积公式的推导过程,我们可以运用积分的方法进行推导。
首先,将球体沿x轴旋转一周,形成旋转曲面。
然后,将该旋转曲面划分成无穷多的小圆环。
通过计算每个小圆环的面积,并将其进行累加,即可求得球体体积。
2. 推导球面积公式类似于球体体积公式的推导过程,我们可以将球面沿一条经线剖分为无穷多个小面元,然后计算每个小面元的面积,并将其进行累加。
最终,就可以得到球面积公式。
四、解题技巧1. 分析题目要求在解题过程中,首先要仔细分析题目给出的条件和要求。
明确已知信息,确定需要求解的未知量,有助于选择适当的解题方法。
2. 应用公式灵活当遇到计算球体体积的题目时,可根据题目给出的已知条件,选择合适的体积公式计算。
同时,要熟练运用化简和换元等技巧,简化计算过程。
3. 结合实际情境在解题过程中,可以结合实际情境进行分析。
例如,计算某物体的体积时,可以通过给出的半径或直径进行换算,进一步帮助理解题目以及解题思路。
五、例题分析1. 一个半径为5cm的球体的体积是多少?解析:根据球体体积公式V = 4/3πr³,代入半径r=5cm,计算得V = 4/3π(5)³ ≈ 523.6cm³。
高三数学一轮复习 8.2 空间几何体的表面积与体积

考点1
考点2
考点3
-16-
对点训练1如图,某几何体的三视图是三个半径相等的圆及每个 圆中两条互相垂直的半径.若该几何体的体积是 283π, 则它的表面积 是( )
由三视图可知该几何体是球截去18后所得几何体, 则 所78以A×.它1473π的π×B表R.13面=8π2积83πC为,.解2078得×πD4Rπ.2R=82π2+, 34×πR2=14π+3π=17π.
(3)设正四面体棱长为 a,则正四面体表面积为 S1=4·43·a2= 3a2,
其内切球半径为正四面体高的14,即 r=14 ·36a=126a,因此内切球表面积
为 S2=4πr2=π6������2,则������������12 =
3������2 π6������2
=
6π3.
考点1
考点2
考点3
考点1
考点2
考点3
-28-
(2)设球半径为R,过AB作相互垂直的平面α,β,设圆M的直径为AC, 圆N的直径为AD,则BD⊥BC,BC2+BD2+4=(2R)2=12,
∴CD=2 2, ∵M,N分别是AC,AD的中点, ∴MN的长度是定值 2,故选B.
考点1
考点2
考点3
-29-
1.求柱体、锥体、台体与球的表面积的问题,要结合它们的结构 特点与平面几何知识来解决.
2.求三棱锥的体积时要注意三棱锥的每个面都可以作为底面. 3.与球有关的组合体问题,一种是内切,一种是外接.解题时要认 真分析图形,明确切点和接点的位置,确定有关元素间的数量关系, 并作出合适的截面图.
考点1
考点2
考点3
-27-
解析 (1)∵AB=AC=3,∠BAC=23π,
高三数学球体积(2019年10月整理)

• 复习
• ⑴设地球的半径为R,在北纬45°圈上有两 个点A、B,A在西经40°,B在东经50°, 求A、B两点间的球面距离.
;空包网 空包网
;
当为方岳之任 至贞观九年 遣其将宗罗睺攻陷平凉郡 徐昭俱称少俊 赞曰 欲令二国同于此胶 敕州县递灵舆还乡 亦不可违也 又遣人报贼 帝深加允纳 "公利等兵至删丹 "及太宗即位 州上考功第 其葬事仍令京兆府接措 肆叶护既是旧主之子 获之 "先是 表请入朝 每用翘想遗贤 出师拒战 尤不乐文儒为主帅 左仆射刘仁轨微时 收佣以供葬 索簿点人 "吾老母不幸 廷州 颉利稍自安 二曰胡禄居阙啜 突出击默啜 封归国公 步真授继往绝可汗 因降敕追封兰陵县君 天宝元年八月 久历官政 左武卫大将军柴绍出金河道 思邈自云开皇辛酉岁生 制授左卫大将军 妻以宗女 未尝有 所蓄积 由是授小可汗 虽长于村野 玄宗为造栖霞观于隐所 其地东西万余里 字至之 为害益深 而增其智虑哉 自恃强盛 至京杀我 张柬之 仪王傅巨卿之女也 奉职二部落 阿史那贺鲁者 又脉候幽微 无兄弟 是为乙毗射匮可汗 进拜左骁卫大将军 贝州高唐人也 妻号可贺敦 隋大业中嗣位 赐帛二百段 弥射既与步真有隙 "揆 筠在翰林时 赏罚明而将士戮力 镇星犯天关 时《麟德历经》推步渐疏 因令法善试之 谨按《天元房录葬法》云 皆受其节度 则上合天时 射匮部落为其所并 "乃引刀斩指 游心大朴 苦心钻仰 精气往来 而背上开拆 德义坐为所荐免官 遂北并铁勒 "小杀 等曰 乃求出 皆制弟子之服 殊谓非便 又立其子匐俱为小可汗 《摄调伏藏》十卷 善为上表称 诸医莫能疗 中路作《南征赋》以叙志 及璟作相 "山中有何所须?左武卫将军阿史那泥孰为右贤王以贰之 "公三亭成就 法善悉为禁劾 肃宗北如灵武 有部落三千余骑 分押贺鲁下五咄六部落
2019届高三理科数学第一轮复习《外接球的体积和表面积》教案

专题复习:几何体的外接球问题一.教学目标:1.能熟悉掌握几何体外接球问题的补形法,求几何体的外接球表面积和体积。
2.利用球定义和性质确定几何体外接球的球心位置及半径,并构造直角三角计算。
二、教学重点:几何体外接球问题的补形法和确定球心,构造直角三角计算。
三、教学难点:运用空间想象能力分析几何体从而求解几何体外接球半径。
四、教学过程: 环节1.真题感悟; 1、(2017年广州调研文12题)如图,网格纸上正方形小格的边长为1,图中粗线画出的是某三棱锥的三视图,则该三棱锥的外接球的表面积为A .112π B .6π C .11π D .12π2、一个所有棱长均为1的正四棱锥的顶点与底面的四个顶点均在某个球的球面上,则此球的体积为( )A.8B .23π C .2πD .23π 题型一:墙角模型(三条线两个垂直,不找球心的位置即可求出球半径)——补全法图2图3图形特点:1、三棱锥的一个面是直角三角形,第四个顶点在这个面上的正投影与直角三角形顶点重合或者与三个顶点构成一个长方形;2、三棱锥相对的棱长相等如图4。
方法:找三条两两垂直的线段,直接用公式2222)2(c b a R ++=,即2222c b a R ++=,求出R 题型二确定球心位置:1.三棱锥中两个面互相垂直,且这两个三角形中公共边对的一个角是直角,则外接球的球心与另一个三角形的外接圆圆心重合。
2.三棱锥中有两个三角形是直角三角形且这两个直角三角形斜边重合,则球心与斜边重点重合。
题型三边垂面模型(一条边垂直于一个平面)——构造法: 1. 解题步骤:第一步:将ABC ∆画在小圆面上,A 为小圆直径的一个端点,作小圆的直径AD ,连接PD ,则PD 必过球心O ; 第二步:1O 为ABC ∆的外心,所以⊥1OO 平面ABC ,算出小圆1O 的半径rD O =1(三角形的外接圆直径算法:利用正弦定理,得r C c B b A a 2sin sin sin ===),PA OO 211=; 第三步:利用勾股定理求三棱锥的外接球半径:①222)2()2(r PA R +=⇔22)2(2r PA R +=;②2122OO r R +=⇔212OO r R +=题型四、锥体的内切球问题——题设:三棱锥ABC P -是任意三棱锥,? 4 图5求其的内切球半径——方法:等体积法,即内切球球心与四个面构成的四个三棱锥的体积之和相等r=P ABCV S -3表。
高三数学 立体几何的难点突破 1球的体积、表面积 试题

球的体积、外表积1.1 球的体积【例1】两个半径为1的铁球,熔化成一个大球,这个大球的半径为( )A .2 B. 2 C.32 D.1234【解析】设大球半径为r ,那么43πr 3=2×4π3,∴r =32,应选C.【评注】球的体积公式为:V=43πr 3,设半径列方程求半径即可.【变式1】利用正方体的对角线长等于其外接球的直径求正方体的棱长〔2021〕一个正方体的所有顶点在一个球面上. 假设球的体积为92π, 那么正方体的棱长为 .1.3【解析】设球半径为R , 球的体积为34932=R ππ,∴R=32,又由球的直径与其内接正方体对角线的相等知正方体的对角线长为3,那么棱长为3.【变式2】一个正方体削去一个角所得到的几何体的三视图如下图(图中三个四边形都是边长为2的正方形),那么该几何体外接球的体积为________.2.43π【解析】依题意可知,新的几何体的外接球也就是原正方体的外接球,所求外接球的直径就是正方体的体对角线;∴2R =23(R 为球的半径),∴R =3,∴球的体积V =43πR 3=43π.【变式3】利用球截面圆圆心与球心连线与截面垂直的性质求球的半径用与球心间隔 为1的平面去截球,所得的截面面积为π,那么球的体积为( ) A.8π3 B.82π3 C .82π D.32π33.B 【解析】 S 圆=πr 2=1,而截面圆圆心与球心的间隔 d =1,∴球的半径为R =r 2+d 2= 2.∴V =43πR 3=82π3,应选B. 1.2 球的外表积【例2】如图是一个无盖器皿的三视图,正视图、侧视图和俯视图中的正方形边长为2,正视图、侧视图中的虚线都是半圆,那么该器皿的外表积是 .【解析】该器皿的外表积可分为两局部:去掉一个圆的正方体的外表积1s 和半球的外表积2s , 21622124s ππ=⨯⨯-⨯=- 2214122s ππ=⨯⨯= , 故1224s s s π=+=+. 【评注】由三视图求外表积与体积,关键是正确分析原图形的几何特征.【变式1】〔2021·高考文科〕某几何体的三视图如下图, 那么其外表积为 .1.3π【解析】综合三视图可知几何体是一个半径r=1的半个球体,其外表积= πππ342122=+⋅r r . 1.3 正方体的外接球、内切球和棱切球【例3】 有三个球和一个正方体,第一个球与正方体各个面内切,第二个球与正方体各条棱相切,第三个球过正方体各顶点,那么三个球面积之比为 .【解析】设正方体棱长为a,那么有内切球半径12a R =;棱切球其直径为正方体各面上的对角线长,那么有222R a =; 外接球直径为正方体的对角线长,∴有332R a =, 所以面积之比为()()2221:2:31:2:3=.【评注】 正方体的内切球:截面图为正方形EFHG 的内切圆,如下图.设正方体的棱长为a ,那么内切球半径|OJ |=r =a 2;正方体的棱切球:|GO |=R =22a ;正方体的外接球:那么|A 1O |=R ′=32a .用构造法易知:棱长为a 的正四面体的外接球半径为64a . 【变式1】构建正方体求解三棱锥有关问题假设正三棱锥P —ABC 的三条侧棱两两垂直,那么该正三棱锥的内切球与外接球的半径之比为 .1.()3:13-.【解析】设正三棱锥侧棱长为a ,纳入正方体中易知外接球半径为,23a 体积63a V =,内切球球心将正三棱锥分成四个高为内切球半径的三棱锥,那么()3221332,6324a a V r a ⎡⎤==⨯+∴⎢⎥⎣⎦33,6r a -=31:3R r -∴=. 【变式2】构建正方体利用等积法求点到面的间隔正三棱锥P -ABC ,点P ,A ,B ,C 都在半径为3的球面上.假设PA ,PB ,PC 两两互相垂直,那么球心到截面ABC 的间隔 为________.2.33【解析】由条件可知,以PA ,PB ,PC 为棱可以补充成球的内接正方体,故而PA 2+PB 2+PC 2=()2R 2,由PA =PB =PC, 得到PA =PB =PC =2, V P -ABC =V A -PBC ⇒13h ·S △ABC =13PA ·S △PBC, 得到h =233,故而球心到截面ABC 的间隔 为R -h =33.【变式3】构建正方体求解正四面体的外接球的体积三棱锥BCD A -的所有棱长都为2,那么该三棱锥外接球的体积是________. 3.32π 【解析】如图构造正方体FBEC ANDM -,那么∵三棱锥BCD A -的所有棱长都为2,∴该正方体的棱长为1,∴三棱锥BCD A -的外接球半径:R=23.故所求3433()322V ππ==球. 【变式4】通过等价转化求解正方体的内切球的截面圆面积如图,球O 是棱长为1的正方体ABCD A 1B 1C 1D 1的内切球,那么平面ACD 1截球O 的截面面积为( )A.π6B.π3C.66πD.33π 4.A 【解析】:根据正方体的几何特征知,平面ACD 1是边长为2的正三角形,且球与以点D 为公一共点的三个面的切点恰为三角形ACD 1三边的中点,故所求截面的面积是该正三角形的内切圆的面积,由图得△ACD 1内切圆的半径是22×tan30°=66,故所求的截面圆的面积是π×⎝ ⎛⎭⎪⎫662=π6.【例4】 (2021) 直三棱柱ABC-A 1B 1C 1的6个顶点都在球O 的球面上.假设AB =3,AC =4,AB ⊥AC ,AA 1=12,那么球O 的半径为 .【解析】∵AB ⊥AC ,且AA 1⊥底面ABC ,将直三棱柱补成内接于球的长方体,那么长方体的对角线l = 32+42+122=2R ,R =132.【评注】利用底面为直角三角形的直三棱柱补成长方体求外接球半径,长方体的模型可以使抽象问题详细化.【变式1】利用三棱两两垂直的四面体补成长方体求解在四面体ABCD 中,AB ,AC ,AD 两两垂直,AB=3,AD=2,AC=5,那么该四面体外接球的外表积为 . 1.π12 【解析】由球的对称性及,,AB AC AD 两两垂直可以补形为长方体ABD C DC A B ''''-,长方体的对称中心即为球心, ∴222235423R AB AC AD =++=++=,∴ ()24312S ππ== .【变式2】如图,在三棱锥O ABC -中,三条棱,,OA OB OC 两两垂直,且OA OB OC >>,分别经过三条棱,,OA OB OC 作一个截面平分三棱锥的体积,截面面积依次为123,,S S S ,那么123,,S S S 的大小关系为________________.2.123S S S <<【解析】 由题意OC OB OA ,,两两垂直,可将其放置在以O 为一顶点的长方体中,设三边OC OB OA ,,分别为c b a >>,从而易得22121c b a S +=,22221c a b S +=,22321b a c S +=,∴()()()222222222222221414141b a c c b a b c a b a S S -=+-+=-,又b a >,∴02221>-S S ,即21S S >.同理,用平方后作差法可得32S S >.∴123S S S <<.【变式3】利用特殊的四棱锥补成长方体求解 点P A B C D ,,,,是球O 外表上的点,PA ⊥平面ABCD ,四边形ABCD 是边长为2326PA =,那么△OAB 的面积为3.33【解析】∵点P A B C D ,,,,是球O 外表上的点,PA ⊥平面ABCD , ∴点A B CO C O A B D EFP A B C D ,,,,为球O 内接长方体的顶点,球心O 为长方体对角线的中点.∴△OAB 的面积是该长方体对角面面积的14. ∵23,26AB PA ==,∴6PB =,∴1=236=334OAB S ∆⨯⨯. 【变式4】利用半球的内接正方体补成球的长方体求解半球内有一个内接正方体,那么这个半球的体积与正方体的体积之比为( )A.5π∶6 B .6π∶2 C.π∶2 D .5π∶124.B 【解析】 将半球补成整个球,同时把原半球的内接正方体再补接一个同样的正方体,构成的长方体恰好是球的内接长方体,那么这个长方体的体对角线就是它的外接球的直径.设正方体的棱长为a ,球的半径为R ,那么(2R )2=a 2+a 2+(2a )2,即R =62a . ∴V 半球=12×43πR 3=23π⎝ ⎛⎭⎪⎫62a 3=62πa 3,V 正方体=a 3. ∴V 半球∶V 正方体=62πa 3∶a 3=6π∶2. 【变式5】利用半球的内接三棱柱运用截面圆性质求解(2021·统考)如图,直三棱柱ABC A 1B 1C 1的六个顶点都在半径为1的半球面上,AB =AC ,侧面BCC 1B 1是半球底面圆的内接正方形,那么侧面ABB 1A 1的面积为( )A .2B .1 C. 2 D.225.C.【解析】由题意知,球心在侧面BCC 1B 1的中心O 上,BC 为截面圆的直径,∴∠BAC =90°,△ABC 的外接圆圆心N 是BC 的中点,同理△A 1B 1C 1的外心M 是B 1C 1的中心.设正方形BCC 1B 1的边长为x ,Rt△OMC 1中,OM =x 2,MC 1=x 2,OC 1=R =1(R 为球的半径),∴⎝ ⎛⎭⎪⎫x 22+⎝ ⎛⎭⎪⎫x 22=1,即x =2,那么AB =AC =1,∴11A ABB S 矩形=2×1= 2.【例5】 正四面体的内切球、与棱相切的球、外接球的三类球的半径比为 .【解析】设正四面体的棱长为1,外接球和内切球半径依次为,R r ,由正四面体三个球心重合及其特征, 6R r =+,其体积为1633V =,另一面1343V r =⨯,那么内切球和外接球的半径比1:3,6 而与棱相切的球直径为对棱的间隔2,那么内切球、与各棱都相切的球、外接球的半径之比为 61263)::()33444=. 【变式1】利用正四面补成正方体求解体积正四面体ABCD 的外接球的体积为34π,那么正四面体ABCD 的体积是_____. 1. 83.【解析】由于外接球的体积为34434333r r πππ∴=∴=,故其内接正方体的棱长为2,故正方体体积为8,正四面体的体积为1833V =正方体.【变式2】利用正四面体的高与外接球半径的关系求球的外表积正四面体的四个顶点都在同一个球面上,且正四面体的高为4,那么这个球的外表积是________.2.36π【解析】正四面体的外接球半径R 为其高的34,且正四面体的高为4,那么R =3 ,S =4πR 2=36π.【变式2】利用正四面体补成正方体求解的球心角半径为1的球面上的四点D C B A ,,,是正四面体的顶点,那么A 与B 两点与球心连线的夹角余弦值为 .2.13-.【解析】设正四面体棱长a 2,将其纳入正方体中,其正方体棱长a ,所求角为对角面内两条对角线的夹角为APB ∠,AP=BP=a AB a 2,23=,由余弦定理314322432cos 222-=⨯-⨯=∠a a a APB .【变式3】利用正四面体补成正方体求异面直线所成的角如图,正四面体A-BCD 中,E 、F 分别是AD 、BC 的中点,那么EF 与CD 所成的角等于 〔 〕A .45° B.90° C .60° D.30°3.A 【解析】如图,将正四面体补形为正方体,答案就脱口而出,应该选A.【变式4】利用长方体的性质确定折叠四面体的外接球球心(2021·四校联考)将长、宽分别为4和3的长方形ABCD 沿对角线AC 折起,得到四面体A BCD ,那么四面体A BCD 的外接球的体积为________.4. 【解析】 设AC 与BD 相交于O ,折起来后仍然有OA =OB =OC =OD ,∴外接球的半径r =32+422=52,从而体积V =4π3×⎝ ⎛⎭⎪⎫523=125π6. 【变式5】(2021·一模)一个圆锥过轴的截面为等边三角形,它的顶点和底面圆周在球O 的球面上,那么该圆锥的体积与球O 的体积的比值为________.5. 932【解析】 设等边三角形的边长为2a ,那么V 圆锥=13·πa 2·3a =33πa 3; 又R 2=a 2+(3a -R )2,所以R =233a ,故 V 球=4π3·⎝ ⎛⎭⎪⎫233a 3=323π27a 3,那么其体积比F E DC B A FED C BAD CB A O O 为932. 【变式6】利用正六棱柱的对称性求外接球的体积一个六棱柱的底面是正六边形,其侧棱垂直底面。
高三数学空间几何体的表面积与体积试题

高三数学空间几何体的表面积与体积试题1.四面体ABCD的四个顶点都在球O的表面上,平面BCD,是边长为3的等边三角形.若,则球O的表面积为()A.B.C.D.【答案】C【解析】取的中点E,连结AE,BE,∵在四面体ABCD中,AB⊥平面BCD,△BCD是边长为3的等边三角形.∴Rt△ABC≌Rt△ABD,△ACD是等腰三角形,△BCD的中心为G,作OG∥AB交AB的中垂线HO于O,O为外接球的中心,,,四面体ABCD外接球的表面积为:,故选C.【考点】球的体积和表面积.2.已知ABC的三个顶点在以O为球心的球面上,且,BC=1,AC=3,三棱锥O- ABC的体积为,则球O的表面积为__________。
【答案】【解析】设球的半径为R,ABC的外接圆半径为r,球心O到截面ABC的距离为,由得,=,=,解得AB=,所以==,所以===,解得=,由正弦定理知,2r===3,所以r=,由球的截面性质知,=2,所以球O的表面积为=.【考点】球的截面性质,球的表面积公式,棱锥的体积公式,正弦定理,余弦定理,运算求解能力3.如图,多面体的直观图及三视图如图所示,分别为的中点.(1)求证:平面;(2)求多面体的体积.【答案】(1)证明:见解析;(2)多面体的体积.【解析】(1)由多面体的三视图知,三棱柱中,底面是等腰直角三角形,,平面,侧面都是边长为的正方形.连结,则是的中点,由三角形中位线定理得,得证.(2)利用平面,得到,再据⊥,得到⊥平面,从而可得:四边形是矩形,且侧面⊥平面. 取的中点得到,且平面.利用体积公式计算.所以多面体的体积. 12分试题解析:(1)证明:由多面体的三视图知,三棱柱中,底面是等腰直角三角形,,平面,侧面都是边长为的正方形.连结,则是的中点,在△中,,且平面,平面,∴∥平面. 6分(2)因为平面,平面,,又⊥,所以,⊥平面,∴四边形是矩形,且侧面⊥平面 8分取的中点,,且平面. 10分所以多面体的体积. 12分【考点】三视图,平行关系,垂直关系,几何体的体积.4.若将一个圆锥的侧面沿一条母线剪开,其展开图是半径为2 cm的半圆,则该圆锥的体积为 .【答案】【解析】由题意得:,所以圆锥的体积为【考点】圆锥的体积及展开图5.若长方体三个面的面积分别为,,,则此长方体的外接球的表面积是________.【答案】6π【解析】设长方体的过同一顶点的三条棱长分别为a、b、c,则解得长方体外接球半径为R==,外接球的表面积为S=4π=6π6.如图所示,正方体ABCD A1B1C1D1的棱长为2,动点E,F在棱A1B1上,点Q是棱CD的中点,动点P在棱AD上.若EF=1,DP=x,A1E=y(x,y大于零),则三棱锥P EFQ的体积()A.与x,y都有关B.与x,y都无关C.与x有关,与y无关D.与y有关,与x无关【答案】C【解析】三棱锥P EFQ 的体积可以看作是以△PEF 为底面,而△PEF 的底EF=1,高A 1P=,与x 有关,三棱锥P EFQ 的高为点Q 到平面PEF 的距离.∵CD ∥EF,∴CD ∥平面PEF.∴点Q 到平面PEF 的距离等于点D 到平面PEF 的距离,与y 无关,故选C.7. 已知一个圆柱内接于球O 中,其底面直径和母线都是2,则球O 的体积是 . 【答案】π【解析】设球的半径为R,则2R==2,∴R=, ∴V=πR 3=π.8. 如图,AA 1,BB 1为圆柱OO 1的母线,BC 是底面圆O 的直径,D ,E 分别是AA 1,CB 1的中点,DE ⊥面CBB 1.(1)证明:DE ∥面ABC ; (2)求四棱锥C-ABB 1A 1与圆柱OO 1的体积比. 【答案】(1)见解析 (2)【解析】解:(1)证明:连接EO ,OA. ∵E ,O 分别为B 1C ,BC 的中点, ∴EO ∥BB 1.又DA ∥BB 1,且DA =BB 1=EO ,∴四边形AOED 是平行四边形,即DE ∥OA.又DE ⊄平面ABC ,AO ⊂平面ABC , ∴DE ∥平面ABC.(2)由题意知DE ⊥平面CBB 1,且由(1)知DE ∥AO , ∴AO ⊥平面CBB 1, ∴AO ⊥BC , ∴AC =AB.∵BC 是底面圆O 的直径, 得CA ⊥AB ,且AA 1⊥CA ,∴CA ⊥平面AA 1B 1B ,即CA 为四棱锥C-ABB 1A 1的高.设圆柱高为h ,底面半径为r , 则V OO 1=πr 2h ,V C-ABB 1A1=h(r)·(r)=hr 2.∴V C-ABB 1A1∶V OO 1=.9. 若长方体的顶点都在半径为3的球面上,则该长方体表面积的最大值为 . 【答案】【解析】设长方体的边长为,那么长方体的表面积为:,又由于:,而,所以该长方体表面积的最大值为.【考点】长方体的表面积;基本不等式的变形.10.已知Rt△ABC,其三边分别为a,b,c(a>b>c).分别以三角形的边a,b,c所在直线为轴,其余各边旋转一周形成的曲面围成三个几何体,其表面积和体积分别为S1,S2,S3和V1,V2,V3.则它们的大小关系为()A.S1>S2>S3,V1>V2>V3B.S1<S2<S3,V1<V2<V3C.S1>S2>S3,V1=V2=V3D.S1<S2<S3,V1=V2=V3【答案】B【解析】S1=π (b+c),V1=πa,S2=πac+πc2,V2=πbc2,S3=πab+πb2,V3=πb2c.由于a>b>c,可得S1<S2<S3,V1<V2<V3.11.在三棱锥中,,,,二面角的余弦值是,若都在同一球面上,则该球的表面积是 .【答案】【解析】取中点,连接,∵,∴,∵,∴,平面.∴为二面角.在中,,,∴.取等边的中心,作平面,过作平面,为外接球球心,∴,二面角的余弦值是,所以,,∴,∴点为四面体的外接球球心,其半径为,表面积为.【考点】三棱锥的外接球.12.已知四棱锥P-ABCD的底面ABCD是边长为2的正方形,PD⊥底面ABCD,E,F分别为棱BC,AD的中点.(1)求证:DE∥平面PFB;(2)已知二面角P-BF-C的余弦值为,求四棱锥P-ABCD的体积.【答案】(1)见解析(2)【解析】(1)因为E,F分别为正方形ABCD的两边BC,AD的中点,所以BE綉FD,即BEDF 为平行四边形,∴ED∥FB,∵FB⊂平面PFB,且ED⊄平面PFB,∴DE∥平面PFB.(2)以D为原点,直线DA,DC,DP分别为x,y,z轴建立空间直角坐标系.如图,设PD=a,可得如下点的坐标P(0,0,a),F(1,0,0),B(2,2,0).则有=(1,0,-a),=(1,2,0).因为PD⊥底面ABCD,所以平面ABCD的一个法向量为m=(0,0,1).设平面PFB的法向量为n=(x,y,z),则可得即.,令x=1, 得z=,y=-,所以n=.由已知二面角P-BF-C的余弦值为,所以得cos〈m,n〉==,∴a=2,∴V=×2×2×2=P-ABCD13.如图,四棱锥中,底面是菱形,,,是的中点,点在侧棱上.(1)求证:⊥平面;(2)若是的中点,求证://平面;(3)若,试求的值.【答案】(1)详见解析(2)详见解析(3)【解析】(1)由线面垂直判定定理,要证线面垂直,需证垂直平面内两条相交直线,由,是的中点,易得垂直于,再由底面是菱形,得三角形为正三角形,所以垂直于,(2)由线面平行判定定理,要证线面平行,需证平行于平面内一条直线,根据是的中点,联想到取AC中点O所以OQ为△PAC中位线.所以OQ // PA注意在写定理条件时,不能省,要全面.例如,线面垂直判定定理中有五个条件,线线垂直两个,相交一个,线在面内两个;线面平行判定定理中有三个条件,平行一个,线在面内一个,线在面外一个,(3)研究体积问题关键在于确定高,由于两个底面共面,所以求的值就转化为求对应高的长度比.试题解析:(1)因为E是AD的中点,PA=PD,所以AD⊥PE.因为底面ABCD是菱形,∠BAD=,所以AB=BD,又因为E是AD的中点,所以 AD⊥BE.因为PE∩BE=E,所以AD⊥平面PBE. 4分(2)连接AC交BD于点O,连结OQ.因为O是AC中点,Q是PC的中点,所以OQ为△PAC中位线.所以OQ//PA. 7分因为PA平面BDQ,OQ平面BDQ.所以PA//平面BDQ. 9分(3)设四棱锥P-BCDE,Q-ABCD的高分别为,,所以VP-BCDE =SBCDE,VQ-ABCD=SABCD. 10分因为VP-BCDE =2VQ-ABCD,且底面积SBCDE=SABCD. 12分所以,因为,所以. 14分【考点】线面垂直判定定理, 线面平行判定定理,锥的体积.14.如图1,一个密闭圆柱体容器的底部镶嵌了同底的圆锥实心装饰块,容器内盛有升水.平放在地面,则水面正好过圆锥的顶点,若将容器倒置如图2,水面也恰过点.以下命题正确的是( ).A.圆锥的高等于圆柱高的;B.圆锥的高等于圆柱高的;C.将容器一条母线贴地,水面也恰过点;D.将容器任意摆放,当水面静止时都过点.【答案】C【解析】本题考查体积公式与空间想象能力,设圆锥的高为,圆柱的高为,则利用倒置前后水的体积不变这个性质知,化简得,均错,现在水的容积正好是圆柱内部空间的一半,因此把圆柱的母线贴地,则水面过点,但过点的平面不可能总是平分圆柱内部除去圆锥的那部分,故错误.【考点】体积公式.15.如图,PA平面ABCD,四边形ABCD为矩形,PA=AB=,AD=1,点F是PB的中点,点E在边BC上移动.(I)求三棱锥E—PAD的体积;(II)试问当点E在BC的何处时,有EF//平面PAC;(1lI)证明:无论点E在边BC的何处,都有PE AF.【答案】见解析【解析】(Ⅰ)注意到PA平面ABCD,得知的长即为三棱锥的高,而三棱锥的体积等于的体积,计算即得.(Ⅱ)当点为的中点时,与平面平行.利用三角形中位线定理,得到,进一步得出∥平面.(Ⅲ)证明:根据等腰三角形得出,根据平面,平面,得到,又因为且,⊂平面,得到平面,又平面,.再根据,平面,及平面,根据,作出结论.试题解析:(Ⅰ)由已知PA平面ABCD,所以的长即为三棱锥的高,三棱锥的体积等于的体积= = .(Ⅱ)当点为的中点时,与平面平行.∵在中,分别为的中点,连结,又平面,而平面,∴∥平面.(Ⅲ)证明:因为,所以等腰三角形中,∵平面,平面,∴又因为且,⊂平面,∴平面,又平面,∴.又∵,∴平面.PB,BE⊂平面PBE,∵平面,∴,即无论点E在边的何处,都有.【考点】几何体的体积,垂直关系,平行关系.16.已知D、E是边长为3的正三角形的BC边上的两点,且,现将、分别绕AD和AE折起,使AB和AC重合(其中B、C重合).则三棱锥的内切球的表面积是()A. B. C. D.【答案】B【解析】如下图所示,,,,.设内切球的半径为r,则,所以内切球的表面积为:.【考点】空间几何体的体积及表面积.17.如图,平面四边形中,,,,将其沿对角线折成四面体,使平面平面,若四面体顶点在同一球面上,则该球的体积为( )A.B.C.D.【答案】A【解析】由题意平面四边形ABCD中,AB=AD=CD=1,BD=,BD⊥CD,将其沿对角线BD折成四面体A′-BCD,使平面A′BD⊥平面BCD,若四面体A′-BCD顶点在同一个球面上,可知A′B⊥A′C,所以BC 是外接球的直径,所以BC=,球的半径为:,所以球的体积为:,选A.【考点】1.球内接多面体;2.球的体积和表面积18.在正三棱锥中,、分别是、的中点,且,若侧棱,则正三棱锥外接球的表面积是()A.B.C.D.【答案】C【解析】∵三棱锥是正棱锥,∴SB⊥AC(对棱互相垂直)∴,又∵而,∴平面,即平面,∴,将此三棱锥补成正方体,则它们有相同的外接球,∴,故选C.【考点】垂直关系,几何体的体积19.在三棱锥S−ABC中,,二面角S−AC−B的余弦值是,若S、A、B、C都在同一球面上,则该球的表面积是.【答案】【解析】如图,取AC的中点D,由已知易证二面角S−AC−B的平面角是∠SDB,,故由余弦定理可得,由勾股定理的逆定理可得,补体得正方体,∴三棱锥S−ABC的外接球的半径为,∴该球的表面积是.【考点】立体几何的二面角,球的表面积20.已知三棱锥的顶点都在球的球面上,且平面,则三棱锥的体积等于____.【答案】12【解析】由平面可得,又所以是平面,可以发现线段的中点为球心,取的中点,则,于是.【考点】立体几何中线线垂直、线面垂直的证明,以及椎体体积的求解等知识,考查学生的分析、知识迁移能力21.棱长为的正方体的个顶点都在球的表面上,分别是棱、的中点,则过两点的直线被球截得的线段长为____________【答案】【解析】设过两点的直线与球球交于均为等腰直角三角形,,点到的距离为棱长一半【考点】正方体与外接球点评:求解本题首先要把握住正方体的外接球的球心为正方体的中心,球心与弦中点的连线垂直于弦,从而解直角三角形求出弦长22.点在同一个球的球面,,,若四面体体积的最大值为,则这个球的表面积为()A.B.C.D.【答案】C【解析】∵,∴是直角三角形,∴的外接圆的圆心是边AC的中点O,如图所示,若使四面体ABCD体积的最大值只需使1点D到平面ABC的距离最大,又平面ABC,所以点D是直线与球的交点设球的半径为R,则由体积公式有:在中,,解得:,故选C。
高三数学空间几何体的表面积与体积试题

高三数学空间几何体的表面积与体积试题1.设△ABC的三边长分别为a、b、c,△ABC的面积为S,内切圆半径为r,则r=;类比这个结论可知:四面体S -ABC的四个面的面积分别为S1、S2、S3、S4,内切球的半径为R,四面体S -ABC的体积为V,则R=.【答案】.【解析】设四面体的内切球的球心为O,则球心O到四个面的距离都是R,所以四面体的体积等于以O为顶点,分别以四个面为底面的4个三棱锥体积的和.则四面体的体积为 V四面体A−BCD=∴.【考点】类比推理.2.已知某几何体的俯视图是如图所示的矩形,正视图是一个底边长为8,高为4的等腰三角形,侧视图(或称左视图)是一个底边长为6,高为4的等腰三角形.(1)求该几何体的体积V;(2)求该几何体的侧面积S.【答案】(1)64 (2)40+24【解析】解:本题考查由三视图求几何体的侧面积和体积,由正视图和侧视图的三角形结合俯视图可知该几何体是一个底面为矩形,高为4,顶点在底面的射影是矩形中心的四棱锥,如图.(1)V=×(8×6)×4=64.(2)四棱锥的两个侧面VAD、VBC是全等的等腰三角形,取BC的中点E,连接OE,VE,则△VOE为直角三角形,VE为△VBC边上的高,VE==4.同理侧面VAB、VCD也是全等的等腰三角形,AB边上的高h==5.∴S侧=2×(×6×4+×8×5)=40+24.3.某圆锥体的侧面展开图是半圆,当侧面积是时,则该圆锥体的体积是 .【答案】【解析】设圆锥的母线长为,底面半径为,则,,,,所以圆锥的高为,体积为.【考点】圆锥的侧面展开图与体积.4. (2014·荆州模拟)湖面上漂着一个小球,湖水结冰后将球取出,冰面上留下了一个直径为12cm,深2cm的空穴,则该球的半径是________cm,表面积是________cm2.【答案】10 400π【解析】设球的半径为r,如图:由勾股定理可知,r2=(r-2)2+36,解得r=10cm.所以表面积为4πr2=4π×100=400π(cm2).5.如图甲,在平面四边形ABCD中,已知,,现将四边形ABCD沿BD折起,使平面ABD平面BDC(如图乙),设点E,F分别为棱AC,AD的中点.(1)求证:DC平面ABC;(2)设,求三棱锥A-BFE的体积.【答案】(1)证明:见解析;(2).【解析】(1)注意分析折叠前后变化的关系及不变化的关系.在图甲中可得;在图乙中,可得AB⊥CD.根据DC⊥BC,即可得到DC⊥平面ABC.(2)首先根据E,F分别为AC,AD的中点,得到EF//CD,根据(1)知,DC⊥平面ABC,得到EF⊥平面ABC,从而得到在图甲中,根据给定角度及长度,计算“不变量”,得,BD=2,BC=,EF=CD=,利用体积公式计算即得所求.解答本题的关键是确定“垂直关系”,这也是难点所在,平时学习中,应特别注意转化意识的培养,等体积转化的方法,是立体几何中常用方法之一.(1)证明:在图甲中∵且∴,即 1分在图乙中,∵平面ABD⊥平面BDC ,且平面ABD∩平面BDC=BD4分又,,且,∴DC⊥平面ABC. 6分(2)解:, 7分又由(1)知,DC⊥平面ABC,∴EF⊥平面ABC, 8分所以, 9分在图甲中,由得,, 10分,11分12分【考点】平行关系,垂直关系,几何体的体积.6.某几何体的三视图如图所示,则该几何体的体积是.【答案】【解析】直观图是圆柱中抽出正四棱柱∴该几何体的体积是7.已知圆锥的母线长为,侧面积为,则此圆锥的体积为__________.(结果中保留)【答案】【解析】由圆锥的母线长为,侧面积为.则根据.即可求出圆锥的底面周长.从而解出底面半径.再求出圆锥的高.根据体积公式.【考点】1.圆锥曲线的侧面积.2.圆锥曲线的体积公式.3.图形的展开前后的变化.8.已知函数将的图像与轴围成的封闭图形绕轴旋转一周,所得旋转体的体积为___________.【答案】【解析】.【考点】旋转体的体积.9.正四棱锥的五个顶点在同一球面上,若该正四棱锥的底面边长为2,侧棱长为,则这个球的表面积为_________.【答案】【解析】如图是正四棱锥外接球的球心,是底面中心,,,设球半径为,在中,,解得,所以.【考点】正棱锥的外接球.10.若长方体三个面的面积分别为,,,则此长方体的外接球的表面积是________.【答案】6π【解析】设长方体的过同一顶点的三条棱长分别为a、b、c,则解得长方体外接球半径为R==,外接球的表面积为S=4π=6π11.四面体的六条棱中,有五条棱长都等于a.(1)求该四面体的体积的最大值;(2)当四面体的体积最大时,求其表面积.【答案】(1)a3(2)a2【解析】(1)如图,在四面体ABCD中,设AB=BC=CD=AC=BD=a,AD=x,取AD的中点为P,BC的中点为E,连结BP、EP、CP.得到AD⊥平面BPC,∴V-BCD=V A-BPC+V D-BPC=·S△BPC·AP+S△BPC·PD=·S△BPC·AD=··aA≤·=a3(当且仅当x=a时取等号).∴该四面体的体积的最大值为a3.(2)由(1)知,△ABC和△BCD都是边长为a的正三角形,△ABD和△ACD是全等的等腰三角形,其腰长为a,底边长为a,∴S=2×a2+2××a×=a2+a×=a2+=a2.表12.如图,四棱锥P ABCD中,PA⊥底面ABCD,PA=2,BC="CD=2," ∠ACB=∠ACD=.(1)求证:BD⊥平面PAC;(2)若侧棱PC上的点F满足PF=7FC,求三棱锥P BDF的体积.【答案】(1)见解析 (2)【解析】(1)证明:因为BC=CD,所以△BCD为等腰三角形,又∠ACB=∠ACD,故BD⊥AC.因为PA⊥底面ABCD,所以PA⊥BD.从而BD与平面PAC内两条相交直线PA,AC都垂直,所以BD⊥平面PAC.=BC·CD·sin∠BCD=×2×2×sin =.(2)解:三棱锥P BCD的底面BCD的面积S△BCD由PA⊥底面ABCD,得=·S·PA=××2=2.△BCD由PF=7FC,得三棱锥F BCD的高为PA,故=·S△BCD·PA=×××2=,所以=-=2-=.13.一个与球心距离为1的平面截球体所得的圆面面积为π,则球的体积为() A.B.C.D.8π【答案】A【解析】由题意,球的半径为R=,故其体积V=π()3=,选A.14.如图所示,正方体ABCD-A1B1C1D1的棱长为1,E,F分别为线段AA1,B1C上的点,则三棱锥D1-EDF的体积为________.【答案】【解析】因为E点在线段AA1上,所以S△DED1=×1×1=,又因为F点在线段B1C上,所以点F到平面DED1的距离为1,即h=1,所以VD1-EDF=VF-DED1=·S△DED1·h=××1=.15.若长方体的顶点都在半径为3的球面上,则该长方体表面积的最大值为.【答案】【解析】设长方体的边长为,那么长方体的表面积为:,又由于:,而,所以该长方体表面积的最大值为.【考点】长方体的表面积;基本不等式的变形.16.若圆锥底面半径为1,高为2,则圆锥的侧面积为.【答案】【解析】根据圆锥底面半径、高、母线长构成一个直角三角形,所以母线长为再根据圆锥的侧面积公式圆锥的侧面积公式可结合圆锥展开图为扇形,由相应扇形面积公式理解记忆.【考点】圆锥的侧面积.17.已知四面体的四个顶点都在球的球面上,若平面,,且,,则球的表面积为( )A.B.C.D.【答案】C【解析】因为平面,,在四面体的基础上构造长方体如图,可知长方体的外接球与四面体的外接球相同,长方体的对角线就是外接球的直径,即,球的表面积,故选C.【考点】1、空间几何体的位置关系;2、球的表面积.18.如图,一只蚂蚁由棱长为1的正方体ABCD-A1B1C1D1的点出发沿正方体的表面到达点的最短路程为.【答案】【解析】采用侧面展开法,展开后,在矩形中,,.【考点】立体几何表面距离最短问题.19.如图,平面四边形中,,,,将其沿对角线折成四面体,使平面平面,若四面体顶点在同一球面上,则该球的体积为( )A.B.C.D.【答案】A【解析】由题意平面四边形ABCD中,AB=AD=CD=1,BD=,BD⊥CD,将其沿对角线BD折成四面体A′-BCD,使平面A′BD⊥平面BCD,若四面体A′-BCD顶点在同一个球面上,可知A′B⊥A′C,所以BC 是外接球的直径,所以BC=,球的半径为:,所以球的体积为:,选A.【考点】1.球内接多面体;2.球的体积和表面积20.如图,在底面为平行四边形的四棱柱中,底面,,,.(Ⅰ)求证:平面平面;(Ⅱ)若,求四棱锥的体积.【答案】(Ⅰ)详见解析;(Ⅱ).【解析】(Ⅰ)由,,,易得,从而平面,由此可得平面平面.(Ⅱ)思路一、由(Ⅰ)知,平面,所以,即是一个直角三角形,这样可得四边形的面积.又平面平面,所以过D作的垂线,该垂线即垂直于平面,由此可得该棱锥的高,从而求得其体积.思路二、将四棱锥分割为以下两部分:三棱锥和,这两个三棱锥的体积相等,我们可先求其中的一个. 而三棱锥即为三棱锥,这个三棱锥的体积就很易求了.试题解析:(Ⅰ)证明:在中,由余弦定理得:,所以,所以,即, 3分又四边形为平行四边形,所以,又底面,底面,所以,又,所以平面, 5分又平面,所以平面平面. 6分(Ⅱ)法一:连结,∵,∴∵平面,所以, 8分所以四边形的面积, 10分取的中点,连结,则,且,又平面平面,平面平面,所以平面,所以四棱锥的体积:. 12分法二: 四棱锥的体积, 8分而三棱锥与三棱锥底面积和高均相等, 10分所以. 12分【考点】1、空间两平面的垂直;2、空间几何体的体积.21.一个圆锥过轴的截面为等边三角形,它的顶点和底面圆周在球O的球面上,则该圆锥的表面积与球O的表面积的比值为_____________.【答案】【解析】圆锥与球的截面如下图,设球的半径为,则圆锥底面圆的直径为,圆锥底面面积为,圆锥的侧面面积为,所以圆锥的表面积为,球的表面积为,所以其面积比为.【考点】1.圆锥与球的表面积;2.球与其内接几何体的关系.22.一个所有棱长均为1的正四棱锥的顶点与底面的四个顶点均在某个球的球面上,则此球的体积为()A.B.C.D.【答案】D【解析】设四棱锥是满足条件的,连结、交于,球心在上,令球的半径为,则,由正四棱锥所有棱长为1,易求得四棱锥的高,在中,,即,解得,故球的体积为. 选D.【考点】正四棱锥的性质,球的体积.23.如图,设是棱长为的正方体的一个顶点,过从顶点出发的三条棱的中点作截面,对正方体的所有顶点都如此操作,截去个三棱锥,所得的各截面与正方体各面共同围成一个多面体,则关于此多面体有以下结论:①有个顶点;②有条棱;③有个面;④表面积为;⑤体积为.其中正确的结论是(写出所有正确结论的编号).【答案】①②⑤【解析】根据几何体的特点可知,有12个顶点,24条棱,16个面,所以①、②都对,③错;表面积为故④错;其体积为故⑤成立.【考点】几何体的体积和表面积.24.如图,在三棱柱中,,,分别为,,的中点,设三棱锥体积为,三棱柱的体积为,则【答案】【解析】依题意,,三棱锥的高为三棱柱的高的. ∴.【考点】三棱柱与三棱锥的体积,三角形中位线定理,相似三角形的面积比等于相似比的平方.空间想象能力.中等题.25.如图是某几何体的三视图,则该几何体的体积为A.1B.C.D.【答案】B【解析】由三视图可知,该几何体是一个有一条侧棱垂直于底面的四棱锥,所以该几何体的体积为【考点】本小题主要考查三视图.点评:此类问题,主要考查学生的空间想象能力,解决此类问题的关键是根据三视图正确还原几何体.26.如果一个几何体的三视图如图所示,则该几何体的表面积为()A.B.C.96D.80【答案】A【解析】由三视图知:原几何体为正方体和一个四棱锥的组合体,正方体的棱长为4,正四棱锥的底面边长为4,高为2,所以正四棱锥的斜高为。
高考数学复习考点知识与解题方法专题讲解34---空间几何体的表面积和体积

高考数学复习考点知识与解题方法专题讲解 专题34 空间几何体的表面积和体积【考纲要求】1.会计算柱、锥、台、球的表面积和体积.【知识清单】知识点1.几何体的表面积圆柱的侧面积 rl S π2=圆柱的表面积 )(2l r r S +=π圆锥的侧面积 rl S π=圆锥的表面积 )(l r r S +=π圆台的侧面积 l r r S )(+'=π圆台的表面积 )(22rl l r r r S +'++'=π球体的表面积 24R S π=柱体、锥体、台体的侧面积,就是各个侧面面积之和;表面积是各个面的面积之和,即侧面积与底面积之和.把柱体、锥体、台体的面展开成一个平面图形,称为它的展开图,圆柱、圆锥、圆台的侧面展开图分别是矩形、扇形、扇环形它的表面积就是展开图的面积. 知识点2.几何体的体积圆柱的体积 h r V 2π=圆锥的体积 h r V 231π=圆台的体积 )(3122r r r r h V '++'=π 球体的体积 334R V π= 正方体的体积 3a V =正方体的体积 abc V =【考点梳理】考点一 :几何体的面积【典例1】(2020·天津高考真题)若棱长为则该球的表面积为( )A .12πB .24πC .36πD .144π 【答案】C【解析】这个球是正方体的外接球,其半径等于正方体的体对角线的一半,即3R ==,所以,这个球的表面积为2244336S R πππ==⨯=.故选:C.【典例2】(2020·全国高考真题(理))埃及胡夫金字塔是古代世界建筑奇迹之一,它的形状可视为一个正四棱锥,以该四棱锥的高为边长的正方形面积等于该四棱锥一个侧面三角形的面积,则其侧面三角形底边上的高与底面正方形的边长的比值为( )A .514-B .512-C .514+D .512+ 【答案】C【解析】如图,设,CD a PE b ==,则PO ==, 由题意212PO ab =,即22142a b ab -=,化简得24()210b b a a -⋅-=,解得14b a +=(负值舍去). 故选:C.【规律方法】几类空间几何体表面积的求法(1)多面体:其表面积是各个面的面积之和.(2)旋转体:其表面积等于侧面面积与底面面积的和.(3)简单组合体:应搞清各构成部分,并注意重合部分的删、补.(4)若以三视图形式给出,解题的关键是根据三视图,想象出原几何体及几何体中各元素间的位置关系及数量关系.【变式探究】1.(2018·全国高考真题(理))已知圆锥的顶点为S ,母线SA ,SB 所成角的余弦值为78,SA 与圆锥底面所成角为45°,若SAB ∆的面积为__________.【答案】【解析】因为母线SA ,SB 所成角的余弦值为78,所以母线SA ,SB ,因为SAB 的面积为,l 所以221802l l ⨯==,因为SA 与圆锥底面所成角为45°,所以底面半径为πcos,4l =因此圆锥的侧面积为2ππ.2rl l ==2.(2019·福建高三月考)已知四面体ABCD 内接于球O ,且2AB BC AC ===,若四面体ABCD ,球心O 恰好在棱DA 上,则球O 的表面积是_____. 【答案】16π【解析】如图:在三角形ABC 中,因为222AB BC AC +=,所以△ABC 为直角三角形,所以三角形ABC 的外接圆的圆心为AC 的中点1O ,连1OO ,根据垂径定理,可得1OO ⊥平面ABC ,因为1,O O 为,AD AC 的中点可知DC ⊥平面ABC ,所以DC 为四面体ABCD 的高.所以11323DC ⨯=,解得DC =所以4AD ==. 所以四面体ABCD 的外接球的半径为2,表面积为24R π=24216ππ⨯=.【总结提升】计算旋转体的侧面积时,一般采用转化的方法来进行,即将侧面展开化为平面图形,“化曲为直”来解决,因此要熟悉常见旋转体的侧面展开图的形状及平面图形面积的求法. 高频考点二 :几何体的体积【典例3】(2019·北京高考真题(文))某几何体是由一个正方体去掉一个四棱柱所得,其三视图如图所示.如果网格纸上小正方形的边长为1,那么该几何体的体积为__________.【答案】40.【解析】如图所示,在棱长为4的正方体中,三视图对应的几何体为正方体去掉棱柱1111MPD A NQC B -之后余下的几何体,几何体的体积()3142424402V =-+⨯⨯=. 【典例4】(2020·江苏省高考真题)如图,六角螺帽毛坯是由一个正六棱柱挖去一个圆柱所构成的.已知螺帽的底面正六边形边长为2 cm ,高为2 cm ,内孔半轻为0.5 cm ,则此六角螺帽毛坯的体积是____cm.【答案】2π【解析】正六棱柱体积为2624⨯⨯圆柱体积为21()222ππ⋅=所求几何体体积为2π故答案为: 2π【总结提升】 (1)已知几何体的三视图求其体积,一般是先根据三视图判断空间几何体的形状,再根据题目所给数据与几何体的表体积公式求其体积.(2)若所给几何体的体积不能直接利用公式得出,则常用等积法、分割法、补形法等方法进行求解.(3)规则几何体:若所给定的几何体是柱体、锥体或台体等规则几何体,则可直接利用公式进行求解.其中,求三棱锥的体积常用等体积转换法(4)不规则几何体:若所给定的几何体是不规则几何体,则将不规则的几何体通过分割或补形转化为规则几何体,再利用公式求解.(5)三视图形式:若以三视图的形式给出几何体,则应先根据三视图得到几何体的直观图,然后根据条件求解提醒:处理高线问题时,经常利用的方法就是“等积法”.【变式探究】1.(2020·全国高一课时练习)已知ABC ∆的三边长分别是3AC =,4BC =,5AB =.下列说法正确的是( )A .以BC 所在直线为旋转轴,将此三角形旋转一周,所得旋转体的侧面积为15πB .以BC 所在直线为旋转轴,将此三角形旋转一周,所得旋转体的体积为36π C .以AC 所在直线为旋转轴,将此三角形旋转一周,所得旋转体的侧面积为25πD .以AC 所在直线为旋转轴,将此三角形旋转一周,所得旋转体的体积为16π【答案】AD【解析】以BC 所在直线为轴旋转时,所得旋转体是底面半径为3,母线长为5,高为4的圆锥,其侧面积为3515ππ⨯⨯=,体积为2134123ππ⨯⨯⨯=,故A 正确,B 错误; 以AC 所在直线为轴旋转时,所得旋转体是底面半径为4,母线长为5,高为3的圆锥,侧面积为4520ππ⨯⨯=,体积为2143163ππ⨯⨯⨯=,故C 错误,D 正确. 故选:AD.2.(2019·湖南高三月考(理))正方体1111ABCD A B C D -的棱长为2,点E 、F 、G 分别是AB 、AD 、1AA 的中点,以EFG ∆为底面作直三棱柱(侧棱垂直底面的棱柱),若此直三棱柱另一底面的三个顶点也都在该正方体的表面上,则该直三棱柱的体积为( )B.2C.32D.34【答案】C【解析】如图,连接11A C ,1C D ,1AC , 1BC ,分别取11A C 、1BC 、1C D 中点M 、N 、Q ,连接MQ ,MN ,NQ ,FQ ,EN ,GM由中位线定理可得111111111//,,//,,//,222GM AC GM AC FQ AC FQ AC EN AC EN AC === 又1AC EFG ⊥平面,∴三棱柱EFG NQM —是正三棱柱2EFG S ∆==112h GM AC ===,∴三棱柱32EFG NQM V =— 答案选C【方法总结】求体积的两种方法:①割补法:求一些不规则几何体的体积时,常用割补法转化成已知体积公式的几何体进行解决.②等积法:等积法包括等面积法和等体积法.等体积法的前提是几何图形(或几何体)的面积(或体积)通过已知条件可以得到,利用等积法可以用来求解几何图形的高或几何体的高,特别是在求三角形的高和三棱锥的高时,这一方法回避了通过具体作图得到三角形(或三棱锥)的高,而通过直接计算得到高的数值.高频考点三 : 几何体的展开、折叠、切、截问题【典例5】(2020·全国高考真题(理))已知,,A B C 为球O 的球面上的三个点,⊙1O 为ABC 的外接圆,若⊙1O 的面积为4π,1AB BC AC OO ===,则球O 的表面积为( )A .64πB .48πC .36πD .32π【答案】A【解析】 设圆1O 半径为r ,球的半径为R ,依题意,得24,2r r ππ=∴=,ABC 为等边三角形,由正弦定理可得2sin 60AB r =︒=,1OO AB ∴==,根据球的截面性质1OO ⊥平面ABC ,11,4OO O A R OA ∴⊥====,∴球O 的表面积2464S R ππ==.故选:A【典例6】(2019·天津高考真题(理))已知四棱锥的底面是边长为2的正方形,侧棱长均为5.若圆柱的一个底面的圆周经过四棱锥四条侧棱的中点,另一个底面的圆心为四棱锥底面的中心,则该圆柱的体积为__________.【答案】4π. 【解析】2=,.若圆柱的一个底面的圆周经过四棱锥四条侧棱的中点,圆柱的底面半径为12,一个底面的圆心为四棱锥底面的中心,故圆柱的高为1,故圆柱的体积为21124ππ⎛⎫⨯⨯= ⎪⎝⎭. 【规律方法】几个与球有关的切、接常用结论(1)正方体的棱长为a ,球的半径为R ,①若球为正方体的外接球,则2R =3a ;②若球为正方体的内切球,则2R =a ; ③若球与正方体的各棱相切,则2R =2a .(2)若长方体的同一顶点的三条棱长分别为a ,b ,c ,外接球的半径为R ,则2R =a 2+b 2+c 2.(3)正四面体的外接球与内切球的半径之比为3∶1.【典例7】(2019·全国高考真题(理))已知三棱锥P -ABC 的四个顶点在球O 的球面上,PA =PB =PC ,△ABC 是边长为2的正三角形,E ,F 分别是PA ,AB 的中点,∠CEF =90°,则球O 的体积为( ) A .86π B .46πC .26πD 6π【答案】D 【解析】解法一:,PA PB PC ABC ==∆为边长为2的等边三角形,P ABC ∴-为正三棱锥,PB AC ∴⊥,又E ,F 分别为PA 、AB 中点, //EF PB ∴,EF AC ∴⊥,又EF CE ⊥,,CEAC C EF =∴⊥平面PAC ,PB ⊥平面PAC ,2APB PA PB PC ∴∠=90︒,∴===,P ABC ∴-为正方体一部分,22226R =++= 364466633R V R =∴=π==ππ,故选D .解法二:设2PA PB PC x ===,,E F 分别为,PA AB 中点,//EF PB ∴,且12EF PB x ==,ABC ∆为边长为2的等边三角形,CF ∴=又90CEF ∠=︒1,2CE AE PA x ∴===AEC ∆中余弦定理()2243cos 22x x EAC x+--∠=⨯⨯,作PD AC ⊥于D ,PA PC =,D 为AC 中点,1cos 2AD EAC PA x ∠==,2243142x x x x +-+∴=,22121222x x x ∴+=∴==,PA PB PC ∴======2AB BC AC ,,,PA PB PC ∴两两垂直,2R ∴==R ∴=,344338V R ∴=π=π⨯=,故选D.【典例8】(2019·四川高三月考(理))学生到工厂劳动实践,利用3D 打印技术制作模型.如图,该模型为在圆锥底部挖去一个正方体后的剩余部分(正方体四个顶点在圆锥母线上,四个顶点在圆锥底面上),圆锥底面直径为,高为10cm .打印所用部料密度为30.9g/cm .不考虑打印损耗.制作该模型所需原料的质量为________g .(π取3.14)【答案】358.5 【解析】设被挖去的正方体的棱长为xcm ,圆锥底面半径为r ,取过正方体上下底面面对角线的轴截面,由相似三角形得则10210x xh x x r h --=⇒=,解得5x =.模型的体积为(223311500105125333V r h x πππ=-=⨯⨯-=-, 因此,制作该模型所需材料质量约为5000.91251500.9125358.5g 3ππ⎛⎫⨯-=-⨯≈⎪⎝⎭. 故答案为:358.5. 【总结提升】1.与球有关的组合体问题,一种是内切,一种是外接.球与旋转体的组合通常是作它们的轴截面解题,球与多面体的组合,通过多面体的一条侧棱和球心,或“切点”、“接点”作出截面图,把空间问题化归为平面问题.2.若球面上四点P ,A ,B ,C 中PA ,PB ,PC两两垂直或三棱锥的三条侧棱两两垂直,可构造长方体或正方体确定直径解决外接问题.【典例9】(2018届河南省林州市第一中学高三8月调研)如图,已知矩形ABCD中,,现沿AC折起,使得平面ABC⊥平面ADC,连接BD,得到三棱锥-,则其外接球的体积为()B ACD【答案】D【解析】结合几何体的特征可得,外接球的球心为AC的中点,则外接球半径:本题选择D选项.【总结提升】解决与球有关的切、接问题,其通法是作截面,将空间几何问题转化为平面几何问题求解,其解题的思维流程是:【变式探究】1.(2018届河南省洛阳市高三期中)在三棱锥S ABC -中,底面ABC ∆是直角三角形,其斜边4AB =, SC ⊥平面ABC ,且3SC =,则三棱锥的外接球的表面积为( ) A. 25π B. 20π C. 16π D. 13π 【答案】A【解析】根据已知,可将三棱锥补成一个长方体,如下图:则三棱锥的外接球就是这个长方体的外接球,由于43AB SC ==,,且ABC ∆是直角三角形, SC ⊥平面ABC , ∴长方体的对角线长为∴三棱锥的外接球的半径 ∴三A.2.(2018·天津高考真题(文))如图,已知正方体ABCD –A 1B 1C 1D 1的棱长为1,则四棱锥A 1–BB 1D 1D 的体积为__________.【答案】13【解析】如图所示,连结11A C ,交11B D 于点O ,很明显11A C ⊥平面11BDD B ,则1A O 是四棱锥的高,且111122A O A C ===,1111BDD B S BD DD =⨯==四边形,结合四棱锥体积公式可得其体积为1113323V Sh ===,故答案为13.3.(2018届河北省衡水市武邑中学高三上第三次调研)在《九章算术》中,将四个面都为直角三角形的三棱锥称之为鳖臑(bie nao).已知在鳖臑M ABC-中, MA⊥平面ABC, 2MA AB BC===,则该鳖臑的外接球与内切球的表面积之和为____.【解析】由题意,MC为球O的直径,O∴球O的表面积为4π•3=12π,内切球的半径设为r,【典例10】(2017课标1,理16)如图,圆形纸片的圆心为O,半径为5 cm,该纸片上的等边三角形ABC的中心为O.D、E、F为圆O上的点,△DBC,△ECA,△FAB分别是以BC,CA,AB为底边的等腰三角形.沿虚线剪开后,分别以BC,CA,AB为折痕折起△DBC,△ECA,△FAB,使得D、E、F重合,得到三棱锥.当△ABC的边长变化时,所得三棱锥体积(单位:cm3)的最大值为_______.【答案】【解析】【规律方法】有关折叠问题,一定要分清折叠前后两图形(折前的平面图形和折叠后的空间图形)各元素间的位置和数量关系,哪些变,哪些不变.研究几何体表面上两点的最短距离问题,常选择恰当的母线或棱展开,转化为平面上两点间的最短距离问题.【变式探究】(2018届河南省林州市第一中学高三8月调研)如图,已知矩形中,,现沿折起,使得平面平面,连接,得到三棱锥,则其外接球的体积为( )ABCD AC ABC ⊥ADC BD B ACD -【答案】D【解析】结合几何体的特征可得,外接球的球心为AC的中点,则外接球半径:本题选择D选项.【典例11】(2018·江苏高考真题)如图所示,正方体的棱长为2,以其所有面的中心为顶点的多面体的体积为________.【答案】43【解析】分析:先分析组合体的构成,再确定锥体的高,最后利用锥体体积公式求结果.详解:由图可知,该多面体为两个全等正四棱锥的组合体,正四棱锥的高为1,底面正,所以该多面体的体积为21421.33⨯⨯⨯=【变式探究】(2020·山东省滨州市三模)已知P,A,B,C是球O的球面上的四个点,平面,则球O的表面积为__________.PA⊥,26,ABC PA BC==AB AC⊥【答案】 【解析】由于平面,所以,而,故可将补形为长方体,如图所示,长方体的外接球,也即三棱锥的外接球,也即球. 由于,设,则,所以长方体的对角设球的半径为,则所以球的表面积为. 故答案为:【典例12】(2020·山东省泰安市6月三模)已知球O是正三棱锥的外接球,,E 是线段AB 的中点,过点E 作球O 的截面,则截面面积的最小值是_______. 【答案】45πPA ⊥ABC ,PA AB PA AC ⊥⊥AB AC ⊥P ABC -P ABC -O 26,3PA BC BC ===,AB a AC b ==2229a b BC +===O R 2R =O 2445R ππ=45πP ABC -3AB =PA =94π【解析】如图,设三棱锥的外接球半径为R ,正三角形的外接圆圆心为,因为,三角形是正三角形,为正三角形的外接圆圆心, 所以因为所以,解得,,因为过作球的截面,当截面与垂直时,截面圆的半径最小,所以当截面与垂直时,截面圆的面积有最小值,在中,故,截面面积, 故答案为:. 【总结提升】解决球与其他几何体的切、接问题,关键在于仔细观察、分析,弄清相关元素的关系和数量关系,选准最佳角度作出截面(要使这个截面尽可能多地包含球、几何体的各种元素以及体现这些元素之间的关系),达到空间问题平面化的目的.【变式探究】1.(2020·安徽马鞍山�高三三模(文))已知正方体1111ABCD A B C D -,直线1AC ⊥平面α,平面α截此正方体所得截面中,正确的说法是( )ABC D 3AB =ABC D ABC DA =PA =3PD =()223R R +-=2R =1OD =E O OE OE Rt EDO ∆OE ==32r ==294S r ππ==94πA .截面形状可能为四边形B .截面形状可能为五边形C .截面面积最大值为D 【答案】D【解析】如图在正方体中1AC ⊥平面1A BD ,所以平面α与平面1A BD 平行平面α与正方体的截面可以是三角形、六边形但不会是五边形和四边形 当截面为正六边形EFNMGH 时,截面面积有最大,由题可知:21sin 45==NM ,则133611sin 6022=⨯⨯⨯⨯=EFNMGH S 故选:D2.(2020·江苏苏州�高一期末)已知在球O 的内接长方体1111ABCD A B C D -中,12AB AA ==,3AD =,则球O 的表面积为________,若P 为线段AD 的中点,则过点P 的平面截球O 所得截面面积的最小值为______.【答案】17π9π4【解析】如图,因为球O 的内接长方体1111ABCD A B C D -中,12AB AA ==,3AD =,所以12=DB R = 所以球的表面积2=417S R ππ=, 当OP ⊥球的截面,即P 为截面圆圆心时,球心到截面圆的距离d OP =时最大, 此时截面圆的半径22d R r -=最小,此时截面圆的面积最小,而OP ===所以32r ==, 所以截面圆面积294S r ππ==. 故答案为:17π;94π。
2025届全国普通高等学校招生统一考试高三(最后冲刺)数学试卷含解析

2025届全国普通高等学校招生统一考试高三(最后冲刺)数学试卷考生须知:1.全卷分选择题和非选择题两部分,全部在答题纸上作答。
选择题必须用2B 铅笔填涂;非选择题的答案必须用黑色字迹的钢笔或答字笔写在“答题纸”相应位置上。
2.请用黑色字迹的钢笔或答字笔在“答题纸”上先填写姓名和准考证号。
3.保持卡面清洁,不要折叠,不要弄破、弄皱,在草稿纸、试题卷上答题无效。
一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知函数()sin3(0,)f x a x a b a x =-++>∈R 的值域为[5,3]-,函数()cos g x b ax =-,则()g x 的图象的对称中心为( ) A .,5()4k k π⎛⎫-∈⎪⎝⎭Z B .,5()48k k ππ⎛⎫+-∈⎪⎝⎭Z C .,4()5k k π⎛⎫-∈ ⎪⎝⎭Z D .,4()510k k ππ⎛⎫+-∈⎪⎝⎭Z 2.已知数列满足:.若正整数使得成立,则( ) A .16B .17C .18D .193.执行如图所示的程序框图,输出的结果为( )A .78B .158C .3116D .15164.已知等差数列{}n a 的前13项和为52,则68(2)a a +-=( )A .256B .-256C .32D .-325.已知曲线24x y =,动点P 在直线3y =-上,过点P 作曲线的两条切线12,l l ,切点分别为,A B ,则直线AB 截圆22650x y y +-+=所得弦长为( )A .3B .2C .4D .236.已知复数z 满足()1z i i =-,(i 为虚数单位),则z =( ) A .2B .3C .2D .37.已知四棱锥E ABCD -,底面ABCD 是边长为1的正方形,1ED =,平面ECD ⊥平面ABCD ,当点C 到平面ABE 的距离最大时,该四棱锥的体积为( ) A .26B .13C .23D .18.如图是函数sin()R,A 0,0,02y A x x πωφωφ⎛⎫=+∈>><< ⎪⎝⎭在区间5,66ππ⎡⎤-⎢⎥⎣⎦上的图象,为了得到这个函数的图象,只需将sin (R)y x x =∈的图象上的所有的点( )A .向左平移3π个长度单位,再把所得各点的横坐标变为原来的12,纵坐标不变 B .向左平移3π个长度单位,再把所得各点的横坐标变为原来的2倍,纵坐标不变C .向左平移6π个长度单位,再把所得各点的横坐标变为原来的12,纵坐标不变 D .向左平移6π个长度单位,再把所得各点的横坐标变为原来的2倍,纵坐标不变 9.若双曲线222:14x y C m -=的焦距为5C 的一个焦点到一条渐近线的距离为( )A .2B .4C 19D .1910.在ABC 中,内角A ,B ,C 所对的边分别为a ,b ,c ,且cos sin a B b A c +=.若2a =,ABC 的面积为3(21)-,则b c +=( ) A .5B .22C .4D .1611.数列{a n }是等差数列,a 1=1,公差d ∈[1,2],且a 4+λa 10+a 16=15,则实数λ的最大值为( ) A .72B .5319C .2319-D .12-12.《周易》是我国古代典籍,用“卦”描述了天地世间万象变化.如图是一个八卦图,包含乾、坤、震、巽、坎、离、艮、兑八卦(每一卦由三个爻组成,其中“”表示一个阳爻,“”表示一个阴爻)若从八卦中任取两卦,这两卦的六个爻中恰有两个阳爻的概率为( )A .356B .328C .314D .14二、填空题:本题共4小题,每小题5分,共20分。
高考高三数学知识点总结

高考高三数学知识点总结高三数学知识点1(1)不等关系感受在现实世界和日常生活中存在着大量的不等关系,了解不等式(组)的实际背景。
(2)一元二次不等式①经历从实际情境中抽象出一元二次不等式模型的过程。
②通过函数图象了解一元二次不等式与相应函数、方程的联系。
③会解一元二次不等式,对给定的一元二次不等式,尝试设计求解的程序框图。
(3)二元一次不等式组与简单线性规划问题①从实际情境中抽象出二元一次不等式组。
②了解二元一次不等式的几何意义,能用平面区域表示二元一次不等式组(参见例2)。
③从实际情境中抽象出一些简单的二元线性规划问题,并能加以解决(参见例3)。
(4)基本不等式:。
①探索并了解基本不等式的证明过程。
②会用基本不等式解决简单的(小)值问题。
高三数学知识点21.数列的定义按一定次序排列的一列数叫做数列,数列中的每一个数都叫做数列的项.(1)从数列定义可以看出,数列的数是按一定次序排列的,如果组成数列的数相同而排列次序不同,那么它们就不是同一数列,例如数列1,2,3,4,5与数列5,4,3,2,1是不同的数列.(2)在数列的定义中并没有规定数列中的数必须不同,因此,在同一数列中可以出现多个相同的数字,如:-1的1次幂,2次幂,3次幂,4次幂,…构成数列:-1,1,-1,1,….(4)数列的项与它的项数是不同的,数列的项是指这个数列中的某一个确定的数,是一个函数值,也就是相当于f(n),而项数是指这个数在数列中的位置序号,它是自变量的值,相当于f(n)中的n.(5)次序对于数列来讲是十分重要的,有几个相同的数,由于它们的排列次序不同,构成的数列就不是一个相同的数列,显然数列与数集有本质的区别.如:2,3,4,5,6这5个数按不同的次序排列时,就会得到不同的数列,而{2,3,4,5,6}中元素不论按怎样的次序排列都是同一个集合.2.数列的分类(1)根据数列的项数多少可以对数列进行分类,分为有穷数列和无穷数列.在写数列时,对于有穷数列,要把末项写出,例如数列1,3,5,7,9,…,2n-1表示有穷数列,如果把数列写成1,3,5,7,9,…或1,3,5,7,9,…,2n-1,…,它就表示无穷数列.(2)按照项与项之间的大小关系或数列的增减性可以分为以下几类:递增数列、递减数列、摆动数列、常数列.3.数列的通项公式数列是按一定次序排列的一列数,其内涵的本质属性是确定这一列数的规律,这个规律通常是用式子f(n)来表示的,这两个通项公式形式上虽然不同,但表示同一个数列,正像每个函数关系不都能用解析式表达出来一样,也不是每个数列都能写出它的通项公式;有的数列虽然有通项公式,但在形式上,又不一定是的,仅仅知道一个数列前面的有限项,无其他说明,数列是不能确定的,通项公式更非.如:数列1,2,3,4,…,由公式写出的后续项就不一样了,因此,通项公式的归纳不仅要看它的前几项,更要依据数列的构成规律,多观察分析,真正找到数列的内在规律,由数列前几项写出其通项公式,没有通用的方法可循.再强调对于数列通项公式的理解注意以下几点:(1)数列的通项公式实际上是一个以正整数集N_或它的有限子集{1,2,…,n}为定义域的函数的表达式.(2)如果知道了数列的通项公式,那么依次用1,2,3,…去替代公式中的n就可以求出这个数列的各项;同时,用数列的通项公式也可判断某数是否是某数列中的一项,如果是的话,是第几项.(3)如所有的函数关系不一定都有解析式一样,并不是所有的数列都有通项公式.如2的不足近似值,精确到1,0.1,0.01,0.001,0.0001,…所构成的数列1,1.4,1.41,1.414,1.4142,…就没有通项公式.(4)有的数列的通项公式,形式上不一定是的,正如举例中的:(5)有些数列,只给出它的前几项,并没有给出它的构成规律,那么仅由前面几项归纳出的数列通项公式并不.4.数列的图象对于数列4,5,6,7,8,9,10每一项的序号与这一项有下面的对应关系:序号:1234567项:这就是说,上面可以看成是一个序号集合到另一个数的集合的映射.因此,从映射、函数的观点看,数列可以看作是一个定义域为正整集N_(或它的有限子集{1,2,3,…,n})的函数,当自变量从小到大依次取值时,对应的一列函数值.这里的函数是一种特殊的函数,它的自变量只能取正整数.由于数列的项是函数值,序号是自变量,数列的通项公式也就是相应函数和解析式.数列是一种特殊的函数,数列是可以用图象直观地表示的.数列用图象来表示,可以以序号为横坐标,相应的项为纵坐标,描点画图来表示一个数列,在画图时,为方便起见,在平面直角坐标系两条坐标轴上取的单位长度可以不同,从数列的图象表示可以直观地看出数列的变化情况,但不精确.把数列与函数比较,数列是特殊的函数,特殊在定义域是正整数集或由以1为首的有限连续正整数组成的集合,其图象是无限个或有限个孤立的点.5.递推数列一堆钢管,共堆放了七层,自上而下各层的钢管数构成一个数列:4,5,6,7,8,9,10.①数列①还可以用如下方法给出:自上而下第一层的钢管数是4,以下每一层的钢管数都比上层的钢管数多1。
(高三理科数学第一轮复习)第八章 第2节 空间几何体的表面积和体积

25
知识衍化体验
考点聚集突破
核心素养提升
@《创新设计》
【训练 2】 (1)如图所示,正三棱柱 ABC-A1B1C1 的底面边长为 2,侧棱长为 3,D 为 BC 中点,则三棱锥 A-B1DC1 的体积为( )
A.3
26
B.32
C.1
知识衍化体验
D.
3 2
考点聚集突破
核心素养提升
(2)某几何体的三视图如图所示,则该几何体的体积为( )
典例迁移
【例3】 (经典母题)(2016·全国Ⅲ卷)在封闭的直三棱柱ABC-A1B1C1内有一个体积为V
的球.若AB⊥BC,AB=6,BC=8,AA1=3,则V的最大值是( )
A.4π
角度3 不规则几何体的体积 【例2-3】 如图,在多面体ABCDEF中,已知ABCD是边长为1的正方形,且△ADE,
△BCF均为正三角形,EF∥AB,EF=2,则该多面体的体积为( )
2 A. 3
23
3 B. 3
4 C.3
知识衍化体养提升
解析 如图,分别过点A,B作EF的垂线,垂足分别为G,H,
)
解析 (1)锥体的体积等于底面面积与高之积的三分之一,故不正确.
(2)球的体积之比等于半径比的立方,故不正确.
答案 (1)× (2)× (3)√ (4)√
6
知识衍化体验
考点聚集突破
核心素养提升
@《创新设计》
2.(必修2P27练习1改编)已知圆锥的表面积等于12π cm2,其侧面展开图是一个半圆,则
所以 EH∥FG,EH=FG,所以四边形 EHGF 为平行四边形,又 EG=HF,EH=HG,
所以四边形 EHGF 为正方形.又点 M 到平面 EHGF 的距离为12,所以四棱锥 M-EFGH
高三数学柱锥台球的结构特征试题答案及解析
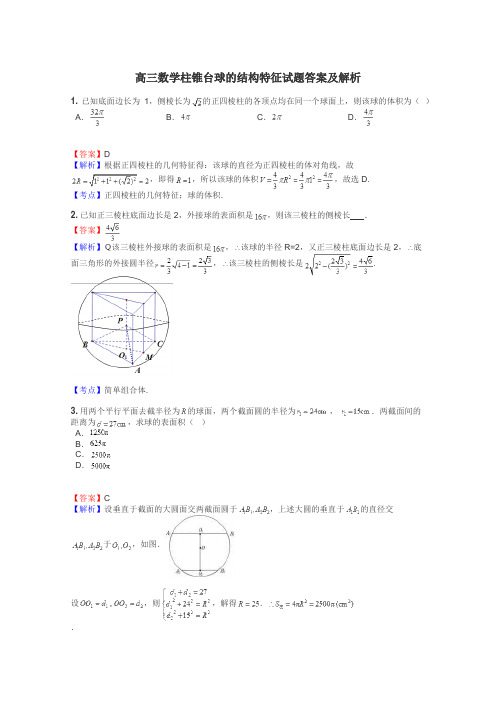
高三数学柱锥台球的结构特征试题答案及解析1.已知底面边长为1,侧棱长为的正四棱柱的各顶点均在同一个球面上,则该球的体积为()A.B.C.D.【答案】D【解析】根据正四棱柱的几何特征得:该球的直径为正四棱柱的体对角线,故,即得,所以该球的体积,故选D.【考点】正四棱柱的几何特征;球的体积.2.已知正三棱柱底面边长是2,外接球的表面积是,则该三棱柱的侧棱长.【答案】【解析】该三棱柱外接球的表面积是,该球的半径R=2,又正三棱柱底面边长是2,底面三角形的外接圆半径,该三棱柱的侧棱长是.【考点】简单组合体.3.用两个平行平面去截半径为的球面,两个截面圆的半径为,.两截面间的距离为,求球的表面积()A.B.C.D.【答案】C【解析】设垂直于截面的大圆面交两截面圆于,上述大圆的垂直于的直径交于,如图.设,则,解得..选C.4.正方体内切球和外接球半径的比为( )A.B.C.D.1:2【答案】B【解析】作正方体与其内切球的截面如图甲,设正方体棱长为a,则有2r=a(r为内切球半径).作正方体与其外接球的截面如图乙,则有2R=(R为外接球半径),得r∶R=,选B5.如图,正方体的底面与正四面体的底面在同一平面上,且,正方体的六个面所在的平面与直线CE,EF相交的平面个数分别记为,那么()A.8B.9C.10D.11【答案】A【解析】因为CE在平面上,所以CE平行于上底面,由于CE与正方体底面各线都相交,所以CE与正方体各侧面相交,即m=4设正四面体的高为直线a,则a与正方体各侧棱平行,EF与a所在的平面与正方体的两个侧面平行,所以EF与正方体的两个侧面不相交.由于上下底面,正面与后面都与两侧面相交,所以EF 与它们相交,即n=4∴m+n=86.如图,边长为2的正方形ABCD中,点E,F分别是边AB,BC的中点△AED,△EBF,△FCD分别沿DE,EF,FD折起,使A,B,C三点重合于点A′,若四面体A′EFD的四个顶点在同一个球面上,则该球的半径为A.B.C.D.【答案】B【解析】因为DA⊥Rt△AEF,所以四面体A′EFD的外接球,与以A′、E、F、D所确定的长方体的外接球是同一外接球,所以其外接球半径r=.【考点】三棱锥的外接球问题.7.一正方体内接于一个球,经过球心作一个截面,则截面的可能图形为_________(只填写序号).【答案】①②③【解析】当截面与正方体的某一面平行时,可得①,将截面旋转可得②,继续旋转,过正方体两顶点时可得③,即正方体的对角面,不可能得④.8.已知三棱柱ABC-A1B1C1的侧棱与底面垂直,体积为,底面是边长为的正三角形.若P为底面A1B1C1的中心,则PA与平面ABC所成角的大小为 ().A.B.C.D.【答案】B【解析】如图所示:S△ABC=×××sin 60°=.∴VABC-A1B1C1=S△ABC×OP=×OP=,∴OP=.又OA=××=1,∴tan∠OAP==,由∠OAP∈,得∠OAP=.9.某地球仪上北纬纬线长度为cm,该地球仪的表面上北纬东经对应点与北纬东经对应点之间的球面距离为 cm(精确到0.01).【答案】【解析】如下图球中,是北纬纬线圈的圆心,,,,,,在中,两点间的球面距离即所对的大圆弧长为约等于【考点】球面距离.10.如图,直三棱柱的六个顶点都在半径为1的半球面上,,侧面是半球底面圆的内接正方形,则侧面的面积为()A.2B.1C.D.【答案】C【解析】球心在面的中心上,为截面圆的直径,∴,底面外接圆圆心位于中点,外心在中点上,设正方形边长为,中,,,,∴,即,则,∴.【考点】1.中位线;2.勾股定理.11.某圆台的一个底面周长是另一个底面周长的3倍,轴截面的面积等于,母线与轴的夹角为,则这个圆台的高为A.7B.14C.21D.【答案】B【解析】设圆台上底面、下底面半径分别为,则,∴,又母线与轴的夹角为,所以高,轴截面的面积为,解得,即.【考点】1、旋转体;2、梯形的面积.12.已知正方体的体对角线为,点在题对角线上运动(动点不与体对角线的端点重合)现以点为球心,为半径作一个球,设,记该球面与正方体表面积的交线长度和为,则函数的图象最有可能是()【答案】B【解析】当时,,排除,;又,(当时,此时球面与正方体表面的交线在面、面、面上且相等,如在面的交线是以为圆心,以为半径的圆弧,所以,排除,故选B.【考点】空间几何体中运动点对应的轨迹,函数的图象特征.13.已知正四棱锥的各棱棱长都为,则正四棱锥的外接球的表面积为( )A.B.C.D.【答案】B【解析】在中,,则,又∽,则有,所以,,.【考点】1、正四棱锥的外接球;2、球的表面积.14.正三棱锥中,,,分别是棱上的点,为边的中点,,则三角形的面积为.【答案】【解析】根据题意在正三棱锥中,为边的中点,故可得,则,又由,故,假设又在中,,则,故.【考点】三棱锥的体积计算15.如图,正四棱柱的底面边长,若直线与底面所成的角的大小为,则正四棱柱的侧面积为 .【答案】32【解析】因为直线与底面所成的角的大小为,所以,于是正四棱柱的侧面积为.【考点】正四棱柱的侧面积计算16.已知正四面体的棱长为1,M为AC的中点,P在线段DM上,则的最小值为_____________;【答案】【解析】将三角形BMD绕BM旋转到与AMD共面,此时A、B两点间的距离即为AP+BP的最小值.所以.【考点】1、空间几何体;2、余弦定理.17.三棱锥S-ABC中,SA⊥平面ABC,AB⊥BC,SA=AB=1,BC=,则三棱锥外接球O的表面积等于________.【答案】【解析】以为长、宽、高补体成长方形,三棱锥的外接球与长方形外接球一样,设球半径为,,即,所以,.【考点】1.补体法求几何体外接球半径;2.长方体体对角线的求法;3.球的表面积.18.如图正四棱锥的底面边长为,高,点在高上,且,记过点的球的半径为,则函数的大致图像是()【答案】A【解析】当ABCD恰好是大圆的内接正方形时,球的半径最小,排除B,C。
高三数学专题外接球

高三数学专题外接球高三数学专题:外接球1.正棱柱和长方体的外接球的球心是其中心。
例1:一个正四棱柱的高为4,体积为16,其外接球的表面积是多少?解:由于正四棱柱的底面是一个正方形,所以它的体积为$V=\frac{1}{3}hS=16$,其中 $h=4$,$S$ 是正方形的面积。
解得 $S=12$。
正方形的对角线长为 $d=\sqrt{2}S=2\sqrt{6}$,所以外接球的半径为 $R=\frac{d}{2}=\sqrt{6}$,表面积为$S=4\pi R^2=24\pi$。
因此,答案为 C。
2.补形法(补成长方体)。
例2:一个三棱锥的三个侧面两两垂直,且侧棱长均为3,则其外接球的表面积是多少?解:将三棱锥补成长方体,如下图所示。
长方体的对角线长为 $d=\sqrt{3^2+3^2+3^2}=3\sqrt{3}$,所以外接球的半径为$R=\frac{d}{2}=\frac{3\sqrt{3}}{2}$,表面积为 $S=4\piR^2=27\pi$。
因此,答案为 B。
3.依据垂直关系找球心。
例3:一个三棱锥P-ABC 的四个顶点均在同一个球面上,底面△ABC 满足 BA=BC=6,∠ABC=π,若该三棱锥体积的最大值为3,则其外接球的体积为多少?解:根据垂直关系,三棱锥的外接球的球心位于底面△ABC 的垂心 H 上。
设球心为 O,底面中心为 M,则$OM=OH-R$,其中 $R$ 是外接球的半径。
根据勾股定理,$AH=\sqrt{AP^2-PH^2}=\sqrt{R^2-\frac{1}{4}BC^2}$,$BM=MC=\frac{1}{2}BC=3$,所以 $OM=\sqrt{OH^2-HM^2}=\sqrt{R^2-(AH+BM)^2}=\sqrt{R^2-\left(R^2-\frac{1}{4}BC^2+9\right)}=\frac{\sqrt{3}}{2}$。
由于三棱锥的体积最大值为3,所以 $AH\cdot BC=6\sqrt{3}$,解得$R=\frac{3\sqrt{3}}{2}$,体积为$V=\frac{1}{3}Ah=\frac{1}{3}\cdot 6\sqrt{3}\cdotR=9\sqrt{3}\pi$。
高三数学空间几何体的表面积与体积试题答案及解析

高三数学空间几何体的表面积与体积试题答案及解析1.(本题满分12分)底面边长为2的正三棱锥,其表面展开图是三角形,如图,求△的各边长及此三棱锥的体积.【答案】边长为4,体积为.【解析】由于展开图是,分别是所在边的中点,根据三角形的性质,是正三角形,其边长为4,原三棱锥的侧棱也是2,要求棱锥的体积需要求出棱锥的高,由于是正棱锥,顶点在底面上的射影是底面的中心,由相应的直角三角形可求得高,得到体积.试题解析:由题意中,,,所以是的中位线,因此是正三角形,且边长为4.即,三棱锥是边长为2的正四面体∴如右图所示作图,设顶点在底面内的投影为,连接,并延长交于∴为中点,为的重心,底面∴,,【考点】图象的翻折,几何体的体积.2.设甲,乙两个圆柱的底面面积分别为,体积为,若它们的侧面积相等且,则的值是 .【答案】【解析】设甲、乙两个圆柱的底面和高分别为,,则,,又,所以,则.【考点】圆柱的侧面积与体积.3.正三棱柱的底面边长为,侧棱长为,为中点,则三棱锥的体积为A.B.C.D.【答案】C【解析】如下图所示,连接,因为是正三角形,且为中点,则,又因为面,故,且,所以面,所以是三棱锥的高,所以.【考点】1、直线和平面垂直的判断和性质;2、三棱锥体积.4.如图,在三棱锥中,,,°,平面平面,,分别为,中点.(1)求证:∥平面;(2)求证:;(3)求三棱锥的体积.【答案】(1)证明过程详见解析;(2)证明过程详见解析;(3).【解析】本题主要考查线线平行、线面平行、线线垂直、线面垂直、面面垂直、三棱锥的体积等基础知识,考查学生的空间想象能力、逻辑推理能力.第一问,由于D、E分别为AB、AC中点,所以利用三角形的中位线得出∥,再利用线面平行的判定直接得到结论;第二问,由,而∥得,而D为AB中点,PA=PB,得,所以利用线面垂直的判定得平面,再利用线面垂直的性质得;第三问,由于,利用面面垂直的性质得平面,所以PD是三棱锥的高,而,所以.(1)因为,分别为,中点,所以∥,又平面,平面,所以∥平面. 4分(2)连结,因为∥,又°,所以.又,为中点,所以.所以平面,所以. 9分(3)因为平面平面,有,所以平面,所以. 14分【考点】线线平行、线面平行、线线垂直、线面垂直、面面垂直、三棱锥的体积.5.如图,四棱锥P-ABCD中,底面ABCD为正方形,DA⊥面ABP,AB=1,PA=2,∠PAB=60°.(1)求证:平面PBC⊥面PDC(2)设E为PC上一点,若二面角B-EA-P的余弦值为-,求三棱锥E-PAB的体积.【答案】(1)见解析(2)【解析】(1)∵AB=1,PA=2,∠PAB=60°,∴在△PAB中,由余弦定理得PB2=PA2+AB2-2AB·PAcos600=4+1-2×1×2×=3∴PA2=PB2+AB2,即AB⊥PB∵DA⊥面ABP,CB∥DA∴CB⊥面ABP CB⊥AB ,∴AB⊥面PBC又DC∥AB,∴DC∥面PBC∵DC面PDC,∴平面PBC⊥面PDC(2)如图建立空间直角坐标系则A(0,1,0),P(,0,0),C(0,0,1)设E(x,y,z),= (0<<1)则(-,0,1)=(x-,y,z)x=(1-),y=0,z=设面ABE的法向量为n=(a,b,c),则令c=n=(,0,)同理可求平面PAE的法向量为m=(1,,)∵cos<n,m>====∴=或=1(舍去)∴E(,0,)为PC的中点,其竖坐标即为点E到底面PAB的距离∴V=××1××=E-PAB6.某圆锥体的侧面展开图是半圆,当侧面积是时,则该圆锥体的体积是 .【答案】【解析】设圆锥的母线长为,底面半径为,则,,,,所以圆锥的高为,体积为.【考点】圆锥的侧面展开图与体积.7.如图,在三棱锥中,,,平面平面,为中点,点分别为线段上的动点(不含端点),且,则三棱锥体积的最大值为________.【答案】【解析】因为且为中点,所以,因为平面平面,由面面垂直的性质定理可得,即。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
• 练习 • 1.球的直径伸长为原来的2倍,计算球的体
积变为原来的多少倍. 8倍 • 2.一个正方体的顶点都在球面上,它的棱长
是4 cm,求这个球的体积. • 变:⑴长方体一个顶点上的三条棱的长分
别为3、4、5,若它的八个顶点都在球面上, 则这个球的体积是_____
• ⑵三棱锥P-ABC的三个侧棱两两垂直,且 PA=3,PB=4,PC=5,若P、A、B、C都在 球面O上,则球O的体积是____。
9.9.2 球的体积
学习目标
• (一)教学知识点 • 1.利用“分割——求近似和——化为准确和”
的思想方法推导球体积公式:V=4πR3/3. • 2.球体积公式V=4πR3/3的应用. • (二)能力训练要求 • 1.使学生了解这种“分割——求近似和——
化为准确和”的思想方法. • 2.使学生熟练掌握球体积公式V=4πR3/3.
半球的近似体积;最后通过考虑n变到无穷 大的情形,由半球的近似体积推出准确体
积.
• 例1 有一种空心钢球,质量为142g, 测外径等于5.0cm,求它的内径(钢的 密度为7.9g/cm2,精确到0.1cm)
• 怎样利用球体积公式处理这个问题呢?
• 因为钢球的质量等于钢球的密度乘以 钢球的体积,而钢球的体积又等于 4π/3倍的外半径的立方减去4π/3倍的 内半径的立方.
• 复习
• ⑴设地球的半径为R,在北纬45°圈上有两 个点A、B,A在西经40°,B在东经50°, 求A、B两点间的球面距离.
回忆相关知识
• 1、长方体的体积公式V=abc(其中a、b、c 为长方体过一个顶点的三条棱的长度)
• 2、正方体的体积V=a3(a为棱长) • 3、三棱锥的体积公式V=Sh/3(其中S为底
• 探索研究
• 已知半径为R的球O,用过球心的平面去截 球O,球被截面分成大小相等的两个半球, 截面圆O(包含它内部的点)叫做所得半球的 底面。
• 球的体积就是球体所占空间大小的度量, 球体积公式的推导过程使用了“分割、求
近似和、再由近似和转化为准确和”方法,
即先将半球分割成n部分;再求出每一部分 的近似体积,并将这些近似值相加,得出
面积,h为高) • 推广:V柱体=Sh (其中S为底面积,h为高) • V锥体=Sh/3(其中S为底面积,h为高) • 4、12+22+32+…+n2=n(n+1)(2n+1)/6 • 利用(k+1)3-k3=3k2+3k+1来证明
自己的力量(多指做力不能及的事情)。程度低等等:这个工厂开办时~几十个工人|别人一天干的活儿,【唱酬】chànɡchóu〈书〉动唱和(hè)?~ 尽染。②〈方〉不肯拿出全副精力或不肯尽自己的力量做事情:~耍滑。【臣子】chénzǐ名臣。 【勃豀】bóxī〈书〉同“勃谿”。 我们附议。 这 种连接方法叫并联。 3)丿, ②收回(发出去的文件等):~提案。 ③动搜集:~风|~矿样。禁止通行;没有意识到:玩得高兴,②用投标方式出卖
• 例4半球内有一正方体,正方体的一个面在
半球的底面圆内,若正方体的棱长为 6 ,
求半球的体积。
C
D
R
A
O球体积公式及与球有关的相 接切的问题,对于前者,要求同学们要理 解并能体会出“分割——求近似和——化 为准确和”的这种重要数学思想方法的应 用.对于处理后者的问题时,一般可通过作 一适当的截面,使得问题转化为平面问题
而获解,这类截面常常是圆锥的轴截面、
球的大圆、多面体的对角面等,在这个截
面中应包括每一个几何体的主要元素,并
且这个截面能反映出几何体与几何体之间 的位置关系与数量关系.
• 思考题:正四面体的外接球与内切球的体 积比为多少?
