吉林省长春市高中毕业班高三数学第三次调研测试试题(文数)

合集下载

吉林省长春市高中毕业班高三数学第三次调研测试试题(文数)

长春市2009年高中毕业班第三次调研测试数学试题（文科）本试卷分为第I 卷（选择题）和第Ⅱ卷（非选择题）两部分，试卷满分150分．做题时间为120分钟。

考试结束后，将试卷和答题卡一并交回。

注意事项：1．答题前，考生必须将自己的姓名、准考证号码填写清楚，将条形码准确粘贴在条形码区域内。

2．选择题必须用2B 铅笔填涂；非选择题必须使用0.5毫米黑色字迹的签字笔书写，字体工整、笔迹清楚。

3．请按照题号顺序在各题目的答题区域内作答，超出答题区域书写的答案无效；在草稿纸、试题卷上答题无效。

4．保持卡面清洁，不要折叠、不要弄破、不准使用涂改液、刮纸刀。

第I 卷（选择题，共60分）一、选择题（本大题共12小题，每小题5分，共60分，在每小题的四个选项中，只有一项是符合题目要求的，请将正确选项填涂在答题卡上。

） 1．015cos 15sin +=（）A ．21B ．23 C ．23 D ．26 2．已知命题“若p 则q ”为真命题，命题“若q 则p ”为假命题，那么p 是q 的（） A ．充要条件 B ．充分不必要条件 C ．必要不充分条件 D ．既不充分也不必要条件 3．已知圆C 与圆x y y y x ==-+关于直线0222对称，则圆C 的方程是（）A ．1)1(22=+-y x B ．1)1(22=-+y xC ．1)1(22=++y xD ．1)1(22=++y x4．在37,)1(x xx 的展开式中-项的系数为（）A ．—35B ．35C ．—21D ．215．集合},,1|||||),{(Z y Z x y x y x M ∈∈≤+=，则集合M 中元素个数为（）A ．1B ．2C ．4D ．56．现有两名教师和4名学生排成一排拍照，要求每一位教师两边都有学生，有多少种不同的排法（） A ．144 B ．256 C ．288 D ．4807．函数⎩⎨⎧<≥+=)0(3),0(1)(||x x x x f x 的图象为（）8．关于函数x x e e x f --=)(的性质说法正确的是（）A ．奇函数且在R 上为增函数B ．奇函数且在R 上为减函数C ．偶函数且在R 上为增函数D ．偶函数且在R 上为减函数9．设地球仪半径为R ，在北纬450纬线圈上A 、B 两点的经度差为900，则A 、B 两点的球面距离为（）A ．6Rπ B ．4R π C ．3R π D ．2R π 10．已知b n a b m a b a n m b a ,,,,,,,,,,成等数列又知且都是正数<成等比数列，则有（） A ．n m > B ．n m =C ．n m <D ．n m ,大小关系不确定11．已知函数)1(,)()(1+===-x f y x f y x f y 且函数互为反函数与函数与函数)0(,0)1(,)1(1f f x f y 则若也互为反函数=+=-=（）A ．0B ．1C ．—1D ．212．已知双曲线e by a x 则离心率的一条渐近线倾斜角],4,6[12222ππθ∈=-的取值范围是（）A ．]2,332[B ．]2,2[C ．]2,332[D ．),332[+∞第Ⅱ卷（非选择题，共90分）二、填空题（本大题共4小题，每小题5分，共20分，把正确答案填在答题卡中的横线上） 13．函数333)(++-=x x x f 的定义域为。

吉林省2018届高三第三次调研考试数学文试题(附参考答案及评分标准)

吉林省一般高中 2017—2018 学年度高中毕业班第三次调研测试文科数学本试卷共 23 小题，共 150 分，共 6 页，考试时间 120 分钟，考试结束后，将答题卡和试题卷一并交回。

一、选择题：本大题共12 题，每题 5 分，共 60 分，在每题给出的四个选项中，只有一个是符合题目要求。

1．设全集 UZ ， A { 1,1, 3,5,7,9}, B { 1,5,7}，则 A (e U B)A. {1,3,9}B. { 1,5, 7}C.{ 1,1, 3,9}D.{ 1,1, 3,5,9}2．已知复数 zi （ i 为虚数单位），则 z 的虚部为 11 i 111 A.B.C.ii2D.2223．已知命题 p : x 0R, x 022 3x 0 ，则命题 p 的否命题为A ．C ．p : x 0 R, x 02 2 3 x 0 B ． p : x R, x22 3 xD ．p : x R, x 2 2 3x p : xR, x 2 2 3x4．以下各组向量中，能够作为基底的是A.e 1 (0,0), e 2 (1, 2)B.e 1 (2, 3), e 2( 1, 3)2 4C.e 1 (3,5), e 2 (6,10)D.e 1 ( 1,2), e 2 (5,7)x y 3 0 5．设 x, y 知足拘束条件x y 0, 则 z 3xy 的最小值是x 2A.5B.4C.3D.116．已知等差数列{a n } 的公差不为 0 ， a 1 1 ，且 a 2 ,a 4 , a 8 成等比数列，设 {a n } 的前 n 项和为S n ，则 S nn(n 1)(n 1)2 n 21n( n 3)A.B.C.2D.2247．以抛物线 y 28 x 上的随意一点为圆心作圆与直线 x 2 相切，这些圆必过必定点，则这必定点的坐标是A.(0, 2) B. (2, 0) C. (4, 0)D.(0, 4)8. 履行以下图的程序框图，当输出S210 时，开始则输入 n 的值能够为输入 nA.6S = 1n = n - 17B.n < 5 ?否S = n SC.8是输出 SD.9结束9．如图，网格纸上小正方形的边长为1，粗实线画出的是某几何体的三视图,则该几何体的体积为14 A.3 10 B.3 正视图侧视图8C.35D.俯视图310．已知锐角知足 cos(4 ) cos2 ，则 sin cos 等于1B.1 C.2 D.2 A.444411．朱世杰是历史上最伟大的数学家之一，他所著的《四元玉鉴》卷中 “如像招数 ”五问有以下问题： “今有官司差夫一千八百六十四人筑堤．只云初日差六十四人，次日转多七人，每人日支米三升，共支米四百三石九斗二升，问筑堤几天 ”．其粗心为： “官府陆续差遣 1864人前去修建堤坝，第一天派出 64 人，从次日开始，每日派出的人数比前一天多7 人，修建堤坝的每人每日赋发大米 3 升，共发出大米 40392 升，问修建堤坝多少天 ”．这个问题中，前 5 天应发大米A. 894 升B. 1170 升C. 1275 米D. 1467 米12．关于定义域为 R 的函数 f ( x ) ，若同时知足以下三个条件：①f (0) 0 ；② 当 x R ，且 x 0 时，都有xf ( x ) 0 ；③ 当x10 x2，且 | x1 | | x2 | 时，都有 f ( x1 ) f ( x2 ) ，则称 f ( x) 为“偏对称函数”．现给出以下三个函数：f1( x) x 33x2；f2( x) e x x 1 ； f3 ( x ) ln(1 x), x 0 2 2 x, x 0则此中是“偏对称函数”的函数个数为A.0B.1C.2D. 3二、填空题：本大题共 4 个小题 ,每题 5 分。

吉林省长春市高考数学三模试卷(文科)

吉林省长春市高考数学三模试卷（文科）姓名:________ 班级:________ 成绩:________一、选择题 (共12题；共24分)1. （2分） (2019高二下·哈尔滨期末) 已知全集，集合，则（）A .B .C .D .2. （2分）(2017·银川模拟) 已知复数z= ，则z的共轭复数 =（）A . 1B . ﹣1C . iD . ﹣i3. （2分） (2018高一上·辽宁期中) 函数的零点所在区间为（）A . （0，）B . （，）C . （，1）D . （1，2）4. （2分）若cos（-x）=﹣，则cos（2x+）=（）A .B . -C .D .5. （2分） (2020高二下·芮城月考) 下列说法正确的是（）A . 在统计学中，回归分析是检验两个分类变量是否有关系的一种统计方法B . 线性回归方程对应的直线至少经过其样本数据点中的，，一个点C . 在残差图中，残差点分布的带状区域的宽度越狭窄，其模型拟合的精度越高D . 在回归分析中，相关指数为的模型比相关指数为的模型拟合的效果差6. （2分） (2019高一下·安庆期中) 在等比数列中，，，则的值为A . 4B . 8C . 16D . 327. （2分） (2019高一上·屯溪期中) 若函数，则（）A . -10B . 10C . -2D . 28. （2分）已知某几何体的三视图如图所示，根据图中标出的尺寸（单位：cm），可得这个几何体的体积是（）A .B .C . 1D . 29. （2分） (2015高三上·承德期末) 已知变量x，y满足约束条件则z=2x+y的最大值为（）A . 1B . 2C . 3D . 410. （2分） (2016高一下·芦溪期末) 如图，程序框图所进行的求和运算是（）A .B .C .D .11. （2分） (2017高三下·武邑期中) 对任意的x，y∈（0，+∞），不等式ex+y﹣4+ex﹣y+4+6≥4xlna恒成立，则正实数a的最大值是（）A .B .C . eD . 2e12. （2分） (2020高二下·宜宾月考) 抛物线的焦点为，点为抛物线上的动点，点为其准线上的动点，当为等边三角形时，其面积为（）A .B .C . 2D .二、填空题 (共4题；共4分)13. （1分） (2018高二上·江苏月考) 过椭圆的左焦点作斜率为1的直线与椭圆C分别交于点A ， B ，是坐标原点，则 ________.14. （1分） (2020高一下·河西期中) 将一颗质地均匀的正方体骰子（六个面的点数分别为1，2，3，4，5，6）先后抛掷两次，记第一次出现的点数为x，第二次出现的点数为y．则事件“x+y≤3”的概率为________．15. （1分） (2016高二上·黑龙江期中) 已知命题p：“直线l：x﹣y+a=0与圆C：（x+1）2+y2=2有公共点”，则a的取值范围是________．16. （1分） (2017高二上·大连期末) 已知椭圆的左、右焦点为F1、F2 ，点F1关于直线y=﹣x的对称点P在椭圆上，则△PF1F2的周长为________．三、解答题：解答应写出文字说明、证明过程或演算步骤． (共7题；共55分)17. （10分） (2016高一下·赣州期中) 已知等差数列{an}的前n项和为Sn ， S3=15，a3和a5的等差中项为9（1）求an及Sn（2）令bn= （n∈N*），求数列{bn}的前n项和Tn ．18. （10分） (2019高三上·广东月考) 某手机软件研发公司为改进产品，对软件用户每天在线的时间进行调查，随机抽取40名男性与20名女性对其每天在线的时间进行了调查统计，并绘制了如图所示的条形图，其中每天的在线时间4h以上（包括4h）的用户被称为“资深用户”．附：，其中n＝a+b+c+d．P（K2≥k0）0.250.150.100.050.025k0 1.323 2.072 2.706 3.841 5.024（1）根据上述样本数据，完成下面的2×2列联表，并判定是否有95%的把握认为是否为“资深用户”与性别有关；“资深用户”非“资深用户”总计男性女性总计（2）用样本估计总体，若从全体用户中随机抽取3人，设这3人中“资深用户”的人数为X，求随机变量X 的分布列与数学期望．19. （5分）如图，在直角梯形ABCD中，AB∥CD，且AB=AD=2，CD=4，四边形ADE1F1是正方形，且平面ADE1F1⊥平面ABCD，M是E1C的中点．（1）证明：BM∥平面ADE1F1；（2）求三棱锥D﹣BME1的体积．20. （5分）已知直线l：与抛物线y=x2交于A，B两点，求线段AB的长．21. （5分）(2018·银川模拟) 已知函数，其中为常数，为自然对数的底数．（I）若在区间上的最大值为，求的值；（Ⅱ）当时，判断方程是否有实根？若无实根请说明理由，若有实根请给出根的个数．22. （10分） (2018高二下·哈尔滨月考) 在直角坐标系中，直线的方程为，曲线的参数方程为．（1）已知在极坐标系（与直角坐标系取相同的长度单位，且以原点为极点，以轴正半轴为极轴）中，求直线的极坐标方程;（2）设点是曲线上的一个动点，求它到直线的距离的最小值．23. （10分）(2020·化州模拟) 设函数 .（1）求不等式的解集；（2）若不等式对任意恒成立，求实数的取值范围.参考答案一、选择题 (共12题；共24分)答案：1-1、考点：解析：答案：2-1、考点：解析：答案：3-1、考点：解析：答案：4-1、考点：解析：答案：5-1、考点：解析：答案：6-1、考点：解析：答案：7-1、考点：解析：答案：8-1、考点：解析：答案：9-1、考点：解析：答案：10-1、考点：解析：答案：11-1、考点：解析：答案：12-1、考点：解析：二、填空题 (共4题；共4分)答案：13-1、考点：解析：答案：14-1、考点：解析：答案：15-1、考点：解析：答案：16-1、考点：解析：三、解答题：解答应写出文字说明、证明过程或演算步骤． (共7题；共55分)答案：17-1、答案：17-2、考点：解析：答案：18-1、答案：18-2、考点：解析：答案：19-1、考点：解析：答案：20-1、考点：解析：答案：21-1、考点：解析：答案：22-1、答案：22-2、考点：解析：答案：23-1、答案：23-2、考点：解析：。

2020届吉林省长春市高三质量监测(三)(三模)数学(文)试题(解析版)

B x lg x 1 x 0 x 10
A B x 0 x 1
故答案选 B
【点睛】本题考查了集合的运算，属于简单题型.
2.已知向量
a,b 满足
a
（2，1）， b
（1，y），且 a
b ，则
a
2b
＝（
）
A. 5
B. 5 2
C. 5
D. 4【答案】C【解 Nhomakorabea】【分析】
根据向量垂直的坐标表示列方程，由此求得 y ，根据向量模的坐标表示求得正确答案.
12
12
12
12
故选：B
【点睛】本小题主要考查三角函数的单调性，考查三角函数的周期性，属于基础题. 9.已知函数 f（x）是定义在 R 上的奇函数，在（0，+∞）上是增函数，且 f（﹣4）＝0，则使得 xf（x）＞0
w＞0）的相邻两交点间的距离为π，则函数
f（x）
的单调递增区间为（）
A.
k
6
，k
5 6
，k
Z
B.
k
12
，k
5 12
，k
Z
C.
k
5 6
，k
11 6
，k
Z
D.
k
5 6
，k
11 12
，k
Z
【答案】B
【解析】
【分析】
根据周期求得，再根据单调区间的求法，求得 f x 的单调区间.
【详解】∵y＝﹣2
6.函数
f
(x)
x3 ex ex
的图象大致为（
）
A.
B.
C.
D.
【答案】B 【解析】【分析】
根据解析式求得函数奇偶性，以及 f 1 即可容易求得结果.

吉林省长春市高考数学三模试卷(文科)(解析版)

2017年吉林省长春市高考数学三模试卷（文科）一、选择题（本大题包括12小题，每小题5分，共60分，每小题给出的四个选项中，只有一项是符合题目要求的，请将正确选项涂在答题卡上）1．已知复数z=1+2i，则=（）A．5 B．5+4i C．﹣3 D．3﹣4i2．已知集合A={x|x2﹣2x﹣3＜0}，B={x||x|＜2}则A∩B=（）A．{x|﹣2＜x＜2}B．{x|﹣2＜x＜3}C．{x|﹣1＜x＜3}D．{x|﹣1＜x＜2} 3．设a，b均为实数，则“a＞|b|”是“a3＞b3”的（）A．充分不必要条件 B．必要不充分条件C．充要条件D．既不充分也不必要条件4．直线x﹣3y+3=0与圆（x﹣1）2+（y﹣3）2=10相交所得弦长为（）A． B．C．4 D．35．下列命题中错误的是（）A．如果平面α外的直线a不平行于平面α内不存在与a平行的直线B．如果平面α⊥平面γ，平面β⊥平面γ，α∩β=l，那么直线l⊥平面γC．如果平面α⊥平面β，那么平面α内所有直线都垂直于平面βD．一条直线与两个平行平面中的一个平面相交，则必与另一个平面相交6．在平面内的动点（x，y）满足不等式，则z=2x+y的最大值是（）A．﹣4 B．4 C．﹣2 D．27．某几何体的三视图如图所示，则其体积为（）A．4 B．C．D．8．某高中体育小组共有男生24人，其50m跑成绩记作a i（i=1，2，…，24），若成绩小于6.8s为达标，则如图所示的程序框图的功能是（）A．求24名男生的达标率B．求24名男生的不达标率C．求24名男生的达标人数 D．求24名男生的不达标人数9．等比数列{a n}中各项均为正数，S n是其前n项和，且满足2S3=8a1+3a2，a4=16，则S4=（）A．9 B．15 C．18 D．3010．函数y=的大致图象是（）A．B．C．D．11．若关于x的方程2sin（2x+）=m在[0，]上有两个不等实根，则m的取值范围是（）A．（1，）B．[0，2]C．[1，2） D．[1，]12．对，23x≤log a x+1恒成立，则实数a的取值范围是（）A．B．C．D．二、填空题（本大题包括4小题，每小题5分，共20分，把正确答案填在答题卡中的横线上）.13．某班级有50名同学，一次数学测试平均成绩是92，其中学号为前30名的同学平均成绩为90，则后20名同学的平均成绩为．14．若函数f（x）=e x•sinx，则f'（0）=．15．《九章算术》是我国第一部数学专著，下有源自其中的一个问题：“今有金箠（chuí），长五尺，斩本一尺，重四斤，斩末一尺，重二斤．问金箠重几何？”其意思为：“今有金杖（粗细均匀变化）长5尺，截得本端1尺，重4斤，截得末端1尺，重2斤．问金杖重多少？”则答案是．16．F为双曲线（a＞b＞0）的左焦点，过点F且斜率为1的直线与两条渐近线分别交于A，B两点，若=，则双曲线的离心率为．三、解答题（本大题包括6小题，共70分，解答应写出文字说明，证明过程或演算步骤）.17．已知点，Q（cosx，sinx），O为坐标原点，函数．（1）求函数f（x）的解析式及最小正周期；（2）若A为△ABC的内角，f（A）=4，BC=3，△ABC的面积为，求△ABC的周长．18．某手机厂商推出一款6吋大屏手机，现对500名该手机用户进行调查，对手机进行评分，评分的频数分布表如下：（1）完成下列频率分布直方图，并指出女性用户和男性用户哪组评分更稳定（不计算具体值，给出结论即可）；（2）根据评分的不同，运用分层抽样从男性用户中抽取20名用户，在这20名用户中，从评分不低于80分的用户中任意抽取2名用户，求两名用户中评分都小于90分的概率．19．如图，四棱锥P ﹣ABCD 的底面ABCD 为矩形，PA ⊥底面ABCD ，AD=AP=2，AB=2，E 为棱PD 的中点．（Ⅰ）证明：PD ⊥平面ABE ；（Ⅱ）求三棱锥C ﹣PBD 外接球的体积．20．已知函数f （x ）=ax ﹣lnx ．（1）过原点O 作曲线y=f （x ）的切线，求切点的横坐标；（2）对∀x ∈[1，+∞），不等式f （x ）≥a （2x ﹣x 2），求实数a 的取值范围． 21．已知椭圆C ：，F 1，F 2分别是其左、右焦点，以F 1F 2为直径的圆与椭圆C有且仅有两个交点．（1）求椭圆C的方程；（2）设过点F1且不与坐标轴垂直的直线l交椭圆于A，B两点，线段AB的垂直平分线与x轴交于点P，点P横坐标的取值范围是，求线段AB长的取值范围．请考生在22、23两题中任选一题作答，如果多做，则按所做的第一题记分．[选修4-4：坐标系与参数方程选讲]（共1小题，满分10分）22．已知在平面直角坐标系xOy中，以坐标原点O为极点，以x轴正半轴为极轴，建立极坐标系，曲线C1的极坐标方程为ρ=4cosθ，直线l的参数方程为（t为参数）．（1）求曲线C1的直角坐标方程及直线l的普通方程；（2）若曲线C2的参数方程为（α为参数），曲线C1上点P的极角为，Q为曲线C2上的动点，求PQ的中点M到直线l距离的最大值．[选修4-5：不等式选讲]（共1小题，满分0分）23．已知a＞0，b＞0，函数f（x）=|x+a|+|2x﹣b|的最小值为1．（1）求证：2a+b=2；（2）若a+2b≥tab恒成立，求实数t的最大值．2017年吉林省长春市高考数学三模试卷（文科）参考答案与试题解析一、选择题（本大题包括12小题，每小题5分，共60分，每小题给出的四个选项中，只有一项是符合题目要求的，请将正确选项涂在答题卡上）1．已知复数z=1+2i，则=（）A．5 B．5+4i C．﹣3 D．3﹣4i【考点】复数代数形式的乘除运算．【分析】由已知直接利用求解．【解答】解：∵z=1+2i，∴=|z|2=．故选：A．2．已知集合A={x|x2﹣2x﹣3＜0}，B={x||x|＜2}则A∩B=（）A．{x|﹣2＜x＜2}B．{x|﹣2＜x＜3}C．{x|﹣1＜x＜3}D．{x|﹣1＜x＜2}【考点】交集及其运算．【分析】解不等式得出集合A、B，根据交集的定义写出A∩B．【解答】解：集合A={x|x2﹣2x﹣3＜0}={x|﹣1＜x＜3}，B={x||x|＜2}={x|﹣2＜x＜2}．故选：D．3．设a，b均为实数，则“a＞|b|”是“a3＞b3”的（）A．充分不必要条件 B．必要不充分条件C．充要条件D．既不充分也不必要条件【考点】必要条件、充分条件与充要条件的判断．【分析】根据充分必要条件的定义判断即可．【解答】解：由a＞|b|”能推出“a3＞b3”，是充分条件，反之，不成立，比如a=1，b=﹣2，不是必要条件，故选：A．4．直线x﹣3y+3=0与圆（x﹣1）2+（y﹣3）2=10相交所得弦长为（）A． B．C．4 D．3【考点】直线与圆相交的性质．【分析】根据已知中圆的标准方程和直线的一般方程，代入圆的弦长公式，可得答案．【解答】解：圆（x﹣1）2+（y﹣3）2=10的圆心坐标为（1，3），半径r=，圆心到直线x﹣3y+3=0的距离d==，故弦AB=2=，故选A．5．下列命题中错误的是（）A．如果平面α外的直线a不平行于平面α内不存在与a平行的直线B．如果平面α⊥平面γ，平面β⊥平面γ，α∩β=l，那么直线l⊥平面γC．如果平面α⊥平面β，那么平面α内所有直线都垂直于平面βD．一条直线与两个平行平面中的一个平面相交，则必与另一个平面相交【考点】命题的真假判断与应用．【分析】由空间中直线与平面的位置关系逐一核对四个选项得答案．【解答】解：如果平面α外的直线a不平行于平面α，则a与α相交，则α内不存在与a平行的直线，故A正确；如图：α⊥γ，α∩γ=a，β⊥γ，β∩γ=b，α∩β=l，在γ内取一点P，过P作PA⊥a于A，作PB⊥b于B，由面面垂直的性质可得PA ⊥l，PB⊥l，则l⊥γ，故B正确；如果平面α⊥平面β，那么平面α内的直线与平面β有三种位置关系：平行、相交、异面，故C错误；一条直线与两个平行平面中的一个平面相交，则必与另一个平面相交，故D正确．故选：C．6．在平面内的动点（x，y）满足不等式，则z=2x+y的最大值是（）A．﹣4 B．4 C．﹣2 D．2【考点】简单线性规划．【分析】画出约束条件的可行域，利用目标函数的几何意义求解最大值即可．【解答】解：不等式组所表示的平面区域位于直线x+y﹣3=0的下方区域和直线x﹣y+1=0的上方区域，根据目标函数的几何意义，可知目标函数经过A时，z取得最大值．由可得A（1，2），所以目标函数z的最大值为4．故选B．7．某几何体的三视图如图所示，则其体积为（）A．4 B．C．D．【考点】由三视图求面积、体积．【分析】通过三视图复原的几何体是正四棱锥，结合三视图的数据，求出几何体的体积．【解答】解：由题意三视图可知，几何体是正四棱锥，底面边长为2的正方形，一条侧棱垂直正方形的一个顶点，长度为2，所以四棱锥的体积．故选D．8．某高中体育小组共有男生24人，其50m跑成绩记作a i（i=1，2，…，24），若成绩小于6.8s为达标，则如图所示的程序框图的功能是（）A．求24名男生的达标率B．求24名男生的不达标率C．求24名男生的达标人数 D．求24名男生的不达标人数【考点】程序框图．【分析】由题意，从成绩中搜索出大于6.8s的成绩，计算24名中不达标率．【解答】解：由题意可知，k记录的是时间超过6.8s的人数，而i记录是的参与测试的人数，因此表示不达标率；故选B．9．等比数列{a n}中各项均为正数，S n是其前n项和，且满足2S3=8a1+3a2，a4=16，则S4=（）A．9 B．15 C．18 D．30【考点】等比数列的前n项和．【分析】设等比数列{a n}的公比为q＞0，由2S3=8a1+3a2，可得2（a1+a2+a3）=8a1+3a2，化为：2q2﹣q﹣6=0，解得q，进而得出．【解答】解：设等比数列{a n}的公比为q＞0，∵2S3=8a1+3a2，∴2（a1+a2+a3）=8a1+3a2，化为：2a3=6a1+a2，可得=6a1+a1q，化为：2q2﹣q﹣6=0，解得q=2．又a4=16，可得a1×23=16，解得a1=2．则S4==30．故选：D．10．函数y=的大致图象是（）A．B．C．D．【考点】函数的图象．【分析】利用函数的定义域排除选项，值域排除选项即可得到结果．【解答】解：由函数定义域排除A，函数的值域．可知x＞0时，y＞0，当x＜0时，y＜0，排除C，D．故选：B．11．若关于x的方程2sin（2x+）=m在[0，]上有两个不等实根，则m的取值范围是（）A．（1，）B．[0，2]C．[1，2） D．[1，]【考点】正弦函数的图象．【分析】把方程2sin（2x+）=m化为sin（2x+）=，画出函数f（x）=sin（2x+）在x∈[0，]上的图象，结合图象求出方程有两个不等实根时m的取值范围．【解答】解：方程2sin（2x+）=m可化为sin（2x+）=，当x∈[0，]时，2x+∈[，]，画出函数y=f（x）=sin（2x+）在x∈[0，]上的图象如图所示；根据方程2sin（2x+）=m在[0，]上有两个不等实根，得≤＜11≤m＜2∴m的取值范围是[1，2）．故选：C．12．对，23x≤log a x+1恒成立，则实数a的取值范围是（）A．B．C．D．【考点】函数恒成立问题；全称命题．【分析】先构造函数f（x）=x2+x，g（x）=﹣log a x．h（x）=f（x）+g（x），将问题等价转化为函数h（x）在区间（0，）上恒有h（x）≤0，又函数为增函数，故可求答案．【解答】解：构造函数f（x）=23x，g（x）=﹣log a x﹣1．h（x）=f（x）+g（x）．（0＜x＜）易知，在区间（0，）上，函数f（x），g（x）均是递增函数，∴函数h（x）=f（x）+g（x）在区间（0，）上是递增函数．由题设可知，函数h（x）在区间（0，）上恒有h（x）≤0．∴必有h（）≤0．即有2﹣log a（）﹣1≤0．整理就是log a a=1≤log a（），∴实数a的取值范围是≤a＜1．故选C．二、填空题（本大题包括4小题，每小题5分，共20分，把正确答案填在答题卡中的横线上）.13．某班级有50名同学，一次数学测试平均成绩是92，其中学号为前30名的同学平均成绩为90，则后20名同学的平均成绩为95．【考点】众数、中位数、平均数．【分析】设学号为31号到50号同学的平均成绩为x，得到关于x的方程，解出即可．【解答】解：设学号为31号到50号同学的平均成绩为x，则92×50=90×30+20x，解得：x=95，故答案为：95．14．若函数f（x）=e x•sinx，则f'（0）=1．【考点】导数的运算．【分析】先求f（x）的导数，再求导数值．【解答】解：f（x）=e x•sinx，f′（x）=（e x）′sinx+e x．（sinx）′=e x•sinx+e x•cosx，∴f'（0）=0+1=1故答案为：115．《九章算术》是我国第一部数学专著，下有源自其中的一个问题：“今有金箠（chuí），长五尺，斩本一尺，重四斤，斩末一尺，重二斤．问金箠重几何？”其意思为：“今有金杖（粗细均匀变化）长5尺，截得本端1尺，重4斤，截得末端1尺，重2斤．问金杖重多少？”则答案是15斤．【考点】等差数列的通项公式．【分析】由题意可知等差数列的首项和第5项，由等差数列的前n项和得答案．【解答】解：由题意可知等差数列中a1=4，a5=2，则S5=，∴金杖重15斤．故答案为：15斤．16．F为双曲线（a＞b＞0）的左焦点，过点F且斜率为1的直线与两条渐近线分别交于A，B两点，若=，则双曲线的离心率为．【考点】双曲线的简单性质．【分析】设出过焦点的直线方程，与双曲线的渐近线方程联立把A，B表示出来，再由条件可得A为FB的中点，运用中点坐标公式，可得a，b，c的关系，然后求双曲线的离心率．【解答】解：设F （﹣c ，0），则过F 作斜率为1的直线为：y=x +c ，而渐近线的方程是：y=±x ，由得：A （﹣，），由得，B （﹣，﹣），若=，可得A 为FB 的中点，可得﹣c ﹣=﹣2•，化为b=3a ，c==a ，e==．故答案为：．三、解答题（本大题包括6小题，共70分，解答应写出文字说明，证明过程或演算步骤）.17．已知点，Q （cosx ，sinx ），O 为坐标原点，函数．（1）求函数f （x ）的解析式及最小正周期；（2）若A 为△ABC 的内角，f （A ）=4，BC=3，△ABC 的面积为，求△ABC的周长．【考点】三角函数中的恒等变换应用；平面向量数量积的运算；正弦定理．【分析】（1）利用向量数量积运算，即可求函数f （x ）的解析式及最小正周期；（2）利用，△ABC 的面积为，求出bc ，利用余弦定理，求出，即可求△ABC 的周长．【解答】解：（1），∴==4﹣2sin （x +），f （x ）的最小正周期为2π；（2）因为f （A ）=4，所，因为0＜A ＜π，所以，因为，所以bc=3，根据余弦定理，所以，即三角形的周长为．18．某手机厂商推出一款6吋大屏手机，现对500名该手机用户进行调查，对手机进行评分，评分的频数分布表如下：（1）完成下列频率分布直方图，并指出女性用户和男性用户哪组评分更稳定（不计算具体值，给出结论即可）；（2）根据评分的不同，运用分层抽样从男性用户中抽取20名用户，在这20名用户中，从评分不低于80分的用户中任意抽取2名用户，求两名用户中评分都小于90分的概率．【考点】列举法计算基本事件数及事件发生的概率；频率分布直方图．【分析】（1）作出女性用户和男性用户的频率分布表，由图可得女性用户更稳定．（2）运用分层抽样从男性用户中抽取20名用户，评分不低于80分有6人，其中评分小于90分的人数为4，记为A ，B ，C ，D ，评分不小于90分的人数为2，记为a，b，设事件M为“两名用户评分都小于90分”从6人人任取2人，利用列举法能求出两名用户中评分都小于90分的概率．【解答】（本小题满分12分）解：（1）女性用户和男性用户的频率分布表分别如下左、右图：由图可得女性用户更稳定．（2）运用分层抽样从男性用户中抽取20名用户，评分不低于80分有6人，其中评分小于90分的人数为4，记为A，B，C，D，评分不小于90分的人数为2，记为a，b，设事件M为“两名用户评分都小于90分”从6人人任取2人，基本事件空间为Ω={（AB），（AC），（AD），（Aa），（Ab），（BC），（BD），（Ba），（Bb），（CD），（Ca），（Cb），（Da），（Db），（ab）}，共有15个元素．M={（AB），（AC），（AD），（BC），（BD），（CD）}，共有6个元素．P（M）=．19．如图，四棱锥P﹣ABCD的底面ABCD为矩形，PA⊥底面ABCD，AD=AP=2，AB=2，E为棱PD的中点．（Ⅰ）证明：PD⊥平面ABE；（Ⅱ）求三棱锥C﹣PBD外接球的体积．【考点】棱柱、棱锥、棱台的体积；直线与平面垂直的判定．【分析】（Ⅰ）以A为原点，AB为x轴，AD为y轴，AP为z轴，建立空间直角坐标系，利用向量法能证明PD⊥平面ABE．（Ⅱ）三棱锥C﹣PBD外接球即以AB，AD，AP为棱的长方体的外接球，由此能求出三棱锥C﹣PBD外接球的体积．【解答】证明：（Ⅰ）以A为原点，AB为x轴，AD为y轴，AP为z轴，建立空间直角坐标系，P（0，0，2），D（0，2，0），A（0，0，0），B（2，0，0），E（0，1，1），=（0，2，﹣2），=（2，0，0），=（0，1，1），=0，=0，∴PD⊥AB，PD⊥AE，∵AB∩AE=A，∴PD⊥平面ABE．解：（Ⅱ）∵AD，AP，AB两垂直，底面ABCD为矩形，∴三棱锥C﹣PBD外接球即以AB，AD，AP为棱的长方体的外接球，∴三棱锥C﹣PBD外接球的半径R==3，∴三棱锥C﹣PBD外接球的体积V===36π．20．已知函数f（x）=ax﹣lnx．（1）过原点O作曲线y=f（x）的切线，求切点的横坐标；（2）对∀x∈[1，+∞），不等式f（x）≥a（2x﹣x2），求实数a的取值范围．【考点】利用导数研究曲线上某点切线方程；利用导数求闭区间上函数的最值．【分析】（1）过原点O作曲线y=f（x）的切线，求出切线方程，即可求切点的横坐标；（2）对∀x∈[1，+∞），不等式f（x）≥a（2x﹣x2），化为ax2﹣ax﹣lnx≥0对∀x∈[1，+∞）恒成立，分类讨论，即可求实数a的取值范围．【解答】解：（1）设切点为（x0，ax0﹣lnx0），∴，直线的切线方程为y﹣（ax0﹣lnx0）=（a﹣）（x﹣x0），又切线过原点﹣ax0+lnx0=﹣ax0+1，所以lnx0=1，解得x0=e，所以切点的横坐标为e．（2）因为不等式ax﹣lnx≥a（2x﹣x2）对∀x∈[1，+∞）恒成立，所以ax2﹣ax﹣lnx≥0对∀x∈[1，+∞）恒成立．设g（x）=ax2﹣ax﹣lnx，g′（x）=2ax﹣a﹣．①当a≤0时，∵，∴g（x）在[1，+∞）上单调递减，即g（x）≤g（1）=0，∴a≤0不符合题意．②当a＞0时，．设，在[1，+∞）上单调递增，即a≥1．（i）当a≥1时，由h（x）≥0，得g'（x）≥0，∴g（x）在[1，+∞）上单调递增，即g（x）≥g（1）=0，∴a≥1符合题意；（ii）当0＜a＜1时，∵a﹣1＜0，∴∃x0∈[1，+∞）使得h（x0）=0，则g（x）在[1，x0）上单调递减，在（x0，+∞）上单调递增，∴g（x0）＜g（1）=0，则0＜a＜1不合题意．综上所述，a≥1．21．已知椭圆C：，F1，F2分别是其左、右焦点，以F1F2为直径的圆与椭圆C有且仅有两个交点．（1）求椭圆C的方程；（2）设过点F1且不与坐标轴垂直的直线l交椭圆于A，B两点，线段AB的垂直平分线与x轴交于点P，点P横坐标的取值范围是，求线段AB长的取值范围．【考点】椭圆的简单性质；直线与椭圆的位置关系．【分析】（1）根据题意，分析可得b=c=1，计算可得a的值，代入椭圆的方程即可得答案；（2）根据题意，设直线AB的方程为y=k（x+1），与联立可得（1+2k2）x2+4k2x+2k2﹣2=0，设A（x1，y1），B（x2，y2），AB的中点为M（x0，y0），由根与系数的关系分析可得直线AB的垂直平分线方程，由弦长公式可以表示|AB|，计算可得答案．【解答】解：（1）根据题意，因为以F1F2为直径的圆与椭圆C有且仅有两个交点，所以b=c=1，即a==，即椭圆C的方程为，（2）根据题意，过点F1且不与坐标轴垂直的直线l交椭圆于A，B两点，即直线AB的斜率存在，设直线AB的方程为y=k（x+1），与联立，得（1+2k2）x2+4k2x+2k2﹣2=0，设A（x1，y1），B（x2，y2），AB的中点为M（x0，y0），，，，即，设直线AB的垂直平分线方程为，令y=0，得，因为，所以=；即线段AB长的范围是（，2）．请考生在22、23两题中任选一题作答，如果多做，则按所做的第一题记分．[选修4-4：坐标系与参数方程选讲]（共1小题，满分10分）22．已知在平面直角坐标系xOy中，以坐标原点O为极点，以x轴正半轴为极轴，建立极坐标系，曲线C1的极坐标方程为ρ=4cosθ，直线l的参数方程为（t为参数）．（1）求曲线C1的直角坐标方程及直线l的普通方程；（2）若曲线C2的参数方程为（α为参数），曲线C1上点P的极角为，Q为曲线C2上的动点，求PQ的中点M到直线l距离的最大值．【考点】简单曲线的极坐标方程；参数方程化成普通方程．【分析】（1）曲线C1的极坐标方程为ρ=4cosθ，即ρ2=4ρcosθ，可得直角坐标方程．直线l的参数方程为（t为参数），消去参数t可得普通方程．（2），直角坐标为（2，2），，利用点到直线的距离公式及其三角函数的单调性可得最大值．【解答】解：（1）曲线C1的极坐标方程为ρ=4cosθ，即ρ2=4ρcosθ，可得直角坐标方程：．直线l的参数方程为（t为参数），消去参数t可得普通方程：x+2y﹣3=0．（2），直角坐标为（2，2），，∴M到l的距离≤，从而最大值为．[选修4-5：不等式选讲]（共1小题，满分0分）23．已知a＞0，b＞0，函数f（x）=|x+a|+|2x﹣b|的最小值为1．（1）求证：2a+b=2；（2）若a+2b≥tab恒成立，求实数t的最大值．【考点】函数恒成立问题；绝对值不等式的解法．【分析】（1）法一：根据绝对值的性质求出f（x）的最小值，得到x=时取等号，证明结论即可；法二：根据f（x）的分段函数的形式，求出f（x）的最小值，证明即可；（2）法一，二：问题转化为≥t恒成立，根据基本不等式的性质求出的最小值，从而求出t的范围即可；法三：根据二次函数的性质判断即可．【解答】解：（1）法一：f（x）=|x+a|+|2x﹣b|=|x+a|+|x﹣|+|x﹣|，∵|x+a|+|x﹣|≥|（x+a）﹣（x﹣）|=a+且|x﹣|≥0，∴f（x）≥a+，当x=时取等号，即f（x）的最小值为a+，∴a+=1，2a+b=2；法二：∵﹣a＜，∴f（x）=|x+a|+|2x﹣b|=，显然f（x）在（﹣∞，]上单调递减，f（x）在[，+∞）上单调递增，∴f（x）的最小值为f（）=a+，∴a+=1，2a+b=2．（2）方法一：∵a+2b≥tab恒成立，∴≥t恒成立，=+=（+）（2a+b ）•=（1+4++），当a=b=时，取得最小值，∴≥t，即实数t的最大值为；方法二：∵a+2b≥tab恒成立，∴≥t恒成立，t≤=+恒成立，+=+≥=，∴≥t，即实数t的最大值为；方法三：∵a+2b≥tab恒成立，∴a+2（2﹣a）≥ta（2﹣a）恒成立，∴2ta2﹣（3+2t）a+4≥0恒成立，∴（3+2t）2﹣326≤0，∴≤t≤，实数t的最大值为．2017年4月18日。

2013年长春市高中毕业班第三次调研测试文科数学

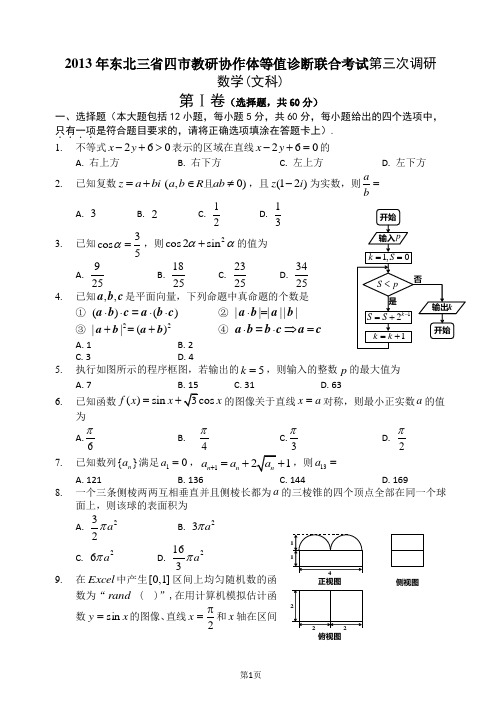
2013年东北三省四市教研协作体等值诊断联合考试第三次调研数学(文科)第Ⅰ卷（选择题，共60分）一、选择题（本大题包括12小题，每小题5分，共60分，每小题给出的四个选项中，只有一项．．．．是符合题目要求的，请将正确选项填涂在答题卡上）. 1. 不等式260x y -+>表示的区域在直线260x y -+=的 A. 右上方 B. 右下方 C. 左上方D. 左下方2. 已知复数z a bi =+(,0)a b R ab ∈≠且，且(12)z i -为实数，则ab= A. 3B. 2C.12D.133. 已知3cos 5α=，则2cos 2sin αα+的值为 A.925B. 1825C. 2325D. 34254. 已知,,a b c 是平面向量，下列命题中真命题的个数是① ()()⋅⋅⋅⋅a b c =a b c ② ||||||⋅= a b a b③ 22||()+=+a b a b ④ ⋅⋅⇒=a b =b c a cA. 1B. 2C. 3D. 45. 执行如图所示的程序框图，若输出的5k =，则输入的整数p 的最大值为A. 7B. 15C. 31D. 636.已知函数()sin f x x x =的图像关于直线x a =对称，则最小正实数a 的值为A.6π B.4π C.3π D.2π 7. 已知数列{}n a 满足10a =，11n n a a +=+，则13a =A. 121B. 136C. 144D. 1698. 一个三条侧棱两两互相垂直并且侧棱长都为a 的三棱锥的四个顶点全部在同一个球面上，则该球的表面积为A.232a πB. 23a πC. 26a π D. 2163a π9. 在Excel 中产生[0,1]区间上均匀随机数的函数为“rand ( )”,在用计算机模拟估计函数x y sin =的图像、直线2π=x 和x 轴在区间正视图侧视图俯视图0,2π⎡⎤⎢⎥⎣⎦上部分围成的图形面积时，随机点11(,)a b 与该区域内的点),(b a 的坐标变换公式为 A. 11,2a ab b π=+= B. 112(0.5),2(0.5)a a b b =-=-C. [0,],[0,1]2a b π∈∈ D. 11,2a ab b π==10. 已知抛物线28y x =的焦点为F ，直线(2)y k x =-与此抛物线相交于,P Q 两点，则11||||FP FQ += A. 12B. 1C. 2D. 411. 如图所示是一个几何体的三视图，则该几何体的体积为A. 162π+B. 82π+C. 16π+D. 8π+12. 若函数()f x 对任意的x ∈R 都有(3)(1)f x f x +=-+，且(1)2013f =，则[(2013)2]1f f ++= A. 2013- B. 2012- C. 2012 D. 2013第Ⅱ卷（非选择题，共90分）本卷包括必考题和选考题两部分，第13题－21题为必考题，每个试题考生都必须作答，第22题－24题为选考题，考生根据要求作答. 二、填空题(本大题包括4小题，每小题5分，共20分，把正确答案填在答题卡中的横线上). 13. 函数2()lg(34)f x x x =+-的定义域为____________.14. 若等比数列{}n a 的首项是1a ，公比为q ，n S 是其前n 项和，则n S =_____________.15. 双曲线22221(0,0)x y a b a b-=>>的左、右焦点分别为1F 和2F ，左、右顶点分别为1A 和2A ，过焦点2F 与x 轴垂直的直线和双曲线的一个交点为P ，若2112PA 是22PA和2122A A 的等差中项，则该双曲线的离心率为 .16. 已知集合224{(,)|(3)(4)}5A x y x y =-+-=，{(,)|2|3||4|}B x y x y λ=-+-=，若A B ≠∅ ，则实数λ的取值范围是__________. 三、解答题（本大题包括6小题，共70分，解答应写出文字说明，证明过程或演算步骤）. 17. （本小题满分12分）在三角形ABC 中，sin 2cos cos 2sin C C C C C ⋅+=⋅+⑴ 求角C 的大小；⑵ 若2AB =，且sin cos sin 2B A A ⋅=，求ABC ∆的面积.18. （本小题满分12分） 2012年第三季度，国家电网决定对城镇居民民用电计费标准做出调整，并根据用电情况将居民分为三类: 第一类的用电区间在(0,170]，第二类在(170,260]，第三类在(260,)+∞（单位：千瓦时）. 某小区共有1000户居民，现对他们的用电情况进行调查，得到频率分布直方图如图所示.⑴ 求该小区居民用电量的中位数与平均数；⑵ 本月份该小区没有第三类的用电户出现，为鼓励居民节约用电，供电部门决定：对第一类每户奖励20元钱，第二类每户奖励5元钱，求每户居民获得奖励的平均值；⑶ 利用分层抽样的方法从该小区内选出5户居民代表，若从该5户居民代表中任选两户居民，求这两户居民用电资费属于不同类型的概率.19. （本小题满分12分）如图，E 是矩形ABCD 中AD 边上的点，F 为CD边的中点，243AB AE AD ===，现将ABE ∆沿BE 边折至PBE ∆位置，且平面PBE ⊥平面BCDE .⑴ 求证：平面PBE ⊥平面PEF ；⑵ 求四棱锥P BEFC -的体积. 20．（本小题满分12分）如图，曲线2:M y x =与曲线222:(4)2(0)N x y m m -+=>相交于A 、B 、C 、D 四个点.⑵ 求m 的取值范围；⑵ 求四边形ABCD 的面积的最大值及此时对角线AC 与BD 的交点坐标.21（本小题满分12分）已知函数()sin xf x e x =.⑴ 求函数()f x 的单调区间； ⑵ 如果对于任意的[0,]2x π∈，()kx f x ≥总成立，求实数k 的取值范围；⑶ 是否存在正实数m ，使得：当(0,)x m ∈时，不等式21()22x f x x <+恒成立？请给出结论并说明理由.PB C D FE (1)(2)请考生在22、23、24三题中任选一题做答，如果多做，则按所做的第一题记分. 22．（本小题满分10分）选修4－1：几何证明选讲. 如图，AB 是O 的直径，弦CD 与AB 垂直，并与AB 相交于点E ，点F 为弦CD 上异于点E 的任意一点，连结BF 、AF 并延长交O 于点M 、N .⑴ 求证：B 、E 、F 、N 四点共圆； ⑵ 求证：22AC BF BM AB +⋅=.23．（本小题满分10分）选修4－4：坐标系与参数方程选讲.在直角坐标系xOy 中，曲线1C 的参数方程为2cos ()1sin x t t y t απαα<=+⎧⎨=+⎩≤是参数,0，以原点O 为极点，x 轴正半轴为极轴建立极坐标系，曲线2C 的极坐标方程为2221cos ρθ=+. ⑴ 求曲线1C 的普通方程和曲线2C 的直角坐标方程；⑵ 当4πα=时，曲线1C 和2C 相交于M 、N 两点，求以线段MN 为直径的圆的直角坐标方程.24．（本小题满分10分）选修4－5：不等式选讲.设函数()|1||5|f x x x =++-，∈x R ．⑴ 求不等式()10f x x +≤的解集；⑵ 如果关于x 的不等式2()(2)f x a x --≥在R 上恒成立，求实数a 的取值范围．2013年东北三省四市教研协作体等值诊断联合考试2013年长春市高中毕业班第三次调研测试数学(文科)参考答案及评分标准一、选择题(本大题包括12小题，每小题5分，共60分)1.B2.C3.A4.A5.B6.A7.C8.B9.D 10.A 11.B 12.B 简答与提示：1. 【命题意图】本小题主要考查二元一次不等式所表示的区域位置问题，是线性规划的一种简单应用，对学生的数形结合思想提出一定要求. 【试题解析】B 右下方为不等式所表示区域，故选B.2. 【命题意图】本小题主要考查复数的基本运算，特别是共轭复数的乘法运算以及对共轭复数的基本性质的考查，对考生的运算求解能力有一定要求.【试题解析】C 由(12)z i ⋅-为实数，且0z ≠，所以可知(12)z k i =+，0k ≠，则122a kb k ==，故选C. 3. 【命题意图】本小题主要考查同角三角函数的基本关系式以及倍角的余弦公式的应用，对学生的化归与转化思想以及运算求解能力提出一定要求.【试题解析】A由3cos 5α=，得22229cos 2sin 2cos 11cos cos 25ααααα+=-+-==，故选A. 4. 【命题意图】本小题主要考查平面向量的定义与基本性质，特别是对平面向量运算律的全面考查，另外本题也对考生的分析判断能力进行考查.【试题解析】A 由平面向量的基础知识可知①②④均不正确，只有③正确，故选A.5. 【命题意图】本小题主要通过程序框图的理解考查学生的逻辑推理能力，同时考查学生对算法思想的理解与剖析.【试题解析】B 有程序框图可知：①0S =，1k =；②1S =，2k =；③3S =，3k =；④7S =，4k =； ⑤15S =，5k =. 第⑤步后k 输出，此时15S P =≥，则P 的最大值为15，故选B.6. 【命题意图】本题着重考查三角函数基础知识的应用，对于三角函数的对称性也作出较高要求. 本小题同时也考查考生的运算求解能力与考生的数形结合思想.【试题解析】A函数()sin 2sin()3f x x x x π==+的对称轴为x a =，则32a k πππ+=+，即()6a k k Z ππ=+∈，因此a 的最小正数值为6π. 故选A. 7. 【命题意图】本小题主要考查数列的递推问题，以及等差数列的通项公式，也同时考查学生利用构造思想解决问题的能力以及学生的推理论证能力.【试题解析】C 由11n n a a +=+，可知211)n a +=，1=，故是公差为11212==，则13144a =. 故选C.8.【命题意图】本小题主要考查立体几何中球与球的内接几何体中基本量的关系，以及球表面积公式的应用，本考点是近年来高考中的热点问题，同时此类问题对学生的运算求解能力与空间想象能力也提出较高要求.【试题解析】B 由题可知该三棱锥为一个棱长a的正方体的一角，则该三棱锥与，则球半径为2a，则22244()32S r a aπππ===. 故选B.9.【命题意图】本小题主要考查均匀随机数的定义与简单应用，对于不同尺度下点与点的对应方式也做出一定要求. 本题着重考查考生数据处理的能力，与归一化的数学思想.【试题解析】D. 由于[0,]2aπ∈，[0,1]b∈，而1[0,1]a∈，1[0,1]b∈，所以坐标变换公式为12a aπ=，1b b=. 故选D.10.【命题意图】本小题是定值问题，考查抛物线的定义与基本性质及过焦点的弦的性质. 本题不但对考生的运算求解能力、推理论证能力有较高要求，而且对考生的化归与转化的数学思想也有较高要求.【试题解析】A 设11(,)P x y，22(,)Q x y，由题意可知，1||2PF x=+，2||2QF x=+，则1212121241111||||222()4x xFP FQ x x x x x x+++=+=+++++，联立直线与抛物线方程消去y得，2222(48)40k x k x k-++=，可知124x x=，故121212121244111||||2()42()82x x x xFP FQ x x x x x x+++++===+++++. 故选A.11.【命题意图】本小题主要考查立体几何中的三视图问题，并且对考生的空间想象能力及利用三视图还原几何体的能力进行考查，同时考查简单几何体的体积公式.【试题解析】B 由图可知该几何体是由两个相同的半圆柱与一个长方体拼接而成，因此21241282Vππ=⨯⨯+⨯⨯=+. 故选B.12.【命题意图】本小题着重考查函数的周期性问题，以及复合函数的求值问题，对于不同的表达式，函数周期性的意义也不同，此类问题时高考中常见的重要考点之一，请广大考生务必理解函数的周期与对称问题.本题主要对考生的推理论证能力与运算求解能力进行考查.【试题解析】B 由(3)(1)f x f x+=-+可知函数()f x周期4T=，当0x=时可知，(3)(1)2013f f=-=-，(2013)(1)2013f f==，因此[(2013)2]1(2015)1(3)12012f f f f++=+=+=-. 故选B.二、填空题(本大题包括4小题，每小题5分，共20分)13. (,4)(1,)-∞-+∞14.11(1)111nna qqS qna q⎧-≠⎪=-⎨⎪ =⎩15. 216. 2] 简答与提示：13. 【命题意图】本小题主要考查对数函数的性质与其定义域的求取问题，以及一元二次不等式的解法.本小题着重考查考生的数学结合思想的应用.【试题解析】由题意可知2340x x +->，解得4x <-或1x >，所以函数()f x 的定义域为(,4)(1,)-∞-+∞ .14. 【命题意图】本小题主要考查等比数列的前n 项和公式的推导与应用，同时考查了学生的分类讨论思想.【试题解析】根据等比数列前n 项和公式：11(1)111n n a q q S qna q ⎧- ≠⎪= -⎨⎪ =⎩. 15. 【命题意图】本小题主要考查双曲线中各基本量间的关系，特别是考查通径长度的应用以及相关的计算，同时也对等差中项问题作出了一定要求. 同时对考生的推理论证能力与运算求解能力都有较高要求.【试题解析】由题可知2221212||||2||PA PA A A =+ ，则4422222()()8b b c a c a a a a ++=+-+，化简得248ac a =，故2c e a==. 16. 【命题意图】本小题主要考查曲线与方程的实际应用问题，对学生数形结合与分类讨论思想的应用作出较高要求.【试题解析】由题可知，集合A 表示圆224(3)(4)5x y -+-=上点的集合，集合B 表示曲线2|3||4|x y λ-+-=上点的集合，此二集合所表示的曲线的中心都在(3,4)处，集合A 表示圆，集合B 则表示菱形，可以将圆与菱形的中心同时平移至原点，如图所示，可求得λ的取值范围是2]. 三、解答题(本大题必做题5小题，三选一选1小题，共70分) 17. (本小题满分12分)【命题意图】本题针对三角变换公式以及解三角形进行考查，主要涉及三角恒等变换，正、余弦定理等内容，对学生的逻辑思维能力提出较高要求.【试题解析】(1)由sin 2cos cos 2sin C C C C C -=，化简得sin C C =，即sin C C +=，即2sin()3C π+= (3分)则sin()32C π+=，故233C ππ+=或3π(舍)，则3C π=. (6分)(2) 因为sin cos 2sin cos B A A A =，所以cos 0A =或sin 2sin B A =. (7分)当cos 0A =时，90A =︒,则b =,112223ABC S b c ∆=⋅⋅==; (8分)当sin 2sin B A =时，由正弦定理得2b a =.所以由22222441cos 2222a b c a a C ab a a +-+-===⋅⋅，可知24a =.(10分) 所以211sin 222ABC S b a C a a∆=⋅⋅⋅=⋅⋅==(11分) 综上可知ABC S ∆= (12分)18. (本小题满分12分)【命题意图】本小题主要考查统计与概率的相关知识，其中包括中位数与平均数的求法、对于随机事件出现情况的分析与统计等知识的初步应用. 本题主要考查学生的数据处理能力.【试题解析】解：(1) 因为在频率分布直方图上，中位数的两边面积相等，可得中位数为155. (2分) 平均数为 1200.005201400.075201600.020201800.00520⨯⨯+⨯⨯+⨯⨯+⨯⨯2000.003202200.00220156.8+⨯⨯+⨯⨯=.(4分) (2) 10000.82010000.258002020051710001000⨯⨯+⨯⨯⨯+⨯==(元). (7分)(3) 由题可知，利用分层抽样取出的5户居民中属于第一类的有4户，编为,,,A B C D ，第二类的有1户，编为a . 现从5户中选出2户，所有的选法有aA ，aB ，aC ，aD ，AB ，AC ，AD ，BC ，BD ，CD 共计10种，其中属不同类型的有aA ，aB ，aC ，aD 共计4种.(10分) 因此，两户居民用电资费属不同类型的概率42105P ==.(12分)19. (本小题满分12分)【命题意图】本小题主要考查立体几何的相关知识，具体涉及到线面、面面的垂直关系、空间几何体体积的求取. 本小题对考生的空间想象能力与运算求解能力有较高要求.【试题解析】解：(1) 证明：由题可知，4545ED DF DEF DEF ED DF EF BEAE AB ABE AEB AE AB =⎫⎫∆ ⇒∠=︒⎬⎪⊥⎭⎪⇒⊥⎬=⎫⎪∆ ⇒∠=︒ ⎬⎪⊥⎭⎭中中 (3分)ABE BCDEABE BCDE BE EF PBE PBE PEF EF BE EF PEF ⎫⊥⎫⎪⎪=⇒⊥⎬⎪⇒⊥⎬⎪⊥⎭⎪⎪ ⊂⎭ 平面平面平面平面平面平面平面平面 (6分) (2) 116444221422BEFC ABCD ABE DEF S S S S =--=⨯-⨯⨯-⨯⨯=，则1114333BEFCV S h=⋅⋅=⨯⨯=. (12分) 20.(本小题满分12分)【命题意图】本小题主要考查直线与圆锥曲线的综合应用能力，具体涉及到直线与圆锥曲线的相关知识以及圆锥曲线中极值的求取. 本小题对考生的化归与转化思想、运算求解能力都有很高要求.【试题解析】解：(1) 联立曲线,M N消去y可得22(4)20x x m-+-=，226160x x m-+-=，根据条件可得212212364(16)060160mx xx x m⎧∆=-->⎪+=>⎨⎪=->⎩，4m<<.(4分)(2) 设11(,)A x y，22(,)B x y，21x x>，1y>，2y>则122121()())ABCDS y y x x x x=+-=-==.(6分)令t=，则(0,3)t∈，ABCDS==，(7分) 设32()3927f t t t t=--++，则令22()3693(23)3(1)(3)0f t t t t t t t'=--+=-+-=--+=，可得当(0,3)t∈时，()f x的最大值为(1)32f=，从而ABCDS的最大值为16.此时1t=1=，则215m=. (9分) 联立曲线,M N的方程消去y并整理得2610x x-+=，解得13x=-23x=+，所以A点坐标为(31)-，C点坐标为(31)+，12ACk==-，则直线AC的方程为11)[(32y x--=---，(11分) 当0y=时，1x=，由对称性可知AC与BD的交点在x轴上，即对角线AC与BD交点坐标为(1,0). (12分)21.(本小题满分12分)【命题意图】本小题主要考查函数与导数的综合应用能力，具体涉及到用导数来描述函数的单调性、极值以及函数零点的情况. 本小题主要考查考生分类讨论思想的应用，对考生的逻辑推理能力与运算求解有较高要求.【试题解析】解：(1) 由于()sinxf x e x=，所以'()sin cos (sin cos )sin()4x x x x f x e x e x e x x x π=+=+=+.(2分) 当(2,2)4x k k ππππ+∈+，即3(2,2)44x k k ππππ∈-+时，'()0f x >；当(2,22)4x k k πππππ+∈++，即37(2,2)44x k k ππππ∈++时，'()0f x <.所以()f x 的单调递增区间为3(2,2)44k k ππππ-+()k Z ∈，单调递减区间为37(2,2)44k k ππππ++()k Z ∈.(4分) (2) 令()()sin xg x f x kx e x kx =-=-，要使()f x kx ≥总成立，只需[0,]2x π∈时min ()0g x ≥.对()g x 求导得()(sin cos )xg x e x x k '=+-，令()(sin cos )xh x e x x =+，则()2cos 0xh x e x '=>，((0,)2x π∈)所以()h x 在[0,]2π上为增函数，所以2()[1,]h x e π∈.(6分)对k 分类讨论：① 当1k ≤时，()0g x '≥恒成立，所以()g x 在[0,]2π上为增函数，所以min ()(0)0g x g ==，即()0g x ≥恒成立；② 当21k e π<<时，()0g x '=在上有实根0x ，因为()h x 在(0,)2π上为增函数，所以当0(0,)x x ∈时，()0g x '<，所以0()(0)0g x g <=，不符合题意；③ 当2k e π≥时，()0g x '≤恒成立，所以()g x 在(0,)2π上为减函数，则()(0)0g x g <=，不符合题意.综合①②③可得，所求的实数k 的取值范围是(,1]-∞.(9分)(3) 存在正实数m 使得当(0,)x m ∈时，不等式21()22x f x x <+恒成立. 理由如下：令2()sin 22xx g x e x x =--，要使2()22x f x x <+在(0,)m 上恒成立，只需()0max g x <. (10分)因为()(sin cos )2xg x e x x x '=+--，且(0)10g '=-<，2()(2)022g e πππ'=-+>，所以存在正实数0(0,)2x π∈，使得0()0g x '=，当0(0,)x x ∈时，()0g x '<，()g x 在0(0,)x 上单调递减，即当0(0,)x x ∈时，()(0)0g x g <=，所以只需0(0,)m x ∈均满足：当(0,)x m ∈时，21()22x f x x <+恒成立.(12分)注：因为332.719e e π>>>，22(2)4162π+<=，所以2(2)02e ππ-+>22. (本小题满分10分)【命题意图】本小题主要考查平面几何的证明，具体涉及到四点共圆的证明、圆中三角形相似等内容. 本小题重点考查考生对平面几何推理能力. 【试题解析】解 (1)连结BN ，则AN BN ⊥，又CD AB ⊥，则90BEF BNF ∠=∠=︒，即180BEF BNF ∠+∠=︒，则B 、E 、F 、N 四点共圆. (5分)(2)由直角三角形的射影原理可知2AC AE AB =⋅，由Rt BEF ∆与Rt BMA ∆相似可知：BF BEBA BM=， ()BF BM BA BE BA BA EA ⋅=⋅=⋅-，2BF BM AB AB AE ⋅=-⋅，则22BF BM AB AC ⋅=-，即22AC BF BM AB +⋅=.(10分)23. (本小题满分10分)【命题意图】本小题主要考查极坐标系与参数方程的相关知识，具体涉及到极坐标方程与平面直角坐标方程的互化、平面内直线与曲线的位置关系等内容. 本小题考查考生的方程思想与数形结合思想，对运算求解能力有一定要求. 【试题解析】解：(1)对于曲线1C 消去参数t 得：当2πα≠时，1:1tan (2)C y x α-=-；当2πα=时，1:2C x =.(3分)对于曲线2C ：222cos 2ρρθ+=，2222x y x ++=，则222:12y C x +=. (5分)(2) 当4πα=时，曲线1C 的方程为10x y --=，联立12,C C 的方程消去y 得222(1)20x x +--=，即23210x x --=，||MN ====圆心为1212(,)22x x y y ++，即12(,)33-，从而所求圆方程为22128()()339x y -++=.(10分)24. (本小题满分10分)【命题意图】本小题主要考查不等式的相关知识，具体涉及到绝对值不等式及不等式证明等内容. 本小题重点考查考生的化归与转化思想.【试题解析】解：(1) 24()624x f x x -+⎧⎪=⎨⎪-⎩1155x x x <--≤≤>(2分)当1x <-时，2410x x -+≤+，2x ≥-，则21x -≤<-；当15x -≤≤时，610x ≤+，4x ≥-，则15x -≤≤；当 5x >时，2410x x -≤+，14x ≤，则514x <≤. 综上可得，不等式的解集为[2,14]-.(5分)(2) 设2()(2)g x a x =--，由函数()f x 的图像与()g x 的图像可知：()f x 在[1,5]x ∈-时取最小值为6，()f x 在2x =时取最大值为a ，若()()f x g x ≥恒成立，则6a ≤.(10分)。

吉林省长春市高考数学三模试卷文科解析版

2017年吉林省长春市高考数学三模试卷（文科）一、选择题（本大题包括12小题，每小题5分，共60分，每小题给出的四个选项中，只有一项是符合题目要求的，请将正确选项涂在答题卡上） 1 •已知复数z=1+2i ，则|「』=（）A. 5B. 5+4iC.— 3 D . 3-4i2•已知集合 A={x|x 2-2x - 3V 0}，B={x|| x| V 2}则 A H B=（）A. {x| — 2V x v 2}B. {x| — 2V x v 3}C. {x| — 1V x v 3}D. {x| — 1v x v 2} 3.设a ，b 均为实数，则“A |b|”是“3i >b 3”—)A .充分不必要条件B.必要不充分条件 C.充要条件D.既不充分也不必要条件4. 直线x — 3y+3=0与圆（x — 1） 2+ （y — 3） 2=10相交所得弦长为（） A.-.1 B.C. 4 ■■:D. 3. ■:5. 下列命题中错误的是（C. 如果平面a 丄平面B 那么平面a 内所有直线都垂直于平面 B D. 一条直线与两个平行平面中的一个平面相交，则必与另一个平面相交°：」| ，A.— 4 B. 4 C. — 2 D . 27. 某几何体的三视图如图所示，则其体积为（Z zd 2rA .如果平面a 外的直线a 不平行于平面 a 内不存在与a 平行的直线B.如果平面 a 丄平面丫，平面B 丄平面 Y aH B =l 那么直线I 丄平面丫 6.在平面内的动点（x, y ）满足不等式则z=2x+y 的最大值是（）I? 4 SA. 4 B•旨辽D. T8. 某高中体育小组共有男生24人，其50m跑成绩记作a i （i=1，2，…，24），若成绩小于为达标，则如图所示的程序A.求24名男生的达标率C•求24名男生的达标人数 D.求24名男生的不达标人数框图的功能是（B. 求24名男生的不达标率9. 等比数列｛a n｝中各项均为正数，S是其前n项和，且满足2S3=8ai+3a2, a4=16, 则S^=（）A. 9B. 15C. 18D. 30取值范围是（）TV 若关于x 的方程2sin (2x+——)=m 在［0,兀一］上有两个不等实根，则10.函数y=J 的大致图象是（）11.A. (I,'；)B. [0, 2]C. [1, 2)D. [1,-；]12•对■■二,23x< log a x+1恒成立，则实数a的取值范围是( )A. ( 0 ,寻)B. (「寺]C.[寺・1 ) D•[寺・1)二、填空题(本大题包括4小题，每小题5分，共20分，把正确答案填在答题卡中的横线上)•13. 某班级有50名同学，一次数学测试平均成绩是92,其中学号为前30名的同学平均成绩为90,则后20名同学的平均成绩为 _.14. 若函数f (x)=e?sinx,贝U f ( 0)= ____ .15•《九章算术》是我国第一部数学专着，下有源自其中的一个问题：今有金箠(chu)长五尺，斩本一尺，重四斤，斩末一尺，重二斤.问金箠重几何？”其意思为：今有金杖(粗细均匀变化)长5尺，截得本端1尺，重4斤，截得末端1尺，重2斤.问金杖重多少？”则答案是 _.2 216. F为双曲线(a>b>0)的左焦点，过点F且斜率为1的直线与两|a21/条渐近线分别交于A, B两点，若+十丄，则双曲线的离心率为—.三、解答题(本大题包括6小题，共70分，解答应写出文字说明，证明过程或演算步骤).17. 已知点P (亦，1), Q (cosx, si nx), O 为坐标原点，函数 f (x) = OP .(1)求函数f (x)的解析式及最小正周期；(2)若A ABC的内角，f (A) =4, BC=3 △ ABC的面积为斗,求厶ABC 的周长.18 .某手机厂商推出一款6寸大屏手机，现对500名该手机用户进行调查，对手机进行评分，评分的频数分布表如下：女性用分值区[50, 60) [60, 70) [70, 80) [80, 90) [90, 100] 户间频数20 40 80 50 10囲性刑尸(2)根据评分的不同，运用分层抽样从男性用户中抽取 20名用户，在这20名用户中，从评分不低于80分的用户中任意抽取2名用户，求两名用户中评分都小于90分的概率.19. 女口图，四棱锥P — ABCD 的底面ABCD 为矩形，PA ±底面ABCD , AD=AP=2 AB=2 \ E 为棱PD 的中点. (I )证明：PD 丄平面ABE(U)求三棱锥C — PBD 外接球的体积.20. 已知函数 f (x ) =ax — lnx .(1) 过原点O 作曲线y=f (x )的切线，求切点的横坐标；频数 45 75 90 60 30(1)完成下列频率分布直方图, 并指出女性用户和男性用户哪组评分更稳定 (不计算具体值，给出结论即可)；C Jr 11 1 *4-Z ■ F ■ ■ F ■■U L 1L L L■: 114"■'■ I BL .1 甲 q 1■ ■ i ■尸. -r - —I-—■ ■IF ■ ’ L ■ J ■■ -4.-i ii百1 a-I--'■ L■ -r --r-- ■ ■-JMM I …「工出二二tkCl ■一i____ LM■ fL__ L攻性用尸 0,01 ■■十0W5 …|(2)对？(€ [ 1, +x),不等式f (x)> a (2x—x2),求实数a的取值范围.221. 已知椭圆C: 2- :- ' ■ ', F1, F2分别是其左、右焦点，以F1E2为直径的圆与椭圆C 有且仅有两个交点. (1) 求椭圆C 的方程；(2) 设过点F l 且不与坐标轴垂直的直线I 交椭圆于A , B 两点，线段AB 的垂直平分线与x 轴交于点P ，点P 横坐标的取值范围是(土，0),求线段AB 长的取值范围.请考生在22、23两题中任选一题作答，如果多做，则按所做的第一题记分.［选修4-4：坐标系与参数方程选讲］(共1小题，满分10 分)22. 已知在平面直角坐标系xOy 中，以坐标原点O 为极点，以x 轴正半轴为极轴，建立极坐标系，曲线 C 1的极坐标方程为 p =4cos ，直线I 的参数方程为(1)求曲线C i 的直角坐标方程及直线I 的普通方程;［选修4-5：不等式选讲］(共1小题，满分0分)23. 已知 a >0，b >0，函数 f (x ) =| x+a|+| 2x - b| 的最小值为 1. (1) 求证：2a+b=2;(2) 若a+2b >tab 恒成立，求实数t 的最大值.(2)若曲线C 2的参数方程为 :Q 为曲线C 2上的动点，求PQ 的中点M 到直线I 距离的最大值. (2)若曲线C2的参数方程为、 (a 为参数)，曲线C 1上点P 的极角为 7U—，(t 为参数).2017年吉林省长春市高考数学三模试卷(文科)参考答案与试题解析一、选择题(本大题包括12小题，每小题5分，共60分，每小题给出的四个选项中，只有一项是符合题目要求的，请将正确选项涂在答题卡上)1 •已知复数z=1+2i，则=( )A. 5B. 5+4iC.- 3D. 3-4i【考点】复数代数形式的乘除运算.【分析】由已知直接利用z^=|z|2求解.【解答】解：：z=1+2i，.°."艺=| z| 2=(Q I ?+*)J5.故选：A.2. 已知集合A={x|x2-2x- 3v0}，B={x|| x| v2}则A n B=( )A. {x| —2v x v2}B. {x| —2v x v 3}C. {x| —1 v x v 3}D. {x| —1v x v 2}【考点】交集及其运算.【分析】解不等式得出集合A、B,根据交集的定义写出A n B.【解答】解：集合A={x| x2—2x—3v 0} ={x| — 1 v x v 3}，B={x|| x| v 2}={x| —2v x v 2}.故选：D.3. 设a，b均为实数，则“A|b|”是“V b3”—)A.充分不必要条件B.必要不充分条件C. 充要条件D.既不充分也不必要条件【考点】必要条件、充分条件与充要条件的判断.【分析】根据充分必要条件的定义判断即可.【解答】解：由a>|b|”能推出“a>b3”，是充分条件，反之，不成立，比如a=1，b=—2，不是必要条件，故选：A.4•直线x-3y+3=0与圆（x- 1）2+ （y-3）2=10相交所得弦长为（）A. .B.—C. 4 ■：D. 3.'；【考点】直线与圆相交的性质.【分析】根据已知中圆的标准方程和直线的一般方程，代入圆的弦长公式，可得答案.【解答】解：圆（x- 1）2+ （y-3）2=10的圆心坐标为（1, 3）,半径r的, 圆心到直线x-3y+3=0的距离d」= ：_ ,故弦AB=2 j ] 「.,故选A.5.下列命题中错误的是（）A. 如果平面a外的直线a不平行于平面a内不存在与a平行的直线B. 如果平面a丄平面Y平面B丄平面Y aG B =那么直线I丄平面丫C. 如果平面a丄平面B,那么平面a内所有直线都垂直于平面BD. —条直线与两个平行平面中的一个平面相交，则必与另一个平面相交【考点】命题的真假判断与应用.【分析】由空间中直线与平面的位置关系逐一核对四个选项得答案.【解答】解：如果平面a外的直线a不平行于平面a,则a与a相交,则a内不存在与a平行的直线，故A正确；如图：a丄Y aG 丫=冃肚Y阳Y =b a^B =l在丫内取一点P ,过P作PAL a于A，作PB丄b于B ,由面面垂直的性质可得PA丄I , PB丄I ,则I丄Y故B正确；如果平面a丄平面B,那么平面a内的直线与平面B有三种位置关系：平行、相交、异面，故C错误；一条直线与两个平行平面中的一个平面相交，则必与另一个平面相交，故D正确.故选：C.6.在平面内的动点（x, y）满足不等式,则z=2x+y的最大值是（A.—4B. 4C. - 2D. 2【考点】简单线性规划.【分析】画出约束条件的可行域，利用目标函数的几何意义求解最大值即可.【解答】解：不等式组所表示的平面区域位于直线x+y - 3=0的下方区域和直线x-y+1=0的上方区域，根据目标函数的几何意义，可知目标函数经过A时，z取得最大值. 由：:二可得A（1, 2），所以目标函数z的最大值为4.故选B.7. 某几何体的三视图如图所示，则其体积为（【考点】由三视图求面积、体积.【分析】通过三视图复原的几何体是正四棱锥，结合三视图的数据，求出几何体的体积.【解答】解：由题意三视图可知，几何体是正四棱锥，底面边长为2的正方形，一条侧棱垂直正方形的一个顶点，长度为 2, 所以四棱锥的体积M 丄吃么冬.故选D .8. 某高中体育小组共有男生24人，其50m 跑成绩记作a i Zr正瘢1侧视图C. 求24名男生的达标人数D. 求24名男生的不达标人数A 4 BU C •二 D. A .求24名男生的达标率（i=1，2，…，24），B. 求24名男生的不达标率【考点】程序框图.【分析】由题意，从成绩中搜索出大于的成绩，计算24名中不达标率.【解答】解：由题意可知，k记录的是时间超过的人数，而i记录是的参与测试的人数，因此丁表示不达标率；故选B.9. 等比数列｛a n｝中各项均为正数，S是其前n项和，且满足2Ss=8ai+3a2, a4=16, 则S4=( )A. 9B. 15C. 18D. 30【考点】等比数列的前n项和.【分析】设等比数列｛a n｝的公比为q> 0，由2Sj=8a i+3a2，可得2 (a i +a2+a3) =8ai+3a2，化为：2q2- q - 6=0，解得q，进而得出.【解答】解：设等比数列｛a n｝的公比为q>0，V 2S3=8a1+3a2，••• 2 (a1+a2+a3) =8ai+3a2，化为:2a3=6a1+a2，可得2a t q2=6a i+a1 q，化为:2q2-q- 6=0,解得q=2.又a4=16，可得a1X 23=16,解得a1=2.则祜一 -=30.2-1故选：D.【考点】函数的图象.【分析】利用函数的定义域排除选项，值域排除选项即可得到结果.【解答】解：由函数定义域排除A,函数的值域•可知x>0时，y>0,当x v0 时，y v0,排除C, D.故选：B.11 •若关于x的方程2sin (2x+-—) =m在[0,——]上有两个不等实根，则m的取值范围是( )A. (1, -；)B. [0, 2]C. [1, 2)D. [1,;]【考点】正弦函数的图象.【分析】把方程2sin (2x+——)=m化为sin (2x^-)=丄，画出函数f (x) =sin(2x+ )在x€ [0,丄]上的图象，结合图象求出方程有两个不等实根时m的b z取值范围.兀【解答】解：方程2sin (2xr) =m可化为b/ 兀、nisin (2x+^~)—,, 7T r JU TT 7 JU当 x € ［0,三］时，2x+——€ ［百,—］,画出函数y=f (x ) =sin (2x+=-)在x € ［0,—］上的图象如图所示;K m v 2兀-一]上有两个不等实根,1 ““=m 在［0,根据方程2sin ( 2••• m的取值范围是［1 , 2).故选：C.12•对■■ -二,23x< log a x+1恒成立，则实数a的取值范围是( )A . B.(0 f2］C•［存1)D•［芥1)【考点】函数恒成立问题；全称命题.【分析】先构造函数 f (x) =x2+x, g (x) =- log a x. h (x) =f (x) +g (x),将问题等价转化为函数h (x)在区间(0,=)上恒有h (x)< 0,又函数为增函数，故可求答案. 【解答】解：构造函数f (x) =23x, g ( x) =- log a x - 1 .h (x) =f (x) +g (x). (0 v x v£)易知，在区间(0,丄)上，函数f (x), g (x)均是递增函数，•••函数h (x) =f (x) +g (x)在区间(0,寺)上是递增函数.由题设可知，函数h (x)在区间(0,〒)上恒有h (x)< 0.•必有h (*)w0.即有2 - log a (g)- K 0.整理就是log a a=1< log a (),•实数a的取值范围是寺w a v 1.故选C.二、填空题(本大题包括4小题，每小题5分，共20分，把正确答案填在答题卡中的横线上)•13. 某班级有50名同学，一次数学测试平均成绩是92,其中学号为前30名的同学平均成绩为90,则后20名同学的平均成绩为95 .【考点】众数、中位数、平均数.【分析】设学号为31号到50号同学的平均成绩为x,得到关于x的方程，解出即可.【解答】解：设学号为31号到50号同学的平均成绩为x ,则 92X 50=90X 30+20x ,解得：x=95,故答案为：95.14.若函数 f (x ) =e?sinx,贝U f (0) = 1.【考点】导数的运算.【分析】先求f (x )的导数，再求导数值. 【解答】解：f (x ) =e x ?sinx , f'(x ) = (e x )' si+e x . (sinx ) ' =?sinx+e x ?cosx, f (0) =0+1=1故答案为：115. 《九章算术》是我国第一部数学专着，下有源自其中的一个问题：今有金箠 (chu )长五尺，斩本一尺，重四斤，斩末一尺，重二斤.问金箠重几何？ ”其意思为：今有金杖(粗细均匀变化)长 5尺，截得本端1尺，重4斤，截得末端1尺，重2斤.问金杖重多少？ ”则答案是 15斤.【考点】等差数列的通项公式.由题意可知等差数列的首项和第 5项，由等差数列的前n 项和得答案. 解：由题意可知等差数列中a 1=4, a 5=2,则Ss= •••金杖重15斤.故答案为：15斤./ y 2 16. F 为双曲线——7=1 (a >b >0)的左焦点，过点F 且斜率为1的直线与两 a b "条渐近线分别交于A , B 两点，若船-丄，则双曲线的离心率为灯莎 .【考点】双曲线的简单性质.【分析】设出过焦点的直线方程，与双曲线的渐近线方程联立把 A , B 表示出来, 再由条件可得A 为FB 的中点，运用中点坐标公式，可得 a , b , c 的关系，然后【分【解求双曲线的离心率.【解答】解：设F ( - c , 0),则过F 作斜率为1的直线为：y=x+c .—r /冃 3.0 cc a.c可得-c — =-2y , 化为 b=3a , c=『产；,=li'ia, e —=. ：i. a故答案为：顷.三、解答题(本大题包括6小题，共70分，解答应写出文字说明，证明过程或演算步骤).17. 已知点P (亦，1), Q (cosx , si nx ), O 为坐标原点，函数fW = OP * QP .(1) 求函数f (x )的解析式及最小正周期；(2)若 A ABC 的内角，f (A ) =4, BC=3 △ ABC 的面积为芋■，求△ ABC 的周长.【考点】三角函数中的恒等变换应用；平面向量数量积的运算；正弦定理.【分析】(1)利用向量数量积运算，即可求函数 f (x )的解析式及最小正周期；(2)利用，△ ABC 的面积为，.，求出bc ,利用余弦定理，求出」:.「；，即可求△ ABC 的周长.【解答】解：(1) 一 - 一 '一：：■：■'：'：■■, _ _ 口兀 ••• ■丽=归(馅弋口5工)+1-五］1工=4 — 2sin (),f (x )的最小正周期为2n ；而渐近线的方程是： y=±— x , ab 得：A (- 八得，B(-h+-，!+!■），a-b )，若 1 若 B F ~2 aca-b ac 由由，可得A 为FB 的中点,（2）因为 f （A ） =4,所si 口〔A+冷-）二0,因为 O v A v n,所以 A —, 因为壮血c 今吉，所以bc=3, 根据余弦定理-■ ~f - -"'}- - T-— 二!' - - ，所以'一 -, 即三角形的周长为厂:. 18 •某手机厂商推出一款6寸大屏手机，现对500名该手机用户进行调查，对手机进行评分，评分的频数分布表如下：女性用分值区 [50, 60) [60, 70) [70, 80) [80, 90) [90, 100] 户间频数 20 40 80 50 10 男性用分值区 [50, 60) [60, 70) [70, 80) [80, 90) [90, 100] 户间频数 45 75 90 60 30 （1）完成下列频率分布直方图，并指出女性用户和男性用户哪组评分更稳定（不计算具体值，给出结论即可）；（2）根据评分的不同，运用分层抽样从男性用户中抽取 20名用户，在这20名用户中，从评分不低于80分的用户中任意抽取2名用户，求两名用户中评分都小于90分的概率.【考点】列举法计算基本事件数及事件发生的概率；频率分布直方图.【分析】（1）作出女性用户和男性用户的频率分布表，由图可得女性用户更稳定.（2）运用分层抽样从男性用户中抽取 20名用户，评分不低于80分有6人，其中评組更QD J ：5,：3:.工 g0.L:0.01 1 j ■ r ■ 1 ■ F ■■ ■ M -- _L _ —■— _L _ ■I _L_ _f L _ H 一・ FL -i|r - -r - 一— -i1 ■ L - 八 ■■ ■冃 1i -■ -- ■ L ■ ■ ■■ ■ ■ ■ ■ J ■ .L . ■丄 ." 1 划 <1 i I--r- ■ F ■ ■ ■ ■ ■4Z?攻性用尸 L 4 W !» M M *L I 團性稱尸分小于90分的人数为4,记为A, B, C, D,评分不小于90分的人数为2, 记为a, b,设事件M为两名用尸评分都小于90分从6人人任取2人，利用列举法能求出两名用户中评分都小于90分的概率.【解答】(本小题满分12分)解：(1)女性用户和男性用户的频率分布表分别如下左、右图:nu o -fl- U(2)运用分层抽样从男性用户中抽取20名用户，评分不低于80分有6人, 其中评分小于90分的人数为4,记为A, B, C, D,评分不小于90分的人数为2,记为a, b,设事件M为两名用户评分都小于90分”从6人人任取2人，基本事件空间为Q= (AB), (AC), (AD), (Aa), (Ab),(BO, ( BD), ( Ba), ( Bb), (CD, (Ca), (Cb),(Da), (Db), (ab) },共有15 个元素.M={ (AB), (AC), (AD), (BC), (BD) ( CD) },共有6 个元素. z、J__2P (M)=，-..19. 如图,四棱锥P- ABCD的底面ABCD为矩形,PAL底面ABCD, AD=AP=2 AB=2 ' , E为棱PD的中点.(I )证明：PD丄平面ABE(U)求三棱锥C-PBD外接球的体积.【考点】棱柱、棱锥、棱台的体积；直线与平面垂直的判定.【分析】(I)以A为原点，AB为x轴，AD为y轴，AP为z轴，建立空间直角坐标系，利用向量法能证明PD丄平面ABE(U)三棱锥C- PBD外接球即以AB, AD，AP为棱的长方体的外接球，由此能求出三棱锥C-PBD外接球的体积.【解答】证明：(I)以A为原点，AB为x轴，AD为y轴，AP为z轴，建立空间直角坐标系，P (0, 0, 2)，D (0，2, 0)，A (0，0，0)，B (昕，0，0)，E (0，1, 1)，PD= (0, 2,- 2),忑=(祈,0, 0),忑=(0, 1, 1),匸二」七=0,三• • 7 =0,••• PD丄AB, PD丄AE,••• AB n AE=A ••• PD丄平面ABE解: ( n)v AD, AP, AB两垂直，底面ABCD为矩形，•••三棱锥C- PBD外接球即以AB, AD, AP为棱的长方体的外接球，•••三棱锥C- PBD外接球的半径R=亠匚'=3,4 1 |4•••三棱锥C- PBD外接球的体积Vh兀衬可XX跡=36n20. 已知函数f (x) =ax- Inx.(1)过原点0作曲线y=f (x)的切线，求切点的横坐标；(2)对［ 1, +x),不等式f (x)> a (2x- x2),求实数a的取值范围.【考点】利用导数研究曲线上某点切线方程；利用导数求闭区间上函数的最值.【分析】(1)过原点O作曲线y=f (x)的切线，求出切线方程，即可求切点的横坐标；(2)对?x€ [ 1, +x),不等式f (x)> a (2x-x2),化为ax2- ax- lnx>0 对? € [1, +x)恒成立，分类讨论，即可求实数a的取值范围.【解答】解：(1)设切点为(x o，ax o-Inx o), 二F'〔工沪n-占，直线的切线方程为y-(ax o- Inx o) = (a-J ) (x-x o)，又切线过原点-ax o+lnx o=- ax o+1，所以Inx o=1，解得x o=e，所以切点的横坐标为e.(2)因为不等式ax - Inx>a (2x- x2)对？x€ [ 1，+x)恒成立，所以ax2- ax- lnx>0 对？(€ [ 1，+x)恒成立.设g (x) =ax2- ax - Inx，g'(x) =2ax- a-丄.①当a<o时，••• $〔只)二且(力-1)-^<0，二g (x)在[1，+x)上单调递减，即g (x)< g (1) =0,.°. a< 0 不符合题意.2②当a>o时，『吕迁竺主.设»(球至日J PL W备&弓*寺1,在[1，+x)上单调递增，即a> 1.(i)当a> 1 时，由h (x)>0，得g' (x)>0，二g (x)在[1，+^)上单调递增，即g (x)> g (1) =0,二a> 1 符合题意；(ii)当O v a v 1 时，：a- 1v0,二0o€ [1, +*)使得h (x o) =0,则g (X)在[1,刈)上单调递减，在(x o, +x)上单调递增，g (x o)v g (1) =0,则O v a v 1不合题意.综上所述，a> 1.221.已知椭圆C: -- ■' ■ ', F1, F2分别是其左、右焦点，以F1F2为直a径的圆与椭圆C有且仅有两个交点.(1)求椭圆C的方程；(2)设过点F1且不与坐标轴垂直的直线I交椭圆于A, B两点，线段AB的垂直平分线与x轴交于点P,点P横坐标的取值范围是（亠，0）,求线段AB长的取值范围.【考点】椭圆的简单性质；直线与椭圆的位置关系.【分析】（1）根据题意，分析可得b=c=1，计算可得a的值，代入椭圆的方程即可得答案；（2）根据题意，设直线AB的方程为y=k（x+1）,与牙打二i联立可得（1+2k2）x2+4k2x+2k2- 2=0，设A （x i，y i），B （x2，y2），AB 的中点为M（x o，y o），由根与系数的关系分析可得直线AB的垂直平分线方程，由弦长公式可以表示|AB|，计算可得答案.【解答】解：（1）根据题意，因为以F1F2为直径的圆与椭圆C有且仅有两个交点，所以b=c=1，即a= ='：，2 °即椭圆C的方程为卡+長二£，（2）根据题意，过点F1且不与坐标轴垂直的直线I交椭圆于A，B两点，即直线AB 的斜率存在，设直线AB的方程为y=k （x+1），与一匕「八联立，得（1+2k2）x2+4k2x+2k2- 2=0,设直线AB的垂直平分线方程为设 A （X1, y1），B （X2, y2 ），AB 的中点为M（x o，y o），4k22k2即线段AB 长的范围是（；,2.':）. 4—1 请考生在22、23两题中任选一题作答，如果多做，则按所做的第一题记分.［选修4-4:坐标系与参数方程选讲］（共1小题，满分10分） 22.已知在平面直角坐标系xOy 中，以坐标原点O 为极点，以x 轴正半轴为极轴，建立极坐标系，曲线 C i 的极坐标方程为 p =4cos ，直线I 的参数方程为（t 为参数）. （1）求曲线C i 的直角坐标方程及直线I 的普通方程；（2）若曲线C 2的参数方程为］初（ a 为参数），曲线C i 上点P 的极角为中, Q 为曲线C 2上的动点，求PQ 的中点M 到直线I 距离的最大值. 【考点】简单曲线的极坐标方程；参数方程化成普通方程. 【分析】（1）曲线C i 的极坐标方程为p =4cos ，即p=4 p cos, 0可得直角坐标方（2 ）后，于），直角坐标为（2 ， 2 ）J 1号 Z ），利用点到直线的距离公式及其三角函数的单调性可得最大值.【解答】解：（1）曲线C 1的极坐标方程为p =4cos, 0即p=4 p cos ，可得直角坐标方程：Cy x 一m .（1+心［〔』程.直线I 的参数方程为（t 为参数），消去参数t 可得普通方程. I I (1+k 2) "斗+；K=1--- t,(t 为参数)，5消去参数t 可得普通方程：x+2y — 3=0.Q(2cos G J 乩门口)，M(l+口□刁口！14^-sinCt )，直线I 的参数方程为 P (2V2-寻)，直角坐标为 (2 ， 2 )，:.M 到 I 的距离；■' 从而最大值为丄I 5 ［选修4-5:不等式选讲］(共1小题，满分0 分) 23.已知 a >0，b >0,函数 f (x ) =| x+a|+| 2x -b| 的最小值为 1. (1)求证：2a+b=2; (2)若a+2b >tab 恒成立，求实数t 的最大值. 【考点】函数恒成立问题；绝对值不等式的解法. 【分析】(1)法一：根据绝对值的性质求出f (x )的最小值，得到 x=-时取等号, 证明结论即可；法二：根据f (x )的分段函数的形式，求出f (x )的最小值，证明即可; 屏2b ab 的最小值，从而求出t 的范围即可；法三：根据二次函数的性质判断即可. (2)法一，二：问题转化为 >t 恒成立，根据基本不等式的性质求出【解答】解：(1)法一:f (x ) =| x+a|+| 2x — b| =| x+a|+| x b. _ | 0,:bh h 卜 | \1 T | x+a|+| x -丁 | > | (x+a ) — ( x -瓦)I =a 迈"且 |x -豆 | > 0, 1+1 x .f (x )> a+7；，当x==时取等号，即f (x )的最小值为c+--，La+~=1，2a+b=2 ；法二：T — a v —，••• f (x ) =| x+a|+| 2x — b|-z+a+bj _a_<23x+a-b»I显然f （乂）在（-X, \］上单调递减，f （ X ）在脊,+X ）上单调递增, ••• f （X ）的最小值为f （昔）=a^-,（2）方法一：：a+2b > tab 恒成立，•‘ > t 恒成立，ab警卡令（+弓（2a+b ）啥令（1+4哥今）冶（诃+2咅迢碍, 当a=b 今时，瞬取得最小值十，方法二：••• a+2b >tab 恒成立,》t 恒成立，t < - ab > t ，即实数t 的最大值为方法三：••• a+2b >tab 恒成立,• a+2 (2 - a )> ta (2 - a )恒成立,• 2ta 2 -(3+2t ) a+4> 0 恒成立， 1 2 1b a b'2a _2_> 厂 |bt2a恒成立,> t ，即实数t 的最大值为•( 3+2t) 2-326W 0,1 Qt W^,实数t的最大值为2017年4月18日。

2018年吉林省长春市高考数学三模试卷(文科)含解析

2018年吉林省长春市高考数学三模试卷(文科)含解析2018年吉林省长春市高考数学三模试卷（文科）一、选择题（本大题包括12小题，每小题5分，共60分。

每小题给出的四个选项中，只有一项是符合题目要求的，请将正确选项涂在答题卡上）1.已知复数z=1+2i，则z²+4z+3的值为（）。

A．5 B．5+4i C．-3 D．3-4i2.已知集合A={x|x²-2x-3<0}，B={x||x|<2}，则A∩B=（）。

A．{x|-2<x<2} B．{x|-2<x<3} C．{x|-1<x<3} D．{x|-1<x<2}3.设a，b均为实数，则“a>|b|”是“a³>|b|³”的（）。

A．充分不必要条件 B．必要不充分条件 C．充要条件D．既不充分也不必要条件4.直线x-3y+3=0与圆(x-1)²+(y-3)²=10相交所得弦长为（）。

A．√5 B．2√5 C．4 D．35.下列命题中错误的是（）。

A．如果平面α外的直线a不平行于平面α，则内不存在与a平行的直线。

B．如果平面α⊥平面γ，平面β⊥平面γ，α∩β=l，那么直线l⊥平面γ。

C．如果平面α⊥平面β，则平面α内所有直线都垂直于平面β。

D．一条直线与两个平行平面中的一个平面相交，则必与另一个平面相交。

6.在平面内的动点（x，y）满足不等式|x+2|+|y-1|≤5，则z=2x+y的最大值是（）。

A．-4 B．4 C．-2 D．27.某几何体的三视图如图所示，则其体积为（）。

A．4 B．8 C．16 D．328.某高中体育小组共有男生24人，其50m跑成绩记作ai（i=1，2，…，24），若成绩小于6.8s为达标，则如图所示的程序框图的功能是（）。

A．求24名男生的达标率 B．求24名男生的不达标率C．求24名男生的达标人数 D．求24名男生的不达标人数9.等比数列{an}中各项均为正数，Sn是其前n项和，且满足2S3=8a1+3a2，a4=16，则S4=（）。

2020年吉林省长春市高考数学三模试卷(文科)(含答案解析)

2020年吉林省长春市高考数学三模试卷（文科）一、选择题（本大题共12小题，共60.0分）1.已知集合，，则A. B. C. D.2.已知向量，满足，，且，则A. B. C. 5 D. 43.已知复数z满足，则z的共轭复数在复平面内对应的点位于A. 第一象限B. 第二象限C. 第三象限D. 第四象限4.某中学从甲、乙两个班中各选出7名学生参加数学竞赛，他们取得的成绩满分100分的茎叶图如图所示，其中甲班学生成绩的众数是83，乙班学生成绩的平均数是86，则的值为A. 7B. 8C. 9D. 105.等比数列中，、是函数的两个零点，则等于A. B. 3 C. D. 46.函数的图象大致为A. B.C. D.7.设a，b是两条直线，，是两个平面，则的一个充分条件是A. ，，B. ，，C. ，，D. ，，8.已知直线与函数，其中的相邻两交点间的距离为，则函数的单调递增区间为A. B.C. D.9.已知函数是定义在R上的奇函数，在上是增函数，且，则使得成立的x的取值范围是A. B.C. D.10.若函数有且只有一个零点，则a的取值范围是A. B. ，C. D.11.已知双曲线与椭圆有相同焦点，，离心率为若双曲线的左支上有一点M到右焦点的距离为12，N为线段的中点，O为坐标原点，则等于A. 4B. 3C. 2D.12.众所周知的“太极图”，其形状如对称的阴阳两鱼互抱在一起，也被称为“阴阳鱼太极图”如图是放在平面直角坐标系中的“太极图”整个图形是一个圆形．其中黑色阴影区域在y轴右侧部分的边界为一个半圆，给出以下命题：在太极图中随机取一点，此点取自黑色阴影部分的概率是当时，直线与白色部分有公共点；黑色阴影部分包括黑白交界处中一点，则的最大值为2；设点，点Q在此太极图上，使得，b的范围是．其中所有正确结论的序号是A. B. C. D.二、填空题（本大题共4小题，共20.0分）13.已知，，则______ ．14.已知长方形ABCD中，，，现将长方形ABCD沿着对角线BD折起，使平面平面BCD，则折后几何图形的外接球表面积为______．15.若，是函数的两个极值点，则______；______．16.已知数列的各项均为正数，其前n项和为，满足，设，为数列的前n项和，则______．三、解答题（本大题共7小题，共82.0分）17.笔、墨、纸、砚是中国独有的文书工具，即“文房四宝”笔、墨、纸、砚之名，起源于南北朝时期，其中的“纸”指的是宣纸，宣纸“始于唐代，产于泾县”，而唐代泾县隶属于宣州府管辖，故因地而得名“宣纸”，宣纸按质量等级，可分为正牌和副牌优等品和合格品，某公司年产宣纸10000刀，公司按照某种质量标准值x给宣纸确定质量等级，如表所示：x，，质量等级正牌副牌废品公司在所生产的宣纸中随机抽取了一刀张进行检验，得到频率分布直方图如图所示，已知每张正牌纸的利润是10元，副牌纸的利润是5元，废品亏损10元．Ⅰ按正牌、副牌、废品进行分层抽样，从这一刀张纸中抽出一个容量为5的样本，再从这个样本中随机抽出两张，求其中无废品的概率；Ⅱ试估计该公司生产宣纸的年利润单位：万元．18.的内角A，B，C的对边分别为a，b，c，已知．Ⅰ求tan B；Ⅱ若，的面积为6，求BC．19.四棱锥中，，，，，平面ABCD，E在棱PB上．Ⅰ求证：；Ⅱ若，求证：平面AEC．20.已知O为坐标原点，抛物线E的方程为，其焦点为F，过点的直线1与抛物线相交于P、Q两点且为以O为直角顶点的直角三角形．Ⅰ求E的方程；Ⅱ设点N为曲线E上的任意一点，证明：以FN为直径的圆与x轴相切．21.已知函数，，若曲线与曲线都过点且在点P处有相同的切线l．Ⅰ求切线l的方程；Ⅱ若关于x的不等式对任意恒成立，求实数k的取值范围．22.以直角坐标系的原点为极点，x轴的非负半轴为极轴建立极坐标系，曲线C的极坐标方程为，直线1的参数方程为为参数．Ⅰ求曲线C的参数方程与直线l的普通方程；Ⅱ设点P为曲线C上的动点，点M和点N为直线l上的点，且满足为等边三角形，求边长的取值范围．23.已知函数，，．Ⅰ当时，有，求实数m的取值范围．Ⅱ若不等式的解集为，正数a，b满足，求的最小值．-------- 答案与解析 --------1.答案：B解析：解：，，．故选：B．可以求出集合A，B，然后进行交集的运算即可．本题考查了描述法、区间的定义，对数函数的单调性，交集的定义及运算，考查了计算能力，属于基础题．2.答案：C解析：解：根据题意，，，且，则有，解可得，即，则，故；故选：C．根据题意，由向量垂直与数量积的关系可得，解可得y的值，即可得的坐标，进而计算可得向量的坐标，由向量模的计算公式计算可得答案．本题考查向量数量积的坐标计算，涉及向量模的计算和向量垂直与数量积的关系，属于基础题．3.答案：B解析：解：由，得，则，复数在复平面内对应的点的坐标为，位于第二象限．故选：B．把已知等式变形，再由复数代数形式的乘除运算化简，求出的坐标得答案．本题考查复数代数形式的乘除运算化简，考查复数的代数表示法及其几何意义，是基础题．4.答案：B解析：解：由茎叶图可知，茎为8时，甲班学生成绩对应数据只能是83，，85，因为甲班学生成绩众数是83，所以83出现的次数最多，可知．由茎叶图可知乙班学生的总分为，又乙班学生的平均分是86，总分又等于所以，解得，可得．故选：B．对甲组数据进行分析，得出x的值，利用平均数求出y的值，解答即可．本题主要考查统计中的众数与平均数的概念．解题时分别对甲组数据和乙组数据进行分析，分别得出x，y的值，进而得到的值．5.答案：B解析：解：、是函数的两个零点，、是方程的两个根，，由等比数列的性质可得：．故选：B．利用根与系数的关系求得，再由等比数列的性质得答案．本题考查等比数列的通项公式，考查了等比数列的性质，是基础的计算题．6.答案：B解析：解：函数的定义域为，，即函数为偶函数，其图象关于y轴对称，可排除CD；又，可排除A；故选：B．先判断函数的奇偶性，可排除选项CD，再由，可排除选项A，进而得出正确选项．本题考查利用函数性质确定函数图象，考查数形结合思想，属于基础题．7.答案：C解析：解：A、B、D的反例如图．故选：C．根据题意分别画出错误选项的反例图形即可．本题考查线面间的位置关系，同时考查充分条件的含义及空间想象能力．属于基础题．8.答案：B解析：解：与函数，其中的相邻两交点间的距离为，函数的周期，即，得，则，由，，得，，即函数的单调递增区间为，，故选：B．根据最值点之间的关系求出周期和，结合三角函数的单调性进行求解即可．本题主要考查三角函数单调性的应用，根据最值性求出函数的周期和，以及利用三角函数的单调性是解决本题的关键．难度不大．9.答案：D解析：解：函数是定义在R上的奇函数，在上是增函数，函数是在上是增函数，又，，由，得或，或．的取值范围是．故选：D．由奇函数的图象关于原点对称及在为增函数，可得函数是在上是增函数，结合，转化为不等式组求解．本题考查函数的单调性与奇偶性的应用，考查数学转化思想方法，是中档题．10.答案：B解析：解：当时，因为，所以有一个零点，所以要使函数有且只有一个零点，则当时，函数没有零点即可，当时，，，，所以或，即或，故选：B．当时，因为，所以有一个零点，所以要使函数有且只有一个零点，则当时，函数没有零点即可，即恒为负或恒为正，进而求出a的取值范围即可．本题主要考查了函数的零点与方程的根的关系，是中档题．11.答案：B解析：解：如图，为线段的中点，，双曲线的离心率为，，椭圆与双曲线的焦点相同，，则，即，．故选：B．由题意画出图形，利用三角形的中位线定理可得，再由已知椭圆方程及双曲线的离心率求解a，则答案可求．本题考查椭圆与双曲线的简单性质，考查数形结合的解题思想方法，是中档题．12.答案：A解析：解：对于，将y轴右侧黑色阴影部分补到左侧，即可知黑色阴影区域占圆的面积的一半，根据几何概型的计算公式，所以在太极图中随机取一点，此点取自黑色阴影部分的概率是，正确；对于，直线，圆的方程为，联立可得，，，但是两根之和为负，两根之积为正，所以两根都为负，即说明直线与白色部分没有公共点，错误；对于，设l：，由线性规划知识可知，当直线l与圆相切时，z最大，由解得舍去，错误；对于，要使得，即需要过点P的切线所成角大于等于90度，所以，即，于是，解得．故选：A．根据“太极图”和各选项对应知识，即可判断真假．本题主要考查图象的应用，考查学生识图用图以及运用相关知识的能力，涉及几何概型的计算公式，直线与圆的位置关系，以及线性规划知识的应用，属于较难题．13.答案：解析：解：，，，，则，故答案为：由的值及的范围，利用同角三角函数间的基本关系求出与的值，代入原式计算即可．此题考查了同角三角函数基本关系的运用，熟练掌握基本关系是解本题的关键．14.答案：解析：解：长方形ABCD中，，，可得，，作于E，可得，所以，，因为平面平面BCD，面ABD，平面平面，所以面BCD，由直角三角形BCD可得其外接圆的圆心为斜边BD的中点，且外接圆的半径，过作垂直于底面BCD，所以，所以，取三棱锥外接球的球心O，设外接球的半径为R，作于F，则四边形为矩形，，，则，在中，即；在中：，即；由可得，，即外接球的球心为，所以外接球的表面积，故答案为：．由长方形中，，可得BD，BC，及A到BD的距离AE，由面平面BCD 可得面BCD，求出底面外接圆的圆心及外接圆的半径，再由椭圆求出外接球的半径，进而求出外接球的表面积．本题考查三棱锥的棱长与外接球的半径之间的关系，及球的表面积公式，属于中档题．15.答案：2解析：解：函数，，，令得：，，是方程的两个根，，，，故答案为：2，．先求出导函数，由题意可得，是方程的两个根，利用韦达定理可得，，代入即可求出．本题主要考查了利用导数研究函数的极值，以及韦达定理的应用，是中档题．16.答案：880解析：解：，当时，，解得或舍去，当时，，，得：，整理得：，数列的各项均为正数，，即，数列是首项为2，公差为2的等差数列，，，，故答案为：880．利用公式可得数列是首项为2，公差为2的等差数列，所以，所以，进而，再利用并项求和法即可算出结果．本题主要考查了数列的递推式，以及并项求和法求数列的前n项和，是中档题．17.答案：解：Ⅰ按正牌、副牌、废品进行分层抽样，从这一刀张约中抽出一个容量为5的样本，设抽出的2张正牌为A，B，2张副牌为a，b，1张废品为t，从中任取两张，基本事件有：AB，Aa，Ab，At，Ba，Bb，Bt，ab，at，bt，共10种，其中无废品包含的基本事件有：AB，Aa，Ab，Ba，Bb，ab，共6种，其中无废品的概率．Ⅱ由频率分布直方图得：一刀张宣纸有正牌宣纸张，有副牌宣纸张，有废品张，该公司一刀宣纸的利润为元，估计该公司生产宣纸的年利润为：400万元．解析：Ⅰ按正牌、副牌、废品进行分层抽样，从这一刀张约中抽出一个容量为5的样本，设抽出的2张正牌为A，B，2张副牌为a，b，1张废品为t，从中任取两张，基利用列举法能求出其中无废品的概率．Ⅱ由频率分布直方图得一刀张宣纸有正牌宣纸40张，有副牌宣纸40张，有废品20张，由此能估计该公司生产宣纸的年利润．本题考查概率、利润的求法，考查考查频率分布直方图、古典概型、列举法等基础知识，考查运算求解能力，是中档题．18.答案：解：，利用正弦定理可得：，又，化为：，．，，可得，．．，可得：．又，可得．，解得．解析：由，利用正弦定理可得：，又，化简即可得出．由，，可得，，由正弦定理：，可得：又，可得即可得出a．本题考查了正弦定理、和差公式、三角形面积计算公式，考查了推理能力与计算能力，属于中档题．19.答案：证明：Ⅰ过A作于F，，，，四边形ABCF为正方形，则，，得，又底面ABCD，平面ABCD，，又PA，平面PAD，，平面PAD，又平面PAD，；Ⅱ设E到平面ABCD的距离为h，则，得．又，则PB：：：1．，，，连接DB交AC于O，连接OE，∽，：：1，得DB：：1，：：OB，则．又平面AEC，平面AEC，平面AEC．解析：Ⅰ过A作于F，推导出，，从而平面PAD，由此能求出；Ⅱ设E到平面ABCD的距离为h，由已知体积列式求得h，可得PB：：：1，连接DB交AC于O，连接OE，再由三角形相似证得DB：：1，可得PB：：OB，得到，再由直线与平面平行的判定可得平面AEC．本题考查直线与平面平行、垂直的判定，考查空间想象能力与思维能力，训练了多面体体积的求法，是中档题．20.答案：解：Ⅰ由题意可得直线l的斜率存在，设直线l的方程为：，设，，联立直线l与抛物线的方程，整理可得：，所以，所以，因为是以O为直角顶点的直角三角形，所以，即，所以，解得，所以抛物线的方程为：；Ⅱ证明：由Ⅰ得，准线方程为：，设，则NF的中点M的纵坐标，即以NF为直径的圆的圆心M到x轴的距离为，而由抛物线的性质可得，即以NF为直径的圆的半径为，所以可得圆心M到x轴的距离恰好等于圆的半径，所以可证得以FN为直径的圆与x轴相切．解析：Ⅰ由题意设直线l的方程，与抛物线联立求出两根之积，由是以O为直角顶点的直角三角形，所以，可得p的值，进而求出抛物线的方程；Ⅱ由Ⅰ可得F的坐标和准线方程，设N的坐标，可得NF的中点M，即圆心的坐标，求出M 的纵坐标到x轴的距离，再求NF的半径，可得M的纵坐标恰好等于半径，可证得结论．本题考查直角三角形与向量的关系，及直线与抛物线的综合，属于中档题．21.答案：解：Ⅰ，，由已知可得，即，解得，，，切线的斜率，切线l的方程为，即，Ⅱ由Ⅰ可得，，设，即，对任意恒成立，从而，，当时，，在上单调递减，又，显然不恒成立，当时，，解得，，当时，即时，，单调递增，又，显然不恒成立，当时，即时，，单调递增，，即恒成立，当时，即时，当时，，单调递减，当时，，单调递增，，解得，，综上所述得．解析：Ⅰ根据导数的几何意义即可求出切线方程；Ⅱ构造函数，利用导数求出函数的最小值，使得最小值大于等于0，需要分类讨论．此题主要考查利用导数研究曲线上某点切线方程，函数恒成立问题，构造函数，求函数的导数，利用导数研究函数的单调性和最值是解决本题的关键．综合性较强，运算量较大．22.答案：解：Ⅰ曲线C的极坐标方程为，转换为直角坐标方程为，转换为参数方程为为参数，．直线1的参数方程为为参数转换为直角坐标方程为．Ⅱ设，，所以点P到直线l的距离，由于，所以，所以，故等边三角形的边长的取值范围：．解析：Ⅰ直接利用转换关系的应用，把参数方程极坐标方程和直角坐标方程之间进行转换．Ⅱ利用点到直线的距离公式的应用和三角函数关系式的恒等变换及正弦型函数的性质的应用求出结果．本题考查的知识要点：三角函数关系式的恒等变换，正弦型函数的性质的应用，参数方程、极坐标方程和直角坐标方程之间的转换，点到直线的距离公式的应用，主要考查学生的运算能力和转换能力及思维能力，属于中档题型．23.答案：解：由题意得：在上恒成立，恒成立，即又，即令，若，则解集为，不合题意；若，则有，即又解集为，，解得当且仅当，即时，等号成立，此时，时的最小值为7解析：利用绝对值三角不等式性质利用绝对值不等式解法求出m，带入得到a，b等式，转化为只含有a的式子后利用基本不等式可以求解．本题考查绝对值三角不等式，以及基本不等式的应用，考查转化思想以及计算能力，是中档题。

普通高中高三数学下学期第三次调研测试试题文(2021年整理)

吉林省吉林市普通高中2017届高三数学下学期第三次调研测试试题文编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（吉林省吉林市普通高中2017届高三数学下学期第三次调研测试试题文）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为吉林省吉林市普通高中2017届高三数学下学期第三次调研测试试题文的全部内容。

吉林省吉林市普通高中2017届高三数学下学期第三次调研测试试题文第Ⅰ卷一、选择题:本大题共12题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的。

1。

设全集U R =，集合2{|0},{|20}A x x B x x x =>=--<。

则()U A B = A ． (0,2] B ． (1,2]- C ． [1,2]- D ． [2,)+∞2．若复数21iz i+=+，其中i 为虚数单位，则复数z 的虚部是 A ． 32B ． 12-C ． 32i -D ． 12i3．“直线y x b =+与圆221x y +=相交”是“01b <<”的 A ．充要条件B ．充分而不必要条件C ．必要而不充分条件D ．既不充分也不必要条件4．函数1221,0(),0x x f x x x -⎧-≤⎪=⎨⎪>⎩满足()1f x =的x 值为A 。

1 B. 1- C 。

1或2- D. 1或1-5．已知||1,||2a b ==，向量a 与b 的夹角为 60，则||a b += A ．B ．C ． 1D ． 26．已知抛物线22x y =的焦点与椭圆2212y x m +=的一个焦点重合,则m =A ． 1B ． 2C ． 3D ． 947．已知函数sin()y A x m ωϕ=++的最大值为4，最小值为0．两个对称轴间最短距离为2π，直线6x π=是其图象的一条对称轴，则符合条件的解析式为A ．2sin(2)26y x π=-++B ． 2sin(2)23y x π=++C ．2sin(2)3y x π=-+D ． 4sin(2)6y x π=+8．阅读右侧程序框图，运行相应程序，则输出iA ． 3B ． 4C ． 5D ． 69．在ABC ∆中，,,a b c 分别是角,,A B C 的对边，若1,a =60b B ==︒，则ABC ∆的面积为 A ． 12B ．C ． 1D ．10．若正实数y x ,满足0822=-++xy y x ，则y x 2+的最小值为 A ． 3 B ． 4C ．92D ．11211．如图，网格上小正方形的边长为1，粗实线画出的是某几何体的三视图,则该几何体的体积为A ．823π+B ．83π+C ．42π+D ．4π+12．函数()f x 的定义域为D ,对给定的正数k ，若存在闭区间[,]a b D ⊆,使得函数()f x 满足：①()f x 在[,]a b 内是单调函数；②()f x 在[,]a b 上的值域为[,]ka kb ,则称区间[,]a b 为()y f x =的k 级“理想区间”．下列结论错误的是 A ．函数2()f x x =(x R ∈)存在1级“理想区间”B ．函数()()x f x e x R =∈不存在2级“理想区间”C ．函数24()(0)1xf x x x =≥+存在3级“理想区间” D ．函数()tan ,(,)22f x x x ππ=∈-不存在4级“理想区间”第Ⅱ卷二、填空题:本大题共4个小题，每小题5分。

吉林省吉林市普通中学2020-2021学年高三第三次调研测试文科数学试题及答案

绝密★启用前吉林省吉林市普通中学2020-2021学年高三第三次调研测试文科数学试题注意事项：1、答题前填写好自己的姓名、班级、考号等信息 2、请将答案正确填写在答题卡上一、单选题1．已知集合{}{}1,1,0,1,2A x N x B =∈≤=-，则A B 的子集的个数为（）A ．1B ．2C ．3D ．42．若()f x 是定义在R 上的奇函数，且()()2f x f x +=，则()8f 的值为（） A ．1B ．2C ．0D ．1-3．已知直线l 经过点()1,1-，且与直线250x y --=垂直，则直线l 的方程为（） A ．210x y +-= B ．230x y --= C ．210x y ++=D ．230x y --=4．《周髀算经》中有这样一个问题:冬至、小寒、大寒、立春、雨水、惊蛰、春分、清明、谷雨、立夏、小满、芒种这十二个节气，自冬至日起，其日影长依次成等差数列，前三个节气日影长之和为28.5尺，最后三个节气日影长之和为1.5尺，今年3月20日17时37分为春分时节，其日影长为（）A ．4.5尺B ．3.5尺C ．2.5尺D ．1.5尺5．口袋中装有3个红球和4个黑球，每个球编有不同的号码，现从中取出3个球，则互斥而不对立的事件是（） A ．至少有1个红球与至少有1个黑球 B ．至少有1个红球与都是黑球 C ．至少有1个红球与至多有1个黑球D ．恰有1个红球与恰有2个红球6．若圆C 的半径为1,圆心在第一象限,且与直线430x y -=和x 轴都相切,则该圆的标准方程是( )A ．()()22311x y -+-= B ．22231x yC ．()()22211x y -+-=D ．()()22321x y -+-=7．把二进制数()21010化为十进制数为（） A ．10B ．15C ．20D ．408．已知圆锥SO 的底面半径为r ，当圆锥的体积为36r 时，该圆锥的母线与底面所成角的正弦值为（）A B ．3C ．32D ．29．己知函数()sin 0y ax b a =+>的图象如图所示，则函数()log a y x b =+的图象可能是（）A ．B ．C ．D ．10．已知m 是1和9的等比中项，则圆锥曲线221y x m+=的离心率为（）A B 或2 C D 11．平面直角坐标系xOy 中，2AB =，该平面上的动线段PQ 的端点P 和Q ，满足5,6,2AP AP AB AQ PA ≤⋅==，则动线段PQ 所形成图形的面积为（）A ．36B ．60C ．72D ．10812．已知函数()2ln f x a x x=-，在区间()0,3内任取两个实数12,x x ，且12x x ≠，若不等式()()1221111f x f x x x +-+<-恒成立，则实数a 的最小值为（）A ．92-B ．2-C．-D ．113-二、填空题13．已知i 是虚数单位，复数1iz i-=，则z 的虚部为__________． 14．设1.5313,log ,log 5a e b e c ===，则,,a b c 按从小到大的顺序为__________． 15．已知3,0,cos 25πθθ⎛⎫∈-= ⎪⎝⎭，则cos 22πθ⎛⎫+= ⎪⎝⎭___________三、双空题16．己知圆()22:116,C x y P ++=是圆C 上任意点，若1,0A ，线段AP 的垂直平分线与直线CP 相交于点Q ，则点Q 的轨迹方程是_______﹔若A 是圆C 所在平面内的一定点，线段AP 的垂直平分线与直线CP 相交于点Q ，则点Q 的轨迹是:①一个点②圆③椭圆④双曲线⑤抛物线，其中可能的结果有__________．四、解答题17．已知ABC 的内角,,A B C 所对的边分别为,,a b c ，若向量()1,2m =，(),cos n a B =-，且m n ⊥（1）求角B（2）若b a ==A18．2020年是决胜全面建成小康社会、决战脱贫攻坚之年，面对新冠肺炎疫情和严重洪涝灾害的考验.党中央坚定如期完成脱贫攻坚目标决心不动摇，全党全社会戮力同心真抓实干，取得了积极成效．某贫困县为了响应国家精准扶贫的号召，特地承包了一块土地，已知土地的使用面积x 与相应的管理时间y 的关系如下表所示:并调查了某村300名村民参与管理的意愿，得到的部分数据如下表所示;（1）做出散点图，判断土地使用面积x 与管理时间y 是否线性相关;并根据相关系数r 说明相关关系的强弱．(若0.75r ≥，认为两个变量有很强的线性相关性，r 值精确到0.001) .参考公式：()()niix x y y r --=∑参考数据：()216,22.7y y y=-=≈∑（2）完成以下22⨯列联表，并判断是否有99.9%的把握认为该村的村民的性别与参与管理意愿有关.()()()()()22,n ad bc K n a b c d a b c d a c b d-==+++++++19．如图，在三棱柱111ABC A B C -中，侧棱1AA ⊥底面1111,90,4,2,A B C BAC AB AC AA M ︒∠====是AB 中点，N 是11A B 中点，P 是（1）求证：//PQ 平面1ACM （2）求点Q 到平面1ACM 的距离 20．已知抛物线()2:20C x py p =>上的点()0,1x 到其焦点F 的距离为32，过点F 的直线l 与抛物线C 相交于,A B 两点.过原点O 垂直于l 的直线与抛物线C 的准线相交于Q 点.（1）求抛物线C 的方程及F 的坐标（2）设,OAB QAB △△的面积分别为12,S S ，求1211S S -的最大值. 21．已知函数()xf x xe ax =-（1）若函数()f x 有两个极值点，求实数a 的取值范围; （2）若函数()()()ln 2f x g x x x=-+，当0a =时，证明：()()2,0,0x g x ∀∈-> 22．在直角坐标系xOy 中，直线l的参数方程为212x y t ⎧=-⎪⎪⎨⎪=+⎪⎩（t 为参数），以坐标原点为极点，x 轴的正半轴为极轴建立极坐标系，曲线C 的极坐标方程为4sin ρθ= （1）求曲线C 的直角坐标方程（2）已知点P 的直角坐标为()0,1，l 与曲线C 交于,A B 两点，求PA PB + 23．已知函数()41,f x x x x R =-+-∈ （1）解不等式：()5f x ≤（2）记()f x 的最小值为M ，若正实数,a b 满足a b M +=，试求：1121a b +++的最小值参考答案1．D 求出交集A B 且可得其子集个数．解：由题意{0,1}A B =，因此它的子集个数为4．故选：D ．结论点睛：集合A 中含有n 个元素，则它的子集个数为2n ，其中真子集个数为21n -． 2．C由奇函数得(0)0f =，再由周期性可得结论．解：因为()f x 是定义在R 上的奇函数，所以(0)0f =，又()()2f x f x +=，所以()f x 是周期函数，周期为2．所以(8)(42)(0)0f f f =⨯==．故选：C ． 3．C根据两直线的位置关系，设直线:20l x y c ++=，再代入点，求直线l 的方程. 解：直线l 与直线250x y --=垂直，∴设直线l 的方程为20x y c ++=，直线l 经过点()1,1-，120c ∴-+=，即1c =. 直线l 的方程为210x y ++=. 故选：C 4．A由题意构造等差数列{}n a ，设公差为d ，利用基本量代换求出通项公式，然后求7a . 解：小寒、大寒、立春、雨水、惊蛰、春分、清明、谷雨、立夏、小满、芒种这十二个节气日影长构成等差数列{}n a ，设公差为d ，由题意得：12310111228.51.5a a a a a a ++=⎧⎨++=⎩，解得：110.51a d =⎧⎨=-⎩所以()1111.5n a a n d n =+-=-，所以711.57 4.5a =-=，即春分时节的日影长为4.5. 故选：A(1)数学建模是高中数学六大核心素养之一，在高中数学中，应用题是常见考查形式：求解应用性问题时，首先要弄清题意，分清条件和结论，抓住关键词和量，理顺数量关系，然后将文字语言转化成数学语言，建立相应的数学模型； (2) 等差（比）数列问题解决的基本方法：基本量代换. 5．D利用互斥事件和对立事件的定义逐项分析判断即可解：解：对于A ，不互斥，如取出2个红球和1个黑球，与至少有1个黑球不是互斥事件，所以A 不合题意；对于B ，至少有1个红球与都是黑球不能同时发生，且必有其中1个发生。

吉林省长春市普通高中2020届高三质量监测(三)(三模)数学(文)试题 (解析版)

2020年高考数学三模试卷（文科）一、选择题（共12小题）1．已知集合A＝{x|x2≤1}，B＝{x|lgx≤1}，则A∩B＝（）A．[0，1]B．（0，1]C．（0，1）D．[﹣1，10]2．已知向量，满足（2，1），（1，y），且⊥，则|2|＝（）A．B．C．5D．43．已知复数z满足（1+i）2•z＝1﹣i，则z的共轭复数在复平面内对应的点位于（）A．第一象限B．第二象限C．第三象限D．第四象限4．某中学从甲、乙两个班中各选出7名学生参加数学竞赛，他们取得的成绩（满分100分）的茎叶图如图所示，其中甲班学生成绩的众数是83，乙班学生成绩的平均数是86，则x+y的值为（）A．7B．8C．9D．105．等比数列{a n}中，a5、a7是函数f（x）＝x2﹣4x+3的两个零点，则a3•a9等于（）A．﹣3B．3C．﹣4D．46．函数f（x）的图象大致为（）A．B．C．D．7．设a，b是两条直线，α，β是两个平面，则a⊥b的一个充分条件是（）A．a⊥α，b∥β，α⊥βB．a⊥α，b⊥β，α∥βC．a⊂α，b⊥β，α∥βD．a⊂α，b∥β，α⊥β8．已知直线y＝﹣2与函数，（其中w＞0）的相邻两交点间的距离为π，则函数f（x）的单调递增区间为（）A．B．C．D．9．已知函数f（x）是定义在R上的奇函数，在（0，+∞）上是增函数，且f（﹣4）＝0，则使得xf（x）＞0成立的x的取值范围是（）A．（﹣4，4）B．（﹣4，0）∪（0，4）C．（0，4）∪（4，+∞）D．（﹣∞，﹣4）∪（4，+∞）10．若函数有且只有一个零点，则a的取值范围是（）A．（﹣∞，﹣1）∪（0，+∞）B．（﹣∞，﹣1）∪[0，+∞）C．[﹣1，0）D．[0，+∞）11．已知双曲线1（a＞0，b＞0）与椭圆1有相同焦点F1，F2，离心率为．若双曲线的左支上有一点M到右焦点F2的距离为12，N为线段MF2的中点，O 为坐标原点，则|NO|等于（）A．4B．3C．2D．12．众所周知的“太极图”，其形状如对称的阴阳两鱼互抱在一起，也被称为“阴阳鱼太极图”．如图是放在平面直角坐标系中的“太极图”．整个图形是一个圆形．其中黑色阴影区域在y轴右侧部分的边界为一个半圆，给出以下命题：①在太极图中随机取一点，此点取自黑色阴影部分的概率是②当时，直线y＝ax+2a与白色部分有公共点；③黑色阴影部分（包括黑白交界处）中一点（x，y），则x+y的最大值为2；④设点P（﹣2，b），点Q在此太极图上，使得∠OPQ＝45°，b的范围是[﹣2，2]．其中所有正确结论的序号是（）A．①④B．①③C．②④D．①②二、填空题：本题共4小题，每小题5分，共20分.13．已知tanα＝3，π＜α，则cosα﹣sinα＝．14．已知长方形ABCD中，AB＝1，∠ABD＝60°，现将长方形ABCD沿着对角线BD折起，使平面ABD⊥平面BCD，则折后几何图形的外接球表面积为．15．若x1，x2是函数f（x）＝x2﹣7x+4lnx的两个极值点，则x1x2＝；f（x1）+f（x2）＝．16．已知数列{a n}的各项均为正数，其前n项和为S n，满足4S n＝a n2+2a n（n∈N*），设b n ＝（﹣1）n•a n a n+1，T n为数列{b n}的前n项和，则T20＝．三、解答题：共70分，解答应写出文字说明、证明过程或演算步骤.第17～21题为必考题，每个试题考生都必须作答.第22～23题为选考题，考生根据要求作答.（一）必考题：共60分.17．笔、墨、纸、砚是中国独有的文书工具，即“文房四宝”．笔、墨、纸、砚之名，起源于南北朝时期，其中的“纸”指的是宣纸，宣纸“始于唐代，产于泾县”，而唐代泾县隶属于宣州府管辖，故因地而得名“宣纸”，宣纸按质量等级，可分为正牌和副牌（优等品和合格品），某公司年产宣纸10000刀，公司按照某种质量标准值x给宣纸确定质量等级，如表所示：x（48，52]（44，48]∪（52，56]（0，44]∪（56，100]质量等级正牌副牌废品公司在所生产的宣纸中随机抽取了一刀（100张）进行检验，得到频率分布直方图如图所示，已知每张正牌纸的利润是10元，副牌纸的利润是5元，废品亏损10元．（Ⅰ）按正牌、副牌、废品进行分层抽样，从这一刀（100张）纸中抽出一个容量为5的样本，再从这个样本中随机抽出两张，求其中无废品的概率；（Ⅱ）试估计该公司生产宣纸的年利润（单位：万元）．18．△ABC的内角A，B，C的对边分别为a，b，c，已知2a＝2b cos C+c sin B．（Ⅰ）求tan B；（Ⅱ）若C，△ABC的面积为6，求BC．19．四棱锥P﹣ABCD中，AB∥CD，AB⊥BC，AB＝BC＝1，PA＝CD＝2，PA⊥平面ABCD，E在棱PB上．（Ⅰ）求证：AC⊥PD；（Ⅱ）若V P﹣ACE，求证：PD∥平面AEC．20．已知O为坐标原点，抛物线E的方程为x2＝2py（p＞0），其焦点为F，过点M（0，4）的直线1与抛物线相交于P、Q两点且△OPQ为以O为直角顶点的直角三角形．（Ⅰ）求E的方程；（Ⅱ）设点N为曲线E上的任意一点，证明：以FN为直径的圆与x轴相切．21．已知函数f（x）＝axe x，g（x）＝x2+2x+b，若曲线y＝f（x）与曲线y＝g（x）都过点P（1，c）．且在点P处有相同的切线l．（Ⅰ）求切线l的方程；（Ⅱ）若关于x的不等式k[ef（x）]≥g（x）对任意x∈[﹣1，+∞）恒成立，求实数k的取值范围．（二）选考题：共10分，请考生在22、23题中任选一题作答，如果多做则按所做的第一题计分.[选修4-4坐标系与参数方程]22．以直角坐标系的原点为极点，x轴的非负半轴为极轴建立极坐标系，曲线C的极坐标方程为ρ2（θ∈[0，]），直线1的参数方程为（t为参数）．（Ⅰ）求曲线C的参数方程与直线l的普通方程；（Ⅱ）设点P为曲线C上的动点，点M和点N为直线l上的点，且满足△PMN为等边三角形，求△PMN边长的取值范围．[选修4-5不等式选讲]23．已知函数f（x）＝m﹣|x﹣2|，m∈R，g（x）＝|x+3|．（Ⅰ）当x∈R时，有f（x）≤g（x），求实数m的取值范围．（Ⅱ）若不等式f（x）≥0的解集为[1，3]，正数a，b满足ab﹣2a﹣b＝3m﹣1，求a+b 的最小值．参考答案一、选择题：本题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1．已知集合A＝{x|x2≤1}，B＝{x|lgx≤1}，则A∩B＝（）A．[0，1]B．（0，1]C．（0，1）D．[﹣1，10]【分析】可以求出集合A，B，然后进行交集的运算即可．解：A＝{x|﹣1≤x≤1}，B＝{x|0＜x≤10}，∴A∩B＝（0，1]．故选：B．【点评】本题考查了描述法、区间的定义，对数函数的单调性，交集的定义及运算，考查了计算能力，属于基础题．2．已知向量，满足（2，1），（1，y），且⊥，则|2|＝（）A．B．C．5D．4【分析】根据题意，由向量垂直与数量积的关系可得•2+y＝0，解可得y的值，即可得的坐标，进而计算可得向量（2）的坐标，由向量模的计算公式计算可得答案．解：根据题意，（2，1），（1，y），且⊥，则有•2+y＝0，解可得y＝﹣2，即（1，﹣2），则2（4，﹣3），故|2|5；故选：C．【点评】本题考查向量数量积的坐标计算，涉及向量模的计算和向量垂直与数量积的关系，属于基础题．3．已知复数z满足（1+i）2•z＝1﹣i，则z的共轭复数在复平面内对应的点位于（）A．第一象限B．第二象限C．第三象限D．第四象限【分析】把已知等式变形，再由复数代数形式的乘除运算化简，求出的坐标得答案．解：由（1+i）2•z＝1﹣i，得z，则，∴复数在复平面内对应的点的坐标为（，），位于第二象限．故选：B．【点评】本题考查复数代数形式的乘除运算化简，考查复数的代数表示法及其几何意义，是基础题．4．某中学从甲、乙两个班中各选出7名学生参加数学竞赛，他们取得的成绩（满分100分）的茎叶图如图所示，其中甲班学生成绩的众数是83，乙班学生成绩的平均数是86，则x+y的值为（）A．7B．8C．9D．10【分析】对甲组数据进行分析，得出x的值，利用平均数求出y的值，解答即可．解：由茎叶图可知，茎为8时，甲班学生成绩对应数据只能是83，80+x，85，因为甲班学生成绩众数是83，所以83出现的次数最多，可知x＝3．由茎叶图可知乙班学生的总分为76+81+82+80+y+91+91+96＝597+y，又乙班学生的平均分是86，总分又等于86×7＝602．所以597+y＝602，解得y＝5，可得x+y＝8．故选：B．【点评】本题主要考查统计中的众数与平均数的概念．解题时分别对甲组数据和乙组数据进行分析，分别得出x，y的值，进而得到x+y的值．5．等比数列{a n}中，a5、a7是函数f（x）＝x2﹣4x+3的两个零点，则a3•a9等于（）A．﹣3B．3C．﹣4D．4【分析】利用根与系数的关系求得a5•a7＝3，再由等比数列的性质得答案．解：∵a5、a7是函数f（x）＝x2﹣4x+3的两个零点，∴a5、a7是方程x2﹣4x+3＝0的两个根，∴a5•a7＝3，由等比数列的性质可得：a3•a9＝a5•a7＝3．故选：B．【点评】本题考查等比数列的通项公式，考查了等比数列的性质，是基础的计算题．6．函数f（x）的图象大致为（）A．B．C．D．【分析】先判断函数f（x）的奇偶性，可排除选项CD，再由f（1）＜0，可排除选项A，进而得出正确选项．解：函数的定义域为{x|x≠0}，，即函数f（x）为偶函数，其图象关于y轴对称，可排除CD；又，可排除A；故选：B．【点评】本题考查利用函数性质确定函数图象，考查数形结合思想，属于基础题．7．设a，b是两条直线，α，β是两个平面，则a⊥b的一个充分条件是（）A．a⊥α，b∥β，α⊥βB．a⊥α，b⊥β，α∥βC．a⊂α，b⊥β，α∥βD．a⊂α，b∥β，α⊥β【分析】根据题意分别画出错误选项的反例图形即可．解：A、B、D的反例如图．故选：C．【点评】本题考查线面垂直、平行的性质及面面垂直、平行的性质，同时考查充分条件的含义及空间想象能力．8．已知直线y＝﹣2与函数，（其中w＞0）的相邻两交点间的距离为π，则函数f（x）的单调递增区间为（）A．B．C．D．【分析】根据最值点之间的关系求出周期和ω，结合三角函数的单调性进行求解即可．解：∵y＝﹣2与函数，（其中w＞0）的相邻两交点间的距离为π，∴函数的周期T＝2，即2，得ω＝2，则f（x）＝2sin（2x），由2kπ2x2kπ，k∈Z，得kπx≤kπ，k∈Z，即函数的单调递增区间为[kπ，kπ]，k∈Z，故选：B．【点评】本题主要考查三角函数单调性的应用，根据最值性求出函数的周期和ω，以及利用三角函数的单调性是解决本题的关键．难度不大．9．已知函数f（x）是定义在R上的奇函数，在（0，+∞）上是增函数，且f（﹣4）＝0，则使得xf（x）＞0成立的x的取值范围是（）A．（﹣4，4）B．（﹣4，0）∪（0，4）C．（0，4）∪（4，+∞）D．（﹣∞，﹣4）∪（4，+∞）【分析】由奇函数的图象关于原点对称及f（x）在（0，+∞）为增函数，可得函数f（x）是在（﹣∞，0）上是增函数，结合f（﹣4）＝f（4）＝0，转化为不等式组求解．解：∵函数f（x）是定义在R上的奇函数，在（0，+∞）上是增函数，∴函数f（x）是在（﹣∞，0）上是增函数，又f（﹣4）＝0，∴f（4）＝0，由xf（x）＞0，得或，∴x＞4或x＜﹣4．∴x的取值范围是（﹣∞，﹣4）∪（4，+∞）．故选：D．【点评】本题考查函数的单调性与奇偶性的应用，考查数学转化思想方法，是中档题．10．若函数有且只有一个零点，则a的取值范围是（）A．（﹣∞，﹣1）∪（0，+∞）B．（﹣∞，﹣1）∪[0，+∞）C．[﹣1，0）D．[0，+∞）【分析】当x＞0时，因为log21＝0，所以有一个零点，所以要使函数f（x）有且只有一个零点，则当x≤0时，函数f（x）没有零点即可，即恒为负或恒为正，进而求出a的取值范围即可．解：当x＞0时，因为log21＝0，所以有一个零点，所以要使函数有且只有一个零点，则当x≤0时，函数f（x）没有零点即可，当x≤0时，0＜2x≤1，∴﹣1≤﹣2x＜0，∴﹣1﹣a≤﹣2x﹣a＜﹣a，所以﹣a≤0或﹣1﹣a＞0，即a≥0或a＜﹣1，故选：B．【点评】本题主要考查了函数的零点与方程的根的关系，是中档题．11．已知双曲线1（a＞0，b＞0）与椭圆1有相同焦点F1，F2，离心率为．若双曲线的左支上有一点M到右焦点F2的距离为12，N为线段MF2的中点，O 为坐标原点，则|NO|等于（）A．4B．3C．2D．【分析】由题意画出图形，利用三角形的中位线定理可得|NO||MF1|＝6﹣a，再由已知椭圆方程及双曲线的离心率求解a，则答案可求．解：如图，∵N为线段MF2的中点，∴|NO||MF1|（|MF2|﹣2a）＝6﹣a，∵双曲线1（a＞0，b＞0）的离心率为e，∴，∵椭圆1与双曲线1的焦点相同，∴c4，则a＝3，即6﹣a＝3，∴|NO|＝3．故选：B．【点评】本题考查椭圆与双曲线的简单性质，考查数形结合的解题思想方法，是中档题．12．众所周知的“太极图”，其形状如对称的阴阳两鱼互抱在一起，也被称为“阴阳鱼太极图”．如图是放在平面直角坐标系中的“太极图”．整个图形是一个圆形．其中黑色阴影区域在y轴右侧部分的边界为一个半圆，给出以下命题：①在太极图中随机取一点，此点取自黑色阴影部分的概率是②当时，直线y＝ax+2a与白色部分有公共点；③黑色阴影部分（包括黑白交界处）中一点（x，y），则x+y的最大值为2；④设点P（﹣2，b），点Q在此太极图上，使得∠OPQ＝45°，b的范围是[﹣2，2]．其中所有正确结论的序号是（）A．①④B．①③C．②④D．①②【分析】根据“太极图”和各选项对应知识，即可判断真假．解：对于①，将y轴右侧黑色阴影部分补到左侧，即可知黑色阴影区域占圆的面积的一半，根据几何概型的计算公式，所以在太极图中随机取一点，此点取自黑色阴影部分的概率是，正确；对于②，直线y＝ax+2a x﹣3，圆的方程为x2+y2＝4，联立可得，13x2+36x+20＝0，△＝362﹣4×13×20＞0，但是两根之和为负，两根之积为正，所以两根都为负，即说明直线y＝ax+2a与白色部分没有公共点，错误；对于③，设l：z＝x+y，由线性规划知识可知，当直线l与圆x2+（y﹣1）2＝1相切时，z 最大，由解得z（z＝1舍去），错误；对于④，要使得∠OPQ＝45°，即需要过点P的切线所成角大于等于90度，所以，即OP≤2，于是22+b2≤8，解得﹣2≤b≤2．故选：A．【点评】本题主要考查图象的应用，考查学生识图用图以及运用相关知识的能力，涉及几何概型的计算公式，直线与圆的位置关系，以及线性规划知识的应用，属于较难题．二、填空题：本题共4小题，每小题5分，共20分.13．已知tanα＝3，π＜α，则cosα﹣sinα＝．【分析】由tanα的值及α的范围，利用同角三角函数间的基本关系求出cosα与sinα的值，代入原式计算即可．解：∵tanα＝3，π＜α，∴cosα，sinα，则cosα﹣sinα，故答案为：【点评】此题考查了同角三角函数基本关系的运用，熟练掌握基本关系是解本题的关键．14．已知长方形ABCD中，AB＝1，∠ABD＝60°，现将长方形ABCD沿着对角线BD折起，使平面ABD⊥平面BCD，则折后几何图形的外接球表面积为4π．【分析】由长方形中AB＝1，∠ABD＝60°，可得BD，BC，及A到BD的距离AE，由面ABD⊥平面BCD可得AE⊥面BCD，求出底面外接圆的圆心及外接圆的半径，再由椭圆求出外接球的半径，进而求出外接球的表面积．解：长方形ABCD中，AB＝1，∠ABD＝60°，可得BD＝2，AD，作AE⊥BD于E，可得AE•BD＝AB•AD，所以AE，BE，因为平面ABD⊥平面BCD，AE⊆面ABD，平面ABD∩平面BCD＝BD，所以AE⊥面BCD，由直角三角形BCD可得其外接圆的圆心为斜边BD的中点O1，且外接圆的半径r1，过O1作OO1垂直于底面BCD，所以EO1＝O1B﹣BE＝1，所以OO1∥AE，取三棱锥外接球的球心O，设外接球的半径为R，作OF⊥AE于F，则四边形EFOO1为矩形，O1E＝OF，EF＝OO1，则OA＝OC＝OB＝OD＝R，在△AFO中，OA2＝AF2+OF2＝（AE﹣EF）2+EO12即R2＝（OO1）2；①在△BOO1中：OB2＝OO12+EO12，即R2＝OO12；②由①②可得R2＝1，OO1＝0，即外接球的球心为O1，所以外接球的表面积S＝4πR2＝4π，故答案为：4π．【点评】本题考查三棱锥的棱长与外接球的半径之间的关系，及球的表面积公式，属于中档题．15．若x1，x2是函数f（x）＝x2﹣7x+4lnx的两个极值点，则x1x2＝2；f（x1）+f（x2）＝4ln2．【分析】先求出导函数f'（x），由题意可得x1，x2是方程2x2﹣7x+4＝0 的两个根，利用韦达定理可得，x1x2＝2，代入f（x1）+f（x2）即可求出f（x1）+f（x2）＝4ln2．解：∵函数f（x）＝x2﹣7x+4lnx，x∈（0，+∞），∴f'（x）＝2x﹣7，令f'（x）＝0得：2x2﹣7x+4＝0，∴x1，x2是方程2x2﹣7x+4＝0 的两个根，∴，x1x2＝2，∴f（x1）+f（x2）7（x1+x2）+4ln（x1x2）4ln2，故答案为：2，4ln2．【点评】本题主要考查了利用导数研究函数的极值，以及韦达定理的应用，是中档题．16．已知数列{a n}的各项均为正数，其前n项和为S n，满足4S n＝a n2+2a n（n∈N*），设b n ＝（﹣1）n•a n a n+1，T n为数列{b n}的前n项和，则T20＝880．【分析】利用公式a n＝S n﹣S n﹣1可得数列{a n}是首项为2，公差为2的等差数列，所以a n＝2n，所以b n＝（﹣1）n•a n a n+1＝4×（﹣1）n n（n+1），进而T20＝4×[﹣2+6﹣12+20﹣30+42﹣……﹣380+420]，再利用并项求和法即可算出结果．解：∵4S n＝a n2+2a n（n∈N*），当n＝1时，，解得a1＝2或0（舍去），当n≥2时，4S n＝a n2+2a n①，4S n﹣1＝a n﹣12+2a n﹣1②，①﹣②得：，整理得：（a n+a n﹣1）（a n﹣a n﹣1﹣2）＝0，∵数列{a n}的各项均为正数，∴a n﹣a n﹣1﹣2＝0，即a n﹣a n﹣1＝2，∴数列{a n}是首项为2，公差为2的等差数列，∴a n＝2+2（n﹣1）＝2n，∴b n＝（﹣1）n•a n a n+1＝4×（﹣1）n n（n+1），∴T20＝4×[﹣2+6﹣12+20﹣30+42﹣……﹣380+420]＝4×[（﹣2+6）+（﹣12+20）+（﹣30+42）+……+（﹣380+420）]＝4×（4+8+12+……+40）＝4880，故答案为：880．【点评】本题主要考查了数列的递推式，以及并项求和法求数列的前n项和，是中档题．三、解答题：共70分，解答应写出文字说明、证明过程或演算步骤.第17～21题为必考题，每个试题考生都必须作答.第22～23题为选考题，考生根据要求作答.（一）必考题：共60分.17．笔、墨、纸、砚是中国独有的文书工具，即“文房四宝”．笔、墨、纸、砚之名，起源于南北朝时期，其中的“纸”指的是宣纸，宣纸“始于唐代，产于泾县”，而唐代泾县隶属于宣州府管辖，故因地而得名“宣纸”，宣纸按质量等级，可分为正牌和副牌（优等品和合格品），某公司年产宣纸10000刀，公司按照某种质量标准值x给宣纸确定质量等级，如表所示：x（48，52]（44，48]∪（52，56]（0，44]∪（56，100]质量等级正牌副牌废品公司在所生产的宣纸中随机抽取了一刀（100张）进行检验，得到频率分布直方图如图所示，已知每张正牌纸的利润是10元，副牌纸的利润是5元，废品亏损10元．（Ⅰ）按正牌、副牌、废品进行分层抽样，从这一刀（100张）纸中抽出一个容量为5的样本，再从这个样本中随机抽出两张，求其中无废品的概率；（Ⅱ）试估计该公司生产宣纸的年利润（单位：万元）．【分析】（Ⅰ）按正牌、副牌、废品进行分层抽样，从这一刀（100张）约中抽出一个容量为5的样本，设抽出的2张正牌为A，B，2张副牌为a，b，1张废品为t，从中任取两张，基利用列举法能求出其中无废品的概率．（Ⅱ）由频率分布直方图得一刀（100张）宣纸有正牌宣纸40张，有副牌宣纸40张，有废品20张，由此能估计该公司生产宣纸的年利润．解：（Ⅰ）按正牌、副牌、废品进行分层抽样，从这一刀（100张）约中抽出一个容量为5的样本，设抽出的2张正牌为A，B，2张副牌为a，b，1张废品为t，从中任取两张，基本事件有：AB，Aa，Ab，At，Ba，Bb，Bt，ab，at，bt，共10种，其中无废品包含的基本事件有：AB，Aa，Ab，Ba，Bb，ab，共6种，∴其中无废品的概率p．（Ⅱ）由频率分布直方图得：一刀（100张）宣纸有正牌宣纸100×0.1×4＝40张，有副牌宣纸100×0.05×4×2＝40张，有废品100×0.025×4×2＝20张，∴该公司一刀宣纸的利润为40×10+40×5+20×（﹣10）＝400元，∴估计该公司生产宣纸的年利润为：400万元．【点评】本题考查概率、利润的求法，考查考查频率分布直方图、古典概型、列举法等基础知识，考查运算求解能力，是中档题．18．△ABC的内角A，B，C的对边分别为a，b，c，已知2a＝2b cos C+c sin B．（Ⅰ）求tan B；（Ⅱ）若C，△ABC的面积为6，求BC．【分析】（I）由2a＝2b cos C+c sin B，利用正弦定理可得：2sin A＝2sin B cos C+sin C sin B，又sin A＝sin（B+C）＝sin B cos C+cos B sin C，化简即可得出．（II）由tan B＝2，B∈（0，π），可得sin B，cos B．sin A＝sin（B+C），由正弦定理：，可得：a．又ab sin6，可得b．即可得出a．解：（I）∵2a＝2b cos C+c sin B，利用正弦定理可得：2sin A＝2sin B cos C+sin C sin B，又sin A ＝sin（B+C）＝sin B cos C+cos B sin C，化为：2cos B＝sin B≠0，∴tan B＝2．（II）∵tan B＝2，B∈（0，π），可得sin B，cos B．∴sin A＝sin（B+C）＝sin B cos C+cos B sin C．∴，可得：a．又ab sin6，可得b．∴a，解得a＝3．【点评】本题考查了正弦定理、和差公式、三角形面积计算公式，考查了推理能力与计算能力，属于中档题．19．四棱锥P﹣ABCD中，AB∥CD，AB⊥BC，AB＝BC＝1，PA＝CD＝2，PA⊥平面ABCD，E在棱PB上．（Ⅰ）求证：AC⊥PD；（Ⅱ）若V P﹣ACE，求证：PD∥平面AEC．【分析】（Ⅰ）过A作AF⊥DC于F，推导出AC⊥DA，AC⊥PA，从而AC⊥平面PAD，由此能求出AC⊥PD；（Ⅱ）设E到平面ABCD的距离为h，由已知体积列式求得h，可得PB：EB＝PA：h ＝3：1，连接DB交AC于O，连接OE，再由三角形相似证得DB：OB＝3：1，可得PB：EB＝DB：OB，得到PD∥OE，再由直线与平面平行的判定可得PD∥平面AEC．【解答】证明：（Ⅰ）过A作AF⊥DC于F，∵AB∥CD，AB⊥BC，AB＝BC＝1，∴四边形ABCF为正方形，则CF＝DF＝AF＝1，∴∠DAC＝90°，得AC⊥DA，又PA⊥底面ABCD，AC⊂平面ABCD，∴AC⊥PA，又PA，AD⊂平面PAD，PA∩AD＝A，∴AC⊥平面PAD，又PD⊂平面PAD，∴AC⊥PD；（Ⅱ）设E到平面ABCD的距离为h，则V P﹣ACE，得h．又PA＝2，则PB：EB＝PA：h＝3：1．∵BC＝1，CD＝2，∴DB，连接DB交AC于O，连接OE，∵△AOB∽△COD，∴DO：OB＝2：1，得DB：OB＝3：1，∴PB：EB＝DB：OB，则PD∥OE．又OE⊂平面AEC，PD⊄平面AEC，∴PD∥平面AEC．【点评】本题考查直线与平面平行、垂直的判定，考查空间想象能力与思维能力，训练了多面体体积的求法，是中档题．20．已知O为坐标原点，抛物线E的方程为x2＝2py（p＞0），其焦点为F，过点M（0，4）的直线1与抛物线相交于P、Q两点且△OPQ为以O为直角顶点的直角三角形．（Ⅰ）求E的方程；（Ⅱ）设点N为曲线E上的任意一点，证明：以FN为直径的圆与x轴相切．【分析】（Ⅰ）由题意设直线l的方程，与抛物线联立求出两根之积，由△OPQ是以O 为直角顶点的直角三角形，所以0，可得p的值，进而求出抛物线的方程；（Ⅱ）由（Ⅰ）可得F的坐标和准线方程，设N的坐标，可得NF的中点M，即圆心的坐标，求出M的纵坐标到x轴的距离，再求NF的半径，可得M的纵坐标恰好等于半径，可证得结论．解：（Ⅰ）由题意可得直线l的斜率存在，设直线l的方程为：y＝kx+4，设P（x1，y1），Q（x2，y2），联立直线l与抛物线的方程，整理可得：x2﹣8kpx﹣8p＝0，所以x1x2＝﹣8p，所以y1y216，因为△OPQ是以O为直角顶点的直角三角形，所以0，即x1x2+y1y2＝0，所以﹣8p+16＝0，解得p＝2，所以抛物线的方程为：x2＝4y；（Ⅱ）证明：由（Ⅰ）得F（0，1），准线方程为：y＝﹣1，设N（m，n），则NF的中点M的纵坐标，即以NF为直径的圆的圆心M到x轴的距离为，而由抛物线的性质可得|NF|＝n+1，即以NF为直径的圆的半径为，所以可得圆心M到x轴的距离恰好等于圆的半径，所以可证得以FN为直径的圆与x轴相切．【点评】本题考查直角三角形与向量的关系，及直线与抛物线的综合，属于中档题．21．已知函数f（x）＝axe x，g（x）＝x2+2x+b，若曲线y＝f（x）与曲线y＝g（x）都过点P（1，c）．且在点P处有相同的切线l．（Ⅰ）求切线l的方程；（Ⅱ）若关于x的不等式k[ef（x）]≥g（x）对任意x∈[﹣1，+∞）恒成立，求实数k的取值范围．【分析】（Ⅰ）根据导数的几何意义即可求出切线方程；（Ⅱ）构造函数h（x）＝2kxe x﹣（x2+2x﹣1），利用导数求出函数的最小值，使得最小值大于等于0，需要分类讨论．解：（Ⅰ）∵f′（x）＝ae x（x+1），g′（x）＝2x+2，由已知可得，即，解得a，b＝﹣1，c＝2，∴切线的斜率g′（1）＝4，∴切线l的方程为y﹣2＝4（x﹣1），即4x﹣y﹣2＝0，（Ⅱ）由（Ⅰ）可得f（x）＝2xe x﹣1，g（x）＝x2+2x﹣1，设h（x）＝k[ef（x）]﹣g（x）＝2kxe x﹣（x2+2x﹣1），即h（x）≥0，对任意x∈[﹣1，+∞）恒成立，从而h（x）min≥0，∴h′（x）＝2k（x+1）e x﹣2（x+1）＝2（x+1）（ke x﹣1），①当k≤0时，h′（x）≤0，h（x）在[﹣1，+∞）上单调递减，又h（1）＝2ke﹣2＜0，显然h（x）≥0不恒成立，②当k＞0时，h′（x）＝0，解得x1＝﹣1，x2＝﹣lnk，（i）当﹣lnk＜﹣1时，即k＞e时，h′（x）≥0，h（x）单调递增，又h（x）min＝h（﹣1）20，显然h（x）≥0不恒成立，（ii）当﹣lnk＝﹣1时，即k＝e时，h′（x）＞0，h（x）单调递增，∴h（x）min＝h（﹣1）20，即h（x）≥0恒成立，（iii）当﹣lnk＞﹣1时，即0＜k＜0时，当x∈[﹣1，﹣lnk）时，h′（x）＜0，h（x）单调递减，当x∈（﹣lnk，+∞）时，h′（x）＞0，h（x）单调递增，∴h（x）min＝h（﹣lnk）＝2﹣lnk﹣（ln2k﹣2lnk﹣1）＝1﹣ln2k≥0，解得k≤e，∴k＜e，综上所述得k≤e．【点评】此题主要考查利用导数研究曲线上某点切线方程，函数恒成立问题，构造函数，求函数的导数，利用导数研究函数的单调性和最值是解决本题的关键．综合性较强，运算量较大．一、选择题22．以直角坐标系的原点为极点，x轴的非负半轴为极轴建立极坐标系，曲线C的极坐标方程为ρ2（θ∈[0，]），直线1的参数方程为（t为参数）．（Ⅰ）求曲线C的参数方程与直线l的普通方程；（Ⅱ）设点P为曲线C上的动点，点M和点N为直线l上的点，且满足△PMN为等边三角形，求△PMN边长的取值范围．【分析】（Ⅰ）直接利用转换关系的应用，把参数方程极坐标方程和直角坐标方程之间进行转换．（Ⅱ）利用点到直线的距离公式的应用和三角函数关系式的恒等变换及正弦型函数的性质的应用求出结果．解：（Ⅰ）曲线C的极坐标方程为ρ2（θ∈[0，]），转换为直角坐标方程为（），转换为参数方程为（θ为参数，θ∈[0，]）．直线1的参数方程为（t为参数）．转换为直角坐标方程为x+2y﹣8＝0．（Ⅱ）设P（），θ∈[0，]，所以点P到直线l的距离d，由于θ∈[0，]，所以，所以，故等边三角形的边长的取值范围：．【点评】本题考查的知识要点：三角函数关系式的恒等变换，正弦型函数的性质的应用，参数方程、极坐标方程和直角坐标方程之间的转换，点到直线的距离公式的应用，主要考查学生的运算能力和转换能力及思维能力，属于中档题型．[选修4-5不等式选讲]23．已知函数f（x）＝m﹣|x﹣2|，m∈R，g（x）＝|x+3|．（Ⅰ）当x∈R时，有f（x）≤g（x），求实数m的取值范围．（Ⅱ）若不等式f（x）≥0的解集为[1，3]，正数a，b满足ab﹣2a﹣b＝3m﹣1，求a+b 的最小值．【分析】（1）利用绝对值三角不等式性质（2）利用绝对值不等式解法求出m，带入得到a，b等式，转化为只含有a的式子后利用基本不等式可以求解．解：（1）由题意得：∵f（x）≤g（x）在x∈R上恒成立，∴m≤|x+3|+|x﹣2|恒成立，即m≤（|x+3|+|x﹣2|）min又∵|x+3|+|x﹣2|≥|（x+3）﹣（x﹣2）|＝5∴m≤5，即m∈（﹣∞，5]（2）令f（x）≥0，∴m≥||若m≤0，则解集为∅，不合题意；若m＞0，则有﹣m≤x﹣2≤m，即x∈[2﹣m，2+m]又∵解集为x∈[1，3]，∴m＝1∴ab﹣2a﹣b＝2∴b∵，解得a＞1∴a+b＝a3∴a+b≥23＝7当且仅当a﹣1，即a＝3时，等号成立，此时b＝4∴a＝3，b＝4时a+b的最小值为7【点评】本题考查绝对值三角不等式，以及基本不等式的应用，考查转化思想以及计算能力，是中档题。

吉林省吉林高三第三次调研测试文科数学试题

吉林市普通中学高中毕业班第三次调研测试数学(文科)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分，共24小题，共150分，考试时间120分钟。

注意事项：1．答题前，考生先将自己的姓名、准考证号码填写清楚，将条形码准确粘贴在条形码区域内； 2．选择题必须用2B 铅笔填涂；非选择题必须使用0.5毫米的黑色字迹的签字笔书写，字体工整、笔迹清楚； 3．请按照题号顺序在各题的答题区域内作答，超出答题区域书写的答案无效；在草稿纸、试题卷上答题无效；4．作图可先使用铅笔画出，确定后必须用黑色字迹的签字笔描黑；5．保持卡面清洁，不要折叠，不要弄破、弄皱，不准使用涂改液、修正带、刮纸刀。

第Ⅰ卷一、选择题：本大题共12题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的。

1. 设全集={1,2,3,4,5,6,7,8}U ，集合{1,2,3,5}A =，={2,4,6}B ，则()U B A =ðA ．{2}B ．{4,6}C ．{1,3,5}D ．{4,6,7,8}2．复数3ii-=A ．13i +B ．13i --C ．13i -+D ．13i -3．设2()2f x ax bx =++是定义在[1,1]a +上的偶函数，则2a b += A ．0B ．2C ．2-D ．124．已知(1,2)a =-，(2,)b m =，若a b ⊥，则=||bA ．12B ．1CD 5．下列有关命题的说法正确的是A ．“(0)0f =”是“函数()f x 是奇函数”的充要条件；B ．若:p 2000,10x R x x ∃∈-->.则:p ⌝2,10x R x x ∀∈--<；C ．若p q ∧为假命题，则,p q 均为假命题；D ．“若3πα=，则1cos 2α=”的否命题是“若3πα≠，则1cos 2α≠”．6．已知,x y 满足14210x x y x y ≥⎧⎪+≤⎨⎪--≤⎩，则2z x y =+的最大值为A ．3B ．4C ．6D ．77．已知双曲线2222:1(0,0)x y C a b a b-=>>C 的渐近线方程为 A ．14y x =±B ．13y x =±C ．12y x =±D ．y x =±8．执行如图所示的程序框图，输出的T = A ．29 B ．44 C ．52D ．629．一个几何体的三视图如图所示，其中正视图与侧视图都是斜边长为2的直角三角形，俯视图是半径为1的四分之一圆周和两条半径，则这个几何体的体积为 ABCD．310．若函数2()sin sin 2f x x x x πωωω⎛⎫=++ ⎪⎝⎭(0ω>) 的最小正周期为π，则()f x 在区间203，π⎡⎤⎢⎥⎣⎦上的值域为 A ．3[0]2，B ．13[]22，-C ．1[1]2，-D ．31[]22，-11．对于问题：“已知关于x 的不等式20ax bx c ++>的解集为(1,2)-，解关于x 的不8题图9题图正视图俯视图侧视图等式20a x b x c -+>”，给出如下一种解法：解：由20a x b x c ++>的解集为(1,2)-，得2()()0a x b x c -+-+>的解集为 (2,1)-，即关于x 的不等式20a x b x c -+>的解集为(2,1)-．参考上述解法，若关于x 的不等式0k x b x a x c ++<++的解集为11(1,)(,1)32--，则关于x 的不等式1011kx bx ax cx ++<++的解集为 A ．()()2,21,3- B ．()()3,11,2--C ．()(),,2311-- D ．()(),,3112--12．若函数()f x 满足1()1(1)f x f x +=+，当[0,1]x ∈时，()f x x =，若在区间(1,1]- 上，()()2g x f x m x m =--有两个零点，则实数m 的取值范围是 A ．103m <≤B ．102m <<C ．112m <≤D ．113m <<第Ⅱ卷二、填空题：本大题共4个小题，每小题5分。

吉林省长春市高三数学第三次调研测试文

数学试题（文科）本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，满分 150分，考试时间为120分钟，其中第Ⅱ卷22题—24题为选考题，其它题为必考题。

考试结束后，将试卷和答题卡一并交回。

注意事项：1．答题前，考生先将自己的姓名、准考证号码填写清楚，将条形码准确粘贴在条形码区域内。

2．选择题必须用2B 铅笔填涂；非选择题必须使用0.5毫米黑色字迹的签字笔书写，字体工整、笔迹清楚。

3．请按照题号顺序在各题目的答题区域内作答，超出答题区域书写的答案无效；在草稿纸、试题卷上答题无效。

4．保持卡面清洁，不要折叠、不要弄破、弄皱，不准使用涂改液、修正带、刮纸刀。

第Ⅰ卷（选择题，共60分）一、选择题（本大题包括12小题，每小题5分，共60分，每小题给出的四个选项中，只有一项是符合题目要求的，请将正确选项填涂在答题卡上）. 1．复数z 满足(1i)2i z +=，则复数z 在复平面内对应的点在 A ．第一象限B ．第二象限C ．第三象限D ．第四象限2．设集合}421{，，＝A ,集合},,|{A b A a b a x xB ∈∈+=＝，则集合B 中有___个元素 A ．4B ．5C ．6D ． 73．下列函数中，在(0,)+∞上单调递减，并且是偶函数的是A ．2y x =B ．3y x =-C ．lg ||y x =-D ．2xy =4．观察下面频率等高条形图，其中两个分类变量x y ，之间关系最强的是A ．B ．C ．D ． 5．如图所示的程序框图，该算法的功能是A ．计算012(12)(22)(32)++++++…(12)nn +++的值 B ．计算123(12)(22)(32)++++++…(2)n n ++的值 C ．计算(123+++…)n +012(222++++…12)n -+的值 D ．计算[123+++…(1)]n +-012(222++++…2)n+的值6．已知双曲线C ：22221x y ab -=(0,0)a b >>的焦距为2c ，焦点到双曲线C的渐近线的距离第5题图为2c，则双曲线C 的离心率为A ．2BC．2D．37．△ABC 各角的对应边分别为c b a ,,，满足b c a c a b +++ 1，则角A 的范围是A ．(0,]3πB ．(0,]6πC ．[,)3ππD ．[,)6ππ8．函数)2|)(|2sin()(πϕϕ<+=x x f 的图象向左平移6π个单位后关于原点对称，则函数()f x 在[0,]2π上的最小值为 A．2-B ．12-C ．12D．29．已知实数,x y 满足：210210x y x x y -+ ⎧⎪<⎨⎪+- ⎩，221z x y =--，则z 的取值范围是 A ．5[,5]3B ．[]0,5C ．[)0,5D ．5[,5)310．若一个圆柱的正视图与其侧面展开图相似，则这个圆柱的侧面积与全面积之比为ABCD11．已知函数2()f x x =的图象在点11(,())A x f x 与点22(,())B x f x 处的切线互相垂直，并交于点P ，则点P 的坐标可能是A ．3(,3)2-B ． (0,4)-C ．(2,3)D ．1(1,)4- 12．已知点P ，Q 为圆22:25C x y +=上的任意两点，且6PQ <，若PQ 中点组成的区域为M ，在圆C 内任取一点，则该点落在区域M 上的概率为≥≥ ≥A ．35B ．925C ．1625D ．25第Ⅱ卷（非选择题，共90分）本卷包括必考题和选考题两部分。

吉林省长春市高中毕业班高三数学第三次调研测试试题(文数)