历年全国中考数学真题分类_001.实数的有关概念
2021年全国中考数学真题分类汇编: 实数的有关概念和性质(含解析)

4.(2021•河北4题)与 结果相同的是( )
A.3﹣2+1B.3+2﹣1C.3+2+1D.3﹣2﹣1
A
1.(2021•绍兴)实数2,0,﹣3, 中,最小的数是( )
A.2B.0C.﹣3D.
C
1.(2021•宁波)在﹣3,﹣1,0,2这四个数中,最小的数是( )
A.﹣3B.﹣1C.0D.2
A
1.(2021•重庆B卷)3的相反数是( )
A.3B. C.﹣3D.
C
8.(2021·安顺、贵阳)如图,已知数轴上A,B两点表示的数分别是a,b,则计算|b|﹣|a|正确的是( )
A.b﹣aB.a﹣bC.a+bD.﹣a﹣b
C{解析}由数轴可知,a<0,b>1,∴|b|=b,|a|=﹣a,∴|b|﹣|a|=b﹣(﹣a)=b+a.
1.(2021•安徽1题)﹣9的绝对值是( )
A.7℃B.﹣7℃C.11℃D.﹣11℃
C
1.(2021·上海)下列实数中,有理数是()
A. B. C. D.
C
1.(2021•新疆)下列实数是无理数的是( )
A.﹣2B.1C. D.2
C
1.(2021•重庆A卷)2的相反数是( )
A.﹣2B.2C. D.
Aቤተ መጻሕፍቲ ባይዱ
1.(2021•泰安)下列各数:﹣4,﹣2.8,0,|﹣4|,其中比﹣3小的数是( )
A.3B.﹣3C. D.
B
1.(2021•黄冈)﹣3的相反数是( )
A.﹣3B. C. D.3
D
1.(2021•菏泽)如图,数轴上点A所表示的数的倒数为( )
A.﹣3B.3C. D.
历年全国中考数学真题分类_01B 实数的有关概念

实数的有关概念一、选择题1. (2011福建泉州,1,3分)-5的倒数是( ).A 、51-B 、51 C 、-5 D 、5 【答案】A 2. (2011广东河源,1,3分)12-的倒数是( ) A .—2 B .2 C .12-D .12 【答案】A3. (2011广东湛江,1,3分)—5的相反数是 A —5 B 5 C 15- D 15【答案】B4. (2011广东湛江,5,3分)第六次全国人口普查显示,湛江市常住人口数约为6990000人,数据6990000用科学记数法表示为A 569.910⨯B 610⨯C 66.9910⨯D 76.9910⨯ 【答案】C5. (2011广东珠海,1,3分)如-43的相反数是 A. 34 B. -43 C.-34 D. 43 【答案】D6. (2011广西桂林,1,3分)2011的倒数是( ).A .12011B .2011C .-2011D .-12011【答案】A7. (2011广西桂林,2,3分)在实数2、0、-1、-2中,最小的实数是( ).A .2B .0C .-1D .-2【答案】D8. (2011贵州毕节,5,3分)毕节地区水能资源丰富,理论蕴藏量达221.21万千瓦,己开发156万千瓦,把己开发水能资源用四舍五入法保留两个有效数学并且用科学计数法表示应记为( )千瓦A .51016⨯B .6106.1⨯C .610160⨯D .71016.0⨯【答案】B9. (2011海南省,1,3分)-3的绝对值是A .-3B .3C .31-D .31 【答案】B10.(2011海南省,9,3分)海南省2010年第六次人口普查数据显示,2010年11月1日零时,全省总人口8671518人.数据8671518用科学记数法(保留三个有效数字)表示应是A .8.7×106B .8.7×107C .8.67×106D .8.67×107【答案】C11. (2011河南,1,3分)-5的绝对值 【 】(A )5 (B )-5 (C )15 (D )15- 【答案】A12. (2011黑龙江省哈尔滨市,1,3分)-6的相反数是( )A .61B .-6C .6D .61- 【答案】C13. (2011湖北十堰,1,3分)下列实数中是无理数的是( )A B C .13D .3.14 【答案】A14. (2011湖北十堰,4,3分)据统计,十堰市2011年报名参加九年级学业考试总人数为26537人,则26537用科学记数法表示为(保留两个有效数字)( )A .2.6×104 B.2.7×104 C. 2.6×105 D. 2.7×105【答案】B15. (湖南湘西,9,3分)下列各数中,是无理数的是( )A.0B.-2 D.12 【答案】C16. (2011江苏常州,1,2分)在下列实数中,无理数是( )A.2B.0 D.13 【答案】 C17. (2011辽宁大连,1,3分)-12的相反数是 A .-2B .-12C .12D .2 【答案】C18. (2011广东深圳,1,3分) -21的相反数是( ) A. -21 B. 21 C. -2 D. 2 【答案】B19. (2011广东深圳,3,3分)今年参加我市初中毕业生学业考试的总人数约为56000人, 这个数据用科学记数法表示为( ).A. 5.6×103B. 5.6×104C. 5.6×105D. 0.56×105【答案】B20.(2011山西,1,2分)6-的值是( )A .-6 B. 16- C. 16D.6 【答案】D21. (2011山西,4,2分)2011年第一季度,我省固定资产投资完成475.6亿元,这个数据用科学记数法可表示为( )A .947.5610⨯元 B. 110.475610⨯元 C. 104.75610⨯元 D. 94.75610⨯元【答案】C22. (2011陕西,1,3分) 32-的相反数是( ) A .23- B .23 C .32 D .32- 【答案】C23. (2011陕西,3,3分) 我国第六次人口普查显示,全国人口为1370536875人,将这个总人口数(保留三个有效数字)用科学计数法表示为( )A .91037.1⨯B .910371.1⨯C .8107.13⨯D .1010137.0⨯ 【答案】A24. (2011天津,3,3分)根据第六次人口普查的统计,截止到2010年11月1日零时,我国总人口约为1370000000人,将1370000000用科学记数法表示为( )A. 100.13710⨯B. 91.3710⨯C.813.710⨯D.713710⨯答案:B25. (2011湖北襄阳,1,3分)-2的倒数是A .-2B .2C .21-D .21 【答案】C26. (2011湖北襄阳,6,3分)下列说法正确的是A .0)2(π是无理数 B .33是有理数 C .4是无理数 D .38-是有理数【答案】D27. (2011广东佛山,1,3)如-2的倒数是 A .-2 B. 2 C 12- D. 12【答案】C28. (2011广东佛山,3,3)下列说法正确的是A .a 一定是正数 B. 20113是有理数C . D.平方等于自身的数只有1【答案】B29. (2010湖南长沙,1,3分) | -2|等于( )A .2B . -2 12C .D .-12【答案】A30. (2011山东莱芜,1,3分)-6的绝对值是 ( )A. -6B. 6C. 61- D. 61 【答案】B31. (2011北京市,1,4分)34-的绝对值是( ) A . 43- B . 43 C . 34- D . 34【答案】D32. (2011北京市,2,4分)我国第六次全国人口普查数据显示,居住在城镇的人口总数达到665 575 306人.将665 575 306用科学记数法表示(保留三个有效数字)约为( )A . 766.610⨯B . 80.66610⨯C . 86.6610⨯D . 76.6610⨯【答案】C33. (2011贵州遵义,1,3分)下列各数中,比-1小的数是A .0 B.-2 C.21 D.1 【答案】B34. (2011贵州遵义,3,3分)某种生物细胞的直径约为0.00056m ,将0.00056用科学记数法表示为A .0.56310-⨯ B. 5.6410-⨯ C. 5.6510-⨯ D. 56510-⨯【答案】B35. (2011广东清远,1,3分)3-的倒数是( )A .3B .3-C .13D .13- 【答案】D36. (2011广东清远,4,3分)据媒体报道,我国因环境问题造成的经济损失每年高达680000000元,这个数用科学计数法可表示为( )A .90.6810⨯B .96.810⨯C .76.810⨯D .76810⨯ 【答案】B37. (2011四川达州,1,3分) 5-的相反数是A 、5-B 、5C 、5±D 、15-【答案】B38. (2011湖南娄底,1,3分)-2011的相反数是A. 2011B. -2011C. 12011D. -12011【答案】A39. (2011湖南娄底,2,3分)2011年4月28日,国家统计局发布2010年第六次全国人口普查主要数据公报,数据显示,大陆31个省、自治区、直辖市和现役军人的人口共1339724852人,大陆总人口这个数据用科学记数法表示(保留3个有效数字)为A. 1.33⨯109人B. 1.34⨯109人C. 13.4⨯108人D. 1.34⨯1010人【答案】B40. (2011内蒙古呼和浩特市,1,3分)如果a 的相反数是2,那么a 等于 ( )A. —2B. 2C. 21D. 21-【答案】A41. (2011内蒙古呼和浩特市,4,3分)用四舍五入法按要求对0.05049分别取近似值,其中错误..的是 ( )A. 0.1(精确到0.1)B. 0.05(精确到百分位)C. 0.05(精确到千分位)D. 0.050(精确到0.001)【答案】C42. (2011福建莆田,1,4分)-2011的相反数是( )A .-2011B .-12011 C .2011 D .12011 【答案】C43. (2011广东肇庆,1,3分)21的倒数是 A .2 B . 2- C .21 D . 21- 【答案】A44. (2011广东肇庆,2,3分)我国第六次人口普查的结果表明,目前肇庆市的人口约为4050000人,这个数用科学记数法表示是A .410405⨯B .5105.40⨯C . 61005.4⨯D . 71005.4⨯ 【答案】C45. (2011广西桂林,1,3分)2011的倒数是( ).A .12011B .2011C .2011-D .12011- 【答案】A46. (2011广西南宁,1,3分)下列所给的数中,是2的相反数的是:(A)-2 (B)21 (C)2 (D)-21 【答案】A47. (2011广西南宁,4,3分)我国第二颗月球探测卫星嫦娥二号于201 1年6月9日奔向距地球1500000km的深空,用科学记数法表示1500000为:(A)1.5 xl06 ( B)O. 15×107 (C)1.5×l07 (D)15×l06【答案】A48. (2011广西梧州,1,3分)-5的相反数是(A )-5 (B )5 (C )15 (D )-15【答案】B49. (2011黑龙江省哈尔滨市,1,3分)-6的相反数是( )A .61B .-6C .6D .61- 【答案】C50. (2011湖北潜江天门仙桃江汉油田,1,3分)31-的倒数是( ) A .31 B .-3 C .3 D .31-【答案】B51. (2011湖北潜江天门仙桃江汉油田,3,3分)第六次人口普查的标准时间是2010年11月1日零时.普查登记的大陆31个省、自治区、直辖市和现役军人的人口共1 339 724 852人.这个数用科学记数法表示为(保留三个有效数字)( )A .1013310.⨯B .1013410.⨯C .910331⨯.D .910341⨯.【答案】D52.(2011江西b 卷,1,3分)下列各数中,最小的是( ).A. 0.1B. 0.11C.0.02D.0.12【答案】C53. (2011江西b 卷,2,3分)根据2010年第六次全国人口普查主要数据公报,广东省常住人口约为10430万人.这个数据可以用科学计数法表示为( ).A. 1.043×108人B. 1.043×107人C.1.043×104人D. 1043×105人【答案】A54. (2011吉林长春,1,3分)2-的绝对值等于(A )12-. (B )12. (C )2-. (D )2. 【答案】(D )55. (2011吉林长春,2,3分)某汽车参展商为参加第8届中国(长春)国际汽车博览会,印制了105000张宣传彩页.105000这个数字用科学记数法表示为(A )410.510⨯. (B )51.0510⨯. (C )61.0510⨯. D )60.10510⨯. 【答案】(B )56. (2011江苏徐州,1,2分)-2的相反数是( )A. 2B.-2C. 12D.-12【答案】A57. (2011江苏徐州,2,2分)2010年我国总人口约为1 370 000 000人,该人口数用科学记数法表示为( )A.110.13710⨯B.91.3710⨯C. 813.710⨯D.713710⨯【答案】B58. (2011辽宁沈阳,1,3分)下列选择项中,既不是正数也不是负数的是A .-1B .0CD .π 【答案】 B59.(2011福建龙岩,1,4分)5的相反数是( )A .15 B. 5 C. 5- D. 15- 【答案】C60. (2011四川广元,5,3分)在《国家长期教育改革和发展规划纲要》中指出,“加大教育投入,提高国家财政性教育经费支出占国内生产总值比例,2012年达到4%”.如果2012年我国国内生产总值为445000亿元,那么2012年国家财政性教育经费支出应为(结果用科学记数法表示)( B )A .178×102亿元B .1.78×104亿元C .1.78×105亿元D .4.45×105亿元【答案】B61. (2011四川眉山,1,3分)-2的相反数是( )A .2B .-2C .21D .-21 【答案】 A62. (2011四川眉山,4,3分)2011年,我市参加中考的学生约为33200人,用科学记数法表示为A. 332×102B.33.2 x103C.3. 32 x l04 D 0. 332 x l05【答案】C63. (2011广西来宾,1,3分)据国家统计局2011年4月28日发布的(2010年第六次人口普查主要数据公报(第1号))我国人口为1370536875人,这一数字用科学记数法表示为(保留四个有效数字)( )A.1.37×910B.1.370×910C.1.371×910D.1.371×810【答案】C64. (2011年铜仁地区,1,4分) -2的相反数是( ) A.21 B. 21- C.-2 D.2. 【答案】D.65. (2011年铜仁地区,2,4分)2011年,某地区有54310人参加中考,将54310用科学记数法(保留2个有效数字)表示为( ) A.54×103B.0.54×105C.5.4×104D.5.5×104 【答案】C.66. (2011福建三明,1,4分)-6的相反数是( )A .-6B .- 16C .16D .6 【答案】D67. (2011福建三明,2,4分)据《2010年三明市国民经济和社会发展统计公报》数据显示,截止2010年底,三明市民用汽车保有量约为98200辆,98200用科学记数法表示正确的是( )A .9.82×103B .98.2×103C .9.82×104D .0.982×104【答案】C68. (2011云南省昆明市,3,3分)据2010年全国第六次人口普查数据公布,云南省常住人口为45966239人,45966239用科学记数法表示且保留两个有效数字为( )A .4.6×107B . 4.6×106C . 4.5×106D . 4.5×107【答案】A69. (2011内蒙古包头,1,3分)21-的绝对值是( ) A .-2 B .21 C .2 D .21- 【答案】B70. (2011内蒙古包头,6,3分)2008年6月1日起全国商品零售场所开始实行“塑料购物袋有偿使用制度”,截止到2011年5月底全国大约节约塑料购物袋6.984亿个,这个数用科学记数法表示约为(保留两个有效数字)( )A .6.9×108个B .6.9×109个C .7×108个D .7.0×108个【答案】D71. (2011内蒙古赤峰,1,3分)-4的相反数是 ( )A .14B .-14C .4D .-4【答案】C72.(2011吉林长春,1,3分)2-的绝对值等于(A )12-. (B )12. (C )2-. (D )2. 【答案】(D )73.(2011吉林长春,2,3分)某汽车参展商为参加第8届中国(长春)国际汽车博览会,印制了105000张宣传彩页.105000这个数字用科学记数法表示为(A )410.510⨯. (B )51.0510⨯. (C )61.0510⨯. D )60.10510⨯. 【答案】(B )74.(2011四川自贡,1,3分)-6的倒数是 ( )A. 6B.-6C.16 D. 16- 【答案】D75.(2011四川雅安1,3分)3-的相反数是( )A 31B 31- C 3 D 3- 【答案】 C76.(2011四川雅安2,3分)光的传播速度为300000km/s ,该数用科学记数法表示为( )A 5103⨯B 6103.0⨯C 6103⨯D 5103-⨯【答案】 A77.(2011山东淄博,1,3分)2011年4月28日,国家统计局公布了第六次全国人口普查结果,总人口为1 339 000 000人,将1 339 000 000用科学记数法表示为( )A .81.33910⨯B .813.3910⨯C .91.33910⨯D .101.33910⨯ 【答案】C78.(2011山东青岛,1,3分)﹣12的倒数是( ). A. 12- B. 12C. ﹣2D. 2 【答案】C79.(2011山东青岛,5,3分) 某种鲸的体重约为1.36×105千克.关于这个近似数,下列说法正确的是( ).A.精确到百分位,有3个有效数字B.精确到个位,有6个有效数字C.精确到千位,有6个有效数字D.精确到千位,有3个有效数字【答案】D80. (2011年青海,15,3分)在 3.14π )A. 3.14ππ【答案】D81. (2011广西崇左,15,3分)今年5月23日从崇左市固投办了解到,自治区统计局日前核准并通报全区各市1~4月份全社会固定资产投资完成情况,其中崇左市1~4月份完成社会固定资产投资共81.97亿元,比去年同期增长53.1%,增幅居全区各市第二位.用科学计数法表示,则81.97亿元可写为( )A .8.197×109元B .81.97×109元C .8.197×108元D .81.97×108元【答案】A82. (2011广西柳州,1,3分)在0,-2, 3A.0B.-2C.3D.【答案】B83. (2011广西百色,1,3分)2011的相反数是A.-2011B.2011C. 12011D. ±2011 【答案】:A84. (2011广西百色,9,3分)我们知道:一个正整数p(P>1)的正因数有两个:1和p ,除此之外没有别的正因数,这样的数p 称为素数,也称质数。
全国中考数学模拟汇编二1实数的有关概念

实数的有关概念A 组:一、 选择题1.(2011双柏县中考模拟)甲型H1N1流感病毒变异后的直径为0.00000013米,将这个数写成科学记数法是( )A .1.3×10-5B .0.13×10-6C .1.3×10-7D .13×10-8【答案】C 2.(2011杭州市余杭中考模拟)改革开放以来,我国国内生产总值由1978年的3645亿元增长到2008年的300670亿元。
将300670用科学记数法表示应为 A.60.3006710⨯ B.53.006710⨯ C.43.006710⨯ D.430.06710⨯【答案】B 3.(2011杭州市进化一中模拟)-2的相反数是( ). A.-2 B.2 C.-21 D.21 【答案】B4.(2011杭州市进化一中模拟)己知1纳米=0.000000001米,则27纳米用科学记数法表示为( ).A. 27×10-9B. 2.7×10-8C. 2.7×10-9D. -2.7×108【答案】B5.(2011萧山区中考模拟)【原创】地球的表面积约为5.1亿Km2,其中陆地面积约为地球表面积的0.29,则地球上陆地面积约为( )A 、721510.km ⨯B 、28105.1km ⨯ C 、291015.0km ⨯ D 、921.510km ⨯【答案】B6.(2011浙江新昌县模拟)61-的相反数是 A .6 B .6- C . 61 D .61- 【答案】C7.(2011浙江舟山市模拟)在-3,0,-2A .-3 B.0 C.-【答案】A8. (2011浙江新昌县模拟)3月11日,日本发生地震和海啸,3月12日,中国红十字会向日本红十字会提供100万元人民币的紧急援助,同时发出慰问电,向日本受灾群众表示诚挚的慰问,对地震遇难者表示深切的哀悼,并表示将根据灾区需求继续提供及时的人道援助. 100万这个数用科学记数法表示为A. 410.01⨯ B. 610.01⨯ C. 510.01⨯ D. 6101.0⨯ 【答案】B9.(2011浙江舟山市模拟)金塘大桥包含主通航孔桥、东通航孔桥、西通航孔桥、非通航孔桥、浅水区引桥、金塘侧引桥、镇海侧引桥,大桥长21.020km ,是目前世界上在恶劣外海环境中建造的最大跨度斜拉桥。
中考数学实数知识点及历年中考真题

中考考点数与式—实数一、考点梳理考点一:实数的分类⎪⎩⎪⎨⎧⎩⎨⎧无限不循环小数—无理数数有限小数或无限循环小—分数整数有理数实数 常见的几种无理数形式:①含π的式子;②构造型:如3.010010001…(每两个1之间多个0)就是一个无限不循环小数;③开方开不尽的数;④三角函数型:如sin45°,tan35°失分点警示:开得尽方的含根号的数属于有理数。
考点二:实数的有关概念1、数轴:(1)三要素:原点、正方向、单位长度。
(2)特征:实数与数轴上的点一一对应;数轴右边的点表示的数总比左边的点表示的数大。
2、相反数:(1)概念:只有符号不同,绝对值相同的两个数。
(2)代数意义:a 、b 互为相反数 ⟺ a+b=0(3)几何意义:数轴上表示互为相反数的两个点到原点的距离相等。
3、绝对值:(1)几何意义:数轴上表示的点到原点的距离(2)运算性质:⎩⎨⎧<-≥=)0a (a )0a (a a ⎩⎨⎧<-≥-=-)()(b a a b b a b a b a ;绝对值的问题经常分类讨论。
(3)非负性:|a|≥0,若|a|+b 2=0,则a=b=0.绝对值等于它本身的数是非负数4、倒数:(1)概念:乘积为1的两个数互为倒数;0没有倒数;(2)若ab=1⇔ a 、b 互为倒数;若ab=-1⇔ a 、b 互为负倒数。
考点三、科学记数法1、定义:把一个大于10的数记成a ×10n 的形式,其中1≤|a |<10,这种记数法叫科学记数法。
例:21000用科学记数法表示为4101.2⨯考点四、平方根、算术平方根和立方根考点五、实数的大小比较(1)数轴比较法:数轴上的两个数,右边的数总比左边的数大.(2)性质比较法:正数>0>负数;两个负数比较大小,绝对值大的反而小.(3)作差比较法:a-b >0 ⟺ a >b ;a-b=0 ⟺ a=b ;a-b <0⟺ a <b.(4)平方法:a >b≥0 ⟺ a 2>b 2.考点六、实数的有关运算1、加法法则:(1)同号两数相加,取相同的符号,并把绝对值相加。
中考数学试题分类大全01_实数的有关概念.pdf

A.4
B. −4
C. 1 4
D. − 1 4
【答案】A 41.(2010 浙江义乌)-2 的相反数是( ▲ )
A.2
B.-2
C.-
D.
【答案】A
42.(2010 重庆)3 的倒数是(
)
A. 1 3
【答案】A
B. − 1 3
C.3
D. − 3
43.(2010 重庆市潼南县)2 的倒数是(
)
A. 1 2
【答案】B
6.(2010 安徽省中中考) 2010 年一季度,全国城镇新增就业人数
为 289 万人,用科学记数法表示 289 万正确的是
…………………………(
)
A)2.89×107. B)2.89×106 .C)2.89×105. D)2.89×104.
【答案】B
学无 止 境
7.(2010 安徽省中中考)下面两个多位数 1248624……、6248624……,都是按照如下方法
【答案】B
33. (2010 台湾)下列选项中,哪一段时间最长? (A) 15 分 (B) 4 小时 (C) 0.3 小时 (D) 11
1020 秒。 【答案】B 34.(2010 台湾) 已知 456456=23a71113b,其中 a、b 均为质数。若 b>a,则 b−a 之 值为何?
(A) 12 (B) 14 (C) 16 (D) 18 。
A.1.3×104
B.1.3×105
C.1.3×106
D.1.3×107
【答案】C
3.(2010
安徽蚌埠二中)记 Sn
= a1
+
a2
++
an
,令Tn
实数概念例题和知识点总结

实数概念例题和知识点总结实数是数学中的一个重要概念,它涵盖了有理数和无理数。
理解实数的概念对于进一步学习数学知识,解决数学问题至关重要。
下面我们通过一些例题来深入理解实数的相关概念,并对重要知识点进行总结。
一、实数的定义和分类实数是有理数和无理数的总称。
有理数包括整数(正整数、0、负整数)和分数(正分数、负分数);无理数是无限不循环小数,例如√2、π等。
二、实数的性质1、实数的有序性:任意两个实数 a 和 b,要么 a < b,要么 a = b,要么 a > b。
2、实数的稠密性:在任意两个不同的实数之间,都存在无穷多个实数。
3、实数的运算封闭性:实数进行加、减、乘、除(除数不为 0)运算,其结果仍然是实数。
三、例题解析例 1:判断下列数哪些是有理数,哪些是无理数?22/7,√5,0,-314,***********(相邻两个 1 之间依次多一个 0)解:22/7 是分数,属于有理数;√5 是无限不循环小数,是无理数;0 是整数,属于有理数;-314 是有限小数,可化为分数,属于有理数;***********(相邻两个 1 之间依次多一个 0)是无限不循环小数,是无理数。
例 2:比较大小:√3 + 1 和 2 +√2解:因为(√3 + 1)²= 3 +2√3 + 1 = 4 +2√3 ,(2 +√2)²=4 +4√2 + 2 = 6 +4√2 。
而 4 +2√3 < 6 +4√2 ,所以√3 + 1 < 2 +√2 。
例 3:已知一个实数的绝对值是√5,求这个实数。
解:设这个实数为 x ,则|x| =√5 ,所以 x =±√5 。
四、实数的运算1、加法:同号两数相加,取相同的符号,并把绝对值相加;异号两数相加,取绝对值较大的数的符号,并用较大的绝对值减去较小的绝对值。
2、减法:减去一个数,等于加上这个数的相反数。
3、乘法:两数相乘,同号得正,异号得负,并把绝对值相乘。
中考数学真题-实数的有关概念与计算

实数的有关概念与计算姓名:__________________ 班级:______________ 得分:_________________一、单选题1.(2021·安徽中考真题)9-的绝对值是( )A .9B .9-C .19D .19- 2.(2021·浙江金华市·中考真题)某超市出售一商品,有如下四种在原标价基础上调价的方案,其中调价后售价最低的是( )A .先打九五折,再打九五折B .先提价50%,再打六折C .先提价30%,再降价30%D .先提价25%,再降价25%3.(2021·山东泰安市·中考真题)下列各数:4-, 2.8-,0,4-,其中比3-小的数是( ) A .4- B .4- C .0 D . 2.8-4.(2021·四川南充市·中考真题)数轴上表示数m 和2m +的点到原点的距离相等,则m 为( ) A .2- B .2 C .1 D .1-5.(2021·四川凉山彝族自治州·中考真题)下列数轴表示正确的是( )A .B .C .D .6.(2021·四川泸州市·中考真题)2021的相反数是( )A .2021-B .2021C .12021-D .120217.(2021·四川乐山市·中考真题)如果规定收入为正,那么支出为负,收入2元记作2+,支出5元记作( ). A .5元 B .5-元 C .3-元 D .7元8.(2021·浙江中考真题)实数2-的绝对值是( )A .2-B .2C .12D .12- 9.(2021·江苏连云港市·中考真题)3-相反数是( )A .13B .3-C .13-D .310.(2021·甘肃武威市·中考真题)中国疫苗撑起全球抗疫“生命线”!中国外交部数据显示,截止2021年3月底,我国已无偿向80个国家和3个国际组织提供疫苗援助.预计2022年中国新冠疫苗产能有望达到50亿剂,约占全球产能的一半,必将为全球抗疫作出重大贡献.数据“50亿”用科学记数法表示为( ) A .8510⨯ B .9510⨯ C .10510⨯ D .85010⨯11.(2021·云南中考真题)某地区2021年元旦的最高气温为9℃,最低气温为2-℃,那么该地区这天的最低气温比最高气温低( )A .7℃B .7-℃C .11℃D .11-℃12.(2021·江苏连云港市·中考真题)2021年5月18日上午,江苏省人民政府召开新闻发布会,公布了全省最新人口数据,其中连云港市的常住人口约为4600000人.把“4600000”用科学记数法表示为( ) A .70.4610⨯ B .74.610⨯ C .64.610⨯D .54610⨯ 13.(2021·浙江温州市·中考真题)计算()22-的结果是( )A .4B .4-C .1D .1-14.(2021·四川泸州市·中考真题)第七次全国人口普查统计,泸州市常住人口约为4 254 000人,将4 254 000用科学记数法表示为( )A .54.25410⨯B .542.5410⨯C .64.25410⨯D .70.425410⨯15.(2021·浙江金华市·中考真题)实数12-,2,3-中,为负整数的是( )A .12-B .C .2D .3-16.(2021·浙江绍兴市·中考真题)实数2,0,3-中,最小的数是( )A .2B .0C .3- D17.(2021·四川中考真题)若a =b =2c =,则a ,b ,c 的大小关系为( ) A .b c a << B .b a c <<C .a c b <<D .a b c <<18.(2021·浙江中考真题)已知,a b 是两个连续整数,1a b <<,则,a b 分别是( )A .2,1--B .1-,0C .0,1D .1,219.(2021·四川凉山彝族自治州· )A .3±B .3C .9±D .920.(2021·浙江温州市·中考真题)第七次全国人口普查结果显示,我国具有大学文化程度的人口超218000000人.数据218000000用科学记数法表示为( )A .621810⨯B .721.810⨯C .82.1810⨯D .90.21810⨯21.(2021·浙江绍兴市·中考真题)第七次全国人口普查数据显示,绍兴市常住人口约为5 270 000人,这个数字5270 000用科学记数法可表示为( )A .70.52710⨯B .65.2710⨯C .552.710⨯D .75.2710⨯22.(2021·四川凉山彝族自治州·中考真题)“天问一号”在经历了7个月的“奔火”之旅和3个月的“环火”探测,完成了长达5亿千米的行程,登陆器“祝融”号火星车于2021年5月15日7时18分从火星发来“短信”,标志着我国首次火星登陆任务圆满成功,请将5亿这个数用科学记数法表示为( )A .7510⨯B .8510⨯C .9510⨯D .10510⨯23.(2021·浙江嘉兴市·中考真题)2021年5月22日,我国自主研发的“祝融号”火星车成功到达火星表面.已知火星与地球的最近距离约为55000000千米,数据55000000用科学记数法表示为( )A .65510⨯B .75.510⨯C .85.510⨯D .80.5510⨯24.(2021·安徽中考真题)《2020年国民经济和社会发展统计公报》显示,2020年我国共资助8990万人参加基本医疗保险.其中8990万用科学记数法表示为( )A .89.9×106B .8.99×107C .8.99×108D .0.899×109二、填空题25.(2021·重庆中考真题)计算:()031p --=_______.26.(2021·云南中考真题)已知a ,b 都是实数,若21(2)0a b ++-=则a b -=_______.27.(2021·山东泰安市·中考真题)2021年5月15日7时18分,天问一号着陆巡视器成功着陆于火星,我国首次火星探测任务着陆火星取得圆满成功.探测器距离地球约3.2亿千米.数据3.2亿千米用科学记数法可以表示为________千米.28.(2021·四川中考真题)中国共产党自1921年诞生以来,仅用了100年时间,党员人数从建党之初的50余名发展到如今约92000000名,成为世界第一大政党.请将数92000000用科学记数法表示为___________.29.(2021·0(1)-=______.30.(2021·0(1)π--=__________.31.(2021·四川自贡市·中考真题)请写出一个满足不等式7x >的整数解_________.32.(2021·四川遂宁市·中考真题)若20a -=,则b a =_____.33.(2021·安徽中考真题)埃及胡夫金字塔是古代世界建筑奇迹之一,其底面是正方形,侧面是全等的等腰1,它介于整数n 和1n +之间,则n 的值是______.三、解答题34.(2021·云南中考真题)计算:201tan 452(3)1)2(6)23-︒-++-+⨯-.35.(2021·浙江金华市·中考真题)计算:()202114sin 45+2-︒-.36.(2021·江苏连云港市·262--.37.(2021·浙江温州市·中考真题)(1)计算:()0438⨯-+-. (2)化简:()()215282a a a -++.38.(2021·四川自贡市·0|7|(2-+.39.(2021·浙江丽水市·中考真题)计算:0|2021|(3)-+--40.(2021·甘肃武威市·中考真题)计算:011(2021)()2cos 452π--+-︒.41.(2021·四川遂宁市·中考真题)计算:()101tan 60232-⎛⎫-+︒--+-- ⎪⎝⎭π42.(2021·重庆中考真题)对于任意一个四位数m ,若千位上的数字与个位上的数字之和是百位上的数字与十位上的数字之和的2倍,则称这个四位数m 为“共生数”例如:3507m =,因为372(50)+=⨯+,所以3507是“共生数”:4135m =,因为452(13)+≠⨯+,所以4135不是“共生数”;(1)判断5313,6437是否为“共生数”?并说明理由;(2)对于“共生数”n ,当十位上的数字是千位上的数字的2倍,百位上的数字与个位上的数字之和能被9整除时,记()3n F n =.求满足()F n 各数位上的数字之和是偶数的所有n . 43.(2021·四川凉山彝族自治州·中考真题)阅读以下材料,苏格兰数学家纳皮尔(J .Npler ,1550-1617年)是对数的创始人,他发明对数是在指数书写方式之前,直到18世纪瑞士数学家欧拉(Evler .1707-1783年)才发现指数与对数之间的联系.对数的定义:一般地.若x a N =(0a >且1a ≠),那么x 叫做以a 为底N 的对数,记作log a x N =,比如指数式4216=可以转化为对数式24log 16=,对数式32log 9=可以转化为指数式239=.我们根据对数的定义可得到对数的一个性质:log ()log log (0,1,0,0)a a a M N M N a a M N ⋅=+>≠>>,理由如下:设log ,log a a M m N n ==,则,n m M a N a ==.m n m n M N a a a +∴⋅=⋅=.由对数的定义得log ()a m n M N +=⋅又log log a a m n M N +=+log ()log log a a a M N M N ∴⋅=+.根据上述材料,结合你所学的知识,解答下列问题:(1)填空:①2log 32=___________;①3log 27=_______,①7log l =________;(2)求证:log log log (0,1,0,0)a a a M M N a a M N N=->≠>>; (3)拓展运用:计算555log 125log 6log 30+-.44.(2021·重庆中考真题)如果一个自然数M 的个位数字不为0,且能分解成A B ⨯,其中A 与B 都是两位数,A 与B 的十位数字相同,个位数字之和为10,则称数M 为“合和数”,并把数M 分解成M A B =⨯的过程,称为“合分解”.例如6092129=⨯,21和29的十位数字相同,个位数字之和为10,609∴是“合和数”.又如2341813=⨯,18和13的十位数相同,但个位数字之和不等于10,234∴不是“合和数”.(1)判断168,621是否是“合和数”?并说明理由;(2)把一个四位“合和数”M 进行“合分解”,即M A B =⨯.A 的各个数位数字之和与B 的各个数位数字之和的和记为()P M ;A 的各个数位数字之和与B 的各个数位数字之和的差的绝对值记为()Q M .令()()()P M G M Q M =,当()G M 能被4整除时,求出所有满足条件的M .。
中考数学专题复习:实数

汇报人:
2023-12-11
目录
• 实数的定义与分类 • 实数的性质 • 实数的运算规则 • 实数在几何中的应用 • 实数在实际生活中的应用 • 中考真题回顾与解析
01
实数的定义与分类
实数的定义
01
实数是有理数和无理数的总称, 通常用字母r表示实数。
02
有理数包括正数、负数和零,而 无理数则是一些无限不循环小数 ,如π、根号2等。
总结词
确定无理数大小,估算在实数范围内值。
详细描述
无理数是指无限不循环小数,不能直接计算,但可以通过估算来确定其大致范围。例如,$\pi$的值 大约在$3.14$和$3.15$之间,$\sqrt{2}$的值大约在$1.4$和$1.5$之间。
中考真题三:实数与三角形
总结词
掌握实数在三角形中的应用。
详细描述
06
中考真题回顾与解析
中考真题一:有理数的混合运算
总结词
掌握运算顺序,灵活运用运算律。
详细描述
有理数的混合运算顺序是先算乘方,再算乘除,最后算加减;同级运算按从左 到右的顺序进行;如果有括号,要先算括号里面的。运算律包括加法交换律、 加法结合律、乘法交换律、乘法结合律和乘法分配律。
中考真题二:无理数的估算
在日常生活中,我们经常使用实数来表示物体的重量。例如,一个苹果重约150 克,一头大象重约5吨等。
在科学研究和工程领域,实数也被广泛应用于表示物体的重量和力等物理量。
用实数表示时间
时间是连续的,无法用有限数量的整数来表示。因此,人们 使用实数来表示时间,例如秒、分、时、日等。
在科学研究、工程技术和金融等领域,人们经常需要精确地 计算时间,这时就需要使用实数来表示时间。
全国中考数学试题分类解析汇编专题1实数的有关概念

全国中考数学试题分类解析汇编专题1:实数的有关概念一、选择题1. (2012北京市4分) 9-的相反数是【 】A .19- B .19 C .9- D .9【答案】D 。
【考点】相反数。
【分析】相反数的定义是:如果两个数只有符号不同,我们称其中一个数为另一个数的相反数,特别地,0的相反数还是0。
因此-9的相反数是9。
故选D 。
2. (2012北京市4分)首届中国(北京)国际服务贸易交易会(京交会)于2012年6月1日闭幕,本届京交会期间签订的项目成交总金额达60 110 000 000美元,将60 110 000 000用科学记数法表示应为【 】A .96.01110⨯B .960.1110⨯C .106.01110⨯D .110.601110⨯【答案】C 。
【考点】科学记数法。
【分析】根据科学记数法的定义,科学记数法的表示形式为a ×10n ,其中1≤|a|<10,n 为整数,表示时关键要正确确定a 的值以及n 的值。
在确定n 的值时,看该数是大于或等于1还是小于1。
当该数大于或等于1时,n 为它的整数位数减1;当该数小于1时,-n 为它第一个有效数字前0的个数(含小数点前的1个0)。
60 110 000 000一共11位,从而60 110 000 000=6.011×1010。
故选C 。
3. (2012天津市3分)据某域名统计机构公布的数据显示,截至2012年5月21日,我国“.NET ”域名注册量约为560 000个,居全球第三位.将560 000用科学记数法表示应为【 】(A )560×103 (B )56×104 (C )5.6×105(D )0.56×106 【答案】C 。
【考点】科学记数法。
【分析】根据科学记数法的定义,科学记数法的表示形式为a ×10n ,其中1≤|a|<10,n 为整数,表示时关键要正确确定a 的值以及n 的值。
历年中考中实数的有关概念和性质真题答案及解析

一、选择题1.(2019湖南怀化,1,4分)下列实数中,哪个数是负数( )D.-1 【答案】D.【解析】解:由于-1<0,所以-1为负数.故选D. 【知识点】实数2.(2019湖南岳阳,1,3分)-2019的绝对值是( ) A .2019 B .-2019 C .12019 D .12019-【答案】A【解析】根据一个负数的绝对值等于它的相反数,得:|-2019|=2019,故选A . 【知识点】有理数,绝对值3.(2019江苏无锡,1,3分)5的相反数是( ) A. -5 B . 5 C .15D .15【答案】A【解析】本题考查了相反数的定义,5相反数为-5 ,故选A. 【知识点】相反数4.(2019山东滨州,1,3分)下列各数中,负数是( ) A .-(-2) B .2--C .(-2)2D .(-2)0【答案】B【解析】∵-(-2)=2,2--=-2,(-2)2=4,(-2)0=1,∴负数是2--.故选B .【知识点】相反数;绝对值;有理数的乘方;零次幂5.(2019山东济宁,1,3分)下列四个实数中,最小的是( ) A .-2 B .-5 C .1 D .4 【答案】B【解析】:根据有理数的大小比较法则可知:-5<-2<1<4. 【知识点】实数的大小比较.6.(2019山东聊城,1,3分) )A. C. 【答案】D(),故选D. 【知识点】相反数7. (2019山东泰安,1,4分) 在实数|-3.14|,-3,π中,最小的数是( )A.-3B.-3C.|-3.14|D.π【答案】B【解析】四个数中,有2个正数:|-3.14|=3.14,π,两个负数:-3,-3,而|-3|=3,|-3|=3≈1.732,∵3>1.732,∴-3<-3,故选B. 【知识点】绝对值,实数比较大小8.(2019山东潍坊,1,3分) 2019的倒数的相反数是( ) A .-2019 B .12019- C .12019D .2019【答案】B【解析】2019的倒数为12019,而12019的相反数为12019-,故选B . 【知识点】有理数,相反数,倒数9.(2019山东潍坊,5,3分)利用教材中的计算器依次按键如下:则计算器显示的结果与下列各数中最接近的一个是( ) A .2.5 B .2.6 C .2.8 D .2.9 【答案】B【解析】由计算器按键可知本题是计算7的近似值,分别计算四个数的平方可得:2.52=6.25,2.62=6.76,2.82=7.84,2.92=8.41,根据计算结果可知最接近于7的数为6.76,所以7≈2.6,故选B .【知识点】计算器的使用,估算10. (2019山东枣庄,11,3分)点O,A,B,C 在数轴上的位置如图所示,O 为原点,AC =1,OA =OB,若点C 所表示的数为a,则点B 所表示的数为( )A.-(a+1)B.-(a -1)C.a+1D.a -1【答案】B【解析】∵点C 所表示的数为a,AC =1,点A 在点C 的左边,∴点A 所表示的数为(a -1),∵OA=OB,∴点A 和点B 所表示的数互为相反数,故点B 所表示的数为-(a -1),故选B 【知识点】数轴表示数,相反数11.(2019山东淄博,6,4分)与下面科学计数器的按键顺序: 对应的任务是( )4y x 21+6ab /c5×6·A.460.6125⨯+ B.450.6126⨯+ C.120.6564⨯÷+ D.1250.646⨯+ 【答案】B【解析】由计算器中输入顺序,对应的任务是450.6126⨯+,故选B.【知识点】用科学计算器计算12.(2019山东淄博,1,4分)比-2小1的实数是( ) A.-3 B.3C.-1D.1【答案】A.【解析】由题意可列出:-2-1=-(2+1)=-3. 即比-2小1的数为-3. 故选A .【知识点】实数的运算,有理数的减法13.(2019四川达州,1,3分) -2019的绝对值是( ) A .2019 B. -2019 C. 20191 D.20191-【答案】A【解析】负数的绝对值是它的相反数,所以-2019的绝对值是-(-2019)=2019 【知识点】绝对值14.(2019四川乐山,1,3分)3-的绝对值是( ) A .3 B .-3C .13D .31-【答案】A【解析】本题考查了有理数的绝对值求法,()333-=--=,故选A. 【知识点】有理数的绝对值15.(2019四川乐山,4,3分)a -一定是( )A .正数B .负数C .0D .以上选项都不正确 【答案】D【解析】本题考查了有理数相反数的求法,a -的符号由字母a 的符号确定:当a 为正数,则a -一定是负数;当a 为0,则a -一定是0;当a 为负数,则a -一定是正数. 【知识点】有理数的相反数16.(2019四川凉山,1,4分)1.-2的相反数是( ) A.2 B.-2 C.21D.21- 【答案】A【解析】-2的相反数是2,故选A. 【知识点】相反数17.(2019四川眉山,1,3分)下列四个数中,是负数的是( )A .|-3|B .-(-3)C .(-3)2D .【答案】D【解析】解:A 、|-3|=3,是正数,故A 不合题意;B 、-(-3)=3,是正数,故B 不合题意;C 、(-3)2=9,是正-是负数,故D符合题意,故选D.数,故C不合题意;D、3【知识点】绝对值;相反数,有理数的乘方,18.(2019四川攀枝花,1,3分)(-1)2等于()A.-1 B.1 C.-2 D.2【答案】B.【解析】负数的隅次方是正数,所以(-1)2=1,故选B.【知识点】乘方的性质19.(2019四川攀枝花,2,3分)在0,-1,2,-3这四个数中,绝对值最小的数是()A.0 B.-1 C.2 D.-3【答案】A.【解析】绝对值最小的数是0,故选A.【知识点】绝对值20.(2019四川省自贡市,1,4分)- 2019的倒数是()A.-2019B.C.D.2019【答案】B.【解析】解:∵a的倒数是,∴-2009的倒数是.故选B.【知识点】倒数.21. (2019四川自贡,7,4分)实数m,n在数轴上对应点的位置如图所示,则下列判断正确的是()A.|m|<1B.1-m>1C.mn>0D.m+1>0【答案】B.【解析】解:由数轴可知,m<-1<0,n>1>0.∴|m|>1,mn<0,m+1<0,-m>0,∴1-m>1.∴选项A,C,D错误,正确的是选项B.故选B.【知识点】数轴,有理数的加法法则,有理数的乘法法则,绝对值3-⨯的结果等于 ( )22. (2019天津,1,3分)计算()9(A) -27 (B)-6 (C) 27 (D)6【答案】A【解析】一正一负相乘,先确定积的符号为负,再把绝对值相乘,绝对值为27.所以答案为 A【知识点】有理数的乘法运算.23. (2019天津,6,3分)估计33的值在( )(A) 2和3之间 (B) 3和4之间 (C) 4和5之间 (D) 5和6之间 【答案】D 【解析】6335363325<<∴<<所以选D【知识点】算术平方根的估算.24.(2019浙江湖州,1,3分)数2的倒数是( )A .-2B .2C .-12D .12 【答案】D .【解析】利用“乘积为1的两个数互为倒数”的概念进行判断,∵2×12=1,∴2的倒数是12,故选D . 【知识点】实数的概念;倒数25.(2019浙江省金华市,1,3分)实数4的相反数是( )A.14-B.-4C.14D.4【答案】B .【解析】由a 的相反数是-a ,得实数4的相反数是-4,故选B . 【知识点】相反数26.(2019浙江金华,4,3分)某地一周前四天每天的最高气温与最低气温如下表,则这四天中温差最大的是( ) A. 星期一 B.星期二 C.星期三 D.星期四【答案】C .【解析】温差=最高气温-最低气温.故选C . 【知识点】温差27. (2019浙江宁波,1,4分) -2的绝对值为( ) A.-12B.2C.12D.-2【答案】B【解析】负数的绝对值是它的相反数,|-2|=2,故选B. 【知识点】绝对值28.(2019浙江衢州,1,3分)在12,0,1,一9四个数中,负数是( )A.12B.0C.1D.-9【答案】D【解析】本题考查负数的概念,不含多重符号的数,含有负号的数是负数,在这四个数中,只有-9带有负号,所以负数是-9,故选D 。
中考数学专题训练:实数的有关概念

中考数学专题训练:实数的有关概念命题点1| 数轴1.(2022·江西)实数a,b在数轴上的对应点的位置如图所示,则下列结论中,正确的是()A.a>b B.a=bC.a<b D.a=-b2.(2022·临沂)如图,A,B位于数轴上原点两侧,且OB=2OA.若点B表示的数是6,则点A表示的数是()A.-2B.-3C.-4D.-53.(2022·北京)实数a,b在数轴上的对应点的位置如图所示,下列结论中正确的是()A.a<-2B.b<1C.a>b D.-a>b4.(2023·连云港)如图,数轴上的点A,B分别对应实数a,b,则a+b______0.(填“>”“<”或“=”)命题点2| 相反数1.(2023·连云港)实数-6的相反数是()A.-16B.16C.-6D.6 2.(2023·青岛)17的相反数是()A.7B.-7C.17D.-173.(2023·宿迁)2 023的相反数是()A.12 023B.-2 023C.2 023D.-12 023命题点3| 倒数1.(2023·泰安)-23的倒数是()A.23B.-23C.32D.-322.(2022·无锡)-15的倒数是()A.-15B.-5C.15D.5命题点4| 绝对值1.(2022·衡阳)-2的绝对值是()A.-2B.2C.12D.-122.(2022·聊城)实数a的绝对值是54,a的值是()A.54B.-54C.±45D.±543.(2022·泰山区检测)-|-2 021|的相反数为() A.-2 021B.2 021C.-12 021D.12 0214.(2022·肥城模拟)若|a-1|与|b-2|互为相反数,则a+b的值为()A.3B.-3C.0D.3或-35.已知x,y,z为有理数,且|x-1|+|y+2|+|z-3|=0,则(x+1)(y-2)(z+3)的值是________.参考答案命题点1| 数轴1.(2022·江西)实数a,b在数轴上的对应点的位置如图所示,则下列结论中,正确的是(C)A.a>b B.a=bC.a<b D.a=-b2.(2022·临沂)如图,A,B位于数轴上原点两侧,且OB=2OA.若点B表示的数是6,则点A表示的数是(B)A.-2B.-3C.-4D.-53.(2022·北京)实数a,b在数轴上的对应点的位置如图所示,下列结论中正确的是(D)A.a<-2B.b<1C.a>b D.-a>b解析:点a在-2的右边,故a>-2,故A选项错误;点b在1的右边,故b>1,故B选项错误;b在a的右边,故b>a,故C选项错误;由数轴得-2<a<-1.5,则1.5<-a<2,1<b<1.5,则-a>b,故D选项正确.故选D.4.(2023·连云港)如图,数轴上的点A,B分别对应实数a,b,则a+b<0.(填“>”“<”或“=”)解析:由数轴可得a<0<b,|a|>|b|,∴a+b<0.故答案为<.命题点2| 相反数1.(2023·连云港)实数-6的相反数是(D)A.-16B.16C .-6D .6解析:-6的相反数是6. 故选D.2.(2023·青岛)17的相反数是( D ) A .7 B .-7 C .17D .-173.(2023·宿迁)2 023的相反数是( B ) A .12 023 B .-2 023 C .2 023 D .-12 023命题点3| 倒数1.(2023·泰安)-23的倒数是( D ) A .23 B .-23 C .32D .-32解析:∵(−23)×(−32)=1, ∴-23的倒数是-32. 故选D.2.(2022·无锡)-15的倒数是( B ) A .-15 B .-5 C .15D .5命题点4| 绝对值1.(2022·衡阳)-2的绝对值是( B ) A .-2 B .2 C .12D .-122.(2022·聊城)实数a 的绝对值是54,a 的值是( D ) A .54 B .-54 C .±45D .±543.(2022·泰山区检测)-|-2 021|的相反数为(B) A.-2 021B.2 021C.-12 021D.12 0214.(2022·肥城模拟)若|a-1|与|b-2|互为相反数,则a+b的值为(A) A.3B.-3C.0D.3或-35.已知x,y,z为有理数,且|x-1|+|y+2|+|z-3|=0,则(x+1)(y-2)(z+3)的值是-48.。
中考数学 专题01 实数的有关概念及运算(原卷版)
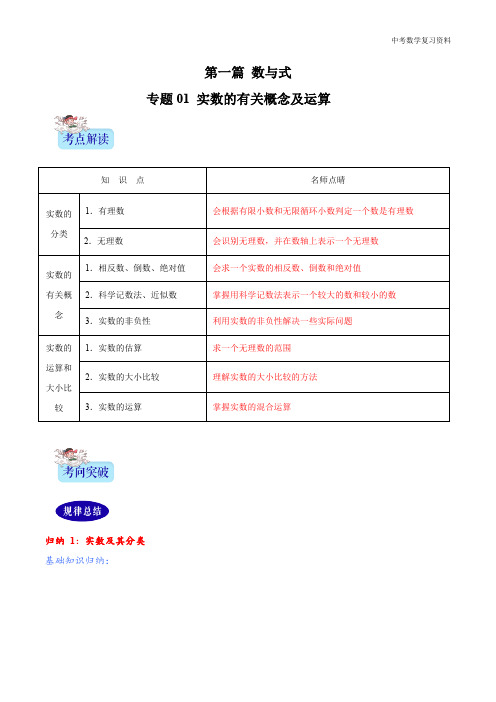
归纳 4:科学记数法与近似数 基础知识归纳:根据科学记数法的定义,科学记数法的表示形式为 a×10n,其中 1≤|a|<10,n 为整数, 表示时关键要正确确定 a 的值以及 n 的值. 基本方法归纳:利用科学记数法表示一个数,在确定 n 的值时,看该数是大于或等于 1 还是小于 1.当该 数大于或等于 1 时,n 为它的整数位数减 1;当该数小于 1 时,-n 为它第一个有效数字前 0 的个数(含小
中考数学复习资料
的克数记为负数,下面检测过的四个排球,在其上方标注了检测结果,其中质量最接近标准的一个是 ( )A.B.Fra bibliotek C.D.
3.(2019 内蒙古通辽市,第 1 题,3 分) 1 的相反数是( ) 2019
A.2019 B. 1 C.﹣2019 D. 1
( )
A.5×106 B.107 C.5×107 D.108 14.(2019 重庆 A,第 8 题,4 分)按如图所示的运算程序,能使输出 y 值为 1 的是( )
A.m=1,n=1 B.m=1,n=0 C.m=1,n=2 D.m=2,n=1
归纳 5:实数的混合运算 基础知识归纳:实数混合运算时,将运算分为三级,加减为一级运算,乘除为二级运算,乘方为三级运 算.同级运算时,从左到右依次进行;不是同级的混合运算,先算乘方,再算乘除,而后才算加减;运算 中如有括号时,先做括号内的运算,按小括号、中括号、大括号的顺序进行 基本方法归纳:实数的混合运算经常涉及到零指数幂、负整数指数幂、特殊角的三角函数值、绝对值的化 简、二次根式等内容,要熟练掌握这些知识. 注意问题归纳:实数的混合运算经常以选择、填空和解答的形式出现,是中考是热点,也是比较容易出错 的地方,在解答此类问题时要注意基本性质和运算的顺序.
中考数学专题复习:实数(含详细参考答案)

中考数学专题复习:实数(含详细参考答案)【基础知识回顾】一、实数的分类:1、按实数的定义分类:实数 有限小数或无限循环数 2、按实数的正负分类:实数【名师提醒:1、正确理解实数的分类。
如:2π是 数,不是 数,722是 数,不是 数。
2、0既不是 数,也不是 数,但它是自然数】二、实数的基本概念和性质1、数轴:规定了 、 、 的直线叫做数轴, 和数轴上的点是一一对应的,数轴的作用有 、 、 等。
2、相反数:只有 不同的两个数叫做互为相反数,a 的相反数是 ,0的相反数是 ,a 、b 互为相反数⇔3、倒数:实数a 的倒数是 , 没有倒数,a 、b 互为倒数⇔4、绝对值:在数轴上表示一个数的点离开 的距离叫做这个数的绝对值。
a =⎪ ⎪ ⎪ ⎪ ⎩ ⎪ ⎪ ⎪ ⎪ ⎨ ⎧ ⎩ ⎨ ⎧ ⎪ ⎪ ⎪ ⎩ ⎪ ⎪ ⎪ ⎨ ⎧ ⎩ ⎨ ⎧ ⎪ ⎩ ⎪ ⎨ ⎧ 正无理数 无理数 负分数 _ 零 正整数 整数 有理数无限不循环小数 ⎩⎨⎧⎩⎨⎧负有理数负零正无理数正实数实数 (a >0)(a <0) 0 (a =0)因为绝对值表示的是距离,所以一个数的绝对值是 数,我们学过的非负数有三个: 、 、 。
【名师提醒:a +b 的相反数是 ,a -b 的相反数是 ,0是唯一一个没有倒数的数,相反数等于本身的数是 ,倒数等于本身的数是 ,绝对值等于本身的数是 】三、科学记数法、近似数和有效数字。
1、科学记数法:把一个较大或较小的数写成 的形式叫做科学记数法。
其中a 的取值范围是 。
2、近似数和有效数字:一般的,将一个数四舍五入后的到的数称为这个数的近似数,这时,从 数字起到近似数的最后一位止,中间所有的数字都叫这个数的有效数字。
【名师提醒:1、科学记数法不仅可以表示较大的数,也可以表示较小的数,其中a 的取值范围一样,n 的取值不同,当表示较大数时,n 的值是原整数数位减一,表示较小的数时,n 是负整数,它的绝对值等于原数中左起第一个非零数字前零的个数(含整数数位上的零)。
2024年中考数学复习专题讲义专题1-实数

A. B. C. D.
7.(2023苏州市中考真题)在比例尺为 的地图上,量得 两地在地图上的距离为 厘米,即实际距离为28000000厘米.数据28000000用科学记数法可表示为________________.
【考点五】实数的运算
1.数的乘方:求n个相同因数a的积的运算叫做乘方,乘方的结果叫幂.在an中,a叫底数,n叫指数.
2.实数的运算:
(1)有理数的运算定律在实数范围内都适用,常用的运算定律有加法结合律 、加法交换律 、乘法交换律 、乘法结合律、 乘法分配律.
(2)运算顺序:先算乘方(开方),再算乘除,最后算加减;有括号的先算括号里面的.
三角形,共得到10个正三角形,称为第三次操作;….根据以上操作,若要得到2023个正
三角形,则需要操作的次数为_______.
三、解答题(共5题)
11.计算: .
12.(2023年苏州市姑苏区一模)计算:
13.(1)如果 , 且 ,求 的值;
(2)已知 、 互为相反数, 、 互为倒数, 的倒数等于它本身,则 的值是多少?
8.(2023江苏泰州中考真题)溶度积是化学中沉淀的溶解平衡常数.常温下 的溶度积约为 ,将数据 用科学记数法表示为__________________.
9.(2023连云港市中考真题)如图,数轴上 点 分别对应实数 ,则 __________0.(用“ ”“ ”或“ ”填空)
10.(2022浙江杭州中考真题)计算: .圆圆在做作业时,发现题中有一个数字被墨水污染了.(1)如果被污染的数字是 ,请计算 .(2)如果计算结果等于6,求被污染的数字.
8.绝对值:数轴上表示数a的点与原点的距离,记作 |a|.
实数的有关概念(含答案)

⎧⎨⎩第1章 数与式第1课 实数的有关概念目的:复习实数有关概念,相反数、绝对值、倒数、数轴、非负数性质、•科学记数法、近似数与有效数字.中考基础知识1.实数的分类2.相反数:只有_______不同的两个数,叫做互为相反数,a 的相反数为______,a-b 的相反数是_______,x+y 的相反数是________,0的相反数为_______,若a ,b 互为相反数,则a+b=________.3.绝对值:几何意义:数a 的绝对值是数a 在数轴上表示的点到_______的距离. 正数的绝对值等于它________. 代数意义 零的绝对值等于________.负数的绝对值等于它的________.│a │=(0)(0)a a a a ≥⎧⎨-<⎩ 4.数轴:0________与数轴上的点是一一对应的,•数轴上的点表示的数左边的总比右边的_________,数轴是沟通几何与代数的桥梁.5.倒数:a (a ≠0)的倒数为________,0_______•倒数,•若a ,•b •互为倒数,•则ab=_____,若a ,b 互为负倒数,则ab=________.6.非负数:│a│≥0,a2≥00.若│a+1│+(c+3)2=0,则a=_______,b=_______,c=________.7.科学记数法:把一个数记作a×10n形式(其中a是具有一位整数的小数,n为自然数).8.近似数与有效数字:一个经过________而得到的近似数,最后一个数在哪一位,就说这个近似数是精确到哪一位的近似数,对于一个近似数,•从左边第一个______数字开始,到最末一位数字止,都是这个近似数的有效数字.备考例题指导例1.填空题(1的倒数为_______,绝对值为________,相反数为_______.(2)若│x-1│=1-x,则x的取值范围是_______,若3x+1有倒数,则x的取值范围是_________.(3)在实数18,π,3,0+1,0.303003……中,无理数有________个.(4)绝对值不大于3的非负整数有________.(5=0,则3x-2y=________.(6)用科学记数法表示-168000=_______,0.000=_________.(7)0.0304精确到千分位等于_______,有_______个有效数字,它们是_______.(8)000保留两个有效数字得到的近似数为________.答案:(1).-2,,(2)x≤1,x≠-13.(3)5.(4)0,1,2,3.(5)7.(6)-1.68×105,2.004×10-4.(7)0.030;2;3,0 (8)2.1×106.例2.已知1<x<4,化简│x-4│解:∵1<x<4,∴x-4<0,1-x<0.原式=│x-4│-│1-x│=4-x+1-x=5-2x.例3.化简│x-2│+│x+3│.解:令x-2=0得x=2,令x+3=0得x=-3.(1)当x<-3时,原式=2-x-x-3=-2x-1;(2)当-3≤x<2时,原式=2-x+x+3=5;(3)当x≥2时,原式=x-2x+x+3=2x+1.分类讨论思想,零点分段法,一般等号取在大于符号中.备考巩固练习1.(,北京)一个数的相反数是3,则这个数是________.2.气温比a℃低3℃记作________.3-a)2与│b-1│互为相反数,则2a b-的值为_______.4.若a2│c-│=0,则a b+c=________.5.计算|47-25|+|35-79|-|29-37|=______________.(注意方法)6.计算│1-a│+│2a+1│+│a│,其中a<-2.7.如果表示a、b两个实数的点在数轴上的位置如图,那么化简│a+b│+果是多少?b a8.按要求取下列各数的近似数:(1)6.286(精确到0.1);(2)1764000(保留三个有效数字);(3)278160(•精确到万位).9.近似数7.60×105精确到_______位,有______个有效数字,近似数7.6×105精确到_______位,有________个有效数字.10.已知a、b、c为实数,且a2+b2+c2=ab+bc+ac,求证a=b=c.答案:1.-3 2.(a-3)℃ 3+1 4.5.原式=47-25+79-35+29-37=17-1+1=17(先去绝对值符号)6.∵a<-2,∴1-a>0,2a+1<0,a<0∴原式=1-a-2a-1-a=-4a7.-2a8.(1)6.286≈6.3 (2)1764000≈1.76×106(3)278160≈28万9.∵7.60×105=760000 ∴近似数7.60×105精确到千位,有三个有效数字7,6,•0;7.6×105精确到万位,有两个有效数字7,610.用配方法和非负数性质,将一个方程转化为三个方程,a2+b2+c2-ab-bc+ac=0 2a2+2b2+2c2-2ab-2bc-2ac=0 (a-b)2+(b-c)2+(a-c)2=0∴a-b=0,b-c=0,a-c=0 ∴a=b=c。
中考数学试题分类汇编知识点01实数的有关概念和性质(2021年整理)

2018年中考数学试题分类汇编知识点01 实数的有关概念和性质编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(2018年中考数学试题分类汇编知识点01 实数的有关概念和性质)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为2018年中考数学试题分类汇编知识点01 实数的有关概念和性质的全部内容。
实数的有关概念和性质一、选择题1。
(2018四川泸州,1题,3分) 在—2,0,12,2四个数中,最小的是( )A.—2 B 。
0 C.12D.2【答案】A【解析】有理数比较大小,负数小于0,0小于正数,因为—2<0〈21<2,故选A【知识点】有理数比较大小2. (2018四川内江,1,3)-3的绝对值为( )A .-3B .3C .-13D .13【答案】B【解析】解:因为负数的绝对值等于它的相反数,所以-3的绝对值为3.故选择B . 【知识点】绝对值;相反数3。
(2018浙江衢州,第1题,3分)-3的相反数是( )A .3B .—3C .13D .13-【答案】A 。
【解析】本题考查了相反数的定义,解题的关键掌握相反数的概念.∵-3的相反数是3,故选A 。
【知识点】相反数;4。
(2018浙江金华丽水,1,3分)在0,1,12-,—1四个数中,最小的数是( ).A . 0B .1C . 12- D . -1【答案】D .【解析】∵—1<12-<0<1,∴最小的数是-1,故选D.【知识点】有理数的大小比较5.(2018山东滨州,2,3分)若数轴上点A、B分别表示数2、-2,则A、B两点之间的距离可表示为( )A.2+(-2) B.2-(-2) C.(-2)+2 D.(-2)-2【答案】B【解析】在数轴上,两点之间的距离等于对应两数之差的绝对值,故A、B两点之间的距离可以表示为)()(2--22--2=【知识点】距离的含义、绝对值的性质6.(2018安徽省,1,4分)8-的绝对值是( )A。
中考数学考点总动员系列 专题01 实数及有关概念(含解析)-人教版初中九年级全册数学试题

考点一:实数及有关概念聚焦考点☆温习理解 一.实数的分类:.⎧⎧⎫⎪⎪⎪⎨⎬⎪⎪⎪⎪⎭⎨⎩⎪⎧⎫⎪⎪⎨⎬⎪⎪⎭⎩⎩正有理数有理数零有限小数和无限循环小数.负有理数实数正无理数无理数无限不循环小数负无理数 注意:在理解无理数时,要注意“无限不循环”,归纳起来有四类: (1)开方开不尽的数,如3,32等;(2)有特定意义的数,如圆周率π,或化简后含有π的数,如23π+等;(3)有特定结构的数…等; (4)某些三角函数,如sin60o等 二.绝对值一个数的绝对值就是表示这个数的点与原点的距离,|a|≥0。
零的绝对值是它本身,也可看成它的相反数,若|a|=a ,则a ≥0;若|a|=-a ,则a ≤0。
三.相反数实数与它的相反数时一对数(只有符号不同的两个数叫做互为相反数,零的相反数是零).从数轴上看,互为相反数的两个数所对应的点关于原点对称,如果a 与b 互为相反数,则有a+b=0,a=-b ,反之亦成立。
四、倒数如果a 与b 互为倒数,则有ab=1,反之亦成立。
倒数等于本身的数是1和-1。
零没有倒数。
五、科学记数法和近似数 1、有效数字一个近似数四舍五入到哪一位,就说它精确到哪一位,这时,从左边第一个不是零的数字起到右边精确的数位止的所有数字,都叫做这个数的有效数字。
2.科学记数法科学记数法的表示形式为a ×10n的形式,其中1≤|a|<10,n 为整数.确定n 的值时,要看把原数变成a 时,小数点移动了多少位,n 的绝对值与小数点移动的位数相同.当原数绝对值>1时,n 是正数;当原数的绝对值<1时,n 是负数. 六、平方根如果一个数的平方等于a ,那么这个数就叫做a 的平方根(或二次方根)。
一个数有两个平方根,他们互为相反数;零的平方根是零;负数没有平方根。
正数a 的平方根记做“a ±”。
正数a 的正的平方根叫做a 的算术平方根,记作“a ”。
正数和零的算术平方根都只有一个,零的算术平方根是零。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
13.(2012浙江绍兴,1,4分)3的相反数是()
A.3B.-3C. D.
【答案】B
14.(2012浙江绍兴,3,4分)据科学家估计,地球的年龄大约是4600000000年,这个数用科学计数法表示为()
A.4.6×108B.46×108C.4.6×109D.0.46×1010
【答案】C
15.(2012浙江绍兴,9,4分)在一条笔直的公路边,有一些树和灯,每相邻的两盏灯之间有3棵树,相邻的树与树、树与灯间的距离都是10m,如图,第一棵树左边5m处有一个路牌,则从此路牌起向右510m~550m之间树与灯的排列顺序是()
【答案】A
8.(2012浙江舟山3,3分)南海资源丰富,其面积约为350万平方千米,相当于我国的渤海、黄海和东海总面积的3倍,其中350万用科学记数法表示为()
(A)0.35×108(B)3.5×107
(C)3.5×106(D)35×105
【答案】C
9.(2012浙江温州,1,4分)给出四个数-1,0,0.5, ,其中为无理数的是()
A.-1B.0C.0.5D.
【答案】D
10.(2012浙江省衢州,1,3分)下列四个数中,最小的数是( )
A.2B.-2C.0D.
【答案】B
11.(2012浙江省衢州,2,3分)衢州市是国家优秀旅游城市,吸引了众多的海内外游客.据衢州市2011年国民经济和社会发展统计公报显示,全年旅游总收入达121.04亿元.将121.04亿元用科学记数法可表示为( )
解答:
解:将四千零七十亿元可写成407000000000,
407000000000=4.07×1011,
故选:C.
点评:
此题考查了科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.
6.(2012•台湾19,3分)如图,数在线的A、B、C、D四点所表示的数分别为a、b、c、d,且O为原点.根据图中各点位置,判断|a﹣c|之值与下列何者不同?( )
【答案】A
3.(2012四川乐山,1,3分)如果规定收入为正,支出为负.收入500元记作500元,那么支出237元应记作()
A. 元B. 元C.237元D.500元
【答案】B
4.(2012•台湾6,3分)如图是利用短除法求出三数8、12、18的最大公因子的过程.利用短除法,求出这三数的最小公倍数为何?( )
解答:
解:104485=1.04485×105.
故选C.
点评:
此题考查科学记数法表示较大的数的方法,准确确定n值是关键.
17.(2012浙江丽水,1,3分)如果零上2 记作+2 ,那么零下3 记作()
A.-3 B.-2 C.+3 D.+2
【答案】A
18.(2012浙江丽水,3,3分)如图,数轴的单位长度为1,如果点A,B表示的数的绝对值相等,那么点A表示的数是()
A.12B.72C.216D.432
考点:
有理数的除法。
专题:
常规题型。
分析:
继续完善短除法,然后根据最小公倍数的求法,把所有的数相乘即可.
解答:
解:如图,完成短除法如下
最小公倍数为2×2×3×2×1×3=72.
故选B.
点评:
本题考查了短除法求最小公倍数的方法,属于小学内容,比较简单,完善短除过程是解题的关键.
A.-4 B.-2 C.0 D.40
【答案】B
19.(2012•义乌市1,3分)﹣2的相反数是( )
A.12.104×109元B.12.104×1010元C.1.2104×1010元D.1.2104×1011元
【答案】C
12.(2012浙江嘉兴,3,4分)南海资源丰富,其面积约为350万平方千米,相当于我国的渤海、黄海和东海总面积的3倍.其中350万用科学计数法表示为()
A.0.35×108B.3.5×107C.3.5×106D.35×105
C、∵|a﹣d|﹣|d﹣c|=AD﹣CD=AC,故本选项错误;
D、∵|a|+|d|﹣|c﹣d|=AO+DO﹣CD=AC,故本选项错误;
故选A.
点评:
本题考查了实数与数轴,知道绝对值的意义是解题的关键.
7.(2012重庆,1,4分)在-3,-1,0,2这四个数中,最小的数是()
A.-3 B.-1 C.0 D.2
【答案】B
16.(2012•宁波)据宁波市统计局年报,去年我市人均生产总值为104485元,104485元用科学记数法表示为( )
A.1.04485×106元B.0.104485×106元C.1.04485×105元D.10.4485×104元
考点:
科学记数法—表示较大的数。
专题:
常规题型。
分析:
科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值是易错点,由于104485有6位,所以可以确定n=6﹣1=5.
一、选择题
1.(2012四川成都,1,3分) 的绝对值是()
A.3 B. C. D.
【答案】A
2.(2012四川成都,5,3分)成都地铁二号线工程即将竣工,通车后与地铁一号线呈“十”字交叉,城市交通通行和转换能力将成倍增长.该工程投资预算约为930 000万元,这一数据用科学记数法表示为()
A. 万元B. 万元C. 万元D. 万元
5.(2012•台湾73分)已知某公司去年的营业额为四千零七十亿元,则此营业额可用下列何者表示?( )
A.4.07×109元B.4.07×1010元C.4.07×1011元D.4.07×1012元
考:
科学记数法—表示较大的数。
分析:
首先将四千零七十亿元可写成407000000000,再利用科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>1时,n是正数;当原数的绝对值<1时,n是负数.
A.|a|+|b|+|c|B.|a﹣b|+|c﹣b|C.|a﹣d|﹣|d﹣c|D.|a|+|d|﹣|c﹣d|
考点:
实数与数轴。
专题:
探究型。
分析:
根据绝对值的性质计算出各绝对值表示的线段长,与|a﹣c|的长进行比较即可.
解答:
解:A、∵|a|+|b|+|c|=AO+BO+CO≠AC,故本选项正确;
B、∵|a﹣b|+|c﹣b|=AB+BC=AC,故本选项错误;
