1.1 锐角三角函数(1)(课时2)课件(浙教版九年级下册)
合集下载
浙教版数学九下1.1锐角三角函数课件

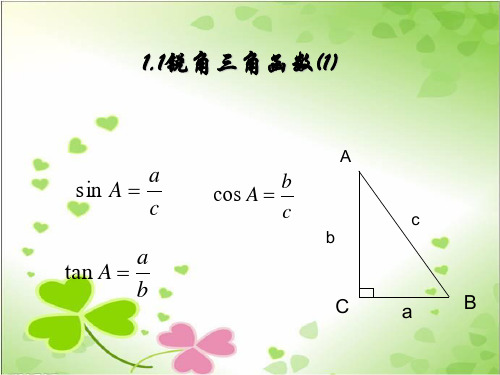
AC 5 5
sin B AC 5 ,cosB BC 2,tan B AC 5 .
AB 3
AB 3
BC 2
延伸:由上面的计算,你能猜想∠A,∠B的正弦、余弦值 有什么规律吗?
结论:一个锐角的正弦等于它余角的余弦,或一个锐角的 余弦等于它余角的正弦.
请同学们拿出
自己的学习工具— 1
2
—一副三角尺,思
AB 5
BC 3
2、 如图,在Rt△ABC中,∠C=90°,BC=2,
AB=3,求∠A,∠B的正弦、余弦、正切值. B
解:在RtABC中,
3
2
AC AB2 BC2 32 22 5,
A
C
sin A BC 2,cos A AC 5 ,tan A BC 2 2 5 .
AB 3
AB 3
c 斜边
B
a 对边
A
bC
例如,当∠A=30°时,我们有
sin A sin 30 1 2
当∠A=45°时,我们有
sin A sin 45 2 2
在图中 ∠A的对边记作a ∠B的对边记作b ∠C的对边记作c
注意
▪ sinA是一个完整的符号,它表示∠A的正弦, 记号里习惯省去角的符号“∠”;
▪ sinA没有单位,它表示一个比值,即直角 三角形中∠A的对边与斜边的比;
,
则sin∠A=___.
b3
5、如图,在△ABC中, AB=CB=5, sinA= ,求△ABC 的面积.
4 5
B
5
5
A
C
如图,在Rt△ABC中,∠C=90°,
我们把锐角A的邻边与斜边的比叫做∠A的
余弦(cosine),记作cosA, 即
1.1 锐角三角函数(1)课件浙教版九年级下册数学
tanα 的值可以大于100吗? D
请求出锐角α 的正切函数
的范围。
A
C
β Eα B
谈谈今天的收获
B
∠A的对边
sinA
斜边
斜边
∠A的对边 cosA
∠A的邻边 斜边
A
∠A的邻边
C
tanA
∠A的对边 ∠A的邻边
回味无穷
• 定义中应该注意的几个问题:
1.sinA,cosA,tanA, 是在直角三角形中定义的, ∠A是 锐角(注意数形结合,构造直角三角形).
2.sinA,cosA,tanA, 是一个完整的符号,表示∠A 的三角函数,习惯省去“∠”号; 3.sinA,cosA,tanA, 是一个比值.注意比的顺序, 且sinA,cosA,tanA, 均﹥0,无单位. 4.sinA,cosA,tanA, 的大小只与∠A的大小有关, 而与直角三角形的边长无关. 5.角相等,则其三角函数值相等;两锐角的三角函数值
12
C
A
C
2.如图,在Rt△ABC中,∠C=90°.
A
B
⑴ 若BC=8,AB=17,求sinA, cosA,tanA的值;
⑵ 若BC︰AB=1︰2 ,求sinA, cosA,tanA的值;
⑶ 若sinA= 5 , 求sinB的值. 13
解后语: 已知直角三角形中的两边或两边之比,
就能求出锐角三角函数值.
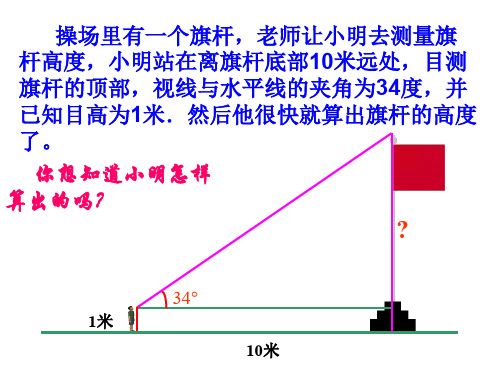
操场里有一个旗杆,老师让小明去测量旗 杆高度,小明站在离旗杆底部10米远处,目测 旗杆的顶部,视线与水平线的夹角为34度,并 已知目高为1米.然后他很快就算出旗杆的高度 了。
你想知道小明怎样 算出的吗?
?
34
1米 10米
第一章 解直角三角形
浙教版初中数学九年级下册1.1《锐角三角函数(1)》 (共16张)课件

(A)扩大2倍 (B)缩小2倍 (C)扩大4倍 (D)没有变化
返回(点我)
1.1 锐角三角函数
——第1课时
自学指导
结合思考题自学P(4)--(5)课内练习前内容,并完 成课内练习 显示练习(点我) 思考下面问题: 1、sinα、cos、tanα 分别代表什么意义,这个α有什么要求? 2、sinα、cos、tanα 的范围分别是什么? 3、sinα、cos、tanα 是不是函数,为什么?
观察归纳
1、了解三角函数的概念; 2、会用符号表示一个锐角的三种三角函数; 3、掌握在直角三角形中,锐角三角函数与边之比的关系; 4、会根据锐角三角函数的定义求锐角三角函数。
sin读音 cos读音 tan读音结论这里邻边指的都是直角边.
探究1
探究2
探究3
在RtΔABC中,如果各边长度都扩大为原来 的2倍,则锐角A的正切值( D )
返回(点我)
1.1 锐角三角函数
——第1课时
自学指导
结合思考题自学P(4)--(5)课内练习前内容,并完 成课内练习 显示练习(点我) 思考下面问题: 1、sinα、cos、tanα 分别代表什么意义,这个α有什么要求? 2、sinα、cos、tanα 的范围分别是什么? 3、sinα、cos、tanα 是不是函数,为什么?
观察归纳
1、了解三角函数的概念; 2、会用符号表示一个锐角的三种三角函数; 3、掌握在直角三角形中,锐角三角函数与边之比的关系; 4、会根据锐角三角函数的定义求锐角三角函数。
sin读音 cos读音 tan读音结论这里邻边指的都是直角边.
探究1
探究2
探究3
在RtΔABC中,如果各边长度都扩大为原来 的2倍,则锐角A的正切值( D )
最新浙教版九年级数学下册课件:1.1锐角三角函数课

B c
a
A b ┌ C
练习:
1、下图中∠ACB=90° ,CD⊥AB 指出∠A的对边、邻边。 B D
A
C
2、1题中如果CD=5,AC=10,则sin∠ACD= sin ∠DCB=
如图:在等腰△ABC 中,AB=AC=5,BC=6. 求: sinB,cosB,tanB
A
5 B 5
┌ 6 D
C
提示:过点A作AD垂直于BC于D.
如图是两个自动扶梯,甲、乙两人分别从1、 2号自动扶梯上楼,谁先到达楼顶?如果AB和 A′B′相等而∠α和∠β大小不同,那么它们的高 度AC 和A′C′相等吗?AB、AC、BC与∠α, A′B′、A′C′、B′C′与∠β之间有什么关系呢?
A A′
3米 3米 β 4米 1
B
a
C C′ 2米
2
B′
想一想
a sin A c b sin B c
b cos A c a cos B c
A
B c a ┌ C
b
sinA=cosB ,cosA=sinB (∠A+∠B=90。)
sin A cos A 1
2 2
sin A tan A cos A
回味无穷
定义中应该注意的几个问题:
1.sinA,cosA,tanA, 是在直角三角形中定义的, ∠A是锐角(注意数形结合,构造直角三角形). 2.sinA,cosA,tanA, 是一个完整的符号,表示∠A 的正切,习惯省去“∠”号; 3.sinA,cosA,tanA, 是一个比值.注意比的顺序, 且sinA,cosA,tanA, 均﹥0,无单位. 4.sinA,cosA,tanA, 的大小只与∠A的大小有关, 而与直角三角形的边长无关. 5.角相等,则其三角函数值相等;两锐角的三角函 数值相等,则这两个锐角相等.
a
A b ┌ C
练习:
1、下图中∠ACB=90° ,CD⊥AB 指出∠A的对边、邻边。 B D
A
C
2、1题中如果CD=5,AC=10,则sin∠ACD= sin ∠DCB=
如图:在等腰△ABC 中,AB=AC=5,BC=6. 求: sinB,cosB,tanB
A
5 B 5
┌ 6 D
C
提示:过点A作AD垂直于BC于D.
如图是两个自动扶梯,甲、乙两人分别从1、 2号自动扶梯上楼,谁先到达楼顶?如果AB和 A′B′相等而∠α和∠β大小不同,那么它们的高 度AC 和A′C′相等吗?AB、AC、BC与∠α, A′B′、A′C′、B′C′与∠β之间有什么关系呢?
A A′
3米 3米 β 4米 1
B
a
C C′ 2米
2
B′
想一想
a sin A c b sin B c
b cos A c a cos B c
A
B c a ┌ C
b
sinA=cosB ,cosA=sinB (∠A+∠B=90。)
sin A cos A 1
2 2
sin A tan A cos A
回味无穷
定义中应该注意的几个问题:
1.sinA,cosA,tanA, 是在直角三角形中定义的, ∠A是锐角(注意数形结合,构造直角三角形). 2.sinA,cosA,tanA, 是一个完整的符号,表示∠A 的正切,习惯省去“∠”号; 3.sinA,cosA,tanA, 是一个比值.注意比的顺序, 且sinA,cosA,tanA, 均﹥0,无单位. 4.sinA,cosA,tanA, 的大小只与∠A的大小有关, 而与直角三角形的边长无关. 5.角相等,则其三角函数值相等;两锐角的三角函 数值相等,则这两个锐角相等.
浙教版数学九年级下册 1.1 锐角三角函数 课件(共18张PPT)

? 求BE的长.
B(山顶)
H
当锐角为30°时,
30°
西坡
其所对的直角边与
斜边之比始终
30°
A
D
B(山顶)
为 1.
C
2
E
东坡
当锐角为45°时,
其所对的直角边
30°
CF
D
B(山顶)
与 斜边之比始 终为 2 .
2
当锐角为50°时,
G 南坡
这个比值是一个确 定的值.
C
HD
任意作一个锐角∠A,在角的边上任意取两点B
与B1分别作BC⊥AC于点C ,B1C1⊥A1C1于点C1.
判断 BC 与 B1C1 是否相等,并说明理由. B1
AB
AB1
B
A
C C1
对于每一个确定的锐角α,在角的边上任意取
一点B作BC⊥AC于点C,比值 BC 是一个确
定的值.
AB
B
A
C
直角三角形中锐角ɑ与其对边与斜边比值关系
ɑ
BC (对边与斜边比值)
1.1锐角三角函数(1)
我关心的是本质 其它都是细节(爱因斯坦)
一 情境创小设红、小强、小颖约好去爬山,他们沿不同倾 斜度的三条道路上山,若山顶与山下的铅垂距离为100 米,你能分别求出他们到达山顶要走的路程吗?
南坡
50°
小颖出发地
西坡
东坡
30°
小红出发地
45°
小强出发地
转化成的数学问题 B(山顶)
2.sinα是一个完整的符号,单独的“sin”没有意义.
练一练
1. 如图△ABC中,∠C=90°,BC=5,AC=12B.
5
计算:(1)sinA= 13.
B(山顶)
H
当锐角为30°时,
30°
西坡
其所对的直角边与
斜边之比始终
30°
A
D
B(山顶)
为 1.
C
2
E
东坡
当锐角为45°时,
其所对的直角边
30°
CF
D
B(山顶)
与 斜边之比始 终为 2 .
2
当锐角为50°时,
G 南坡
这个比值是一个确 定的值.
C
HD
任意作一个锐角∠A,在角的边上任意取两点B
与B1分别作BC⊥AC于点C ,B1C1⊥A1C1于点C1.
判断 BC 与 B1C1 是否相等,并说明理由. B1
AB
AB1
B
A
C C1
对于每一个确定的锐角α,在角的边上任意取
一点B作BC⊥AC于点C,比值 BC 是一个确
定的值.
AB
B
A
C
直角三角形中锐角ɑ与其对边与斜边比值关系
ɑ
BC (对边与斜边比值)
1.1锐角三角函数(1)
我关心的是本质 其它都是细节(爱因斯坦)
一 情境创小设红、小强、小颖约好去爬山,他们沿不同倾 斜度的三条道路上山,若山顶与山下的铅垂距离为100 米,你能分别求出他们到达山顶要走的路程吗?
南坡
50°
小颖出发地
西坡
东坡
30°
小红出发地
45°
小强出发地
转化成的数学问题 B(山顶)
2.sinα是一个完整的符号,单独的“sin”没有意义.
练一练
1. 如图△ABC中,∠C=90°,BC=5,AC=12B.
5
计算:(1)sinA= 13.
1最新浙教版初中数学九年级下册精品课件.1 锐角三角函数

在直角三角形中共有五个元素:边a,b,c, 锐角∠A,∠B.这五个
元素之间有如下等量关系:
(1)三边之间关系: a2 +b2 =c2 (勾股定理)
(2)锐角之间关系: ∠A+∠B=90°
(3)边角之间关系:
B
正 弦 函 数 : sin A
A的 对 斜边
边
a c
余 弦 函 数 : cos
A
A的 邻 斜边
450 ┌ 600 ┌
老师期望: 你能对伴随九个学年的这副三角尺所具有的功能来个 重新认识和评价. 根据上面的计算,完成<特殊角的三角函数值表>
做一做
B
2 1
45°
A
C
1
sin45 ° = 2
2
cos45°= 2
2
tan45°= 1
做一做
B
2
3
60°
A
C
1
sin60°= 3
2
cos60°= 1
练习
1.某商场有一自动扶梯,其倾斜角为300,高为7m,扶梯的长
度是多少?
B
2.如图,在Rt△ABC中,∠C=90°,
c
∠A,∠B ,∠C的对边分别是a,b,c.
求证:sin2A+cos2A=1.
A
a
┌
b
C
老师期望:
sin2A+cos2A=1它反映了同角之间的三角函数的关系,且它更具 有灵活变换的特点,若能予以掌握,则将有益于智力开发.
B
sin A a , cos A b ,
c
c
c
sin B b , cosB a ,
九年级数学下册 第一章 解直角三角形 1.1 锐角三角函数(第1课时)正弦、余弦、正切函数课件 (新版)浙教

下面图1和图2中各有一个比较陡的梯子,你能把它 们找出来吗?说说你的理由。
2020/1/1
精品课件
3
图1
图2
一样长的梯子的陡、梯子的放置角度(倾 斜角)、垂直高度和水平宽度它们之间有什么 关系?
2020/1/1
精品课件
4
梯子越陡——倾斜角__越_大__ 倾斜角越大——垂直高度与梯子长的比_越_大_ 倾斜角越大——水平宽度与梯子长的比__越_小__ 倾斜角越大——垂直高度与水平宽度的比_越_大___
,
4
5
另一边OA上有一点P(b,4),若sin α= ,则b=
________.
2020/1/1
精品课件
20
4 如图,在Rt△ABC中,∠C=90°,AB=6,
cosB= 2 ,则BC的长为________. 3
1 5 如图,已知Rt△ABC中,∠C=90°,AC=4,tanA = 2 ,则 BC的长是( )
2020/1/1
精品课件
12
练习1
1 把Rt△ABC三边的长度都扩大为原来的3倍,则锐
角A的正弦函数值( )
1
A.不变
B.缩小为原来的 3
C.扩大为原来的3倍 D.不能确定
2 在Rt△ABC中,∠C=90°,AC=12,
BC =5,则sin A的值为( )
A. 5 12
B. 12 5
C. 12 13
3
5
5
5
4
5
解析:A.
B.
C.
D.
在Rt△ABC中,∠45C=90°,则∠A+∠B=90°,
则cos B=sin A= .故选B.
2020/1/1
精品课件
2020/1/1
精品课件
3
图1
图2
一样长的梯子的陡、梯子的放置角度(倾 斜角)、垂直高度和水平宽度它们之间有什么 关系?
2020/1/1
精品课件
4
梯子越陡——倾斜角__越_大__ 倾斜角越大——垂直高度与梯子长的比_越_大_ 倾斜角越大——水平宽度与梯子长的比__越_小__ 倾斜角越大——垂直高度与水平宽度的比_越_大___
,
4
5
另一边OA上有一点P(b,4),若sin α= ,则b=
________.
2020/1/1
精品课件
20
4 如图,在Rt△ABC中,∠C=90°,AB=6,
cosB= 2 ,则BC的长为________. 3
1 5 如图,已知Rt△ABC中,∠C=90°,AC=4,tanA = 2 ,则 BC的长是( )
2020/1/1
精品课件
12
练习1
1 把Rt△ABC三边的长度都扩大为原来的3倍,则锐
角A的正弦函数值( )
1
A.不变
B.缩小为原来的 3
C.扩大为原来的3倍 D.不能确定
2 在Rt△ABC中,∠C=90°,AC=12,
BC =5,则sin A的值为( )
A. 5 12
B. 12 5
C. 12 13
3
5
5
5
4
5
解析:A.
B.
C.
D.
在Rt△ABC中,∠45C=90°,则∠A+∠B=90°,
则cos B=sin A= .故选B.
2020/1/1
精品课件
(浙教版)数学九下:1.1《锐角三角函数》ppt课件(2)

2 2 2 2
45°
a tan 45 1 a
仔细观察,说说你发现 30°、45°、60°角的正弦值、余弦值和正切值如下表: 这张表有哪些规律? 锐角a 30° 三角函数 sin a
1 2
45°
2 2
60°
3 2
cos a
tan a
3 2
3 3
2 2
1 2
1
3
例1求下列各式的值:
(1)cos260°+sin260°
1.2锐角三角函数
B
∠A的对边
sinA 斜边
斜边 ∠A的对边
cosA
∠A的邻边 斜边
A
∠A的邻边
C
tanA
∠A的对边 ∠A的邻边
活 动 1
两块三角尺中有几个不同的锐 角?分别求出这几个锐角的正 弦值、余弦值和正切值. 60° 30° 45° 45°
设30°所对的直角边长为a,那么斜边长为2a 另一条直角边长=
1 2sin A cos A
sin 230 + tan 245 + sin 260 1 2 cosห้องสมุดไป่ตู้45 + tan30 cos30
2、已知:α为锐角,且满
足 3tan 数。 3、在Rt△ABC中,∠C=90°,化简
2
-4tan + 3 =0 ,求α的度
1-2sinAcosA
=0
=1
应用生活
例2:操场里有一个旗杆,老师让小明去测量旗杆
高度,小明站在离旗杆底部10米远处,目测旗杆的顶 部,视线与水平线的夹角为30度,并已知目高为1.65 米.然后他很快就算出旗杆的高度了。
你想知道小明怎样 算出的吗?
1.1锐角三角函数(第一课时)课件(共17张PPT)浙教版数学九年级下册

cosA=
=
∠的邻边
温馨提醒:以正弦为例
sinA(省去角的符号),
30°的正弦表示为sin30°,比值 叫做∠A的正切值,记做tanA,即
斜边
∠BAC的正弦表示为sin∠BAC
,∠1的正弦表示为:sin∠1.
tanA=
∠的对边
∠的邻边
=
概念运用
①BC=8,AC=6
概念
cosA=
= ,
tanA=
4
3
sinA=
4
5
3
= ,
5
= .
解后反思:在直角三角
形中,已知什么条件可
以求三角函数值?
课堂练习
1.如图,在Rt△ABC中,∠ACB=90°,作CD⊥AB于
点D,若BC=5,BD=4,求sin∠A.
C
A
B
思路1:求AB的长
思路2:等角转化
△BCD∽△BAC
B"
P
C" Q
图(1)
图(2)
角为30°
’’ 1
""
=
= =
’’ 2
"
’’
3 "
=
=
=
’’
2
"
’’
3 ""
=
=
=
’’
3
"
请先按暂停键!
思考完成后
再按回播放键!
边的比值为定值
探索规律
当∠PAQ发生改变时,刚才所获得的发现是否还成立呢?
解:设AB=5k,AC=3k,
锐角三角函数课件(浙教版)

第一章 解直角三角形
1.1 锐角三角函数
2024/9/18
比值 BC 叫做∠α的正弦 ,记做sinα. AB
比值
AC AB
叫做∠α的余弦,记做cosα.
比值
BC AC
叫做∠α的正切,记做tanα.
B
α
AC
sin BC cos AC
AB
AB
tan BC
AC
锐角α的正弦、余弦、正切 统称为∠α的三角函数
结论正确的是( D )
B
பைடு நூலகம்
A.sinA= 4 5
C.sinA=
3 4
B.sinA=
3 5
5
D.以上结论都不正确 A
3 C
2、如图,在Rt△ABC中,∠ACB=90°,作CD⊥AB于D,
若BD=2,BC=3.则sinA= 2 .
C
3
3
A
D2 B
3.如图,在△ABC中,AB=15,AC=13, S△ABC=84, 求sinA的值。 C
• 如图,在Rt⊿ABC中,∠C=Rt∠
sin BC
AB
sin
A
A的对边 斜边
A
cos AC
AB
cos
A
A的邻边 斜边
tan BC
AC
tan
A
A的对边 A的邻边
B
∠AB 的 对邻
C边
例1 在Rt⊿ABC中,∠C=Rt∠,AC=4,BC=3,求
∠A的正弦、余弦和正切。
B
变式1:在Rt⊿ABC中,∠C=Rt∠,BC:AB=3:5,
A
B
求锐角∠A的余弦。
C
A
变式2:在Rt⊿ABC中,∠C=Rt∠,s
1.1 锐角三角函数
2024/9/18
比值 BC 叫做∠α的正弦 ,记做sinα. AB
比值
AC AB
叫做∠α的余弦,记做cosα.
比值
BC AC
叫做∠α的正切,记做tanα.
B
α
AC
sin BC cos AC
AB
AB
tan BC
AC
锐角α的正弦、余弦、正切 统称为∠α的三角函数
结论正确的是( D )
B
பைடு நூலகம்
A.sinA= 4 5
C.sinA=
3 4
B.sinA=
3 5
5
D.以上结论都不正确 A
3 C
2、如图,在Rt△ABC中,∠ACB=90°,作CD⊥AB于D,
若BD=2,BC=3.则sinA= 2 .
C
3
3
A
D2 B
3.如图,在△ABC中,AB=15,AC=13, S△ABC=84, 求sinA的值。 C
• 如图,在Rt⊿ABC中,∠C=Rt∠
sin BC
AB
sin
A
A的对边 斜边
A
cos AC
AB
cos
A
A的邻边 斜边
tan BC
AC
tan
A
A的对边 A的邻边
B
∠AB 的 对邻
C边
例1 在Rt⊿ABC中,∠C=Rt∠,AC=4,BC=3,求
∠A的正弦、余弦和正切。
B
变式1:在Rt⊿ABC中,∠C=Rt∠,BC:AB=3:5,
A
B
求锐角∠A的余弦。
C
A
变式2:在Rt⊿ABC中,∠C=Rt∠,s
新浙教版九年级数学下册第一章《锐角三角函数的计算(1)》公开课课件

课外拓展
2、求证:对于任何锐角α,sin =tanα
cos
w用科学计算器求锐角的三角函数值, 要用到三个键: sin cos tan
w例如,求 sin160,cos420, tan850 和sin720 38′25″的按键 盘顺序如下:
w例如,求sin160,cos420, tan850 和sin720 38′25″的按键盘顺序如 下:
D
随堂练习
w6 如图,根据图中已知 数据,求△ABC其余各边 A
20
的长,各角的度数和 B 550 △ABC的面积.
250
C
A
w7 如图,根据图中已 知数据,求AD.
250 550┌
B 20 C
D
随堂练习
w8 如图,根据图中已知
数据,求△ABC其余各边 A 的长,各角的度数和 a
△ABC的面积.
1.2三角函数的有关计算(1) 由角求三角函数值
锐角三角函数
sinAcoBs a, c
tanA= a
b
coAs sinBb, c
wB, tanA·tanB=1.
w同角之间的三角函数关系: wsin2A+cos2A=1.
B
c
a
┌
b
C
w特殊角300,450,600角的三角函数值.
及其三角函数 求另一边
求另一边
sin A a , c
acsin A. c a . sin A
B
ca ┌
A bC
cos A b , c
bccoA.s c b . cos A
A
tan A a , b
abtaA n. b a . tan A
α β┌
《锐角三角函数》PPT课件 (公开课)2022年浙教版 (2)

AC
练习拓展,层层递进
• 例1.在Rt⊿ABC中,∠C=Rt∠,AB=5,BC=3, 求锐角∠A的各三角函数值(书P5)
A
正弦 余弦 正切
∠A
sinA= 3 5
c
o
sA=
4 5
tanA= 3 4
C
B
∠B
sinB= 4 5
cosB= 3 tanB= 4
5
3
变
• 在Rt⊿ABC中,∠C=Rt∠,AC=8,BC=6,求 锐角∠A的各三角函数值(书P6作业题2)
列出方程后,还必须找出符合方程的未知数的值.
能使方程左右两边的值相等 的未知数的值叫方程的解.
例1: 判断下列t的值是不是
方程2t+1=7-t的解: (1) t=-2 (2) t=1 (3) t=2
3、小强、小杰、张明参加投篮比赛,每人投20次.小强投进10个
球,小杰比张明多投进2个,三人平均每人投进14个球.问小杰和
运用已学的知识,根据下列问题中的条件,分别列
出方程:
1、一件衣服按 8 折销售的售价为72元,这件衣服的原价是多
少元? 设这件衣服的原价为x元,可列出方程
_0__.8_x____7_2_;
2、物体在水下,水深每增加米承受的压力就会增加1个大气
压.当“蛟龙”号下潜至3500米时,它承受的压力约为340个
2x 12 14
设第一次射击的成绩为x个, 可列方程为____3_______
0.8x72
观察你所列的方程,这些方
340 1 x500 10.33
程之间有什么共同的特点?
★方程两边都是整式;
2x 12 14 3
★方程中只含有一个未知数; ★未知数的指数是一次。
2022年浙教初中数学九下《锐角三角函数》PPT课件2
1、这节课我们学了什么?
2、今后在涉及直角三角形的 边角 关系时,你会选择什么方法去解 决?
作业:
1、课内练习1、2,作业题第1题
2、你能用所学知识分别求出30 ° 、45°、 60 °的三角
函数 值吗?
C
思考题:
1、若y=sinA+3,则y取值范围为________ A
B
2、如图,在Rt Δ ABC中, ∠B=90 °,则sinA =____
如图, △ABC中, ∠C=90 °,CD⊥AB,垂足
为D.
1 、若已知AD=6,AC=10,求sinB的值
2 、若已知AD=4,BD=8,求tanA的值
根据三角函数定义,你能确定锐 角A的正弦与余弦三角函数值 的 取值范围吗?
并找一找∠A的四个三角函数之间 有何关系?
0sinA1,0cosA1
小结:
2、如图所示的长方形分割成四个大小相同 的正方形。已知正方形的边长为a,则tan = ____ , sin =______
你真正理解了吗?
3、等腰三角形的腰长为5cm,底 边长为8cm,则它的底角的正切 值是____.
1
4、已知sinA= 2 ,求cosA, tanA的值.
祝你成功﹗ C
A
D
B
A=
b
c
tan
A=
a
b
cot
A=
b
a
这四个函数统称为锐角A的三角函数.
例:求出如图所示的Rt△ABC 中你会求∠A的四个三角函数值 A 吗?∠B的呢?
8
C
B
6
你记住了吗?
相信自己能行﹗
y
1、如图所示:则sin =_____, cos = ______, tan = _____。
2、今后在涉及直角三角形的 边角 关系时,你会选择什么方法去解 决?
作业:
1、课内练习1、2,作业题第1题
2、你能用所学知识分别求出30 ° 、45°、 60 °的三角
函数 值吗?
C
思考题:
1、若y=sinA+3,则y取值范围为________ A
B
2、如图,在Rt Δ ABC中, ∠B=90 °,则sinA =____
如图, △ABC中, ∠C=90 °,CD⊥AB,垂足
为D.
1 、若已知AD=6,AC=10,求sinB的值
2 、若已知AD=4,BD=8,求tanA的值
根据三角函数定义,你能确定锐 角A的正弦与余弦三角函数值 的 取值范围吗?
并找一找∠A的四个三角函数之间 有何关系?
0sinA1,0cosA1
小结:
2、如图所示的长方形分割成四个大小相同 的正方形。已知正方形的边长为a,则tan = ____ , sin =______
你真正理解了吗?
3、等腰三角形的腰长为5cm,底 边长为8cm,则它的底角的正切 值是____.
1
4、已知sinA= 2 ,求cosA, tanA的值.
祝你成功﹗ C
A
D
B
A=
b
c
tan
A=
a
b
cot
A=
b
a
这四个函数统称为锐角A的三角函数.
例:求出如图所示的Rt△ABC 中你会求∠A的四个三角函数值 A 吗?∠B的呢?
8
C
B
6
你记住了吗?
相信自己能行﹗
y
1、如图所示:则sin =_____, cos = ______, tan = _____。
2022年浙教初中数学九下《锐角三角函数》PPT课件6

名师指津
1. 一个实数的立方根表示为3 a,根指数 3 不能省略. 2. 一个实数的立方根的结果总是唯一的. 3. 3 -a=-3 a(a 为一切实数).
1.1 锐角三角函数(1)
取宝物比赛
10m
10
(1)
1m
5m
(2)
梯子在上升变陡的过程中,倾 斜角,铅直高度与梯子的比,水 平宽度与梯子的比,铅直高度与 水平宽度的比,都发生了什么变 化?
铅
直
高
倾斜角
度
水平宽度
梯子在上升变陡的过程中,倾 斜角,铅直高度与梯子的比,水 平宽度与梯子的比,铅直高度与 水平宽度的比,都发生了什么变 化?
想一想
B
B1
(1)直角三角形AB1C1和直角三 角 形ABC有什么关系?
BC
B 1C 1 A C
AC1 BC
(2) A B 和 A B 1 , A B 和A B 1 , A C
和B
A
1C C
1 1
有什么关系?
A
(3)如果改变B在梯子上的位置
呢?
C C1
B
∠A的对边
sinA
斜边
斜边
∠A的对边 cosA
【解析】 (1)∵3x3+24=0,∴3x3=-24,
∴x3=-8,∴x=3 -8=-2. (2)∵1000(x-1)3=-27, ∴(x-1)3=-0.027,
∴x-1=3 -0.027=-0.3, ∴x=0.7. 【答案】 (1)x=-2 (2)x=0.7
【典例 2】 计算:
3 (1)
0.125;
的比_越__大__
铅 直 高
度
水平宽度
想一想
B
A
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(3) 3 cos30 0
2 sin45 + tan45 cos600
0 0.
计算: (1)sin600-cos450;(2)cos600+tan600;
2 (3) sin 450 + sin 600 - 2 cos450. 2
2 2 0 (4) sin 30 + cos2 600 - 2 cos2 450. 2
┌
600
┌
老师期望: 你能对伴随九个学年的这副三角尺所具有的功能来个 重新认识和评价. 根据这副三角板你能记住这三个角的三角函数值吗?
老师提示: 例1 计算:
(1)2sin300-3cos600; (2) cos2450+tan600. sin600; cos2450表示 (cos450)2, 其余类推.
课内练习3
1、课文P9 T3
2、课文P10 T4—5
小结
B
看图说话: 直角三角形三边的关系. 直角三角形两锐角的关系. 直角三角形边与角之间的关系. 特殊角300,450,600角的三角函数 值. 互余两角之间的三角函数关系. 同角之间的三角函数关系
c a A b ┌ C
300,450,600角的三角函数值
通过课前预习、自学P7-9完成填空
特殊角的三角函数值表
锐角α 三角函数
30°
1 2
45°
2 2 2 2
60°
3 2 1 2
正弦sinα 要能记 住有多 好 余弦cosα 正切tanα
3 2 3 3
1
3
这张表还可以看出许多 知识之间的内在联系?
300 450 450
300
450
450
┌
600
┌
做一做
(1) cos2450+ sin2450 (2) cos2600+ sin2600 你发现了什么?对于任意锐角A,是否都有cos2A+ sin2A=1 ?请说明理由.
讨论
作业:
1、作业本(2) 2、预习课文P10——11
例2 如图,在Rt△ABC 中,∠C=90°, AB
6
BC 3
求∠A的度数.
B
A
CБайду номын сангаас
课内练习2 在Rt△ABC 中,∠C=90°,AC=6,BC 2 3 则 ∠A= ∠B=
例3。一位同学的手臂长65cm,当他高 举双臂时,指尖高出头顶35cm。问当他 的手臂与水平成60度角时,指尖高出头 顶多少cm(精确到0。1cm)?
