华南理工-大学物理练习题-刚体力学,习题三
2021大学物理B-第3章刚体力学练习题 (1)

第三章 刚体力学一、 选择题1、一轻绳跨过一具有水平光滑轴、质量为M 的定滑轮,绳的两端分别悬有质量为m 1 和m 2 的物体(m 1<m 2),如图所示.绳与轮之间无相对滑动.若某时刻滑轮沿逆时针方向转动,则绳中的张力[ ](A) 处处相等. (B) 左边大于右边.(C) 右边大于左边. (D) 哪边大无法判断.2、将细绳绕在一个具有水平光滑轴的飞轮边缘上,现在在绳端挂一质量为m 的重物,飞轮的角加速度为β.如果以拉力2mg 代替重物拉绳时,飞轮的角加速度将[ ](A) 小于β . (B) 大于β,小于2β. (C) 大于2β. (D) 等于2β.3、如图所示,一匀质细杆可绕通过上端与杆垂直的水平光滑固定轴O 旋转,初始状态为静止悬挂.现有一个小球自左方水平打击细杆.设小球与细杆之间为非弹性碰撞,则在碰撞过程中对细杆与小球这一系统[ ](A) 只有机械能守恒. (B) 只有动量守恒.(C) 只有对转轴O 的角动量守恒.(D) 机械能、动量和角动量均守恒.4、如图所示,一根匀质细杆可绕通过其一端O 的水平轴在竖直平面内自由转动,杆长5/3m 。
今使杆从与竖直方向成︒60角由静止释放(g 取10m/s 2),则杆的最大角速度为 [ ] (A )3rad/s ; (B)πrad/s ; 3.0rad/s ; (D)3/2rad/s 。
5、对一个绕固定水平轴O 匀速转动的转盘,沿图示的同一水平直线从相反方向射入两颗质量相同、速率相等的子弹,并停留在盘中,则子弹射入后转盘的角速度应[ ](A) 增大;(B) 减小;(C) 不变;(D) 无法确定。
6、一根长为l 、质量为M 的匀质棒自由悬挂于通过其上端的光滑水平轴上。
现有一质量为m 的子弹以水平速度v 0射向棒的中心,并以v 0/2的水平速度穿出棒,此后棒的最大偏转角恰为90°,则v 0的大小为 [ ] (A)34gl m M ; (B)2gl ; (C)gl m M 2; (D)22316mgl M 。
大学物理试题库刚体力学 Word 文档

大学物理试题库刚体力学 Word 文档大学物理试题库刚体力学word文档第三章刚体力学一、刚体运动学(定轴转动)---角位移、角速度、角加速度、线量与角量的关系1、刚体做定轴转动,下列表述错误的是:【】a;各质元具备相同的角速度;b:各质元具备相同的角加速度;c:各质元具备相同的线速度;d:各质元具备相同的角位移。
2、半径为0.2m的飞轮,从静止开始以20rad/s2的角加速度做定轴转动,则t=2s时,飞轮边缘上一点的切向加速度a?=____________,法向加速度an=____________,飞轮转过的角位移为_________________。
3、刚体任何复杂的运动均可理解为_____________和______________两种运动形式的合成。
二、转动惯量1、刚体的转动惯量与______________和___________________有关。
2、长度为l,质量为m的光滑木棒,顾其一端a点旋转时的转动惯量ja=_____________,拖其中心o点旋转时的转动惯量jo=_____________________。
3、半径为r、质量为m的光滑圆盘拖其中心轴(旋转轴盘面)旋转的转动惯量j=___________。
4、【】两个匀质圆盘a和b的密度分别就是?a和?b,若?a??b,但两圆盘的质量和厚度相同,如两盘对通过盘心垂直于盘面轴的转动惯量各为ja和jb则:(a)ja?jb;(b)ja?jb(c)ja?jb(d)不能确定三、刚体动力学----旋转定理、动能定理、角动量定理、角动量动量1、一短为l的轻质细杆,两端分别紧固质量为m和2m的小球,此系统在直角平面内可以绕开中点o且与杆横向的水平扁平紧固轴(o轴)旋转.已经开始时杆与水平成60°角,处在静止状态.无初输出功率地释放出来以后,杆球这一刚体系统拖o轴旋转.系统拖o轴的转动惯量j=___________.释放出来后,当杆转至水平边线时,刚体受的合外力矩m=______;角加速度______.2、一个能绕固定轴转动的轮子,除受到轴承的恒定摩擦力矩mr外,还受到恒定外力矩m的作用.若m=20nm,轮子对固定轴的转动惯量为j=15kgm2.在t=10s内,轮子的角速度由??=0增大到?=10rad/s,则mr=_______.3、【】银河系有一可以视作物的天体,由于引力汇聚,体积不断膨胀。
《大学物理学》刚体部分练习题解答

解答一、选择题:1.B2.B3.B4.C5.D6.D7.B8.C9.A 10. D 11.A 12.D 13.A 14.B 15.A三.计算题1.解:由于组合轮是一个整体,有12J J J =+。
应用牛顿运动定律:对物体A ,1111m g T m a -=;对物体B ,2222T m g m a -=,对组合轮,应用转动定律:12T R T r J α-=。
考虑到:1a R α=,2a r α=,解得:121221212122221212m R m r a g R J J m R m r m R m r a g r J J m R m r -⎧=⋅⎪+++⎪⎨-⎪=⋅⎪+++⎩;21222112212122121122221212J J m r m R rT m gJ J m R m r J J m R m R rT m gJ J m R m r ⎧+++=⋅⎪+++⎪⎨+++⎪=⋅⎪+++⎩。
2.解:由于飞轮的质量全部分布在轮缘上,有:2J m R =;而力矩为恒力矩,有:()3200102/6020/53rad s t ωππα-⋅===; 闸瓦给飞轮的正压力: 1.25 2.5'0.5l F FN F l ⨯⨯===, ∴0.42.50.250.25f M NR F F μ==⋅⨯=;由转动定律:M J α=,有:2f M mR α=→2200.25600.253F π=⋅⋅,有314F N =。
3. 解:由角动量守恒定律:200()2J m r J ωω+=,得 2J m r =。
由于 :310/m kg s t-=所以 :5323235105s 1101100.1110m J t r ----⨯====⨯⨯⨯⨯⨯ 4.解:设圆盘相对于地面的角速率为0ω,则人相对于地面的角速率为0vRωω∆=+。
应用角动量守恒定律:200J mR ωω+=,有:22000vJ mR mR Rωω∆++⋅=, 解得: 202mR vJ mR Rω∆=-⋅+。
2012华南理工大学华南理工大学理论力学考试试卷

五、平面机构如图所示,在某一瞬时,杆 AB 水平,杆 OA 垂直,杆 OA 的角速 度为ω = 2 rad / s ,角加速度为α = 2rad / s2 ,OA = AB = R = 2r = 1m ,轮子
在圆弧槽中作无滑动滚动。试求该瞬时轮心 B 和轮边缘 C 点的速度以及 B 点 的加速度大小。 (15 分)
一、判断题 (正确打“√”,错误打“×”,每小题 2 分,共 10 分)
1、平面任意力系,只要主矢 FR ≠ 0 ,最后必可简化为一合力。
(
)
2、刚体在 3 个力的作用下平衡,这 3 个力不一定在同一个平面内。 ( )
3、某刚体作平面运动时,若 A 和 B 是其平面图形上的任意两点,则速度投
影定理 [vrA ]AB = [vrB ]AB 恒成立。
A
D
v1
v2
α M1
M2
B
C
5、图示匀质细杆的端点 A、B 在固定圆环中沿壁运动。已知:杆长为 L、质量 为 m,质心 C 的速度大小 vC 为常数,圆环半径为 r。试求惯性力系向圆心 O 简化的结果,并在图中标明方向。
《 理论力学 》64 学时 A 卷 第 4 页 共 7 页
四、图示支架由 AC、ED 和滑轮组成,各处均由铰链连接。滑轮半径 r = 30cm , 上面吊着重 P = 1kN 的物体。试求 A、E 处的约束反力。(每取一次研究对象 要画受力图再列平衡方程) (15 分)
其适用条件是 ( )。
A、 A、B 两点均在 y 轴上;
B、 y 轴垂直于 A、B 连线;
C、 x 轴垂直于 A 、B 连线; D、 y 轴不垂直于 A、B 连线。
大学物理第三章刚体力学基础习题答案

方向竖直向下
3-15 由角动量守恒得
mul J mvl 1 1 2 1 2 2 mu m v J 因弹性碰撞,系统机械能守恒: 2 2 2 1 1 2 2 又: J M 2l Ml 12 3 6mu M 3m u 联立可得: v M 3m l M 3m
2 2 2 1 mv l [m( l ) M l 2 ] 3 3 3
o
2 l 3
6mv (4m 3M ) l
v
m
A
3-9 电风扇在开启电源后,经过t1时间到达了额定 转速,此时相应的角速度为 0。当关闭电源后,经 过t2时间风扇停转。已知风扇转子的转动惯量为 J, 并假定摩擦力矩和电机的电磁力矩均为常量,试根据 已知量推算电机的电磁力矩。 解: 设电机的电磁力矩为M,摩擦力矩为Mf
1
0
t1
3-9 (1)
mg T ma
T mg sin 30 ma
g 2 a m/s 4
方向竖直向下
T2 N 2
mg
(2)
mg T1 ma
T2 mg sin 300 ma
T1r T2r J
a r
T1
1
mg
J k m r2
g 联立求解得: a 22 k
质点运动 m 质 量 力 F 刚体定轴转动 2 J r 转动惯量 m dm 力矩 M Fr sin
dp dL F m a F 第二定律 转动定律 M J M dt dt p mv 动 量 角动量 L J t t2 动量定理 t Fdt mv2 mv1 角动量定理 t Mdt J 2 J1 1 动量守恒 F 0, mv 恒矢量 角动量守恒 M 0, J 恒矢量 力矩的功 W Md 力 的 功 W F dr
大学物理习题答案03刚体运动学

⼤学物理习题答案03刚体运动学⼤学物理练习题三⼀、选择题1.⼀⼒学系统由两个质点组成,它们之间只有引⼒作⽤。
若两质点所受外⼒的⽮量和为零,则此系统(A) 动量、机械能以及对⼀轴的⾓动量都守恒。
(B) 动量、机械能守恒,但⾓动量是否守恒不能断定。
(C) 动量守恒,但机械能和⾓动量守恒与否不能断定。
(D) 动量和⾓动量守恒,但机械能是否守恒不能断定。
[ C ]解:系统=0合外F,内⼒是引⼒(保守内⼒)。
(1)021 F F,=0合外F ,动量守恒。
(2)2211r F r F A =合。
21F F,但21r r时0A 外,因此E不⼀定守恒。
(3)21F F,2211d F d F M =合。
两⼒对定点的⼒臂21d d 时,0 合外M,故L 不⼀定守恒。
2. 如图所⽰,有⼀个⼩物体,置于⼀个光滑的⽔平桌⾯上,有⼀绳其⼀端连结此物体,另⼀端穿过桌⾯中⼼的⼩孔,该物体原以⾓速度ω在距孔为R 的圆周上转动,今将绳从⼩孔往下拉。
则物体 (A) 动能不变,动量改变。
(B) 动量不变,动能改变。
(C) ⾓动量不变,动量不变。
(D) ⾓动量改变,动量改变。
(E)⾓动量不变,动能、动量都改变。
[ E ]解:合外⼒(拉⼒)对圆⼼的⼒矩为零,⾓动量O Rrmv L 守恒。
r 减⼩,v 增⼤。
因此p 、E k 均变化(m不变)。
3. 有两个半径相同,质量相等的细圆环A 和B 。
A 环的质量分布均匀,B 环的质量分布不均匀。
它们对通过环⼼并与环⾯垂直的轴的转动惯量分别为J A 和J B ,则(A)A J >B J (B) A J < B J(C) A J =B J (D) 不能确定A J 、B J 哪个⼤。
[ C ]解:2222mR dm R dm R dm r J, J 与m 的分布⽆关。
另问:如果是椭圆环,J 与质量分布有关吗?(是)4. 光滑的⽔平桌⾯上,有⼀长为2L 、质量为m 的匀质细杆,可绕过其中点且垂直于杆的竖直光滑固定轴O ⾃由转动,其转动惯量为31mL 2,起初杆静⽌。
东华理工大学 物理练习试卷答案 刚体力学

J 00 J
J0 2mR2 /5,
2
J 2m( R / 2 )2 /5
40
2 T0 T 4 0 4
14. 一块方板,可以绕通过其一个水平边的光滑
固定轴自由转动.最初板自由下垂.今有一小团粘 土,垂直板面撞击方板,并粘在板上。对粘土和 方板系统,如果忽略空气阻力,在碰撞中守恒的 绕木板转轴的角动量 量是 ________________. (动能、 绕木板转轴的角动量、 机械能、 动量)
E p EK J
1 2
EK EP 0
2
Ep J
1 2
2
M J
即角速度从小到大,角加速度从大到小
7、一水平圆盘可绕通过其中心的固定竖直轴转动,盘上站着一个 人.把人和圆盘取作系统,当此人在盘上随意走动时,若忽略轴 的摩擦,此系统 [ C ] (A)动量守恒. (B)机械能守恒. (C) 对转轴的角动量守恒. (D) 动量、机械能和角动量都守恒. (E) 动量、机械能和角动量都不守恒.
2m 得 k 2 L 2 mg df dmg rdr 2
L
dM rdf
2m g 2 2 M dM r dr m gL 2 L 3 0
L
18.如图所示,一轻绳绕过一轻滑轮,绳的一端被一质量为m 的 人抓住,绳的另一端悬挂一质量为 m / 2的物体,定滑轮的质 量为 M ,半径为R,可视为匀质圆盘。设人从静止开始相对绳 匀速向上爬行时,绳子与滑轮间无相对滑动, 求物体上升的加速度。
8、如图所示,一静止的均匀细棒,长为L、质量为M,可绕通过 棒的端点且垂直于棒长的光滑固定轴O在水平面内转动,转动 1 ML 惯量为 。一质量为m、速率为v的子弹在水平面内沿与棒 3 1 v 垂直的方向射出并穿出棒的自由端,设穿过棒后子弹的速率 2 B 为 ,则此时棒的角速度应为[ ]。 1
大学物理刚体习题

大学物理刚体习题(总13页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--习 题第三章 刚体的转动刚体的定轴转动47. 一定滑轮半径为R ,质量为M ,用一质量不计的绳绕在滑轮上,另一端系一质量为m 的物体并由静止释放,这时滑轮的角加速度为1β,若不系物体而用一力F = mg 拉绳子使滑轮转动,这时角加速度为2β,这时有()1β2β()1β2β (C )1β2β(D )无法判断 分析由转动定律M I β=本题中I 不变β的大小完全取决于M 的大小而 M TR =系物体m 时 : T mg <不系物体而用一力F = mg 时: TF mg ==因此力矩变大所以有12ββ<mF选49.一飞轮的转动惯量为J ,t = 0时角速度为0ω,轮子在转动过程中受到一力矩2ωk M-=,则当转动角速度为0/3ω时的角加速度β = 从0ω到0/3ω飞轮转动经过的时间t ∆= 解: (1) 求β当0/3ω时, 20()3M k ω=-由 M J β=, 可得此时 209k MJ J ωβ==-(2) d M J J dt ωβ== 2d k J dt ωω-=分离变量,两边积分32td kdt Jωωωω-=⎰⎰解得: 02J t k ω∆=50.长为l 的均匀直棒可绕其下端与棒垂直的水平光滑轴在竖直平面内转动。
抬起一端使与水平夹角为60=θ,棒对轴的转动惯量为231ml J =,由静止释放直棒,则t = 0时棒的β=?;水平位置时的β=?这时的ω=(1)求β 据转动定律M J β=, MJβ= 0t =时, cos 602lM mg =︒水平位置时, 2lM mg =代入MJβ=,可别解得034glβ= 和 32g l β= (2)求ωd d d d M J J J J dt d dt d ωωθωβωθθ====将cos 2l M mg θ=和213J ml =代入化简并积分得, 0033cos 2g d d l ωπθθωω=⎰⎰ 60可求得332g l ω=(本题还可用动能定律机械能守恒方便求解ω)2211sin 60223l mg ml ω︒=⋅ 332g lω⇒=51.一飞轮以min /600rev 的转速转动,其转动惯量为25.2m kg J ⋅=,以恒定力矩使飞轮在一分钟内停止转动,求该力矩M 。
华南理工大学大学物理习题答案

1.答案:37.4%;不是; 。
2.答案: 。
3.答案: 。
三、计算题
1.答案:(1) ;(2) ;(3) 。
2.答案:(1) ,熵增加;(2) , 。
3.答案:(1) ;(2) ;(3) J/K。
4.答案: 。
习题四
一、选择题
1.B;2.C;3.C;4.B;5.D。
二、填空题
1.答案:10 cm;(/6) rad/s;/3。
2.答案:(b,f);(a,e)。
3.答案: ; 。
4.答案: ; 。
5.答案:802Hz
三、计算题
1.答案:证明(略),
2.答案:(1) , ;(2) , ;
(3) 。
3.答案:(1) ;(2) 。
5.答案:(1)4000条;(2)0.5mm;(3) 。
三、计算题
1.答案: 。
2.答案:(1)648.2nm;(2)0.15。
3.答案:(1) ;(2) 。
4.答案: 。
5.答案:546nm。
习题七
一、选择题
1.D;2.B;3.B;4.C;5.D。
二、填空题
1.答案:3mm。
2.答案: 。
3.答案: ; 。
2.答案: ;垂直。
3.答案:(1)双折射;(2)相等;(3)相等。
4.答案:355nm;396nm。
三、计算题
1.答案:
2.答案:2/5.
3.答案:(1)48.4°;(2)41.6°。
4.答案:54.7°
5.答案:
习题九
一、选择题
1.B;2.A;3.A;4.C;5.A。
二、填空题
1.答案: ; ; 。
3.答案:小于;大于。
大学物理第3章-刚体力学习题解答

大学物理第3章-刚体力学习题解答第3章 刚体力学习题解答3.13 某发动机飞轮在时间间隔t 内的角位移为):,:(43s t rad ct bt at θθ-+=。
求t 时刻的角速度和角加速度。
解:23212643ct bt ct bt a dt d dtd -==-+==ωθβω3.14桑塔纳汽车时速为166km/h ,车轮滚动半径为0.26m ,发动机转速与驱动轮转速比为0.909, 问发动机转速为每分多少转?解:设车轮半径为R=0.26m ,发动机转速为n 1, 驱动轮转速为n 2, 汽车速度为v=166km/h 。
显然,汽车前进的速度就是驱动轮边缘的线速度,909.0/2212Rn Rn v ππ==,所以:min/1054.1/1024.93426.014.3210166909.02909.013rev h rev n R v ⨯=⨯===⨯⨯⨯⨯π3.15 如题3-15图所示,质量为m 的空心圆柱体,质量均匀分布,其内外半径为r 1和r 2,求对通过其中心轴的转动惯量。
解:设圆柱体长为h ,则半径为r ,厚为dr 的薄圆筒的质量dm 为:2..dm h r dr ρπ=对其轴线的转动惯量dI z 为232..z dI r dm h r dr ρπ==212222112..()2r z r I h r r dr m r r ρπ==-⎰ 3.17 如题3-17图所示,一半圆形细杆,半径为,质量为,求对过细杆二端轴的转动惯量。
解:如图所示,圆形细杆对过O 轴且垂直于圆形细杆所在平面的轴的转动惯量为mR 2,根据垂直轴定理z x y I I I =+和问题的对称性知:圆形细杆对过轴的转动惯量为12mR 2,由转动惯量的可加性可求得:半圆形细杆对过细杆二端轴的转动惯量为:214AA I mR '=3.18 在质量为M ,半径为R 的匀质圆盘上挖出半径为r 的两个圆孔,圆孔中心在半径R 的中点,求剩余部分对过大圆盘中心且与盘面垂直的轴线的转动惯量。
大学物理刚体习题

大学物理刚体习题在大学物理的学习中,刚体是一个重要的概念。
刚体是指物体内部各点之间没有相对位移,不发生形变,整体运动状态一致的理想化模型。
在解决物理问题时,刚体的性质为我们提供了极大的便利。
以下是一些常见的大学物理刚体习题。
一、基本概念题1、什么是刚体?列举一些常见的刚体实例。
2、刚体在什么情况下可以被视为刚体?其基本性质是什么?3、描述刚体的运动,并解释相关概念,如转动、角速度、角加速度等。
二、刚体的动力学问题4、一个刚体绕固定轴转动,在某时刻受到一个外力矩的作用,求该刚体接下来的运动状态。
41、一个刚体在平面上做纯滚动,如何计算其加速度和速度?411、一个刚体在重力场中处于平衡状态,求其重心的位置。
三、刚体的静力学问题7、一个刚体受到两个大小相等、方向相反的力作用,求该刚体的平衡状态。
71、一个刚体在平面上受到一个力矩的作用,求该刚体的转动效果。
711、一个刚体在三个不在同一直线上的力作用下处于平衡状态,求该刚体的重心位置。
四、刚体的运动学问题10、一个刚体绕固定轴转动,其角速度与时间成正比,求该刚体的角加速度和转速。
101、一个刚体在平面上做纯滚动,其速度与时间成正比,求该刚体的加速度和转速。
1011、一个刚体受到一个周期性外力矩的作用,求该刚体的运动状态。
以上就是一些常见的大学物理刚体习题。
解决这些问题需要我们深入理解刚体的性质和相关的物理概念,如力、力矩、重心等。
通过这些习题的练习,我们可以更好地掌握刚体的相关知识,提高我们的物理水平。
大学物理刚体力学标题:大学物理中的刚体力学在物理学的研究中,大学物理是引领我们探索自然界规律的重要途径。
而在大学物理中,刚体力学是一个相对独特的领域,它专注于研究物体在受到外力作用时的质点运动规律。
本文将探讨大学物理中的刚体力学。
一、刚体概念及特性刚体是指物体内部各质点之间没有相对位移,形状和体积不发生变化的理想化物体。
在刚体力学中,我们通常将刚体视为一个整体,研究其宏观运动规律。
刚体力学_习题三,华工大物上习题,资料参考答案,华南理工

姓名 班级 序号刚体力学1.半径为 1.5m r =的飞轮,初角速度0=10rad/s ω,角加速度25rad/s α=-,若初始时刻角位移为零,则在何时角位移再次为零,而此时边缘上点的线速度为多少? 2.一质量为m 的物体悬于一条轻绳的一端,绳另一端绕在一轮轴的轴上,如图所示.轴水平且垂直于轮轴面,其半径为r ,整个装置架在光滑的固定轴承之上.当物体从静止释放后,在时间t 内下降了一段距离S .试求整个轮轴的转动惯量(用m 、r 、t 和S 表示)。
3. 如图所示,物体1和2的质量分别为m 1与m 2,滑轮的转动惯量为J ,半径为r , 物体2与桌面间的摩擦系数为μ,设绳子与滑轮间无相对滑动,滑轮与转轴无摩擦。
求系统的加速度a 及绳中的张力T 1和T 2。
4.一个转动惯量为J 的圆盘绕一固定轴转动,初角速度为0ω。
设它所受阻力矩与转动角速度成正比M k ω=- (k 为正常数)。
求(1)它的角速度从0ω变为0/2ω所需时间;(2)在上述过程中阻力矩所做的功。
5.如图所示,滑轮的转动惯量J =0.5kg ⋅m 2,半径r =30cm ,弹簧的劲度系数k =2.0N/m ,重物的质量m =2.0kg 。
当此滑轮——重物系统从静止开始启动,开始时弹簧没有伸长。
滑轮与绳子间无相对滑动,其它部分摩擦忽略不计。
问物体能沿斜面下滑多远?当物体沿斜面下滑1.00m 时,它的速率有多大?6.一长为1 m 的均匀直棒可绕过其一端且与棒垂直的水平光滑固定轴转动.抬起另一端使棒向上与水平面成60°,然后无初转速地将棒释放.已知棒对轴的转动惯量为231ml,其中m 和l 分别为棒的质量和长度.求:(1) 放手时棒的角加速度; (2) 棒转到水平位置时的角速度.7.一根长为l 、质量为M 的匀质棒自由悬挂于通过其上端的光滑水平轴上。
现有一质量为m 的子弹以水平速度v0射向棒的中心,并以v0/2的水平速度穿出棒,此后棒的最大偏转角恰为90︒,求v0的大小。
华南理工大学大学物理习题试卷、习题册详细答案(下册)

3.答案:(1) ;(2) 。
4.答案:(1) , 线的方向为逆时针方向;(2) , 的方向指向轴心。
5.答案:(1) ;(2) 。
习题七
一、选择题
1.B;2.D;3.B;4.B;5.A。
二、填空题
1.答案: ; 。
2.答案: ; ; ; 。
3.答案: 。
4.答案: 。
5.答案:0.91c; 。
3.答案:(1)5个, ;(2)9个, ;(3)5;(4)18。
4.答案:10; ; 。
5.答案:
三、计算题
1.答案:(1) ;
(2) ;
(3)能级跃迁图如图所示。
2.答案:(1) , ;
(2) 。
3.答案:(1)0.19;(2)0.40。
4.答案:(1) ;
(2)在 (即 )处概率最小,其值均为零。
3.答案: 。
4.答案: ;方向沿轴向上。
习题四
一、选择题
1.D;2.B;3.A;4.A。
二、填空题
1.答案: ;M = 0。
2.答案:(1) ;(2) 。
3.答案:(1)霍尔;(2) 。
4.答案: ; 。
5.答案: 。
三、计算题
1.答案: ,方向:垂直于ab向上。
2.答案:(1) ;
(2)线圈法线与 成 或 角时。
3.答案:(1) ,方向水平向左;(2) ;
(3) ,方向水平向右。
4.答案: 。
5.答案: 。
习题六
一、选择题
1.C;2.B;3.B;4.D;5.A。
二、填空题
1.答案:方向;常;变。
2.答案:a;b;c;c;b;a。
3.答案: 。
华南理工大学大学物理各章节习题及答案汇编
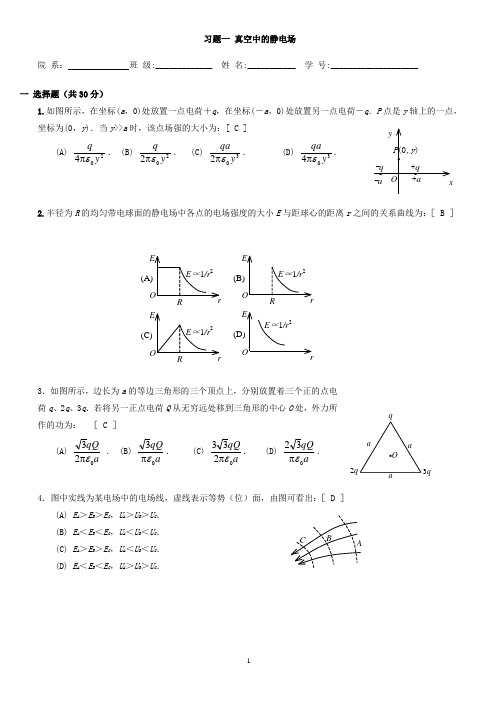
习题一 真空中的静电场院 系: 班 级:_____________ 姓 名:___________ 学 号:____________________一 选择题(共30分)1.如图所示,在坐标(a ,0)处放置一点电荷+q ,在坐标(-a ,0)处放置另一点电荷-q .P 点是y 轴上的一点,坐标为(0,y ).当y >>a 时,该点场强的大小为:[ C ] (A)204y q επ. (B)202y q επ. (C)302y qa επ. (D) 304yqa επ.2.半径为R 的均匀带电球面的静电场中各点的电场强度的大小E 与距球心的距离r 之间的关系曲线为:[ B ]3.如图所示,边长为a 的等边三角形的三个顶点上,分别放置着三个正的点电荷q 、2q 、3q .若将另一正点电荷Q 从无穷远处移到三角形的中心O 处,外力所作的功为: [ C ](A) a qQ 023επ . (B) a qQ 03επ. (C) a qQ 0233επ. (D) aqQ 032επ.4.图中实线为某电场中的电场线,虚线表示等势(位)面,由图可看出:[ D ] (A) E A >E B >E C ,U A >U B >U C . (B) E A <E B <E C ,U A <U B <U C . (C) E A >E B >E C ,U A <U B <U C . (D) E A <E B <E C ,U A >U B >U C .E Or(D) E ∝1/r 23q2q5.半径为R 的“无限长”均匀带电圆柱面的静电场中各点的电场强度的大小E 与距轴线的距离r 的关系曲线为: [ B ]6.在边长为a 的正方体中心处放置一电荷为Q 的点电荷,则正方体顶角处的电场强度的大小为: (A)2012a Q επ. (B) 206a Q επ. (C) 203a Q επ. (D) 20aQεπ. [C ]7.图示为一具有球对称性分布的静电场的E ~r 关系曲线.请指出该静电场是由下列哪种带电体产生的. (A) 半径为R 的均匀带电球面. [ B ](B) 半径为R 的均匀带电球体.(C) 半径为R 的、电荷体密度为=A r (A 为常数)的非均匀带电球体. (D) 半径为R 的、电荷体密度为=A/r (A 为常数)的非均匀带电球体.8.选无穷远处为电势零点,半径为R 的导体球带电后,其电势为U 0,则球外离球心距离为r 处的电场强度的大小为(A) 302r U R . (B) R U 0. (C) 20r RU . (D) r U 0. [ C ]9. 设有一“无限大”均匀带正电荷的平面.取x 轴垂直带电平面,坐标原点在带电平面上,则其周围空间各点的电场强度E随距平面的位置坐标x 变化的关系曲线为(规定场强方向沿x 轴正向为正、反之为负):[C ]10. 一个静止的氢离子(H +)在电场中被加速而获得的速率为一静止的氧离子(O +2)在同一电场中且通过相同的路径被加速所获速率的:(A) 2倍. (B) 22倍. (C) 4倍. (D) 42倍. [ B ]E O rE ∝1/rE Or(D) E ∝1/rR E Or(C) E ∝1/rE Or(A) E ∝1/rO R rE E ∝1/r 2OxE (A)OxE (C)OxE (B)OxE (D)E ∝1/|x|E ∝x11.如图所示,一个电荷为q 的点电荷位于立方体的A 角上,则通过侧面abcd的电场强度通量等于:(A) 06εq . (B) 012εq . (C) 024εq . (D) 048εq. [ C ]二 填空题1.电荷分别为q 1,q 2,q 3的三个点电荷分别位于同一圆周的三个点上,如图所示.设无穷远处为电势零点,圆半径为R ,则b 点处的电势U =___________ . ()32102281q q q R++πε2.图中所示以O 为心的各圆弧为静电场的等势(位)线图,已知U 1<U 2<U 3,在图上画出a 、b 两点的电场强度的方向,并比较它们的大小.E a = E b (填<、=、>).3.两根相互平行的“无限长”均匀带正电直线1、2,相距为d ,其电荷线密度分别为λ1和λ2如图所示,则场强等于零的点与直线1的距离a 为_____________ .d 211λλλ+4.如图所示,两同心带电球面,内球面半径为r 1=5 cm ,带电荷q 1=3×10-8C ;外球面半径为r 2=20 cm , 带电荷q 2=-6×108C ,设无穷远处电势为零,则空间另一电势为零的球面半径r = __________________.10 cm5.已知某静电场的电势函数U =a ( x 2+ y ),式中a 为一常量,则电场中任意点的电场强度分量E x =-2ax ,E y = -a ,E z = 0.6.如图所示.试验电荷q ,在点电荷+Q 产生的电场中,沿半径为R 的整个圆弧的3/4圆弧轨道由a 点移到d 点的过程中电场力作功为 0 ;从d 点移到无穷远处的过程中,电场力作功为qQ / (4πε0R ).7.一个带电荷q 、半径为R 的金属球壳,壳内是真空,壳外是介电常量为ε 的无限大各向同性均匀电介质,则此球壳的电势U =________________.Rqεπ48.在点电荷q 的电场中,把一个-1.0×10-9C 的电荷,从无限远处(设无限远处电势为零)移到离该点电荷距离 0.1 m 处,克服电场力作功 1.8×10-5 J ,则该点电荷q =-2×10-7库伦.(真空介电常量0=8.85×10-12C 2·N -1·m -2)A b caq2 q 1 q 3OOU 1U 2U 3abλ2a d 12q 1 q 2 r 1r 2+Q R q d∞三 计算题1.厚度为d 的“无限大”均匀带电导体板两表面单位面积上电荷之和为σ.试求图示离左板面距离为a 的一点与离右板面距离为b 的一点之间的电势差.解:选坐标如图.由高斯定理,平板内、外的场强分布为:E = 0 (板内) )2/(0εσ±=x E (板外)1、2两点间电势差⎰=-2121d x E U U x x x d b d d d a d 2d 22/2/02/)2/(0⎰⎰+-+-+-=εσεσ )(20a b -=εσ 2.一环形薄片由细绳悬吊着,环的外半径为R ,内半径为R /2,并有电荷Q 均匀分布在环面上.细绳长3R ,也有电荷Q 均匀分布在绳上,如图所示,试求圆环中心O 处的电场强度(圆环中心在细绳延长线上).解:先计算细绳上的电荷在O 点产生的场强.选细绳顶端作坐标原点O ,x 轴向下为正.在x 处取一电荷元 d q = d x = Q d x /(3R ) 它在环心处的场强为 ()20144d d x R qE -π=ε ()20412d x R R xQ -π=ε 整个细绳上的电荷在环心处的场强()203020116412RQx R dx R Q E R εεπ=-π=⎰ 圆环上的电荷分布对环心对称,它在环心处的场强E 2=0由此,合场强 i R Qi E E20116επ== 方向竖直向下.3.电荷Q (Q >0)均匀分布在长为L 的细棒上,在细棒的延长线上距细棒中心O 距离为a 的P 点处放一电荷为q (q >0 )的点电荷,求带电细棒对该点电荷的静电力. 解:沿棒方向取坐标Ox ,原点O 在棒中心处.求P 点场强: ()()20204d 4d d x a xx a q E -π=-π=ελε 3分 ()⎰--π=2/2/204d L L x a xE ελ()2202/2/0414L a Qx a L L -π=-⋅π=-εελ 4分 方向沿x 轴正向. 点电荷受力:==qE F ()2204πL a qQ-ε 方向沿x 轴正方向. 3分1σda1σd abxOO R 3RR /2E 1xR3R x xOPL+Q OaP O L/2L/2d x d q a。
大学物理练习册习题及答案4

习题及参考答案第3章 刚体力学参考答案思考题3-1刚体角动量守恒的充分而必要的条件是 (A )刚体不受外力矩的作用。
(B )刚体所受合外力矩为零。
(C)刚体所受的合外力和合外力矩均为零。
(D)刚体的转动惯量和角速度均保持不变。
答:(B )。
3-2如图所示,A 、B 为两个相同的绕着轻 绳的定滑轮。
A 滑轮挂一质量为M 的物体, B 滑轮受拉力F ,而且F =Mg 。
设A 、B 两 滑轮的角加速度分别为βA 和βB ,不计滑轮 轴的摩擦,则有(A )βA = βB (B )βA > βB(C )βA < βB (D )开始时βA = βB ,以后βA < βB 答:(C )。
3-3关于刚体对轴的转动惯量,下列说法中正确的是(A )只取决于刚体的质量,与质量的空间分布和轴的位置无关。
(B)取决于刚体的质量和质量的空间分布,与轴的位置无关。
(C )取决于刚体的质量、质量的空间分布和轴的位置。
(D)只取决于转轴的位置,与刚体的质量和质量的空间分布无 答:(C )。
3-4一水平圆盘可绕通过其中心的固定铅直轴转动,盘上站着一个人,初始时整个系统处于静止状态,当此人在盘上随意走动时,若忽略轴的摩擦,则此系统(A)动量守恒; (B)机械能守恒; (C)对转轴的角动量守恒;(D)动量、机械能和角动量都守恒; (E)动量、机械能和角动量都不守恒。
答:(C )。
3-5光滑的水平桌面上,有一长为2L 、质量为m 的匀质细杆,可绕过其中点o 且垂直于杆的竖直光滑固定轴自由转动,其转动惯量为213mL,起初杆静止,桌面上有两个质量均为m 的小球,各自在 垂直于杆的方向上,正对着杆的一端,以相同速率v 相向 运动,如图所示,当两小球同时与杆的两个端点发生完全非弹性碰撞后,就与杆粘在一起转动,则这一系统碰撞后的转动角速度应为AMF思考题3-2图v思考题3-5图(A)23L v (B)45L v (C)67L v (D)89L v (E)127L v答:(C )。
大学物理刚体力学测试题答案

选择题答案及解析
• 答案:D
• 解析:根据刚体的转动惯量公式,对于一个质量均匀分布的细杆,其转动惯量与质量、长度和质心到转轴的距离有关。故 D选项正确。
选择题答案及解析
• 答案:A • 解析:根据刚体的动能定理,当刚
体受到的合外力矩不为零时,刚体 的角速度会发生变化。故A选项正 确。
填空题答案及解析
有挑战性
部分题目难度较大,需要学生具备较强的分 析问题和解决问题的能力。
测试题答案解析总结
要点一
详细解析
每道题目都附有详细的答案解析,帮助学生理解解题思路 和方法。
要点二
举一反三
答案解析中还提供了相关题型的解题技巧,有助于学生触 类旁通。
THANKS
感谢观看
难题
考查学生的综合运用能力和创新思维,难度较大,需要较高的解题技巧。
测试题目的目标
01
检验学生对刚体力学基本概念和公式的掌握程度。
02
评估学生对刚体力学知识的应用能力。
提高学生的综合运用能力和创新思维。
03
02
测试题内容选Leabharlann 题选择题1答案:C1
选择题2答案:B
2
选择题3答案:D
3
填空题
填空题1答案
• 答案
10 N·m
• 解析
根据刚体的转动动能公式,当刚体的转动惯量为1 kg·m²,角速度为10 rad/s时,其转 动动能为0.5×1×10²=50 J。由于题目中要求的是力矩,因此需要将动能转换为力矩,
即50 J=10 N·m。故填空题1的答案是10 N·m。
填空题答案及解析
• 答案
2 kg·m²
04
测试题总结
测试题特点总结
华理工大学大学物理习题之 刚体力学习题详解

习题三一、选择题1.一根长为l 、质量为M 的匀质棒自由悬挂于通过其上端的光滑水平轴上。
现有一质量为m 的子弹以水平速度v 0射向棒的中心,并以v 0/2的水平速度穿出棒,此后棒的最大偏转角恰为90︒,则v 0的大小为 [ ](A; (B; (C(D )22163M glm 。
答案:A 解:11122,1122J J J J Mg l ωωωω=+⎧⎪⎨=⋅⎪⎩ 22211, 243l m l J m J M l ⎛⎫=== ⎪⎝⎭ 0012/2v v l l ω==,0021/21/22v v l l ωω===,111121()2J J J J ωωωω-== 21122J Mgl ω=, 2112J J Mgl J ω⎛⎫⋅= ⎪⎝⎭, 22114J Mgl Jω= 22202244143v ml l Mgl Ml ⎛⎫ ⎪⎝⎭=⋅,Mgl M v m =⋅202163,2202163M v gl m =,所以 340gl m Mv =2.圆柱体以80rad/s 的角速度绕其轴线转动,它对该轴的转动惯量为24kg m ⋅。
在恒力矩作用下,10s 内其角速度降为40rad/s 。
圆柱体损失的动能和所受力矩的大小为 [ ](A )80J ,80N m ⋅; (B )800J ,40N m ⋅;(C )4000J ,32N m ⋅;(D )9600J ,16N m ⋅。
答案:D解:800=ω,40=ω,10=t ,4J =2201122k E J J ωω-∆=- 22011()4(64001600)9600(J)22k E J ωω∆=-=⨯⨯-=M 恒定,匀变速,所以有0t ωωα=-,0tωωα-=,08040416N m 10M J J tωωα--==⋅=⨯=⋅3.一个转动惯量为J 的圆盘绕一固定轴转动,初角速度为0ω。
设它所受阻力矩与转动角速度成正比M k ω=- (k 为正常数)。
大学物理刚体习题

7 ml 48
2
(2)
6 g sin 由(1)、(2)得: 2 7l 应用质心运动定理: N mg ma c l$方向: mg sin Nl macl t$方向: mg cos Nt mact
(3) (4)
上页 下页 返回 退出
l 2 6 g sin a cl (5) 4 7 l l l 4 mg cos 3 g cos a (6) ct 4 4 J 7 o 13 N mg sin , 由 (3)(4)(5)(6) 可解得: l 7
(2)角动量定理
与同向
dL d ( J ) M 或 Mdt J 2 2 J 1 1 dt dt
当刚体(系统)所受外力矩为零时,则刚体(系统) 对此轴的总角动量为恒量。
(3)角动量守恒定律
M 0
J i i
恒量
上页 下页 返回 退出
例题 1 一轻绳跨过一定滑轮,滑轮视为圆盘,绳的两端 分别悬有质量为m1和m2的物体1和2,m1< m2 如图所示 。设滑轮的质量为 m , 半径为 r , 所受的摩擦阻力矩为 M 。绳与滑轮之间无相对滑动。试求物体的加速度和绳 的张力。
解:滑轮具有一定的转动惯 量。在转动中受到阻力矩 的作用,两边的张力不再 相等,设物体1这边绳的张 力为T1、 T1’(T1’= T1) ,
M
碰撞过程角动量守恒,得:
3 mv 4 L = ( Jm+ JM )ω 2 1 3 2 JM = 3 M L Jm = m ( 4 L )
3L 4 M θ m L
ω
3 mv L 3 mv 4 =9 4 2 1 = 2 9 mL 1 M L m L M L +3 +3 16 16
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
姓名 班级 序号
刚体力学
1.半径为 1.5m r =的飞轮,初角速度0=10rad/s ω,角加速度25rad/s α=-,若初始时刻角坐标为零,则在何时角坐标再次为零,而此时边缘上点的线速度为多少?
2.一质量为m 的物体悬于一条轻绳的一端,绳另一端绕在一轮轴的轴上,如图所示.轴水平且垂直于轮轴面,其半径为r ,整个装置架在光滑的固定轴承之上.当物体从静止释放后,在时间t 内下降了一段距离S .试求整个轮轴的转动惯量(用m 、r 、t 和S 表示)。
3. 如图所示,物体1和2的质量分别为m 1与m 2,滑轮的转动惯量为J ,半径为r , 物体2与桌面间的摩擦系数为μ,设绳子与滑轮间无相对滑动,滑轮与转轴
无摩擦。
求系统的加速度a 及绳中的张力T 1和T 2。
4.一个转动惯量为J 的圆盘绕一固定轴转动,初角速度为0ω。
设它所受阻力矩与转动角速
度成正比M k ω=- (k 为正常数)。
求
(1)它的角速度从0ω变为0/2ω所需时间;(2)在上述过程中阻力矩所做的功。
5.如图所示,滑轮的转动惯量J =0.5kg ⋅m 2,半径r =30cm ,弹簧的劲度系数k =2.0N/m ,重物的质量m =2.0kg 。
当此滑轮——重物系统从静止开始启动,
开始时弹簧没有伸长。
滑轮与绳子间无相对滑动,其它部分摩
擦忽略不计。
问物体能沿斜面下滑多远?当物体沿斜面下滑1.00m 时,它的速率有多大?
6.一长为1 m 的均匀直棒可绕过其一端且与棒垂直的水平光滑固定轴转动.抬起另一端使棒向上与水平面成60°,然后无初转速地将棒释放.已知棒对轴的转动惯量为231ml ,其中m 和l 分别为棒的质量和长度.求:
(1) 放手时棒的角加速度; (2) 棒转到水平位置时的角速度.
7.一根长为l 、质量为M 的匀质棒自由悬挂于通过其上端的光滑水平轴上。
现有一质量为m 的子弹以水平速度v 0射向棒的中心,并以v 0/2的水平速度穿出棒,
此后棒的最大偏转角恰为90︒,求v 0的大小。
8. 在自由旋转的水平圆盘上,站一质量为m 的人。
圆盘半径为R ,转动惯量为J ,角速度为ω。
如果这人由盘边走到盘心,则角速度的变化 ∆ω 和系统动能的变化∆E k 各为多少?
9. 一根质量为 m 、长度为 L 的匀质细直棒,平放在水平桌面上。
若它与桌面间的滑动摩擦系数为μ,在0t =时,使该棒绕过其一端的竖直轴在水平
桌面上旋转,其初始角速度为ω0,求棒停止转动所需时间。
10、如图,框架AA 可绕铅直轴OO 自由转动,转动惯量为J 1。
在框架中间支承一个转子B ,其对OO 轴的转动惯量为J 2,开始时框架不动,转子有一角速度ω0,由于支承处有摩擦,于是框架也被带着转动起来,若经过时间t 以后,转子相对于框架的角速度变为零,求支承处的摩擦力矩(设为常量)。
m m M 0v 0/2v l。
