一线三等角模型、双垂直模型(自己总结)
初中几何 一线三等角模型
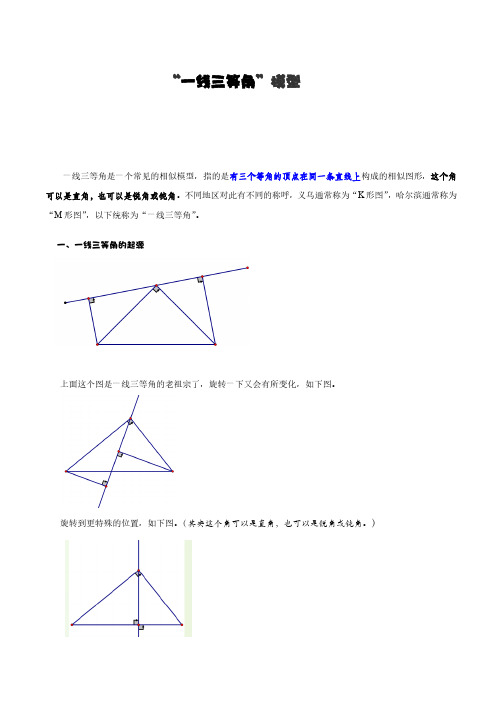
一、一线三等角的起源上面这个图是一线三等角的老祖宗了,旋转一下又会有所变化,如下图。
旋转到更特殊的位置,如下图。
(其实这个角可以是直角,也可以是锐角或钝角。
)“一线三等角”模型一线三等角是一个常见的相似模型,指的是有三个等角的顶点在同一条直线上构成的相似图形,这个角可以是直角,也可以是锐角或钝角。
不同地区对此有不同的称呼,义乌通常称为“K 形图”,哈尔滨通常称为“M 形图”,以下统称为“一线三等角”。
二、一线三等角的两种基本类型1.三等角都在直线的同侧2.三等角分居直线的两侧l三、一线三等角的性质1.一般情况下,由∠1=∠2=∠3,易得△AEC∽△BDE. 2.当等角所对的边相等时,两个三角形全等。
如图,当CE=ED时,易得△AEC≌△BDE.3.“中点型一线三等角”的特殊性质如图,当∠1=∠2=∠3且D 是BC 的中点时,△BDE ∽△CFD ∽△DFE .如图,加画两条垂线......,“一线三等角”就与“四边形中的半角模型”联系在一起了。
半角模型:EF =EM +FN . 4.“中点型一线三等角”的变式 如图,当∠1=∠2且∠AOC =90°+21∠BAC 时,点O 是△ABC 的内心.易证∠4=∠5=∠6,以下就省略了。
四、一线三等角的常用构图下面以等腰三角形为例说明一线三等角的常见构图。
由于角顶点位置的改变,或角绕顶点旋转会产生各种各样的变式,但万变不离其宗:构造相似三角形列比例式解决问题。
当然,特殊情况下也可能是全等。
五、一线三等角的应用1.一线三等角应用的三个层次⑴初级阶段:图形中已经存在“一线三等角”,直接应用模型解题;⑵中级阶段:图形中存在“一线二等角”,补上“一等角”构造此模型;⑶高级阶段:图形中只有直线上的一个角,补上“二等角”构造此模型。
2.在张角问题中,构造“一线三等角”是基本手段之一。
对坐标系中的张角问题,在x轴或y轴(也可以是平行于x轴或y轴的直线)上构造“一线三等角”是解决问题的关键。
(完整版)一线三等角模型、双垂直模型(自己总结)

t i me an dAl l t h i ng si n如图,AB=12米,CA ⊥AB 于点A ,DB ⊥AB 于点B ,且AC=4米,点P 从B 向A 运动,每分钟走1米,点Q 从B 点向D 运动,每分钟走2米,P 、Q 两点同时出发,运动几分钟后,△CPA 与△PQB 全等?如图①所示,在△ABC 中,∠C=90°,AC=BC ,过点C 在△ABC 外作直线MN ,AM ⊥MN于点M ,BN ⊥MN 于点N .(1)求证:MN=AM +BN .(2)如图②.若过点C 直线MN 与线段AB 相交,AM ⊥MN 于点M ,BN ⊥MN 于N ,(1)中的结论是否仍然成立?说明理由.图① 图②me an dAh i ng si nt he i rb ei n ga re go 如图,已知∠B=∠C=90°,M 是BC 的中点,DM 平分∠ADC.(1)求证:AM 平分∠DAB(2)试说明线段DM 与AM 有怎样的位置关系?(3)线段CD 、AB 、AD 间有怎样的关系?直接写出结果。
如图,△ABE ≌△EDC ,E 在BD 上,AB ⊥BD ,垂足为B ,△AEC 是等腰直角三角形吗?为什么?man d【练3】正方形ABCD,E 是BC 上一点,AE EF,交∠DCH 的平分线于点F ,求证AE=EF⊥如图所示,在中,,点D 在边AB 上,使,过点D 作,分ABC Rt ∆ 90=∠ABC AC EF ⊥别交AC 于点E ,CB 的延长线于点F 。
求证:AB=BF 。
(8分)如图(1),已知AB ⊥BD ,ED ⊥BD ,AB=CD ,BC=DE ,(1)试判断AC 与CE 的位置关系,并说明理由.(2)若将CD 沿CB 方向平移得到图②③④⑤的情形,其余条件不变,此时第(1)问中ACan dAl l t g sgo od fo r与CE 的位置关系还成立吗?结论还成立吗?请任选一个说明理由.如图,在△ABC 中,AB=AC ,DE 是过点A 的直线,BD ⊥DE 于D ,CE ⊥DE 于点E ;(2)若B. C 在DE 的两侧(如图所示),其他条件不变,AB 与AC 仍垂直吗?若是请给出证明;若不是,请说明理由。
一线三等角模型、双垂直模型[自己总结]课件.doc
![一线三等角模型、双垂直模型[自己总结]课件.doc](https://img.taocdn.com/s3/m/88448e3590c69ec3d4bb752c.png)
如图所示,在RtABC中,ABC90,点D在边AB上,使,过点D作EFAC,分别
交AC于点E,CB的延长线于点F。求证:AB=BF。(8分)
如图(1),已知AB⊥BD,ED⊥BD,AB=CD,BC=DE,
(1)试判断AC与CE的位置关系,并说明理由.
(2)若将CD沿CB方向平移得到图②③④⑤的情形,其余条件不变,此时第(1)问中AC与
CE的位置关系还成立吗?结论还成立吗?请任选一个说明理由.
如图,在△ABC中,AB=AC,DE是过点A的直线,BD⊥DE于D,CE⊥DE于点E;
.专业知识编辑整理.
(2)试说明线段DM与AM有怎样的位置关系?
(3)线段CD、AB、AD间有怎样的关系?直接写出结果。
如图,△ABE≌△EDC,E在BD上,AB⊥BD,垂足为B,△AEC是等腰直角三角形吗?
为什么?
【练3】正方形ABCD,E是BC上一点,AEEF,交∠DCH的平分线于点F,求证AE=EF
.专业知识编辑整理.
N于点M,BN⊥MN于点N.
(1)求证:MN=AM+BN.
(2)如图②.若过点C直线MN与线段AB相交,AM⊥MN于点M,BN⊥MN于N,(1)中的
结论是否仍然成立?说明理由.
图①格式.
如图,已知∠B=∠C=90°,M是BC的中点,DM平分∠ADC.
(1)求证:AM平分∠DAB
.WORD完美格式.
如图,AB=12米,CA⊥AB于点A,DB⊥AB于点B,且AC=4米,点P从B向A运动,
每分钟走1米,点Q从B点向D运动,每分钟走2米,P、Q两点同时出发,运动几分钟
后,△CPA与△PQB全等?
如图①所示,在△ABC中,∠C=90°,AC=BC,过点C在△ABC外作直线MN,AM⊥M
最全相似模型专题(中考数学必考)

几何模型09——相似模型三角形相似是每一年中考必考的知识点,相似模型主要包括:“A”型和“X”型相似,母子模型相似(共边共角型),一线三等角,双垂直模型和旋转相似,中考命题者经常把这些模型放在圆,四边形,或函数图象当中,特别要留意母子模型相似的一种特殊情况:射影定理中的知二求四和一线三垂直(k型相似),下面对这些类型做如下总结:一、“A”型和“X”型相似例1.如图,在△ABC中,点D是AC上的点,且AD=2CD,过D作DE∥BC交AB于E,过D作DF∥AB交BC于F.(1)若BC=15,求线段DE的长.(2)若△ADE的面积为16,求△CDF的面积.变式1.如图,在△ABC中,点D,E,F分别在AB,BC,AC边上,DE∥AC,EF∥AB.(1)求证:△BDE∽△EFC.(2)设,①若BC=12,求线段BE的长;②若△EFC的面积是20,求△ABC的面积.变式2.如图,Rt△ABC中,∠C=90°,AB=14,AC=7,D是BC上一点,BD=8,DE⊥AB,垂足为E,求线段DE的长.变式3.如图,AB为半圆O的直径,C为BA延长线上一点,CD切半圆O于点D,连接OD.作BE⊥CD于点E,交半圆O于点F.已知CE=12,BE=9.(1)求证:△COD∽△CBE.(2)求半圆O的半径r的长.变式4.如图,AG是∠HAF的平分线,点E在AF上,以AE为直径的⊙O交AG于点D,过点D作AH的垂线,垂足为点C,交AF于点B.(1)求证:直线BC是⊙O的切线;(2)若AC=2CD,设⊙O的半径为r,求BD的长度.变式5.如图,在矩形ABCD中,AB=6,BC=8,沿直线MN对折,使A、C重合,直线MN 交AC于O.(1)求证:△COM∽△CBA;(2)求线段OM的长度.变式6.如图,已知AB为⊙O的直径,F为⊙O上一点,AC平分∠BAF且交⊙O于点C,过点C作CD⊥AF于点D,延长AB、DC交于点E,连接BC、CF.(1)求证:CD是⊙O的切线;(2)若AD=6,DE=8,求BE的长;变式7.如图,在△ABC中,∠C=90°,点O在CB上,⊙O经过点C,且与AB相切于点D,与CB的另一个交点为E.(1)求证:DE∥OA;(2)若AB=10,tan∠DEO=2,求⊙O的半径.例2.如图,在Rt△ABC中,∠A=90°,AC=9,BC=15.(1)求BC边上的高AD的长度;(2)正方形的一边FG在BC上,另两个顶点E、H分别在边AB、AC上,求正方形EFGH 的边长.(相似比等于高之比)例3.如图,⊙O的半径为5,点P在⊙O外,PB交⊙O于A、B两点,PC交⊙O于D、C 两点.求证:PA•PB=PD•PC(割线定理);变式1.如图,在△ABC中,AB=AC,以AC为直径的⊙O交AB于点D,交BC于点E.(1)求证:BE=CE;(2)若BD=2,BE=3,求AC的长.变式2.如图,以△ABC 的边BC 为直径的⊙O 分别交AB ,AC 于点D ,E ,且点E 是的中点,连接DE .(1)求证:△ABC 是等腰三角形.(2)若BC =10,CE =6,求线段AD 的长.变式3.如图,在△ABC 中,AB =AC ,以AB 为直径的半圆O 分别交BC ,AC 于点D ,E ,连结EB ,OD ,DE .(1)求证:OD ⊥EB .(2)若DE =,AB =10,求AE 的长.例4.如图,在△ABC 中,D ,E 分别是边AC ,AB 的中点,BD 与CE 交于点O ,连接DE . 求证:2OE CO OD BO ==变式1.如图,AB 、CD 相交于点O ,连接AC 、BD ,点E 、F 分别为AC 、BD 的中点,连接OE 、OF ,若∠A =∠D ,OA =OF =6,OD =9,求OE 的长.变式2.如图,已知圆O,弦AB、CD相交于点M.(1)求证:AM•MB=CM•MD;(相交弦定理)(2)若M为CD中点,且圆O的半径为3,OM=2,求AM•MB的值.变式3.如图,在⊙O中,弦AB、CD相交于点P,且PD<PC.(1)求证:△P AD∽△PCB;(2)若P A=3,PB=8,CD=10,求PD.例5.如图,过△ABC的边AC的中点D作直线交AB于E,交BC的延长线于F.求证:=;(梅捏劳斯定理特殊情况)变式1.如图,已知△ABC的边AB上有一点D,边BC的延长线上有一点E,且AD=CE.DE 交AC于点F,试证明:AB•DF=BC•EF.变式2.如图,△ABC中,D为BC的中点,过D的直线交AC于E,交AB的延长线于F.求证:=.变式3.如图,△ABC中,D是BC边的中点,过点D的直线交AB于点E,交AC的延长线于点F,且BE=CF.求证:AE=AF.二、共边共角型相似例1.如图,在△ABC中,D为BC边上的一点,且∠CAD=∠B.(1)求证:;(2)若AC=2,BC=4,设△ADC面积为S1,△ABD面积为S2,求证:S2=3S1.变式1.如图,在△ABC中,D为边AB上一点,∠ACD=∠B,若AC=6,BC=5,CD=4,求AD,AB的长.变式2.如图,已知正方形ABCD中,BE平分∠DBC且交CD边于点E,将△BCE绕点C顺时针旋转到△DCF的位置,并延长BE交DF于点G.(1)求证:△BDG∽△DEG;(2)若EG•BG=4,求BE的长.变式3.如图,在Rt△ABC中,∠C=90°,以AB上一点O为圆心,OA的长为半径作⊙O,交AC、AB分别于D,E两点,连接BD,且∠A=∠CBD.若CD=1,BC=2,求AD 的长度.例2.如图,在菱形ABCD中,G是BD上一点,连接CG并延长交BA的延长线于点F,交AD于点E.(1)求证:AG=CG.(2)求证:AG2=GE•GF.变式1.如图,点P是菱形ABCD的对角线BD上一点,连接CP并延长,交AD于点E,交BA的延长线于点F.(1)求证:PC2=PE•PF;(2)若菱形边长为8,PE=2,EF=6,求FB的长.例3.如图,CD是⊙O的切线,点C在直径AB的延长线上.(切割线模型)(1)求证:∠CAD=∠BDC;(2)若BD=AD,AC=3,求CD的长.变式1.如图,O为线段PB上一点,以O为圆心,OB长为半径的⊙O交PB于点A,点C 在⊙O上,连接PC,满足PC2=P A•PB.若AB=3P A,求的值.例4.如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于D.(1)(射影定理)求证:AC2=AD•AB;BC2=BD•BA;CD2=AD•BD;(2)若AD=2,DB=8,求AC,BC,CD的长;(知二求四)(3)若AC=6,DB=9,求AD,CD,BC的长;(知二求四)(4)求证:AC•BC=AB•CD.(等面积法)变式1.如图,AB是⊙O的直径,点C是圆上一点,连接AC和BC,过点C作CD⊥AB于点D.若CD=4,BD=3,求⊙O的半径长.(直径所对的圆周角为直角)变式2.如图,在Rt△ABC中,∠BAC=90°,∠BAD=∠C,点D在BC边上,以AD为直径的⊙O交AB于点E,交AC于点F.已知:AB=6,AC=8,求AF的长.变式3.在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O交AB于点D,点E是边BC的中点,连结DE.(1)求证:DE是⊙O的切线;(2)若AD=4,BD=9,求⊙O的半径.例4.如图,以△ABC的一边AB为直径作⊙O,⊙O与BC边的交点恰好为BC的中点D,过点D作⊙O的切线交AC于点E.(1)求证:DE⊥AC;(2)若AB=3DE,求tan∠ACB的值.(射影定理知二求四)(3)若AB=5CE,求tan∠ACB的值.(射影定理知二求四)变式1.如图,四边形ABCD内接于⊙O,对角线AC为⊙O的直径,过点C作AC的垂线交AD的延长线于点E,点F为CE的中点,连接DB,DC,DF.(1)求证:DF是⊙O的切线;(2)若AC=2DE,求tan∠ABD的值.三、双垂直例1.如图,在矩形ABCD中,点E在边BC上,AF⊥DE,垂足为F,AD=4,CE=2,DE =2,求DF的长.变式1.如图,点P是正方形ABCD边AD上一点,Q是边BC延长线上一点,若AB=12,P A=5,PQ⊥BP.求CQ的长.变式2.如图,△ABC中,BD、CE分别是AC、AB边上的高,若AE=5,AD=6,CD=2.求EB的长.变式3.如图,在Rt△ABC中,∠ABC=90°,E是边AC上一点,且BE=BC,过点A作BE的垂线,交BE的延长线于点D,求证:△ADE∽△ABC.四、一线三等角例1.已知:如图,△ABC中,∠BAC=90°,AB=AC=1,点D是BC边上的一个动点(不与B,C点重合),∠ADE=45°.(1)求证:△ABD∽△DCE;(2)设BD=x,AE=y,求y关于x的函数关系式;例2.如图,E是正方形ABCD的边AB上的点,过点E作EF⊥DE交BC于点F.(1)求证:△ADE∽△BEF;(2)若AB=6,AE=2,求线段CF的长.变式1.如图,将一个直角的顶点P放在矩形ABCD的对角线BD上滑动,并使其一条直角边始终经过点A,另一条直角边与边BC相交于点E.且AD=8,DC=6,则=.五、旋转相似例1.如图,在锐角三角形ABC中,点D,E分别在边AC,AB上,AG⊥BC于点G,AF⊥DE于点F,∠EAF=∠GAC.(1)求证:△ADE∽△ABC;(2)若AD=3,AB=5,求的值.变式1.如图,△ABC和△CEF中,AB=BC,CF=EF,∠CBA=∠CFE=90°,E在△ABC 内,∠CAE+∠CBE=90°,连接BF.(1)求证:△CAE∽△CBF;(2)若BE=1,AE=2,求EF的长.。
完整版几何模型一线三等角模型

一线三等角模型一 . 一线三等角看法“一线三等角” 是一个常有的相似模型, 指的是有 三个等角的极点在同一条直线上构成的相似图形, 这个角能够是直角, 也能够是锐角或钝角。
不同样地区对此有不同样的称呼, “K 形图”,“三垂直”,“弦图”等,以下称为“一线三等角” 。
二 . 一线三等角的分类全等篇CDDCAPBAPB锐角直角DDDCAPB同侧钝角DAABPPBABPCC相似篇C异侧DCDCAPBA PB锐角直角DDCA PB同侧钝角DDABPABPABPCCC异侧三、“一线三等角”的性质1. 一般情况下,如图 3-1 ,由∠ 1=∠ 2=∠ 3,易得△ AEC ∽△ BDE.2. 当等角所对的边相等时,则两个三角形全等. 如图 3-1 ,若 CE=ED ,则△ AEC ≌△ BDE.3.中点型“一线三等角”如图 3-2,当∠ 1=∠2=∠3,且 D 是 BC 中点时,△ BDE∽△ CFD∽△ DFE.4. “中点型一线三等角“的变式(认识)如图 3-3,当∠ 1=∠2 且BOC 901BAC 时,点O是△ABC的内心.能够考虑构2造“一线三等角”.如图 3- 4“中点型一线三等角”平时与三角形的内心或旁心相关,BOC901BAC 这是内心的性质,反之未必是内心. 2在图 3-4(右图)中,若是延长BE 与 CF,交于点 P ,则点 D 是△ PEF 的旁心 .5.“一线三等角”的各种变式(图 3-5 ,以等腰三角形为例进行说明)图 3-5其实这个第 4 图,延长 DC 反而好理解 . 相当于两侧型的,不延长理解,以为是一种新式的,同侧穿越型?无论怎么变,都是由三等角确定相似三角形来进行解题四、“一线三等角”的应用1.“一线三等角”应用的三种情况 .a.图形中已经存在“一线三等角”,直接应用模型解题;b.图形中存在“一线二等角”,不上“一等角”构造模型解题;c. 图形中只有直线上一个角,不上“二等角”构造模型解题.领悟:感觉最后一种情况出现比很多,特别是压轴题中,经常会有一个特别角或指导该角的三角函数值时,我经常构造“一线三等角”来解题.2.在定边对定角问题中,构造一线三等角是基本手段,特别是直角坐标系中的张角问题,在 x 轴或 y 轴(也能够是平行于 x 轴或 y 轴的直线)上构造一线三等角解决问题更是重要的手段 .3.构造一线三等角的步骤:找角、定线、构相似坐标系中,要讲究“线”的特别性如图 3-6 ,线上有一特别角,就考虑构造同侧型一线三等角自然只加这两条线平时是不够的,为了利用这个特别角导线段的关系,过 C 、D两点作直线 l 的垂线是必不能少的。
双垂直模型结论及证明

双垂直模型结论及证明双垂直模型听起来就像是一门深奥的科学,但其实呢,它也可以用一种轻松的方式来理解。
想象一下,你在玩积木,想要把一堆零碎的块拼在一起,结果发现有两个特别的块,像是交叉的两根线,一垂直一水平。
咱们就可以从这儿开始聊聊双垂直模型了。
这个模型的核心在于它如何处理数据,哎,这就像咱们生活中那些矛盾的事情,明明在一个方向上走,却总有一些意想不到的转折。
咱们得理解,双垂直模型主要是用来分析两个变量之间的关系。
就好比你和你的朋友,大家都是独立的个体,但当你们聚在一起的时候,就会产生各种有趣的化学反应。
这个模型就像是揭开了这种“化学反应”的神秘面纱,让人们可以清晰地看到各种关系。
有人可能会问,这个模型到底有什么用?它在很多领域都有应用,比如经济学、社会学,甚至在市场营销中也能看到它的身影。
就像是每次你想买个新手机,都会先比较一下各个品牌之间的优缺点,双垂直模型就是在帮助你理清这些复杂的关系。
咱们再深入一层,这个模型的结论是,两个变量之间的互动关系可以用一种简单明了的方式呈现出来。
比如说,你的工作效率和休息时间之间的关系,明明休息了之后,你的效率会更高,但如果你休息得太久,那效率又会掉下去。
哎,这种现象就像是喝咖啡,喝多了会心慌,但适量喝又能提神。
这个模型的魅力就在于,它能把这种复杂的互动关系用简单的图表和公式表达出来,真是太神奇了。
咱们来聊聊这个模型的证明部分。
证明就像是在解一道难题,有时需要一些巧妙的方式来显示出事情的真相。
你知道吗?很多时候,科学家们就是通过观察和实验来验证模型的准确性。
就像是你在厨房做菜,尝一尝再加点盐,最后调到一个恰到好处的味道。
双垂直模型的证明过程也是如此,得经过一系列的数据收集、分析,再加上一点运气,最终得到一个可靠的结论。
就算有时候结果不如预期,但这些数据也能让你明白哪里出了问题。
而这个模型的应用不仅限于理论,实际上,它对实际操作也有很大的帮助。
想象一下,如果你是一位商家,想要推出新产品,使用这个模型来分析目标客户的偏好,就能更精准地制定营销策略。
一线三等角模型、双垂直模型(自己总结)

如图,ABT2米,CA丄AB于点A, DB丄AB于点B,且AC=4米,点P从B向A运动, 每分钟走1米,点Q从B点向D运动,每分钟走2米,P、Q两点同时出发,运动几分钟后,A CPA与A POB全等?如图①所示,在A ABC中,ZC=90°, AC=BC,过点C在△ ABC外作直线MN,AM丄MN于点M, BN丄MN于点N.⑴求证:MN二AM + BN.(2)如图②.若过点C直线MN与线段AB相交,AM丄MN于点M, BN丄MN于N, (1)中的结论是否仍然成立?说明理由.图②图①B N如图,已知ZB=ZC=90°, M是BC的中点,DM平分ZADC.(1)求证:AM平分ZDAB(2)试说明线段DM与AM有怎样的位置关系?(3)线段CD、AB、AD间有怎样的关系?直接写出结果。
如图,ZkABE竺Z\EDC, E在BD上,AB丄BD,垂足为B, A AEC是等腰直角三角形吗?为什么?【练3】正方形ABCD,E是BC上一点,AE丄EF,交ZDCH的平分线于点F,求证AE=EF如图所示,在RtMBC中,ZABC=W,点D在边AB上,使,过点D作刃7丄AC,分别交AC于点E, CB的延长线于点F。
求证:AB=BF» (8分)如图(1),己知AB丄BD, ED丄BD, AB二CD, BC=DE,(1) 试判断AC与CE的位置关系,并说明理由.(2) 若将CD沿CB方向平移得到图②③④⑤的情形,其余条件不变,此时第(1)问中AC 与CE的位置关系还成立吗?结论还成立吗?请任选一个说明理由.如图,在ZkABC 中,AB=AC, DE 是过点A 的直线,BD 丄DE 于D, CE 丄DE 于点E : ⑵若B. C 在DE 的两侧(如图所示),其他条件不变,AB 与AC 仍垂直吗?若是请给出证 明;若不是,请说明理由。
⑴若B. C 在DE 的同侧(如图所示)且AD=CE.求证:AB 丄AC ;如图,"03=90。
一线三等角模型结论及证明

一线三等角模型结论及证明
摘要
一线三等角模型是几何学中的重要概念,它指的是在一个给定的直线上,存在三个等角,它们的夹角均为120度。
本文将详细阐述一线三等角模型的结论及证明,以及如何使用它来解决实际问题。
一、定义
一线三等角模型是几何学中的重要概念,它指的是在一个给定的直线上,存在三个等角,它们的夹角均为120度。
二、结论
一线三等角模型的结论如下:
1、如果在一条直线上有三个等角,则它们的夹角均为120度。
2、如果三条直线的夹角均为120度,则它们共线。
三、证明
1、证明一:假设在一条直线上有三个等角,设它们的夹角为α,β,γ,则有
α+β+γ=360°,由等角性质可知α=β=γ=120°,得证。
2、证明二:假设三条直线的夹角均为120°,设它们的夹角分别为α,β,γ,则有α+β+γ=360°,此时α=β=γ=120°,由此可知,三条直线共线,得证。
四、实际应用
一线三等角模型可以用来解决实际问题,比如,在建筑设计中,可以根据一线三等角模型设计出美观的建筑结构,如三角形的屋顶,具有特殊的视觉效果。
结论
一线三等角模型是几何学中的重要概念,它指的是在一个给定的直线上,存在三个等角,
它们的夹角均为120度。
本文详细阐述了一线三等角模型的结论及证明,并且给出了如何使用它来解决实际问题的实例。
2024中考数学常见几何模型归纳总结—三角形中的倒角模型-高分线模型、双(三)垂直模型

2024中考数学常见几何模型归纳总结—三角形中的倒角模型-高分线模型、双(三)垂直模型近年来各地考试中常出现一些几何倒角模型,该模型主要涉及高线、角平分线及角度的计算(内角和定理、外角定理等)。
熟悉这些模型可以快速得到角的关系,求出所需的角。
本专题高分线模型、双垂直模型、子母型双垂直模型(射影定理模型)进行梳理及对应试题分析,方便掌握。
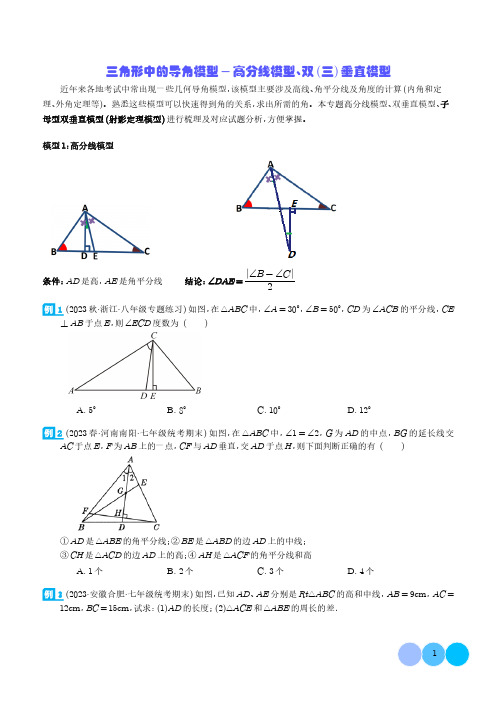
模型1:高分线模型条件:AD 是高,AE 是角平分线结论:∠DAE=2B C∠∠-例1.(2023秋·浙江·八年级专题练习)如图,在ABC 中,30A ∠=︒,50B ∠=︒,CD 为ACB ∠的平分线,CE AB ⊥于点E ,则ECD ∠度数为()A .5︒B .8︒C .10︒D .12︒【答案】C 【分析】依据直角三角形,即可得到40BCE ∠=︒,再根据30A ∠=︒,CD 平分ACB ∠,即可得到BCD ∠的度数,再根据DCE BCD BCE ∠=∠-∠进行计算即可.【详解】解:50,B CE AB ∠=︒⊥ ,40BCE ∴∠=︒,又30A ∠=︒ ,CD 平分ACB ∠,1118050305022()BCD BCA ∴∠=∠=⨯︒-︒-︒=︒,504010DCE BCD BCE ∴∠=∠-∠=︒-︒=︒,故选:C .【点睛】本题考查的是三角形内角和定理,熟知三角形内角和是180︒是解答此题的关键.例2.(2023春·河南南阳·七年级统考期末)如图,在△ABC 中,∠1=∠2,G 为AD 的中点,BG 的延长线交AC 于点E ,F 为AB 上的一点,CF 与AD 垂直,交AD 于点H ,则下面判断正确的有()①AD 是△ABE 的角平分线;②BE 是△ABD 的边AD 上的中线;③CH 是△ACD 的边AD 上的高;④AH 是△ACF 的角平分线和高A .1个B .2个C .3个D .4个【答案】B【详解】解:①根据三角形的角平分线的概念,知AG 是△ABE 的角平分线,故此说法错误;②根据三角形的中线的概念,知BG 是△ABD 的边AD 上的中线,故此说法错误;③根据三角形的高的概念,知CH 为△ACD 的边AD 上的高,故此说法正确;④根据三角形的角平分线和高的概念,知AH 是△ACF 的角平分线和高线,故此说法正确.故选:B .【点睛】本题考查了三角形的角平分线、三角形的中线、三角形的高的概念,注意:三角形的角平分线、中线、高都是线段,且都是顶点和三角形的某条边相交的交点之间的线段.透彻理解定义是解题的关键.例3.(2023·安徽合肥·七年级统考期末)如图,已知AD 、AE 分别是Rt △ABC 的高和中线,AB =9cm ,AC =12cm ,BC =15cm ,试求:(1)AD 的长度;(2)△ACE 和△ABE 的周长的差.【答案】(1)AD 的长度为365cm ;(2)△ACE 和△ABE 的周长的差是3cm .【分析】(1)利用直角三角形的面积法来求线段AD 的长度;(2)由于AE 是中线,那么BE =CE ,再表示△ACE 的周长和△ABE 的周长,化简可得△ACE 的周长﹣△ABE 的周长=AC ﹣AB 即可.【详解】解:(1)∵∠BAC =90°,AD 是边BC 上的高,∴S △ACB =12AB•AC =12BC•AD ,∵AB =9cm ,AC =12cm ,BC =15cm ,∴AD =AB AC CB ⋅=91215⨯=365(cm ),即AD 的长度为365cm ;(2)∵AE 为BC 边上的中线,∴BE =CE ,∴△ACE 的周长﹣△ABE 的周长=AC+AE+CE ﹣(AB+BE+AE )=AC ﹣AB =12﹣9=3(cm ),即△ACE 和△ABE 的周长的差是3cm .【点睛】此题主要考查了三角形的面积,关键是掌握直角三角形的面积求法.例4.(2023·广东东莞·八年级校考阶段练习)如图,在ABC 中,AD ,AE 分别是ABC 的高和角平分线,若30B ∠=︒,50C ∠=︒.(1)求DAE ∠的度数.(2)试写出DAE ∠与C B ∠-∠关系式,并证明.(3)如图,F 为AE 的延长线上的一点,FD BC ⊥于D ,这时AFD ∠与C B ∠-∠的关系式是否变化,说明理由.【答案】(1)10︒(2)()12DAE C B ∠=∠-∠(3)不变,理由见解析【分析】(1)根据三角形内角和求出BAC ∠,根据角平分线的定义得到50BAE ∠=︒,根据高线的性质得到90ADE ∠=︒,从而求出60BAD ∠=︒,继而根据角的和差得到结果;(2)根据角平分线的定义得到12BAE BAC ∠=∠,根据三角形内角和求出119022EAC B C ∠=︒-∠-∠,根据角的和差得到结果;(3)过A 作AG BC ⊥于G ,结合(2)知1()2EAG C B ∠=∠-∠,证明FD AG ∥,得到AFD EAG ∠=∠,即可证明.【详解】(1)解:∵30B ∠=︒,50C ∠=︒,∴1805030100BAC ∠=︒-︒-︒=︒,∵AE 平分BAC ∠,∴1502BAE CAE BAC ∠=∠=∠=︒,∵AD 是高,∴90ADE ∠=︒,∵30B ∠=︒,∴60BAD ∠=︒,∴10DAE BAD BAE ∠=∠-∠=︒;(2)()12DAE C B ∠=∠-∠,证明如下:∵AE 平分BAC ∠,∴12EAC BAC ∠=∠,∵180BAC B C ∠=︒-∠-∠,∴()11101902822B C B C EAC ︒-∠-∠-∠︒-==∠∠,∴EAD EAC DAC ∠=∠-∠()11090922B C C =︒∠---∠︒-∠()12C B =∠-∠;(3)不变,理由是:如图,过A 作AG BC ⊥于G ,由(2)可知:1()2EAG C B ∠=∠-∠,AG BC ⊥ ,90AGB ∠=︒,FD BC ⊥ ,90FDC ∴∠=︒,AGD FDC ∴∠=∠,FD AG ∴∥,AFD EAG ∴∠=∠,1()2AFD C B ∴∠=∠-∠.【点睛】本题主要考查三角形的内角和定理、角平分线的性质、直角三角形的性质和平行线的判定与性质,熟练掌握三角形的内角和定理和角平分线的性质是解题的关键.模型2:双垂直模型结论:①∠A =∠C ;②∠B =∠AFD =∠CFE ;③AB CD AE BC ⋅=⋅。
三角形中的导角模型-高分线模型、双(三)垂直模型(学生版)
三角形中的导角模型-高分线模型、双(三)垂直模型近年来各地考试中常出现一些几何导角模型,该模型主要涉及高线、角平分线及角度的计算(内角和定理、外角定理等)。
熟悉这些模型可以快速得到角的关系,求出所需的角。
本专题高分线模型、双垂直模型、子母型双垂直模型(射影定理模型)进行梳理及对应试题分析,方便掌握。
模型1:高分线模型条件:AD是高,AE是角平分线结论:∠DAE=∠B-∠C21(2023秋·浙江·八年级专题练习)如图,在△ABC中,∠A=30°,∠B=50°,CD为∠ACB的平分线,CE ⊥AB于点E,则∠ECD度数为()A.5°B.8°C.10°D.12°2(2023春·河南南阳·七年级统考期末)如图,在△ABC中,∠1=∠2,G为AD的中点,BG的延长线交AC于点E,F为AB上的一点,CF与AD垂直,交AD于点H,则下面判断正确的有()①AD是△ABE的角平分线;②BE是△ABD的边AD上的中线;③CH是△ACD的边AD上的高;④AH是△ACF的角平分线和高A.1个B.2个C.3个D.4个3(2023·安徽合肥·七年级统考期末)如图,已知AD、AE分别是Rt△ABC的高和中线,AB=9cm,AC= 12cm,BC=15cm,试求:(1)AD的长度;(2)△ACE和△ABE的周长的差.4(2023·广东东莞·八年级校考阶段练习)如图,在△ABC中,AD,AE分别是△ABC的高和角平分线,若∠B=30°,∠C=50°.(1)求∠DAE的度数.(2)试写出∠DAE与∠C-∠B关系式,并证明.(3)如图,F为AE的延长线上的一点,FD⊥BC于D,这时∠AFD与∠C-∠B的关系式是否变化,说明理由.模型2:双垂直模型结论:①∠A=∠C;②∠B=∠AFD=∠CFE;③AB⋅CD=AE⋅BC。
初中数学几何模型(五)一线三等角模型

初中数学几何模型(五)一线三等角模型一线三等角模型:指有三个相等角的顶点在同一直线上构成的相似或全等(相等角所对的边相等)图形,相等的角可以是锐角,也可以是直角或钝角。
(一)全等1、相等的三个角和全等三角形在直线同侧。
已知:如图,点A、B、C在同一直线上,∠1=∠2=∠3,且CD=CE,则△ACD≌△BEC。
证明:∵∠BCD=∠1+∠D,∠BCD=∠3+∠BCE,∠1=∠3,∴∠D=∠BCE,∵∠1=∠2,CD=CE,∴△ACD≌△BEC(AAS)。
2、相等的三个角和全等三角形在直线异侧。
已知:如图,点A、B、C在同一直线上,∠1=∠2=∠3,且CD=CE,则△ACD ≌△BEC。
证明:∵∠2=∠D+∠ACD,∠3=∠BCE+∠ACD,∠2=∠3,∴∠D=∠BCE,∵∠2=∠1,∴∠DAC=∠CBE,∵CD=CE,∴△ACD≌△BEC(AAS)。
一线三等角结论1:当等角所对边相等时,则两个三角形全等。
(二)相似1、相等的三个角和相似三角形在直线同侧。
已知:如图,点A、B、C在同一直线上,∠1=∠2=∠3,则△ACD∽△BEC。
证明:∵∠BCD+∠1+∠D,∠BCD=∠3+∠BCE,∠1=∠3,∴∠D=∠BCE,∵∠1=∠2,∴△ACD∽△BEC。
2、相等的三个角和相似三角形在直线异侧。
已知:如图,点A、B、C在同一直线上,∠1=∠2=∠3,则△ACD∽△BEC。
证明:∵∠1=∠D+∠ACD,∠3=∠BCE+∠ACD,∠1=∠3,∴∠D=∠BCE,∵∠1=∠2,∴∠DAC=∠CBE,∴△ACD∽△BEC。
一线三等角结论2:一线三等角两个三角形相似。
(三)一线三等角变式:中点型如图,点C在相等AB上,且AC=BC,∠1=∠2=∠3。
求证:△ACD∽△BEC∽△CED证明:∵∠1=∠2=∠3,∴△ACD ∽△BEC ,∴AD BC =CD CE , ∵AC=BC ,∴AD AC =CD CE ,∵∠1=∠3,∴△ACD ∽△CED ,∴△ACD ∽△BEC ∽△CED ,∴∠4=∠5=∠8,∠9=∠6=∠7。
(完整版)几何模型:一线三等角模型
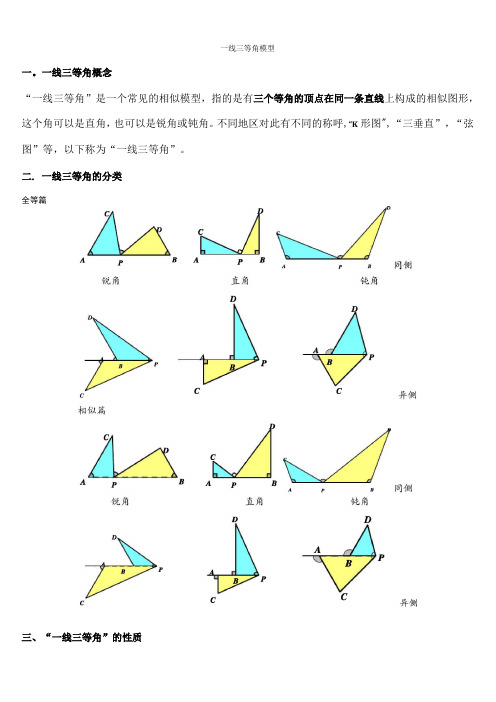
一线三等角模型一。
一线三等角概念“一线三等角”是一个常见的相似模型,指的是有三个等角的顶点在同一条直线上构成的相似图形,这个角可以是直角,也可以是锐角或钝角。
不同地区对此有不同的称呼,“K形图",“三垂直”,“弦图”等,以下称为“一线三等角”。
二. 一线三等角的分类全等篇三、“一线三等角”的性质1。
一般情况下,如图3—1,由N 仁Z2=Z3,易得△AECs^BDEo2. 当等角所对的边相等时,则两个三角形全等.如图3.中点型“一线三等角 如图3—2,当Z1=Z2=Z3,且D 是BC 中点时,△BDEs^CFDs^DFE 。
4。
“中点型一线三等角“的1如图3—4“中点型一线三等角”通常与三角形的内心或旁心相关,ZBOC 二90。
+A BAC 这是内心的^2 性质,反之未必是内心.在图3-4(右图)中,如果延长BE 与CF ,交于点P,则点D 是APEF 的旁心.图3—5其实这个第4图,延长DC 反而好理解•相当于两侧型的,不延长理解,以为是一种新型的,同 侧穿越型?不管怎么变,都是由三等角确定相似三角形来进行解题四、“一线三等角”的应用1•“一线三等角”应用的三种情况.图3-1图3-3图3-4+Ja。
图形中已经存在“一线三等角”,直接应用模型解题;b。
图形中存在“一线二等角”,不上“一等角”构造模型解题;c・图形中只有直线上一个角,不上“二等角”构造模型解题。
体会:感觉最后一种情况出现比较多,尤其是压轴题中,经常会有一个特殊角或指导该角的三角函数值时,我经常构造“一线三等角”来解题.2。
在定边对定角问题中,构造一线三等角是基本手段,尤其是直角坐标系中的张角问题,在x轴或y轴(也可以是平行于x轴或y轴的直线)上构造一线三等角解决问题更是重要的手段。
在DC的延檢銭上截眼匚E二J3•构造一线三等角的步骤:找角、定线、构相似1IJttnZAEP=aaZPFB=啦-工上则以’唾二ZPFB=a二ZAPE』所I^APAEwABPF.在CP±WCE=则曲厶斗EOunZBFD=⑶“则ZAEC-ZBFD=ZAPB•所I^APAE«ABPF・坐标系中,要讲究“线"的特殊性如图3—6,线上有一特殊角,就考虑构造同侧型一线三等角(完整版)几何模型:一线三等角模型当然只加这两条线通常是不够的,为了利用这个特殊角导线段的关系,过C、D两点作直线I的垂线是必不可少的。
初中数学双垂直模型

初中数学双垂直模型
初中数学双垂直模型是指在平面直角坐标系内,两条直线互相垂直,并且与某一直线的两个垂线互相垂直的模型。
在初中数学中,双垂直模型是一个重要的概念,它与坐标系、勾股定理等知识密切相关。
在学习双垂直模型时,我们需要了解什么是垂直,并学会判断两条直线是否垂直。
同时,我们还需要掌握如何求出两条垂直直线之间的夹角,并能够运用这个知识解决一些相关问题。
在实际应用中,双垂直模型常常用于解决建筑、制图、几何学等领域的问题。
例如,在建筑设计中,设计师需要掌握双垂直模型的相关知识,以确保建筑物的结构稳定;在制图中,双垂直模型则可以用来确定坐标轴的方向和位置;在几何学中,双垂直模型是学习正交投影等重要概念的基础。
总之,初中数学双垂直模型是一个重要的概念,它不仅是学习坐标系、勾股定理等知识的基础,还在实际应用中有着广泛的应用。
因此,我们应该认真学习和掌握这个概念,以提高我们的数学水平和应用能力。
- 1 -。
全等典型模型:“一线三等角”模型

《三角形证明》题型解读11 全等典型模型:“一线三等角”模型【知识梳理】(一)“一线三等角模型”题型特征:图形的某条线段上出现三个相等的角,如图中∠B=∠2=∠C解题方法:只要题目再出现一组等边(BE=AC 或EF=AE 或BF=EC ),必证△BEF ≌△CAE (AAS 或ASA )(二)“三垂直模型”(“一线三直角模型”)1.基本图形题型特征:图形的某条线段上出现三个直角,如图中∠B=∠AED=∠C=90°解题方法:只要题目再出现一组等边(AB=EC 或BE=DC 或AE=DE ),必证△ABE ≌△ECD (AAS 或ASA )2.两种变化图形(1)“交叉型”三垂直模型(2)“L 型”三垂直模型【典型例题】 例1.如图,在△ABC 中,AB=AC=2,∠B=40º,点D 在线段BC 上运动(点D 不与点B 、C 重合),连接AD ,作∠ADE=40º,DE 交线段AC 于点E .(1)当∠BDA=115°时,∠EDC=________,∠AED=___________;(2)线段DC 的长度为何值时,△ABD ≌△DCE ,请说明理由; (3)在点D 的运动过程中,△ADE 的形状可以是等腰三角形吗?若可以,求∠BDA 的度数;若不可以,请说明理 由.证∠1+∠2=°,∠2+∠A=°,∴∠1=∠A 又∠B=∠C ,若AB ≅FC若AB ~FC 21A B F E D C 证∠1+∠2=°,∠2+∠A=°,∴∠1=∠A 又∠B=∠C ,若AB ≅EC若AB ~EC 21A B CE D 证明:∵∠1+∠2=90°,∠2+∠A=90°,∴∠1=∠A 又∵∠B=∠C ,若其中有一组边相等,则证ABE ≅FCD;若没有边相等,则证ABE ~FCD;C (1(2ED CB A(1)若有等边,则△ABE≌△BDC(AAS )(2)若无等边,则△ABE∽△BDC(AA )D CA CE D B例2.如图,长方形ABCD 中,E 在AD 上,且EF ⊥EC ,EF=EC ,DE=2,长方形的周长为16,求AE 的长..例3.在△ABC 中AB =AC ,∠BAC =90°,分别过B 、C 作过A 点的直线的垂线,垂足为D 、E .(1)求证:△AEC ≌△BDA ;(2)如果CE =2,BD =4,求ED 的长是多少?例4.(1)已知,如图①,在△ABC 中,∠BAC=90°,AB=AC ,直线m 经过点A ,BD ⊥m 于点D ,CE ⊥m 于点E ,求证:DE=BD+CE ;(2)如图②,将(1)中的条件改为:在△ABC 中,AB=AC ,D 、A 、E 三点都在直线m 上,且有∠BDA=∠AEC=∠BAC=α,其中α为任意钝角,请问结论DE=BD+CE 是否成立?若成立,请你给出证明;若不成立,请说明理由.例5.如图,正方形ABCD 中,P 、Q 分别是边AB 、BC 上的两个动点,P 、Q 同时分别从A 、B 出发,点P 沿AB 向B 运动;点Q 沿BC 向C 运动,速度都是1个单位长度/秒.运动时间为t 秒.连结AQ 、DP 相交于点F ,求证:AQ ⊥DP ;A C E D BA B C D E F 图F E DC B A。
一线三等角模型体会

一线三等角模型体会
1.“一线三等角"应用的三种情况。
a.图形中已经存在一线三等角,直接应用模型解题;
b.图形中存在“一线二等角”,补上“一等角”构造模型解题;C.图形中只有直线上一个角,补上“二等角”构造模型解题.
2.在定边对定角问题中,构造一线三等角是基本手段。
3.构造一线三等角的步骤:找角、定线、构相似。
如上图,线上有一特殊角,
就考虑构造同侧型一线三等角,当然只加这两条线通常是不够的,为了利用这个特殊角与线段的关系,过C、D两点作直线的垂线是必不可少的。
例如图2,已知E是矩形ABCD的边AB上一点,EFLDE交BC于点F,试说
明:△ADE~△BFE。
析:要证明ΔADE 与ΔBFE相似,已经知道∠A=∠B=90°,只需要再找出另外一对相等的角即可。
解答:在矩形ABCD中,∠A=∠B=90°∵EF⊥DE
∴∠DEF=90°,∠2+∠3=90°
又∵∠1+∠3=90°
∴∠1=∠2
∴ΔADE∽ΔBFE
小结:此时,在直线AB上,∠A=∠DEF=∠B=90°,一条线上有3个直角,两边的ΔADE与ΔBFE相似。
这个相似的基本图形像字母K,可以称为“K”型相似,但更因为图形的结构特征是一条线上有3个垂直关系,也常被称为“一线三垂直”。
通过例题,我们已经证明,“一线三垂直”可以得出相似三角形,那普通的3个等角又会怎样呢?
此时,一条线上的三个等角由90°变成了60°,两边的三角形依然相似。
那么,更一般的等角呢?。
几何模型:一线三等角模型

一线三等角模型一.一线三等角概念“一线三等角”是一个常见的相似模型,指的是有三个等角的顶点在同一条直线上构成的相似图形,这个角可以是直角,也可以是锐角或钝角。
不同地区对此有不同的称呼,“K 形图”,“三垂直”,“弦图”等,以下称为“一线三等角”。
二.一线三等角的分类全等篇同侧锐角直角钝角P异侧相似篇A同侧锐角直角钝角P异侧三、“一线三等角”的性质1.一般情况下,如图 3-1,由∠1=∠2=∠3,易得△AEC∽△BDE.2.当等角所对的边相等时,则两个三角形全等.如图 3-1,若 CE=ED,则△AEC≌△BDE.3.中点型“一线三等角”如图 3-2,当∠1=∠2=∠3,且 D 是 BC 中点时,△BDE∽△CFD∽△DFE.4.“中点型一线三等角“的变式(了解) 如图 3-3,当∠1=∠2 且1902BOC BAC ∠=︒+∠时,点 O 是△ABC 的内心.可以考虑构造“一线三等角”.如图 3-4“中点型一线三等角”通常与三角形的内心或旁心相关,1902BOC BAC ∠=︒+∠这是内心的性质,反之未必是内心.在图 3-4(右图)中,如果延长 BE 与 CF ,交于点 P ,则点 D 是△PEF 的旁心.5.“一线三等角”的各种变式(图 3-5,以等腰三角形为例进行说明 )图 3-5其实这个第 4 图,延长 DC 反而好理解.相当于两侧型的,不延长理解,以为是一种新型的,同侧穿越型?不管怎么变,都是由三等角确定相似三角形来进行解题四、“一线三等角”的应用1.“一线三等角”应用的三种情况.a.图形中已经存在“一线三等角”,直接应用模型解题;b.图形中存在“一线二等角”,不上“一等角”构造模型解题;c.图形中只有直线上一个角,不上“二等角”构造模型解题.体会:感觉最后一种情况出现比较多,尤其是压轴题中,经常会有一个特殊角或指导该角的三角函数值时,我经常构造“一线三等角”来解题.2.在定边对定角问题中,构造一线三等角是基本手段,尤其是直角坐标系中的张角问题,在 x 轴或 y 轴(也可以是平行于 x 轴或 y 轴的直线)上构造一线三等角解决问题更是重要的手段.3.构造一线三等角的步骤:找角、定线、构相似坐标系中,要讲究“线”的特殊性如图 3-6,线上有一特殊角,就考虑构造同侧型一线三等角当然只加这两条线通常是不够的,为了利用这个特殊角导线段的关系,过 C、D 两点作直线 l 的垂线是必不可少的。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
如图,AB=12米,CA⊥AB于点A,DB⊥AB于点B,且AC=4米,点P从B向A运动,每分钟走1米,点Q从B点向D运动,每分钟走2米,P、Q两点同时出发,运动几分钟后,⊥CPA与⊥PQB全等?
如图①所示,在△ABC中,∠C=90°,AC=BC,过点C在△ABC外作直线MN,AM⊥M N于点M,BN⊥MN于点N.
(1)求证:MN=AM+BN.
(2)如图②.若过点C直线MN与线段AB相交,AM⊥MN于点M,BN⊥MN于N,(1)中的结论是否仍然成立?说明理由.
图①图②
如图,已知∠B=∠C=90°,M是BC的中点,DM平分∠ADC.
(1)求证:AM平分∠DAB
(2)试说明线段DM与AM有怎样的位置关系?
(3)线段CD、AB、AD间有怎样的关系?直接写出结果。
如图,⊥ABE⊥⊥EDC,E在BD上,AB⊥BD,垂足为B,⊥AEC是等腰直角三角形吗?为什么?
【练3】正方形ABCD,E 是BC 上一点,AE ⊥EF,交∠DCH 的平分线于点F ,求证AE=EF
如图所示,在ABC Rt ∆中, 90=∠ABC ,点D 在边AB 上,使,过点D 作AC EF ⊥,分别交AC 于点E ,CB 的延长线于点F 。
求证:AB=BF 。
(8分)
如图(1),已知AB ⊥BD ,ED ⊥BD ,AB=CD ,BC=DE ,
(1)试判断AC 与CE 的位置关系,并说明理由.
(2)若将CD 沿CB 方向平移得到图⊥⊥⊥⊥的情形,其余条件不变,此时第(1)问中AC 与CE 的位置关系还成立吗?结论还成立吗?请任选一个说明理由.
如图,在⊥ABC中,AB=AC,DE是过点A的直线,BD⊥DE于D,CE⊥DE于点E;
(2)若B.C在DE的两侧(如图所示),其他条件不变,AB与AC仍垂直吗?若是请给出证明;若不是,请说明理由。
(1)若B.C在DE的同侧(如图所示)且AD=CE.求证:AB⊥AC;
如图,
∠AOB,OA=OB,直线l经过点O,分别过A、B两点作l
90
=
BD⊥
AC⊥交l于点C,l 交l于点D。
求证:AC=OD。
(6分)
如图,在⊥ACB中,⊥ACB=90゜,CD⊥AB于D.
(1)求证:⊥ACD=⊥B;
(2)若AF平分⊥CAB分别交CD、BC于E.F,求证:⊥CEF=⊥CFE.
如图,已知:AB⊥BD,ED⊥BD,AB=CD,BC=DE,那么AC与CE有什么关系?写出你的猜想并说明理由。
如图1,在⊥ABC中,AB=AC,点D是BC的中点,点E在AD上。
(1)求证:BE=CE;
(2)如图2,若BE的延长线交AC于点F,且BF⊥AC,垂足为F,⊥BAC=45⊥,原题设其它条件不变。
求证:⊥AEF⊥⊥BCF.。
