高中数学竞赛练习—几何—题目1-10
高中数学竞赛练习—几何—题目1-10

最新高中数学奥数竞赛试题几何(1):设D是ABC的边BC上的一点,点P在线段AD上,过点D作一直线分别与线段AB、PB交于点M、E,与线段AC、PC的延长线交于点F、N。
如果DE=DF,求证:DM=DN几何(2)设点D为等腰ABC∆的底边BC上一点,F为过A、D、C三点的圆在ABC∆内的弧上一点,过B、Array D、F三点的圆与边AB交于点E。
求证:CD EF DF AE BD AF⋅+⋅=⋅几何(3):如图所示,在△ABC中,90,,∠=︒是边CA上的两点,ABC D G Array连接BD,BG . 过点A,G分别作BD的垂线,垂足分别为E,F,连接CF. 若BE=EF,求证:ABG DFC∠=∠.几何(4):如图,在ABC∆中,60A∠=︒, ABC∆的内切圆I分别切边,AB AC于点,D E,直线DE分别与直线BI CI,相交于点F G,, 证明:12FG BC=.B几何(5):在△ABC中,BC>AB,BD平分ABC交AC于D,如图,CP垂直BD,垂足为P,AQ垂直BP,Q为垂足。
M是AC中点,E 是BC中点。
若△PQM的外接圆O与AC 的另一个交点为H,求证: O、H、E、M 四点共圆。
C A几何(6):如图,ABC的内切圆I分别切BC、AC于点M、N,点E、F分别为边AB、AC的中点,D 是直线EF与BI的交点。
证明:M、N、D三点共线。
D A几何(7)ee、Ie分别是ABC∆的外接圆和内切圆;证明:过O 上的任意一点D,都可以作一个三角形DEF,使得Oe、Ie分别是DEF∆的外接圆和内切圆.几何(8)如图,过ABC ∆的外心O 任作一直线,分别交边,AB AC 于,M N ,F E ,分别是,BN CM 的中点.证明:EOF A ∠=∠.几何(9):设000,,AA BB CC 是ABC ∆的三条角平分线,自0A 作01A A ∥0BB ,02A A ∥0CC ,12,A A 分别在,AC AB 上,直线123A A BC A =I ;类似得到点33,B C .证明:333,,A B C 三点共线.33几何(10):一张纸上画有一个半径为R的圆O和圆内一个定点A,且OA=a,折叠纸片,使圆周上某一点A'刚好与点A重合.这样的每一种折法,都留下一条折痕.当A'取遍圆周上所有点时,求所有折痕所在直线上点的集合.几何(1):设D 是ABC ∆的边BC 上的一点,点P 在线段AD 上,过点D 作一直线分别与线段AB 、PB 交于点M 、E ,与线段AC 、PC 的延长线交于点F 、N 。
高中数学立体几何测试题(10套)

∴ BD ∥平面 PMN ,
位置关系为
平行
。
∴ O 到平面 PMN 的距离即为 BD 到平面 PMN 的距离。
11 、a,b 为异面直线,且 a,b 所成角为 40 °,直线 c 与 a,b 均异面,且所成角均为
∵ BD ⊥ AC , MN ∥ BD
∵ PA⊥面 ABCD
θ,若这样的 c 共有四条,则 θ的范围为 (70 °, 90° ) 。
D
C
A
B
D1 A1
C1 B1
17 、 已知异面直线 a, b 的公垂线段 AB 的中点为 O,平面 满足 a∥ , b∥ , 且 O , M 、 N 是 a, b 上的任意两点, MN ∩ = P,求证: P 是 MN 的中
点
A aM
O
P
BN b
.
立几面测试 001
参考答 案
一、 1- 8 ACDDBDBA
2、已知 m, n 为异面直线, m∥平面 , n∥平面 , ∩ =l ,则 l( ) ( A)与 m, n 都相交 ( B)与 m,n 中至少一条相交 ( C)与 m, n 都不相交 ( D )与 m, n 中一条相交
3、已知 a, b 是两条相交直线, a∥ ,则 b 与 的位置关系是 ( )
A 、 b∥
PAM
∵ AB=2 , BM=1 , CM=1
∴ AM= 5 ,
P
A H
O
.
B
F M
B
D N C
立几面测试 003
一、选择题
1.异面直线是指
(A) 在空间内不能相交的两条直线
(B) 分别位于两个不同平面的两条直线
(C) 某一个平面内的一条直线和这个平面外的一条直线
高一数学竞赛几何篇试题

高一数学竞赛几何篇试题一、选择题(每题5分,共30分)1. 在直角三角形ABC中,∠C=90°,若AB=10,AC=6,则BC的长度为多少?A. 8B. 12C. 14D. 162. 已知圆的半径为5,圆心到直线的距离为3,问直线与圆的位置关系是什么?A. 相切B. 相交C. 相离D. 无法确定3. 在平面直角坐标系中,点A(-1,2)和点B(3,-1),求直线AB的斜率。
A. -1B. 1C. 2D. 34. 一个正六边形的内角是多少?A. 120°B. 135°C. 150°D. 160°5. 已知三角形ABC的三边长分别为a, b, c,且满足a^2 + b^2 =c^2,这个三角形是什么类型的三角形?A. 锐角三角形B. 直角三角形C. 钝角三角形D. 等腰三角形6. 一个球的体积是V,那么它的表面积是多少?A. 4πVB. 2π√VC. 4π√VD. V^(2/3)二、填空题(每题5分,共20分)1. 已知点P(2,3)关于直线x=1的对称点是Q,求点Q的坐标。
2. 一个正方体的体积是27立方米,求它的表面积。
3. 若圆心在原点,半径为r的圆的方程是(x-h)^2 + (y-k)^2 = r^2,当h=0,k=0,r=1时,圆的方程是________。
4. 在三角形ABC中,若∠A=60°,AB=2,AC=3,求BC的长度。
三、解答题(每题25分,共50分)1. 已知椭圆的长轴为2a,短轴为2b,焦点在x轴上,且a=5,b=3,求椭圆的标准方程。
2. 在平面直角坐标系中,点M(-1,-1),点N(1,1),求以MN为直径的圆的方程,并计算圆的面积。
结束语以上试题覆盖了高中数学竞赛中几何部分的常见题型,希望同学们能够通过练习这些题目,提高自己的几何解题能力。
记住,几何问题往往需要空间想象力和逻辑推理能力,不断练习是提高解题技巧的关键。
全国高中数学联赛二试平面几何赛题精选

历年全国高中数学联赛二试几何题汇总1 (类似九点圆)如图,在锐角∆ABC 中,AB<AC ,AD 是边BC 上的高,P 是线段AD 内一点。
过P 作PE ⊥AC ,垂足为E ,作PF ⊥AB ,垂足为F 。
1O 、2O 分别是∆BDF 、∆CDE 的外心。
求证:1O 、2O 、E 、F 四点共圆的充要条件为P 是∆ABC 的垂心。
证明:连BP 、CP 、1O 2O 、E 2O 、EF 、F 1O 。
因为PD ⊥BC ,PF ⊥AB ,则B 、D 、P 、F 四点共圆,且BP 为该圆的直径。
又因为1O 是∆BDF 的外心,故1O 在BP 上且是BP 的中点。
同理可证,C 、D 、P 、E 四点共圆,且2O 是CP 的中点。
于是,1O 2O 平行于BC ,则∠P 2O 1O =∠PCB 。
因为AF*AB = AP*AD = AE*AC ,所以B 、C 、E 、F 四点共圆。
充分性:设P 是∆ABC 的垂心,由于PE ⊥AC ,PF ⊥AB ,所以,B 、1O 、P 、E 四点共线,C 、2O 、P 、F 四点共线,∠F 2O 1O =∠FCB =∠FEB = ∠FE 1O ,故1O 、2O 、E 、F 四点共圆 必要性:设1O 、2O 、E 、F 四点共圆,则∠1O 2O E + ∠EF 1O = π注意到∠P 2O 1O =∠PCB=∠ACB - ∠ACP ,又因为2O 是直角∆CEP 的斜边中点,也就是∆CEP 的外心,所以∠P 2O E=2∠ACP 。
ABDCEFP1O 2O因为1O 是直角∆BFP 的斜边中点,也就是∆BFP 的外心,从而∠PF 1O =2π - ∠BF 1O = 2π- ∠ABP 因为B 、C 、E 、F 四点共圆,所以∠AFE =∠ACB ,∠PFE =2π- ∠ACB 于是,由∠1O 2O E + ∠EF 1O = π得: (∠ACB - ∠ACP+ 2∠ACP )+ (2π - ∠ABP +2π- ∠ACB) = π , 即∠ABP =∠ACP 。
高中数学竞赛与强基计划试题专题:解析几何

高中数学竞赛与强基计划试题专题:解析几何一、单选题1.(2020·北京·高三强基计划)从圆224x y +=上的点向椭圆22:12x C y +=引切线,两个切点间的线段称为切点弦,则椭圆C 内不与任何切点弦相交的区域面积为()A .2πB .3πC .4πD .前三个答案都不对2.(2022·北京·高三校考强基计划)内接于椭圆22149x y +=的菱形周长的最大值和最小值之和是()A .B .CD .上述三个选项都不对3.(2020·湖北武汉·高三统考强基计划)已知直线1211::22l y x l y x =-=,,动点P 在椭圆22221(0)x y a b a b +=>>上,作1//PM l 交2l 于点M ,作2//PN l 交1l 于点N .若22PM PN +为定值,则()A .2ab =B .3ab =C .2a b =D .3a b=4.(2020·北京·高三强基计划)设直线3y x m =+与椭圆2212516x y +=交于A ,B 两点,O 为坐标原点,则OAB面积的最大值为()A .8B .10C .12D .前三个答案都不对5.(2022·贵州·高二统考竞赛)如图,1C ,2C 是离心率都为e 的椭圆,点A ,B 是分别是2C 的右顶点和上顶点,过A ,B 两点分别作1C 的切线1l ,2l .若直线1l ,2l 的斜率分别为1k ,2k ,则12k k 的值为()A .2eB .21e -C .21e -D .21e 6.(2020·湖北武汉·高三统考强基计划)过椭圆22149x y +=的中心作两条互相垂直的弦AC 和BD ,顺次连接,,,A B C D 得一四边形,则该四边形的面积可能为()A .10B .12C .14D .167.(2019·贵州·高三校联考竞赛)设椭圆C :()222210x y a b a b +=>>的左、右焦点分别为12,F F ,其焦距为2c .点322c N ⎛⎫⎪ ⎪⎝⎭在椭圆的内部,点M 是椭圆C 上的动点,且112||MF MN F +<恒成立,则椭圆C 的离心率的取值范围是()A .⎛ ⎝⎭B .⎫⎪⎪⎝⎭C .⎫⎪⎪⎝⎭D .⎝⎭二、多选题8.(2022·贵州·高二统考竞赛)如图,M ,N 分别是Rt ABC △两直角边上的动点,P 是线段MN 的中点,则以下结论正确的是()A .当△AMN 的面积为定值时,点P 的轨迹为双曲线一支B .当|MN |为定值时,点P 的轨迹为一圆弧C .当||||AM AN +为定值时,点P 的轨迹为不含端点线段D .当△AMN 的周长为定值时,点P 的轨迹为抛物线9.(2020·北京·高三校考强基计划)已知A ,B 分别为双曲线2214x y -=的左、右顶点,P 为该曲线上不同于A ,B 的任意一点设,,∠=∠= PAB PBA PAB αβ的面积为S ,则()A .tan tan αβ⋅为定值B .tantan22αβ⋅为定值C .tan()S αβ⋅+为定值D .cot()S αβ⋅+为定值10.(2020·北京·高三校考强基计划)已知点(1,1),(1,0)A Q ,P 为椭圆22143x y +=上的动点,则||||PA PQ +的()A .最大值为4B .最大值为4C .最小值为4-D .最小值为4三、填空题11.(2022·江苏南京·高三强基计划)设F ,l 分别为双曲线()22411212x y --=的右焦点与右准线,椭圆Γ以F和l 为其对应的焦点及准线,过F 作一条平行于y =的直线,交椭圆Γ于A 、B 两点,若Γ的中心位于以AB 为直径的圆外,则椭圆离心率e 的范围为___________.12.(2018·山东·高三竞赛)若直线65280x y --=交椭圆22221x ya b+=(0a b >>,且2a 、b 为整数)于点A 、C .设()0,B b 为椭圆的上顶点,而ABC 的重心为椭圆的右焦点2F ,则椭圆的方程为______.13.(2022·新疆·高二竞赛)设z 为复数,若方程2297--=z z 表示一条圆锥曲线,则此曲线的离心率=e ___________.14.(2021·全国·高三竞赛)已知集合{}22(,)|||||,0,(,)|1,044x y A x y x y t t B x y m m ⎧⎫=+>=+≤<<⎨⎩≤⎬⎭满足B A ⊆,若P 为集合B 的边界线C 上任意一点,12F F 、为曲线C 的焦点,I 为12PF F △的内心,直线1IF 和2IF 的斜率分别为12k k 、,且1213k k ⋅=-则t 的最小值为________.15.(2021·全国·高三竞赛)已知ABCD Y 的四个顶点均在双曲线2214y x -=上,点(0,1)P 在边AB 上,且12AP PB =,则ABCD Y 的面积等于_______.四、解答题16.(2022·湖北武汉·高三统考强基计划)设F 为椭圆C :22194x y +=的左焦点,P 为椭圆C 上的一点(1)作正方形FPAB (F ,P ,A ,B 按逆时针排列)当P 沿着椭圆运动一周,求动点B 的轨迹方程.(2)设()3,2Q 为椭圆外一点,求PQ PF +的取值范围.17.(2018·全国·高三竞赛)一束直线12,,l l 的每条均过xOy 平面内的抛物线2:C y x =的焦点,()1i l i ≥与抛物线C 交于点i A 、i B .若1l 的斜率为1,()2i l i ≥的斜率为1+2014l 的解析式.18.(2018·福建·高三竞赛)已知1F 、2F 分别为椭圆()2222:10x y C a b a b +=>>的左、右焦点,点3P ⎛⎫ ⎪⎝⎭在椭圆C 上,且12F PF △的垂心为5,33H ⎛⎫- ⎪ ⎪⎝⎭.(1)求椭圆C 的方程;(2)设A 为椭圆C 的左顶点,过点2F 的直线l 交椭圆C 于D 、D 两点.记直线AD 、AE 的斜率分别为1k 、2k ,若1212k k +=-,求直线l 的方程.19.(2018·江西·高三竞赛)若椭圆221259x y +=上不同的三点()11,A x y ,94,5B ⎛⎫ ⎪⎝⎭,()22,C x y 到椭圆右焦点的距离顺次成等差数列,线段AC 的中垂线l 交x 轴于点T ,求直线BT 的方程.20.(2018·湖北·高三竞赛)已知O 为坐标原点,()1,0N ,点M 为直线=1x -上的动点,MON ∠的平分线与直线MN 交于点P ,记点P 的轨迹为曲线E .(1)求曲线E 的方程;(2)过点11,22Q ⎛⎫-- ⎪⎝⎭作斜率为k 的直线l ,若直线l 与曲线E 恰好有一个公共点,求k 的取值范围.21.(2021·全国·高三竞赛)过抛物线22y px =(p 为不等于2的质数)的焦点F ,作与x 轴不垂直的直线l 交抛物线于M 、N 两点,线段MN 的垂直平分线交MN 于P 点,交x 轴于Q 点.(1)求PQ 中点R 的轨迹L 的方程;(2)证明:L 上有无穷多个整点(横、纵坐标均为整数的点),但L 上任意整点到原点的距离均不是整数.22.(2021·全国·高三竞赛)已知椭圆22:12+=x E y 的右焦点为(c,0)F ,上顶点为M ,圆222:()(0)F x c y r r -+=>,问:椭圆E 上是否存在两点P 、Q 使得圆F 内切于三角形MPQ 若存在,求出直线PQ 的方程;若不存在,请说明理由.23.(2021·全国·高三竞赛)如图所示,()(),0P a b a b <<为抛物线2:4F y x =外一点,过P 引抛物线Γ的两条切线PA PB 、,切点分别为A 、B .在线段PA 上取两点D 、E ,使得PD AE =.若过D 、E 两点的直线12l l 、分别切抛物线Γ于M 、N 两点(异于A ).求四边形MNAB 面积的最大值.24.(2021·全国·高三竞赛)已知椭圆22122:1(0)x y C a b a b+=>>,其右焦点为F ,过F 作直线l 交椭圆1C 于A 、B 两点(l 与x 轴不重合),设线段AB 中点为D ,连结OD (O 为坐标原点),直线OD 交椭圆1C 于M 、N 两点,若A 、M 、B 、N 四点共圆,且||8||3MN OD =,求椭圆1C 的离心率.25.(2018·甘肃·高三竞赛)已知椭圆2222:1x y C a b+=过点()0,2M ,且右焦点为()2,0F .(1)求椭圆C 的方程;(2)过点F 的直线l 与椭圆C 交于,A B 两点,交y 轴于点P .若,PA mAF PB nBF ==,求证:m n +为定值;(3)在(2)的条件下,若点P 不在椭圆C 的内部,点Q 是点P 关于原点O 的对称点,试求三角形QAB 面积的最小值.26.(2018·山东·高三竞赛)已知圆22:4O x y +=与曲线:3C y x t =-,(),A m n ,(),B s p ,(),,,m n s p *∈N 为曲线C 上的两点,使得圆O 上任意一点到点A 的距离与到点B 的距离之比为定值()1k k >,求t 的值.27.(2022·福建·高二统考竞赛)已知椭圆C :()222210x y a b a b+=>>的离心率为12,1A 、2A 分别为椭圆C 的左、右顶点,1F 、2F 分别为椭圆C 的左、右焦点,B 为椭圆C 的上顶点,且11BA F ∆的外接圆半径为3.(1)求椭圆C 的方程;(2)设与x 不垂直的直线l 交椭圆C 于P 、Q 两点(P 、Q 在x 轴的两侧),记直线1A P 、2PA 、2A Q 、1QA 的斜率分别为1k 、2k 、3k 、4k .已知()142353k k k k +=+,求2F PQ ∆面积的取值范围.28.(2022·新疆·高二竞赛)如图,已知ABC 内接于抛物线2:=E x y ,且边,AB AC 所在直线分别与抛物线2:4=M y x 相切,F 为抛物线M 的焦点.求证:(1)边BC 所在直线与抛物线M 相切;(2)A ,C ,B ,F 四点共圆.(2021·全国·高三竞赛)已知(2,1)S 为椭圆22Γ:182x y+=上的点,对椭圆Γ上的任意两点P 、Q ,用如下办法定义它们的“和”P Q +:过点S 作一条平行于PQ (若点P 与Q 重合,则直线PQ 表示椭圆Γ在P 处的切线)的直线l 与椭圆Γ交于不同于S 的另一点,记作P Q +(若l 与椭圆Γ相切,则规定S 为P Q +).并规定n nP P P P=+++个.29.若点(0,P Q ,求P Q +、2P 以及100P 的坐标.30.在椭圆Γ上是否存在不同于S 的点P ,满足3P S =?若存在,求出所有满足条件的点P 的坐标;若不存在,请说明理由.高中数学竞赛与强基计划试题专题:解析几何答案一、单选题1.(2020·北京·高三强基计划)从圆224x y +=上的点向椭圆22:12x C y +=引切线,两个切点间的线段称为切点弦,则椭圆C 内不与任何切点弦相交的区域面积为()A .2πB .3πC .4πD .前三个答案都不对【答案】A【分析】算出椭圆内与切点弦不相交的点的边界的方程,从而可求区域的面积.【详解】设圆224x y +=上一点为(2cos ,2sin )P θθ,则对应切点弦所在直线l 的方程为2cos 2sin 12xy θθ⋅+⋅=即cos 2sin 1x y θθ+=,1≥,故椭圆C 内不与任何切点弦相交的区域面积即为椭圆2241x y +=围成的面积,其面积为1ππ122⨯⨯=.2.(2022·北京·高三校考强基计划)内接于椭圆22149x y +=的菱形周长的最大值和最小值之和是()A.B.CD .上述三个选项都不对【答案】D【分析】求出椭圆的极坐标方程,设内接于椭圆22149x y +=的菱形为ABCD ,()12,,,2A B πρθρθ⎛⎫+ ⎪⎝⎭,分别求出22,OA OB ,再根据222AB OA OB =+,结合三角恒等变换化简,再根据三角函数的性质求出AB 的最大值和最小值,即可得解.【详解】解:由22149x y +=,得229436x y +=,化为极坐标方程为223645cos ρθ=+,设内接于椭圆22149x y +=的菱形为ABCD ,则OA OB ⊥,设()12,,,2A B πρθρθ⎛⎫+ ⎪⎝⎭,则22123645cos OA ρθ==+,22222363645sin 45cos 2OB ρπθθ==+⎛⎫++ ⎪⎝⎭,所以2221222363645cos 45sin AB ρρθθ=+=+++2223613361325162025sin cos 36sin 24θθθ⨯⨯==+++,当2sin 20θ=时,2AB 取得最大值,即AB所以菱形的周长的最大值为当2sin 21θ=时,2AB 取得最小值,即AB 的最小值为13,所以菱形的周长的最小值为13,所以内接于椭圆22149x y +=的菱形周长的最大值和最小值之和是1313=.3.(2020·湖北武汉·高三统考强基计划)已知直线1211::22l y x l y x =-=,,动点P 在椭圆22221(0)x y a b a b +=>>上,作1//PM l 交2l 于点M ,作2//PN l 交1l 于点N .若22PM PN +为定值,则()A .2ab =B .3ab =C .2a b =D .3a b=【答案】C【分析】根据四边形OMPN 是平行四边形,得到2222PM PN OM ON +=+为定值,然后将取特殊位置(),0P a ,()0,P b 求解.,易知由四边形OMPN 是平行四边形,所以2222PM PN OM ON +=+为定值,取点(),0P a 时,由()1212y x a y x ⎧=-⎪⎪⎨⎪=-⎪⎩,解得24a x a y ⎧=⎪⎪⎨⎪=-⎪⎩,所以,24a a M ⎛⎫- ⎪⎝⎭,由对称性得:,24a a N ⎛⎫ ⎪⎝⎭,所以22258OM ON a +=,取点()0,P b 时,由1212y x b y x ⎧=+⎪⎪⎨⎪=-⎪⎩,解得2x bb y =-⎧⎪⎨=⎪⎩,所以,2b M b ⎛⎫- ⎪⎝⎭,由对称性得:,2b N b ⎛⎫ ⎪⎝⎭,所以22252OM ON b +=,所以225582a b =,即2a b =,4.(2020·北京·高三强基计划)设直线3y x m =+与椭圆2212516x y +=交于A ,B 两点,O 为坐标原点,则OAB面积的最大值为()A .8B .10C .12D .前三个答案都不对【答案】B【分析】联立直线方程和椭圆方程后消元,利用公式可求面积的表达式,再利用基本不等式可求面积的最大值.【详解】由22312516y x m x y =+⎧⎪⎨+=⎪⎩可得22241150254000x mx m ++-=,()22222500424125400160024116000m m m ∆=-⨯-=⨯->,故m而241241AB ==,故1122ABOS AB ==△2224120210241m m+-⨯==,当且仅当m=等号成立,故OAB面积的最大值为10,5.(2022·贵州·高二统考竞赛)如图,1C,2C是离心率都为e的椭圆,点A,B是分别是2C的右顶点和上顶点,过A,B两点分别作1C的切线1l,2l.若直线1l,2l的斜率分别为1k,2k,则12k k的值为()A.2e B.21e-C.21e-D.21e【答案】C【详解】不妨设22122:1x yCa b+=,222222:x yCa bλ+=(0,1)a bλ>>>,∴,(,0)(0,)A aB bλλ,11:()l y k x aλ=-代入1C的方程得:()2222322422211120b a k x a k x a k a bλλ+-+-=,()()()23222224222111Δ240a kb a k a k a bλλ=--+-=,化简得()221221bkaλ=-.22:l y k x bλ=+代入22221x ya b+=得()22222222222220b a k x a bk x a b a bλλ+-+-=.()()()222222222222Δ240a bkb a k a b a bλλ=-+-=.化简得()222221bkaλ-=.∴422124bk ka=,∴222212221b a ck k ea a-===-,6.(2020·湖北武汉·高三统考强基计划)过椭圆22149x y+=的中心作两条互相垂直的弦AC和BD,顺次连接,,,A B C D得一四边形,则该四边形的面积可能为()A.10B.12C.14D.16【答案】B【分析】设()11,A x y,()22,B x y,设x轴正方向旋转到与向量OA 同向所转过的角为α,利用三角函数的定义表示,A B的坐标,代入椭圆方程,求得223636,OA OB关于α的函数表达式,进而得到223636OA OB关于α的函数表达式,利用三角函数恒定变形化简,然后利用三角函数的性质求得其取值范围,进而得到四边形面积的取值范围,从而做出选择.【详解】设()11,A x y ,()22,B x y ,设x 轴正方向旋转到与向量OA同向所转过的角为α,并根据题意不妨设OA 到OB 为逆时针旋转π2,则11cos ,sin .x OA y OA αα⎧=⎪⎨=⎪⎩,22cos sin ,2sin cos .2x OB OB y OB OB πααπαα⎧⎛⎫=+=- ⎪⎪⎪⎝⎭⎨⎛⎫⎪=+= ⎪⎪⎝⎭⎩22149x y +=,229436x y +=,2222369cos 4sin 5cos 4OA ααα=+=+, 22223694cos 5sin 4sin OBααα=+=+,2222236362516925cos sin 36sin 23636,44OA OBααα⎡⎤=+=+∈⎢⎥⎣⎦,∴36136,2OA OB ⎡⎤∈⎢⎥⎣⎦,1442,1213ABCD S OA OB ⎡⎤=∈⎢⎥⎣⎦,当4πα=时取到最小值14413,当0α=时取得最大值12.只有选项B 中的12在此范围内7.(2019·贵州·高三校联考竞赛)设椭圆C :()222210x y a b a b +=>>的左、右焦点分别为12,F F ,其焦距为2c .点322c N ⎛⎫⎪ ⎪⎝⎭在椭圆的内部,点M 是椭圆C上的动点,且112||MF MN F +<恒成立,则椭圆C 的离心率的取值范围是()A.⎛ ⎝⎭B.⎫⎪⎪⎝⎭C.,121⎛⎫⎪ ⎪⎝⎭D.⎝⎭【答案】D【详解】由322c N ⎛⎫ ⎪ ⎪⎝⎭在椭圆的内部,得22229142c c a b +<,即222222924b c a c a b +<,从而422441590a a c c -+>,得到4291540e e -+>,因此()()2231340e e -->.因为0<e <1,所以3e 2-4<0,故3e 2<1,得到0e <<.又由112||MF MN F +<恒成立,即22||a MN MF +-<恒成立,等价于()2max2||a MN MF +-<,亦即22a NF +<,等价于2a ,即2a e >.e <<二、多选题8.(2022·贵州·高二统考竞赛)如图,M ,N 分别是Rt ABC △两直角边上的动点,P 是线段MN 的中点,则以下结论正确的是()A .当△AMN 的面积为定值时,点P 的轨迹为双曲线一支B .当|MN |为定值时,点P 的轨迹为一圆弧C .当||||AM AN +为定值时,点P 的轨迹为不含端点线段D .当△AMN 的周长为定值时,点P 的轨迹为抛物线【答案】ABC【详解】建立如图的直角坐标设(),P x y ,则(2,0)M x ,(0,2)N y ,0x >,0y >,对于A ,当Rt △AMN 面积为定值()20k k >时,12222x y k ⋅⋅=,∴(0)x y k k ⋅=>轨迹为双曲线一支,所以A 正确.对于B ,若2(0)MN d d =>,则222222444x y d x y d +=⋅+=,(0,0)x y >>是一圆弧,所以B 正确.对于C ,当2(0)AM AN t t +=>时,222(0,0)x y t x y +=>>,即(0,0)x y t x y +=>>为空端点线段,所以C 正确.对于D ,当Rt △AMN 的周长为定值2C 时,则222x y C ++,即(0,0)x y C x y +=>>,()C x y =-+,∴22222222x y C Cx Cy xy x y +=--+++,所以2(22)2x C y Cx C -=-,2222Cx C y x C-=-轨迹为双曲线一支,所以D 错误.9.(2020·北京·高三校考强基计划)已知A ,B 分别为双曲线2214x y -=的左、右顶点,P 为该曲线上不同于A ,B 的任意一点设,,∠=∠= PAB PBA PAB αβ的面积为S ,则()A .tan tan αβ⋅为定值B .tantan22αβ⋅为定值C .tan()S αβ⋅+为定值D .cot()S αβ⋅+为定值【答案】AC【分析】利用三角换元得到P 的坐标为2,tan ,0,cos 2P πθθθ⎛⎫⎛⎫∈⎪ ⎪⎝⎭⎝⎭,利用斜率公式可求,αβ与θ的关系,化简后可得,αβ的关系,故可判断AB 的正误,根据面积公式可求S (用θ表示),故可判断CD 的正误.【详解】不妨设2,tan ,0,cos 2P πθθθ⎛⎫⎛⎫∈⎪ ⎪⎝⎭⎝⎭,则tan sin tan 22(1cos )(2)cos θθαθθ==+--,tan sin tan 22(1cos )2cos θθβθθ=-=---,1||tan 2tan 2S AB θθ=⋅⋅=,因此2114tan ,tan ,221t t S t t αβ==-=-,其中tan 2t θ=.对于选项A ,1tan tan 4αβ=-为定值.对于选项B ,由于22224tantan22tan tan 1tan tan tantan 2222αβαβαβαβ=⎛⎫-++ ⎪⎝⎭,因此若tantan22αβ为定值,则tantan 22αβ+为定值,从而tan 2α和tan 2β是确定的值,矛盾,对于选项C ,D ,有()2112122tan()115122t t t t t tαβ--+==-+⋅,因此tan()S αβ⋅+是定值,cot()S αβ⋅+不是定值.10.(2020·北京·高三校考强基计划)已知点(1,1),(1,0)A Q ,P 为椭圆22143x y +=上的动点,则||||PA PQ +的()A.最大值为4B.最大值为4C.最小值为4-D.最小值为4【答案】BD【分析】利用椭圆的定义可求||||PA PQ +的最值.【详解】注意到Q 为椭圆的右焦点,设其椭圆的左焦点为(1,0)Q '-,则()()||||||44||PA PQ PA PQ PA PQ +=+-=-''+,而||PA PQ -'的取值范围是,AQ AQ ''-⎡⎤⎣⎦,即[,因此所求最大值为4,最小值为4三、填空题11.(2022·江苏南京·高三强基计划)设F ,l 分别为双曲线()22411212x y --=的右焦点与右准线,椭圆Γ以F 和l 为其对应的焦点及准线,过F作一条平行于y =的直线,交椭圆Γ于A 、B 两点,若Γ的中心位于以AB 为直径的圆外,则椭圆离心率e 的范围为___________.【答案】⎫⎪⎪⎭【详解】由双曲线方程可知其焦准距为3,则椭圆Γ的焦准距23b c=(同侧焦点和准线),如图,设椭圆中心为O,建立平面直角坐标系,设F :()222210x y a b a b+=>>,()11,A x y ,()22,B x y ,直线AB方程:)y x c =+,联立直线AB 和椭圆Γ可得:()222222223630b a x a cx a c a b +++-=,由韦达可得:212222212226+=-+33=+3a x x b a a c x x b a ⋅⎧⎪⎪⎨⎪⎪⎩,由椭圆中心O 位于以AB 为直径的圆外,则有12120OA OB x x y y ⋅=+>,结合韦达定理可得:222242222422222233330333a c a b b a c a b b b a b a b a----+=>+++,所以422441030a a c c -+<,即423e 10e 40-+<,e 1<<,12.(2018·山东·高三竞赛)若直线65280x y --=交椭圆22221x ya b+=(0a b >>,且2a 、b 为整数)于点A 、C .设()0,B b 为椭圆的上顶点,而ABC 的重心为椭圆的右焦点2F ,则椭圆的方程为______.【答案】2212016x y +=【详解】设()11,A x y ,()22,C x y ,由题意ABC 的重心为椭圆的右焦点2F ,整理得213x x c +=,21y y b +=-.由()11,A x y ,()22,C x y 在直线65280x y --=上,得到212165y y x x -=-.由()11,A x y ,()22,C x y 在椭圆()222210x y a b a b +=>>上,得到2211221x y a b +=,2222221x y a b+=.两式相减并整理得()()()()2212122121635y y y y b b a x x x x c +---==⋅+-,整理得225a bc =.①本号资料全部来源于微信公#众号:数学第六感因为()11,A x y ,()22,C x y 在直线65280x y --=上,所以有1165280x y --=,2265280x y --=.将123x x c +=,12y y b +=-代入得()635560c b ⨯---=,整理得18556c b +=.②联立①②,且注意到a 、b 为整数,解得2c =,4b =,220a =.故所求的椭圆方程为2212016x y +=.13.(2022·新疆·高二竞赛)设z 为复数,若方程2297--=z z 表示一条圆锥曲线,则此曲线的离心率=e ___________.【答案】4【详解】令||,|3|,|3|=-=+=z a z b z c ,则27-=a bc .由复数的几何意义知222218+=+b c a .所以由前两式知2()32-=b c,即||-=b c ,故||3||3||6--+=<z z .因此z6的双曲线,14.(2021·全国·高三竞赛)已知集合{}22(,)|||||,0,(,)|1,044x y A x y x y t t B x y m m ⎧⎫=+>=+≤<<⎨⎩≤⎬⎭满足B A ⊆,若P 为集合B 的边界线C 上任意一点,12F F 、为曲线C 的焦点,I 为12PF F △的内心,直线1IF 和2IF 的斜率分别为12k k 、,且1213k k ⋅=-则t 的最小值为________.【详解】因为12F F 、为曲线C 的焦点,I 为12PF F △的内心,若曲线C 的方程为22221x y a b +=,则I 的轨迹方程为22221x y c bc c a +=⎛⎫ ⎪+⎝⎭,故有22121.3bc c a c k k ⎛⎫ ⎪+⎝⎭=-=-⋅可知::2:a b c =,所以3m =.设(2cos )P θθ为曲线C上一点,则有|2cos ||t θθ≥+恒成立,即t ≥15.(2021·全国·高三竞赛)已知ABCD Y 的四个顶点均在双曲线2214y x -=上,点(0,1)P 在边AB 上,且12AP PB =,则ABCD Y 的面积等于_______.【答案】4【分析】由对称性,知O 为平行四边形的中心,设()00,A x y ,得()002,32B x y --,将点A 、B 的坐标代入双曲线方程,求得A 、B 的坐标,利用等面积法知4ABCD AOB S S = △,代入即可求解.【详解】由平行四边形的对称性与双曲线的对称性,知O 为平行四边形的中心,由A 、B 、C 、D 四点在两支双曲线上各有两点,不妨设A 、D 在左支上,B 、C 在右支上,如图:考虑A 、B 关于双曲线中心的对称点,A B '',因为单支双曲线上不存在四点构成平行四边形,知,A C B D =''=,所以ABCD Y 的对称中心为O .设()00,A x y ,由12AP PB =,得()002,32B x y --.将点A 、B 的坐标代入双曲线方程得()22002020*******y x y x ⎧-=⎪⎪⎨-⎪-=⎪⎩,解得:00814x y ⎧=⎪⎪⎨⎪=-⎪⎩或00814x y ⎧=-⎪⎪⎨⎪=-⎪⎩所以A B x x ⎧=⎪⎪⎨⎪=⎪⎩或A B x x ⎧=⎪⎪⎨⎪=⎪⎩.故242||21ABCDADB AOB A B S S S OP x x ===⋅-=⨯⨯YV V.四、解答题16.(2022·湖北武汉·高三统考强基计划)设F 为椭圆C :22194x y +=的左焦点,P 为椭圆C上的一点(1)作正方形FPAB (F ,P ,A ,B 按逆时针排列)当P 沿着椭圆运动一周,求动点B 的轨迹方程.(2)设()3,2Q 为椭圆外一点,求PQ PF +的取值范围.【答案】(1)((22=149x x -+.(2)【详解】(1)如图所示,将椭圆C绕其左焦点()F 逆时针旋转90 ,得到椭圆'C,注意到在正方形FPAB 中,点B 可以看成也是由点P 绕点F 逆时针旋转90 而形成的,由于点P 在椭圆C 上运动,则点B 在椭圆'C 上运动.求B 的轨迹方程,也就是求椭圆'C 的方程.注意到椭圆'C的中心坐标为(,从而'C的方程为((22=149x x +.(2)如图所示,|||||PQ PFQF +≥当且仅当,,P F Q 三点共线,即P 运动到1P 位置时,等号成立.记椭圆C 的右焦点为)E,注意到()||||=||2||=||||6PQ PF PQ a PE PQ PE ++--+,显然有||||||=PQ PE QE -≤从而||||6PQ PF +≤+,当且仅当,,P E Q 三点共线,即P 运动到2P 位置时,等号成立.||||6PQ PF ≤+≤即PQ PF+的取值范围17.(2018·全国·高三竞赛)一束直线12,,l l 的每条均过xOy 平面内的抛物线2:C y x =的焦点,()1i l i ≥与抛物线C 交于点i A 、i B .若1l 的斜率为1,()2i l i ≥的斜率为1+2014l 的解析式.【答案】((()()201520152014201411112411y x -⎛⎫=⋅- ⎪⎝⎭-【详解】易知抛物线焦点1,04P ⎛⎫⎪⎝⎭.设()1:1,2,4i i l y k x i ⎛⎫=-= ⎪⎝⎭ ,并与2y x =联立知点i A 、i B 的横坐标i A x 、i B x 满足关于x 的方程()2222120216i i i k k x k x -++=且i i A B x x ≠.则i ii i A B A B x =-=221i i k k +=.从而,当2i≥时,有1111i i k k -==+.记{}n F 满足121F F ==及递推关系21n n n F F F ++=+则{}n F 为斐波那契数列其通项公式为n nn F ⎡⎤⎛⎥=- ⎥⎝⎭⎝⎭⎦.下面证明:1i i iF k F +=对一切正整数i 成立.由2111F k F ==,知i=1时结论成立.设i=t 时结论成立.则121111111t t t t t t t t t F F F F k k F F F +++++++=+=+==即i=t+1时结论也成立.由数学归纳法知1i i iF k F +=对一切正整数i 成立.特别地,201520142014F k F =.从而,2014l的解析式为((()()201520152014201411112411y x +-⎛⎫=⋅- ⎪⎝⎭-.【注】本题亦可用不动点方法求数列{}i k 的通项.18.(2018·福建·高三竞赛)已知1F 、2F 分别为椭圆()2222:10x y C a b a b +=>>的左、右焦点,点3P ⎛⎫ ⎪⎝⎭在椭圆C 上,且12F PF △的垂心为5,33H ⎛⎫- ⎪ ⎪⎝⎭.(1)求椭圆C 的方程;(2)设A 为椭圆C 的左顶点,过点2F 的直线l 交椭圆C 于D 、D 两点.记直线AD 、AE 的斜率分别为1k 、2k ,若1212k k +=-,求直线l 的方程.【答案】(1)22143x y +=(2)()21y x =-【详解】设()1,0F c -,()2,0F c .由12F PF的垂心为53H ⎫-⎪⎪⎝⎭,得12F H PF ⊥.所以12531F H PF k k -⋅==-,224593c -=,解得21c =.由点P ⎫⎪⎪⎝⎭在椭圆C 上,得2224119a b +=.结合2221a b c -==,解得24a =,23b =.所以椭圆C 的方程为22143x y +=.(2)由(1)知()2,0A -,()21,0F .若l 的斜率不存在,则由对称性,知120k k +=,不符合要求.若l 的存在,设为k ,则l 的方程为()1y k x =-.由()221143y k x x y ⎧=-⎪⎨+=⎪⎩,得()22224384120k x k x k +-+-=.①设()11,D x y ,()22,E x y ,则2122843k x x k +=+,212241243k x x k -=+.所以()()1212121212112222k x k x y y k k x x x x --+=+=+++++()()()12121234331122222x x k k x x x x ⎡⎤++⎛⎫=-+-=⋅-⎢⎥⎪++++⎢⎥⎝⎭⎣⎦()()221222121222834344322412824244343k x x k k k k k x x x x k k ⎡⎤⎛⎫+⎢⎥ ⎪⎡⎤+++⎝⎭⎢⎥=⋅-=⋅-⎢⎥⎢⎥-+++⎢⎥⎣⎦+⨯+⎢⎥++⎣⎦()222222238161221122412161612k k k k k k k k k k ⎡⎤++⎛⎫+⎢⎥=⋅-=⋅-=- ⎪-+++⎢⎥⎝⎭⎣⎦.又1212k k +=-,因此2k =,直线l 的方程为()21y x =-.19.(2018·江西·高三竞赛)若椭圆221259x y +=上不同的三点()11,A x y ,94,5B ⎛⎫ ⎪⎝⎭,()22,C x y 到椭圆右焦点的距离顺次成等差数列,线段AC 的中垂线l 交x 轴于点T ,求直线BT 的方程.【答案】252064x y -=【详解】用a 、b 、c 分别表示椭圆的半长轴、半短轴及半焦距之长度,则5a =,3b =,4c =,右焦点为()4,0F ,且准线方程为2a x c=,由21AFca a x c=-,22CF c a a x c=-,得1455AF x =-,2455CF x =-,根据等差性质,2AF CF BF +=,而95BF =,即12441855555x x ⎛⎫⎛⎫-+-= ⎪ ⎪⎝⎭⎝⎭,所以128x x +=.①设线段AC 的中点为D ,则其坐标为124,2y y D +⎛⎫ ⎪⎝⎭,又设点T 的坐标为()0,0T x ,则AC 的中垂线DT 的方程为()12121242y y x xy x y y +--=---.因()0,0T x 在此直线上,故有()1212012042y y x xx y y +--=---,即()221201242y y x x x --=-.②又根据A 、B 在椭圆上,得()221192525y x =-,()222292525y x =-,所以()()22121212925y y x x x x -=-+-,据①,即有()22121236225y y x x -=--.③再据②③得06425x =,即点T 的坐标为64,025T ⎛⎫⎪⎝⎭,于是直线BT 的方程为252064x y -=.20.(2018·湖北·高三竞赛)已知O 为坐标原点,()1,0N ,点M 为直线=1x -上的动点,MON ∠的平分线与直线MN 交于点P ,记点P 的轨迹为曲线E .(1)求曲线E 的方程;(2)过点11,22Q ⎛⎫-- ⎪⎝⎭作斜率为k 的直线l ,若直线l 与曲线E 恰好有一个公共点,求k 的取值范围.【答案】(1)()201y x x =≤<(2)11,132⎧⎫+⎪⎪⎛⎤-⎨⎬⎥⎝⎦⎪⎪⎩⎭ 【详解】(1).设()(),,1,P x y M t -,易知01x ≤<.因为OP 平分MON ∠,所以OM MP PN ON==,所以)11,x x +-①)0y t y -=-.②由①②可得21y t x =-,代入①得到11x x +=-E 的方程为()201y x x =≤<.(2).记()()1,1,1,1A B -,则11,3QA QB k k ==-.直线l 的方程为1122y k x ⎛⎫+=+ ⎪⎝⎭,与抛物线方程2y x =联立,消去x 得()21102ky y k -+-=当直线l 与抛物线2y x =相切于点T 时,()1210k k ∆=--=,解得1,2k =当1k k ==T y =T 在曲线E 上;当212k k ==时,T y =,切点T 不在曲线E 上.若直线l 与曲线E 恰好有一个公共点,则有QB QA k k k <≤或k =,故所求k的取值范围为1,13⎛⎤-⋃ ⎥⎝⎦⎪⎪⎩⎭.21.(2021·全国·高三竞赛)过抛物线22y px =(p 为不等于2的质数)的焦点F ,作与x 轴不垂直的直线l 交抛物线于M 、N 两点,线段MN 的垂直平分线交MN 于P 点,交x 轴于Q 点.(1)求PQ 中点R 的轨迹L 的方程;(2)证明:L 上有无穷多个整点(横、纵坐标均为整数的点),但L 上任意整点到原点的距离均不是整数.【答案】(1)24()(0)y p x p y =-≠;(2)证明见解析.【详解】(1)抛物线22y px =的焦点为(,0)2p ,设l 的直线方程为()(0)2p y k x k =-≠.由得222y pxp y k x ⎧=⎪⎨⎛⎫=- ⎪⎪⎝⎭⎩得222221(2)04k x pk p x p k -++=.设M 、N 的横坐标分别为12x x 、,由21222pk p x x k ++=,得22122222,()2222P Px x pk p pk p p px y k k k k+++===-=,而PQ l ⊥,故PQ 的斜率为1k -,PQ 的方程为2212()2p pk py x k k k +-=--.代入0Q y =得222223222Q pk p pk px p k k ++=+=.设动点R 的坐标为(),x y ,则:21()21()22p Q P Qp x x x p k p y y y k ⎧=+=+⎪⎪⎨⎪=+=⎪⎩,因此222()4(0)p p x p y y k-==≠,故PQ 中点R 的轨迹L 的方程为24()(0)y p x p y =-≠.(2)显然对任意非零整数t ,点2((41),)p t pt +都是L 上的整点,故L 上有无穷多个整点.反设L 上有一个整点(),x y 到原点的距离为整数()0m m ≥,不妨设0,0x y >>,则:22224()x y m y p x p ⎧+=⎨=-⎩①②,因为p 是奇质数,于是|p y ,从②可推出|p x ,再由①可推出|p m .令111,,x px y py m pm ===,则有22211121141x y m y x ⎧+=⎨=-⎩③④,由③,④得2211114x x m -+=,于是2211(81)(8)17x m +-=,即()()111181881817x m x m +++-=,于是111181817,8181x m x m ++=+-=,得111x m ==,故10y =,有10y py ==,但L 上的点满足0y ≠,矛盾!因此,L 上任意点到原点的距离不为整数.22.(2021·全国·高三竞赛)已知椭圆22:12+=x E y 的右焦点为(c,0)F ,上顶点为M ,圆222:()(0)F x c y r r -+=>,问:椭圆E 上是否存在两点P 、Q 使得圆F 内切于三角形MPQ 若存在,求出直线PQ的方程;若不存在,请说明理由.【答案】存在,PQ的方程为(260x y +-+-=.【详解】假设这样的P 、Q 存在,且设()()1122,,,P x y Q x y ,由题意知(0,1),(1,0)M F ,所以直线()111:10MP y x x y x --+=.因为该直线与圆F 相切,则d r =r =,两边平方化简得()()2222111111x y r x y ⎡⎤+-=+-⎣⎦,整理得()()()()22221111111210r x ryx y -+--+-=.因为()221121x y =-,消去1x 得()()()()()2222111112111210r y r yx y -⋅-+--+-=.因为11y ≠,两边同时除以11y -,得()()()()221111211120r y r y x -⋅++---=,整理得()()221121310x ryr -+-+-=,即点P 在直线()()2221310x r y r -+-+-=上.同理,点Q 也在直线()()2221310x r y r -+-+-=上,因此直线PQ 的方程为()()2221310x r y r -+-+-=.又因为直线PQ 圆Fr=,解得r =因此直线PQ 存在且直线PQ的方程为(260x y +-+-=.23.(2021·全国·高三竞赛)如图所示,()(),0P a b a b <<为抛物线2:4F y x =外一点,过P 引抛物线Γ的两条切线PA PB 、,切点分别为A 、B .在线段PA 上取两点D 、E ,使得PD AE =.若过D 、E 两点的直线12l l 、分别切抛物线Γ于M 、N 两点(异于A ).求四边形MNAB 面积的最大值.【详解】设()()()()11220000,,,,,,,A x y B x y M x y N x y '',则直线AP 的方程为()112y y x x =+,直线BP 的方程为()222y y x x =+,故有121242y y a y y b ⎧=⎪⎪⎨+⎪=⎪⎩,同理可得1010,22E D y y y yy y '++==,又因为PD AE =,所以1E D y y b y +=+,即002y y b +'=,故12121200424AB MN y y k k x x y y b y y '-=====-++,因此//AB MN .直线AB 的方程为22by x a =+,直线MN 的方程为0000004y y y x y y y y '''=+++,即0022y y by x '=+,故两平行线间的距离d ',||AB ===||MN =所以00|4|1(||||))24MNABy y a S d AB MN '-=⋅+=⋅,其中0204a y y b ≤'≤,可令22004,b a A b y y X '-=-=,则:1(4MNAB S A X =-218=+3183⎛≤ ⎝⎭当22001(4)9b y y b a '-=-时取到最大值.24.(2021·全国·高三竞赛)已知椭圆22122:1(0)x y C a b a b+=>>,其右焦点为F ,过F 作直线l 交椭圆1C 于A 、B 两点(l 与x 轴不重合),设线段AB 中点为D ,连结OD (O 为坐标原点),直线OD 交椭圆1C 于M 、N 两点,若A 、M 、B 、N 四点共圆,且||8||3MN OD =,求椭圆1C 的离心率.【分析】先将椭圆与直线联立,结合韦达定理表示出D 坐标,再结合直线OD 交椭圆1C 于M 、N 两点,若A 、M 、B 、N 四点共圆,且||8||3MN OD =,求出2,3M ⎛ ⎝⎭再代入椭圆求出a ,进而求出离心率.【详解】不妨设椭圆1C 的半焦距1c =,则221b a =-,椭圆右焦点为(1,0)F .设:1l x ky =+,将1x ky =+,代入22221x ya b+=消去x 化简整理得()()()222222222110a k k a y a ky a -++---=.显然,方程判别式Δ0>,设()(),,,A A B B A x y B x y .由韦达定理知()2222221A B a k y y a k k a-+=--+,从而()()22222222222211122222A B D A B a k x x ax ky ky a k k a a k k a ⎛⎫-+==++=-+= ⎪ ⎪-+-+⎝⎭,()2222211D D a k x y k a k k a--==--+,于是()22222222221,a k a D a k k a a k k a ⎛⎫-- ⎪ ⎪-+-+⎝⎭.所以直线OD 的方程为()221a x y a k =--.设圆AMBN 的方程为222:0C x y Dx Ey F ++++=,直线l 直线MN 的方程为()232:(1)01a C x ky x y a k ⎛⎫--+= ⎪ ⎪-⎝⎭,由于3C 经过12C C 、的交点,且123C C C 、、均为二次曲线,则存在常数12λλ、,使得()()2222212222(1)11a x y x ky x y x y Dx Ey Fa b a k λλ⎛⎫⎛⎫--+=+-+++++ ⎪ ⎪ ⎪-⎝⎭⎝⎭,比较方程两边xy 系数知()2201a k a k -+=-,即2221a k a =-,由对称性不妨设k =.代入点D 的坐标得1,22D a ⎛- ⎪ ⎪⎝⎭,又||8||3MN OD =,得点2,3M ⎛ ⎝⎭,而M 在1C上,故22222311a a ⎛⎛⎫ ⎪ ⎝⎭⎝⎭+=-,解得a =于是1C的离心率为3c e a ==.25.(2018·甘肃·高三竞赛)已知椭圆2222:1x y C a b+=过点()0,2M ,且右焦点为()2,0F .(1)求椭圆C 的方程;(2)过点F 的直线l 与椭圆C 交于,A B 两点,交y 轴于点P .若,PA mAF PB nBF ==,求证:m n +为定值;(3)在(2)的条件下,若点P 不在椭圆C 的内部,点Q 是点P 关于原点O 的对称点,试求三角形QAB 面积的最小值.【详解】(1)由题意b=2,c=2,所以28a =,椭圆C 的方程为22184x y +=.(2)设A 、B 、P 的坐标分别为()()()1122,,,,0,x y x y t .由PA mAF = 知121m x m =+,11ty m=+.又点A 在椭圆C 上,则22211184m t m m ⎛⎫⎛⎫ ⎪ ⎪++⎝⎭⎝⎭+=,整理得222840m m t +-+=.由PB nBF =,同理得到222840n n t +-+=.由于A 、B 不重合,即m n ≠,故m 、n 是二次方程222840x x t +-+=的两根,所以m+n=-4,为定值.(3)依题意,直线l 的方程为12x yt+=,即()22t y x =--,与椭圆C 的方程联立,消去y 并整理,得()2222244160t xt x t +-+-=,()()42221642416321280t t tt ∆=-+-=+>,所以221212224416,22t t x x x x t t -+=⋅=++,而1212122QAB S t x x t x x ∆=⋅⋅-=⋅-()()22222121212=4QAB S t x x t x x x x ∆⎡⎤=-+-⎣⎦()42222216166422t t tt t ⎡⎤-⎢⎥=-⎢⎥++⎣⎦()2222321282t t t +=⋅+.()2243212t ⎡⎤⎢⎥=-⎢⎥+⎣⎦由已知,点P 不在椭圆C 的内部,得2t ,即24t ,所以2QAB S ∆的最小值为82563299⨯=,故三角形QAB 面积的最小值为163.26.(2018·山东·高三竞赛)已知圆22:4O x y +=与曲线:3C y x t =-,(),A m n ,(),B s p ,(),,,m n s p *∈N 为曲线C 上的两点,使得圆O 上任意一点到点A 的距离与到点B 的距离之比为定值()1k k >,求t 的值.【答案】43t =【详解】设(),P x y 为圆O 上任意一点,则由题意知PA k PB=.即222PA k PB =,于是()()()()22222x m y n k x s y p ⎡⎤-+-=-+-⎣⎦,整理得()()()()22222222222222111k s m kp nmn k s p x y x y k k k --+-++--=---.因此点P 的轨迹是一个圆.因为(),P x y 为圆上任意一点,所以此圆与圆22:4O x y +=必为同一个圆,于是有()22201k s m k --=-,()22201k p nk --=-,()()22222241mn k s p k +-+=-,整理得20k s m -=,20k p n -=,所以()()()()()22222424222222222411m n k s p k sk p k s p ks p k k +-++-+==+=--.因为s ,*p N ∈,所以21s ≥,21p ≥,从而22242k s p =≤+.又因为1k >,所以1s p ==,22k =,2m n ==.因此将()2,2A ,()1,1B ,代入3y x t =-,得43t =.27.(2022·福建·高二统考竞赛)已知椭圆C :()222210x y a b a b+=>>的离心率为12,1A 、2A 分别为椭圆C 的左、右顶点,1F 、2F 分别为椭圆C 的左、右焦点,B 为椭圆C 的上顶点,且11BA F ∆的外接圆半径为3.(1)求椭圆C 的方程;(2)设与x 不垂直的直线l 交椭圆C 于P 、Q 两点(P 、Q 在x 轴的两侧),记直线1A P 、2PA 、2A Q 、1QA 的斜率分别为1k 、2k 、3k 、4k .已知()142353k k k k +=+,求2F PQ ∆面积的取值范围.【答案】(1)2211612x y +=(2)0,2⎛ ⎝⎭【详解】(1)由椭圆C 的离心率为12,知12c a =,于是112BF a c OF ===,所以1=30F BO ∠︒,1=60BFO ∠︒,11=120BF A ∠︒,又AB ===,且11BA F ∆所以11==2sin sin1203AB BF A ∠⨯︒,解得=2c ,因此,=4a,b =所以,椭圆C 的方程为2211612x y +=.(2)如图,易知直线l 斜率不为0,设l 方程为x ty m =+,由22=++=11612x ty m x y ⎧⎪⎨⎪⎩,得()2223463480t y mty m +++-=,设()11,P x y ,()22,Q x y ,则122634mt y y t -+=+,212234834m y y t -=+,由(1)知,()14,0A -,()24,0A ,所以122211111222111134441643PA PA y y y y k k k k x x x y ⋅=⋅=⋅===-+---,同理,123434OA QA k k k k ⋅=⋅=-,因为()142353k k k k +=+,所以()2323335443k k k k --=+,()2323233543k k k k k k +-⋅=+,由l 与x 不垂直可得230k k +≠,所以23920k k =-,即22920PA QA k k ⋅=-,所以121294420y y x x ⋅=---,()()1212209440y y ty m ty m ++-+-=,于是()()()()22121292094940t y y t m y y m ++-++-=,()()()222223486920949403434m mt t t m m t t --+⋅+-⋅+-=++,整理得2340m m --=,解得1m =-或=4m ,因为P 、Q 在x 轴的两侧,所以2122348034m y y t -=<+,44m -<<,又1m =-时,直线l 与椭圆C 有两个不同的交点,因此1m =-,直线l 恒过点()1,0D -,。
高中数学竞赛 几何专题练习题

.高中数学竞赛——平面几何典型例题,,相交于点过点的一条直线分别与,相交于点1.如图,与,,ADDO⊙⊙OO⊙⊙OC2121︵︵上,的弧的延长线交于点,点在上,,点在的弧与线段BDADPDBPQMACO⊙O⊙21MN?OD,与线段的延长线交于点.是的外心,且QDABCBCON△四点共圆.,,求证:,PQMN OPQADBO2O1CMN??,,,的内平分角线的对称点分别为,是2.设内一点,点关于BA??BACO?O△ABC????,相交于一点..证明:,BBAACCC A'C'BO'ABC)内,的弧Γ(不含点如图,在3.中,,点在的外接圆AEBCABC△?ABC?BAC?90△.,于点,连接,,连接并延长至点使得连接交圆ΓEDBFDFEC?AE??EC?CAFEAC三点共的外心为记.求证:O,A,CO△DEF线.AΓFDBCE O;...,于的弦交圆,为中点,过引圆,4.如图,已知等圆与圆交于PAABBOOOOCDOO2121,三线交于一点..求证:的弦交圆于,过引圆CQABEFQEPOOO12EACQPOO21DFB.的内心依次记为,,,内接于圆,5.四边形II,,II,ABCABDBCD△△△ABCDACD△DABC.是圆内接四边形试证:IIII DCAB DI B I A CI C I D ABAG,BG,CG?A,?B,?C的角平分线对称的三条,证明的重心为分别关于6.已知G△ABC直线交于一点.P;...和分别交圆于在内.射线和7.梯形是圆内接梯形..PBGBCDGABCDAGAB∥CD△和.于.过且平行于的直线分别交和RABBDQBCGS四点共圆.、、求证:若平分,则、RPQCBDBG?S,分别内分,,是正六边形的两条对角线,点,8.如图,设MCEABCDEFACACNCE3AMCN,共线.使,求证:,BM??N ACCE3EDNFCMBA9.如图,一圆交的边分别于与,与,与,如果由点AB,,BCCACBBAACABC△211221AB,C的垂线也相交于一点.的垂线相交于一点,则过点分别引ABCA,BC,CB,A,2,22111AC2B1CB12POBCAA21;...C,DAD,BCF,G分别是上的两个点,弦10.已知,交于点为直径的半圆是以EABOAC,BD?AEF,?BEG的垂心分别为,,若延长线上的点,且满足BE??AEAF?BGHH,21F,K,G 三点共线.上;⑵证明⑴的交点在圆KBHAH,O2111.锐角中,,分别是其外心、垂心,求证:的外心在直线ABBOHO、H△△ABCC?B??上.12.已知的外心为,,为的外接圆上且在内部的任意一PABC?O90?A????ABCOBC点,以为直径的圆分别与,交于点,,,分别与,或其延EABPBDPCACOAOEOD长线交于点,,求证,,三点共线.AFFGG AEDFOGPCB;..。
竞赛数学高中试题及答案

竞赛数学高中试题及答案试题一:多项式问题题目:已知多项式 \( P(x) = x^3 - 3x^2 + 2x - 5 \),求 \( P(2) \) 的值。
解答:将 \( x = 2 \) 代入多项式 \( P(x) \) 中,得到:\[ P(2) = 2^3 - 3 \times 2^2 + 2 \times 2 - 5 = 8 - 12 + 4 -5 = -5 \]试题二:几何问题题目:在直角三角形 ABC 中,角 C 是直角,若 \( AB = 10 \) 且\( AC = 6 \),求斜边 BC 的长度。
解答:根据勾股定理,直角三角形的斜边 \( BC \) 可以通过以下公式计算:\[ BC = \sqrt{AB^2 - AC^2} = \sqrt{10^2 - 6^2} = \sqrt{100 - 36} = \sqrt{64} = 8 \]试题三:数列问题题目:给定数列 \( a_n = 2n - 3 \),求数列的前 5 项。
解答:根据数列公式 \( a_n = 2n - 3 \),我们可以计算出前 5 项:\[ a_1 = 2 \times 1 - 3 = -1 \]\[ a_2 = 2 \times 2 - 3 = 1 \]\[ a_3 = 2 \times 3 - 3 = 3 \]\[ a_4 = 2 \times 4 - 3 = 5 \]\[ a_5 = 2 \times 5 - 3 = 7 \]数列的前 5 项为:-1, 1, 3, 5, 7。
试题四:概率问题题目:一个袋子里有 5 个红球和 3 个蓝球,随机抽取 2 个球,求抽到一个红球和一个蓝球的概率。
解答:首先计算总的可能组合数,即从 8 个球中抽取 2 个球的组合数:\[ \text{总组合数} = \binom{8}{2} = \frac{8 \times 7}{2} = 28 \]然后计算抽到一个红球和一个蓝球的组合数:\[ \text{有利组合数} = \binom{5}{1} \times \binom{3}{1} = 5 \times 3 = 15 \]所以,抽到一个红球和一个蓝球的概率为:\[ P = \frac{\text{有利组合数}}{\text{总组合数}} =\frac{15}{28} \]试题五:函数问题题目:若函数 \( f(x) = x^2 - 4x + 4 \),求 \( f(x) \) 的最小值。
高中奥林匹克竞赛数学平面几何100题——珍藏版

高中数学联赛难度几何题100道第一题:学习证明角平分 (4)第二题:学习证明四点共圆 (5)第三题:学习证明角的倍数关系 (6)第四题:证明线与圆相切 (7)第五题:证明垂直 (8)第六题:证明线段相等 (9)第七题:证明线段为比例中项 (10)第八题:证明垂直 (11)第九题:证明线段相等 (12)第十题:证明角平分 (13)第十一题:证明垂直 (14)第十二题:证明线段相等 (15)第十三题:证明角相等 (16)第十四题:证明中点 (17)第十五题:证明线段的二次等式 (18)第十六题:证明角平分 (19)第十七题:证明中点 (20)第十八题:证明角相等 (21)第十九题:证明中点 (22)第二十题:证明线段相等 (23)第二十一题:证明垂直 (24)第二十二题:证明角相等 (25)第二十三题:证明四点共圆 (26)第二十四题:证明两圆相切 (27)第二十五题:证明线段相等 (28)第二十六题:证明四条线段相等 (29)第二十七题:证明线段比例等式 (30)第二十八题:证明角的倍数关系 (31)第二十九题:证明三线共点 (32)第三十题:证明平行 (33)第三十一题:证明线段相等 (34)第三十二题:证明四点共圆 (35)第三十三题:证明三角形相似 (36)第三十四题:证明角相等 (37)第三十五题:证明内心 (38)第三十六题:证明角平分 (39)第三十七题:证明垂直 (40)第三十八题:证明面积等式 (41)第三十九题:证明角平分 (42)第四十题:证明角相等 (43)第四十二题:证明中点 (45)第四十三题:证明角相等 (46)第四十四题:证明垂直 (47)第四十五题:证明角相等 (48)第四十六题:证明垂直 (49)第四十七题:证明四点共圆 (50)第四十八题:证明四点共圆 (51)第四十九题:证明四点共圆 (52)第五十题:证明角平分 (53)第五十一题:证明线段相等 (54)第五十二题:证明两圆外切 (55)第五十三题:证明垂直 (56)第五十四题:证明垂直 (57)第五十五题:证明垂直 (58)第五十六题:证明垂直 (59)第五十七题:证中点 (60)第五十八题:证明角相等 (61)第五十九题:证明角相等 (62)第六十题:证明四点共圆 (63)第六十一题:证明四点共圆 (64)第六十二题:证明四点共圆 (65)第六十三题:证明角相等 (66)第六十四题:证明角的倍数关系 (67)第六十五题:证明中点 (68)第六十六题:伪旁切圆 (69)第六十七题:证明垂直 (70)第六十八题:证明平行 (71)第六十九题:证明圆心在某线上 (72)第七十题:证明三线共点 (73)第七十一题:证明垂直 (74)第七十二题:证明垂直 (75)第七十三题:证明中点 (76)第七十四题:证明垂直 (77)第七十五题:证明垂直 (78)第七十六题:证明三线共点 (79)第七十七题:证明平行 (80)第七十八题:证明平行 (81)第七十九题:证明三线共点、证明垂直 (82)第八十题:证明三点共线(牛顿定理) (83)第八十一题:证明角平分 (84)第八十二题:证明角相等 (85)第八十三题:证明三点共线 (86)第八十四题:证明四圆共点 (87)第八十六题:证明线段相等 (89)第八十七题:证明角相等 (90)第八十八题:证明线段相等 (91)第八十九题:证明线段相等 (92)第九十题:证明线段相等 (93)第九十一题:证明中点 (94)第九十二题:证明四点共圆 (95)第九十三题:证明西姆松定理及逆定理 (96)第九十四题:证明线段的和差关系等式 (97)第九十五题:证明角相等 (98)第九十六题:证明托勒密定理及逆定理 (99)第九十七题:证明线段的和差关系等式 (100)第九十八题:证明角相等 (101)第九十九题:证明四点共圆 (102)第一百题:证明两三角形共内心 (103)第一题:证明角平分已知PE 、PF 是⊙O 的切线,A 、B 是一组对径点,PB 交⊙O 于另一点C ,直线AF 、BE 交于D 点。
高中数学趣味知识竞赛题库

高中数学趣味知识竞赛题库一、选择题(1 - 10题)1. 设集合A={xx^2-3x + 2=0},B={xax - 2=0},若B⊆ A,则a所有可能的值构成的集合为()- A. {1,2}- B. {1,(2)/(3)}- C. {0,1,2}- D. {0,1,(2)/(3)}- 解析:- 先求解集合A,对于方程x^2-3x + 2 = 0,因式分解得(x - 1)(x - 2)=0,解得x = 1或x = 2,所以A={1,2}。
- 因为B⊆ A,当B=varnothing时,ax-2 = 0无解,此时a = 0;当B≠varnothing时,若x=(2)/(a)=1,则a = 2;若x=(2)/(a)=2,则a = 1。
所以a所有可能的值构成的集合为{0,1,2},答案是C。
2. 函数y=log_a(x + 3)-1(a>0,a≠1)的图象恒过定点A,若点A在直线mx+ny + 1 = 0上,其中mn>0,则(1)/(m)+(2)/(n)的最小值为()- A. 8- B. 6- C. 4- D. 10- 解析:- 对于函数y=log_a(x + 3)-1,令x+3 = 1,即x=-2,此时y=-1,所以定点A(-2,-1)。
- 因为点A在直线mx + ny+1 = 0上,所以-2m - n+1 = 0,即2m + n = 1。
- 又因为mn>0,所以m>0,n>0。
- 则(1)/(m)+(2)/(n)=(2m +n)((1)/(m)+(2)/(n))=2+(4m)/(n)+(n)/(m)+2=(4m)/(n)+(n)/(m)+4。
- 根据基本不等式(4m)/(n)+(n)/(m)≥slant2√(frac{4m){n}×(n)/(m)} = 4,当且仅当(4m)/(n)=(n)/(m)时等号成立。
- 所以(1)/(m)+(2)/(n)≥slant4 + 4=8,答案是A。
高中数学竞赛与强基计划试题专题:立体几何

高中数学竞赛与强基计划试题专题:立体几何一、单选题1.(2020·北京·高三强基计划)如图,设P 为单位立方体1111ABCD A B C D -的棱1AB 上的一点,则11PA PC +的最小值为()AB C .2D .前三个答案都不对2.(2022·贵州·高二统考竞赛)平面α与长方体的六个面所成的角分别为(1,2,3,6)i i θ= ,则612sin i i θ=∑的值为()A .2B .3C .4D .6二、填空题3.(2019·全国·高三竞赛)已知P 是ABC 所在平面α外一点,则PA ⊥平面α,PB PC ==,3tan 2PBC ∠=.则点A 到平面PBC 的距离的最大值是______.4.(2019·全国·高三竞赛)在三棱柱111ABC A B C -中,底面边长和侧棱长均相等,1160BAA CAA ==∠∠︒.则异面直线1AB 与1BC 所成的角为_______.5.(2018·全国·高三竞赛)已知三棱锥S-ABC 的底面是以AB 为斜边的等腰直角三角形,且SA=SB=SC=AB=2.则三棱锥S-ABC 外接球表面积为__________.6.(2020·江苏·高三竞赛)在长方体1111ABCD A B C D -中,4AB =,1BC CC ==M 是1BC 的中点,N 是1MC 的中点.若异面直线AN 与CM 所成的角为θ,距离为d ,则2020sin d θ=__________.7.(2021·浙江·高二竞赛)在ABC 中,30B C ∠=∠=︒,BC =P ,Q 分别在线段AB 和AC 上,1AP =,AQ =直线AD BC ⊥于D .现将三角形ABC 沿着AD 对折,当平面ADB 与平面ADC 的二面角为60︒时,则线段PQ 的长度为______.8.(2022·浙江·高二竞赛)在正四棱锥S ABCD -中,M 在棱SC 上且满足2SM MC =.过AM 作截面将此四棱锥分成上,下两部分,记上,下两部分的体积分别为1V ,2V ,则21V V 的最大值为______.9.(2022·广西·高二统考竞赛)若长方体的长、宽、高都是自然数,且所有棱长之和等于它的体积,则称此长方体为“完美长方体”,“完美长方体”的体积的最大值为______.10.(2022·福建·高二统考竞赛)如图,P 为长方体1111ABCD A B C D -的对角线1BD 上一点,平面APC ∥平面11DA C ,若12AA AD =,则二面角P -AB -C 的正切值为___________.11.(2022·新疆·高二竞赛)已知二面角l αβ--的平面角为60︒,A ,D 为直线l 上的两点,射线DB 在平面α内,射线DC 在平面β内,已知=45,=30BDA CDA ∠∠︒︒,则cos ∠BDC 等于___________.12.(2022·江苏南京·高三强基计划)在棱长为6的正四面体ABCD 中,M 为面BCD 上一点,且5AM =,设异面直线AM 与BC 所成的角为α,则cos α的最大值为___________.13.(2019·全国·高三竞赛)E 、F 分别是正四面体ABCD 的棱BD 、CD 的中点,则平面ABC 和平面AEF 所成二面角的余弦值是______.14.(2018·全国·高三竞赛)在三棱锥-P ABC 中,已知PA ⊥底面ABC .若BPC BAC ∠=∠,且AB AC >,则BCA PBC ∠-∠=______.15.(2019·全国·高三竞赛)在空间四边形ABCD 中,AC a = ,BD b = ,E 、F 分别是AB 、CD 上的点,使得2012AE CF EB FD==.则EF =______(用a 、b 表示).16.(2019·全国·高三竞赛)在边长为1的正方体1111ABCD A B C D -中,点E 、F 、G 分别为棱1AA 、11C D 、BC 的中点.则四面体1B EFG 的体积为______.17.(2018·全国·高三竞赛)已知三棱锥-P ABC 的底面ABC ∆是边长为6的正三角形,PA ⊥平面ABC ,4PA =,若点Q 满足()12PQ PA PB PC =++ ,则三棱锥Q ABC -的体积为______.18.(2018·全国·高三竞赛)设正三棱柱ABC A B C '''-的体积为V ,点 P Q 、分别在棱 AA CC ''、上,满足AP C Q '=.则四面体BPQB '的体积为______.19.(2018·全国·高三竞赛)在正四棱锥P ABCD -中,已知11 A C 、,分别为 PA PC 、中点.则11A BC DP ABCD V V 三棱锥正四棱锥--=______.20.(2018·全国·高三竞赛)一个粮仓大致可看做一个圆台,其上底半径为3米,下底半径为6米,米.一只吃饱了的老鼠在锻炼身体,它打算从圆台下底圆周上的点A 出发,绕圆台侧面慢跑一周,再回到点A .为了使路程最短,这只老鼠至少要跑______米.21.(2019·全国·高三竞赛)在四棱锥P ABCD -中,已知四边形ABCD 为矩形,且4AB =,3BC =,5PA PB PC PD ====,AC 与PD 交于点O ,M 为边PC 的中点.则OM 与平面PBC 所成的角为______.22.(2018·全国·高三竞赛)在正四棱锥P ABCD -中,已知3AB =,且侧面PAD 侧面CPD 所成二面角大小为3π2.该四棱锥外接球的体积为______.23.(2018·全国·高三竞赛)用一块边长为2的正方形纸片(顶点为A 、B 、C 、D ,中心为O )折成一个正四棱锥O ABCD -.当该四棱锥体积最大时,二面角--A OB C 的平面角的大小为______.24.(2019·全国·高三竞赛)已知四面体ABCD 的四个面DBC DCA DAB ABC ∆∆∆∆、、、的面积分别为12、21、28、37,顶点D 到面ABC ∆的距离为h.则h=__________.25.(2020·浙江·高三竞赛)如图所示,在单位正方体上有甲、乙两个动点,甲从P 点匀速朝P '移动;乙从Q 点匀速出发朝Q '移动,到达Q '后速度保持不变并折返.现甲、乙同时出发,当甲到达P '时,乙恰好在到达Q '后折返到Q ,则在此过程中,甲、乙两点的最近距离为__________.26.(2018·河北·高二竞赛)若123A A A △的三边长分别为8、10、12,三条边的中点分别是B 、C 、D ,将三个中点两两连结得到三条中位线,此时所得图形是三棱锥A-BCD 的平面展开图,则此三棱锥的外接球的表面积是________.27.(2019·四川·高三校联考竞赛)已知正四棱锥Γ的高为3,侧面与底面所成角为3π,先在Γ内放入一个内切球O 1,然后依次放入球234,,,O O O ,使得后放入的各球均与前一个球及Γ的四个侧面均相切,则放入所有球的体积之和为_____.三、解答题28.(2022·贵州·高二统考竞赛)甲乙二人轮流给一个正方体的棱涂色,首先,甲任选3条棱涂成红色,然后乙从余下的9条棱中任选3条涂成绿色,接着甲从余下的6条棱中任选3条涂成红色,最后乙将余下的3条棱涂成绿色,如果甲能将某个面上的4条边全都涂成红,甲就获胜,试问甲有必胜策略吗?说明理由.29.(2018·全国·高三竞赛)在三棱锥O ABC -中,已知OA OB OC ==AC =,2AB =,且OB AC ⊥.以O 为球心、1为半径作一个球.则三棱锥O ABC -不在球内部的部分体积为______.30.(2021·全国·高三竞赛)证明:如下构造的空间曲线Γ的任意五等分点组都不在同一球面上,曲线Γ的构造:作周长为l 的圆O ,在圆O 上取 AmB 使 15l AmB <的长度25l <,并以AB 为轴将 AmB 旋转180︒得弧 Am B ',在圆O 上取 BnC ,使 AmB 的长度 BnC +的长度25l <,并以BC 为轴将 BnC 旋转θ度()0180θ︒<<︒得弧 Bn C',这样,由弧 Am B Bn C CrA ''、、组成的曲线便是空间曲线.(如图所示)高中数学竞赛与强基计划试题专题:立体几何答案一、单选题1.(2020·北京·高三强基计划)如图,设P 为单位立方体1111ABCD A B C D -的棱1AB 上的一点,则11PA PC +的最小值为()AB C .22-D .前三个答案都不对【答案】A 【分析】如图,将11A B A 和11C B A △翻折到同一平面后可求11PA PC +的最小值.【详解】如图,将11A B A 和11C B A △翻折到同一平面.可得所求最小值为11AC ==.2.(2022·贵州·高二统考竞赛)平面α与长方体的六个面所成的角分别为(1,2,3,6)i i θ= ,则612sin i i θ=∑的值为()A .2B .3C .4D .6【答案】C【详解】解法1.取平面α与长方体的一个面平行或重合,则在(1,2,36)i i θ=⋯中有两个为0,四个为2π,所以612sin i i θ=∑=20+41=⨯⨯ 4.解法2.建立如图的空间坐标系D xyz -,取α的法向量为()000,,n x y z = ,长方体相邻三个面的法向量为1(1,0,0)= n ,2(0,1,0)n = ,3(0,0,1)n = ,∴612cos i i θ=∑2221231232n n n n n n n n n n n n ⎡⎤⎛⎫⎛⎫⎛⎫⋅⋅⋅⎢⎥ ⎪ ⎪ ⎪=++⎢⎥ ⎪ ⎪ ⎪⋅⋅⋅⎝⎭⎝⎭⎝⎭⎢⎥⎣⎦22200022222222200000000022x y z x y z x y z x y z ⎛⎫=++= ⎪++++++⎝⎭,∴612sin i i θ=∑=6-612cos i i θ=∑624=-=.二、填空题3.(2019·全国·高三竞赛)已知P 是ABC 所在平面α外一点,则PA ⊥平面α,PB PC ==,3tan 2PBC ∠=.则点A 到平面PBC 的距离的最大值是______.【答案】2【详解】如图,作PD BC ⊥于点D ,联结AD ,作AF PD ⊥于点F.因为PA ⊥平面ABC ,BC PD ⊥,所以,BC AD BC ⊥⇒⊥平面PAD ⇒平面PAD ⊥平面PBC .由AF PD ⊥,得AF ⊥平面PBC .于是,AF 即为点A 到平面PBC 的距离.因为3tan 2PBC ∠=,所以,sin PBD ∠.又sin PD PB PBD =∠=在Rt PAD中,122AF PD ≤=.4.(2019·全国·高三竞赛)在三棱柱111ABC A B C -中,底面边长和侧棱长均相等,1160BAA CAA ==∠∠︒.则异面直线1AB 与1BC 所成的角为_______.【答案】arccos 6.【详解】在平面11BB C C 中,将1BC 平移至1DB ,则1AB D ∠即为所求的角设三棱柱底面边长和侧棱长均为1.在1AB D ∆中,11AB B D AD 22211111cos 2AB B D AD AB D AB B D +-∠=⋅=于是,1AB D ∠=.5.(2018·全国·高三竞赛)已知三棱锥S-ABC 的底面是以AB 为斜边的等腰直角三角形,且SA=SB=SC=AB=2.则三棱锥S-ABC 外接球表面积为__________.【答案】163π【详解】如图,设三棱锥S-ABC 外接球球心为O ,半径为R由SA=SB=SC=AB=2,知S 在平面ABC 内的投影为ABC ∆的外心,即AB 的中点H.由OA=OB=OC ,知O 在平面ABC 内的投影也为AB 的中点H.于是,S 、O 、H 三点共线.又由OA=OB=OS ,知O 为SAB ∆的外心.因此,22323R OA ==⨯⨯=.故所求为21643ππ⨯=⎝⎭.6.(2020·江苏·高三竞赛)在长方体1111ABCD A B C D -中,4AB =,1BC CC ==M 是1BC 的中点,N 是1MC 的中点.若异面直线AN 与CM 所成的角为θ,距离为d ,则2020sin d θ=__________.【答案】1616【详解】因为1CM BC ⊥,故90θ=︒.过点M 作ME AN ⊥于点E ,则ME CM ⊥,故d ME =.因为4AB =,3BN =,所以5AN =,则4sin 5d ME MN ANB ==∠=,从而可得2020sin 1616d θ=.故答案为:1616.7.(2021·浙江·高二竞赛)在ABC 中,30B C ∠=∠=︒,BC =P ,Q 分别在线段AB 和AC 上,1AP =,AQ =直线AD BC ⊥于D .现将三角形ABC 沿着AD 对折,当平面ADB 与平面ADC 的二面角为60︒时,则线段PQ 的长度为______.【分析】先根据二面角的定义,得到△BCD 为等边三角形,得到BC 的长度,然后在折后的立体图形中,在△PAQ 和△BAC 中利用余弦定理即可求得线段PQ 的长度.【详解】因为折叠前后,AD 与DB ,CD 的垂直关系保持不变,∴∠BDC 为二面角B —AD —C 的平面角,依题意可知60BDC ∠=︒,在折叠前的图形中30B C ∠=∠=︒,BC =∴BD CD ==∴在折叠后,△ABC为等边三角形,∴BC =,所以222222cos 22AP AQ PQ AB AC BC PAQ AP AQ AB AC+-+-∠==⋅⋅,又∵AP=1,AQ =AD =1,AB =AC =2,258=,解得PQ =.8.(2022·浙江·高二竞赛)在正四棱锥S ABCD -中,M 在棱SC 上且满足2SM MC =.过AM 作截面将此四棱锥分成上,下两部分,记上,下两部分的体积分别为1V ,2V ,则21V V 的最大值为______.【答案】78【详解】设过AM 的平面交SB,SD 于G,P ,将平面MGAP 延伸,交BC,CD 于E ,F ,则A ,E ,F 共线.设BG x SB =,21,211FC DP EC x FD PS EB x⋅⋅=⋅=- ,又FC CE CE CE FD DA BC CE BE ===-,而()2113,11221BE X DP BE x CE x PS CE x -⎛⎫=∴=⋅-= ⎪--⎝⎭,由于()1123ASM G ASC P ASC ASC B ASC S d d V SG SP V S d SB SD ---⋅+⎛⎫==+ ⎪⋅⎝⎭()122143541335355535x x x x x ⎛⎫--⎛⎫=-+=++ ⎪ ⎪ ⎪--⎝⎭⎝⎭,140,,5,333x y x ⎡⎤⎡⎤∈∴-∈⎢⎥⎢⎥⎣⎦⎣⎦,185,159V V ⎡⎤∴∈⎢⎥⎣⎦,21111718V V V V V V V -∴==-≤.9.(2022·广西·高二统考竞赛)若长方体的长、宽、高都是自然数,且所有棱长之和等于它的体积,则称此长方体为“完美长方体”,“完美长方体”的体积的最大值为______.【答案】120【详解】设长、宽、高分别为a 、b 、c ,且1a b c ≥≥≥,则()4++=a b c abc ,()4+=4b c a bc -,>4bc ,2>4b bc ≥.由a b ≥得()22844b b c b ≥-≥-,故()23,420,b b ≥⎧⎪⎨-≤⎪⎩从而38b ≤≤.因此,()(),,=10,3,2a b c ,()6,4,2,()24,5,1,()14,6,1,()9,8,1,所求最大值为2451=120⨯⨯.10.(2022·福建·高二统考竞赛)如图,P 为长方体1111ABCD A B C D -的对角线1BD 上一点,平面APC ∥平面11DA C ,若12AA AD =,则二面角P -AB -C 的正切值为___________.【答案】2【详解】如图,设1O 、O 分别为长方体上、下底面矩形对角线的交点,因为平面APC ∥平面11DA C ,平面11D DBB ⋂平面APC OP =,平面11D DBB ⋂平面111DA C DO =,所以1OP DO ∥,又11OB DO ∥,所以O 、P 、1B 三点共线,设Q 为1DO 与1D B 的交点,则Q 为1D P 的中点,P 为QB 的中点,因此113BP BD =,作PH DB ⊥于H ,HR AB ⊥于R ,则PH ⊥平面ABCD ,PR AB ⊥,∠PRH 为二面角P -AB -C 的平面角,由12AA AD =,113BP BD =,可得11233PH DD AD ==,13RH AD =,所以tan 2PH PRH HR∠==,二面角P -AB -C 的正切值为2.11.(2022·新疆·高二竞赛)已知二面角l αβ--的平面角为60︒,A ,D 为直线l 上的两点,射线DB 在平面α内,射线DC 在平面β内,已知=45,=30BDA CDA ∠∠︒︒,则cos ∠BDC 等于___________.【答案】8【详解】在α平面中,过点A 作DA 的垂线,交射线DB 于点B ,交射线DC 于点C ,设1DA =,则1,33====AB DB AC DC ,则=60BAC ∠︒是二面角M l N --的平面角;在BDC 中,利用余弦定理得21033=-∠BC BDC ,同理在BAC 中,2=BC ,所以cos 8+∠=BDC .12.(2022·江苏南京·高三强基计划)在棱长为6的正四面体ABCD 中,M 为面BCD 上一点,且5AM =,设异面直线AM 与BC 所成的角为α,则cos α的最大值为___________.【答案】15【详解】过A 作底面BCD 的垂线AH ,H 为垂足,则AH =由5AM =,可知AM 是以AH 为旋转轴的圆锥的母线,且M 所在的底面圆周半径=1r ,由最小角定理知,AM 与BC 所成角α的最小值为AM 与面BCD 所成线面角,即当α最小时,()max 1cos 5α=.13.(2019·全国·高三竞赛)E 、F 分别是正四面体ABCD 的棱BD 、CD 的中点,则平面ABC 和平面AEF 所成二面角的余弦值是______.【详解】设正四面体的棱长为1,平面ABC 与平面AEF 所成二面角的大小为θ,易知EF BC ,过点A 作BC 的平行线AP ,则EF BC AP ,且AP 就是平面ABC 和平面AEF 所成二面角的棱,易知,60PAC ACB ∠=∠=︒,30CAF ∠=︒,PAF AFE ∠=∠,AE AF ==1122EF BC ==,故cos AFE ∠=,由三面角余弦定理得cos cos cos CAF PAC PAF ∠=∠⋅∠+sin sin cos PAC PAF θ∠⋅∠⋅1222θ⇒=+cos 33θ⇒=.14.(2018·全国·高三竞赛)在三棱锥-P ABC 中,已知PA ⊥底面ABC .若BPC BAC ∠=∠,且AB AC >,则BCA PBC ∠-∠=______.【答案】2π.【详解】如图,作AD BC ⊥于点D ,联结PD .显然,PD AD >.故可在线段PD 上取一点E ,使得DE DA =,联结BE 、CE .易证ABC EBC S S ∆∆≌.从而,BEC BAC BPC ∠=∠=∠.故P 、B 、C 、E 四点共圆.这表明,点E 在ABC ∆外.由AB AC >,知ACB ∠为钝角.从而,CED PBC ∠=∠.故22BCA PBC CAD CED ππ∠-∠=+∠-∠=.15.(2019·全国·高三竞赛)在空间四边形ABCD 中,AC a = ,BD b =,E 、F 分别是AB 、CD 上的点,使得2012AE CFEB FD==.则EF =______(用a 、b 表示).【答案】20122013a b+.【详解】如图,EF EB BC CF =++.记2012λ=.则1111AE EB EB AB EB AB λλλ=⇒=⇒=++,11CF CF CF CD FD CD λλλλλ=⇒=⇒=++.故11111111EF EB BC CF AB BC BC CD λλλλ=++=+++++++()()1111111AC BD AB BC BC CD AC BD λλλλλλλλ+=+++=+=+++++.将2012λ=,AC a = ,BD b =代入即得20122013a b EF +=.16.(2019·全国·高三竞赛)在边长为1的正方体1111ABCD A B C D -中,点E 、F 、G 分别为棱1AA 、11C D 、BC 的中点.则四面体1B EFG 的体积为______.【答案】316【详解】如图,过点E 作1B G 的平行线,与11A D 交于点E '.则111111=3E FB B EFG B E FG GE FB V V V S BB '''∆==⋅四面体四面体四面体.由题设得114A E '=.在正方体底面上,有11511511911242242216E FB S ∆'⎛⎫=+-⨯⨯-⨯⨯= ⎪⎝⎭.故1316B EFG V 四面体=.17.(2018·全国·高三竞赛)已知三棱锥-P ABC 的底面ABC ∆是边长为6的正三角形,PA ⊥平面ABC ,4PA =,若点Q 满足()12PQ PA PB PC =++,则三棱锥Q ABC -的体积为______.【答案】【详解】记ABC ∆的中心点为O .则()()()()11302222OA OB OC PQ PA PB PC PO OA PO OB PO OC PO PO OQ ⎡⎤++=⇒=++=+++++=⇒=⎣⎦.故11111==22323ABC Q ABC P ABC V V S PA ∆--=⨯⋅⨯⨯三棱锥三棱锥18.(2018·全国·高三竞赛)设正三棱柱ABC A B C '''-的体积为V ,点 P Q 、分别在棱 AA CC ''、上,满足AP C Q '=.则四面体BPQB '的体积为______.【答案】13V【详解】1V V V V 3BPQB P BB Q A BB Q A BB C V -'--'''====四面体三棱锥三棱锥三棱锥.19.(2018·全国·高三竞赛)在正四棱锥P ABCD -中,已知11 A C 、,分别为 PA PC 、中点.则11A BC D P ABCDV V 三棱锥正四棱锥--=______.【答案】14【详解】注意到11124A ABD P ABD P ABCD V V V ---==三棱锥三棱锥正四棱锥.同理,114C ABD P ABCD V V --=三棱锥正四棱锥.又11111448B A C D B ACP P ABC P ABCDV V V V ----===三棱锥三棱锥三棱锥三棱锥同理11C 18D A P P ABCD V --=三棱锥正四棱锥.故11111122484A BC D P ABCDV V --=-⨯-⨯=三棱锥正四棱锥.20.(2018·全国·高三竞赛)一个粮仓大致可看做一个圆台,其上底半径为3米,下底半径为6米,米.一只吃饱了的老鼠在锻炼身体,它打算从圆台下底圆周上的点A 出发,绕圆台侧面慢跑一周,再回到点A .为了使路程最短,这只老鼠至少要跑______米.【答案】103π+【详解】将此圆台的侧面展开,得到一个圆环的一部分,如图,在展开图中,弧 AD 和弧 EF分别对应圆台的下底和上底,点()A D 是老鼠的出发点.假设圆环的内半径为r ,外半径为R ,所对的圆心角为α,显然,23r απ=⨯,26R απ=⨯,()()22263R r -+=-.解得4r =,8R =,32πα=.作AB 与弧 EF切于点B ,DC 与弧 EF 切于点C .由图像,知A B C D →→→为最短路线,其中,B C →这一段路线在弧 EF上.计算得AB ==且易知3AOB COD π∠=∠=,56BOC AOB COD πα∠=-∠-∠=.故弧 BC的长为510463ππ⨯=.于是,最短路线长度为101033ππ+=+(米).21.(2019·全国·高三竞赛)在四棱锥P ABCD -中,已知四边形ABCD 为矩形,且4AB =,3BC =,5PA PB PC PD ====,AC 与PD 交于点O ,M 为边PC 的中点.则OM 与平面PBC 所成的角为______.【答案】【详解】取边BC 的中点E ,则OE BC ⊥,PE BC ⊥.从而,BC POE 平面⊥.过点O 作OF PE ⊥,则OF PBC ⊥平面.于是,OMF ∠为所求.因为OM 为Rt POC ∆斜边的中线,所以,52OM =.又OP OE OF PE ⋅==sin OF OMF OM ∠=故OM 与平面PBC 所成的角为22.(2018·全国·高三竞赛)在正四棱锥P ABCD -中,已知3AB =,且侧面PAD 侧面CPD 所成二面角大小为3π2.该四棱锥外接球的体积为______.【答案】243π16【详解】分别过点C 、A 作PD 的垂线,则垂线必交于PD 上一点Q ,且2π3AQC ∠=,AQ CD =.因为AC ==,所以sin180120sin1202AC AQ CQ ︒-︒==⋅=︒,DQ ==由222PQ PC CQ =-,得2PC =.设O 为正方形ABCD 的中心,则四棱锥外接球的球心O '必在直线PO 上,PO 与球交于另一点P '.又122CO AC ==,则32PO ==.由23CO P O PO='=,知()1924R PO P O =+='.故34243ππ316V R ==球.23.(2018·全国·高三竞赛)用一块边长为2的正方形纸片(顶点为A 、B 、C 、D ,中心为O )折成一个正四棱锥O ABCD -.当该四棱锥体积最大时,二面角--A OB C 的平面角的大小为______.【答案】2π3【详解】如图,作AE OB ⊥于点E ,连接CE.则CE OB ⊥,AEC ∠为所求二面角的平面角.设H 为底面中心.则OH ⊥平面ABCD .作HF AB ⊥,连接OF .由三垂线定理得OF AB ⊥.设2AB x =.则BF x =,AH HC ==,OH =故O ABCDV -==≤=正四棱锥由均值不等式的等号成立条件,知当且仅当x =O ABCD V -正四棱锥取最大值.又3OF ==,OF AB AE OB ⋅=⋅,则43OF AB AE CE OB ⋅===.而AC ==,故由余弦定理得2221cos 22AE CE AC AEC AE EC +-∠==-⋅.因为0πAEC <∠<,所以,2π3AEC ∠=.24.(2019·全国·高三竞赛)已知四面体ABCD 的四个面DBC DCA DAB ABC ∆∆∆∆、、、的面积分别为12、21、28、37,顶点D 到面ABC ∆的距离为h.则h=__________.【答案】37【详解】注意到,222212212837++=.因此,四面体ABCD 为直角四面体.故3ABC DA DB DC h S ∆⋅⋅===25.(2020·浙江·高三竞赛)如图所示,在单位正方体上有甲、乙两个动点,甲从P 点匀速朝P '移动;乙从Q 点匀速出发朝Q '移动,到达Q '后速度保持不变并折返.现甲、乙同时出发,当甲到达P '时,乙恰好在到达Q '后折返到Q ,则在此过程中,甲、乙两点的最近距离为__________.6611【详解】设甲、乙的速度分别为1v 、2v ,在此过程中,1232v v =,即1223v v =.不妨设13v 、22v =,则总的时间为1.设在时间为0t 末,甲、乙之间的距离最短,即此时P 、Q 分别达到M 、N 点.分两种情况讨论:路程前半程与路程后半程.(1)路程前半程:010,2t ⎡⎤∈⎢⎥⎣⎦,则02QN t =,03PM t =,0MH t =,02PH t ,2200122QH t t =+-,进而有222001223213333MN t t t ⎛⎫=-+=-+≥ ⎪⎝⎭,故63MN ≥013t =时取等号).(2)路程后半程:01,12t ⎡⎤∈⎢⎥⎣⎦,则()021QN t =-,03PM t ,0MH t =,02PH t ,2200122QH t t =+-,进而有222007661114511111111MN t t t ⎛⎫=-+=-+≥ ⎪⎝⎭,故66MN ≥0711t =时取等号).666>6611.26.(2018·河北·高二竞赛)若123A A A △的三边长分别为8、10、12,三条边的中点分别是B 、C 、D ,将三个中点两两连结得到三条中位线,此时所得图形是三棱锥A-BCD 的平面展开图,则此三棱锥的外接球的表面积是________.【答案】772π【详解】由已知,四面体A-BCD 的三组对棱的长分别是4、5、6.构造长方体使其面对角线长分别为4、5、6,设长方体的长、宽、高分别为x 、y 、z ,外接球半径为R ,则222222222456x y x z y z ⎧+=⎪+=⎨⎪+=⎩,得()22227722R x y z =++=,故2778R =,所以772S π=.27.(2019·四川·高三校联考竞赛)已知正四棱锥Γ的高为3,侧面与底面所成角为3π,先在Γ内放入一个内切球O 1,然后依次放入球234,,,O O O ,使得后放入的各球均与前一个球及Γ的四个侧面均相切,则放入所有球的体积之和为_____.【答案】1813π【详解】设侧面与底面所成角为θ.记球Oi 的半径为ri ,体积为Vi ,i =1,2,3,….因为1cos 2θ=,故1113cos r h r r θ=+=,即1113r h ==.定义12n n s r r r =+++ ,由于132(2)n n r h s n -=-,所以()132n n n r r r +-=,即113n n r r +=,所以113n n r -⎛⎫= ⎪⎝⎭.故333111441333i nnni i i i i V r ππ-===⎛⎫==⋅ ⎪⎝⎭∑∑∑,所以118lim 13ni n i V π→∞==∑.三、解答题28.(2022·贵州·高二统考竞赛)甲乙二人轮流给一个正方体的棱涂色,首先,甲任选3条棱涂成红色,然后乙从余下的9条棱中任选3条涂成绿色,接着甲从余下的6条棱中任选3条涂成红色,最后乙将余下的3条棱涂成绿色,如果甲能将某个面上的4条边全都涂成红,甲就获胜,试问甲有必胜策略吗?说明理由.【答案】甲没有必胜策略,理由见解析【详解】将正方体的12条棱分成4组:{}{}112334223441,,,,,A B B B A A A B B B A A ,{}334112,,A B B B A A ,{}441223,,A B B B A A.当甲第一次涂红3条棱后,由抽屈原理知,上述4组棱中总有一组的3条棱均未被涂红.乙只要将这一组的3条棱涂绿,则正方体的6个面就各有一条绿边.可见,甲没有必胜策略.29.(2018·全国·高三竞赛)在三棱锥O ABC -中,已知OA OB OC ==AC =,2AB =,且OB AC ⊥.以O 为球心、1为半径作一个球.则三棱锥O ABC -不在球内部的部分体积为______.【答案】239π-.【详解】考虑棱长为的正方体将点O 置于正方体的中心,A 、B 、C 可置于正方体的三个顶点,该三个顶点在正方体的同一个面上.故球与三棱锥相交的部分是球体的112.从而,所求体积为321421212339ππ-⨯=-.30.(2021·全国·高三竞赛)证明:如下构造的空间曲线Γ的任意五等分点组都不在同一球面上,曲线Γ的构造:作周长为l 的圆O ,在圆O 上取 AmB 使 15l AmB <的长度25l <,并以AB 为轴将 AmB 旋转180︒得弧Am B ',在圆O 上取 BnC ,使 AmB 的长度 BnC +的长度25l <,并以BC 为轴将 BnC 旋转θ度()0180θ︒<<︒得弧 Bn C',这样,由弧 Am B Bn C CrA ''、、组成的曲线便是空间曲线.(如图所示)【详解】设12345A A A A A 、、、、是曲线Γ的任一五等分点组.#本号资*料全部来源于微信公众号:数学第六感由曲线Γ的构造知,曲线Γ的长度为 ,l AmB 的长度 1,5CrA>的长度35l >,那么至少有一个分点不妨设为1A ,落在弧 Am B '内(不包括端点),同时至少有三个分点,不妨设为234A A A 、、,落在 CrA内(不包括端点).又由曲线Γ的构造知 Am B '与弧 CrA在同一平面内,从而1234A A A A 、、、四点在同一平面内.由平面几何知识知,234A A A 、、三点只能确定唯一的圆O ,而1A 不在圆O 上,所以1234A A A A 、、、四点不共圆.于是1234A A A A 、、、四点必不共球面,否则过1234A A A A 、、、的平面与1234A A A A 、、、所在的球的截面是圆,即1234A A A A 、、、四点共圆,矛盾.故12345A A A A A 、、、、不可能共球面,即曲线Γ的任意五等分点组都不在同一球面上.。
全国高中数学竞赛试题及答案

全国高中数学竞赛试题及答案试题一:函数与方程1. 已知函数\( f(x) = 2x^3 - 3x^2 + x - 5 \),求\( f(x) \)的极值点。
2. 求解方程\( x^2 - 4x + 3 = 0 \)的所有实根。
3. 判断函数\( g(x) = \frac{1}{x} \)在区间\( (0, +\infty) \)上的单调性。
试题二:解析几何1. 已知椭圆\( \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 \),其中\( a > b > 0 \),求椭圆的焦点坐标。
2. 求圆\( (x - h)^2 + (y - k)^2 = r^2 \)的切线方程,已知切点坐标为\( (m, n) \)。
3. 证明点\( P(x_1, y_1) \)和点\( Q(x_2, y_2) \)的连线\( PQ \)的中点坐标为\( \left(\frac{x_1 + x_2}{2}, \frac{y_1 +y_2}{2}\right) \)。
试题三:数列与级数1. 已知等差数列的首项\( a_1 = 3 \),公差\( d = 2 \),求第10项\( a_{10} \)。
2. 求等比数列\( b_1, b_2, b_3, \ldots \)的前\( n \)项和,其中\( b_1 = 1 \),公比\( r = 3 \)。
3. 判断数列\( c_n = \frac{1}{n(n + 1)} \)的收敛性。
试题四:概率与统计1. 从5个红球和3个蓝球中随机抽取3个球,求至少有2个红球的概率。
2. 抛掷一枚均匀硬币4次,求正面朝上的次数为2的概率。
3. 某工厂生产的产品中有2%是次品,求从一批产品中随机抽取10个产品,至少有1个是次品的概率。
试题五:组合与逻辑1. 有5个不同的球和3个不同的盒子,将球分配到盒子中,每个盒子至少有一个球,求不同的分配方法总数。
2. 证明:对于任意的正整数\( n \),\( 1^2 + 2^2 + 3^2 + \ldots + n^2 = \frac{n(n + 1)(2n + 1)}{6} \)。
高中联赛难度几何题100道(精华双图版)

高中联赛难度几何题100道(精华双图版)第一题:证明角平分已知PE 、PF 是⊙O 的切线,A 、B 是一组对径点,PB 交⊙O 于另一点C ,直线AF 、BE 交于D 点。
求证:PCE PCD ∠=∠。
第二题:证明四点共圆如图,AB 是⊙O 的直径,C ,D 是圆上异于A 、B ,且在AB 同侧的两点,分别过C 、D 作⊙的O 切线,它们交于点E ,线段AD 与BC 的交点为F ,线段AB 与EF 的交点为M ,求证:E 、C 、M 、D 四点共圆。
第三题:证明角的倍数关系如图,PE 、PF 是以AB 为直径圆的切线E 、F 是切点,PB 交圆于C 点,AF 、BE 交于D 点,AB 是直径。
求证:ACD DPE ∠=∠2。
第四题:证明线与圆相切已知:ABC ∆中,︒=∠90A ,AD 切⊙ABC ,AD 交BC 延长线于D ,E 是A 关于BC 的对称点,BE AY ⊥于Y ,X 是AY 中点,延长BX 交⊙ABC 于J ,求证:BD 切AJD ∆外接圆。
第五题:证明垂直已知四边形ABCD 内接于以BD 为直径的圆,设'A 为A 关于BD 为对称点,'B 是B 关于AC 对称点,直线AC 交'DB 于Q ,直线DB 交'CA 于P 。
求证:AC PQ ⊥。
第六题:证明线段相等已知:BC 、BD 是⊙O 切线,C 、D 是切点,BJA 是割线,A 、J 在圆上,J 离B 较近,AO DE ⊥于E ,交AB 于F ,AC 交DE 于G ,求证:FG DF =。
第七题:证明线段为比例中项已知ABC ∆中,BC AC =,M 是AB 的中点,FG 经过点M ,且CFG ∆与ABC ∆有相同的内心。
求证:GM FM AM ⨯=2。
第八题:证明垂直已知:ABC ∆为非直角三角形,AD 平分BAC ∠,D 在BC 上,AC DF ⊥于F ,AB DE ⊥于E ,CE 交BF 于P 。
高中数学竞赛几何专题练习题
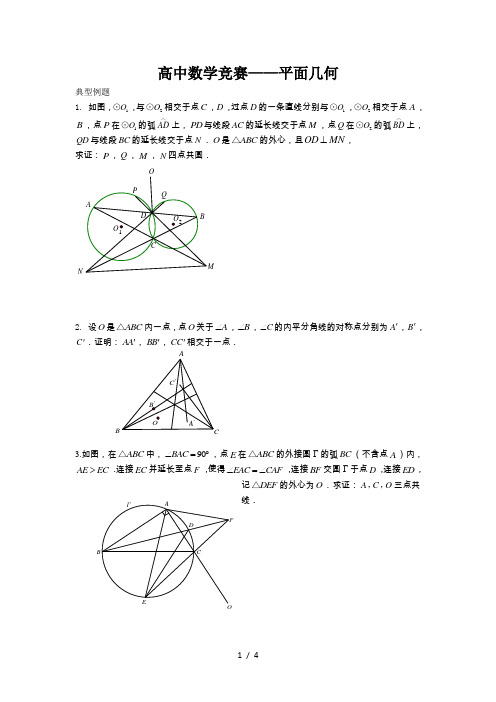
高中数学竞赛——平面几何典型例题1. 如图,1O ⊙,与2O ⊙相交于点C ,D ,过点D 的一条直线分别与1O ⊙,2O ⊙相交于点A ,B ,点P 在1O ⊙的弧AD ︵上,PD 与线段AC 的延长线交于点M ,点Q 在2O ⊙的弧BD ︵上,QD 与线段BC 的延长线交于点N .O 是ABC △的外心,且MN OD ⊥,求证:P ,Q ,M ,N 四点共圆.N2. 设O 是ABC △内一点,点O 关于A ∠,B ∠,C ∠的内平分角线的对称点分别为A ',B ',C '.证明:AA ',BB ',CC '相交于一点.B3.如图,在ABC △中,90BAC ∠=︒,点E 在ABC △的外接圆Γ的弧BC (不含点A )内,AE EC >.连接EC 并延长至点F ,使得EAC CAF ∠=∠,连接BF 交圆Γ于点D ,连接ED ,记DEF △的外心为O .求证:A C O ,,三点共线.ΓFEDCB AO4.如图,已知等圆1O 与圆2O 交于A ,B ,O 为AB 中点,过O 引圆1O 的弦CD 交圆2O 于P ,过O 引圆2O 的弦EF 交圆1O 于Q .求证:AB ,CQ ,EP 三线交于一点.5.四边形ABCD 内接于圆,BCD △,ACD △,ABD △,ABC △的内心依次记为,,,A B C D I I I I .试证:A B C D I I I I 是圆内接四边形.I DI CI BI ADCBA6. 已知ABC △的重心为G ,证明,,AG BG CG 分别关于,,A B C ∠∠∠的角平分线对称的三条直线交于一点P .7.梯形ABCD 是圆内接梯形.AB CD ∥.G 在BCD △内.射线AG 和BG 分别交圆于P 和Q .过G 且平行于AB 的直线分别交BD 和BC 于R 和S .求证:若BG 平分CBD ∠,则P 、Q 、R 、S 四点共圆.8.如图,设AC ,CE 是正六边形ABCDEF 的两条对角线,点M ,N 分别内分AC ,CE ,使AM CN AC CE ==,求证:B ,M ,N 共线. NMFEDC BA9.如图,一圆交ABC △的边,,BC CA AB 分别于1A 与2A ,1B 与2B ,1C 与2C ,如果由点111,,A B C 分别引,,BC CA AB 的垂线相交于一点,则过点2,22,A B C 的垂线也相交于一点.B10. 已知,C D 是以AB 为直径的半圆O 上的两个点,弦,AD BC 交于点E ,,F G 分别是,AC BD 延长线上的点,且满足AF BG AE BE ⋅=⋅,若,AEF BEG ∆∆的垂心分别为12,H H ,证明⑴12,AH BH 的交点K 在圆O 上;⑵,,F K G 三点共线.11.锐角ABC △中,B C ∠=∠,O H 、分别是其外心、垂心,求证:BOH △的外心在直线AB 上.12. 已知ABC ∆的外心为O ,90A ∠<︒,P 为OBC ∆的外接圆上且在ABC ∆内部的任意一点,以OA 为直径的圆分别与AB ,AC 交于点D ,E , OD ,OE 分别与PB ,PC 或其延长线交于点F ,G ,求证A ,F ,G 三点共线.FG ED P OC。
高中联赛难度几何100题及其解答(修订版)

高中联赛难度几何 100 题及其解答解答人:文武光华数学工作室 田开斌第一题、如图,P 为⊙O 外一点,PA 、PB 分别切⊙O 于 A 、B ,PCD 为⊙O 一条割线,CO 交⊙O 于另一点 E ,AC 、EB 交于点 F ,证明:CD 平分∠ADF。
F证明方法一:如图,延长 ED 交 CA 于 K ,根据条件知四边形 CADB 为调和四边形,故ED 、EC 、EA 、EB 构成一组调和线束,进而知 K 、C 、A 、F 构成一组调和点列。
而 KD⊥CD, 故 CD 平分∠ADF 。
PF证明方法二:如图,连结 OA 、OB 、AB 、BC ,因为∠AFB = ∠ACE − ∠BEC =∠AOE−∠BOC=180°−∠AOC−∠BOC=∠APC,且PA = PB ,故点 P 为△ABF 的外心。
于是知222∠PFA = ∠PAC = ∠PDA ,所以 P 、A 、D 、F 四点共圆。
又PA = PF ,故 CD 平分∠ADF。
F第二题、如图,AB 为⊙O直径,C、D 为⊙O上两点,且在 AB 同侧,⊙O在C、D 两处的切线交于点 E,BC、AD 交于点 F,EF 交AB 于M,证明:E、C、M、D 四点共圆。
B证明:如图,延长 AC、BD 交于点 K,则BC⊥AK,AD⊥BK,从而知 F 为△KAB 的垂心。
又在圆内接六边形 CCADDB 中使用帕斯卡定理,知 K、E、F 三点共线,从而KM⊥AB于M。
于是知∠CMF = ∠CAF = ∠CDE,所以 E、C、M、D 四点共圆。
B第三题、如图,AB 为⊙O 直径,C 、D 为⊙O 上两点,且在 AB 同侧,⊙O 在 C 、D 两处的切线交于点 E ,BC 、AD 交于点 F ,EB 交⊙O 于点 G ,证明:∠CEF = 2∠AGF 。
B证明:如图,根据条件知∠CFD =AB +CD =(180°−A C )+(180°−BD ) = ∠CAB + ∠DBA =22∠ECF + ∠EDF ,且EC = ED ,故点 E 为△CFD 外心。
高中数学几何题竞赛试题

高中数学几何题竞赛试题一、选择题(每题3分,共15分)1. 在直角三角形ABC中,∠C=90°,若AB=5,AC=3,则BC的长度是:A. 4B. 3C. 2D. 无法确定2. 已知圆的半径为r,圆心O到直线l的距离为d,若圆与直线l相切,则d与r的关系是:A. d = rB. d > rC. d < rD. d ≠ r3. 在正六边形ABCDEF中,若AB=2,则对角线AC的长度是:A. 2B. 2√3C. 4D. 4√34. 若一个正方体的表面积为S,棱长为a,则a与S的关系是:A. a = √SB. a = SC. a = S/6D. a = √(S/6)5. 已知椭圆的长轴为2a,短轴为2b,焦点到中心的距离为c,若a=5,b=3,则c的值是:A. 4B. 2C. √7D. √(25-9)二、填空题(每题4分,共20分)6. 在三角形ABC中,若∠A=60°,AB=AC=6,则BC的长度是______。
7. 已知圆柱的底面半径为r,高为h,若圆柱的体积为V,则V与r和h的关系是V=______。
8. 若一个圆锥的底面半径为r,高为h,且圆锥的体积为V,则圆锥的底面积是______。
9. 已知一个球的体积为V,半径为R,则R与V的关系是R=______。
10. 若一个正多边形的边数为n,且其内角为x,则x与n的关系是x=______。
三、解答题(每题10分,共30分)11. 已知三角形ABC的三个顶点坐标分别为A(2,3),B(5,6),C(1,1),求三角形ABC的面积。
12. 已知圆的方程为(x-3)²+(y-4)²=25,求圆心到直线3x+4y-20=0的距离。
13. 已知一个正四面体的棱长为a,求其外接球的半径。
四、证明题(每题10分,共25分)14. 证明:在直角三角形中,斜边的中线等于斜边的一半。
15. 证明:对于任意一个三角形,其内角和为180°。
高中数学竞赛专题练习:立体几何

竞赛试题选讲之 立体几何一、选择题部分1. (吉林预赛)正方体ABCD -A 1B 1C 1D 1中,过顶点A 1作直线l ,使l 与直线AC 和直线BC 1所成的角均为60°,则这样的直线l 的条数为 ( C ) A. 1 B. 2 C. 3 D. 大于32、(陕西赛区预赛)如图2,在正方体1111ABCD A B C D -中,P 为棱AB 上一点,过点P 在空间作直线l ,使l 与平面ABCD 和平面AB 11C D 均成030角,则这样的直线l 的条数为 ( B )A. 1 B .2 C. 3 D .43.(集训试题)设O 是正三棱锥P-ABC 底面是三角形ABC 的中心,过O 的动平面与PC 交于S ,与PA 、PB 的延长线分别交于Q 、R ,则和式PSPR PQ 111++( ) A .有最大值而无最小值B .有最小值而无最大值C .既有最大值又有最小值,两者不等D .是一个与面QPS 无关的常数解:设正三棱锥P-ABC 中,各侧棱两两夹角为α,PC 与面PAB 所成角为β,则v S-PQR =31S △PQR ·h=21(31PQ ·PRsin α)·PS ·sin β。
另一方面,记O 到各面的距离为d ,则v S-PQR =v O-PQR +v O-PRS +v O-PQS ,31S △PQR ·d=31△PRS ·d+31S △PRS ·d+31△PQS ·d=213⋅d PQ ·PRsin α+213⋅d PS ·PRsin α+213⋅d PQ ·PS ·sin α,故有:PQ ·PR ·PS ·sin β=d(PQ ·PR+PR ·PS+PQ ·PS),即dPS PR PQ βsin 111=++=常数。
高中数学联赛几何题

几何专题1.线段AB平行于两等圆的连心线并与两圆相交(交点都在AB内),分别过A,B作靠近自己的一圆的两切线,设这四条切线围成的四边形包含两圆.求证,这个四边形有内切圆.2.ABCV的内切圆与AB,AC边分别切于P,Q点,设RS是平行于AB的中位线,而T是直线PQ与RS的交点.求证,T在角B的平分线上.3.设K,L分别是ABCV的边AC,CB上的旁切圆切点.求证,线段KL,AB的中点连线:(1)平分ABCV的周长;(2)平行于ABCÐ的角平分线.4. 以O 为圆心的圆的两条弦AC 与BD 交于K 点,设M,N 分别是三角形AKB,CKD 的外心.求证:OM=KN .5. ABC V 的三条高是,,AD BE CF .求证:以三角形,,AEF BFD CDE 的垂心为顶点的三角形与DEF V 全等.6. 设AD,BE,CF 是锐角三角形ABC 的三条高,123,,O O O 分别是三角形AEF,BFD,CDE 的内心,而123,,T T T 分别是ABC V 的内切圆与三边BC,CA,AB 的切点.求证:六边形132132T O T OT O 的各边全都相等.B7. 等腰三角形ABC 的顶角120C? ,D ,E 为底边AB 上两点满足60DCE? (点D 靠近点A ,点E靠近点B ),F ,G 分别为边AC ,BC 上两点,满足,ADFCDB BEG CEA ?行= .求证:ADF BEG CDE S S S +=V V V8. ABCD 是非等腰的梯形.1A 是BCD V 外接圆与直线AC 异于点C 的交点.类似定义111,,B CD 点.求证:1111A B C D 也是梯形.9. 圆内接四边形的两对角线交于P 点,四边的中点依次为K,L,M,N .求证:三角形PKL ,PLM ,PMN ,PNK 的外接圆半径都相等.B爱数学 高中2015年11. 锐角三角形ABC 的三边BC ,AC ,AB 上分别取点111,,A B C 使得射线111,,A A B B C C 为111A B C V 的三条内角平分线.试证:111,,AA BB CC 是三角形ABC 的三条高12. 锐角三角形ABC 的两边AB,BC 分别向外做两个矩形ABMN ,BCKL 满足MB BCAB BL=.求证:直线AL,CM,NK 共点.D13. 如图,1O e 过2O e 的圆心,由1O e 上的点C 作2O e 的两条切线,分别另交1O e 于A,B 两点.求证:直线AB 与两圆的连心线垂直.14. 如图,12,O O e e 相交于E ,F 两点,过平面上一点O 做1O e 的2条切线OA ,OB 与2O e 的两条切线OC ,OD ;若AOB COD ? ,证明:EOC FOB ? .15. 12,O O e e 交于A,B 两点,一条公切线(靠近点B )的切点为E ,F ,直线AB 与EF 交于M 点.在AM 的延长线上取点K 使得KM M A =,直线KE 与1O e 交于E ,C 两点,直线KF 与2O e 交于F ,D 两点.证明:CDA 共线.16. ABC V 中H 为垂心,I 为内心,O 为外心,K 是内切圆与BC 边的切点.若//IO BC ,求证://AO HK .17. O e 为斜边为AB 的直角三角形ABC 的外接圆,设K 是劣弧BC的中点,N 是线段AC 的中点,M 是射线KN 与O e 的交点,O e 在A,C 处的切线交于E 点.求证:EMK Ð为直角.18. 12,O O e e 交于AB 两点,过B 的直线分别另交12,O O e e 于K ,M 点.直线PQ 与1O e 切于Q 点并平行于AM ,直线PR 与2O e 切于R 点并平行于AK ,点P ,Q 位于直线KM 的不同侧.求证: (1)点A 在直线QR 上:(2)点P 在直线KM 上19. 正方形1111A B C D 在正方形ABCD 内,又2222,,,A B C D 分别是1111AA BB CC DD 、、、的中点.试证:2222A B C D 也是正方形.20. 设ABC V 的边AB 、AC 上分别有N 、K 两点,且N 、K 、C 、B共圆于O e ,若ABC V 与ANK V 的外接圆还交于异于点A 的点M ,求证:AM OM ^.C21. 设四边形ABCD 有内切圆O e ,求证:OAB V 、OBC V 、OCD V 、ODA V 的垂心共线.22. 如图,凸四边形ADPE 中,ADPAEP ? ,延长AD 至点B ,延长AE 至点C ,使得DPBEPC ? ,记ADE V 的外心为点1O ,ABC V 的外心为点2O ,且两外接圆不相切,求证:直线12O O 平分AP .B23. 两圆12O O e e 、相交于P 、Q 两点,且离点P 近的公切线分别与12O O e e 、切于点A 、B .过点P 作1O e 的切线,与2O e 交于点C ,又AP 延长之后与BC 交于点R ,证明:PQR V 的外接圆与直线BP 、BR 相切.24. 设O e 的内接四边形ABCD ,E 是对角线交点,P 是四边形内任意异于E 的一点,,,,PAB PBC PCD PDA V V V V 的外心分别是1233O O O O 、、、,设1324O O O O 、交于点Q ,求证:O E Q 、、共线25. 已知AD 是锐角ABC V 的一条高,P 是AD 上某一点,延长BP交AC 于点M ,延长CP 交AB 于点N ,又MN 与AP 交于点Q ,过Q 做任一直线交PN 于点E ,交AM 于点F ,求证:EDA FDA ? .26. 证明斯坦纳定理:ABC V 外接圆上一点P 与ABC V 垂心H 的连线PH 被P 关于ABC V 的西姆松线平分延长PD 交外接圆于Q ,延长AH 交BC 于M 交外接圆于N 则HM=MN ,只需证明AQ 平行EF ,由AQPN 为等腰梯形推 出结论B C27.证明牛顿线:四边形ABCD对边交点分别为E,F,对角线AC中点为M,BD中点为N,EF中点为O,则M,N,O三点共线28.六边形ABCDEF中各边中点分别为A’B’C’D’E’F’证明:A’D’,B’E’,C’F’交于一点的充要条件是三角形ACE面积等于三角形BDF面积29.四边形蝴蝶定理:四边形ABCD满足AB=AD,BC=CD,对角线AC,BD相交于O,过O做任俩直线分别交四边于P、Q、R、S,PQ、RS交BD于M、N,证明:OM=ON30. 如图,两个正方形(边长不一定相等)重叠,边之间的交点为12121212,,,,,,,A A B B C C D D ,证明:2222A C B D31. 证明:将三角形的各内角三等分,靠近某一边的两条三分角线相交得一交点则三交点构成正三角形.C求证:直线AT 关于BC ,BT 关于CA ,CT 关于AB 的对称线交于一点.33. ABC V 的角平分线1AA 上取点X ,设BX 交AC 于点1B ,直线CX 交AB 于1C ,线段11A B 与1CC 交于P 点,线段11AC 与1BB 交于Q 点.求证:PAC QAB ? .34. 锐角ABC V 的内切圆I 切BC 于点K ,AD 为ABC V 的高,M 为AD 的中点,直线KM 交I e 于另一点N ,求证:NK 平分BNC Ð.CBC35.如图,非正三角形ABC中,O为外心,三条高AD,BE,CF交于点H,直线ED和AB交于点M,FD和AC交于点N .求证:OH MN^.36.ABCV的内切圆BC于D,E在线段AD在圆内的部分上,设线段EB,CE分别与圆交于点F、G,求证:AD,BG,CF共点.B C。
历年全国高中数学联赛《平面几何》专题真题汇编

历年全国高中数学联赛《平面几何》专题真题汇编1、如图,在锐角三角形ABC 的BC 边上有两点E 、F ,满足∠BAE =∠CAF ,作FM ⊥AB ,FN ⊥AC (M 、N 是垂足),延长AE 交三角形ABC 的外接圆于D .证明:四边形AMDN 与三角形ABC 的面积相等.2、如图:⊿ABC 中,O 为外心,三条高AD 、BE 、CF 交于点H ,直线ED 和AB 交于点M ,FD 和AC 交于点N 。
求证:(1)OB ⊥DF ,OC ⊥DE ;(2)OH ⊥MN 。
【解析】证明:(1)∵A 、C 、D 、F 四点共圆 ∴∠BDF =∠BAC又∠OBC =21(180°-∠BOC )=90°-∠BAC∴OB ⊥DF . (2)∵CF ⊥MA∴MC 2-MH 2=AC 2-AH 2 ① ∵BE ⊥NA∴NB 2-NH 2=AB 2-AH 2 ② ∵DA ⊥BC∴BD 2-CD 2=BA 2-AC 2 ③ ∵OB ⊥DF∴BN 2-BD 2=ON 2-OD 2 ④ ∵OC ⊥DE∴CM 2-CD 2=OM 2-OD 2 ⑤ ①-②+③+④-⑤,得NH 2-MH 2=ON 2-OM 2 MO 2-MH 2=NO 2-NH 2 ∴OH ⊥MN∵1-=DF OB k k ∴OB ⊥DF 同理可证OC ⊥DE . 在直线BE 的方程)(b x a cy -=中令x =0得H (0,a bc -)∴ac ab bc a c b a bc a a bc k OH++=+++=32222直线DF 的方程为x bc a acab y +-=2由⎪⎪⎩⎪⎪⎨⎧--=+-=)(2c x c a y x bc a ac ab y 得N (22222222,2c bc a ac abc c bc a bc c a -+--++) 同理可得M (22222222,2b bc a ab abc b bc a c b b a -+--++) ∴bc a ac ab bc a bc a b c bc a c b a k MN3)3)()(())((222222++-=++-+-=∵k OH ·k MN =-1,∴OH ⊥MN .3、如图,在⊿ABC 中,∠A=60°,AB>AC ,点O 是外心,两条高BE 、CF 交于H点,点M 、N 分别在线段BH 、HF 上,且满足BM=CN ,求OH NH MH +的值。
新高中数学竞赛习题之平面几何

欢迎阅读第一讲注意添加平行线证题在同一平面内,不相交的两条直线叫平行线.平行线是初中平面几何最基本的,也是非常重要的图形.在证明某些平面几何问题时,若能依据证题的需要,添加恰当的平行线,则能使证明顺畅、简洁.添加平行线证题,一般有如下四种情况.1 为了改变角的位置大家知道,两条平行直线被第三条直线所截,同位角相等,内错角相等,同旁内角互补.利用这些性质,例1设∠BAP答:由则很顺畅例2证明:由有来.∠2,例3、N、Q证明:于K、G由显然,PD =FD=GD,可知PG∥EC.由CE平分∠BCA,知GP平分∠FGA.有PK=PM.于是,PM+PN=PK+KQ=PQ.这里,通过添加平行线,将PQ“掐开”成两段,证得PM=PK,就有PM+PN=PQ.证法非常简捷.3 为了线段比的转化由于“平行于三角形一边的直线截其它两边,所得对应线段成比例”,在一些问题中,可以通过图3添加平行线,实现某些线段比的良性转化.这在平面几何证题中是会经常遇到的.例4 设M 1、M 2是△ABC 的BC 边上的点,且BM 1=CM 2.任作一直线分别交AB 、AC 、AM 1、AM 2于P 、Q 、N 1、N 2.试证:APAB +AQ AC =11AN AM +22AN AM . 证明:如图4,若PQ ∥BC ,易证结论成立. 若PQ 与BC 不平行,设PQ 交直线BC 于D .过点A 作PQ 的平行线交直线BC 于E .由BM 1=CM 2,可知BE +CE =M 1E +M 2E ,易知 AP AB =DE BE ,AQ AC =DE CE ,. 例5EDA . ,例6果BM 2+CN 2=DM 2+DN 2,求证:AD 2=41(AB 2+AC 2). 证明:如图6,过点B 作AC 的平行线交ND 延长线于E .连ME .由BD =DC ,可知ED =DN .有 △BED ≌△CND . 于是,BE =NC . 显然,MD 为EN 的中垂线.有 EM =MN .由BM 2+BE 2=BM 2+NC 2=MD 2+DN 2=MN 2=EM 2,可知△BEM 为直角三角形,∠MBE =90°.有 ∠ABC +∠ACB =∠ABC +∠EBC =90°. 于是,∠BAC =90°.A PEDC M 2M 1B Q N 1N 2图4图6A N C DE B M所以,AD 2=221⎪⎭⎫ ⎝⎛BC =41(AB 2+AC 2). 这里,添加AC 的平行线,将BC 的以D 为中点的性质传递给EN ,使解题找到出路. 例7 如图7,AB 为半圆直径,D 为AB 上一点,分别在半圆上取点E 、F ,使EA =DA, FB =DB .过D 作AB 的垂线,交半圆于C .求证:CD 平分EF .证明:如图7,分别过点E 、F 作AB 的垂线,G 、H 为垂足,连FA 、EB . 易知 DB 2=FB 2=AB ·HB , AD 2=AE 2=AG ·AB .二式相减,得 DB 2-AD 2=AB ·(HB -AG ),或 (DB -AD )·AB =AB ·(HB -AG ).于是,DB -AD =HB -AG ,或 DB -HB =AD -AG . 就是DH =GD .例8例9OE 显然,∠FKQ =∠EKP ,可知 ∠FOQ =∠EOP .由OF =OE ,可知 Rt △OFQ ≌Rt △OEP . 则OQ =OP .于是,OK 为PQ 的中垂线,故 QK =KP .所以,AK 平分BC .综上,我们介绍了平行线在平面几何问题中的应用.同学们在实践中应注意适时添加平行线,让平行线在平面几何证题中发挥应有的作用.练习题1. 四边形ABCD 中,AB =CD ,M 、N 分别为AD 、BC 的中点,延长BA 交直线NM 于E ,延长CD 交直线NM 于F .求证:∠BEN =∠CFN .A G D O HB FC E 图7(提示:设P 为AC 的中点,易证PM =PN .)2. 设P 为△ABC 边BC 上一点,且PC =2PB .已知∠ABC =45°,∠APC =60°.求∠ACB . (提示:过点C 作PA 的平行线交BA 延长线于点D .易证△ACD ∽△PBA .答:75°)3. 六边开ABCDEF 的各角相等,FA =AB =BC ,∠EBD =60°,S △EBD =60cm 2.求六边形ABCDEF 的面积.(提示:设EF 、DC 分别交直线AB 于P 、Q ,过点E 作DC 的平行线交AB 于点M .所求面积与EMQD 面积相等.答:120cm 2)4. AD 为Rt △ABC 的斜边BC 上的高,P 是AD 的中点,连BP 并延长交AC 于E .已知AC :AB =k .求AE :EC .(提示:过点A 作BC 的平行线交BE 延长线于点F .设BC =1,有AD =k ,DC =k 2.答:211k) 5. ABF .(6. c1. (F .)7. .8. △、DE (9. AD OM =(.)1 ,1.1 例1 且∠但因则可得EB =EF ,从而获取. 证明:如图1,延长AD 与△ABC 的外接圆相交于点F ,连结CF 与BF ,则∠BFA =∠BCA =∠ABC =∠AFC ,即∠BFD =∠CFD .故BF :CF =BD :DC .又∠BEF =∠BAC ,∠BFE =∠BCA ,从而∠FBE =∠ABC =∠ACB =∠BFE .故EB =EF .作∠BEF 的平分线交BF 于G ,则BG =GF .图1因∠GEF =21∠BEF =∠CEF ,∠GFE =∠CFE ,故△FEG ≌△FEC .从而GF =FC . 于是,BF =2CF .故BD =2CD . 1.2 利用四点共圆 例2 凸四边形ABCD 中,∠ABC =60°,∠BAD =∠BCD =90°, AB =2,CD =1,对角线AC 、BD交于点O ,如图2.则sin ∠AOB =____.分析:由∠BAD =∠BCD =90°可知A 、B 、C 、D 四点共圆,欲求sin ∠AOB ,联想到托勒密定理,只须求出BC 、AD 即可.解:因∠BAD =∠BCD =90°,故A 、B 、C 、D 四点共圆.延长BA 、CD 交于P ,则∠ADP =∠ABC =60°. 设解得 又S 例3 △ABC 须证AC AH 交点).证明: 又 ∴ 442 构造相关的辅助圆解题有些问题貌似与圆无关,但问题的题设或结论或图形提供了某些与圆的性质相似的信息,此时可大胆联想构造出与题目相关的辅助圆,将原问题转化为与圆有关的问题加以解决.2.1 联想圆的定义构造辅助圆例4 如图4,四边形ABCD 中,AB ∥CD ,AD =DC =DB =p ,BC =q .求对角线AC 的长. 分析:由“AD =DC =DB =p ”可知A 、B 、C 在半径为p 的⊙D 上.利用圆的性质即可找到AC 与p 、q 的关系. 解:延长CD 交半径为p 的⊙D 于E 点,连结AE .显然A 、B 、C 在⊙D 上.A B C DP O 图2A E DC B∵AB ∥CD ,∴BC =AE .从而,BC =AE =q .在△ACE 中,∠CAE =90°,CE =2p ,AE =q ,故 AC =22AE CE -=224q p -.2.2例5 A 侧,解:C (4,0).、Q (1+ AD 2.3 例6 BM ·BN 证明: 以 BM 即 AB 2例7 AD 和证明:EF 2即 EP 22.4 例8 如图8,△ABC 与△A 'B 'C '的三边分别为a 、b 、c 与a '、 b '、c ',且∠B =∠B ',∠A +∠A =180°.试证:aa '=bb '+cc '. 分析:因∠B =∠B ',∠A +∠A '=180°,由结论联想到托勒密定理, 构造圆内接四边形加以证明. 证明:作△ABC 的外接圆,过C 作CD ∥AB 交圆于D ,连结AD 和BD , 如图9所示. ∵∠A +∠A '=180°=∠A +∠D ,∠BCD =∠B =∠B ', (1)(2)图8A C A'B'C'c b a'c'b'A∴∠A '=∠D ,∠B '=∠BCD .∴△A 'B 'C '∽△DCB . 有DC B A ''=CB C B ''=DBC A '', 即 DC c '=aa '=DBb '. 故DC =''a ac ,DB =''a ab . 又AB ∥DC ,可知BD =AC =b ,BC =AD =a .从而,由托勒密定理,得 AD ·BC =AB ·DC +AC ·BD ,即 a 2=c ·''a ac +b ·''a ab . 故aa '=bb '+cc '.1. (提示:DCBD .) 2. BAC (CAD =∠DAE 3. 在△(=10°,4.如图求证:G 、H .5. 如图且AC =(得△6.已知求证:(AC =AN ·AM .)7. 若正五边形ABCDE 的边长为a ,对角线长为b ,试证:a b -ba =1. (提示:证b 2=a 2+ab ,联想托勒密定理作出五边形的外接圆即可证得.)第三讲 点共线、线共点在本小节中包括点共线、线共点的一般证明方法及梅涅劳斯定理、塞瓦定理的应用。
高中联赛难度几何题100道

.第一题:证明角平分4第二题:证明四点共圆5第三题:证明角的倍数关系6第四题:证明线与圆相切7第五题:证明垂直8第六题:证明线段相等9第七题:证明线段为比例中项10第八题:证明垂直11第九题:证明线段相等12第十题:证明角平分13第十一题:证明垂直14第十二题:证明线段相等15第十三题:证明角相等16第十四题:证明中点17第十五题:证明线段的二次等式18第十六题:证明角平分19第十七题:证明中点20第十八题:证明角相等21第十九题:证明中点22第二十题:证明线段相等23第二十一题:证明垂直24第二十二题:证明角相等25第二十三题:证明四点共圆26第二十四题:证明两圆相切27第二十五题:证明线段相等28第二十六题:证明四条线段相等29第二十七题:证明线段比例等式30第二十八题:证明角的倍数关系31第二十九题:证明三线共点32第三十题:证明平行33第三十一题:证明线段相等34第三十二题:证明四点共圆35第三十三题:证明三角形相似36第三十四题:证明角相等37第三十五题:证明内心38第三十六题:证明角平分39第三十七题:证明垂直40第三十八题:证明面积等式41第三十九题:证明角平分42第四十题:证明角相等43第四十一题:证明中点44第四十二题:证明中点45第四十三题:证明角相等46第四十四题:证明垂直47第四十六题:证明垂直49第四十七题:证明四点共圆50第四十八题:证明四点共圆51第四十九题:证明四点共圆52第五十题:证明角平分53第五十一题:证明线段相等54第五十二题:证明两圆外切55第五十三题:证明垂直56第五十四题:证明垂直57第五十五题:证明垂直58第五十六题:证明垂直59第五十七题:证中点60第五十八题:证明角相等61第五十九题:证明角相等62第六十题:证明四点共圆63第六十一题:证明四点共圆64第六十二题:证明四点共圆65第六十三题:证明角相等66第六十四题:证明角的倍数关系67第六十五题:证明中点68第六十六题:伪旁切圆69第六十七题:证明垂直70第六十八题:证明平行71第六十九题:证明圆心在某线上72第七十题:证明三线共点73第七十一题:证明垂直74第七十二题:证明垂直75第七十三题:证明中点76第七十四题:证明垂直77第七十五题:证明垂直78第七十六题:证明三线共点79第七十七题:证明平行80第七十八题:证明平行81第七十九题:证明三线共点、证明垂直82 第八十题:证明三点共线〔牛顿定理〕83 第八十一题:证明角平分84第八十二题:证明角相等85第八十三题:证明三点共线86第八十四题:证明四圆共点87第八十五题:证明角平分88第八十六题:证明线段相等89第八十七题:证明角相等90第八十八题:证明线段相等91第九十题:证明线段相等93第九十一题:证明中点94第九十二题:证明四点共圆95第九十三题:证明西姆松定理与逆定理96 第九十四题:证明线段的和差关系等式97 第九十五题:证明角相等98第九十六题:证明托勒密定理与逆定理99 第九十七题:证明线段的和差关系等式100 第九十八题:证明角相等101第九十九题:证明四点共圆102第一百题:证明两三角形共内心103第一题:证明角平分已知PE 、PF 是⊙O 的切线,A 、B 是一组对径点,PB 交⊙O 于另一点C ,直线AF 、BE 交于D 点。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
设D是ABC的边BC上的一点,点P在线段AD上,过点D作一直线分别与线段AB、PB交于点M、E,与线段AC、PC的延长线交于点F、N。
如果DE=DF,求证:DM=DN设点D为等腰ABC∆的底边BC上一点,F为过A、D、C三点的圆在ABC∆内的弧上一点,过B、Array D、F三点的圆与边AB交于点E。
求证:CD EF DF AE BD AF⋅+⋅=⋅如图所示,在△ABC中,90,,∠=︒是边CA上的两点,ABC D G Array连接BD,BG . 过点A,G分别作BD的垂线,垂足分别为E,F,连接CF. 若BE=EF,求证:ABG DFC∠=∠.几何(4):如图,在ABC∆中,60A∠=︒, ABC∆的内切圆I分别切边,AB AC于点,D E,直线DE分别与直线BI CI,相交于点F G,, 证明:12FG BC=.B几何(5):在△ABC中,BC>AB,BD平分ABC交AC于D,如图,CP垂直BD,垂足为P,AQ垂直BP,Q为垂足。
M是AC中点,E 是BC中点。
若△PQM的外接圆O与AC 的另一个交点为H,求证: O、H、E、M 四点共圆。
C A几何(6):如图,ABC的内切圆I分别切BC、AC于点M、N,点E、F分别为边AB、AC的中点,D 是直线EF与BI的交点。
证明:M、N、D三点共线。
D A几何(7)∆的外接圆和内切圆;证明:过O 上的任意一点D,都可以作一个三角形DEF,使得O、I分别是DEF∆的外接圆和内切圆.如图,过ABC ∆的外心O 任作一直线,分别交边,AB AC 于,M N ,F E ,分别是,BN CM 的中点.证明:EOF A ∠=∠.设000,,AA BB CC 是ABC ∆的三条角平分线,自0A 作01A A ∥0BB ,02A A ∥0CC ,12,A A 分别在,AC AB 上,直线123A A BC A =;类似得到点33,B C .证明:333,,A B C 三点共线.33几何(10):一张纸上画有一个半径为R的圆O和圆内一个定点A,且OA=a,折叠纸片,使圆周上某一点A'刚好与点A重合.这样的每一种折法,都留下一条折痕.当A'取遍圆周上所有点时,求所有折痕所在直线上点的集合.设D 是ABC ∆的边BC 上的一点,点P 在线段AD 上,过点D 作一直线分别与线段AB 、PB 交于点M 、E ,与线段AC 、PC 的延长线交于点F 、N 。
如果DE=DF ,求证:DM=DN证明:对AMD ∆和直线BEP 用梅涅劳斯定理得:1(1)AP DE MBPD EM BA⋅⋅=,对AFD ∆和直线NCP 用梅涅劳斯定理得:1(2)AC FN DPCF ND PA ⋅⋅=, 对AMF ∆和直线BDC 用梅涅劳斯定理得:1(3)AB MD FCBM DF CA⋅⋅= (1)(2)(3)式相乘得:1DE FN MDEM ND DF⋅⋅=,又DE=DF ,所以有DM DNDM DE DN DE=--,所以DM=DN 。
设点D 为等腰ABC ∆的底边BC 上一点,F 为过A 、D 、C 三点的圆在ABC ∆内的弧上一点,过B 、D 、F 三点的圆与边AB 交于点E 。
求证:CD EF DF AE BD AF ⋅+⋅=⋅ 设AF 的延长线交BDF 于K ,AEF AKBAEF AKB∠=∠∴∆∆因此,EK BK AE AKAF AB AF AB==。
于是要证(1), 只需证明:(2)CD BK DF AK BD AB ⋅+⋅=⋅ 又注意到KBD KFD C ∠=∠=∠。
我们有1sin 2DCK S CD BK C ∆=⋅⋅∠进一步有1sin 21sin 2ABD ADK S BD AB CS AK DF C∆∆=⋅⋅∠=⋅⋅∠因此要证(2),只需证明(3)ABD DCK ADKS S S ∆∆∆=+ 而(3)//(4)ABC AKC S S BK AC∆∆⇔=⇔ 事实上由BKA FDB KAC ∠=∠=∠知(4)成立,得证。
如图所示,在△ABC中,90,,ABC D G∠=︒是边CA上的两点,连接BD,BG . 过点A,G分别作BD的垂线,垂足分别为E,F,连接CF. 若BE=EF,求证:ABG DFC∠=∠.证:作Rt ABC的外接圆w,延长BD、AE分别交w于K、J.连接BJ、CJ、KJ、FJ. 易知BAJ KBC∠=∠,故BJ=KC.于是四边形BJCK是等腰梯形,又AJ垂直平分BF,故BJ=FJ,故四边形FJCK是平行四边形.设AE与BG的交点为M,FC与JK的交点为N,则M、N分别是BG和FC的中点,于是sin sin, sin sinAB MAG JKC FK AG BAM BKJ CK∠∠===∠∠又BAG FKC∠=∠,于是BAG∆∽FKC∆,所以ABG DFC∠=∠.EFGD几何(4):如图,在ABC ∆中,60A ∠=︒, ABC ∆的内切圆I 分别切边,AB AC 于点,D E ,直线DE 分别与直线BI CI ,相交于点F G ,, 证明:12FG BC =.证法一:分别连接CF BG ID IE AI ,,,,, 则A D I E 、、、四点共圆.所以12IDE A ∠=∠,从而1902BDF A ∠=︒+∠, 又1118022BIC B C A ∠=︒-∠+∠︒+∠()=90,所以BDF BIC ∠=∠.又 DBF CBI ∠=∠,得FDB ∆∽CIB ∆.所以FB DBCB IB=. 又由 DBI FBC ∠=∠,得 IDB ∆∽CFB ∆,所以 CF BF ⊥, 从而1302FCG A ∠=∠=︒.同理BG GC ⊥,所以B C F G 、、、四点共圆,由此 sin FGBC FCG=∠,所以12FG BC =.证法二:因为1()2BIG B C ∠=∠+∠,又因为1801()22A BDG ADEBC ︒-∠∠=∠==∠+∠,所以B D I G 、、、四点共圆,因此 90BGC BDI ∠=∠=︒.同理90CFB ∠=︒,所以B C F G 、、、四点共圆.又 19090()302FCG FBC BCI B C ∠=︒-∠-∠=︒-∠+∠=︒,所以1sin 2FG BC FCG BC =∠=.BB几何(5):在△ABC 中,BC >AB ,BD 平分ABC ∠交AC 于D ,如图,CP 垂直BD ,垂足为P ,AQ 垂直BP ,Q 为垂足。
M 是AC 中点,E 是BC 中点。
若△PQM 的外接圆O 与AC 的另一个交点为H ,求证: O 、H 、E 、M 四点共圆。
作AQ 延长线交BC 于N ,则Q 为AN 中点,又M 为AC 中点,故QM //BC 。
所以12PQM PBC ABC ∠=∠=∠。
同理,12MPQ ABC ∠=∠。
所以 QM= PM 。
又因为Q 、H 、P 、M 共圆,所以PHC PHM PQM ∠=∠=∠,故PHC PBC ∠=∠。
所以P 、H 、B 、C 四点共圆,90BHC BPC ∠=∠=,故12HE BC EP ==。
结合OH =OM ,知OE 为HP 中垂线,易知EHO EPO OPM ∠=∠=∠,所以O 、H 、E 、M 四点共圆。
CA几何(6):如图,ABC ∆的内切圆I 分别切BC 、AC 于点M 、N ,点E 、F 分别为边AB 、AC 的中点,D 是直线EF 与BI 的交点。
证明:M 、N 、D 三点共线。
连接AD ,则易知90ADB ∠=。
连接AI 、DM ,DM 与AC 交于点G 。
因为ABI DBM∠=∠,所以AB BI BD BM =,故ABI DBM ∆∆,从而1902DMB AIB ACB ∠=∠=+∠ 连接IG 、IC 、IM ,则1902IMG DMB ACB GCI ∠=∠-=∠=∠所以I 、M 、C 、G 四点共圆,从而IG AC ⊥,因此G 与N 重合,即M 、N 、D 三点共线。
DAID C BAF E NM几何(7)已知O 、I 分别是ABC ∆的外接圆和内切圆;证明:过O 上的任意一点D ,都可以作一个三角形DEF ,使得O 、I 分别是DEF ∆的外接圆和内切圆.证:如图,设OI d =,,R r 分别是ABC ∆的外接圆和内切圆半径,延长AI 交O 于K ,则2sin2A KI KB R ==,sin 2rAI A =,延长OI 交O 于,M N ;则()()2R d R d IM IN AI KI Rr +-=⨯=⨯=,即222R d Rr -=;过D 分别作I 的切线,DE DF ,,E F 在O 上,连EF ,则DI 平分EDF ∠,只要证,EF 也与I 相切;设DIO P =,则P 是EF 的中点,连PE ,则2sin2D PE R =,sin 2r DI D =,()()22ID IP IM IN R d R d R d ⋅=⋅=+-=-,所以2222sin 2sin 22R d R d D DPI R PE DI r --==⋅==, 由于I 在角D 的平分线上,因此点I 是DEF ∆的内心, (这是由于,()()0011180180222D EPEI PIE P F +∠=∠=-∠=-∠=,而 2D PEF ∠=,所以2EFEI ∠=,点I 是DEF ∆的内心). 即弦EF 与I 相切.N F几何(8)如图,过ABC ∆的外心O 任作一直线,分别交边,AB AC 于,M N ,F E ,分别是,BN CM 的中点.证明:EOF A ∠=∠. 先证引理:如图,过O 的直径KL 上的两点,A B 分别作弦,CD EF ,连,CE DF ,分别交,K L 于,M N ,若OA OB =,则MA NB =.引理证明:设CD EF P =,直线,CE DF 分别截PAB ∆,据梅涅劳斯定理,1AC PE BM CP EB MA ⋅⋅=,1BF PD ANFP DA NB⋅⋅=; 则MA AC AD PE PF BM NB BE BF PC PD AN⋅⋅⋅⋅=⋅⋅⋅⋅ ……① 而由相交弦,得PC PD PE PF ⋅=⋅ ……② 若O 的半径为R ,OA OB a ==,则22AC AD AK AL R a BK BL BE BF ⋅=⋅=-=⋅=⋅ …③,据①②③得,MA MB NB NA =,即1MA MA AB ABNB NB AB AB+===+.因此MA NB =.引理得证.回到本题,如下图(两图都适用),延长MN 得直径1KK ,在直径上取点1M ,使1OM OM =,设11CM O A =,连1A B 交1KK 于1N ,由引理,11MN M N =,(右图中则是11M N MN =)因此,O 是1NN 的中点,故,OE OF 分别是1NBN ∆及1MCM ∆的中位线,于是得1EOF BA C A ∠=∠=∠.11几何(9):设000,,AA BB CC 是ABC ∆的三条角平分线,自0A 作01A A ∥0BB ,02A A ∥0CC ,12,A A 分别在,AC AB 上,直线123A A BC A =;类似得到点33,B C .证明:333,,A B C 三点共线.证明:据梅尼劳斯逆定理,只要证,3333331CA AB BC B C A B C A⋅⋅= …… ①由于直线123A A A 截ABC∆,得2313211BA CA AA A B A A AC ⋅⋅=,所以 321321CA A A A CA BBA AA =⋅…… ②; 同理有321321AB B B B A B C CB BB =⋅ …… ③,321321BC C C C BC A AC CC =⋅…… ④. 由020BC BA BA BC =⋅,020AA AA AC AI =⋅,得200200AA AA AC BC BA BA BC AI⋅=⋅⋅ … ⑤ 又由010AA AA AB AI =⋅,010CA CA CB CB =⋅,得100100A CCA CB AIAA AA AB BC⋅=⋅⋅… ⑥ 据②、⑤、⑥得23000030000CA CA CA AC CB A BBA BC AB A B ⎛⎫=⋅⋅= ⎪ ⎪⎝⎭; 同理可得,23030CB CB B A B A ⎛⎫= ⎪⎝⎭,23030AC AC C B C B ⎛⎫= ⎪⎝⎭…… ⑦ 由于ABC ∆的三条角平分线000,,AA BB CC 共点,由塞瓦定理,0000001CA AB BC B C A B C A⋅⋅= …… ⑧,于是由⑦、⑧得, 23033003330001CA CA AB BC AB BC B C A B C A B C A B C A ⎛⎫⋅⋅=⋅⋅= ⎪ ⎪⎝⎭,即①成立,因此结论得证.33几何(10):一张纸上画有一个半径为R的圆O和圆内一个定点A,且OA=a,折叠纸片,使圆周上某一点A'刚好与点A重合.这样的每一种折法,都留下一条折痕.当A'取遍圆周上所有点时,求所有折痕所在直线上点的集合.解:对于⊙O上任意一点A',连AA',作AA'的垂直平分Array线MN,连OA'.交MN于点P.显然OP+P A=OA'=R.由于点A在⊙O内,故OA=a<R.从而当点A'取遍圆周上所有点时,点P的轨迹是以O、A为焦点,OA=a为焦距,R(R>a)为长轴的椭圆C.而MN上任一异于P的点Q,都有OQ+QA=OQ+QA'>OA'.故点Q在椭圆C外.即折痕上所有的点都在椭圆C上及C外.反之,对于椭圆C上或外的一点S,以S为圆心,SA为半径作圆,交⊙O于A',则S在AA'的垂直平分线上,从而S在某条折痕上.最后证明所作⊙S与⊙O必相交.1︒当S在⊙O外时,由于A在⊙O内,故⊙S与⊙O必相交;2︒当S在⊙O内时(例如在⊙O内,但在椭圆C外或其上的点S'),取过S'的半径OD,则由点S'在椭圆C外,故OS'+S'A≥R(椭圆的长轴).即S'A≥S'D.于是D在⊙S'内或上,即⊙S'与⊙O必有交点.于是上述证明成立.综上可知,折痕上的点的集合为椭圆C上及C外的所有点的集合.。
