第三章一维定态问题
曾谨言《量子力学导论》第二版的课后答案

+a
= 2mω a 2 ⋅
得 a2 = (3)
π = mωπ a 2 = n h 2
代入(2) ,解出
E n = nℏω ,
积分公式:
n = 1, 2 , 3 , ⋯ a 2 − u 2 du = u a2 u a2 − u2 + arcsin + c 2 2 a
(4)
∫
2π
1.4 设一个平面转子的转动惯量为 I,求能量的可能取值。 提示:利用
)
[ (
) (
)
]
其 中 T 的 第 一 项 可 化 为 面 积 分 , 而 在 无 穷 远 处 归 一 化 的 波 函 数 必 然 为 0 。 因 此
ℏ2 T= d 3 r∇ψ * ⋅ ∇ψ ∫ 2m
结合式(1) 、 (2)和(3) ,可知能量密度
(3)
w=
且能量平均值
ℏ2 ∇ψ * ⋅ ∇ψ + ψ *Vψ , 2m
(1)
1 mω 2 x 2 。 2
−a
0 a x (2)
a = 2 E / mω 2 ,
x = ± a 即为粒子运动的转折点。有量子化条件
+a
∫ p ⋅ dx = 2 ∫
nh 2ℏn = mωπ mω
−a
1 2m( E − mω 2 x 2 ) dx = 2mω 2 ∫ a 2 − x 2 dx 2 −a
∫= 1, 2 , ⋯ , pϕ 是平面转子的角动量。转子的能量 E = pϕ / 2I 。
解:平面转子的转角(角位移)记为 ϕ 。
.
它的角动量 pϕ = I ϕ (广义动量) , pϕ 是运动惯量。按量子化条件
∫
∴
因而平面转子的能量
量子力学第三章

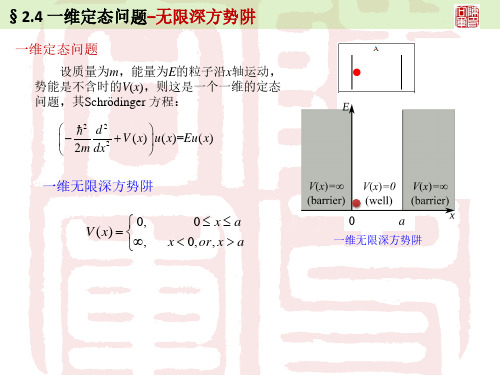
当 x a 或x 0,方程中含有 x 项
因 (x) 及 E 有限
( x) 0
(3)
从物理考虑,粒 子不能透过无穷 高的势壁
13
一维无限深势阱 方程(1)
当 0 xa
Chapter 3 One dimensional Problems of Schrodinger Eq.
Chapter 3 One dimensional Problems of Schrodinger Eq.
束缚态:0<E<V0
0, V ( x) V0
d 2 k 2 0 dx 2 2mE k
General Solution
V(x)
x a/2 x a/2
I
V 定理3:设 V x 具有空间反演不变性, x V x 。
4
Chapter 3 One dimensional Problems of Schrodinger Eq.
宇称
空间反射:空间矢量反向的操作。
r r
(r , t ) (r , t )
归一化条件
A 2
a
17
一维无限深势阱
Chapter 3 One dimensional Problems of Schrodinger Eq.
推导:
| n x | dx
2
a 2
0
| n | dx | n | dx | n | dx
2 2 2 0 a
ˆ 定义:空间反射算符,又称宇称算符 P :
ˆ (r , t ) (r , t ) P
5
Chapter 3 One dimensional Problems of Schrodinger Eq.
Chapter 3-1 一维定态问题(上)

当n分别是奇数和偶数时,满足 偶函数 → ψn ( −x) =ψn ( x) (n为奇数) (n为偶数)
奇函数 → ψn ( −x) =−ψn ( x)
即n是奇数时,波函数是x的偶函数,我们称 这时的波函数具有偶宇称;当n为偶数时, 波函数是x的奇函数,我们称这时的波函数具 有奇宇称。本征函数所具有的这种确定的奇 偶性(宇称)是由势函数 对原点的这种对称性 而来的。关于这个问题,后面将就普遍情形 作专门讨论。
a.势U(x)中第一类不连续性的存在并不改 变加于函数的标准条件。事实上, 按Schrodinger 方程 ψ ′′ = (U − ε )ψ 在势的每一个不连续点,U出现一有限量的突 ψ 也如此,但ψ ′′ 的积分在这些点上保 然跳跃, ′′ 持连续: 因此ψ ′及ψ (理由更充足)处处连续。 (证明见:曾《量子力学导论》p53)
节点数 : 按定义,所谓节点,即本征函数 的零点(端点除外),从图可以看出 ψ n 与x轴相 交(n-1)次,即ψ n 有(n-1)个节点。
§3.2.3 有限深对称方势阱
⎧ ⎪ 0, ⎪ V (x) = ⎨ ⎪V , ⎪ 0 ⎩ a x < 2 a x ≥ 2
(1)
a为阱宽,为势阱高度。 以下讨论束缚态情况 ( 0 < E < V0 ) , 前例可看成 是 V0 ≥ E 的极限情况。
⎧ d 2ψ + α 2ψ = 0 ( x < a) ⎪ 2 ⎨ dx ⎪ ψ =0 ( x ≥ a) ⎩
(3)
在 x < a 区域内的通解是
ψ = A sin α x + B cos α x
(4)
亦可取为ψ = c sin(α x +δ ) , c 和 δ 待定。
第3章 一维定态问题

2 d ( x) 2mE 2 2 k ( x) 0 令: k 2 则: 2 dx
通解:
x Aeikx Beikx C coskx D sin kx
A, B, C, D 为常数,由标准条件和归一化条件确定。 ka ka a ka ka a C cos D sin 0 x C cos D sin 0 x 2 2 2 2 2 2
(3)能量间隔:
(n 1) 2 2 2 n 2 2 2 2 2 E n E n1 En (2n 1) 2 2 2m a 2m a 2m a2
n一定, a一定,
a En 0
En 2n 1 n En 2 0 En n En
2
V
a 时 2
d 2 ( x) 2 x x ( x ) ( x ) A ' e B ' e dx2
由有限条件,当
x a 2 x
( x) 0
粒子不可以进入Ⅱ区
I区: V 0
2 d 薛定谔方程: ( x) 2m E ( x) 0 dx2 2
( x)
E2
1 ( x)
n 1, 2,
a n sin x n 1, 2,3 2 a
E1
非对称二维无限深势阱
0 0 x a,0 y b V ( x, y) others
2 n12 n2 En ( 2 2) 2m a b 2
( p) ( p)
2
2
4 a
pa cos 2 2 2 2 2 a p
2
3
8.非对称一维无限深势阱
4 ( x)
V ( x)
2.6 一维定态问题

§2.6 一维定态问题一.一维定态波函数的一般性质对一维定态问题,薛定谔方程为定理一:设是方程的一个解,对应能量为E,则也是方程的一个解,对应能量也为E。
证明:,对方程两边取复共轭,利用满足相同的方程,对应的能量都是E。
定理二:设具有空间反射不变性,即,如为方程的一个解,对应能量为E;则也为方程的一个解,对应能量也是E。
定理三:当时,如无简并,方程的解有确定的宇称。
即偶宇称:,或奇宇称:。
证明:因为和都是能量E的解,二者应表示同样的状态。
因此应只差一常数。
,则所以,,,。
二.一维无限深势阱,,,,令,方程的解为:,利用边界条件:得:,即:,,(时,,无物理意义), 对应的波函数为:。
利用归一化条件: , 得:,归一化后的波函数为:。
束缚态:无穷远处为零的波函数所描述的状态。
基态:体系能量最低的态。
三.一维线性谐振子一维线性谐振子的势能为,体系的薛定谔方程为,进行如下变量代换:,,薛定谔方程变为:,变系数二级常微分方程。
,方程变为,解为,时,有限,将写成如下形式:,带入原方程将H按展成幂级数,时,有限,要求幂级数只有有限项。
级数只有有限项的条件是:,线性谐振子的能级为:,线性谐振子的能量为分离值,相邻能级的间距为。
零点能:,。
厄密多项式:递推公式: (1)(2)(3)(4)对应的波函数为:,归一化常数:四.势垒贯穿;薛定谔方程为,,(a)时令,方程变为:,,在区域,波函数:在区域,波函数:在区域,波函数:对投射波,不应有向左传播的波,即:。
利用波函数及微商在和的连续条件,我们有:::,解方程组:利用几率流密度公式:得出入射波、透射波、反射波的几率流密度入射波几率流密度:透射波几率流密度:反射波几率流密度:投射系数:反射系数:(b) 时令,方程变为:,方程的解形式为:利用边界条件得:其中双曲正弦函数,双曲余弦函数投射系数:隧道效应:粒子在能量E小于势垒高度时仍能贯穿势垒的现象。
按经典力学:,如,则动能为负。
量子力学讲义及资料第三章: 一维定态问题

第三章: 一维定态问题[1]对于无限深势阱中运动的粒子(见图3-1)证明2a x = )()(22226112πn a x x -=-并证明当∞→n 时上述结果与经典结论一致。
[解]写出归一化波函数:()axn a x n πsin2=ψ (1) 先计算坐标平均值:xdx axn a xdx a x n a xdx x a aa)(⎰⎰⎰-==ψ=02022cos 11sin 2ππ利用公式:2sin cos sin ppxp px x pxdx x +-=⎰ (2) 得2cos sin cos ppxp px x pxdx x +-=⎰ (3) 22cos 22sin 221022aa x n n a a x n x n a x a x a=⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛-=ππππ 计算均方根值用()x x x x x ,)(222-=-以知,可计算2xdx ax n x a dx a x n x a dx x x a a)(⎰⎰⎰-==ψ=022222022cos 11sin 2ππ利用公式px ppx x p px x p pxdx x sin 1cos 2sin 1cos 3222-+=⎰ (5) aa x n x n a a x n n a x n a x a x 0222222cos222sin 22311πππππ⋅⎪⎭⎫⎝⎛-⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛--=222223πn a a -= ()22222222223⎪⎭⎫ ⎝⎛--=-=-a n a a x x x x π)(2222212πn a a -=(6) 在经典力学的一维无限深势阱问题中,因粒子局限在(0,a )范围中运动,各点的几率密度看作相同,由于总几率是1,几率密度a1=ω。
210a xdx a xdx x aa ===⎰⎰ω 312202a dx x a x a==⎰()22222222223⎪⎭⎫⎝⎛--=-=-a n a a x x x x π)(故当∞→n 时二者相一致。
量子力学导论第3章答案

第三章一维定态问题3.1)设粒子处在二维无限深势阱中,⎩⎨⎧∞<<<<=其余区域,0,0 ,0),(by a x y x V 求粒子的能量本征值和本征波函数。
如b a = ,能级的简并度如何? 解:能量的本征值和本征函数为m E y x n n 222π =)(2222bn an y x +,2,1, ,sinsin2==y x y x nn n n byn axn abyx ππψ若b a =,则 )(222222y x n nn n ma E yx +=πayn axn ay x nn yx ππψsinsin2=这时,若y x n n =,则能级不简并;若y x n n ≠,则能级一般是二度简并的(有偶然简并情况,如5,10==y x n n 与2,11''==y x n n )3.2)设粒子限制在矩形匣子中运动,即⎩⎨⎧∞<<<<<<=其余区域 ,0,0,0 ,0),,(cz b y a x z y x V 求粒子的能量本征值和本征波函数。
如c b a ==,讨论能级的简并度。
解:能量本征值和本征波函数为)(222222222cn bn an mnn n Ez y x zyx++=π ,,3,2,1,, ,sinsinsin8==z y x z y x n n n czn byn axn abcn n n zy x πππψ当c b a ==时,)(2222222z y x n n n mann n Ezyx++=πayn ayn axn a n n n z y x zy x πππψsinsinsin223⎪⎭⎫⎝⎛=z y x n n n ==时,能级不简并;z y x n n n ,,三者中有二者相等,而第三者不等时,能级一般为三重简并的。
z y x n n n ,,三者皆不相等时,能级一般为6度简并的。
如 ⎩⎨⎧→++=++→++=++)9,6,3()10,5,1(2086161210)11,3,1()9,7,1(10438652222222222223.3)设粒子处在一维无限深方势阱中,⎩⎨⎧><∞<<=ax 0, ,0 ,0),(x ax y x V 证明处于定态)(x n ψ的粒子)61(12)x -(x ,22222πn aa x -==讨论∞→ n 的情况,并于经典力学计算结果相比较。
一维定态的简并问题

一维定态的简并问题
一维定态的简并问题是一个涉及到量子力学和量子统计力学的概念。
在这个问题中,我们考虑一个粒子在一维无限深势阱中的定态,也就是粒子在一维空间中被限制在了一个特定的区域内。
根据量子力学的原理,粒子的能量是由其动能和势能共同决定的。
在一维无限深势阱中,粒子的势能是无限大的,因此其能量是由动能决定的。
当粒子处于定态时,其能量是确定的,而动能也是确定的,因此粒子的波函数在一维空间中是有规律的。
然而,当粒子处于不同的量子态时,其波函数可能会表现出不同的规律性。
在某些情况下,不同的量子态可能会有相同的能量,这就是所谓的能级简并。
在一维无限深势阱中,能级简并通常出现在高激发态,因为高激发态的粒子具有更多的动量和能量,因此其波函数在一维空间中的规律性更加复杂。
简并问题在一维定态中是存在的,但并不是所有的一维定态都会有简并现象。
有些一维定态是没有简并的,也就是说它们的能量是唯一的,不会出现能级简并的情况。
这种现象被称为非简并性定理。
这个定理在一维无限深势阱中成立,但在其他情况下可能不成立。
总之,一维定态的简并问题是一个涉及到量子力学和量子统计力学的概念。
在这个问题中,我们需要考虑粒子在一维空间中的运动和能量分布,以及不同量子态之间的相互作用和简并现象。
2020年物理竞赛—量子力学A版—第三章 一维定态问题 一维势散射问题34PPT 课件

新坐标下 Schrodinger 方程改写为:
该式是新坐标下一维线性 谐振子Schrödinger 方程,于是可以利用已 有结果得:
d2 dx2
(
x)
2
2
[
E
1 2
2
x2
V0
]
(
x)
0
d2 dx2
(
x)
2
2
[
E
1 2
2
x2
]
(
x)
0
其中 E E V0
能量本征值:
En
(n
1 2
)
En En V0
然而,量子情况与此不 同,对于基态,其几率密度 是: ω0(ξ) = |ψ0(ξ)|2
= N02 exp[-ξ2] (1)在ξ= 0处找到粒子的 几率最大; (2)在|ξ|≧1处,即在阱外 找到粒子的几率不为零,与 经典情况完全不同。
5. 几率分布
分析波函数可知量子力学的谐振子波函数ψn有 n 个节点,在节 点处找到粒子的几率为零。而经典力学的谐振子在 [-a, a] 区间每 一点上都能找到粒子,没有节点。
ωn(ξ)
n=2
|10|2
ω0(ξ)
n=1
-1 0 1
n=0
-1 1
-4 -2
24
当线性谐振子处在前几个量子态时,几率分布与经典情况差别很大。当 量子数增大时,相似性随之增加。
(三)例
例1. 求三维谐振子能级,并讨论它的简并情况。
解: l (1)三维谐振子 Hamilton 算符
Hˆ
2
2
d2
(5)求归一化常数
(I)作变量代换,因为ξ=αx, 所以dξ=αdx;
chapt3一维定态问题

推论:一维束缚态的波函数必为实函数(当然
可保留一相位因子)。
证
(−
h2 2m
d2 dx2
+
V(x))un (x)
=
Enun (x)
令 un (x) = Rn (x) + iIn (x)( R n (x), In (x) 都是实函数) 则
x > 0 中。
定义: a. 反射份额 b. 透射份额
R=
jR ji
,现
R=1;
T = jT ji
,现
T=0。
T+R =1
3. 在区域 x > 0 ,概率密度为
ρ = uE(x) 2 = D 2 e−2Κx
在这一区域,经典粒子是不能到达的。这是量 子物理学的结论。它可能带来经典物理学认为 不可能出现的物理现象。
范围内有 n 个节点(即有 n 个 x 点使
un (xi ) = 0,不包括边界点或∞远)。
基态无节点(当然处处不为零的波函数没 有这性质,如 eimφ (它是简并的),同样, 多体波函数由于反对称性,而可能无这性质)
(4)在无穷大位势处的边条件:根据坐标空 间的自然条件,波函数应单值,连续,平方可积,
所以,
B→0
于是,当 V0 → ∞ , 方程有解
u(x)
=
⎧A ⎨ ⎩
sin 0
kx
x<0 x>0
这表明,在无穷大的位势处,波函数为0, 边界上要求波函数连续,但并不要求再计及导 数的连续性。当然,概率密度和概率通量矢总 是连续的。
§3.2 隧穿效应和扫描隧穿显微镜 (1)阶梯位势:讨论最简单的定态问题
一维定态问题无限深方势阱
u(x)
2
=
2
sin 2
nπ
a a
0
x, ,
0≤ x≤a x < 0,or, x > a
n = 1, 2,3,
概率分布不均匀,存在概率为零的节点。 但:概率分布不随时间变化!
§2.4 一维定态问题–无限深方势阱
结论:
(3) 束缚在势阱中的粒子的能量是量子化的
=E
E=n
π2 2
2ma2
n2 ,
平均值
∫ = E
+∞
ψ
−∞
*
(r
,
t
)
−
2
2m
∇2
+V
(r,t) ψ
(r , t )dτ
总能能算符:
Hˆ
=−
2
∇2
+V
(r,t)
pˆ 2 =
+V (r,t)
2m
2m
称为粒子的哈密顿算符。
§2.5 力学量的平均值、算符表示—平均值
含时薛定谔方程:
i
∂ψ
∂t
=
−
2
2m
∇2
+ V (r,t) ψ
(1) 粒子的位置 r
例如:一维无限深方势阱
粒子的位置是不确定的,取值在[0, a]之间。 但粒子的概率分布是确定的,是
u(x)
2
=
2 sin2 nπ a a 0
x, ,
0≤ x≤a x < 0,or, x > a
n = 1, 2,3,
所以,可以得到粒子位置的平均值 (假设粒子处在基态 n =1 态):
2
∇2 2m
+ V (r,t)ψ
量子力学 曾谨言 第五版 第三章知识点

所以,当 V ( x) 为实函数时,一维定态波函数可取为实函数。 下面一条性质涉及空间反射变换和宇称。 做空间反射变换:
x → −x
ψ ( x) → ψ (− x)
ˆ 代表空间反射变换: P ˆψ ( x= ) ,用算符 P
ψ (− x)
宇称本征方程:
ˆψ ( x) = λψ ( x) P
可证 λ 为实数。只有当 λ 为实数时,该方程才是本征方程。因为按照基本假定,本征值与测量值相对
1
作者:张宏标(任课教师)
东北师范大学本科生物理专业量子力学课程讲稿 Lectures on Quantum Mechanics for undergraduates of physical major
称为它的简并度。 (ii)、当 V ( x) 为实函数时,一维定态波函数可取为实函数。 [证] 分能级无简并和有简并两种情况来证明 (1)、能级无简并情况:对应能级 E ,只有一个独立的本征波函数。 设ψ ( x) 为能量值为 E 的本征波函数,能量本征方程:
作者:张宏标(任课教师) 2
东北师范大学本科生物理专业量子力学课程讲稿 Lectures on Quantum Mechanics for undergraduates of physical major
应,而测量值总是实数。
ˆ 的本征值 λ 。 宇称(Parity) :空间反射变换算符 P
宇称的可能取值:
因此,在 x = x0 点,ψ ′( x) 不连续, 连接条件为:
ψ ′( x0 + ε ) −ψ ′( x0 − ε ) = −
2mV0 ψ ( x0 ) 。 2
′ −ψ 2ψ 1′ = (v)、若ψ 1 ( x) 和ψ 2 ( x) 都是能级本征值 E 所对应的本征波函数,则有ψ 1ψ 2 常数 。 ′ = ψ 2ψ 1′ 。 而对于束缚态(即 lim ψ ( x) → 0 ) ,则为ψ 1ψ 2
03一维定态问题

2 2 2 2 2 (nx ny nz ), nx , ny , nz 1, 2,... 2 2ma
可见简并度取决于(nx,ny,nz)使得nx2+ny2+nz2= n’x2+n’y2+n’z2 的(nx,ny,nz)组个数,基态无简并, 其他例如第一激发态(1,1,2),(1,2,1),(2,1,1)三 重简并,......
Quantum mechanics
小
结
除了求解束缚态以外,还有一类问题即一维散射问题,束 缚定态的能量本征值一般由方程结合边界条件,波函数 连接条件确定,是分立的,而且束缚态本身满足平方可积 条件,一定是可归一的.散射态则一定不可归一,其能量本 征值是连续的(取决于入射粒子).设粒子从势垒左边入射, 其波函数ψ的渐近行为如下给出:
第三章一维定态问题
12/88
Quantum mechanics
习题解答
0,0 x a V ( x) , x 0, x a
3,设粒子处于一维无限深方势阱中运动,即
对处于第n个定态ψn(x)的粒子计算坐标和动量的期望值x,p以及 相应的涨落⊿x,⊿p.讨论当n→∞的情况,并与经典力学比较.
2
n d n x x2 H n ( x) (1) e e n dx
即H1(x)=1,H2(x)=2x等,能量本征函数ψn(x),的宇称性质 ψn(-x),=(-1)nψn(x),其中基态无节点,必为偶宇称态,又是 最小不确定态.此外,谐振子问题也可在动量表象中求解.
第三章一维定态问题
4/88
2
2
(0)
δ-势阱(γ为负)存在唯一的一个束缚态.δ-势问题的求解也 可在动量表象中进行.另外,如果求解δ-势的散射问题,则 可知其透射振幅在k复平面正虚轴上的极点对应于δ-势 阱的束缚态.其实,束缚态在散射振幅的极点里,这是一个 普遍的事实.
大学课件 量子力学 一维定态问题

(4)由归一化条件定系数 A
| m |2 dx
a
| I |2 dx a a
|
II m
|2
dx
a
| III |2 dx
a
a
|
II m
|2
dx
a
a
a
a
| A |2 sin2 m xdx 1
2a
| A |2 cos 2 m xdx 1
(3)宇称
1)空间反射:空间矢量反射的操作
r r
(r ,
t)
(r,
t
)
2)如果有:
(r, t) (r, t)
(r, t) (r, t)
称波函数具有正宇称(或偶宇称);
(r,
t)
(r ,
t
)
称波函数具有负宇称(或奇宇称);
3)如果在空间反射下,
(r, t) (r, t)
则波函数没有确定的宇称。
ψ(-a) = ψ(a) = 0。
在阱外U(x)->∞,连
续性和有限性条
则解为:
件要求
I 0, II A sin(x ), III 0.
因为势壁无限高,从物理上考虑,粒子不 能透过势壁,
按波函数的统计解释,要求在阱壁上和阱 外波函数为0.
使用波函数标准条件 :连续性
1)波函数连续性:
与上面波函数连续性条件导出的结果 A sin(-αa + δ)= 0 矛盾,二者 不能同时成立。所以波函数导数在有无穷跳跃处不连续。
Asin(a )0 Asin(a )0
Asin(a )cos Asin(a )cos
Acos(a )sin 0 Acos(a )sin 0
第三章一维定态问题

中运动,求粒子的能级和对应的波函数。
解: U (x)与t 无关,是定态问题。其定态S—方程
2
d 2 (x) U (x) (x) E (x)
2m dx2
在各区域的具体形式为
x0
2 2m
d2 dx2
1(x)
U
( x) 1 ( x)
E 1 ( x)
1
0xa
2 2m
d2 dx2
2
(
x)
E
等式两边除以(x, y, z) X ( x)Y ( y)Z(z)
1 2 d2
1 2 d2
1 2 d2
X
2
dx2
X
V1( x)
Y
2
dy2
Y V2( y)
Z
2
dz2
Z
V3(z)
E
2 [
2
d2 dx 2
V1 ( x)]X ( x)
Ex X (x)
2 d 2
[
2
dy 2
V2 ( y)]Y ( y)
E yY ( y)
2 d 2
[ 2 dz 2 V3 ( z )]Z ( z ) Ez Z ( z )
其中
E Ex Ey Ez
返回
(二)一维无限深势阱
0, V ( x)
| x | a | x | a
V(x)
I
II
III
求解 S — 方程 分四步:
-a 0 a
(1)列出各势域的一维S—方程
(2)解方程
(3)使用波函数标准条件定解
(4)定归一化系数
(1)列出各势域的 S — 方程
2
2
一维问题

b) (3.4 3.4b
b)式表明阱中的动量谱是两个在全实轴上反向运动的单色 de 3.4b (3.4
Broglie 波叠加而成的驻波。
显然,两种结果很不相同。究竟谁正确?或是两者都对?两者都 错?实际的文献讨论中,几种观点全有表述。事实上,波函数、动量
̇̇ 算符及 Schrodinger 方程都应当定义在整个 x 轴上,而不只是定义在势
参考文献
[1] 泡利物理学讲义,第 5 卷:波动力学,第二章,§7。 洪铭熙等 译,人民教育出版社, 1982 年。W. Pauli , 《Handbuch der Physik》, eds. by H. Geiger and K. Scheel, Vol. 24/1, Springer, Berlin, 1933。 他于 1956-1958 年在苏黎世联邦工业大 学物理学位课程两次授课中,依然如此讲法。 [2] L.N.Cooper,《物理世界(上、下) 》 ,杨基方等译,海洋出版社, 1984。第 184 页。 [3] 朗道和栗弗席茨,量子力学(非相对论理论) ,上册,§22, 高
π ( x+a )ℏ ⎞ nπ ⎞ i ⎛ nπ ( x+a )ℏ i⎛n ⎧ ⎤ -Ent ⎟ - ⎜ + En t ⎟ ⎜ ⎟ ⎟ 1 ⎡ 2a 2a ℏ⎜ ℏ⎜ ⎝ ⎠ ⎝ ⎠⎥ ⎪ ⎢ e e , ⎪ ψn ( x ) = ⎨ 2i a ⎢ ⎥ ⎣ ⎦ ⎪ 0, ⎪ ⎩
− iE n t ℏ
,
这里出现两个待定系数 A 、 α 和一个待定参数 k (它的数值将决定阱 中粒子的能量) 。为了确定它们,利用两个边界条件 ψ ( ±a ) = 0 (加上 总几率归一条件,一共也是三个) ,即
⎧ ⎪ sin ( ka + α ) = 0 ⎨ ⎪ ⎩ sin ( -ka + α ) = 0
一维运动问题的一般分析

第三章 一维势场中的粒子§3.1 一维运动问题的一般分析一维问题的实际背景是平面型固体器件,“超晶格”,以及从高维问题约化下来的一维问题。
3.1.1 一维定态Schrödinger 方程的解的一般特征一维定态Schrödinger 方程是222(),2d V x E m dx ψψψ-+= 或者写为二阶常微分方程的标准形式 ()2222()0.d m E V x dxψψ+-= 在经典力学的意义上E T V =+,其中T 是动能,永远0≥,因此我们永远有0E V -≥。
而在量子力学里由于有不确定关系的缘故,我们完全谈不上粒子在某点处有多大的动能,因此即使在0E V -<的区域里,波函数仍然有非零解。
然而方程在0E V -<的区域和0E V ->的区域解的特征是完全不同的。
我们把0E V ->的区域称为经典允许区,0E V -<的区域称为经典禁戒区。
把方程重写为22212(),d m E V dxψψ=-- 并假设ψ是实函数。
画出()vs ()x x ψ的曲线,那么我们发现:在经典允许区(0->E V 即>E V )里,()x ψ在横轴上方是向上凸的,在横轴下方是向下凹的;在经典禁戒区(0-<E V 即<E V )里,()x ψ在横轴上方是向下凹的,在横轴下方是向上凸的。
所以,在经典允许区里()x ψ呈现出振荡式的行为,而在经典禁戒区里()x ψ通常是单调变化的。
这样一个直观的图像对于我们理解以后的问题很有帮助。
3.1.2 关于一维定态Schrödinger 方程的解的基本定理朗斯基(Wronski)定理:若势能()V x 在-∞<<+∞x 上没有奇点,ψ1()x 和ψ2()x 都是一维定态Schrödinger 方程的解,而且属于相同的能量,那么12121212ψψψψψψψψ''∆≡≡-=''常数, 其中/d dx ψψ'≡。
3.1一维定态的一般性质

(x)
V
(x)
(x)
E
(x)
可见, (x)也是属于E的解,即可能有简并。
由此得推论:若V (x) V (x),且解无简并,则解
必有确定的宇称,即波函数具有奇偶性。
此时, (x)与 (x)表示同一个态(可相差一个
任意常数)
宇称算符一般用P来表 示,其作用是 Pf (r ) f (r )
按照前面的讨论,有
成立)
证明:
[分析]如何证明导数连续?在边界处 导数相等即可,可由Schrodinger方程出发。
由方程
d2 dx2
(
x)
2m 2
[
E
V
(
x)]
(
x)
在V (x)连续区, (x)、 '(x)的连续性是显然的。
在x ~ a邻域,对方程积分并取
a
lim dx ( 0,是个小量)
0 a
得 '(a 0 ) '(a 0 )
即
(x) 1 [ f (x) g(x)], (x) 1 [ f (x) g(x)]
2
2
则完备得证
该定理告诉我们:在存在着简并时,可以通过 一定组合构造出对应于能量本征值E的确定宇 称解。
定理5:对于阶梯形方位势(在a处跃变)
V (x) VV12
xa xa
V(x) V2 V1 0
ax
若V2 V1 有限,则定态波函数 (x) 及其导数 '(x) 必是连续的(若 |V2 V1 | ,则定理不
一维定态问题数学处理简单,便于得到 严格解。作为量子体系,同样可展现量子 问题的主要特征,因而是处理复杂问题的 基础。 所谓一维运动就是指在某一方向上的运动。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
II k
Asin k
1)波函数连续:
I 0, II A sin(x ), III 0.
V(x)
I (a) II (a) Asin(a ) 0,
I
II
III
II (a) III (a)
Asin(a ) 0.
2)波函数导数连续:
-a 0 a
在边界 x = -a,势有无穷跳跃,波函数微商不连续。这是因为:
Ex X(x)
[
2
2
d2 dy2
V2 ( y)]Y ( y)
E yY ( y)
[
2
2
d2 dz 2
V3 (z)]Z (z)
Ez Z(z)
令 ψ(x,y,z) = X(x) Y(y) Z(z)
E = Ex + Ey + Ez
于是S-方程化为三个常微分方程:
所谓一维运 动就是指在 某一方向上 的运动。
第三章 一维定态问题
§1 一维无限深势阱
§1
§2 线性谐振子
§2
§3 一维势散射问题
§3
在继续阐述量子力学基本原理之前,先用 Schrodinger 方程来处理一类简单的问题——一维 定态问题。其好处有四:
(1)有助于具体理解已学过的基本原理; (2)有助于进一步阐明其他基本原理; (3)处理一维问题,数学简单,从而能对结果进行
2
2
d2 dx 2
(
x)
V
(
x )
(
x)
E ( x)
d2 dx 2
( x)
2
2
[V ( x)
E ]
( x)
0
势V(x)分为三个区域,
用 I 、II 和 III
表示,
其上的波函数分别为 ψI(x),ψII(x) 和 ψIII (x)。则方程为:
d 2
dx 2
I (x)
2
2
(V
2
E )
I (x)
0
x a
2
2
2
V
( x,
y,
z)
( x,
y,
z)
E
( x,1( x) V2( y) V3(z)
令: (x, y, z) X(x)Y ( y)Z(z)
2 2
d2
dx2
d2 dy2
d2 dz2
X ( x)Y (
y)Z(z)
V1( x) V2(
y) V3(z)
1 2 d 2
X
2
dx2
X
V1( x)
Y
2
dy2
Y V2( y)
Z
2
dz2
Z
V3(z)
E
[ 2
2
d2 dx 2
V1 ( x)]X ( x)
Ex X (x)
2 d 2
[
2
dy 2
V2 ( y)]Y ( y)
E yY ( y)
2 d 2
[ 2 dz 2 V3 ( z )]Z ( z ) Ez Z ( z )
其中
E Ex Ey Ez
返回
(二)一维无限深势阱
0, V ( x)
| x | a | x | a
V(x)
I
II
III
求解 S — 方程 分四步:
-a 0 a
(1)列出各势域的一维S—方程
(2)解方程
(3)使用波函数标准条件定解
(4)定归一化系数
(1)列出各势域的 S — 方程
( x,
y,
z)
E
( x,
y,
z)
YZ
2 2
d2 dx2
X V1( x)
XZ
2 2
d2 dy2
Y V2( y)
XY
2 2
d2 dz 2
Z V3(z)
E ( x,
y, z)
等式两边除以(x, y, z) X ( x)Y ( y)Z(z)
1 2 d 2
1 2 d 2
III
a
1。单值,成立; 2。有限:当x
-∞, ψ 有限条件要求
C2=0。
d2 dx 2
I
2
I
0
d2
dx
2
II
2 II
0
d2
dx
2
III
2 III
0
I II
C1e x C2e x
A sin(x )
III B1e x B2e x
(3)使用波函数标准条件
I C1e x
Acos(a )sin 0 Acos(a )sin 0
(1) (2)
(1)+(2)
cos(a) sin 0 (3)
(2)-(1)
sin(a) cos 0 (4)
两种情况:
由(4)式
I . sin 0 0 则 cos 1
csionsa00 scionsa00
sin a 0
a n
Hˆ [ 2 2 V ( x, y, z)] ( x, y, z) E ( x, y, z) 2
此方程是一个二阶偏微分方程。若势可写成:
V(x,y,z) = V1(x) + V2(y) + V3(z)
形式,则 S-方程可在直角坐标系中分离变量。
[
2
2
d2 dx 2
V1 ( x)]X ( x)
若ψI(-a)’ = ψII(-a)’, 则有,0 = A αcos(-αa + δ)
与上面波函数连续条件导出的结果 A sin(-αa + δ)= 0 矛盾,二 者不能同时成立。所以波函数导数在有无穷跳跃处不连续。
Asin(a )0 Asin(a )0
Asin(a )cos Asin(a )cos
d 2
dx 2
II ( x)
2
2
E
II
(
x
2 )
0
a xa
d2 dx 2
III ( x )
2
2
(V
E )
III ( x )
0
xa
方程可 简化为:
d2 dx 2
I
2
I
0
d2
dx
2
II
2 II
0
d2
dx
2
III
2 III
0
V(x)
I
II
-a 0
III a
V(x)
I
II
-a 0
细致讨论,量子 体系的许多特征都可以在这些一 维问题中展现出来; (4)一维问题还是处理各种复杂问题的基础。
§1 一维无限深势阱
返回
(一)一维运动 (二)一维无限深势阱 (三)宇称 (四)讨论
(一) 一维运动
当粒子在势场 V(x,y,z) 中运动时,其 Schrodinger 方程为:
n a
(n 0,1,2, )
因
2
2 2
E
所以
E
2 2
2
2
2
n
a
2
n2 22 2 a 2
En
II n
Asinx Asin n
a
x
n2 22 E n 2a2
II n
Asin n
a
x
(n 0,1,2, )
讨论
当n
0时 :
0,
E0 0
0 II
A
s
in
0
x
状态不存在
0
当n
k时 :
2
2
2
(V
E)
I (a)
lim
C1e
a
0
所以
I 0
同 理 : III 0
从物理考虑,粒子不能透过无穷高的势壁。
根据波函数的统计解释,要求在阱壁上和阱壁 外波函数为零,特别是
ψ(-a) = ψ(a) = 0。
则解为:
I 0, II A sin(x ), III 0.
使用标准条件 3。连续:
