12网络单纯形法演示
02-2单纯形法

+ +x3 x2 +
5 2 x4
= 30 = 8 = 6
0 比值
1 x1
0 3 x1 z
-2x4 + x5 = 12 ③ 4 min
1 + 2x4 +x5 = 42 x3 + 2 x4 - 1 x5 = 4 3 3 1 + 2 x4 = 6 x4 + 1 x5 = 4 -2 3 3
1 2
x4
(2.1)
xn+1, xn+2, … , xn+m 称为人工变量。
初始基本可行解:( 人造基本解 )
X0 = ( 0, 0, … , 0, b1, b2, …, bm )T
n个
22
第2 章
单纯形法
2.3 人工变量法
基本思想:
人造解 X0 不是原LP问题的基本可行解。 但若能通过单纯形法的迭代步骤,将虚拟 的人工变量都替换出去,都变为非基变量(即 人工变量xn+1 = xn+2 = … = xn+m = 0),则X0的 前n个分量就构成原LP问题的一个基本可行解。
解
3 x1 1 0 3 -3 1 0 3 -3
5 x2 0 2 4 -5 0 1 0 0
0 x3 1 0 0 0 1 0 0 0
0 x4 0 1 0 0 0 1/2 -2 5/2
0 x5 0 0 1 0 0 0 1 0
比 值
6 min 9 8
4 min
19
第2 章
单纯形法
2.2 单纯形法的计算过程 cj
基 解
cj
cn xn
x1 1 0
┇
x2 … xm 0 … 1 …
Network Simplex Method网络单纯形法-精选文档54页

Optimality
• If no arc like ki exists, then your prices can not be undercut
– A competitor could break even at best
Algebraic Description (Step 1)
• Each step begins with a feasible tree solution x defined by a tree T.
• Requirements
– The amount entering a node minus the amount leaving it is equal to its demand
– The amount shipped over any arc is nonnegative
Example
-5 1
3 1
0
12
1 43
33 0
0
2 5 -2
LP Formulation
• Let c be a row vector and x a column vector indexed by the set of arcs
– cij is the cost of shipping over ij – xij is the amount to ship over ij
– You want to ship as much as possible – You must also adjust the rest of your
schedule to conform with demand
Example
01
4 5
3
52
网络单纯形算法

5
基本流
基本结构包含生成树 T,弧的集合L,弧集U, T ∪L ∪U = A. 对每个 (i,j) ∈ L, xij= 0. 对每个 (i,j)∈U, xij= uij. 选择在T中的弧流,以便每个结点满足它的供应/需求约 束. 如果流也满足上下界限制,基本结构也是可行的. 基本结构也可能不可行. 实际上,这就是对偶单纯形算法 的正常情况下.
看动画.
10
另一种替换计算单纯形乘子的方法
令πi 是在T中从结点i到结点1 (根结点)的路径的代价. 如果 (j,k) 反向的,那么使用代 价-cjk. 什么是结点4的单纯形乘子? 什么是结点6的单纯形乘子?
11
最优化条件(又一次)
生成树解的最优化条件: 以下条件是最小代价流问题的最优解的条件,对于对 偶问题,π是最佳的. 1. 基本流 x 是可行的 2. π 是单纯形乘子向量 3. For 每个非树弧(i,j) a. 如果 cπij> 0, 那么 xij= 0 b. 如果cπij< 0, 那么 xij= uij 如果弧(5,6)满足最优条件, 在弧(5,6)上的流是什么?
16
生成树,部分生成树解
结点1是根结点. 树从 根结点"悬挂".
17
结点深度和前驱
,其他
18
线
在进行深度优先搜索 的时候,获得线. 在深度优先搜索中, 每个结点指向下一个 结点.
19
寻找圈
procedure IDENTIFY CYCLE; begin 设置 i : = k 且 j : = l; while i ≠j do begin
在单纯形方法中,我们如何避免成圈?(或者说如果环绕 圈发送的流总数是0,我们做什么?) 单纯形方法的最坏情况性能是什么? 在实践中,加速性能的好的启发式方法是什么?
网络单纯形算法

11
5
39
跟随从结点8开始的线 跟随从结点 开始的线
1 8 3 10 6 9 7 2 12
什么是 thread(8)?
11
5
40
跟随从结点8开始的线 跟随从结点 开始的线
1 8 3 10 6 9 7 2 12
什么是 thread(3)?
11
5
41
跟随从结点8开始的线 跟随从结点 开始的线
1 8 3 10 6 9 7 2 12
什么是 thread(10)?
11
5
42
跟随从结点8开始的线 跟随从结点 开始的线
1 8 3 10 6 9 7 2 12
什么是 thread(11)?Biblioteka 11543
跟随从结点8开始的线 跟随从结点 开始的线
1 8 3 10 6 9 7 2 12
什么是 thread(6)?
11
5
44
停止规则
1
停止规则: 停止规则 当depth(当 当 前结点) 前结点 ≤ depth(8)的时 的时 候停止
为了计算流,向上 为了计算流, 迭代树, 迭代树,寻找流能 唯一确定的弧. 唯一确定的弧
3
2
2 4
在弧(5,3)中的流是 中的流是 在弧 什么? 什么?
3
计算生成树流
1 1 -6 2 1 3 6 -4 7
在弧(3,2)中的流是 中的流是 在弧 什么? 什么?
3
2
2 4
3
5 3
4
计算生成树流
1 1 -6 2 7 6 -4
7
depth = 1
3 10
8 6
depth = 1
2
11
最优化方法之单纯形法PPT课件

3 5
4 2
1 0
0 1
9 8
x3 9 3x1 0 x4 8 5x1 0
x1 3
x1 1.6
第5页/共76页
x1取min3,1.6 1.6,
即x4 0 x4出基
得到新基
3 5
1
0
• 迭代(求新的基本可行解)
3 4 1 0 9
5
2
0
1
8
主元素
3 4 1 0 9
1
25 0
s.t 3x1 4x2 x3 9
5x1 2x2 x4 8
x1, x2 , x3 , x4 0
• 找初始基可行解
系数的增广矩阵
取初始可行基为B1
1
0
0 1
3 4 1 0 9
A
5
2
0
1
8
得基可行解 X (0) (0 0 9 8)T
目标函数值 z(0) 0
• 判断是否最优解?能否找到另一个基可行解使目标函数 值下降?
x3
3 14
x4
3 2
x1
-
1 7
x3
2 7 x4 1
x2
3 2
5 14
x3
3 14
x4
x1
1
1 7
x3
-
2
7
x4
代入目标函数:
z
17.5
5 14
x3
25 14
x4
最优解: X * (1 1.5 0 0)T z* 17.5
第10页/共76页
X (0) (0 0 9 8)T z(0) 0
x1, x2 , x3 , x4 , x5 0
zj cj cBB1Pj cj
图论动画-网络单纯形算法-46页PPT精选文档

T
L
-6
U
4
4
5
没有弧违反最
-4
优条件.
32
寻找圈
1
8
3
6
10
11
7 2
9
12
5
33
使用深度和前驱
01
8
23
6
10
11
7 2
9
12
54
depth(5) = 4;
depth(3) = 2;
用 pred(5) 替换结点5
34
使用深度和前驱
01
8
23
6
10
11
7 2
9 3 12 5
depth(9) = 3;
T L U
4
4, 0
5
下一个生成树
是什么?
21
旋转(pivot)之后
u14, x14
1
4,2
2
2, 1 4,3
3
3,0 5, 3
3,3 1, 0
更新的生成树
T L U
4
4, 0
5
在旋转中,一条
弧加入到 T, 而
另一条弧从 T 删
除.
22
更新乘子
0
-4
1
0
0
32
4
-2
0
34
4
2
0
5
3
-2
当前乘子和即约代价
4, $2 3, $5
2, $4
3, $4
3 1, $4
5, $5
最小代价流问题
-4 4
4, $2
5 -3
T L U
17
生成树流
单纯形法基本原理及实例演示

③计算各非基变量xj的检验数j=Cj-CBPj ′,若所有j≤0,则问题已得
到最优解,停止计算,否则转入下步。
④在大于0的检验数中,若某个k所对应的系数列向量Pk≤0,则此问
题是无界解,停止计算,否则转入下步。
⑤根据max{j|j>0}=k原则,确定xk为换入变量(进基变量),再按 规则计算:=min{bi/aik| aik>0}=bl/ aik 确定xBl为换出变量。建 立新的单纯形表,此时基变量中xk取代了xBl的位置。
⑥以aik为主元素进行迭代,把xk所对应的列向量变为单位列向量,即 aik变为1,同列中其它元素为0,转第③ 步。
线性规划的例子
max z 4x1 3x2 2x1 2x2 1600 5x1 2.5x2 2500 x1 400 x1, x2 0
线性规划--标准化
● 引入变量:s1,s2,s3
检验系数区
Z=CBB-1b
初始单纯形表
迭代 基变 次数 量
CB
x1
x2
s1
s2
s3
50 100 0 0 0
比值
b bi ai 2
1 Zj=CBNj j cj zj
Z=CBB-1b
初始单纯形表
基
迭代 次数
变
CB
x1
X2
s1
s2 S3
量
50 100 0 0 0
比值
b bi ai 2
1 1 1 0 0 300
C向量
max z 50 100 0 0
CB
CN
x1
x2
0•
1 1 1
1 0 0
0 1 0
单纯形法的矩阵描述课件PPT

单纯形法的基本概念
单纯形法是一种求解线性规划问题的 算法。
它通过迭代的方法,不断寻找最优解 ,直到找到最优解或确定无解为止。
单纯形法的步骤
01
初始化
设置初始单纯形表格,选择一个初始基可行解。
02 03
迭代
通过迭代的方式,不断寻找最优解。在每次迭代中,根据单纯形表格进 行相应的操作,包括进基、离基、换基等步骤,直到找到最优解或确定 无解。
初始解选择
选择合适的初始解,避免 陷入循环的可能性。
算法终止条件
设置合适的终止条件,在 循环发生之前提前结束算 法。
启发式搜索策略
引入启发式搜索策略,指 导算法跳过可能导致循环 的解。
处理特殊情况的方法
异常处理
针对特殊情况,如输入数据错误、 矩阵奇异等情况,设计异常处理 机制。
边界情况处理
对算法边界情况进行特殊处理,确 保算法的正确性和稳定性。
生产调度
通过单纯形法,企业可以优化生 产调度,合理安排生产任务,提
高生产线的协同作业能力。
在金融投资组合中的应用
投资组合优化
单纯形法可用于优化金融投资组合,帮助投资者 选择最佳的投资组合方案,降低投资风险。
风险控制
在金融投资中,单纯形法可以帮助投资者控制风 险,通过分散投资降低资产波动。
收益最大化
单纯形法的矩阵描述课件
目 录
• 单纯形法简介 • 单纯形法的矩阵描述 • 单纯形法的实现 • 单纯形法的改进与优化 • 单纯形法的应用 • 总结与展望
01 单纯形法简介
线性规划问题
01
线性规划问题是在一组线性不等 式约束下,最大化或最小化一个 线性目标函数的问题。
02
线性规划问题在运筹学、经济学 、管理学等领域有广泛的应用。
单纯形法原理以及步骤
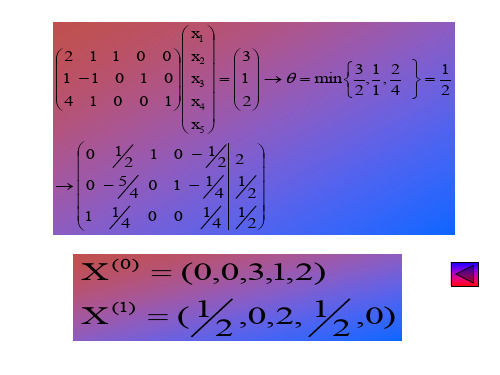
,0)
4、单纯形法迭代原理
单纯形法是沿顶点寻找线性规划问题最优解的一种有效方法。该方法主要包括: 确定初始基可行解(即起始顶点);从一个基可行解转移到另一个基可行解; 最优性检验三项内容。
1. 确定初始基可行解
对标准形式的线性规划问题
max z = ∑jn=1 cjxj
(1-6)
∑jn=1 Pjxj = b
0 0 … 0 amj 0 … 1 bm
bl alj
xj
min
bi aij
aij>
0
x1
2 1 1 1 4 1
1 0 0
0 1 0
0 0 1
x2 x3 x4
3 1 2
min
3, 2
1 1
,
2 4
1 2
x5
0
1 2
1
0
54
0
1
1 4
0
0
1 2
2
1
1 4
X (1) (x10 a1 j , x20 a2 j ,, xm0 amj ,0,, ,,0)T
由于Pj≤ 0,对任意的 0
xi0 aij 0
无限增大时,目标函数值无限增加,所以,线性规划问题具有无界解。
返回
第四节 单纯形法计算步骤
1.求初始基可行解,列出单纯形表 2. 最优性检验 3. 基变换(从一个基转换到另一个基) 4. 重复步骤2和3,求出最优解
…
xl 变为非基变量
xk 变为基变量
4 . 重复第2、3步,直到求出最优解(或计算结束)。
例:用表格式单纯形法求解下列线性规划问题。
max z =20x1 + 8x2 + 6x3
运筹学-单纯形法ppt课件

基本解中最多有m个非零分量。
基本解的数目不超过
C个nm。
n!
m!n
m!
定义 在线性规划问题的一个基本可行解中,如果所有的基变量都取正值,则 称它为非退化解,如果所有的基本可行解都是非退化解。称该问题为非退化的 线性规划问题;若基本可行解中,有基变量为零,则称为退化解,该问题称为 退化的线性规划问题。
Cnm
上述结论说明: 线性规划的最优解可通过有限次运算在基可行解中获得.
;.
8
2 单纯形法
(1)单纯形法的引入 例1
Max Z=40X1 +50X2
X1 +2X2 +X3
=30
3X1 +2X2 +X4 =60
2X2 X1 … X5 0
+X5 =24
;.
9
解:(1)、确定初始可行解
B = ( P3 P4 P5 ) = I
表
示
0 10 I C N B C -1 B N B -1 N-C B B -B 1-1 -C B B -B 1b -b 1
BN I b
CB CN 0
0
I
B-1N
B-1
B-1b
0
CN -CB B-1N
-CB B-1
CBB-1b
;.
27
对应I 式的单纯形表—— I 表(初始单纯形表)
价值系数cj
a2m1
amm1
a1m2 a2m2
amm2
a1n a2n amn
非 基 向 量
X B x1 x2 xm T
X N xm1 xm2 xn T
基变量
非基变量
;.
3
AX b
单纯形法与对偶定理

单纯形法与对偶定理单纯形法⼀般oi 中遇到的线性规划问题都长这样⽐如某⼀些⽹络流问题,以及⼆分图最⼤权匹配啥的,结合对偶定理,可以有很多很强的结论以及⼀个最⼩费⽤流的线性规划式⼦现在考虑怎么做这类问题不妨先引⼊⼀个基变量(松弛变量)⽐如说现在的系数矩阵是⽐如说现在的系数矩阵是x 11x 12x 13x 14...x 1n +1x 21x 22x 23x 24...x 2n +1x 31x 32x 33x 34...x 3n +1x 41x 42x 43x 44...x 4n +1...x m 1x m 2x m 3x m 4...x mn +1对于第i ⾏x i ,n +1=b i −n∑j =1x i ,j ∗a i ,j 不妨将第x i ,k 表⽰出来x i ,k =x i ,n +1+∑j != k x i ,j ∗a i ,j −b i−a i ,k给你要最⼤化的式⼦带来的价值是这样可以吧x i ,n +1的值给去x i ,k ,这样的操作叫做转轴之后就可以⽤这个过程来时⽬标函数有最⼤值有⼀个例题吧很容易列出线性规划式⼦max :c 1∗x 1+c 2∗x 2+...+c n ∗x n a 11∗x 1+a 12∗x 2+...+a 1n ∗x n <=b 1..a m 1∗x 1+a m 2∗x 2+...+a mn ∗x n <=b m就是⼀个板⼦题#include<bits/stdc++.h>#define MAXN 500#define eps 1e-7typedef double ll;const ll inf = 1e18;using namespace std;int n,m;ll a[MAXN][MAXN];int id[MAXN];void out(){for(int i = 1 ; i <= n ; i++)printf("%.2f " , a[0][i]); puts("");for(int i = 1 ; i <= m ; i++){ for(int j = 1 ; j <= n ; j++){ printf("%.2f " , a[i][j]); }printf("%.2f " , a[i][0]); puts(""); }}void plot(int x , int y){ swap(id[x + n] , id[y]);double t = a[x][y]; a[x][y] = 1;for(int j = 0 ; j <= n ; j++)a[x][j] /= t; for(int i = 0 ; i <= m ; i++){if(i == x || a[i][y] < eps)continue; t = a[i][y] , a[i][y] = 0;for(int j = 0 ; j <= n ; j++)a[i][j] -= a[x][j] * t; }}bool simplex(){for(int i = 1 ; i <= n ; i++)id[i] = i; int x = 0, y = 0; int cnt = 0; ll minl; while(1){x = y = 0 , minl = inf; cnt++;for(int i = 1 ; i <= n ; i++)if(a[0][i] > eps){x = i;break;} if(!x)break;for(int i = 1 ; i <= m ; i++)if(a[i][x] > eps && minl > a[i][0] / a[i][x])minl = a[i][0] / a[i][x] , y = i; if(!y) {puts("Unbounded"); return false;} plot(y , x); }return true;}int main(){while(scanf("%d%d",&n,&m) == 2){ memset(a , 0 ,sizeof(a));for(int i = 1 ; i <= n ; i++)cin>>a[0][i]; for(int i = 1 ; i <= m ; i++){for(int j = 1 ; j <= n ; j++)cin>>a[i][j]; cin>>a[i][0]; }simplex();printf("Nasa can spend %d taka.\n",(int)ceil(-a[0][0]*m)); }}对偶定理考虑⼀个基本的线性规划模型{}{max :c 1∗x 1+c 2∗x 2+...+c n ∗x n a 11∗x 1+a 12∗x 2+...+a 1n ∗x n <=b 1..a m 1∗x 1+a m 2∗x 2+...+a mn ∗x n <=b mx i >=0其系数矩阵为a 11a 12...a 1n a 21a 22...a 2n a 31a 32...a 3n..a m 1a m 2...a mn那么上⾯这个线性规划模型的对偶问题的系数矩阵为上述系数矩阵的转置矩阵a 11a 12...a 1n a 21a 22...a 2n a 31a 32...a 3n..a m 1a m 2...a mnT 即:a 11a 21...a m 1a 12a 22...a m 2a 13a 32...a m 3..a 1n a 2n ...a nm那么线性规划模型对偶过来就是max :b 1∗y 1+b 2∗y 2+...+b m ∗y m a 11∗x 1+a 21∗x 2+...+a m 1∗x n <=c 1..a 1n ∗y 1+a 2n ∗y 2+...+a nm ∗y m <=c my i >=0基本上⼤多数的线性规划模型都可以通过对x i 的转换化成标准形式不过还是应该列个表:并且注意:原问题有⽆界解等价于对偶问题⽆可⾏解但是对偶问题⽆可⾏解时,原问题可能为⽆界解或者⽆可⾏解线性规划在⽹络流中的应⽤全⼳模矩阵(任何⼀个⾏数列数相同的⼦矩阵的值都是+1/-1)有⼀个很好的性质,对于⼀个线性规划模型的系数矩阵是⼀个全⼳模矩阵,那么有每⼀个单纯形法的调整系数都应当为(-1,0,1)线性规划对偶性--->>可以通过很显然的式⼦推导推导出---->>(最⼤流 = 最⼩割)部分题⽬没有很显然的建图,⼀般是转线性规划,然后看⼀看是不是⼀个全⼳模矩阵,如果是,就可以使⽤⽹络流解决有⼀个可以判断是否是全⼳模矩阵的⽅法直接考虑差分,对于每⼀个约束 + 表⽰⼊,-表⽰出,直接建图,跑⼀个最⼩最⼩费⽤流就好了也可以直接对偶掉,做⼀个单纯形法线性规划与特殊的整数规划前40分可以直接dp 掉还有⼀道题Codeforces 375E,有O (n 3)的dp 做法,但是线性规划可以很快的做掉。
Network Simplex Method网络单纯形法

Example
-5 1
4 5
3
12
7
43
33 1
9
5 5 -2
12 13 14 23 25 35 54
1 1 1 1 0 0 0 0
2
1
0
0 1 1 0
0
3 0 1 0 1 0 1 0
4
0
0
1
0
0
0
1
5 0 0 0 0 1 1 1
LP Formulation (2)
Network
• A network is a collection of nodes connected by arcs
• Each node has a demand for the commodity
– Nodes that are sources of the commodity have a negative demand
– For all ji in T, yi = yj + cji – If the price was lower then you would lose
money – If the price was higher then a competitor could
undercut your price
Problem / Solution
• A competitor could still undercut your price
– If there was an arc ki not in T with yi > yk + cki
• You don’t want to lose business, so you also plan to ship over ki
12网络单纯形法演示

去掉弧(2,1),将 T 分成两部分
更新的乘子与检验数
给树的一端节点增 加Δ不会影响除 (2,1) 外 树 弧 的 检 验 数。为什么?
Δ应多 大才能 使 (2,1) 的检验 数为 0?
更新的乘子与检验数
这个树解 是最优解 么?
将一条违背弧加入到生成树中构成回路
沿回路发送流量
将弧(3,4)加入生成树中
回路是 什么? 可以发 送多大 流量?
沿回路发送 1 单位流量。
下一棵 生成树 是什 么?
下一棵生成树解
更新乘子
更新的生成树
当前乘子
如何修 改乘子 呢?
更新乘子
更新乘子
当前乘子
Δ应该 多大?
最优解
更新的乘子
当前生 成树是 否最优 解?
这是最优解
没有弧 违背最 优性条 件。
注意:(i,j)的检 验数是:
cij-πi+πj
具有弧费用的生 成树。如何选择节 点势使树的检验 数为 0?
注意:(i,j)的检 验数是:
cij-πi+πj
计算生成树的单纯形乘子
计算生成树的单纯形乘子
在最小费用流问题 中有一个多余的约 束。
可以自主确定π1, 令π1=0。
节点2的单纯形乘 子是什么?
将一条违背弧加入到生成树中构成回路
沿回路发送流量
将(2,1)加入树中。
回路是 什么? 可以发 送多少 流量?
沿回路发送 2 单位流量。
下一棵 生成树 是什 么?
经过一轮迭代后
更新乘子
更新的生成树
在迭代中, 加入 T 中 一条弧,从 T 中去掉 一条弧。
当前乘子与检验数
如何使 c*=0 且 其他树 弧检验 数为 0?
线性规划模型的单纯形法PPT课件

大化
目标函数中添加“惩罚因子”-M(M是任意大的正 数)为人工变量系数,只要人工变量>0,则目标函 数不可能实现最优。
第19页/共57页
max Z 2x1 3x2 0x3 0x4 0x5 Mx6 Mx7
x1 x2 x3 x6 350
x1
x4
x7
125
2x1 x2 x5 600
cj-zj 0 1/2M -M 0 -1/2M+1 0 -M 50M
-2
+600
第23页/共57页
表3-13 最优单纯形表3
cj
-2 -3 0 0 0 -M -M
CB XB x1 x2 x3 x4 x5 x6 x7 b
-3 x2 0 1 -2 0 -1 2 0 100
-2 x1 1 0 1 0 1 -1 0 250
cj-zj 20+M 30+M 0 0 -M 0
30 x2 0 20 x1 1 -M a 0
1 0.1 -0.3 0 0 6 0 0 1 0 0 30 0 -0.1 -0.7 -1 1 4
cj-zj
0
0 -3- -11- -M 0
0.1M 0.7M
由检验数全部≤0,可判定但前解应为最优解,但在基 变量中,有不为0 的人工变量,说明没有可行解。
(2)无界解。如果存在一个检验数大于零, 但对应列中的系数向量的每一个元素都小于 或等于零,则此线性规划模型是无界的。
(3)无穷多最优解。基变量中无人工变量, 且无2的情况,非基变量中的检验数有零,则 此线性规划模型有无穷多最优解。
第25页/共57页
无可行解在大M法中判断:检验数全部小于等于零且 有人工变量为基变量,则此线性规划模型无可行解。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
cij-πi+πj
具有弧费用的生 成树。如何选择节 点势使树的检验 数为 0?
注意:(i,j)的检 验数是:
cij-πi+πj
计算生成树的单纯形乘子
计算生成树的单纯形乘子
在最小费用流问题 中有一个多余的约 束。
可以自主确定π1, 令π1=0。
节点2的单纯形乘 子是什么?
弧 (2,6) 流 量 多大?
弧 (7,1) 的 流 量多大?
计算一棵生成树流
计算一棵生成树流
弧 (1,2) 流 量 多大?
注意:有两种 方法计算弧 (1,2) 的 流 量 , 结果都是 4。这 是不是巧合?
计算生成树的单纯形乘子
计算生成树的单形乘子
具有弧费用的生 成树。如何选择节 点势使树的检验 数为 0?
15.053
网络单纯形法演示
计算一棵生成树流
一棵有供应和 需求的树。(假 定其他弧流量 是 0)。
弧 (4,3) 的 流 量 多大?
计算一棵生成树流
计算一棵生成树流
要计算流量, 重复观察树, 找出流量是 唯一确定的 弧。
弧(5,3)流量多 大?
弧 (3,2) 的 流 量多大?
计算一棵生成树流
计算一棵生成树流
将一条违背弧加入到生成树中构成回路
沿回路发送流量
将(2,1)加入树中。
回路是 什么? 可以发 送多少 流量?
沿回路发送 2 单位流量。
下一棵 生成树 是什 么?
经过一轮迭代后
更新乘子
更新的生成树
在迭代中, 加入 T 中 一条弧,从 T 中去掉 一条弧。
当前乘子与检验数
如何使 c*=0 且 其他树 弧检验 数为 0?
计算生成树的单纯形乘子
节点 4 的单纯 形乘子是什 么?
节点 5 的单纯 形乘子是什 么?
计算生成树的单纯形乘子
网络单纯形算法
这是这棵树有 关的单纯形乘 子。他们不依 靠弧流量,也 不依靠非树弧 费用。
最小费用流问题
生成树流量
单纯形乘子与检验数
一棵初始生成树解
初始单纯形乘子与 检验数。
什么弧违 背最优条 件?
(1,2)的检验数是 c12-π1+π2 =0.
故5-0+π2=0.
节点 7 的单纯形 乘子是什么?
计算生成树的单纯形乘子
(1,2)的检验数是 c71-π7+π1 =0.
故-6-π7+0=0.
节点 3 的单纯形 乘子是什么?
计算生成树的单纯形乘子
节点 6 的单纯 形乘子是什 么?
计算生成树的单纯形乘子
回路是 什么? 可以发 送多大 流量?
沿回路发送 1 单位流量。
下一棵 生成树 是什 么?
下一棵生成树解
更新乘子
更新的生成树
当前乘子
如何修 改乘子 呢?
更新乘子
更新乘子
当前乘子
Δ应该 多大?
最优解
更新的乘子
当前生 成树是 否最优 解?
这是最优解
没有弧 违背最 优性条 件。
去掉弧(2,1),将 T 分成两部分
更新的乘子与检验数
给树的一端节点增 加Δ不会影响除 (2,1) 外 树 弧 的 检 验 数。为什么?
Δ应多 大才能 使 (2,1) 的检验 数为 0?
更新的乘子与检验数
这个树解 是最优解 么?
将一条违背弧加入到生成树中构成回路
沿回路发送流量
将弧(3,4)加入生成树中
