福建省平潭县高中数学 3.1.3 概率的基本性质2导学案 新人教A版必修3
高中数学 第三章 概率 3.1.3 概率的基本性质教案 新人教A版必修3(2021年整理)
福建省莆田市高中数学第三章概率3.1.3 概率的基本性质教案新人教A版必修3编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（福建省莆田市高中数学第三章概率3.1.3 概率的基本性质教案新人教A版必修3）的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。
本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为福建省莆田市高中数学第三章概率3.1.3 概率的基本性质教案新人教A版必修3的全部内容。
3.1。
3 概率的基本性质一、教学目标：1、知识与技能：（1）正确理解事件的包含、并事件、交事件、相等事件，以及互斥事件、对立事件的概念；（2）概率的几个基本性质:1)必然事件概率为1，不可能事件概率为0,因此0≤P（A)≤1；2）当事件A与B互斥时，满足加法公式：P（A∪B）= P(A）+ P（B）；3）若事件A与B为对立事件，则A∪B为必然事件，所以P(A∪B)= P（A)+ P（B)=1，于是有P（A)=1—P（B）(3)正确理解和事件与积事件，以及互斥事件与对立事件的区别与联系。
2、过程与方法：通过事件的关系、运算与集合的关系、运算进行类比学习，培养学生的类化与归纳的数学思想。
3、情感态度与价值观：通过数学活动，了解教学与实际生活的密切联系，感受数学知识应用于现实世界的具体情境，从而激发学习数学的情趣。
二、重点与难点：概率的加法公式及其应用,事件的关系与运算.三、学法与教学用具：1、讨论法，师生共同讨论，从而使加深学生对概率基本性质的理解和认识;2、教学用具：投灯片四、教学设计:1、创设情境:(1）集合有相等、包含关系，如{1，3｝={3，1｝，｛2，4｝С｛2,3，4，5｝等；（2）在掷骰子试验中，可以定义许多事件如：C1=｛出现1点｝，C2=｛出现2点}，C3=｛出现1点或2点｝，C4=｛出现的点数为偶数｝……师生共同讨论：观察上例，类比集合与集合的关系、运算，你能发现事件的关系与运算吗?2、基本概念:（1)事件的包含、并事件、交事件、相等事件见课本P115；（2）若A∩B为不可能事件，即A∩B=ф，那么称事件A与事件B互斥；（3)若A∩B为不可能事件，A∪B为必然事件,那么称事件A与事件B互为对立事件；（4）当事件A与B互斥时，满足加法公式：P(A∪B)= P(A）+ P（B）;若事件A与B为对立事件,则A∪B为必然事件，所以P(A∪B)= P（A）+ P(B）=1，于是有P（A）=1—P(B）．3、例题分析：例1 一个射手进行一次射击，试判断下列事件哪些是互斥事件？哪些是对立事件?事件A：命中环数大于7环；事件B：命中环数为10环；事件C：命中环数小于6环；事件D：命中环数为6、7、8、9、10环。
高中数学 3.1.3概率的基本性质教案 新人教A版必修3
3.1.3 概率的基本性质教学目标知识与技能：（1）正确理解事件的包含、并事件、交事件、相等事件，以及互斥事件、对立事件的概念；（2）概率的几个基本性质：1）必然事件概率为1，不可能事件概率为0，因此0≤P(A)≤1；2）当事件A与B互斥时，满足加法公式：P(A∪B)= P(A)+ P(B)；3）若事件A与B为对立事件，则A∪B为必然事件，所以P(A∪B)= P(A)+ P(B) =1于是有P(A)=1-P(B)（3）正确理解和事件与积事件，以及互斥事件与对立事件的区别与联系.过程与方法：通过事件的关系、运算与集合的关系、运算进行类比学习，培养学生的类化与归纳的数学思想。
情感态度与价值观：通过数学活动，了解教学与实际生活的密切联系，感受数学知识应用于现实世界的具体情境，从而激发学习数学的情趣。
学情分析在学生了解频率的基础上，通过师生共同讨论类比频率的性质,利用频率与概率的关系得到了概率的几个基本性质,这里的推导并不是严格的数学证明,仅仅是形式上的一种解释,因为频率稳定在概率附近仅仅是一种描述,没有给出严格的定义。
重点难点教学重点：概率的加法公式及其应用.教学难点：事件的关系与运算.教学过程教学活动（1）两个集合存在着包含与相等的关系,集合可以进行交、并、补运算，你还记得子集、相等集、交集、并集和补集的含义及其符号表示吗？（2）我们可以把一次试验可能出现的结果看成一个集合，那到必然事件对应全集，随机事件对应子集，不可能事件对应空集，从而可以类比集合的关系与运算；分析事件之间的关系与运算，使我们对概率有进一步的理解。
在掷骰子试验中,我们用集合的形式定义如下事件：C1={出现1点}，C2={出现2点}，C3={出现3点}，C4={出现4点}，C5={出现5点}，C 6={出现6点}， D1={出现的点数不大于1}，D2={出现的点数大于3}，D3={出现的点数小于5}，E={出现的点数小于7}，F={出现的点数大于6}，G={出现的点数为偶数}，H={出现的点数为奇数},……等等思考1、上述事件哪些是必然事件，哪些是随机事件，哪些是不能事件？思考2、如果事件C1发生，则一定有哪些事件发生？在集合中，集合C1与这些集合之间的关系怎样描述？思考3、分析事件C1与事件D1之间的包含关系，按集合关系这两个事件之间的关系应怎样描述？思考4、如果事件C5发生或C6发生，就意味着哪个事件发生？反之成立吗？思考5、类似地当且仅当事件A发生且事件B发生时，事件C发生，则称事件C为事件A与B的交事件（或积事件）.思考6、两个集合的交可能为空集，两个事件的交事件也可能为不可能事件，即：A∩B= ϕ，此时，称事件A与事件B互斥，那么在一次试验中，事件A与事件B互斥的含义怎样理解？上述事件中能找出这样的例子吗？思考7、若A∩B为不可能事件, A ∪ B为必然事件,则称事件A与事件B互为对立事件，那么在一次试验中，事件A与事件B互为对立事件的含义怎么理解？能举出例子吗？思考8、事件A与事件B的积事件、和事件，分别对应两个集合的交、并，那么事件A与事件B互为对立事件时对应集合是什么关系？思考9、若事件A与事件B相互对立，那么事件A与事件B互斥吗？反之呢？例1、一个射手进行一次射击,试判断下列事件哪些是互斥事件?哪些是对立事件?事件A：命中环数大于7环；事件B：命中环数为10环；事件C：命中环数小于6环；事件D：命中环数为6、7、8、9、10环。
高中数学3.1.3概率的基本性质导学案新人教A版必修3
概率的基天性质【学习目标】1．理解、掌握事件间的包含关系和相等关系．2．掌握事件的交、并运算，理解互斥事件和对峙事件的看法及关系．3．掌握概率的性质，并能用之解决相关问题．【学习要点】概率的性质课前预习案【知识链接】在掷骰子试验中，我们用会合形式定义以下事件：C1＝{ 出现 1 点} ，C2＝{ 出现 2 点} ，C3＝ { 出现 3点} ， C4＝{ 出现 4 点} ，C5＝{ 出现 5 点} ，C6＝{出现 6 点} ，D1＝{ 出现的点数不大于1}，D2＝{ 出现的点数大于4} ，D3 ＝ { 出现的点数小于6} ，E＝ { 出现的点数小于7} ， F＝ { 出现的点数大于6} ， G＝ { 出现的点数为偶数 } ， H＝ { 出现的点数为奇数} ．1．假如事件C1 发生，则必定有哪些事件发生？反之建立吗？在会合中，会合C1 与这些会合之间的关系如何描绘？2．假如事件“ C2发生或 C4 发生或 C6 发生”，就意味着哪个事件发生？3．事件 D2 与事件 H 同时发生，意味着哪个事件发生？4．事件 D3 与事件 F 能同时发生吗？5．事件 G 与事件 H 能同时发生吗？这两个事件有什么关系？【知识梳理】1．事件的关系(1) 包含关系．一般地，关于事件件 A 包含于事件A 与事件 B，假如事件A____ ，则事件B) ，记作 ____(或 A B) ．不行能事件记作B 必定____，这时称事件B 包含事件____，任何事件都包含不行能事件，即A( 或称事______．知识拓展：类比会合，事件 B 包含事件 A 可用图表示，以下图．(2)相等关系．一般地，若 ______ ，且 ______，那么称事件 A 与事件 B 相等，记作 A ＝ B．知识拓展：类比会合，事件 A 与事件 B 相等可用图表示，以下图．2．事件的运算(1) 并事件．若某事件 C 发生当且仅当事件A 记作 C＝______( 或 C＝ A ＋ B) ．知识拓展：类比会合的运算，事件 A 与事件发生 ____ 事件 B 发生，则称此事件为事件 A 与事件B 的并事件可用图表示，即以下图的暗影部分．B 的 ____( 或和事件) ，(2) 交事件．若某事件 C 生当且当事件 A 生 ____事件 B 生，称此事件事件 A 与事件 B 的交事件( 或事件)，作 C＝______( 或 C＝ AB) ．知拓展：比会合，事件 A 与事件 B 的交事件可用表示，即如所示的暗影部分．(3)互斥事件．若 A____B ______(A∩B＝ )，那么称事件 A 与事件 B 互斥，其含是，事件 A 与事件 B 在任何一次中 ______生．教点 1：①事件 A 、事件 B 互斥是指事件 A 与事件 B 在一次中不会同生，即事件 A 与 B 互不包含，A B，B A ．A 与B 两个事件同生的概率0.②假如事件 A 与事件 B 是互斥事件，那么③与会合比，可用表示，如所示．(4)立事件．若 A∩B____事件， A∪ B____事件，那么称事件 A 与事件 B 互立事件，其含是：事件 A 与事件 B 在任何一次中 ______一个生．教点 2：① 立事件的特点：一次中，不会同生，且必有一个事件生．② 立事件是特别的互斥事件，即立事件是互斥事件，但互斥事件不必定是立事件．③从会合角度看，事件 A 的立事件，是全集中由事件 A 所含果成的会合的集．3．概率的几个性(1) 范．任何事件的概率P(A) ∈ ______.(2) 必定事件的概率．必定事件的概率P(A) ＝ ____.(3)不行能事件的概率．不行能事件的概率P(A) ＝ ____.(4)概率加法公式．假如事件 A 与事件 B 互斥，有 P(A ∪ B) ＝ ______.教点3：①事件 A 与事件 B 互斥，假如没有一条件，加法公式将不可以用．②假如事件A1 ， A2 ，⋯， An 相互互斥，那么P(A1 ＋ A2 ＋⋯＋ An) ＝ P(A1) ＋ P(A2) ＋⋯＋ P(An) ，即相互互斥事件和的概率等于其概率的和．③在求某些稍复的事件的概率，可将其分解成一些概率易求的相互互斥的事件，化整零，化易．(5)立事件的概率．若事件 A 与事件 B 互立事件，那么 A ∪ B 必定事件，有P(A ∪ B) ＝ ______＋ ______＝ 1.教点4：①公式使用的前提必是立事件，否不可以使用此公式．②当一事件的概率不易直接求，但其对峙事件的概率易求时，可运用此公式，即便用间接法求概率．思虑：若事件 A 与事件 B 不互斥，则 P(A ∪ B) ＝P(A) ＋ P(B) 建立吗？自主小测1、同时投掷两枚硬币，向上边都是正面为事件M，向上边起码有一枚是正面为事件N，则有 ()A．M N B．M N C．M＝N D．M＜N2、投掷一枚平均的正方体骰子，事件P＝ { 向上的点数是 1} ，事件 Q＝ { 向上的点数是 3 或 4} ，M＝{向上的点数是 1 或 3} ，则 P∪Q＝ __________， M∩Q＝ __________.3、在 30 件产品中有28 件一级品， 2 件二级品，从中任取 3 件，记“3件都是一级品”为事件 A，则 A 的对峙事件是 __________ ．4、事件 A 与 B 是对峙事件，且 P(A) ＝ 0.6，则 P(B) 等于 ()A． 0.4 B ．0.5C． 0.6D． 15、已知 P(A) ＝ 0.1，P(B) ＝ 0.2，且 A 与 B 是互斥事件，则P(A ∪ B) ＝ __________.课上导教案事件与会合之间的对应关系：会合事件必定事件不行能事件 ( )事件 B 包含于事件A(B A)事件 B 与事件 A 相等 (B＝A)事件 B 与事件 A 的并事件 (B ∪A)事件 B 与事件 A 的交事件 (B∩A)事件 B 与事件 A 互斥 (B∩A＝)事件 A 的对峙事件【例题解说】【例题 1】判断以下各事件是不是互斥事件，假如是互斥事件，那么是不是对峙事件，并说明原因．某小组有 3 名男生和 2 名女生，从中任选 2 名同学去参加演讲竞赛，此中：(1)恰有 1 名男生和恰有 2 名男生；(2)起码有 1 名男生和起码有 1 名女生；【当堂检测】1．从装有 5 个红球和 3 个白球的口袋内任取 3 个球，那么，互斥而不对峙的事件是()A ．起码有一个红球与都是红球B．起码有一个红球与都是白球C．起码有一个红球与起码有一个白球D．恰有一个红球与恰有两个红球2．甲、乙两人下棋，甲获胜的概率是40%，甲不输的概率为 90%，则甲、乙两人下成和棋的概率为 ()A． 60% B ．30%C． 10% D ．50%3．从一箱产品中随机地抽取一件，设事件 A ＝ { 抽到一等品 } ，且已知 P(A) ＝ 0.65，则事件“抽到的不是一等品”的概率为 ()A． 0.7 B ．0.65C． 0.35 D ．0.34．一个射手进行一次射击，试判断以下事件哪些是互斥事件；哪些是对峙事件．事件 A ：命中环数大于7 环；事件 B ：命中环数为10 环；事件 C：命中环数小于 6 环；事件 D：命中环数为 6,7,8,9,10 环．5 某公事员去外处开会，他乘火车、轮船、汽车、飞机去的概率分别是 0.3,0.2,0.1,0.4 ，求：(1)他乘火车或乘飞机去的概率；(2)他不乘轮船去的概率．【问题与收获】【知识链接】1、【提示】若 C1 发生，则必定发生的事件有D1、D3 、E、 H，反之若D1 、 D3、 E、H 分别建立，能推出 C1 发生的只有D1.从会合的看法看，事件C1 是事件 D3、 E、 H 的子集，会合 C1 与会合 D1 相等．2、【提示】意味着事件 G 发生．3、【提示】C5 发生．4、【提示】不可以．5、【提示】事件 G 与事件 H 不可以同时发生，但必有一个发生．知识梳理答案： 1． (1) 发生发生 B A A (2)B A A B2． (1) 或并事件A∪ B(2) 且A∩B (3)∩ 不行能事件不会同时(4)不行能必定有且仅有3． (1)[0,1](2)1(3)0 (4)P(A) ＋P(B) (5)P(A) P(B)自主小测答案1、 A 事件 N 包含两种结果：向上边都是正面或向上边是一正一反．则当 M 发生时，事件 N 必定发生．则有 M N.2、{ 向上的点数是1或3或4}{ 向上的点数是 3}3、起码有一件是二级品4、 A P(B) ＝ 1－P(A) ＝ 0.4.5、0.3 P(A ∪ B)＝ P(A) ＋P(B) ＝ 0.1＋ 0.2＝ 0.3.事件与会合之间的对应关系事件与会合之间的对应关系以下表：事件会合必定事件全集不行能事件 ( )空集 ()事件 B 包含于事件 A(B A)会合 B包含于会合 A(B A)事件 B 与事件 A 相等 (B＝A)会合 B与会合 A 相等 (B ＝A)事件 B 与事件 A 的并事件 (B ∪A)会合 B与会合 A 的并集 (B∪ A)事件 B 与事件 A 的交事件 (B∩A)会合 B与会合 A 的交集 (B ∩A)事件 B 与事件 A 互斥 (B∩A＝)会合B与会合A的交集为空集(B∩A＝)事件 A 的对峙事件会合A的补集()例题答案：【例题 1】解： (1)是互斥事件．原因是在所选的 2 名同学中，“恰有 1 名男生”本质是选出“1名男生和 1 名女生”，它与“恰有 2 名男生”不行能同时发生，因此是互斥事件．不是对峙事件．原因是入选出的 2 名同学都是女生时，这两个事件都没有发生，因此不是对峙事件．(2) 不是互斥事件．原因是“起码有1 名男生”包含“1名男生、1 名女生”和“2名都是男生”这两种结果，“起码有 1 名女生”包含“1名女生、 1 名男生”和“2名都是女生”这两种结果，入选出的是 1 名男生、 1 名女生时，它们同时发生．这两个事件也不是对峙事件．原因是这两个事件能同时发生，因此不是对峙事件．(3)是互斥事件．原因是“起码有 1 名男生”包含“1名男生、 1 名女生”和“2名都是男生”这两种结果，它与“全部是女生”不行能同时发生．是对峙事件．原因是这两个事件不可以同时发生，且必有一个发生，因此是对峙事件．【例题 2】解： (1)设“射中 10 环”为事件 A，“射中 7 环”为事件 B ，则“射中 10 环或 7 环”的事件为A ∪ B，事件 A 和事件 B 是互斥事件，故 P(A ∪B) ＝ P(A) ＋P(B) ＝ 0.21＋ 0.28＝0.49，因此射中 10 环或 7 环的概率为 0.49.(2)设“射中 7 环以下”为事件 C，“射中 7 环或 8 环或 9 环或 10 环”为事件 D，则 P(D) ＝ 0.21＋ 0.23＋ 0.25＋ 0.28＝ 0.97.又事件 C 和事件 D 是对峙事件，则 P(C)＝ 1－P(D) ＝ 1－0.97＝ 0.03.因此射中7 环以下的概率是0.03.【例题 3】正解：记事件“出现1点”“出现2点”“出现3点”“出现5点”分别为A1，A2，A3，A4，由题意知这四个事件相互互斥．则A∪B＝ A1∪A2 ∪A3∪A4.11112故 P(A ∪B) ＝ P(A1 ∪ A2 ∪ A3 ∪ A4) ＝P(A1) ＋P(A2) ＋ P(A3) ＋ P(A4) ＝＋＋＋＝ .66663。
人教A版高中数学必修三3.1.3《概率的基本性质》》导学案
3.对立事件：事件“A不发生”称为A的对立事件，记作_________,对立事件也称为 ________,在每一次试验中，相互对立的事 件A与事件 不会_______ ___,并且一定____________.
精讲互动
例1．判断下列给出的每对事件是否为互斥事件，是否为对立事件，并说明理由。
从40张扑克牌（红桃、黑桃、方块、梅花点数从1~10各10张）中，任取一张。
（1）“抽出红桃”与“抽出黑桃”；
（2）“抽出红色牌”与“抽出黑色牌”；
（3）“抽出的牌点数为5的倍数”与“抽出的牌点数大于9”。
例2 .解读课本例5和例6
4.互斥事件的概率加法公式：
（1）在一个随机试验中，如果随机事件A和事件B是互斥事件，那么有P(A+B)=_________
(2)如果随机事件 中任意两个是互斥事件，那么有 ____________。
5.对立事件的概率运算： _____________。
探索新知：
1.如何从集合的角度理解互斥事件？
2.互斥 事件与对立事件有何异同？
§3.1.3概率的基本性质1
授课
时间
第周星期第
目标
1理解互斥事件、对立事件的定义，会判断所给事件的类 型；
2.掌握互斥事件的概率加法公式并会应用。
重点难点
重点：概率的加法公式及其应用；事件的关系与运算
难点：互斥事件与对立事件的区别与联系
学习
过程
与方
法
自主学习
1.互斥事件：在一个随机试验中，把一次试验下___________的两个事件A与B称作互斥事件。
高中数学 第三章 概率 3.1.3 概率的基本性质学案 新人教A版必修3-新人教A版高一必修3数学学
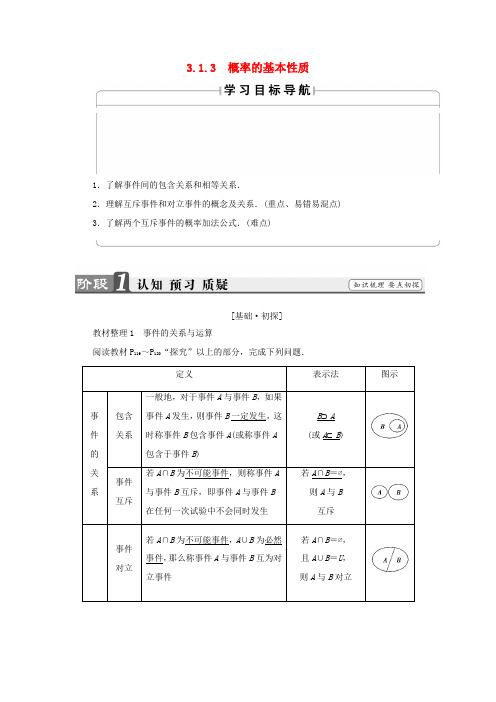
3.1.3 概率的基本性质1．了解事件间的包含关系和相等关系．2．理解互斥事件和对立事件的概念及关系．(重点、易错易混点)3．了解两个互斥事件的概率加法公式．(难点)[基础·初探]教材整理1 事件的关系与运算阅读教材P119～P120“探究”以上的部分，完成下列问题．定义表示法图示事件的关系包含关系一般地，对于事件A与事件B，如果事件A发生，则事件B一定发生，这时称事件B包含事件A(或称事件A包含于事件B)B⊇A(或A⊆B)事件互斥若A∩B为不可能事件，则称事件A与事件B互斥，即事件A与事件B在任何一次试验中不会同时发生若A∩B＝∅，则A与B互斥事件对立若A∩B为不可能事件，A∪B为必然事件，那么称事件A与事件B互为对立事件若A∩B＝∅，且A∪B＝U，则A与B对立事件的运算并事件若某事件发生当且仅当事件A或事件B发生，则称此事件为事件A与事件B的并事件(或和事件)A∪B(或A＋B)交事件若某事件发生当且仅当事件A发生且事件B发生，则称此事件为事件A与事件B的交事件(或积事件)A∩B(或AB)同时抛掷两枚硬币，向上面都是正面为事件M，向上面至少有一枚是正面为事件N，则有( )A．M⊆N B．M⊇NC．M＝N D．M＜N【解析】事件N包含两种结果：向上面都是正面或向上面是一正一反．则当M发生时，事件N一定发生，则有M⊆N.故选A.【答案】 A教材整理2 概率的性质阅读教材P120“探究”以下的部分，完成下列问题．1．概率的取值范围为[0,1]．2．必然事件的概率为1，不可能事件的概率为0.3．概率加法公式：如果事件A与事件B互斥，则P(A∪B)＝P(A)＋P(B)．特例：若A与B为对立事件，则P(A)＝1－P(B)，P(A∪B)＝1，P(A∩B)＝0.4．概率的加法公式的含义(1)使用条件：A，B互斥．(2)推广：若事件A1，A2，…，A n彼此互斥，则P(A1＋A2＋…＋A n)＝P(A1)＋P(A2)＋…＋P(A n)．(3)在求某些复杂的事件的概率时，可将其分解为一些概率较易求的彼此互斥的事件，化整为零，化难为易．1．判断(正确的打“√”，错误的打“×”)(1)互斥事件一定对立．( )(2)对立事件一定互斥．( )(3)互斥事件不一定对立．( )(4)事件A与B的和事件的概率一定大于事件A的概率．( )(5)事件A与B互斥，则有P(A)＝1－P(B)．( )(6)若P(A)＋P(B)＝1，则事件A与事件B一定是对立事件．( )【答案】(1)×(2)√(3)√(4)×(5)×(6)×2．P(A)＝0.1，P(B)＝0.2，则P(A∪B)等于( )A．0.3 B．0.2C．0.1 D．不确定【解析】由于不能确定A与B互斥，则P(A∪B)的值不能确定．【答案】 D3．一商店有奖促销活动中有一等奖与二等奖两个奖项，其中中一等奖的概率为0.1，中二等奖的概率为0.25，则不中奖的概率为________．【解析】中奖的概率为0.1＋0.25＝0.35，中奖与不中奖互为对立事件，所以不中奖的概率为1－0.35＝0.65.【答案】0.65[小组合作型]互斥事件与对立事件的判定( ) A．至多两件次品B．至多一件次品C．至多两件正品D．至少两件正品(2)把红、黑、蓝、白4张纸牌随机地分发给甲、乙、丙、丁4个人，每人分得1张，事件“甲分得红牌”与事件“乙分得红牌”是( )A．对立事件B．不可能事件C．互斥但不对立事件D．以上答案都不对【精彩点拨】根据互斥事件及对立事件的定义判断．【尝试解答】(1)“至少有两件次品”的否定是“至多有一件次品”，故选B.(2)“甲分得红牌”与“乙分得红牌”不会同时发生，但分得红牌的还可能是丙或丁，所以不是对立事件．故选C.【答案】(1)B (2)C判断互斥事件和对立事件时，主要用定义来判断.当两个事件不能同时发生时，这两个事件是互斥事件；当两个事件不能同时发生且必有一个发生时，这两个事件是对立事件.[再练一题]1．某小组有3名男生和2名女生，从中任选2名同学参加演讲比赛，判断下列每对事件是不是互斥事件，如果是，再判断它们是不是对立事件：(1)“恰有1名男生”与“恰有2名男生”；(2)“至少有1名男生”与“全是男生”；(3)“至少有1名男生”与“全是女生”；(4)“至少有一名男生”与“至少有一名女生”．【解】从3名男生和2名女生中任选2人有如下三种结果：2名男生，2名女生，1男1女．(1)“恰有1名男生”指1男1女，与“恰有2名男生”不能同时发生，它们是互斥事件；但是当选取的结果是2名女生时，该两事件都不发生，所以它们不是对立事件．(2)“至少1名男生”包括2名男生和1男1女两种结果，与事件“全是男生”可能同时发生，所以它们不是互斥事件．(3)“至少1名男生”与“全是女生”不可能同时发生，所以它们互斥，由于它们必有一个发生，所以它们是对立事件．(4)“至少有1名女生”包括1男1女与2名女生两种结果，当选出的是1男1女时，“至少有1名男生”与“至少有1名女生”同时发生，所以它们不是互斥事件．事件的运算A＝{出现1点}，B＝{出现3点或4点}，C＝{出现的点数是奇数}，D＝{出现的点数是偶数}．(1)说明以上4个事件的关系；(2)求两两运算的结果．【精彩点拨】解答时抓住运算定义．【尝试解答】在投掷骰子的试验中，根据向上出现的点数有6种基本事件，记作A i ＝{出现的点数为i}(其中i＝1,2，…，6)．则A＝A1，B＝A3∪A4，C＝A1∪A3∪A5，D＝A2∪A4∪A6.(1)事件A与事件B互斥，但不对立，事件A包含于事件C，事件A与D互斥，但不对立；事件B与C不是互斥事件，也不对立；事件B与D不是对立事件，也不是互斥事件；事件C与D是互斥事件，也是对立事件．(2)A∩B＝∅，A∩C＝A，A∩D＝∅.A∪B＝A1∪A3∪A4＝{出现点数1或3或4}，A∪C＝C＝{出现点数1或3或5}，A∪D＝A1∪A2∪A4∪A6＝{出现点数1或2或4或6}．B∩C＝A3＝{出现点数3}，B∩D＝A4＝{出现点数4}．B∪C＝A1∪A3∪A4∪A5＝{出现点数1或3或4或5}．B∪D＝A2∪A3∪A4∪A6＝{出现点数2或3或4或6}．C∩D＝∅，C∪D＝A1∪A2∪A3∪A4∪A5∪A6＝{出现点数1,2,3,4,5,6}．事件间运算方法：1利用事件间运算的定义.列出同一条件下的试验所有可能出现的结果，分析并利用这些结果进行事件间的运算.2利用Venn图，借助集合间运算的思想，分析同一条件下的试验所有可能出现的结果，把这些结果在图中列出，进行运算.[再练一题]2．掷一枚骰子，下列事件：A＝{出现奇数点}，B＝{出现偶数点}，C＝{点数小于3}，D＝{点数大于2}，E＝{点数是3的倍数}．求：(1)A∩B，BC；(2)A∪B，B＋C；(3)记H是事件H的对立事件，求D，A C，B∪C，D＋E.【解】(1)A∩B＝∅，BC＝{出现2点}．(2)A∪B＝{出现1,2,3,4,5或6点}，B＋C＝{出现1,2,4或6点}．(3)D＝{点数小于或等于2}＝{出现1或2点}；A C＝BC＝{出现2点}；B∪C＝A∪C＝{出现1,2,3或5点}；D＋E＝{出现1,2,4或5点}．[探究共研型]互斥事件和对立事件的关系探究1【提示】在一次试验中，事件A和它的对立事件只能发生其中之一，并且必然发生其中之一，不可能两个都不发生．探究2 互斥事件和对立事件有何区别和联系？【提示】(1)对立事件一般是针对两个事件来说的，一般两个事件对立，则这两个事件是互斥事件；反之，若两个事件是互斥事件，则这两个事件未必是对立事件．(2)对立事件是特殊的互斥事件，若事件A，B是对立事件，则A与B互斥，而且A∪B 是必然事件．某射手在一次射击训练中，射中10环，9环，8环，7环的概率分别为0.21,0.23,0.25,0.28，计算这个射手在一次射击中：(1)射中10环或7环的概率；(2)不够7环的概率．【精彩点拨】先设出事件，判断是否互斥或对立，然后再使用概率公式求解．【尝试解答】(1)设“射中10环”为事件A，“射中7环”为事件B，由于在一次射击中，A与B不可能同时发生，故A与B是互斥事件．“射中10环或7环”的事件为A∪B.故P(A∪B)＝P(A)＋P(B)＝0.21＋0.28＝0.49.所以射中10环或7环的概率为0.49.(2)不够7环从正面考虑有以下几种情况：射中6环，5环，4环，3环，2环，1环，0环，但由于这些概率都未知，故不能直接求解，可考虑从反面入手，不够7环的反面大于等于7环，即7环，8环，9环，10环，由于此两事件必有一个发生，另一个不发生，故是对立事件，可用对立事件的方法处理．设“不够7环”为事件E ，则事件E 为“射中7环或8环或9环或10环”，由(1)可知“射中7环”、“射中8环”等彼此是互斥事件，所以P (E )＝0.21＋0.23＋0.25＋0.28＝0.97，从而P (E )＝1－P (E )＝1－0.97＝0.03.所以不够7环的概率是0.03.1．对于一个较复杂的事件，一般将其分解成几个简单的事件，当这些事件彼此互斥时，原事件的概率等于这些事件概率的和．并且互斥事件的概率加法公式可以推广为：P (A 1∪A 2∪…∪A n )＝P (A 1)＋P (A 2)＋…＋P (A n )．其使用的前提条件仍然是A 1，A 2，…，A n 彼此互斥．故解决此类题目的关键在于分解事件及确立事件是否互斥．2．“正难则反”是解决问题的一种很好的方法，应注意掌握，如本例中的第(2)问，直接求解比较麻烦，则可考虑求其对立事件的概率，再转化为所求．[再练一题]3．甲、乙两人下棋，和棋的概率为12，乙获胜的概率为13，求： (1)甲获胜的概率；(2)甲不输的概率．【解】 (1)“甲获胜”和“和棋或乙获胜”是对立事件，所以“甲获胜”的概率P ＝1－12－13＝16. (2)法一：设事件A 为“甲不输”，可看成是“甲获胜”“和棋”这两个互斥事件的并事件，所以P (A )＝16＋12＝23.法二：设事件A 为“甲不输”，可看成是“乙获胜”的对立事件，所以P (A )＝1－13＝23.1．如果事件A ，B 互斥，记A －，B －分别为事件A ，B 的对立事件，那么( )A ．A ∪B 是必然事件B.A －∪B －是必然事件C.A －与B －一定互斥D.A －与B －一定不互斥【解析】 用集合的Venn 图解决此类问题较为直观，如图所示，A －∪B －是必然事件．【答案】 B2．从一批产品中取出三件产品，设A ＝{三件产品全不是次品}，B ＝{三件产品全是次品}，C ＝{三件产品至少有一件是次品}，则下列结论正确的是( )A ．A 与C 互斥B ．任何两个均互斥C ．B 与C 互斥D ．任何两个均不互斥【解析】 ∵从一批产品中取出三件产品包含4个基本事件．D 1＝{没有次品}，D 2＝{1件次品}，D 3＝{2件次品}，D 4＝{3件次品}，∴A ＝D 1，B ＝D 4，C ＝D 2∪D 3∪D 4，故A 与C 互斥，A 与B 互斥，B 与C 不互斥．【答案】 A3．甲、乙两人下棋，甲获胜的概率为40%，甲不输的概率为90%，则甲、乙两人下成和棋的概率为( )A ．60%B ．30%C ．10%D ．50%【解析】 甲不输棋包含甲获胜或甲、乙两人下成和棋，则甲、乙两人下成和棋的概率为90%－40%＝50%.【答案】 D4．从4名男生和2名女生中任选3人去参加演讲比赛，所选3人中至少有1名女生的概率为45，那么所选3人中都是男生的概率为________. 【解析】 设A ＝{3人中至少有1名女生}，B ＝{3人都为男生}，则A ，B 为对立事件，所以P (B )＝1－P (A )＝15. 【答案】 155．盒子里装有6个红球，4个白球，从中任取3个球．设事件A 表示“3个球中有1个红球，2个白球”，事件B 表示“3个球中有2个红球，1个白球”．已知P (A )＝310，P (B )＝12，求“3个球中既有红球又有白球”的概率． 【解】 记事件C 为“3个球中既有红球又有白球”，则它包含事件A “3个球中有1个红球，2个白球”和事件B “3个球中有2个红球，1个白球”，而且事件A 与事件B 是互斥的，所以P (C )＝P (A ∪B )＝P (A )＋P (B )＝310＋12＝45.。
福建省平潭县高中数学 3.1.2 概率的意义导学案 新人教A版必修3
达标训练 1. 课本 p129 练习 1 2. 课本 p132 练习 1 2 3 3. 已知射手甲射中靶的概率为 0.9，因此我们认为即使射手甲比较优秀，他射击 10 发子弹也不可能全中，其中必有一发不中，试判断这种认识是否正确.
作业 布置 学习 小结 / 教 学 反思
1．习题 3-1 A 3，B 组 2. 教辅资料
1
例 2．抛一枚硬币（质地均匀） ，连续出现 5 次正面向上，有人认为下次出现反面 向 上的概率大于 1/2，这种理解正确吗？
例 3．为了增强学生对世园会的了解和认识，某校决定在全校 3000 名学生中随机抽 取 10 名学生举行一次有关西安世园会的知识问卷，小明认为被选取的可能性为
1 ， 不可能抽到他，所以他就不想去查阅、咨询有关世园会的知识，你认为他的 300
2
3
2 ．问题 1：抛掷 1 0 次硬币，是否一定是 5 次“正面朝上”和 5 次“5 次反面朝上”?
3. 问题 2：有四个阉，其中两个分别代表两件奖品，四个人按排序依次抓阉来决定 这两件奖品的归属.先抓的人中奖率一定大吗？ 学习 过程 与方 法
4.阅读课本 p127-130，你发现了什么问题？
精讲互动 例 1． （1）某厂产品的次品率为 0.02，问“从该厂产品中任意地抽取 100 件，其中 一定有 2 件次品”这一说法对不对？为什么？ （2）一次抽奖活动中，中奖的概率为 0.3，解释该概率的含义； （3）某种病治愈的概率是 0.3，那么，现有 10 人得这种病，在治疗中前 7 人没 有治愈，后 3 人一定能治愈吗？
§3.1.2 概率的意义
授课 时间 学习 目标 重点 难点 第 周 星期 第 节 课型 新授课 主备课 人 刘百波
高中数学 第3章 概率 3.1.3 概率的基本性质学案 新人教A版必修3
学习资料3.1。
3 概率的基本性质学习目标核心素养1.了解事件间的包含关系和相等关系．2．理解互斥事件和对应事件的概念及关系．（难点、易混点)3．会用互斥事件与对立事件的概率公式求概率．（重点）4．了解并事件与交事件的概念，会进行事件的运算.1．通过互斥事件与对立事件的学习，体会逻辑推理素养．2．借助概率的求法，提升数学运算素养。
1．事件的关系与运算(1）事件的关系：定义表示法图示包含关系一般地，对于事件A与事件B，如果事件A发生,则事件B一定发生，这时称事件B包含事件A（或称事件A包含于事件B)B⊇A（或A⊆B）相等关系A⊆B且B⊆A A＝B事件互斥若A∩B为不可能事件，则称事件A与事件B互斥A∩B＝∅事件对立若A∩B为不可能事件,A∪B为必然事件，那么称事件A与事件B互为对立事件A∩B＝∅且A∪B＝U (2）事件的运算:定义表示法图示并事件若某事件发生当且仅当事件A发生或事件B发生，则称此事件为事件A与事件B的并事件（或和事件）A∪B（或A＋B）交事件若某事件发生当且仅当事件A发生且事件B发生，则称此事件为事件A与事件B的交事件(或积事件）A∩B(或AB）（1)概率的取值范围：［0，1］．（2）必然事件的概率为1，不可能事件的概率为0。
(3）概率加法公式为:如果事件A与B为互斥事件，则P（A∪B)＝P(A）＋P(B）．（4）若A与B为对立事件,则P（A)＝1－P(B）．P(A∪B)＝1,P(A∩B）＝0。
思考:互斥事件与对立事件有什么区别和联系？[提示]判断对象区别联系A,B是互斥事件A∩B＝∅若A，B是对立事件，则A，B一定互斥A，B是对立事件A∩B＝∅,A∪B＝Ω1．同时掷两枚硬币，向上面都是正面为事件A，向上面至少有一枚是正面为事件B，则有（）A．A⊆B B．A⊇BC．A＝B D．A<BA[由事件的包含关系知A⊆B。
]2．掷一枚骰子，观察结果，A＝{向上的点数为1},B＝｛向上的点数为2｝，则()A．A⊆B B．A＝BC．A与B互斥D．A与B对立C[由于事件A与B不可能同时发生，故A、B互斥．］3．一批产品共有100件,其中5件是次品，95件是合格品．从这批产品中任意抽取5件,现给出以下四个事件：事件A:“恰有一件次品”;事件B：“至少有两件次品”；事件C：“至少有一件次品";事件D：“至多有一件次品”．并给出以下结论：①A∪B＝C；②D∪B是必然事件;③A∪B＝B；④A∪D＝C。
高中数学3.1.3概率的基本性质导学案(无答案)新人教版必修3
3.1.3 概率的基本性质【学习目标】1、了解事件间各种关系的概念，会判断事件间的关系；2、了解两个互斥事件的概率加法公式，知道对立事件的公式，会用公式进行简单的概率计算；3、通过学习，进一步体会概率思想方法应用于实际问题的重要性。
重点：事件间的关系，概率的加法公式。
难点：互斥事件与对立事件的区别与联系。
【课前导学】阅读课本P119--121，完成下列问题1、一般地，对于事件A和事件B,如果事件A发生，则事件B一定发生，称事件B _______________ A (或事件A __________ 事件B),记作B A (或A B)；特殊地，不可能事件记为，任何事件都包含。
2、两个事件A，B中，若A B,且B A，那么称事件A与事件B ______________ ，记作_________3、某事件发生当且仅当事件A发生或者事件B发生称为事件A和事件B的_________ 事件，记作 _______ .4、某事件发生当且仅当事件A发生且事件B发生称为事件A和事件B的―—事件，记为5、事件A与事件B的交事件的特殊情况，当A A B=(不可能事件)时，称事件A与事件B 。
(即两事件不能同时发生)6、在两事件互斥的条件上，再加上事件A U事件B为必然事件，则称事件A与事件B为_____________ 事件。
(即事件A和事件B有且只有一个发生)7、集合间的关系可以用Venn图来表示。
类似，事件间的关系我们也可以用图形来表示。
8、区别互斥事件与对立事件：从图像上我们也可以看出对立事件是互斥事件的特例，但互斥事件并非都是对立事件。
概率的基本性质：1、任何事件的概率P(A) , 0 W P(A) W 11)必然事件B 一定发生，则P(B)= ________ ; 2)不可能事件C 一定不发生，则p(C)= _________3)随机事件A发生的概率为_____________ ; 4)若A B,则p(A) ___________ P(B)5)、特别地,，若A与B为对立事件，则A U B为必然事件，P(A U B) = 1 = P(A) +「P(B)即P(A) = _______2、概率的加法公式(1)互斥事件时同时发生的概率：当事件A与B互斥时，A U B发生的概率为_____________ ;(2)对立事件有一个发生的概率：当事件A与B对立时，A发生的概率为 _________________【课中导学】例1、试判断下列事件哪些是互斥事件？哪些是对立事件？1、一个射手进行一次射击，事件A:命中环数大于7环；事件B:命中环数为10环;事件C:命中环数小于6环；事件D:命中环数为6、7、8、9、10环.2、从40张扑克牌（红桃，黑桃，方块，梅花点数从1-10各10张）中，任取一张。
高中数学 3.1.3概率的基本性质教案 新人教A版必修3
课题：书法---写字基本知识课型：新授课教学目标：1、初步掌握书写的姿势，了解钢笔书写的特点。
2、了解我国书法发展的历史。
3、掌握基本笔画的书写特点。
重点：基本笔画的书写。
难点：运笔的技法。
教学过程：一、了解书法的发展史及字体的分类：1、介绍我国书法的发展的历史。
2、介绍基本书体：颜、柳、赵、欧体，分类出示范本，边欣赏边讲解。
二、讲解书写的基本知识和要求：1、书写姿势：做到“三个一”：一拳、一尺、一寸（师及时指正）2、了解钢笔的性能：笔头富有弹性；选择出水顺畅的钢笔；及时地清洗钢笔；选择易溶解的钢笔墨水，一般要固定使用，不能参合使用。
换用墨水时，要清洗干净；不能将钢笔摔到地上，以免笔头折断。
三、基本笔画书写1、基本笔画包括：横、撇、竖、捺、点等。
2、教师边书写边讲解。
3、学生练习，教师指导。
（姿势正确）4、运笔的技法：起笔按，后稍提笔，在运笔的过程中要求做到平稳、流畅，末尾处回锋收笔或轻轻提笔，一个笔画的书写要求一气呵成。
在运笔中靠指力的轻重达到笔画粗细变化的效果，以求字的美观、大气。
5、学生练习，教师指导。
（发现问题及时指正）四、作业：完成一张基本笔画的练习。
板书设计：写字基本知识、一拳、一尺、一寸我的思考：通过导入让学生了解我国悠久的历史文化，激发学生学习兴趣。
这是书写的起步，让学生了解书写工具及保养的基本常识。
基本笔画书写是整个字书写的基础，必须认真书写。
课后反思：学生书写的姿势还有待进一步提高，要加强训练，基本笔画也要加强训练。
课题：书写练习1课型：新授课教学目标：1、教会学生正确书写“杏花春雨江南”6个字。
2、使学生理解“杏花春雨江南”的意思，并用钢笔写出符合要求的的字。
重点：正确书写6个字。
难点：注意字的结构和笔画的书写。
教学过程：一、小结课堂内容，评价上次作业。
二、讲解新课：1、检查学生书写姿势和执笔动作（要求做到“三个一”）。
2、书写方法是：写一个字看一眼黑板。
（老师读，学生读，加深理解。
[精品]新人教A版必修三高中数学第三章3.1.3概率的基本性质导学案
![[精品]新人教A版必修三高中数学第三章3.1.3概率的基本性质导学案](https://img.taocdn.com/s3/m/4cd1c1d09e314332396893c2.png)
3．13 概率的基本性质1．理解、掌握事件间的包含关系和相等关系．2．掌握事件的交、并运算，理解互斥事件和对立事件的概念及关系．3．掌握概率的性质，并能用之解决有关问题．1．事件的关系(1)包含关系．一般地，对于事件A与事件B，如果事件A，则事件B一定，这时称事件B包含事件A(或称事件A包含于事件B)，记作(或A B)．不可能事件记作，任何事件都包含不可能事件，即．类比集合，事件B包含事件A可用图表示，如图所示．(2)相等关系．一般地，若，且，那么称事件A与事件B相等，记作A＝B．类比集合，事件A与事件B相等可用图表示，如图所示．【做一做1】同时抛掷两枚硬币，向上面都是正面为事件M，向上面至少有一枚是正面为事件N，则有( )A．M N B．M N．M＝N D．M＜N 2．事件的运算(1)并事件．若某事件发生当且仅当事件A发生事件B发生，则称此事件为事件A与事件B的(或和事件)，记作＝(或＝A＋B)．类比集合的运算，事件A与事件B的并事件可用图表示，即如图所示的阴影部分．(2)交事件．若某事件发生当且仅当事件A发生事件B发生，则称此事件为事件A与事件B的交事件(或积事件)，记作＝(或＝AB)．类比集合，事件A与事件B的交事件可用图表示，即如图所示的阴影部分．(3)互斥事件．若AB为(A∩B＝)，那么称事件A与事件B互斥，其含义是，事件A与事件B在任何一次试验中发生．①事件A、事件B互斥是指事件A与事件B在一次试验中不会同时发生，即事件A与B互不包含，A B，B A．②如果事件A与事件B是互斥事件，那么A与B这两个事件同时发生的概率为0[]③与集合类比，可用图表示，如图所示．(4)对立事件．若A∩B为事件，A∪B为事件，那么称事件A与事件B互为对立事件，其含义是：事件A与事件B在任何一次试验中一个发生．①对立事件的特征：一次试验中，不会同时发生，且必有一个事件发生．②对立事件是特殊的互斥事件，即对立事件是互斥事件，但互斥事件不一定是对立事件．③从集合角度看，事件A的对立事件，是全集中由事件A所含结果组成的集合的补集．【做一做2－1】抛掷一枚均匀的正方体骰子，事件P＝{向上的点数是1}，事件Q＝{向上的点数是3或4}，M＝{向上的点数是1或3}，则P∪Q＝，M∩Q＝【做一做2－2】在30件产品中有28件一级品，2件二级品，从中任取3件，记“3件都是一级品”为事件A，则A的对立事件是．3．概率的几个性质(1)范围．任何事件的概率P(A)∈(2)必然事件的概率．必然事件的概率P(A)＝(3)不可能事件的概率．不可能事件的概率P(A)＝(4)概率加法公式．如果事件A与事件B互斥，则有P(A∪B)＝①事件A与事件B互斥，如果没有这一条件，加法公式将不能应用．②如果事件A1，A2，…，A n彼此互斥，那么P(A1＋A2＋…＋A n)＝P(A1)＋P(A2)＋…＋P(A n)，即彼此互斥事件和的概率等于其概率的和．③在求某些稍复杂的事件的概率时，可将其分解成一些概率较易求的彼此互斥的事件，化整为零，化难为易．(5)对立事件的概率．若事件A与事件B互为对立事件，那么A∪B为必然事件，则有P(A∪B)＝＋＝1①公式使用的前提必须是对立事件，否则不能使用此公式．②当一事件的概率不易直接求，但其对立事件的概率易求时，可运用此公式，即使用间接法求概率．【做一做3－1】事件A与B是对立事件，且P(A)＝06，则P(B)等于( )A．04 B．05 ．06 D．1 【做一做3－2】已知P(A)＝01，P(B)＝02，且A与B是互斥事件，则P(A∪B)＝答案：1．(1)发生发生B A A(2)B A A B【做一做1】 A 事件N包含两种结果：向上面都是正面或向上面是一正一反．则当M发生时，事件N一定发生．则有M N 2．(1)或并事件A∪B(2)且A∩B(3)∩不可能事件不会同时(4)不可能必然有且仅有【做一做2－1】 {向上的点数是1或3或4} {向上的点数是3}【做一做2－2】至少有一件是二级品3．(1)[0,1] (2)1 (3)0 (4)P(A)＋P(B) (5)P(A) P(B) 【做一做3－1】 A P(B)＝1－P(A)＝04【做一做3－2】 03 P(A∪B)＝P(A)＋P(B)＝01＋02＝031．若事件A与事件B不互斥，则P(A∪B)＝P(A)＋P(B)不成立剖析：否定一个等式不成立，只需举出一个反例即可．例如：抛掷一枚均匀的正方体骰子，向上的点数是1或2或3或4或5或6为事件A，且A＝B，则A∪B表示向上的点数是1或2或3或4或5或6，则P(A)＝P(B)＝P(A∪B)＝1，P(A)＋P(B)＝1＋1＝2，所以此时P(A∪B)≠P(A)＋P(B)，即P(A∪B)＝P(A)＋P(B)不成立．上例中P(A∪B)＝P(A)＋P(B)不成立的原因是事件A与事件B不是互斥事件．其实对于任意事件A与B，有P(A∪B)＝P(A)＋P(B)－P(A∩B)(不要求证明也不要求会用)，那么当且仅当A∩B＝，即事件A与事件B是互斥事件时，P(A∩B)＝0，此时才有P(A∪B)＝P(A)＋P(B)成立．2．事件与集合之间的对应关系剖析：事件与集合之间的对应关系如下表：)()B A＝)＝([|||||]题型一判断互斥(对立事件)【例题1】判断下列各事件是否是互斥事件，如果是互斥事件，那么是否是对立事件，并说明理由．某小组有3名男生和2名女生，从中任选2名同去参加演讲比赛，其中：(1)恰有1名男生和恰有2名男生；(2)至少有1名男生和至少有1名女生；(3)至少有1名男生和全是女生．反思：判断互斥事件和对立事件时，主要用定义判断．当两个事件不能同时发生时，这两个事件是互斥事件；当两个事件不能同时发生且必有一个发生时，这两个事件是对立事件．题型二概率加法公式的应用【例题2】某射手在一次射击训练中，射中10环，9环，8环，7环的概率分别为021，023,025,028，计算这个射手在一次射击中：(1)射中10环或7环的概率； (2)射中7环以下的概率．分析：(1)利用互斥事件的概率加法公式解决；(2)转化为求对立事件的概率．反思：求复杂事件的概率通常有两种方法：一是将所求事件转化成彼此互斥的事件的并(如本题(1))，二是先求对立事件的概率，进而再求所求事件的概率(如本题(2))．题型三 易错辨析【例题3】 抛掷一枚质地均匀的骰子，向上的一面出现1点、2点、3点、4点、5点、6点的概率都是16，记事件A 为“出现奇数”，事件B 为“向上的点数不超过3”，求P (A ∪B )．错解：设向上的一面出现1点、2点、3点、4点、5点、6点分别记为事件1，2，3，4，5，6，则它们两两是互斥事件，且A ＝1∪3∪5，B ＝1∪2∪3P (1)＝P (2)＝P (3)＝P (4)＝P (5)＝P (6)＝16则P (A )＝P (1∪3∪5)＝P (1)＋P (3)＋P (5)＝16＋16＋16＝12P (B )＝P (1∪2∪3)＝P (1)＋P (2)＋P (3)＝16＋16＋16＝12故P (A ∪B )＝P (A )＋P (B )＝12＋12＝1错因分析：错解的原因在于忽视了“和事件”概率公式应用的前提条件，由于“朝上一面的数是奇数”与“朝上一面的数不超过3”这二者不是互斥事件，即出现1或3时，事件A，B同时发生，所以不能应用公式P(A∪B)＝P(A)＋P(B)求解．答案：【例题1】解：(1)是互斥事件．理由是在所选的2名同中，“恰有1名男生”实质是选出“1名男生和1名女生”，它与“恰有2名男生”不可能同时发生，所以是互斥事件．不是对立事件．理由是当选出的2名同都是女生时，这两个事件都没有发生，所以不是对立事件．(2)不是互斥事件．理由是“至少有1名男生”包括“1名男生、1名女生”和“2名都是男生”这两种结果，“至少有1名女生”包括“1名女生、1名男生”和“2名都是女生”这两种结果，当选出的是1名男生、1名女生时，它们同时发生．这两个事件也不是对立事件．理由是这两个事件能同时发生，所以不是对立事件．(3)是互斥事件．理由是“至少有1名男生”包括“1名男生、1名女生”和“2名都是男生”这两种结果，它与“全是女生”不可能同时发生．是对立事件．理由是这两个事件不能同时发生，且必有一个发生，所以是对立事件．【例题2】解：(1)设“射中10环”为事件A，“射中7环”为事件B，则“射中10环或7环”的事件为A ∪B ，事件A 和事件B 是互斥事件，故P (A ∪B )＝P (A )＋P (B )＝021＋028＝049， 所以射中10环或7环的概率为049(2)设“射中7环以下”为事件，“射中7环或8环或9环或10环”为事件D ，则P (D )＝021＋023＋025＋028＝097 又事件和事件D 是对立事件， 则P ()＝1－P (D )＝1－097＝003 所以射中7环以下的概率是003【例题3】 正解：记事件“出现1点”“出现2点”“出现3点”“出现5点”分别为A 1，A 2，A 3，A 4，由题意知这四个事件彼此互斥．则A ∪B ＝A 1∪A 2∪A 3∪A 4故P (A ∪B )＝P (A 1∪A 2∪A 3∪A 4)＝P (A 1)＋P (A 2)＋P (A 3)＋P (A 4)＝16＋16＋16＋16＝231．从装有5个红球和3个白球的口袋内任取3个球，那么，互斥而不对立的事件是( )A ．至少有一个红球与都是红球B ．至少有一个红球与都是白球[。
福建省平潭县高中数学 3.1.3 概率的基本性质2导学案 新人教A版必修3
例3．(选讲)袋中有红、黄、白3种颜色的球各一只，每次从中任取1只，有放回的抽取3次，求：
（1）3只球颜色全相同的概率；
（2）3只球颜色不全相同的概率。
达标训练
1.课本p151练习1 2
2.选择教辅资料
作业
布置
1.习题3-2 9，10，11
2.预习下一节内容
学习小结/教学
反思
1复习：(1)互斥事件：.
(2)事件A+B：给定事件A，B，规定A+B为，事件A+B发生是指事件A和事件B________。
(3)对立事件：事件“A不发生”称为A的对立事件，记作_________,对立事件也称为________,在每一次试验中，相互对立的事件A与事件 不会__________,并且一定____________.
§3.1.3概率的基本性质2
授课
时间
第周星期第节
课型
习题课
主备课人
刘百波
学习
目标
1理解互斥事件与对立事件的概念，会判断所给事件的类型；
2.能利用互斥事件与对立事件的概率公式进行相应的概率运算。
重点难点
重点：概率的加法公式及其应用；事件的关系与运算
难点：互斥事件与对立事件的区别与联系
学习
过程
与方
法
自主学习
(4)互斥事件的概率加法公式：
（1）在一个随机试验中，如果随机事件A和事件B是互斥事件，那么有P(A+B)=_________.
(2)如果随机事件 中任意两个是互斥事件，那么有 ____________。
(5)对立事件的概率运算： _____________。
2探索新知：
阅读教材p147例7，你得到的结论是什么？
福建省平潭县高中数学 第三章复习导学案 新人教A版必修3
授课时间第周星期第节课型复习课主备课人刘百波学习目标1．掌握概率的基本性质2．学会古典概型和几何概型简单运用重点难点重点古典概型、几何概型的相关知识点难点古典概型、几何概型的具体应用学习过程与方法自主学习1.本章的知识建构如下：2.概率的基本性质：1）必然事件概率为1，不可能事件概率为0，因此0≤P(A)≤1；2）当事件A与B互斥时，满足加法公式：P(A∪B)= P(A)+ P(B)；3）若事件A与B为对立事件，则A∪B为必然事件，所以P(A∪B)= P(A)+ P(B)=1，于是有P(A)=1—P(B)；（巧妙的运用这一性质可以简化解题）4）互斥事件与对立事件的区别与联系：我们可以说如果两个事件为对立事件则它们一定互斥，而互斥事件则不一定是对立事件3.古典概型（1）正确理解古典概型的两大特点：1）试验中所有可能出现的基本事件只有有限个；2）每个基本事件出现的可能性相等；（2）掌握古典概型的概率计算公式：P（A）=总的基本事件个数包含的基本事件个数A4.几何概型（1）几何概率模型：如果每个事件发生的概率只与构成该事件区域的长度（面积或体积）成比例，则称这样的概率模型为几何概率模型；（2）几何概型的概率公式：P（A）=积）的区域长度（面积或体试验的全部结果所构成积）的区域长度（面积或体构成事件A；（3）几何概型的特点：1）试验中所有可能出现的结果（基本事件）有无限多个；2）每个基本事件出现的可能性相等．随机事件频率概率，概率的意思义与性质应用概率解决实际问题古典概型几何概型随机数与随机模拟5.古典概型和几何概型的区别相同：两者基本事件的发生都是等可能的；不同：古典概型要求基本事件有有限个，几何概型要求基本事件有无限多个.精讲互动例1、柜子里装有3双不同的鞋，随机地取出2只，试求下列事件的概率（1）取出的鞋子都是左脚的;（2）取出的鞋子都是同一只脚的（选作）变式：（1）取出的鞋一只是左脚的，一只是右脚的；（2）取出的鞋不成对例2、取一根长为3 m的绳子，拉直后在任意位置剪断，那么剪得两段的长度都不小于1m 的概率有多大？达标训练1. 课本p161 复习题三 A组：1 2 3 4 5 62. 教辅资料作业布置1.复习题三 A组：7 、8、 9、10 、112.教辅资料学习小结/教学反思。
高中数学 (3.1.3 概率的基本性质)教案 新人教A版必修3
课题：3.1.3 概率的基本性质教学目标：（1）正确理解事件的包含、并事件、交事件、相等事件,以及互斥事件、对立事件的概念；通过事件的关系、运算与集合的关系、运算进行类比学习,培养学生的类比与归纳的数学思想.（2）概率的几个基本性质：①必然事件概率为1,不可能事件概率为0,因此0≤P(A)≤1；②当事件A与B互斥时,满足加法公式：P(A∪B)=P(A)+P(B)；③若事件A与B为对立事件,则A∪B为必然事件,所以P(A∪B)=P(A)+P(B)=1,于是有P(A)=1-P(B).（3）正确理解和事件与积事件,以及互斥事件与对立事件的区别与联系,通过数学活动,了解数学与实际生活的密切联系,感受数学知识应用于现实世界的具体情境,从而激发学习数学的情趣.教学重点：概率的加法公式及其应用.教学难点：事件的关系与运算.教学方法：讲授法课时安排1课时教学过程一、导入新课：全运会中某省派两名女乒乓球运动员参加单打比赛,她们夺取冠军的概率分别是2/7和1/5,则该省夺取该次冠军的概率是2/7+1/5,对吗？为什么？为解决这个问题,我们学习概率的基本性质.二、新课讲解：Ⅰ、事件的关系与运算１、提出问题在掷骰子试验中,可以定义许多事件如：C1={出现1点},C2={出现2点},C3={出现3点},C4={出现4点},C5={出现5点},C6={出现6点},D1={出现的点数不大于1},D2={出现的点数大于3},D3={出现的点数小于5},E={出现的点数小于7},F={出现的点数大于6},G={出现的点数为偶数},H={出现的点数为奇数},……类比集合与集合的关系、运算说明这些事件的关系和运算,并定义一些新的事件.(1)如果事件C1发生,则一定发生的事件有哪些？反之,成立吗？(2)如果事件C2发生或C4发生或C6发生,就意味着哪个事件发生？(3)如果事件D2与事件H同时发生,就意味着哪个事件发生？(4)事件D3与事件F能同时发生吗？(5)事件G与事件H能同时发生吗？它们两个事件有什么关系？２、活动：学生思考或交流,教师提示点拨,事件与事件的关系要判断准确．３、讨论结果：(1)如果事件C1发生,则一定发生的事件有D1,E,D3,H,反之,如果事件D1,E,D3,H分别成立,能推出事件C1发生的只有D1.(2)如果事件C2发生或C4发生或C6发生,就意味着事件G发生.(3)如果事件D2与事件H同时发生,就意味着C5事件发生.(4)事件D3与事件F不能同时发生.(5)事件G与事件H不能同时发生,但必有一个发生.４、总结：由此我们得到事件A,B的关系和运算如下：①如果事件A发生,则事件B一定发生,这时我们说事件B包含事件A（或事件A包含于事件B）,记为B⊇A（或A⊆B）,不可能事件记为∅,任何事件都包含不可能事件.②如果事件A发生,则事件B一定发生,反之也成立,（若B⊇A同时A⊆B）,我们说这两个事件相等,即A=B.如C1=D1.③如果某事件发生当且仅当事件A发生或事件B发生,则称此事件为事件A与B的并事件（或和事件）,记为A∪B或A+B.④如果某事件发生当且仅当事件A发生且事件B发生,则称此事件为事件A与B的交事件（或积事件）,记为A∩B或AB.⑤如果A∩B为不可能事件（A∩B=∅）,那么称事件A与事件B互斥,即事件A与事件B在任何一次试验中不会同时发生.⑥如果A∩B为不可能事件,A∪B为必然事件,那么称事件A与事件B互为对立事件,即事件A与事件B在一次试验中有且仅有一个发生.Ⅱ、概率的几个基本性质１、提出以下问题:（1）概率的取值范围是多少?（2）必然事件的概率是多少?（3）不可能事件的概率是多少?（4）互斥事件的概率应怎样计算?（5）对立事件的概率应怎样计算?２、活动：学生根据试验的结果,结合自己对各种事件的理解,教师引导学生,根据概率的意义: （1）由于事件的频数总是小于或等于试验的次数,所以,频率在0—1之间,因而概率的取值范围也在0—1之间.（2）必然事件是在试验中一定要发生的事件,所以频率为1,因而概率是1.（3）不可能事件是在试验中一定不发生的事件,所以频率为0,因而概率是0.（4）当事件A与事件B互斥时,A∪B发生的频数等于事件A发生的频数与事件B发生的频数之和,互斥事件的概率等于互斥事件分别发生的概率之和.（5）事件A与事件B互为对立事件,A∩B为不可能事件,A∪B为必然事件,则A∪B的频率为1,因而概率是1,由（4）可知事件B的概率是1与事件A发生的概率的差.３、讨论结果：（1）概率的取值范围是0—1之间,即0≤P(A)≤1.（2）必然事件的概率是1.如在掷骰子试验中,E={出现的点数小于7},因此P(E)=1.（3）不可能事件的概率是0,如在掷骰子试验中,F={出现的点数大于6},因此P(F)=0. （4）当事件A与事件B互斥时,A∪B发生的频数等于事件A发生的频数与事件B发生的频数之和,互斥事件的概率等于互斥事件分别发生的概率之和,即P(A∪B)=P(A)+P(B),这就是概率的加法公式.也称互斥事件的概率的加法公式.（5）事件A与事件B互为对立事件,A∩B为不可能事件,A∪B为必然事件,P(A∪B)=1.所以1=P(A)+P(B),P(B)=1-P(A),P(A)=1-P(B).如在掷骰子试验中,事件G={出现的点数为偶数}与H={出现的点数为奇数}互为对立事件,因此P(G)=1-P(H).三、例题讲解：例：如果从不包括大小王的52张扑克牌中随机抽取一张,那么取到红心（事件A）的概率是41,取到方块（事件B ）的概率是41,问： （1）取到红色牌（事件C ）的概率是多少？（2）取到黑色牌（事件D ）的概率是多少？活动：学生先思考或交流,教师及时指导提示,事件C 是事件A 与事件B 的并,且A 与B 互斥,因此可用互斥事件的概率和公式求解,事件C 与事件D 是对立事件,因此P(D)=1-P(C). 解：（1）因为C=A∪B,且A 与B 不会同时发生,所以事件A 与事件B 互斥,根据概率的加法公式得P(C)=P(A)+P(B)=21. （2）事件C 与事件D 互斥,且C∪D 为必然事件,因此事件C 与事件D 是对立事件,P(D)=1-P(C)=21. 四、课堂练习：教材第１２１页练习：１、２、３、４、５五、课堂小结：1.概率的基本性质是学习概率的基础.不可能事件一定不出现,因此其概率为0,必然事件一定发生,因此其概率为1.当事件A 与事件B 互斥时,A∪B 发生的概率等于A 发生的概率与B 发生的概率的和,从而有公式P （A∪B）=P （A ）+P （B ）；对立事件是指事件A 与事件B 有且仅有一个发生.2.在利用概率的性质时,一定要注意互斥事件与对立事件的区别与联系,互斥事件是指事件A 与事件B 在一次试验中不会同时发生,其具体包括三种不同的情形：（1）事件A 发生且事件B 不发生；（2）事件A 不发生且事件B 发生；（3）事件A 与事件B 同时不发生,而对立事件是指事件A 与事件B 有且仅有一个发生,其包括两种情形:①事件A 发生B 不发生；②事件B 发生事件A 不发生,对立事件是互斥事件的特殊情形.六、课后作业：习题3.1A 组5,B 组1、2.预习教材３.２.１板书设计教学反思：。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
授课时间第周星期第节课型习题课
主备课
人
刘百波
学习目标1理解互斥事件与对立事件的概念，会判断所给事件的类型；2.能利用互斥事件与对立事件的概率公式进行相应的概率运算。
重点难点重点：概率的加法公式及其应用；事件的关系与运算难点：互斥事件与对立事件的区别与联系
学习过程与方法自主学习
1复习：(1)互斥事件： .
(2)事件A+B：给定事件A，B，规定A+B为，事件A+B发生是指事件A和
事件B________。
(3)对立事件：事件“A不发生”称为A的对立事件，记作_________,对立事件也称为________,在每一次试验中，相互对立的事件A与事件A不会__________,并且
一定____________.
(4)互斥事件的概率加法公式：
（1）在一个随机试验中，如果随机事件A和事件B是互斥事件，那么有P(A+B)=_________.
(2)如果随机事件
n
A
A
A,
,
,
2
1
中任意两个是互斥事件，那么有
=
+
+
+)
(
2
1n
A
A
A
P ____________。
(5)对立事件的概率运算：=
)
(A
P_____________。
2探索新知：
阅读教材p147例7，你得到的结论是什么？
精讲互动
例1．某公司部门有男职工4名，女职工3名，由于工作需要，需从中任选3名职工出国洽谈业务，判断下列每对事件是否为互斥事件，如果是，再判断它们是否为对立事件：
（1）至少1名女职工与全是男职工；
（2）至少1名女职工与至少1名男职工；
（3）恰有1名女职工与恰有1名男职工；
（4）至多1名女职工与至多1名男职工。
例2．课本p148 例8
例3．(选讲)袋中有红、黄、白3种颜色的球各一只，每次从中任取1只，有放回的抽取3次，求：
（1）3只球颜色全相同的概率；
（2）3只球颜色不全相同的概率。
达标训练
1.课本p151 练习1 2
2.选择教辅资料
作业布置1. 习题3-2 9，10，11
2. 预习下一节内容
学习小结/教学
反思。