《有理数的加法》课件ppt 北师大版七年级上
合集下载
北师大版七年级数学上册 2.2.1有理数的加法 课件(共25张PPT)
表示法，可推算出图2所表示的算式是( B )
A.(+3)+(+6)
B.(+3)+(-6)
C.(-3)+(+6)
D.(-3)+(-6)
温故知新
课堂导学
核心素养分层练
PART
03
核心素养分层练
让学习变的简单
1.3+(-5)的结果是( B )
A.2
B.-2
C.8
D.-8
2.气温由-3 ℃上升了4 ℃后的气温是( B )
-27
；
(2)(-21)+15=
-6
；
(3)(-55)+0=
(4)38+(-38)=
-55
；
0
.
6.计算：
(1)
−
+
−
；
(2)
(1)- .
(3)
−
+ +1；
(3) .
−
+ +(-1)；
(2)- .
(4)
−
+ .
(4)-
.
7.小邱同学做这样一道题“计算 − + ■ ”，其中“■”是被墨水污染看
版本：北师版
年级：七年级上册
第二章
2.2
有理数及其运算
有理数的加减运算
第一课时
有理数的加法
学习目标
1.了解有理数加法的意义，理解有理数加法法则的
A.(+3)+(+6)
B.(+3)+(-6)
C.(-3)+(+6)
D.(-3)+(-6)
温故知新
课堂导学
核心素养分层练
PART
03
核心素养分层练
让学习变的简单
1.3+(-5)的结果是( B )
A.2
B.-2
C.8
D.-8
2.气温由-3 ℃上升了4 ℃后的气温是( B )
-27
；
(2)(-21)+15=
-6
；
(3)(-55)+0=
(4)38+(-38)=
-55
；
0
.
6.计算：
(1)
−
+
−
；
(2)
(1)- .
(3)
−
+ +1；
(3) .
−
+ +(-1)；
(2)- .
(4)
−
+ .
(4)-
.
7.小邱同学做这样一道题“计算 − + ■ ”，其中“■”是被墨水污染看
版本：北师版
年级：七年级上册
第二章
2.2
有理数及其运算
有理数的加减运算
第一课时
有理数的加法
学习目标
1.了解有理数加法的意义，理解有理数加法法则的
课件有理数的加法PPT_北师大版七年级数学上册PPT精品课件[完整版]
![课件有理数的加法PPT_北师大版七年级数学上册PPT精品课件[完整版]](https://img.taocdn.com/s3/m/820501fbbed5b9f3f80f1c1e.png)
则：
（千米）.
答：第二天勘察队在出发点的下游 千米处.
重难易错
7.计算：
（1）（+1.2）+（-0.3）=
（2）（-3.5）+
=
（3）
=
（4）
=
0.9 ； ；
； .
8.下列各式运算正确的是（ D ） A. （-7）+（-7）=0 B. C. 0+（-101）=101 D.
三级检测练
一级基础巩固练 9. 下列运算过程正确的是（ D ） A. （-3）+（-4）=-3+-4=… B. （-3）+（-4）=-3+4=… C. （-3）+（-4）=3+（-4）=… D. （-3）+（-4）=-（3+4）=…
；
第7课 知识点2 有理数加法的应用
（2）（-19）+（-3）=-（19+3）=-22.
（3）
=
；
有理数的加法（1）
（2）
=
；
（2）绝对值相等的两个数的和等于0.
.
（1）若x的相反数是3，y=5，则x+y=
；
（2）（-19）+（-3）=-（19+3）=-22.
新课学习
知识点1 借助数轴比较有理数的大小 1.（1）同号两数相加，取相同的符号，并把绝对值相加.
解：-35+50=15（℃）.
两个点分别在原点的两侧，这两个点表示的有理数的和是2+（-3）=-1或-2+3=1.
答：求得的和中最小的是-12.
（4） 李老师在4张纸条上分别写上4个有理数：|-3|，-（+4），+|-9|，-8，他让同学们从中抽取2张，并求出其和.
课件有理数的加法ppt_北师大版七年级数学上册ppt
二级能力提升练
11. 已知a是最大的负整数，b是绝对值最小的整数，c
是最小的正整数，则a+b+c等于（ B ）
A. -1
B. 0
C. 1
D. 2
12. 填空：
（1）绝对值小于2的所有整数的和是 0
；
（2）已知a是最小的正整数，b是a的相反数，c的绝
对值为3，则a+b+c=
3或-3 .
13.小虫从某点A出发在一直线上来回爬行，假定向右爬
小虫从某点A出发在一直线上来回爬行，假定向右爬行的路程记为正数，向左爬行的路程记为负数，爬行的各段路程依次为：（单位：
厘米）+5，-3，+10，
（2）小虫离开原点最远是多少厘米？
第二章 第8课 有理数的加法（2）
答：小虫最后回到出发点A.
有理数及其运算
（1）绝对值小于2的所有整数的和是
；
答：从A地出发到收工时共耗油33.
(2)若每千米耗油0.5升,从A地出发到收工时共 耗油多少升? （2）|+10|+|-3|+|+4|+|+2|+|-8|+|+13|+
|-2|+|+12|+|+8|+|+5| =10+3+4+2+8+13+2+12+8+5=67， 67×0.5=33.5 （升）. 答：从A地出发到收工时共耗油33.5升.
(1)问收工时距A地多远?
第二次爬行距离原点是（+5）+（-3）=2（cm），
第四次爬行距离原点是（+12）+（-8）=4（cm），
新北师大版七年级数学上册《有理数的加法法则》公开课课件
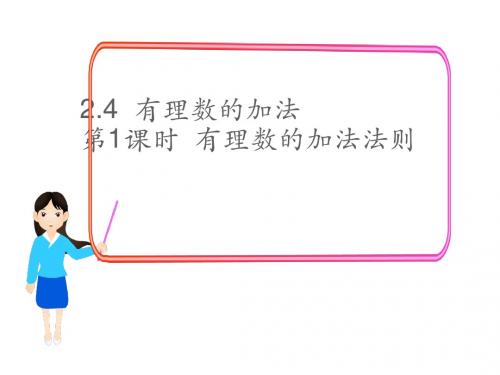
星期一
进出货情况
+5 +3 +8 -2 -4 -6
库存变化
星期二
合 计
提出问题：星期一该建筑工地仓库的水泥库存是增加了还 是减少了？星期二呢？请先列出算式，然后借 助于数轴算出结果。
合作交流
+5 -2
星期一：仓库进货5吨，再出货2吨（即进货-2吨），这一天库存是增加还是减少？
-9 -8 -7 -6 -5 –4 -3 –2 -1 0 1 2 3 4 5 6 7 8 9
(+11)+(- 6) 8 (- = 11)+(+6)
=+2
=-2
趁热打铁
☞
3、计算：
（1）（－42）+（+17）；（2）0+（－39.98）； （3）（+7.3）+（+3.7）；（4）（－ ）+0.4
1 3
例题解析
☞
（2）4+（－5）
例2、在数轴上表示下列有理数的运算，并求出运算的结果。 （1）（－3）+（－4）
那天的库存是多少吨？ -5 -9 -8 -7 -6 -5 –4 -3 –2 -1 0 1 2 3 4 5 6 7 8 9 （-5）+ 0 = －5
结论：一个数同零相加，仍得这个数。
交流反思
☞
有理数加法法则
1、同号两数相加，取相同的符号，并把绝对值相加。
2、异号两数相加，取绝对值较大的加数
的符号，并用较大的绝对值减去较小 的绝对值。
解：(1)
-4
-3
-9 -8 -7 -6 -5 –4 -3 –2 -1 0 1 2 3 4 5 6 7 8 9
(-3)+(-4)= -7
进出货情况
+5 +3 +8 -2 -4 -6
库存变化
星期二
合 计
提出问题：星期一该建筑工地仓库的水泥库存是增加了还 是减少了？星期二呢？请先列出算式，然后借 助于数轴算出结果。
合作交流
+5 -2
星期一：仓库进货5吨，再出货2吨（即进货-2吨），这一天库存是增加还是减少？
-9 -8 -7 -6 -5 –4 -3 –2 -1 0 1 2 3 4 5 6 7 8 9
(+11)+(- 6) 8 (- = 11)+(+6)
=+2
=-2
趁热打铁
☞
3、计算：
（1）（－42）+（+17）；（2）0+（－39.98）； （3）（+7.3）+（+3.7）；（4）（－ ）+0.4
1 3
例题解析
☞
（2）4+（－5）
例2、在数轴上表示下列有理数的运算，并求出运算的结果。 （1）（－3）+（－4）
那天的库存是多少吨？ -5 -9 -8 -7 -6 -5 –4 -3 –2 -1 0 1 2 3 4 5 6 7 8 9 （-5）+ 0 = －5
结论：一个数同零相加，仍得这个数。
交流反思
☞
有理数加法法则
1、同号两数相加，取相同的符号，并把绝对值相加。
2、异号两数相加，取绝对值较大的加数
的符号，并用较大的绝对值减去较小 的绝对值。
解：(1)
-4
-3
-9 -8 -7 -6 -5 –4 -3 –2 -1 0 1 2 3 4 5 6 7 8 9
(-3)+(-4)= -7
北师大版七年级上册数学.1有理数的加法法则课件
（1）（－2）＋（－3）=-5
○ － ○ －
○ － ○ － ○ －
○ － ○ －○ －○ － ○ －
（2）（－3）＋2＝ －1
○ － ○ －
○ －
○+ ○+
○ － ○+ ○ － ○+
○ －
○ －
○ －
（3）（－4）＋4＝ 0
○ －
○ － ○ －
○○++ ○ ○++
○ － ○+ ○ － ○+ ○ － ○+ ○ － ○+
5. |-5|+|+3|=_8__; |-11| - |-6|=__5_.
在小学我们已经学习了正有理数及0的加法 运算，前面我们又学习了负有理数。负有理数怎 样参加加法运算呢？让我们一起来学习。为此， 我们来看一个大家熟悉的实际问题：
某班举行知识比赛，平分标准是：答对一题
得1分，答错一题扣1分，不回答得0分。
你能从上面的两个算式中发现什么？
同号两数相加,取相同的 符号，并把绝对值相加.
情况2：异号两数相加 (3)先向东移动5个单位，再向西移动３个 单位，结果向东移动了２个单位，那么
+5 -3 -9 -8 -7 -6 -5 –4 -3 –2 -1 0 1 2 3 4 5 6 7 8 9
+2
列算式得：（+5）+（-3）= +2
（3）5 +（－5） （4）0 +（－2）
解：（1）180+（－10）第一步：确定符号 异号两数相加，
正可号 以（省＋略）==1+7（0 180－10）取第大绝的二对绝步值对：较值确大减的去定数较和的小的符的绝号绝对对。值值。用较
北师大版数学七年级上册《有理数的加法法则》名师精品课件
小结：
本节课学习了什么内容？（有理数的加法法则） 有理数加法计算的一般步骤是什么？（先确定符号，再计算绝对值） 有理数的加法与算术数加法的最大区别是什么？（符号）
作业 （1）第26页A组、B组题做在作业本上。
思考题 （3）
：1)a+|a|=0，a是什么数？
2)若|a+1|=2，那么a=?
课后练习 见本课时练习
（4） 0+ 5
例1 计算下列各题（说明理由） ：
（1）（－3.5）+（+7）（异号两数相加）
=（7-3.5） （取绝对值较大的数的
=3.5
符号，并用较大的绝对 值减去较小的绝对值）
（2) （－11）+（－9）（同号两数相加）
=-（11+9） （取相同的符号，并把
=-20
绝对值相加）
（3） 2 ( 2)
2.4 有理数的加法 第1课时 有理数的加法法则
如果你是仓库管理员，将怎样记录每天仓库内进出货的情况和库存变化？
引例：尝试完成下列问题：
一建筑工地仓库记录星期一和星期二水泥的进货和出货数量如下， 其中进货为正，出货为负（单位：吨）：
日期 星期一 星期二 合计
进出货情况
+5
-2
+3
-4
库存变化
问题1：你能得出这两天水泥进货和出货的合计数量吗？ 问题2：这种运算方式与小学里有何不同呢？ 问题3：你能列出算式表示这两天水泥进货和出货的合计数量来得出结果？
3+(-2)=1
-1 0 1 2 3
4+(-4)=0
-1 0 1 2 3 4
练习1：口算 (1)、(+5)+(+3)； (－5)+(－3)； (+11)+(－6)； (－4)+0； (2)、(+5)+(－3 ) ； (－5)+(+3)； (－11)+(+6)；
《有理数的加法》PPT课件 (公开课)2022年北师大版 (13)
7．计算： (1)(－5)＋(－9); (1)原式＝－14
(3)＋8＋(－11); (3)原式＝－3
(2)0＋(－5)； (2)原式＝－5
(4)7＋(－7)． (4)原式＝0
8．计算： (＋16)＋(－25)＋(＋24)＋(－35)＝[__(＋__1_6_)__＋_(_＋__2_4_)__]＋ [(__(－__2_5_)__)＋(__(_－__3_5_) _)]＝(＋40)＋(－60)＝__－__2_0___.从中可 知，先把____正____数和____负____数分别相加，比较简便．
9．用运算律计算使运算简便，那么计算：(－39.2)＋(－ 231)＋(－60.8)＝[(－39.2)＋_(_－__6_0_.8_)_]＋_(_－__2_3_1_)_.
ቤተ መጻሕፍቲ ባይዱ
10．下列运用运算律变形正确的是( B )
A．2＋(－7)＝7＋(－2) B．3＋(－8)＋5＝3＋5＋(－8) C．[6＋(－13)]＋4＝[6＋(－4)]＋13 D.13＋(－2)＋(－23)＝(13＋23)＋(－2)
5．下列运算错误的有( C )
①(－21)＋(－21)＝0；②(－6)＋(＋4)＝－10；
③0＋(－13)＝－13； ④(＋56)＋(－16)＝23.
A．0 个
B．1 个
C．2 个
D．3 个
6．两数相加，其和小于每一个加数，那么( B )
A．这两个加数必有一个加数是 0 B．这两个加数必是两个负数 C．这两个加数一正一负，且负数的绝对值较大 D．这两个加数的符号不能确定
15．潜水艇原来停在海面下500米处，先上浮150米，又下 潜200米，再上浮100米，这时潜水艇在海面下多少米处( B )
A．350 B．450 C．550 D．650
北师大版数学七年级上册2.4.1有理数的加法法则课件
4
2
(- 5 )+(-1 5 )=
（1）快速说出上面算式结果的符号； （2）快速说出上面算式结果的绝对值.
新知再探
根据刚才得的探究，你有什么想法？ 你能举出与上面不同类型的例子吗？
牛刀小试
（+1.2）+（-3.7）= （+2.8）+（-5.2）=
（-43）+（+37;(+1 5 )=
.
小结
1、你学会了什么新知识？ 2、你掌握了什么新方法？ 3、你还有什么新问题？
小结:
确定类型 定符号 绝对值
同号
相同符号
异号(绝对值 不相等) 取绝对值较大 的加数的符号
相加 相减
异号(互为相 反数)
与0相加
结果是0 仍是这个数
人越是高兴的事情，越爱隐藏；越是痛苦的事情，越爱小题大作。 岁寒，然后知松柏之后凋也。——《论语·子罕》 白发无凭吾老矣！青春不再汝知乎？年将弱冠非童子，学不成名岂丈夫？俞良弼 懒人无法享受休息之乐。——拉布克 梯子的梯阶从来不是用来搁脚的，它只是让人们的脚放上一段时间，以便让别一只脚能够再往上登。 所谓成长，就是逼着你一个人，踉踉跄跄的受伤，跌跌撞撞的坚强。
（1）快速说出上面算式的符号；
（2）快速说出上面算式的绝对值.
牛刀小试
请直接说出下列各式的结果：（+23）+（23）= （-100）+（+100）=
（+（2.-83））++（0=-2.8）= 0+（（-6-40）.8）= +0.8=
1.同号两数相加,取相同的符号,并把 绝对值相加.
2.绝对值不相等的异号两数相加,取绝 对值较大的加数的符号,并用较大的绝对值 减去较小的绝对值.
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
-5
-4
-3
-2
-1
0
1
2
3(-2)+Fra bibliotek-3)=-5-5 -4 -3 -2 -1 0 1
(-3)+2=-1
-5 -4 -3 -2 -1 0 1
2
3
2
3
3+(-2)=1
-5 -4 -3 -2 -1 0 1
(-4)+4=0
2
3
两个有理数相加，和的符号如何确定？ 两个有理数相加，和的符号如何确定？ 和的绝对值如何确定
注意：
异号绝对值不等的 两数相加，分步思考： ①确定和的符号； ②确定和的 绝对值，写出所得和； ③相反数相加直接 得出零。
计算： 计算： （1） （-25）+（-7） ） ） （ ） （2） （-13）+5 ） ） （3） （-23）+0 ） ） （4） ） 45+（-45） （ ）
• 填入输出结果：
4、 向东走3米，再向西走5米， 、 向东走 米 再向西走 米 两次一共向东走了多少米 ？
-5
3 -3 -2 -1 0 1 2 3
＋
4
-2
3+（-5）=-2 （ ）
二、有理数加法的类型
1. 5 + 3 = 8 2.（-5）+（-3）= - 8 2.（ 3. （-3）+（-2）= - 5 ） （ ） 4. 5+（-3）=2 （ ） 5. 3+（-5）=-2 （ ）
总结提高 小结
1、掌握有理数的加法法则， 、掌握有理数的加法法则， 加法法则 正确地进行加法运算。 正确地进行加法运算。 2、两个有理数相加， 2、两个有理数相加，首先 加法类型， 判断加法类型 判断加法类型，再确定和的符 号，最后确定和的绝对值。 最后确定和的绝对值。 3、注意异号绝对值 、注意异号绝对值 不等的两数相加。 不等的两数相加。
计算下列各式： 例1 计算下列各式： 1、（ ）+（-1 ） 2、180 +（－ ） 、（-10） （ （－10） 、（ 、 （－ 3、5+（－ ） （－5） 4、0 +（－ 2） 、 （－ 、 （－ ） 解： 1、（ 、（-10）+（-1 ） （同号两数相加） 、（ ） （ =-（ （取相同的符号） （ ） =-（10 + 1） （把绝对值相加） （ ） =- 11
• 例3：利用有理数加法解决下列实际 ： 问题1 一人一个月工资可得800元， 问题 、一人一个月工资可得 元 奖金可得500元，这个人一个月收入 奖金可得 元 多少元？ 多少元？ 解：规定收入为正，则 规定收入为正， （＋800）＋（＋500）＝＋1300 （＋800）＋（＋500）＝＋1300 800）＋（＋500）＝＋ 答：这个人一个月收入1300元。 这个人一个月收入1300元 1300
问题2、一个人向东走了 问题 、一个人向东走了200米，又向 米 西走了300米，结果他是向东走还是向 西走了 米 西走，向东或向西走了多少米？ 西走，向东或向西走了多少米？
解：规定向东走为正，向西走为负， 规定向东走为正，向西走为负， ：（＋200）＋（－300）＝－100 200）＋（－300）＝－ 则：（＋200）＋（－300）＝－100 这个人向西走了100 100米 答：这个人向西走了100米。
-3
-8 -7 -6
＋
-5 -4
-5
-3
-2
-1
0
1
-8
（-5）+（-3）=-8
一、有理数加法的意义
-3 5
-1 0 1 2 3 4 5 6
＋
2
5+（-3）=2 （ ） 3、 向东走 米，再向西走 米， 、 向东走5米 再向西走3米 两次一共向东走了多少米？ 两次一共向东走了多少米？
一、有理数加法的意义
（3） 0 +（ -0﹒1 ） ） （ ﹒
练习2（口答） 练习 （口答） 1、 （+4）+（-7） =－3 、 ） （ ） － 2、 （-8）+（-3） =－11 、 ） （ ） － 3、（ ）+（+5） =－4 、（-9） （ ） 、（ － 4、 （--6）+（+6） 、 ） （ ） 5、 （-7）+0 、 ） =－7 － 6、 8+（-1） =7 、 （ ） － 7、（ ）+1 =－6 、（-7） 、（ 8、 0+（-10） =－10 、 （ ） － =0
例2： 计算 ：
（1） （-3）+（-9） ） ） （ ） （2） （-1/2)+(+1/3) ）
解：（1）（ ）+ （-9） （3） 0 +（ -0﹒1 ） ）（-3） ：（ ）（ ） ） （ ﹒ =-（3+9） （ ） =-12 ）（-1/2）+（+1/3） （2）（ ）（ ） （ ） =-（1/2-1/3） （ ） =-1/6 = -0﹒1 ﹒
一、有理数加法的意义
1、向东走5米，再向东走 米， 、向东走 米 再向东走3米 两次一共向东走了多少米？ 两次一共向东走了多少米？
5
-1 0 1 2 3 4
＋
5 6
3
7 8
8
(+5)+(+3)=8
一、有理数加法的意义
2、向西走5米，再向西走 米， 、向西走 米 再向西走3米 两次一共向东走了多少米？ 两次一共向东走了多少米？
同号两数相加
6 3+（-2）=1 （ ）
7. 5+（-5）=0 （ ） 8 4+（-4）=0 （ ）
异号两数相加
9.（-5）+0=-5 （ ）
一数和零相加
三、有理数加法法则
1、 同号两数相加，取相同的符号， 、 同号两数相加，取相同的符号， 并把绝对值相加。 并把绝对值相加。 2、 绝对值不相等的异号两数相加， 、 绝对值不相等的异号两数相加 异号两数相加， 取绝对值较大的加数的符号， 取绝对值较大的加数的符号，并用较 大的绝对值减去较小的绝对值。 大的绝对值减去较小的绝对值。互为 的两个数相加得0。 相反数 的两个数相加得 。 3、 一个数同 相加，仍得这个数。 、 一个数同0相加 仍得这个数。 相加， 注意：1、确定和的符号； 2、确定和的绝对值。
2、180 +（－ ） （绝对值不相等的异号两数相加） 、 （－10） （－
=+（ （ ） （取绝对值较大的加数符号） =+（180 – 10） （ ） （用较大的绝对值减去较小的绝对值） =170 3、5+（－ ） （互为相反数的两数相加） （－5） 、 （－ =0
4、0 +（－ 2） （一个数同0相加） 、 （－ ）
•
＋5
＋（－4） ＋（－ ）
0 输入 －1 －3
输出
让每条线上的三个数之和为零
-49
复习
1、如果向东走5米记作 米， 、如果向东走 米记作 米记作+5米 那么向西走3米记作＿＿. 米记作＿＿ 那么向西走 米记作＿＿ 2、已知 、已知a=-5，b=+3， ， ， ︱a︳+︱b︱=＿＿ ︳ ︱ ︱ ＿＿ 已知a=-5，b=+3， 已知 ， ， ︱a︱-︱b︱=＿＿ ︱ ︱ ︱ ＿＿
不久前， 不久前，中国足球队在客场与卡塔 尔的比赛中，上半场输了一个球， 尔的比赛中，上半场输了一个球，下半 场经过艰苦奋战进了一个球， 场经过艰苦奋战进了一个球，这场比赛 中国队净胜球数是多少？ 中国队净胜球数是多少？ 如果把赢一个球记作 +1 输一个球记作 －1
则净胜球为 （+1）+（-1）=0 ） （ ）
• 单机游戏 • 英雄无敌6：/zt/hmm6/
如果+1表示为 如果 表示为 －1表示为 表示为
0
（－2）+（－3） =－5 ） （ ） －
（－3）+2 =－1 ）
3+（－2）=1
（-4）+4 =0 ）
=-2
练习1： 练习 ：计算下列各式 1. (＋11) ＋(＋9)= ＋（11＋9） ＋20 ＋ ＋ ＋ ） ＝ 2. (－8) ＋(－2) ＝ （8＋2） －10 － － － ＋ ） ＝ 3. (－12) ＋(＋4) ＝－（12－4） －8 － ＋ － ） ＝ ＋ － ） 4. (＋7) ＋(－6) ＝ （7－6） ＋1 ＋ － ＝ 0 5. (＋100) ＋(－100) ＝ ＋ － 6. (－18) ＋0＝－18 － ＝