矩形谐振腔讲义
合集下载
《矩形谐振腔》课件
矩形谐振腔的设计
1
设计参数
2
包括谐振腔尺寸、波导位置、材料选择
等。
3
一般步骤
确定频率、计算谐振腔尺寸、优化设工具等。
矩形谐振腔的应用
微波和微纳电子学
矩形谐振腔在微波电路和微纳电子学中广泛应用， 用于滤波、频率选择和放大等。
量子计算
矩形谐振腔是量子计算中的关键元件，用于存储和 操作量子比特。
参考文献
相关研究论文
1. "矩形谐振腔的设计与制作"，XXX期刊，2020 年。
网络资源
2. "如何设计优秀的矩形谐振腔"，微电子论坛， https://www.***.com
谐振模式的定义
谐振模式是矩形谐振腔中特定频率下的电磁场分布形态，不同模式对应不同的场分布和电磁能量分布。
不同谐振模式的特点
TE10
最简单的模式，电场仅沿一个方向震荡。
TM11
电场和磁场都存在，和波导边界垂直。
TE01
场与波导边界垂直，纵向波动不变。
TE20
正方形波导才有的模式，电场沿两个方向震荡。
实验
1
测量共振频率
通过改变谐振腔的尺寸，测量不同谐振
测量Q值
2
模式的共振频率。
通过测量共振峰的宽度，计算谐振腔的 品质因数（Q值）。
结论
1 优点与不足
2 未来发展趋势
矩形谐振腔具有结构简单、易于制作的优点， 但波导的存在会引入损耗。
随着技术的不断进步，矩形谐振腔将在量子 计算和通信领域发挥越来越重要的作用。
《矩形谐振腔》PPT课件
矩形谐振腔是微波和微纳电子学中常见的元件。本课件将详细介绍矩形谐振 腔的定义、工作原理、谐振模式以及设计和应用。
高二物理竞赛课件：矩形截面谐振腔
Ez A3 sin kx x sin ky y cos kz z
再考虑:
x
L1,
Ex x
0
m
kx L1
y z
再由 E
L2 , Ex 0, L3, Ex 0,
0 得kx A1
ky
kz
n
Lp2
L3
ky A2 kz A3
m, n,
0
p
0,1,2,3
两个独立常数由激励谐振的信号强度来确定
谐振频率 mnp
(C3coskz z D3sinkz z)
若u Ex ,
x
0, Ex x
0, D1
0
y 0, Ex 0,C2 0.
z 0, Ex 0, C3 0.
Ex A1 cos kx x sin ky y sin kz z
A1 C1D2D3
同理: Ey A2 sin kx x cos ky y sin kz z
解:设导体板在xoz平面.法线沿y轴.根据导体表面边界条件:
Et 0, Hn 0 即：Ex Ez 0, H y 0
y
H
E
z
x
因此沿z方向传播,电场沿y方向偏振的电磁波可以传播.而另
一种偏振即 E 平行于导体面的偏振不能存在.
3
-Q
B
5
+Q 4
Q
A
-Q 3
1 -Q 2 +Q
4
+Q -Q
③ 对每一组值，有两个独立偏振波型.
④若 L1 L2 L3 .最低振荡频率的波模为(1,1,0)
f1,1,0
2
1
1 1. L12 L22
1,1,0
2
矩形谐振腔内部TE与TM模场分布的演示课件
电磁场与电磁波课程专题研究：矩形波导、矩形谐振腔内部TE 与TM 模场分布的演示课件A Demo of Field Distribution for TE and TM Modes in Rectangular Waveguid e and Rectangular Resonator信息与通信工程 3071102304 叶彬彬Abstract :本问题的提出是因为自己在学习场分布时对这个问题就不太了解，在完成老师布置的画出11TE 模场分布的作业的时候就曾经尝试过用MATLAB 去解决 ，但是当时没有成功。
借专题研究这个机会又把这个问题重新拾起，不但对加深自己的理解有帮助，也希望为后来学这门课的同学做出一个好的演示。
场分布的公式参照了电磁场与电磁波（第二版）陈抗生著 高等教育出版社，on pages: 270, 383-3841、 场分布描述a) 矩形谐振腔TE 模场分布公式,,cos()sin()cos()x mnp m n p n m x n y p z E A b a b lππππ=∑ ,,sin()cos()sin()y mnpm n pm m x n y p z E A a a b l ππππ=-∑ 0z E =,,1sin()cos()cos()x mnp m n p m p m x n y p z H jA a l a b lπππππωμ=∑ ,,1cos()sin()cos()y mnp m n p m p m x n y p z H jA b l a b lπππππωμ=∑ 22,,cos()cos()sin()z mnp m n pn m m x n y p z b a H jA a b l πππππωμ⎛⎫⎛⎫+ ⎪ ⎪⎝⎭⎝⎭=-∑ b) 矩形谐振腔TM 模场分布公式2,,cos()sin()sin()x mnp m n pmp m x n y p z E B la a b l ππππωμ=-∑ 2,,sin()cos()sin()y mnp m n pnp m x n y p z E B lb a b l ππππωμ=-∑22,,sin()sin()cos()z mnp m n pn m m x n y p z b a E B a b l πππππωε⎛⎫⎛⎫+ ⎪ ⎪⎝⎭⎝⎭=∑ ,,sin()cos()cos()x mnp m n p n m x n y p z H jB b a b lππππ=∑ ,,cos()sin()cos()y mnpm n pm m x n y p z H jB a a b l ππππ=-∑ 0z H =c) 矩形波导TE 模场分布公式(),πππcos()sin() z j t k z x mnm n n m n E A x y e b a bω-=∑ (),πππsin()cos() z j t k z y mnm nm m n E A x y e a a b ω-=-∑ 0z E =(),πππsin()cos() z j t k z z x mnm n k m m n H A x y e a a bωωμ-=∑ (),πππcos()sin() z j t k z z y mnm nk n m n H A x y e b a b ωωμ-=∑ 222()22,πππj cos()cos() z j t k z z mn m nn m m n H A x y e b a a b ωωμ-⎡⎤=-+⎢⎥⎣⎦∑ d) 矩形波导TM 模场分布公式(),πππcos()sin() z j t k z z x mnm n k m m n E B x y e a a bωωε-=-∑ (),πππsin()cos() z j t k z z y mnm nk n m n E B x y e b a b ωωε-=-∑ 222()22,πππsin()sin() z j t k z z mnm n n m m n E B x y e j b a a bωωε-⎛⎫=+ ⎪⎝⎭∑ (),πππsin()cos() z j t k z x mn m n n m n H B x y e b a bω-=∑(),πππcos()sin() z j t k z y mnm nm m n H B x y e a a b ω-=-∑H=zk=其中矩形波导的色散关系为zmn2、MATLAB绘图实现有以上的场分布公式后就可以利用MATLAB将场分布图绘出，用的是MESH和QUIVER两个函数。
43矩形谐振腔-PPT课件
则
m m n E E cos sin sin z x y
a b
第四章 微波谐振器
§4.3 矩形谐振腔
在与z=0相距ι处再放一短路板，形成腔体. 则有边界条件 所以
E 0 x z l
p p l p 或 ( 0 , 1 , 2 , 3 ) l
则腔体内TMmnp模的纵向电场为
m n p E E sin x sin y cos z z m a b l
第四章 微波谐振器
§4.3 矩形谐振腔
腔体内TMmnp模的其它场分量为
E p m m n p m E cos x sin y sin z x 2 a b l K cl a
2 2 2
2
2
不同的m,n,p对应不同的TEmnp模，m,n不能同时为零。 工作于TEmnp模的矩形腔具有多谐性。
第四章 微波谐振器
§4.3 矩形谐振腔
2. TMmnp模
H 0 E 0 z z
行波状态下矩形波导TMmn模的纵向电场分量
m n j z E E sin x sin y e z 0 a b
H j 2 H m 0 m n H H cos x cos y sin z z m a b
令 得
(4-29)
在与z=0相距ι处再放一短路板，形成腔体，
则有边界条件
H 0 zz l
第四章 微波谐振器
§4.3 矩形谐振腔
n 2 m K c a b
2
2
矩形谐振腔PPT课件
Hx
k2jkzkz2
Hz x
jkz z
Hy
k2jkzkz2
Hz y
jk z
z
Hx
k2
1 kz2
(Hz x z
)
Hy
k2
1 kz2
(Hz y z
)
Ex
j
k2 kz2
Hz y
Ey
j
k2 kz2
Hz x
Ez 0
2020/6/10
.
14
第九章 导行电磁波
H z ( x ,y ,z ) c o s ( m a x ) c o s ( n b y ) ( D 1 e jk z z D 2 e jk z z )
因为随着频率升高，必须减小 LC 谐振电路的电感量和电 容量，但是当 LC 很小时，分布参数的影响不可忽略。电容器 的引线电感、线圈之间以及器件之间的分布电容必须考虑。
随着频率升高，回路的电磁辐射效应显著，电容器中的 介质损耗也随之增加，这些因素导致谐振电路的品质因素 Q 值显著下降。
在米波以上的微波波段，经常使用相应波段的传输线来构 成谐振器件。
衰减常数 Pl
2P
[Np m]
P l 单位长度波导壁的功率损耗
P 单位长度波导壁的传输功率
TE10
b
Rs
[12b( fc)2]
1( fc)2
af
TM
f
11
2020/6/10
电磁场. 理论
3
第九章 导行电磁波
9-5 矩形谐振腔
研究波导谐振腔的意义
在米波以上的微波波段，集总参数的LC谐振电路无法使用。
m 、 n 和 p 取不同的值，可得不同模式的TM波，称为 TMmnp 模式。
§5-3 矩形谐振腔 微波技术基础 课件 PPT
Et
H
t
1
K
2 c
1
K
2 c
z
j
t Ez
waz t
Ez
§5－3 矩形谐振腔——一、电磁场的表示式——TM模
▪
TMmnp场分量为：Ex Em
1
K
2 c
p
l
m
a
cos m
a
x sin n
b
y sin p
l
z
Ey
Em
1
K
2 c
p
l
n sin m
b a
x cos n
b
（三）等效电导G0
▪ 以TE101模为例
取上壁内表面中心点与下壁内表面中心点之间的连线作为积分线
则
B b
Um
E dl
A
0 Eydy Emb
已求得：
s H
2
ds
H
2 m
2l 2
2b a3 l3
al a2 l 2
2
G0 Rs
s H ds Rs
U
2 m
2
2b a3 l3 al a2 l 2 2b2 a2 l 2
2E0
K
2 c
m
a
cos m
a
x sin n
b
y sin
p
l
z
Em
Kc2
m
a
cos m
a
xsin n
b
y sin
p
l
z
b) Er zl 0
l p 或 p ( p 0,1,2,3,...)
l
Ez
Em
sin
《矩形谐振腔》课件
优化算法
采用遗传算法、粒子群算法等优化算 法，对矩形谐振腔进行优化设计，以 提高其性能。
04
矩形谐振腔的制造工艺
加工工艺流程
切割与成型
使用切割机和成型机对材料进行 精确加工，得到矩形谐振腔的初 步形状。
组装与调试
将各部分组合在一起，并进行必 要的调整和测试，以确保其性能 达标。
01
材料准备
选择合适的材料，如铜、铝或不 锈钢，确保其物理和化学属性满 足谐振腔的设计要求。
03
表面处理不均匀
表面处理过程中可能出现不均 匀的情况，影响电磁性能。解 决策略包括加强工艺控制和增 加后处理工序。
04
组装误差
部件组装时可能出现误差，导 致性能下降。应对措施包括采 用精密的测量设备和严格的组 装流程管理。
05
矩形谐振腔的性能测试与分析
测试设备与方法
01
测试设备
02
高精度频谱分析仪
分析频率响应曲线，确定矩形谐振腔的工作频 带和带宽。
测试结果分析
阻抗匹配
测量矩形谐振腔的输入和输出阻抗。
分析阻抗匹配情况，判断矩形谐振腔是否具有良好的 能量传输效率。
测试结果分析
01
群时延
02
测量矩形谐振腔在不同频率下的群时延。
03 分析群时延曲线，评估矩形谐振腔对信号的畸变 程度。
结果与讨论
雷达制导
在雷达制导系统中，矩形谐振腔可用于信号处理和目标识别，提高制导精度和抗干扰能力。
其他领域的应用
微波测量
矩形谐振腔可用于微波测量领域，如微波频谱分析、微波传感器等。
电子对抗
在电子对抗中，矩形谐振腔可用于信号干扰和欺骗，提高电子设备的抗干扰能力。
采用遗传算法、粒子群算法等优化算 法，对矩形谐振腔进行优化设计，以 提高其性能。
04
矩形谐振腔的制造工艺
加工工艺流程
切割与成型
使用切割机和成型机对材料进行 精确加工，得到矩形谐振腔的初 步形状。
组装与调试
将各部分组合在一起，并进行必 要的调整和测试，以确保其性能 达标。
01
材料准备
选择合适的材料，如铜、铝或不 锈钢，确保其物理和化学属性满 足谐振腔的设计要求。
03
表面处理不均匀
表面处理过程中可能出现不均 匀的情况，影响电磁性能。解 决策略包括加强工艺控制和增 加后处理工序。
04
组装误差
部件组装时可能出现误差，导 致性能下降。应对措施包括采 用精密的测量设备和严格的组 装流程管理。
05
矩形谐振腔的性能测试与分析
测试设备与方法
01
测试设备
02
高精度频谱分析仪
分析频率响应曲线，确定矩形谐振腔的工作频 带和带宽。
测试结果分析
阻抗匹配
测量矩形谐振腔的输入和输出阻抗。
分析阻抗匹配情况，判断矩形谐振腔是否具有良好的 能量传输效率。
测试结果分析
01
群时延
02
测量矩形谐振腔在不同频率下的群时延。
03 分析群时延曲线，评估矩形谐振腔对信号的畸变 程度。
结果与讨论
雷达制导
在雷达制导系统中，矩形谐振腔可用于信号处理和目标识别，提高制导精度和抗干扰能力。
其他领域的应用
微波测量
矩形谐振腔可用于微波测量领域，如微波频谱分析、微波传感器等。
电子对抗
在电子对抗中，矩形谐振腔可用于信号干扰和欺骗，提高电子设备的抗干扰能力。
矩形波导谐振腔的谐振频率PPT课件
波源，没有外源分布，即 0
,导波系统内
的场量随时间作正弦变化 ,0则,J导 0波系统内的电磁场
可以表示为
第5页/共69页
图7-2 任意截面的均匀导波系统
E(x, y, z） E(x, y）e z
H(x, y, z） H(x, y）e z
(7-1) (7-2)
第6页/共69页
式中 为传播常数。一般情况下， j 。下
第14页/共69页
显然，平行双导线、同轴线以及带状线等能够 建立静电场，因此他们可以传播TEM波，而由单根 导体构成的金属波导中不可能存在静电场，因此 金属波导不可能传播TEM 波。
由式(7-5)可知，对于ETz M波，根据方程H (z 70-
8a)和导波系统的边界条件，求出 后，再考虑
到
Ex， 可kc2得ETxzM波的其他横向Ey场 分kc2量E为yz
(7-31)
Ez
E0
sin mπ a
x sin nπ b
y e jkz z
将
式
（
7
-
3
1
）以及 Ex
j kz E0
k
2 c
mπ a
cos mπ x sin nπ y ejkzz
代a 入 式 b（ 7-5）中，并
加上因子
（令 ），求得矩形波 Ey
j
kz E0 kc2
nπ b
sin
mπ a
a b
第28页/共69页
当工作频率f fc 时，即k 2 kc2 时 ， 为出纯虚数，
j jkz ，电磁波可以在波导中沿z 方向传播。
其中
kz
k 2 kc2
k
1
fc f
矩形谐振腔讲义
二、品质因数Q0
2 1 W We Wm | H| dv 2 v
(31-7)
而导体壁损耗
1 1 2 PL | J s | Rs ds Rs | H |2 ds S 2 S 2
(31-8)
式中Rs是表面电阻率， 有限电导率所对应的谐振腔Q值
Rs
0 , H 为切向磁场。因此， 2
y
Ey
j
z
0
k
E0 x E0 0 x 1 E y z z Hx j j sin sin cos = j cos l 0 z 0 l a l 2l a E E0 0 1 E y x z x z Hz j j 0 cos sin j cos sin x a a l 2a a l
§5.1 矩形谐振腔
Rectangular Resonator
讨论谐振腔的主要指标是谐振频率 0 、品质因数 Q 和电导G。谐振腔的讨论思路是:理想腔—耦合腔—非 理想腔，如图(31-2)所示。 在研究谐振频率f0时，采用不计及腔损耗，即腔壁 由理想导体构成。但是，当研究Q时,则必须考虑损耗 的因素。 耦合腔和实际腔反映了谐振腔的具体应用。
一、谐振频率0
可见,谐振腔在三个方向都是纯驻波，而传输线kc是 二维谐振。
传输线—二维 kc 传输腔—三维 k
图 31-3 二维谐振和三维谐振
一、谐振频率0
进一步,如果讨论的是传输型谐振腔，即
l p
( p 1,2,3,)
则有
(31-4)
0
2 m n p a b l
第5章1、2矩形谐振腔
5
2016/4/15
第五章 微波谐振腔
5.1 简介
两块相对放置的导体板也可构成微波谐 振腔，如果导体板的尺度远大于微波波长。 r r
这种腔体被称为开放式微波谐振腔。
这两种谐振腔在毫米波、远 红外和光波频段有广泛用途 。 利用介质材料参数的周期性 或非周期性变化，可以构成所谓 分布反馈谐振腔。
2016/4/15
m m n m m n ) sin( x)cos ( y) sin(t z ) D' ( ) sin( x)cos ( y) sin(t z ) a a b a a b
E y ( x, y, z, t ) (
2016/4/15
m m n ) sin ( x)cos( y) D' sin (t z ) D' sin (t z ) a a b
b2
a1
2016/4/15 4
第五章 微波谐振腔
5.1 简介
2a
圆波导
两块相对放置的导体板也可构成微波谐 振腔，如果导体板的尺度远大于微波波长。 这种腔体被称为开放式微波谐振腔。
r
r
当电磁波波长较短时，很容易实现这种 谐振腔。在光学系统中，这种谐振腔称为 FP 腔。 优点是品质因数高（选频特性好）。
(5-2)
(1) 由边界条件 Ex(x,y,z = 0, t) 0 可得：D' = D' = D'
(2) 由边界条件 Ex(x,y,z = l, t) 0 ，和 D' = D' = D' 可得： = p / l
(
(p = 1,2,3, … 是否可取零待定)
m 2 n 2 m 2 n 2 p 2 ) ( ) 2 ( ) ( ) ( ) 2 a b a b l
2016/4/15
第五章 微波谐振腔
5.1 简介
两块相对放置的导体板也可构成微波谐 振腔，如果导体板的尺度远大于微波波长。 r r
这种腔体被称为开放式微波谐振腔。
这两种谐振腔在毫米波、远 红外和光波频段有广泛用途 。 利用介质材料参数的周期性 或非周期性变化，可以构成所谓 分布反馈谐振腔。
2016/4/15
m m n m m n ) sin( x)cos ( y) sin(t z ) D' ( ) sin( x)cos ( y) sin(t z ) a a b a a b
E y ( x, y, z, t ) (
2016/4/15
m m n ) sin ( x)cos( y) D' sin (t z ) D' sin (t z ) a a b
b2
a1
2016/4/15 4
第五章 微波谐振腔
5.1 简介
2a
圆波导
两块相对放置的导体板也可构成微波谐 振腔，如果导体板的尺度远大于微波波长。 这种腔体被称为开放式微波谐振腔。
r
r
当电磁波波长较短时，很容易实现这种 谐振腔。在光学系统中，这种谐振腔称为 FP 腔。 优点是品质因数高（选频特性好）。
(5-2)
(1) 由边界条件 Ex(x,y,z = 0, t) 0 可得：D' = D' = D'
(2) 由边界条件 Ex(x,y,z = l, t) 0 ，和 D' = D' = D' 可得： = p / l
(
(p = 1,2,3, … 是否可取零待定)
m 2 n 2 m 2 n 2 p 2 ) ( ) 2 ( ) ( ) ( ) 2 a b a b l
43矩形谐振腔
(4-32)
第四章 微波谐振器
§4.3 矩形谐振腔
下面的关系式成立
K 2K c 22, Kc2ma2nb2
K2m a2nb 2pl2
不同的m,n,p对应不同的TEmnp模，m,n不能同时为零。 工作于TEmnp模的矩形腔具有多谐性。
Hm 2a l2 21a4bH l4m 2a2l2al b
第四章 微波谐振器
§4.3 矩形谐振腔
在腔体前后壁(z=0,z=ι)的内表面上
H 1 2H x12H m 2a l2 2si2 n ax
在腔体左右壁(x=0,x=a)的内表面上
H 2 2H z12H m 2si2n lx
第四章 微波谐振器
§4.3 矩形谐振腔
在与z=0相距ι处再放一短路板，形成腔体.
则有边界条件
Exzl 0
所以 lp 或 p (p0 ,1 ,2 ,3 )
l
则腔体内TMmnp模的纵向电场为
E z E m s im a nx s in b ny c o p ls z
第四章 微波谐振器
§4.3 矩形谐振腔
腔体内TMmnp模的其它场分量为
E x K E m c 2p lm ac o m ax s s in b n y s ip ln z E y K E m c 2p ln b s im a n x c o n by s s ip ln z H x jm E K c 2 n bs im a n x c o n by s c o p lz s
H xH ma lsi a nx co lsz
矩形谐振腔讲义课件
电导率
电导率影响电磁波在介质中的传播损耗，进而影响腔体的Q值。
介电常数
介电常数决定了电磁波在介质中的传播速度，从而影响谐振频率。
损耗角正切值
损耗角正切值反映了介质的能量损耗特性，对腔体的Q值有重要影 响。
矩形谐振腔的表面涂层
涂层材料
涂层材料的电导率、介电常数 和磁导率都会影响腔体的性能
。
涂层厚度
涂层厚度需精确控制，以确保 其对电磁波的反射特性的影响
矩形谐振腔讲义课件
contents
目录
• 矩形谐振腔概述 • 矩形谐振腔的基本原理 • 矩形谐振腔的设计与优化 • 矩形谐振腔的制造工艺 • 矩形谐振腔的性能测试与评估 • 矩形谐振腔的应用实例
01
矩形谐振腔概述
定义与特性
定义
矩形谐振腔是一种具有特定边界条件 的空腔，通常由金属壁围成，可以在 其中产生电磁波的共振。
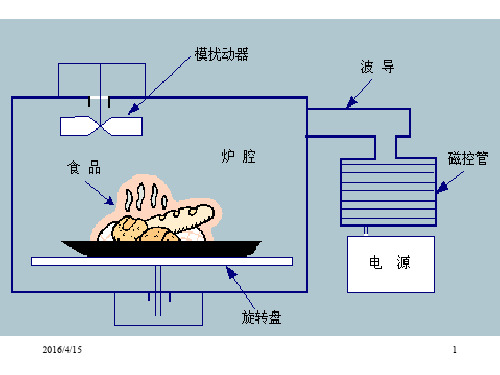
矩形谐振腔可用于微波加热，快速均匀 地加热物质，广泛应用于食品加工和材 料处理。
VS
医疗领域
在医疗领域，矩形谐振腔可用于微波治疗 和诊断，例如肿瘤热疗和微波成像。
THANKS
感谢观看
制造流程
材料准备
根据设计图纸准备相应的材料 ，并进行必要的处理如清洗、 矫直等。
组装调试
将加工好的各个部件进行组装 ，并进行必要的调试和测试， 确保性能符合要求。
设计图纸
根据需求和规格，设计矩形谐 振腔的图纸，包括腔体尺寸、 形状、接口等。
加工成型
按照设计图纸对材料进行加工 ，形成矩形谐振腔的各个部件 。
质量检测
对制造完成的矩形谐振腔进行 质量检测，包括尺寸、外观、 电气性能等方面的检测。
05
矩形谐振腔讲义
x sin 2 l
l
1 2 z dxdydz ablE0 8
计算导体Q值时有六个面需要考虑
PL (1) ( 2) (3) 2 2 2
b b a 1 Re 2 H x 0 0 2 a
2
(31-31)
0 0
2
dxdy 2 z 0
b 0
l
0 0 2
2
g
l
所以，TE101模Ey最终写成
E y E0 sin x sin z a l
(31-27)
现在采用Maxwell方程组解出
四、矩形腔TE101模的场和λ0
E j 0 H 1 H j
0 x
0
i
2
2 E0 0 2 l 2 x 2 z 0 E0 a + 2 cos sin dxdz 2 0 0 2a a l 8 l a
五、TE101模的Q值
结合上面三种情况可知
2
(31-1)
一、谐振频率0
理 想 腔 耦 合 腔 非 理 想 腔 G 介 质
C
G o
L
G o L C
C L G o
G
Q
G 0
图 31-2 谐振腔研究的思路框图
一、谐振频率0
但是在求解中,它与传输线不同。在传输线中z是优 势方向:即。从概念上讲：x、y方向是驻波，而z方向 假定是行波。
传 输 线
y
谐 振 腔
y -z
-z
0
x
x 0
d E 2 kx E0 2 dx d 2E 2 ky E0 2 dy d 2E 2E 0 2 dz 2 2 kx ky k c2 kc k 2 2
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
§5.1 矩形谐振腔
Rectangular Resonator
讨论谐振腔的主要指标是谐振频率0、品质因数Q
和电导G。谐振腔的讨论思路是:理想腔—耦合腔—非 理想腔，如图(31-2)所示。
在研究谐振频率f0时，采用不计及腔损耗，即腔壁 由理想导体构成。但是，当研究Q时,则必须考虑损耗 的因素。
耦合腔和实际腔反映了谐振腔的具体应用。
四、矩形腔TE101模的场和λ0
图 31-6 TE101模的场结构
五、TE101模的Q值
W W em a x 1 2 V E 2 d v 1 20 l0 b 0 a E 0 2 s i n 2 a x s i n 2 lz d x d y d z 1 8 a b lE 0 2
ab l2
(2)
l
2 0
b
2
l
0
Hz
dydz 2
x0
0
b 0
E02
2
0
2l
2
sin2
axdydz
20E02 42
bl a2
(3)
l
2 0
a 0
Hx 2 Hz 2
l
dxdz 2 0
a 0
E0
2
0
2l
2
sin2
ax
cos2
lzdxdz
l
+2 0
a 0
E0
2
2a0
计算导体Q值时有六个面需要考虑
(31-31)
PL
1 2
Re
b
2 0
a 0
Hx
2
l
dxdy 2
z0
0
b 0
Hz
2 dydz
x0
2
l 0
a 0
Hx 2 Hz 2 dxdz
(1)
b
2 0
a 0
Hx
2
b
dxdy 2
z0
0
a 0
E02
2
0
2l
2
sin2
axdxdyຫໍສະໝຸດ 20E02 42矩形腔TE101模是最基本而重要的模式，它是由传 输线TE10模在z方向加两块短路板而构成的金属封闭 盒。
图 31-5 矩形TE101模
四、矩形腔TE101模的场和λ0
已经知道，TE10模Ey中Emsinaxejz
首先在z=0处放一块金属板(全反射),则有
(31-25)
E y E m s ia n x e jz e jz 2 jm E s ia n x siz n
令E0=-2jEm而且在 z处l 放一块金属板(全反射)，
即
。sin这 l时有0
l2 g p p1,2,(31-26)
四、矩形腔TE101模的场和λ0
l
1 2
，p g其中
min，l 这12 时g 对应
2 g l
所以，TE101模Ey最终写成
。则p 1
Ey E0sinaxsinl z
现在采用Maxwell方程组解出
一、谐振频率0
谐振腔中谐振频率0(或f0)和谐振波长0是最基本 参数，但是要注意0是不变量，而0则与媒质r0有
关。
在一个封闭系统中，电能与磁能相等称之为谐振。
谐 振 腔 的 规 律 同 样 服 从 Maxwell 方 程 组 ， 可 导 出
Helmholtz方程。
2Ek2E0
(31-1)
一、谐振频率0
Q0
2 W
Wr
0W
PL
(31-6)
W表示谐振腔的平均储能，WT表示一个周期T内
谐振腔的能量损耗。WT=TPL，PL表示一个周期内平 均损耗功率。式(31-6)对于低频和高频均适用的。
平均储能在谐振时有一特点，即腔内所储的电能等 于所储的磁能。
二、品质因数Q0
WW eW m1 2v|H |2dv
2
cos2
x
a
sin2
lzdxdz
20E02 82
a l
l a
五、TE101模的Q值
(31-27)
四、矩形腔TE101模的场和λ0
Ej0H
i j k
H j
1
0 x y z
0 Ey 0
Hx
j 1 Ey 0 z
jE00l sinaxcoslz =j
E0
0
2l
sinaxcoslz
Hz
j 1 Ey x
jE0 acosaxsinlz
j E0
2a0 cosaxsinlz
四、矩形腔TE101模的场和λ0
归纳起来TE101模的场
Ey
E
0
sin
a
x
sin
l
z
Hx
j
E0
0
2a
s
in
x
a
cos
l
z
Hz
j
E0
0
2a
cos
x
a
sin
l
z
(31-28)
四、矩形腔TE101模的场和λ0
从概念上来考察矩形波导，Ey和Hz在z方向行波
同时出现最大值；
而TE101模
中Ey和只差，一负Ey号~s，，in最使l z大 值Hz 对~c有应os行最a 波z小 传值S输z。的在12 E实相yH功位z 率方；面而， TE101模中相位差90°，因此Sz只有虚功率。如果研究
传输线—二维 kc
传输腔—三维 k
图 31-3 二维谐振和三维谐振
一、谐振频率0
进一步,如果讨论的是传输型谐振腔，即
l p
(p 1 ,2 ,3 , ) (31-4)
则有
0
2 m2n2p2 a b l
1
1c22pl2
(31-5)
二、品质因数Q0
品质因数又称Q值，它反映谐振腔储能与损耗之间
的关系。
k
2 y
E
0
d 2E 2E 0 dz 2
k
2 x
k
2 y
k
2 c
k c2 k 2 2
y -z
x
0
d 2E dx 2
k
2 x
E
0
d 2E dy 2
k
2 y
E
0
d 2E dz 2
k
2 z
E
0
k
2
k
2 x
k
2 y
k
2 z
一、谐振频率0
可见,谐振腔在三个方向都是纯驻波，而传输线kc是 二维谐振。
理想腔
C
Go L
耦合腔
Go L
C
非理想腔 G-介 质
C G
L Go
图 31-2 谐振腔 研究Q 的思G0 路框图
一、谐振频率0
但是在求解中,它与传输线不同。在传输线中z是优 势方向:即。从概念上讲：x、y方向是驻波，而z方向
假定是行波。
传输线
谐振腔
y -z
x
0
d 2E dx 2
k
2 x
E
0
d 2E dy 2
Ey和Hz也有类似情况。
四、矩形腔TE101模的场和λ0
由于
k2 2 0 2kx 2ky 2kz2 a 2 l 2
可知
0
2al a2 l2
(31-29)
其场结构如图31-6所示。值得提出：如果是TE10p模，
只要作代换
即l 可 pl ， l 这时有
0
2al
pa2 l2
(31-30)
而导体壁损耗
(31-7)
P L1 2S|Js|2R sds1 2R s S|H |2ds
(31-8)
式中Rs是表面电阻率， Rs 20为, H切 向磁场。因此，
有限电导率所对应的谐振腔Q值
Q0R0s
V|H|2dv2
S|H|2ds
|H|2dv
V
S|H|2ds
(31-9)
四、矩形腔TE101模的场和λ0
Rectangular Resonator
讨论谐振腔的主要指标是谐振频率0、品质因数Q
和电导G。谐振腔的讨论思路是:理想腔—耦合腔—非 理想腔，如图(31-2)所示。
在研究谐振频率f0时，采用不计及腔损耗，即腔壁 由理想导体构成。但是，当研究Q时,则必须考虑损耗 的因素。
耦合腔和实际腔反映了谐振腔的具体应用。
四、矩形腔TE101模的场和λ0
图 31-6 TE101模的场结构
五、TE101模的Q值
W W em a x 1 2 V E 2 d v 1 20 l0 b 0 a E 0 2 s i n 2 a x s i n 2 lz d x d y d z 1 8 a b lE 0 2
ab l2
(2)
l
2 0
b
2
l
0
Hz
dydz 2
x0
0
b 0
E02
2
0
2l
2
sin2
axdydz
20E02 42
bl a2
(3)
l
2 0
a 0
Hx 2 Hz 2
l
dxdz 2 0
a 0
E0
2
0
2l
2
sin2
ax
cos2
lzdxdz
l
+2 0
a 0
E0
2
2a0
计算导体Q值时有六个面需要考虑
(31-31)
PL
1 2
Re
b
2 0
a 0
Hx
2
l
dxdy 2
z0
0
b 0
Hz
2 dydz
x0
2
l 0
a 0
Hx 2 Hz 2 dxdz
(1)
b
2 0
a 0
Hx
2
b
dxdy 2
z0
0
a 0
E02
2
0
2l
2
sin2
axdxdyຫໍສະໝຸດ 20E02 42矩形腔TE101模是最基本而重要的模式，它是由传 输线TE10模在z方向加两块短路板而构成的金属封闭 盒。
图 31-5 矩形TE101模
四、矩形腔TE101模的场和λ0
已经知道，TE10模Ey中Emsinaxejz
首先在z=0处放一块金属板(全反射),则有
(31-25)
E y E m s ia n x e jz e jz 2 jm E s ia n x siz n
令E0=-2jEm而且在 z处l 放一块金属板(全反射)，
即
。sin这 l时有0
l2 g p p1,2,(31-26)
四、矩形腔TE101模的场和λ0
l
1 2
，p g其中
min，l 这12 时g 对应
2 g l
所以，TE101模Ey最终写成
。则p 1
Ey E0sinaxsinl z
现在采用Maxwell方程组解出
一、谐振频率0
谐振腔中谐振频率0(或f0)和谐振波长0是最基本 参数，但是要注意0是不变量，而0则与媒质r0有
关。
在一个封闭系统中，电能与磁能相等称之为谐振。
谐 振 腔 的 规 律 同 样 服 从 Maxwell 方 程 组 ， 可 导 出
Helmholtz方程。
2Ek2E0
(31-1)
一、谐振频率0
Q0
2 W
Wr
0W
PL
(31-6)
W表示谐振腔的平均储能，WT表示一个周期T内
谐振腔的能量损耗。WT=TPL，PL表示一个周期内平 均损耗功率。式(31-6)对于低频和高频均适用的。
平均储能在谐振时有一特点，即腔内所储的电能等 于所储的磁能。
二、品质因数Q0
WW eW m1 2v|H |2dv
2
cos2
x
a
sin2
lzdxdz
20E02 82
a l
l a
五、TE101模的Q值
(31-27)
四、矩形腔TE101模的场和λ0
Ej0H
i j k
H j
1
0 x y z
0 Ey 0
Hx
j 1 Ey 0 z
jE00l sinaxcoslz =j
E0
0
2l
sinaxcoslz
Hz
j 1 Ey x
jE0 acosaxsinlz
j E0
2a0 cosaxsinlz
四、矩形腔TE101模的场和λ0
归纳起来TE101模的场
Ey
E
0
sin
a
x
sin
l
z
Hx
j
E0
0
2a
s
in
x
a
cos
l
z
Hz
j
E0
0
2a
cos
x
a
sin
l
z
(31-28)
四、矩形腔TE101模的场和λ0
从概念上来考察矩形波导，Ey和Hz在z方向行波
同时出现最大值；
而TE101模
中Ey和只差，一负Ey号~s，，in最使l z大 值Hz 对~c有应os行最a 波z小 传值S输z。的在12 E实相yH功位z 率方；面而， TE101模中相位差90°，因此Sz只有虚功率。如果研究
传输线—二维 kc
传输腔—三维 k
图 31-3 二维谐振和三维谐振
一、谐振频率0
进一步,如果讨论的是传输型谐振腔，即
l p
(p 1 ,2 ,3 , ) (31-4)
则有
0
2 m2n2p2 a b l
1
1c22pl2
(31-5)
二、品质因数Q0
品质因数又称Q值，它反映谐振腔储能与损耗之间
的关系。
k
2 y
E
0
d 2E 2E 0 dz 2
k
2 x
k
2 y
k
2 c
k c2 k 2 2
y -z
x
0
d 2E dx 2
k
2 x
E
0
d 2E dy 2
k
2 y
E
0
d 2E dz 2
k
2 z
E
0
k
2
k
2 x
k
2 y
k
2 z
一、谐振频率0
可见,谐振腔在三个方向都是纯驻波，而传输线kc是 二维谐振。
理想腔
C
Go L
耦合腔
Go L
C
非理想腔 G-介 质
C G
L Go
图 31-2 谐振腔 研究Q 的思G0 路框图
一、谐振频率0
但是在求解中,它与传输线不同。在传输线中z是优 势方向:即。从概念上讲：x、y方向是驻波，而z方向
假定是行波。
传输线
谐振腔
y -z
x
0
d 2E dx 2
k
2 x
E
0
d 2E dy 2
Ey和Hz也有类似情况。
四、矩形腔TE101模的场和λ0
由于
k2 2 0 2kx 2ky 2kz2 a 2 l 2
可知
0
2al a2 l2
(31-29)
其场结构如图31-6所示。值得提出：如果是TE10p模，
只要作代换
即l 可 pl ， l 这时有
0
2al
pa2 l2
(31-30)
而导体壁损耗
(31-7)
P L1 2S|Js|2R sds1 2R s S|H |2ds
(31-8)
式中Rs是表面电阻率， Rs 20为, H切 向磁场。因此，
有限电导率所对应的谐振腔Q值
Q0R0s
V|H|2dv2
S|H|2ds
|H|2dv
V
S|H|2ds
(31-9)
四、矩形腔TE101模的场和λ0