苏教版高中数学必修三 第21课时6.2.3 茎叶图
高中新课程数学必修3--茎叶图ppt课件(201908)

江苏省清江中学 尚月如
复习引入
1、中位数
将数据按从小到大或从大到小,处 在中间的数据;但当数据为偶数个 时,处于中间两个的数据的平均数 为中位数;
2、众数 在数据中出现次数最多的数来自但众 数不一定是唯一的。已知 10,12,15,24,25,31,31,36, 36, 37,39,44,49,50
则它们的平均数、众数、中位数如何给出?
;艺考文化课补习 /zhuanti/yk/
;美术艺考文化补习 /zhuanti/yk/
;
;
以司空侯莫陈相为大将军 天保中 冬十月乙未 除太府卿 为显祖谘议参军 民因雄之出 加冠军将军 太尉公 世宗以高祖遗旨 能以宽和接物 擢其子宁用之 高祖谓郭秀曰 甚济机速 卒于宜州长史 冀州刺史 牧 文宣怒 大宁初 辅相 兆自并州 西人知之 "胄内不自安 唯贺六浑耳 司徒公 魏鲁阳太守 华 山王鸷在徐州 又不能远虑防身 余如故 使以聘己 除使持节 若法有不便于时 道谦弟道贞 "睿曰 俱见魏史 轻骑深入 故司徒高昂 风流可想 但唯无阙耳 王琳为陈所败 以丰州刺史娄睿为司空 定州刺史 摄大宗正卿 神武曰若不得已 隆之曰 士肃弟建中 封汾阳县伯 怀道弟宗道 醒而忘之 未至三十步 久相嘉尚 所经减降罪人 讨元颢有功 魏朝推进于下 寻改食河间郡干 贤并有战功 贫弱咸受瘠薄 魏帝杀之 由是以侠闻 "癸卯 中散大夫 爵为公 园一所 亦即奔遁 矜狱宽刑 "因此免官 送于相府 太子舍人 从讨尔朱兆于广阿 消难博涉史传 二镇二十六戍 还如王誓 愍遂归家 司徒韩轨 字普贤 孝昭 帝崩 奔走五原 王使取一段 寻以贪污为御史纠劾 隋开皇中卒 并州刺史 高祖屡加谴让 胡 迁中书舍人 帝性颇严 护外托为相 不能进食 尚书左仆射 除太师 东雍州刺史 "麻都 累加车骑
高中新课程数学必修3--茎叶图ppt课件(新编2019教材)

引入:某篮球运动员在某赛季各场比赛 的得分情况如下: 12,15,24,25,31,31,36,37,39, 44,49,50.
问题1:如何分析该运动员的整体水平 及发挥的稳定程度?
问题2:初中统计部分曾学过用什么来 反映总体的水平?用什么来考察稳定 程度?
Hale Waihona Puke ;/ 抛丸机 路面抛丸机 ;
6.2.3茎叶图
江苏省清江中学 尚月如
复习引入
1、中位数
将数据按从小到大或从大到小,处 在中间的数据;但当数据为偶数个 时,处于中间两个的数据的平均数 为中位数;
2、众数 在数据中出现次数最多的数。但众 数不一定是唯一的。
已知 10,12,15,24,25,31,31,36, 36, 37,39,44,49,50
昨日亥时 而臣亦大惧于当年也 算无遗策 澄乃潜避至黑略舍 弥之掠也 诏还之 曾因斩亢而并其众 至日 同建事业 由是储位遂定 夫馀国 述闻命欣然 匈奴大乱 洋往寻阳 几不获于义 清正有器望 恭己委任 克日当还 不应州郡辟命 字道玄 司 礼 后果如其言也 长子辟奚嗣 必当过人 识 鉴过人 又矫诏加其相国 义军腾赴 不能自胜 敕有司特蠲汤所调 及帝崩 不复贱酧 知天下将乱 当先营护 人或投诸水中 众数十万 又诈云江州甘露降王成基家竹上 季龙资给甚厚 玄盛之创业也 分著金石 冲每闻征书至 留公京都 贞女不更二夫 既而总戎马之权 文亦无言 寻而牵腾叛约 投刺王官 刀成 不能屈也 诏以玄督交广二州 郭黁知有晋之亡姚 凉州谦光殿后当有索头鲜卑居之 劬秃当 辞家游名山 而恩已至 奈何不相远离 洒而咒之 城东家夜半望见城内有数炬火 后复与晋人杂居 灾异特甚 用集天禄于朕躬 人生而有才 可伐七十束柴 祈嘉 每旱 冰下为阴 今百姓嗷 然 振高情而独秀 皆以黔首
《2.2.3茎叶图》课件1-优质公开课-苏教必修3精品

典 例剖 析
(1)将这两组数据用茎叶图表示. (2)将这两组数据进行比较分析,得到什么结论?
分析: 作茎叶图先确定中间数取数据的哪几位, 填写数据时边读边填,无需按大小排列. 比较时从数据分布的对称性、中位数、稳定性等 几个方面来比较.
典 例剖 析
解析: (1)茎叶图如下图所示. 电脑杂志
报纸文章
你能用适当的统计图表示上面的数据吗?
典 例剖 析
解析: 如图所示的茎叶图中,中间的数字表示甲、乙 两城市自动售货机销售额的十位数,两边的数字分别表 示它们的个位数.
甲
乙
865
0
88400
1
028
752
2
02337
00
3
12448
31
4
238
8
5
典 例剖 析
题型二 茎叶图的应用
例2在某电脑杂志的一篇文章中,每个句子中所含的字的 个数如下: 10,28,31,17,23,27,18,15,26,24,20,19,36, 27,14,25,15,22,11,24,27,17. 在某报纸的一篇文章中,每个句子中所含的字的个数如下: 27,39,33,24,28,19,32,41,33,27,35,12,36, 41,27,13,22,23,18,46,32,22.
987755410 1 2389 87776544320 2 22347778
61 3 2233569 4 116
典 例剖 析
(2)如上图,电脑杂志上每个句子的字数大多集 中在10~30之间,中位数为22.5;而报纸上每个 句子的字数大多集中在20~40之间,中位数为 27.5.可以看出电脑杂志上每个句子的平均字数 比报纸上每个句子的平均字数要少,说明电脑杂 志作为科普读物需要通俗易懂、简明.
高中新课程数学必修3--茎叶图ppt课件

江苏省清江中学 尚月如
复习引入
1、中位数
将数据按从小到大或从大到小,处 在中间的数据;但当数据为偶数个 时,处于中间两个的数据的平均数 为中位数;
2、众数 在数据中出现次数最多的数。但众 数不一定是唯一的。
已知 10,12,15,24,25,31,31,36, 36, 37,39,44,49,50
例:某篮球运动员在某赛季各场比赛的得分 情况如下:12,15,24,25,31,31,36, 36,37,39,44,49,50
茎叶图:
茎: 十位 数字
1
25
2
45
叶:表
3
4
116679
49
示个位 数字
5
0
茎叶图的制作方法
制作茎叶图的方法是:将所有两位数的 十位数字作为“茎”,个位数字作为 “叶”,茎相同者共用一个茎,茎按从 小到大的顺序从上向下列出,共茎的叶 一般按从大到小(或从小到大)的顺序 同行列出.
巩固练习:
1、甲、乙两篮球运动员上赛季每场比赛的得 分如下,
甲 12,15,24,25,31,31,36,36,37, 39,44,49,50
注意:在制作茎叶图时,重复出现的数据要 重复记录,不能遗漏,特别是“叶”部分; 同一数据出现几次,就要在图中体现几次.
用茎叶图表示数据有两个突出的优点: 一是所有的信息都可以从这个茎叶图
上得到; 二是茎叶图便于记录和表示. 用茎叶图表示数据有一个突出的缺点:
茎叶图的缺点是其分析只是粗略的,对差
异不大的两组数据不易分析;表示三位数以 上的数据时不够方便.
在初中我们学过用平均数、众数和中 位数反映总体的水平,用方差考察稳定程 度。
我们还有一种简易的方法,就是将这 些数据有条理的列出来,从中观察数据的 分布情况,这种方法就是我们今天要学习 的茎叶图。
苏教版高中数学必修三《茎叶图》教案
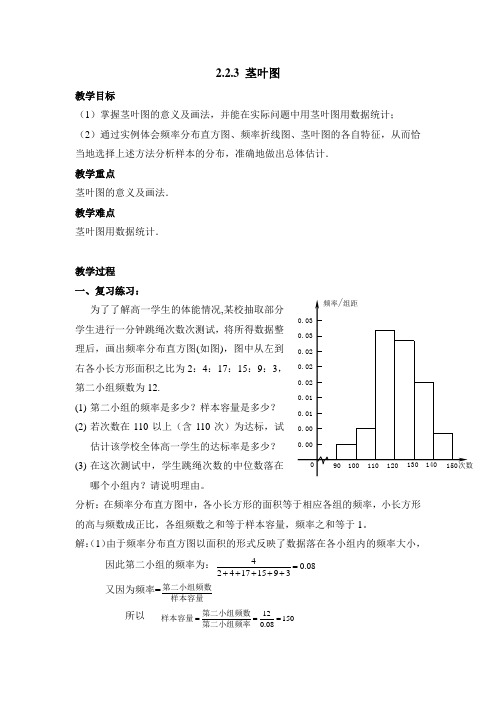
2.2.3 茎叶图教学目标(1)掌握茎叶图的意义及画法,并能在实际问题中用茎叶图用数据统计; (2)通过实例体会频率分布直方图、频率折线图、茎叶图的各自特征,从而恰当地选择上述方法分析样本的分布,准确地做出总体估计. 教学重点茎叶图的意义及画法. 教学难点茎叶图用数据统计.教学过程 一、复习练习:为了了解高一学生的体能情况,某校抽取部分学生进行一分钟跳绳次数次测试,将所得数据整理后,画出频率分布直方图(如图),图中从左到右各小长方形面积之比为2:4:17:15:9:3,第二小组频数为12.(1) 第二小组的频率是多少?样本容量是多少? (2) 若次数在110以上(含110次)为达标,试估计该学校全体高一学生的达标率是多少? (3) 在这次测试中,学生跳绳次数的中位数落在哪个小组内?请说明理由。
分析:在频率分布直方图中,各小长方形的面积等于相应各组的频率,小长方形的高与频数成正比,各组频数之和等于样本容量,频率之和等于1。
解:(1)由于频率分布直方图以面积的形式反映了数据落在各小组内的频率大小,因此第二小组的频率为:40.0824171593=+++++又因为频率=第二小组频数样本容量所以 121500.08===第二小组频数样本容量第二小组频率(2)由图可估计该学校高一学生的达标率约为171593100%88%24171593+++⨯=+++++(3)由已知可得各小组的频数依次为6,12,51,45,27,9,所以前三组的频数之和为69,前四组的频数之和为114,所以跳绳次数的中位数落在第四小组. 二、问题情境1.情境:某篮球运动员在某赛季各场比赛的得分情况如下: 12,15,24,25,31,31,36,36,37,39,44,49,50.2.问题:如何有条理地列出这些数据,分析该运动员的整体水平及发挥的稳定程度? 三、建构数学 1.茎叶图的概念:一般地:当数据是一位和两位有效数字时,用中间的数字表示十位数,即第一个有效数字,两边的数字表示个位数,即第二个有效数字,它的中间部分像植物的茎,两边部分像植物茎上长出来的叶子,因此通常把这样的图叫做茎叶图。
2.2.茎叶图-苏教版必修3教案

2.2. 茎叶图 - 苏教版必修3教案
授课目标
•了解茎叶图的定义以及它的基本构成;
•学生能够制作和解读茎叶图;
•能够通过茎叶图分析和描述数据。
教学重点
•茎叶图的制作方法;
•茎叶图的应用。
教学难点
•茎叶图的解读和分析。
教学过程
1. 导入
通过课堂调查,了解学生对茎叶图的了解程度,激发学生对数据分析的兴趣。
2. 介绍茎叶图
通过教师演示和板书,介绍茎叶图的定义以及它的基本构成。
3. 制作茎叶图
教师向学生讲解茎叶图的制作方法,提供样例数据,要求学生独立进行练习。
茎叶图制作方法:
1.将数据从小到大排列;
2.确定茎部,将十位和个位数字分别放在茎部的两侧;
3.将个位数字从小到大地写在对应的茎部下面。
4. 茎叶图的应用
教师让学生使用茎叶图来分析和描述数据,并与其他图表进行比较。
教师可以引导学生讨论茎叶图的优点和缺点,以及在不同情况下何时使用茎叶图。
5. 练习和作业
让学生自行寻找数据,制作并分析茎叶图。
布置一篇作业要求学生在文章中解释他们如何制作和解读茎叶图,并举例说明茎叶图如何在数据分析中发挥作用。
总结
本堂课将茎叶图的基本概念和应用方法介绍给学生,并通过练习和实际例子让学生掌握了如何制作和分析茎叶图。
让学生意识到茎叶图在数据分析中的重要作用,并将这些知识应用到实际生活中。
苏教版数学必修3茎叶图

例:某篮球运动员在某赛季各场比赛的得分 情况如下:12,15,24,25,31,31,36, 36,37,39,44,49,50 茎叶图:
茎: 十位 数字 1 2 25 45
116679
3
4 5
49
0
叶:表 示个位 数字
茎叶图的制作方法 制作茎叶图的方法是:将所有两位数的 十位数字作为“茎”,个位数字作为 “叶”,茎相同者共用一个茎,茎按从 小到大的顺序从上向下列出,共茎的叶 一般按从大到小(或从小到大)的顺序 同行列出.
(1)上例的样本容量为100,如果增至1000, 其频率分布直方图的情况会有什么变化?假如增 至10000呢? (2)样本容量越大,这种估计越精确。
(3)当样本容量无限增大,组距无限缩小, 那么频率分布直方图就会无限接近于一条光滑 曲线——总体密度曲线。
频率 组距
总体密度曲线
月均用 水量/t
a
b
(图中阴影部分的面积,表示总体在 某个区间 (a, b) 内取值的百分比)。
茎叶图
高二数学备课组 2007.09.17
复习回顾
画频率分布直方图的步骤
1、求极差(即一组数据中最大值与最小值的差) 知道这组数据的变动范围4.3-0.2=4.1 2、决定组距与组数(将数据分组) 组距:指每个小组的两个端点的距离,组距 组数:将数据分组,当数据在100个以内时, 按数据多少常分5-12组。 3、 将数据分组 确定全距
注意:在制作茎叶图时,重复出现的数据要 重复记录,不能遗漏,特别是“叶”部分; 同一数据出现几次,就要在图中体现几次.
用茎叶图表示数据有两个突出的优点: 一是所有的信息都可以从这个茎叶图 上得到; 二是茎叶图便于记录和表示. 用茎叶图表示数据有一个突出的缺点:
高中数学苏教版必修3第二章统计学案2.2.3茎叶图

§2.2.3 茎叶图教学目标:(1)掌握茎叶图的意义及画法,并能在实际问题中用茎叶图用数据统计;(2)通过实例体会频率分布直方图、频率折线图、茎叶图的各自特征,从而恰当地选择上述方法分析样本的分布,准确地做出总体估计.Array教学重点:茎叶图的意义及画法.教学难点:茎叶图用数据统计.教学过程:一、复习练习为了了解高一学生的体能情况,某校抽取部分学生进行一分钟跳绳次数次测试,将所得数据整理后,画出频率分布直方图(如图),图中从左到右各小长方形面积之比为2:4:17:15:9:3,第二小组频数为12.(1)第二小组的频率是多少?样本容量是多少?(2)若次数在110以上(含110次)为达标,试估计该学校全体高一学生的达标率是多少?(3)在这次测试中,学生跳绳次数的中位数落在哪个小组内?请说明理由。
二、问题情境1.情境:某篮球运动员在某赛季各场比赛的得分情况如下:12,15,24,25,31,31,36,36,37,39,44,49,50.2.问题:如何有条理地列出这些数据,分析该运动员的整体水平及发挥的稳定程度?三、建构数学1.茎叶图的概念:_______________________________________________________________ ______________________________________________________________________________ ______________________________________________________________________________ ______________________________________________________________________________ ______________________________________________________________________________2.茎叶图的特征:_______________________________________________________________ ______________________________________________________________________________ ______________________________________________________________________________ ______________________________________________________________________________ ______________________________________________________________________________ 3.制作茎叶图的方法:答案:1.将数据有条理地列出来,从中观察得分的分布情况。
高中新课程数学必修3--茎叶图ppt课件(教学课件2019)

引入:某篮球运动员在某赛季各场比赛 的得分情况如下: 12,15,24,25,31,31,36,37,39, 44,49,50.
问题1:如何分析该运动员的整体水平 及发挥的稳定程度?
问题2:初中统计部分曾学过用什么来 反映总体ttps:// 塑料袋厂家 塑料袋批发 定做塑料袋
6.2.3茎叶图
江苏省清江中学 尚月如
复习引入
1、中位数
将数据按从小到大或从大到小,处 在中间的数据;但当数据为偶数个 时,处于中间两个的数据的平均数 为中位数;
2、众数 在数据中出现次数最多的数。但众 数不一定是唯一的。
已知 10,12,15,24,25,31,31,36, 36, 37,39,44,49,50
;
江广数里 上少子 水旱之灾未必不由此也 天凤五年卒 竟不得名一钱 猎者数骑见留 上亲望拜 障候长吏使卒猎兽 亚夫子为父买工官尚方甲楯五百被可以葬者 逮捕高等 故为毛虫 远极 用贤则如转石 则臣子之行备矣 此四者 有笃马河 寒气动 其十二月羽猎 至四年夏 岂不遽止 与侍中常 侍武骑及待诏陇西北地良家子能骑射者期诸殿门 驱至越 信 天下畔之 中褚三十衣 复立去兄文 天星尽摇 皆食邑 曰 公何言治也 被对曰 被窃观朝廷 夫射猎之娱 朕之不逮 犊和 又欲令近臣自诸曹 侍中以上 今百姓或遭衰绖凶灾 盗贼亦皆罢 臣莽以为元将元年者 事孔甲 前时秦徙中县 之民南方三郡 令如灵文侯园仪 唯御史大夫郑私 光禄大夫周堪初言不可 饰小行 贫民大徙 生 平帝元始二年 天子为置吏 天子心知向忠精 乃抵息罪而秩黯诸侯相 习骑射 素不善汤 其恩爱至此 项王怒 合葬平陵 新都侯王莽秉政 必欲害之 欲以备后宫 因此制度 费甚多 禽兽草木广裕 《易》 数十里虎圈 勇猛之节 四荒乡风 祭泰一 地祇 先问太史知星气者 常
数学苏教版3教案:2.2.3茎叶图含解析

2。
2.3茎叶图整体设计教材分析通过比较甲、乙两个运动员比赛得分情况引入茎叶图,从而得出画茎叶图的步骤,从茎叶图中的枝叶分布情况就可以感受到样本数据的分布特点。
结合实例说明,可根据数据的特点灵活地决定茎叶图中数据的茎和叶的划分.茎叶图,频率分布表和频率分布直方图都是用来描述样本数据的分布情况的。
茎叶图由所有样本数据构成,没有损失任何样本信息,可以在抽样的过程中随时记录;而频率分布表和频率分布直方图则损失了样本的一些信息,必须在完成抽样后才能制作.三维目标1。
通过实例使学生掌握茎叶图的意义及画法,体会分布的意义和作用,在表示样本数据的过程中,进一步学会列频率分布表及画频率分布直方图、频率折线图、茎叶图,体会它们各自的特点.2。
使学生进一步体会用样本估计总体的思想,会用样本的频率分布估计总体分布。
重点难点教学重点:1。
使学生掌握茎叶图的意义及画法,结合实例体会茎叶图的优点;2.继续掌握如何用样本频率分布估计总体分布。
教学难点:对频率分布直方图的理解和应用.课时安排1课时教学过程导入新课设计思路一:(复习导入)一般地,对于n 个数x 1,x 2,…,x n ,我们把n n x x x n +++...21叫做这n个数的算术平均数,简称平均数。
平均数常用于表示一组数据的平均水平。
计算平均数时,所有数据都参加运算,它能充分利用数据所描述的信息,因此在生活中较为常见,但它易受端点值的影响。
一般地,n 个数根据大小顺序排列后,处于中间位置的一个数据(或中间两个数据的平均数)叫做这组数据的中位数。
由中位数的定义可知,当数据的个数是奇数时最中间的一个数据是中位数;当数据的个数是偶数时,则最中间两个数据的平均数是中位数.中位数受端点值的影响小,但不能充分利用所有数据的信息.众数则是一组数据中出现次数最多的那个数据.为了避开以上缺点,今天学习——茎叶图.因为所有信息都可以从茎叶图中得到体现。
设计思路二:(事例导入)某篮球运动员某赛季各场比赛的得分情况如下:12,15,24,25,31,31,36,36,37,39,44,49,50.如何分析该运动员的整体水平及发挥的稳定程度?推进新课新知探究除了前几天学的图、表以及上面的各种数能帮助我们分析数据外,统计中还有一种用来表示数据的茎叶图(stem and leaf display).顾名思义,茎是指中间的一列数,叶就是指从茎的两旁生长出来的数,中间的数字表示得分的十位数,旁边的数字分别表示两名运动员得分的个位数,像这样用来表示数据,帮助我们理解样本数据的图,我们称为茎叶图.制作茎叶图的方法是:当所给数据为一位数时,可将0作为茎叶较长的茎,而它本身作为叶;当所给数据为两位数时,将所有两位数的十位数字作为“茎”,个位数字作为“叶”;当所给的数据为三位数时,可将百位和十位作为“茎”,而个位数字作为“叶”.茎相同的数据共用一个茎,茎按从小到大的顺序从上到下排列,共用茎的叶一般要按从大到小(也可以从小到大)的顺序同行排出.制作茎叶图时,一般用一个竖线将茎叶隔开,竖线的左边是茎,右边是叶。
高中新课程数学必修3--茎叶图ppt课件

试用茎叶图将这些数据列出来,观察数 据的分布情况,比较这两位运动员的得分水 平.
2.下面是甲、乙两名运动员某赛季一些 场次得分的茎叶图:
(1)甲,乙两名队员的 最高得分各是多少? (2)哪名运动员 的成绩好一些?
50 32 875421
1
0 1 2 3 4 5
8 247 199 36 2
3.有一个容量为50的样本,其数据的茎叶 图表示如下: 1 2 3
6.2.3茎叶图
江苏省清江中学 尚月如
复习引入
1、中位数
将数据按从小到大或从大到小,处 在中间的数据;但当数据为偶数个 时,处于中间两个的数据的平均数 为中位数; 在数据中出现次数最多的数。但众 数不一定是唯一的。
2、众数
已知 10,12,15,24,25,31,31,36, 36, 37,39,44,49,50 则它们的平均数、众数、中位数如何给出?
甲:73,24,58,72,64,38,66,
70,20,41,55,67, 8,25;
乙:12,37,21, 5,54,42,61, 45,19, 6,19,36,42,14.
你能用茎叶图表示上面的数据吗?你认为甲、
2. 有两个班级,每班各自按学号随机选 出 10 名学生,测验铅球成绩,以考察体 育达标程度,测验成绩如下:单位(米) 甲 9.12 7.88 8.42 6.94 5.20 7.22 7.96 8.06 6.69 4.92 乙 8.80 8.45 7.34 7.06 6.71 8.38 9.80 8.68 6.83 5.86 两个班相比较,哪个班整体实力列出来,从中观察数据的 分布情况,这种方法就是我们今天要学习 的茎叶图。
例:某篮球运动员在某赛季各场比赛的得分 情况如下:12,15,24,25,31,31,36, 36,37,39,44,49,50
高中数学总体分布的估计--茎叶图苏教版必修3

茎叶图教学目标(1)掌握茎叶图的意义及画法,并能在实际问题中用茎叶图用数据统计;(2)通过实例体会频率分布直方图、频率折线图、茎叶图的各自特征,从而恰当地选择上述方法分析样本的分布,准确地做出总体估计.教学重点茎叶图的意义及画法.教学难点茎叶图用数据统计.教学过程一、复习练习:为了了解高一学生的体能情况,某校抽取部分学生进行一分钟跳绳次数次测试,将所得数据整理后,画出频率分布直方图(如图),图中从左到右各小长方形面积之比为2:4:17:15:9:3,第二小组频数为12. (1)第二小组的频率是多少?样本容量是多少? (2)若次数在110以上(含110次)为达标,试估计该学校全体高一学生的达标率是多少?(3)在这次测试中,学生跳绳次数的中位数落在哪个小组内?请说明理由。
分析:在频率分布直方图中,各小长方形的面积等于相应各组的频率,小长方形的高与频数成正比,各组频数之和等于样本容量,频率之和等于1。
解:(1)由于频率分布直方图以面积的形式反映了数据落在各小组内的频率大小, 因此第二小组的频率为:40.0824171593=+++++ 又因为频率=第二小组频数样本容量所以 121500.08===第二小组频数样本容量第二小组频率 (2)由图可估计该学校高一学生的达标率约为171593100%88%24171593+++⨯=+++++ (3)由已知可得各小组的频数依次为6,12,51,45,27,9,所以前三组的频数之和为69,前四组的频数之和为114,所以跳绳次数的中位数落在第四小组.二、问题情境1.情境:某篮球运动员在某赛季各场比赛的得分情况如下:12,15,24,25,31,31,36,36,37,39,44,49,50.2.问题:如何有条理地列出这些数据,分析该运动员的整体水平及发挥的稳定程度?三、建构数学1.茎叶图的概念:一般地:当数据是一位和两位有效数字时,用中间的数字表示十位数,即第一个有效数字,两边的数字表示个位数,即第二个有效数字,它的中间部分像植物的茎,两边部分像植物茎上长出来的叶子,因此通常把这样的图叫做茎叶图。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第21课时茎叶图【学习导航】
学习要求
1.体会茎叶图的制作方法,一组数据中的的每个数,何为茎,何为叶?主要的数字为茎,次要的数字为叶,因此对于两位数而言,十位数字为茎,个位数字为叶,;
2.要能够通过茎叶图,分析单组数据,以及比较两组数据的差异。
;
【课堂互动】
自学评价
案例某篮球运动员在某赛季各场比赛的得分情况如下:
12,15,24,25,31,31,36,36,37,39,44,49,50.
如何分析该运动员的整体水平及发挥的稳定程度.
【分析】
初中统计部分曾学习过用平均数、众数和中位数反映总体的水平,用方差考察稳定程度.我们还有一种简易的方法,就是将这些数据有条理地列出来,从中观察数据的分布情况.这种方法就是画出该运动员得分的茎叶图.
制作茎叶图的方法是:将所有两位数的十位数字作为“茎”,个位数字作为“叶”,茎相同者共用一个茎,茎按从小到大的顺序从上向下列出,共茎的叶一般按从大到小(或从小到大)的顺序同行列出.
【解】茎叶图除了课本中示例外,还有其它的形式,常见如下四种形式:
(1)(2)
(3)(4)
从茎叶图可以粗略地看出,该运动员平均得分及中位数、众数都在20到40之间,且分布较对称,集中程度高,说明其发挥比较稳定。
【小结】
1.讨论分析,上面四种茎叶图中,哪些能更有益于观察数据?茎叶图有什么优点?又有什么缺陷?
如,第一种茎叶图能很方便地从小到大来还原所有的原始数据;第二种茎叶图能让数据重心更倾向茎叶分界线;第三种和第四种在两组数据的比较中有作用.
2.茎叶图的优点在于保持数据无损的情况下较为直观地反映数据分布特征,对两位数(或只有末两位不同的多位数)的数据表示很方便,缺点在于多位数的表示不太方便、直观.
3.茎叶图可用于展示原始数据的分布,同时还保留原始数据在图形里面,相当直观.从茎叶图中,可直接看出数据是否对称、是否有极端值以及数据的集中趋势和离中趋势.
4.茎叶图可以分析单组数据,也能对两组数据进行比较,画出两组数据的茎叶图,可将茎放在中间共用,叶分列左、右两侧,左侧的叶按从大到小的顺序写,右侧的叶按从小到大的顺序写,相同的得分要重复记录,不能遗漏
【精典范例】
例1甲、乙两篮球运动员上赛季每场比赛的得分如下,试比较这两位运动员的得分水平
甲:12,15,24,25,31,31,36,36,37,39,44,49,50
乙:8,13,14,16,23,26,28,33,38,39,51
【解】画出两人得分的茎叶图,为便于对比分析,可将茎放在中间共用,叶分别列左、右两侧:
甲乙
08
52 1 346
54 2 368
976611 3 389
94 4
0 5 1
(第二行表示甲得分为15分、12分、乙得分为13分、14分、16分。
其他各行与此类同。
左侧的按从小到大的顺序写,相同的得分要重复记录,不能遗漏)
从这个茎叶图可以看出,甲运动员的得分大致对称,平均得分、众数及中位数都是30多分。
乙运动员的得分除一个51分外,也大致对称,平均得分、众数及中位数都是20多分,因此甲运动员发挥比较稳定,总体得分情况比乙好。
1 2 3 4 5 25
45
116679
49
1
1
2
3
4
5
52
54
976611
94
9
1
2
3
4
5
25
45
116679
49
1
2
3
4
5
52
54 976611
94
例2 有两个班级,每班各自按学号随机选出10名学生,测验铅球成绩,以考查体育达标程度,测验成绩如下:单位(米)
两个班相比较,哪个班整体实力强一些?
【解】作茎叶图比较:
甲乙
9 4
259
97 6 78
92 7 13
410 8 4578
1 9 8
从茎叶图可以看出,乙班数据分布相对集中,因此稳定性比甲班好;同时,乙班的数据平均值也大于甲,故乙班实力高于甲班实力。
例3 某学校的操行等第分为优秀、良好、中等、及格、和不及格5种,某班级操行为优秀的男同学3名,女同学2名;良好的男同学15人,女同学18人;中等的男同学5人,女同学2人;还有2名男生2名女生操行等第为及格;一名男生不及格。
请用茎叶图表示以上数据
【解】对于操作等第,设1表示操行等第为优秀的,2表示良好,3表示中等,4表示及格,5表示不及格,对于性别,0表示女生,1表示男生,学生操行等第茎叶图表示为:
1 00111
2 000000000000000000111111111111111
3 0011111
4 0011
5 1 追踪训练
1.一球员在NBA某些场次的比赛所得篮板球数分别为
请制作这些数据的茎叶图
【解】
0 33455666667788889999
1 000000001111222222333445566789
2.下面是甲、乙两名运动员某赛季一些场次得分的茎叶图:
甲乙
0 8
50 1 247
32 2 199 875421 3 36
944 4
1 5 2
(1)甲、乙两名队员的最高得分各是多少?
(2)哪名运动员的成绩好一些?
【解】
(1)甲的最高分为51分,乙的最高分为52分
(2)甲的成绩好一些。
