[09][ch5][地面观测元素归算至椭球面1]
第五章_地球椭球与测量计算

§5.1.2 垂线偏差及其基本公式
天文方位角与大地方位角之间的关系式:
应用大地测量学
) A ( ( 5-14 L) sin
A ( tan 5-15 )
以上公式称为拉普拉斯方程式。
§5.1.2 垂线偏差及其基本公式
应用大地测量学
椭球短轴与地球某一固定历元的地轴不平行,起始大 地子午面和起始天文子午面也不平行,将产生欧拉角,设 为 X , Y , 。此时垂线偏差公式( 5-8)及拉普拉斯方程式 Z (5-15)扩展为:
一是椭球参数的选择(椭球的大小和形状);
二是确定椭球与地球的相关位置,即椭球的定位(椭球与 大地水准面包围的大地体应当最密合)。
应用ቤተ መጻሕፍቲ ባይዱ地测量学
§5.1 地球椭球及其定位
具有一定几何参数,经过定位,在全球范围内与大地 体最为接近、密合最好的椭球称为地球椭球。 在某一地区与大地水准面密合最好的椭球,称为参考 椭球。
应用大地测量学
§5.1.3 椭球定位
椭球定位通过大地原点的天文观测实现。对于大地原点:
B0= ψ 0-ξ 0
L0= λ 0-η 0· secψ 0 A0= α 0-η 0· tanψ 0
H0= H0常+ζ 0
初期定位时,ξ 0,η 0,ζ 0未知,可取为0。称为一点定位。
根据大地测量和天文测量数据,在 ξ 0,η 0,ζ 0值。称为多点定位。
2 e e' ( 1 e 5-4) 2 e' e 1 e'
e 2f f
2
(5-52 )
应用大地测量学
§5.1.1 椭球的几何参数及其关系
几种椭球几何参数
克拉索夫斯基椭球 1980国家大地坐标系 WGS-84 a b e2 6378245 6356863.01877 6378140 6356755.28816 6378137 6356752.3142 0.00669437999013 0.00673949674227 1:298.257223563
大地测量学重要名词解释简答题

大地测量学基础一、名词解释1、大地测量学:是指在一定的时间与空间参考系中,测量和描绘地球形状及其重力场并监测其变化,为人类活动提供关于地球的空间信息的一门学科。
2、天球:是指以地球质心O(或测站)为中心,半径r为任意长度的一个假想的球体。
3、大地基准:指用以描述地球形状的参考椭球的参数,以及参考椭球在空间中的定位及定向,还有在描述这些位置时所采用的单位长度的定义。
4、岁差:地球绕地轴旋转,由于日、月等天体的影响,地球的旋转轴在空间围绕黄级发生缓慢移动。
5、章动:地球旋转轴在岁差的基础上叠加18.6年的短期周圆周运动,振幅为9.21秒,这种现象称为章动。
6、极移:地球自转使地球体自身内部结构的相对位置变化,从而导致极点在地球表面上的位置随时间而变化,这种现象被称为极移。
7、恒星时(ST):以春分点作为基本参考点,由春分点周日视运动确定的时间,称为恒星时。
8、真太阳时MT:以真太阳作为基本参考点,由其周日视运动确定的时间,称为真太阳时。
一个真太阳日就是真太阳连续两次经过某地的上中天(上子午圈)所经历的时间。
9、大地水准面:假想海洋处于完全静止的平衡状态时海水面延伸到大陆地面以下所形成的闭合曲面,叫大地水准面。
10、正常椭球:与地球质量相等且质量分布均匀的椭球。
11、正常重力加速度:正常椭球对其表面与外部点所产生的重力加速度。
12、正常位水准面:相应于正常重力加速度的重力等位面。
13、理论闭合差:由水准面不平行而引起的水准环线闭合差,称为理论闭合差。
14、正常椭球面:是大地水准面的规则形状(一般指旋转椭球面)。
因此引入正常椭球后,地球重力位被分成正常重力位和扰动位两部分,实际重力也被分成正常重力和重力异常两部分。
15、总的地球椭球:一个和整个大地体最为密合的。
总地球椭球中心和地球质心重合,总的地球椭球的短轴与地球地轴相重合,起始大地子午面和起始天文子午面重合,总地球椭球和大地体最为密合。
16、参考椭球:具有确定参数(长半径 a和扁率α),经过局部定位和定向,同某一地区大地水准面最佳拟合的地球椭球。
第19讲 地面观测值归算到参考椭球面概要

u cos A ucoscosA usinsinA cosA sinA
z z ' cos A sin A
4.地面观测长度归算至椭球面
用测距仪测得的
长度是连接地面两点
间的直线斜距,将其
归算到椭球面,称为 斜距归算。
4.地面观测长度归算至椭球面
线方向所加的改正,称为截
面差改正,以δ3表示
原因:由于相对法截线不重
合而采用大地线代替产生的
2.水平观测方向归算到椭球面
③ 截面差改正
2 2 e S ' ' '' cos B1 sin 2 A1 计算公式: 3 2 12N1
使用范围: 一等三角测量
δ3为0的情况:
A1=0º ,90º ,180º ,270º 照准点与测站点在同一子午
第19讲 地面观测值归算
教学目标
知识目标
了解地面观测值归算的意义和要求 掌握水平观测方向归算到椭球面的方法 了解天顶距观测值的归算方法 掌握地面长度观测值归算至椭球面的方法 了解垂线偏差的计算公式
技能目标 能够进行水平方向观测值的归算 能够进行地面长度观测值的归算
1.归算的意义和要求
bb′=H2θ
Ka R Ka R BR N2
bb′=H2
Ka R Ka Kb cos B2
Ka Kb OKb OKa
N 2e 2 sin B2 N1e 2 sin B1
N2e2 (sin B2 sin B1 )
2、水平观测方向归算到椭球面
② 标高差改正
sin B1 sin B2 cos B2 ( B2 B1 )
地面观测元素归算至椭球面1

m 1 1、垂线偏差改正( )
Z P [图形]
N AR1A 的方向值 弧长OR1 A b R1 A0 AR的方向值 弧长OR
R
R1 1 R 1 R1 R
Z A
法
u
Z1
P
M
线
u
O1
m
A
K a R1 1
R
大地水平面
O
S
二、水平观测方向归算至椭球面
通过归算,为在椭球面上的 水平坐标 计算提供观测数据。
推算 平差
大地坐标 (L,B)
推算 平差 平面坐标 (X,Y)
一、归算的意义和要求
2、归算的要求
1)以椭球面法线为基准线。 2)以椭球面为基准面。
Significance and request of reduction
垂线偏差u
3)椭球面两点连线用大地线。
M
u
Z1
q
m
z1 法
线
P
u
O1
什么情况下垂线 偏差改正为 0 ?
q 90 z1
R1 1 R
A
O
大地水平面
二、水平观测方向归算至椭球面
Reduction of horizontal directional observations to the ellipsoid
1、垂线偏差改正(1 )
垂线偏差分量ξ、η: 查图内插得到 测站点至目标点的大 地方位角A:概略计 算得到 照准目标的垂直角α1 :
M
u
Z1
q
m
z1 法
线
P
u
O1
q 90 z1
R1 1 R
第四章 4将地面观测值归算至椭球面
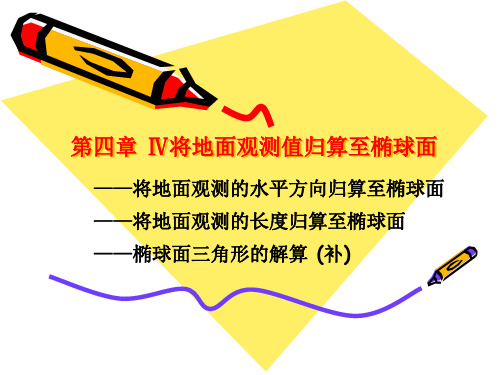
r ⋅ sin A = C
在旋转椭球面上, 在旋转椭球面上,大地线各点的平行圈半径 与大地线在该点的大地方位角的正弦的乘积 等于常数。式中常数C也叫大地线常数 也叫大地线常数。 等于常数。式中常数 也叫大地线常数。
克莱劳方程的应用
r ⋅ sin A = C
对于同一条大地线上的各点因要保持同一个c 对于同一条大地线上的各点因要保持同一个c值,而使点 上的大地线方位角与平行圈半径两者间的变动互为制约。 上的大地线方位角与平行圈半径两者间的变动互为制约。 •当大地线穿越赤道时 当大地线穿越赤道时 C = a sin A0 赤道是大地线 c = a •当大地线达极小平行圈时 当大地线达极小平行圈时 子午圈是大地线 c = 0
1 h2 由: S = D − 2D
S 得:d h = − d S h
计算取值精度分析
R2 d S dR = Hm S
若: dS/S=10-6, Hm=1km, R=6370km, 得: dR=40.6km。
由此可见, 概略值6370km上下各 上下各40km的范围内,即使 的范围内, 由此可见,在R概略值 概略值 上下各 的范围内 测距边高出于投影面1000m,仍能保证边长归化高达百万 测距边高出于投影面 , 分之一精度。在我国任何地方、 分之一精度。在我国任何地方、任何方位的椭球面的曲率 半径均在6370km±40km以内,都可以按圆球半径 以内, 半径均在 ± 以内 R=6370km归算测距边长。 归算测距边长。 归算测距边长
S dh = − dS h
若: S=2km, h=500m, 得: dh=4mm。
dS=1mm
可见,高差的准确求定对测距边的改平至为重要, 可见,高差的准确求定对测距边的改平至为重要,尤其是 在短边和高差较大的情况下。 在短边和高差较大的情况下。
【2019年整理】地面观测元素归算至椭球面

5.5.地面观测元素归算至椭球面
一、归算的意义和要求 二、水平观测方向归算至椭球面 三、观测天顶距的归算 四、地面观测长度归算至椭球面 五、天文经纬度与大地经纬度的关系 六、天文方位角与大地方位角的关系
二、水平观测方向归算至椭球面
Reduction of horizontal directional observations to the ellipsoid
2.大地线是一条曲面曲线 ,该曲线上任意一点的主 法线与曲面法线重合。
内容回顾
大地线
▪ 性质 1.大地线是椭球面上两点 间的最短线。
2.大地线是无数法截线弧 素的连线。
3.椭球面上的大地线是双 重弯曲的曲线。
4.大地线一般位于相对法 截线之间。
5.5.地面观测元素归算至椭球面
一、归算的意义和要求 二、水平观测方向归算至椭球面 三、观测天顶距的归算 四、地面观测长度归算至椭球面 五、天文经纬度与大地经纬度的关系 六、天文方位角与大地方位角的关系
二、水平观测方向归算至椭球面
Reduction of horizontal directional observations to the ellipsoid
1、垂线偏差改正(1)
[Z图形]P N
AR1A的方向值 弧长OR1
AR的方A向0 值
R1 弧长OR
M
R
m
R1 1 R
1 R1 R
A弧R1长bO R1 弧长OR
M
R
m
R1 1 R
1 R1 R
K a R1 1
R
Z A u
法
Z1
线
u
A
大地水平面
P
O1 O
S
大地测量学第四章 8将椭球面上的元素化算至高斯平面
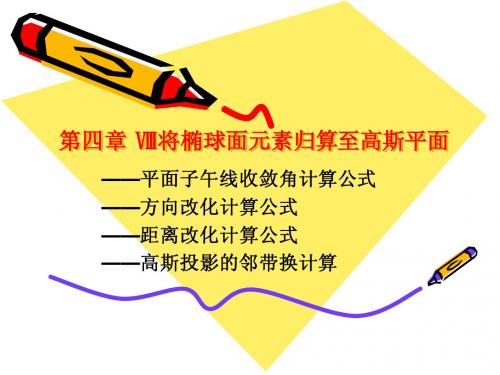
2、柯西.黎曼条件 柯西.
正形条件长度比m与方位角 无关 即满足: 正形条件长度比 与方位角A无关,即满足: F = 0 与方位角 无关,
∂x ∂y , = ∂q ∂l ∂x ∂y = − ∂l ∂q
E =G
上一讲应掌握的内容
3、什么是高斯投影坐标正、反算? 、什么是高斯投影坐标正、反算? 高斯投影坐标正 4、高斯投影必须满足以下三个条件 、高斯投影必须满足以下三个条件 (1)中央子午线投影后为直线,两侧的投影对称于中央子午线 中央子午线投影后为直线, 中央子午线投影后为直线 (2)中央子午线投影后长度不变 中央子午线投影后长度不变 中央子午线投影后长度不变 ∂y ∂x ∂x ∂y (3)投影具有正形性质,即正形投影条件 投影具有正形性质, 投影具有正形性质 , = = − ∂l ∂q ∂l ∂q 5、 5、高斯投影坐标正算推导思路 • 由第一个条件可知: 由第一个条件可知: x = m 0 + m 2l 2 + m 4l 4 + L
(2 + 5 t 2 + 3t 4 ) y 5 f f
B f 先 由 x计 算 出
二、方向改化计算公式
大地线描写形曲线与其弦线之间的夹角, (一)定义:大地线描写形曲线与其弦线之间的夹角, 叫方向改化。 曲改直” 叫方向改化。 “曲改直” 椭球面△网归算到平面上,所有的方向都必须加方向改化
(二)方向改化公式推导
1、方向改化近似公式的推导 、 在球面上四边形ABED的内角之和等于 °+ε 的内角之和等于360° 在球面上四边形 的内角之和等于 由于是等角投影, 由于是等角投影,所以这两个四边形内角之和应该 相等,即 相等,
3 6 0 0 + ε = 3 6 0 + δ ab + δ ba
大地测量学基础(将地面观测值归算至椭球面)
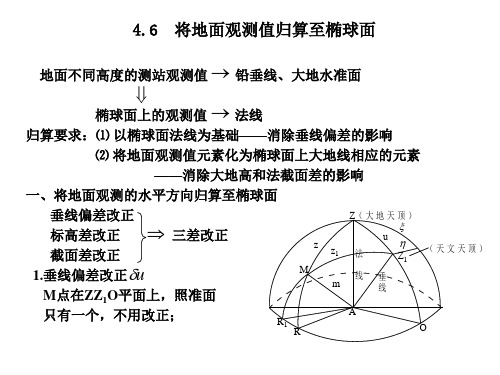
(3)任意投影
ab 1 ab
2. 按经纬网投影形状分类 方位投影;圆锥投影
3. 圆柱(椭圆柱)投影 正轴投影;斜轴投影;横轴投影
四、高斯投影 分带、以中央子午线为基准,横轴椭圆柱面等角投影 高斯—克吕格投影。
小结: (1)概念:长度比、主方向、变形椭圆、长度变形; (2)掌握:长度、方向、角度、面积变形的计算公式
目的:经过u,h , g 三差改正,地面的水平方向观测值 椭
A
球面上相应大地线的方向值。
D
说明:⑴ u h g
B C
⑵ 三差改正 意义(目的) 主要关系量
数值
一等 二等 三四等
垂线偏差 化为法线为基准 ,
的方向观测值
0.05 ~ 0.1 加 加 酌情
标高差 化为椭球面上法 截线的方向值
F1,F2就是“一定的数学法则 ”
二、地图投影的变形
1. 长度比 m lim P1' P2 ' P P P1P2 0 1 2
N X
P2
P1
p'2 p'1
m ds
O
dS
S
Y
一般情况下,长度比是一个变量,随点位、方向而变化。
2. 主方向和变形椭圆 主方向:投影后一点的长度比依方向不同而变化。其中最
(
dnA dS n
)
1
Sn n!
(
dA dS
)1
S
(
d2A dS 2
)1
S2 2!
(
d3A dS 2
)1
S3 3!
一阶导数推导大地线微分方程
dB dS
1 M
c os A
V3 c
c os A
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
ξ 《规范》规定,水平方 θ
Z
向归算时,各项改正要 Z
q 计算到: 线 M u
m
A
u
η
z1 法
1
P
一等 二等
0.001秒 0.01秒 0.1秒 O
O1
M
uθ η
Z1
P
ξ
q
m
z1 法
线
u
O1
什么情况下垂线 偏差改正为 0 ?
q 90 − z1
R1 −δ1 R
A
大地水平面
O
二、水平观测方向归算至椭球面
Reduction of horizontal directional observations to the ellipsoid
1、垂线偏差改正(δ1 )
A
大地水平面
O
二、水平观测方向归算至椭球面
Reduction of horizontal directional observations to the ellipsoid
1、垂线偏差改正(δ1 )
[量级]
δ 1 = −(ξ sin A − η cos A) cot z1 = −(ξ sin A − η cos A) tan α 1
二、水平观测方向归算至椭球面
Reduction of horizontal directional observations to the ellipsoid
将水平观测方向归算至椭球面,通常需要进行垂线偏差改正 、标高差改正和截面差改正,简称三差改正。
1、垂线偏差改正(δ1)
( Correction for deflection of the vertical ) [定义]地面上以铅垂线为准的水平方向观测值,归算为以椭球面 法线为准的水平方向值时,顾及测站点垂线偏差影响所加的改正。
为0情况: 1)照准点在椭球面上, ⇔ H 2 = 0, δ 2 = 0 2)照准点与观测点同经度或纬度, ⇔ A = 0 、 、 、 ,δ 2 = 0 90 180 270
θ
A A
A δ2 b′ 1 b S
H2
确定水平坐标的流程
水平方向 垂直角 地面距离 天文经纬度 天文方位角
已知坐标 (L,B) 水平方向 垂直角 地面距离 大地经纬度 大地方位角
已知坐标 (X,Y) 水平方向 垂直角 地面距离 平面方位角
布设水平 观测 地面上观 归算 椭球面上 归算 高斯平面 的元素 控制网 测元素 的元素
1、归算的意义
2、标高差改正(δ2 )
[公式推导] 因:
B
θ
A
N
′ A1 ≈ A1
视三角形 Abb′ 为球面三角形,由 正弦定理,可得:
A b′ N 1 δ 2 b N S ′ A A 1 b′
A 1
H2
sin δ 2 sin A1 = bb′ S
δ2
S
b
O
Ka
A
KB
δ2
″
sin A1 = bb′ ρ ′′ S
二、水平观测方向归算至椭球面
Z1
P
ξ
线
u
O1
=R
R +δ1 = R 1
⇔ −δ1 = R − R 1
A
Ka R1 −δ1
R
大地水平面
O
S
二、水平观测方向归算至椭球面
Reduction of horizontal directional observations to the ellipsoid
m 1、垂线偏差改正(δ1 )
Z P [图形]
Reduction of horizontal directional observations to the ellipsoid
2、标高差改正(δ2 )
B
[图形]
A A
θ
H2
N
b δ2 b ′
O
Ka
Kb
二、水平观测方向归算至椭球面
Reduction of horizontal directional observations to the ellipsoid
Reduction of horizontal directional observations to the ellipsoid
2、标高差改正(δ2 )
[公式推导] sin A1 ″ δ 2 = bb′ ρ ′′ S bb′ ≈ H 2θ
Ka R Ka R ≈ θ≈ N2 BR
B
θ
A A
A δ2 b′ 1 b S
q 90 − z1
R1 −δ1 R
A
三四等
大地水平面
二、水平观测方向归算至椭球面
Reduction of horizontal directional observations to the ellipsoid
1、垂线偏差改正(δ1 )
[实际计算说明]
Z
A
δ 1 = −(ξ sin A − η cos A) cot z1 = −(ξ sin A − η cos A) tan α 1
第九讲
地面观测元素归 算至椭球面
内容回顾
相对法截线
形成原因 椭球面上两点的法线不在 同一平面上。 位置规律 纬度高的点对纬度低的点 的法截线偏上,反之,则 偏下。 造成问题 造成椭球面上几何图形的 破裂。
LA < LB < LC,BA < BC < BB
内容回顾
大地线
定义 1.大地线是一条曲面曲线 ,该曲线上任意一点的相 邻两弧素,位于该点的同 一法截面中。 2.大地线是一条曲面曲线 ,该曲线上任意一点的主 法线与曲面法线重合。
二、水平观测方向归算至椭球面
Reduction of horizontal directional observations to the ellipsoid
1、垂线偏差改正(δ1 )
Z P [图形]
Z
A
法
N ARA 方 值= 弧 OR1 的 向 长 1
A0 AR的方向值= 弧长OR
= R1
M
m
uθ η
一、归算的意义和要求
Significance and request of reduction
一 维
高程控制网
H常
传统大地测量
点位三维坐标
二 维
水平控制网
(L,B)
一、归算的意义和要求
Significance and request of reduction
确定水平坐标的流程
布设水平 控制网
一、二等三角点中心标石埋设图
H2
N2
O
K a R = K a K b cos B2
K a K b = OK b − OK a = N 2 e 2 sin B2 − N1e 2 sin B1 ≈ N 2 e (sin B2 − sin B1 )
2
R 90 − B2
Ka
Kb
二、水平观测方向归算至椭球面
Reduction of horizontal directional observations to the ellipsoid
大地水平面
O
二、水平观测方向归算至椭球面
Reduction of horizontal directional observations to the ellipsoid
1、垂线偏差改正(δ1 )
[量级]
Z
A
δ 1 = −(ξ sin A − η cos A) cot z1 = −(ξ sin A − η cos A) tan α 1
O
R 90 − B
Ka
δ2
″
H 2e 2 ρ ′′ = sin 2 A1 cos 2 B2 2M 2
KB
二、水平观测方向归算至椭球面
Reduction of horizontal directional observations to the ellipsoid
2、标高差改正(δ2 )
[量级]
B
H 2e 2 ρ ′′ δ 2″ = sin 2 A1 cos 2 B2 2M 2
1、垂线偏差改正(δ1 )
[公式推导] 在球面三角形 MZZ1中,
Z
A
uθ η
Z1
P
ξ
sin ( A − θ ) sin q = sin u sin z1
在球面三角形 MRR1中,
q
M
m
z1 法
线
u
O1
sin( −δ1 ) = cos z1 sin q
合并得:
q 90 − z1
R1 −δ1 R
A
− 1 = ξ sin A − θ cos z1 δ 1δ= −(u sin( A − η ) cotA) cot z1 = ξ sin A cos cos cos A α = −(u (sin A − η θ − A) tansin θ ) cot z1 1
垂线偏差u
本节学习要求
理解并掌握各项改正的定义、 公式中各符号的含义、量级及 应用范围,部分公式要求画图 推导。
5.5.地面观测元素归算至椭球面 5.5.地面观测元素归算至椭球面
一、归算的意义和要求 二、水平观测方向归算至椭球面 三、观测天顶距的归算 四、地面观测长度归算至椭球面 五、天文经纬度与大地经纬度的关系 六、天文方位角与大地方位角的关系
内容回顾
大地线
性质 1.大地线是椭球面上两点 间的最短线。 2.大地线是无数法截线弧 素的连线。 3.椭球面上的大地线是双 重弯曲的曲线。 4.大地线一般位于相对法 截线之间。
