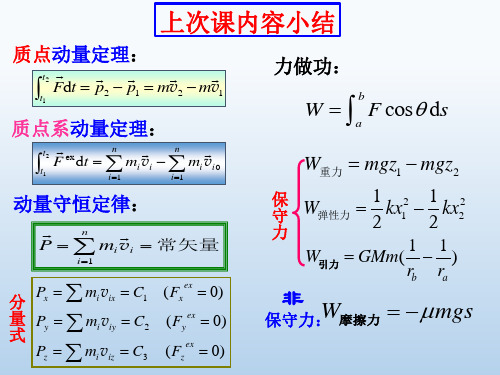
大学物理2-6动能定理
大学物理2-6碰撞

系统损失的机械能
1 m1m2 2 2 E (1 e ) (v10 v20 ) 2 m1 m2
例题2-18 在碰撞实验中,常用如图所示的仪器.A为一 小球,B为蹄状物,质量分别为m1和m2.开始时,将A 球从张角θ处落下,然后与静止的B物相碰撞,嵌入B 中一起运动,求两物到达最高处的张角φ. 解:(1)小球A从开始位置下落h, 而到最低位置,这是小球与蹄状物 B碰撞前的过程,此过程机械能守 恒.
§2-6
碰撞
特点:碰撞时间短 碰撞体间的作用力 >> 外力(外力可略) 正碰:碰撞前后的速度都沿着球心的联线(碰撞体 可作球体) 设 v10和v20分别表示两球在碰撞前的速度,v1和 v2 分别表示两球在碰撞后的速度, m1和 m2 分别为两球 的质量。
v10
v20
f1
v1
v2
m2
f2
质心
质心运动定理
动量守恒定律 动能定理 成对力的功 势能 机械能守恒定律
§2-5 质点系的功能原理
§2-6 碰撞
§2-7 质点的角动量和角动量守恒定律 §2-8 对称性和守恒定律
m1
碰撞前
m2
m1
m2
碰撞时
m1
应用动量守恒定律得
m1v10 m2v20 m1v1 m2v2
碰撞后
牛顿的碰撞定律:碰撞后两球的分离速 度 (v2 v1 ) ,与碰撞前两球的接近速度 (v10 v20 ) 成正 比,比值由两球的材料性质决定。
恢复系数
e 0,碰撞后两球以同一速度运动,并不分开,
(1 e)m1 (v10 v20 ) v2 v20 m1 m2
大学物理-动能定理

4. 势能曲线
Ep (h)
E
Eh
Ep
o
H H h
重力势能
Ep
E
o
Ek
Ep
3-4 动能定理
Ep (x)
AE
B
Ek
Ep
o
x
弹性势能
Ek 0
x
引力势能
26
势能曲线的作用:
3-4 动能定理
(1)根据势能曲线的形状可以讨论物体的运动。
(2)利用势能曲线,可以判断物体在各个位置 所受保守力的大小和方向。
力提供园周运动的向心力而不做功,摩擦力做负
功使滑块动能减少。
W
1 mv2 2
1 2
mv0
2
(1)
34
3-4 动能定理
v2 N m
(2)
R
N m dv
(3)
dt
将式(2)代入式(3),整理变形为
v2 dv dv d v dv R dt dt d R d
分离变量并积分,得
做功,它们所做元功之和为
dA fij dri f ji drj
因
fij f ji
mi
drji
dri
rij
rij drij
所以
fij
dA fij (dri drj ) fij drij
f ji m j drj
讨论:内力做功的特点
14
成对力的功
对它所作的功为零.
非保守力:力所作的功与路径有关. (例如摩擦力)
23
3. 势能
3-4 动能定理
大学物理功-动能定理-保守力的功

解: 抛体在重力场中运动,
m g 是一恒量,
y
但m 的轨迹是一抛物线, 取一元位移d r
dr b
a
m g 与位移的夹角θ时时在变 在这一元段内写出元功
mg
x
dA Fdrmgdr
m gdscosmgdy
b
b
b
A
Fdr
a
Fcosds mg
a
a
dy
m g(ybya) 9
解:(1)建坐标系如图
l-a O
fμ m(lg x)/l l l μmg
A f afdra l (lx)dx μm(g lx)2l μm(g la)2
a x
2l
a 2l
注意:摩擦力作负功! 21
(2)对链条应用动能定理:
l-x O
A= AP+ Af 1 2m2v 1 2m0 2v
x
v0
0AP+ Af
1m2v 2
x
A Pa lp d r a lm l x gd m x(l2 2 g l a 2 )
前已得出: Af
μm (gl a)2
2l
m(lg 2a2)μ m(lg a)21m2v
2l
2l
2
得 v
g l
1
(l2 a 2)μ (l a )22
13
3) A为合外力作功的代数和,不是合外力中某 一个力的功。动能定理中的速度必须相对同一 个惯性系。
4)通过作功,质点与外界进行能量交换。 如果 外力对物体做正功,质点动能增加; 如果 外力对物体做负功,质点的动能减少,
即物体克服外力作功,是以减少自身的动能为 代价。
所以,动能是物体因运动而具有的作功的本领。
动能定理教案大学物理

一、教学目标1. 知识与技能:(1)理解动能的概念,掌握动能的表达式和计算方法。
(2)掌握动能定理的表述和推导过程,能够运用动能定理分析实际问题。
(3)了解动能定理在物理学中的应用,如运动学、动力学等领域。
2. 过程与方法:(1)通过实验探究,体会动能定理的物理意义。
(2)运用数学工具,推导动能定理的表达式。
(3)通过实例分析,提高学生运用动能定理解决实际问题的能力。
3. 情感态度与价值观:(1)培养学生对物理学的兴趣,激发学生的求知欲。
(2)培养学生严谨的学术态度,提高学生的科学素养。
(3)引导学生关注物理现象,培养发现问题、分析问题和解决问题的能力。
二、教学重点与难点1. 教学重点:(1)动能定理的表述和推导过程。
(2)动能定理的应用。
2. 教学难点:(1)动能定理的推导过程。
(2)动能定理在复杂问题中的应用。
三、教学过程1. 导入新课(1)回顾动能的概念和计算方法。
(2)提出问题:如何解释物体在受到外力作用下动能的变化?2. 动能定理的推导(1)回顾功的定义和计算方法。
(2)通过实验探究,验证功与动能变化的关系。
(3)运用数学工具,推导动能定理的表达式。
3. 动能定理的应用(1)分析动能定理在运动学中的应用,如速度、加速度、位移等。
(2)分析动能定理在动力学中的应用,如牛顿第二定律、能量守恒定律等。
(3)通过实例分析,提高学生运用动能定理解决实际问题的能力。
4. 课堂小结(1)总结动能定理的表述和推导过程。
(2)强调动能定理在物理学中的应用。
(3)布置课后作业,巩固所学知识。
5. 课后作业(1)完成课后习题,巩固动能定理的基本概念和推导过程。
(2)分析实际问题,运用动能定理解决问题。
四、教学反思1. 教学过程中,注重启发学生思考,引导学生主动探究。
2. 运用多种教学方法,如实验探究、实例分析等,提高学生的学习兴趣。
3. 注重培养学生运用动能定理解决实际问题的能力,提高学生的综合素质。
4. 课后及时反思,总结教学经验,不断改进教学方法。
大学物理教案_动能定理

课时:2课时教学目标:1. 理解动能定理的概念,掌握其表达式和物理意义。
2. 能够运用动能定理解决实际问题,分析物体运动状态。
3. 培养学生逻辑思维能力和分析问题的能力。
教学重点:1. 动能定理的概念和表达式。
2. 动能定理的应用。
教学难点:1. 动能定理的理解和应用。
2. 复杂问题中动能定理的应用。
教学过程:一、导入1. 回顾牛顿第二定律和功的定义,引出动能定理。
2. 提问:动能定理与牛顿第二定律和功有何关系?二、新课讲授1. 动能定理的概念:物体动能的变化等于物体所受合外力所做的功。
2. 动能定理的表达式:ΔE_k = W3. 动能定理的物理意义:动能定理揭示了物体运动状态与外力做功之间的关系。
4. 动能定理的应用:a. 计算物体在一段时间内的动能变化。
b. 确定物体运动状态。
c. 分析物体受力情况。
三、例题分析1. 例题1:一个质量为m的物体,从高度h自由落下,求落地时的速度。
2. 例题2:一辆质量为m的汽车,从静止开始加速,在时间t内通过距离s,求汽车所受合外力。
3. 例题3:一个物体在水平面上做匀速直线运动,求物体所受合外力。
四、课堂练习1. 练习1:一个质量为m的物体,从高度h自由落下,求落地时的动能。
2. 练习2:一辆质量为m的汽车,从静止开始加速,在时间t内通过距离s,求汽车所受合外力。
3. 练习3:一个物体在水平面上做匀速直线运动,求物体所受合外力。
五、总结1. 总结动能定理的概念、表达式和物理意义。
2. 强调动能定理的应用。
教学反思:1. 本节课通过引入牛顿第二定律和功的概念,引出动能定理,使学生更容易理解动能定理的物理意义。
2. 通过例题分析和课堂练习,使学生掌握动能定理的应用,提高学生的实际操作能力。
3. 在教学过程中,注重培养学生的逻辑思维能力和分析问题的能力,使学生能够灵活运用动能定理解决实际问题。
大学物理第二章动能定理
例题3. 如图,一轻绳跨过一定滑轮,两边分别拴有质量
为m及M的物体,M离地面的高度为h: (1)若滑轮质量及
摩擦力不计,m与桌面的摩擦也不计,开始时两物体均静
止,求M落到地面时的速度(m始终在桌面上); (2)若m与
桌面的静摩擦系数和滑动摩擦系数均为,结果又如何?
解:
m
(1)不计摩擦,系统(m,M,地球)机械能守恒:
v
m
0 M f c
f
s
s
Wf Wf 0
N
v c
N
WN WN 0
质点系动能定理:
质点系的动能的增量等于作用于质点系的一切外力与
内力做功之和.
W ex
W in
n i1
1 2
mi vi2
n i1
1 2
mi vi20
2.2.1 质点系动量定理
作用于质点系的合外力的冲量等于质点系动量的增量.
t2
系统内所有质点对同一参考点角动量的矢量和称为
质点系的角动量.
L Li ri pi ri mivi
i
i
i
dL dt
d dt
Li
i
Mi外
i
Mi内
i
0
M外
M 外
dL dt
积分得:
t2 t1
M外dt
L2
L1
注意:只有外力矩对质点系的角动量变化有贡献,
内力矩对质点系的角动量变化没有贡献.
W
F dr
l
F dr
acb
F dr
bda
0
a
c
F dr F dr F dr
acb
adb
bda
d
动能定理角动量定理

注意 1)守恒条件: M 0
能否为 Mdt 0 ?
2)与动量守恒定律对比:
当
F 0
时,
当
M
0
时,
p
恒矢量
L 恒矢量
彼此独立
《大学物理C》
第三章 刚体定轴转动
角动量守恒定律适用于以下情况:
(1)对于单一刚体:J、 均不变, 则匀速转动
(2) 对于系统: Ji、 均可以变化,但
角动量守恒
角动量守恒;
角动量守恒;
机械能不守恒 .
机械能不守恒 .
圆锥摆系统 动量不守恒; 角动量守恒; 机械能守恒 .
《大学物理C》
第三章 刚体定轴转动
注意:区分两类冲击摆
角动量守恒
(1)
O
l v0
m M
质点
质点 柔绳无切向力
➢水平方向: Fx = 0 , px 守恒
mv0 = (m+M)v
➢ 对 O点:
解 碰撞前 M 落在
A点的速度
vM (2gh)1 2
碰撞后的瞬间, M、
N具有相同的线速度
N
u l
B
2
M
h
C
A
l/2 l
《大学物理C》
第三章 刚体定轴转动
角动量守恒
vM (2gh)1 2
u l
2
N
C
M h
A
B
l/2
l
解得
mvM
l 2
J
2mu
l 2
1 12
ml 2
1 2
ml 2
mvMl 2 ml 2 12 ml2
6m(2gh)1 2 2 (m 6m)l
演员 N 以 u 起 跳, 达到的高度
大学物理能量及能量守恒定律

物体在场中某点的势能等于将物体从该点移到 零势点过程中保守力做的功。
3)保守力为其相关势能梯度的负值:
F
d A F d l Fldl d E p
m
θ
dl
l
Fl
dE p Fl dl
保守力在 l 方向投影
F 保 grad E p E p
v0 m
mv
2 0
4 J
x (m)
1
4
7 9
E 守恒,当 Ek=0时
E
p
max
E 0 4J
E p 4J
作曲线
2)要
F
知运动范围
dE p dx 0
x 1
dE p dx
0
势能曲线斜率为负:
1 x 4,
x 9
3) x = 4m 处,势能最小
ml
2
2
所以棒撞击地板时的角速度是
;
3g l
练习3.
如图所示, 已知: M , l , m , , v0 ;击中
求:击中时 ; max ? o
3 4
3 4
l处
(只列方程)
分两个阶段求解,各遵循什么规律? 1)相撞: 质点
l
M
v0
定轴刚体
c
对 O 轴角动量守恒
1 4
i
A
i
i内
0
2.变力的功
dr
微元分析法:
ds
P
b
F r
取微元过程
P
r
以直代曲
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
ab Fτ
ds
ab maτ
ds
b
a
m
d d
v t
d
s
vb va
mv d v
1 2
m vb2
1 2
m va2
定义质点的动能为:Ek
1 mv2 2
动能定理
质点动能定理:合外力对质点所做的功等于质点 动能的增量。
Aab Ekb Eka Ek
几点注意: a.合力做正功时,质点动能增大;反之,质
点动能减小。
b.动能的量值与参考系有关。
c.动能定理只适用于惯性系。 d.功是一个过程量,而动能是一个状态量。
动能定理
(3)质点系动能定理
多个质点组成的质点系,既要考虑外力,又要 考虑质点间的相互作用力(内力)。
二质点组成的 系统
推 广
多个质点组成 的系统
两个质点在外力及内
力作F用1下如图所示F:2
m1
f1 2
下从a运动到b。
b
a
怎样计算这个力
的功呢?
采用微元分割法
动能定理
第1段近似功: A1 F1 r1
第2段近似功: A2 F2
r2
Δ
r3
Δ
r4
Δ r2
F4
Δ r1
F3
a
F2
F1
Δ ri
b Fi
第i 段近似功:
Δ Ai Fi • ri
总功近似:
Aab Δ Ai Fi • ri
i
i
F
N
F
300
(a)
100
fr
(b)
G
动能定理
解: 木箱所受的力为:拉力F ,方向与斜面成100 角向上;重力G ,方向竖直向下;斜面对木箱的支 持力N ,方向垂直于斜面向上,斜面对木箱的摩擦 力 fr 方向和斜面平行,与木箱运动方向相反, 如图 (b).已知l=3m,每个力所作的功可计算如下。
(1)拉力F 所做的功A1
动能定理
用d当A 表ri示,称0 为时元,可功用。d r表示,称为元位移; Ai
元功: d A F d r
总功:
Aab
lim
r 0
i
Fi ri
b F dr
a
在数学形式上,力的功等于力F 沿路径L
从a到b的线积分。
动能定理
(2)质点动能定理
根据功的积分形式
Aab
ab
F
d r
(3)如改用起重机把木箱吊上汽车,这时所用拉力
F 的大小至少要等于重力 G 。在这个拉力 F
的作用下,木箱移动的竖直距离是 l sin 30o 。因此
拉力所作的最小功为
A Fl sin 30 980 3 0.5J 1.47103 J
动能定理
它等于重力 所作的功,而符号相反。与(1) 中 F 作的功相比较,用了起重机能够少作功。为了 把木箱装上汽车,我们所需要做的最小功等于克服 重力所作的功,其大小为1.47×103J, 这对于斜面或 是利用起重机甚至其他机械都是一样的。机械不能 省功,但能省力。在(1)中拉力 F 多作的功
功率P:力d在A单位F时 间 d内r做的F功,v用P 表示
dt dt
功率是反映力做功快慢的物理量。
在国际单位制中,功的单位是N•m,叫做焦(J), 功率的单位是J/s ,叫做W(瓦)。
动能定理
2. 能量
能量是反映各种运动形式共性的物理量,各种运 动形式的相互转化用能量来量度。各种运动形式的 相互转化遵循能量的转换和守恒定律。
f21
m2
动能定理
对m1运用质点动能定理:
b1 a1
F1
dr1
b1 a1
f12 dr1
1 2
m1v12b
1 2
m1v12a
对m2运用质点动能定理:
b
2
a2
F2
d
r2
b2
a2
f21d r2
1 2
m2v22b
1 2
m2v22a
F1Biblioteka 2m1f1 2f21
m2
动能定理
作为系统考虑时,得到:
A1 Fl cos10 700 3 0.985J 2.07 103 J
重力 G 所做的功A2
A2 Gl sin30 98030.5J -1.47103 J
动能定理
正压力 N 所做的功A3
A3 Nl cos 90 0 摩擦力 f r 所作的功A4;分析木箱的受力,由
于木箱在垂直于斜面方向上没有运动,根据牛顿第 二定律得
动能定理
例题2-10 装有货物的木箱,重G=980N,要把它 运上汽车。现将长l=3m的木板搁在汽车后部,构成一
斜面,然后把木箱沿斜面拉上汽车。斜面与地面成30o
角,木箱与斜面间的滑动摩擦系数=0.20,绳的拉力
与 斜 面 成 10o 角 , 大 小 为 700N , 如 图 (a) 所 示 。 求:(1)木箱所受各力所作的功;(2)合外力对木箱 所作的功;(3)如改用起重机把木箱直接吊上汽车能 不能少做些功?
§2-6 动能定理
1. 功的概念
功是表示力对空间累积效应的物理量。
功是能量变 化的量度。 物体在力 的F作用下发生一无限小的位移
dr
(元位移)时,d此A力对(它F做co的s功 )定d义r为
其中为力与位移的夹角。可以把上式写成两个
矢量的标积
dA F dr
功是标量,没有方向,但有正负。
动能定理
当0</2时,dA>0,力对物体做正功。 当=/2时, dA=0,力对物体不做功。 当/2<时,dA<0,力对物体做负功。
2.07 103 J 1.47 103 J 0.60 103 J
起的是什么作用呢?我们说:第一,为了克服摩擦 力,用去435J的功,它最后转变成热量;第二,余 下的165J的功将使木箱的动能增加。
动能定理
b1
a1
F d
1
r
1
b
2
a2
F 2
d
r 2
b1
a1
f12
d
r1
b2
a2
f 21d r2
1 2
m1v12b
1 2
m2v22b
1 2
m1v12a
1 2
m2v22a
A外 A内 Ekb Eka Ek
质点系动能定理:所有外力与所有内力对质点系 做功之和等于质点系总动能的增量。
推广:上述结论适用多个质点。
N F sin10 G cos 30 0 N=G cos 30-F sin10 727N
由此可求得摩擦力
fr N 0.20 727N 145N
A4=frl cos180 145 3J 435J
动能定理
(2)根据合力所作功等于各分力功的代数和,算 出合力所作的功
A A1 A2 A3 A4 165J
只有在能量的转换和守恒定律发现以后,人们才 认识功、动能和势能的真实含义。二十世纪初,爱 因斯坦建立了狭义相对论,得到了“质能关系”, 进一步揭示能量和质量的相当性,对于能量的认识 更深入了一步。
与机械运动对应的的能量是机械能。
动能定理
3. 牛顿第二定律的又一积分形式
(1)变力的功
物体在变力的作用
