电磁场边界条件
电磁场的边界条件

将⑧代入⑨,得: sin 2 cos 1 sin 1 cos 2 sin(1 2 ) rs sin 2 cos 1 sin 1 cos 2 sin(1 2 )
2n1 cos 1 ts n1 cos 1 n2 cos 2
对绝大多数物质, 1 2
所以得到方程:
E1 y z E1' y z E2 y z
z 0
⑥
代入边界条件,可得:
k1 cos 1 A1s k1' cos 1' A1' s k2 cos 2 A2 s
k1 k1' 整理得: cos 1 A1s cos 1' A1' s cos 2 A2 s k2 k2' k1 sin 2 将 代入上式,得: k2 sin 1
AB BC CD DA
针对麦克斯韦 方程组积分形 式的第三个与 第四个方程, 建立如左图模 型,积分可得
E2t CD ( E2 n DF E1n FA) 0
E1t E2t 同理可得 H1t =H 2t
电磁场边界条件
(1)电场强度E 在分界面上的平行分量连续。
从右图可以看出, 对于s光:
Ex 0 E y ES Ez 0
根据几何关系,可知:
k x k sin 1 , k y 0, k z k cos 1
对于单色平面光波: E0 e E
i[t ( k x x k y y k z z )]
将上面的结论带 i[1t ( k sin 1 x k cos1 z )] E E0 e 入方程可得: 对于s光,可以分解为:
i ( k2 sin 2 x )
电磁场的边界条件

媒质2
§8
2.7.1 边界条件一般表达式 D ) dS C H dl S ( J en ( H 1 H 2 ) J S t B en ( E1 E 2 ) 0 dS C E dl S t e n (B1 B 2 ) 0 S B dS 0 en (D1 D 2 ) S S D dS V ρdV en 分界面上的电荷面密度
媒质1 媒质2 分界面上的电流面密度
§8
边界条件的推证 (1) 电磁场量的法向边界条件
媒质 1 媒质 2
en
ΔS
D1
Δh
在两种媒质的交界面上任取一
点P,作一个包围点P 的扁平圆柱 曲面S,如图表示。 令Δ h →0,则由
S
P
D2
即 同理 ,由
S
D dS ρdV
V
(D1 D2 ) en S S S
d
x
π ez sin( z ) cos(t k x x ) (A/m) 0 d k x E0
(2) z = 0 处导体表面的电流密度为
J S ez H
z 0
πE0 ey sin(t k x x) 0 d
(A/m)
z = d 处导体表面的电流密度为
J S (ez ) H
4 30
107 cos(15 108 t ) A/m
可见,在 z = 0 处,磁场强度的切向分量是连续的,因为在分界面 上(z = 0)不存在面电流。
§8
例 2.7.2 如图所示,1区的媒质参数为1 5 0、1 0、 1 0, 2区的媒质参数为 2 0、2 0、 2 0。若已知自由空间的电 场强度为 E2 ex 2 y ey 5z ez (3 z ) V/m
《电磁场理论》5.6 磁介质分界面上的边界条件

J ms | a M 2 (e ) 0 I ]e z J ms | b M 2 e [( 1) 0 2 b
在垂直于z轴平面内的磁化电流为
Im
S
Jm dS
2 b
J ms dl (
1) I ( 1) I 0 0 0
B
B
0
B
I
0 I B e ( 0 )
0 I H e (0 ) B I H0 e 0 (0 )
13
(2)磁介质中的磁化强度为 ( 0 ) I M ( 1) H e 0 ( 0 ) 则磁化电流密度为 1 d 1 d ( 0 ) I ( M )e z [ ]e z 0 J m M d d ( 0 ) 在磁介质的表面上,当 0时,磁化电流面密度为
8
求磁化电流:
( 1 0 ) I 介质磁化强度为: M e H 20 0
B
体磁化电流为:
e
e
ez
J m M M rM
面磁化电流为:
0 z Mz
J sm
( 1 0 ) I ( 1 0 ) I e e ez M n 20 20
l
H 1 dl H 2 2 I
H1 I 2 e
I b
O a
3
2
1
0 I B1 H 1 e 2
11
0 a时 (3 )
H
l
3
dl H 3 2 0
H3 0
I b
3.5 电磁场的边界条件(一)

E1t E1 E1n
( 7 aˆ 124 aˆ 95 aˆ ) 50 x 50 y 50 z
根据边界条件: E1t E2t
D1n D2n 0
30E1n 0 E2n
E2 n
( 279 50
aˆ x
372 50
aˆ y
465 50
aˆz )
得: E2 E2t E2n 5.72aˆx 4.96aˆy 11.2aˆz
A B
故: 1 S 2 S
该式表明:在两种媒质分界面处, 标量电位是连续的。
因为:E
D1n D2n S
2
2
n
S
1
1
n
S
S
在理想导体表面上:
S
C
(常数)
例1: 试求两个平行板电容器的电场强度。
解:忽略边缘效应 图(a) 电场方向与分界面垂直
3.5 电磁场的边界条件(一)
1. 电场法向分量的边界条件 2. 电场切向分量的边界条件 3. 标量电位的边界条件
决定分界面两侧电磁场变化关系的方程称为边界条件。
1. 电场法向分量的边界条件
如图所示,在柱形闭合面上应 用电场的高斯定律
S D dS nˆ1D1S nˆ2D2S S S
小结:
1. 电场法向分量的边界条件 D1n D2n S
2. 电场切向分量的边界条件 E1t E2t
3. 标量电位的边界条件
1 S 2 S
合回路abcd ,在此回路上应用法拉第电磁
感应定律
l
E
dl
S
B t
dS
因为: l E dl E1t l E2tl
B dS B lh 0
S t
电磁场的边界条件与电磁波的辐射和传播

电磁场的边界条件与电磁波的辐射和传播[摘要]:本文结合相关示意图简要总结了电磁场的边界条件,在参考大量相关文献的基础上,由边界条件出发分析了交变电磁场传播的原理,联系实际解释了电磁场的辐射和传播。
关键字:电磁场;电磁波;边界条件;辐射;传播。
一、电磁场的边界条件电磁场在两种不同媒质分界面上,从一侧过渡到另一侧时,场矢量E、D、B、H一般都有一个跃变。
电磁场的边界条件就是指场矢量的这种跃变所遵从的条件,也就是两侧切向分量之间以及法向分量之间的关系。
电磁场的边界条件可以由麦克斯韦方程组的积分形式推出,它实际上是积分形式的极限结果。
这些边界条件是:n·(D1-D2)=ρs; (1)n×(E1-E2)=0; (2)n·(B1-B2)=0; (3)n×(H1-H2)=J)s。
(4)式中n为两媒质分界面法线方向的单位矢量,场矢量E、D、B、H的下标1或2分别表示在媒质1或2内紧靠分界面的场矢量,ρ为分界面上的自由电荷面密度,J为分界面上的传导电流面密度。
式(1)表示在分界面两侧电位移矢量D的法向分量的差等于分界面上的自由电荷面密度。
当分界面上无自由电荷时,两侧电位移矢量的法向分量相等,即其法向分量是连续的。
式(2)表示在分界面两侧电场强度E的切向分量是连续的。
式(3)表示在分界面两侧磁通密度B的法向分量是连续的。
式(4)表示在分界面两侧磁场强度H的切向分量的差等于分界面上的表面传导电流面密度。
当分界面上无表面传导电流时,两侧磁场强度的切向分量相等,即其切向分量是连续的。
当媒质2为理想导体时,E2、D2、B2、H2等于零,式(1)表示D1的法向分量等于自由电荷面密度;式(2)表示E1无切向分量.式(3)表示B1的法向分量为零;式(4)表示H1的切向分量等于表面传导电流面密度,并且与电流方向正交。
二、电磁波的辐射和传播电磁波的产生与发射是通过天线来实现的。
由振荡电路产生的强大交变讯号通过互感耦合到天线上,天线就有交变电流产生,如下图所示。
电磁场电磁场的媒质边界条件

ars
nr S S
环路围面法向
3 电场强度的关系
rr r nnErrr 2EElrrr 22aErrnrs1
rr
l 0,l
nr r
r E1
r as
nr
r as
0
rE1 0
n E2 n E1 0 E2t E1t
两种媒质界面处电场强度的切向分量相等 (无条件连续)
4 电通密度的关系
以理想导体为边界的区域中,空间电磁场 可以看成是源电荷、电流激发场与导体表面 感应电荷,电流激发场(散射场)的叠加。 在一定条件下,散射场可以等效为位于导体 区域内等效像电荷、电流激发的场,等效像 电荷、电流的分布决定于导体的边界条件。 这种通过寻找像电荷电流求解空间区域电磁 场分布的方法称为镜像法。
l r
Hr2
H1 l
r as
r
nr
Jrl ,
rH1
l
r
ars
as
r Jl
n
r as
n H2 n H1 Jl
H2t H1t J l
在两种媒质界面处,磁场强度的切向分量是 有条件连续的。
4 磁通密度的关系
nr
rr B2 B1
0 Bn2 Bn1 0
在两种媒质的界面处,磁通密度矢量的法向分量 无条件连续。
T? ? 1 f
3 理想导体内部的电磁场
• 理想导体内部不存在电场,只要电场不为 零,在电场的作用下就会有自由电荷分布, 另外导体内的电流密度会成为无穷大,这是 不符合物理的。
• 由麦克斯韦第二方程可得理想导体中的时变 磁场也必为零。
r E
0,
r B
0,
r
Bt
r B
时变电磁场的边界条件

时变电磁场的边界条件
1、在任何边界上电场强度的切向分量是连续的(条件:磁感应强度的变化率有限)
2、在任何边界上,磁感应强度的法向分量是连续的
3、电通密度的法向分量边界条件与媒质特性有关。
两种理想介质形成的边界上,电通密度的法向分量是连续的
4、磁场强度的切线分量边界条件也与媒质特性有关。
在一般边界上,磁场强度的切向分量是连续的(条件:电通密度的时间变化率有限)。
但在理想导电体表面上可以形成表面电流,此时磁场强度的切向分量是不连续的
5、理想导体内部不可能存在电场,否则将会导致无限大的电流;理想导体内部也不可能存在时变磁场,否则这种时变磁场在理想导体内部会产生时变电场。
在理想导体内部也不可能存在时变的传导电流,否则这种时变的传导电流在理想导体内部会产生时变磁场。
所以,在理想导电体内部不可能存在时变电磁场及时变的传导电流,它们只可能分布在理想导电体的表面。
6、在任何边界上,电场强度的切向分量及磁感应强度的法向分量是连续的,因此理想导体表面上不可能存在电场切向分量及磁场法向分量,只可能存在法向电场及切向磁场,也就是说,时变电场必须垂直于理想导电体的表面,而时变磁场必须与其表面相切。
7、无源区中的正弦电磁场被其边界上的电场切向分量或磁场切向分量唯一地确定。
电磁场的边界条件

2.7 电磁场的边界条件
第二章 电磁场的基本规律
二、理想导体表面上的边界条件
理想导体 E、D、B、H=0
n×H1=JS n×E1=0 n•B1=0 n•D1=ρS
n×(H1-H2)=JS n×(E1-E2)=0 n•(B1-B2)=0 n•(D1-D2)=ρS
2.7 电磁场的边界条件
第二章 电磁场的基本规律
一、边界条件的一般形式
磁场强度H的边界条件 1 2
H C
dl H1
l H2
l JS
N l
l (N n)l
n H1 h
H2 Δl
n×(H1-H2)=JS
2.7 电磁场的边界条件
第二章 电磁场的基本规律
电场强度E的边界条件
n×(E1-E2)=0
磁感应强度B的边界条件
S B dS B1nS B2nS 0 1
n
B1
ΔS h
n•(B1-B2)=0
2
B2
2.7 电磁场的边界条件
第二章 电磁场的基本规律
电位移矢分界面两侧,电场强度的切向分 量和磁感应强度的法向分量总是连续的;若分 界面上不存在面电流和面电荷,则磁场强度的 切向分量和电位移矢量的法向分量是连续的
电磁场的边界条件

也可以表示为标量形式:
可见, 的切向分量在不同的媒质分界面上不连续, H 与分界面上的传导电流面密度有关。
②、E 的边界条件
en
(E1 E2 ) 0 E E 1t 2t
结论: E 切向连续。
③ D 的边界条件
1
dv
n
D2
D1 h 0
D dS
s
2
电磁场的边界条件
1 什么是边界条件?
2 为什么要研究边界条件? 3 如何讨论边界条件?
在两种不同媒质的分界面上,场矢量E, D, B, H
各自满足的关系,称为电磁场的边界条件。
在实际的电磁场问题中,总会遇到两种不
同媒质的分界面(例如:空气与玻璃的分界面、 导体与空气的分界面等),边界条件在处理电 磁场问题中占据着十分重要的地位。
或
B 1n B 2n D 1n D 2n
2.理想导体与介质的分界面,电导率 , 假设I为介质,II为理想导体。 此时
E 2 0 , B 2 0, D 2 0, H 2 0
en en en en
H1 Js E1 0 B1 0 D 1 ρ s
dS )
由于
D t
有限,故 lim S
h 0
D t
dS 0
而 lim
h 0
J dS
s
h 0
lim
(J S )
h 0
lim
( J e p l h ) J s e p l
en ( H 1
H2) Js
H 1t H 2t J s
数
, ,
电磁场边界条件分析
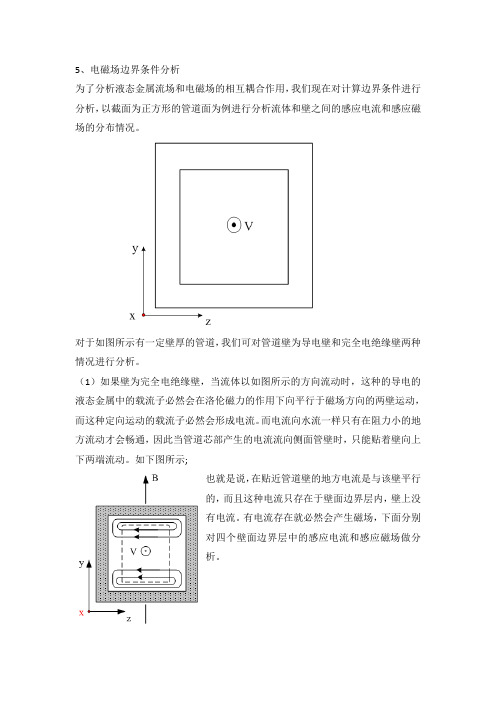
5、电磁场边界条件分析为了分析液态金属流场和电磁场的相互耦合作用,我们现在对计算边界条件进行分析,以截面为正方形的管道面为例进行分析流体和壁之间的感应电流和感应磁场的分布情况。
对于如图所示有一定壁厚的管道,我们可对管道壁为导电壁和完全电绝缘壁两种情况进行分析。
(1)如果壁为完全电绝缘壁,当流体以如图所示的方向流动时,这种的导电的液态金属中的载流子必然会在洛伦磁力的作用下向平行于磁场方向的两壁运动,而这种定向运动的载流子必然会形成电流。
而电流向水流一样只有在阻力小的地方流动才会畅通,因此当管道芯部产生的电流流向侧面管壁时,只能贴着壁向上下两端流动。
如下图所示;也就是说,在贴近管道壁的地方电流是与该壁平行的,而且这种电流只存在于壁面边界层内,壁上没有电流。
有电流存在就必然会产生磁场,下面分别对四个壁面边界层中的感应电流和感应磁场做分析。
侧面有J y≠0 该感应电流会产生感应磁场,根据右手螺旋定则贴近壁处的感应磁场应该是有两个方向。
对于管道的上半部,感应磁场方向与速度方向相同,管道下半部,感应磁场方向与速度方向相反。
也就是说在侧面壁上感应磁场有:bx≠0,by=0,bz≠0。
但是这里只考虑的是管道的一面截面,而管道应该是这样的很多个截面沿着x轴方向的组合,因此整体考虑的话,bz=0。
J z=0J x=0上下壁面有Jz≠0 分析同上,可知上下壁面的感应磁场为:bz≠0,bx=0,by=0Jx=0Jy=0(2)如果壁时导电的,当芯部流体产生的感应电流流经侧面面壁时必然会通过该壁,从而在管道壁中也有感应电流存在。
如下图所示:侧面壁有Jz≠0 导电壁不像完全电绝缘壁那样,在该侧面边界层内不存在平行于壁的电流,只存在与垂直于壁的电流。
分析可知bx≠0,by=0,bz=0且侧面上半部和下半部的感应磁场方向相反。
Jy=0 Jx=0上下壁面有,对于壁的电导率比流体的电导率高的情况,就相当于壁是良导体,因此芯部产生的感应电流不会存在于壁面边界层中,而只能在管道壁中。
第3讲 电磁场的边界条件

tan1 H1t / H1n 1 / B1n 1 tan2 H2t / H2n 2 / B2n 2
第三讲 电磁场的边界条件
【例1】 电介质透镜可以用来使电场平直化。如 图所示电介质透镜左侧表面为圆柱面,右侧表面 为平面。若区域1中点P(r,45°,z)处电场为
E1 e 5 e 3 为了使区域3中的电场 E3 与x轴平行,则透镜电介
• 场矢量的折射关系
tan1 E1t / E1n 1 / D1n 1 tan2 E2t / E2n 2 / D2n 2
en E1 0
en D1 S
第三讲 电磁场的边界条件
三、几种常见边界条件
2、恒定电场的边界条件
场矢量的边界条件
S J dS 0 C E dl 0
第三讲 电磁场的边界条件
三、几种常见边界条件
1、静电场的边界条件
• 一般形式
en (E1 E2 ) 0
en (D1 D2 ) S
• 两种电介质分界面
媒质1
en 1
E1
1
媒质2 E2
2
2
en (E1 E2 ) 0
• 导体与电介质分界面
en (D1 D2 ) 0
质相对介电常数应为多少?
【解】由边界条件,若 E3 平行于x轴,则E2也必平行于x轴。 在左侧圆柱面分界面上,由电场边界条件:
E1t E2t E1 E2 E2 3
D1n D2n 1E1 2 E2 E2
要使合成波E2 平行于x轴,则必有
5
r2
第三讲 电磁场的边界条件
三、几种常见边界条件
3、恒定磁场的边界条件
2-7 电磁场的边界条件

ห้องสมุดไป่ตู้
解: ⑴ 电介质分界面,分界面上 E 的切向分量连续,z 0 处
E1 (0, t ) ex [60cos(15108 t ) 20cos(15108 t )]V / m ex 80cos(15108 t )V / m
E2 (0, t ) ex Acos(15108 t ) V / m
2.7
电磁场的边界条件
求解由不同媒质所构成的各区域中的电磁场问题。
电磁场矢量 E、 D、 H、 B 在不同媒质分界面上各自满足的关系,称为
电磁场的边界条件。
1. 磁场强度 H 的边界条件
在媒质分界面上,包围P点作一矩形回路l 。 令 l2 0,根据麦氏第一方程 D 1 1 1 2 2 2 l H dl SJ dS S t dS H dl ( H1 H 2 ) e dl H dl 0 ep l l2 l1 en D lim dS 0 lim J dS J e p dl e S h 0 t S l1 h 0
顶面
D1 en dS
D2 en dS S dS
S
可得 en ( D1 D2 ) S
D1n D2n S
D 的法向分量不连续。
当 S 0 时,
en ( D1 D2 ) 0
D1n D2n 0
磁场矢量穿过不存在面电流的分界面时,方向发生变化与磁介质
参数的关系。
总结:电磁场的边界条件 ①在两种媒质分界面上,如果存在面电流,使 H 的切向分量不连续, 其不连续量由 en ( H1 H 2 )确定。若分界面上不存在面电流,则 JS 的切向分量是连续的。 H
电磁场边界条件

解:(1)磁场强度
r
Q
r E
0
H t
ex
E y z
ez
Ey x
0
H t
可求得
r
H t
E0
0
r [ex
d
cos(
d
z)
cos(t
kx)
r ez
k
sin(
d
z)sin(t kx)]
r H
r ex
0d
E0
cos(
d
z) sin(t
r kx) ez
k
0
E0
sin(
d
z) cos(t
kx)
2)两导体表面的面电流密度
D2 )
0
s
相应的标量形式为
H1t H2t B1n B2n
E1t E2t D1n D2n
2.7.2 两种特殊情况的边界条件
1、理想导体表面上的边界条件
理想导体是指σ→∞,所以在理想导体内部不存在电场
。此外,理想导体内部也不存在磁场。理想导体内部不存 在电磁场,即所有场量为零。设 e是n 理想导体的外法向矢
θ1=1.09°,B1 / B2=0.052。由此可见,铁磁材料内部的磁感应强 度远大于外部的磁感应强度,同时外部的磁感应线几乎与铁磁 材料表面垂直。
例1、在两导体平板(z=0和z=d)之间的空气中传播的
电磁波,已知其电场强度为
r E
ery E0
sin(
d
z) cos(t
kx)
式中k为常数,求:(1)磁场强度;(2)两导体表面的面电流 密度和面电荷密度。
s
en
D |zd
ez
D |zd
电磁场三类边界条件

电磁场三类边界条件电磁场三类边界条件电磁场的边界条件是指在介质边界处,电场和磁场的变化情况。
根据边界条件的不同,可以将其分为三类:第一类边界条件、第二类边界条件和第三类边界条件。
下面将详细介绍这三类边界条件。
一、第一类边界条件第一类边界条件也称为零法向电场和零切向磁场边界条件。
它是指在介质表面上,法向于表面的电场强度和切向于表面的磁感应强度均为零。
1. 零法向电场在介质表面上,由于介质内部和外部存在不同的电荷分布情况,因此会产生一个法向于表面方向的电场。
而当这个电场穿过介质表面时,就会发生反射和折射现象。
为了描述这种现象,我们需要引入一个重要的物理量——法向于表面方向上的电通量密度。
根据高斯定理可知,在任意一个闭合曲面内部,通过该曲面的总电通量等于该曲面所包围空间内部所有自由电荷之代数和。
因此,在介质表面附近,我们可以将其看作一个微小的闭合曲面。
则在该曲面上的电通量密度可以表示为:$$\vec{D_1}\cdot\vec{n}=\rho_s$$其中,$\vec{D_1}$表示介质1内部的电位移矢量,$\vec{n}$表示介质表面法向矢量,$\rho_s$表示表面自由电荷密度。
当我们将这个式子应用于介质表面时,可以得到:$$D_{1n}=\rho_s$$其中,$D_{1n}$表示介质1内部法向于表面方向上的电场强度。
由于介质表面上不存在自由电荷,因此$\rho_s=0$。
因此,在第一类边界条件下,法向于介质表面方向上的电场强度为零。
2. 零切向磁场在介质表面上,由于介质内部和外部存在不同的磁场分布情况,因此会产生一个切向于表面方向的磁感应强度。
而当这个磁场穿过介质表面时,就会发生反射和折射现象。
为了描述这种现象,我们需要引入一个重要的物理量——切向于表面方向上的磁通量密度。
根据安培环路定理可知,在任意一个闭合回路上,通过该回路的总磁通量等于该回路所包围空间内部所有电流之代数和。
因此,在介质表面附近,我们可以将其看作一个微小的闭合回路。
电磁场三类边界条件

电磁场三类边界条件介绍在电磁学中,边界条件是解决电磁场问题时的重要问题之一。
电磁场三类边界条件指的是麦克斯韦方程组在不同介质之间的边界上的满足条件。
这些条件在电磁场问题的求解中起到了关键的作用。
在本文中,我们将详细探讨电磁场三类边界条件的定义和应用。
一、第一类边界条件第一类边界条件也称为电磁场的法向边界条件。
其主要定义了电场和磁场在边界上的法向分量之间的关系。
具体表达如下:1.在介质边界上,电场的法向分量E n1和E n2满足:E n1=E n2;2.在介质边界上,磁场的法向分量H n1和H n2满足:H n1=H n2。
第一类边界条件体现了介质边界上的电场和磁场的连续性。
二、第二类边界条件第二类边界条件也称为电磁场的切向边界条件。
其主要定义了电场和磁场在边界上的切向分量之间的关系。
具体表达如下:1.在介质边界上,电场的切向分量E t1和E t2满足:E t1ϵ1=E t2ϵ2;2.在介质边界上,磁场的切向分量H t1和H t2满足:H t1μ1=H t2μ2。
其中,ϵ1和ϵ2分别为两个介质的介电常数,μ1和μ2分别为两个介质的磁导率。
第二类边界条件体现了介质边界上的电场和磁场的连续性和切向分量之间的比例关系。
三、第三类边界条件第三类边界条件也称为电磁场的混合边界条件。
其主要定义了电场和磁场在边界上的法向分量和切向分量之间的关系。
具体表达如下:1.在介质边界上,电场的法向分量E n1和E n2满足:E n1=E n2;2.在介质边界上,磁场的法向分量H n1和H n2满足:H n1=H n2;3.在介质边界上,电场的切向分量E t1和E t2满足:E t1ϵ1=E t2ϵ2;4.在介质边界上,磁场的切向分量H t1和H t2满足:H t1μ1=H t2μ2。
第三类边界条件综合了第一类和第二类边界条件,体现了介质边界上的电场和磁场的连续性以及法向分量和切向分量之间的比例关系。
四、应用举例电磁场三类边界条件在电磁学中的应用非常广泛,下面我们以几个实际问题为例,说明其应用方法:例一:平行板电容器考虑一对平行金属板构成的电容器,两板之间填充了介电常数为ϵ的均匀介质。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
电磁场边界条件
电磁场边界条件是指电磁场的变化情况在物体的表面上的变化情况,它决定了电磁场的变化特性。
它是电磁场的基本规律,在物理学中有着重要的地位。
它的主要内容有:无磁性介质的电磁场边界条件,有磁性介质的电磁场边界条件和电磁辐射的边界条件。
无磁性介质的电磁场边界条件由电场强度和磁场强度的法向分量构成;有磁性介质的电磁场边界条件由电场强度和磁场强度的法向分量以及介质的磁导率构成;电磁辐射的边界条件由电磁辐射的波功率流密度和波向分量构成。
电磁场边界条件的求解是物理学中最重要的问题之一。
