数值方法C++代码大全上(包括二分法迭代法牛顿法等等)
常用数学算法C语言实现

常用数学算法C语言实现C语言中有许多常用的数学算法,包括排序算法、查找算法、线性代数算法等等。
下面将介绍其中一些常用的数学算法的C语言实现。
1. 冒泡排序算法(Bubble Sort)冒泡排序是一种简单的排序算法,它的原理是通过相邻元素之间的比较和交换来实现排序。
具体实现如下:```cvoid bubbleSort(int arr[], int n)int i, j;for (i = 0; i < n-1; i++)for (j = 0; j < n-i-1; j++)if (arr[j] > arr[j+1])int temp = arr[j];arr[j] = arr[j+1];arr[j+1] = temp;}}}```2. 二分查找算法(Binary Search)二分查找算法是一种效率较高的查找算法,它要求查找的数组必须已经排序。
具体实现如下:```cint binarySearch(int arr[], int left, int right, int x)if (right >= left)int mid = left + (right - left) / 2;if (arr[mid] == x) return mid;if (arr[mid] > x) return binarySearch(arr, left, mid - 1, x);return binarySearch(arr, mid + 1, right, x);}return -1;```3. 矩阵相乘算法(Matrix Multiplication)矩阵相乘算法用于计算两个矩阵的乘积,它的实现需要使用多层循环来依次计算各个元素的值。
具体实现如下:```cvoid matrixMultiplication(int mat1[][N], int mat2[][N], int res[][N])int i, j, k;for (i = 0; i < N; i++)for (j = 0; j < N; j++)res[i][j] = 0;for (k = 0; k < N; k++)res[i][j] += mat1[i][k] * mat2[k][j];}}}```这只是其中一些常用的数学算法的C语言实现,还有很多其他算法,包括快速排序、最大公约数算法、素数判断算法等等。
c语言二分查找算法代码

c语言二分查找算法代码C语言二分查找算法是一种非常常用的查找算法,也是一种高效的算法,特别是当数据规模非常大时,它的优势体现得更加明显。
通过对待查找的数据进行二分割,然后迭代比对的方式,二分查找算法能够在较短的时间内准确地定位目标所在的索引位置。
本文将介绍C语言二分查找算法的代码实现,以及如何通过该算法查找并定位数据目标。
1.基本思想C语言二分查找算法是利用了待查找的数据有序的特性,通过将数据逐渐逼近目标值,最终定位目标所在的位置。
具体实现过程如下:(1)首先确定数据的中间位置。
(2)将待查找的目标值与中间位置的值进行比较。
(3)如果目标值等于中间位置的值,则返回中间位置的索引。
(4)如果目标值小于中间位置的值,则将数据的范围缩小到第一项到中间项之间的数据。
(5)如果目标值大于中间位置的值,则将数据的范围缩小到中间项到最后一项之间的数据。
(6)重复以上步骤,直到找到目标值。
二分查找算法的核心思想就是不断缩小数据的范围,将数据迭代划分为两部分,缩小搜索的范围,以快速定位目标值所在的索引位置。
2.代码实现C语言实现二分查找算法虽然简单,但是需要考虑很多边界条件,才能保证算法的正确性和鲁棒性。
下面,我们将介绍二分查找算法的代码实现。
(1)基本二分查找算法```c int binary_search(int *arr, int num, intvalue) { int low = 0, high = num - 1, mid;while(low <= high) { mid = (low + high)/ 2; if(arr[mid] == value)return mid; else if(arr[mid] > value) high = mid - 1; else low = mid+ 1; } return -1; } ```该算法的基本思路已经在上面进行了分析。
该代码实现中,arr为待查找的有序数据,num为数据的个数,value为待查找的目标值。
数值方法C++代码大全上(包括二分法迭代法牛顿法等等)

数值方法C++代码大全上(包括二分法迭代法牛顿法等等)1.二分法#include#include#include //调用fabs函数。
double f(double x) //定义函数F(x)。
{return 2*x*x*x-x-1;}void main(){double a,b,w,x;cout<<"请输入方程根的区间[a,b]及误差w:";cin>>a>>b>>w;x=(a+b)/2;while(fabs(f(x))>w&&fabs(a-b)>w){ //用while循环控制中值折算的条件。
if(f(x)*f(b)<0) a=x; //进行二分,缩小求值范围。
else if(f(a)*f(x)<0) b=x;x=(a+b)/2;}cout<<x<<endl;< p="">}2.迭代法#include#include#include#includeusing namespace std;typedef double (*pFun)(double x);double getIterativeValue(double x){return pow((x+1)/2,(double)1.0/3);}double Solve(pFun f,double x,double e,int n){double res;while(n--){res = f(x);if(fabs(res - x) < e){outPrint("第%d次次迭代以后返回值为:%0.7lf \n",10-n,res); break;}elsex = res;outPrint("第%d次迭代以后x值为:%0.7lf\n ",10-n,x);}return res;}int main(){cout << setprecision(7);double x,e;cout << "输入初值和精度:" << endl;cin >> x >> e;cout << Solve(getIterativeValue,x,e,10) << endl;system("pause");return 0;3.牛顿法#include#include#include#includeusing namespace std;typedef double (*pFun)(double x);double getIterativeValue(double x){return pow((x+1)/2,(double)1.0/3);}double Solve(pFun f,double x,double e,int n){double res;while(n--){res = f(x);if(fabs(res - x) < e){printf("第%d次次迭代以后返回值为:%0.7lf \n",10-n,res); break;}elsex = res;printf("第%d次迭代以后x值为:%0.7lf\n ",10-n,x);}return res;}int main()cout << setprecision(7);double x,e;cout << "输入初值和精度:" << endl;cin >> x >> e;cout << Solve(getIterativeValue,x,e,10) << endl; return 0;}4.高斯消元法#include#include#define N 10 //矩阵大小范围/** 使用已经求出的x,向前计算x(供getx()调用)* float a[][] 系数矩阵* float x[] 方程组解* int i 解的序号* int n 矩阵大小* return 公式中需要的和*/float getm(float a[N][N], float x[N], int i, int n) {float m = 0;int r;for(r=i+1; r<="">{m += a[i][r] * x[r];}return m;}* 解方程组,计算x* float a[][] 系数矩阵* float b[] 右端项* float x[] 方程组解* int i 解的序号* int n 矩阵大小* return 方程组的第i个解*/float getx(float a[N][N], float b[N], float x[N], int i, int n){float result;if(i==n-1) //计算最后一个x的值result = float(b[n-1]/a[n-1][n-1]);else //计算其他x值(对于公式中的求和部分,需要调用getm()函数)result = float((b[i]-getm(a,x,i,n))/a[i][i]);return result;}void main()//float a[N][N] = {{2,1,1},{1,3,2},{1,2,2}}; //float b[N] = {4,6,5};float a[N][N]; //系数矩阵float b[N]; //右端项float x[N]; //方程组解int i,j,k;int n=N; //矩阵大小/*用户手工输入矩阵*/printf("请输入系数矩阵的大小:"); scanf("%d", &n);printf("请连续输入矩阵值:");for(i=0; i<="" p="">{for(j=0; j<="" p="">scanf("%f", &a[i][j]);}printf("请输入右端项:");for(i=0; i<="" p="">{scanf("%f", &b[i]);}/*显示原始矩阵*/printf("\n原始矩阵\n");for(i=0; i<="" p="">{for(j=0; j<="" p="">printf("%f ",a[i][j]);printf("\t|\t%f\n",b[i]);}printf("\n\n");/*进行高斯消去*/for(j=0; j<="" p="">{for(i=j+1; i<="" p="">{float m = (float)(a[i][j]/a[j][j]); for(k=j; k<="" p="">{a[i][k] = a[i][k]-m*a[j][k];}b[i] = b[i]-m*b[j];}}/*显示处理后矩阵*/printf("高斯消去后矩阵\n");for(i=0; i<="" p="">{for(j=0; j<="" p="">printf("%f ",a[i][j]);printf("\t|\t%f\n",b[i]);}/*回代方式解方程组*/for(i=n-1; i>=0; i--){x[i] = getx(a,b,x,i,n);}/*显示方程组解*/printf("\n\n方程组解\n");for(i=0; i<="" p="">{printf("x%d = %f\n", i+1,x[i]);}}5.高斯先列主元消元法采用高斯先列主元消元法求解线性方程组AX=b方法说明(以4阶为例):(1)第1步消元——在增广矩阵(A,b)第一列中找到绝对值最大的元素,将其所在行与第一行交换,再对(A,b)做初等行变换使原方程组转化为如下形式:,注:“*”代表非0。
计算方法(各种方法的程序源代码)

第一章求根公式法:#include<stdio.h>#include<math.h>main(){int a,b,c;double x1,x2,d=0.0;printf("请输入a,b,c的值:\n");scanf("%d,%d,%d",&a,&b,&c);d=b*b-4*a*c;if(d>=0){if(d>0){x1=(-b+sqrt(d))/(2*a);x2=(-b-sqrt(d))/(2*a);printf("方程的两根为x1=%f,x2=%f\n",x1,x2);}else{ x1=-b/(2*a);x2=x1;printf("方程的两根为x1=%f,x2=%f\n",x1,x2);}}else{printf("方程无实根\n");}return 0;}二分法:#include<stdio.h>#include<math.h>double f(double x){double y;y=x*x*x-2*x-5;return y;}main(){double a=2.0,b=3.0,x;if(f(a)*f(b)<0.0){do{x=(a+b)/2.0;if(f(a)*f(x)<0.0){b=x;continue;}if(f(x)*f(b)<0.0)a=x;}while(fabs(a-b)>0.01);}else printf("没有实根");printf("实根为%f",x);return 0;}第二章拉格朗日插值:#include <iostream>#include <iomanip>#include <stdlib.h>using namespace std;#define N 100void lagrange(){int n,k,m,q=1;float x[N],y[N],xx,yyy1,yyy2,yy1,yy2,yy3;cout<<"请输入X的个数:";cin>>n;for(k=0;k<=n-1;k++){cout<<"请输入X"<<k<<"的值:";cin>>x[k];cout<<"请输入Y"<<k<<"的值:";cin>>y[k];}system("cls");cout<<"则Xi与Yi表格如下:"<<endl;cout<<"Xi"<<"";for(k=0;k<=n-1;k++)cout<<setiosflags(ios::left)<<setw(10)<<x[k]; cout<<endl;cout<<"Yi"<<"";for(k=0;k<=n-1;k++)cout<<setiosflags(ios::left)<<setw(10)<<y[k]; cout<<endl;while(q){cout<<"请输入所求x的值:";cin>>xx;while(xx>x[k-1]||xx<x[0]){cout<<"输入错误,请重新输入:";cin>>xx;}for(k=0;k<=n-1;k++){if(xx<x[k]){m=k-1;k=n-1;}}yyy1=y[m]*((xx-x[m+1])/(x[m]-x[m+1]))+y[m+1]*((xx-x[m])/(x[m+1]-x[m] ));cout<<"则拉格朗日分段线性插值为:"<<yyy1<<endl;for(k=0;k<=n-1;k++){if(xx<x[k]){m=k-1;k=n-1;}}if((xx-x[m])>(x[m+1]-xx))m=m+1;else m=m;yy1=y[m-1]*((xx-x[m])*(xx-x[m+1]))/((x[m-1]-x[m])*(x[m-1]-x[m+1])); yy2=y[m]*((xx-x[m-1])*(xx-x[m+1]))/((x[m]-x[m-1])*(x[m]-x[m+1])); yy3=y[m+1]*((xx-x[m-1])*(xx-x[m]))/((x[m+1]-x[m-1])*(x[m+1]-x[m])); yyy2=yy1+yy2+yy3;cout<<"则拉格朗日分段二次插值为:"<<yyy2<<endl;cout<<"是否输入其余要求x的值[是(1),否(0)]:";cin>>q;}system("cls");}void main(){lagrange();}牛顿插值:#include<stdio.h>#include<math.h>main(){float a[]={0,1,2,3,4},b[]={3,6,11,18,27};float f[5],x,t,m,n,s=0;int i,j,k,l;printf("请输入x的值:");scanf("%f",&x);f[0]=b[0];for(i=1;i<5;i++){m=0;for(j=0;j<=i;j++){t=1;for(k=0;k<=i;k++){if(k!=j) t=t/(a[j]-a[k]);}m=m+b[j]*t;}n=1;for(l=0;l<i;l++) n=n*(x-a[l]);s=s+m*n;}s=s+f[0];printf("s=%f",s);return 0;}线性和二次插值法:#include<stdio.h>#include<math.h>main(){floata[]={0.4,0.5,0.6,0.7,0.8,0.9},b[]={-0.916291,-0.693147,-0.510826,-0.3566 75,-0.223144,-0.105361};float x,t,m,p1=0.0,p2=0.0,p3=0.0;int i,j;printf("请输入x的值");scanf("%f",&x);for(i=0;i<2;i++){t=0.0;for(j=0;j<2;j++){if(j!=i) t=t+((x-a[j])/(a[i]-a[j]))*b[i];}p1=p1+t;}printf("线性插值的结果为:%f",p1);for(i=0;i<3;i++){m=1.0;for(j=0;j<3;j++){if(j!=i) m=m*((x-a[j])/(a[i]-a[j]));}p2=p2+m*b[i];}printf("取0.4,0.5,0.7,的二次插值的结果为:%f",p2); for(i=1;i<4;i++){m=1.0;for(j=1;j<4;j++){if(j!=i) m=m*((x-a[i])/(a[i]-a[j]));}p3=p3+m*b[i];}printf("取0.5,0.6,0.7的二次插值的结果为:%f",p3);return 0;}直线拟合法:#include<stdio.h>#include<math.h>main(){float X[5]={-2,-1,0,1,2},Y[5]={0,0.2,0.5,0.8,1.0}; float a=0,b=0,c=0,d=0,m,n;int i;for(i=0;i<5;i++){a=a+X[i];b=b+Y[i];c=c+X[i]*X[i];d=d+X[i]*Y[i];};m=(b*c-a*d)/(5*c-a*a);n=(5*d-c*a)/(5*c-a*a);float x,y;printf("请输入X的值");scanf("%f",&x);y=m+n*x;printf("拟合后代入x的值得出的结果为:%f",y); return 0;}第三章复化辛甫生算法:#include<stdio.h>#include<math.h>float f(float x){float y;y=3*x*x+2*x;return y;}main(){float a,b,h,s;int k=1,n;printf("请输入a,b,n");scanf("%f,%f,%d",&a,&b,&n);h=(b-a)/n;s=f(b)-f(a);for(float x=a;k<n;k++){x=x+h/2;s=s+4*f(x);x=x+h/2;s=s+2*f(x);}s=(h/6)*s;printf("s=%f",s);}龙贝格算法:#include<stdio.h>#include<string.h>#include<math.h>#include<conio.h>#include<stdlib.h>float f(float x){return (2*x);}float r(float a,float b){int k=1;float s,x,t1,t2,s1,s2,c1,c2,r1,r2,h=b-a,p;t1=h*(f(a)+f(b))/2;while(1){s=0;x=a+h/2;do{s+=f(x);x+=h;}while(x<b);t2=(t1+h*s)/2.0;if(fabs(t2-t1)<p)return(t2);s2=t2+(t2-t1)/3.0;if(k==1){t1=t2;s1=s2;h/=2;k+=1;continue;}c2=s2+(s2-s1)/15.0;if(k==2){c1=c2;t1=t2;s1=s2;h/=2.0;k+=1;continue;}r2=c2+(c2-c1)/63;if(k==3){r1=r2;c1=c2;t1=t2;s1=s2;h/=2;k+=1;continue;};if(fabs(s1-s2)<p)return(s2);r1=r2;c1=c2;t1=t2;s1=s2;h/2;k+=1;return(r1);}}main(){int i;float a,b,p,s,clrsca();printf("\n input integrate f(x) the begin:");scanf("%f",&a);printf("\n input integrate f(x) the end:"); scanf("%f",&b);printf("\n input p:");scanf("%f",&p);s=r(a,b);printf("the result is:%f",s);getch();return(s);}变步长积分法:#include<stdio.h>#include<math.h>void main(){double k,a,b;int kk,n;double sum[100],t[100];printf("方程为f(x)=x/(4+x^2),积分区间为[0,1]\n");printf("请输入预定精度a的值\n");scanf("%lf",&a);t[0]=0.1;t[1]=0.1088;for(k=1.0,kk=1;fabs(t[kk]-t[kk-1])>=a;k++,kk++){for(n=1,sum[kk+1]=0;n<=pow(2.0,k);n++){b=(2*n-1)/pow(2.0,k+1);sum[kk+1]+=b/(4+b*b);}t[kk+1]=0.5*t[kk]+(1/pow(2.0,k+1))*sum[kk+1];}printf("\n方程利用变步长梯形法积分后的积分值为%f\n",t[kk]);}第四章:欧拉法:#include<stdio.h>#include<math.h>#include<string.h> #include<stdlib.h> float f(float x,float y){ float f;f=x+y;return f;};main(){float x[6],y[6],h;int n;printf("请输入x[0],y[0],h的值:");scanf("%f%f%f",&x[0],&y[0],&h);for(n=1;n<6;x[0]=x[n],y[0]=y[n],n++){ x[n]=x[0]+h;y[n]=y[0]+h*f(x[0],y[0]);printf("%f,%f",x[n],y[n]);printf("\n");}return 0;}改进欧拉法:#include<stdio.h>#include<math.h>#include<string.h>#include<stdlib.h>float f(float x,float y){float f;f=x+y;return f;};main(){float x[6],y[6],h,yp,ye;int n;printf("请输入x[0],y[0],h的值:");scanf("%f%f%f",&x[0],&y[0],&h);for(n=1;n<6;x[0]=x[n],y[0]=y[n],n++){ x[n]=x[0]+h;yp=y[0]+h*f(x[0],y[0]);ye=y[0]+h*f(x[n],yp);y[n]=(yp+ye)/2;printf("%f,%f",x[n],y[n]);printf("\n");}return 0;}四阶龙格库塔法:#include<stdio.h>#include<math.h>#include<string.h>float f(float x,float y){float f;f=x+y;return f;}main(){float x[11],y[11],h,k1,k2,k3,k4;printf("请分别输入x[0],y[0],h的值:");scanf("%f%f%f",&x[0],&y[0],&h);for(int n=1;n<11;x[0]=x[n],y[0]=y[n],n++){ x[n]=x[0]+h;k1=f(x[0],y[0]);k2=f(x[0]+h/2,y[0]+h*k1/2);k3=f(x[0]+h/2,y[0]+h*k2/2);k4=f(x[n],y[0]+h*k3);y[n]=y[0]+h*(k1+2*k2+2*k3+k4)/6;printf("%f,%f",x[n],y[n]);printf("\n");}return 0;}第六章迭代法:#include<stdio.h>#include<math.h>#include<string.h>double F1(double x);double Newton(double x0, double e); int main(){double x0 = 0.5;double e = 10E-6;printf("x = %f\n", Newton(x0, e));getchar();return 0;}double F1(double x){return log(x+2)/log(10);}double Newton(double x0, double e) {double x1;do{x1 = x0;x0 =F1(x1);} while (fabs(x0 - x1) > e);return x0;}埃特金加速法:#include<stdio.h>#include<conio.h>#include<math.h>#define h 1.E-10 double f(double x0) {x0=exp(-x0);return x0;}double sub(double x) {if(x>=0)return x;else return -x;}main(){double x0=0.5,x,s=0.0; do{x=f(x0);s=sub(x-x0);x0=x;}while(s>h); printf("x=%f",x); getch();return 0;}快速弦截法:#include<stdio.h>#include <math.h>float f(float x){float y;y=x*exp(x)-1;return (y);}float xpoint(float x1,float x2){float y;y=(x1*f(x2)-x2*f(x1)) / (f(x2) - f(x1));return (y) ;}float root(float x1, float x2) {int i;float x,y,y1;y1=f(x1);do{x=xpoint(x1,x2);y=f(x);if(y*y1>0){y1=y;x1=x;}elsex2=x;}while(fabs(y)>=0.0000001); return (x);}main(){float x1,x2,f1,f2,x;do{printf("input x1,x2:\n");scanf("%f,%f",&x1,&x2);f1=f(x1);f2=f(x2);}while(f1*f2>=0);x=root(x1,x2);printf("A root of equation is %8.4f\n",x); }第七章高斯消去法:#include<stdio.h>#include<math.h>main(){float a[10][10],b[10],m[10][10],x[10],sum; int i,j,k,n;printf("the top exp:");scanf("%d",&n);printf("\n");for(i=0;i<n;i++){for(j=0;j<n;j++){scanf("%f",&a[i][j]);}for(i=0;i<n;i++){scanf("%f",&b[i]);}for(k=0;k<n-1;k++){if(a[k][k]==0)printf("error");else {for(i=k+1;i<n;i++){m[i][k]=a[i][k]/a[k][k];} };a[i][k]=m[i][k];b[i]=b[i]-m[i][k]*b[k];for(j=k+1;j<n;j++)a[i][j]=a[i][j]-m[i][k]*a[k][j];};if(a[n-1][n-1]==0)printf("error");else x[n-1]=b[n-1]/a[n-1][n-1];b[n-1]=x[n-1];for(i=n-2;i>=0;i--){sum=0;for(j=i+1;j<n;j++){sum+=a[i][j]*x[j];}x[i]=(b[i]-sum)/a[i][i];b[i]=x[i];}for(i=0;i<n;i++)printf("%f\n",x[i]);}return 0;}选主元消去法:#include<stdio.h>#include<math.h>main(){float a[10][10],b[10],s,t,e,sum; int i,j,k,n,m;printf("The top exp is "); scanf("%d",&n);for(i=0;i<n;i++)for(j=0;j<n;j++)scanf("%f",&a[i][j]);for(i=0;i<n;i++)scanf("%f",&b[i]);scanf("%f",&e);k=0;do{t=a[k][k];for(i=k;i<n;i++){if(fabs(t)<fabs(a[i][k])){t=a[i][k];m=i;}else m=k;}if(fabs(t)<e)printf("det A = 0\n");else {if(m!=k){for(j=0;j<n;j++){s=a[m][j];a[m][j]=a[k][j];a[k][j]=s;}s=b[m];b[m]=b[k];b[k]=s;}for(i=k+1;i<n;i++)for(j=k+1;j<n;j++){a[i][k]=a[i][k]/a[k][k];a[i][j]=a[i][j]-a[i][k]*a[k][j];b[i]=b[i]-a[i][k]*b[k];}}k++;}while(k<n-2);if(fabs(a[n-1][n-1])<e)printf("det A = 0\n");else {b[n-1]=b[n-1]/a[n-1][n-1];for(i=n-2;i>=0;i--){sum=0;for(k=i+1;k<n;k++){sum+=a[k][j]*b[j];}b[i]=(b[i]-sum)/a[i][i];}}for(i=0;i<n;i++)printf("%f\n",b[i]);}追赶法:#include<stdio.h>#include<math.h>main(){int i,j,k,n;float d[10][10],g[10],a[10],b[10],c[10],x[10],y[10],f[10];printf("the top exp is ");scanf("%d",&n);scanf("%f,%f,%f,%f",&d[0][0],&d[0][1],&d[n-1][n-2],&d[n-1][n-1]); for(i=1;i<n-1;i++)for(j=i-1;j<=i+1;j++)scanf("%f",&d[i][j]);for(i=0;i<n;i++)scanf("%f",&g[i]);for(i=1;i<n-1;i++)a[i]=d[i][i-1];for(i=0;i<n;i++)b[i]=d[i][i];for(i=0;i<n-1;i++)c[i]=d[i][i+1];f[0]=c[0]/b[0];for(k=1;k<n-1;k++)f[k]=c[k]/(b[k]-a[k]*f[k-1]);y[0]=g[0]/b[0];for(i=1;i<n;i++)y[i]=(g[i]-a[i]*y[i-1])/(b[i]-a[i]*f[i-1]); x[n-1]=y[n-1];for(i=n-2;i>=0;i--)x[i]=y[i]-f[i]*x[i+1];for(i=0;i<n;i++)printf("%f\n",x[i]);}。
线性方程组的数值算法C语言实现(附代码)

线性方程组AX=B 的数值计算方法实验一、 实验描述:随着科学技术的发展,线性代数作为高等数学的一个重要组成部分,在科学实践中得到广泛的应用。
本实验的通过C 语言的算法设计以及编程,来实现高斯消元法、三角分解法和解线性方程组的迭代法(雅可比迭代法和高斯-赛德尔迭代法),对指定方程组进行求解。
二、 实验原理:1、高斯消去法:运用高斯消去法解方程组,通常会用到初等变换,以此来得到与原系数矩阵等价的系数矩阵,达到消元的目的。
初等变换有三种:(a)、(交换变换)对调方程组两行;(b)、用非零常数乘以方程组的某一行;(c)、将方程组的某一行乘以一个非零常数,再加到另一行。
通常利用(c),即用一个方程乘以一个常数,再减去另一个方程来置换另一个方程。
在方程组的增广矩阵中用类似的变换,可以化简系数矩阵,求出其中一个解,然后利用回代法,就可以解出所有的解。
2、选主元:若在解方程组过程中,系数矩阵上的对角元素为零的话,会导致解出的结果不正确。
所以在解方程组过程中要避免此种情况的出现,这就需要选择行的判定条件。
经过行变换,使矩阵对角元素均不为零。
这个过程称为选主元。
选主元分平凡选主元和偏序选主元两种。
平凡选主元:如果()0p pp a ≠,不交换行;如果()0p pp a =,寻找第p 行下满足()0p pp a ≠的第一行,设行数为k ,然后交换第k 行和第p 行。
这样新主元就是非零主元。
偏序选主元:为了减小误差的传播,偏序选主元策略首先检查位于主对角线或主对角线下方第p 列的所有元素,确定行k ,它的元素绝对值最大。
然后如果k p >,则交换第k 行和第p 行。
通常用偏序选主元,可以减小计算误差。
3、三角分解法:由于求解上三角或下三角线性方程组很容易所以在解线性方程组时,可将系数矩阵分解为下三角矩阵和上三角矩阵。
其中下三角矩阵的主对角线为1,上三角矩阵的对角线元素非零。
有如下定理:如果非奇异矩阵A 可表示为下三角矩阵L 和上三角矩阵U 的乘积: A LU = (1) 则A 存在一个三角分解。
C语言常用数值计算算法(素数、公约数、级数、方程根和定积分)
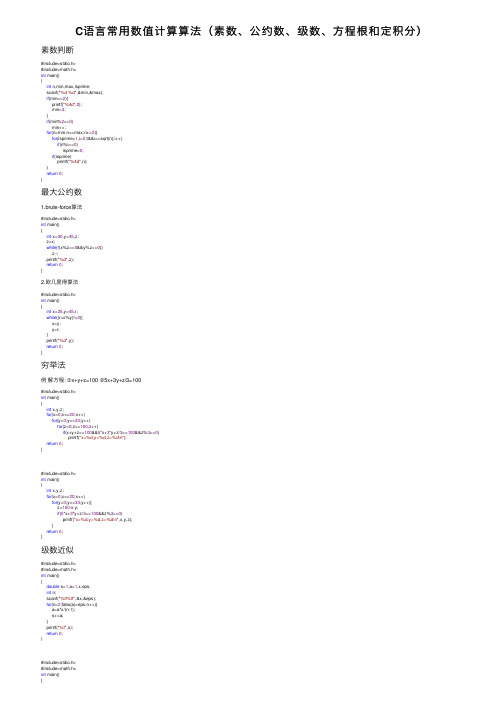
C语⾔常⽤数值计算算法(素数、公约数、级数、⽅程根和定积分)素数判断#include<stdio.h>#include<math.h>int main(){int n,min,max,isprime;scanf("%d %d",&min,&max);if(min<=2){printf("%4d",2);min=3;}if(min%2==0)min++;for(n=min;n<=max;n+=2){for(isprime=1,i=2;t&&i<=sqrt(n);i++)if(n%i==0)isprime=0;if(isprime)printf("%4d",n);}return0;}最⼤公约数1.brute-force算法#include<stdio.h>int main(){int x=30,y=45,z;z=x;while(!(x%z==0&&y%z==0))z--;printf("%d",z);return0;}2.欧⼏⾥得算法#include<stdio.h>int main(){int x=35,y=45,r;while((r=x%y)!=0){x=y;y=r;}printf("%d",y);return0;}穷举法例解⽅程: ①x+y+z=100 ②5x+3y+z/3=100#include<stdio.h>int main(){int x,y,z;for(x=0;x<=20;x++)for(y=0;y<=33;y++)for(z=0;z<=100;z++)if(x+y+z==100&&5*x+3*y+z/3==100&&z%3==0)printf("x=%d,y=%d,z=%d\n");return0;}#include<stdio.h>int main(){int x,y,z;for(x=0;x<=20;x++)for(y=0;y<=33;y++){z=100-x-y;if(5*x+3*y+z/3==100&&z%3==0)printf("x=%d,y=%d,z=%d\n",x,y,z);}return0;}级数近似#include<stdio.h>#include<math.h>int main(){double s=1,a=1,x,eps;int n;scanf("%lf%lf",&x,&eps);for(n=2;fabs(a)>eps;n++){a=a*x/(n-1);s+=a;}printf("%f",s);return0;)#include<stdio.h>#include<math.h>int main(){double sum,x,eps=1e-6,fn,tn;int s=1,n=2;scanf("%lf",&x);s=fn=x;do{s=-s;fn=fn*(2*n-3)/(2*n-2)*x*x;tn=sign*fn/(2*n-1);sum=sum+tn;n++;}while(fabs(tn)>eps);printf("%f",sum);⼀元⾮线性⽅程求根⼀、⽜顿迭代法 1.基本概念:如果函数连续,且待求零点孤⽴,那么在零点周围存在⼀个区域,当初值在这个邻域内时,⽜顿法收敛。
(完整版)非常全的C语言常用算法

一、基本算法1.交换(两量交换借助第三者)例1、任意读入两个整数,将二者的值交换后输出。
main(){int a,b,t;scanf("%d%d",&a,&b);printf("%d,%d\n",a,b);t=a; a=b; b=t;printf("%d,%d\n",a,b);}【解析】程序中加粗部分为算法的核心,如同交换两个杯子里的饮料,必须借助第三个空杯子。
假设输入的值分别为3、7,则第一行输出为3,7;第二行输出为7,3。
其中t为中间变量,起到“空杯子”的作用。
注意:三句赋值语句赋值号左右的各量之间的关系!【应用】例2、任意读入三个整数,然后按从小到大的顺序输出。
main(){int a,b,c,t;scanf("%d%d%d",&a,&b,&c);/*以下两个if语句使得a中存放的数最小*/if(a>b){ t=a; a=b; b=t; }if(a>c){ t=a; a=c; c=t; }/*以下if语句使得b中存放的数次小*/if(b>c) { t=b; b=c; c=t; }printf("%d,%d,%d\n",a,b,c);}2.累加累加算法的要领是形如“s=s+A”的累加式,此式必须出现在循环中才能被反复执行,从而实现累加功能。
“A”通常是有规律变化的表达式,s在进入循环前必须获得合适的初值,通常为0。
例1、求1+2+3+……+100的和。
main(){int i,s;s=0; i=1;while(i<=100){s=s+i; /*累加式*/i=i+1; /*特殊的累加式*/}printf("1+2+3+...+100=%d\n",s);}【解析】程序中加粗部分为累加式的典型形式,赋值号左右都出现的变量称为累加器,其中“i = i + 1”为特殊的累加式,每次累加的值为1,这样的累加器又称为计数器。
C语言复习---迭代法,牛顿迭代法,二分法求根

C语⾔复习---迭代法,⽜顿迭代法,⼆分法求根⼀:⽤迭代法求 x=√a。
求平⽅根的迭代公式为:X(n+1)= (Xn+a/Xn) /2。
#define _CRT_SECURE_NO_WARNINGS#include <stdio.h>#include <stdlib.h>#include <math.h>int main(){double x1, x2;float a;scanf("%f", &a);x2 = 1.0;do{x1 = x2;x2 = (x1 + a / x1) / 2;} while (fabs(x1-x2)>pow(10,-5));printf("value:%lf", x2);system("pause");return0;}⼆:⽤求⽅程在1.5附近的根(2x3-4x2+3x-6=0)例:⽅程求根⽜顿迭代法求⽅程 f(x)=x3+x2-3x-3=0在1.5附近的根f(x)=x^3+x^2-3x-3f'(x)=3x^2+2x-3x(n+1)=xn-f(xn)/f'(xn)令x1=1.5x2=1.777778x3=1.733361x4=1.732052x5=1.732051x6=1.732051如果精确到0.000001,则x=1.732051准确值=根号3重要公式#include <stdio.h>#include <stdlib.h>#include <math.h>int main(){double x1=0, x2;double fx1, fx2;x2 = 1.5;while (fabs(x1 - x2)>=1e-6){x1 = x2;fx1 = 2 * x1*x1*x1 - 4 * x1*x1 + 3 * x1 - 6; //f(xn)fx2 = 6 * x1*x1 - 8 * x1 + 3; //f(xn)'x2 = x1 - fx1 / fx2;}printf("value:%lf", x2);system("pause");return0;}三:⼆分法求⽅程的根给定精确度ξ,⽤⼆分法求函数f(x)零点近似值的步骤如下:1确定区间[a,b],验证f(a)·f(b)<0(这是前提,选取的区间必须满⾜这个条件),给定精确度ξ. 2求区间(a,b)的中点c.3计算f(c).(1) 若f(c)=0,则c就是函数的零点;(2) 若f(a)·f(c)<0,则令b=c;(3) 若f(c)·f(b)<0,则令a=c.(4) 判断是否达到精确度ξ:即若|a-b|<ξ,则得到零点近似值a(或b),否则重复2-4.#include <stdio.h>#include <stdlib.h>#include <math.h>double fx(double x){return2 * x*x*x - 4 * x*x + 3 * x - 6;}int main(){double x1 , x2;double fx1, fx2;double e = 1e-6;do{printf("enter (x1,x2):\n");scanf("%lf", &x1);scanf("%lf", &x2);if (x1>x2){double temp = x1;x1 = x2;x2 = temp;}fx1 = fx(x1);fx2 = fx(x2);} while (fx1*fx2>0);if (fabs(fx1) < e)printf("solution1:%lf\n", x1);else if (fabs(fx2) < e)printf("solution2:%lf\n", x2);else{while (fabs(x1 - x2) >= e){double mid = (x1 + x2) / 2;if (fx(mid)*fx2 < 0)x1 = mid;elsex2 = mid;}printf("solution3:%lf", x2);}system("pause");return0;}。
C语言求解一元二次方程的解源码(迭代法,二分法,牛顿迭代法)

#include <stdio.h>#include <stdlib.h>#include <math.h>#define maxint 32767.0#define minint -32768.0#define accuracy 0.0000001//精确度,值越小计算结果越精确float a,b,c;//系数float dt;//b^2-4acfloat x1=0.0,x2=0.0;//方程的解void read();void setDt();int assertX();void binarySolution();void interation();void newtonInteration();double f(double x);double f1(double x);double absolute(double x);void accurate();int main(void){int end=1;while(end!=0)//继续运算{accurate();printf("按任意键继续(输入0退出):\n");scanf("%d",&end);}}//读取a,b,cvoid read(){printf("请输入方程ax^2+bx+c=0的系数a,b,c:\n");printf("请输入二次项系数a:");while(0==scanf("%f",&a)||a==0){while('\n' != getchar()){}printf("输入无效!请重新输入二次项系数a:");}printf("请输入一次项系数b:");while(0==scanf("%f",&b)){while('\n' != getchar()){}printf("输入无效!请重新输入一次项系数b:");}printf("请输入常数项c:");while(0==scanf("%f",&c)){while('\n' != getchar()){}printf("输入无效!请重新输入常数项c:");}}//计算dtvoid setDt(){dt=b*b-4*a*c;}//判断是否有解int assertX(){if(dt>=0) return 1;return 0;}//循环计算控制void accurate(){read();setDt();int method=0;printf("请选择求解方法:\n\t1.二分法\n\t2.迭代法\n\t3.牛顿迭代法\n请选择:");while((0==scanf("%d",&method))||(method!=1&&method!=2&&method!=3)){while('\n' != getchar()){}printf("输入无效!请重新选择:");}if(!assertX()){printf("该方程无解!\n");}else{switch(method){case 1:binarySolution();break;case 2:interation();break;case 3:newtonInteration();break;}printf("方程%fx^2+%fx+%f=0的解为:x1=%.10f x2=%.10f\n",a,b,c,x1,x2); }}//二分法void binarySolution(){double min=minint,temp=(-1.0*b)/(2*a),max=maxint,middle=0.0;//求解X1while((max-temp)>=accuracy){middle=(max+temp)/2;if(a>0)//开口向上{if(f(middle)>0)max=middle;elsetemp=middle;}else//开口向下{if(f(middle)>0)temp=middle;elsemax=middle;}}x2=temp;//求解X2temp=(-1.0*b)/(2*a);while((temp-min)>=accuracy){middle=(min+temp)/2;if(a>0)//开口向上{if(f(middle)>0)min=middle;elsetemp=middle;}else//开口向下{if(f(middle)>0)temp=middle;elsemin=middle;}}x1=temp;}//迭代法void interation(){//求解X1,在曲线对称轴处选择初始点double index=(-1.0*b)/(2*a),temp;if(b!=0)//b不等于0时进行迭代{temp=index;index=-1.0*(a*temp*temp+c)/b;while((absolute(index-temp))>accuracy) {temp=index;index=-1.0*(a*temp*temp+c)/b;}x1=index;x2=(-1.0*b)/a-x1;}else//b=0时ax^2+c=0直接求解{x1=sqrt(-1.0*c/a);x2=-x1;}}//牛顿迭代法void newtonInteration(){//求解X1,在曲线对称轴右侧选取初始点double index=(-1.0*b)/(2*a)+10,temp; temp=index;index=temp-f(temp)/f1(temp);while((absolute(index-temp))>accuracy) {temp=index;index=temp-f(temp)/f1(temp);}x1=index;//求解X2,在曲线对称轴左侧选取初始点index=(-1.0*b)/(2*a)-10,temp;temp=index;index=temp-f(temp)/f1(temp);;while((absolute(index-temp))>accuracy) {temp=index;index=temp-f(temp)/f1(temp);}x2=index;}//函数f(x)double f(double x){return a*x*x+b*x+c;}//函数f(x)的一次导函数double f1(double x){return 2.0*a*x+b;}//求解绝对值double absolute(double x) {if(x<=0) return (-1.0*x); return x*1.0;}。
数值计算课程设计程序代码

这是本人做的数值计算课程设计的程序源代码。
代码均为C++语言编写。
前面十个程序代码分别为十种数值算法,最后一个程序代码头文件“”的源代码。
这十个程序有大部分要用到头文件“”,具体请查看程序的头文件包含申明语句。
这个头文件中包含矩阵常用运算的函数,可像matlab中一样方便的使用矩阵。
1.二分法解非线性方程#include<iostream>#include<cmath>using namespace std;//二分法解非线性方程double F(double x) //待解的f(x){ return x*sin(x)-1;}int main(){double a,b,ya,yb,delta,t,yt,err;cout<<"请依次输入区间(a,b)的左右端点值及精度要求delta : ";cin>>a>>b>>delta;int i,max1;ya=F(a); yb=F(b);if(ya*yb>0)return 0;max1=1+int(log(b-a)-log(delta)/log(2));for(i=1;i<=max1;i++){t=(a+b)/2;yt=F(t);if(yt==0){a=t;b=t;}else if(yb*yt>0){b=t;yb=yt;}else{a=t;ya=yt;}if(b-a<delta)break;}t=(a+b)/2;err=fabs(a-b);cout<<"方程的解为:"<<t<<endl;cout<<"误差: err = "<<err<<endl;return 0;}2.高斯列主元消去法解线性方程组#include<iostream>#include"matrix.h"using namespace std;//高斯列主元消去法解线性方程组int main(){matrix A,X; //A用来保存线性方程组的增广矩阵,X保存方程组的解int i,j,k,l,n;double temp;cout<<"请输入线性方程组的维数: n = "; cin>>n;A(n,n+1); cout<<"请输入线性方程组的增广矩阵:\n A = "<<endl;A.input();for(i=1;i<=n;i++) //行变换为上三角形{temp=A(i,i); k=0;for(j=i+1;j<=n;j++) //选列主元{if(fabs(A(j,i))>fabs(temp)){temp=A(j,i);k=j;}}if(k>i)A.M_h(i,k); //选主元后行交换for(j=i+1;j<=n;j++){temp=-A(j,i)/A(i,i);A.M_h(temp,i,j);}}//cout<<"测试:A=\n";A.print(8);for(i=n;i>=1;i--) //回代求解{temp=0;for(j=1;j<=n-i;j++)temp+=A(i,i+j)*X(i+j);X(i)=(A(i,n+1)-temp)/A(i,i);}cout<<"线性方程组的解为(从x1到xn顺序排列): \nX = "<<endl;X.print(8);return 0;}3.龙贝格积分算法#include<iostream>#include"matrix.h"using namespace std;//龙贝格积分算法double F(double x)//被积函数{return (x*x+x+1)*cos(x);}double power(double a,int n) //a的n次方{double temp=1;for(int i=0;i<n;i++)temp*=a;return temp;}int main(){matrix R; //R为龙贝格积分表double a,b,tol,err=1,x,h,s;int i,n,m=1,j,k;cout<<"请依次输入下限a,上限b,精度tol,积分表行数n: ";cin>>a>>b>>tol>>n;h=b-a;R=E(n);R(1,1)=(F(a)+F(b))*h/2;for(i=1;i<n&&err>tol;i++){h=h/2;s=0;for(j=1;j<=m;j++){x=a+h*(2*j-1);s+=F(x);}R(i+1,1)=R(i,1)/2+h*s;m=2*m;for(k=1;k<=i;k++){R(i+1,k+1)=R(i+1,k)+(R(i+1,k)-R(i,k))/(power(4,k)-1);}err=fabs(R(i,i)-R(i+1,k)); //注意:结束循环时,k=i+1。
牛顿迭代法c++代码

牛顿迭代法c++代码牛顿迭代法是一种数值计算方法,用于求解非线性方程的根。
它是通过不断迭代逼近的方式来逐步逼近方程的根。
在数学上,给定一个函数f(x),我们希望找到一个近似的解x*,使得f(x*)=0。
牛顿迭代法的基本思想是利用切线逼近函数曲线,求得切线与x轴的交点,将该交点作为新的近似解,不断迭代直到满足精度要求。
牛顿迭代法的迭代公式为:x_n+1 = x_n - f(x_n)/f'(x_n)。
下面是一个用C++实现牛顿迭代法的示例代码:```cpp#include <iostream>#include <cmath>double f(double x) {return x*x - 2; // 求解方程x^2 - 2 = 0}double f_derivative(double x) {return 2*x; // 方程f(x) = x^2 - 2的导数为2x}double newton_method(double x0, double epsilon, intmax_iterations) {double x = x0;int iteration = 0;while (iteration < max_iterations) {double fx = f(x);double f_derivative_x = f_derivative(x);if (std::abs(fx) < epsilon) {std::cout << "Found solution: x = " << x << std::endl;return x;}if (std::abs(f_derivative_x) < epsilon) {std::cout << "Derivative is close to zero. Exiting." << std::endl;return std::numeric_limits<double>::quiet_NaN(); // 返回NaN表示迭代失败}x = x - fx/f_derivative_x;++iteration;}std::cout << "Maximum iterations reached. Exiting." << std::endl;return std::numeric_limits<double>::quiet_NaN(); // 返回NaN 表示迭代失败}int main() {double x0 = 1.0; // 初始值double epsilon = 1e-6; // 精度要求int max_iterations = 1000; // 最大迭代次数double root = newton_method(x0, epsilon, max_iterations);return 0;}```以上代码中,我们定义了两个函数f(x)和f_derivative(x),分别表示了要求解的非线性方程和该方程的导数。
数值分析算法C语言程序

数值分析算法C语言程序数值分析是研究数学问题的近似解法的一门学科,其中包括了各种数值方法和算法。
本文将介绍数值分析中的常见算法,并给出相应的C语言程序。
1.二分法(Bisection Method)二分法是一种求函数零点的简单且常用的方法。
该方法的基本思想是通过不断将区间进行二分,并比较中点处函数值的正负来找到零点所在的区间。
```c#include <stdio.h>double f(double x)return x * x - 2;double bisection(double a, double b, double eps)double c;while ((b - a) > eps)c=(a+b)/2;if (f(c) == 0)break;}else if (f(a) * f(c) < 0)b=c;}elsea=c;}}return c;int maidouble a = 0.0;double b = 2.0;double result = bisection(a, b, eps);printf("The root is: %lf\n", result);return 0;```2.牛顿迭代法(Newton's Method)牛顿迭代法是一种高效的求函数零点的方法。
该方法的基本思想是通过对函数进行线性逼近,不断逼近函数的零点。
```c#include <stdio.h>#include <math.h>double f(double x)return x * x - 2;double df(double x)return 2 * x;double newton(double x0, double eps) double x = x0;double deltaX = f(x) / df(x);while (fabs(deltaX) > eps)deltaX = f(x) / df(x);x = x - deltaX;}return x;int maidouble x0 = 2.0;double result = newton(x0, eps); printf("The root is: %lf\n", result); return 0;```3.高斯消元法(Gaussian Elimination)高斯消元法是一种用于求解线性方程组的方法。
数值分析-代码

注:凡“in.open("C:\\Users\\Administrator\\Desktop\\data-拉格朗日插值.txt")”等里面的路径自己合理修改。
1-1.拉格朗日插值(用一系列已知点求近似函数,并估计未知点的函数值)#include<fstream.h>#include<stdlib.h>int n; //插值节点个数double *X,*Y;//插值节点数组double x;//估计点void read(){double temp;ifstream in;in.open("C:\\Users\\Administrator\\Desktop\\data-拉格朗日插值.txt");if(!in){cout<<"can not open the file !"<<endl;exit(0);}in>>n;X=new double[n];Y=new double[n];for(int i=0;i<n;i++){in>>temp;X[i]=temp;cout<<temp<<" ";in>>temp;Y[i]=temp;cout<<temp<<"\n";}in>>temp;x=temp;cout<<"x="<<temp<<endl;in.close();}void main(){double t,y=0;read();for(int k=0;k<n;k++){t=1;for(int i=0;i<n;i++)if(k!=i)t=(x-X[i])/(X[k]-X[i])*t;y=y+t*Y[k];}cout<<"y="<<y<<endl;}1-2.埃特金逐步插值法(同上)#include<fstream.h>#include<stdlib.h>double *X,*Y; //插值节点(x,y)double x; //带估点int n; //N个插值点,插n-1次。
数值分析中的各种公式C 代码

二分法2.2 算法步骤步骤1:准备计算f(x)在有根区间[a,b]端点处的值f(a),f(b).步骤2:二分计算f(x)在区间中点(a+b)/2处的值f((a+b)/2).步骤3:判断若f((a+b)/2)=0,则(a+b)/2即是根,计算过程结束,否则检验;若f((a+b)/2)f(a)<0,则以(a+b)/2代替b,否则以(a+b)/2代替a.反复执行步骤2和步骤3,直到区间[a,b]的长度小于允许误差e,此时中点(a+b)/2即为所求近似根。
2.3 程序流程图3 实验结果分析#include"stdio.h"void main(){float a,b,e,x,c;int k=0,n=1;scanf("%f,%f,%f",&a,&b,&e);while(n==1){x=(a+b)/2;c=(x*x*x-x-1)*(a*a*a-a-1);if(c<0){b=x;if(b-a<=e){printf("%f,%d\n",x,k);break;}else k++;}else{ if(c==0) { printf("%f,%d\n",x,k);break;}else { a=x; if(b-a<=e) { printf("%f,%d\n",x,k);break;}else k++;}}}}高斯塞德尔迭代法求方程组解 高斯主元素消去法求方程组解2.2 算法步骤高斯塞德尔迭代法:步骤1:给定初值)0(1)0(2)0(1,...,,n x x x ,精度ε,最大容许迭代次数M,令k=1。
步骤2:对 i=1,2,…,n 依此计算)0()1()0()1(01)0()1()1().(i i ii i iinj j j ij iix x x x e a x a xx→-=-=∑≠=步骤3:求出 e=}{max 1i ni e ≤≤,若 e<ε,则输出 )0(i x (i=1,2,..,n ),停止计算。
数值计算方法实验程序源代码

上机实验1. 秦九韶算法:编程求多项式P(x)=(((0.0625x+0.0425) x+1.912) x+2.1296在x=1.0处的值。
#include "stdio.h"main(){static float a[]={2.1296,1.912,0.0425,0.0625};float y;int i;float x=1.0;clrscr();y=a[3];for (i=2;i>=0;i--)y=y*x+a[i];printf("x=%4.2f,y=%6.4f",x,y);}2. 二分法:方程f(x)=x3-x-1=0,利用逐步搜索法确定一个有根区间。
#include "stdio.h"#include "math.h"#define f(x) (x*(x*x-1)-1)#define e 0.005main(){int i=0;float x,a=1,b=1.5,y=f(a);if(y*f(b)>=0){printf("\nThe range is error!"); return;}elsedo{ x=(a+b)/2;printf("\nx%d=%6.4f",i,x);i++;if (f(x)==0) break;if(y*f(x)<0)b=x;elsea=x;}while(fabs(b-a)>e);printf("\nx=%4.2f",x);} #include "stdio.h"#include "math.h"#define f(x) ((x*x-1)*x-1)main(){int i;float x,a=1,b=1.5,y=f(a);if(y*f(b)>=0){printf("\nThe range is error!"); return;}elsefor(i=0;i<=6;i++)/*次数限制结束*/ {x=(a+b)/2;printf("\nx%d=%6.4f",i,x);if (f(x)==0) break;if(y*f(x)<0)b=x;elsea=x;}printf("\nx=%4.2f",x);}3. 迭代法:(1) 求方程f(x)=x-10x+2=0的一个根#include "stdio.h"#include "math.h"main(){float x0,x1=1;int i=1;do{x0=x1;x1=log10(x0+2);printf("\nx%d=%6.4f",i,x1);i++;}while(fabs(x1-x0)>=0.00005);printf("\nx=%6.4f",x1);printf("\nf(x)=%6.4f",fabs(x1-pow(10,x1)+2)) ;} (2) 求方程x=e-x在0.5附近的根。
数值计算(二分法、简单迭代法、Newton迭代法、弦截法(割线法、双点弦法))解读

2.2 简单迭代法
思想:迭代法是一种逐次逼近的方法,它是固定公式反复校正跟的近似值,使之逐步精确,最后得到精度要求的结果。
步骤:1.构造迭代公式f(x),迭代公式必须是收敛的。
2.计算x1,x1=f(x0).
3.判断|x1-x0|是否满足精度要求,如不满足则重复上述步骤。
k
xk
f(xk)
1
-1.01393
0.0415678
2
-1.0002
0.000607777
3
-0.999999
-3.11969e-006
4
-1
2.11001e-010
表4-2
区间[1.5,1.8]结果x=1.69028
k
xk
f(xk)
1
1.64403
-0.676455
2
1.68071
-0.151106
14
1.69029
1
1.725
8
1.69043
15
1.69029
2
1.6875
9
1.69014
16
1.69029
3
1.70625
10
1.69028
17
1.69028
4
1.69687
11
1.69036
18
1.69028
5
1.69219
12
1.69032
6
1.68984
13
1.6903
表1-3
简单
初值-1.5
12
-1.50489
18
-1.50505
表2-1
二分法牛顿不动点代码

#include<stdio.h>#include<math.h>#define true 1#define false 0#define ZERO 1.0E-20//二分法f1(){ double A,FA,B,FB,C,P,FP,TOL;int I,NO,OK,FLAG;FILE *OUP[1];double absval(double);double F(double);void INPUT(int *, double *, double *, double *, double *, double *, int *);void OUTPUT(FILE **, int *);INPUT(&OK, &A, &B, &FA, &FB, &TOL, &NO);if (OK) {OUTPUT(OUP, &FLAG);I = 1; /*步骤一*/OK = true; /* 步骤二*/while ((I<=NO) && OK) {C = (B - A) / 2.0; /* 步骤三*/P = A + C;/* 步骤四*/FP = F(P);if (FLAG == 2) fprintf(*OUP,"%3d %15.8e %15.7e \n",I,P,FP);if ((absval(FP)<ZERO) || (C<TOL)) {fprintf(*OUP,"\nApproximate solution P = %11.8f \n",P);fprintf(*OUP,"with F(P) = %12.8f\n",FP);fprintf(*OUP,"Number of iterations = %3d",I);fprintf(*OUP," Tolerance = %15.8e\n",TOL);OK = false;}else { I++; /* 步骤五*/ /* 步骤六*/if ((FA*FP) > 0.0) {A = P; FA = FP;}else {B = P; FB = FP;}}}if (OK) { fprintf(*OUP,"\nIteration number %3d",NO);fprintf(*OUP," gave approximation %12.8f\n",P);fprintf(*OUP,"F(P) = %12.8f not within tolerance : %15.8e\n",FP,TOL);}fclose(*OUP);}return 0;} /* 步骤七*/double F(double X) /* 所求函数*/{double f;f = ( X + 4.0 ) * X * X - 10.0;return f;}void INPUT(int *OK, double *A, double *B, double *FA, double *FB, double *TOL, int *NO) { double X;char AA;printf("二分法.\n");printf("是否继续输入?\n");printf("Enter Y or N\n");scanf("%c",&AA);if ((AA == 'Y') || (AA == 'y')) {*OK = false;while (!(*OK)) {printf("输入A,B的值\n");scanf("%lf %lf", A, B);if (*A > *B) {X = *A; *A = *B; *B = X;}if (*A == *B) printf("A 不等于B\n");else {*FA = F(*A);*FB = F(*B);if (*FA*(*FB) > 0.0) printf("F(A) 和F(B) 有相同的符号\n");else *OK = true;}}*OK = false;while(!(*OK)) {printf("输入容许误差值\n");scanf("%lf", TOL);if (*TOL <= 0.0) printf("Tolerance must be positive\n");else *OK = true;}*OK = false;while (!(*OK)) {printf("输入允许的最大迭代次数\n");scanf("%d", NO);if (*NO <= 0) printf("Must be positive integer\n");else *OK = true;}}else {printf("The program will end so that the function F can be created\n");*OK = false;}}void OUTPUT(FILE **OUP, int *FLAG)/*输出函数*/{ char NAME[30];printf("选择输出目标\n");printf("1. Screen\n");printf("2. Text file\n");printf("Enter 1 or 2\n");scanf("%d", FLAG);if (*FLAG == 2) {printf("Input the file name in the form - drive:name.ext\n");printf("A:OUTPUT.DTA\n");scanf("%s", NAME);*OUP = fopen(NAME, "w");}else *OUP = stdout;fprintf(*OUP,"Bisection Method\n");printf("选择输出结果的数量\n");printf("1. Answer only\n");printf("2. All intermeditate approximations\n");printf("Enter 1 or 2\n");scanf("%d", FLAG);if (*FLAG == 2) fprintf(*OUP, " I P F(P)\n"); }double absval(double val) /*绝对值函数*/{if (val >= 0) return val;else return -val;}//不动点迭代法void f2(){ double TOL,P0,P;int I,NO,FLAG,OK;//char AA;FILE *OUP[1];void INPUT(int *, double *, double *, int *);void OUTPUT(FILE **, int *);double absval(double);double G(double );INPUT(&OK, &P0, &TOL, &NO);if (OK) {OUTPUT(OUP, &FLAG);I = 1; OK = true; /* 步骤一*//* 步骤二*/while((I<=NO) && OK) {/*步骤三*/P = G(P0);if (FLAG == 2) fprintf(*OUP, "%3d %15.8e\n", I, P);/* 步骤四*/if (absval(P-P0) < TOL) {/* procedure completed successfully */fprintf(*OUP, "\nApproximate solution P = %12.8f\n", P);fprintf(*OUP, "Number of iterations = %3d", I);fprintf(*OUP, " Tolerance = %14.8e\n",TOL);OK = false;}else { I++;/* 步骤五*//* 步骤六*/ P0 = P; }}if (OK) {/* 步骤七*/fprintf(*OUP, "\nIteration number %3d", NO);fprintf(*OUP, " gave approximation %12.8f\n", P);fprintf(*OUP, "not within tolerance %14.8e\n",TOL);}fclose(*OUP);}}double G(double X) /* 所求函数*/{ double g;g = X*X*X+4*X*X-10;return g;}void INPUT(int *OK, double *P0, double *TOL, int *NO)/*输入函数*/{ char AA;printf("This is the Fixed-Point Method.\n");printf("Has the function G been created in the program immediately preceding\n");printf("the INPUT function?\n");printf("Enter Y or N\n");scanf("%c",&AA);if ((AA == 'Y') || (AA == 'y')) {*OK = false;printf("Input initial approximation\n");scanf("%lf",P0);while(!(*OK)) {printf("Input tolerance\n");scanf("%lf", TOL);if (*TOL <= 0.0) printf("Tolerance must be positive\n");else *OK = true;}*OK = false;while (!(*OK)) {printf("Input maximum number of iterations - no decimal point\n");scanf("%d", NO);if (*NO <= 0) printf("Must be positive integer\n");else *OK = true;}}else {printf("The program will end so that the function G can be created\n");*OK = false;}}void OUTPUT(FILE **OUP, int *FLAG);/*输出函数*//* 绝对值函数*/double __cdecl absval(double val);//牛顿法void f3(){ double x0,x,f,tg;int n = 0;printf("请输入初始值x:");scanf("%lf",&x0);while(1) {printf("第%d次迭代:\n",n);printf("x值为%f:\n",x);f=cos(x0)-(x0);tg=-sin(x0)-1;x=x0-f/tg;if(fabs(x-x0)<=1e-4){ break;}x0=x;n++;}}void main(){int i;printf("选择计算方法:1、二分法;2、不动点迭代法;3、牛顿法");scanf("%d",&i);switch(i){case 1:f1();case 2:f2();case 3:f3();}}。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
#define N 10 //矩阵大小范围
/*
*使用已经求出的x,向前计算x(供getx()调用)
* float a[][]系数矩阵
* float x[]方程组解
* int i解的序号
* int n矩阵大小
* return公式中需要的和
*/
float getm(float a[N][N], float x[N], int i, int n)
1.
#include<iostream.h>
#include <stdio.h>
#include <math.h> //调用fabs函数。
double f(double x) //定义函数F(x)。
{
return 2*x*x*x-x-1;
}
void main()
{
double a,b,w,x;
cout<<"请输入方程根的区间[a,b]及误差w:";
typedef double (*pFun)(double x);
double getIterativeValue(double x)
{
return pow((x+1)/2,(double)1.0/3);
}
double Solve(pFun f,double x,double e,int n)
{
double res;
cin>>a>>b>>w;
x=(a+b)/2;
while(fabs(f(x))>w&&fabs(a-b)>w){ //用while循环控制中值折算的条件。
if(f(x)*f(b)<0) a=x; //进行二分,缩小求值范围。
else if(f(a)*f(x)<0) b=x;
x=(a+b)/2;
}
cout<<x<<endl;
printf("请连续输入矩阵值:");
for(i=0; i<n; i++)
{
for(j=0; j<n; j++)
scanf("%f", &a[i][j]);
}
printf("请输入右端项:");
for(i=0; i<n; i++)
{
scanf("%f", &b[i]);
}
/*显示原始矩阵*/
printf("\n原始矩阵\n");
else //计算其他x值(对于公式中的求和部分,需要调用getm()函数)
result = float((b[i]-getm(a,x,i,n))/a[i][i]);
return result;
}
void main()
{
//float a[N][N] = {{2,1,1},{1,3,2},{1,2,2}};
cout << Solve(getIterativeValue,x,e,10) << endl;
system("pause");
return 0;
}
3.
#include <iostream>
#include <cmath>
#include <iomanip>
#include <stdio.h>
using namespace std;
}
2.
#include <iostream>
#include <cmath>
#include <iomanip>
#include <stdio.h>
using namespace std;
typedef double (*pFun)(double x);
double getIterativeValue(double x)
break;
}
else
x = res;
outPrint("第%d次迭代以后x值为:%0.7lf\n ",10-n,x);
}
return res;
}
int main()
{
cout << setprecision(7);
double x,e;
cout << "输入初值和精度:" << endl;
cin >> x >> e;
//float b[N] = {4,6,5};
float a[N][N]; //系数矩阵
float b[N]; //右端项
float x[N]; //方程组解
int i,j,k;
int n=N; //矩阵大小
/*用户手工输入矩阵*/
printf("请输入系数矩阵的大小:");
scanf("%d", &n);
* loat a[N][N], float b[N], float x[N], int i, int n)
{
float result;
if(i==n-1) //计算最后一个x的值
result = float(b[n-1]/a[n-1][n-1]);
for(i=0; i<n; i++)
{
for(j=0; j<n; j++)
printf("%f ",a[i][j]);
{
return pow((x+1)/2,(double)1.0/3);
}
double Solve(pFun f,double x,double e,int n)
{
double res;
while(n--)
{
res = f(x);
if(fabs(res - x) < e)
{
outPrint("第%d次次迭代以后返回值为:%0.7lf \n",10-n,res);
{
float m = 0;
int r;
for(r=i+1; r<n; r++)
{
m += a[i][r] * x[r];
}
return m;
}
/*
*解方程组,计算x
* float a[][]系数矩阵
* float b[]右端项
* float x[]方程组解
* int i解的序号
* int n矩阵大小
}
int main()
{
cout << setprecision(7);
double x,e;
cout << "输入初值和精度:" << endl;
cin >> x >> e;
cout << Solve(getIterativeValue,x,e,10) << endl;
return 0;
}
4.
#include <stdio.h>
while(n--)
{
res = f(x);
if(fabs(res - x) < e)
{
printf("第%d次次迭代以后返回值为:%0.7lf \n",10-n,res);
break;
}
else
x = res;
printf("第%d次迭代以后x值为:%0.7lf\n ",10-n,x);
}
return res;
