凹凸性、渐近线、作图30页PPT文档
合集下载
经济数学课件 4.3函数的凹凸性

x
《经济数学基础》配套课件
定义4.3.3、4.3.4
若 lim f ( x) b,lim f ( x) b 或 lim f (x) b,
x
x
x
则称直线 y = b 为曲线 y = f (x) 的水平渐近线.
若 lim f (x) , lim f ( x) 或 lim f ( x) ,
0
0
f (x)
凹的∪
拐点 (0,1)
凸的∩
拐点 (2 3 ,1127)
凹的∪
凹区间为(,0《],经[2济3数,学基), 础凸》区配套间课为件[0, 2 3]
凹凸区间为(,0], [0, 2 3], [2 3 ,). 《经济数学基础》配套课件
例 求曲线
的拐点.
2
5
解:
y
1 3
x
3
,
y
2 9
x
3
x ( ,0) 0
2. 求
并求出 及
为 0 和不存在
的点 ;
3. 列表判别增减及凹凸区间 , 求出极值和拐点 ;
4. 求渐近线 ;
5. 确定某些特殊点 , 描绘函数图形 .
《经济数学基础》配套课件
例5. 描绘函数
的图形.
解: 1) 定义域为
图形对称于 y 轴.
2)
求关键点 y 1
2
x
e
x2 2
,
y
1
e
x2
2 (1
(0, )
y
不存在
y凹
0
凸
因此点 ( 0 , 0 ) 为曲线
的拐点 .
《经济数学基础》配套课件
练习. 求曲线
的凹凸区间及拐点.
第8节 曲线的凹凸性及渐近线

2
2
那么称在Ⅰ上的图形是(向上)凹的(或凹弧);
如果恒有
f ( x1 x2 ) f (x1) f (x2)
2
2
那么称在Ⅰ上的图形是(向上)凸的(或凸弧)。
定义:设函数 y f x在a,b内可导,则
1.如果曲线y f x在a,b内任意点的切线总位于 曲线的下方,则称曲线y f x在a,b上是凹的.
1.确定函数的定义域并求f x; 2.求出f x 0和f x不存在的点x0; 3.对于2中的每一个x0,检查f x在x0左、右两侧
邻近的符号.
例3.求曲线y 2x3 3x2 12 x 14的凹凸区间和拐点 .
解 函数的定义域为 (, ).
y y
6x2 0
6x 12, ,得x1
y 1 2
第八节 曲线的凹凸性及渐近线
一、曲线的凹凸性及拐点的判定定理 二、曲线的渐近线
一、曲线的凹凸性及其判别法
y y f (x)
y y f (x)
o
x x x1 x2 12
x
2
o x1 x1 x2 x2 x
2
定义 设在区间Ⅰ上连续,如果对Ⅰ上任意两点 x1, x2,
恒有 f ( x1 x2 ) f (x1) f (x2)
拐点是曲线凹与凸的分界点.由定理知,在拐点左右两侧
f x的符号必然异号,因而在拐点处有f x 0或者f x 不存在;反过来,f x 0的点和f x不存在的点可能是 曲线的拐点,究竟是否拐点,还要看该点处f x的符号是
否异号.
例1.判定曲线 y x3的凹凸性.
解 函数的定义域为 (, ).
y' 3x2 , y'' 6x. x 0 y'' 0.
函数的凹凸性与作图

机动 目录 上页 下页 返回 结束
6)绘图
x ( , 1) 1 (1,1)
y
1
无 定 义
(1, 3) 3
(3 , )
2
(极大)
0
(极小)
铅直渐近线 斜渐近线 特殊点
x 1 1 5 y x 4 4
( x 3) 2 y 4( x 1)
x
y
0 9 4
2 1 4
3) 判别曲线形态
x y y y
0 0
1 2
(0 , 1)
1
0
1 2 e
(1, )
(极大)
机动
(拐点)
目录 上页 下页 返回 结束
x y y y
0 0
1 2
(0 , 1)
1
0
1 2 e
(1, )
(极大)
(拐点)
4) 求渐近线
y
A
1 2
lim y 0
( k x b)
f ( x) b k lim [ ] x x x f ( x) k lim x x
(或 x )
f ( x) b lim x[ k ]0 x x x f ( x) b lim [ k ]0 x x x
b lim [ f ( x) k x]
y
C M
y f ( x)
y kxb
L
PN
有渐近线
但抛物线
x y 0 a b
无渐近线 .
o
y
x
x
o
机动
目录
上页
下页
返回
结束
1. 水平与铅直渐近线 若 则曲线
6)绘图
x ( , 1) 1 (1,1)
y
1
无 定 义
(1, 3) 3
(3 , )
2
(极大)
0
(极小)
铅直渐近线 斜渐近线 特殊点
x 1 1 5 y x 4 4
( x 3) 2 y 4( x 1)
x
y
0 9 4
2 1 4
3) 判别曲线形态
x y y y
0 0
1 2
(0 , 1)
1
0
1 2 e
(1, )
(极大)
机动
(拐点)
目录 上页 下页 返回 结束
x y y y
0 0
1 2
(0 , 1)
1
0
1 2 e
(1, )
(极大)
(拐点)
4) 求渐近线
y
A
1 2
lim y 0
( k x b)
f ( x) b k lim [ ] x x x f ( x) k lim x x
(或 x )
f ( x) b lim x[ k ]0 x x x f ( x) b lim [ k ]0 x x x
b lim [ f ( x) k x]
y
C M
y f ( x)
y kxb
L
PN
有渐近线
但抛物线
x y 0 a b
无渐近线 .
o
y
x
x
o
机动
目录
上页
下页
返回
结束
1. 水平与铅直渐近线 若 则曲线
《函数凹凸性》PPT课件

y cos x sin x .
令 y 0,
得
x1
3 4
,
x2
7 4
.
f (3) 2 0, f (7) 2 0,
4
4
中值定理与导数的应用
10
在[0,2]内曲线有拐点为 (3 ,0), (7 ,0).
4
4
中值定理与导数的应用
11
二、渐近线
定义: 当曲线 y f ( x) 上的一动点 P 沿着曲线 移向无穷点时, 如果点 P 到某定直线 L 的距离 趋向于零, 那么直线 L 就称为曲线 y f ( x) 的 一条渐近线.
22
lim
x0
f
(x)
4( x 1)
lim[
x0
x2
2]
,
得铅直渐近线 x 0.
列表确定函数升降区间,凹凸区间及极值点和拐点:
x (,3) 3 (3,2) 2 (2,0) 0 (0,)
f ( x)
0 不存在
f (x)
0
f (x)
拐点
(3, 26) 9
极值点
3
间
断 点
中值定理与导数的应用
解 D : (,), 无奇偶性及周期性.
f ( x) (3x 1)(x 1), f ( x) 2(3x 1).
令 f ( x) 0, 得驻点 x 1 , x 1. 3
令 f ( x) 0,
得特殊点 x 1 . 3
补充点: A (1,0),
B (0,1), C (3 , 5). 28
f (x)在点 x0处二阶导数不存在 .
中值定理与导数的应用
6
例2 求曲线 y 3x4 4x3 1的拐点及
凹、凸的区间.
高等数学导数应用二凹凸拐点图形PPT课件

从而, 点 (x0, f (x0 )) 为曲线 y f (x) 的拐点 .
你能由以上的几个定理归纳出 求曲线拐点的步骤吗?
第28页/共56页
求拐点一般步骤
求曲线 y f (x) 拐点的一般步骤 : (1) 求 f (x) 的定义域 (或确定讨论区间 ) ; (2) 计算 f (x) , f (x) , (如需要可求出 f (x)) ; (3) 求拐点可疑点 : 使 f (x) 0 的点和 f (x) 不存在的点 ; (4) 根据定理判别可疑点是 否确为拐点 .
且仅在孤立点处出现 f (x) 0 .
第24页/共56页
于是 f (x) (x0 , x0x ) , f (x) (x0 x, x0 ) , 故 f (x) 在 x x0 处取极小值, 从而必有 f (x0 ) ( f (x)) xx0 0 .
使 f (x) 0 及 f (x) 不存在的点 ,
第26页/共56页
定理 ( 判别拐点的充分条件 )
设 f (x) C( I ) , f (x) 在 U(x0 ) (x0 I )内三阶可导. 若 f (x0 ) 0 , 且 f (x0 ) 0 , 则
点 (x0 , f (x0 )) 为曲线 y f (x) 的拐点 .
第27页/共56页
证 由于 f (x0 ) 0 , 故不妨设 f (x0 ) 0 .
成立 , 则称曲线
y f (x) 在区间 I 上是凹的 ;
第9页/共56页
例1
分析立方抛物线 y x3 的凹凸性.
分析
f ( x1 x2 ) x13 3x12 x2 3x1x22 x23
2
8
1( 2
f
(x1)
f
(x2 ))
3.5凹凸性与函数图形描绘PPT课件

3.5 曲线的凹凸性与函数作图
• 一.曲线的凹凸性及拐点 • 二.函数图形的描绘
一、凹凸性及拐点
y
y f (x) B
凹
A
oa
bx
y f (x)
y
B
凸
A oa
bx
1.定义 设函数f(x)在区间I上除端点外都可导,
x0为I的任一内点,若对 x I( x x0 ),恒有
f (x) f (x0 )(x x0 ) f (x0 ) ( f (x) f (x0)(x x0) f (x0)) 则称函数曲线 y 在f (区x)间I上是(向上)凹 的. (凸)
5 补充点,如与坐标轴的 交点、间断点、始点、 终点.
6 光滑连接各点,绘出函 数图形。
例5
作函数 ( x)
1
x2
e2
的图形.
2
解 1 [0,), (偶函数, 图形关于y轴对称)
2 ( x)
令 ( x) 0,
x
x2
e 2,
2
(
x)
(
x
1)(
x
1)
e
x2 2
.
2
得驻点 x 0,
令 ( x) 0,
得 x 1, x 1.
3°列表确定函数增减区间,凹凸区间及极值点 与拐点:
x
( x) ( x) ( x)
0 (0,1) 1 (1,)
0
0
1 2
拐点
(1, 1 ) 2e
4 lim ( x) lim
1
x2
e 2 0,
得水平渐近线
y 0.
x
x 2
( x)
1
x2
e2
2
写在最后
• 一.曲线的凹凸性及拐点 • 二.函数图形的描绘
一、凹凸性及拐点
y
y f (x) B
凹
A
oa
bx
y f (x)
y
B
凸
A oa
bx
1.定义 设函数f(x)在区间I上除端点外都可导,
x0为I的任一内点,若对 x I( x x0 ),恒有
f (x) f (x0 )(x x0 ) f (x0 ) ( f (x) f (x0)(x x0) f (x0)) 则称函数曲线 y 在f (区x)间I上是(向上)凹 的. (凸)
5 补充点,如与坐标轴的 交点、间断点、始点、 终点.
6 光滑连接各点,绘出函 数图形。
例5
作函数 ( x)
1
x2
e2
的图形.
2
解 1 [0,), (偶函数, 图形关于y轴对称)
2 ( x)
令 ( x) 0,
x
x2
e 2,
2
(
x)
(
x
1)(
x
1)
e
x2 2
.
2
得驻点 x 0,
令 ( x) 0,
得 x 1, x 1.
3°列表确定函数增减区间,凹凸区间及极值点 与拐点:
x
( x) ( x) ( x)
0 (0,1) 1 (1,)
0
0
1 2
拐点
(1, 1 ) 2e
4 lim ( x) lim
1
x2
e 2 0,
得水平渐近线
y 0.
x
x 2
( x)
1
x2
e2
2
写在最后
函数性态的研究(最值、凹凸性与渐近线).ppt

驻点
可能最值
极值点处 端点处
f 不存在的点
(应是f 的连续点)
(3) 如何判定:
驻点
可能最值
极值点处 端点处
f
不存在的点
(应是f 的连续点)
(3) 如何判定: 若 f (x)C ,则
只要比较 f 在驻点、 f 不存在的点、端点处的值, 最大者为最大值,最小者为最小值.
两个结论:
两个结论:
(1) 若 f (x)C[a, b] ,且在 (a, b) 内有唯一极值点 x0 ,
(6)
f
二阶连续可导, y sin
f ( x2 ) ,
求d2y .
dx 2
推广到一般情况: 设 f ( x) 在 x0 处有 n 阶导数, f ( x0 ) f (x0 ) f (n1)(x0 ) 0 ,且 f (n)( x0 ) 0 .则
10 n为奇数时,点 x0 为非极值点; 20 n为偶数时,
“ f ( x) 0 ”为 f ( x) 0 ”,则为严格凹函数. 反之未必成立,即 Thm 7 及注仅是充分条件,非必要.
例 9 证: ( x y)lnx y xlnx ylny , x, y0且 x y ;
2
Proof. 设 f ( x) xlnx , x0 ,(Step1 找准函数, )
Def. 2 设 f ( x) C[a, b] .对 x 1 , x2 (a, b) ,
及 0 1 ,若总有
f ( x1 (1 )x2) f (x1) (1 ) f (x2) (a, b) 内的凸函数; f ( x1 (1 )x2) f (x1) (1 ) f (x2) (a, b) 内的凹函数.
补充作业 (1)
ae2x cos x, x 0,
微积分4.4曲线的凹凸性、拐点与渐近线

动点M沿着曲线无限远离原点 y
y=ƒ(x)
移动时, 若该动点M到某直线L 的距离无限趋近于零 (如右图),
αM˘• Q •
•
L: y=ax+b
则称此直线L是曲线 y = ƒ(x)
o »α
x
的渐近线.
曲线 y = ƒ(x) 的渐近线按其与 x 轴的位置关系, 可分为
以下三种:
18
1.水平渐近线
定义4.4.5 如果曲线 y = ƒ(x)的定义域是无限区间, 且有
x -
x
两边同除以 x 并取极限有
f (x) lim[ a]0 x x-
或 lim[f(x)a]0 x x
即
f(x) lim a x x-
或 lim f(x) a x x
从而得到求 y = ƒ(x) 的斜渐近线 y = ax + b 的公式为:
a
f (x) lim
x x
或
b
lim[
x
f
( x)
lim
1
x x 1
x x1
所 以 y x 1 是 曲 线 的 一 条 斜 渐 近 线 .
25
四*. 函数图形的描绘
借助于一阶导数的符号, 可以确定函数图形在哪个区间 上上升, 在哪个区间上下降, 在什么地方有极值点; 借助于 二阶导数的符号, 可以确定函数图形在哪个区间上为凹, 在哪个区间上为凸, 在什么地方有拐点. 知道了函数图形 的升降、凹凸以及极值点和拐点后, 也就可以掌握函数的 性态, 并把函数的图形画得准确.
ax]
a
f (x) lim
x x
b
lim [
x
f
(x)
ax]
凹凸性、渐近线、作图资料

[解] 定义域:(,), 是偶函数.
因 为 lim e x2 0, 所 以 直 线y 0 x
是 水 平 渐 近 线.
y 2xex2
y 2ex2 (2x2 1)
令 y 0 驻点:x 0
令 y 0 x 1
10/15/2019
令 y '' 0, 得 x 1 , 没有二阶导数不存在的点 列表如下:5
x
(,
1 )
5
y '' -
y凸
1
5
0
8 25
拐点
(1 , ) 5
+
凹
在 x 1 两侧 y ''符号发生改变,则(1 , 8 )是拐点.
5
5 25
1
例3.求曲线 y x3 的拐点.
1
解:函数 y x3 的定义域为 (, )
函数的凹凸性、渐近线 与作图
一、函数的凹凸性 二、曲线的渐近线 三、函数作图
10/15/2019
1
一、函数的凹凸性
若在某区间内,曲线上每一点的切线都位 于该曲线的下方,则称曲线在该区间内是凹的; 若曲线上每一点的切线都位于该曲线的上方,
则称曲线在该区间内是凸的.
(a)中曲线上任意两点的割线在曲线的上方
f (x2 )
则称f (x)在该区间上的图形是凸的.
10/15/2019
4
凹曲线的一阶导数变化规律:
若 f (x)是凹函数,则 f (x)单调增加;
10/15/2019
5
凸曲线的一阶导数变化规律:
若 f (x)是凸函数,则 f (x)单调减少.
10/15/2019
6
因 为 lim e x2 0, 所 以 直 线y 0 x
是 水 平 渐 近 线.
y 2xex2
y 2ex2 (2x2 1)
令 y 0 驻点:x 0
令 y 0 x 1
10/15/2019
令 y '' 0, 得 x 1 , 没有二阶导数不存在的点 列表如下:5
x
(,
1 )
5
y '' -
y凸
1
5
0
8 25
拐点
(1 , ) 5
+
凹
在 x 1 两侧 y ''符号发生改变,则(1 , 8 )是拐点.
5
5 25
1
例3.求曲线 y x3 的拐点.
1
解:函数 y x3 的定义域为 (, )
函数的凹凸性、渐近线 与作图
一、函数的凹凸性 二、曲线的渐近线 三、函数作图
10/15/2019
1
一、函数的凹凸性
若在某区间内,曲线上每一点的切线都位 于该曲线的下方,则称曲线在该区间内是凹的; 若曲线上每一点的切线都位于该曲线的上方,
则称曲线在该区间内是凸的.
(a)中曲线上任意两点的割线在曲线的上方
f (x2 )
则称f (x)在该区间上的图形是凸的.
10/15/2019
4
凹曲线的一阶导数变化规律:
若 f (x)是凹函数,则 f (x)单调增加;
10/15/2019
5
凸曲线的一阶导数变化规律:
若 f (x)是凸函数,则 f (x)单调减少.
10/15/2019
6
第四节 曲线的凹向,渐近线及图像的描绘-PPT文档资料

(1) f(x)0,则f(x)在[a,b]上的图形是上凹的;
(2) f(x)0,则f(x)在[a,b]上的图形是下凹的.
上一页下一页 返回
例1 判 断 曲 线 y x 3的 凹 向 . DR
解 y3x2, y6x, 当x0时,y 0, 曲 线 在 ( ,0 ] 为 下 凹 的 ; 当x0时,y 0, 曲 线 在 [ 0 , ) 为 上 凹 的 ; 注意到, 点 ( 0 , 0 ) 是 曲 线 由 下 凹 变 上 凹 的 分 界 点 .
上一页下一页 返回
三、作图举例
例5 作函 f(x)数 4(x x 21)2的图 . 形 解 D:x0, 非奇非偶函数,且无对称性.
f(x)4(xx3 2),
f(x)8(xx4 3).
令f(x)0, 得驻 x点 2,
令 f(x)0, 得特殊 x点 3.
lx i m f(x)lx i [m 4(x x 21)2] 2
上一页下一页 返回
上一页下一页 返回
lx i0m f(x)lx i0[m 4(x x 21)2] , 得铅垂渐近x线0.
列表确定函数升降区间,凹向区间及极值点和拐点:
x ( ,3) 3 (3,2)2 (2,0) 0 (0,)
f(x) 0
不存在
f(x)
0
f (x)
拐点
(3, 26) 9
上一页下一页 返回
例2 求 曲 线 y 3 x 4 4 x 3 1 的 拐 点 及 凹 向 .
解 D :(, )
y1x 2 31x 2 2, y36x(x2).
令y0,
得x1
0,
x2
2. 3
3
x (,0)
0
(0, 2 3)
高数课件14凹凸性

凹凸性与光滑性 的应用:在优化 问题、微分方程 等领域有广泛应 用
凹凸性与函数的单调性
凹凸性:函数在某点处的二阶导数符号决定了该点的凹凸性
单调性:函数在某点处的一阶导数符号决定了该点的单调性
凹凸性与单调性的关系:凹凸性与单调性是函数在某点处的二阶导数和一阶导数的符号决定的
凹凸性与单调性的应用:在解决实际问题时,可以利用凹凸性与单调性来判断函数的极值和拐 点
利用极限判断: 如果极限存在且 大于0,则为凹 函数;如果极限 存在且小于0, 则为凸函数。
03
凹凸性的性质
凹凸函数的性质
01 02
03 04
05 06
凸函数:对于任意x1, x2, y1, y2,若x1 < x2,则f(x1) < f(x2) 凹函数:对于任意x1, x2, y1, y2,若x1 < x2,则f(x1) > f(x2) 凸函数的二阶导数大于等于0
正二阶导数:函数在该点处 为凸函数
负二阶导数:函数在该点处 为凹函数
注意事项:凹凸性判定法只 适用于二阶可导的函数
06
凹凸性的扩展知识
凹凸性的连续性和可微性
凹凸性的连续性:凹凸性是函数 在某点附近的局部性质,与函数 的连续性无关
凹凸性的可导性:凹凸性是函数 在某点附近的局部性质,与函数 的可导性无关
凹凸性与函数极值的关系
凹凸性是函数在某点附近的性质,与函数在该点的极值有关 凸函数在极小值点处具有凹性,凹函数在极大值点处具有凸性 凸函数的极小值点处,其导数大于等于0 凹函数的极大值点处,其导数小于等于0 凸函数的极小值点处,其二阶导数大于等于0 凹函数的极大值点处,其二阶导数小于等于0
感谢观看
汇报人:
曲线的凹凸性、拐点与渐近线

x1 x2 f ( x 1 ) f ( x2 ) f( ) , 2 2 则称 f ( x )在 I 上的图形是(向上)凸的(凸弧)。 x x y y f( )
如果恒有
1
2
f ( x1 ) f ( x2 ) f ( x1 ) 2 x x2 f( 1 ) 2 x1 x2 2
f ( x2 )
2013-9-12 9
§2.4.2 曲线的凹凸性、拐点与渐近线
注 如果 f ( x) (1)lim 不存在; x x f ( x) (2)lim a , 但 lim[ f ( x ) ax ]不存在, x x x 则可以判断y f ( x )不存在斜渐近线。
2013-9-12
§2.4.2 曲线的凹凸性、拐点与渐近线
1.函数的凹凸性与拐点 定义1:设 f ( x )在区间 I 上连续,如果对于 I 上任意两点 x1 , x2, x1 x2 f ( x 1 ) f ( x2 ) 恒有 f( ) , 2 2 则称 f ( x )在 I 上的图形是(向上)凹的(凹弧);
2013-9-12
13
§2.4.2 曲线的凹凸性、拐点与渐近线
x2 例8 求曲线 f ( x ) 的渐近线。 x 1
2013-9-12
14x x 来自则直线 y C 是曲线 y f ( x )的水平渐近线。
(2)垂直渐近线 若曲线 y f ( x )在点 x0处间断,且 lim f ( x ) 或 lim f ( x ) ,
x x0 x x0
则直线 x x0是曲线 y f ( x )的垂直渐近线。 f ( x) (3)斜渐近线 若 lim a , lim[ f ( x ) ax ] b, x x x 则直线y ax b是曲线 y f ( x )的斜渐近线。
如果恒有
1
2
f ( x1 ) f ( x2 ) f ( x1 ) 2 x x2 f( 1 ) 2 x1 x2 2
f ( x2 )
2013-9-12 9
§2.4.2 曲线的凹凸性、拐点与渐近线
注 如果 f ( x) (1)lim 不存在; x x f ( x) (2)lim a , 但 lim[ f ( x ) ax ]不存在, x x x 则可以判断y f ( x )不存在斜渐近线。
2013-9-12
§2.4.2 曲线的凹凸性、拐点与渐近线
1.函数的凹凸性与拐点 定义1:设 f ( x )在区间 I 上连续,如果对于 I 上任意两点 x1 , x2, x1 x2 f ( x 1 ) f ( x2 ) 恒有 f( ) , 2 2 则称 f ( x )在 I 上的图形是(向上)凹的(凹弧);
2013-9-12
13
§2.4.2 曲线的凹凸性、拐点与渐近线
x2 例8 求曲线 f ( x ) 的渐近线。 x 1
2013-9-12
14x x 来自则直线 y C 是曲线 y f ( x )的水平渐近线。
(2)垂直渐近线 若曲线 y f ( x )在点 x0处间断,且 lim f ( x ) 或 lim f ( x ) ,
x x0 x x0
则直线 x x0是曲线 y f ( x )的垂直渐近线。 f ( x) (3)斜渐近线 若 lim a , lim[ f ( x ) ax ] b, x x x 则直线y ax b是曲线 y f ( x )的斜渐近线。
函数的凹凸性与作图.ppt

机动 目录 上页 下页 返回 结束
例5:证明不等式
例5.4 例5.5
1 (xn yn ) ( x y )n (x 0, y 0, x y, n 1)
2
2
证明:设 f (t) tn (t 0,n 1) 则
f (t) ntn1, f (t) n(n 1)tn2,
当 t 0,n 1 时,有 f (t) 0
x x x k lim f (x)
x x
(或x )
lim [ f (x) k b ] 0
x x
x
b lim [ f (x) kx]
x (或x )
机动 目录 上页 下页 返回 结束
例2. 求曲线
的渐近线 .
解: y
x3
, lim y ,
(x 3)(x 1) x3
(或x 1)
即上述 f(t)为下凸函数,于是对任意 x 0, y 0 有:
1 (xn yn) ( x y)n
2
2
二、 曲线的渐近线
定义3 . 若曲线 C上的点M 沿着曲线无限地远离原点
时, 点 M 与某一直线 L 的距离趋于 0, 则称直线 L 为
曲线C 的渐近线 .
y
y f (x)
或为“纵坐标差” C M y k x b
例如, 双曲线
L PN
o
x
有渐近线
x y0
y
ab
但抛物线
无渐近线 .
ox
机动 目录 上页 下页 返回 结束
1. 水平与铅直渐近线
若
则曲线
有水平渐近线 y b.
(或x )
若
则曲线
有垂直渐近线 x x0 .
(或x x0 )
4.6函数的凹凸渐近线图形
例5 求曲线y x2 的渐近线. 1 x
解 无水平渐近线,x=-1为垂直渐近线.
又 lim f ( x) lim x 1
x x
x 1 x
所以
lim [ f (x) ax] lim [ x2 x] 1
x
x 1 x
所 以 b 1
a1
于是曲线有斜渐近线 y x 1
注意: 如果
(1) lim f ( x) 不存在; x x
第六节 函数的凸性(concavity) 、曲线的拐点
(point of inflexion)及渐近线(asymptote)
一、函数的凸性、曲线的拐点
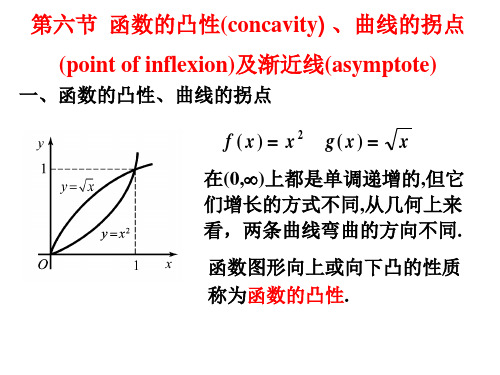
f (x) x2 g(x) x
在(0,)上都是单调递增的,但它 们增长的方式不同,从几何上来 看,两条曲线弯曲的方向不同.
函数图形向上或向下凸的性质 称为函数的凸性.
y
g(x) x 1
o f (x) x2 1
x
C
B
D A
f '( x) 0
递增
y
y
o
x1
x1 x2 2
x x2
图形上任意弧段在弦的下方
f
x1
2
x2
f x1
2
f x2
o
x1 x1 x2
x2
x
2
图形上任意弧段在弦的上方
f
x1
2
x2
f x1
2
f x2
定义1:设 f (x)在区间 I 上连续,
驻点、不可导点等; 4.确定函数的单调区间、极值点、凸凹区间以及拐点; 5.求函数的渐近线; 6.综合以上讨论画出函数图像。
下凸、单调增, 上凸、单调增,
下凸、单调减, 上凸、单调减,
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(1)求函数的定义域; (2)求二阶导数; (3)求定义域内使二阶导数等于零
或二阶导数不存在的点; (4)检验各点两侧二阶导数的符号,如果
符号不同,该点就是拐点的横坐标;
(5)求出拐点的纵坐标.
例2.求曲线 y5x33x27x1凹、凸区间 及拐点.
解:函数的定义域为 (,)
y'15x26x7, y''30x6
为 曲 线 yf(x)的 拐 点 .
y
y f(x)
定理1:(拐点必要条件)
设 f (x)有二阶导数,
(•x0, f(x0)
若(x0, f (x0 ))为 f (x)的
x
拐点,则有f (x0 ) 0.
o x0
2020/4/3
7
定理2(拐点的充分条件)
设f 在点x0的某邻域内有二阶, 导 若f 在x0两侧异号 ,则(x0, f (x0))是f 的一 个拐点 .
(1)若 在 (a, b)内f(x)0, 则f(x)在 [a, b]是 凹 函 数 ;
(2)若 在 (a, b)内f(x)0, 则f(x)在 [a, b]是 凸 函 数 .
2020/4/3
6
(三 ) 拐点
设 点 (x0,f(x0))是 曲 线 yf(x)上 的 一 个 点 ,
在 该 点 两 侧 曲 线 凹 凸 性 相 反 ,则 称 点 (x0,f(x0))
x1 , x2恒 有 :
f
x1
2
x2
f ( x1 ) 2
f (x2)
则 称 f (x)在 该 区 间 上 的 图 形 是 凹 的 ;如 果 恒 有 :
f
x1
2
x2
f ( x1 ) f ( x2 ) 2
则 称 f (x)在 该 区 间 上 的 图 形 是 凸 的 .
2020/4/3
3
凹曲线的一阶导数变化规律:
-5
0
5
x
ezplot('x*(x-1)*y=1',[-10 10])
10
21
(2)水平渐近线 若limf(x)b,则 直y线 b是 曲
x (x )
yf(x)的水平渐 . 近线
注意:只有当函数的定义域是无穷区间时, 其曲线才有可能存在水平渐近线.
2020/4/3
22
对于函数 f (x) sin x
2020/4/3
8
例1.判断曲线 y x 4 的凹凸性.
解:
y 4 x3 , y 12x2
当x 0时,y 0; x 0时 , y 0,
y Ox
故曲线 y x 4 在 (, ) 上是凹的.
说明:若在某点二阶导数为0,在其两侧二 阶导数不变号,则曲线的凹凸性不变 .
求拐点的一般步骤:
lim fxax b
x
则 yaxb是曲线 yfx的一条斜渐近线.
y'
1
2
x 3,
y
''
2
5
x3
2
3
9
9x3 x2
当 x 0 时, y '' 不存在. 当 x 0 时, y '' 0; 当 x 0 时, y '' 0, 在 x 0 的两侧,y '' 的符号发生改变.点
( 0 , 0 ) 是该曲线的拐点.
y=x1/3
3
2
1
y
0
-1
-2
--310
-5
0
5
y
y f(x)
P
•
ykxb
o
2020/4/3
M
x
17
曲线渐近线的分类 (1)铅直渐近线
y xa
若 lim f ( x ) ( ) x a
(或 lim f ( x) ( ))
x a
oa x
则直线 xa
y f(x)
为 曲 线 y f ( x )的
铅直渐近线.
2020/4/3
18
y
ytaxn y ycoxt
一、函数的凹凸性
若在某区间内,曲线上每一点的切线都位 于该曲线的下方,则称曲线在该区间内是凹的; 若曲线上每一点的切线都位于该曲线的上方,
则称曲线在该区间内是凸的.
(a)中曲线上任意两点的割线在曲线的上方
(b)中曲线上任意两点的割线在曲线的下方
2020/4/3
2
(一) 凹凸性定义
设 f (x)在 区 间 I上 连 续,如 果 对 I上 任 意 两 点
若 f( x ) 是 凹 函 数 , 则 f ( x ) 单 调 增 加 ;
2020/4/3
4
凸曲线的一阶导数变化规律:
若 f( x ) 是 凸 函 数 ,则 f ( x ) 单 调 减 少 .
2020/4/3
5
(二)凹凸性的判定 定理1:( 用二阶导数判定函数的凹凸性 )
设 函 数 f(x )在 [a ,b ]上 连 续 ,在 (a ,b )内 二 阶 可 导 , 那 么
y
0
-5
-10 -10
2020/4/3
-5
0
5
x
ezplot('x*y=1',[-10 10])
10
15
作业
P108 习题4 20(2)(3) 21
预习:P112—115
2020/4/3
16
二、曲线的渐近线
如 果 曲 线 上 一 动 点 沿 曲 线 趋 于 无 穷 远 时 , 动 点 与 某 一 直 线 的 距 离 趋 于 零 ,则 称 该 直 线 为 曲 线 的 一 条 渐 近 线 .
令 y '' 0, 得 x 1 , 没有二阶导数不存在的点 列表如下:5
x ( ,1 )
5
y '' -
y凸
1
5
0
8 2
5
拐点
(1 , ) 5
+
凹
在x
1 5
两侧 y
'' 符号发生改变,则 ( 1 , 8 )是拐点.
5 25
1
例3.求曲线 y x 3 的拐点.
1
解:函数 y x 3 的定义域为 (,)
2
o
2
x
o
2
x
2020/4/3
19
例5.求曲线 f (x) 1 的铅直渐近线.
x(x 1)
解 因为 lim 1 ,
x0 x(x 1)
lim 1 x1 x(x 1)
所以 x 0 和x 1 是曲线的0 x=0 x=1
-5
-10 -10
2020/4/3
10
x
x=linspace(-10,10);
y=nthroot(x,3);
plot(x,y)
2020/4/3
13
例4.求曲线 y 1 的拐点.
x
解 函数 y 1 的定义域为 (,0)U(0,)
x
y'
1 x2
,
y''
2 x3
由于 y
1 x
在x
0
处没有定义,所以该曲线
没有拐点.
y=1/x 10
5
x
由于 lim sin x 0
x x
所以, y 0 是曲线的一条水平渐近线.
y=sinx/x 1
0.5
y
0
-0.5
-200 -100
0
100 200
x
2020/4/3
23
(3)斜渐近线
如果曲线 y f (x) 有
f x
lim a0,
x x
或
f x
lim a0, x x
lim fxax b
x
或二阶导数不存在的点; (4)检验各点两侧二阶导数的符号,如果
符号不同,该点就是拐点的横坐标;
(5)求出拐点的纵坐标.
例2.求曲线 y5x33x27x1凹、凸区间 及拐点.
解:函数的定义域为 (,)
y'15x26x7, y''30x6
为 曲 线 yf(x)的 拐 点 .
y
y f(x)
定理1:(拐点必要条件)
设 f (x)有二阶导数,
(•x0, f(x0)
若(x0, f (x0 ))为 f (x)的
x
拐点,则有f (x0 ) 0.
o x0
2020/4/3
7
定理2(拐点的充分条件)
设f 在点x0的某邻域内有二阶, 导 若f 在x0两侧异号 ,则(x0, f (x0))是f 的一 个拐点 .
(1)若 在 (a, b)内f(x)0, 则f(x)在 [a, b]是 凹 函 数 ;
(2)若 在 (a, b)内f(x)0, 则f(x)在 [a, b]是 凸 函 数 .
2020/4/3
6
(三 ) 拐点
设 点 (x0,f(x0))是 曲 线 yf(x)上 的 一 个 点 ,
在 该 点 两 侧 曲 线 凹 凸 性 相 反 ,则 称 点 (x0,f(x0))
x1 , x2恒 有 :
f
x1
2
x2
f ( x1 ) 2
f (x2)
则 称 f (x)在 该 区 间 上 的 图 形 是 凹 的 ;如 果 恒 有 :
f
x1
2
x2
f ( x1 ) f ( x2 ) 2
则 称 f (x)在 该 区 间 上 的 图 形 是 凸 的 .
2020/4/3
3
凹曲线的一阶导数变化规律:
-5
0
5
x
ezplot('x*(x-1)*y=1',[-10 10])
10
21
(2)水平渐近线 若limf(x)b,则 直y线 b是 曲
x (x )
yf(x)的水平渐 . 近线
注意:只有当函数的定义域是无穷区间时, 其曲线才有可能存在水平渐近线.
2020/4/3
22
对于函数 f (x) sin x
2020/4/3
8
例1.判断曲线 y x 4 的凹凸性.
解:
y 4 x3 , y 12x2
当x 0时,y 0; x 0时 , y 0,
y Ox
故曲线 y x 4 在 (, ) 上是凹的.
说明:若在某点二阶导数为0,在其两侧二 阶导数不变号,则曲线的凹凸性不变 .
求拐点的一般步骤:
lim fxax b
x
则 yaxb是曲线 yfx的一条斜渐近线.
y'
1
2
x 3,
y
''
2
5
x3
2
3
9
9x3 x2
当 x 0 时, y '' 不存在. 当 x 0 时, y '' 0; 当 x 0 时, y '' 0, 在 x 0 的两侧,y '' 的符号发生改变.点
( 0 , 0 ) 是该曲线的拐点.
y=x1/3
3
2
1
y
0
-1
-2
--310
-5
0
5
y
y f(x)
P
•
ykxb
o
2020/4/3
M
x
17
曲线渐近线的分类 (1)铅直渐近线
y xa
若 lim f ( x ) ( ) x a
(或 lim f ( x) ( ))
x a
oa x
则直线 xa
y f(x)
为 曲 线 y f ( x )的
铅直渐近线.
2020/4/3
18
y
ytaxn y ycoxt
一、函数的凹凸性
若在某区间内,曲线上每一点的切线都位 于该曲线的下方,则称曲线在该区间内是凹的; 若曲线上每一点的切线都位于该曲线的上方,
则称曲线在该区间内是凸的.
(a)中曲线上任意两点的割线在曲线的上方
(b)中曲线上任意两点的割线在曲线的下方
2020/4/3
2
(一) 凹凸性定义
设 f (x)在 区 间 I上 连 续,如 果 对 I上 任 意 两 点
若 f( x ) 是 凹 函 数 , 则 f ( x ) 单 调 增 加 ;
2020/4/3
4
凸曲线的一阶导数变化规律:
若 f( x ) 是 凸 函 数 ,则 f ( x ) 单 调 减 少 .
2020/4/3
5
(二)凹凸性的判定 定理1:( 用二阶导数判定函数的凹凸性 )
设 函 数 f(x )在 [a ,b ]上 连 续 ,在 (a ,b )内 二 阶 可 导 , 那 么
y
0
-5
-10 -10
2020/4/3
-5
0
5
x
ezplot('x*y=1',[-10 10])
10
15
作业
P108 习题4 20(2)(3) 21
预习:P112—115
2020/4/3
16
二、曲线的渐近线
如 果 曲 线 上 一 动 点 沿 曲 线 趋 于 无 穷 远 时 , 动 点 与 某 一 直 线 的 距 离 趋 于 零 ,则 称 该 直 线 为 曲 线 的 一 条 渐 近 线 .
令 y '' 0, 得 x 1 , 没有二阶导数不存在的点 列表如下:5
x ( ,1 )
5
y '' -
y凸
1
5
0
8 2
5
拐点
(1 , ) 5
+
凹
在x
1 5
两侧 y
'' 符号发生改变,则 ( 1 , 8 )是拐点.
5 25
1
例3.求曲线 y x 3 的拐点.
1
解:函数 y x 3 的定义域为 (,)
2
o
2
x
o
2
x
2020/4/3
19
例5.求曲线 f (x) 1 的铅直渐近线.
x(x 1)
解 因为 lim 1 ,
x0 x(x 1)
lim 1 x1 x(x 1)
所以 x 0 和x 1 是曲线的0 x=0 x=1
-5
-10 -10
2020/4/3
10
x
x=linspace(-10,10);
y=nthroot(x,3);
plot(x,y)
2020/4/3
13
例4.求曲线 y 1 的拐点.
x
解 函数 y 1 的定义域为 (,0)U(0,)
x
y'
1 x2
,
y''
2 x3
由于 y
1 x
在x
0
处没有定义,所以该曲线
没有拐点.
y=1/x 10
5
x
由于 lim sin x 0
x x
所以, y 0 是曲线的一条水平渐近线.
y=sinx/x 1
0.5
y
0
-0.5
-200 -100
0
100 200
x
2020/4/3
23
(3)斜渐近线
如果曲线 y f (x) 有
f x
lim a0,
x x
或
f x
lim a0, x x
lim fxax b
x
