类比探究专题训练
类比探究(习题及答案)
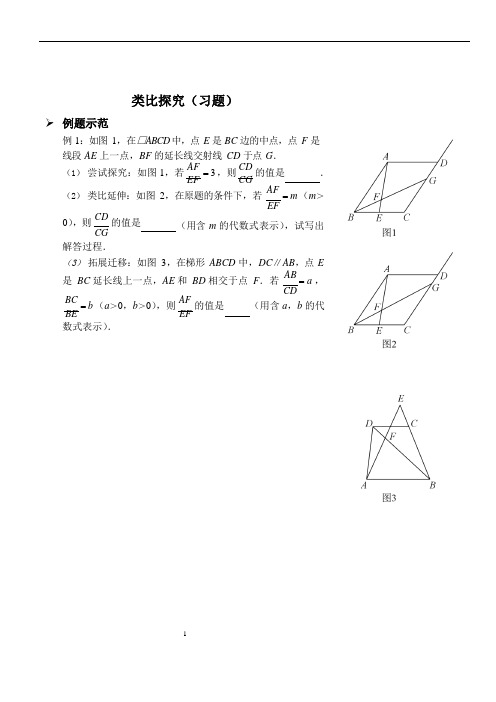
➢例题示范类比探究(习题)例1:如图1,在□ABCD 中,点E 是BC 边的中点,点F 是线段AE 上一点,BF 的延长线交射线CD 于点G.(1)尝试探究:如图1,若AF= 3 ,则CD的值是.EF CG(2)类比延伸:如图2,在原题的条件下,若AF=m (m>EF0),则CD的值是CG解答过程.(用含m 的代数式表示),试写出(3)拓展迁移:如图3,在梯形ABCD 中,DC∥AB,点E是BC 延长线上一点,AE 和BD 相交于点F.若AB=a ,CDBC=b(a>0,b>0),则AF的值是(用含a,b 的代BE EF 数式表示).1【思路分析】根据特征确定问题结构,设计方案解决第一问.问题背景是平行四边形,且已知线段比例关系,考虑通过相似传递比例关系,进而求 CD的值.CG构造相似利用作平行线的方法,即过中点 E 作 EH ∥AB 交 BG于点 H ,可得“A ”字型相似△BEH ∽△BCG ,“X ”型相似△EFH ∽△AFB ,结合 AF= 3 ,可得 CG =2EH ,AB =3EH ,故EFCD = 3 .CG 2类比第一问思路,解决第二问.分析不变特征,此时平行四边形、中点特征均不变,变化的是 AF ,EF 的比例,照搬第一问思路,过点 E 作 EH ∥AB 交BG 于点 H ,同样可得△BEH ∽△BCG ,△EFH ∽△AFB ,此时 CG =2EH ,AB =mEH ,故 CD = m.CG 2照搬思路解决第三问.虽然此问中图形、中点 E 、比例关系均发生变化,但 DC ∥AB 不变,依然可利用相似来整合条件,可照搬前面思路处理, 依然构造平行.过点 E 作 EH ∥AB 交 BD 的延长线于点 H ,可得△BCD ∽△BEH ,△AFB ∽△EFH ,可得 BC = CD,BE EHAF = AB ,结合 AB = a , BC = b ,可知 EF EH CD BE AF = AB = a ⋅CD = ab . EF EH EH212 3➢巩固练习1.如图1,一副直角三角板满足AB=BC,AC=DE,∠ABC=∠DEF=90°,∠EDF=30°.【操作】将三角板DEF 的直角顶点E 放置于三角板ABC 的斜边AC 上,再将三角板DEF 绕点E 旋转,并使边DE 与边AB 交于点P,边EF 与边BC 交于点Q.【探究】在旋转过程中,(1)如图2,当CE=1时,EP 与EQ 满足怎样的数量关系?EA并给出证明.(2)如图3,当CE= 2 时,EP 与EQ 满足怎样的数量关系?EA并给出证明.(3)根据你对(1),(2)的探究结果,试写出当CE=m时,EAEP 与EQ 满足的数量关系式为.3,=2.如图1,在等边三角形ABC 中,线段AD 为其内角角平分线,过点D 的直线B1C1⊥AC 于C1,交AB 的延长线于B1.(1)请你探究:AC =CD AC1 C1D 是否都成立?AB BD AB1DB1(2)请你继续探究:如图2,若△ABC 为任意三角形,线段AD 为其内角角平分线,请问AC=CD一定成立吗?并证明AB BD你的判断.(3)如图3,在Rt△ABC 中,∠ACB=90°,AC=8,AB=40,3E 为AB 上一点且AE=5,CE 交其内角角平分线AD 于F.试求DF的值.FA43.如图1,将两个完全相同的三角形纸片ABC 和DEC 重合放置,其中∠C =90°,∠B =∠E =30°.(1) 操作发现如图 2,固定△ABC ,使△DEC 绕点 C 旋转,当点 D 恰好落在 AB 边上时,填空:①线段 DE 与 AC 的位置关系是 ;②设△BDC 的面积为 S 1,△AEC 的面积为 S 2,则 S 1 与 S 2 的数量关系是.图 1图 2(2) 猜想论证当△DEC 绕点 C 旋转到图 3 所示的位置时,小明猜想(1) 中 S 1 与 S 2 的数量关系仍然成立,并尝试分别作出了△BDC 和△AEC 中 BC ,CE 边上的高,请你证明小明的猜想.(3) 拓展探究如图 4 , 已知∠ ABC =60°, 点 D 是其角平分线上一点, BD =CD =4,DE ∥AB 交 BC 于点 E .若在射线 BA 上存在点 F , 使 S △DCF =S △BDE ,请直.接.写.出.相应的 BF 的长.5➢思考小结总结类比探究问题中的常见结构①旋转结构始终含有等腰结构(正方形、等腰直角三角形等),并且经过旋转后,能将各条件重新组合应用.②中点结构平行夹中点(类)倍长中线中位线始终含有中点,常考虑利用中点结构补全图形,然后将所证目标放在一个较大的背景下(等腰三角形、直角三角形、等腰直角三角形等)研究.③直角结构始终含有直角,常构造直角与斜直角配合,得到同角的余角相等;再配合构造的其他直角证明相似,所求目标往往和比例关系相关.6④平行结构所求目标为线段间的比例关系,题目中没有相似三角形,往往考虑利用平行线构造相似求解.78 3 3 【参考答案】 ➢ 巩固练习1. (1)EP =EQ ,证明略;(2) EP = 1EQ ,证明略;2 (3) EP = 1EQ .m2. (1)都成立,证明略; (2)一定成立,证明略;(3) DF = 5 .FA 83. (1)①DE ∥AC ;②S 1=S 2.(2) 证明略; (3) BF 的长为4 3或 .38。
类比探究与动点问题专项训练(二)(含答案)
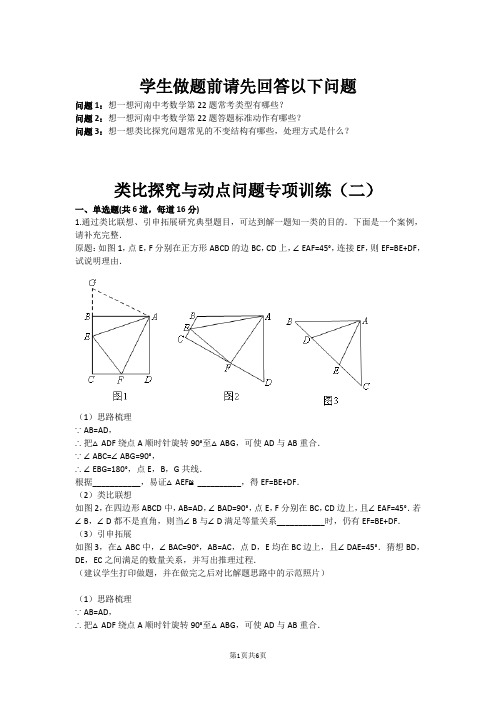
学生做题前请先回答以下问题问题1:想一想河南中考数学第22题常考类型有哪些?问题2:想一想河南中考数学第22题答题标准动作有哪些?问题3:想一想类比探究问题常见的不变结构有哪些,处理方式是什么?类比探究与动点问题专项训练(二)一、单选题(共6道,每道16分)1.通过类比联想、引申拓展研究典型题目,可达到解一题知一类的目的.下面是一个案例,请补充完整.原题:如图1,点E,F分别在正方形ABCD的边BC,CD上,∠EAF=45°,连接EF,则EF=BE+DF,试说明理由.(1)思路梳理∵AB=AD,∴把△ADF绕点A顺时针旋转90°至△ABG,可使AD与AB重合.∵∠ABC=∠ABG=90°,∴∠EBG=180°,点E,B,G共线.根据___________,易证△AEF≌__________,得EF=BE+DF.(2)类比联想如图2,在四边形ABCD中,AB=AD,∠BAD=90°,点E,F分别在BC,CD边上,且∠EAF=45°.若∠B,∠D都不是直角,则当∠B与∠D满足等量关系___________时,仍有EF=BE+DF.(3)引申拓展如图3,在△ABC中,∠BAC=90°,AB=AC,点D,E均在BC边上,且∠DAE=45°.猜想BD,DE,EC之间满足的数量关系,并写出推理过程.(建议学生打印做题,并在做完之后对比解题思路中的示范照片)(1)思路梳理∵AB=AD,∴把△ADF绕点A顺时针旋转90°至△ABG,可使AD与AB重合.∵∠ABC=∠ABG=90°,∴∠EBG=180°,点E,B,G共线.根据___________,易证△AEF≌__________,得EF=BE+DF.A.AAS,△AGEB.SAS,△AGEC.SAS,△AEGD.SSS,△AGE答案:C解题思路:见第3题中解析试题难度:三颗星知识点:中考数学几何中的类比探究2.(上接第1题)(2)类比联想如图2,在四边形ABCD中,AB=AD,∠BAD=90°,点E,F分别在BC,CD边上,且∠EAF=45°.若∠B,∠D都不是直角,则当∠B与∠D满足等量关系_________时,仍有EF=BE+DF.( )A.∠B=∠DB.∠B+∠D=180°C.∠B-∠D=90°D.∠B=2∠D答案:B解题思路:见第3题中解析试题难度:三颗星知识点:中考数学几何中的类比探究3.(上接第1,2题)(3)引申拓展如图3,在△ABC中,∠BAC=90°,AB=AC,点D,E均在BC边上,且∠DAE=45°,则BD,DE,EC之间满足的数量关系为( )A.DE=BD+ECB.C. D.答案:C解题思路:试题难度:三颗星知识点:中考数学几何中的类比探究4.如图,在平行四边形ABCD中,AB=5,BC=10,F为AD的中点,CE⊥AB于点E,设.(1)当时,求CE的长;(2)当时,①设,能够得到,求k的值;②连接CF,当的值最大时,求BE的长.(建议学生打印做题,并在做完之后对比解题思路中的示范照片)(1)当α=60°时,EF的长为( )A.5B.C. D.答案:A解题思路:见第6题中解析试题难度:三颗星知识点:中点结构5.(上接第4题)(2)①当时,设,能够得到,则k的值为( )A. B.C. D.3答案:D解题思路:见第6题中解析试题难度:三颗星知识点:中点结构6.(上接第4,5题)(2)②连接CF,当的值最大时,BE的长为( )A. B.C. D.5答案:B解题思路:试题难度:三颗星知识点:直角三角形斜边中线等于斜边一半。
类比探究专题(一)——平行结构(含答案).docx

学生做题前请先回答以下问题问题1:类比探究问题的处理思路是什么?类比探究专题(一)一一平行结构一、单选题(共6道,每道16分)1.如图1, D是厶ABC的边BC上一点,过点D的一条直线交AC于点F,交BA的延长线于点E.AE(1)若BD二CD, CF=2AF,则巧童的值为()£A.2B. 21羽C. WD. 3答案:B 解题思路:如图,过点川作?tG" EC,交DE于点G,易得ZUFaAC肋,A A EG^ABED,.AG_AF _\ AG _ AE** ~CD~CF = 29 ~BD~~BE f设BD=CD=a,^\AG = -f2a.AE _ AG _ 2^ _ 1BE BD a 2即空的值为二BE 2难度:三颗星知识点:平行结构AE2.(上接第1题)(2)如图2,若BD=CD, CF=mAF,则巧应的值为((用含m的代数式表示)A.叨B.血丄C.2/D•加图2答案:D解题思路:如图,过点川作?1G" EG交DE于点G,易得△MGSACFZ), /\AEG^/\BED f.AG _,4F _ 1 AG _ AE** ~CD~CF = m9丽一旋’ 设BD=CD=a,则AG = -,ma.AE _AG _ 1即空的值为丄.BE m试题难度:三颗星知识点:平行结构3.(上接第1, 2题)(3)如图3,将原题改为“过点D的一条直线交AC的延长线于点F,交AEAB 于点E",若BD=nCD, CF=mAF,则的值为()(用含m, n的代数式表示)答案:c解题思路:如图,过点M 作AGllBC,交DE 的延长线于点G,易得厶0妙厶677), AAEG^ABED,.AG_AF _ 1 AG _ AE"~CD = CF~m 9 ~BD~1E 9设 BD= nCD=na f 则AG =—,ma・血 ■ ■ 卫G…BE BD na即竺 的值为 1---- ■BE mn 试题难度:三颗星知识点:平行结构4. 已知AD 是△ ABC 的中线,将BC 边所在直线绕点D 顺时针旋转°角,交AB 边于点M’交射线AC 于点N,设观二如'泗=陀(存0,尸0)1+1=2丄+丄显C.X 尹D.x 尹 °答案:c解题思路: (1)如图1, X 歹满足的函数关系式为(1+1 = 42B .X歹 图11如图,过点C作CEllAB,交胚V于点£,则厶NCES△也4胚・CN _ CE…AN = AM'・・・血)是厶ABC的中线,・\BD=CD・'/CEll BM,易得△3D遊△(?%,/. CE=BM,・CN _ BM"AN = AM'*.* AAf = xAB f AN = JL4C (x h 0, y h 0),BAI = AB—AAI = AB—x^4B , CN — AN— AC — \-AC- AC,•r.vAC — AC AB一xABvAC xAB整理得丄+丄=2,x y即丄与丄满足的函数关系式为2+丄=2・X V X V试题难度:三颗星知识点:平行结构5.(上接第4题)(2)如图2,当G是AD上任意一点时(点G不与点A重合),过点G的直线交AB 边于点皿' ,交AC 边于点“,设丄与丄AG=mAD,AM i = x i AB f百旷*^0(x70,”工0),则卍"满足的函数关系式为()丄+丄=2丄+丄工A.卅才 B .X ,X 21 12 —+ —=—— D 卅 y' m答案:D解题思路:如图,过点D 作MM"交43的延长线于点交47于点N,AM AD AN•' AG = utiD , AXf — x f AB , AV = X'r AC (x r h 0, y r h 0), JAf = AN = y^AC (x^O, y 0)由(1)可知,-+- = 2, x y.1 1 1 12 ..—+ — = ----- + ---- =—. x r v r wx mv m即丄与丄满足的函数关系式为1+1=- x v x v m6. (上接第4, 5题)(3)如图3,当G 是AD 上任意一点时(点G 不与点A 重合),过点G 的直线交 AB 边于点加,交 AC的延长线于点“,设CT难度:三颗星知识点:平行结构图2丄+丄乜 丄+丄/C.0 0D.* 歹" 答案:D解题思路:如图,过点。
类比探究问题(习题及答案)

类比探究问题(习题)>例题示范例1:如图1,在正方形ABCD中,E, F分别是BC, CD上的点, 且ZE4F=45。
,则有结论EF=BE+DF成立.(1)如图2,在四边形ABCD中,AB=AD. ZB=ZD=90。
, E, F分别是BC, CD上的点,且ZEAF是ZB4D的一半,那么结论EF二BE+DF 是否仍然成立?若成立,请证明;若不成立,请说明理山.⑵ 如图3,若恪(1)中的条件改为:在四边形ABCD 4^,AB=AD.ZB+上ADC=180。
,延长SC到点E,延长CD到点F,使得ZEAF 仍然是ZBAD的一半,则结论EF二BE+DF是否仍然成立?若成立,请证明;若不成立,请写出它们之间的数量关系,并证明.图1D图2F思路分析:1.题目中有旋转结构,可以类比.题U结论思路:如图1,延长CB到G,使BG二DF,根据已知条件容易证明^ ABG幻△ADF,由此可以推出ZBAG=ZD4F, AG=AF.而Z EAF』ABAD.2 所以得到ZDAF+ZBAE二ZEAF,进一步得到ZEAF二上EAG, 所以故EF=EG=BE+BG=BE+DF ・2.类比上面思路,解决笫一问•如图2,延长CB到G,使BG=DF, 根据已知条件容易证明^ABG^^ADF.山此可以推出ZBAG=ZD4F, AG=AF.而Z EAF=_ ZBAD,2 所以得到ZDAF+ZBAE二ZEAF,进一步得到ZEAF二上EAG, 所以△故EF=EG=BE+BG=BE+DF ・3.照搬思路解决第二问•结论EF=BE+DF不成立,应为EF=BE-DF.如图3,在BC上截取BG=DF, 山于ZB+ZAQC=180。
,Z/1DF+Z/IDC=18O^ 可以得到ZB=ZADF,所以△ABG幻△ADF,山此可以推出ZBAG=ZD4F, AG=AF.而Z EAF』ZBAD.2 所以得到ZEAF=ZEAG,所以△AEF竺△AEG,A)90。
△ADF空△ABG (SAS)I AAEF^AAEG (SAS)I故EF=EG=BE-BG=BE-DF ・D>巩固练习1.如图1,在正方形ABCD和正方形CGEF (CG>BC)中,点C, G在同一直线上,M是AE的中点.(1)探究线段MD, MF的位置关系及数量关系,并证明.(2)若将图1中的正方形CGEF绕点C顺时针旋转,使D, C, G三点在同一直线上,如图2,其他条件不变,则(1)中得到的两个结论是否发生变化?请写出你的猜想并加以证明.(3)若将图1中的正方形CGEF绕点C顺时针旋转,使正方形CGEF的对角线CE恰好与正方形ABCD的边在同一直线上,如图3,其他条件不变,则(1)中得到的两个结论是否发生变化?请写出你的猜想并加以证明.图2E2.在△ABC中,已知BC >AC.动点D绕△ABC'的顶点A逆时针旋转,丄LAD=BC,连接CD. E, F分别为AB, CD的中点,直线EF与直线AD眈分别交于点M, N.如图1,当点D旋转到BQ 的延长线上时,点N恰好与点Fifi合,取AC的中点H,连接HE, HF.根据三角形中位线定理和平行线的性质,可得结论ZAMF二ZBNE (无需证明).(1)当点D旋转到图2中的位置时,ZAMFLj ZBNE有何数量关系?请写出猜想,并给出证明.(2)当点Q旋转到图3中的位置时,ZAMF与ZBNE有何数量关系?请直接写出结论.3.已知AABC,以△ABC的边4C为直角边向外作等腰直角三角形ABE和等腰直角三角形ACD AB=AE. AC=AD. ZBAE= ZCAD=90\ M 是BC中点,连接AM, DE.(1)如图1,在△ABC中,当ZB4C二90。
类比探究题-中考数学专题训练

专题七 类比探究题类型一 线段数量关系问题(2018·河南)(1)问题发现如图①,在△OAB 和△OCD 中,OA =OB ,OC =OD ,∠AOB=∠COD=40°,连接AC ,BD 交于点M.填空: ①ACBD的值为________; ②∠AMB 的度数为________; (2)类比探究如图②,在△OAB 和△OCD 中,∠AOB=∠COD=90°,∠OAB=∠OCD=30°,连接AC 交BD 的延长线于点M.请判断ACBD 的值及∠AMB 的度数,并说明理由;(3)拓展延伸在(2)的条件下,将△OCD 绕点O 在平面内旋转,AC ,BD 所在直线交于点M ,若OD =1,OB =7,请直接写出当点C 与点M 重合时AC 的长.【分析】 (1)①证明△COA≌△DOB(SAS),得AC =BD ,比值为1;②由△COA≌△DOB,得∠CAO=∠DBO,根据三角形的内角和定理,得∠AMB=180°-(∠DBO+∠OAB+∠ABD)=180°-140°=40°;(2)根据两边的比相等且夹角相等可得△AOC∽△BOD,则AC BD =OCOD =3,由全等三角形的性质得∠AMB 的度数;(3)正确画出图形,当点C 与点M 重合时,有两种情况:如解图①和②,同理可得△AOC∽△BOD,则∠AMB =90°,ACBD =3,可得AC 的长.【自主解答】解:(1)问题发现①1【解法提示】∵∠AOB=∠COD=40°, ∴∠COA=∠DOB. ∵OC=OD ,OA =OB , ∴△COA≌△DOB(SAS), ∴AC=BD , ∴ACBD=1. ②40°【解法提示】∵△COA≌△DOB, ∴∠CAO=∠DBO. ∵∠AOB=40°, ∴∠OAB+∠ABO=140°,在△AMB 中,∠AMB=180°-(∠CAO+∠OAB+∠ABD)=180°-(∠DBO+∠OAB+∠ABD)=180°-140°=40°. (2)类比探究ACBD=3,∠AMB=90°,理由如下: 在Rt△OCD 中,∠DCO=30°,∠DOC=90°, ∴OD OC =tan 30°=33, 同理,得OB OA =tan 30°=33,∵∠AOB=∠COD=90°, ∴∠AOC=BOD , ∴△AOC∽△BOD, ∴AC BD =OCOD=3,∠CAO=∠DBO. ∴∠AMB=180°-∠CAO-∠OAB-MBA =180°-(∠DAB+∠MBA+∠OBD)=180°-90°=90°. (3)拓展延伸①点C 与点M 重合时,如解图①, 同理得△AOC∽△BOD, ∴∠AMB=90°,ACBD =3,设BD =x ,则AC =3x , 在Rt△COD 中,∵∠OCD=30°,OD =1, ∴CD=2, ∴BC=x -2.在Rt△AOB 中,∠OAB=30°,OB =7. ∴AB=2OB =27,在Rt△AMB 中,由勾股定理,得AC 2+BC 2=AB 2, 即( 3 x)2+(x -2)2=(27)2, 解得x 1=3,x 2=-2(舍去), ∴AC=33;②点C 与点M 重合时,如解图②,同理得:∠AMB=90°,ACBD =3,设BD =x ,则AC =3x ,在Rt△AMB 中,由勾股定理,得AC 2+BC 2=AB 2, 即(3x)2+(x +2)2=(27)2解得x 1=-3,解得x 2=2(舍去). ∴AC=2 3.综上所述,AC 的长为33或2 3.图①图② 例1题解图1.(2016·河南) (1)发现如图①,点A 为线段BC 外一动点,且BC =a ,AB =b.填空:当点A 位于________________时,线段AC 的长取得最大值,且最大值为__________(用含a ,b 的式子表示). (2)应用点A 为线段BC 外一动点,且BC =3,AB =1,如图②所示,分别以AB ,AC 为边,作等边三角形ABD 和等边三角形ACE ,连接CD ,BE.①请找出图中与BE 相等的线段,并说明理由; ②直接写出线段BE 长的最大值. (3)拓展如图③,在平面直角坐标系中,点A 的坐标为(2,0),点B 的坐标为(5,0),点P 为线段AB 外一动点,且PA =2,PM =PB ,∠BPM=90°,请直接写出线段AM 长的最大值及此时点P 的坐标.2.(2015·河南)如图①,在Rt△ABC 中,∠B=90°,BC =2AB =8,点D ,E 分别是边BC ,AC 的中点,连接DE.将△EDC 绕点C 按顺时针方向旋转,记旋转角为α. (1)问题发现①当α=0°时,AE BD =2;②当α=180°时,AE BD =2;(2)拓展探究试判断:当0°≤α<360°时,AEBD 的大小有无变化?请仅就图②的情形给出证明.(3)解决问题当△EDC 旋转至A ,D ,E 三点共线时,直接写出线段BD 的长.3.(2014·河南) (1)问题发现如图①,△ACB 和△DCE 均为等边三角形,点A ,D ,E 在同一直线上,连接BE. 填空:①∠AEB 的度数为__________;②线段AD ,BE 之间的数量关系为______________. (2)拓展探究如图②,△ACB 和△DCE 均为等腰直角三角形,∠ACB=∠DCE=90°,点A ,D ,E 在同一直线上,CM 为△DCE 中DE 边上的高,连接BE ,请判断∠AEB 的度数及线段CM ,AE ,BE 之间的数量关系,并说明理由. (3)解决问题如图③,在正方形ABCD 中,CD =2,若点P 满足PD =1,且∠BPD=90°,请直接写出点A 到BP 的距离.4.(2018·南阳二模)在△ABC中,∠ACB是锐角,点D在射线BC上运动,连接AD,将线段AD绕点A逆时针旋转90°,得到AE,连接EC.(1)操作发现若AB=AC,∠BAC=90°,当D在线段BC上时(不与点B重合),如图①所示,请你直接写出线段CE和BD 的位置关系和数量关系是______________,______________;(2)猜想论证在(1)的条件下,当D在线段BC的延长线上时,如图②所示,请你判断(1)中结论是否成立,并证明你的判断.(3)拓展延伸如图③,若AB≠AC,∠BAC≠90°,点D在线段BC上运动,试探究:当锐角∠ACB等于________度时,线段CE和BD之间的位置关系仍成立(点C,E重合除外)?此时若作DF⊥AD交线段CE于点F,且当AC=32时,请直接写出线段CF的长的最大值是____.5.已知,如图①,△ABC,△AED是两个全等的等腰直角三角形(其顶点B,E重合),∠BAC=∠AED=90°,O为BC的中点,F为AD的中点,连接OF.(1)问题发现①如图①,OFEC=_______;②将△AED 绕点A 逆时针旋转45°,如图②,OFEC =_______;(2)类比延伸将图①中△AED 绕点A 逆时针旋转到如图③所示的位置,请计算出OFEC 的值,并说明理由.(3)拓展探究将图①中△AED 绕点A 逆时针旋转,旋转角为α,0°≤α≤90°,AD =2,△AED 在旋转过程中,存在△ACD 为直角三角形,请直接写出线段CD 的长.类型二 图形面积关系问题(2017·河南)如图①,在Rt△ABC 中,∠A=90°,AB =AC ,点D ,E 分别在边AB ,AC 上,AD =AE ,连接DC ,点M ,P ,N 分别为DE ,DC ,BC 的中点. (1)观察猜想图①中,线段PM 与PN 的数量关系是________,位置关系是________; (2)探究证明把△AD E 绕点A 逆时针方向旋转到图②的位置,连接MN ,BD ,CE ,判断△PMN 的形状,并说明理由; (3)拓展延伸把△ADE 绕A 在平面内自由旋转,若AD =4,AB =10,请直接写出△PMN 面积的最大值.图①图② 例2题图【分析】 (1)利用三角形的中位线定理得出PM =12CE ,PN =12BD ,进而判断出BD =CE ,即可得出结论,再利用三角形的中位线定理得出PM∥CE,继而得出∠DPM=∠DCA,最后用互余即可得出结论;(2)先判断出△ABD≌△ACE,得出BD =CE ,同(1)的方法得出PM =12BD ,PN =12BD ,即可得出PM =PN ,同(1)的方法即可得出结论;(3)先判断出MN 最大时,△PMN 的面积最大,进而求出AN ,AM ,即可得出MN 最大=AM +AN ,最后用面积公式即可得出结论. 【自主解答】解:(1)∵点P ,N 是BC ,CD 的中点, ∴PN∥BD,PN =12BD.∵点P ,M 是CD ,DE 的中点, ∴PM∥CE,PM =12CE.∵AB=AC ,AD =AE , ∴BD =CE , ∴PM=PN. ∵PN∥BD, ∴∠DPN=∠ADC, ∵PM∥CE, ∴∠DPM=∠DCA. ∵∠BAC=90°, ∴∠ADC+∠ACD=90°,∴∠MPN=∠DPM+∠DPN=∠DCA+∠ADC=90°,(2)由旋转知,∠BAD=∠CAE, ∵AB=AC ,AD =AE , ∴△ABD≌△ACE(SAS), ∴∠ABD=∠ACE,BD =CE.同(1)的方法,利用三角形的中位线定理,得PN =12BD ,PM =12CE ,∴PM=PN ,∴△PMN 是等腰三角形, 同(1)的方法得,PM∥CE, ∴∠DPM=∠DCE, 同(1)的方法得,PN∥BD, ∴∠PNC=∠DBC.∵∠DPN=∠DCB+∠PNC=∠DCB+∠DBC,∴∠MPN=∠DPM+∠DPN=∠DCE+∠DCB+∠DBC=∠BCE+∠DBC=∠ACB+∠ACE+∠DBC=∠ACB+∠ABD +∠DBC=∠ACB+∠ABC. ∵∠BAC=90°, ∴∠ACB+∠ABC=90°, ∴∠MPN=90°,∴△PMN 是等腰直角三角形,例2题解图(3)如解图,同(2)的方法得,△PMN 是等腰直角三角形, ∴当MN 最大时,△PMN 的面积最大, ∴DE∥BC 且DE 在顶点A 上面, ∴MN 最大=AM +AN , 连接AM ,AN ,在△ADE 中,AD =AE =4,∠DAE=90°,在Rt△ABC 中,AB =AC =10,AN =52, ∴MN 最大=22+52=72,∴S △PMN 最大=12PM 2=12×12MN 2=14×(72)2=492.1.(2013·河南)如图①,将两个完全相同的三角形纸片ABC 和DEC 重合放置,其中∠C=90°,∠B=∠E =30°. (1)操作发现如图②,固定△ABC,使△DEC 绕点C 旋转,当点D 恰好落在AB 边上时,填空: ①线段DE 与AC 的位置关系是______________;②设△BDC 的面积为S 1,△AEC 的面积为S 2,则S 1与S 2的数量关系是______________. (2)猜想论证当△DEC 绕点C 旋转到如图③所示的位置时,小明猜想(1)中S 1与S 2的数量关系仍然成立,并尝试分别作出了△BDC 和△AEC 中BC ,CE 边上的高,请你证明小明的猜想. (3)拓展探究已知∠ABC=60°,点D 是角平分线上一点,BD =CD =4,DE∥AB 交BC 于点E(如图④).若在射线BA 上存在点F ,使S △DCF =S △BDE ,请直接写出相应的BF 的长.2.已知Rt△ABC 中,BC =AC ,∠C=90°,D 为AB 边的中点,∠EDF=90°,将∠EDF 绕点D 旋转,它的两边分别交AC ,CB(或它们的延长线)于E ,F.当∠EDF 绕点D 旋转到DE⊥AC 于E 时,如图①所示,试证明S △DEF +S △CEF =12S △ABC .(1)当∠EDF 绕点D 旋转到DE 和AC 不垂直时,如图②所示,上述结论是否成立?若成立,请说明理由;若不成立,试说明理由.(2)直接写出图③中,S△DEF,S△CEF与S△ABC之间的数量关系.3.(2018·郑州模拟)如图①所示,将两个正方形ABCD和正方形CGFE如图所示放置,连接DE,BG. (1)图中∠DCE+∠BCG=__________°;设△DCE的面积为S1,△BCG的面积为S2,则S1与S2的数量关系为______________;猜想论证:(2)如图②所示,将矩形ABCD绕点C按顺时针方向旋转后得到矩形FECG,连接DE,BG,设△DCE的面积为S1,△BCG的面积为S2,猜想S1和S2的数量关系,并加以证明;(3)如图③所示,在△ABC中,AB=AC=10 cm,∠B=30°,把△ABC沿AC翻折得到△AEC,过点A作AD 平行CE交BC于点D,在线段CE上存在点P,使△ABP的面积等于△ACD的面积,请写出CP的长.4.(2018·驻马店一模)如图①,△ABC与△CDE都是等腰直角三角形,直角边AC,CD在同一条直线上,点M,N分别是斜边AB,DE的中点,点P为AD的中点,连接AE,BD,PM,PN,MN.(1)观察猜想图①中,PM与PN的数量关系是______________,位置关系是______________;(2)探究证明将图①中的△CDE绕着点C顺时针旋转α(0°<α<90°),得到图②,AE与MP,BD分别交于点G,H,判断△PMN的形状,并说明理由;(3)拓展延伸把△CDE绕点C任意旋转,若AC=4,CD=2,请直接写出△PMN面积的最大值.参考答案类型一 针对训练1.解:(1)∵点A 为线段BC 外一动点,且BC =a ,AB =b ,∴当点A 位于CB 的延长线上时,线段AC 的长取得最大值,且最大值为BC +AB =a +b. (2)①CD=BE ,理由:∵△ABD 与△ACE 是等边三角形, ∴AD=AB ,AC =AE ,∠BAD=∠CAE=60°, ∴∠BAD+∠BAC=∠CAE+∠BAC,即∠CAD=∠EAB. 在△CAD 和△EAB 中,⎩⎪⎨⎪⎧AD =AB ∠CAD=∠EAB AC =AE ,∴△CAD≌△EAB,∴CD=BE.②∵线段BE 长的最大值等于线段CD 的最大值,由(1)知,当线段CD 的长取得最大值时,点D 在CB 的延长线上, ∴线段BE 长的最大值为BD +BC =AB +BC =4;(3)∵将△APM 绕着点P 顺时针旋转90°得到△PBN,连接AN ,如解图①, 则△APN 是等腰直角三角形, ∴PN=PA =2,BN =AM.∵点A 的坐标为(2,0),点B 的坐标为(5,0), ∴OA=2,OB =5,∴AB=3,∴线段AM长的最大值等于线段BN长的最大值,∴当点N在线段BA的延长线时,线段BN取得最大值,最大值为AB+AN.∵AN=2AP=22,∴线段AM的长最大值为22+3.如解图②,过点P作PE⊥x轴于点E.∵△APN是等腰直角三角形,∴PE=AE=2,∴OE=BO-AB-AE=5-3-2=2-2,∴P(2-2,2).图①图②第1题解图2.解:(1)①当α=0°时,∵在Rt△ABC中,∠B=90°,∴AC=AB2+BC2=(8÷2)2+82=4 5.∵点D、E分别是边BC、AC的中点,∴AE=45÷2=25,BD=8÷2=4,∴AEBD=254=52.②如解图①,当α=180°时,得可得AB∥DE,∵ACAE=BCBD,∴AEBD=ACBC=458=52.(2)当0°≤α≤360°时,AEBD的大小没有变化.∵∠ECD=∠ACB, ∴∠ECA=∠DCB. 又∵EC DC =AC BC =52,∴△ECA∽△DCB, ∴AE BD =EC DC =52.图①图②图③ 第2题解图(3)①如解图②,∵AC=45,CD =4,CD⊥AD,∴AD=AC 2-CD 2=(45)2-42=80-16=8. ∵AD=BC ,AB =DC ,∠B=90°, ∴四边形ABCD 是矩形, ∴BD=AC =4 5.③如解图③,连接BD ,过点D 作AC 的垂线交AC 于点Q ,过点B 作AC 的垂线交AC 于点P , ∵AC=45,CD =4,CD⊥AD,∴A D =AC 2-CD 2=(45)2-42=80-16=8, ∵点D 、E 分别是边BC 、AC 的中点, ∴DE=12AB =12×(8÷2)=12×4=2,∴AE=AD -DE =8-2=6, 由(2),可得AE BD =52,∴BD=652=1255.综上所述,BD 的长为45或1255. 3.解:(1)∵△ACB 和△DCE 均为等边三角形, ∴CA=CB ,CD =CE ,∠ACB=∠DCE=60°, ∴∠ACD=∠BCE. 在△ACD 和△BCE 中, ⎩⎪⎨⎪⎧AC =BC ∠ACD=∠BCE CD =CE, ∴△ACD≌△BCE(SAS),∴∠ADC=∠BEC. ∵△DCE 为等边三角形,∴∠CDE=∠CED=60°. ∵点A ,D ,E 在同一直线上,∴∠ADC=120°, ∴∠BEC=120°,∴∠AEB=∠BEC-∠CED=60°. ②∵△ACD≌△BCE,∴AD=BE. (2)∠AEB=90°,AE =BE +2CM. 理由如下:∵△ACB 和△DCE 均为等腰直角三角形, ∴CA=CB ,CD =CE ,∠ACB=∠DCE=90°. ∴∠ACD=∠BCE. 在△ACD 和△BCE 中, ⎩⎪⎨⎪⎧CA =CB ∠ACD=∠BCE CD =CE, ∴△ACD≌△BCE(SAS), ∴AD=BE ,∠ADC=∠BEC.∵△DCE 为等腰直角三角形,∴∠CD E =∠CED=45°. ∵点A ,D ,E 在同一直线上, ∴∠ADC=135°,∴∠BEC=135°, ∴∠AEB=∠BEC-∠CED=90°. ∵CD=CE ,CM⊥DE,∴DM=ME. ∵∠DCE=90°,∴DM=ME =CM , ∴AE=AD +DE =BE +2CM.(3)∵PD=1,∴点P 在以点D 为圆心,1为半径的圆上.∵∠BPD=90°,∴点P在以BD为直径的圆上,∴点P是这两圆的交点.①当点P在如解图①所示位置时,连接PD,PB,PA,作AH⊥BP,垂足为H,过点A作AE⊥AP,交BP于点E.∵四边形ABCD是正方形,∴∠ADB=45°,AB=AD=DC=BC=2,∠BAD=90°,∴BD=2.∵DP=1,∴BP= 3.∵∠BPD=∠BAD=90°,∴点A、P、D、B在以BD为直径的圆上,∴∠APB=∠ADB=45°.∴△PAE是等腰直角三角形.又∵△BAD是等腰直角三角形,点B,E,P共线,AH⊥BP,∴由(2)中的结论可得:BP=2AH+PD,∴3=2AH+1,∴AH=3-1 2;②当点P在如解图②所示位置时,连接PD、PB、PA、作AH⊥BP,垂足为H,过点A作AE⊥AP,交PB的延长线于点E,同理可得:BP=2AH-PD,∴3=2AH-1,∴AH=3+1 2.综上所述,点A到BP的距离为3-12或3+12.图①图② 第3题解图4.解:(1)①∵AB=AC ,∠BAC=90°, 线段AD 绕点A 逆时针旋转90°得到AE , ∴AD=AE ,∠BAD=∠CAE, ∴△BAD≌△CAE, ∴CE=BD ,∠ACE =∠B, ∴∠BCE=∠BCA+∠ACE=90°,∴线段CE ,BD 之间的位置关系和数量关系为CE =BD ,CE⊥BD; (2)(1)中的结论仍然成立.证明如下: 如解图①,∵线段AD 绕点A 逆时针旋转90°得到AE , ∴AE=AD ,∠DAE=90°. ∵AB=AC ,∠BAC=90°, ∴∠CAE=∠BAD, ∴△ACE≌△ABD, ∴CE=BD ,∠ACE=∠B, ∴∠BCE=90°,∴线段CE ,BD 之间的位置关系和数量关系为CE =BD ,CE⊥BD; (3)45°;34.过A 作AM⊥BC 于M ,过点E 作EN⊥MA 交MA 的延长线于N ,如解图②. ∵线段AD 绕点A 逆时针旋转90°得到AE , ∴∠DAE=90°,AD =AE ,∴∠NAE=∠ADM,易证得Rt△AMD≌Rt△ENA, ∴NE=AM.∵CE⊥BD,即CE⊥MC,∴∠MCE=90°, ∴四边形MCEN 为矩形, ∴NE=MC ,∴AM=MC , ∴∠ACB=45°. ∵四边形MCEN 为矩形, ∴Rt△AMD∽Rt△DCF, ∴MD CF =AMDC,设DC =x , ∵在Rt△AMC 中,∠ACB=45°,AC =32,∴AM=CM =3,MD =3-x ,∴3-x CF =3x ,∴CF=-13x 2+x =-13(x -32)2+34,∴当x =32时,CF 有最大值,最大值为34.故答案为45°,34;图①图② 第4题解图5.解:(1)①∵△A BC ,△AED 是两个全等的等腰直角三角形, ∴AD=BC.∵O 为BC 的中点,F 为AD 的中点, ∴AF=OC.∵∠BAC=∠AED=90°,AB =AC ,AE =DE , ∴∠DAE=∠CBA=45°, ∴AD∥BC,∴四边形AFOC 是平行四边形, ∴OF=AC =22EC ,∴OF EC =22; 故答案:22; ②∵AO=22AC ,∠BAO=∠CAO=45°,∠DAE=45°, ∴∠DAE=∠CAO. ∵AE=AC , ∴AF=AO , ∴AF AE =AO AC,∴△AFO∽△AEC, ∴OF EC =AO AC =22; 故答案:22. (2)OF =22EC. 理由:在等腰直角△ADE 中,F 为AD 的中点, ∴AF=12AD =22AE.在等腰直角△ABC 中,O 为BC 的中点, 如解图①,连接AO , ∴AO=22AC ,∠BAO=∠CAO=45°. ∴∠DAE=45°,∴∠DAE=∠CAO,即∠DAO=∠CAE. ∵AE=AC , ∴AF=AO , ∴AF AE =AO AC, ∴△AFO∽△AEC, ∴OF EC =AO AC =22; (3)∵△ABC 和△AED 是两个全等的等腰直角三角形, ∴AD=BC =2, ∴ED=AE =AB =AC =1,当△ACD 为直角三角形时,分两种情况:图①图②图③ 第5题解图①当AD 与AB 重合时,如解图②,连接CD. 当△ACD 为直角三角形时,AD⊥AC, 即将△ADE 绕点A 逆时针旋转45°. ∵AD=2,AC =1,∴由勾股定理可得CD =(2)2+12=3; ②当AE 与AC 重合时,如解图③, 当△ACD 为直角三角形时,AC⊥CD,即将△ADE 绕点A 逆时针旋转90°,此时CD =AC =1. 综上所述,CD 的长为3或1. 类型二 针对训练1.解:(1)①△DEC 绕点C 旋转到点D 恰好落在AB 边上, ∴AC=CD.∵∠BAC=90°-∠B=90°-30°=60°. ∴△ACD 是等边三角形, ∴∠ACD=60°,又∵∠CDE=∠BAC=60°, ∴∠ACD=∠CDE, ∴DE∥AC;②∵∠B=30°,∠C=90°, ∴CD=AC =12AB ,∴BD=AD =AC ,根据等边三角形的性质,△ACD 的边AC ,AD 上的高相等,∴△BDC 的面积和△AEC 的面积相等(等底等高的三角形的面积相等),即S 1=S 2; (2)∵△DEC 是由△ABC 绕点C 旋转得到, ∴BC=CE ,AC =CD ,∠DCE=∠ACB=90°, ∵∠ACN+∠ACE=180°, ∴∠ACN=∠DCM.在△ACN 和△DCM 中,⎩⎪⎨⎪⎧∠ACN=∠DCM,∠N=∠CMD=90°,AC =CD∴△ACN≌△DCM(AAS), ∴AN=DM ,∴△BDC 的面积和△AEC 的面积相等(等底等高的三角形的面积相等),即S 1=S 2;第1题解图(3)如解图,过点D 作DF 1∥BE 交BA 于点F 1,易求得四边形BEDF 1是菱形,∴BE=DF 1,且BE ,DF 1边上的高相等,此时S△DCF 1=S △BDE ; 过点D 作DF 2⊥BD.∵∠ABC=60°,F 1D∥BE 交BA 于点F 2, ∴∠F 2F 1D =∠ABC=60°.∵BF 1=DF 1,∠F 1BD =12∠ABC=30°,∠F 2DB =90°,∴∠F 1DF 2=∠ABC=60° ∴△DF 1F 2是等边三角形, ∴DF 1=DF 2.∵BD=CD ,∠ABC=60°,点D 是角平分线上一点, ∴DBC=∠DCB=12×60°=30°,∴∠CDF 1=180°-∠BCD=180°-30°=150°, ∠CDF 2=360°-150°-60°=150°, ∴∠CDF 1=∠CDF 2. 在△CDF 1和△CDF 2中, ⎩⎪⎨⎪⎧DF 1=DF 2∠CDF 1=∠CDF 2CD =CD, ∴△CDF 1≌△CDF 2(SAS),∴点F 2也是所求的点. ∵∠ABC=60°,点D 是角平分线上一点,DE∥AB, ∴∠DBC=∠BDE=∠ABD=12×60°=30°.又∵BD=4,∴BE=12×4÷cos 30°=2÷32=433,∴BF 1=433,BF 2=BF 1+F 1F 2=433+433=833.故BF 的长为433或833.2.解:当∠EDF 绕D 点旋转到DE⊥AC 时,四边形CEDF 是正方形;设△ABC 的边长AC =BC =a ,则正方形CEDF 的边长为12a ,∴S △ABC =12a 2,S 正方形CEDF =(12a)2=14a 2,即S △DEF +S △CEF =12S △ABC ;(1)上述结论成立;理由如下: 连接CD ,如解图①所示.∵AC=BC ,∠ACB=90°,D 为AB 中点,∴∠B=45°,∠DCE=12∠ACB=45°,CD⊥AB,CD =12AB =BD ,∴∠DCE=∠B,∠CDB=90° ∵∠EDF=90°, ∴∠1=∠2, 在△CDE 和△BDF 中, ⎩⎪⎨⎪⎧∠1=∠2CD =BD∠DCE=∠B, ∴△CDE≌△BDF(ASA),∴S △DEF +S △CEF =S △ADE +S △BDF =12S △ABC ;图①图② 第2题解图(2)S △DEF -S △CEF =12S △ABC ;理由如下:连接CD ,如解图②所示,同(1)得:△DEC≌△DFB,∠DCE=∠DBF =135°, ∴S △DEF =S 五边形DBFEC , S △CFE +S △DBC , =S △CFE +12S △ABC ,∴S △DEF -S △CFE =12S △ABC .∴S △DEF 、S △CEF 、S △ABC 的关系是S △DEF -S △CEF =12S △ABC .3.解:(1)如解图①中,∵四边形ABCD 、EFGC 都是正方形, ∴∠BCD=∠ECG=90°.∵∠BCG+∠BCD+∠DCE+∠ECG=360°, ∴∠BCG+∠ECD=180°.图①图②图③ 第3题解图如解图①,过点E 作EM⊥DC 于点M ,过点G 作GN⊥BN 交BN 的延长线于点N , ∴∠EMC=∠N=90°.∵四边形ABCD 和四边形ECGF 均为正方形, ∴∠BCD=∠DCN=∠ECG=90°,CB =CD ,CE =CG ,∴∠1=90°-∠2,∠3=90°-∠2, ∴∠1=∠3. 在△CME 和△CNG 中, ⎩⎪⎨⎪⎧∠EMC=∠GNC ∠1=∠3EC =CG, ∴△CME≌△CNG(ASA), ∴EM=GN.又∵S 1=12CD·EM,S 2=12CB·GN,∴S 1=S 2;故答案为180°,S 1=S 2; (2)猜想:S 1=S 2,证明:如解图②,过点E 作EM⊥DC 于点M ,过点B 作BN⊥GC 交GC 的延长线于点N , ∴∠EMC=∠N=90°.∵矩形CGFE 由矩形ABCD 旋转得到的, ∴CE=CB ,CG =CD ,∵∠ECG=∠ECN=∠BCD=90°,∴∠1=90°-∠2,∠3=90°-∠2,∴∠1=∠3. 在△CME 和△CNB 中, ⎩⎪⎨⎪⎧∠EMC=∠BNC ∠1=∠3EC =CB, ∴△CME≌△CNB(AAS). ∴EM=BN.又∵S 1=12CD·EM,S 2=12CG ·BN ,∴S 1=S 2;(3)如解图③,作DM⊥AC 于M ,延长BA ,交EC 于N , ∵AB=AC =10 cm ,∠B=30°, ∴∠ACB=∠ABC=30°, ∴∠BAC=120°,根据翻折的性质,得∠ACE=∠ACB=30°, ∵AD∥CE,∴∠DAC=∠ACE=30°, ∴∠BAD=90°,DM =12AD ,∴BN⊥EC.∵AD=tan∠ABD·AB,AB =10 cm , ∴AD=tan 30°×10=103 3 (cm),∴DM=12×1033=533(cm).∵S △ABP =12AB·PN,S △ADC =12AC·DM,S △ABP =S △ADC ,AB =AC ,∴PN=DM =533.在Rt△ANC 中,∠ACN=30°,AC =10 (cm), ∴NC=cos∠ACN·AC=cos 30°×10=53(cm). ∵在EC 上到N 的距离等于533的点有两个,∴P′C=103 3 cm ,P ″C =203 3 cm.∴CP 的长为103 3 cm 或203 3 cm.4.解:(1)PM =PN ,PM⊥PN,理由如下: 如解图①,延长AE 交BD 于O , ∵△ACB 和△ECD 是等腰直角三角形, ∴AC=BC ,EC =CD ,∠ACB=∠ECD=90°. 在△ACE 和△BCD 中, ⎩⎪⎨⎪⎧AC =BC ,∠ACE=∠BCD=90°,CE =CD ,∴△ACE≌△BCD(SAS), ∴AE=BD ,∠EAC=∠CBD,∵∠EAC+∠AEC=90°,∠AEC=∠BEO, ∴∠CBD+∠BEO=90°, ∴∠BOE =90°,即AE⊥BD,∵点M 、N 分别是斜边AB 、DE 的中点,点P 为AD 的中点, ∴PM=12BD ,PN =12AE ,∴PM=PN.∵PM∥BD,PN∥AE,AE⊥BD,∴∠NPD=∠EAC,∠MPA=∠BDC,∠EAC+∠BDC=90°, ∴∠MPA+∠NPC=90°,∴∠MPN=90°, 即PM⊥PN.图①图② 第4题解图(2)△PMN 为等腰直角三角形,理由如下: 如解图②,设AE 交BC 于点O. ∵△ACB 和△ECD 是等腰直角三角形, ∴AC=BC ,EC =CD ,∠AC B =∠ECD=90°, ∴∠ACB+∠BCE=∠ECD+∠BCE, ∴∠ACE=∠BCD, ∴△ACE≌△BCD, ∴AE=BD ,∠CAE =∠CBD. 又∵∠AOC=∠BOE,∠CAE=∠CBD, ∴∠BHO=∠ACO=90°.∵点P ,M ,N 分别为AD ,AB ,DE 的中点, ∴PM=12BD ,PM∥BD,PN =12AE ,PN∥AE,∴PM=PN ,∴∠MGE+∠BHA=180°, ∴∠MGE=90°, ∴∠MPN=90°,∴PM⊥PN,即△PMN 为等腰直角三角形.(3)由(2)可知△PMN 是等腰直角三角形,PM =12BD ,∴当BD 的值最大时,PM 的值最大,△PMN 的面积最大, ∴当B ,C ,D 共线时,BD 的最大值为BC +CD =6, ∴PM=PN =3,∴△PMN 面积的最大值为12×3×3=92.。
类比探究专题 全

D类比探究之图形变化1. (2011福建南平)(1)操作发现:如图1,在矩形ABCD 中,E 是BC 的中点,将△ABE 沿AE 折叠后得到△AFE ,点F 在矩形ABCD 内部,延长AF 交CD 于点G .猜想线段GF 与GC 有何数量关系?并证明你的结论. (2)类比探究:如图2,将(1)中的矩形ABCD 改为平行四边形,其它条件不变,(1)中的结论是否仍然成立?请说明理由.图1 图22.(2011北京)在□ABCD中,∠BAD的平分线交直线BC于点E,交直线DC于点F.(1)在图1中证明CE=CF;(2)若∠ABC=90°,G是EF的中点(如图2),直接写出∠BDG的度数;(3)若∠ABC=120°,FG∥CE,FG=CE,分别连结DB、DG(如图3),求∠BDG 的度数.图1 图2 图33.(2011大连)在△ABC中,∠A=90°,点D在线段BC上,∠EDB=12∠C,BE⊥DE,垂足为E,DE与AB相交于点F.(1)当AB=AC时(如图1),①∠EBF=_______°;②探究线段BE与FD的数量关系,并加以证明;(2)当AB=kAC时(如图2),求B EF D的值(用含k的式子表示).图1 图24. (2009武汉)如图1,在中,,于点,点是边上一点,连接交于,交边于点. (1)求证:; (2)当为边中点,时,如图2,求的值;(3)当为边中点,时,请直接写出的值.图1 图2R t A B C △90B A C ∠=°AD BC ⊥D O A C B O A D F O E O B ⊥B C E A B F C O E △∽△O A C 2A C AB =O F O E O AC A C n A B=O F O El类比探究之图形运动1.(2008河北)如图1,的边在直线上,,且;的边也在直线上,边与边重合,且.(1)在图1中,请你通过观察、测量,猜想并写出与所满足的数量关系和位置关系;(2)将沿直线向左平移到图2的位置时,交于点,连接,.猜想并写出与所满足的数量关系和位置关系,请证明你的猜想;(3)将沿直线向左平移到图3的位置时,的延长线交的延长线于点,连接,.你认为(2)中所猜想的与的数量关系和位置关系还成立吗?若成立,给出证明;若不成立,请说明理由.图1 图2A B C△B C l A C B C⊥A C B C=E F P△F P l E F A C EF FP=A B A PE F P△l E P A C Q A P BQ BQ A PE F P△l E P A CQ A P BQ BQ A P4. (2009辽宁抚顺)已知:如图所示,直线M A N B M AB ∠∥,与N B A ∠的平分线交于点C ,过点C 作一条直线l 与两条直线M A N B 、分别相交于点D E 、. (1)如图1所示,当直线l 与直线M A 垂直时,猜想线段A D B E A B 、、之间的数量关系,请直接写出结论,不用证明;(2)如图2所示,当直线l 与直线M A 不垂直且交点D E 、都在A B 的同侧时,(1)中的结论是否成立?如果成立,请证明;如果不成立,请说明理由; (3)当直线l 与直线M A 不垂直且交点D E 、在A B 的异侧时,(1)中的结论是否仍然成立?如果成立,请说明理由;如果不成立,那么线段A D B E A B 、、之间还存在某种数量关系吗?如果存在,请直接写出它们之间的数量关系.图1 图2 备用图备用图5. (2009河北)在图1至图3中,点B 是线段AC 的中点,点D 是线段CE 的中点.四边形BCGF 和CDHN 都是正方形.AE 的中点是M .(1)如图1,点E 在AC 的延长线上,点N 与点G 重合时,点M 与点C 重合,求证:FM =MH ,FM ⊥MH ;(2)将图1中的CE 绕点C 顺时针旋转一个锐角,得到图2,求证:△FMH 是等腰直角三角形;(3)将图2中的CE 缩短到图3的情况,△FMH 还是等腰直角三角形吗?(不必说明理由)图1A HC (M )D EB FG (N )G图2AHC DBFNMAHCD图3 BFG MN5. (2011辽宁沈阳)已知,△ABC 为等边三角形,点D 为直线BC 上一动点(点D 不与B 、C 重合).以AD 为边作菱形ADEF ,使∠DAF =60°,连接CF . (1)如图1,当点D 在边BC 上时, ①求证:∠ADB =∠AFC ;②请直接判断结论∠AFC =∠ACB +∠DAC 是否成立;(2)如图2,当点D 在边BC 的延长线上时,其他条件不变,结论∠AFC =∠ACB +∠DAC 是否成立?请写出∠AFC 、∠ACB 、∠DAC 之间存在的数量关系,并写出证明过程;(3)如图3,当点D 在边CB 的延长线上时,且点A 、F 分别在直线BC 的异侧,其他条件不变,请补全图形,并直接写出∠AFC 、∠ACB 、∠DAC 之间存在的等量关系. 图1 图2 图3类比探究之阅读理解1. (2009青海)请阅读,完成证明和填空.九年级数学兴趣小组在学校的“数学长廊”中兴奋地展示了他们小组探究发现的结果,内容如下:(1)如图1,正三角形ABC 中,在A B A C 、边上分别取点M N 、,使B M A N =,连接B N C M 、,发现B N C M =,且60N O C ∠=°. 请证明:60N O C ∠=°.(2)如图2,正方形A B C D 中,在A B B C 、边上分别取点M N 、,使A M B N =,连接A N D M 、,那么A N =,且D O N ∠=度.(3)如图3,正五边形A B C D E 中,在A B B C 、边上分别取点M N 、,使A M B N =,连接A N E M 、,那么A N =,且E O N ∠=度. (4)在正n 边形中,对相邻的三边实施同样的操作过程,也会有类似的结论. 请大胆猜测,用一句话概括你的发现: .图1图2图36.(2009黑龙江齐齐哈尔)如图1,在四边形ABCD中,AB=CD,E、F分别是BC、AD的中点,连接EF并延长,分别与BA、CD的延长线交于点M、N,则∠BME=∠CNE(不需证明).(温馨提示:在图1中,连接BD,取BD的中点H,连接HE、HF,根据三角形中位线定理,证明HE=HF,从而∠1=∠2,再利用平行线性质,可证得∠BME=∠CNE.)问题一:如图2,在四边形ADBC中,AB与CD相交于点O,AB=CD,E、F分别是BC、AD的中点,连接EF,分别交DC、AB于点M、N,判断△OMN 的形状,请直接写出结论;问题二:如图3,在△ABC中,AC>AB,D点在AC上,AB=CD,E、F分别是BC、AD的中点,连接EF并延长,与BA的延长线交于点G,若∠EFC=60°,连接GD,判断△AGD的形状并证明.图1图2图37. (2009浙江嵊州)(1)阅读理解:课外兴趣小组活动时,老师提出了如下问题: 如图,△ABC 中,若AB =5,AC =3,求BC 边上的中线AD 的取值范围.小明在组内经过合作交流,得到了如下的解决方法:延长AD 到E ,使得DE =AD ,再连接BE (或将△ACD 绕点D 逆时针旋转180°得到△EBD ),把AB 、AC 、2AD 集中在△ABE 中,利用三角形的三边关系可得2<AE <8,则1<AD <4.感悟:解题时,条件中若出现“中点”“中线”字样,可以考虑构造以中点为对称中心的中心对称图形,把分散的已知条件和所求证的结论集中到同一个三角形中. (2)问题解决:受到(1)的启发,请你证明下面命题:如图,在△ABC 中,D 是BC 边上的中点,DE ⊥DF ,DE 交AB 于点E ,DF 交AC 于点F ,连接EF . ①求证:BE +CF >EF ;②若∠A =90°,探索线段BE 、CF 、EF 之间的等量关系,并加以证明. (3)问题拓展:如图,在四边形ABDC 中,∠B +∠C =180°,DB =DC ,∠BDC =120°,以D 为顶点作一个60°角,角的两边分别交AB 、AC 于E 、F 两点,连接EF ,探索线段BE 、CF 、EF 之间的数量关系,并加以证明.6.(2010江苏连云港)如果一条直线把一个平面图形的面积分成相等的两部分,我们把这条直线称为这个平面图形的一条面积等分线.例如,平行四边形的一条对角线所在的直线就是平行四边形的一条面积等分线.(1)三角形的中线、高线、角平分线分别所在的直线一定是三角形的面积等分线的有________;(2)如图1,梯形ABCD中,AB∥DC,如果延长DC到E,使CE=AB,连接AE,那么有S梯形ABCD=S△ADE.请你给出这个结论成立的理由,并过点A作出梯形ABCD的面积等分线(不写作法,保留作图痕迹);(3)如图2,四边形ABCD中,AB与CD不平行,S△ADC>S△ABC,过点A 能否作出四边形ABCD的面积等分线?若能,请画出面积等分线,并给出证明;若不能,说明理由.图1图2。
2021年中考数学总复习 直线形综合 类比探究型专题训练(不用相似)(含答案与解析)

类比探究型几何综合题专题训练(不用相似)【类型1】通过位置变化(图形变换)进行类比探究〖例1〗已知:如图,等边△AOB的边长为4,点C为OA中点.(1)如图1,将OC绕点O顺时针旋转,使点C落到OB边的点D处,设旋转角为α(0°<α≤360°).则此时α=;此时△COD是三角形(填特殊三角形的名称).(2)如图2,固定等边△AOB不动,将(1)中得到的△OCD绕点O逆时针旋转,连接AC,BD,设旋转角为β(0°<β≤360°).①求证:AC=BD;②当旋转角β为何值时,OC∥AB,并说明理由;③当A、C、D三点共线时,直接写出线段BD的长.〖例2〗现有与菱形有关的三幅图,如图:(1)(感知)如图①,AC是菱形ABCD的对角线,∠B=60°,E、F分别是边BC、CD上的中点,连结AE、EF、AF.若AC=2,则CE+CF的长为.(2)(探究)如图②,在菱形ABCD中,∠B=60°.E是边BC上的点,连结AE,作∠EAF=60°,边AF交边CD于点F,连结EF.若BC=2,求CE+CF的长.(3)(应用)在菱形ABCD中,∠B=60°.E是边BC延长线上的点,连结AE,作∠EAF=60°,边AF交边CD延长线于点F,连结EF.若BC=2,EF⊥BC时,借助图③求△AEF的周长.〖尝试练习〗1.如图1,等边△ABC与等边△BDE的顶点B重合,D、E分别在AB、BC上,AB=2√2,BD=2.现将等边△BDE从图1位置开始绕点B顺时针旋转,如图2,直线AD、CE相交于点P.(1)在等边△BDE旋转的过程中,试判断线段AD与CE的数量关系,并说明理由;(2)在等边△BDE顺时针旋转180°的过程中,当点B到直线AD的距离最大时,求PC的长;(3)在等边△BDE旋转一周的过程中,当A、D、E三点共线时,求CE的长.2.△ABC中,∠BAC=90°,AB=AC,点D为直线BC上一动点(点D不与B,C重合),以AD 为边在AD右侧作正方形ADEF,连接CF.(1)探究猜想如图1,当点D在线段BC上时,①BC与CF的位置关系为:;②BC、CD、CF之间的数量关系为:;(2)深入思考如图2,当点D在线段CB的延长线上时,结论①、②是否仍然成立?若成立,请给予证明;若不成立,请你写出正确结论再给予证明.(3)拓展延伸如图3,当点D在线段BC的延长线上时,正方形ADEF对角线交于点O.若已知AB=2√2,CD=14BC,请求出OC的长.3.如图1,正方形ABCD与正方形AEFG有公共的顶点A,且正方形AEFG的边AE,AG分别在正方形ABCD的边AB,AD上,显然BE=DG,BE⊥DG.(1)将图1的正方形AEFG绕点A转动一定的角度到图2的位置.求证:①BE=DG;②BE⊥DG;(2)如图3,若点D,G,E在同一条直线上,且正方形ABCD的边长是4√2,正方形AEFG的边长为3√2,求BE的长.【类型2】通过形状变化进行类比探究〖例3〗如图1,在△ABC中,AB=AC,∠BAC=α.D为BC边上一点(不与点B,C重合),将线段AD绕点A逆时针旋转α,得到AE,连接DE,CE.(1)求证:CE=BD;(2)若α=60°,其他条件不变,如图2.请猜测线段AC,CD,CE之间的数量关系,并说明理由;(3)若α=90°,其他条件不变,如图3,请写出∠ACE的度数及线段AD,BD,CD之间的数量关系,并说明理由.〖例4〗如图1,在正方形ABCD中,点P是对角线BD上的一点,点E在AD的延长线上,且PC=PE,PF交CD于点F.(1)求证:∠PCD=∠PED;(2)连接EC,求证:EC=√2AP;(3)如图2,把正方形ABCD改成菱形ABCD,其他条件不变,当∠DAB=60°时,请直接写出线段EC和AP的数量关系.〖尝试练习〗4.已知菱形ABCD和菱形DEFG有公共的顶点D,C点在DE上,且∠ADC=∠EDG,连接AE,CG,如图1.(1)试猜想AE与CG有怎样的数量关系(直接写出关系,不用证明);(2)将菱形DEFG绕点D按顺时针方向旋转,使点E落在BC边上,如图2,连接AE和CG.你认为(1)中的结论是否还成立?若成立,请给出证明;若不成立,请说明理由;(3)在(2)的条件下,如果∠ADC=∠EDG=90°,如图3,你认为AE和CG是否垂直?若垂直,请给出证明;若不垂直,请说明理由.5.已知在平行四边形ABCD中,AB≠BC,将△ABC沿直线AC翻折,点B落在点E处,AD与CE相交于点O,联结DE.(1)如图1,求证:AC∥DE;(2)如图2,如果∠B=90°,AB=√3,BC=√6,求△OAC的面积;(3)如果∠B=30°,AB=2√3,当△AED是直角三角形时,求BC的长.6.如图,在平行四边形ABCD中,∠BAD的平分线交BC于点E,交DC的延长线于F,以EC、CF为邻边作平行四边形ECFG.(1)求证:四边形ECFG是菱形;(2)连结BD、CG,若∠ABC=120°,则△BDG是等边三角形吗?为什么?(3)若∠ABC=90°,AB=10,AD=24,M是EF的中点,求DM的长.【自主反馈】7.如图1,△ABC是等边三角形,点D,E分别是BC,AB上的点,且BD=AE,AD与CE交于点F.(1)求∠DFC的度数;(2)将CE绕着点C逆时针旋转120°,得到CP,连接AP,交BC于点Q.①补全图形(图2中完成);②用等式表示线段BE与CQ的数量关系,并证明.8.已知△ABC是等腰三角形.(1)如图1,若△ABC,△ADE均是顶角为42°的等腰三角形,BC、DE分别是底边,求证:△ABD≌△ACE;(2)如图2,若△ABC为等边三角形,将线段AC绕点A逆时针旋转90°,得到AD,连接BD,∠BAC的平分线交BD于点E,连接CE.①求∠AED的度数;②试探究线段AE、CE、BD之间的数量关系,并证明.9.在Rt△ABC中,∠ABC=90°,∠BAC=30°,将△ABC绕点A顺时针旋转一定的角度α得到△AED,点B、C的对应点分别是E、D.(1)如图1,当点E恰好在AC上时,求∠CDE的度数;(2)如图2,若α=60°时,点F是边AC中点,求证:DF=BE;(3)如图3,点B、C的坐标分别是(0,0),(0,2),点Q是线段AC上的一个动点,点M是线段AO上的一个动点,是否存在这样的点Q、M使得△CQM为等腰三角形且△AQM为直角三角形?若存在,请直接写出满足条件的点M的坐标;若不存在,请说明理由.10.在等腰直角三角形纸片ABC中,点D是斜边AB的中点,AB=10,点E为BC上一点,将纸片沿DE折叠,点B的对应点为点B'.(1)如图①,连接CD,则CD的长为;(2)如图②,B'E与AC交于点F,DB'∥BC.①求证:四边形BDB'E为菱形;②连接B'C,则△B'FC的形状为;(3)如图③,则△CEF的周长为.11.已知正方形ABCD,以CE为边在正方形ABCD外部作正方形CEFG,连AF,H是AF的中点,连接BH,HE.(1)如图1所示,点E在边CB上时,则BH,HE的关系为;(2)如图2所示,点E在BC延长线上,(1)中的结论是否仍然成立?若成立,请证明;若不成立,请给出新的结论并证明.(3)如图3,点B,E,F在一条直线上,若AB=13,CE=5,直接写出BH的长.12.(1)操作发现:如图1,在矩形ABCD中,E是BC的中点,将△ABE沿AE折叠后得到△AFE,点F在矩形ABCD内部,延长AF交CD于点G.猜想线段GF与GC有何数量关系?并证明你的结论.(2)简单应用:在(1)中,如果AB=4,AD=6,求CG的长.(3)类比探究:如图2,将(1)中的矩形ABCD改为平行四边形,其它条件不变,(1)中的结论是否仍然成立?请说明理由.13.我们知道,平行四边形的对边平行且相等,利用这一性质,可以为证明线段之间的位置关系和数量关系提供帮助.重温定理,识别图形(1)如图①,我们在探究三角形中位线DE和第三边BC的关系时,所作的辅助线为“延长DE到点F,使EF=DE,连接CF”,此时DE与DF在同一直线上且DE=12DF,又可证图中的四边形为平行四边形,可得BC与DF的关系是,于是推导出了“DE∥BC,DE=12BC”.寻找图形,完成证明(2)如图②,四边形ABCD和四边形AEFG都是正方形,△BEH是等腰直角三角形,∠EBH=90°,连接CF、CH.求证CF=√2BE.构造图形,解决问题(3)如图③,四边形ABCD和四边形AEFG都是菱形,∠ABC=∠AEF=120°,连接BE、CF.直接写出CF与BE的数量关系.类比探究型几何综合题专题训练(不用相似)答案与解析〖例1〗解:(1)如图1,∵△AOB是等边三角形,∴AO=BO=AB,∠AOB=60°,∵将OC绕点O顺时针旋转,使点C落到OB边的点D处,∴OC=OD,∠COD=∠AOB=60°=α,∴△COD是等边三角形,答案为:60°,等边;(2)①∵△COD是等边三角形,∴OC=OD,∠COD=∠AOB=60°,∴∠AOC=∠BOD,又∵AO=BO,∴△AOC≌△BOD(SAS),∴AC=BD;②如图2,当点C在点O的上方时,若OC∥AB,∴∠AOC=∠OAB=60°=β,如图2﹣1,当点C在点O的下方时,若OC∥AB,∴∠ABO=∠BOC=60°,∴β=360°﹣60°﹣60=240°,综上所述:β=60°或240°;③如图3,当点D在线段AC上时,过点O作OE⊥AC于E,∵等边△AOB的边长为4,点C为OA 中点,∴AO=AB=OB=4,OC=OD=CD=2,∵∠AOB=∠COD=60°,∴∠AOC=∠BOD,∴△AOC≌△BOD(SAS),∴AC=BD,∵OE⊥CD,OC=OD,∴CE=DE=1,∴OE=√OC2−CE2=√3,∴AE=√OA2−OE2=√13,∴AC=AE+CE=1+√13=BD;如图4,当点C在线段AD上时,过点O作OF⊥AD于F,同理可求DF=CF=1,AF=√13,∴AC=BD=√13﹣1,综上所述:BD=√13+1或√13﹣1.〖例2〗解:(1)感知:∵四边形ABCD是菱形,∴BC=CD=AB=2,∵E,F分别是边BC,CD的中点,∴CE=12BC,CF=12CD=1,∴CE+CF=2.故答案为:2.(2)探究:如图,连结AC.∵四边形ABCD是菱形,∴AB=BC,AB∥CD.∴∠B+∠BCD=180°.∵∠B=60°,∴△ABC是等边三角形,∠BCD=120°.∴∠BAC=∠ACB=60°,AB=AC.∴∠ACF=∠B=60°.∵∠EAF=60°,∴∠BAC﹣∠CAE=∠EAF﹣∠CAE.∴∠BAE=∠CAF.∴△ABE≌△ACF(ASA).∴BE=CF.∴CE+CF=BC=2.(3)应用:如图所示:∵四边形ABCD是菱形,∴AB=BC,AB∥CD.∴∠B+∠BCD=180°.∵∠B=60°,∴△ABC是等边三角形,∠BCD=120°.∴∠BAC=∠ACB=60°,AB=AC.∴∠CAD=∠B=60°.∵∠EAF=60°,∴∠CAD﹣∠DAE=∠EAF﹣∠DAE.∴∠CAE=∠DAF.∵∠ACE=∠ADF,AC=AD∴△ACE≌△ADF(ASA).∴CE=DF,AE=AF,∵∠EAF=60°,∴△AEF为等边三角形,∵EF⊥BC,∠ECF=60°,∴CF=2CE,∵CD=BC=2,∴CE=2,∴EF=√CF2−CE2=2√3,∴△AEF的周长为6√3.〖尝试练习〗1.解:(1)AD=CE,理由:∵△ABC与△BDE都是等边三角形,∴AB=BC,BD=BE,∠ABC=∠DBE =60°,∴∠ABD =∠CBE , ∴△ABD ≌△CBE (SAS ),∴AD =CE ;(2)如图2,过点B 作BH ⊥AD 于H ,在Rt △BHD 中,BD >BH ,∴当点D ,H 重合时,BD =BH ,∴BH ≤BD ,∴当BD ⊥AD 时,点B 到直线AD 的距离最大,∴∠EDP =90°﹣∠BDE =30°,同(1)的方法得,△ABD ≌△CBE (SAS ), ∴∠BEC =∠BDA =90°,EC =AD ,在Rt △ABD 中,BD =2,AB =2√2, 根据勾股定理得,AD =√AB 2−BD 2=2, ∴CE =2,∵∠BEC =90°,∠BED =60°, ∴∠DEP =90°﹣60°=30°=∠EDP ,∴DP =EP ,如图2﹣1,过点P 作PQ ⊥DE 于Q , ∴EQ =12DE =1,在Rt △EQP 中,∠PEQ =30°, ∴EP =EQcos ∠DEP =2√33, ∴PC =2−2√33; (3)①当点D 在AE 上时,如图3,∴∠ADB =180°﹣∠BDE =120°,∴∠BDE =60°, 过点B 作BF ⊥AE 于F ,在Rt △BDF 中,∠DBF =30°,BD =2, ∴DF =1,BF =√3,在Rt △ABF 中,根据勾股定理得,AF =√AB 2−BF 2=√5,AD =AF ﹣DF =√5﹣1,∴CE =AD =√5﹣1; ②当点D 在AE 的延长线上时,如图4,同①的方法得,AF =√5,DF =1,∴AD =AF +DF =√5+1,∴CE =AD =√5+1, 即满足条件的CE 的长为√5+1和√5﹣1. 2.解:(1)①正方形ADEF 中,AD =AF , ∵∠BAC =∠DAF =90°,∴∠BAD =∠CAF ,又∵AB=AC ,∴△DAB ≌△FAC (SAS ),∴∠ABC =∠ACF ,∵AB =AC ,∠BAC =90°,∴∠ABC =∠ACB =45°,∴∠ACB +∠ACF ═45°+45°=90°, 即BC ⊥CF ;②△DAB ≌△FAC ,∴CF =BD ,∵BC =BD +CD , ∴BC =CF +CD ;故答案为:BC =CF +CD ;(2)CF ⊥BC 成立;BC =CD +CF 不成立,CD =CF +BC .理由如下:∵正方形ADEF 中,AD =AF ,∵∠BAC =∠DAF =90°,∴∠BAD =∠CAF ,又∵AB=AC , ∴△DAB ≌△FAC (SAS ),∴∠ABD =∠ACF , ∵∠BAC =90°,AB =AC ,∴∠ACB =∠ABC =45°.∴∠ABD =180°﹣45°=135°,∴∠BCF =∠ACF ﹣∠ACB =135°﹣45°=90°,∴CF ⊥BC .∵CD =DB +BC ,DB =CF ,∴CD =CF +BC .(3)过点A 作AH ⊥BC 于点H ,过点E 作EM ⊥BD 于点M ,EN ⊥CF 于点N , ∵∠BAC =90°,AB =AC =2√2, ∴BC =4,∴CD =14BC =1,∴BD =5, 由(2)同理可证得△DAB ≌△FAC ,∴BC ⊥CF ,CF =BD =5,∵四边形ADEF 是正方形,∴OD =OF ,∵∠DCF =90°,∴DF =√CD 2+CF 2=√26,∴OC =√262.3.证明:(1)如图2,延长DG交BE于H,∵四边形ABCD,四边形AEFG是正方形,∴AB=AD,AG=AE,∠DAB=∠GAE=90°,∴∠DAG=∠BAE,∴△DAG≌△BAE(SAS),∴BE=DG,∠ADG=∠ABE,∵∠C+∠CBA+∠ABE+∠BHD+∠CDH=360°,∴90°+90°+∠ADG+∠CDH+∠BHD=360°,∴∠BHD=90°,∴DG⊥BE;(2)如图3,连接BD,∵正方形ABCD的边长是4√2,正方形AEFG的边长为3√2,∴BD=√2AD=8,GE=√2AE=6,∵BD2=DE2+BE2,∴64=(6+BE)2+BE2,∴BE=√23﹣3.〖例3〗证明:(1)∵将线段AD绕点A逆时针旋转α,∴AD=AE,∠DAE=α,∴∠BAC=∠DAE,∴∠BAD=∠CAE,又∵AB=AC,AD=AE,∴△BAD≌△CAE(SAS)∴BD=CE;(2)AC=CD+CE,理由如下:∵AB=AC,∠BAC=60°∴△ABC是等边三角形,∴AC=BC,由(1)可知:BD=CE,∴BC=BD+CD=CE+CD,∴AC=CD+CE;(3)∠ACE=45°,BD2+CD2=2AD2,理由如下:∵AB=AC,∠BAC=90°,∴∠ABC=∠ACB=45°,∵△BAD≌△CAE∴∠ACE=∠ABC=45°,∴∠BCE=∠ACE+∠ACB=90°,∴CE2+CD2=DE2,∵AD=AE,∠DAE=90°,∴DE2=2AD2,∴CE2+CD2=2AD2,∴BD2+CD2=2AD2.〖例4〗(1)证明:∵四边形ABCD是正方形,∴AD=DC,∠ADP=∠CDP=45°,又∵PD=PD,∴△ADP≌△CDP(SAS),∴∠PAD=∠PCD,AP=CP,∵PC=PE,∴AP=PE,∴∠PAD=∠PED,∴∠PCD=∠PED;(2)证明:∵四边形ABCD是正方形,∴∠ADC=∠EDF=90°,由(1)知,∠PCD=∠PED,∵∠CFP=∠EFD(对顶角相等),∴180°﹣∠CFP﹣∠PCD=180°﹣∠EFD﹣∠PED,即∠CPF=∠EDF=90°,∵PC=PE,∴△CPE是等腰直角三角形,∴EC=√2CP,由(1)知,AP=CP,∴EC=√2AP;(3)解:AP=CE;理由如下:∵四边形ABCD是菱形,∠DAB=60°,∴AB=BC,∠ABP=∠CBP =60°,∠BAD=∠BCD,∠EDC=∠DAB=60°,又∵PB=PB,∴△ABP≌△CBP(SAS),∴PA =PC,∠BAP=∠BCP,∴∠DAP=∠DCP,∵PC=PE,∴PA=PE,∴∠DAP=∠AEP,∴∠DCP =∠AEP,∵∠CFP=∠EFD,∴180°﹣∠CFP﹣∠PCF=180°﹣∠EFD﹣∠AEP,即∠CPF=∠EDF=60°,∴△EPC是等边三角形,∴PC=EC,∴EC=AP,〖尝试练习〗4.解:(1)AE=CG,理由如下:∵四边形ABCD和四边形DEFG都是菱形,∴DA=DC,DE=DG,又∵∠ADE=∠CDG,∴△DAE≌△DCG(SAS),∴AE=CG;(2)成立,理由如下:∵∠ADC=∠EDG,∴∠ADC﹣∠EDC=∠EDG﹣∠EDC,即∠ADE=∠CDG,又∵DA=DC,DE=DG,∴△DAE≌△DCG(SAS),∴AE=CG;(3)AE⊥CG,理由如下:延长线段AE、GC交于点H,∵AD∥BC,∴∠CEH=∠DAE,由(2)可知,△DAE ≌△DCG ,∴∠DAE =∠DCG ,∴∠CEH =∠DCG , ∵四边形ABCD 是菱形,∠ADC =90°,∴四边形ABCD 是正方形,∴∠BCD =90°,∴∠ECH +∠DCG =90°,∴∠ECH +∠CEH =90°,∴∠CHE =90°,∴AE ⊥CG . 5.(1)证明:由折叠的性质得:△ABC ≌△△ AEC ,∴∠ACB =∠ACE ,BC =EC ,∵四边形ABCD 是平行四边形,∴AD =BC ,AD ∥BC .∴EC =AD ,∠ACB =∠CAD ,∴∠ACE =∠CAD ,∴OA =OC ,∴OD =OE ,∴∠ODE =∠OED ,∵∠AOC =∠DOE ,∴∠CAD =∠ACE =∠OED =∠ODE ,∴AC ∥DE ; (2)解:∵平行四边形ABCD 中,∠B =90°,∴四边形ABCD 是矩形,∴∠CDO =90°,CD =AB =√3,AD =BC =√6,由(1)得:OA =OC ,设OA =OC =x ,则OD =√6﹣x ,在Rt △OCD 中,由勾股定理得:(√3)2+(√6﹣x )2=x 2,解得:x =3√64,∴OA =3√64, ∴△OAC 的面积=12OA ×CD =12×3√64×√3=9√28;(3)解:分两种情况:①如图3,当∠EAD =90°时,延长EA 交BC 于G ,∵AD =BC ,BC =EC ,∴AD =EC , ∵AD ∥BC ,∠EAD =90°,∴∠EGC =90°, ∵∠B =30°,AB =2√3,∴∠AEC =30°, ∴GC =12EC =12BC ,∴G 是BC 的中点, 在Rt △ABG中,BG =√32AB =3,∴BC =2BG =6;②如图4,当∠AED =90°时∵AD =BC ,BC =EC ,∴AD =EC ,由折叠的性质得:AE =AB ,∴AE =CD ,又∵AC=AC ,∴△ACE ≌△CAD (SSS ), ∴∠ECA =∠DAC ,∴OA =OC ,∴OE =OD ,∴∠OED =∠ODE ,∴∠AED =∠CDE , ∵∠AED =90°,∴∠CDE =90°,∴AE ∥CD , 又∵AB ∥CD ,∴B ,A ,E 在同一直线上, ∴∠BAC =∠EAC =90°,∵Rt △ABC 中,∠B =30°,AB =2√3,∴AC =√33AB =2,BC =2AC =4;综上所述,当△AED 是直角三角形时,BC 的长为4或6.6.证明:(1)∵AF 平分∠BAD ,∴∠BAF =∠DAF ,∵四边形ABCD 是平行四边形, ∴AD ∥BC ,AB ∥CD ,∴∠DAF =∠CEF ,∠BAF =∠CFE ,∴∠CEF =∠CFE ,∴CE =CF , 又∵四边形ECFG 是平行四边形, ∴四边形ECFG 为菱形;(2)△BDG 是等边三角形,理由如下:∵四边形ABCD 是平行四边形,∴AB ∥DC ,AB =DC ,AD ∥BC ,∵∠ABC =120°,∴∠BCD =60°,∠BCF =120°,由(1)知,四边形CEGF 是菱形,∴CE =GE ,∠BCG =12∠BCF =60°,∴CG =GE =CE ,∠DCG =120°,∵EG ∥DF ,∴∠BEG =120°=∠DCG ,∵AE 是∠BAD 的平分线,∴∠DAE =∠BAE ,∵AD ∥BC , ∴∠DAE =∠AEB ,∴∠BAE =∠AEB ,∴AB =BE ,∴BE =CD ,∴△BEG ≌△DCG (SAS ),∴BG =DG ,∠BGE =∠DGC ,∴∠BGD =∠CGE ,∵CG =GE =CE ,∴△CEG 是等边三角形, ∴∠CGE =60°,∴∠BGD =60°,∵BG =DG , ∴△BDG 是等边三角形;(3)如图2中,连接BM ,MC ,∵∠ABC =90°,四边形ABCD 是平行四边形,∴四边形ABCD 是矩形,又由(1)可知四边形ECFG 为菱形,∠ECF=90°,∴四边形ECFG为正方形.∵∠BAF=∠DAF,∴BE=AB=DC,∵M为EF中点,∴∠CEM=∠ECM=45°,∴∠BEM=∠DCM=135°,∴△BME≌△DMC(SAS),∴MB=MD,∠DMC=∠BME.∴∠BMD=∠BME+∠EMD=∠DMC+∠EMD=90°,∴△BMD是等腰直角三角形.∵AB=10,AD=24,∴BD=√AB2+AD2=26,∴DM=√22BD=13√2.【自主反馈】7.解:(1)∵△ABC是等边三角形,∴AB=AC=BC,∠BAC=∠B=∠ACB=60°,又∵BD=AE,∴△ABD≌△CAE(SAS),∴∠BAD=∠ACE,∵∠BAD+∠DAC=60°,∴∠DFC=∠ACE+∠DAC=60°;(2)①根据题意补全图形如图2所示:②线段BE与CQ的数量关系为:CQ=12BE;理由如下:∵CE绕着点C逆时针旋转120°,得到CP,∴CE=CP,∠ECP=120°,∵∠DFC=60°,∴AD∥CP,∴∠ADC=∠DCP,∵△ABD≌△CAE,∴CE=AD,∴AD=CP,∴△ADQ≌△PCQ(AAS),∴CQ=DQ=12CD,∵AB=BC,BD=AE,∴BE=CD,∴CQ=12BE.8.解:(1)∵△ABC,△ADE均是顶角为42°的等腰三角形,BC、DE分别是底边,∴AB=AC,AD=AE,∠BAC=∠DAE,∴∠BAD=∠CAE,∴△ABD≌△ACE(SAS);(2)①∵△ABC是等边三角形,∴AB=AC,∠BAC=60°,由旋转知,AC=AD,∠CAD=90°,∴AB=AD,∠BAD=∠BAC+∠CAD=150°,∴∠D=12(180°﹣∠BAD)=15°,∵AE是∠BAC的平分线,∴∠CAE=12∠BAC=30°,∴∠DAE=∠CAD+∠CAE=120°,∴∠AED=180°﹣∠D﹣∠DAE=45°;②BD=2CE+√2AE;证明:如图,∵△ABC是等边三角形,∴AB=AC,∵AE是∠BAC的角平分线,∴∠BAE=∠CAE,∵AE=AE,∴△BAE≌△CAE(SAS),∴BE=CE,过点A作AF⊥AE交DE于F,∴∠EAF=90°,由旋转知,∠CAD=90°,∴∠CAE=∠DAF,由①知,∠AED=45°,∴∠AFE=45°=∠AEF,∴AE=AF,∴EF=√2AE,∵AC=AD,∴△ACE≌△ADF(SAS),∴DF=CE,∴BD=BE+EF+DF=CE+√2AE+CE =2CE+√2AE.9.解:(1)∵∠ABC=90°,∠BAC=30°,∴∠ACB=60°,∵△ABC绕点A顺时针旋转α得到△AED,点E恰好在AC上,∴CA=AD,∠EAD=∠BAC=30°,∴∠ACD=∠ADC=12(180°﹣30°)=75°,∵∠EDA=∠ACB=60°,∴∠CDE=∠ADC﹣∠EDA=15°;(2)连接BF,∵点F是边AC中点,∴BF=AF=12AC,∵∠BAC=30°,∴BC=12AC,∴∠FBA=∠BAC=30°,∵△ABC绕点A顺时针旋转60°得到△AED,∴∠BAE=∠CAD=60°,CB=DE,∠DEA=∠ABC=90°,∴DE =BF ,延长BF 交AE 于点G ,则∠BGE =∠GBA +∠BAG =90°, ∴∠BGE =∠DEA ,∴BF ∥ED ,∴四边形BFDE 是平行四边形,∴DF =BE ; (3)∵点B 、C 的坐标分别是(0,0),(0,2), ∴BC =2,∵∠ABC =90°,∠BAC =30°, ∴AC =4,AB =2√3,若∠QMA =90°,CQ =MQ 时,如图3,设CQ =QM =x ,∠CAB =30°,∴AQ =2x ,AM =√3x , ∴AC =x +2x =3x =4,∴x =43,∴AM =43√3,∴BM =AB ﹣AM =2√3﹣4√33=2√33,∴点M (2√33,0); 若∠AQM =90°,CQ =QM 时,如图4, 设CQ =QM =x ,∠CAB =30°, ∴AQ =√3x ,AM =2x , ∴AC =x +√3x =4,∴x =2√3﹣2,∴AM =4√3﹣4, ∴BM =2√3﹣(4√3﹣4)=4﹣2√3, ∴点M (4﹣2√3,0);综上所述:M (2√33,0)或(4﹣2√3,0).10.(1)解:∵△ABC 是等腰直角三角形,点D 是斜边AB 的中点,AB =10,∴CD =12AB =5(2)①证明:由折叠的性质得:B 'D =BD ,B 'E =BE ,∠B 'DE =∠BDE ,∵DB '∥BC ,∴∠B 'DE =∠BED ,∴∠BDE =∠BED ,∴BD =BE ,∴B 'D =BE ,∴四边形BDB 'E 是平行四边形,又∵B 'D =BD ,∴四边形BDB 'E 为菱形;②解:∵△ABC 是等腰直角三角形,点D 是斜边AB 的中点,∴CD =12AB =BD , 由折叠的性质得:B 'D =BD ,∴CD =B 'D ,∴∠DCB '=∠DB 'C ,∵∠ACB =90°,∴AC ⊥BC ,∵DB '∥BC ,∴DB '⊥AC ,∴∠ACB '=90°﹣∠DB 'C ,由①得:四边形BDB 'E 为菱形, ∴AB ∥B 'E ,∵CD ⊥AB ,∴CD ⊥B 'E ,∴∠EB 'C =90°﹣∠DCB ',∴∠ACB '=∠EB 'C , ∴FB '=FC ,即△B 'FC 为等腰三角形;(3)解:连接B 'C ,如图③所示:∵△ABC 是等腰直角三角形,点D 是斜边AB 的中点,AB =10,∴BC =√22AB =5√2,∠B =45°,CD =12AB =BD ,∠ACD =12∠ACB =45°,由折叠的性质得:B 'D =BD ,∠B '=∠B =45°,∴CD =B 'D ,∴∠DCB '=∠DB 'C ,∴∠FCB '=∠FB 'C ,∴CF =B 'F ,∴△CEF 的周长=EF +CF +CE =EF +B 'F +CE =B 'E +CE =BE +CE =BC =5√2; 11.解:(1)BH ⊥HE ,BH =HE ;理由如下: 延长EH 交AB 于M ,如图1所示: ∵四边形ABCD 和四边形CEFG 是正方形,∴AB ∥CD ∥EF ,AB =BC ,CE =FE ,∠ABC =90°,∴∠AMH =∠FEH ,∵H 是AF 的中点,∴AH =FH ,∴△AMH ≌△FEH (AAS ), ∴AM =FE =CE ,MH =EH ,∴BM =BE , ∵∠ABC =90°,∴BH ⊥HE ,BH =12ME =HE ;(2)结论仍然成立.BH ⊥HE ,BH =HE .理由如下:延长EH 交BA 的延长线于点M ,如图2所示:∵四边形ABCD 是正方形,四边形EFGC 是正方形,∴∠ABE =∠BEF =90°,AB =BC ,AB ∥CD ∥EF ,CE =FE ,∴∠HAM =∠HFE ,∴△AHM ≌△FHE (ASA ),∴HM =HE ,AM =EF =CE ,∴BM =BE ,∵∠ABE =90°, ∴BH ⊥EH ,BH =12EM =EH ;(3)延长EH 到M ,使得MH =EH ,连接AH 、BH ,如图3所示:同(2)得:△AMH ≌△FEH (SAS ),∴AM =FE =CE ,∠MAH =∠EFH , ∴AM ∥BF ,∴∠BAM +∠ABE =180°,∴∠BAM +∠CBE =90°,∵∠BCE +∠CBE =90°∴∠BAM =∠BCE ,∴△ABM ≌△CBE (SAS ),∴BM =BE ,∠ABM =∠CBE ,∴∠MBE =∠ABC =90°,∵MH =EH ,∴BH ⊥EH ,BH =12EM =MH =EH ,在Rt △CBE 中,BE =√CB 2−CE 2=12,∵BH =EH ,BH ⊥EH ,∴BH =√22BE =6√2.12.解:(1)GF =GC .理由如下:如图1,连接GE , ∵E 是BC 的中点, ∴BE =EC ,∵△ABE 沿AE 折叠后得到△AFE ,∴BE =EF ,∴EF =EC ,∵四边形ABCD 是矩形,∴∠C =∠B =90°,∴∠EFG =90°,∴Rt △GFE ≌Rt △GCE (HL ),∴GF =GC ; (2)设GC =x ,则AG =4+x ,DG =4﹣x , 在Rt △ADG 中,62+(4﹣x )2=(4+x )2, 解得x =94.∴GC =94;(3)(1)中的结论仍然成立.证明:如图2,连接FC ,∵E 是BC 的中点,∴BE =CE ,∵将△ABE 沿AE 折叠后得到△AFE ,∴BE =EF ,∠B =∠AFE ,∴EF =EC ,∴∠EFC =∠ECF ,∵矩形ABCD 为平行四边形,∴∠B =∠D , ∵∠ECD =180°﹣∠D ,∠EFG =180°﹣∠AFE =180°﹣∠B =180°﹣∠D ,∴∠ECD =∠EFG ,∴∠GFC =∠GFE ﹣∠EFC =∠ECG ﹣∠ECF =∠GCF ,∴∠GFC =∠GCF ,∴FG =CG ;即(1)中的结论仍然成立.13.解:(1)∵AE =CE ,DE =EF ,∠AED =∠CEF ,∴△AED ≌△CEF (SAS ), ∴AD =CF ,∠ADE =∠F ,∴BD ∥CF ,∵AD =BD ,∴BD =CF ,∴四边形BCFD 是平行四边形,∴DF =BC ,DF ∥BC , (2)证明:∵四边形ABCD 是正方形∴AB =BC ,∠ABC =90°,即∠ABE +∠CBE =90° ∵△BEH 是等腰直角三角形,∴EH =2BE =2BH ,∠BEH =∠BHE =45°, ∠EBH =90°,即∠CBH +∠CBE =90° ∴∠ABE =∠CBH , ∴△ABE ≌△CBH (SAS ), ∴AE =CH ,∠AEB =∠CHB ,∴∠CHE =∠CHB ﹣∠BHE =∠CHB ﹣45°=∠AEB ﹣45°, ∵四边形AEFG 是正方形, ∴AE =EF ,∠AEF =90°,∴EF =HC ,∠FEH =360°﹣∠AEF ﹣∠AEB ﹣∠BEH =225°﹣∠AEB , ∴∠CHE +∠FEH =∠AEB ﹣45°+225°﹣∠AEB =180°, ∴EF ∥HC 且 EF =HC , ∴四边形EFCH 是平行四边形, ∴CF =EH =√2BE ;(3)CF=√3BE,如图,过点B作BH,使∠EBH=120°,且BH=BE,连接EH、CH,则∠BHE=∠BEH=30°,∵∠ABC=∠EBH=120°,∴∠ABE=∠CBH,∵AB=BC,BE=BH,∴△AEB≌△CHB(SAS),∴CH=AE=EF,∠CHB=∠AEB,∵∠CHE=∠CHB﹣∠BHE=∠AEB﹣30°,∠FEH=360°﹣∠AEF﹣∠AEB﹣∠BEH=210°﹣∠AEB,∴∠CHE+∠FEH=180°,∴CH∥EF且CH=EF,∴四边形EFCH是平行四边形,∴CF=EH,过B作BN⊥EH于N,在△EBH中,∠EBH=120°,BH=BE,∴∠BEN=30°,EH=2EN,BE,∴EN=√32∴EH=√3BE,∴CF=EH=√3BE.。
类比探究(人教版)(含答案)

类比探究(人教版)一、单选题(共9道,每道11分)1.如图1,△ABC的边BC在直线l上,AC⊥BC,且AC=BC;△EFP的边FP也在直线l上,边EF与边AC重合,且EF=FP.如图1,易证AB=AP,且AB⊥AP.(1)将△EFP沿直线l向左平移到图2的位置时,EP交AC于点O,连接AP,BO.则BO与AP所满足的数量及位置关系是( )A.相等但不垂直B.不相等但垂直C.相等且垂直D.不相等也不垂直答案:C解题思路:试题难度:三颗星知识点:类比探究2.(上接第1题)(2)将△EFP沿直线l继续向左平移到图3的位置时,EP的延长线交AC 的延长线于点O,连接AP,BO.此时,BO与AP的数量关系和位置关系是( )A.相等但不垂直B.不相等但垂直C.相等且垂直D.不相等也不垂直答案:C解题思路:试题难度:三颗星知识点:类比探究3.已知:如图,在Rt△ABC中,AB=BC,∠ABC=90°.一块等腰直角三角板的直角顶点放在斜边AC的中点O处,将三角板绕点O旋转,三角板的两直角边分别交AB,BC或其延长线于点E,F,图1,图2是旋转三角板所得图形的两种情况.(1)如图1,当点E和点F分别在AB和BC边上时,OE和OF的大小关系是( )A.OE>OFB.OE=OFC.OE<OFD.无法确定答案:B解题思路:试题难度:三颗星知识点:类比探究4.(上接第3题)(2)如图2,当点E和点F分别在AB和BC边的延长线上时,OE和OF的大小关系是( )A.OE>OFB.OE=OFC.OE<OFD.无法确定答案:B解题思路:试题难度:三颗星知识点:类比探究5.如图1,在正方形ABCD和正方形CGEF(CG>BC)中,点B,C,G在同一直线上,点M是AE的中点。
(1)探究线段MD,MF的位置关系,并证明。
解题思路:(1)小明猜测MD⊥MF,看到图1中M是AE的中点,并且AD∥EF,考虑延长DM交EF于点H,如下图,先利用全等三角形的判定定理_____,证明_____,由全等的性质可以得到_____,所以CD=EH,进而可以得到FD=FH,在等腰△DFH中,由等腰三角形三线合一可以得到_____,从而证明结论。
类比探究综合测试(通用版)(含答案)

类比探究综合测试(通用版)试卷简介:测试学生在处理类比探究问题过程中,有没有类比照搬的意识,能否根据题干或者问与问之间的联系,照搬辅助线,照搬思路来解决问题,同时考查学生对于类比探究中中点结构、旋转结构、平行结构这三种特殊结构的处理思路。
一、单选题(共6道,每道16分)1.如图1,△ABC和△BDE均为等腰直角三角形,BA⊥AC,ED⊥BD,点D在AB边上.连接EC,取EC的中点F,连接AF,DF.为了证明AF⊥DF,AF=DF,我们只需要延长DF交线段AC于点G,说明AF是等腰直角三角形ADG的中线即可.现将△BDE旋转至如图2所示的位置,使点E在AB的延长线上,点D在CB的延长线上,其他条件不变,类比上面的做法,为了证明AF⊥DF,AF=DF,我们需要作的辅助线是( )A.连接ADB.过点C作CG⊥DF,交DF的延长线于点GC.延长DF交AC的延长于点G,连接ADD.延长DF到G,使DF=FG,连接CG,AD,AG答案:D解题思路:在图1中,给出的辅助线达到的一个效果就是保证F是等腰直角三角形ADG斜边的中点,满足DF=FG.若在图2中达到同样的效果,需要延长DF到G,使DF=FG,这样再连接AD,AG之后才能保证F是等腰直角三角形ADG斜边的中点.试题难度:三颗星知识点:中考数学几何中的类比探究2.(上接第1题)在试题1图2的证明中,说明△ADG是等腰直角三角形之前,证明AD=AG 需要直接使用到某对三角形全等,则判定这对三角形全等的条件是( )A.AASB.ASAC.SSSD.SAS答案:D解题思路:要证明AD=AG,我们需要证明△ABD≌△ACG.根据上一题的分析,如图,延长DF到G,使DF=FG,连接CG,AD,AG,容易证明△DEF≌△GCF,∴CG=ED=BD,∠DEF=∠GCF,∴DE∥CG,∴∠GCD=∠BDE=90°,∴∠GCA=∠DBA=135°.又∵AC=AB,∴△ABD≌△ACG(SAS).(为了证明AF⊥DF,AF=DF,接下来需要根据得出的条件,说明∠DAG=90°,进而说明AF是等腰直角三角形ADG斜边上的中线)试题难度:三颗星知识点:中考数学几何中的类比探究3.如图1,在正方形ABCD中,点E,F分别为DC,BC边上的点,且满足∠EAF=45°,连接EF.利用旋转的思想很容易证明DE+BF=EF;如图2,将Rt△ABC沿斜边翻折得到△ADC,点E,F分别为DC,BC边上的点,且.则DE,BF,EF之间的数量关系为( )A. B.C.DE+2BF=EFD.DE+BF=EF答案:D解题思路:在图1中,旋转思想考虑了两个方面,一个是AB=AD,能够实现旋转,一个是,能够将角度放在一起,所以图1中的证明是将△DAE旋转,使得AD 与AB重合,这是一种思想,作辅助线的时候是延长CB到点G,使得BG=DE,最后证明GF=EF.图2中有同样的两个结构:AB=AD,,所以照搬分析图1的思路来研究数量关系.如图,延长CB到点G,使得BG=DE,连接AG.易证△ADE≌△ABG,∴AE=AG,BG=DE,∠DAE=∠BAG,∴∠DAE+∠BAF=∠BAG+∠BAF=∠GAF.∵,∴∠GAF=∠EAF.又∵AF=AF,∴△GAF≌△EAF,∴GF=EF,∴EF=GB+BF=DE+BF,即DE,BF,EF满足的数量关系是DE+BF=EF.试题难度:三颗星知识点:类比探究问题4.(上接第3题)如图3,在四边形ABCD中,AB=AD,E,F分别为DC,BC边上的点,且满足,当∠ABC与∠ADC满足( )时,可使得DE+BF=EF.A.∠ABC=∠ADCB.∠ABC+∠ADC=180°C.∠ABC=2∠ADC-180°D.∠ABC+2∠ADC=270°答案:B解题思路:试题3中图1和图2的证明,都是利用旋转的思想来证明DE+BF=EF,从作辅助线开始到结束,整个分析有以下几点:延长CB到点G,使得BG=DE,证明△ABG≌△ADE(SAS),导出∠GAF=∠EAF,进而证明△GAF≌△EAF(SAS),之后导出线段关系.若在图3中用此方法证明,首先延长CB到点G,使得BG=DE,要证明△ABG和△ADE全等,需要保证∠ABG=∠ADE,也就是需要∠ABC+∠ADC=180°,所以需要添加的条件是∠ABC+∠ADC=180°.添加条件之后的证明如下:如图,延长CB到点G,使得BG=DE,连接AG.∵∠ABC+∠ADC=180°,∠ABC+∠ABG=180°,∴∠ABG=∠ADE.又∵AB=AD,BG=DE,∴△ADE≌△ABG,∴AE=AG,BG=DE,∠DAE=∠BAG,∴∠DAE+∠BAF=∠BAG+∠BAF=∠GAF.∵,∴∠GAF=∠EAF.又∵AF=AF,∴GF=EF,∴EF=GB+BF=DE+BF.试题难度:三颗星知识点:类比探究问题5.如图,D是△ABC的边BC上一点,过点D的一条直线交AC于点F,交BA的延长线于点E.若BD=2CD,CF=mAF,则的值是( )A. B.C. D.答案:B解题思路:如图,过点D作DG∥AC,交AB于点G.设CD=a,BD=2a,AF=b,CF=mb.∵△BDG∽△BCA,∴∴,BG=2AG.设AG=c,BG=2c,∴,即∴∴试题难度:三颗星知识点:中考数学几何中的类比探究6.如图,D是△ABC的边BC上一点,过点D的一条直线交AC的延长线于点F,交AB于点E.若BD=aCD,CF=bAF,则的值是( )A. B.C. D.答案:D解题思路:如图,过点D作DG∥AC,交AB于点G.设CD=m,BD=am,AF=n,CF=bn.∵△BDG∽△BCA,∴∴,BG=aAG.设AG=c,BG=ac,∵△EAF∽△EGD,∴,即∴∴.试题难度:三颗星知识点:中考数学几何中的类比探究。
类比探究专题训练

类比探究专题训练1. 已知OM 是∠AOB 的平分线,点P 是射线OM 上一点,点C ,D 分别在射线OA ,OB 上,连接PC ,PD . (1)发现问题如图1,当PC ⊥OA ,PD ⊥OB 时,则PC 与PD 的数量关系是_________. (2)探究问题如图2,点C ,D 在射线OA ,OB 上滑动,且∠AOB =90°,当PC ⊥PD 时,PC 与PD 在(1)中的数量关系还成立吗?说明理由.图1CBA ODM P图2D OBPM A C2. 如图,AD ∥BC ,若∠ADP =∠α,∠BCP =∠β,射线OM 上有一动点P .(1)当点P 在A ,B 两点之间运动时,∠CPD 与∠α,∠β之间有何数量关系?请说明理由.(2)如果点P 在A ,B 两点外侧运动时(点P 与点A ,B ,O 三点不重合),请你直接写出∠CPD 与∠α,∠β之间的数量关系.备用图ON MD CBA3. 已知:如图,直线a ∥b ,直线c 与直线a ,b 分别相交于C ,D 两点,直线d与直线a ,b 分别相交于A ,B 两点,点P 在直线AB 上运动(不与A ,B 两点重合).(1)如图1,当点P 在线段AB 上运动时,总有:∠CPD =∠PCA +∠PDB ,请说明理由;(2)如图2,当点P 在线段AB 的延长线上运动时,∠CPD ,∠PCA ,∠PDB 之间有怎样的数量关系,并说明理由;(3)如图3,当点P 在线段BA 的延长线上运动时,∠CPD ,∠PCA ,∠PDB 之间又有怎样的数量关系(只需直接给出结论)?图1d DC B AP abc 图2c baP A B C Dd 图3c baP A BC Dd4. 综合与实践:(1)如图,已知:在等腰直角△ABC 中,∠BAC =90°,AB =AC ,直线m 经过点A ,BD ⊥直线m ,CE ⊥直线m ,垂足分别为点D ,E .小明观察图形特征后猜想线段DE ,BD 和CE 之间存在DE =BD +CE 的数量关系,请你判断他的猜想是否正确,并说明理由.(2)如图,将(1)中的条件改为:△ABC 为等边三角形,D ,A ,E 三点都在直线m 上,并且有∠BDA =∠AEC =∠BAC =60°,请问结论DE =BD +CE 是否成立?并说明理由.(3)如图,若将(1)中的三角形变形为一般的等腰三角形,△ABC 中,AB =AC ,∠BAC =α,其中α为任意锐角或钝角,D ,A ,E 三点都在直线m 上.问:满足什么条件时,结论DE =BD +CE 仍成立?直接写出条件即可.EDCBAm图1BD A CEm图2mA BCDE图35. 在△ABC 中,∠ACB =90°,AC =BC ,直线MN 经过点C ,且AD ⊥MN 于D ,BE ⊥MN 于E .(1)当直线MN 绕点C 旋转到图1的位置时,△ADC 和△CEB 全等吗?请说明理由.(2)聪明小亮发现,当直线MN 绕点C 旋转到图1的位置时,可得DE =AD +BE ,请你说明其中的理由.(3)小亮将直线MN 绕点C 旋转到图2的位置,线段DE ,AD ,BE 之间存在着什么的数量关系,请写出这一关系,并说明理由.的图1EDCBAMN 图2EDC BAMN6. 阅读理解:如图1,在△ABC 中,若AB =10,BC =8.求AC 边上的中线BD的取值范围.小聪同学是这样思考的:延长BD 至E ,使DE =BD ,连接CE .利用全等将边AB 转化到CE ,在△BCE 中利用三角形三边关系即可求出中线BD 的取值范围.在这个过程中小聪同学证三角形全等用到的判定方法是______________;中线BD 的取值范围是_______________.(2)问题解决:如图2,在△ABC 中,点D 是AC 的中点,点M 在AB 边上,点N 在BC 边上,若DM ⊥DN .求证:AM +CN >MN .(3)问题拓展:如图3,在△ABC 中,点D 是AC 的中点,分别以AB ,BC 为直角边向△ABC 外作等腰直角三角形ABM 和等腰直角三角形BCN ,其中∠ABM =NBC =∠90°,连接MN ,探索BD 与MN 的关系,并说明理由.图1ED C BANM图2ABC D 图3NMD C BA7. 乐乐和数学小组的同学们研究了如下问题,请你也来试一下吧!点C 是直线l 1上一点,在同一平面内,乐乐他们把一个等腰直角三角板ABC 任意摆放,其中直角顶点C 与点C 重合,过点A 作直线l 2⊥l 1,垂足为点M ,过点B 作l 3⊥l 1垂足为N .(1)如图1时,线段BN ,AM 与MN 之间的数量关系是__________________(不必说明理由);(2)当直线l 2,l 3,位于点C 的右侧时,如图2,判断线段BN ,AM 与MN 之间的数量关系,并说明理由;(3)当直线l 2,l 3,位于点C 的左侧时,如图3,请你补全图形,并直接写出线段BN ,AM ,MN 之间的数量关系.图1图2图3l 3NMl 1l 2ABCl 3C BAl 2l 1MNl 3l 2l 1MN8. (1)如图1,在四边形ABCD 中,AB =AD ,∠B =∠D =90°,E ,F 分别是边BC ,CD 上的点,且∠EAF =12∠BAD .请直接写出线段EF ,BE ,FD 之间的数量关系:____________;(2)如图2,在四边形ABCD 中,AB =AD ,∠B +∠D =180°,E ,F 分别是边BC ,CD 上的点,且∠EAF =12∠BAD ,(1)中的结论是否仍然成立?请写出证明过程;(3)在四边形ABCD 中,AB =AD ,∠B +∠D =180°,E ,F 分别是边BC ,CD所在直线上的点,且∠EAF =12∠BAD .请直接写出线段EF ,BE ,FD 之间的数量关系:______________.图1FE D CBAABCD E F图2ABCD备用图ABCD备用图9.认真阅读下面关于三角形内外角平分线所夹的探究片段,完成所提出的问题.探究1:如图1,在△ABC中,O是∠ABC与∠ACB的平分线BO和CO的交点,通过分析发现∠BOC=90°+12∠A,理由如下:∵BO和CO分别是∠ABC和∠ACB的角平分线,∴∠1=12∠ABC,∠2=12∠ACB,∴∠1+∠2=12(∠ABC+∠ACB)=12(180°-∠A)=90°-12∠A,∴∠BOC=180°-(∠1+∠2)=180°-(90°-12∠A)=90°+12∠A.(1)探究2:如图2中,O是∠ABC与外角∠ACD的平分线BO和CO的交点,试分析∠BOC与∠A有怎样的关系?请说明理由.(2)探究3:如图3中,O是外角∠DBC与外角∠ECB的平分线BO和CO 的交点,则∠BOC与∠A有怎样的关系?(直接写出结论)(3)拓展:如图4,在四边形ABCD中,O是∠ABC与∠DCB的平分线BO 和CO的交点,则∠BOC与∠A+∠D有怎样的关系?(直接写出结论)图1CBAO12图2CBAOD 图3EDOAB C图4DCBAO10. (1)如图1,已知四边形ABCD 为长方形,∠CAB 和∠ABD 的平分线恰好交于CD 边上的点E ,试判断:AB ___________AC +BD (填﹥,﹤或=); (2)如图2,已知AC ∥BD ,EA ,EB 分别平分∠CAB 和∠ABD ,CD 过点E ,且CD ⊥AC 试探究AB ,AC 与BD 之间的数量关系,并说明理由; (3)如图3,在(2)题中,如果没有“CD ⊥AC ”这个条件,(2)题的结论还成立吗,请说明理由.图1EDCBAEDCBA图2图3ABCDE11. 已知:如图所示,直线MN ∥GH ,另一直线交GH 于A ,交MN 于B ,且∠MBA =80°,点C 为直线GH 上一动点,过点C 的直线交MN 于点D ,且∠GCD =50°.(1)如图1,当点C 在点A 右边且点D 在点B 左边时,∠DBA 的平分线与∠DCA 的平分线交于点P ,求∠BOC 的度数;(2)如图2,当点C 在点A 右边且点D 在点B 右边时,∠DBA 的平分线与∠DCA 的平分线交于点P ,求∠BPC 的度数;(3)当点C 在点C 左边且点D 在点B 左边时,∠DBA 的平分线与∠DCA 的平分线所在直线交于点P ,请直接写出∠BPC 的度数,不说明理由.图1图2图3DCBAMNGHP PH GNMABCDHGNMAB12. 如图1,在△ABC 中,∠ACB 为锐角,点D 为射线BC 上一动点,连接AD ,以AD 为直角边且在AD 的上方作等腰直角三角形ADF ,连接CF . (1)若AB =AC ,∠BAC =90°.①当点D 在线段BC 上时(与点B 不重合),试探究CF 与BD 的数量关系和位置关系,并说明理由.②当点D 在线段BC 的延长线上时,①中的结论是否仍然成立,请在图2中画出相应图形并直接写出你的猜想.(2)如图3,若AB ≠AC ,∠BAC ≠90°,∠BCA =45°,点D 在线段BC 上运动,试探究CF 与BC 的位置关系,并说明理由.图1DC BAF图2ABC图3DC BAF13. 已知△ABC 是直角三角形,∠BAC =90°,AB =AC ,直线l 经过点A ,分别过点B ,C 向直线l 作垂线,垂足分别为D ,E .(1)如图1,当点B ,C 位于直线l 同侧时,证明:△ABD ≌△CAE . (2)如图2,若点B ,C 在直线l 的异侧,其他条件不变,△ABD ≌△CAE 是否依然成立?请说明理由.(3)图形变式:如图3,锐角△ABC 中,AB =AC ,直线l 经过点A ,点D ,E 分别在直线l 上,点B ,C 位于l 的同一侧,如果∠CEA =∠ADB = ∠BAC ,请找到图中的全等三角形,并直接写出线段ED ,EC ,DB 的数量关系.的图1lA BCDE图2ED CBA ll图3ECA DB14. 平面内的两条直线有相交和平行两种位置关系.(1)观察与思考:如图1,若AB ∥CD ,点P 在AB ,CD 外部,∠BPD ,∠B ,∠D 之间的数量关系为__________________. (2)猜想与证明:①将点P 移到AB ,CD 内部,如图2,则∠BPD ,∠B ,∠D 之间有何数量关系?请证明你的结论;②在图2中,将直线AB 绕点B 逆时针方向旋转一定角度交直线CD 于点Q ,如图3,则∠BPD ,∠B ,∠PDQ ,∠BQD 之间有何数量关系?请证明你的结论.(3)拓展与应用:在图4中,∠A +∠B +∠C +∠D +∠E +∠F =___________.图1A B CDOPABCD P图2AB C DP Q图3AB CDEF 图415. 已知直线AB ∥CD ,点M ,N 分别在直线AB ,CD 上,点E 为平面内一点.(1)如图1,∠BME ,∠E ,∠END 的数量关系为______(直接写出答案); (2)如图2,∠BME =m °,EF 平分∠MEN ,NP 平分∠END ,EQ ∥NP ,求 ∠FEQ 的度数(用含m 的式子表示);(3)如图3,点G 为CD 上一点,∠BMN =n ∠EMN ,∠GEK =n ∠GEM ,EH ∥MN 交AB 于点H ,探究∠GEK ,∠BMN ,∠GEH 之间的数量关系(用含n 的式子表示).图1图2图3A BC DMENFQ PNME DCBA KH GA BCDE N M。
类比探究综合检测(北师版)(含答案).docx

类比探究综合检测(北师版)一、单选题(共7道,每道14分)1.如图,在RtA ABC中,AB二BC, ZABC=90°. 一块等腰直角三角板的直角顶点放在斜边AC的小点0处,将三角板绕点0旋转,图2,图2是旋转三角板所得图形的两种情况,三角板的两直角边分别交AB, BC或其延长线于点E, F,图1,图2可以证明出0E与OF之间有相同的数量关系,则这个数量关系为()A3OE = -OFA. 4B. = OF4 5OS = -OF OE = -OFC. 3D. 4答案:B 解题思路:观察到两间都有中点,且是直角加中点,所以考虑利用直角三角形斜边的中线等于斜边一半进行类比,OE=OF,证明如下:如图1,连接P0,T20是等腰Rt△九BC斜边的中线,.\BO^OA=OC, BO1AC,ZOB4=ZOCB=45。
, 又T Z£OF=90°,・•・ ZBOE=ZCOF,:.ABOE^ACOF (ASA),・•・ OE=OF.如图2,连接20,•・• BO是等腫Rt△肋C斜边的中线,:,BO=OA=OC f BO1AC, AOBA=AOCB=45°f 又•・• ZEOF=90。
,・•・ ZB0E=ZC0F,ZOBA=ZOCB=45°f•••乙OBE=ZOCF=\35。
,:.ABOE^ACOF (ASA),・•・ OE=OF.故选B.试题难度:三颗星知识点:类比探究问题2.(上接笫1题)在证明图1,图2屮0E与OF Z间的数量关系时,小明发现直接连接B0 即可类比解决两问,你能说出小明的思路吗?()①全等;②再证全等;③等角对等边;④等边对等角;⑤等腰直角三角形的性质.A.①②⑤B.①⑤C.⑤①D.①③④答案:C解题思路:由第1题的解题思路知,答案选C.试题难度:三颗星知识点:类比探究问题3.(上接第1, 2题)在小明同学的证明过程中,需要证明三角形全等,请问他所依据的判定定理是()A.SASB.ASAC.SSSD.SSA答案:B解题思路:由第1题的解题思路知,答案选B.试题难度:三颗星知识点:类比探究问题4•如图,直线AM//BN, ZMAB与ZNBA的平分线交于点C,过点C作一条直线'与两条直线MA, NB分别相交于点D, E.如图1所示,当直线/与直线MA垂直时,则线段AD, BE, ABZ间的数量关系是()图1A,A52=^D24-552 B.曲<AD + BEAB = AD-^BS^AB = AD + 2BSC答案:C 解题思路:如图,延长〃(7交£\「于点F・£V,・・・ZD 毎+ZEB4=180。
类比探究专项训练(三)(含答案)

类比探究专项训练(三)一、单选题(共5道,每道20分)1.在等边三角形ABC中,点E在直线AB上,点D在直线BC上,且CE=DE.为判断AE和BD 之间的关系,小明准备分情况进行讨论.当E是AB中点时,如图1,小明发现,由于E是AB边的中点,利用三线合一可以得到AE=BE,∠ECB=30°,再由CE=DE可以得到∠D=30°,进而得到∠BED=30°,就可以得到BD=BE=AE.但是当E不是AB中点时,就不能照搬上述方式进行证明,此时小明想到了另外一种方式:过点E作EF∥BC,交AC于点F,也能证明AE=BD.(1)当E是线段AB上除端点和中点外的任一点时,如图2,按照上述辅助线证明AE=BD,证明过程中需要使用一对三角形全等,则证明此对三角形全等不能使用的条件是( )A.AASB.ASAC.SASD.SSS答案:D解题思路:1.解题要点①要在图2中照搬小明的思路,需要明白小明的思路在图1中是怎么证明的.考虑不能利用E是中点带来的结论,所以证明时,要避开中点带来的结论(AE=BE,∠ECB=30°),用其他条件来讨论.过点E作EF∥BC,交AC于点F,则△AEF是等边三角形,AE=EF=AF,能够证明△EFC≌△DBE,EF=BD,进而得到AE=BD.②在图2中,同样作出辅助线,如图所示,照搬①中的证明思路,先得到△AEF是等边三角形,AE=EF,再证明△EFC≌△DBE.关键在于判断三角形全等能够使用的条件有哪些.由题意得,BE=FC.∵∠ABC=∠AFE=60°,∴∠DBE=∠EFC=120°.∵∠D+∠DEB=60°,∠ECD+∠ECF=60°,∠D=∠ECD,∴∠DEB=∠ECF.同时∠D=∠ECD=∠CEF,即两个三角形中,三组内角分别对应相等,同时BE=CF,CE=DE,则证明△EFC≌△DBE可以使用AAS,ASA,SAS,不能使用的是SSS.③思考前面的证明过程,不变的特征是:△ABC是等边三角形,CE=DE.作平行线是为了得到等边三角形,进而得到全等三角形.④整个证明的路线图是:作辅助线;判断等边三角形(△AEF);证明△EFC≌△DBE.2.解题过程我们利用SAS来证明AE=BD,具体过程如下:如图,过点E作EF∥BC,交AC于点F.则∠AEF=∠ABC=∠A=60°,∴△AEF是等边三角形,∴AE=EF=AF,∴BE=FC.∵CE=DE,∴∠D=∠ECD.∵∠ABC=∠ACB,∴∠D+∠DEB=∠ECD+∠ECF,∴∠DEB=∠ECF,∴△EFC≌△DBE(SAS),∴EF=BD,∴AE=BD.试题难度:三颗星知识点:中考数学几何中的类比探究2.(上接第1题)(2)当点E在BA的延长线上时,如图3,点D在BC边上,且CE=DE,按照下面的操作,能够证明AE=BD的是( )A.直接证明△EAC≌△BDEB.①过点A作AF∥BC,交EC于点F;②△AEF是等边三角形;③△AFC≌△BDEC.①过点E作EF∥BC,交CA的延长线于点F;②△AEF是等边三角形;③△EFC≌△DBED.①过点A作AF∥BC,交EC于点F,连接DF;②四边形FDBE是等腰梯形答案:C解题思路:1.解题要点此题中△ABC是等边三角形及CE=DE没有发生变化,所以可照搬(1)中的思路.作辅助线;判断等边三角形(△AEF);证明△EFC≌△DBE.作出的辅助线是:过点E作EF∥BC,交CA的延长线于点F.2.解题过程完整的证明过程如下:如图,过点E作EF∥BC,交CA的延长线于点F.则∠AEF=∠B=∠EAF=∠BAC=60°,∴△AEF是等边三角形,∴AE=EF=AF,∴BE=FC.∵CE=DE,∴∠EDC=∠ECD,∴∠B+∠BED=∠ACB+∠FCE.∵∠B=∠ACB,∴∠BED=∠FCE,∴△EFC≌△DBE(SAS),∴EF=BD,∴AE=BD.试题难度:三颗星知识点:中考数学几何中的类比探究3.正方形ABCD中,O是对角线AC的中点,P是对角线AC上一动点,连接PB.(1)过点P作PF⊥CD于点F,PE⊥PB,交CD(或CD的延长线)于点E,如图1和图2所示,则DF和EF之间的数量关系是( )A. B.C.DF=EFD.答案:C解题思路:①题目当中的一个明显特征是,∠BPE是斜直角,通过补成弦图的方式来处理问题:如图,延长FP,交AB于点G.则四边形AGFD是矩形,△AGP是等腰直角三角形.此时能够证明△PFE≌△BGP,∴EF=PG=AG=DF.②由于在图1和图2中,PB⊥PE没有发生变化,PF⊥CD也没有发生变化,所以可以通过相同的思路分析(相同的辅助线,相同的证明思路).2.解题过程以图1为例,如图,延长FP,交AB于点G.易知四边形AGFD是矩形,△AGP是等腰直角三角形,∴AG=DF=PG,AD=GF=AB,∴BG=PF.又∵∠EFP=∠PGB,∠EPF=90°-∠GPB=∠PBG,∴△PFE≌△BGP,∴EF=PG,∴DF=EF.试题难度:三颗星知识点:中考数学几何中的类比探究4.(上接第3题)(2)在(1)中,当点P在线段OA上时,如图所示,则线段PA,PC,CE 之间的数量关系为( )A. B.C. D.答案:D解题思路:①由于PA,PC都是斜放置的线段,所以考虑借助图形中出现的等腰直角三角形,将PA,PC转到正方形的边上,利用正方形和等腰直角三角形边长之间的关系对目标进行研究.②借助于(1)中作出的辅助线,能够得到.这样就把PA,PC,CE之间的关系转化为三条线段CF,EF,CE之间的关系.③整个思考过程:DF=EF;利用等腰直角三角形的线段关系:;CF=CE+EF.2.解题过程如图,由(1)可知DF=EF.在等腰直角三角形AGP中,,在等腰直角三角形PFC中,,而CF=CE+EF,∴,∴,即线段PA,PC,CE之间的数量关系为.试题难度:三颗星知识点:中考数学几何中的类比探究5.(上接第3,4题)(3)在(1)中,当点P在线段OC上时(不与点O,C重合),类比(2)中的做法,可以判断线段PA,PC,CE之间的数量关系为( )A. B.C. D.答案:C解题思路:1.解题要点(2)和(3)的区别仅在于点P在线段OA上和点P在线段OC上.PF⊥CD,PE⊥PB没有发生变化,所以可照搬(2)中的思路.2.解题过程如图,延长FP,交AB于点G,由(1)可知DF=EF.在等腰直角三角形AGP中,,在等腰直角三角形PFC中,,而CF=EF-CE,∴,∴,即线段PA,PC,CE之间的数量关系为.试题难度:三颗星知识点:中考数学几何中的类比探究。
八下类比探究专题训练
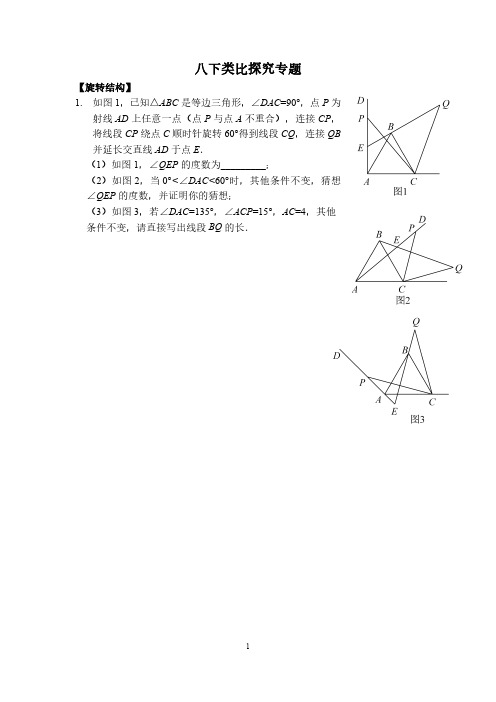
八下类比探究专题【旋转结构】1.如图1,已知△ABC是等边三角形,∠DAC=90°,点P为射线AD上任意一点(点P与点A不重合),连接CP,将线段CP绕点C顺时针旋转60°得到线段CQ,连接QB 并延长交直线AD于点E.(1)如图1,∠QEP的度数为_________;(2)如图2,当0°<∠DAC<60°时,其他条件不变,猜想∠QEP的度数,并证明你的猜想;(3)如图3,若∠DAC=135°,∠ACP=15°,AC=4,其他条件不变,请直接写出线段BQ的长.2.已知:点D是等腰直角三角形ABC斜边BC所在直线上一点(不与点B重合),连接AD.(1)如图1,当点D在线段BC上时,将线段AD绕点A逆时针旋转90°得到线段AE,连接CE.求证:BD=CE,BD⊥CE;(2)如图2,当点D在线段BC延长线上时,探究AD,BD,CD三条线段之间的数量关系,写出结论并说明理由;(3)若BD CD,直接写出∠BAD的度数.图1图2备用图3.如图,在△ABC中,∠ABC为锐角,点M为射线BA上一点,连接CM,以CM为直角边且在CM的下方(沿CM顺时针方向)作等腰直角三角形CMN,∠MCN=90°,连接BN.(1)若AC=BC,∠ACB=90°.①如图1,当点M在线段AB上(与点A不重合)时,则BN与AM的数量关系为__________,位置关系为_________;②当点M在线段BA的延长线上时,①的结论是否仍然成立,请在图2中画出相应图形并说明理由.(2)如图3,若AC≠BC,∠ACB≠90°,∠ABC=45°,点M在线段AB上运动,请判断BN与AB的位置关系,并说明理由.4.如图1,在△ABC中,AB=AC,射线BP从BA所在位置开始绕点B顺时针旋转,旋转角为α(其中α<∠ABC).(1)当∠BAC=60°时,将BP旋转到图2位置,点D在射线BP上,若∠CDP=120°,则∠ACD_____∠ABD(填“>”、“=”、“<”),线段BD,CD 与AD之间的数量关系是____________;(2)当∠BAC=90°时,将BP旋转到图3位置,点D在射线BP上,若∠CDP=90°,求证:BD-CD AD;(3)当∠BAC=120°时,将BP旋转到图4位置,点D在射线BP上,若∠CDP=60°,请直接写出线段BD,CD与AD之间的数量关系(不必证明).图1图2图3图45.发现:如图1,点B是线段AD上的一点,分别以AB,BD为边向外作等边三角形ABC和等边三角形BDE,连接AE,CD,相交于点O.①线段AE与CD的数量关系为_________;∠AOC的度数为___________.②△CBD可看作△ABE经过怎样的变换得到的?________________.(2)应用:如图2,若点A,B,D不在一条直线上,(1)中的结论①还成立吗?请说明理由;(3)拓展:在四边形ABCD中,AB=AC,∠BAC=90°,∠ADC=45°,若AD=8,CD=6,请直接写出B,D两点之间的距离.6.已知:△ABC 是等腰直角三角形,动点P 在斜边AB 所在的直线上,以PC 为直角边作等腰直角三角形PCQ ,其中∠PCQ =90°,探究并解决下列问题:(1)如图1,若点P 在线段AB 上,且AC =1+3,PA =2,则:①线段PB =_________,PC =_________;②猜想:PA 2,PB 2,PQ 2三者之间的数量关系为__________;(2)如图2,若点P 在AB 的延长线上,在(1)中所猜想的结论仍然成立,请你利用图2给出证明过程;(3)若动点P 满足13PA PB ,求PCAC 的值.(提示:请利用备用图进行探求)7.(1)如图1,O是等边△ABC内一点,连接OA,OB,OC,且OA=3,OB=4,OC=5,将△BAO绕点B顺时针旋转后得到△BCD,连接OD.求:①旋转角是__________度;②线段OD的长为__________;③求∠BDC的度数.(2)如图2所示,O是等腰直角△ABC(∠ABC=90°)内一点,连接OA,OB,OC,∠AOB=135°,OA=1,OB=2,求OC的长.小明同学借用了图1的方法,将△BAO绕点B顺时针旋转后得到△BCD,请你继续用小明的思路解答,或是选择自己的方法求解.8.已知,在△ABC中,∠BAC=90°,AB=AC,点D为直线BC上一动点(点D不与B,C重合),以AD 为边作正方形ADEF,连接CF.(1)观察猜想如图1,当点D在线段BC上时可以证明△ABD≌△ACF,则①BC与CF的位置关系为______________;②BC,DC,CF之间的数量关系为______________.(2)类比探究如图2,当点D在线段BC的延长线上时,其他条件不变,(1)中①②结论是否仍然成立?若成立,请给予证明;若不成立,请你写出正确结论再给予证明.(3)拓展延伸如图3,当点D在线段BC的反向延长线上时,且点A,F分别在直线BC的两侧,其他条件不变.①BC,DC,CF之间的数量关系为_______________;②若正方形ADEF的边长为3,对角线AE,DF相交于点O,连接OC,则OC的长度为___________.1.(1)阅读理解:如图1,在△ABC中,若AB=10,AC=6,求BC边上的中线AD的取值范围.解决此问题可以用如下方法:延长AD到点E使DE=AD,再连接BE(或将△ACD绕着点D逆时针旋转180°得到△EBD),把AB,AC,2AD集中在△ABE中,利用三角形三边的关系即可判断.中线AD的取值范围是__________.(2)问题解决:如图2,在△ABC中,D是BC边上的中点,DE⊥DF于点D,DE交AB于点E,DF交AC于点F,连接EF,求证:BE+CF>EF.(3)问题拓展:如图3,在四边形ABCD中,∠B+∠D=180°,CB=CD,∠BCD=140°,以C为顶点作一个70°角,角的两边分别交AB,AD于E,F两点,连接EF,探索线段BE,DF,EF之间的数量关系,并加以证明.1.数学课上,张老师出示了问题:如图1,四边形ABCD是正方形,∠DAB=∠ABC=∠BCD=∠CDA=90°,AB=BC=CD=DA,AB∥CD,AD∥BC,点E是边BC的中点,∠AEF=90°,且EF交正方形外角∠DCG的平分线CF于点F,求证:AE=EF.经过思考,小明展示了一种正确的解题思路:取AB的中点M,连接ME,则AM=EC,易证△AME≌△ECF,所以AE=EF.在此基础上,同学们作了进一步的研究:(1)小颖提出:如图2,如果把“点E是边BC的中点”改为“点E是边BC上(除B,C外)的任意一点”,其他条件不变,那么结论“AE=EF”仍然成立,你认为小颖的观点正确吗?如果正确,写出证明过程;如果不正确,请说明理由.(2)小华提出:如图3,点E是BC的延长线上(除C点外)的任意一点,其他条件不变,结论“AE=EF”仍然成立.你认为小华的观点正确吗?如果正确,写出证明过程;如果不正确,请说明理由.2.提出问题:如图1,将三角板放在正方形ABCD上,使三角板的直角顶点P在对角线AC上,一条直角边经过点B,另一条直角边交边DC于点E,求证:PB=PE.分析问题:学生甲:如图1,过点P作PM⊥BC,PN⊥CD,垂足分别为M,N.通过证明两三角形全等,进而证明两条线段相等.学生乙:连接DP,如图2,很容易证明PD=PB,然后再通过“等角对等边”证明PE=PD,就可以证明PB=PE了.解决问题:请你选择上述一种方法给予证明.问题延伸:如图3,移动三角板,使三角板的直角顶点P 在对角线AC上,一条直角边经过点B,另一条直角边交DC的延长线于点E,PB=PE还成立吗?若成立,请证明;若不成立,请说明理由.【新定义】1.联想三角形外心(外心是三角形三条边的垂直平分线的交点,即三角形外接圆的圆心)的概念,我们可引入如下概念.定义:到三角形的两个顶点距离相等的点,叫做此三角形的准外心.举例:如图1,若PA =PB ,则点P 为△ABC 的准外心.应用:如图2,CD 为等边三角形ABC 的高,准外心P 在高CD 上,且12PD AB ,求∠APB 的度数.探究:已知△ABC 为直角三角形,斜边BC =5,AB =3,准外心P 在AC 边上,试探究P A 的长.2.定义:我们把三角形被一边中线分成的两个三角形叫做“朋友三角形”.性质:“朋友三角形”的面积相等.如图1,在△ABC 中,CD 是AB 边上的中线,那么△ACD和△BCD 是“朋友三角形”,并且ACD BCD S S △△.应用:如图2,在直角梯形ABCD 中,∠ABC =90°,AD ∥BC ,AB=AD =4,BC =6,点E 在BC 上,点F 在AD 上,BE=AF ,AE 与BF 交于点O .(1)求证:△AOB 和△AOF 是“朋友三角形”;(2)连接OD ,若△AOF 和△DOF 是“朋友三角形”,求四边形CDOE 的面积.拓展:如图3,在△ABC 中,∠A =30°,AB =8,点D 在线段AB 上,连接CD ,△ACD 和△BCD 是“朋友三角形”,将△ACD 沿CD 所在直线翻折,得到△A'CD ,若△A'CD与△ABC 重合部分的面积等于△ABC 面积的14,则△ABC 的面积是__________(请直接写出答案).3.如图1,我们把对角线互相垂直的四边形叫做垂美四边形.(1)概念理解:如图2,在四边形ABCD中,AB=AD,CB=CD,问四边形ABCD是垂美四边形吗?请说明理由.(2)性质探究:试探索垂美四边形ABCD两组对边AB2,CD2与BC2,AD2之间的数量关系.猜想结论:(要求用文字语言叙述)_____________________,写出证明过程(先画出图形,写出已知、求证).(3)问题解决:如图3,分别以Rt△ACB的直角边AC和斜边AB为边向外作正方形ACFG和正方形ABDE,连接CE,BG,GE,已知AC=4,AB=5,求GE的长.4.我们定义:在△ABC 中,把AB 绕点A 顺时针旋转α(0°<α<180°)得到AB′,把AC 绕点A 逆时针旋转β得到AC′,连接B′C′.当α+β=180°时,我们称△AB′C′叫△ABC 的“旋补三角形”,△AB′C′的边B′C′上的中线AD 叫做△ABC 的“旋补中线”.下面各图中,△AB′C′均是△ABC 的“旋补三角形”,AD 均是△ABC 的“旋补中线”.(1)如图1,若△ABC 为等边三角形,BC =8,则AD 的长等于________;(2)如图2,若∠BAC =90°,求证:AD =12BC ;(3)如图3,若△ABC 为任意三角形,(2)中结论还成立吗?如果成立,给予证明;如果不成立,说明理由.5.我们把两条中线互相垂直的三角形称为“中垂三角形”.例如图1、图2、图3中,AF,BE是△ABC的中线,AF⊥BE,垂足为P,像这样的三角形均为“中垂三角形”.设BC=a,AC=b,AB=c.特例探索(1)如图1,当∠ABE=45°,c=a=_____,b=_____;如图2,当∠ABE=30°,c=4时,a=________,b=________.归纳证明(2)请你观察(1)中的计算结果,猜想a2,b2,c2三者之间的关系,用等式表示出来,并利用图3证明你发现的结论.拓展应用(3)如图4,在□ABCD中,点E,F分别是AD,BC的中点,BE⊥AC于点H,若AD=AB=3,求AF的长.。
类比探究专题(一)——平行结构(含答案)

学生做题前请先回答以下问题问题1:类比探究问题的处理思路是什么?以下是问题及答案,请对比参考:问题1:类比探究问题的处理思路是什么?答:类比探究问题的处理思路为:(1)类比探究往往会围绕一个不变结构进行考查.类比探究中常见的不变结构有:中点结构、直角结构、旋转结构、平行结构.(2)若不属于常见结构类型,则需要我们尝试着去寻找不变结构解决问题.①根据题干条件,结合支干条件先解决第一问.②类比解决下一问.如果不能,分析条件变化,寻找不变特征.③结合所求目标,依据不变特征尝试找不变结构,大胆猜测、尝试、验证.若属于类比探究常见的结构类型,调用结构类比解决.类比探究专题(一)——平行结构一、单选题(共6道,每道16分)1.如图1,D是△ABC的边BC上一点,过点D的一条直线交AC于点F,交BA的延长线于点E.(1)若BD=CD,CF=2AF,则的值为( )A.2B.C. D.答案:B解题思路:试题难度:三颗星知识点:平行结构2.(上接第1题)(2)如图2,若BD=CD,CF=mAF,则的值为( ) (用含m的代数式表示)A. B.C. D.答案:D解题思路:试题难度:三颗星知识点:平行结构3.(上接第1,2题)(3)如图3,将原题改为“过点D的一条直线交AC的延长线于点F,交AB于点E”,若BD=nCD,CF=mAF,则的值为( )(用含m,n的代数式表示)A. B.C. D.答案:C解题思路:试题难度:三颗星知识点:平行结构4.已知AD是△ABC的中线,将BC边所在直线绕点D顺时针旋转角,交AB边于点M,交射线AC于点N,设.(1)如图1,满足的函数关系式为( ) A. B.C. D.答案:C解题思路:试题难度:三颗星知识点:平行结构5.(上接第4题)(2)如图2,当G是AD上任意一点时(点G不与点A重合),过点G的直线交AB边于点,交AC边于点,设,则满足的函数关系式为( )A. B.C. D.答案:D解题思路:试题难度:三颗星知识点:平行结构6.(上接第4,5题)(3)如图3,当G是AD上任意一点时(点G不与点A重合),过点G 的直线交AB边于点,交AC的延长线于点,设,则满足的函数关系式为( )A. B.C. D.答案:D解题思路:试题难度:三颗星知识点:平行结构。
类比探究专项训练(二)(含答案)

类比探究专项训练(二)一、单选题(共6道,每道16分)1.探究问题:(1)方法感悟:如图1,在正方形ABCD中,E,F分别为边CD,BC上的点,且满足∠EAF=45°,连接EF,求证:DE+BF=EF.关于证明上述结论的辅助线的作法,下列说法不合适的是( )A.延长CB到G,使BG=DE,连接AGB.过点A作AG⊥AE,交CB的延长线于点GC.将△ADE绕点A顺时针旋转90°得到△ABG(之后证明点G,B,F在同一条直线上)D.过点A作AG⊥EF于点G答案:D解题思路:1.解题要点①分析题目特征,属于类比探究中对旋转结构的考查.最终的目标是将DE和BF拼接起来,有下列几种实现方式:A选项:延长CB到G,使BG=DE,连接AG,可以得到△ADE≌△ABG(SAS),之后利用△AGF≌△AEF(SAS)可以证明结论;B选项:过点A作AG⊥AE,交CB的延长线于点G,可以得到△ADE≌△ABG(ASA),之后利用△AGF≌△AEF(SAS)可以证明结论;C选项:将△ADE绕点A顺时针旋转90°得到△ABG,利用∠ABG+∠ABC=180°说明点G,B,F在同一条直线上,进而证明△AGF≌△AEF(SAS),之后可以证明结论;所以答案选D.②利用选项A中的辅助线分析上述证明过程,可分为以下几步:辅助线描述;△ADE≌△ABG;∠GAF=∠EAF;△AGF≌△AEF.2.解题过程利用选项A中的辅助线来证明DE+BF=EF.如图,延长CB到G,使GB=DE,连接AG.在正方形ABCD中,AB=AD,∠ABG=∠ADE=90°,∵BG=DE,∴△ADE≌△ABG,∴AG=AE,∠GAB=∠EAD.∵∠EAF=45°,∴∠BAF+∠EAD=45°,∴∠BAF+∠GAB=45°,∴∠GAF=∠EAF,∴△AGF≌△AEF,∴GF=EF,即BG+BF=EF,∴DE+BF=EF.试题难度:三颗星知识点:中考数学几何中的类比探究2.(上接第1题)(2)方法迁移:如图2,将Rt△ABC沿斜边翻折得到△ADC,E,F分别为边CD,BC上的点,且满足.则DE,BF,EF之间的数量关系为( )A. B.DE+BF=EFC.2DE+BF=EFD.DE+2BF=EF答案:B解题思路:1.解题要点①照搬(1)中的思路:辅助线描述;△ADE≌△ABG;∠GAF=∠EAF;△AGF≌△AEF.②辅助线同样是:延长CB到G,使得BG=DE,连接AG.③能够按照①中的框架操作的关键特征在于:AB=AD,∠ABC+∠ADC=180°,能够实现旋转,即能够得到△ADE≌△ABG;,能够保证△AGF≌△AEF.不变特征是:AB=AD,∠ABC+∠ADC=180°,.2.解题过程如图,延长CB到G,使得BG=DE,连接AG.∵△ADC是由Rt△ABC沿斜边AC翻折得到的,∴AB=AD,∠ABC=∠ADC=90°.∵BG=DE,∴△ADE≌△ABG,∴AG=AE,∠GAB=∠EAD.∵,∴∠BAF+∠EAD=∠EAF,∴∠BAF+∠GAB=∠EAF,∴∠GAF=∠EAF,∴△AGF≌△AEF,∴EF=GF=BG+BF,∴DE+BF=EF.试题难度:三颗星知识点:中考数学几何中的类比探究3.(上接第1,2题)(3)问题拓展:如图3,在四边形ABCD中,AB=AD,E,F分别为边CD,BC上的点,且满足,则当∠B和∠D满足( )时,DE+BF=EF成立.A.∠B=∠DB.∠B+∠D=180°C.∠B=2∠DD.∠B+∠D=120°答案:B解题思路:1.解题要点照搬(1),(2)中的思路:辅助线描述;△ADE≌△ABG;∠GAF=∠EAF;△AGF≌△AEF.发现在作出辅助线之后,要证明△ADE≌△ABG,缺少角度条件.与前面的不变特征相比较,若要结论仍成立,需要让∠ABC+∠D=180°.2.解题过程当“∠B+∠D=180°”时,完整的证明过程如下:如图,延长CB到G,使得BG=DE,连接AG.∵∠ABC+∠D=180°,∴∠ABG=∠D.∵AB=AD,BG=DE,∴△ADE≌△ABG,∴AG=AE,∠GAB=∠EAD.∵,∴∠BAF+∠EAD=∠EAF,∴∠BAF+∠GAB=∠EAF,∴∠GAF=∠EAF,∴△AGF≌△AEF,∴EF=GF=BG+BF,∴DE+BF=EF.试题难度:三颗星知识点:中考数学几何中的类比探究4.(1)如图1,在正方形ABCD的边AB上任取一点E,过点E作EF⊥AB,交BD于点F,取DF的中点G,连接EG,CG.为了研究线段EG和CG之间的数量和位置关系,可通过作辅助线:延长EG,交AD的延长线于点H,连接EC,HC,来进行分析.则得到的结论是( )A.EG=CG且EG⊥CGB.EG=CG但EG与CG不垂直C.EG⊥CG但EG≠CGD.答案:A解题思路:1.解题要点利用题干中给出的辅助线信息继续研究,寻找进一步的结论来说明EG和CG之间的关系.由“平行+中点”可以得到DH=EF=BE,则△CBE≌△CDH(SAS),进而得到△ECH是等腰直角三角形,所以EG=CG且EG⊥CG.2.解题过程如图,延长EG,交AD的延长线于点H,连接EC,HC.由题意得,EF∥AD,△BEF是等腰直角三角形.∵G是DF的中点,∴FG=DG.∵DH∥EF,∴∠DHG=∠FEG,∠EFG=∠HDG,∴△EFG≌△HDG,∴DH=EF=BE,EG=HG.∵BC=DC,∠EBC=∠HDC=90°,∴△CBE≌△CDH,∴EC=HC,∠BCE=∠DCH,∴∠ECH=∠ECD+∠DCH=∠ECD+∠BCE=90°,∴△ECH是等腰直角三角形.∵EG=HG,∴EG=CG且EG⊥CG.试题难度:三颗星知识点:中考数学几何中的类比探究5.(上接第4题)(2)在图1的基础上,将△BEF绕点B逆时针旋转90°,其他条件不变,如图2,为了证明EG和CG之间的数量和位置关系仍成立,类比(1)中的辅助线和证明思路,需要作出的辅助线是( )A.延长EG,交AD于点H,连接HCB.延长BG,交AD于点H,连接HCC.延长EG,交CD的延长线于点HD.延长EF,交DA的延长线于点H,连接HC答案:C解题思路:1.解题要点①要类比(1)中的辅助线和证明思路,需要明白(1)中的辅助线和思路带给我们什么.首先能够得到全等,利用的是“平行+中点”,也即是“EF∥CD,FG=DG”.那么此题中也应该利用“平行+中点”,所以需要延长EG,交CD的延长线于点H.其次是△CBE≌△CDH,进而得到△ECH是等腰直角三角形.而在此题中△CBE和△CDH是不存在的,但是可以直接利用EC=HC判断△ECH是等腰直角三角形.②比较两问的特点,都是观察到G是DF的中点,从“平行+中点”入手判断结论,证明框架是:辅助线(平行+中点);△CBE≌△CDH(EC=HC,∠ECH=90°);△ECH是等腰直角三角形.2.解题过程完整地证明结论的过程如下:如图,延长EG,交CD的延长线于点H.由题意得,EF∥CD,FG=DG,∴∠H=∠GEF,∠EFG=∠HDG,∴△EFG≌△HDG,∴HD=EF=BE,EG=HG.∵CB=CD,∴EC=HC,∴△ECH是等腰直角三角形.∵EG=HG,∴EG=CG且EG⊥CG.试题难度:三颗星知识点:中考数学几何中的类比探究6.(上接第4,5题)(2)在图1的基础上,将△BEF绕点B逆时针旋转180°,其他条件不变,如图3,为了证明EG和CG之间的数量和位置关系仍成立,类比(1),(2)中的辅助线和证明思路,需要证明两个直角三角形全等,则判断该三角形全等时使用的条件是( )A.AASB.ASAC.HLD.SAS答案:D解题思路:1.解题要点照搬(1),(2)中的证明思路:辅助线(平行+中点);△CBE≌△CDH(EC=HC,∠ECH=90°);△ECH是等腰直角三角形.2.解题过程如图,延长EG,交AD于点H,连接EC,HC.由题意得,F,B,D三点共线,EF∥AD,∴∠DHG=∠FEG,∠F=∠HDG.∵FG=DG,∴△FEG≌△DHG,∴DH=EF=BE,EG=HG.∵BC=DC,∠HDC=∠EBC=90°,∴Rt△BEC≌Rt△DHC,∴EC=HC,∠ECB=∠HCD,∴∠ECH=∠ECB+∠BCH=∠HCD+∠BCH=90°,∴△ECH是等腰直角三角形.∵EG=HG,∴EG=CG且EG⊥CG,故证明过程中,判断两个直角三角形全等时使用的条件是SAS.试题难度:三颗星知识点:中考数学几何中的类比探究。
中考数学专题之类比探究实战演练(含答案)
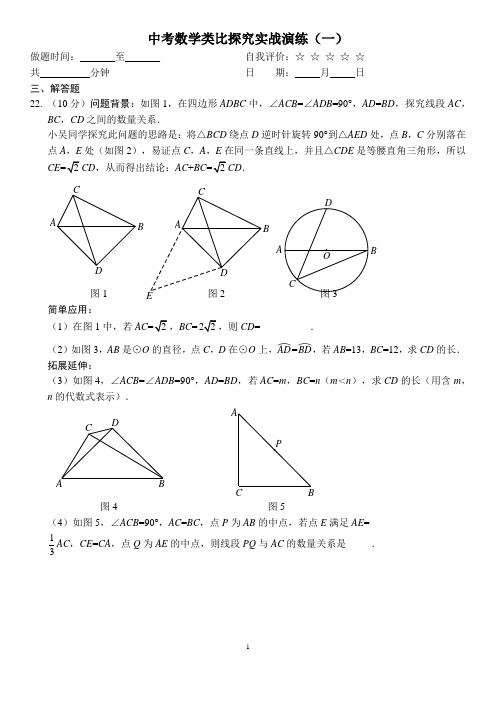
三、解答题22. (10分)问题背景:如图1,在四边形ADBC 中,∠ACB =∠ADB =90°,AD =BD ,探究线段AC ,BC ,CD 之间的数量关系.小吴同学探究此问题的思路是:将△BCD 绕点D 逆时针旋转90°到△AED 处,点B ,C 分别落在点A ,E 处(如图2),易证点C ,A ,E 在同一条直线上,并且△CDE 是等腰直角三角形,所以CECD ,从而得出结论:AC +BCCD .图1图2 简单应用:(1)在图1中,若AC ,BC =CD =__________.(2)如图3,AB 是⊙O 的直径,点C ,D 在⊙O 上,AD ︵=BD ︵,若AB =13,BC =12,求CD 的长.拓展延伸:(3)如图4,∠ACB =∠ADB =90°,AD =BD ,若AC =m ,BC =n (m <n ),求CD 的长(用含m ,n 的代数式表示).图4图5(4)如图5,∠ACB =90°,AC =BC ,点P 为AB 的中点,若点E 满足AE = 13AC ,CE =CA ,点Q 为AE 的中点,则线段PQ 与AC 的数量关系是_____. DC BADCBBAE DCBA三、解答题22. (10分)如图1,在Rt △ABC 中,∠ACB =90°,AC =BC ,点D ,E 分别在AC ,BC 边上,DC =EC ,连接DE ,AE ,BD ,点M ,N ,P 分别是AE ,BD ,AB 的中点,连接PM ,PN ,MN . (1)BE 与MN 的数量关系是___________;(2)将△DEC 绕点C 逆时针旋转到如图2的位置,判断(1)中的结论是否仍然成立,如果成立,请写出证明过程,若不成立,请说明理由;(3)若CB =6,CE =2,在将图1中的△DEC 绕点C 逆时针旋转一周的过程中,当B ,E ,D 三点在一条直线上时,请直接写出MN 的长.中考数学类比探究实战演练(三)做题时间:_______至_______ 自我评价:☆ ☆ ☆ ☆ ☆ 共__________分钟 日 期:_____月_____日 三、解答题22. (10分)已知正方形ABCD 与正方形CEFG ,M 是AF 的中点,连接DM ,EM .(1)如图1,点E 在CD 上,点G 在BC 的延长线上,请判断DM ,EM 的数量关系与位置关系,并直接写出结论;(2)如图2,点E 在DC 的延长线上,点G 在BC 上,(1)中结论是否仍然成立?请证明你的结论;(3)将图1中的正方形CEFG 绕点C 旋转,使D ,E ,F 三点在一条直线上,若AB =13,CE =5,请画出图形,并直接写出MF 的长.图1PNM EDCBA图2PNME D CBA备用图E DCBA中考数学类比探究实战演练(四)做题时间:_______至_______ 自我评价:☆☆☆☆☆共__________分钟日期:_____月_____日三、解答题22.(10分)如图,在Rt△ABC中,∠ACB=90°,BC=nAC,CD⊥AB于D,点E是直线AC上一动点,连接DE,过点D作FD⊥ED,交直线BC于点F,连接EF.(1)探究发现:如图1,若n=1,点E在线段AC上,则tan∠EFD=____.(2)数学思考:①如图2,若点E在线段AC上,则tan∠EFD=_______(用含n的代数式表示).②当点E在直线AC上运动时,①中的结论是否仍然成立?若成立,请给予证明;若不成立,请说明理由.从“点E是线段AC延长线上的任意一点”或“点E是线段AC反向延长线上的任意一点”中,任选一种情况,在图3中画出图形,给予相应的证明或理由.(3)拓展应用:若ACBC=DF=CE的长.图1ABCDE FGM图2MGF EDCBA图1E DCBA图2E DA图3DCBAABCD备用图【参考答案】中考数学类比探究实战演练(一)22.(1)3;(2)CD的长为2;(3)CD的长为)2n m-;(4AC=AC=.中考数学类比探究实战演练(二)22.(1)BE MN;(2)成立,理由略;(3)MN11.中考数学类比探究实战演练(三)23.(1)DM=EM,DM⊥EM;(2)(1)中的结论仍成立,证明略;(3)MF,图形略.中考数学类比探究实战演练(四)22.(1)1;(2)①1n;②成立,证明略;(3)CE或中考数学类比探究实战演练(五)做题时间:_______至_______ 自我评价:☆☆☆☆☆共__________分钟日期:_____月_____日三、解答题22.(10分)在菱形ABCD中,∠BAD=120°,点O为射线CA上的动点,作射线OM与直线BC相交于点E,将射线OM绕点O逆时针旋转60°,得到射线ON,射线ON与直线CD相交于点F.(1)如图1,点O与点A重合时,点E,F分别在线段BC,CD上,请直接写出CE,CF,CA 三条线段之间的数量关系;(2)如图2,点O在CA的延长线上,且OA=13AC,E,F分别在线段BC的延长线和线段CD的延长线上,请写出CE,CF,CA三条线段之间的数量关系,并说明理由;(3)点O在线段AC上,若AB=6,BO=CF=1时,请直接写出BE的长.图1F ENM (O )D C B A图2FENMO DC BA备用图DCBA【参考答案】22.(1)CA=CE+CF;(2)CF-CE=43AC,理由略;(3)BE的长为3,5或1.中考数学类比探究实战演练(六)做题时间:_______至_______ 自我评价:☆☆☆☆☆共__________分钟日期:_____月_____日三、解答题22.(10分)已知:△ABC是等腰三角形,CA=CB,0°<∠ACB≤90°,点M在边AC上,点N在边BC上(点M,点N不与所在线段端点重合),BN=AM,连接AN,BM.射线AG∥BC,延长BM 交射线AG于点D,点E在直线AN上,且AE=DE.(1)如图,当∠ACB=90°时.①求证:△BCM≌△ACN;②求∠BDE的度数.(2)当∠ACB=α,其他条件不变时,∠BDE的度数是__________(用含α的代数式表示);(3)若△ABC是等边三角形,AB=N是BC边上的三等分点,直线ED与直线BC交于点F,请直接..写出线段CF的长.B C DAEM N GBA GC备用图1备用图2AB CG中考数学类比探究实战演练(七)做题时间:_______至_______ 自我评价:☆ ☆ ☆ ☆ ☆ 共__________分钟 日 期:_____月_____日 三、解答题22. (10分)已知在Rt △ABC 中,∠BAC =90°,CD 为∠ACB 的平分线,将∠ACB 沿CD 所在的直线对折,使点B 落在点B′处,连接AB′,BB′,延长CD 交BB′于点E ,设∠ABC =2α(0°<α<45°). (1)如图1,若AB =AC ,求证:CD =2BE ;(2)如图2,若AB ≠AC ,试求CD 与BE 的数量关系(用含α的式子表示);(3)如图3,将(2)中的线段BC 绕点C 逆时针旋转角(α+45°),得到线段FC ,连接EF 交BC 于点O ,设△COE 的面积为S 1,△COF 的面积为S 2,求12SS (用含α的式子表示).中考数学类比探究实战演练(八)做题时间:_______至_______ 自我评价:☆ ☆ ☆ ☆ ☆ 共__________分钟 日 期:_____月_____日 三、解答题图1ABCDEB′图22αABCD E B′B′E D CB A2α图3OF22. (10分)在Rt △ABC 中,∠ACB =90°,AB,AC =2,过点B 作直线m ∥AC ,将△ABC 绕点C 顺时针旋转得到△A′B′C (点A ,B 的对应点分别为A′,B′),射线CA′,CB′分别交直线m 于点P ,Q .(1)如图1,当P 与A′重合时,求∠ACA′的度数.(2)如图2,设A′B′与BC 的交点为M ,当M 为A′B′的中点时,求线段PQ 的长.(3)在旋转过程中,当点P ,Q 分别在CA′,CB′的延长线上时,试探究四边形P A′B′Q 的面积是否存在最小值.若存在,求出四边形P A′B′Q 的最小面积;若不存在,请说明理由.图1QmB′A′ (P )BC AM图2A′AC B P B′mQ备用图AC Bm中考数学类比探究实战演练(九)做题时间:_______至_______ 自我评价:☆ ☆ ☆ ☆ ☆ 共__________分钟 日 期:_____月_____日 三、解答题22. (10分)问题背景:如图1,等腰△ABC 中,AB =AC ,∠BAC =120°,作AD ⊥BC 于点D ,则D为BC 的中点,∠BAD =21∠BAC =60°,于是2BC BDAB AB==迁移应用:如图2,△ABC 和△ADE 都是等腰三角形,∠BAC =∠DAE =120°,D ,E ,C 三点在同一条直线上,连接BD . ①求证:△ADB ≌△AEC ;②请直接写出线段AD ,BD ,CD 之间的等量关系式.拓展延伸:如图3,在菱形ABCD 中,∠ABC =120°,在∠ABC 内作射线BM ,作点C 关于BM 的对称点E ,连接AE 并延长交BM 于点F ,连接CE ,CF . ①求证:△CEF 是等边三角形; ②若AE =5,CE =2,求BF 的长.图1图2图3D B AEDBA FEMDCBA中考数学类比探究实战演练(十)做题时间:_______至_______ 自我评价:☆ ☆ ☆ ☆ ☆ 共__________分钟 日 期:_____月_____日 三、解答题22. (10分)在正方形ABCD 中,点E ,F 分别在边BC ,CD 上,且∠EAF =∠CEF =45°.(1)将△ADF 绕着点A 顺时针旋转90°,得到△ABG (如图1). 求证:△AEG ≌△AEF .(2)若直线EF 与AB ,AD 的延长线分别交于点M ,N (如图2). 求证:EF 2=ME 2+NF 2.(3)将正方形改为长与宽不相等的矩形,若其余条件不变(如图3),请你直接写出线段EF ,BE ,DF 之间的数量关系.中考数学类比探究实战演练(十一)做题时间:_______至_______ 自我评价:☆ ☆ ☆ ☆ ☆ 共__________分钟 日 期:_____月_____日图1G FE D CB A N图2M FE D CB A 图3FED CBA三、解答题22. (10分)【操作发现】(1)如图1,△ABC 为等边三角形,先将三角板中的60°角与∠ACB 重合,再将三角板绕点C 按顺时针方向旋转(旋转角大于0°且小于30°).旋转后三角板的一直角边与AB 交于点D .在三角板斜边上取一点F ,使CF =CD ,线段AB 上取点E ,使∠DCE =30°,连接AF ,EF . ①求∠EAF 的度数;②DE 与EF 相等吗?请说明理由. 【类比探究】(2)如图2,△ABC 为等腰直角三角形,∠ACB =90°,先将三角板的90°角与∠ACB 重合,再将三角板绕点C 按顺时针方向旋转(旋转角大于0°且小于45°).旋转后三角板的一直角边与AB 交于点D .在三角板另一直角边上取一点F ,使CF =CD ,线段AB 上取点E ,使∠DCE =45°,连接AF ,EF .请直接写出探究结果:①∠EAF 的度数;②线段AE ,ED ,DB 之间的数量关系.图1图2中考数学类比探究实战演练(十二)做题时间:_______至_______ 自我评价:☆ ☆ ☆ ☆ ☆ 共__________分钟 日 期:_____月_____日 三、解答题22. (10分)数学活动课上,某学习小组对有一内角为120°的平行四边形ABCD (∠BAD =120°)进行探究:将一块含60°的直角三角板如图放置在平行四边形ABCD 所在平面内旋转,且60°角的顶点始终与点C 重合,较短的直角边和斜边所在的两直线分别交线段AB ,AD 于点E ,F (不包FDE CBAABCEF D括线段的端点). (1)初步尝试如图1,若AD =AB ,求证:①△BCE ≌△ACF ;②AE +AF =AC . (2)类比发现如图2,若AD =2AB ,过点C 作CH ⊥AD 于点H ,求证:AE =2FH . (3)深入探究如图3,若AD =3AB ,探究得:3AE AFAC的值为常数t ,则t =_______.图1 图2 图3F EDC B A HF EDBAF EDCB A三、解答题22. (10分)小华遇到这样一个问题:在菱形ABCD 中,∠ABC =60°,边长为4,在菱形ABCD 内部有一点P ,连接PA ,PB ,PC ,求PA +PB +PC 的最小值.小华是这样思考的:要解决这个问题,首先应想办法将这三条端点重合于一点的线段分离,然后再将它们连接成一条折线,并让折线的两个端点为定点,这样依据“两点之间,线段最短”,就可以求出这三条线段和的最小值了.他先后尝试了翻折、旋转、平移的方法,发现通过旋转可以解决这个问题.他的做法是:如图1,将△APC 绕点C 顺时针旋转60°,恰好旋转至△DEC ,连接PE ,BD ,则BD 的长即为所求.(1)请你写出在图1中,PA +PB +PC 的最小值为________. (2)参考小华思考问题的方法,解决下列问题:①如图2,在△ABC 中,∠ACB =30°,BC =6,AC =5,在△ABC 内部有一点P ,连接PA ,PB ,PC ,求PA +PB +PC 的最小值.②如图3,在正方形ABCD 中,AB =5,P 为对角线BD 上任意一点,连接PA ,PC ,请直接写出PA +PB +PC 的最小值(保留作图痕迹).图1PADBECB CPA图2P图3DCBA三、解答题22.(10分)在△ABC中,∠A=90°,点D在线段BC上,∠EDB=12∠C,BE⊥DE,垂足为E,DE与AB相交于点F.(1)如图1,若点D与点C重合,AB=AC,探究线段BE与FD的数量关系.(2)如图2,若点D与点C不重合,AB=AC,探究线段BE与FD的数量关系,并加以证明.(3)如图3,若点D与点C不重合,AB=kAC,求BEFD的值(用含k的式子表示).图1图2图3CB(D)AFECB DAFECB DAFE三、解答题22. (10分)问题背景:已知∠EDF 的顶点D 在△ABC 的边AB 所在直线上(不与A ,B 重合),DE 交AC 所在直线于点M ,DF 交BC 所在直线于点N ,记△ADM 的面积为S 1,△BND 的面积为S 2.(1)初步尝试:如图1,当△ABC 是等边三角形,AB =6,∠EDF =∠A ,且DE ∥BC ,AD =2时,则S 1·S 2=_____________.(2)类比探究:在(1)的条件下,先将点D 沿AB 平移,使AD =4,再将∠EDF 绕点D 旋转至如图2所示位置,求S 1·S 2的值.(3)拓展延伸:当△ABC 是等腰三角形时,设∠B =∠A =∠EDF =α.①如图3,当点D 在线段AB 上运动时,设AD =a ,BD =b ,求S 1·S 2的表达式(结果用a ,b 和α的三角函数表示);②如图4,当点D 在BA 的延长线上运动时,设AD =a ,BD =b ,直接写出S 1·S 2的表达式,不必写出解答过程.图1 图2 图3图4中考数学类比探究实战演练(十六)做题时间:_______至_______ 自我评价:☆ ☆ ☆ ☆ ☆ 共__________分钟 日 期:_____月_____日F三、解答题22. (10分)点A ,B 分别是两条平行线m ,n 上任意一点,在直线n 上找一点C ,使BC =kAB ,连接AC ,在直线AC 上任取一点E ,作∠BEF =∠ABC ,EF 交直线m 于点F .(1)如图1,当∠ABC =90°,k =1时,判断线段EF 和EB 之间的数量关系,并证明.(2)如图2,当∠ABC =90°,k ≠1时,(1)中的结论还成立吗?若成立,请证明;若不成立,请重新判断线段EF 和EB 之间的数量关系.(3)如图3,当0°<∠ABC <90°,k =1时,探究EF 和EB 之间的数量关系,并证明.图1 图2 图3中考数学阅读理解问题实战演练(一)做题时间:_______至_______ 自我评价:☆ ☆ ☆ ☆ ☆ 共__________分钟 日 期:_____月_____日 三、解答题22. (10分)我们定义:如果一个三角形一条边上的高等于这条边,那么这个三角形叫做“等高底”三角形,这条边叫做这个三角形的“等底”. (1)概念理解:如图1,在△ABC 中,AC =6,BC =3,∠ACB =30°,试判断△ABC 是否是“等高底”三角形,请说明理由.mnAF CB EmnA F E CBB CEF A nm(2)问题探究:如图2,△ABC 是“等高底”三角形,BC 是“等底”,作△ABC 关于BC 所在直线的对称图形得到△A′BC ,连接AA′交直线BC 于点D .若点B 是 △AA′C 的重心,求BCAC的值. (3)应用拓展:如图3,已知l 1∥l 2,l 1与l 2之间的距离为2.“等高底”△ABC 的“等底”BC 在直线l 1上,点A 在直线l 2上,有一边的长是BC 的2倍.将△ABC 绕点C 按顺时针方向旋转45°得到△A′B′C ,A′C 所在直线交l 2于点D ,求CD 的值.中考数学阅读理解问题实战演练(二)做题时间:_______至_______ 自我评价:☆ ☆ ☆ ☆ ☆ 共__________分钟 日 期:_____月_____日 三、解答题 22. (10分)定义:我们知道,四边形的一条对角线把这个四边形分成了两个三角形,如果这两个三角形相似(不全等),我们就把这条对角线叫做这个四边形的“相似对角线”. 理解:(1)如图1,已知Rt △ABC 在正方形网格中,请你只用无刻度的直尺在网格中找到一点D ,使四边形ABCD 是以AC 为“相似对角线”的四边形(保留画图痕迹,找出3个即可);(2)如图2,在四边形ABCD 中,∠ABC =80°,∠ADC =140°,对角线BD 平分∠ABC .求证:BD 是四边形ABCD 的“相似对角线”; 运用:(3)如图3,已知FH 是四边形EFGH 的“相似对角线”,∠EFH =∠HFG = 30°,连接EG ,若△EFG的面积为FH 的长.图1ABC图2DA′AB C图3l 2l 1A′D B′ABC【参考答案】中考数学类比探究实战演练(六)22.(1)①证明略;②∠BDE的度数为90°;(2)α或(180°-α);(3)CF中考数学类比探究实战演练(七)22.(1)证明略;(2)CD=2BE·tan2α;(3)12sin(45)S Sα=︒-.中考数学类比探究实战演练(八)22.(1)∠ACA′的度数为60°;(2)线段PQ的长为72;(3)四边形P A′B′Q的最小面积为3.中考数学类比探究实战演练(九)22.(1+BD=CD;(2)①证明略;②BF的长为图1ABC图2AB CD图3EF GH中考数学类比探究实战演练(十)22. (1)证明略;(2)证明略;(3)EF 2=2(BE 2+DF 2).中考数学类比探究实战演练(十一)22. (1)①∠EAF =120°;②DE 与EF 相等,理由略;(2)①∠EAF =90°;②DB 2+AE 2=ED 2.中考数学类比探究实战演练(十二)22. (1)证明略;(2)证明略;(3.中考数学类比探究实战演练(十三)22. (1)(2)①PA +PB +PC ;②PA +PB +PC (. 中考数学类比探究实战演练(十四)22. (1)12BE FD =; (2)12BE FD =,证明略;(3)2BE k FD =.中考数学类比探究实战演练(十五)22. (1)12;(2)S 1·S 2的值为12;(3)①22121()sin 4S S ab α⋅=;②22121()sin 4S S ab α⋅=.中考数学类比探究实战演练(十六)22. (1)EF =EB ,证明略; (2)不成立,1EF EB k=;(3)EF =EB ,证明略.中考数学阅读理解问题实战演练(一)22. (1)△ABC 是“等高底”三角形,理由略;(2)2AC BC =;(3)CD的值为3,2.中考数学阅读理解问题实战演练(二)22.(1)图略;(2)证明略;(3)FH的值为.21。
类比探究专项训练(六)(含答案)
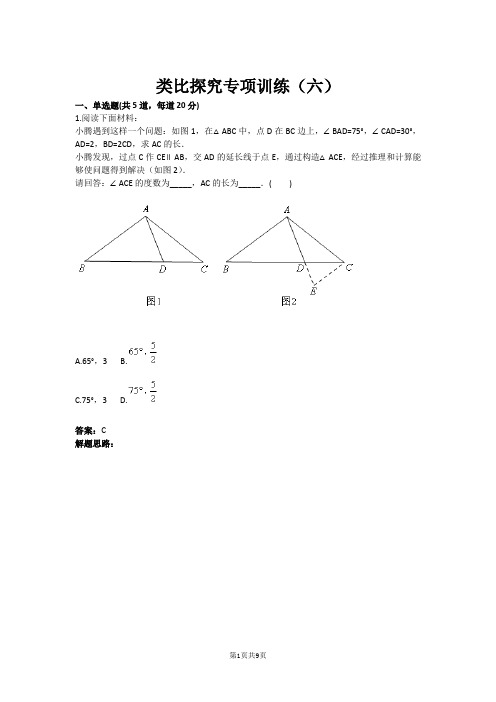
类比探究专项训练(六)一、单选题(共5道,每道20分)1.阅读下面材料:小腾遇到这样一个问题:如图1,在△ABC中,点D在BC边上,∠BAD=75°,∠CAD=30°,AD=2,BD=2CD,求AC的长.小腾发现,过点C作CE∥AB,交AD的延长线于点E,通过构造△ACE,经过推理和计算能够使问题得到解决(如图2).请回答:∠ACE的度数为_____,AC的长为_____.( )A.65°,3B.C.75°,3D.答案:C解题思路:试题难度:三颗星知识点:中考数学几何中的类比探究2.(上接第1题)参考小腾思考问题的方法,解决问题:如图3,在四边形ABCD中,∠BAC=90°,∠CAD=30°,∠ADC=75°,AC与BD交于点E,AE=2,BE=2DE,则BC的长为( )A.6B.C. D.答案:C解题思路:试题难度:三颗星知识点:中考数学几何中的类比探究3.问题背景:如图1,在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠D=90°.E,F分别是边BC,CD上的点,且∠EAF=60°.求证:EF=BE+DF.关于证明上述结论的辅助线的作法,有如下说法:①延长FD到G,使DG=BE,连接AG;②过点A作AG⊥EF于点G;③将△ABE绕点A逆时针旋转120°得到△ADG(之后证明点G,D,F在同一条直线上).其中可以证明结论的是( )A.①B.②③C.①③D.①②③答案:C解题思路:试题难度:三颗星知识点:全等三角形的判定与性质4.(上接第3题)探索延伸:如图2,在四边形ABCD中,AB=AD,E,F分别是边BC,CD上的点,且,则当∠B和∠D满足什么条件时,EF=BE+DF成立?( )A.∠B=∠DB.∠B+∠D=180°C.∠B=2∠DD.∠B+∠D=120°答案:B解题思路:试题难度:三颗星知识点:全等三角形的判定与性质5.(上接第3,4题)实际应用:如图3,在某次军事演习中,舰艇甲在指挥中心(O处)北偏西30°的A处,舰艇乙在指挥中心南偏东70°的B处,并且两舰艇到指挥中心的距离相等.接到行动指令后,舰艇甲向正东方向以60海里/小时的速度前进,舰艇乙沿北偏东50°的方向以80海里/小时的速度前进.1.5小时后,指挥中心观测到甲、乙两舰艇分别到达E,F处,且两舰艇之间的夹角为70°,则此时两舰艇之间的距离为( )海里.A. B.210C.300D.条件不够,无法计算答案:B解题思路:试题难度:三颗星知识点:中考数学几何中的类比探究。
中考数学专项训练:类比探究与拓展应用

专项训练1.小圆同学对图形旋转前后的线段之间、角之间的关系进行了拓展探究.(一)猜测探究在ABC △中,AB AC =,M 是平面内任意一点,将线段AM 绕点A 按顺时针方向旋转与BAC ∠相等的角度,得到线段AN ,连接NB .(1)如图1,若M 是线段BC 上的任意一点,请直接写出NAB ∠与MAC ∠的数量关系是 ,NB 与MC 的数量关系是 ;(2)如图2,点E 是AB 延长线上点,若M 是CBE ∠内部射线BD 上任意一点,连接MC ,(1)中结论是否仍然成立?若成立,请给予证明,若不成立,请说明理由.(二)拓展应用如图3,在△111A B C 中,118A B =,11160A B C ∠=︒,11175B AC ∠=︒,P 是11B C 上的任意点,连接1A P ,将1A P 绕点1A 按顺时针方向旋转75︒,得到线段1AQ ,连接1B Q .求线段1B Q 长度的最小值.2.在图1,2,3中,已知ABCD ,120ABC ∠=︒,点E 为线段BC 上的动点,连接AE ,以AE 为边向上作菱形AEFG ,且120EAG ∠=︒.(1)如图1,当点E 与点B 重合时,CEF ∠= ︒;(2)如图2,连接AF .①填空:FAD ∠ EAB ∠(填“>”,“ <”,“=” );②求证:点F 在ABC ∠的平分线上;(3)如图3,连接EG ,DG ,并延长DG 交BA 的延长线于点H ,当四边形AEGH 是平行四边形时,求BC AB的值.3.【问题探究】(1)如图1,ABC △和DEC △均为等腰直角三角形,90ACB DCE ∠=∠=︒,点B ,D ,E 在同一直线上,连接AD ,BD .①请探究AD 与BD 之间的位置关系: ;②若10AC BC ==,2DC CE ==,则线段AD 的长为 ;【拓展延伸】(2)如图2,ABC ∆和DEC ∆均为直角三角形,90ACB DCE ∠=∠=︒,21AC =,7BC =,3CD =,1CE =.将DCE △绕点C 在平面内顺时针旋转,设旋转角BCD ∠为(0360)αα︒<︒,作直线BD ,连接AD ,当点B ,D ,E 在同一直线上时,画出图形,并求线段AD 的长.4.如图1,正方形ABDE和BCFG的边AB,BC在同一条直线上,且2AB BC=,取EF的中点M,连接MD,MG,MB.(1)试证明DM MG⊥,并求MBMG的值.(2)如图2,将图1中的正方形变为菱形,设2(090)EABαα∠=<<︒,其它条件不变,问(1)中MBMG的值有变化吗?若有变化,求出该值(用含α的式子表示);若无变化,说明理由.5.如图1,菱形ABCD 的顶点A ,D 在直线上,60BAD ∠=︒,以点A 为旋转中心将菱形ABCD 顺时针旋转(030)αα︒<<︒,得到菱形AB C D ''',B C ''交对角线AC 于点M ,C D ''交直线l 于点N ,连接MN .(1)当//MN B D ''时,求α的大小.(2)如图2,对角线B D ''交AC 于点H ,交直线l 与点G ,延长C B ''交AB 于点E ,连接EH .当HEB '△的周长为2时,求菱形ABCD 的周长.6.思维启迪:(1)如图1,A ,B 两点分别位于一个池塘的两端,小亮想用绳子测量A ,B 间的距离,但绳子不够长,聪明的小亮想出一个办法:先在地上取一个可以直接到达B 点的点C ,连接BC ,取BC 的中点P (点P 可以直接到达A 点),利用工具过点C 作CD AB ∥交AP 的延长线于点D ,此时测得200CD =米,那么A ,B 间的距离是米.思维探索:(2)在ABC △和ADE △中,AC BC =,AE DE =,且AE AC <,90ACB AED ∠=∠=︒,将ADE △绕点A 顺时针方向旋转,把点E 在AC 边上时ADE △的位置作为起始位置(此时点B 和点D 位于AC 的两侧),设旋转角为α,连接BD ,点P 是线段BD 的中点,连接PC ,PE .①如图2,当ADE △在起始位置时,猜想:PC 与PE 的数量关系和位置关系分别是 ;②如图3,当90α=︒时,点D 落在AB 边上,请判断PC 与PE 的数量关系和位置关系,并证明你的结论;③当150α=︒时,若3BC =,1DE =,请直接写出2PC 的值.7.综合与实践动手操作:第一步:如图1,正方形纸片ABCD 沿对角线AC 所在的直线折叠,展开铺平.在沿过点C 的直线折叠,使点B ,点D 都落在对角线AC 上.此时,点B 与点D 重合,记为点N ,且点E ,点N ,点F 三点在同一条直线上,折痕分别为CE ,CF .如图2.第二步:再沿AC 所在的直线折叠,ACE △与ACF △重合,得到图3. 第三步:在图3的基础上继续折叠,使点C 与点F 重合,如图4,展开铺平,连接EF ,FG ,GM ,ME .如图5,图中的虚线为折痕.问题解决:(1)在图5中,BEC 的度数是,AE BE的值是 . (2)在图5中,请判断四边形EMGF 的形状,并说明理由;(3)在不增加字母的条件下,请你以图中5中的字母表示的点为顶点,动手画出一个菱形(正方形除外),并写出这个菱形: .8.如图,在直角坐标系中,直线132y x=−+与x轴,y轴分别交于点B,点C,对称轴为1x=的抛物线过B,C两点,且交x轴于另一点A,连接AC.(1)直接写出点A,点B,点C的坐标和抛物线的解析式;(2)已知点P为第一象限内抛物线上一点,当点P到直线BC的距离最大时,求点P的坐标;(3)抛物线上是否存在一点Q(点C除外),使以点Q,A,B为顶点的三角形与ABC△相似?若存在,求出点Q的坐标;若不存在,请说明理由.题9.已知抛物线2342y ax x =++的对称轴是直线3x =,与x 轴相交于A ,B 两点(点B 在点A 右侧),与y 轴交于点C .(1)求抛物线的解析式和A ,B 两点的坐标;(2)如图1,若点P 是抛物线上B 、C 两点之间的一个动点(不与B 、C 重合),是否存在点P ,使四边形PBOC 的面积最大?若存在,求点P 的坐标及四边形PBOC 面积的最大值;若不存在,请说明理由;(3)如图2,若点M 是抛物线上任意一点,过点M 作y 轴的平行线,交直线BC 于点N ,当3MN =时,求点M 的坐标.10.如图,抛物线2542y mx mx =−−与x 轴交于1(A x ,0),2(B x ,0)两点,与y 轴交于点C ,且21112x x −=. (1)求抛物线的解析式;(2)若1(P x ,1)y ,2(Q x ,2)y 是抛物线上的两点,当12a x a +,292x 时,均有12y y ,求a 的取值范围;(3)抛物线上一点(1,5)D −,直线BD 与y 轴交于点E ,动点M 在线段BD 上,当BDC MCE ∠=∠时,求点M 的坐标.11.如图,抛物线2y ax bx c =++经过(3,0)A −,(1,0)B ,(0,3)C 三点.(1)求抛物线的函数表达式;(2)如图1,P 为抛物线上在第二象限内的一点,若PAC △面积为3,求点P 的坐标;(3)如图2,D 为抛物线的顶点,在线段AD 上是否存在点M ,使得以M ,A ,O 为顶点的三角形与ABC △相似?若存在,求点M 的坐标;若不存在,请说明理由.12.若二次函数2y ax bx c =++的图象与x 轴、y 轴分别交于点(3,0)A 、(0,2)B −,且过点(2,2)C −.(1)求二次函数表达式;(2)若点P 为抛物线上第一象限内的点,且4PBA S =△,求点P 的坐标;(3)在抛物线上(AB 下方)是否存在点M ,使ABO ABM ∠=∠?若存在,求出点M 到y 轴的距离;若不存在,请说明理由.13.综合与探究如图,抛物线26y ax bx =++经过点(2,0)A −,(4,0)B 两点,与y 轴交于点C ,点D 是抛物线上一个动点,设点D 的横坐标为(14)m m <<.连接AC ,BC ,DB ,DC .(1)求抛物线的函数表达式;(2)BCD △的面积等于AOC △的面积的34时,求m 的值; (3)在(2)的条件下,若点M 是x 轴上一动点,点N 是抛物线上一动点,试判断是否存在这样的点M ,使得以点B ,D ,M ,N 为顶点的四边形是平行四边形?若存在,请直接写出点M 的坐标;若不存在,请说明理由.14.如图,在平面直角坐标系中,抛物线22(0)y ax bx a =++≠与x 轴交于A ,B 两点(点A 在点B 的左侧),与y 轴交于点C ,抛物线经过点(2,3)D −−和点(3,2)E ,点P 是第一象限抛物线上的一个动点.(1)求直线DE 和抛物线的表达式;(2)在y 轴上取点(0,1)F ,连接PF ,PB ,当四边形OBPF 的面积是7时,求点P 的坐标;(3)在(2)的条件下,当点P 在抛物线对称轴的右侧时,直线DE 上存在两点M ,N (点M 在点N 的上方),且22MN =,动点Q 从点P 出发,沿P M N A →→→的路线运动到终点A ,当点Q 的运动路程最短时,请直接写出此时点N 的坐标.15.如图1,在平面直角坐标系中,抛物线233373848y x x =+−与x 轴交于点A 、B (点A 在点B 右侧),点D 为抛物线的顶点,点C 在y 轴的正半轴上,CD 交x 轴于点F ,CAD ∆绕点C 顺时针旋转得到CFE ∆,点A 恰好旋转到点F ,连接BE .(1)求点A 、B 、D 的坐标;(2)求证:四边形BFCE 是平行四边形;(3)如图2,过顶点D 作1DD x ⊥轴于点1D ,点P 是抛物线上一动点,过点P 作PM x ⊥轴,点M 为垂足,使得PAM △与1DD A △相似(不含全等).①求出一个满足以上条件的点P 的横坐标;②直接回答这样的点P 共有几个?。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(2012一测)21、如图1,直角∠EPF的顶点和正方形ABCD的顶点C重合,两直角边PE,PF分别和AB,AD所在直线交于点E和F,易得△PBE≌△PDF,故结论“PE=PF”成立;(1)如图2,若点P在正方形ABCD的对角线AC上,其他条件不变,(1)中的结论是否仍然成立?说明理由;(2)如图3,将(2)中的“正方形”改为“矩形”,其他条件不变,若AB=m,BC=n,直接写出PFPE的值。
(2013一测)22.(本题10分)(1)问题背景如图1,Rt△ABC中,∠BAC=90°,AB=AC,∠ABC的平分线交直线AC于D,过点C作CE⊥BD,交直线BD 于E.请探究线段BD与CE的数量关系.(事实上,我们可以延长CE与直线BA相交,通过三角形的全等等知识解决问题.)结论:线段BD与CE的数量关系是______________________(请直接写出结论);(2)类比探索在(1)中,如果把BD改为∠ABC的外角∠ABF的平分线,其他条件均不变(如图2),(1)中的结论还成立吗?若成立,请写出证明过程;若不成立,请说明理由;(3)拓展延伸在(2)中,如果AB≠AC,且AB=nAC(0<n<1),其他条件均不变(如图3),请你直接写出BD与CE的数量关系.结论:BD=_____CE(用含n的代数式表示).DECBAFAB CEDF BECAD图1 图2 图3G FED C B AABC DEFGH KL IJGF EDCBA(2015一测)22.(本题10分)如图①,正方形AEFG 的边长为1,正方形ABCD 的边长为3,且点F 在AD 上. (1)求;(2)把正方形AEFG 绕点A 按逆时针方向旋转45°得图②,求图②中的;(3)把正方形AEFG 绕点A 旋转一周,在旋转的过程中,存在最大值与最小值,请直接写出最大值,最小值.(2017二测)22.(10分)问题发现:如图1,在△ABC 中,∠C =90°,分别以AC ,BC 为边向外侧作正方形ACDE 和正方形BCFG .(1)△ABC 和△DCF 面积的关系是______________;(请在横线上填写“相等”或“不等”) (2)拓展探究:若∠C ≠90°,(1)中的结论还成立吗?若成立,请结合图2给出证明;若不成立,请说明理由;(3)解决问题:如图3,在四边形ABCD 中,AC ⊥BD ,且AC 与BD 的和为10,分别以四边形ABCD 的四条边为边向外侧作正方形ABFE 、正方形BCHG 、正方形CDJI ,正方形DALK ,运用(2)的结论,图中阴影部分的面积和是否有最大值?如果有,请求出最大值,如果没有,请说明理由.图1图2 图33.(2016·山东省德州市·4分)我们给出如下定义:顺次连接任意一个四边形各边中点所得的四边形叫中点四边形.(1)如图1,四边形ABCD中,点E,F,G,H分别为边AB,BC,CD,DA的中点.求证:中点四边形EFGH是平行四边形;(2)如图2,点P是四边形ABCD内一点,且满足PA=PB,PC=PD,∠APB=∠CPD,点E,F,G,H分别为边AB,BC,CD,DA的中点,猜想中点四边形EFGH的形状,并证明你的猜想;(3)若改变(2)中的条件,使∠APB=∠CPD=90°,其他条件不变,直接写出中点四边形EFGH的形状.(不必证明)4.(2016广西南宁)已知四边形ABCD是菱形,AB=4,∠ABC=60°,∠EAF的两边分别与射线CB,DC相交于点E,F,且∠EAF=60°.(1)如图1,当点E是线段CB的中点时,直接写出线段AE,EF,AF之间的数量关系;(2)如图2,当点E是线段CB上任意一点时(点E不与B、C重合),求证:BE=CF;(3)如图3,当点E在线段CB的延长线上,且∠EAB=15°时,求点F到BC的距离.10.(2015浙江嘉兴,24,14分)类比等腰三角形的定义,我们定义:有一组邻边相等的凸四边形叫做“等邻边四边形”.⑴概念理解如图1,在四边形ABCD中添加一个条件使得四边形ABCD是“等邻边四边形”.请写出你添加的一个条件.⑵问题探究①小红猜想:对角线互相平分的“等邻边四边形”是菱形. 她的猜想正确吗?请说明理由.②如图2,小红画了一个Rt△ABC,其中∠ABC=90°,AB=2,BC=1,并将Rt△ABC沿∠ABC的平分线BB方向平移得到A B C,连接AA,BC.小红要使平移后的四边形ABC A是“等邻边四边形”,应平移多少距离(即线段BB的长)?⑶应用拓展AC AB.试探究如图3,“等邻边四边形”ABCD中,AB=AD,∠BAD+∠BCD=90°,AC,BD为对角线,2BC,CD,BD的数量关系.11.(2015山东临沂,25,11分)如图1,在正方形ABCD的外侧,作两个等边三角形ADE和DCF,连接AF,BE(1)请判断:AF与BE的数量关系是,位置关系是;(2)如图2,若将条件“两个等边三角形ADE和DCF”变成“两个等腰三角形ADE和DCF,且EA=ED=FD=FC”,第(1)问中的结论是否仍然成立?请作出判断并给予证明;(3)若三角形ADE和DCF为一般三角形,且AE=DF,ED=FC,第(1)问中的结论都能成立吗?请直接写出你的判断。
20.(2015山东潍坊,23,12分)如图1,点O是正方形ABCD两对角线的交点. 分别延长OD到点G,OC到点E,使OG=2OD,OE=2OC,然后以OG、OE为邻边作正方形OEFG,连接AG,DE.(1)求证:DE⊥AG;OE F G,如图2. (2)正方形ABCD固定,将正方形OEFG绕点O逆时针旋转α角(0°<α<360°)得到正方形'''OAG是直角时,求α的度数;①在旋转过程中,当∠'AF长的最大值和此时α的度数,直接写出结果不必说明理由.②若正方形ABCD的边长为1,在旋转过程中,求'4. (2015眉山市,25,9分)如图,在矩形ABCD 中,E 是AB 边的中点,沿EC 对折矩形ABCD ,使B 点落在点P 处,折痕为EC ,连结AP 并延长AP 交CD 于F 点, (1)求证:四边形AECF 为平行四边形;(2)若△AEP 是等边三角形,连结BP ,求证:EPC APB ∆≅∆; (3)若矩形ABCD 的边AB=6,BC=4,求△CPF 的面积2. (2015黑龙江牡丹江,26,8分)已知四边形ABCD 是正方形,等腰直角△AEF 的直角顶点E 在直线BC上(不与点B ,C 重合),FM ⊥AD ,交射线AD 于点M.(1)当点E 在边BC 上,点M 在边AD 的延长线上时,如图①,求证:AB+BE=AM ;(提示:延长MF ,交边BC 的延长线于点H.)(2)当点E 在边C B 的延长线上,点M 在边A D 上时,如图②;当点E 在边B C 的延长 线上,点M 在边A D 上时,如图③.请分别写出线段A B ,B E ,A M 之间的数量关系,不需要证明;(3)在(1),(2)的条件下,若BE=3,∠AFM =15°,则AM = .PBCD24. (2014浙江省台州市,9,4分)如图,F 是正方形ABCD 的边CD 上的一个动点,BF 的垂直平分线交对角线AC 于点E ,连接BE ,BF ,则EBF 的度数是 ··································································· ( ) A .45°B .50°C .60°D .不确定11. (2014重庆B 卷,18,4分)如图,在边长为62的正方形ABCD 中,E 是AB 边上一点,G 是AD 延长线一点,BE =DG ,连接EG ,CF ⊥EG 交EG 于点H ,交AD 于点F ,连接CE 、BH .若BH =8,则FG =_____________.18题图GHABC DE F 10. (2014年山东省日照市24,3分)(1)如图1,在正方形ABCD 中,E 是AB 上一点,F 是AD 延长线上一点,且DF=BE .求证:CE=CF ;(2)如图2,在正方形ABCD 中,E 是AB 上一点,G 是AD 上一点,如果∠GCE=45°,请你利用(1)的结论证明:GE=BE+GD . (3)运用(1)(2)解答中所积累的经验和知识,完成下题: 如图3,在直角梯形ABCD 中,AD ∥BC (BC >AD ),∠B=90°,AB=BC ,E 是AB 上一点,且∠DCE=45°,BE=4,DE=10,求直角梯形ABCD 的面积.ABC DEFM13.(2014山东威海 24,11分)猜想与证明:如图①摆放矩形纸片ABCD 与矩形纸片ECGF ,使B ,C ,G 三点在一条直线上,CE 在边CD 上.连结AF ,若M 为AF 的中点,连结DM ,ME ,试猜想DM 与ME 的关系,并证明你的结论.拓展与延伸:(1)若将“猜想与证明”中的纸片换成正方形纸片ABCD 与正方形纸片ECGF ,其它条件不变,则DM 和ME 的关系为_______;(2)如图②摆放正方形纸片ABCD 与正方形纸片ECGF ,使点F 在边CD 上,点M 仍为AF 的中点,试证明(1)中的结论仍然成立.如图,在Rt △ABC 中,∠B =90°,AC =60,AB =30.D 是AC 上的动点,过D 作DF ⊥BC 于F ,过F 作FE ∥AC ,交AB 于E .设CD =x ,DF =y . (1)求y 与x 的函数关系式;(2)当四边形AEFD 为菱形时,求x 的值; (3)当△DEF 是直角三角形时,求x 的值.ABCD EFGM 图②ABCDEFG M图①DA11.(2014年江西省抚州市24,10分)【试题背景】已知:l∥m∥n∥k,平行线l与m、m与n、n与k之间的距离分别为d1、d2、d3,且d 1 =d3 = 1,d2 = 2 . 我们把四个顶点分别在l、m、n、k这四条平行线上的四边形称为“格线四边形”.【探究1】⑴如图1,正方形ABCD为“格线四边形”,BE l⊥于点E,BE的反向延长线交直线k于点F. 求正方形ABCD的边长.【探究2】⑵矩形ABCD为“格线四边形”,其长:宽= 2 :1 ,则矩形ABCD的宽为 .(直接写出结果即可)【探究3】⑶如图2,菱形ABCD为“格线四边形”且∠ADC=60°,△AEF是等边三角形,AE⊥k于点E,∠AFD=90°,直线DF分别交直线l、k于点G、M. 求证:EC DF=.【拓展】⑷如图3,l∥k,等边三角形ABC的顶点A、B分别落在直线l、k上,AB⊥k于点B,且AB=4 ,∠ACD=90°,直线CD分别交直线l、k于点G、M,点D、E分别是线段GM、BM上的动点,且始终保持AD=AE,DH l⊥于点H.猜想:DH在什么范围内,BC∥DE?并说明此时BC∥DE的理由.5、(2013年江西省)某数学活动小组在作三角形的拓展图形,研究其性质时,经历了如下过程:●操作发现:在等腰△ABC中,AB=AC,分别以AB和AC为斜边,向△ABC的外侧作等腰直角三角形,如图1所示,其中DF⊥AB于点F,EG⊥AC于点G,M是BC的中点,连接MD和ME,则下列结论正确的是(填序号即可)①AF=AG=21AB;②MD=ME;③整个图形是轴对称图形;④∠DAB=∠DMB.●数学思考:在任意△ABC中,分别以AB和AC为斜边,向△ABC的外侧..作等腰直角三角形,如图2所示,M是BC的中点,连接MD和ME,则MD和ME具有怎样的数量和位置关系?请给出证明过程;●类比探索:在任意△ABC中,仍分别以AB和AC为斜边,向△ABC的内侧作等腰直角三角形,如图3所示,M是BC 的中点,连接MD和ME,试判断△MED的形状.答:.第22题图。
