大学物理 电场和电场强度
大学物理 第一章静止电荷的电场(必看)

q2d (A) 2 S 0
Байду номын сангаас
)。
q2d (B) S 0 q2d (D) S 0
q2 F Eq 2S 0
q2d (C) 2 S 0
d
d
q E 2 0 2S 0
q 2d A Fd 2S 0
量等于该闭合面内所包围的电荷代数和除以真空的
介电常数,数学表达式为
1 E ds
s
0 ( s面内)
q
典型电荷的电场
(1)点电荷
E
q 4 0 r
2
er
(2)半径为R 、带电量为Q均匀带电球面
E0
E Q 4 0 r
2
rR
er
rR
(3)均匀带电无限长直线
E 2 0 r
2 ES 2 xS
底面
E
x
0
0
d x 时: 2 q DS
2 ES DS
0
D E 2 0
例 题 15 15、如图所示,一无限长的均匀带电圆柱体,
体电荷密度为 ,截面半径为 R 。
求:
(1)柱内( r R )电场强度分布?
(2)柱外(r R)的电场强度分布?
直线中垂线的P点到带电直线中心o的距离
OP L
时,P点的电场强度大小。 解(1)
dE
E
L 2 L 2
y
L r ax 2
o
x
1 1 ( ) L 4 0 ( a x) 2 4 0 a a L 2
dq 4 0 r 2 dx
大学物理知识点归纳

大学物理第十一章:真空中的静电场一、电场强度:数值上等于单位正电荷在该点受到的电场力的大小,也等于单位面积电通量的大小(即电场线密度);方向与该点的受力方向(或者说电场线方向)一致。
二、电场强度的计算:a)点电荷的电场强度:b)电偶极子中垂线上任意一点的电场强度:(表示点到电偶极子连线的距离)c)均匀带电直棒:无限长(=0)无限ii.非均匀电场E穿过曲面S的电通量:四、高斯定理a)b)表述:真空中任何静电场中,穿过任一闭合曲面的电通量,在数值上等于该闭合曲面内包围的电荷的代数和除以;c)理解:1.高斯定理表达式左边的E是闭合面上处的电场强度,他是由闭合面内外全部电荷共同产生的,即闭合曲面外的电荷对空间各点的E有贡献,要影响闭合面上的各面元的同量。
2.通过闭合曲面的总电量只决定于闭合面内包围的电荷,闭合曲面外部的电荷对闭合面的总电通量无贡献。
d)应用:1.均匀带电球面外一点的场强相当于全部电荷集中于球心的点电荷在该点的电场强度。
2.均匀带电球面内部的电场强度处处为零。
五、电势a)静电场环路定理:在静电场中,电场强度沿任意闭合路径的线积分等于零。
b)电场中a点的电势:1.无穷远为电势零点:2.任意b点为电势零点:电场中任意一点的电场强度等于该点点势梯度的负值。
第十二章a)导体内部,电场强度处处为零;导体表明的电场强度方向垂直该处导体表面;电场线不进入导体内部,b)c)d)e)a)i.b)导体空腔内有带电体(电量为q)的情况i.空腔导体原来不带电,空腔外表面感应电荷为q,空腔内表面感应电荷为-q。
如果空腔导体原来带电量Q,则内外表面电荷量分别加上Q。
三、A、B为两个任意带电平面:,四、静电场中的电介质:a)电介质中的电场强度:i.ii.电介质极化后,介质内部任意一处,合电场强度,但不等于0,这是电场中的电介质与电场中的导体静电平衡后的重要区别。
五、电介质中的高斯定理:a)其中六、有电介质存在时静电场的分析计算:i.由介质中的高斯定理先计算空间的分布,再由求得空间电场的分布。
大学物理常用公式(电场磁场 热力学)

第四章 电 场一、常见带电体的场强、电势分布2)均匀带电球面(球面半径 )的电场:3)无限长均匀带电直线(电荷线密度为): E = ,方向:垂直于带电直线。
2r( rR ) 4)无限长均匀带电圆柱面(电荷线密度为):E =2r (rR )5)无限大均匀带电平面(电荷面密度为)的电场: E =/20 ,方向:垂直于平面。
二、静电场定理 1、高斯定理:e = ÑE v dS v = q 静电场是有源场。
Sq 指高斯面内所包含电量的代数和;E 指高斯面上各处的电场强度,由高斯面内外的全 部电荷产生; Ñ E vdS v 指通过高斯面的电通量,由高斯面内的电荷决定。
2、环路定理: Ñ E v dl v =0 静电场是保守场、电场力是保守力,可引入电势能三、求场强两种方法1、利用场强势叠加原理求场强 分离电荷系统: E v = E v i ;连续电荷系统: E v = dE v i =12、利用高斯定理求场强 四、求电势的两种方法n1、利用电势叠加原理求电势 分离电荷系统:U =U i ;连续电荷系统: U = dU i =1电势零点v v 2、利用电势的定义求电势 U =电势零点Edl五、应用vv b点电荷受力: F = qE电势差: U ab =U a -U b = b EdraE =1 qU =q4r 24r1)点电荷:E =0 (rR ) q2 (rR ) 4r 2U =q (r R ) 4r q (r R ) 4Ra 点电势能:W a = qU a由 a 到 b 电场力做功等于电势能增量的负值 A ab = -W = -(W b -W a )六、导体周围的电场1、静电平衡的充要条件: 1)、导体内的合场强为 0,导体是一个等势体。
2)、导体表面的场强处处垂直于导体表面。
E v ⊥表面。
导体表面是等势面。
2、静电平衡时导体上电荷分布: 1)实心导体: 净电荷都分布在导体外表面上。
大学物理电磁学公式

大学物理电磁学公式大学物理电磁学是物理学中的一个重要分支,研究电场和磁场以及它们之间的相互作用。
在学习和研究电磁学的过程中,我们经常会接触到一系列重要的公式。
以下是一些常见的大学物理电磁学公式的详细介绍。
1. 库仑定律(Coulomb's Law):库仑定律描述了两个点电荷之间相互作用力的大小和方向。
它的数学表达式为:F = k * |q1 * q2| / r²其中,F为两个电荷所受的力,k为库仑常数,q1和q2分别为两个电荷的大小,r为两个电荷之间的距离。
2. 电场强度(Electric Field Intensity):电场强度描述了电荷在某一点周围的电场的强弱。
对于一个点电荷,其电场强度的数学表达式为:E = k * |q| / r²其中,E为电场强度,k为库仑常数,q为电荷的大小,r为点电荷到被测点之间的距离。
3. 电势能(Electric Potential Energy):电势能描述了电荷由于存在于电场中而具有的能量。
对于一个点电荷,其电势能的数学表达式为:U = k * |q1 * q2| / r其中,U为电势能,k为库仑常数,q1和q2分别为两个电荷的大小,r为两个电荷之间的距离。
4. 电势差(Electric Potential Difference):电势差描述了电场中两个点之间的电势能的差异。
对于两个点电荷之间的电势差,其数学表达式为:ΔV = V2 - V1 = -∫(E · dl)其中,ΔV为电势差,V1和V2分别为两个点的电势,E为电场强度,dl为路径元素。
5. 电场线(Electric Field Lines):电场线用于可视化电场的分布情况。
电场线从正电荷流向负电荷,并且密集的电场线表示电场强度较大,稀疏的电场线表示电场强度较小。
6. 电场的高斯定律(Gauss's Law for Electric Fields):电场的高斯定律描述了电场通过一个闭合曲面的总通量与该闭合曲面内的电荷量之间的关系。
大学物理 静电场总结

5. 电势定义:
a
Wpa q0
ur r E dl
a
静电场力作的功与电势差、电势能之间的关系:
b ur r
Aab qE dl q(a b ) (Wpb Wpa ) a
6. 电势分布的典型结论
1) 点电荷: q 4 0r
2) 均匀带电圆环轴线上:
4 0
q R2 x2
3) 均匀带电球面的电势分布:
1)平行板电容器 C 0S
d
2) 电容器的串并联:
串联 1 1 1 1
C C1 C2
Cn
并联 C C1 C2 Cn
4. 电场能量
电容器的静电能: W Q2
2C
电场能量密度:
w
1 2
0E2
各向同性的电介质:
电介质 电位移
D ε0E P
D ε0εr E εE
Gauss定理
2. 静电平衡时导体上的电荷分布 1) 实心导体: 电荷只分布在表面,导体内部没有净电荷.
2) 空腔导体: • 腔内无电荷 电荷分布在外表面,内表面无电荷. •:腔内有电荷: 腔体内表面所带的电量和腔内带电体所带 的电量等量异号。 • 接地空腔导体 外表面不带电, 静电屏蔽 :
3. 电容 C Q
q
4
q
0R
L L rR L L rR
40r
4) 无限长均匀带电直线: ln rB 20 r
(B 0)
7. 电势的计算 叠加法 定义法
第6章 静电场中的导体与电介质
1. 导体的静电平衡条件:
电场描述: ⑴ 导体内部任意一点的场强为零。 ⑵ 导体表面处的场强方向与该处表面垂直.
电势描述: 导体是一等势体,表面是一等势面.
大学物理电场电场强度

Q1
d
r
Байду номын сангаас观察点
.P
库仑定律: • 1785年,法国库仑(C.A.Coulomb) 库仑
库仑定律
真空中两个静止的点电荷之间的作用力(静电力), 与它们所带电量的乘积成正比,与它们之间的距离的平方 成反比,作用力沿着这两个点电荷的连线。
F21 ——电荷q1作用于电荷q2的力。
q1q2 F21 F12 k 2 r0 r 1 k 4 0
F31 1 40 q1q3 r2
F3
q3 0.3m j q2
F31
0.6m
9.0 109 140 N
6.5 10 8.6 10 N
5 5
0.62
i
0.52m
q1
x
力 F31 沿x轴和y轴的分量分别为
Fx F31 cos 30 120N
引力
q1q2 1 q1q2 注意:只适用两 r0 r 2 3 个点电荷之间 4 0 r 4 0 r
静电力的叠加原理 作用于某电荷上的总静电力等于其他点电荷单独 存在时作用于该电荷的静电力的矢量和。 数学表达式
离散状态
N F Fi i 1
r10
ri 0
dF
A q0 B
q0
A
FB
(1)点电荷的电场
3.电场强度的计算
(2)场强叠加原理和点电荷系的电场 (3)连续分布电荷的电场
(1)点电荷的电场
1 q0 q F r 3 4 0 r
E
F 1 q E r 3 q0 40 r
E
q 源点
q0
E
场点
大学物理——电场强度与电势
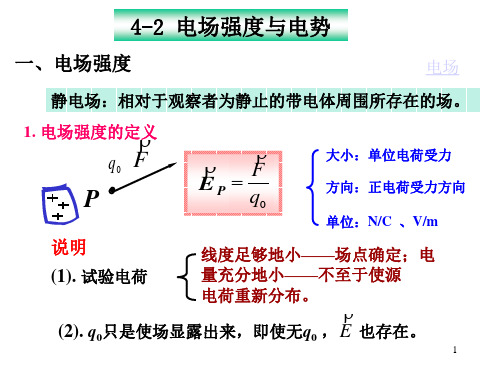
例题
均匀带电细棒,长 L ,电荷线密度 , 求:中垂面上的场强 。 r dQ
y
dQ dy
解 : dE 4 r 3 0
r1
L0
dE dE x i dE y j E dE i dE x j 0 dE y
L L L
E r
2
3、场强叠加原理
(1)点电荷系的场强 Q2
点电荷的场强
点 电 Q1 荷
试验电荷 F2 Q
0
E
F F
1
Q 4 0 r
2
r0
由定义
F F3 F1 F2 E E1 E2 E3 Q0 Q0 Q0 Q0
L
E E //
x xQ dQ x dQ cos dE 2 L 3 L r 4 r 40 r 0 (1) x 0 xQ i
dE
E
L
dE 0
E0
4 0 x R
2
2
3
2
Q (2)R <<x E 2 4 0 x
dE
P
x
r
R
O
dr
9
讨论 (1) 当R >> x ,圆板可视为无限大薄板
E 2 0
(2)
E1
E1 E2
E1 E2
EI E1 E2 0 EII E1 E2 0 EIII E1 E2 0
E2
(3) 补偿法
10
例 已知圆环带电量为q ,杆的线密度为 ,长为L
qq 0 1 1 A r 4 0 1 r2
大学物理一复习 第五章 静电场和习题小结

q 4 π
0
dr r
2
r
q
1 q ( ) 4 r r 4 r q
0 0
r
E
V
q 4 π 0r
q 0, V 0 q 0, V 0
三、电势叠加原理
点电荷系
Va
q1
q2
a
E dl
V1 V 2 V n
第 五 章 静电场
Nothing in life is to be feared. It is only to be understood. ----(Marie Curie)
本章参考作业:P190
5-1,5-2、5-9①、5-14、5-21、 5-23、5-26、5-27、5-30。
学 习 要 点
的大小处处相等,且有
cos 1
cos 0
(目的是把“ E ”从积分号里拿出来)
计算高斯面内的电荷,由高斯定理求 E。
高斯定理运用举例: ---计算有对称性分布的场强
掌握所有 例题
1、球对称——球体、球面、球壳等。 2、轴对称——无限长直线、圆柱体、圆柱面。 3、面对称——无限大均匀带电平面。
E
0
R
r
三、面对称——无限大均匀带电平面。
例6、求无限大均匀带电平面的场 分布。已知面电荷密度为
o
p
dE
dE
解:对称性分析: 垂直平面 E
选取闭合的柱形高斯面
左底 侧
右底
侧 0
左底
E S
S'
E S
右底
2 ES
