数学人教版八年级下册矩形练习题
人教版八年级数学下册矩形的性质和判定 同步练习

初中数学试卷矩形的性质和判定同步练习1.矩形的对边,对角线且,四个角都是,即是图形又是图形。
2.矩形的面积是60,一边长为5,则它的一条对角线长等于。
3.如果矩形的一边长为8,一条对角线长为10,那么这个矩形面积是__________。
4. 矩形的一内角平分线把矩形的一条边分成3和5两部分,则该矩形的周长是___________.5. 矩形的两条对角线的夹角是60°,一条对角线与矩形短边的和为15,那么矩形对角线的长为_______,短边长为_______.6.如图,已知在平面直角坐标系中,O为坐标原点,四边形OABC是矩形,点A、C的坐标分别为A(10,0)、C(0,4),点D是OA的中点,点P在BC边上运动,当△ODP是腰长为5的等腰三角形时,点P的坐标为。
7.若一个直角三角形的两条直角边分别为5和12,则斜边上的中线等于 .8.平行四边形没有而矩形具有的性质是()A.对角线相等B.对角线互相垂直C.对角线互相平分D.对角相等9.下列叙述错误的是()A.平行四边形的对角线互相平分B.平行四边形的四个内角相等。
C.矩形的对角线相等。
D.有一个角时90º的平行四边形是矩形10.下列检查一个门框是否为矩形的方法中正确的是()A.测量两条对角线是否相等B.用曲尺测量对角线是否互相垂直C.用曲尺测量门框的三个角是否都是直角D.测量两条对角线是否互相平分11.矩形ABCD对角线相交于点O,如果△ABC周长比△AOB周长大10cm,则AD长是()A.5cmB.7.5cmC.10cmD.12.5cm12.下列图形中对称轴有2条的图形是()A.平行四边形B.等边三角形C.矩形D.直角三角形二、解答题:13.如图,已知矩形ABCD的两条对角线相交于O,∠AOD=120°,AB=4cm,求此矩形的面积.14.平行四边形ABCD,E是CD的中点,△ABE是等边三角形.求证:四边形ABCD是矩形.15.如图,矩形ABCD中,EF⊥EB,EF=EB,ABCD周长为22cm,CE=3cm.求:DE的长.16.如图,矩形ABCD中,DE=AB,CF⊥DE.求证:EF=EB.17.如图,矩形ABCD中,点E、F分别在AB、CD上,BF//DE,若AD=12cm,AB=7cm,且AE:EB=5:2,求阴影部分.18.如图,矩形ABCD中,对角线AC、BD相交于O,AE⊥BD,垂足为E,已知AB=3,AD=4,求△AEO的面积.19.矩形ABCD中,E是CD上一点,且AE=CE,F是AC上一点FH⊥AE于H,FG⊥CD于G.求证:FH+FG=AD.20.在平行四边形ABCD中,对角线AC、BD相交于O,EF过点O,且AF⊥BC.求证:四边形AFCE是矩形21.平行四边形ABCD中,对角线AC、BD相交于点O,点P是四边形外一点,且PA⊥PC,PB⊥PD,垂足为P.求证:四边形ABCD为矩形.参考答案1.相等;互相平分;相等;直角;轴对称;中心对称;2.12;3.48;4.22或26;5.10,5;6.(2,4),(3,4),(8,4);7.6.5;8.A 9.B 10.C 11.C 12.C 13.163cm 2;14.证明:∵AE =BE (等边△),∠DEA =∠EAB =60º=∠ABE =∠CEB (内错角相等). DE =CE (E 中点);∴△ADE ≌△BCE (两边夹一角相等),∠C =∠D (对应角相等), ∠C +∠D =180º(同旁内角互补),∠C =∠D =90º,同理∠A =∠B =90º;所以 平行四边形ABCD 是矩形.(四个角是直角).15.∵四边形ABCD 是矩形,∴AD=BC ,DC=AB ,∠D=∠C=90°,∵EF ⊥EB ,∴∠FEB=90°,∴∠DEF+∠CEB=90°,∠CEB+∠CBE=90°,∴∠DEF=∠CBE , 在△DEF 和△CBE 中,∠D =∠C ,∠DEF =∠CBE ,EF =EB ,∴△DEF ≌△CBE (AAS ), ∴DE=BC ,DF=CE=3cm ,∵矩形ABCD 的ABCD 周长为22cm ,∴2(BC+DE+EC )=22,∴DE+DE+3=11,∴DE=4.16.∵∠AED=∠FDC ,∠DAE=∠DFC=90°∴∠ADE=∠FCD又∵DE=AB=CD ∴△ADE ≌△FCD ∴DF=AE ∴EF=DE-DF=AB-AE=BE 。
人教版八年级数学下册--18_2_1 矩形(第2课时 矩形的判定)练习】

第十八章平行四边形18.2.1 矩形(第二课时矩形的判定)精选练习一.选择题(共10小题)1.四边形ABCD的对角线AC、BD互相平分,要使它成为矩形,可添加条件()A.AB=CD B.AC=BD C.AB∥CD D.AC⊥BD2.如图,要使▱ABCD为矩形,则可以添加的条件是()A.AC⊥BD B.AC=BD C.∠AOB=60°D.AB=BC3.已知▱ABCD,下列条件中,不能判定这个平行四边形为矩形的是()A.∠A=∠B B.∠A=∠C C.AC=BD D.AB⊥BC4.如图,在平行四边形ABCD中,对角线AC、BD相交于点O.下列条件不能判定平行四边形ABCD 为矩形的是()A.∠ABC=90°B.AC=BD C.AD=AB D.∠BAD=∠ADC5.如图,在▱ABCD中,对角线AC与BD相交于点O,对于下列条件:①∠1+∠3=90°;②BC2+CD2=AC2;③∠1=∠2;④AC⊥BD.能判定四边形ABCD是矩形的个数是()A.1个B.2个C.3个D.4个6.在四边形ABCD中,AD∥BC,下列选项中,不能判定四边形ABCD为矩形的是()A.AD=BC且AC=BD B.AD=BC且∠A=∠BC.AB=CD且∠A=∠C D.AB∥CD且AC=BD7.在平行四边形ABCD中,对角线AC、BD交于O点,下列条件中不能判定平行四边形ABCD是矩形的是()A.AC=BD B.AB⊥BCC.OA=OB=OC=OD D.AC⊥BD8.如图,平行四边形ABCD的对角线AC与BD相交于点O,添加一个条件使平行四边形ABCD为矩形的是()A.AD=AB B.AB⊥AD C.AB=AC D.CA⊥BD9.如图,在▱ABCD中,对角线AC、BD相交于点O,若再添加﹣个条件使▱ABCD成为矩形,则该条件不可以是()A.AC=BD B.AO=BO C.∠BAD=90°D.∠AOB=90°10.在数学活动课上,老师和同学们判断一个四边形门框是否为矩形,下面是某合作学习小组的4位同学拟定的方案,其中正确的是()A.测量对角线是否相互平分B.测量其中四边形的三个角都为直角C.测量一组对角是否都为直角D.测量两组对边是否分别相等二.填空题(共5小题)11.如图,D、E、F是△ABC各边中点,请在△ABC中添加一个条件:,使四边形DF AE是矩形.12.如图,请添加一个条件使平行四边形ABCD成为矩形,这个条件可以是(写出一种情况即可).13.如图,在△ABC中,AB=AC,点D在BC边上,DF∥AB,DE∥AC,则当∠B=°时,四边形AEDF是矩形.14.如图,已知直角三角形ABC,∠ABC=90°,小明想做一个以AB、BC为边的矩形,于是进行了以下操作:(1)测量得出AC的中点E;(2)连接BE并延长到D,使得ED=BE;(3)连接AD和DC.则四边形ABCD即为所求的矩形.理由是.15.如图,连接四边形ABCD各边中点,得到四边形EFGH,还要添加条件,才能保证四边形EFGH是矩形.三.解答题(共2小题)16.如图,在四边形ABCD中,∠B=∠C.点E、F、G分别在边AB、BC、CD上,AE=GF=GC.(1)求证:四边形AEFG是平行四边形;(2)当∠FGC与∠EFB满足怎样的关系时,四边形AEFG是矩形.请说明理由.17.如图,在△ABC中,AD是中线,E是AD的中点,过点A作AF∥BC交CE的延长线于点F,连接BF.(1)求证:四边形AFBD是平行四边形;(2)当△ABC满足什么条件时,四边形AFBD是矩形?并给出证明.第十八章平行四边形18.2.1 矩形(第二课时矩形的判定)精选练习答案一.选择题(共10小题)1.四边形ABCD的对角线AC、BD互相平分,要使它成为矩形,可添加条件()A.AB=CD B.AC=BD C.AB∥CD D.AC⊥BD【解答】解:需要添加的条件是AC=BD,理由如下:∵四边形ABCD的对角线AC、BD互相平分,∴四边形ABCD是平行四边形,∵AC=BD,∴平行四边形ABCD是矩形(对角线相等的平行四边形是矩形);故选:B.2.如图,要使▱ABCD为矩形,则可以添加的条件是()A.AC⊥BD B.AC=BD C.∠AOB=60°D.AB=BC【解答】解:因为有一个角是直角的平行四边形是矩形;对角线相等的平行四边形是矩形,故选:B.3.已知▱ABCD,下列条件中,不能判定这个平行四边形为矩形的是()A.∠A=∠B B.∠A=∠C C.AC=BD D.AB⊥BC【解答】解:A、∵四边形ABCD是平行四边形,∴AD∥BC,∴∠A+∠B=180°,∵∠A=∠B,∴∠A=∠B=90°,∴▱ABCD为矩形,故选项A不符合题意;B、∠A=∠C不能判定▱ABCD为矩形,故选项B符合题意;C、∵四边形ABCD是平行四边形,AC=BD,∴▱ABCD是矩形,故选项C不符合题意;D、∵AB⊥BC,∴∠B=90°,∴▱ABCD为矩形,故选项D不符合题意;故选:B.4.如图,在平行四边形ABCD中,对角线AC、BD相交于点O.下列条件不能判定平行四边形ABCD 为矩形的是()A.∠ABC=90°B.AC=BD C.AD=AB D.∠BAD=∠ADC【解答】解:A.根据有一个角是直角的平行四边形是矩形能判定平行四边形ABCD为矩形,故此选项不符合题意;B.根据对角线相等的平行四边形是矩形能判定平行四边形ABCD为矩形,故此选项不符合题意;C.根据邻边相等的平行四边形是菱形能判定平行四边形ABCD为菱形,不能判定平行四边形ABCD 为矩形,故此选项符合题意;D.∵平行四边形ABCD中,AB∥CD,∴∠BAD+∠ADC=180°,又∵∠BAD=∠ADC,∴∠BAD=∠ADC=90°,根据有一个角是直角的平行四边形是矩形能判定平行四边形ABCD为矩形,故此选项不符合题意.故选:C.5.如图,在▱ABCD中,对角线AC与BD相交于点O,对于下列条件:①∠1+∠3=90°;②BC2+CD2=AC2;③∠1=∠2;④AC⊥BD.能判定四边形ABCD是矩形的个数是()A.1个B.2个C.3个D.4个【解答】解:①∵∠1+∠3=90°,∴∠ABC=90°,∴▱ABCD是矩形,故①正确;②∵四边形ABCD是平行四边形,∴AB=CD,∵BC2+CD2=AC2,∴BC2+AB2=AC2,∴∠ABC=90°,∴▱ABCD是矩形,故②正确;③∵四边形ABCD是平行四边形,∴OA=OC=AC,OB=OD=BD,∵∠1=∠2,∴OA=OB,∴AC=BD,∴▱ABCD是矩形,故③正确;④∵四边形ABCD是平行四边形,AC⊥BD,∴▱ABCD是菱形,故④错误;能判定四边形ABCD是矩形的个数有3个,故选:C.6.在四边形ABCD中,AD∥BC,下列选项中,不能判定四边形ABCD为矩形的是()A.AD=BC且AC=BD B.AD=BC且∠A=∠BC.AB=CD且∠A=∠C D.AB∥CD且AC=BD【解答】解:A.∵AD∥BC,AD=BC,∴四边形ABCD是平行四边形,∵AC=BD,∴平行四边形ABCD是矩形,故选项A不符合题意;B.∵AD∥BC,AD=BC,∴四边形ABCD是平行四边形,∴∠A+∠B=180°,∵∠A=∠B,∴∠A=∠B=90°,∴平行四边形ABCD是矩形,故选项B不符合题意;C.∵AD∥BC,∴∠A+∠B=∠C+∠D=180°,∵∠A=∠C,∴∠B=∠D,∴四边形ABCD是平行四边形,∴AB=CD,∴不能判定四边形ABCD为矩形,故选项C符合题意;D、∵AD∥BC,AB∥CD,∴四边形ABCD是平行四边形,∵AC=BD,∴四边形ABCD是矩形,故选项D不符合题意;故选:C.7.在平行四边形ABCD中,对角线AC、BD交于O点,下列条件中不能判定平行四边形ABCD是矩形的是()A.AC=BD B.AB⊥BCC.OA=OB=OC=OD D.AC⊥BD【解答】解:A.∵四边形ABCD是平行四边形,又∵AC=BD,∴平行四边形ABCD是矩形,故本题选项不符合题意;B.∵AB⊥BC,∴∠ABC=90°,∵四边形ABCD是平行四边形,∴平行四边形ABCD是矩形,故本选项不符合题意;C.∵AO=OB=OC=OD,∵AC=BD,∵四边形ABCD是平行四边形,∴平行四边形ABCD是矩形,故本题选项不符合题意;D.∵四边形ABCD是平行四边形,又∵AC⊥BD,∴平行四边形ABCD是菱形,不是矩形,故本题选项符合题意;故选:D.8.如图,平行四边形ABCD的对角线AC与BD相交于点O,添加一个条件使平行四边形ABCD为矩形的是()A.AD=AB B.AB⊥AD C.AB=AC D.CA⊥BD【解答】解:A、∵平行四边形ABCD中,AD=AB,∴平行四边形ABCD是菱形,故选项A不符合题意;B、∵AB⊥AD,∴∠BAD=90°,∴平行四边形ABCD是矩形,故选项B符合题意;C、平行四边形ABCD中,AB=AC,不能判定平行四边形ABCD是矩形,故选项C不符合题意;D、∵平行四边形ABCD中,CA⊥BD,∴平行四边形ABCD是菱形,故选项D不符合题意;故选:B.9.如图,在▱ABCD中,对角线AC、BD相交于点O,若再添加﹣个条件使▱ABCD成为矩形,则该条件不可以是()A.AC=BD B.AO=BO C.∠BAD=90°D.∠AOB=90°【解答】解:A、∵四边形ABCD是平行四边形,AC=BD,∴平行四边形ABCD是矩形,故选项A不符合题意;B、∵四边形ABCD是平行四边形,∴AO=CO,BO=DO,∵AO=BO,∴AC=BD,∴平行四边形ABCD是矩形,故选项B不符合题意;C、∵四边形ABCD是平行四边形,∠BAD=90°,∴平行四边形ABCD是矩形,故选项C不符合题意;D、∵∠AOB=90°,∴AC⊥BD,∵四边形ABCD是平行四边形,∴平行四边形ABCD是菱形,故选项D不符合题意;故选:D.10.在数学活动课上,老师和同学们判断一个四边形门框是否为矩形,下面是某合作学习小组的4位同学拟定的方案,其中正确的是()A.测量对角线是否相互平分B.测量其中四边形的三个角都为直角C.测量一组对角是否都为直角D.测量两组对边是否分别相等【解答】解:A、对角线是否相互平分,能判定平行四边形,故选项A不符合题意;B、其中四边形中三个角都为直角,能判定矩形,故选项B符合题意;C、一组对角是否都为直角,不能判定形状,故选项C不符合题意;D、两组对边是否分别相等,能判定平行四边形,故选项D不符合题意;故选:B.二.填空题(共5小题)11.如图,D、E、F是△ABC各边中点,请在△ABC中添加一个条件:∠A=90°(答案不唯一),使四边形DF AE是矩形.【解答】解:添加条件:∠A=90°;理由如下:∵E、D、F分别是AB、BC、AC的中点,∴DE是△ABC的中位线,AE=AB,AF=AC,∴DE∥AC,DE=AC,∴DE=AF,∴四边形AEDF是平行四边形,∵∠A=90°,∴平行四边形AEDF是矩形,故答案为:∠A=90°(答案不唯一).12.如图,请添加一个条件使平行四边形ABCD成为矩形,这个条件可以是AC=BD或∠ABC=90°(写出一种情况即可).【解答】解:若使平行四边形ABCD变为矩形,可添加的条件是:AC=BD;(对角线相等的平行四边形是矩形)∠ABC=90°.(有一个角是直角的平行四边形是矩形)故答案为:AC=BD或∠ABC=90°.13.如图,在△ABC中,AB=AC,点D在BC边上,DF∥AB,DE∥AC,则当∠B=45°时,【解答】解:当∠B=45°时,四边形AEDF是矩形.∵DF∥AB,DE∥AC,∴四边形AEDF是平行四边形,∵AB=AC,∴∠B=∠C=45°,∴∠A=90°,∴四边形AEDF是矩形.故答案为45.14.如图,已知直角三角形ABC,∠ABC=90°,小明想做一个以AB、BC为边的矩形,于是进行了以下操作:(1)测量得出AC的中点E;(2)连接BE并延长到D,使得ED=BE;(3)连接AD和DC.则四边形ABCD即为所求的矩形.理由是有一个角是直角的平行四边形为矩形.【解答】解:∵E是AC的中点,∴AE=CE,∵ED=BE,∴四边形ABCD是平行四边形,又∵∠ABC=90°,∴平行四边形ABCD为矩形,故答案为:有一个角是直角的平行四边形为矩形.15.如图,连接四边形ABCD各边中点,得到四边形EFGH,还要添加AC⊥BD条件,才能保证【解答】解:∵G、H、E分别是BC、CD、AD的中点,∴HG∥BD,EH∥AC,∴∠EHG=∠1,∠1=∠2,∴∠2=∠EHG,∵四边形EFGH是矩形,∴∠EHG=90°,∴∠2=90°,∴AC⊥BD.故还要添加AC⊥BD,才能保证四边形EFGH是矩形.三.解答题(共2小题)16.如图,在四边形ABCD中,∠B=∠C.点E、F、G分别在边AB、BC、CD上,AE=GF=GC.(1)求证:四边形AEFG是平行四边形;(2)当∠FGC与∠EFB满足怎样的关系时,四边形AEFG是矩形.请说明理由.【解答】(1)证明:在梯形ABCD中,AB=DC,∠B=∠C,∵GF=GC,∴∠C=∠GFC,∠B=∠GFC,∴AB∥GF,即AE∥GF,∵AE=GF,∴四边形AEFG是平行四边形.(2)解:当∠FGC=2∠EFB时,四边形AEFG是矩形,理由:∵∠FGC+∠GFC+∠C=180o,∠GFC=∠C,∠FGC=2∠EFB,∴2∠GFC+2∠EFB=180°,∴∠BFE+∠GFC=90°.∴∠EFG=90°.∵四边形AEFG是平行四边形,∴四边形AEFG是矩形.17.如图,在△ABC中,AD是中线,E是AD的中点,过点A作AF∥BC交CE的延长线于点F,连接BF.(1)求证:四边形AFBD是平行四边形;(2)当△ABC满足什么条件时,四边形AFBD是矩形?并给出证明.【解答】解:(1)证明:∵E为AD的中点,D为BC中点,∴AE=DE,BD=CD,∵AF∥CD,∴∠AFE=∠DCE,∠F AE=∠CDE,在△AFE和△DCE中,∠AFE=∠DCE,∠F AE=∠CDE,AE=DE∴△AFE≌△DCE(AAS),∴AF=CD,∴AF=BD,∵AF∥BD,∴四边形AFBD为平行四边形;(2)当△ABC满足条件AB=AC时,四边形AFBD是矩形,证明:∵AB=AC,D为BC中点,即AD为BC边上的中线,∴AD⊥BC,即∠ADB=90°,∵四边形AFBD为平行四边形,∴四边形AFBD为矩形.。
人教版八年级下册数学 矩形 同步检测

18.2.1矩形同步检测一、选择题1.如图,矩形ABCD的两条对角线相交于点O,∠AOD=60°,AD =4,则AC的长是( )A. 4B. 8C. 43D. 832.如图,矩形纸片ABCD中,AB=4,BC=8,将纸片折叠,使点C 与点A重合,折痕为EF,点D的对应点为G,连接DG,则图中阴影部分面积是()A. 5B. 3C. 365D. 1853.矩形具有而平行四边形不一定具有的性质是()A. 对边平行B. 对边相等C. 对角线互相平分D. 对角线相等4.如图所示,矩形ABCD的对角线交于O,AE⊥BD于E,∠1:∠2=2:1,则∠1的度数为().A. 22.5°B. 45°C. 30°D. 60°5.E为矩形ABCD的边CD上的一点,AB=AE=4,BC=2,则∠BEC 是().A. 15°B. 30°C. 60°D. 75°6.一个矩形和一个平行四边形的边分别相等,若矩形面积为这个平行四边形的面积的2倍,则平行四边形的锐角的度数为().A. 15°B. 30°C. 45°D. 60°7.已知E、F分别是矩形ABCD的对边BC和AD上的点,且BE=1BC,3 AD,连结AC、EF,那么().AF=23A. AC平分EF,但EF不平分ACB. AC与EF互相平分C. EF平分AC,但AC不平分EFD. AC与EF不会互相平分8.如图,在△ABC中,∠ACB=90°,CD⊥AB,垂足为点D,点E 是AB的中点,CD=DE=a,则AB的长为( )A. 2aB. 22aC. 3aD. 43a39.如图,在△ABC中,∠BAC=90°,AD是BC边上的高,E、F分别是AB、AC边的中点,若AB=8,AC=6,则△DEF的周长为()A. 12B. 13C. 14D. 1510.如图,在△ABC中,∠ACB=90°, ∠ABC=60°, BD平分∠ABC ,P点是BD的中点,若AD=6, 则CP的长为( )A. 3.5B. 3C. 4D. 4.5二、填空题11.如图,△ABC中,AD是高,E、F分别是AB、AC的中点.若AB=8,AC=6,则四边形AEDF的周长为.12.如图,90∆中,5,6∆的顶∠=︒,已知ABCMON===, ABCAC BC AB点,A B分别在边,OM ON上,当点B在边ON上运动时,点A随之在边OM上运动,ABC∆的形状保持不变,在运动过程中,点C到点O的最大距离为____________.13.如图,将长方形纸片ABCD折叠,折痕为EF,若AB=2,BC=3,则阴影部分的周长为____________.14.如图,矩形ABCD中,对角线AC的中点为O,过O作EF⊥AC,分别交AB、DC于E、F,若AB=4,BC=2,那么线段EF的长为_____.15.如图,矩形ABCD内有一点E,连接AE,DE,CE,使AD=ED=EC,若∠ADE=20°,则∠AEC=____.16.如图,矩形ABCD中,对角线AC、BD交于点O,点E是BC 上一点,且AB=BE,∠1=15°,则∠2=________°.三、解答题17.已知:如图,在△ABC中,AD BC⊥,⊥,垂足为点D,BE AC垂足为点E ,M 为AB 边的中点,连结ME 、MD 、ED .(1)猜想△MED 的形状,并说明理由.(2)若4AB =,30DBE ∠=︒,求△MED 的面积.18.如图,已知矩形ABCD 的周长为20,AB =4,点E 在BC 上,点F 在CD 上,且AE ⊥EF ,AE =EF .求CF 的长.19.如图,在矩形ABCD 中,F 是BC 边上的一点,AF 的延长线交DC 的延长线于G ,DE ⊥AG 于E ,且DE=DC ,根据上述条件,请你在图中找出一对全等三角形,并证明你的结论.20.如图,在矩形ABCD中,连接对角线AC,BD,延长BC至点E,使BC=CE,连接DE.求证:DE=AC.21.如图,在矩形ABCD中,对角线AC、BD相交于点O,点E、F 分别是AO、AD的中点,若AB=60cm,BC=80cm,则△AEF的周长是多少?22.如图,把矩形纸片ABCD沿EF折叠,使点B落在边AD上的点B′处,点A落在点A′处;(1)求证:B′E=BF;(2)设AE=a,AB=b,BF=C,试猜想a,b,c之间的一种关系,并给予证明.参考答案1.B【解析】因为∠AOD=60°,AD=4,,矩形ABCD,AC=BD, ,∠BDA=60°,所以AO=DO=AD所以AC=8.故选B.2.D【解析】过点G作GH⊥AD于点H,由题意知,AF=FC,AB=CD=AG=4,BC=AD=8,在Rt△ABF中,由勾股定理知AB2+BF2=AF2,即42+(8﹣AF)2=AF2,解得AF=5,∵∠BAF+∠FAE=∠FAE+∠EAG=90°,∴∠BAF=∠EAG,∵∠B=∠AGE=90°,AB=AG,∴△BAF≌△GAE,∴AE=AF=5,ED=GE=3,∵S△GAE=12AG•GE=12AE•GH∴GH=125,∴S△GED= 12ED•GH= 12×3×125= 185,故选D.3.D【解析】矩形的对角线相等,而平行四边形的对角线不一定相等.故选D.4.B【解析】∵四边形ABCD为矩形,AE⊥BD,∴∠2+∠ABD=∠ADB+∠ABD =∠EAD+∠ADB=90°,∴∠ADB=∠2,∠1+∠OAD+∠ADB=90°,∵四边形ABCD是矩形,∴AO=OD,∴∠OAD=∠ADB=∠2,∴∠1+2∠2=90°,∵∠1:∠2=2:1,∴2∠2=∠1,∴2∠1=90°,∴∠1=45°,故选B.5.D【解析】∵在Rt△ADE中,AD=2,AE=4,∴∠AED=30°,∵AB∥CD,∴∠EAB=∠AED=30°,∵AB=AE,∴∠AEB=75°,∴∠BEC=180°-∠AED-∠AEB=180°-30°-75°=75°.故选D.【点睛】本题考查了矩形的性质,含30度角的直角三角形等,熟记矩形的性质和含30度角的直角三角形的性质是解题的关键.6.B【解析】如图,矩形ABCD与平行四边形BCFG中,BG=AB,过点G作GH⊥BC,垂足为H,∵S矩形ABCD=BC·AB=2S平行四边形BCFG=2BC·GH,∴BG=2GH,∵△BGH是Rt△,∠BHG=90°,∴∠GBH=30°,故选B.【点睛】本题考查了矩形的面积、平行四边形的面积以及直角三角形中,30度角所对直角边等于斜边的运用,根据已知条件推导出平行四边形的高与一边的关系是解题的关键.7.B【解析】∵四边形ABCD 是矩形,∴AD=BC ,AD//BC ,∴∠DAC=∠ACB ,∵BE=13BC ,AF=23AD ,∴AF=CE , 又∵∠AOF=∠COE ,∴△AOF ≌△COE ,∴AO=CO ,FO=EO ,即AC 与EF 互相平分,故选B.8.B【解析】CD ⊥AB ,CD =DE =a,所以222a a a +=点E 是AB 的中点,CE=1,2AB 所以2故选B.9.A【解析】试题解析:在ABC 中,由勾股定理可得:22226810.BC AB AC +=+= AD 是BC 边上的高,E 、F 分别是AB 、AC 边的中点,则:1115,4, 3.222EF BC DE AB DF AC ======DEF 的周长为:45312.DE EF DF ++=++= 点睛:直角三角形的性质:直角三角形斜边的中线等于斜边的一半.10.B【解析】试题分析:∵∠ACB =90°,∠ABC =60°,∴∠A =30°,∵BD 平分∠ABC ,∴∠ABD =12∠ABC =30°,∴∠A =∠ABD ,∴BD =AD =6,∵在Rt △BCD 中,P 点是BD 的中点,∴CP =12BD =3.故选B .11.14【解析】试题解析:∵AD 是高,90ADB ADC ∴∠=∠=,∵E 、F 分别是AB 、AC 的中点,11,22ED EB AB DF FC AC ∴====, ∵AB=8,AC=6,∴AE+ED=8,AF+DF=6,∴四边形AEDF 的周长为8+6=14,故答案为:14.12.7【解析】试题解析:如图,取AB 的中点D ,连接CD .∵AC=BC=5,AB=6.∵点D是AB边中点,∴BD=12AB=3,∴CD=2222=53BC BD--=4;连接OD,OC,有OC≤OD+DC,当O、D、C共线时,OC有最大值,最大值是OD+CD,又∵△AOB为直角三角形,D为斜边AB的中点,∴OD=12AB=3,∴OD+CD=3+4=7,即OC=7.13.10【解析】∵AE=ME,AB=MN,BF=NF,∴ME+DE+MN+CD+CF+NF=AE+DE+AB+CD+CF+BF=AD+AB+CD+BC=2+3+2+3=10.点睛:本题主要考查了折叠问题以及矩形的性质的运用,解题时注意:折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.14.5【解析】如图,连接CE ,∵点O 是矩形ABCD 对角线AC 的中点,EF ⊥AC ,∴AE=CE ,AO=12AC=222242255AB BC +=+==.设AE=x ,则CE=x ,BE=4x -,在Rt △BCE 中,由勾股定理可得:CE2=BE2+BC2,即()22242x x =-+, 解得: 2.5x =,即AE=2.5,∴在Rt △AOE 中,OE=()222252.552AE AO -=-=, ∵点O 是矩形ABCD 对角线AC 的中点,∴点O 是矩形的对称中心,∴EF=2OE=5.点睛:由矩形是关于对角线中点成中心对称的可得:EF=2OE ,AO=12AC ,从而把求EF 的长转化为求OE 的长,进一步转化为求AE 的长,连接CE ,由已知得到CE=AE ,就可把问题转化到Rt △CEB 中求CE 的长,这样利用勾股定理建立方程即可解得AE ,从而求得EF.15.120°(180°【解析】在△ADE中,∵∠ADE=20°,AD=ED,∴∠AED=12-20°)=80°,∵四边形ABCD是矩形,∠ADE=20°,∴∠EDC=90°-20°=70°,在△DEC中,∵ED=EC,∴∠DEC=180°-70°×2=40°,∴∠AEC=∠AED+∠DEC=80°+40°=120.16.30【解析】∵四边形ABCD是矩形,∴∠ABC=∠BAD=90°,OB=OD,OA=OC,AC=BD,∴OB=OC,OB=OA,∴∠OCB=∠OBC,∵AE平分∠BAD,∴∠BAE=∠DAE=45°,∴∠AEB=180°−90°−45°=45°,∵∠1=15°,∴∠OCB=∠AEB−∠EAC=45°−15°=30°,∴∠OBC=∠OCB=30°,∴∠AOB=30°+30°=60°,∵OA=OB,∴△AOB是等边三角形,∴AB=OB,∵∠BAE=∠AEB=45°,∴AB=BE,∴OB=BE,∴∠OEB=∠EOB,∵∠OBE=30°,∠OBE+∠OEB+∠BEO=180°,∴∠OEB=75°,∵∠AEB=45°,∴∠2=∠OEB−∠AEB=30°,故答案为:30.点睛:本题考查了矩形的性质,等边三角形的性质,等腰三角形的性质的综合应用,能求出∠OEB和∠AEB的度数是解此题的关键. 17.(1)等腰三角形;(2【解析】试题分析:(1)由于AD⊥BC,BE⊥AC,所以△ADB和△ABE是直角三角形,又因为M为AB边的中点,所以ME=MD=1AB,2所以△MED为等腰三角形;(2)由条件知∠EMD=2∠DAC=60°,从而可得等腰三角形DME是边长为2的等边三角形可得到问题答案.试题解析:(1)猜测△MED 为等腰三角形,理由如下.由题意可得,DM 是RT △ABD 斜边上的中线, ∴1DM AB BM 2==,EM 是Rt ABE 斜边上的中线, ∴1EM AB BM 2==,∴DM EM =,∴MED 为等腰三角形.(2)由(1)中可得:DM BM =,EM BM =,∴MBD MDB ∠∠=,MBE MEB ∠∠=,∴AMD MBD MDB 2MDB ∠∠∠∠=+=,AME MBE MEB 2MBE ∠∠∠∠=+=, ∴()EMB AMD AME 2MBD MBE 2DBE ∠∠∠∠∠∠=-=-=,∴在等腰MED 中,EMD 2DBE 60∠∠==︒,∴MED 是等边三角形,边长为AB DM BM 22===, ∴DEM S =点睛:本题考查了直角三角形斜边上的中线等于斜边的一半的性质、等边三角形的判定和性质和等边三角形的面积计算,题目综合性很好.18.2cm【解析】试题分析:根据已知条件易证△ABE ≌△ECF ,根据全等三角形的性质可得CE=AB=4cm ,根据矩形的周长为20cm 可得2(4+4+BE )=20,B E=2cm ,再由全等三角形的性质可得CF=BE=2cm.试题解析:∵AE⊥EF,∴∠AFE=90°,∴∠AEB+∠BAE =90°,而∠AEB+∠CEF=90°,∴∠BAE=∠CEF,又∠ABE=∠ECF=90°,AE=EF,∴Rt△ABE≌Rt△ECF,∴CE=AB=4cm又∵矩形ABCD周长为20cm∴2(4+4+BE)=20∴BE=2cm∴CF=BE=2cm19.详见解析.【解析】由已知条件易得:∠DEA=∠ABF=90°,∠DAE=∠AFB,DE=DC=AB,从而可得:△ABF≌△DEA.试题解析:图中:△ABF≌△DEA,证明如下:∵四边形ABCD为矩形,∴∠B=90°,AB=DC.∵DE⊥AG于E,DE=DC,∴∠AED=90°=∠B,AB=DE.∵四边形ABCD为矩形,∴AD∥CB.∴∠DAE=∠AFB.,∴△ABF≌△DEA(AAS).20.证明见解析【解析】试题分析:证明CD是线段BE的垂直平分线,得到DB=DE,又因为DB=AC,则得证.试题解析:∵四边形ABCD是矩形,∴AC=BD,∠BCD=90°,∵BC=CE,∴DC是BE的中垂线,∴BD=DE,∴DE=AC.21.△AEF的周长是90cm.【解析】试题分析:先根据勾股定理求出AC的长,由矩形的性质可知:矩形的两条对角线相等,可得BD=AC,即可得OD的长,在△AOD中,根据E、F分别是AO、AD在中点,分别求出AE、EF、AF的长,即可得△AEF的周长.试题解析:在Rt△ABC中,=100cm,在矩形ABCD中BD=AC=100cm,AD=BC=80cm,∵点E、F分别是AO、AD的中点,∴EF是△AOD的中位线,∴EF=12OD=14BD=25,AF=12AD=12BC=40cm,AE=12AO=14AC=25,∴△AEF的周长=AE+AF+EF=90cm.22.(1)证明见解析;(2)a,b,c三者存在的关系是a+b>c,理由见解析.【解析】(1)首先根据题意得B′F=BF,∠B′FE=∠BFE,接着根据平行线的性质和等腰三角形的判定即可证明B′E=BF;(2)解答此类题目时要仔细读题,根据三角形三边关系求解分类讨论解答,要提高全等三角形的判定结合勾股定理解答.证明:(1)由题意得B′F=BF,∠B′FE=∠BFE,在矩形ABCD中,AD ∥BC,∴∠B′EF=∠BFE,∴∠B′FE=∠B'EF,∴B′F=BE,∴B′E=BF;解:(2)答:a,b,c三者关系不唯一,有两种可能情况:(ⅰ)a,b,c三者存在的关系是a2+b2=c2.证明:连接BE,则BE=B′E,由(1)知B′E=BF=c,∴BE=c.在△ABE中,∠A=90°,∴AE2+AB2=BE2,∵AE=a,AB=b,∴a2+b2=c2;(ⅱ)a,b,c三者存在的关系是a+b>c.证明:连接BE,则BE=B′E.由(1)知B′E=BF=c,∴BE=c,在△ABE中,AE+AB>BE,∴a+b>c.“点睛”此题以证明和探究结论形式来考查矩形的翻折、等角对等边、三角形全等、勾股定理等知识.第一,较好考查学生表述数学推理和论证能力,第(1)问重点考查了学生逻辑推理的能力,主要利用等角对等边、翻折等知识来证明;第二,试题呈现显示了浓郁的探索过程,试题设计的起点低,图形也很直观,也可通过自已动手操作,寻找几何元素之间的对应关系,形成较为常规的方法解决问题,第(2)问既考查了学生对勾股定理掌握的程度又考查学生的数学猜想和探索能力,这对于培养学生创新意识和创新精神十分有益;第三,解题策略多样化在本题中得到了充分的体现.。
2020-2021学年人教版八年级下册数学 18.2.1矩形 同步练习 (含解析)

18.2.1矩形同步练习一.选择题1.如图,要使平行四边形ABCD成为矩形,需要添加的条件是()A.∠A+∠B=180°B.∠B+∠C=180°C.∠A=∠B D.∠B=∠D2.如图,矩形ABCD的长BC=20cm,宽AB=15cm,∠ABC的平分线BE交AD于点E,则AE、ED的长分别为()A.15cm和5cm B.10cm和5cm C.9cm和6cm D.8cm和7cm3.取一张长方形纸片,过长方形的任意一个顶点将纸片折叠(只折一次),那么折痕和该顶点所在的长方形的两边所成角的关系是()A.互余B.互补C.相等D.不确定4.如图,在矩形ABCD中,AB=2,对角线AC与BD相交于点O,AE⊥BD,垂足为E.若BE =EO,则AD的长是()A.6B.2C.3D.25.如图,在矩形ABCD中,对角线BD的垂直平分线MN交AD于点M,交BC于点N,连接BM、DN.若AB=4,AD=8,则MD的长为()A.3B.4C.5D.66.如图,E、F分别是矩形ABCD边上的两点,设∠ADE=α,∠EDF=β,∠FDC=γ,若∠AED =α+β,下列结论正确的是()A.α=βB.α=γC.α+β+2γ=90°D.2α+γ=90°7.如图,矩形ABCD的对角线AC与BD交于点O,过点O作BD的垂线分别交AD、BC于E、F两点.若AC=2,∠DAO=30°,则FC的长度为()A.1B.2C.D.8.如图,把一块含有30°角的直角三角板ABC的直角顶点放在矩形桌面CDEF的一个顶点C 处,桌面的另一个顶点F与三角板斜边相交于点F,如果∠1=50°,那么∠AFE的度数为()A.10°B.20°C.30°D.40°9.如图,在矩形纸片ABCD中,AB=3,BC=2,沿对角线AC剪开(如图①);固定△ADC,把△ABC沿AD方向平移(如图②),当两个三角形重叠部分的面积最大时,移动的距离AA′等于()A.1B.1.5C.2D.0.8或1.210.如图,在矩形ABCD中,AD=AB,∠BAD的平分线交BC于点E,DH⊥AE于点H,连接BH并延长交CD于点F,连接DE交BF于点O,下列结论:①AE=AD;②∠AED=∠CED;③BH=HF;④CF=DF;⑤BC﹣CF=2HE,其中正确的有()A.5个B.4个C.3个D.2个二.填空题11.如图在矩形ABCD对角线AC,BD相交于点O,若∠ACB=30°,AB=2,则BD的长为.12.如图,矩形ABCD中,AD=2,AB=3,过点A、C作相距为2的平行线段AE,CF,分别交CD,AB于点E,F,则DE的长是.13.如图,在矩形ABCD中,AB=8,AD=6,点E,F都在CD上,点P在AD上,连接PE,若EF=PE,∠FBP=∠ABP,2∠APB+∠DPE=180°,则线段AP的长为.14.如图,在矩形ABCD中,点E、F分别在边AD、AB上,△CEF为等腰直角三角形,CE=EF,∠CEF=90°,∠BAD的平分线交CF于点H,连接BH.若BH=,AF=,则△ABH的面积为.15.如图,矩形ABCD,O为对角线交点,以AO,AB为邻边作平行四边形ABC1O,AC1交OB 于点O1;以AO1,AB为邻边作平行四边形ABC2O1…,若S矩形ABCD=a,则=.三.解答题16.如图,点E在矩形ABCD的边BC上,延长EB到点F,使BF=CE,连接AF.求证:AD =EF.17.如图,在平行四边形ABCD中,P是AB上一点(不与点A,B重合),CP=CD,过点P作PQ⊥CP,交AD于点Q,连接CQ,∠BPC=∠AQP.(1)求证:四边形ABCD是矩形;(2)当AP=3,AD=9时,求AQ和CQ的长.参考答案一.选择题1.解:A、当∠A+∠B=180°时,不可判断平行四边形ABCD成为矩形;B、当∠B+∠C=180°时,不可判断平行四边形ABCD成为矩形;C、当∠A=∠B时,∠A=∠B=90°,可判定平行四边形ABCD是矩形;D、当∠B=∠D时,不可判断平行四边形ABCD是矩形;故选:C.2.解:∵四边形ABCD是矩形,∴AD∥BC,AD=BC=20cm,∴∠AEB=∠EBC,∵BE平分∠ABC,∴∠ABE=∠EBC=45°,∴∠AEB=∠ABE,∴AB=AE=15cm,∴DE=AD﹣AE=5cm,故选:A.3.解:如图所示:∵四边形ABCD是长方形,∴∠BAD=90°,∵AE是任意一条折痕,∴∠BAE+∠DAE=90°,即折痕和该顶点所在的长方形的两边所成角的关系是互余;故选:A.4.解:∵四边形ABCD是矩形,∴OB=OD,OA=OC,AC=BD,∴OA=OB,∵BE=EO,AE⊥BD,∴AB=AO,∴OA=AB=OB,即△OAB是等边三角形,∴∠ABD=60°,∴∠ADE=90°﹣∠ABD=30°,∴AD=AB=2,故选:B.5.解:∵对角线BD的垂直平分线MN交AD于点M,交BC于点N,∴MB=MD,设MD长为x,则MB=DM=x,在Rt△AMB中,BM2=AM2+AB2即x2=(8﹣x)2+42,解得:x=5,∴MD长为5.故选:C.6.解:∵四边形ABCD是矩形,∴∠A=∠ADC=90°,∵∠ADE=α,∠EDF=β,∠FDC=γ,∴α+β+γ=90°,∵∠AED+α=90°,∠AED=α+β,∴2α+β=90°,∴α+β+γ=2α+β,∴α=γ,故选:B.7.解:∵四边形ABCD是矩形,∴OA=OD,∴∠OAD=∠ODA=30°,∴∠AOD=120°,∵EF⊥BD,∠AEO=120°,∴∠EDO=30°,∠DEO=60°,∵四边形ABCD是矩形,∴∠OBF=∠OCF=30°,∠BFO=60°,∴∠FOC=60°﹣30°=30°,∴OF=CF,又∵Rt△BOF中,BO=BD=AC=,∴OF=tan30°×BO=1,∴CF=1,故选:A.8.解:∵四边形CDEF为矩形,∴EF∥DC,∴∠AGE=∠1=50°,∵∠AGE为△AGF的外角,且∠A=30°,∴∠AFE=∠AGE﹣∠A=20°.故选:B.9.解:如图,设A′B′交AC于点E,tan∠DAC==,设AA′=x,A′D=2﹣x,∵AD=2,DC=3,∴=,∴A′E=x,∵两个三角形重叠部分的面积是S=AE×A′D=x(2﹣x)=﹣(x﹣1)2+,解当x=1时,阴影部分的面积最大,AA′=1,故选:A.10.解:①设AB=a,则AD=a,∵AE平分∠BAD,∴∠BAE=45°,∴BA=BE.∴在Rt△ABE中,AE=a,∴AE=BE.①正确;②∵DH⊥AH,∠DAE=45°,AD=a,∴DH=AH=a.∴DH=DC.根据到角两边距离相等的点在角的平分线上定理可知DE平分∠AEC,即②∠AED=∠CED 正确;③∵AH=AB=a,∴∠ABH=∠AHB.∵AB∥CD,∴∠ABF+∠DFB=180°.又∠AHB+∠BHE=180°,∴∠BHE=∠HFD.∠HEB=∠FDH=45°,又BE=DH=a,∴△BHE≌△HFD(AAS),∴BH=HF,③正确;④由△BHE≌△HFD得到HE=DF,HE=AE﹣AH=,则CF=a﹣()=2a﹣,∴,即CF=DF,∴④错误;⑤BC=a,CF=2a﹣,HE=,∴BC﹣CF=2HE,∴⑤正确;综上所述,正确的是①②③⑤共4个.故选:B.二.填空题11.解:在矩形ABCD中,∠ABC=90°,∵∠ACB=30°,AB=2,∴AC=2AB=2×2=4,∵四边形ABCD是矩形,∴BD=AC=4.故答案为:4.12.解:∵四边形ABCD是矩形,∴AB∥CD,∴∠F AH=∠AED,∵∠ADE=∠AHF=∠DAF=90°,AD=2,FH=2,∴AD=FH,∴△ADE≌△F AH(AAS),∴AF=AE,∵AE∥CF,AF∥EC,∴四边形AECF是平行四边形,∵AF=AE,∴四边形AECF是菱形,设DE=x,则BF=x,CE=CF=3﹣x,在Rt△BCF中,(3﹣x)2=x2+22,解得x=;故答案为:.13.解:分别延长PE、BF,交于点G,∵四边形ABCD是矩形,AB=8,AD=6,∴∠A=∠C=∠D=90°,BC=AD=6,AB=CD=8,∵2∠APB+∠DPE=180°,∴∠APB=∠GPB.在△P AB和△PGB中,,∴△P AB≌△PGB(ASA),∴PG=P A,∠A=∠G=90°,在△DPG和△EFG中,,∴△DPE≌△GFE(AAS),∴DP=DG,∴PE+GE=DE+EF,即PG=DF,∴PG=DF=P A,即CF=8﹣DF=8﹣AP,∴GF=DP=AD﹣AP,即BF=8﹣GF=8﹣(6﹣AP)=2+AP,∵∠C=90°,∴BC2+CF2=BF2,即62+(8﹣AP)2=(2+AP)2,∴AP=.故答案为:.14.解:如图,连接EH,延长AH交DC的延长线于N,∵∠AEF+∠AFE=90°,∠AEF+∠DEC=90°,∴∠AFE=∠DEC,在△AEF和△DCE中,,∴△AEF≌△DCE(SAS),∴AE=CD,DE=AF=,∴AE=CD=AB,∵AH平分∠BAD,∴∠BAH=∠DAH=45°,∵∠ADC=90°,∴∠DAN=∠N=45°,∴AD=DN,∴AF=CN,在△AFH和△NCH中,,∴△AFH≌△NCH(AAS),∴FH=HC,又∵∠ABC=90°,∴BH=FH=HC=,∴CF=2,设BF=x,则AB=+x,∴AD=2+x=BC,∵CF2=BF2+BC2,∴40=x2+(2+x)2,∴x=2,(负值舍去),∴BF=2,BC=4,∴BF=2AF,∴S△AFH=S△BFH,∵S△BFC=×BF×BC=×2×4=8,∴S△BFH=4,S△AFH=2,∴S△ABH=2+4=6,故答案为:6.15.解:∵四边形ABCD是矩形,四边形ABC1O是平行四边形,∴S△ABO=S矩形ABCD,S△ABO=S,∴S=S矩形ABCD=,同理可得:平行四边形ABC2O1的面积=,平行四边形ABC3O2的面积=,…∴平行四边形ABC2020O2019的面积=.故答案为:.三.解答题16.证明:∵四边形ABCD是矩形,∴AD=BC,∵EF=BF+BE,∵BC=CE+BE,BF=CE,∴EF=BC,∴AD=EF.17.(1)证明:∵∠BPQ=∠BPC+∠CPQ=∠A+∠AQP,∠BPC=∠AQP,∴∠CPQ=∠A,∵PQ⊥CP,∴∠A=∠CPQ=90°,∴平行四边形ABCD是矩形;(2)解:∵四边形ABCD是矩形,∴∠D=∠CPQ=90°,在Rt△CDQ和Rt△CPQ中,,∴Rt△CDQ≌Rt△CPQ(HL),∴DQ=PQ,设AQ=x,则DQ=PQ=12﹣x,在Rt△APQ中,AQ2+AP2=PQ2,∴x2+32=(9﹣x)2,解得:x=4,∴AQ的长是4.设CD=AB=CP=y,则PB=y﹣3,在Rt△PCB中,根据勾股定理列方程,求出y=15.在Rt△CDQ中,CQ==5.。
新人教版八年级数学下矩形练习题

八年级 张老师组稿 姓名 学号 2010.05.15一、选择题(仔细读题,一定要选择最佳答案哟!)1.如图1中(1),把一个长为m 、宽为n 的长方形(m n >)沿虚线剪开,拼接成图(2),成为在一角去掉一个小正方形后的一个大正方形,则去掉的小正方形的边长为( )A .2m n -B .m n -C .2m D .2n 2.如图2.在矩形ABCD 中,1=AB ,3=AD ,AF 平分DAB ∠,过C 点作BD CE ⊥于E ,延长AF 、EC 交于点H ,下列结论中:①FH AF =;②BF BO =;③ CH CA =;④ED BE 3=,正确的( )A .②③B .③④C .①②④D .②③④3.如图3,矩形纸片ABCD 中,AB =4,AD =3,折叠纸片使AD 边与对角线BD 重合,折痕为DG , 则AG 的长为( )A .1B .34C .23D .24、如图4,EF 过矩形ABCD 对角线的交点O ,交AB 、CD 于E 、F ,则阴影部分的面积是矩形面积的( )。
A 、51B 、41C 、31D 、1035、如图5,矩形ABCD 中,AB=8㎝,把矩形沿直线AC 折叠,使点B 落在点E 处,AE 交DC 于F ,若AF=425㎝,则AD 长为( )。
A 、4㎝ B 、5㎝ C 、6㎝ D 、7㎝6.如图6,长方形ABCD 中,E 点在BC 上,且AE平分∠BAC 。
若BE=4,AC =15,则 AEC 面积为( )(A ) 15 (B ) 30 (C ) 45 (D ) 60 。
图 1 图 2 图3O HE F D C A B图4 图5 图6二、填空题(试一试,你一定能成功哟!)1.若将4根木条钉成的矩形木框变形为平行四边形形状,并使面积为矩形面积的一半,则这个平行四边形的一个最小内角是______度。
2.如果用4个相同的长为3宽为1的长方形,拼成一个大的长方形,那么这个大的长方形的周长可以是_____.3.矩形内有一点P到各边的距离分别为1、3、5、7,则该矩形的最大面积为平方单位.4.一个矩形的对角线等于长边的一半与短边的和,则短边与长边的比为。
2020-2021学年人教版八年级下册数学 18.2.1矩形 同步习题(含解析)

18.2.1矩形同步习题一.选择题1.矩形具有而一般平行四边形不具有的性质是()A.对角线互相平分B.对角相等C.对边相等D.对角线相等2.如图,在矩形ABCD中,两条对角线AC与BD相交于点O,AB=3,OA=2,则AD的长为()A.5B.C.D.3.若直角三角形斜边上的高和中线长分别是4cm,6cm,则它的面积是()A.12cm2B.24cm2C.15cm2D.48cm24.如图,在矩形ABCD中,AD=6,对角线AC与BD相交于点O,AE⊥BD,垂足为E,DE=3BE.求AE的长()A.B.3C.D.5.如图,矩形ABCD的对角线AC、BD交于点O,M、N分别为BC、OC的中点,AB=6,∠ACB=30°则MN的长为()A.3B.4C.5D.66.如图所示,矩形ABCD中,BC=2AB,E为BC上的一点,且AE=AD,则∠EDC的度数是()A.30°B.75°C.45°D.15°7.如图,矩形ABCD的对角线AC、BD相交于点O,E是边BC的中点,AO=,AD=4,则OE的长为()A.1B.C.2D.8.如图,四边形ABCD是矩形,∠BDC的平分线交AB的延长线于点E,若AD=4,AE=10,则AB的长为()A.4.2B.4.5C.5.2D.5.59.如图,长方形ABCD中,F是BC上(不与B、C重合)的任意一点,图中面积相等的三角形有()A.3对B.4对C.5对D.6对10.如图,矩形ABCD中,∠BOC=120°,BD=12,点P是AD边上一动点,则OP的最小值为()A.3B.4C.5D.6二.填空题11.如图,在矩形ABCD中,对角线AC、BD相交于点O,∠OAD=55°,则∠OBA的度数为.12.如图,在矩形ABCD中,AC,BD交于点O,M,N分别为AB,OA的中点.若MN=2,CD=4,则∠ACB的度数为.13.如图,四边形OABC是矩形,点A的坐标为(4,0),点C的坐标为(0,2),把矩形OABC 沿OB折叠,点C落在点D处,则点D的坐标为.14.如图,点E是矩形ABCD内任一点,若AB=4,BC=7.则图中阴影部分的面积为.15.如图所示,在矩形ABCD中,AB=6,AD=8,P是AD上的动点,PE⊥AC,PF⊥BD 于F,则PE+PF的值为_____.三.解答题16.如图,在矩形ABCD中,点F是BC边上一点,DE⊥AF于E,且DE=DC,求证:△ABF ≌△DEA.17.如图,矩形ABCD中,AB=1,BC=2,点E在AD上,点F在BC边上,FE平分∠DFB.(1)判断△DEF的形状,并说明理由;(2)若点F是BC的中点,求AE的长.18.如图,已知E是矩形ABCD一边AD的中点,延长AB至点F,连接CE,EF,CF,得到△CEF.且CD=1,AF=2,CF=3.(1)求BC的长;(2)求证:CE⊥EF.参考答案一.选择题1.解:A、矩形、平行四边形的对角线都是互相平分的.,故本选项不符合;B、矩形、平行四边形的对角都是相等的,故本选项不符合;C、矩形、平行四边形的对边都是相等的,故本选项不符合;D、矩形的对角线相等,平行四边形的对角线不一定相等,故本选项符合;故选:D.2.解:∵矩形ABCD中,两条对角线AC与BD相交于点O,OA=2,∴AC=2AO=4,又∵AB=3,∠ABC=90°,∴BC==,∴AD=BC=,故选:D.3.解:∵直角三角形斜边上中线长6cm,∴斜边=2×6=12(cm),∴面积=×12×4=24(cm2).故选:B.4.解:∵DE=3BE,∴BD=4BE,∵四边形ABCD是矩形,∴BO=DO=BD=2BE,∴BE=EO,又∵AE⊥BO,∴AB=AO,∴AB=AO=BO,∴△ABO是等边三角形,∴∠ABO=60°,∴∠ADB=30°,又∵AE⊥BD,∴AE=AD=3,故选:B.5.解:∵四边形ABCD是矩形,∴AO=CO=BO=DO,∠ABC=90°,∵∠ACB=30°,∴∠BAC=60°,∴△ABO是等边三角形,∴BO=AB=6,∵M、N分别为BC、OC的中点,∴MN=BO=3,故选:A.6.解:∵四边形ABCD是矩形,∴AD∥BC,AD=BC,∠B=∠ADC=90°,∵BC=2AB,AE=AD,∴AE=2AB,∴∠AEB=30°,∵AD∥BC,∴∠DAE=∠AEB=30°,∵AD=AE,∴∠ADE=75°,∴∠EDC=15°,故选:D.7.解:∵四边形ABCD是矩形,∴AO=CO,AC=2AO=2,∠ADC=90°,∴CD===2,∵E是边BC的中点,∴OE是△BCD的中位线,∴OE=CD=1,故选:A.8.解:如图,∵四边形ABCD是矩形,∴CD∥AB,∴∠1=∠E.又∵∠BDC的平分线交AB的延长线于点E,∴∠1=∠2,∴∠2=∠E.∴BE=BD.∵AE=10,∴BD=BE=10﹣AB.在直角△ABD中,AD=4,BD=10﹣AB,则由勾股定理知:AB==.∴AB=4.2.故选:A.9.解:∵四边形ABCD是矩形,∴AD∥BC,S△ABD=S△BCD=S矩形ABCD,∴S△ABD=S△AFD=S矩形ABCD,S△ABF=S△BFD,∴S△ADF=S△BCD,S△ABE=S△DEF,故选:C.10.解:∵四边形ABCD是矩形,∴OA=OB=OC=OD=BD=6,∵∠BOC=120°=∠AOD,∴∠OAD=∠ODA=30°,当OP⊥AD时,OP有最小值,∴OP=OD=3,故选:A.二.填空题11.解:∵矩形ABCD中,对角线AC,BD相交于点O,∴∠DAB=90°,DB=AC,OD=OB=OA=OC,∵∠OAD=55°,∴∠ODA=∠OAD=55°,∴∠OBA=90°﹣∠ADB=90°﹣55°=35°,故答案为:35°.12.解:∵四边形ABCD是矩形,∴AB=CD=4,AO=CO,BO=DO,AC=BD,∴AO=BO,∵M,N分别为AB,OA的中点,∴BO=2MN=4,∴AO=BO=AB=4,∴△ABO是等边三角形,∴∠BAC=60°,∴∠ACB=30°,故答案为:30°.13.解:设BD与OA交于点E,作DF⊥OA于点F,∵点A的坐标为(4,0),点C的坐标为(0,2),∴OC=2,OA=4,∵四边形ABCD是矩形,∴BC∥OA,∴∠CBO=∠AOB,由翻折变换的性质可知,∠DBO=∠CBO,∴∠OBD=∠AOB,∴BE=OE,在Rt△EAB中,设BE=OE=x,则AE=4﹣x,由勾股定理得22+(4﹣x)2=x2,解得x=,即BE=,∴OE=BE=,在Rt△ODE中,OD=OC=2,DE=BD﹣BE=4﹣=,由OE•DF=OD•DE得וDF=×2×,∴DF=,在Rt△ODF中,由勾股定理得OF2=OD2﹣DF2=22﹣()2=,∴OF=,∴点D的坐标为(,﹣),故答案为:(,﹣).14.解:∵四边形ABCD是矩形,∴AD=BC=7,设两个阴影部分三角形的底为AD,BC,高分别为h1,h2,则h1+h2=AB,∴S△EAB+S△ECD=AD•h1+BC•h2=AD(h1+h2)=AD•AB=矩形ABCD的面积=×7×4=14;故答案为:14.15.解:连接OP,∵四边形ABCD是矩形,∴∠DAB=90°,AC=2AO=2OC,BD=2BO=2DO,AC=BD,∴OA=OD=OC=OB,∴S△AOD=S△DOC=S△AOB=S△BOC=14S矩形ABCD=14×6×8=12,在Rt△BAD中,由勾股定理得:BD=22226810 AB AD+=+=,∴AO=OD=5,∵S△APO+S△DPO=S△AOD,∴×AO×PE+×DO×PF=12,∴5PE+5PF=24,PE+PF=24 5,故答案为:24 5.三.解答题16.证明:如图,连接DF,∵四边形ABCD是矩形,∴DC⊥CF,又∵DE=DC,DE⊥AF,∴DF平分∠CFE,∴∠CFD=∠DFE,∵CB∥AD,∴∠CFD=∠ADF,∠AFB=∠DAE,∴∠DF A=∠ADF,∴AF=AD,在△ABF和△DEA中,,∴△ABF≌△DEA(ASA).17.解:(1)△DEF是等腰三角形,理由如下:∵四边形ABCD是矩形,∴AB=CD,AD=BC,AD∥BC,∠C=90°,∴∠BFE=∠DEF,∵FE平分∠DFB,∴∠BFE=∠DFE,∴∠DEF=∠DFE,∴DE=DF,∴△DEF是等腰三角形;(2)∵AB=1,BC=2,∴CD=1,AD=2,∵点F是BC的中点,∴FC==1,Rt△DCF中,∠C=90°,∴DF=,∴DE=DF=,∴AE=AD﹣DE=2﹣.18.(1)解:∵四边形ABCD是矩形,CD=1,∴AB=1,∠ABC=∠FBC=90°,∵AF=2,∴BF=1,∵Rt△CBF中,∠FBC=90°,BF=1,CF=3,∴根据勾股定理得CF2=BC2+BF2,∴BC===,∴BC的长是;(2)证明:矩形ABCD中,AD=BC=,∵E是AD的中点,∴AE=DE=,∵Rt△AEF中,∠A=90°,AE=1,AF=2,∴根据勾股定理得,EF==,∵Rt△CDE中,∠D=90°,CD=1,DE=1,∴根据勾股定理得,EC==,∵△CEF中,EC=,EF=,CF=3,∴CE2+EF2=CF2,∴△CEF是直角三角形,∴CE⊥EF.。
人教版八年级数学下册第02课 矩形的性质与判定 同步练习题

初中数学试卷第02课矩形的性质与判定同步练习题【例1】如图,在矩形ABCD中,点E是BC上一点,AE=AD,DF⊥AE,垂足为F.求证:DF=DC.【例2】如图,在矩形ABCD中,对角线BD的垂直平分线MN与AD相交于点M,与BC相交于点N,连接BM,DN.(1)求证:四边形BMDN是菱形;(2)若AB=4,AD=8,求MD的长.【例3】如图,已知在△ABC中,AC=3,BC=4,AB=5,点P在AB上(不与A、B重合),过P作PE⊥AC,PF⊥BC,垂足分别是E、F,连接EF,M为EF的中点.(1)请判断四边形PECF的形状,并说明理由;(2)随着P点在边AB上位置的改变,CM的长度是否也会改变?若不变,请你求CM的长度;若有变化,请你求CM的变化范围.【例4】如图,在矩形ABCD中,对角线AC,BD相交于点O,点E,F分别在边AD,BC上,且DE=CF,连接OE,OF.求证:OE=OF.【例5】如图,△ABC中,点O是边AC上一个动点,过O作直线MN∥BC.设MN交∠ACB的平分线于点E,交∠ACB 的外角平分线于点F.(1)求证:OE=OF;(2)若CE=12,CF=5,求OC的长;(3)当点O在边AC上运动到什么位置时,四边形AECF是矩形?并说明理由.课堂同步练习一、选择题:1、如图,四边形ABCD为平行四边形,延长AD到E,使DE=AD,连接EB,EC,DB,添加一个条件,不能使四边形DBCE 成为矩形的是( )A.AB=BEB.DE⊥DCC.∠ADB=90°D.CE⊥DE第1题图第2题图第4题图2、如图是一张矩形纸片ABCD,AD=10cm,若将纸片沿DE折叠,使DC落在DA上,点C的对应点为点F,若BE=6cm,则DC的长是()A.4cmB.6cmC.8cmD.10cm3、若顺次连接四边形ABCD各边的中点所得到的四边形是矩形,则该四边形ABCD一定是()A.菱形B.对角线互相垂直的四边形C.矩形D.对角线相等的四边形4、如图,把一个长方形纸片沿EF折叠后,点D、C分别落在D′、C′的位置,若∠EFB=65°,则∠AED′等于()A.50°B.55°C.60°D.65°5、如图.矩形ABCD中.E在AD上.且EF⊥EC.EF=EC.DE=2.矩形的周长为16.则AE的长是()A.3B.4C.5D.7第5题图第6题图第7题图6、如图,E是矩形ABCD中BC边的中点,将△ABE沿AE折叠到△AFE,F在矩形ABCD内部,延长AF交DC于G 点,若∠AEB=55°,则∠DAF=( )A.40°B.35°C.20°D.15°7、如图,将矩形纸片ABCD沿EF折叠,使点B与CD的中点重合,若AB=2,BC=3,则△FCB′与△B′DG的面积之比为( )A.9:4B.3:2C.4:3D.16:98、如图,矩形ABCD沿着直线BD折叠,使点C落在C′处,BC′交AD于E,AD=8,AB=4,则DE长为( )A.3B.4C.5D.6第8题图第9题图9、如图,在矩形ABCD中,AB=2,BC=4,对角线AC的垂直平分线分别交AD、AC于点E、O,连接CE,则CE的长为( )A.3B.3.5C.2.5D.2.810、如图,矩形ABCD中,AE平分∠BAD交BC于E,∠CAE=15°,则下列结论:△ODC是等边三角形;②BC=2AB;③∠AOE=135°;④S△AOE=S△COE.其中正确的结论的个数有( )A.1B.2C.3D.4第10题图第11题图第12题图11、在矩形ABCD中,点A关于∠B的角平分线的对称点为E,点E关于∠C的角平分线的对称点为F,若AD=,AB=3,则S △ADF=()A.2B.3C.3D.12、如图,在矩形ABCD中,O为AC中点,EF过O点,且EF⊥AC分别交DC于F,交AB于E,点G是AE中点,且∠AOG=30°.①DC=3OG;②OG=BC;③△OGE是等边三角形;④S△AOE=S矩形ABCD.则结论正确的个数为( )A.1B.2C.3D.4二、填空题:13、若矩形的一个角的平分线分一边为4cm和3cm的两部分,则矩形的周长为cm.14、如图,矩形ABCD的对角线AC,BD相交于点O,CE∥BD,DE∥AC,若AC=4 cm,则四边形CODE的周长为。
人教版 八年级数学下册 18.2.1 矩形 培优练习(含答案)
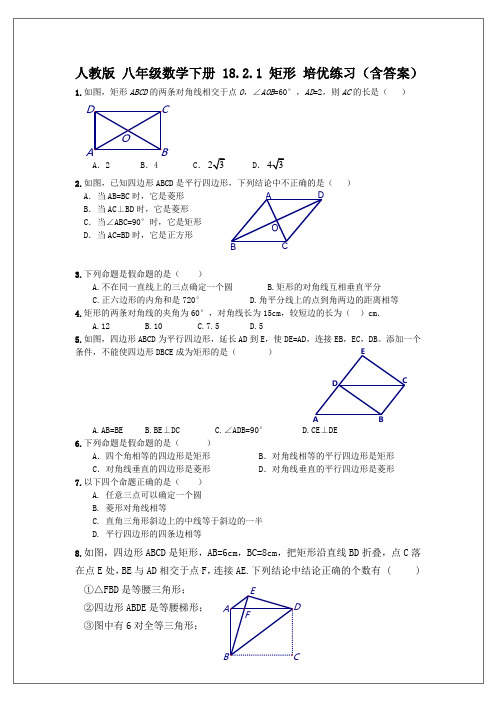
人教版 八年级数学下册 18.2.1 矩形 培优练习(含答案)1.如图,矩形ABCD 的两条对角线相交于点O ,∠AOB =60°,AD =2,则AC 的长是( )A .2B .4C .23D .432.如图,已知四边形ABCD 是平行四边形,下列结论中不正确的是( )A .当AB=BC 时,它是菱形B .当AC ⊥BD 时,它是菱形 C .当∠ABC=90°时,它是矩形D .当AC=BD 时,它是正方形3.下列命题是假命题的是( ) A.不在同一直线上的三点确定一个圆 B.矩形的对角线互相垂直平分 C.正六边形的内角和是720° D.角平分线上的点到角两边的距离相等4.矩形的两条对角线的夹角为60°,对角线长为15cm ,较短边的长为( )cm . A.12 B.10 C.7.5 D.55.如图,四边形ABCD 为平行四边形,延长AD 到E ,使DE=AD ,连接EB ,EC ,DB 。
添加一个条件,不能使四边形DBCE 成为矩形的是( )A.AB=BEB.BE ⊥DCC.∠ADB=90°D.CE ⊥DE 6.下列命题是假命题的是( )A .四个角相等的四边形是矩形B .对角线相等的平行四边形是矩形C .对角线垂直的四边形是菱形D .对角线垂直的平行四边形是菱形 7.以下四个命题正确的是( ) A. 任意三点可以确定一个圆 B. 菱形对角线相等C. 直角三角形斜边上的中线等于斜边的一半D. 平行四边形的四条边相等8.如图,四边形ABCD 是矩形,AB=6cm ,BC=8cm ,把矩形沿直线BD 折叠,点C 落在点E 处,BE 与AD 相交于点F ,连接AE.下列结论中结论正确的个数有 ( ) ①△FBD 是等腰三角形; ②四边形ABDE 是等腰梯形; ③图中有6对全等三角形;BC O DAOD C B A A B C DEF EDA④四边形BCDF的周长为532;⑤AE的长为145cm.A.2个B.3个 C.4个D.5个9.如图,点P是矩形ABCD的边AD上的一动点,矩形的两条边AB、BC的长分别是6和8,则点P到矩形的两条对角线AC和BD的距离之和是( )A.4.8 B.5 C.6 D.7.2二、填空题(共有7道小题)10.如图,在矩形ABCD中,对角线AC,BD交于点O,已知∠AOD=120°,AB=4,则AC的长为。
人教版初二数学下册矩形性质练习

矩形的性质练习一、选择——基础知识运用1.如图,矩形的两条对角线的一个交角为60°,两条对角线的长度的和为20cm,则这个矩形的一条较短边的长度为()A.10cm B.8cm C.6cm D.5cm2.如图,在矩形ABCD中,DE平分∠ADC交BC于点E,EF⊥AD交AD于点F,若EF=3,AE=5,则AD等于()A.5 B.6 C.7 D.83.Rt△ABC中,∠C=90°,锐角为30°,最短边长为5cm,则最长边上的中线是()A.5cm B.15cm C.10cm D.2.5cm4.如图,在△ABC中,CF⊥AB于F,BE⊥AC于E,M为BC的中点,EF=7,BC=10,则△EFM的周长是()A.17 B.21 C.24 D.275.如图,在矩形ABCD中,AF⊥BD于E,AF交BC于点F,连接DF,则图中面积相等但不全等的三角形共有()A.2对B.3对C.4对D.5对6.如图,在平面直角坐标系中,矩形OABC,OA=3,OC=6,将△ABC沿对角线AC翻折,使点B落在点B′处,AB′与y轴交于点D,则点D的坐标为()A.(0, B.(0, C.(0, D.(0,二、解答——知识提高运用7.如果把电视屏幕看作一个长方形平面,建立一个直角坐标系,若左下方的点的坐标是(0,0),右下方的点的坐标是(32,0),左上方的点的坐标是(0,28),则右上方的点的坐标是。
8.长方形ABCD面积为12,周长为14,则对角线AC的长为。
9.如图,自矩形ABCD的顶点C作CE⊥BD,E为垂足,延长EC至F,使CF=BD,连接AF,求∠BAF的大小。
10.如图,在△ABC中,∠BAC>90°,DC⊥DB,BE⊥EC,F为BC上的一个动点,猜想:当F为于BC上的什么位置时,△FDE是等腰三角形,并证明你的猜想是正确的。
11.如图,在矩形ABCD中,AD=12,AB=7,DF平分∠ADC,AF⊥EF。
2021年人教版八年级数学下册《矩形》同步基础练习卷(含答案)

2021年人教版八年级数学下册《矩形》同步基础练习卷一、选择题1.下列关于矩形的说法,正确的是( )A.对角线相等的四边形是矩形B.对角线互相平分的四边形是矩形C.矩形的对角线互相垂直且平分D.矩形的对角线相等且互相平分2.在□ABCD中,AC交BD于点O,再添加一个条件,仍不能判定四边形ABCD是矩形的条件是( )A.AB=ADB.OA=OBC.AC=BDD.DC⊥BC3.如图,四边形ABCD的对角线AC,BD相交于点O,已知下列6个条件:①AB∥DC;②AB=DC;③AC=BD;④∠ABC=90°;⑤OA=OC;⑥OB=OD.则不能使四边形ABCD成为矩形的是( )A.①②③B.②③④C.②⑤⑥D.④⑤⑥4.如图,要使平行四边形ABCD成为矩形,需添加的条件是( )A.AB=BCB.AC⊥BDC.AC=BDD.∠1=∠25.如图,顺次连接四边形ABCD各边中点得四边形EFGH,要使四边形EFGH为矩形,应添加的条件是( )A.AB∥DCB.AC=BDC.AC⊥BDD.AB=DC6.在数学活动课上,老师和同学们判断一个四边形门框是否为矩形,下面是某合作学习小组的4位同学拟定的方案,其中正确的是( )A.测量对角线是否相互平分B.测量两组对边是否分别相等C.测量一组对角是否为直角D.测量四边形的其中三个角是否都为直角7.有下列说法:①四个角都相等的四边形是矩形;②有一组对边平行,有两个角为直角的四边形是矩形;③两组对边分别相等且有一个角为直角的四边形是矩形;④对角线相等且有一个角是直角的四边形是矩形;⑤对角线互相平分且相等的四边形是矩形;⑥一组对边平行,另一组对边相等且有一角为直角的四边形是矩形.其中,正确的个数是()A.2个 B.3个C.4个 D.5个8.检查一个门框是否为矩形,下列方法中正确的是()A.测量两条对角线,是否相等B.测量两条对角线,是否互相平分C.测量门框的三个角,是否都是直角D.测量两条对角线,是否互相垂直9.如图,将矩形纸片ABCD沿对角线BD折叠一次,则图中全等三角形有()A.2对B. 3对C. 4对D.5对10.如图,将矩形ABCD沿对角线BD折叠,使点C和点C′重合,若AB=2,则C′D的长为()A.1B.2C.3D.411.如图,在矩形ABCD中,DE平分∠ADC交BC于点E,EF⊥AD交AD于点F,若EF=3,AE=5,则AD等于()A.5B.6C.7D.812.如图,矩形ABCD中,E在AD上,EF⊥EC,EF=EC,DE=2,矩形周长为16,则AE长是( )A.3B.4C.5D.7二、填空题13.如图,要使平行四边形ABCD是矩形,则应添加的条件是__________(添加一个条件即可).14.如图,把一张矩形纸片ABCD沿EF折叠,点C、D分别落在C/、D/的位置上,EC′交AD于G,已知∠EFG=56°,那么∠BEG= .15.如图,在矩形ABCD中,AE⊥BD于E,∠DAE=3∠EAB,则∠ACD的度数为.16.如图,点E是矩形ABCD内任一点,若AB=3,BC=4.则图中阴影部分的面积为.17.如图,△ABC中,若∠ACB=90°,∠B=55°,D是AB的中点,则∠ACD= °.18.如图是叠放在一起的两张长方形卡片,图中有∠1、∠2、∠3,则其中一定相等的是_____三、解答题19.如图,四边形ABCD是平行四边形,AC,BD交于点O,∠1=∠2.求证:四边形ABCD是矩形.20.如图,四边形ABCD的对角线AC、BD交于点O,已知O是AC的中点,AE=CF,DF∥BE.(1)求证:△BOE≌△DOF;(2)若2OD=AC,则四边形ABCD是什么特殊四边形?请证明你的结论.21.如图,在△ABC中,AB=AC,AD是BC边上的中线,AE∥BC,CE⊥AE,垂足为E.(1)求证:△ABD≌△CAE.(2)连结DE,线段DE与AB之间有怎样的位置关系和数量关系?请证明你的结论.22.如图,将平行四边形ABCD的边DC延长到点E,使CE=DC,连接AE,交BC于点F。
人教版八年级数学下《矩形》拔高练习

《矩形》拔高练习一、选择题(本大题共5小题,共25.0分)1.(5分)一个矩形的长是宽的2倍,对角线的长是,那么这个矩形的长等于()A.2B.C.1D.22.(5分)如图,在△ABC中,∠BAC=90°,点D在BC延长线上,且AD=BC,若∠D=40°,则∠B=()A.10°B.20°C.30°D.40°3.(5分)如图,矩形ABCD中,AB=3,AD=9,点E在边AD上,AE=1,过E、D两点的圆的圆心O在边AD的上方,直线BO交AD于点F,作DG⊥BO,垂足为G.当△ABF与△DFG全等时,⊙O的半径为()A.B.C.D.4.(5分)如图,点A、D、G、M在半圆上,四边形ABOC、DEOF、HMNO均为矩形,设BC=a,EF=b,HN=c,则a、b、c三者间的大小关系为()A.a>b>c B.a<b<c C.a=b=c D.a>c>b 5.(5分)下列说法正确的有()个①一组对边平行且一组对角相等的四边形是平行四边形;②一组对边相等且有一个角是直角的四边形是矩形;③三角形的中位线平行于三角形的第三边且等于第三边的一半;④两条对角线相等的四边形是矩形.A.1B.2C.3D.4二、填空题(本大题共5小题,共25.0分)6.(5分)直角三角形斜边上的高与中线分别为8cm和10cm,则它的面积是cm2.7.(5分)矩形ABCD的对角线AC、BD相交于点O,∠AOD=120°,AC=8,则△ABC的周长为.8.(5分)如图,矩形OABC的顶点A,C分别在坐标轴上,B(8,7),D(5,0),点P是边AB或边BC上的一点,连接OP,DP,当△ODP为等腰三角形时,点P的坐标为.9.(5分)如图,在矩形ABCD中,以A为圆心,AD长为半径作圆,交AB于点E,F为BC的中点,过点F作AB的平行线,交于点G,则∠AGF的度数为.10.(5分)如图,∠MON=90°,矩形ABCD的顶点A、B分别在边OM、ON 上,当B在边ON上运动时,A随之在OM上运动,矩形ABCD的形状保持不变,其中AB=4,BC=2,运动过程中点D到点O的最大距离是.三、解答题(本大题共5小题,共50.0分)11.(10分)如图是某居民小区的一块长为2a米,宽为b米的长方形空地,为了美化环境,准备在这个长方形的四个顶点处修建一个半径为a米的扇形花台,然后在花台内种花,其余种草.如果建造花台及种花费用每平方米需要资金100元,种草每平方米需要资金50元,那么美化这块空地共需资金多少元?12.(10分)过矩形ABCD的对角线AC的中点O作EF⊥AC,交BC边于点E,交AD边于点F,分别连接AE,CF.(1)求证:四边形AECF是菱形;(2)若AB=3,∠DCF=30°,求EF的长.13.(10分)把一张形状是矩形的纸片剪去其中某个角,剩下的部分是一个多边形,则这个多边形的内角和是多少?14.(10分)如图,长方形AOBC在直角坐标系中,点A在y轴上,点B在x 轴上,已知点C的坐标是(8,4).(1)对角线AB的垂直平分线MN交x轴于点M,连接AM,求线段AM的长;(2)在x轴上是否存在一个点P,使△P AM为等腰三角形?如果有请直接写出符合题意的所有点P的坐标.15.(10分)如图,在矩形ABCD中,AC,BD交于点O,延长BC到点E,使CE=BC,连接AE交CD于点F.若AD=10,求OF的长.《矩形》拔高练习参考答案与试题解析一、选择题(本大题共5小题,共25.0分)1.(5分)一个矩形的长是宽的2倍,对角线的长是,那么这个矩形的长等于()A.2B.C.1D.2【分析】设矩形的宽是a,则长是2a,再根据勾股定理求出a的值即可.【解答】解:设矩形的宽是a,则长是2a,∵对角线的长是5cm,∴a2+(2a)2=()2,解得a=1,∴这个矩形的长=2a=2.故选:D.【点评】本题考查的是勾股定理,熟知在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键.2.(5分)如图,在△ABC中,∠BAC=90°,点D在BC延长线上,且AD=BC,若∠D=40°,则∠B=()A.10°B.20°C.30°D.40°【分析】取BC的中点E,连接AE,根据直角三角形的性质得到AE=BC=BE,根据等腰三角形的性质,三角形的外角的性质计算.【解答】解:取BC的中点E,连接AE,∵∠BAC=90°,点E是BC的中点,∴AE=BC=BE,∴∠B=∠EAB,∵AD=BC,∴AE=AD,∴∠AED=∠D=40°,∴∠B=20°,故选:B.【点评】本题考查的是直角三角形的性质,等腰三角形的性质,掌握在直角三角形中,斜边上的中线等于斜边的一半是解题的关键.3.(5分)如图,矩形ABCD中,AB=3,AD=9,点E在边AD上,AE=1,过E、D两点的圆的圆心O在边AD的上方,直线BO交AD于点F,作DG⊥BO,垂足为G.当△ABF与△DFG全等时,⊙O的半径为()A.B.C.D.【分析】根据全等三角形的性质得到BF=DF,根据矩形的性质得到∠A=90°,根据勾股定理得到AF=4,连接OE,OD,则OE=OD,过O作OH⊥AD于H,则HE=HD=4,根据相似三角形的性质得到OH=,根据勾股定理列方程即可得到结论.【解答】解:∵△ABF与△DFG全等,∴BF=DF,∵AD=9,∴BF=9﹣AF,∵四边形ABCD是矩形,∴∠A=90°,∴AB2+AF2=BF2,即32+AF2=(9﹣AF)2,解得:AF=4,∵AE=1,∴EF=3,DE=8,连接OE,OD,则OE=OD,过O作OH⊥AD于H,则HE=HD=4,∴FH=1,∵∠A=∠OHF=90°,∠AFB=∠OFH,∴△ABF∽△HOF,∴,即,∴OH=,在Rt△ODH中,OD==,故选:B.【点评】本题考查了矩形的性质,全等三角形的性质,相似三角形的判定和性质,勾股定理,正确的作出辅助线是解题的关键.4.(5分)如图,点A、D、G、M在半圆上,四边形ABOC、DEOF、HMNO均为矩形,设BC=a,EF=b,HN=c,则a、b、c三者间的大小关系为()A.a>b>c B.a<b<c C.a=b=c D.a>c>b【分析】由题意可得MO=NH,DO=EF,AO=BC,且MO=DO=AO,即可求a=b=c.【解答】解:如图:连接OM,OD,OA∵四边形ABOC、DEOF、HMNO均为矩形∴MO=NH,DO=EF,AO=BC∵MO=DO=AO∴a=b=c故选:C.【点评】本题考查了矩形的性质,熟练运用矩形的性质解决问题是本题的关键.5.(5分)下列说法正确的有()个①一组对边平行且一组对角相等的四边形是平行四边形;②一组对边相等且有一个角是直角的四边形是矩形;③三角形的中位线平行于三角形的第三边且等于第三边的一半;④两条对角线相等的四边形是矩形.A.1B.2C.3D.4【分析】根据平行四边形的判定,矩形的判定,三角形的中位线定理即可一一判断;【解答】解:①一组对边平行且一组对角相等的四边形是平行四边形;正确,可以证明两组对角分别相等.②一组对边相等且有一个角是直角的四边形是矩形;错误;③三角形的中位线平行于三角形的第三边且等于第三边的一半;正确;④两条对角线相等的四边形是矩形.错误,应该是两条对角线相等的平行四边形是矩形;故选:B.【点评】本题考查平行四边形的判定,矩形的判定,三角形的中位线定理等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.二、填空题(本大题共5小题,共25.0分)6.(5分)直角三角形斜边上的高与中线分别为8cm和10cm,则它的面积是80 cm2.【分析】根据直角三角形斜边上中线性质求出斜边长,再根据直角三角形的面积公式求出面积即可.【解答】解:∵直角三角形的斜边上的中线为10,∴斜边为2×10=20,∵直角三角形斜边上的高为8,∴此直角三角形的面积为=80cm2,故答案为:80.【点评】本题考查了直角三角形斜边上中线性质的应用,注意:直角三角形斜边上中线等于斜边的一半.7.(5分)矩形ABCD的对角线AC、BD相交于点O,∠AOD=120°,AC=8,则△ABC的周长为12+4.【分析】根据矩形性质求出AO=BO=4,得出等边三角形AOB,求出AB,即可求出答案.【解答】解:∵四边形ABCD是矩形,AC=8,∴AC=BD,AC=2AO,BD=2BO,∠ABC=90°,∴AO=BO=OC=4,∵∠AOD=120°,∴∠AOB=60°,∴△AOB是等边三角形,∴AB=AO=4,∴BC==4,∴△ABC的周长是4+4+4+4=12+4,故答案为:12+4.【点评】本题考查了矩形性质,等边三角形的性质和判定的应用,注意:矩形的对角线相等且互相平分.8.(5分)如图,矩形OABC的顶点A,C分别在坐标轴上,B(8,7),D(5,0),点P是边AB或边BC上的一点,连接OP,DP,当△ODP为等腰三角形时,点P的坐标为(8,4)或(,7).【分析】分两种情形分别讨论即可解决问题;【解答】解:∵四边形OABC是矩形,B(8,7),∴OA=BC=8,OC=AB=7,∵D(5,0),∴OD=5,∵点P是边AB或边BC上的一点,∴当点P在AB边时,OD=DP=5,∵AD=3,∴P A==4,∴P(8,4).当点P在边BC上时,只有PO=PD,此时P(,7).综上所述,满足条件的点P坐标为(8,4)或(,7).故答案为(8,4)或(,7).【点评】本题考查矩形的性质、坐标与图形性质、等腰三角形的判定等知识,解题的关键是学会用分类讨论的思想思考问题,属于中考常考题型.9.(5分)如图,在矩形ABCD中,以A为圆心,AD长为半径作圆,交AB于点E,F为BC的中点,过点F作AB的平行线,交于点G,则∠AGF的度数为150°.【分析】由题意可证四边形GHBF是矩形,即可得GM=BC=AD=AG,利用三角函数求出∠GAB的值,继而求出∠AGF的值.【解答】解:连接AG,作GM⊥AB于点M.∴GM∥BF,GM⊥GF.由题意知GF∥AB,AB⊥BC,∴四边形GHBF是矩形.∴∠FGH=90°,GH=BC.∵AG=AD,AD=BC,∴GM=AG∵sin∠GAB==∴∠GAB=30°.∵GF∥AB,∴∠AGF=150°.故答案为150°【点评】本题考查了矩形的性质,锐角三角函数,添加恰当的辅助线构造直角三角形是本题的关键.10.(5分)如图,∠MON=90°,矩形ABCD的顶点A、B分别在边OM、ON上,当B在边ON上运动时,A随之在OM上运动,矩形ABCD的形状保持不变,其中AB=4,BC=2,运动过程中点D到点O的最大距离是2+2.【分析】取AB的中点E,连接OD、OE、DE,根据直角三角形斜边上的中线等于斜边的一半可得OE=AB,利用勾股定理列式求出DE,然后根据三角形任意两边之和大于第三边可得OD过点E时最大.【解答】解:如图:取线段AB的中点E,连接OE,DE,OD∵AB=4,点E是AB的中点,∠AOB=90°∴AE=BE=2=OE∵四边形ABCD是矩形∴AD=BC=2,∠DAB=90°∴DE==2∵OD≤OE+DE∴当点D,点E,点O共线时,OD的长度最大.∴点D到点O的最大距离=OE+DE=2+2故答案为:2+2【点评】本题考查了矩形的性质,直角三角形斜边上的中线等于斜边的一半,勾股定理,三角形三边关系,确定出OD过AB的中点时值最大是解题的关键.三、解答题(本大题共5小题,共50.0分)11.(10分)如图是某居民小区的一块长为2a米,宽为b米的长方形空地,为了美化环境,准备在这个长方形的四个顶点处修建一个半径为a米的扇形花台,然后在花台内种花,其余种草.如果建造花台及种花费用每平方米需要资金100元,种草每平方米需要资金50元,那么美化这块空地共需资金多少元?【分析】根据所需资金=花台需要的资金+草地需要的资金,可求解.【解答】解:由题意可得:花台的面积为πa2平方米,草地的面积为(2ab﹣πa2)平方米∴美化这块空地共需资金=100×πa2+50×(2ab﹣πa2)=(50πa2+100ab)元【点评】本题考查了矩形的性质,用正确的代数式表达草地面积是本题的关键.12.(10分)过矩形ABCD的对角线AC的中点O作EF⊥AC,交BC边于点E,交AD边于点F,分别连接AE,CF.(1)求证:四边形AECF是菱形;(2)若AB=3,∠DCF=30°,求EF的长.【分析】(1)根据菱形的判定与性质即可求出答案.(2)根据含30度的直角三角形的性质以及等边三角形的性质与判定即可求出答案.【解答】解:(1)由矩形ABCD可知:∠F AO=∠ECO,AO=CO,在△AOF与△COE中,,∴△AOF≌△COE(ASA),∴OE=OF,∴四边形AECF是平行四边形,∵EF⊥AC,∴四边形AECF是菱形;(2)∵∠DCF=30°,AB=CD=3,∴∠FCE=60°,CE=2∵CF=CE,∴△EFC是等边三角形,∴EF=2;【点评】本题考查矩形的性质,解题的关键是熟练运用矩形的性质以及含30度的直角三角形的性质,本题属于基础题型.13.(10分)把一张形状是矩形的纸片剪去其中某个角,剩下的部分是一个多边形,则这个多边形的内角和是多少?【分析】把一张形状是矩形的纸片剪去其中某一个角,剩下的部分的形状可能是三角形或四边形或五边形,再根据多边形的内角和定理判断即可.【解答】解:把一张形状是矩形的纸片剪去其中某一个角,剩下的部分的形状可能是三角形或四边形或五边形,故这个多边形的内角和可能是180°或360°或540°.【点评】本题考查了多边形的内角和定理,判断剩下的部分的形状可能是三角形或四边形或五边形是解题的关键.14.(10分)如图,长方形AOBC在直角坐标系中,点A在y轴上,点B在x 轴上,已知点C的坐标是(8,4).(1)对角线AB的垂直平分线MN交x轴于点M,连接AM,求线段AM的长;(2)在x轴上是否存在一个点P,使△P AM为等腰三角形?如果有请直接写出符合题意的所有点P的坐标.【分析】(1)设AM=x,则BM=x,OM=8﹣x,根据勾股定理列方程得:AO2+OM2=AM2,则42+(8﹣x)2=x2,解出即可;(2)△P AM为等腰三角形时,分情况进行讨论:①以A为圆心,以AM为半径画圆;②以M为圆心,以MA为半径,画圆;③作AM的垂直平分线;确定点P的位置,分别计算可得结论.【解答】解:(1)由题意得:OA=4,OB=8,∵MN是AB的垂直平分线,∴AM=BM,设AM=x,则BM=x,OM=8﹣x,Rt△AOM中,由勾股定理得:AO2+OM2=AM2,∴42+(8﹣x)2=x2,解得:x=5,∴AM=5;(2)如图,①当AP1=AM=5时,OM=OP1=3,此时P1(﹣3,0);②当AM=P2M=P3M=5时,此时P2(﹣2,0),P3(8,0);③如图,作AM的垂直平分线,交AM于E,交x轴于P4,∴EM=,sin∠EP4M==sin∠OAM=,∴P4M=,∴OP4=﹣3=,此时P4(﹣,0),综上,△P AM为等腰三角形,点P的坐标是(﹣3,0)或(﹣2,0)或(8,0或(﹣,0).【点评】本题考查的是矩形的性质,等腰三角形的判定,勾股定理,线段垂直平分线的性质,同时与方程相结合解决问题,灵活运用分情况讨论思想是解题的关键.15.(10分)如图,在矩形ABCD中,AC,BD交于点O,延长BC到点E,使CE=BC,连接AE交CD于点F.若AD=10,求OF的长.【分析】首先根据矩形的性质证得△ADF≌△ECF,然后判定OF为△ACE的中位线,从而求得OF的值.【解答】解:∵四边形ABCD是矩形,∴BC=AD,OA=OB=OC=OD,∠ADF=∠BCF=∠BAD=∠ABC=90°,∴∠ECF=90°,∵CE=BC,AD=10,∴EC=BC=AD=10,在△ADF和△ECF中,∴△ADF≌△ECF(AAS),∴AF=EF,即F为AE的中点,、∴OF为△ACE的中位线,∴OF=CE=5.【点评】本题考查了矩形的性质,解题的关键是根据矩形的性质判定三角形全等并证得OF为△ACE的中位线,难度不大.。
人教版数学八年级下《18.2.1矩形》课时练习含答案

八年级下册18.2.1矩形课时练习一.选择题(共15小题)1.一个长方形在平面直角坐标系中三个顶点的坐标为(﹣1,﹣1),(﹣1,2),(3,﹣1),则第四个顶点的坐标为()A.(2,2)B.(3,2)C.(3,3)D.(2,3)答案:B知识点:坐标与图形性质;矩形的性质解析:解答:解:如图可知第四个顶点为:即:(3,2).故选B.分析:本题可在画出图后,根据矩形的性质,得知第四个顶点的横坐标应为3,纵坐标应为2.本题考查学生的动手能力,画出图后可很快得到答案.2.如图,矩形ABCD中,AB=1,AD=2,M是CD的中点,点P在矩形的边上沿A⇒B⇒C⇒M 运动,则△APM的面积y与点P经过的路程x之间的函数关系用图象表示大致是下图中的()A. B.C. D.答案:A知识点:函数的图像;分段函数;矩形的性质解析:解答:解:点P由A到B这一段中,三角形的AP边上的高不变,因而面积是路程x的正比例函数,当P到达B点时,面积达到最大,值是1.在P由B到C这一段,面积随着路程的增大而减小;到达C点,即路程是3时,最小是;由C到M这一段,面积越来越小;当P到达M时,面积最小变成0.因而应选第一个选项.故选A.分析:根据每一段函数的性质,确定其解析式,特别注意根据函数的增减性,以及几个最值点,确定选项比较简单.本题考查了分段函数的画法,是难点,要细心认真.3.如图,矩形ABCD中,AB=3,BC=5.过对角线交点O作OE⊥AC交AD于E,则AE 的长是()A.1.6B.2.5C.3D.3.4答案:D知识点:线段垂直平分线的性质;勾股定理;矩形的性质解析:解答:解:连接EC,由矩形的性质可得AO=CO,又因EO⊥AC,则由线段的垂直平分线的性质可得EC=AE,设AE=x,则ED=AD﹣AE=5﹣x,在Rt△EDC中,根据勾股定理可得EC2=DE2+DC2,即x2=(5﹣x)2+32,解得x=3.4.故选D.分析:利用线段的垂直平分线的性质,得到EC与AE的关系,再由勾股定理计算出AE的长.本题考查了利用线段的垂直平分线的性质.矩形的性质及勾股定理综合解答问题的能力,在解上面关于x的方程时有时出现错误,而误选其它选项.4.一次数学课上,老师请同学们在一张长为18厘米,宽为16厘米的矩形纸板上,剪下一个腰长为10厘米的等腰三角形,且要求等腰三角形的一个顶点与矩形的一个顶点重合,其它两个顶点在矩形的边上,则剪下的等腰三角形的面积为多少平方厘米()A.50B.50或40C.50或40或30D.50或30或20答案:C知识点:等腰三角形的性质;勾股定理;矩形的性质解析:解答:解:如图四边形ABCD是矩形,AD=18cm,AB=16cm;本题可分三种情况:①如图(1):△AEF中,AE=AF=10cm;S△AEF=•AE•AF=50cm2;②如图(2):△AGH中,AG=GH=10cm;在Rt△BGH中,BG=AB﹣AG=16﹣10=6cm;根据勾股定理有:BH=8cm;∴S△AGH=AG•BH=×8×10=40cm2;③如图(3):△AMN中,AM=MN=10cm;在Rt△DMN中,MD=AD﹣AM=18﹣10=8cm;根据勾股定理有DN=6cm;∴S△AMN=AM•DN=×10×6=30cm2.故选C.分析:本题中由于等腰三角形的位置不确定,因此要分三种情况进行讨论求解,①如图(1),②如图(2),③如图(3),分别求得三角形的面积.题主要考查了等腰三角形的性质.矩形的性质.勾股定理等知识,解题的关键在于能够进行正确的讨论.5.菱形具有而矩形不具有性质是()A.对角线相等B.对角线互相平分C.对角线互相垂直D.对角线平分且相等答案:C知识点:菱形的性质;矩形的性质解析:解答:解:A.菱形的对角线不一定相等,矩形的对角线一定相等,故本选项错误;B.菱形和矩形的对角线均互相平分,故本选项错误;C.菱形的对角线互相垂直,而矩形的对角线不一定互相垂直(互相垂直时是正方形),故本选项正确;D.菱形和矩形的对角线均互相平分且相等,故本选项错误.故选C.分析:由于菱形的对角线互相垂直平分,矩形的对角线互相平分且相等,据此进行比较从而得到答案.本题考查矩形与菱形的性质的区别:矩形的对角线互相平分且相等,菱形的对角线互相平分.垂直且平分每一组对角.6.在矩形ABCD中,AB=1,AD=3,AF平分∠DAB,过C点作CE⊥BD于E,延长AF.EC交于点H,下列结论中:①AF=FH;②BO=BF;③CA=CH;④BE=3ED.正确的是()A.②③B.③④C.①②④D.②③④答案:D知识点:矩形的性质;角平分线的性质;等腰三角形的性质;等边三角形的性质。
人教版八年级下册数学试题:18.2.1矩形专题练习试题(无答案)

矩 形一、定义:1、 是矩形。
2、边的性质有: 。
。
3、角的性质有: 。
4、对角线的性质有: 。
矩形判定方法:5、从定义的角度来看判定定理有: 。
6、从角的角度来看判定定理有: 。
7、从对角线角度来看判定定理有: 。
8、直角三角形斜边上的中线等于 。
9、30º的角所对的直角边等于 。
二、填空选择题1、矩形的两条对角线的夹角为60°,较短的边长为4.5厘米,则对角线长为 。
2、已知矩形的一条对角线与一边的夹角为30°,则矩形两条对角线相交所得的四个角的度数分别为 、 、 、 .3、已知矩形的一条对角线长为10cm ,两条对角线的一个交角为120°,则矩形的边长分别为 cm , cm , cm , cm .4、如图、在矩形ABCD 中,点E 、F 分别在边AB 、CD 上,BF ∥DE 。
若AD=12cm ,AB=7cm ,且AE ︰EB= 5︰2,则四边形EBFD 的面积为 2cm 6、如图、周长为68cm 的矩形ABCD 被分成7个全等的矩形,则矩形的面积为 。
7、如图3,有一个长方形纸片沿EF 折叠后,点D ,C 分别落在G ,H 的位置上,若∠EFB=650,则∠AEG 等于( )A :500 B :550 C :600 D :6508、已知:如图,矩形ABCD 中,AB=3cm ,AD=4cm ,P 为AD 上的一动点,PE ⊥AC,PF ⊥BD ,则PE+PF 的值为( )A :512 B :2 C :25 D :513 9、已知:如图,矩形ABCD 中,DE ⊥AC 于E ,∠ADE ︰∠EDC=3︰2则∠BDE 的度数是( )A :150B :360C :540D :18010、如图,矩形纸片ABCD 中,AD =9,AB =3,将其折叠,使点D 与点B 重合,折痕为EF ,那么折痕EF 的长为________.11、矩形纸片ABCD 中,AB=8cm ,把矩形纸片沿直线AC 折叠,点B 落在点E 处,AE 交DC 于点F ,若AF=cm 425,则AD 的长为( )A 、cm 4B 、cm 5C 、cm 6D 、cm 712、矩形ABCD 中,AB=8cm ,AD=10cm ,点E 在CD 上,将△ADE 沿AE 折叠,使D 落在BC 边上的F 处, EC 长 。
矩形的判定(分层作业)-八年级数学下册(人教版)(解析版)

人教版初中数学八年级下册18.2.2矩形的判定同步练习夯实基础篇一、单选题:1.下列给出的判定中不能判定一个四边形是矩形的是()A .有三个角是直角B .对角线互相平分且相等C .对角线互相垂直且相等D .一组对边平行且相等,一个角是直角【答案】C【分析】利用矩形的判定方法即可对各选项进行判断,得到符合题意的选项.【详解】解:A 、有三个角是直角的四边形是矩形,该选项说法正确,不合题意;B 、对角线互相平分且相等的四边形是矩形,该选项说法正确,不合题意;C 、对角线互相平分且相等的四边形是矩形,该选项原说法错误,符合题意;D 、一组对边平行且相等,一个角是直角的四边形是矩形,该选项说法正确,不合题意;故选:C .【点睛】此题考查了矩形的判定,矩形的判定方法有:有一个角是直角的平行四边形是矩形;三个角都是直角的四边形是矩形;对角线相等的平行四边形是矩形,熟练掌握矩形的判定方法是解本题的关键.2.如图,四边形ABCD 是平行四边形,添加下列条件,能判定这个四边形是矩形的是()A .=BAD ABCB .AB BDC .AC BD D .=A B BC【答案】A【分析】由矩形的判定和平行四边形的性质分别对各个选项进行判断即可;【详解】解:A 、∵四边形ABCD 是平行四边形,+=180°ABC BAC ,=ABC BAC ∵,==90°ABC BAC ,平行四边形ABCD 是矩形,故选项A 符合题意;B 、∵四边形ABCD 是平行四边形,AB BD ,++=180°BAD ABD DBC ,90ABD ,90°BAD ,选项B 不能判定这个平行四边形为矩形,故选项B 不符合题意;C 、∵四边形ABCD 是平行四边形,AC BD ,平行四边形ABCD 是菱形,故选项C 不符合题意;D 、∵四边形ABCD 是平行四边形,=A B BC ,平行四边形ABCD 是菱形,故选项D 不符合题意;故选:A .【点睛】本题考查了矩形的判定、菱形的判定、平行四边形的性质等知识,熟练掌握矩形的判定是解题的关键.3.如图,矩形ABCD 的对角线AC ,BD 相交于点O ,过点O 作OE AC 交AD 于E ,若4,8AB BC ,则AE 的长为()A .3B .4C .5D .【答案】C 【分析】根据矩形ABCD ,得到AD =BC =8,∠ADC =90°,OA =OC ,从而得证△AOE ≌△COE ,AE =CE ,设AE =x ,则EC =x ,DE =8-x ,利用勾股定理计算即可.【详解】如图,连接EC ,∵矩形ABCD ,OE AC ,4,8AB BC ,∴AD =BC =8,AB =CD =4,∠ADC =90°,OA =OC ,∵OE AC ,∴∠AOE =∠COE =90°,∵OE=OE ,∴△AOE ≌△COE ,AE =CE ,设AE =x ,则EC =x ,DE =8-x ,在Rt △DEC 中,222CE DE CD ,∴222(8)4x x ,∴x =5,∴AE =5,故选C.【点睛】本题考查了矩形的性质,三角形全等的判定和性质,勾股定理,熟练掌握矩形的性质,三角形全等,勾股定理是解题的关键.4.如图,平行四边形ABCD的对角线AC,BD相交于点O, AOB是等边三角形,OE BD交BC于点E,CD=2,则CE的长为()DA.1B C.235.如图,在四边形ABCD 中,对角线AC BD ,垂足为O ,点E 、F 、G 、H 分别为边AD 、AB 、BC 、CD 的中点.若8AC ,6BD ,则四边形EFGH 的面积为()A .48B .24C .32D .12∴EF ∥GH ,FG ∥HE 且EF ⊥FG .四边形EFGH 是矩形.∴四边形EFGH 的面积=EF •EH =3×4=12,即四边形EFGH 的面积是12.故选:D .【点睛】本题考查的是中点四边形.解题时,利用了矩形的判定以及矩形的性质,矩形的判定定理有:(1)有一个角是直角的平行四边形是矩形;(2)有三个角是直角的四边形是矩形;(3)对角线互相平分且相等的四边形是矩形.6.如图,在四边形ABCD 中,点E ,F ,G ,H 分别是AD ,BD ,BC ,CA 的中点,若四边形EFGH 是矩形,则四边形ABCD 需满足的条件是()A .AB DCB .AC BD C .AC BD D .AB DC∵//EF AB ,//HE CD ,∴AB CD ,故选:A .【点睛】本题考查矩形的判定定理,三角形中位线的定义和性质,关键是利用三角形中位线定理证明四边形EFGH 是平行四边形,再利用 FE HE 推出AB CD .7.如图,在直角三角形ABC 中,90ACB ,3AC ,4BC ,点M 是边AB 上一点(不与点A ,B 重合),作ME AC 于点E ,MF BC 于点F ,则EF 的最小值是()A .2B .2.4C .2.5D .2.6【答案】B 【分析】根据题意可证四边形ECFM 是矩形,得EF =CM ,再由垂线段最短得CM 最短进而可得EF 最短,最后进行计算即可.【详解】连接CM ,∵ME AC ,MF BC ,∴ MEC = MFC =90°,当CM AB ,1122ABC S AC BC AB CM △,∴113422CM AB , ABC 中,二、填空题:8.如图,平行四边形ABCD中,对角线AC,BD相交于点O,欲使四边形ABCD变成矩形,则还需添加______.(写出一个合适的条件即可)【答案】AC=BD(答案不唯一)【分析】根据矩形的判定条件求解即可.【详解】解:添加条件AC=BD,利用如下:∵四边形ABCD是平行四边形,∴OA=OC,OB=OD,又∵AC=BD,∴平行四边形ABCD是矩形,故答案为:AC=BD(答案不唯一).【点睛】本题主要考查了矩形的判定,熟知矩形的判定条件是解题的关键.9.一个木匠要制作矩形的踏板.他在一个对边平行的长木板上分别沿与长边垂直的方向锯两次,就能得到矩形踏板.理由是______.【答案】三个角都是直角的四边形是矩形(或:“有一个角是直角的平行四边形是矩形”)【分析】使用矩形的判定定理,有三个角是直角的四边形是矩形【详解】因为木板的对边平行,在进行两次锯开时都是沿着垂直于对边的方向,所以会出现4个直角,有三个角是直角的四边形是矩形.故答案是三个角是直角的四边形是矩形.【点睛】本题考查矩形的判定,需要熟记矩形的判定定理并灵活运用.10.如图,顺次连接四边形ABCD 各边中点得四边形EFGH ,要使四边形EFGH 为矩形,AC 与BD 应满足的的条件是___________.,,,E F G H ∵分别为,,CD AD AB 1,2EF AC GH EF GH AC 四边形EFGH 为平行四边形,要使平行四边形EFGH 为矩形,则AC BD,.故答案为:AC BD【点睛】本题考查了三角形中位线定理、平行四边形的判定、矩形的判定,熟练掌握三角形中位线定理是解题关键.AB CD,PM、PN、QM、QN分别为角平分线,则四边形PMQN是__________.11.如图,//∴四边形PMQN是平行四边形,∵∠NPM=90°,∴四边形PMQN是矩形.故答案为:矩形.【点睛】此题主要考查了矩形的判定和平行线的性质,解题关键是根据角平分线和平行线的性质得出90°角和平行四边形.12.如图,矩形ABCD中,BE⊥AC于点E,若∠ACB=23°,则∠DBE=_______度.【答案】44【分析】由矩形的性质可知∠OBC=∠ACB=23°,则可求得∠AOB度数,由直角三角形的性质可得∠DBE的度数.【详解】解:∵四边形ABCD是矩形∴AC=BD,OA=OC,OB=OD,∴OB=OC,∴∠ACB=∠OBC=23°,∵∠AOB=∠ACB+∠OBC=46°,且BE⊥AC,∴∠DBE=44°.故答案为:44【点睛】本题主要考查矩形的性质,等腰三角形的性质,利用矩形的对角线相等且平分求得∠OBC的度数是解题的关键.13.如图,在面积为36的四边形ABCD中,∠ADC=∠ABC=90°,AD=CD,DP⊥AB于点P,则DP的长是_____【答案】6【分析】作DE⊥BC,交BC延长线于E,如图,则四边形BEDP为矩形,再利用等角的余角相等得到∠ADP=∠CDE,则可利用“AAS”证明△ADP≌△CDE,得到DP=DE,S△ADP=S△CDE,所以四边形BEDP为正方形,S四边形ABCD=S正方形BEDP,根据正方形的面积公式得到DP2=36,易得DP=6.【详解】如图,作DE⊥BC,交BC延长线于E,∵DP⊥AB,ABC=90°,∴四边形BEDP为矩形,∴∠PDE=90°,即∠CDE+∠PDC=90°,∵∠ADC=90°,即∠ADP+∠PDC=90°,∴∠ADP=∠CDE,在△ADP和△CDE中APD CED ADP CDE AD DC===,∴△ADP ≌△CDE ,∴DP =DE ,S △ADP =S △CDE ,∴四边形BEDP 为正方形,S 四边形ABCD =S 正方形BEDP ,∴DP 2=36,∴DP =6.故答案为6.【点睛】本题考查了全等三角形的判定与性质:全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具.在判定三角形全等时,关键是选择恰当的判定条件.也考查了正方形和矩形的性质.本题的关键的作辅助线构造两个全等的三角形.三、解答题:14.如图,在ABC 中,AB AC ,AD 平分BAC 交BC 于点D ,分别过点A 、D 作AE BC ∥、DE AB ∥,AE 与DE 相交于点E ,连接CE .(1)求证:AE BD ;(2)求证:四边形ADCE 是矩形.【答案】(1)见解析(2)见解析【分析】(1)根据AE BC ∥、DE AB ∥证明四边形ABDE 为平行四边形,即可得出答案;(2)由等腰三角形的性质得出BD CD ,AD BC ,得出AE CD ,90ADC ,先证出四边形ADCE 是平行四边形.再证明四边形ADCE 是矩形即可.【详解】(1)证明:∵AE BC ∥、DE AB ∥,∴四边形ABDE 是平行四边形,∴AE BD ;(2)证明:∵AB AC ,AD 平分BAC ,∴BD CD ,AD BC ,∵AE BD ,∴AE CD ,∵AE CD ∥,∴四边形ADCE 是平行四边形,∵AD BC ,∴90ADC∴四边形ADCE 是矩形.【点睛】本题主要考查了平行四边形的判定与性质、矩形的判定、等腰三角形的性质;熟练掌握平行四边形的判定与性质,由等腰三角形的性质得出BD CD ,AD BC ,是解决问题的关键.15.如图,四边形ABCD 是平行四边形,过点D 作DE AB 于点E ,点F 在边CD 上,CF AE ,连接AF ,BF .(1)求证:四边形BFDE 是矩形.(2)若AF 是DAB 的平分线.若6CF ,8BF ,求DC 的长.DAF DFA ,10AD FD ,10616DC DF FC .【点睛】本题考查了平行四边形的性质,矩形的性质和判定,角平分线的定义,等角对等边,能综合运用定理进行推理是解此题的关键.16.如图,在四边形ABCD 中,AD BC ,90ABC BCD .对角线,AC BD 交于点,O DE 平分ADC 交BC 于点E ,连接OE .(1)求证:四边形ABCD 是矩形;(2)若2CD ,DBC =30 ,求△BED 的面积.17.如图,在ABCD Y 中,对角线AC ,BD 相交于点O ,AE BD 于点E ,DF AC 于点F ,且AE DF .(1)求证:四边形ABCD 是矩形.(2)若:4:5BAE EAD ,求EAO 的度数.∴904050OBA OAB ,∴504010EAO OAB BAE .【点睛】本题考查了矩形的判定与性质、平行四边形的性质、全等三角形的判定与性质、等腰三角形的性质等知识;熟练掌握矩形的判定与性质,证明三角形全等是解题的关键.能力提升篇一、单选题:1.如图,点P 是Rt ABC 中斜边(AC 不与A ,C 重合)上一动点,分别作PM AB 于点M ,作PN BC 于点N ,点O 是MN 的中点,若9AB ,12BC ,当点P 在AC 上运动时,则BO 的最小值是()A .3B .3.6C .3.75D .4【点睛】本题主要考查矩形的判定与性质,垂线段最短,勾股定理及面积法等知识,熟练掌握矩形的判定与性质是解题的关键.2.如图,在Rt ABC △中,90A ,M 为BC 的中点,H 为AB 上一点,过点C 作CG AB ∥,交HM 的延长线于点G ,若10AC ,8AB ,则四边形ACGH 周长的最小值是()A .28B .26C .22D .18【答案】A 【分析】通过证明BMH CMG △≌△可得BH CG ,可得四边形ACGH 的周长即为AB AC GH ,进而可确定当MH AB 时,四边形ACGH 的周长有最小值,通过证明四边形ACGH 为矩形可得H G 的长,进而可求解.【详解】解:CG AB ∥∵,B MCG ,M ∵是BC 的中点,BM CM ,在BMH V 和CMG V 中,B MCG BM CM BMH CMG,()BMH CMG ASA △≌△,HM GM ,BH CG ,10AC ∵,8AB ,四边形ACGH 的周长18AC CG AH GH AB AC GH GH ,当GH 最小时,即MH AB 时四边形ACGH 的周长有最小值,90A ∵,MH AB ,GH AC ∥,四边形ACGH 为矩形,10GH ,四边形ACGH 的周长最小值为181028 ,故选:A .【点睛】本题主要考查轴对称 最短路径问题,全等三角形的判定与性质,确定GH 的值是解题的关键.3.在矩形ABCD 中,对角线AC 、BD 相交于点O ,AE 平分BAD 交BC 于点E ,15CAE .连接OE ,则下面的结论:①DOC 是等边三角形;②BOE △是等腰三角形;③2BC AB ;④150 AOE ;⑤AOE COE S S ,其中正确的结论有()A.2个B.3个C.4个D.5个二、填空题:4.如图,在平行四边形ABCD 中,90A ,10AD ,=8AB ,点P 在边AD 上,且BP BC ,点M 在线段BP 上,点N 在线段BC 的延长线上,且=PM CN ,连接MN 交CP 于点F ,过点M 作ME CP 于E ,则=EF ___________.,根据等角对等边可得5.如图,在矩形ABCD 中,4AB cm ,12AD cm ,点P 从点A 向点D 以每秒1cm 的速度运动,Q 以每秒4cm 的速度从点C 出发,在B 、C 两点之间做往返运动,两点同时出发,点P 到达点D 为止(同时点Q 也停止),这段时间内,当运动时间为______时,P 、Q 、C 、D 四点组成矩形.【答案】2.4s 或4s 或7.2s【分析】根据已知可知:点Q 将由,C B C B C 根据矩形的性质得到AD ∥BC ,设过了t 秒,当AP=BQ 时,P 、Q 、C 、D 四点组成矩形,在点Q 由C B 的过程中,则PA=t ,BQ=12-4t ,求得t=2.4(s ),在点Q 由B C 的过程中,t=4(t-3),求得t=4(s ),在点Q 再由C B 中,t=12-4(t-6),求得t=7.2(s ),在点Q 再由B C 的过程中,t=4(t-9),t=13(s ),故此舍去,从而得到结论.【详解】解:根据已知可知:点Q 由,C B C B C在点Q第一次到达点B过程中,∵四边形ABCD是矩形,∴AD∥BC,,则四边形APQB是矩形,则以P、Q、C、D四点为顶点组成矩形.若AP BQ设过了t秒,则PA=t,BQ=12-4t,∴t=12-4t,∴t=2.4(s),的过程中,在点Q由B C设过了t秒,则PA=t,BQ=4(t-3),t=4(t-3),解得:t=4(s),在点Q再由C B过程中,设过了t秒,则PA=t,BQ=12-4(t-6),t=12-4(t-6),解得:t=7.2(s),的过程中,在点Q再由B C设过了t秒,则PA=t,BQ=4(t-9),t=4(t-9),解得:t=13(s)>12(s),故此舍去.故答案为:2.4s或4s或7.2s;【点睛】本题考查了矩形的性质与判定,此题属于动点型题目.解题时要注意数形结合与方程思想的应用.三、解答题:6.如图,在平行四边形ABCD 中,过点D 作DE AB 于点E ,点F 在边CD 上,CF AE ,连接AF BF ,.(1)求证:四边形BFDE 是矩形.(2)已知60DAB AF ,是DAB 的平分线,若6AD ,则□ABCD 的面积为______.7.如图,在Rt ABC 中,90,5,3ACB AB BC ,D 是AC 的中点,CE AB ∥,动点P 以每秒1个单位长度的速度从点B 出发向点A 移动,连接PD 并延长交CE 于点F ,设点P 移动的时间为t 秒.(1)求AB与CE之间的距离;(2)当t为何值时,四边形PBCF为平行四边形;(3)当4PF 时,求t的值.【点睛】此题考查了平行四边形的判定与性质、矩形的判定与性质以及勾股定理的运用,熟练掌握平行四边形的判定与性质是解本题的关键.。
人教版数学八年级下册:《18.2.2矩形的判定》练习含答案

《矩形的判定》练习题一、选择——基础知识运用1.在四边形ABCD中,AC、BD交于点O,在下列各组条件中,不能判定四边形ABCD为矩形的是()A.AB=CD,AD=BC,AC=BDB.AO=CO,BO=DO,∠A=90°C.∠A=∠C,∠B+∠C=180°,AC⊥BDD.∠A=∠B=90°,AC=BD2.检查一个门框是否为矩形,下列方法中正确的是()A.测量两条对角线,是否相等B.测量两条对角线,是否互相平分C.测量门框的三个角,是否都是直角D.测量两条对角线,是否互相垂直3.在四边形ABCD中,AC与BD相交于点O,且OA=OC,OB=OD.如果再增加条件AC=BD,此四边形一定是()A.正方形B.矩形C.菱形D.都有可能4.有下列说法:①四个角都相等的四边形是矩形;②有一组对边平行,有两个角为直角的四边形是矩形;③两组对边分别相等且有一个角为直角的四边形是矩形;④对角线相等且有一个角是直角的四边形是矩形;⑤对角线互相平分且相等的四边形是矩形;⑥一组对边平行,另一组对边相等且有一角为直角的四边形是矩形.其中,正确的个数是()A.2个B.3个C.4个D.5个5.已知:线段AB,BC,∠ABC=90°.求作:矩形ABCD.以下是甲、乙两同学的作业:对于两人的作业,下列说法正确的是()A.两人都对B.两人都不对C.甲对,乙不对D.甲不对,乙对)二、解答——知识提高运用6.已知,平行四边形ABCD中,AB=5,AD=12,BD=13.求证:平行四边形ABCD是矩形。
7.如图所示,在□ABCD中,E为AD的中点,△CBE是等边三角形,求证:□ABCD是矩形。
8.已知:在△ABC中,∠A=90°,D,E分别是AB,AC上任意一点,M,N,P,Q分别是DE,BE,BC,CD的中点,求证:四边形PQMN是矩形。
9.如图,□ABCD与□ABEF中,BC=BE,∠ABC=∠ABE,求证:四边形EFDC是矩形。
【初中数学】人教版八年级下册第2课时 矩形的判定(练习题)

人教版八年级下册第2课时矩形的判定(356)1.如图,四边形ABCD的对角线AC,BD相交于点O,AD//BC,AC=BD.试添加一个条件:,使四边形ABCD为矩形.2.如图,已知平行四边形ABCD中,E是BC的中点,连接AE并延长,交DC的延长线于点F,且AF=AD,连接BF,求证:四边形ABFC是矩形.3.如图,平行四边形ABCD中,延长边AB到点E,使BE=AB,连接DE,BD和EC,设DE交BC于点O,∠BOD=2∠A.求证:四边形BECD是矩形.4.如图,在△ABC中,AB=3,AC=4,BC=5,P为边BC上一动点,PE⊥AB于点E,PF⊥AC于点F,M为EF的中点,则AM的最小值为()A.54B.52C.53D.655.矩形ABCD中,AB=2cm,BC=5cm,P,Q分别为AD,BC上的动点,点P从点D出发向点A运动,运动到点A停止,点Q同时从点B出发向点C运动,运动到点C停止,点P,Q的速度都是1cm/s,设点P,Q运动的时间为t s.(1)如图①,连接PQ,AQ,CP,当t=四边形ABQP是矩形;(2)如图②,当点P,Q运动1s时,连接AQ,CP,BP,DQ,AQ交BP于点H,CP交DQ于点F,得到四边形HPFQ.求证:四边形HPFQ是矩形6.如图,以△ABC(∠BAC≠60∘)的三边为边在BC的同一侧分别作三个等边三角形,即△ABD,△BCE,△ACF,请回答下列问题:(1)四边形ADEF是什么特殊形状的四边形?(2)当△ABC满足什么条件时,四边形ADEF是矩形?(3)为什么题中有条件∠BAC≠60∘?7.如图,在△ABC中,AB=AC,D为BC的中点,AE//BC,DE//AB.求证:四边形ADCE 为矩形.8.如图,在四边形ABCD中,AB//CD,∠BAD=90∘,AB=5,BC=12,AC=13.求证:四边形ABCD是矩形.9.已知:如图,在△ABC中,AB=AC,AD⊥BC,垂足为D,AN是△ABC的外角∠CAM的平分线,CE⊥AN,垂足为E,猜想四边形ADCE的形状,并给予证明.10.如图所示,四边形ABCD的对角线互相平分.如果要使它成为矩形,那么需要添加的条件可以是()A.AB=CDB.AD=BCC.AB=BCD.AC=BD11.如图,在平行四边形ABCD中,请添加一个条件:,使得平行四边形ABCD成为矩形.12.如图,工人师傅砌门时,要想检验门框ABCD是否符合设计要求(即门框是不是矩形),在确保两组对边分别平行的前提下,只要测量出对角线AC,BD的长度,然后看它们是否相等就可以判断了.(1)当AC(填“等于”或“不等于”)BD时,门框符合要求;(2)这种做法的根据是.13.如图所示,四边形ABCD是平行四边形,AC,BD交于点O,∠1=∠2. 求证:四边形ABCD是矩形.参考答案1.【答案】:答案不唯一,如AD=BC等【解析】:四边形ABCD的对角线AC=BD,所以只需添加条件使四边形ABCD是平行四边形即可.因为AD//BC,所以可以添加AD=BC,即一组对边平行且相等的四边形是平行四边形2.【答案】:证明:∵四边形ABCD是平行四边形,∴AB//CD,AD=BC,∴∠BAE=∠CFE,∠ABE=∠FCE.∵E为BC的中点,∴EB=EC,∴△ABE≌△FCE,∴AB=CF.∵AB//CF,∴四边形ABFC是平行四边形.∵AF=AD,∴BC=AF,∴四边形ABFC是矩形3.【答案】:证明:在平行四边形ABCD中,AD=BC,AB=CD,AB//CD,则BE//CD.又∵AB=BE,∴BE=CD,∴四边形BECD为平行四边形,∴OD=OE,OC=OB.∵四边形ABCD为平行四边形,∴∠A=∠BCD.又∵∠BOD=2∠A,∠BOD=∠OCD+∠ODC,∴∠OCD=∠ODC,∴OC=OD,∴OC+OB=OD+OE,即BC=ED,∴平行四边形BECD为矩形4.【答案】:D【解析】:连接AP.∵在△ABC中,AB=3,AC=4,BC=5,∴AB2+AC2=BC2,即∠BAC=90∘.又∵PE⊥AB于点E,PF⊥AC于点F,∴四边形AEPF是矩形,∴EF=AP.∵M是EF的中点,∴AM=12EF=12AP.∵AP的最小值为直角三角形ABC斜边上的高,等于125,∴AM的最小值是655(1)【答案】52【解析】:∵四边形ABCD是矩形,∴AD=BC=5,AD//BC,∠B=90∘,当AP=BQ时,四边形ABQP是矩形,即5−t=t,解得t=52(2)【答案】证明:在矩形ABCD中,AD=BC,AD//BC.∵当t=1时,PD=BQ=1cm,∴四边形DPBQ是平行四边形,∴BP//DQ.∵AD=BC,AD//BC,DP=BQ,∴AP=CQ,AP//CQ,∴四边形APCQ是平行四边形,∴AQ//CP,∴四边形HPFQ是平行四边形.∵在矩形ABCD中,∠ADC=∠ABQ=90∘,AD=BC=5cm,AB=CD=2cm,由勾股定理得:CP=√5cm,BP=2√5cm,∴BP2+CP2=BC2,∴∠BPC=90∘,∴四边形HPFQ是矩形6(1)【答案】解:四边形ADEF是平行四边形.理由:∵△ABD,△EBC都是等边三角形,∴AD=BD=AB,BC=BE=EC, ∠DBA=∠EBC=60∘∴∠DBE+∠EBA=∠ABC+∠EBA,∴∠DBE=∠ABC.在△DBE和△ABC中,∵BD=BA,∠DBE=∠ABC,BE=BC,∴△DBE≌△ABC,∴DE=AC.又∵△ACF是等边三角形,∴AC=AF,∴DE=AF.同理可证:AD=EF,∴四边形ADEF是平行四边形(2)【答案】∵四边形ADEF是矩形,∴∠DAF=90∘,∴∠BAC=360∘−∠DAF−∠DAB−∠FAC=360∘−90∘−60∘−60∘=150∘,∴当∠BAC=150∘时,四边形ADEF是矩形(3)【答案】当∠BAC=60∘时,以A,D,E,F为顶点的四边形不存在.理由如下:若∠BAC=60∘,则∠DAF=360∘−∠BAC−∠DAB−∠FAC=360∘−60∘−60∘−60∘=180∘.此时,A,D,E,F四点共线,∴此时以A,D,E,F为顶点的四边形不存在7.【答案】:证明:∵AE//BC,DE//AB,∴四边形ABDE是平行四边形,∴AE=BD.∵D为BC的中点,∴BD=DC,∴AE=DC.∵AE//DC,∴四边形ADCE是平行四边形.又∵AB=AC,D为BC的中点,∴AD⊥CD,∴平行四边形ADCE为矩形8.【答案】:证明:四边形ABCD中,AB//CD,∠BAD=90∘,∴∠ADC=90∘.又∵△ABC中,AB=5,BC=12,AC=13,满足132=52+122,∴△ABC是直角三角形,且∠B=90∘,∴四边形ABCD是矩形9.【答案】:解:四边形ADCE是矩形.证明:∵AB=AC,AD⊥BC,∴∠BAD=∠CAD.∵AN是△ABC的外角∠CAM的平分线,∴∠MAN=∠CAN,∴∠DAN=12∠BAC+12∠MAC=90∘.∵CE⊥AN,AD⊥BC,∴∠ADC=∠AEC=90∘,∴四边形ADCE是矩形.10.【答案】:D【解析】:对角线互相平分的四边形是平行四边形,要想使其成为矩形,只需满足对角线相等或有一个角是直角即可11.【答案】:答案不唯一,如∠A=90∘12.【答案】:等于;对角线相等的平行四边形是矩形13.【答案】:∵∠1=∠2,∴BO=CO,即2BO=2CO.∵四边形ABCD是平行四边形,∴AO=CO,BO=DO,∴AC=2CO,BD=2BO,∴AC=BD.∵四边形ABCD是平行四边形,∴四边形ABCD是矩形【解析】:∵∠1=∠2,∴BO=CO,即2BO=2CO.∵四边形ABCD是平行四边形,∴AO=CO,BO=DO,∴AC=2CO,BD=2BO,∴AC=BD.∵四边形ABCD是平行四边形,∴四边形ABCD是矩形。
人教版八年级下册数学 18.2.1 矩形 同步测试题(含答案)

18.2.1 矩形同步测试题1.如图,四边形ABCD的对角线互相平分,要使它变为矩形,需要添加的条件是( )A.AB=CDB.AD=BCC.∠AOB=45°D.∠ABC=90°2.如图,小贤为了体验四边形的不稳定性,将四根木条用钉子钉成一个矩形框架ABCD,B与D两点之间用一根橡皮筋拉直固定,然后向右扭动框架,观察所得四边形的变化,下列判断错误的是( )A.四边形ABCD由矩形变为平行四边形B.BD的长度增大C.四边形ABCD的面积不变D.四边形ABCD的周长不变3.如图,在矩形ABCD中(AD>AB),点E是BC上一点,且DE=DA,AF⊥DE,垂足为点F,在下列结论中,不一定正确的是( )A.△AFD≌△DCEB.AF=ADC.AB=AFD.BE=AD-DF4.如图,点E是矩形ABCD的边AD延长线上的一点,且AD=DE,连接BE交CD于点O,连接AO,下列结论中不正确的是( )A.△AOB≌△BOCB.△BOC≌△EODC.△AOD≌△EODD.△AOD≌△BOC5.如图,在矩形ABCD中,AB=3,将△ABD沿对角线BD折叠,得到△EBD,DE与BC 交于点F,∠ADB=30°,则EF=( )A. B.2 C.3 D.36.如图,在矩形ABCD中,对角线AC,BD交于点O,以下说法错误的是( )A.∠ABC=90°B.AC=BDC.OA=OBD.OA=AD7.(2016·菏泽)在▱ABCD中,AB=3,BC=4,连接AC,BD,当▱ABCD的面积最大时,下列结论正确的有( )①AC=5;②∠BAD+∠BCD=180°;③AC⊥BD;④AC=BD.A.①②③B.①②④C.②③④D.①③④8.如图,P是矩形ABCD的对角线AC的中点,E是AD的中点.若AB=6,AD=8,则四边形ABPE的周长为( )A.14B.16C.17D.189.如图,在Rt△ABC中,∠ACB=90°,D,E分别为AC,AB边的中点,连接DE,CE.则下列结论中不一定正确的是( )A.ED∥BCB.ED⊥ACC.∠ACE=∠BCED.AE=CE10.如图,在矩形ABCD中,O为AC的中点,EF过O点且EF⊥AC分别交DC,AB于点F,E,点G是AE的中点,且∠AOG=30°,则下列结论正确的有( )①DC=3OG;②OG=BC;③△OGE是等边三角形;④S△AOE=S矩形ABCD.A.1个B.2个C.3个D.4个11.图,AB=6,O是AB的中点,直线l经过点O,∠1=120°,P是直线l上一点,当△APB 为直角三角时,AP= .12.如图,在矩形ABCD中,AC与BD交于点O,BE⊥AC,CF⊥BD,垂足分别为E,F.求证:BE=CF.13.如图,AC为矩形ABCD的对角线,将边AB沿AE折叠,使点B落在AC上的点M处,将边CD沿CF折叠,使点D落在AC上的点N处.(1)求证:四边形AECF是平行四边形;(2)若AB=6,AC=10,求四边形AECF的面积.14.如图所示,以△ABC的三边为边在BC的同侧分别作三个等边三角形,即△ABD,△BCE,△ACF,连接DE,EF.请回答下列问题:(1)四边形ADEF是什么四边形?并说明理由.(2)当△ABC满足什么条件时,四边形ADEF是矩形?15.如图,在矩形ABCD中,AB=12 cm,BC=6 cm,点P沿AB边从点A开始向点B 以2 cm/s的速度移动,点Q沿DA边从点D开始向点A以1 cm/s的速度移动,如果P,Q同时出发,用t(s)表示移动的时间(0≤t≤6).(1)当t为何值时,△QAP为等腰三角形?(2)求四边形QAPC的面积,并探索一个与计算结果有关的结论.参考答案1.【答案】D解:因为四边形ABCD的对角线互相平分,所以四边形ABCD为平行四边形,A,B 两选项为平行四边形具有的性质,C选项添加后也不一定是矩形,根据矩形的定义知D可以.故选D.2.【答案】C3.【答案】B4.【答案】A解:∵四边形ABCD是矩形,∴AD=BC,∠ADO=∠EDO=∠C=90°.∵AD=DE,∴BC=DE.在△BOC与△EOD中,∠BOC=∠DOE,∠C=∠EDO=90°,BC=DE,∴△BOC≌△EOD.故B选项正确.在△AOD和△EOD中,AD=DE,∠ADO=∠EDO=90°,OD=OD,∴△AOD≌△EOD.故C选项正确.由B,C知△AOD≌△BOC,故D选项正确.而A选项中两三角形明显不全等.5.【答案】A6.【答案】D7.【答案】B解:当▱ABCD的面积最大时,四边形ABCD为矩形,得出∠BAD=∠ABC=∠BCD=90°,AC=BD,根据勾股定理求出AC,即可得出结论.8.【答案】D 9.【答案】C10.【答案】C解:根据直角三角形斜边上的中线等于斜边的一半可得OG=AG=GE=AE,再根据等边对等角可得∠OAG=30°,根据直角三角形两锐角互余求出∠GEO=60°,从而判断出△OGE是等边三角形,判断出③正确;设AE=2a,则OE=a,利用勾股定理求出AO的长,从而得到AC的长,再求出BC的长,然后利用勾股定理求出AB=3a,从而判断出①正确,②错误;再根据三角形的面积公式和矩形的面积公式列式判断出④正确.11.【答案】3或3或3解:当∠APB=90°时,分两种情况讨论.情况一:如图①,∵O为AB中点,∴PO=AB,AO=BO.∴PO=BO.∵∠1=120°,∴∠PBA=30°.∴AP=AB=3;情况二:如图②,∵AO=BO,∠APB=90°,∴PO=BO.∵∠1=120°,∴∠BOP=60°.∴△BOP为等边三角形.∴BP=AB=3.∴AP===3.当∠BAP=90°时,如图③,∵∠1=120°,∴∠AOP=60°,∴∠APO=30°,∴PO=2AO=6.∴AP===3.当∠ABP=90°时,如图④,∵∠1=120°,∴∠BOP=60°,∴∠BPO=30°,∴PO=2BO=6.∴BP===3.∴AP===3.12.证明:∵四边形ABCD为矩形,∴AC=BD.∴BO=CO.∵BE⊥AC于E,CF⊥BD于F,∴∠BEO=∠CFO=90°.又∵∠BOE=∠COF,∴△BOE≌△COF.∴BE=CF.13.(1)证明:由折叠知AM=AB,CN=CD,∠FNC=∠D=90°,∠AME=∠B=90°,∴∠ANF=90°,∠CME=90°.∵四边形ABCD为矩形,∴AB=CD,AD∥BC.∴∠FAN=∠ECM,AM=CN.∴AM-MN=CN-MN,即AN=CM.在△ANF和△CME中,∴△ANF≌△CME(ASA).∴AF=CE.又∵AF∥CE,∴四边形AECF是平行四边形.(2)解:∵AB=6,AC=10,∴BC=8.设CE=x,则EM=BE=8-x,CM=10-6=4. 在Rt△CEM中,(8-x)2+42=x2,解得x=5. ∴四边形AECF的面积为CE·AB=5×6=30.14.解:(1)四边形ADEF是平行四边形.理由:∵△ABD,△BEC都是等边三角形,∴BD=AB,BE=BC,∠DBA=∠EBC=60°.∴∠DBE=60°-∠EBA,∠ABC=60°-∠EBA, ∴∠DBE=∠ABC.∴△DBE≌△ABC.∴DE=AC,又∵△ACF是等边三角形,∴AC=AF.∴DE=AF.同理可得△ABC≌△FEC,∴EF=BA=DA.∵DE=AF,DA=EF,∴四边形ADEF为平行四边形.(2)若四边形ADEF为矩形,则∠DAF=90°,∵∠DAB=∠FAC=60°,∴∠BAC=360°-∠DAB-∠FAC-∠DAF=360°-60°-60°-90°=150°.∴当△ABC满足∠BAC=150°时,四边形ADEF是矩形.15.解:(1)由题意得DQ=t cm,AP=2t cm,∴AQ=(6-t)cm.若△QAP为等腰三角形,则只能是AQ=AP,于是6-t=2t,∴t=2.故当t=2时,△QAP为等腰三角形.(2)S四边形QAPC=S矩形ABCD-S△CDQ-S△BPC=12×6-×12t-×(12-2t)×6=72-6t-36+6t=36(cm2).结论:在点P,Q的移动过程中,四边形QAPC的面积始终不变,为36 cm2.。
2020届人教版八年级数学下册-18.2.1矩形(2)同步练习试题(含解析)

18.2.1矩形(2)同步练习姓名:__________班级:__________学号:__________本节应掌握和应用的知识点1.有一个角是直角的平行四边形是矩形.2.对角线相等的平行四边形是矩形.3.有三个角是直角的四边形是矩形.基础知识和能力拓展训练一、选择题1.下列叙述错误的是()A. 平行四边形的对角线互相平分B. 对角线互相平分的四边形是平行四边形C. 矩形的对角线相等D. 对角线相等的四边形是矩形2.如图,四边形ABCD的对角线AC、BD相交于点O,且AC=BD,则下列条件能判定四边形ABCD为矩形的是()A. AB=CDB. OA=OC,OB=ODC. AC⊥BDD. AB∥CD,AD=BC3.如已知:线段AB,BC,∠ABC = 90°. 求作:矩形ABCD. 以下是甲、乙两同学的作业:对于两人的作业,下列说法正确的是()A. 两人都对B. 两人都不对C. 甲对,乙不对D. 甲不对,乙对4.矩形ABCD中,E,F,M为AB,BC,CD边上的点,且AB=6,BC=7,AE=3,DM=2,EF⊥FM,则EM的长为()A. 5B. 52C. 6D. 625.如图,E,F分别是矩形ABCD边AD、BC上的点,且△ABG,△DCH的面积分别为15和20,则图中阴影部分的面积为()A. 15B. 20C. 35D. 406.如图,矩形ABCD中,BC=2AB,对角线相交于O,过C点作CE⊥BD交BD于E点,H为BC 中点,连接AH交BD于G点,交EC的延长线于F点,下列5个结论:①EH=AB;②∠ABG=∠HEC;③△ABG≌△HEC;④S△GAD=S四边形GHCE;⑤CF=BD.正确的有()个A. 2B. 3C. 4D. 57.如图所示,四边形ABCD中,AD∥BC,∠B=90°,E为AB上一点,分别以ED,EC为折痕将两个角(∠A,∠B)向内折起,点A,B恰好落在CD边的点F处.若AD=3,BC=5,则EF的值是 ()A. 15B. 215C. 17D. 2178.如图,E是矩形ABCD中BC边的中点,将△ABE沿AE折叠到△AFE,F在矩形ABCD内部,延长AF交DC于G点,若∠AEB=55°,则∠DAF=()A. 40°B. 35°C. 20°D. 15°9.如图,在矩形ABCD中,点E在AD上,且EC平分∠BED,AB=2,∠ABE=45°,则DE的长为( )A. 2-2B.-1 C.-1 D. 2-10.有一块矩形的牧场如图1,它的周长为700米.将它分隔为六块完全相同的小矩形牧场,如图2,每一块小矩形牧场的周长是()A. 150米B. 200米C. 300米D. 400米二、填空题11.如图,在四边形ABCD中,AC,BD相交于点O,AO=OC,BO=OD,∠ABC=90°,则四边形ABCD是________;若AC=5cm,则BD=________.12.平行四边形ABCD的对角线相交于点O,分别添加下列条件:①∠ABC=90°;②AC⊥BD;③AB=BC;④AC平分∠BAD;⑤AO=DO.使得四边形ABCD是矩形的条件有________13.如图,矩形ABCD中,AB=8cm,BC=3cm,E是DC的中点,BF=12FC,则四边形DBFE的面积为_______ cm2.14.如图,在△ABC,AB=AC,点D为BC的中点,AE是∠BAC外角的平分线,DE//AB交AE 于E,则四边形ADCE的形状是___________.15.已知:如图,矩形ABCD中,E,F是CD的两个点,EG⊥AC,FH⊥AC,垂足分别为G,H,若AD=2,DE=1,CF=2,且AG=CH,则EG+FH=_____.16.如图,在矩形ABCD中,对角线AC、BD相交于点O,点E、F分别是AO、AD的中点,若AB=6 cm,BC=8 cm,则△AEF的周长为________cm.三、解答题17.如图,Rt△ABE与Rt△DCF关于直线m对称,已知∠B=90°,∠C=90°,连接EF,AD,点B,E,F,C在同一条直线上.求证:四边形ABCD是矩形.18.如图,在△ABC中,AB=AC=5,BC=6,AD为BC边上的高,过点A作AE∥BC,过点D作DE∥AC,AE与DE交于点E,AB与DE交于点F,连结BE.求四边形AEBD的面积19.如图,在▱ABCD中,过点D作DE⊥AB于点E,点F在边CD上,CF=AE,连接AF,BF. (1)求证:四边形BFDE是矩形;(2)若CF=6,BF=8,DF=10,求证:AF是∠DAB的平分线.20.如图,将矩形ABCD沿对角线BD折叠,使点C落在点E处,BE与AD交于点F.⑴求证:ΔABF≌ΔEDF;⑵将折叠的图形恢复原状,点F与BC边上的点G正好重合,连接DG,若AB=6,BC=8,求DG的长.21.如图,在▱ABCD中,各内角的平分线分别相交于点E,F,G,H.(1)求证:△ABG≌△CDE;(2)猜一猜:四边形EFGH是什么样的特殊四边形?证明你的猜想;(3)若AB=6,BC=4,∠DAB=60°,求四边形EFGH的面积.22.如图,△ABC中,点O是边AC上一个动点,过O作直线MN∥BC.设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F.(1)求证:OE=OF;(2)若CE=8,CF=6,求OC的长;(3)当点O在边AC上运动到什么位置时,四边形AECF是矩形?并说明理由.参考答案1.D【解析】A. 平行四边形的对角线互相平分,正确,不符合题意;B. 对角线互相平分的四边形是平行四边形,正确,不符合题意;C. 矩形的对角线相等,正确,不符合题意;D. 对角线相等的四边形是矩形,也可能是等腰梯形,也可能是一般四边形,故错误,符合题意,故选D.2.B【解析】解:A.由AB=DC,AC=BD无法判断四边形ABCD是矩形.故错误;B.∵OA=OC,OB=OD,∴四边形ABCD是平行四边形,∵AC=BD,∴四边形ABCD是矩形.故正确;C.由AC⊥BD,AC=BD无法判断四边形ABCD是矩形,故错误.D.由AB∥CD,AC=BD无法判断四边形ABCD是矩形,故错误.故选B.点睛:本题考查矩形的判定方法、熟练掌握矩形的判定方法是解决问题的关键,记住对角线相等的平行四边形是矩形,有一个角是90度的平行四边形是矩形,有三个角是90度的四边形是矩形,属于中考常考题型.3.A【解析】由甲同学的作业可知,CD=AB,AD=BC,∴四边形ABCD是平行四边形,又∵∠ABC=90°,∴▱ABCD是矩形.所以甲的作业正确;由乙同学的作业可知,CM=AM,MD=MB,∴四边形ABCD是平行四边形,又∵∠ABC=90°,∴▱ABCD是矩形.所以乙的作业正确;故选A.4.B【解析】过E作EG⊥CD于G,∵四边形ABCD是矩形,∴∠A=∠D=90°,又∵EG ⊥CD ,∴∠EGD=90°,∴四边形AEGD 是矩形,∴AE=DG ,EG=AD ,∴EG=AD=BC=7,MG=DG −DM=3−2=1,∵EF ⊥FM ,∴△EFM 为直角三角形,∴在Rt △EGM 中,故选B.点睛:本题考查了矩形的判定、勾股定理等知识,过E 作EG ⊥CD 于G ,利用矩形的判定可得,四边形AEGD 是矩形,则AE=DG ,EG=AD ,于是可求MG=DG-DM=1,在Rt △EMG 中,利用勾股定理可求EM .5.C【解析】试题解析:连接EF ,由图可知AFE EBA S S =V V ,那么AFE AGE EBA AGE S S S S -=-V V V V , 所以ABG EFG S S =V V ,同理, CDH EFH S S =V V ,则=152035EFG EFH S S S +=+=V V 阴影, 故本题应选C.6.B【解析】试题解析:由图可知, 12EH BC =,因为12AB BC = ,所以EH AB = ,故①正确;因为EH HC = ,所以HEC HCE ∠=∠ ,由于90HCE EBC ∠+∠=︒ , 90EBC ABG ∠+∠=︒ ,所以ABG HCE ∠=∠ ,则ABG HEC ∠=∠ ,故②正确; 在△ABG 与△HEC 中, 45BAG DHC EHC ∠=∠=︒<∠ ,从而两三角形不全等,故③错误;过点A 作AM ⊥BG 于点M ,由图可知2ABG BGH S S =V V ,而12AMG ABG S S ≠V V ,即 AMG BGH S S ≠V V ,则GAD GHCE S S ≠V 四边形 ,故④错误;因为90F EGH ∠+∠=︒ , 45EGH GBH ∠=∠+︒ , GBH DAC ∠=∠,所以 45F DAC ∠+∠=︒ ,又因为45DAC CAF ∠+∠=︒ ,所以F CAF ∠=∠ ,则 CF BD =,故⑤正确.综上所述,正确的结论有3个,故选B.点睛:矩形的对角线相等且相互平分.7.A【解析】先根据折叠的性质得EA =EF ,BE =EF ,DF =AD =3,CF =CB =5,则AB =2EF ,DC =8,再作DH ⊥BC 于H ,因为AD ∥BC , ∠B =90°,则可判定四边形ABHD 为矩形,所以DH =AB =2EF ,HC =BC -AD =2,然后在Rt △DHC 中,利用勾股定理计算出DH =所以EF 8.C【解析】∵△ABE沿AE折叠到△AEF,∴∠BAE=∠FAE,∵∠AEB=55°,∠ABE=90°,∴∠BAE=90°−55°=35°,∴∠DAF=∠BAD−∠BAE−∠FAE=90°−35°−35°=20°,故答案为:20°,故选C.9.A【解析】∵四边形ABCD是矩形,∴AD∥BC.∴∠DEC=∠BCE.∵EC平分∠DEB,∴∠DEC=∠BEC.∴∠BEC=∠ECB.∴BE=BC.∵四边形ABCD是矩形,∴∠A=90°.∵∠ABE=45°,∴∠ABE=AEB=45°.∴AB=AE=2.∵由勾股定理得:BE==,∴BC=BE=.∴DE=AD-AE=BC-AB=-2故选:A.点睛:本题考查了矩形的性质、角平分线的性质、等腰三角形的性质、勾股定理的应用等知识;要学会添加常用的辅助线,构造特殊三角形来解决问题.熟练掌握矩形的性质、等腰三角形的判定与性质是解决问题的关键.10.C【解析】试题分析:根据题意设小长方形的长为x,宽为y,则可知2(2x+3y)=700,且2y+x=2x,解得y=50,x=100,所以小长方形的周长为300米.故选:C.11.矩形 5cm【解析】试题解析:∵AO=OC,BO=OD,∴四边形ABCD是平行四边形.∵∠ABC=90°,∴四边形ABCD是矩形。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
新人教版数学八年级下册18.2.1矩形课时练习一.选择题(共15小题)1.一个长方形在平面直角坐标系中三个顶点的坐标为(﹣1,﹣1),(﹣1,2),(3,﹣1),则第四个顶点的坐标为()A.(2,2)B.(3,2)C.(3,3)D.(2,3)答案:B知识点:坐标与图形性质;矩形的性质解析:解答:解:如图可知第四个顶点为:即:(3,2).故选B.分析:本题可在画出图后,根据矩形的性质,得知第四个顶点的横坐标应为3,纵坐标应为2.本题考查学生的动手能力,画出图后可很快得到答案.2.如图,矩形ABCD中,AB=1,AD=2,M是CD的中点,点P在矩形的边上沿A⇒B⇒C⇒M 运动,则△APM的面积y与点P经过的路程x之间的函数关系用图象表示大致是下图中的()A. B.C. D.答案:A知识点:函数的图像;分段函数;矩形的性质解析:解答:解:点P由A到B这一段中,三角形的AP边上的高不变,因而面积是路程x的正比例函数,当P到达B点时,面积达到最大,值是1.在P由B到C这一段,面积随着路程的增大而减小;到达C点,即路程是3时,最小是;由C到M这一段,面积越来越小;当P到达M时,面积最小变成0.因而应选第一个选项.故选A.分析:根据每一段函数的性质,确定其解析式,特别注意根据函数的增减性,以及几个最值点,确定选项比较简单.本题考查了分段函数的画法,是难点,要细心认真.3.如图,矩形ABCD中,AB=3,BC=5.过对角线交点O作OE⊥AC交AD于E,则AE 的长是()A.1.6B.2.5C.3D.3.4答案:D知识点:线段垂直平分线的性质;勾股定理;矩形的性质解析:解答:解:连接EC,由矩形的性质可得AO=CO,又因EO⊥AC,则由线段的垂直平分线的性质可得EC=AE,设AE=x,则ED=AD﹣AE=5﹣x,在Rt△EDC中,根据勾股定理可得EC2=DE2+DC2,即x2=(5﹣x)2+32,解得x=3.4.故选D.分析:利用线段的垂直平分线的性质,得到EC与AE的关系,再由勾股定理计算出AE的长.本题考查了利用线段的垂直平分线的性质.矩形的性质及勾股定理综合解答问题的能力,在解上面关于x的方程时有时出现错误,而误选其它选项.4.一次数学课上,老师请同学们在一张长为18厘米,宽为16厘米的矩形纸板上,剪下一个腰长为10厘米的等腰三角形,且要求等腰三角形的一个顶点与矩形的一个顶点重合,其它两个顶点在矩形的边上,则剪下的等腰三角形的面积为多少平方厘米()A.50B.50或40C.50或40或30D.50或30或20答案:C知识点:等腰三角形的性质;勾股定理;矩形的性质解析:解答:解:如图四边形ABCD是矩形,AD=18cm,AB=16cm;本题可分三种情况:①如图(1):△AEF中,AE=AF=10cm;S△AEF=•AE•AF=50cm2;②如图(2):△AGH中,AG=GH=10cm;在Rt△BGH中,BG=AB﹣AG=16﹣10=6cm;根据勾股定理有:BH=8cm;∴S△AGH=AG•BH=×8×10=40cm2;③如图(3):△AMN中,AM=MN=10cm;在Rt△DMN中,MD=AD﹣AM=18﹣10=8cm;根据勾股定理有DN=6cm;∴S△AMN=AM•DN=×10×6=30cm2.故选C.分析:本题中由于等腰三角形的位置不确定,因此要分三种情况进行讨论求解,①如图(1),②如图(2),③如图(3),分别求得三角形的面积.题主要考查了等腰三角形的性质.矩形的性质.勾股定理等知识,解题的关键在于能够进行正确的讨论.5.菱形具有而矩形不具有性质是()A.对角线相等B.对角线互相平分C.对角线互相垂直D.对角线平分且相等答案:C知识点:菱形的性质;矩形的性质解析:解答:解:A.菱形的对角线不一定相等,矩形的对角线一定相等,故本选项错误;B.菱形和矩形的对角线均互相平分,故本选项错误;C.菱形的对角线互相垂直,而矩形的对角线不一定互相垂直(互相垂直时是正方形),故本选项正确;D.菱形和矩形的对角线均互相平分且相等,故本选项错误.故选C.分析:由于菱形的对角线互相垂直平分,矩形的对角线互相平分且相等,据此进行比较从而得到答案.本题考查矩形与菱形的性质的区别:矩形的对角线互相平分且相等,菱形的对角线互相平分.垂直且平分每一组对角.6.在矩形ABCD中,AB=1,AD=3,AF平分∠DAB,过C点作CE⊥BD于E,延长AF.EC交于点H,下列结论中:①AF=FH;②BO=BF;③CA=CH;④BE=3ED.正确的是()A.②③B.③④C.①②④D.②③④答案:D知识点:矩形的性质;角平分线的性质;等腰三角形的性质;等边三角形的性质。
解析:解答:解:∵AB=1,AD=3,∴BD=AC=2,OB=OA=OD=OC=1.∴△OAB,△OCD为正三角形.AF平分∠DAB,∴∠FAB=45°,即△ABF是一个等腰直角三角形.∴BF=AB=1,BF=BO=1.∵AF平分∠DAB,∴∠FAB=45°,∴∠CAH=45°﹣30°=15°.∵∠ACE=30°(正三角形上的高的性质)∴∠AHC=15°,∴CA=CH由正三角形上的高的性质可知:DE=OD÷2,OD=OB,∴BE=3ED.故选D.分析:这是一个特殊的矩形:对角线相交成60°的角.利用等边三角形的性质结合图中的特殊角度解答.本题主要考查了矩形的性质及正三角形的性质.7.如图,矩形ABCD的两条对角线相交于点O,∠AOB=60°,AB=2,则矩形的对角线AC 的长是()A.2B.4C.2D.4答案:B知识点:矩形的性质;等边三角形的判定与性质解析:解答:解:因为在矩形ABCD中,所以AO=AC=BD=BO,又因为∠AOB=60°,所以△AOB是等边三角形,所以AO=AB=2,所以AC=2AO=4.故选B.分析:本题的关键是利用等边三角形和矩形对角线的性质求长度.本题难度中等,考查矩形的性质.8.已知AC为矩形ABCD的对角线,则图中∠1与∠2一定不相等的是()A. B.C. D.答案:D知识点:矩形的性质;三角形的外角性质解析:解答:解:A项的对顶角相等;B,C项不确定;D项一定不相等,因为∠1=∠ACD,∠2>∠ACD.故选D.分析:根据矩形的性质,利用排除法可求解.本题主要是利用三角形的外角>和它不相邻的任一内角可知,∠1与∠2一定不相等.9.如图,矩形ABCD的周长为20cm,两条对角线相交于O点,过点O作AC的垂线EF,分别交AD,BC于E,F点,连接CE,则△CDE的周长为()A.5cmB.8cmC.9cmD.10cm答案:D知识点:矩形的性质;线段垂直平分线的性质解析:解答:解:∵ABCD为矩形,∴AO=OC.∵EF⊥AC,∴AE=EC.∴△CDE的周长=CD+DE+EC=CD+DE+AE=CD+AD=10(cm)故选D.分析:∵△CDE的周长=CD+DE+EC,又EC=AE,∴周长=CD+AD.本题的关键是利用线段垂直平分线的性质求出AE=CE,进而求三角形的周长.10.如图,在矩形ABCD中,E为CD的中点,连接AE并延长交BC的延长线于点F,则图中全等的直角三角形共有()A.6对B.5对C.4对D.3对答案:C知识点:矩形的性质;直角三角形全等的判定解析:解答:解:图中全等的直角三角形有:△AED≌△FEC,△BDC≌△FDC≌△DBA,共4对.故选C.分析:先找出图中的直角三角形,再分析三角形全等的方法,然后判断它们之间是否全等.本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、SSA、HL.注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.11.如图,将矩形ABCD沿AE折叠,若∠BAD′=30°,则∠AED′等于()A.30°B.45°C.60°D.75°答案:C知识点:矩形的性质;翻折变换(折叠问题)解析:解答:解:根据题意得:∠DAE=∠EAD′,∠D=∠D′=90°.∵∠BAD′=30°,∴∠EAD′=(90°﹣30°)=30°.∴∠AED′=90°﹣30°=60°.故选C.分析:根据折叠的性质求∠EAD′,再在Rt△EAD′中求∠AED′.已知图形的折叠,就是已知图形全等,就可以得到一些相等的角.12.矩形ABCD中的顶点A.B.C.D按顺时针方向排列,若在平面直角坐标系内,B.D两点对应的坐标分别是(2,0).(0,0),且A.C两点关于x轴对称,则C点对应的坐标是()A.(1,1) B.(1,﹣1) C.(1,﹣2) D.(,﹣)答案:B知识点:矩形的性质;关于x轴、y轴对称的点的坐标解析:解答:解:已知B,D两点的坐标分别是(2,0).(0,0),则可知A,C两点的横坐标一定是1,且关于x轴对称,则A,C两点纵坐标互为相反数,设A点坐标为:(1,b),则有:,解得b=1,所以点A坐标为(1,1)点C坐标为(1,﹣1).故选B.分析:根据关于x轴对称,横坐标不变,纵坐标互为相反数和平行四边形的性质,确定C 点对应的坐标.此题考查知识点比较多,要注意各个知识点之间的联系,并能灵活应用.13.如图,在矩形ABCD中,EF∥AB,GH∥BC,EF.GH的交点P在BD上,图中面积相等的四边形有()A.3对B.4对C.5对D.6对答案:C知识点:矩形的性质;全等三角形的判定解析:解答:解:在矩形ABCD中,∵EF∥AB,AB∥DC,∴EF∥DC,则EP∥DH;故∠PED=∠DHP;同理∠DPH=∠PDE;又PD=DP;所以△EPD≌△HDP;则S△EPD=S△HDP;同理,S△GBP=S△FPB;则(1)S梯形BPHC=S△BDC﹣S△HDP=S△ABD﹣S△EDP=S梯形ABPE;(2)S□AGPE=S梯形ABPE﹣S△GBP=S梯形BPHC﹣S△FPB=S□FPHC;(3)S梯形FPDC=S□FPHC+S△HDP=S□AGPE+S△EDP=S梯形GPDA;(4)S□AGHD=S□AGPE+S□HDPE=S□PFCH+S□PHDE=S□EFCD;(5)S□ABFE=S□AGPE+S□GBFP=S□PFCH+S□GBFP=S□GBCH故选C.分析:本题考查了矩形的性质,得出△EPD≌△HDP,则S△EPD=S△HDP,通过对各图形的拼凑,得到的结论.本题是一道结论开放题,掌握矩形的性质,很容易得到答案.14.将矩形ABCD沿AE折叠,得到如图所示的图形,已知∠CED′=60°,则∠AED的大小是()A.60°B.50°C.75°D.55°答案:A知识点:矩形的性质;翻折变换(折叠问题)解析:解答:解:∵∠AED′是△AED沿AE折叠而得,∴∠AED′=∠AED.又∵∠DEC=180°,即∠AED′+∠AED+∠CED′=180°,又∠CED′=60°,∴∠AED==60°.故选A.分析:根据折叠前后对应部分相等得∠AED′=∠AED,再由已知求解.图形的折叠实际上相当于把折叠部分沿着折痕所在直线作轴对称,所以折叠前后的两个图形是全等三角形,重合的部分就是对应量.15.如图,在宽为20m,长为30m的矩形地面上修建两条同样宽的道路,余下部分作为耕地.根据图中数据,计算耕地的面积为()A.600m 2B.551m 2C.550m 2D.500m 2答案:B 知识点:矩形的性质解析:解答:解:30×20﹣30×1﹣20×1+1×1=600﹣30﹣20+1=551(平方米)答:耕地的面积为551平方米.故选B .分析:要计算耕地的面积,只要求出小路的面积,再用矩形的面积减去小路的面积即可.解答此题的关键是正确求出小路的面积,要注意两条小路重合的面积最后要加上.二.填空题(共5小题)1.如图,把一个矩形纸片OABC 放入平面直角坐标系中,使OA 、OC 分别落在x 轴、y 轴上,连接OB ,将纸片OABC 沿OB 折叠,使点A 落在A′的位置上.若OB =,21=OC BC ,求点A′的坐标为 .答案:53 ,54 知识点:坐标与图形性质;矩形的性质;翻折变换(折叠问题)解析:解答:解:∵OB =5,21=OC BC ∴BC =1,OC =2设OC 与A′B 交于点F ,作A′E ⊥OC 于点E∵纸片OABC 沿OB 折叠∴OA =OA′,∠BAO =∠BA′O =90°∵BC ∥A′E∴∠CBF =∠FA′E∵∠AOE =∠FA′O∴∠AOE =∠CBF∴△BCF ≌△OA′F∴OA′=BC =1,设A′F =x∴OF =2﹣x∴A′F =,OF =∵A′E =A′F×OA′÷OF =∴OE =∴点A’的坐标为(53-,54). 故答案为:(53-,54).分析:由已知条件可得:BC =1,OC =2.设OC 与A′B 交于点F ,作A′E ⊥OC 于点E ,易得△BCF ≌△OA′F ,那么OA′=BC =1,设A′F =x ,则OF =2﹣x .利用勾股定理可得A′F =,OF =,利用面积可得A′E =A′F×OA′÷OF =,利用勾股定理可得OE =,所以点A’的坐标为().解决本题的关键是利用三角形的全等得到点A′所在的三角形的一些相关的线段的长度,进而利用面积的不同表示方法和勾股定理得到所求的点的坐标.2.在矩形ABCD 中,A (4,1),B (0,1),C (0,3),则点D 的坐标为 .答案:(4,3)知识点:坐标与图形性质;矩形的性质解析:解答:解:因为AB=4,BC=2,则AD=BC=2,CD=AB=4.∴D的坐标为(4,3).故答案为:(4,3).分析:画出草图,根据A,B,C的位置与矩形的性质来确定出D的位置.此题主要考查学生对坐标的特点及矩形的性质的掌握情况.3.如图,一张矩形纸片沿AB对折,以AB中点O为顶点将平角五等分,并沿五等分的折线折叠,再沿CD剪开,使展开后为正五角星(正五边形对角线所构成的图形),则∠OCD 等于_________.答案:126°知识点:矩形的性质;翻折变换(折叠问题);三角形内角和定理解析:解答:解:展开如图:∵∠COD=360°÷10=36°,∠ODC=36°÷2=18°,∴∠OCD=180°﹣36°﹣18°=126°.故选C.分析:按照如图所示的方法折叠,剪开,把相关字母标上,易得∠ODC和∠DOC的度数,利用三角形的内角和定理可得∠OCD的度数.解决本题的关键是能够理解所求的角是五角星的哪个角,解题时可以结合正五边形的性质解决.4.如图,点A、D、G、M在半⊙O上,四边形ABOC、DEOF、HMNO均为矩形.设BC=a,EF=b,NH=c,则a、b、c的大小关系为_________________.答案:a =b =c知识点:矩形的性质;垂径定理解答:解答:解:连接OM 、OD 、OA 、根据矩形的对角线相等,得BC =OA ,EF =OD ,NH =OM .再根据同圆的半径相等,得a =b =c .分析:本题主要根据矩形的性质以及垂径定理进行做题.此题主要能够根据矩形的对角线相等把线段进行转换,根据同圆的半径相等即可证明.5.如图,矩形ABCD 沿AE 折叠,使D 点落在BC 边上的F 点处,如果∠BAF =60°,则∠AEF =______.答案:75°知识点:矩形的性质;翻折变换(折叠问题)解析:解答:解:∵∠EAF 是∠DAE 折叠而成,∴∠EAF =∠DAE ,∠ADC =∠AFE =90°,∠EAF =260902∠BAF 90︒︒︒-=-=15°, 在△AEF 中∠AFE =90°,∠EAF =15°,∠AEF =180﹣∠AFE ﹣∠EAF =180°﹣90°﹣15°=75°.分析:根据矩形的性质,求出∠EAF =15°,从而得出∠AEF 的度数即可.本题考查了矩形的性质,图形的折叠实际上相当于把折叠部分沿着折痕所在直线作轴对称,所以折叠前后的两个图形是全等三角形,复合的部分就是对应量.三.解答题(共5小题)1.如图,EF过矩形ABCD对角线的交点O,且分别交AB、CD于E、F,那么阴影部分的面积是矩形ABCD的面积是多少?1答案:4知识点:矩形的性质解析:解答:解:∵四边形为矩形,∴OB=OD=OA=OC,在△EBO与△FDO中,∠EOB=∠DOF,OB=OD,∠EBO=∠FDO,△EBO≌△FDO,∴阴影部分的面积=S△AEO+S△EBO=S△AOB,∵△AOB与△ABC同底且△AOB的高是△ABC高的,∴S△AOB=S△OBC=S矩形ABCD.分析:本题主要根据矩形的性质,得△EBO≌△FDO,再由△AOB与△OBC同底等高,得出结论.本题考查矩形的性质,矩形具有平行四边形的性质,又具有自己的特性,要注意运用矩形具备而一般平行四边形不具备的性质.2.如图,顺次连接圆内接矩形各边的中点,得到菱形ABCD,若BD=8,DF=4,则菱形ABCD的边长为多少?答案:8知识点:垂径定理;菱形的性质;矩形的性质;勾股定理解析:解答:解:如图,连接OM,根据菱形的对角线互相垂直平分,得OD=4,即圆的半径是8,在直角△AOM中,OM=8,AM=4根据勾股定理,得OA =43,在直角△AOD 中,根据勾股定理得到:AD =1648+=8即菱形的边长是8.分析:根据菱形的性质和勾股定理求解.综合运用了菱形的性质以及勾股定理.3.如图,矩形的长与宽分别为a 和b ,在矩形中截取两个大小相同的圆作为圆柱的上下底面,剩余的矩形作为圆柱的侧面,刚好能组合成一个没有空隙的圆柱,则a 和b 要满足什么数量关系?答案:12a π+=b 知识点:相切两圆的性质;矩形的性质解析:解答:解:组成圆柱后,圆柱的底面周长=剩余长方形的长.2b 2a a -π=, 整理得12a π+=b . 分析:利用圆柱的底面周长和剩余长方形的长之间的等量关系列出方程计算.解决本题的关键是得到圆柱的底面周长和剩余长方形的长之间的等量关系.4.如图,在矩形ABCD 中,AB =2AD ,E 是CD 上一点,且AE =AB ,则∠CBE 的度数是多少?5.答案:15°知识点:矩形的性质;三角形内角和定理;等腰三角形的性质解析:解答:解:∵AB=2AD,AE=AB.∴AE=2AD.∴直角△ADE中∠AED=30°.∵AB∥CD∴∠EAB=∠AED=30°.又∵AE=AB.∴∠AEB=∠ABE=230180︒︒-=75°.∴∠CBE=15°.分析:根据矩形的性质∠EAB=∠AED=30°,再根据等腰三角形的性质,利用三角形内角和定理求解.解答此题要熟悉矩形的性质,直角三角形特殊角的判定.5.矩形ABCD的两条对角线相交于点O,∠AOB=60°,则对角线AC与边BC所成的角是多少度?答案:30°知识点:矩形的性质;等腰三角形的性质解析:解答:解:根据矩形的对角线相等且互相平分得到:OB=OC.则∠ACB=∠OBC.∵∠AOB=∠ACB+∠OBC∴∠ACB=30°.故选B.分析:根据矩形的对角线的性质,结合等腰三角形的性质求解.本题主要考查了矩形的对角线相等且平分.即对角线把矩形分成了四个等腰三角形.。
