燕庆明 信号与系统 习题答案
电子教案《信号与系统》(第四版_燕庆明)(含习题解答)6.3

6.3 线性系统的稳定性
一、稳定的概念
稳定:充要条件是
h(t)
dt
,即H(s)的全部极点
位于S的左半平面;
临界稳定: H(s)在虚轴上有单极点,其余极点均在
S的左半平面;
不稳定: H(s)只要有一个极点位于S的右半平面。
信号与系统 6.3-2
例
图1
二、稳定性判据
信号与系统 6.3-3
必要条件: H( s )的分母多项式
D(s) ansn an-1sn-1 a1s a0
的全部系数非零且均为正实数。 充要条件:对二阶系统,D(s) a2s2 a1s a0 的全部 系数非零且为正实数。 充要条件:对三阶系统,D(s) a3s3 a2s2 a1s a0 的 各项系数全为正,且满足
a1a2 a0a3
信号与系统 6.3-4
例 导弹跟踪系统H (s) Nhomakorabeas3
34.5s2 119.7s 98.1 35.714s2 119.741s 98.1
N (s) D(s)
显然
a1a2 > a0a3
故系统稳定。
练习: 判别稳定性
1. D(s) s2 3s 2 2. D(s) s3 s2 4s 10 3. D(s) s3 4s2 5s 6
end
信号与系统课后习题参考答案

信号与系统课后习题参考答案1试分别指出以下波形就是属于哪种信号?题图1-11-2试写出题1-1图中信号得函数表达式。
1-3已知信号与波形如题图1-3中所⽰,试作出下列各信号得波形图,并加以标注。
题图1-3⑴⑵⑶⑷⑸⑹⑺⑻⑼1-4已知信号与波形如题图1-4中所⽰,试作出下列各信号得波形图,并加以标注。
题图1-4⑴⑵⑶⑷⑸⑹⑺⑻⑼1-5已知信号得波形如题图1-5所⽰,试作出信号得波形图,并加以标注。
题图1-51-6试画出下列信号得波形图:⑴⑵⑶⑷1-7试画出下列信号得波形图:⑴⑵⑶⑷⑸⑹1-8试求出以下复变函数得模与幅⾓,并画出模与幅⾓得波形图。
⑴⑵⑶⑷1-9已知信号,求出下列信号,并画出它们得波形图。
1-10试作出下列波形得奇分量、偶分量与⾮零区间上得平均分量与交流分量。
题图1-101-11试求下列积分:⑴⑵⑶⑷⑸⑹1-12试求下列积分:⑴⑵⑴(均为常数)⑵⑶⑷⑸⑹⑺⑻1-14如题图1-14中已知⼀线性时不变系统当输⼊为时,响应为。
试做出当输⼊为时,响应得波形图。
题图1-14 1-15已知系统得信号流图如下,试写出各⾃系统得输⼊输出⽅程。
题图1-151-16已知系统⽅程如下,试分别画出她们得系统模拟框图。
⑴⑵⑶1-17已知⼀线性时不变系统⽆起始储能,当输⼊信号时,响应,试求出输⼊分别为与时得系统响应。
第⼆章习题2-1试计算下列各对信号得卷积积分:。
⑴(对与两种情况)⑵⑶⑷⑸⑹2-2试计算下列各对信号得卷积与:。
⑴(对与两种情况)⑵⑶⑷⑸⑹2-3试计算下图中各对信号得卷积积分:,并作出结果得图形。
题图2-32-4试计算下图中各对信号得卷积与:,并作出结果得图形。
题图2-42-5已知,试求:⑴⑵⑶2-7系统如题图2-7所⽰,试求系统得单位冲激响应。
已知其中各⼦系统得单位冲激响应分别为:题图2-72-8设已知LTI 系统得单位冲激响应,试求在激励作⽤下得零状态响应。
2-9⼀LTI 系统如题图2-9所⽰,由三个因果LTI ⼦系统级联⽽成,且已知系统得单位样值响应如图中。
信号与系统课后习题答案

习 题 一 第一章习题解答基本练习题1-1 解 (a) 基频 =0f GCD (15,6)=3 Hz 。
因此,公共周期3110==f T s 。
(b) )30cos 10(cos 5.0)20cos()10cos()(t t t t t f ππππ+==基频 =0f GCD (5, 15)=5 Hz 。
因此,公共周期5110==f T s 。
(c) 由于两个分量的频率1ω=10π rad/s 、1ω=20 rad/s 的比值是无理数,因此无法找出公共周期。
所以是非周期的。
(d) 两个分量是同频率的,基频 =0f 1/π Hz 。
因此,公共周期π==01f T s 。
1-2 解 (a) 波形如图1-2(a)所示。
显然是功率信号。
t d t f TP T TT ⎰-∞→=2)(21lim16163611lim 22110=⎥⎦⎤⎢⎣⎡++=⎰⎰⎰∞→t d t d t d T T T W(b) 波形如图1.2(b)所示。
显然是能量信号。
3716112=⨯+⨯=E J (c) 能量信号 1.0101)(lim101025=-===⎰⎰∞∞---∞→T t ttT e dt edt eE J(d) 功率信号,显然有 1=P W1-3 解 周期T=7 ,一个周期的能量为 5624316=⨯+⨯=E J 信号的功率为 8756===T E P W 1-5 解 (a) )(4)2()23(2t tt δδ=+; (b) )5.2(5.0)5.2(5.0)25(5.733-=-=----t e t e t et tδδδ(c) )2(23)2()3sin()2()32sin(πδπδπππδπ+-=++-=++t t t t 题解图1-2(a) 21题解图1-2(b) 21(d) )3()3()(1)2(-=----t e t t et δδε。
1-6 解 (a) 5)3()94()3()4(2-=+-=+-⎰⎰∞∞-∞∞-dt t dt t t δδ(b) 0)4()4(632=+-⎰-dt t t δ(c) 2)]2(2)4(10[)]42(2)4()[6(63632=+++-=+++-⎰⎰--dt t t dt t t t δδδδ(d)3)3(3)(3sin )(1010=⋅=⎰⎰∞-∞-dt t Sa t dt ttt δδ。
信号与系统教程燕庆明答案

信号与系统教程燕庆明答案【篇一:信号与系统课后习题】t)?tf(t?td),tf(t?t0)?yf(t?t0)?,yf(t?t0)?(t?t0)f(t?t0)。
(3)令g(t)?f(t?t0),t[g(t)]?g(?t)?f(?t?t0),tf(t?t0)? yf(t?t0),yf(t?t0)?f(?t?t0)1.2.已知某系统输入f(t)与输出y(t)的关系为y(t)?f(t)判断该系统是否为线性时不变系统?解:设t为系统运算子,则y(t)可以表示为y(t)?t[f(t)]?f(t),不失一般性,设f(t)?f1(t)?f2(t)t[f1(t)]?f1(t)?y1(t),t[f(t)]?f1(t)?f2(t)?y(t),显然其不相等,即为非线性时不变系统。
df(t)tf(x)dx(2):[y(t)]2?y(t)?f(t) 1.3判断下列方程所表示系统的性(1):y(t)?0dt(3):y(t)?2y(t)?3y(t)?f(t)?f(t?2)(4):y(t)?2ty(t)?2y(t)?3f(t) 线性非线性时不变线性时不变线性时变1.4。
试证明方程y(t)+ay(t)=f(t)所描述的系统为线性系统。
证明:不失一般性,设输入有两个分量,且f1(t)→y1(t),f2(t)→y2(t) 则有y1(t)+ay1(t)=f1(t),y2(t)+ay2(t)=f2(t) 相加得y1+ay1(t)+y2(t)+ay2(t)=f1(t)+f2(t) 即d[y1(t)+y2(t)]+a[y1(t)+y2(t)] dt=f1(t)+f2(t)可见f1(t)+f2(t)→y1(t)+y2(t)即满足可加性,齐次性是显然的。
故系统为线性的。
1.5。
证明1.4满足时不变性。
证明将方程中的t换为t-t0,t0为常数。
即y(t-t0)+ay(t-t0)=f(t-t0) 由链导发则,有dy(t?t0)dtd(t?t0)dy(t?t0)d(t?t0)dy(t?t0)dy(t?t0)1从而又因t0为常数,故所以有 ??dtd(t?t0)dtdtd(t?t0)dy(t?t0)ay(tt0)f(tt0)即满足时不变性f(t-t0)→y(t-t0) dty(t)?y(t?t0)f(t)?f(t??t)?所以ttlimf(t)?f(t??t)limy(t)?f(t?t0)既有 f(t)?y(t) ?t0t0tt1.7 若有线性时不变系统的方程为y(t)+ay(t)=f(t)在非零f(t)作用下其响应y(t)=1-e-t,试求方程y(t)+ay(t)=2f(t)+f(t)的响应。
信号与系统(第5版) 燕庆明 37635 习题解答

《信号与系统》(第5版)习题解答燕庆明鲁纯熙高等教育出版社2014年8月目录第1章习题解析 (2)第2章习题解析 (6)第3章习题解析 (16)第4章习题解析 (24)第5章习题解析 (32)第6章习题解析............................................................................ 错误!未定义书签。
第7章习题解析 (50)第1章习题解析1-1 题1-1图示信号中,哪些是连续信号?哪些是离散信号?哪些是周期信号?哪些是非周期信号?哪些是有始信号?(c) (d)题1-1图解 (a)、(c)、(d)为连续信号;(b)为离散信号;(d)为周期信号;其余为非周期信号;(a)、(b)、(c)为有始(因果)信号。
1-2 给定题1-2图示信号f ( t ),试画出下列信号的波形。
[提示:f ( 2t )表示将f ( t )波形压缩,f (2t )表示将f ( t )波形展宽。
] (a) 2 f ( t - 2 )(b) f ( 2t )(c) f ( 2t ) (d) f ( -t +1 )题1-2图解 以上各函数的波形如图p1-2所示。
图p1-21-3 如图1-3图示,R 、L 、C 元件可以看成以电流为输入,电压为响应的简单线性系统S R 、S L 、S C ,试写出各系统响应电压与激励电流函数关系的表达式。
题1-3图解 各系统响应与输入的关系可分别表示为)()(t i R t u R R ⋅= t t i L t u L L d )(d )(= ⎰∞-=t C C i Ct u ττd )(1)(1-4 如题1-4图示系统由加法器、积分器和放大量为-a 的放大器三个子系统组成,系统属于何种联接形式?试写出该系统的微分方程。
S R S L S C题1-4图解 系统为反馈联接形式。
设加法器的输出为x ( t ),由于)()()()(t y a t f t x -+=且)()(,d )()(t y t x t t x t y '==⎰故有 )()()(t ay t f t y -='即)()()(t f t ay t y =+'1-5 已知某系统的输入f ( t )与输出y ( t )的关系为y ( t ) = | f ( t )|,试判定该系统是否为线性时不变系统?解 设T 为系统的运算子,则可以表示为)()]([)(t f t f T t y ==不失一般性,设f ( t ) = f 1( t ) + f 2( t ),则)()()]([111t y t f t f T ==)()()]([222t y t f t f T ==故有)()()()]([21t y t f t f t f T =+=显然)()()()(2121t f t f t f t f +≠+即不满足可加性,故为非线性时不变系统。
信号与系统课后习题答案

f 2 (−1) (t) =
δ (t − 2) − δ (t − 3)
*
t ε e(−t+1) (t + 1)dt
−∞
= [δ (t − 2) − δ (t − 3)]* (1 − e−(t+1) )ε (t + 1)
= (1 − e−(t−2+1) )ε (t − 2 + 1) − (1 − e−(t−3+1) )ε (t − 3 + 1)
) − iL (t) − uC (t) R1
R2
状态方程为:
⎪⎪⎧u&C (t) ⎨
=
f (t) R1C
−
uC (t) R1C
−
iL (t) C
⎪⎪⎩i&L
(t)
=
uC
(t)
− R2iL L
(t)
1.17 写出题图 1.8 系统的输入输出方程。
解: (b)系统框图等价为:
⎧x′′(t) = f (t) − 3x′(t) − 2 y(t)
x2(0-)=1 时,y2(t)=4e-t-2e-3t,t≥0 则 x1(0-)=5,x2(0-)=3 时,系统的零输入响应: yx(t)=y(t)=5y1(t)+3y2(t)=22e-t 十 9e-3t,t≥0
1.22 在题 1.21 的基础上,若还已知 f(t)=ε(t),x1(0-)=0,x2(0-)=0 时,有 y(t)=2+e-t+2e-3t,t≥0 试求当 f(t)=3ε(t),x1(0-)=2,x2(0-)=5 时的系统响应 y(t)。 解: 记,f(t)=ε(t),x1(0-)=0,x2(0-)=0 时,系统响应 yf(t)=y(t)=2+e-t+2e-3t,t≥0 则当 f(t)=3ε(t),x1(0-)=2,x2(0-)=5 时的系统全响应 y(t)为: y(t)=3yf(t)+2y1(t)+5y2(t)
信号与系统燕庆眀第一章

本次课重点
掌握信号的定义 重点学会分析与判断信号的类别与性质
30
电子信息与计算机工程系
习题
a、c、d a、b、c a、b、c
b
d
31
电子信息与计算机工程系
§1.5 系统的概念
系统是指由若干个相互关联、相互作用的事物,按 照一定的规律组成,并且对外具有某种特定功能的 整体。
激励
系统
h(.)
时限信号:若在时间区间 ( t1 , t2 ) 内 f (t) ≠0 ,而在此区间 外 f (t)=0 的信号。
25
电子信息与计算机工程系
§1.3.2 信号分析与处理
时域法 信号表现出一定波形的时间特性,如出现时 间的先后、持续时间的长短、重复周期的大 小及随时间变化的快慢等。 频域法 任意信号在一定条件下总可以分解为许多不 同频率的正弦分量,即具有一定的频率成分 (频谱)。 信号的频谱分析就是研究信号的频率特性。
f (t ) f (t )
T
t
f (t )
T
t
① t 与 t +T 的值相等 周期信号三重含义: ② 延时T,波形相同
③ 波形按T周期重复
22
t
电子信息与计算机工程系
§1.3.1 信号的分类——连续信号与离散信号
连续信号(Continuous-time signals)指在所讨论的时间 模拟信号? 内,对任意时刻值除若干个不连续点外都有定义的信号。 数字信号? ( Analog signals )模拟信号:定义域值域均连续的信号 离散信号( Discrete-time signals)是指只在某些不连续 规定的时刻有定义,而在其他时刻没有定义的信号。
电子教案-信号与系统第四版(含习题解答)-信号与系统电子教案

第7章 离散系统的时域分析 7.1 离散信号与离散系统 7.2 卷积和 Z变换的主要性质 8.3 系统的Z域分析 8.4 系统函数H(Z)与稳定性 8.5 数字滤波器的概念
← 返回总目录 ← 返回上一页 ← 返回本讲第一页 ← 结束本讲放映
目录
第1章 基础概念 1.1 历史的回顾 1.2 应用领域 1.3 信号的概念 1.4 基本信号和信号处理 1.5 系统的概念 1.6 线性时不变系统
第2章 连续系统的时域分析
2.1 系统的微分方程及其响应 2.2 阶跃信号与阶跃响应 2.3 冲激信号与冲激响应 2.4 卷积及其应用 2.5 二阶系统的分析
普通高等教育“十一五”国家级规划教材
(高职高专辅助教学媒体)
燕庆明 主编
高等教育出版社 高等教育电子音像出版社
2007年
前言
“信号与系统”课程是高职高专院校电子信息类各专业的必修课,是“电 路分析”课程后的又一门重要的主干课程。为了帮助教师组织教学,提高教 学效率,我们以教材《信号与系统》(第4版)(燕庆明主编,高等教育出版 社,2007.12)为蓝本,编制了信号与系统电子教案、全书习题解答、 MATLAB仿真和实验指导。参与本教案制作的有燕庆明、鲁纯熙和顾斌杰。
本教案采用PowerPoint制作,应用方便、灵活。其中共设置8章(可讲授 60学时左右)。各校教师可根据实际需要增减有关内容。使用中有何建议可 与我们联系。不当之处,请批评指正。
Tel: (0510)88392227 作者 2007.9
使用说明
运行环境:Office 2000以上。 请安装Office工具中的公式编辑器。 按钮使用: 下列按钮在单击时可超链接到相应幻灯片。
燕庆明-信号与系统作业题答案

1-2 已知某系统的输入f ( t )与输出y ( t )的关系为y ( t ) = | f ( t )|,试判定该系统是否为线性时不变系统?解 设T 为系统的运算子,则可以表示为 )()]([)(t f t f T t y == 则 )()()]([111t y t f t f T == )()()]([222t y t f t f T == 不失一般性,设f ( t ) = f 1( t ) + f 2( t ),故有 )()()]([)(21t f t f t f T t y +==)()(21t f t f +≠ 即不满足可加性,为非线性系统。
)]([)()()()]([00000t t f T t t f t t y t t f t t f T -=-=--=-故为时不变系统,综合起来为非线性时不变系统1-3 判断下列方程所表示的系统的性质。
(b) )2()()(3)(2)(-+'=+'+''t f t f t y t y t y (c) )(3)(2)(2)(t f t y t y t t y =+'+''解 (b )是线性常系数微分方程,为线性时不变系统; (c)是线性微分方程,但不是常系数,为线性时变系统。
1-11 由图f(t)画出的f(2t-2)波形)0,2()22()0,2()(),1,5.1()22()1,1()()1,5.1()22()1,1()(),0,1()22()0,0()(的的的的的的的的-→--→--→-→t f t f t f t f t f t f t f t f1-15 计算下列结果)0)3(3(0d )3()()(21d )()3πcos(d )()3πcos()(21200=-≠=-+=-=-⎰⎰⎰-∞∞--t t t t t t c t t t t t b δδδδω时1-17 计算下列各式211])([1d )(d )(d )]()([)()(2)(2)()()]([)()()1()(02222=+='-+='+='+=+-=-=-=-∞+∞--∞+∞--∞+∞------⎰⎰⎰t t t t t t t tt e t t e t t e t t t e b t e t e t t t e dtd dt t d te dt d a δδδδεεδδεεε2-3 设有二阶系统方程 0)(4)(4)(=+'+''t y t y t y 在某起始状态下的0+起始值为2)0(,1)0(='=++y y ,试求零输入响应。
信号与系统课后习题与解答第一章

1-1 分别判断图1-1所示各波形是连续时间信号还是离散时间信号,若是离散时间信号是否为数字信号?图1-1图1-2解 信号分类如下:⎪⎪⎩⎪⎪⎨⎧⎩⎨⎧--⎩⎨⎧--))(散(例见图数字:幅值、时间均离))(连续(例见图抽样:时间离散,幅值离散))(连续(例见图量化:幅值离散,时间))(续(例见图模拟:幅值、时间均连连续信号d 21c 21b 21a 21图1-1所示信号分别为 (a )连续信号(模拟信号); (b )连续(量化)信号; (c )离散信号,数字信号; (d )离散信号;(e )离散信号,数字信号; (f )离散信号,数字信号。
1-2 分别判断下列各函数式属于何种信号?(重复1-1题所示问) (1))sin(t e at ω-; (2)nT e -; (3))cos(πn ;(4)为任意值)(00)sin(ωωn ;(5)221⎪⎭⎫⎝⎛。
解由1-1题的分析可知: (1)连续信号; (2)离散信号;(3)离散信号,数字信号; (4)离散信号; (5)离散信号。
1-3 分别求下列各周期信号的周期T : (1))30t (cos )10t (cos -; (2)j10t e ;(3)2)]8t (5sin [;(4)[]为整数)(n )T nT t (u )nT t (u )1(0n n ∑∞=-----。
解 判断一个包含有多个不同频率分量的复合信号是否为一个周期信号,需要考察各分量信号的周期是否存在公倍数,若存在,则该复合信号的周期极为此公倍数;若不存在,则该复合信号为非周期信号。
(1)对于分量cos (10t )其周期5T 1π=;对于分量cos (30t ),其周期15T 2π=。
由于5π为21T T 、的最小公倍数,所以此信号的周期5T π=。
(2)由欧拉公式)t (jsin )t (cos e t j ωωω+= 即)10t (jsin )10t (cos e j10t +=得周期5102T ππ==。
信号与系统燕庆明第三版课后答案

信号与系统燕庆明第三版课后答案【篇一:信号与系统课后习题】t)?tf(t?td),tf(t?t0)?yf(t?t0)?,yf(t?t0)?(t?t0)f(t?t0)。
(3)令g(t)?f(t?t0),t[g(t)]?g(?t)?f(?t?t0),tf(t?t0)? yf(t?t0),yf(t?t0)?f(?t?t0)1.2.已知某系统输入f(t)与输出y(t)的关系为y(t)?f(t)判断该系统是否为线性时不变系统?解:设t为系统运算子,则y(t)可以表示为y(t)?t[f(t)]?f(t),不失一般性,设f(t)?f1(t)?f2(t)t[f1(t)]?f1(t)?y1(t),t[f(t)]?f1(t)?f2(t)?y(t),显然其不相等,即为非线性时不变系统。
df(t)t??f(x)dx(2):[y(t)]2?y(t)?f(t) 1.3判断下列方程所表示系统的性(1):y(t)?0dt(3):y(t)?2y(t)?3y(t)?f(t)?f(t?2)(4):y(t)?2ty(t)?2y(t)?3f(t) 线性非线性时不变线性时不变线性时变1.4。
试证明方程y(t)+ay(t)=f(t)所描述的系统为线性系统。
证明:不失一般性,设输入有两个分量,且f1(t)→y1(t),f2(t)→y2(t) 则有y1(t)+ay1(t)=f1(t),y2(t)+ay2(t)=f2(t) 相加得y1+ay1(t)+y2(t)+ay2(t)=f1(t)+f2(t) 即d[y1(t)+y2(t)]+a[y1(t)+y2(t)] dtt)+y2(t)即满足可加性,齐次性是显然的。
故系统为线性的。
1.5。
证明1.4满足时不变性。
证明将方程中的t换为t-t0,t0为常数。
即y(t-t0)+ay(t-t0)=f(t-t0) 由链导发则,有dy(t?t0)? dtd(t?t0)dy(t?t0)d(t?t0)dy(t?t0)dy(t?t0)?1从而又因t0为常数,故所以有 ??dtd(t?t0)dtdtd(t?t0)dy(t?t0)?ay(t?t0)?f(t?t0)即满足时不变性f(t-t0)→y(t-t0) dty(t)?y(t?t0)f(t)?f(t??t)?所以?t?tlimf(t)?f(t??t)limy(t)?f(t?t0)既有 f(t)?y(t) ??t?0?t?0?t?t1.7 若有线性时不变系统的方程为y(t)+ay(t)=f(t)在非零f(t)作用下其响应y(t)=1-e-t,试求方程y(t)+ay(t)=2f(t)+f(t)的响应。
信号与系统课后答案(PDF)
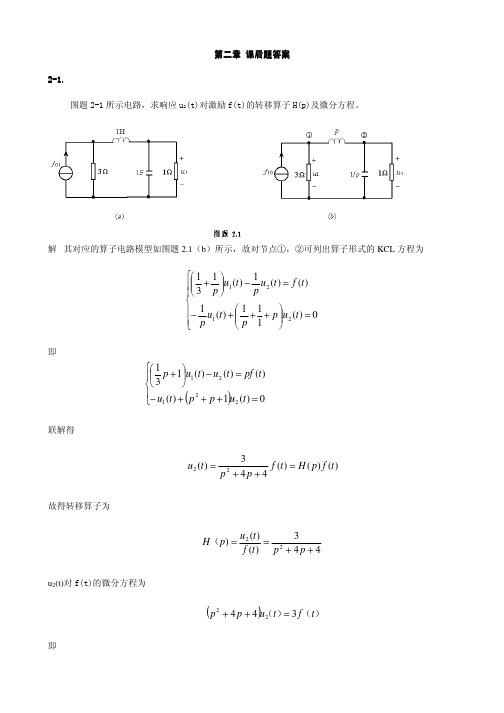
第二章第二章 课后题答案课后题答案2-1.1.图题2-1所示电路,求响应u 2(t)对激励f(t)的转移算子H(p)及微分方程。
解 其对应的算子电路模型如图题2.1(b )所示,故对节点①,②可列出算子形式的KCL 方程为= +++−=−+0)(111)(1)()(1)(1312121t u p p t u p t f t u p t u p即()=+++−=−+0)(1)()()()(13122121t u p p t u t pf t u t u p联解得)()()(443)(22t f p H t f p p t u =++=故得转移算子为443)()()22++==p p t f t u p H (u 2(t)对f(t)的微分方程为())()(t f t u p p 34422=++即)(t f t u t u dt d t u dt d 3)(4)(4)(22222=++2-2图题2-2所示电路,求响应i(t)对激励f(t)的转移算子H(p)及微分方程。
解 其对应的算子电路模型如图2.2(b)所示。
故得)()(t f p p p p pp t f t i 3011101022221.01)(2+++=+×++=故得转移算子为30111010)()()(2+++==p p p t f t i p Hi(t)对f(t)的微分方程为)()1010()()3011(2t f p t i p p +=++即)(10)(10)(30)(11)(22t f t f dt d t i t i dt d t i dt d +=++2-3图题2-3所示电路,已知u C (0-)=1 V, i(0-)=2 A。
求t>0时的零输入响应i(t)和u C (t)。
解 其对应的算子电路模型如图题2.3(b)所示。
故对节点N 可列写出算子形式的KCL 方程为0)(2312= ++t u p p C又有uc(t)=pi(t),代入上式化简,即得电路的微分方程为=====++−+−+1)0()0(2)0()0(0)()23(2c cu u i i t i p p电路的特征方程为0232=++p p故得特征根(即电路的自然频率)为p 1=-1,p 2=-2。
信号与系统 燕庆明 课后习题

1
计算:
2.1 设有如下函数 f( t ),试分别画出它们的波形。 (a) f( t ) = 2( t 1 ) 2( t 2 ) (b) f( t ) = sint[( t ) ( t 6 )]
2-2 试用阶跃函数的组合表示题 2-4 图所示信号。 解(a) f( t ) = ( t ) 2( t 1 ) + ( t 2 )
f
(t
t0 ) 即满足时不变性
f(t-t0)→y(t-t0)
1.6.试一般性地证明线性时不变系统具有微分特性。
证明 设 f(t)→y(t),则 f(t-Δt)→y(t-Δt)又因为 f (t) f (t t) y(t) y(t t0 ) 所以
t
t
lim f (t) f (t t) lim y(t) f (t t0 ) 既有 f '(t) y'(t)
h(t) x1(t) [ (t) (t)] (t) 2e3t (t) 阶跃响应
s(t)
t
h( )d
1 (1
2e 3t
) (t)
0
3
3.6LTI系统的冲激响应如图(a),若输入信号f (t)如图(b)所示三角波,求零状态响应?
本题用图形扫描计算卷积即y(t) h(t) f (t) 0(t 0),
(7)=2 t
3-1 如图 2-1 所示系统,试以 uC( t )为输出列出其微分方程。
解 由图示,有
iL
uC R
C
duC dt
又 iL
1 L
t
0(uS uC )dt 故
1 L
信号和系统课后习题答案解析

完美.格式.编辑专业.资料.整理第一章习题参考解答1.1 绘出下列函数波形草图。
(1) ||3)(t et x -=(2) ()⎪⎪⎨⎧<≥=02021)(n n n x n n(3) )(2sin )(t t t x επ=(4) )(4sin )(n n n x επ=(5) )]4()([4cos )(--=-t t t et x tεεπ(6) )]4()1([3)(---=n n n x nεε(7) t t t t x cos)]2()([)(πδδ--=(8) )]1()3([)(--+=n n n n x δδ完美.格式.编辑专业.资料.整理(9) )2()1(2)()(-+--=t t t t x εεε(10) )5(5)]5()([)(-+--=n n n n n x εεε(11) )]1()1([)(--+=t t dtdt x εε (12) )()5()(n n n x --+-=εε(13) ⎰∞--=td t x ττδ)1()((14) )()(n n n x --=ε1.2 确定下列信号的能量和功率,并指出是能量信号还是功率信号,或两者均不是。
(1) ||3)(t et x -=解 能量有限信号。
信号能量为:()⎰⎰⎰⎰∞-∞-∞∞--∞∞-+===02022||2993)(dt edt edt e dt t xE ttt ∞<=⋅-⋅+⋅⋅=∞-∞-9)21(92190202tte e(2) ()⎪⎩⎪⎨⎧<≥=02021)(n n n x n n解 能量有限信号。
信号能量为:()∞<=+=+==∑∑∑∑∑∞=--∞=∞=--∞=∞-∞=35)41(4])21[(2)(0102122n n n nn n n n n n xE(3) t t x π2sin )(=完美.格式.编辑专业.资料.整理 解 功率有限信号。
周期信号在(∞-∞,)区间上的平均功率等于在一个周期内的平均功率,t π2sin 的周期为1。
《信号与系统教程》教学指导书--燕庆明(可编辑)

《信号与系统教程》教学指导书--燕庆明教育科学“十五”国家规划课题研究成果《信号与系统教程》教学指导书燕庆明高等教育出版社书书书内容提要本书是与燕庆明主编《信号与系统教程》相配套的教学指导书。
书中明确了主教材各章的教学目标和教学重点,并对重点给予指导。
内容精炼,例题丰富。
书中除了对全书的习题进行解析外,还编写了!套模拟试题,为学生自学检测提供帮助。
本书适合于高等学校电子信息类专业的教师和学生作为“信号与系统”课程的教学参考书和学习指导书。
" 图书在版编目(!"#)数据"《信号与系统教程》教学指导书#燕庆明$ ?北京:高等教育出版社, %&&’ %" *+,-/&0 /&’&1 /." 信?" 燕?" 信号系统 /高等学校 /! " #教学参考资料" 2-3$4$" 中国版本图书馆 5*6数据核字(%&&’)第&331’号出版发行" 高等教育出版社" " " " " " " " 购书热线" && /40&101!!社" " 址" 北京市西城区德外大街0号免费咨询" !&& /!& /&13!邮政编码" &&& 网" " 址" 7889:# #::: 7;9 ; ?总" " 机" && /!%&%!!33 " " " " " 7889:# #::: 7;9 @A ?经" " 销" 新华书店北京发行所印" " 刷"开" " 本" .!. B34&" #4 版" " 次" " " 年" 月第版印" " 张" 3$1 印" " 次" " " 年" 月第次印刷字" " 数" .& &&& 定" " 价" % 1&元本书如有缺页、倒页、脱页等质量问题,请到所购图书销售部门联系调换。
《信号与系统》习题参考答案

《信号与系统》习题参考答案(1)2—1(1) 01()()()()(1)()ta at x t h t x u t d e d e u t aτττττ∞---∞*=⋅-==-⎰⎰ (2) 00()()(cos sin )()x t h t t d ωτωτδττ∞-∞*=+⋅-⎰0000(cos sin )()cos sin t t t d t t ωωδττωω∞-∞=+⋅-=+⎰(3) 当0t <时 ()()0x t h t *=当01t ≤<时 20()()(1)2tt x t h t d t ττ*=+=+⎰当12t ≤<时 13()()(1)2x t h t d ττ*=+=⎰ 当23t ≤<时 12213()()(1)22t x t h t d t t ττ-*=+=-++⎰ 当3t ≥时 ()()0x t h t *= (4) 当0t <时 ()()0x t h t *=当0t ≥时 01()()sin 2(1cos 2)2tx t h t d t ττ*==-⎰ (5) 22222(2)2(4)241()()(2)2t t t t t t t x t h t e d e d e ee ττττ-----*=-=-+⎰⎰ (6)()x t at b =+11212()()()()()(2)3363tt x t h t a b d a tb t a t a bττδ-*=+++*--=++⎰2—2(1) [][][][2](2)[2]x n h n nu n n n u n δ*=*-=--(2) 10[][](2)[](21)[]nin i x n h n u n u n +=*==-∑(3) 当0n ≥时 1111[][]2()()232i n in i x n h n --=-∞*==∑ 当0n <时 111[][]2()223n i n i n i x n h n --=-∞*==⋅∑ (4) 当0n <时 [][]0x n h n *=当0n ≥时 110[][]()[]n n nin ii x n h n u n βααββα++-=-*==-∑(5) 当07n ≤≤时 071[][](1)[1(1)]2in i n x n h n -=-*=-=--∑ 当70n -≤≤时 71[][](1)[(1)1]2ni n i x n h n -=-*=-=--∑ 2—3(1) 12()()[(1)(1)][(5)(5)]x t x t u t u t t t δδ*=+--*++- (6)(4)(4)(6)u t u t u t u t =++--+-- (2) 123()()()x t x t x t **{[(6)(4)][(4)(6)]}*[u t u t u t u t =+-++---11()()]22t t δδ++- ( 6.5)( 4.5)( 5.5)( 3.5)( 3.5)( 5.5)u t u t u t u t u t u t =+-+++-++--- ( 4.5)( 6.5)u t u t +---(3) 1311()()[(1)(1)][()()]22x t x t u t u t t t δδ*=+--*++- ( 1.5)(0.5)(0.5)( 1.5)u t u t u t u t =+--++-- 2—4 0(3)331()(3)1t k k t tk k y t eu t k e e e e∞-----=-∞=-∞=-=⋅=-∑∑311A e-=- 2—5(1) 当2t ≥时 ()()0x t h t *= 当20t -<<时 11()()2t x t h t d t τ+-*==+⎰当02t <<时 11()()2t x t h t d t τ-*==-⎰(2) 当01t <<时 1()()22(1)tx t h t d t τ*==-⎰ 当10t -<<时 01()()22(1)2t tx t h t d d t t t ττ+*=+=-++=+⎰⎰当21t -<<-时 11()()2t x t h t d t τ+-*==+⎰当 1t ≥ 或 2t <-时 ()()0x t h t *=此题也可利用性质,先对()x t 积分,对()h t 微分,'()()()y t x t dt h t =*⎰(3) 当0t <时 (1)1()()1t x t h t e dt +∞--*==⎰当0t ≥时 1(1)(1)11()()22t t t t t x t h t e dt e dt e ++∞-----+*=+=-⎰⎰(4) 当t π< 或 5t π>时 ()()0x t h t *= 当3t ππ<<时 0()()sin 1cos t x t h t d t πττ-*==+⎰当35t ππ<<时 23()()sin 1cos t x t h t d t ππττ-*==--⎰(5) 当01t <<时 2211()()222()22x t h t t t t *=-=--当12t <≤时 2231()()264[2()]22x t h t t t t *=-+-=---()()x t h t *是以2为周期的周期函数 2—7(1) 111[][1]()[]()[1]22nn h n Ah n u n A u n ---=--111()[()()][1]()22nn n A u n n δδ-=+--=12A =(2) 111[][][][1][][]h n h n Ah n h n h n n δ---*-*-=*11[][][1]2h n n n δδ-∴=-- (3) 11[][][]2[[][1]][]nx n h n h n u n u n h n --**=--* 2[]2[[][4]]2[[1][5]]nn x n u n u n u n u n -∴=------2—8(1) 0()3()y t y t =(2) 00()()(2)y t y t y t =-- (3) 0()(1)y t y t =- (4) 0()()y t y t =-(5) 0()()dy t y t dt=(6) 202()()d y t y t dt =2—9 12111[][]()[]()[1]222n n x n h n u n u n -*=-+--1()([][1])[]2nu n u n n δ=---=1221[][][][]([][])*[]y n x n h n h n x n h n h n =**=* []*([][])[][]n n n n n u n u n u n u n δαβαβ=+=+ 2—10(1) 341201[][]((0.5))[3]2(1())[3]2n nn n x n x n u n u n ++=*=+=-+∑ (2) 4123[][][]2(1(0.5))[3]([][1])n x n x n x n u n n n δδ+**=-+*-- 43312(1(0.5))[3]2(1(0.5))[2]()[3]2n n n u n u n u n +++=-+--+=+ (3) 23[][][3]([][1])[3][2][3]x n x n u n n n u n u n n δδδ*=+*--=+-+=+ 2—11(1) 12345[][]([][][])[]h n h n h n h n h n h n =*-*+ (2) 34[][][1]h n h n nu n *=- 234[][][](1)[][1][]h n h n h nn u n n u n u n -*=+--= 12345[][]([][][])[]h n h n h n h n h n h n =*-*+514()([][3])*[][]2nu n u n u n hn =--+ 4[]6[1]7[2][]4[3]5[]6[1]7[2]4[3]n n u n n n n n u n n δδδδδδδ=+-+-++-=+-+---(1)'()()(2)(2)()(2)tt y t e x d x t y t x t τττ---∞=--+-=-+-⎰(2)()(2)t h t eu t --=- (2)当1t ≤时 ()0y t =当14t <≤时 1(2)(1)2()1t t y t e d e ττ+----==-⎰当4t >时 1(2)(4)(1)2()t t t t y t e d e e ττ+-------==-⎰2—13(1)213()()()()(1)[()](1)[()](1)h t h t h t u t t t u t t u t δδδ**=*-*-=-*-=-- 1213()()()()()()(1)h t h t h t h t h t u t u t =+**=--(2)1(10)1(02)()3(23)0t t t y t t t +-<<⎧⎪<<⎪=⎨-<<⎪⎪⎩其余2—14(1)因果、稳定 (2)非因果、非稳定 (3)非因果、稳定 (4)非因果、稳定 (5)非因果、稳定 (6)因果、稳定 (7)因果、非稳定 2—15(1)因果、稳定 (2)非因果、稳定 (3)非因果、非稳定 (4)非因果、稳定 (5)因果、非稳定 (6)非因果、稳定 (7)因果、稳定 2—16(1)对 (2)对()h t dt ∞-∞=+∞⎰(3)错 例如单位冲激响应(1)t δ-是因果的,但LTI 系统的逆系统(1)t δ+不是因果的。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《信号与系统》(第3版)习题解析高等教育出版社目录第1章习题解析 (2)第2章习题解析 (6)第3章习题解析 (16)第4章习题解析 (23)第5章习题解析 (31)第6章习题解析 (41)第7章习题解析 (49)第8章习题解析 (55)第1章习题解析1-1 题1-1图示信号中,哪些是连续信号?哪些是离散信号?哪些是周期信号?哪些是非周期信号?哪些是有始信号?(c) (d)题1-1图解 (a)、(c)、(d)为连续信号;(b)为离散信号;(d)为周期信号;其余为非周期信号;(a)、(b)、(c)为有始(因果)信号。
1-2 给定题1-2图示信号f ( t ),试画出下列信号的波形。
[提示:f ( 2t )表示将f ( t )波形压缩,f (2t )表示将f ( t )波形展宽。
] (a) 2 f ( t - 2 )(b) f ( 2t )(c) f ( 2t ) (d) f ( -t +1 )题1-2图解 以上各函数的波形如图p1-2所示。
图p1-21-3 如图1-3图示,R 、L 、C 元件可以看成以电流为输入,电压为响应的简单线性系统S R 、S L 、S C ,试写出各系统响应电压与激励电流函数关系的表达式。
题1-3图解 各系统响应与输入的关系可分别表示为)()(t i R t u R R ⋅= t t i L t u L L d )(d )(= ⎰∞-=t C C i Ct u ττd )(1)(1-4 如题1-4图示系统由加法器、积分器和放大量为-a 的放大器三个子系统组成,系统属于何种联接形式?试写出该系统的微分方程。
S R S L S C题1-4图解 系统为反馈联接形式。
设加法器的输出为x ( t ),由于)()()()(t y a t f t x -+=且)()(,d )()(t y t x t t x t y '==⎰故有 )()()(t ay t f t y -='即)()()(t f t ay t y =+'1-5 已知某系统的输入f ( t )与输出y ( t )的关系为y ( t ) = | f ( t )|,试判定该系统是否为线性时不变系统?解 设T 为系统的运算子,则可以表示为)()]([)(t f t f T t y ==不失一般性,设f ( t ) = f 1( t ) + f 2( t ),则)()()]([111t y t f t f T ==)()()]([222t y t f t f T ==故有)()()()]([21t y t f t f t f T =+=显然)()()()(2121t f t f t f t f +≠+即不满足可加性,故为非线性时不变系统。
1-6 判断下列方程所表示的系统的性质。
(1) ⎰+=t f tt f t y 0d )(d )(d )(ττ (2) )()(3)()(t f t y t y t y '=+'+''(3) )(3)()(2t f t y t y t =+'(4) )()()]([2t f t y t y =+'解 (1)线性;(2)线性时不变;(3)线性时变;(4)非线性时不变。
1-7 试证明方程)()()(t f t ay t y =+'所描述的系统为线性系统。
式中a 为常量。
证明 不失一般性,设输入有两个分量,且)()()()(2211t y t f t y t f →→,则有)()()(111t f t ay t y =+')()()(222t f t ay t y =+'相加得)()()()()()(212211t f t f t ay t y t ay t y +=+'++'即[][])()()()()()(d d212121t f t f t y t y a t y t y t +=+++可见)()()()(2121t y t y t f t f +→+即满足可加性,齐次性是显然的。
故系统为线性的。
1-8 若有线性时不变系统的方程为)()()(t f t ay t y =+'若在非零f ( t )作用下其响应t t y --=e 1)(,试求方程)()(2)()(t f t f t ay t y '+=+'的响应。
解 因为f ( t ) →t t y --=e 1)(,由线性关系,则)e 1(2)(2)(2t t y t f --=→由线性系统的微分特性,有t t y t f -='→'e )()(故响应t t t t y t f t f ----=+-=→'+e 2e )e 1(2)()()(2第2章习题解析2-1 如图2-1所示系统,试以u C ( t )为输出列出其微分方程。
题2-1图解 由图示,有 t u C R u i d d CC L +=又⎰-=tt u u L i 0C S L d )(1故C CC S )(1u C R u u u L ''+'=-从而得)(1)(1)(1)(S C C C t u LC t u LC t u RC t u =+'+''2-2 设有二阶系统方程0)(4)(4)(=+'+''t y t y t y在某起始状态下的0+起始值为2)0(,1)0(='=++y y试求零输入响应。
解 由特征方程λ2 + 4λ + 4 =0得 λ1 = λ2 = -2则零输入响应形式为t e t A A t y 221zi )()(-+=由于y zi ( 0+ ) = A 1 = 1-2A 1 + A 2 = 2所以A 2 = 4故有0,)41()(2zi ≥+=-t e t t y t2-3 设有如下函数f ( t ),试分别画出它们的波形。
(a) f ( t ) = 2ε( t -1 ) - 2ε( t -2 )(b) f ( t ) = sin πt [ε( t ) - ε( t -6 )]解 (a)和(b)的波形如图p2-3所示。
图p2-32-4 试用阶跃函数的组合表示题2-4图所示信号。
题2-4图解 (a) f ( t ) = ε( t ) - 2ε( t -1 ) + ε( t -2 )(b) f ( t ) = ε( t ) + 2ε( t -T ) + 3ε( t -2T )2-5 试计算下列结果。
(1) t δ( t - 1 )(2)⎰∞∞--t t t d )1(δ (3) ⎰∞--0d )()3πcos(t t t δω (4)⎰+---003d )(e t t t δ解 (1) t δ( t - 1 ) = δ( t - 1 )(2)1d )1(d )1(=-=-⎰⎰∞∞-∞∞-t t t t t δδ(3) 21d )()3πcos(d )()3πcos(00=-=-⎰⎰∞∞--t t t t t δδω (4)1d )(d )(e d )(e 00003003===-⎰⎰⎰+-+-+---t t t t t t t t δδδ2-6 设有题2-6图示信号f ( t ),对(a)写出f ' ( t )的表达式,对(b)写出f " ( t )的表达式,并分别画出它们的波形。
题2-6图解 (a)20,21≤≤t f ' ( t ) = δ( t - 2 ), t = 2-2δ( t - 4 ), t = 4(b) f " ( t ) = 2δ( t ) - 2δ( t - 1 ) - 2δ( t - 3 ) + 2δ( t - 4 )图p2-62-7 如题2-7图一阶系统,对(a)求冲激响应i 和u L ,对(b)求冲激响应u C 和i C ,并画出它们的波形。
题2-7图解 由图(a)有Ri t u t i L -=)(d d S 即)(1d d S t u Li L R t i =+ 当u S ( t ) = δ( t ),则冲激响应)(e 1)()(t L t i t h t L Rε⋅==- 则电压冲激响应)(e )(d d )()(L t L R t t i L t u t h t L Rεδ⋅-===- 对于图(b)RC 电路,有方程R u i t u CC S C d d -=即S C C11i Cu RC u =+' 当i S = δ( t )时,则)(e 1)()(C t Ct u t h RC tε⋅==-同时,电流)(e 1)(d d C C t RCt t u C i RCtεδ⋅-==-2-8 设有一阶系统方程)()()(3)(t f t f t y t y +'=+'试求其冲激响应h ( t )和阶跃响应s ( t )。
解 因方程的特征根λ = -3,故有)(e )(31t t x t ε⋅=-当h ( t ) = δ( t )时,则冲激响应)(e 2)()]()([)()(31t t t t t x t h t εδδδ⋅-=+'*=-阶跃响应)()e 21(31d )()(30t h t s t t εττ-+==⎰2-9 试求下列卷积。
(a) ε( t + 3 ) * ε( t - 5 )(b) δ( t ) * 2(c) t e -t ⋅ε( t ) * δ' ( t )解 (a) 按定义ε( t + 3 ) * ε( t - 5 ) =⎰∞∞---+ττετεd )5()3(t考虑到τ < -3时,ε( τ + 3 ) = 0;τ > t -5时,ε( t -τ - 5 ) = 0,故ε( t + 3 ) * ε( t - 5 ) =2,2d 53>-=⎰--t t t τ也可以利用迟延性质计算该卷积。
因为ε( t ) * ε( t ) = t ε( t )f1( t-t1 ) * f2( t-t2 ) = f( t-t1-t2 )故对本题,有ε( t + 3 ) * ε( t- 5 ) = ( t + 3 - 5 )ε( t + 3 - 5 ) = ( t- 2 )ε( t- 2 ) 两种方法结果一致。
(b) 由δ( t )的特点,故δ( t ) * 2 = 2(c) t e-t⋅ε( t ) * δ'( t ) = [t e-tε( t )]' = ( e-t-t e-t )ε( t )2-10对图示信号,求f1( t ) * f2( t )。
题2-10图解(a)先借用阶跃信号表示f1( t )和f2( t ),即f1( t ) = 2ε( t ) - 2ε( t- 1 )f2( t ) = ε( t ) -ε( t- 2 )故f1( t ) * f2( t ) = [2ε( t ) - 2ε( t- 1 )] * [ε( t ) -ε( t- 2 )]因为ε( t ) * ε( t ) = ⎰t0d1τ= tε( t )故有f 1( t ) * f 2( t ) = 2t ε( t ) - 2( t - 1 )ε( t - 1 ) -2( t - 2 )ε( t - 2 ) + 2( t - 3 )ε( t - 3 )读者也可以用图形扫描法计算之。
