第三章 时域分析法
合集下载
自控第三章 时域分析法
wdtp = nЛ
欠阻尼二阶系统的性能指标
第一次峰值 : n=1 所以: tp=Л / wd 峰值时间定性分析 wn↗→wd= wn(1-ζ 2)1/2 ↗→tp ↘ ζ ↘→wd= wn(1-ζ 2)1/2 ↗→tp ↘
峰值时间越小, 快速性越好.
欠阻尼二阶系统的性能指标
3. 超调量σ % h（tp）- h（∞） σ % = ————————— *100% h（∞） 由h(t)求出h(tp)和h(∞), 代入定义式即得.
三、一阶系统的单位脉冲响应
K（S）= G（S）R（S） = 1 /（TS+1） k（t）= L
-1
[ K（S）]
= e-t/T/T
T越小 → 响应的持续时间越短 → 快速性越好。
四、三种响应之间的关系
δ (t) = d/dt [u(t)] = d2/dt2 [r(t)] k(t) = d/dt [h(t)] = d2/dt2 [Ct(t)]
欠阻尼二阶系统的性能指标
h(tp)=1-(1-ζ 2)-1/2e–ζ =1-(1-ζ 2)-1/2e–ζ =1+(1-ζ =1+(1-ζ =1+ h(∞) = 1 σ% = e
2 1/2
Wntp Wntp
sin(wdtp+θ ) sin(Л +θ )
2
)-1/2e–ζ Wntp sinθ 2 )-1/2e–ζ Wntp w (1-ζ 2)1/2/w n n
eSS= 1 - h（∞）= 0
一阶系统在单位阶跃输入下的稳态误差为0。
二、一阶系统的单位斜坡响应
Ct(S)= G(S)R(S)
= 1/[(TS+1)S2] Ct(t)= L-1[Ct(S)] = t - T + e-t/T 稳态误差 : eSS= T 一阶系统在单位斜坡输入下的稳态误差为T。它只能通过 减小时间常数T来减小，而不能最终消除。
欠阻尼二阶系统的性能指标
第一次峰值 : n=1 所以: tp=Л / wd 峰值时间定性分析 wn↗→wd= wn(1-ζ 2)1/2 ↗→tp ↘ ζ ↘→wd= wn(1-ζ 2)1/2 ↗→tp ↘
峰值时间越小, 快速性越好.
欠阻尼二阶系统的性能指标
3. 超调量σ % h（tp）- h（∞） σ % = ————————— *100% h（∞） 由h(t)求出h(tp)和h(∞), 代入定义式即得.
三、一阶系统的单位脉冲响应
K（S）= G（S）R（S） = 1 /（TS+1） k（t）= L
-1
[ K（S）]
= e-t/T/T
T越小 → 响应的持续时间越短 → 快速性越好。
四、三种响应之间的关系
δ (t) = d/dt [u(t)] = d2/dt2 [r(t)] k(t) = d/dt [h(t)] = d2/dt2 [Ct(t)]
欠阻尼二阶系统的性能指标
h(tp)=1-(1-ζ 2)-1/2e–ζ =1-(1-ζ 2)-1/2e–ζ =1+(1-ζ =1+(1-ζ =1+ h(∞) = 1 σ% = e
2 1/2
Wntp Wntp
sin(wdtp+θ ) sin(Л +θ )
2
)-1/2e–ζ Wntp sinθ 2 )-1/2e–ζ Wntp w (1-ζ 2)1/2/w n n
eSS= 1 - h（∞）= 0
一阶系统在单位阶跃输入下的稳态误差为0。
二、一阶系统的单位斜坡响应
Ct(S)= G(S)R(S)
= 1/[(TS+1)S2] Ct(t)= L-1[Ct(S)] = t - T + e-t/T 稳态误差 : eSS= T 一阶系统在单位斜坡输入下的稳态误差为T。它只能通过 减小时间常数T来减小，而不能最终消除。
时域分析法
§ 3.2 一阶系统的时间响应
一、一阶系统的数学模型 数学模型
其中时间常数T＝1 / K
二、一阶系统的单位阶跃响应
对于单位阶跃输入
xi
(t )
1(t ),
Xi
(s)
1 s
故系统单位阶跃响应象函数为
1
1 s
s
T
1
A s
s
B 1
1 s
s
1
1
T
T
T
取拉氏反变换得系统单位阶跃响应为
1t
xo (t) 1 e T
，为闭环极点的实部； ，为闭环极点的虚部；
欠阻尼二阶系统的单位阶跃响应的象函数为
。
将上式进行拉氏反变换，单位阶跃响应为
(3.33)
x0 (t) 1
e n t
1 2
(n
1 2 n
cosdt sin dt)
1
ent
1 2
(sin
c osd t
cos
sin d t )
1
e nt
1
2
sin(
则
Xo
s
Xo Xi
s s
X
i
s
1 1 Ts 1
1
T
s
1 T
进行拉氏反变换
x0
(t
)
1 T
t
eT
四、响应之间的关系 对线性定常系统，输入之间存在微积分关系，其响
应间也存在相应微积分关系。
作用：在测试系统时，可由一种信号推断几种信号的相应响应。
§ 3.3 二阶系统的时间响应
一、典型二阶系统的数学模型
决定。
在稳态下，输出 x0 (t) 和输入 xi (t) 之间不存在误差，即系统
第三章_时域分析方法
第3章时域分析法基本要求3－1 时域分析基础3－2 一、二阶系统分析与计算3－3 系统稳定性分析3－4 稳态误差分析计算返回主目录基本要求1熟练掌握一、二阶系统的数学模型和阶跃响应的特点。
熟练计算性能指标和结构参数，特别是一阶系统和典型欠阻尼二阶系统动态性能的计算方法。
2了解一阶系统的脉冲响应和斜坡响应的特点。
3正确理解系统稳定性的概念，能熟练运用稳定性判据判定系统的稳定性并进行有关的参数计算、分析。
4正确理解稳态误差的概念，明确终值定理的应用条件。
5熟练掌握计算稳态误差的方法。
6掌握系统的型次和静态误差系数的概念。
控制系统的数学模型是分析、研究和设计控制系统的基础，经典控制论中三种分析（时域，根轨迹，频域）、研究和设计控制系统的方法，都是建立在这个基础上的。
3－1 时域分析基础一、时域分析法的特点它根据系统微分方程，通过拉氏变换，直接求出系统的时间响应。
依据响应的表达式及时间响应曲线来分析系统控制性能，并找出系统结构、参数与这些性能之间的关系。
这是一种直接方法，而且比较准确，可以提供系统时间响应的全部信息。
二、典型初始状态，典型外作用1. 典型初始状态通常规定控制系统的初始状态为零状态。
即在外作用加于系统之前，被控量及其各阶导数相对于平衡工作点的增量为零，系统处于相对平衡状态。
2. 典型外作用①单位阶跃函数1(t)tf(t)⎩⎨⎧<≥==0t 00t 1)t (1)t (f 其拉氏变换为：s 1dt e 1)s (F )]t (f [L 0st===⎰∞-其数学表达式为：t②单位斜坡函数0t 0t 0t)t (1t )t (f <≥⎩⎨⎧=.=其拉氏变换为：2sts 1dt e t )s (F )]t (f [L ===⎰∞-f(t)其数学表达式为：③单位脉冲函数000)()(=≠⎩⎨⎧∞==t t t t f d 其数学表达式为：其拉氏变换为：1)()]([==s F t f L ⎰+∞∞-=1)(dt t d 定义：图中1代表了脉冲强度。
自动控制原理-第3章-时域分析法
系统响应达到峰值所需要的时间。
调节时间
系统响应从峰值回到稳态值所需的时间。
振荡频率
系统阻尼振荡的频率，反映系统的动态性能。
系统的阶跃响应与脉冲响应
阶跃响应
系统对阶跃输入信号的响应，反映系 统的动态性能和稳态性能。
脉冲响应
系统对脉冲输入信号的响应，用于衡 量系统的冲激响应能力和动态性能。
03
一阶系统时域分析
01
单位阶跃响应是指系统在单位阶跃函数作为输入时的
输出响应。
计算方法
02 通过将单位阶跃函数作为输入，代入一阶系统的传递
函数中，求出系统的输出。
特点
03
一阶系统的单位阶跃响应是等值振荡的，其最大值为1，
达到最大值的时间为T，且在时间T后逐渐趋于0。
一阶系统的单位脉冲响应
定义
单位脉冲响应是指系统在单 位脉冲函数作为输入时的输
无法揭示系统结构特性
时域分析法主要关注系统的动态行为和响应，难以揭示系统的结构特 性和稳定性。
对初值条件敏感
时域分析法的结果对系统的初值条件较为敏感，初值条件的微小变化 可能导致计算结果的较大偏差。
感谢您的观看
THANKS
计算简便
时域分析法通常采用数值积分方法进 行计算，计算过程相对简单，易于实 现。
时域分析法的缺点
数值稳定性问题
对于某些系统，时域分析法可能存在数值稳定性问题，例如数值积分 方法的误差累积可能导致计算结果失真。
计算量大
对于高阶系统和复杂系统，时域分析法需要进行大量的数值积分计算， 计算量较大，效率较低。
自动控制原理-第3章-时域 分析法
目录
• 时域分析法概述 • 时域分析的基本概念 • 一阶系统时域分析 • 二阶系统时域分析 • 高阶系统时域分析 • 时域分析法的优缺点
调节时间
系统响应从峰值回到稳态值所需的时间。
振荡频率
系统阻尼振荡的频率，反映系统的动态性能。
系统的阶跃响应与脉冲响应
阶跃响应
系统对阶跃输入信号的响应，反映系 统的动态性能和稳态性能。
脉冲响应
系统对脉冲输入信号的响应，用于衡 量系统的冲激响应能力和动态性能。
03
一阶系统时域分析
01
单位阶跃响应是指系统在单位阶跃函数作为输入时的
输出响应。
计算方法
02 通过将单位阶跃函数作为输入，代入一阶系统的传递
函数中，求出系统的输出。
特点
03
一阶系统的单位阶跃响应是等值振荡的，其最大值为1，
达到最大值的时间为T，且在时间T后逐渐趋于0。
一阶系统的单位脉冲响应
定义
单位脉冲响应是指系统在单 位脉冲函数作为输入时的输
无法揭示系统结构特性
时域分析法主要关注系统的动态行为和响应，难以揭示系统的结构特 性和稳定性。
对初值条件敏感
时域分析法的结果对系统的初值条件较为敏感，初值条件的微小变化 可能导致计算结果的较大偏差。
感谢您的观看
THANKS
计算简便
时域分析法通常采用数值积分方法进 行计算，计算过程相对简单，易于实 现。
时域分析法的缺点
数值稳定性问题
对于某些系统，时域分析法可能存在数值稳定性问题，例如数值积分 方法的误差累积可能导致计算结果失真。
计算量大
对于高阶系统和复杂系统，时域分析法需要进行大量的数值积分计算， 计算量较大，效率较低。
自动控制原理-第3章-时域 分析法
目录
• 时域分析法概述 • 时域分析的基本概念 • 一阶系统时域分析 • 二阶系统时域分析 • 高阶系统时域分析 • 时域分析法的优缺点
语音信号处理课件__第03章时域分析
SNRdB 6.02B 4.77 20log10 (
x
xmax
)
(3-11)
3.1 语音信号的短时处理方法 脉冲编码调制
若是xmax取为4倍方差(δx)
SNRdB 6.02B 7.27
取样之位数 8 16 24
(3-12)
数字信号的信噪比 41 dB 89 dB 137 dB
3.1 语音信号的短时处理方法 脉冲编码调制
一个数字信号取样之后，变成离散时间信号，接下来就是要用数字 方式来表示这个离散时间信号上的每个取样值。 一个电位波形会有固定的电压范围，一个取样值可以是在此电压范 围内的任何电位。如果只能用固定数目的位来表示这些取样值，那 么这些二进数字就只能代表固定的几个电位值，这个转换就是量化 (quantization)，而转换之后只允许存在的几个电位值就是量化阶 数(quantization level)。 执行量化转换的硬件电路，就是量化器（quantizer)。以二进数字 表示的信号就是数字信号(digital signal)，而这种将信号波形转 变成二进数字的方法，就叫脉冲编码调制(pulse code modulation, PCM)。
3.1 语音信号的短时处理方法
预处理 平滑滤波器：D/A后面的低通滤波器是平滑滤 波器，对重构的语音波形的高次谐波起平滑 作用，以去除高次谐波失真。 预加重：
现象:由于语音信号的平均功率谱受声门激励和口 鼻辐射的影响，高频端大约在800 Hz以上按6dB/ 倍频程跌落，为此要在预处理中进行预加重。 目的:提升高频部分，使信号的频谱变得平坦，以 便于进行频谱分析或声道参数分析。 位置:预加重可在A/D变换前的反混叠滤波之前进行， 这样不仅能够进行预加重，而且可以压缩信号的动 态范围，有效地提高信噪比。
x
xmax
)
(3-11)
3.1 语音信号的短时处理方法 脉冲编码调制
若是xmax取为4倍方差(δx)
SNRdB 6.02B 7.27
取样之位数 8 16 24
(3-12)
数字信号的信噪比 41 dB 89 dB 137 dB
3.1 语音信号的短时处理方法 脉冲编码调制
一个数字信号取样之后，变成离散时间信号，接下来就是要用数字 方式来表示这个离散时间信号上的每个取样值。 一个电位波形会有固定的电压范围，一个取样值可以是在此电压范 围内的任何电位。如果只能用固定数目的位来表示这些取样值，那 么这些二进数字就只能代表固定的几个电位值，这个转换就是量化 (quantization)，而转换之后只允许存在的几个电位值就是量化阶 数(quantization level)。 执行量化转换的硬件电路，就是量化器（quantizer)。以二进数字 表示的信号就是数字信号(digital signal)，而这种将信号波形转 变成二进数字的方法，就叫脉冲编码调制(pulse code modulation, PCM)。
3.1 语音信号的短时处理方法
预处理 平滑滤波器：D/A后面的低通滤波器是平滑滤 波器，对重构的语音波形的高次谐波起平滑 作用，以去除高次谐波失真。 预加重：
现象:由于语音信号的平均功率谱受声门激励和口 鼻辐射的影响，高频端大约在800 Hz以上按6dB/ 倍频程跌落，为此要在预处理中进行预加重。 目的:提升高频部分，使信号的频谱变得平坦，以 便于进行频谱分析或声道参数分析。 位置:预加重可在A/D变换前的反混叠滤波之前进行， 这样不仅能够进行预加重，而且可以压缩信号的动 态范围，有效地提高信噪比。
自动控制原理-第3章
响应曲线如图3-2所示。图中
为输出的稳态值。
第三章 线性系统的时域分析 法
图 3-2 动态性能指标
第三章 线性系统的时域分析 法
动态性能指标通常有以下几种:
延迟时间td: 指响应曲线第一次达到稳态值的一半所需的时间
上升时间tr: 若阶跃响应不超过稳态值, 上升时间指响应曲线从 稳态值的10%上升到90%所需的时间; 对于有振荡的系统, 上升时 间定义为响应从零第一次上升到稳态值所需的时间。上升时间越 短, 响应速度越快。
可由下式确定: (3.8)
振荡次数N: 在0≤t≤ts内, 阶跃响应曲线穿越稳态值c(∞)次 一半称为振荡次数。
上述动态性能指标中, 常用的指标有tr、ts和σp。上升时间tr 价系统的响应速度; σp评价系统的运行平稳性或阻尼程度; ts是同
时反映响应速度和阻尼程度的综合性指标。 应当指出, 除简单的一 、二阶系统外, 要精确给出这些指标的解析表达式是很困难的。
中可以看出, 随着阻尼比ζ的减小, 阶跃响应的振荡程度加剧。 ζ =0时是等幅振荡, ζ≥1时是无振荡的单调上升曲线, 其中临界阻尼 对应的过渡过程时间最短。 在欠阻尼的状态下, 当0.4＜ζ＜0.8时过
渡过程时间比临界阻尼时更短, 而且振荡也不严重。 因此在 控制工程中, 除了那些不允许产生超调和振荡的情况外, 通常都希
第三章 线性系统的时域分析法 4. 脉冲函数 脉冲函数(见图3-1(d))的时域表达式为
(3.4)
式中,h称为脉冲宽度, 脉冲的面积为1。若对脉冲的宽度取趋于 零的极限, 则有
(3.5) 及
(3.6)
称此函数为理想脉冲函数, 又称δ函数(见图3-1(e))。
第三章 线性系统的时域分析 法
第3章 时域分析法
6．稳态误差 在图3-6所示单位阶跃响应曲线中，对单位阶跃响应的稳态误差可以用ess来表 示，通常用ess反映系统跟踪输入时的稳态精度。
稳态误差ess：对单位负反馈系统，当t→∞时，系统单位阶跃响应的实际稳态 值与给定值之差，即
ess1= 1 − c(∞) 如果c(∞)为1, 则系统的稳态误差为零。
函数的图形如图3-5所示。
t 0
图3-5 正弦函数图形
3.2 阶跃响应的性能指标
（1）动态过程。动态过程也称过渡过程或瞬态过程，指系统在典型输入信 号作用下，其输出量从初始状态到最终状态的过程。根据系统结构和参数 选择的情况，动态过程表现为衰减、发散和等幅振荡几种形式。显然，一 个可以正常运行的控制系统，其动态过程必须是衰减的，即系统必须是稳 定的，动态过程除提供系统稳定的信息外，还可以提供其响应速度和阻尼 情况等信息，这些信息是用系统动态性能描述的 。
（2）稳态过程。稳态过程也称系统的稳态响应，指系统在典型输入信号 作用下，当t→∞时，其输出量的表现形式。稳态过程表征系统输出量最终复 现输入量的程度，提供系统稳态误差的信息，用系统的稳态性能描述。在分 析系统性能时，认为当系统的输出对其输入的复现进入允许的误差范围以后， 系统进入稳态。
由此可见，控制系统在典型输入信号作用下的性能指标由动态性能指标和稳 态性能指标两部分组成，一般认为阶跃输入对系统来说是最为严峻的工作状 态，如果系统在阶跃函数作用下的动态性能满足要求，那么在其他输入形式 作用下的动态性能也能满足要求。
时间ts。稳态值称为误差带，可以是5%或2%，前者称为5%误差带， 后者称为2%误差带。
5．峰值时间
在图3-6所示单位阶跃响应曲线中，对单位阶跃响应的峰值时间可以用tp来 表示，通常用tp评价系统的响应速度，也反映系统的局部快速性。
时域分析法
16:19
一般的控制系统多数为高阶系统，但是它们有可 能在一定的条件下用二阶系统去近似。因此，对 于二阶系统的分析具有重要的实际意义。在系统 的分析与设计中，通常将二阶系统的响应特性作 为一种基准。
16:19
二阶系统传递函数的标准形式
某随动系统方块图
如图所示随动系统的微分方程式：
TM
d
2c t
/ TM
s2
n2 2ns
n2
3.4.4
其中 n为无阻尼自然振荡角频率(固有频率)； 称为阻尼比；
均为二阶系统的特征参数，是系统本身的固有特性。
16:19
二阶系统的特征方程
s2
2
ns
2 n
0
3.4.5
由上式解得二阶系统的二个特征根(即闭环极点)为：
s1,2 n jn 1 2 3.4.6
当0 1时，特征根为一对实部为
16:19
当-1< <0 ，特征根是位于右半平面的共轭复根，呈发散振荡 状态。如图3 .6(e)所示。
当 < -1，呈单调发散状态。如图3 .6(f)所示 P53图3.7表明了极点分布与n、 的关系图。
16:19
二阶系统的单位阶跃响应 1. 欠阻尼状态
令r t 1t，则有Rs 1
s
二阶系统在单位阶跃函数作用下输出：
16:19
3.1 线性定常系统的时间响应及 暂态响应性能指标
一、时间响应
线性系统的动态方程
an y(n) (t) an1 y(n1) (t) L a1y&(t) a0 y(t) bm x(m) (t) bm1x(m1) (t) L b1x&(t) b0x(t)
经过拉氏变换得
时域分析法
动,试分析系统在x扰动下的特性。
解:
系统闭环传递函数：
r+ -
K
x
+
1
y
+
s(1+Ts)
Y(s)
1
G( s ) X ( s ) Ts2 s K
K
1
T
K s2 1 s K
TT
1 K
s2
n2 2ns n2
其中 2
1 KT
n
K T
y( t )
1
1
K
1 1 2
e n t
sin( d t
,m
n
写成零极点形式： m
kg (s zi )
(s) n1
i 1 n2
, n1 2n2 n, m n
(s p j ) (s2 2 l nl s nl 2 )
j 1
l 1
其单位阶跃响应函数为：
C(s)
(s) 1 s
a0 s
n1 j1
aj s pj
n2 l 1
l (s lnl ) lnl 1 l 2 s2 2 l nl s nl 2
第三章 时域分析法
主要内容： 1. 控制系统的时间响应 2. 误差分析和计算 3. 稳定性分析（劳斯判据）
系统分析：对控制系统的稳定性、误差和动态 特性等方面的指标进行分析，即分析系统的稳 定性、准确性和快速性。
dny
d n1 y
dy
dmx
d m1 x
dx
an dt n an1 dt n1 L a1 dt a0 y bm dt m bm1 dt m1 L b1 dt b0 x
——相角
极点的虚部决定系统的震荡频率：
解:
系统闭环传递函数：
r+ -
K
x
+
1
y
+
s(1+Ts)
Y(s)
1
G( s ) X ( s ) Ts2 s K
K
1
T
K s2 1 s K
TT
1 K
s2
n2 2ns n2
其中 2
1 KT
n
K T
y( t )
1
1
K
1 1 2
e n t
sin( d t
,m
n
写成零极点形式： m
kg (s zi )
(s) n1
i 1 n2
, n1 2n2 n, m n
(s p j ) (s2 2 l nl s nl 2 )
j 1
l 1
其单位阶跃响应函数为：
C(s)
(s) 1 s
a0 s
n1 j1
aj s pj
n2 l 1
l (s lnl ) lnl 1 l 2 s2 2 l nl s nl 2
第三章 时域分析法
主要内容： 1. 控制系统的时间响应 2. 误差分析和计算 3. 稳定性分析（劳斯判据）
系统分析：对控制系统的稳定性、误差和动态 特性等方面的指标进行分析，即分析系统的稳 定性、准确性和快速性。
dny
d n1 y
dy
dmx
d m1 x
dx
an dt n an1 dt n1 L a1 dt a0 y bm dt m bm1 dt m1 L b1 dt b0 x
——相角
极点的虚部决定系统的震荡频率：
自动控制原理第3章
例1. 系统特征方程式为
s 6 s 12 s 11 s 6 0
4 3 2
例2. 系统特征方程式为
s 3 s 2 s s 5s 6 0
5 4 3 2
特殊情况:
1) 劳斯行列表中某一行左边第一个数为零,其余 不为零或没有. 例: 例:
s 4 3s 3 s 2 3S 1 0
-
1/s
k/(s+5)(s+1)
例:系统特征方程式:
2 s 3 T s 2 10 s 100 0 s
4
按稳定要求确定T的临界值.
六.系统的相对稳定性
§3-3 控制系统的稳态误差
一.误差及稳态误差的定义 系统的误差为 e(t)=被控量的希望值－被控量的实际值 常用的误差定义有两种
二.线性定常系统稳定的充分必要条件
线性定常系统微分方程为:
a0
d dt
n 1
n
n
c (t )
d a dt
1
n 1
c (t ) n 1
d a dt
2
n2 n2
c (t )
d a dt
3
n3 n3
c ( t ) ........
a
d dt
m m
c (t )
a
n
c (t )
第三章 控制系统的时域分析法
§3-1 引言
一. 典型输入信号 1、阶跃函数
r(t)
r (t ) {
0 A
t0 t0
A
t
2、斜坡函数
r(t) {
r(t)
0 At
t0 t0
斜率＝A
自动控制原理 第三章时域分析方法
位脉冲响应，由此可以求得系统的传递函数。
总结与分析：
一阶系统对典型试验信号的响应 输入信号x(t) 输出响应y(t)
1 2 3
t
1() δ(t)
t T Te t / T
1 et /T
1 T
et /T
l 线性定常系统对输入信号导数的响应，可以通过 把系统对输入信号的响应进行微分求得； l 系统对输入信号积分的响应，可以通过把系统对原 输入信号的响应进行积分求得，而积分常数则由初 始条件决定。
3.1.1 控制系统的输入信号
● 在分析和设计控制系统时，需要有一个对各种
系统性能进行比较的基础。
● 从实际应用中抽象出一些典型的输入信号，它
们具有广泛的代表性和实际意义。
● 通过比较各类系统对这些典型试验信号的响
应来分析它们的性能。
常用的典型试验信号：
r(t) A t (a) 阶跃信号
r(t)
1 E
实验方法求取一阶系统的传递函数：
63.2％ T
1 Ts 1
对一阶系统的单位阶跃响应曲线， 1、直接从达到稳态值的63.2%对应的时间求出一阶 系统的时间常数；
2、从t＝0处的切线斜率求得系统的时间常数。 思考题：
若系统增益K不等于1，系统的稳态值应是多少？如何用实
验方法从响应曲线中求取K值？
3.2.2单位斜坡响应
2、系统的稳态响应为y(∞)=t－T，是一个与输入斜 坡函数斜率相同但时间迟后T的斜坡函数。
3、输出总是小于输入，误差逐步从零增大到时间 常数T并保持不变，因此T也是稳态误差。系统 的时间常数T越愈小，系统跟踪输入信号的稳态 误差也越小。
3.2.3 单位脉冲响应
1 R( s) L[ ( t )] 1 Y ( s) G ( s) R( s) G (s ) Ts 1 系统输出量的拉氏变换式就是系统的传递函数
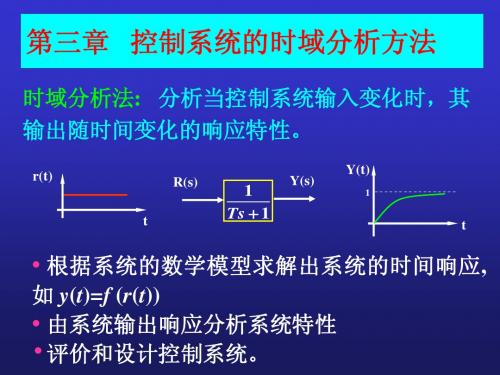
总结与分析：
一阶系统对典型试验信号的响应 输入信号x(t) 输出响应y(t)
1 2 3
t
1() δ(t)
t T Te t / T
1 et /T
1 T
et /T
l 线性定常系统对输入信号导数的响应，可以通过 把系统对输入信号的响应进行微分求得； l 系统对输入信号积分的响应，可以通过把系统对原 输入信号的响应进行积分求得，而积分常数则由初 始条件决定。
3.1.1 控制系统的输入信号
● 在分析和设计控制系统时，需要有一个对各种
系统性能进行比较的基础。
● 从实际应用中抽象出一些典型的输入信号，它
们具有广泛的代表性和实际意义。
● 通过比较各类系统对这些典型试验信号的响
应来分析它们的性能。
常用的典型试验信号：
r(t) A t (a) 阶跃信号
r(t)
1 E
实验方法求取一阶系统的传递函数：
63.2％ T
1 Ts 1
对一阶系统的单位阶跃响应曲线， 1、直接从达到稳态值的63.2%对应的时间求出一阶 系统的时间常数；
2、从t＝0处的切线斜率求得系统的时间常数。 思考题：
若系统增益K不等于1，系统的稳态值应是多少？如何用实
验方法从响应曲线中求取K值？
3.2.2单位斜坡响应
2、系统的稳态响应为y(∞)=t－T，是一个与输入斜 坡函数斜率相同但时间迟后T的斜坡函数。
3、输出总是小于输入，误差逐步从零增大到时间 常数T并保持不变，因此T也是稳态误差。系统 的时间常数T越愈小，系统跟踪输入信号的稳态 误差也越小。
3.2.3 单位脉冲响应
1 R( s) L[ ( t )] 1 Y ( s) G ( s) R( s) G (s ) Ts 1 系统输出量的拉氏变换式就是系统的传递函数
线性系统的时域分析法
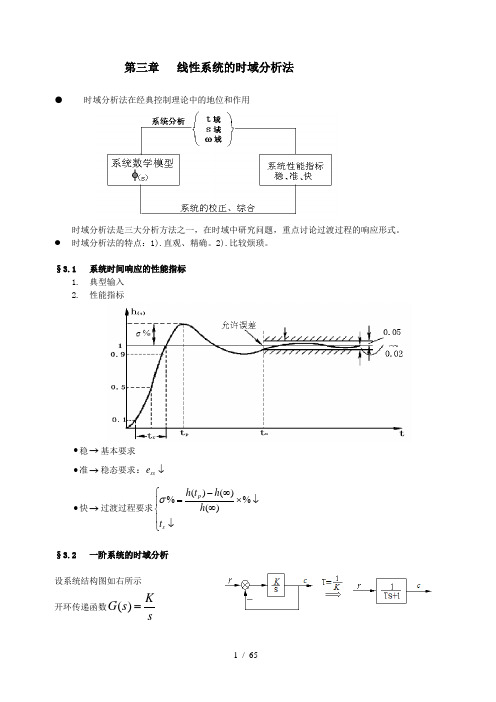
第三章 线性系统的时域分析法●时域分析法在经典控制理论中的地位和作用时域分析法是三大分析方法之一，在时域中研究问题，重点讨论过渡过程的响应形式。
时域分析法的特点：1).直观、精确。
2).比较烦琐。
§3.1 系统时间响应的性能指标1. 典型输入2. 性能指标•稳→基本要求 •准→稳态要求↓ss e ：•快→过渡过程要求⎪⎩⎪⎨⎧↓↓⨯∞∞-=sp t h h t h %)()()(%σ§3.2 一阶系统的时域分析设系统结构图如右所示 开环传递函数sK s G =)(闭环传递函数)1(11111)(T Ts Ts T K s K s K s K s -=+=+=+=+=Φλ :)(1)(时t t r =Ts sTs s T s R s s C 111)1(1)()()(+-=+=Φ=1)(,0)0( 1)(1=∞=-=∴-c c e t c t TTc e T t c t T 1)0( 1)(1='='-依)(t h 特点及s t 定义有：95.01)(1=-=-s t Ts et h05.095.011=-=-s t Te305.0ln 1-==-s t TT t s 3=∴一阶系统特征根1s T=-分布与时域响应的关系：21110 ()().(). ()s C s s R s h t t s s s •==Φ===时11() ()1()at a s a C s h t e s s a s s a•===-+=-+--时例1已知系统结构图如右其中：12.010)(+=s s G加上H K K ,0环节，使s t 减小为原来的0.1倍，且总放大倍数不变，求H K K ,0解：依题意，要使闭环系统02.00.21.0*=⨯=s t ，且闭环增益=10。
11012.0)101(10 1012.01012.010112.010.)(1)(.(s)0000+++=++=+++=+=Φs K K K K s K s K s K s G K s G K HH H H H令 101011002.01012.00⎪⎪⎩⎪⎪⎨⎧=+==+=H H K K K K T 联立解出⎩⎨⎧==109.00K K H 例2已知某单位反馈系统的单位阶跃响应为at e t h --=1)(求(1).闭环传递函数)(s Φ；(2).单位脉冲响应；(3).开环传递函数。
第三章 时域分析法
1 h()
0.9 h()
td
0.5 h()
td
0.1 h()
0 tr tp
ts
单位阶跃响应曲线
响延应迟曲时线间第t一d ：次
达到稳态值的一 半所需的时间。
0.02或 0.05上升时间 tr :
响应曲线从稳态值 的 10%上升到 9t 0%，所需的时间。
峰值时间 t p :响应曲
线达到超调量的第一个 峰值所需要的时间。
s2 = -n - n 2 -1 = -1/ T2
R(s)
22 nn
ss((ss 22nn))
C(s)
29
二阶系统的传递函数
开环传递函数：
G(s) =
n2
s(s 2n )
闭环传递函数：
C(s) R(s)
=
s2
n2 2ns
n2
30
二阶系统的特征方程为
s2 2ns n2 = 0
解方程求得特征根：
s1,2 = -ns n 2 -1
s1,s2完全取决于 ，n两个参数。
h(tp)于终值之差的 百分比，即
单位阶跃响应曲线
tr 或t p 评价系统的响应速度；
% = h(tp ) - h() 100%
h()
t s 同时反映响应速度和阻尼程度的综合性指标。
% 评价系统的阻尼程度或振荡最大峰值。
17
注意事项：
%, ts及ess三项指标是针对阶跃响应
而言的，对于非阶跃输入，则只有
=
t
- T(1-
-1t
eT
)
=
t
-
T
-1t
Te T
因为
-1t
e(t) = r(t) - c(t) = T (1- e T )
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
单位斜坡响应曲线如图所示：
c(t)
r(t)=t
T T
引入误差的概念：0
t
当时间t趋于无穷时，系统单位阶跃响应的实
际稳态值与给定值之差。即：
e h h()
ss
0
一阶系统单位斜坡响应存在稳态误差
ess=t-(t-T)=T 从曲线上可知，一阶系统单位斜坡响应达到 稳态时具有和输入相同的斜率，只要在时间 上滞后T,这就存在着ess=T的稳态误差。
e wn t sin(
1 2
1 2 wnts ) 0.05或0.02
不易求出ts，但可得出wnts与ξ的关系曲线：
调节时间不连续的示意图
ξ值的微小变化可引起调节时间ts显著的变化。
当ξ=0.68（5%误差带）或ξ=0.76（2%误差 带），调节时间ts最短。所以通常的控制系统 都设计成欠阻尼的。 曲线的不连续性，是由于ξ值的微小变化可引 起调节时间显著变化而造成的。 近似计算时，常用阻尼正弦振荡的包络线衰减 到误差带之内所需时间来确定ts。
故kt 0.3
三.一阶系统的单位斜坡响应 R(t) t, R(s) 1
s2
C(s) (s) R(s) 1 1 1 T T 2
Ts 1 s2 s2 s Ts 1 拉氏反变换，单位斜坡响应为
Ct (t) (t T ) Tet/T (t 0) 其中t T为稳态分量，Tet/T为暂态分量。
写为
C(s)
w2 n
1/TT 12
R(s) s2 2 w s w2 (s 1/ T )(s 1/ T )
n
n
1
2
1
(T s 1)(T s 1)
1
2
1
T1 1
T2
wn wn
wn
2 1) 2 1)
式中：
1 w ( 2 1); 1 w (
T
n
T
n
1
2
w2 1 且设T T
所以应取n=1。
于是w t ,t
dp
p
w d
w n
当wn一定时，ξ越小，tp越小；
1 2
当ξ一定时，wn越大，tp越小。
3.超调量σ%
h(t ) 1 ewntp sin( )
p
1 2
sin( ) sin 1 2
tp wn
1 2
h(t p ) 1 e / 1 2 设h() 1
-1/T 0
T表征系统惯性大小的重要参数。
二.一阶系统的单位阶跃响应 当r(t) 1(t)时，R(s) 1 ,
s
则C(s) (s) R(s) 1 1 1 T
Ts 1 s s Ts 1
对C(s)进行拉氏反变换 h(t) 1 et /T t T , h(T ) 0.632 t 2T , h(2T ) 0.865 t 3T , h(3T ) 0.950 t 4T , h(4T ) 0.982
延迟时间td:响应曲线第一次到达终值一半 所需的时间。
二.峰值时间tp
响应曲线超过稳态值h(∞)达到第一个峰值 所需的时间。
三.调节时间ts
在稳态值h(∞)附近取一误差带，通常取
5%h(), 2%h()
响应曲线开始进入并保持在误差带内所需 的最小时间，称为调节时间。
ts越小，说明系统从一个平衡状态过渡到 另一个平衡状态所需的时间越短。
R(s)
100/s
C(s)
kt
解：系统的闭环传递函数
(s) 100 / s 1/ kt
1
100 s
kt
0.01s 1 kt
当kt
0.1时, (s)
10 0.1s 1
显然时间常数T 0.1秒.
因此调节时间为ts 3T 0.3秒，
如果要求ts
0.1秒, ts
3T
3 0.01 kt
0.1,
t
r
w d
w 1 2 n
当wn一定时，ξ越小，tr越小；
当ξ一定时，wn越大，tr越小。
2.峰值时间tp
h(t) 1 ewnt[coswdt
1 2 sin wdt] ①
h(t) 1 ewnt sin(w t ) ②
1 2
d
对①式两边求导，并令其=0，得：
h' (t) wnewnt (coswdt
h' (t)
2wn 1 2
e wn t
sin wdt
wn
1 2 ewnt sin wdt
∴ h' (t) (
2wn 1 2
wn
1 2 )ewnt sin wdt
wn
1 2
e wn t
sin wdt
0
sin wdt p 0
wdt p n (n 0,1,2, )
tp为输出响应达到第一个峰值所对应的时间
下面具体讨论欠阻尼二阶系统动态性能指标。
1.上升时间tr
h(t ) 1,则1 ewntr sin(w t ) 1
r
1 2
dr
e wntr
sin(w t ) 0
1 2
dr
1
0, e wntr 0,
1 2
w t n (n 0,1,2, ) dr
由定义知：tr为输出响应第一次到达稳态值所 需时间，所以应取n=1。
% 0没有超调，非周期响应，
惯性环节亦称非周期环节。
曲线
C(t)
1 1/T斜率
0.632
h(t) 1 et/T
0
T
t
t 3T (5%误差带) s
t 4T (2%误差带) s
T越小，系统的快速性越好。
例1.一阶系统的结构图如图所示，若kt=0.1,试 求系统的调节时间ts，如果要求ts 0.1秒。 试求反馈系数应取多大？
1 2
sin(wd t )
arctg
h(t)
曲线：
1 2 或 arccos
1
0
t
欠阻尼二阶系统的单位阶跃响应曲线是按指 数规律衰减到稳定值的，衰减速度取决于特 征值实部-ξwn的大小，而衰减振荡的频率， 取决于特征根虚部wd的大小。
角的定义
上图绘出了不同ξ值下，二阶系统的单位阶 跃响应曲线。直观地看，ξ越大，超调量 σ%越小，响应的振荡性越弱，平稳性越好； 反之，ξ越小，振荡性越强，平稳性越差。 当ξ＝0时，系统的零阻尼响应为：
负实部的共轭复根 s w jw 1 2
1, 2
n
n
系统的单位阶跃响应具有衰减振荡特性，称
为欠阻尼状态。(如图a)
s1
wn
s2
0
(a)
s2 s1 0
(c)
s1,2
0
(b)
s1
0
s2
(d )
2.当ξ=1时，特征方程具有两个相等的负实 根，称为临界阻尼状态。（如图b）
3.当ξ>1时，特征方程具有两个不相等的负 实根，称为过阻尼状态。（如图c）
时，ts 4.75T1 ,当T1 4T2 ， 1.25 时， ts 3.3T1
当 T1 4T2 ， 1.25 时，ts 3T1 由此可见，当 T1 4T2 ， 二阶系统可近似等效为一阶系统，调节时间可用3T1
来估算。
当
1
时，临界阻尼二阶系统
1 T1
1 T2
n ，则
c(s)
s
n2
n 2
第三章 时域分析法
3-1 控制系统的时域指标 3-2 一阶系统的时间响应 3-3 二阶系统分析 3-4 控制系统的稳定性和代数判据 3-5 稳态误差的分析和计算
3-1 控制系统的时域指标
所谓时域分析法，就是在时间域内研究控制系统性能 的方法，它是通过拉氏变换直接求解系统的微分方程， 得到系统的时间响应，然后根据响应表达式和响应曲 线分析系统的动态性能和稳态性能。
则 % h(t p ) h() 100% e / 1 2 100%
h()
所以超调量是阻尼比ξ的函数，与无阻尼振 荡频率wn的大小无关。
σ%与ξ的关系曲线
ξ增大，σ%减小，通常为了获得良好的平 稳性和快速性，阻尼比ξ取在0.4-0.8之间, 相应的超调量25%-2.5%。
4.调节时间ts
根据定义：
4.当ξ=0时，系统有一对共轭纯虚根，系统 单位阶跃响应作等幅振荡，称为无阻尼或 零阻尼状态。（如图d）
下面，分过阻尼（包括临界阻尼）和欠阻 尼（包括零阻尼）两种情况，来研究二阶 系统的单位阶跃响应。
二.二阶系统的单位阶跃响应
1.过阻尼情况。
当ξ>1时，二阶系统的闭环特征方程有两
个不相等的负实根，这时闭环传递函数可
Wn无阻尼振荡频率或固有频率，也叫自然振 荡频率。
当系统输入为单位阶跃信号时，系统的输 出量为
C(s)
s2
wn2
2wn s
wn2
1 s
1 s
(s
s wn wn )2
wd2
(s
wn wn )2
wd2
拉氏反变换
h(t) 1 ewnt (coswd t
1 2 sin wd t)
1
e wnt
控制系统的时域性能指标，是根据系统在 单位阶跃函数作用下的时间响应——单位 阶跃响应确定的，通常以h（t）表示。 实际应用的控制系统，多数具有阻尼振荡 的阶跃响应，如图3-1所示：
h(t)
1.0 0.5 td
0 tr tp ts
误差带5%或2%
h()
一.上升时间tr
响应曲线从零首次上升到稳态值h(∞)所需 的时间，称为上升时间。对于响应曲线无 振荡的系统，tr是响应曲线从稳态值的10% 上升到90 %所需的时间。
1 2
sin wdt)
wd ewnt ( sin wdt