06磁介质磁化和介质中安培环路定理
合集下载
3磁介质中的安培环路定理

单位: T m A-1
在均匀的磁介质
B
(非铁磁质)中
M
磁场强度与磁感
H
应强度成正比,
Is
同向。
Ic
§3.磁介质中安培环路定理 / 三、几个结论
4.结论4
磁介质(非铁磁介质)中,磁化强度 与磁场强度具有线性关系。
M
κ m
H
κ 为磁化率。 m
电介质中 P κ 0E
5.结论5
相对磁导率与磁化率之间的关系
§3.磁介质中安培环路定理 / 二、环路定理
H B M
0
H dl Ic
②. H 既与磁感应强度 B 有关,又与磁化
强度 M 有关,所以 H 又是混合物理量。
③.磁场强度的单位与 M 相同,
安培/米,A/m
④.若 H d l 0 不一定环路上各点的
H 为 0,因为 H 是环路内、外电流共同 产生的。
R
由螺线管的磁场
r
B
分布可知,管内 的场各处均匀一
H
致,管外的场为0;
I
§3.磁介质中安培环路定理 / 四、解题方法
1.介质内部
作 abcda 矩形回路,回 路内的传导电 流代数和为:
B
a
b
H
d
cI
I c n ab I 在环路上应用介质中的环路定理:
H dl
H dl H dl H dl H dl
第三节
磁介质中的 安培环路定理
一、问题的提出
在真空中的安培环路定理中:
B dl 0 I
将其应用在磁介质中时,I为所有电流的
代数和;
B dl 0 (I c I s )
如果求 B
B = Bo + B’
在均匀的磁介质
B
(非铁磁质)中
M
磁场强度与磁感
H
应强度成正比,
Is
同向。
Ic
§3.磁介质中安培环路定理 / 三、几个结论
4.结论4
磁介质(非铁磁介质)中,磁化强度 与磁场强度具有线性关系。
M
κ m
H
κ 为磁化率。 m
电介质中 P κ 0E
5.结论5
相对磁导率与磁化率之间的关系
§3.磁介质中安培环路定理 / 二、环路定理
H B M
0
H dl Ic
②. H 既与磁感应强度 B 有关,又与磁化
强度 M 有关,所以 H 又是混合物理量。
③.磁场强度的单位与 M 相同,
安培/米,A/m
④.若 H d l 0 不一定环路上各点的
H 为 0,因为 H 是环路内、外电流共同 产生的。
R
由螺线管的磁场
r
B
分布可知,管内 的场各处均匀一
H
致,管外的场为0;
I
§3.磁介质中安培环路定理 / 四、解题方法
1.介质内部
作 abcda 矩形回路,回 路内的传导电 流代数和为:
B
a
b
H
d
cI
I c n ab I 在环路上应用介质中的环路定理:
H dl
H dl H dl H dl H dl
第三节
磁介质中的 安培环路定理
一、问题的提出
在真空中的安培环路定理中:
B dl 0 I
将其应用在磁介质中时,I为所有电流的
代数和;
B dl 0 (I c I s )
如果求 B
B = Bo + B’
磁介质中的安培环路定理
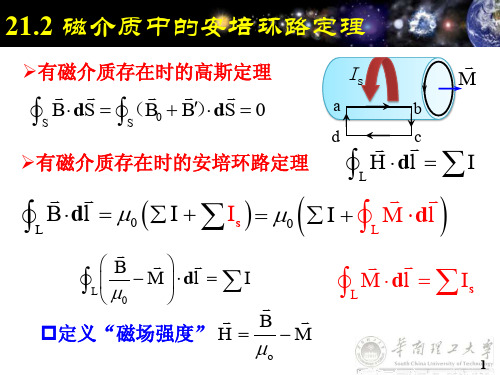
L
L
B M dl I L 0 B M 定义“磁场强度” H
L
M dl I s
o
1
磁化率
实验指出: M m H
均匀的各向同性的磁介质
系数m称为“磁化率”。
H
B
解:
L
H dl I
ab H n ab I
则:H nI
B
a
d
. . .
× × ×
I
b
B o r H nI
c
5
均匀的各向同性的磁介质
2
例题1
一半径为R1的无限长圆柱形直导线,外面包一层半 径为R2,相对磁导率为r 的圆筒形磁介质。通过导 线的电流为I0 。求磁场强度和磁感应强度的分布。 解: 0 r R1 H dl 2π rH
L
r
r
R1
R2
I0
I 2 π r 2 π R1
R1 r R2 r R2
H dl H 2π r I
L
Ir H 2 π R12
B 0 H
0 Ir
2πR12
B 0 H
0 I
2π r
B 0 r H
0 r I
2π r
例题2
有两个半径分别为R1和R2的“无限长”同轴圆筒形 导体,在它们之间充以相对磁导率为μr 的磁介质。 当两圆筒通有相反方向的电流I时,试求磁感强度。 解: d R1 , B 0 R1 d R2 H dl I
0
M
B
介质中的安培环路定理14.3铁磁质

例1:一无限长螺线管,通以电流I,管内充有相对磁 导率为 r的各向同性的均匀介质,若单位长度线圈 B H ,及面磁化电流密度。 匝数为n,求介质中的 和
解:由于螺线管无限长, 故管外磁场为零,管内 磁场均匀,B 和 H 与管轴线平行
j M (r 1) H (r 1)nI
j ' 0 即磁化电流和传导电流方向相同 顺磁质 r 1 故
r 1 故 j ' 0 即磁化电流和传导电流方向相反 抗磁质
例2:长直单芯电缆的芯是一根 半径为R 的金属导体,它与外壁 之间充满均匀磁介质,电流从芯 流过再沿外壁流回。求介质中磁 场强度及磁感应强度。
(2)铁磁质在没有传导电流存在时也可以有磁性
这种磁性叫做剩磁 (3)一次磁化过程损耗的能量与磁滞回线包围的面 积成正比
三、铁磁质的分类
1 按矫顽力HC分 软磁材料:磁滞回线窄而长,Br , Hc都小;
硬磁材料:磁滞回线较宽,Br , Hc较大;
B
Hc
Hc
B
Hc
H
Hc
H
作变压器的软磁材料
作永久磁铁的硬磁材料
弱磁质的磁化特点:
B
tg
H
(1) 0为一常数, B-H曲线为一直线, 斜率 tg 0
H (2) B-H曲线具有可逆性, B ; H B ; H 0 B 0
2. 铁磁质的磁化曲线 将螺绕环中充满铁磁质: 开始时I=0, H=0, B=0; 然 后增大电流 I H 测B
2 按磁滞回线形状分
B
Br
B
Bs
H
-H c
Br
o
Hc
磁介质的磁化规律

外圆柱面内一点到轴的垂直距离是 I I I
r1,以r1为半径作一圆,取此圆为积 分回路,根据安培环路定理有Biblioteka Hdl H
2r1 0
dl
I
H I
2r1
B
0 H
0
I
2 r1
(2)设在圆柱体内一点到轴的垂直距离是r2,则
以r2为半径作一圆,根据安培环路定理有
H
d
l
H
2r2
0
d
l
H
2r2=I
r 2 2
迈斯纳效应:完全抗磁性
处于迈斯纳态的超导体会表现出完美抗磁性,或超抗磁性,意思是 超导体深处(离表面好几个穿透深度的地方)的总磁场非常接近零。 亦即是它们的磁化率 = −1。抗磁性体的定义为能产生自发磁化的 物料,且磁化方向与外加场直接相反。然而,超导体中抗磁性的基 本来源与一般材料的非常不同。在一般材料中,抗磁性是原子核旁 电子的轨道自旋,与外加磁场间电磁感应的直接结果。在超导体中, 完全抗磁性的原因是表面的超导电流所引起的,电流的流动方向与
的基本物理量。
例1 在均匀密绕的螺绕环内充满均匀的顺磁介质,
已知螺绕环中的传导电流为I ,单位长度内匝数 n ,环
的横截面半径比环的平均半径小得多,磁介质的相对磁 导率为 。求环内的磁场强度和磁感应强度。
解:在环内任取一点,
过该点作一和环同心、 半径为 的圆r形回路。
r
H dl NI
式中 为N螺绕环上线圈
进动 pm
L e
进动
pm
e
L
pm
pm
B0
进动 B0
可以证明:不论电子原来 的磁矩与磁场方向之 间的夹角是何值,在外磁场 B0中,电子角动量 L进 动这的种转等向 效总 圆是 电和 流的磁磁力矩矩的M方的向方永向远构与成右B0手的螺方旋向关相系反。。
磁介质中的高斯定理和安培环路定理.

B 0(H M ) 0(H mH) 0(1 m)H
在各B向0H同r0H性r H介质r中H10B.rH为m磁相关导对系 率磁:B导 率。0D r电H介0质rHE中
E
在真空 中 r 1, B0 0H
3.明确几点:
①. H 是 一辅助物理量,描述磁场的基本物理量仍然
是 B。H是 为消除磁化电流的影响而引入的,
B 和H 的名字张冠李戴了。
4
②. H 既与磁感应强度B 有关,又与磁化强度M 有
关,所以H 又是混合物理量。
③.磁场强度 的单 位与磁化强度相同,安培/米,A/m
④.若 H dl 0不一定环路内无电流。
或由 I s (r 1)I c
求 Is;
9
例1:长直螺线管半径为 R ,通有电流 I,线圈密度 为 n , 管内插有半径为 r ,相对磁导率为 r 磁介质, 求介质内和管内真空部分的磁感应强度 B 。
解: 由螺线管的磁场分布 可知,管内的场各处均匀
R
r
a Bb
一致,管外的场为0;
H
1.介质内
10
H dl H dl 0
bc
da
因为 cd 段处在真空中,真
a
B ab H b
空中的 M = 0;B = 0 ,
有 H dl 0
d
c d
Ic
cd H dl
H dl
Hdl cos H dl H ab I c
§12.2 磁介质中的高斯定理和安培环路定理
1
一、磁介质中的高斯定理
磁介质放在磁场中,磁介质受到磁场的作用要产
磁介质的磁化和介质中的安培环路定理简化
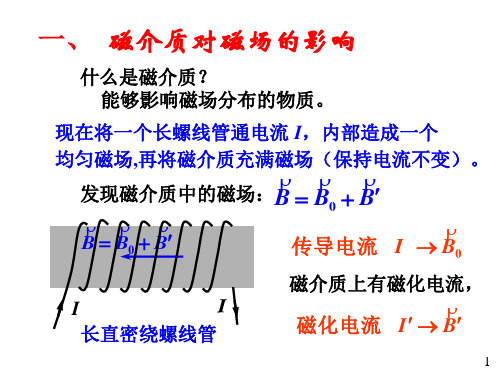
物理意义
M d l I s
积分关系
磁化强度
束缚面电流
磁化强度沿任一回路的环流,等于穿过此回路的 束缚电流 IS的代数和。 IS与L环绕方向成右旋者为正, 反之为负。 与电介质中对比的公式 P dS q'
S
S
电极化强度
束缚电荷
10
可以象研究电介质与电场的相互影响一样,通过 引入适当的物理量加以简化。 4.磁介质中的安培环路定理
顺磁质
顺磁质的
m分 i 分 S 分
m分≠0,称为分子固有磁矩。
3
一般由于分子的热运动, m分 完全是混乱的, 不显磁性。 但是在外磁场中, m分 会发生转向而排列,
这就是顺磁质被“磁化”。 外磁场越强,转向排列越整齐。 顺磁质内部的各 S N 分子等效磁矩 m分 S 有一定程度的排列, 分子等效电流 i 使 顺磁质内部的磁场加强; 而且顺磁质会被磁铁吸引。
磁化电流 I B
1
实验发现:充各种磁介质,磁介质内的磁场 有的比真空时弱, 有的比真空时强。
B内 r B0
r
……该磁介质的相对磁导率
(1)抗磁质
(2)顺磁质
(3)铁磁质
r 略<1 (铜,银,氢等) r 略>1 (铝,锰,氧等) r >>1 (铁,钴,镍等)
……磁介质的磁导率。
实验表明: M B
在各向同性的顺磁质、 抗磁质内,有线性关系
r 1 M B
0 r
对顺磁质: M 平行于 B 对抗磁质: M 反平行于 B (对铁磁质: M 和 B 呈非线性关系)
8
3.磁化强度与磁化电流 Is的关系 在 外磁场作用下,介质中的分子电流可等效成介 质表面的磁化电流 Is,它产生附加磁场,但无热效应。 定义: 沿磁介质轴线方向上单位长度的磁化电流称为 磁化电流密度 js 。 Is
M d l I s
积分关系
磁化强度
束缚面电流
磁化强度沿任一回路的环流,等于穿过此回路的 束缚电流 IS的代数和。 IS与L环绕方向成右旋者为正, 反之为负。 与电介质中对比的公式 P dS q'
S
S
电极化强度
束缚电荷
10
可以象研究电介质与电场的相互影响一样,通过 引入适当的物理量加以简化。 4.磁介质中的安培环路定理
顺磁质
顺磁质的
m分 i 分 S 分
m分≠0,称为分子固有磁矩。
3
一般由于分子的热运动, m分 完全是混乱的, 不显磁性。 但是在外磁场中, m分 会发生转向而排列,
这就是顺磁质被“磁化”。 外磁场越强,转向排列越整齐。 顺磁质内部的各 S N 分子等效磁矩 m分 S 有一定程度的排列, 分子等效电流 i 使 顺磁质内部的磁场加强; 而且顺磁质会被磁铁吸引。
磁化电流 I B
1
实验发现:充各种磁介质,磁介质内的磁场 有的比真空时弱, 有的比真空时强。
B内 r B0
r
……该磁介质的相对磁导率
(1)抗磁质
(2)顺磁质
(3)铁磁质
r 略<1 (铜,银,氢等) r 略>1 (铝,锰,氧等) r >>1 (铁,钴,镍等)
……磁介质的磁导率。
实验表明: M B
在各向同性的顺磁质、 抗磁质内,有线性关系
r 1 M B
0 r
对顺磁质: M 平行于 B 对抗磁质: M 反平行于 B (对铁磁质: M 和 B 呈非线性关系)
8
3.磁化强度与磁化电流 Is的关系 在 外磁场作用下,介质中的分子电流可等效成介 质表面的磁化电流 Is,它产生附加磁场,但无热效应。 定义: 沿磁介质轴线方向上单位长度的磁化电流称为 磁化电流密度 js 。 Is
10.2磁介质中的安培环路定理

H
B
(2)作永久磁铁的硬磁材料
C
还用于磁电式电表中的永磁铁。 耳机中的永久磁铁,永磁扬声器。
(3)作存储元件的矩磁材料 锰镁铁氧体,锂锰铁氧体
C
Br=BS ,Hc不大,磁滞回线是矩形。 用于记忆元件,当+脉冲产生H>HC使磁芯呈+B态, 则–脉冲产生H< – HC使磁芯呈– B态,可做为二进制 的两个态。
s
S
B
B
s
B dS ( Bo B ) dS 0
s s
磁介质中的高斯定理
通过磁场中任一闭合曲面的总磁通量为零
3、磁场强度、磁介质中的安培环路定理
L
B dl 0 ( I 0 I s )
L
M dl I s B dl 0 I 0 0 M dl L L L L L B L ( 0 M ) dl I 0 L
解: r R
I
R
2 LH dl H 2 r I r 2 I R
H
I
0
Ir H 2R 2
Ir B 2R 2
r
rR
H I
H 2r I
2r
I
0 I B 2r
R
0
H
0 I 2R
r
H
I 2R
B
I 2R
O
R
r
O
R
r
H
C
H
C
B
H
H
H
钨钢,碳钢,铝镍钴合金 矫顽力(Hc)大(>102A/m),剩磁Br大 磁滞回线的面积大,损耗大。
§7.7磁介质中的安培环路定理

Chapter 7.
作者:杨茂田
§7. 7 磁介质中的安培环路定理
§ 11.2 磁介质中的安培环路定理 § 7.7 磁介质中的安培环路定理
卵磷脂
Chapter 7.
作者:杨茂田
§7. 7 磁介质中的安培环路定理
一、磁场强度H的安培环路定理
B dl 0 ( I s
L
( L内)
0
( r R3 )
r
磁介质内: H I 2 r
I
M m H ( 1) I 0 2 r
(解毕)
R3
R2 R1
Chapter 7.
作者:杨茂田
§7. 7 磁介质中的安培环路定理
有磁介质时求磁场问题的一般方法:
自由电流(传导电流)I0i 分布
H dl
I 0i )
L
I 0i
r
Is:被L包围的总磁化电流; I0i:被L包围的自由电流;
B
Is=
m M B r 0
is
L
dI s n Sdl cos is
S
dl
B, M
Chapter 7.
作者:杨茂田
§7. 7 磁介质中的安培环路定理
pm dN pm M lim n pm V 0 V dV
( L)
B
L
I0 dl i ) I 0 i ) B dl 0 ( I s M
L
is
L
L
( L内)
( L内)
S
dl
B, M
Chapter 7.
作者:杨茂田
作者:杨茂田
§7. 7 磁介质中的安培环路定理
§ 11.2 磁介质中的安培环路定理 § 7.7 磁介质中的安培环路定理
卵磷脂
Chapter 7.
作者:杨茂田
§7. 7 磁介质中的安培环路定理
一、磁场强度H的安培环路定理
B dl 0 ( I s
L
( L内)
0
( r R3 )
r
磁介质内: H I 2 r
I
M m H ( 1) I 0 2 r
(解毕)
R3
R2 R1
Chapter 7.
作者:杨茂田
§7. 7 磁介质中的安培环路定理
有磁介质时求磁场问题的一般方法:
自由电流(传导电流)I0i 分布
H dl
I 0i )
L
I 0i
r
Is:被L包围的总磁化电流; I0i:被L包围的自由电流;
B
Is=
m M B r 0
is
L
dI s n Sdl cos is
S
dl
B, M
Chapter 7.
作者:杨茂田
§7. 7 磁介质中的安培环路定理
pm dN pm M lim n pm V 0 V dV
( L)
B
L
I0 dl i ) I 0 i ) B dl 0 ( I s M
L
is
L
L
( L内)
( L内)
S
dl
B, M
Chapter 7.
作者:杨茂田
磁介质中的环路定理

∫ H ⋅ dl H= 2πr
= nI
r
O
B = µH = µ0µr H
例2:一无限长载流圆柱体,通有电流I,设电流I均匀 一无限长载流圆柱体, 分布在整个横截面上. 分布在整个横截面上.柱体的磁导率为μ,柱外为真 空.求:柱内外各区域的磁场强度和磁感应强度。 柱内外各区域的磁场强度和磁感应强度。 解:
Is = ML = ∫ M ⋅ dl
L
∫l B ⋅ dl
l
= µ 0 ( NI + ∫ M ⋅ dl )
l
l
∫(
l
B
µ0
− M ) ⋅ dl = NI = ∑ I
∫ H ⋅ dl = ∑I
传
( H磁场强度)
磁介质中的安培环路定理 磁介质中的安培环路定理 中的安培环路
∫ H ⋅ dl = ∑I
l
传
注意: 各向同性磁介质 注意 各向同性磁介质
充满各向同性介质的磁场
与介质有关的磁化电流产生 与介质有关的磁化电流产生 磁化电流 顺磁质 抗磁质 铁磁质
B = µr B0
介质的相对磁导率
µ r ≥1 µr ≤1 µr>> 1
二、磁介质的磁化 分子圆电流和磁矩 顺 磁 质 的 磁 化 磁 磁
I0 Is
m
I
Is
B0
磁质
磁
B = B0 + B '
无外磁场时抗磁质分子磁矩为零 无外磁场时抗磁质分子磁矩为零 抗 磁 质 的 磁 化
H = B
磁化率) M = κH κ(磁化率)
µ0
−M =
B
µ0
− κH
B = µ0 (1 + κ ) H
磁介质的磁化和介质中的安培环路定理

5
H dl H dl 0
bc
da
cd 段处,B = 0 ,
a
B ab H b
有
H
cd
dl
0
H dl H dl H
ab
d
dl H ab
ab
c d Ic
Ic
H ab Ic nabI, H nI
B 0r H 0rnI
2、管内真空中
H nI
作环路 abcda ; 在环路上应用介质 真空中 r 1
垂直于轴的平面内取圆为安培回路:
r R1
H1
2rH1
I
2R12
I
R12
r
r 2
B1
r10 I 2R12
r
同理 R1 r R1
I
H2 2r
B2
r 2 0 I 2r
R2 r H3 0 B3 0 第7页/共10页
I
R1 R2
I
H
r
R1
R2
7
超导简介
1911年,荷兰物理学家H·K ·昂纳斯及其助手首先发 现在温度降至液氦的沸点(4.2K)以下时,水银的电 阻为0。在低温下某些物质失去电阻的性质,为超导体。
2003 年再次送入地球轨道,观察暗物质和反物质。
高温超导现已达到 -153°C。
第10页/共10页
10
•还可制造超导磁悬浮列车,世界上最快的磁悬浮列
车时速超过500公里/小时。
第9页/共10页
9
• 无损耗输电:传统输电过程中总要产生一部分焦耳 热损耗,一般在 10%~20%,如果采用超导体输电,几 乎没有电能损失,而且不需要升压,可以不用变压器
设备,也不必架设高压线,可以在地下管道中。甚至 可以直接传输直流电。
大学物理学8.11 磁介质中的安培环路定理

这就是磁介质中安培环路定理
例:长直螺线管半径为 R ,通有电 流 I,线圈密度为 n , 管内插有半径为 r ,相对磁导率为 r 的磁介质,求介质 内和管内真空部分的磁感应强度 B 。
解:
R
由螺线管的磁 r
B
场分布可知,管内的
H
场各处均匀一致,管
外的场为0
I
1.介质内部
B
作 abcda
矩形回路,回路内
a
b H
的传导电流代数和
d
cI
为
I c n ab I
在环路上应用介质中的环路定理:
H dl
H dl H dl H dl H dl
ab
bc
cd
da
∵在bc和da段路径上 Hdl , cos 0 a
H dl H dl 0
H nI
由 B 0r H 有 B 0rnI
B b
H cI
ห้องสมุดไป่ตู้
2.管内真空
d
中 作环路
a
abcda ; 在环路上
应用介质中的安培
环路定理,同理有
H nI
c bB
H I
由 B 0r H 和真空中 r 1
有
B 0H 0nI
课后作业 习题8.20
bc
da
d
B b
H cI
又因为 cd 段处在管外的真空中, 管外的场,B = 0 ,所以 H = 0 ;
H dl 0
cd
H dl H dl
ab
Hdl cos
a
ab
H dl H ab I c ab
例:长直螺线管半径为 R ,通有电 流 I,线圈密度为 n , 管内插有半径为 r ,相对磁导率为 r 的磁介质,求介质 内和管内真空部分的磁感应强度 B 。
解:
R
由螺线管的磁 r
B
场分布可知,管内的
H
场各处均匀一致,管
外的场为0
I
1.介质内部
B
作 abcda
矩形回路,回路内
a
b H
的传导电流代数和
d
cI
为
I c n ab I
在环路上应用介质中的环路定理:
H dl
H dl H dl H dl H dl
ab
bc
cd
da
∵在bc和da段路径上 Hdl , cos 0 a
H dl H dl 0
H nI
由 B 0r H 有 B 0rnI
B b
H cI
ห้องสมุดไป่ตู้
2.管内真空
d
中 作环路
a
abcda ; 在环路上
应用介质中的安培
环路定理,同理有
H nI
c bB
H I
由 B 0r H 和真空中 r 1
有
B 0H 0nI
课后作业 习题8.20
bc
da
d
B b
H cI
又因为 cd 段处在管外的真空中, 管外的场,B = 0 ,所以 H = 0 ;
H dl 0
cd
H dl H dl
ab
Hdl cos
a
ab
H dl H ab I c ab
磁介质中的安培环路定理

产生磁场:
I
Bdl o I o I
有磁介质
B
C
的总场 传导电流 分布电流
分子磁矩 m I 'π r 2
A LD
n(单位体积分子磁矩数)
I n π r2LI ' nmL
M m nm
V
I ML BC M dl
I'
r
Cr
l M dl l B dl 0 ( I l M dl )
第二节 磁介质中的安培环路定理 磁场强度
一、有介质时的高斯定理
介质中的磁感应强度:
B B外 B
无论是什么电流激发的磁场,其磁力线均是无头
无尾的闭合曲线。
∴ 通过磁场中任意闭合曲面的磁通量为零。
即: BdS 0
二、有介质时的安培环路定理
在有介质的空间,传导电流与磁化电流共同
例:长直螺线管ห้องสมุดไป่ตู้充满均匀磁介质r单位长度上
的匝数为n,通有电流I 。求管内的磁感应强度。
解:管外磁场为零,取图示的回路
L H dl Ii
L
ab H n ab I
B
I
...
则:H nI
B or H nI
B
a
b
× × × ×M
d c nˆ
相对磁导率 r 1 磁 导 率 0r
1 顺磁质
r 1 抗磁质
1 铁磁质
(非常数)
各向同性磁介质
B 0r H H
H和 B的区别: B是描述磁场作为物质与其它物质交换动量的物理量;
H是描述磁场能量传输的物理量;
磁介质中安培环路定理

5)求出Fx Fx dF sin
b I2
力的方向向右
(1)Fx
dF sin
0
0I1I2 sin Rd 0 2R sin
0I1I2
2
(2)Fx
2
dF sin
0
2 0I1I2 sin Rd 0 2R sin
0I1I2
AB C
dFA
3106 N / cm
___________,
dFB
_____0_______,
dl
dl
dFC _3__1_0__6_N__/_c_m.
dl
(0 4 107 )
IA
IB
IC
dFA I ABAdl
BA
BAB
BCA
0IB 2d
0IC 2 2d
dd
dFA 30I 2 dl 4d
4) r>c
I I I 0
B0
例7 一无限长圆柱形铜导体(磁导率0),半径为R, 通有均匀分布的电流I,导体外充满相对磁导率r的磁
介质。今有一矩形平面S(长1m,宽2R),位置如右 图中画斜线部分所示,求通过该矩形平面的磁通量.
解:
r
R
:
B1
0 Ir 2R 2
r
R
:
B2
0r I 2r
2R R 2R
0I 0I 30 I
H dl
I I 3I
例4 如图,电荷q (>0)均匀地分布在一个半径为R的薄 球壳外表面上,若球壳以恒角速度 0绕Z轴转动,则 沿着Z轴从-到+ 磁感应强度的线积分
q00
B dl ___2___
B dl
B dl
L
b I2
力的方向向右
(1)Fx
dF sin
0
0I1I2 sin Rd 0 2R sin
0I1I2
2
(2)Fx
2
dF sin
0
2 0I1I2 sin Rd 0 2R sin
0I1I2
AB C
dFA
3106 N / cm
___________,
dFB
_____0_______,
dl
dl
dFC _3__1_0__6_N__/_c_m.
dl
(0 4 107 )
IA
IB
IC
dFA I ABAdl
BA
BAB
BCA
0IB 2d
0IC 2 2d
dd
dFA 30I 2 dl 4d
4) r>c
I I I 0
B0
例7 一无限长圆柱形铜导体(磁导率0),半径为R, 通有均匀分布的电流I,导体外充满相对磁导率r的磁
介质。今有一矩形平面S(长1m,宽2R),位置如右 图中画斜线部分所示,求通过该矩形平面的磁通量.
解:
r
R
:
B1
0 Ir 2R 2
r
R
:
B2
0r I 2r
2R R 2R
0I 0I 30 I
H dl
I I 3I
例4 如图,电荷q (>0)均匀地分布在一个半径为R的薄 球壳外表面上,若球壳以恒角速度 0绕Z轴转动,则 沿着Z轴从-到+ 磁感应强度的线积分
q00
B dl ___2___
B dl
B dl
L
二磁介质中的安培环路定理传导电流磁化电流

第 15 章
磁介质
(Magnetism medium)
(4)
1
§15-1 磁介质的分类
1.磁介质的种类
在考虑物质与磁场的相互影响时,我们把所有的物 质都称为磁介质。
电场中,电介质极化后,在均匀电介质表面出现 极化电荷,于是电介质中的电场为
与此类似E,磁Eo场中E, 磁E介ro 质磁化后,在均匀磁介
en
M
a
b
l
图15-6
M dl Mab Jab I内 (15-5) l Jab 闭合路径l所包围的磁化电流的代数和
可见,磁化强度的环流(磁化强度沿闭合路径l的线 积分)等于该闭合路径l所包围的磁化电流的代数和。
11
§15 -3 磁介质中的磁场 磁场强度 一.磁介质中的磁场
顺磁质分子的固有磁矩pm虽不为零,但由于分子 的热运动,分子磁矩取每一个方向的概率是一样的, 因
此对一块顺磁质来说,分子磁矩的矢量和为零,故也不
显磁性。
4
电子进动与附加磁矩
在外磁场Bo作用下, 分子中的电子受到洛仑兹 力的作用,除了绕核运动和自旋外,还要附加一个以外 磁场方向为轴线的转动,从而形成进动。
图15-5
JLS=| pmi| =磁介质中分子磁矩的矢量和
按磁化强度的定义 ,有
M
pmi J
V
(15-3)
即磁化电流面密度J 等于磁化强度M的大小 。
10
一般情况下, J=M可 写成下面的矢量式:
J M en (15-4)
取如图15-6所示的 矩形闭合路径l, 则磁化 强度的环流为
B=Bo+B =rBo (15-1)
传导 磁化 电流 电流
二.磁介质中的安培环路定理
磁介质
(Magnetism medium)
(4)
1
§15-1 磁介质的分类
1.磁介质的种类
在考虑物质与磁场的相互影响时,我们把所有的物 质都称为磁介质。
电场中,电介质极化后,在均匀电介质表面出现 极化电荷,于是电介质中的电场为
与此类似E,磁Eo场中E, 磁E介ro 质磁化后,在均匀磁介
en
M
a
b
l
图15-6
M dl Mab Jab I内 (15-5) l Jab 闭合路径l所包围的磁化电流的代数和
可见,磁化强度的环流(磁化强度沿闭合路径l的线 积分)等于该闭合路径l所包围的磁化电流的代数和。
11
§15 -3 磁介质中的磁场 磁场强度 一.磁介质中的磁场
顺磁质分子的固有磁矩pm虽不为零,但由于分子 的热运动,分子磁矩取每一个方向的概率是一样的, 因
此对一块顺磁质来说,分子磁矩的矢量和为零,故也不
显磁性。
4
电子进动与附加磁矩
在外磁场Bo作用下, 分子中的电子受到洛仑兹 力的作用,除了绕核运动和自旋外,还要附加一个以外 磁场方向为轴线的转动,从而形成进动。
图15-5
JLS=| pmi| =磁介质中分子磁矩的矢量和
按磁化强度的定义 ,有
M
pmi J
V
(15-3)
即磁化电流面密度J 等于磁化强度M的大小 。
10
一般情况下, J=M可 写成下面的矢量式:
J M en (15-4)
取如图15-6所示的 矩形闭合路径l, 则磁化 强度的环流为
B=Bo+B =rBo (15-1)
传导 磁化 电流 电流
二.磁介质中的安培环路定理
12-2 磁介质中的安培环路定理

0
即
H 0
或
B0
例2 在均匀密绕的螺绕环内充满均匀的顺磁介质, 已知螺绕环中的传导电流为 I ,单位长度内匝数 n , 环的横截面半径比环的平均半径小得多,磁介质的 相对磁导率和磁导率分别为 和 r 。求环内的磁 场强度和磁感应强度。
解:在环内任取一点, 过该点作一和环同心、 半径为 r 的圆形回路。
B H M o
通常写成
B 0 ( H M )
M mH
实验证明: 各向同性磁介质
m
只与介质的性质有关称为磁介质的磁化率
M mH
代入
如果介质是均匀介质 如果介质是不均匀的 位置的函数
m m
是常数 是空间
B 0 ( H M )
r
H d l NI
式中 N为螺绕环上线圈的总匝数。由对称性可 知,在所取圆形回路上各点的磁感应强度的大小相 等,方向都沿切线。
H d l NI
H 2r NI
NI H nI 2r
r
当环内是真空时 B0 0 H 当环内充满均匀介质时 B H 0 r H B r B0
12-2 磁场强度
磁介质中的安培环路定理
一.有磁介质时的安培环路定理 无磁介质时的磁场安培环路定理
L
B0 dl 0
(L内)
I
穿过回路 的总电流
0
有磁介质时的磁场安培环路定理
B dl 0 ( I i I S )
L
穿过回路 的总电流
注意!这里 B 是导线中的传导电流激发的磁场和
r 1 r 1 r >>1
顺磁质 抗磁质 铁磁质
即
H 0
或
B0
例2 在均匀密绕的螺绕环内充满均匀的顺磁介质, 已知螺绕环中的传导电流为 I ,单位长度内匝数 n , 环的横截面半径比环的平均半径小得多,磁介质的 相对磁导率和磁导率分别为 和 r 。求环内的磁 场强度和磁感应强度。
解:在环内任取一点, 过该点作一和环同心、 半径为 r 的圆形回路。
B H M o
通常写成
B 0 ( H M )
M mH
实验证明: 各向同性磁介质
m
只与介质的性质有关称为磁介质的磁化率
M mH
代入
如果介质是均匀介质 如果介质是不均匀的 位置的函数
m m
是常数 是空间
B 0 ( H M )
r
H d l NI
式中 N为螺绕环上线圈的总匝数。由对称性可 知,在所取圆形回路上各点的磁感应强度的大小相 等,方向都沿切线。
H d l NI
H 2r NI
NI H nI 2r
r
当环内是真空时 B0 0 H 当环内充满均匀介质时 B H 0 r H B r B0
12-2 磁场强度
磁介质中的安培环路定理
一.有磁介质时的安培环路定理 无磁介质时的磁场安培环路定理
L
B0 dl 0
(L内)
I
穿过回路 的总电流
0
有磁介质时的磁场安培环路定理
B dl 0 ( I i I S )
L
穿过回路 的总电流
注意!这里 B 是导线中的传导电流激发的磁场和
r 1 r 1 r >>1
顺磁质 抗磁质 铁磁质
物理学下磁介质中的安培环路定理

未来研究方向和挑战
复杂磁场下的安培环路定理研究
在实际应用中,磁场往往是非常复杂的,如何准确描述和 计算复杂磁场下的安培环路定理是一个重要的研究方向。
磁化电流的精确测量和控制
磁化电流是磁介质磁化程度的量度,如何精确测量和控制 磁化电流对于理解和应用安培环路定理具有重要意义。
新型磁材料的开发和应用
随着科技的发展,新型磁材料不断涌现,如何将这些新型磁材料应用 于安培环路定理中,发挥其独特优势,是一个具有挑战性的课题。
磁介质性质
磁介质具有磁化性,即在外磁场 作用下,磁介质内部会产生附加 磁场,使原磁场发生变化。
磁化现象与磁化强度
磁化现象
磁介质在外磁场作用下,其内部磁偶 极子会重新排列,产生附加磁场,这 种现象称为磁化。
磁化强度
磁化强度是描述磁介质磁化程度的物 理量,表示单位体积内磁偶极子的磁 矩矢量和。
分类及特点分析
磁感应强度B描述了磁场对磁介质的作用力大小,而磁场强度H则描述了磁场的源强 度。
边界条件对磁场分布影响分析
在两种不同磁介质的分界面上, 磁场的切向分量连续,即磁场线
与分界面平行。
磁场的法向分量在分界面两侧会 发生跃变,跃变的大小与两种磁
介质的磁导率差异有关。
边界条件对磁场分布的影响可以 通过麦克斯韦方程组中的边界条
变压器工作原理简述
变压器基本结构
由铁芯和线圈组成,通过电磁感应实 现电压变换。
工作原理
当原线圈中通入交流电时,会在铁芯 中产生交变磁场,进而在副线圈中感 应出电动势。安培环路定理可用于分 析变压器中的磁场分布和漏磁现象。
其他电磁设备设计优化方向
电磁铁
利用安培环路定理分析电磁铁 的磁场分布和吸力特性,优化
大学物理电磁学部分磁介质的磁化和介质中的安培环路定理省名师优质课赛课获奖课件市赛课一等奖课件

S
0
S
q0
1
0
P dS
S
S
( 0 E
P)
def
dS
S
q0
D 0E P
SD dS q0 S
16
• B, H , M 之间旳关系
M
def
BmHFra bibliotekH M
0
B 0 (1 m )H
r
(1
m
)
B 0r H H
r 称为相对磁导率
0r 磁导率
• P、D、E 之间旳关系:
P
def
0r H
H
B 0r
r 1 m相对磁导率。
0 r 为磁导率
D
H H
电介质中
0 r E
E
在各向同性介质中 B.H 关系 :B 0r H H
在真空 中 r 1, B0 0H
顺即磁介BB0质:Br
介质中旳磁感应强度是真空中旳r倍。
B 0 , r 1
抗磁介质: B B0,0 r 1
就要受到磁场旳力矩作用,
力矩旳方向力图使分子磁矩旳方
向沿外场转向。各分子磁矩都在一定
B0
程度上沿外磁场方向排列起来.
分子磁矩旳矢量和: m 0
从导体横截面看,导体内部分子电流两两反向,相
互抵消。导体边沿分子电流同向,未被抵消旳分子电流
沿着柱面流动 。 ⊙ B0 等效
分子电流可等 B0 效成磁介质表
( B
0 I 0
L M ) dl
M dl
L
I
L 0
L
• 定义H:磁B场 强 M度
0
12
B
( M ) dl I
L
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
r
致,管外的场为零;
a Bb
H
1.介质内部 作 abcda 矩形回路。
d Ic
回路内的传导电流代数和为: I c n ab I
在环路上应用介质中的环路定理:
H dl H dl H dl H dl H dl
ab
bc
cd
da
∵在bc和da段路径上 H dl , cos 0
i
产生反向电子附加磁矩 B
结论:不论电子的轨道磁矩方向如
f核
v
fL
i
e
Bm
B0
f核
i
e
v
fL
B
m
何,附加磁场总与外场反向,
分子电流可等效成磁介质 表面的磁化电流 Is, Is产 生附加磁场。
⊕
B0
等 效 Is
B0
B
5
二、介质中的高斯定理
磁介质放在磁场中,磁介质受到磁场的作用产生
附任加一磁点场的。总磁强为:B
介质中的磁感应强度
1.磁介质的分类
顺磁介质: B
B0, r
1
抗磁介质: B B0,0 r 1
是真空中的r倍。
铁磁介质: B B0, r 1
2
2.磁介质的磁化机制
N
类似电介质的讨论,从物质
i
电结构来说明磁性的起源。
S
相当于一 磁偶极子
整个分子磁矩是其中各个电子的轨道磁矩和自旋磁 矩以及核的自旋磁矩的矢量和(核自旋磁矩常可忽略)
常数为 r2的 磁介质,且r2 >r1。求B和 H的分布?
解:根据轴对称性,以轴上一点为圆心在
垂直于轴的平面内取圆为安培回路:
r R1
H1
2rH1
I
2R12
I
R12
r
r 2
B1
r10 I 2R12
r
同理 R1 r R1
I
H2 2r
B2
r 2 0 I 2r
R2 r H3 0 B3 0
10
H dl H dl 0
bc
da
因为 cd 段处在真空中,真
a
B ab H b
空中的M =0;B = 0 ,
有 H dl 0
d
c d
Ic
cd H dl
H dl
Hdl cos H dl H ab I c
ab
ab
ab
H ab Ic nabI, H nI
B
0r 7
H dl
L
L
I
• 定义:磁场强度
磁介质中的环路定理
H
B
0r
物理意义:磁场强度沿闭合路径的线积分,等于环路 所包围的传导电流的代数和。
2.明确几点: ①. H是一辅助物理量,描述磁场的基本物理量仍然 是BB和。HH的是名为字消张除冠磁李化戴电了流。的影响而引入的,
②.磁场强度的单位:安培/米,A/m
③. H是环路内、外电流共同产生的。
8
在各向同性的均匀磁介质中
B 0r H H
0
r
为磁导率
B 0r H H
在各向同性介质中
B.H
关系:B
• 定义:H磁场 强B度
0r
电介质中
D
0
r
E
E
0r H H
在真空中 r 1, B0 0H
3.应用介质中安培环路定理解题方法
1.场对称性分析; 2.选取环路;
I
R1 R2
I
H
r
R1
R2
12
顺磁质:由具有固有磁矩的分子组成。分子中各电子的 磁矩不完全抵消,整个分子具有一定的固有磁矩。
抗磁质:分子中各电子的磁矩完全抵消,整个分子不 具有固有的磁矩。
1.顺磁质的磁化机制
磁介质是由大量分子或原子组成,无外场时,顺磁
质分子的磁矩排列杂乱无章,介质内分子磁矩的矢量
和 m 。0
3
有外磁场时,力矩的方向力图使分子磁
有磁介质的总磁场
磁化电流 传导电流
可以象研究电介质与电场的相互影响一样,通过引
入适当的物理量加以简化。
在各向同性均 匀介质中:
B r B0
B dl 0r I
(I
I )
r
I
B0 I B'
B
dl
I
B B0 B'
D dS q0
L 0r
L
H dl I L L
S
S
• 定义:磁场强度 H
3.求环路 内dl Ic 求 H; 由 B 0r H 求 B 9
例1:长直螺线管半径为 R ,通有电流 I,线圈密度为
n , 管内插有半径为 r ,相对磁导率为 r 磁介质,求介
质内和管内真空部分的磁感应强度 B 。
解:由螺线管的磁场分布可
R
知,管内的场各处均匀一
矩的方向沿外场转向。各分子磁矩都在
一定程度上沿外磁场方向排列起来.
B0
从导体横截面看,导体内部分子电流两
两反向,相互抵消。导体边缘分子电流同
向,未被抵消的分子电流沿着柱面 流动 。
⊙B0
B0 分子电流可等效成
等 效 Is
B
磁介质表面的磁化 电流 Is, Is产生附加 磁场。
B B0 B B0
B 0r H 0rnI
H nI
2.管内真空中
作环路 abcda ; 在环路上应用介质 中的安培环路定理,同理有:
真空中 r 1
B 0H 0nI
11
例2:如图载流无限长磁介质圆柱其磁导为 r1,外面
有半径为 R2的无限长同轴圆柱面,该面也通有电流 I, 圆柱面外为真空,在R1<r<R2区域内,充满相对介质
B0
B'
量为磁零力。线无头B无dS尾。0穿过任何一个闭合曲面的磁通 s 二、磁介质中的安培环路定理
1.磁介质中的安培环路定理
在真空中的安培环路定理中:
B0 dl
在介质中: B dl 0 (I I)
0 I
磁化电流
有磁介质的总磁场
传导电流
6
在介质中: B dl 0 (I I)
磁化电流 Is 可产生附加磁场,但无热效应,因为无
宏观电荷的移动,磁化电流束缚在介质表面上,不可
引出,因此,磁化电流也称为束缚电流。
4
2.抗磁质的磁化机制
对抗磁介质来说,无外磁场时,各 B0
电子的磁矩矢量和为 零,分子磁矩为
零 ,分子不显磁性。
加外磁场后,电子受的向心力
为核力和洛仑兹力的叠加,
f心 f核 fL f核
磁介质的磁化 磁介质中的高斯定 理和安培环路定理
(第五章第5、6节)
1
一、磁介质的磁化现象
凡是能与磁场发生相互作用的物质叫磁介质。
磁场中放入磁介质 磁介质发生磁化 出现磁化电流
产生附加磁场
磁介质内部的总场强 B B0
在各向同性均匀介质中:B
r 称为相对磁导率。
B r B0
即
B B0
r
