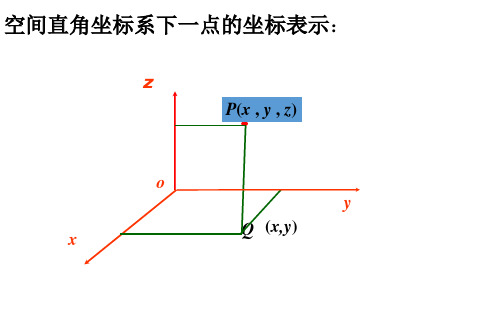
柱坐标系与球坐标系简介

xy＝ ＝ρρcsions
θ， θ，
z＝z，
求出ρ，θ即可．
(2)已知柱坐标系中的柱坐标化为直角坐标，利用公式
xy＝ ＝ρρcsions
θ， θ，
z＝z，
x，y，z即可．
求出
上一页
返回首页
下一页
【自主解答】 (1)设M的柱坐标为(ρ，θ，z)，
则由11＝ ＝ρρcsions
θ， θ，
z＝1，
解之得，ρ＝ 2，θ＝π4，
之间的一种对应关系．把建立上述对应关系的坐标系叫做
柱坐标系 ，有序数组(ρ，θ，z)叫做点 P 的柱坐标，记作
P(ρ，θ，z) ，其中 ρ≥0,0≤θ<2π，－∞＜Z＜＋∞.
图 1-4-1
上一页
返回首页
下一页
已知点A的柱坐标为(1,0,1)，则点A的直角坐标为( )
A．(1,1,0)
B．(1,0,1)
上一页
返回首页
下一页
1．由直角坐标化为球坐标时，我们可以设点M的球坐标为(r，φ，θ)，再利 用变换公式
xy＝＝rrssiinn
φcos φsin
θ， θ，
z＝rcos φ
求出r，θ，φ.
2．利用r2＝x2＋y2＋z2，tan θ＝yx，cos φ＝zr，特别注意由直角坐标求球坐标 时，应首先看明白点所在的象限，准确取值，才能无误．
上一页
返回首页
下一页
【自主解答】 设点的直角坐标为(x，y，z)，
x＝2sin34πcos34π＝2× 22×－ 22＝－1， 则y＝2sin34πsin34π＝2× 22× 22＝1，
z＝2cos34π＝2×－ 22＝－ 2，
因此点M的直角坐标为(－1,1，－ 2)．
上一页
返回首页
下一页
1．根据球坐标系的意义以及与空间直角坐标系的联系，首先要明确点的
下一页
3．已知一个点的球坐标为2，34π，π4，则它的高低角为(
)
A．－π4
3π B. 4
π
π
C.2
D.3
【解析】 ∵φ＝34π，∴它的高低角为π2－φ＝－π4.
【答案】 A
上一页
返回首页
下一页
4．设点 M 的直角坐标为(1,1， 2)，则点 M 的柱坐标为________，球坐标 为________.
【答案】
2，π4，
2
2，π4，π4
上一页
返回首页
下一页
5．已知点P的柱坐标为
2，π4，5
，点B的球坐标为
6，π3，π6，求这两个
点的直角坐标．
上一页
返回首页
下一页
【解】 设点P的直角坐标为(x1，y1，z1)，
则x1＝ 2cos π4＝1，
y1＝ 2sin π4＝1，z＝5.
设点B的直角坐标为(x2，y2，z2)，
(2)y＝ρsin θ＝ 2sin34π＝1，
z＝2，
因此所求点的直角坐标为(－1,1,2).
上一页
返回首页
下一页
将点的球坐标化为直角坐标 已知点M的球坐标为2，34π，34π，求它的直角坐标．
【思路探究】 球坐标 x―＝―rs―in―φ―co―sz＝θ―，r―cyo―＝s ―φrs―in―φs―in―θ→， 直角坐标
则x2＝
6sin
π 3cos
π6＝
6× 23× 23＝346，
上一页
返回首页
下一页
y2＝
6sin
π 3sin
π6＝
6× 23×12＝342，
z2＝
6cos
π3＝
6×12＝
6 2.
所以点P的直角坐标为(1,1,5)，点B的直角坐标为346，342， 26.
上一页
返回首页
下一页
球坐标(r，φ，θ)中角φ，θ的边与数轴Oz，Ox的关系，注意各自的限定范围，即
0≤φ≤π，0≤θ<2π.
2．化点的球坐标(r，φ，θ)为直角坐标(x，y，z)，需要运用公式
x＝rsin φcos θ， y＝rsin φsin θ， z＝rcos φ，
转化为三角函数的求值与运算．
上一页
返回首页
下一页
点 P 的球坐标，记做 P(r，φ，θ)，其中 r≥0,0≤φ≤π，0≤θ＜2π.
上一页
返回首页
下一页
已知点A的球坐标为3，π2，π2，则点A的直角坐标为(
)
A．(3,0,0)
B．(0,3,0)
C．(0,0,3)
D．(3,3,0)
【解析】
∵x＝3×sin
π 2
×cos
π2＝0，y＝3×sin
π2×sin
x＝ρcos θ， θ，z)，代入变换公式y＝ρsin θ，
z＝z，
求ρ；也可以利用ρ2＝x2＋y2，求ρ.利用tan θ
＝yx，求θ，在求θ的时候特别注意角θ所在的象限，从而确定θ的取值． 2．点的柱坐标和直角坐标的竖坐标相同．
上一页
返回首页
下一页
[再练一题]
1．根据下列点的柱坐标，分别求直角坐标：
π2 ＝3，z＝3×cos
π2＝0，
∴直角坐标为(0,3,0)．故选B.
【答案】 B
上一页
返回首页
下一页
[小组合作型] 点的柱坐标与直角坐标互化
(1)设点M的直角坐标为(1,1,1)，求它的柱坐标系中的坐标； (2)设点N的柱坐标为(π，π，π)，求它的直角坐标．
上一页
返回首页
下一页
【思路探究】 (1)已知直角坐标系中的直角坐标化为柱坐标，利用公式
因此点C的柱坐标为
2，π4，0.
上一页
返回首页
下一页
(2)由于r＝ x2＋y2＋z2＝ 12＋12＋0＝ 2.
又cos φ＝zr＝0，∴φ＝π2.
又tan θ＝yx＝1，∴θ＝π4，
故点C的球坐标为
2，π2，π4.
上一页
返回首页
下一页
[构建·体系]
— 柱坐标系 柱、球坐标系—— 球坐标系
— 柱坐标、球坐标的互化
上一页
返回首页
下一页
[再练一题] 3．若本例中条件不变，求点C的柱坐标和球坐标．
上一页
返回首页
下一页
【解】 易知C的直角坐标为(1,1,0)．
设点C的柱坐标为(ρ，θ，0)，球坐标为(r，φ，θ)，其中0≤φ≤π，0≤θ<2π.
(1)由于ρ＝ x2＋y2＝ 12＋12＝ 2.
又tan θ＝yx＝1，∴θ＝π4，
因此，点M的柱坐标为
2，π4，1.
上一页
返回首页
下一页
(2)设N的直角坐标为(x，y，z)，
x＝ρcos θ， 则由y＝ρsin θ，
z＝z，
x＝πcos π， 得y＝πsin π，
z＝π，
∴xy＝ ＝－0，π， z＝π，
因此，点N的直角坐标为(－π，0，π)．
上一页
返回首页
下一页
百度文库
1．由直角坐标系中的直角坐标求柱坐标，可以先设出点M的柱坐标为(ρ，
(1)
2，5π，3 6
；(2)
2，34π，2 .
上一页
返回首页
下一页
【解】 设点的直角坐标为(x，y，z)．
x＝ρcos
θ＝2cos56π＝－
3，
(1)y＝ρsin θ＝2sin56π＝1，
z＝3，
因此所求点的直角坐标为(－ 3，1,3)．
上一页
返回首页
下一页
x＝ρcos θ＝
2cos34π＝－1，
上一页
返回首页
下一页
【解析】 由坐标变换公式，可得ρ＝ x2＋y2＝ 2，tan θ＝yx＝1，θ＝π4(点 (1,1)在平面xOy的第一象限)，
r＝ x2＋y2＋z2＝ 12＋12＋ 22＝2.
由rcos φ＝z＝ 2，
得cos φ＝ r2＝ 22，φ＝π4.
∴点M的柱坐标为
2，π4，
2，球坐标为2，π4，π4.
教材整理 1 柱坐标系
阅读教材 P16～P17“思考”及以上部分，完成下列问题．
一般地，如图 1-4-1，建立空间直角坐标系 Oxyz.设 P 是空间任意一点．它
在 Oxy 平面上的射影为 Q，用(ρ，θ)(ρ≥0,0≤θ<2π)表示点 Q 在平
面 Oxy 上的极坐标，这时点 P 的位置可用有序数组(ρ，θ，z)(z ∈R)表示．这样，我们建立了空间的点与有序数组 (ρ，θ，z)
上一页
返回首页
下一页
1．在空间直角坐标系中，点P的柱坐标为2，π4，3，P在xOy平面上的射影 为Q，则Q点的坐标为( )
A．(2,0,3)
C.
2，π4，3
B.2，π4，0 D．( 2，π4，0)
【解析】 由点的空间柱坐标的意义可知，选B.
【答案】 B
上一页
返回首页
下一页
2．柱坐标P16，π3，5转换为直角坐标为(
C．(0,1,1)
D．(1,1,1)
【解析】 ∵x＝ρcos θ＝1，y＝ρsin θ＝0，z＝1， ∴直角坐标为(1,0,1)，故选B.
【答案】 B
上一页
返回首页
下一页
教材整理 2 球坐标系
阅读教材 P17～P18，完成下列问题． 一般地，如图 1-4-2，建立空间直角坐标系 Oxyz.设 P
是空间任意一点，连接 OP，记|OP|＝r，OP 与 Oz 轴正向
图1-4-2
所夹的角为 φ.设 P 在 Oxy 平面上的射影为 Q，Ox 轴按逆时针方向旋转到 OQ 时
所转过的 最小正角 为 θ.这样点 P 的位置就可以用有序数组 (r，φ，θ) 表
示．这样，空间的点与有序数组 (r，φ，θ) 之间建立了一种对应关系．把建立
上述对应关系的坐标系叫做球坐标系(或空间极坐标系)，有序数组(r，φ，θ)叫做
[再练一题] 2．若例2中“点M的球坐标改为M3，56π，53π”，试求点M的直角坐标．
上一页
返回首页
下一页
【解】 设M的直角坐标为(x，y，z)，
x＝rsin
φcos
θ＝3sin56πcos53π＝34，
则y＝rsin
φsin
θ＝3sin56πsin53π＝－3
4
3，
z＝rcos φ＝3cos56π＝－323，
阶
阶
段
段
一
三
四 柱坐标系与球坐标系简介
学
阶 段 二
业 分 层 测
评
上一页
返回首页
下一页
1．了解柱坐标系、球坐标系的意义，能用柱坐标系、球坐标系刻画简单 问题中的点的位置．(重点)
2．知道柱坐标、球坐标与空间直角坐标的互化关系与公式，并用于解 题．(难点、易错点)
上一页
返回首页
下一页
[基础·初探]
)
A．(5,8,8 3)
B．(8,8 3，5)
C．(8 3，8,5)
D．(4,8 3，5)
上一页
返回首页
下一页
【解析】
由公式xy＝ ＝ρρcsions
θ， θ
z＝z，
x＝16cosπ3＝8， 得y＝16sinπ3＝8 3，
z＝5， 即P点的直角坐标为(8,8 3，5)． 【答案】 B
上一页
返回首页
∴因此M的直角坐标为34，－3 4 3，－3 2 3.
上一页
返回首页
下一页
空间点的直角坐标化为球坐标
已知长方体ABCD-A1B1C1D1中，底面正方形ABCD的边长为1，棱 AA1的长为 2 ，如图1-4-3所示，建立空间直角坐标系Axyz，Ax为极轴，求点C1 的直角坐标和球坐标．
【思路探究】 先确定C1的直角坐标，再根据空间直角 坐标系与球坐标系的联系，计算球坐标．
图1-4-3
上一页
返回首页
下一页
【自主解答】 点C1的直角坐标为(1,1， 2)． 设C1的球坐标为(r，φ，θ)，其中r≥0,0≤φ≤π，0≤θ<2π， 由x＝rsin φcos θ，y＝rsin φsin θ，z＝rcos φ， 得r＝ x2＋y2＋z2＝ 12＋ 22＋12＝2. 由z＝rcos φ，∴cos φ＝ 22，φ＝π4， 又tan θ＝yx＝1，∴θ＝π4， 从而点C1的球坐标为2，π4，π4.