平行线的判定和性质经典题
平行线的判定及性质

平行线的判定、性质专练
姓名:
例1:如图所示:AD∥BC,∠A=∠C,试说明AB∥DC.
变式:如图所示:AB∥DC,∠A=∠C,试说明AD∥BC.
变式2:如图,点E为DF上的点,点B为AC上的点,∠1= ∠2,∠C= ∠D,求证:DF ∥AC
变式3:如图,点B、E分别在AC、DF上,BD、CE均与AF相交,∠1=∠2,∠C=∠D,试问:∠A与∠F相等吗?请说出你的理由。
变式4:如图,已知∠A=∠F,∠C=∠D,求证:BD//CE.
例2:已知AB ∥CD,GP,HQ 分别平分∠EGB, ∠EHD,判断GP 与HQ 是否平行?
变式1:如图11,直线AB 、CD 被EF 所截,∠1 =∠2,∠CNF =∠BME。
求证:AB∥CD,MP∥NQ.
F 2
A B C D Q E 1 P M N 图11
变式2:已知AB∥CD,GP,HQ分别平分∠AGF, ∠EHD,判断GP与HQ是否平行?
例3:如图,已知AB∥CD,∠1=∠2,求证∠E=∠F.
变式1:如图,已知∠E=∠F,∠1=∠2,:求证AB∥CD .
变式2:如图,已知AB∥CD,∠E=∠F,:求证∠1=∠2.
变式3:如图,已知AB∥CD, AF∥DE, :求证∠1=∠2.
变式4:如图,已知∠1=∠2, AF∥DE, :求证AB∥CD.。
专题01 平行线的判定和性质(解析版)

2022-2023学年浙教版七年级数学下册精选压轴题培优卷专题01 平行线的判定和性质一.选择题(共10小题,满分20分,每小题2分)1.(2分)(2022秋•沙坪坝区期末)如图,直线AB,CD被直线EF所截,AB∥CD,∠1=113°,则∠2的度数为( )A.23°B.67°C.77°D.113°解:∵AB∥CD,∴∠CFE=∠1=113°,∠2=180°﹣∠CFE=180°﹣113°=67°,故选:B.2.(2分)(2023春•九龙坡区校级月考)将一块三角板和一块直尺如图放置,若∠1=50°,则∠2的度数为( )A.110°B.120°C.130°D.140°解:如图,∵∠3=∠1,∴∠2=∠A+∠3=140°.故选:D.3.(2分)(2022秋•青云谱区校级期末)如图,已知长方形纸片ABCD,点E,F在AD边上,点G,H在BC边上,分别沿EG,FH折叠,使点D和点A都落在点M处,若α+β=119°,则∠EMF的度数为( )A.57°B.58°C.59°D.60°解:∵长方形ABCD,∴AD∥BC,∴∠DEG=α,∠AFH=β,∴∠DEG+∠AFH=α+β=119°,由折叠得:∠DEM=2∠DEG,∠AFM=2∠AFH,∴∠DEM+∠AFM=2×119°=238°,∴∠FEM+∠EFM=360°﹣238°=122°,在△EFM中,∠EMF=180°﹣(∠FEM+∠EFM)=180°﹣122°=58°,故选:B.4.(2分)(2022春•殷都区校级月考)如图,AB∥CD,则图中α,β,γ三者之间的关系是( )A.α+β+γ=180°B.α﹣β+γ=180°C.α+β﹣γ=180°D.α+β+γ=360°解:如图,延长AE交直线CD于F,∵AB∥CD,∴∠α+∠AFD=180°,∵∠AFD=∠β﹣∠γ,∴∠α+∠β﹣∠γ=180°,故选:C.5.(2分)(2022•绿园区校级模拟)如图,已知锐角∠AOB,按下列步骤作图:①在射线OA上取一点C,以点O为圆心,OC长为半径作,交射线OB于点D,连接CD;②分别以点C,D为圆心,CD长为半径作弧,交于点M.N;③连MN,OM.则下列结论错误的是( )A.∠COM=∠COD B.若OM=MN,则∠AOB=30°C.MN∥CD D.MN<3CD解:连接ON,MD,由作法得CM=CD=DN,∴∠COM=∠COD,所以A选项正确;∵OM=ON,∴当OM=MN时,△OMN为等边三角形,∴∠MON=60°,∵∠AOB=∠MOA=∠NOB=×60°=20°,所以B选项错误;∵,∴∠MDC=∠DMN,∴MN∥CD,所以C选项正确;∵CM+CD+DN>MN,∴3CD>MN,所以D选项正确.故选:B.6.(2分)(2019秋•淮阴区期末)如图,将长方形ABCD沿线段EF折叠到EB'C'F的位置,若∠EFC'=100°,则∠DFC'的度数为( )A.20°B.30°C.40°D.50°解:由翻折知,∠EFC=∠EFC'=100°,∴∠EFC+∠EFC'=200°,∴∠DFC'=∠EFC+∠EFC'﹣180°=200°﹣180°=20°,故选:A.7.(2分)(2021春•奉化区校级期末)如图,AD∥BC,∠D=∠ABC,点E是边DC上一点,连接AE交BC的延长线于点H.点F是边AB上一点.使得∠FBE=∠FEB,作∠FEH的角平分线EG交BH于点G,若∠DEH =100°,则∠BEG的度数为( )A.30°B.40°C.50°D.60°解:设FBE=∠FEB=α,则∠AFE=2α,∠FEH的角平分线为EG,设∠GEH=∠GEF=β,∵AD∥BC,∴∠ABC+∠BAD=180°,而∠D=∠ABC,∴∠D+∠BAD=180°,∴AB∥CD,∠DEH=100°,则∠CEH=∠FAE=80°,∠AEF=180°﹣∠FEG﹣∠HEG=180°﹣2β,在△AEF中,80°+2α+180﹣2β=180°故β﹣α=40°,而∠BEG=∠FEG﹣∠FEB=β﹣α=40°,故选:B.8.(2分)(2022•博望区校级一模)如图是一款手推车的平面示意图,其中AB∥CD,∠1=24°,∠2=76°,则∠3的度数为( )A.104°B.128°C.138°D.156°解:如图:∵AB∥CD,∠1=24°,∴∠A=∠1=24°,∵∠2=76°,∠2+∠4=180°,∴∠4=180°﹣∠2=180°﹣76°=104°,∴∠3=∠4+∠A=104°+24°=128°.故选:B.9.(2分)(2022秋•南岗区校级期中)如图,AB∥CD∥EF,则下列各式中正确的是( )A.∠1+∠2+∠3=180°B.∠1+∠2=180°+∠3C.∠1+∠3=180°+∠2D.∠2+∠3=180°+∠1解:∵AB∥CD∥EF,∴∠2+∠BDC=180°,∠3=∠CDE,又∠BDC=∠CDE﹣∠1,∴∠2+∠3﹣∠1=180°.故选:D.10.(2分)(2022春•青秀区校级期中)已知AB∥CD,点E在BD连线的右侧,∠ABE与∠CDE的角平分线相交于点F,则下列说法正确的是( )①∠ABE+∠CDE+∠E=360°;②若∠E=80°,则∠BFD=140°;③如图(2)中,若∠ABM=∠ABF,∠CDM=∠CDF,则6∠BMD+∠E=360°;④如图(2)中,若∠E=m°,∠ABM=∠CDF,则∠M=()°.A.①②④B.②③④C.①②③D.①②③④解:∵AB∥CD,∴∠ABE+∠BEG=180°,∠CDE+∠DEG=180°,∴∠ABE+∠BEG+∠CDE+∠DEG=360°,即∠ABE+∠BED+∠CDE=360°,①正确,∵∠BED=80°,∠ABE+∠BED+∠CDE=360°,∴∠ABE+∠CDE=280°,∵AB∥CD,∴∠ABF=∠BFH,∠CDF=∠DFH,∴∠BFD=∠BFH+∠DFH=∠ABF+∠CDF=(∠ABE+∠CDE)=140°,②正确,与上同理,∠BMD=∠ABM+∠CDM=(∠ABF+∠CDF),∴6∠BMD=2(∠ABF+∠CDF)=∠ABE+∠CDE,∴6∠BMD+∠E=360°,③正确,由题意,④不一定正确,∴①②③正确,故选:C.二.填空题(共10小题,满分20分,每小题2分)11.(2分)(2022秋•朝阳区校级期末)如图,已知AC∥BD,∠CAE=30°,∠DBE=35°,则∠AEB等于 65° .解:过点E作EF∥AC,∵AC∥BD,∴AC∥EF∥BD,∴∠AEF=∠CAE=30°,∠BEF=∠DBE=35°,∴∠AEB=∠AEF+∠BEF=65°.故答案为:65°.12.(2分)(2022秋•宛城区校级期末)如图,把一个长方形纸片沿OG折叠后,C,D两点分别落在C',D'两点处,若∠AOD':∠D'OG=4:3,则∠BGO= 54 度.解:∵∠AOD':∠D'OG=4:3,设∠AOD'=4x,则∠D'OG=3x,由翻折可知∠DOG=∠D'OG=3x∵∠AOD'+∠D'OG+∠DOG=180°,即10x=180°,解得x=18°,∵AD∥BC,∴∠BGO=∠DOG=3x=54°,故答案为:54.13.(2分)(2022秋•沙坪坝区校级期末)如图,直线GH分别与直线AB,CD相交于点G,H,且AB∥CD.点M在直线AB,CD之间,连接GM,HM,射线GH是∠AGM的平分线,在MH的延长线上取点N,连接GN,若∠N=∠BGM,∠M=∠N+∠HGN,则∠MHG的度数为 45° .解:过M作MF∥AB,过H作HE∥GN,如图:设∠BGM=2α,∠MHD=β,则∠N=∠BGM=2α,∴∠AGM=180°﹣2α,∵GH平分∠AGM,∴∠MGH=∠AGM=90°﹣α,∴∠BGH=∠BGM+∠MGH=90°+α,∵AB∥CD,∴MF∥AB∥CD,∴∠M=∠GMF+∠FMH=∠BGM+∠MHD=2α+β,∵∠M=∠N+∠HGN,∴2α+β=×2α+∠HGN,∴∠HGN=β﹣α,∵HE∥CN,∴∠GHE=∠HGN=β﹣α,∠EHM=∠N=2α,∴∠GHD=∠GHE+∠EHM+∠MHD=(β﹣α)+2α+β=2β+α,∵AB∥CD,∴∠BGH+∠GHD=180°,∴(90°+α)+(2β+α)=180°,∴α+β=45°,∴∠MHG=∠GHE+∠EHM=(β﹣α)+2α=α+β=45°,故答案为:45°.14.(2分)(2022•苏州模拟)如图,把一张长方形纸片ABCD沿EF折叠,∠1=50°,则∠FGE= 80 °.解:由折叠得∠GEF=∠DEF,∵AD∥BC∴∠DEF=∠1∴∠GEF=∠1∵∠FGE+2∠1=180°,∴∠FGE=180°﹣2×50°=80°,故答案为:80.15.(2分)(2022春•大荔县校级月考)如图,在三角形ABC中,点D、E分别在AB、BC上,连接DE,且DE∥AC,∠1=∠2,若∠B=50°,则∠BAF的度数为 130° .解:∵DE∥AC,∴∠2=∠C,∵∠1=∠2,∴∠1=∠C,∴AF∥BC,∴∠B+∠BAF=180°,∵∠B=50°,∴∠BAF=180°﹣50°=130°.故答案为:130°.16.(2分)(2022秋•新会区校级期末)如图,将长方形ABCD沿EF翻折,再沿ED翻折,若∠FEA″=105°,则∠CFE= 155 度.解:由四边形ABFE沿EF折叠得四边形A′B′FE,∴∠A′EF=∠AEF.∵∠A′EF=∠A′ED+∠DEF,∠AEF=180°﹣∠DEF.∴∠A′ED+∠DEF=180°﹣∠DEF.由四边形A′B′ME沿AD折叠得四边形A″B″ME,∴∠A′ED=∠A″ED.∵∠A″ED=∠A″EF+∠DEF=105°+∠DEF,∴∠A′ED=105°+∠DEF.∴105°+∠DEF+∠DEF=180°﹣∠DEF.∴∠DEF=25°.∵AD∥BC,∴∠DEF=∠EFB=25°.∴∠CFE=180°﹣∠EFB=180°﹣25°=155°.故答案为:155.17.(2分)(2022春•思明区校级期末)如图,将长方形纸片ABCD沿EF折叠后,点A,B分别落在A',B'的位置,再沿AD边将∠A'折叠到∠H处,已知∠1=50°,则∠FEH= 15 °.解:由折叠可知:∠BFE=∠B'FE,∠AEF=∠A'EF,∠A'EG=∠HEG,∵∠1+∠BFE+∠B'FE=180°,∠1=50°,∴∠BFE=65°,∵AD∥BC,∴∠AEF+∠BFE=180°,∴∠AEF=115°,∴∠A'EF=115°,过B'作B'M∥AD,则∠DGB'=∠GB'M,∵AD∥BC,∴∠MB'F=∠1,∴∠1+∠DGB'=∠GB'F=90°,∴∠DGB'=90°﹣50°=40°,∴∠A'GE=∠DGB'=40°,∵∠A'=90°,∴∠HEG=∠A'EG=90°﹣40°=50°,∴∠A'EH=2×50°=100°,∴∠FEH=∠A'EF﹣∠A'EH=115°﹣100°=15°.故答案为:15.18.(2分)(2021秋•南岗区校级期中)如图,直线MN与直线AB、CD分别交于点E、F,AB∥CD,∠BEF与∠EFD的角平分线交于点P,EP与CD交于点G,点H是MN上一点,且GH⊥EG,连接PH,K是GH上一点使∠PHK=∠HPK,作PQ平分∠EPK,交MN于点Q,∠HPQ:∠QFP=3:2,则∠EHG= 30° .解:∵AB∥CD,∴∠BEF+∠EFD=180°,∵∠BEF与∠EFD的角平分线交于点P,∴∠PEF=∠BEF,∠PFE=∠EFD,∴∠PEF+∠PFE=(∠BEF+∠EFD)=90°,∵∠EPF=180°﹣(∠PEF+∠PFE)=90°,∵GH⊥EG,∴∠EGH=∠EPF=90°,∴FP∥HG,∴∠FPH=∠PHK,∠QFP=∠EHG,设∠PHK=x°,则∠FPH=∠HPK=∠PHK=x°,∠FPK=∠FPH+∠HPK=2x°,∴∠EPK=∠EPF+∠FPK=90°+2x°,∵PQ平分∠EPK,∴∠QPK=∠EPK=(90°+2x°)=45°+x°,∴∠HPQ=∠QPK﹣∠HPK=45°,∵∠HPQ:∠QFP=3:2,∴∠QFP=30°,∴∠EHG=∠QFP=30°;故答案为:30°.19.(2分)(2021秋•香坊区校级期中)已知AB∥CD,∠ACD=60°,∠BAE:∠CAE=2:3,∠FCD=4∠FCE,若∠AEC=78°,则∠AFC= 88° .解:∵AB∥CD,∴∠CAB=180°﹣∠ACD=180°﹣60°=120°,∵∠BAE:∠CAE=2:3,∴∠CAE=120×=72°,∵∠AEC=78°,∴∠ACE=180°﹣∠AEC﹣∠CAE=180°﹣78°﹣72°=30°,设∠FCE=x,则∠FCD=4x,∴∠ACF=∠ACD﹣∠FCD=60°﹣4x,∴∠ACE=∠ACF+∠ECF=60°﹣3x,∴60°﹣3x=30°,∴x=10°,∴∠ACF=60°﹣40°=20°,∴∠AFC=180°﹣∠ACF﹣∠CAE=180°﹣20°﹣72°=88°,故答案是:88°.20.(2分)(2021春•东港区校级期末)把一张对边互相平行的纸条,折成如图所示,EF是折痕,若∠EFB=32°,则下列结论:①∠C'EF=32°;②∠AEC=148°;③∠BGE=64°;④∠BFD=116°.正确的有 3 个.解:∵AC′∥BD′,∴∠C′EF=∠EFB=32°,所以①正确;∵∠C′EF=∠FEC,∴∠C′EC=2×32°=64°,∴∠AEC=180°﹣64°=116°,所以②错误;∴∠BFD=∠EFD′﹣∠BFE=180°﹣2∠EFB=180°﹣64°=116°,所以④正确;∵∠BGE=∠C′EC=2×32°=64°,所以③正确.故答案为3.三.解答题(共7小题,满分60分)21.(6分)(2022秋•长安区校级期末)如图,直线CD、EF交于点O,OA,OB分别平分∠COE和∠DOE,已知∠1+∠2=90°,且∠2:∠3=2:5.(1)求∠BOF的度数;(2)试说明AB∥CD的理由.解:(1)∵OA,OB分别平分∠COE和∠DOE,∴,,∵∠COE+∠DOE=180°,∴∠2+∠AOC=90°,∵∠COE=∠3,∴,∴,∵∠2:∠3=2:5,∴,∴,∴∠2=40°,∴∠3=100°,∴∠BOF=∠2+∠3=140°;(2)∵∠1+∠2=90°,∠2+∠AOC=90°,∴∠1=∠AOC,∴AB∥CD.22.(6分)(2022秋•市北区校级期末)如图,已知∠1+∠2=180°,∠B=∠E.(1)试猜想AB与CE之间有怎样的位置关系?并说明理由.(2)若CA平分∠BCE,∠B=50°,求∠A的度数.解:(1)AB∥CE,∵∠1+∠2=180°(已知),∴DE∥BC(同旁内角互补,两直线平行),∴∠ADF=∠B(两直线平行,同位角相等),∵∠B=∠E(已知),∴∠ADF=∠E(等量代换),∴AB∥CE(内错角相等,两直线平行).(2)∵AB∥CE,∴∠B+∠BCE=180°,∵∠B=50°,∴∠BCE=130°,∵CA平分∠BCE,∴∠ACE==65°,∵AB∥CE,∴∠A=∠ACE=65°.23.(6分)(2022秋•荆门期末)如图,在△ABC中,AD⊥BC于D,G是BA延长线上一点,AH平分∠GAC.且AH∥BC,E是AC上一点,连接BE并延长交AH于点F.(1)求证:AB=AC;(2)猜想并证明,当E在AC何处时,AF=2BD.(1)证明:∵AH平分∠GAC,∴∠GAF=∠FAC,∵AH∥BC,∴∠GAF=∠ABC,∠FAC=∠C,∴∠ABC=∠C,∴AB=AC.(2)解:当AE=EC时,AF=2BD.理由:∵AB=AC,AD⊥BC,∴BD=DC,∵AF∥BC,∴∠FAE=∠C,∵∠AEF=∠CEB,AE=EC,∴△AEF≌△CEB(ASA),∴AF=BC=2BD.24.(10分)(2022秋•南关区校级期末)已知AM∥CN,点B在直线AM、CN之间,∠ABC=88°.(1)如图1,请直接写出∠A和∠C之间的数量关系: ∠A+∠C=88° .(2)如图2,∠A和∠C满足怎样的数量关系?请说明理由.(3)如图3,AE平分∠MAB,CH平分∠NCB,AE与CH交于点G,则∠AGH的度数为 46° .解:(1))过点B作BE∥AM,如图,∵BE∥AM,∴∠A=∠ABE.∵BE∥AM,AM∥CN,∴BE∥CN.∴∠C=∠CBE.∵∠ABC=88°.∴∠A+∠C=∠ABE+∠CBE=∠ABC=88°.故答案为:∠A+∠C=88°;(2)∠A和∠C满足:∠C﹣∠A=92°.理由:过点B作BE∥AM,如图,∵BE∥AM,∴∠A=∠ABE.∵BE∥AM,AM∥CN,∴BE∥CN.∴∠C+∠CBE=180°.∴∠CBE=180°﹣∠C.∵∠ABC=88°.∴∠ABE+∠CBE=88°.∴∠A+180°﹣∠C=88°.∴∠C﹣∠A=92°.(3)设CH与AB交于点F,如图,∵AE平分∠MAB,∴∠GAF=∠MAB.∵CH平分∠NCB,∴∠BCF=∠BCN.∵∠B=88°,∴∠BFC=88°﹣∠BCF.∵∠AFG=∠BFC,∴∠AFG=88°﹣∠BCF.∵∠AGH=∠GAF+∠AFG,∴∠AGH=(∠BCN﹣∠MAB).由(2)知:∠BCN﹣∠MAB=92°,∴∠AGH=×92°=46°.故答案为:46°.25.(10分)(2022春•铜梁区校级月考)课题学习:平行线的“等角转化”功能.(1)阅读理解:如图1,已知点A是BC外一点,连接AB、AC,求∠B+∠BAC+∠C的度数.阅读并补充下面推理过程.解:过点A作ED∥BC,∴∠B= ∠EAB ,∠C= ∠DAC ,∵∠EAB+∠BAC+∠DAC=180°,∴∠B+∠BAC+∠C=180°.解题反思:从上面的推理过程中,我们发现平行线具有“等角转化”的功能,将∠BAC、∠B、∠C“凑”在一起,得出角之间的关系,使问题得以解决.(2)方法运用:如图2,已知AB∥ED,求∠B+∠BCD+∠D的度数;(3)深化拓展:已知AB∥CD,点C在点D的右侧,∠ADC=50°,BE平分∠ABC,DE平分∠ADC,BE,DE所在的直线交于点E,点E在直线AB与CD之间.①如图3,点B在点A的左侧,若∠ABC=36°,求∠BED的度数.②如图4,点B在点A的右侧,且AB<CD,AD<BC.若∠ABC=n°,求∠BED度数.(用含n的代数式表示)解:(1)∵ED∥BC,∴∠B=∠EAB,∠C=∠DAC(两直线平行,内错角相等);故答案为:∠EAB;∠DAC;(2)过C作CF∥AB,∵AB∥DE,∴CF∥DE,∴∠D+∠FCD=180°,∵CF∥AB,∴∠B+∠FCB=180°,∴∠B+∠FCB+∠FCD+∠D=360°,∴∠B+∠BCD+∠D=360°;(3)①过E作EG∥AB,∵AB∥DC,∴EG∥CD,∴∠GED=∠EDC,∵DE平分∠ADC,∴,∴∠GED=25°,∵BE平分∠ABC,∴,∵GE∥AB,∴∠BEG=∠ABE=18°,∴∠BED=∠GED+∠BEG=25°+18°=43°;②过E作PE∥AB,∵AB∥CD,∴PE∥CD,∴∠PED=∠EDC=25°,∵BE平分∠ABC,∠ABC=n°,∴,∵AB∥PE,∴∠ABE+∠PEB=180°,∴,∴.26.(10分)(2022春•铁东区校级月考)如图1为北斗七星的位置图,如图2将北斗七星分别标为A,B,C,D,E,F,G,将A,B,C,D,E,F顺次首尾连接,若AF恰好经过点G,且B,G,C在一条直线上,若AF∥DE,∠B=∠C+9°,∠D=∠E=105°.(1)求∠F的度数.(2)计算∠B﹣∠CGF的度数是 115° .(3)连接AD,当∠ADE与∠CGF满足怎样数量关系时,BC∥AD.并说明理由,解:(1)∵AF∥DE,∴∠F+∠E=180°,∴∠F=180°﹣105°=75°;(2)延长DC交AF于K,可得:∠B﹣∠CGF=∠C+10°﹣∠CGF=∠GKC+10°=∠D+9°=114°,故答案为:114°;(3)当∠ADE+∠CGF=180°时,BC∥AD,∵AF∥DE,∴∠GAD+∠ADE=180°,∠ADE+∠CGF=180°,∴∠GAD=∠CGF,∴BC∥AD.27.(12分)(2022春•江汉区校级月考)如图1,直线l分别交直线AB、CD于点EF(点在点F的右侧).若∠1+∠2=180°.(1)求证:AB∥CD;(2)如图2,点H在直线AB、CD之间,过点H作HG⊥AB于点G,若FH平分∠EFD,∠2=120°,求∠FHG的度数.(3)如图3,直线MN与直线AB、CD分别交于点M、N,若∠EMN=120°,点P为线段EF上一动点,Q 为直线CD上一动点,请直接写出∠PMN与∠MPQ,∠PQF之间的数量关系.(题中的角均指大于0°且小于180°的角)(1)证明:∵∠1+∠2=180°,∠2+∠DFE=180°,∴∠1=∠DFE(同角的补角相等),∴AB∥CD(同位角相等,两直线平行);(2)解:如图所示,过点H作HP∥AB,则HP∥AB∥CD,∵GH∥AB,即∠EGH=90°,∴∠PHG=180°﹣∠EGH=90°,∵∠2=120°,∴∠EFD=180°﹣∠2=60°,∵FH平分∠EFD,∴∠HFD=30°,∵PH∥CD,∴∠PHF=∠HFD=30°,∴∠FHG=∠PHF+∠PHG=120°;(3)解:如图3﹣1,当点Q在线段FN上时,过点P作PH∥AB,则PH∥AB∥CD,∴∠EMP=∠MPH,∠PQF=∠HPQ,∴∠MPQ+∠PMN﹣∠PQF=∠MPQ﹣∠HPQ+∠PMN=∠MPH+∠PMN=∠EMP+∠PMN=∠EMN=120°;如图3﹣2,当点Q在FN的延长线上时,过点P作PH∥AB,则PH∥AB∥CD,∴∠EMP=∠MPH,∠PQF=∠HPQ,∴∠MPQ+∠PMN﹣∠PQF=∠MPQ+∠PMN﹣∠HPQ=∠MPH+∠PMN=∠EMP+∠PMN=∠EMN=120°;如图3﹣3(1),当点Q在NF的延长线上且点Q在直线MP的右侧时,过点P作PH∥AB,则PH∥AB∥CD,∴∠EMP=∠MPH,∠PQF+∠HPQ=180°,∴∠MPQ+∠PMN+∠PQF=∠MPQ+180°﹣∠HPQ+∠PMN=∠MPH+∠PMN+180°=∠EMP+∠PMN+180°=∠EMN+180°=300°;如图3﹣3(2),当点Q在NF的延长线上且点Q在直线MP的右侧时,过点P作PH∥AB,则PH∥AB∥CD,∴∠EMP+∠MPH=180°,∠PQF=∠HPQ,∴∠MPQ﹣∠PMN﹣∠PQF=∠MPQ﹣∠PMN﹣∠HPQ=∠MPH﹣∠PMN=180°﹣∠EMP﹣∠PMN=180°﹣∠EMN=60°;综上,∠PMN与∠MPQ,∠PQF之间的数量关系为:∠MPQ+∠PMN﹣∠PQF=120°或∠MPQ+∠PMN+∠PQF=300°或∠MPQ+∠PMN﹣∠PQF=60°。
平行线典型例题

一.解答题(共21小题)
1.如图,AD⊥BC于D,EG⊥BC于G,∠E=∠1,可得AD平分∠BAC.
理由如下:∵AD⊥BC于D,EG⊥BC于G,(已知)
∴∠ADC=∠EGC=90°,(垂直的定义),
∴AD∥EG,(同位角相等,两直线平行)
∴∠1=∠2,(两直线平行,内错角相等)
∠E=∠3,(两直线平行,同位角相等)
解答:
解:AD与BC平行;理由如下:
∵BE∥DF,
∴∠B+∠BCD=180°(两直线平行,同旁内角互补)
∵∠B=∠D,
∴∠D+∠BCD=180°,
点评:
本题考查了平行线的性质及判定,熟记定理是正确解题的关键.
4.如图,已知BE∥DF,∠B=∠D,则AD与BC平行吗?试说明理由.
考点:
平行线的判定与性质.
专题:
探究型.
分析:
利用两直线平行,同旁内角互补可得∠B+∠C=180°,即∠C+∠D=180°;根据同旁内角互补,两直线平行可证得AD∥BC.
这是一道结论开放的探究性问题,由于E点位置的不确定性,可引起对E点不同位置的分类讨论。本题可分为AB,CD之间或之外。
结论:①∠AEC=∠A+∠C②∠AEC+∠A+∠C=360°③∠AEC=∠C-∠A④∠AEC=∠A-∠C⑤∠AEC=∠A-∠C⑥∠AEC=∠C-∠A.
例、如图,将三角板的直角顶点放在直角尺的一边上,∠1=30°,∠2=50°,则∠3的度数为( )
(3)如图3,点 、 是直线CM、DN内部的一个点,连结 、 、 .
试求 的度数;
(4)若按以上规律,猜想并直接写出 … 的度数(不必写出过程).
例、如图,已知直线l1∥l2,且l3和l1、l2分别交于A、B两点,点P在AB上.
平行线的判定及性质 例题及练习

平行线的判定及性质一、【基础知识精讲】1、平行线的判定(1)平行公理:经过直线外一点,有且只有一条直线与已知直线平行. (2)平行公理的推论:平行于同一条直线的两条直线. (3)在同一平面内,垂直于同一条直线的两条直线. (4)同位角相等,两直线平行. (5)内错角相等,两直线平行.(6)同旁内角互补,两直线平行.3、平行线的性质(1)两直线平行,同位角相等. (2)两直线平行,内错角相等.(3)两直线平行,同旁内角互补.二、【例题精讲】专题一:余角、补角、对顶角与三线八角例题1:∠A的余角与∠A的补角互为补角,那么2∠A是()A.直角 B.锐角 C.钝角 D.以上三种都有可能【活学活用1】如图2-79中,下列判断正确的是()A.4对同位角,2对内错角,4对同旁内角B.4对同位角,2对内错角,2对同旁内角C.6对同位角,4对内错角,4对同旁内角D.6对同位角,4对内错角,2对同旁内角【活学活用2】如图2-82,下列说法中错误的是( )A.∠3和∠5是同位角B.∠4和∠5是同旁内角C.∠2和∠4是对顶角D.∠1和∠2是同位角【活学活用3】如图,直线AB与CD交于点O,OE⊥AB于O,图中∠1与∠2的关系是()A.对顶角B.互余C.互补D相等例题2:如果两个角的两边分别平行,而其中一个角比另一个角的4倍少30°,那么这两个角分别是_______.【活学活用4】如图,∠AOC +∠DOE +∠BOF = .专题二:平行线的判定例题3:如图,已知∠EFB+∠ADC=180°,且∠1=∠2,试说明DG ∥AB.1 2A BCDF E G【活学活用】1、长方体的每一对棱相互平行,那么这样的平行棱共有 ( )A .9对B .16对 C.18对 D .以上答案都不对2、已知:如图2-96,DE ⊥AO 于E,BO ⊥AO,FC ⊥AB 于C ,∠1=∠2,求证:DO ⊥AB.3、如图2-97,已知:∠1=∠2=,∠3=∠4,∠5=∠6.求证:AD ∥BC.4、如图2—101,若要能使AB ∥ED ,∠B 、∠C 、∠D 应满足什么条件?ABCDOE F5、同一平面内有四条直线a 、b 、c 、d ,若a ∥b ,a ⊥c ,b ⊥d ,则c 、d 的位置关系为( ) A.互相垂直 B .互相平行 C.相交 D .没有确定关系专题三:平行线的性质1、如图,110,ABC ACB BO ∠+∠=、CO 分别平分ABC ∠和,ACB EF ∠过点O 与BC 平行,则BOC ∠= . 2、如图,AB //CD ,BC //DE ,则∠B+∠D = .3、如图,直线AB 与CD 相交于点O ,OB 平分∠DOE .若60DOE ∠=,则∠AOC 的度数是 .4、 如图,175,2120,375∠=∠=∠=,则4∠= .13 425、如图,//AB CD ,直线EF 分别交AB 、CD 于E 、F ,ED 平分BEF ∠,若172∠=,则2∠= .【例题讲解】例1:如图,已知:AD ∥BC, ∠AEF=∠B,求证:AD ∥EF 。
2、平行线的判定和性质练习题
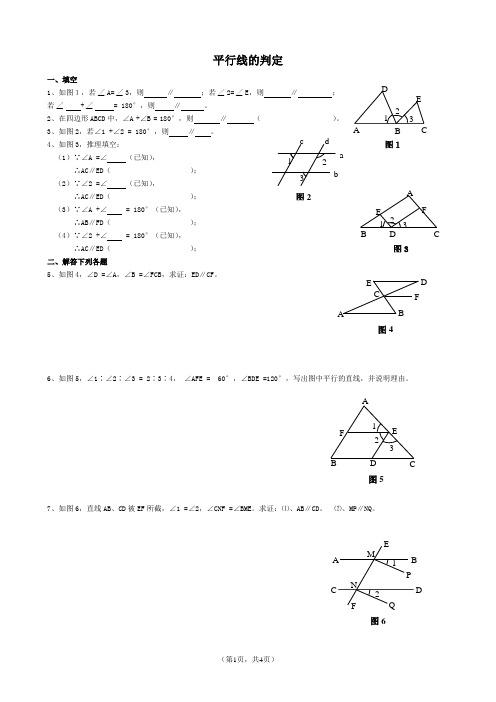
一、填空1、如图1,若∠A=∠3,则 ∥ ;若∠2=∠E ,则 ∥ ;若∠ +∠ = 180°,则 ∥ 。
2、在四边形ABCD 中,∠A +∠B = 180°,则 ∥ ( )。
3、如图2,若∠1 +∠2 = 180°,则 ∥ 。
4、如图3,推理填空:(1)∵∠A =∠ (已知),∴AC∥ED( ); (2)∵∠2 =∠ (已知),∴AC∥ED( ); (3)∵∠A +∠ = 180°(已知), ∴AB∥FD( ); (4)∵∠2 +∠ = 180°(已知), ∴AC∥ED( ); 二、解答下列各题5、如图4,∠D =∠A,∠B =∠FCB,求证:ED∥CF。
6、如图5,∠1∶∠2∶∠3 = 2∶3∶4, ∠AFE = 60°,∠BDE =120°,写出图中平行的直线,并说明理由。
7、如图6,直线AB 、CD 被EF 所截,∠1 =∠2,∠CNF =∠BME。
求证:⑴、AB∥CD。
⑵、MP∥NQ。
a bc d 1 23 图2AB CED12 3 图11 2 3 AF CDB E图3E BAFD C图41 32 A E CD BF 图5F2A B CDQE1 P MN 图6一、填空1、如图1,已知∠1 = 100°,AB∥CD,则∠2 = ,∠3 = ,∠4 = 。
2、如图2,直线AB 、CD 被EF 所截,若∠1 =∠2,则∠AEF +∠CFE = 。
3、如图3所示:⑴、若EF∥AC,则∠A +∠ = 180°,∠F + ∠ = 180°( )。
⑵、若∠2 =∠ ,则AE∥BF。
⑶、若∠A +∠ = 180°,则AE∥BF。
4、如图4,AB∥CD,∠2 = 2∠1,则∠2 = 。
5、如图5,AB∥CD,EG⊥AB 于G ,∠1 = 50°,则∠E = 。
6、如图6,AB∥CD,AC⊥BC,图中与∠CAB 互余的角有 。
七年级数学下册平行线的性质【十大题型】(举一反三)(人教版)

专题5.2 平行线的性质【十大题型】【人教版】【题型1 平行线的判定与性质的运用(计算与证明)】 (1)【题型2 平行线的判定与性质(书写过程)】 (5)【题型3 平行线与三角尺(直角顶点在平行线上)】 (9)【题型4 平行线与三角尺(直角顶点不在平行线上)】 (11)【题型5 平行线的判定与性质综合(角度之间的数量关系)】 (16)【题型6 平行线的判定与性质综合(求定值)】 (21)【题型7 平行线的判定与性质综合(规律问题)】 (31)【题型8 平行线的性质(折叠问题)】 (36)【题型9 平行线的应用(转角问题)】 (41)【题型10 平行线的判定与性质综合(旋转)】 (46)【知识点平行线的性质】【例1】(2022·西藏·林芝市广东实验中学七年级期中)如图,点D,E在AC上,点F,G分别在BC,AB上,且DG∥BC,∠1=∠2.(1)求证:DB∥EF;(2)若EF∠AC,∠1=50°,求∠ADG的度数.【答案】(1)见解析(2)∠ADG=40°【分析】(1)利用两直线平行,内错角相等,再根据同位角相等,两直线平行即可得证;(2)先求出∠C,再根据两直线平行,同位角相等,即可得解.(1)证明:∠DG∥BC,∠∠1=∠DBC.又∠∠1=∠2,∠∠2=∠DBC,∠DB∥EF.(2)∠EF∠AC,∠∠CEF=90°.∠∠2=∠1=50°,∠∠C=90°-50°=40°.∠DG∥BC,∠∠ADG=∠C=40°.【点睛】本题考查平行线的判定和性质.熟练掌握平行线的性质和判定是解题的关键.【变式1-1】(2022·湖北·五峰土家族自治县中小学教研培训中心七年级期末)已知:如图,AE⊥BC,FG⊥BC,∠CEA=∠FGB,∠D=∠ABC+50°,∠CBD=70°.(1)求证:AB∥CD;(2)求∠C的度数.【答案】(1)证明见解析(2)∠C=30°【分析】(1)先证明AE∥GF,可得∠EAB=∠FGB,再证明∠CEA=∠EAB,从而可得答案;(2)由AB∥CD,可得∠D+∠CBD+∠ABC=180°,再把∠D=∠ABC+50°,∠CBD=70°代入进行计算即可.(1)证明:∵AE⊥BC,FG⊥BC,∠AE∥GF,∴∠EAB=∠FGB,∵∠CEA=∠FGB,∴∠CEA=∠EAB,∠AB∥CD;(2)解:由(1)得,AB∥CD,∴∠D+∠CBD+∠ABC=180°,∵∠D=∠ABC+50°,∠CBD=70°,∠∠ABC+70°+∠ABC+50°=180°∴∠ABC=30°,∴∠C=∠ABC=30°.【点睛】本题考查的是平行线的判定与性质,方程思想的应用,掌握“平行线的判定与性质”是解本题的关键.【变式1-2】(2022·重庆·巴川初级中学校七年级期中)如图,∠ABC中,∠BAC的角平分线交BC于D,点F在BA的延长线上,点E在线段CD上,EF与AC相交于点G,且∠BDA+∠CEG=180°.(1)求证:AD∥EF;(2)若点H在FE的延长线上,且∠EDH=∠C,则∠F与∠H相等吗?请说明理由.【答案】(1)见详解(2)∠F=∠H,说明见详解【分析】(1)根据∠BDA+∠CEG=180°,∠DEF+∠CEG=180°,可得∠BDA=∠DEF,根据同位角相等,两直线平行可判定AD∥EF;(2)根据∠EDH=∠C,可得DH∥AC,继而得到∠H=∠EGC,由对顶角∠AGF=∠EGC,可得∠H=∠AGF,由(1)AD∥EF可得∠DAG=∠AGF,∠BAD=∠F,再因为AD是∠BAC的角平分线,有∠DAG=∠BAD,即可证明∠F=∠H.(1)证明:∠∠BDA+∠CEG=180°,∠DEF+∠CEG=180°,∠∠BDA=∠DEF,∠AD∥EF.(2)解:∠F=∠H,理由如下:∠∠EDH=∠C,∠DH∥AC,∠∠H=∠EGC,∠∠AGF=∠EGC,∠∠H=∠AGF,∠AD∥EF,∠∠DAG=∠AGF,∠BAD=∠F,又∠AD是∠BAC的角平分线,∠∠DAG=∠BAD,∠∠F=∠H.【点睛】本题考查了平行线的判定与性质,角平分线的定义,熟练掌握并应用平行线的判定与性质是解答本题的关键.【变式1-3】(2022·湖北·武汉市新洲区阳逻街第一初级中学三模)如图,已知AD⊥BC,EF⊥BC,∠1=∠2.(1)求证:EF∥AD;(2)求证:∠BAC+∠AGD=180°.【答案】(1)见解析(2)见解析【分析】(1)根据垂直得出∠EFB=∠ADB=90°,根据平行线的判定得出EF∥AD;(2)根据平行线的性质得出∠1=∠BAD,由∠1=∠2得出∠2=∠BAD,根据平行线的判定得出DG∥BA,再根据平行线的性质即可得解.【详解】(1)证明:∠AD⊥BC,EF⊥BC,∠∠EFB=90°,∠ADB=90°(垂直的定义),∠∠EFB=∠ADB(等量代换),∠EF∥AD(同位角相等,两直线平行);(2)证明:∠EF∥AD,∠∠1=∠BAD(两直线平行,同位角相等),又∵∠1=∠2(已知),∠∠2=∠BAD(等量代换),∠DG∥BA(内错角相等,两直线平行),∠∠BAC+∠AGD=180°(两直线平行,同旁内角互补).【点睛】本题主要考查了平行线的判定与性质,熟记平行线的判定定理与性质定理是解题的关键.【题型2 平行线的判定与性质(书写过程)】【例2】(2022·黑龙江·哈尔滨市风华中学校七年级期中)如图,∠1=∠2,∠A=∠D.求证:∠B=∠C.(请把下面证明过程补充完整)证明:∵1=∠2(已知)又∵∠1=∠3(____________)∴∠2=∠3(____________)∴AE∥FD(_____________)∴∠A=∠_____(______________)∵∠A=∠D(已知)∴∠D=∠BFD(等量代换)∠_____∥CD(__________________)∴∠B=∠C(____________)【答案】对顶角相等;等量代换;内错角相等,两直线平行;BFD;两直线平行,内错角相等;AB;内错角相等,两直线平行;两直线平行,内错角相等.【分析】先利用对顶角的性质证明∠2=∠3,再证明AE∥FD,可证明∠A=∠BFD,可得∠D=∠BFD,再证明AB∥CD,从而可得答案.【详解】证明:∵1=∠2(已知)又∵∠1=∠3(对顶角相等)∴∠2=∠3(等量代换)∴AE∥FD(内错角相等,两直线平行)∴∠A=∠BFD(两直线平行,内错角相等)∵∠A=∠D(已知)∴∠D=∠BFD(等量代换)∠AB∥CD(内错角相等,两直线平行)∴∠B=∠C(两直线平行,内错角相等)【点睛】本题考查的是对顶角的性质,平行线的判定与性质,熟练的利用平行线的判定与性质进行证明是解本题的关键.【变式2-1】(2022·黑龙江·哈尔滨市萧红中学校七年级阶段练习)阅读并完成下面的证明过程:已知:如图,AB∥EF,∠1=∠2,BE、CE分别平分∠ABC和∠BCD,求证:BE⊥CE.证明:∠BE、CE分别平分∠ABC和∠BCD.∠ABC∠∠ABE=∠EBC=12∠2=________=1∠BCD(角平分线定义)2又∠∠1=∠2,∠∠1=∠ECD()∠EF∥CD()又∠AB∥EF(已知)∠________________()∠∠ABC+∠BCD=180°()(∠ABC+∠BCD)=90°,∠∠ABE+∠2=12又∠AB∥EF,∠∠ABE=∠BEF()∠∠BEF+∠1=90°,∠∠BEC=90°,∠BE⊥CE()【答案】∠ECD;等量代换;内错角相等,两直线平行;AB∥CD;如果两条直线都与第三条直线平行,那么这两条直线也互相平行;两直线平行,同旁内角互补;两直线平行,内错角相等;垂直定义.【分析】根据平行线的性质、平行线的判定以及垂直的定义进行分析即可解答.【详解】证明:∠BE、CE分别平分∠ABC和∠BCD.∠ABC∠∠ABE=∠EBC=12∠BCD(角平分线定义)∠2=∠ECD=12又∠∠1=∠2,∠∠1=∠ECD(等量代换)∠EF∥CD(内错角相等,两直线平行)又∠AB∥EF(已知)∠AB∥CD(如果两条直线都与第三条直线平行,那么这两条直线也互相平行)∠∠ABC+∠BCD=180°(两直线平行,同旁内角互补)(∠ABC+∠BCD)=90°,∠∠ABE+∠2=12又∠AB∥EF,∠∠ABE=∠BEF(两直线平行,内错角相等)∠∠BEF+∠1=90°,∠∠BEC=90°,∠BE⊥CE(垂直定义).故答案为:∠ECD;等量代换;内错角相等,两直线平行;AB∥CD;如果两条直线都与第三条直线平行,那么这两条直线也互相平行;两直线平行,同旁内角互补;两直线平行,内错角相等;垂直定义.【点睛】本题主要考查了平行线的判定与性质、垂直的定义等知识点,灵活运用平行线的判定与性质是解答本题的关键.【变式2-2】(2022·湖南·株洲景炎学校七年级期中)完成下面证明过程并写出推理根据:已知:如图所示,∠BAP与∠APD互补,∠1=∠2.求证:∠E=∠F.证明:∠∠BAP与∠APD互补(已知),即∠BAP+∠APD=180°,∠____________∥_____________(_____________________),∠∠BAP=∠APC(_____________________).又∠∠1=∠2,∠∠BAP-∠1=∠APC-∠2(等式的性质),即∠3=∠4,∠____________∥_____________(_____________________),∠∠E=∠F(_____________________).【答案】AB;CD;同旁内角互补,两直线平行;两直线平行,内错角相等;AE;FP;内错角相等,两直线平行;两直线平行,内错角相等【分析】根据平行线的判定与性质,结合图形完成填空即可求解.【详解】∠∠BAP与∠APD互补(已知),即∠BAP+∠APD=180°,∠AB∥CD(同旁内角互补,两直线平行),∠∠BAP=∠APC(两直线平行,内错角相等).又∠∠1=∠2,∠∠BAP-∠1=∠APC-∠2(等式的性质),即∠3=∠4,∠AE∥FP(内错角相等,两直线平行),∠∠E=∠F(两直线平行,内错角相等)故答案为:AB;CD;同旁内角互补,两直线平行;两直线平行,内错角相等;AE;FP;内错角相等,两直线平行;两直线平行,内错角相等.【点睛】本题考查了平行线的性质与判定进行证明,掌握平行线的性质与判定是解题的关键.【变式2-3】(2022·重庆·巴川初级中学校七年级期中)推理填空:完成下面的证明过程.如图,已知∠1+∠2=180°,∠B=∠DEF,求证:.DE∠BC证明:∠∠1+∠2=180°()∠2=∠3(_______________________________)∠∠1+∠3=180°∠______∥______(_____________________________)∠∠B=______(________________________________)∠∠B=∠DEF(已知)∠∠DEF=_______ (_______________________)∠DE∠BC()【答案】已知;对顶角相等;AB;EF;同旁内角互补,两直线平行;∠EFC;两直线平行,同位角相等;∠EFC;等量代换;内错角相等,两直线平行【分析】由于∠1+∠2=180°,∠2=∠3,则∠1+∠3=180°,根据同旁内角互补,两直线平行得到AB∥EF,则利用平行线的性质得∠B=∠CFE,由于∠B=∠DEF,所以∠DEF=∠CFE,于是根据平行线的判定得到DE∥BC.【详解】证明:∠∠1+∠2=180°(已知)∠2=∠3(对顶角相等)∠∠1+∠3=180°∠AB∥EF(同旁内角互补,两直线平行)∠∠B=∠EFC(两直线平行,同位角相等)∠∠B=∠DEF(已知)∠∠DEF=∠EFC(等量代换)∠DE∥BC(内错角相等,两直线平行)【点睛】本题考查了平行线的判定与性质:内错角相等,两直线平行;同旁内角互补,两直线平行;两直线平行,同位角相等.掌握平行线的判定与性质是解题的关键.【题型3 平行线与三角尺(直角顶点在平行线上)】【例3】(2022·辽宁·阜新实验中学七年级期末)如图,含有30°角的直角三角板的两个顶点E、F放在一个长方形的对边上,点E为直角顶点,∠EFG=30°,延长EG交CD于点P,如果∠3=65°,那么∠2的度数是()A.100°B.105°C.115°D.120°【答案】C【分析】根据直角三角形两锐角互余得到∠1=25°,根据平角的定义得到∠AEF=90°-∠1=65°,根据平行线的性质即可得到结论.【详解】解:∠∠D=90°,∠3=65°,∠∠1=25°,∠∠FEG=90°,∠∠AEF=90°-∠1=65°,∠AD∥BC,∠∠2=180°-∠AEF=115°,故选:C.【点睛】本题考查了直角三角形两锐角互余和平行线的性质,关键是得出∠AEF与∠2互补.【变式3-1】(2022·浙江·金华市第四中学九年级阶段练习)将一直角三角板与两边平行的纸条如图所示放置,下列结论:(1)∠1=∠2;(2)∠3=∠2;(3)∠2+∠4=90°;(4)∠4+∠5=180°,其中正确的个数是()A.1B.2C.3D.4【答案】D【分析】根据两直线平行同位角相等,内错角相等,同旁内角互补,及直角三角板的特殊性解答.【详解】解:∠纸条的两边平行,∠(1)∠1=∠2(两直线平行,同位角相等);(2)∠3=∠4(两直线平行,内错角相等);(4)∠4+∠5=180°(两直线平行,同旁内角互补)均正确;又∠直角三角板与纸条下线相交的角为90°,∠(3)∠2+∠4=90°,正确.故选:D.【点睛】本题考查平行线的性质,正确识别“三线八角”中的同位角、内错角、同旁内角是正确答题的关键.【变式3-2】(2022·山东青岛·七年级期中)将一块直角三角板ABC按如图方式放置,其中∠ABC=30°,A,B两点分别落在直线m、n上,∠1=20°,添加下列哪一个条件可使直线m∥n ()A.∠2=20°B.∠2=30°C.∠2=45°D.∠2=50°【答案】D【分析】根据平行线的判定定理求解即可.【详解】解:由平行线的判定可知,当∠2=∠ABC+∠1时,m∥n,即∠2=∠ABC+∠1=30°+20°=50°,故选:D.【点睛】本题考查了平行线的判定,熟练掌握平行线的判定定理是解题的关键.【变式3-3】(2022·河南南阳·二模)小明把一副三角板按如图所示方式摆放,直角边CD与直角边AB相交于点F,斜边DE∥BC,∠B=30°,∠E=45°,则∠CFB的度数是()A.95°B.115°C.105°D.125°【例4】(2022·全国·八年级专题练习)如图,a∥b,一块含45°的直角三角板的一个顶点落在直线b上,若∠1=58°54′,则∠2的度数为()A.103°6′B.104°6′C.103°54′D.104°54′【答案】C【分析】设∠2的同位角为∠3,∠3的邻补角为∠5,三角板的一个锐角为∠4,根据等腰三角板的特点可求出∠4,根据三角形内角和即可求出∠5,再根据平角的性质即可求出∠3,进而根据两直线平行同位角相等即可求出∠2.【详解】设∠2的同位角为∠3,∠3的邻补角为∠5,三角板的一个锐角为∠4,如图,∠直角三角板含一个45°的锐角,∠该三角板为等腰三角形,∠∠4=45°,∠∠1=58°54′,又∠在三角形中有∠1+∠4+∠5=180°,∠∠5=180°-(∠1+∠4)=180°-(58°54′+45°)=180°-103°54′=76°6′,∠∠3+∠5=180°,∠∠3=180°-∠5=180°-76°6′=103°54′,∠a∥b,∠∠2=∠3,∠∠2=103°54′,故选:C.【点睛】本题主要考查了平行线的性质以及三角形的内角和等知识,掌握两直线平行同位角相等是解答本题的关键.【变式4-1】(2022·山西晋中·七年级期末)用一块含60°角的直角三角板和一把直尺按图中所示的方式放置,其中直尺的直角顶点与三角板的60°角顶点重合,直尺两边分别与三角板的两条直角边相交,若∠1=50°,则∠2的度数为()A.25°B.22.5°C.20°D.15°【答案】C【分析】如图,根据题意得到∠C=90°,AB∠DE,∠CDF=60°.先根据三角形内角和求出∠ABC=40°,再根据平行的性质求出∠CDE=40°,即可求出∠2=20°.【详解】解:如图,由题意得∠C=90°,AB∠DE,∠CDF=60°.∠∠C=90°,∠1=50°,∠∠ABC=180°-∠C-∠1=40°,∠AB∠DE,∠∠CDE=∠CBA=40°,∠∠CDF=60°∠∠2=∠CDF-∠CDE=20°.故选:C【点睛】本题考查了三角形的内角和定理,平行线的性质,熟知两个定理并理解题意得到已知条件是解题的关键.【变式4-2】(2022·福建·莆田市城厢区南门学校七年级阶段练习)如图,AB∥CD,将一副直角三角板作如下摆放,∠GEF=60°,∠MNP=45°.下列结论:①GE∥MP;②∠EFN=150°;③∠BEF=75°;④∠AEG=∠PMN.其中正确的是_______.【答案】①②③④【分析】①由题意得∠G=∠MPN=∠MPG=90°,利用内错角相等,两直线平行即可判定GE∥MP;②由题意得∠EFG=30°,利用邻补角即可求出∠EFN的度数;③过点F作FH⊥AB,可得FH∥CD,从而得到∠HFN=∠MNP=45°,可求得∠EFN=105°,再利用平行线的性质即可求出∠BEF;④利用角的计算可求出∠AEG=45°,从而可判断.【详解】解:①∵∠G=∠MPN=∠MPG=90°,∴GE∥MP,故①正确;②∵∠EFG=30°,∴∠EFN=180°−30°=150°,故②正确;③过点F作EH∥AB,如图,∵AB∥CD,∴FH∥CD,∴∠HFN=∠MNP=45°,∴∠EFN=150°−45°=105°,∵FH∥AB,∴∠BEF=180°−105°=75°;故③正确;④∵∠GEF=60°,∠BEF=75°,∴∠AEG=180°−60°−75°=45°,∴∠AEG=∠PMN=45°,故④正确.故答案为:①②③④.【点睛】本题考查平行线的性质与判定,解题的关键是熟记平行线的判定条件与性质并灵活运用.【变式4-3】(2022·山东淄博·期末)如图所示,将一直角三角板放在AB,CD两条平行线之间:(1)图甲中,容易求得∠1+∠2=90°,请直接写出图乙中∠1,∠2的数量关系;(2)请问图丙中∠1,∠2的数量关系是什么?并加以说明;(3)请直接写出图丁中∠1,∠2的数量关系.【答案】(1)∠1+∠2=270°(2)∠2-∠1=90°;见解析(3)∠1=∠2+90°【分析】(1)过三角板的直角顶点作AB的平行线MN,得AB∥MN∥CD.根据两直线平行,同旁内角互补,即可得∠1,∠2的关系.(2)过三角板的直角顶点作AB的平行线MN,得AB∥MN∥CD.根据两直线平行,内错角相等,平角互补,即可得∠1,∠2的关系.(3)过点O作AB的平行线MN,得AB∥MN∥CD,据两直线平行,内错角相等,即可得∠1,∠2的关系.(1)如图,过三角板的直角顶点作AB的平行线MN,得AB∥MN∥CD∠∠1+∠3=180°,∠2+∠4=180°又∠∠3+∠4=90°∠∠1+∠3+∠2+∠4=180°+180°∠∠1+∠2=360°−90°=270°∠∠1+∠2=270°.(2)如图,过三角板的直角顶点作AB的平行线MN,得AB∥MN∥CD∠∠1=∠3,∠2+∠4=180°又∠∠3+∠4=90°∠∠1+180°−∠2=90°∠∠2−∠1=90°.(3)如图,过点O作AB的平行线MN,得AB∥MN∥CD∠∠MOC=∠2∠∠1=90°+∠MOC∠∠1=90°+∠2.【点睛】本题考查平行线的性质,解题的关键是掌握两直线平行,内错角相等,同旁内角互补;平角互补.【题型5 平行线的判定与性质综合(角度之间的数量关系)】【例5】(2022·黑龙江鹤岗·七年级期末)如图①,AB∥CD,M为平面内一点,若BM∠MC,则易证∠ABM与∠DCM互余.(1)如图②,AB∥CD.点M在射线EA上运动,猜想点M在点A和D之间时,∠BMC与∠ABM、∠DCM之间的数量关系,并证明.(2)在(1)的条件下,当点M在射线EA的其它位置上时(不与点E,A,D重合)请直接写出∠BMC与∠ABM、∠DCM之间的数量关系.又∠AB∥CD,∠MF∥CD,∠∠DCM=∠FMC,∠∠ABM+∠DCM=∠BMF+∠CMF=∠BMC;(2)解:当点M在E、A两点之间时,如图3,∠BMC=∠DCM-∠ABM;过M作MF∥AB,交EC于F,则∠ABM=∠BMF,又∠AB∥CD,∠MF∥CD,∠∠DCM=∠FMC,∠∠BMC=∠CMF-∠BMF=∠DCM-∠ABM;当点M在AD的延长线上时,如图4,∠BMC=∠ABM-∠DCM.过M作MF∥AB,交EC于F,则∠ABM=∠BMF,又∠AB∥CD,∠MF∥CD,∠∠DCM=∠FMC,∠∠BMC=∠BMF-∠CMF=∠ABM-∠DCM.【点睛】本题考查了平行线的判定和性质,关键是构建平行线,利用平行线的性质进行解答.解题时注意分类思想的运用.【变式5-1】(2022·辽宁·兴城市第二初级中学七年级阶段练习)已知,点A,点B分别在线段MN,PQ上,且∠ACB-∠MAC=∠CBP.(1)如图1,求证:MN∥PQ;(2)分别过点A和点C作直线AG、CH使AG∥CH,以点B为顶点的直角∠DBI的两边分别与直线CH,AG交于点F和点E,如图2,试判断∠CFB、∠BEG之间的数量关系,并证明;(3)在(2)的条件下,若BD和AE恰好分别平分∠CBP和∠CAN,并且∠ACB=80°,求∠CFB 的度数.(直接写出答案)【答案】(1)见解析(2)∠CFB−∠BEG=90°,证明见解析(3)∠CFB=130°【分析】(1)过C作CE∥MN,根据平行线的判定和性质即可得到结论;(2)过B作BR∥AG,根据平行线的性质得到∠BEG=∠EBR,∠RBF+∠CFB=180°,等量代换即可得到结论;(3)过E作ES∥MN,根据平行线的性质得到∠NAE=∠AES,∠QBE=∠BES,根据角平分线的定义得到∠NAE=∠EAC,∠CBD=∠DBP,根据四边形的内角和即可得到结论.(1)解:如图,过C作CE∥MN,∠∠1=∠MAC,∠∠2=∠ACB-∠1,∠∠2=∠ACB-∠MAC,∠∠ACB-∠MAC=∠CBP,∠∠2=∠CBP,∠CE∥PQ,∠MN∥PQ;(2)如图,过B作BR∥AG,∠AG∥CH,∠BR∥HF,∠∠BEG=∠EBR,∠RBF+∠CFB=180°,∠∠EBF=90°,∠∠BEG=∠EBR=90°-∠RBF,∠∠BEG=90°-∠RBF=90°-(180°-∠CFB),∠∠CFB-∠BEG=90°;(3)如图,过E作ES∥MN,∠MN∥PQ,∠ES∥PQ,∠∠NAE=∠AES,∠QBE=∠BES,∠BD和AE分别平分∠CBP和∠CAN,∠∠NAE=∠EAC,∠CBD=∠DBP,∠∠CAE=∠AES,∠∠EBD=90°,∠∠EBQ+∠PBD=∠EBC+∠CBD=90°,∠∠QBE=∠EBC,∠∠EBC=∠BES,(360°−∠ACB),∠∠AEB=∠AES+∠BES=∠CAE+∠EBC=12∠∠ACB=80°,∠∠AEB=140°,∠∠BEG=40°,∠∠CFB-∠BEG=90°,∠∠CFB=130°.【点睛】本题考查了平行线的判定和性质,余角的性质,四边形的内角和,正确的作出辅助线是解题的关键.【变式5-2】(2022·湖北·宜昌市第九中学七年级期中)如图,∠1=∠2,∠D=∠CMG.(1)求证:AD∥NG;(2)若∠A+∠DHG=180°,试探索:∠ANB,∠NBG,∠1的数量关系;(3)在(2)的条件下,若∠ANB:∠BNG=2:1,∠1=100°,∠NBG=130°,求∠A的度数.【答案】(1)见解析(2)∠NBG+∠1−∠ANB=180°(3)∠A=105°【分析】(1)由∠1=∠2,∠1=∠GFC,得到∠2=∠CFG,于是得到CM∥DE,根据平行线的性质得到∠D=∠ACM,等量代换得到∠CMG=∠ACM,于是得到结论.(2)过B作BP∥AN交NG于P,由于AD∥NG,于是得到∠D=∠DHG,等量代换得到∠A+∠D=180°,得到AN∥DH,根据平行线的判定得到BP∥CM,由平行线的性质得到∠PBG+∠1=180°,等量代换即可得到结论;(3)由∠1+∠PBG=180°,∠1=100°,得到∠PBG=80°,由于∠NBG=130°,于是得到∠ANB=∠NBP=50°,根据已知条件得到∠ANB:∠BNG=2:1,即可得到结论.(1)证明:∠∠1=∠2,∠1=∠GFC,∠∠2=∠CFG,∠CM∥DE,∠∠D=∠ACM,∠∠D=∠CMG,∠∠CMG=∠ACM,∠AD∥NG;(2)解:∠NBG−∠ANB+∠1=180°;理由如下:过B作BP∥AN交NG于P,∠∠ANB=∠NBP,∠AD∥NG,∠∠D=∠DHG,∠∠A+∠DHG=180°,∠∠A+∠D=180°,∠AN∥DH,又∠CM∠DH,∠BP∥CM,∠∠PBG+∠1=180°,∠∠PBG=∠NBG−∠NBP=∠NBG−∠ANB,∠∠NBG−∠ANB+∠1=180°;(3)解:∠∠1+∠PBG=180°,∠1=100°,∠∠PBG=80°,∠∠NBG=130°,∠∠ANB=∠NBP=50°,∠∠ANB:∠BNG=2:1,∠∠BNP=25°,∠∠ANG=75°,∠∠A=105°.【点睛】本题考查了平行线的判定和性质,对顶角的性质,正确的作出辅助线是解题的关键.【变式5-3】(2022·湖北·潜江市高石碑镇第一初级中学七年级期中)如图1,AB∥CD,直线AE分别交AB、CD于点A、E.点F是直线AE上一点,连结BF,BP平分∠ABF,EP平分∠AEC,BP与EP交于点P.(1)若点F是线段AE上一点,且BF∠AE,求∠P的度数;(2)若点F 是直线AE 上一动点(点F 与点A 不重合),请写出∠P 与∠AFB 之间的数量关系并证明. 【答案】(1)45°(2)当F 点在A 点上方时,∠BPE =12∠AFB ,当F 点在A 点下方时,∠BPE =90°﹣12∠AFB【分析】(1)过点P 作PQ ∥AB ,过点F 作FH ∥AB ,由平行线的性质得∠ABP +∠CEP =∠BPE ,∠ABF +∠CEF =∠BFE ,再由垂直定义和角平分线定义求得结果;(2)分三种情况:点F 在EA 的延长线上时,点F 在线段AE 上时,点F 在AE 的延长线上时,分别进行探究便可.(1)解:过点P 作PQ ∥AB ,过点F 作FH ∥AB ,∠AB ∥CD ,∠AB ∥CD ∥PQ ∥FH ,∠∠ABP =∠BPQ ,∠CEP =∠EPQ ,∠ABF =∠BFH ,∠CEF =∠EFH ,∠∠ABP +∠CEP =∠BPQ +∠EPQ =∠BPE ,∠ABF +∠CEF =∠BFH +∠EFH =∠BFE ,∠BF ∠AE ,∠∠ABF +∠CEF =∠BFE =90°,∠BP 平分∠ABF ,EP 平分∠AEC ,∠∠ABP +∠CEP =12(∠ABF +∠CEF )=45°, ∠∠BPE =45°;(2)①当点F 在EA 的延长线上时,∠BPE =12∠AFB ,理由如下:如备用图1,过点P作PQ∥AB,过点F作FH∥AB,过点P作PQ∥AB,过点F作FH∥AB,过点P 作PQ ∥AB ,过点F 作FH ∥AB ,∠AB ∥CD ,∠AB ∥CD ∥PQ ∥FH ,∠∠ABP =∠BPQ ,∠CEP =∠EPQ ,180°﹣∠ABF =∠BFH ,∠AEC =∠EFH ,∠∠CEP +∠ABP =∠EPQ +∠BPQ =∠BPE ,∠BFH ﹣∠EFH =180°﹣∠ABF ﹣∠AEC =∠AFB , ∠BP 平分∠ABF ,EP 平分∠AEC ,∠∠CEP +∠ABP =12(∠AEC +∠ABF )=12(180°﹣∠AFB ), ∠∠BPE =90°﹣12∠AFB ;综上,当E 点在A 点上方时,∠BPE =12∠AFB ,当E 点在A 点下方时,∠BPE =90°﹣12∠AFB . 【点睛】此题考查平行线的性质:两直线平行内错角相等,两直线平行同位角相等,两直线平行同旁内角互补,以及角平分线的性质,在相交线问题中通常作平行线利用平行线的性质解答,将角度转化由此求出答案.解题中运用分类思想解答问题.【题型6 平行线的判定与性质综合(求定值)】【例6】(2022·湖南·株洲二中七年级期末)实验证明,平面镜反射光线的规律是:射到平面镜上的光线和被反射出的光线与平面镜所夹的锐角相等.如图1,一束光线m 射到平面镜a 上,被a 反射后的光线为n ,则入射光线m 、反射光线n 与平面镜a 所夹的锐角∠1=∠2.(1)如图2,一束光线m 射到平面镜a 上,被a 反射到平面镜b 上,又被b 反射.若被b 反射出的光线n 与光线m 平行,且∠1=50°,则∠2= °,∠3= °.(2)请你猜想:当射到平面镜a 上的光线m ,经过平面镜a 、b 的两次反射后,入射光线m 与反射光线n 平行时,两平面镜a 、b 间的夹角∠3的大小是否为定值?若是定值,请求出∠3,若不是定值,请说明理由.(3)如图3,两面镜子的夹角为α°(0<α<90),进入光线与离开光线的夹角为β°(0<β<90).试探索α与β的数量关系,并说明理由.【答案】(1)100;90;(2)90°(3)2α+β=180°【分析】(1)根据平面镜反射光线的规律得∠1=∠4=50°,再利用平角的定义得∠5=80°,然后利用平行线的性质计算出∠2=100°,则∠6=40°,再利用三角形内角和定理计算∠3;(2)当∠3=90°时,根据三角形内角和定理得∠4+∠6=90°,则2∠4+2∠6=180°,利用平角的定义得到∠2+∠5=180°,然后根据平行线的判定得到m∥n;(3)由(1)可得,∠5=180°-2∠2,∠6=180°-2∠3,再根据∠2+∠3=180°-∠α,即可得出∠β=180°-∠5-∠6=2(∠2+∠3)-180°=2(180°-∠α)-180°=180°-2∠α.(1)解:如图:∠∠1=∠4=50°,∠∠5=180°-2×50°=80°,∠m∥n∠∠2+∠5=180°,∠∠2=100°,(180°-∠2)=40°,∠∠6=12∠∠3=180°-∠4-∠6=90°;故答案为:100,90;(2)当∠3=90°时,m∥n理由如下:∠∠3=90°,∠∠4+∠6=90°,∠2∠4+2∠6=180°,∠∠2+∠5=180°,∠m∥n;(3)解:如图3,由(1)可得,∠5=180°-2∠2,∠6=180°-2∠3,∠∠2+∠3=180°-∠α,∠∠β=180°-∠5-∠6=2(∠2+∠3)-180°=2(180°-∠α)-180°=180°-2∠α,∠α与β的数量关系为:2α+β=180°,故答案为:2α+β=180°.【点睛】本题考查了平行线的判定与性质以及三角形内角和定理,解题时注意:同旁内角互补,两直线平行;两直线平行,同旁内角互补.【变式6-1】(2022·河北保定·七年级阶段练习)如图,直线AB∠CD,点M,N分别在直线AB,CD 上,H为直线CD下方一点.(1)如图1,MH和NH相交于点H,求证:∠MHN=∠AMH−∠CNH.(温馨提示:可过点H 作AB的平行线)(2)延长HN至点G,∠BMH的平分线ME和∠GND的平分线NE相交于点E,HM与CD相交于点F.①如图2,若∠BME=50°,∠END=30°,求∠MHN的度数;②如图2,当点F在点N左侧时,若∠BME的度数为x°,∠END的度数为y°,且x+y的值是一个定值,请问∠MHN的度数是否会随x的变化而发生改变?若不变,求出∠MHN的度数;若变化,请说明理由.③如图3,当点N在点F左侧时,②中其他条件不变,请问∠MHN的度数是否会随x的变化而发生改变?若不变,直接写出....∠MHN的度数;若变化,请说明理由.【答案】(1)见解析(2)①20°;②不变,180°−2(x°+y°);③不变,2(x°+y°)−180°【分析】(1)过点H作HQ∥AB.可得HQ∥CD,从而得到∠AMH=∠MHQ,∠CNH=∠NHQ,即可求证;(2)①根据∠BME=50°,∠END=30°,可得∠BMH=100°,∠GND=60°,从而得到∠AMH=180°−∠BMH=80°,∠CNH=60°.再由∠MHN=∠AMH−∠CNH,即可求解;②根据题意可得∠AMH=180°−2x°,∠CNH=2y°,再由∠MHN=∠AMH−∠CNH,即可求解;③过点H作OH∠AB,根据平行线的性质,可证得∠MHN=∠OHM−∠OHN=∠BMH−∠DNH.从而得到∠MHN=2x°+2y°−180°=2(x°+y°)−180°,即可求解.(1)证明:如图,过点H作HQ∥AB.∠HQ∥AB且AB∥CD,∠HQ∥CD,∠∠AMH=∠MHQ,∠CNH=∠NHQ,∠∠MHN=∠MHQ−∠NHQ=∠AMH−∠CNH;(2)解:①ME平分∠BMH,∠BME=50°,∠∠BMH=100°,∠NE平分∠DNG,∠DNE=30°,∠∠GND=60°,∠∠AMH=180°−∠BMH=80°,∠CNH=60°.由(1)可知:∠MHN=∠AMH−∠CNH=80°−60°=20°.∠∠MHN=20°;②∠ME平分∠BMH,∠BME=x°,∠∠BMH=2x°,∠NE平分∠DNG,∠DNE=y°,∠∠GND=2y°,∠∠AMH=180°−2x°,∠CNH=2y°,∠∠MHN=180°−2x°−2y°=180°−2(x°+y°).∠x+y为一个定值,∠∠MHN不会随x的变化而发生改变,度数为180°−2(x°+y°);③不变,∠MHN的度数为2(x°+y°)−180°.理由如下:如图,过点H作OH∥AB,∠∠BMH=∠OHM,∠AB∥CD,∠OH∥CD,∠∠DNH=∠OHN,∠∠MHN=∠OHM−∠OHN=∠BMH−∠DNH.∠ME平分∠BMH,∠BME=x°,∠∠BMH=2x°∠NE平分∠DNG,∠DNE=y°,∠∠GND=2y°,∠∠DNH=180°−2y°,∠∠MHN=2x°−(180°−2y°),∠∠MHN=2x°+2y°−180°=2(x°+y°)−180°.∠x+y为一个定值,∠∠MHN不会随x的变化而改变.【点睛】本题主要考查了平行线的性质和判定,有关角平分线的计算,熟练掌握平行线的性质和判定,利用类比思想解答是解题的关键.【变式6-2】(2022·福建龙岩·七年级期末)如图1,点A、D分别在射线BM、CN线上,BM∥CN,BM∠BC于点B,AE平分∠BAD交BC于点E,连接DE,∠1+∠2=90°.(1)求证:AE∠ED;(2)求证:DE平分∠ADC;(3)如图2,∠EAM和∠EDN的平分线交于点F,试猜想∠F的值是否为定值,若是,请予以证明;若不是,请说明理由.【答案】(1)见解析(1)证明:如图1,过点E作EG∥BM,则∠1=∠3,∠BM∥CN,∠EG∥CN,∠∠4=∠2,∠∠3+∠4=∠1+∠2=90°,∠∠AED=90°,∠AE∠ED.(2)证明:∠ AE平分∠BAD,∠∠BAD=2∠1,∠BM∥CN,∠∠BAD+∠CDA=180°,∠2∠1+∠CDA,(3)∠F为定值.证明:如图2,过点F作FH∥BM,设∠AFH=α,∠DFH=β,∠BM∥CN,∠FH∥CN,∠∠α+∠β=∠6+∠7,∠∠EAM和∠EDN的平分线交于点F,∠∠α+∠β=12(180°−∠1)+12(180°−∠2)=180°−12(∠1+∠2)=180°−45°=135°,∠∠F=∠α+∠β=135°,∠∠F为定值,∠F=135°,故答案为:∠F=135°.【点睛】本题主要考查垂线、角平分线的性质,解题的关键是掌握垂垂线的概念和角平分线与∠CFM互补(1)如图1,试判断直线AB与直线CD的位置关系,并说明理由.(2)如图2,∠BEF与∠EFD的平分线交于点P,EP的延长线与CD交于点G,H是MN上一点,且GH⊥EG,求证:PF∥GH.(3)如图3,在(2)的条件下,连接PH,K是GH上一点,使∠PHK=∠HPK,作PQ平分∠EPK,求证:∠HPQ的大小是定值.【答案】(1)平行;理由见解析(2)见解析(3)见解析【分析】(1)根据同旁内角互补,两条直线平行,即可判断直线AB与直线CD平行;(2)先根据两条直线平行,同旁内角互补,再根据∠BEF与∠EFD的角平分线交于点P,可得∠EPF=90°,进而证明PF∥GH;(3)根据角平分线定义,及角的和差计算即可求得∠HPQ的度数.(1)解:结论:AB∥CD;理由如下:∠∠MEB与∠CFM互补,∠MEB=∠AEF,∠∠AEF与∠CFM互补,∠AB∥CD.(2)∠EG平分∠BEF,∠∠PEF=1∠BEF,2又∠FP平分∠EFD,∠∠EFP=1∠EFD,2由(1)知AB∥CD,∠∠BEF+∠EFD=180°,∠∠PEF+∠EFP=90°,∠∠EPF=90°,【例7】(2022·辽宁·鞍山市第十四中学七年级阶段练习)如图,已知AB//CD,若按图中规律继续划分下去,则∠1+∠2+⋯+∠n等于()A.n•1800B.2n•1800C.(n−1)•1800D.(n−1)2•1800【答案】C【分析】根据第1个图形∠1+∠2=180°,第2个图形∠1+∠2+∠3=2×180°,第,3个图形∠1+∠2+∠3+∠4=3×180°…,进而得出答案.【详解】(1)∠AB∠CD,∠∠1+∠2=180°(两直线平行,同旁内角互补);(2)过点E作一条直线EF平行于AB,∠AB∠CD,∠AB∠EF,CD∠EF,∠∠1+∠AEF=180°,∠FEC+∠3=180°,∠∠1+∠2+∠3=360°;(3)过点E、F作EM、FN平行于AB,∠AB∠CD,∠AB∠EM∠FN∠CD,∠∠1+∠AEM=180°,∠MEF+∠EFN=180°,∠NFC+∠4=180°;∠∠1+∠2+3+∠4=540°;(4)中,根据上述规律,显然作(n-1)条辅助线,运用(n-1)次两条直线平行,同旁内角互补.即可得到n个角的和是180°(n-1).故选:C.【点睛】此题主要考查了平行线的性质,正确得出图中变化规律是解题关键.【变式7-1】(2022·湖南·邵阳市第六中学八年级阶段练习)如图,已知直线AE,BF被直线AB所截,且AE//BF,AC1,BC1分别平分∠EAB,∠FBA;AC2,BC2分别平分∠BAC1和∠ABC1;AC3,BC3分别平分∠BAC2,∠ABC2…依次规律,得点C n,则∠C n的度数为()A.90−902n B.180−902n−1C.902n−1D.1802nAB∠CD.试求:(1)图(1)中∠A+∠C的度数,并说明理由.(2)图(2)中∠A+∠APC+∠C的度数,并说明理由.(3)图(3)中∠A+∠AEF+∠EFC+∠C的度数,并简要说明理由.(4)按上述规律,∠A+……+∠C(共有n个角相加)的和为【答案】(1)180°,理由见解析;(2)360°,理由见解析;(3)540°,理由见解析;(4)180°(n-1)【分析】(1)据两直线平行,同旁内角互补可得∠A+∠C=180°;(2)沿P作一条平行A B、CD的平行线PM,由两直线平行,同旁内角互补可得∠A+∠APM=180°,∠MPC+∠C=180°,故∠A+∠APC+∠C=360°;(3)根据第二题,同理可得∠A+∠AEF+∠EFC+∠C=540°;(4)由以上规律,有两个角时,和为180°;有三个角时和为360°;有四个角时和为540°…故可得有n个角时,和为180°(n-1).【详解】解:(1)∠AB∠CD,∠∠A+∠C=180°(两直线平行,同旁内角互补);(2)过点P作一条直线PM平行于AB,∠AB∠CD,∠AB∠PM,∠CD∠PM∠AB,∠∠A+∠APM=180°,∠MPC+∠C=180°,∠∠A+∠APC+∠C=360°;(3)分别过点E、F作EM、FN平行于AB,∠AB∠CD,∠AB∠EM∠FN∠CD,∠∠A+∠AEM=180°,∠MEF+∠EFN=180°,∠NFC+∠C=180°;∠∠A+∠AEF+∠EFC+∠C=540°;(4)由以上规律,有两个角时,和为180°;有三个角时和为360°;有四个角时和为540°…故可得有n个角时,和为180°(n-1).【点睛】本题主要考查两直线平行,同旁内角互补的性质,并考查学生通过计算总结规律的能力,是一道好题.【变式7-3】(2022·浙江·七年级阶段练习)阅读并探究下列问题.(1)如图①,将长方形纸片剪两刀,其中AB∥CD,则∠2与∠1、∠3有何关系?请进行证明.(2)如图②,将长方形纸片剪四刀,其中AB∥CD,则∠1、∠2、∠3、∠4、∠5的关系为.(3)如图③,将长方形纸片剪2016刀,其中AB∥CD,则共剪出个角.若将剪出的角(∠A、∠C除外)分别用∠E1、∠E2、∠E3…表示,则被剪出的这些角的关系为.(4)如图④,直线AB∥CD,∠EF A=∠HMN=x°,∠FGH=3x°,∠CNP=y°|2x+y−102|+√x+y−72=0由上述结论求∠GHM的度数.【答案】(1)∠1+∠3=∠2,证明见解析;(2)∠1+∠3+∠5=∠2+∠4;(3)2017,∠A+∠C+∠E2+∠E4+…+∠E2014=∠E1+∠E3+…+∠E2015.(4)48°.【分析】(1)过E点作EF∠AB,则EF∠CD,根据两直线平行,内错角相等得到∠AEF=∠1,∠CEF=∠3,即有∠2=∠1+∠3;(2)分别过E、G、F分别作EM∠AB,GN∠AB,FP∠AB,根据两直线平行,内错角相等,同(1)一样易得到∠2+∠4=∠1+∠3+∠5;(3)综合(1)(2)易得开口向左的角的度数的和等于开口向右的角的度数的和.(4)利用(3)的结论得到∠BFG+∠GHM+∠MND=∠FGH+∠HMN,易计算出∠GHM.。
平行线的性质与判定经典题型

平行线的性质与判定经典题型1.在三角形ABC中,角B等于角ACB,CD平分角ACB 并交AB于点D,AE与DC平行并交BC延长线于点E。
已知角E等于36度,求角B的度数。
2.在图中,如果AB平行于CD,则角α、β、γ之间的关系是什么?3.在图中,AB平行于CD且CD平行于PN,角ABC等于50度,角CPN等于150度。
求角BCP的度数。
4.在图中,直线AB和CD被直线EF所截。
如果角BMN 等于角DNF且角1等于角2,那么MQ平行于NP。
为什么?5.在图中,将一个长方形纸片沿EF折叠后,点D和C分别落在D'和C'的位置。
如果角EFB等于65度,则角AED'等于多少度?6.在图中,如果角1等于角2且角C等于角D,则角A等于角F。
为什么?7.在图中,已知角1加角2等于180度,角3等于角B。
试判断角AED和角ACB的大小关系,并说明理由。
8.已知AB平行于CD,分别探讨下列四个图形中角APC和角PAB、角PCD的关系。
从所得四个关系中任选一个并说明理由。
9.在图中,已知角1等于角2,角3等于角4,角5等于角6.证明AD平行于BC。
10.在图中,已知CD垂直于AB于点D,EF垂直于AB于点F,角DGC等于105度,角BCG等于75度。
求角1加角2的度数。
11.在图中,AD垂直于BC于点D,EF垂直于BC于点F,EF交AB于点G,交CA的延长线于点E,且角1等于角2.AD是否平分角BAC?说明理由。
12.在图中,如果AB平行于CD且角1等于角2,则角E等于角F。
为什么?13.在图中,DB平行于FG平行于EC,角ABD等于60度,角ACE等于36度,AP平分角BAC。
求角PAG的度数。
14.在图中,AB平行于CD,角1等于115度,角2等于140度。
求角3的度数。
15.已知:AC平行于DE,DC平行于EF,CD平分角BCD。
证明:EF平分角BED。
16.已知:AB平行于CD,角1等于角B,角2等于角D。
平行线的判定与性质练习题

平行线的判定与性质练习题平行线的判定与性质练习题平行线是几何学中的基本概念之一,它在我们的日常生活中无处不在。
从道路上的交叉口到建筑物的设计,平行线都扮演着重要的角色。
在几何学中,我们需要学会判定平行线,并掌握它们的性质。
下面,我将给大家提供一些平行线的判定与性质练习题,希望能帮助大家更好地理解和应用平行线的知识。
练习题一:判定平行线1. 在下图中,判断线段AB和线段CD是否平行。
A-----B| |C-----D2. 在下图中,判断线段AB和线段EF是否平行。
A-----B| || |E-----F3. 在下图中,判断线段AB和线段CD是否平行。
A-----B\ /\ /C-----D练习题二:平行线的性质1. 若两条平行线被一条横线所截,那么对应的内角互补。
2. 若两条平行线被一条横线所截,那么对应的外角相等。
3. 若两条直线分别与一条平行线相交,那么对应的内角相等。
4. 若两条直线分别与一条平行线相交,那么同旁内角互补。
练习题三:平行线的应用1. 若两条平行线被一条横线所截,且已知其中一个内角的度数为60°,求对应的内角和外角的度数。
2. 若两条平行线被一条横线所截,且已知其中一个外角的度数为120°,求对应的内角和另一个外角的度数。
3. 若两条直线分别与一条平行线相交,且已知其中一个内角的度数为70°,求对应的内角和同旁内角的度数。
4. 若两条直线分别与一条平行线相交,且已知其中一个同旁内角的度数为45°,求对应的内角和另一个同旁内角的度数。
通过以上练习题,我们可以加深对平行线的判定与性质的理解。
判定平行线需要观察线段的走向,若两条线段的走向相同,即不相交且不重合,则可以判定它们为平行线。
而平行线的性质则是通过观察线段之间的关系得出的。
掌握这些性质可以帮助我们解决更复杂的几何问题。
在应用平行线的过程中,我们可以根据已知条件利用平行线的性质进行推导。
平行线的判定专项练习60题

1.已知:如图,BE平分∠ ABC,∠ 1=∠2.求证: BC∥DE.2.如图,已知∠ A=∠F,∠ C=∠D,试说明BD∥CE.3.如图所示, AB⊥BC,BC⊥CD,BF 和 CE是射线,并且∠ 1=∠2,试说明BF∥CE.4.如图, AB⊥BC,∠ 1+∠2=90°,∠ 2=∠3,求证: BE∥DF.5.如图, OP平分∠ MON, A、B 分别在 OP、 OM上,∠ BOA=∠BAO,那么 AB平行于 ON吗若平行,请写出证明过程;若不平行,请说明理由.6.已知:如图,∠ 1=∠2,∠ A=∠C.求证: AE∥BC.7.已知,如图 B、 D、 A 在一直线上,且∠ D=∠E,∠ ABE=∠D+∠E, BC是∠ ABE的平分线,求证: DE∥BC.8.如图,已知∠ AEC=∠A+∠C,试说明: AB∥CD.9.如图,已知AC∥ED, EB平分∠ AED,∠ 1=∠2,求证: AE∥BD.10.如图,直线AB、 CD与直线 EF 相交于 E、 F,已知:∠ 1=105°,∠ 2=75°,求证: AB∥CD.11.如图,∠ D=∠A,∠ B=∠FCB,求证: ED∥CF.12.如图,已知AB⊥BC,CD⊥BC,∠ 1=∠2,求证: EB∥FC.13.如图所示所示,已知BE是∠B 的平分线,交AC于 E,其中∠ 1=∠2,那么DE∥BC吗为什么14.如图,已知∠ C=∠D,DB∥EC.AC与 DF平行吗试说明你的理由.15.如图, AC⊥AE,BD⊥BF,∠ 1=35°,∠ 2=35°,求证: AE∥BF.16.如图,已知AB∥CD,∠ 1=∠2,求证: BE∥CF.17.已知∠ BAD=∠DCB,∠ 1=∠3,求证: AD∥BC.18.如图, AD是三角形 ABC的角平分线, DE∥CA,并且交AB与点 E,∠ 1=∠2, DF与 AB 是否平行为什么19.如图,已知:∠ C=∠DAE,∠ B=∠D,那么AB平行于 DF吗请说明理由.20.如图,已知点 B 在 AC上, BD⊥BE,∠ 1+∠C=90°,问射线CF与 BD平行吗说明理由.21.已知∠1的度数是它补角的 3 倍,∠2 等于 45°,那么AB∥CD 吗为什么22.已知:如图,BDE是一条直线,∠ ABD=∠CDE,BF 平分∠ ABD, DG平分∠ CDE,求证: BF∥DG.23.如图,四边形ABCD中,∠ A=∠C=90°, BF、 DE分别平分∠ ABC、∠A DC.判断 DE、 BF 是否平行,并说明理由.24.如图,若∠ CAB=∠CED+∠CDE,求证: AB∥CD.25.如图, CD⊥AB,GF⊥AB,∠ 1=∠2.试说明DE∥BC.26.如图所示,∠ CAD=∠ACB,∠ D=90°, EF⊥CD.试说明:∠ AEF=∠B.27.已知:如图所示,C,P,D 三点在同一条直线上,∠BAP+∠APD=180°,∠E=∠F,求证:∠ 1=∠2.28.如图,∠ D=∠1,∠ E=∠2,DC⊥EC.求证: AD∥BE.29.如图,在四边形ABCD中,∠ A=∠C, BE平分∠ ABC, DF平分∠ ADC,试说明BE∥DF.30.已知:如图,∠ 1=∠2,∠ A=∠F,则∠C与∠D相等吗试说明理由.31.如图,在四边形ABCD中,∠ A=∠C=90°,∠ 1=∠2,∠ 3=∠4,求证: BE∥DF.32.如图,已知∠ 1=∠2求证:a∥b.33.如图, DE⊥AO 于 E,BO⊥AO 于 O,FC⊥AB 于 C,∠ 1=∠2,找出图中互相平行的线,并加以说明.34.如图,已知∠ 1=∠2,∠ C=∠CDO,求证: CD∥OP.35.如图,已知DE平分∠ BDF, AF 平分∠ BAC,且∠ 1=∠2.求证( 1)DF∥AC;(2)DE∥AF.36.如图, AD平分∠ BAC, EF平分∠ DEC,且∠ 1=∠2,试说明DE与 AB的位置关系.37.如图,在△ ABC 中,点 D在 AB 上,∠ ACD=∠A,∠ BDC 的平分线交BC于点 E.求证: DE∥AC.38.如图, AB 与 CD相交于点O,并且∠ A=∠1,试问∠2 与∠B 满足什么关系时, AC∥BD 说明理由.39.如图,已知∠ 1=∠A,∠ 2=∠B,那么MN与 EF 平行吗如果平行,请说明理由.40.如图,直线 AB、 CD被直线 EF 所截,∠ 1+∠4=180°,求证: AB∥CD.41.如图所示,已知:∠ 1=∠2,∠ E=∠F.试说明AB∥CD.42.如图,已知EF⊥CD于 F,∠ GEF=25°,∠ 1=65°,则AB与 CD平行吗请说明理由.43.如图,已知∠ 1=∠2=90°,∠ 3=30°,∠ 4=60°,图中有几对平行线说说你的理由.44.直线 AB, CD被直线 EF 所截,∠ 1=∠2,直线AB 和 CD平行吗为什么45.已知:如图, AD⊥BC,EF⊥BC,∠ 1=∠2.求证: AB∥GF.46.如图,已知B、C、 D 三点在同一条直线上,∠ B=∠1,∠ 2=∠E,试说明AD∥CE.47.直线 AB、 CD与 GH交于 E、F, EM平分∠ BEF, FN平分∠ DFH,∠BEF=∠DFH,求证: EM∥FN.48.如图所示,∠ ABC=∠BCD,BE、 CF分别平分∠ ABC 和∠ BCD,请你说出BE与 CF 的位置关系,并说出你的理由.49.如图,若∠ 1=∠2,请判断DB与 EC的位置关系,并说明理由.50.如图,在△ ABC 中, CD⊥AB,垂足为D,点 E 在 BC上, EF⊥AB,垂足为F.(1) CD与 EF 平行吗为什么(2)如果∠ 1=∠2,DG∥BC 吗为什么51.如图,已知:HG平分∠ AHM, MN平分∠ DMH,且∠ AHM=∠DMH.问: GH与 MN有怎样的位置关系,请说明理由.(请注明每一步的理由)52.已知:如图,∠ C=∠1,∠2 和∠D互余, BE⊥FD 于点 G.求证: AB∥CD.53.如图,直线AB, CD被 EF所截,∠ 3=∠4,∠ 1=∠2,EG⊥FG.求证: AB∥CD.54.已知:如图,CD是直线, E 在直线 CD上,∠ 1=130°,∠ A=50°,求证:AB∥CD.55.如图,已知∠ 1=∠2,∠ DAB=∠DCA,且DE⊥AC,BF⊥AC,问:(1)AD∥BC 吗(2)AB∥CD 吗为什么56.如图,四边形 ABCD,∠ 1=30°,∠ B=60°, AB⊥AC,则 AD与 BC一定平行吗 AB与 CD呢若平行请说明理由,反之则不用说明理由.57.已知:如图,∠ A=∠F,∠ C=∠D.求证: BD∥CE.58.如图, AD⊥BC 于点 D,∠ 1=2,∠ CDG=∠B,请你判断 EF 与 BC的位置关系,并加以证明,要求写出每步证明的理由.59.已知:如图,CE平分∠ ACD,∠ 1=∠B,求证: AB∥CE.60.如图,已知∠ 1=∠2,∠ 3=∠4,可以判定哪两条直线平行平行线的判定 60 题参考答案 :4.∵ AB⊥BC,∴∠ 3+∠4=90°.1.∵ BE 平分∠ ABC,∵∠ 2=∠3,∠ 1+∠2=90°,∴∠ 1=∠3,∴∠ 1=∠4,∵∠ 1=∠2,∴BE∥DF.∴∠ 2=∠3,5. AB平行于 ON.∴BC∥DE证明:∵ OP 平分∠ MON,2.∵∠ A=∠F(已知),∴∠ BOA=∠NOA,∴AC∥DF(内错角相等,两直线平行),∵∠ BOA=∠BAO,∴∠ C=∠CEF(两直线平行,内错角相等),∴∠ BAO=∠NOA,∵∠ C=∠D(已知),∴AB∥ON∴∠ D=∠CEF(等量代换),6.∵∠ 1=∠2,∴BD∥CE(同位角相等,两直线平行).∴DC∥AB,3.∵ AB⊥BC(已知),∴∠ A+∠ADC=180°.∴∠ ABC=90°(垂直定义);又∵∠ A=∠C,∵BC⊥CD(已知),∴∠ ADC+∠C=180°,∴∠ BCD=90°(垂直定义),∴AE∥BC.∴∠ ABC=∠DCB;7.∵ BC是∠ ABE 的平分线,∵∠ 1=∠2(已知),∴∠ ABC=∠CBE(角平分线定义),∴∠ ABC﹣∠ 2=∠DCB﹣∠ 1,∵∠ ABE=∠D+∠E=∠ABC+∠CBE,∠ D=∠E,即∠ FBC=∠ECB,∴∠ ABC=∠D,∴BF∥CE(内错角相等,两直线平行)∴DE∥BC8.过点 E 作 EF∥AB.∴AE∥BF.∵EF∥AB,16.∵ AB∥CD,∴∠ A=∠AEF;∴∠ ABC=∠BCD(两直线平行,内错角相等);又∵∠ AEC=∠A+∠C,∵∠ 1=∠2,∴∠ AEC=∠AEF+∠C;∴∠ ABC﹣∠ 1=∠BCD﹣∠ 2,而∠ AEC=∠AEF+∠CEF,即∠ EBC=∠BCF,∴∠ CEF=∠C,∴BE∥CF(内错角相等,两直线平行).∴EF∥CD,17.∵∠ BAD=DCB,∠ 1=∠3(已知),∴AB∥CD.∴∠ BAD﹣∠ 1=∠DCB﹣∠ 3(等式性质),即∠ 2=∠4,9.∵ AC∥ED,∴AD∥BC(内错角相等,两直线平行)∴∠ 1=∠4;18.DF∥AB.∵∠ 1=∠2,理由:∵ DE∥CA,∴∠ 2=∠4;∴∠ 1=∠CAD,又∵ EB 平分∠ AED,∵AD是三角形 ABC的角平分线,∴∠ 3=∠4;∴∠ BAD=∠CAD,∴∠ 2=∠3,∵∠ 1=∠2,∴AE∥BD∴∠ 2=∠BAD,10.∵∠ 1+∠BEF=180°,∠ 1=105°,∴DF∥AB∴∠ BEF=75°,19.AB∥DF( 2 分)∵∠ 2=75°,理由:∵∠ C=∠DAE,(已知)∴∠ BEF=∠2,∴AD∥BC,(内错角相等,两直线平行)( 2 分)∴AB∥CD.∴∠ D=∠DFC,(两直线平行,内错角相等)11.∵∠ D=∠A,∴∠ B=∠D,(已知)∴ED∥AB;∴∠ B=∠DFC,(2 分)∵∠ B=∠BCF,∴AB∥DF(同位角相等,两直线平行)∴AB∥CF;20.CF∥BD.理由如下:∴ED∥CF.∵BD⊥BE,12.∵ AB⊥BC,CD⊥BC(已知),∴∠ 1+∠2=90°;∴∠ ABC=∠BCD=90°(垂直定义);∵∠ 1+∠C=90°,又∵∠ 1=∠2(已知),∴∠ 2=∠C.∴∠ ABC﹣∠ 1=∠BCD﹣∠ 2(等量减等量,差相等),∴CF∥BD.∴∠ EBC=∠FCB,21.AB∥CD.( 1 分)∴EB∥FC(内错角相等,两直线平行)理由如下:13.∵ BE 是∠B 的平分线,∵∠ 1+∠MNC=180°,∠ MNC=∠1,∴∠ 1=∠CBE,∴∠ 1=135°.(2 分)∵∠ 1=∠2,又∵∠ AMN=∠2=45°,(3 分)∴∠ 2=∠CBE,∴∠ 1+∠AMN=180°.( 4 分)∴DE∥BC.∴AB∥CD14. AC与 DF平行,理由如下:22.∵ BF 平分∠ ABD, DG平分∠ CDE,∵BD∥EC,∴∠ 1=∠ABD,∠ 2=∠CDE,∴∠ DBC+∠C=180°,又∵∠ ABD=∠CDE,又∠ C=∠D,∴∠ 1=∠2,∴∠ DBC+∠D=180°,∴BF∥DG(同位角相等,两直线平行).∴AC∥DF.23.ED∥BF;证明如下:15.∵ AC⊥AE,BD⊥BF,∵四边形 ABCD中,∠ A=∠C=90°,∴∠ 1+∠3=∠2+∠4=90°,∴∠ ADC+∠ABC=180°,∵∠ 1=35°,∠ 2=35°,∵BF、 DE分别平分∠ ABC、∠ ADC,∴∠ 3=∠4,∴∠ ADC+∠ABC=2∠ADE+2∠ABF=180°,∴∠ ADE+∠ABF=90°,又∵∠ A=90°,∠ ADE+∠AED=90°,∴∠ AED=∠ABF,∴ED∥BF(同位角相等,两直线平行).24.在△ ECD中∵∠ C+∠CED+∠CDE=180°(三角形内角和定理)又∵∠ CAB=∠CED+∠CDE(已知),∴∠ C+∠CAB=180°(等量代换),∴AB∥CD(同旁内角互补,两直线平行)25.∵ CD⊥AB,GF⊥AB,,∵∠ 1=∠DGF,又∵∠ 1=∠2,∴∠ 2=∠DGF,∴DB∥EC,∴∠ DBA=∠C,∴∠ C=∠D31.∵四边形ABCD中,∠ A=∠C=90°,∴∠ ABC+∠CDA=180°,∵∠ 1=∠2,∠ 3=∠4,∴∠ 2+∠3=90°,∴CD∥FG,∵∠ A=90°,∴∠ 2=∠DCG;∴∠ 1+∠AEB=90°,又∵∠ 1=∠2,∵∠ 1=∠2,∴∠ DCG=∠1,∴∠ AEB=∠3,∴DE∥BC∴BE∥FD.26.∵∠ CAD=∠ACB,32.∵∠ 1=∠2,∠ 2=∠3,∴AD∥BC,∴∠ 1=∠3,∵EF⊥CD,∴a∥b.∴∠ EFC=90°33.CF∥OD.∵∠ D=90°,理由:∵ DE⊥AO,BO⊥AO,∴∠ EFC=∠D,∴AD∥EF,∴DE∥BO,∴∠ 3=∠2,∴BC∥EF,∵∠ 1=∠2,∴∠ AEB=∠B.∴∠ 1=∠3,27.∵∠ E=∠ F,∴CF∥OD∴AE∥FP,34.∵∠ DOB是△ COD的外角,∴∠ PAE=∠APF;又∵∠ BAP+∠APD=180°,∴∠ C+∠CDO=∠DOB,又∵∠ DOB=∠1+∠2,∴AB∥CD,而∠ 1=∠2,∠ C=∠CDO,∴∠ BAP=∠APC,即∠ 2+∠PAE=∠1+∠APF;∴∠ 2=∠C,∴∠ 2=∠1∴CD∥OP28.∵ DC⊥EC,35.( 1)∵ DE平分∠ BDF,AF 平分∠ BAC,∴∠ 1+∠2=90°,∴∠ BDF=2∠1,∠ BAC=2∠2,又∠ D=∠1,∠ E=∠2,又∵∠ 1=∠2,∴∠ D+∠1+∠E+∠2=180°.∴∠ BDF=∠BAC,根据三角形的内角和定理,得∴DF∥AC;∠A+∠B=180°,∴AD∥BE ( 2)∵A F 平分∠ BAC,∴∠ BAF=∠2.29.∵∠ A+∠ABC+∠C+∠CDA=360°又∵∠ 1=∠2,而∠ A=∠C,BE平分∠ ABC, DF 平分∠ CDA∴∠ 1=∠BAF,∴2∠A+2∠ABE+2∠ADF=360°∴DE∥AF.即∠ A+∠ABE+∠ADF=180°36.DE∥AB,又∠ A+∠ABE+∠AEB=180°∵AD平分∠BAC,∴∠ AEB=∠ADF∴BE∥DF30.∠ C=∠D.理由如下:∵∠ A=∠F,∴∠ BAC=2∠1,∵EF 平分∠ DEC,∴∠ DEC=2∠2,∵∠ 1=∠2,∴DF∥AC,∴∠ BAC=∠DEC,∴∠ D=∠DBA.∴DE∥AB.37.∵∠ BDE+∠CDE=∠A+∠ACD,又 DE是∠ BDC的平分线,∠ ACD=∠A,∴∠ A=∠BDE,∴DE∥AC.38.∠2与∠B相等时, AC∥BD.理由如下:∵∠ A=∠1,∠ 1=∠2,∴∠ A=∠2,∵∠ 2=∠B,∴∠ A=∠B,∴AC∥BD.39. MN与 EF平行.理由如下:∵∠ 1=∠A,∴MN∥AB,∵∠ 2=∠B,∴E F∥AB,∴M N∥EF.40.∵∠ 1+∠2=180°,∠ 1+∠4=180°,∴∠ 2=∠4,∴AB∥CD.41.∵∠ E=∠F,∴BE∥CF,∴∠ EBC=∠BCF,∵∠ 1=∠2,∴∠ CBA=∠DCB,∴AB∥CD.42.∵ EF⊥CD 于 F,∴∠ EFG=90°,∵∠ GEF=25°,∴∠ EGF=65°,∵∠ 1=65°,∴∠ 1=∠EGF,∴AB∥CD.43.图中共有 2 对平行线.①AB∥C D.理由如下:∵∠ 1=∠2=90°,∴AB∥CD(在同一平面内,如果两条直线同时垂直于同一条直线,那么这两条直线平行);②∵∠ 2=90°,∴∠ 4+∠5=90°,又∵∠ 3=30°,∠ 4=60°,∴∠ 3=∠5,∴E F∥HG(同位角相等,两直线平行).综上所述,图中共有 2 对平行线,它们是:AB∥CD、EF∥HG 44.AB∥CD,理由:∵∠1=∠2,∠1=∠3,∴∠ 2=∠3,∴A B∥CD.45.∵ AD⊥BC,EF⊥BC(已知),∴∠ ADB=∠EFC=90°(垂直的定义),∴∠ B=90°﹣∠ 1(直角三角形两锐角互余),∠G FC=90°﹣∠ 2(互余的定义),∵∠ 1=∠2(已知),∴∠ B=∠GFC(等角的余角相等),∴AB∥GF(同位角相等,两直线平行)46.∵∠ B=∠1,∴AB∥DE(同位角相等,两直线平行),∴∠ 2=∠ADE(两直线平行,内错角相等)∵∠ 2=∠E,∴∠ E=∠ADE,∴AD∥CE(内错角相等,两直线平行).47.∵ EM平分∠ BEF, FN平分∠DFH,∴∠ BEF=2∠MEF,∠DFH=2∠NFH,∵∠ BEF=∠DFH,∴∠ MEF=∠NF H,∴EM∥FN48.BE∥CF,理由是:∵ BE, CF 分别平分∠ ABC 和∠ BCD,∴∠ 1=∠ABC,∠ 2=∠BCD,∵∠ ABC=∠BCD,∴∠ 1=∠2,∴BE∥CF.49. DB与 EC的位置关系是平行,理由:∵∠ 1=∠3,∠ 2=∠4(对顶角相等),又∵∠ 1=∠2,∴∠ 3=∠4,∴BD∥EC.50.( 1)CD∥EF,理由是:∵ CD⊥AB,EF⊥AB,∴∠ CDF=∠EFB=90°,∴CD∥EF.(2)DG∥BC,理由是:∵ CD∥EF,∴∠ 2=∠BCD,∵∠ 1=∠2,∴∠ 1=∠BCD,∴DG∥BC.51.GH∥MN.理由如下:∵HG平分∠ AHM, MN平分∠ DNH(已知),∴∠ GHM∠AHM,∠ NMH=∠DMH(角平分线定义),而∠ AHM=∠DMH(已知)∴∠ GHM=∠NMH(等量代换),∴GH∥MN.(内错角相等,两直线平行)52.∵ BE⊥FD,∴∠ EGD=90°,∴∠ 1+∠D=90°,又∠2和∠D 互余,即∠ 2+∠D=90°,∴∠ 1=∠2,即∠ BAD+∠B=180°,又已知∠ C=∠1,∴AD∥BC.∴∠ C=∠2,( 2) AB与 CD不一定平行.∴AB∥CD57.∵∠ A=∠F,53.∵ EG⊥FG,∴AC∥DF,∴∠ G=90°,∴∠ C=∠FEC,∴∠ 1+∠3=90°,∵∠ C=∠D,∵∠ 1=∠2,∠ 3=∠4,∴∠ D=∠FEC,∴∠ 1+∠2+∠3+∠4=180°,∴BD∥CE.∴AB∥CD.58. EF 与 BC的位置关系是垂直关系.54.:∵∠ 1+∠2=180°,∠ 1=130°,证明:∵∠ CDG=∠B(已知),∴∠ 2=50°,∴DG∥AB(同位角相等,两直线平行),∵∠ A=50°,∴∠ 1=∠DAB(两直线平行,内错角相等),∴∠ A=∠2,又∠ 1=2(已知),∴AB∥CD.∴EF∥AD(内错角相等,两直线平行),55.( 1)∵ DE⊥AC,BF⊥AC,∴∠ EFB=∠ADB(两直线平行,同位角相等),∴∠ AED=∠CFB=90°,又 AD⊥BC于点 D(已知),∴∠ DAE+∠1=90°,∠ BCF+∠2=90°,∴∠ ADB=90°,∵∠ 1=∠2,∴∠ EFB=∠ADB=90°,∴∠ DAE=∠BCF,所以 EF与 BC的位置关系是垂直.∴AD∥BC;59.∵ CE 平分∠ ACD,( 2)AB∥CD.∴∠ 1=∠2,理由如下:∵∠ DAE=∠BCF,∠ DAB=∠DCB,∵∠ 1=∠B,∴∠ DAB﹣∠ DAE=∠DCB﹣∠ BCF,∴∠ 2=∠B,即∠ CAB=∠ACD,∴AB∥CE.∴AB∥CD.60.∵∠ 1=∠2,56.( 1) AD与 BC一定平行.理由如下:∴AB∥CD,∵AB⊥AC,∵∠ 3=∠4,∴∠ BAC=90°,∴AD∥BC,∵∠ 1=30°,∠ B=60°,故可以判定 AB∥CD,AD∥BC.∴∠ 1+∠BAC+∠B=180°,。
平行线的判定与性质(重点题专项讲练)(人教版)(解析版)
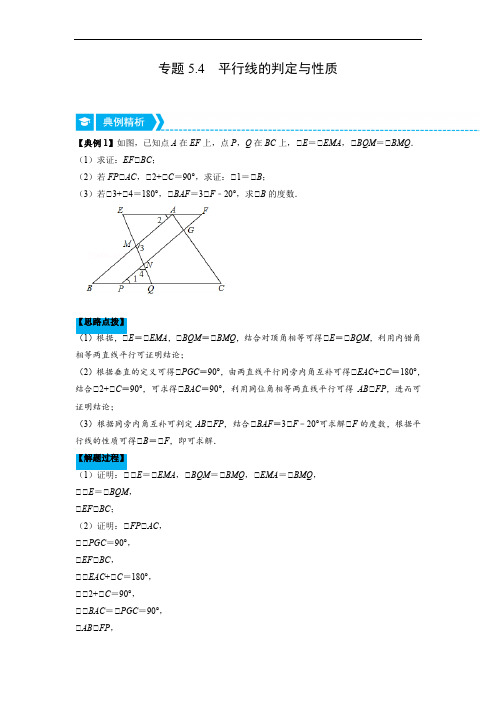
专题5.4 平行线的判定与性质【典例1】如图,已知点A在EF上,点P,Q在BC上,∠E=∠EMA,∠BQM=∠BMQ.(1)求证:EF∠BC;(2)若FP∠AC,∠2+∠C=90°,求证:∠1=∠B;(3)若∠3+∠4=180°,∠BAF=3∠F﹣20°,求∠B的度数.【思路点拨】E=∠EMA,∠BQM=∠BMQ,结合对顶角相等可得∠E=∠BQM,利用内错角相等两直线平行可证明结论;(2)根据垂直的定义可得∠PGC=90°,由两直线平行同旁内角互补可得∠EAC+∠C=180°,结合∠2+∠C=90°,可求得∠BAC=90°,利用同位角相等两直线平行可得AB∠FP,进而可证明结论;(3)根据同旁内角互补可判定AB∠FP,结合∠BAF=3∠F﹣20°可求解∠F的度数,根据平行线的性质可得∠B=∠F,即可求解.【解题过程】E=∠EMA,∠BQM=∠BMQ,∠EMA=∠BMQ,∠∠E=∠BQM,∠EF∠BC;(2)证明:∠FP∠AC,∠∠PGC=90°,∠EF∠BC,∠∠EAC+∠C=180°,∠∠2+∠C=90°,∠∠BAC=∠PGC=90°,∠AB∠FP,∠∠1=∠B;(3)解:∠∠3+∠4=180°,∠4=∠MNF,∠∠3+∠MNF=180°,∠AB∠FP,∠∠F+∠BAF=180°,∠∠BAF=3∠F﹣20°,∠∠F+3∠F﹣20°=180°,解得∠F=50°,∠AB∠FP,EF∠BC,∠∠B=∠1,∠1=∠F,∠∠B=∠F=50°.1.(2021•鞍山一模)如图,∠1=∠2=∠3=56°,则∠4的度数是()A.56°B.114°C.124°D.146°【思路点拨】根据对顶角相等得到∠2=∠5,结合∠1=∠2,得到∠1=∠5,即可判定l1∠l2,根据平行线的性质得出∠6=56°,再根据邻补角的定义求解即可.【解题过程】解:如图,∠∠1=∠2,∠2=∠5,∠∠1=∠5,∠l1∠l2,∠∠3=∠6,∠∠3=56°,∠∠6=56°,∠∠4+∠6=180°,∠∠4=180°﹣56°=124°,故选:C.2.(2021•雁塔区校级模拟)如图,在三角形ABC中,CD平分∠ACB,∠1=∠2=36°,则∠3=()A.36°B.52°C.72°D.80°【思路点拨】由平行线的判定定理可得AC∠DE,由平行线的性质可得∠ACB=∠3,由平分线的定义可得∠ACB=2∠1=72°,即得∠3的度数.【解题过程】解:∠∠1=∠2=36°,∠AC∠DE,∠∠ACB=∠3,∠CD平分∠ACB,∠∠ACB=2∠1=72°,∠∠3=72°.故选:C.3.(2021春•单县期末)如图,AB∠BC于点B,DC∠BC于点C,DE平分∠ADC交BC于点E,点F为线段CD延长线上一点,∠BAF=∠EDF,则下列结论正确的有()∠∠BAD+∠ADC=180°;∠AF∠DE;∠∠DAF=∠F.A.3个B.2个C.1个D.0个【思路点拨】∠证明AB∠CD,可做判断;∠根据平行线的判定和性质可做判断;∠根据AF∠ED得内错角相等和同位角相等,再由角平分线的定义得∠ADE=∠CDE,从而可做判断.【解题过程】解:∠∠AB∠BC,DC∠BC,∠AB∠CD,∠∠BAD+∠ADC=180°,故∠正确;∠∠AB∠CD,∠∠AFD+∠BAF=180°,∠∠BAF=∠EDF,∠∠AFD+∠EDF=180°,∠AF∠DE,故∠正确;∠∠AF∠ED,∠∠DAF=∠ADE,∠F=∠CDE,∠DE平分∠ADC,∠∠ADE=∠CDE,∠∠DAF=∠F,故∠正确;故选:A.4.(2021春•德宏州期末)如图所示,AC∠BC,DC∠EC,则下列结论:∠∠1=∠3;∠∠ACE+∠2=180°;∠若∠A=∠2,则有AB∠CE;∠若∠2=∠E,则有∠4=∠A.其中正确的有()A.∠∠∠B.∠∠∠C.∠∠D.∠∠∠∠【思路点拨】由已知可得∠1+∠2=90°,∠3+∠2=90°,等量代换即可得出∠结论;延长EC,如图1,由已知条件可得∠1+∠5=90°,∠1+∠2=90°,可得∠2=∠5,根据平角的性质可得∠ACE+∠5=180°,等量代换即可得出∠结论;由已知条件可得∠A=∠2,∠ACE+∠2=180°,等量代换可得∠A+∠ACE=180°,根据平行线的判定即可得出∠结论;由平行线的性质可得∠E=∠4,由已知条件∠2=∠E,∠2=∠A,等量代换可得∠4=∠A.即可得出∠结论.【解题过程】证明:∠AC∠BC,DC∠EC,∠∠1+∠2=90°,∠3+∠2=90°,∠∠1=∠3.故结论∠正确;延长EC,如图1,∠DC∠CE,AC∠BC,∠∠1+∠5=90°,∠1+∠2=90°,∠∠2=∠5,∠∠ACE+∠5=180°,∠∠ACE+∠2=180°.故结论∠正确;∠∠A=∠2,∠ACE+∠2=180°,∠∠A+∠ACE=180°,∠AB∠CE.故结论∠正确;∠AB∠CE,∠∠E=∠4,∠∠2=∠E,∠2=∠A,∠∠4=∠A.故结论∠正确.所以结论正确的有∠∠∠∠.故选:D.5.(2021春•汉川市期末)如图,AD∠BC,∠B=∠D,延长BA至点E,连接CE,∠EAD∠EAD+∠ECD;∠若和∠ECD的角平分线交于点P.下列三个结论:∠AB∠CD;∠∠AOC=12∠E=60°,∠APC=70°,则∠D=80°.其中结论正确的个数有()A.0B.1C.2D.3【思路点拨】∠EAD,∠E=∠根据平行线的性质与判定即可判断;∠∠AOC=∠EAP+∠E,而∠EAP==12∠ECD,即可判断;∠利用平行线的性质和角平分线定义即可判断.【解题过程】解:∠AD∠BC,∠∠BAD+∠B=180o,∠∠B=∠D,∠∠BAD+∠D=180o,∠AB∠CD,故∠正确;∠AB∠CD,∠∠ECD=∠E,∠AP平分∠EAD,∠EAD∠∠EAP=12∠∠AOC=∠EAP+∠E,∠∠AOC=1∠EAD+∠ECD,故∠正确;2∠∠ECD=∠E=60o,∠CP平分∠ECD,∠ECD=30°,∠∠ECP=12∠∠APC=70°,∠AOE=∠COP,∠∠EAP=40°,∠AP平分∠EAD,∠∠EAD=2∠EAP=80°,∠AB∠CD,∠∠D=∠EAD=80°,故∠正确;故选:D.6.(2021春•夏津县期末)如图,CB平分∠ACD,∠2=∠3,若∠4=60°,则∠5的度数是.【思路点拨】由∠2与∠3间关系,可得到AB与CD的位置关系,利用角平分线的性质和平行线的性质可求得∠5度数.【解题过程】解:∠CB平分∠ACD,∠ACD..∠∠1=∠2=12∠∠2=∠3,∠AB∠CD.∠∠5=∠2,∠4=∠ACD=60°.∠∠5=∠2=30°.故答案为:30°.7.(2021秋•嵩县期末)如图,AE∠CF,∠ACF的平分线交AE于点B,G是CF上的一点,∠GBE的平分线交CF于点D,且BD∠BC,下列结论:∠BC平分∠ABG;∠AC∠BG;∠与∠DBE互余的角有2个;∠若∠A=α,则∠BDF=180°−α.其中正确的是.(请把正确结论的序号都填上)8【思路点拨】根据平行线的性质得出∠A和∠ACB的关系,再根据角平分线的性质找出图中相等的角,由等角的余角相等即可得出结论.【解题过程】解:∠CBD=90°,∠∠ABC+∠EBD=90°,又∠∠DBG=∠EBD,∠∠ABC=∠CBG,∠BC平分∠ABG,∠∠正确,∠∠GBC=∠ABC=∠ACB,∠AC∠BG,∠∠正确,∠∠DBE=∠DBG,∠与∠DBE互余的角有∠ABC,∠GBC,∠ACB,∠GCB,有4个,∠∠错误,∠∠BDF=180°﹣∠BDG,∠BDG=90°﹣∠CBG=90°﹣∠ACB,又∠∠ACB=12×(180°﹣α)=90°−α2,∠∠BDF=180°﹣[90°﹣(90°−α2)]=180°−α2,∠∠错误,故答案为:∠∠.8.(2021春•凤山县期末)如图,已知∠1=∠2,∠C=∠F.请指出∠A与∠D的数量关系,并说明理由.【思路点拨】根据∠1=∠2,∠3=∠2,可得∠1=∠3,得BF∠CE,根据平行线的性质得∠ABF=∠C,由∠C =∠F,得∠ABF=∠F,即可得出AC∠DF,得∠A和∠D的数量关系是相等.【解题过程】解:∠A和∠D的数量关系是相等.理由是:如图,∠∠1=∠2,∠3=∠2,∠∠1=∠3,∠BF∠CE,∠∠ABF=∠C,∠∠C=∠F,∠∠ABF=∠F,∠AC∠DF,∠∠A=∠D.9.(2021春•陇县期末)如图,∠AEM+∠CDN=180°,EC平分∠AEF.若∠EFC=62°,求∠C的度数.【思路点拨】根据同角的补角相等可得出∠AEM=∠CDM,利用“同位角相等,两直线平行”可得出AB∠CD,由“两直线平行,同旁内角互补”及∠EFC=62°可求出∠AEF=118°,结合角平分线的定义可求出∠AEC的度数,再利用“两直线平行,内错角相等”即可求出∠C的度数.【解题过程】解:∠∠CDM+∠CDN=180°,又∠∠AEM+∠CDN=180°,∠∠AEM=∠CDM,∠AB∠CD,∠∠AEF+∠EFC=180°,∠∠EFC=62°,∠∠AEF=118°,∠EC平分∠AEF,∠∠AEC=59°,∠AB∠CD,∠∠C=∠AEC=59°.10.(2021春•江都区校级期中)已知:如图,CD∠AB,FG∠AB,垂足分别为D、G,点E 在AC上,且∠1=∠2.(1)那么DE与BC平行吗?为什么?(2)如果∠B=40°,且∠A比∠ACB小10°,求∠DEC的度数.【思路点拨】(1)根据CD∠AB,FG∠AB,可判定CD∠FG,利用平行线的性质可知∠2=∠BCD,已知∠1=∠2,等量代换得∠1=∠BCD,故可证DE与BC平行;(2)根据三角形内角和求出∠ACB=75°,再根据平行线的性质即可求解.【解题过程】解:(1)DE∠BC,理由如下:∠CD∠AB,FG∠AB,∠CD∠FG.∠∠2=∠BCD,又∠∠1=∠2,∠∠1=∠BCD,∠DE∠BC;(2)∠∠B=40°,∠ACB﹣10°=∠A,∠∠ACB+(∠ACB﹣10°)+40°=180°,∠∠ACB=75°,由(1)知,DE∠BC,∠∠DEC+∠ACB=180°,∠∠DEC=105°.11.(2021春•老河口市期末)如图,已知∠1=∠BDC,∠2+∠3=180°.(1)求证:AD∠CE;(2)若DA平分∠BDC,CE∠AE于E,∠F AB=55°,求∠1的度数.【思路点拨】(1)根据同位角相等,两直线平行可判定AB∠CD,得到∠2=∠ADC,等量代换得出∠ADC+∠3=180°,即可根据同旁内角互补,两直线平行得解;(2)由CE∠AE,AD∠CE得出∠DAF=∠CEF=90°,再根据平行线的性质即可求出∠ADC =∠2=35°,再根据角平分线的定义即可得解.【解题过程】(1)证明:∠∠1=∠BDC,∠AB∠CD,∠∠2=∠ADC,∠∠2+∠3=180°,∠∠ADC+∠3=180°,∠AD∠CE;(2)解:∠CE∠AE于E,∠∠CEF=90°,由(1)知AD∠CE,∠∠DAF=∠CEF=90°,∠∠ADC=∠2=∠DAF﹣∠F AB,∠∠F AB=55°,∠∠ADC=35°,∠DA平分∠BDC,∠1=∠BDC,∠∠1=∠BDC=2∠ADC=70°.12.(2021春•镇江期中)已知:如图所示,∠BAC和∠ACD的平分线交于E,AE交CD于点F,∠1+∠2=90°.(1)求证:AB∠CD;(2)试探究∠2与∠3的数量关系,并说明理由.【思路点拨】(1)根据角平分线定义得出∠BAC=2∠1,∠ACD=2∠2,根据∠1+∠2=90°得出∠BAC+∠ACD =180°,根据平行线的判定得出即可;(2)根据平行线的性质和角平分线定义得出∠1=∠3,即可求出答案.【解题过程】(1)证明:∠∠BAC和∠ACD的平分线交于E,∠∠BAC=2∠1,∠ACD=2∠2,∠∠1+∠2=90°,∠∠BAC+∠ACD=180°,∠AB∠CD;(2)解:∠2+∠3=90°,理由如下:∠AF平分∠BAC,∠∠BAF=∠1,∠AB∠CD,∠∠BAF=∠3,∠∠1=∠3,∠∠1+∠2=90°,∠∠2+∠3=90°.13.(2021秋•禅城区期末)已知:如图,点B、C在线段AD的异侧,点E、F分别是线段AB、CD上的点,∠AEG=∠AGE,∠C=∠DGC.(1)求证:AB∠CD;(2)若∠AGE+∠AHF=180°,求证:∠B=∠C;(3)在(2)的条件下,若∠BFC=4∠C,求∠D的度数.【思路点拨】(1)由对顶角相等可得∠AGE=∠DGC,从而可得∠AEG=∠C,则可判定AB∠CD;(2)由平角的定义可得∠AGE+∠EGH=180°,从而可求得∠EGH=∠AHF,则可判定EC∠BF,则有∠B=∠AEG,从而可求证;(3)由(2)得BF∠EC,则有∠C+∠BFC=180°,从而可求∠C的度数,利用三角形的内角和即可求∠D的度数.【解题过程】(1)证明:∠∠AEG=∠AGE,∠C=∠DGC,∠AGE=∠DGC,∠∠AEG=∠C,∠AB∠CD;(2)证明:∠∠AGE+∠EGH=180°,∠AGE+∠AHF=180°,∠∠EGH=∠AHF,∠EC∠BF,∠∠B=∠AEG,∠AB∠CD,∠∠C=∠AEG,∠∠B=∠C;(3)解:∠BF∠EC,∠∠C+∠BFC=180°,∠∠BFC=4∠C,∠∠C+4∠C=180°,解得∠C=36°,∠∠C=∠DGC,∠∠DGC=36°,∠∠D=180°﹣∠C﹣∠DGC=108°.14.(2021秋•南岗区期末)已知:在四边形ABCD中,∠B=∠D,点E在边BC的延长线上,连接AE交CD于点F,若∠BAF+∠AFC=180°.(1)如图1,求证:AD∠BC;(2)如图2,过点D作DG∠AE交BE的延长线于点C,若∠G=∠B,在不添加任何辅助线的情况下,请直接写出图2中除∠B以外的四个与∠G相等的角.【思路点拨】(1)由已知条件可得AB∠CD,从而有∠B=∠ECD,则可求得∠D=∠ECD,即可得AD∠BC;(2)利用平行线的性质进行求解即可.【解题过程】(1)证明:∠∠BAF+∠AFC=180°,∠AB∠CD,∠∠B=∠ECD,∠∠D=∠ECD,∠AD∠BC;(2)∠DG∠AE,∠∠G=∠AEB,由(1)得AD∠BC,∠∠AEB=∠DAE,∠ADC=∠DCG,∠∠G=∠DAE,∠∠B=∠ADC,∠G=∠B,∠∠G=∠ADC=∠DCG,综上所述,所∠G相等的角有:∠AEB,∠DAE,∠ADC,∠DCG.15.(2021秋•安居区期末)如图,∠ADE+∠BCF=180°,AF平分∠BAD,∠BAD=2∠F.(1)AD与BC平行吗?请说明理由.(2)AB与EF的位置关系如何?为什么?(3)若BE平分∠ABC.试说明:∠∠ABC=2∠E;∠∠E+∠F=90°.【思路点拨】(1)由∠ADE+∠BCF=180°结合邻补角互补,可得出∠BCF=∠ADC,再利用“同位角相等,两直线平行”可得出AD∠BC;(2)根据角平分线的定义及∠BAD=2∠F,可得出∠BAF=∠F,再利用“内错角相等,两直线平行”可得出AB∠EF;(3)∠由AB∠EF,利用“两直线平行,内错角相等”可得出∠ABE=∠E,结合角平分线的定义可得出∠ABC=2∠E;∠由AD∠BC,利用“两直线平行,同旁内角互补”可得出∠BAD+∠ABC=180°,再结合∠BAD =2∠F,∠ABC=2∠E可得出∠E+∠F=90°.【解题过程】解:(1)AD∠BC,理由如下:∠∠ADE+∠BCF=180°,∠ADE+∠ADC=180°,∠∠BCF=∠ADC,(2)AB∠EF,理由如下:∠AF平分∠BAD,∠BAD=2∠F,∠BAD=∠F,∠∠BAF=12∠AB∠EF.(3)∠∠ABC=2∠E,理由如下:∠AB∠EF,∠∠ABE=∠E.∠BE平分∠ABC,∠∠ABC=2∠ABE=2∠E.∠∠E+∠F=90°,理由如下:∠AD∠BC,∠∠BAD+∠ABC=180°.∠∠BAD=2∠F,∠ABC=2∠E,∠2∠E+2∠F=180°,∠∠E+∠F=90°.16.(2021春•铁西区期末)如图,直线MN分别与直线AC、DG交于点B、F,且∠1=∠2.∠ABF 的角平分线BE交直线DG于点E,∠BFG的角平分线FC交直线AC于点C.(1)请直接写出直线AC与DG的位置关系;(2)求证:BE∠CF;(3)若∠C=35°,求∠BED的度数.【思路点拨】(1)由对顶角相等可得∠ABF=∠1,从而有∠ABF=∠2,即可得AC∠DG;(2)求出∠1=∠BFG,根据平行线的判定得出AC∠DG,求出∠EBF=∠BFC,根据平行线的判定得出即可;(3)根据平行线的性质得出∠C=∠CFG=∠BEF=35°,再求出答案即可.【解题过程】解:(1)AC∠DG,理由如下:∠∠ABF=∠1,∠1=∠2,∠∠ABF=∠2,∠AC∠DG;(2)由(1)知AC∠DG,∠∠ABF=∠BFG,∠∠ABF的角平分线BE交直线DG于点E,∠BFG的角平分线FC交直线AC于点C,∠∠EBF=12∠ABF,∠CFB=12∠BFG,∠∠EBF=∠CFB,∠BE∠CF.(3)∠AC∠DG,∠C=35°,∠∠C=∠CFG=35°,∠BE∠CF,∠∠CFG=∠BEG=35°,∠∠BED=180°﹣∠BEG=145°.17.(2021春•广陵区校级期中)如图1,直线MN与直线AB、CD分别交于点E、F,∠1与∠2互补.(1)试判断直线AB与直线CD的位置关系,并说明理由;(2)如图2,∠AEF与∠EFC的角平分线交于点P,EP延长线与CD交于点G,点H是MN 上一点,且PF∠GH,试判断直GH与EG的位置关系,并说明理由.【思路点拨】(1)利用邻补角的定义及已知得出∠1=∠CFE,即可判定AB∠CD;(2)利用(1)中平行线的性质推知∠AEF+∠EFC=180°,然后根据角平分线的性质、三角形内角和定理证得∠EPF=90°,即EG∠PF,故结合已知条件PF∠GH,易证GH∠EG;【解题过程】解:(1)AB∠CD,理由如下:∠∠1与∠2互补,∠∠1+∠2=180°,又∠∠2+∠CFE=180°,∠∠1=∠CFE,∠AB∠CD;(2)GH∠EG,理由如下:由(1)知,AB∠CD,∠∠AEF+∠EFC=180°.又∠∠AEF与∠EFC的角平分线交于点P,∠∠FEP+∠EFP=1(∠BEF+∠EFD)=90°,2∠∠EPF=90°,即EG∠PF,∠PF∠GH,∠GH∠EG.18.(2021秋•嵩县期末)图1展示了光线反射定律:EF是镜面AB的垂线,一束光线m射到平面镜AB上,被AB反射后的光线为n,则入射光线m,反射光线n与垂线EF所夹的锐角θ1=θ2.(1)在图1中,证明:∠1=∠2.(2)图2中,AB,BC是平面镜,入射光线m经过两次反射后得到反射光线n,已知∠1=30°,∠4=60°,判断直线m与直线n的位置关系,并说明理由.(3)图3是潜望镜工作原理示意图,AB,CD是平行放置的两面平面镜.请解释进入潜望镜的光线m为什么和离开潜望镜的光线n是平行的?【思路点拨】(1)根据角的关系解答即可;(2)求出∠5+∠6=180°,根据平行线的判定得出即可;(3)根据平行线的性质和平均的定义得到∠5=∠6,根据平行线的判定得出即可.【解题过程】(1)证明:∠∠AFE=∠BFE=90°,∠θ1=θ2.(2)解:直线m∠直线n,理由:如图2,∠∠1=∠2=30°,∠3=∠4=60°,∠∠5=180°﹣∠1﹣∠2=120°,∠6=180°﹣∠3﹣∠4=60°,∠∠5+∠6=180°,∠直线m∠直线n;(3)解:∠AB∠CD,∠∠2=∠3,∠∠1=∠2,∠3=∠4,∠∠1=∠2=∠3=∠4,∠180°﹣∠1﹣∠2=180°﹣∠3﹣∠4,即:∠5=∠6,∠m∠n.19.(2021秋•上蔡县期末)已知:如图,AB∠CD∠GH,GH过点P.(1)如图1,若∠BAP=40°,∠DCP=30°,则∠APC=(直接写出结果);(2)如图2,直线MN分别交AB于点E,交CD于点F,点P在线段EF上,点Q在射线FC上.若∠MEB=110°,∠PQF=50°,求∠EPQ的度数;(3)如图3,点P在射线FN上,点Q在射线FD上,∠AEF的平分线交CD于点O.若∠PQF= 1∠MEB,试判断OE与PQ是否平行?并说明理由.2(1)依据平行线的性质,即可得到∠APG =∠BAP =40°,∠CPG =∠DCP =30,再根据∠APC =∠APG +∠CPG 进行计算即可;(2)利用邻补角的定义可得∠BEP =180°﹣110°=70°,利用(1)的结论即可得∠EPQ 的度数; (3)根据对顶角相等以及角平分线的定义可得∠PQF =12∠MEB =12∠AEF =∠AEO ,再根据平行线的性质∠AEO =∠EOF ,可得∠PQF =∠EOF ,根据内错角相等两直线平行即可得OE ∠PQ .【解题过程】解:(1)∠AB ∠CD ∠GH ,∠∠APG =∠BAP =40°,∠CPG =∠DCP =30,∠∠APC =∠APG +∠CPG =40°+30°=70°,故答案为:70°;(2)∠∠MEB =110°,∠∠BEP =180°﹣110°=70°,由(1)可得:∠EPQ =∠EPG +∠QPG =∠BEP +∠PQF =70°+50°=120°;(3)OE ∠PQ .理由:∠∠PQF =12∠MEB ,∠MEB =∠AEF ,∠∠PQF =12∠MEB =12∠AEF ,∠EO 平分∠AEF .∠∠PQF =12∠AEF =∠AEO , ∠AB ∠CD ,∠∠AEO =∠EOF ,∠∠PQF =∠EOF ,∠OE ∠PQ .20.(2021春•汉阳区期中)如图1,已知两条直线AB ,CD 被直线EF 所截,分别交于点E ,F ,EM 平分∠AEF 交CD 于点M ,且∠FEM =∠FME .(1)直线AB 与直线CD 的位置关系是 ;(2)如图2,点G 是射线FD 上一动点(不与点F 重合),EH 平分∠FEG 交CD 于点H ,过点H 作HN ∠EM 于点N ,设∠EHN =α,∠EGF =β.∠当点G 在运动过程中,若β=56°,求α的度数;∠当点G 在运动过程中,α和β之间有怎样的数量关系?请写出你的猜想,并加以证明.【思路点拨】(1)根据角平分线的性质可得∠AEM=∠FEM,由已知条件∠FEM=∠FME,等量代换可得∠AEM=∠FME,由平行线的判定即可得出答案;(2)由平行线的性质可得β=∠GEB,由平角的性质可得∠AED=180°﹣∠GEB,根据角平分线的性质可得∠CEF=12∠AEF,∠FEH=12∠FEG,由∠CEH=∠CEF+∠FEH可计算出度数,根据垂线的性质可得α+∠CEH=90°,代入计算即可得出答案;(3)证明方法同(2).【解题过程】证明:(1)∠EM平分∠AEF,∠∠AEM=∠FEM,∠∠FEM=∠FME,∠∠AEM=∠FME,∠AB∠CD.故答案为:AB∠CD;(2)∠∠AB∠CD,∠β=∠GEB=56°,∠∠AEG=180°﹣∠GEB=180°﹣56°=124°,∠EH平分∠FEG,EM平分∠AEF,∠∠CEF=12∠AEF,∠FEH=12∠FEG,∠∠CEH=∠CEF+∠FEH=12∠AEF+12∠FEG=12(∠AEF+∠FEG)=12∠AED=12×124°=62°,∠HN∠EM,∠α+∠CEH=90°,∠α=90°﹣∠CEH=90°﹣62°=28°;∠a=12β.理由如下:∠AB∠CD,∠β=∠GEB,∠∠AED=180°﹣∠GEB=180°﹣β,∠EH平分∠FEG,EM平分∠AEF,∠∠CEF=12∠AEF,∠FEH=12∠FEG,∠∠CEH=∠CEF+∠FEH=12∠AEF+12∠FEG=12(∠AEF+∠FEG)=12∠AEG=12(180°−β),∠HN∠EM,∠α+∠CEH=90°,∠α+12(180°−β)=90°,即a=12β.21.(2021秋•南岗区校级期中)已知,直线EF分别与直线AB、CD相交于点G、H,并且∠AGE+∠DHE=180°.(1)如图1,求证:AB∠CD.(2)如图2,点M在直线AB、CD之间,连接MG、HM,当∠AGM=32°,∠MHC=68°时,求∠GMH的度数.(3)只保持(2)中所求∠GMH的度数不变,如图3,GP是∠AGM的平分线,HQ是∠MHD 的平分线,作HN∠PG,则∠QHN的度数是否改变?若不发生改变,请求出它的度数.若发生改变,请说明理由.(本题中的角均为大于0°且小于180°的角)【思路点拨】(1)先由邻补角得到∠AGE+∠BGE=180°,然后结合∠AGE+∠DHE=180°得到∠BGE=∠DHE,最后得证AB∠CD;(2)先由AB∠CD得到∠AGH+∠CHG=180°,即∠AGM+∠MGH+∠MHG+∠MHC=180°,再结合∠MGH+∠MHG+∠GMH=180°得到∠GMH=∠AGM+∠MHC,最后结合已知条件得到∠GMH的大小;(3)先由(2)得到∠AGM+∠MHC=∠GMH=100°,∠MGH+∠MHG=80°,然后结合角平分线的定义得到∠MGP和∠MHQ,再结合HN∠PG得到∠GHN=∠PGH,最后由∠QHN=∠GHN﹣∠GHQ求得∠QHN的大小.【解题过程】(1)证明:∠∠AGE +∠BGE =180°,∠AGE +∠DHE =180°,∠∠BGE =∠DHE ,∠AB ∠CD .(2)解:∠AB ∠CD ,∠∠AGH +∠CHG =180°,即∠AGM +∠MGH +∠MHG +∠MHC =180°,∠∠MGH +∠MHG +∠GMH =180°,∠∠GMH =∠AGM +∠MHC ,∠∠AGM =32°,∠MHC =68°,∠∠GMH =100°.(3)解:∠QHN 的度数不发生改变,理由如下,由(2)得,∠AGM +∠MHC =∠GMH =100°,∠∠MGH +∠MHG =80°,∠GP 、HQ 分别平分∠MGA 和∠MHD ,∠∠MGP =12∠MGA ,∠MHQ =12∠MHD =12(180°﹣∠MHC )=90°−12∠MHC , ∠∠PGH =∠MGP +∠MGH =12∠MGA +∠MGH , ∠HN ∠PG , ∠∠GHN =∠PGH =12∠MGA +∠MGH ,∠∠QHN =∠GHN ﹣∠GHQ =(12∠MGA +∠MGH )﹣(∠MHQ ﹣∠MHG )=12∠MGA +∠MGH ﹣∠MHQ +∠MHG =12∠MGA +80°﹣∠MHQ ,∠∠QHN =12∠MGA +80°﹣(90°−12∠MHC )=﹣10°+12(∠MGA +∠MHC )=﹣10°+12×100°=40°.22.(2021秋•香坊区校级期中)点E 在射线DA 上,点F 、G 为射线BC 上两个动点,满足∠DBF =∠DEF ,∠BDG =∠BGD ,DG 平分∠BDE .(1)如图1,当点G 在F 右侧时,求证:BD ∠EF ;(2)如图2,当点G 在BF 左侧时,求证:∠DGE =∠BDG +∠FEG ;(3)如图3,在(2)的条件下,P 为BD 延长线上一点,DM 平分∠BDG ,交BC 于点M ,DN 平分∠PDM ,交EF 于点N ,连接NG ,若DG ∠NG ,∠B ﹣∠DNG =∠EDN ,求∠B 的度数.【思路点拨】(1)通过证明∠DBF=∠EFG,利用同位角相等,两直线平行即可得出结论;(2)过点E作GH∠BD,交AD于点H,利用(1)的结论和平行线的性质即可得出结论;(3)设∠BDM=∠MDG=α,则∠BDG=∠EDG=∠DGB=2α,∠PDE=180°﹣4α,∠PDM =180°﹣α;利用已知条件用含α的式子表示∠PDN,∠EDN,∠GDN,∠DNG,再利用∠B ﹣∠DNG=∠EDN,得到关于α的方程,解方程求得α的值,则∠B=180°﹣4α,结论可求.【解题过程】证明:(1)∠DG平分∠BDE,∠∠BDG=∠ADG.又∠∠BDG=∠BGD,∠∠ADG=∠DGB.∠AD∠BC.∠∠DEF=∠EFG.∠∠DBF=∠DEF,∠∠DBF=∠EFG.∠BD∠EF.(2)过点G作GH∠BD,交AD于点H,如图,∠BD∠EF,∠GH∠EF.∠∠BDG=∠DGH,∠GEF=∠HGE,∠∠DGE=∠DGH+∠HGE,∠∠DGE=∠BDG+∠FEG.(3)设∠BDM=∠MDG=α,则∠BDG=∠EDG=∠DGB=2α,∠PDE=180°﹣4α.∠∠PDM=180°﹣α.∠DN平分∠PDM∠∠PDN=∠MDN=90°−α2.∠∠EDN=∠PDN−∠PDE=90°−α2−(180°−4α)=72α−90°.∠∠GDN=∠MDN﹣∠MDG=90°−α2−α=90°−32α.∠DG∠ON,∠∠DNG=90°.∠∠DNG=90°−(90°−32α)=32α.∠DE∠BF,∠∠B=∠PDE=180°﹣4α.∠∠B﹣∠DNG=∠EDN,∠180°−4α−32α=72α−90°,解得:α=30°.∠∠B=180°﹣4α=60°.。
平行线性质练习题30题

平行线性质练习题1. 已知直线AB和CD平行,若BE平分∠ABC,求证:BE也平分∠ECD。
2. 在平行线l1和l2之间,有一条横穿它们的直线l3,形成了八个角。
求证:同旁内角互补。
3. 若直线a ∥ b,直线b ∥ c,求证:直线a ∥ c。
4. 已知直线AB ∥ CD,点E在AB上,点F在CD上,且∠BEF = 120°,求∠EFD的度数。
5. 在平行线l1和l2上分别取点A、B、C、D,若AB = CD,BC = DA,求证:四边形ABCD是平行四边形。
6. 已知直线l1 ∥ l2,点P在l1上,点Q在l2上,若PQ垂直于l1,求证:PQ也垂直于l2。
7. 在平行线l1和l2之间,有一条横穿它们的直线l3,形成了八个角。
求证:内错角相等。
8. 若直线a ∥ b,直线c与a、b都相交,且∠1 = ∠2,求证:直线c ∥ b。
9. 已知直线AB ∥ CD,点E在AB上,点F在CD上,且∠AEF = 30°,求∠CFD的度数。
10. 在平行线l1和l2上分别取点A、B、C、D,若AB = CD,AD = BC,求证:四边形ABCD是矩形。
11. 已知直线l1 ∥ l2,点P在l1上,点Q在l2上,若PQ = QR,PR = QR,求证:∠PQR = 90°。
12. 在平行线l1和l2之间,有一条横穿它们的直线l3,形成了八个角。
求证:同位角相等。
13. 若直线a ∥ b,直线c与a、b都相交,且∠1 + ∠2 = 180°,求证:直线c ∥ a。
14. 已知直线AB ∥ CD,点E在AB上,点F在CD上,且∠BEF = 135°,求∠EFD的度数。
15. 在平行线l1和l2上分别取点A、B、C、D,若AB = CD,AC= BD,求证:四边形ABCD是菱形。
16. 已知直线l1 ∥ l2,点P在l1上,点Q在l2上,若PQ垂直于l1,且PQ = QR,求证:PR垂直于l2。
平行线的判定与性质(含答案)-

22.平行线的判定与性质知识纵横在同一平面内,不相交的两条直线叫做平行线(parallel lines).角是平面几何图形中最活跃的元素,前面我们已学习过特殊角、•数量关系角等角的知识。
当两条直线相交或分别与第三条直线相交,就产生对顶角、同位角、内错角、同旁内角等位置关系角,进一步丰富了角的知识,它们在角的计算与证明中有广泛的应用。
与平行线相关的问题一般都是平行线的判定与性质的综合运用,主要体现在如下两个方面:1.由角定角 已知角的关系−−−→判定两直线平行−−−→性质确定其他角的关系.2.由线定线 已知两直线平行−−−→性质角的关系−−−→判定确定其他两直线平行.例题求解【例1】如图,AB ∥CD,AC ⊥BC,图中与∠CAB 互余的角有_______个.(2003年安徽省中考题)思路点拨 充分运用对顶角、平行线性质等与角相关的知识,借助互余的概念判断。
解:3个 提示:分别为∠BCD,∠ABC,∠EBF. 【例2】如图,平行直线AB 、CD 与相交直线EF 、GH 相交,图中的同旁内角共有( • ).A.4对B.8对C.12对D.16对 (第11届“希望杯”邀请赛试题) 思路点拨 每一个“三线八角”基本图形都有两对同旁内角,从对原图形进行分解入手。
解:选D 提示:原图形可分解出如下8个基本图形.BFDG E C AB FHD GECA【例3】如图,已知∠B=25°,∠BCD=45°,∠CDE=30°,∠E=10°,求证:AB∥EF思路点拨解本例的困难在于图形中没有“三线八角”,考虑创造条件,在图中添置“三线八角”或作出与AB或CD平行的直线。
解:过C点作CG∥AB,过点D作DH∥AB,可证得∠HDE=10°=∠DEF,故HD∥EF,•又HD∥AB,所以AB∥EF.【例4】如图,在△ABC中,CE⊥AB于E,DF⊥AB于F,AC∥ED,CE是∠ACB的平分线.•求证:∠EDF=∠BDF.思路点拨综合运用角平分线、垂直(vertical)的定义、平行线的判定与性质等知识,因图形复杂,故需恰当分解图形.解:提示:由DF∥CE得,∠BDF=∠BCE,∠FDE=∠DEC,由AC∥DE得,∠DEC=∠ECA【例5】探究:(1)如图a,若AB∥CD,则∠B+∠D=∠E,你能说明为什么吗?(2)反之,若∠B+∠D=∠E,直线AB与CD有什么位置关系?请证明;(3)若将点E移至图b所示位置,此时∠B、∠D、∠E之间有什么关系?请证明;(4)若将E点移至图c所示位置,情况又如何?(5)在图d中,AB∥CD,∠E+∠G与∠B+∠F+∠D又有何关系?(6)在图e中,若AB∥CD,又得到什么结论?B F DE CAB FDECAB (a)DE CA B (b)DEC A(c)B D EC A B (d)F DG E C A F 2E nE 2F n-1F 1B(e)DE 1CA思路点拨:已知AB ∥CD,连结AB 、CD 的折线内折或外折;或改变E 点位置、•或增加折线的条数,通过适当地改变其中的一个条件,就能得出新的结论,给我们创造性的思考留下了极大的空间。
第5章《相交线与平行线》 大题专项提升训练:平行线的判定和性质(含答案)

人教版七年级下册第5章《相交线与平行线》大题专项提升训练平行线的判定和性质1.如图,AE平分∠BAD,DF平分∠CDA,且AE∥DF,求证:AB∥CD.2.如图,AD⊥CB于D,EF⊥CB于F,∠1=∠2,∠BAC=70°,求∠AGD的度数.3.如图,已知∠1+∠2=180°,∠3=108°.求∠4的度数.4.如图,已知AB=CD,∠1=∠2.求证:BC=DA.5.如图,∠1=∠2,∠C=∠D.求证:∠A=∠F.6.如图,已知∠1+∠2=180°,∠DEF=∠A,试判断∠ACB与∠DEB的大小关系,并对结论进行说明.7.已知:如图,C,D是直线AB上两点,∠1+∠2=180°,DE平分∠CDF,EF∥AB,(1)求证:CE∥DF;(2)若∠DCE=130°,求∠DEF的度数.8.如图,D,E分别是三角形ABC的边AB,BC上的点,DE∥AC,点F在DE的延长线上,且∠DFC=∠A.(1)求证:AB∥CF;(2)若∠ACF比∠BDE大40°,求∠BDE的度数.9.如图,在△ABC中,EF⊥AB,CD⊥AB.(1)求证:EF∥CD;(2)若点G在AC边上,∠1=∠2,求证:∠DGC+∠GCB=180°.10.如图,在三角形ABC中,AD⊥BC于点D,点E是AB上一点,EF⊥BC于点F,点G是AC上一点,连接DG,且∠1=∠2.求证:AB∥DG.11.如图,在三角形ABC中,AD⊥BC,EF⊥BC,垂足分别为D、F.G为AC上一点,E为AB上一点,∠1=∠2.求证:DG∥AB.12.如图,在三角形ABC中,EF⊥AB,∠ADG=∠B,若点G在AC边上,∠1=∠2,判断CD与AB的位置关系,并说明理由.13.如图,在三角形ABC中,∠1=∠2,点E,F,G分别在BC,AB,AC上,且EF⊥AB,GD∥BC交AB于点D.请判断CD与AB的位置关系,并说明理由.14.如图,在三角形ABC中,点D、F在边BC上,点E在边AB上,点G在边AC上,AD∥EF,∠1+∠FEA=180°.求证:∠CDG=∠B.15.如图,在三角形ABC中,CD⊥AB,垂足为点D,F为BC上的点,FG⊥AB,垂足为点G,点E在AC上,连接DE,若∠EDC=∠BFG.求证:∠B=∠ADE.16.如图,在三角形ABC中,点D、F在BC边上,点E在AB边上,点G在AC边上,EF与GD的延长线交于点H,∠CDG=∠B,∠1+∠FEA=180°.(1)EH与AD平行吗?请说明理由;(2)若∠BAD=30°,求∠H的度数.17.如图,在三角形ABC中,点D,F在边BC上,点E在边AB上,点G在边AC上,EF与GD的延长线交于点H,∠1=∠B,∠2+∠3=180°.(1)判断EH与AD的位置关系,并说明理由.(2)若∠DGC=58°,且∠H=∠4+10°,求∠H的度数.参考答案1.【解答】证明:∵AE平分∠BAD,DF平分∠CDA,∴∠DAE=∠BAD,∠ADF=∠CDA又∵AE∥DF,∴∠DAE=∠ADF,∴∠BAD=∠CDA,∴AB∥CD.2.【解答】解:∵EF∥AD(已知),∴∠2=∠3(两直线平行,同位角相等);∵∠1=∠2(已知),∴∠1=∠3(等量代换);∴DG∥AB(内错角相等,两直线平行).∴∠BAC+∠AGD=180°(两直线平行,同旁内角互补).∵∠BAC=70°,∴∠AGD=110°.3.【解答】解:给图中各角标上序号,如图所示.∵∠1+∠2=180°,∠2+∠5=180°,∴∠1=∠5,∴AB∥CD,∴∠3=∠6.∵∠4+∠6=180°,∠3=108°,∴∠4=180°﹣108°=72°.4.【解答】证明:在△ABC与△CDA中,,∴△ABC≌△CDA(SAS),∴BC=DA.5.【解答】证明:∵∠1=∠2,∠2=∠3,∴∠1=∠3.∴BD∥CE.∴∠ABD=∠C.又∠C=∠D,∴∠D=∠ABD.∴DF∥AC.∴∠A=∠F.6.【解答】解:∠ACB与∠DEB相等,理由如下:证明:∵∠1+∠2=180°(已知),∠1+∠DFE=180°(邻补角定义),∴∠2=∠DFE(同角的补角相等),∴AB∥EF(内错角相等两直线平行),∴∠BDE=∠DEF(两直线平行,内错角相等),∵∠DEF=∠A(已知),∴∠BDE=∠A(等量代换),∴DE∥AC(同位角相等两直线平行),∴∠ACB=∠DEB(两直线平行,同位角相等).7.【解答】(1)证明:∵∠1+∠2=180°,C,D是直线AB上两点,∴∠1+∠DCE=180°,∴∠2=∠DCE,∴CE∥DF;(2)解:∵CE∥DF,∠DCE=130°,∴∠CDF=180°﹣∠DCE=180°﹣130°=50°,∵DE平分∠CDF,∴∠CDE=∠CDF=25°,∵EF∥AB,∴∠DEF=∠CDE=25°.8.【解答】(1)证明:∵DE∥AC,∴∠BDE=∠A,∵∠DFC=∠A,∴∠DFC=∠BDE,∴AB∥CF.(2)解:∵DE∥AC,∴∠ACF+∠DFC=180°,由(1)中已证∠DFC=∠BDE,∴∠ACF+∠BDE=180°,又∵∠ACF比∠BDE大40°,∴∠BDE+40°+∠BDE=180°,∴∠BDE=70°.9.【解答】证明:(1)∵EF⊥AB,CD⊥AB,∴∠BFE=∠CDB=90°,∴EF∥CD;(2)∵EF∥CD,∴∠2=∠BCD,∵∠1=∠2,∴∠1=∠BCD,∴DG∥BC,∴∠DGC+∠GCB=180°.10.【解答】证明:∵EF⊥BC,AD⊥BC,∴EF∥AD,∴∠1=∠BAD,∵∠1=∠2,∴∠BAD=∠2,∴AB∥DG.11.【解答】证明:∵AD⊥BC,EF⊥BC,∴∠ADB=∠EFB=90°,∴AD∥EF,∴∠2=∠3,∵∠1=∠2,∴∠1=∠3,∴DG∥AB.12.【解答】解:CD⊥AB.理由如下:∵∠ADG=∠B,∴DG∥BC,∴∠1=∠DCB,∵∠1=∠2,∴∠2=∠DCB,∴CD∥EF,∴∠CDB=∠EFB,∵EF⊥AB,∴∠EFB=90°,∴∠CDB=90°,∴CD⊥AB.13.【解答】解:CD⊥AB.理由如下:∵DG∥BC,∴∠1=∠DCB.∵∠1=∠2,∴∠2=∠DCB.∴CD∥EF.∴∠CDB=∠EFB.∵EF⊥AB,∴∠EFB=90°.∴∠CDB=90°.∴CD⊥AB.14.【解答】证明:∵AD∥EF,(已知),∴∠2=∠3,(两直线平行,同位角相等),∵∠1+∠FEA=180°,∠2+∠FEA=180°,∴∠1=∠2(同角的补角相等),∴∠1=∠3(等量代换),∴DG∥AB(内错角相等,两直线平行),∴∠CDG=∠B.(两直线平行,同位角相等).15.【解答】证明:如图所示:∵FG⊥AB,CD⊥AB,∴∠FGB=∠CDB=90°,∴FG∥CD,∴∠BFG=∠BCD,又∵∠EDC=∠BFG,∴∠BCD=∠EDC,∴DE∥BC,∴∠B=∠ADE.16.【解答】解:(1)平行,理由如下:∵∠CDG=∠B,∴AB∥DG,∴∠BAD=∠1,∵∠1+∠FEA=180°,∴∠BAD+∠FEA=180°,∴EH//AD;(2)由(1)得EH//AD,∠1=∠BAD,∴∠H=∠1,∴∠BAD=∠H,∵∠BAD=30°,∴∠H=30°.17.【解答】解:(1)EH∥AD,理由如下:∵∠1=∠B,∴AB∥GD,∴∠2=∠BAD,∵∠2+∠3=180°,∴∠BAD+∠3=180°,∴EH∥AD;(2)由(1)得AB∥GD,∴∠2=∠BAD,∠DGC=∠BAC,∵∠DGC=58°,∴∠BAC=58°,∵EH∥AD,∴∠2=∠H,∴∠H=∠BAD,∴∠BAC=∠BAD+∠4=∠H+∠4=58°,∵∠H=∠4+10°,∴∠4+10°+∠4=58°,解得:∠4=24°,∴∠H=34°.。
5.平行线的判定与性质

1. (2011 江苏省徐州市) 如图,AB CD AB ∥,与DE 交于点F ,4070B D ∠=︒∠=︒,,则E ∠=__________.答案:302. (2011 江苏省扬州市) 如图,C 岛在A 岛的北偏东60°方向,在B 岛的北偏西45°方向,则从C 岛看A B 、两岛的视角ACB ∠=__________°.答案:1053. (2011 辽宁省本溪市) 如图,AB CD ∥,直线MN 分别交AB 、CD 于点E 、F ,EG 平分AEF ∠,EG FG ⊥于点G .若50BEM ∠=°,则CFG ∠=_____________度.北答案:654. (2011 辽宁省大连市) 如图,直线1115a b ∠=︒∥,,则2∠=_________︒.答案:65;5. (2011 内蒙古鄂尔多斯市) 如图,直线12l l ∥,365∠=°,2130∠=°,则1∠为()A .50°B .55°C .60°D .65°答案:D6. (2011 青海省西宁市) 如图,将三角形的直角顶点放在直尺的一边上,130∠=︒,320∠=︒,则2∠=___________.答案:50︒7. (2011 山东省德州市) 如图,直线12l l ∥,1=402=75∠,∠,则3∠等于( )(A )55 (B )60(C )65 (D )70答案:C8. (2011 山东省菏泽市) 一次数学活动课上,小聪将一副三角板按图中方式叠放,则∠α等于( )A.30°B.45°C.60°D.75° l 1l 21 2 3答案:D9. (2011 山东省济南市) 如图,直线l 与直线a 、b 分别交于点A 、B ,a b ∥,若170∠=°,则2∠____________度.答案:11010. (2011 山东省济宁市) 如图,AE BD ∥,1120240∠=∠=°,°,则C ∠的度数是( )A.10° B.20° C.30° D.40°30°45°α答案:B11. (2011 山东省聊城市) 如图,已知a b ∥,150∠=°,则2∠的度数是( )A .40°B .50°C .120°D .130°答案:D12. (2011 山东省临沂市) 如图,已知AB CD ∥,170∠=°,则2∠的度数是( )A .60° B.70° C .80° D .110°A BDC 1 2 cab1 2答案:D13. (2011 山东省枣庄市) 如图,直线AB ∥CD ,∠A =70︒,∠C =40︒,则∠E 等于( )A .30° B.40°C .60° D.70°答案:A14. (2011 山东省淄博市) 如图,直线AB ,CD 分别与直线AC 相交于点A ,C ,与直线BD 相交于点B ,D .若12∠=∠,375∠=°,求4∠的度数.A C BDE答案:解:12∠=∠AB CD ∴∥34∴∠=∠375∠=°475∴∠=°15. (2011 山西省) 如图所示,AOB ∠的两边OA 、OB 均为平面反光镜,35AOB =∠,在OB 上有一点E ,从E 点射出一束光线经OA 上的点D 反射后,反射光线DC 恰好与OB 平行,则DEB ∠的度数是( )A .35B .70C .110D .120答案:B16. (2011 陕西省) 如图,AC BD AE ∥,平分BAC ∠交BD 于点E .若164∠=°,则2∠=_________.答案:122°17. (2011 广东省肇庆市) 如图,已知直线a ∥b ∥c ,直线m 、n 与a 、b 、c 分别交于点A 、C 、E 、B 、D 、F ,AC = 4,CE = 6,BD = 3,则BF =( )A. 7B. 7.5C. 8D. 8.5答案:B18. (2011 四川省泸州市) 如图,1∠与2∠互补,3135∠=︒,则4∠的度数是( )(A )45︒ (B )55︒ (C )65︒ (D )75︒abcA B C D E F m n答案:A19. (2011 四川省绵阳市) 如图,AB CD CP ∥,交AB 于O ,AO PO =,若50C ∠=°,则A ∠=_____度.答案:25°20. (2011 新疆建设兵团) 如图,AB ∥CD ,AD 和BC 相交于O 点,∠A =40°,∠AOB =75°.则∠C 等于( )A .40°B .65°C .75°D .115°答案:B21. (2011 新疆乌鲁木齐) 如图,AD 与BC 相交于点O ,AB CD ∥,若3060B D ∠=∠=°,°,则BOD ∠= ______度.答案:9022. (2011 云南省大理市) 如图,l 1∥l 2,∠1=120°,则∠2= .答案:60︒23. (2011 浙江省湖州市) 如图,已知CD 平分130ACBDE AC ∠∠=︒,∥,,则2∠= 度.l 1l 2 l 312答案:6024. (2011 浙江省丽水市) 如图,把一块含有45°角的直角三角板的两个顶点放在直尺的对边上.如果120∠=°,那么2∠的度数是( )A .30°B .25°C .20°D .15°答案:B25. (2011 浙江省宁波市) 如图所示,3720AB CD E C ∠=∠=∥,°,°,则EAB ∠的度数为( )D2 1ABE CA .57° B.60° C.63° D.123°答案:A26. (2011 浙江省绍兴市) 如图,已知AB ∥CD ,BC 平分∠ABE ,∠C =34°,则∠BED 的 度数是( )A .17°B .34°C .56°D .68°答案:D27. (2011 浙江省温州市) 如图,1402803a b ∠=∠=∠=∥,°,°, 度.A DB CE答案:12028. (2011 重庆市) 如图,8060AB CD C CAD ∠=∠=∥,°,°,则BAD ∠的度数等于() A .60° B.50° C.45° D.40°A BD C答案:D29. (2011 山东省日照市) 如图,已知直线AB CD ∥,125C ∠=°,45A ∠=°,那么E ∠的大小为( )A .70°B .80°C .90°D .100°答案:B30. (2011 山东省泰安市) 如图,l ∥m ,等腰直角三角形ABC 的直角顶点C 在直线m 上,若∠β=20°,则∠α的度数为( )A .25°B .30°C .20°D .35°答案:A。
平行线的性质知识点及练习题

平行线的性质知识点及练习题1、平行线的性质:性质1:两直线平行,同位角相等;性质2:两直线平行,内错角相等;性质3:两直线平行,同旁内角互补。
几何符号语言:∵AB ∥CD∴∠1=∠2〔两直线平行,内错角相等〕∵AB ∥CD ∴∠3=∠2〔两直线平行,同位角相等〕∵AB ∥CD ∴∠4+∠2=180°〔两直线平行,同旁内角互补〕2、两条平行线的距离如图,直线AB ∥CD ,EF ⊥AB 于E ,EF ⊥CD 于F ,那么称线段EF 的长度为两平行线AB 与CD 间的距离。
注意:直线AB ∥CD ,在直线AB 上任取一点G ,过点G 作CD 的垂线段GH ,那么垂线段GH 的长度也就是直线AB 与CD 间的距离。
3、命题:⑴命题的概念:判断一件事情的语句,叫做命题。
⑵命题的组成每个命题都是题设、结论两局部组成。
题设是事项;结论是由事项推出的事项。
命题常写成“如果……,那么……〞的形式。
具有这种形式的命题中,用“如果〞开场的局部是题设,用“那么〞开场的局部是结论。
有些命题,没有写成“如果……,那么……〞的形式,题设和结论不明显。
对于这样的命题,要经过分析才能找出题设和结论,也可以将它们改写成“如果……,那么……〞的形式。
注意:命题的题设〔条件〕局部,有时也可用“……〞或者“假设……〞等形式表述;命题的结论局部,有时也可用“求证……〞或“那么……〞等形式表述。
4、平行线的性质与判定①平行线的性质与判定是互逆的关系两直线平行同位角相等;两直线平行内错角相等;两直线平行同旁内角互补。
其中,由角的相等或互补〔数量关系〕的条件,得到两条直线平行〔位置关系〕这是平行线的判定;由平行线〔位置关系〕得到有关角相等或互补〔数量关系〕的结论是平行线的性质。
典型例题:∠1=∠B ,求证:∠2=∠C证明:∵∠1=∠B 〔〕∴DE ∥BC 〔同位角相等,两直线平行〕 ∴∠2=∠C 〔两直线平行,同位角相等〕注意,在了DE ∥BC ,不需要再写一次了,得到了DE ∥BC ,这可以把它当作条件来用了典型例题:如图,AB ∥DF ,DE ∥BC ,∠1=65°求∠2、∠3的度数A B C DEF 1 2 3 4 A EG B C FH D A D F BE C 1 2 3解答:∵DE ∥BC 〔〕∴∠2=∠1=65°〔两直线平行,内错角相等〕∵AB ∥DF 〔〕∴AB ∥DF 〔〕∴∠3+∠2=180°〔两直线平行,同旁内角互补〕∴∠3=180°-∠2=180°-65°=115°平行线的性质练习题一、选择题:(每题3分,共12分)1、如图1所示,AB ∥CD,那么与∠1相等的角(∠1除外)共有( ) D C B A 1ED C BA O F E D C BA (1) (2) (3) 〔4〕2、如图2所示,DE ∥BC,CD 是∠ACB 的平分线,∠B=72°,∠ACB=40°,•那么∠BDC 等于( )°°°°3、以下说法:①两条直线平行,同旁内角互补;②同位角相等,两直线平行;•③内错角相等,两直线平行;④垂直于同一直线的两直线平行,其中是平行线的性质的是( )A.①B.②和③C.④D.①和④4、如图3所示,CD ∥AB,OE 平分∠AOD,OF ⊥OE,∠D=50°,那么∠BOF 为( )°°°°二、填空题:(每题3分,共12分)5、如图4所示,n m //,∠2=50°,那么∠1= °,∠3= °,∠4= °6、把命题“邻补角的平分线互相垂直〞改写成“如果……,那么……。
第二章第02讲 平行线的判定和性质(10类热点题型讲练)(解析版)
第02讲平行线的判定和性质(10类热点题型讲练)1.掌握同位角、内错角、同旁内角的位置关系;2.掌握利用同位角、内错角、同旁内角判定判定两条直线平行的条件,并能解决一些问题;3.掌握平行线的性质与判定的综合运用;4.体会平行线的性质与判定的区别与联系.知识点01 同位角、内错角、同旁内角的概念1.同位角、内错角和同旁内角:填空:(1)如图,∠1和∠5,分别在直线AB,CD的上方(同一方),在直线EF的右侧(同侧).具有这种位置关系的一对角是同位角.(2)如图,∠3和∠5,在直线AB,CD之间,在直线EF的两侧.具有这种位置关系的一对角叫做内错角.(3)如图,∠3和∠6,在直线AB,CD之间,在直线EF的同侧.具有这种位置关系的一对角叫做同旁内角.【总结】(1)同位角:在被截直线的同一方向,截线的同侧的一对角.(2)内错角:在被截直线的内侧,截线的两侧的一对角.(3)同旁内角:在被截直线的内侧,截线的同侧的一对角.知识点02 平行线的定义及表示(1)定义:在同一平面内内,不相交的两条直线.(2)表示:平行用“∥”符号表示,读作“平行于”.1.同一平面内,两条直线的位置关系:(1)平行 (2)相交2.利用直尺和三角尺画平行线:一“落”、二“靠”、三“移”、四“画”.【注意】平行线的画法四字诀1.“落”:三角板的一边落在已知直线上;2.“靠”:用直尺紧靠三角板的另一边;3.“移”:沿直尺移动三角板,直至落在已知直线上的三角板的一边经过已知点;4.“画”:沿三角板过已知点的边画直线.知识点03 平行公理及推论(1)平行公理:经过直线外一点,有且只有一条直线与这条直线平行.(2)推论:如果两条直线都与第三条直线平行,那么这两条直线也互相平行.即如果b∥a,c∥a,那么b∥c.【注意】平行公理(1)“有且只有”强调直线的存在性和唯一性.(2)前提条件“经过直线外一点”,若点在直线上,不可能有平行线.知识点04 平行线的判定方法平行线的判定方法1:(1)文字表述:两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.简单说成:同位角相等,两直线平行.(2)几何语言:∵∠1=∠5(或者∠2=∠6,∠4=∠8,∠3=∠7),∴AB∥CD.平行线的判定方法2:(1)文字表述:两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.简单说成:内错角相等,两直线平行.(2)几何语言:∵∠2=∠8(或者∠3=∠5),∴AB∥CD.平行线的判定方法3:(1)文字表述:两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.简单说成:同旁内角互补,两直线平行.(2)几何语言:∵∠2+∠5=180°(或者∠3+∠8=180°),∴AB∥CD.平行线的其他判定方法:(1)在同一平面内,平行于同一条直线的两条直线平行.(2)在同一平面内,垂直于同一条直线的两条直线平行.【总结】判定两直线平行的方法方法一:平行线的定义:在同一平面内,不相交的两条直线就是平行线.方法二:平行公理的推论:如果两条直线都与第三条直线平行,那么这两条直线也互相平行.方法三:同位角相等,两直线平行.方法四:内错角相等,两直线平行.方法五:同旁内角互补,两直线平行.方法六:同一平面内,垂直于同一条直线的两条直线平行.知识点05 平行线的性质(1)文字表达:①两条平行线被第三条直线所截,同位角相等,内错角相等,同旁内角互补;②简单说成:两直线平行,同位角相等;两直线平行,内错家相等;两直线平行,同旁内角互补;(2)几何语言表述:已知,如图所示,若AB∥CD,则①同位角:∠1=∠5(或∠2=∠6,∠4=∠8,∠3=∠7);②内错角:∠2=∠8(或∠3=∠5);③同旁内角:∠2+∠5=180°(或∠3+∠8=180°).题型01 同位角、内错角、同旁内角的辨别【例题】(2023上·黑龙江哈尔滨·七年级校考期中)如图,下列结论正确的是( )A .5Ð与4Ð是对顶角B .1Ð与3Ð是同位角C .2Ð与3Ð是同旁内角D .1Ð与2Ð是同旁内角【答案】D【分析】本题考查同位角同旁内角、对顶角,根据同位角、同旁内角、对顶角的定义进行判断,熟练掌握各角的定义是解题的关键.【详解】A 、5Ð与23Ð+Ð是对顶角,故本选项错误,不符合题意;B 、1Ð与34Ð+Ð是同位角,故本选项错误,不符合题意;C 、2Ð与3Ð没有处在两条被截线之间,故本选项错误,不符合题意;D 、1Ð与2Ð是同旁内角;故本选项正确,符合题意;故选:D .【变式训练】1.(2023上·四川巴中·七年级四川省巴中中学校考阶段练习)如图所示,有下列五种说法:①1Ð和4Ð是同位角;②3Ð和5Ð是内错角;③2Ð和6Ð是同旁内角;④5Ð和2Ð是同位角;⑤1Ð和3Ð是同旁内角;其中正确的是( )A .①②③⑤B .①②③④C .①②③④⑤D .①②④⑤【答案】D 【分析】本题考查了同位角、 内错角以及同旁内角的定义,根据内错角、 同位角以及同旁内角的定义寻找出各角之间的关系, 再比照五种说法判断对错, 即可得出结论 .【详解】解: 根据内错角、 同位角以及同旁内角的定义分析五种说法 .①1Ð和4Ð是同位角, 即①正确;②3Ð和5Ð是内错角, 即②正确;③2Ð和6Ð是内错角, 即③不正确;④5Ð和2Ð是同位角, 即④正确;⑤1Ð和3Ð是同旁内角, 即⑤正确 .2.(2023下·广东河源·七年级期中)如图,a ,b ,c 三条直线两两相交,下列说法错误的是( )A .1Ð与2Ð是同位角B .2Ð与4Ð是内错角C .3Ð与4Ð是对顶角D .1Ð与3Ð是同旁内角【答案】B 【分析】本题考查相交直线所成相关角的概念,解答关键是熟知同位角、内错角、同旁内角、对顶角的相关概念和判断方法.【详解】解:A .1Ð与2Ð是直线a 、直线b 被直线c 所截,所得到的同位角,因此选项A 不符合题意;B .2Ð与4Ð是直线a 、直线c 被直线b 所截,所得到的同位角,因此选项B 符合题意;C .3Ð与4Ð是对顶角,因此选项C 不符合题意;D .1Ð与3Ð是直线b 、直线c 被直线a 所截,所得到的同旁内角,因此选项D 不符合题意;故选:B .题型02 同位角相等,两直线平行【例题】根据要求完成下面的填空:如图,直线AB ,CD 被EF 所截,若已知12Ð=Ð.23Ð=ÐQ (______),又12Ð=ÐQ (已知),\Ð______=Ð______,∴______∥______(______).【详解】23Ð=ÐQ (对顶角相等),又12Ð=ÐQ (已知),AB CD \∥(同位角相等,两直线平行),故答案为:对顶角相等,1,3,AB ,CD ,同位角相等,两直线平行.【变式训练】1.请完成下面的推理过程并在括号里填写推理依据:如图,129023,,AB BC ^=°Ð+ÐÐ=Ð,BE 与DF 平行吗?为什么?解:BE DF ∥.理由如下:∵AB BC ^(已知),∴ABC Ð=________°即34Ð+Ð=________°( )又∵1290Ð+Ð=°( ),且23ÐÐ=(已知)∴14Ð=Ð( )∴BE DF ∥( )【详解】解:BE DF ∥.理由如下:∵AB BC ^(已知),∴90ABC Ð=°,即3490Ð+Ð=°(等量代换)又∵1290Ð+Ð=°(已知),且23ÐÐ=(已知)∴14Ð=Ð(等角的补角相等)∴BE DF ∥(同位角相等,两直线平行).故答案为:90,90,等量代换,已知,等角的补角相等,同位角相等,两直线平行.2.如图,已知AC AE ^,BD BF ^,135Ð=°,235Ð=°.AC 与BD 平行吗?AE 与BF 平行吗?阅读下面的解答过程,并填空或填写理由.解:AC 与BD 平行;AE 与BF 平行,理由如下:Q 135Ð=°,235Ð=°\12Ð=Ð\(________)∥(________)(________________________);又Q AC AE^\EAC 90Ð=o\1EAB EAC Ð=Ð+Ð=(________)o同理可得2FBG FBD Ð=Ð+Ð=(________)o∴(________)∥(________)(_____________________________).【详解】解:AC 与BD 平行;AE 与BF 平行,理由如下:Q 135Ð=°,235Ð=°\12Ð=Ð\AC ∥BD (同位角相等,两直线平行);又Q AC AE^\90EAC Ð=°\1125EAB EAC Ð=Ð+Ð=°同理可得2125FBG FBD Ð=Ð+Ð=°\AE ∥BF (同位角相等,两直线平行).题型03 内错角相等,两直线平行【例题】如图,EF 交AD 于O ,AB 交AD 于A ,CD 交AD 于D ,12Ð=Ð,34ÐÐ=,试判断AB 和CD 的位置关系,并说明为什么.【详解】解:AB CD P .理由:12Ð=ÐQ ,34ÐÐ=,23ÐÐ=,14\Ð=Ð,∴AB CD P .【变式训练】1.推理填空:已知:如图AB BC ^于B ,CD BC ^于C ,12Ð=Ð,求证:BE CF ∥.证明:∵AB BC ^于B ,CO ∴139024Ð+Ð=°Ð+Ð=,∴1Ð与3Ð互余,2Ð与4Ð又∵12Ð=Ð( ),(1)求BOF Ð的度数;(2)试说明AB CD ∥的理由.【详解】(1)∵OA OB ,分别平分∴12AOE AOC COE ÐÐÐÐ==,∵180COE DOE Ð+Ð=°,题型04 同旁内角互补,两直线平行【例题】如图,已知直线AB CD 、被直线EF 所截,GE 平分AEF Ð,GF 平分EFC Ð,1290Ð+Ð=°,AB CD ∥吗?为什么?解:∵GE 平分AEF Ð,GF 平分EFC Ð(已知),∴2AEF ÐÐ=___________,2EFC ÐÐ=___________,∴AEF EFC ÐÐ+=___________( ),∵1290Ð+Ð=°( ),∴AEF EFC ÐÐ+=___________°,∴AB CD ∥.【详解】解:GE Q 平分AEF Ð,GF 平分EFC Ð(已知),21AEF \Ð=Ð,22EFC Ð=Ð,2(12)AEF EFC \Ð+Ð=Ð+Ð(等量代换)1290Ð+Ð=°Q (已知),180AEF EFC \Ð+Ð=°,AB CD \∥.【变式训练】1.如图,160,260,3120°°°Ð=Ð=Ð=.试说明,DE BC DF ∥∵160260,°°Ð=Ð=∴12Ð=Ð(等量代换)证明:∵12180Ð+Ð=°,∴a ∥______(______).∵13Ð=Ð,∴a ∥______(______).∴b c ∥(______).【详解】证明:∵12180Ð+Ð=°,∴a ∥b (同旁内角互补,两直线平行).∵13Ð=Ð,∴a ∥ c (同位角相等,两直线平行).∴b c ∥(如果两条直线都与第三条直线平行,那么这两条直线也互相平行).题型05 平行线及平行公理【详解】解:因为Ð13Ð=Ð(对顶角相等)所以Ð2=Ð3(等量代换)所以a ∥c (同位角相等,两直线平行)又因为a b ∥(已知)1.如图所示,直线AB CD ,相交于点O ,OD 平分EOB Ð,OF 平分AOE Ð,GH CD ^,垂足为点H ,GH 与FO 平行吗?说明理由.(1)判断CD与AB的位置关系;(2)求证:DF BE∥.^【详解】(1)解:∵AB MN∥.∴CD AB题型06添加一条件使两条直线平行Ð=Ð【答案】EAB【分析】本题主要考查了平行线的判定.要判断的位置关系,根据平行线的判定定理解答即可.∵180CDB B Ð+Ð=°,∴AB CD ∥(同旁内角互补,两直线平行);故答案为:EAB C Ð=Ð(答案不唯一).【变式训练】【答案】①②④【分析】根据平行线的判定条件,逐一判断即可解答.【详解】解:①12Ð=Ð,能判断【答案】250Ð=°.(答案不唯一)【分析】根据平行线的判定和性质进行解答即可.【详解】解:可以添加条件Ð∵EF MN ^,∴90EFM Ð=°【点睛】本题主要考查了平行线的判定和性质,解题的关键是熟练掌握平行线的判定,内错角相等,两直线平行;同位角相等,两直线平行;同旁内角互补,两直线平行.题型07 根据平行线的性质求角度【例题】(2023下·新疆阿克苏·七年级校考期末)如图,AB CD ∥,直线EF 分别交AB 、CD 于点E 、F ,EG 平分AEF Ð,135Ð=°,求2Ð的度数.【答案】110°【分析】根据平行线的性质、角平分线的定义结合平角的定义即可求解.【详解】解:如图所示,∵AB CD ∥,135Ð=°∴3135Ð=Ð=°∵EG 平分AEFÐ∴3435Ð=Ð=°∴21803535110Ð=°-°-°=°.【点睛】本题主要考查了平行线的性质、角平分线的定义,熟练掌握平行线的性质、求出3135Ð=Ð=°是关键.【变式训练】1.(2023下·浙江金华·七年级校联考期末)如图,点E 在BC 的延长线上,连接DE ,作CED Ð的角平分线分别交线段AD ,DC 于点F ,点G ,已知AB CD ∥,AD BC ∥.(1)试说明2BED DFE Ð=Ð;(2)若105B Ð=°,28DFE Ð=°,求CDE Ð的度数.【答案】(1)见解析(2)19CDE Ð=°【分析】(1)根据角平分线的性质得出2BED BEF Ð=Ð,根据平行线的性质可得DFE BEF Ð=Ð;(2)根据平行线的性质可得105DCE B Ð=Ð=°,根据平行线的性质得出105ADC DCE Ð=Ð=°,180ADE BED Ð+Ð=°,根据(1)的结论得出256BED DFE Ð=Ð=°,180124ADE BED Ð=°-Ð=°,进而根据CDE ADE ADC Ð=Ð-Ð,即可求解.【详解】(1)解:∵EF 平分CED Ð,∴2BED BEF Ð=Ð,∵AD BC∥∴DFE BEF Ð=Ð,(2)解:∵AB CD ∥,105B Ð=°,∴105DCE B Ð=Ð=°,∵AD BC ∥,∴105ADC DCE Ð=Ð=°,180ADE BED Ð+Ð=°.∵28DFE Ð=°,∴256BED DFE Ð=Ð=°,∴180124ADE BED Ð=°-Ð=°,∴12410519CDE ADE ADC Ð=Ð-Ð=°-°=°.【点睛】本题考查了平行线的性质,角平分线的定义,熟练掌握平行线的性质是解题的关键.2.(2023下·贵州黔南·七年级统考期末)如图,已知AB CD ∥,AD BC ∥,90DCE Ð=°,点E 在线段AB 上,90FCG Ð=°,点F 在直线AD 上,90AHG Ð=°.(1)图中与D Ð相等的角有__________;(2)若25ECF Ð=°,求BCD Ð的度数;(3)在(2)的条件下,点C (点C 不与B ,H 两点重合)从点B 出发,沿射线BG 的方向运动,其他条件不变,求BAF Ð的度数.【答案】(1)DCG Ð,ECF Ð,BÐ(2)155°(3)25°或155°【分析】(1)根据同角的余角相等以及平行线的性质,即可得到与D Ð相等的角;(2)根据25ECF Ð=°,90DCE Ð=°,可得65FCD Ð=°,再根据90BCF Ð=°,即可得到6590155BCD Ð=°+°=°;(3)分两种情况讨论:当点C 在线段BH 上;点C 在BH 延长线上,根据平行线的性质,即可得到BAF Ð的度数为25°或155°.【详解】(1)解:AD BC ∥Q ,D DCG \Ð=Ð,90FCG Ð=°Q ,90DCE Ð=°,ECF DCG \Ð=Ð,D ECF \Ð=Ð,AB DC Q ∥,DCG B \Ð=Ð,D B \Ð=Ð;\与D Ð相等的角为DCG Ð,ECF Ð,B Ð;(2)解:25ECF Ð=°Q ,90DCE Ð=°,65FCD \Ð=°,90BCF Ð=°Q ,6590155BCD \Ð=°+°=°;(3)解:分两种情况进行讨论:①如图a ,当点C 在线段BH 上时,点F 在DA 的延长线上,此时25ECF DCG B Ð=Ð=Ð=°,AD BC ∥Q ,25BAF B \Ð=Ð=°;②如图b ,当点C 在BH 的延长线上时,点F 在线段AD 上.25B Ð=°Q ,AD BC ∥,18025155BAF \Ð=°-°=°,综上所述,BAF Ð的度数为25°或155°.【点睛】本题考查了平行线的性质,熟练掌握平行线的性质定理是解题关键.题型08平行线的性质在生活中的应用【答案】120°/120度【分析】首先过B作BF AE∥,根据100Ð=°Q,A\Ð=Ð=°,100ABF A又160ABC Ð=°Q ,16010060FBC \Ð=°-°=°,AE CD ∥Q ,FB CD \∥,180********C FBC \Ð=°-Ð=°-°=°,故答案为:120°.【点睛】此题主要考查了平行线性质,关键是掌握两直线平行,同旁内角互补;两直线平行,内错角相等.【变式训练】【答案】17°/17度【分析】由平行线的性质可知D B C M B C M B D Ð=Ð-Ð求解即可.【详解】解:∵MN EF ∥,∴160M B C Ð=Ð=°.【答案】30°/30度【分析】过点B 作BF CE ∥.先利用平行线的性质和垂直的定义、角的和差关系求出CBF Ð,再利用平行线的性质和角的和差关系求得结论.【详解】解:过点B 作BF CE ∥.CE l ∥Q ,BF l \∥.190ABF \Ð=Ð=°.140ABC Ð=°Q ,1409050CBF \Ð=°-°=°.BF CE ∥Q ,50ECB CBF \Ð=Ð=°.DCE DCB BCE\Ð=Ð-Ð8050=°-°30=°.故答案为:30°.【点睛】本题主要考查了平行线的性质,掌握平行线的性质和角的和差关系是解决本题的关键.题型09 平行线的性质与判定综合应用【答案】(1)见解析;(2)F BMF DNFÐ=Ð-Ð;(3)20【分析】本题主要考查平行线的判定和性质,作辅助线是解题的关键.(1)过点E作EF AB∥,根据平行线的性质可求解;(2)如图②,过F作FH AB∥,根据平行线的性质即可得到结论;∥,根据平行线的性质即可得到结论.(3)如图③,过C作CG AB【详解】(1)证明:如图①,过点E作EF AB∥,则MEF BMEÐ=Ð,∥,又∵AB CD∥,∴EF CD\Ð=Ð,NEF DNEMEN MEF NEF\Ð=Ð+Ð,Ð=Ð+Ð;即MEN BME DNE(2)解:BMF MFN FNDÐ=Ð+Ð.P,证明:如图②,过F作FK AB\Ð=Ð,BMF MFK∥,∵AB CDP,∴FK CD\Ð=Ð,FND KFN\Ð=Ð-Ð=Ð-Ð,MFN MFK KFN BMF FND即:BMF MFN FND Ð=Ð+Ð.故答案为:BMF MFN FND Ð=Ð+Ð;(3)如图③,过C 作CG AB ∥,18060GCA BAC \Ð=°-Ð=°,∵AB DE ∥,∴CG DE ∥,80GCD CDE \Ð=Ð=°,20ACD \Ð=°,故答案为:20.【变式训练】1.(2023上·湖南岳阳·八年级校考开学考试)如图,12Ð=Ð,BAE BDE Ð=Ð,点F 在DE 的延长线上,点C 在AB 的延长线上,且EA 平分BEF Ð.(1)求证:AB DE ∥;(2)若40BAE Ð=°,求EBD Ð.【答案】(1)见解析(2)40°【分析】(1)根据对顶角相等结合题意推出1ABE Ð=Ð,根据“同位角相等,两直线平行”即可判定AB DE ∥;(2)根据平行线的性质结合题意推出AEF BDE Ð=Ð,即可判定AE BD P ,根据平行线的性质及角平分线的定义求解即可.【详解】(1)证明:∵2ABE Ð=Ð(对顶角相等),又12Ð=Ð(已知),∴1ABE Ð=Ð(等量代换),∴AB DE ∥(同位角相等,两直线平行);(2)解:由(1)已证AB DE ∥可得:40BAE AEF Ð=Ð=°(两直线平行,内错角相等),又∵BAE BDE Ð=Ð,∴AEF BDE Ð=Ð(等量代换),∴AE BD P (同位角相等,两直线平行),∴AEB EBD Ð=Ð(两直线平行,内错角相等),又∵EA 平分BEF Ð,∴AEB AEF Ð=Ð,∴40EBD AEB AEF BAE Ð=Ð=Ð=Ð=°,∴40Ð=°EBD .【点评】此题考查了平行线的判定与性质,熟记平行线的判定定理与性质定理是解题的关键.2.(2023下·江苏泰州·七年级校考期中)如图,在ABC V 中,点D 、F 在BC 边上,点E 在AB 边上,点G 在AC 边上,EF 与GD 的延长线交于点H ,BDH B Ð=Ð,AEH ADH Ð=Ð.(1)EH 与AD 平行吗?为什么?(2)若40H Ð=°,求BAD Ð的度数.【答案】(1)平行,见解析(2)40°【分析】(1)EH AD ∥,理由如下:由已知条件,BDH B Ð=Ð,根据平行线的判定可得AB GH ∥,根据平行线的性质得180BAD ADH Ð+Ð=°,等量代换得到180BAD AEH Ð+Ð=°,即可得出答案;(2)结合(1)根据平行线的性质即可得解.【详解】(1)EH AD ∥,理由如下:BDH B Ð=ÐQ ,AB GH \∥,180BAD ADH \Ð+Ð=°,AEH ADH Ð=ÐQ ,180BAD AEH \Ð+Ð=°,EH AD \∥;(2)180BAD ADH Ð+Ð=°Q ,又EH AD Q ∥,180H ADH \Ð+Ð=°,H BAD \Ð=Ð,40H Ð=°Q ,40BAD \Ð=°.【点睛】此题考查了平行线的判定与性质,熟记平行线的判定与性质定理是解题的关键.题型10 根据平行线的性质与判定探究角的关系(1)123ÐÐÐ、、之间的关系为(2)如果点P 在A 、B 两点之间运动时,(3)如果点P (点P 和A 、【答案】(1)123Ð+Ð=Ð(2)123Ð+Ð=Ð(3)123Ð-Ð=Ð或2Ð-Ð∴52Ð=Ð(两直线平行,内错角相等),∵345Ð=Ð+Ð,∴123Ð+Ð=Ð(等量代换);故答案为:123Ð+Ð=Ð;(2)解:由(1)的证明过程知,123ÐÐÐ、、之间的关系不发生变化;故答案为:123Ð+Ð=Ð;(3)解:过点P 作1PQ l ∥,∵12l l ∥,∴21PQ l l ∥∥;当点P 在AB 延长线上时,如左图,则24ÐÐ=,134CPQ Ð=Ð=Ð+Ð,∴132Ð=Ð+Ð,即123Ð-Ð=Ð;当点P 在BA 延长线上时,如右图,∵21PQ l l ∥∥,∴14Ð=Ð,234DPQ Ð=Ð=Ð+Ð,∴231Ð=Ð+Ð,即213Ð-Ð=Ð;综上,123Ð-Ð=Ð或213Ð-Ð=Ð.故答案为:123Ð-Ð=Ð或213Ð-Ð=Ð.【变式训练】(1)图中CBD Ð= °;(2)当ACB ABD Ð=Ð时,ABC Ð=(3)随点P 位置的变化,图中APB Ð【答案】(1)60P;(1)求证:AB CD(2)点G是射线MD上的一个动点∥交直线AB于点N,设HN EMβ=°①点G在点F右侧,且70∵EH 平分FEG Ð,∴HEF HEG Ð=Ð,∵HN EM ∥,∴EHN HEM HEF FEM Ð=Ð=Ð+Ð,∵FEM FME Ð=Ð,∴EHN HEF FME αÐ=Ð+Ð=,∵()180********EGF FME GEM FME FEM HEF FME HEF Ð=°-Ð-Ð=°-Ð-Ð-Ð=°-Ð+Ð,∴1802βα=°-,∵70β=°,∴701802α°=°-,解得55α=°.②α和β之间的数量关系为2βα=或1802βα=°-.理由如下:当点G 在点F 的右侧,由(2)得1802αβ=°-,当点G 在点F 的左侧时,如图2,∵EH 平分FEG Ð,∴HEF HEG Ð=Ð,∵HN EM ∥,∴EHN HEM Ð=Ð,∵FEM FME Ð=Ð,∴()222EGF FME GEM FEM GEM GEM HEG GEM GEM HEG HEM Ð=Ð+Ð=Ð+Ð=Ð+Ð+Ð=Ð+Ð=Ð,∴2EGF EHN Ð=Ð,即2βα=,综上所述,α和β之间的数量关系为2βα=或1802βα=°-.【点睛】本题考查角平分线的定义,平行线的性质,利用数形结合和分类讨论的思想是解题关键.一、单选题1.(2023下·云南昭通·七年级统考阶段练习)如图,下列条件不能判定AB CD P 的是( )A .13Ð=ÐB .35Ð=ÐC .12180Ð+Ð=°D .15Ð=Ð【答案】B 【分析】根据平行线的判定定理,对各项逐一进行判断即可.【详解】解:A 、13Ð=Ð,根据同位角相等,两直线平行可判定AB CD P ,故此选项不符合题意;B 、35Ð=Ð,对顶角相等,不能判定AB CD P ,故此选项符合题意;C 、12180Ð+Ð=°,根据同旁内角互补,两直线平行可判定AB CD P ,此选项不符合题意;D 、15Ð=Ð,根据内错角相等,两直线平行可判定AB CD P ,故此选项不符合题意;故选:B .【点睛】本题考查了平行线的判定定理,解题的关键是正确识别“三线八角”中的同位角、内错角、同旁内角,不能遇到相等或互补关系的角就误认为具有平行关系,只有同位角相等、内错角相等、同旁内角互补,才能推出两被截直线平行.2.(2023下·广东江门·七年级统考期末)如图所示,以下说法错误的是( )A .1Ð与2Ð是同位角B .4Ð与3Ð是同位角C .5Ð与3Ð是内错角D .4Ð与5Ð是同旁内角【答案】C 【分析】根据同位角、内错角、同旁内角的定义逐项判断即可.【详解】解:A 、1Ð与2Ð是同位角,正确,不符合题意;B 、4Ð与3Ð是同位角,正确,不符合题意;C 、5Ð与3Ð不是内错角,错误,符合题意;D 、4Ð与5Ð是同旁内角,正确,不符合题意,故选:C .【点睛】本题考查同位角、内错角、同旁内角,解答的关键是理解定义:如果两条直线被第三条直线所截所形成的的角,在两条被截直线之间且在截线两侧的两个角互为内错角;在两条被截直线同一方且在截线同侧的两个角互为同位角;在两条被截线之间且在截线同侧的两个角互为同旁内角.3.(2023上·陕西铜川·八年级统考期末)如图,下列推理及括号中所注明的推理依据错误的是( )A .∵AD BC ∥,180BAD D \Ð+Ð=°(两直线平行,同旁内角互补)B .∥Q AB CD ,180BCD ABC \Ð+Ð=°(两直线平行,同旁内角互补)C .13Ð=ÐQ ,AB CD \∥(内错角相等,两直线平行)D .DAM CBM Ð=ÐQ ,AD BC \∥(同位角相等,两直线平行)【答案】A【分析】本题考查的是平行线的判定与性质,利用平行线的判定方法与性质逐一分析即可得到答案,熟记平行线的判定方法与平行线的性质是解本题的关键.【详解】解:∵AD BC ∥,180BAD ABC \Ð+Ð=°(两直线平行,同旁内角互补),故A 符合题意;∥Q AB CD ,180BCD ABC \Ð+Ð=°(两直线平行,同旁内角互补),故B 不符合题意;13Ð=ÐQ ,AB CD \∥(内错角相等,两直线平行),故C 不符合题意;DAM CBM Ð=ÐQ ,AD BC \∥(同位角相等,两直线平行),故D 不符合题意;故选A4.(2023上·陕西榆林·八年级校考期末)如图,直线a b P ,直线l 与直线a 相交于点P ,与直线b 相交于点Q ,PM l ^于点P ,若155Ð=°,则2Ð的度数为( )A .35°B .55°C .125°D .145°【答案】A 【分析】本题考查了平行线性质,根据两直线平行,同位角相等,平角的定义计算即可.【详解】如图,∵a b P ,155Ð=°,∵34180,2+Ð=°ÐÐ+Ð∴180324а--Ð==Ð故选A .5.(2023上·四川宜宾·七年级四川省宜宾市第二中学校校考阶段练习)平分BAC Ð,A C CE ^A .1个【答案】D 【分析】①根据平行线的传递性可以判断出来内角互补可得2BAC Ð+Ð212180Ð+Ð=°,可求得结果;二、填空题【答案】①②④【分析】根据同位角的定义,逐一判断选项,即可得到答案.【详解】解:①∠1和∠2在两条直线的同侧,也在第三条直线的同侧,故它们是同位角;②∠1和∠2在两条直线的同侧,也在第三条直线的同侧,故它们是同位角;【答案】B DAB Ð=Ð【分析】根据“内错角相等,两直线平行【详解】解:由“内错角相等,两直线平行【答案】36°/36度【分析】由对顶角相等可得Ð件可求得B Ð,即可求解.【详解】解:如图,1108Ð=°Q ,31108\Ð=Ð=°,∵l AB ∥,3180A \Ð+Ð=°,2B Ð=Ð,【答案】3或7.5或12【分析】本题考查了平行线的性质.分类讨论Ð的大小即可求解.性质确定旋转角AFE∥时,如图所示:【详解】解:①当DE BC30AFE Ð=°∴30310t ==秒②当DE AB ∥时,如图所示:∵45FHD A Ð=Ð=°,∴45HFD Ð=°45AFE HFD EFD Ð=Ð+Ð=°+∴757.510t ==秒180120AFE E Ð=°-Ð=°∴1201210t ==秒综上所述:t 的值为3或7.5或12三、解答题11.(2023上·新疆克孜勒苏·七年级统考期末)如图,已知12180Ð+Ð=°,3B Ð=Ð,试判断C Ð与AED Ð的大小关系,请补全证明过程,即在横线处填上结论或理由.解:AED C Ð=Ð.理由如下:∵12180Ð+Ð=°(已知),1180DFE Ð+Ð=°(_______),∴2DFE Ð=Ð(_______),∴AB ∥ _______(_______),∴3ADE Ð=Ð(_______),∵3B Ð=Ð(已知),∴∠_______=Ð_______(_______),∴_______∥_______(_______),C AED Ð=Ð(_______).【答案】平角的定义;等量代换;EF ;内错角相等,两直线平行;两直线平行,内错角相等:ADE ;B ;等量代换;DE ;BC ,同位角相等,两直线平行;两直线平行,同位角相等【分析】本题考查了平行线的判定与性质,根据证明的思路,把证明过程填写完整即可.【详解】AED C Ð=Ð.理由如下:∵12180Ð+Ð=°(已知),1180DFE Ð+Ð=°(平角的定义),∴2DFE Ð=Ð(等量代换),∴AB EF ∥(内错角相等,两直线平行),∴3ADE Ð=Ð(两直线平行,内错角相等),∵3B Ð=Ð(已知),∴ADE B Ð=Ð(等量代换),∴DE BC ∥(同位角相等,两直线平行),∴C AED Ð=Ð(两直线平行,同位角相等).故答案为:平角的定义;等量代换;EF ;内错角相等,两直线平行;两直线平行,内错角相等:ADE ;B ;等量代换;DE ;BC ,同位角相等,两直线平行;两直线平行,同位角相等.12.(2023上·吉林长春·七年级统考期末)在下列解答中,填空(理由或数学式).如图,已知直线b c ∥,1116Ð=°,3=4ÐÐ.(1)求AOB Ð的度数;(2)求证:直线a c ∥.解:(1)∵1116Ð=° (已知)∴2116Ð=°( ).∵b c ∥(已知),∴2AOB Ð=Ð( ).故答案为:已知;内错角相等,两直线平行;如果两条直线都和第三条直线平行,那么这两条直线也互相平行.13.(2023上·吉林长春·七年级校考期末)如图,已知AB CD P ,AC 与BD 相交于点E ,从点E 引一条射线EF 交线段AB 于点F ,若180AFE DCB Ð+Ð=°,A AEF Ð=Ð,求证:DCA ACB Ð=Ð.证明:∵AB CD P (已知),∴180ABC DCB Ð+Ð=°(两直线平行,同旁内角互补),又∵180AFE DCB Ð+Ð=°(已知),∴AFE ABC Ð=Ð(____________________),∴EF ∥__________(____________________),∴Ð=AEF __________(____________________),∵AB CD P (已知),∴A DCA Ð=Ð(____________________),∵A AEF Ð=Ð(已知),∴DCA ACB Ð=Ð(____________________).【答案】见解析【分析】本题考查平行线的性质与判定,根据题目已知条件及现有步骤结合平行线的判定和性质定理,即可得到答案.【详解】证明:AB CD P (已知),∴180ABC DCB Ð+Ð=°(两直线平行同旁内角互补),又∵180AFE DCB Ð+Ð=°(已知),∴AFE ABC Ð=Ð(同角的补角相等);∴ EF BC ∥(同位角相等,两直线平行),∴AEF ACB Ð=Ð(两直线平行,同位角相等),∵AB CD P (已知),∴A DCA Ð=Ð(两直线平行,内错角相等),∴A AEF Ð=Ð(已知),∴DCA ACB Ð=Ð(等量代换),故答案为:同角的补角相等;BC ;同位角相等,两直线平行;ACB Ð;两直线平行,同位角相等;两直线平行,内错角相等;等量代换.14.(2023上·重庆沙坪坝·八年级统考期中)已知:如图,在ABC V 中,点D 在BC 边上,EF AD ∥分别交AB ,CB 于点E ,F ,DG 平分ADC Ð,12180Ð+Ð=°,(1)求证:AB DG ∥;(2)若40B Ð=°,60DAC Ð=°,求DGC Ð的度数.【答案】(1)见解析(2)100°【分析】本题考查了平行线的性质与判定、角平分线的定义、三角形的外角性质,熟练掌握平行线的性质和判定,是解决本题的关键.平行线的性质:两直线平行,内错角相等;两直线平行,同位角相等;两直线平行,同旁内角互补;平行线的判定:内错角相等,两直线平行;同位角相等,两直线平行;同旁内角互补,两直线平行.三角形的外角性质:三角形的外角等于与它不相邻的两个内角的和.【详解】(1)证明:∵EF AD ∥,∴1180BAD Ð+Ð=°.∵12180Ð+Ð=°.∴2BAD Ð=Ð.∴AB DG ∥;(2)解:∵AB DG ∥,40B Ð=°,∴40GDC B Ð=Ð=°,∵DG 平分ADC Ð,∴240GDC Ð=Ð=°,又∵60DAC Ð=°,∴2100DGC DAC Ð=Ð+Ð=°.15.(2023上·四川遂宁·七年级射洪中学校联考阶段练习)如图1,直线AD EF P ,点B C ,分别在EF 和AD 上,A ABC Ð=Ð,BD 平分CBF Ð.【探索】如图②,AM 平分BAC Ð,CAM CMA Ð=Ð,点E 在射线AB 上,点F 在线段CM 上,若AEF C Ð=Ð,求证:EF AC ∥.【拓展】如图③,将【探索】中的点F 移动到线段CM 的延长线上,其他条件不变,若357CAM MEF Ð=Ð=°,请直接写出AME Ð的度数.【答案】感知:BAM Ð;BAM Ð;探索:见解析;拓展:76AME =°∠【分析】感知:根据角平分线定义和平行线的性质进行解答即可;探索:先证明AB CD P ,得出AEF EFD Ð=Ð,在证明EFD C Ð=Ð,根据平行线的判定得出结论即可;拓展:根据角平分线定义得出57BAM CAM ==°∠∠, 257114BAC =´°=°∠,根据平行线的性质求出18066C BAC =°-=°∠∠,求出661947AEM =°-°=°∠,最后根据平行线的性质求出结果即可.【详解】解:感知:∵AM 平分BAC Ð,(已知),∴CAM BAM Ð=Ð(角平分线的定义),∵AB CD P (已知),∴CMA BAM Ð=Ð(两直线平行,内错角相等)∴CAM CMA Ð=Ð(等量代换).故答案为:BAM Ð;BAM Ð.探索:∵AM 平分BAC Ð,∴CAM BAM Ð=Ð,∵CAM CMA Ð=Ð,∴A BAM CM =Ð∠,∴AB CD P ,∴AEF EFD Ð=Ð,∵AEF C Ð=Ð,∴EFD C Ð=Ð,∴EF AC ∥.拓展:∵357CAM MEF Ð=Ð=°,∴根据探索可知:57BAM CAM ==°∠∠,19MEF =°∠,∴257114BAC =´°=°∠,根据探索可知:AB CD P ,∴18066C BAC =°-=°∠∠,∴66AEF C ==°∠∠,∴661947AEM =°-°=°∠,∵AB CD P ,∴57AMC BAM ==°∠∠,47DME AEM ==°∠∠,∴18076AME AMC DME =°--=°∠∠∠.【点睛】本题主要考查了平行线的判定和性质,角平分线的定义,几何图形中的角度计算,解题的关键是熟练掌握平行线的判定方法,内错角相等,两直线平行;同位角相等,两直线平行;同旁内角互补,两直线平行.平行线的性质,两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补.17.(2023上·内蒙古乌海·八年级统考期末)综合与实践:问题:如图1,直线AB 、BC 、AC 两两相交,交点分别为点A 、B 、C ,点D 在线段AB 上,过点D 作DE BC ∥交AC 于点E ,过点E 作EF AB ∥交BC 于点F .(1)若65ABC Ð=°,求DEF Ð的度数.请将下面的解答过程补充完整,并填空(理由或数学式)解:∵DE BC ∥,∴DEF Ð= ______(______),∵EF AB ∥,∴______ ABC =Ð(______),∴DEF ABC Ð=Ð(______),∵65ABC Ð=°,∴65DEF Ð=°.探究:如图2,直线AB 、BC 、AC 两两相交,交点分别为点A 、B 、C ,点D 在线段AB 的延长线上,过点D 作DE BC ∥交AC 于点E ,过点E 作EF AB ∥交BC 于点F .(2)在图2中,若65ABC Ð=°,求DEF Ð的度数并说明理由.(3)猜想:如果ABC Ð的两边分别平行于DEF Ð的两边,直接写出ABC Ð与DEF Ð这两个角之间有怎样的数量关系?【答案】(1)EFC Ð;两直线平行,内错角相等;EFC Ð;两直线平行,同位角相等;等量代换;(2)115DEF Ð=°,理由见解析;(3)ABC DEF Ð=Ð或180ABC DEF Ð+Ð=°【分析】本题主要考查平行线的性质,解答的关键是熟记平行线的性质并灵活运用.(1)由平行线的性质可得DEF EFC Ð=Ð,EFC ABC Ð=Ð,则有DEF ABC Ð=Ð,即可得解;(2)由平行线的性质得65ABC ADE Ð=Ð=°,180ADE DEF Ð+Ð=°,则可求DEF Ð得度数.(3)根据平行线的性质分析,即可获得答案.【详解】解:(1)∵DE BC ∥,∴DEF EFC Ð=Ð(两直线平行,内错角相等),∵EF AB ∥,∴EFC ABC Ð=Ð(两直线平行,同位角相等),∴DEF ABC Ð=Ð(等量代换),∵65ABC Ð=°,∴65DEF Ð=°.故答案为:EFC Ð;两直线平行,内错角相等;EFC Ð;两直线平行,同位角相等;等量代换;(2)115DEF Ð=°,理由如下:∵DE BC ∥,∴65ABC ADE Ð=Ð=°(两直线平行,同位角相等),∵EF AB ∥,∴180ADE DEF Ð+Ð=°(两直线平行,同旁内角互补),∴180115DEF ADE Ð=°-Ð=°;(3)ABC DEF Ð=Ð或180ABC DEF Ð+Ð=°,理由如下:如图1,ABC Ð的两边分别平行于DEF Ð的两边时,ABC DEF Ð=Ð;如图2,ABC Ð的两边分别平行于DEF Ð的两边时,180ABC DEF Ð+Ð=°.18.(2023上·全国·八年级专题练习)如图,线段AB 与线段CD 平行,P 是平面内一点,连接PA PD ,,射线AM DN ,分别平分BAP CDP ÐÐ,.(1)当点P 在线段DA 的延长线上时:①在图1中,依题意补全图形;②请直接写出直线AM 与直线DN 的位置关系:___________;(2)如图2,当点P 在直线AB 与直线CD 之间时,射线AM ,DN 交于点Q ,探究P Ð与AQD Ð的数量关系,。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
平行线的判定和性质经典题
一.选择题(共18小题)
1.如图所示,同位角共有()
3.下列说法中正确的个数为()
①不相交的两条直线叫做平行线
②平面内,过一点有且只有一条直线与已知直线垂直
③平行于同一条直线的两条直线互相平行
4.在同一平面内,有8条互不重合的直线,l1,l2,l3…l8,若l1⊥l2,l2∥l3,l3⊥l4,l4∥l5…
6.如图所示,AC⊥BC,DE⊥BC,CD⊥AB,∠ACD=40°,则∠BDE等于()
8.下列所示的四个图形中,∠1和∠2是同位角的是()
11.如图所示,BE∥DF,DE∥BC,图中相等的角共有()
13.如图所示,DE∥BC,DC∥FG,则图中相等的同位角共有()
14.如图所示,AD∥EF∥BC,AC平分∠BCD,图中和α相等的角有()
15.如果两个角的两边分别平行,而其中一个角比另一个角的4倍少30°,那么这两个角
16.把直线a 沿水平方向平移4cm ,平移后的像为直线b ,则直线a 与直线b 之间的距离为
17.
(2009•宁德)在下列四个汽车标志图案中,能用平移变换来分析其形成过程的图案是
18.(2004•烟台)
4根火柴棒摆成如图所示的象形“口”字,平移火柴棒后,原图形变成的象形文字是( )
二.填空题(共12小题)
19.已知∠α和∠β的两边互相平行,且∠α=60°,则∠β= _________ .
20.(2004•西宁)如图,AD∥EG∥BC,AC∥EF,则图中与∠1相等的角(不含∠1)有 _________ 个;若∠1=50°,则∠AHG= _________ 度.
第20题 第21题 第22题
21.(2009•永州)如图,直线a 、b 分别被直线c 、b 所截,如果∠1=∠2,那么∠3+∠4= _________ 度.直线a 、b 分别被直线c 、b 所截.
22.(2010•抚顺)如图所示,已知a∥b,∠1=28°,∠2=25°,则∠3= _________ 度.
23.如图,已知BO 平分∠CBA,CO 平分∠ACB,MN∥BC,且过点O ,若AB=12,AC=14,则△AMN 的周长是 _________ .
第23题第24题
24.(1)如图1,在长方形ABCD中,AB=3cm,BC=2cm,则AB与CD之间的距离为_________ cm;
(2)如图2,若∠_________ =∠_________ ,则AD∥BC;
(3)如图3,DE∥BC,CD是∠ACB的平分线,∠ACB=50°,则∠EDC=_________ 度;
25.已知直线a∥b,点M到直线a的距离是5cm,到直线b的距离是3cm,那么直线a和直线b之间的距离为_________ .
26.如图,已知AB∥CD∥EF,BC∥AD,AC平分∠BAD,那么图中与∠AGE相等的角有_________ 个.
第26题第27题
27.如图所示,AD∥EF∥BC,AC∥EN,则图中与∠1相等的角有_________ 个.
28.如图:直角△ABC中,AC=5,BC=12,AB=13,则内部五个小直角三角形的周长为
_________ .
第28题第29题第30题
29.如图,将网格中的三条线段沿网格线平移后组成一个首尾相接的三角形,至少需要移动_________ 格.
30.如图,面积为12cm2的△ABC沿BC方向平移至△DEF位置,平移的距离是边BC长的两倍,则图中的四边形ACED的面积是_________ cm2.
平行线的判定和性质经典题
参考答案与试题解析
一.选择题(共18小题)
1.如图所示,同位角共有()
2.如图所示,将一张长方形纸对折三次,则产生的折痕与折痕间的位置关系是()
3.下列说法中正确的个数为()
①不相交的两条直线叫做平行线
②平面内,过一点有且只有一条直线与已知直线垂直
③平行于同一条直线的两条直线互相平行
4.在同一平面内,有8条互不重合的直线,l1,l2,l3…l8,若l1⊥l2,l2∥l3,l3⊥l4,l4∥l5…
6.如图所示,AC⊥BC,DE⊥BC,CD⊥AB,∠ACD=40°,则∠BDE等于()
7.如图,AB∥CD,且∠BAP=60°﹣α,∠APC=45°+α,∠PCD=30°﹣α,则α=()
8.下列所示的四个图形中,∠1和∠2是同位角的是()
10.如图,AB∥CD∥EF,AF∥CG,则图中与∠A(不包括∠A)相等的角有()
11.如图所示,BE∥DF,D E∥BC,图中相等的角共有()
13.如图所示,DE∥BC,DC∥FG,则图中相等的同位角共有()
14.如图所示,AD∥EF∥BC,AC平分∠BCD,图中和α相等的角有()
15.如果两个角的两边分别平行,而其中一个角比另一个角的4倍少30°,那么这两个角
16.把直线a沿水平方向平移4cm,平移后的像为直线b,则直线a与直线b之间的距离为
17.(2009•宁德)在下列四个汽车标志图案中,能用平移变换来分析其形成过程的图案是
18.(2004•烟台)
4根火柴棒摆成如图所示的象形“口”字,平移火柴棒后,原图形变成的象形文字是( )
二.填空题(共12小题)
19.已知∠α和∠β的两边互相平行,且∠α=60°,则∠β= 60°或120° .
20.(2004•西宁)如图,AD∥EG∥BC,AC∥EF,则图中与∠1相等的角(不含∠1)有 5 个;若∠1=50°,则∠AHG=130 度.
21.(2009•永州)如图,直线a、b分别被直线c、b所截,如果∠1=∠2,那么∠3+∠4= 180 度.直线a、b分别被直线c、b所截.
22.(2010•抚顺)如图所示,已知a∥b,∠1=28°,∠2=25°,则∠3=53 度.
23.如图,已知BO平分∠CBA,CO平分∠ACB,MN∥BC,且过点O,若AB=12,AC=14,则△AMN 的周长是26 .
24.(1)如图1,在长方形ABCD中,AB=3cm,BC=2cm,则AB与CD之间的距离为 2 cm;(2)如图2,若∠ 1 =∠ 2 ,则AD∥BC;
(3)如图3,DE∥BC,CD是∠ACB的平分线,∠ACB=50°,则∠EDC=25 度;
25.已知直线a∥b,点M到直线a的距离是5cm,到直线b的距离是3cm,那么直线a和直线b之间的距离为2cm或8cm .
26.如图,已知AB∥CD∥EF,BC∥AD,AC平分∠BAD,那么图中与∠AGE相等的角有 5 个.
27.如图所示,AD∥EF∥BC,AC∥EN,则图中与∠1相等的角有 5 个.
28.如图:直角△ABC中,AC=5,BC=12,AB=13,则内部五个小直角三角形的周长为30 .
29.如图,将网格中的三条线段沿网格线平移后组成一个首尾相接的三角形,至少需要移动9 格.
30.如图,面积为12cm2的△ABC沿BC方向平移至△DEF位置,平移的距离是边BC长的两倍,则图中的四边形ACED的面积是36 cm2.。
