勾股定理与旋转问题专题课件
合集下载
勾股定理数学优秀ppt课件
实际应用
在建筑、工程等领域，经常需要利用勾股定理求解直角三角形的边长问题，如计算梯子抵墙 时的长度等。
判断三角形类型问题
判断是否为直角三角形
01
若三角形三边满足勾股定理公式，则该三角形为直角三角形。
判断直角三角形的直角边和斜边
02
在直角三角形中，斜边是最长的一边，通过勾股定理可以判断
哪条边是斜边，哪条边是直角边。
06
总结回顾与展望未来
关键知识点总结回顾
勾股定理的定义和表达式
在直角三角形中，直角边的平方和等于斜边的平方，即a²+b²=c²。
勾股定理的证明方法
通过多种几何图形（如正方形、梯形等）的面积关系来证明勾股定 理。
勾股定理的应用场景
在几何、三角学、物理学等领域中广泛应用，如求解三角形边长、 角度、面积等问题。
勾股定理与其他数学定理关系探讨
与三角函数关系
勾股定理是三角函数的基础，通 过勾股定理可以推导出正弦、余 弦、正切等三角函数的基本关系。
与向量关系
在向量空间中，勾股定理可以表示 为两个向量的点积等于它们模长的 平方和，这进一步揭示了勾股定理 与向量的紧密联系。
与几何图形关系
勾股定理在几何图形中有着广泛的 应用，如求解直角三角形、矩形、 菱形等图形的边长、面积等问题。
勾股定理是数学中的基本定理之一， 也是几何学中的基础概念，对于理 解三角形、圆等几何形状的性质具 有重要意义。
历史发展及应用
历史发展
勾股定理最早可以追溯到古埃及时期，但最为著名的证明是由 古希腊数学家毕达哥拉斯学派给出的。在中国，商高在周朝时 期就提出了“勾三股四弦五”的勾股定理的特例。
应用
勾股定理在几何、三角、代数、物理等多个领域都有广泛应用， 如求解三角形边长、角度、面积等问题，以及力学、光学等领 域的计算。
在建筑、工程等领域，经常需要利用勾股定理求解直角三角形的边长问题，如计算梯子抵墙 时的长度等。
判断三角形类型问题
判断是否为直角三角形
01
若三角形三边满足勾股定理公式，则该三角形为直角三角形。
判断直角三角形的直角边和斜边
02
在直角三角形中，斜边是最长的一边，通过勾股定理可以判断
哪条边是斜边，哪条边是直角边。
06
总结回顾与展望未来
关键知识点总结回顾
勾股定理的定义和表达式
在直角三角形中，直角边的平方和等于斜边的平方，即a²+b²=c²。
勾股定理的证明方法
通过多种几何图形（如正方形、梯形等）的面积关系来证明勾股定 理。
勾股定理的应用场景
在几何、三角学、物理学等领域中广泛应用，如求解三角形边长、 角度、面积等问题。
勾股定理与其他数学定理关系探讨
与三角函数关系
勾股定理是三角函数的基础，通 过勾股定理可以推导出正弦、余 弦、正切等三角函数的基本关系。
与向量关系
在向量空间中，勾股定理可以表示 为两个向量的点积等于它们模长的 平方和，这进一步揭示了勾股定理 与向量的紧密联系。
与几何图形关系
勾股定理在几何图形中有着广泛的 应用，如求解直角三角形、矩形、 菱形等图形的边长、面积等问题。
勾股定理是数学中的基本定理之一， 也是几何学中的基础概念，对于理 解三角形、圆等几何形状的性质具 有重要意义。
历史发展及应用
历史发展
勾股定理最早可以追溯到古埃及时期，但最为著名的证明是由 古希腊数学家毕达哥拉斯学派给出的。在中国，商高在周朝时 期就提出了“勾三股四弦五”的勾股定理的特例。
应用
勾股定理在几何、三角、代数、物理等多个领域都有广泛应用， 如求解三角形边长、角度、面积等问题，以及力学、光学等领 域的计算。
《17.1勾股定理 勾股定理的应用 》课件
1．了解勾股定理的发现过程，掌握勾股定 理的内容，会用面积法证明勾股定理。 2．培养在实际生活中发现问题总结规律的 意识和能力。 3．介绍我国古代在勾股定理研究方面所取 得的成就，激发爱国热情，勤奋学习。 重点：勾股定理的内容及证明。 难点：勾股定理的证明。
（一）、课前准备（2分钟）
1、直角△ABC的主要性质是：∠C=90°（用几何
c2 = a2 + b2
有一种特殊的直角三角形， 已知一边可以求另外两边长
A
A
c a
a
C
45° b
B
C
c
30°
b
B
a:b:c=1:1:√2
a:b:c=1:√3:2
a= 5 cm时求b=？c=？ c= 6 cm时求b=？a=？
勾股小常识：勾股数
1、 基本勾股数如：大家一定要熟记
3、4、5 5、12、13 7、24、25
（2）在长方形ABCD中，宽AB为1m，长BC为 2m ，求AC长．
A
D
1m
B
2m
C
在Rt△ ABC中，∠B=90°,由勾股定理可知：
AC AB2 BC2 12 22 5
活动2 问题
（1）在长方形ABCD中AB、BC、AC大小关系？
D
C
AB＜BC＜AC
AC 2 AB2 BC 2
AB
2、下列说法正确的是（ D ）
A.若a、b、c是△ABC的三边，则: a2 b2 c2
B.若a、b、c是Rt△ABC的三边，则 a2 b2 c2 C.若a、b、c是Rt△ABC的三边，A 90 ， 则 a2 b2 c2
D.若a、b、c是Rt△ABC的三边，C 90 ，
则 a2 b2 c2
《勾股定理》PPT优质课件(第1课时)
A． 3
B．3
C． 5
D．5
E
课堂检测
基础巩固题
1. 若一个直角三角形的两直角边长分别为9和12，则斜边的
长为（ C）
A.13
B.17
C. 15
D.18
2.若一个直角三角形的斜边长为17，一条直角边长为15，则
另一直角边长为（ A ）
A.8
B.40
C.50
D.36
3.在Rt△ABC中，∠C=90°，若a︰b=3︰4，c=100，则 a= _6_0___，b = __8_0___.
课堂检测
4．如图，所有的四边形都是正方形，所有的三角形都是直角三角 形，其中最大的正方形的边长为7cm,则正方形A，B，C，D的面 积之和为_____4_9_____cm2 ．
C D
B A
7cm
课堂检测
能力提升题
在Rt△ABC中，AB＝4，AC＝3，求BC的长.
解：本题斜边不确定，需分类讨论：
当AB为斜边时，如图，BC 42 32 7;
形，拼成一个新的正方形.
探究新知 剪、拼过程展示：
b
a ca
朱实
b 朱实 黄实朱实
c 〓b
ba
朱实
a
M a P bb
N
探究新知 “赵爽弦图”
c
朱实
b
朱实
黄实 朱实
a
朱实
证明：∵S大正方形＝c2， S小正方形＝(b-a)2,
∴S大正方形＝4·S三角形＋S小正方形，
探究新知
毕达哥拉斯证法：请先用手中的四个全等的直角三角形按图 示进行拼图，然后分析其面积关系后证明吧.
因此设a=x,c=2x,根据勾股定理建立方程得 (2x)2-x2=152，
与勾股定理相关的旋转问题
例3 如图，在等腰直角三角形ABC中，∠ABC=90°，D为AC 边上的中点，过点D作DE⊥DF，交AB于点E，交BC于点F。求 证：AE2+CF2=DE2+DF2.
即学即练 已知凸四边形ABCD中，∠ABC =∠ADC = 45°，AC＝AD，
求证：BD2=2AB2+BC2.
小结
1.这节课你学到了哪些解题的思想和方法? 2.本节课你还有什么困惑?
与勾股定理相关的旋转问题
学习目标
1.掌握与勾股定理相关的旋转问题模型； 2.会用旋转法做辅助线，构造直角三角形 使用勾股定理； 3.掌握与勾股定理相关的旋转问题的解题 方法和技巧。
方法指导：对于条件较分散而题中又含 公共顶点相等的边（一般是相邻的边） 时，常采用旋转法，将分散条件集中到 一个三角形中去。
例1 如图，在△ABC中，∠BAC=90°，AB=AC，点D，E在BC 上，且∠DAE=45°，求证：CD2+BE2=DE2.
即学即练 如图，等腰直角三角形ABC中，点D在斜边BC上，求证：
BD2+CD2=2AD2.
例2 如图所示，在△ABC中，∠ACB=90°，AC=BC，P是 △ABC内一点，且PA=3，PB=1，PC=2，求∠BPC的度数。
即学即练 如图，P是等边三角形ABC内一点。
（1）若PA=4，PC=3，PB=5，求∠APC； （2）若∠APB：∠BPC：∠CPA=5：6：7，则以PA、PB、PC 为边的三角形的三个角分别是多少？
即学即练 如图，P是正方形ABCD内一点，且 PA 1, PB 2, PC 3 ，
求∠APB的度数。
勾股定理与旋转
1 如图正方形ABCD 的边长为3，E 为CD 边上的一点，DE=1,以点A 为中心，把∆时针旋转90º得∆ABE ´，连接EE ´，则EE ´的长为＿＿＿＿＿2如图，P 为等边三角形内一点，PC=5,PB=12, ∠BPC=150º （1）求PA 的长（2）将⊿BAP 绕点B 顺时针旋转60º，请画出旋转后的图形，并标出相应点的字母，连接CA ＇,则∆BA ´P 为＿＿三角形，∆PA ´C 为＿＿三角形，PA ´=＿＿＿(3) PC ， PA ´ ，A ´C 之间有何等量关系3 ∆ABC 中，∠BAC=90º AB=AC ∠EAD=45º （1）当点在线段上时，求证BE ²＋CF ²=EF ²(2)将∆ABE 绕＿＿点＿＿时针旋转＿＿度,得∆ACE ´，连接DE ´，则∠E ´CD=＿＿∠1＋∠2=＿＿＿ ∠E ´AD=∠2＋∠3=＿＿＿ ∆ AED ≌∆＿＿（3）当点E 在线段BC 上时，D 在BC 延长线上时，上述结论是否还成立，若成立，请证明，若不成立，请说明理由BCDEEABC PABCDE4, ∆ABC 中， ∠ACB=90º，AC=BC ，点P 是∆ABC 内一点，且PA=6，PB=2，PC=4，求∠BPC 的度数5、 P 是正方形ABCD 内一点，连接PA,PB,PC （1）将∆PAB 绕点B 顺时针旋转90º到∆P ´CB 的位置，若PA=2，PB=4，∠APB=135º ,求PP ´及PC 的长6 如图，Rt ∆ABC 中，AC=BC ， ∠ACB=90º ，AP ²+QB ²=PQ ²，将∆ACP 绕点C 逆时针旋转90º得∆CBP ´，连QP ´（1）求证PQ=P ´Q （2）求证∆CPQ ≌CP ´Q （3）求∠PCQBCAPCDBAPBCQPAP7 正∆ABC 中，P 为内部一点（1）若PA=3，PB=4，PC=5，求∠APB （2）若PA ²＋PB ²=PC ²，求∠APB8、如图1，P 是正三角形ABC 内的一点，且PA=6，PB=8，PC=10，求∠APB 的度数。
1勾股定理(第1课时)(教学PPT课件(华师大版))28张
正方形中小方格的个数，你有什么猜想？
1955年希腊发行的一枚纪念邮票.
讲授新课
知识点一 直角三角形三边的关系
视察正方形瓷砖铺成的地面.
（1）正方形P的面积是
1
（2）正方形Q的面积是
1
平方厘米；
（3）正方形R的面积是
2
平方厘米.
平方厘米；
上面三个正方形的面积之间有什么关系？
等腰直角三角形ABC三边长度之间存在什么关系吗？
程.
b
a
b
a
c
c
b
c
c
a
a
b
讲授新课
证明：大正方形的面积=(a+b)2.
四个个全等的直角三角形和小正方形的面积
1
2
2
之和= 4 ab c 2ab c .
2
b
由题可知(a+b)2=2ab+c2，
a
c
化简可得a2+b2=c2.
我们利用拼图的方法，将形的问题
与数的问题结合起来，再进行整式
A的面积
B的面积
C的面积
左图
4
9
13
右图
16
9
25
结论：以直角三角形两直角边为边长的小正方形的面积的和，等于以斜边为边长的正方形的面积.
SA+SB=SC
讲授新课
猜想:两直角边a、b与斜边 c 之间的关系？
A
a
B b
c
a2+b2=c2
C
讲授新课
概念总结
由上面的探索可以发现：对于任意的直角三角形，如果它的两
数学（华东师大版）
八年级 上册
第14章 勾股定理
1955年希腊发行的一枚纪念邮票.
讲授新课
知识点一 直角三角形三边的关系
视察正方形瓷砖铺成的地面.
（1）正方形P的面积是
1
（2）正方形Q的面积是
1
平方厘米；
（3）正方形R的面积是
2
平方厘米.
平方厘米；
上面三个正方形的面积之间有什么关系？
等腰直角三角形ABC三边长度之间存在什么关系吗？
程.
b
a
b
a
c
c
b
c
c
a
a
b
讲授新课
证明：大正方形的面积=(a+b)2.
四个个全等的直角三角形和小正方形的面积
1
2
2
之和= 4 ab c 2ab c .
2
b
由题可知(a+b)2=2ab+c2，
a
c
化简可得a2+b2=c2.
我们利用拼图的方法，将形的问题
与数的问题结合起来，再进行整式
A的面积
B的面积
C的面积
左图
4
9
13
右图
16
9
25
结论：以直角三角形两直角边为边长的小正方形的面积的和，等于以斜边为边长的正方形的面积.
SA+SB=SC
讲授新课
猜想:两直角边a、b与斜边 c 之间的关系？
A
a
B b
c
a2+b2=c2
C
讲授新课
概念总结
由上面的探索可以发现：对于任意的直角三角形，如果它的两
数学（华东师大版）
八年级 上册
第14章 勾股定理
《勾股定理》 完整版PPT课件
弦
勾
勾
股
股
证法三： 伽菲尔德证法:
a bc
a
c
1、整体看
b
2、分割看
有趣的总统证法
美国第二十任总统伽菲尔德的证法在数学史上被传为佳话
人们为了纪念他对勾股定理直观、简捷、易懂、明了的证明，
就把这一证法称为“总统”证法。 D
bc c
C a
Aa
bD
勾股定理
如果直角三角形两直角边分别为a，b，斜边
为c，那么 a2 + b2 = c2
练习
1.在RtABC中，AB=c，BC=a，AC=b，
B=90
(1)已知a=6,b=10,求c的长度（ B ）
A6
B8
C 10 D 12
(2)已知a=24,c=7,求b的长度（ D ）.
A 20
B 11 C 13
D 25
A
c
b
B
a
C
2.在Rt△ABC中, a=5,c=13,
则下列计算正确的是 （ B ）
2 、运用“勾股定理”应注意什么问题？ 3、你还有什么疑惑或没有弄懂的地方？
拓展
在波平如静的湖面上,有一朵美丽的红莲 ,它高出
水面1米 ,一阵大风吹过,红莲被吹至一边,花朵齐
及水面,如果知道红莲移动A
x2+22=(x+1)2
1
C
2
H
┓
?x
B
美丽的勾股树
（×）
（2）若a、b、c为Rt△ABC的三边,则a2+b2=c2.
（×）
C不一定代表 直角三角形
的斜边哦
练习
4.求下列直角三角形中未知边的长: 5
(精选幻灯片)勾股定理ppt课件
2 2 22
“总统证法”． 比较上面二式得 c2=a2+b2
16
1.求下列图中表示边的未知数x、y、z的值.
81 144
144 169
z
625 576
①
②
③
17
做一做：
A
625
P
C
B
400
P的面积 =___2_2__5________ AB=_2__5_______ BC=__2_0_______
b c
a2+b2=c2吗？
• 1881年，伽菲尔 德就任美国第二
A b 1 E aB ∵ S梯形ABCD= 2 a+b2
十任总统.后来， 1
人们为了纪念他 对勾股定理直观、 简捷、易懂、明
= (a2+2ab+b2) 2
又∵ S梯形 ABCD=S
AED+S
EBC+S
CED
了的证明，就把 这一证法称为
1 1 11 = ab+ ba+ c2= (2ab+c2)
33
34
C A
（2）在图2-2中，正 方形A，B，C中各含 有多少个小方格？它 们的面积各是多少？
B C
图2-1
A
（3）你能发现图2-1 中三个正方形A，B， C的面积之间有什么
B 图2-2
关系吗？
（图中每个小方格代表一个单位面积） SA+SB=SC
即：两条直角边上的正方形面积之和等于
斜边上的正方形的面积
3
s1 s2
s3
返 拼回 图 4
合作 & 交S流1+☞S2=S3
a等²+腰a直²=角c三²角形两直角边
“总统证法”． 比较上面二式得 c2=a2+b2
16
1.求下列图中表示边的未知数x、y、z的值.
81 144
144 169
z
625 576
①
②
③
17
做一做：
A
625
P
C
B
400
P的面积 =___2_2__5________ AB=_2__5_______ BC=__2_0_______
b c
a2+b2=c2吗？
• 1881年，伽菲尔 德就任美国第二
A b 1 E aB ∵ S梯形ABCD= 2 a+b2
十任总统.后来， 1
人们为了纪念他 对勾股定理直观、 简捷、易懂、明
= (a2+2ab+b2) 2
又∵ S梯形 ABCD=S
AED+S
EBC+S
CED
了的证明，就把 这一证法称为
1 1 11 = ab+ ba+ c2= (2ab+c2)
33
34
C A
（2）在图2-2中，正 方形A，B，C中各含 有多少个小方格？它 们的面积各是多少？
B C
图2-1
A
（3）你能发现图2-1 中三个正方形A，B， C的面积之间有什么
B 图2-2
关系吗？
（图中每个小方格代表一个单位面积） SA+SB=SC
即：两条直角边上的正方形面积之和等于
斜边上的正方形的面积
3
s1 s2
s3
返 拼回 图 4
合作 & 交S流1+☞S2=S3
a等²+腰a直²=角c三²角形两直角边
勾股定理ppt课件
创设情境 数学是科技发展中最重要的学科，2002年全球最顶级数学家大 会在北京召开，大会会徽是：
赵爽弦图
数学文化 赵爽，名婴，字君卿，是我国三国时期杰出的数学家， 他在注解《周髀算经》时给出的这个图.
创设情境 请你观察这个图中有哪些基本几何图形？2002年的数学家大会为 什么用这个图作为会徽呢？
继续探究
1.如图，表格中左、右各有一组图，每组图中的三个正方形的面积分 别是多少，它们之间有什么关系？（设表格中每个小正方形面积为1）
C A
B
C A
B
继续探究 2.观察图形，请完成下面表格：
两个图中正 方形C的面积 如何求呢？
项目
左图 右图 A、B、C 面积关系
A的面积 4 16
B的面积 9 9
A
8
B 6
C
应用新知
例2 如图，图中所有的三角形都是直角三角形，四边形都是正方形，已知正方形 B，D的边长分别是16，12，SE=625，S1=400，求正方形A、C的边长. 解：依题意，得SB=162=256，SD=122=144， ∵S1=SA+SB且S1=400， ∴SA=S1-SB=400-256=144， ∴正方形A的边长为 144 12， ∵SE=S1+S2且SE=625，S1=400， ∴S2=SE-S1=625-400=225， ∵S2=SC+SD，∴SC=S2-SD=225-144=81， ∴正方形C的边长 81 9 .
证明2： 如图，四个全等直角三角形拼成
如图所示的正方形，直角边为a、
b，斜边为c. S四个直角三角形面积和= 4 1 ab 2ab，
2
S四个直角三角形面积和=(a+b)2-c2
《勾股定理》数学教学PPT课件(10篇)
= (DE+CE)·( DE- BE)
=BD·
CD.
D
B
E
C
课堂小
结
利用勾股定理解
决实际问题
勾股定理
的应用
构造直角三角形
解决实际问题
第十七章 勾股定理
17.1 勾股定理
第3课时
利用勾股定理作图和计算
知识要点
1.勾股定理与数轴、坐标系
2.勾股定理与网格
3.勾股定理与几何图形
新知导入
想一想：
我们知道数轴上的点有的表示有理数，有的表示无理数，你
能在数轴上画出表示 13 的点吗？
如果能画出长为 13 的线段，就能在数轴上画出表示 13 的
2
点.容易知道，长为
的线段是两条直角边的长都为1的直角三
角形的斜边.
长为 13 的线段能是直角边的长为正整数的直角三角形的
斜边吗？
新知导入
想一想：
利用勾股定理，可以发现，直角边的长为正整数2, 3
知识
的直角三角形的斜边长为
AC2+BC2=AB2
由上面的例子，我们猜想：
命题1 如果直角三角形的两条直角边长分别为a,b，斜边
长为c,那么a2+b2=c2.两直角边的平方和等于斜边的平方.
a
c
b
课程讲授
1
勾股定理
下面让我们跟着以前的数学家们用拼图法来证明这一猜想.
c
证明：∵S大正方形＝c2，
S小正方形＝(b-a)2,
b
a
b-a
例 如图是由4个边长为1的正方形构成的“田字格”，只用没有刻
度的直尺在这个“田字格”中最多可以作出长度为
8
_____条．
=BD·
CD.
D
B
E
C
课堂小
结
利用勾股定理解
决实际问题
勾股定理
的应用
构造直角三角形
解决实际问题
第十七章 勾股定理
17.1 勾股定理
第3课时
利用勾股定理作图和计算
知识要点
1.勾股定理与数轴、坐标系
2.勾股定理与网格
3.勾股定理与几何图形
新知导入
想一想：
我们知道数轴上的点有的表示有理数，有的表示无理数，你
能在数轴上画出表示 13 的点吗？
如果能画出长为 13 的线段，就能在数轴上画出表示 13 的
2
点.容易知道，长为
的线段是两条直角边的长都为1的直角三
角形的斜边.
长为 13 的线段能是直角边的长为正整数的直角三角形的
斜边吗？
新知导入
想一想：
利用勾股定理，可以发现，直角边的长为正整数2, 3
知识
的直角三角形的斜边长为
AC2+BC2=AB2
由上面的例子，我们猜想：
命题1 如果直角三角形的两条直角边长分别为a,b，斜边
长为c,那么a2+b2=c2.两直角边的平方和等于斜边的平方.
a
c
b
课程讲授
1
勾股定理
下面让我们跟着以前的数学家们用拼图法来证明这一猜想.
c
证明：∵S大正方形＝c2，
S小正方形＝(b-a)2,
b
a
b-a
例 如图是由4个边长为1的正方形构成的“田字格”，只用没有刻
度的直尺在这个“田字格”中最多可以作出长度为
8
_____条．
旋转与勾股定理的三种题型ppt课件
11
变式3： 如图P是正方形ABCD内一点，点P到正方形的三 个顶点A、B、C的距离分别为PA=1，PB=2，PC=3。求此 正方形ABCD面积。 变式4：正方形ABCD内一点P，使得PA：PB：PC= 1：2：3，求∠APB的度数。
12
下课了!
诲 •悟性的高低取决于有无悟“心 人 ”,其实,人与人的差别就在于你 不 是否去思考, 去发现，去总结。 倦
由勾股定理的逆定理知∠APPl=90o
∠APB=∠APPl+∠BPPl=900+600=1500
10
变式1：如图，P是正三角形ABC内的一点，且 PA=6，PB=8，PC=10，求∠APB的度数。
变式2：如图1，P是正三角形ABC内的一点，且 PA=3a，PB=4a，PC=5a，求∠APB的度数。
7
（一）正三角形类型 在正ΔABC中，P为ΔABC内一点，将ΔABP绕A点按逆时针 方向旋转600，使得AB与AC重合。经过这样旋转变化， 将图（1-1-a）中的PA、PB、PC三条线段集中于图（1-1b）中的一个ΔP'CP中，此时ΔP'AP也为正三角形。
8
例3
如图，点P是等边△ABC内一点，且PA=3， PB=4，PC=5，求∠APB的度数。
23
解：如图，延长AB交KF于点O，延长AC交GM于点P， 所以，四边形AOLP是正方形， 边长AO=AB+AC=3+4=7， 所以，KL=3+7=10，LM=4+7=11， 因此，矩形KLMJ的面积为10×11=110． 故选C．
24
(2011·温州中考)我国汉代数学家赵爽为了证明勾股定理， 创制了一幅“弦图”，后人称其为“赵爽弦图”(如图1).图2 由弦图记 图中正方形ABCD，正方形EFGH，正方形MNKT的面积分别为S1， S2,S3,若S1+S2+S3=10，则S2的值是_____.
变式3： 如图P是正方形ABCD内一点，点P到正方形的三 个顶点A、B、C的距离分别为PA=1，PB=2，PC=3。求此 正方形ABCD面积。 变式4：正方形ABCD内一点P，使得PA：PB：PC= 1：2：3，求∠APB的度数。
12
下课了!
诲 •悟性的高低取决于有无悟“心 人 ”,其实,人与人的差别就在于你 不 是否去思考, 去发现，去总结。 倦
由勾股定理的逆定理知∠APPl=90o
∠APB=∠APPl+∠BPPl=900+600=1500
10
变式1：如图，P是正三角形ABC内的一点，且 PA=6，PB=8，PC=10，求∠APB的度数。
变式2：如图1，P是正三角形ABC内的一点，且 PA=3a，PB=4a，PC=5a，求∠APB的度数。
7
（一）正三角形类型 在正ΔABC中，P为ΔABC内一点，将ΔABP绕A点按逆时针 方向旋转600，使得AB与AC重合。经过这样旋转变化， 将图（1-1-a）中的PA、PB、PC三条线段集中于图（1-1b）中的一个ΔP'CP中，此时ΔP'AP也为正三角形。
8
例3
如图，点P是等边△ABC内一点，且PA=3， PB=4，PC=5，求∠APB的度数。
23
解：如图，延长AB交KF于点O，延长AC交GM于点P， 所以，四边形AOLP是正方形， 边长AO=AB+AC=3+4=7， 所以，KL=3+7=10，LM=4+7=11， 因此，矩形KLMJ的面积为10×11=110． 故选C．
24
(2011·温州中考)我国汉代数学家赵爽为了证明勾股定理， 创制了一幅“弦图”，后人称其为“赵爽弦图”(如图1).图2 由弦图记 图中正方形ABCD，正方形EFGH，正方形MNKT的面积分别为S1， S2,S3,若S1+S2+S3=10，则S2的值是_____.
《勾股定理》说课PPT
教学目标
1.【知识与技能】
①理解并掌握勾股定理的内容和证明，能够灵活运 用勾股定理及其计算； ②通过观察分析，大胆猜想，并探索勾股定理，培 养学生动手操作、合作交流、逻辑推理的能力。
2.【过程与方法】
在探索勾股定理的过程中，让学生经历“观察-猜想 -归纳-验证”的数学思想，并体会数形结合和从特 殊到一般的思想方法。
深入探究 网络信息
要求学生利用网格画一个两直角边分别 为2、3的三角形，用不同的方法求面积，以 及探究直角三角形三边存在的关系。
（2+3）2-4*1/2*2*3=13=22+32 或4*1/2*2*3+1=13
利用正方形网格让学生感知其的实用性及便 捷性。
2
规律猜想 直达快车
由上面探究我们可以得出在直角三角形中，两直角 边的平方和等于斜边的平方。由此提出命题：如果 一个三角形是直角三角形，那么其两直角边的平方 和等于斜边的平方。分析并根据命题画图，写出已 知和求证。画图：a2+b2=c2。联想到用字母表示数字 的方法，贯彻代数的应用思想。
数字验证 拼图效果
证明勾股定理：证明该命题的方法有很多，先让学 生进行讨论回答。展示分割拼接的过程，展示拼图 出的效果，鼓励学生代表作示范演示，然后介绍古 代数学家赵爽的的证明方法，老师通过准备的PPT进 行演示。
实践应用 拓展提高
1.出示题目①在△ABC中，∠C=900，AC=21m,BC=28m. i 求△ABC的面积 ii斜边AB的长 iii 求高CD. 引导学生进行解决问题 ②媒体课件演示FLASH小动画片：某楼房三楼失火，消防 员赶来救火，了解到每层楼高3米，消防员取来6.5米长 的云梯，如果梯子底部离墙基距离为2.5米。问：消防员 能否进入三楼救火? 布置作业 试一试：你能把两个边长分别为5、12的正方形经过切割 后拼接成一个正方形吗？如果可以，那么所得到的新正 方形的边长为多少呢？
勾股定理与旋转
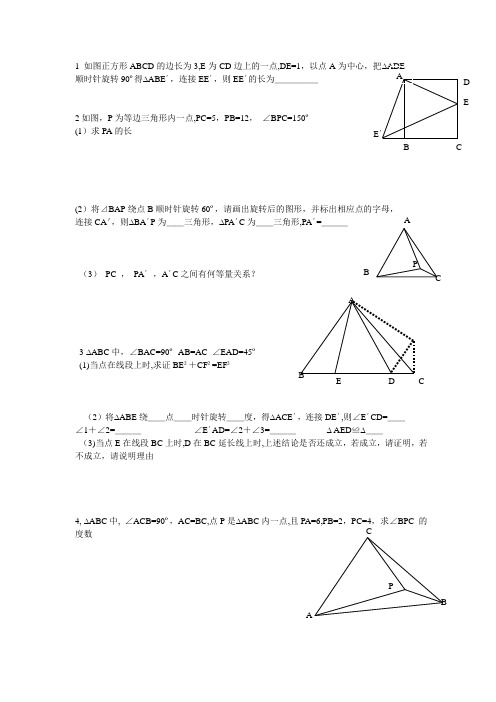
1 如图正方形ABCD 的边长为3,E 为CD 边上的一点,DE=1，以点A顺时针旋转90º得∆ABE ´，连接EE ´，则EE ´的长为＿＿＿＿＿2如图，P 为等边三角形内一点,PC=5，PB=12， ∠BPC=150º (1）求PA 的长(2）将⊿BAP 绕点B 顺时针旋转60º，请画出旋转后的图形，并标出相应点的字母，连接CA ＇，则∆BA ´P 为＿＿三角形，∆PA ´C 为＿＿三角形,PA ´=＿＿＿（3） PC ， PA ´ ，A ´C 之间有何等量关系？3 ∆ABC 中，∠BAC=90º AB=AC ∠EAD=45º (1)当点在线段上时,求证BE ²＋CF ²=EF ²（2）将∆ABE 绕＿＿点＿＿时针旋转＿＿度，得∆ACE ´，连接DE ´,则∠E ´CD=＿＿∠1＋∠2=＿＿＿ ∠E ´AD=∠2＋∠3=＿＿＿ ∆ AED ≌∆＿＿（3)当点E 在线段BC 上时,D 在BC 延长线上时,上述结论是否还成立，若成立，请证明，若不成立，请说明理由4, ∆ABC 中, ∠ACB=90º，AC=BC,点P 是∆ABC 内一点,且PA=6,PB=2，PC=4，求∠BPC 的度数B CD EE A B CPA B CD E BC AP5、 P 是正方形ABCD 内一点，连接PA ，PB,PC （1）将∆PAB 绕点B 顺时针旋转90º到∆P ´CB 的位置，若PA=2，PB=4，∠APB=135º ，求PP ´及PC 的长6 如图，Rt ∆ABC 中,AC=BC ， ∠ACB=90º ,AP ²+QB ²=PQ ²，将∆ACP 绕点C 逆时针旋转90º得∆CBP ´，连QP ´(1）求证PQ=P ´Q (2)求证∆CPQ ≌CP ´Q （3）求∠PCQ7 正∆ABC 中，P 为内部一点(1）若PA=3，PB=4，PC=5，求∠APB (2）若PA ²＋PB ²=PC ²，求∠APB8、如图1,P 是正三角形ABC 内的一点，且PA=6，PB=8,PC=10,求∠APB 的度数。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
C NP
BM
A
PPT学习交流
13
A
• 求∠BPC
P
B
C
PPT学习交流
6
• 练习1.P是正三角形ABC内一点，且
PA=6,PB=8,PC=10.
• 求∠APB
A
P
B
C
PPT学习交流
7
• 练习2.P是正三角形ABC内一点，且
PA=3a,PB=4a,PC=5a.
• 求∠APB
A
P
B
C
PPT学习交流
8
• 练习3.在四边形ABCD中，∠ABC=30°， ∠ADC=60°，AD=CD.
• (1)请画出旋转后的图形，说出此时△APB绕
点B旋转了多少度。
A
D
P
B
C
PPT学习交流
4
• (2)求出PG的长度。
• (3)猜想△PGC的形状，并说明理由
• (4)求∠APB
A
D
• (5)求出此正方形ABCD的面积
P
B
C
PPT学习交流
5
• 3.P为正三角形ABC内一点，且 PA=5,PB=4,PC=3.
• 求证：BD2=AB2+BC2
A
D
B
C
PPT学习交流
9
• 练习4.等腰直角三角形ABC的斜边上取两点M、
Байду номын сангаас
N，使得∠MCN=45°
• 求证：MN2=AM2+BN2
C
AM
N
B
PPT学习交流
10
• 练习5、在等腰Rt△ABC中，∠CAB=90°,P是 三角形内一点，且PA=1,PB=3,PC2=7
• 求：∠CPA的大小？ C
P
A
B
PPT学习交流
11
• 练习6.如图所示，△ABC是等腰直角三角形
，AB=AC，D是斜边BC的中点，E、F分别是AB
、AC边上的点，且DE⊥DF，若BE=12，CF=5
．求线段EF的长。
B
D
E
A
FC
PPT学习交流
12
• 练习7、如图，在△ABC中，∠B=90°，M为AB 上一点，AM=BC，N为BC上一点，CN=BM，连 接AN、CM交于点P。求∠APM的大小。
勾股定理与旋转问题专题
PPT学习交流
1
• 1.在△ABC中，∠ACB=90°，AC=BC，P是 △ABC内一点，PB=1，PC=2,PA=3.
• 求∠BPC
C
P
A
B
PPT学习交流
2
P' C
P
A
B
PPT学习交流
3
• 2.P是正方形ABCD内一点，PA=1,PB=2,PC=3, 以B为旋转中心，将△ABP按顺时针方向旋转， 使得点A与C重合，点P旋转到点G.
BM
A
PPT学习交流
13
A
• 求∠BPC
P
B
C
PPT学习交流
6
• 练习1.P是正三角形ABC内一点，且
PA=6,PB=8,PC=10.
• 求∠APB
A
P
B
C
PPT学习交流
7
• 练习2.P是正三角形ABC内一点，且
PA=3a,PB=4a,PC=5a.
• 求∠APB
A
P
B
C
PPT学习交流
8
• 练习3.在四边形ABCD中，∠ABC=30°， ∠ADC=60°，AD=CD.
• (1)请画出旋转后的图形，说出此时△APB绕
点B旋转了多少度。
A
D
P
B
C
PPT学习交流
4
• (2)求出PG的长度。
• (3)猜想△PGC的形状，并说明理由
• (4)求∠APB
A
D
• (5)求出此正方形ABCD的面积
P
B
C
PPT学习交流
5
• 3.P为正三角形ABC内一点，且 PA=5,PB=4,PC=3.
• 求证：BD2=AB2+BC2
A
D
B
C
PPT学习交流
9
• 练习4.等腰直角三角形ABC的斜边上取两点M、
Байду номын сангаас
N，使得∠MCN=45°
• 求证：MN2=AM2+BN2
C
AM
N
B
PPT学习交流
10
• 练习5、在等腰Rt△ABC中，∠CAB=90°,P是 三角形内一点，且PA=1,PB=3,PC2=7
• 求：∠CPA的大小？ C
P
A
B
PPT学习交流
11
• 练习6.如图所示，△ABC是等腰直角三角形
，AB=AC，D是斜边BC的中点，E、F分别是AB
、AC边上的点，且DE⊥DF，若BE=12，CF=5
．求线段EF的长。
B
D
E
A
FC
PPT学习交流
12
• 练习7、如图，在△ABC中，∠B=90°，M为AB 上一点，AM=BC，N为BC上一点，CN=BM，连 接AN、CM交于点P。求∠APM的大小。
勾股定理与旋转问题专题
PPT学习交流
1
• 1.在△ABC中，∠ACB=90°，AC=BC，P是 △ABC内一点，PB=1，PC=2,PA=3.
• 求∠BPC
C
P
A
B
PPT学习交流
2
P' C
P
A
B
PPT学习交流
3
• 2.P是正方形ABCD内一点，PA=1,PB=2,PC=3, 以B为旋转中心，将△ABP按顺时针方向旋转， 使得点A与C重合，点P旋转到点G.