等腰梯形的性质
等腰梯形课件

图形定义
总结词
通过图形展示等腰梯形的特点。
详细描述
在PPT中插入一个等腰梯形的图形,并标注出它的两腰、底边和两个底角,以便 学生更好地理解等腰梯形的定义。
性质和定理
总结词
介绍等腰梯形的一些重要性质和定理 。
详细描述
在PPT中列出等腰梯形的一些重要性 质和定理,如“等腰梯形的两腰相等 ”、“等腰梯形的两底角相等”等, 并给出相应的证明过程。
步骤四
连接底边的两个端点,完成等 腰梯形的作图。
等腰梯形和其他图形的联系
与平行四边形的联系
等腰梯形可以看作是一个平行四边形 去掉一个直角三角形后形成的。
与三角形的联系
等腰梯形可以看作是由两个三角形组 成的,其中一个是直角三角形,另一 个是等腰三角形。
THANKS 感谢观看
在建筑设计中的应用
建筑设计中的等腰梯形元素
在建筑设计中,等腰梯形经常被用作窗户、门洞或其他装饰 元素的形状,以增加建筑的美观性和设计感。
等腰梯形在结构设计中的应用
在某些建筑结构中,等腰梯形的设计可以使结构更加稳定和 安全,例如桥梁的斜拉索或高层建筑的支撑结构。
在日常生活中的应用
日常生活中的等腰梯形物品
等腰梯形的面积和周长之间没有直接的关系,它们分别由不同的公式计
算得出。
02
面积与周长的独立性
在等腰梯形中,改变上底、下底和高的长度会影响面积,同时的,改变一个不会影响另一个。
03
实际应用
在解决几何问题时,需要综合考虑面积和周长的关系,以得出正确的结
论。
04 等腰梯形的实际应用
在几何图形中的应用
等腰梯形在几何证明中的应用
等腰梯形是几何图形中的一种,它在解决几何问题,特别是关于角度、边长和面 积的问题时非常有用。例如,利用等腰梯形的性质证明某些角度相等或边长相等 。
等腰梯形的性质定理和判定定理及其证明最新版

2
C
E
知识拓展:用下面方法证明等腰梯形的判定定理
⑴如图,分别延长梯形ABCD的腰BA、CD设它 们相交于点E.通过证明Δ EAD 和Δ EBC是
等腰三角形,来证明定理
已知:在梯形ABCD中,AD∥BC,∠B=∠C
求证:AB=CD 证明:∵∠B=∠C ∴EB=EC
又∵ AD∥BC ∴∠1=∠B, ∠2=∠C
现代人每天生活在纷繁、复杂的社会当中,紧张、高速的节奏让人难得有休闲和放松的时光。人们在奋斗事业的搏斗中深感身心的疲惫。然而,如果你细心观察,你会发现作 为现代人,其实人们每天都在尽可能的放松自己,调整生活节奏,追求充实快乐的人生。看似纷繁的社会里,人们的生活方式其实也不复杂。大家在忙忙碌碌中体味着平凡的 人生乐趣。由此我悟出一个道理,那就是----生活简单就是幸福。生活简单就是幸福。一首优美的音乐、一支喜爱的歌曲,会让你心境开朗。你可以静静地欣赏你喜爱的音乐, 可以在流荡的旋律中回忆些什么,或者什么都不去想;你可以一个人在房间里大声的放着摇滚,也可以在网上用耳麦与远方的朋友静静地共享;你还可以一边放送着音乐,一 边做着家务....生活简单就是幸福。一杯清茶,或一杯咖啡,放在你的桌边,你的心情格外的怡然。你可以浏览当天的报纸,了解最新的国内外动态,哪怕是街头趣闻;或者捧 一本自己喜欢的杂志、小说,从字里行间获得那种特别的轻松和愉悦....生活简单就是幸福。经过精心的烹制,一桌可心的菜肴就在你的面前,你招呼家人快来品尝,再备上最 喜欢的美酒,这是多么难得的享受!生活简单就是幸福。春暖花开的季节,或是清风送爽的金秋,你和家人一起,或是朋友结伴,走出户外,来一次假日的郊游,享受大自然 带给你的美丽、芬芳。吸一口新鲜的空气,忘却都市的喧嚣,身心仿佛受到一番洗涤,这是一种什么样的轻松感受!生活简单就是幸福。你参加朋友们的一次聚会,那久违的 感觉带给你温馨和激动,在觥酬交错之间你享受与回味真挚的友情。朋友,是那样的弥足珍贵....生活简单就是幸福。周末的夜晚,一家老小围坐在电视机旁,尽享团圆的欢乐 现代人越来越会生活,越来越会用各种不同的方式来放松自己。垂钓、上网、打牌、玩球、唱卡拉OK、下棋.....不一而足。人们根据自己的兴趣爱好寻找放松身心的最佳方式, 在相对固定的社交圈子里怡然的生活,而且不断的扩大交往的圈子,结交新的朋友有时,你会为新添置的一套漂亮时装而快乐无比;有时,你会为孩子的一次小考成绩优异而 倍感欣慰;有时,你会为刚参加的一项比赛拿了名次而喜不自胜;有时,你会为完成了上司交给的一个任务而信心大增生活简单就是幸福!生活简单就是幸福,不意味着我们 放弃了对目标的追逐,是在忙碌中的停歇,是身心的恢复和调整,是下一步冲刺的前奏,是以饱满的精力和旺盛的热情去投入新的“战斗”的一个“驿站”;生活简单就是幸 福,不意味着我们放弃了对生活的热爱,是于点点滴滴中去积累人生,在平平淡淡中寻求充实和快乐。放下沉重的负累,敞开明丽的心扉,去过好你的每一天。生活简单就是 幸福!我的心徜徉于春风又绿的江南岸,纯粹,清透,雀跃,欣喜。原来,真正的愉悦感莫过于触摸到一颗不染的初心。人到中年,初心依然,纯真依然,情怀依然,幸甚至 哉。生而为人,芳华刹那,真的不必太多要求,一盏茶,一本书,一颗笃静的心,三两心灵知己,兴趣爱好一二,足矣。亦舒说:“什么叫做理想生活?不用吃得太好穿得太 好住得太好,但必需自由自在,不感到任何压力,不做工作的奴隶,不受名利的支配,有志同道合的伴侣,活泼可爱的孩子,丰衣足食,已经算是理想。”时间如此猝不及防, 生命如此仓促,忠于自己的内心才是真正的勇敢,以不张扬的姿态,将自己活成一道独一无二的风景,才是最大的成功。试问,你有多久没有靠在门槛上看月亮了,你有多久 没有在家门口的那棵大树下乘凉了,你有多久没有因为一个人一件事而心生感动了,你又有多久没有审视自己的内心了?与命运的较量中,我们被迫前行,却忘记了来时的方
等腰梯形的性质

Rt △ABE ≌Rt △DCF
A
D
关键:分割
两个全等的 一直个角平三行角四形边形
一个一等个腰矩三形角形
BE
)1
EF
过 作上一底腰两的端平点行作线高也是是梯梯形形 常用的辅辅助助线线。。
C
第三页,编辑于星期三:十五点 五十七分。
猜想:等腰梯形的两 条对角线之间有什么 数量关系?
发现:等腰梯形的
两条对角线相等。
作业:
1.完成练习纸
2.书P94练习题22.5/2、3、
第十三页,编辑于星期三:十五点 五十七分。
AC=BD
第十一页,编辑于星期三:十五点 五十七分。
方法比知识更重要
解决梯形问题的基本思路和方法:
通过添加适当的辅助线,把梯形问题转化为平行四边 形和三角形的问题来解决。
常画的辅助线有以下几种:
A
D
A
D
A
D
O
B
E
CB E F
作一腰平行线 E 作高线
CB
C
E
作对角线的平行线
A B
D
C 延长两腰
第十二页,编辑于星期三:十五点 五十七分。
第六页,编辑于星期三:十五点 五十七分。
1、如图,梯形ABCD中,AD∥BC,
AB=DC,则∠A= ∠D,∠C= ∠。B
x+3x=180°
A
D
\ 3x /
2、如图,梯形ABCD中,AD∥BC,
∠A:∠B=3:1,则∠D=
13度5 。
3、如图,梯形ABCD中,AD∥BC,
AB=DC,若AC=3cm,则BD=
验证
第四页,编辑于星期三:十五点 五十七分。
八年级数学等腰梯形的判定1

性质一:等腰梯形同一底上的两个角相等。 性质二:等腰梯形的对角线相等。 逆命题: 同一底上的两个角相等的梯形
是等腰梯形。
逆命题:对角线相等的梯形是等腰梯形。
逆命题: 同一底上的两个角相等的梯形 是等腰梯形。 A D
已知: 在梯形ABCD 中, AD//BC,
∠ B= ∠ C.
B (3) C
(2 )
3、已知: 在梯形ABCD 中,AD//BC, E为BC中点,EF 垂直 A B, EG垂直CD,EF=EG。 求证: 梯形ABCD为等腰梯形? A F B E D G C
逆命题:对角线相等的梯形为等腰梯形。
已知: 在梯形ABCD 中, AD//BC,AC=BD
求证: 梯形ABCD为等腰梯形。 A D
∠ACB= ∠DBC.
求证: 梯形ABCD是等腰梯形
A O B C D
请把你的收获告诉大家,
让我们一起分享!
判定一:同一底上的两角相等的梯形为
等腰梯形。
判定二:对角线相等的梯形为等腰梯形.
A B
D C
A B
A B
D
C D C B
A
D
C A B D B
A
D C
C
请各位老师提出宝贵意见
三寸人间 / 三寸人间
求证 : 梯形ABCD为等 腰梯形. (1) (2)
已知:
在梯形ABCD 中,AD//BC, ∠ B= ∠ C.
求证 :
梯形ABCD为等腰梯形.Fra bibliotekA DB
E
C
已知:
在梯形ABCD 中,AD//BC, ∠ B= ∠ C.
求证 :
梯形ABCD为等腰梯形.
A
等腰梯形的性质与判定

直角梯形
A
DBC来自(1)定义法:两条腰相等的梯形是等腰梯形。 (2)定理:同一底上的两个内角相等的梯形是等腰梯形。 (3)定理:对角线相等的梯形是等腰梯形。
A A D B B
图1
D
C
图2
C
一组对边平行而
四边形
等腰梯形
梯形
另一组对边不平行
直角梯形
二、等腰梯形的性质 (1)两底平行,两腰相等 AD∥BC, AB=CD (2)同底上两角相等 ∠A= ∠D, ∠B= ∠C (3)对角线相等 AC=BD B A D
C
(4)是轴对称图形
证明:等腰梯形同一底上两个角相等
C
等腰梯形的判定方法
1、定义法:两条腰相等的梯形是等腰梯形。
2、定理:同一底上的两个内角相等的梯形是等腰梯形。 3、定理:对角线相等的梯形是等腰梯形。
同一底上的两个内角相等的梯形是等腰梯形
已知:如图, 在梯形ABCD中,AD∥BC,∠B=∠C。 求证:梯形ABCD是等腰梯形。 证明:如图,过点D作DE//AB,交BC于点E,则 ∠1=∠B. ∵AD//BC, DE//AB. ∴四边形ABED是平行四边形. ∴AB=DE(平行四边形对边相等). ∵ ∠B =∠C ∴∠1=∠C ∴DE=DC(等角对等边) ∴ AB=DC(等量代换) ∴梯形ABCD是等腰梯形
D
B
E
F
C
辅助线:作高
E
证明3:延长BA,CD相交点E. ∵ ∠B =∠C ∴ BE=CE(等角对等边) ∴ ∠1 =∠B, ∠2 =∠C (两直线平行,同位角相等) ∴ ∠1 =∠2 (等量代换) ∴ AE=DE(等角对等边) ∴ BE -AE=DE-CE 即AB=DC ∴梯形ABCD是等腰梯形
等腰梯形的性质定理和判定定理及其证明

等腰梯形的性质定理和判定定理及其证明等腰梯形是指具有两边边长相等的梯形。
在等腰梯形的性质定理和判定定理中,我们会探讨一些关于其边长,角度,和对角线的性质。
下面,我将解释等腰梯形的性质定理和判定定理,并给出它们的证明。
性质定理1:等腰梯形的两个底角是相等的。
证明:考虑一个等腰梯形ABCD,其中AB和CD是底边,BC和AD是斜边。
假设∠A和∠B是两个底角。
首先,我们可以根据等腰梯形的性质,得到AB=CD。
接着,我们可以通过等边三角形来证明∠BAD≌∠CBA。
因为AB=CD,所以三角形ABC和三角形DCA是等边三角形。
因此,∠ABC≌∠CDA和∠CAB≌∠DAC。
我们可以通过相邻角的和等于180度的原理,得到∠BAD+∠ABC+∠CAB=180度和∠CBA+∠CDA+∠DAC=180度。
由于∠ABC≌∠CDA和∠CAB≌∠DAC,所以∠BAD+∠ABC+∠CAB=∠BAD+∠CDA+∠DAC。
因此,根据相等的角度和等于相等的角度之和,我们得到∠BAD+∠ABC+∠CAB=∠CBA+∠CDA+∠DAC。
将等腰梯形的性质AB=CD和∠BAD+∠ABC+∠CAB=∠CBA+∠CDA+∠DAC代入其中,我们可以得到∠BAD=∠CBA。
因此,等腰梯形的两个底角是相等的。
性质定理2:等腰梯形的两个对角线相等。
证明:考虑一个等腰梯形ABCD,其中AB和CD是底边,BC和AD是斜边。
我们需要证明AC=BD。
我们已经知道∠BAD=∠CBA。
因此,∠BAD和∠CBA是等腰梯形的两个底角,根据性质定理1,我们可以知道∠A=∠D和∠B=∠C。
我们可以通过相同边上的相等角来证明∠BAD≌∠BCD和∠ABD≌∠ACD。
因为∠A=∠D和∠B=∠C,所以AB//CD。
根据平行线的性质,我们得到∠ABD≌∠CDA和∠ACD≌∠BDA。
因此,根据等腰三角形的定义,我们可以知道三角形ABD和三角形CAD是等腰三角形。
因此,AD=BD和AC=CD。
等腰梯形和直角梯形及其性质

艺术创作
在绘画、雕塑等艺术创作 中,等腰梯形和直角梯形 的组合可以创造出独特的 视觉效果和艺术美感。
建筑设计
在建筑设计中,等腰梯形 和直角梯形的组合可以用 于构建独特的外观和结构, 如塔楼、拱门等。
THANK YOU
感谢聆听
详细描述
等腰梯形具有轴对称性,即沿一条经 过两腰中点的直线对折,两侧能够完 全重合。此外,等腰梯形的两个底角 相等,并且两条腰也相等。
面积计算
总结词
等腰梯形的面积可以通过上底、下底和高的长度来计算。
详细描述
等腰梯形的面积可以用公式 `(上底 + 下底) * 高 / 2` 来计算 。这个公式基于梯形面积的一般定义,即“上底加下底后乘 高再除以2”。
02
直角梯形
定义
直角梯形:一个四边形,其中一对相对边是平行的,并且另一对相对边是垂直的 。
定义中的关键词:平行、垂直。
性质
相对边平行
直角梯形的一组对
只有一个直角
直角梯形中只包含一个直角。
面积计算
面积公式
上底
下底
高
面积 = (上底 + 下底) × 高 ÷ 2。
直角梯形在生活中的应用
楼梯设计
直角梯形可以作为楼梯的形状 ,利用其斜边作为踏步,提供 平稳的上下楼梯体验。
斜坡
直角梯形可以作为斜坡的形状 ,用于车辆或人员上下坡的通 道。
排水系统
在排水设计中,直角梯形可以 用于设计沟渠和下水道,以实 现顺畅的排水效果。
等腰梯形与直角梯形的综合应用
01
02
03
机械零件
八年级数学等腰梯形的性质
思
考
1、用一块面积为800 cm 2 的等腰
梯形彩纸做风筝 ,为牢固起见,
用竹条作梯形的对角线,对角
线恰好互相垂直,那么至少需 要竹条 80 cm
A
D
解: ∵四边形ABCD是等腰梯形
∴设AC=BD=x
B
C
又∵AC⊥BD
∴ 1 x 2 = 800
2
解得:x=40
∴至少需要竹条 80 cm
“横断面”的概念
3
S2
5
4
D、S1 = S2
7
练习二
3、如图:若a=4 , b=6 , c=7 ,d=3 , 以它们为边作梯形,其中a∥b , 你认为这样的梯形能作出吗?
若能请作出图形,若不能,
Aa D
c
d
请说明 解: 这样的梯形不能作出
B
Hb C
过A点作AH∥CD 交BC于H点,得到 AHCD
∴AH=CD=d=3 , AD=HC= a = 4
A、m>h B、m<h C、m=h D、不能确定 B 解:
D
h
EC H
2 1 2 1 2 1
∟
过D作DH∥AC交BC 延长线于H点 ∴ BD=DH
∵AC⊥BD
又过D作DE ⊥ BH于E点
∴BD ⊥ DH
∴ DE= BH
又∵ AD ∥ BH , DH ∥ AC ∴四边形ACHD是平行四边形
= (BC+CH)
“横断面”的概念
梯形的性质应用1
横断面
梯形的性思质应用考
2、河流的一个横断面,如图,根据下表中的测量数据计算断面面积
离河一岸的距离(m) 0 2 3 5 9 11
水 深(m)
等腰梯形知识点总结

等腰梯形知识点总结一、定义等腰梯形是一个四边形,它具有两组对边相等的性质。
具体地说,等腰梯形的两条底边和两条斜边都是相等的。
这意味着等腰梯形的上底和下底、左斜边和右斜边是相等的。
二、性质1. 对边性质:等腰梯形的两组对边是相等的,即上底等于下底,左斜边等于右斜边。
2. 对角性质:等腰梯形的对角线交点平分底边。
3. 对角线性质:等腰梯形的对角线长度相等。
三、面积等腰梯形的面积可以通过以下公式来计算:\[ S = \frac{(a + b) \times h} {2} \]其中,a和b分别表示上底和下底的长度,h表示等腰梯形的高。
四、周长等腰梯形的周长可以通过以下公式来计算:\[ C = a + b + 2l \]其中,a和b分别表示上底和下底的长度,l表示等腰梯形的斜边的长度。
五、性质证明1. 等腰梯形的对角线性质证明:等腰梯形的两对角线相等。
我们可以证明这一性质,从而利用等腰三角形的性质来得证。
证明:连接等腰梯形上底和下底的中点,可以得到两个等腰三角形。
因为等腰三角形的性质是两个底角相等,所以等腰梯形的两对角线相等。
2. 等腰梯形的面积计算证明:等腰梯形的面积可以通过将其视为一个矩形和两个直角三角形的和来进行计算。
具体来说,我们可以将等腰梯形的上底和下底之和视为矩形的长度,高为等腰梯形的高;而等腰梯形的底边与高构成两个直角三角形,通过计算这两个直角三角形的面积并加上矩形的面积,就可以得到等腰梯形的面积。
六、应用等腰梯形在现实生活中有许多应用。
例如,等腰梯形的性质常常用于建筑和工程设计中,用来计算各种结构的面积和周长。
此外,等腰梯形的性质还可以在数学题中用来解决各种几何问题。
七、总结等腰梯形是一个重要的几何概念,具有多种性质和应用。
通过本文的介绍,我们可以了解到等腰梯形的定义、性质、面积和周长的计算方法,以及它在现实生活中的应用。
掌握了这些知识,我们可以更好地理解和运用等腰梯形的概念,在解决各种数学问题和实际应用中发挥作用。
等腰梯形的性质及证明(教案)

等腰梯形的性质及证明第一章:等腰梯形的定义及基本性质1.1 等腰梯形的定义引导学生复习梯形的定义,引入等腰梯形的概念。
通过实物模型或图形,让学生观察并理解等腰梯形的特征。
1.2 等腰梯形的边长关系引导学生观察等腰梯形的两条腰和底边的关系。
证明等腰梯形的两条腰长相等。
1.3 等腰梯形的对角线性质引导学生观察等腰梯形的对角线。
证明等腰梯形的对角线互相平分。
第二章:等腰梯形的内角性质2.1 等腰梯形的内角和引导学生复习四边形的内角和定理。
证明等腰梯形的内角和为360度。
2.2 等腰梯形的对角线与内角的关系引导学生观察等腰梯形的对角线与内角的关系。
证明等腰梯形的对角线与内角相等。
第三章:等腰梯形的对称性质3.1 等腰梯形的轴对称性引导学生复习轴对称性的概念。
证明等腰梯形具有轴对称性。
3.2 等腰梯形的中心对称性引导学生复习中心对称性的概念。
证明等腰梯形具有中心对称性。
第四章:等腰梯形的角平分线性质4.1 等腰梯形的角平分线定义引导学生复习角平分线的定义。
引入等腰梯形的角平分线概念。
4.2 等腰梯形的角平分线性质引导学生观察等腰梯形的角平分线。
证明等腰梯形的角平分线互相平分。
第五章:等腰梯形的应用5.1 等腰梯形的面积计算引导学生复习梯形的面积计算公式。
推导等腰梯形的面积计算公式。
5.2 等腰梯形的应用实例给出等腰梯形的实际应用题目。
引导学生运用等腰梯形的性质和证明结果解决实际问题。
第六章:等腰梯形的判定6.1 等腰梯形的判定条件引导学生复习四边形的判定条件。
引入等腰梯形的判定条件,即两条腰相等。
6.2 等腰梯形的判定方法给出等腰梯形的判定方法。
通过实际例子,让学生学会运用判定方法判断一个四边形是否为等腰梯形。
第七章:等腰梯形的相似性质7.1 等腰梯形的相似性质引导学生复习相似图形的性质。
引入等腰梯形的相似性质,即对应角相等,对应边成比例。
7.2 等腰梯形的相似证明给出等腰梯形的相似证明方法。
通过实际例子,让学生学会运用相似性质证明两个等腰梯形相似。
初中数学 等腰梯形有哪些全等性质

初中数学等腰梯形有哪些全等性质等腰梯形是一个重要的几何形状,在初中数学中学习它的全等性质可以帮助我们更好地理解和应用几何知识。
下面将介绍等腰梯形的全等性质,并解释它们的证明过程。
1. 全等性质1:等腰梯形的两个底角相等。
证明:设等腰梯形ABCD和A'B'C'D'的底边AB和A'B'相等,且底角∠DAB和∠D'A'B'相等。
我们需要证明∠DCB和∠D'C'B'也相等。
首先,连接AC和A'C'。
由于等腰梯形的底边平行,我们可以得知∠ADC和∠A'D'C'是对应角,它们相等。
又因为∠DAB和∠D'A'B'相等,所以∠DAC和∠D'A'C'也相等。
接下来,考虑三角形ADC和A'D'C'。
我们已经知道∠DAC和∠D'A'C'相等,底边AD和A'D'相等,且底边DC和C'D'相等。
根据第一个全等性质(SAS),我们可以得知三角形ADC和A'D'C'全等。
因此,∠DCB和∠D'C'B'也相等。
2. 全等性质2:等腰梯形的两个腿相等。
证明:设等腰梯形ABCD和A'B'C'D'的底边AB和A'B'相等,且腿BC和B'C'相等。
我们需要证明腿AD和A'D'也相等。
首先,连接AC和A'C'。
由于等腰梯形的底边平行,我们可以得知∠ADC和∠A'D'C'是对应角,它们相等。
又因为∠DAB和∠D'A'B'相等,所以∠DAC和∠D'A'C'也相等。
接下来,考虑三角形ADC和A'D'C'。
等腰梯形的性质

O
O
O
在等腰梯形中下列结论:(1)两腰相等(2)两 底平行(3)对角线相等(4)两底相等
其中正确的是( )
A. 1个
C. 3个
150分
B. 2个
D. 4个
在等腰梯形ABCD中,AD ∥BC,AB=DC若∠B=45 , A AB=6cm,BC=10cm,
O
则梯形的面积为(
2
400分 )
2
D
B
2
C
A.20cm B.15cm
C.12cm D.16cm
2
作 业 如图,在等腰梯形ABCD中,
AD∥BC,AB=DC若 ∠A=60 ,AD=5cm,BC=9cm,
O
求线段BC的长?
A
D
(用两种方法)
B
C
继续加油!
恭喜你,答对了!
继续加油!
继续加油!
继续加油!
继续加油!
继续加油!
B
大 比拼
开
筋 脑
动 你 的
对于等腰梯形,下面结论错误 的是( )
A.只有一组相等的对边
50分
B.只有一条对称轴
C.只有一组相等的内角 D.两条对角线相等
等腰梯形的一个角为120 ,上底为10,下 底为30 ,则它的腰长为( )
0
A.10
300分
B .30
C .40
D .20
如图等腰梯形ABCD中,AD∥BC,
第 五 中 松学 孙 岩
定义:一组对边平行,而另一组对边不平行的 四边形,叫做梯形。
上底
腰
高
腰
下底
上底和下底与位置无关,与两边长短有关。
上底
上 底
梯形与等腰梯形的性质与计算

梯形与等腰梯形的性质与计算梯形是一个几何形状,具有两对平行边,其中一对边较长,另一对边较短。
在梯形中,这两对平行边通过非平行的边连接。
等腰梯形是特殊的梯形,具有两对平行边等长的性质。
一、梯形的性质梯形的性质有以下几点:1. 对角线长度关系:梯形的对角线是两个非平行边之间的连线。
在任意梯形中,对角线之间的长度有一个重要的关系:对角线之和等于两底边长度之和。
即,对于梯形ABCD,有AC + BD = AB + CD。
2. 平行边关系:在梯形中,两对平行边之间的长度关系存在一个特殊的比例关系:两个平行边的长度之比等于与这两个平行边平行的两条高的长度之比。
即,对于梯形ABCD,若AD∥BC,则有AD/BC = AH/DH。
3. 高的长度关系:在梯形中,两条平行边之间的高具有相等的性质。
即,对于梯形ABCD,若AD∥BC,则有AH = DH。
二、等腰梯形的性质等腰梯形是一种特殊的梯形,具有两对平行边等长的性质。
在等腰梯形中,除了满足梯形的性质外,还有以下几个特点:1. 对角线长度关系:等腰梯形的对角线长度相等。
即,对于等腰梯形ABCD,有AC = BD。
2. 底角与顶角关系:等腰梯形的底角(梯形两个底边与其对应的邻边之间的角)相等,顶角(梯形两个非平行边之间的角)也相等。
即,对于等腰梯形ABCD,∠A = ∠C,∠B = ∠D。
三、梯形和等腰梯形的计算梯形和等腰梯形的计算可以利用其各个部分的性质来进行。
以下是计算梯形和等腰梯形常用的公式:1. 梯形的面积计算:梯形的面积可以通过将其分割成一个矩形和两个直角三角形,并计算各个部分的面积来获得。
梯形的面积公式为:面积= (上底+ 下底)×高 / 2。
2. 等腰梯形的面积计算:等腰梯形的面积可以通过将其分割成两个等腰直角三角形和一个矩形,并计算各个部分的面积来获得。
等腰梯形的面积公式为:面积 = (上底 + 下底) ×高 / 2。
3. 梯形的周长计算:梯形的周长可以通过将其各边长度相加来获得。
等腰梯形的面积计算与性质

等腰梯形的面积计算与性质等腰梯形是一种具有特殊性质的四边形,其两边平行,并且两对邻边长度相等。
在本文中,我们将讨论等腰梯形的面积计算方法以及其性质。
一、等腰梯形的面积计算要计算等腰梯形的面积,我们需要知道其两条平行边的长度以及高的长度。
假设等腰梯形的上底长为a,下底长为b,高为h。
等腰梯形的面积计算公式如下:面积 = (上底 + 下底) ×高 ÷ 2根据这个公式,我们可以将a、b和h的值代入,计算出等腰梯形的面积。
例如,如果上底长为5cm,下底长为8cm,高为6cm,那么根据面积计算公式,我们可以进行如下计算:面积 = (5 + 8) × 6 ÷ 2= 13 × 6 ÷ 2= 78 ÷ 2= 39cm²所以,该等腰梯形的面积为39平方厘米。
二、等腰梯形的性质除了面积计算,等腰梯形还有其他一些特殊性质:1. 等腰梯形的对角线相等:等腰梯形的两条对角线长度相等。
这是因为等腰梯形具有对称性,两条边平行且长度相等,所以对角线也相等。
2. 等腰梯形的内角性质:等腰梯形的内角有一些特殊性质。
两个腰之间的内角相等,两个底之间的内角相等,且这两个内角的和等于180度。
3. 等腰梯形的高线性质:等腰梯形的高线被平分,即将等腰梯形分成两个全等的直角三角形。
4. 等腰梯形的周长:等腰梯形的周长等于上底、下底和两腰的长度之和。
即周长 = 上底 + 下底 + 2 ×腰长。
通过对等腰梯形的面积计算和性质的了解,我们可以更好地理解和应用等腰梯形。
无论是在几何学中还是实际生活中,等腰梯形都有其特殊的应用。
这些应用包括建筑设计、制作家具、计算地表面积等等。
总结:等腰梯形是一种具有特殊性质的四边形,其面积计算可以使用面积计算公式进行。
除了面积计算,等腰梯形还有一些特殊性质,如对角线相等、内角性质、高线性质和周长计算。
通过对等腰梯形的研究和应用,我们可以更好地理解和利用这个几何形状。
八年级数学等腰梯形的性质

在地理测量中,等腰梯形可用于测量 地形高度、计算面积等,其简单的几 何形状能够方便测量和计算。
06 总结与展望
对等腰梯形性质的总结
等腰梯形的定义:等腰梯形是一组对 边平行且另一组对边相等的四边形。
等腰梯形的性质
等腰梯形的两腰相等。
等腰梯形同一底上的两个内角相等。 等腰梯形的对角线相等。
等腰梯形是轴对称图形,对称轴是上下底中 点的连线所在直线(过两底中点的直线)。
在土地测量中,等腰梯形可以 用来表示某块土地的形状,通 过计算其面积可以确定土地的 面积和价值等信息。
05 等腰梯形在生活中的应用
建筑领域中的应用
建筑设计
等腰梯形可用于建筑设计中的门 窗、楼梯、走廊等部分,其对称 性和稳定性使得建筑物更加美观 和实用。
桥梁设计
在桥梁设计中,等腰梯形可用于 桥墩、桥台等部分,其结构稳定 性能够增强桥梁的承重能力和安 全性。
等腰梯形的上下底边平行,因此 同旁内角互补,即相邻两个内角
的度数之和为180度。
03 等腰梯形的判定方法
通过边长判定等腰梯形
两条腰相等
两条对角线相等
在等腰梯形中,两条腰的长度是相等 的,这是判定等腰梯形的基本条件。
在等腰梯形中,两条对角线的长度也 是相等的。
上底和下底平行
等腰梯形的上底和下底必须是平行的, 这也是等腰梯形的一个重要特征。
该公式是计算等腰梯形面积的基本方 法,适用于所有已知上底、下底和高 的情况。
面积计算方法的推导过程
推导等腰梯形面积的计算方法,可以 通过将等腰梯形划分为两个等高的直 角三角形和一个矩形来进行。
然后,根据三角形和矩形的面积计算 公式,可以分别求出两个直角三角形 的面积和矩形的面积。
等腰梯形的性质及证明(教案)

等腰梯形的性质及证明第一章:等腰梯形的定义及基本性质1.1 等腰梯形的定义引导学生回顾梯形的定义,引入等腰梯形的概念。
通过实物模型或图形,让学生观察和描述等腰梯形的特征。
1.2 等腰梯形的边长关系引导学生测量和记录等腰梯形的上底、下底和斜边的长度。
分析等腰梯形上底和下底的长度关系,引导学生发现等腰梯形的两底边相等。
1.3 等腰梯形的对角线性质引导学生测量和记录等腰梯形的对角线长度。
分析等腰梯形对角线的长度关系,引导学生发现等腰梯形的对角线相等。
第二章:等腰梯形的角性质2.1 等腰梯形的底角性质引导学生观察等腰梯形的底角,并测量和记录底角的大小。
分析等腰梯形底角的大小关系,引导学生发现等腰梯形的底角相等。
2.2 等腰梯形的顶角性质引导学生观察等腰梯形的顶角,并测量和记录顶角的大小。
分析等腰梯形顶角的大小关系,引导学生发现等腰梯形的顶角相等。
第三章:等腰梯形的对称性质3.1 等腰梯形的轴对称性质引导学生观察等腰梯形的对称性,并画出对称轴。
分析等腰梯形的轴对称性质,引导学生发现等腰梯形是轴对称图形。
3.2 等腰梯形的中心对称性质引导学生观察等腰梯形的对称性,并画出中心对称点。
分析等腰梯形的中心对称性质,引导学生发现等腰梯形是中心对称图形。
第四章:等腰梯形的判定4.1 等腰梯形的判定条件引导学生回顾梯形的定义,引入等腰梯形的判定条件。
通过实例和图形,让学生判断和验证等腰梯形的判定条件。
4.2 等腰梯形的判定定理引导学生学习和理解等腰梯形的判定定理。
通过证明和实例,让学生掌握和应用等腰梯形的判定定理。
第五章:等腰梯形的应用5.1 等腰梯形的面积计算引导学生学习和理解等腰梯形的面积计算公式。
通过实例和练习,让学生应用面积计算公式计算等腰梯形的面积。
5.2 等腰梯形的实际应用引导学生思考和讨论等腰梯形在实际生活中的应用。
通过实例和问题,让学生解决实际问题,并应用等腰梯形的性质和判定。
第六章:等腰梯形的构造与应用6.1 等腰梯形的构造方法介绍使用直尺和圆规构造等腰梯形的方法。
初中数学等腰梯形的性质知识点详解

初中数学等腰梯形的性质知识点详解初中数学等腰梯形的性质知识点详解对于数学的学习中,下面是对等腰梯形的性质知识点的内容讲解,学习。
等腰梯形的性质①两底平行,两腰相等②等腰梯形在同一底上的两个角相等③等腰梯形的两条对角线相等④等腰梯形是轴对称图形,只有一条对称轴,一底的垂直平分线是它的对称轴通过上面对数学中等腰梯形的性质知识点的内容讲解学习,相信同学们已经能很好的掌握了吧,希望同学们会从中学习的更好。
初中数学相关的角与性质知识点详解对于数学的学习中,下面是对相关的角与性质知识点的内容讲解,学习。
相关的角与性质相关的角:1、对顶角:一个角的两边分别是另一个角的两边的反向延长线,这两个角叫做对顶角。
2、互为补角:假如两个角的和是一个平角,这两个角做互为补角。
3、互为余角:假如两个角的和是一个直角,这两个角叫做互为余角。
4、邻补角:有公共顶点,一条公共边,另两条边互为反向延长线的两个角做互为邻补角。
注意:互余、互补是指两个角的数量关系,与两个角的位置无关,而互为邻补角那么要求两个角有特殊的位置关系。
角的性质1、对顶角相等。
2、同角或等角的余角相等。
3、同角或等角的补角相等。
通过上面对数学中相关的角与性质知识点的内容讲解学习,相信同学们已经能很好的掌握了吧,希望同学们会从中学习的更好。
初中数学菱形的定义与性质知识点详解下面是教师对数学中菱形的定义与性质相关知识讲解,希望给同学们的复习学习提供很好的帮助。
菱形的定义与性质1、定义:邻边相等的平行四边形是菱形。
2、性质:〔1〕菱形的四边形都相等。
〔2〕菱形的对角线互相垂直,并且每一条对角线平分一组对角,〔3〕菱形的面积等于对角线乘积的一半。
〔4〕菱形既是中心对称图形,又是轴对称图形,有2条对称轴。
相信上面对数学中菱形的定义与性质知识的讲解学习,同学们已经能很好的掌握了吧,希望同学们在考试中获得优异成绩。
初中数学梯形定义知识点详解下面是教师对数学中梯形定义相关知识讲解,希望给同学们的复习学习提供很好的帮助。
等腰梯形所具备的条件

等腰梯形所具备的条件等腰梯形是一种特殊的梯形,它具备以下条件:1. 平行边相等:等腰梯形的上下底边是平行的,且长度相等。
这意味着梯形的两条平行边的长度是相等的。
2. 对角线相等:等腰梯形的两条对角线的长度相等。
对角线是连接梯形的非相邻顶点的线段,因此等腰梯形的两条对角线长度相等。
3. 对角线互相垂直:等腰梯形的两条对角线互相垂直。
这意味着两条对角线的交点是一个直角。
4. 两组相等的内角:等腰梯形的上底角和下底角相等,且左斜边角和右斜边角相等。
这意味着梯形的两组内角的度数是相等的。
等腰梯形是一个特殊的四边形,它具备上述条件。
这些条件使得等腰梯形具有一些独特的性质和特点。
等腰梯形的平行边长度相等,这意味着梯形的上下底边的长度是相等的。
这样的性质使得等腰梯形在建筑设计中具有一定的应用价值。
例如,我们常见的楼梯就是由等腰梯形组成的,通过调整梯形的大小和角度,可以设计出美观、稳定的楼梯结构。
等腰梯形的对角线长度相等,这意味着梯形的两条对角线的长度是相等的。
这个性质在几何证明中经常被使用。
例如,在证明两个三角形相似或全等时,我们可以利用等腰梯形的对角线相等性质来推导出结论。
等腰梯形的两条对角线互相垂直,这意味着两条对角线的交点是一个直角。
这个性质在解决一些几何问题时非常有用。
例如,在求解等腰梯形的面积时,我们可以利用对角线垂直的性质将梯形分解为两个直角三角形,从而简化计算过程。
等腰梯形的两组内角相等。
这个性质在解决一些几何问题时也非常有用。
例如,在证明两个三角形相似或全等时,我们可以利用等腰梯形的内角相等性质来推导出结论。
总结起来,等腰梯形具备平行边相等、对角线相等、对角线互相垂直和两组内角相等四个条件。
这些条件使得等腰梯形具有一些特殊的性质和特点,对于几何学的研究和应用具有重要意义。
通过研究和应用等腰梯形的性质,我们可以更好地理解和解决与梯形相关的问题。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
A
HD
如图7, 延长等腰梯形的两腰 相交于点E,
由∠B=∠C,AD∥BC,可知
△EBC和△EAD都是等腰三角形。
B
图7 F
C 因此从点E作两底的垂线必平分两 底。根据等腰三角形是轴对称图形,
可得等腰梯形也是轴对称图形。过
这也是研究梯形常用的
两底中点的直线是它的对称轴。
辅助线作法,即延长梯
形的两腰交于一点,得
∴ ∠DEC=∠B
∴ ∠B=∠C
等腰梯形的性质1:等腰梯形在同一底上的两个内角相等。
A
D
已知:如图6,在梯形ABCD中,AD∥BC,
AB=DC。
BE
F
图6
求证:∠B=∠C 。
C 证明:过A、D分别作AE⊥BC,DF⊥BC , 垂
足分别为E、F ∴AE∥DF,∠AEB= ∠DFC=900 ∵ AD∥BC
梯形的性质
上面的几幅图中有你熟悉的图形吗?
两组对边分别平行
四边形 只有一组对边平行
平行四边形 梯形
一、梯形 1、梯形的定义:
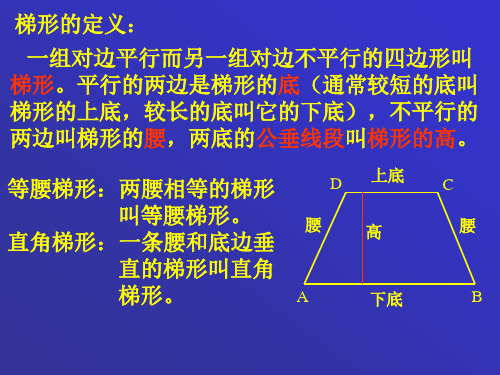
一组对边平行而另一组对边不平 行的四边形叫做梯形。
梯形
平行四边形
底角 上底
认识梯
腰高
腰
形
下底 底角
一组对边平行,另一组对边 不平行的四边形,叫做梯形。
2、梯形的有关概念:
2.等腰梯形有哪些性质?.
1)等腰梯形的一组对边平行,两腰相等。 2)等腰梯形同一底上的两个底角相等,对角线相等。
3)等腰梯形为轴对称图形,对称轴是连接两底中 心的直线。
3.今天我们在研究梯形问题时,用了哪些方法将梯形问 题转化为其他图形问题? 常用方法有平移一腰、作两高线、延长两腰。
如图,在等腰梯形ABCD中,AB//DC,E是DC延长线上的 D C
1、连接梯形两腰中点的线段叫作梯形的中位线。 试问:梯形的中位线与梯形的上、下底有何关系?
(即:EF与AB、CD有什么关系?) A
D
EF =
1( 2
AB+CD)
E B
F C
结论:梯形的中位线长等于上底和下底之和的一半。
六.反思与小结
1.我们今天学习了哪几种特殊的梯形?主要研究了哪种 梯形? (直角梯形和等腰梯形,主要研究了等腰梯形)
两组对边分别平行
平行四边形
四边形
只有一组对边平行 梯形
有一个角是直角 两腰相等
直角梯形 等腰梯形
在半透明的方格纸上,画一个等腰梯形ABCD, 过两底边AD、BC的中点E、F画一条直线,将 等腰梯形ABCD沿直线EF对折,你发现了什么?
AE
D
O
B
F
C
在等腰梯形中再画出梯 形的两条对角线,你认 为又出现了哪些相等的
(1)梯形平行的两边叫做梯形的底(通常把较短 的底叫上底,较长的底叫做下底)。
AE
D
H
G
B G F HC 图1
E
F
图2
(2)不平行的两边叫梯形的腰。 (3)两底的距离叫做梯形的高。
3、两种特殊的梯形:
A
DA
D
矩形
B
图3
CB
图4
C
(1)一腰垂直于底的梯形叫做直角梯形(如图3)。
(2)两腰相等的梯形叫做等腰梯形(如图4)。
在△ABC和△DCB中
AB DC ABC DCB BC CB
∴ △ABC≌△DCB (SAS)
∴ AC=DB
(OB = OC OA = OD)
等腰梯形的两条对角线相等
符号语言 ∵在等腰梯形ABCD中,AD∥BC
∴AC=BD.
A
D
B
C
四边形ABCD是等腰梯形,延长两腰BA, CD后交于点E,问△ EBC和△ EAD的形状如何?
A
D
O
B
CE
1、梯形有关概念及其性质 2、等腰梯形的性质
边
角
等腰梯形
两底平行 两腰相等
同一底上的两 个内角相等 (对角互补, 同一腰上的两 个角也互补)
对角线
两条对角线 相等
对称性 轴对称图形
3、(等腰)梯形常用的辅助线添法
平移一腰
作高
延长两腰
连结对角线
平移对角线
4、转化思想பைடு நூலகம்
借助添加辅助线将梯形转化为三角形和平行四边形、矩形;将复杂问题转 化为简单问题;将未知转化为已知。
证明:∵ABCD是等腰梯形
E
∴ ∠ B= ∠ C
(等腰梯形同一条底边上的两个内角相等)
∴EB = EC
∴ △ EBC是等腰三角形
A
D
∵ AD∥ BC
∴ ∠ B= ∠EAD ∠ C = ∠EDA
又∵ ∠ B= ∠ C
B
C
∴∠EAD = ∠EDA
∴EA = ED
∴ △ EAD是等腰三角形
如图,等腰梯形ABCD中,AD∥BC,对角线 AC=BC+AD,求∠ACB的度数。
等腰梯形同一底上的两个底角相等
符号语言
∵在等腰梯形ABCD中,AD∥BC ∴∠A=∠D, ∠B=∠C.
A
D
B
C
如图,梯形ABCD中,AD∥BC,AB=CD, ∠B=60°,AB⊥AC,那么∠ACD=____, ∠D=_______。
A
D
B
C
2、等腰梯形的对称性:
E
等腰梯形为什么是轴对称图形?
它的对称轴是什么?
这也是研究梯形
时常用的辅助线作法, 即从同一底的两端作 另一底的垂线段,它 可把梯形分成一个矩 形和两个直角三角形 (如果是等腰梯形, 所得到的两个直角三 角形全等)。
∴四边形AEFD是平行四边形 ∴AE=DF 在Rt△ABE和Rt△DCF中
AE DF
AB DC
∴ Rt△ABE≌Rt△DCF
∴ ∠B=∠C
关系?
二、等腰梯形的性质
对称性
等腰梯形是轴对称图形。
对称轴——两底中点所在直线
边
等腰梯形两底平行,两腰相等。
角 对角线
等腰梯形同一底边上的两个内角相等。 等腰梯形的两条对角线相等。
1、等腰梯形的性质1:等腰梯形在同一底上的两个内角相等
已知:如图5,在梯形ABCD中,
A
D
AD∥BC,AB=DC。
求证:∠B=∠C 。
B
E
图5
证明:过点D作DE∥AB,交BC于点E,
C 得到△DEC。
∵ AD∥BC,DE∥AB
∴四边形ABED是平行四边形
研究梯形时,
常常需要添加适当 的辅助线,把梯形 转化成平行四边形 和三角形,此处是 移动一腰,即从梯 形的一个顶点作一 腰的平行线。
∴ AB=DE ∵ AB=DC
∴ DE=DC ∴ ∠DEC=∠C ∵ DE∥AB
到两个三角形(如果是
等腰梯形,则得到两个
分别以梯形两底为底的
等腰三角形)。
3、等腰梯形的性质2:等腰梯形的两条对角线相等。
A
D
已知:如图8,在梯形ABCD中, AD∥BC,AB=DC 。
O
求证:AC=BD
证明:在梯形ABCD中
B
图8
C
∵ AB=DC,
∴ ∠ABC=∠DCB(等腰梯形在同
一底上的两个内角相等)。
E
一点,BE=BC,试说明∠A和∠E的关系。
A
B
如图:已知在等腰梯形ABCD中, AD ∥ BC, AB=DC =4,AD =3,BC =7,求∠ B的度数。
