专题 染色问题与染色方法
小学奥数杂题染色问题【三篇】
小学奥数杂题染色问题【三篇】
解析：对房间染色，使最下面的两个房间染成黑色，与黑色相邻的
房染成白色，
则图中有7个黑色房间和5个白色房间．
如果要想不重复地走过每一个房间，黑色与白色房间数应该相等．故题中的想法是不能实现的．
点评：完成本题也可根据要求据图中的房间实际找下路线，看是
否能够找到．
【第二篇】
展览会有36个展室(如图),每两相邻展室之间均有门相通.能不能从入
口进去,不重复地参观完全部展室后,从出口出来呢?
答案：
不能.对展室实行染色,使相邻两房间分别是黑色和白色的.此时入
口处展室的颜色与出口处展室的颜色是相同的,而不重复参观完36个
展室,入口与出口展室的颜色应该不相同.
【第三篇】
染色问题基本解法：
三面涂色和顶点相关 8个顶点。
两面染色和棱长相关。
即新棱长（棱长-2）×12
一面染色和表面积相关。
同样用新棱长计算表面积公式（棱长-2）×（棱长-2）*6
0面染色和体积相关。
用新棱长计算体积公式（棱长-2）×（棱长-2）×（棱长-2）
长方体的解法和立方体同理，即计算各种公式前长、宽、高都要先减2再利用公式计算。
排列组合题型全归纳 专题06 染色问题(原卷版)
专题06染色问题【方法技巧与总结】涂色问题常用方法：(1)根据分步计数原理，对各个区域分步涂色，这是处理区域染色问题的基本方法；(2)根据共用了多少种颜色讨论，分别计算出各种情形的种数，再用分类计数原理求出不同的涂色方法种数；(3)根据某两个不相邻区域是否同色分类讨论.从某两个不相邻区域同色与不同色入手，分别计算出两种情形的种数，再用分类计数原理求出不同涂色方法总数.k 种颜色圆周染色问题如图，把一个圆分成(2)n n ≥个扇形，每个扇形用k 种颜色之一染色，要求相邻扇形不同色，有(1)(1)(1)n n n a k k =-+-⨯-种方法.正常着色定理如图，用k （k 为正整数）种颜色给图的n 个顶点着色，则正常着色的方法为：,(1)(1)(1),2n n n k F k k n =-+--≥，1,k F k =.【典型例题】例1．（2023·全国·高三专题练习）如图是某届国际数学家大会的会标，现在有4种颜色给其中5个小区域涂色，规定每个区域只涂一种颜色，相邻区域颜色不相同，则不同的涂色方案种数为（）A．72B．48C．36D．24例2．（2023·全国·高三专题练习）如图，湖北省分别与湖南、安徽、陕西、江西四省交界，且湘、皖、陕互不交界，在地图上分别给各省地域涂色，要求相邻省涂不同色，现有5种不同颜色可供选用，则不同的涂色方案数为（）A．480B．600C．720D．840例3．（2023·全国·高三专题练习）给图中A，B，C，D，E，F六个区域进行染色，每个区域只染一种颜色，且相邻的区域不同色.若有4种颜色可供选择，则共有（）种不同的染色方案.A．96B．144C．240D．360例4．（2023·全国·高三专题练习）有4种不同颜色的涂料，给图中的6个区域涂色，要求相邻区域的颜色不相同，则不同的涂色方法共有（）A．1512种B．1346种C．912种D．756种例5．（2023·全国·高三专题练习）在一个正六边形的六个区域涂色（如图），要求同一区域同一种颜色，相邻的两块区域（有公共边）涂不同的颜色，现有5种不同的颜色可供选择，则不同涂色方案有（）A．720种B．2160种C．4100种D．4400种例6．（2023·全国·高三专题练习）用红、黄、蓝、绿、橙五种不同颜色给如图所示的5块区域A、B、C、D、E涂色，要求同一区域用同一种颜色，有共公边的区域使用不同颜色，则共有涂色方法（）A．120种B．720种C．840种D．960种例7．（2023秋·重庆沙坪坝·高三重庆八中校考开学考试）用黑白两种颜色随机地染如图所示表格中5个格子，每个格子染一种颜色，并且从左到右数，不管数到哪个格子，总有黑色格子不少于白色格子的染色方法种数为（）A ．6B ．10C ．16D ．20例8．（2023·全国·高三专题练习）在如图所示的5个区域内种植花卉，每个区域种植1种花卉，且相邻区域种植的花卉不同，若有6种不同的花卉可供选择，则不同的种植方法种数是（）A ．1440B ．720C ．1920D ．960例9．（2023·全国·高三专题练习）如图，用五种不同的颜色给图中的O ，A ，B ，C ，D ，E 六个点涂色（五种颜色不一定用完），要求每个点涂一种颜色，且图中每条线段的两个端点涂不同的颜色，则不同的涂法种数是（）A ．480B ．720C ．1080D ．1200例10．（2023·全国·高三专题练习）用五种不同颜色给三棱柱111ABC A B C -的六个顶点涂色，要求每个顶点涂一种颜色，且每条棱的两个顶点涂不同颜色，则不同的涂法有（）A ．840种B ．1200种C ．1800种D ．1920种例11．（2023·全国·高三专题练习）正方体六个面上分别标有A 、B 、C 、D 、E 、F 六个字母，现用5种不同的颜色给此正方体六个面染色，要求有公共棱的面不能染同一种颜色，则不同的染色方案有（）种.A ．420B ．600C ．720D ．780例12．（2023春·内蒙古赤峰·高二赤峰二中校考阶段练习）如图，某伞厂生产的太阳伞的伞篷是由太阳光的七种颜色组成，七种颜色分别涂在伞篷的八个区域内，且恰有一种颜色涂在相对区域内，则不同颜色图案的此类太阳伞最多有（）.A．40320种B．5040种C．20160种D．2520种例13．（2023·全国·高三专题练习）如图，用四种不同的颜色给图中的A，B，C，D，E，F，G七个点涂色，要求每个点涂一种颜色，且图中每条线段的两个端点涂不同颜色，则不同的涂色方法有（）A．192B．336C．600D．以上答案均不对例14．（2023·全国·高三专题练习）如图所示，将一个四棱锥的每一个顶点染上一种颜色，并使同一条棱上的两端异色，如果只有5种颜色可供使用，则不同的染色方法种数是()A．420B．210C．70D．35例15．（2023·全国·高二专题练习）如图，给图中的A，B，C，D，E，F六个点涂色，要求每个点涂一种颜色，且图中每条线段的两个端点涂不同颜色，若有四种颜色可供选择，则不同的涂色方法共有______种.例16．（2023·全国·高三专题练习）如图，用四种不同颜色给图中的A，B，C，D，E，F，G，H八个点涂色，要求每个点涂一种颜色，且图中每条线段上的点颜色不同，则不同的涂色方法有___________种.例17．（2023·全国·高三专题练习）如图，一个地区分为5个行政区域，现给地图着色，要求相邻区域不得使用同一种颜色，共有5种颜色可供选择，则不同的着色方法共有________种(以数字作答)．例18．（2023·全国·高三专题练习）如图，用4种不同的颜色给图中的8个区域涂色，每种颜色至少使用一次，每个区域仅涂一种颜色，且相邻区域所涂颜色互不相同，则区域A，B，C，D和1A，1B，1C，1D分别各涂2种不同颜色的涂色方法共有_________种；区域A，B，C，D和1A，1B，1C，1D分别各涂4种不同颜色的涂色方法共有_________种.例19．（2023·陕西宝鸡·统考一模）七巧板是古代劳动人民智慧的结晶.如图是某同学用木板制作的七巧板，它包括5个等腰直角三角形､一个正方形和一个平行四边形.若用四种颜色给各板块涂色，要求正方形板块单独一色，其余板块两块一种颜色，而且有公共边的板块不同色，则不同的涂色方案有______种.例20．（2023秋·甘肃张掖·高三高台县第一中学校考阶段练习）如图，节日花坛中有5个区域，现有4种不同颜色的花卉可供选择，要求相同颜色的花不能相邻栽种，则符合条件的种植方案有_____________种.例21．（2023·高二课时练习）如图，用5种不同的颜色给图中的A、B、C、D、E、F6个不同的点涂色，要求每个点涂1种颜色，且图中每条线段的两个端点涂不同的颜色，则不同的涂色方法共有______种.例22．（2023·全国·高三专题练习）在如图所示的十一面体ABCDEFGHI中，用3种不同颜色给这个几何体各个顶点染色，每个顶点染一种颜色，要求每条棱的两端点异色，则不同的染色方案种数为__________．例23．（2023·全国·高二专题练习）埃及胡夫金字塔是古代世界建筑奇迹之一，它的形状可视为一个正四棱锥，如图所示．将一个正四棱锥的每一个顶点染上一种颜色，并使同一条棱的两端异色，如果只有5种颜色可供使用，求不同的染色方法种数．例24．（2023·全国·高三专题练习）如图，一个正方形花圃被分成5份．(1)若给这5个部分种植花，要求相邻两部分种植不同颜色的花，已知现有5种颜色不同的花，求有多少种不同的种植方法？(2)若向这5个部分放入7个不同的盆栽，要求每个部分都有盆栽，问有多少种不同的放法？例25．（2023·全国·高三专题练习）用()3,n n n N *≥∈种不同的颜色给如图所示的A 、B 、C 、D 四个区域涂色．（1）若相邻区域能用同一种颜色，则图①有多少种不同的涂色方案？（2）若相邻区域不能用同一种颜色，当6n =时，图①、图②各有多少种不同的涂色方案？（3）若相邻区域不能用同一种颜色，图③有180种不同的涂色方案，求n 的值．例26．（2023·全国·高二专题练习）如图所示的A ，B ，C ，D 按照下列要求涂色．（1）用3种不同颜色填涂图中A，B，C，D四个区域，且使相邻区域不同色，若按从左到右依次涂色，有多少种不同的涂色方案？（2）若恰好用3种不同颜色给A，B，C，D四个区域涂色，且相邻区域不同色，共有多少种不同的涂色方案？（3）若有3种不同颜色，恰好用2种不同颜色涂完四个区域，且相邻区域不同色，共有多少种不同的涂色方案？例27．（2023·全国·高二专题练习）（1）从5种颜色种选出3种颜色，涂在一个四棱锥的五个顶点上，每一个顶点涂一种颜色，并使同一条棱上的两个顶点异色，则不同的涂色方法有______种；（2）从5种颜色种选出4种颜色，涂在一个四棱锥的五个顶点上，每一个顶点涂一种颜色，并使同一条棱上的两个顶点异色，则不同的涂色方法有______种．。
(完整版)染色问题的计数方法
染色问题的计数方法河北张家口市第三中学王潇与染色问题有关的试题新颖有趣,其中包含着丰富的数学思想,染色问题,解题方法技巧性强且灵活多变,故这类问题有利于培养学生的创新思维能力,分析问题与观察问题的能力,有利于开发学生的智力。
一、区域染色问题1.根据乘法原理，对各个区域分步染色，这是处理这类问题的基本的方法。
例1要用四种颜色给四川、青藏、西藏、云南四省（区）的地图染色（图1）每一省（区）一种颜色，只要求相邻的省（区）不同色，则不同染色的方法有多少种？分析先给西藏青海云南四川四川染色有4种方法，再给青海染色有3种方法，接着给西藏染色有2种方法，最后给云南染色有2种方法，根据乘法原理，不同的染色方法共有4×3×2×2＝48种2.根据共用了多少种颜色分类讨论，分别计算出各种情形的种数，再用加法原理求出不同年拾方法种数。
例2 （2003年全国高考题）如图2，一个地区分为5个行政区域，现给地图着色，要求相邻区域不得使用同一颜色，现有4种颜色可供选择，则不同的着色方法共有多少种？分析 依题意至少要12345图2选用3种颜色。
（1） 当选用三种颜色时，区域2与4必须同色，区域3与5必须同色，有34A 种。
（2） 当用四种颜色时，若区域2与4同色，则区域3与5不同色，有44A 种；若区域3与5同色，则区域2与4不同色，有44A 种，故用四种颜色时共有244A 种。
由加法原理可知满足题意的着色方法共有34A ＋244A ＝24＋2×24＝72种。
3 根据某两个不相邻区域是否同色分类讨论，从某两个不相邻区域同色与不同色入手，分别计算出两种情形的种数，再用加法原理求出不同染色方法数。
例3 用红、黄、蓝、白、黑五种颜色涂在“田”字形的四个小方格内（图3），每格涂一种颜色，相邻的两格涂不同的颜色，如果颜色可以反复使用，共有多少种不同的涂色方法？1234图3（1）四格涂不同的颜色，方法数为45A ；（2）有且仅有两格涂相同的颜色，即只有一组对角小方格涂相同颜色，涂法种数为21245C A ； （3）两组对角小方格涂相同颜色，涂法种数为25A 。
初中数学重点梳理：染色问题
染色问题知识定位染色是分类的直观表现，在数学竞赛中有大批以染色面目出现的问题，这类问题的特点是知识点少，逻辑性强，技巧性强，其内部蕴藏着深刻的数学思想。
同时，染色作为一种解题手段也在数学竞赛中广泛使用。
将问题中的对象适当进行染色，有利于我们观察、分析对象之间的关系，像国际象棋的棋盘那样，我们可以把被研究的对象染上不同的颜色，许多隐藏的关系会变得明了，再通过对染色图形的处理达到对原问题的解决，这种解题方法称为染色法。
知识梳理知识梳理1.染色问题解答染色问题，并不需要具备更多的数学知识，只需要具有缜密的思考能力和较强的分析能力。
纵观各种染色试题，它与我们经常使用的数学方法紧密联系。
大体上有如下几种方法：奇偶分析、归纳法、反证法、抽屉原理、构造法、组合计数等。
常见的染色方式有：点染色、线段染色、小方格染色和对区域染色。
例题精讲【试题来源】【题目】用任意的方式将平面上的每一点染上黑色或白色(称为二染色).求证：一定存在长为1的线段，它的两个端点同色。
【答案】在平面上任作一个边长为1的正三角形，设三个顶点为A，B，C，由于平面上的每点只着黑、白两色之一，根据抽屉原理，A，B，C三点中必有两点同色，以这两同色点为端点的线段长度恰为1.【解析】在平面上任画一条长为1的线段，如图，若A，B两点同色，则结论已成立.若A，B 两点不同色，为确定起见不妨设A为黑色，B为白色，以AB为边作正三角形ABC，则AB=BC=CA=1.这时C点要么是黑点，要么是白点.若C为黑点，则AC为两个端点同色的长为1的线段.若C为白点，则BC为两个端点同色的长为1的线段.上述分析过程，其实已完成了证明过程，不过思路一旦找出，出现边长为1的正三角形的顶点A，B，C三点的构想是个关键，为此可得出如下简化的证明.【知识点】染色问题【适用场合】当堂例题【难度系数】3【试题来源】【题目】对平面上的点黑白二染色后，一定存在三顶点同色的直角三角形.【答案】见解析【解析】对平面上的点黑白二染色，根据例1的结论，存在边长为a(a＞0)的线段AB，它的两个端点同色(不妨设A，B同黑).以AB为边作正方形ABCD，对角线AC，BD交于点O，如图，如果D，O，C中有一个黑点，则该点与A，B构成三顶点同黑色的直角三角形.如果D，O，C全白色，则△DOC就是三顶点全为白色的直角三角形.因此，二染色平面上一定存在顶点同色的直角三角形.【知识点】染色问题【适用场合】当堂例题【难度系数】3【试题来源】【题目】用任意的方式，对平面上的每个点染黑色或白色，求证：一定存在一个边长为1或3的正三角形，它的三个顶点同色.【答案】见解析【解析】若存在边长为1且顶点同色的正三角形，则问题得证.若不存在边长为1且顶点同色的正三角形，则一定存在长为1的线段AB ，两端点A ，B 异色.以AB =1为底作腰长为2的等腰三角形ABC ，则C 与A 或B 总有一对是异色的.不妨设长为2的线段AC 两端点异色(见图(a )).取AC 的中点O ，则O 必与A ，C 之一同色(见图(b ))，不妨设O 与A 同色.由于不存在边长为1的同色顶点的正三角形，所以以AO 为一边的等边三角形的另外的顶点D 和E 必与A 异色.此时，△ECD 就是一个边长为3的顶点同色的正三角形.评注 事实上，当将平面分成宽度为23的水平带状区域，且每个区域含下沿直线，不含上沿直线，使相邻的带状区域染上不同颜色，对这样的平面二染色，任意边长为1的正三角形的三个顶点均不同色，但存在边长为3的三顶点同色的三角形.由例3可得更一般的结论：平面上点二染色后，要么存在边长为a (a ＞0)三顶点同色的正三角形，要么存在边长为3 a 三顶点同色的正三角形.【知识点】染色问题 【适用场合】当堂练习题 【难度系数】3【试题来源】【题目】连接圆周上9个不同点的36条线段染成红色或蓝色，假设9点中每3点所确定的三角形都至少含有一条红色边.证明有4点，其中每两点的连线都是红色.【答案】见解析【解析】设9个点依次为v1，v2，…，v9，首先证明必存在一点，设为v1，从v 1出发的红色线段不是5条.事实上，若不然，如果都是5条，则共有红色线段295不是整数，矛盾.若从v1出发的红色线段至少有6条，设v1v2，v1v3，v1v4，v1v5，v1v6，v 1v7均为红色，则由第26讲例8评注可知，连结v2，v3，v4，v5，v6，v7的线段中必有同色三角形.由题意知它只能为红色三角形，设为v2v3v4，则v1，v 2，v3，v4四点中两两皆连红线.若从v1出发的红色线段至多4条，则v1出发的蓝色线段至少有4条，设为v 1v2，v1v3，v1v4，v1v5，则v2，v3，v4，v54点必然两两连红线.否则，例如若v2v3是蓝色的，则△v1v2v3是蓝色三角形，与题设至少有一边为红色矛盾.以上各例中，染色都是作为问题条件给出的，有时，染色方法也作为一种分类手段，因此，用形象直观地染色进行分类，也就成了一种很有特色的解题方法.【知识点】染色问题【适用场合】随堂课后练习【难度系数】3【试题来源】【题目】某桥牌俱乐部约定，四个人在一起打牌，同一方的两个人必须都曾合作过，或都不曾合作过.试证：只要有五个人，就一定能凑齐四个人，按照约定在一起打牌.【答案】见解析【解析】本题证明采用构造一个涂色模型，使它与原问题间有一一对应的关系.如果模型中的问题证明了，那么原问题也相应地证明了.证明五个人对应为空间五个点，如两个人合作过，那么对应两点连结红色线段，如两人不曾合作过，那么对应两点连结蓝色线段.因此原问题等价于证明涂色模型：空间五个点(无三点在一条直线上)，两两连线，涂上红色或蓝色之一.证明必存在两条无公共端点的同色线段.设五个点为A1，A2，A3，A4，A5，不失一般性，不妨设A1A2为红色.观察△A3A4A5三条边的颜色.(1)如果△A3A4A5中有一条边为红色，设为A3A4，那么A1A2与A3A4是满足条件的两条线段；(2)如果△A3A4A5的三条边均为蓝色，此时如A1A3，A1A4，A1A5与A2A3，A2A4，A2A5中如果有一条蓝色线段，那么问题就获证.如以A1A3是蓝色线段为例，那么A1A3与A4A5是满足条件的两条线段.反之，如果此时六条线段均为红色，如取A1A3与A2A4就是满足条件的两条线段.由于无公共端点的同色线段存在，证得原命题成立.【知识点】染色问题【适用场合】阶段测验【难度系数】3【试题来源】【题目】把平面划分成形为全等正六边形的房间，并按如下办法开门：若三面墙汇聚于一点，那么在其中两面墙上各开一个门，而第三面墙不开门.证明：不论沿多么曲折的路线走回原来的房间，所穿过的门的个数一定是偶数.【答案】见解析【解析】为方便起见，我们把有公共门的两个房间叫做相邻的.用两种不同的颜色涂平面上的这些房间，使相邻的房间的颜色不同(如图).注意，从某种颜色的房间走到同种颜色的房间，必须经过另一种颜色的房间.显然，从任一房间走到同种颜色的房间，必定经过偶数个门.这样，利用图形和不同的颜色就可以解出这道题.【知识点】染色问题【适用场合】课后两周练习【难度系数】3【试题来源】【题目】有一个2003⨯2003的棋盘和任意多个l⨯2及1⨯3的矩形纸片，规定l⨯2的纸片只能沿着棋盘的格线水平地放置，而1⨯3的纸片只能沿着棋盘的格线铅直地放置. 请问是否可依上述规定取用一些纸片不重叠地盖满整个棋盘？【答案】不可以【解析】先将棋盘的每一行黑白交错涂色，即第一行，第二行，第三行，…，依次为黑色，白色，黑色，….经过这样涂色后，开始时棋盘的黑白方格数之差为2003个.沿着棋盘的格线水平地放置1⨯2的纸片，每放上一个l⨯2的纸片，就能盖住黑白方格各一个，所以这个操作并不会改变黑白方格数之差；而每一个1⨯3的矩形纸片沿着棋盘的格线铅直地放置，所覆盖的三个方格都是同一颜色，所以每放置一片l⨯3的矩形纸片，棋盘的黑白方格数之差就增加3个或减少3个.因为2003不是3的倍数，所以，依题述规定取用一些1⨯2及l⨯3的矩形纸片是不可能不重叠地盖满整个棋盘的.【知识点】染色问题【适用场合】课后一个月练习【难度系数】3【试题来源】【题目】证明：如图，用15块4×1的矩形瓷砖与1块2×2的方形瓷砖，不能覆盖8×8的正方形地面(瓷砖不许断开！).【答案】见解析【解析】本例题有多种证法.一个共同点是：“不能覆盖”的证明，通常借助于反证法.证法1将8×8的正方形地面的小方格，用黑、白色涂之，染色法如图.于是，每一块4×1瓷砖，不论怎样辅设，都恰好盖住两个白格两个黑格.15块4×1瓷砖共盖住30个白格和30个黑格.一块2×2瓷砖，无论怎么放，总是盖住“三白一黑”或“三黑一白”，即只能盖住奇数个白格和奇数个黑格.而盘中的黑白格总数相等(全为32个).所以用15块4×1砖与1块2×2砖不能完全覆盖8×8地面.证法2将8×8的正方形地面的小方格.用代号为1，2，3，4的四种颜色涂之，染色法如(a).这时，4×1砖每次总能盖住1，2，3，4四色；而2×2砖不论放何处，总是不能同时盖住1，2，3，4四色.故是不可能的.证法3同样用四色涂之，涂法如(b).用反证法，设4×1砖横着盖住i 色的有x i 块，竖着盖住的有y 块.2×2砖盖住阴影格处(不妨假定，余仿此).假定能够盖住.那么有：⎩⎨⎧=+=+,144,16421y x y x 相减得4(x 1－x 2)=2.因为x 1与x 2均为整数，这是不可能的.【知识点】染色问题 【适用场合】当堂例题 【难度系数】3【试题来源】【题目】（1）用1×1，2×2，3×3三种型号的正方形地板砖铺设23×23的正方形地面，请你设计一种辅设方案，使得1×1的地板砖只用一块．（2）请你证明：只用2×2，3×3两种型号的地板砖，无论如何铺设都不能铺满23×23的正方形地面而不留空隙．【答案】见解析【解析】(1)首先用12块地板砖与6块地板砖能铺成的长方形地面, 再利用4个的板块,恰用1块地板砖,可以铺满的正方形地面. (2)我们将的大正方形分成23行23列共计529个的小方格,再将第1行,第4行,第7行,第10行,第13行,第16行,第19行,第22行这八行染红色,其余的15行都染白色,任意或的小正方块无论怎样放置(边线与大正方形格线重合),每块或的正方块都将盖住偶数块的白色小方格.假设用及的正方形地板砖可以铺满后正方形地面,则它们盖住的白色的小方格总数为偶数个.然而地面染色后共有(奇数)个的白色小方格,矛盾.所以,只用,两种型号地板砖无论如何铺设,都不能铺满的正方形地面而不留空隙.【知识点】染色问题【适用场合】当堂例题【难度系数】3【试题来源】【题目】如图，对A，B，C，D，E，F，G七个区域分别用红、黄、绿、蓝、白五种颜色中的某一种来着色，规定相邻的区域着不同的颜色．那么有种不同的着色方法．【答案】2880【解析】对这五个区域,我们分五步依次给予着色:(1)区域A共有5种着色方式;(2)区域B因不能与区域A同色,故共有4种着色方式;(3)区域C因不能与区域B同色,故共有4种着色方式;(4)区域D因不能与区域A,B,C同色,故共有2种着色方式;(5)区域E因不能与区域A,D同色,故共有3种着色方式.(6)区域F因不能与区域D,E同色,故共有3种着色方式.(7)区域G因不能与区域A,E,F同色,故共有2种着色方式.于是,根据乘法原理共有种不同的着色方式.因此，本题正确答案是:2880.【知识点】染色问题【适用场合】随堂课后练习【难度系数】3【试题来源】【题目】一块2×2的方格由4个1×1的方格构成，每个小方格被涂上红、绿两种颜色之一．如果要求绿色小方格的上方和右方不能与红色方格邻接．且上述四个小方格可以全部不涂绿色，也可全部涂上绿色．则可能的涂色方法共有种．【答案】2880【解析】对这五个区域，我们分五步依次给予着色：（1）区域A共有5种着色方式；（2）区域B因不能与区域A同色，故共有4种着色方式；（3）区域C因不能与区域B同色，故共有4种着色方式；（4）区域D因不能与区域A，B，C同色，故共有2种着色方式；（5）区域E因不能与区域A，D同色，故共有3种着色方式．（6）区域F因不能与区域D，E同色，故共有3种着色方式．（7）区域G因不能与区域A，E，F同色，故共有2种着色方式．于是，根据乘法原理共有5×4×4×2×3×3×2=2880种不同的着色方式．故答案为：2880．【知识点】染色问题【适用场合】当堂例题【难度系数】3【试题来源】【题目】在9×9的方格表中，有29个小格被染上了黑色，如果m表示至少包含5个黑色小方格的行的数目，n表示至少包含5个黑色小方格的列的数目，试确定m+n的最大值．【答案】10【解析】∵m表示至少包含5个黑色小方格的行的数目，∴5m小于29，∴m的最大值为5，当m=5时，则n的最大值为5．故m+n的最大值为5+5=10．【知识点】染色问题【适用场合】当堂例题【难度系数】3【试题来源】【题目】将凸五边形ABCDE的5条边和5条对角线染色，且满足任意有公共顶点的两条线段不同色，求颜色数目的最小值．【答案】5【解析】由于顶点A是4条线段AB，AC，AD，AE的公共点，因此至少需要4种颜色．若只有4种颜色，不妨设为红、黄、蓝、绿，则每个顶点引出的4条线段的颜色包含红、黄、蓝、绿各一种，因此，红色的线段共有条，矛盾．所以，至少需要5种颜色．下面的例子说明5种颜色可以将这10条线段染为满足条件的颜色．将AB，CE 染为1号颜色；将BC，DA染为2号颜色；将CD，EB染为3号颜色；将DE，AC染为4号颜色；将EA，BD染为5号颜色，则任意有公共顶点的两条线段不同色．综上所述，颜色数目的最小值为5．【知识点】染色问题【适用场合】当堂例题【难度系数】3【试题来源】【题目】有10个表面涂满红漆的正方体，其棱长分别为2，4，6，…，20.若把这些正方体全部锯成棱长为1的小正方体，求有多少个至少一面有漆的小正方体.【答案】8000【解析】【知识点】染色问题【适用场合】随堂课后练习【难度系数】3【试题来源】【题目】将直线上的每一个点都染上红、黄两色中的一种，证明：必存在同颜色的三个点，使得其中一点是另两点为端点的线段的中点.【答案】见解析【解析】【知识点】染色问题【适用场合】当堂例题【难度系数】3【试题来源】【题目】某班有50个学生，男女各占一半，他们围成一圈，席地而坐开营火晚会，求证：必能找到一位两旁都是女生的学生.【答案】见解析【解析】【知识点】染色问题【适用场合】课后两周练习【难度系数】3【试题来源】【题目】若由“L”形的4个小方格，无重迭地拼成一个4×n的矩形.试证：n必为偶数.【答案】见解析【解析】【知识点】染色问题【适用场合】随堂课后练习【难度系数】3【试题来源】【题目】将一个棱长分别为36厘米、54厘米和72厘米的长方体切割成一些大小相同、棱长是整数厘米的正方体，然后给这些正方体的表面涂色。
(完整版)染色问题的计数方法
染色问题的计数方法河北张家口市第三中学王潇与染色问题有关的试题新颖有趣,其中包含着丰富的数学思想,染色问题,解题方法技巧性强且灵活多变,故这类问题有利于培养学生的创新思维能力,分析问题与观察问题的能力,有利于开发学生的智力。
一、区域染色问题1.根据乘法原理，对各个区域分步染色，这是处理这类问题的基本的方法。
例1要用四种颜色给四川、青藏、西藏、云南四省（区）的地图染色（图1）每一省（区）一种颜色，只要求相邻的省（区）不同色，则不同染色的方法有多少种？分析先给西藏青海云南四川四川染色有4种方法，再给青海染色有3种方法，接着给西藏染色有2种方法，最后给云南染色有2种方法，根据乘法原理，不同的染色方法共有4×3×2×2＝48种2.根据共用了多少种颜色分类讨论，分别计算出各种情形的种数，再用加法原理求出不同年拾方法种数。
例2 （2003年全国高考题）如图2，一个地区分为5个行政区域，现给地图着色，要求相邻区域不得使用同一颜色，现有4种颜色可供选择，则不同的着色方法共有多少种？分析 依题意至少要12345图2选用3种颜色。
（1） 当选用三种颜色时，区域2与4必须同色，区域3与5必须同色，有34A 种。
（2） 当用四种颜色时，若区域2与4同色，则区域3与5不同色，有44A 种；若区域3与5同色，则区域2与4不同色，有44A 种，故用四种颜色时共有244A 种。
由加法原理可知满足题意的着色方法共有34A ＋244A ＝24＋2×24＝72种。
3 根据某两个不相邻区域是否同色分类讨论，从某两个不相邻区域同色与不同色入手，分别计算出两种情形的种数，再用加法原理求出不同染色方法数。
例3 用红、黄、蓝、白、黑五种颜色涂在“田”字形的四个小方格内（图3），每格涂一种颜色，相邻的两格涂不同的颜色，如果颜色可以反复使用，共有多少种不同的涂色方法？1234图3（1）四格涂不同的颜色，方法数为45A ；（2）有且仅有两格涂相同的颜色，即只有一组对角小方格涂相同颜色，涂法种数为21245C A ； （3）两组对角小方格涂相同颜色，涂法种数为25A 。
专题06 染色问题(解析版)
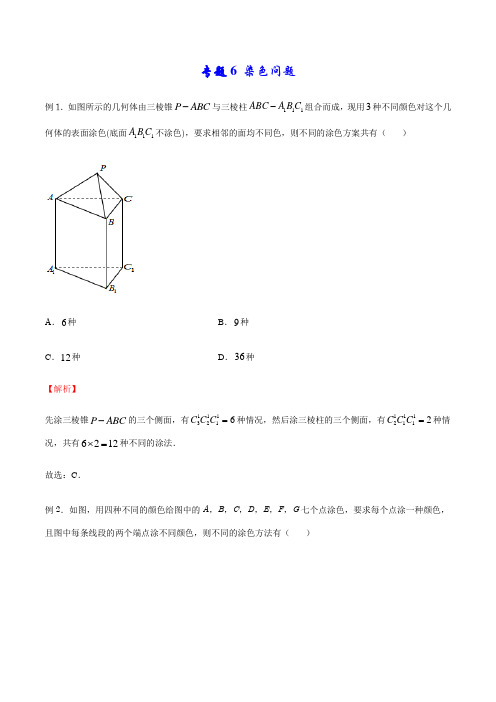
专题6 染色问题例1．如图所示的几何体由三棱锥P ABC -与三棱柱111ABC A B C -组合而成，现用3种不同颜色对这个几何体的表面涂色(底面111A B C 不涂色)，要求相邻的面均不同色，则不同的涂色方案共有（ ）A ．6种B ．9种C ．12种D ．36种【解析】 先涂三棱锥P ABC -的三个侧面，有1113216C C C =种情况，然后涂三棱柱的三个侧面，有1112112C C C =种情况，共有6212⨯=种不同的涂法．故选：C ．例2．如图，用四种不同的颜色给图中的A ，B ，C ，D ，E ，F ，G 七个点涂色，要求每个点涂一种颜色，且图中每条线段的两个端点涂不同颜色，则不同的涂色方法有（ ）A ．192种B ．336种C ．600种D ．624种【解析】 由题意，点E ，F ，G 分别有4，3，2种涂法，（1）当A 与F 相同时，A 有1种涂色方法，此时B 有2种涂色方法，①若C 与F 相同，则C 有1种涂色方法，此时D 有3种涂色方法；②若C 与F 不同，则D 有2种涂色方法.故此时共有()432121312240⨯⨯⨯⨯⨯⨯+⨯=种涂色方法.（2）当A 与G 相同时，A 有1种涂色方法，①若C 与F 相同，则C 有1种涂色方法，此时B 有2种涂色方法，D 有2种涂色方法；②若C 与F 不同，则C 有2种涂色方法，此时B 有2种涂色方法，D 有1种涂色方法.故此时共有()4321122221192⨯⨯⨯⨯⨯⨯+⨯⨯=种涂色方法.（3）当A 既不同于F 又不同于G 时，A 有1种涂色方法.①若B 与F 相同，则C 与A 相同时，D 有2种涂色方法，C 与A 不同时，C 和D 均只有1种涂色方法； ②若B 与F 不同，则B 有1种涂色方法，（i ）若C 与F 相同，则C 有1种涂色方法，此时D 有2种涂色方法；（ii ）若C 与F 不同，则必与A 相同，C 有1种涂色方法，此时D 有2种涂色方法.故此时共有()()43211121111212168⨯⨯⨯⨯⨯⨯+⨯+⨯⨯+⨯=⎡⎤⎣⎦种涂色方法.综上，共有240192168600++=种涂色方法.故选：C.例3．现有6种不同的颜色，给图中的6个区域涂色，要求相邻区域不同色，则不同的涂色方法共有（ ）A ．720种B ．1440种C ．2880种D ．4320种【解析】 根据题意分步完成任务：第一步：完成3号区域：从6种颜色中选1种涂色，有6种不同方法；第二步：完成1号区域：从除去3号区域的1种颜色后剩下的5种颜色中选1种涂色，有5种不同方法；第三步：完成4号区域：从除去3、1号区域的2种颜色后剩下的4种颜色中选1种涂色，有4种不同方法；第四步：完成2号区域：从除去3、1、4号区域的3种颜色后剩下的3种颜色中选1种涂色，有3种不同方法；第五步：完成5号区域：从除去1、2号区域的2种颜色后剩下的4种颜色中选1种涂色，有4种不同方法；第六步：完成6号区域：从除去1、2、5号区域的3种颜色后剩下的3种颜色中选1种涂色，有3种不同方法；⨯⨯⨯⨯⨯=种.所以不同的涂色方法：6543434320故选：D.例4．将5种不同的花卉种植在如图所示的四个区域中，每个区域种植一种花卉，且相邻区域花卉不同，则不同的种植方法种数是（）．A．420 B．180 C．64 D．25【解析】由题意，由于规定一个区域只涂一种颜色，相邻的区域颜色不同，可分步进行区域A有5种涂法，B有4种涂法，⨯⨯⨯=种，A，D不同色，D有3种，C有2种涂法，有5432120⨯⨯=种，A，D同色，D有1种涂法，C有3种涂法，有54360共有180种不同的涂色方案．故选：B．例5．用红、黄、蓝、绿、橙五种不同颜色给如图所示的5块区域A、B、C、D、E涂色，要求同一区域用同一种颜色，有共公边的区域使用不同颜色，则共有涂色方法（）A ．120种B ．720种C ．840种D ．960种【解析】 法一：A 有5种颜色可选，B 有4种颜色可选，D 有3种颜色可选，若CA 同色，E 有4种颜色可选；若CB 同色，E 有4种颜色可选；若C 与A 、B 都不同色，则C 有2种颜色可选，此时E 有4种颜色可选，故共有()5434424960⨯⨯⨯++⨯=种．法二：当使用5种颜色时，有55120A =种涂色方法；当使用4种颜色时，必有两块区域同色，可以是AC ，BC ，AE ，BE ，CE ，共有455600A =种涂色方法；当使用3种颜色时，只能是AC 同色且BE 同色，AE 同色且BC 同色，ACE 同色，BCE 同色，共有354240A =种涂色方法，∴共有120600240960++=种涂色方法.故选：D.例6．如图，某伞厂生产的太阳伞的伞篷是由太阳光的七种颜色组成，七种颜色分别涂在伞篷的八个区域内，且恰有一种颜色涂在相对区域内，则不同颜色图案的此类太阳伞最多有（ ）.A．40320种B．5040种C．20160种D．2520种【解析】先从7种颜色中任意选择一种，涂在相对的区域内，有177C=种方法，再将剩余的6种颜色全部涂在剩余的6个区域内，共有66A种方法，由于图形是轴对称图形，所以上述方法正好重复一次，所以不同的涂色方法，共有66725202A⨯=种不同的涂法.故选：D.例7．如图所示，将四棱锥S-ABCD的每一个顶点染上一种颜色，并使同一条棱上的两端异色，如果只有5种色可供使用，则不同的染色方法种数为（）A．240 B．360 C．420 D．960【解析】⨯⨯=种染色方法.由题设，四棱锥S-ABCD的顶点S、A、B所染的颜色互不相同，它们共有54360设5种颜色为1，2，3，4，5，当S、A、B染好时，不妨设其颜色分别为1、2、3，若C染2，则D可染3或4或5，有3种染法；若C染4，则D可染3或5，有2种染法，若C染5，则D可染3或4，有2种染法.⨯=（种）.可见，当S、A、B已染好时，C、D还有7种染法，故不同的染色方法有607420故选：C⨯方格纸中每个小方格染三种颜色之一，使得每种颜色的小方格的个数相等.若相例8．如图所示，将3333邻两个小方格的颜色不同，称他们的公共边为“分割边”，则分割边条数的最小值为( )A．33 B．56 C．64 D．78【解析】记分隔边的条数为L，首先将方格按照按图分三个区域，分别染成三种颜色，粗线上均为分隔边，此时共有56条分隔边，即56L =，其次证明：56L ≥，将将方格的行从上至下依次记为1233,,,A A A ，列从左至右依次记为1233,,B B B ，行i A 中方格出现的颜色数记为()i n A ，列i B 中方格出现的颜色个数记为()i n B ，三种颜色分别记为123,,c c c ，对于一种颜色j c ，设()j n c 为含有j c 色方格的行数与列数之和，定义当i A 行含有j c 色方格时，(),1i j A c δ=，否则(),0i j A c δ=，类似的定义(),i j B c δ，所以()()()()()()()3333331111,,i i i ji j j i i i j n A n B A c B c n c δδ====⎫+=+=⎪⎭∑∑∑∑， 由于染j c 色的格有21333633⨯=个，设含有j c 色方格的行有a 个，列有b 个，则j c 色的方格一定再这个a 行和b 列的交叉方格中，从而363ab ≥，所以()()3839(1,2,3)j j n c a b n c j =+≥≥>⇒≥=①，由于在行i A 中有()i n A 种颜色的方格，于是至少有()1i n A -条分隔边，类似的，在列i B 中有()i n B 种颜色的方格，于是至少有()1i n B -条分隔边， 则()()()()()()()3333113311166i i i ii i i L n A n B n A n B ===≥-+-=+-∑∑∑② ()3166j j n c ==-∑③下面分两种情形讨论，(1)有一行或一列所有方格同色，不妨设有一行均为1c 色，则方格的33列均含有1c 的方格，又1c 色的方格有363个,故至少有11行有1c 色方格，于是()1113344n c ≥+=④由①③④得()()()123664439396656L n c n c n c ≥++-≥++-=，(2)没有一行也没有一列的所有方格同色,则对任意133i ≤≤均有()()2,2i i n A n B ≥≥，从而，由式②知：()()()33166334666656i i i L n A n B =≥+-≥⨯-=>∑，综上，分隔边条数的最小值为56.故选：B.例9．如图给三棱柱ABC DEF -的顶点染色，定义由同一条棱连接的两个顶点叫相邻顶点，规定相邻顶点不得使用同一种颜色，现有4种颜色可供选择，则不同的染色方法有_________________.【解析】首先先给顶点,,A B C 染色，有3424A =种方法，再给顶点D 染色，①若它和点B 染同一种颜色，点E 和点C 染相同颜色，点F 就有2种方法，若点E 和点C 染不同颜色，则点E 有2种方法，点F 也有1种方法，则,,DEF 的染色方法一共有2214+⨯=种方法，②若点D 和点B 染不同颜色，且与点C 颜色不同，则点D 有1种方法，点E 与点C 颜色不同，则点E 有1种方法，则点F 有1种方法，此时有1种方法；若最后E 与C 相同，则F 有2种方法，则共有2种方法；点D 与点C 颜色相同，则点D 有1种方法，则点E 有2种方法，则点F 有2种方法，共有224⨯=种方法，所以点D 和点B 染不同，颜色共有1247++=种方法，所以点,,D E F 的染色方法一共有4711+=种，所以共有2411264⨯=种方法.故答案为：264例10．现用五种不同的颜色，要对如图中的四个部分进行着色，要求公共边的两块不能用同一种颜色，共有__________种不同着色方法【解析】先排I ，有5种方法；然后排II,IV ，最后排III ：①当II,IV 相同时，方法有44⨯种，故方法数有54480⨯⨯=种.②当II,IV 不同时，方法有433⨯⨯种，故方法数有5433180⨯⨯⨯=种.综上所述，不同的着色方法数有80180260+=种.故答案为：260例11．如图所示的五个区域中，中心区E 域是一幅图画，现要求在其余四个区域中涂色．．．．．．．．．，有四种颜色可供选择．要求每个区域只涂一种颜色且相邻区域所涂颜色不同，则不同的涂色方法种数为______．【解析】分三种情况：（1）用四种颜色涂色，有4424A =种涂法；（2）用三种颜色涂色，有34248A =种涂法；（3）用两种颜色涂色，有2412A =种涂法；所以共有涂色方法24481284++=.故答案为：84例12．从红、黄、蓝、黑四种颜色中选出3种颜色，给如图所示的六个相连的圆涂色，若每种颜色只能涂两个圆，且相邻两个圆所涂颜色不能相同，则不同的涂色方案的种数是________.【解析】从红、黄、蓝、黑四种颜色中选出3种颜色有4种选法.因为每种颜色只能涂两个圆，且相邻两个圆所涂颜色不能相同，分两类：一类是，前三个圆用3种颜色，有336A =种方法，后3个圆也有3种颜色，有11224C C =种方法，此时不同方法有6×4=24方法； 二类是，前3个圆2种颜色，后3个圆2种颜色，共有11326C C =方法.综上可知，所有的涂法共有()4246120⨯+=种方法.故答案为： 120例13．如图一个正方形花圃被分成5份．若给这5个部分种植花，要求相邻两部分种植不同颜色的花，已知现有红、黄、蓝、绿4种颜色不同的花，则不同的种植方法有_________种【解析】先对E 部分种植，有4种不同的种植方法；再对A 部分种植，又3种不同的种植方法；对C 部分种植进行分类：①若与A 相同，D 有2种不同的种植方法，B 有2种不同的种植方法，共有432248⨯⨯⨯=（种）， ②若与A 不同，C 有2种不同的种植方法，D 有1种不同的种植方法，B 有1种不同的种植方法，⨯⨯⨯⨯=（种），共有4321124综上所述，共有72种种植方法．故答案为：72.例14．现有五种不同的颜色，要对图形中的四个部分进行着色，要求有公共边的两块不能用同一种颜色，不同的涂色方法有_______种．【解析】依题意，I、II、III区域有共同边颜色互不相同，按I、II、III、IV顺序着色，则区域I有5种着色方法，区域II有4种着色方法，区域III有3种着色方法，IV只与II、III相邻，因此区域IV有3种着色方法，根据分步乘法计数原理，不同的着色方法种数为⨯⨯⨯=.5433180故答案为：180例15．现将如图所示的5个小正方形涂上红、黄两种颜色，其中3个涂红色，2个涂黄色，若恰有两个相邻的小正方形涂红色，则不同的涂法共有__________种(用数字作答).【解析】当涂红色两个相邻的小正方形在两端时是有12224A A =， 当涂红色两个相邻的小正方形在不在两端时是有122A =，则不同的涂法种数共有426+=种．故答案为：6．例16．四色猜想是近代数学难题之一，四色猜想的内容是：“任何一张地图最多用四种颜色就能使具有共同边界的国家着上不同的颜色”，如图，一张地图被分成了五个区域，每个区域只使用一种颜色，现有4种颜色可供选择（四种颜色不一定用完），则满足四色猜想的不同涂色种数为__________【解析】设五个区域分别为,,,,A B C D E ，依题意由公共边的两个区域颜色不同，用四种颜色进行涂色则有两个区域颜色相同，可以是A 与C ，A 与E ，B 与E 同色，有涂色方法44372A =；或用三种颜色涂色，则有2组颜色同色，为A 与C 同色，B 与E 同色，有涂色方法3424A =，根据分类加法原理，共有涂色方法722496+=.故答案为：96.例17．如图，将标号为1，2，3，4，5的五块区域染上红、黄、绿三种颜色中的一种，使得相邻区域(有公共边)的颜色不同，则不同的染色方法有______种.【解析】对于1，有三种颜色可以安排；若2和3颜色相同，有两种安排方法，4有两种安排，5有一种安排，此时共有322112⨯⨯⨯=；若2和3颜色不同，则2有两种，3有一种.当5和2相同时，4有两种；当5和2不同，则4有一种，此时共有()322118⨯⨯+=⎡⎤⎣⎦，综上可知，共有121830+=种染色方法.故答案为：30.例18．某城市在中心广场建造一个花圃，花圃分为6个部分.现要栽种4种不同颜色的花，每部分栽种一种且相邻部分不能栽种同样颜色的花，则不同的栽种方法有______种.（用数字作答）【解析】由题意，6个部分.栽种4种不同颜色的花，必有2组颜色相同的花，若2、5同色，则3、6同色或4、6同色，所以共有44248A =种栽种方法；若2、4同色，则3、6同色，所以共有4424A =种栽种方法；若3、5同色，则2、4同色或4、6同色，所以共有44248A =种栽种方法；所以共有482448120++=种栽种方法.故答案为：120例19．给图中A ，B ，C ，D ，E ，F 六个区域进行染色，每个区域只染一种颜色，且相邻的区域不同色.若有4种颜色可供选择，则共有___种不同的染色方案.【解析】解：要完成给图中A、B、C、D、E、F六个区域进行染色，染色方法可分两类，第一类是仅用三种颜色染色，即AF同色，BD同色，CE同色，则从四种颜色中取三种颜色有344C=种取法，三种颜色染三个区域有3 36A=种染法，共4624⨯=种染法；第二类是用四种颜色染色，即AF，BD，CE中有一组不同色，则有3种方案(AF不同色或BD不同色或CE不同色），先从四种颜色中取两种染同色区有2412A=种染法，剩余两种染在不同色区有2种染法，共有312272⨯⨯=种染法．∴由分类加法原理得总的染色种数为247296+=种．故答案为：96．20．如图，用4种不同的颜色对图中5个区域涂色（4种颜色全部使用），要求每个区域涂一种颜色，相邻的区域不能涂相同的颜色，则不同的涂色方法有种.（用数字作答）例21．给如图染色，满足条件每个小方格染一种颜色，有公共边的小方格颜色不能相同，则用4种颜色染色的方案有__种，用5种颜色染色的方案共有__种.【解析】（1）根据题意，若用4种颜色染色时，先对A 、B 区域染色有1143C C 种，再对C 染色： ①当C 同B 时，有1122C C 种；②当C 同A 时，有111322C C C +种；③当C 不同A 、B 时，有111232()C C C +种； 综合①②③共有11111111114322322232[()]252C C C C C C C C C C ++++=种； （2）根据题意，若用5种颜色染色时，先对A 、B 区域染色有1154C C 种，再对C 染色：①当C 同B 时，有1133C C 种；②当C 同A 时，有111433C C C +种；③当C 不同A 、B 时，有11113423()C C C C +种；综合①②③，共有1111111111154334333423[()]1040C C C C C C C C C C C ++++=种. 故答案为：252；1040.例22．如图，用四种不同的颜色给三棱柱ABC A B C '''-的六个顶点涂色，要求每个点涂一种颜色．若每个底面的顶点涂色所使用的颜色不相同，则不同的涂色方法共有________种；若每条棱的两个端点涂不同的颜色，则不同的涂色方法共有________种．【解析】（1）由题得每个底面的顶点涂色所使用的颜色不相同，则不同的涂色方法共有3344576A A =；（2）若B '，A '，A ，C 用四种颜色，则有4424A =； 若B '，A '，A ，C 用三种颜色，则有33442222192A A ⨯⨯+⨯⨯=；若B '，A '，A ，C 用两种颜色，则有242248A ⨯⨯=.所以共有2419248++=264种．故答案为：①576；②264.。
五年级上奥数试题——第七讲染色与操作
第七讲染色与操作问题教学目标1. 掌握染色问题的分析思路和典型的染色方法；2. 理解操作问题的解题方法。
经典精讲染色问题这里的染色问题不是要求如何染色，然后问有多少种染色方法的那类题目，它指的是一种解题方法。
染色方法是一种将题目研究对象分类的形象化方法，通过将问题中的对象适当染色，我们可以更形象地观察分析出其中所蕴含的关系，再经过一定的逻辑推理，便能得出问题的答案。
这类问题不需要太多的数学知识，但技巧性、逻辑性较强，要注意学会几种典型的染色方法。
【例1】 六年级一班全班有35名同学，共分成5排，每排7人，坐在教室里，每个座位的前后左右四个位置都叫作它的邻座。
如果要让这35名同学各人都恰好坐到他的邻座上去，能办到吗？为什么？【分析】 划一个57 的方格表，其中每一个方格表示一个座位。
将方格黑白相间地染上颜色，这样黑色座位与白色座位都成了邻座。
因此每位同学都坐到他的邻座相当于所有白格的坐到黑格，所有黑格的坐到白格。
但实际上图中有17个黑格，18个白格，黑格与白格的个数不相等，故不能办到。
【例2】 右图是学校素质教育成果展览会的展室，每两个相邻的展室之间都有门相通。
有一个人打算从A 室开始依次而入，不重复地看过各室展览之后，仍回到A 室，问他的目的能否达到，为什么？【分析】 采用染色法。
如右下图，共有9个展览室，对这9个展览室，黑白相间地进行染色，从白室A 出发走过第1扇门必至黑室，再由黑室走过第2扇门至白室，由于不重复地走遍每一间展览室，因此将走过黑白相间的8个展览室，再回到白室A ，共走过9扇门。
由于走过奇数次门至黑室，走过偶数次门至白室。
现在，走过9扇门，必至黑室，所以无法回到原来的白室A 。
A[巩固] 有一次车展共6636⨯=个展室，如右图，每个展室与相邻的展室都有门相通，入口和出口如图所示。
参观者能否从入口进去，不重复地参观完每个展室再从出口出来?[分析] 如右下图，对每个展室黑白相间染色，那么每次只能从黑格到白格或从白格到黑格。
四年级数学奥数题知识点《染色问题》专项训练及答案
四年级数学奥数题知识点《染色问题》专项训练
及答案
题型：染色问题难度：★★
如图，把A、B、C、D、M这五个部分用5种不同的颜色染色，且相邻的部分不能使用同一种颜色，有的颜色也可以不用，不相邻的部分可以使用同一种颜色，那么这幅图一共有多少种不同的染色方法?
【答案解析】
如果5种颜色全部使用，那么共有5×4×3×2×1=120种染色方法。
如果只使用4种颜色，可以是B和D同色，也可以是A和C 同色，那么共有5×4×3×2×2=240种染色方法。
如果只使用3种颜色，那么有B和D同色并且A和C同色，共有5×4×3=60种染色方法。
120+240+60=420，所以这幅图一共有420种不同的染色方法。
题型：染色问题难度：★★
如图，9条小线段组成了4个小三角形，现在将每条线段分别染上红、黄、蓝三种颜色之一，使得每个三角形三条边的颜色互不相同，那么共有多少种不同的染色方式?
【答案解析】
任选一个小三角形的一条边，当这条边的颜色确定时，这个小三角形的染色方法有2种，同时每种方法都会确定与其相邻的小三角形的一条边的颜色。
24×3=48，所以共有48种不同的染色方式。
染色问题
什么是染色问题这里的染色问题不是要求如何染色，然后问有多少种染色方法的那类题目，它指的是一种解题方法。
染色方法是一种将题目研究对象分类的形象化方法，通过将问题中的对象适当染色，我们可以更形象地观察分析出其中所蕴含的关系，再经过一定的逻辑推理，便能得出问题的答案。
这类问题不需要太多的数学知识，但技巧性、逻辑性较强，要注意学会几种典型的染色方法。
染色问题基本解法：三面涂色和顶点有关 8个顶点。
两面染色和棱长有关。
即新棱长（棱长-2）×12一面染色和表面积有关。
同样用新棱长计算表面积公式（棱长-2）×（棱长-2）*60面染色和体积有关。
用新棱长计算体积公式（棱长-2）×（棱长-2）×（棱长-2）长方体的解法和立方体同理，即计算各种公式前长、宽、高都要先减2再利用公式计算。
染色问题的解题思路染色问题是数奥解题中的难点，这类问题初看起来好像无从着手，其实只要认真思考问题也很容易解决，下面就染色问题的解题思路说一下。
图一首先，拿到一道题先认真观察，看这个题的突破点。
什么是染色问题的突破点呢？那就是找染色区域中的一个最多，这个最多是指一个区域，其他区域与它连接的最多。
例如图一中A区域A与B、C、D、E、 F连接最广所以A为特殊区域。
找到这个区域问题就容易解决了。
这个区域可以任意添色就是染最多的颜色。
本题中有4种颜色那么A可以染4种颜色了。
完成这个事件需要A、B、C、D、E、F6步所以用乘法原理。
这道题找到了最特殊的A 区域第二特殊区域和第三区域的确定也就容易了，C区域是与A相连，连接区域的数量仅次于A区域图一中的C和E区域都可以做第二个特殊区域了，但只能选一个，我们把C当成第二特殊的区域，则C可以染3种颜色。
区域B跟A、C相连那么 B可以染2种。
D与A、C、E相连则只能选1种，对吗？我们仔细观察，按顺序说A----4，C------3，B-------2，D 则连接A、C当A 选色后C有3种可能，D在A、C选色后只有2种可能。
染色问题
染色问题 （一）一．基本方法染色问题的本质是对集合的元素进行分类的问题，染色可以使分类更直观、更形象．染色问题主要有两类：一类使借助染色方法解决问题；二类是问题的条件是用染色的方式给出的．常见的染色问题有对区域的染色（包括对方格，三角形的染色），对线段的染色，对点的染色．常用思想方法是整体思想，抽屉原理，考虑极端情形，数学归纳法，构造思想等． 二．例题精选（一）．k 染色平面问题将平面上的点用不超过k 种颜色给每一个点染一种颜色，这样的平面叫做k 染色平面．１．坐标平面上若干个整点，将一些整点染红色，一些染蓝色，证明：总可以有一种染法使每行、每列两种颜色点数之差不超过１．２．对于任意的a >0，二染色平面上必存在斜边长为a 且内角分别为︒︒︒90,60,30的三顶点同色的三角形．R R R R RR R RR BB B BBBB B B B B B B B B R R R R RR BＲ４．求证：二染色平面上，一定存在一个边长为1或3的正三角形，它的三个顶点同色．（若用三染色平面呢？）（二）．平面图形的染色问题５．已知⊿ABC 为正三角形，G 为三条线段AB 、BC 、CA （包括A 、B 、C ）上的所有点的集合，将G 中的一些点染上黑色，其余点染白色，试证：至少存在一个正三角形 ABC 的内接直角三角形，三顶点是同色的． 关键：在2,,,,,===EACE FCBF DBAD F E D CA BC AB 且上取点则D ，E ，F 必有两点同色，不妨设为E ，F 同为黑色，若BC 上还有黑色点，命题的证．否则ＢＣ上除点Ｆ全为白色点，若ＡＢ上有白色点，得证．否则ＡＢ上全为 黑色点，则Ｅ在ＡＢ上的射影Ｇ为黑色点，再在ＡＢ上取 另一点Ｈ，则三角形ＦＧＨ是直角三角形．６．正九边形的一些顶点染上白色，另一些染上黑色．证明：存在两个全等的三角形，每一个三角形的顶点染有同一颜色．解：九个顶点中至少有5个顶点颜色相同，设为白色，5个白色顶点能构成10个顶点同为白色三角形，然后绕正九边形中心旋转，每次旋转)8,,1,0(92 =k k π，上述10个三角形，9次旋转后构成90个三角形。
小学奥数——染色问题（答案）
⼩学奥数——染⾊问题（答案）第9讲染⾊问题【知识要点】染⾊⽅法是⼀种对题⽬所研究的对象⽤直观形象的染⾊来进⾏分类的⽅法。
象国际象棋的棋盘那样，我们可以把研究的对象染上不同的颜⾊，使问题变得浅显明了、⼀⽬了然，有利于我们观察、分析对象之间的关系，再利⽤奇偶性、抽屉原理等多种知识对染⾊图形进⾏分析，从⽽达到对原问题的解决。
【典型例题】例1、教室中有7排位⼦，每排7张，每张位⼦上坐⼀个同学，如果⼀周后，每个同学都必须和他相邻的（前、后、左、右）某⼀个同学换位⼦，问：这种交换可能成功吗？为什么？解：如右图所⽰⿊⽩相间涂⾊，⽩⾊共有25个，⿊⾊24个，要实现题意要求，⼀个⽩⾊位置必须和⼀个⿊⾊位置互换，⿊⽩座位应该⼀样多才⾏，所以办不到。
例2、如图是⼀所房⼦的⽰意图,图中数字表⽰房间号码,每间房⼦都与隔壁的房间相通.问能否从1号房间开始,不重复的⾛遍所有房间⼜回到1号房间? 解：如图所⽰每⼀个奇数号房间旁边⼀定是偶数号房间，反之亦然，那么奇数号房间⼀定⾛到偶数号，偶数号⼀定⾛到奇数号，从⼀号开始⾛奇数步⼀定是到偶数号房间，⾛偶数步⼀定是到奇数号房间，要不重复的⾛遍所有房间回到1号房间，共要⾛9步，应该⾛到偶数号房间，⽽1是奇数，所以办不到。
例3、⼀个8?8国际象棋(下图)去掉对⾓上两格后,是否可以⽤31个2?1的“⾻牌” (形如 )把象棋盘上的62个⼩格完全盖住?解：任意⼀个2?1的“⾻牌”⼀定是⼀⽩⼀⿊的，所以若要⽤31个这样的⾻牌覆盖这个棋盘，⽩⿊格数应该⼀样多，⽽此棋盘中有32个⿊格，30个⽩格，所以办不到。
例4、线段AB 的两个端点，⼀个标以红⾊，⼀个标以蓝⾊。
在此线段中任意插⼊2008个分点，每个分点任意涂上红⾊或蓝⾊，这样分得2009条不重叠的⼩线段，如果把两端涂⾊不同的线段叫做奥运线段，奥运线段的条数是奇数还是偶数？解：原本的线段AB 就是⼀条奥运线段，然后不管中间插⼊的点是什么颜⾊的，都会破坏原来的奥运线段从⽽变成⼀条两端同⾊⼀条奥运线段，再然后如果在⼀条奥运线段中间插⼊任意颜⾊的点，奥运线段会被破坏，但是⼜会⽣成⼀条较短的，那么奥运线段的数量总数不变；如果在⼀条两端同⾊的线段中间插⼊不同⾊ 1 2 3 4 5 6 7 8 9的点，⼀下就增加2条奥运线段，不改变奥运线段数量的奇偶性。
(完整版)染色问题的计数方法
染色问题的计数方法河北张家口市第三中学 王潇与染色问题有关的试题新颖有趣 ,其中包含着丰富的数 学思想 ,染色问题 ,解题方法技巧性强且灵活多变 ,故这类问题 有利于培养学生的创新思维能力 ,分析问题与观察问题的能 力,有利于开发学生的智力。
一、 区域染色问题1. 根据乘法原理，对各个区域分步染色，这是处理这 类问题的基本的方法。
例 1 要用四种颜色给四川、青藏、西藏、云南四 省（区）的地图染色（图 1）每一省（区）一种颜色，只要 求相邻的省（区）不同色，则不同染色的方法有多少种？法，再给青海染色有 3 种方法，接着给西藏染色有 2 种方法， 最后给云南染色有 2 种方法，根据乘法原理，不同的染色方 法共有 4×3×2×2＝48 种2. 根据共用了多少种颜色分类讨论，分别计算出各种 情形的种数，再用加法原理求出不同年拾方法种数。
例 2 （2003 年全国高考题）如图 2，一个地区分为 5 个行 政区域，现给地图着色，要求相邻区域不得使用同一颜色，种方（1）当选用三种颜色时，区域2 与4 必须同色，3区域3 与5 必须同色，有A4种。
（2）当用四种颜色时，若区域2 与4 同色，则区域3与5不同色，有A44种；若区域3 与5 同色，则区域2与4 不同色，有A44种，故用四种颜色时共有2 A44种。
3由加法原理可知满足题意的着色方法共有A43＋2A44＝24＋2× 24＝72 种。
3 根据某两个不相邻区域是否同色分类讨论，从某两个不相邻区域同色与不同色入手，分别计算出两种情形的种数，再用加法原理求出不同染色方法数。
例3 用红、黄、蓝、白、黑五种颜色涂在“田”字形的四个小方格内（图3），每格涂一种颜色，相邻的两格涂不同的颜色，如果颜色可以反复使用，共有多少种不同的涂色方法？2134图31）四格涂不同的颜色，方法数为A45 ；（2）有且仅有两格涂相同的颜色，即只有一组对角小方格 涂相同颜色，涂法种数为 2C 15A24； （ 3）两组对角小方格涂相同颜色，涂法种数为 A52 。
小学奥数——染色问题(答案)
第9讲 染色问题【知识要点】染色方法是一种对题目所研究的对象用直观形象的染色来进行分类的方法。
象国际象棋的棋盘那样，我们可以把研究的对象染上不同的颜色，使问题变得浅显明了、一目了然，有利于我们观察、分析对象之间的关系，再利用奇偶性、抽屉原理等多种知识对染色图形进行分析，从而达到对原问题的解决。
【典型例题】例1、教室中有7排位子，每排7张，每张位子上坐一个同学，如果一周后，每个同学都必须和他相邻的（前、后、左、右）某一个同学换位子，问：这种交换可能成功吗？为什么？ 解：如右图所示黑白相间涂色，白色共有25个，黑色24个，要实现题意要求，一个白色位置必须和一个黑色位置互换，黑白座位应该一样多才行，所以办不到。
例2、如图是一所房子的示意图,图中数字表示房间号码,每间房子都与隔壁的房间相通.问能否从1号房间开始,不重复的走遍所有房间又回到1号房间? 解：如图所示每一个奇数号房间旁边一定是偶数号房间，反之亦然，那么奇数号房间一定走到偶数号，偶数号一定走到奇数号，从一号开始走奇数步一定是到偶数号房间，走偶数步一定是到奇数号房间，要不重复的走遍所有房间回到1号房间，共要走9步，应该走到偶数号房间，而1是奇数，所以办不到。
例3、一个8⨯8国际象棋(下图)去掉对角上两格后,是否可以用31个2⨯1的“骨牌” (形如 )把象棋盘上的62个小格完全盖住?解：任意一个2⨯1的“骨牌”一定是一白一黑的，所以若要用31个这样的骨牌覆盖这个棋盘，白黑格数应该一样多，而此棋盘中有32个黑格，30个白格，所以办不到。
例4、线段AB 的两个端点，一个标以红色，一个标以蓝色。
在此线段中任意插入2008个分点，每个分点任意涂上红色或蓝色，这样分得2009条不重叠的小线段，如果把两端涂色不同的线段叫做奥运线段，奥运线段的条数是奇数还是偶数？ 解：原本的线段AB 就是一条奥运线段，然后不管中间插入的点是什么颜色的，都会破坏原来的奥运线段从而变成一条两端同色一条奥运线段，再然后如果在一条奥运线段中间插入任意颜色的点，奥运线段会被破坏，但是又会生成一条较短的，那么奥运线段的数量总数不变；如果在一条两端同色的线段中间插入不同色 1 2 3 4 5 6 7 8 9的点，一下就增加2条奥运线段，不改变奥运线段数量的奇偶性。
小学奥数模块教程染色问题(一)
染色问题（一）染色问题是一种将题目研究对象分类的形象化方法，通过将问题中的对象适当染色，我们可以更形象地观察分析出其中蕴含的关系，再经过一定的逻辑推理，便能得出问题的答案。
因此，这里的染色问题指的是一种解题方法。
这类问题不需要太多的数学知识，但技巧性、逻辑性较强，要注意学会集中典型的染色方法。
根据具体题目的研究对象，染色方法大致可以分为对点染色、对线段染色、对方格染色和对区域染色。
对方格染色常用的是黑白方格相间染色，也叫自然染色。
例1如右图，在5×5方格的A格中有一只爬虫，它每次总是朝上下左右方向爬到相邻的方格中。
那么他能否不重复的爬满每个方格再回A到A格中？解：有小虫的爬法，可黑白相间对方格自然染色，于是小虫只能由黑格爬到白格或白格爬到黑格。
所以它由A出发回到A，即黑格爬到黑格，必须经过偶数步。
而小方格为5×5=25个，每格爬过一次，就应该为25步，不是偶数。
于是这只爬虫不可能不重复地爬遍每格再回到A格。
例2 有一次车展有6×6=36个展室，如图。
每格展室与相邻的展室都有门相通，入口和出口如图所示。
参观者能否从入口进去，不重复地参观完每格展室在从出口出来？解：如图，对每个展室黑白相间染色，同样每次只能冲黑格到白格或者从白格到黑格。
入口和出口都是白格，故线路黑白相间，首位都是白格，于是应该白格比合格多1个，而实际上白格、黑格都是18个，故不能做到不重复走遍每个展室。
例3 右图是某一套房子的平面图，共12个房间，每相邻两间房间都有门相通。
请问，你能从某个房间出发，不重复地走完每个房间吗？解：如图所示，将房间黑白相间染色，发现只有5个黑格、7个白格。
因为每次只能从黑到白或者白到黑，路线必然是黑白相间，显然应该从多的白格开始。
但路线上1白1黑......直至5白5黑后还多余2白格，不可能从白到黑。
故无法实现不重复地走遍每个房间。
小结：染色问题的解题技巧主要在于染色具体方案的构造，其基本原则是使题目条件出现一定的规律，以利于解题。
染色问题总结
染色问题总结引言染色是一种常见的化学处理方法，广泛应用于纺织、造纸、印刷等行业。
通过给纤维或纸张上色，可以使其具有各种色彩，满足不同的需求。
然而，在染色过程中，常常会遇到一些问题，例如颜色不均匀、染色剂渗透不足等。
本文将对染色问题进行总结，分析常见问题的原因，并提出解决方案。
1. 颜色不均匀的问题1.1 问题描述颜色不均匀是染色过程中常见的问题之一。
在染色后，织物或纸张上出现颜色深浅不一的现象，影响了产品的质量。
1.2 原因分析1.2.1 染料分散性差：染料的分散性差会导致在染色过程中染料分布不均匀。
这可能由于染料粒子过大、分散剂使用不当等原因引起。
1.2.2 温度不均匀：染色温度不均匀会导致不同部位的颜色上色不一致。
可能是因为染缸加热方式不合理或温度传递不均匀等原因。
1.2.3 染色时间不足：染色时间过短，染料无法充分渗入纤维或纸张中，导致颜色不均匀。
1.3 解决方案1.3.1 使用分散性好的染料：选择分散性好的染料，可以提高染料在溶液中的分散性，减少颜色不均匀的问题。
1.3.2 控制染色温度：染色过程中要控制好温度，使得染缸内温度均匀分布。
1.3.3 延长染色时间：根据染料和纤维或纸张的特性，可以适当延长染色时间，确保染料充分渗入。
2. 染色剂渗透不足的问题2.1 问题描述在染色过程中，有时会出现染料渗透不足的问题。
即染料未能完全渗透到纤维或纸张的内部，导致染色效果不理想。
2.2 原因分析2.2.1 纤维或纸张密度大：纤维或纸张的密度大会阻止染料渗透，使得染料无法充分吸附。
2.2.2 纤维或纸张表面处理不当：纤维或纸张表面的处理不当，如有杂质、油污等，会减少染料的渗透性。
2.2.3 染料质量不佳：染料质量不佳，可能含有不溶于水的颗粒物或杂质，影响染料的渗透。
2.3 解决方案2.3.1 选择适应纤维或纸张的染料：根据纤维或纸张的特性选择适应的染料，可以提高染料的渗透性。
2.3.2 对纤维或纸张进行表面处理：在染色前对纤维或纸张进行表面处理，清除杂质和油污等，提高染料的渗透性。
小升初数学思维拓展几何图形专项训练专题12-染色问题
专题12-染色问题小升初数学思维拓展几何图形专项训练（知识梳理+典题精讲+专项训练）1、这里的染色问题不是要求如何染色，然后问有多少种染色方法的那类题目，它指的是一种解题方法．染色方法是一种将题目研究对象分类的形象化方法，通过将问题中的对象适当染色，我们可以更形象地观察分析出其中所蕴含的关系，再经过一定的逻辑推理，便能得出问题的答案．这类问题不需要太多的数学知识，但技巧性、逻辑性较强，要注意学会几种典型的染色方法．染色问题基本解法：三面涂色和顶点有关，8个顶点．两面染色和棱长有关．即新棱长（棱长-2）×12一面染色和表面积有关．同样用新棱长计算表面积公式（棱长-2）×（棱长-2）×60面染色和体积有关．用新棱长计算体积公式（棱长-2）×（棱长-2）×（棱长-2）长方体的解法和立方体同理，即计算各种公式前长、宽、高都要先减2再利用公式计算。
【典例一】已知一个大正方体木块能分割成若干个棱长是1cm的小正方体木块，在这个大正方体木块的6个面上涂红色，在分割成的若干个棱长是1cm的小正方体大木块中，两面涂红色的共有108块，那么只有一面涂红色的有几块？【分析】根据两面涂色的小正方体的个数=正方体的棱长数⨯（棱长2)-，可得大正方体的棱长；接下来再根据一2)-即可得到答案。
面涂色的小正方体的个数=正方体的面数⨯（棱长2【解答】解：大正方体的棱长为：10812211()÷+=cm26(112)486⨯-=（块)答：只有一面涂红色的有486块。
【点评】本题主要考查了染色问题，解题的关键是根据两面涂色的小正方体的个数=正方体的棱长数⨯（棱长2)-，求出大正方体的棱长。
【典例二】图中的立体由26个小正立方体组成，外露的部分（包括底部）漆上油漆后再拆散，问有多少个小正立方体有三面漆了油漆？【分析】小正立方体有三面漆了油漆的在大立方体的顶点处，由于大正方体在涂油漆前少了一个角，从而空出一个小正方体，却导致增加了两个小正方体倍涂色三个面；据此得解．【解答】解：三面漆了油漆的在大立方体的顶点处，由于大正方体在涂油漆前少了一个角，从而空出一个小正方体，却导致增加了两个小正方体倍涂色三个面；-+=（个)81310答：有10个小正立方体有三面漆了油漆．【点评】本题考查了学生观察的能力以及找规律的能力，关键是换角度思考，先数出涂色的面数．【典例三】给图中的各点（小圆圈）涂上颜色，相连接的两个点的颜色要不相同，最少要用几种颜色？【分析】图中有5个正方形，每个正方形只要保证每条对角线上的两的点同色，另一条与它不同色即可，这样只需要两种颜色，据此解答．【解答】解：根据分析画图如下：答：最少要用两种颜色．【点评】本题实际是著名的四色问题，四色问题是1852年英国数学家费南希斯 格里斯提出的，结论是：“不论多么复杂的地图，只要用不多于四种颜色就可以解决着色问题．”一．选择题（共8小题）1．一个棱长是3厘米的正方体，表面全部涂上红油漆，然后切成棱长是1厘米的小正方体，有3面是红色的小正方体有()个。
排列组合专题之染色问题3
排列组合专题之染色问题【引例】引例1．在一个正六边形的6个区域栽种观赏植物，如右图，要求同一块中种同一种植物，相邻的两块种不同的植物．现有四种不同的植物可供选择，则有________种栽种方案．引例2．某城市在中心广场建造一个花圃，花圃分为6个部分（如图），现要栽种4种不同颜色的花，每部分栽种一种且相邻部分不能栽种同样颜色的花，不同的栽种方法有_____种．（以数字作答）【分析】首先栽种第1部分，有14C 种栽种方法；然后问题就转化为用余下3种颜色的花，去栽种周围的5个部分（如右图所示），此问题和引例1是同一题型，因此我们有必要对这一题型的解法做一深入探讨。
【剖析】为了深入探讨这一题型的解法，（1）让我们首先用m （m≥3）种不同的颜色（可供选择），去涂4个扇形的情形（要求每一个扇形着一种颜色，相邻扇形着不同颜色），如图所示以1和3（相间）涂色相同与否为分类标准：①1和3涂同一种颜色，有m 种涂法；2有m-1种涂法,4也有m-1种涂法,∴ 共有 (1)(1)m m m ⋅-⋅-种涂法。
②1和3涂不同种颜色，有2m A 种涂法;2有m-2种涂法，4也有m-2种涂法，∴ 共有 2(2)(2)m A m m ⋅-⋅-种涂法。
综合①和②，共有(1)(1)m m m ⋅-⋅-+2(2)(2)m A m m ⋅-⋅-432463m m m m =-+-种涂法。
（２）下面来分析引例1以A 、C 、E （相间）栽种植物情况作为分类标准：①A 、C 、E 栽种同一种植物，有4种栽法；B 、D 、F 各有3种栽法，∴ 共有 4×3×3×3＝108 种栽法。
②A 、C 、E 栽种两种植物,有222432C C A 种栽法（24C 是4种植物中选出2种，23C 是A 、C 、E3个区域中选出2个区域栽种同一种植物，22A 是选出的2种植物排列），B 、D 、F 共有3×2×2 种栽法（注：若A 、C 栽种同一种植物，则B 有3 种栽法，D 、F 各有2种栽法），222432322432C C A ∴⨯⨯⨯=共有种栽法。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
竞赛讲座14-染色问题与染色方法1．小方格染色问题最简单的染色问题是从一种民间游戏中发展起来的方格盘上的染色问题.解决这类问题的方法后来又发展成为解决方格盘铺盖问题的重要技巧.例1 如图29-1(a),3行7列小方格每一个染上红色或蓝色.试证:存在一个矩形,它的四个角上的小方格颜色相同.证明由抽屉原则,第1行的7个小方格至少有4个不同色,不妨设为红色(带阴影)并在1、2、3、4列（如图29-1（b））.在第1、2、3、4列（以下不必再考虑第5，6，7列）中，如第2行或第3行出现两个红色小方格，则这个问题已经得证；如第2行和第3行每行最多只有一个红色小方格（如图29-1（c）），那么在这两行中必出现四角同为蓝色的矩形，问题也得到证明.说明：（1）在上面证明过程中除了运用抽屉原则外，还要用到一种思考问题的有效方法，就是逐步缩小所要讨论的对象的范围，把复杂问题逐步化为简单问题进行处理的方法.（2）此例的行和列都不能再减少了.显然只有两行的方格盘染两色后是不一定存在顶点同色的矩形的.下面我们举出一个3行6列染两色不存在顶点同色矩形的例子如图29-2.这说明3行7列是染两色存在顶点同色的矩形的最小方格盘了.至今,染k 色而存在顶点同色的矩形的最小方格盘是什么还不得而知.例2 (第2届全国部分省市初中数学通讯赛题)证明:用15块大小是4×1的矩形瓷砖和1块大小是2×2的矩形瓷砖，不能恰好铺盖8×8矩形的地面.分析将8×8矩形地面的一半染上一种颜色，另一半染上另一种颜色，再用4×1和2×2的矩形瓷砖去盖，如果盖住的两种颜色的小矩形不是一样多，则说明在给定条件不完满铺盖不可能.证明如图29-3，用间隔为两格且与副对角线平行的斜格同色的染色方式，以黑白两种颜色将整个地面的方格染色.显然，地面上黑、白格各有32个.每块4×1的矩形砖不论是横放还是竖盖，且不论盖在何处，总是占据地面上的两个白格、两个黑格，故15块4×1的矩形砖铺盖后还剩两个黑格和两个白格.但由于与副对角线平行的斜格总是同色，而与主对角线平行的相邻格总是异色，所以，不论怎样放置，一块2×2的矩形砖，总是盖住三黑一白或一黑三白.这说明剩下的一块2×2矩形砖无论如何盖不住剩下的二黑二白的地面.从而问题得证.例3 （1986年北京初二数学竞赛题）如图29-4（1）是4个1×1的正方形组成的“L”形，用若干个这种“L”形硬纸片无重迭拼成一个m×n（长为m个单位，宽为n个单位）的矩形如图29-4（2）.试证明mn必是8的倍数.证明∵m×n矩形由“L”形拼成，∴m×n是4的倍数，∴m、n中必有一个是偶数，不妨设为m.把m×n矩形中的m列按一列黑、一列白间隔染色（如图29-4（2）），则不论“L”形在这矩形中的放置位置如何（“L”形的放置，共有8种可能），“L”形或占有3白一黑四个单位正方形（第一种），或占有3黑一白四个单位正方形（第二种）.设第一种“L”形共有p个，第二种“L”形共q个，则m×n矩形中的白格单位正方形数为3p+q，而它的黑格单位正方形数为p+3q.∵m为偶数，∴m×n矩形中黑、白条数相同，黑、白单位正方形总数也必相等.故有3p+q=p+3q，从而p=q.所以“L”形的总数为2p个，即“L”形总数为偶数，所以m×n 一定是8的倍数.2．线段染色和点染色下面介绍两类重要的染色问题.(1) 线段染色.较常见的一类染色问题是发样子组合数学中图论知识的所谓“边染色”（或称“线段染色”），主要借助抽屉原则求解.例4 （1947年匈牙利数学奥林匹克试题）世界上任何六个人中，一定有3个人或者互相认识或者互相都不认识.我们不直接证明这个命题，而来看与之等价的下述命题例5 （1953年美国普特南数学竞赛题）空间六点，任三点不共线，任四点不共面，成对地连接它们得十五条线段，用红色或蓝色染这些线段（一条线段只染一种颜色）.求证:无论怎样染,总存在同色三角形.证明设A、B、C、D、E、F是所给六点.考虑以A为端点的线段AB、AC、AD、AE、AF，由抽屉原则这五条线段中至少有三条颜色相同，不妨设就是AB、AC、AD，且它们都染成红色.再来看△BCD的三边，如其中有一条边例如BC是红色的，则同色三角形已出现（红色△ABC）；如△BCD三边都不是红色的，则它就是蓝色的三角形，同色三角形也现了.总之,不论在哪种情况下,都存在同色三角形.如果将例4中的六个人看成例5中六点,两人认识的连红线,不认识的连蓝线,则例4就变成了例5.例5的证明实际上用染色方法给出了例4的证明.例6 (第6届国际数学奥林匹克试题)有17位科学家,其中每一个人和其他所有人的人通信,他们的通信中只讨论三个题目.求证:至少有三个科学家相互之间讨论同一个题目.证明用平面上无三点共线的17个点A1,A2,…，A17分别表示17位科学家.设他们讨论的题目为x,y,z,两位科学家讨论x连红线,讨论y连蓝线,讨论z连黄线.于是只须证明以这17个点为顶点的三角形中有一同色三角形.考虑以A1为端点的线段A1A2,A1A3,…，A1A17，由抽屉原则这16条线段中至少有6条同色，不妨设A1A2，A1A3，…，A1A7为红色.现考查连结六点A2，A3，…，A7的15条线段，如其中至少有一条红色线段，则同色（红色）三角形已出现；如没有红色线段，则这15条线段只有蓝色和黄色，由例5知一定存在以这15条线段中某三条为边的同色三角形（蓝色或黄色）.问题得证.上述三例同属图论中的接姆赛问题.在图论中,将n点中每两点都用线段相连所得的图形叫做n点完全图,记作k n.这些点叫做“顶点”，这些线段叫做“边”.现在我们分别用图论的语言来叙述例5、例6.定理1 若在k6中，任染红、蓝两色，则必有一只同色三角形.定理2 在k17中,任染红、蓝、黄三角，则必有一只同色三角形.（2）点染色.先看离散的有限个点的情况.例7 （首届全国中学生数学冬令营试题）能否把1，1，2，2，3，3，…，1986，1986这些数排成一行，使得两个1之间夹着一个数，两个2之间夹着两个数，…，两个1986、之间夹着一千九百八十六个数？请证明你的结论.证明将1986×2个位置按奇数位着白色，偶数位着黑色染色，于是黑白点各有1986个.现令一个偶数占据一个黑点和一个白色，同一个奇数要么都占黑点，要么都占白点.于是993个偶数，占据白点A1=993个，黑色B1=993个.993个奇数，占据白点A2=2a个，黑点B2=2b个，其中a+b=993.因此，共占白色A=A1+A2=993+2a个.黑点B=B1+B2=993+2b个，由于a+b=993（非偶数！）∴a≠b，从而得A≠B.这与黑、白点各有1986个矛盾. 故这种排法不可能.“点”可以是有限个，也可以是无限个，这时染色问题总是与相应的几何问题联系在一起的.例8 对平面上一个点，任意染上红、蓝、黑三种颜色中的一种.证明:平面内存在端点同色的单位线段.证明作出一个如图29-7的几何图形是可能的,其中△ABD、△CBD、△AEF、△GEF 都是边长为1的等边三角形，CG=1.不妨设A点是红色，如果B、E、D、F中有红色，问题显然得证.当B、E、D、F都为蓝点或黄点时，又如果B和D或E和F同色，问题也得证.现设B和D异色E和F异色,在这种情况下,如果C或G为黄色或蓝点,则CB、CD、GE、GF中有两条是端点同色的单位线段，问题也得证.不然的话,C、G均为红点，这时CG是端点同色的单位线段.证毕.还有一类较难的对区域染色的问题，就不作介绍了.练习二十九1．6×6的方格盘，能否用一块大小为3格，形如的弯角板与11块大小为3×1的矩形板，不重迭不遗漏地来铺满整个盘面.2．（第49届苏联基辅数学竞赛题）在两张1982×1983的方格纸涂上红、黑两种颜色，使得每一行及每一列都有偶数个方格是黑色的.如果将这两张纸重迭时，有一个黑格与一个红格重合，证明至少还有三个方格与不同颜色的方格重合.3．有九名数学家，每人至多会讲三种语言，每三名中至少有2名能通话，那么其中必有3名能用同一种语言通话.4．如果把上题中的条件9名改为8名数学家，那么，这个结论还成立吗？为什么？5．设n=6（r-2）+3（r≥3），求证：如果有n名科学家，每人至多会讲3种语言，每3名中至少有2名能通话，那么其中必有 r名能用同一种语言通话.6．（1966年波兰数学竞赛题）大厅中会聚了100个客人，他们中每人至少认识67人，证明在这些客人中一定可以找到4人，他们之中任何两人都彼此相识.7．（首届全国数学冬令营试题）用任意方式给平面上的每一个点染上黑色或白色.求证：一定存在一个边长为1或的正三角形，它三个顶点是同色的.练习二十九１．将１、４行染红色、２、５行染黄色、３、６行染蓝色，然后就弯角板盖住板面的不同情况分类讨论．２．设第一张纸上的黑格Ａ与第二张纸上的红格Ａ′重合．如果在第一张纸上Ａ所在的列中，其余的黑格（奇数个）均与第二张纸的黑格重合，那么由第二张纸上这一列的黑格个数为偶数，知必有一黑格与第一张纸上的红格重合，即在这一列，第一张纸上有一方格Ｂ与第二张纸上不同颜色的方格Ｂ′重合．同理在Ａ、Ｂ所在行上各有一个方格Ｃ、Ｄ，第二张纸上与它们重合的方格Ｃ′、Ｄ′的颜色分别与Ｃ、Ｄ不同．３．把９名数学家用点Ａ１，Ａ２，…，Ａ９表示．两人能通话，就用线连结，并涂某种颜色，以表示不同语种。
两人不通话，就不连线．（１）果任两点都有连线并涂有颜色，那么必有一点如Ａ１，以其为一端点的８条线段中至少有两条同色，比如Ａ１Ａ２、Ａ１Ａ３．可见Ａ１，Ａ２，Ａ３之间可用同一语言通话．②如情况①不发生，则至少有两点不连线，比如Ａ１、Ａ２．由题设任三点必有一条连线知，其余七点必与Ａ１或Ａ２有连线．这时七条线中，必有四条是从某一点如Ａ１引出的．而这四条线中又必有二条同色，则问题得证．４．结论不成立，如图所示（图中每条线旁都有一个数字，以表示不同语种）．５．类似于第３题证明．６．用点Ａ１、Ａ２、…、Ａ１００表示客人，红、蓝的连线分别表示两人相识或不相识，因为由一个顶点引出的蓝色的线段最多有３２条，所以其中至少有三点之间连红线．这三个点（设为Ａ１、Ａ２、Ａ３）引出的蓝色线段最多为９６条．去掉所有这些蓝色的线段（连同每条线段上的一个端点ＡＩ，Ｉ≠１，２，３），这样，在图中至少还剩下四个点，除Ａ１、Ａ２、Ａ３外，设第四点为Ａ４，这四个点中Ａ１，Ａ２，Ａ３每一个点与其它的点都以红色的线段相连，于是客人Ａ１、Ａ２、Ａ３、Ａ４彼此两两相识．７．先利用右图证明＂若平面上有两个异色的点距离为２，地么必定可以找到符合题意的三角形＂．再找长为２端点异色的线段．以Ｏ（白色）为圆心，４为半径作圆．如圆内皆白点，问题已证．否则圆内有一黑点Ｐ，以ＯＰ为底作腰长为２的三角形ＯＰＲ，则Ｒ至少与Ｏ、Ｐ中一点异色，这样的线段找到．。